Modeling Cell Selectivity of Antimicrobial Peptides: How Is the Selectivity Influenced by Intracellular Peptide Uptake and Cell Density

Antimicrobial peptides (AMPs) are known to attack bacteria selectively over their host cells. Many attempts have been made to use them as a template for designing peptide antibiotics for fighting drug-resistant bacteria. A central concept in this endeavor is “peptide selectivity,” which measures the “quality” of peptides. However, the relevance of selectivity measurements has often been obscured by the cell-density dependence of the selectivity. For instance, the selectivity can be overestimated if the cell density is larger for the host cell. Furthermore, recent experimental studies suggest that peptide trapping in target bacteria magnifies the cell-density dependence of peptide activity. Here, we propose a biophysical model for peptide activity and selectivity, which assists with the correct interpretation of selectivity measurements. The resulting model shows how cell density and peptide trapping in cells influence peptide activity and selectivity: while these effects can alter the selectivity by more than an order of magnitude, peptide trapping works in favor of host cells at high host-cell densities. It can be used to correct selectivity overestimates.

Introduction

Antimicrobial peptides (AMPs) are naturally-occurring peptide antibiotics and attack bacteria selectively over host cells (1–3). AMPs are mostly cationic and have stronger binding affinity for bacterial membranes, which carry a large fraction of anionic lipids (1–4). Their amphiphilic structure enables them to attach to and perturb membranes (1–5). While membrane perturbation is not the sole mechanism of action, it is the first decisive event they induce (1, 2, 5). Indeed, AMPs are multitasking molecules: they are pore formers, metabolic inhibitors (1, 2), and/or immunomodulators (6–8). Their membrane-perturbing ability has, however, spurred many attempts to use them as a template for designing potent peptide antibiotics, especially for fighting conventional drug-resistant bacteria (1, 2, 4, 9). Developing bacterial resistance against membrane-perturbing peptides would involve “costly” redesigning of their membranes (1). Nevertheless, pathogens can evolve antimicrobial resistance (10, 11). Consequences of this need to be considered in our endeavor in searching for potent peptide antibiotics. Despite this challenge, the therapeutic potential of these multitasking molecules has generated interest in designing optimized peptides [see a recent review (7) and references therein].

A central concept in assessing peptide potency is “peptide selectivity.” For a given peptide, it is quantified by the ratio of a minimum hemolytic concentration (MHC) to a minimum inhibitory concentration (MIC) [see for instance; (9)]. For large MHC/MIC, there is a range of peptide concentration at which a given peptide is active against bacteria only. The requirement of a minimum peptide concentration (either MIC or MHC) for membrane rupture suggests that cell density is a control parameter for peptide activity and selectivity, as recently discussed (12, 13). Increasing the cell density is equivalent to reducing the amount of peptides available to each cell. As a result, MICs and MHCs increase as the cell density increases; the ratio MHC/MIC is cell-density dependent.

A related quantity is a threshold coverage of peptides on membranes (3, 14–17). Let P/L be the molar ratio of bound peptides to lipids. At the MIC or MHC, P/L reaches the threshold value, P/L*, beyond which bound peptides permeabilize the membrane. The value of P/L* depends on the type of peptide and lipid (3, 14–17). It is typically larger for lipid membranes mimicking bacterial membranes.

The correct interpretation of selectivity measurements has often been obscured by the cell-density dependence of the selectivity (12, 13, 18). For instance, the selectivity can be overestimated if the cell density is larger for the host cell. Furthermore, a number of recent studies highlight the effect of peptide trapping inside (dead) cells on peptide activity and selectivity (19–21). It was shown that each cell can absorb ~10⁷ peptides (19–21). Often referred to as an inoculum effect [see (19–22) and references therein], this enhances population survivability (21), since it lowers the peptide concentration in the solution. As a result, the MIC obtained for a bacterial culture increases more rapidly with the cell density (21), compared to what corresponding model membranes would suggest (12, 13).

Here we offer a biophysical model of peptide activity and selectivity that assists with the correct interpretation of selectivity measurements. Our primary goal is to present a theoretical model, which can be used to predict peptide activity and selectivity under a variety of conditions, once their biophysical parameters are characterized. Indeed, an experimental approach to the relationship between peptide selectivity and cell densities is complex in a multi-species cultures, despite its relevance in biological and medical contexts. Our model will be beneficial for clarifying the relevance of selectivity measurements under controlled conditions.

Here we consider two approaches to quantifying cell selectivity (MHC/MIC). Imagine measuring MICs and MHCs in separate cell cultures (each containing a single species) and combining them into MHC/MIC. In this work, the resulting selectivity is referred to as “noncompetitive selectivity.” Alternatively, one can measure MICs and MHCs in a multi-species cell culture containing both bacteria and host cells and then calculate MHC/MIC. The resulting (competitive) selectivity is generally different from the corresponding noncompetitive one (12). If the competitive selectivity reflects adequately the competition between host cells and bacteria in binding peptides, the noncompetitive one can be exaggerated, when the host cell density is high, as correctly referred to as an experimental “illusion” by Matsuzaki (18).

Consistent with earlier studies (12, 13, 19–21), our results suggest that both MICs and MHCs increase with cell densities C_cell; in a low cell-density limit, they become C_cell-independent, i.e., intrinsic to a given peptide. Our results also show that peptide trapping increases both MICs and MHCs, magnifying their cell-density dependence, since the competition for peptides between cells is now stronger. This is a key feature highlighted in recent experiments (19–21) but left out in earlier theoretical studies (12, 13). The net effect of peptide trapping on peptide selectivity is that it tends to enhance the selectivity in the large host-cell density limit. With the parameter choices used, noncompetitive selectivity can be exaggerated by an order of magnitude. Our model also offers a systematic approach to correcting the selectivity for exaggeration; a noncompetitive selectivity can be corrected into a corresponding competitive one.

Theoretical Model

In this section, we discuss how peptide selectivity depends on cell density. We first introduce a few key parameters relevant in this work. Let C_p be the total concentration of peptides. Recall that P/L is the molar ratio of membrane-bound peptides to lipids; (P/L)_B for bacterial membranes and (P/L)_H for host cell membranes. At a certain value of C_p, denoted as $C_{\text{p}}^{*}$, P/L reaches a threshold value required for membrane rupture, (P/L)*; $C_{\text{p}}^{*}$ is either MIC or MHC. Also, the cell density, C_cell, is a key parameter for peptide activity and selectivity (12, 13, 19–21); C_cell = C_B for bacteria and C_cell = C_H for host cells. A related quantity is the surface area of each cell, A_cell (12): A_cell = A_B or A_cell = A_H for bacteria and host cells, respectively. Doubling A_cell for given C_cell is equivalent to doubling C_cell for given A_cell. Similarly, a_B and a_H are the lipid headgroup area for bacterial and host-cell membranes, respectively. Finally, N_p is the number of trapped peptides per cell: N_pB and N_pH for bacteria and host cells, respectively.

The cell-density dependence of peptide activity, especially for a mixture of bacterial and host cells, is illustrated in Figure 1 [see (13) for a homogeneous case]. Here, the concentric circles in blue represent bacterial cells and the pink ones stand for host cells. Figure 1(i) shows a single-cell limit at an MIC. The introduction of a host cell will reduce the amount of peptides for the existing bacterial cell as shown in (ii). The extra number of peptides to maintain at the MIC is equal to (P/L)_H × A_H/a_H; similarly, in (iii), the number of peptides that should be added is ${(P/L)}_{\text{B}}^{*}\times A_{\text{B}}/a_{\text{B}}+2{(P/L)}_{\text{H}}\times A_{\text{H}}/a_{\text{H}}$.

FIGURE 1

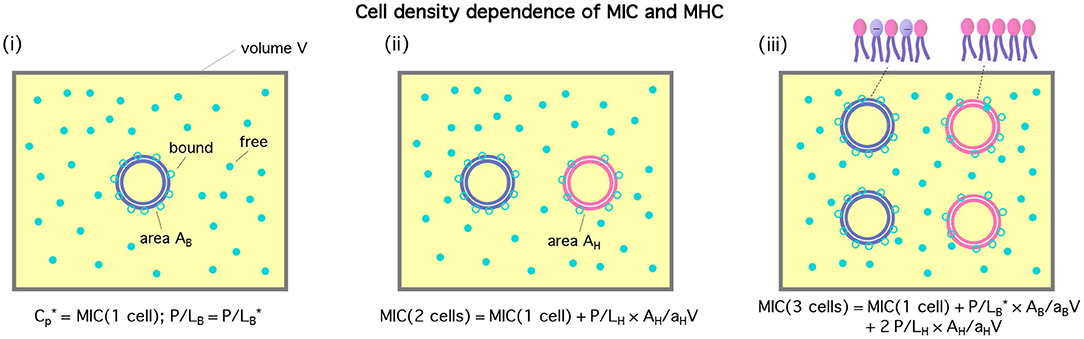
Figure 1. Cell-density dependence of $C_{\text{p}}^{*}$, i.e., either MIC or MHC. Cells are represented by two concentric circles and peptides by filled (free) or unfilled circles (bound) circles; if the blue circles represent bacterial cells, the pink ones stand for host cells. Let A_cell = A_B or A_H be the bacterial or host cell surface area, respectively. The progression from (i)–(iii) suggests that $\text{MIC}(C_{\text{cell}})=\text{MI}{\text{C}}_0+A_{\text{B}}/a_{\text{B}}\times {(P/L)}_{\text{B}}^{*}{C}_{\text{B}}+A_{\text{H}}/a_{\text{H}}\times {(P/L)}_{\text{H}}{C}_{\text{H}}$. If we exchange the role between bacterial and host cells, we arrive at $\text{MHC}(C_{\text{cell}})=\text{MH}{\text{C}}_0+A_{\text{H}}/a_{\text{H}}\times {(P/L)}_{\text{H}}^{*}{C}_{\text{H}}+A_{\text{B}}/a_{\text{B}}\times {(P/L)}_{\text{B}}{C}_{\text{B}}$. The figure was adapted with permission from (12), Copyright (2015) American Chemical Society, and from (13) with permission from The Royal Society of Chemistry.

A number of studies have unambiguously shown that (dead) cells can absorb a large number of peptides (~10⁷-10⁸) (19– 21). This enhances the so-called “inoculum” effect: it amplifies the cell-density dependence of MICs and MHCs, since it increases the number of peptides consumed by each cell. Along the line of what was done recently (13), this effect can be taken into account. Recall that N_pB and N_pH are the number of absorbed peptides per cell in bacterial and host cells, respectively. Our consideration replies on the following justifiable simplification: N_pB = 0 below MIC and similarly N_pH = 0 below MHC. Prior to membrane rupture, penetration of peptides into a cell is expected to be a rare event, since it involves overcoming a large free energy barrier for crossing an otherwise intact cell membrane.

Following the reasoning in Figure 1 and taking into account peptide trapping, one can arrive at

$\begin{array}{l}\text{MIC}(C_{\text{B}},C_{\text{H}})={\text{MIC}}_0+\left[{\left(\frac{P}{L}\right)}_{\text{B}}^{*}\frac{A_{\text{B}}}{a_{\text{B}}}+N_{\text{pB}}^{*}\right]C_{\text{B}}\\ +{\left(\frac{P}{L}\right)}_{\text{H}}\frac{A_{\text{H}}}{a_{\text{H}}}{C}_{\text{H}}& (\mathrm{1a})\end{array}$

$\begin{array}{l}\text{MHC}(C_{\text{B}},C_{\text{H}})={\text{MHC}}_0+\left[{\left(\frac{P}{L}\right)}_{\text{H}}^{*}\frac{A_{\text{H}}}{a_{\text{H}}}+N_{\text{pH}}^{*}\right]C_{\text{H}}\\ +\left[{\left(\frac{P}{L}\right)}_{\text{B}}\frac{A_{\text{B}}}{a_{\text{B}}}+N_{\text{pB}}\right]C_{\text{B}}& (\mathrm{1b})\end{array}$

Here MIC₀ and MHC₀ are, respectively, MIC and MHC in the low-cell density (or single-cell) limit: C_cell → 0 (C_cell is either C_B or C_H). The term inside […] can be interpreted as the total number of peptides consumed per cell; recall $N_{\text{p}}^{*}$ is the value of N_p at $C_{\text{p}}^{*}$ (e.g., either MIC or MHC). It is assumed that MHC > MIC: peptides are selective, i.e., at the MIC, host cells remain intact. This has to be understood with caution. If MICs and MHCs are measured separately in a noncompetitive way, MICs can be larger than MHCs. This is, however, irrelevant for our discussion here. As a result of this inequality, the relations in Equation (1) are not fully symmetric with respect to the exchange between the subscripts “B” and “H.”

It is worth noting that the values of (P/L)_B and (P/L)_H depend on the total concentration of peptides and cell densities. They are determined by chemical equilibrium between free and bound peptides [see the Appendix]. In contrast, ${(P/L)}_{\text{B}}^{*}$ and ${(P/L)}_{\text{H}}^{*}$ are constants, which are set by the membrane-peptide parameters (3, 14–16).

Finally, note that the term [(P/L)_B (A_B/a_B) + N_pB] in Equation (1b) is larger than […] in Equation (1a), since the former is evaluated at a larger value of C_p above the MIC. In this case, however, pore formation in bacterial membranes will alter the energetics of peptide binding. In the limit C_H ≫ C_B, as is often the case, this will not limit the applicability of Equation (1b), since this term has a minimal impact on the MHC.

For a noncompetitive or homogeneous case, the last term in Equations (1a,b) will disappear. It is worth noting that the values of MIC₀, MHC₀, $N_{\text{pB}}^{*}$, and $N_{\text{pH}}^{*}$ can be obtained from noncompetitive measurements. If (P/L)* is not known, the number of peptides consumed per cell, i.e., the term inside […] in Equation (1), can be viewed as a fitting parameter. See below for a competitive case.

It will be instructive to compare the two terms inside […] in Equation (1): the number of membrane-bound peptides and the number of adsorbed peptides per cell. For this consideration, we invoke some simplification: a cell viewed as a sack of molecules enclosed by a bilayer. For E. coli as a representative bacterium, $A_{\text{B}}\approx 12\text{μ}{\text{m}}^2$, twice the area of each lipid layer (either inner or outer) in the cytoplasmic membrane. Since $a_{\text{B}}\approx a_{\text{H}}\approx 70{\AA }^2$, $A_{\text{B}}/a_{\text{B}}\approx 1.7\times 10^7$. For the peptide melittin, ${(P/L)}_{\text{B}}^{*}\approx 0.02$ and ${(P/L)}_{\text{H}}^{*}\approx 0.01$ (14–16). We thus find ${(P/L)}_{\text{B}}^{*}(A_{\text{B}}/a_{\text{B}})\approx 3.4\times 10^5$. This number is much smaller than $N_{\text{pB}}\approx 10^7$-10⁸ (21). The presence of outer membranes will not change this inequality. For human red blood cells as representative host cells, A_H ≈ 17A_B and $A_{\text{H}}/a_{\text{H}}\approx 2.9\times 10^8$. As a result, we obtain ${(P/L)}_{\text{H}}^{*}(A_{\text{H}}/a_{\text{H}})\approx 2.9\times 10^6$, which is smaller than $N_{\text{pH}}\approx 10^7$ (19, 20). The main source of inoculum effects is the trapping of peptides inside dead cells (i.e., for P/L > (P/L)*).

A full analysis of Equation (1) is involved, since it requires the determination of four unknowns: (P/L)_B, (P/L)_H, N_pB, and N_pH, as a function of C_p [see (12, 13) for earlier efforts]; also the energetics of peptide trapping including peptide binding to intracellular components has yet to be understood in a quantitative manner.

In some relevant limits, we can use Equation (1) to map out a few scenarios regarding peptide selectivity. In the competitive case, if C_H ≫ C_B as in whole blood, Equation (1) can be approximated as

$\begin{array}{ll}\text{MIC}(C_{\text{B}},C_{\text{H}})\approx {\text{MIC}}_0+{\left(\frac{P}{L}\right)}_{\text{H}}\frac{A_{\text{H}}}{a_{\text{H}}}{C}_{\text{H}},& (\mathrm{2a})\end{array}$

$\begin{array}{ll}\text{MHC}(C_{\text{B}},C_{\text{H}})\approx {\text{MHC}}_0+\left[{\left(\frac{P}{L}\right)}_{\text{H}}^{*}\frac{A_{\text{H}}}{a_{\text{H}}}+N_{\text{pH}}^{*}\right]C_{\text{H}}& (\mathrm{2b})\end{array}$

Here (P/L)_H in Equation (2a) is to be evaluated at C_p = MIC.

In Equation (2), MIC₀ and MHC₀ can be viewed as fitting parameters. In a more systematic approach, they can be related to binding energy, w, which characterizes the interaction of a peptide with a membrane (see the Appendix); in this work, w_B and w_H are the binding energy for bacterial and host-cell membranes, respectively.

Chemical equilibrium between free and bound peptides [see Equation A3 in the Appendix and the SI of (12)] leads to¹

$\begin{array}{ll}\text{MIC}(C_{\text{B}},C_{\text{H}})\approx \frac{1}{v_{\text{p}}}·\frac{\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{1-\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{e}^{w_{\text{H}}/k_{\text{B}}T}+{\left(\frac{P}{L}\right)}_{\text{H}}\frac{A_{\text{H}}}{a_{\text{H}}}{C}_{\text{H}}.& (3)\end{array}$

Here, v_p is the volume occupied by each peptide in the bulk and A_p is the peptide area on the membrane surface.

We can use Equation (3) to eliminate (P/L)_H in Equation (2a) by equating the first terms in these two equation²; similarly, ${(P/L)}_{\text{H}}^{*}$ in Equation (2b) can be eliminated in favor of (MHC)₀:

$\begin{array}{ll}\text{MIC}(C_{\text{B}},C_{\text{H}})\approx {\text{MIC}}_0+\left(\frac{{\text{MIC}}_0{v}_{\text{p}}}{{\text{MIC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}\frac{A_{\text{H}}}{A_{\text{p}}}\right)C_{\text{H}},& (\mathrm{4a})\end{array}$

$\begin{array}{l}\text{MHC}(C_{\text{B}},C_{\text{H}})\approx {\text{MHC}}_0\\ +\left(\frac{{\text{MHC}}_0{v}_{\text{p}}}{{\text{MHC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}\frac{A_{\text{H}}}{A_{\text{p}}}+N_{\text{pH}}^{*}\right)C_{\text{H}}.& (\mathrm{4b})\end{array}$

The MIC in Equation (4a) increases linearly with C_H. It can be strikingly different from the corresponding noncompetitive MIC in the limit C_B → 0: MIC₀. For sufficiently large C_H, the former can be much larger than the latter.

The ratio MHC/MIC becomes

$\begin{array}{l}\frac{\text{MHC}}{\text{MIC}}\approx \frac{{\text{MHC}}_0+\left[{\left(\frac{P}{L}\right)}_{\text{H}}^{*}\frac{A_{\text{H}}}{a_{\text{H}}}+N_{\text{pH}}^{*}\right]C_{\text{H}}}{{\text{MIC}}_0+\left[\frac{{\text{MIC}}_0{v}_{\text{p}}}{{\text{MIC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}\frac{A_{\text{H}}}{A_{\text{p}}}\right]C_{\text{H}}}\\ =\frac{{\text{MHC}}_0+\left(\frac{{\text{MHC}}_0{v}_{\text{p}}}{{\text{MHC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}\frac{A_{\text{H}}}{A_{\text{p}}}+N_{\text{pH}}^{*}\right)C_{\text{H}}}{{\text{MIC}}_0+\left(\frac{{\text{MIC}}_0{v}_{\text{p}}}{{\text{MIC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}\frac{A_{\text{H}}}{A_{\text{p}}}\right)C_{\text{H}}}.& (5)\end{array}$

This implies that peptide trapping in host cells enhances peptide selectivity. Compared to the case $N_{\text{pH}}^{*}\approx 0$, more peptides will be needed in order for (P/L)_H to reach ${(P/L)}_{\text{H}}^{*}$ for $N_{\text{pH}}^{*}\gg 1$. Since the second term inside […] in the numerator of Equation (5) is larger than the first term roughly by an order of magnitude, the effect of peptide trapping on the selectivity is up to about 10-fold.

Note that the MHC in Equation (4b) holds for a host-cell only case as well. In contrast, the MIC for a bacterial-cell only case becomes

$\begin{array}{ll}\text{MIC}(C_{\text{B}})={\text{MIC}}_0+\left(\frac{{\text{MIC}}_0{v}_{\text{p}}}{{\text{MIC}}_0{v}_{\text{p}}+e^{w_{\text{B}}/k_{\text{B}}T}}\frac{A_{\text{B}}}{A_{\text{p}}}+N_{\text{pB}}^{*}\right)C_{\text{B}}.& (6)\end{array}$

This can be obtained from Equation (4b) by exchanging the role of host cells with that of bacteria.

The main advantage of Equations (4), (5), and (6) is that P/L* is not shown explicitly. It is absorbed into MIC₀ or MHC₀, which are experimentally more accessible. Also it is worth noting that the use of Equation (4) or Equation (5) would not necessarily require measurements of such biophysical parameters as v_p, w_H, w_B, $N_{\text{pH}}^{*}$, and $N_{\text{pB}}^{*}$. The term inside (…) on the right-hand side of Equations (4) and (6) as a whole can be viewed as a fitting parameter. It is a slope of either MIC or MHC curve as a function of the cell density and can be obtained from the corresponding homogeneous case. See the last section for relevant points.

Results

We have analyzed Equations (4) and (5) to clarify inoculum effects on peptide activity and selectivity. For lipid bilayers mimicking cell membranes, the parameters in these equations have been characterized (12–16). They are, however, not known for real cells. In particular, the interdependence between w, P/L*, and $C_{\text{p}}^{*}$ is elusive because of the complexities of cell structures. For instance, w_B for Gram-negative bacteria should take into account the peptide interaction with their outer membrane (OM), among others. Recall that this is an effective parameter, in which microscopic details (e.g., peptide charge, peptide interaction with the OM, and the presence of cholesterol in the host-cell membrane) are subsumed. This has only recently been mapped out theoretically for lipid bilayers (13). Here we do not attempt to calculate the effective binding energy w (either w_B or w_H) for real cells and to use it in the computation of MIC₀ and MHC₀. Instead, we start with conveniently-chosen but biophysically-relevant values of MIC₀ and MHC₀. The resulting analysis will not involve (P/L)* explicitly. For simplicity, the number of trapped peptides N_p is chosen to be the same for bacteria and host cells: $N_{\text{p}}=0,10^7,5\times 10^7$.

Otherwise, we have used peptide parameters relevant for the peptide melittin (12–16): peptide charge Q = 5, $A_{\text{p}}=400{\AA }^2$, and $v_{\text{p}}={33}^3{\AA }^3$. For this peptide, w was mapped out for model membranes, mimicking bacterial and host-cell membranes: w_B = −16.6k_BT and w_H = −6.72k_BT (13). They are used as representative binding energy. Also, $a_{\text{B}}=74{\AA }^2$, $a_{\text{H}}=71{\AA }^2$, $A_{\text{B}}=1.2\times {10}^9{\AA }^2=12\mu {\text{m}}^2$ as for E. coli, and A_H = A_B or A_H = 17A_B as for human red blood cells (12).

We have plotted our results for MICs and MHCs in Figure 2. For this, we have chosen the parameters as follows: MIC₀ = 1μM and MHC₀ = 5μM. Figure 2A shows the MIC as a function of C_B in units of 5 × 10⁹cells/mL obtained in a noncompetitive way. In all cases, the MIC increases linearly from MIC₀ = 1μM, as C_B increases, as expected from Equation (1). The inset recaptures the MIC data in linear plot. It indicates a linear relationship between the MIC and C_B. The MIC curve is steeper for a larger value of N_p. This is well aligned with recent experiments (21). The inoculum effect increases the slope of the MIC curves, not the “y”-intercept, which coincides with cell-density independent MIC₀.

FIGURE 2

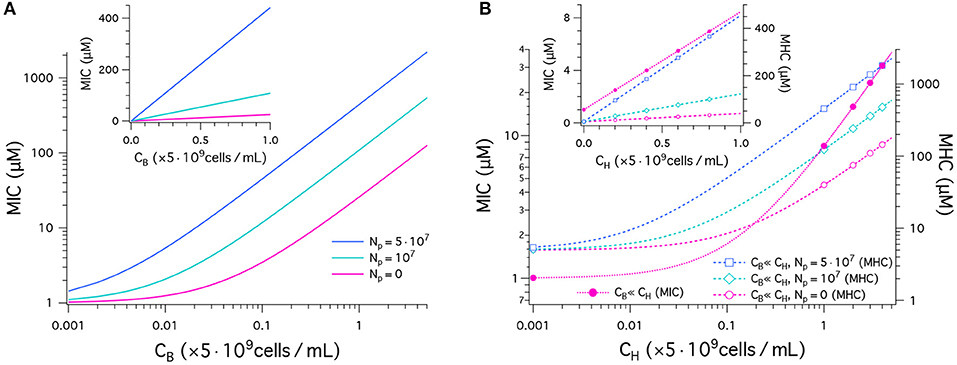
Figure 2. Peptide activity, i.e., MICs and MHCs. We have chosen the parameters as follows: (MIC)₀ = 1μM and (MHC)₀ = 5μM; w_B = −16.6k_BT and w_H = −6.72k_BT; $A_{\text{p}}=400^2$; $v_{\text{p}}={33}^{3\text{ 3}}$; $A_{\text{B}}=1.2\times {10}^{9\text{ 2}}$ and A_H = 17 × A_B. The number of trapped peptides N_p is chosen to be the same for bacteria and host cells: $N_{\text{p}}=0,10^7,5\times 10^7$. (A) This graph shows the results for MICs as a function of C_B in units of 5 × 10⁹cells/mL obtained in a noncompetitive way. In all cases, the MIC increases from MIC₀ = 1, as C_B increases (Equation 1). The MIC is higher for a larger value of N_p. The sensitivity of the MIC to N_p is better captured in the linear plot in the inset; all the curves indicate a linear relationship between the MIC and C_B. (B) MICs (left axis) and MHCs (right axis) are shown as a function of C_H given in units of 5 × 10⁹cells/mL obtained in a competitive way. Various symbols are used to distinguish between different choices of N_p. If C_H ≫ C_B, MICs are roughly independent of N_p; in this case, MHCs are approximately the same for the competitive and noncompetitive cases. As C_H increases, the MIC increases up to 40-fold from MIC₀ at C_H = 0 (Equation 4a). Similarly MHCs increase as a function of C_H, more rapidly for larger N_p (Equation 4b); for $N_{\text{p}}=10^7$, the MHC increases by up to two orders of magnitude. The inset graph recaptures the data in a linear plot.

In Figure 2B, MICs (left axis) and MHCs (right axis) are shown as a function of C_H given in units of 5 × 10⁹cells/mL obtained in a competitive way. They are represent by dashed lines with symbols. First, note that MHCs are approximately the same for the competitive and noncompetitive cases as long as C_H ≫ C_B; also MICs are insensitive to C_B and N_p, if C_H ≫ C_B and MHC₀ > MIC₀ (see Equation 4). This is distinct from larger MICs for larger N_p in the noncompetitive case in Figure 2A. As C_H increases, the MIC increases up to 40-fold from MIC₀ at C_H = 0 (Equation 4A). This is consistent with the observation that peptide interactions with host cells diminish peptide activity in vivo (24). Similarly, MHCs increase as a function of C_H, more rapidly for larger N_p (Equation 4B and the inset graph). For $N_{\text{p}}=10^7$, the MHC increases by up to two orders of magnitude.

Figure 3 displays our results for peptide selectivity, which combines the graphs in Figures 2A and B. The graph in Figure 3A shows our results for MHC/MIC as a function of C_B obtained in a noncompetitive way. In all cases presented by various colors, the ratio MHC/MIC or the selectivity decreases, as C_B increases. The selectivity is higher for larger values of C_H. Also, it is higher for larger N_p if $C_{\text{B}}\lesssim 0.07\times 10\times 10^9\text{cells}/\text{mL}$ but is smaller if $C_{\text{B}}\gtrsim 0.07\times 10\times 10^9\text{cells}/\text{mL}$. Peptide trapping increases both MHC and MIC. At low C_B, the net effect is to enhance the selectivity; at high C_B, it reduces the selectivity, since lots of peptides are trapped in bacteria and “wasted.”

FIGURE 3

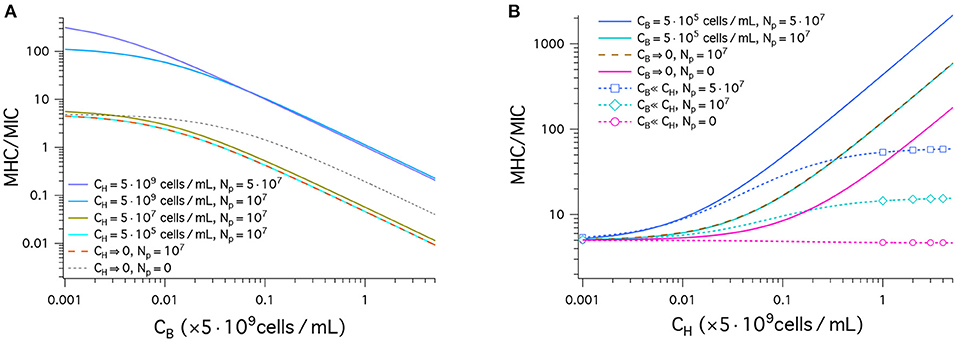
Figure 3. Cell selectivity of antimicrobial peptides, i.e., MHC/MIC. We have used the same parameters as in Figure 2: (MIC)₀ = 1μM, and (MHC)₀ = 5μM; w_B = −16.6k_BT, and w_H = −6.72k_BT; $A_{\text{p}}=400^2$; $v_{\text{p}}={33}^{3\text{ 3}}$; $A_{\text{B}}=1.2\times {10}^{9\text{ 2}}$ and A_H = 17 × A_B; $N_{\text{p}}=0,10^7,5\times 10^7$ (the same for bacteria and host cells). (A) This graph shows MHC/MIC as a function of C_B in units of 5 × 10⁹cells/mL obtained in a noncompetitive way. In all cases, the selectivity decreases, as C_B increases. The selectivity is higher for larger values of C_H. It is also larger for larger N_p unless C_H = 0 (black dashed) or $C_{\text{B}}\gtrsim 0.07\times 5\times 10^9$ (compare the top two curves). Also note that there is no essential difference between the two cases: $C_{\text{H}}=0,N_{\text{p}}=10^7$ (tangerine) and $C_{\text{H}}=5\times 10^5\text{cells}/\text{mL},N_{\text{p}}=10^7$ (cyan). This means that the latter case falls in the single-cell limit. (B) MHC/MIC are shown as a function of C_H given in units of 5 × 10⁹cells/mL. Competitive (dashed lines with various symbols) and noncompetitive (solid lines) cases are compared. For the competitive case, Equation (4) was used, which holds for C_H ≫ C_B. The competitive selectivity increases as C_H increases, except for N_p = 0 (magenta). In all noncompetitive cases shown, the selectivity increases as C_H increases. In all cases, the selectivity is higher for larger N_p. In the noncompetitive case, the presence of 5 × 10⁵cells/mL does not change the selectivity with reference to the corresponding limiting case C_B → 0; at this density of bacterial cells, MIC ≈ MIC₀. Compared to the corresponding competitive selectivity, the noncompetitive selectivity is overestimated, more so for larger C_H; for $C_{\text{H}}=5\times 10^9\text{cells}/\text{mL}$, the latter is exaggerated by an order of magnitude.

Also note that there is no essential difference between the two cases: $C_{\text{H}}=0,N_{\text{p}}=10^7$ (tangerine) and $C_{\text{H}}=5\times 10^5\text{cells}/\text{mL},N_{\text{p}}=10^7$ (cyan). This means that the latter case falls in the single-cell limit.

In Figure 3B, the results for MHC/MIC are shown as a function of C_H. Competitive (dashed line with various symbols) and noncompetitive (solid lines) cases are compared. For the competitive case, Equation (4) was used, which holds for C_H ≫ C_B. The competitive selectivity increases as C_H increases, except for N_p = 0 (magenta). In all noncompetitive cases, the selectivity increases as C_H increases; the presence of $C_{\text{B}}=5\times 10^5\text{cells}/\text{mL}$ does not change the selectivity with reference to the corresponding limiting case C_B → 0, since at this density of bacterial cells, MIC ≈ MIC₀. In both the competitive and noncompetitive cases shown, the selectivity is higher for larger N_p: peptide trapping enhances the selectivity.

Similarly to what earlier studies suggest (12, 18), the results in Figure 3B show how peptide selectivity can be mistakenly estimated. Compared to the corresponding competitive selectivity, the noncompetitive selectivity is overestimated, more so for larger C_H; for $C_{\text{H}}=5\times 10^9\text{cells}/\text{mL}$, the latter is exaggerated by an order of magnitude.

These results also clear up possible confusions. Even in the presence of a large amount of host cells, the selectivity measured in a competitive environment is not an experimental artifact. It just reflects correctly the cell-density dependence of the selectivity, as discussed in the section 2.

Discussions and Conclusions

We have discussed the cell-density dependence of peptide activity and selectivity. For this, we have combined physical arguments, which relate peptide activity and selectivity to cell density, and a Langmuir-type model, in which the amount peptide binding (or trapping) is dictated by an effective binding energy. This combined effort produced a predictive model for peptide activity and selectivity. It can be used to calculate MICs, MHCs, and MHC/MIC, once a few key biophysical parameters are characterized, which include the number of trapped peptides per cell (19–21) and peptide-membrane interactions.

Alternatively, our model can be used as a fitting model for analyzing data. For instance, the “y”-intercept and the “slope” can be extracted from noncompetitive measurements of MICs or MHCs vs. cell density. This will determine (MIC)₀ or (MHC)₀ as well as the terms inside (…) on the right-hand side of Equations (4b) and (6). This information can be used in Equation (4) (or more generally Equation 1), which represents a heterogeneous mixture of bacteria and host cells.

This consideration, however, would necessitate prior knowledge about one of $N_{\text{pB}}^{*}$ and ${(P/L)}_{\text{B}}^{*}$ (or equivalently w_B). To see this, notice that homogeneous measurements lead to the value of the sum of the two terms inside (…) in Equation (6). If ${(P/L)}_{\text{B}}^{*}$ is known, as is most obvious for pure-lipid membranes (3, 17), $N_{\text{pB}}^{*}$ can be extracted from noncompetitive measurements.

An alternative but possibly less practical approach is to measure several MICs in a competitive setting. By fitting the data to Equation (4a) will produce the coefficient of C_H. One can then obtain MIC, MHC, and MHC/MIC as a function of C_B or C_H, the density of bacteria or host cells, respectively. For instance, in whole blood, $C_{\text{H}}\approx 5\times 10^9\text{cells}/\text{mL}$. The density of bacteria depends on the degree and location of infection. It ranges from 1 colony-forming unit (CFU/mL) (in blood stream) to 10⁹CFU/mL (in soft tissue or peritonea) [see a recent review (20) and relevant references therein]. Graphs similar to those in Figure 2 or Figure 3 will be beneficial for understanding the activity and selectivity of antimicrobial peptides in varying biological environments.

As pointed out in a number of earlier studies (12, 18–20), the selectivity measured noncompetitively is often much larger than the corresponding competitive one, if the host cell density is much larger than the bacterial cell density. The results in Figure 3 offer a quantitative picture of how the selectivity can be excessively overestimated. It can, however, be corrected, since noncompetitive measurements can be converted into competitive ones. For instance, suppose that noncompetitive measurements led to w_B = −16.6k_BT, w_H = −6.72k_BT, $N_{\text{p}}=10^7$, MIC₀ = 1μM, and MHC₀ = 5μM, as in Figure 3. In the presence of $C_{\text{B}}=5\times 10^5\text{cells}/\text{mL}$ and $C_{\text{H}}=5\times 10^9\text{cells}/\text{mL}$ (C_B ≪ C_H), these parameters choices would lead to the following noncompetitive selectivity: MHC/MIC ≈ 100 (Equation 1 and Figure 3). It can be corrected graphically (Figure 3) or mathematically (Equation 4) into the corresponding competitive selectivity MHC/MIC ≈ 10.

As a final remark, we wish to mention that peptide activity against live cells is time-dependent, as observed in recent experiments (21). Accordingly, the density of bacterial cells, is a dynamic quantity. Furthermore, heterogeneous absorption of peptides in cells was shown to have a nontrivial consequence on population survivability. Because of the stochastic nature of molecular interactions occurring on the cell surface and inside, some cells absorb a large number of peptides (~10⁷-10⁸) (19–21), thus reducing the availability of peptides to the rest and contributing favorably to population survivability (21). Also, the density of peptides can change with time, depending on how fast the host cells produce them (21). It is also influenced by peptide degradation by protease (20, 24). Its effect on peptide activity is similar to what we expect from peptide trapping. Taking into all these known and unknown details goes beyond the scope of what can be done at present. Future considerations are warranted.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

B-YH and BRS conducted the research. B-YH wrote the manuscript. BRS, SN, and ST-A commented on the manuscript. SN helped solve the peptide binding equations. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by NSERC (Canada) (B-YH) and the National Institute of Health (R15-GM124640) (ST-A).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the reviewers for their useful comments on the relevance of our work to selectivity measurements in multi-species cultures and on bacterial resistance against antimicrobial peptides, and for bringing relevant work to our attention (22).

Footnotes

1. ^Here (P/L)_H is to be evaluated at the peptide concentration C_p = MIC. As a result, w_H in this expression corresponds to (P/L)_H smaller than ${(P/L)}_{\text{H}}^{*}$. Here we ignore the possible dependence of w_H on (P/L)_H. For pure-lipid membranes, this dependence can, in principle, be mapped out (13). If we use the final expression in Equation (4a) as a fitting model, this issue becomes irrelevant.

2. ^The origin of the cell-density dependent term in Equation (3) is obvious from the illustration in Figure 1. At the low-cell density limit, Equation (3) is equivalent to saying that

$\begin{array}{ll}{\text{MIC}}_0=\frac{1}{v_{\text{p}}}·\frac{\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{1-\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{e}^{w_{\text{H}}/k_{\text{B}}T}& (7)\end{array}$

This can be obtained from Equation (A3) in the Appendix. More directly, chemical equilibrium at C_p = MIC₀ in the low-cell density limit requires

$\begin{array}{l}\ln \left(v_{\text{p}}{\text{MIC}}_0\right)=\frac{w_{\text{B}}}{k_{\text{B}}T}+\ln \frac{\frac{A_{\text{p}}}{a_{\text{B}}}{\left(\frac{P}{L}\right)}_{\text{B}}^{*}}{1-\frac{A_{\text{p}}}{a_{\text{B}}}{\left(\frac{P}{L}\right)}_{\text{B}}^{*}}\\ =\frac{w_{\text{H}}}{k_{\text{B}}T}+\ln \frac{\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{1-\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}.& (8)\end{array}$

The second term in each line is the entropic chemical potential of bound peptides in units of k_BT (23). The second equality leads to Equation (7), which shows the relationship between the total peptide concentration, i.e., MIC₀, and (P/L)_H. Equation (7) can readily be solved for (P/L)_H:

$\begin{array}{ll}{\left(\frac{P}{L}\right)}_{\text{H}}=\frac{{\text{MHC}}_0{v}_{\text{p}}}{{\text{MHC}}_0{v}_{\text{p}}+e^{w_{\text{H}}/k_{\text{B}}T}}.& (9)\end{array}$

This is used in the transition from Equations (2A) to (4A).

References

1. Zasloff M. Antimicrobial peptides of multicellular organisms. Nature. (2002) 415:389–95. doi: 10.1038/415389a

CrossRef Full Text | Google Scholar

2. Brogden KA. Antimicrobial peptides: pore formers or metabolic inhibitors in bacteria? Nat Rev Microbiol. (2005) 3:238–50. doi: 10.1038/nrmicro1098

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Melo MN, Ferre R, Castanho MARB. Antimicrobial peptides: linking partition, activity and high membrane-bound concentrations. Nat Rev Microbiol. (2009) 7:245–50. doi: 10.1038/nrmicro2095

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Epand RM Epand RF. Biophysical analysis of membrane-targeting antimicrobial peptides: membrane properties and the design of peptides specifically targeting gram-negative bacteria. In: Wang G, editor. Antimicrobial Peptides Discovery, Design and Novel Therapeutic Strategies. Wallingford: CABI (2010).

Google Scholar

5. Matsuzaki K. Why and how are peptide-lipid interactions utilized for self-defense? Magainins and tachyplesins as archetypes. Biochim Biophys Acta. (1999) 1462:1–10. doi: 10.1016/s0005-2736(99)00197-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hancock RE, Haney EF, Gill EE. The immunology of host defence peptides: beyond antimicrobial activity. Nat Rev Immunol. (2016) 16:321–34. doi: 10.1038/nri.2016.29

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mookherjee N, Anderson MA, Haagsman HP, Davidson DJ. Antimicrobial host defence peptides: functions and clinical potential. Nat Rev Drug Discov. (2020) 19:311–32. doi: 10.1038/s41573-019-0058-8

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hancock REW, Sahl HG. Antimicrobial and host-defense peptides as new anti-infective therapeutic strategies. Nat Biotechnol. (2006) 24:1551–7. doi: 10.1038/nbt1267

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jiang Z, Vasil AI, Hale JD, Hancock REW, Vasil ML, Hodges RS. Effects of net charge and the number of positively charged residues effects on the biological activity of amphipathic α-helical cationic antimicrobial peptides. Biopolymers. (2007) 90:369–83. doi: 10.1002/bip.20911

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Perron GG, Zasloff M, Bell G. Experimental evolution of resistance to an antimicrobial peptide. Proc R Soc B. (2006) 273:251–6. doi: 10.1098/rspb.2005.3301

CrossRef Full Text | Google Scholar

11. Peschel A, Sahl HG. The co-evolution of host cationic antimicrobial peptides and microbial resistance. Nat Rev Microbiol. (2006) 4:529–36. doi: 10.1038/nrmicro1441

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bagheri A, Taheri-Araghi A, Ha BY. How cell concentrations are implicated in cell selectivity of antimicrobial peptides. Langmuir. (2015) 31:8052–62. doi: 10.1021/acs.langmuir.5b01533

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Nourbakhsh S, Taheri-Araghi S, Ha BY. Toward building a physical model for membrane selectivity of antimicrobial peptides: making a quantitative sense of the selectivity. Soft Matter. (2019) 15:7509–26. doi: 10.1039/c9sm00930b

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lee MT, Chen FY, Huang HW. Energetics of pore formation induced by membrane active peptides. Biochemistry. (2004) 43:3590–9. doi: 10.1021/bi036153r

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lee M, Hung W, Chen F, Huang HW. Many-body effect of antimicrobial peptides: on the correlation between Lipid's spontaneous curvature and pore formation. Biophys J. (2005) 89:4006–16. doi: 10.1529/biophysj.105.068080

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Huang HW. Molecular mechanism of antimicrobial peptides: the origin of cooperativity. Biochim Biophys Acta Biomembr. (2006) 1758:1292–302. doi: 10.1016/j.bbamem.2006.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Melo MN, Ferre R, Feliu L, Bardají E, Planas M, Castanho MARB. Prediction of antibacterial activity from physicochemical properties of antimicrobial peptides. PLoS ONE. (2011) 6:e28549. doi: 10.1371/journal.pone.0028549

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Matsuzaki K. Control of cell selectivity of antimicrobial peptides. Biochim Biophys Acta Biomembr. (2009) 1788:1687–92. doi: 10.1016/j.bbamem.2008.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Savini F, Luca V, Bocedi A, Massoud R, Park Y, Mangoni ML, et al. Cell-density dependence of host-defense peptide activity and selectivity in the presence of host cells. ACS Chem Biol. (2017) 12:52–6. doi: 10.1021/acschembio.6b00910

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Savini F, Bobone S, Roversi D, Mangoni ML, Stella W. From liposomes to cells: filling the gap between physicochemical and microbiological studies of the activity and selectivity of host-defense peptides. Peptide Sci. (2018) 110:e24041–1-14. doi: 10.1002/pep2.24041

CrossRef Full Text | Google Scholar

21. Snoussi M, Talledo JP, Rosario NAD, Mohammadi S, Ha BY, Košmrlj A, Taheri-Araghi S. Heterogeneous absorption of antimicrobial peptide LL37 in Escherichia coli cells enhances population survivability. eLife. (2018) 7:e38174. doi: 10.7554/eLife.38174

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Loffredo MR, et al. Inoculum effect of antimicrobial peptides. (2020) Available online at: https://www.biorxiv.org/content/10.1101/2020.08.21.260620v1.full

Google Scholar

23. Dill K, Bromberg S. Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience. 2nd Edition. New York, NY: Garland Science.

Google Scholar

24. Starr CG, He J, Wimley WC. Host cell interactions are a significant barrier to the clinical utility of peptide antibiotics. ACS Chem Biol. (2016) 11:3391–9. doi: 10.1021/acschembio.6b00843

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix

Here we present a Langmuir model of peptide binding [see (23) and the SI of (12)]. Let μ_B and μ_H be the chemical potential of bound peptides, and σ_B and σ_H their planar density, on the bacterial and host-cell surface, respectively. The planar density is related to P/L through σ_Ba_B = (P/L)_B and σ_Ha_H = (P/L)_H. Recall that w_B and w_H are the peptide binding energy for bacterial and host-cell membranes, respectively. In general, the binding energy depends on the value of P/L mainly through the interaction between bound peptides. In recent studies (13), it was estimated at P/L = (P/L)*. The resulting binding energy can be used to find (P/L)*, i.e., either MIC or MHC.

Let v_p be the volume occupied by each peptide in the bulk and A_p the area occupied by each bound peptide on the membrane surface. In the presence of two types of cells, we find

$\begin{array}{l}{\mu }_{\text{B}}=w_{\text{B}}+k_{\text{B}}T\ln \left(\frac{{\sigma }_{\text{B}}{A}_{\text{p}}}{1-{\sigma }_{\text{B}}{A}_{\text{p}}}\right)\\ {\mu }_{\text{H}}=w_{\text{H}}+k_{\text{B}}T\ln \left(\frac{{\sigma }_{\text{H}}{A}_{\text{p}}}{1-{\sigma }_{\text{H}}{A}_{\text{p}}}\right)& (\mathrm{A1})\end{array}$

as well as

$\begin{array}{ll}{\mu }_{\text{free}}=k_{\text{B}}T\ln \left\{\left[C_{\text{p}}-\left(C_{\text{B}}{\sigma }_{\text{B}}{A}_{\text{B}}+C_{\text{H}}{\sigma }_{\text{H}}{A}_{\text{H}}\right)\right]v_{\text{p}}\right\}.& (\mathrm{A2})\end{array}$

In equilibrium, μ_B = μ_H = μ_free. We thus arrive at

$\begin{array}{ll}{C}_{\text{p}}={\left(\frac{P}{L}\right)}_{\text{B}}\frac{A_{\text{B}}}{a_{\text{B}}}{C}_{\text{B}}+{\left(\frac{P}{L}\right)}_{\text{H}}\frac{A_{\text{H}}}{a_{\text{H}}}{C}_{\text{H}}+\frac{1}{v_{\text{p}}}\frac{\frac{A_{\text{p}}}{a_{\text{B}}}{\left(\frac{P}{L}\right)}_{\text{B}}}{1-\frac{A_{\text{p}}}{a_{\text{B}}}{\left(\frac{P}{L}\right)}_{\text{B}}}{e}^{w_{\text{B}}/k_{\text{B}}T}& (\mathrm{A3a})\end{array}$

$\begin{array}{ll}{C}_{\text{p}}={\left(\frac{P}{L}\right)}_{\text{B}}\frac{A_{\text{B}}}{a_{\text{B}}}{C}_{\text{B}}+{\left(\frac{P}{L}\right)}_{\text{H}}\frac{A_{\text{H}}}{a_{\text{H}}}{C}_{\text{H}}+\frac{1}{v_{\text{p}}}\frac{\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{1-\frac{A_{\text{p}}}{a_{\text{H}}}{\left(\frac{P}{L}\right)}_{\text{H}}}{e}^{w_{\text{H}}/k_{\text{B}}T}.& (\mathrm{A3b})\end{array}$

In this expression, we eliminated the planar density in favor of P/L. These equations can be solved simultaneously for the two unknowns: (P/L)_H and (P/L)_B for a given value of C_p. The value of C_p at which ${(P/L)}_{\text{H}}={(P/L)}_{\text{H}}^{*}$ (${(P/L)}_{\text{B}}={(P/L)}_{\text{B}}^{*})$ is an MHC (MIC). If evaluated at P/L*, the last term in Equations A3(a) and (b) is the $C_{\text{p}}^{*}$ in the low-cell density limit: either MHC₀ or MIC₀.