Design of circulating temperature control system for rubber and plastic industry based on mechatronics

Introduction: In the modern rubber and plastics industry, temperature control becomes a key factor affecting product quality and production efficiency. However, the existing temperature control system generally has the problem of temperature lag and high energy consumption. Aiming at the problem of poor control effect of current temperature control system, a new circulating temperature control system for plastic industry was proposed in this study.

Methods: Firstly, fuzzy neural network and improved particle swarm optimization algorithm were introduced in this study, and then the hybrid algorithm was combined with mechatronics technology to design and implement a set of rubber and plastic industry cycle temperature control system.

Results: According to the test data, the improved algorithm performed well in both scenarios. Compared with the comparison algorithm, the improved algorithm has the following parameters: tuning time (scenario 1:513s, scenario 2:521s), overshoot (scenario 1:2.5%, scenario 2:2.3%), steady-state error (scenario 1:005, scenario 2:004) and absolute integral error (scenario 1:008, scenario 2: 0.007) has been significantly optimized. Simulation analysis shows that the proposed temperature control system has stronger anti-interference ability and lower energy consumption (0.6 hour energy consumption: 1086.5J, energy saving rate: 38.7%).

Discussion: The results show that the cyclic temperature control system of rubber and plastics industry is superior to the comparison system in terms of temperature control performance, anti-interference ability and energy consumption. The research not only improves the accuracy and efficiency of temperature control systems in the rubber and plastics industry, but also promotes the promotion of green and sustainable production methods. This is essential to promote the high-quality development of the plastics and rubber industry.

1 Introduction

In the modern rubber and plastic industry, with the rapid development of economy, the demand for rubber products and plastic products has increased sharply, and the market competition has become increasingly fierce (Bandewad et al., 2023). The temperature control in the process of rubber and plastic processing is a key link, which directly affects the quality and production efficiency of the product. In the rubber and plastic industry, temperature control systems (TCS) are faced with unique challenges. Different from general stochastic dynamic systems, the rubber and plastic processing process has significant nonlinear, time-varying and uncertain characteristics (Chauhan et al., 2024a). These characteristics stem from the fact that the thermophysical properties of rubber and plastic materials change significantly with temperature, as well as the complex chemical reactions during processing. These characteristics make temperature control difficult to describe and predict through simple mathematical models, so designing an effective control strategy requires a deep understanding and quantification of these specific characteristics (Chauhan et al., 2024b).

Numerous academics and engineers have done a great deal of research on the creation and use of temperature control devices since the turn of the century, when circulating temperature control technology first emerged. For example, Chen and Hu suggested a TCS based on adaptive enhanced genetic algorithm to better adjust the greenhouse’s temperature to improve plant growth rate. The outcomes demonstrated that the technology could successfully regulate the greenhouse’s temperature and encourage plant growth (Chen and Hu, 2022). In addition, Lyngfelt et al. (2022) suggested a TCS for fluidized bed boilers with the goal to solve the issue of high temperature volatility in these boilers. According to the findings of the empirical analysis, this TCS outperformed the classical control system in terms of temperature control (Lyngfelt et al., 2022). However, despite the achievements, a comprehensive and systematic design theory has not been formed so far. Existing TCS mostly suffers from the problems of temperature lag, high energy consumption (EC) and complicated operation, which is difficult to meet the modern rubber and plastic industry’s demand for high precision, high efficiency and low EC. In recent years, the research of temperature control technology not only focuses on hardware design and implementation, but also gradually deepens into the optimization and innovation of temperature control algorithm. In terms of temperature monitoring and control of microfluidic devices, Dos-Reis-Delgado et al. (2023) reviewed the latest progress and challenges, emphasizing the importance of high-precision temperature control for improving the performance of microfluidic systems (Dos-Reis-Delgado et al., 2023). Meanwhile, in the field of processing, Fernandes et al. adopted internal cooling tools to achieve temperature control during the processing of Inconel 718, thus enhancing sustainability (Fernandes et al., 2024). These studies show that temperature control technology is gradually developing in a more efficient and environmentally friendly direction.

Current research mainly focuses on the hardware design and implementation of TCS, while the optimization and innovation of temperature control algorithm is relatively insufficient. Despite the widespread usage of the conventional proportional-integral-derivative (PID) technique, achieving the optimal control effect in the complex and dynamic industrial environment can frequently be challenging. For example, Ghamari et al. (2022) proposed a PID controller (PIDC) based on ant optimization algorithm to improve the performance of buck converter. Patil et al. (2024) reviewed PID controller tuning methods based on intelligent and natural heuristic algorithms and pointed out the potential of these methods in improving control performance in industrial applications. In addition, Coskun and StiIK applied intelligent PID control to industrial electro-hydraulic systems to achieve higher control accuracy and stability (Coskun and İtik, 2023). Liu et al. (2023) proposed a general industrial temperature control system based on fuzzy fractional order PID controller, providing a new solution for complex industrial temperature control problems. In summary, although cyclic temperature control technology has made some progress, the optimization and innovation of temperature control algorithm still need to be strengthened.

In view of the above background and status quo, the study designs and realizes a set of efficient and accurate circulating TCS in rubber and plastic industry by introducing fuzzy neural network and combining with mechatronics technology (MT). The goal of the study is to enhance the rubber and plastic industry’s production efficiency and product quality while also resolving issues with the current TCS. The research’s novelty lies in incorporating intricate algorithms into the design of circulating TCS in the rubber and plastic industries, and in optimizing the system’s response time and accuracy through control. Concurrently, the intelligent and modular design of TCS is realized to enhance the system’s expandability and maintainability when integrated with MT.

2 Methods and materials

2.1 Temperature control algorithm based on improved PSO and fuzzy PID

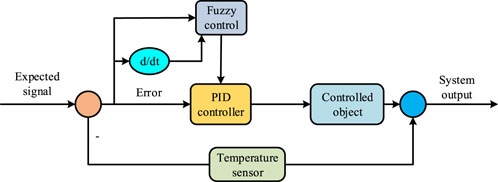
An improved control technique that blends fuzzy logic (FL) with conventional PID control strategy is called the fuzzy PID control algorithm (FPIDCA). It is frequently challenging for the typical PIDC to accomplish the required control effect in circulating TCS in the rubber and plastic industries because of the nonlinearity, time-varying, and uncertainty of the processing process. The FPIDCA introduces FL to change the PIDC’s settings online, which increases the control system’s robustness and adaptability. Figure 1 depicts its control flow.

Figure 1

Figure 1. Control flow of FPIDCA.

The creation of the FL controller in Figure 1, which includes the fuzzification of input variables, the creation of fuzzy rules, and the defuzzification of output variables, is crucial to the design of the fuzzy PIDC. The error change rate and the system error are typically among the input variables. To get at the fuzzy control quantities, they are first fuzzified into fuzzy sets and then reasoned using fuzzy rules. The defuzzification process then transforms the fuzzy control quantity into the actual PID parameter adjustment quantity, realizing the dynamic adjustment of the PIDC. Through fuzzy reasoning, the adjustment amount of PID parameters can be obtained as shown in Equation 1.

$\left\{\begin{array}{l}\Delta K_p={\displaystyle \sum _{i=1}^n}\mu A_i\left(e\right)\mu B_i\left(ec\right)C_i\\ \Delta K_i={\displaystyle \sum _{i=1}^n}\mu A_i\left(e\right)\mu B_i\left(ec\right)D_i\\ \Delta K_d={\displaystyle \sum _{i=1}^n}\mu A_i\left(e\right)\mu B_i\left(ec\right)E_i\end{array}\right.(1)$

In Equation 1, $A_i$, $B_i$, $C_i$, $D_i$, and $E_i$ denote the fuzzy sets of error, error change rate, and PID parameter adjustment, respectively. $\mu A_i\left(e\right)$ and $\mu B_i\left(ec\right)$ denote the affiliation functions of the corresponding fuzzy sets of error and error change rate, respectively. Ultimately, Equation 2 displays the PIDC’s parameters.

$\left\{\begin{array}{l}{K}_p={K_p}^{\prime }+\Delta K_p\\ K_i={K_i}^{\prime }+\Delta K_i\\ K_d={K_d}^{\prime }+\Delta K_d\end{array}\right.(2)$

In Equation 2, $K_d$, $K_i$ and $K_p$ are the initial parameters of the PIDC. To provide more precise and reliable temperature management, the FPIDCA may thus dynamically modify the PID parameters in accordance with the system’s current state. When it comes to circulating TCS in the rubber and plastic industry, the FPIDCA outperforms the classic PID control method in terms of resilience and adaptability, but its performance is still constrained by the affiliation function selection and fuzzy rule formulation. The study presents the particle swarm optimization (PSO) algorithm to optimize the fuzzy PIDC’s parameters in an effort to further improve its performance. PSO is a group intelligence-based optimization algorithm that solves optimization problems by mimicking the social behaviors of biological groups, like fish schools and flocks of birds. PSO updates the particle’s position and velocity iteratively in order to find the optimal solution, with each particle serving as a potential solution to the problem. Equation 3 displays the particle velocity update formula.

$v_{id}^{k+1}=\omega v_{id}^k+c_1{r}_1\left(p_{id}^k-x_{id}^k\right)+c_2{r}_2\left(p_{gd}^k-x_{gd}^k\right)(3)$

In Equation 3, $v_{id}^{k+1}$ denotes the speed of the $k+1$ th iteration of the $i$ th particle in the $d$ th dimension. $\omega$ is the inertia weight (IW). $c_1$ and $c_2$ are learning factors. $r_1$ and $r_2$ are random numbers between [0, 1]. $p_{id}^k$ is the best position found so far by the $i$ th particle in the $d$ th dimension. $p_{gd}^k$ is the best position found so far by all particles on the $d$ th dimension. $x_{id}^k$ is the position of the $i$ th particle at the $k$ th iteration on the $d$ th dimension. Equation 4 lists the particle position update formula.

$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}(4)$

In Equation 4, $x_{id}^{k+1}$ denotes the position of the $i$ th particle at the $k+1$ th iteration in the $d$ th dimension. By using PSO for fuzzy PIDC parameter optimization, the iterative search of PSO can identify the ideal parameter combinations. The parameters of the controller can be encoded as the particle positions. Its specific steps are shown in Figure 2.

Figure 2

Figure 2. Specific steps of fuzzy PID optimization by PSO algorithm.

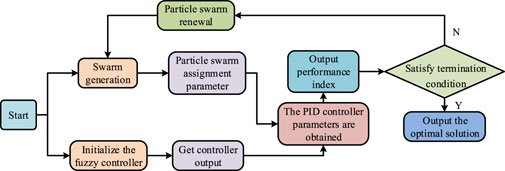
In Figure 2, the process of optimizing fuzzy PID by particle swarm algorithm (PSA) includes the steps of initializing particle swarm, evaluating particle fitness, updating particle velocity and position, and judging termination conditions. Among them, the design of the fitness function (FF) is the key, which can reflect the control performance of the fuzzy PIDC in circulating TCS in rubber and plastic industry, such as control accuracy, response speed, stability and so on. Equation 5 presents the expression of the FF.

$F\left(X\right)=\alpha \cdot Accuracy\left(X\right)+\beta \cdot ReponseTime\left(X\right)+\gamma \cdot Stability\left(X\right)(5)$

In Equation 5, $F\left(X\right)$ is the FF for evaluating the performance of particle $X$ (a set of fuzzy PIDC parameters). $\alpha$, $\beta$, $\gamma$ are the weighting coefficients, which are used to balance the weights between control accuracy, response speed and stability. $Accuracy\left(X\right)$, $ReponseTime\left(X\right)$ and $Stability\left(X\right)$ are functions to evaluate the control accuracy, response speed and stability respectively. Through the iterative search of the PSA, the combination of fuzzy PIDC parameters that makes the FF optimal can be found to further improve the performance of the TCS (Rajamani et al., 2023). Nevertheless, the PSA has drawbacks including limited convergence accuracy and an easy way to enter a local optimal state. To further enhance the effectiveness of PSO optimized fuzzy PIDC in circulating TCS in rubber and plastic industry, the study proposes an improved particle swarm optimization (IPSO). Moreover, it is combined with the FPIDCA to form the IPSO-FZPID temperature control algorithm. The algorithm aims to find the optimal fuzzy PIDC parameter combinations more efficiently by improving the search mechanism of the PSA, so as to improve the TCS’s overall performance. In the IPSO-FZPID temperature control algorithm, during the iteration process of the PSA, the adaptive adjustment strategy of introducing the IW $w$ and acceleration coefficients $c_1$ and $c_2$ is studied. This enables it to better reflect the actual control effect of fuzzy PIDC in circulating TCS in rubber and plastic industry. The adaptive tuning equation is shown in Equation 6.

$\left\{\begin{array}{l}w=w_{\max }-\frac{\left(w_{\max }-w_{\min }\right)\cdot iter}{ite{r}_{\max }}\\ c_1={c_1}_{start}+\frac{\left(c_{1end}-{c_1}_{start}\right)\cdot iter}{ite{r}_{\max }}\\ c_2={c_2}_{start}+\frac{\left(c_{2end}-{c_2}_{start}\right)\cdot iter}{ite{r}_{\max }}\end{array}\right.(6)$

In Equation 6, $iter$ is the current iteration number. $ite{r}_{\max }$ is the maximum iterations. $w_{\max }$ and $w_{\min }$ are the maximum and minimum values of IWs, respectively. ${c_1}_{start}$, $c_{1end}$, ${c_2}_{start}$ and $c_{2end}$ are the start and end values of the acceleration coefficients, respectively. The specific operation flow of IPSO-FZPID temperature control algorithm is shown in Figure 3.

Figure 3

Figure 3. Specific operation flow of IPSO-FZPID temperature control algorithm.

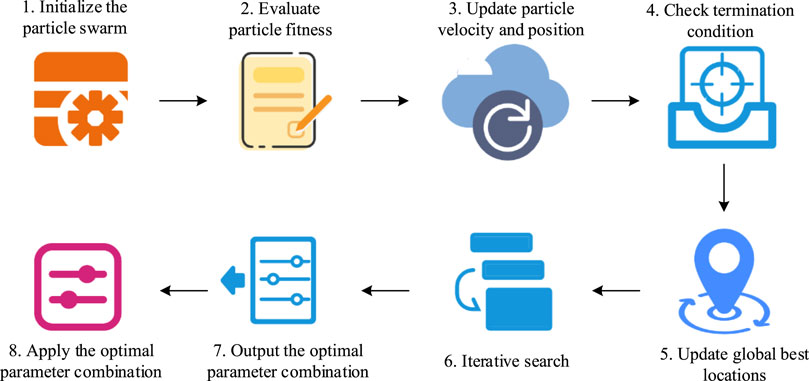
In Figure 3, the operation process of IPSO-FZPID temperature control algorithm is mainly divided into eight steps. The initialization of the particle swarm and the measurement of its size and particle dimensions in relation to the fuzzy PIDC’s parameter count constitute the first step. Compute each particle’s fitness value for evaluation based on the FF in the second step. The third step is to update the velocity and position of each particle using the update formula of IPSO, and to ensure that the updated particle positions are still within the valid parameter range. Verifying that the termination condition has been satisfied is the fourth step. The iteration ends if it is satisfied. If not, carry out the fifth step as before. The particle with the highest fitness value is identified in the fifth phase, which involves updating the global best position to that particle’s location and comparing the fitness values of all current particles. Repeating steps 2 through 5 until the termination condition is met is the sixth step. At the conclusion of the iteration, the seventh step is to output the global best position as the fuzzy PIDC’s ideal parameter combination. To achieve more precise and consistent temperature control in the rubber and plastic industries, the eighth stage involves applying the ideal parameter combination to the fuzzy PIDC in the circulating TCS. The innovation of this research is to combine IPSO algorithm with FZPID, and improve the response time and accuracy of cyclic TCS through control optimization. By dynamically adjusting PID parameters, the IPSO algorithm can better adapt the fuzzy PID controller to the complex and changing industrial environment, so as to improve the accuracy and stability of temperature control. At the same time, by combining with mechatronics technology, the intelligent and modular design of TCS is realized, and the scalability and maintainability of the system are improved.

2.2 Design of circulating TCS in rubber and plastic industry combining mechatronics and IPSO-FZPID algorithm

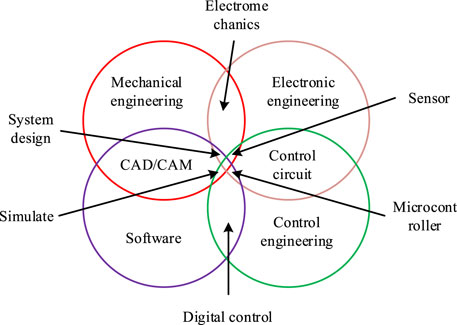
In the circulating TCS in rubber and plastic industry, the application of mechatronics can combine the traditional mechanical temperature control equipment with advanced electronic control technology to realize more accurate and efficient temperature control. However, the temperature control algorithm plays an important role, so the study combines the IPSO-FZPID algorithm and mechatronics to propose a new type of circulating TCS in rubber and plastic industry. Therefore, the research combines IPSO-FZPID algorithm and mechatronics to propose a new circulating TCS in rubber and plastic industry. Among them, mechatronics is a cross-discipline combining mechanical technology and electronic technology. It covers many fields such as mechanical design, electronic technology, control theory, computer technology and so on (Wang et al., 2023). The principle of MT is shown in Figure 4.

Figure 4

Figure 4. Technical principle of mechatronics.

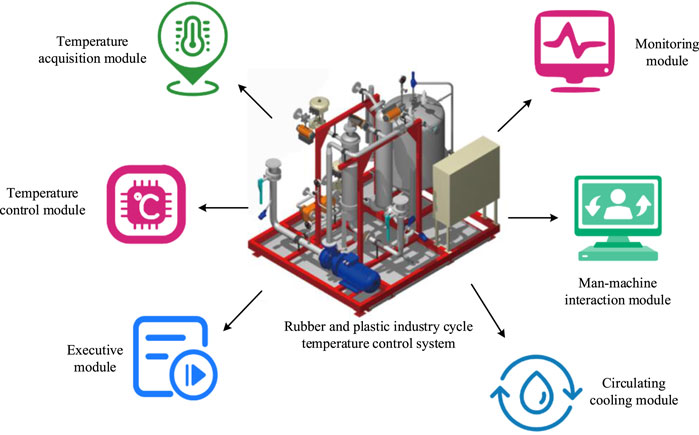
In Figure 4, MT is a kind of technology that organically combines mechanical technology, sensor technology and other technologies, and comprehensively applies them in practice. It is the combination of mechanical engineering and automation. By affixing or integrating the information processing and control capabilities of electronic devices onto mechanical equipment, it realizes the intelligence and humanization of mechanical devices (Kuru et al., 2023). In addition, the design of a mechatronics system involves several aspects, including the mechanical body, sensor devices, information processing devices, and actuators. The synergistic work of these components enables the system to be optimized for the convenience of the user. In circulating TCS in rubber and plastic industry, mechatronics is able to combine traditional mechanical temperature control equipment with electronic control technology to achieve more efficient temperature control (Baghli et al., 2023; Petrosian et al., 2023). Moreover, IPSO-FZPID algorithm can accurately control the temperature of TCS. Therefore, the study proposes circulating TCS in rubber and plastic industry that combines both. The system combines various technologies such as mechanical, electronic and control to achieve accurate control of temperature in the production process. The proposed circulating TCS mainly consists of temperature acquisition module, temperature control module, actuator module and circulating cooling module. Its structure is shown in Figure 5.

Figure 5

Figure 5. Structure diagram of circulating TCS in rubber and plastic industry.

In Figure 5, the TCS mainly includes six modules. Among them, the temperature acquisition module is responsible for real-time acquisition of temperature data during the rubber and plastic processing. After being processed by the signal conditioning circuit, the temperature data are transferred to the temperature control module. The research uses a low-pass filter for noise suppression throughout the temperature acquisition process to reduce the effect of sensor noise on the temperature data. Equation 7 displays the low-pass filter’s transfer function.

$H\left(s\right)=\frac{{\omega }_c}{s+{\omega }_c}(7)$

In Equation 7, ${\omega }_c$ is the cutoff frequency and $s$ is the complex variable of Laplace transform. The temperature control module is the core of the system, which receives temperature data from the temperature acquisition module. After data preprocessing, the IPSO-FZPID temperature control algorithm is applied to accurately control the temperature based on the preset temperature setpoint and the current actual temperature value. The study uses Kalman filter to process the dynamic temperature data to provide more accurate temperature estimation. Equation 8 displays the state update and covariance update formulae for the Kalman filter.

$\left\{\begin{array}{l}{\stackrel{⌢}{x}}_{k\left|k\right.}={\stackrel{⌢}{x}}_{k\left|k-1\right.}+K_k\left(z_k-H{\stackrel{⌢}{x}}_{k\left|k-1\right.}\right)\\ P_{k\left|k\right.}=\left(I-K_{k}H\right)P_{k\left|k\right.-1}\end{array}\right.(8)$

In Equation 8, ${\stackrel{⌢}{x}}_{k\left|k\right.}$ is the current state estimate. $z_k$ is the observation value. $H$ is the observation matrix. $K_k$ is the Kalman gain. $P_{k\left|k\right.}$ is the estimated covariance matrix. The IPSO-FZPID algorithm combines the advantages of IPSO and FPIDCA, and calculates the optimal control parameters by dynamically adjusting the PID parameters to adapt to the complex and changing industrial environment. Afterwards, these control parameters are converted into control signals and sent to the actuator module for precise regulation of the heating power or cooling flow. The actuator module drives the corresponding actuators according to the control signals from the temperature control module. These actuators adjust the heating power or cooling flow rate to realize the precise regulation of the temperature during the machining process. The dynamic response model of the actuators is shown in Equation 9.

$\tau \frac{dy}{dt}+y=K{u}_1(9)$

In Equation 9, $y$ is the output and $u_1$ is the input control signal. $\tau$ is the time constant and $K$ is the gain. The circulating cooling module is responsible for the recycling of the cooling medium, which is delivered to the part to be cooled by a pump. The heat is absorbed and then dissipated through heat sinks or cooling towers and then re-circulated. The cooling medium’s heat transmission in the circulating cooling module can be explained by a one-dimensional heat transfer equation. Equation 10 displays the particular expression.

$\frac{\mathrm{\partial }T}{\mathrm{\partial }t}={\alpha }^{\prime }\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{x}^2}-u_2\frac{\mathrm{\partial }T}{\mathrm{\partial }x}(10)$

In Equation 10, $T$ is temperature. $t$ is time. $x$ is position. ${\alpha }^{\prime }$ is thermal diffusivity. $u_2$ is the fluid velocity. In addition, the system is equipped with a human-computer interaction module that allows the operator to conveniently set temperature set-points, monitor real-time temperature profiles, view historical data, and perform system troubleshooting. Lastly, a monitoring module is also included in the system to track the real-time functioning of critical components and guarantee the system’s stable operation. Once abnormal conditions are detected, the system will automatically alarm and take appropriate protective measures to avoid the expansion of the fault on the production impact. The whole system through the coordinated work of the modules, to achieve a precise and efficient control of the temperature in the rubber and plastic processing. In addition to lowering EC and environmental pollutants, this successfully raises product quality and manufacturing efficiency.

3 Results

3.1 Comparative performance analysis of IPSO-FZPID temperature control algorithm

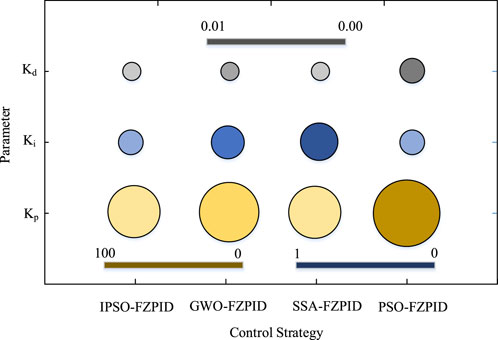
The FZPID parameters are optimized in this work through the use of IPSO. Through performance comparisons with the Grey Wolf Optimizer Fuzzy PID Controller (GWO-FZPID), Sparrow Search Algorithm-Fuzzy PID Controller (SSA-FZPID), and Particle Swarm Optimization-Fuzzy PID Controller (PSO-FZPID) algorithms, the study examines the effectiveness of this method’s optimized FZPID algorithm. These algorithms were chosen as benchmarks primarily because of their broad applicability and effectiveness in dealing with complex optimization problems. GWO algorithm seeks the optimal solution by simulating the social rank and hunting behavior of gray wolves, SSA algorithm simulates the foraging and warning behavior of sparrows, and traditional PSO algorithm optimizes parameters by information sharing and iterative updating among particles. The performance of these algorithms has been established through simulation experiments and literature review, and has a certain representativeness. The comparative test’s special experimental setting is separated into two main sections: software and hardware. To guarantee the high efficiency of the algorithm operation, the hardware is a high-performance server outfitted with an Intel Xeon processor and large-capacity RAM. The software is based on the MATLAB/Simulink platform to build a simulation environment, using its powerful numerical computation and dynamic system simulation capabilities, to assess the performance of the algorithm and comparative analysis. The dataset used in the study is a homemade dataset that collects a variety of scenarios of temperature changes during rubber and plastic processing. To guarantee test findings are accurate and fair, all comparison algorithms are executed in the same experimental setup. The controller parameters obtained from the four algorithms are first compared and the results are shown in Figure 6.

Figure 6

Figure 6. PIDC parameters obtained by different methods.

In Figure 6, the K_p values of IPSO-FZPID, GWO-FZPID, SSA-FZPID, and PSO-FZPID algorithms are 31.18, 21.45, 52.36, and 22.48, respectively. The K_i values of these four algorithms are 0.392, 0.578, 0.273, and 0.271, respectively. The K_d values of these four algorithms are 0.060, 0.048, 0.083, 0.045. The study computes the tuning time (TT), peak time (PT), and rise time (RT) dynamic characteristic indexes under the unit-step response after acquiring the parameters of the four algorithms. This allows for an evaluation of the algorithms’ performance. These metrics can reflect the response speed and stability of the controller. Figure 7 displays the unit step curves for each of the four methods in the data set.

Figure 7

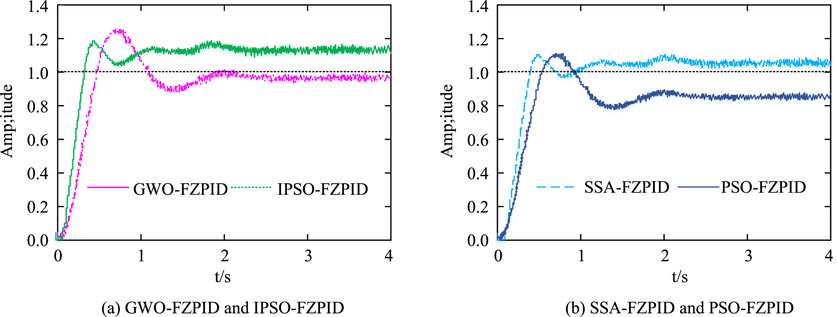
Figure 7. Comparison results of dynamic characteristics of four PIDC’s. (A) GWO-FZPID and IPSO-FZPID (B) SSA-FZPID and PSO-FZPID.

In Figure 7, the TT, PT, and RT of the proposed IPSO-FZPID algorithm of the study are 0.513s, 0.478s, and 0.443s, respectively. The TT, PT, and RT of the GWO-FZPID algorithm are 0.638s, 0.629s, and 0.613s, respectively. The TT, PT, and RT of the SSA-FZPID algorithm are 1.836s, 0.721s, and 0.633s, respectively. The TT, PT, and RT of PSO-FZPID algorithm are 1.391s, 0.811s, and 0.724s, respectively. The aforementioned findings show that the action object responds more quickly and that the research-proposed IPSO-FZPID algorithm performs better in terms of control than the comparative algorithms. To verify the performance of the fuzzy PID algorithm proposed by the study, the study also compares and analyzes its temperature control error with the comparison algorithm in two different scenarios. Figure 8 displays the analysis’s findings. Two scenarios are set up to further verify the performance of IPSO-FZPID algorithm. Scenario 1 simulates conventional temperature changes during rubber and plastic processing, while Scenario 2 simulates a more complex and dynamic environment of temperature changes, including more external disturbances and uncertainties. The main difference between the two scenarios is the complexity and degree of uncertainty of temperature change. The temperature changes in scenario 1 are relatively smooth, while the temperature changes in scenario 2 are more dramatic and unpredictable. The choice of these two scenarios is based on the actual needs of the rubber and plastics processing industry and is designed to cover a wide range of situations from fast response to stability control. These two scenarios were chosen mainly based on their universality and representation in rubber and plastic processing, as well as their ease of simulation and implementation in a simulation environment.

Figure 8

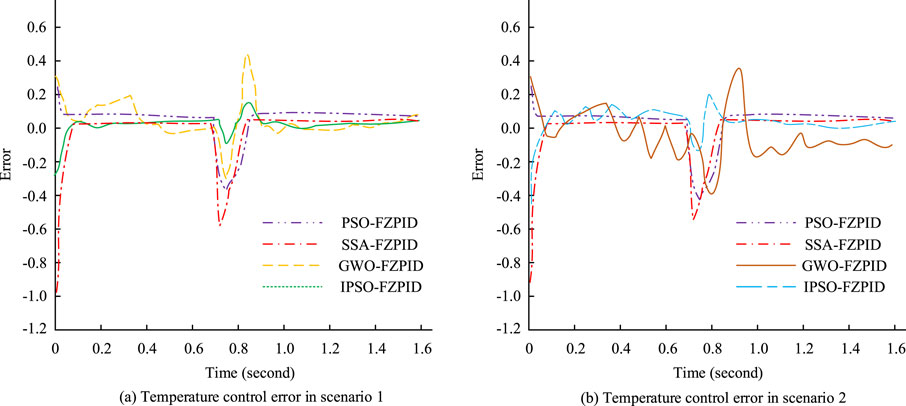
Figure 8. Comparison curve of temperature control errors. (A) Temperature control error is scenario 1 (B) Temperature control error is scenario 2.

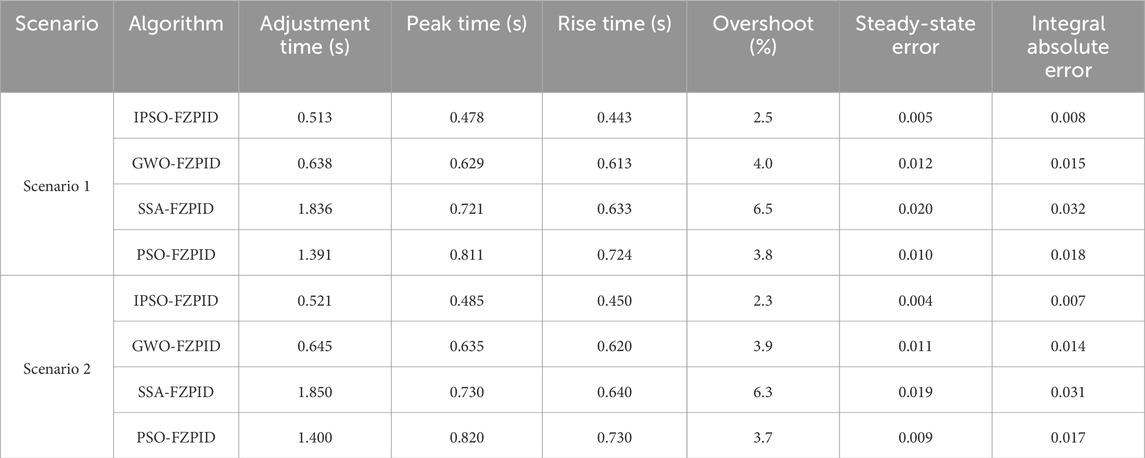
In Figure 8A, in Scenario 1, the overall average error value of temperature control of the IPSO-FZPID algorithm is 0.05, while the overall average error value of temperature control of the GWO-FZPID algorithm, SSA-FZPID algorithm, and PSO-FZPID algorithm are 0.08, 0.25, and 0.13, respectively. The overall average error value of the IPSO-FZPID algorithm’s temperature control is shown in Figure 8B as being substantially better than that of the comparative algorithms. The above results indicate that the IPSO-FZPID algorithm has better temperature control, which further illustrates the superiority of the performance of the proposed IPSO-FZPID algorithm of the study. Finally the study compares the four algorithms in two scenarios in terms of TT, PT, above time, overshooting amount, steady state error, and integral absolute error. Table 1 displays the results of the comparison.

Table 1

Table 1. Performance comparison of the four algorithms in two scenarios.

The data in Table 1 show that the IPSO-FZPID algorithm performs well in both scenarios. In scenario 1, the adjustment time of IPSO-FZPID is only 0.513 s, which is about 20%, 72%, and 63% faster than the GGO-FZPID’s 0.638 s, SSA-FZPID’s 1.836 s, and PSO-FZPID’s 1.391 s, respectively. At the same time, it also has the lowest overshoot, only 2.5%, far lower than the other algorithms of 4.0%, 6.5% and 3.8%. In terms of steady-state error and absolute error, IPSO-FZPID also leads other algorithms with excellent performance of 0.005 and 0.008, respectively. In Scenario 2, IPSO-FZPID remains ahead despite fluctuations in performance metrics. Its adjustment time is the fastest, 0.521 s. The lowest overshoot was 2.3%. The steady-state error is also the smallest, 0.004. These data once again prove the stability and superiority of IPSO-FZPID algorithm in two scenarios, showing its great potential in the field of control. The above data show that the IPSO-FZPID algorithm is superior to GWO-FZPID, SSA-FZPID and PSO-FZPID in terms of response speed, stability and control accuracy, and it is the preferred algorithm for rubber and plastic industryTCS.

3.2 Simulation analysis of circulating TCS in rubber and plastic industry

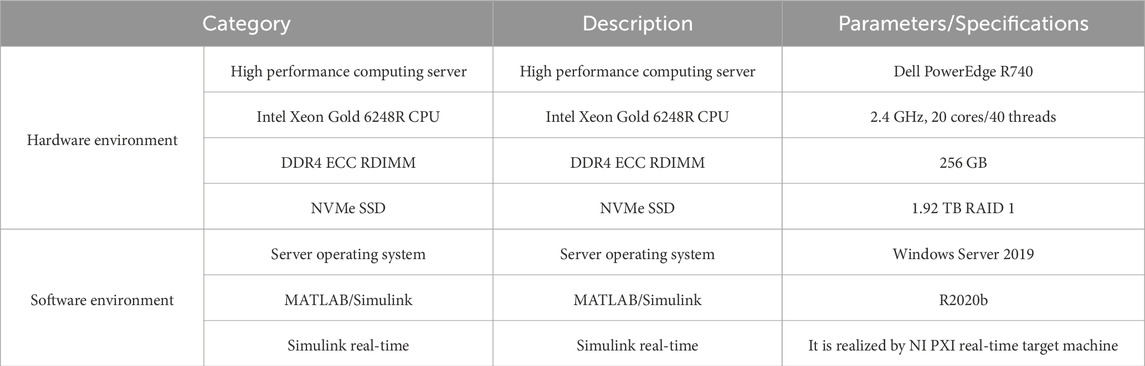
After verifying the superiority of IPSO-FZPID algorithm, in order to analyze the effectiveness of the application of circulating TCS in rubber and plastic industry proposed by the study, the study is simulated. Table 2 displays the simulation environment.

Table 2

Table 2. Simulation environment configuration of circulating TCS in rubber and plastic industry.

In the simulation environment of Table 2, the study compares this TCS with GWO-FZPID TCS and SSA-FZPID TCS for comparison experiments. The comparison indexes are simulation results and anti-interference effect, system EC, and system energy-saving rate. Figure 9 displays the comparison findings of the four TCS’s actual temperature fluctuations. In this study, the evaluation of anti-interference performance mainly considers two types of interference: first, the sudden temperature change caused by environmental factors in the processing environment is simulated; The second is the internal parameter disturbance of the system, which simulates the temperature fluctuation caused by internal factors such as controller parameters or sensor errors. In order to evaluate the anti-interference ability of the system, the study introduced these two types of interference in the simulation environment, and recorded the recovery time of the system after interference (that is, the time from the occurrence of interference to the system to reach a stable state again) and the maximum temperature fluctuation. By comparing the recovery time and temperature fluctuation amplitude under the control of different algorithms, the anti-interference performance of the system can be evaluated quantitatively.

Figure 9

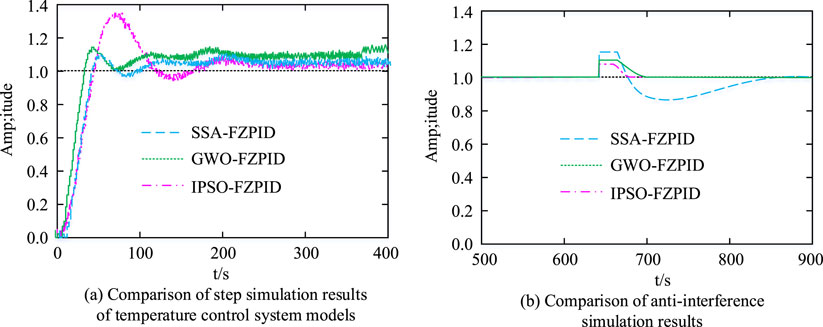
Figure 9. Comparison of simulation results and anti-interference effect of the three systems. (A) Comparison of step simulation results of temperature control sysstem models (B) comparison if anti-interference simulation results.

In Figure 9A, the overall performance of the proposed IPSO-FZPID TCS of the study is better. Its TT, PT, and RT are 50.6s, 47.5s, and 43.6s, respectively, which are better than the comparison system. Additionally, in Figure 9B, the research proposed IPSO-FZPID TCS is more resistant to interference. It is able to return to normal within 30.5s after encountering disturbances. Moreover, it only fluctuates up to 1.08, which is better than the comparison TCS. The experimental results show that IPSO-FZPID TCS exhibits stronger anti-interference ability and stability in the presence of interference. When the system encounters external disturbances, IPSO-FZPID TCS can quickly restore stability and effectively suppress temperature fluctuations, which is essential to ensure product quality in rubber and plastic processing. In contrast, the comparison algorithm has poor performance in anti-interference ability and stability, and is prone to large temperature fluctuations, which affect product quality and production efficiency. The three systems’ energy-saving rates and EC are also put to the test in this investigation. In Figure 10, the test results are displayed. In this study, the calculation of energy consumption is based on the system energy consumption model in the simulation environment. By simulating the temperature regulation process under the control of different algorithms, the model records the actual working time and power output of heating and cooling equipment, and then calculates the total energy consumption. In order to verify the accuracy of the results, the experiment was repeated several times in the simulation environment, and the average value was taken as the final result. In addition, although the energy consumption data in the study was based on simulation, the simulation model has been calibrated with actual data to ensure that it approximates real-world energy consumption.

Figure 10

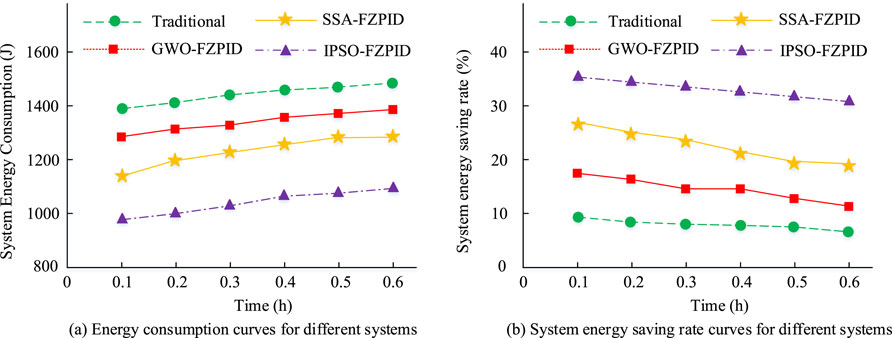
Figure 10. Comparison of EC and energy-saving rates of the three systems. (A) Energy consumption curves for different sysytems (B) system energy saving rate curves for different systems.

In Figure 10A, the IPSO-FZPID TCS has the lowest overall EC. Moreover, its EC at 0.6 h is 1,086.5 J, which is significantly better than 1,244.3 J of SSA-FZPID system, 1,381.5 J of GWO-FZPID system, and 1,431.7 J of conventional TCS. In Figure 10B, IPSO-FZPID TCS has the highest EC energy-saving rate. Moreover, its EC energy-saving rate at 0.6 h is 32.7%, which is significantly better than the comparison system. The outcomes indicate that the proposed IPSO-FZPID TCS of the study performs better in terms of EC dimension.

4 Discussion

The study designed and implemented an efficient circulating TCS in rubber and plastic industry by introducing fuzzy neural network and IPSO algorithm combined with MT. The experimental results indicated that the IPSO-FZPID temperature control algorithm TT (0.513s) was approximately 20%–70% faster than other algorithms, with the lowest overshooting (2.5%), and also significantly better than other algorithms in terms of steady state error (0.005) and integral absolute error (0.008). The results verified the effectiveness of the IPSO algorithm in optimizing the parameters of the fuzzy PIDC. Its dynamic tuning ability was especially outstanding when dealing with complex and changing industrial environments. The above results were similar to those of Dogruer and Can (2022). Further analyzing the simulation results, the IPSO-FZPID TCS not only performed well in the dynamic characteristics of temperature control, but also showed obvious advantages in the anti-interference ability. In the event of external interference, the system could quickly restore stability, effectively suppressing temperature fluctuations, which was crucial for ensuring product quality in rubber and plastic processing. In addition, from the perspective of EC, IPSO-FZPID TCS had the lowest overall EC. Moreover, its EC at 0.6 h was 1,086.5 J, which was significantly better than that of SSA-FZPID system (1,244.3 J), GWO-FZPID system (1,381.5 J), and conventional TCS (1,431.7 J). The IPSO-FZPID TCS significantly reduced the overall EC of the system and improved the energy utilization efficiency through more accurate temperature control, which is in line with the requirements of modern industrial sustainable development. The results coincided with the conclusions obtained by Suid’s team (Suid and Ahmad, 2022).

Furthermore, it is evident from comparing the research findings with the most recent studies that an increasing academics are starting to focus on the use of intelligent algorithms in TCSs. For example, some research demonstrated that predictive control algorithms based on deep learning showed strong predictive ability and optimization potential in complex industrial processes (Agarwal et al., 2023). However, these algorithms were often demanding in terms of computational resources and complicated in the model training process. In contrast, the IPSO-FZPID algorithm used in the study reduced the computational complexity and hardware resource requirements while maintaining high efficiency, which makes it easier to generalize the application in real industrial environments. In addition, the study emphasized the application of MT in TCS. By integrating sensors, controllers and actuators, the intelligent and modular design of the system was realized.

5 Conclusion

To solve the current problem of poor temperature control in rubber and plastic industry, a set of circulating TCS in rubber and plastic industry based on IPSO-FZPID algorithm and MT was successfully designed and realized. The outcomes indicated that the system was superior to the traditional TCS and other comparative algorithms in terms of response speed, stability and accuracy of temperature control. Meanwhile, the system also demonstrated strong anti-interference ability and low EC, which provided strong support for the green and sustainable development of rubber and plastic industry. However, the study still has some shortcomings. One, the IPSO algorithm performs well in optimizing the parameters of the fuzzy PIDC, but its performance is still affected by factors such as the initial parameter settings and the number of iterations. Second, the TCS in real industrial environments may face more unknown and complex disturbances, which require further validation and optimization of the robustness of the algorithm. To further improve the TCS’s performance, more sophisticated optimization algorithms and effective intelligent control techniques can be investigated in the future. Meanwhile, the cooperation with industry will be strengthened to transform the research results into practical applications and contribute to the high-quality development of rubber and plastic industry.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HC: Conceptualization, Data curation, Methodology, Writing–original draft, Writing–review and editing. WL: Formal Analysis, Software, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agarwal, S., Tyagi, M., and Garg, R. K. (2023). Conception of circular economy obstacles in context of supply chain: a case of rubber industry. Int. J. Prod. Perform. Manag. 72 (4), 1111–1153. doi:10.1108/ijppm-12-2020-0686

CrossRef Full Text | Google Scholar

Baghli, F. Z., Lakhal, Y., and El Kadi, Y. A. (2023). The efficiency of an optimized PID controller based on ant colony algorithm (ACO-PID) for the position control of a multi-articulated system. J. Robotics Control 4 (3), 289–298. doi:10.18196/jrc.v4i3.17709

CrossRef Full Text | Google Scholar

Bandewad, G., Datta, K. P., Gawali, B. W., and Pawar, S. N. (2023). Review on discrimination of hazardous gases by smart sensing technology. Artif. Intell. Appl. 1 (2), 70–81. doi:10.47852/bonviewaia3202434

CrossRef Full Text | Google Scholar

Chauhan, S., Vashishtha, G., Zimroz, R., and Kumar, R. (2024b). A crayfish optimised wavelet filter and its application to fault diagnosis of machine components. Int. J. Adv. Manuf. Technol. 135, 1825–1837. doi:10.1007/s00170-024-14626-0

CrossRef Full Text | Google Scholar

Chauhan, S., Vashishtha, G., Zimroz, R., Kumar, R., and Gupta, M. K. (2024a). Optimal filter design using mountain gazelle optimizer driven by novel sparsity index and its application to fault diagnosis. Appl. Acoust. 225, 110200. doi:10.1016/j.apacoust.2024.110200

CrossRef Full Text | Google Scholar

Chen, Q., and Hu, X. (2022). Design of intelligent control system for agricultural greenhouses based on adaptive improved genetic algorithm for multi-energy supply system. Energy Rep. 8, 12126–12138. doi:10.1016/j.egyr.2022.09.018

CrossRef Full Text | Google Scholar

Coskun, M. Y., and İtik, M. (2023). Intelligent PID control of an industrial electro-hydraulic system. ISA Trans. 139 (3), 484–498. doi:10.1016/j.isatra.2023.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Dogruer, T., and Can, M. S. (2022). Design and robustness analysis of fuzzy PID controller for automatic voltage regulator system using genetic algorithm. Trans. Inst. Meas. Control 44 (9), 1862–1873. doi:10.1177/01423312211066758

CrossRef Full Text | Google Scholar

Dos-Reis-Delgado, A. A., Carmona-Dominguez, A., Sosa-Avalos, G., Jimenez-Saaib, I. H., Villegas-Cantu, K. E., Gallo-Villanueva, R. C., et al. (2023). Recent advances and challenges in temperature monitoring and control in microfluidic devices. Electrophoresis 44 (1), 268–297. doi:10.1002/elps.202200162

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandes, G. H. N., Barbosa, L. M. Q., França, P. H. P., Ferreira, E. R., Martins, P. S., and Machado, Á. R. (2024). Enhancing sustainability in Inconel 718 machining: temperature control with internally cooled tools. Int. J. Adv. Manuf. Technol. 131 (5), 2771–2789. doi:10.1007/s00170-023-12296-y

CrossRef Full Text | Google Scholar

Ghamari, S. M., Narm, H. G., and Mollaee, H. (2022). Fractional-order fuzzy PID controller design on buck converter with antlion optimization algorithm. IET Control Theory and Appl. 16 (3), 340–352. doi:10.1049/cth2.12230

CrossRef Full Text | Google Scholar

Kuru, K., Ansell, D., Hughes, D., Watkinson, B. J., Gaudenzi, F., Jones, M., et al. (2023). Treatment of nocturnal enuresis using miniaturised smart mechatronics with artificial intelligence. IEEE J. Transl. Eng. Health Med. 12 (3), 204–214. doi:10.1109/jtehm.2023.3336889

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Xue, D., and Zhang, S. (2023). General type industrial temperature system control based on fuzzy fractional-order PID controller. Complex and Intelligent Syst. 9 (3), 2585–2597. doi:10.1007/s40747-021-00431-9

CrossRef Full Text | Google Scholar

Lyngfelt, A., Pallares, D., Cl, L., Lind, F., Thunman, H., and Leckner, B. (2022). Achieving adequate circulation in chemical looping combustion─ design proposal for a 200 mwth chemical looping combustion circulating fluidized bed boiler. Energy and Fuels 36 (17), 9588–9615. doi:10.1021/acs.energyfuels.1c03615

CrossRef Full Text | Google Scholar

Patil, R. S., Jadhav, S. P., and Patil, M. D. (2024). Review of intelligent and nature-inspired algorithms-based methods for tuning PID controllers in industrial applications. J. Robotics Control (JRC) 5 (2), 336–358. doi:10.18196/jrc.v5i2.20850

CrossRef Full Text | Google Scholar

Petrosian, A. R., Petrosyan, R. V., Pilkevych, I. A., and Graf, M. S. (2023). Efficient model of PID controller of unmanned aerial vehicle. J. Edge Comput. 2 (2), 104–124. doi:10.55056/jec.593

CrossRef Full Text | Google Scholar

Rajamani, M. P. E., Rajesh, R., and Willjuice Iruthayarajan, M. (2023). Design and experimental validation of PID controller for buck converter: a multi-objective evolutionary algorithms based approach. IETE J. Res. 69 (1), 21–32. doi:10.1080/03772063.2021.1905564

CrossRef Full Text | Google Scholar

Suid, M. H., and Ahmad, M. A. (2022). Optimal tuning of sigmoid PID controller using nonlinear sine cosine algorithm for the automatic voltage regulator system. ISA Trans. 128 (6), 265–286. doi:10.1016/j.isatra.2021.11.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Xu, S., and Hu, H. (2023). PID controller for PMSM speed control based on improved quantum genetic algorithm optimization. IEEE Access 11 (3), 61091–61102. doi:10.1109/access.2023.3284971

CrossRef Full Text | Google Scholar