- Mechanical Engineering Department, Bucknell University, Lewisburg, PA, United States
This paper reports on preliminary observations of an investigation of flows associated with models that mimic serrations on the leading edge of barn owl feathers. The objective was to use particle image velocimetry measurements to determine the capacity of singular and multiple curved (three-dimensional) serration models to modify the noise-reducing indicators of a narrow-channeled flow past a cylinder. Four models were tested: 3 singular serration models of respective angles of inclination, α = 24°, 27.5° and 31°, and a model consisting of an array of 3 serrations of α = 24°, 27.5° and 31°. Each case was subjected to flow of Reynolds number (based on the serration height and maximum velocity of the flow) of ∼2,000, simulating the flow regime of local flow around barbs of real barn owl flights. A planar particle image velocimetry technique was used to capture the midspan plane velocities to determine the effects of each model. The results show that using singular serration models of inclination angles than 30° may lead to disorganized spatial structures and enhanced turbulence levels. On the other hand, an array of only 3 curved serrations of different geometries can modify the spatial flow structure into a well-ordered one, resulting in a 50% reduction in turbulence intensities. These initial results suggest that under complex flow conditions, the insertion of single and multiple curved serrations can lead to significant flow changes that may result in potential noise modifications.
1 Introduction
In many applications of fluid dynamics, several flow control systems have been contrived to manipulate flows for some desired effect (Abdolahipour, 2023; Shahrokhi et al., 2024; Bhaduri et al., 2024). While some of the main goals of control include transition delay, lift enhancement, drag reduction and turbulence augmentation (Gad-el-Hak, 2001), noise suppression has gained currency as a major objective for a number of reasons. The operations of many engineering systems such as high-speed trains, wind turbines, industrial fan assemblies, aircraft frames and automobiles, are often accompanied by a high level of noise production. Such noise intensities have been particularly noted to have potentially harmful effects to both human wellbeing (Wagner et al., 2017) and structural integrity (Cao et al., 2023). Thus, there is an increasing demand to develop technologies to promote silent system operation.
One prospective avenue of exploration has been biomimicry. Several research works have shown that barn owls have a distinctive ability to fly silently (Bachmann et al., 2007; Wagner et al., 2017; Wang et al., 2019). In fact, their silent flight is so remarkable that one study indicates that their flyover noise generation is barely captured by many sensitive microphones (Wagner et al., 2017). The inspiration from such noiseless flights have led many to study barn owl wing and feather morphology so as to adapt its features to solve some engineering noise problems. The literature indicates that the silent flight of the barn owl is due to a soft downy coating on the wings and legs, and wings marked by comb-like fringes (called serrations) at the leading edges, and fringes at the trailing edges (Graham, 1934; Wang et al., 2019; Rong and Liu, 2022). While all of these features are essential component of the owl’s unique ability, this work focusses on the serrations on the wings for noise mitigation.
The serrations in question are hooks that occur at the outer vanes of the leading edges of outermost wing feathers (Bachmann and Wagner, 2011). As vanes of feathers consist of barbs, each serration can be seen as a single barb ending that bends upwards (Bachmann et al., 2007; Bachmann and Wagner, 2011), forming a three-dimensional structure that requires several quantitative geometric measures to define them. Accordingly, Bachmann and Wagner (2011) have suggested definitions of lengths, angles of inclination and tilt, profile, curvature, and orientation at the leading edge to sufficiently characterize singular and groups of serrations.
Despite the three-dimensional complexity of serrations, they have been conventionally represented as simplified two-dimensional models that are only mean approximations of length and shapes. Using those simplified model shapes such as rectangular slits, triangular flaps, saw tooth, iron, chopped root, and chopped peak shapes, many researchers have studied the flow and acoustic field, deducing several conclusions about the effect of serrations (Qaissi et al., 2023; Zhou et al., 2020; ITO, 2009). These effects include the passive control of transitions from laminar to turbulence (Rao et al., 2017), geometry dependence of noise reduction attributes (Zhou et al., 2020), and the suppression of large-scale vortex structures (Cao et al., 2022). Despite the stock of knowledge accrued from these research works, flow measurements around more natural models of serrations and conditions of flow are rare. This therefore begs the question as to the value of the characteristic three-dimensional complex curvature associated with natural serrations.
Subsequently, more recently, some studies have explored more realistic models of barn owl feathers. However, the information found in these publications have been limited. For instance, Rong and Liu (2022) tried to incorporate feather-feather interactions through using fore wing and hind wing models, but failed to account for three-dimensional properties of serrations. Juknevicius, Chong, and Woodhead (2017), on the other hand, considered the effects of curvature in their model serrations. However, their work only reported aeroacoustic performance, and no fluid dynamic effects. While the research group of Brücker and Wagner (Muthuramalingam et al., 2020; Midmer et al., 2024), has produced some of the most detailed flow data of the flow around 3D-curved serration models, their work presented the bulk effect of a cascade of serrations subject to uniform flow. Consequently, the physics of singular serrations are unknown. More importantly, the effects of the complex geometries of multiple naturally shaped serrations under less ideal flow conditions remain a mystery. Yet such non-ideal conditions are practically relevant in scenarios requiring noise mitigation, such as the operation of cooling fans and electronic components in narrow spaces and under high load conditions (Sun et al., 2023). Thus, this work meets the need for characterizing and understanding the potential utility of singular or multiple serrations for noise or flow control measures.
This work therefore seeks to add more to the current understanding of flow phenomenon around serrations similar to that of a barn owl. Specifically, this paper aims at using particle image velocimetry measurements to determine the flow effects of singular and multiple curved serration models in modifying the noise-reducing indicators of flow structures under narrow-channeled flow conditions. This is part of a research program that seeks to provide a comprehensive characterization of the flow and acoustic field associated with a more naturally shaped serration network. It is expected this work will provide some insight into distinctive characteristics that might contribute to flow control in general, and specifically for noise reduction.
2 Materials and methods
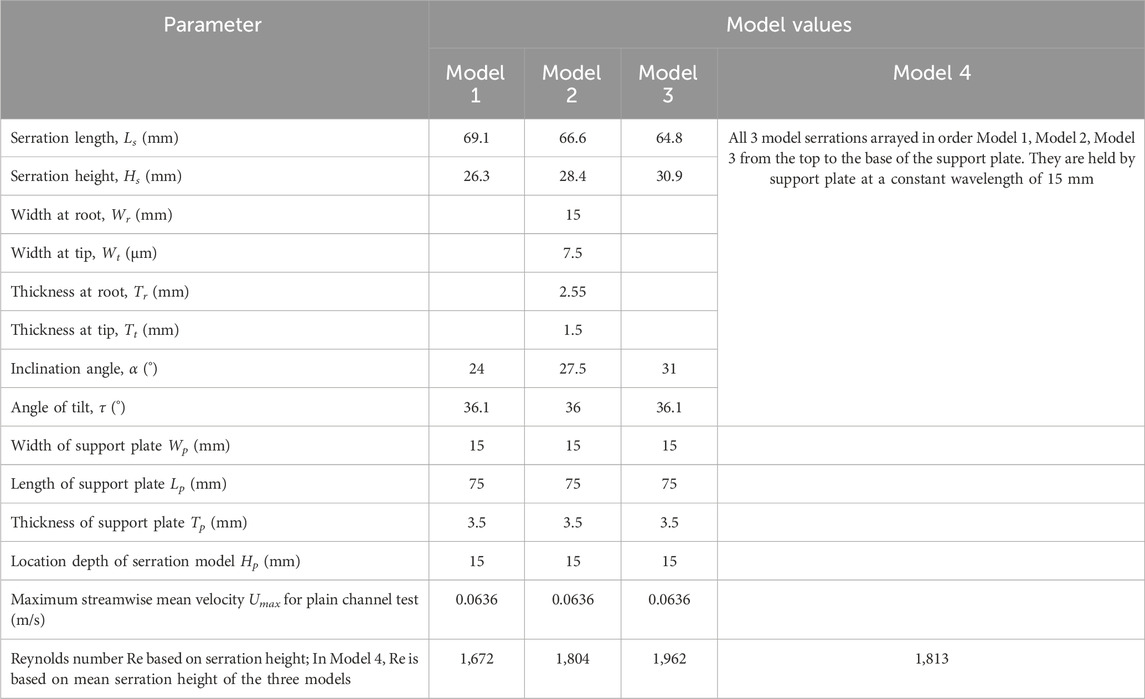
The experimental system utilized in this work consists of models of serrations, a recirculating flume with qualified upstream conditions, and a particle image velocimetry system. The models of serrations were fabricated by first generating geometric computer aided design (CAD) draft using SolidWorks software (SolidWorks Corp, Dassault Systémes, France). The designs were based on published measurements of barbs of barn owls (Bachmann and Wagner, 2011). In designing each of the models, a 500 μm base plate of 85 μm thickness was first created, and extended as a 2,000 μm lofted straight beam to a tapered tip of 250 μm × 50 μm cross-section. The beam was then bent to the requisite inclination angle α, and tilt angle τ. The CAD draft was then scaled up uniformly by thirty-fold, making it conveniently large for testing. The model was then 3D-printed into a rigid solid model with final values dimensions summarized in Table 1.
As shown in Table 1, the relevant parameters are serration length, widths at the root and tip of the barbs, thickness at the root and tips, inclination angle α, and the tilt angle τ. These parameters are explicitly defined schematically in Figure 1A. Three basic models of singular serrations were developed for 3 different angles of inclination 24°, 27.5°, and 31°, while maintaining the same mean tilt angle of ∼ 31°. All of the values were chosen to comport with typical values measured from barn owl feather serrations (Bachmann and Wagner, 2011). For convenience, the singular serration models are hereafter labelled Model 1, Model 2, and Model 3, per specifications in Table 1. An additional model (labelled Model 4) was created to simulate an array of variant serrations made up of the geometries in Models 1, 2 and 3. To facilitate the installation of each of the models, a support plate of length Lp = 75 mm, width Wp = 15 mm, and thickness Tp = 3.5 mm, was used (Figure 1B). Each of the 3 basic models was attached to the support plate at a distance Hp = 30 mm from one edge (Figure 1C) to form a model assembly. In the specific case of Model 4, the model assembly consisted of the combination of all singular serration models at a wavelength of 15 mm as indicated in Figure 1D and Table 1.
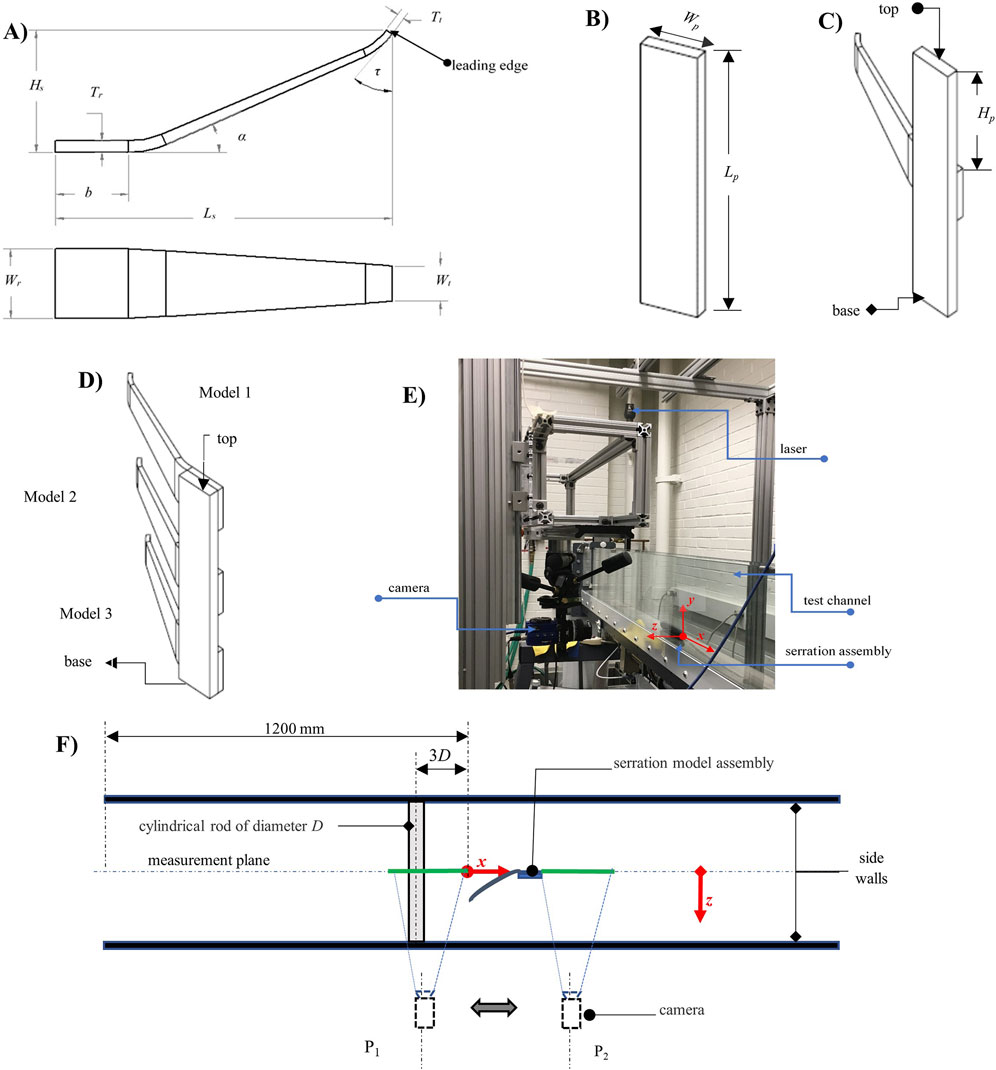
Figure 1. This shows geometric configurations of the test models and arrangement. Parameters are defined in Table 1. In (A), 2D projected views of serrations are shown. The geometric parameters (defined in Table 1) are indicated. Figure (B) is the supporting plate of the serration model, (C) is a sample assembly of models 1, 2 and 3; and (D) is the assembly for model 4. In (E) and (F), the arrangement of the models relative to the test channel, coordinate directions and PIV system are shown. In (F), the two main positions of the PIV camera are shown as P1 and P2 in a top view. The diameter of the rod D is 15.9 mm.
The flow tests were carried out in a recirculating hydraulic flume with a test section of length 2.5 m, width 0.08 m, and of transparent acrylic walls to facilitate optically-based measurements. Regarding the system of coordinate directions, the rectangular Cartesian system employed is defined relative to the test channel. This is expressed in Figures 1E, F. The flow was directed in the streamwise (x) direction, with the wall-normal and spanwise directions denoted by y and z respectively. The origins of x, y, z, are respectively located 1.2 m away from the channel entrance, on the bottom wall of the channel, and in the midspan of the test channel.
To test each model serration, the respective serration model assembly (Figures 1C, D) was installed downstream of the cylinder, as indicated in Figures 1E, F. The leading edge of each model (i.e., the tip) was located at x = 0. As this location is only 1.2 m downstream off the channel entrance, any flow speed corresponding to Reynolds numbers of barn owl flights will not be fully developed. Additionally, for each of the tests, pressure-driven water flow was conducted through the flume in an open channel flow of mean depth 0.08 m at the location of measurement. This flow depth gives rise to a low aspect ratio (or narrow) open channel flow (Arthur, 2023a) that is associated with complex secondary flow effects. Under both developing and secondary flow conditions, the underlying flow may be deemed less controlled; however, such flow is that which may be arguably encountered in nature (Arthur, 2023a), and relevant in industrial applications requiring noise reduction (Sun et al., 2023). In order to generate significant vortical disturbance in the flow that can be modified by serrations (Midmer et al., 2024), a circular rod of diameter D = 15.9 mm and length ∼79 mm was installed in the channel (Figure 1F). The central axis of the cylinder was located at a streamwise distance of 72.5D from the entrance of the test channel, and at a gap G (i.e., wall-normal distance between the axis and the channel bottom wall) of 2.83D.
The characterization of velocity for the flow region was done using a two-dimensional particle image velocimetry (PIV) technique. The PIV system consisted of a camera, laser, programable timing unit, and a computer. Both camera and laser were attached to a traversing mechanism so that they could be moved at a given distance within an uncertainty limit of ± 0.5 mm, without altering the spatial location or orientation between the camera and laser planes of measurement. Additionally, seeding of the flow was accomplished using silver-coated hollow glass spheres of mean diameter 10 μm and specific gravity 1.4. The specific components (along with accessories) utilized in this work are the same as those used in a previous work (Arthur, 2023b). The reader is therefore referred to that publication for detailed descriptions. For each round of PIV test, 1,500 pairs of instantaneous images were recorded with the camera at a rate of ∼ 5 Hz. They were thereafter transferred to the computer where a DaVis-10.2 PIV software was used for processing.
With a field of view of 96.2 mm × 67.3 mm in the x and y directions, the ensuing scale factor was 29.78 pixels per mm. Processing of the images was initiated by a single pass cross-correlation vector calculation wherein the interrogation area was set to a size of 64 pixels × 64 pixels at 50% overlap. Multiple passes of post-processing were then followed for vector validation and noise reduction. This involved a four-pass spatial median filtering conditioned to robustly and automatically remove and iteratively replace (single and groups of) spurious vectors. For these post-processing schemes, each image was subdivided into 32 pixels × 32 pixels with 50% overlap. In the end, the processing yielded 180 vectors × 126 vectors with the distances between neighboring vectors being 0.56 mm in both x and y directions. This value is far less than 1% of the boundary layer thickness (as will be noted in Section 3.1). With other relevant precautions taken (e.g., the interrogation window being at four times bigger than the maximum particle displacement, and that there were at least 10 particle images per interrogation window) to assure low random errors, such a resolution is considered sufficient to compute and interpret the spatial organization of vortices with adequate accuracy (Rahgozar et al., 2013; Adrian and Westerweel, 2011).
Processed instantaneous velocity vector data measurements were analyzed so as to extract requisite statistics of turbulence. Accordingly, time-averaged velocities and turbulent intensities in the streamwise direction were computed. Only these are reported in this work. They are reported herein as U and u respectively. The corresponding evaluations in the wall-normal directions are also presented as V and v respectively. Following the method of assessment described in Wieneke (2015), the uncertainties of these statistics were estimated at 95% confidence level, and found to be ± 1.5% and ± 2% of the respective maximum values of (U, V) and (u, v).
For each test condition, the flow speed was kept constant. With this bulk flow, six series of open-channel test flows were conducted for: (1) an empty (plain) channel flow case (nothing mounted in the flow); (2) the case of the channel only having a cylindrical rod installed ∼ 72.5D from the entrance of the test channel; (3) the case where Model 1 was installed downstream of the cylindrical rod; (4) the case of Model 2 installed downstream of the cylindrical rod; (5) the case of Model 3 set downstream of the cylindrical rod; and (6) Model 4 mounted downstream of the cylindrical rod. For each round, two sections of the flow were captured to study regions of streamwise locations at
3 Results and discussion
The results for this work are summarized in Figures 2, 3. This is given in terms of time-averaged (mean) flow parameters (velocities and vorticities), turbulence intensities (velocity fluctuations), and the spatial correlation of the velocity fluctuations. Thus, the data is non-transient. In general, all the plots are shown in dimensionless units, using the maximum streamwise mean velocity in the plain channel flow Umax, the cylindrical rod diameter D, and boundary layer thickness δ, as the normalizing parameters. It is pointed out that using D instead of the serration height as the normalizing length parameter particularly marks a significant departure from other studies (Muthuramalingam et al., 2020; Midmer et al., 2024). However, this is considered as a reasonable and appropriate choice, giving the commonality of D in all serration test cases, as opposed to the multiple serration heights used.
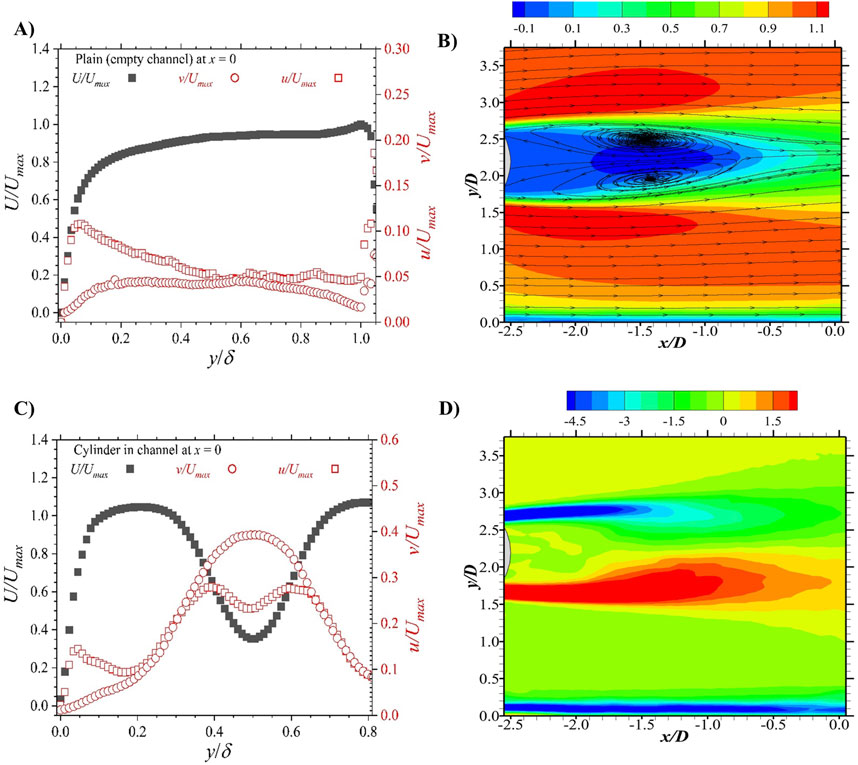
Figure 2. These plots qualify the flow prior to the insertion of serration test models. In (A, C), normalized one-dimensional wall-normal variations of flow profiles extracted at the x = 0 are shown for an empty channel case and for channel with the upstream cylindrical rod. These are plotted for mean streamwise velocity (U), streamwise turbulent intensity (u) and wall-normal turbulent intensity (v) profiles. Plots in (B) and (D) are contour plots, respectively of normalized U superimposed with streamlines (B), and mean spanwise vorticity (D). These plots capture flow with a cylindrical rod inserted upstream (shown partially as grey section within map). Note that the plots are normalized using the maximum streamwise mean velocity Umax, the boundary layer thickness δ and the rod diameter D.
Figure 3. These characterize planar flow effects due to serration models. Charts in (A, B) show the variation of normalized streamwise turbulence intensity (u/Umax) and wall-normal turbulence intensity (v/Umax). These are averaged over the area upstream of model (designated as ‘pre-model’: −0.5 ≤ x/D ≤ 0 and 0 ≤ y/D ≤ 3.75); and the area downstream of the model (designated as ‘post-model’: 4.0 ≤ x/D ≤ 4.5 and 0 ≤ y/D ≤ 3.75). The plots in (C) represent normalized mean spanwise vorticity (ΩzD/Umax). This is shown for the case of a cylinder installation (on the left), and additional installations of Models 1, 2, 3, 4 respectively (from left to right). The plots in (D) are the two-point spatial autocorrelation functions of the streamwise fluctuating velocities (Ruu). This is also demonstrated for the case of a cylinder installation (on the left), and additional installations of Models 1, 2, 3, 4 respectively (from left to right). Note that for isocontours of Ruu, the contour levels for each of the plots are 0.5, 0.6, 0.7, 0.8, and 0.9, respectively, in an inward direction towards the core.
3.1 Baseline flow conditions
In Figure 2 the qualification of the inlet flow conditions is presented for the cases of an empty channel flow (2A), and a channel flow with a cylindrical rod installed (2B – D). As these two cases are baseline, conditions, the plots may be used subsequently as references to assess flow cases where the serrations are installed. In the specific case of Figures 2A, C, one-dimensional profiles are extracted at x = 0 (i.e., the streamwise location of the subsequently mounted leading edge of a serration model), representing a characterization of the approach flow locations. The plots in Figure 2B, D on the other hand, are the contours of whole flow fields of the approach flow region.
The profiles in Figure 2A indicate streamwise mean velocities that form a boundary layer with a thickness δ of 71.9 mm, a depth-averaged streamwise velocity of 0.0551 m/s, and a maximum streamwise mean velocity Umax of 0.0636 m/s. With such flow velocities, the local Reynolds numbers associated with the serration heights are expected to be less than 2000, and thus within the regime expected of flows around barbs of real barn owl flights (Midmer et al., 2024). It is noteworthy that Umax is located below the water surface (flow depth of 79 mm). This is in accordance with the velocity-dip phenomenon commonly observed in narrow channel flows (Arthur, 2023a; Kundu, 2017). This phenomenon is generally thought to occur due to the transport of energy and momentum by strong free surface vortex, resulting in a downward motion at channel centerline, and consequently the retardation of velocity at the free surface (Mahananda et al., 2022). While this is an underlying occurrence in the present experiments, Figure 2A indicates that the dipping effect is still restricted to the immediate regions of the free surface. On the other hand, the plots of turbulence intensities in Figure 2A show that at the edge of the boundary layer, the background turbulence are 5% and 2% in the streamwise and wall-normal directions respectively. These values are relatively low in comparison with other developing narrow channel flows (Arthur, 2023a). Indeed, even the maxima close to the solid wall boundary are significantly lower than that of other open channel flows (E.g., Nezu and Rodi, 1986; Arthur, 2023a), and therefore, not expected to affect the observations recorded in this work). In summary, the baseline plain flow is one of a conventional developing open channel boundary layer flow in a narrow channel with persistent but low background disturbances.
In Figures 2B–D, the plots show the effect of mounting a cylinder at x =
3.2 Effects of serrations
The question that follows then is, what happens when a serration is inserted into the present flow? To provide some preliminary answers to this query, attention is now turned to Figure 3. In Figures 3A, B, the results are shown in terms of comparisons of area-averaged turbulence intensities (Midmer et al., 2024). The turbulence intensities are averaged over the area upstream of the location of model insert, i.e., −0.5 ≤ x/D ≤ 0 and 0 < y/D ≤ 3.75; and the area downstream of the model insert, i.e., 4.0 ≤ x/D ≤ 4.5 and 0 ≤ y/D ≤ 3.75. These areas were selected to compare clear effects immediately preceding and following the installation of serrations. This is an important assessment, as turbulence intensity has been noted elsewhere to be an important indicator of flow-generated noise (Midmer et al., 2024), and may well be so for the midspan planar evaluations presented here. Figures 3A, B show that in the absence of serrations, the streamwise and wall-normal turbulence intensities diminish by about the same margin (∼ 36%) downstream of the flow past the cylinder. However, by installing the Models 1 and 2 serrations, respectively, at x = 0, the reductions in turbulence intensities are cut by half (average of ∼ 19%) in both streamwise and wall-normal directions. This means that inserting a single model serration with an inclination angle less than 30° in the flow may agitate the flow, generating more turbulence in its wake, with likely effect of noise increment. On the other hand, a serration model of 31° inclination angle leads to a rather different result – no effect on the streamwise turbulence levels, but marked reductions (53%) in the wall-normal direction (Figure 3B). The results also demonstrate that by utilizing multiple (even just 3) serrations with different geometric shapes, further reduction (∼48%) in turbulence intensities is possible, with the potential for noise reduction.
In Figure 3C, mean spanwise vorticities (Ωz = ∂V/∂x − ∂U/∂y) are shown in normalized terms (ΩzD/Umax) as contour plots of the same region. The contours are plotted to provide a comparative indication of the location, extent and intensity of organized vortex cores for the cases of an upstream cylinder installation, and for the respective installations of Models 1, 2, 3, and 4. The results show that as expected, vortices shed (due to flow moving past a mounted cylinder) dissipate further downstream (>7D) with traces of positive vorticity values spanning a wall-normal location of 0.75 <y/D < 2.25. However, the installation of the models alters the vorticity map, with notable thin linear streaks of vortex cores aligned at an angle in the wall-normal direction. The results of Model 1, 2, and 3 indicate that as the angles of inclinations increase, the thin vortex streaks tend to shift towards the location of the models. Model 4 results, on the other hand, are less streaky and more scattered.
The order, extent and orientation of the large-scale structures are assessed further using two-point spatial autocorrelation functions of the streamwise fluctuating velocities (Ruu). This is done following the same procedure outlined in Arthur (2022). Correlation functions are computed for all test cases, centered around the locations close to the presence of streaky vortex cores as observed in Figure 3C. In Figure 3D, sample isocontours are shown as representative of several other contours that were extracted. For the plots shown, each of the contours are centered at (x/D = 4.25, y/D = 1.19). For clarity, the contour levels shown are 0.5, 0.6, 0.7, 0.8, and 0.9, respectively, in an inward direction towards the core. In general, the cylinder case is the most elongated, while Model 1 is the least. Additionally, while the contours obtained for cases of the cylinder, Model 3 and Model 4 are symmetrical and more elongated along the streamwise direction, that of Models 1 and 2 are not so. Interpreting these results in terms of the organization of coherent structures of the flow, the plots indicate that the installation of singular or multiple serrations lead to different outcomes of spatial structural organization. The single serrations with the least angle of inclination tends to devolve the order of the spatial structures, while larger angles result in a more organized structure in the streamwise direction, relative to the wall-normal. This order grows with the use of multiple serrations.
4 Conclusion
This research was carried out to study the flow around singular and multiple curved model serration of a barn owl’s feather. The objective was to obtain insight into the flow control effects of such serrations in a narrow-channeled flow domain. To that end, a planar particle image velocimetry technique was used to obtain velocity measurements of an open channel flow around three singular serration models of three different angles of inclination (i.e., 24°, 27.5°, and 31°); and the flow around a model of an array of those three angles of inclinations. Each of these model tests were conducted using a vortically disturbed flow source (i.e., flow past a cylinder). A planar particle image velocimetry technique was used to capture velocities in the midspan plane at several sections in order to map out the approach flow as well as the flow features further downstream of each model. The data presented herein are the preliminary observations of the tests.
The results show that a single model serration with an inclination angle less than 30° in the flow, may agitate the flow, generating more turbulence, and streaky vortex cores with disorganized spatial structures in the wall-normal direction. On the other hand, a single serration model of 31° results in limited but more organized system of vortical activity in the wall-normal direction, culminating in less turbulence in that direction. The data also shows that by using multiple geometrically shaped serrations, an organized streak of vortex core is formed, along with 50% reduction in turbulence intensities.
While merely indicative and requiring confirmation through direct measurement of the acoustic field, these observations point to singular serrations, resulting in further noise generation along the stream of a complex flow condition, or at best maintaining the noise level in that direction. The results also suggest the need to use an array of serrations to ensure significant reductions in noise levels under those flow conditions.
It should however be pointed out that the data presented here are not time-resolved. Additionally, the models tested are rigid bodies. Thus, details of transient flow phenomena are lacking. Furthermore, it is likely that the fluid structure interactions of flexible serrations would have led to a different outcome. Thus, a more comprehensive study is required in the future to assess these issues. Nonetheless, the present report serves as a useful introductory study into the flow effects of curved serrations.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
JA: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdolahipour, S. (2023). Effects of low and high frequency actuation on aerodynamic performance of a supercritical airfoil. Front. Mech. Eng. 9, 1290074. doi:10.3389/fmech.2023.1290074
Adrian, R. J., and Westerweel, J. (2011). Particle image velocimetry. no. 30. NY, USA: Cambridge University Press.
Arthur, J. K. (2022). Coherent structures of a turbulent flow bounded by a compact permeable wall. Fluids 7 (5), 158. doi:10.3390/fluids7050158
Arthur, J. K. (2023a). PIV measurements of open-channel turbulent flow under unconstrained conditions. Fluids 8 (4), 135. doi:10.3390/fluids8040135
Arthur, J. K. (2023b). A narrow-channeled backward-facing step flow with or without a pin–fin insert: flow in the separated region. Exp. Therm. Fluid Sci. 141, 110791. doi:10.1016/j.expthermflusci.2022.110791
Bachmann, T., Klän, S., Werner, B., Klaas, M., Schröder, W., and Wagner, H. (2007). Morphometric characterisation of wing feathers of the barn owl Tyto alba pratincola and the pigeon Columba livia. Front. Zoology 4, 1–15. doi:10.1186/1742-9994-4-23
Bachmann, T., and Wagner, H. (2011). The three-dimensional shape of serrations at barn owl wings: towards a typical natural serration as a role model for biomimetic applications. J. Anat. 219 (2), 192–202. doi:10.1111/j.1469-7580.2011.01384.x
Bhaduri, S., Ray, A., De, A., and Sugarno, M. I. (2024). Flow control in a confined supersonic cavity flow using subcavity. Front. Mech. Eng. 10, 1378433. doi:10.3389/fmech.2024.1378433
Cao, H., Zhou, T., Zhang, Y., and Zhang, M. (2022). An experimental investigation of aerodynamic and aeroacoustic performance of a wind turbine airfoil with trailing edge serrations. J. Acoust. Soc. Am. 151 (2), 1211–1222. doi:10.1121/10.0009570
Cao, S., Zhang, Z., Wu, X., He, Y., and Zhang, Q. (2023). Exploring the suppression mechanism of wind buffeting noise with bionic structures featuring leading-edge serrations and surface ridges. J. Low Freq. Noise, Vib. Act. Control 42 (4), 1718–1732. doi:10.1177/14613484231185416
Graham, R. R. (1934). The silent flight of owls. Aeronautical J. 38 (286), 837–843. doi:10.1017/s0368393100109915
ITO, S. (2009). Aerodynamic influence of leading-edge serrations on an airfoil in a low Reynolds number-A study of an owl wing with leading edge serrations. J. Biomechanical Sci. Eng. 4 (1), 117–123. doi:10.1299/jbse.4.117
Jiang, H., and Cheng, L. (2021). Large-eddy simulation of flow past a circular cylinder for Reynolds numbers 400 to 3900. Phys. Fluids 33 (3). doi:10.1063/5.0041168
Juknevicius, A., Pei Chong, T., and Woodhead, P. C. (2017). “Leading edge noise reduction of thin aerofoil by the straight and curved serrations of the add-on type,” in 23rd AIAA/CEAS aeroacoustics conference, 3491.
Kundu, S. (2017). Prediction of velocity-dip-position at the central section of open channels using entropy theory. J. Appl. Fluid Mech. 10 (1), 221–229. doi:10.18869/acadpub.jafm.73.238.26403
Mahananda, M., Hanmaiahgari, P. R., and Ram, B. (2022). On the turbulence characteristics in developed and developing rough narrow open-channel flow. J. Hydro-environment Res. 40, 17–27. doi:10.1016/j.jher.2021.11.003
Midmer, A., Brücker, C., Weger, M., Wagner, H., and Bleckmann, H. (2024). Interaction of barn owl leading edge serrations with freestream turbulence. Bioinspiration and Biomimetics 19 (3), 036014. doi:10.1088/1748-3190/ad3a4f
Muthuramalingam, M., Talboys, E., Wagner, H., and Bruecker, C. (2020). Flow turning effect and laminar control by the 3D curvature of leading edge serrations from owl wing. Bioinspiration and Biomimetics 16 (2), 026010. doi:10.1088/1748-3190/abc6b4
Nezu, I., and Rodi, W. (1986). Open-channel flow measurements with a laser Doppler anemometer. J. hydraulic Eng. 112 (5), 335–355. doi:10.1061/(asce)0733-9429(1986)112:5(335)
Price, S. J., Sumner, D., Smith, J. G., Leong, K., and Paidoussis, M. P. (2002). Flow visualization around a circular cylinder near to a plane wall. J. Fluids Struct. 16 (2), 175–191. doi:10.1006/jfls.2001.0413
Qaissi, K., Elsayed, O., Faqir, M., and Essadiqi, E. (2023). Aerodynamic optimization of trailing-edge-serrations for a wind turbine blade using taguchi modified additive model. Energies 16 (3), 1099. doi:10.3390/en16031099
Rahgozar, S., Maciel, Y., and Philipp, S. (2013). Spatial resolution analysis of planar PIV measurements to characterise vortices in turbulent flows. J. Turbul. 14 (10), 37–66. doi:10.1080/14685248.2013.851386
Rao, C., Ikeda, T., Nakata, T., and Liu, H. (2017). Owl-inspired leading-edge serrations play a crucial role in aerodynamic force production and sound suppression. Bioinspiration and biomimetics 12 (4), 046008. doi:10.1088/1748-3190/aa7013
Rong, J., and Liu, H. (2022). Aeroacoustic interaction between owl-inspired trailing-edge fringes and leading-edge serrations. Phys. Fluids 34 (1). doi:10.1063/5.0078974
Shahrokhi, S. S., Taeibi Rahni, M., and Akbari, P. (2024). Aerodynamic design of a double slotted morphed flap airfoil– a numerical study. Front. Mech. Eng. 10, 1371479. doi:10.3389/fmech.2024.1371479
Sun, Z., Chai, P., Tian, J., Du, Z., and Ouyang, H. (2023). Aerodynamic noise characteristics of axial flow fan in narrow space and noise reduction based on flow control. J. Eng. Gas Turbines Power 145, 10. doi:10.1115/1.4063127
Wagner, H., Weger, M., Klaas, M., and Schröder, W. (2017). Features of owl wings that promote silent flight. Interface focus 7 (1), 20160078. doi:10.1098/rsfs.2016.0078
Wang, Y., Zhao, K., Lu, X.-Y., Song, Y.-B., and Bennett, G. J. (2019). Bio-inspired aerodynamic noise control: a bibliographic review. Appl. Sci. 9 (11), 2224. doi:10.3390/app9112224
Wieneke, B. (2015). PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 26 (7), 074002. doi:10.1088/0957-0233/26/7/074002
Keywords: barn owl, angle of inclination, tilt angle, curved serration, flow control, particle image velocimetry
Citation: Arthur JK (2024) Particle image velocimetry study of the flow control effects of singular and multiple curved serration models. Front. Mech. Eng. 10:1452996. doi: 10.3389/fmech.2024.1452996
Received: 21 June 2024; Accepted: 17 October 2024;
Published: 28 October 2024.
Edited by:
Ram Balachandar, University of Windsor, CanadaReviewed by:
Arash Shams Taleghani, Ministry of Science, Research and Technology, IranSabal Bista, University of Windsor, Canada
Majed Etemadi, University of Windsor, Canada
Copyright © 2024 Arthur. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James K. Arthur, amFtZXMuYXJ0aHVyQGJ1Y2tuZWxsLmVkdQ==
 James K. Arthur
James K. Arthur