- 1Department of Mechanical and Industrial Engineering, Indian Institute of Technology Roorkee, Roorkee, India
- 2Department of Design, Indian Institute of Technology Roorkee, Roorkee, India
Fragment-induced penetrating injuries pose a significant threat in modern combat. Explosions from explosive devices generate metallic fragments that can lethally penetrate various body regions, with the head being particularly most vulnerable to fatality in terms of penetration. Hence, understanding the head’s response to fragment impact is crucial. To this end, this study investigated the ballistic response of an anatomically accurate anthropometric head surrogate to fragment impact. The head surrogate comprised simulants for the three major layers of the head (skin, skull, and brain). Using a pneumatic gas gun, we impacted chisel-nosed fragment simulating projectiles (FSPs) of 1.10-g and 2.79-g on the head surrogate. We analyzed the ballistic response of the head surrogate in terms of ballistic limit velocities (V50), energy densities (E50/A), and failure mechanisms in each layer. The results indicated sensitivity to the FSP size. The 1.10-g FSP had a ∼41% higher V50 and a ∼63% higher E50/A compared to the 2.79-g FSP. Additionally, each head surrogate layer exhibited distinct failure mechanisms. The skin simulant failed due to a combination of shearing and elastic hole enlargement, forming a cavity smaller than the size of the FSP. The skull simulant fractured, creating a cavity at the entry point matching the FSP size. The brain simulant failure involved shearing of the cavity and penetration of fractured skull fragments. We also observed no significant difference in response when introducing a flexible neck attachment on which the head surrogate was mounted. Furthermore, comparisons of an anthropometric (close-shape) head surrogate with a simplified open-shaped head surrogate revealed the minimal influence of the head curvature on the response due to the localized nature of fragment penetration. These findings provide a comprehensive understanding of the head surrogate’s mechanical response to fragment impact. The insights from this work hold significant value in the assessment of penetrating head injury, especially against small fragments. The results can be applied in modern warhead design and forensic investigations.
1 Introduction
Safeguarding military personnel from ballistic threats is a crucial aspect in asymmetric conflicts. The primary cause of penetrating injuries to military personnel in modern warfare is fragments generated from the explosion of various explosive ammunitions (Breeze and Powers, 2017; Breeze and Clasper, 2013; Regasa et al., 2018; Bowyer et al., 1995; Carr et al., 2017). These fragments exhibit irregular shapes and sizes and are termed natural fragments to distinguish them from well-designed or pre-formed projectiles. “Natural fragments” will be referred to simply as “fragments” in this work for brevity.
Even though fragments are the primary cause of penetrating injuries in warfare, existing literature on penetrating injuries to biological tissues predominantly focuses on larger projectiles such as bullets (Mahoney et al., 2018; Oehmichen et al., 2004; Mahoney et al., 2017a; Thali M. et al., 2002; Riva et al., 2019; Sterzik et al., 2017; Riva et al., 2021; Euteneuer et al., 2019; Taylor et al., 2022). However, the response of biological tissues against bullets cannot be inferred for fragments as they exhibit different characteristics, both geometrical and mechanics of interaction (Kneubuehl, 2011; Van der Voort et al., 2016; Breeze and Carr, 2016a). Fragments with irregular shapes and sizes are generally composed of a single material, unlike bullets that are meticulously engineered for aerodynamic efficiency with standardized shapes, sizes, and compositions (Kneubuehl, 2011; Bhatnagar, 2006). Fragments primarily penetrate tissues through a piercing mechanism, whereas bullets mainly cause crushing and pulsating cavitation in the tissues (Van der Voort et al., 2016; Shuker, 2019). Moreover, bullets exhibit deformation behavior, while fragments typically do not deform due to their hardness (Riva et al., 2019; Berryman, 2019). Hence, there is a notable gap in research on the response of biological tissues against the fragment’s impact. It is imperative to comprehend how fragments interact with biological tissues, organs, or their surrogate, particularly in terms of ballistic limit velocities and the associated failure mechanisms.
Because natural fragments vary in shape and size, testing each shape and size configuration of the fragment against the biological tissues or their surrogates is practically not possible due to the countless number of potential configurations of fragments. Identifying this challenge, NATO has suggested some fragment simulating projectiles (FSPs). These FSPs come in various shapes and sizes based on the most generic shapes and sizes of naturally generated fragments in the battlefield (NATO and NATO Standardization Agreement, 2003; Bolduc and Jager, 2016).
Fragment penetration in various body parts can prove lethal, in which the head is most vulnerable (Champion et al., 2003; Vakil and Singh, 2017; Van Wyck et al., 2015). Penetrating head injuries pose a significant threat in modern warfare, with a high probability (70%–90%) of death (Champion et al., 2003; Vakil and Singh, 2017; Van Wyck et al., 2015). Even when survival occurs, severe life-threatening injuries, infections, and long-term risks such as epilepsy are common (Carr et al., 2015). Therefore, understanding the ballistic response of the head to penetrating impacts is important. While there are several studies examining the response of the head or head surrogate against bullet impact (Mahoney et al., 2018; Oehmichen et al., 2004; Mahoney et al., 2017a; Thali M. et al., 2002; Riva et al., 2019; Sterzik et al., 2017; Riva et al., 2021; Euteneuer et al., 2019; Taylor et al., 2022; Carr et al., 2015), research on the head response against FSPs is particularly scarce. Existing studies (Watkins et al., 1988; Li et al., 2023) on the impact of small fragments on human or animal head surrogates often report the energy required for fragments to penetrate the head. These investigations, however, lack a comprehensive analysis of experimental ballistic limit velocities, failure mechanisms, and resulting injury patterns.
To address this objective, we conducted experimental investigations on an anatomically correct anthropometric head surrogate subjected to FSP impact. We opted for the head surrogate comprising the skin, skull, and brain simulants due to limitations in ethical constraints in accessing post-mortem human subjects (PMHS), monkeys, and pigs and the challenges in scaling rodent data to human responses (Breeze and Carr, 2016b). Tissue-mimicking simulants (Breeze and Carr, 2016b; Carr et al., 2018; Jussila et al., 2005) were chosen as they offer repeatability of experiments compared to PMHS and animals (Breeze and Carr, 2016b). PMHS and animals often exhibit subject-specific variabilities, requiring a substantial number of experiments to obtain reliable results (Breeze and Carr, 2016b). We determine the ballistic limit velocities (V50) and corresponding energies (E50) and analyze the failure patterns. Moreover, we conducted two comparative analyses. First, we compared the response of the anthropometric head surrogate attached to a rigid neck attachment versus a flexible neck attachment. Second, we compared the responses of the anthropometric (close-shape) head surrogate and an open-shape head surrogate. These comparative investigations aimed to elucidate how variations in neck attachment flexibility and head surrogate geometry (curvature) affect their response to FSPs. The results of this work have applications in various engineering purposes, such as providing insights into ballistic limit velocities, energy densities, macroscopic failure patterns, and failure mechanisms related to penetrating head injuries.
2 Methods
2.1 Fragment simulating projectiles (FSPs) and the experimental setup
NATO has recommended various sizes and shapes of FSPs in NATO STANAG 2920 (NATO and NATO Standardization Agreement, 2003; Bolduc and Jager, 2016), including rectangular, spherical, right-circular cylindrical, and chisel-nosed cylindrical. Among these, chisel-nosed cylindrical FSPs are considered the most versatile (Breeze and Carr, 2016c). In this study, two chisel-nosed cylindrical FSPs of different sizes, 1.10-g and 2.79-g, were prepared in accordance with NATO STANAG 2920 (Figure 1). Note that we have used the term “sizes” as opposed to “masses” of FSPs throughout the manuscript wherever we compared the two FSPs. The term “size” is generally used for the different dimensions of identical shaped FSPs (Bhatnagar, 2006; Breeze et al., 2013a; Breeze et al., 2013b; Breeze et al., 2015). The FSPs were fabricated from mild steel (density = 7,860 kg/m³; elastic modulus = 210 GPa; Poisson’s ratio = 0.3) using turning and grinding processes.

Figure 1. Photograph depicting FSPs and sabot (A) two chisel-nosed cylindrical FSPs prepared following NATO STANAG 2920; (B) schematic of FSPs depicting dimensions; (C) assembly of the split-sabot and FSP.
The FSPs were launched on the head surrogate using a pneumatic gas gun setup (Figure 2). The complete setup included an air compressor, a pressure vessel, a pressure gauge, a pneumatic actuator, a seamless barrel, and a target-holding fixture. Atmospheric air was compressed using the air compressor and stored in the pressure vessel at the required pressure. A single barrel with a fixed length of 5 m and an internal diameter of 25 mm was used. Split sabots were utilized to accommodate different-sized FSPs in the fixed-diameter barrel. The split sabots, composed of symmetrical halves, were made of nylon material (Figure 1B). Sabots were designed with an external diameter equal to the internal diameter of the barrel. The internal side of the sabot featured a cavity with the size matching that of the specific FSP.
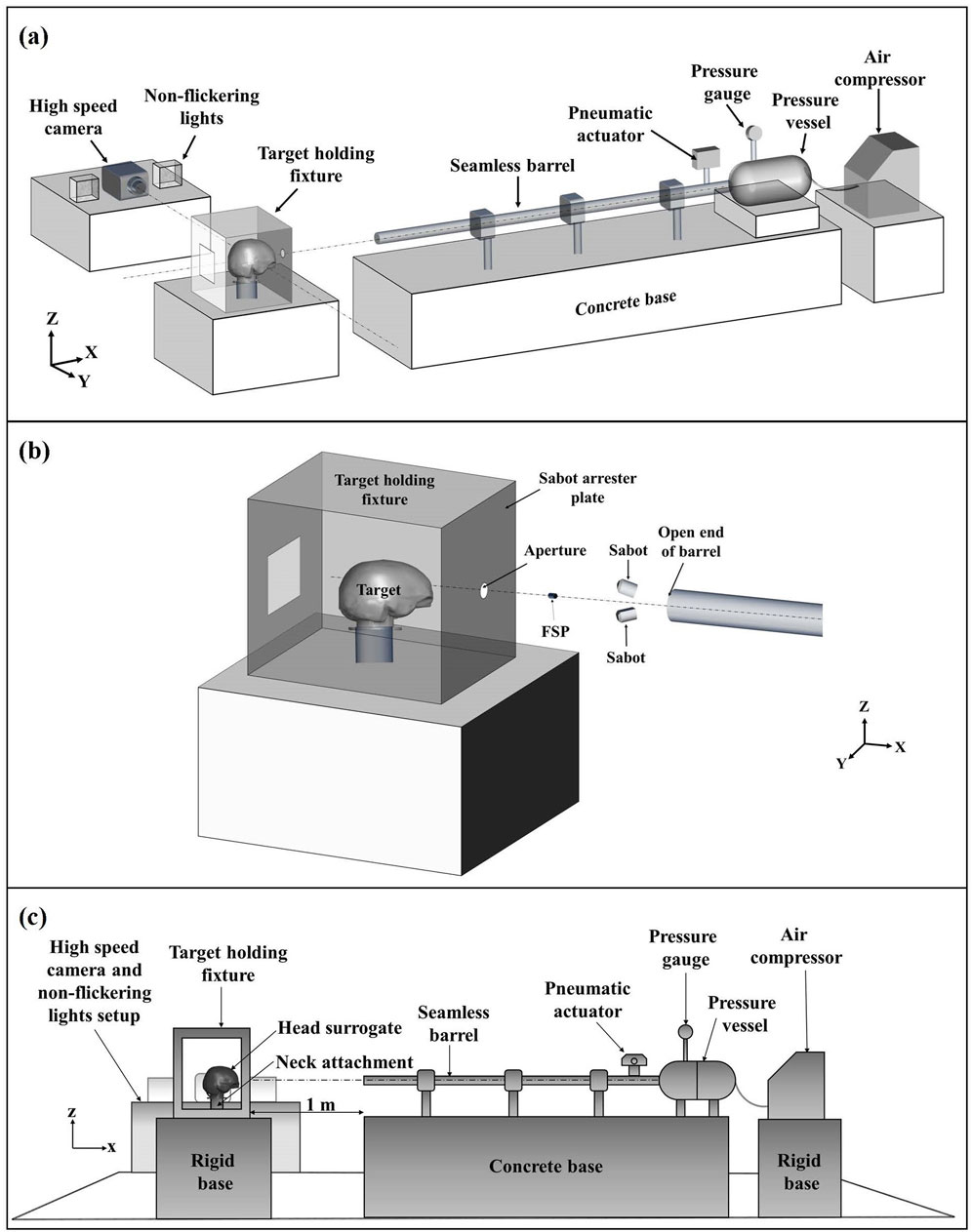
Figure 2. Schematic illustration of the experimental setup: (A) complete experimental setup; (B) close-up view of FSP–target during FSP flight; (C) side view of the experimental setup depicting the placement of the head surrogate. Fragment velocities were estimated from the high-speed images. The target-holding fixture was kept on a rigid base at ∼1 m distance from the open end of the barrel.
The sabots, containing FSPs, were positioned at some distance in the barrel and accelerated by the quick release of compressed air from the pressure vessel. Compressed air was released by triggering the pneumatic actuator, which opened the passage between the pressure vessel and the barrel. The sabots were designed for stability during travel in the barrel, while minimizing their mass to achieve higher velocity. The desired FSP velocity was attained by adjusting the pressure in the pressure vessel and the distance of the sabot inside the barrel from the open end (i.e., effective barrel length). The variation in FSP velocity for a given set of pressure and effective barrel length was within ±5 m/s.
Upon exiting the barrel, the sabot opened and detached the FSP to move separately. The FSP, having less frontal drag and weight, moved faster than the sabot. As they continued their trajectory, the sabot’s motion was constrained by a sabot arrester plate attached to the front of the target-holding fixture (Figure 2B). In contrast, the FSP impacted the target by passing through a small aperture provided in the sabot arrester plate (Figure 2B). The target-holding fixture was kept on a rigid base at a distance of ∼1 m from the open end of the barrel.
2.2 Tissue simulants and head surrogate
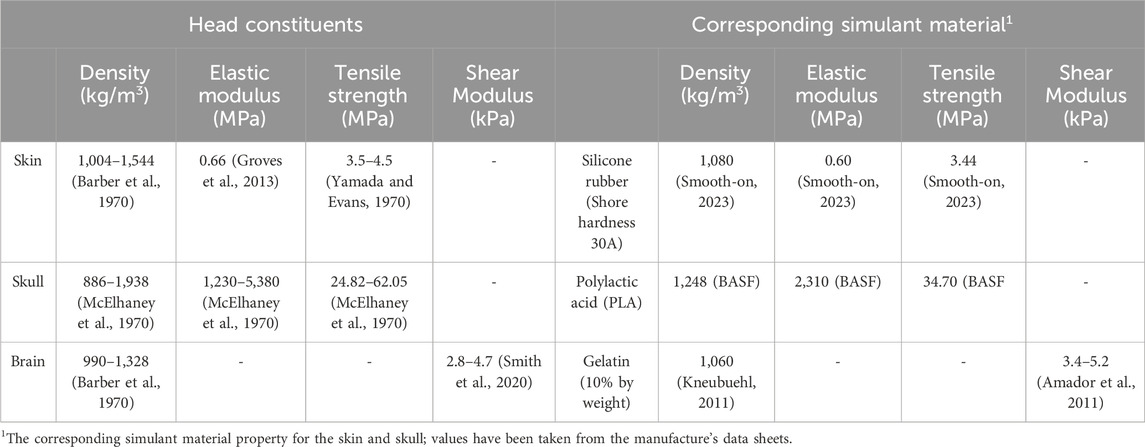
A head surrogate based on the geometry of the global human body models consortium’s (GHBMC) head (Gayzik F. et al., 2011; Gayzik F. S. et al., 2011; Mao et al., 2013) was used in this work. The GHBMC head model’s geometry is based on a 50th percentile male volunteer. In the development of the head surrogate, three primary layers of the head were employed: skin, skull, and brain. The choice of simulants for each layer was based on their mechanical characteristics, such as stress–strain response, elastic modulus, and failure strength. The selection of simulants aimed to ensure agreement with the distinctive properties of the corresponding biological tissue (Table 1). The subsequent section provides a breakdown of each layer of the simulant and the overall head surrogate model.
2.2.1 Skin simulant
For the skin simulant (Figure 3A), a two-part silicone compound (Smooth-On, Inc., USA) with a shore hardness of 30A was utilized. This specific material was chosen due to the similarity of its stress–strain response to human skin (Chanda et al., 2017; Chanda and Upchurch, 2018; Marechal et al., 2021). The skin simulant was prepared in two symmetrical parts, tailored to the anthropometric shape of the head, and maintained a thickness of 3 mm. This thickness selection was in line with the average thickness of human skin documented in existing literature (Chanda, 2018; Sperrazza and Kokinakis, 1968; Yoganandan and Pintar, 1997).
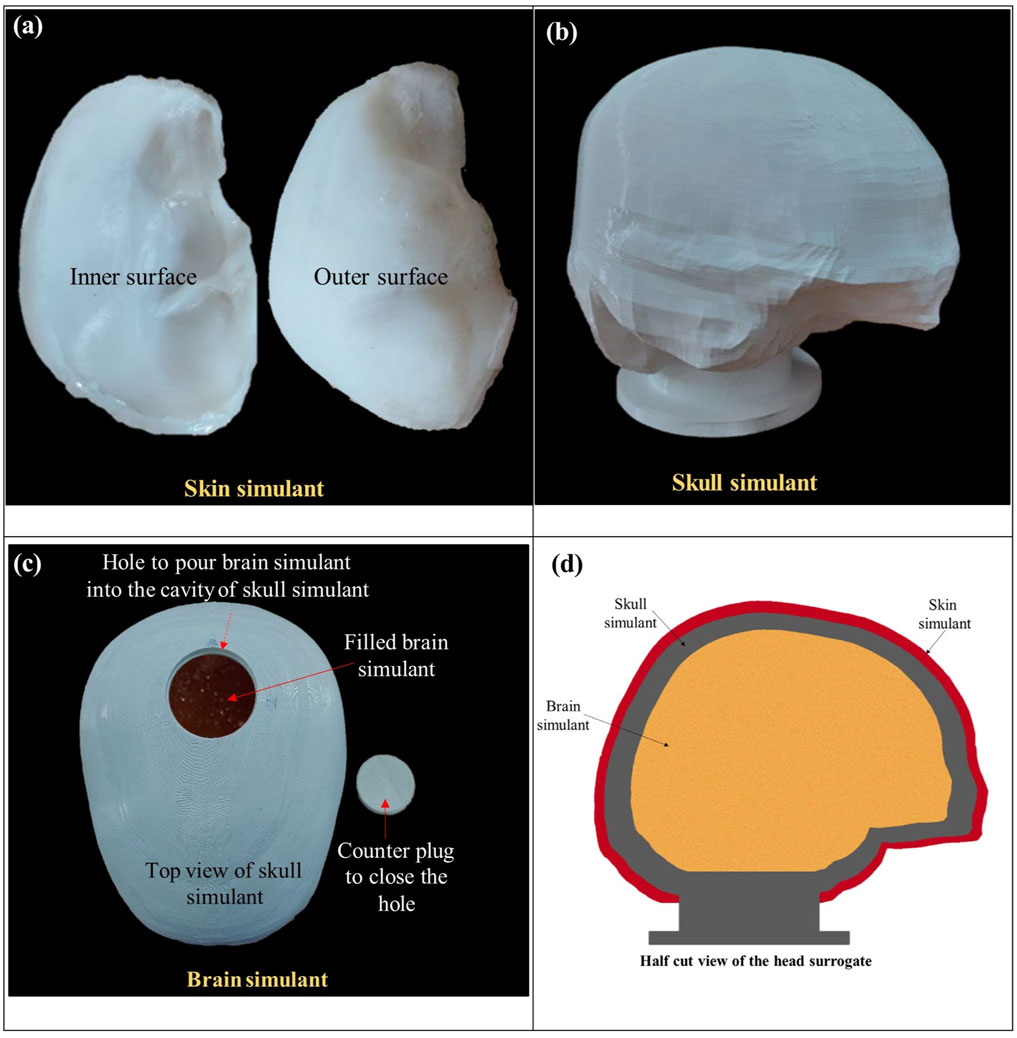
Figure 3. Photographs of the individual layers of the skin, skull, and brain simulants, depicted in (A–C), respectively. Panel (D) illustrates a schematic of a half-cut view of the head surrogate, presenting the arrangement of the layers.
To prepare the skin simulant, both components of the silicone material were blended in an equal proportion (i.e., 1:1) by weight. The mixture was stirred continuously during the preparation to prevent the formation of air bubbles or lumps and ensure homogeneity in each sample. The resulting mixture was poured into a custom-made mold of polylactic acid (PLA). The mold was created by 3D printing of the inner and outer layers of the scalp of the GHBMC head model. After pouring the mixture into the mold, the mixture was left to cure at room temperature for 16 h.
2.2.2 Skull simulant
The skull simulant (Figure 3B) was fabricated through 3D printing of the inner and outer skull components of the GHBMC head model. PLA with 100% infill density was used for 3D printing. PLA was chosen due to the resemblance of its mechanical properties with those of the human skull, including density, tensile strength, and elastic modulus (Falland-Cheung et al., 2017; Singh et al., 2024). Moreover, PLA was also a suitable candidate material in terms of availability and ease of printing. An opening was made at the top of the skull simulant, accompanied by a counter plug. This opening served the purpose of pouring the brain simulant inside the skull simulant.
2.2.3 Brain simulant
Ballistic gelatin fabricated in accordance with the Fackler model (10% concentration by weight) (Jussila, 2004) was used as a brain simulant (Figure 3C). Ballistic gelatin was prepared using gelatin powder with a bloom strength of 250. In the process, a homogeneous mixture of gelatin powder and cold water was prepared in a 10:90 ratio. The mixture was heated and continuously stirred to maintain the homogeneity. Subsequently, the mixture was poured into the skull simulant through the top opening, and the assembly was kept in the refrigerator at 4°C for 24 h to allow the curing before testing. The 10% ballistic gelatin is commonly used as a brain simulant due to its similarity in elastic modulus and density to the actual brain (Riva et al., 2021; Farrer et al., 2015). Furthermore, ballistic gelatin exhibits behavior comparable to that of the brain in terms of cavity formation, depth of penetration, and deformation (Dąbrowska et al., 2016; Mabbott et al., 2016).
2.2.4 Head surrogate
The head surrogate was developed by assembling all the layers. After filling the brain simulant inside the skull simulant, the top opening of the skull simulant was closed and sealed using the counter plug. Afterward, the skin simulant was glued over the skull simulant. Figure 3D illustrates a schematic of a half-cut view of the head surrogate, showcasing all three layers after assembly.
2.3 Neck attachment
Head surrogates in ballistic testing often feature different attachments as the neck to hold the head surrogate, broadly categorized as rigid and flexible neck attachments (Mahoney et al., 2018; Carr et al., 2015; Rodriguez-Millan et al., 2023; Miranda-Vicario et al., 2018). Rigid neck attachments, such as simple blocks or rods, fix the head surrogate in place with little or no movement (Mahoney et al., 2018; Mahoney et al., 2017a; Carr et al., 2015; Mahoney et al., 2020). On the contrary, flexible neck attachments, with a mass similar to that of an actual neck, have the capability to deform or bend, mimicking an actual neck’s response to external loading (Rodriguez-Millan et al., 2023; Miranda-Vicario et al., 2018; Freitas et al., 2014). The literature lacks information on the effects of both types of neck attachments on the ballistic response of head surrogates against FSPs. Therefore, we utilized both rigid and flexible neck attachments with the head surrogate and examined their respective effects.
This investigation was based on the hypothesis of whether FSP impact can cause flexion or extension (i.e., bending of the neck in forward and backward directions, respectively) of the neck attachment and affect the ballistic response of the head surrogate. This type of neck bending has been observed in some previous studies involving blunt (Nightingale et al., 2015; Ivancic, 2013) impact and ballistic impact using larger projectiles such as bullets (Tse et al., 2017). Furthermore, the testing of FSP with the head–neck surrogate is challenging and sometimes destructive due to the dynamic nature of events. Dummies are also sought in the evaluation of actual warheads. In such a scenario, fragments may travel haphazardly and may potentially damage the biofidelic flexible necks such as the Hybrid-III neck. These flexible dummy necks are costly, difficult to manufacture, and may get damaged due to the direct impact of fragments on the neck attachment. Hence, simpler, rigid neck attachments are desired, provided the results are comparable to that of the flexible neck attachment.
The head surrogate was mounted on the neck attachments, and the head and neck assembly were held at the target-holding fixture. Two types of neck attachments were employed. The rigid neck attachment (Figure 4A) was a rigid solid cylinder made of aluminum, matching the mass and size of an average human neck. The flexible neck attachment (Figure 4B) was a Hybrid-III neck (Humanetics, Farmington Hills, MI).

Figure 4. Head surrogate model mounted on (A) a rigid neck attachment and (B) a flexible neck attachment.
2.4 Ballistic testing and estimation of ballistic limit velocities
The target-holding fixture, housing the head–neck surrogate, was positioned at a distance of ∼1 m from the open end of the barrel to allow for adequate time for sabot opening and FSP separation. High-speed videography of the ballistic events was done using a high-speed camera (Phantom v411, Vision Research, Inc., Wayne, NJ). The high-speed camera was strategically oriented perpendicular to the trajectory of the FSP (Figure 2A). A frame rate ranging between 10,000 and 13,000 frames per second was set, contingent upon the desired resolution.
High-speed images were used to determine the velocity of the FSP. A calibration of pixels to millimeters at the plane of the FSP’s travel path was performed to obtain a pixel-to-millimeter conversion scale. Subsequently, pixel coordinates at the central point of the FSP were recorded for each frame. The distance traveled by the FSP in each frame was calculated by multiplying the pixel-to-millimeter scale with the difference in pixel coordinates between successive frames. The velocity of the FSP in a specific frame was determined by dividing the distance traveled in that frame by the time interval between two frames. Velocities of FSP were nearly constant in all the frames. However, velocity calculations were executed for multiple frames immediately before the impact, and an average velocity value was reported to uphold the accuracy. It should be noted that, in this work, the rotational velocity of the FSP was not considered because we did not observe (qualitatively, from the high-speed images) significant rotation or spin of the FSPs. The experimental setup used in this work was not capable of generating spin on the fragment. Nguyen et al. (2021) and Cunniff (2014) also suggest that the rotational velocity of small FSPs such as the ones used in this work is generally insignificant (<∼2% of total energy).
In the context of ballistic impact analysis, two parameters, namely, threshold velocity (Vth) and ballistic limit velocity (V50), are vital for evaluating the effectiveness of a projectile against the target to be defected. Vth represents the minimum projectile velocity among all impact velocities resulting in target perforation. Conversely, a more statistically robust parameter, V50, is used to address data scatter in experiments. V50 is defined as the projectile velocity corresponding to a 50% probability of perforation.
In this study, we defined perforation as the perforation of both the skin and skull simulants and subsequent penetration into the brain simulant. This classification is based on the premise that projectile penetration into the brain following perforation of the skin and skull layers is typically considered lethal (Van Wyck et al., 2015; Maiden, 2009).
We estimated the V50 values following the NATO STANAG 2920 (NATO and NATO Standardization Agreement, 2003; Bolduc and Jager, 2016). NATO STANAG 2920 defines V50 as the arithmetic mean of six impact velocities around the Vth. Among these six velocities, three correspond to the maximum velocities, resulting in non-perforation, while the remaining three correspond to the minimum velocities, causing perforation. The velocity spread, defined by the difference between the maximum and minimum velocities among the six velocities, was 6 m/s and 24 m/s for the 1.10-g and 2.79-g FSPs, respectively. This velocity spread falls within the acceptable range (<40 m/s) stipulated by NATO STANAG 2920 (NATO and NATO Standardization Agreement, 2003; Bolduc and Jager, 2016; Nguyen et al., 2020).
2.5 Anthropometric (close-shape) vs. open-shape head surrogate models
The simulant layers of a head surrogate (i.e., skin, skull, and brain) are typically arranged in two ways to prepare the head surrogate: first, as an open-shape model, by stacking various layers in the form of rectangle cross-sectioned samples (Riva et al., 2019; Sterzik et al., 2017; Riva et al., 2021; Mahoney et al., 2017b), and second, as close-shape anatomically accurate models with layers having geometry close to the actual organ (Mahoney et al., 2018; Mahoney et al., 2017a; Thali M. et al., 2002; Carr et al., 2015). The first approach allows for better imaging of the ballistic event and projectile penetration (Riva et al., 2021; Mahoney et al., 2017b) and facilitates the investigation of the interaction of the projectile with various layers. This, in turn, provides mechanistic insights (e.g., failure mechanisms). Open-shaped models are easier to build and manufacture. Hence, they are economical in terms of cost, time, and resources. Open-shape surrogates do not capture the effects due to the geometry of the head (e.g., head curvature). However, the level of abstraction in open-shape surrogates is generally sufficient to reasonably estimate ballistic limit velocities and energies required for various levels of penetration and perforation into the head surrogate. The second approach allows for accurate anatomical representation, which better captures the geometric effects and enables the mounting of head protective equipment such as helmets (Mahoney et al., 2018; Mahoney et al., 2017b). Open-shape head surrogates are unconstrained at the edges, except for the bottom surface resting on the fixture. In contrast, close-shape head surrogates completely enclose the brain within the skull, with the skin layer covering it externally. Although it is relatively costly and time-consuming to build close-shape head surrogates, it is a better approximation of real-world scenarios such as experiments using post-mortem human subjects. However, imaging of skull and brain simulants is not possible with the close-shape head surrogate.
In our previous study (Pandey et al., 2024), we explored the response of an open-shape head surrogate (Figure 5), benefiting from its advantages in visualization and simplification. However, a lingering question is how much does this simplification influence the results. To address this, we compared the response of an anthropometric (close-shape) head surrogate with the findings from our earlier study on the open-shape head surrogate.
3 Results
3.1 Threshold velocity (Vth), ballistic limit velocity (V50), and corresponding energy densities (Eth/A, E50/A)
Table 2 shows the raw experimental velocity data for both perforation and non-perforation cases. Table 3 presents the calculated values of Vth, V50, Eth/A, and E50/A. Markedly, the values of Vth and V50 exhibited proximity, with a difference of within ∼10% for both FSPs. Therefore, our subsequent discussions in the manuscript will focus solely on V50.

Table 2. Raw experimental data for the 1.10-g and 2.79-g FSPs. The first column with numbers presents the velocity of the specific FSP in m/s, and the second column depicts the outcome of impact (i.e., perforation and non-perforation). P: perforation, NP: non-perforation.
The V50 for the 1.10-g FSP represented a ∼41% increase compared to the V50 of the 2.79-g FSP. The corresponding energies (E50) for both FSPs fell within the range of 10–14 J. The energy density (E50/A), calculated as the energy of the FSP divided by its presented cross-sectional area, was ∼63% higher for the 1.10-g FSP than for the 2.79-g FSP. This disparity in the energy density can be attributed to the smaller cross-sectional area of the 1.10-g FSP.
3.2 Failure pattern
3.2.1 Skin simulant failure
The failure of the skin simulant resulted from a combination of cavity shearing and elastic hole enlargement. The final size of the created cavity in the skin simulant was smaller than the size of the FSP. The failed surfaces, showcasing cavities created by both FSPs in the skin simulant, are illustrated in Figure 6. Each zoomed view of the cavity (Figures 6A, B) features an ellipse (yellow) enclosing the final cavity and a dotted circle (red) indicating the actual size of the respective FSP. It is evident from the figures that the final size of the cavity is smaller than the size of the FSP. The sheared surface was distinctly visible in the zoomed view of a sectioned cavity of the skin simulant (Figure 6C).

Figure 6. Sheared surface of the skin simulant (A) cavity created by the 1.10-g FSP; (B) cavity created by the 2.79-g FSP; (C) zoomed view of the internal surface of the cavity visible after sectioning along the cavity.
3.2.2 Skull simulant failure
The failure of the skull simulant occurred due to crushing by the FSP. Figure 7 depicts the failed surface of the skull simulant. In complete perforation cases, the material of the skull simulant in front of the FSP failed due to a localized and dynamic compressive loading by the FSP. The failed material of the skull simulant further broke into smaller pieces and created a circular cavity. The diameter of the fractured cavity in the skull simulant was close to the diameter of the FSP (Figures 7A, B). In most of the partial perforation cases, the FSP rebounded after the impact. However, in some cases of partial perforation, the FSP got stuck in the skull simulant (Figure 7C).

Figure 7. Failed surface of the skull simulant (A) cavity generated by the 1.10-g FSP; (B) cavity generated by the 2.79-g FSP; (C) stuck FSP in the skull simulant.
3.2.3 Brain simulant failure
The FSP penetrated into the brain simulant after passing through the fractured cavity of the skull simulant. The failure of the brain simulant took place through the shearing of a permanent cavity up to the depth of penetration of the FSP. As the brain simulant was entirely enclosed within the skull simulant, imaging the cavity of the brain simulant was not possible. Therefore, a schematic illustrating the cavity is presented in Figure 8A. Furthermore, additional damage of the brain simulant arose due to the penetration of broken pieces of the skull simulant in the brain simulant (Figures 8A, B).
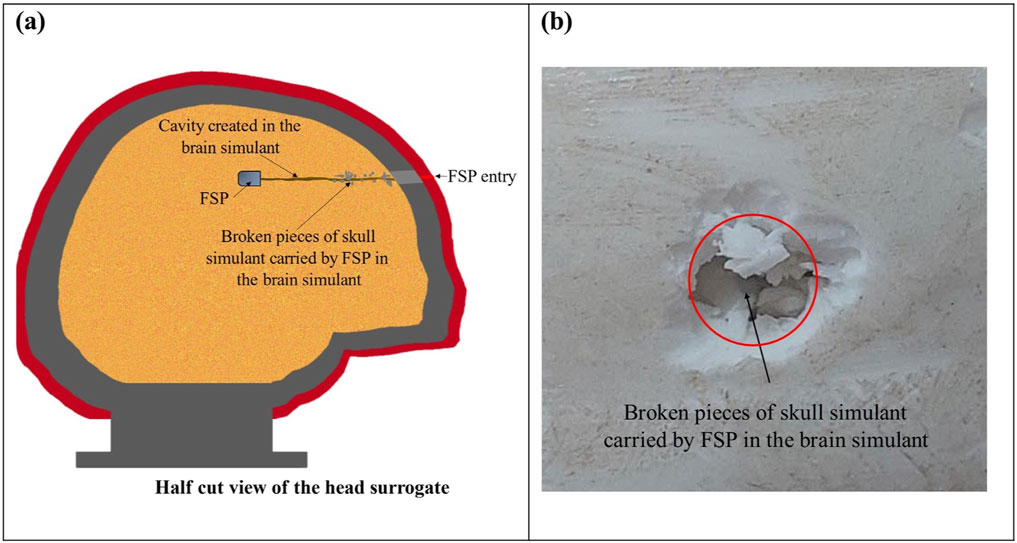
Figure 8. Damage of the brain simulant: (A) a schematic representing the internal view of the head surrogate with the sheared cavity in the brain simulant after perforation; (B) the visible broken piece of the skull simulant penetrated in the brain simulant.
3.3 Effect of the flexibility of the neck attachment on the ballistic response of the head surrogate
To examine the effect of neck attachment flexibility on the head surrogate’s ballistic response, we attached a flexible neck attachment to the head surrogate. The head surrogate was subjected to the impact of a 2.79-g FSP. The raw experimental data for the flexible neck attachment are tabulated in Table 4.
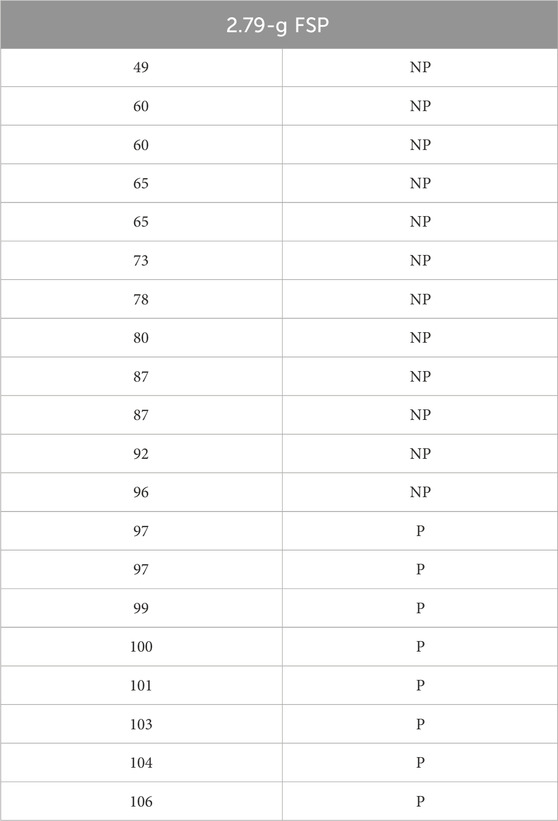
Table 4. Raw experimental data for the 2.79-g FSP’s impact on the head surrogate with a flexible neck attachment. The first column with numbers presents the velocity of the specific FSP in m/s, and the second column depicts the outcome of impact (i.e., perforation and non-perforation). P: perforation, NP: non-perforation.
Table 5 outlines the Vth and V50 obtained with both types of neck attachments. It was observed that there was no significant alteration in the V50 of the head surrogate when transitioning from a rigid neck attachment to a flexible one. The discrepancy in the obtained V50 using these two types of neck attachments was ∼10%. The flexible neck attachment showed a similar response as the rigid neck attachment due to negligible bending in the neck attachment after the impact of the FSP on the head surrogate. The variance in V50 was primarily attributed to the difference in the velocity spread near the Vth (Tables 2 and 4), which influenced the calculation of V50. Moreover, there was no marked distinction in the failure pattern (Figure 9).

Figure 9. Photographs depicting the failed surface of each layer of the head surrogate with a rigid neck attachment and a flexible neck attachment.
3.4 Comparison of the response of the anthropometric (close-shape) and open-shape head surrogates
To assess the effect of geometric curvature, the results from this study on an anthropometric (close-shape) head surrogate were compared to the results from our previous work (Pandey et al., 2024) on an open-shape head surrogate. Table 6 shows the V50 values obtained for both types of head surrogates. The findings from the anthropometric head surrogate experiments revealed that the V50 values were in proximity (within ∼18%) with those obtained from the open-shape head surrogate model for both FSPs.
Figure 10 displays the failed surface of various layers from both the head surrogate types. The failure patterns observed in each layer of the anthropometric head surrogate were consistent with those seen in the open-shape head surrogate. In both types of head surrogates, the skin simulant exhibited failure through the shearing of a cavity with size smaller than the size of the FSP. For the skull simulant, both head surrogate models showed failure by fracturing a circular cavity with a size equivalent to the FSP size. Lodging of the FSP in the skull simulant in a few partial perforation cases was also consistent. Similar to the brain simulant failure in the anthropometric head surrogate, the brain simulant in the open-shape head surrogate failed through shearing and additional damage due to the penetration of broken pieces of the skull simulant into the brain simulant.
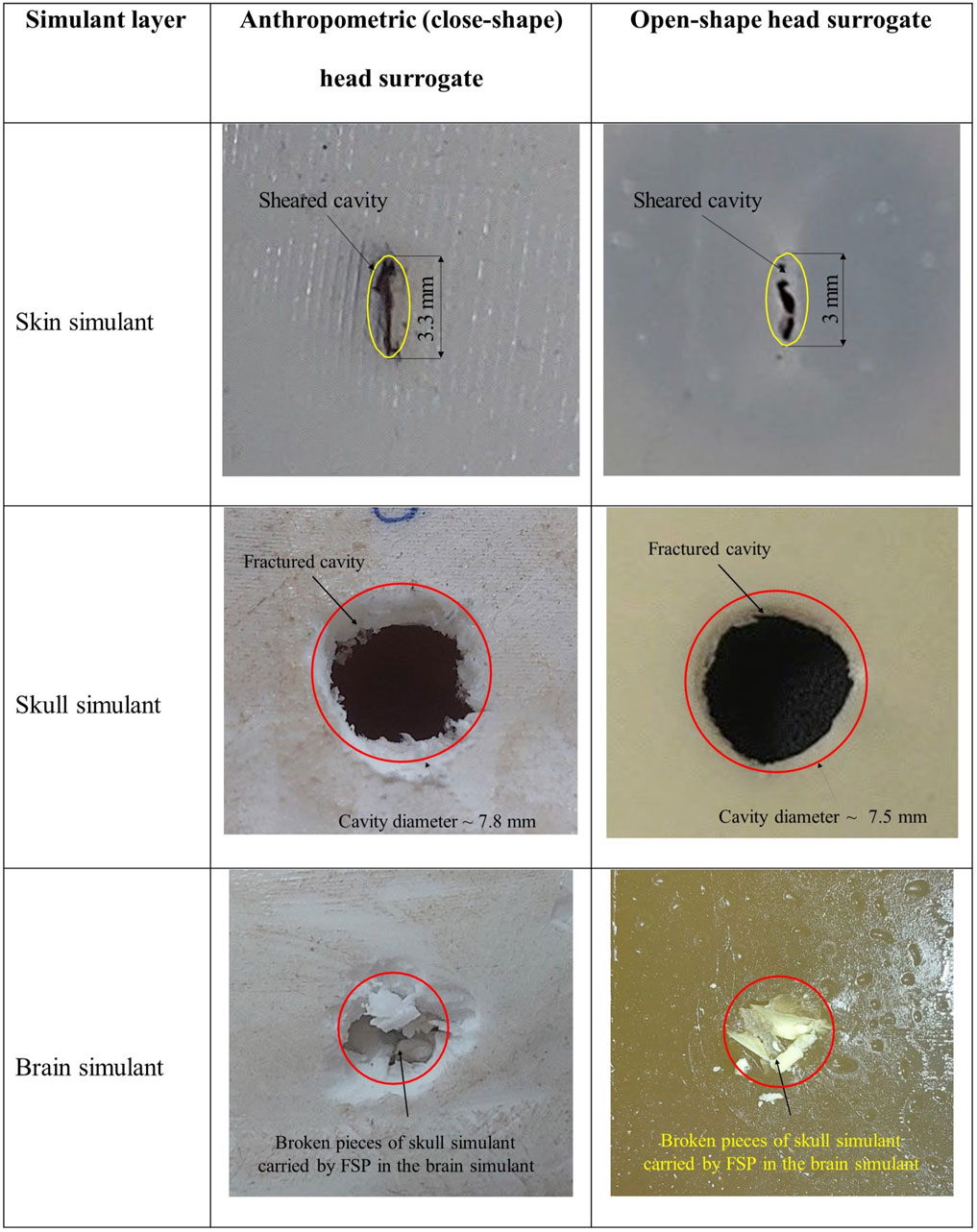
Figure 10. Photographs depicting representative failed surface of each layer of anthropometric (closed-shape) and open-shape head surrogates.
4 Discussion
We investigated the ballistic response of an anthropometric head surrogate model under the impact of two chisel-nosed FSPs weighing 1.10-g and 2.79-g. Although fragments are the prevalent source of combat injuries (Breeze and Powers, 2017; Breeze and Clasper, 2013; Regasa et al., 2018; Bowyer et al., 1995; Carr et al., 2017), the current literature lacks sufficient information elucidating the response of the head or head surrogate under the impact of fragments, particularly against NATO-specified chisel-nosed FSPs. We present V50 and E50/A required for penetrating the head surrogate and analyze the failure patterns in various tissue simulant layers of the head surrogate. We investigate the influence of the neck attachment’s flexibility and the head surrogate’s geometry (curvature) on the head surrogate’s response. This study aims to fill a gap in the existing literature by comprehensively investigating the aforementioned aspects. It should be noted that, in this study, we assessed unprotected situations, recognizing that in tactical warfare, injuries can occur during as well as after active combat.
V50 and E50/A values exhibited an inversely proportional relationship with the size of the FSP (Table 3). As the size of FSP decreased from 2.79-g to 1.10-g, the values of V50 and E50/A increased by ∼41% and ∼63%, respectively. This variation can be ascribed to the change in the sectional density (mass of projectile divided by its presented area). Sectional density is a vital parameter for comparing the V50 of different projectiles as it accounts for the sizes and mass of all projectiles (Breeze and Clasper, 2013; Breeze et al., 2013b). Projectiles with higher sectional density typically tend to have lower V50 values (Breeze and Clasper, 2013; Jussila et al., 2005; Breeze et al., 2013b; Pullen et al., 2021; Pandey et al., 2023). Consequently, the larger FSP (i.e., the 2.79-g FSP) offered a lower V50 (Table 3).
Energies (E50) corresponding to the V50 were in the range of 10–14 J (Table 3). The comparable value of E50 observed can be due to the small variation of the FSP sizes (i.e., 1.10-g and 2.79-g) investigated in this study. Moreover, E50 exhibits an inherent relationship between mass and velocity, so its variation might be relatively less than that of V50. The E50 values obtained in this study are consistent with the values in the limited literature on fragment energy required for penetration in the head. For instance, Watkins et al. (1988) reported ∼19 J of energy needed by a 1.045-g steel sphere for penetration in a head surrogate made of dried human skull with chamois leather as the skin simulant and gelatin as the brain simulant. Li et al. (2023) recorded 12–22 J as the energy range required for goat head penetration by 1.2-g steel spherical and cubical fragments. In the standards of NATO’s MSIAC (Munitions Safety Information Analysis Center) (Van der Voort et al., 2016; Tomasello et al., 2023) and the UK’s ESTC (Explosives Storage and Transport Committee) (Oei Su Cheok, 2005), the threshold energy of small fragments to cause lethal penetration is 15–20 J.
The energy of the projectile is used as a criterion for lethal penetration or casualty. There are differences in opinion among the authors on the threshold energy of projectiles to produce casualty (Kneubuehl, 2011; Rettinger, 2017; Henderson, 2010). A conventional standard of 80 J of bullet energy was suggested earlier for incapacitating a human on the battlefield, a notion primarily influenced by the perspectives of German artillery (Rettinger, 2017). However, it is important to acknowledge that the nuanced dynamics of small fragment interactions diverge significantly from the mechanisms observed with larger projectiles such as bullets. Unlike bullets, which induce tissue crushing and create pulsating cavities, small fragments tend to interact more locally, penetrating primarily through the piercing mechanism (Van der Voort et al., 2016; Breeze and Carr, 2016a; Shuker, 2019; Kneubuehl, 1994). Consequently, small fragments may cause lethal penetration at energy levels lower than those typically associated with larger projectiles such as bullets. As seen in this study, fragments can penetrate tissues at energy levels substantially below the 80 J threshold.
The failure mechanism observed in the skin simulant involved a sequence of events initiated by shearing of the cavity, followed by elastic hole enlargement. Upon impact, the skin simulant underwent stretching in the direction of the FSP, reaching a point where a cavity was sheared. Subsequently, during the perforation process, the skin simulant attempted elastic recovery but was impeded by the presence of the rigid FSP. This resulted in the lateral stretching of the skin simulant, which elastically recovered once the perforation process was completed, the typical phenomenon termed elastic hole enlargement (Rosenberg and Dekel, 2012). The resulting cavity was elliptical, with its longer side aligned along the nose length of the FSP (Figure 6). Notably, the final size of the cavity was smaller than that of the respective FSP, owing to the shearing of the cavity while in a stretched state, followed by elastic recovery. This observation of smaller cavities is consistent with that of existing literature on cavity formation in the skin due to projectile penetration (Kneubuehl et al., 2011; Serraino et al., 2020; Inchingolo et al., 2011; Baptista et al., 2014; Carr et al., 2014).
The failure of the skull simulant was attributed to the compressive loading exerted by the FSP upon impact. This loading generated a compressive stress wave at the point of impact, which subsequently reflected as a tensile wave from the rear surface of the skull simulant. The skull simulant failed when these reflected tensile waves reached the skull simulant’s tensile strength. Consequently, the material beneath the FSP was fractured into smaller pieces, facilitating the penetration of the FSP into the brain simulant. A circular cavity was created in the skull simulant (Figure 7). The diameter of the cavity closely matched the diameter of the respective FSP. This pattern of circular cavity formation, where the diameter matches that of the penetrating projectile, aligns with findings in existing literature (Smith et al., 2015; Żochowski et al., 2023; Caister et al., 2020; Kieser et al., 2014)
Following the fracture of the cavity in the skull simulant, the FSP penetrated into the brain simulant. After penetration, the FSP sheared a permanent cavity in the brain simulant (Figure 8). The smaller pieces of the fractured skull simulant were also carried into the brain simulant by the FSP. As a result, besides the direct threat posed by the FSP, the brain was also subjected to a potential injury from the skull simulant fragments. Numerous studies have documented the presence of skull fragments along the wound path in brains or brain simulants (Riva et al., 2019; Mahoney et al., 2020; Mahoney et al., 2017b; Thali M. J. et al., 2002; Karger et al., 1998).
It was noted that a flexible neck attachment did not significantly alter the V50 (Table 5) or the failure pattern of the head surrogate (Figure 9). The discrepancy in V50 obtained with these two neck attachments was ∼10%. The flexible neck attachment behaved similarly to the rigid neck attachment. Despite the introduction of a flexible neck attachment, negligible bending in neck attachment was observed due to the large difference in mass between the FSP and the head surrogate (Figure 11). The head surrogate, weighing ∼3.5 kg, was considerably heavier than the FSPs (i.e., 1.10–2.79 g). This large difference in mass played a crucial role in determining the momentum (product of mass and velocity) transfer during impact. Initially, the head surrogate and neck attachment arrangement were at rest (V = 0 m/s). Following the principle of conservation of momentum, a significant transfer of momentum after impact can potentially cause the head surrogate–neck parenchyma to move or bend (V > 0 m/s) depending on the boundary conditions (Nightingale et al., 2015; Ivancic, 2013; Tse et al., 2017). However, when the FSP impacted the head surrogate, the head surrogate’s momentum changed insignificantly due to the relatively small momentum transferred by the FSP. This small change in the head surrogate momentum was not enough to create a significant motion in the head surrogate–neck parenchyma.
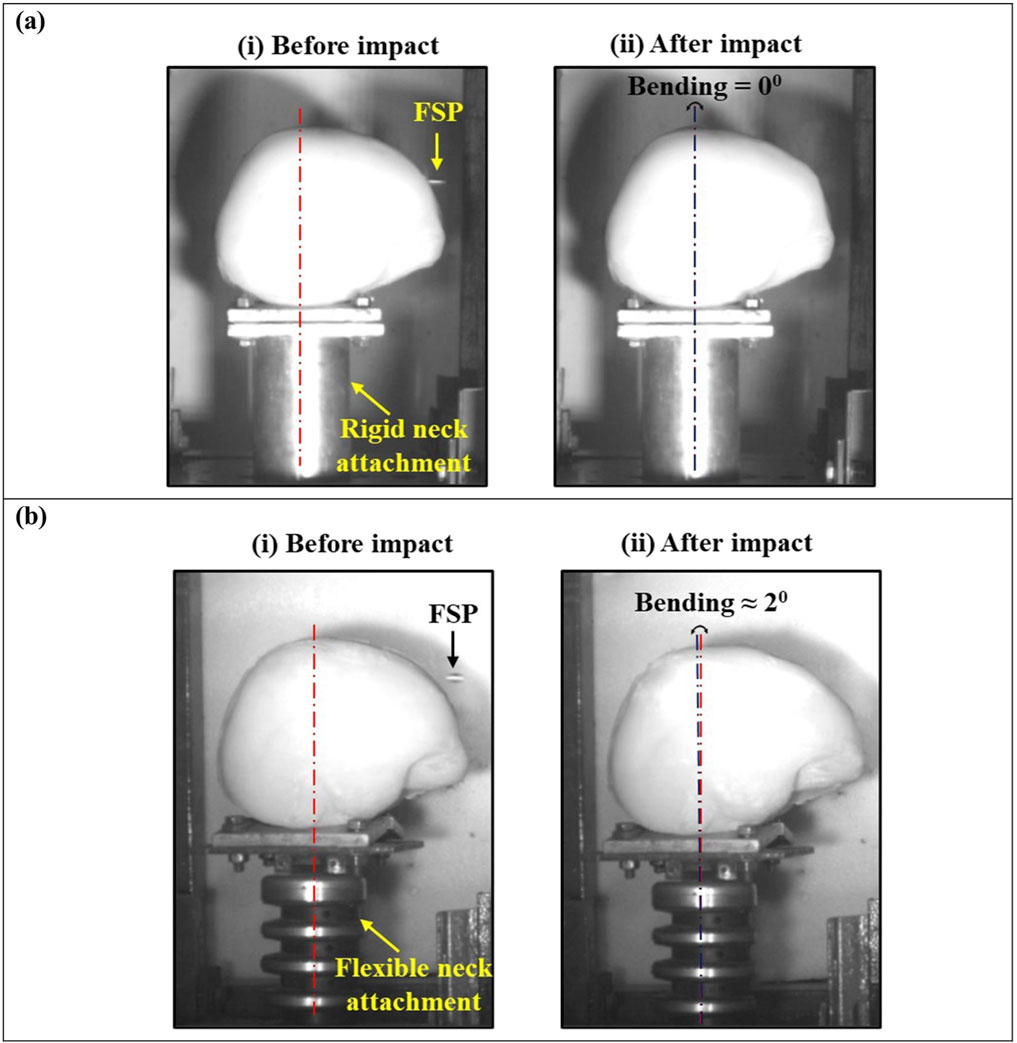
Figure 11. Bending of neck attachment due to impact of FSP in (A) a rigid neck attachment and (B) a flexible neck attachment.
The variance in V50 in both cases was primarily due to differences in the velocity spread in the six velocities considered for calculating it (Table 4). Therefore, rigid neck attachments can effectively be employed in experiments involving small fragments without affecting the outcomes due to their lack of flexibility. Rigid neck attachments offer advantages in terms of cost-effectiveness, availability, and maintenance ease.
No significant variation was observed when comparing the response of the open-shape simplified head surrogate with the anthropometric (close-shape) head surrogate. Comparable V50 values were obtained in both cases, differing by ∼18% for the 2.79-g FSP and ∼11% for the 1.10-g FSP (Table 6). Few previous studies demonstrating the geometric effects of the targets on V50 velocity (Stargel, 2005; Pasquali and Gaudenzi, 2017) on metallic and composite structures have indicated that the ballistic limit increases with the target curvature due to enhanced material compression compared to planar targets. The difference in V50 velocity obtained in this work can be attributed to either geometric effects or the experimental spread in the minimum and maximum velocities used for V50 calculation. The velocity spread, defined by the difference between the maximum and minimum velocities among these six velocities, was 15 m/s and 24 m/s for the open-shape and close-shape head surrogates, respectively. This velocity spread falls within the acceptable range (<40 m/s) stipulated by NATO STANAG 2920 (NATO and NATO Standardization Agreement, 2003; Bolduc and Jager, 2016; Nguyen et al., 2020). Although the velocity spread was within the acceptable range, a more extensive set of experiments in the future, with a narrower velocity range, could potentially reduce the observed difference between the V50 values. We believe that additional data with a narrower range of velocities are needed to fully attribute the difference in V50 velocity to the geometric effects.
The failure patterns observed in each layer of the anthropometric head surrogate resembled those seen in the corresponding layers of the open-shaped head surrogate (Figure 10). In both cases, the skin simulant failed by shearing an elliptical cavity with a diameter smaller than the diameter of the respective FSP, the bone simulant failed by fracturing a circular cavity with a diameter close to the diameter of the corresponding FSP, and the brain simulant failed by shearing a permanent cavity and experiencing additional damage from the penetration of broken pieces of the skull simulant. Furthermore, the penetration time for both types of head surrogates was found to be within 200 µs (Figure 12). It should be noted that the wave propagation response tends to prevail up to ∼200 µs, as highlighted in previous studies (Sutar and Ganpule, 2020; Ganpule et al., 2013). Only after this time frame three-dimensional geometric effects, such as head curvature, become more prominent in the structural response. These results imply that the geometrical curvature of the skull exerts a minimal influence under the impact of small fragments due to the localized nature of the response, where geometric effects play a less important role.

Figure 12. Time taken for the penetration of FSP (A) in the anthropometric (close-shape) head surrogate and (B) in the open-shape head surrogate.
The findings from this study are useful in the evaluation of penetrating head injuries and in defining the lethality criteria, particularly in relation to small fragments. The results will be useful in the design of modern warheads for producing fragments of optimum size. Furthermore, data generated in this work can be utilized for the calibration and validation of computational head models against small projectile impact. Additionally, the observed failure patterns and the shapes and sizes of cavities in different layers of head surrogates can be utilized in forensic investigations and autopsies to identify the type of projectile involved.
5 Limitations
This work has certain limitations. The head surrogate model employed lacked complexity, such as the heterogeneous and anisotropic nature of tissues and intricate structures such as thin layers found in the human head. A human head consists of various layers, including the cranial meninges and the wavy cranial sutures, which are composed of collagen fibers connecting different sections of the skull. These layers are relatively thin, typically measuring between 0.5 and 1 mm, and their morphology and mechanical properties are not fully documented in the literature. As a result, developing surrogate materials that accurately replicate these layers is challenging. Additionally, 3D printing of such surrogate materials with small thicknesses and complex structures is difficult. To streamline the experimental procedures and data analysis, we excluded these layers from our study. Furthermore, we did not investigate the effect of fragment nose shape on the ballistic response. Our earlier work (Pandey et al., 2023) on an isolated skin simulant may provide valuable insights in this regard. In this work, we did not consider the spin (i.e., rotational velocity) of the fragment. Future studies incorporating a wider range of fragment sizes, different fragment shapes, fragment spin, and more biofidelic head–neck surrogates will further enhance the understanding regarding the response of the head surrogate against small fragments.
6 Conclusion
To investigate the ballistic response of the head against fragments, an anatomically correct anthropometric head surrogate was developed and subjected to the impact of 1.10-g and 2.79-g chisel-nosed FSPs. The key findings are as follows:
• The lighter FSP (1.10-g) exhibited higher ballistic limit velocities (V50) compared to the heavier FSP (2.79-g), with V50 values of 159 m/s and 85 m/s, respectively.
• The energy density (E50/A) corresponding to V50 was also higher for the 1.10-g FSP (0.61 J/mm2) than for the 2.79-g FSP (0.23 J/mm2).
• Each layer of the head surrogate failed differently. The skin simulant failed by shearing a cavity, followed by elastic hole enlargement, resulting in a cavity with size smaller than the size of FSP. The skull fractured, creating a circular cavity with a diameter of cavity at the entry point close to the size of the FSP. The brain simulant failed due to shearing and penetration of broken skull fragments.
• The flexible neck attachment exhibited negligible bending after impact, resulting in no considerable change in the head surrogate’s response compared to the response of the head surrogate with a rigid neck attachment.
• No significant influence of head curvature was observed on the overall response of the head surrogate due to the localized nature of fragment penetration.
Taken together, the results unveil critical details on fragment penetration thresholds (velocities and energy densities) in the head surrogate and the mechanics of fragment interaction with each simulated tissue layer of the head surrogate. These insights hold significant value in assessment of penetrating head injury.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
PP: conceptualization, data curation, formal analysis, investigation, methodology, visualization, and writing–original draft. SG: conceptualization, funding acquisition, supervision, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Armaments Research Board (grant number ARMREB-ASE-2018-198). SG acknowledges financial support from the Armaments Research Board under the grant ARMREB-ASE-2018-198.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amador, C., Urban, M. W., Chen, S., Chen, Q., An, K.-N., and Greenleaf, J. F. (2011). Shear elastic modulus estimation from indentation and SDUV on gelatin phantoms. IEEE Trans. Biomed. Eng. 58, 1706–1714. doi:10.1109/tbme.2011.2111419
Baptista, M. V., d'Ávila, S. C., and d'Ávila, A. M. M. (2014). Histopathological detection of entry and exit holes in human skin wounds caused by firearms. J. Forensic Leg. Med. 25, 49–52. doi:10.1016/j.jflm.2014.04.017
Barber, T. W., Brockway, J. A., and Higgins, L. S. (1970). The density of tissues in and about the head. Acta neurol. Scand. 46, 85–92. doi:10.1111/j.1600-0404.1970.tb05606.x
BASF (2024). Forward AM ultrafuse PLA technical data sheet. Available at: https://move.forward-am.com/hubfs/AES%20Documentation/Standard%20Filaments/PLA/TDS/Ultrafuse_PLA_TDS_EN_v4.4.pdf.
Berryman, H. E. (2019). A systematic approach to the interpretation of gunshot wound trauma to the cranium. Forensic Sci. Int. 301, 306–317. doi:10.1016/j.forsciint.2019.05.019
Bhatnagar, A. (2006). “Bullets, fragments and bullet deformation,” in Lightweight ballistic composites (Elsevier), 29–71.
Bolduc, M., and Jager, H. (2016). Summary of newly ratified NATO standard AEP 2920. Sys. Sym. PASS, 25–40.
Bowyer, G., Cooper, G., and Rice, P. (1995). Management of small fragment wounds in war: current research. Ann. R. Coll. Surg. Engl. 77, 131–134. doi:10.1097/00005373-199603001-00037
Breeze, J., Carr, D., Mabbott, A., Beckett, S., and Clasper, J. (2015). Refrigeration and freezing of porcine tissue does not affect the retardation of fragment simulating projectiles. J. Forensic Leg. Med. 32, 77–83. doi:10.1016/j.jflm.2015.03.003
Breeze, J., and Carr, D. J. (2016a). “Energised fragments, bullets and fragment simulating projectiles,” in Blast injury science and engineering (Springer), 219–226.
Breeze, J., and Carr, D. J. (2016b). “Physical models: tissue simulants,” in Blast injury science and engineering (Springer), 145–153.
Breeze, J., and Carr, D. J. (2016c) “Energised fragments, bullets and fragment simulating projectiles,” in Blast injury science and engineering: a guide for clinicians and researchers, 219–226.
Breeze, J., and Clasper, J. C. (2013). Determining the velocity required for skin perforation by fragment simulating projectiles: a systematic review. BMJ Mil. Health 159, 265–270. doi:10.1136/jramc-2013-000070
Breeze, J., Hunt, N., Gibb, I., James, G., Hepper, A., and Clasper, J. (2013a). Experimental penetration of fragment simulating projectiles into porcine tissues compared with simulants. J. Forensic Leg. Med. 20, 296–299. doi:10.1016/j.jflm.2012.12.007
Breeze, J., James, G., and Hepper, A. (2013b). Perforation of fragment simulating projectiles into goat skin and muscle. BMJ Mil. Health 159, 84–89. doi:10.1136/jramc-2013-000065
Caister, A., Carr, D. J., Campbell, P., Brock, F., and Breeze, J. (2020). The ballistic performance of bone when impacted by fragments. Int. J. Leg. Med. 134, 1387–1393. doi:10.1007/s00414-020-02299-9
Carr, D., Kieser, J., Mabbott, A., Mott, C., Champion, S., and Girvan, E. (2014). Damage to apparel layers and underlying tissue due to hand-gun bullets. Int. J. Leg. Med. 128, 83–93. doi:10.1007/s00414-013-0856-1
Carr, D., Lindstrom, A.-C., Jareborg, A., Champion, S., Waddell, N., Miller, D., et al. (2015). Development of a skull/brain model for military wound ballistics studies. Int. J. Leg. Med. 129, 505–510. doi:10.1007/s00414-014-1073-2
Carr, D. J., Lewis, E., and Horsfall, I. (2017). A systematic review of military head injuries. BMJ Mil. Health 163, 13–19. doi:10.1136/jramc-2015-000600
Carr, D. J., Stevenson, T., and Mahoney, P. F. (2018). The use of gelatine in wound ballistics research. Int. J. Leg. Med. 132, 1659–1664. doi:10.1007/s00414-018-1831-7
Champion, H. R., Bellamy, R. F., Roberts, C. P., and Leppaniemi, A. (2003). A profile of combat injury. J. Trauma. Acute Care Surg. 54, S13–S19. doi:10.1097/01.ta.0000057151.02906.27
Chanda, A. (2018). Biomechanical modeling of human skin tissue surrogates. Biomimetics 3, 18. doi:10.3390/biomimetics3030018
Chanda, A., Unnikrishnan, V., Flynn, Z., and Lackey, K. (2017). Experimental study on tissue phantoms to understand the effect of injury and suturing on human skin mechanical properties. Proc. Inst. Mech. Eng. H. J. Eng. Med. 231, 80–91. doi:10.1177/0954411916679438
Chanda, A., and Upchurch, W. (2018). Biomechanical modeling of wounded skin. J. Compos. Sci. 2, 69. doi:10.3390/jcs2040069
Cunniff, P. M. (2014). “A method to describe the statistical aspects of armor penetration, human vulnerability and lethality due to fragmenting munitions,” in International symposium on ballistics.
Dąbrowska, A., Rotaru, G. M., Derler, S., Spano, F., Camenzind, M., Annaheim, S., et al. (2016). Materials used to simulate physical properties of human skin. Technol 22, 3–14. doi:10.1111/srt.12235
Euteneuer, J., Gosch, A., Cachée, P., and Courts, C. (2019). Evaluation of the backspatter generation and wound profiles of an anatomically correct skull model for molecular ballistics. Int. J. Leg. Med. 133, 1839–1850. doi:10.1007/s00414-019-02120-2
Falland-Cheung, L., Waddell, J. N., Li, K. C., Tong, D., and Brunton, P. (2017). Investigation of the elastic modulus, tensile and flexural strength of five skull simulant materials for impact testing of a forensic skin/skull/brain model. J. Mech. Behav. Biomed. Mat. 68, 303–307. doi:10.1016/j.jmbbm.2017.02.023
Farrer, A. I., Odéen, H., de Bever, J., Coats, B., Parker, D. L., Payne, A., et al. (2015). Characterization and evaluation of tissue-mimicking gelatin phantoms for use with MRgFUS. J. Ther. ultrasound 3, 9–11. doi:10.1186/s40349-015-0030-y
Freitas, C. J., Mathis, J. T., Scott, N., Bigger, R. P., and MacKiewicz, J. (2014). Dynamic response due to behind helmet blunt trauma measured with a human head surrogate. Int. J. Med. Sci. 11, 409–425. doi:10.7150/ijms.8079
Ganpule, S., Alai, A., Plougonven, E., and Chandra, N. (2013). Mechanics of blast loading on the head models in the study of traumatic brain injury using experimental and computational approaches. Biomech. Model. Mechanobiol. 12, 511–531. doi:10.1007/s10237-012-0421-8
Gayzik, F., Moreno, D., Geer, C., Wuertzer, S., Martin, R., and Stitzel, J. (2011a). Development of a full body CAD dataset for computational modeling: a multi-modality approach. Ann. Biomed. Eng. 39, 2568–2583. doi:10.1007/s10439-011-0359-5
Gayzik, F. S., Moreno, D. P., Vavalle, N. A., Rhyne, A. C., and Stitzel, J. D. (2011b). “Development of the global human body models consortium mid-sized male full body model,” in International workshop on human subjects for biomechanical research, national highway traffic safety administration.
Groves, R. B., Coulman, S. A., Birchall, J. C., and Evans, S. L. (2013). An anisotropic, hyperelastic model for skin: experimental measurements, finite element modelling and identification of parameters for human and murine skin. J. Mech. Behav. Biomed. Mater. 18, 167–180. doi:10.1016/j.jmbbm.2012.10.021
Henderson, J. (2010). Lethality criteria for debris generated from accidental explosions. London (United Kingdom): Ministry of defence.
Inchingolo, F., Tatullo, M., Marrelli, M., Inchingolo, A. D., Pinto, G., Inchingolo, A. M., et al. (2011). Short report of an unusual ballistic trauma. Int. J. Surg. Case Rep. 2, 272–274. doi:10.1016/j.ijscr.2011.08.009
Ivancic, P. C. (2013). Neck injury response to direct head impact. Accid. Analysis and Prev. 50, 323–329. doi:10.1016/j.aap.2012.05.008
Jussila, J. (2004). Preparing ballistic gelatine—review and proposal for a standard method. Forensic Sci. Int. 141, 91–98. doi:10.1016/j.forsciint.2003.11.036
Jussila, J., Leppäniemi, A., Paronen, M., and Kulomäki, E. (2005). Ballistic skin simulant. Forensic Sci. Int. 150, 63–71. doi:10.1016/j.forsciint.2004.06.039
Karger, B., Puskas, Z., Ruwald, B., Teige, K., and Schuirer, G. (1998). Morphological findings in the brain after experimental gunshots using radiology, pathology and histology. Int. J. Leg. Med. 111, 314–319. doi:10.1007/s004140050178
Kieser, D. C., Riddell, R., Kieser, J. A., Theis, J.-C., and Swain, M. V. (2014). Bone micro-fracture observations from direct impact of slow velocity projectiles. J. Archives Mil. Med. 2. doi:10.5812/jamm.15614
Kneubuehl, B. P. (2011). Wound ballistics: basics and applications. Springer Science and Business Media.
Kneubuehl, B. P., Coupland, R. M., Rothschild, M. A., and Thali, M. J. (2011). “Wound ballistics and forensic medicine,” in Wound ballistics (Springer), 253–303.
Li, Z., Peng, Y., Yang, H., Li, N., and Huang, X. (2023). Simulation and experimental studies of debris penetrating skull. J. Biomech. 151, 111551. doi:10.1016/j.jbiomech.2023.111551
Mabbott, A., Carr, D., Champion, S., and Malbon, C. (2016). Comparison of porcine thorax to gelatine blocks for wound ballistics studies. Int. J. Leg. Med. 130, 1353–1362. doi:10.1007/s00414-015-1309-9
Mahoney, P., Carr, D., Arm, R., Gibb, I., Hunt, N., and Delaney, R. J. (2018). Ballistic impacts on an anatomically correct synthetic skull with a surrogate skin/soft tissue layer. Int. J. Leg. Med. 132, 519–530. doi:10.1007/s00414-017-1737-9
Mahoney, P. F., Carr, D., Delaney, R., Hunt, N., Harrison, S., Breeze, J., et al. (2017a). Does preliminary optimisation of an anatomically correct skull-brain model using simple simulants produce clinically realistic ballistic injury fracture patterns? Int. J. Leg. Med. 131, 1043–1053. doi:10.1007/s00414-017-1557-y
Mahoney, P. F., Carr, D. J., Delaney, R. J., and Gibb, I. E. (2020). Shooting through windscreens: ballistic injury assessment using a surrogate head model—two case reports. Int. J. Leg. Med. 134, 1409–1417. doi:10.1007/s00414-019-02170-6
Mahoney, P. F., Carr, D. J., Miller, D., and Teagle, M. (2017b). The effect of helmet materials and simulated bone and tissue layers on bullet behaviour in a gelatine model of overmatch penetrating head injury. Int. J. Leg. Med. 131, 1765–1776. doi:10.1007/s00414-017-1665-8
Maiden, N. (2009). Ballistics reviews: mechanisms of bullet wound trauma. Forensic Sci. Med. Pathol. 5, 204–209. doi:10.1007/s12024-009-9096-6
Mao, H., Zhang, L., Jiang, B., Genthikatti, V. V., Jin, X., Zhu, F., et al. (2013). Development of a finite element human head model partially validated with thirty five experimental cases. J. Biomech. Eng. 135, 111002. doi:10.1115/1.4025101
Marechal, L., Balland, P., Lindenroth, L., Petrou, F., Kontovounisios, C., and Bello, F. (2021). Toward a common framework and database of materials for soft robotics. Soft Robot. 8, 284–297. doi:10.1089/soro.2019.0115
McElhaney, J. H., Fogle, J. L., Melvin, J. W., Haynes, R. R., Roberts, V. L., and Alem, N. M. (1970). Mechanical properties of cranial bone. J. Biomech. 3, 495–511. doi:10.1016/0021-9290(70)90059-x
Miranda-Vicario, A., Bravo, P., and Coghe, F. (2018). Experimental study of the deformation of a ballistic helmet impacted with pistol ammunition. Compos. Struct. 203, 233–241. doi:10.1016/j.compstruct.2018.07.012
NATO, NATO Standardization Agreement (2003). Stanag 2920: ballistic test method for personal armour materials and combat clothing. 2nd ed. NATO Standardization Agency.
Nguyen, T.-T., Breeze, J., and Masouros, S. D. (2021). Penetration of energized metal fragments to porcine thoracic tissues. J. Biomech. Eng. 144. doi:10.1115/1.4053212
Nguyen, T.-T. N., Meek, G., Breeze, J., and Masouros, S. D. (2020). Gelatine Backing affects the performance of single-layer ballistic-resistant materials against blast fragments. Front. Bioeng. Biotechnol. 8, 744. doi:10.3389/fbioe.2020.00744
Nightingale, R. W., Myers, B. S., and Yoganandan, N. (2015). Neck injury biomechanics, Accidental injury: biomechanics and prevention, 259–308.
Oehmichen, M., Meissner, C., König, H., and Gehl, H.-B. (2004). Gunshot injuries to the head and brain caused by low-velocity handguns and rifles: a review. Forensic Sci. Int. 146, 111–120. doi:10.1016/j.forsciint.2004.06.023
Oei Su Cheok, W. K. J. (2005). “Weapon danger area variation with incapacitation criteria,” in DSTA horizons (Singapore: Defence Science and Technology Agency), 96–101.
Pandey, P., Joshi, Y., Khan, M., Iqbal, M., and Ganpule, S. (2024). Experimental investigation of the ballistic response of head surrogate against fragment simulating projectiles. Exp. Mech. 64, 85–104. doi:10.1007/s11340-023-01010-4
Pandey, P. K., Harmukh, A., Khan, M. K., Iqbal, M. A., and Ganpule, S. G. (2023). Ballistic response of skin simulant against fragment simulating projectiles. Def. Technol. 30, 70–82. doi:10.1016/j.dt.2023.04.009
Pasquali, M., and Gaudenzi, P. (2017). Effects of curvature on high-velocity impact resistance of thin woven fabric composite targets. Compos. Struct. 160, 349–365. doi:10.1016/j.compstruct.2016.10.069
Pullen, A., Kieser, D. C., and Hooper, G. (2021). Validation of Roebuck 1518 synthetic chamois as a skin simulant when backed by 10% gelatin. Int. J. Leg. Med. 135, 909–912. doi:10.1007/s00414-020-02408-8
Regasa, L. E., Kaplan, D. A., Martin, E. M. M., Langbein, J., Johnson, F., and Chase, L. C. (2018). Mortality following hospital admission for US active duty service members diagnosed with penetrating traumatic brain injury, 2004–2014. J. Head Trauma Rehabilitation 33, 123–132. doi:10.1097/HTR.0000000000000380
Rettinger, G. (2017). The “80 Joule criterion” reconsidered today. Forensic Sci. Int. 276, 64–70. doi:10.1016/j.forsciint.2017.04.020
Riva, F., Fracasso, T., Guerra, A., and Genet, P. (2021). Practical application of synthetic head models in real ballistic cases. Int. J. Leg. Med. 135, 2567–2579. doi:10.1007/s00414-021-02671-3
Riva, F., Lombardo, P., Zech, W.-D., Jackowski, C., and Schyma, C. (2019). Individual synthetic head models in wound ballistics—a feasibility study based on real cases. Forensic Sci. Int. 294, 150–159. doi:10.1016/j.forsciint.2018.11.020
Rodriguez-Millan, M., Rubio, I., Burpo, F., Olmedo, A., Loya, J., Parker, K., et al. (2023). Impact response of advance combat helmet pad systems. Int. J. Impact Eng. 181, 104757. doi:10.1016/j.ijimpeng.2023.104757
Serraino, S., Milone, L., Picone, D., Argo, A., Salerno, S., and Midiri, M. (2020). “Imaging for ballistic trauma: other applications of forensic imaging in the living,” in Radiology in forensic medicine (Springer), 169–180.
Shuker, S. T. (2019). Emergency treatment of blast, shell fragment and bullet injuries to the central midface complex. J. Maxillofac. Oral Surg. 18, 124–130. doi:10.1007/s12663-018-1107-2
Singh, A., Kumar, D., and Ganpule, S. (2024). Biomechanical response of head surrogate with and without the helmet. J. Biomech. Eng. 146, 031001. doi:10.1115/1.4062968
Smith, D. R., Guertler, C. A., Okamoto, R. J., Romano, A. J., Bayly, P. V., and Johnson, C. L. (2020). Multi-excitation magnetic resonance elastography of the brain: wave propagation in anisotropic white matter. J. biomechanical Eng. 142, 071005. doi:10.1115/1.4046199
Smith, M. J., James, S., Pover, T., Ball, N., Barnetson, V., Foster, B., et al. (2015). Fantastic plastic? Experimental evaluation of polyurethane bone substitutes as proxies for human bone in trauma simulations. Leg. Med. 17, 427–435. doi:10.1016/j.legalmed.2015.06.007
Smooth-on (2023). “Dragon Skin™ series addition cure silicone rubber compounds,” in Technical bulletin, smooth-on. Available at: www.smooth-on.com/products/dragon-skin-30/.
Sperrazza, J., and Kokinakis, W. (1968). Ballistic limits of tissue and clothing. Ann. N. Y. Acad. Sci. 152, 163–167. doi:10.1111/j.1749-6632.1968.tb11973.x
Stargel, D. S. (2005). Experimental and numerical investigation into the effects of panel curvature on the high velocity ballistic impact response of aluminum and composite panels. College Park: University of Maryland.
Sterzik, V., Kneubuehl, B. P., Bohnert, M., Riva, F., and Glardon, M. (2017). Bullet fragmentation preceding a contour shot: case study and experimental simulation. Int. J. Leg. Med. 131, 173–177. doi:10.1007/s00414-016-1462-9
Sutar, S., and Ganpule, S. (2020). Investigation of wave propagation through head layers with focus on understanding blast wave transmission. Biomech. Model. Mechanobiol. 19, 875–892. doi:10.1007/s10237-019-01256-9
Taylor, S. C., Ondruschka, B., Kieser, D. C., Hammer, N., Lee, M., Hooper, G. J., et al. (2022). Ballistic trauma caused by military rifles: experimental study based on synthetic skull proxies. Med. Pathology 18, 30–36. doi:10.1007/s12024-021-00432-7
Thali, M., Kneubuehl, B., Dirnhofer, R., and Zollinger, U. (2002a). The dynamic development of the muzzle imprint by contact gunshot: high-speed documentation utilizing the skin–skull–brain model. Forensic Sci. Int. 127, 168–173. doi:10.1016/s0379-0738(02)00117-2
Thali, M. J., Kneubuehl, B. P., Zollinger, U., and Dirnhofer, R. (2002b). The “Skin–skull–brain model”: a new instrument for the study of gunshot effects. Forensic Sci. Int. 125, 178–189. doi:10.1016/s0379-0738(01)00637-5
Tomasello, K., Jacq, C., Baker, E., and Sharp, M. (2023). “NATO AC326 subgroup B ammunition systems design and assessment–insensitive munitions test STANAG updates,” in 2019 insensitive munitions and energetic materials technology symposium, 21–24. Seville, Spain.
Tse, K. M., Tan, L. B., Yang, B., Tan, V. B. C., and Lee, H. P. (2017). Effect of helmet liner systems and impact directions on severity of head injuries sustained in ballistic impacts: a finite element (FE) study. Med. and Biol. Eng. and Comput. 55, 641–662. doi:10.1007/s11517-016-1536-3
Vakil, M. T., and Singh, A. K. (2017). A review of penetrating brain trauma: epidemiology, pathophysiology, imaging assessment, complications, and treatment. Emerg. Radiol. 24, 301–309. doi:10.1007/s10140-016-1477-z
Van der Voort, M. M., Baker, E. L., Schultz, E., and Sharp, M. W. (2016). Projection criteria for insensitive munitions and hazard classification, MSIAC report O-168.
Van Wyck, D., Grant, G., and Laskowitz, D. (2015). Penetrating traumatic brain injury: a review of current evaluation and management concepts. J. Neurol. Neurophysiol. 6, 336–343. doi:10.4172/2155-9562.1000336
Watkins, F., Pearce, B., and Stainer, M. (1988). Physical effects of the penetration of head simulants by steel spheres. J. Trauma. Acute Care Surg. 28, S40–S54. doi:10.1097/00005373-198801001-00011
Yoganandan, N., and Pintar, F. A. (1997). Biomechanics of penetrating trauma. Crit. Rev. Biomed. Eng. 25, 485–501. doi:10.1615/critrevbiomedeng.v25.i6.10
Keywords: head surrogate, fragment, impact, ballistic limit velocity, failure
Citation: Pandey PK and Ganpule SG (2024) Evaluation of an anthropometric head surrogate exposed to chisel-nosed fragment simulating projectile impact. Front. Mech. Eng. 10:1446479. doi: 10.3389/fmech.2024.1446479
Received: 09 June 2024; Accepted: 14 October 2024;
Published: 31 October 2024.
Edited by:
Marco Eugeni, Sapienza University of Rome, ItalyReviewed by:
Chengxing Yang, Central South University, ChinaMichele Pasquali, Sapienza University of Rome, Italy
Copyright © 2024 Pandey and Ganpule. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. G. Ganpule, Z2FucHVsZUBtZS5paXRyLmFjLmlu
 Punit Kumar Pandey
Punit Kumar Pandey S. G. Ganpule
S. G. Ganpule