Toward compound fault diagnosis via EMAGAN and large kernel augmented few-shot learning

Bearings are essential in machinery. Damage to them can cause financial losses and safety risks at industrial sites. Therefore, it is necessary to design an accurate diagnostic model. Although many bearing fault diagnosis methods have been proposed recently, they still cannot meet the requirements of high-accurate prediction of bearing faults. There are several challenges in this: 1) In practical settings, gathering sufficient and balanced sample data for training diagnostic network models proves challenging. 2) The damage to bearings in real industrial production sites is not singular, and compound faults are also a huge challenge for diagnostic networks. To address these issues, this study introduces a novel fault diagnosis model called EMALKNet that integrates DCGAN with Efficient Multi-Scale Attention (EMAGAN) and RepLKNet-XL, enhancing the detection and analysis of bearing faults in industrial machinery. This model employs EMAGAN to explore the underlying distribution of raw data, thereby enlarging the fault sample pool and enhancing the model’s diagnostic capabilities; The large kernel structure of RepLKNet-XL is different from the current mainstream small kernel and has stronger representation extraction ability. The proposed method has been validated on the Paderborn University dataset and the Huazhong University of Science and Technology dataset.

1 Introduction

Bearings are a key component that can withstand and reduce friction in mechanical equipment. Bearings play a crucial role in today’s engineering applications and daily life, finding extensive applications across diverse mechanical devices (Huang et al., 2019; Zhu et al., 2021; Du et al., 2024; Fan et al., 2024; Zhang and Wu, 2024). However, in the industrial generation, the long-term work of many mechanical equipment will lead to various types of bearing failures, which have a great impact on production (Schwendemann et al., 2021; Li et al., 2024). It is crucial to design an accurate mechanical equipment prediction and maintenance system based on bearing fault diagnosis to avoid economic losses and personnel injuries caused by bearing damage (Du et al., 2022b; Jia et al., 2023; Zhu and Fang, 2024).

Technological advancements have broadened the use of artificial intelligence across numerous domains. Particularly in fault diagnosis, deep learning (DL) has become an essential technique for predicting and diagnosing bearing issues (Chen et al., 2019; Du et al., 2022a). Pan et al. (2023) proposed the SENet-TSCNN model, integrating squeeze-excitation networks with a dual-stream CNN architecture, demonstrating high precision and robust generalization in fault diagnosis. An and Wang (2022) introduced a rolling bearing fault diagnosis method combining an overlapping group sparse model with a deep compound convolutional neural network. Convex optimization was applied to the sparse optimization model to extract fault characteristics from compound bearings, which were then diagnosed and classified using a novel deep compound convolutional neural network model. This method effectively detects and classifies faults in rolling bearings under both steady and varying conditions. However, these methods have been validated only with enough, single-fault datasets. This means that bearing fault diagnosis still needs to overcome the following two challenges: 1) Model training demands substantial data, yet operational bearings typically remain fault-free, leading to scarce and imbalanced sample data (Ruan et al., 2021). 2) In industrial environments, bearings often experience multiple concurrent faults (Xu et al., 2022).

To address the small sample issue, this paper introduces the Deep Convolutional Generative Adversarial Networks with Efficient Multi-Scale Attention (EMAGAN). Research indicates that Variable Auto Encoders (VAE) can address this problem by capturing essential features and reconstructing new samples resembling the originals. However, VAE training can be challenging and may yield low-fidelity samples (Zhang et al., 2021). Similar to VAE, there is also a Generative Adversarial Network (GAN). GAN can also generate new data similar to real data distribution, which has been proven by scholars to be helpful for expanding the sample size of bearing fault diagnosis (Shao et al., 2019; Zhang et al., 2020; Peng et al., 2021). However, GAN training often faces stability issues and can produce low-quality samples. In contrast, this paper introduces Efficient Multi-Scale Attention (EMA) in Deep Convolutional Generative Adversarial Networks (DCGAN) to enhance the balance between global structure and local details, resulting in more realistic image generation (Ouyang et al., 2023).

To address the challenges posed by compound faults to diagnostic models, this paper uses RepLKNet-XL as a classification model. Huang et al. (2018) employed a Deep Decoupling Convolutional Neural Network (DDCNN) to automatically and effectively identify and decouple compound faults in rotating machinery. However, this method necessitates manual design of decoupling and merging strategies between labels, relying on the expertise and domain knowledge of experienced professionals. Chen et al. (2023) proposed an integrated approach for diagnosing compound faults in industrial robots, utilizing two compact transformer networks for accurate fault detection in noisy settings. However, this approach is complex and requires a substantial dataset. Conversely, this paper highlights that RepLKNet-XL excels in extracting global features and analyzing the intrinsic characteristics of samples, showcasing its robust diagnostic capabilities.

The contributions of our work include the following.

1. It introduces a model that combines EMAGAN and RepLKNet-XL to diagnose compound bearing faults, enhancing the model’s diagnostic capabilities by expanding fault samples and leveraging the strong feature extraction of RepLKNet-XL’s large kernel structure.

2. Introducing EMA into Deep Convolutional Generation adversarial Network (DCGAN), the stability and convergence speed of GAN can be improved. EMALKNet leverages EMAGAN to generate additional fault samples, effectively addressing the challenge of data scarcity and imbalance.

3. By utilizing the large kernel structure of RepLKNet-XL, the model is capable of extracting more robust features from the data, contributing to its superior performance in diagnosing compound bearing faults under various conditions.

2 Fundamental theory

2.1 Continuous wavelet transform

In this paper, the sample data consists of the bearing’s vibration signal, characterized as a 1D time series. To facilitate better feature extraction, the 1D data is converted into 2D images using continuous wavelet transform (CWT) (Antoine et al., 1993; Zhao et al., 2023). At present, the image recognition technology is more mature, the use of image classification can achieve good fault diagnosis results. Compared with Fourier transform, CWT converts data into 2D image can retain both frequency information and time information. The expression of wavelet transform is:

$CW{T}_x\left(p,q\right)=\frac{1}{\sqrt{p}}{\int }_{-\infty }^{+\infty }{\psi }_{p,q}\left(\frac{t-q}{p}\right)x\left(t\right)dt(1)$

In Eq. 1, ’p’ and ’q’ are defined as the scale and displacement parameters of the signal, respectively, with $\psi$ serving as the wavelet basis function. The experiments described in this document employ the compound Morlet wavelet for the wavelet basis.

$\phi \left(t;{\omega }_0,\sigma \right)={\pi }^{-1/4}{e}^{i{\omega }_{0}t}{e}^{-\frac{t^2}{2{\sigma }^2}}(2)$

Where Formula 2, $\omega$ serves as the frequency parameter, influencing the wavelet function’s frequency, while $\sigma$ is a scale parameter that governs the wavelet’s spread in the time domain and impacts its bandwidth.

2.2 Theory of DCGAN

Deep Convolutional Generative Adversarial Network (DCGAN), a variation of the GAN, comprises a Generator (G) and a Discriminator (D). Generate samples similar to real data by randomly inputting noise of a specified size into generator G, and optimize G’s performance in the direction of deceiving the discriminator. The discriminator D continuously optimizes network parameters to distinguish between real sample data and generated data. The two constantly engage in adversarial training and progress together (Goodfellow et al., 2014). To evaluate the effectiveness of both the generator and discriminator simultaneously and provide feedback, the following loss function is introduced:

${\min }_G{\max }_{D}V\left(D,G\right)=E_{x\sim p_{\text{data\hspace{0.17em}}\left(x\right)}}\left[\log D\left(x\right)\right]+E_{Z\sim P_z\left(z\right)}\left[\log \left(1-D\left(G\left(z\right)\right)\right)\right](3)$

where $x\sim p_{\text{data\hspace{0.17em}}(x)}$ denotes that x takes the dataset of real images and $Z\sim P_z(z)$ denotes that it takes the randomly generated noisy data. Eq. 3 visually expresses the adversarial relationship between D and G. For D, the loss function needs to be maximized, and for G, the loss function needs to be minimized (Goodfellow et al., 2014; Wang et al., 2017). Compared with GAN, DCGAN can better learn the feature representation of images by introducing convolutional layer, batch normalization and full convolutional network structure, thus improving the quality and stability of generated images (Radford et al., 2015).

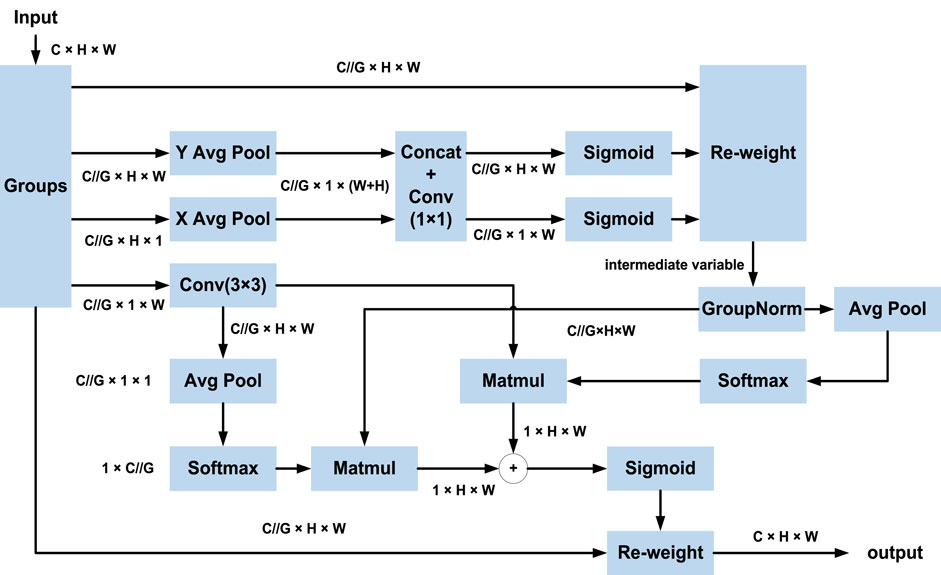
2.3 Efficient multiscale attention module for cross-space learning

The EMA module’s structure, illustrated in Figure 1, operates by initially grouping a feature $X\in R^{C\times H\times W}$ into $X=\left[X_0,X_{i,\dots ..}{X}_{G-1}\right],X\in R^{C//G\times H\times W}$. It then calculates attention weight descriptors from the grouped feature map using a parallel subnet consisting of three separate branches. The first two of the three parallel branches are grouped and encoded in two spatial directions, respectively, which are first average pooled, then connected along the height direction and simultaneously convolved using a $1\times 1$ size convolution kernel, and finally activated by a sigmoid. The final branch in the network employs a single $3\times 3$ convolutional kernel to encapsulate multi-scale features. This arrangement preserves precise spatial information in the channel during the extraction of attention weight descriptors. The outputs from the two parallel branches are then merged following cross-spatial learning, enhancing pixel-level pairwise relationships and emphasizing the overall context across all pixels.

$\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left[S_n\right]}=\sqrt{n}\sqrt{{\displaystyle \sum _{m=0}^{k-1}}\frac{m^2}{k}-{\left({\displaystyle \sum _{m=0}^{k-1}}\frac{m}{k}\right)}^2}=\sqrt{\frac{n\left(k^2-1\right)}{12}}=O\left(k\sqrt{n}\right)(4)$

Figure 1

Figure 1. EMA structure diagram.

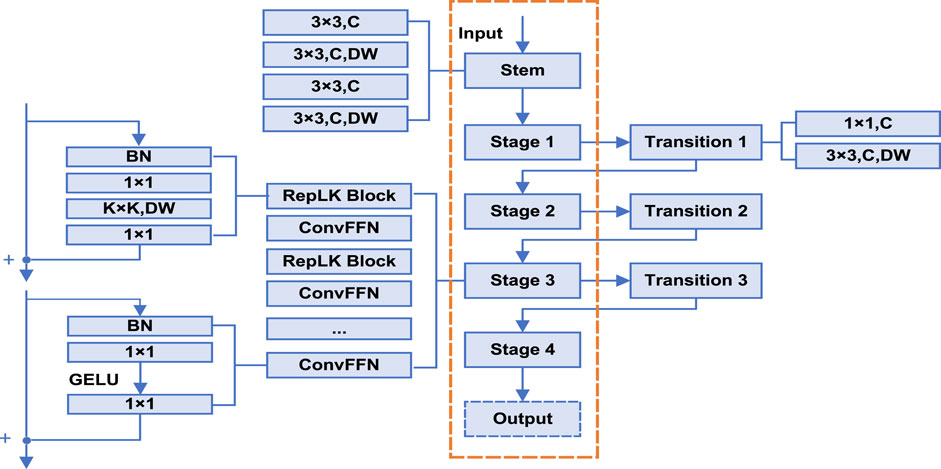
2.4 RepLKNet classification model

RepLKNet is an oversized kernel classification model (Ding et al., 2022), which applies multiple oversized kernels, such as $31\times 31$ convolutional kernels, in CNN to effectively improve the actual sensory field of the network. Post-experimentation, it was found that enhancing the actual sensory field significantly boosts the network’s accuracy in diagnosing faults. The network’s structure is depicted in Figure 2. The “Stem” denotes the initial layer where multiple convolutional layers are employed early on to enhance detail capture. The stem sequence starts with a $3\times 3$ convolution featuring 2$\times$ downsampling, followed by a $3\times 3$ depth-wise (DW) convolutional layer to detect low-level patterns, a $1\times 1$ convolution, and another depth-wise $3\times 3$ convolution for further low-level pattern analysis. In Figure 2, Stages 1–4 are composed of multiple RepLK blocks, each featuring shortcuts and DW K $\times$ K large kernels. Additionally, a $1\times 1$ convolution is applied both before and after each DW convolution. Each large DWconv is reparameterised with a $5\times 5$ kernel. Besides the large convolutional layers that ensure ample receptive field and spatial information aggregation, the depth of the model also significantly influences its representational capabilities. Increasing the depth by using a $1\times 1$ conv layer provides more nonlinearities and information communication across channels. Drawing inspiration from the feed-forward networks (FFNs) prevalent in transformers and MLPs, a CNN-like ConvFFN block is crafted, incorporating shortcuts, dual $1\times 1$ batch normalization (BN) layers, and GELU activation. Transition in the figure is then a transition block consisting of $1\times 1$conv and 2$\times$downsampling of $3\times 3$conv. In this configuration, B represents the number of RepLK blocks, C is the channel dimension, and K denotes the kernel size. There are four RepLK blocks in the network structure, so the RepLKNet architecture consists of [B1; B2; B3; B4], [C1; C2; C3; C4], [K1; K2; K3; K4].

Figure 2

Figure 2. The architecture of RepLKNet.

3 Proposed method

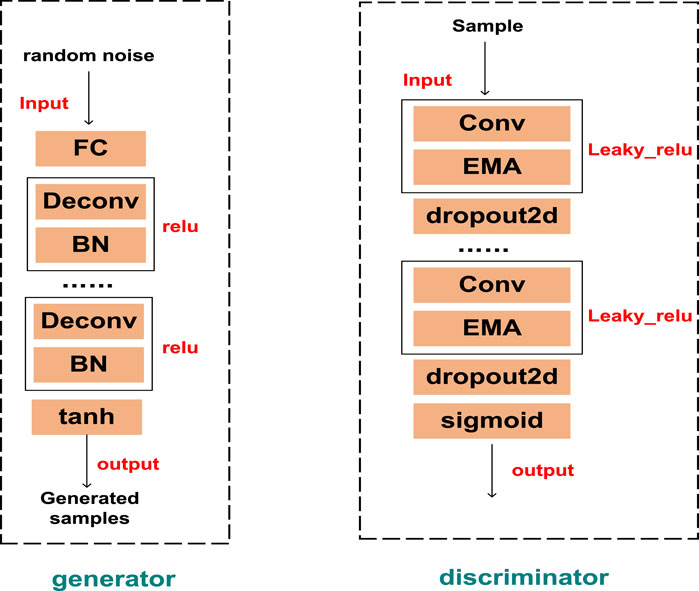
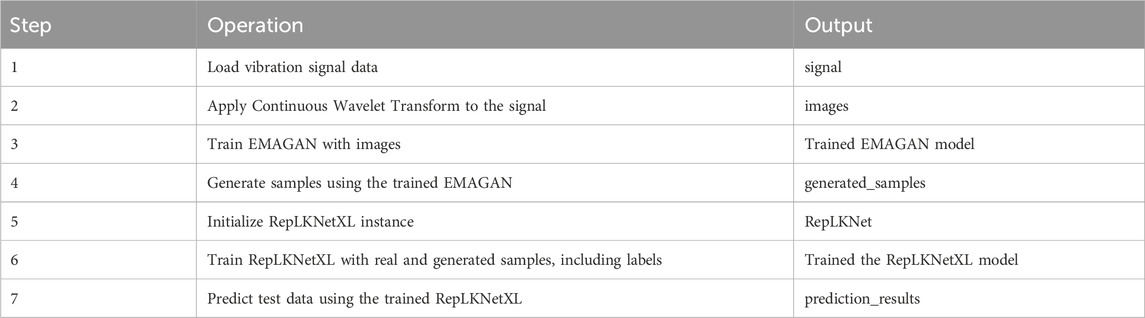
As mentioned above, DCGAN consists of G and D. The two are constantly fighting against each other, and ideally they will promote each other to enhance the ability of extracting image features. Therefore when only EMA is added to D, the discriminative ability of D will be improved, and D is more likely to find defects in G-generated samples, which will lead to more realistic G-generated samples. Figure 3 is the structure of G of EMAGAN designed in this paper, which consists of one fully connected layer, three inverse convolutional layers, three BN layers, and the activation function used is tanh. The structure of D of EMAGAN designed in this paper is shown in Figure 3, which consists of two convolutional layers, two EMA modules, one fully connected layer and one BN layer, and the activation function used is leaky_relu function and sigmoid function, and the EMA modules act after the two convolutional layers respectively. After passing random noise into the trained EMAGAN, it can be obtained to generate new samples, and subsequently the dataset can be preprocessed. The processed data is fed into the RepLKNet classification model mentioned above, and the parameters of the RepLKNet classification model are set to B = [2; 2; 18; 2], C = [256; 512; 1024; 2048], and K = [27; 27; 27; 13]. From Eq. 4, it’s clear that when weights are uniform, the effective receptive field size increases linearly with the kernel size, K (Luo et al., 2016). Thus when K = [27; 27; 27; 13], RepLKNet can obtain higher feature integration capability and more compound capture patterns, which helps to extract features that help to extract more global and compound features. Figure 4 shows the overall diagnostic flow of the model. The pseudo-code for this method is detailed in Table 1.

Figure 3

Figure 3. Flowchart of GAN. Left is the generator and right is the discriminator.

Figure 4

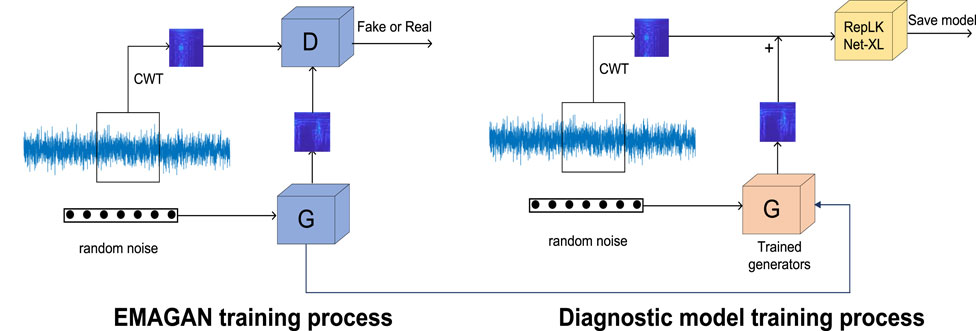
Figure 4. General schematic of the suggested approach. On the left is EMAGAN’s training process, and on the right is RepLKNet-XL, using the trained G to expand the sample, and completing the diagnosis.

Table 1

Table 1. Proposed methodology in pseudocode format.

4 Experimental design

The experimental platform in this paper is a server based on NVIDIA RTX4090 24G and Intel Xeon Gold 6430.

4.1 Introduction and pre-processing of dataset

The Paderborn dataset is used for the experiments in this paper. The dataset was gathered and released by the University of Paderborn using the rolling bearing condition test bed at the Department of Design and Drive Technology. The test bench is composed of five parts: motor, torque measuring shaft, rolling bearing test module, flywheel, and load motor. The dataset includes data for normal bearings, single fault bearings, multiple single fault bearings, and compound fault bearings. Motor current is recorded at a frequency of 64 kHz, vibration signals at 64 kHz, mechanical parameters at 4 kHz, and temperature at 1 Hz (Lessmeier et al., 2016). The data bearing type collected in this dataset is the 6203 bearing. To be closer to the real situation, the data samples selected in this paper are all real damage samples.

Once the dataset is selected, the initial step involves processing the original vibration signal. The sampling formula used in this study is detailed below:

$sample=\frac{\text{\hspace{0.17em}point\_num\hspace{0.17em}}-\text{\hspace{0.17em}sample\_size\hspace{0.17em}}}{\text{\hspace{0.17em}stride\hspace{0.17em}}}+1(5)$

where stride represents the sampling step size, point_num indicates the total count of vibration points, and sample_size refers to the vibration count at each sampling point. In this experiment, the stride and sample_size are set at 900, with each dataset file containing 200 sampling points. The vibration data sampled from the window was then converted into a time-frequency plot using Eq. 5, and the image size was compressed to $64\times 64$ to reduce the amount of computation.

4.2 Case 1: low speed and high torque fault diagnosis based on the data set of Paderborn University

4.2.1 Experiment 1: methods for comparison

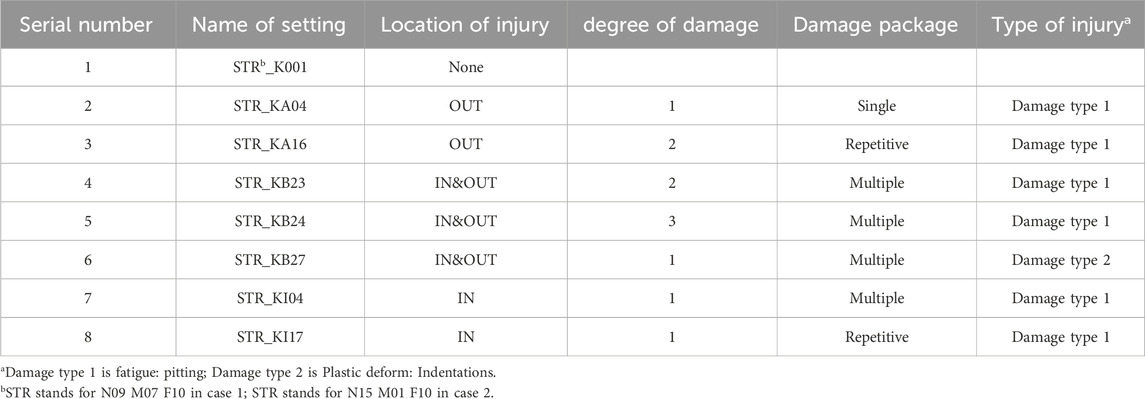
EMALKNet diagnostic effect of this summary of the samples taken for the experiment as Table 2, all the eight kinds of data are real damage data. In the table, the bearing code N09 indicates that the bearing speed is 900rpm, M07 indicates that the torque is 0.7Nm, F10 indicates that the radial force is 10n, and the last three digits indicate the bearing code; for the combination of damages, Single indicates a single fault, Repetitive indicates that the same kind of damages occurs in several places, and Multiple indicates that a mixture of multiple damages; IN indicates the damage of the inner ring of the bearing, and OUT indicates the damage of the outer ring.

Table 2

Table 2. This is the data set selected for case 1 and case 2.

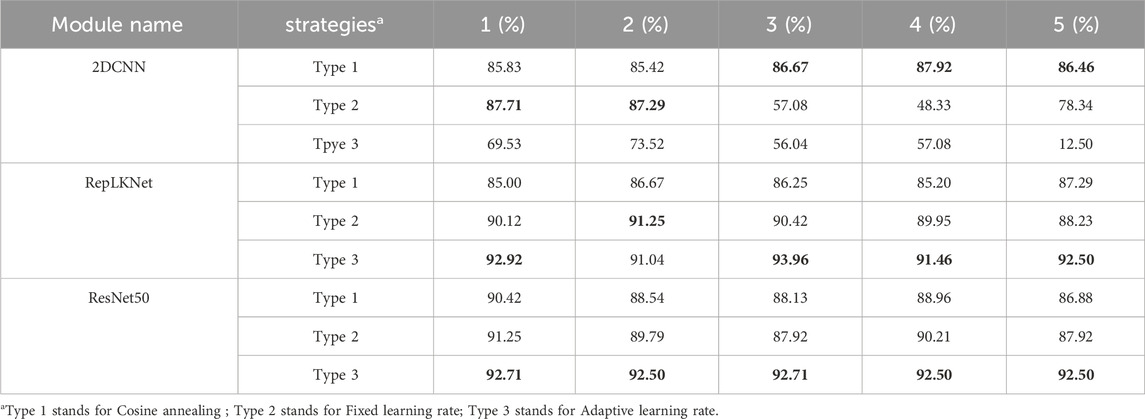
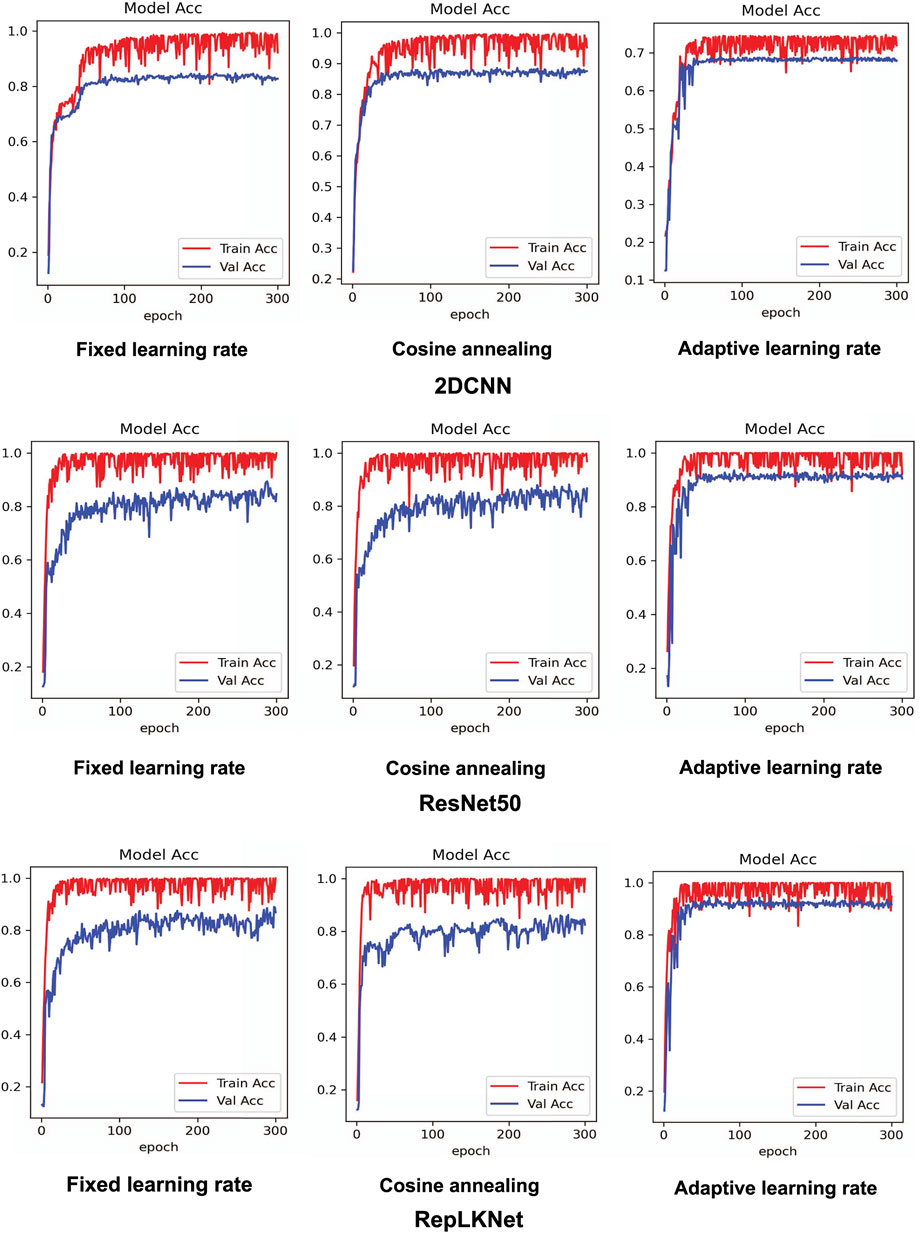
In this section, the paper details a comparative experiment designed to showcase the diagnostic strengths of the proposed model and underline its enhancements relative to existing methods. The experiment was selected to compare 2DCNN (a), ResNet50 (b), RepLKNet-XL (f) and proposed EMALKNet (h) model. Before the formal experiment began, we conducted a pre-experiment to assess the effects of different learning strategies on these models’ convergence speed and accuracy. The models chosen for this pre-experiment were 2DCNN, ResNet50, and (EMAGAN)RepLKNet. The models were trained using three distinct strategies: fixed learning rate, adaptive learning rate, and cosine annealing. For each training category, 200 samples were utilized, maintaining a 7:3 ratio between the training and validation sets. The training process consisted of 300 uniform rounds, and this procedure was replicated five times. The experiment followed these parameters consistently, and the results are depicted in the accuracy image shown in Figure 6. Table 3 illustrates the results of the comparison. From the analysis of Table 3, it can be concluded that cosine annealing is the optimal strategy for 2DCNN, while the adaptive learning rate strategy yields the best results for ResNet50 and (EMAGAN)RepLKNet. Furthermore, as observed from Figure 5, all three models achieve good convergence after only 200 rounds of training.

Table 3

Table 3. Pre-experimental results. In bold is the optimal result of each experiment.

Figure 5

Figure 5. The performance of different learning strategies in three models.

Referring to the pre-experiment results and To simulate the small sample situation, the samples used in the formal experiments are the same as those in the pre-experiment, the batch_size is uniformly set to 64, and the epochs are uniformly set to 200. The ratio of training set and validation set is set as 7:3. The learning strategy for 2DCNN uses cosine annealing, and the rest of the model learning strategies use Adaptive learning rate. Mixup (Zhang et al., 2017) is also introduced to enhance the data in the experiments. Mixup serves to allow the model to disrupt the order of the incoming samples in each validation set during the validation process, so as to improve the model’s generalisation ability. The G learning rate in EMAGAN was set to 0.0002, G was set to 0.00002, the number of samples used was 200 and batch_size was set to 64. The samples used in EMALKNet are expanded with real and generated samples in the ratio of 1:4.

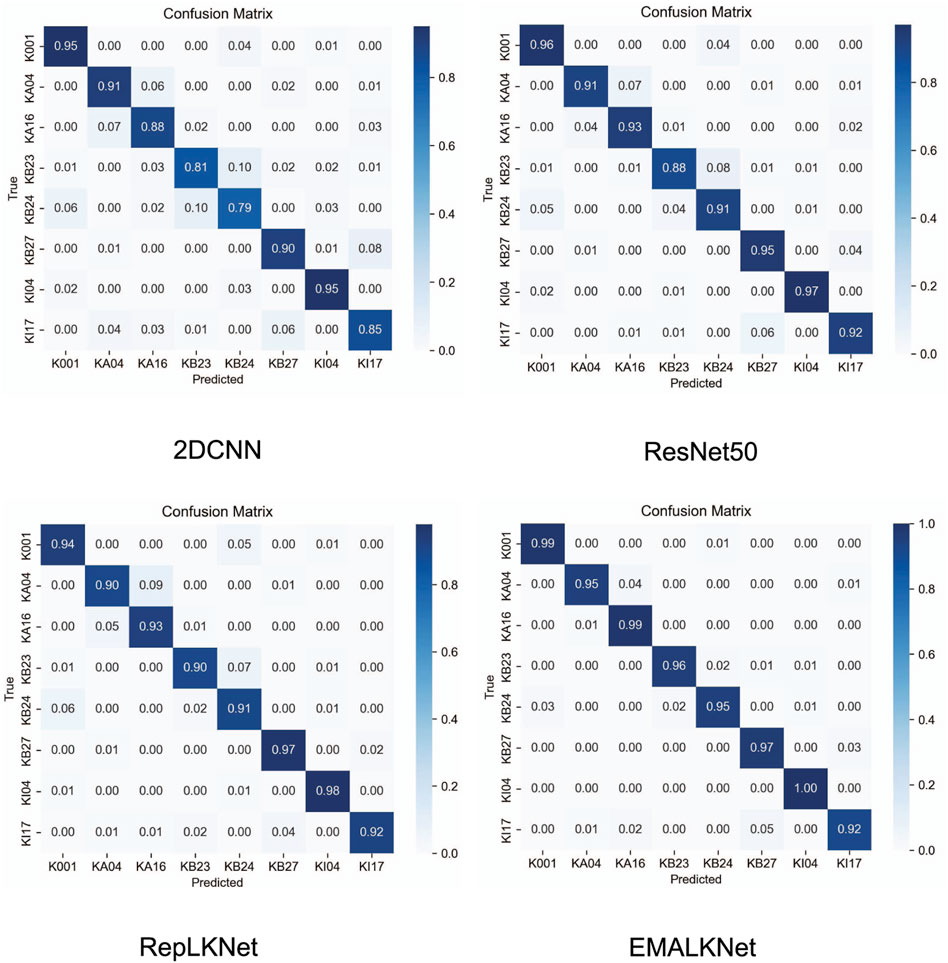
Figure 6; Table 4 show the diagnostic effectiveness of each model under real sample conditions, where the samples used for diagnosis were obtained by randomly re-sampling from the dataset with 300 of each data selection. Specifically, 2DCNN has the highest accuracy of only 88.25%, ResNet50 and RepLKNet have relatively better accuracies of 92.88% and 93.08%, respectively, whereas the diagnostic method proposed in this paper is as high as 96.71%, which is higher than those of the other three models by 8.64%, 3.83%, and 3.63%, respectively.

Figure 6

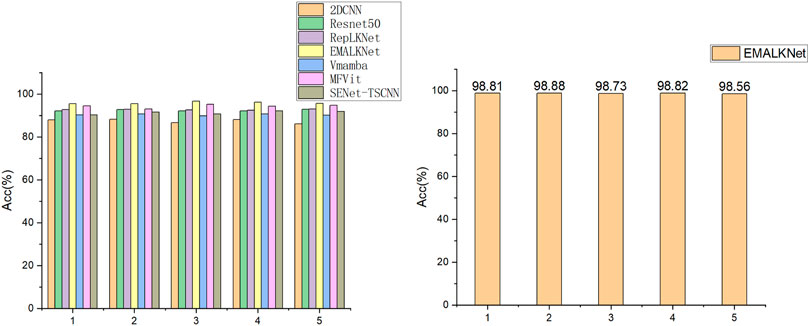
Figure 6. The left is a comparison of all the models in case 1. The right is On the right is the result of case 2.

Table 4

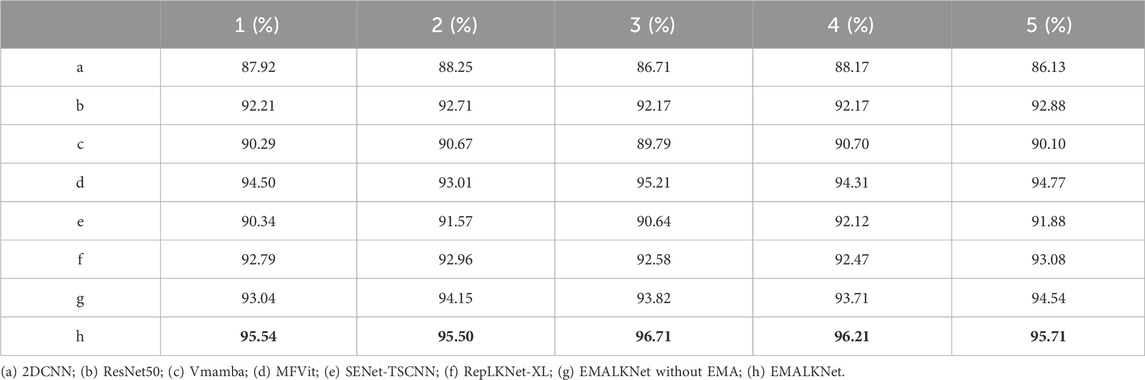
Table 4. This is the results of the formal experiment in Case 1. In bold is the optimal result of each experiment.

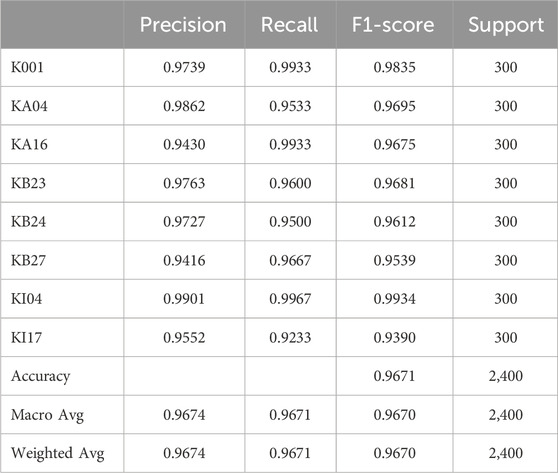
In this experiment, we evaluated the performance of a compound bearing fault diagnosis model that identifies and classifies different types of faults through machine learning classification tasks. The results are shown in the Table 5. The results show that the model exhibits high accuracy and recall in various categories, with K001, KA04, and KI04 achieving an accuracy of over 97%, demonstrating the effectiveness of the model in identifying these specific types of faults. The overall accuracy of the model is 96.71%, with macro average accuracy, recall rate, and F1 score all exceeding 96.7%, indicating that the model has high accuracy and reliability in handling compound fault diagnosis tasks.

Table 5

Table 5. The evaluation indicators of the EMALKNet model.

The results demonstrate that the model introduced in this study effectively handles compound fault diagnosis, even with limited samples. The significant improvement compared to the RepLKNet model underscores that employing GANs and their derivatives to augment sample sizes can successfully mitigate the challenge of insufficient samples in fault diagnosis. Meanwhile, by analysing the confusion matrices of the four models in Figure 7, it is not difficult to find that EMALKNet also outperforms the other three models in the diagnosis of two same faults, KB23 and KB24, with different damage levels, which further illustrates that the large kernel feature of RepLKNet has a stronger help in the extraction ability of fault samples.

Figure 7

Figure 7. Confusion matrix of test results for the four models.

In addition to the aforementioned three classical algorithms, this study further evaluates three cutting-edge fault diagnosis methods: (c) VMamba, (d) MF-Vit and (e) SENet-TSCNN. SENet-TSCNN integrates Squeeze-and-Excitation Networks with Two-Stream Convolutional Neural Networks, utilizing Continuous Wavelet Transform to transform raw data into time-frequency images for diagnostic purposes (Pan et al., 2023). MF-Vit employs both discrete and continuous wavelet transformations to process raw vibration signals, coupled with a vision transformer model to detect faults (Xu et al., 2023). VMamba, a vision-based network, amalgamates state-space models with 2D selective scanning to foster efficient visual representation learning (Liu et al., 2024). The experimental design of this section adhered to the original parameter settings of these methodologies. Results are delineated in Table 4. Comparative analysis reveals that the accuracy of the method developed in this paper surpasses those of VMamba (c), MF-Vit (d), and SENet-TSCNN (e) by 6.01%, 1.5%, and 4.59%, respectively. In comparison with the most advanced current methods, these findings underscore the distinct advantages of EMALKNet in performing composite fault diagnosis under conditions of limited sample sizes.

4.2.2 Experiment 2: ablation study on the EMAGAN

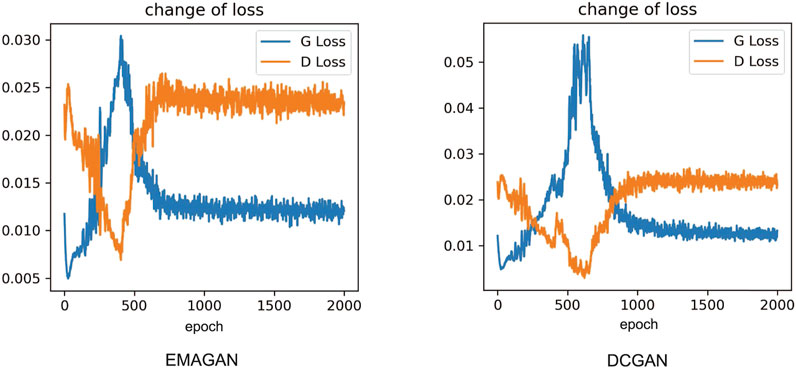
An ablation experiment was designed in this vignette, and the data set selected for this experiment is the same as that of Experiment One. Under the same conditions, the dataset in Table 2 is learnt and new samples are generated using EMAGAN and DCGAN respectively, and the size of the learnt dataset is also 200. The G learning rate in EMAGAN was set to 0.0002, G was set to 0.00002, the number of samples used was 200 and batch_size was set to 64. The loss function image for EMAGAN and DCGAN are shown in Figure 8. Through comparison, it can be found that the EMAGAN designed in this paper starts to converge stably at about 500 epochs, which is 300 epochs earlier than that of DCGAN. 800 samples are generated by DCGAN, and the 800 samples are randomly divided into the training set and the validation set according to the ratio of 7:3 with the original 200 samples. Then RepLKNet is used for classification, and 300 real samples are randomly selected to test the diagnostic effect of RepLKNet in the real sample situation. The experiment was repeated five times and compared with the results of EMALKNet. The comparison results are shown in Table 4, from which it can be seen that EMALKNet (d) is 2.05% more accurate than EMALKNet without EMA (g). Combined with the loss function in Figure 8 it can be seen that EMAGAN has stronger feature extraction capability and better convergence and excellent sample expansion capability than DCGAN, which are all due to EMA’s cross-latitude interaction and multi-scale attention.

Figure 8

Figure 8. Loss function for EMAGAN and DCGAN.

4.3 Case 2: high speed and low torque fault diagnosis based on the data set of Paderborn University

This subsection reevaluated the performance of the proposed method by selecting samples with varying conditions from the University of Paderborn dataset. The sample data selected for this experiment are shown in Table 2, where the bearing code N15 indicates that the bearing speed is 1500 rpm, M01 indicates that the torque is 0.1 Nm, F10 indicates that the radial force is 10n, and the last three digits indicate the bearing code. The difference between experiment 1 and experiment 2 is that the speed of experiment 2 is faster, and the operating conditions of the two are very different. The training strategy and sample processing method are the same as experiment 1. The experiment was repeated for five times. Figure 6 shows the results of the five experiments, and the diagnostic accuracy rate is all about 98.8%, which proves that EMALKNet still has high diagnostic accuracy even under the two different working conditions of faster rotating speed and smaller torque. It shows that EMALKNet has strong generalization and stability.

4.4 Case 3:composite fault diagnosis fault diagnosis based on the data set of HUST

4.4.1 Introduction of dataset

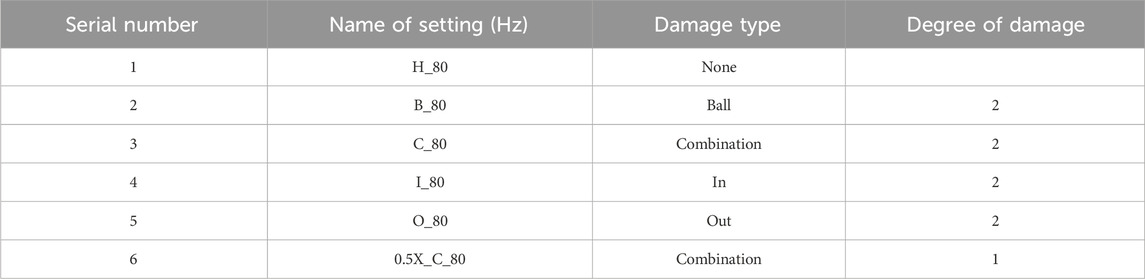
The dataset utilized in this study was sourced from Huazhong University of Science and Technology (HUST) and was generated using the Spectra-Quest mechanical fault simulator, specifically designed for bearing failure analysis. The data pertains to an ER-16K bearing model, featuring an axle diameter of 38.52 mm and a ball diameter of 7.94 mm. Data acquisition was conducted at a sampling frequency of 25.6 kHz, capturing data points under various operational states, including health, inner ring failure, outer ring failure, rolling element failure, and compound failure. For each condition, a total of 262,144 data points were recorded (Zhao et al., 2024). In this experiment, the data set simulates the bearing diagnosis under the noise condition. The selected data sets for this analysis are detailed in Table 6, with “H” denoting healthy bearings and “B” indicating damaged bearings. “C” represents mixed damage conditions; “I” signifies damage to the bearing’s inner ring; “O” denotes outer ring damage. “0.5X” was used to describe moderate injury, while more severe injuries were categorized differently. A constant operating frequency of 80 Hz was maintained throughout the experiments.

Table 6

Table 6. This table is the data set selected for case 3.

4.4.2 Contrast experiment

The experimental data were initially transformed into time-frequency representations using wavelet transformation, resulting in 300 samples. Out of these, 200 samples were selected for further augmentation via EMAGAN-based synthesis. Subsequently, these 200 augmented samples were randomly divided into a training set and a validation set, maintaining a ratio of 7:3. The remaining 100 samples were reserved for the testing phase, with the test accuracy being the primary metric of evaluation. All other experimental configurations were consistent with those outlined in Case 1. In this experiment, a comparative analysis is conducted, encompassing the examination of three traditional methodologies alongside three state-of-the-art approaches. The ablation experiment was also designed. The experimental results are summarized in Table 7.

Table 7

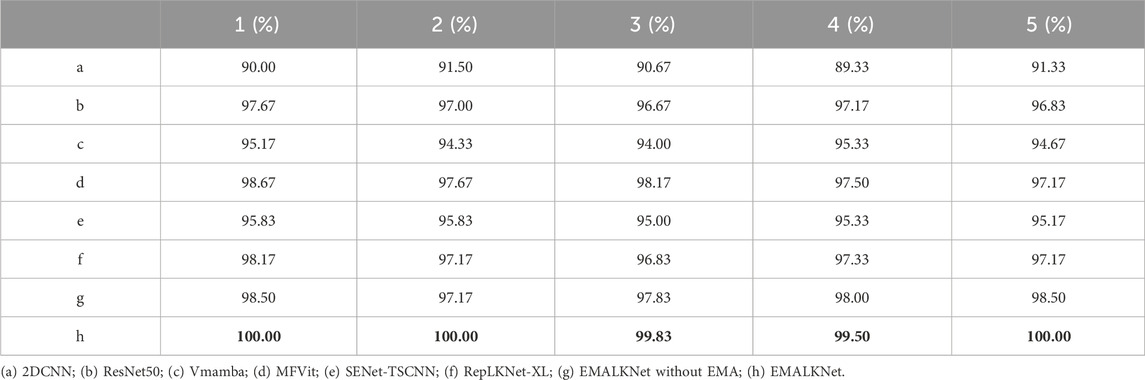
Table 7. This is the results of the formal experiment in Case 3. In bold is the optimal result of each experiment.

Through comparative analysis, it has been observed that the method proposed in this paper still exhibits excellent diagnostic performance on the HUST dataset, with the highest accuracy reaching 100% and the lowest being 99.5%. The diagnostic accuracy has seen an improvement of 8.7%, 2.33%, 2.83%, 4.83%, 1.33%, and 4.17% compared to 2DCNN, ResNet50, RepLKNet-XL, Vmamba, MFVit, and SENet-TSCNN, respectively. Furthermore, the ablation study indicates that the accuracy of EMALKNet is 1.5% higher than that of EMALKNet without EMA, which underscores the superior feature extraction capability of EMAGAN.

5 Discussion of the limitations of this method

While the proposed method exhibits certain superiority in the diagnosis of compound faults in bearings under small sample conditions, it is not without its limitations. Initially, the extensive architecture of the method’s large core network is substantial, demanding significant computational resources, which implies the requirement for sophisticated computational equipment for practical implementation. Additionally, the method introduced in this paper shares some inherent limitations with existing approaches; for example, in case 1, the diagnostic performance on the KI17 dataset is comparable to other methods and does not effectively address the diagnosis of the “Plastic deform: Indentations” type of damage. Finally, in real-world industrial environments, bearing speeds and operating conditions may fluctuate in real time, a challenge that the method presented in this paper has yet to overcome.

6 Conclusion

This study presents a cutting-edge approach for diagnosing bearing faults in machinery with limited sample availability by introducing a new model called EMALKNet that integrates EMAGAN with RepLKNet-XL. This innovation leverages the Efficient Multi Scale Attention mechanism within a Deep Convolutional Generative Adversarial Network framework to enhance sample quality and quantity, effectively overcoming traditional challenges of data scarcity and imbalance. The model’s utilization of RepLKNet-XL’s large kernel structure enables it to extract compound fault features with high precision, improving accuracy and robustness in fault diagnosis under compound and real conditions.

Future research can focus on enhancing the model’s adaptability across various industrial settings and optimizing real-time processing capabilities for widespread practical application.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://mb.uni-paderborn.de/kat/forschung/kat-datacenter/bearing-datacenter and https://github.com/CHAOZHAO-1/HUSTbearing-dataset.

Author contributions

WX: Writing–original draft, Writing–review and editing, Data curation, Software. ZZ: Writing–original draft. ZW: Writing–review and editing. TW: Writing–original draft. ZH: Writing–review and editing. SD: Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, F., and Wang, J. (2022). Rolling Bearing Fault Diagnosis Algorithm Using Overlapping Group Sparse-Deep Complex Convolutional Neural Network. Nonlinear. Dynamics. 108, 2353–2368. doi:10.1007/s11071-022-07314-9

CrossRef Full Text | Google Scholar

Antoine, J.-P., Carrette, P., Murenzi, R., and Piette, B. (1993). Image Analysis With Two-Dimensional Continuous Wavelet Transform. Signal Process. 31, 241–272. doi:10.1016/0165-1684(93)90085-o

CrossRef Full Text | Google Scholar

Chen, C., Liu, C., Wang, T., Zhang, A., Wu, W., and Cheng, L. (2023). Compound fault Diagnosis for Industrial Robots Based on Dual-Transformer Networks. J. Manuf. Syst. 66, 163–178. doi:10.1016/j.jmsy.2022.12.006

CrossRef Full Text | Google Scholar

Chen, Z., Gryllias, K., and Li, W. (2019). Mechanical fault diagnosis using convolutional neural networks and extreme learning machine. Mech. Syst. signal Process. 133, 106272. doi:10.1016/j.ymssp.2019.106272

CrossRef Full Text | Google Scholar

Ding, X., Zhang, X., Han, J., and Ding, G. (2022). “Scaling up your Kernels to 31x31: Revisiting Large Kernel Design in cnns,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 11963–11975.

Google Scholar

Du, N. T., Dien, N. P., and Cuong, N. H. (2022a). “Detection Fault Symptoms of Rolling Bearing Based on Enhancing Collected Transient Vibration Signals,” in The AUN/SEED-Net Joint Regional Conference in Transportation, Energy, and Mechanical Manufacturing Engineering. Editors A.-T. Le, V.-S. Pham, M.-Q. Le, and H.-L. Pham (Singapore: Springer Nature Singapore), 373–384.

CrossRef Full Text | Google Scholar

Du, N. T., Dien, N. P., and Nga, N. T. T. (2022b). Gear Fault Detection in Gearboxes Operated in Non-Stationary Conditions Based on Variable Sideband Analysis without a Tachometer. Front. Mech. Eng. 8. doi:10.3389/fmech.2022.10212221021222

CrossRef Full Text | Google Scholar

Du, N. T., Trung, P. T., Cuong, N. H., and Dien, N. P. (2024). Automatic Rolling Bearings Fault Classification: A Case Study at Varying Speed Conditions. Front. Mech. Eng. 10. doi:10.3389/fmech.2024.1341466

CrossRef Full Text | Google Scholar

Fan, C., Peng, Y., Shen, Y., Guo, Y., Zhao, S., Zhou, J., et al. (2024). Variable Scale Multilayer Perceptron for Helicopter Transmission System Vibration Data Abnormity Beyond Efficient Recovery. Eng. Appl. Artif. Intell. 133, 108184. doi:10.1016/j.engappai.2024.108184

CrossRef Full Text | Google Scholar

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative Adversarial Nets. Adv. neural Inf. Process. Syst. 27. doi:10.5555/2969033.2969125

CrossRef Full Text | Google Scholar

Huang, R., Liao, Y., Zhang, S., and Li, W. (2018). Deep decoupling Convolutional Neural Network for Intelligent Compound Fault Diagnosis. Ieee Access 7, 1848–1858. doi:10.1109/access.2018.2886343

CrossRef Full Text | Google Scholar

Huang, T., Fu, S., Feng, H., and Kuang, J. (2019). Bearing Fault Diagnosis Based on Shallow Multi-Scale Convolutional Neural Network With Attention. Energies 12, 3937. doi:10.3390/en12203937

CrossRef Full Text | Google Scholar

Jia, L., Chow, T. W., and Yuan, Y. (2023). Gtfe-net: A Gramian Time Frequency Enhancement CNN For Bearing Fault Diagnosis. Eng. Appl. Artif. Intell. 119, 105794. doi:10.1016/j.engappai.2022.105794

CrossRef Full Text | Google Scholar

Lessmeier, C., Kimotho, J. K., Zimmer, D., and Sextro, W. (2016). Condition Monitoring of Bearing Damage in Electromechanical Drive Systems By Using Motor Current Signals of Electric Motors: A Benchmark Data Set For Data-Driven Classification. PHM Soc. Eur. Conf. 3. doi:10.36001/phme.2016.v3i1.1577

CrossRef Full Text | Google Scholar

Li, S., Peng, Y., Shen, Y., Zhao, S., Shao, H., Bin, G., et al. (2024). Rolling Bearing Fault Diagnosis Under Data Imbalance and Variable Speed Based On Adaptive Clustering Weighted Oversampling. Reliab. Eng. Syst. Saf. 244, 109938. doi:10.1016/j.ress.2024.109938

CrossRef Full Text | Google Scholar

Liu, Y., Tian, Y., Zhao, Y., Yu, H., Xie, L., Wang, Y., et al. (2024). Vmamba: Visual state space model. arXiv preprint arXiv:2401.10166.

Google Scholar

Luo, W., Li, Y., Urtasun, R., and Zemel, R. (2016). Understanding the Effective Receptive Field in Deep Convolutional Neural Networks. Adv. neural Inf. Process. Syst. 29. doi:10.5555/3157382.3157645

CrossRef Full Text | Google Scholar

Ouyang, D., He, S., Zhang, G., Luo, M., Guo, H., Zhan, J., et al. (2023). “Efficient Multi-Scale Attention Module with Cross-Spatial Learning,” in ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Pan, W., Sun, Y., Cheng, R., and Cao, S. (2023). A Senet-Tscnn Model Developed for Fault Diagnosis Considering Squeeze-Excitation Networks and Two-Stream Feature Fusion. Meas. Sci. Technol. 34, 125117. doi:10.1088/1361-6501/acf3351361-6501/acf335

CrossRef Full Text | Google Scholar

Peng, C., Li, L., Chen, Q., Tang, Z., Gui, W., and He, J. (2021). A fault diagnosis Method for Rolling Bearings Based on Parameter Transfer Learning Under Imbalance Data Sets. Energies 14, 944. doi:10.3390/en14040944

CrossRef Full Text | Google Scholar

Radford, A., Metz, L., and Chintala, S. (2015). Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv Prepr. arXiv:1511.06434.

Google Scholar

Ruan, D., Song, X., Gühmann, C., and Yan, J. (2021). Collaborative Optimization OF CNN and GAN FOR Bearing Fault Diagnosis Under Unbalanced Datasets. Lubricants 9, 105. doi:10.3390/lubricants9100105

CrossRef Full Text | Google Scholar

Schwendemann, S., Amjad, Z., and Sikora, A. (2021). Bearing Fault Diagnosis With Intermediate Domain Based Layered Maximum Mean Discrepancy: A New Transfer Learning Approach. Eng. Appl. Artif. Intell. 105, 104415. doi:10.1016/j.engappai.2021.104415

CrossRef Full Text | Google Scholar

Shao, S., Wang, P., and Yan, R. (2019). Generative adversarial networks for data augmentation in machine fault diagnosis. Comput. Industry 106, 85–93. doi:10.1016/j.compind.2019.01.001

CrossRef Full Text | Google Scholar

Wang, K., Gou, C., Duan, Y., Lin, Y., Zheng, X., and Wang, F.-Y. (2017). Generative adversarial Networks: Introduction and Outlook. IEEE/CAA J. Automatica Sinica 4, 588–598. doi:10.1109/JAS.2017.7510583

CrossRef Full Text | Google Scholar

Xu, J., Zhou, L., Zhao, W., Fan, Y., Ding, X., and Yuan, X. (2022). Zero-Shot Learning for Compound Fault Diagnosis of Bearings. Expert Syst. Appl. 190, 116197. doi:10.1016/j.eswa.2021.116197

CrossRef Full Text | Google Scholar

Xu, Z., Tang, X., and Wang, Z. (2023). A Multi-Information Fusion Vit Model and its Application to the Fault Diagnosis Of Bearing With Small Data Samples. Machines 11, 277. doi:10.3390/machines11020277

CrossRef Full Text | Google Scholar

Zhang, H., Cisse, M., Dauphin, Y. N., and Lopez-Paz, D. (2017). mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412.

Google Scholar

Zhang, S., Ye, F., Wang, B., and Habetler, T. G. (2021). Semi-Supervised Bearing Fault Diagnosis and Classification Using Variational Autoencoder-Based Deep Generative Models. IEEE Sensors J. 21, 6476–6486. doi:10.1109/JSEN.2020.3040696

CrossRef Full Text | Google Scholar

Zhang, W., Li, X., Jia, X.-D., Ma, H., Luo, Z., and Li, X. (2020). Machinery Fault Diagnosis With Imbalanced Data Using Deep Generative Adversarial Networks. Measurement 152, 107377. doi:10.1016/j.measurement.2019.107377

CrossRef Full Text | Google Scholar

Zhang, Z., and Wu, L. (2024). Graph Neural Network-Based Bearing Fault Diagnosis Using Granger Causality Test. Expert Syst. Appl. 242, 122827. doi:10.1016/j.eswa.2023.122827

CrossRef Full Text | Google Scholar

Zhao, C., Zio, E., and Shen, W. (2024). Domain Generalization for Cross-Domain Fault Diagnosis: An Application-Oriented Perspective and a Benchmark Study. Reliab. Eng. Syst. Saf. 245, 109964. doi:10.1016/j.ress.2024.1099642024.109964

CrossRef Full Text | Google Scholar

Zhao, H., Liu, J., Chen, H., Chen, J., Li, Y., Xu, J., et al. (2023). Intelligent Diagnosis Using Continuous Wavelet Transform and Gauss Convolutional Deep Belief Network. IEEE Trans. Reliab. 72, 692–702. doi:10.1109/TR.2022.3180273

CrossRef Full Text | Google Scholar

Zhu, H., and Fang, T. (2024). Compound Fault Diagnosis of Rolling Bearings With Few-Shot Based on Dcgan-Replknet. Meas. Sci. Technol. 35, 066105. doi:10.1088/1361-6501/ad24b5

CrossRef Full Text | Google Scholar

Zhu, X., Qian, Z., Chen, X., Liu, L., Sheng, C., and Gu, W. (2021). Electrohydrodynamics-Printed Silver Nanoparticle Flexible Pressure Sensors with Improved Gauge Factor. IEEE Sensors J. 21, 5836–5844. doi:10.1109/JSEN.2020.3038086

CrossRef Full Text | Google Scholar