Influence of the dimple cross-sectional profile on the behavior of gas parallel slider bearings

This paper studies the effect of the dimple cross-sectional profile on the behavior of gas parallel slider bearings using the numerical method. The numerical method is performed in MATLAB software. The influence of geometrical parameters of dimples on the dimensionless average pressure is studied for different dimple cross-sectional profiles. The geometrical parameters of dimples include dimple depth, dimple area density, transversal textured ratio, and longitudinal textured ratio. It is found that the hydrodynamic lubrication of dimple-textured gas parallel slider bearings is controlled by the dimple depth, dimple area density, transversal textured ratio, longitudinal textured ratio, and dimple cross-sectional profile. Furthermore, the impact of sliding speed on the hydrodynamic lubrication is studied for different dimple cross-sectional profiles. The results indicate that the optimum sliding speed for maximizing the hydrodynamic pressure is controlled by the dimple cross-sectional profile.

1 Introduction

The improvement of product performance could cause technological innovation (Mitrovic et al., 2014; Chen et al., 2017; Marinkovc et al., 2024). Surface texturing has been successfully used for the improvement of product performance. The role of surface texturing includes increasing the storage of the lubricant (Ibatan et al., 2015), increasing the load capacity (Murthy et al., 2007), improving the anti-wear ability (Mao et al., 2020), and reducing friction (Grützmacher et al., 2019). Recently, many studies have been conducted on textured products. Wu et al. (2023) applied three types of surface textures to the guidance of thrust ball bearings. It was shown that the oil storage of the bearing raceway could be increased by applying the surface texture to the guiding. By optimizing the parameters, Guo et al. (2023) studied the friction force, load force, and leakage of journal bearings with V-shaped textures. The optimization parameters included the ratio of the texture width, the angle of the texture, and the depth of the texture. Zhao and Zhang (2023) concluded that the surface texture had an important influence on the reduction effect of wear in non-magnetic plastic and brittle materials. By fabricating the chevron-shaped texture in different positions, Schnell et al. (2023) investigated the impact of partial texturing on the frictional behavior of journal bearings. They found that the textures located in the high-load region could produce the lowest friction. Wang et al. (2023) studied the behavior of elliptical bearings. They showed that the surface texture could reduce the end leakage. Boidi et al. (2021) found that the frictional behavior of the bearing could be improved by employing the fast texturing technique. Chen et al. (2021) established a mathematical model to study the behavior of mechanical seals with multi-scale composite textures. The results showed that the lubrication behavior of mechanical seals could be improved by means of surface texture. Feldman et al. (2007) optimized the texturing parameters in order to obtain the maximum stiffness and efficiency of the textured hydrostatic gas seal. Rajput et al. (2021) studied the impact of the surface texture on the piston ring. They found that the surface texture could reduce the friction of piston rings. Obikawa et al. (2011) investigated the impact of the surface texture on the tool rake face. The results showed that the surface texture could reduce the friction coefficient and friction force. Qiu et al. (2012); Qiu et al. (2013) investigated the effect of texture shape on the performance of fully textured gas parallel slider bearings. They found that surface texture could improve the load capacity and stiffness of gas parallel slider bearings and reduce the friction coefficient. However, Qiu et al. (2014) investigated the accuracy of the compressible Reynolds equation for predicting the local pressure of textured gas parallel slider bearings. Liu et al. (2021) investigated the performance of partially textured gas parallel slider bearings with orientation ellipse dimples. They showed that the long axis of the ellipse dimple should be placed parallel to the sliding direction to obtain the maximum average pressure. When the rarefaction effect was considered, Murthy et al. (2007) investigated the performance of textured gas parallel slider bearings.

The influence of groove cross-sectional profiles on the behavior of gas parallel slider bearings has been studied (Liu et al., 2023). However, the influence of the dimple cross-sectional profile on the behavior of gas parallel slider bearings has not yet been studied. This paper aims to study the influence of dimple cross-sectional profiles on the behavior of gas parallel slider bearings.

2 Analytical model

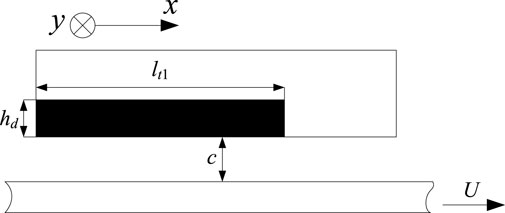
The schematic diagram of gas parallel slider bearings with dimples is shown in Figure 1. The upper slider is fixed. The relative speed between two sliders is $U$, and the lubricant between two sliders is the ideal gas. The dimples are partially textured in the upper slider. The minimum distance between the two sliders is $c$. Each dimple is marked with depth $h_d$. The length of the textured slider along the $x$ direction is $l_{t1}$.

Figure 1

Figure 1. Schematic diagram of dimple-textured gas parallel slider bearings.

Figure 2 presents the schematic diagram of the upper slider. The lower slider is marked with length $l$. The upper slider has $n\times m$ ($n=l/l_1$; $m=l/l_2$) imaginary cells. The imaginary cells are marked with length $l_1$ and width $l_2$. The textured length along the $x$ direction is $l_{t1}$, and the textured length along the $y$ direction is $l_{t2}$. The radius of the dimple is $r$. In Figure 2C, the dimple cross-sectional profile is triangle. In Figure 2D, the dimple cross-sectional profile is rectangle. In Figure 2E, the dimple cross-sectional profile is parabolic.

Figure 2

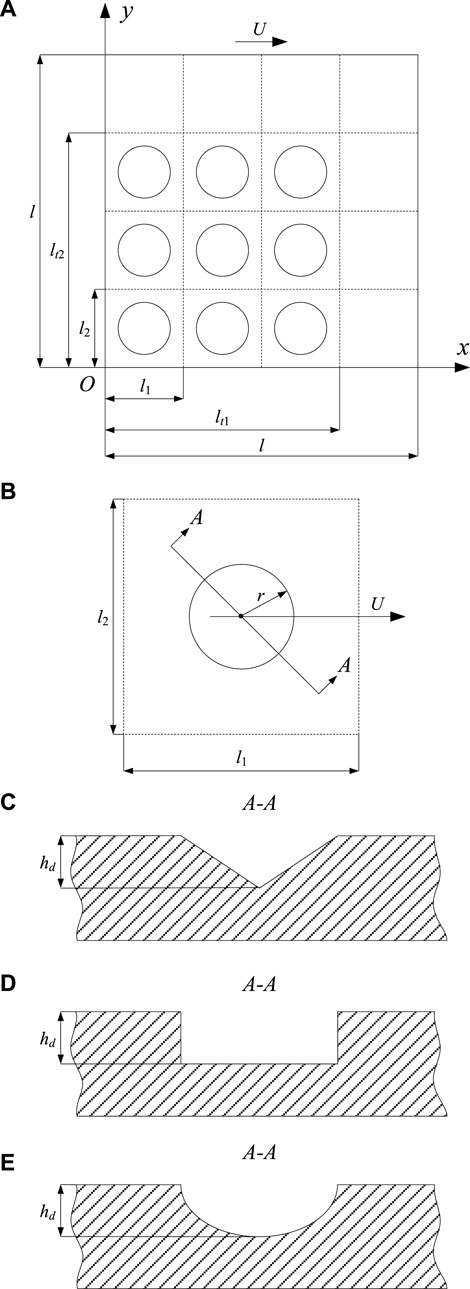
Figure 2. Schematic diagram of the lower slider. (A) Dimple distribution on the lower slider surface, (B) dimple in an imaginary cell, (C) cross-sectional profile of a triangular dimple, (D) cross-sectional profile of a rectangular dimple, and (E) cross-sectional profile of a parabolic dimple.

The dimple area ratio is defined as

$s_p=\frac{\pi r^2}{l_1{l}_2}.(1)$

The transversal textured ratio is defined as

$f_{t1}=\frac{l_{t1}}{l}.(2)$

The longitudinal textured ratio is defined as

$f_{t2}=\frac{l_{t2}}{l}.(3)$

The lubrication equation of dimple textured gas parallel slider bearings is expressed as (Liu et al., 2021)

$\frac{\partial }{\partial x}\left(p{h}^3\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(p{h}^3\frac{\partial p}{\partial y}\right)=6\mu U\frac{\partial \left(ph\right)}{\partial x},(4)$

where $h$ is the lubricant thickness, $p$ is the hydrodynamic pressure, and $\mu$ is the viscosity.

The dimensionless parameters are introduced by

$X=\frac{x}{w_0},Y=\frac{y}{w_0},P=\frac{p}{p_a},H=\frac{h}{c},(5)$

where $p_a$ is the atmospheric pressure and $w_0$ is the referenced parameter.

The dimensionless lubrication equation of dimple textured gas parallel slider bearings is expressed as

$\frac{\partial }{\partial X}\left(P{H}^3\frac{\partial P}{\partial X}\right)+\frac{\partial }{\partial Y}\left(P{H}^3\frac{\partial P}{\partial Y}\right)=\mathrm{\Lambda }\frac{\partial \left(PH\right)}{\partial X},(6)$

where $\mathrm{\Lambda }=6\mu U{w}_0/\left(p_a{c}^2\right)$.

For the triangular dimples, the dimensionless lubricant thickness $H$ is expressed as

$H=\left\{\begin{array}{l}1+\frac{\left(\sqrt{s_p{L}_1{L}_2}-\sqrt{\pi }\sqrt{X_1^2+Y_1^2}\right)H_d}{\sqrt{s_p{L}_1{L}_2}},\\ X_1^2+Y_1^2\le \frac{s_p{L}_1{L}_2}{\pi },X\le f_{t1}L,\text{and\hspace{0.17em}}Y\le f_{t2}L\\ 1,\text{elsewhere}\end{array}\right..(7)$

For the rectangular dimples, it is expressed as

$H=\left\{\begin{array}{l}1+H_d,\\ X_1^2+Y_1^2\le \frac{s_p{L}_1{L}_2}{\pi },X\le f_{t1}L,\text{and\hspace{0.17em}}Y\le f_{t2}L\\ 1,\text{elsewhere}\end{array}\right..(8)$

For the parabolic dimples, it is expressed as

$H=\left\{\begin{array}{l}1+H_d-\frac{\pi \left(X_1^2+Y_1^2\right)H_d}{s_p{L}_1{L}_2},\\ X_1^2+Y_1^2\le \frac{s_p{L}_1{L}_2}{\pi },X\le f_{t1}L,\text{and\hspace{0.17em}}Y\le f_{t2}L\\ 1,\text{elsewhere}\end{array}\right.,(9)$

where

$\left.\begin{array}{l}{X}_1=X-\left(n_1+\frac{1}{2}\right)L_1\\ Y_1=Y-\left(m_1+\frac{1}{2}\right)L_2\end{array}\right\},(10)$

$n_1=fix\left(X/L_1\right),(11)$

$m_1=fix\left(Y/L_2\right).(12)$

Here, $L_1=l_1/w_0$ is the dimensionless length of imaginary cells, $L_2=l_2/w_0$ is the dimensionless width of imaginary cells, fix is the integer function, $H_d=h_d/c$ is the dimensionless dimple depth, and $L=l/w_0$ is the dimensionless slider length.

The dimensionless boundary condition is expressed as (Liu et al., 2021)

$P\left(0,Y\right)=P\left(L,Y\right)=P\left(X,0\right)=P\left(X,L\right)=1.(13)$

The multi-grid finite element method (Liu et al., 2021) is used to solve Equation 6, and the dimensionless average pressure $P_{av}$ is obtained. The dimensionless average pressure $P_{av}$ can be computed as

$P_{av}=\frac{p_{av}}{p_a}=\frac{{\int }_0^L{\int }_0^{L}PdXdY}{L^2}.(14)$

3 Result and discussions

When the program is performed, some computing parameters are given as $n=10$, $m=10$, $w_0=0.05\text{\hspace{0.17em}mm}$, $c=8\times {10}^{-4}\text{\hspace{0.17em}mm}$, $l=2.5\text{\hspace{0.17em}mm}$, $p_a=0.101325\text{\hspace{0.17em}MPa}$, and $\mu =1.8\times {10}^{-5}\text{\hspace{0.17em}Pa}\cdot \mathrm{s}$.

Figure 3 shows the pressure distribution of dimple-textured gas parallel slider bearings. It is observed from Figure 3 that the maximum pressure of gas parallel slider bearings with rectangular dimples is larger than that of gas parallel slider bearings with triangular dimples and parabolic dimples. This result implies that the pressure distribution of dimple-textured gas parallel slider bearings is controlled by the dimple cross-sectional profile.

Figure 3

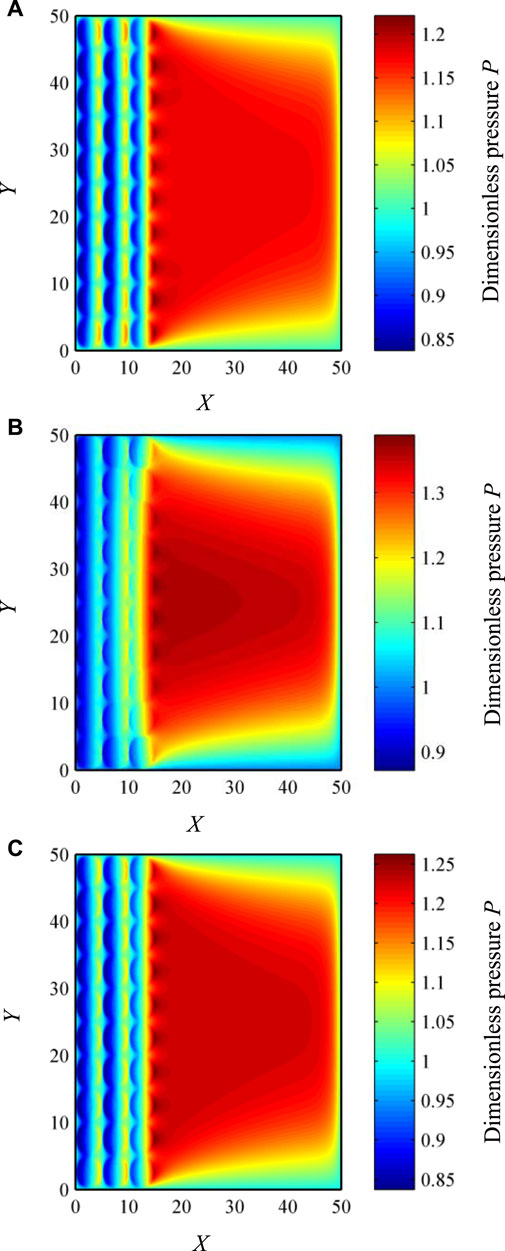
Figure 3. Pressure distributions of gas parallel slider bearings ($H_d=2$, $s_p=0.7$, $f_{t1}=0.3$, $f_{t2}=1$, and $U=12\mathrm{m}/\mathrm{s}$). (A) Triangular dimples, (B) rectangular dimples, and (C) parabolic dimples.

Figure 4 presents the effect of dimensionless dimple depth on the dimensionless average pressure for different dimple cross-sectional profiles. It is observed that the dimensionless average pressure first increases and then decreases with the increase in the dimensionless dimple depth. This result implies that there exists an optimum dimensionless dimple depth to maximize the dimensionless average pressure for different dimple cross-sectional profiles. For the triangle dimples, the optimum dimensionless dimple depth is 5; for the rectangular dimples, it is 2; and for the parabolic dimples, it is 3. Therefore, the optimum dimple depth for maximizing the average pressure is controlled by the dimple cross-sectional profile.

Figure 4

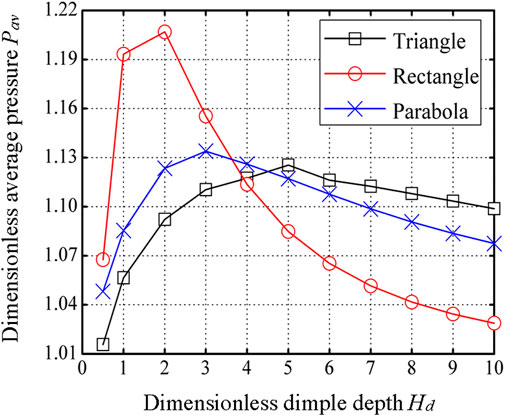
Figure 4. Effect of dimensionless dimple depth on the dimensionless average pressure for dimensionless dimple cross-sectional profiles ($s_p=0.7$, $f_{t1}=0.3$, $f_{t2}=1$, and $U=12\mathrm{m}/\mathrm{s}$).

The effect of dimple area density on the dimensionless average pressure is shown in Figure 5 for different dimple cross-sectional profiles. It is observed that the dimensionless average pressure increases with an increase in the dimple area density. Hence, the dimples should be fabricated as large as possible in order to obtain the maximum hydrodynamic pressure based on the actual processing technology.

Figure 5

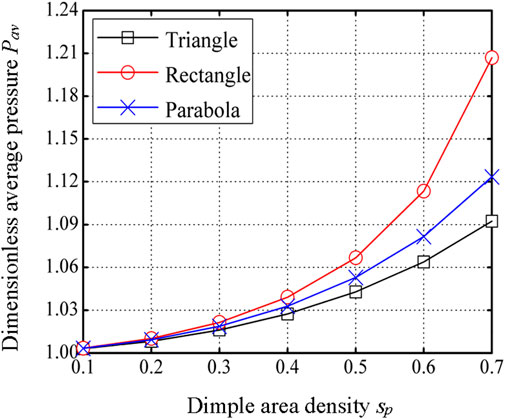
Figure 5. Effect of dimple area density on the dimensionless average pressure for different dimple cross-sectional profiles ($H_d=2$, $f_{t1}=0.3$, $f_{t2}=1$, and $U=12\mathrm{m}/\mathrm{s}$).

Figure 6 presents the effect of the transversal textured ratio on the dimensionless average pressure for different dimple cross-sectional profiles. It is observed from Figure 6 that the dimensionless average pressure for $f_{t1}<1$ is larger than that for $f_{t1}=1$. This result implies that partial texturing along the $x$ direction could produce a larger hydrodynamic pressure than full texturing along the $x$ direction. Therefore, partial texturing along the $x$ direction may be a good choice for maximizing the hydrodynamic pressure. It is also observed from Figure 6 that the optimum transversal textured ratio for maximizing the hydrodynamic pressure is controlled by the dimple cross-sectional profile.

Figure 6

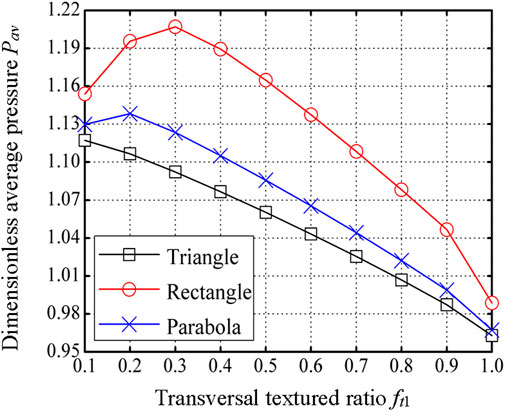
Figure 6. Effect of the transversal textured ratio on the dimensionless average pressure for different dimple cross-sectional profiles ($H_d=2$, $s_p=0.7$, $f_{t2}=1$, and $U=12\mathrm{m}/\mathrm{s}$).

Figure 7 presents the effect of the longitudinal textured ratio on the dimensionless average pressure for different dimple cross-sectional profiles. It is observed that the dimensionless average pressure increases with the increase in the longitudinal textured ratio. This result implies that full texturing along the $y$ direction could produce a larger hydrodynamic pressure than partial texturing along the $y$ direction. Therefore, full texturing along the $y$ direction may be a good choice for maximizing the hydrodynamic pressure.

Figure 7

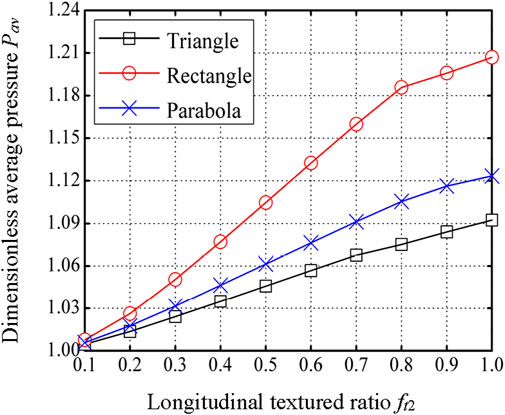
Figure 7. Effect of the longitudinal textured ratio on the dimensionless average pressure for different dimple cross-sectional profiles ($H_d=2$, $s_p=0.7$, $f_{t1}=0.3$, and $U=12\mathrm{m}/\mathrm{s}$).

Figure 8 presents the effect of sliding speed on the dimensionless average pressure for different dimple cross-sectional profiles. It is observed that the dimensionless average pressure first increases and then decreases with the increase in the sliding speed. This result implies that the sliding speed should not be chosen too large or too small in order to obtain the maximum hydrodynamic pressure. It is also observed that the optimum sliding speed for maximizing the hydrodynamic pressure is controlled by the dimple cross-sectional profile.

Figure 8

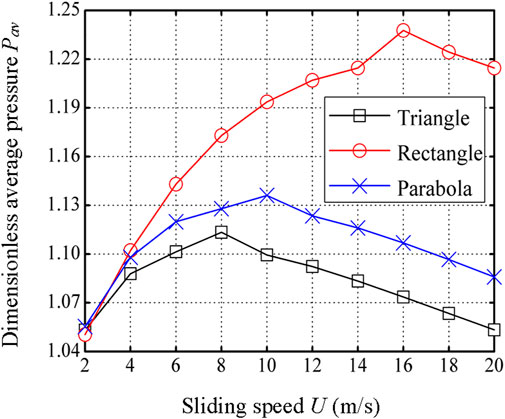
Figure 8. Effect of sliding speed on the dimensionless average pressure for different dimple cross-sectional profiles ($H_d=2$, $s_p=0.7$, $f_{t1}=0.3$, and $f_{t2}=1$).

4 Conclusion

In this investigation, we identify the effect of the dimple cross-sectional profile on the behavior of gas parallel slider bearings using the numerical method. First, we identify the effect of cross-sectional profiles and dimple geometrical parameters on the hydrodynamic pressure of gas parallel slider bearings. The geometrical parameters of dimples include dimple depth, dimple area density, transversal textured ratio, and longitudinal textured ratio. Next, we identify the effect of cross-sectional profiles and sliding speed on the hydrodynamic pressure of gas parallel slider bearings. Based on the present investigation, the following findings are obtained:

(1) The optimum dimple depth for maximizing the average pressure is controlled by the dimple cross-sectional profile.

(2) The average pressure increases with the increase in the dimple area density.

(3) Partial texturing along the $x$ direction could produce a larger hydrodynamic pressure than full texturing along the $x$ direction. Full texturing along the $y$ direction could produce a larger hydrodynamic pressure than partial texturing along the $y$ direction.

(4) The optimum transversal textured ratio for maximizing the hydrodynamic pressure is controlled by the dimple cross-sectional profile.

(5) The optimum sliding speed for maximizing the hydrodynamic pressure is controlled by the dimple cross-sectional profile.

In essence, this investigation represents an effort to expand the research scope of surface texture. The findings of the present investigation are useful for the design of dimple-textured gas parallel slider bearings. In this paper, the surface roughness of gas parallel slider bearings is not considered. In subsequent research, we will study the effect of dimple cross-sectional profiles on the behavior of gas parallel slider bearings with surface roughness.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

XiL: writing–original draft. XuL: writing–original draft. CY: writing–original draft. HK: writing–original draft. ZZ: writing–original draft. YC: writing–original draft. WQ: writing–original draft. BH: writing–original draft. FL: writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Scientific Research Project of Hunan Province Education Department (grant no. 23C0893), Scientific Research Project of Hunan Applied Technology University in 2023 (no. 11), Planning Project of China Private Education Association (School Development) in 2023 (Research on the Integration of Engineering Education Certification and Curriculum Ideological and Political Construction of Private Universities—Taking Robot Engineering as an example, grant no. CANFZG23355), and Teaching Research Reform Project of Hunan Applied Technology University in 2023 (Research on the Integration of Engineering Education Certification and Curriculum Ideological and Political Construction of Private Universities—Taking Mechanical Design, Manufacturing and Automation as an example, grant no. 35).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boidi, G., Grutzmacher, P. G., Kadiric, A., Profito, F. J., Machado, I. F., Gachot, C., et al. (2021). Fast laser surface texturing of spherical samples to improve the frictional performance of elasto-hydrodynamic lubricated contacts. Friction 9 (5), 1227–1241. doi:10.1007/s40544-020-0462-4

CrossRef Full Text | Google Scholar

Chen, P., Li, J., Shi, Z., and Xiang, X. (2017). Numerical optimization of gourd-shaped surface texture and experiment of tribological performance. J. Central South Univ. 24, 2773–2782. doi:10.1007/s11771-017-3691-6

CrossRef Full Text | Google Scholar

Chen, T. Y., Ji, J. H., Fu, Y. H., Yang, X. P., Fu, H., and Fang, L. (2021). Tribological performance of UV picosecond laser multi-scale composite textures for C/SiC mechanical seals: theoretical analysis and experimental verification. Ceram. Int. 47 (16), 23162–23180. doi:10.1016/j.ceramint.2021.04.312

CrossRef Full Text | Google Scholar

Feldman, Y., Kligerman, Y., and Etsion, I. (2007). Stiffness and efficiency optimization of a hydrostatic laser surface textured gas seal. J. Tribol. 129 (2), 407–410. doi:10.1115/1.2540120

CrossRef Full Text | Google Scholar

Grützmacher, P. G., Profito, F. J., and Rosenkranz, A. (2019). Multi-scale surface texturing in tribology-current knowledge and future perspectives. Lubricants 7 (11), 95. doi:10.3390/lubricants7110095

CrossRef Full Text | Google Scholar

Guo, J., Ding, B., Wang, Y. F., and Han, Y. F. (2023). Co-optimization for hydrodynamic lubrication and leakage of V-shape textured bearings via linear weighting summation. Phys. Scr. 98, 125218. doi:10.1088/1402-4896/ad07be

CrossRef Full Text | Google Scholar

Ibatan, T., Uddin, M. S., and Chowdhury, M. A. K. (2015). Recent development on surface texturing in enhancing tribological performance of bearing sliders. Surf. Coatings Technol. 272, 102–120. doi:10.1016/j.surfcoat.2015.04.017

CrossRef Full Text | Google Scholar

Liu, F. X., Li, Z. L., Yang, C. J., Wu, H. B., Yin, 1 H. Z., and Jiang, S. (2021). Hydrodynamic lubrication of partially textured gas parallel slider bearings with orientation ellipse dimples. Math. Problems Eng. 2021, 1–7. doi:10.1155/2021/4441892

CrossRef Full Text | Google Scholar

Liu, F. X., Yang, C. J., Xu, S. W., Xie, K., Xie, D. Z., Han, B. H., et al. (2023). Influence of geometrical shape on the lubrication performance of partially micro-grooved gas-lubricated parallel slider bearings. Mechanika 29 (3), 252–257. doi:10.5755/j02.mech.32384

CrossRef Full Text | Google Scholar

Mao, B., Siddaiah, A., Liao, Y., and Menezes, P. L. (2020). Laser surface texturing and related techniques for enhancing tribological performance of engineering materials: a review. J. Manuf. Process. 53, 153–173. doi:10.1016/j.jmapro.2020.02.009

CrossRef Full Text | Google Scholar

Marinkovc, A., Stojanovic, B., Gachot, C., and Lazovi, T. (2024). Analysis of lubrication regimes for porous sliding bearing. Lubricants 12 (6), 184. doi:10.3390/lubricants12060184

CrossRef Full Text | Google Scholar

Mitrovic, S., Babic, M., Miloradović, N., Bobic, I., Stojanovic, B., Dzunic, D., et al. (2014). Wear characteristics of hybrid composites based on Za27 alloy reinforced with silicon carbide and graphite particles. Tribol. industry 36 (1), 204–210.

Google Scholar

Murthy, A., Etsion, I., and Talke, F. (2007). Analysis of surface textured air bearing sliders with rarefaction effects. Tribol. Lett. 28, 251–261. doi:10.1007/s11249-007-9269-y

CrossRef Full Text | Google Scholar

Obikawa, T., Kamio, A., Takaoka, H., and Osada, A. (2011). Micro-texture at the coated tool face for high performance cutting. Int. J. Mach. Tools Manuf. 51, 966–972. doi:10.1016/j.ijmachtools.2011.08.013

CrossRef Full Text | Google Scholar

Qiu, M., Bailey, B., Stoll, R., and Raeymaekers, B. (2014). The accuracy of the compressible Reynolds equation for predicting the local pressure in gas-lubricated textured parallel slider bearings. Tribol. Int. 72, 83–89. doi:10.1016/j.triboint.2013.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, M., Delic, A., and Raeymaekers, B. (2012). The effect of texture shape on the load-carrying capacity of gas-lubricated parallel slider bearings. Tribol. Lett. 48, 315–327. doi:10.1007/s11249-012-0027-4

CrossRef Full Text | Google Scholar

Qiu, M., Minson, B., and Raeymaekers, B. (2013). The effect of texture shape on the friction coefficient and stiffness of gas-lubricated parallel slider bearings. Tribol. Int. 67, 278–288. doi:10.1016/j.triboint.2013.08.004

CrossRef Full Text | Google Scholar

Rajput, H., Atulkar, A., and Porwal, R. (2021). Optimization of the surface texture on piston ring in four-stroke IC engine. Mater. Today Proc. 44, 428–433. doi:10.1016/j.matpr.2020.09.752

CrossRef Full Text | Google Scholar

Schnell, G., Studemund, H., Thomas, R., and Seitz, H. (2023). Experimental investigations on the friction behavior of partially femtosecond laser-textured journal bearing shells. Tribol. Int. 188, 108764. doi:10.1016/j.triboint.2023.108764

CrossRef Full Text | Google Scholar

Wang, L. L., Duan, J. D., He, M. X., Liu, Y. A., and Bao, Y. L. (2023). Study on antifriction mechanism of surface textured elliptical bearings. J. Tribol. 145 (1), 1–20. doi:10.1115/1.4055197

CrossRef Full Text | Google Scholar

Wu, C., Yang, K., Ni, J., Lu, S. G., Yao, L. D., and Li, X. L. (2023). Investigations for vibration and friction torque behaviors of thrust ball bearing with self-driven textured guiding surface. Friction 11 (6), 894–910. doi:10.1007/s40544-022-0627-4

CrossRef Full Text | Google Scholar

Zhao, X. D., and Zhang, Y. M. (2023). Analysis of the tribological and dynamic performance of textured bearings under contaminated conditions. Tribol. Int. 187, 108732. doi:10.1016/j.triboint.2023.108732

CrossRef Full Text | Google Scholar