- 1Institute of Aircraft Propulsion Systems, University of Stuttgart, Stuttgart, Germany
- 2MTU Aero Engines AG, Munich, Germany
- 3MTU Maintenance Hannover GmbH, Langenhagen, Germany
During service, civil turbofans experience environmentally induced deterioration. Predicting this in a digital service twin model is computationally challenging due to the need to model both deterioration mechanisms and environmental conditions. For compressor erosion, a key challenge is to model particle ingestion throughout a flight mission (FM). During ground operations, these particles may be airborne or deposited on runways and taxiways. This work assesses the impact of the latter on turbofan core compressor deterioration during a mission. The airflow field in front of the engine intake is approximated using potential flow theory. Comparisons with measurements show that the predicted air velocity near the engine is underestimated since the inlet ground vortices generated from viscous effects are neglected. The forces acting on the particles are derived from the flow field. It turns out that most particles are lifted from the ground during take-off (TO). Yet only smaller particles below
1 Introduction
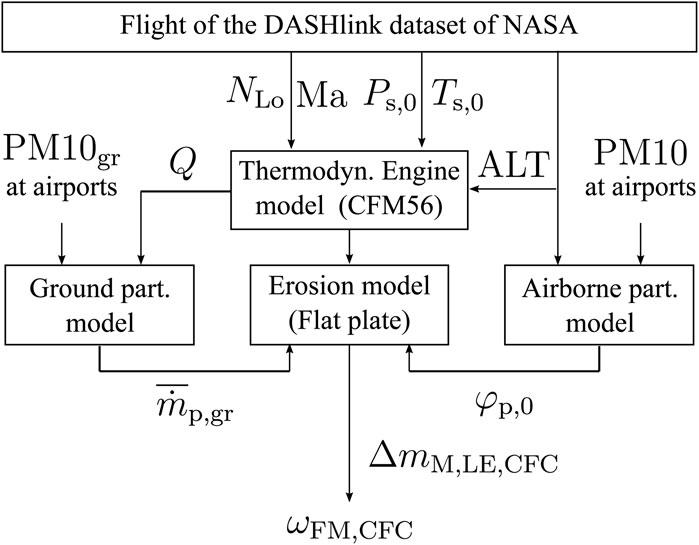
Engine maintenance constitutes a relevant part of the operating costs of airlines (International Air Transport Association). The work scope, cost, and timing of the engine maintenance actions depend, among others, on the type of engine, its distance from the ground, the way it is operated, and the environment in which it is operated. All these contribute to deterioration mechanisms such as erosion, fouling, corrosion, and abrasion, simultaneously interacting in a complex way (Saravanamuttoo, 1994; Kurz and Brun, 2000; Hamed et al., 2006). Together with a limited base of in-service data, this made the derivation of cause–effect relationships difficult for a long time. Consequently, a model-based prediction of engine maintenance type and intervals is still a challenge. Today, the increased amount of digitally available data, such as Automatic Dependent Surveillance—Broadcast (ADS-B) or Continuous Engine Operational Data (CEOD), provides additional details of individual aircraft operations. This stipulates the generation of so-called digital twins, which duplicate the real existing engine throughout its service life by a digitally created model representing its time-dependent characteristics (Klein et al., 2022). In doing so, the digital twins combine suitable analytical, numerical, and artificial intelligence models, providing useful information about the system state that is not accessible through data analysis. The requirement to predict the service life of whole fleets of engines in acceptable computational times makes computationally efficient modeling indispensable. The outcome of the digital twin used is a comparison of flight missions (FMs) in terms of their severity, i.e., the degree of hardware deterioration experienced by the engines during these missions.
The impact of the engine installation on the experienced severity is indicated in Richardson et al. (1979). In this study, it is reported that the elevated center engine of McDonnell Douglas DC-10 aircraft experiences a reduced rate of deterioration compared to the engines mounted under the wings. With the type of engine and its installation being fixed for a particular aircraft type, the severity of a flight mission will depend on its operational details and ambient conditions. Hence, the fixed installation aspects and the varying operational factors have to be discussed separately. This is demonstrated using solid particle erosion as an example for the deterioration mechanism, which has been widely investigated experimentally and numerically. Flat plate experiments provide an established source of empirical data for solid particle erosion. Dimensional analysis (Lorenz et al., 2022) shows that applying the erosion data derived from flat plate experiments to the computation of the material loss during a mission for a given combination of solid particles and engine part materials requires the following components:
1. A statistically relevant number of impacts on a flat plate surface element
2. A suitable relation of the surface setback to the particle size
3. A suitable relation of the surface elements to the particle size
4. A representative impact angle
5. A representative kinetic energy of the impacting particle.
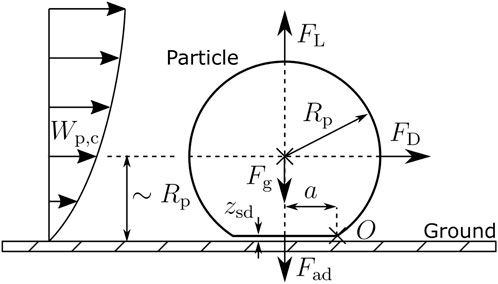
The numerical investigation of the erosion severity requires modeling three basic processes involved with solid particle erosion of turbofan engines. The first process embraces all aspects influencing the ingestion of particles by the engine. The second process is the transport of the particles in the working fluid within the engine. The third process is the impact of the particles on the gas path surfaces, including its consequences for the surface and the particles. The process of engine wear by solid particle erosion thus begins with the transport of particles from their original position in the engine’s environment into the engine’s inlet. During airborne flight segments, only particles suspended in the air can be ingested. However, during flight segments performed on the ground, both particles dissolved in the air and particles lying on airport pavements can be ingested by the engine. This leads to the question about the importance of runway and taxiway particle ingestion to aircraft engine compressor deterioration. Early experimental investigations show that the engine height above the ground, engine power setting, and atmospheric circulation are key to the formation of vortices extending from the inlet to the ground surface and that the surface structure plays a decisive role in the lifting of objects from the surface (Rodert and Garrett, 1955). The factors influencing the lifting force on an object lying on the surface have been investigated in Glenny and Pyestock (1970) based on the system shown in Figure 1A. Dimensional analysis of this system resulted in the approximate nondimensional expression shown in Equation 1.
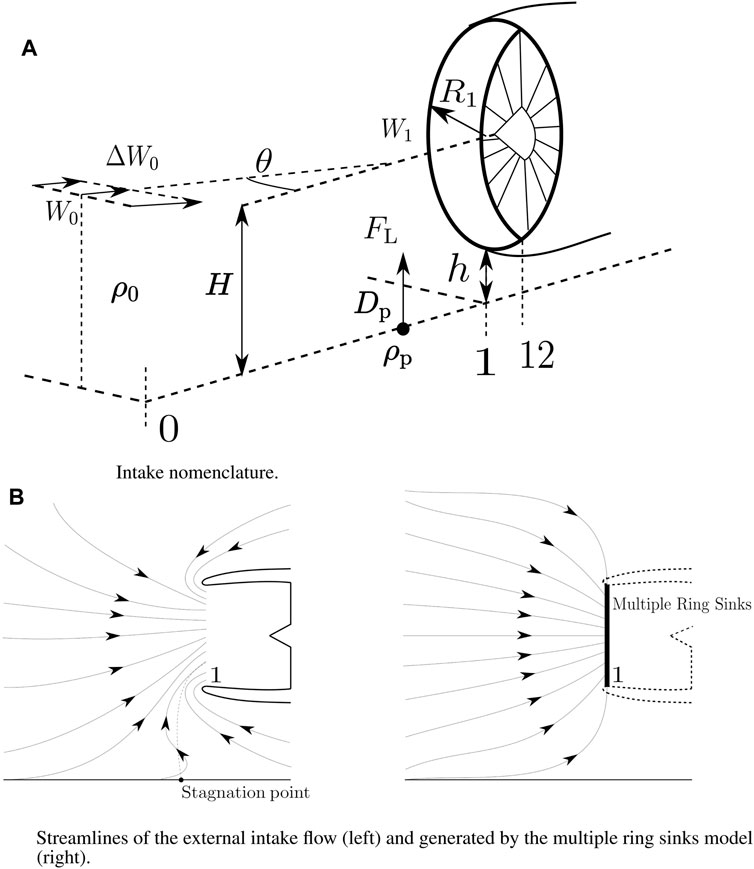
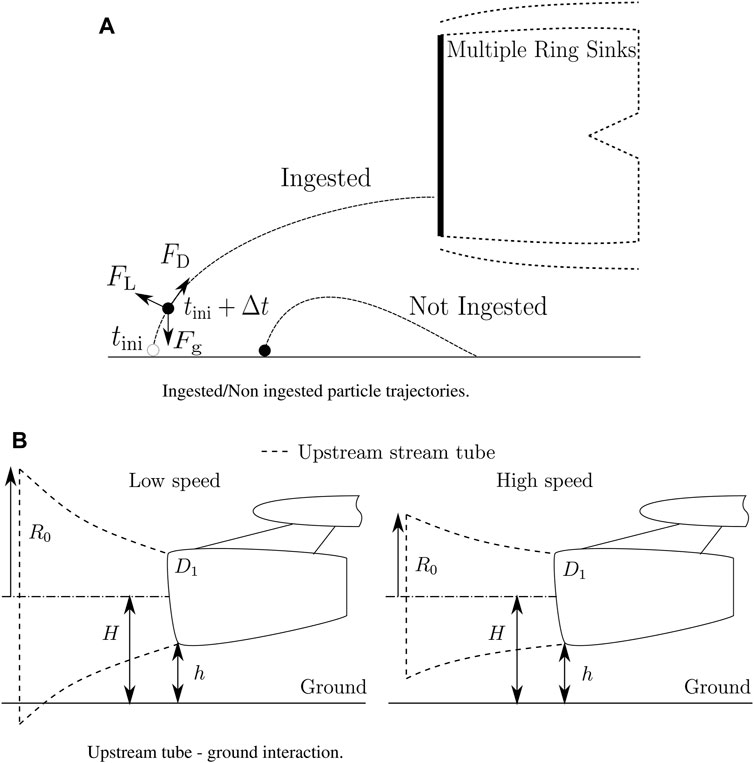
Figure 1. (A) Intake nomenclature. (B) Streamlines of the external intake flow (left) and generated by the multiple ring sink model (right).
Hence, it is postulated in Glenny and Pyestock (1970) that high-bypass ratio engines featuring large inlet diameters
2 Digital twin model
The applied fast computing engine digital twin model is documented in Brandes et al. (2021a); Scarso et al. (2022). Its general structure is shown in Figure 2. It is generated using state-of-the-art performance synthesis and compressor mean line methods. The performance synthesis model represents an engine similar to a CFM56 engine (Brandes et al., 2021b). Performance synthesis is run à priori to give a table of engine non-dimensional parameters. Similarly, the compressor mean line model is run à priori to derive a set of compressor non-dimensional inter-blade row data, including flow angles and velocities. For a given flight condition and power setting, the engine model provides all gas path parameters needed to compute the mission severity parameter of the core flow compressors. The power setting is commanded by an aircraft model at every point of the flight mission. The non-dimensional low-pressure shaft speed
It is assumed that all solid particles ingested by the engine are like Arizona Road Dust (
3 Air velocity field around and in the engine intake
A typical streamline pattern of the external intake airflow is shown in Figure 1B. This is the result of the intake geometry, the position of the intake relative to the ground, the power setting of the engine, and a potential cross-wind. The streamline pattern is not symmetric because of the proximity to the ground and the intake/nacelle shape. It has a stagnation point on the ground with the corresponding stagnation streamline. The flow to the right-hand direction of the stagnation streamline is flowing opposite to the main intake flow direction and features high curvature at the intake lip. The flow to the left of the stagnation streamline follows the main intake flow direction and is characterized by a lower degree of curvature. The numerical computation of this flow field with high spatial resolution is not suitable in the context of digital twin modeling. Modeling the intake velocity field around the engine intake through a potential flow generated by
It is assumed that air density and axial velocity are evenly distributed at the intake throat. Hence, the volumetric air mass flow,
The multiple ring sinks absorb airflow from all directions. To model the flow through the intake contour, only the forward half of the absorption by the multiple ring sinks is included. With these assumptions, the volumetric mass flow satisfies Equation 4.
Since the inlet velocity
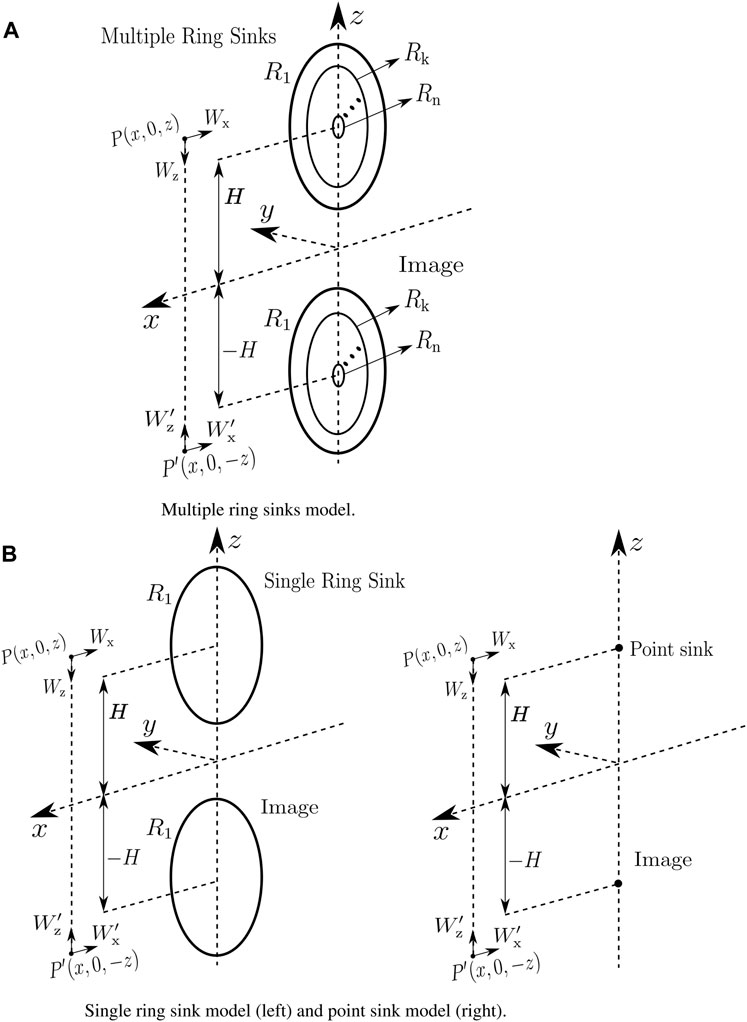
Figure 3. (A) Multiple ring sink model. (B) Single-ring sink model (left) and point sink model (right).
According to Hess and Smith (1967), this results in the velocity potential
The predicted and measured air velocities along the intake centerline
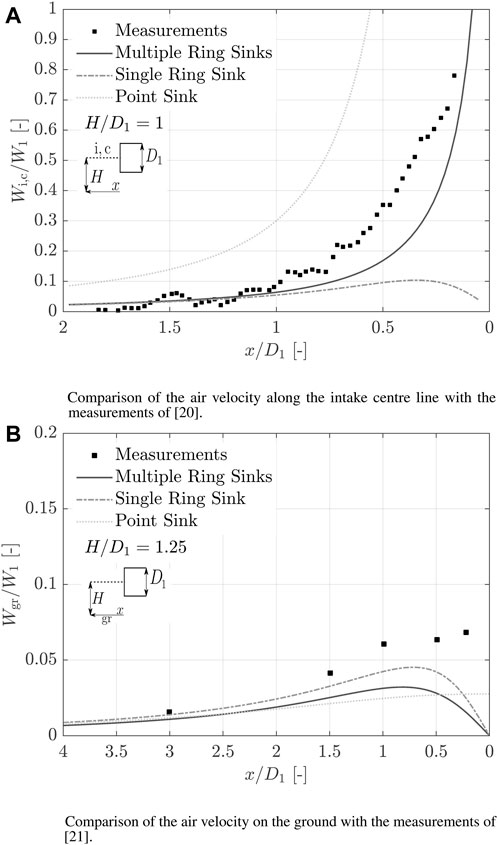
Figure 4. (A) Comparison of the air velocity along the intake center line with the measurements by Secareanu et al. (2005). (B) Comparison of the air velocity on the ground with the measurements of Colehour and Farquhar (1971).
4 Particle detachment model
The particles lying on the ground are assumed to be Arizona Road Dust
The gravity force is given by Equation 8, with
According to El-Batsh (2001), the drag force acting on a small spherical particle is given in Equation 9. As shown in Figure 5, the flow velocity
In Equation 9,
The Knudsen number
The lifting force
Assuming a linear velocity profile, the velocity gradient
The surface energy per unit area,
where
The considered values and references are reported in Table 1. The radius
where the composite Young’s modulus of the asphalt surface and the silica particle is given by Equation 17
The Poisson’s ratio
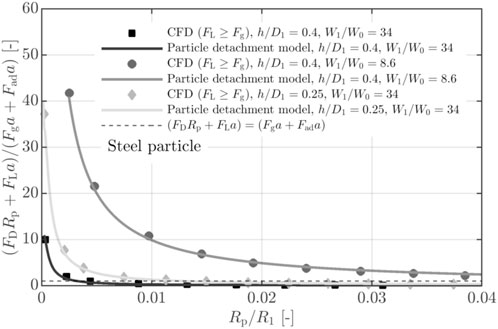
Figure 6. Comparison of the particle detachment model with that of MacManus and Slaby (2015).
5 Particle trajectory
The trajectory of a particle picked up by the intake flow from the ground is crucial for determining whether this particle is ingested into the engine. It is assumed that the particle does not bounce after being detached from the ground and that the lifting force is constant and acting on the particle for a distance equal to its radius
From Equation 18, the amount of the initial lifting velocity perpendicular to the ground surface
Once a particle is detached from the ground, its motion in a three-dimensional flow field is represented using the Boussinesq–Basset–Oseen equation. For particles of a density three or more orders of magnitude greater than the fluid density, the three-dimensional change in the velocity vector
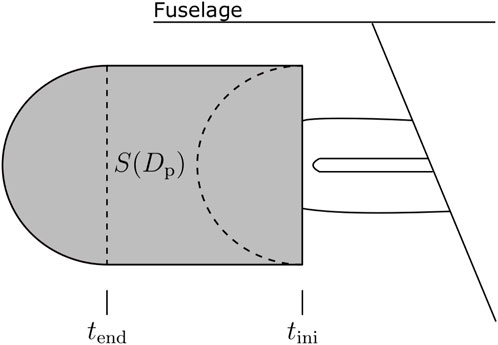
The ingestion fraction (
6 Amount of the runway and taxiway particles ingested
In static ground operation, the upstream stream tube of the intake flow is intersected by the ground surface, as shown in Figure 1B. With static ground operation marking the starting point
For each operating point, from the starting point
7 Impact of the engine power setting on the maximum size of ingested particles
The maximum ingested particle size at take-off and idle power settings is investigated for a non-moving aircraft. The engine volume flow
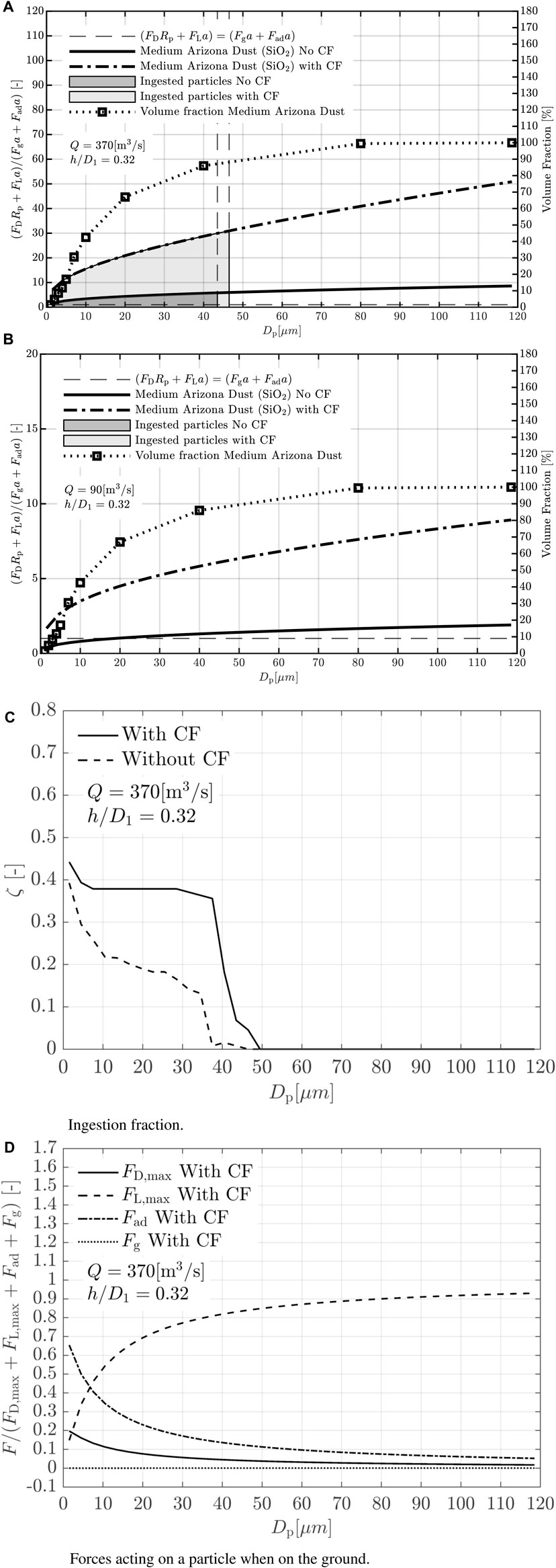
Figure 9. (A) Maximum ingested particle diameter during take-off. (B) Maximum ingested particle diameter during taxi. (C) Ingestion fraction. (D) Forces acting on a particle when on the ground.
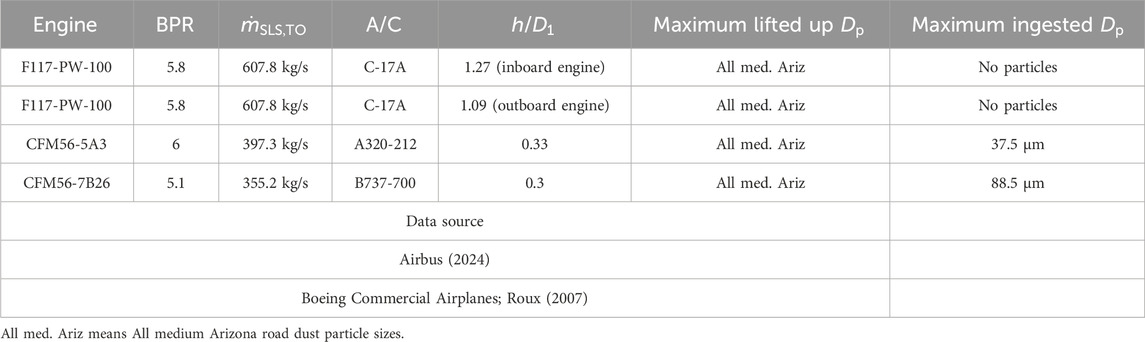
8 Impact of engine position on the maximum ingested particle diameter
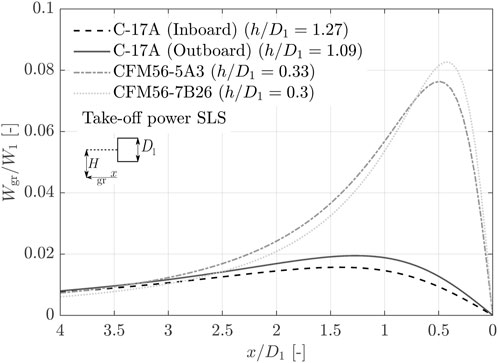
The impact of engine position on the maximum ingested ground particle size is investigated using three engines with varying heights above the ground. The analysis assumes a maximum power setting at sea level static (SLS) operation. Publicly available data for these engines and their installations are provided in Table 2. Among the engines considered, one is mounted on a high-wing aircraft configuration (F117-PW-100 mounted on the C-17A). For this engine, both inboard and outboard positions on the wing are examined. Additionally, two other engines are considered, representing a low-wing aircraft configuration: the CFM56-5A3 mounted on the A320-212 and the CFM56-7B26 mounted on the B737-700. For the high-wing aircraft engine positions, no runway and taxiway particles are ingested even if all particle sizes of the medium Arizona Road Dust are lifted up from the ground (see Table 2). This is due to the high nondimensional engine height
9 Impact of ground particles on the mission severity
The model described in Sections 3–5 is applied to a single flight mission considering different levels of ground particle concentrations
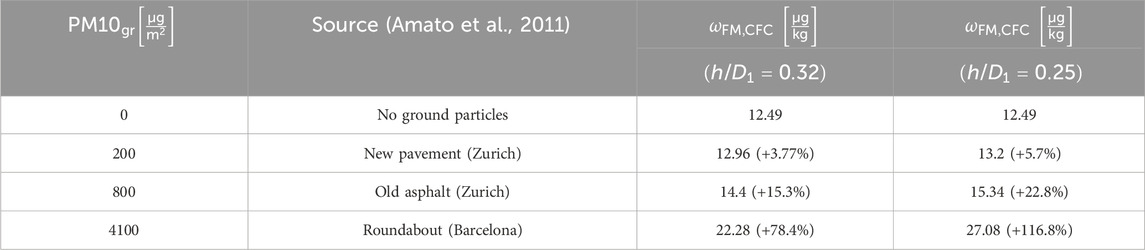
Table 3. Flight mission severity parameter calculated for one mission with different ground particle concentrations and two different
10 Impact of ground particles on flight segment severity
The severity of segments from a sample of 100 flight missions from NASA’s DASHlink dataset has been investigated. These missions, all operated by the same aircraft in 2002, occurred between various airports across the United States. The distance between departure and arrival airports is maintained at under 1,000 km (540 NM) to ensure that the severity experienced during ground operations, where ingestion of taxiway and runway particles is a concern, remains significant. Engine conditions are kept constant across all missions to prevent erosion accumulation and chord length reduction between flights. Suspended particle concentrations during the missions are calculated using the exponential altitude dependency as described in Hobbs (1993), scaled with daily PM10 levels at the departure and arrival airports to provide a realistic variation of suspended particle concentrations. Figure 11 shows the severity of each flight segment for the 100 sampled missions. All the departure and arrival airports of the selected missions are assumed to have PM10 ground particle load of either
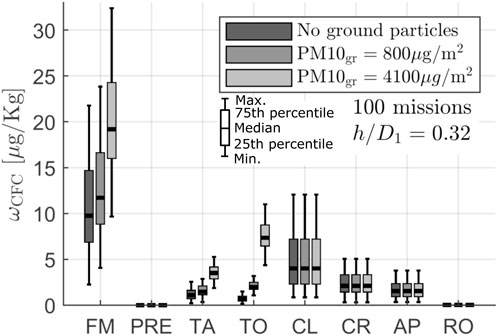
Figure 11. Impact of the flight segment on the mission severity parameter. The severity parameters calculated for the entire FM are shown on the left side.
11 Conclusion
It has been demonstrated that a simplified ingestion model of the taxiway and runway particles is suitable for investigating flight mission severity with regard to core flow compressor erosion. Its computational efficiency allows for the investigation of numerous missions in a short time, making it suitable for integration with a digital twin model. However, the model may underestimate the number of particles ingested due to its limited ability to reflect the complex inlet flow features such as ground vortices generated from viscous effects. The application of this model reveals that mission severity with regard to core compressors is affected by the ingestion of taxiway and runway particles. Key impacting factors include ground particle concentrations, engine height above the ground, and power settings. It is found that ground particles are ingested during take-off acceleration only. For very high ground particle concentrations, the influence of the take-off segment on overall mission severity becomes significant for engines operating flights traveling less than 1,000 km (540 NM). Thus, the ground particle concentration is a crucial boundary condition for understanding engine deterioration due to solid particle erosion.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.
Author contributions
SSc: conceptualization, investigation, methodology, validation, visualization, writing–original draft, and writing–review and editing. SSt: conceptualization and writing–review and editing. JM: writing–review and editing. NS: writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The project on which this paper is based was funded by MTU Aero Engines Holding AG.
Acknowledgments
The authors are grateful to MTU Aero Engines for insightful assistance and for funding this research project. The authors acknowledge the American Project Discovery in Aeronautics Systems Health (DASHlink) of the National Aeronautics and Space Administration (NASA) for the allowance to use their datasets to underpin this research. The authors would also like to acknowledge the United States Environmental Protection Agency (EPA) and the website Visual crossing for their availability to provide the vital data for this research.
Conflict of interest
Author JM was employed by MTU Aero Engines AG. Author NS was employed by MTU Maintenance Hannover GmbH.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Airbus (2024). A320 aircraft characteristics airport and maintenance planning. Available at: https://aircraft.airbus.com/en/customer-care/fleet-wide-care/airport-operations-and-aircraft-characteristics/aircraft-characteristics (Accessed March 16, 2024).
Amato, F., Pandolfi, M., Moreno, T., Furger, M., Pey, J., Alastuey, A., et al. (2011). Sources and variability of inhalable road dust particles in three european cities. Elsevier Atmos. Environ. 45 (37), 6777–6787. doi:10.1016/j.atmosenv.2011.06.003
Boeing Commercial Airplanes Airplane characteristics for airport planning. Available at: https://www.boeing.com/commercial/airports/plan-manuals (Accessed March 16, 2024).
Brandes, T., Koch, C., and Staudacher, S. (2021b). Estimation of aircraft engine flight mission severity caused by erosion. J. Turbomach. 143 (11), 2021. doi:10.1115/1.4051000
Brandes, T., Scarso, S., Koch, C., and Staudacher, S. (2021a). “Data-driven analysis of engine mission severity using non-dimensional groups,” in Proceedings of ASME Turbo Expo 2021: tirtual eonference. GT2021-58673.
Colehour, J. L., and Farquhar, B. W. (1971). Inlet vortex. J. Aircr. 8 (1), 39–43. doi:10.2514/3.44224
Das, S. K., Sharma, M. M., and Schechter, R. S. (1995). Adhesion and hydrodynamic removal of colloidal particles from surfaces. Part. Sci. Technol. 13 (3-4), 227–247. doi:10.1080/02726359508906680
El-Batsh, H. (2001). Modeling particle deposition on compressor and turbine blade surfaces. Vienna: Vienna University of Technology. [Dissertation].
Glenny, D. E., and Pyestock, N. G. T. E. (1970). Ingestion of debris into intakes by vortex action. Ministry of technology. London: Aeronautical research council, C.P.1114.
Hamed, A., Tabakoff, W. C., and Wenglarz, R. V. (2006). Erosion and deposition in turbomachinery. J. Propuls. Power 22 (2), 350–360. doi:10.2514/1.18462
Hess, J. L., and Smith, A. M. O. (1967). Calculation of potential flow about arbitrary bodies. Elsevier Prog. Aerosp. Sci. 8, 1–138. doi:10.1016/0376-0421(67)90003-6
Hinds, W. C., and Zhu, Y. (1998). Aerosol technology: properties, behavior, and measurement of airborne particles. Chem. Environ. Health Saf.
Hobbs, P. V. (1993). Aerosol-cloud-climate interactions. 1st ed. San Diego, California (USA): Academic Press, Inc.
Hooi, C. G., Lagor, F. D., and Paley, D. A. (2015). Flow sensing, estimation and control for rotorcraft in ground effect. MT (USA): IEEE Aerospace Conference, Big Sky.
International Air Transport Association Airline maintenance cost executive commentary FY2022 data. Available at: https://www.iata.org/(Accessed March 16, 2024).
Klein, M., Staudacher, S., Abu-Taa, K., and Schwengler, J. (2022). Digital service twin to assess engine deterioration and remaining part life. Rotterdam, Netherlands: Proceedings of ASME Turbo Expo. GT2022-82113.
Kurz, R., and Brun, K. (2000). Degradation in gas turbine systems. Munich, Germany: Proceedings of ASME Turbo Expo.
Leighton, D., and Acrivos, A. (1985). The lift on a small sphere touching a plane in the presence of a simple shear flow. J. Appl. Math. Phys. (ZAMP) 36, 174–178. doi:10.1007/bf00949042
Li, Q., Rudolph, V., and Peukert, W. (2006). London-van der Waals adhesiveness of rough particles. Elsevier Powder Technol. 161 (3), 248–255. doi:10.1016/j.powtec.2005.10.012
Lorenz, M., Klein, M., Hartmann, J., Koch, C., and Staudacher, S. (2022). Prediction of compressor blade erosion experiments in a cascade based on flat plate specimen. Front. Im. Mech. Eng. 8. doi:10.3389/fmech.2022.925395
Lyne, Å. L., Krivosheeva, O., and Birgisson, B. (2013). Adhesion between bitumen and aggregate: implementation of spectroscopic ellipsometry characterisation and estimation of hamaker’s constant. Mater. Struct. 46 (10), 1737–1745. doi:10.1617/s11527-012-0012-2
MacManus, D. G., and Slaby, M. (2015). Intake ground vortex and computational modelling of foreign object ingestion. Aeronauticla J. 119 (1219), 1123–1145. doi:10.1017/s0001924000011167
Nakayama, A., and Jones, J. R. (1996). Vortex formulation in inlet flow near a wall. Reno, Nevada (USA): AIAA 34th Aerospace Sciences Meeting and Exhibit.
NASA Dashlink sample flight data. Available at: https://c3.nasa.gov/dashlink/projects/85/(Accessed March 16, 2024).
Richardson, J. H., Sallee, G. P., and Smakula, F. K. (1979). “Causes of high pressure compressor deterioration in service,” in 15th Joint Propulsion jonference, pas cegas (USA: Nevada).
Rivera, J. L., Sutherland, J. W., and Allen, J. S. (2013). Lift-off behavior of micro and nanoparticles in contact with a flat surface. J. Fluids Eng. 135 (10), 1–6. doi:10.1115/1.4024563
Rodert, L. A., and Garrett, F. B. (1955). Ingestion of foreign objects into turbine engines by vortices. NACA TN: National Advisory Committee for Aeronautics.
Saravanamuttoo, H. I. H. (1994). “Erosion, corrosion and foreign object damage in gas turbines,” in AGARD-CP-558 (Rotterdam ,Netherlands: North Atlantic Treaty Organization). Technical Evaluator’s Report.
Scarso, S., Staudacher, S., Keller, C., and Mathes, J. (2022). Mission severity assessment based on 1hz engine data. Rotterdam, Netherlands: Proceedings of ASME Turbo Expo. GT2022-80923.
Secareanu, A., Moroianu, D., Karlsson, A., and Fuchs, L. (2005). Experimental and numerical study of ground vortex interaction in an air-intake. Reno, Nevada (USA): 43rd AIAA Aerospace Sciences Meeting and Exhibit.
Soltani, M., and Ahmadi, G. (1994). On particle adhesion and removal mechanisms in turbulent flows. J. Adhesion Sci. Technol. 8 (7), 763–785. doi:10.1163/156856194x00799
Tsai, C. J., Pui, D. Y. H., and Liu, B. Y. H. (1991). Elastic flattening and particle adhesion. Aerosol Sci. Technol. 15 (4), 239–255. doi:10.1080/02786829108959531
United States Environmental Protection Agency (EPA) Air quality index daily values report. Available at: https://www.epa.gov/outdoor-air-quality-data/air-quality-index-daily-values-report (Accessed March 16, 2024).
Vincent, B. (1973). The van der Waals attraction between colloid particles having adsorbed layers. II Calculation of interaction curves. J. Colloid Interface Sci. 42 (2), 270–285. doi:10.1016/0021-9797(73)90290-7
Xu, L. Typical values of Young’s elastic modulus and Poisson’s ratio for pavement materials. Available at: https://www.academia.edu/15702729 (Accessed March 16, 2024).
Zoeteweij, M. L., van der Donck, J. C. J., and Versluis, R. (2009). Particle removal in linear shear flow: model prediction and experimental validation. J. Adhesion Sci. Technol. 23 (6), 899–911. doi:10.1163/156856109x411247
Nomenclature
Keywords: digital twin, erosion, compressor deterioration, runway and taxiway particles, engine deterioration, particle ingestion
Citation: Scarso S, Staudacher S, Mathes J and Schwarz N (2024) A model to assess the importance of runway and taxiway particles to aircraft engine compressor deterioration. Front. Mech. Eng. 10:1420472. doi: 10.3389/fmech.2024.1420472
Received: 20 April 2024; Accepted: 30 July 2024;
Published: 22 August 2024.
Edited by:
Zhigang Zuo, Tsinghua University, ChinaReviewed by:
Zhiyi Yu, Beijing Institute of Technology, ChinaDavid John Rajendran, Cranfield University, United Kingdom
Copyright © 2024 Scarso, Staudacher, Mathes and Schwarz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefano Scarso, c3RlZmFuby5zYzk1QGdtYWlsLmNvbQ==
 Stefano Scarso
Stefano Scarso Stephan Staudacher
Stephan Staudacher Jürgen Mathes2
Jürgen Mathes2