Analysis of the wake mechanism in external flow around tandem bluff bodies with different aspect ratios

The interaction mechanism of external flow with two inline rectangular cylinders having different aspect ratios under the impact of gap spacing (G) is the subject of this research. The gap spacing between the cylinders was varied from 0.25 to 20 times their size. Both cylinders were vertically mounted, with the first having a higher aspect ratio than the second. The results revealed five distinct flow patterns under the influence of G: single slender body, shear layer reattachment, intermittent shedding, binary vortex street, and single-row vortex street. The mean pressure on both cylinders was found to vary due to changes in flow patterns. Both cylinders bore the same shedding frequency but had different pressure variations. The second cylinder placed in the wake of first experienced negative average drag force for some spacing values, while the first cylinder had positive average drag values for all chosen G. Due to the change in flow pattern from shear layer reattachment to intermittent shedding flow, the negative drag force on the second cylinder jumped to a positive drag. It was also observed that the rms values of drag and lift force coefficients, as well as their amplitudes for the second cylinder, were mostly higher than corresponding values for the first cylinder at all selected G. This study revealed that G = 4 and 8 are the critical gap spacing values due to sudden changes in fluid force parameters.

1 Introduction

Computational fluid dynamics (CFD) is an interesting, complex, state-of-the-art field due to the rapid development of computer technology and newly developed numerical techniques and programming languages. One of the most significant aspects of CFD is the analysis of fluid–solid interactions and resulting outcomes. Much research has examined fluid flow around bluff bodies (commonly termed “cylinders”). The study of the wake structure mechanism behind cylindrical objects is important to many practical applications in various engineering disciplines. For example, such cylindrical objects appear in most civil designs, such as high-rise buildings, chimneys, suspension bridges, and many internal and external supporting components of such structures. Electronic chips are mostly rectangular/square in cross section, thus resembling rectangular cylinders. The flow mechanism and characteristics behind these objects depend on parameters such as the blockage ratio (B), Reynolds number (Re), inflow velocities, shape, size, arrangement, and quantity of structures in the flow field.

Many numerical and experimental studies relevant to circular and rectangular/square cylindrical structure flow characteristics are apparent from the literature. Mittal and Raghuvanshi (2001) conducted numerical analysis of vortex shedding behind circular cylinders for laminar flows by considering Re ranging from 60 to 100. They found that, as the Re increases the average drag coefficient (CD_mean) decreases while the Strouhal number (St) increases. Belloli et al. (2014) experimentally analyzed flow around circular cylinders at high Re up to 6 × 10⁵ and found that drag was approximately 0.85 for the flat surface conditions at Re = 10⁵ and dropped to 0.3 at Re = 2.5 × 10⁵. Kuzmina and Marchevsky (2021) simulated flow interactions with circular cylinders by considering Re ranging from 20 to 200. The two flow regimes they observed were i) stable, where the flow was symmetric, and ii) vortex shedding, where they observed the von Karman vortex street. Furthermore, the separation point changed with a variation in Re. Comparing the fluid flow features, it is apparent that the circular cylinder displayed an unfixed boundary layer detachment, but the square/rectangular cylinder displayed a stable detachment point only from its edges. Due to this detachment phenomenon, the flow modes and wake structure mechanism differ in both geometries. Zhang and Zhang (2012) analyzed low-Re flow past a square cylinder that ranged from 25 to 150. They found two stable symmetric vortices behind the cylinder at Re = 25 and 50, indicating steady flow. They also found that pressure gradually rose while moving toward the cylinder from the inlet and dropped in the down-wake area. Perumal et al. (2012) studied the flow around a single square cylinder by considering Re ranging from 4 to 150. They found laminar, steady, and slightly separated flow from the cylinder at extremely low Re. At higher Re, the flow split into a pair of symmetrical vortices about the channel central line. They also observed that the flow appeared uniform at low B while, for moderated B = 10, an instability developed within the flow field for Re = 51. Ahmad et al. (2021) analyzed the flow characteristics around a rectangular cylinder at low aspect ratios (AR) and Re. They found that, for AR = 0.05, the vortex formed instantly behind the back surface of the cylinder. They also reported the sinusoidal nature of drag coefficient (CD) for all AR. Islam et al. (2012) conducted numerical simulations of rectangular cylinder flows with distinct aspect ratios by considering Re = 100, 150, 200, and 250 and AR varying from 0.15 to 4. They observed that the results for AR = 0.15 at Re = 100 indicated dual parallel rows of clockwise and anticlockwise vortices. At AR = 0.5, the vortices appeared at the top and bottom sides of the cylinder for a shorter duration. Octavianty et al. (2016) experimentally studied the radiation of sound and flow structure around a rectangular cylinder at various Re and AR with Mach numbers ((Ma) below 0.16. According to this research, the vortex formation region was extremely close to the back surface of the cylinder where the maximum spectrum line (SPL) occurred.

In the case of multiple obstacles, gap spacing (G) is another important parameter which significantly affects flow characteristics. Several studies have examined the combined effects of Re and G on fluid flows around two inline circular or square or rectangular cylinders (Shiraishi et al., 1986; Su et al., 2002; Su et al., 2004; Kuo et al., 2008; Huang et al., 2012; Mithun and Tiwari, 2014; Gnatowska et al., 2020; Rajpoot et al., 2021; Shui et al., 2021; Wang et al., 2022). Important findings of these studies are highlighted in Table 1. From fluid–solid interaction analyses in the literature, it is well-known that bluff bodies of similar dimensions, if arranged differently, such as side-by-side, staggered, or tandem to the incoming flow, have significant differences in fluid force behavior as well as near wakes formed behind them. Chakraborty et al. (2022) analyzed the influence of gap spacing on flow past two circular cylinders placed side by side by considering Re = 5 × 10⁵ and G = 2 to 14. They observed that the pressure at the front of both cylinders was greater than the pressure on the back, resulting in a positive drag force for all G. Sarvghad et al. (2011) also conducted a numerical simulation of flow over similarly arranged cylinders by considering Re = 100 and 200 and 1.5 $\le$ G $\le$ 4. They categorized the flow in different patterns they termed biased flow, flip-flopping, synchronized anti-phase vortex shedding, and in-phase asymmetric. Adeeb et al. (2018) observed the flow around two side-by-side square cylinders by considering Re = 100, G = 1.5 to 5, and corner radii (R/D) = 0 to 0.5. They observed that, for 0 $\le$ R/D $\le$ 0.5, at G $\le$ 1.5, the wake of both cylinders joined and functioned as an isolated wake structure for all R/D choices. Ma et al. (2017) analyzed the wake of two side-by-side square cylinders at Re in the range of 16–200 and G = 0 to 10. It was found that, when Re was low, the wake flow after both cylinders was steady state. When Re increased, the recirculation bubbles appeared within the downstream region attached with cylinders. These bubbles grew as unstable modes and dominated the steady mode. The flow became transient and vortex shedding was then observed. Burattini and Agrawal (2013) observed the interaction of wakes of two square cylinders placed side by side by considering Re = 73 and G = 0.5 to 6. It was reported that, with changing G, vortex shedding was much affected. Lee et al. (2019) reported an isolated bluff-body flow pattern for G $\le$ 0.5, an asymmetric wake flow pattern for 0.75 $\le$ G $\le$ 1.25, a transitional flow pattern for 1.5 $\le$ G $\le$ 1.75, and a dual street flow pattern for G $\ge$ 2 for flow-past rectangular cylinders arranged side by side. Fluid flow-past staggered cylinders strongly depended on G and inclination angle ($\alpha$) between cylinders. Ye et al. (2019) observed flow induced vibrations in the case of two circular cylinders in a staggered configuration at Re = 200, G = 5 to 7 with $\alpha$ = 0$°$ to 90 $°$. They reported that, at G = 5, the vortices’ generation and attachment with the second cylinder was much influenced by an inclined angle of 0$°$ to 35$°$ ; however, for an inclined angle beyond these values, the flow structure was not much varied. Aboueian and Sohankar (2017) numerically analyzed the shedding frequency in the case of flow past two staggered square cylinders by considering Re = 150, G = 0.1 to 6, and $\alpha$ = 45$°$. They reported that the variations in gap spacing are directly related to the shedding frequencies. According to Alam et al. (2016), the wake flow around two staggered square cylinders is very dependent on the angle of inclination between cylinders. Small angles greatly impact flow characteristics, while larger angles more weakly influence flow characteristics.

TABLE 1

TABLE 1. Fluid flow characteristics around two bluff bodies reported in literature.

When multiple objects (more than two) appear in the fluid flow stream, the resulting forces and flow structure may significantly differ from those seen in case of two or a single body even at the same Reynolds number or gap spacings. Alam et al. (2017) observed the flow around three tandem circular cylinders by considering Re = 200, gap spacing between first and second cylinder (G₁) = 3.5 to 5.25, and gap spacing between the second and third cylinder (G₂) in the range 3.6–5.5. They categorized the flow structures as in-phase, antiphase, and intermediate, depending on G₁ and G₂. Eizadi et al. (2022) analyzed the transitions in the wake of six circular obstacles placed inline at Re = 40 to 180 and G = 0.5 to 18. They concluded that wake transitions of multiple cylinders depend not only on Re but also on G. Song et al. (2017) observed the flow patterns and force variations over four inline square cylinders by considering Re = 300 and G = 1.5 to 8. They reported that, when G $<$ 3.5, CD_mean values for the downstream cylinders increased sharply with increasing G. For G > 3.5, the CD_mean values of the downstream cylinders decreased gradually with increasing G. Islam et al. (2018) investigated different aspect ratio effects on the flow around three inline cylinders at Re = 150, AR = 0.25 to 3, and G = 0.5 to 7. They observed that, at all G, the CL_rms of all cylinders decreased with increasing AR. Rahman et al. (2021) numerically computed the forces on three rectangular cylinders by considering 60 $\le$ Re $\le$ 180, AR = 0.25 to 4, and G = 1.5. They reported that the shedding frequencies of all cylinders increased while CD_mean decreased due to the increase in AR at all Re.

Studies describing the fluid flow around other geometries like airfoils have also been conducted (Bajalan et al., 2011; Mirzaei et al., 2012; Rangan and Santanu Ghosh, 2022; Abdolahipour, 2023). Another aspect of fluid–solid interactions is flow control around bluff bodies. Utilizing flow control strategies, efficient devices have been designed to save energy by minimizing flow-induced forces and controlling wake flow structures. Among various available flow controlling strategies, flow control through modulated pulse jet (Abdolahipour et al., 2021; Abdolahipour et al., 2022) and plasma actuator (Salmasi et al., 2013; Mohammadi and Taleghani, 2014; Taleghani et al., 2018) are frequently studied by researchers.

It can be concluded from this literature that the flow characteristics of multiple bodies are influenced by many parameters, including Re, G, B, AR, and $\alpha$. Among these, fluid flows around rectangular bodies have been less investigated, especially vertically mounted bodies. Information about cases when both cylinders have different AR is very rare. From an application point of view, bluff bodies with rectangular cross sections are particularly important because, for example, most civil structures have rectangular cross sections and are vertically assembled. Electronic devices mostly have rectangular cross-sectional internal components. Flow around such bodies differs from flow around circular/square cross-sectional bodies. Hence, the current study will explore the fluid flow characteristics around two tandem rectangular bodies with different aspect ratios. The main focus will be on the effects of aspect ratios and varying gap spacing between cylinders on vorticity patterns, pressure variations, streamline behavior, and variations in fluid forces behavior. This study will also enhance our understanding of the dependence of the flow characteristics of both bodies on each other. Furthermore, it will help in designing flow control strategies for similar bodies placed in cross flows.

2 Numerical method

The current analysis utilizes the well-known numerical methodology, the lattice Boltzmann method (LBM). The simplified nature, easy implementation, and accuracy features of LBM make it more suitable than conventional methods for simulating fluid dynamics problems (Mohammad, 2011). This method involving two main steps, streaming and collision, has several advantages over the Navier–Stokes (NS) solvers. It has an explicit nature with conditional stability conditions (Chen and Doolen, 1998). The nonlinearity appearance in the case of NS equations does not appear in this method because the Boltzmann equation (BE) is quasi-linear. Pressure can be obtained through a simple procedure from the equation of state instead of dealing with the Laplace equation in each time step. LBM contains a variety of discrete models for simulating fluid flows. The current study is based upon the well-known two-dimensional nine-velocity directions (D2Q9, D indicates dimensions and Q the number of velocity directions) model (Figure 1) (Sukop and Throne, 2006).

FIGURE 1

FIGURE 1. D2Q9 lattice model.

The discrete BE along a specified direction is

$\frac{\partial f}{\partial t}+e_i\nabla f_i=\frac{1}{\tau }\left(f_i^{eq}-f_i\right),(1)$

where $t$ = time, $f_i$ = distribution function, $\tau$ = parameter for relaxation time, and $f_i^{eq}$ = the equilibrium distribution function.

After discretization through finite differencing, the lattice Boltzmann equation (LBE) takes the following form:

$f_i\left(x+∆x,t+∆t\right)=-\omega \left[f_i\left(x,t\right)-f_i^{eq}\left(x,t\right)\right],(2)$

where $\omega =\frac{∆t}{\tau }$, $\tau$ is the relaxation time, and $∆t$ = $∆x$ = 1 (Wolf-Gladrow, 2000).

For the current study, the following form of $f_i^{eq}$ is considered:

$f_i^{eq}=\rho w_i\left[1+3\left(e_i.u\right)-\frac{3}{2}{u}^2+\frac{9}{4}{\left(e_i.u\right)}^2\right],(3)$

where $\rho$ is density, u is fluid velocity, and $w_i$ are weighting coefficients (see Table 2).

TABLE 2

TABLE 2. Weighting coefficients for the D2Q9 model.

Here, w₀ are weight-associated with rest particle, w_a are weights for particles moving along the axis, and w_d are weights for particles moving diagonally.

Density and velocity are expressed in terms of $f_i$ as

$\rho ={\sum }_{i=0}^{i=n}{f}_i,(4)$

$\rho u={\displaystyle \sum _{i=0}^{i=n}}{e_{i}f}_i.(5)$

The fluid kinematic viscosity is expressed as

$\nu =\frac{\left(2\tau -1\right)}{6}.(6)$

The values of $e_i$ are given as

$e_i=\left\{\begin{array}{l}\left(0,0\right),i=0,\\ c\left(-\mathit{cos}\frac{i\pi }{2},-\mathit{sin}\frac{i\pi }{2}\right),i=1to4,\\ \sqrt{2}c\left(-\mathit{cos}\frac{\left(2i+1\right)\pi }{2},-\mathit{sin}\frac{\left(2i+1\right)\pi }{2}\right),i=5to8.\end{array}\right.(7)$

For some recent developments of LBM schemes regarding applications in different fields, readers are referred to Noori et al. (2019) and Noori et al. (2020).

3 Problem statement

The problem’s schematic diagram considered in this study is shown in Figure 2. This figure depicts a channel containing the two tandem rectangular cylinders placed in a fluid stream to be analyzed here. The height of the first cylinder (C₁) is h₁ and of the second cylinder (C₂) is h₂, and the width of both cylinders is denoted by D. In this study, h₁ and h₂ are discretized so as to have 40 and 30 lattices, respectively, while the width D has 20 lattices. Each cylinder is of a different aspect ratio (AR = height of cylinder/width of cylinder): the first cylinder has AR = 2:1 while the second has AR = 3:2. X_u = 10D is the distance from the channel entrance position to C₁, and X_d = 20D is the distance from C₂ to the domain outlet. The distance from the upper surface of C₁ to the upper boundary is Y_u = 8D, while Y_b = 8D is the distance from the lower surface of C1 to the lower boundary of the domain. These lengths are selected based on the recommendations of previous research in order to have a minimal effect of domain size on results (Perumal et al., 2012). Channel length L varies as the gap between cylinders (G = s/D) varies, while the height H is fixed. All lengths in this study are non-dimensionalized using the characteristic length (D = 20).

FIGURE 2

FIGURE 2. Geometry of the problem.

The boundary conditions in this study are applied in terms of distribution functions. At the inlet position, uniform incoming flow ($u=U_{in},v=0$) is assumed (Islam et al., 2012). The convective boundary condition in terms of distribution functions given as $\frac{\partial f_i}{\begin{array}{c}\partial t\end{array}}+U_{in}\frac{\partial f_i}{\partial x}=0$ is used at the outlet boundary (Ahmad et al., 2021). The surface of each cylinder as well as the upper and lower walls of the domain is treated through the no-slip boundary condition, mathematically expressed as ($u=v=0$). In LBM simulations, the no-slip condition is applied in terms of the bounce back rule in which the particles which stream into the wall are bounced back in the opposite direction inside the fluid stream. For example, the particles with distribution functions f₇, f₄, and f₈ streaming toward the lower wall bounce back as f₇ = f₅, f₄ = f₂, and f₈ = f₆. A similar procedure was also adopted for other directions for fluid particles hitting the solid walls (Rahman et al., 2021). Although the geometry considered in the current study has smooth boundaries, LBM is also a suitable choice for curved or moving boundaries (Tao et al., 2018; Marson et al., 2021).

4 Grid independence and code validation study

4.1 Grid independence

In order to ensure grid independence, we considered three different grid sizes (10, 20, and 40 points) around the outer surface of a single square cylinder at Re = 100 (Table 3). In terms of percentage variation, the values of physical variables like CDmean, St, and CLrms are more significantly impacted by the 10-point grid than the 40-point results. In comparison, the 20-point grid produced superior outcomes relative to 10 points. Furthermore, the convergence of a 40-point grid required significantly longer time, and there was no great variation in results at 20- and 40-point grid sizes. Therefore, we considered the 20-point grid for analysis for this study. This grid size follows recommendations based on lattice Boltzmann simulations for both single and multiple objects (Islam et al., 2018; Rahman et al., 2021). Note that the uniform meshing ($\Delta x=\Delta t=1$) is selected in the whole computational domain because the standard LBM considers such meshing for simulations without any need to use external mesh generators (Perumal et al., 2012). It is easy to apply and, in the case of rectangular obstacles, uniform meshing is an optimal choice to ensure accurate results in less computational time.

TABLE 3

TABLE 3. Impact of spatial resolution on the physical properties of flow past a single square cylinder at Re = 100.

4.2 Code validation

For code validation, we performed computations for flow around a single square cylinder and quantitatively compared our results with the experimental and numerical results of other research considering Re = 100 (Table 4). Note that the results for the geometry considered in current work are not available in the literature. Therefore, the code validation study was performed for flow around a single square cylinder. This was based on the fact that the flow around a single cylinder serves as a benchmark problem for flow around bluff bodies. This practice was adopted in most previously published studies. Table 4 demonstrates good agreement among the current results and with those of other studies. Some minor deviations in results also appear. Note that the exact matching of results is not possible because several parameters, including the accuracy of the underlying numerical technique, mesh size, domain dimensions, and the dimensions of cylinders influence the outcomes. The overall agreement of current and previous results indicates that the current code calculated the results efficiently. Furthermore, we refer readers for the details of quantitative as well as qualitative validation in the case of flow around two and more inline arranged cylinders to Abbasi et al. (2018) and Abbasi et al. (2020).

TABLE 4

TABLE 4. Code validation in terms of single square cylinder at Re = 100.

It may therefore be concluded that our code is well established and that we can use it for flow around tandem arranged cylinders, done in the present study.

5 Results and discussion

The flow around two tandem rectangular cylinders with distinct aspect ratios was simulated at Re = 100 by considering different values of G progressively varying from 0.25 to 20. From previous studies, we can conclude that the flow structure mechanism around multiple rectangular cylinders appears to be a complicated phenomenon that depends on several parameters, including Re, G, and AR (Islam et al., 2018; Rahman et al., 2021). In the current study, the resulting flow regimes are specified into different patterns in terms of the creation of different shape vortices, wake structure mechanism, and the behavior of shear layers detaching from cylinder corners and interacting with each other. These different flow patterns depend on increasing values of G in this study. The prominent flow patterns observed in this study are the single slender body (SSB) flow found in the range G = 0.25–0.75, the shear layer reattachment (SLR) flow found in the range G = 1–4, the intermittent shedding (IS) flow mode found in the range G = 4.25–5.25, and the binary vortex street (BVS) flow found for G = 5.5–20, except at G = 8 where the single-row vortex street (SRVS) flow was observed. Similar flow patterns have been reported by Zdravkovich (1987) for flow around tandem bodies with different characteristics. In the following subsections, a comprehensive illustration for each flow pattern is presented and discussed.

5.1 Single slender body

The flow pattern noticed here at smaller gaps between two tandem rectangular cylinders is the SSB flow in the range 0.25 $\le$ G $\le$ 0.75 (Figure 3). In Figure 3A, the corresponding vorticity contour of SSB is presented. This contour shows that the free shear layers that split off the front edges of C₁ do not rejoin with C₂ but instead roll up within the wake of C₂ while, within the space in the cylinders, a steady flow can be observed. An isolated vortex row appears within the down-wake region of the cylinders, similar to the flow around a solo body. Zdravkovich (1987) also classified such a flow pattern as a single slender body occurring in the range between 1 < G < 1.8 for coupled inline circular cylinders. This kind of flow pattern is also known as an isolated blunt body (Shui et al., 2021). Figure 3B presents the pressure and streamline contour for this flow pattern—it is obvious that the pressure is higher on the leading surface area of the C₁ and lower at the rear side of the C₂. This indicates that the existence of the C₁ has a major role in suppressing pressure on C₂. In Figure 3B, the streamlines graph shows that an elongated recirculating vortex at the upper side of C₂ is formed while, in the wake adjacent to C₂, a large D-type recirculating eddy appears. The size and shape of vortices as well as recirculating eddies are sufficiently larger than those of a single square cylinder case due to the increased aspect ratios of these cylinders. In Figure 3C, the variation in drag coefficients with time is presented. The CD for C₁ is almost constant while, for C₂, it appears to be sinusoidal after some time steps. This is because the shear layers pass smoothly around C₁ but roll up in the wake of C₂. It can also be observed that the drag force is positive for C₁ and negative for C₂ acting as a thrust force. Huang et al. (2012) also observed such a drag tendency around two 2:1 rectangular cylinders. In Figure 3D, the lift coefficients for both cylinders are presented against time. The CL graph depicts the C₁ CL having higher amplitude than C₂. In that case, the flow boundary layer detaching for the C₁ corners spread over a larger region than C₂. Another reason is the impact of AR, which indicates that a cylinder with high AR tends to face more lift than a cylinder with low AR. Moreover, CL becomes periodic for both cylinders after smooth behavior at initial time steps. Figures 3E,F present the spectrum energy of lift coefficient for both cylinders. The St value for both cylinders (shown on peaks of spectrum graph) indicates that the shedding frequency is much dependent on Re and G. The power spectrum graphs of both cylinders depict a similar peak value, indicating the dominant wake frequency behind the cylinders. This St value is comparatively lower than other flow patterns found in this study. It also indicates a relatively uniform and predictable vortex shedding pattern, with vortices shedding regularly.

FIGURE 3

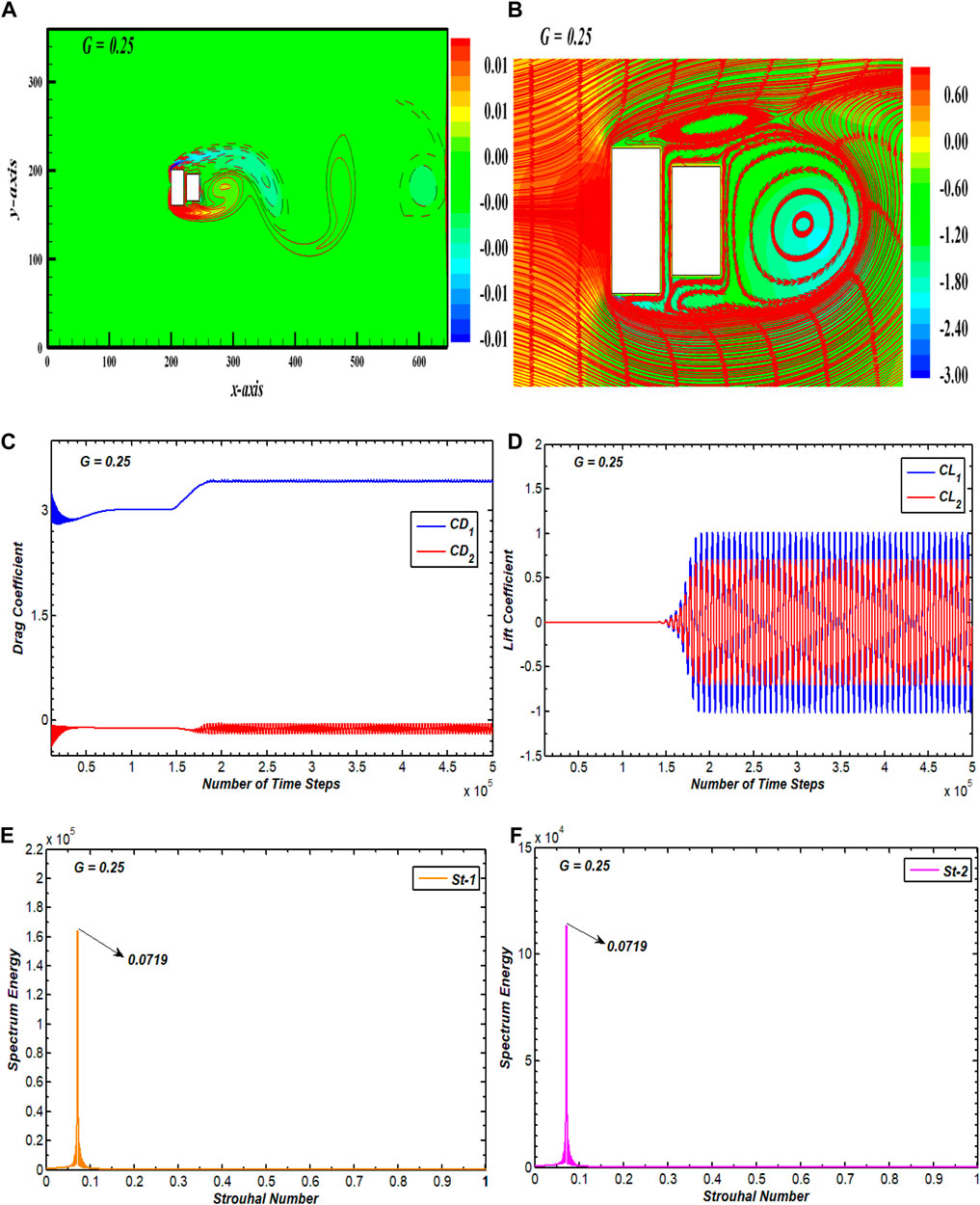
FIGURE 3. (A) Vorticity contour, (B) pressure streamlines, (C, D) drag and lift coefficients, and (E, F) spectral energy of CL for single slender body flow.

5.2 Shear layer reattachment

The second flow regime seen from current simulation results is SLR flow which extents in the range 1 $\le$ G $\le$ 4 (Figure 4). In Figure 4A, the associated vorticity pattern for SLR flow is presented at G = 1 as a representative case. The vorticity graph depicts inner shear layers splitting from C₁ rejoin at upstream side of C₂ and also move within the gap region. The vortices shed only in the wake of C₂ like the previous flow pattern. However, now the vortices behind the rear cylinder are stronger, with reduced size and greater number compared to SSB flow. According to Zdravkovich (1987), this flow pattern appears within the range 1.2 < G < 3.4 for coupled inline circular cylinders of same size. In Figure 4B, the pressure and streamline graph is presented for SLR flow. The pressure graph shows that, in this case, while the maximum pressure is at the front face of C₁, but C₂ is also subjected to some pressure due to the fluid being forced to flow inside the gap region as distance between cylinders increased. As the flow passes away from the cylinders, the pressure drops, implying a region of low pressure in the wake behind the cylinders. In Figure 4B, the streamline pattern shows elongated recirculating eddies developing around the upper, lower, and rear areas of C₂. In the wake adjacent to C₂, the size of the recirculating eddy appears to be smaller than the SSB case because of the reduced size of the vortices within wake region. Figure 4C presents the variation in drag coefficients with time. The CD graph shows almost similar behavior to the SSB flow case—higher drag on C₁ than on C₂. This might be due to the fact that the AR of the cylinders affects the CD, with the higher AR cylinder probably experiencing higher drag force. In Figure 4D, the lift coefficients are presented against time for the SLR flow pattern. The graph shows that CL is periodic for both cylinders. The amplitude of consecutive CL cycles is now sufficiently higher than the SSB case. This is due to the SLR and increase in the spacing ratio that results in changing the lift force signals. Figures 4E,F present the power spectrum of the lift coefficient for both cylinders. This graph of both cylinders depicts a peak value similar to the SSB flow pattern. However, here the St values are significantly greater than those for a SSB flow pattern. This is due to the SLR flow case, which leads to a more complicated flow pattern and a higher shedding frequency.

FIGURE 4

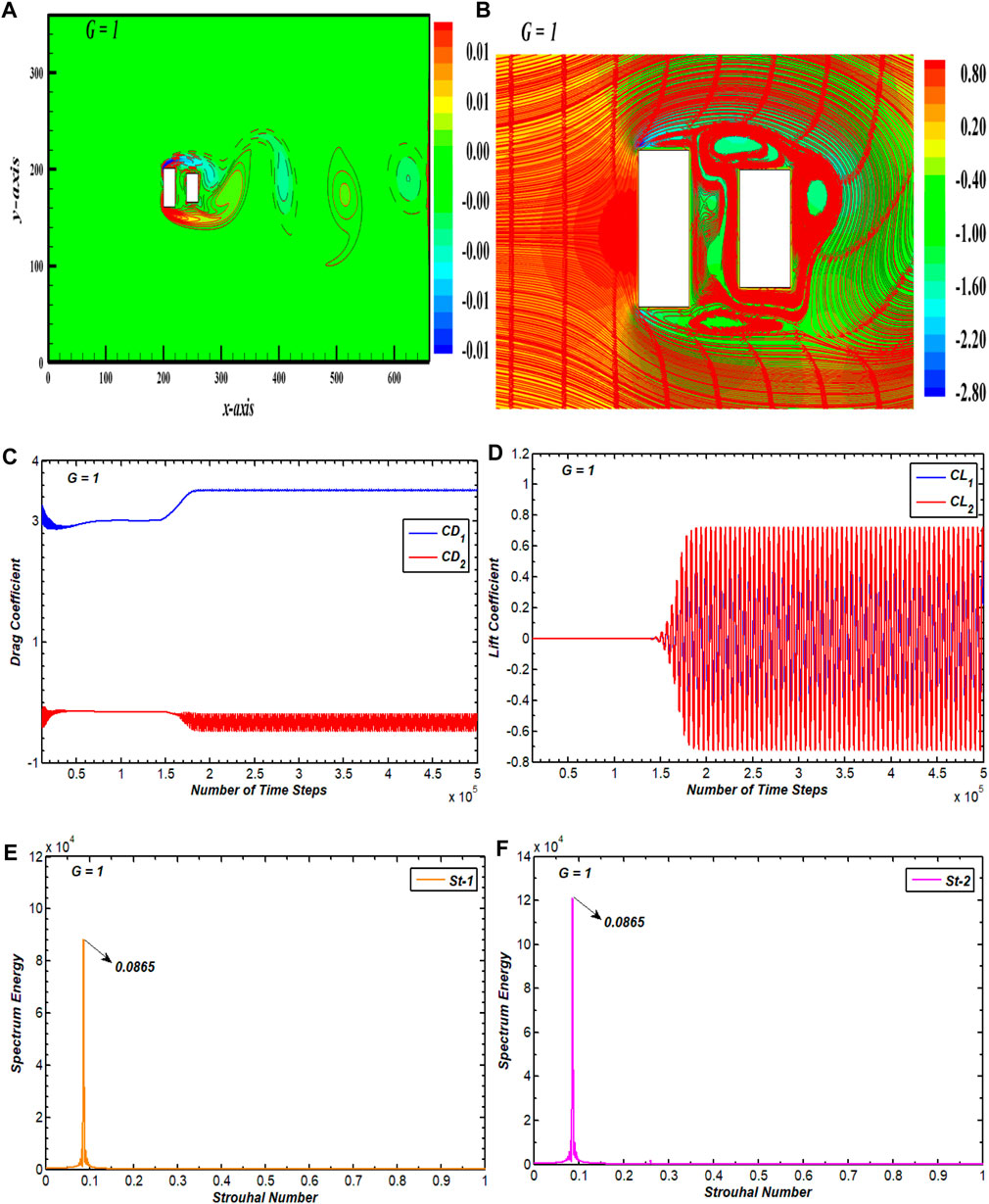
FIGURE 4. (A) Vorticity contour, (B) pressure streamlines, (C, D) drag and lift coefficients, and (E, F) power spectrum of CL for alternate reattachment flow.

5.3 Intermittent shedding

With increased distance between the cylinders, the flow structure mechanism and interactions of separated flow with C₂ become entirely different from the SSB and SLR flow patterns (see Figure 5). In Figure 5A, the vorticity contour shows that the boundary layers separated out of the top and bottom sides of C₁ join to form vortices in the gap before interacting with C₂ because of the larger space between the cylinders. After that, these vortices impinge on C₂ and form a vortex street in its wake (Figure 5A). There seems no definite pattern for movement of vortices, as was in case of SSB and SLR patterns. Furthermore, the structures of vortices in street differ from each other, and it can also be observed that the strength of vortices in this case is increased more than those seen in previous flow patterns. The pressure exhibits a fluctuating pattern, with alternating regions of maximum and minimum pressure (Figure 5B). These pressure variations correspond to irregularly shedding vortices. At the back of C₁, the pressure reduces, implying the creation of a low-pressure zone, followed by a rapid increase in pressure as the flow merges to C₂. The pressure becomes minimal in the near wake zone of C₂. These alternately repeated pressure patterns generate a characteristic waviness in the pressure contour. From Figure 5B, the location, size, and behavior of the vortices shedding from both cylinders along with the wake pattern behind the cylinders is indicated by streamlines. These show that the fluid detachment occurs at the leading edges of C₁ and that a recirculating eddy appears behind C₁. The fluid then moves toward C₂ where it splits again, forming another recirculating eddy in the near lower corner of C₂. Both cylinders generate their own eddies because of the wider gap between them. The streamlines emerging from the bottom frontal edge of C₁ move toward the upper frontal corner of C₂, indicating irregularity of fluid movement within the gap. A similar trend prevails in the wake region, as indicated by streamlines. Due to such chaos and amalgamation in flow, this flow pattern is classified as IS flow, and it is seen in the range 4.25 $\le$ G $\le$ 5.25 in the current study. This disorder in flow structure also affects the drag and lift forces (Figures 5C,D). The smooth variations observed in the case of these force coefficients for SSB and SLR flow patterns no longer exist due to IS. The CD graph shows an irregular pattern with random dips and peaks due to the flow transitions from one vortex shedding pattern to another. The consecutive drag signals switch from low to high values onto C₂, and the amplitude of the CD curves increases compared to C₁ as time progresses. In Figure 5D, CL exhibits periodic variations, with CL switching from lower to higher amplitude cycles over time. Initially, the amplitude of CL curves for C₂ are higher than C₁, which becomes almost similar as time advances. CL further exhibits variations with G between the cylinders in this case. For lower values of G, the cylinders’ wakes merge more strongly, leading to larger CL amplitude. For large G, the CL amplitude decreases, implying a weaker interaction between the cylinders’ wakes. The spectral energy plots for both cylinders show a similar peak value, indicating that the vortices shed with similar frequency from both cylinders. Multiple peaks appear, indicating an irregular attachment of the shear layers and an inconsistency of shedding vortices among the cylinders and after C₂. Islam et al. (2018) also reported such behavior in St for three inline rectangular cylinders. Such flow characteristics were also observed by Zdravkovich (1987) for coupled circular cylinders in tandem arrangement for the spacing range 3.4 < G < 3.8.

FIGURE 5

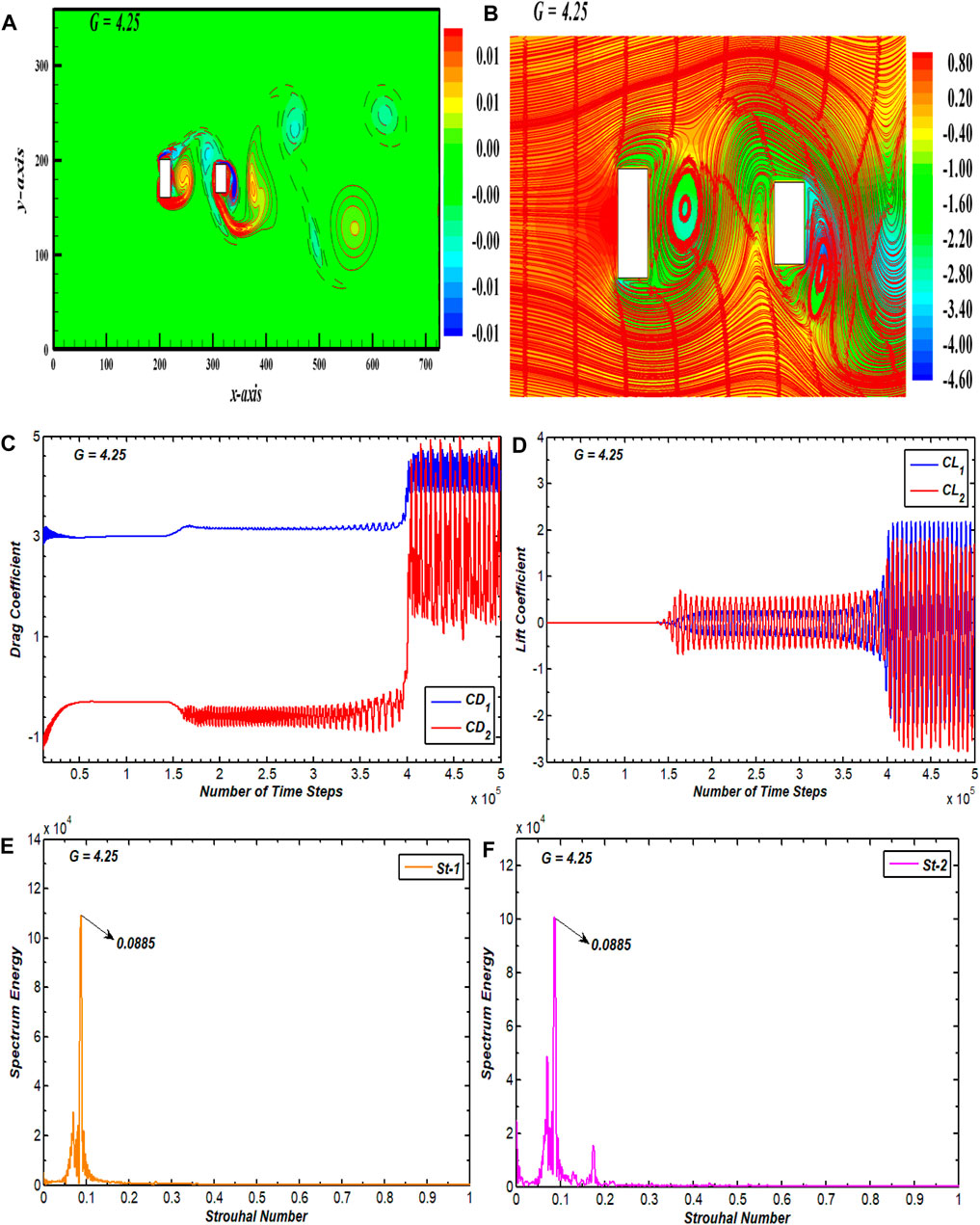
FIGURE 5. (A) Vorticity contour, (B) pressure streamlines, (C, D) drag and lift coefficients, and (E, F) power spectrum of CL for intermittent shedding flow.

5.4 Binary vortex street

The BVS flow pattern ranges over the spacing values G = 5.5–20, except for G = 8, where a single-row vortex street (SRVS) pattern appeared (discussed in the next section) (Figure 6). In Figure 6A, the associated vorticity pattern for BVS is given, depicting that each cylinder generates its own vortex street and that the vortex street behind C₂ is binary because the movement of the vortices is in a parallel dual line of clockwise and anticlockwise vortices. The vortices after C₂ are elliptically shaped with almost similar sizes. Zdravkovich (1987) also reported similar characteristics of BVS for flow-past coupled tandem circular cylinders for the spacing range G > 3.4 to 3.8. Figure 6B shows that the pressure varies randomly inside the domain in this flow pattern. Instead of a minimal pressure zone in the back of C₂, as was seen in previous flow patterns, the pressure now seems minimal at the corners of C₁. This distribution of pressure corresponds to the single cylinder case. This can be attributed to the increased gap spacing in which wake interference effects are minimized. This phenomenon becomes more prominent in BVS flow as G further increases. The streamlines in contour show larger recirculation zones within the gaps and after C₂. In this case, the eddies appearing within the gap region and after C₂ differ in shape and size due to changed vortex structures from the other flow patterns in this study. The CD for C₁ has periodic variations, while the CD for C₂ has initial fluctuating behavior which eventually settles to being periodic (Figure 6C). The lift coefficients become periodic for both cylinders after a short interval of linear behavior (Figure 6D). The CL oscillations have sufficiently higher amplitudes than SSB, SLR, and IS flow patterns due to the elliptically shaped vortices appearing after the cylinders. The periodic oscillation of the lift force demonstrates the domination of wake frequency within the spectrum energy graph (Figures 6E,F). There thus appears only a single peak in each case of the power spectrum plot.

FIGURE 6

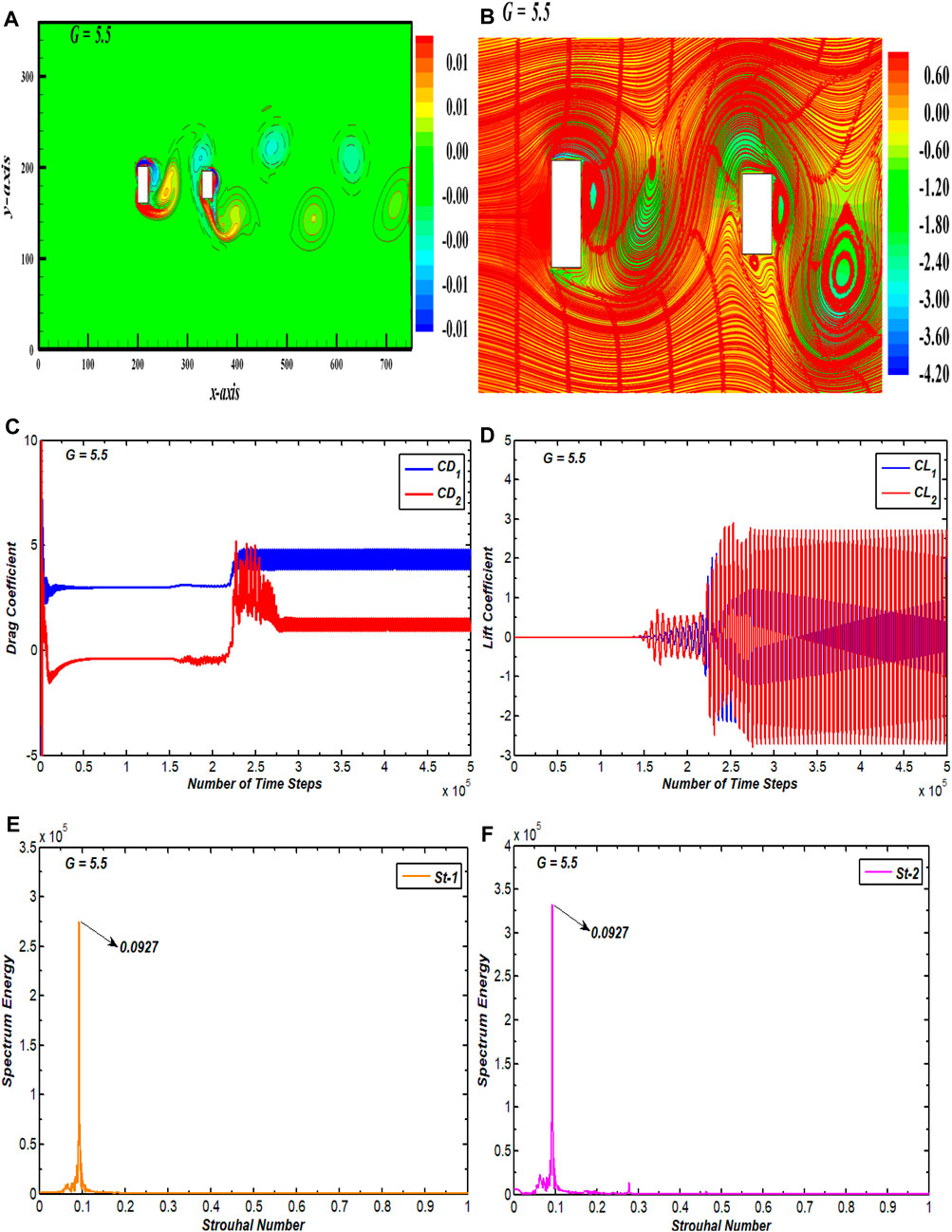
FIGURE 6. (A) Vorticity profile, (B) pressure streamlines, (C, D) drag and lift coefficients, and (E, F) power spectrum of CL for binary vortex street flow.

5.5 Single-row vortex street

The SRVS flow pattern in the wake of both cylinders is observed at only one gap spacing value—G = 8 in this study (Figure 7). The corresponding vorticity contour for the SRVS flow pattern is presented in Figure 7A, which shows that the vortices travel in a single row throughout the computational domain. The vortices in the wake of each cylinder are elongated and merge in the wake of C₂. The pressure seems to be higher at the front surface of C₁ and minimal at the corners and at back surface of C₂ (Figure 7B). Here, the stagnation point is generated, showing that the flow is slowed due to the presence of the cylinder. The flow separates from the corners of the cylinders, indicating a low-pressure area. The lowest pressure value appears at back surface of C₂. This low-pressure area causes the periodic shedding of vortices in the wake of each cylinder. In Figure 7B, the streamlines depict a distinct pattern of alternating vortex shedding from each cylinder. The streamlines appear to be curvy and firmly packed together in the center of the wake, indicating the existence of strong vorticity. Due to this, the drag as well as lift coefficients appear to be significantly impacted for both cylinders (Figures 7C,D). Since each cylinder sheds its own SRVS, the lift on the second cylinder is more stabilized than the IS and BVS flow pattern. The amplitude of consecutive cycles of the lift coefficients for both cylinders lessen compared to the IS and BVS flow patterns. This can be attributed to the individual shedding of vortices from both cylinders in a single row. A comparison with the SSB and SLR flow patterns reveals a significant rise in the amplitude of consecutive CL cycles for both cylinders due to the elongated recirculating regions of vorticity in the wake of both cylinders. These graphs also show that the amplitude of both force coefficients is higher in the case of second cylinder than of first. This is due to wake interference effect of C₁ on the second cylinder. Due to SRVS flow pattern and the smooth passage of vortices in the domain, the power spectrum of the lift coefficient graph for both cylinders indicates a similar peak value (Figures 7E,F).

FIGURE 7

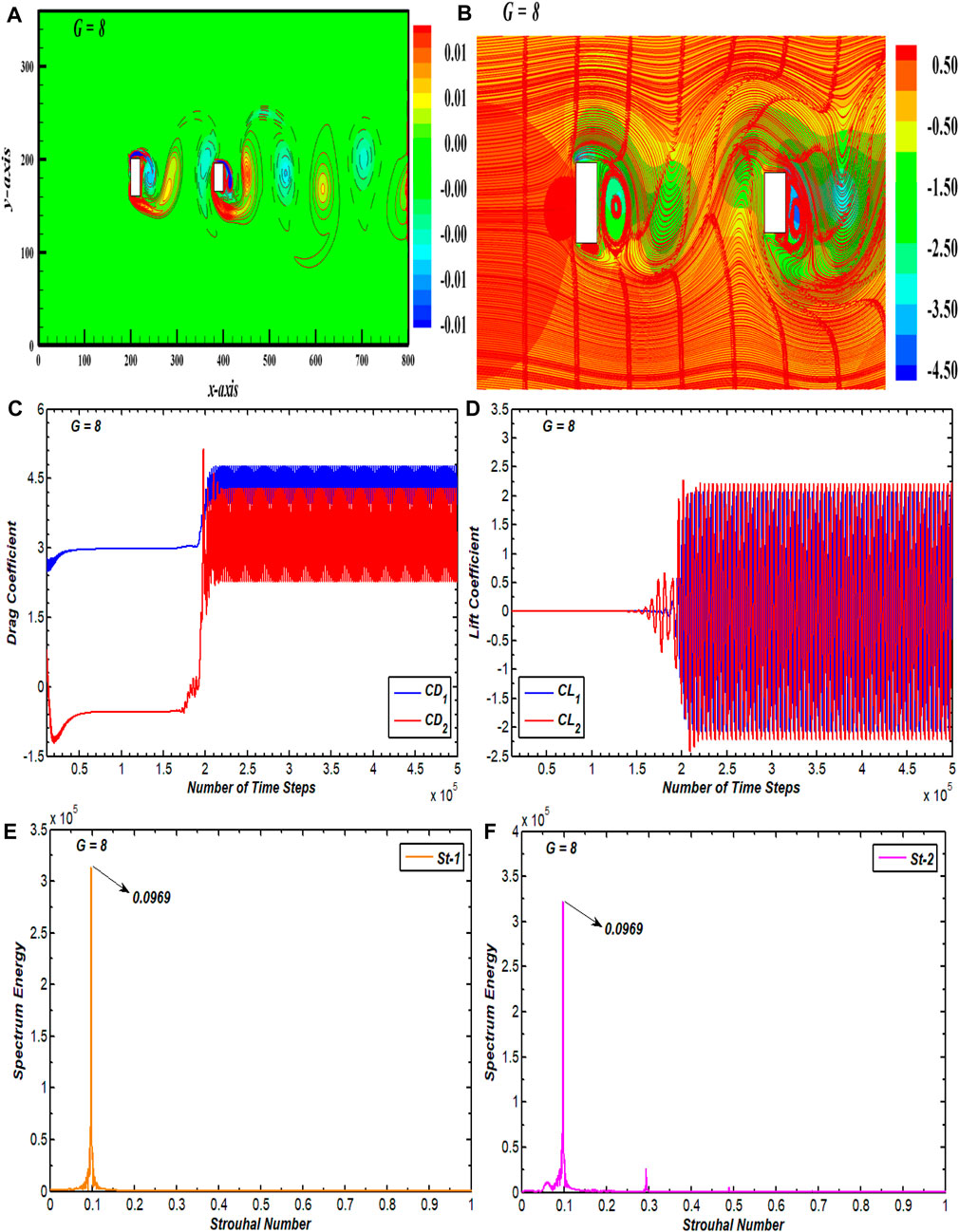
FIGURE 7. (A) Vorticity profile, (B) pressure streamlines, (C, D) drag and lift coefficients, and (E, F) power spectrum of CL for single vortex street flow.

6 Force statistics

Variations of various fluid force parameters acting on both cylinders with varying gap spacing is presented in this section in order to analyze the influence of G on the forces. The parameters considered for this purpose are CD_mean, St, CD_rms, CL_rms, amplitude of the drag coefficient (CD_amp), and amplitude of the lift coefficient (CL_amp). Figure 8 presents the effect of G on variations of these parameters at Re = 100.

FIGURE 8

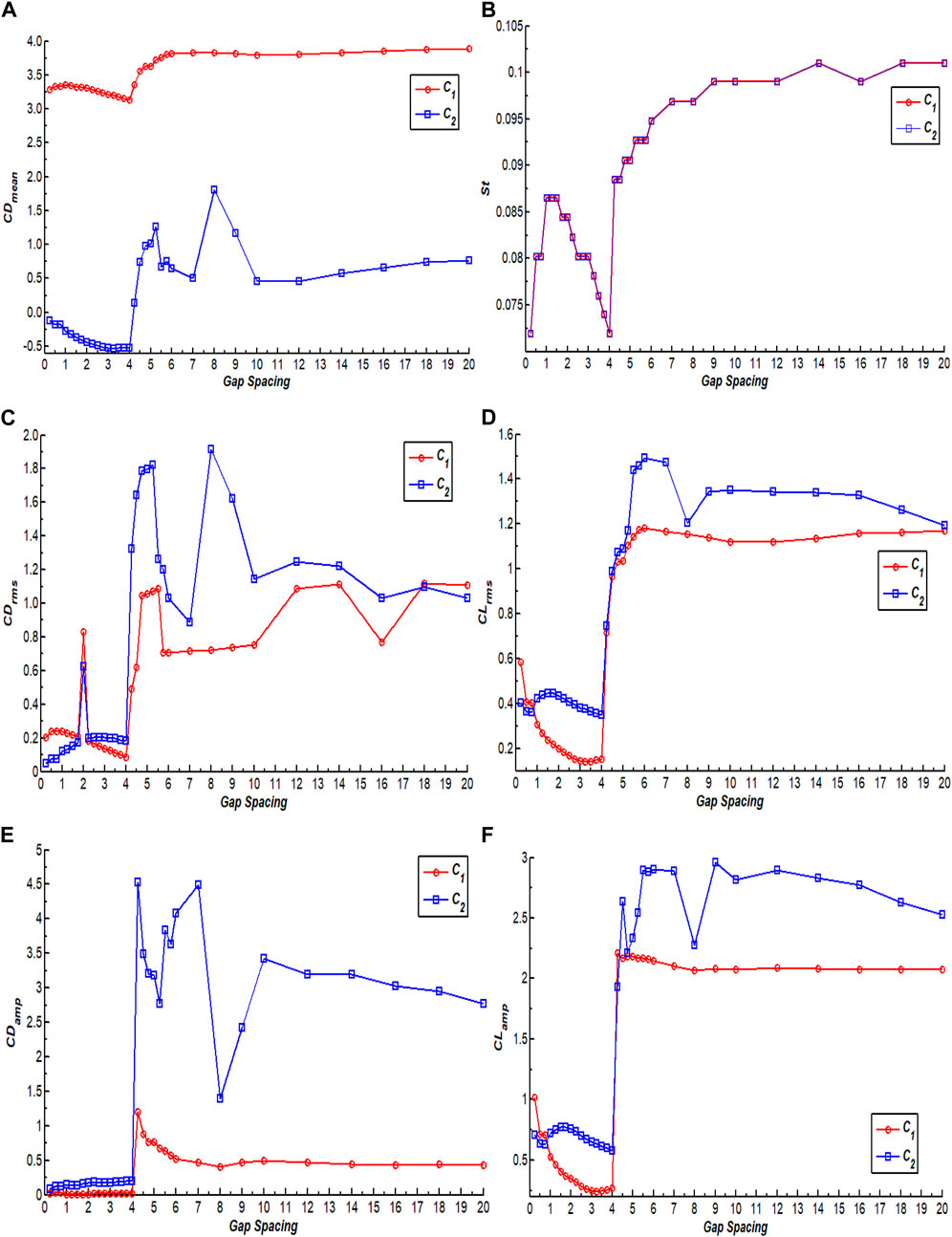
FIGURE 8. Gap spacing effect on the variation of (A) CD_mean, (B) St, (C) CD_rms, (D) CL_rms, (E) CD_amp, and (F) CL_amp.

The variation of CD_mean for flow around two tandem rectangular cylinders with increasing G is presented in Figure 8A. It can be observed that CD_mean of C₁ is greater than CD_mean of C₂ for all chosen values of G because the incoming flow initially interacts with C₁ and thus exerts maximum drag force on C₁. Another possible reason that C₁ experiences significantly higher drag force than C₂ is that it has higher AR. Relating the variations of drag force coefficient, it is apparent that the change in flow patterns significantly affects the drag force. In the range G = 0.25 to 1, the average drag on C₁ slightly increases and then shows decreasing behavior until G = 4. It then increases with increasing G and approaches its maximum value at G = 20. Note that, at G = 1, the flow pattern changes from SSB to SLR, while after G = 4, the flow pattern changes from SLR to IS. The CD_mean of C₂ is negative and initially decreases until G = 4. Huang et al. (2012) also observed the negative value of CD_mean for C₂ for flowing past 2:1 rectangular cylinders in tandem at Re = 200. After G = 4, it jumps from negative to positive values due to a change in flow pattern from SLR to IS. The negative values of CD_mean indicate that the drag force acts as a thrust force, thus generating a backflow due to narrow gaps between cylinders. The minimum value of CD_mean for both cylinders can be seen at G = 4, while the maximum for C₂ occurs at G = 8, and CD_mean of C₁ is maximum at G = 20. Figure 8A also shows that, after G = 10, the influence of gap spacing on CD_mean of both cylinders decreases. Figure 8B presents the variation of St of both cylinders with G. Both cylinders have same St for all G, indicating that the vortices shed from both cylinders with same frequency notwithstanding whether both cylinders have different ARs. Rahman et al. (2021) also found similar behavior in St for flow past three rectangular cylinders. Initially for G = 0.25 to 0.75, St shows increasing behavior. SSB flow was observed in this range of gap spacing. In the range G = 1.75 to 4, it shows decreasing behavior, which indicates that the shedding frequency decreases due to the push of shear layers inside the gaps between cylinders. After that it increases with increasing G and approaches the local maximum value for both cylinders at G = 14. The minimum value of St can be observed at G = 4 for both cylinders where the SLR flow pattern was seen. The variation of CD_rms of both cylinders at different values of G is presented in Figure 8C. Initially, when G = 0.25 to 1, the CD_rms of C₁ slightly increased and then showed decreasing behavior in the range G = 1.25 to 1.75 where the SLR flow is observed. The CD_rms of C₂ show increasing behavior in the range G = 0.25 to 1.75. The CD_rms of both cylinders jump to higher values at G = 2 and then again show decreasing behavior until G = 4. After G = 4, it jumps to higher values due to a change in flow pattern from SLR to IS. The CD_rms of both cylinders show a mix of increasing and decreasing behaviors as G increases further. The minimum value of CD_rms for both cylinders can be noticed at G = 4, while the maximum value of CD_rms of C₁ appears at G = 18, and CD_rms of C₂ is maximum at G = 8 where the SRVS flow pattern was reported. The effect of varying G on CL_rms of both cylinders is shown in Figure 8D. This graph depicts that, in the range G = 0.25 to 4, the CL_rms of C₁ shows decreasing behavior. After that, it increases with increasing G and thus approaches its local maximum value at G = 6. The CL_rms of C₂ shows decreasing behavior initially in the SSB flow pattern regime and, after that, slightly increases and then shows decreasing behavior until G = 4. The CL_rms curves then show an increasing trend to higher values for both cylinders. Note that the IS flow pattern is observed in this range. At G = 4.5 to 7.75, the value of CL_rms of C₂ increases and then suddenly decreases, which can be observed at G = 8 because of flow pattern change from BVS to SRVS flow. The variation of CD_amp for both cylinders with varying G is shown in Figure 8E. It can be observed that, until G = 4, CD_amp for both cylinders is almost constant, indicating little change in amplitude of drag force in this spacing range. After G = 4, CD_amp jumps to the highest values for both cylinders due to the appearance of the IS flow pattern. Note that, in this flow pattern, the vortices appear to be in an irregular pattern in the wake of both cylinders. This graph also shows that the higher spacing values result in higher amplitude drag force than the smaller spacing values. The variation of CL_amp of both cylinders shown in Figure 8F indicates that the C₂ bears higher amplitude than C₁ at almost all spacing values. This is due to the wake interference effects of C₁ on C₂. Shui et al. (2021) also reported similar results in CL_amp for flow around two tandem square cylinders. Initially, CL_amp corresponding to C₁ decreased until G = 4 but, after G = 4, it suddenly increased to a higher value and became almost independent of G, showing negligible modifications. In the range G = 0.25 to 0.75, the CL_amp of C₂ shows decreasing behavior. After G = 4, the CL_amp of both cylinders has sudden jumps (Figure 8F). The minimum value of CL_amp of both cylinders can be observed at G = 4 where the SLR flow pattern is observed. Its maximum value for C₁ appears at G = 4.25 and the maximum value for C₂ at G = 9.

7 Conclusion

Numerical calculations were performed to analyze the fluid flow around two vertically positioned rectangular cylinders in tandem arrangement using the lattice Boltzmann method. The cylinders considered in this study were of different aspect ratios. The main goal of this study was to determine the wake structures under the effect of gap spacing in the range G = 0.25 to 20 at Re = 100. The results were presented and discussed in the form of vorticity contour visualizations, pressure streamline contours, variation of drag, and lift coefficient against time. Fluid force parameters of average drag coefficient, Strouhal number, rms values of drag, lift coefficients, and the amplitudes of these force coefficients were also analyzed under the impact of changing gaps between cylinders. The important findings of this study are:

(1) Bearing various characteristics, five different wake flow patterns were observed in this study depending on various ranges of gap spacings: i) single slender body, ii) shear layer reattachment, iii) intermittent shedding, iv) binary vortex street, and v) single-row vortex street.

(2) The single slender body flow pattern, observed in the range G = 0.25 to 0.75, consists of single vortex street in the down wake area of C₂, without any gap flow, similar to the flow around a single bluff body. The fluid forces in this flow pattern varied periodically with similar amplitude as time proceeded.

(3) In the range G = 1 to 4, the shear layer reattachment flow was observed. In this flow pattern, the strength of vortices increased in the down wake region. The amplitude of lift force coefficient on both cylinders also increased more than single slender body flow. The secondary cylinder interaction frequency impact was also observed in this flow pattern.

(4) In the range G = 4.25 to 5.25, the intermittent shedding flow pattern was observed. In this flow pattern, the vortices did not exhibit any proper pattern, but instead chaos was observed in the flow structure. The CD varied irregularly with random dips and peaks due to the flow structure transitions between larger and smaller sized vortices.

(5) The binary vortex street flow pattern was found in the range G = 5.5 to 20 except at G = 8, where the single-row vortex street flow pattern was observed. In the binary vortex flow pattern, both cylinders generated their own vortex street, while the vortex street in the down wake region traveled in a double row of parallel vortices. The vortex formation region enlarged in this range of gap spacing, corresponding to both flow patterns, which resulted in higher magnitude drag and lift forces on cylinders.

(6) It was observed that C₂ experienced negative drag in the spacing range between G = 0.25 to 4, while C₁ had positive values of CD_mean for all G. The negative drag force on C₂ jumped to positive as the flow pattern changed from shear layer reattachment to intermittent shedding flow. Furthermore, the CL_rms, CD_rms, CL_amp, and CD_amp for C₂ were mostly higher than corresponding values on C₁ for all values of G.

(7) Although C₂ was shielded by C₁ and faces low pressure at smaller spacing values, it was also subjected to pressure change due to the changes in flow patterns as gap spacing progressively increased. Furthermore, the magnitude of pressure on both cylinders changed due to change in flow patterns.

(8) At G = 4 and 8, the fluid force parameters like CD_mean, St, CD_rms, CL_rms, CD_amp, and CL_amp achieved either maximum or minimum values or had sudden jumps in values. The flow structure at these spacing values also exhibits complexity. Both spacing values are hence critical for fluid flow dynamics around the geometry considered in this study.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

WA: conceptualization, project administration, supervision, and writing–review and editing. ME: formal analysis, methodology, validation, and writing–original draft. HR: visualization and writing–review and editing. ZU: funding acquisition, resources, and writing–review and editing. MH: funding acquisition, supervision, and writing–review and editing. KS: funding acquisition and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by King Saud University, Riyadh, Saudi Arabia, under Researchers Supporting Project Number RSP2024R18.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors and, the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, W. S., Islam, S. U., Faiz, L., and Rahman, H. (2018). Numerical investigation of transitions in flow states and variation in aerodynamic forces for flow around square cylinders arranged inline. Chin. J. Aeronautics 31 (11), 2111–2123. doi:10.1016/j.cja.2018.08.020

CrossRef Full Text | Google Scholar

Abbasi, W. S., Mahmood, R., and Naheed, A. (2020). On the wake interference effects for flow around tandem bodies. J. Braz. Soc. Mech. Sci. Eng. 42, 53. doi:10.1007/s40430-019-2137-5

CrossRef Full Text | Google Scholar

Abdolahipour, S. (2023). Effects of low and high frequency actuation on aerodynamic performance of a supercritical airfoil. Front. Mech. Eng. 9, 1290074. doi:10.3389/fmech.2023.1290074

CrossRef Full Text | Google Scholar

Abdolahipour, S., Mani, M., and Taleghani, A. S. (2021). Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Phys. Scr. 96, 125012. doi:10.1088/1402-4896/ac2bdf

CrossRef Full Text | Google Scholar

Abdolahipour, S., Mani, M., and Taleghani, A. S. (2022). Experimental investigation of flow control on a high-lift wing using modulated pulse jet vortex generator. J. Aerosp. Eng. 35 (5). doi:10.1061/(ASCE)AS.1943-5525.0001463

CrossRef Full Text | Google Scholar

Abograis, A., and Alshayji, A. (2013). Reduction of fluid forces on a square cylinder using passive control methods. Boston, USA: COMSOL Conference.

Google Scholar

Aboueian, J., and Sohankar, A. (2017). Identification of flow regimes around two staggered square cylinders by a numerical study. Theory Comput. Fluid Dyn. 31, 295–315. doi:10.1007/s00162-017-0424-2

CrossRef Full Text | Google Scholar

Adeeb, E., Haider, B. A., and Sohn, C. H. (2018). Flow interference of two side-by-side square cylinders using IB-LBM- Effect of corner radius. Results Phys. 10, 256–263. doi:10.1016/j.rinp.2018.05.039

CrossRef Full Text | Google Scholar

Ahmad, S., Islam, S. U., Nazeer, G., and Zhou, C. Y. (2021). Numerical investigation of Strouhal number discontinuity and flow characteristics around single rectangular cylinder at low aspect ratios and Reynolds numbers. J. Braz. Soc. Mech. Sci. Eng. 43 (315), 1–26. doi:10.1007/s40430-021-03040-2

CrossRef Full Text | Google Scholar

Alam, Md. M., Bai, H., and Zhou, Y. (2016). The wake of two staggered square cylinders. J. Fluid Mech. 801, 475–507. doi:10.1017/jfm.2016.303

CrossRef Full Text | Google Scholar

Alam, Md. M., Derakhshandeh, J. F., Zheng, Q., Rehman, S., Ji, C., and Zafar, F. (2017). “The flow around three tandem circular cylinders,” in The world congress on Advances in Structural Engineering and Mechanics (ASEM 17), Ilsan(Seoul), Korea, August 28 - September 1, 2017.

Google Scholar

Bajalan, S., Shadaram, A., Hedayat, N., and Taleghani, A. S. (2011). Experimental study of frequency behavior for a circular cylinder behind an airfoil. World Acad. Sci. Eng. Technol. Int. J. Aerosp. Mech. Eng. 5, 2349–2353.

Google Scholar

Belloli, M., Giappino, S., Morganti, S., Muggiasca, S., and Zasso, A. (2014). Vortex induced vibrations at high Reynolds numbers on circular cylinders. Ocean. Eng. 94, 140–154. doi:10.1016/j.oceaneng.2014.11.017

CrossRef Full Text | Google Scholar

Burattini, P., and Agrawal, A. (2013). Wake interaction between two side-by-side square cylinders in channel flow. Comput. Fluids 77, 134–142. doi:10.1016/j.compfluid.2013.02.014

CrossRef Full Text | Google Scholar

Chakraborty, S., Chaterjee, S., and Kumar, R. (2022). Effect of gap ratio on flow influenced actions of two circular cylinders in side-by-side arrangement. J. Mines, Metals Fuels 70 (3A), 15–20. doi:10.18311/jmmf/2022/30662

CrossRef Full Text | Google Scholar

Chen, S., and Doolen, G. D. (1998). Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364. doi:10.1146/annurev.fluid.30.1.329

CrossRef Full Text | Google Scholar

Eizadi, H., An, H., Zhu, H., Chang, L., and Cheng, L. (2022). Wake transitions of six tandem circular cylinders at low Reynolds numbers. Phys. Fluids 34 (2), 1–49. doi:10.1063/5.0080268

CrossRef Full Text | Google Scholar

Gnatowska, R., Sobczyk, J., and Wodziak, W. (2020). Stability of flow around two rectangular cylinders in tandem. Appl. Phys. Mech. Material Eng. 138 (2), 295–298. doi:10.12693/APhysPolA.138.295

CrossRef Full Text | Google Scholar

Huang, Z., Xi, G., and Zhang, W. (2012). Numerical simulation of spacing effects on the flow past two 2:1 rectangular cylinders in tandem at Re = 200. Proc. Am. Soc. Mech. Eng. 2012, 1–9. doi:10.1115/FEDSM2012-72157

CrossRef Full Text | Google Scholar

Islam, S. U., Manzoor, R., Ying, Z. C., and Islam, Z. U. (2018). Numerical investigation of different aspect ratios for flow past three inline rectangular cylinders. J. Braz. Soc. Mech. Sci. Eng. 40, 410. doi:10.1007/s40430-018-1334-y

CrossRef Full Text | Google Scholar

Islam, S. U., Zhou, C. Y., Shah, A., and Xie, P. (2012). Numerical simulation of flow past rectangular cylinders with different aspect ratios using the incompressible lattice Boltzmann method. J. Mech. Sci. Technol. 26 (4), 1027–1041. doi:10.1007/s12206-012-0328-4

CrossRef Full Text | Google Scholar

Kuo, C. H., Chein, S. M., and Hsieh, H. J. (2008). Self-sustained oscillations between two tandem cylinders at Reynolds number 1000. Exp. Fluids 44, 503–517. doi:10.1007/s00348-007-0409-9

CrossRef Full Text | Google Scholar

Kuzmina, K., and Marchevsky, I. (2021). Flow simulation around circular cylinder at low Reynolds numbers. J. Phys. Conf. Ser. 1715, 1–7. doi:10.1088/1742-6596/1715/1/012067

CrossRef Full Text | Google Scholar

Lee, S. J., Mun, G. S., Park, Y. G., and Ha, M. Y. (2019). A numerical study on fluid flow around two side-by-side rectangular cylinders with different arrangements. J. Mech. Sci. Technol. 33 (7), 3289–3300. doi:10.1007/s12206-019-0624-3

CrossRef Full Text | Google Scholar

Ma, S., Kang, C.-W., Lim, T.-B. A., Wu, C.-H., and Tutty, O. (2017). Wake of two side-by-side square cylinders at low Reynolds numbers. Phys. Fluids 29, 1–23. doi:10.1063/1.4979134

CrossRef Full Text | Google Scholar

Marson, F., Thorimbert, Y., Chopard, B., Ginzburg, I., and Latt, J. (2021). Enhanced single-node lattice Boltzmann boundary condition for fluid flows. Phys. Rev. E 103 (5), 053308. doi:10.1103/physreve.103.053308

PubMed Abstract | CrossRef Full Text | Google Scholar

Mirzaei, M., Taleghani, A. S., and Shadaram, A. (2012). Experimental study of vortex shedding control using plasma actuator. Appl. Mech. Mater. 186, 75–86. doi:10.4028/www.scientific.net/amm.186.75

CrossRef Full Text | Google Scholar

Mithun, M. G., and Tiwari, S. (2014). Flow past two tandem square cylinders vibrating transversely in phase. Jpn. Soc. Fluid Mech. 46, 055509–055532. doi:10.1088/0169-5983/46/5/055509

CrossRef Full Text | Google Scholar

Mittal, S., and Raghuvanshi, A. (2001). Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Int. J. Numer. Methods Fluid 35, 421–447. doi:10.1002/1097-0363(20010228)35:4<421::aid-fld100>3.0.co;2-m

CrossRef Full Text | Google Scholar

Mohammad, A. A. (2011). Lattice Boltzmann method: fundamentals and engineering applications with computer codes. Berlin: Springer.

Google Scholar

Mohammadi, M., and Taleghani, A. S. (2014). Active flow control by dielectric barrier discharge to increase stall angle of a naca0012 airfoil. Arabian J. Sci. Eng. 39, 2363–2370. doi:10.1007/s13369-013-0772-1

CrossRef Full Text | Google Scholar

Noori, M. S., Rahni, M. T., and Taleghani, A. S. (2020). Effects of contact angle hysteresis on drop manipulation using surface acoustic waves. Theor. Comput. Fluid Dyn. 34, 145–162. doi:10.1007/s00162-020-00516-0

CrossRef Full Text | Google Scholar

Noori, S. M. S., Rahni, M. T., and Taleghani, S. A. S. (2019). Multiple-relaxation time color-gradient lattice Boltzmann model for simulating contact angle in two-phase flows with high density ratio. Eur. Phys. J. Plus 134, 399. doi:10.1140/epjp/i2019-12759-x

CrossRef Full Text | Google Scholar

Norberg, C. (1993). Flow around rectangular cylinders: pressure forces and wake frequencies. J. Wind Eng. Industrial Aerodynamics 49, 187–196. doi:10.1016/0167-6105(93)90014-f

CrossRef Full Text | Google Scholar

Octavianty, R., Asai, M., and Inasawa, A. (2016). Experimental study on vortex shedding and sound radiation from a rectangular cylinder at low Mach numbers. Jpn. Soc. Aeronautical Space Sci. 59 (5), 261–268. doi:10.2322/tjsass.59.261

CrossRef Full Text | Google Scholar

Okajima, A. (1982). Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398. doi:10.1017/s0022112082003115

CrossRef Full Text | Google Scholar

Perumal, D. A., Kumar, V. S., and Dass, K. A. (2012). Numerical simulation of viscous flow over a square cylinder using lattice Boltzmann method. ISRN Math. Phys. 2012, 1–16. doi:10.5402/2012/630801

CrossRef Full Text | Google Scholar

Rahman, H., Islam, S. U., Abbasi, W. S., Manzoor, R., Amin, F., and Alam, Z. (2021). Numerical computations for flow patterns and force statistics of three rectangular cylinders. Math. Problems Eng. 2021, 1–12. doi:10.1155/2021/9991132

CrossRef Full Text | Google Scholar

Rajpoot, R. S., Anirudh, K., and Dhinakaran, S. (2021). Numerical investigation of unsteady flow across tandem cylinders near a moving wall at Re = 100. Case Stud. Therm. Eng. 26, 1–14. doi:10.1016/j.csite.2021.101042

CrossRef Full Text | Google Scholar

Rangan, M. L. N. V. K., and Santanu Ghosh, S. (2022). A face-based immersed boundary method for compressible flows using a uniform interpolation stencil. Front. Mech. Eng. 8, 903492. doi:10.3389/fmech.2022.903492

CrossRef Full Text | Google Scholar

Saha, A. K., Muralidhar, k., and Biswas, G. (2000). Transition and chaos in two-dimensional flow past a square cylinder. J. Eng. Mech. 126, 523–532. doi:10.1061/(asce)0733-9399(2000)126:5(523)

CrossRef Full Text | Google Scholar

Salmasi, A., Shadaram, A., and Taleghani, A. S. (2013). Effect of plasma actuator placement on the airfoil efficiency at poststall angles of attack. IEEE Trans. Plasma Sci. 41 (10), 3079–3085. doi:10.1109/tps.2013.2280612

CrossRef Full Text | Google Scholar

Sarvghad, , Hesam, M., and Navid, N. (2011). Numerical simulation of flow over two side-by-side circular cylinders. J. Hydrodynamics 23 (6), 792–805. doi:10.1016/S1001-6058(10)60178-3

CrossRef Full Text | Google Scholar

Shiraishi, N., Matsumoto, M., and Shirato, H. (1986). On aerodynamic instabilities of tandem structures. J. Wind Eng. Industrial Aerodynamics 23, 437–447. doi:10.1016/0167-6105(86)90061-9

CrossRef Full Text | Google Scholar

Shui, Q., Duan, C., Wang, D., and Gu, Z. (2021). New insights into numerical simulations of flow around two tandem square cylinders. AIP Adv. 11, 1–14. doi:10.1063/5.0042797

CrossRef Full Text | Google Scholar

Sohankar, A., Davidson, L., and Norberg, C. (1995). “Numerical simulation of unsteady flow around a square two-dimensional cylinder.” in. Twelfth Australasian Fluid Mechanics Conference the University of Sydney, Australia, 4-8 December 2022, 517–520.

Google Scholar

Song, Y., Zhu, R., Simon, T. W., and Xie, G. (2017). Computational fluid dynamics modeling patterns and force characteristics of flow over in-line four square cylinders. Therm. Sci. 21 (00), 2553–2563. doi:10.2298/tsci170211035s

CrossRef Full Text | Google Scholar

Su, Z., Liu, Y., and So, R. M. C. (2004). Numerical simulation of two tandem circular cylinders in a turbulent flow. Flow-Induced Vib. 2004, 297–302.

Google Scholar

Su, Z. D., Guo, Z. L., So, R. M. C., and Liu, Y. (2002). “Two- and three-dimensional study of two tandem circular cylinders in a cross flow,” in Conference on Bluff Body Wakes and Vortex-Induced Vibrations, Port Douglas, Australia, 17-20 December 2002, 1–5.

Google Scholar

Sukop, M. C., and Throne, D. T. (2006). Lattice Boltzmann modeling: an introduction for geo-scientists and engineers. Berlin: Springer.

Google Scholar

Taleghani, A. S., Abdollah Shadaram, A., Mirzaei, M., and Abdolahipour, S. (2018). Parametric study of a plasma actuator at unsteady actuation by measurements of the induced flow velocity for flow control. J. Braz. Soc. Mech. Sci. Eng. 40, 173. doi:10.1007/s40430-018-1120-x

CrossRef Full Text | Google Scholar

Tao, S., He, Q., Chen, B., Yang, X., and Huang, S. (2018). One-point second-order curved boundary condition for lattice Boltzmann simulation of suspended particles. Comput. Math. Appl. 76 (7), 1593–1607. doi:10.1016/j.camwa.2018.07.013

CrossRef Full Text | Google Scholar

Wang, J., Shan, X., and Liu, J. (2022). First instability of the flow past two tandem cylinders with different diameters. Phys. Fluids 34, 1–19. doi:10.1063/5.0098204

CrossRef Full Text | Google Scholar

Wolf-Gladrow, D. A. (2000). Lattice-gas cellular automata and lattice Boltzmann models: an introduction. Berlin: Springer.

Google Scholar

Ye, Z.-H., Sun, X., and Zhang, J.-Z. (2019). Flow-induced vibrations of two staggered circular cylinders at low Reynolds number. J. Vib. Test. Syst. Dyn. 3 (1), 39–53. doi:10.5890/jvtsd.2019.03.004

CrossRef Full Text | Google Scholar

Zdravkovich, M. M. (1987). The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261. doi:10.1016/s0889-9746(87)90355-0

CrossRef Full Text | Google Scholar

Zhang, Z., and Zhang, X. (2012). Direct simulation of low-Re flow around a square cylinder by numerical manifold method for Navier-Stokes equations. J. Appl. Math. 2012, 1–14. doi:10.1155/2012/465972

CrossRef Full Text | Google Scholar

Nomenclature