Concurrent product layout design optimization and dependency management using a modified NSGA-III approach

The complexity of mechatronic systems has increased with the significant advancements of technology in their components which makes their design more challenging. This is due to the need for incorporating expertise from different domains as well as the increased number and complexity of components integrated into the product. To alleviate the burden of designing such products, many industries and researchers are attracted to the concept of modularization which is to identify a subset of system components that can form a module. To achieve this, a novel product-related dependency management approach is proposed in this paper with the support of an augmented design structure matrix. This approach makes it possible to model positive and negative dependencies and to compute the combination potency between components to form modules. This approach is then integrated into a modified non-dominated sorting genetic algorithm III to concurrently optimize the design and identify the modules. The methodology is exemplified through the case study of a layout design of an automatic greenhouse. By applying the proposed methodology to the case study, it was possible to generate concepts that decreased the number of modules from 9 down to 4 while ensuring the optimization of the design performance.

1 Introduction

The need for incorporation of a multidisciplinary engineering approach makes the mechatronic design a complex task to achieve (Torry-Smith et al., 2013; Mohebbi et al., 2014). To obtain a final design, one must go through the whole design process composed of conceptual design, preliminary design, and detailed design. In each of these phases, one of the main challenges is to find near-optimal solutions considering the information available. The problem statement of a mechatronic design usually presents multiple conflicting objectives which makes the design task even more complex Many researchers in the field of engineering design (Zhang et al., 2023), evolutionary computation (Xia and Li, 2020), and generative design are still working to solve the complex real-life design problems coupled with optimization such as mechatronic design (Dehghani and Trojovský, 2023). Therefore, from a design perspective, there still is a crucial need for a better methodology to model (Chouinard et al., 2020), manage, and evaluate a design (Mohebbi et al., 2018).

One of the new trends in engineering research and development is product modularity. According to (Gershenson et al., 2003), the precise definition of product modularity has not been unanimously defined among the research community. However, most definitions share the same idea that combining or regrouping components into modules increases the modularity of a product. Many benefits come with modularization as it becomes easier to replace a part when it is broken or when the system needs to be upgraded. Moreover, it is also easier to redesign the layout of the product by changing the position of the modules or testing different modules to compare their performance. Additionally, modularity allows for the development of product families which reduces the number of parts to be dealt with by both the designer and the company. The impact of modularity on product and product process performances has also been evaluated up to a certain degree with more empirical studies (Piran et al., 2016; Vickery et al., 2016). Generally, modularity improves design and development.

In this work, concepts from engineering design and evolutionary computation are combined to overcome issues related to module identification during the layout design phase. Module identification can be seen as combining two or more components, subsystems, or systems to form a module. To achieve module identification, one must face three main issues.

The first issue is to correctly model the product-related dependencies (Torry-Smith et al., 2014; Chouinard et al., 2019). A component’s dependency can be defined as how a component affects another one. The dependency between two components can be detrimental. For example, a heat source close to a heat sensor will cause the heat sensor to capture erroneous values of the environment. The dependency can also be beneficial such as a heat source close to a fan that can help regulate the temperature of a room.

The second issue is to define the combination compatibility between components. The combination of two components implies that they are physically integrated to form a module. Considering that two components can have both beneficial and detrimental dependencies at the same time, it can be difficult to decide whether they should be combined or not within the same module.

The last issue is to identify modules that do not deteriorate the design optimizer performance. Hence, the module identification methods must be well integrated into the design optimization process. For example, evolutionary computation has operators such as crossover that will need to be adapted to maintain the design space exploration capabilities of the evolutionary algorithm.

The main objective of this paper is to integrate module identification during the design optimization process. The contribution lies in module identification based on product-related dependency management and complex number design structure matrix (DSM) representation which are used to evaluate the combination compatibility between components. The module identification utilizes an evolutionary algorithm to generate and evaluate modules. The methodology is then validated through a case study in which the layout design of an automatic greenhouse is of concern.

The remaining part of the paper will be structured as follows: Section 2 presents a brief literature review of modular design combined with design optimization. Section 3 describes the proposed methodology. Section 4 presents the layout design of an autonomous greenhouse as a case study. Section 5 reports the results and analysis of the layout design of an autonomous greenhouse. Finally, Section 6 concludes this paper.

2 Literature review on product modules identification

This section will describe a brief state-of-the-art survey on the use of modularity and genetic algorithms in product design. Afterward, it will be easier to position the work presented in this paper and identify its contributions.

2.1 Modularity, genetic algorithm, and product design

Even though product modularity has beneficial effects on design and development, there are still many research topics that need to be studied. One of the main challenges, mentioned by (Hölttä-Otto and de Weck, 2007), is evaluating when to favor a modular design or an integral design. Many researchers are working on overcoming this challenge. For example, AlGeddawy et al. (2017), achieved a modular design based on the design for assembly. To do this, a combination of Cladistics which is a classification tool used in biology, design structure matrix (DSM), and the principle of product granularity level was used. This methodology allows the designer to have a compromise between modularity and integration. Moreover, Hölttä et al. (2005), mentioned that there is a tradeoff between modularity and the performance of the product. If the constraints and performances of the product are more rigid, an integral design seems to be more adequate. However, if the performance requirements are flexible, a modular design can be favored for product variety, ease of re-design, maintenance, repairs, etc. From this, it is possible to realize that the degree of modularity depends on the product specifications and purposes. To evaluate the degree of modularity needed, many papers can be found in the literature. For an exhaustive literature review, it is recommended to look at Gershenson et al. (2004) as well as a more recent review of Bonvoisin et al. (2016). In this section, a brief literature review will be done about the motivation and evaluation of the degree of modularity.

Yu et al. (2003) automatically developed modular product architectures through DSM clustering. DSM clustering was achieved using a specialized genetic algorithm (GA) to manage the different possible clusters. The minimum description length was used as the objective function, which is a model that approximates the system. Xiaogang et al. (2006) used a GA to reorganize the DSM to bring the values closer to the diagonal. A coordination cost function that was computed with the modified DSM was used to evaluate which cluster was better. Wrigley et al. (2019) optimized the layout of a light water modular nuclear reactor power plant. Module identification was done by translating the process and instrumentation diagram into a DSM. Then, a clustering algorithm reorganized the DSM to form modules that are fed to a GA for layout optimization. Cheng et al. (2012) presented a modularization method based on axiomatic design and design structure matrix. The axiomatic design was used to decompose the system and DSMs were used to evaluate the interaction between design parameters. Finally, a GA optimized the minimal description length for DSM clustering to achieve design parameters’ module identification. In these works, module identification is achieved by reorganizing the DSM and clustering components based on component-component interactions. The issue with these methodologies is that the effect of modularization on the design performance is not included in the design optimization or even design selection. Hence, the set of modules found with DSM clustering is not necessarily the optimal set of possible modules in terms of design performance.

Tseng et al. (2008) designed a product with a green life cycle using a GA algorithm that optimizes the likelihood of two components being in the same module based on the concept of liaison intensity. Consequently, the idea is to maximize the liaison intensity in a module and to minimize the liaison intensity between modules. Paras et al. (2018) used a grouping GA to redesign used products in the garment industry. The product was divided into a manageable number of parts. Then, the grouping GA combined different parts to achieve the redesign requirements. The objective called design fitness is a weighted sum of four garment specific objectives. Xiao et al. (2009) uses a GA combined with fuzzy pattern recognition for module decomposition. The objective function is the proximity of the pattern of a solution with a user-defined ideal pattern. Since the objective is to find a near user-defined ideal pattern, the near-optimal pattern is not guaranteed since it is user-dependent. Meng et al. (2007) achieved module identification for product families using a single objective GA. The single objective is a weighted sum aggregation of four different objectives related to a modular design for product families. Shan et al. (2008), Shan and Chen (2009), Shan and Chen (2011) used the weighted sum of four types of DSM for a model formulation which is functional, geometrical, physical, and auxiliary. Then, the optimization of an objective function based on the life cycle of the product and two principles of modular design were done with particle swarm optimization, improved particle swarm optimization, and harmony search algorithms. Kreng and Lee (2004) offered a four-phase methodology. The first phase is analyzing the functional and physical interactions between components. Phase two is finding the proper modularity metrics or modular drivers which will guide the modularity process. The third phase consists of modeling the modularization using a non-linear programming model. The final phase is optimizing the objective function using a grouping GA that clusters components into modules. In these works, the optimization considers modular metrics as well as product-related metrics. However, they use a single objective optimization for a multi-objective optimization problem which means they will converge on one design based on the selection of promising designs. Furthermore, the design performance is not included in the optimization process.

Xu et al. (2018) used a two-step methodology for the modular design filament winding process equipment. The first step is to find the modules from components using a grouping GA and modular driving forces. The second step is to optimize the performance requirement using a non-dominated sorting genetic algorithm II and the modules found in the first step. Even though multi-objective optimization is used, the modularization process and design optimization are done separately. As mentioned above, this could lead to a set of suboptimal modules. Wei et al. (2015) used three principles for modular design: interaction within a module, interactions between modules, and components affecting the same functional requirements should be combined into a module. To identify modules, a multi-objective optimization is done where all three principles are concurrently optimized using the improved strength Pareto evolutionary algorithm. Finally, to choose the best set from the Pareto set, a fuzzy selection mechanism is used to eliminate the bias from human selection. However, the design performance is not included in the optimization process. Zheng et al. (2023) proposed an improved genetic algorithm named NSGA2-FCM to identify modules in a product. The authors use the FBS mapping to break down the function and structure aspects of the system and highlight their dependencies for the module identification process. The proposed methodology has been tested on a beer fermenter. Even though this method uses FBS mapping to calculate the affinity between two modules, it does not explicitly optimize the design performance while identifying the modules. Furthermore, the number of modules seems to be a parameter that is given by the user. Consequently, the methodology does not optimize the level of modularity.

Ali et al. (2023) present a generic modularization framework based on the conceptual model of a product. The principle is to use a conceptual knowledge graph to find the dependencies between the different components. Then, the knowledge graph is encoded as chromosomes with the linear linkage encoding in order to feed it to the genetic algorithm. The framework proposed many options for objective functions that have been found in the literature. All of these objective functions are for modularization, consequently, the optimization of the design performance is not taken into account. Furthermore, the difference between positive and negative dependencies might be considered in the knowledge graph, but it is not explicitly shown in their methodology and their online shop case study.

Wang et al. (2023) present a methodology to identify the impact of product structural characteristics on modularity based on a data-driven model. The data is created by generating many random structural DSM that represent virtual products. This method has been developed by the authors due to the difficulty of finding data. Then, the module identification is done with the aid of a hierarchical clustering algorithm. Based on these results, the authors were able to discuss the impact of the number of parts and average number of connected nodes on the product’s modular performance. This work uses binary DSM to represent the structural properties of the product. Hence, they can define that between two components there is a dependency, however, they do not consider if the dependency is positive or negative. This could lead to the formation of a module that increases the modular performance of the product but decreases its functional performance.

As mentioned by Gershenson et al. (2004), there is a need for flexibility in the modularization of a product to consider modules in the early design stages such as layout design. Moreover, Bonvoisin et al. (2016) also express a lack of flexibility during the modularization process. Metrics and methods for modularization are often problem-specific which restricts their use.

2.2 Main objective and contributions

The main objective of this paper is to offer a tool that allows the user to evaluate the effects of modularization on the design performance while optimizing the design performance.

As mentioned in the literature review, one of the main challenges that designers face is to know when to design a system that is composed of multiple changeable and replaceable subsystems (modular design) instead of a system that cannot be easily decomposed into subsystems (integral design). In the literature review, multiple ways are proposed to overcome this, but to the best of the authors’ knowledge, there is no approach that fully integrates the modularization with the multi-objective design performance optimization. Indeed, most of them use a two-step strategy where the first step is to identify the modules and the second step is to optimize the design. Therefore, the design performance is not necessarily used as a driver to evaluate if a modular design is better than an integral design.

The main contribution of this work is to use the power of genetic algorithms and design performances to create, evaluate, and rank designs with different levels of modularity. The original aspects of the developed methodology can be listed as follows:

• Formation of modules during design optimization allows to have a GA with a diverse population in terms of level of modularity.

• The GA has an elitist mechanism that evaluates if modularization is favored or not based on design performances. In other words, designs of different levels of modularity are compared together based on multiple design performances. Hence, allowing a direct comparison of modular designs and integral designs.

• Multi-objective optimization which leads to a Pareto front containing multiple near-optimal solutions with different levels of modularity. Hence, the user can have a better overview of the trade-offs of choosing a modular design instead of an integral design.

Therefore, the main objective of the developed approach is to present the usability and feasibility of evaluating the level of modularity needed for a specific system based on design performances in one multi-objective optimization run. The proposed approach could greatly help designers find the proper level of modularity while keeping an adequate design performance.

Within the scope of this paper, the modularization of an autonomous greenhouse was done with a GA and design performances. This paper details the steps followed for the development of this approach.

3 System design description

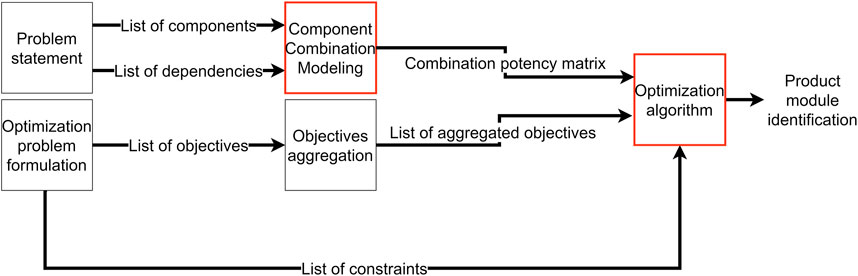
Figure 1 shows the overview of the methodology as well as the contribution of this paper. Although the problem statement and optimization problem formulation have been treated in detail in our previous work (Law-Kam Cio et al., 2020), a summary will be presented in Section 4 for completeness. However, the main focus will be the component combination modeling, as well as its integration into the optimization algorithm.

Figure 1

Figure 1. Overview of the methodology. The red squares represent the places of focus in this paper.

3.1 Modeling components’ dependencies

To model component dependencies, A DSM with complex arrays will be used which was developed in the authors’ previous work (Chouinard et al., 2020). This augmented DSM uses complex numbers to differentiate negative and positive dependencies. By treating negative and positive dependencies separately, it is possible to aggregate multiple DSMs together while avoiding the loss of information caused by sign cancellation. Indeed, often the negative dependencies are represented by negative numbers and positive dependencies by positive ones. Hence, during the aggregation, the summation of negative and positive dependencies might be 0 which can lead the designer to falsely believe that there are no dependencies between two components. The arrays of the DSM are described as:

$\mathbf{\text{DS}}{\mathbf{M}}^{*}=\left[{\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right]$

where the real part $a_{ij}$ describes the positive dependency and the imaginary part $b_{ij}$ shows the negative dependency amongst component $i$ and component $j$ . This notation has the advantage of conserving and accumulating positive and negative dependencies separately during the aggregation of matrices. In this methodology, the chosen aggregation method is a weighted sum of all the DSMs.

3.2 Modeling the component combination

For the DSM aggregation process, a matrix named expert combination matrix (ECM) is added to take into consideration the designer’s experience in combining components. ECM is introduced to reflect on the feasibility of combining two components into a module. This also includes evaluating if the effort needed to combine two components consumes too many resources in terms of time and cost even though there are no clear adverse effects. Once DSM* is obtained, a matrix called combination potency matrix (CPM) can be computed that can be described as:

$\mathbf{\text{CPM}}=\left[\mathbf{f}\left({\mathbf{a}}_{\text{ij}}+{\mathbf{b}}_{\text{ij}}\mathbf{j}\right)\right]=\left[\frac{{\mathbf{a}}_{\text{ij}}}{{\mathbf{b}}_{\text{ij}}}\right]$

where $a_{ij}+b_{ij}j$ is found in the DSM*. The idea is to find a function $f\left(.\right)$ that allow the quantification of the combination potency based on the complex number notation.

The concept of complex DSMs has not been widely used. Hence, there is no formulation of $f\left(a_{ij}+b_{ij}j\right)$ given in the literature, therefore in this work, a simple ratio $f\left(a_{ij}+b_{ij}j\right)=\frac{a_{ij}}{b_{ij}}$ will be used. The chosen function is based on a simple and intuitive view of the matter. Indeed, a ratio of positive dependencies and negative dependencies gives a range of values from 0 to $\infty$, where 0 means that there is no combination potency between two components and $\infty$ means that there is a high combination potency. A scale of numerical and qualitative values is shown based on the different values of the real and imaginary parts:

$\left\{\begin{array}{c}\left\{\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)=\mathbf{\infty }|{\mathbf{a}}_{\mathbf{\text{ij}}}>\mathbf{0}\hspace{0.17em}\mathbf{\text{and\hspace{0.17em}}}{\mathbf{b}}_{\mathbf{\text{ij}}}=\mathbf{0}\right\}\to \mathbf{H}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{c}\mathbf{o}\mathbf{m}\mathbf{b}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{p}\mathbf{o}\mathbf{t}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{y}\\ \left\{\mathbf{1}<\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)<\mathbf{\infty }|{\mathbf{a}}_{\mathbf{\text{ij}}}>{\mathbf{b}}_{\mathbf{\text{ij}}}\right\}\to \mathbf{C}\mathbf{o}\mathbf{m}\mathbf{b}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{p}\mathbf{o}\mathbf{t}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{y}\\ \left\{\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)=\mathbf{1}|{\mathbf{a}}_{\mathbf{\text{ij}}}=\mathbf{0}\hspace{0.17em}\mathbf{\text{and\hspace{0.17em}}}{\mathbf{b}}_{\mathbf{\text{ij}}}=\mathbf{0}\right\}\to \mathbf{\text{Independent}}\\ \left\{\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)=\mathbf{1}|{\mathbf{a}}_{\mathbf{\text{ij}}}={\mathbf{b}}_{\mathbf{\text{ij}}}\ne \mathbf{0}\right\}\to \mathbf{\text{Neutral}}\\ \left\{\mathbf{0}<\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)<\mathbf{1}|{\mathbf{a}}_{\mathbf{\text{ij}}}<{\mathbf{b}}_{\mathbf{\text{ij}}}\right\}\to \mathbf{L}\mathbf{o}\mathbf{w}\mathbf{c}\mathbf{o}\mathbf{m}\mathbf{b}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{p}\mathbf{o}\mathbf{t}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{y}\\ \left\{\mathbf{f}\left({\mathbf{a}}_{\mathbf{\text{ij}}}+{\mathbf{b}}_{\mathbf{\text{ij}}}\mathbf{j}\right)=\mathbf{0}|{\mathbf{a}}_{\mathbf{\text{ij}}}=\mathbf{0}\hspace{0.17em}\mathbf{\text{and\hspace{0.17em}}}{\mathbf{b}}_{\mathbf{\text{ij}}}>\mathbf{0}\right\}\to \mathbf{N}\mathbf{o}\mathbf{c}\mathbf{o}\mathbf{m}\mathbf{b}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{p}\mathbf{o}\mathbf{t}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{y}\end{array}\right.$

It is important to mention the difference between cases 3 and 4. The combination process of case 3 should be easier than the one for case 4, since in case 3, the two components are independent due to the absence of dependencies. Moreover, in case 4 the designers need to deal with adverse effects. For this reason, the numerical value for case 3 is slightly higher than for case 4 which is why the numerical value for case 3 is represented by the “1⁺” symbol. Hence, even though the numerical value of case 3 would be mathematically undefined. From a coding point of view, it is possible to catch this exception in an if statement and assign its numerical value to 1.00001 to respect the “1⁺” symbol assigned to case 3.

3.3 Integrating the component combination in evolutionary computation

The chosen evolutionary algorithm in this work is a modified version of the non-dominated sorting genetic algorithm -III (NSGA-III) (Deb and Jain, 2014). Part of these modifications is presented in a previous work of the authors (Law et al., 2020). The components’ combination has also a chance of being performed during the reproduction phase of the NSGA-III (See Figure 2). There is a probability associated with the occurrence of the combination operator just like the mutation operator. The components’ combination is done on a clone of a random individual from the population. Here, the individual represents a design. Hence, the population is composed of many designs that compete with one another in order to find a set of near-optimal designs.

Figure 2

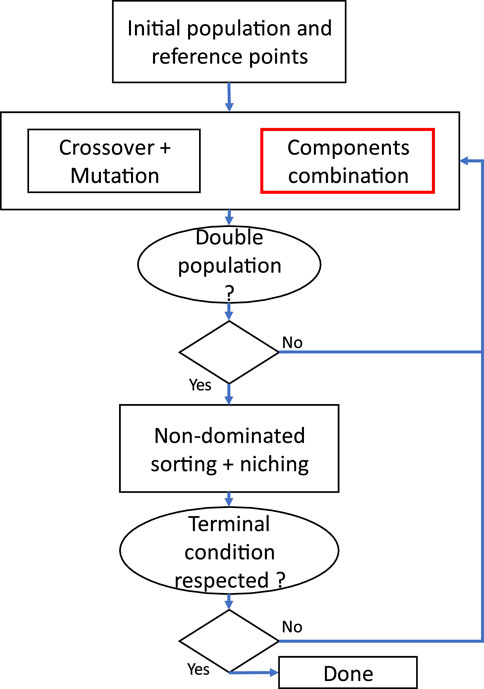
Figure 2. Overview of the modified NSGA-III algorithm. The red square represents the added operator.

From Figure 2, not only the methodology allows individuals with modules to compete with individuals without modules, but it also allows competition between modules. Hence, it is possible to evaluate the effect of modularization on the design performance (i.e., objectives), thus, if a specific module is beneficial, it will improve one or more objectives. Using this strategy, the algorithm will favor optimal modules, if they exist, based on the design performance. However, the optimization algorithm must be adapted to achieve this.

The component combination happens within an individual (i.e., a design). Hence, the population will be composed of many individuals that formed different modules during the optimization. To keep track of the individuals’ modules, each individual will have a combination tracker vector (CTV). To be more precise, the CTV is used to know which components are combined into a module and to adapt operators and/or mechanisms of the optimization algorithm. To better understand how CTV is modified throughout the optimization process, Table 1 represents the formation of a module of one individual after 2 component combinations. Initially, the CTV is generated by assigning one component (first column) to one module (second column). Hence, at the beginning, every module contains a unique component. The third column shows the impact of combining two modules on the CTV. The combination is formed by integrating the seventh component (seventh module) with the second one (second module) which is why the CTV’s module ID of the 3^rd column, seventh row is changed to 2. Moreover, the module ID of the third column, eighth^, and ninth rows are changed to seven and eight, respectively, to keep track of the total number of modules. The last column represents how the CTV will be changed if another component is added to the module. The ninth component is also integrated with the second component which is why the index of the third column, ninth row is 2. The module is now formed of the second, seventh^, and ninth components.

Table 1

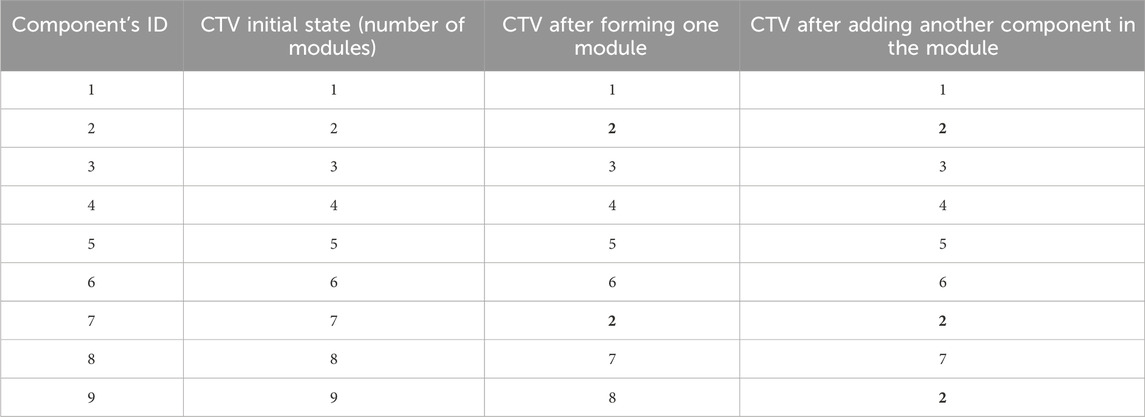
Table 1. Example of the use of CTV. Impact of forming a module on the CTV (third column). Impact of including a component into an existing module (fourth column).

The CTV also offers another advantage. As mentioned earlier, some evolutionary operators will be affected by the combination of components. For this implementation, the crossover operator is the only one that has a conflict with the combination of components. Indeed, applying a crossover operator between two solutions with different combinations is most likely to output an implausible individual. In this work, an implausible individual is defined as an individual with too many or too few components. This is where the CTV can be useful. To avoid implausible individuals, a crossover between two individuals can happen if their CTVs are identical. In other words, the crossover operation can happen when two individuals have identical modules. However, if their CTVs are not identical, but share an identical module at the crossover point, an exchange between these identical modules will be done. Otherwise, no crossover operator is done between the two individuals. This modification of the crossover operation is done to ensure the exploration of the design space.

4 Case study: autonomous greenhouse layout design

In Law et al. (2020), Law-Kam Cio et al. (2020), the authors proposed a case study based on components’ placement and dependencies for the layout design of an autonomous greenhouse. This case study was chosen because it can greatly benefit from modularity. Indeed, by integrating components into modules, it is possible to reduce the volume occupied by components which will increase the volume allocated for the growth of the plants. Hence, the autonomous greenhouse will better fulfill its main function which is to ensure the growth and survival of plants. The formulation will briefly be presented here.

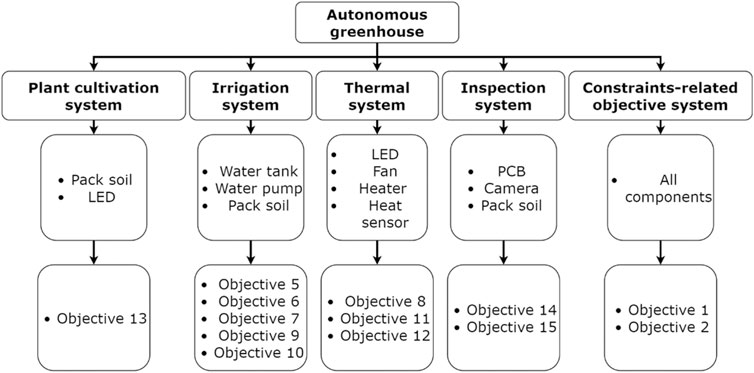
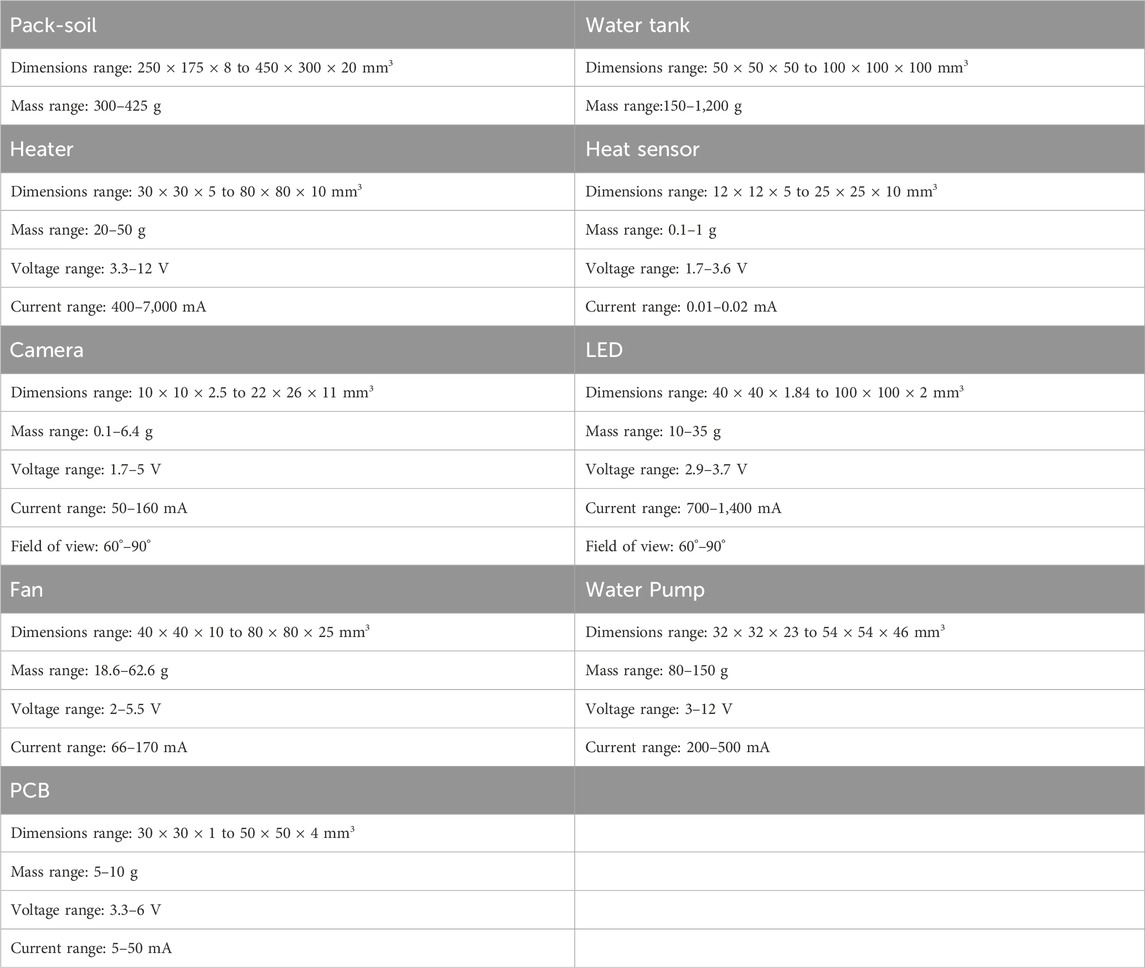
There are nine main components for the autonomous greenhouse design. First, the pack soil contains the seeds and the artificial soils needed for the growth of plants. Second, a water distribution system composed of a water tank and a water pump is needed to make sure the pack soil receives the necessary nutritious water to grow and survive. Third, LEDs act as artificial sunlight to allow photosynthesis and to give a growth direction. Fourth, to avoid the plant freezing, a heater, heat sensor, and fan are used to control the whole greenhouse temperature. Finally, an inspection system composed of a camera and PCB board is used to give information about the health and condition of plants to the operator of the greenhouse. The PCB board contains sensors that give information about the gas concentration of the greenhouse’s environment (i.e., O₂, CO₂, etc.).

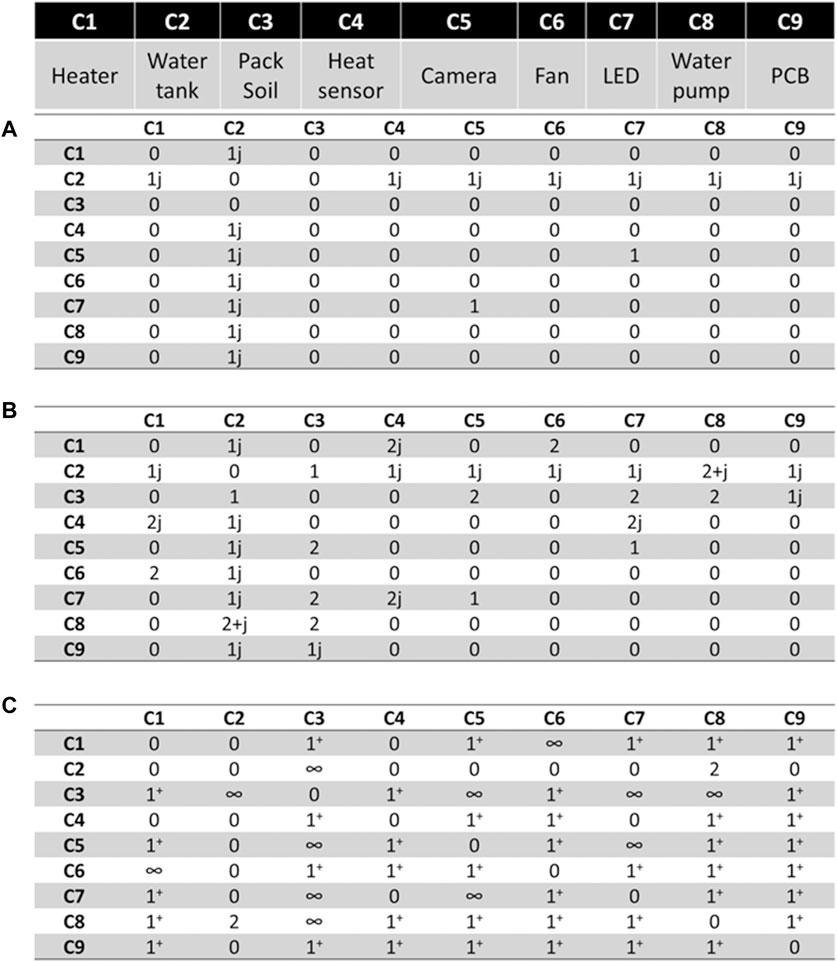
The new DSMs are presented in Figure 3. The DSMs have been modified using the following adaptation of the complex scale presented in (Chouinard et al., 2020).

$\left\{\begin{array}{c}Complexvalue=0+2j\to Detrimental\\ Complexvalue=0+1j\to Undesirable\\ Complexvalue=0+0j\to Neutral\\ Complexvalue=1+0j\to Desirable\\ Complexvalue=2+0j\to Necessary\end{array}\right.$

Figure 3

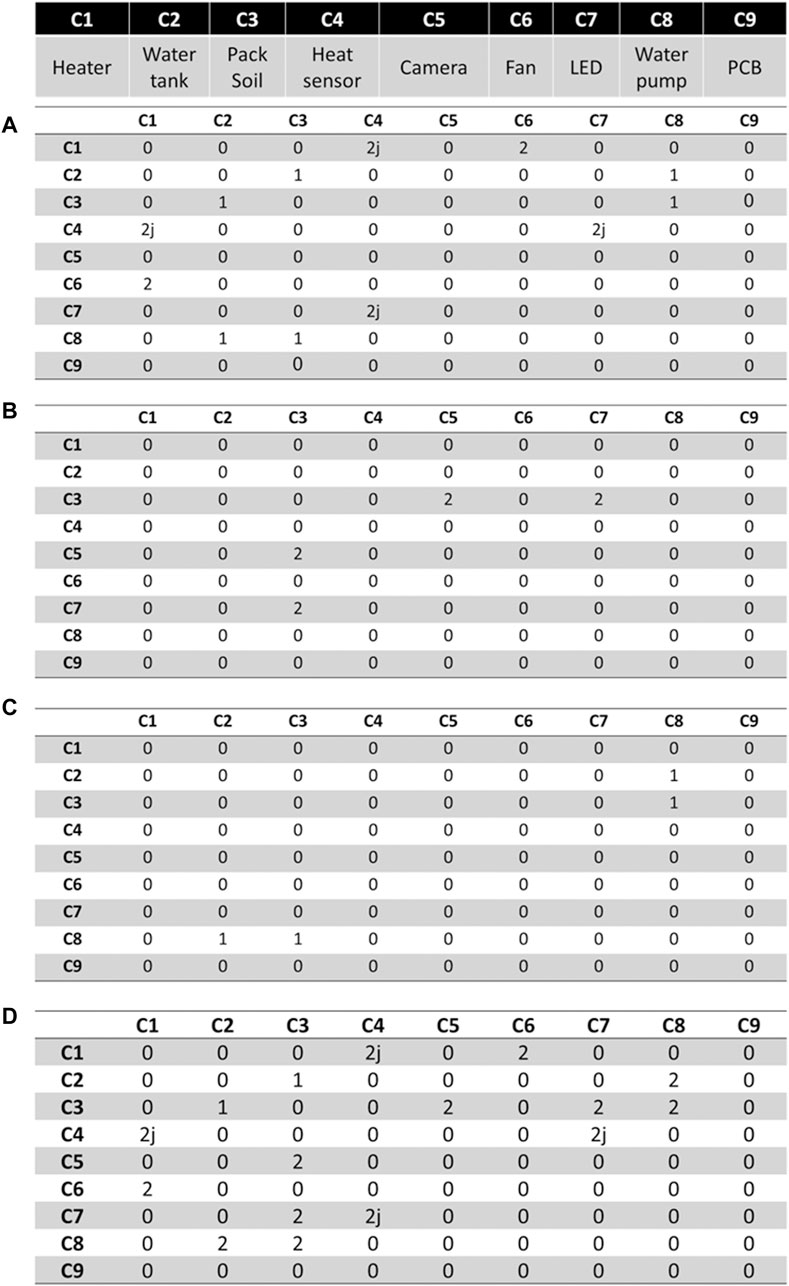
Figure 3. DSMs of the layout design of an autonomous greenhouse. DSM of closeness (A) DSM of the field of view (B) DSM of physical connections (C) Aggregated DSM (D).

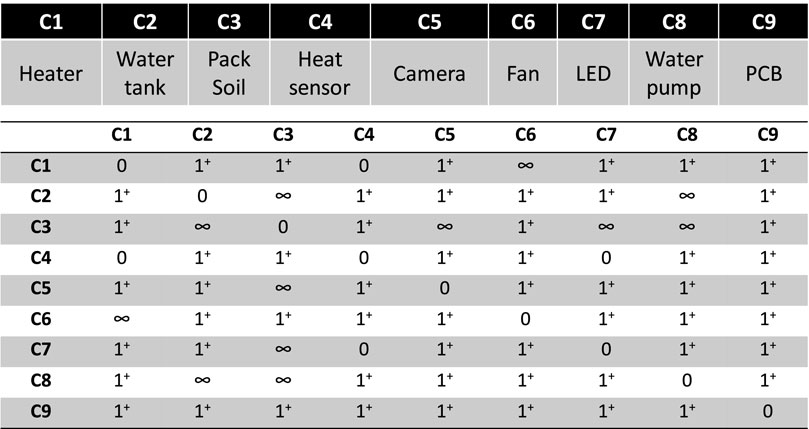
Using the formulation, the layout design of most systems can be modeled by three matrices. The first one is the closeness matrix which represents how far or close a component should be from another one. The second matrix is the field of view (FOV) matrix which indicates that a component needs to be within or outside of the FOV of another one. The last one is the physical connection matrix and defines the number of connections between two components. The aggregation of these three matrices is computed using the weighted sum approach. Using the aggregated matrix, the CPM is calculated and shown in Figure 4. In this case study, it is important to note that there is a difference between the closeness and the combination of two components. To illustrate this, the water tank will be taken as an example. The water tank could be close to the LEDs without any consequences. However, combining the water tank and the LEDs is not favored for reasons such as water and electronics are not compatible, and their combination can be troublesome, but possible.

Figure 4

Figure 4. CPM of the layout design of an autonomous greenhouse.

To input this sort of information, the ECM is used since its purpose is to include expert knowledge about the physical integration between components as mentioned above. Hence, the water tank and electric components have a value of 1j since such a combination is not favored since it would make the design and development more complex. Furthermore, a value of one is given to the ECM element of the LED and the camera to avoid lens flare since the light could prevent the camera from achieving its functional requirement. Including the ECM in the aggregation process, the new aggregated matrix and CPM are given in Figure 5. It is possible to see that the input of the designer on the combination of components has an important impact on the CPM. For example, the LED and camera have high combination potency as opposed to their potency being neutral before.

Figure 5

Figure 5. Integrating the ECM. ECM (A) New aggregated matrix (B) New CPM (C).

In this paper, the objective function from the authors’ previous work has been used and reported in Table 2 to obtain layout designs of an autonomous greenhouse. This table shows the relationship between the dependencies found using product-related dependency management and the objective functions. These objectives treat information about the placement and size of components to ensure the survival and growth of the plants. DX, DY, and DZ represent the dimensions of a component, and PX, PY, and PZ their position within the greenhouse. Finally, M, V, and A are the mass, voltage, and current of a component, respectively.

Table 2

Table 2. Dependencies and objective functions of the layout design of an autonomous greenhouse.

Furthermore, the strategy for the aggregation of objectives is illustrated in Figure 6. The methodology used to aggregate these objectives uses axiomatic design to identify the subsystems and components of the greenhouse. Then based on the dependencies and objective functions of the layout design (Table 2) and the axiomatic design, the objective functions are aggregated by associating them to subsystems. More details of this methodology can be found in the author’s previous work (Law et al., 2020).

Figure 6

Figure 6. Objectives aggregation of the layout design of an autonomous greenhouse.

5 Results and discussion

The simulation parameters are presented in Table 3. The parameters above the thick line are the algorithm parameters of the modified NSGA-III. The reference vector size and population size have been chosen based on the recommendation of Deb and Jain (2014). The rest of the parameters were fine-tuned by trials and errors. The probabilities of combination and mutation were defined so that the modularity process would not be done too quickly to allow the comparison of different levels of modularity within a simulation run. The design parameters in light gray are from the authors’ previous work (Law-Kam Cio et al., 2020). For completeness, the components’ parameters from Law-Kam Cio et al. (2020) are also reported in Table 4. It is important to mention that the modularization process starts only when the entire population is constraints-free. By doing so, it is possible to compare the feasible non-modular designs to feasible modular designs. If the modularization process is better, the non-modular design should completely disappear after a while.

Table 3

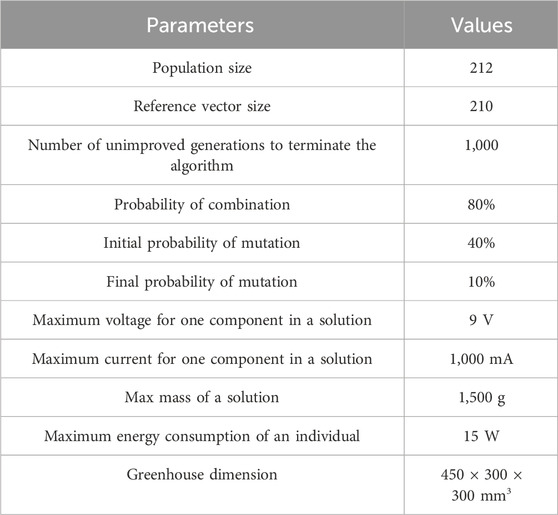
Table 3. Simulation parameters. The first 6 parameters are algorithm parameters and the other ones are design parameters.

Table 4

Table 4. Components’ parameters.

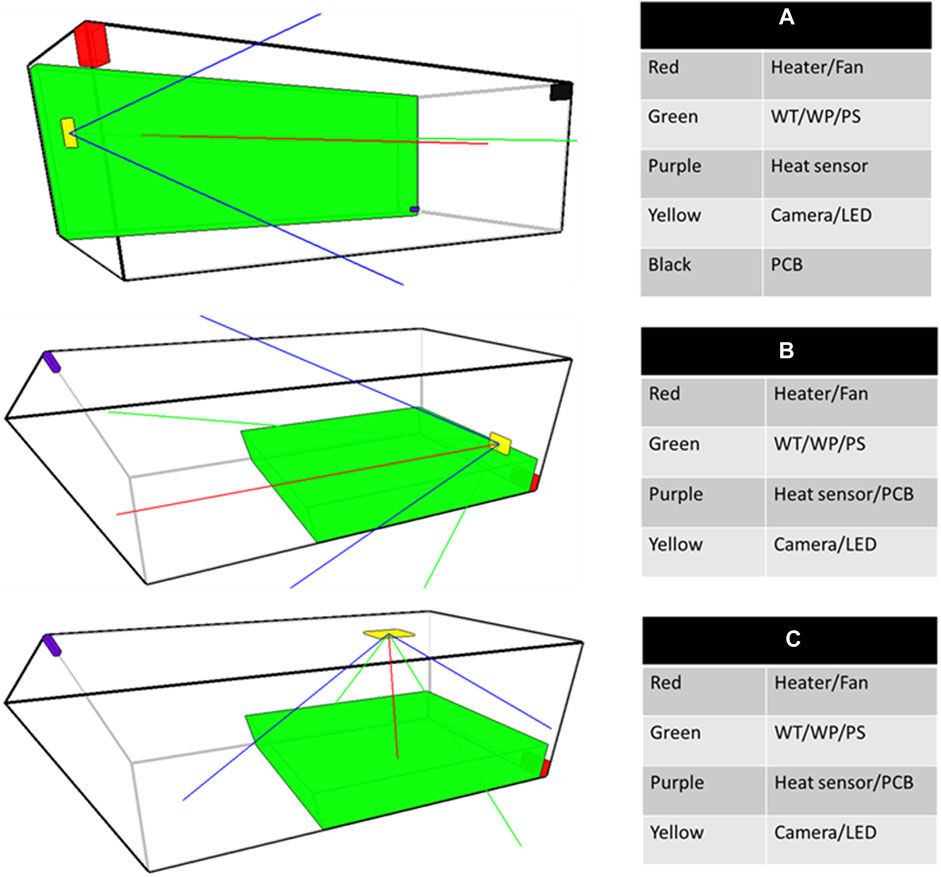
To show the applicability of the methodology presented above, a comparison of simulation runs done with and without the modularization process is carried out. Figure 7 shows different examples of layouts of 10 simulation runs without modularization. Ten simulation runs were done for reproducibility purposes. Hence, there were many duplicated layouts and similar layouts that were outputted from these simulations runs. Therefore, the presented layouts in Figure 7 are the most common and near-optimal ones. By analyzing the layouts of this study case, it is possible to notice that the optimization of the layout unveils clusters of components. Indeed, all the examples show physical proximity between the pack soil, water tank, and water pump. The same conclusion can be made for the heater and the fan as well as the camera and the LED. As for the heat sensor and the PCB, only layout A of Figure 7 shows a possible combination. The red, blue, and green lines in each figure are for the line of sight and field of view of the components. The red lines are the line of sight of the component starting from the center of the component. The blue and green lines are the field of view of the components in the form of a cone.

Figure 7

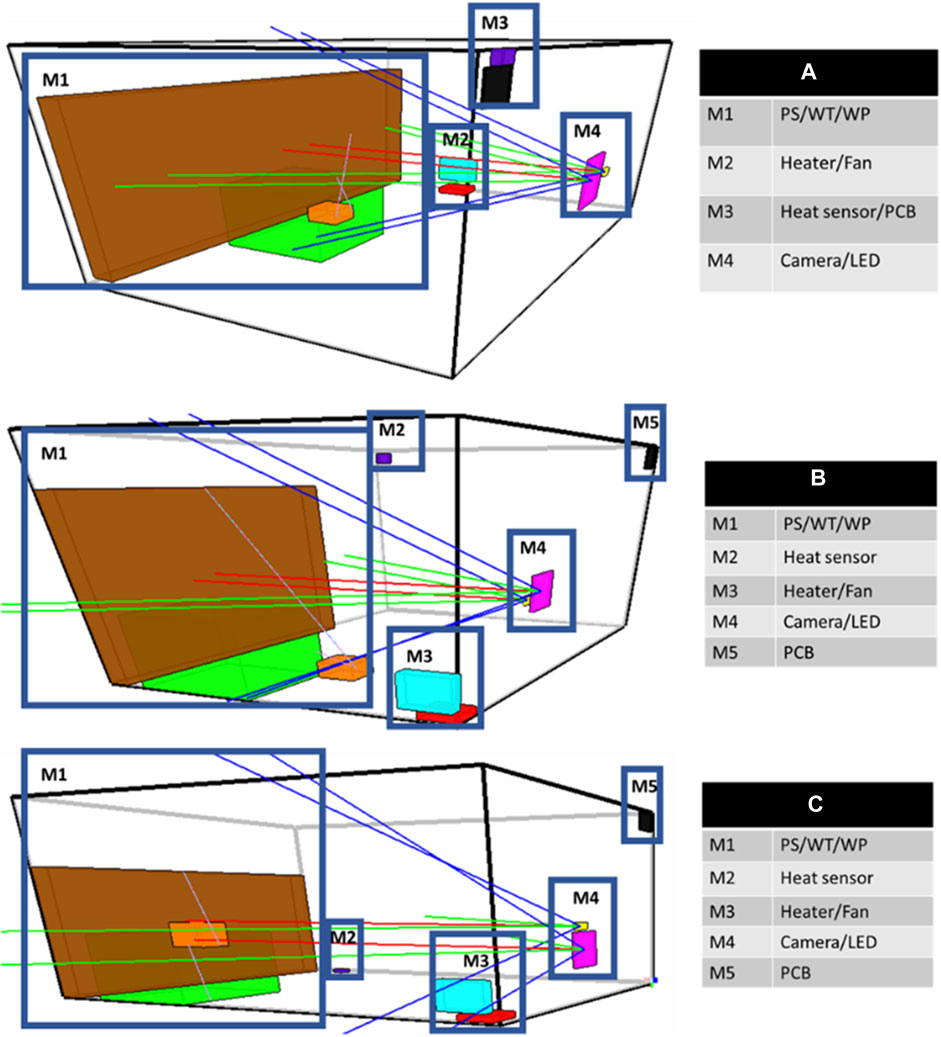
Figure 7. Examples of layouts are generated without modularization. Highlighting the possible modules. (A–C) show multiple solutions with different possible modules.

Figures 8–10 show the results of 10 simulation runs. The layouts were chosen to show the different levels of modularization while achieving the functional requirements.

Figure 8

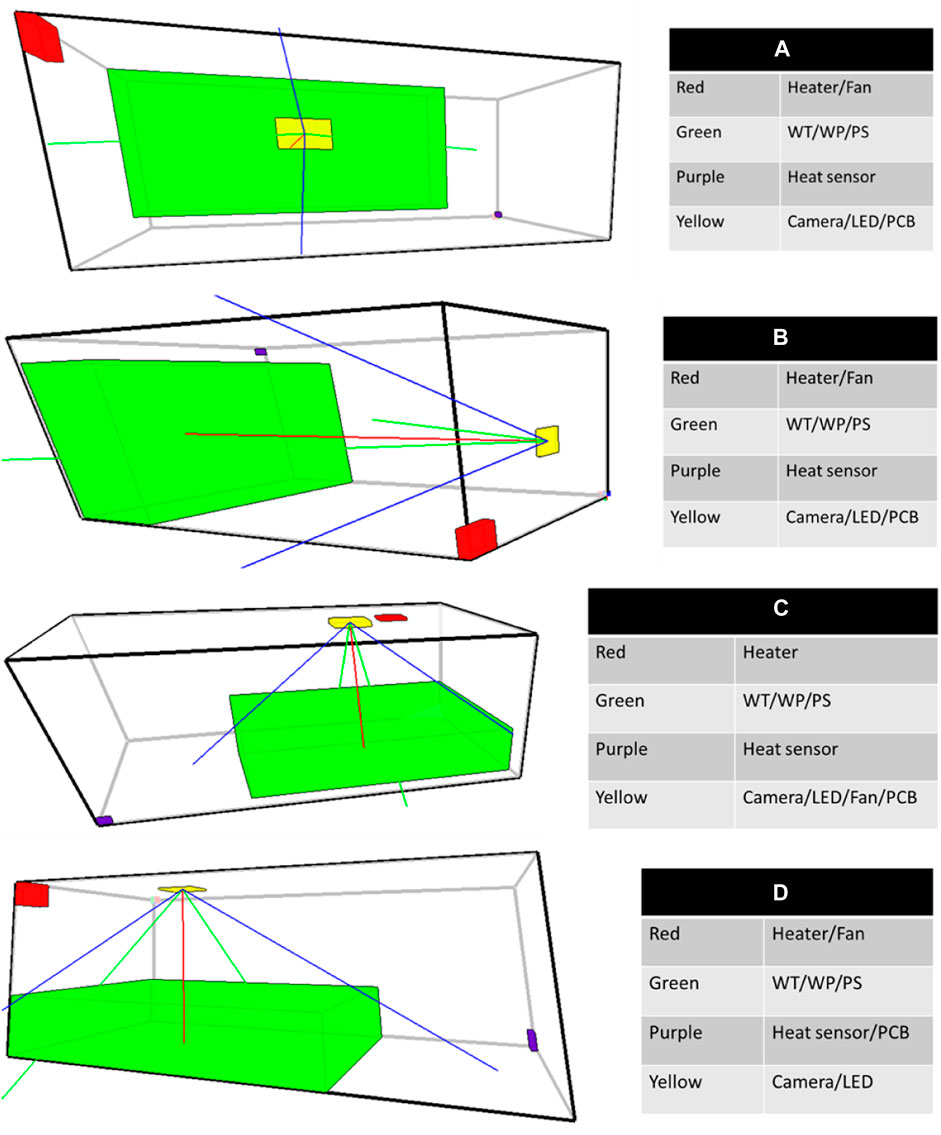
Figure 8. Examples of highly modular layouts. (A–D) show the different solutions with the same modularity level.

Figure 9

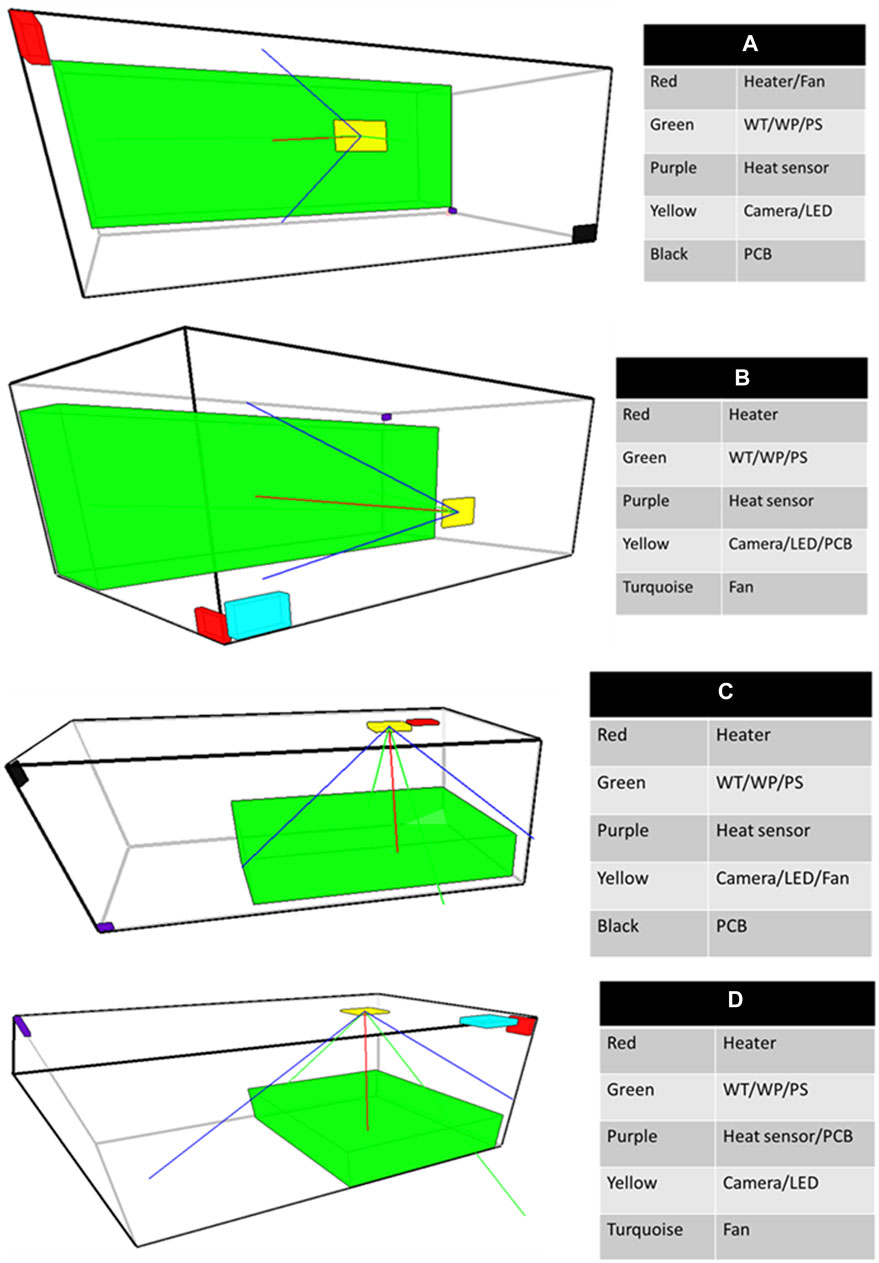
Figure 9. Examples of moderate modular layouts. (A–D) show the different solutions with the same modularity level.

Figure 10

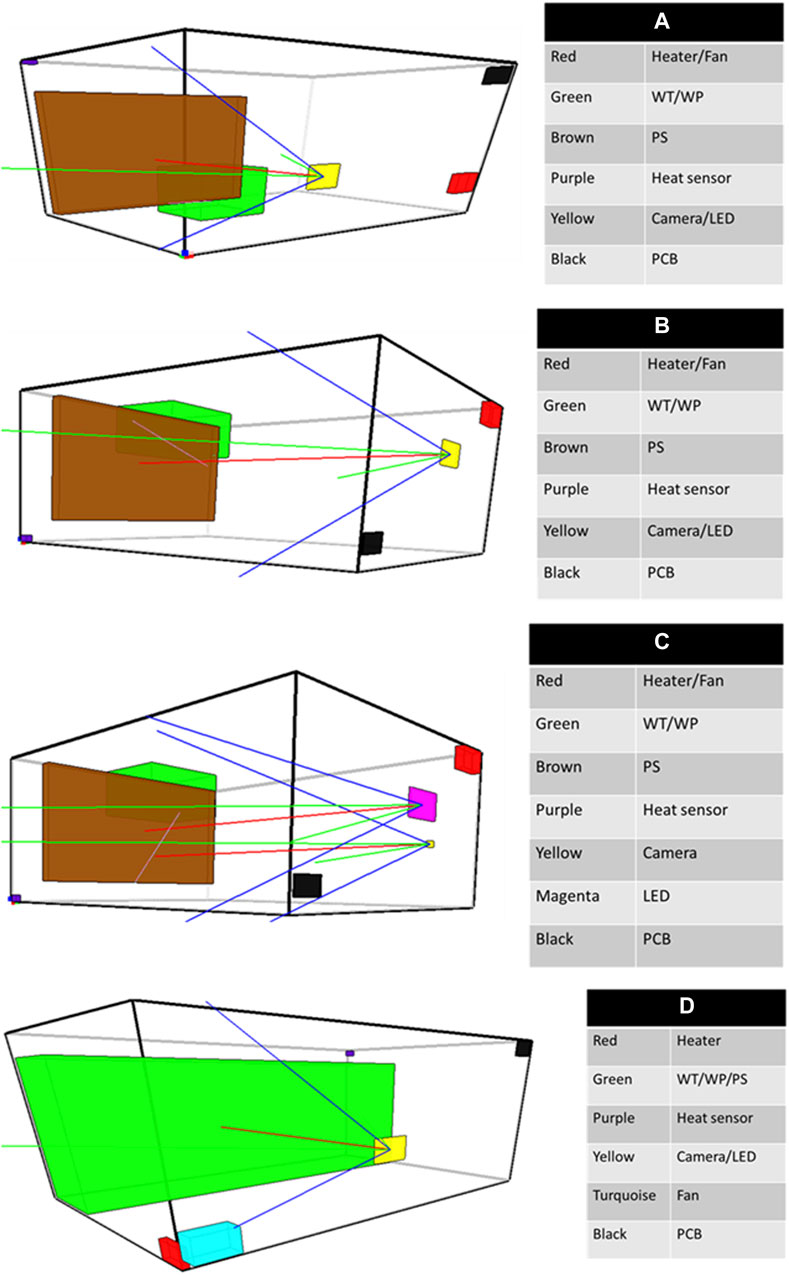
Figure 10. Examples of low modular layouts. (A–D) show the different solutions with the same modularity level.

Figure 8 shows four examples of highly modular layouts of an autonomous greenhouse. These layouts have four modules. As expected from the CPM as well as the modules identified from Figure 7, the water tank and pack soil are combined due to their high combination potency for each layout. For the same reason, it is possible to see that the camera and LED are also combined. For layout D, the heat sensor and the PCB are combined. The CPM shows that this combination can happen without impacting the system performance and layout A of Figure 7 shows that their combination can be expected. Looking at the CPM, the combination of the heater and fan is most likely to happen. This is confirmed as it is possible to see all the layouts of Figure 8 except C has the heater and fan combined. For layout C, the heater is the only component of its module, and the fan is combined with the camera, LED, and PCB. Furthermore, layouts A and B include the PCB with the module composed of the camera and LED. These combinations were expected since the PCB has an independent dependency with all the components except the water tank. Finally, the water pump is combined with the water tank and pack soil even though the designer’s suggestion was to avoid combining these two components in the ECM. This goes to show that their combination would greatly benefit the design performances even if it can also be difficult to achieve by the designer.

Figure 9 shows four examples of moderate modular layouts. The number of modules for these layouts is 5. It is possible to see that the water tank, water pump, and pack soil still form a module for every layout. The heater and fan module have only been present in layout A. For the other layouts, the fan is either combined with the camera and LED module (layout C) or is a module of its own (layout B and D). The separation of the heater and fan was not expected, considering that the CPM shows an infinite combination potency between these components. However, it seems that the combination of these two simply did not happen due to the stochastic nature of the optimization because layouts B and D show that the heater and fan are really close to one another similarly to the layouts of Figure 7. As for layout C, the fan simply got combined with the camera and LED first. Then, the combination of the heater with this module was not optimal since the heater would be closer to the heat sensor.

Figure 10 shows four examples of low modular layouts. This shows more than five modules. These layouts are similar to the layout of Figure 7. Indeed, it is still possible to see a tendency to combine the water tank, water pump, and pack soil into a module. The same goes for the heater and fan as well as the camera and LED. Hence, in the layouts of Figure 10, some of these modules have been made or partially made.

In all the examples of Figures 8–10, the water tank and water pump have been combined even though the designer indicated that this combination is not suggested in the ECM. The reason why this combination is preferred can be explained by objectives 1, 7, and 9 of Table 2 which greatly benefit from this combination. Indeed, these objectives are mainly related to the length and volume of the tubes needed to do the water distribution. By combining the water tank and water pump, the length of the tubes does not need to be handled with the overall design of the greenhouse but solely in the design within the module composed of the water tank and water pump. Furthermore, this combination also leads to the improvement of the objectives 13 and 14 of Table 2. These two objectives are related to avoiding the obstruction of the view of the camera and the lighting of the LED. By having the tubes, water tank, and water pump inside one module, it is possible to reduce the obstructed area as can be seen by comparing the designs without modularization A, B, and C of Figure 7 with the low modular designs A, B, and C of Figure 10. Furthermore, it is possible to observe, in higher modular designs (Figures 8, 9), that the improvement of objectives 1,7,9, 13, and 14 is greatly increased since combining the water tank, water pump, and pack soil reduces the overall volume and the obstruction of the camera and LED. The reason is that the water tank and water pump can increase their volume by increasing the width and length of the module while decreasing its height. Hence, the optimization shows the designer that this combination is more advantageous for the design of a greenhouse even if it must overcome negative dependencies.

It is possible to observe the benefits of modularity on the layout design of an autonomous greenhouse by analyzing the results of Figures 8–10. The more modular is the layout, the more available space there is for the growth of the plants. Furthermore, the module containing the pack soil and the water tank usually has a bigger volume that implies more seeds and/or more water can be used to grow plants. Finally, the field of view of the camera and LED projecting on the pack soil are less obstructed by other components. This is mainly due to the combination of the pack soil, water tank, and water pump since the water tank and water pump contributed the most to the obstruction of fields of view as shown in Figure 7.

It is important to mention that some of the outputted layouts were poor. Layout A from Figure 11 cannot be used to ensure the growth and survival of the plants due to the undesired direction of the camera and LED module. The filming and illumination of the plant cannot be fulfilled adequately with this configuration. Layout B also shows this problem as well as the heater and fan module being blocked by the pack soil, water tank, and water pump module. This can cause a suboptimal performance of the fan which can lead to a local heat point or cold point. Layout C also shows this problem.

Figure 11

Figure 11. Examples of inadequate layouts. (A–C) show different inadequate solutions.

6 Limitations and future works

The presented results showed that the proposed methodology achieved module identification while ensuring the functional requirements of the product. However, the methodology could be improved by overcoming one of the issues, which is the absence of an exploratory mechanism (e.g., niching techniques) among the set of modules integrated into the optimization algorithm. Indeed, the formation of one module can prevent the formation of another one. Hence, it is possible to obtain a local optimal set of modules if it takes over the population. A local optimal can also mislead the designer and cause the final product to be less optimal or to not fulfill the customers’ needs. To overcome this issue, a niching mechanism such as an adapted version of the crowding distance based on the CTV might be a solution in future works.

Another issue is that the CPM has static values that depend on the designers’ weight assignments and the chosen computation method. Hence, the probability of combining two components is greatly impacted by the designers. In the case where the designer input is inaccurate, two mechanisms could be explored to rectify this. The first one is the exploration and study of the computation method other than the ratio between positive and negative dependencies. The second one is to make the CPM values dynamic and learn through trials using reinforcement learning algorithms.

Lastly, a comparative study between the proposed methodology and other methodology should be done. To make sure that the comparative study is valid, the current state-of-the-art modularity methods and evolutionary algorithms should be adapted to offer many concepts with different levels of modularity.

7 Conclusion

This paper presents a methodology to concurrently optimize a product design while identifying modules. The methodology uses complex DSM to evaluate the combination potency between components based on their positive and negative dependencies. The combination potency is then summarized into a matrix called a combination potency matrix (CPM). The CPM is then integrated into a modified version of the NSGA-III to simultaneously accomplish the module identification and layout design optimization of an autonomous greenhouse. The proposed methodology allowed us to find concepts of the layout of an autonomous greenhouse with different levels of modularization. The modularization process was able to reduce the number of physical components from 9 down to a minimum of 4 modules. The benefits of the modularization for the autonomous greenhouse are more space for the growth of the plants, lower obstruction of the filming and illuminating of the camera and LED, respectively, and larger pack-soil and water tank which means more seeds can be planted. The proposed methodology was able to obtain these benefits while ensuring the fulfillment of the functional requirements of the autonomous greenhouse. However, poor concepts were still found due to the conflict between modules and objectives functions as well as the definition of the dominance in the non-dominated sorting. To improve the proposed methodology some modifications as been suggested such as a dynamic CPM as well as including diversity among the set of modules.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Y-SL: Conceptualization, Formal-analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft. GB: Funding-acquisition, Formal-analysis, Methodology, Project-administration, Resources, Supervision, Validation, Writing–review and editing. AV: Conceptualization, Funding-acquisition, Formal-analysis, Methodology, Project-administration, Resources, Supervision, Validation, Writing–review and editing. AM: Funding-acquisition, Formal-analysis, Project-administration, Resources, Supervision, Validation, Visualization, Writing–review and editing. SA: Conceptualization, Funding-acquisition, Formal-analysis, Methodology, Project-administration, Resources, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors would like to acknowledge the financial support of the Fond de recherche du Québec–Nature et Technologies (FRQNT).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AlGeddawy, T., Samy, S. N., and ElMaraghy, H. (2017). Best design granularity to balance assembly complexity and product modularity. J. Eng. Des. 28 (7-9), 457–479. doi:10.1080/09544828.2017.1325859

CrossRef Full Text | Google Scholar

Ali, S. J., Michael Laranjo, J., and Bork, D. (2023). “A generic and customizable genetic algorithms-based conceptual model modularization framework,” in International conference on enterprise design, operations, and computing (Berlin, Heidelberg: Springer), 39–57.

CrossRef Full Text | Google Scholar

Bonvoisin, J., Halstenberg, F., Buchert, T., and Stark, R. (2016). A systematic literature review on modular product design. J. Eng. Des. 27 (7), 488–514. doi:10.1080/09544828.2016.1166482

CrossRef Full Text | Google Scholar

Cheng, Q., Zhang, G., Gu, P., and Shao, X. (2012). A product module identification approach based on axiomatic design and design structure matrix. Concurr. Eng. 20 (3), 185–194. doi:10.1177/1063293x12453350

CrossRef Full Text | Google Scholar

Chouinard, U., Achiche, S., and Baron, L. (2019). Integrating negative dependencies assessment during mechatronics conceptual design using fuzzy logic and quantitative graph theory. Mechatronics 59, 140–153. doi:10.1016/j.mechatronics.2019.03.009

CrossRef Full Text | Google Scholar

Chouinard, U., Law-Kam Cio, Y.-S., Vadean, A., and Achiche, S. (2020). “Concurrent modeling of positive and negative dependencies in the design structure matrix using complex numbers,” in DS 103: proceedings of the 22nd international DSM conference (DSM 2020) (Cambridge, Massachusetts: MIT).

CrossRef Full Text | Google Scholar

Deb, K., and Jain, H. (2014). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: solving problems with box constraints. IEEE Trans. Evol. Comput. 18 (4), 577–601. doi:10.1109/TEVC.2013.2281535

CrossRef Full Text | Google Scholar

Dehghani, M., and Trojovský, P. (2023). Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 8. doi:10.3389/fmech.2022.1126450

CrossRef Full Text | Google Scholar

Gershenson, J. K., Prasad, G. J., and Zhang, Y. (2003). Product modularity: definitions and benefits. J. Eng. Des. 14 (3), 295–313. doi:10.1080/0954482031000091068

CrossRef Full Text | Google Scholar

Gershenson, J. K., Prasad, G. J., and Zhang, Y. (2004). Product modularity: measures and design methods. J. Eng. Des. 15 (1), 33–51. doi:10.1080/0954482032000101731

CrossRef Full Text | Google Scholar

Hölttä, K., Suh, E. S., and de Weck, O. (2005). “Tradeoff between modularity and performance for engineered systems and products,” in DS 35: Proceedings ICED 05, the 15th International Conference on Engineering Design, Melbourne, Australia, 15.-18.08. 2005, 449–450.

Google Scholar

Hölttä-Otto, K., and de Weck, O. (2007). Degree of modularity in engineering systems and products with technical and business constraints. Concurr. Eng. 15 (2), 113–126. doi:10.1177/1063293x07078931

CrossRef Full Text | Google Scholar

Kreng, V. B., and Lee, T.-P. (2004). Modular product design with grouping genetic algorithm—a case study. Comput. and Industrial Eng. 46 (3), 443–460. doi:10.1016/j.cie.2004.01.007

CrossRef Full Text | Google Scholar

Law, Y.-S., Ma, Y., Vadean, A., Beltrame, G., and Achiche, S. (2020). “Objective reduction using axiomatic design and product-related dependencies: a layout synthesis of an autonomous greenhouse case study,” in Proceedings of the ASME 2020 international design engineering technical Conferences and Computers and Information in engineering conference, Virtual, Online, 17-19 August 2020.

Google Scholar

Law-Kam Cio, Y.-S., Ma, Y., Vadean, A., Beltrame, G., and Achiche, S. (2020). Evolutionary layout design synthesis of an autonomous greenhouse using product-related dependencies. Artif. Intell. Eng. Des. Analysis Manuf. EDAM, 1–16. doi:10.1017/S0890060420000384

CrossRef Full Text | Google Scholar

Meng, X., Jiang, Z., and Huang, G. Q. (2007). On the module identification for product family development. Int. J. Adv. Manuf. Technol. 35 (1), 26–40. doi:10.1007/s00170-006-0712-2

CrossRef Full Text | Google Scholar

Mohebbi, A., Achiche, S., and Baron, L. (2018). Multi-criteria fuzzy decision support for conceptual evaluation in design of mechatronic systems: a quadrotor design case study. Res. Eng. Des. 29 (3), 329–349. doi:10.1007/s00163-018-0287-6

CrossRef Full Text | Google Scholar

Mohebbi, A., Baron, L., Achiche, S., and Birglen, L. (2014). “Trends in concurrent, multi-criteria and optimal design of mechatronic systems: a review,” in Innovative Design and Manufacturing (ICIDM), Proceedings of the 2014 International Conference on: IEEE, Montreal, QC, Canada, 13-15 August 2014, 88–93.

CrossRef Full Text | Google Scholar

Paras, M. K., Wang, L., Chen, Y., Curteza, A., Pal, R., and Ekwall, D. (2018). A sustainable application based on grouping genetic algorithm for modularized redesign model in apparel reverse supply chain. Sustainability 10 (9), 3013. doi:10.3390/su10093013

CrossRef Full Text | Google Scholar

Piran, F. A. S., Lacerda, D. P., Camargo, L. F. R., Viero, C. F., Dresch, A., and Cauchick-Miguel, P. A. (2016). Product modularization and effects on efficiency: an analysis of a bus manufacturer using data envelopment analysis (DEA). Int. J. Prod. Econ. 182, 1–13. doi:10.1016/j.ijpe.2016.08.008

CrossRef Full Text | Google Scholar

Shan, Q., and Chen, Y. (2009). “Research on numerical module identification approaches,” in 2009 Eighth IEEE/ACIS International Conference on Computer and Information Science, Shanghai, China, 01-03 June 2009, 672–676.

CrossRef Full Text | Google Scholar

Shan, Q., and Chen, Y. (2011). Harmony search algorithm and its application to product module identification. Adv. Mater. Res. 225-226, 1100–1104. doi:10.4028/scientific.net/AMR.225-226.1100

CrossRef Full Text | Google Scholar

Shan, Q., Chen, Y., and Yan, G. (2008). “Product module identification based on PSO,” in 2008 International Symposium on Information Science and Engineering, Shanghai, China, 20-22 December 2008, 231–235.

Google Scholar

Torry-Smith, J. M., Mortensen, N. H., and Achiche, S. (2014). A proposal for a classification of product-related dependencies in development of mechatronic products. Res. Eng. Des. 25 (1), 53–74. doi:10.1007/s00163-013-0161-5

CrossRef Full Text | Google Scholar

Torry-Smith, J. M., Qamar, A., Achiche, S., Wikander, J., Mortensen, N. H., and During, C. (2013). Challenges in designing mechatronic systems. J. Mech. Des. 135 (1), 011005. doi:10.1115/1.4007929

CrossRef Full Text | Google Scholar

Tseng, H.-E., Chang, C.-C., and Li, J.-D. (2008). Modular design to support green life-cycle engineering. Expert Syst. Appl. 34 (4), 2524–2537. doi:10.1016/j.eswa.2007.04.018

CrossRef Full Text | Google Scholar

Vickery, S. K., Koufteros, X., Dröge, C., and Calantone, R. (2016). Product modularity, process modularity, and new product introduction performance: does complexity matter? Prod. Operations Manag. 25 (4), 751–770. doi:10.1111/poms.12495

CrossRef Full Text | Google Scholar

Wang, S., Liu, D.-Z., He, C., Zou, G.-Y., and Li, Z.-K. (2023). Impacts of product structural characteristics on modular performance with virtual DSM data mining. J. Eng. Des. 34 (7), 462–486. doi:10.1080/09544828.2023.2232983

CrossRef Full Text | Google Scholar

Wei, W., Liu, A., Lu, S. C. Y., and Wuest, T. (2015). A multi-principle module identification method for product platform design. J. Zhejiang University-SCIENCE A 16 (1), 1–10. doi:10.1631/jzus.A1400263

CrossRef Full Text | Google Scholar

Wrigley, P. A., Wood, P., Stewart, P., Hall, R., and Robertson, D. (2019). Module layout optimization using a genetic algorithm in light water modular nuclear reactor power plants. Nucl. Eng. Des. 341, 100–111. doi:10.1016/j.nucengdes.2018.10.023

CrossRef Full Text | Google Scholar

Xia, X., and Li, S. (2020). Research on improved chaotic particle optimization algorithm based on complex function. Front. Phys. 8. doi:10.3389/fphy.2020.00368

CrossRef Full Text | Google Scholar

Xiao, Y., Luo, G., Ma, J., Hao, L., and Sun, H. (2009). “An approach for module decomposition based on fuzzy pattern recognition,” in 2009 IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong, China, 08-11 December 2009, 1528–1532.

CrossRef Full Text | Google Scholar

Xiaogang, X., Chao, L., Jian, Y., and Yahua, C. (2006). “An analytical method based on design structure matrix for modular identification,” in 2006 7th International Conference on Computer-Aided Industrial Design and Conceptual Design, Hangzhou, China, 17-19 November 2006, 1–4.

CrossRef Full Text | Google Scholar

Xu, X., Zhang, W., and Ding, X. (2018). Modular design method for filament winding process equipment based on GGA and NSGA-II. Int. J. Adv. Manuf. Technol. 94 (5), 2057–2076. doi:10.1007/s00170-017-0929-2

CrossRef Full Text | Google Scholar

Yu, T.-L., Yassine, A. A., and Goldberg, D. E. (2003). “A genetic algorithm for developing modular product architectures,” in ASME 2003 international design engineering technical Conferences and Computers and Information in engineering conference, Chicago, Illinois, USA, 2-6 September 2003, 515–524.

CrossRef Full Text | Google Scholar

Zhang, H., Gou, J., Yin, P., Su, X., and Yuan, X. (2023). Film-cooling hole optimization and experimental validation considering the lateral pressure gradient. Front. Mech. Eng. 8. doi:10.3389/fmech.2022.973293

CrossRef Full Text | Google Scholar

Zheng, H., Guo, H., Pang, T., Guo, Z., and Guo, X. (2023). A module classification method for light industrial equipment based on improved NSGA2-FCM algorithm. Sci. Rep. 13 (1), 13789. doi:10.1038/s41598-023-39116-3

PubMed Abstract | CrossRef Full Text | Google Scholar