Direct yaw moment control of eight-wheeled distributed drive electric vehicles based on super-twisting sliding mode control

This paper proposed a novel direct yaw moment control (DYC) system to enhance vehicle stability and handling performance in various driving conditions and overcome the chattering problem of traditional sliding mode control. Accordingly, a DYC strategy is developed for eight-wheeled DDEVs by utilizing a super-twisting sliding mode (STSM) algorithm. Initially, a three-degrees-of-freedom model, nonlinear tire model, and motor model are established for vehicles. Subsequently, the reference yaw rate is obtained based on the reference model of the vehicle to serve as a control target. The DYC strategy is then established using the error between the actual yaw rate and the reference yaw rate as the input. Moreover, a traditional sliding mode (SM) controller is developed to enhance vehicle stability. A second-order SM controller is designed by incorporating a STSM control algorithm to address the chattering problem associated with traditional SM controllers. The algorithm adaptively adjusts the sliding surface and controls the gains based on the dynamic state of the vehicle. The effectiveness of the proposed control strategy is validated via hardware-in-the-loop simulations.

1 Introduction

Electric vehicles (EVs) offer significant advantages, including enhanced energy efficiency, superior powertrain dynamics, and reduced emissions, all of which contribute to a more sustainable transportation system (Zhai et al., 2011; De Novellis et al., 2013). In particular, while full-electric vehicles with on-board motor configurations share some benefits such as improved energy management and advanced torque control, distributed drive electric vehicles (DDEVs) with in-wheel motor technology excel by allowing more precise and independent torque manipulation. DDEVs achieve an advanced form of dynamic control through the use of in-wheel motors (Chen et al., 2018; Liang et al., 2023). These motors independently control the torque at each wheel, distributing torque according to the performance and traction conditions of each wheel, thus improving vehicle handling and stability (Pugi et al., 2017; Lenzo et al., 2019). This system permits one side to drive, while the other side applies brakes, enhancing the ability of the direct yaw moment control (DYC) (Tahami et al., 2004; Sun et al., 2022). Currently, most DDEVs use hierarchical control structures for the DYC. The upper layer is dedicated to motion tracking and employs a control algorithm to calculate the required control force. The lower torque-allocation control layer is responsible for distributing the torque to each wheel (Li et al., 2015; Hu et al., 2019; Zhao et al., 2021).

The use of proportional–integral (PI) control to calculate an appropriate control signal has been discussed (Fujimoto et al., 2006). Fujimoto et al. (2006) presented a simple control algorithm that is highly reliable and well suited for establishing accurate mathematical models for linear steady-state systems. However, the vehicle system, which is nonlinear and subject to parameter uncertainty, falls under the category of a nonlinear time-varying system. The simulation results presented by Jonasson et al. (2011) demonstrated significant discrepancies in the control outcomes of a proportional–integral–derivative (PID) controller under different operating conditions. In a DYC based on a linear quadratic regulator (LQR) (Ding et al., 2017), the system performance is influenced by unmodeled dynamics and parameter uncertainties. To address this problem, a robust LQR with variable gains was proposed (Wang et al., 2018). An additional control term was introduced into the traditional LQR feedback contribution to restrict the closed-loop tracking error near the origin of the state space. A torque vectoring controller is developed for an electric vehicle with dual front-wheel electric machines, utilizing an LPV gain-scheduled vehicle dynamics controller along with a torque and slip limiter to enhance traction control (Kaiser et al., 2014). Furthermore, a linear parameter-varying H∞ controller was designed using the linear matrix inequality (LMI) approach to tackle the parameter uncertainty problem (Hang et al., 2019). The controller was designed to generate the steering angles of the front and rear wheels, as well as yaw moments. Vignati et al. (2022) explored the synergistic coordination of active rear steering and torque vectoring enabled by independent electric motors at the rear axle in order to optimize vehicle handling and stability during cornering, employing phase portraits to analyze the impact on vehicle dynamics.

Recently, owing to its strong robustness to uncertainties and nonlinearities, sliding mode (SM) control has been widely applied in vehicle dynamic control. Adaptive fuzzy sliding mode control was proposed for implementing DYC (Ding et al., 2017). The weight coefficients of the sideslip angle and yaw rate were dynamically adjusted in real time using fuzzy control. An improved adaptive SM control scheme was proposed to improve the control stability by fully utilizing the DYC of four-wheeled electric vehicles (Nguyen et al., 2020). A quantitative stability index was derived, and a sliding mode (SM) controller was designed to track the desired control variables of a two-degrees-of-freedom vehicle model. To address the chattering problem inherent in the first-order SM control, a second-order SM control was developed by implementing the power integrator technique in conjunction with a nonlinear disturbance observer (Ding et al., 2017). An integral SM (ISM) formulation was proposed for torque vectoring control of a fully electric vehicle. An analysis of the controller performance, including chattering and irregular control actions was also included (Goggia et al., 2014). To combat stability problems arising from actuator faults and uncertainties in road friction, a novel SM controller with an adaptive PI sliding surface was developed. The primary objective of the developed controller was to generate a virtual control signal that can effectively counteract these problems (Subroto et al., 2020). Wang et al. (2022) designed a controller by utilizing the ISM control technique to achieve the desired yaw moment by regulating both the yaw rate and sideslip angle. A novel SM reaching law was developed to reduce chattering and enhance the convergence of state variables, and its effectiveness was confirmed through theoretical analysis. Moreover, a fuzzy compensation and preview angle-enhanced sliding model controller were proposed to enhance the tracking accuracy and robustness of mobile robots using the Kalman algorithm to evaluate the centroid slip angle and yaw rate (Li et al. (2021). To effectively handle external disturbances and parameter changes, the SM control method utilized switching functions. However, the benefits of SM control are hindered by oscillations caused by chattering. Chattering adversely affects control systems. It has been reported that mechanical parts can experience fatigue, which quickly leads to system destruction (Boiko et al., 2007; Zhang et al., 2022). Consequently, numerous strategies have been devised to mitigate chattering and enhance controller performance. These techniques include the reaching law, higher-order SM, and fractional SM.

Research on chattering problems has primarily focused on incorporating suitable filters into the SM control. Therefore, this paper presents a design solution for a super-twisting SM (STSM) controller and proves its stability using the Lyapunov method. Hardware-in-the-loop (HIL) simulation comparisons of the two designed controllers indicate that the controller based on the super-twisting algorithm exhibits superior control performance. The designed controller is insensitive to uncertainties and nonlinearity in the vehicle parameters, along with its ability to effectively and rapidly control the yaw rate of the vehicle while efficiently suppressing the chattering phenomenon caused by traditional SM control. The remainder of this paper is organized as follows. Chapter 2 establishes the vehicle models employed in this study. The DYC system is thoroughly described in Chapter 3. Chapter 4 validates the proposed methodology using simulation experiments. Finally, Chapter 5 presents the main conclusions of this study.

2 Vehicle modeling

2.1 3-DOF dynamic model

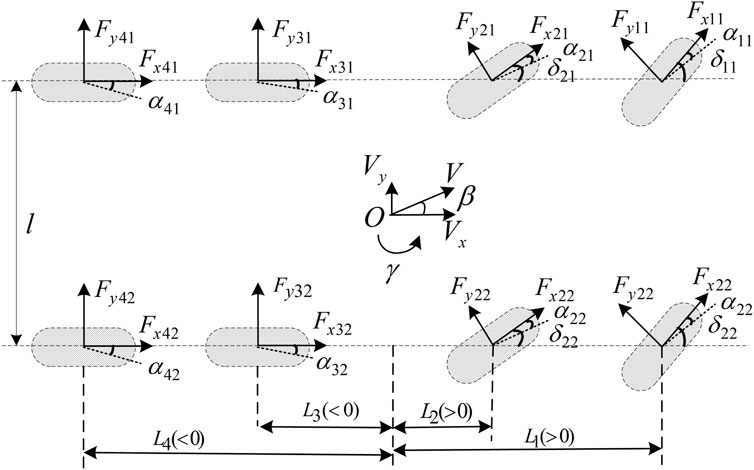
This study examined an eight-wheeled distributed drive electric vehicle (8W-DDEV) with four-wheel front steering. A three-degrees-of-freedom (3-DOF) model of an 8W-DDEV is proposed, which assumes a vehicle driving on a level road with negligible pitch, vertical, and roll motions and disregards the effects of the steering and suspension systems (Zhang et al., 2022). Consequently, the lateral, longitudinal and yaw motions can be considered, and a 3-DOF model is constructed, as shown in Figure 1.

FIGURE 1

FIGURE 1. 3-Dof model of the 8W-DDEV.

In Figure 1, O represents the vehicle’s center of gravity, the x-axis points in the direction of the vehicle’s forward movement, and the y-axis points to the driver’s left side. The equation for the vehicle lateral motion can be expressed as (Rajamani, 2011)

$\begin{array}{l}m\left({\dot{V}}_y+V_x\gamma \right)=F_{y11}\cos {\delta }_{11}+F_{x11}\sin {\delta }_{11}+F_{y12}\cos {\delta }_{12}+F_{x12}\sin {\delta }_{12}+F_{y21}\cos {\delta }_{21}\\ +F_{x21}\sin {\delta }_{21}+F_{y22}\cos {\delta }_{22}+F_{x22}\sin {\delta }_{22}+F_{y31}+F_{y32}+F_{y41}+F_{y42}\end{array}.\mathrm{(1)}(\mathrm{})$

The equation for the vehicle longitudinal motion can be expressed as

$\begin{array}{l}m\left({\dot{V}}_x-V_y\gamma \right)=-F_{y11}\sin {\delta }_{11}+F_{x11}\cos {\delta }_{11}-F_{y12}\sin {\delta }_{12}+F_{x12}\cos {\delta }_{12}-F_{y21}\sin {\delta }_{21}\\ +F_{x21}\cos {\delta }_{21}-F_{y22}\sin {\delta }_{22}+F_{x22}\cos {\delta }_{22}+F_{x31}+F_{x32}+F_{x41}+F_{x42}\end{array}.\mathrm{(2)}(\mathrm{})$

where m denotes the vehicle mass; V_x and V_y denote the velocities along the x- and y-axis, respectively; γ denotes the yaw rate; F_xij and F_yij denote the longitudinal force and lateral force of the wheels, respectively (i = 1, 2, 3, 4 for the ith-axis, j = 1, 2 for the left and right wheels); and δ_ij denotes the steering angle of the first two axles (i = 1, 2 for the ith-axis, j = 1, 2 for the left and right wheels).

The equation for the vehicle yaw motion can be expressed as

$\begin{array}{l}{I}_z\dot{\gamma }=M+L_1\left(F_{y11}\cos {\delta }_{11}+F_{x11}\sin {\delta }_{11}+F_{y12}\cos {\delta }_{12}+F_{x12}\sin {\delta }_{12}\right)+\\ L_2\left(F_{y21}\cos {\delta }_{21}+F_{x21}\sin {\delta }_{21}+F_{y22}\cos {\delta }_{22}+F_{x22}\sin {\delta }_{22}\right)-L_3\left(F_{y31}+F_{y32}\right)-L_4\left(F_{y41}+F_{y42}\right)\end{array}.(3)$

where I_z represents the moment of inertia of the vehicle, L_i denotes the distance of the ith axis from the center of mass (i = 1, 2, 3, 4), and M indicates the direct yaw moment, given by

$M=\frac{l}{2}\left(F_{x12}\cos {\delta }_{12}-F_{x11}\cos {\delta }_{11}+F_{x22}\cos {\delta }_{22}-F_{x21}\cos {\delta }_{21}+F_{x32}-F_{x31}+F_{x42}-F_{x41}\right).(4)$

2.2 The tire and wheel model

To simplify the study, the vehicle suspension is considered rigid, and the vehicle body is assumed to have uniform density. The vertical wheel load is computed by separating it into static and dynamic components, with dynamic load variations accounting for changes due to vehicle acceleration, deceleration, and steering. Factors such as vehicle climb and obstacle navigation have been omitted for simplicity, and the analysis only focuses on load changes during horizontal surface travel. Additionally, the model excludes the lateral tilting and pitching motions of the vehicle, with the wheel load being influenced solely by longitudinal and lateral accelerations. The vertical wheel load can be expressed as follows:

$\begin{array}{l}{F}_{z11}=\frac{L_b^2-L_a\cdot L_1}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}-\frac{m{a}_{y}h}{W}\right)-\frac{L_a}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z12}=\frac{L_b^2-L_a\cdot L_1}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}+\frac{m{a}_{y}h}{W}\right)-\frac{L_a}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z21}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1-L_2\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}-\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1-L_2\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z22}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1-L_2\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}+\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1-L_2\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z31}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1+L_3\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}-\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1+L_3\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z32}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1+L_3\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}+\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1+L_3\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z41}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1+L_4\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}-\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1+L_4\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2},\\ F_{z42}=\frac{L_b^2-L_a\cdot L_1-\left(L_a-4L_1\right)\left(L_1+L_4\right)}{4L_b^2-L_a^2}\cdot \left(\frac{mg}{2}+\frac{m{a}_{y}h}{W}\right)-\frac{L_a-4\left(L_1+L_4\right)}{4L_b^2-L_a^2}\cdot \frac{m{a}_{x}h}{2}\end{array}.(5)$

where F_zij (i = 1, 2, 3, and 4 for the ith-axis, j = 1, 2 for the left and right wheels) denotes the vertical load of the tires; g denotes gravitational acceleration; a_x and a_y denote the longitudinal and lateral accelerations, respectively; $h$ denotes the height of the center of gravity, and W is the wheelbase. Consequently, L_a and L_b² can be expressed as

$L_a=\left(L_1-L_2\right)+\left(L_1-L_3\right)+\left(L_1+L_4\right).(6)$

${L_b}^2={\left(L_1-L_2\right)}^2+{\left(L_1-L_3\right)}^2+{\left(L_1+L_4\right)}^2.(7)$

Given the requirement of nonlinear tire forces in vehicle dynamic control, it is inevitable that a linear tire model will not suffice. However, because of the complexity of the calculation involving numerous fitting parameters in Pacejka Magic Formula, this study opts for the Dugoff tire model for the tire force calculation (Ding et al., 2010). The Dugoff tire model accurately describes the nonlinearity of the lateral force of the tire and requires fewer parameters. The description is as follows:

$\left\{\begin{array}{l}{F}_{y\text{ij}}=C_{\text{ij}}\tan {\alpha }_{\text{ij}}f\left(\lambda \right)\\ f\left(\lambda \right)=\left\{\begin{array}{cc}\left(2-\lambda \right)\lambda ,& \text{if\hspace{0.17em}}\lambda <1\\ 1,& \text{if\hspace{0.17em}}\lambda \ge 1\end{array}\right.\\ \lambda ={\mu }_{\text{ij}}{F}_{z\text{ij}}/\left(2C_{\text{ij}}\left|\tan {\alpha }_{\text{ij}}\right|\right)\end{array}\right..(8)$

The slip angle of each tire is calculated using the following equation.

$\left\{\begin{array}{l}{\alpha }_{11}={\delta }_{11}-\left(\beta +L_1\gamma /V_x\right)\\ {\alpha }_{12}={\delta }_{12}-\left(\beta +L_1\gamma /V_x\right)\\ {\alpha }_{21}={\delta }_{21}-\left(\beta +L_2\gamma /V_x\right)\\ {\alpha }_{22}={\delta }_{22}-\left(\beta +L_2\gamma /V_x\right)\\ {\alpha }_{31}={\alpha }_{32}=-\beta +L_3\gamma /V_x\\ {\alpha }_{41}={\alpha }_{42}=-\beta +L_3\gamma /V_x\end{array}\right.(9)$

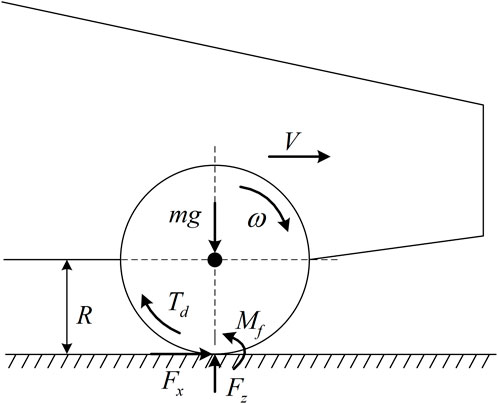
Each in-wheel motor is an independent drive unit that requires a force analysis for each wheel. The single-wheel model is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Single wheel model.

The expression for the wheel torque can be determined from Figure 2:

$I_w\dot{\omega }=T_d-F_{x}R-M_f(10)$

where I_w denotes the moment of inertia for the wheel (including the in-motor), ω signifies the wheel angular velocity, R denotes the wheel radius, M_f indicates the resisting moment of the wheel, and T_d denotes the wheel torque.

The torque of the rolling resistance exerted on the wheel is

$F_x=\frac{T_d}{R}(11)$

The torque applied to the wheels by the motor can be approximated as follows:

$T_d=i_c{T}_e(12)$

where T_e indicates motor torque, and i_c indicates the transmission ratio of the reducer.

As the primary focus of the research is on the dynamics control of the vehicle and the formulation of a yaw torque control strategy, the control system is particularly concerned with the output characteristics of the in-wheel motors (Carello et al., 2021). To maintain the clarity and scope of the study, a simplified treatment of other powertrain components has been adopted, and as such, extensive consideration of features such as power/torque limitations of the electric motors (EMs), power limitations of the energy storage system (ESS), or asymmetries of the powertrain in acceleration and deceleration phases is not included. To simplify the depiction of the torque dynamic response, the model used a first-order system in which the motor output torque can be expressed as follows:

$T_e=\frac{1}{\tau s+1}{T}_{ref}(13)$

where τ denotes the response time constant of the motor, and T_ref indicates the reference torque of the motor.

2.3 Reference model

In this study, the control objective is to determine the yaw rate of the vehicle. Therefore, it is necessary to calculate the reference yaw rate and establish a reference model for the vehicle. The equation for the vehicle reference model is as follows (Cai et al., 2022):

$\left\{\begin{array}{l}m\left({\dot{V}}_y+V_x\cdot \gamma \right)=F_{y1}\cos {\delta }_1+F_{y2}\cos {\delta }_2+F_{y3}+F_{y4}\\ I_z\dot{\gamma }=F_{y1}\cos {\delta }_1\cdot L_1+F_{y2}\cos {\delta }_2\cdot L_2+F_{y3}\cdot L_3+F_{y4}\cdot L_4\end{array}\right..(14)$

When sideslip angle is small, it can be approximated as

$\beta =\arctan \frac{V_y}{V_x}\approx \frac{V_y}{V_x}.(15)$

Assuming the longitudinal speed V_x is constant, then $\dot{\beta }={\dot{V}}_y/V_x$; when the steering angle δ is not large, $\cos {\delta }_1\approx 1$, $\cos {\delta }_2\approx 1$. Eq. 14 can be simplified as

$\left\{\begin{array}{l}\dot{\beta }=\frac{1}{m{V}_x}\left(F_{y1}+F_{y2}+F_{y3}+F_{y4}\right)-\gamma \\ \dot{\gamma }=\frac{1}{I_z}\left(F_{y1}{L}_1+F_{y2}{L}_2+F_{y3}{L}_3+F_{y4}{L}_4\right)\end{array}\right..(16)$

The tire lateral force can be directly proportional to the slip angle of tire, which is expressed as

$\left\{\begin{array}{l}{F}_{y1}=C_1{\alpha }_1\\ F_{y2}=C_2{\alpha }_2\\ F_{y3}=C_3{\alpha }_3\\ F_{y4}=C_4{\alpha }_4\end{array}\right..(17)$

If the vehicle operates under stable conditions, the changes in the yaw rate and sideslip angle are gradual. Consequently, in Eq. 16 it can be assumed that $\dot{\gamma }=0$ and $\dot{\beta }=0$. By applying this assumption to Eqs 14–17, the reference yaw rate to improve the maneuverability can be derived as follows:

${\gamma }_{ref}=\frac{V_x/L}{1+K{V}_x^2}{\delta }_1.(18)$

where $L$ denotes the equivalent wheelbase, which can be expressed as

$L=\frac{\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}{C}_i\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left(C_i{L}_i^2\right)-{\left[\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left(C_i{L}_i\right)\right]}^2}{C_1\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left[C_i\left(L_1-L_i\right)\right]+a_s{C}_2\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left[C_i\left(L_2-L_i\right)\right]}.(19)$

where $a_s$ denotes the constant ratio of the wheel angles of the two front axles.

$K$ is the stability factor, which can be expressed as

$K=-\frac{m\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left(C_i{L}_i\right)}{\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}{C}_i\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left(C_i{L}_i^2\right)-{\left[\underset{i=1}{\overset{4}{\mathrm{\Sigma }}}\left(C_i{L}_i\right)\right]}^2}.(20)$

The vehicle’s lateral motion can be influenced by the road friction coefficient, which must satisfy the following expression:

${\gamma }_{ref}\le \left|\left(\mu \cdot g\right)/V_x\right|.(21)$

where μ denotes the road friction coefficient. Eq. 21 reflects the fundamental physical limitation imposed on a vehicle’s yaw rate by tire-road friction during steering. Specifically, it conveys the maximum achievable yaw rate before tire slip occurs, which is dictated by the coefficient of friction between the tires and the road surface. This boundary condition is vital for improving the vehicle handling performance and ensuring the vehicle lateral stability.

By combining Equations 18 and (21), the reference yaw rate for improving maneuverability can be obtained as follows:

${\gamma }_{ref}=\text{sign}\left({\delta }_1\right)\cdot \min \left(\left|\left(\mu \cdot g\right)/V_x\right|,\left|\frac{V_x/L}{1+K{V}_x^2}{\delta }_1\right|\right).(22)$

where ${\gamma }_{ref}$ denotes the conventional reference yaw rate, which is widely adopted as a control objective for enhancing vehicle performance. In this paper, the reference yaw rate ${\gamma }_{ref}$ in Eq. 22 is used as the control objective of the DYC system. This control objective improves maneuverability by providing precise control of the vehicle direction changes and actively managing the balance between understeer and oversteer for stability. It also adapts to different driving conditions and preferences, ensuring predictable vehicle behavior and enhancing the driver’s handling experience.

In practice, calculating the reference yaw rate in real-time requires measuring the steering wheel angle, the longitudinal vehicle speed, and the road friction coefficient. The vehicle speed and the steering wheel angle can be readily measured using onboard sensors that are standard in modern vehicles. Determining the surface friction coefficient, however, is less straightforward and typically involves estimation algorithms that leverage sensor data such as wheel slip, vehicle acceleration, and potentially additional inputs from advanced sensor systems like optical or infrared pavement scanners (Ahn et al., 2012).

3 Design of DYC strategy

3.1 Structure of DYC strategy

To satisfy the control objectives, a lateral dynamic control algorithm is developed to calculate the reference yaw moment. The DYC approach is adopted, as shown in Figure 3 (Cai et al., 2021). First, the reference yaw rate is calculated based on the motion state of the vehicle using the algorithm outlined in Section 2. Subsequently, the yaw moment is computed using a tracking controller. The tracking controller is developed by utilizing STSM algorithm and nonlinear tire models, for overcoming the chattering problem of conventional SMC and improving the vehicle stability in the non-linear region of tire force. Additionally, the torque-distribution module generates additional torque for each in-wheel motor. A tire force distribution method with the optimization objective of tire utilization is used to improve the safety margin of tire forces (Guo et al., 2019). Furthermore, HIL simulations, including double lane change test and steering wheel angle sinusoidal input test, were performed to validate the effectiveness of the control strategy.

FIGURE 3

FIGURE 3. Structure of the DYC strategy.

3.2 Design of the traditional SM controller

The first step in designing an SM controller is to select a sliding surface (Ding et al., 2017). Note that the actual yaw rate should approach its reference values, and the yaw rate SM controller can then be designed with the sliding surface established as

$s_{\gamma }=\gamma -{\gamma }_{ref}.(23)$

By applying the equal convergence law, the derivative of $s_{\gamma }$ can be expressed as

${\dot{s}}_{\gamma }=-k_{\gamma }\text{sign}\left(s_{\gamma }\right).(24)$

where $k_{\gamma }$ denotes the coefficient of the equal convergence law.

Based on Equations 14–(17), (23), and (24), the feedback yaw moment under SM control can be obtained as follows:

$\begin{array}{l}{M}_z=I_z\left[-k_{\gamma }\text{sign}\left(\gamma -{\gamma }_{ref}\right)+{\dot{\gamma }}_{ref}\right]-\left(L_1{C}_1+L_2{C}_2-L_3{C}_3-L_4{C}_4\right)\beta \\ -\left(L_1^2{C}_1+L_2^2{C}_2+L_3^2{C}_3+L_4^2{C}_4\right)\frac{\gamma }{V_x}+\left(L_1{C}_1+a_s{L}_2{C}_2\right){\delta }_1\end{array}.(25)$

The Lyapunov function is defined as

$V=\frac{1}{2}{s}^2.(26)$

Then,

$\dot{V}=s\dot{s}=-k_{\gamma }\text{sgn}\left(s\right)\cdot s.(27)$

Taking $k_{\gamma }>0$, $\dot{V}\le 0$, the system given by Eq. 25 is stable.

In general, the value of $k_{\gamma }$ should be sufficiently large for the system to approach the SM surface quickly and accurately. However, when $k_{\gamma }$ is too large, the system experiences severe chattering.

Eq. 25 is derived from traditional SM control and employs a linear tire model. The method is effective in situations where the road friction coefficient is high, and the lateral acceleration remains within tolerable limits. However, when the vehicle tires enter the nonlinear region, the linear tire model used in Eq. 17 fails to accurately depict the lateral force of the tire. This discrepancy can lead to excessive yaw moments and compromise vehicle stability. Furthermore, the chattering on the sliding surface becomes more pronounced. To address these problems, an STSM control approach is employed to compute the yaw moment.

3.3 Design of the STSM controller

Owing to the nonlinearity of the tire force representation, the lateral force in Eq. 3 must be calculated using a nonlinear tire model. The disturbance caused by the external environment is denoted as d(t). Therefore, Eq. 3 can be written as follows:

$\dot{\gamma }=f\left(\gamma \right)+Mz+d\left(t\right).(28)$

where $f\left(\gamma \right)$ is the sum of lateral moments generated by the lateral force of the tire.

$f\left(\gamma \right)=L_1\left(F_{y11}+F_{y12}\right)+L_2\left(F_{y21}{F}_{y22}\right)-L_3\left(F_{y31}+F_{y32}\right)-L_4\left(F_{y41}+F_{y42}\right).(29)$

The lateral force of each tire is calculated using Eqs 5–9.

The sliding surface is defined as

$s_{\gamma }=\gamma -{\gamma }_{ref}.(30)$

The design of the second-order SM controller based on the STSM algorithm is as follows (Gonzalez et al., 2011):

$M_z=-\left(k_1{\left|s_2\right|}^{\frac{1}{2}}\text{sign}\left(s_2\right)+\int k_2\text{sign}\left(s_2\right)\mathrm{d}t\right)-f\left(\gamma \right).(31)$

By employing the sliding surface in Eq. 30 and the second-order SM controller in Eq. 31, there exist gains k₁ > 0 and k₂ > 0 that ensure the global stability of the systems in Eqs 1 and (3).

Taking the derivative of Eq. 30 gives

${\dot{s}}_2=\dot{\gamma }-{\dot{\gamma }}_{ref}=f\left(\gamma \right)+Mz+d\left(t\right).(32)$

Assuming that the disturbance d(t) is continuously differentiable, there exists a positive constant L satisfying the condition

$\left|\dot{d}\left(t\right)\right|\le L.(33)$

Substituting Eq. 31 into (32) produces:

${\dot{s}}_2=-k_1{\left|s_2\right|}^{\frac{1}{2}}\text{sign}\left(s_2\right)-\int k_2\text{sign}\left(s_2\right)\mathrm{d}t+d\left(t\right).(34)$

A variable replacement is performed in Eq. 34 by letting

$z_1=s_2.(35)$

$z_2=-\int k_2\text{sign}\left(s_2\right)\mathrm{d}t+d\left(t\right).(36)$

Therefore, Eq. 34 can be transformed into

${\dot{z}}_1=-k_1{\left|s_2\right|}^{\frac{1}{2}}\text{sign}\left(s_2\right)+z_2.(37)$

${\dot{z}}_2=-k_2\text{sign}\left(s_2\right)+\dot{d}\left(t\right).(38)$

The Lyapunov function is defined as

$V_2={\xi }^{\mathrm{T}}P\xi .(39)$

${\xi }^{\mathrm{T}}=\left[{\xi }_1,{\xi }_2\right]=\left[{\left|z_1\right|}^{\frac{1}{2}}\text{sign}\left(z_1\right),z_2\right].(40)$

where p is a positive-definite constant matrix.

The following adaptive gain is designed for the controller:

$\left\{\begin{array}{l}{\dot{k}}_1=\left\{\begin{array}{cc}\alpha \sqrt{\frac{\sigma }{2}},& ‖s‖⩾\epsilon \\ 0,& ‖s‖<\epsilon \end{array}\right.\\ k_2=k_1\\ k_1>\frac{{\left(2L+\nu +4\right)}^2-12\left(4L+1\right)}{12\nu }\end{array}\right..(41)$

where $\alpha$, $\sigma$, $\epsilon$, and $\nu$ are all greater than zero.

The following Lyapunov candidates are chosen:

$V\left({\xi }_1,{\xi }_2,k_1\right)=V_0+\frac{1}{2\sigma }{\left(k_1-k_1^{*}\right)}^2.(42)$

$V_0={\xi }^{\mathrm{T}}P\xi =\left[\begin{array}{cc}{\xi }_1^{\mathrm{T}}& {\xi }_2^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}\nu +4& -2\\ -2& 1\end{array}\right]\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right].(43)$

where $k_1^{*}$ denotes a sufficiently large constant. Matrix p is clearly positive and definite.

The derivation of V₀ yields

${\dot{V}}_0\left(={\dot{\xi }}^{\mathrm{T}}P\xi +{\xi }^{\mathrm{T}}P\stackrel{.}{\xi }\right)⩽-\frac{1}{{‖s‖}^{\frac{1}{2}}}{\xi }^{\mathrm{T}}Q\xi .(44)$

$Q=\left[\begin{array}{cc}{Q}_{11}& Q_{12}\\ Q_{21}& 4\end{array}\right].(45)$

$Q_{11}=\nu k_1+2\left(2k_1-k_2\right)+4L,k_1>\frac{{\left(2L+\nu +4\right)}^2-12\left(4L+1\right)}{12\nu }$

Q is positive definite, and the minimum Q eigenvalue satisfies ${\lambda }_{\min }\left\{Q\right\}>2$.

For positive definite matrices p and Q, the following inequality relationship exists:

$\begin{array}{c}{\lambda }_{\min }\left\{P\right\}{‖\xi ‖}^2⩽{\xi }^{\mathrm{T}}P\xi ⩽{\lambda }_{\max }\left\{P\right\}{‖\xi ‖}^2\\ {\lambda }_{\min }\left\{Q\right\}{‖\xi ‖}^2⩽{\xi }^{\mathrm{T}}Q\xi ⩽{\lambda }_{\max }\left\{Q\right\}{‖\xi ‖}^2\end{array}.(46)$

where ${\lambda }_{\min }\left\{\right\}$ indicates the minimum eigenvalue of the matrix, and ${\lambda }_{\max }\left\{\right\}$ indicates the maximum eigenvalue of the matrix.

According to Eqs 44 and (46),

${\dot{V}}_0\left(=-\frac{1}{{‖s‖}^{\frac{1}{2}}}{\xi }^{\mathrm{T}}Q\xi \right)⩽-\frac{{\lambda }_{\min }\left\{Q\right\}}{{‖s‖}^{\frac{1}{2}}}{‖\xi ‖}^2⩽-\frac{{\lambda }_{\min }^{\frac{1}{2}}\left\{P\right\}}{{\lambda }_{\max }\left\{P\right\}}{V}_0^{\frac{1}{2}}.(47)$

The derivation of Eq. 42 yields

$\begin{array}{l}\dot{V}⩽-\frac{{\lambda }_{\min }^{\frac{1}{2}}\left\{P\right\}}{{\lambda }_{\max }\left\{P\right\}}{V}_0^{\frac{1}{2}}-\frac{\alpha }{\sqrt{2\sigma }}\left|k_1-k_1^{*}\right|+\frac{1}{\sigma }\left(k_1-k_1^{*}\right){\dot{k}}_1+\frac{\alpha }{\sqrt{2\sigma }}\left|k_1-k_1^{*}\right|\\ ⩽-\frac{{\lambda }_{\min }^{\frac{1}{2}}\left\{P\right\}}{{\lambda }_{\max }\left\{P\right\}}{V}_0^{\frac{1}{2}}-\frac{\alpha }{\sqrt{2\sigma }}\left|k_1-k_1^{*}\right|-\left(\frac{{\dot{k}}_1}{\sigma }-\frac{\alpha }{\sqrt{2\sigma }}\right)\left|k_1-k_1^{*}\right|\\ ⩽-{\kappa }_0{V}^{\frac{1}{2}}-\left(\frac{{\dot{k}}_1}{\sigma }-\frac{\alpha }{\sqrt{2\sigma }}\right)\left|k_1-k_1^{*}\right|\\ ⩽-{\kappa }_0{V}^{\frac{1}{2}}+{\eta }_0\end{array}.(48)$

${\kappa }_0=\min \left\{\frac{{\lambda }_{\min }^{\frac{1}{2}}\left\{P\right\}}{{\lambda }_{\max }\left\{P\right\}},\alpha \right\}.(49)$

${\eta }_0=-\left(\frac{\stackrel{.}{k_1}}{\sigma }-\frac{\alpha }{\sqrt{2\sigma }}\right)\left|k_1-k_1^{*}\right|.(50)$

Thus, the controller is stable. Furthermore, ξ₁ and ξ₂ can converge in finite time, and the slip mode surface also converges in finite time.

4 Simulation verification

4.1 Hardware-in-the-loop simulation platform

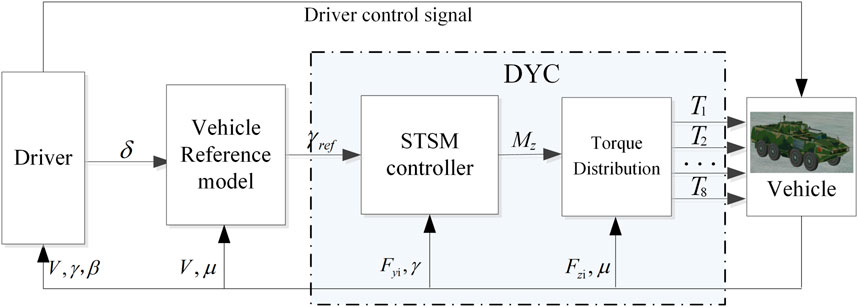
HIL simulations were performed to validate the effectiveness of the control strategy. The structure of the HIL simulation platform comprises a driver control system, controller system, motor drive system, and dynamic vehicle simulation system, as shown in Figure 4 (Cai et al., 2021; Toropov et al., 2023).

FIGURE 4

FIGURE 4. Structure of HIL simulation platform.

On the HIL simulation platform, the driver sends control signals to the controller system through the control system, which includes the dSPACE simulation system and the actual vehicle controller, and executes the control strategy based on the driving inputs and state information gathered from the real-time vehicle simulation dynamics model. Subsequently, the controller sends torque commands to the motor-drive system. The motor drive system then transfers the actual output torque of the motor to a real-time vehicle simulation model to propel the vehicle. Information exchange between various systems occurs through the Controller Area Network (CAN) and FlexRay buses.

4.2 Double lane change test

The double lane change test is a vehicle handling stability test that simulates a vehicle changing lanes or avoiding a sudden obstacle to assess vehicle handling stability in an emergency. With the controllers in Eqs 25 and (31) and without control, the double lane change maneuver was conducted under the condition of a low road friction coefficient. The simulation conditions are as follows: the road friction coefficient was set to 0.3, the vehicle velocity was 70 km/h, and the distance was 220 m. Figure 5 illustrates the simulation results, where Figure 5A presents the yaw rate, Figure 5B depicts the sideslip angle, Figure 5C illustrates the vehicle trajectory, and Figure 5D shows the steering wheel angle.

FIGURE 5

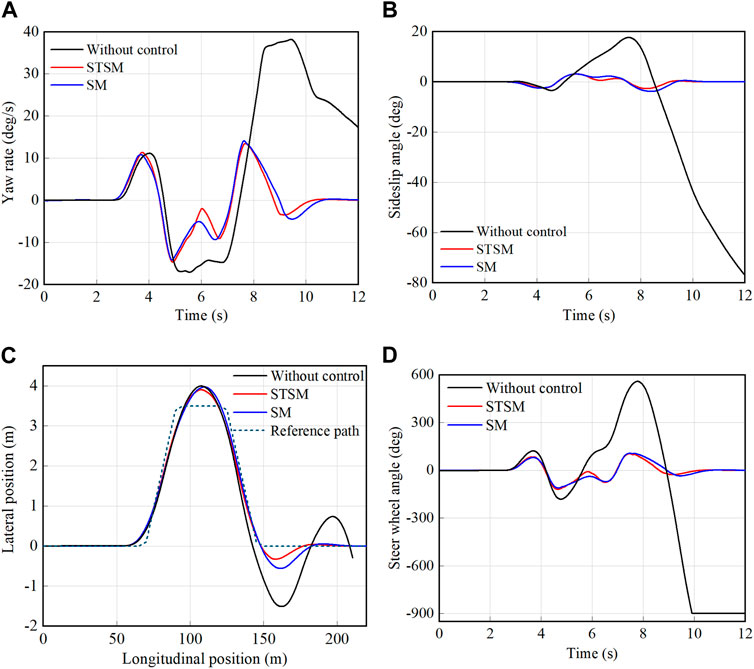
FIGURE 5. Simulation results of double lane change test. (A) yaw rate (B) sideslip angle (C) vehicle trajectory (D) steering wheel angle.

Based on the simulation results, it is evident that, without control, the vehicle trajectory deviates significantly from the reference trajectory. Additionally, the yaw rate experiences considerable fluctuations, the vehicle sideslip angle surpasses the stable range, and the steering wheel angle reaches its maximum limit. This indicates a complete loss of control by the driver. However, when the SM and STSM controllers were implemented, the vehicle steering stability improved, enabling the vehicle to closely follow the reference trajectory. Furthermore, in comparing the two controllers, it can be observed that the vehicle using the STSM algorithm exhibits smaller trajectory deviations, lower side-slip angles, and faster tracking of the yaw rate. Consequently, the control effect of the STSM controller is superior to that of the SM controller.

4.3 Steering wheel angle sinusoidal input test

The sinusoidal input test of the steering wheel angle is a critical experimental method implemented to assess the lateral dynamic response of a vehicle, crucial for examining its dynamic stability, maneuverability, and responsive performance. Recognized as one of the essential handling experiments, the sinusoidal test is a proven approach to validate the control capabilities of a vehicle under various operational scenarios. In the experiment, with the road friction coefficient set to 0.3 and the vehicle velocity maintained at 50 km/h, a sinusoidal input was applied to the steering wheel angle to induce lateral dynamics. The specific frequency and time range were selected to exemplify the vehicle behavior within a typical operational range and to provide a clear, reproducible assessment of system performance. This approach enables a focused analysis on the immediate response and stabilization of the vehicle, which is further supported by the simulation results shown in Figure 6.

FIGURE 6

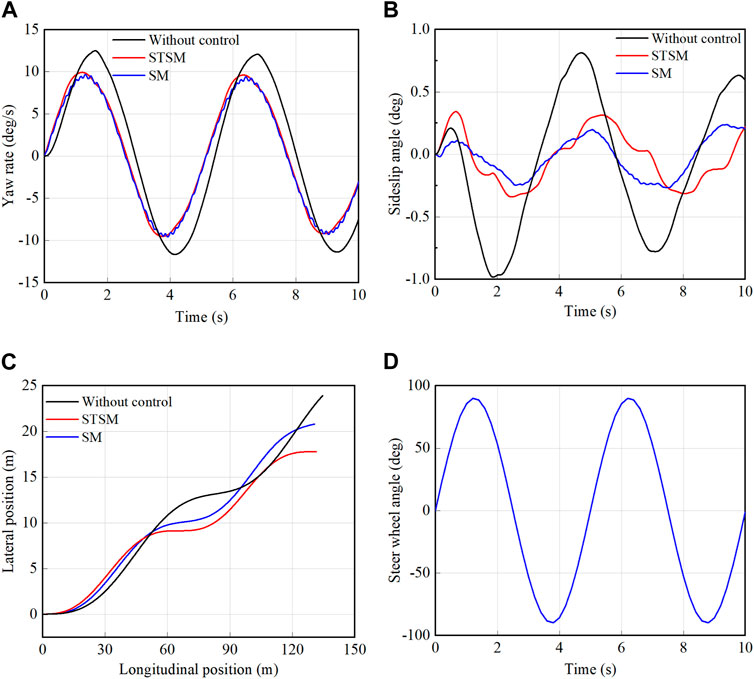
FIGURE 6. Simulation results of steering wheel angle sinusoidal input test. (A) yaw rate (B) sideslip angle (C) vehicle trajectory (D) steering wheel angle.

From the simulation results shown in Figure 6, it can be observed that the experimental results differ for vehicles with STSM, SM, and without control, although the steering inputs are the same. From Figure 5C, the vehicle with STSM exhibits the smallest lateral distance, which means that the vehicle has the best steering ability, followed by the vehicle with ST control, and the vehicle without control has the largest lateral displacement and the worst steering ability. In terms of the yaw rate, the vehicle without control has the largest yaw rate, and the yaw rates of the vehicles with SM and STSM control are approximately the same; however, the yaw rate of the SM control exhibits some fluctuation and chattering, which is avoided by STSM control. From Figure 5B, the vehicle without control has a larger lateral slip angle, and the lateral slip angle is significantly reduced after control is adopted. However, the lateral slip angle of the vehicle with the SM control still exhibits a certain amount of chattering. Therefore, in the case of continuous steering, the vehicle with the STSM control achieved excellent control performance.

5 Conclusion

This study presents a comprehensive DYC system that utilizes the STSM algorithm to enhance the handling stability of 8W-DDEVs. The STSM method is carefully designed to overcome the chattering phenomenon commonly found in traditional SM control, improving control accuracy and vehicle maneuverability. Extensive HIL simulations conducted in the study confirm that the STSM control strategy significantly improves the yaw rate tracking capability and vehicle stability compared with the traditional SM method. The proposed STSM method is characterized by fast convergence speed and reduced chattering effect, and shows remarkable potential in improving the accuracy and robustness of DYC systems.

The results provide a solid foundation for the practical improvement of DYC system performance and a crucial step forward in optimizing vehicle performance. It is expected that future research phases will transition from simulation testing to empirical testing on real vehicles, a necessary step to validate and improve the applicability and effectiveness of STSM control strategies under real-world conditions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZL: Methodology, Writing–original draft. LC: Writing–original draft. JL: Validation, Writing–review and editing. YZ: Software, Writing–review and editing. CL: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This paper was supported by the Equipment Pre-Research Project of China, Grant No. 301051102.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahn, C., Peng, H., and Tseng, H. E. (2012). Robust estimation of road friction coefficient using lateral and longitudinal vehicle dynamics. Veh. Syst. Dyn. 50, 961–985. doi:10.1080/00423114.2012.659740

CrossRef Full Text | Google Scholar

Bartolini, G., Ferrara, A., and Usai, E. (1998). Chattering avoidance by second-order sliding mode control. IEEE Trans. Autom. Contr. 43, 241–246. doi:10.1109/9.661074

CrossRef Full Text | Google Scholar

Boiko, I., Fridman, L., Pisano, A., and Usai, E. (2007). Analysis of chattering in systems with second-order sliding modes. IEEE Trans. Autom. Contr. 52, 2085–2102. doi:10.1109/tac.2007.908319

CrossRef Full Text | Google Scholar

Cai, L., Liao, Z., Wei, S., and Li, J. (2021). “Improvement of maneuverability and stability for eight wheel independently driven electric vehicles by direct yaw moment control,” in Proceedings of the 2021 24th International Conference on Electrical Machines and Systems, Gyeongju, Korea, 31 October 2021 - 03 November 2021.

CrossRef Full Text | Google Scholar

Cai, L., Liao, Z., Wei, S., and Li, J. (2022). Novel direct yaw moment control of multi-wheel hub motor driven vehicles for improving mobility and stability. IEEE Trans. Ind. Appl. 59, 591–600. doi:10.1109/tia.2022.3211831

CrossRef Full Text | Google Scholar

Carello, M., de Carvalho Pinheiro, H., Longega, L., and Di Napoli, L. (2021). Design and modelling of the powertrain of a hybrid fuel cell electric vehicle. SAE Int. J. Adv. Curr. Pract. Mobil. 3, 2878–2892. doi:10.4271/2021-01-0734

CrossRef Full Text | Google Scholar

Chen, L., Chen, T., Xu, X., Cai, Y., Jiang, H., and Sun, X. (2018). Multi-objective coordination control strategy of distributed drive electric vehicle by orientated tire force distribution method. IEEE Access 6, 69559–69574. doi:10.1109/access.2018.2877801

CrossRef Full Text | Google Scholar

De Novellis, L., Sorniotti, A., and Gruber, P. (2013). Wheel torque distribution criteria for electric vehicles with torque-vectoring differentials. IEEE Trans. Veh. Technol. 63, 1593–1602. doi:10.1109/tvt.2013.2289371

CrossRef Full Text | Google Scholar

Ding, N., and Taheri, S. (2010). A modified Dugoff tire model for combined-slip forces. Tire Sci. Technol. 38, 228–244. doi:10.2346/1.3481696

CrossRef Full Text | Google Scholar

Ding, S., Liu, L., and Zheng, W. X. (2017). Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 64, 6752–6762. doi:10.1109/tie.2017.2682024

CrossRef Full Text | Google Scholar

Ding, S., and Sun, J. (2017). Direct yaw-moment control for 4WID electric vehicle via finite-time control technique. Nonlinear Dyn. 88, 239–254. doi:10.1007/s11071-016-3240-0

CrossRef Full Text | Google Scholar

Fujimoto, H., Takahashi, N., Tsumasaka, A., and Noguchi, T. (2006). “Motion control of electric vehicle based on cornering stiffness estimation with yaw-moment observer,” in Proceedings of the 9th IEEE International Workshop on Advanced Motion Control, Istanbul, Turkey, March 2006, 27–29.

Google Scholar

Goggia, T., Sorniotti, A., De Novellis, L., Ferrara, A., Gruber, P., Theunissen, J., et al. (2014). Integral sliding mode for the torque-vectoring control of fully electric vehicles: theoretical design and experimental assessment. IEEE Trans. Veh. Technol. 64, 1701–1715. doi:10.1109/tvt.2014.2339401

CrossRef Full Text | Google Scholar

Gonzalez, T., Moreno, J. A., and Fridman, L. (2011). Variable gain super-twisting sliding mode control. IEEE Trans. Autom. Contr. 57, 2100–2105. doi:10.1109/tac.2011.2179878

CrossRef Full Text | Google Scholar

Guo, L., Ge, P., and Sun, D. (2019). Torque distribution algorithm for stability control of electric vehicle driven by four in-wheel motors under emergency conditions. IEEE Access 7, 104737–104748. doi:10.1109/access.2019.2931505

CrossRef Full Text | Google Scholar

Hang, P., Chen, X., and Luo, F. (2019). LPV/H∞ controller design for path tracking of autonomous ground vehicles through four-wheel steering and direct yaw-moment control. Int. J. Automot. Technol. 20, 679–691. doi:10.1007/s12239-019-0064-1

CrossRef Full Text | Google Scholar

Hu, J., Hu, Z., Fu, C., and Nan, F. (2019). Integrated control of AFS and DYC for in-wheel-motor electric vehicles based on operation region division. Int. J. Veh. Des. 79, 221–247. doi:10.1504/ijvd.2019.103594

CrossRef Full Text | Google Scholar

Jonasson, M., Andreasson, J., Solyom, S., and Stensson Trigell, A. (2011). Utilization of actuators to improve vehicle stability at the limit: from hydraulic brakes toward electric propulsion. J. Dyn. Sys., Meas. Control. 133, 051003. doi:10.1115/1.4003800

CrossRef Full Text | Google Scholar

Kaiser, G., Liu, Q., Hoffmann, C., Korte, M., and Werner, H. (2014). LPV torque vectoring for an electric vehicle with experimental validation. IFAC Proc. Vol. 47, 12010–12015. doi:10.3182/20140824-6-za-1003.00163

CrossRef Full Text | Google Scholar

Lenzo, B., Bucchi, F., Sorniotti, A., and Frendo, F. (2019). On the handling performance of a vehicle with different front-to-rear wheel torque distributions. Veh. Syst. Dyn. 57, 1685–1704. doi:10.1080/00423114.2018.1546013

CrossRef Full Text | Google Scholar

Li, J., Wang, J., Peng, H., Hu, Y., and Su, H. (2021). Fuzzy-torque approximation-enhanced sliding mode control for lateral stability of mobile robot. IEEE Trans. Syst. Man. Cybern. Syst. 52, 2491–2500. doi:10.1109/tsmc.2021.3050616

CrossRef Full Text | Google Scholar

Li, L., Jia, G., Chen, J., Zhu, H., Cao, D., and Song, J. (2015). A novel vehicle dynamics stability control algorithm based on the hierarchical strategy with constrain of nonlinear tyre forces. Veh. Syst. Dyn. 53, 1093–1116. doi:10.1080/00423114.2015.1025082

CrossRef Full Text | Google Scholar

Liang, J., Feng, J., Fang, Z., Lu, Y., Yin, G., Mao, X., et al. (2023). An energy-oriented torque-vector control framework for distributed drive electric vehicles. IEEE Trans. Transp. Electrification 9, 4014–4031. doi:10.1109/tte.2022.3231933

CrossRef Full Text | Google Scholar

Nguyen, N. P., Oh, H., Kim, Y., Moon, J., Yang, J., and Chen, W. H. (2020). Fuzzy-based super-twisting sliding mode stabilization control for under-actuated rotary inverted pendulum systems. IEEE Access 8, 185079–185092. doi:10.1109/access.2020.3029095

CrossRef Full Text | Google Scholar

Pugi, L., Grasso, F., Pratesi, M., Cipriani, M., and Bartolomei, A. (2017). Design and preliminary performance evaluation of a four wheeled vehicle with degraded adhesion conditions. Int. J. Elec. Hybrid. Veh. 9, 1–32. doi:10.1504/ijehv.2017.082812

CrossRef Full Text | Google Scholar

Rajamani, R. (2011). Vehicle dynamics and control. 2. New York, USA: Springer Science and Business Media, 15–37.

Google Scholar

Subroto, R. K., Wang, C. Z., and Lian, K. L. (2020). Four-wheel independent drive electric vehicle stability control using novel adaptive sliding mode control. IEEE Trans. Ind. Appl. 56, 5995–6006. doi:10.1109/tia.2020.2977598

CrossRef Full Text | Google Scholar

Sun, P., Trigell, A. S., Drugge, L., and Jerrelind, J. (2022). Energy efficiency and stability of electric vehicles utilising direct yaw moment control. Veh. Syst. Dyn. 60, 930–950. doi:10.1080/00423114.2020.1841903

CrossRef Full Text | Google Scholar

Tahami, F., Farhangi, S., and Kazemi, R. (2004). A fuzzy logic direct yaw-moment control system for all-wheel-drive electric vehicles. Veh. Syst. Dyn. 41, 203–221. doi:10.1076/vesd.41.3.203.26510

CrossRef Full Text | Google Scholar

Toropov, E., Tumasov, A., Vashurin, A., Butin, D., and Stepanov, E. (2023). Hardware-in-the-Loop testing of vehicle’s electronic stability control system. Appl. Eng. Lett. 8, 70–79. doi:10.18485/aeletters.2023.8.2.4

CrossRef Full Text | Google Scholar

Vignati, M., and Sabbioni, E. (2022). A cooperative control strategy for yaw rate and sideslip angle control combining torque vectoring with rear wheel steering. Veh. Syst. Dyn. 60, 1668–1701. doi:10.1080/00423114.2020.1869273

CrossRef Full Text | Google Scholar

Wang, H., Han, J., and Zhang, H. (2022). Lateral stability analysis of 4WID electric vehicle based on sliding mode control and optimal distribution torque strategy. Actuators 11, 244. doi:10.3390/act11090244

CrossRef Full Text | Google Scholar

Wang, Z., Montanaro, U., Fallah, S., Sorniotti, A., and Lenzo, B. (2018). A gain scheduled robust linear quadratic regulator for vehicle direct yaw moment control. Mechatronics 51, 31–45. doi:10.1016/j.mechatronics.2018.01.013

CrossRef Full Text | Google Scholar

Zhai, H., Frey, H. C., and Rouphail, N. M. (2011). Development of a modal emissions model for a hybrid electric vehicle. Transp. Res. Part D. Transp. Environ. 16, 444–450. doi:10.1016/j.trd.2011.05.001

CrossRef Full Text | Google Scholar

Zhang, Z., Ma, X., Liu, C., and Wei, S. (2022). Dual-steering mode based on direct yaw moment control for multi-wheel hub motor driven vehicles: theoretical design and experimental assessment. Def. Technol. 18, 49–61. doi:10.1016/j.dt.2020.05.004

CrossRef Full Text | Google Scholar

Zhao, J., Wang, X., Liu, T., Liang, Z., Hua, X., and Wang, Y. (2021). Hierarchical control for cornering stability of dual-motor RWD vehicles with electronic differential system using PSO optimized SOSMC method. Adv. Eng. Inf. 50, 101413. doi:10.1016/j.aei.2021.101413

CrossRef Full Text | Google Scholar