Lubrication subjected to effects of electric and magnetic fields: recent research progress and a generalized MEMT-field Reynolds equation

Electric and magnetic fields have been used in various ways to enhance the performance of lubrication systems. The presence of these fields can significantly change the properties of lubricants. The rapid adoption of electric vehicles (EVs) has presented new lubrication-related challenges due to the presence of electric current. There is an urgent need for an in-depth study of lubrication systems subjected to such fields. This paper highlights recent research works on several key areas of lubrication involving electric or magnetic fields, which are:1) electric double layer in lubrication, 2) electrorheological fluids, 3) magnetorheological fluids, 4) ferrofluids, and 5) typical fluids used in the current EVs and typical surface failures of bearing components in EVs. Commonly used lubricants in each area are reviewed; lubrication mechanisms and related mathematical models are summarized; methods for and results from numerical analyses and experimental explorations are discussed; and common features of lubrications in different fields are explored. Based on the current research progress in these fields and the classic generalized Reynolds equation, a generalized mechanical-electro-magnetic-thermal-field (MEMT-field) Reynolds equation is proposed to describe the aforementioned lubrication scenarios and the effects of coupled mechanical, electric, magnetic, and thermal fields, which can be solved with a numerical iteration method.

1 Introduction

The presence of electric or magnetic field can significantly change the flow characteristics of lubricants made of special fluids. Applications have been developed to use these features to enhance lubrication. On the other hand, improper use of electric or magnetic field can be detrimental. The rapid adoption of electric vehicles (EVs) has presented new lubrication-related challenges due to the presence of electrical current (Chen Y. et al., 2020). It is important to have an in-depth understanding of lubrication systems subjected to electric and magnetic fields and under the influences of charged particles.

In the field of lubrication, four types of electric/magnetic lubrications have been studied extensively, which are the electric double layer (EDL) lubrication, electrorheological (ER) fluid lubrication, magnetorheological (MR) fluid lubrication, and ferrofluids lubrication. The electric double layer (EDL) often appears at the interface of an ionic fluid and a solid surface. The charge on the solid surface adsorbs the nearby counter-ions and repels identical ions in the flowing fluid, forming an adsorbed layer near the surface as liquid molecules move (Fang et al., 2023). The electric double layer can lead to a reduction of the coefficient of friction and an improvement in the load carrying capacity of the lubricant (Palacio and Bhushan, 2010). A numerical model for EDL lubrication has been proposed (Zhang and Umehara, 1998), in which the electric force is expressed as a function of electric potential. The EDL lubrication is commonly used with water-based lubricants, and it still draws wide research attention currently.

Electrorheological (ER) fluids consist of a suspension of micron-size particles in a low-electrical-conductivity liquid, usually a dielectric oil (Khusid and Acrivos, 1995). The ER fluid responds to the excitation of an external electric field by creating chain-like structures between exciting poles (Michalec et al., 2018), thus changing the rheological properties of the ER fluid. The response time is generally around 10 ms and is strongly dependent on particle size, magnitude of the excitation source, along with the viscosity, electric conductivity, and dielectric constant of the ER fluid (Hao, 2001). A Bingham-type model has been widely used to describe this non-Newtonian rheological change when an ER fluid is subjected to an external electric field (Bossis and Brady, 1984; Parthasarathy and Klingenberg, 1996). The controllable rheological variation makes ER fluids ideal lubricants for many advanced lubrication systems.

Magnetorheological (MR) fluids and ferrofluids both fall into the category of ferrohydrodynamic fluids. The rheological response of an MR fluid results from the magnetic-particle polarization induced in the presence of a magnetic field; induced dipoles can form chain structures aligned with the exerted magnetic field (Moles, 2015). The rheology of MR fluids can be rapidly and reversibly varied from the state of a Newtonian-like fluid to that of a stiff semisolid by controlling the magnetic field (Simon et al., 2001). Similar to ER fluids, a Bingham-type model can also be used to describe this rheological change (De Vicente et al., 2011; Gołdasz and Sapiński, 2015). Compared with the ER fluids, the MR fluids inherently have higher yield strengths and are capable of generating greater fluid forces (Bompos and Nikolakopoulos, 2011). Like the ER fluids, the MR fluids can also improve the performance of lubrication.

Ferrofluids used as lubricants are usually comprised of ferromagnetic particles. An external magnetic field can significantly change the rheological properties of a ferrofluid without forming a chain structure, i.e., the field controls its rheology while simultaneously maintaining its fluidity (Prajapati, 1995). When a ferrofluid is used, the system load capacity can be enhanced by viscosity increase in the magnetic field; the lubricant can be retained at desired locations to prevent leakage and contamination; fine magnetic particles may help reduce wear of rubbing surfaces (Deysarkar and Clampitt, 1988; Säynätjoki and Holmberg, 1993; Prajapati, 1995; Uhlmann et al., 2002). These advantages make ferrofluid lubricants more promising than traditional oil-based lubricants in many applications.

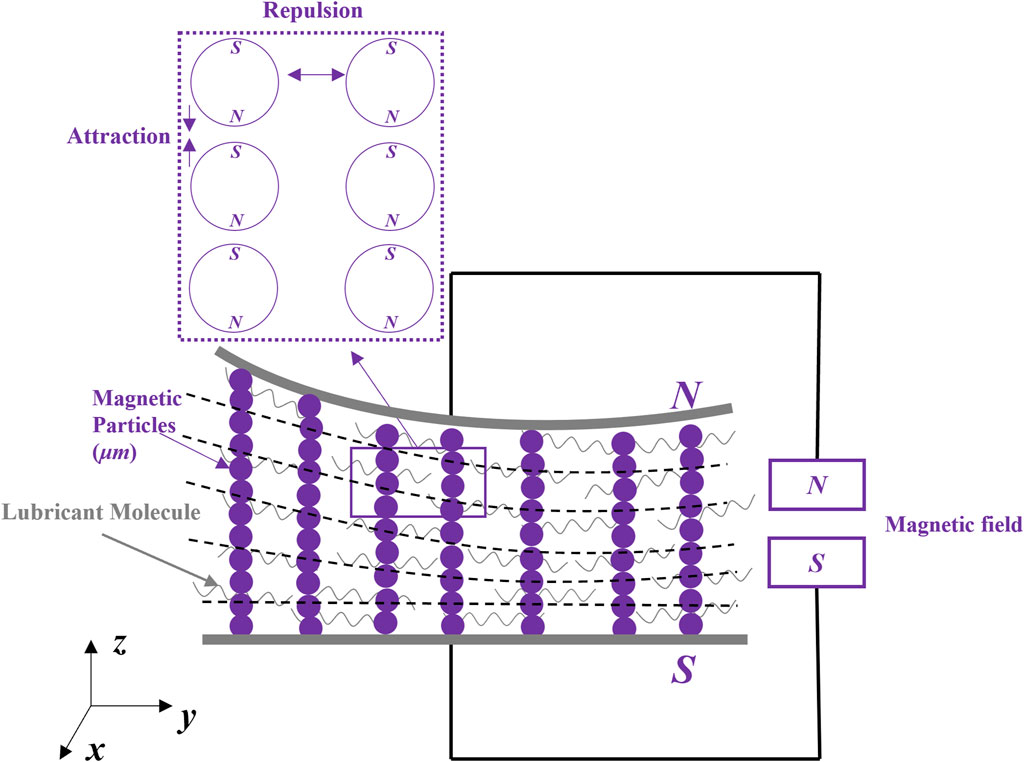
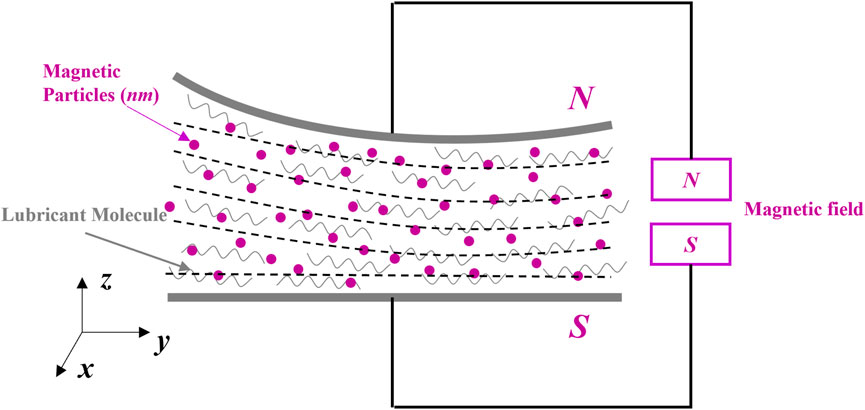
Figure 1 shows the formations of four lubrication types mentioned above, with the conventional hydrodynamic lubrication presented as a reference. From the left, the first one illustrates a regular lubrication case with a conventional oil. The next is the EDL lubrication, where some ions in the lubricant are attached strongly in the stern layers and others are free in the diffuse layers. The next is the ER lubrication, for which an external electric field is exerted, and electrical particles are aligned to form chains. A similar phenomenon also appears in the MR fluid lubrication under an external magnetic field, in which magnetic particles also form lines along the magnetic field direction. However, the magnetic particles in the ferrofluid lubrication, far right, should retain their fluidity in the carrier fluid.

FIGURE 1

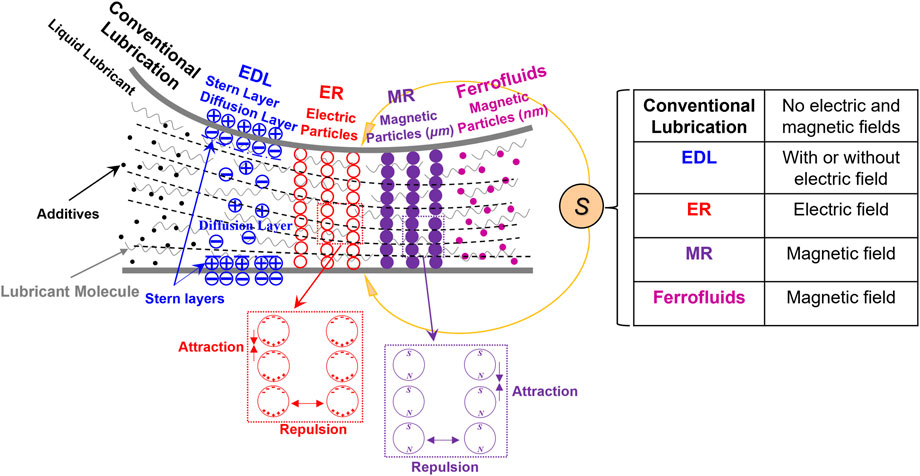
FIGURE 1. Formations of different lubrications in various fields. Here, S means the source, which can be an electric field or magnetic field, or no external field.

Electric vehicles (EVs) have gained increasing momentum during recent years as a viable solution to reduce emissions and promote a cleaner environment, showing promising advantages in a trend to replace vehicles using the internal combustion engine (ICE) (Farfan-Cabrera, 2019; Shah et al., 2021a; Sanguesa et al., 2021; Rodríguez et al., 2022). Regarding mechanical performance, lubricants used in EVs may come into direct contact with electric units and circuits, exposing them to electric and magnetic fields. However, these lubrication systems can be vulnerable under certain circumstances and experience failures (He et al., 2020). These failure phenomena in EVs raise a huge demand on explorations of new lubrication strategies for EVs. A robust lubrication technology is crucial for energy efficiency and EV durability (Tung et al., 2020). Safe EVs for future transportation require in-depth research on component lubrication behaviors under an electric field.

This paper reviews the mechanisms and formations of the lubrications mentioned above, revisits the numerical models for these lubrication systems in electric and/or magnetic fields, and discusses related numerical simulations and experimental explorations. EV lubrication systems and their potential failure modes will also be briefly evaluated. A primary purpose of such an extensive cross-field review is to explore the common features of lubrication in different fields, so as to identify an integrated approach for future lubrication research for EVs and other mechanical systems involving electric and magnetic fields. At the end, a generalized mechanical-electro-magnetic-thermal-field (MEMT-field) Reynolds equation is proposed from modification and extension of existing models, and from consideration of the electric and magnetic forces and the field effects.

2 Electric double layer (EDL)

Electrostatic charges on a solid surface create an electrical potential. When an ionic liquid is in contact with the solid surface, counter ions in the ionic liquid will be attracted by the electrostatic field and become balancing charges. The rearrangement of electrostatic charges and ions is called the electric double layer (EDL). EDL usually occurs at the interfaces of ceramic tribo-pair and water-based lubricants, which often shows low friction and high load capacity (Xu and Kato, 2000; Phillips and Zabinski, 2004). In the EDL lubrication, hydrodynamic lubrication is believed to occur on very thin water film, and experimental results showed the influences of EDL structures on fluid viscosity and lubrication friction coefficient (Chen et al., 2002; Phillips and Zabinski, 2004). Elton (1948) attributed the apparent increase in viscosity to the resistance to shear of the double layer and termed it the “electroviscous effect.” For lubrication systems with EDL structures, the existence of the EDL resists the flow and makes the load carrying capacities increase (Li, 2005). The EDL structure can form spontaneously and can be reconstructed by changing the ionic concentration in a lubricant or by applying an external electric field on the friction pair (Wang et al., 2006). Both numerical and experimental research have been mainly focused on the effect of the EDL on enhancing the performance of water lubrication systems.

2.1 Lubricants used in EDL

The key to form the EDL structure in lubrication is the existence of ions in the lubricant, and the EDL is less obvious in nonionic fluids or fluids with very few ions (Xie et al., 2015). Ionic liquids (ILs) are room-temperature molten salts that consist of organic cations and inorganic or organic anions (Cai et al., 2020), which make them ideal additives in a fluid to form the EDL in lubrication. Due to their good solubility in water, they are widely used in water-based lubricants. Commonly used cations including 1,3-dialkylimidazolium, N-alkylpyridinium, alkylammonium, alkylphosphonium, and common anions including Cl⁻, Tf₂N⁻, BF₄⁻, PF₆⁻ (Cai et al., 2020). Oil-miscible ILs have been developed by adding proper alkyl chains to both cations and anions, which made it possible for ILs to become additives in oil-based lubricants (Zhou and Qu, 2017). Quaternary ammonium and phosphonium cations, along with halogen-free anions like phosphate, sulfonate, orthoborate, and carboxylate, have been synthesized and tested as additives in base oils (Cowie et al., 2017). Generally, more carbon atoms in the alkyl groups on the cation lead to a higher solubility of ILs in nonpolar oils by diluting the charge density and increasing intermolecular London dispersion forces (Barnhill et al., 2014). Oil-based ILs decompose without producing ash and remain stable at high temperatures. Their ability to create a strong EDL structure similar to pure ILs enables effective lubrication of diverse solid surfaces (Silvester et al., 2021). Phosphonium-based ILs have been explored, and some of them show synergistic interactions with such traditional additives as ZDDP (Qu et al., 2012; Yu et al., 2012; Qu et al., 2015).

2.2 Structure and electric properties of EDL

EDL consists of the Stern layer (compact layer) and the diffuse layer. In the Stern layer, the ions are strongly attracted to the solid surface and are immobile. The diffuse layer is over the Stern layer. Due to the drop of net charge density, the ions in this layer are mobile. A typical EDL structure is illustrated in Figure 2. There are two EDL structures between the upper and lower solid surfaces of a lubricated gap, and in Figure 2, the dashed line connected to the electrical source indicates that an optional external electric field can also be added to enhance the EDL effects (Kailer et al., 2011). The border between the Stern layer and the diffusion layer is defined as the slipping plane. The electrical potential at the slipping plane, called the zeta potential, $\zeta$, can be measured experimentally (Bai et al., 2006). Film thickness, $h$, is defined between two slip planes. The stern layer is very thin, compared to film thickness.

FIGURE 2

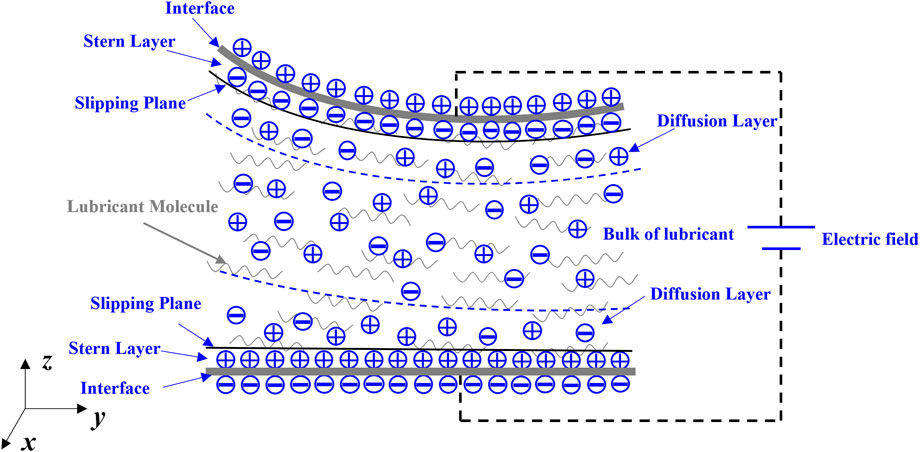
FIGURE 2. Formation of the EDL in lubrication, dash line connected to the electric field means an external electric field is optional.

From the Maxwell equation, the local net charge density per unit volume, ${\rho }_e$, can be described by the Poisson equation, Eq. 1 (Zhang and Umehara, 1998):

${\rho }_e=-\frac{\epsilon {\nabla }^2\psi }{4\pi }(1)$

where $\epsilon$ is the absolute dielectric constant, and $\psi$ is the electric potential. Multiple methods can be used to simulate $\psi$ (Zhang and Umehara, 1998; Zuo et al., 2012a; Chen Q. D. et al., 2020). Here discussed below is the method by Zhang and Umehara (1998). The electric potential, $\psi$ between the EDLs of two EDL structures on both side of the gap along the film thickness direction (the z direction) is given by:

$\psi =\left\{\begin{array}{c}\zeta e^{\left(-\chi z\right)},0\le z\le h/2\\ \zeta e^{\left(-\chi \left(h-z\right)\right)},h/2\le z\le h\end{array}\right.(2)$

where $h$ is the film thickness, and $\chi$ is the Debye double layer thickness. Based on the Helmgoltz-Smoluvhowski theory, the streaming potentials, $E_x$ and $E_y$ in the x and y directions are:

$E_x=-\frac{\zeta \epsilon }{4\pi {\eta }_a\lambda }\frac{\partial p}{\partial x}(3)$

$E_y=-\frac{\zeta \epsilon }{4\pi {\eta }_a\lambda }\frac{\partial p}{\partial y}(4)$

where ${\eta }_a$ is the apparent viscosity of the fluid, $p$ is the pressure, and $\lambda$ is the specific conductance. Thus, the differential electro-kinetic forces, $d{R}_x$ and $d{R}_y$, in the x and y directions, can be given by:

$d{R}_x=E_x{\rho }_e(5)$

$d{R}_y=E_y{\rho }_e(6)$

2.3 Mathematical model of EDL in lubrication

Prieve and Bike (1987; Bike and Prieve, 1990) first proposed a model for electrohydrodynamic lubrication with a thin EDL film. Later, Zhang and Umehara (1998) developed a hydrodynamic lubrication theory including a modified Reynolds equation with the consideration of the EDL. The latter is briefly summarized here. Combining the electro-kinetic forces with the viscous force and pressure gradient, the force equilibrium equations in the x and y directions are:

$\eta \frac{{\partial }^2{u}_x}{\partial z^2}-\frac{\partial p}{\partial x}-\frac{E_x\epsilon }{4\pi }\frac{{\partial }^2\psi }{\partial z^2}=0(7)$

$\eta \frac{{\partial }^2{u}_y}{\partial z^2}-\frac{\partial p}{\partial y}-\frac{E_y\epsilon }{4\pi }\frac{{\partial }^2\psi }{\partial z^2}=0(8)$

The boundary conditions of the lubricant flows are:

$\begin{array}{c}u\left(0\right)=U_1;v\left(0\right)=V_1;\psi \left(0\right)=\zeta \\ u\left(h\right)=U_2;v\left(h\right)=V_2;\psi \left(h\right)=\zeta \end{array}(9)$

Here, the no-slip conditions are used for velocity in Eq. 9, while the velocity boundary condition considering the Navier slip has also been studied (Li and Jin, 2008). Using integration, the flow velocities in the x and y directions are:

$u=\frac{z^2}{2\eta }\frac{\partial p}{\partial x}-\frac{hz}{2\eta }\frac{\partial p}{\partial x}+\frac{E_x\epsilon }{\eta 4\pi }\left(\psi -\zeta \right)+\frac{U_2-U_1}{h}z+U_1(10)$

$v=\frac{z^2}{2\eta }\frac{\partial p}{\partial y}-\frac{hz}{2\eta }\frac{\partial p}{\partial y}+\frac{E_y\epsilon }{\eta 4\pi }\left(\psi -\zeta \right)+\frac{V_2-V_1}{h}z+V_1(11)$

Based on velocities from Eqs. 10, 11, the flow rates in the x and y directions are:

$q_x=\frac{1}{\eta }\left\{-\frac{h^3}{12}\frac{\partial p}{\partial x}-\frac{E_x\epsilon \zeta }{4\pi }\left[h-\frac{2}{\chi }\left(1-e^{-\chi h/2}\right)\right]\right\}+\frac{U_1+U_2}{2}h(12)$

$q_y=\frac{1}{\eta }\left\{-\frac{h^3}{12}\frac{\partial p}{\partial y}-\frac{E_y\epsilon \zeta }{4\pi }\left[h-\frac{2}{\chi }\left(1-e^{-\chi h/2}\right)\right]\right\}+\frac{V_1+V_2}{2}h(13)$

By assuming that the fluid is incompressible and the flows are in a steady state, based on the continuity equation, the governing equation for the EDL lubrication model can be obtained as:

$\frac{\partial }{\partial x}\left(\frac{h^3}{12{\eta }_a}\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{12{\eta }_a}\frac{\partial p}{\partial y}\right)=\frac{U_1+U_2}{2}\frac{\partial h}{\partial x}+\frac{V_1+V_2}{2}\frac{\partial h}{\partial y}(14)$

where ${\eta }_a$ is the apparent viscosity defined by:

${\eta }_a=\eta +\frac{3{\epsilon }^3{\zeta }^2\left\{3-\frac{2}{\chi }\left(1-e^{-\chi h/2}\right)\right\}}{4{\pi }^2\lambda h^3}(15)$

The second term can be considered as the viscosity increment caused by the EDL.

2.4 Numerical simulations of the EDL effects

With the modified Reynolds equation discussed in the previous section, Zhang and Umehara (1998) calculated the hydrodynamic load and friction coefficient of infinitely wide plane bearings. Wong et al. (2003) studied the EDL effect on water lubrication of metal-ceramic friction pairs under a high pressure. The numerical simulations results showed that the EDL effect was only significant for a water-film thickness of less than approximately 100 nm. As the zeta-potential increases, the minimum film thickness increases (Figure 3A), while the friction coefficient decreases (Figure 3B). Chun and Ladd (2004) pointed out that the substantial difference in the electroviscous forces predicted by constant-charge and constant-potential boundary conditions was caused by the Debye–Hückel approximation. By assuming that the ion concentration obeyed the equilibrium Boltzmann distribution, Bai et al. (2006) calculated the local net charge density of lubricants and further derived the expression of electric field intensity. As a result, a new equation to calculate apparent viscosity was derived. Li (2009), Li and Jin (2008) considered boundary slip and stress-jump boundary conditions; they derived an apparent viscosity equation expressed explicitly as a function of the Debye length, electro-viscosity, and slip length, as well as a stress-jump parameter. The coupled effects of the EDL and slip/stress jump boundary were also studied, Chakraborty and Chakraborty (2011) pointed out that the flow and consequent ion migration caused by the EDL effect can increase the load capacity of a slider bearing.

FIGURE 3

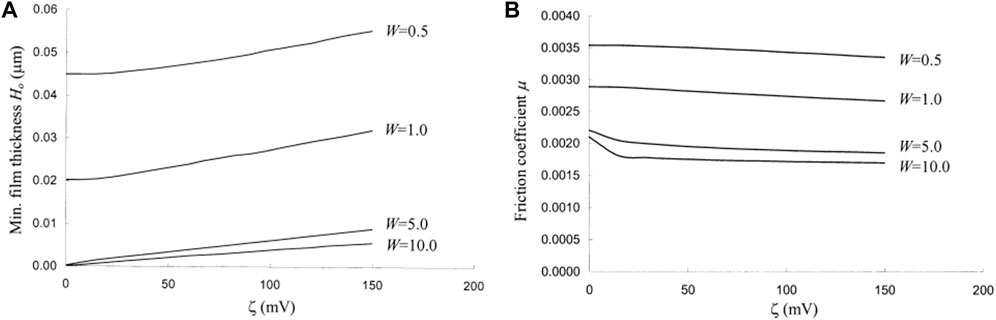
FIGURE 3. (A) Influence of the zeta-potential on the minimum film thickness (B) Influence of the zeta-potential on friction coefficient (W is the load). With permission to re-use (Wong et al., 2003).

Under certain conditions, the EDLs on the two solid/ions liquid interfaces can be asymmetrical. Zuo et al. (2012b) derived a numerical model considering asymmetrical EDLs and came to a conclusion that the larger the sum of the two zeta potentials is, the larger the pressure increment. Later, their numerical model was modified for the cases where the lubrication film was very thin and the two EDLs were overlapped (Zuo et al., 2012a). Based on the asymmetrical EDL numerical model, Chen et al. (2013) calculated the film thickness and the pressure distribution of the elastohydrodynamically formed water film in a line contact used a viscosity-pressure relationship.

Recently, several new numerical models have been developed via more realistic assumptions. Jing et al. (2017) proposed a model based on the nonlinear Poisson-Boltzmann equation without using the Debye–Hückel approximation, and the new model also considered the variation in the bulk electrical conductivity of the lubricant under the influence of the EDL. Chen Q. D. et al. (2020) developed an asymmetrical EDL lubrication model using the Poisson equation to determine the electric field and the Nernst equation to express the ionic concentration. Fang et al. (2020) combined EDL effect with the average flow Reynolds equation, conducted lubrication simulation in roughness surface, showed the EDL effect and asperity contact work together to balance the out applied load. Later, Fang and Ma (2023) proposed a model, based on surface-force effects, to analyze the boundary lubricated contact behavior of smooth and rough surfaces, and the results showed that a relatively low normal load could be supported by the EDL and the van der Waals effect, whereas a high normal load was supported by the hydration effect.

2.5 Experiments on EDL in lubrication

Experiments work on EDL focuses on the structure, controllability, and lubrication performances. Different EDL structures in SiC and Si₃N₄ tributaries caused different lubrication results (Chen et al., 2002). The overlap of EDLs between two like-charged surfaces would develop a repulsive pressure (Gong et al., 1999), Oogaki et al. (2009) did experiments and extended this repulsive pressure theory to the contact between two soft but repulsive surfaces with a finite roughness. Arora and Cann (2010) measured film thickness and friction behaviors of four imidazolium ionic liquids, and the EDL was found to be the reason for the similar friction coefficients in the boundary lubrication regime. An external field can change the structure and properties of an EDL. Luo et al. (2004) experimentally investigated the formation of an ordered layer by applying an external electric field. Wang et al. (2006) conducted experiments to study the changes of viscosity and friction coefficient due to different strengths of an external electric field. Gajewski and Glogowski (2010) tested the performance of a ZDDP-oil blend under an external DC electric field and made several predictions on the EDL structures at the earthed metal shaft.

Liu et al. (2019) explained the nature of the EDLs in solvents with weak or without polarity based on the experiment results of CuS nanoparticle additives. Dong et al. (2020) showed that a self-assembled EDL with the proton-type ionic-liquid additives could result in a continuous boundary protective film to reduce shear damping in the horizontal direction. The EDL effect has also been studied from the angle of tribochemistry, revealing that an applied electric potential could promote redox reactions and change the EDL structure (Spikes, 2020). Kailer et al. (2011) investigated the tribological behavior of sintered SiC under electric potentials and found that the cathodic polarization of the ceramic surfaces modified the EDL structures and affected the chemical-chemical reactions of SiC with water; an EDL could cause enhanced near-surface viscosity that stabilized hydrodynamic lubrication conditions.

In conclusion of issues of EDL in lubrication, EDL phenomenon usually appears in the lubricant systems with ionic-liquid additives. The balance of electrostatic charges on a solid surface and counter ions in the fluid forms the EDL structures along the lubrication borders. Within the EDL regime, the surface area exhibits a notably higher concentration of the ionic liquid, compared with that in the bulk solution. This concentration variation plays a pivotal role in improving the load-carrying capacity and lowering friction coefficient (Zhou et al., 2009). The electric forces induced by EDLs are portions of the overall force field, and a modified Reynolds equation has been re-visited. Both numerical simulations and experiments have been conducted to evaluate the effects of EDL structures on lubrication performance.

3 Electrorheological (ER) fluids

Electrorheological (ER) fluids are composed of suspensions of electrically polarizable particles in a non-conducting carrier liquid (Stejskal, 2015). Winslow (1949) first discovered the ER effect where the apparent viscosity of an ER fluid changed in response to an applied electric field and predicted its application in various fields. Due to the dielectric constant contrast between the particles and the liquid, each particle would be polarized under an electrostatic field with an effective dipole moment (Wen et al., 2008). The induced dipole-dipole interaction can cause particles to form fibrous structures along the applied field direction. It requires a significant work to break these fibers and to make the suspended particles flow (Rankin et al., 1998). As a result, the apparent viscosity is enhanced. The controllability of the rheological property of an ER fluid makes it an ideally “smart” lubricant to program the performance of bearings and other tribological systems.

3.1 Components of ER fluids

Three major components of a typical ER fluid are a carrier liquid, additives, and ER particles. ER fluids contains two phases, i.e., a dispersed phase (solid particles) and a continuous phase (nonaqueous/nonpolar liquids) (Zhao and Yang, 2013). In terms of the miscibility of dispersed phases, ER fluids can divide into two categories, which are the heterogeneous ER fluids with solid particulates and homogeneous ER fluids with liquid particulates (Hao, 2011). The solid particles are usually referred to inorganic metal oxide particles, ferroelectric particles, or some other inorganic or organic polarizable particles (Jolly and Carlson, 2000). Homogeneous ER fluids usually contain low-molecular weight liquid crystals or polymeric liquid crystals, they have the advantage that they display no sedimentation or flocculation (Richtering, 2001). The containing liquids of ER fluids are usually be mineral or silicone oils, or other organic oils with additives, and the additives can be any polar material that can enhance the ER effect and/or the stability of the particle suspension (Hao, 2001).

3.2 Mechanisms of ER fluids

3.2.1 Forces in ER fluids

The Stokesian dynamics method (Bossis and Brady, 1984; Brady and Bossis, 1988; Bonnecaze and Brady, 1992; Baxter-Drayton and Brady, 1996) can be used to model an ER fluid in lubrication. Possible forces in an working ER fluid include hydrodynamic forces, electrostatic forces, Brownian forces, short-range repulsive forces, van der Waals forces, and other colloidal forces (Parthasarathy and Klingenberg, 1996). However, the two major forces of them are the hydrodynamic forces, in vector ${\mathbf{F}}^{\mathbf{H}}$, and the interparticle electrostatic forces, in vector ${\mathbf{F}}^{\mathbf{P}}$. When neglecting the inertial effect on the low Reynolds-number flows, the motion of the particles can be described as:

${\mathbf{F}}^{\mathbf{H}}+{\mathbf{F}}^{\mathbf{P}}=0(16)$

The hydrodynamic forces, ${\mathbf{F}}^{\mathbf{H}}$, on spheres in a suspension, can be calculated as (Brenner, 1966; Bonnecaze and Brady, 1992):

${\mathbf{F}}^{\mathbf{H}}=-{\mathbf{R}}_{FU}\cdot \left(\mathbf{U}-{\mathbf{U}}^{\infty }\right)+{\mathbf{R}}_{FE}:{\mathbf{L}}^{\infty }(17)$

where $\mathbf{U}$ is the particle translational/rotational velocity vector; ${\mathbf{U}}^{\infty }$ is the imposed flow velocity tensor at infinity evaluated at the particle center; ${\mathbf{L}}^{\infty }$ is the symmetric (and traceless, by virtue of continuity) portion of the velocity gradient tensor; ${\mathbf{R}}_{FU}$ and ${\mathbf{R}}_{FE}$ are the hydrodynamic resistance matrices that relate the hydrodynamic force/torque on the particles to their motion relative to the fluid and to the imposed shear flow, respectively.

3.2.2 Electrostatic forces

Multiple methods, based on simplified physical models, have been used to calculate the electrostatic forces (Parthasarathy and Klingenberg, 1996). The simplest physical model is the idealized electrostatic polarization model that contains dielectric spheres, characterized with diameter $d=2a$, $a$ is the particle radius), dielectric constant ${\epsilon }_p$, and a Newtonian continuous phase of a fluid with dielectric constant ${\epsilon }_c$ and viscosity ${\eta }_c$. Both the liquid and particle phases are assumed to be uncharged and have zero conductivity when there is no external electric field. In this model, the force, ${\mathbf{F}}^{el}$, on a given particle can be calculated by the following integration over the sphere surface area, $A$, at a determined electrical potential, as:

${\mathbf{F}}^{el}={\displaystyle \underset{A}{\int }}{\sigma }^M\cdot ndA(18)$

where ${\sigma }^M={\epsilon }_0{\epsilon }_c\left[\text{EE}-\left(1/2\right)E^2\mathrm{\delta }\right]$ is the Maxwell stress tensor, $\mathbf{E}=-\mathbf{\nabla }\psi$ is the local electric field, ${\epsilon }_0$ is the absolute dielectric constant and $\mathrm{\delta }$ is the unit tensor. When considering a uniform electric field, ${\mathbf{E}}_0$, the exact ${\mathbf{F}}^{el}$ between two isolated spheres is:

${\mathbf{F}}_{ij}^{el}\left(r_{ij},{\theta }_{ij}\right)=\frac{3}{16}\pi {\epsilon }_0{\epsilon }_c{\sigma }^2{\beta }^2{E}_0^2{\left(\frac{\sigma }{r_{ij}}\right)}^4\left[\begin{array}{c}\left(2f_{\parallel }{\cos }^2{\theta }_{ij}-f_{\perp }{\sin }^2{\theta }_{ij}\right){\mathbf{e}}_r+\\ \left(f_{\mathrm{\Gamma }}\sin 2{\theta }_{ij}\right){\mathbf{e}}_{\theta }\end{array}\right](19)$

where $\beta$ is $\left({\epsilon }_p-{\epsilon }_c\right)/\left({\epsilon }_p+2{\epsilon }_c\right)$, ${\mathbf{e}}_r$ and ${\mathbf{e}}_{\theta }$ are the unit vectors in the $r$ and $\theta$ directions, respectively, and $f_{\parallel }$, $f_{\perp }$, $f_{\mathrm{\Gamma }}$ are the dimensionless functions describing the influences of higher order multipole moments. Bonnecaze and Brady (1992) employed electrostatic energy $\vartheta$ to calculate the electrostatic forces (Eq. 20):

${\mathit{F}}_i^{el}=-\frac{\partial \vartheta }{\partial {\mathbf{x}}_i}(20)$

where ${\mathbf{x}}_i$ is the particle’s position. Thus, for a system with $N$ particles, the ensemble average $〈\mathbf{x}{\mathbf{F}}^{\mathbf{P}}〉$ for a statistically homogeneous suspension is given by:

$〈\mathbf{x}{\mathbf{F}}^{\mathbf{P}}〉=\frac{1}{N}{\displaystyle {\sum }_{\alpha }^N}{\mathbf{x}}_{\alpha }{\mathbf{F}}_{\alpha }^{el}(21)$

When considering the conductivities of both the particles and the bulk fluid, the Maxwell-Wagnel model can be used if the permittivity and conductivity of the individual phases are assumed to be constants (Parthasarathy and Klingenberg, 1996). In addition, Foulc et al. (1994) investigated the effect of nonlinear electrical conduction in ER fluids.

3.2.3 Rheology of ER fluids

The bulk stress $〈\mathbf{\Sigma }〉$ of a statistically homogeneous suspension containing $N$ particles in volume $V$ is (Batchelor, 1970; Batchelor, 1977; Brady and Bossis, 1988; Bonnecaze and Brady, 1992):

$〈\mathbf{\Sigma }〉=\mathbf{IT}+2\eta {\mathbf{L}}^{\infty }+\frac{N}{V}\left(〈{\mathbf{S}}^{\mathbf{H}}〉+〈{\mathbf{S}}^{\mathbf{P}}〉-〈\mathbf{x}{\mathbf{F}}^{\mathbf{P}}〉\right)(22)$

where $\mathbf{IT}$ is an isotropic term, and the second term is the contribution of the fluid to the stress. The presence of the particles makes the contributions shown in the last term. The hydrodynamic and particle stresslets, ${\mathbf{S}}^{\mathbf{H}}$ and ${\mathbf{S}}^{\mathbf{P}}$ are the symmetric and traceless first moments of the force distributions on a particle due to the shear flow and the interparticle forces, respectively (Eqs. 23, 24):

$〈{\mathbf{S}}^{\mathbf{H}}〉=-〈{\mathbf{R}}_{SU}\cdot {\mathbf{R}}_{FU}^{-1}\cdot {\mathbf{R}}_{FE}-{\mathbf{R}}_{SE}〉:{\mathbf{L}}^{\infty }(23)$

$〈{\mathbf{S}}^{\mathbf{P}}〉=-〈{\mathbf{R}}_{SU}\cdot {\mathbf{R}}_{FU}^{-1}\cdot {\mathbf{F}}^{\mathbf{P}}〉(24)$

where ${\mathbf{R}}_{SU}$ and ${\mathbf{R}}_{SE}$ are the configuration-dependent resistance matrices that relate the particle stresslets to particle velocities and the rate of strain. For a monolayer system, the bulk shear in the $xy$ plane is (${\mathbf{U}}^{\infty }=\dot{\gamma }y{\mathbf{e}}_x$), the total relative viscosity, ${\eta }^T$, is the proportionality between the $yx$ components of the bulk stress $〈\mathbf{\Sigma }〉$ and shear rate $\dot{\gamma }$ represented by:

${\eta }^T=\frac{〈\mathbf{\Sigma }〉}{\dot{\gamma }}(25)$

which can be calculated as:

${\eta }^T={\eta }^H+{\eta }^{S^P}+{\eta }^{XF}(26)$

where

${\eta }^H=1+\frac{5}{3}{\varphi }_A\frac{1}{N}{\displaystyle {\sum }_{\alpha =1}^N}{\left({\mathbf{S}}_{\alpha }^H\right)}_{yx}(27)$

${\eta }^{S^P}=\frac{5}{3}{\varphi }_A\frac{1}{MaN}{\displaystyle {\sum }_{\alpha =1}^N}{\left({\mathbf{S}}_{\alpha }^H\right)}_{yx}(28)$

${\eta }^{XF}=\frac{5}{3}{\varphi }_A\frac{1}{MaN}{\displaystyle {\sum }_{\alpha }^N}{\left({\mathbf{x}}_{\alpha }{\mathbf{F}}_{\alpha }^{el}\right)}_{yx}(29)$

In Eqs. 25–29, ${\varphi }_A$ is the areal fraction of the monolayer, $\frac{5}{3}{\varphi }_A$ is the monolayer equivalence of the Einstein viscosity, $\dot{\gamma }$ is the shear rate, ${\eta }^H$ is the hydrodynamic viscosity, ${\eta }^{S^P}$ is the particle viscosity, and ${\eta }^{XF}$ is the $\mathbf{x}{\mathbf{F}}^{\mathbf{P}}$ viscosity. The combination of ${\eta }^{S^P}$ and ${\eta }^{XF}$ can be referred to as the ER viscosity, ${\eta }^{ER}$. $Ma$ is the Mason number, which represents the relative importance of the viscous shear forces to the electrostatic forces. The magnitude of the electrostatic polarization force and hydrodynamic force can be written as (Marshall et al., 1989):

$F^P=12\pi {\epsilon }_c{a}^2{\beta }^2{E}^2(30)$

$F^H=6\pi {\eta }_c{a}^2\dot{\gamma }(31)$

where $E$ is the magnitude of the electric field strength, $\beta =\left({\epsilon }_p-{\epsilon }_c\right)/\left({\epsilon }_p+2{\epsilon }_c\right)$. The expression of $Ma$ is:

$Ma=\frac{{\eta }_c\gamma }{2{\epsilon }_c{\left(\beta E\right)}^2}(32)$

A numerical simulation result is shown in Figure 4, where the total viscosities have been converted into the shear stresses by multiplying them with their corresponding $Ma$. The shear-stress shear-rate plot has the asymptotic feature of the Bingham plastic model for shear stress. The shear stress approaches a constant value, or the Bingham yield stress, at small $Ma$ values or low shear rates. When $Ma$ is large ($Ma=\infty$ ), the viscosity increases linearly as a Newtonian fluid.

FIGURE 4

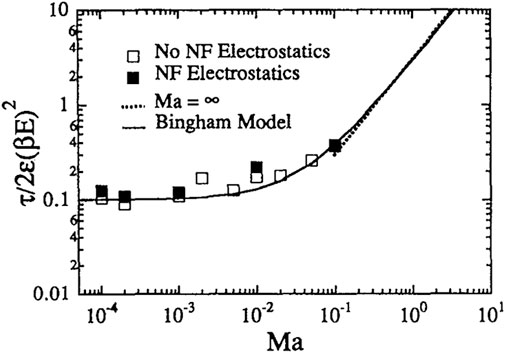
FIGURE 4. Shear stress for the monolayer simulation. Ma is the Mason number. The solid line is for the results from the Bingham shear-stress model, assuming a constant plastic viscosity. NF indicates that near-field electrostatic interactions were included. With permission to re-use (Bonnecaze and Brady, 1992).

By comparing the experimental data over the range of $0.09\le \varphi \le 0.34$, where $\varphi$ is volumetric fraction, Parthasarathy and Klingenberg (1996) found that the ER-fluid viscosity $\eta$, normalized by fluid viscosity ${\eta }_0$, could be described fairly well in the form expressed below:

$\frac{\eta }{{\eta }_0}=\frac{M{a}^{*}}{Ma}+1(33)$

where $M{a}^{*}$ is a material constant, equivalent to a dimensionless dynamic yield stress; for their system, $M{a}^{*}\propto {\varphi }_A$. Rewriting Eq. 33 as $\eta =\left(M{a}^{*}/Ma\right){\eta }_0+{\eta }_0$, then multiplying it by the shear rate $\dot{\gamma }$, result in a form similar to the widely used Bingham model, which can be utilized here to simplify the rheology modeling for ER fluids:

$\begin{array}{c}\dot{\gamma }=0,\tau <{\tau }_0\\ \tau ={\tau }_0\left(E\right)+{\eta }_0\dot{\gamma },\tau >{\tau }_0\end{array}(34)$

The Bingham model, Eq. 34, requires two main parameters, yield stress ${\tau }_0\left(E\right)$, beyond which a solidified ER fluid breaks and starts to behave like a fluid (Sheng and Wen, 2012), and original fluid viscosity ${\eta }_0$ without the applied electric potential, where $E$ is the applied electric field strength. When shear stress $\tau$ is smaller than the yield stress, ${\tau }_0$, the fluid remains at rest. When the shear stress is larger than the yield stress, the fluid starts to flow, and the shear stress has a linear relationship with the shear rate. It is important to determine the yield stress of an ER fluid. Winslow (1949) first summarized the square relationship between the yield stress and the intensity of the applied electric field. Later, ${\tau }_0\left(E\right)$ is often represented as:

${\tau }_0\left(E\right)=\alpha E^{\beta }(35)$

where $\alpha$ and $\beta$ are empirical parameters, and $\beta$ is usually chosen as 2.0.

Besides the typical Bingham model, a quasi-Bingham model (Jang and Tichy, 1997) has also been widely used:

$\tau ={\eta }_0\dot{\gamma }+\frac{2{\tau }_0}{\pi \dot{\gamma }}\arctan \left(\frac{\dot{\gamma }}{{\dot{\gamma }}_0}\right)(36)$

where ${\dot{\gamma }}_0$ is a constant. When ${\dot{\gamma }}_0=0$, Eq. 36 is converted to the typical Bingham model; when, ${\dot{\gamma }}_0=\mathrm{\infty }$ it becomes the Newtonian fluid rheology model. The apparent viscosity of ER fluids can be written as:

${\eta }_a=\frac{\tau }{\dot{\gamma }}(37)$

3.3 Mathematical model of ER fluids lubrication

A modified Reynolds equation for ER fluids lubrication has been developed by Tichy and his colleagues (Tichy, 1991; Dorier and Tichy, 1992; Tichy, 1993; Jang and Tichy, 1997) based on the Bingham model, which is briefly repeated here. Consider an ER lubrication geometry system shown in Figure 5. The momentum equations in the $x$ and $y$ directions are:

$\frac{\partial {\tau }_{zx}}{\partial z}=\frac{\partial p}{\partial x}(38)$

$\frac{\partial {\tau }_{zy}}{\partial z}=\frac{\partial p}{\partial y}(39)$

where $\tau$ is calculated from constitutive equation Eq. 37, and represented by:

${\tau }_{zx}=\eta \left(\dot{\gamma }\right)\frac{\partial u}{\partial z}(40)$

${\tau }_{zy}=\eta \left(\dot{\gamma }\right)\frac{\partial v}{\partial z}(41)$

FIGURE 5

FIGURE 5. Formation of ER fluid lubrication.

By combining the momentum and constitutive equations and using the boundary conditions, a nonlinear equation to calculate $\dot{\gamma }$ can be obtained as:

${\dot{\gamma }}^2=\frac{1}{{\eta }^2\left(\dot{\gamma }\right)}\left\{\begin{array}{c}{\left[\frac{\partial p}{\partial x}\left(z-\frac{f_1^{\prime }\left(h\right)}{f_1^{\prime }\left(h\right)}\right)+\frac{U_2-U_1}{f_2^{\prime }\left(h\right)}\right]}^2\\ +{\left[\frac{\partial p}{\partial y}\left(z-\frac{f_1^{\prime }\left(h\right)}{f_2^{\prime }\left(h\right)}\right)+\frac{V_2-V_1}{f_2^{\prime }\left(h\right)}\right]}^2\end{array}\right\}(42)$

with

$f_1^{\prime }\left(z;x,y\right)={\int }_0^z\frac{z}{\eta \left(\dot{\gamma }\right)}dz(43)$

$f_2^{\prime }\left(z;x,y\right)={\int }_0^z\frac{1}{\eta \left(\dot{\gamma }\right)}dz(44)$

subjected to the boundary conditions of the lubrication system (Eq. 45):

$\begin{array}{c}u\left(0\right)=U_1;v\left(0\right)=V_1\\ u\left(h\right)=U_2;v\left(h\right)=V_2\end{array}(45)$

Now, the velocities can be solved as:

$u=\frac{\partial p}{\partial x}{f}_3^{\prime }\left(z\right)+\frac{U_2-U_1}{f_2^{\prime }\left(h\right)}{f}_2^{\prime }\left(z\right)+U_1(46)$

$v=\frac{\partial p}{\partial y}{f}_3^{\prime }\left(z\right)+\frac{V_2-V_1}{f_2^{\prime }\left(h\right)}{f}_2^{\prime }\left(z\right)+V_1(47)$

with

$f_3^{\prime }\left(z;x,y\right)=f_1^{\prime }\left(z\right)-\frac{f_1^{\prime }\left(h\right)}{f_2^{\prime }\left(h\right)}{f}_2^{\prime }\left(z\right)(48)$

The continuity equation of the fluid element is:

$\frac{\partial q_x}{\partial x}+\frac{\partial q_y}{\partial y}=0(49)$

The mass flow rates in the $x$ and $y$ directions can be obtained by integration:

$q_x={\displaystyle {\int }_0^h}udh=f_4^{\prime }\left(h\right)\frac{\partial p}{\partial x}+\left(U_2-U_1\right)f_5^{\prime }\left(h\right)+U_{1}h(50)$

$q_y={\displaystyle {\int }_0^h}vdh=f_4^{\prime }\left(h\right)\frac{\partial p}{\partial y}+\left(V_2-V_1\right)f_5^{\prime }\left(h\right)+V_{1}h(51)$

Substitute Eqs. 50, 51 into the continuity equation, Eq. 49, the modified Reynolds equation for an ER fluid can be written as follows:

$\begin{array}{c}\frac{\partial }{\partial x}\left[f_4^{\prime }\left(h\right)\frac{\partial p}{\partial x}\right]+\frac{\partial }{\partial y}\left[f_4^{\prime }\left(h\right)\frac{\partial p}{\partial x}\right]=\\ \frac{\partial \left(U_1-U_2\right)f_5^{\prime }\left(h\right)}{\partial x}+\frac{\partial \left(V_1-V_2\right)f_5^{\prime }\left(h\right)}{\partial y}-\frac{\partial \left(U_{1}h\right)}{\partial x}-\frac{\partial \left(V_{1}h\right)}{\partial y}\end{array}(52)$

where

$f_4^{\prime }\left(z;x,y\right)={\int }_0^z{f}_3^{\prime }\left(z\right)dz(53)$

$f_5^{\prime }\left(z;x,y\right)=\frac{1}{f_2^{\prime }\left(h\right)}{\int }_0^z{f}_2^{\prime }\left(z\right)dz(54)$

3.4 Numerical simulations of ER-fluid lubrication

In 1991, Tichy (1991) used the Bingham model calculated the lubrication behavior of journal bearings lubricated with an ER fluid. The pressure distribution against yield stress ${\tau }_0$ is showed in Figure 6. Later, Dimarogonas and Kollias (1992) investigated the controllability of the stability properties of ER-fluid-lubricated bearings, and the numerical results showed that an applied electric could considerably change the lubrication behaviors of the bearings. Dorier and Tichy (1992) calculated several lubrication flows and revealed non-monotonic trends in the load and flow rate behaviors as functions of stress parameter. Jang and Tichy (1997) proposed a dimensionless modified Reynolds equation for ER-fluid lubrication and obtained spring and damping coefficients for the journal bearing.

FIGURE 6

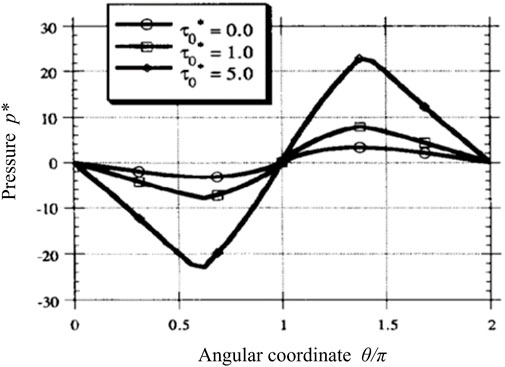
FIGURE 6. Squeeze film damper, dimensionless pressure distribution, low eccentricity ratio $\mathit{\epsilon }=\mathbf{0.25}$. With permission to re-use. (Tichy, 1991).

Zhun and Ke-Qin, (2002) emphasized that the primary factors affecting the performance of ER-fluid-lubricated journal bearings under low shear-rate conditions were the apparent viscosity and the movement of the yield surface within the bearing clearance. The yield surface distinguishes the yield and non-yield region of an ER fluid in lubrication. Peng and Zhu (2005), Peng and Zhu (2006) used a modified Bingham model to describe the ER fluid for journal bearings and solved the fluid equation using CFD techniques. The results showed that the ER effects increase the film pressure and load-carrying capacity (Figure 7). Basavaraja et al. (2010) pointed out that using ER fluids as lubricants could partially compensate the reduction in the film thickness caused by journal misalignments. Lee (2015) made a time-transient nonlinear analysis of a rigid rotor supported by an ER lubricated plain journal bearing, and the results show that an increased electric field strength could lead to a greater loading capacity for the bearing operated at certain clearance ratios.

FIGURE 7

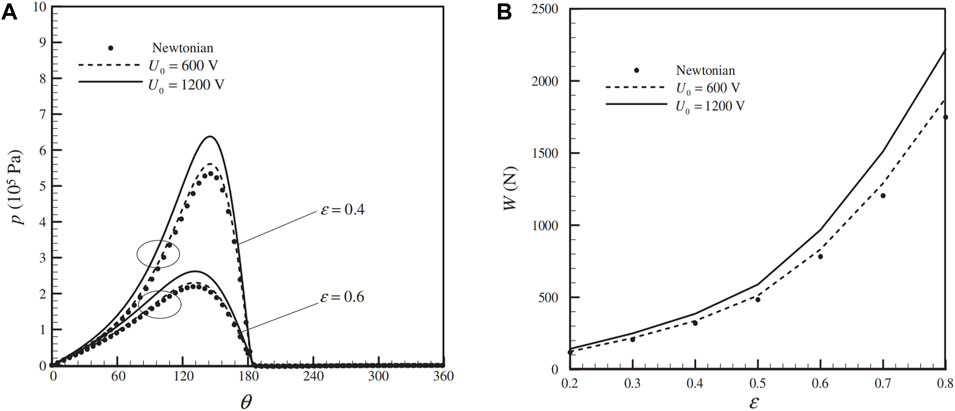
FIGURE 7. (A) Film pressure $p$ as a function of circumferential position angle $\theta$ for different applied electric voltages $U_0$, $\epsilon$ is eccentricity ratio; (B) Load capacity $W$ vs. $\epsilon$ at different $U_0$. With permission to re-use (Peng and Zhu, 2005).

Christidi-Loumpasefski et al. (2018) studied the stiffness and damping dynamic coefficients of the journal bearing with ER lubrication and obtained these coefficients as functions of the applied electric field. Mutra and Srinivas (2019) focused on the unbalance response of a rotor system lubricated with an ER fluid. Both gyroscopic effects and nonlinear bearing forces were considered, and the effect of externally applied electric field on the dynamic response was studied.

Recently, numerical modeling of ER lubrication has been further extended to more bearing systems. A group of researchers (Kumar and Sharma, 2019; Agrawal and Sharma, 2021; Singh et al., 2022) calculated the ER-fluid lubrication behavior of textured conical hybrid journal bearings, textured multi-lobe hole-entry hybrid journal bearings, and spherically recessed hydrostatic thrust bearing. Kumar et al. (2021a, 2022) simulated the impact of ER fluids on symmetric journal bearings and hybrid journal bearings.

3.5 Experimental research on ER-fluid lubrication

Many experimental works have been conducted to study the performances of tribopairs lubricated with ER fluids. Nikolakopoulos and Papadopoulos (1998) conducted an experiment to test a high-speed journal bearing with a small radial clearance lubricated with an ER fluid, and the results gave good agreement with the corresponding numerical solutions. Their work also demonstrated that items like eccentricity, attitude angle, and stiffness coefficients were all functions of the applied electric field. Lingard et al. (1989) studied the wear in ER fluid lubrication on a laboratory wear tester and indicated that ER fluids could lead to more severe wear compared to those lubricated with conventional commercial oils in the pin-on-disc and disc-on-disc test configurations. They summarized that the wear of an ER-fluid-lubricated surface could be characterized as adhesive interaction of asperity, extensive delamination, and the generation of large numbers of spherical particles. Park et al. (1996) conducted pin-on-disc experiments, and their results showed that both wear rate and friction coefficients increased with particle concentration. Barber et al. (2005) demonstrated, using a pin-on-disc tester worked in a hydrostatic lubrication, that friction and wear of sliding components could be controlled by an applied electric voltage. Moreover, the analysis of microscopic surface topographic changes due to wear of the pin specimen indicated that ER fluid could stabilized wear and friction at a higher wear rate as compared to the case lubricated only with the carrier liquid (Choi et al., 2010).

To conclude the work related to ER-fluid lubrication, the working mechanisms of ER fluids are based on the polarization of electrical particles due to the difference in dielectric constants of electrical particles and carrier fluid. This polarization behavior leads to the formation of chain structures of particles along the applied electric field. As a result, the rheology of an ER fluid is changed, viscosity increased, and load capacity improved. Besides, the behaviors of ER fluids can be controlled by an external electric field, which makes them suitable for many lubrication scenarios. In simulations, the rheology of ER fluids is often described by a Bingham model. A modified Reynolds equation has been derived by using the rheological model. ER fluids have been widely researched with both numerical and experimental approaches. In numerical modeling, the performances of ER fluids used in multiple types of bearings have been simulated along with the properties of these lubrication systems. The focus of experimental work has been on the wear performance and the controllability of ER fluid lubrication.

4 Magnetorheological (MR) fluids

An MR fluid is composed of ferromagnetic or paramagnetic particles dispersed within a carrier fluid (Margida et al., 1996). The size of the solid particles is in the order of micrometers. Without an external magnetic field, the magnetic particles are arbitrarily distributed, and MR fluid behaves like a Newtonian fluid. Under an external magnetic field, the viscosity and yield stress of the MR fluid change due to queuing of magnetic particles, and the MR fluid behave like a non-Newtonian fluids (Gołdasz and Sapiński, 2015). The functionality of MR fluids is due to the magnetic permeability mismatch between the solid particles and the liquid (De Vicente et al., 2011). By adjusting the external magnetic field, the rheological features of MR fluids are controlled. The interesting nature of MR fluids has attracted a great deal of research on the employments and applications of these fluids (Ahamed et al., 2018). Among them, using MR fluids as lubricants in journal bearing and other lubrication systems has been a major focus (Elsaady et al., 2020).

4.1 Components of MR fluids

MR fluids are basically non colloidal solid-in-liquid suspensions of micro-sized magnetizable particles, an insert base fluid, and other additives (Baranwal and Deshmukh, 2012). Typically, carrier liquids can be petroleum base oil, silicone, polyesters, polyethers, water, synthetic hydrocarbon oils, and others (Carlson and Jolly, 2000). Metals or ceramics, such as the iron–cobalt alloy, carbonyl iron, nickel–zinc ferrites, and ferrite-polymers, can be used as magnetic particles (Ashtiani et al., 2015). Additives are often used as auxiliary materials to improve the MR effect through increasing re-dispersibility and reducing sedimentation ratio and oxidation, frequently used additives include oleic acid, silica nanoparticles, and stearic acid (Pei and Peng, 2022).

4.2 Mechanisms for MR fluids and mathematical modeling

Like ER fluids, the working mechanisms of MR fluids can be explained by a particle magnetization model. Under an external magnetic field, polarization can be induced in the suspended particles to form dipole moments (Jolly et al., 1999). As the dipole-dipole interaction increases, the particles align to form chains along the flux lines of the magnetic field (Felt et al., 1996).

The ratio between Stokesian hydrodynamic and dipolar magnetostatic forces acting on the particles can also be represented by a Mason number (Ramos et al., 2011). The definition of Mason number $Ma$ in the MR fluids can be different, two of them, which has been widely used, are (Volkova et al., 2000; Klingenberg et al., 2007):

$Ma=\frac{8{\eta }_0\gamma }{{\mu }_0{\mu }_{cr}{\left(\beta H\right)}^2}(55)$

$Ma=\frac{{\eta }_0\gamma }{2{\mu }_0{\mu }_{cr}{\left(\beta H\right)}^2}(56)$

where ${\mu }_0$ is the permeability of vacuum, ${\mu }_{cr}$ is the relative permeability of the continuous phase, $\beta =\left({\mu }_{\mathit{pr}}-{\mu }_{cr}\right)/\left({\mu }_{\mathit{pr}}+2{\mu }_{cr}\right)$ is a contrast factor, ${\mu }_{\mathit{pr}}$ is the relative permeability of the particles, and $H$ is the magnetic-field strength.

The basic formation of MR fluid lubrication is shown in Figure 8. Experimental and numerical results also support the use of a non-Newtonian model for MR fluids (Pei and Peng, 2022). Several models have been used to calculate viscosity of MR fluids (Kumar et al., 2021b), and the most popular models for MR fluid lubrication systems are the Bingham model and the Herschel–Bulkley model. In the Bingham model, shear stress $\tau$ can be approximated as:

$\begin{array}{c}\dot{\gamma }=0,\tau <{\tau }_0\\ \tau ={\tau }_0\left(H\right)+{\eta }_0\dot{\gamma },\tau >{\tau }_0\end{array}(57)$

which is the same as Eq. 34, where ${\tau }_0$ is the yield stress, $\dot{\gamma }$ is the shear rate, and ${\eta }_0$ is the viscosity of the fluid without magnetic field. ${\tau }_0\left(H\right)$ is a function of external magnetic field, which can be obtained from experimental data (Bompos and Nikolakopoulos, 2011). Then the apparent viscosity, ${\eta }_a$, can be represented as:

${\eta }_a={\eta }_0+{\tau }_0\left(H\right)/\dot{\gamma }(58)$

FIGURE 8

FIGURE 8. Formation of MR fluid lubrication.

In the Herschel-Bulkley model, $\tau$ is represented as:

$\tau ={\tau }_0\left(H\right)+K{\dot{\gamma }}^n(59)$

where $K$ and $n$ are model constants. If $n=1$, Eq. 59 becomes Eq. 57, and $K$ becomes the fluid viscosity without the applied magnetic field; if $n>1$, the MR fluid is shear thickening; and if $n<1$, the MR fluid is shear thinning (Wang et al., 2015). The apparent viscosity is then given as:

${\eta }_a={\tau }_0{\dot{\gamma }}^{-1}+K{\dot{\gamma }}^{n-1}(60)$

Based on Tichy’s theory (Tichy, 1991; Dorier and Tichy, 1992; Tichy, 1993; Jang and Tichy, 1997), a modified Reynolds equation can be obtained, which is similar to that discussed in the previous section for the ER fluids.

4.3 Numerical simulations of MR-fluid lubrication

In 2008, Gertzos et al. (2008) used the commercial CFD software, Fluent, to simulate the hydrodynamic journal-bearing lubricated by MR fluids. The rheological property of the MR fluid was described by an extended Herschel–Bulkley model. The Navier-Stokes equation was solved, instead of the Reynolds equation, due to the high density of the MR particles in the fluid. The results showed that the values of load carrying capacity, the film pressure, and the frictional force of the MR fluid were larger than those produced by a Newtonian fluid, and that they increase with the yield stress. Bompos and Nikolakopoulos (2011) built an integrated MR fluid journal-bearing simulation model with ANSYS based on the CFD and finite element method. Amperes law was used to calculate the magnetic field generated by different current densities. The presence of a magnetic field can increase attitude angle, means an enhancement of the load-carrying capacity, or reduction of the Sommerfeld number, which is reciprocal of load capacity, whereas friction coefficient can also be increased by the magnetic field. It should be mentioned that MR fluid lubrication makes friction more dependent on the bearing structure in terms of width over diameter, L/D, and shifts the attitude angle-Sommerfeld number curves towards the high load or low Sommerfeld number side. Based on previous studies, Bompos and Nikolakopoulos (2015) conducted numerical simulations to examine the effect of artificial textures on the performances of the journal bearings lubricated by MR fluid.

The external magnetic field may alter the yield stress of an MR fluid. Lampaert and Van Ostayen (2019b) presented a mathematical model to predict the load and stiffness of a planar hydrostatic bearing lubricated with a Bingham plastic fluid. The model showed that the yield stress of an MR fluid was about proportional to intensity of the magnetic field. In order to improve the efficiency of numerical simulation, they (2020) also proposed an “exact” thin-film lubrication simulation model for the Bingham plastic fluid. This new model was less computationally demanding since it had a lower number of degrees of freedom needed and required no numerical regularization for the Bingham plastic fluid model. Lampaert et al. (2020) assessed the lubrication of a hybrid journal bearing via this new model and the finite element method, which demonstrated that both yield stress and viscosity increase as functions of the applied magnetic field.

A group of researchers also extended the use of MR-fluid lubrication to more types of journal bearings. Sharma and Tomar (2021) considered the lubricant flow via an orifice restrictor in the bearing clearance space and solved a modified Reynolds equation along with a restrictor flow equation to determine the performance of an MR-fluid lubricated hybrid hole-entry spherical journal bearing with micro-grooves. The MR fluid lubrication improved the minimum fluid-film thickness, and the micro-grooves on the surface of the hybrid spherical journal bearing significantly enhanced the stiffness coefficients. Sahu and Sharma (2019) used a simulation model and examined the thermal effects on the performance of an MR-fluid lubricated slot-entry journal bearing. When the temperature of the MR fluid rose, the viscous structure of the MR fluid became weaker, and the fluid resistance against movement decreased. Sahu et al. (2022) studied the behavior of an MR-fluid lubricated journal bearing with surface irregularities under misalignment conditions, and they reported that the mutual effects of surface irregularities and MR particles enhanced the minimum fluid film thickness and increased the damping capabilities of the bearing system.

4.4 Experimental research on MR-fluid lubrication

Numerous experiments have been conducted on testing the performances of MR-fluid lubrication systems in recent years. Wang et al. (2017) set up a test stand and measured rotordynamic coefficients of an MR-fluid-lubricated floating-ring bearing, the bearing separates the MR fluid into two lubricant films, inner film and outer film. Their results showed that stiffness and damping of the outer film increased as the external magnetic field was enhanced, which indicated that the bearing could achieve a semi-active control by changing the external magnetic field. Vaz et al. (2017) conducted experiments to investigate variations of the frictional force developed in the journal bearing lubricated with an MR fluid, revealing that friction became higher as the magnetic field strength got stronger. Lampaert and Van Ostayen (2019a) built an experimental apparatus to measure the load capacity of a hydrostatic bearing lubricated with an MR fluid. The results were compared to those from a numerical model and an analytical model, all three yielded similar characteristics in the same order of magnitude. Compared with experimental results, the inaccuracy of the analytical model was attributed to its coarse assumptions, and that in the numerical model to the material model. Quinci et al. (2021) used a dedicated test rig to assess the behavior of the bearing lubricated with an MR fluid. Compared to oil lubrication, the bearing lubricated with the MR fluid had thicker fluid films at low speeds and beneficial pressure distribution. Figure 9 shows the coefficient of friction from both experiments data and FEM simulations. The results indicate that the use of MR fluid may lead to increased friction losses.

FIGURE 9

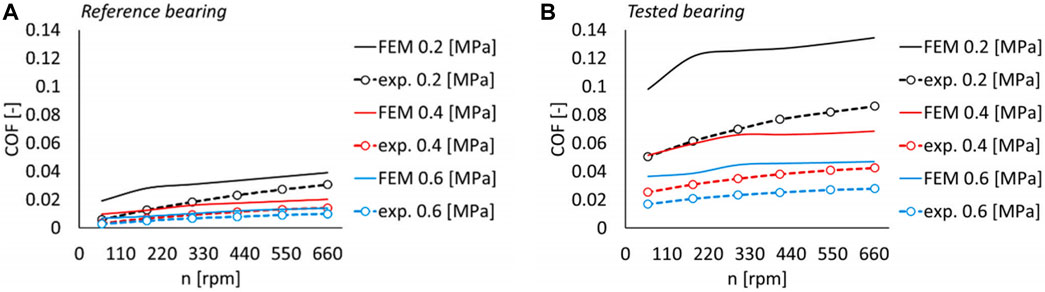
FIGURE 9. Coefficient of friction at different speeds and applied loads for (A) reference (SAE 30 mineral oil lubricated) and (B) Tested (MR-fluid lubricated) bearings (Both FEM and experimental results are plotted). With permission to re-use (Quinci et al., 2021).

In summary, the MR-fluid lubrication utilizes chains of particles formed, due to the magnetic permeability mismatch between the solid particles and the carrier fluid, under an external magnetic field. The polarization of magnetic particles changes the rheology of MR fluids and causes viscosity to increase. This change can be controlled by the intensity of the magnetic field and improve the load capacity of the lubrication system. Non-Newtonian viscosity models can be used to simplify the rheology model. Modified Reynolds equation, similar to that for the ER fluids, can be derived and used to analyze MR lubrication problems. Numerical simulations have been conducted to examine the ability of MR fluids to lubricate different bearings. Experiment results show that MR fluids can enhance lubrication performances of different bearings.

5 Ferrofluids

A ferrofluid is a kind of magnetic fluids of synthesized colloidal mixtures of a non-magnetic carrier liquid and permanently magnetized solid particles (Rinaldi et al., 2005). Compared to the MR fluids, solid particles in the ferrofluids are on the order of nanometers, about 3–15 nm, which are relatively smaller, while the size of those in a usual MR fluid is well above 1 μm (1–20 μm) (Vékás, 2008). By applying an external magnetic field, the rheological properties of ferrofluids are changed, and ferrofluids can be confined, positioned, shaped, and controlled at desired places (Huang et al., 2011). Using ferrofluid as the lubricant under an appropriate magnetic field can gain the merits of increasing load capacity and film thickness.

5.1 Components of ferrofluids

Ferrofluids can be treated as colloidal suspension of single-domain magnetic particles and a base liquid. These magnetic nanoparticles could be Fe, Co, iron oxide (γ-Fe2O3, Fe3O4) or MnZn ferrites (Genc and Derin, 2014). In order to prevent agglomeration due to van der Walls interactions, the particles are usually coated (Odenbach, 2013). The coating could be surfactant molecules or an electric shell. For particles coated with surfactant agents, steric repulsion between particles acts as a physical barrier. For particles coated with electric shells, electrostatic repulsion exists between particles, the pH of the carrier liquid depends on the sign of the surface charge of the particles. Both steric and electrostatic repulsion prevent particle agglomeration (Scherer and Neto, 2005). The carrier liquid could be either polar or non-polar, such as water, ethylene glycol, transformer oil, and engine oil, etc. (Kole and Khandekar, 2021).

5.2 Mechanisms of ferrofluids

The small-size magnetic particles in ferrofluids can prevent fluids from forming sediment in the gravitational field or in moderate magnetic field gradients (Odenbach, 2004). As mentioned before, these particles are also covered with a surfactant layer to prevent agglomeration due to van der Waals interactions, and hence, ferrofluids can maintain fluidity in high magnetic field gradients, and the particles can be treated as small permanent magnets in the carrier liquid (Odenbach, 2004). There is no chains structure in ferrofluids. An energy factor, $\lambda$, can be defined, based on the Brownian thermal energy and magnetic polarization energy of individual particles, to show the difference between an MR fluids and a ferrofluid (Eq. 61) (Olabi and Grunwald, 2007):

$\lambda =\frac{{\mu }_0{P}_{mag}^{2}V}{12kT}(61)$

where ${\mu }_0$ is the permeability of vacuum, $P_{mag}$ is polarization, $V$ is particle volume, $k$ is Bolzmann’s constant, and $T$ is temperature. When $\lambda$ is larger than 1, the magnetization energy is larger than thermal energy, and the fluid should have MR functionality. Otherwise, the thermal energy is larger, and the magnetic field would guide the particles according to the flux density, the fluid should have the ferrofluid functionality (Olabi and Grunwald, 2007).

Since the magnetic particles in a ferrofluid are not interacting with each other, the magnetic moment is fixed within the particles. When a ferrofluid is subjected to an external magnetic field, as the magnetic moments of particles tending to align with the magnetic field direction, the rotation caused by viscous dissipation would lead to a misalignment of particles magnetic moments and the magnetic field. This misalignment gives rise to a magnetic torque that counteracts the mechanical torque due to the shear flow. Thus, the free rotation of the particles is hindered and, macroscopically, an increase in viscosity can be observed (Odenbach, 2004). This mechanism of rheological variations makes the flow of a ferrofluid controlled by the gradient and direction of the magnetic field.

5.3 Mathematical model of ferrofluids lubrication

Several flow models have been proposed to describe the behaviors of ferrofluids (Neuringer and Rosensweig, 1964; Jenkins, 1969; Shliomis, 1971). Among them, the Neuringer–Rosensweig model represents a pioneering effort of ferrofluid–lubrication research and has been widely used. Here, the procedure (Osman et al., 2001) to derive the Neuringer–Rosensweig model is briefly re-visited.

The core concept of the Neuringer-Rosensweig model is the consideration of the magnetic body force. Ferrofluids are non-conductive, and the induced magnetic force ${\mathbf{f}}_m$ is:

${\mathbf{f}}_m={\mu }_{0}M\nabla H(62)$

where ${\mu }_0$ is the permeability of a free space or air, $M$ is the magnetization of the ferrofluid, and $H$ is the magnetic field intensity.

Consider a typical ferrofluids lubrication system shown in Figure 10. By treating the magnetic force as an external body force, the momentum equation can be written as:

$\frac{\partial p}{\partial x}=\eta \frac{{\partial }^{2}u}{\partial z^2}+f_{mx}(63)$

$\frac{\partial p}{\partial y}=\eta \frac{{\partial }^{2}v}{\partial z^2}+f_{my}(64)$

where $u$ and $v$ are the velocities in the $x$ and $y$ directions, $p$ is the pressure, and $\eta$ is the viscosity of ferrofluids. Assume $M$ is independent of temperature, and $H$ does not change along the film thickness direction. A new pressure expressed $p^{\prime }$ can be introduced as:

$p^{\prime }=p-{\mu }_{0}MH(65)$

FIGURE 10

FIGURE 10. Formation of ferrofluid lubrication.

The momentum equation can be written as:

$\frac{\partial p^{\prime }}{\partial x}=\eta \frac{{\partial }^{2}u}{\partial z^2}(66)$

$\frac{\partial p^{\prime }}{\partial y}=\eta \frac{{\partial }^{2}v}{\partial z^2}(67)$

By considering the boundary conditions (Eq. 68):

$\begin{array}{c}u\left(0\right)=U_1;v\left(0\right)=V_1\\ u\left(h\right)=U_2;v\left(h\right)=V_2\end{array}(68)$

The velocity profiles can be obtained as:

$u=\frac{1}{2\eta }\frac{\partial p^{\prime }}{\partial x}\left(z^2-zh\right)+\frac{U_2-U_1}{h}z+U_1(69)$

$v=\frac{1}{2\eta }\frac{\partial p^{\prime }}{\partial y}\left(z^2-zh\right)+\frac{V_2-V_1}{h}z+V_1(70)$

Combing velocity profiles, Eqs. 69, 70, with the continuity equation, a modified Reynolds equation can be written as follows for the ferrofluids (Eq. 71):

$\frac{\partial }{\partial x}\left(\frac{h^3}{12\eta }\frac{\partial p^{\prime }}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{12\eta }\frac{\partial p^{\prime }}{\partial y}\right)=\frac{U_1+U_2}{2}\frac{\partial h}{\partial x}+\frac{V_1+V_2}{2}\frac{\partial h}{\partial y}(71)$

5.4 Numerical simulations of ferrofluids lubrication

Major numerical models used to calculate ferrofluid lubrication systems are Neuringer-Rosensweig model, Shliomis model, and Jenkins model (Huang and Wang, 2016). Numerous numerical simulations have been conducted using Neuringer-Rosensweig model. Tipei (1982) considered magnetization $M$ as a function of magnetic field intensity $H$ and film thickness direction $z$, and derived a more general pressure differential equation. Equation 65 is a particular case when $\partial M/\partial T=0$ and $\partial H/\partial z=0$. When applying the model to investigate the lubrication performance of short bearings, the results showed that in the modeled ferrofluid lubrication, the active area of the load-supporting film was increased, and bearing stiffness and stability were improved. Shat and others (Bhat and Deheri, 1991; Bhat and Deheri, 1993; Shah and Bhat, 2000; Shah, 2003) researched the squeeze-film performances for two approaching surfaces with various physical configurations, including step plates, annular plates, and curved circular plates. Numerical results indicated that the pressure and load capacity both increased with the increasing magnetization parameter. Osman et al. (2001), Osman et al. (2003), Osman (2004) tested different magnetic field models for ferrofluid-lubricated bearings and took the elastic deformation and non-Newtonian fluids characteristic into consideration. Their results showed that a shear thickening non-Newtonian ferrofluid could increase the load-carrying capacity and decrease the friction coefficient at high eccentricity ratios of the journal bearings. Hsu et al. (2013), Hsu et al. (2014) examined the combined effects of stochastic surface roughness and a magnetic field on short and long journal bearings lubricated with ferrofluids. For the short bearings, introducing longitudinal roughness can increase load capacity, but for the long bearings, the lubrication performance can be improved by transverse roughness. These observations are similar to what shown in conventional elastohydrodynamic lubrication of rough surfaces (Zhu and Wang, 2013; Wang and Zhu, 2019).

The Shliomis model (Shliomis, 1971) considered the effects of rotation of magnetic particles, magnetic moments, and particle volume concentration into the ferrofluid flow model. Walker and Buckmaster (1979) made several assumptions to simplify the Shliomis model and found that the Brownian motion of the particles, together with rotation of the magnetic particles, produces the rotational viscosity, which could support stronger loads. Shukla and Kumar (1987) used the Shliomis model and calculated the ferrofluid lubrication performances of squeeze-film bearings and slider bearings in the presence of a transverse magnetic field. They revealed that as the strength of applied magnetic field increased, the load capacity of bearings increased, but the coefficient of friction decreased. The cavitation effects were also investigated using the Shliomis model, and results showed that the application of the magnetic field to the ferrofluid would not affect the point of cavitation (Chandra et al., 1992; Sinha et al., 1993). By neglecting the magnetic moment relaxation time and assuming a saturated ferrofluid, Shah and Bhat (2005a) derived a modified Shliomis model to include the rotation of magnetic particles in a squeeze film, the load capacity and response time were found to increase with increasing values of the ferrite-particle concentration and the strength of the applied magnetic field. By applying the averaged momentum principle, a governing equation based on the Shliomis model could be derived to include the influences of convective fluid inertia forces. The results showed that the effect of the fluid inertia forces enhanced the load capacity (Lin, 2012; Lin, 2013; Lin et al., 2013).

The Jenkins model (Jenkins, 1969; Jenkins, 1971) used the isothermal static equilibrium theory for ferrofluids, obtained integrals of the linear momentum equations, and identified the magnetic energy density function for ferrofluids to determine the governing equations of the system. Compared with the Neuringer–Rosensweig model, in the Jenkins model, the body-force density due to the self-field is separated from the external body forces, such as that caused by an external magnetic field (Huang and Wang, 2016). Shah and Bhat (2003a, 2003b, 2004, 2005b) studied the performance of different ferrofluid lubrication systems numerically using Jenkins model. For a ferrofluid lubricated parallel-plate squeeze-film bearing, the load-carrying capacity was found to increase with increasing values of the rotation parameters (Shah and Bhat, 2003b). The slip velocity effect was theoretically analyzed in two different slider bearings, and the results stated that an increased slip parameter could help reduce load capacity and friction (Shah and Bhat, 2003a; Shah and Bhat, 2005b). As the strength of the magnetic field increases, the load capacity increases and the coefficient of friction decreases in a slider bearing with its stator having a circular convex-pad surface (Shah and Bhat, 2004). Based on the Jenkins model, Patel and Deheri (2011) studied the effect of surface roughness on a slider bearing with a slip velocity. It was found that the negatively skewed roughness could help increase the load capacity. Laghrabli et al. (2017) created a magnetic field by diplaced finite wire to study the hydrodynamic lubrication by ferrofluids of finite journal bearings, and got the numerical solution of the Jenkins model. Figure 11 shows the influence of magnetic force on load capacity and attitude angle. Compared with non magnetic fluid case, ferrofluids can provide higher load capacities, and the increase of magnetic force coefficient causes an increase in the attitude angle.

FIGURE 11

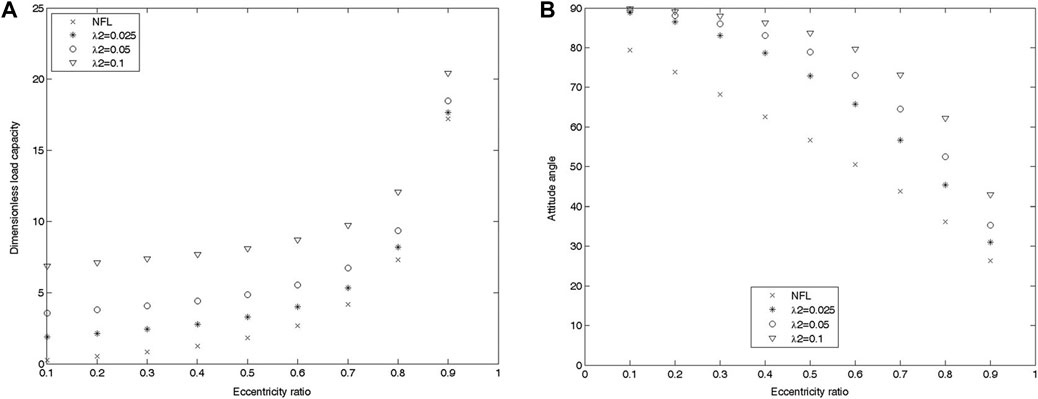
FIGURE 11. (A) Effect of the magnetic force coefficient ${\lambda }_2$ on dimensionless load capacity. NFL, nonmagnetic lubricant. (B) Effect of the magnetic force coefficient ${\lambda }_2$ on attitude angle. NFL, nonmagnetic lubricant. With permission to re-use (Laghrabli et al., 2017).

5.5 Experimental research on ferrofluids lubrication

Experimental studies on ferrofluid lubrication have been mainly focused on the tribological performances of different ferrofluids. Wang et al. (2008) investigated Mn_0.78Zn_0.22Fe₂O₄ nanoferromagnetic as the additive in 46^# turbine oil using a four-ball friction and wear tester. It is shown that the ferrofluid yielded a much better friction reduction and anti-wear ability than the base oil. Huang et al. (2009) prepared ferrofluid composes of different Fe₃O₄ additives in α-olefinic hydrocarbon synthetic oil (PAO4) and evaluated their tribological performances in a four-ball tester. The use of ferrofluids increased the maximum non-seizure load and reduces the wear scar diameter compared to what the carrier liquid did. Later, they prepared Fe₃O₄-based ferrofluids with different saturation of magnetizations by the co-precipitation technique and tested the performances of the ferrofluids on a ring-on-cylinder tester. The experimental results indicated that ferrofluids had a good friction-reduction ability subjected to an external magnetic field, compared with the carrier liquid, and the proper magnet field distribution could be suitable for the fixation of the lubricant in the contact zone of the friction pairs (Huang et al., 2011).

Xu et al. (2020) used a commercial Fe₃O₄-based ferrofluid as the lubricant to improve the operation performance of a thrust ball bearing under starved lubrication conditions on a tribo-tester, and experiment results showed ferrofluid could easily be restricted on the ring surface, even at high rotational speed, by the external magnetic field. Thus, lubricant usage could be reduced, and starvation could be avoided or delayed. Recently, Sahoo et al. (2022) proposed to use inverse ferrofluids that were dispersions of non-magnetic particles (typically silica or polystyrene) in a ferrofluid to lubricate tribo-pairs, in which the amount of lubricant was small and the lubricated region highly confined. The proposed ferrofluids were composed of non-magnetic solid particles, such as MoS₂, polytetrafluoroethylene, or silica dispersed in polyalphaolefin. An MCR-302 tribometer with a ball-on-three-plate configuration in steel-steel contacts (AISI 316) was used for these experiments. With appropriate magnetic field gradients, the prepared ferrofluids could be driven to the region of interest and thus controlled the friction locally.

For ferrofluid lubrication, magnetic particles in the base-liquid carriers are much smaller than those in the MR fluids. Under an external magnetic field, the nano-sized magnetic particles do not form chain structures, and the ferrofluids can maintain fluidity. The rheological properties of ferrofluids can be controlled by an external magnetic field, which can help increase load capacity. Mathematical models have been developed to describe the magnetic force on magnetic particles, and a modified Reynolds equation based on the Neuringer-Rosensweig model has been briefly derived in this section. Numerical simulations based on different models and various lubrication situations have been conducted. Experimental research has been focused on the performances of ferrofluids with different lubrication properties.

6 Electric vehicles (EVs) lubrication

Compared to internal combustion engine vehicles (ICEVs), EVs have an average total energy use that is 3.4 times lower, and the CO₂ emissions per kilometer of an ICE vehicle can be up to 4.5 times higher than that of an EV (Holmberg and Erdemir, 2019). Leading consumer concerns regarding EVs including driving range, charging time, accessibility to charging infrastructure, and vehicle cost (Van Rensselar, 2019).

The distinctive design configurations of EVs have created substantial impact on driveline lubrication requirements pertaining to electrical and heat transfer characteristics, energy efficiency, and the presence of electric currents and magnetic fields (Shah et al., 2021b). Main components to be lubricated in EVs include electric-motor system bearings, steering system bearings, wheel bearings, constant-velocity joints, the transmission system, and among others (Farfan-Cabrera, 2019; Hemanth et al., 2021). The presence of the electric and magnetic fields in EVs can potentially lead to various forms of bearing damage and lubrication failures (Gahagan, 2017; Chen Y. et al., 2020). Enhancing the lubrication systems in EVs requires thorough research into the intricate interactions between tribological components and electric and magnetic fields to ensure performance and durability.

6.1 Lubricants used in EVs

Lubricated contacts in EVs are likely to be exposed to stray currents (Spikes, 2020), and the operation of power electronics may subject lubricants of EVs to an elevated temperature (Johnson et al., 2004). Thus, it is crucial to assess the electrical and thermal properties of the lubricant used in EVs (Shah et al., 2022). Moreover, there is a heightened need for anticorrosion capabilities due to the direct interaction between lubricants and copper components (Gahagan, 2017). Compared to ICEVs, the shaft of the electric motor in EVs is usually subjected to a higher rotation rates, which requires the use of lubricants with low viscosity to facilitate high torque transferring, minimize friction, and enhance cooling performance (Van Rensselar, 2019; Parenago et al., 2022). In developing lubricants for EVs, special attention should be paid to thermal conductivity, material compatibility, copper corrosion, electrical resistivity, aeration, and wear (McCoy, 2021).

Multiple conventional transmission oils have been used for EV lubrication (Taylor, 2021). Test results showed that conventional automatic transmission fluids can maintain good electrical compatibility in electrified drivelines, and the higher the content of antioxidant additives is, the lower the variations of electrical conductivity with the oxidation (Rodríguez et al., 2022).

However, due to the working environment differences between EVs and ICEs, new lubricants suitable for EVs are still needed to satisfy the special requirements of the EVs. Besides the fluidic performance, both the electrical and thermal properties of lubricants should be well controlled (Chen Y. et al., 2020).

The electrical properties of a lubricant includes electrical conductivity, dielectric constant (permittivity), and dielectric strength, which are dependent on both base oils and lubricant additive package (Gahagan, 2017). A too low electrical conductivity of the lubricant can lead to accumulation of electric charges and sparking; on the contrary, current leakage can arise short circuits when the conductivity is too high (Parenago et al., 2022). Tang et al. (2013) pointed out that transmission lubricant need to have a relatively low electrical conductivity and found a hybrid electric transmission fluid consisting of a dispersant/detergent additive system, which shows low electrical conductivities and excellent anti-oxidation durability. Gahagan (2017) developed and tested an electric dual-clutch transmission fluid that had a low electrical conductivity and dielectric constant along with a good compatibility with typical electrical insulating materials and enhanced protection against copper corrosion. Nano particles have been used to mitigate harmful electrical current discharges by enhancing lubricant insulation or conductivity (Ahmed Abdalglil Mustafa et al., 2022).

High thermal conductivity is essential for driveline fluids in electrified powertrains, which helps take heat away from metal wings, cools the motor, and allows more current to pass through the motor to increase the torque output (McCoy, 2021). Rivera et al. (2022) tested the cooling performance of three automatic transmission fluids, indicated that both the base oil molecular structure and antioxidant property have a great influence on thermal conductivity. Beyer et al. (2019) emphasized the importance of the new lubricant requirements for electrical properties, copper corrosivity, heat transfer ability, and material compatibility, when the lubricant is in contact with electric motors. A recent review summarized and presented, in tabular forms, of the tribological performances of common electrically and thermally conductive lubricants (Bustami et al., 2023).

The efficiency requirement of EVs demands a low viscosity to reduce churning and pumping losses (Tung et al., 2020). Lubricants with low viscosity also have high heat transfer property. However, a low viscosity may also result in potential problems with hardware protection, low-temperature sealing, and volatility (Newcomb, 2023). To address these issues, additives with improved chemistry are needed to encounter wear and fatigue, and redesign of seals may be necessary to ensure proper functionality at low temperatures (Tokozakura et al., 2022).

6.2 Failures of EVs lubrication

Optimal lubrication systems for EVs should be designed to resist potential failure of both electromechanical and electrical components (Parenago et al., 2022). In EVs, the induced shaft voltages and currents can lead to premature failures in components like bearings, seals, pads, and gears, and they can also result in electromagnetic interference and radio frequency interference that destabilize the motor’s operation (He et al., 2020). Approximately 40%–60% of all early motor failures are bearing related (Walther and Holub, 2014). Besides, the highly fluctuating charged environment in EVs can cause electrical breakdown of lubricants in improper lubrication systems (Chen Y. et al., 2020). These lubrication failures of bearings and the electrically induced bearing damage (EIBD) are the main failure modes discussed in this paper.

The primary failure mechanisms of electrical breakdown of lubricants are degradation, microbubble formation, and electrowetting (Chen Y. et al., 2020; He et al., 2020). The degradation of a lubricant occurs due to the impact of discharge currents, leading to a decrease in dielectric strength and a change in the chemical composition (Romanenko et al., 2016). The voltage across the bearing induces an electric discharge current, which imbues chemical decomposition of the components of the grease, including additives and thickeners, and generates particles with reduced dielectric strengths (Romanenko et al., 2016). The high temperature during bearing operation may further induce oxidation of the base oil and thickener, which increases the amount of acidic species and high-viscosity products in lubricants (Yu and Yang, 2011). Evaporation of volatile oxidation products at a high temperature also causes the loss of base oil (Komatsuzakl et al., 2000). Degradation alters the lubricant components, causing a reduced bearing load-carrying capacity. The ineffective lubricant film formed by degraded lubricants results in contact fatigue wear on bearing rolling surfaces, and finally, a shorter bearing life (Yu and Yang, 2011). Experimental results showed the generation of microbubbles in charged lubricant films (Luo et al., 2006; Xie et al., 2008; Xie et al., 2009; Xie et al., 2010). The main reason for microbubbles formation was attributed to the local overheating due to electro-thermal effect (Xie et al., 2008). The dielectrophoretic force, the pressure difference force due to the residual pressure near the contact region, and viscous drag force are the dominant forces responsible for the bubble motion (Xie et al., 2009). The collapse of bubbles in a higher-pressure region could cause noise, vibration, and damage to bearing systems (Dowson and Taylor, 1979). In addition, electric field emission at the interface of the microbubbles and the liquid could initiate electrical breakdown, which may also cause failure in lubricants (Qian et al., 2005). Electrowetting is the phenomenon that the contact angle of partially wetting liquid droplets on surfaces could be altered by the applied voltage (Mugele and Baret, 2005). In lubricants, electrowetting-induced interfacial tension could change the fluidic behavior of the lubricants (McHale et al., 2019), potentially leading to lubricant spread and breakdown when subjected to high electrostatic stress (Mugele and Baret, 2005).

The EIBD stems from a dissymmetrical effect when voltage differences are created between the shaft and the bearing housing, and electric current breaks through the lubrication system (Ahmed Abdalglil Mustafa et al., 2022). The passage of current induces localized surface heating (Prashad, 2001b), which may reach temperatures high enough to cause some local damage. Under severe operating conditions, such as high speeds, torques, and temperatures, electric currents can further exacerbate the situation and reduce bearings service lives by triggering more severe adhesive, abrasive, and oxidative wear (Farfan-Cabrera et al., 2023). Although bearings are designed to operate in the hydrodynamic regime, there are asperity contacts. Electric charges can be accumulated on the surfaces up to the threshold limit at which discharge leaks at the asperity contacts, then the current tends to flow through the asperity contacts along paths of least resistance (Prashad, 1988). Bearing currents mainly depend on the magnitude of the shaft voltage and bearing impedance (Prashad, 1987). Tribo-pairs under electric fields can act as capacitors, the voltage between these tribo-pairs would rise until it reaches the dielectric breakdown voltage of the lubricant film, resulting in a significant current surge (Chen Y. et al., 2020). In specific, dielectric breakdown can be initiated by thermally generated electrons within a high electric field that acquire enough kinetic energy to ionize molecules within the fluid (Gahagan, 2017). These current discharges usually happen through the bearing balls and raceways, causing significant energy dispersion and various degrees of EIBD within a short time (Ahmed Abdalglil Mustafa et al., 2022). In EVs’ electric motors, when bearing lubrication-film breakdown happens, a leakage current path can be established through both the motor bearings and load bearings (Hadden et al., 2016).

Electrical breakdown would also cause arcing across asperity contacts, which may result in surface damage in bearings (Spikes, 2020). Arcing occurs when current-conducting paths are disrupted due to asperities separating because of increased film thickness, vibration effects, or a combination of these factors, or by the presence of a high-resistivity lubricant (Prashad, 1987). As a result, surfaces damages will be caused by the arc welding and high temperature effect (Prashad, 1988).

Typical morphological damages to bearing component surfaces include: i) pitting, ii) frosting, iii) fluting, iv) spark tracks, v) welding, and vi) brinelling (Costello, 1993; Boyanton and Hodges, 2002; Silva and Cardoso, 2005). Pitting of bearings in EVs, which is due to the electric discharge between surfaces caused by the concentration of current at spots as small as several micrometers in diameter (Sunahara et al., 2011), could result in noise and vibration in motors. Micro arcing or flash causes local metal melting and produce pitting, leading to washboard-like marks on bearing surfaces (Suzumura, 2016). Rough surface asperity contacts could further accelerate pitting failure in lubrication systems (Pu et al., 2016).

Frosting, also known as micro-spalling, originates from either adhesive or abrasive wear to the material surface. This kind of wear is induced by insufficient lubrication related to electric discharges, which is generally imperceptible to the naked eye and is microscopically characterized as small “craters” (Plazenet et al., 2018). Pits of frosting are smaller than those of pitting, but they may merge with damage progression, and then, surfaces become stain-like, similarly to a shot-peened or sand-blasted surface, looking like etched or frosted glass (McCloskey, 1995).

Fluting, or washboarding, is seen as a pattern of multiple gray lines across bearing raceways, the washboard appearance is a secondary damage, as it becomes visible over time (Oliver et al., 2017). Bearing current flow intrigued by capacitive coupling is normally the root causes of bearing fluting (Boyanton and Hodges, 2002). Ball vibration of bearings is believed to enhance the scratch marks of the raceway, which also induces fluting (Liu, 2014).

The appearance of spark tracks is that of scratches in the babbitted surface, which looks very irregular and is often askew to the direction of rotation (Costello, 1991). Under magnification, the bottoms of the tracks are sometimes melted, and the corners are sharp (Costello, 1993). The formation of spark tracks has a close relation to shaft voltages and bearing current, and the appearance of craters are due to spark erosion on the track surfaces (Prashad, 2001a). Heavy stray welding current from momentarily contact between the rotor and the stator is a main cause of welding, which appears as spot-welded marks (Costello, 1993). A before-and-after vibration analysis revealed the change occurred in a bearing that had suffered the welding current damage (Hisey, 2014).

Brinelling is related to bearing static vibration, which may be a consequence of the operation of damaged surfaces. Bearing electric current is another cause of brinelling (Silva and Cardoso, 2005). True brinelling happens when loads are over the elastic limit given to the bearing materials. Indentations in the raceways are called Brinell marks and can lead to vibration noise. False brinelling is similar to true brinelling but has no macroscopic plastic deformation (Liu and Zhang, 2020).

6.3 Lubricants behaviors in EVs

Fundamental research on the intricate interactions between lubricants and electric/magnetic fields in EVs is essential to address lubrication system failures effectively. The presence of an electric field generates electrostatic interaction in lubrication systems, which may affect the frictional behavior at tribo-pairs (Xie et al., 2015). EDL and ER structures may form under electrostatic forces. The stern layer of EDL can be further divided into “inner” and “outer Helmholtz” planes. In the inner plane, a layer of water dipoles may align with the electric field and adhere to the electrode surface. Hydrated ions of opposite charges are attracted to the electrode surface by electrostatic forces in the outer plane (Spikes, 2020). For ER structures, the electrostatic forces between particles are the main reason for the polarized chain structures (Davis and Ginder, 1995). Shear thickening controlled by the electric field and electrostatic particle-interaction-induced interparticle friction forces are considered to play an important role in the origin of lateral shear resistance of ER fluids (Tian et al., 2011). If lubricants containing magnetic particles are used, the electric and magnetic fields in EVs may also induce magnetic interactions and result in the MR effects or ferrofluid properties. The MR performance is due to the magnetic dipole induced on each particle in the fluid by the application of an external magnetic field, as well as the interaction between these dipoles and the magnetic field itself (Dassisti and Brunetti, 2022). Under a magnetic field, the particles in ferrofluids should experience a magnetic volumetric force, both the translational and rotational motions of these particles are then transferred to the corresponding ferrofluid by the shear mechanism, spin diffusion, and rotational friction (Dalvi et al., 2022). Theories mentioned in the previous sections can offer valuable insights into the study of these complex interactions in the lubrication systems of EVs.

Besides electrostatic and magnetic interactions, the electric field in EVs can cause structural changes of lubricant molecules or transferred-film formations (He et al., 2020). Research showed the influence of such events, triggered by applied electric field, on wear and friction performance (Lavielle, 1994; Csapo et al., 1996). Another rising concern is the influence of the external electric field on chemical reactions and physical absorption occurred at material surfaces, which can lead to changes in friction and wear performances of the system (Chen Y. et al., 2020). For chemical reactions, the applied electrode potential on tribo-pairs could promote redox reactions at dubbing surfaces, involving either oxygen in air or lubricant additives. The physical absorption of ionic and polarizable species can be controlled by changing the surface charge distribution of metal and oxide-covered metal surfaces (Spikes, 2020).

7 Generalized MEMT-field Reynolds equation

The lubrication issues discussed in previous sections largely fall into one or more types of EDL, ER fluids, MR fluids, ferrofluids, and conventional lubrications. Table 1 summarized the Reynolds equations of these cases. Compared to the original expressions in references, the same boundary conditions are used in the equations in this table. For EDL and ferrofluid conditions, the electric and magnetic forces were described as body forces in the Reynolds equation. For ER and MR lubrications, a non-Newtonian model was used to represent the rheology changes caused by particle polarizations. It should be noted that Table 1 only summarized one model for each situation, and other numerical models and modified Reynolds equations may also be used to analyze these lubrication problems. Extending the view of lubrication modeling to a wider scope of fluid-mechanics studies, the effects of electromagnetic fields can be analyzed through coupling the Maxwell and the Navier-Stocks equations via the Lorentz force (Duan, 2012; Thompson et al., 2014).

TABLE 1

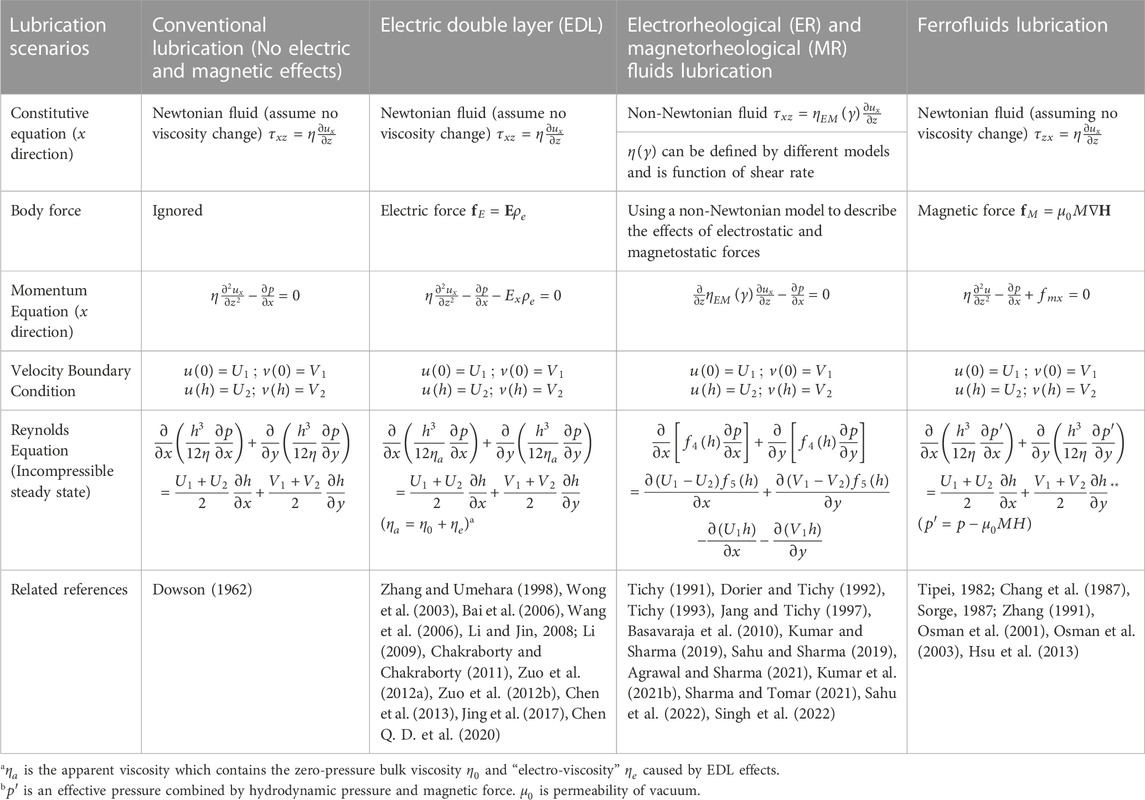
TABLE 1. Modified Reynolds equations of different lubrication scenarios (steady state; incompressible).

Based on previous discussions, a generalized MEMT-field Reynolds equation can be derived, following the work by Dowson (1962), for the lubrication problems in all these major fields. Here, the gravitational and inertia forces are ignored. The effects of electromagnetic fields are coupled through the Lorentz forces on charged particles, and through the fluid density and non-Newtonian viscosity.

7.1 Force equilibrium

Figure 12 shows all the forces involved in a lubrication system subjected to electric and magnetic fields. In a fluid element marked with the cuboidal volume, the electric and magnetic fields should induce volumetric Lorentz (electromagnetic) force ${\mathbf{F}}_L$. Other forces are due to pressure and shear stresses. The force balance in the x and y directions is:

$\begin{array}{c}pdydz-\left(p+\frac{\partial p}{\partial x}dx\right)dydz+\left({\tau }_{zx}+\frac{\partial {\tau }_{zx}}{\partial z}dz\right)dydx-{\tau }_{zx}dydx+F_{Lx}dxdydz=0\\ pdxdz-\left(p+\frac{\partial p}{\partial x}dy\right)dxdz+\left({\tau }_{zy}+\frac{\partial {\tau }_{zy}}{\partial z}dz\right)dydx-{\tau }_{zy}dydx+F_{Ly}dxdyd=0\end{array}(72)$

which can be summarized as:

$\begin{array}{c}-\frac{\partial p}{\partial x}+\frac{\partial {\tau }_{zx}}{\partial z}+F_{Lx}=0\\ -\frac{\partial p}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+F_{Ly}=0\end{array}(73)$

where $p$ is pressure, $\tau$ is shear stress. For given electromagnetic fields, the Lorentz force components are:

$\begin{array}{c}{F}_{Lx}={\rho }_e\left[E_x+{\left(\overline{\mathbf{V}}\times \mathbf{B}\right)}_x\right]\\ F_{Ly}={\rho }_e\left[E_y+{\left(\overline{\mathbf{V}}\times \mathbf{B}\right)}_y\right]\end{array}(74)$

where the Lorentz forces are elementary average volumetric forces related to average volumetric charge density ${\rho }_e$ and average particle velocity $\overline{\mathbf{V}}$. Separate the Lorentz forces into the electric and magnetic forces. The expressions of electric force ${\mathbf{f}}_E$ in the x and y directions are:

$\begin{array}{c}{f}_{Ex}={\rho }_e{E}_x\\ f_{Ey}={\rho }_e{E}_y\end{array}(75)$

FIGURE 12

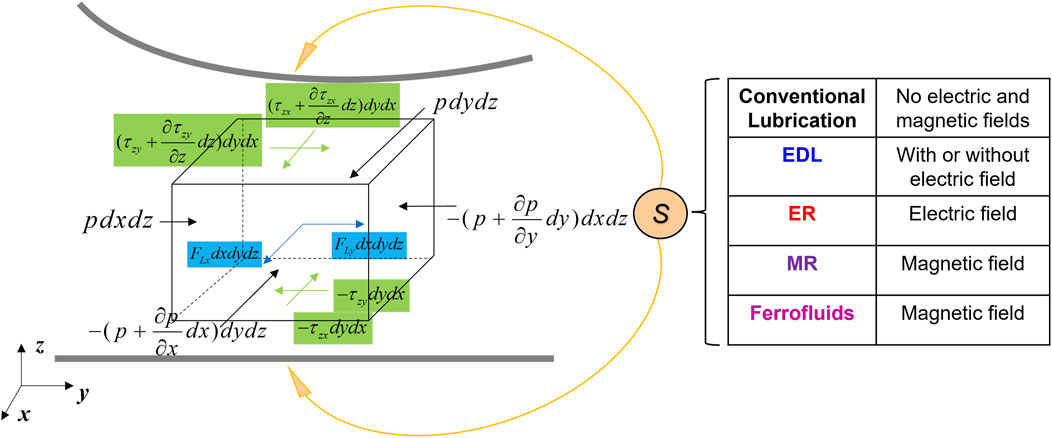
FIGURE 12. Forces on fluid element under electric and magnetic fields. Here, S means the source, which can be an electric field, or a magnetic field, or an electromagnetic field or no external field.

Magnetic force ${\mathbf{f}}_M$ in the x and y directions are:

$\begin{array}{c}{f}_{Mx}={{\rho }_e\left(\overline{\mathbf{V}}\times \mathbf{B}\right)}_x\\ f_{My}={{\rho }_e\left(\overline{\mathbf{V}}\times \mathbf{B}\right)}_y\end{array}(76)$

Substituting electric force ${\mathbf{f}}_E$ and magnetic force ${\mathbf{f}}_M$ into Eq. 73 results in:

$\begin{array}{c}-\frac{\partial p}{\partial x}+\frac{\partial {\tau }_{zx}}{\partial z}+f_{Ex}+f_{Mx}=0\\ -\frac{\partial p}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+f_{Ey}+f_{My}=0\end{array}(77)$

7.2 Constitutive equation

Generally, a non-Newtonian viscosity model is expected due to the effects of electric, magnetic, and thermal fields. Here, the viscosity behavior in the electromagnetic field is summarized as ${\eta }_{EM}\left(\gamma ,T\right)$, which is determined by temperature $T$, shear rate $\gamma$, and subjected to pressure p, electric field intensity $E$, and magnetic field intensity $H$. The shear-stress and shear-rate relationship can be expressed as:

$\begin{array}{c}{\tau }_{zx}={\eta }_{EM}\left(\gamma ,T\right)\frac{\partial u}{\partial z}\\ {\tau }_{zy}={\eta }_{EM}\left(\gamma ,T\right)\frac{\partial v}{\partial z}\end{array}(78)$

where $\gamma$ is shear rate, u and v are the velocities in the x and y directions. Then, substituting Eq. 78 into Eq. 77, the equilibrium equation can be re-written as:

$\begin{array}{c}-\frac{\partial p}{\partial x}+\frac{\partial }{\partial z}\left({\eta }_{EM}\left(\gamma ,T\right)\frac{\partial u}{\partial z}\right)+f_{Ex}+f_{Mx}=0\\ -\frac{\partial p}{\partial y}+\frac{\partial }{\partial z}\left({\eta }_{EM}\left(\gamma ,T\right)\frac{\partial v}{\partial z}\right)+f_{Ey}+f_{My}=0\end{array}(79)$

7.3 Integration to the generalized MEMT-field Reynolds equation

The velocity boundary conditions used here are:

$\begin{array}{c}u\left(0\right)=U_1;v\left(0\right)=V_1;w\left(0\right)=W_1\\ u\left(h\right)=U_2;v\left(h\right)=V_2;w\left(h\right)=W_2\end{array}(80)$

Integrating Eq. 79 with respect to z and dividing the result by ${\eta }_{EM}\left(\gamma ,T\right)$ lead to the following, in which pressure remains constant across the lubricant film:

$\begin{array}{c}\frac{\partial u}{\partial z}=\frac{z}{{\eta }_{EM}\left(\gamma ,T\right)}\frac{\partial p}{\partial x}+f_1\left(z\right)+f_3\left(z\right)+\frac{A_1}{{\eta }_{EM}\left(\gamma ,T\right)}\\ \frac{\partial v}{\partial z}=\frac{z}{{\eta }_{EM}\left(\gamma ,T\right)}\frac{\partial p}{\partial y}+f_2\left(z\right)+f_4\left(z\right)+\frac{A_2}{{\eta }_{EM}\left(\gamma ,T\right)}\end{array}(81)$

where $f_1\sim f_4$ are each a function of z, related to the electric and magnetic forces, represented by:

$\begin{array}{c}{f}_1\left(z\right)=-\frac{{\int }_0^z{f}_{Ex}dz}{{\eta }_{EM}\left(\gamma ,T\right)};f_2\left(z\right)=-\frac{{\int }_0^z{f}_{Ey}dz}{{\eta }_{EM}\left(\gamma ,T\right)}\\ f_3\left(z\right)=-\frac{{\int }_0^z{f}_{Mx}dz}{{\eta }_{EM}\left(\gamma ,T\right)};f_4\left(z\right)=-\frac{{\int }_0^z{f}_{My}dz}{{\eta }_{EM}\left(\gamma ,T\right)}\end{array}(82)$

In the integration process, if velocity is involved in the electric and magnetic forces calculation, the velocity profiles from the previous iteration can be used. Therefore, f₁ ∼ f₄ from Eq. 82 have no current-step velocity components. Integrating Eq. 81 with respect to z finds the velocity components of the current-step as follows,

$\begin{array}{c}u=\frac{\partial p}{\partial x}{f}_5\left(z\right)+f_6\left(z\right)+f_8\left(z\right)+A_1{f}_{10}\left(z\right)+B_1\\ v=\frac{\partial p}{\partial y}{f}_5\left(z\right)+f_7\left(z\right)+f_9\left(z\right)+A_2{f}_{10}\left(z\right)+B_2\end{array}(83)$

where $A_1$, $A_2$, $B_1$, $B_2$ are integration constants, and $f_5\sim f_{10}$ are all functions of z, represented by:

$\begin{array}{c}{f}_5\left(z\right)={\int }_0^z\frac{z}{{\eta }_{EM}\left(\gamma ,T\right)}dz;f_6\left(z\right)={\int }_0^z{f}_1\left(z\right)dz\\ f_7\left(z\right)={\int }_0^z{f}_2\left(z\right)dz;f_8\left(z\right)={\int }_0^z{f}_3\left(z\right)dz\\ f_9\left(z\right)={\int }_0^z{f}_4\left(z\right)dz;f_{10}\left(z\right)={\int }_0^z\frac{1}{{\eta }_{EM}\left(\gamma ,T\right)}dz\end{array}(84)$

Substituting the boundary conditions for velocities, the integration constants can be solved (Eq. 85):

$\begin{array}{c}{A}_1=\frac{U_2-U_1-f_5\left(h\right)\frac{\partial p}{\partial x}-f_6\left(h\right)-f_8\left(h\right)}{f_{10}\left(h\right)};B_1=U_1\\ A_2=\frac{V_2-V_1-f_5\left(h\right)\frac{\partial p}{\partial y}-f_7\left(h\right)-f_9\left(h\right)}{f_{10}\left(h\right)};B_2=V_1\end{array}(85)$

As a result, the velocities can be represented as:

$u=f_{11}\left(z\right)\frac{\partial p}{\partial x}+\frac{U_2-U_1-f_6\left(h\right)-f_8\left(h\right)}{f_{10}\left(h\right)}{f}_{10}\left(z\right)+f_6\left(z\right)+f_8\left(z\right)+U_1(86)$

$v=f_{11}\left(z\right)\frac{\partial p}{\partial y}+\frac{V_2-V_1-f_7\left(h\right)-f_9\left(h\right)}{f_{10}\left(h\right)}{f}_{10}\left(z\right)+f_7\left(z\right)+f_9\left(z\right)+V_1(87)$

where

$f_{11}\left(z\right)=f_5\left(z\right)-\frac{f_5\left(h\right)}{f_{10}\left(h\right)}{f}_{10}\left(z\right)(88)$

Note that the coefficients in the right-hand side terms in Eqs. 86, 87 contain the velocity components from the previous iteration step if these terms are related to velocity.

The mass continuity equation is:

$\frac{\partial \rho \left(p,T,E,H\right)}{\partial t}+\frac{\partial \left[\rho \left(p,T,E,H\right)u\right]}{\partial x}+\frac{\partial \left[\rho \left(p,T,E,H\right)v\right]}{\partial y}+\frac{\partial \left[\rho \left(p,T,E,H\right)w\right]}{\partial z}=0(89)$

where density $\rho$ is a function of pressure $p$, temperature $T$, electric field intensity $E$, and magnetic field intensity $H$. Integrating this mass continuity equation with respect to z, between the limits of the gap, yields:

${\int }_0^h\frac{\partial \rho }{\partial t}dz+{\int }_0^h\frac{\partial \left(\rho u\right)}{\partial x}dz+{\int }_0^h\frac{\partial \left(\rho v\right)}{\partial y}dz+{\left(\rho w\right)}_0^h=0(90)$

Substitute velocity gradients and velocities expressions into Eq. 90 and calculate the integrations result in the following generalized MEMT-field Reynolds equation. Detailed derivation is in the Supplementary material.

$\begin{array}{c}\frac{\partial }{\partial x}\left(\left[F_2+G_1\right]\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\left[F_2+G_1\right]\frac{\partial p}{\partial y}\right)=h\left[\frac{\partial {\left(\rho U\right)}_2}{\partial x}+\frac{\partial {\left(\rho V\right)}_2}{\partial y}\right]\\ -\frac{\partial }{\partial x}\left(\frac{\left(U_2-U_1\right)\left(F_3+G_2\right)}{F_0}+U_1{G}_3\right)-\frac{\partial }{\partial y}\left(\frac{\left(V_2-V_1\right)\left(F_3+G_2\right)}{F_0}+V_1{G}_3\right)\\ -\frac{\partial }{\partial x}\left(F_4+G_4\right)-\frac{\partial }{\partial y}\left(F_6+G_6\right)-\frac{\partial }{\partial x}\left(F_5+G_5\right)-\frac{\partial }{\partial y}\left(F_7+G_7\right)\\ +{\int }_0^h\frac{\partial \rho }{\partial t}dz+{\left(\rho W\right)}_2-{\left(\rho W\right)}_1\end{array}(91)$

where the $F$ and $G$ functions are:

$\begin{array}{c}{F}_0=f_{10}\left(h\right);F_1=f_5\left(h\right)\\ F_2={\int }_0^h\rho z\left(\frac{z}{{\eta }_{EM}\left(\gamma ,T\right)}-\frac{f_5\left(h\right)}{{\eta }_{EM}\left(\gamma ,T\right)f_{10}\left(h\right)}\right)dz;F_3={\int }_0^h\frac{z\rho }{{\eta }_{EM}\left(\gamma ,T\right)}dz\\ F_4={\int }_0^{h}z\rho f_1\left(z\right)dz-\frac{f_6\left(h\right)F_3}{F_0};F_5={\int }_0^{h}z\rho f_3\left(z\right)dz-\frac{f_8\left(h\right)F_3}{F_0}\\ F_6={\int }_0^{h}z\rho f_2\left(z\right)dz-\frac{f_7\left(h\right)F_3}{F_0};F_7={\int }_0^{h}z\rho f_4\left(z\right)dz-\frac{f_9\left(h\right)F_3}{F_0}\\ \begin{array}{c}{G}_1={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_{11}\left(z\right)dz;G_2={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_{10}\left(z\right)dz;G_3={\int }_0^{h}z\frac{\partial \rho }{\partial z}dz\\ G_4={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_6\left(z\right)dz-\frac{f_6\left(h\right)G_2}{F_0};G_5={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_8\left(z\right)dz-\frac{f_8\left(h\right)G_2}{F_0}\\ G_6={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_7\left(z\right)dz-\frac{f_7\left(h\right)G_2}{F_0};G_7={\int }_0^{h}z\frac{\partial \rho }{\partial z}{f}_9\left(z\right)dz-\frac{f_9\left(h\right)G_2}{F_0}\end{array}\end{array}(92)$

The generalized MEMT-field Reynolds equation, Eq. 91, resembles format of the classic generalized Reynolds equation by Dowson (1962) because the two terms on the left-hand side describe the flows due to pressure gradient, the first three terms on the right-hand side are the “shear” flow terms, and the last three terms are the “squeeze” flow terms, although the fluid viscosity and density have been augmented to include the effect of electromagnetic fields. However, the terms containing $F_4$, $G_4$, $F_6$, and $G_6$ represent the effect of the electric forces; terms containing $F_5$, $G_5$, $F_7$ and $G_7$ represent the effect of the magnetic forces.

In most engineering applications, the boundary surface velocity in the x and y directions are constant, or not stretchable. For a liquid lubricant, the density variation across the film can be neglected, i.e., $\partial \rho /\partial z=0$, and thus, all $G$ functions are zero. In this way, the generalized MEMT-field Reynolds equation can be reduced to the following.

$\begin{array}{c}\frac{\partial }{\partial x}\left(F_2\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(F_2\frac{\partial p}{\partial y}\right)=U_2\frac{\partial \left(\rho h\right)}{\partial x}+V_2\frac{\partial \left(\rho h\right)}{\partial y}\\ -\left(U_2-U_1\right)\frac{\partial }{\partial x}\left(\frac{F_3}{F_0}\right)-\left(V_2-V_1\right)\frac{\partial }{\partial y}\left(\frac{F_3}{F_0}\right)\\ -\frac{\partial }{\partial x}{F}_4-\frac{\partial }{\partial y}{F}_6-\frac{\partial }{\partial x}{F}_5-\frac{\partial }{\partial y}{F}_7+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(93)$

The generalized MEMT-field Reynolds equation, Eq. 91 or Eq. 93, fully couples the effects of different fields, such as mechanical flow, electric, magnetic, and thermal fields, in a lubrication system under the support of the Maxwell equations for the Lorentz forces and the energy equation for temperature, solvable with a numerical iteration method. The field-related f functions can be defined following the approach of the mechanical-electrical-magnetic-chemical-thermal (MEMCT) theory (Zhang et al., 2018; Wang and Zhu, 2019) and quantified with experiments on fluid properties in electromagnetic fields.

7.4 Discussion

The generalized MEMT-field Reynolds equation (Eq. 91) can be degenerated into the classic Reynolds equation and each specific scenario discussed in Sections 2–5 under specific conditions.

7.4.1 Conventional lubrication

In a conventional lubrication system without electric and magnetic forces, functions related to electric and magnetic fields, $f_1\sim f_4$, $f_6\sim f_9$, $F_4\sim F_7$ and $G_4\sim G_7$ are zero. In this way, Eq. 91 can be written as:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\left[F_2+G_1\right]\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\left[F_2+G_1\right]\frac{\partial p}{\partial y}\right)=h\left[\frac{\partial {\left(\rho U\right)}_2}{\partial x}+\frac{\partial {\left(\rho V\right)}_2}{\partial y}\right]\\ -\frac{\partial }{\partial x}\left[\frac{\left(U_2-U_1\right)\left(F_3+G_2\right)}{F_0}+U_1{G}_3\right]-\frac{\partial }{\partial y}\left[\frac{\left(V_2-V_1\right)\left(F_3+G_2\right)}{F_0}+V_1{G}_3\right]\\ +{\int }_0^h\frac{\partial \rho }{\partial t}dz+{\left(\rho W\right)}_2-{\left(\rho W\right)}_1\end{array}(94)$

This is the same as the generalized Reynolds equation for fluid-film lubrication derived by Dowson (1962). Further, if viscosity and density variations across the lubricant film are ignored, the remaining $G$ functions are also zero, and the other $f$ and $F$ functions can be simplified to:

$\begin{array}{c}{f}_5\left(z\right)=\frac{z^2}{2\eta },f_{10}\left(z\right)=\frac{z}{\eta },f_{11}\left(x\right)=\frac{z^2-hz}{2\eta }\\ F_0=f_{10}\left(h\right)=\frac{h}{\eta },F_1=f_5\left(h\right)=\frac{h^2}{2\eta },F_2=\frac{\rho h^3}{12\eta },F_3=\frac{\rho h^2}{2\eta }\end{array}(95)$

Besides, if the boundary velocities are constants, generalized Reynolds equation Eq. 94 can be reduced to:

$\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial y}\right)=\left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}+\frac{\partial \left(\rho h\right)}{\partial t}(96)$

Eq. 96 a popular form of the Reynolds equation for fluid lubrication, widely used for solving various types of isothermal lubrication problems (Wang and Zhu, 2019).

7.4.2 EDL in lubrication

When lubricants form the EDL structures under an electric field and there is no magnetic field, functions related to magnetic field, $f_3$, $f_4$, $f_8$, $f_9$, $F_5$, $F_7$, $G_5$ and $G_7$ are zero. Assume there are no viscosity and density changes across the film, $f$ and $F$ functions can be simplified to the same expression as Eq. 95. If boundary velocities are constants, the generalized MEMT-field Reynolds equation reduces to:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial y}\right)=\left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}\\ -\frac{\partial F_4}{\partial x}-\frac{\partial F_6}{\partial y}+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(97)$

Choose the same method as stated by Zhang and Umehara (1998) to calculate the functions related to electric forces, the electric forces in the x and y directions are:

$\begin{array}{c}{f}_{Ex}={\rho }_e{E}_x=-\frac{E_x\epsilon }{\eta 4\pi }\frac{{\partial }^2\psi }{\partial z^2}\\ f_{Ey}={\rho }_e{E}_y=-\frac{E_y\epsilon }{\eta 4\pi }\frac{{\partial }^2\psi }{\partial z^2}\end{array}(98)$

As a result, $f_1$, $f_2$, $f_6$, $f_7$, $F_4$, $F_6$ become:

$\begin{array}{c}{f}_1\left(z\right)=\frac{E_x\epsilon }{\eta 4\pi }\frac{\partial \psi }{\partial z};f_2\left(z\right)=\frac{E_y\epsilon }{\eta 4\pi }\frac{\partial \psi }{\partial z}\\ f_6\left(z\right)=\frac{E_x\epsilon }{4\pi \eta }\left[\psi \left(z\right)-\psi \left(0\right)\right];f_7\left(z\right)=\frac{E_y\epsilon }{4\pi \eta }\left[\psi \left(z\right)-\psi \left(0\right)\right]\\ F_4=\frac{E_x\rho \epsilon \zeta }{4\pi \eta }\left[h-\frac{2}{\chi }\left(1-e^{\left(-\chi h/2\right)}\right)\right];F_6=\frac{E_y\rho \epsilon \zeta }{4\pi \eta }\left[h-\frac{2}{\chi }\left(1-e^{\left(-\chi h/2\right)}\right)\right]\end{array}(99)$

Equation 97 is then:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial y}\right)=\\ \left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}-\frac{\partial }{\partial x}\left\{\frac{\rho E_x\epsilon \zeta }{4\pi \eta }\left[h-\frac{2}{\chi }\left(1-e^{-\chi h/2}\right)\right]\right\}\\ -\frac{\partial }{\partial y}\left\{\frac{\rho E_y\epsilon \zeta }{4\pi \eta }\left[h-\frac{2}{\chi }\left(1-e^{-\chi h/2}\right)\right]\right\}+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(100)$

In references (Zhang and Umehara, 1998), an apparent viscosity ${\eta }_a$ is usually used to combine the effect of the electric forces with viscosity as:

${\eta }_a=\eta +{\eta }_e(101)$

where $\eta$ is the viscosity of bulk fluid and ${\eta }_e$ is usually called the “electro-viscosity” caused by the EDL effects. Following the details given in Section 2.3 and rearranging terms, Eq. 100 can be summarized as:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12{\eta }_a}\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12{\eta }_a}\frac{\partial p}{\partial y}\right)\\ =\left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(102)$

If the system is in the steady state and the fluid incompressible, this equation is the same as the one derived by Zhang and Umehara (1998).

7.4.3 ER and MR fluids in lubrication

In the usual ER or MR lubrication modeling, the electric forces or magnetic forces are not included; therefore, $f_1\sim f_4$, $f_6\sim f_9$, $F_4\sim F_7$ and $G_4\sim G_7$ are zero. Assuming that there is no density change across the film, and a non-Newtonian viscosity model determined by the electric, magnetic, and temperature field is used, Eq. 91 is reduced to:

$\begin{array}{c}\frac{\partial }{\partial x}\left(F_2\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(F_2\frac{\partial p}{\partial y}\right)=\frac{\partial \left(U_2\rho h\right)}{\partial x}+\frac{\partial \left(V_2\rho h\right)}{\partial y}\\ -\frac{\partial }{\partial x}\left[\frac{\left(U_2-U_1\right)F_3}{F_0}\right]-\frac{\partial }{\partial y}\left[\frac{\left(V_2-V_1\right)F_3}{F_0}\right]+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(103)$

Compare to the modified Reynolds equation for ER or MR fluids, Eq. 52,

$\begin{array}{c}{F}_2=-\rho f_4^{\prime }\left(z\right)\\ \frac{\partial \left(U_2\rho h\right)}{\partial x}-\frac{\partial }{\partial x}\left[\frac{\left(U_2-U_1\right)F_3}{F_0}\right]=-\left(\frac{\partial \rho \left(U_1-U_2\right)}{\partial x}{f}_5^{\prime }\left(h\right)-\frac{\partial \left(U_1\rho h\right)}{\partial x}\right)\\ \frac{\partial \left(V_2\rho h\right)}{\partial y}-\frac{\partial }{\partial y}\left[\frac{\left(V_2-V_1\right)F_3}{F_0}\right]=-\left(\frac{\partial \rho \left(V_1-V_2\right)}{\partial y}{f}_5^{\prime }\left(h\right)-\frac{\partial \left(V_1\rho h\right)}{\partial y}\right)\end{array}(104)$

Substitute Eq. 104 into Eq. 103, and for the steady state lubrication with an incompressible fluid, the above becomes the same expression as Eq. 52, the one given by Dorier and Tichy (1992), which uses a Bingham-like viscous fluid.

7.4.4 Ferrofluids in lubrication

When considering the ferrofluid effect alone, only the magnetic forces are applied to particles, no electric forces are expected, and thus, $f_1$, $f_2$, $f_6$, $f_7$, $F_4$, $F_6$, $G_4$ and $G_6$ are zero. Assuming that there are no viscosity and density changes across the film, $f$ and $F$ functions can be simplified to the same expression as Eq. 95. If boundary velocities are constants, Eq. 91 reduces to:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\eta }\frac{\partial p}{\partial y}\right)=\left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}\\ -\frac{\partial F_5}{\partial x}-\frac{\partial F_7}{\partial y}+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(105)$

Using the Neuringer-Rosensweig model (Tipei, 1982) to process the magnetic force, when magnetization $M$ and magnetic field intensity $H$ are independent of temperature and film thickness direction. The magnetic force in the x and y directions are:

$\begin{array}{c}{f}_{Mx}={\mu }_{0}M\frac{\partial H}{\partial x}\\ f_{My}={\mu }_{0}M\frac{\partial H}{\partial y}\end{array}(106)$

In this way, $f_3$, $f_4$, $f_8$, $f_9$, $F_5$, and $F_7$ become:

$\begin{array}{c}{f}_3\left(z\right)=-\frac{{\mu }_{0}Mz}{\eta }\frac{\partial H}{\partial x};f_4\left(z\right)=-\frac{{\mu }_{0}Mz}{\eta }\frac{\partial H}{\partial y}\\ f_8\left(z\right)=-\frac{{\mu }_{0}M{z}^2}{2\eta }\frac{\partial H}{\partial x};f_9\left(z\right)=-\frac{{\mu }_{0}M{z}^2}{2\eta }\frac{\partial H}{\partial y}\\ F_5=-\frac{\rho h^3{\mu }_{0}M}{12\eta }\frac{\partial H}{\partial x};F_7=-\frac{\rho h^3{\mu }_{0}M}{12\eta }\frac{\partial H}{\partial y}\end{array}(107)$

Introducing the concept of generalized pressure, $p^{\prime }=p-{\mu }_{0}MH=p-p_M$, with $f_{Mx}=\partial p_M/\partial x;f_{My}=\partial p_M/\partial y,$ where $p_M$ is the effective pressure due to the magnetic forces, Eq. 105 can be written as:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12\eta }\frac{\partial p^{\prime }}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12\eta }\frac{\partial p^{\prime }}{\partial y}\right)\\ =\left(\frac{U_2+U_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial x}+\left(\frac{V_2+V_1}{2}\right)\frac{\partial \left(\rho h\right)}{\partial y}+\frac{\partial \left(\rho h\right)}{\partial t}\end{array}(108)$

In steady-state incompressible lubrication, Eq. 108 is the same as the equation derived by Osman et al. (2001), only the velocity expressions are different.

In magnetohydrodynamics lubrication, an electrically conducting fluid flows subjected to a magnetic field. The magnetic force exerted on the fluid may involve velocity. Instead of generalized pressure, a new function representing the effect of the magnetic force could be derived and added in the modified Reynolds equation (Hughes and Elco, 1962; Lin et al., 2009; Jadhav et al., 2019).

7.4.5 Generalized pressure term and a different form of the generalized MEMT-field Reynolds equation

The format of Eq. 108 suggests that an effective pressure could also be defined for the cases where the electric force also exists if this new effective pressure is independent of film thickness direction z. In this way, both electric and magnetic forces can be represented by similar effective pressure gradients as:

$\begin{array}{c}{f}_{Ex}=\frac{\partial p_E}{\partial x};f_{Ey}=\frac{\partial p_E}{\partial y}\\ f_{Mx}=\frac{\partial p_M}{\partial x};f_{My}=\frac{\partial p_M}{\partial y}\end{array}(109)$

where $p_E$ and $p_M$ are effective pressures due to electric and magnetic forces, independent of z along the film thickness direction. As a result, a generalized pressure $p^{\prime }$ can be structured as:

$p^{\prime }=p-p_E-p_M(110)$

Reasoning from Eq. 108, a different form of the generalized MEMT-field Reynolds equation with generalized pressure terms can be obtained:

$\begin{array}{c}\frac{\partial }{\partial x}\left(\left[F_2+G_1\right]\frac{\partial p^{\prime }}{\partial x}\right)+\frac{\partial }{\partial y}\left(\left[F_2+G_1\right]\frac{\partial p^{\prime }}{\partial y}\right)=U_2\frac{\partial \left(\rho h\right)}{\partial x}+V_2\frac{\partial \left(\rho h\right)}{\partial y}\\ -\left(U_2-U_1\right)\frac{\partial }{\partial x}\left(\frac{F_3+G_2}{F_0}\right)-U_1\frac{\partial G_3}{\partial x}-\left(V_2-V_1\right)\frac{\partial }{\partial y}\left(\frac{F_3+G_2}{F_0}\right)-V_1\frac{\partial G_3}{\partial y}\\ +{\int }_0^h\frac{\partial \rho }{\partial t}dz+\rho \frac{\partial h}{\partial t}\end{array}(111)$

where $p^{\prime }$ should possess the nature of the fluid pressure, independent of z along the film thickness direction. This equation resembles the classic generalized Reynolds equation (Dowson, 1962), revealing an analogy between certain variables pertaining to the mechanical and electromagnetic fields, similar to that in solid systems which crosses different fields (Zhang and Wang, 2022) and that in fluid mechanics (Kambe, 2014; Marner, 2019).

8 Summary and conclusion

This paper presents an overview of the studies of four lubrication areas subjected to electric and magnetic fields, which are those about electric double layer (EDL), electrorheological (ER) fluids, magnetorheological (MR) fluids, and ferrofluids, as well as lubrication issues in electric vehicles (EVs). It includes a discussion on the mechanisms and benefits of electric and magnetic fields in these scenarios, as well as typical lubricants used in each system, and highlights the analyses of the effects of electric and magnetic fields in the numerical research and experimental work in each area. This paper has also visited current EV requirements for lubricants properties and the common failures in EV lubrication. A generalized MEMT-field Reynolds equation is derived for all four scenarios mentioned above from the summary of the theories for each of the four areas. The results of this study can be concluded as follows.

1) The presence of electric and magnetic fields can change the rheological properties of lubricants, which usually increases the lubricant viscosity. As a result, the load-carrying capacity of the lubrication system can be enhanced.

2) In the EDL lubrication, the effect of the electric field is represented by an electric force. For ER and MR fluids, non-Newtonian empirical models are commonly used to describe the rheological changes due to the electric and magnetic fields. The magnetic forces exerted on magnetic particles are added to the ferrofluid lubrication to simulate the magnetic effects.

3) The electrical environment of EVs brings about new requirements for lubrication system design and lubricant development. The existence of shaft voltage and bearing current can induce many failures. Both experimental and numerical investigations are needed for a more fundamental understanding of lubricant behaviors in EVs.

4) The review suggests a possibility to extend the current understanding of lubrication to electromagnetic fields with an integrated theory. Starting from the classic generalized Reynolds equation, a set of three forms of the generalized MEMT-field Reynolds equation, Eqs. 91, 93, 111, has been derived for the coupled effects of electric, magnetic, thermal, and mechanical fields. Given the fact that the lubrication in EVs may involve two or more of these fields, this equation set may prove instrumental in designing advanced EV lubricants and tribo-pairs.

Author contributions

XW: Conceptualization, Investigation, Writing–original draft, Writing–review and editing, Methodology. QW: Conceptualization, Investigation, Writing–review and editing, Methodology, Supervision, Writing–original draft. NR: Writing–review and editing, Conceptualization. RE: Writing–review and editing, Conceptualization.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was supported by Valvoline Global Operations.

Acknowledgments

The authors sincerely thank Valvoline Global Operations and Center for Surface Engineering and Tribology for their research support.

Conflict of interest

NR and RE are associated with Valvoline Global Operations.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2023.1334814/full#supplementary-material

References

Agrawal, N., and Sharma, S. C. (2021). Effect of the ER lubricant behaviour on the performance of spherical recessed hydrostatic thrust bearing. Tribol. Int. 153, 106621. doi:10.1016/j.triboint.2020.106621

CrossRef Full Text | Google Scholar

Ahamed, R., Choi, S. B., and Ferdaus, M. M. (2018). A state of art on magneto-rheological materials and their potential applications. J. Intelligent Material Syst. Struct. 29, 2051–2095. doi:10.1177/1045389x18754350

CrossRef Full Text | Google Scholar

Ahmed Abdalglil Mustafa, W., Dassenoy, F., Sarno, M., and Senatore, A. (2022). A review on potentials and challenges of nanolubricants as promising lubricants for electric vehicles. Lubr. Sci. 34, 1–29. doi:10.1002/ls.1568

CrossRef Full Text | Google Scholar

Arora, H., and Cann, P. M. (2010). Lubricant film formation properties of alkyl imidazolium tetrafluoroborate and hexafluorophosphate ionic liquids. Tribol. Int. 43, 1908–1916. doi:10.1016/j.triboint.2010.03.011

CrossRef Full Text | Google Scholar

Ashtiani, M., Hashemabadi, S. H., and Ghaffari, A. (2015). A review on the magnetorheological fluid preparation and stabilization. J. Magnetism Magnetic Mater. 374, 716–730. doi:10.1016/j.jmmm.2014.09.020

CrossRef Full Text | Google Scholar

Bai, S. X., Huang, P., Meng, Y. G., and Wen, S. Z. (2006). Modeling and analysis of interfacial electro-kinetic effects on thin film lubrication. Tribol. Int. 39, 1405–1412. doi:10.1016/j.triboint.2005.12.004

CrossRef Full Text | Google Scholar

Baranwal, D., and Deshmukh, T. (2012). MR-fluid technology and its application-a review. Int. J. Emerg. Technol. Adv. Eng. 2, 563–569.

Google Scholar

Barber, G., Jiang, Q., Zou, Q., and Carlson, W. (2005). Development of a laboratory test device for electrorheological fluids in hydrostatic lubrication. Tribotest 11, 185–191. doi:10.1002/tt.3020110302

CrossRef Full Text | Google Scholar

Barnhill, W. C., Qu, J., Luo, H. M., Meyer, H. M., Ma, C., Chi, M. F., et al. (2014). Phosphonium-organophosphate ionic liquids as lubricant additives: effects of cation structure on physicochemical and tribological characteristics. Acs Appl. Mater. Interfaces 6, 22585–22593. doi:10.1021/am506702u

PubMed Abstract | CrossRef Full Text | Google Scholar

Basavaraja, J. S., Sharma, S. C., and Jain, S. C. (2010). A study of misaligned electrorheological fluid lubricated hole-entry hybrid journal bearing. Tribol. Int. 43, 1059–1064. doi:10.1016/j.triboint.2009.12.052

CrossRef Full Text | Google Scholar

Batchelor, G. (1970). The stress system in a suspension of force-free particles. J. fluid Mech. 41, 545–570. doi:10.1017/s0022112070000745

CrossRef Full Text | Google Scholar

Batchelor, G. (1977). The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. fluid Mech. 83, 97–117. doi:10.1017/s0022112077001062

CrossRef Full Text | Google Scholar

Baxter-Drayton, Y., and Brady, J. F. (1996). Brownian electrorheological fluids as a model for flocculated dispersions. J. Rheology 40, 1027–1056. doi:10.1122/1.550772

CrossRef Full Text | Google Scholar

Beyer, M., Brown, G., Gahagan, M., Higuchi, T., Hunt, G., Huston, M., et al. (2019). Lubricant concepts for electrified vehicle transmissions and axles. Tribol. Online 14, 428–437. doi:10.2474/trol.14.428

CrossRef Full Text | Google Scholar

Bhat, M. V., and Deheri, G. M. (1991). Squeeze film behaviour in porous annular discs lubricated with magnetic fluid. Wear 151, 123–128. doi:10.1016/0043-1648(91)90352-U

CrossRef Full Text | Google Scholar

Bhat, M. V., and Deheri, G. M. (1993). Magnetic-fluid-based squeeze film in curved porous circular discs. J. Magnetism Magnetic Mater. 127, 159–162. doi:10.1016/0304-8853(93)90210-S

CrossRef Full Text | Google Scholar

Bike, S. G., and Prieve, D. C. (1990). Electrohydrodynamic lubrication with thin double-layers. J. Colloid Interface Sci. 136, 95–112. doi:10.1016/0021-9797(90)90081-X

CrossRef Full Text | Google Scholar

Bompos, D., and Nikolakopoulos, P. (2015). Static performance of surface textured magnetorheological fluid journal bearings. Tribol. Industry 37, 340.

Google Scholar

Bompos, D. A., and Nikolakopoulos, P. G. (2011). CFD simulation of magnetorheological fluid journal bearings. Simul. Model. Pract. Theory 19, 1035–1060. doi:10.1016/j.simpat.2011.01.001

CrossRef Full Text | Google Scholar

Bonnecaze, R. T., and Brady, J. F. (1992). Dynamic simulation of an electrorheological fluid. J. Chem. Phys. 96, 2183–2202. doi:10.1063/1.462070

CrossRef Full Text | Google Scholar

Bossis, G., and Brady, J. F. (1984). Dynamic simulation of sheared suspensions. I. General method. J. Chem. Phys. 80, 5141–5154. doi:10.1063/1.446585

CrossRef Full Text | Google Scholar

Boyanton, H. E., and Hodges, G. (2002). Bearing fluting [motors]. Ieee Ind. Appl. Mag. 8, 53–57. doi:10.1109/Mia.2002.1028391

CrossRef Full Text | Google Scholar

Brady, J. F., and Bossis, G. (1988). Stokesian dynamics. Annu. Rev. fluid Mech. 20, 111–157. doi:10.1146/annurev.fl.20.010188.000551

CrossRef Full Text | Google Scholar

Brenner, H. (1966). Hydrodynamic resistance of particles at small Reynolds numbers. Adv. Chem. Eng. 6, 287–438. doi:10.1016/S0065-2377(08)60277-X

CrossRef Full Text | Google Scholar

Bustami, B., Rahman, M. M., Shazida, M. J., Islam, M., Rohan, M. H., Hossain, S., et al. (2023). Recent progress in electrically conductive and thermally conductive lubricants: a critical review. Lubricants 11, 331. doi:10.3390/lubricants11080331

CrossRef Full Text | Google Scholar

Cai, M. R., Yu, Q. L., Liu, W. M., and Zhou, F. (2020). Ionic liquid lubricants: when chemistry meets tribology. Chem. Soc. Rev. 49, 7753–7818. doi:10.1039/d0cs00126k

PubMed Abstract | CrossRef Full Text | Google Scholar

Carlson, J. D., and Jolly, M. R. (2000). MR fluid, foam and elastomer devices. Mechatronics 10, 555–569. doi:10.1016/S0957-4158(99)00064-1

CrossRef Full Text | Google Scholar

Chakraborty, J., and Chakraborty, S. (2011). Combined influence of streaming potential and substrate compliance on load capacity of a planar slider bearing. Phys. Fluids 23, 082004. doi:10.1063/1.3624615

CrossRef Full Text | Google Scholar

Chandra, P., Sinha, P., and Kumar, D. (1992). Ferrofluid lubrication of a journal bearing considering cavitation. Tribol. Trans. 35, 163–169. doi:10.1080/10402009208982104

CrossRef Full Text | Google Scholar

Chang, H., Chi, C., and Zhao, P. (1987). A theoretical and experimental study of ferrofluid lubricated four-pocket journal bearings. J. Magnetism Magnetic Mater. 65, 372–374. doi:10.1016/0304-8853(87)90074-6

CrossRef Full Text | Google Scholar

Chen, M., Kato, K. J., and Adachi, K. (2002). The comparisons of sliding speed and normal load effect on friction coefficients of self-mated Si3N4 and SiC under water lubrication. Tribol. Int. 35, 129–135. doi:10.1016/S0301-679X(01)00105-0

CrossRef Full Text | Google Scholar

Chen, Q. D., Shyu, S. H., and Li, W. L. (2020). An overlapped electrical double layer model for aqueous electrolyte lubrication with asymmetric surface electric potentials. Tribol. Int. 147, 106283. doi:10.1016/j.triboint.2020.106283

CrossRef Full Text | Google Scholar

Chen, Y., Jha, S., Raut, A., Zhang, W. Y., and Liang, H. (2020). Performance characteristics of lubricants in electric and hybrid vehicles: a review of current and future needs. Front. Mech. Switzerl. 6, 571464. doi:10.3389/fmech.2020.571464

CrossRef Full Text | Google Scholar

Chen, Y. J., Zuo, Q. Y., and Huang, P. (2013). Influence of electric double layers on elastohydrodynamic lubricating water film in line contact. Proc. Institution Mech. Eng. Part N-Journal Nanomater. Nanoeng. Nanosyst. 227, 196–198. doi:10.1177/1740349913479588

CrossRef Full Text | Google Scholar

Choi, S. B., Sohn, J. W., Han, Y. M., and Lee, C. H. (2010). Wear characteristics under boundary lubrication contacts in phosphorated starch-based electrorheological fluid. Tribol. Trans. 53, 256–265. doi:10.1080/10402000903312331

CrossRef Full Text | Google Scholar

Christidi-Loumpasefski, O. O., Tzifas, I., Nikolakopoulos, P. G., and Papadopoulos, C. A. (2018). Dynamic analysis of rotor-bearing systems lubricated with electrorheological fluids. Proc. Institution Mech. Eng. Part K-Journal Multi-Body Dyn. 232, 153–168. doi:10.1177/1464419317725932

CrossRef Full Text | Google Scholar

Chun, B., and Ladd, A. C. (2004). The electroviscous force between charged particles: beyond the thin-double-layer approximation. J. Colloid Interface Sci. 274, 687–694. doi:10.1016/j.jcis.2004.03.066

PubMed Abstract | CrossRef Full Text | Google Scholar

Costello, M. J. (1991). “Shaft voltages and rotating machinery,” in Industry Applications Society 38th Annual Petroleum and Chemical Industry Conference, Toronto, ON, Canada, 09-11 September 1991, 71–78.

Google Scholar

Costello, M. J. (1993). Shaft voltages and rotating machinery. Ieee Trans. Industry Appl. 29, 419–426. doi:10.1109/28.216553

CrossRef Full Text | Google Scholar

Cowie, S., Cooper, P. K., Atkin, R., and Li, H. (2017). Nanotribology of ionic liquids as lubricant additives for alumina surfaces. J. Phys. Chem. C 121, 28348–28353. doi:10.1021/acs.jpcc.7b09879

CrossRef Full Text | Google Scholar

Csapo, E., Zaidi, H., and Paulmier, D. (1996). Friction behaviour of a graphite-graphite dynamic electric contact in the presence of argon. Wear 192, 151–156. doi:10.1016/0043-1648(95)06788-4

CrossRef Full Text | Google Scholar

Dalvi, S., Van Der Meer, T. H., and Shahi, M. (2022). Numerical evaluation of the ferrofluid behaviour under the influence of three-dimensional non-uniform magnetic field. Int. J. Heat Fluid Flow 94, 108901. doi:10.1016/j.ijheatfluidflow.2021.108901

CrossRef Full Text | Google Scholar

Dassisti, M., and Brunetti, G. (2022). “Introduction to magnetorheological fluids,” in Reference module in materials science and materials engineering (Elsevier).

Google Scholar

Davis, L., and Ginder, J. (1995). “Electrostatic forces in electrorheological fluids,” in Progress in electrorheology: science and technology of electrorheological materials (Springer).

CrossRef Full Text | Google Scholar

De Vicente, J., Klingenberg, D. J., and Hidalgo-Alvarez, R. (2011). Magnetorheological fluids: a review. Soft matter 7, 3701–3710. doi:10.1039/c0sm01221a

CrossRef Full Text | Google Scholar

Deysarkar, A. K., and Clampitt, B. H. (1988). Evaluation of ferrofluids as lubricants. J. Synthetic Lubr. 5, 105–114. doi:10.1002/jsl.3000050203

CrossRef Full Text | Google Scholar

Dimarogonas, A. D., and Kollias, A. (1992). Electrorheological fluid-controlled smart journal bearings. Tribol. Trans. 35, 611–618. doi:10.1080/10402009208982163

CrossRef Full Text | Google Scholar

Dong, R., Yu, Q. L., Bai, Y. Y., Wu, Y., Ma, Z. F., Zhang, J. Y., et al. (2020). Towards superior lubricity and anticorrosion performances of proton-type ionic liquids additives for water-based lubricating fluids. Chem. Eng. J. 383, 123201. doi:10.1016/j.cej.2019.123201

CrossRef Full Text | Google Scholar

Dorier, C., and Tichy, J. (1992). Behavior of a bingham-like viscous-fluid in lubrication flows. J. Newt. Fluid Mech. 45, 291–310. doi:10.1016/0377-0257(92)80065-6

CrossRef Full Text | Google Scholar

Dowson, D. (1962). A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 4, 159–170. doi:10.1016/s0020-7403(62)80038-1

CrossRef Full Text | Google Scholar

Dowson, D., and Taylor, C. M. (1979). Cavitation in bearings. Annu. Rev. Fluid Mech. 11, 35–65. doi:10.1146/annurev.fl.11.010179.000343

CrossRef Full Text | Google Scholar

Duan, R. (2012). Green's function and large time behavior of the Navier–Stokes–Maxwell system. Analysis Appl. 10, 133–197. doi:10.1142/s0219530512500078

CrossRef Full Text | Google Scholar

Elsaady, W., Oyadiji, S. O., and Nasser, A. (2020). A review on multi-physics numerical modelling in different applications of magnetorheological fluids. J. Intelligent Material Syst. Struct. 31, 1855–1897. doi:10.1177/1045389X20935632

CrossRef Full Text | Google Scholar

Elton, G. (1948). Electroviscosity. I. The flow of liquids between surfaces in close proximity. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 194, 259–274. doi:10.1098/rspa.1948.0079

CrossRef Full Text | Google Scholar

Fang, Y., and Ma, L. (2023). Mechanic model of water-based boundary lubricated contact based on surface force effects. Friction 11, 93–108. doi:10.1007/s40544-021-0579-0

CrossRef Full Text | Google Scholar

Fang, Y. F., Ma, L. R., and Luo, J. B. (2020). Modelling for water-based liquid lubrication with ultra-low friction coefficient in rough surface point contact. Tribol. Int. 141, 105901. doi:10.1016/j.triboint.2019.105901

CrossRef Full Text | Google Scholar

Fang, Y. F., Xuan, H., Ren, H. L., Fu, S. J., and Lin, T. L. (2023). Numerical study on thin film lubrication performance with imperfect coating under the effect of the electrical double layer in point contact. Lubricants 11, 274. doi:10.3390/lubricants11070274

CrossRef Full Text | Google Scholar

Farfan-Cabrera, L. I. (2019). Tribology of electric vehicles: a review of critical components, current state and future improvement trends. Tribol. Int. 138, 473–486. doi:10.1016/j.triboint.2019.06.029

CrossRef Full Text | Google Scholar

Farfan-Cabrera, L. I., Erdemir, A., Cao-Romero-Gallegos, J. A., Alam, I., and Lee, S. (2023). Electrification effects on dry and lubricated sliding wear of bearing steel interfaces. Wear 516, 204592. doi:10.1016/j.wear.2022.204592

CrossRef Full Text | Google Scholar

Felt, D. W., Hagenbuchle, M., Liu, J., and Richard, J. (1996). Rheology of a magnetorheological fluid. J. Intelligent Material Syst. Struct. 7, 589–593. doi:10.1177/1045389x9600700522

CrossRef Full Text | Google Scholar

Foulc, J. N., Atten, P., and Felici, N. (1994). Macroscopic model of interaction between particles in an electrorheological fluid. J. Electrost. 33, 103–112. doi:10.1016/0304-3886(94)90065-5

CrossRef Full Text | Google Scholar

Gahagan, M. P. (2017). Lubricant technology for hybrid electric automatic transmissions. SAE Technical Paper 2017-01-2358, Available at: https://doi.org/10.4271/2017-01-2358.

Google Scholar

Gajewski, J. B., and Glogowski, M. J. (2010). Base oil and its blends with ZDDP and their effect on tribocharging, braking torque and electrical double layers in a friction junction. Tribol. Lett. 38, 179–185. doi:10.1007/s11249-010-9588-2

CrossRef Full Text | Google Scholar

Genc, S., and Derin, B. (2014). Synthesis and rheology of ferrofluids: a review. Curr. Opin. Chem. Eng. 3, 118–124. doi:10.1016/j.coche.2013.12.006

CrossRef Full Text | Google Scholar

Gertzos, K. P., Nikolakopoulos, P. G., and Papadopoulos, C. A. (2008). CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant. Tribol. Int. 41, 1190–1204. doi:10.1016/j.triboint.2008.03.002

CrossRef Full Text | Google Scholar

Gołdasz, J., and Sapiński, B. (2015). Insight into magnetorheological shock absorbers. Cham: Springer.

Google Scholar

Gong, J. P., Kagata, G., and Osada, Y. (1999). Friction of gels. 4. Friction on charged gels. J. Phys. Chem. B 103, 6007–6014. doi:10.1021/jp990256v

CrossRef Full Text | Google Scholar

Hadden, T., Jiang, J. W., Bilgin, B., Yang, Y., Sathyan, A., Dadkhah, H., et al. (2016). “A review of shaft voltages and bearing currents in EV and HEV motors,” in IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23-26 October 2016, 1578–1583.

CrossRef Full Text | Google Scholar

Hao, T. (2001). Electrorheological fluids. Adv. Mater. 13, 1847. doi:10.1002/1521-4095(200112)13:24<1847::Aid-Adma1847>3.0.Co;2-A

CrossRef Full Text | Google Scholar

Hao, T. (2011). Electrorheological fluids: the non-aqueous suspensions. Netherlands: Elsevier.

Google Scholar

He, F., Xie, G. X., and Luo, J. B. (2020). Electrical bearing failures in electric vehicles. Friction 8, 4–28. doi:10.1007/s40544-019-0356-5

CrossRef Full Text | Google Scholar

Hemanth, G., Suresha, B., and Ananthapadmanabha, (2021). Hybrid and electric vehicle tribology: a review. Surf. Topogr. Prop. 9, 043001. doi:10.1088/2051-672X/ac2bf6

CrossRef Full Text | Google Scholar

Hisey, D. a. S. (2014). Welding electrical hazards: an update. Weld. World 58, 171–191. doi:10.1007/s40194-013-0103-x

CrossRef Full Text | Google Scholar

Holmberg, K., and Erdemir, A. (2019). The impact of tribology on energy use and CO2 emission globally and in combustion engine and electric cars. Tribol. Int. 135, 389–396. doi:10.1016/j.triboint.2019.03.024

CrossRef Full Text | Google Scholar

Hsu, T. C., Chen, J. H., Chiang, H. L., and Chou, T. L. (2013). Lubrication performance of short journal bearings considering the effects of surface roughness and magnetic field. Tribol. Int. 61, 169–175. doi:10.1016/j.triboint.2012.12.016

CrossRef Full Text | Google Scholar

Hsu, T.-C., Chen, J.-H., Chiang, H.-L., and Chou, T.-L. (2014). Combined effects of magnetic field and surface roughness on long journal bearing lubricated with ferrofluid. J. Mar. Sci. Technol. 22, 6. doi:10.6119/JMST-013-0207-4

CrossRef Full Text | Google Scholar

Huang, W., Shen, C., Liao, S. J., and Wang, X. L. (2011). Study on the ferrofluid lubrication with an external magnetic field. Tribol. Lett. 41, 145–151. doi:10.1007/s11249-010-9693-2

CrossRef Full Text | Google Scholar

Huang, W., and Wang, X. L. (2016). Ferrofluids lubrication: a status report. Lubr. Sci. 28, 3–26. doi:10.1002/ls.1291

CrossRef Full Text | Google Scholar

Huang, W., Wang, X. L., Ma, G. L., and Shen, C. (2009). Study on the synthesis and tribological property of Fe3O4 based magnetic fluids based magnetic fluids. Tribol. Lett. 33, 187–192. doi:10.1007/s11249-008-9407-1

CrossRef Full Text | Google Scholar

Hughes, W., and Elco, R. (1962). Magnetohydrodynamic lubrication flow between parallel rotating disks. Journal of Fluid Mechanics 13, 21–32. doi:10.1017/S0022112062000464

CrossRef Full Text | Google Scholar

Jadhav, S., Thakre, G. D., and Sharma, S. C. (2019). Influence of MHD lubrication and textured surface in EHL line contact. Frontiers in Mechanical Engineering 5, 33. doi:10.3389/fmech.2019.00033

CrossRef Full Text | Google Scholar

Jang, S., and Tichy, J. A. (1997). Internal damper characteristics of rotor system with submerged ER fluid journal bearing. Int. J. Rotating Mach. 3, 61–71. doi:10.1155/s1023621x97000079

CrossRef Full Text | Google Scholar

Jenkins, J. (1971). Some simple flows of a para-magnetic fluid. J. de Physique 32, 931–938. doi:10.1051/jphys:019710032011-12093100

CrossRef Full Text | Google Scholar

Jenkins, J. T. (1969). A theory of magnetic fluids. Arch. Ration. Mech. Anal. 46, 42–60. The Johns Hopkins University. doi:10.1007/BF00251867

CrossRef Full Text | Google Scholar

Jing, D., Pan, Y., and Wang, X. (2017). The effect of the electrical double layer on hydrodynamic lubrication: a non-monotonic trend with increasing zeta potential. Beilstein J. Nanotechnol. 8, 1515–1522. doi:10.3762/bjnano.8.152

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, R. W., Evans, J. L., Jacobsen, P., Thompson, J. R. R., and Christopher, M. (2004). The changing automotive environment: high-temperature electronics. Ieee Trans. Electron. Packag. Manuf. 27, 164–176. doi:10.1109/Tepm.2004.843109

CrossRef Full Text | Google Scholar

Jolly, M. R., Bender, J. W., and Carlson, J. D. (1999). Properties and applications of commercial magnetorheological fluids. J. Intelligent Material Syst. Struct. 10, 5–13. doi:10.1177/1045389X9901000102

CrossRef Full Text | Google Scholar

Jolly, M. R., and Carlson, J. D. (2000). “Composites with field-responsive rheology,” in Comprehensive composite materials. Editor C. Z Anthony Kelly (Oxford: Pergamon).

CrossRef Full Text | Google Scholar

Kailer, A., Amann, T., Krummhauer, O., Herrmann, M., Sydow, U., and Schneider, M. (2011). Influence of electric potentials on the tribological behaviour of silicon carbide. Wear 271, 1922–1927. doi:10.1016/j.wear.2010.12.011

CrossRef Full Text | Google Scholar

Kambe, T. (2014). “On fluid Maxwell equations,” in Frontiers of fundamental physics and physics education research (Cham: Springer).

CrossRef Full Text | Google Scholar

Khusid, B., and Acrivos, A. (1995). Effects of conductivity in electric-field-induced aggregation in electrorheological fluids. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 52, 1669–1693. doi:10.1103/physreve.52.1669

PubMed Abstract | CrossRef Full Text | Google Scholar

Klingenberg, D. J., Ulicny, J. C., and Golden, M. A. (2007). Mason numbers for magnetorheology. J. Rheology 51, 883–893. doi:10.1122/1.2764089

CrossRef Full Text | Google Scholar

Kole, M., and Khandekar, S. (2021). Engineering applications of ferrofluids: a review. J. Magnetism Magnetic Mater. 537, 168222. doi:10.1016/j.jmmm.2021.168222

CrossRef Full Text | Google Scholar

Komatsuzakl, S., Uematsu, T., and Kobayashl, Y. (2000). Change of grease characteristics to the end of lubricating life. NLGI Spokesm. 63, 22–29.

Google Scholar

Kumar, A., and Sharma, S. C. (2019). Textured conical hybrid journal bearing with ER lubricant behavior. Tribol. Int. 129, 363–376. doi:10.1016/j.triboint.2018.08.040

CrossRef Full Text | Google Scholar

Kumar, S., Kumar, V., and Singh, A. K. (2021a). Analysis of electrorheological fluid operated symmetric journal bearing. J. Tribol. 30, 100–115.

Google Scholar

Kumar, S., Kumar, V., and Singh, A. K. (2022). Dynamic performance analysis of ER fluid lubricated journal bearing. AIP Conf. Proc. 2357, 100001. AIP Publishing LLC. doi:10.1063/5.0080603

CrossRef Full Text | Google Scholar

Kumar, S., Sehgal, R., Wani, M. F., and Sharma, M. D. (2021b). Stabilization and tribological properties of magnetorheological (MR) fluids: a review. J. Magnetism Magnetic Mater. 538, 168295. doi:10.1016/j.jmmm.2021.168295

CrossRef Full Text | Google Scholar

Laghrabli, S., El Khlifi, M., Nabhani, M., and Bou-Saïd, B. (2017). Ferrofluid lubrication of finite journal bearings using Jenkins model. Lubr. Sci. 29, 441–454. doi:10.1002/ls.1379

CrossRef Full Text | Google Scholar

Lampaert, S. G. E., and Van Ostayen, R. a. J. (2019a). Experimental results on a hydrostatic bearing lubricated with a magnetorheological fluid. Curr. Appl. Phys. 19, 1441–1448. doi:10.1016/j.cap.2019.09.004

CrossRef Full Text | Google Scholar

Lampaert, S. G. E., Quinci, F., and Van Ostayen, R. a. J. (2020). Rheological texture in a journal bearing with magnetorheological fluids. J. Magnetism Magnetic Mater. 499, 166218. doi:10.1016/j.jmmm.2019.166218

CrossRef Full Text | Google Scholar

Lampaert, S. G. E., and Van Ostayen, R. a. J. (2019b). Load and stiffness of a hydrostatic bearing lubricated with a Bingham plastic fluid. J. Intelligent Material Syst. Struct. 30, 3056–3065. doi:10.1177/1045389X19873426

CrossRef Full Text | Google Scholar

Lampaert, S. G. E., and Van Ostayen, R. a. J. (2020). Lubrication theory for Bingham plastics. Tribol. Int. 147, 106160. doi:10.1016/j.triboint.2020.106160

CrossRef Full Text | Google Scholar

Lavielle, L. (1994). Electric-field effect on the friction of a polyethylene terpolymer film on a steel substrate. Wear 176, 89–93. doi:10.1016/0043-1648(94)90201-1

CrossRef Full Text | Google Scholar

Lee, Y. B. (2015). Behavior analysis of controllable electrorheology fluid plain journal bearings. J. Dyn. Syst. Meas. Control-Transactions Asme 137, 061013. doi:10.1115/1.4029369

CrossRef Full Text | Google Scholar

Li, W. (2005). Effects of electrodouble layer (EDL) and surface roughness on lubrication theory. Tribol. Lett. 20, 53–61. doi:10.1007/s11249-005-7792-2

CrossRef Full Text | Google Scholar

Li, W. L. (2009). Derivation of modified Reynolds equation: a porous media model with effects of electrokinetics. J. Tribology-Transactions Asme 131. doi:10.1115/1.3140610

CrossRef Full Text | Google Scholar

Li, W. L., and Jin, Z. (2008). Effects of electrokinetic slip flow on lubrication theory. Proc. Institution Mech. Eng. Part J J. Eng. Tribol. 222, 109–120. doi:10.1243/13506501jet369

CrossRef Full Text | Google Scholar

Lin, J., Hung, C., Hsu, C., and Lai, C. (2009). Dynamic stiffness and damping characteristics of one-dimensional magneto-hydrodynamic inclined-plane slider bearings. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology 223, 211–219. doi:10.1243/13506501JET498

CrossRef Full Text | Google Scholar

Lin, J. R. (2012). Derivation of ferrofluid lubrication equation of cylindrical squeeze films with convective fluid inertia forces and application to circular disks. Tribol. Int. 49, 110–115. doi:10.1016/j.triboint.2011.11.006

CrossRef Full Text | Google Scholar

Lin, J. R. (2013). Fluid inertia effects in ferrofluid squeeze film between a sphere and a plate. Appl. Math. Model. 37, 5528–5535. doi:10.1016/j.apm.2012.09.030

CrossRef Full Text | Google Scholar

Lin, J. R., Lin, M. C., Hung, T. C., and Wang, P. Y. (2013). Effects of fluid inertia forces on the squeeze film characteristics of conical plates-ferromagnetic fluid model. Lubr. Sci. 25, 429–439. doi:10.1002/ls.1206

CrossRef Full Text | Google Scholar

Lingard, S., Bullough, W. A., and Shek, W. M. (1989). Tribological performance of an electro-rheological fluid. J. Phys. D-Applied Phys. 22, 1639–1645. doi:10.1088/0022-3727/22/11/012

CrossRef Full Text | Google Scholar

Liu, C., Friedman, O., Li, Y., Li, S., Tian, Y., Golan, Y., et al. (2019). Electric response of CuS nanoparticle lubricant additives: the effect of crystalline and amorphous octadecylamine surfactant capping layers. Langmuir 35, 15825–15833. doi:10.1021/acs.langmuir.9b01714

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W. (2014). The prevalent motor bearing premature failures due to the high frequency electric current passage. Eng. Fail. Anal. 45, 118–127. doi:10.1016/j.engfailanal.2014.06.021

CrossRef Full Text | Google Scholar

Liu, Z. P., and Zhang, L. (2020). A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 149, 107002. doi:10.1016/j.measurement.2019.107002

CrossRef Full Text | Google Scholar

Luo, J. B., He, Y., Zhong, M., and Jin, Z. M. (2006). Gas bubble phenomenon in nanoscale liquid film under external electric field. Appl. Phys. Lett. 89. doi:10.1063/1.2213979

CrossRef Full Text | Google Scholar

Luo, J. B., Shen, M. W., and Wen, S. Z. (2004). Tribological properties of nanoliquid film under an external electric field. J. Appl. Phys. 96, 6733–6738. doi:10.1063/1.1806259

CrossRef Full Text | Google Scholar

Margida, A. J., Weiss, K. D., and Carlson, J. D. (1996). Magnetorheological materials based on iron alloy particles. Int. J. Mod. Phys. B 10, 3335–3341. doi:10.1142/S0217979296001781

CrossRef Full Text | Google Scholar

Marner, F. (2019). Potential-based formulations of the Navier-Stokes equations and their application. Durham: Durham University.

Google Scholar

Marshall, L., Zukoski, C. F., and Goodwin, J. W. (1989). Effects of electric-fields on the rheology of non-aqueous concentrated suspensions. J. Chem. Society-Faraday Trans. I 85, 2785–2795. doi:10.1039/f19898502785

CrossRef Full Text | Google Scholar

Mccloskey, T. H. (1995). “Troubleshooting bearing and lube oil system problems,” in Proceedings of the 24th Turbomachinery Symposium. Texas A&M University. Turbomachinery Laboratories.

Google Scholar

Mccoy, B. (2021). Next generation driveline lubricants for electrified vehicles. Tribol. Lubr. Technol. 77, 38–40.

Google Scholar

Mchale, G., Orme, B. V., Wells, G. G., and Ledesma-Aguilar, R. (2019). Apparent contact angles on lubricant-impregnated surfaces/SLIPS: from superhydrophobicity to electrowetting. Langmuir 35, 4197–4204. doi:10.1021/acs.langmuir.8b04136

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalec, M., Svoboda, P., Krupka, I., and Hartl, M. (2018). Tribological behaviour of smart fluids influenced by magnetic and electric field-A review. Tribol. industry 40, 515–528. doi:10.24874/ti.2018.40.04.01

CrossRef Full Text | Google Scholar

Moles, N. C. (2015). Actively controllable hydrodynamic journal bearing design using magnetorheological fluids. Doctoral dissertation, University of Akron.

Google Scholar

Mugele, F., and Baret, J. C. (2005). Electrowetting: from basics to applications. J. Physics-Condensed Matter 17, R705–R774. doi:10.1088/0953-8984/17/28/R01

CrossRef Full Text | Google Scholar

Mutra, R. R., and Srinivas, J. (2019). Rotor vibration control studies with electrorheological fluid lubricant in floating ring bearings. Noise Vib. Worldw. 50, 157–165. doi:10.1177/0957456519843512

CrossRef Full Text | Google Scholar

Neuringer, J. L., and Rosensweig, R. E. (1964). Ferrohydrodynamics. Phys. Fluids 7, 1927–1937. doi:10.1063/1.1711103

CrossRef Full Text | Google Scholar

Newcomb, T. (2023). A brief review of the rapid transformation of driveline lubricants for hybrid electric and electric vehicles. Front. Mech. Switzerl. 9, 1139385. doi:10.3389/fmech.2023.1139385

CrossRef Full Text | Google Scholar

Nikolakopoulos, P. G., and Papadopoulos, C. A. (1998). Controllable high speed journal bearings, lubricated with electro-rheological fluids. An analytical and experimental approach. Tribol. Int. 31, 225–234. doi:10.1016/s0301-679x(98)00025-5

CrossRef Full Text | Google Scholar

Odenbach, S. (2004). Recent progress in magnetic fluid research. J. Physics-Condensed Matter 16, R1135–R1150. doi:10.1088/0953-8984/16/32/R02

CrossRef Full Text | Google Scholar

Odenbach, S. (2013). Ferrofluids and their applications. MRS Bull. 38, 921–924. doi:10.1557/mrs.2013.232

CrossRef Full Text | Google Scholar

Olabi, A. G., and Grunwald, A. (2007). Design and application of magneto-rheological fluid. Mater. Des. 28, 2658–2664. doi:10.1016/j.matdes.2006.10.009

CrossRef Full Text | Google Scholar

Oliver, J. A., Guerrero, G., and Goldman, J. (2017). Ceramic bearings for electric motors eliminating damage with new materials. Ieee Ind. Appl. Mag. 23, 14–20. doi:10.1109/Mias.2016.2600692

CrossRef Full Text | Google Scholar

Oogaki, S., Kagata, G., Kurokawa, T., Kuroda, S., Osada, Y., and Gong, J. P. (2009). Friction between like-charged hydrogels-combined mechanisms of boundary, hydrated and elastohydrodynamic lubrication. Soft Matter 5, 1879–1887. doi:10.1039/b815102d

CrossRef Full Text | Google Scholar

Osman, T. A. (2004). Effect of lubricant non-Newtonian behavior and elastic deformation on the dynamic performance of finite journal plastic bearings. Tribol. Lett. 17, 31–40. doi:10.1023/B:Tril.0000017416.95176.30

CrossRef Full Text | Google Scholar

Osman, T. A., Nada, G. S., and Safar, Z. S. (2001). Effect of using current-carrying-wire models in the design of hydrodynamic journal bearings lubricated with ferrofluid. Tribol. Lett. 11, 61–70. doi:10.1023/A:1016657914947

CrossRef Full Text | Google Scholar

Osman, T. A., Nada, G. S., and Safar, Z. S. (2003). Different magnetic models in the design of hydrodynamic journal bearings lubricated with non-Newtonian ferrofluid. Tribol. Lett. 14, 211–223. doi:10.1023/A:1022869432202

CrossRef Full Text | Google Scholar

Palacio, M., and Bhushan, B. (2010). A review of ionic liquids for green molecular lubrication in nanotechnology. Tribol. Lett. 40, 247–268. doi:10.1007/s11249-010-9671-8

CrossRef Full Text | Google Scholar

Parenago, O. P., Lyadov, A. S., and Maksimov, A. L. (2022). Development of lubricant formulations for modern electric vehicles. Russ. J. Appl. Chem. 95, 765–774. doi:10.1134/S1070427222060015

CrossRef Full Text | Google Scholar

Park, W. C., Choi, S. B., Cheong, C. C., Suh, M. S., and Yeo, M. S. (1996). Boundary lubrication characteristics of silica-based electro-rheological fluids. J. Intelligent Material Syst. Struct. 7, 511–516. doi:10.1177/1045389x9600700507

CrossRef Full Text | Google Scholar

Parthasarathy, M., and Klingenberg, D. J. (1996). Electrorheology: mechanisms and models. Mater. Sci. Eng. R-Reports 17, 57–103. doi:10.1016/0927-796x(96)00191-X

CrossRef Full Text | Google Scholar

Patel, N. D., and Deheri, G. (2011). Effect of surface roughness on the performance of a magnetic fluid based parallel plate porous slider bearing with slip velocity. J. Serbian Soc. Comput. Mech. 5, 104–118.

Google Scholar

Pei, P., and Peng, Y. B. (2022). Constitutive modeling of magnetorheological fluids: a review. J. Magnetism Magnetic Mater. 550, 169076. doi:10.1016/j.jmmm.2022.169076

CrossRef Full Text | Google Scholar

Peng, J., and Zhu, K. Q. (2005). Hydrodynamic characteristics of ER journal bearings with external electric field imposed on the contractive part. J. Intelligent Material Syst. Struct. 16, 493–499. doi:10.1177/1045389x05052312

CrossRef Full Text | Google Scholar

Peng, J., and Zhu, K. Q. (2006). Effects of electric field on hydrodynamic characteristics of finite-length ER journal bearings. Tribol. Int. 39, 533–540. doi:10.1016/j.triboint.2005.03.017

CrossRef Full Text | Google Scholar

Phillips, B. S., and Zabinski, J. S. (2004). Ionic liquid lubrication effects on ceramics in a water environment. Tribol. Lett. 17, 533–541. doi:10.1023/B:Tril.0000044501.64351.68

CrossRef Full Text | Google Scholar

Plazenet, T., Boileau, T., Caironi, C., and Nahid-Mobarakeh, B. (2018). A comprehensive study on shaft voltages and bearing currents in rotating machines. Ieee Trans. Industry Appl. 54, 3749–3759. doi:10.1109/Tia.2018.2818663

CrossRef Full Text | Google Scholar

Prajapati, B. L. (1995). Magnetic-fluid-based porous squeeze films. J. Magnetism Magnetic Mater. 149, 97–100. doi:10.1016/0304-8853(95)00346-0

CrossRef Full Text | Google Scholar

Prashad, H. (1987). Effect of operating parameters on the threshold voltages and impedance response of non-insulated rolling element bearings under the action of electrical currents. Wear 117, 223–240. doi:10.1016/0043-1648(87)90257-2

CrossRef Full Text | Google Scholar

Prashad, H. (1988). The effects of current leakage on electroadhesion forces in rolling friction and magnetic-flux density distribution on the surface of rolling element bearings. J. Tribology-Transactions Asme 110, 448–455. doi:10.1115/1.3261649

CrossRef Full Text | Google Scholar

Prashad, H. (2001a). Appearance of craters on track surface of rolling element bearings by spark erosion. Tribol. Int. 34, 39–47. doi:10.1016/S0301-679x(00)00133-X

CrossRef Full Text | Google Scholar

Prashad, H. (2001b). Tribology in electrical environments. Lubr. Sci. 13, 359–369. doi:10.1002/ls.3010130407

CrossRef Full Text | Google Scholar

Prieve, D. C., and Bike, S. G. (1987). Electrokinetic repulsion between two charged bodies undergoing sliding motion. Chem. Eng. Commun. 55, 149–164. doi:10.1080/00986448708911924

CrossRef Full Text | Google Scholar

Pu, W., Zhu, D., Wang, J. X., and Wang, Q. J. (2016). Rolling-sliding contact fatigue of surfaces with sinusoidal roughness. Int. J. Fatigue 90, 57–68. doi:10.1016/j.ijfatigue.2016.04.007

CrossRef Full Text | Google Scholar

Qian, J., Joshi, R. P., Kolb, J., Schoenbach, K. H., Dickens, J., Neuber, A., et al. (2005). Microbubble-based model analysis of liquid breakdown initiation by a submicrosecond pulse. J. Appl. Phys. 97. doi:10.1063/1.1921338

CrossRef Full Text | Google Scholar

Qu, J., Bansal, D. G., Yu, B., Howe, J. Y., Luo, H. M., Dai, S., et al. (2012). Antiwear performance and mechanism of an oil-miscible ionic liquid as a lubricant additive. Acs Appl. Mater. Interfaces 4, 997–1002. doi:10.1021/am201646k

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, J., Barnhill, W. C., Luo, H. M., Meyer, H. M., Leonard, D. N., Landauer, A. K., et al. (2015). Synergistic effects between phosphonium-alkylphosphate ionic liquids and zinc dialkyldithiophosphate (ZDDP) as lubricant additives. Adv. Mater. 27, 4767–4774. doi:10.1002/adma.201502037

PubMed Abstract | CrossRef Full Text | Google Scholar

Quinci, F., Litwin, W., Wodtke, M., and Van Den Nieuwendijk, R. (2021). A comparative performance assessment of a hydrodynamic journal bearing lubricated with oil and magnetorheological fluid. Tribol. Int. 162, 107143. doi:10.1016/j.triboint.2021.107143

CrossRef Full Text | Google Scholar

Ramos, J., Klingenberg, D. J., Hidalgo-Alvarez, R., and De Vicente, J. (2011). Steady shear magnetorheology of inverse ferrofluids. J. Rheology 55, 127–152. doi:10.1122/1.3523481

CrossRef Full Text | Google Scholar

Rankin, P. J., Ginder, J. M., and Klingenberg, D. J. (1998). Electro- and magneto-rheology. Curr. Opin. Colloid and Interface Sci. 3, 373–381. doi:10.1016/S1359-0294(98)80052-6

CrossRef Full Text | Google Scholar

Richtering, W. (2001). “Polymer-based electrorheological fluids,” in Encyclopedia of materials: science and technology. Editor K. H. J. B. A. R. W. C. A. M. C. F. A. B. I. A. E. J. K. A. S. M. A. P VEYSSIÈRE (Oxford: Elsevier).

CrossRef Full Text | Google Scholar

Rinaldi, C., Chaves, A., Elborai, S., He, X. W., and Zahn, M. (2005). Magnetic fluid rheology and flows. Curr. Opin. Colloid and Interface Sci. 10, 141–157. doi:10.1016/j.cocis.2005.07.004

CrossRef Full Text | Google Scholar

Rivera, N., Viesca, J. L., García, A., Prado, J. I., Lugo, L., Battez, A. H., et al. (2022). Cooling performance of fresh and aged automatic transmission fluids for hybrid electric vehicles. Applied Sciences 12, 8911. doi:10.3390/app12178911

CrossRef Full Text | Google Scholar

Rodríguez, E., Rivera, N., Fernández-González, A., Pérez, T., González, R., and Battez, A. H. (2022). Electrical compatibility of transmission fluids in electric vehicles. Tribol. Int. 171, 107544. doi:10.1016/j.triboint.2022.107544

CrossRef Full Text | Google Scholar

Romanenko, A., Muetze, A., and Ahola, J. (2016). Effects of electrostatic discharges on bearing grease dielectric strength and composition. Ieee Trans. Industry Appl. 52, 4835–4842. doi:10.1109/Tia.2016.2596239

CrossRef Full Text | Google Scholar

Sahoo, R., Ussa-Aldana, P., Lancon, D., Rondelez, F., Morillas, J., Hidalgo-Alvarez, R., et al. (2022). Design of smart lubricants using the inverse ferrofluid approach. Tribol. Int. 166, 107346. doi:10.1016/j.triboint.2021.107346

CrossRef Full Text | Google Scholar

Sahu, K., and Sharma, S. C. (2019). Magneto-rheological fluid slot-entry journal bearing considering thermal effects. J. Intelligent Material Syst. Struct. 30, 2831–2852. doi:10.1177/1045389x19873401

CrossRef Full Text | Google Scholar

Sahu, K., Sharma, S. C., and Ram, N. (2022). Misalignment and surface irregularities effect in MR fluid journal bearing. Int. J. Mech. Sci. 221, 107196. doi:10.1016/j.ijmecsci.2022.107196

CrossRef Full Text | Google Scholar

Sanguesa, J. A., Torres-Sanz, V., Garrido, P., Martinez, F. J., and Marquez-Barja, J. M. (2021). A review on electric vehicles: technologies and challenges. Smart Cities 4, 372–404. doi:10.3390/smartcities4010022

CrossRef Full Text | Google Scholar

Säynätjoki, M., and Holmberg, K. (1993). Magnetic fluids in sealing and lubrication–A state of the art review. J. Synthetic Lubr. 10, 119–132. doi:10.1002/jsl.3000100203

CrossRef Full Text | Google Scholar

Scherer, C., and Neto, A. M. F. (2005). Ferrofluids: properties and applications. Braz. J. Phys. 35, 718–727. doi:10.1590/S0103-97332005000400018

CrossRef Full Text | Google Scholar

Shah, R., and Bhat, M. (2004). Ferrofluid lubrication of a slider bearing with a circular convex pad. J. Natn.Sci.Foundation Sri Lanka 32 (3and4), 139–148. doi:10.4038/jnsfsr.v32i3-4.2433

CrossRef Full Text | Google Scholar

Shah, R., Gashi, B., González-Poggini, S., Colet-Lagrille, M., and Rosenkranz, A. (2021a). Recent trends in batteries and lubricants for electric vehicles. Adv. Mech. Eng. 13, 168781402110217. doi:10.1177/16878140211021730

CrossRef Full Text | Google Scholar

Shah, R., Gashi, B., and Rosenkranz, A. (2022). Latest developments in designing advanced lubricants and greases for electric vehicles-An overview. Lubr. Sci. 34, 515–526. doi:10.1002/ls.1605

CrossRef Full Text | Google Scholar

Shah, R., Tung, S., Chen, R., and Miller, R. (2021b). Grease performance requirements and future perspectives for electric and hybrid vehicle applications. Lubricants 9, 40. doi:10.3390/lubricants9040040

CrossRef Full Text | Google Scholar

Shah, R. C. (2003). Ferrofluid lubrication in step bearing with two steps. Industrial Lubr. Tribol. 55, 265–267. doi:10.1108/00368790310496392

CrossRef Full Text | Google Scholar

Shah, R. C., and Bhat, M. (2003a). Analysis of a porous exponential slider bearing lubricated with a ferrofluid considering slip velocity. J. Braz. Soc. Mech. Sci. Eng. 25, 264–267. doi:10.1590/s1678-58782003000300008

CrossRef Full Text | Google Scholar

Shah, R. C., and Bhat, M. (2003b). Ferrofluid lubrication of a parallel plate squeeze film bearing. Theor. Appl. Mech. 2003, 221–240. doi:10.2298/tam0303221s

CrossRef Full Text | Google Scholar

Shah, R. C., and Bhat, M. V. (2000). Squeeze film based on magnetic fluid in curved porous rotating circular plates. J. Magnetism Magnetic Mater. 208, 115–119. doi:10.1016/s0304-8853(99)00570-3

CrossRef Full Text | Google Scholar

Shah, R. C., and Bhat, M. V. (2005a). Ferrofluid squeeze film between curved annular plates including rotation of magnetic particles. J. Eng. Math. 51, 317–324. doi:10.1007/s10665-004-1770-9

CrossRef Full Text | Google Scholar

Shah, R. C., and Bhat, M. V. (2005b). Lubrication of porous parallel plate slider bearing with slip velocity, material parameter and magnetic fluid. Industrial Lubr. Tribol. 57, 103–106. doi:10.1108/00368790510595066

CrossRef Full Text | Google Scholar

Sharma, S. C., and Tomar, A. K. (2021). Study on MR fluid hybrid hole-entry spherical journal bearing with micro-grooves. Int. J. Mech. Sci. 202, 106504. doi:10.1016/j.ijmecsci.2021.106504

CrossRef Full Text | Google Scholar

Sheng, P., and Wen, W. J. (2012). Electrorheological fluids: mechanisms, dynamics, and microfluidics applications. Annu. Rev. Fluid Mech. 44 (44), 143–174. doi:10.1146/annurev-fluid-120710-101024

CrossRef Full Text | Google Scholar

Shliomis, M. (1971). Effective viscosity of magnetic suspensions. Zh. Eksp. Teor. Fiz. 61, s1971d–s1971.

Google Scholar

Shukla, J. B., and Kumar, D. (1987). A theory for ferromagnetic lubrication. J. Magnetism Magnetic Mater. 65, 375–378. doi:10.1016/0304-8853(87)90075-8

CrossRef Full Text | Google Scholar

Silva, J. L., and Cardoso, A. M. (2005). “Bearing failures diagnosis in three-phase induction motors by extended Park's vector approach,” in 31st Annual Conference of IEEE Industrial Electronics Society, 2005. IECON 2005, Raleigh, NC, USA, 06-10 November 2005, 6.

CrossRef Full Text | Google Scholar

Silvester, D. S., Jamil, R., Doblinger, S., Zhang, Y. X., Atkin, R., and Li, H. (2021). Electrical double layer structure in ionic liquids and its importance for supercapacitor, battery, sensing, and lubrication applications. J. Phys. Chem. C 125, 13707–13720. doi:10.1021/acs.jpcc.1c03253

CrossRef Full Text | Google Scholar

Simon, T. M., Reitich, F., Jolly, M. R., Ito, K., and Banks, H. T. (2001). The effective magnetic properties of magnetorheological fluids. Math. Comput. Model. 33, 273–284. doi:10.1016/S0895-7177(00)00244-2

CrossRef Full Text | Google Scholar

Singh, A. K., Kumar, V., Singh, S. J., Sharma, N., and Choudhary, D. (2022). A comparative performance assessment of hydrostatic thrust bearings operating with electrorheological lubricant. Industrial Lubr. Tribol. 74, 892–900. doi:10.1108/Ilt-01-2022-0034

CrossRef Full Text | Google Scholar

Sinha, P., Chandra, P., and Kumar, D. (1993). Ferrofluid lubrication of cylindrical rollers with cavitation. Acta Mech. 98, 27–38. doi:10.1007/Bf01174291

CrossRef Full Text | Google Scholar

Sorge, F. (1987). A numerical approach to finite journal bearings lubricated with ferrofluid. J. Tribology-Transactions Asme 109, 77–82. doi:10.1115/1.3261331

CrossRef Full Text | Google Scholar

Spikes, H. A. (2020). Triboelectrochemistry: influence of applied electrical potentials on friction and wear of lubricated contacts. Tribol. Lett. 68, 90–27. doi:10.1007/s11249-020-01328-3

CrossRef Full Text | Google Scholar

Stejskal, J. (2015). Polymers of phenylenediamines. Prog. Polym. Sci. 41, 1–31. doi:10.1016/j.progpolymsci.2014.10.007

CrossRef Full Text | Google Scholar

Sunahara, K., Ishida, Y., Yamashita, S., Yamamoto, M., Nishikawa, H., Matsuda, K., et al. (2011). Preliminary measurements of electrical micropitting in grease-lubricated point contacts. Tribol. Trans. 54, 730–735. doi:10.1080/10402004.2011.597543

CrossRef Full Text | Google Scholar

Suzumura, J. (2016). Prevention of electrical pitting on rolling bearings by electrically conductive grease. Q. Rep. RTRI 57, 42–47. doi:10.2219/rtriqr.57.1_42

CrossRef Full Text | Google Scholar

Tang, T. H. Z., Devlin, M., Mathur, N., Henly, T., and Saathoff, L. (2013). Lubricants for (hybrid) electric transmissions. Sae Int. J. Fuels Lubr. 6, 289–294. doi:10.4271/2013-01-0298

CrossRef Full Text | Google Scholar

Taylor, R. I. (2021). Energy efficiency, emissions, tribological challenges and fluid requirements of electrified passenger car vehicles. Lubricants 9, 66. doi:10.3390/lubricants9070066

CrossRef Full Text | Google Scholar

Thompson, R. J., Wilson, A., Moeller, T., and Merkle, C. L. (2014). A strong conservative Riemann solver for the solution of the coupled Maxwell and Navier–Stokes equations. J. Comput. Phys. 258, 431–450. doi:10.1016/j.jcp.2013.10.041

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, M. L., Jiang, J. L., Pesika, N., Zeng, H. B., Israelachvili, J., et al. (2011). Reversible shear thickening at low shear rates of electrorheological fluids under electric fields. Phys. Rev. E 83, 011401. doi:10.1103/PhysRevE.83.011401

PubMed Abstract | CrossRef Full Text | Google Scholar

Tichy, J. A. (1991). Hydrodynamic lubrication theory for the Bingham plastic-flow model. J. Rheology 35, 477–496. doi:10.1122/1.550231

CrossRef Full Text | Google Scholar

Tichy, J. A. (1993). Behavior of a squeeze film damper with an electrorheological fluid. Tribol. Trans. 36, 127–133. doi:10.1080/10402009308983141

CrossRef Full Text | Google Scholar

Tipei, N. (1982). Theory of lubrication with ferrofluids - application to short bearings. J. Lubr. Technology-Transactions Asme 104, 510–515. doi:10.1115/1.3253274

CrossRef Full Text | Google Scholar

Tokozakura, D., Sano, T., Nakamura, T., Tada, A., Susukida, Y., Moritani, H., et al. (2022). Development of transaxle fluid for electrified vehicles: validating optimized viscosity through targeted hardware testing. SAE Technical Paper, 2022-01-1103. Available at: https://doi.org/10.4271/2022-01-1103.

CrossRef Full Text | Google Scholar

Tung, S. C., Woydt, M., and Shah, R. (2020). Global insights on future trends of hybrid/EV driveline lubrication and thermal management. Front. Mech. Switzerl. 6, 571786. doi:10.3389/fmech.2020.571786

CrossRef Full Text | Google Scholar

Uhlmann, E., Spur, G., Bayat, N., and Patzwald, R. (2002). Application of magnetic fluids in tribotechnical systems. J. Magnetism Magnetic Mater. 252, 336–340. doi:10.1016/S0304-8853(02)00724-2

CrossRef Full Text | Google Scholar

Van Rensselar, J. (2019). The tribology of electric vehicles. Tribol. Lubr. Technol. 75, 34–43. doi:10.1016/j.triboint.2019.06.029

CrossRef Full Text | Google Scholar

Vaz, N., Binu, K., Serrao, P., Hemanth, M., Jacob, J., Roy, N., et al. (2017). Experimental investigation of frictional force in a hydrodynamic journal bearing lubricated with magnetorheological fluid. J. Mech. Eng. Automation 7, 131–134. doi:10.5923/j.jmea.20170705

CrossRef Full Text | Google Scholar

Vékás, L. (2008). Ferrofluids and magnetorheological fluids. Adv. Sci. Technol. 54, 127–136. Trans Tech Publ. doi:10.4028/www.scientific.net/ast.54.127

CrossRef Full Text | Google Scholar

Volkova, O., Bossis, G., Guyot, M., Bashtovoi, V., and Reks, A. (2000). Magnetorheology of magnetic holes compared to magnetic particles. J. Rheology 44, 91–104. doi:10.1122/1.551075

CrossRef Full Text | Google Scholar

Walker, J. S., and Buckmaster, J. D. (1979). Ferrohydrodynamic thrust-bearings. Int. J. Eng. Sci. 17, 1171–1182. doi:10.1016/0020-7225(79)90100-9

CrossRef Full Text | Google Scholar

Walther, H. C., and Holub, R. A. (2014). “Lubrication of electric motors as defined by IEEE standard 841-2009, shortcomings and potential improvement opportunities,” in 2014 IEEE Petroleum and Chemical Industry Technical Conference (PCIC), San Francisco, CA, USA, 08-10 September 2014, 91–98.

CrossRef Full Text | Google Scholar

Wang, J., and Zhu, D. (2019). Interfacial mechanics: theories and methods for contact and lubrication. Boca Raton, FL: CRC Press.

Google Scholar

Wang, L. J., Guo, C. W., and Yamane, R. (2008). Experimental research on tribological properties of Mn 0.78Zn0.22 Fe2O4 magnetic fluids. J. Tribology-Transactions Asme 130. doi:10.1115/1.2913539

CrossRef Full Text | Google Scholar

Wang, X. H., Li, H. G., Li, M., Bai, H. Y., Meng, G., and Zhang, H. (2015). Dynamic characteristics of magnetorheological fluid lubricated journal bearing and its application to rotor vibration control. J. Vibroengineering 17, 1912–1928.

Google Scholar

Wang, X. H., Li, H. G., and Meng, G. (2017). Rotordynamic coefficients of a controllable magnetorheological fluid lubricated floating ring bearing. Tribol. Int. 114, 1–14. doi:10.1016/j.triboint.2017.04.002

CrossRef Full Text | Google Scholar

Wang, X. J., Bai, S. X., and Huang, P. (2006). Theoretical analysis and experimental study on the influence of electric double layer on thin film lubrication. Front. Mech. Eng. 1, 370–373. doi:10.1007/s11465-006-0040-0

CrossRef Full Text | Google Scholar

Wen, W., Huang, X., and Sheng, P. (2008). Electrorheological fluids: structures and mechanisms. Soft Matter 4, 200–210. doi:10.1039/b710948m

PubMed Abstract | CrossRef Full Text | Google Scholar

Winslow, W. M. (1949). Induced fibration of suspensions. J. Appl. Phys. 20, 1137–1140. doi:10.1063/1.1698285

CrossRef Full Text | Google Scholar

Wong, P. L., Huang, P., and Meng, Y. (2003). The effect of the electric double layer on a very thin water lubricating film. Tribol. Lett. 14, 197–203. doi:10.1023/A:1022320531293

CrossRef Full Text | Google Scholar

Xie, G. X., Guo, D., and Luo, J. B. (2015). Lubrication under charged conditions. Tribol. Int. 84, 22–35. doi:10.1016/j.triboint.2014.11.018

CrossRef Full Text | Google Scholar

Xie, G. X., Luo, J. B., Liu, S. H., Guo, D., Li, G., and Zhang, C. H. (2009). Effect of liquid properties on the growth and motion characteristics of micro-bubbles induced by electric fields in confined liquid films. J. Phys. D-Applied Phys. 42, 115502. doi:10.1088/0022-3727/42/11/115502

CrossRef Full Text | Google Scholar

Xie, G. X., Luo, J. B., Liu, S. H., Guo, D., and Zhang, C. H. (2010). Bubble generation in a nanoconfined liquid film between dielectric-coated electrodes under alternating current electric fields. Appl. Phys. Lett. 96. doi:10.1063/1.3443633

CrossRef Full Text | Google Scholar

Xie, G. X., Luo, J. B., Liu, S. H., Zhang, C. H., and Lu, X. C. (2008). Micro-bubble phenomenon in nanoscale water-based lubricating film induced by external electric field. Tribol. Lett. 29, 169–176. doi:10.1007/s11249-007-9288-8

CrossRef Full Text | Google Scholar

Xu, J. G., and Kato, K. (2000). Formation of tribochemical layer of ceramics sliding in water and its role for low friction. Wear 245, 61–75. doi:10.1016/S0043-1648(00)00466-X

CrossRef Full Text | Google Scholar

Xu, M. C., Dai, Q. W., Huang, W., and Wang, X. L. (2020). Using magnetic fluids to improve the behavior of ball bearings under starved lubrication. Tribol. Int. 141, 105950. doi:10.1016/j.triboint.2019.105950

CrossRef Full Text | Google Scholar

Yu, B., Bansal, D. G., Qu, J., Sun, X. Q., Luo, H. M., Dai, S., et al. (2012). Oil-miscible and non-corrosive phosphonium-based ionic liquids as candidate lubricant additives. Wear 289, 58–64. doi:10.1016/j.wear.2012.04.015

CrossRef Full Text | Google Scholar

Yu, Z. Q., and Yang, Z. G. (2011). Fatigue failure analysis of a grease-lubricated roller bearing from an electric motor. J. Fail. Analysis Prev. 11, 158–166. doi:10.1007/s11668-010-9422-z

CrossRef Full Text | Google Scholar

Zhang, B., and Umehara, N. (1998). Hydrodynamic lubrication theory considering electric double layer for very thin water film lubrication of ceramics. Jsme Int. J. Ser. C-Mechanical Syst. Mach. Elem. Manuf. 41, 285–290. doi:10.1299/jsmec.41.285

CrossRef Full Text | Google Scholar

Zhang, X., and Wang, Q. J. (2022). A unified analogy-based computation methodology from elasticity to electromagnetic-chemical-thermal fields and a concept of multifield sensing. ASME Open J. Eng. 1. doi:10.1115/1.4053910

CrossRef Full Text | Google Scholar

Zhang, X., Wang, Q. J., and Shen, H. (2018). A multi-field coupled mechanical-electric-magnetic-chemical-thermal (MEMCT) theory for material systems. Comput. Methods Appl. Mech. Eng. 341, 133–162. doi:10.1016/j.cma.2018.07.005

CrossRef Full Text | Google Scholar

Zhang, Y. (1991). Static characteristics of magnetized journal bearing lubricated with ferrofluid. J. Tribology-Transactions Asme 113, 533–537. doi:10.1115/1.2920656

CrossRef Full Text | Google Scholar

Zhao, C., and Yang, C. (2013). Electrokinetics of non-Newtonian fluids: a review. Adv. Colloid Interface Sci. 201-202, 94–108. doi:10.1016/j.cis.2013.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, F., Liang, Y., and Liu, W. (2009). Ionic liquid lubricants: designed chemistry for engineering applications. Chem. Soc. Rev. 38, 2590–2599. doi:10.1039/b817899m

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y., and Qu, J. (2017). Ionic liquids as lubricant additives: a review. Acs Appl. Mater. Interfaces 9, 3209–3222. doi:10.1021/acsami.6b12489

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, D., and Wang, Q. J. (2013). Effect of roughness orientation on the elastohydrodynamic lubrication film thickness. J. Tribology-Transactions Asme 135, 031501. doi:10.1115/1.4023250

CrossRef Full Text | Google Scholar

Zhun, Z., and Ke-Qin, Z. (2002). Characteristics of electrorheological fluid flow in journal bearings. Chin. Phys. Lett. 19, 273–275. doi:10.1088/0256-307x/19/2/341

CrossRef Full Text | Google Scholar

Zuo, Q. Y., Huang, P., and Su, F. H. (2012a). Theory analysis of asymmetrical electric double layer effects on thin film lubrication. Tribol. Int. 49, 67–74. doi:10.1016/j.triboint.2011.12.021

CrossRef Full Text | Google Scholar

Zuo, Q. Y., Ping, H., and Gyimah, G. K. (2012b). The effect of asymmetrical electric double layer on pressure of hydrodynamic lubricating film. Adv. Mater. Res. 393-395, 1536–1540. Trans Tech Publ. doi:10.4028/www.scientific.net/amr.393-395.1536

CrossRef Full Text | Google Scholar