Buckling response of functionally graded multilayer graphene platelet-reinforced composite plates with circular/elliptical cutouts supporting on an elastic foundation under normal and shear loads

The present article deals with the buckling response of functionally graded multilayer graphene platelet-reinforced composite (FG-GPL RC) rectangular plates with circular/elliptical cutouts resting on a Winkler-type elastic foundation under uniaxial and biaxial normal and shear loads. Rule of mixtures and the Halpin–Tsai approach are applied to obtain the effective Poisson’s ratio, mass density, and elastic modulus of the reinforced composite. The governing equations are developed by applying the third-order shear deformation plate theory. Then, the finite element procedure is used to solve the problem. Four different types of graphene platelet distributions, namely, UD, FG-X, FG-V, and FG-O, are considered. A broad range of factors such as plate aspect ratio, plate slenderness ratio, applying uniaxial and biaxial normal and shear loads to the plate, several Winkler elastic foundation stiffness parameters, different displacement boundary conditions, the effect of size of the circular cutout and orientation of the elliptical cutout, and the influence of GPL weight fraction are discussed in several tabular and graphical data in detail.

1 Introduction

The increasing usage of composite materials, such as carbon nanotube (CNT) and graphene-reinforced composite (GRC) structures, due to their countless applications and superior material properties, has led to several studies and articles investigating the different aspects and behaviors of these appreciable materials. GRC structures have several advantages, such as lightweight, flexibility, transparency, energy absorbency, and electrical and thermal conductivity, and their foreseeable wide application in different industries has attracted significant attention in recent years. Adding a low content of nanofiller reinforcements with a specific distribution pattern to the matrix can surprisingly improve the structural behavior. Hence, several research studies have been carried out on the structural analyses of shell- and plate-type structures reinforced with graphene platelets (GPLs). Those studies mentioned here are related to the behavior of structures that are reinforced by GPLs. In detail, Song et al. (2018), by applying the first-order shear deformation theory (FSDT), showed that the weight fraction of nanofillers and GPL distribution pattern are two main factors affecting the bending and buckling behaviors of the FG-GPL RC plates. Shen et al. (2018) investigated FG-GRC-laminated cylindrical panels and noticed that the piece-wise FG pattern of graphene reinforcement may enhance the buckling forces and the post-buckling strength. The governing equations for the post-buckling responses of the panels were proposed based on Reddy’s higher-order shear deformation shell theory and von Kármán strain–displacement relationships. Shen et al. (2017) employed the higher-order shear deformation plate theory (HSDT) to present the thermal post-buckling of FG-GPL-laminated plates supporting on an elastic medium. They presented that the critical buckling temperature of the plates may be enhanced by the FG graphene reinforcement distribution pattern of the structure. Song et al. (2017) examined the buckling and post-buckling responses of the uniaxially and biaxially compressed FG-GPL RC plates and revealed that by adding only 1.0 wt% GPLs, the FG-X structure achieved the highest critical buckling force up to 5.55 times that of the neat epoxy plate. In their study, theoretical formulations were proposed based on the FSDT and von Kármán-type nonlinear kinematics and included the effect of an initial geometric imperfection. A two-step perturbation technique was employed to determine the asymptotic post-buckling solutions, and the biaxial compressive post-buckling equilibrium paths of both perfect and imperfect plates simply supported on all edges. Babaei and Asemi (2020) applied the Hamilton principle, FSDT, and finite element method (FEM) to study the influence of the volume fraction of CNTs on the displacements of annular sector plate and observed that enhancing the volume fraction of CNTs from 0.11 to 0.17 causes a reduction of more than 36% in the transverse displacements. Asemi et al. (2020) used the Hamilton principle based on FSDT and FEM to derive the governing equations of motion of FG porous annular sector plates reinforced by GPLs for three various types of porosity patterns. They revealed that in the case of the GPLA pattern, the transverse displacement is decreased by 91% by adding only 1 wt% of GPLs to the metal matrix. Abedini Baghbadorani and Kiani (2021) applied FSDT of shells and Donnell kinematic relationships and Hamilton principle to derive the governing equations for the free vibrations and the boundary conditions of GPL-RC cylindrical shells. They showed that when the inner and outer layers of the GPL-RC cylindrical shells have the maximum content of reinforcements, maximum frequencies are obtained. Thai et al. (2019) proposed the NURBS procedure based on the four-variable refined plate theory to analyze FG-GPL RC plates and proved that the structures with FG-O and FG-X patterns lead to the minimum and maximum amounts of natural frequencies and buckling loads, respectively. Jafari and Kiani (202) presented the free vibration behavior of thick, multilayer composite plates with different distribution patterns of GPLs and obtained the same results as Thai et al. (2019). They applied a quasi-3D plate model which captures the thickness stretching effects and non-uniform shear strains through the thickness. With the aid of the Navier solution, suitable for plates with all edges simply supported, Fourier expansions were implemented for the essential variables of the displacement field. Closed-form expressions were provided to obtain the natural frequencies of FG-GPL RC plates. Yang et al. (2017a) investigated the buckling and post-buckling behaviors of functionally graded multilayer nanocomposite beams reinforced with a low content of GPLs resting on an elastic foundation. The nonlinear governing equations of the beam on an elastic foundation were derived within the framework of the first-order shear deformation beam theory and then converted into a nonlinear algebraic system by using the differential quadrature method. They showed that GPLs with a bigger surface area and comprising fewer single-GPL laminates may provide better reinforcing influence; however, for GPL aspect ratios and width-to-thickness ratios more than 4 and 1000, critical buckling force and post-buckling path will be almost identical. Furthermore, many studies have been implemented to show that functionally graded nanofiller distribution patterns also play a key role in the structural response of composite structures (Pradhan and Phadikar, 2010; Lei et al., 2015; Zhang et al., 2015; Bui et al., 2016; Lin et al., 2017; Ansari et al., 2018; García-Macías et al., 2018; Lin et al., 2018; Muni Rami Reddy et al., 2018; Shahrjerdi and Yavari, 2018; Yang et al., 2018; Nguyen et al., 2019; Thai et al., 2019; Hung et al., 2021; Saiah et al., 2022).

Many studies have investigated the effect of an elastic foundation on the structural behavior of composite structures to show that the existence of an elastic foundation can exhibit better performance of the structure. For example, Asemi et al. (2014) achieved highly accurate results by employing a three-dimensional elasticity-graded element to study the buckling response of FG annular sector plates. Their results revealed that the size and location of buckling deformations are mainly influenced by how the plate is partially rested on the elastic foundation. Shariyat and Asemi (2014b) observed that applying an elastic medium as the foundation leads to higher buckling forces and causes narrower, local, and shorter buckling deformations. Mohammadi et al. (2014) investigated the buckling response of a GPL sheet resting on an elastic foundation subjected to thermal conditions and shear loads using the differential quadrature method (DQM). Fattahi et al. (2019) studied the buckling behavior of GPL sheets resting on an elastic Pasternak and Winkler medium and revealed that critical axial buckling forces of the rested GPL sheet for the Pasternak foundation were greater than those obtained for the Winkler foundation.

Structural members, including plates, beams, and shells, are often subjected to different load conditions that may cause the buckling phenomenon. Several research studies have been conducted to investigate the buckling problem of composite structures under different loading conditions, including uniaxial and biaxial normal and shear loads. For example, Asemi et al. (2013) presented the buckling of heterogeneous FGM plates subjected to different normal and shear forces by applying a 3D elasticity approach. Asemi et al. (2015) applied a 3D elasticity-based graded FEM to study the shear buckling analysis of FGM annular sector plates. Fan et al. (2020) applied the Gurtin–Murdoch surface theory of elasticity to analyze the buckling behavior of FGM skew nanoplates subjected to shear loads.

Composite plates find application as a structural member in various fields, like automobiles, space vehicles, submarines, and many others, where a high strength and stiffness-to-weight ratio are desired. Sometimes, holes and cutouts of various shapes are unavoidable in these types of plates for their proper functioning. These structural members are usually subjected to in-plane loading. With geometrical discontinuities, these composite plates with holes are more vulnerable due to an increase in stress near discontinuities (holes), which results in the buckling phenomenon. Therefore, the buckling analysis of these structures for better safety and evaluation of the load-bearing capacity of these composite plates is essential. Limited studies have been conducted on the structural analyses of these composite structures to find the effect of cutout size and shape on their behavior. For example, Lakshmi Narayana et al. (2018) conducted a numerical study using FEM to show the effects of different shapes of cutouts on the thermal buckling response of graphite/epoxy-laminated plates. They found that for a plate with an elliptical cutout, the values of the critical buckling temperatures are enhanced by increasing the cutout orientation from a horizontal case to a vertical case. Geng et al. (2020) analyzed the buckling of FG-GPL RC plates with a circular hole subjected to normal loads based on the FSDT and FE approaches for three different GPL distribution patterns. Ashrafi et al. (2013) showed that stresses around the circular cutout of FGM plates under biaxial tensions may be considerably decreased by the FG distribution of the material properties. Asemi et al. (2016a) applied FEM to provide mechanical stress distribution of FGM plates around the circular cutout and natural frequencies of the plate. Alashkar et al. (2022) utilized computational modeling to study the effect of circular cutouts’ diameter and arrangements on the buckling response of FGM plates. The obtained results denoted that horizontal arrangements exhibit the highest critical buckling loads and best buckling performance.

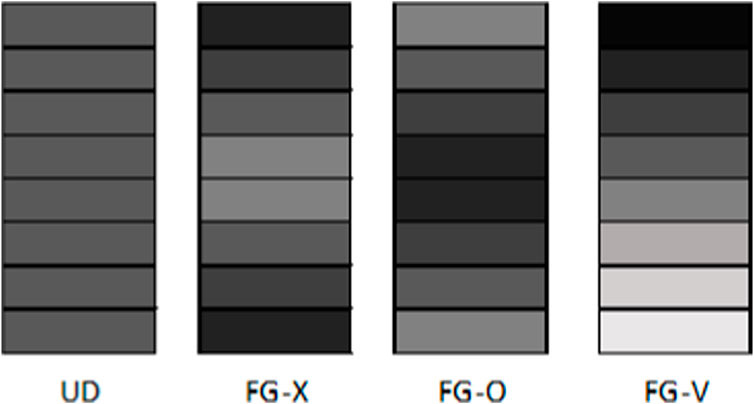
Reviewing relevant articles showed that several research studies have been conducted on the behaviors of the composite structures reinforced by CNTs and GPLs. However, fewer studies have been conducted to study the effects of circular/elliptical cutouts on the buckling response of composite structures, especially FG-GRC plates. Due to the various industrial applications of graphene platelet-reinforced composite plates in mechanical and aerospace engineering, the need to fill the void of how circular and elliptical cutouts influence the buckling response of GPL RC plates is sensed. Particularly, the effect of shear loads and elliptical-shaped cutouts on the buckling response of plates is less investigated. Furthermore, plates on an elastic foundation are common structural elements employed in many civil engineering applications, such as foundations, storage tanks, swimming pools, floor systems of buildings and highways, and airfield pavements. Therefore, the influence of biaxial normal and shear loads and elastic foundation on the buckling response of FG-GPL RC plates with circular/elliptical cutouts is studied for the first time in the present work. In addition, most of the previous studies are based on FSDT and CLPT, which are suitable for moderately thick and thin plates, respectively. FSDT overestimates the buckling loads for thick plates rather than the third-order shear deformation plate theory (TSDT). Hence, in the present study, the governing equations are derived applying the TSDT to investigate the influence of a broad range of factors such as plate aspect ratio, plate width/thickness ratio, size and shape of the cutout, uniaxial and biaxial normal and shear loads, several Winkler elastic foundation stiffness parameters, different boundary conditions, and GPL nanofiller weight fraction on the buckling loads of FG-GPL RC plates. The influence of four major graphene platelet (GPL) distribution patterns, namely, UD, FG-X, FG-V, and FG-O, on the buckling response of plates is investigated. Rule of mixtures and the Halpin–Tsai approach are applied to obtain the effective Poisson’s ratio, mass density, and elastic modulus of the reinforced composite. The finite element procedure is employed to solve the problem.

2 Problem modeling

2.1 Geometry and material properties of an FG-GPL RC plate

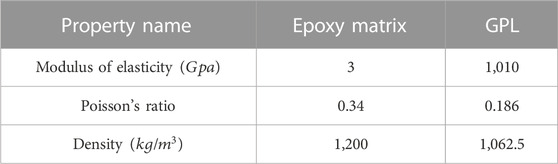
We combine the advantages of both FGM and GPL using a functionally graded graphene platelet-reinforced composite (FG-GPL RC) structure. GPLs and isotropic epoxy are considered the reinforcement and the matrix of the composite media, respectively. An FG-GPL RC plate with length a, width b, total thickness h, and a circular cutout with radius r, as shown in Figure 1, is assumed in this paper. The plate is resting on a Winkler elastic foundation, where k_w indicates the stiffness of the Winkler elastic foundation. The plate is constructed of $N_L$ layers with identical thickness t. GPLs in each individual layer are uniformly distributed, but their volume fraction changes from layer to layer, which leads to a functionally graded pattern. Therefore, each individual layer of the GPL RC plate is isotropic and homogeneous. Figure 2 shows the five uniform or functionally graded distribution patterns of GPL nanofillers. UD denotes the uniform distribution, and FG-X, FG-O, FG-V, and FG-Λ show the functionally graded patterns of GPLs. The UD distribution 1) denotes a homogeneous and isotropic multilayer plate in which nanofillers are uniformly dispersed across the thickness of the plate. The GPL volume fraction is dispersed symmetrically and linearly in FG-X 2) and FG-O 3) distributions, in which the GPL amount gradually changes from the top or bottom surfaces to the middle layer. The unsymmetrical patterns are FG-V 4) and FG-Λ 5) distributions. An adequately large number of layers, $\left(N_L\right)$, leads to a gentle and connected distribution pattern along the plate thickness. The volume fraction $V_{GPL}$ of the kth layer for different GPL patterns is given as follows (Jafari and Kiani, 2021):

$\left\{\begin{array}{l}{UD:V}_{GPL}^{\left(k\right)}=V_{GPL}^{*},\\ {FG-X:V}_{GPL}^{\left(k\right)}=2V_{GPL}^{*}\frac{\left|2k-N_L-1\right|}{N_L},\\ {FG-O:V}_{GPL}^{\left(k\right)}=2V_{GPL}^{*}\left(1-\frac{\left|2k-N_L-1\right|}{N_L}\right),\\ {FG-V:V}_{GPL}^{\left(k\right)}=V_{GPL}^{*}\frac{2k-1}{N_L},\end{array}\right.(1)$

FIGURE 1

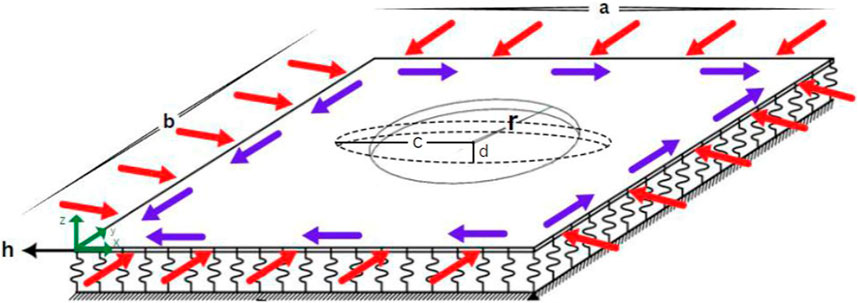
FIGURE 1. Geometrical schematic of the FG-GPL RC plate with circular/elliptical cutouts under uniaxial and biaxial normal and shear loads resting on the Winkler elastic foundation.

FIGURE 2

FIGURE 2. Various GPL patterns in an FG-GPL RC plate.

where $N_L$ is total number of layers and assumed to be an even number. $V_{GPL}^{*}$ is the average magnitude of the volume fraction of GPLs and can be evaluated based on the weight fraction of GPLs $\left(W_{GPL}\right)$, density of the matrix $\left({\rho }_m\right)$, and GPLs $\left({\rho }_{GPL}\right)$.

$V_{GPL}^{*}=\frac{W_{GPL}}{W_{GPL}+\frac{{\rho }_{GPL}}{{\rho }_m}-\left(1-W_{GPL}\right)}.(2)$

In the aforementioned equations, the subscripts (m) and (GPL) stand for the matrix and GPLs, respectively. The effective elastic modulus of the nanocomposite plate is obtained through the Halpin–Tsai model, which is dependent on the geometry of the nanoplatelets (Ma and Jin, 2022; Mollaei et al., 2023). Hence, the elasticity modulus of the kth layer of the plate, which is denoted by $E^{\left(k\right)}$, is regarded as

$E^{\left(k\right)}=\frac{3}{8}\left(\frac{1+{\xi }_L^{GPL}{\eta }_L^{GPL}{V}_{GPL}^{\left(k\right)}}{1-{\eta }_L^{GPL}{V}_{GPL}^{\left(k\right)}}\right)E_m+\frac{5}{8}\left(\frac{1+{\xi }_W^{GPL}{\eta }_W^{GPL}{V}_{GPL}^{\left(k\right)}}{1-{\eta }_W^{GPL}{V}_{GPL}^{\left(k\right)}}\right)E_m.(3)$

In Eq. 3, the elasticity modulus of the matrix is shown by $E_m$. The two parameters ${\eta }_L^{GPL}$ and ${\eta }_W^{GPL}$ in Eq. 3 depend on the elastic properties of the constituents and the geometry of the platelets:

${\eta }_L^{GPL}=\frac{E_{GPL}-E_m}{E_{GPL}+{\xi }_L^{GPL}{E}_m},(4)$

${\eta }_W^{GPL}=\frac{E_{GPL}-E_m}{E_{GPL}+{\xi }_W^{GPL}{E}_m}.(5)$

The other two parameters, ${\xi }_L^{GPL}$ and ${\xi }_W^{GPL}$, in Eqs 4, 5 depend on the geometrical dimensions of the nanofillers:

${\xi }_L^{GPL}=\frac{a_{GPL}}{t_{GPL}},(6)$

${\xi }_W^{GPL}=\frac{b_{GPL}}{t_{GPL}},(7)$

where $a_{GPL}$, $b_{GPL}$, and $t_{GPL}$ are assumed to be the length, width, and thickness of GPLs, respectively.

The simple rule of mixture estimation is used to evaluate the Poisson’s ratio and the mass density of the kth layer of the nanocomposite plate (Cong and Duc, 2018; Esmaeili et al., 2022; Farsadi et al., 2022):

$v^{\left(k\right)}=v_{GPL}{V}_{GPL}^{\left(k\right)}+v_m{V}_m^{\left(k\right)},(8)$

${\rho }^{\left(k\right)}={\rho }_{GPL}{V}_{GPL}^{\left(k\right)}+{\rho }_m{V}_m^{\left(k\right)},(9)$

where

$V_m^{\left(k\right)}=1-V_{GPL}^{\left(k\right)},(10)$

where $v_{GPL}$, ${\rho }_{GPL}$ and $v_m$, ${\rho }_m$ are the Poisson’s ratio and mass density of the GPL and matrix, respectively.

In addition, the rigidity modulus $G^{\left(k\right)}$ of the kth layer is as follows:

$G^{\left(k\right)}=\frac{E^{\left(k\right)}}{2\left(1+v^{\left(k\right)}\right)}.(11)$

2.2 Governing equations of an FG-GL RC plate

The governing equations of the plate resting on an elastic foundation are derived applying the third-order shear deformation plate theory. Hence, the displacement field $\left(u,v,w\right)$ is assumed as

$u\left(x,y,z\right)=u_0\left(x,y\right)+\frac{5}{4}\left(z-\frac{4}{3h^2}{z}^3\right){\varnothing }_x\left(x,y\right)+\left(\frac{1}{4}z-\frac{5}{3h^2}{z}^3\right)w_{0,x},(12)$

$v\left(x,y,z\right)=v_0\left(x,y\right)+\frac{5}{4}\left(z-\frac{4}{3h^2}{z}^3\right){\varnothing }_y\left(x,y\right)+\left(\frac{1}{4}z-\frac{5}{3h^2}{z}^3\right)w_{0,y},(13)$

$w\left(x,y,z\right)=w_0\left(x,y\right),(14)$

where $u_0$, $v_0$, and $w_0$ represent the displacements at $z=0$ (the midplane of a plate); ${\varnothing }_x$ and ${\varnothing }_y$ are the transverse normal rotations of the $y$ and $x$ axes. The finite element procedure is used to estimate the eigenvalue buckling forces of the FG-GPL RC plate. A four-node element with seven DOFs per node is employed for modeling the plate. The displacement field of an individual node $i$ is as follows:

$Q_e^i={\left\{u_{0i}{v}_{0i}{w}_i{\varnothing }_{xi}{\varnothing }_{yi}\frac{{\partial w}_{0i}}{\partial x}\frac{{\partial w}_{0i}}{\partial y}\right\}}^T,i=1,\dots ,4.(15)$

Among the displacement components, $w$ is estimated by the Hermitian shape functions and the other components by the Lagrangian functions. Hence, the displacement components may be presented as follows:

$\left\{u_0,v_0,{\varnothing }_x,{\varnothing }_y\right\}=\left\{{\displaystyle \sum _{i=1}^4}{\psi }_i{u}_{oi},{\displaystyle \sum _{i=1}^4}{\psi }_i{v}_{oi},{\displaystyle \sum _{i=1}^4}{\psi }_i{\varnothing }_{xi},{\displaystyle \sum _{i=1}^4}{\psi }_i{\varnothing }_{yi}\right\},(16)$

$w={\mathrm{\Xi }}_1{w}_{01}+{\mathrm{\Xi }}_2\frac{{\partial w}_{01}}{\partial x}+{\mathrm{\Xi }}_3\frac{{\partial w}_{01}}{\partial y}+\dots +{\mathrm{\Xi }}_{10}{w}_{04}+{\mathrm{\Xi }}_{11}\frac{{\partial w}_{04}}{\partial x}+{\mathrm{\Xi }}_{12}\frac{{\partial w}_{04}}{\partial y},(17)$

$\frac{\partial w}{\partial x}=\frac{\partial }{\partial x}\left({\mathrm{\Xi }}_1{w}_{01}+{\mathrm{\Xi }}_2\frac{{\partial w}_{01}}{\partial x}+{\mathrm{\Xi }}_3\frac{{\partial w}_{01}}{\partial y}+\dots +{\mathrm{\Xi }}_{10}{w}_{04}+{\mathrm{\Xi }}_{11}\frac{{\partial w}_{04}}{\partial x}+{\mathrm{\Xi }}_{12}\frac{{\partial w}_{04}}{\partial y}\right),(18)$

$\frac{\partial w}{\partial y}=\frac{\partial }{\partial y}\left({\mathrm{\Xi }}_1{w}_{01}+{\mathrm{\Xi }}_2\frac{{\partial w}_{01}}{\partial x}+{\mathrm{\Xi }}_3\frac{{\partial w}_{01}}{\partial y}+\dots +{\mathrm{\Xi }}_{10}{w}_{04}+{\mathrm{\Xi }}_{11}\frac{{\partial w}_{04}}{\partial x}+{\mathrm{\Xi }}_{12}\frac{{\partial w}_{04}}{\partial y}\right),(19)$

where ${\psi }_i$ is the Lagrangian shape function and ${\mathrm{\Xi }}_i$ is the Hermitian function. The components of ${\psi }_i$ and ${\mathrm{\Xi }}_i$ are presented in Appendix A.

The displacement field of an element is approximated by using its nodal values:

${\mathit{U}}_{\mathbf{0}}={\mathbf{\Delta }}_{\mathit{{\rm H}}}{\mathit{Q}}_{\mathit{e}},(20)$

where ${\mathbf{\Delta }}_{\mathit{{\rm H}}}$ is the shape function matrix; ${\mathit{U}}_{\mathbf{0}}$ and ${\mathit{Q}}_{\mathit{e}}$ are expressed as follows:

${\mathbf{U}}_{\mathbf{0}}={\left\{u_0,v_0,w_0,{\varnothing }_x,{\varnothing }_y,w_{0,x},w_{0,y}\right\}}^T,(21)$

${\mathit{Q}}_{\mathit{e}}={\left\{{\mathit{Q}}_e^1{\mathit{Q}}_e^2{\mathit{Q}}_e^3{\mathit{Q}}_e^4\right\}}^T.(22)$

The strains of the plate when it is subjected to in-plane pre-buckling loads may be expressed as

$\left\{\begin{array}{c}\epsilon \\ \gamma \end{array}\right\}=\left\{\begin{array}{c}{\epsilon }^{\left(0\right)}\\ {\gamma }^{\left(0\right)}\end{array}\right\}+z\left\{\begin{array}{c}{\epsilon }^{\left(1\right)}\\ 0\end{array}\right\}+z^2\left\{\begin{array}{c}0\\ {\gamma }^{\left(2\right)}\end{array}\right\}+z^3\left\{\begin{array}{c}{\epsilon }^{\left(3\right)}\\ 0\end{array}\right\}+\left\{{\epsilon }_P^G\right\},(23)$

with

${\epsilon }^{\left(0\right)}=\left\{\begin{array}{c}\frac{{\partial u}_0}{\partial x}\\ \frac{{\partial v}_0}{\partial y}\\ \frac{{\partial u}_0}{\partial y}+\frac{{\partial v}_0}{\partial x}\end{array}\right\},{\epsilon }^{\left(1\right)}=\frac{1}{4}\left\{\begin{array}{c}5\left(\frac{{\partial \varnothing }_x}{\partial x}+\frac{{\partial }^{2}w}{\partial x^2}\right)\\ 5\left(\frac{{\partial \varnothing }_y}{\partial y}+\frac{{\partial }^{2}w}{\partial y^2}\right)\\ \left(\frac{{\partial \varnothing }_x}{\partial y}+2\frac{{\partial }^{2}w}{\partial x\partial y}+\frac{{\partial \varnothing }_y}{\partial x}\right)\end{array}\right\},{\epsilon }^{\left(3\right)}=\frac{-5}{{3h}^2}\left\{\begin{array}{c}\frac{{\partial \varnothing }_x}{\partial x}+\frac{{\partial }^{2}w}{\partial x^2}\\ \frac{{\partial \varnothing }_y}{\partial y}+\frac{{\partial }^{2}w}{\partial y^2}\\ \frac{{\partial \varnothing }_x}{\partial y}+2\frac{{\partial }^{2}w}{\partial x\partial y}+\frac{{\partial \varnothing }_y}{\partial x}\end{array}\right\},(24)$

${\gamma }^{\left(0\right)}=\frac{1}{4}\left\{\begin{array}{c}{5\varnothing }_x+\frac{\partial w}{\partial x}\\ {5\varnothing }_y+\frac{\partial w}{\partial y}\end{array}\right\},{\gamma }^{\left(2\right)}=\frac{-5}{h^2}\left\{\begin{array}{c}{\varnothing }_x+\frac{\partial w}{\partial x}\\ {\varnothing }_y+\frac{\partial w}{\partial y}\end{array}\right\};{\epsilon }_P^G=\left\{\begin{array}{c}\frac{1}{2}{\left(\frac{\partial w}{\partial x}\right)}^2+\frac{z^2}{2}{\left(\frac{{\partial \varnothing }_x}{\partial x}\right)}^2+\frac{z^2}{2}{\left(\frac{{\partial \varnothing }_y}{\partial x}\right)}^2\\ \frac{1}{2}{\left(\frac{\partial w}{\partial y}\right)}^2+\frac{z^2}{2}{\left(\frac{{\partial \varnothing }_x}{\partial y}\right)}^2+\frac{z^2}{2}{\left(\frac{{\partial \varnothing }_y}{\partial y}\right)}^2\\ \begin{array}{c}\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}+z^2\frac{{\partial \varnothing }_x}{\partial x}\frac{{\partial \varnothing }_x}{\partial y}+z^2\frac{{\partial \varnothing }_y}{\partial x}\frac{{\partial \varnothing }_y}{\partial y}\\ 0\\ 0\end{array}\end{array}\right\}.(25)$

By substituting Eq. 15 into Eqs 24, 25, the strain components may be presented as

$\epsilon =\left({\mathbf{\Delta }}_1+{\mathbf{\Delta }}_2+{\mathbf{\Delta }}_3\right){\mathit{Q}}_{\mathit{e}},\gamma =\left({\mathbf{\Delta }}_4+{\mathbf{\Delta }}_5\right){\mathit{Q}}_{\mathit{e}},(26)$

with

${\mathbf{\Delta }}_1={\displaystyle \sum _i^4}\left[\begin{array}{ccccc}{\psi }_{i,x}& 0& 0& 0& 0\\ 0& {\psi }_{i,y}& 0& 0& 0\\ {\psi }_{i,y}& {\psi }_{i,x}& 0& 0& 0\end{array}\right],(27)$

${\mathbf{\Delta }}_2=\frac{1}{4}{\displaystyle \sum _{i=1}^4}\left[\begin{array}{ccccccc}0& 0& {\left({\mathrm{\Xi }}_{\left(3i-2\right),x}\right)}_{,x}& {5\psi }_{i,x}& 0& {\left({\mathrm{\Xi }}_{\left(3i-1\right),x}\right)}_{,x}& {\left({\mathrm{\Xi }}_{\left(3i\right),x}\right)}_{,x}\\ 0& 0& {\left({\mathrm{\Xi }}_{\left(3i-2\right),y}\right)}_{,y}& 0& 5{\psi }_{i,y}& {\left({\mathrm{\Xi }}_{\left(3i-1\right),y}\right)}_{,y}& {\left({\mathrm{\Xi }}_{\left(3i\right),y}\right)}_{,y}\\ 0& 0& 2{\left({\mathrm{\Xi }}_{\left(3i-2\right),x}\right)}_{,y}& 5{\psi }_{i,y}& 5{\psi }_{i,x}& 2{\left({\mathrm{\Xi }}_{\left(3i-1\right),x}\right)}_{,y}& 2{\left({\mathrm{\Xi }}_{\left(3i\right),x}\right)}_{,y}\end{array}\right],(28)$

${\mathbf{\Delta }}_4=\frac{5}{4}{\displaystyle \sum _{i=1}^4}\left[\begin{array}{ccccccc}0& 0& {\mathrm{\Xi }}_{\left(3i-2\right),x}& {\psi }_i& 0& {\mathrm{\Xi }}_{\left(3i-1\right),x}& {\mathrm{\Xi }}_{3i,x}\\ 0& 0& {\mathrm{\Xi }}_{\left(3i-2\right),y}& 0& {\psi }_i& {\mathrm{\Xi }}_{\left(3i-1\right),y}& {\mathrm{\Xi }}_{3i,y}\end{array}\right],(29)$

${\mathbf{\Delta }}_5=-\frac{5}{h^2}{\displaystyle \sum _{i=1}^4}\left[\begin{array}{ccccccc}0& 0& {\mathrm{\Xi }}_{\left(3i-2\right),x}& {\psi }_i& 0& {\mathrm{\Xi }}_{\left(3i-1\right),x}& {\mathrm{\Xi }}_{3i,x}\\ 0& 0& {\mathrm{\Xi }}_{\left(3i-2\right),y}& 0& {\psi }_i& {\mathrm{\Xi }}_{\left(3i-1\right),y}& {\mathrm{\Xi }}_{3i,y}\end{array}\right].(30)$

The stress–strain relationships based on Hooke’s law are as follows:

$\sigma ={\mathit{D}}_m\left({\epsilon }^{\left(0\right)}+{z\epsilon }^{\left(1\right)}+z^3{\epsilon }^{\left(3\right)}\right),\mathit{\tau }={\mathit{D}}_s\left({\gamma }^{\left(0\right)}+z^2{\gamma }^{\left(2\right)}\right),(31)$

with

$\sigma ={\left\{{\sigma }_x,{\sigma }_y{,\tau }_{xy}\right\}}^T,\tau ={\left\{{\tau }_{xz},{\tau }_{yz}\right\}}^T,(32)$

${\mathit{D}}_m=\frac{E}{1-v^2}\left[\begin{array}{ccc}1& v& 0\\ v& 1& 0\\ 0& 0& \frac{\left(1-v\right)}{2}\end{array}\right],{\mathit{D}}_s=\frac{E}{2\left(1+v\right)}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].(33)$

The elastic strain energy of the plate and Winkler elastic foundation is written as follows:

$U=\frac{1}{2}{\displaystyle \sum ^{N_E}}{\displaystyle \underset{V_e}{\int }}{\epsilon }^T\sigma dV+\frac{1}{2}{k}_w{\displaystyle \sum ^{N_E}}{\displaystyle \underset{S_e}{\int }}{w}^{2}dS(34)$

or in the matrix form

$U=\frac{1}{2}{\displaystyle \sum ^{N_E}}{\mathit{Q}}_e^T{\mathit{K}}_e^p{\mathit{Q}}_e+\frac{1}{2}{\displaystyle \sum ^{N_E}}{\mathit{Q}}_e^T{\mathit{K}}_e^w{\mathit{Q}}_e,(35)$

where the stiffness matrices corresponding to the strain energy of deformation of element ${\mathit{K}}_e^p$ and elastic foundation ${\mathit{K}}_e^w$ are given as

${\mathit{K}}_e^p={\displaystyle \underset{S_e}{\int }}\left[\begin{array}{c}{\mathbf{\Delta }}_1^T\mathit{A}{\mathbf{\Delta }}_{\mathbf{1}}+{\mathbf{\Delta }}_1^T\mathit{{\rm B}}{\mathbf{\Delta }}_{\mathbf{2}}+{\mathbf{\Delta }}_1^T\mathit{E}{\mathbf{\Delta }}_{\mathbf{3}}+{\mathbf{\Delta }}_2^T\mathit{{\rm B}}{\mathbf{\Delta }}_{\mathbf{1}}+{\mathbf{\Delta }}_2^T\mathit{D}{\mathbf{\Delta }}_{\mathbf{2}}+{\mathbf{\Delta }}_2^T\mathit{F}{\mathbf{\Delta }}_{\mathbf{3}}+{\mathbf{\Delta }}_3^T\mathit{E}{\mathbf{\Delta }}_{\mathbf{1}}+\\ {\mathbf{\Delta }}_3^T\mathit{F}{\mathbf{\Delta }}_{\mathbf{2}}+{\mathbf{\Delta }}_3^T\mathit{F}{\mathbf{\Delta }}_{\mathbf{2}}+{\mathbf{\Delta }}_3^T\mathit{H}{\mathbf{\Delta }}_{\mathbf{3}}+{\mathbf{\Delta }}_4^T{\mathit{A}}^{\prime }{\mathbf{\Delta }}_{\mathbf{4}}+{\mathbf{\Delta }}_4^T{\mathit{{\rm B}}}^{\prime }{\mathbf{\Delta }}_{\mathbf{5}}+{\mathbf{\Delta }}_5^T{\mathit{{\rm B}}}^{\prime }{\mathbf{\Delta }}_{\mathbf{4}}+{\mathbf{\Delta }}_5^T{\mathit{D}}^{\prime }{\mathbf{\Delta }}_{\mathbf{5}}\end{array}\right]dS,(36)$

${\mathit{K}}_e^w={\displaystyle \underset{S_e}{\int }}{\mathbf{\Delta }}_6^T{k}_w{\mathbf{\Delta }}_{\mathbf{6}}dS,(37)$

${\mathbf{\Delta }}_{\mathbf{6}}={\left[\begin{array}{ccccccccccccccc}0& 0& 0& 0& 0& 0& 0& ...& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& ...& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& {\mathrm{\Xi }}_1& 0& 0& {\mathrm{\Xi }}_2& {\mathrm{\Xi }}_3& ...& 0& 0& {\mathrm{\Xi }}_{10}& 0& 0& {\mathrm{\Xi }}_{11}& {\mathrm{\Xi }}_{12}\\ 0& 0& 0& 0& 0& 0& 0& ...& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& ...& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& {\mathrm{\Xi }}_{1,x}& 0& 0& {\mathrm{\Xi }}_{2,x}& {\mathrm{\Xi }}_{3,x}& ...& 0& 0& {\mathrm{\Xi }}_{10,x}& 0& 0& {\mathrm{\Xi }}_{11,x}& {\mathrm{\Xi }}_{12,x}\\ 0& 0& {\mathrm{\Xi }}_{1,y}& 0& 0& {\mathrm{\Xi }}_{2,y}& {\mathrm{\Xi }}_{3,y}& ...& 0& 0& {\mathrm{\Xi }}_{10,y}& 0& 0& {\mathrm{\Xi }}_{11,y}& {\mathrm{\Xi }}_{12,y}\end{array}\right]}_{7*24},(38)$

where

$\left(\mathit{A},\mathit{B},\mathit{D},\mathit{E},\mathit{F},\mathit{H}\right)={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left(1,z,z^2,z^3,z^4{,z}^6\right){\mathit{D}}_{m}dz,(39)$

$\left({\mathit{A}}^{\prime },{\mathit{B}}^{\prime },{\mathit{D}}^{\prime }\right)={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left(1,z^2,z^4\right){\mathit{D}}_{s}dz.(40)$

The geometric strain energy due to in-plane pre-buckling loads is obtained as

$U^G=\frac{1}{2}{\displaystyle \sum ^{N_E}}{\displaystyle \underset{V_e}{\int }}{\widehat{\sigma }}_0^T{\epsilon }_P^{G}dV.(41)$

By substituting the geometric strain into Eq. 41, we obtain

$U^G=\frac{1}{2}{\displaystyle \sum ^{N_E}}{\displaystyle \underset{S_e}{\int }}{\left({\overline{\epsilon }}_P^G\right)}^T{\sigma }_0{\overline{\epsilon }}_P^{G}dS,(42)$

where

${\overline{\epsilon }}_P^G=\left\{\begin{array}{c}{w}_{0,x}\\ w_{0,y}\\ \begin{array}{c}{\varnothing }_{x,x}\\ {\varnothing }_{x,y}\\ \begin{array}{c}{\varnothing }_{y,x}\\ {\varnothing }_{y,y}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& \frac{\partial }{\partial x}& 0& 0& 0\\ 0& 0& 0& \frac{\partial }{\partial y}& 0& 0& 0\\ 0& 0& 0& 0& \frac{\partial }{\partial x}& 0& 0\\ 0& 0& 0& 0& \frac{\partial }{\partial y}& 0& 0\end{array}\right]\left\{\begin{array}{c}u\\ v\\ \begin{array}{c}w\\ {\varnothing }_x\\ {\varnothing }_y\\ w_{0,x}\\ w_{0,y}\end{array}\end{array}\right\}={\mathbf{\Delta }}_P^G{\mathit{Q}}_e,(43)$

${\sigma }_0=diag\left(h\stackrel{\sim }{\sigma },\frac{h^3}{12}\stackrel{\sim }{\sigma },\frac{h^3}{12}\stackrel{\sim }{\sigma }\right),\stackrel{\sim }{\sigma }={\left[{\sigma }_x^0{\tau }_{xy}^0;{\tau }_{xy}^0{\sigma }_y^0\right]}^T.(44)$

Then, Eq. 42 becomes

$U^G=\frac{1}{2}{\displaystyle \sum ^{N_E}}{\mathit{Q}}_e^T{\mathit{K}}_e^{Gp}{\mathit{Q}}_e,(45)$

with

${\mathit{K}}_e^{Gp}={\displaystyle \underset{S_e}{\int }}{\left({\mathbf{\Delta }}_P^G\right)}^T{\sigma }_0{\mathbf{\Delta }}_P^{G}dS.(46)$

For the buckling problem, after assembly of element matrices, we derive the following equation:

$\left\{K^P+K^w-{\lambda }_b\left(K^{GP}\right)\right\}Q=0,(47)$

where $K^P$, $K^w$, and $K^{GP}$ are the global stiffness matrix, stiffness matrix of the elastic foundation, and global geometric stiffness matrix, respectively. Eq. 47 should be solved to obtain the buckling mode shapes and buckling forces ${\lambda }_b$.

3 Parametric and comparison studies

A FG-GPL RC plate, as shown in Figure 1, with width $b=1m$ is considered. As studied in Song et al. (2017), Thai et al. (2019), and Jafari and Kiani (2021), results and values for free vibration and buckling analysis of a functionally graded multilayer GPL RC plate with a total number of layers $N_L$ ≥10 provide accurate and acceptable results. In the present study, to achieve more accurate results, the total number of layers is considered to be $N_L$ = 20. Other required data, geometric ratios, and boundary conditions are given in each table. GPL nanofillers considered in this paper have a length of $a_{\text{GPL}}$ = 2.5 μm, width of ${\mathrm{b}}_{\text{GPL}}$ = 1.5 μm, and thickness of ${\mathrm{t}}_{\text{GPL}}$ = 1.5 nm. The other required material properties such as elastic modulus and Poisson’s ratio of epoxy matrix and GPL reinforcement are provided in Table 1.

TABLE 1

TABLE 1. Mechanical properties of the epoxy matrix and GPLs.

Three boundary conditions for different loadings are considered:

$\text{Clamped\hspace{0.17em}for\hspace{0.17em}normal\hspace{0.17em}loads}:\left\{\begin{array}{c}\text{At\hspace{0.17em}}\mathrm{x}=0,\mathrm{a}:\mathrm{v}=\mathrm{w}={\varnothing }_x={\varnothing }_y=w_{0,x}=w_{0,y}=0,\\ \text{At\hspace{0.17em}}\mathrm{y}=0,\mathrm{b}:\mathrm{u}=\mathrm{w}={\varnothing }_x={\varnothing }_y=w_{0,x}=w_{0,y}=0,\end{array}\right.(48)$

$\text{Simply}-\text{supported\hspace{0.17em}for\hspace{0.17em}normal\hspace{0.17em}loads}:\left\{\begin{array}{c}\text{At\hspace{0.17em}}\mathrm{x}=0,\mathrm{a}:\mathrm{v}=\mathrm{w}={\varnothing }_y=w_{0,y}=0,\\ \text{At\hspace{0.17em}}\mathrm{y}=0,\mathrm{b}:\mathrm{u}=\mathrm{w}={\varnothing }_x=w_{0,y}=0,\end{array}\right.(49)$

$\text{Clamped\hspace{0.17em}for\hspace{0.17em}shear\hspace{0.17em}loads}:\left\{\begin{array}{c}\text{At\hspace{0.17em}}\mathrm{x}=0,\mathrm{a}:\mathrm{u}=\mathrm{w}={\varnothing }_x={\varnothing }_y=w_{0,x}=w_{0,y}=0,\\ \text{At\hspace{0.17em}}\mathrm{y}=0,\mathrm{b}:\mathrm{v}=\mathrm{w}={\varnothing }_x={\varnothing }_y=w_{0,x}=w_{0,y}=0.\end{array}\right.(50)$

3.1 Verification of results

In order to validate the accuracy of the results of the present study, the critical buckling load ratios $\left(N_{cr}^C/N_{cr}^M\right)$ are recalculated and compared as shown in Table 2 with those from Song et al. (2017). A comparative study is carried out for the critical buckling load ratios of a simply supported FG-GPL RC plate without cutouts and with the same material properties listed in Table 1. Here, $N_{cr}^C$ and $N_{cr}^M$ are critical buckling loads of the plates with and without GPLs, respectively. Geometric dimensions of the plate are $a=0.45m$, $a/b=1$, and $a/h=10$. The number of layers, $N=10$, and 1.0 wt% GPLs are used for comparing results. It can be seen that the present results are in good agreement with those obtained by Song et al. (2017).

TABLE 2

TABLE 2. Comparison of the critical buckling load ratio ($N_{cr}^C/N_{cr}^M$) for a simply supported FG-GPL RC plate under uniaxial compression.

3.2 Numerical results and discussion for buckling loads of an FG-GPL RC plate with circular/elliptical cutouts

In this section, several numerical examples are demonstrated to study the effects of different factors on the buckling behavior of an FG-GPL RC plate with a cutout.

The effect of different thickness ratios ($b/h$) and GPL patterns on the buckling response of a multilayered FG-GPL RC plate with a circular cutout under uniaxial compression is shown in Table 3. The cutout radius is assumed to be $r/b=0.2$ and the plate aspect ratio is $a/b=1$, while the plate is fully clamped at all edges. The first four buckling loads are reported in Table 3. This table reveals that with the same volume fraction and same width-to-thickness ratio, the FG-X distribution pattern results in the highest buckling values, while the FG-O distribution pattern results in the lowest values. Hence, UD and FG-V distribution patterns result in intermediate values. In addition, results show that when the plate slenderness ratio increases, the buckling loads decrease, as expected. The influence of GPL weight fraction and distribution pattern of nanofillers on the buckling loads of the FG-GPL RC plate with a circular cutout is provided in Table 4. The buckling loads of the pure epoxy plate are tabulated for comparison purposes. As can be seen in the table, by dispersing only a low amount of GPL nanofillers, the buckling loads can remarkably improve. By dispersion of only 0.5 wt% and 1.0 wt% GPLs for the FG-X plate, the buckling load enhanced 2.97 and 4.84 times, respectively. The effects of two different boundary conditions and GPL patterns on the buckling loads of the plate under uniaxial compression are compared in Table 5. This table shows the first four buckling loads of the plate for $a/b=1$, $b/h=20$, and circular cutout radius $r/b=0.2$. As can be seen in this table, buckling forces are higher for the boundary conditions that restrict more degrees of freedom (DOFs). Values tabulated in Table 6 are provided to indicate the effect of the $a/b$ ratio and GPL pattern on the buckling load results of the FG-GPL RC clamped plate with a circular cutout under uniaxial load. Results denote that by increasing the plate aspect ratio from 1 to 2, the buckling loads enhanced up to 99.6% for the FG-X plate, but by changing the aspect ratio from 2 to 4, the buckling loads decreased by 7.8%. This can be justified by investigating the pre-buckling stresses of the plates with different aspect ratios. In this case, for plates with a/b = 4, the magnitude of the compressive stresses around the hole is more than the plates with a/b = 2. Results of Tables 3–6 denote that the stiffness of the outer layers generally has the most remarkable effect on the stiffness of the composite structure. Therefore, as shown previously, the structure with the FG-X gradient pattern shows the highest stiffness and buckling capabilities, and UD, FG-V, and FG-O patterns in the sequence have lower values.

TABLE 3

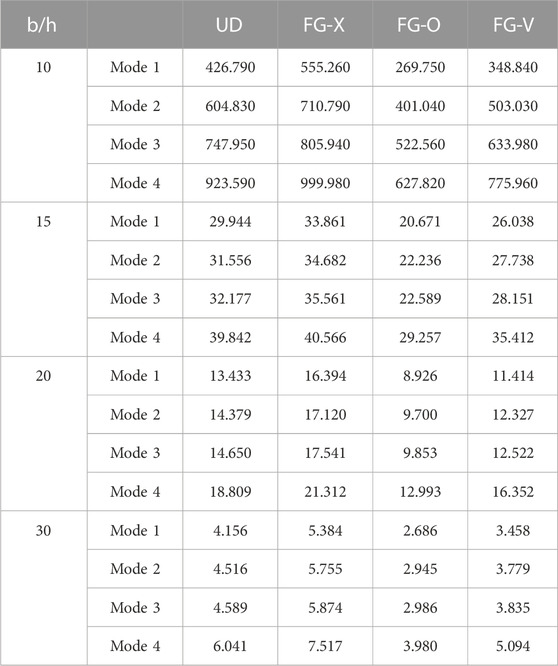
TABLE 3. Effect of the b/h ratio on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($a/b=1$; $r/b=0.2$, CCCC, uniaxial load, and 1.0 wt%).

TABLE 4

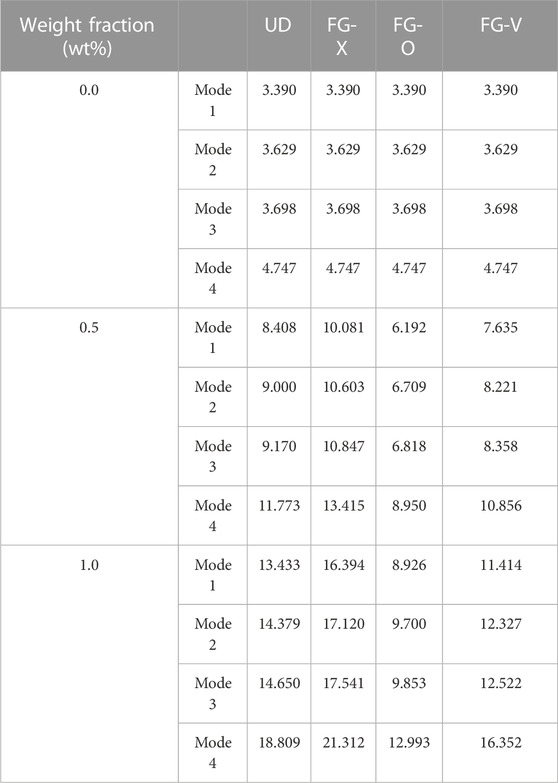
TABLE 4. Effect of the GPL weight fraction and GPL pattern on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($a/b=1$; $b/h=20$; $r/b=0.2$, CCCC, and uniaxial load).

TABLE 5

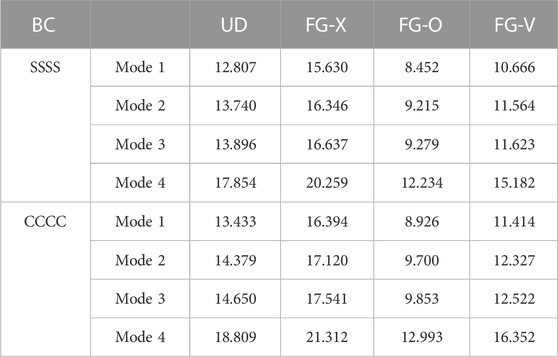
TABLE 5. Effect of different boundary conditions and GPL patterns on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($a/b=1$; $b/h=20$; $r/b=0.2$, uniaxial load, and 1.0 wt%).

TABLE 6

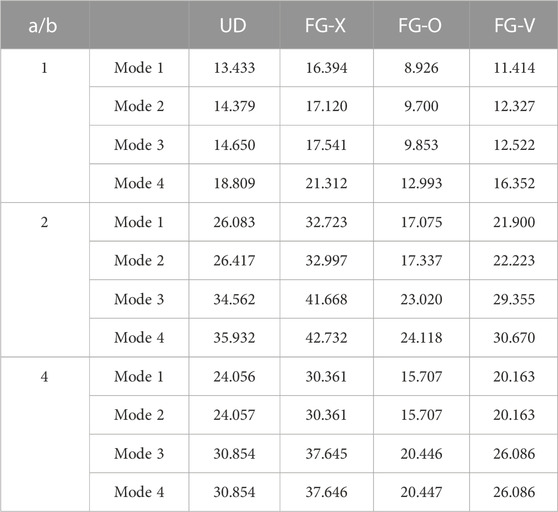
TABLE 6. Effect of the plate aspect ratio and GPL pattern on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($b/h=20$; $r/b=0.2$, CCCC, uniaxial load, and $1.0wt.\%$).

Table 7 presents the buckling loads for three different radiuses of the circular cutout of the FG-GPL RC plate under uniaxial load. As expected, with the reduction in the cutout radius, the buckling loads are increased. For example, by increasing the cutout radius-to-width ratio ($r/b)$ from 0.1 to 0.3, the buckling loads are decreased by 22.3%. This is due to the fact that for larger cutouts, the pre-buckling compressive stresses are more than smaller cutouts. Table 8 lists the first four buckling loads for the FG-GPL RC plate under uniaxial load with a circular cutout resting on the Winkler-type elastic foundation. Values are provided for several elastic foundation stiffness parameters and a plate with CCCC supports. The comparison of the values in Table 8 with those without an elastic foundation (Table 3) denotes that applying an elastic foundation postpones the buckling phenomenon. For example, the buckling loads are increased by 42.6% for the FG-GPL RC plate when the elastic foundation stiffness is increased from 0 to 1 $\left(\raisebox{1ex}{$GN$}\!\left/ \!\raisebox{-1ex}{$m^3$}\right.\right)$.

TABLE 7

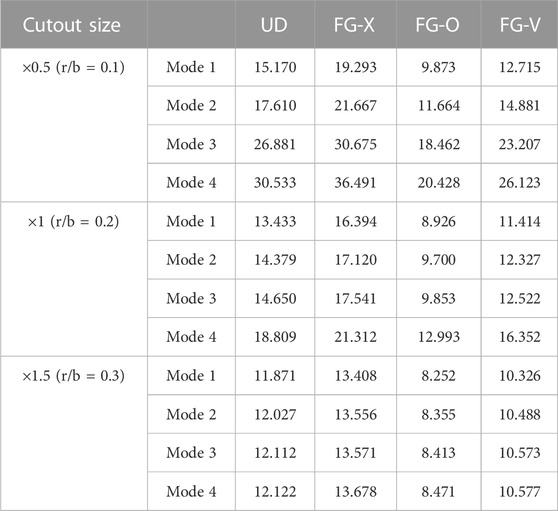
TABLE 7. Effect of the circular cutout radius and GPL pattern on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($a/b=1$; $b/h=20$, CCCC, uniaxial load, and 1.0 wt%).

TABLE 8

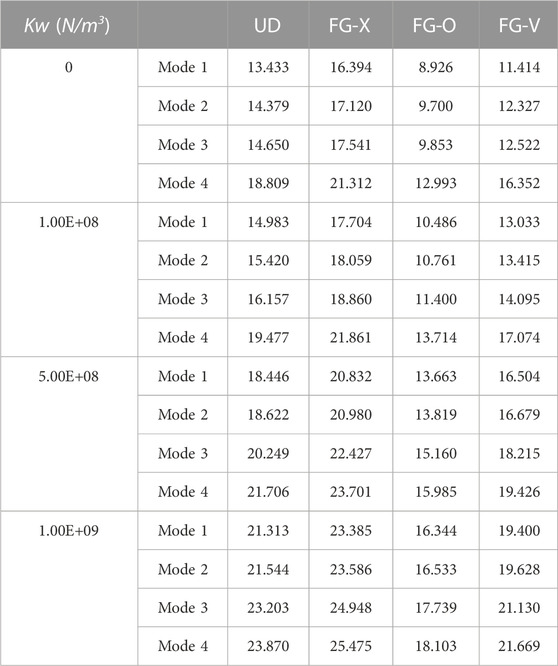
TABLE 8. Effect of the Winkler elastic foundation and GPL pattern on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout ($a/b=1$; $b/h=20$; $r/b=0.2$, CCCC, uniaxial load, and 1.0 wt%).

Buckling loads of the FG-GPL RC plate under uniaxial and biaxial normal loads are compared with those resting on an elastic foundation in Table 9 for two different plate aspect ratios and four GPL patterns. As can be seen in the table, for the plate aspect ratio of 1, the buckling loads of uniaxial and biaxial compressions are almost identical for the plate without an elastic foundation. For the higher plate aspect ratios ($a/b=2$), the buckling load of the plate under biaxial load is considerably lower compared to those under uniaxial load. For all aspect ratios, by adding an elastic foundation to the plate, the buckling loads are increased for both uniaxial and biaxial compressions. Values provided in Table 10 are tabulated with the intent of comparing the critical buckling loads of the FG-GPL RC plate under uniaxial load with different shapes of cutout with/without an elastic foundation. The effect of the elliptical cutout orientation of the plate under uniaxial load is also investigated. The elliptical cutout is considered to have the same area as the circular cutout with $r/b=0.2$. Here, c and d are the semi-major and semi-minor radius of the elliptical cutout, and their radius-to-width ratios are assumed to be 0.3 and $0.133$, respectively. As seen in Table 10, if the major radius of the elliptical cutout is parallel to the direction of the applied load, the critical buckling load of the UD pattern is approximately 2.39 times lower compared to those when the semi-major radius of the elliptical cutout is perpendicular to the applied load. Furthermore, in this case, the buckling loads are lower than the case of the plate with the circular cutout. Results show that the influence of the elastic foundation on the plate with an elliptical cutout is more remarkable compared to the plate with a circular cutout. For example, when the plate with an elliptical cutout is embedded in an elastic foundation, the critical buckling load of the plate with the UD pattern is approximately 1.73 times greater compared with the plate without an elastic foundation, while for the plate with a circular cutout, it is approximately 1.37 times higher. Buckling loads of the FG-GPL RC plate under shear loads are compared with those resting on the elastic foundation, as shown in Table 11, for two different plate aspect ratios, different shapes of cutouts, and four GPL patterns. By increasing the aspect ratio from 1 to 2, the critical shear buckling load of the plate without an elastic foundation and for the UD pattern reduces by 1.83 times, while that of the plate resting on an elastic foundation reduces by 1.55 times. As can be seen from this table, the shear buckling loads of plates with circular and elliptical cutouts are almost identical. Figure 3, Figure 4, and Figure 5 show the first four buckling mode shapes of the full-clamped FG-GPL RC plate discussed in previous numerical tables. Mode shape results indicate that the elastic foundation with higher stiffness generates more slender and local buckling waves.

TABLE 9

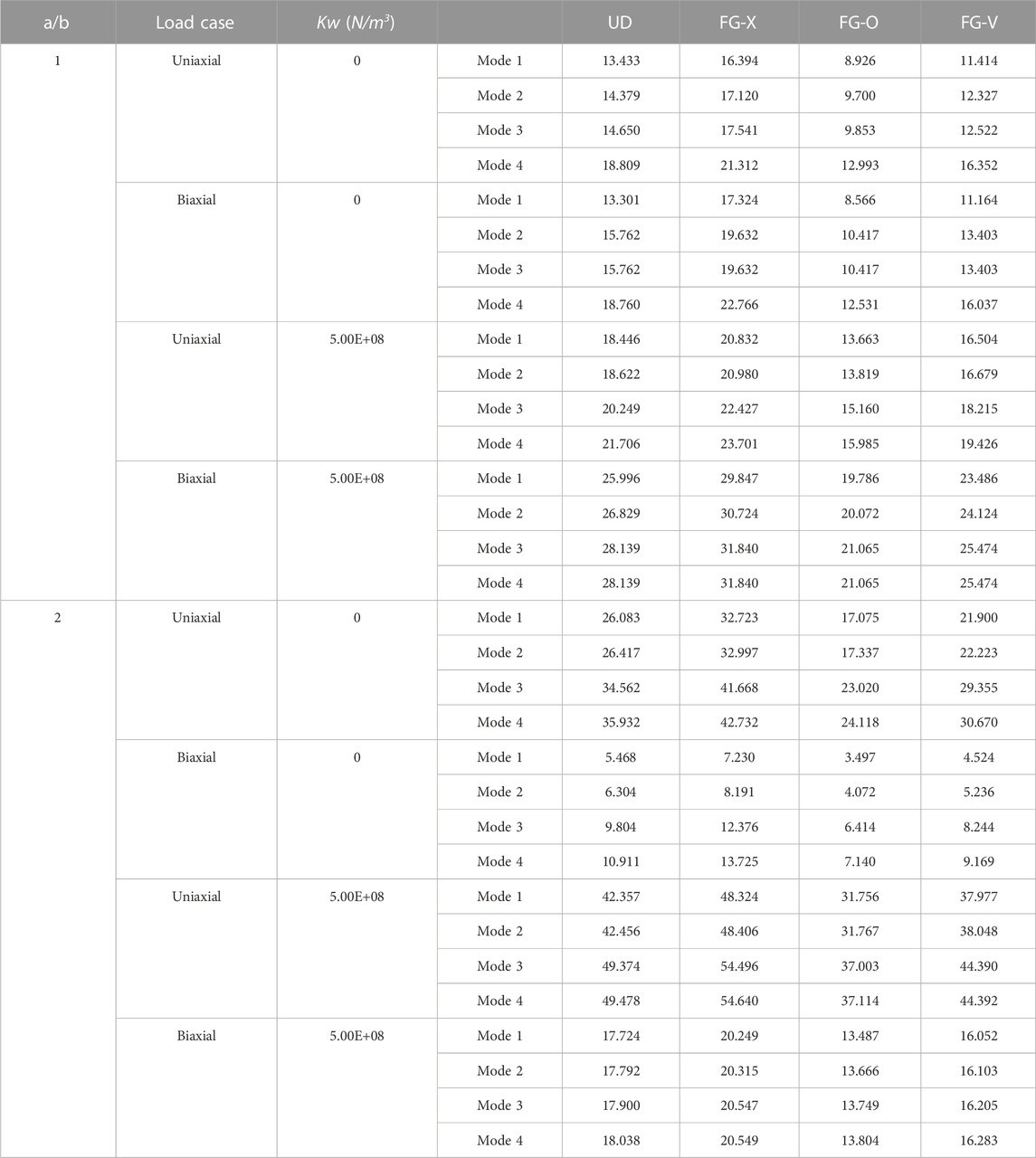
TABLE 9. Influence of uniaxial and biaxial normal loads on the buckling load $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with a circular cutout resting on an elastic foundation ($b/h=20$; $r/b=0.2$, CCCC, and 1.0 wt%).

TABLE 10

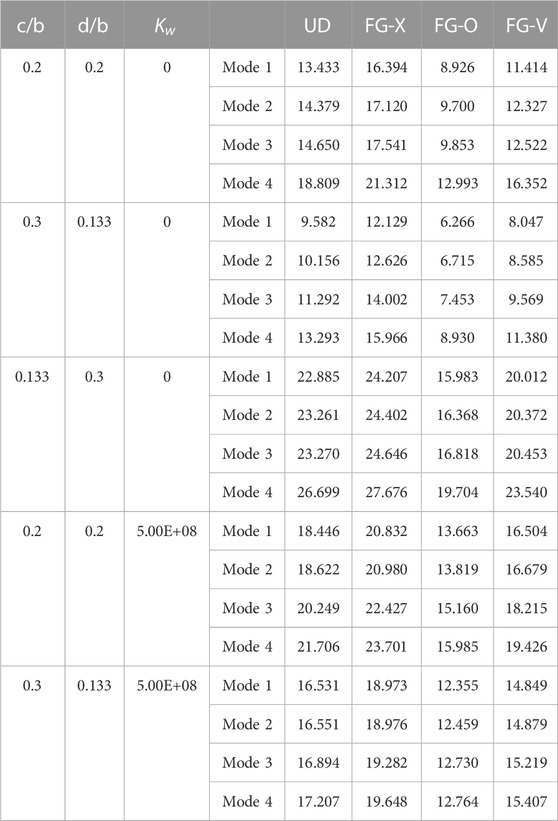
TABLE 10. Buckling loads $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with circular/elliptical cutouts under uniaxial load resting on an elastic foundation ($a/b=1$; $b/h=20$, CCCC, and 1.0 wt%).

TABLE 11

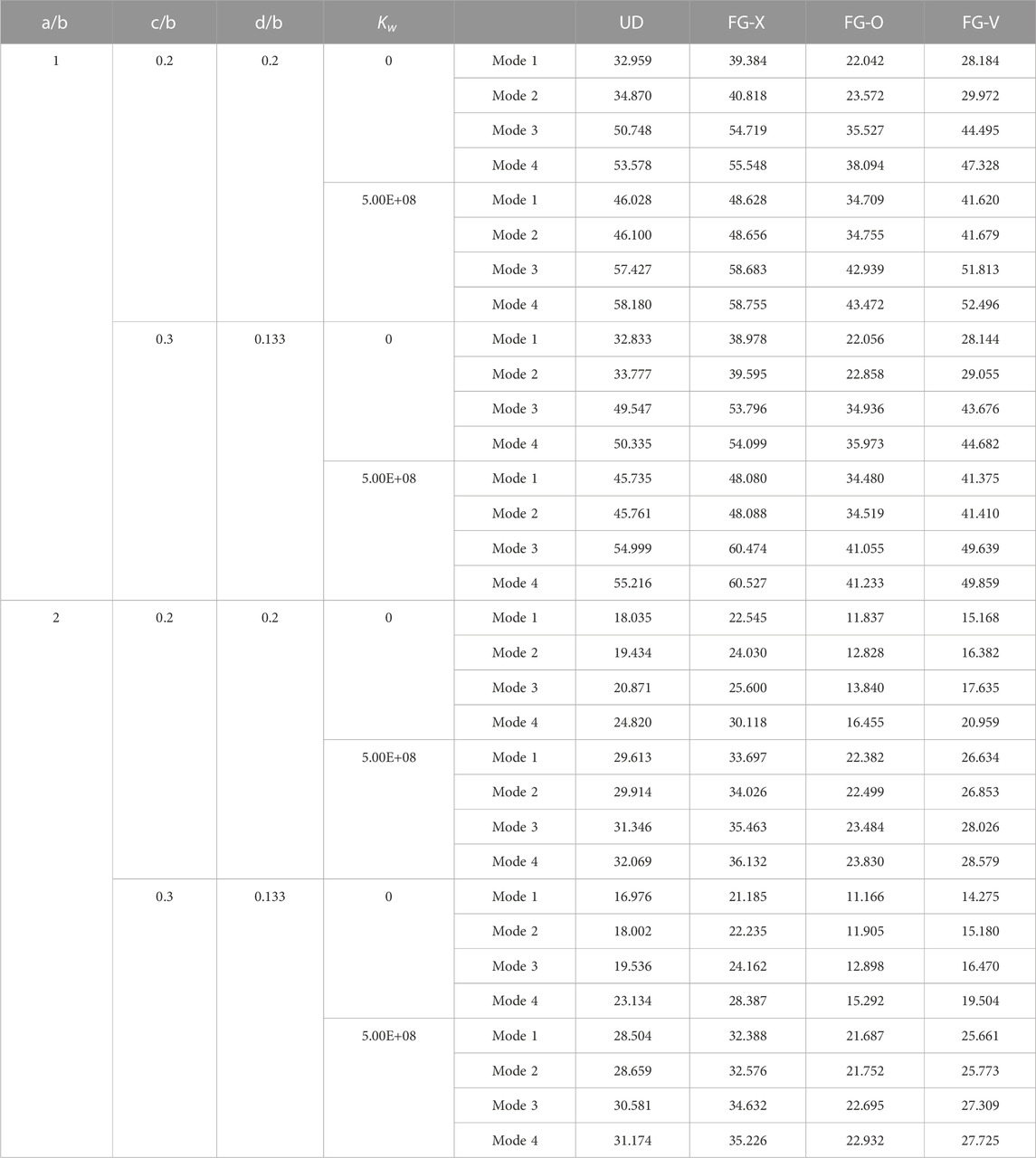
TABLE 11. Shear buckling loads $\left(\raisebox{1ex}{$MN$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ of the FG-GPL RC plate with circular/elliptical cutouts resting on an elastic foundation ($b/h=20$, CCCC, and 1.0 wt%).

FIGURE 3

FIGURE 3. First four buckling mode shapes of the FG-GPL RC plate with a circular cutout under different loads with/without an elastic foundation ($a/b=1$; $b/h=20$; $r/b=0.2$, CCCC, and 1.0 wt%).

FIGURE 4

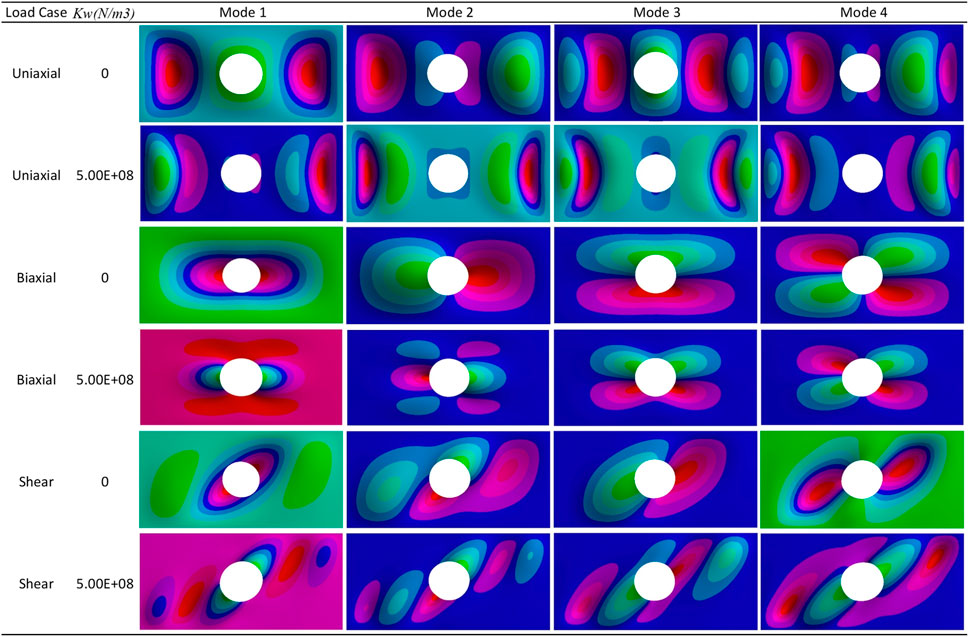
FIGURE 4. First four buckling mode shapes of the FG-GPL RC plate with a circular cutout under different loads with/without an elastic foundation ($a/b=2$; $b/h=20$; $r/b=0.2$, CCCC, and 1.0 wt%).

FIGURE 5

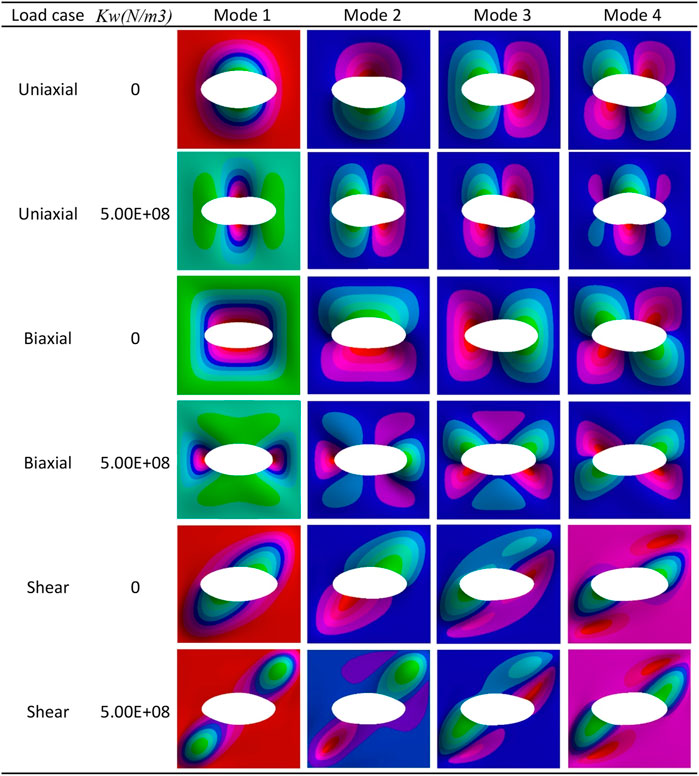
FIGURE 5. First four buckling mode shapes of the FG-GPL RC plate with an elliptical cutout under different loads with/without an elastic foundation ($a/b=1$; $b/h=20$; $c/b=0.3$; $d/b=0.133$, CCCC, and 1.0 wt%).

4 Conclusion

A set of numerical studies has been conducted to describe the buckling behavior of a functionally graded multilayer GPL-reinforced composite plate with circular/elliptical cutouts resting on a Winkler-type elastic foundation under uniaxial and biaxial normal and shear loads. Formulations are proposed based on the third-order shear deformation plate theory and finite element procedure. A broad range of factors such as plate aspect ratio, plate width/thickness ratio, size of the circular cutout, applying uniaxial and biaxial normal and shear loads, several Winkler elastic foundation stiffness parameters, different displacement boundary conditions, circular and elliptical cutouts, orientation of the elliptical cutout, and influence of the GPL weight fraction have been investigated for four GPL distribution patterns to analyze the buckling behavior of the FG-GPL RC plates. The main conclusions of the present study are summarized as follows:

➢ In general, the stiffness of the outer layers has the most remarkable effect on the stiffness of the composite structure. Therefore, as described previously, the structure with the FG-X gradient pattern presented the highest stiffness and buckling capabilities, and UD, FG-V, and FG-O patterns in the sequence have lower values.

➢ By dispersing a low content of GPL nanofillers to the matrix, the buckling loads can remarkably improve. For example, by dispersion of only 0.5 wt% and 1.0 wt% GPLs in the epoxy matrix, the FG-X plate buckling load enhanced 2.97 and 4.84 times, respectively.

➢ By increasing the cutout radius-to-width ratio ($r/b$ ) from $0.1$ to 0.3, the buckling loads decreased by 22.3%.

➢ Buckling loads increased by 42.6% for the FG-GPL RC plate when the elastic foundation stiffness increased from 0 to 1 $\left(\raisebox{1ex}{$GN$}\!\left/ \!\raisebox{-1ex}{$m^3$}\right.\right)$.

➢ If the major axis of the elliptical cutout is parallel to the direction of the applied load, the critical buckling load for the plate with the UD pattern is approximately 2.39 times lower than that when the semi-major radius of the elliptical cutout is perpendicular to the applied load.

➢ The influence of the elastic foundation on the plate with an elliptical cutout is more remarkable compared to the plate with a circular cutout. When the plate with an elliptical cutout is embedded in an elastic foundation, the critical buckling load of the plate with the UD pattern is approximately 1.73 times greater compared with that of the plate without an elastic foundation, while for the plate with a circular cutout, it is approximately 1.37 times higher.

➢ By increasing the plate aspect ratio from 1 to 2, the critical shear buckling load of the plate without an elastic foundation for the UD pattern reduces by 1.83 times, while that of the plate resting on an elastic foundation reduces by 1.55 times.

➢ The shear buckling loads of the plates with circular and elliptical cutouts with an equal area are almost identical.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AK: formal analysis, investigation, software, validation, writing–original draft, and writing–review and editing. MB: data curation, formal analysis, investigation, methodology, software, validation, writing–original draft, and writing–review and editing. KA: conceptualization, data curation, formal analysis, investigation, methodology, supervision, validation, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abedini Baghbadorani, A., and Kiani, Y. (2021). Free vibration analysis of functionally graded cylindrical shells reinforced with graphene platelets. Compos. Struct. 276, 114546. doi:10.1016/j.compstruct.2021.114546

CrossRef Full Text | Google Scholar

Alashkar, A., Elkafrawy, M., Hawileh, R., and AlHamaydeh, M. (2022). Buckling analysis of functionally graded materials (FGM) thin plates with various circular cutout arrangements. J. Compos. Sci. 6 (9), 277. doi:10.3390/jcs6090277

CrossRef Full Text | Google Scholar

Ansari, R., Torabi, J., and Hassani, R. (2018). In-plane and shear buckling analysis of FG-CNTRC annular sector plates based on the third-order shear deformation theory using a numerical approach. Comput. &Amp; Math. Appl. 75 (2), 486–502. doi:10.1016/j.camwa.2017.09.022

CrossRef Full Text | Google Scholar

Asemi, K., Ashrafi, H., and Shariyat, M. (2016a). Three-dimensional stress and free vibration analyses of functionally graded plates with circular holes by the use of the graded finite element method. J. Appl. Mech. Tech. Phys. 57 (4), 690–700. doi:10.1134/s0021894416040131

CrossRef Full Text | Google Scholar

Asemi, K., Babaei, M., and Kiarasi, F. (2020). Static, natural frequency and dynamic analyses of functionally graded porous annular sector plates reinforced by graphene platelets. Mech. Based Des. Struct. Mach. 50 (11), 3853–3881. doi:10.1080/15397734.2020.1822865

CrossRef Full Text | Google Scholar

Asemi, K., Salehi, M., and Akhlaghi, M. (2014). Three dimensional biaxial buckling analysis of functionally graded annular sector plate fully or partially supported on Winkler elastic foundation. Aerosp. Sci. Technol. 39, 426–441. doi:10.1016/j.ast.2014.04.011

CrossRef Full Text | Google Scholar

Asemi, K., Salehi, M., and Akhlaghi, M. (2015). Three dimensional graded finite element elasticity shear buckling analysis of FGM annular sector plates. Aerosp. Sci. Technol. 43, 1–13. doi:10.1016/j.ast.2015.02.009

CrossRef Full Text | Google Scholar

Asemi, K., Shariyat, M., Salehi, M., and Ashrafi, H. (2013). A full compatible three-dimensional elasticity element for buckling analysis of FGM rectangular plates subjected to various combinations of biaxial normal and shear loads. Finite Elem. Analysis Des. 74, 9–21. doi:10.1016/j.finel.2013.05.011

CrossRef Full Text | Google Scholar

Ashrafi, H., Asemi, K., and Shariyat, M. (2013). A three-dimensional boundary element stress and bending analysis of transversely/longitudinally graded plates with circular cutouts under biaxial loading. Eur. J. Mech. - a/Solids 42, 344–357. doi:10.1016/j.euromechsol.2013.07.009

CrossRef Full Text | Google Scholar

Babaei, M., and Asemi, K. (2020). Static, dynamic and natural frequency analyses of functionally graded carbon nanotube annular sector plates resting on viscoelastic foundation. SN Appl. Sci. 2 (10), 1652. doi:10.1007/s42452-020-03421-7

CrossRef Full Text | Google Scholar

Bui, T. Q., Do, T. V., Ton, L. H. T., Doan, D. H., Tanaka, S., Pham, D. T., et al. (2016). On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos. Part B Eng. 92, 218–241. doi:10.1016/j.compositesb.2016.02.048

CrossRef Full Text | Google Scholar

Cong, P. H., and Duc, N. D. (2018). New approach to investigate the nonlinear dynamic response and vibration of a functionally graded multilayer graphene nanocomposite plate on a viscoelastic Pasternak medium in a thermal environment. Acta Mech. 229 (9), 3651–3670. doi:10.1007/s00707-018-2178-3

CrossRef Full Text | Google Scholar

Esmaeili, H. R., Kiani, Y., and Beni, Y. T. (2022). Vibration characteristics of composite doubly curved shells reinforced with graphene platelets with arbitrary edge supports. Acta Mech. 233 (2), 665–683. doi:10.1007/s00707-021-03140-z

CrossRef Full Text | Google Scholar

Fan, F., Lei, B., Sahmani, S., and Safaei, B. (2020). On the surface elastic-based shear buckling characteristics of functionally graded composite skew nanoplates. Thin-Walled Struct. 154, 106841. doi:10.1016/j.tws.2020.106841

CrossRef Full Text | Google Scholar

Farsadi, T., Rahmanian, M., and Kurtaran, H. (2022). Nonlinear stability of multilayered graphene platelet-reinforced functionally graded wing-like plates. Acta Mech. 233 (8), 3233–3252. doi:10.1007/s00707-022-03238-y

CrossRef Full Text | Google Scholar

Fattahi, A. M., Safaei, B., and Ahmed, N. A. (2019). A comparison for the non-classical plate model based on axial buckling of single-layered graphene sheets. Eur. Phys. J. Plus 134 (11), 555. doi:10.1140/epjp/i2019-12912-7

CrossRef Full Text | Google Scholar

García-Macías, E., Rodríguez-Tembleque, L., and Sáez, A. (2018). Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos. Struct. 186, 123–138. doi:10.1016/j.compstruct.2017.11.076

CrossRef Full Text | Google Scholar

Geng, X., Zhao, L., and Zhou, W. (2020). Finite-element buckling analysis of functionally graded GPL-reinforced composite plates with a circular hole. Mech. Based Des. Struct. Mach. 49 (7), 1028–1044. doi:10.1080/15397734.2019.1707688

CrossRef Full Text | Google Scholar

Hung, D. X., Tu, T. M., and Hao, T. D. (2021). Free vibration analysis of laminated CNTRC plates using the pb2-ritz method. J. Mech. Eng. 18 (1), 213–232. doi:10.24191/jmeche.v18i1.15181

CrossRef Full Text | Google Scholar

Jafari, P., and Kiani, Y. (2021). Free vibration of functionally graded graphene platelet reinforced plates: a quasi 3D shear and normal deformable plate model. Compos. Struct. 275, 114409. doi:10.1016/j.compstruct.2021.114409

CrossRef Full Text | Google Scholar

Lakshmi narayana, A., Vijaya Kumar, R., and Krishnamohana Rao, G. (2018). Thermal buckling analysis of laminated composite plate with square/rectangular, elliptical/circular cutout. Mater. Today Proc. 5 (2), 5354–5363. doi:10.1016/j.matpr.2017.12.121

CrossRef Full Text | Google Scholar

Lei, Z., Zhang, L., and Liew, K. (2015). Free vibration analysis of laminated FG-CNT reinforced composite rectangular plates using the kp-Ritz method. Compos. Struct. 127, 245–259. doi:10.1016/j.compstruct.2015.03.019

CrossRef Full Text | Google Scholar

Lin, F., Xiang, Y., and Shen, H. S. (2017). Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites – a molecular dynamics simulation. Compos. Part B Eng. 111, 261–269. doi:10.1016/j.compositesb.2016.12.004

CrossRef Full Text | Google Scholar

Lin, H. G., Cao, D. Q., and Xu, Y. Q. (2018). Vibration, buckling and aeroelastic analyses of functionally graded multilayer graphene-nanoplatelets-reinforced composite plates embedded in piezoelectric layers. Int. J. Appl. Mech. 10 (03), 1850023. doi:10.1142/s1758825118500230

CrossRef Full Text | Google Scholar

Ma, R., and Jin, Q. (2022). Stability of functionally graded graphene-reinforced composite laminated thick plates in thermal environment. Acta Mech. 233 (10), 3977–3996. doi:10.1007/s00707-022-03300-9

CrossRef Full Text | Google Scholar

Mohammadi, M., Farajpour, A., Moradi, A., and Ghayour, M. (2014). Shear buckling of orthotropic rectangular graphene sheet embedded in an elastic medium in thermal environment. Compos. Part B Eng. 56, 629–637. doi:10.1016/j.compositesb.2013.08.060

CrossRef Full Text | Google Scholar

Mollaei, S., Babaei, M., and Asemi, K. (2023). Torsional buckling of functionally graded graphene reinforced composite laminated cylindrical panel. Archive Appl. Mech. 93 (2), 427–435. doi:10.1007/s00419-022-02132-2

CrossRef Full Text | Google Scholar

Muni Rami Reddy, R., Karunasena, W., and Lokuge, W. (2018). Free vibration of functionally graded-GPL reinforced composite plates with different boundary conditions. Aerosp. Sci. Technol. 78, 147–156. doi:10.1016/j.ast.2018.04.019

CrossRef Full Text | Google Scholar

Nguyen, H. N., Tan, T. C., Luat, D. T., Phan, V. D., Thom, D. V., and Minh, P. V. (2019). Research on the buckling behavior of functionally graded plates with stiffeners based on the third-order shear deformation theory. Materials 12 (8), 1262. doi:10.3390/ma12081262

PubMed Abstract | CrossRef Full Text | Google Scholar

Pradhan, S. C., and Phadikar, J. K. (2010). Scale effect and buckling analysis of multilayered graphene sheets based on nonlocal continuum Mechanics. J. Comput. Theor. Nanosci. 7 (10), 1948–1954. doi:10.1166/jctn.2010.1565

CrossRef Full Text | Google Scholar

Saiah, B., Bachene, M., Guemana, M., Chiker, Y., and Attaf, B. (2022). On the free vibration behavior of nanocomposite laminated plates contained piece-wise functionally graded graphene-reinforced composite plies. Eng. Struct. 253, 113784. doi:10.1016/j.engstruct.2021.113784

CrossRef Full Text | Google Scholar

Shahrjerdi, A., and Yavari, S. (2018). Free vibration analysis of functionally graded graphene-reinforced nanocomposite beams with temperature-dependent properties. J. Braz. Soc. Mech. Sci. Eng. 40 (1), 25. doi:10.1007/s40430-017-0943-1

CrossRef Full Text | Google Scholar

Shariyat, M., and Asemi, K. (2014b). Three-dimensional non-linear elasticity-based 3D cubic B-spline finite element shear buckling analysis of rectangular orthotropic FGM plates surrounded by elastic foundations. Compos. Part B Eng. 56, 934–947. doi:10.1016/j.compositesb.2013.09.027

CrossRef Full Text | Google Scholar

Shen, H. S., Xiang, Y., and Fan, Y. (2018). Postbuckling of functionally graded graphene-reinforced composite laminated cylindrical panels under axial compression in thermal environments. Int. J. Mech. Sci. 135, 398–409. doi:10.1016/j.ijmecsci.2017.11.031

CrossRef Full Text | Google Scholar

Shen, H. S., Xiang, Y., and Lin, F. (2017). Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin-Walled Struct. 118, 229–237. doi:10.1016/j.tws.2017.05.006

CrossRef Full Text | Google Scholar

Song, M., Yang, J., and Kitipornchai, S. (2018). Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 134, 106–113. doi:10.1016/j.compositesb.2017.09.043

CrossRef Full Text | Google Scholar

Song, M., Yang, J., Kitipornchai, S., and Zhu, W. (2017). Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int. J. Mech. Sci. 131 (132), 345–355. doi:10.1016/j.ijmecsci.2017.07.017

CrossRef Full Text | Google Scholar

Thai, C. H., Ferreira, A., Tran, T., and Phung-Van, P. (2019). Free vibration, buckling and bending analyses of multilayer functionally graded graphene nanoplatelets reinforced composite plates using the NURBS formulation. Compos. Struct. 220, 749–759. doi:10.1016/j.compstruct.2019.03.100

CrossRef Full Text | Google Scholar

Yang, J., Chen, D., and Kitipornchai, S. (2018). Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 193, 281–294. doi:10.1016/j.compstruct.2018.03.090

CrossRef Full Text | Google Scholar

Yang, J., Wu, H., and Kitipornchai, S. (2017a). Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 161, 111–118. doi:10.1016/j.compstruct.2016.11.048

CrossRef Full Text | Google Scholar

Zhang, L., Lei, Z., and Liew, K. (2015). Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos. Struct. 120, 189–199. doi:10.1016/j.compstruct.2014.10.009

CrossRef Full Text | Google Scholar

Appendix

A four-noded Lagrangian quadrangular element is used. The associated linear Lagrangian interpolation functions in terms of the natural coordinates $\left(\xi ,\eta \right)$ are as follows:

$\left\{\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right\}=\frac{1}{4}\left\{\begin{array}{c}\left(1-\xi \right)\left(1-\eta \right)\\ \left(1+\xi \right)\left(1-\eta \right)\\ \left(1+\xi \right)\left(1+\eta \right)\\ \left(1-\xi \right)\left(1+\eta \right)\end{array}\right\}.(\mathrm{A1})$

In addition, the Hermitian interpolation functions in terms of the natural coordinates $\left(\xi ,\eta \right)$ are as follows:

$\left\{\begin{array}{c}{\mathrm{\Xi }}_1\\ {\mathrm{\Xi }}_2\\ \begin{array}{c}{\mathrm{\Xi }}_3\\ {\mathrm{\Xi }}_4\\ \begin{array}{c}{\mathrm{\Xi }}_5\\ {\mathrm{\Xi }}_6\\ \begin{array}{c}{\mathrm{\Xi }}_7\\ {\mathrm{\Xi }}_8\\ \begin{array}{c}{\mathrm{\Xi }}_9\\ {\mathrm{\Xi }}_{10}\\ {\mathrm{\Xi }}_{11}\\ {\mathrm{\Xi }}_{12}\end{array}\end{array}\end{array}\end{array}\end{array}\right\}=\frac{1}{8}\left\{\begin{array}{c}\begin{array}{c}\left(1-\xi \right)\left(1-\eta \right)\left(2-\xi -\eta -{\xi }^2-{\eta }^2\right)\\ \left(\xi +1\right)\left(1-\eta \right){\left(1-\xi \right)}^2\end{array}\\ \left(\eta +1\right)\left(1-\xi \right){\left(1-\eta \right)}^2\\ \begin{array}{c}\left(1+\xi \right)\left(1-\eta \right)\left(2+\xi -\eta -{\xi }^2-{\eta }^2\right)\\ \left(\xi -1\right)\left(1-\eta \right){\left(1+\xi \right)}^2\\ \begin{array}{c}\left(\eta +1\right)\left(1+\xi \right){\left(1-\eta \right)}^2\\ \left(1+\xi \right)\left(1+\eta \right)\left(2+\xi +\eta -{\xi }^2-{\eta }^2\right)\\ \begin{array}{c}\left(\xi -1\right)\left(1+\eta \right){\left(1+\xi \right)}^2\\ \left(\eta -1\right)\left(1+\xi \right){\left(1+\eta \right)}^2\\ \begin{array}{c}\left(1-\xi \right)\left(1+\eta \right)\left(2-\xi +\eta -{\xi }^2-{\eta }^2\right)\\ \left(\xi +1\right)\left(1+\eta \right){\left(1-\xi \right)}^2\\ \left(\eta -1\right)\left(1-\xi \right){\left(1+\eta \right)}^2\end{array}\end{array}\end{array}\end{array}\end{array}\right\}.(\mathrm{A2})$