Real area of contact and tractions on the patterned surfaces generated by spinodal decomposition and amplified instability

Past decades featured significant advancements in additive and micromanufacturing that facilitated the creation of functional patterned surfaces with impressive spatial resolutions. However, these techniques are expensive and require a considerable amount of time and energy, and hence lack scalability to practical surfaces. Recent techniques employing spinodal decomposition and instabilities amplified via centrifugal acceleration offer viable and cheaper alternatives. The patterns created by those techniques, however, vary randomly in geometry. When interfacing those patterned surfaces with other components and under self-contact scenarios, geometric variations lead to stress concentration and abrupt failure around the contact. In this study, we investigate numerically real contact areas, contact tractions, and stress concentration. We generate patterned surfaces in congruence with actual surfaces created by those techniques. Then, we conduct normal-contact analyses of those surfaces boundary element method (BEM) under nominal mean pressures ranging from 0.001E* to E*, where E* is the contact modulus. We record real contact areas and stress concentration as a function of nominal mean pressures. We compare these values with the analytical solutions from sinusoidally-patterned and randomly rough surfaces. Randomness in pattern geometry is primarily influenced by the processing parameters such as the degree of anisotropy in spinodal decomposition and acceleration in amplified instabilities. To understand the influence of the processing parameters, we perform a parametric study. We find isotropic spinodal decomposition creates patterns that deliver contact area and traction distributions similar to randomly rough surfaces, and lead to high-stress concentrations. Such high-stress concentrations are expected to occur under self-contact loading scenarios, and thus can explain the compromised resilience and strength in recently-proposed spinodal metamaterials. For patterned surfaces created by amplified instabilities, high-stress concentrations are obtained for the surfaces created at high accelerations. At high accelerations, increased elastic instabilities and stochastic growth result in a more skewed and broader distribution in heights. Therefore, high-stress concentrations are inevitable. To account for combined loading scenarios, we conduct additional simulations on the same surface patterns with frictional pre-sliding contacts. We find the frictional tractions play a secondary role in stress concentrations where the primary factor is the processing parameters determining the degree of randomness in pattern geometry.

1 Introduction

Surface patterning has found widespread use in tailoring contact properties such as wettability (Bico et al., 2001), adhesion (Davis and Crosby, 2011), stiffness (Perris et al., 2021), and friction (Eriten et al., 2016; Afshar-Mohajer and Zou, 2020). Conventional methods of surface patterning such as additive manufacturing (Askari et al., 2020), micro/nanofabrication (Dong et al., 2018; Wang et al., 2022), and ultra-precision machining (Yu et al., 2011) require a significant amount of resources, energy and time. Hence, alternative patterning techniques are currently sought for more sustainability, scalability, energy efficiency, and cost-effectiveness. Several examples of such methods include selective etching during spinodal decomposition (Hodge et al., 2007; Lee and Mohraz, 2010), amplified Rayleigh-Taylor instabilities during sol-gel transitions (Marthelot et al., 2018; Jambon-Puillet et al., 2021), pulsed laser patterning (Chen et al., 2020), patterns induced by plate buckling (Holmes et al., 2008; Davis and Crosby, 2011), and force-triggered patterns in mechano-responsive hydrogels (Matsuda et al., 2019; Mu et al., 2022). However, surface patterns obtained by these efficient and scalable techniques inherently have randomness in geometry, and geometric randomness deters their performance under contact loading. For instance, taller asperities with smaller curvatures co-exist with shorter and blunter asperities due to inherent randomness in the manufacturing process. This randomness is expected to lead to a reduction in the real area of contact and thus high-stress concentrations and failure in contact applications.

In this paper, we simulate the contact performance of surfaces created by two of those alternative surface patterning techniques, namely, spinodal decomposition and Rayleigh-Taylor instability methods, and study the influence of processing parameters on the real area of contact, contact tractions, and stress concentration factors. Surface patterns created by spinodal decomposition are the product of the decomposition of two phases interrupted at an arbitrary time and the removal of one of the phases selectively. Spinodal architectures are shown to facilitate multifunctionality and tunability in stiffness when used in 3D lattices, metamaterials, and cellular materials (Vidyasagar et al., 2018; Guell Izard et al., 2019; Hsieh et al., 2019; Kumar et al., 2020; Portela et al., 2020). As a clear advantage over conventional microstructures (e.g., discrete walls and beam struts), the spinodal topography reduces stress concentrations and promotes resilience in those metamaterials. However, the spinodal microstructures are prone to self-contact loading. For instance, unconfined compression tests on metamaterials with various spinodal topography (Portela et al., 2020) deliver nearly fully-recoverable strains under cyclic loading, and thus validate resilience. When examined carefully, however, self-contact among internal structures and failure around contacts are observed in several of those tests. Those internal failures clearly compromise the load-bearing capacity of those materials at subsequent loading cycles. Our study will reveal the performance of spinodal topographies under contact loading.

The other patterning technique we will study is the amplified Rayleigh-Taylor instability method. In this method, patterns are seeded as droplets in thin films of polymer blends, and centrifugal accelerations are adjusted by a rotating drum to amplify instabilities during the sol-gel transition and control heights and curvatures of hairs extending from initial droplets (Marthelot et al., 2018; Jambon-Puillet et al., 2021). In Ref. (Jambon-Puillet et al., 2021), the probability density functions (PDF) of the initial droplet heights and final hair heights formed at different rotating speeds are reported. The initial droplets form patterns with narrow height distribution; i.e., more uniform heights whereas the hair heights formed after additional rotations possess much broader distribution; i.e., random heights. This broadening in PDF of heights is expected to decrease the real area of contact and increase stress concentrations under contact loading.

Inspired by those observations, this paper investigates numerically the real area of contact, contact tractions, and stress concentration factors of patterned surfaces formed by spinodal decomposition and amplified instabilities. We first generate patterned surfaces in congruence with actual surfaces created by those processing techniques (Section 2.1). Then, we conduct normal and tangential-contact analyses of those surfaces via the boundary element method (Section 2.2 and Section 2.3). At each simulation, we record the real area of contact and stress concentration factor as a function of nominal mean pressures (Section 3). We then compare these values with the analytical solutions from the sinusoidally-patterned and randomly rough surfaces. Randomness in pattern geometry is primarily influenced by the processing parameters such as the degree of anisotropy in spinodal decomposition and acceleration in amplified instabilities. To understand the influence of the processing parameters and combined loading on contact tractions, we also present a parametric study (Section 4). To our best knowledge, systematic analysis of the performance of surfaces patterned by efficient and scalable manufacturing methods is currently missing in the literature.

2 Materials and methods

2.1 Generation of the surface geometry

First, we employ Numerical Python (NumPy) package to generate surface geometries consisting of the patterns created by two methods: i) spinodal decomposition and ii) amplified instabilities via material acceleration.

2.1.1 Spinodal decomposition

Surface patterns created by spinodal decomposition are the product of the decomposition of two phases interrupted at an arbitrary time and the selective discarding of one of the phases. The Cahn-Hilliard equation governs the spatiotemporal diffusion and evolution of phases, which can be quantified by the local concentration $\varphi \left(\mathbf{r},t\right)$ at position r on the surface and time t (Cahn, 1961), where the magnitude of ϕ ranges from 0 to 1 and 0 and 1 denote distinct material phases, Γ is the penalty parameter for interphases, D is the effective diffusivity, and $f\left(\varphi \right)$ is the free energy functional quantified by the total energy of a particular phase distribution in space.

$\frac{\partial \varphi \left(\mathbf{r},t\right)}{\partial t}=D{\nabla }^2\left[\left(\frac{df\left(\varphi \left(\mathbf{r},t\right)\right)}{d\varphi \left(\mathbf{r},t\right)}-\mathrm{\Gamma }{\nabla }^2\varphi \left(\mathbf{r},t\right)\right)\right](1)$

While creating the surfaces via spinodal decomposition, the partial differential equation given in Eq. 1 should be numerically solved for $\varphi \left(\mathbf{r},t_f\right)$ where t_f is an arbitrarily long time, and then one of the phases, say close to 0 values, are spatially eliminated. In practice, the elimination process involves a selective material removal process such as chemical etching, and thus perfect separation of phases is not possible, especially around the interphases where $0<\varphi \left(\mathbf{r},t_f\right)<1$. Therefore, this imperfect etching will result in surface patterns. Here, we assume that the height of those surface patterns will scale with the magnitude of $\varphi \left(\mathbf{r},t_f\right)$, i.e., the spots with $\varphi \left(\mathbf{r},t_f\right)=1$ will constitute the surface peaks thanks to no etching and the spots with $\varphi \left(\mathbf{r},t_f\right)=0$ will experience maximum etching and thus form the valleys. The bottleneck in the generation of surfaces in this manner is the long simulation times needed for sufficient spatiotemporal evolution of phase distribution, and the sensitivity of the final patterns to the initial values. Cahn had shown that solution to Eq. 1 can be approximated by a superposition of Fourier components growing or diminishing according to their wavelengths (Cahn, 1961). Assuming slowly-varying amplitudes for those components, spatial variation of phase can be approximated as a Gaussian random field (spinodoid) as done elsewhere (Kumar et al., 2020), where n_i and Γ_i are the direction and phase angles of the ith component of the series, k is the wave number that we set to 2π, and m is the number of waves taken as 1,000 in this study.

$\varphi \left(\mathbf{r}\right)=\sqrt{\frac{2}{m}}\sum _{i=1}^m\cos \left(k{\mathbf{n}}_i\cdot \mathbf{r}+{\mathrm{\Gamma }}_i\right)(2)$

Obviously, the approximate series representation given in Eq. 2 provides the concentration ϕ(r) and thus surface heights much quicker than the full Cahn-Hilliard equation does. Besides, Kumar et al. (2020) showed that limiting the directions of the components n_i would lead to anisotropic patterns, and thus the creation of various topographies is possible with a single expression. To generate the concentrations as a function of position, we first select the direction vector n_i residing on the surface spanned by e₁ and e₂ basis vectors in x and y directions. Direction vector has a unit-norm and can be described by a single angle Θ_i = cos⁻¹ (e₁ ⋅n_i) as n_i = (cos Θ_i, sin Θ_i) in e₁ and e₂ basis. Thus, the selection of the direction vector is reduced to the choice of the angle Θ. If that angle is chosen randomly within the range [0, π/2], then the direction of wave components will be randomly distributed in the first quadrant defined by x > 0 ∧ y > 0 surface plane and the resultant surface patterns will be isotropic. Limiting the upper bound of that range to a particular angle θ, in contrast, will lead to strong directionality and thus anisotropy in the concentrations and surface patterns. After selecting the direction vector, phase angle Γ_i is randomly assigned from the range [0, 2π] to each wave. Summing the expressions for all waves as in Eq. 2 then yields the concentration ϕ(x, y) over the discretized surface plane. We then scale the concentrations uniformly to obtain a target of 0.1 [a.u.] for the root-mean-square (rms) of surface heights; i.e., h (x, y) = Cϕ(x, y) such that h_rms = 0.1. The surface plane xy is 10 × 10 [a.u.] in dimension so that surface slopes $\approx 0.1/10$ are practically sound. Since k = 2π yields wavelengths of unity in each wave component, 10 × 10 surface plane will guarantee about 10 surface peaks per direction and thus enable statistical analyses of the contact parameters, especially in isotropic surface case ($\approx 100$ surface peaks). The xy plane is discretized into 512 × 512 points, which is a compromise between accuracy and computational efficiency in the contact analyses compared to the finer discretizations (e.g., mesh convergence study reveals less than 5% difference from the finest discretization of 2048 × 2048). Figure 1 shows the surface heights h (x, y) for two representative surfaces created by this procedure. All physical lengths in x and y directions and height h (x, y) in Figure 1 are normalized by window size L, 10 [a.u.]. As shown in Figure 1A, limiting the angle Θ ≤ θ = π/180 delivers an anisotropic surface geometry where height variations in y direction are minimal compared to the variations in x. That surface as an extreme example resembles a 2D sine wave profile. When the direction vector is selected randomly in all possible directions; i.e., Θ ≤ θ = π/2, isotropic distribution of the surface heights is achieved (Figure 1B).

FIGURE 1

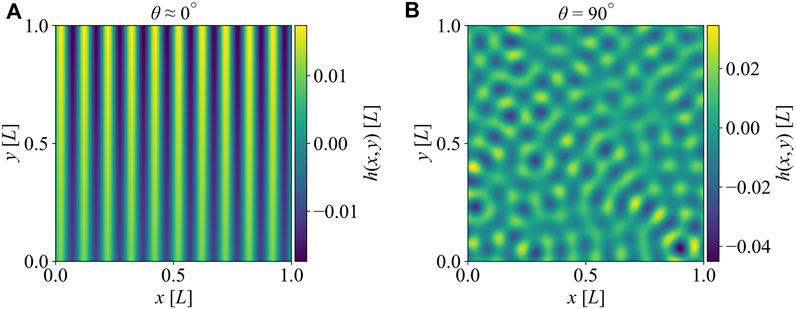
FIGURE 1. Surface heights h (x, y) generated by spinodal decomposition. (A) The surface with θ ≈ 0° (anisotropic surface). (B) The surface with θ = 90° (isotropic surface).

2.1.2 Amplified instability

Surfaces generated by amplified instability employ dynamics of a rotating drum to amplify instabilities and pattern formation in thin films of polymer blends such as polydimethylsiloxane (PDMS) and vinylpolysiloxane (VPS-8) (Jambon-Puillet et al., 2021). Here, we simulate this pattern formation by following the physical processes and corresponding equations reported in (Marthelot et al., 2018; Jambon-Puillet et al., 2021). In this process, one first coats a drum of radius R with a thin layer of polymer melt (PDMS + VPS-8) with surface tension γ and density ρ. Then, the drum is rotated at a slow speed Ω₁ to induce Rayleigh-Taylor instabilities in the polymer melt and form an initial hexagonal array of “pendant droplets”. The wavelengths and heights of this initial pattern depend on the characteristic length $l_c=\sqrt{\gamma /(\rho R{\mathrm{\Omega }}_1)}$, a measure of capillary length for the melt (Marthelot et al., 2018). The profile of individual droplets can be found by the Young–Laplace equation Eq. 3 that describes the balance of hydrostatic pressure due to the centrifugal acceleration and the effect of the surface tension of the melt (Ku et al., 1968), where s is the arc length, φ(s) is the angle between the tangent vector to s and the vertical axis, and r(s) and z(s) are the radial and height coordinates defining the droplet as shown in Figure 2.

$\frac{d^2\phi \left(s\right)}{d{s}^2}=\frac{-\cos \phi \left(s\right)}{{\ell }_c^2}+\frac{d}{ds}\left(\frac{\cos \phi \left(s\right)}{r\left(s\right)}\right),\frac{dz\left(s\right)}{ds}=\cos \phi \left(s\right),\frac{dr\left(s\right)}{ds}=\sin \phi \left(s\right)(3)$

Solving Eq. 3 with properly selected boundary conditions delivers the axisymmetric initial droplet profile, z(s) and r(s). As in (Jambon-Puillet et al., 2021), we use the following boundary conditions: φ(0) = φ(s_f) = −π/2, r (s_f) = 0, z (0) = 0, and z (s_f) = h₀, where s_f is the total arc length and h₀ is the maximum height of the initial droplet. The first two of those boundary conditions relate to vanishing slopes of the profile at the edge (s = 0) and symmetry axis (s = s_f) of the profile, and the last three follow from the coordinate definitions and instability-driven initial height, h₀ at the axisymmetry axis. Setting h₀ to a given value, one can use the shooting method to solve Eq. 3 and initially unknown total arc length s_f, and obtain individual droplet profile as shown in Figure 2. Note that r_f denotes a radial extent of the initial droplet. Marthelot et al. (2018) and Jambon-Puillet et al. (2021) show that theoretical solution to Eq. 3 captures well the profile of experimentally manufactured droplet by Rayleigh-Taylor instability. Because we assume the initial droplets are perfectly axisymmetric, we can simply render 3D shape of droplets h (x, y) in discretized xy plane for a single unit: there exists ${(x_i)}_{0\le i<2n-1}$ and ${(y_j)}_{0\le j<2n-1}$ such that, for any a = 0, 1, 2, …, n−1 satisfies $\{h(x_i,y_j)|r_a\le {\left({(x_i-x_n)}^2+{(y_j-y_n)}^2\right)}^{0.5}<r_{a+1}\}=\frac{z(r_{a+1})-z(r_a)}{r_{a+1}-r_a}\left({\left({(x_i-x_n)}^2+{(y_j-y_n)}^2\right)}^{0.5}-r_a\right)+z(r_a)$, where x_i and y_j denote the ith point of x and jth point of y, respectively, on the discretized xy plane (i.e., linear interpolation). The half-profile of droplet shown in Figure 2 is discretized with n number of points, and r_a denotes the ath point in discretized r, e.g., z (r₀) = h₀ and z (r_n−1) = 0. There is no droplet growth between the droplets, and the film thickness of the elastomers after droplet generation is very thin, so we assume the surface patch between the droplets and hairs is perfectly flat; i.e., for any i, j which does not satisfy $r_a\le {\left({(x_i-x_n)}^2+{(y_j-y_n)}^2\right)}^{0.5}<r_{a+1}$, h (x_i, y_j) = 0. Repeating this procedure for many such droplets and distributing them in a hexagonal array over the surface would form the initial pattern. In line with the experimental findings of (Jambon-Puillet et al., 2021), we select h₀ from a log-normal distribution with 0.034l_c of mean and 0.36l_c of standard deviation and obtain the profile of 115 droplets. We then repeat those droplets with a wavelength of $\mathrm{\Lambda }=2\pi \sqrt{2}{l}_c$ over the surface with 10Λ × 10Λ area 0.0373 m × 0.0373 m in physical dimensions). The surface is discretized into 1,024 × 1,024 points. This discretization is determined by the comparison with the case of 2024 × 2024 discretization in the same manner for the spinodal surface.A subsequent increase in the rotational speed of the drum leads to a further increase in the heights of the initially seeded droplets. Increasing acceleration promotes this growth while simultaneous curing and thus the formation of elastic resistance balances inertial forces and prevents stripping of partially-cured polymer blend from the drum surface. Resulting droplet profiles look like elongated versions of the initial profiles, “stretched hairs” (Jambon-Puillet et al., 2021) (see Figure 2 for an example). Jambon-Puillet et al. (2021) utilized minimization of energy and provided an estimation for the ratio of final to initial maximum heights of the droplets, $\epsilon =h_0^{*}/h_0$, as a function of effective acceleration defined by $g_{\text{eff}}=R({\mathrm{\Omega }}_2^2-{\mathrm{\Omega }}_1^2)$ where Ω₂ is the increased rotation speed of the drum, where β ≈ 0.29 and α = ρg_effh₀/G is a nondimensional parameter estimated for each droplet of height h₀ and shear modulus G.

$\epsilon \left(\alpha \right)=\frac{1}{3}\left(\beta \alpha +g\left(\alpha \right)+\frac{{\beta }^2{\alpha }^2}{g\left(\alpha \right)}\right),g\left(\alpha \right)=\sqrt[3]{{\beta }^3{\alpha }^3+\left(3/2\right)\left(9+\sqrt{12{\beta }^3{\alpha }^3+81}\right)}(4)$

Note that α is a measure of acceleration-induced pressure in terms of the elasticity of the partially-cured blend. Assuming lubrication theory, droplet shapes forming under the influence of gravity and surface tension were previously discussed in (Lister et al., 2010). In particular, the profile of an individual droplet at equilibrium can be expressed as Eq. 5, where J₀ is the Bessel function of the first kind of order 0 and r_f is the total radial length.

$z\left(r\right)=\epsilon h_0\frac{{\mathrm{J}}_0\left(r_f/l_c\right)-{\mathrm{J}}_0\left(r\sqrt{\epsilon }/l_c\right)}{{\mathrm{J}}_0\left(r_f/l_c\right)-1}(5)$

Jambon-Puillet et al. (2021) found that Eq. 5 approximated the measured profiles of the stretched hairs reasonably well. We employ Eq. 5 to obtain the profiles of individual stretched hairs as shown in Figure 2. To obtain the final surface patterns (e.g., Figure 3B), we repeat this procedure for all 115 droplets. The histogram of the peak heights of the stretched hairs shown in Figure 3B agrees reasonably well with the measured histograms reported in (Jambon-Puillet et al., 2021). Thus, our assumptions on the acceleration-induced shape changes of initial droplets deliver surface patterns similar to the ones obtained in practice. Note that the stretch ɛ, the growth factor of the peak height for each droplet Eq. 5 is a strong function of the parameter α and thus effective acceleration. As detailed by Jambon-Puillet et al. (2021), axisymmetric profiles given by Eqs 3–5 are obtained when α ≲ 8. Therefore, in this study, we investigate surface patterns for effective acceleration values residing within that limit. Lastly, the initial and final profiles of the droplets simulated by this process (Figure 3) exhibit clear differences. All physical lengths in x and y directions and height h (x, y) in Figure 1 are normalized by window size L, 0.0373 m. The stretch in heights due to increased acceleration is accompanied by shrinkage in radial extent as illustrated for an individual droplet in Figure 2. Both of those changes in geometry lead to an increase in curvature. Hence, effective acceleration as a surface processing parameter is expected to have a prominent influence on contact mechanics. We will study this more in Section 4.

FIGURE 2

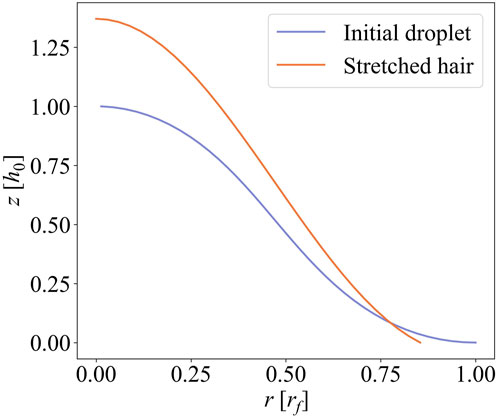
FIGURE 2. Representative profiles of the initial droplet and stretched hair. The initial droplet is given at Ω₁ = 41.9 rad/s, and the stretched droplet is obtained at g_eff = 137 m/s². h₀ and r_f denote the maximum heights and radial extent of the profiles of an initial droplet, respectively.

FIGURE 3

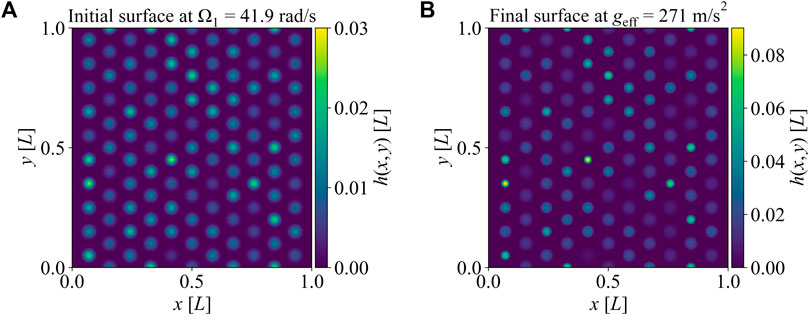
FIGURE 3. The images of the surface patterns generated by amplified instability. (A) The surface generated by Rayleigh-Taylor instability at the initial drum rotation speed of Ω₁ = 41.9 rad/s. The surface has 115 droplets. (B) The surface generated by increasing the drum rotation speed further at g_eff = 271 m/s².

2.2 Normal contact analysis

2.2.1 Numerical simulations

To simulate the elastic response of patterned surfaces under normal contact, we employ TAMAAS, an open-source C++-based Python Library developed by the Computational Solid Mechanics Laboratory at EPFL (Frérot et al., 2020). We simulate non-adhesive elastic contact and so utilize the conjugate gradient-based contact scheme (Polonsky and Keer, 1999) and boundary integral method. For that, as explained in the previous section, we first generate surfaces simulating the patterns created by the spinodal decomposition and amplified instability. Patterned surfaces are treated as rigid punches repeating periodically outside the xy domain to be pressed on elastic half-space. We assign 1 [a.u.] for Young’s modulus E and 0.5 for Poisson’s ratio ν of the elastic half-space. We then impose the nominal mean contact pressures p₀ ranging from 0.001E* to E* and solve for the contact pressures at each grid point, p (x, y). All pressure units are normalized to the contact modulus E* = E/(1 − ν²).

Figure 4 shows representative contact pressure distributions obtained from the isotropic spinodal patterned surface and the initial surface generated by the amplified instability. Both surfaces are imposed to nominal mean contact pressures p₀ of 3.16 × 10⁻²E*. One can see that only a minute portion of the nominal contact area is load-bearing and local contact pressures can attain very high values up to 2.5E* at the peaks of both surface patterns hinting at inevitable stress concentrations and potential failure. Both features are signatures of randomly rough surfaces. We will show in Section 3 that surface patterning via the two methods mentioned in the previous section can lead to a reduction in contact areas and stress concentrations comparable to randomly rough surfaces. To quantify the real area of contact A_r, we estimate the sum of grid areas with non-zero pressures, and obtain the real mean contact pressure p_r as $\frac{p_0{A}_0}{A_r}$. Since peak heights and curvatures vary within nominal contact areas of both patterns, there will be local areas with much larger pressures than p_r. To study stress concentrations at those locations, we define $p_{\mathit{conc}}=\frac{p_r+3p_{\mathit{rms}}(x,y)}{p_0}$, where p_rms denote the rms of contact pressures. This definition captures stress concentrations well without potential amplification and error due to discretization (especially under light loading).

FIGURE 4

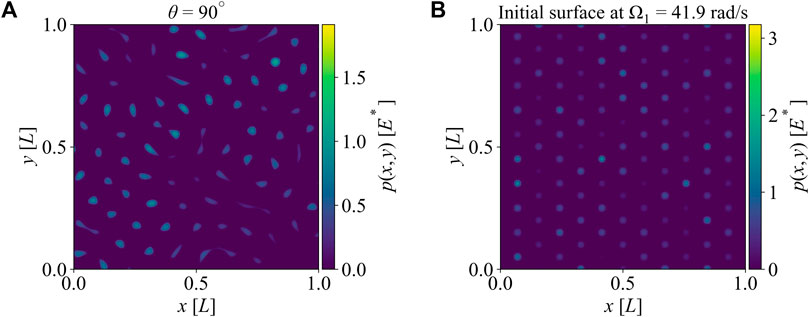
FIGURE 4. The images of the local pressures over the surfaces. (A) The local pressure for the surface generated by spinodal decomposition at θ = 90° (isotropic surface) (B) The local pressure for the surface generated by amplified instability at Ω₁ = 41.9 rad/s.

2.2.2 Theoretical contact models

To verify, compare and contrast our numerical results with existing contact theories, we will adopt the following models for different cases.

• For comparison to the anisotropic spinodal surface, we will use 2D-sinusoidal contact formulations (Johnson, 1985). This choice is apparent from Figure 1A, which is created by limiting the direction vector to within θ ≈ 0° and thus surface heights vary along the x-axis only. The ratio of real to nominal areas of contact A_r/A₀ and the contact pressures p(x) for 2D-sinusoidal surface h (x, y) ≈ z(x) = Δ cos (2πx/λ) are given as Eqs 6, 7, where a is the half contact width at each peak, and p* = πE*Δ/λ;

$\frac{A_r}{A_0}=\frac{2a}{\lambda }=\left\{\begin{array}{cc}\frac{2}{\pi }{\sin }^{-1}\left(\sqrt{\frac{p_0}{p^{*}}}\right)\hfill & p_0<p^{*}\hfill \\ 1\hfill & p_0\ge p^{*}\hfill \end{array}\right.(6)$

$p\left(x\right)=\left\{\begin{array}{cc}\max \left(\frac{2p_0\cos \left(\frac{\pi x}{\lambda }\right)}{{\sin }^2\left(\frac{\pi a}{\lambda }\right)}\sqrt{{\sin }^2\left(\frac{\pi a}{\lambda }\right)-{\sin }^2\left(\frac{\pi x}{\lambda }\right)},0\right)\hfill & p_0<p^{*}\hfill \\ p_0+p^{*}\cos \left(2\pi x/\lambda \right)\hfill & p_0\ge p^{*}\hfill \end{array}\right.(7)$

• For comparison to isotropic spinodal surfaces, we adopt discrete Greenwood-Williamson model (GW model) because randomly-sampled spinodal surfaces tend to possess an average wave number of k = 2π (Eq. 2) leading to well-separated surface peaks, and thus we can describe the curvature of the peaks separately and treat them as non-interacting asperities under light loading (Greenwood and Williamson, 1966). Assuming elliptical Hertzian contact for each peak, the normal load $P_i^s$ carried by asperity i and the contact area of asperity i, $A_i^s$, follow as Eq. 8, where $R_{e,i}^s$, $h_i^s$ and ${\delta }_i=h_i^s-d$ are the effective radius of curvature, height, and compression of asperity i, d is the separation between the mean of surface patterns and the undeformed surface of the half-plane, and N is the number of load-bearing asperities.

$P_i^s=\frac{4}{3}{E}^{*}{\left(R_{e,i}^s\right)}^{1/2}{\left({\delta }_i\right)}^{3/2},A_i^s=\sum _{i=1}^N\pi {\delta }_i{R}_{e,i}^s(8)$

The effective radius of curvature $R_e^s=1/K^s$ is defined as ${\left[{\kappa }_1{\kappa }_2\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)\right]}^{-1/3}$, where κ₁ and κ₂ are the relative principal curvature of the contact (Greenwood, 1997). Note that in our case κ₁ and κ₂ are equal to the principal curvatures of the generated spinodal surface because the counter elastic surface is ideally flat. This effective radius of curvature definition delivers accurate estimations for mildly elliptical contacts as the majority of the contact areas obtained from the spinodal patterns. The asperities are identified by a 9-point peak-picking algorithm.

• For comparison to surfaces generated by the amplified instability method, we adopt discrete GW model for the same basis as in the isotropic spinodal surface: The droplets and hairs created by this method can be assumed as isolated asperities. We can estimate the normal load $P_i^s$ carried by asperity i and the contact area $A_i^s$ of asperity i by using Eq. 8. We should note that for this case the effective radius of curvature $R_e^s=1/\kappa$ is obtained from $\kappa =|z^{″}|/{(1+z^{\prime 2})}^{3/2}$, where z = z(r) is axisymmetric. The profiles of the initial droplets and subsequent hairs are given by Eqs 3–5.

2.3 Tangential contact analysis

We conduct the combined normal and tangential contact analysis via Tamaas to study the effect of shear tractions on the stress concentration factor. We simulate the 3D non-adhesive elastic contact under combined normal and tangential loading by the conjugate gradient method (Polonsky and Keer, 1999). The mechanical properties are the same as the normal loading simulations. The value of 0.5 for Poisson’s ratio allows us to remove the elastic mismatch (Patil and Eriten, 2015) and enables us to verify the numerical simulations against the theoretical Cattaneo–Mindlin model for a sphere-on-flat contact (Johnson, 1985). To limit shear tractions, Coulomb friction model with friction coefficient μ is used. We assign boundary conditions with two nominal tractions: mean pressure p₀ in z direction (normal to the surface); and mean shear traction q_x in x direction (in our case, q_y = 0). In tangential contact analysis, we set the mean pressure p₀ at 0.0316E* and mean shear traction at q_x = 0.7 μp₀. Note that this selection of mean shear traction delivers significant contributions to stress concentrations without leading to gross sliding.

After each simulation, we obtain x, y, and z components of tractions, namely, t_x (x, y), t_y (x, y), and t_z (x, y), and compute an equivalent traction $|\mathbf{t}(x,y)|=\sqrt{t_x^2+t_y^2+t_z^2}$ at each grid point in contact. Then, we define $p_{\mathit{conc}}=\frac{t_r+3t_{\mathit{rms}}}{p_0}$, where t_r and t_rms denote the mean and standard deviation of equivalent tractions. To simulate the influence of the increasing shear tractions on the stress concentration, we vary the friction coefficient μ from 0 to 0.625. Note that perfect elastic similarity, fully-recoverable deformations, and no damage assumptions of the model result in contact areas being unaltered during the shear loading. Therefore, the definition of stress concentration is congruent to the one for the normal contact analysis when t_x = t_y = 0; i.e., μ = 0 case.

3 Results

3.1 Real area of contact and mean contact pressures

3.1.1 Spinodal decomposition

Figures 5A, B show the real area of contact normalized by the nominal area A_r/A₀ and real mean contact pressure p_r as a function of mean pressure p₀ for two extreme cases: θ ≈ 0° and θ = 90°. Note that those cases correspond respectively to the most anisotropic (2D sinusoidal) and isotropic patterns shown in Figure 1. For each case, 20 randomly sampled surfaces are realized with randomly selected direction vectors and phase angle per wave components Eq. 2. The mean and ± 1 standard deviation of the responses of those 20 surfaces are shown in Figure 5 and the subsequent figures. As expected for both cases, the real area of contact is less than a few percent of the nominal area at light loading (p₀ ≈ 10⁻³E*). Around that light-loading asymptote, discrete GW simulations overlap nearly perfectly with the numerical solutions, which further verifies the numerical modeling. 2D sine contact theory correlates with the numerical solutions of the anisotropic case even at heavier loads reaching up to p₀ ≈ E*. At that level of loading, complete contact condition is attained; i.e., A_r ∼ A₀. 2D sine contact theory also predicts that complete contact is reached when p₀ = p* = πE*Δ/λ, which is $\approx 0.55E^{*}$ for the 2D surfaces rendered. At p₀ = 0.55E*, the mean of numerical solutions is A_r/A₀ ≈ 0.85 suggesting 15% deviation from the theory, which is pretty close to the complete contact. This comparison with theory confirms our expectation on anisotropic cases resembling 2D-sinusoidal wavy patterns whereas isotropic cases delivering contact performance similar to randomly rough surfaces.

FIGURE 5

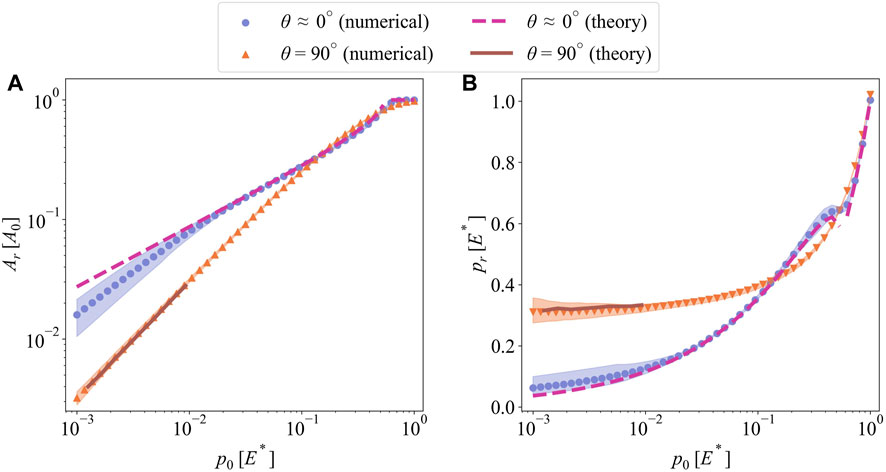
FIGURE 5. (A) The real area of contact A_r and (B) the real mean contact pressure p_r as a function of nominal mean pressure p₀ for the surfaces generated by spinodal decomposition with θ ≈ 0° (anisotropic) and θ = 90° (isotropic).

Reduction in the real load-bearing areas leads the inevitable increase in real mean contact pressures. Figure 5B shows the real mean contact pressures p_r obtained from the simulations and contact theories. The real mean contact pressures at light loading (p₀ < 0.01E*) are constant around 0.3E* for the isotropic patterns. Discrete GW model predicted similar values. The continuous form of GW model with randomly rough surfaces also predicts a constant real mean contact pressure independent of the applied load. This is thanks to the proportional increase of load-bearing areas with increasing load. For the anisotropic case, real mean contact pressures increase nonlinearly with the applied load and 2D sinusoidal contact solution captures that change reasonably well. At heavier loads (p₀ > 0.1E*), both anisotropic and isotropic patterns deliver similar real areas of contact and mean contact pressures. At that asymptote, sensitivity to the initial patterns is lost through long-range interactions, shape alterations, and mergers among contact patches. Similar observations were reported elsewhere with detailed numerical analysis of sinusoidal contacts (Yastrebov et al., 2014).

3.1.2 Amplified instability

Figures 6A, B show the real area of contact and the real mean contact pressure for the surfaces generated by amplified instability. Numerical simulations and corresponding discrete GW model predictions are plotted for three different instability cases. The first case is the initial surface rendered at Ω₁ = 41.9 rad/s, and the second and third cases are created with incrementally increased rotating speeds corresponding to effective accelerations of g_eff = 137 m/s² and g_eff = 271 m/s², respectively. The second and third surfaces are originated from the same initial surfaces. Note that initial heights are selected randomly from an experimentally-measured distribution, which then leads to a slightly different set of peaks for each surface patterns. Twenty surfaces are rendered at each case to determine statistically-relevant contact parameters numerically. The discrete GW model is obtained for one of those surfaces delivering mean values of the contact parameters shown in Figure 6. The shaded area represents the mean ± 1 standard deviation of numerical results for 20 surfaces per case. Similar to spinodal surfaces, all of the cases deliver contact areas much smaller than the nominal area under light loading. Besides, the real area of contact seems proportional to the applied load, which leads to constant real mean contact pressures at that extreme (p₀ < 0.01E*). The real area of contact is consistently the smallest for high effective acceleration cases and highest for the initial surfaces, and vice versa is true for the real mean contact pressure. As the effective acceleration increases, so do the stretch of initial droplets and the height of individual hairs. Besides, the curvature for stretched hairs increases with the effective acceleration as shown in Figure 2. Both of those changes in geometry lead to less contact area and more stress concentration.

FIGURE 6

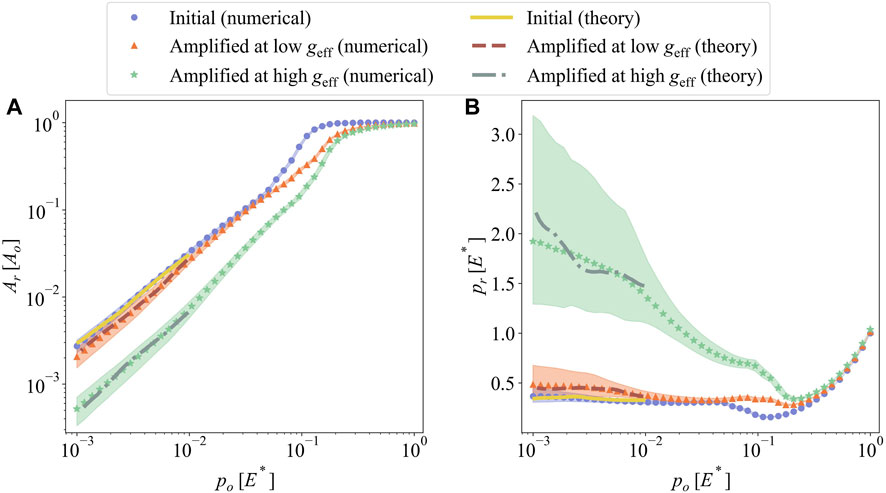
FIGURE 6. (A) The real area of contact A_r and (B) the real mean contact pressure p_r as a function of nominal mean pressure p₀ for the surfaces generated by amplified instability at three stages: after initial rotation, after low and after high effective acceleration g_eff.

The real mean contact pressure p_r for the initial surfaces and the surfaces created at low g_eff is almost constant from 0.35E* to 0.45E*, while the surfaces created at high g_eff show decreasing real mean contact pressure for p₀ < 0.1E*. This will be discussed in detail in Section 4 with the asperity curvatures and asperity heights. In Eq. 4, the stretch ɛ increases as α increases, and α is linearly proportional to the initial droplet height h₀. Consequently, the variance in the initial surface’s asperity heights may result in a wider range of variance in amplified surfaces. We can see the shaded area is getting larger as the increased rotating speed Ω₂ is getting higher.

3.2 Stress concentration

The real mean contact pressures shown above ranged from 0.05E* to 2.0E* at light loading. Such high pressures can be accommodated without failure only by highly flexible soft materials. The stress concentration at the peaks of surface patterns discussed above, however, will result in actual contact patches experiencing much larger pressures than p_r, and thus permanent deformation and catastrophic failure is possible even for soft materials. Here, we investigate the stress concentrations p_conc over the surfaces generated by the spinodal decomposition and amplified instability.

3.2.1 Spinodal decomposition

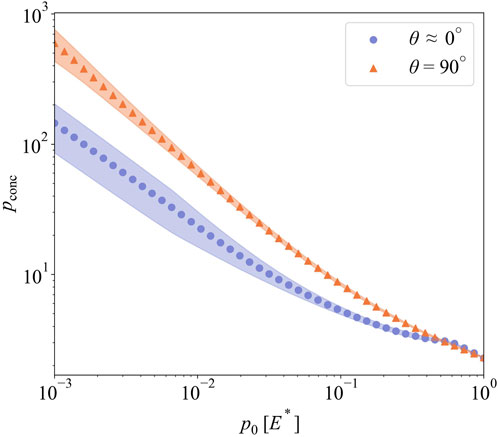
Figure 7 shows the evolution of stress concentration p_conc on anisotropic and isotropic spinodal surfaces as a function of applied nominal pressure p₀. As defined in Section 2, p_conc is essentially the ratio of maximum and real mean contact pressures. The stress concentration for both the anisotropic and isotropic surface patterns starts at values ranging from 200 to 800, decreases monotonically with increasing nominal pressures, and converges to about 2 under heavy loading. The factor of 2 is common to any wavy pattern at the inception of complete contact. Except for that heavy-loading asymptote, isotropic patterns experience higher stress concentration than anisotropic patterns.

FIGURE 7

FIGURE 7. The stress concentration for the surfaces generated by spinodal decomposition.

3.2.2 Amplified instability

Figure 8 shows the evolution of stress concentration p_conc on the surfaces created by amplified instability as a function of applied nominal pressure p₀. Three cases of amplified instability are investigated as above: after initial rotation, after low, and after high effective acceleration. Similar to the spinodal surfaces, stress concentration starts at high values ranging around from 10³ to 10⁴ under low nominal pressures, decreases monotonically, and approaches 2 under high nominal pressures. The patterns created at high effective acceleration (g_eff = 271 m/s²) exhibit higher stress concentration than the other patterns. This is because the initial droplets get taller and sharper as effective acceleration increases (see, for example, Figure 2).

FIGURE 8

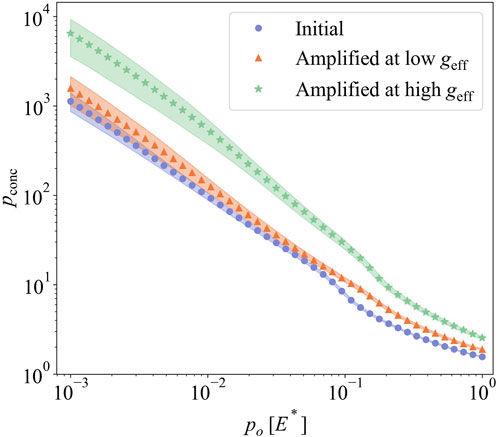
FIGURE 8. The stress concentration for the surface generated by amplified instability from numerical results.

4 Parametric study and discussion

Surface patterns created by the spinodal decomposition and amplified instability deliver contact responses that inherently depend on processing parameters. For instance, limiting the spinodal decomposition by angle θ controls the degree of anisotropy in the resulting patterns. As shown in Figure 7, isotropic patterns experience about 2.5 times the stress concentration that fully anisotropic (2D-sine wave) patterns do under light loading. For patterns created by amplified instability, increasing effective acceleration results in taller and sharper peaks and that leads to more than 3-fold increase in stress concentration compared to the initial droplets under light loading (Figure 8). Those differences vanish under heavy loading due to all surfaces approaching complete contact conditions. Next, we conduct a parametric study to determine the sensitivity of the contact responses to the above-mentioned processing parameters.

4.1 Influence of anisotropy in spinodal decomposition

To investigate the influence of anisotropic spinodal decomposition on the contact response, we simulate 20 surfaces generated using Eq. 2 at $\theta =\left\{0.02°,15°,30°,60°,90°\right\}$. Recall that as θ increases, the resulting surfaces evolve from 2D-sinusoidal to isotropic random patterns. We study the contact response under a low nominal contact pressure, p₀ = 0.001E* since the sensitivity to surface patterns is maximum at light loading. Figure 9A shows the real area of contact A_r (left y-axis) and the real mean contact pressure p_r (right y-axis) for all surfaces as a function of θ. The real area of contact decreases monotonically as θ increases. That reduction in load-bearing areas is naturally accompanied by the increase in the real mean contact pressures and the stress concentration. As seen in Figure 9B, the stress concentration is close to 200 for the anisotropic patterns (θ ≈ 0°) and 800 for the isotropic patterns (θ = 90°). The sensitivity of the real contact pressures and stress concentration on the degree of anisotropy, i.e., parameter θ stems from the decomposition patterns. For low θ values, the phase decomposition occurs preferentially along a single axis, and thus resulting patterns possess peaks with two very contrasting curvatures. Very high peak curvatures are obtained along the direction where decomposition is possible, and very low curvatures (nearly flat) along the orthogonal direction where decomposition is suppressed. Therefore, even though the surface heights are scaled to the same rms height values, the peaks of the patterns are sharper for isotropic cases than the ones for anisotropic. Eventually, the sharper peaks experience higher stress and thus higher stress concentrations. To illustrate this on the simulated surfaces, we plot in Figures 9C, D the rms of the peak heights σ^s and the mean effective curvatures ${\bar{K}}^s$ for different θ. The rms of peak heights is almost the same for all of the cases except for θ ≈ 0° cases. For that case, the surface pattern is an almost perfect 2D sine wave, and thus peak picking and statistics on heights and curvatures are not reliable. In contrast, the average effective curvature increases significantly from θ = 15° case to 60° and settles to a plateau afterward. This stark increase in average effective curvatures leads to sharper peaks and higher real contact pressures. Note that GW model assuming a random distribution of peak heights also predicts that $p_r\approx \chi E^{*}{\left({\sigma }^s{\bar{K}}^s\right)}^{0.5}$, where χ is a constant that depends on peak height distributions. Normal distribution captures well the distribution of the peaks for all the θ cases, so χ = 0.25. In Figure 9A, we show that a simple expression of p_r given by the GW model captures the trend of numerical simulations for all θ cases. That in turn informs us that surfaces created by spinodal decomposition nearly always possess peaks with a degree of randomness in their heights and curvatures, which then lead to contact response similar to randomly rough surfaces. The only way to prevent this is to inhibit decomposition perfectly along certain directions and thus obtain more deterministic patterns like the 2D sine waves shown in Figure 1A.

FIGURE 9

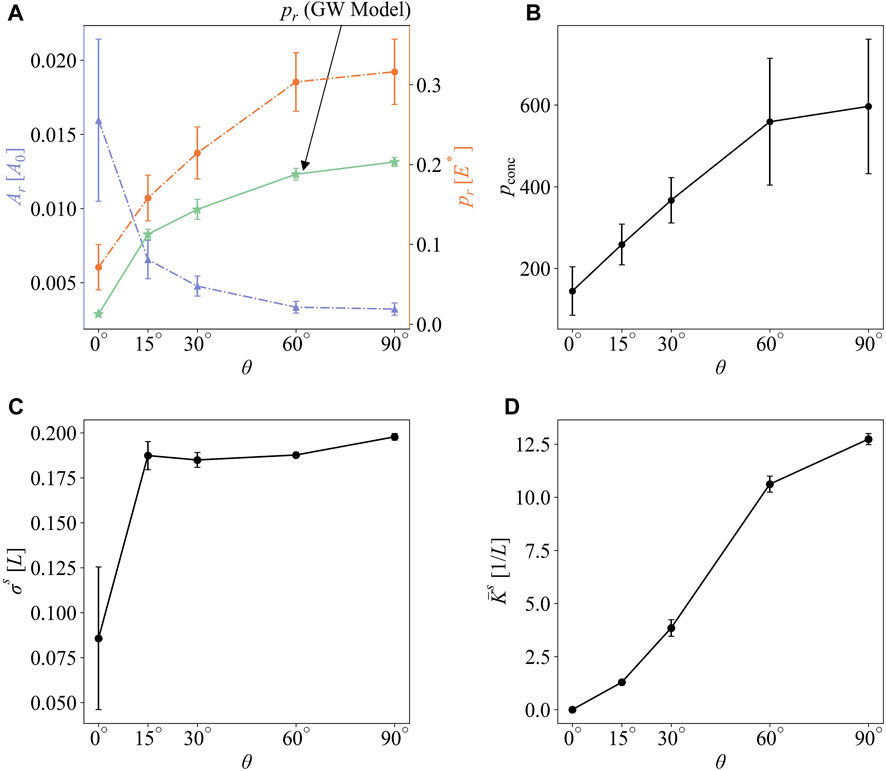
FIGURE 9. (A) The real area of contact (left, blue) and real mean contact pressure (right, orange), (B) the stress concentration, (C) the rms asperity height, and (D) the average effective curvature of asperity vs. directional parameter θ.

4.2 Influence of acceleration in amplified instability

The extent of stretch ɛ by effective centrifugal acceleration is a function of α = ρg_effh₀/G. For identical material and droplet height, α is proportional to the effective centrifugal acceleration g_eff, but inversely proportional to the elastic resistance of the drop G. The elastic resistance of the drop G depends on curing time and temperature, and thus determining its value is difficult during processing. Because of those difficulties, we will use the combined nondimensional parameter ρg_effl_c/G instead in the parametric study, where the characteristic length $l_c=\sqrt{\gamma /(\rho R{\mathrm{\Omega }}_1)}$ at a given initial rotating speed Ω₁. The combined parameter will be more sensitive to the effective acceleration applied during patterning, and thus can be treated as a processing parameter. We create 5 different surfaces using Eq. 5 corresponding to the nondimensional parameter ρg_effl_c/G = {1.48, 2.24, 3.14, 4.04, 4.92} and simulate it under light loading p₀ = 0.001E*. Lower bound 1.48 and upper bound 4.92 are the cases amplified at low g_eff and high g_eff in Figure 6, respectively, and those correspond to the actual surfaces with hair height pdfs reported by (Jambon-Puillet et al., 2021) in Figures 4B, C. For the largest ρg_effl_c/G case at 4.92, the average α is 5.44 < 8, which guarantees that most of the hair patterns exhibit stretches in line with the Eq. 4. Figure 10A shows the real contact area A_r (left y-axis) and the real mean contact pressure p_r (right y-axis). The real contact area gets smaller as ρg_effl_c/G increases, and the real mean contact pressure and stress concentration increase. The stress concentration at ρg_effl_c/G = 4.92 is about four times the stress concentration at ρg_effl_c/G = 1.48 (Figure 10B). Those trends in the real contact area, real mean contact pressure, and stress concentration can be linked to the rms peak height and curvature variations with ρg_effl_c/G parameter. At small values of ρg_effl_c/G corresponding to effective accelerations, the hair heights are fairly uniform (Figure 3A), whereas at high ρg_effl_c/G the hair heights are widely distributed as shown in Figure 3B, which leads to higher rms peak heights (Figure 10C). Moreover, as the droplet is stretched under higher effective acceleration, the reduction in the radial extent of the droplet leads to a sharper peak; i.e., increased curvature (Figure 10D). At high ρg_effl_c/G, the patterned surfaces feature highly-contrasting tall and sharp hairs coexisting with short and flat hairs. This can be directly observed from the increase of standard deviations in rms asperity heights and curvatures with increasing effective acceleration. Since tall and sharp hairs bear most of the load under light loading, real contact pressures are significantly high. With increasing load, shorter and flatter hairs start load bearing and the pressures drop. For highly-contrasting hairs as at high ρg_effl_c/G, recruiting more of those shorter and flatter hairs with further loading could lead to steep increase in real contact areas and thus reduction in real contact pressures. This can be seen in Figure 6B where pr decreases with applied nominal pressures until close to a complete contact condition. As GW model predicted p_r for the spinodal surface, it also predicts p_r for the surface generated by amplified instability reasonably well. Unlike the distribution of asperity heights for spinodal surfaces, the exponential function captures the distribution of asperity heights for amplified instability, so χ = 0.56. In Figure 10A, the predicted p_r indicated by an arrow compares well with the BEM estimations.

FIGURE 10

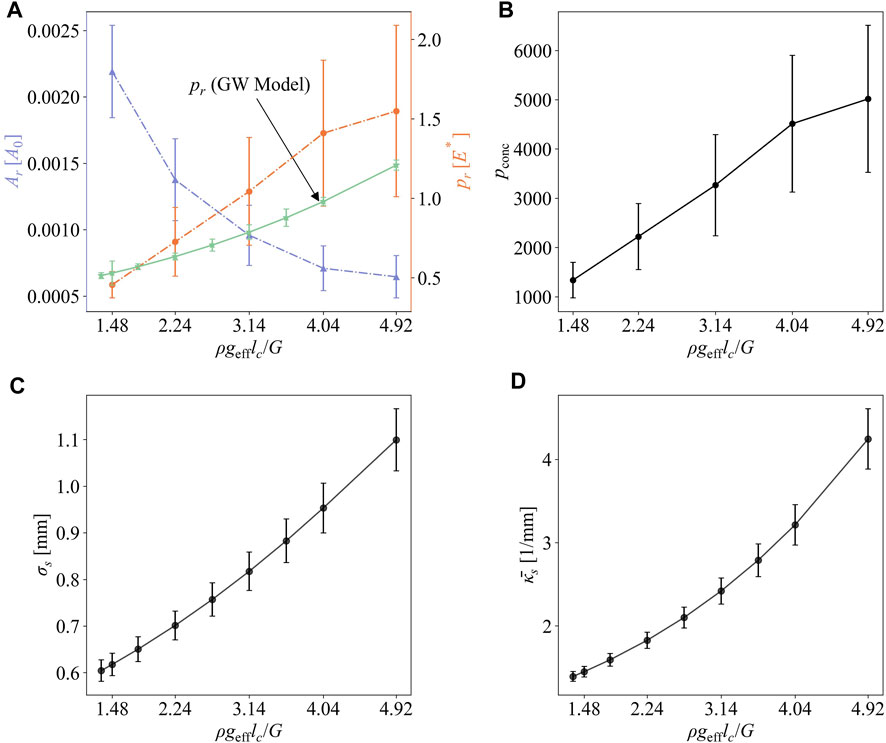
FIGURE 10. (A) The real area of contact (left, light blue) and real mean contact pressure (right, orange), (B) the stress concentration, (C) the rms asperity height, and (D) the average curvature of asperity vs. ρg_effl_c/G.

4.3 Influence of tangential loading

Lastly, we study the influence of combined loading on the above-mentioned stress concentration factors. Figure 11 shows the percent increment of stress concentration factors as a function of friction coefficient μ for three surface patterns: the isotropic spinodal patterned surface (θ = 90°), the anisotropic spinodal patterned surface (θ ≈ 0°) and the initial droplets generated by the amplified instability. Note that we simulate each surface at a mean pressure of p₀ = 0.0316E* and a mean shear traction of q_x = 0.7 μp₀, which corresponds to pre-sliding contact globally. Therefore, increasing friction coefficients simulate an increase in applied shear traction. Since the percent increment is estimated with respect to the stress concentration factors under pure normal loading, p_conc,0, it reveals the influence of added shear traction. It can be observed that the stress concentration factors increase with increasing shear tractions for all cases, but the increment is limited to 5% compared to the values for pure normal loading. Those findings confirm that the frictional tractions play a secondary role in stress concentrations where the primary factor is the processing parameters determining the degree of randomness in pattern geometry.

FIGURE 11

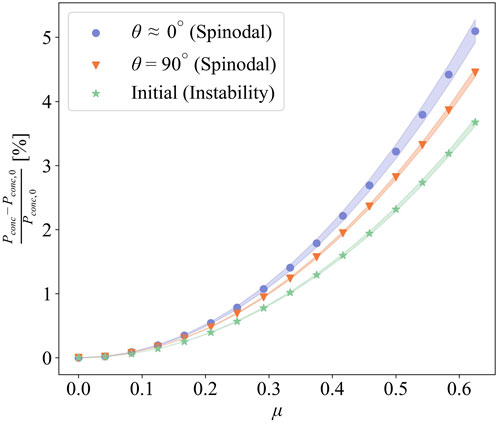
FIGURE 11. Percent increment of stress concentration as a function of friction coefficient in three representative surfaces.

5 Discussion and conclusion

In this paper, we have studied the real contact areas and tractions on the patterned surfaces generated by spinodal decomposition and amplified instability and reported how geometric randomness in the resulting patterns leads to stress concentrations under contact loading. On the surfaces generated by spinodal decomposition, the isotropic patterns deliver smaller real contact areas and thus higher real mean contact pressures and stress concentrations compared to the anisotropic patterns. Commonly, surfaces and metamaterials produced by spinodal decomposition are made of metals or ceramics. The stress concentration factors we report here suggest that nominal stresses are amplified by orders of magnitude in such surfaces under external or self-contact loading. Hence, local yielding or fracture is inevitable. Those local failures will hinder mechanical strength and resilience, and thus durability of the materials. On the surfaces generated by amplified instability, a similar reduction in the real contact area and increase in stress concentrations occur with increasing effective acceleration during patterning. At higher effective accelerations, the hair patterns exhibit broader variation in both height and curvature, and thus some hairs carry tractions that are 3 orders of magnitude higher than the nominal mean contact pressures. In general, the amplified instability method is used in patterning gels and elastomers. Both groups of materials have specific material formulations that can sustain large deformations without permanent failure. For instance, ultra-stretchable double network hydrogels can be synthesized to withstand stretches up to 100. Such hydrogels would be safe under contact loading even when patterned at the highest effective acceleration.

It is noteworthy that the stress concentrations reported here should be taken as an upper bound since we simulated linear elastic contact but in practice nonlinear material properties and failure would limit local tractions and deformations. The authors are currently working on experimental investigation of the above-mentioned surface patterns and the subsequent modeling will incorporate relevant material and failure models to inspect contact response more realistically.

Data availability statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.

Author contributions

WL and ME contributed to the conception and design of the study. WL conducted numerical simulations and analyses and wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research is partially funded by the US National Science Foundation (award numbers: CMMI-CAREER-1554146 and CMMI-2224380).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afshar-Mohajer, M., and Zou, M. (2020). Multi-scale in situ tribological studies of surfaces with 3d textures fabricated via two-photon lithography and replica molding. Adv. Mater. Interfaces 7, 2000299. doi:10.1002/admi.202000299

CrossRef Full Text | Google Scholar

Askari, M., Hutchins, D. A., Thomas, P. J., Astolfi, L., Watson, R. L., Abdi, M., et al. (2020). Additive manufacturing of metamaterials: A review. Addit. Manuf. 36, 101562. doi:10.1016/j.addma.2020.101562

CrossRef Full Text | Google Scholar

Bico, J., Tordeux, C., and Quéré, D. (2001). Rough wetting. Europhys. Lett. 55, 214–220. doi:10.1209/epl/i2001-00402-x

CrossRef Full Text | Google Scholar

Cahn, J. W. (1961). On spinodal decomposition. Acta Metall. 9, 795–801. doi:10.1016/0001-6160(61)90182-1

CrossRef Full Text | Google Scholar

Chen, S., Richter, B., Sridharan, K., Pfefferkorn, F., and Eriten, M. (2020). Patterning and fusion of alumina particles on S7 tool steel by pulsed laser processing. J. Manuf. Process. 60, 107–116. doi:10.1016/j.jmapro.2020.10.044

CrossRef Full Text | Google Scholar

Davis, C. S., and Crosby, A. J. (2011). Mechanics of wrinkled surface adhesion. Soft Matter 7, 5373–5381. doi:10.1039/c1sm05146f

CrossRef Full Text | Google Scholar

Dong, L., King, W. P., Raleigh, M., and Wadley, H. N. (2018). A microfabrication approach for making metallic mechanical metamaterials. Mater. Des. 160, 147–168. doi:10.1016/j.matdes.2018.09.008

CrossRef Full Text | Google Scholar

Eriten, M., Usta, A. D., and Liu, L. (2016). Tuning the dissipation in friction dampers excited by depolarized waves across patterned surfaces. J. Vib. Acoust. 138. doi:10.1115/1.4033343

CrossRef Full Text | Google Scholar

Frérot, L., Anciaux, G., Rey, V., Pham-Ba, S., and Molinari, J.-F. (2020). Tamaas: A library for elastic-plastic contact of periodic rough surfaces. J. Open Source Softw. 5, 2121. doi:10.21105/joss.02121

CrossRef Full Text | Google Scholar

Greenwood, J. (1997). Analysis of elliptical hertzian contacts. Tribol. Int. 30, 235–237. doi:10.1016/s0301-679x(96)00051-5

CrossRef Full Text | Google Scholar

Greenwood, J. A., and Williamson, J. P. (1966). Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 295, 300–319. doi:10.1098/rspa.1966.0242

CrossRef Full Text | Google Scholar

Guell Izard, A., Bauer, J., Crook, C., Turlo, V., and Valdevit, L. (2019). Ultrahigh energy absorption multifunctional spinodal nanoarchitectures. Small 15, 1903834. doi:10.1002/smll.201903834

CrossRef Full Text | Google Scholar

Hodge, A., Biener, J., Hayes, J., Bythrow, P., Volkert, C., and Hamza, A. (2007). Scaling equation for yield strength of nanoporous open-cell foams. Acta Mater. 55, 1343–1349. doi:10.1016/j.actamat.2006.09.038

CrossRef Full Text | Google Scholar

Holmes, D. P., Ursiny, M., and Crosby, A. J. (2008). Crumpled surface structures. Soft Matter 4, 82–85. doi:10.1039/b712324h

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsieh, M.-T., Endo, B., Zhang, Y., Bauer, J., and Valdevit, L. (2019). The mechanical response of cellular materials with spinodal topologies. J. Mech. Phys. Solids 125, 401–419. doi:10.1016/j.jmps.2019.01.002

CrossRef Full Text | Google Scholar

Jambon-Puillet, E., Piéchaud, M. R., and Brun, P.-T. (2021). Elastic amplification of the Rayleigh–taylor instability in solidifying melts. Proc. Natl. Acad. Sci. 118, e2020701118. doi:10.1073/pnas.2020701118

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, K. L. (1985). Contact Mechanics. Cambridge University Press.

Google Scholar

Ku, T., Ramsey, J., and Clinton, W. (1968). Calculation of liquid droplet profiles from closed-form solution of young-laplace equation. IBM J. Res. Dev. 12, 441–447. doi:10.1147/rd.126.0441

CrossRef Full Text | Google Scholar

Kumar, S., Tan, S., Zheng, L., and Kochmann, D. M. (2020). Inverse-designed spinodoid metamaterials. npj Comput. Mater. 6, 73–10. doi:10.1038/s41524-020-0341-6

CrossRef Full Text | Google Scholar

Lee, M. N., and Mohraz, A. (2010). Bicontinuous macroporous materials from bijel templates. Adv. Mater. 22, 4836–4841. doi:10.1002/adma.201001696

PubMed Abstract | CrossRef Full Text | Google Scholar

Lister, J. R., Rallison, J. M., and Rees, S. J. (2010). The nonlinear dynamics of pendent drops on a thin film coating the underside of a ceiling. J. fluid Mech. 647, 239–264. doi:10.1017/s002211201000008x

CrossRef Full Text | Google Scholar

Marthelot, J., Strong, E., Reis, P. M., and Brun, P.-T. (2018). Designing soft materials with interfacial instabilities in liquid films. Nat. Commun. 9, 4477–7. doi:10.1038/s41467-018-06984-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsuda, T., Kawakami, R., Namba, R., Nakajima, T., and Gong, J. P. (2019). Mechanoresponsive self-growing hydrogels inspired by muscle training. Science 363, 504–508. doi:10.1126/science.aau9533

PubMed Abstract | CrossRef Full Text | Google Scholar

Mu, Q., Cui, K., Wang, Z. J., Matsuda, T., Cui, W., Kato, H., et al. (2022). Force-triggered rapid microstructure growth on hydrogel surface for on-demand functions. Nat. Commun. 13, 6213. doi:10.1038/s41467-022-34044-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Patil, D. B., and Eriten, M. (2015). Frictional energy dissipation in spherical contacts under presliding: effect of elastic mismatch, plasticity and phase difference in loading. J. Appl. Mech. 82. doi:10.1115/1.4029020

CrossRef Full Text | Google Scholar

Perris, J., Xu, Y., Kartal, M. E., Gadegaard, N., and Mulvihill, D. M. (2021). Tailorable and repeatable normal contact stiffness via micropatterned interfaces. Tribol. Lett. 69, 106–112. doi:10.1007/s11249-021-01473-3

CrossRef Full Text | Google Scholar

Polonsky, I., and Keer, L. (1999). A numerical method for solving rough contact problems based on the multi-level multi-summation and conjugate gradient techniques. Wear 231, 206–219. doi:10.1016/s0043-1648(99)00113-1

CrossRef Full Text | Google Scholar

Portela, C. M., Vidyasagar, A., Krödel, S., Weissenbach, T., Yee, D. W., Greer, J. R., et al. (2020). Extreme mechanical resilience of self-assembled nanolabyrinthine materials. Proc. Natl. Acad. Sci. 117, 5686–5693. doi:10.1073/pnas.1916817117

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidyasagar, A., Krödel, S., and Kochmann, D. M. (2018). Microstructural patterns with tunable mechanical anisotropy obtained by simulating anisotropic spinodal decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 474, 20180535. doi:10.1098/rspa.2018.0535

CrossRef Full Text | Google Scholar

Wang, C., Vangelatos, Z., Grigoropoulos, C. P., and Ma, Z. (2022). Micro-engineered architected metamaterials for cell and tissue engineering. Mater. Today Adv. 13, 100206. doi:10.1016/j.mtadv.2022.100206

CrossRef Full Text | Google Scholar

Yastrebov, V. A., Anciaux, G., and Molinari, J.-F. (2014). The contact of elastic regular wavy surfaces revisited. Tribol. Lett. 56, 171–183. doi:10.1007/s11249-014-0395-z

CrossRef Full Text | Google Scholar

Yu, D., Wong, Y., and Hong, G. (2011). Ultraprecision machining of micro-structured functional surfaces on brittle materials. J. micromechanics microengineering 21, 095011. doi:10.1088/0960-1317/21/9/095011

CrossRef Full Text | Google Scholar