Highly underexpanded rarefied jet flows

A highly underexpanded jet outflow into the background in transition and scattering regimes is studied computationally. The direct simulation Monte Carlo method and Navier–Stokes equations are used. The main parameters’ impact on the jet flow is analyzed. It is shown that a drastic flow structure transformation occurs in a relatively narrow Reynolds numbers’ range, 5 ≤ Re_L ≤ 30, featuring the jet–surrounding gas interaction. At Re_L = 5, a shock wave structure that is typical for the underexpanded jet degenerates completely. The existing empirical expressions application for the estimation of the characteristic dimensions of the shock wave structure in the transition regime leads to significant inaccuracy. For the considered parameters’ range, the approaches based on the direct simulation Monte Carlo method and Navier–Stokes (NS) equations’ solution lead to similar results in the nozzle region, where the flow regime is hydrodynamic. Nevertheless, the NS approach employment for the assessment of flow parameters within rarefied shock layers is debatable.

1 Introduction

Supersonic underexpanded gas jets have been the subject of research since the 1960s (Dulov and Lukyanov, 1984; Avduevski et al., 1989; Franquet et al., 2015; Sutton and Biblarz, 2017). A jet expansion is characterized by the expansion ratio n = p_a/p_∞, where p_a is the gas pressure at the nozzle outlet and p_∞ is the background gas pressure. Highly underexpanded jets (n ≫ 1) are associated with the spacecraft rocket engines’ operation in the rarefied Earth and other planets’ atmosphere. The study of such jets is necessary for minimizing contamination and spacecraft surface damage caused by the jets (Cai et al., 2022) and for optimizing the operations during a spacecraft launch and landing. A special case is the outflow of rarefied jets from low-thrust engines used in the spacecraft control systems (Micci and Ketsdever, 2000). Such jets are characterized by moderate values of the Reynolds number Re_∗, calculated by the parameters of the nozzle throat, and a wide range of Reynolds number Re_L, which determines the jet–environment interaction regime.

In cluster beam deposition technologies (Hagena, 1980; 1987) and vacuum gas jet technologies of nanostructured film deposition (Bykov et al., 2019; Starinskiy et al., 2022), a highly underexpanded jet is formed when flowing from a source/crucible into a low-pressure chamber. The gas dynamic parameters of the jet have a decisive influence on the cluster synthesis processes, and their evaluation is necessary for technologies’ optimization. A significant part of the operating range of vacuum technologies corresponds to low and moderate Reynolds numbers Re_∗ and Re_L.

Experimental studies of underexpanded gas jets at low Re_L have been carried out and described in a large number of publications, such as in Rebrov et al. (1971), Volchkov et al. (1973), Kisliakov et al. (1975), and Dubrovin et al. (2022). Despite that, theoretical studies related to n ≫ 1 and Re_L < 100 parameters’ range are quite insufficient. Simulations for this range are challenging due to the following reasons. The flow regime in the mixing region is transitional in terms of the Knudsen number or even a free molecular one. At some locations, non-equilibrium effects arise, which complicate the entire jet flow calculation using traditional methods based on the solution of the Navier–Stokes (NS) equations. The use of computational approaches based on the kinetic gas models, such as the direct simulation Monte Carlo (DSMC) method (Bird, 1994; 2013), is optimal for low values of Re_L which include outflow into the vacuum (Re_L = 0) (Sharipov, 2004; Varoutis et al., 2008; Bykov and Zakharov, 2022). However, the DSMC method is resource intensive. On the one hand, it requires the simulation of a dense flow in the chamber and nozzle, and on the other hand, for n ≫ 1, a sufficiently large computational domain is required in the jet expansion region both in the axial and radial directions that requires the employment of additional simulation techniques, such as the use of radial weight factors that can lead to the violation of conservation laws (Bird, 1994); another way is to employ supercomputer systems (Kashkovsky et al., 2023). The use of hybrid approaches, which implies matching the solution of the NS equations for a hydrodynamic region and the kinetic approach for a rarefied region (George, 2000; Schwartzentruber and Boyd, 2015; Suss et al., 2023), is also possible. However, it does not solve the problem since a large jet expansion region simulation is its most resource-intensive part. The question on the correct solution match at the corresponding transition boundary also arises (Tcheremissine, 2023).

The aim of this work is to study a highly underexpanded jet flow in the mentioned parameters’ range (n ≫ 1, Re_L < 100). The study involves the analysis of the main parameter impact on the flow structure inside a conical nozzle and an expanding jet, refinement of Re_L values for which there are no shock waves in the mixing region, discussion on the suitability of the available empirical expressions for estimating jet dimensions, and analysis of a correctness of flow modeling using the NS approach.

The study is organized as follows. In the next section, the problem statement is formulated and the approaches used are described. The third section is devoted to the analysis of simulation results. The last section draws the conclusions.

2 Problem statement

2.1 Geometry and flow parameters

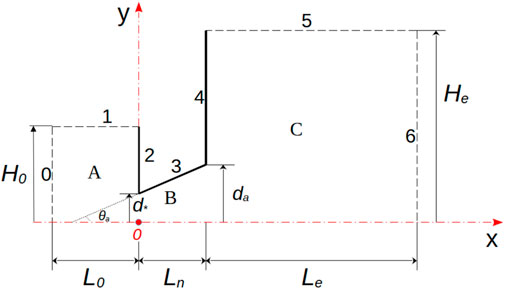
The argon outflow from a conical nozzle into the background gas is considered (Figure 1). The computational domain consists of a chamber, in which the stagnation gas parameters (p₀ and T₀) are fixed (domain A), a diverging conical nozzle (domain B), and the region of jet expansion outside the nozzle (domain C). The nozzle is a divergent cone with length L_n = 6 mm, throat diameter d_∗ = 1 mm, outlet diameter d_a = 3.6 mm, and nozzle half-angle θ_a ≈ 12.2°. The throat corresponds to the minimum cross-section of the nozzle’s conical part. In the considered geometry, it coincides with the coordinates’ origin, as shown in Figure 1.

FIGURE 1

FIGURE 1. Computational domain (not to scale).

The chamber (stagnation) pressure, p₀, and the background gas pressure, p_∞, are varied at close values of gas temperatures in the chamber and background T₀/T_∞∼ 1 (Table 1).

TABLE 1

TABLE 1. Main flow parameters.

The flow in the nozzle is determined by the Reynolds number Re_∗, calculated from the parameters of the gas in the throat or by the corresponding Knudsen number Kn_∗. The interaction of the outflowing gas with ambient gas is characterized by the Reynolds number Re that is determined by environmental parameters, the characteristic jet size, and the characteristic outflow velocity. Re_∗ and Re are related to each other. When the gas in the chamber and background gas are the same and their temperatures are equal, the additional dimensionless parameters that determine the flow are the expansion ratio n, Mach number at the nozzle outlet, M_a, and Prandtl number, Pr (Dulov and Lukyanov, 1984). The considered flow parameters are summarized in Table 1.

The Reynolds number in the nozzle throat is determined as

${\mathrm{R}\mathrm{e}}_{\ast }=\frac{{\rho }_{\ast }{v}_{\ast }{d}_{\ast }}{\mu \left(T_{\ast }\right)},(1)$

where ρ_∗ and v_∗ are the gas mass density and velocity in the throat (averaged over the section), respectively, and μ(T_∗) is the gas viscosity at the throat temperature T_∗. The Knudsen number (Bird, 1994) can be estimated as

${\mathrm{K}\mathrm{n}}_{\ast }=\frac{2\left(5-2\omega \right)\left(7-2\omega \right)}{15\sqrt{\pi }}\sqrt{\frac{\gamma }{2}}\frac{{\mathrm{M}}_{\ast }}{{\mathrm{R}\mathrm{e}}_{\ast }},(2)$

where γ = 1.67 is the specific heat ratio, ω is the exponent in the viscosity–temperature dependence, and M_∗ is the Mach number in the throat. For estimation of the main parameters, it is assumed that M_∗ = 1.

The Reynolds number characterizing the flow regime in the expansion region is defined as Re = ρ_∞v_mL/μ_∞ = αRe_L (Dulov and Lukyanov, 1984). Herein, ρ_∞ and μ_∞ are the density and viscosity of the ambient gas, respectively; v_m is the maximum outflow velocity; L is the characteristic size of the underexpanded jet, estimated as the distance to the Mach disk, x_c, or to the corresponding intersection point of an oblique shock and axis (see Section 3.2); Re_L is defined as

${\mathrm{R}\mathrm{e}}_L={\mathrm{R}\mathrm{e}}_{\ast }/\sqrt{N},(3)$

where N = p₀/p_∞ is the nozzle pressure ratio. The parameter α is a weak function of the Mach number at the nozzle outlet, specific heat ratio, and half-angle and is of the order of unity. Therefore, instead of Re, parameter Re_L is frequently used (Rebrov et al., 1971; Dulov and Lukyanov, 1984). The corresponding Knudsen number (Dulov and Lukyanov, 1984) can be estimated as

${\mathrm{K}\mathrm{n}}_L={\lambda }_{\infty }/L\approx 1/{\mathrm{R}\mathrm{e}}_L.(4)$

where λ_∞ is the mean free path of molecules in the ambient gas. Equation 4 assumes an equality of the stagnation and ambient temperatures.

As shown in Table 1, the considering regimes of the nozzle flow are hydrodynamic, while the regime of the jet with a background interaction is transitional in terms of the Knudsen number.

2.2 DSMC method parameters

The Bird’s classical algorithm using the no time counter (NTC) scheme (Bird, 1994; Bird, 2013) is employed in DSMC simulations. Elastic collisions are described by the variable hard sphere (VHS) model, for which the collision diameter was determined by the particle relative velocity c as

$d=d_{\mathit{ref}}{\left(c_{\mathit{ref}}/c\right)}^{\omega -1/2},(5)$

where, for argon, d_ref = 4.17 ⋅ 10^–10 m, c_ref = 558.3 m/s, (T_ref = 273 K), and ω = 0.81 (Bird, 1994). This equation implies that μ ∼ T^ω (Eq. 6).

The dimensions of domain (A) are L₀ = 2d_∗ and H₀ = 1.35d_∗, and the dimensions of domain (C) are L_e = 330d_∗ and H_e = 45d_∗. At the boundaries 0 and 1, the gas is assumed to be at rest. Diffuse reflection with total energy accommodation and temperature T₀ is assumed at boundaries 2, 3, and 4. The conditions at boundaries 5 and 6 are similar to the “gas at rest” condition: incident particles are removed from the simulation, and the particles flowing into this region correspond to a semi-Maxwellian distribution function with parameters p_∞ and T_∞.

A zone mesh with a different number of cells within each zone is used in the simulations. The zones are of a rectangular or triangular shape and consist of rectangular and triangular cells. The DSMC mesh for the whole domain and nozzle region is shown in Supplementary Figure S1. The number of zones varies from 272 to 400, the total number of cells varies from 10⁶ to 3.5 ⋅ 10⁶, and the number of computing particles varies from 5 ⋅ 10⁸ to 10⁹, depending on the simulation case. Additional verification simulations, in which the number of cells in the nozzle and the area adjacent to it varies, showed the practical absence of dependence of the solution with a further decrease in cell size. The in-house DSMC code (Bykov and Gorbachev, 2019) is employed, and the algorithm is parallelized by the spatial decomposition method and performed on the Polytechnic Tornado cluster of the supercomputer center of the Peter the Great St. Petersburg Polytechnic University.

The code verification was performed in several previous works, such as in Bykov and Gorbachev (2019) and Bykov and Zakharov (2022). Herein, we present a comparison of flow through nozzle DSMC results against solution results of the NS equations.

2.3 Simulation using the Navier–Stokes equations

Supersonic jet modeling was performed using the OpenFOAM package, version 2112, distributed under the GNU GPL license. A set of equations describing the transient flow of viscous compressible gas was used—the mass conservation equation (continuity equation), momentum conservation equation (motion equation), and energy conservation equation—which were closed by the ideal gas law and Newtonian law for viscous stress tensor (Greenshields et al., 2009).

The power law of dependency of viscosity on temperature for argon was used as follows:

$\mu =A{T}^{\omega },(6)$

where ω is as given in (5), A = 2.25 ⋅ 10^–7, and the viscosity units are Pa⋅s.

An unsteady viscous gas flow solver rhoCentralFOAM was used. It is based on the Kurganov–Tadmor central-upstream difference scheme. The rhoCentralFOAM solves momentum and mass conservation equations using the time separation approach. The inviscid equations are solved explicitly to obtain the predicted variable value. Then, the diffusion terms are added in the form of implicit corrections to the original inviscid equations (Greenshields et al., 2009).

The computational domain for NS simulations was taken to be the same as that for DSMC (see Figure 1). At the inlet and outlet sections (borders 0 and 6), the soft boundary conditions are used as

$\partial V_n/\partial n=0,\partial p/\partial n=0,\partial T/\partial n=0.(7)$

where $\vec{n}$ is the unit normal vector of the surface, $\vec{V}$ is the gas velocity, and V_n is the normal component of the surface velocity vector. On the walls (1, 2, 3, and 4), isothermal with T₀ temperature and no-slip boundary conditions are applied as

$T=T_0,\vec{V}=0.(8)$

Although the conditions at boundary 1 inside the chamber between the DSMC and NS approaches differs, they lead to the same mass flux through the throat.

The outer boundary (5) represents a far field with fixed pressure. In the case of an inflow, the temperature boundary condition is switched from a zero normal gradient to a fixed value at T = T_∞:

$\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{fl}\mathrm{o}\mathrm{w}:\partial V_n/\partial n=0,p=p_{\infty },\partial T/\partial n=0,(9)$

$\mathrm{I}\mathrm{n}\mathrm{fl}\mathrm{o}\mathrm{w}:\partial V_n/\partial n=0,p=p_{\infty },T=T_{\infty }.(10)$

The problem is solved using the transient approach, where at the initial moment, discontinuity in the pressure field is assumed: a high pressure p₀ at chamber (A) and a low pressure p_∞ in nozzle (B) and expansion region (C). During computation, steady fields are obtained.

A 2D structured mesh with approximately 200,000 cells with near-surface layer resolution is used. The computational mesh is shown in Supplementary Figure S2. To see the cell size effect, additional simulations are performed, which show that the solution obtained on the 200,000 cells mesh is not dependent on the cell size.

3 Results

3.1 Nozzle flow

The simulation results, of both the DSMC and NS, show a non-monotonic behavior of the gas dynamic parameters inside the nozzle (Figures 2, 3). In the paraxial region of the nozzle, the density and temperature maxima and the minimum Mach number are observed. The behavior of the parameters in the flow regions near the nozzle wall and near the axis significantly differs. These features of the flow are due to the following factors.

FIGURE 2

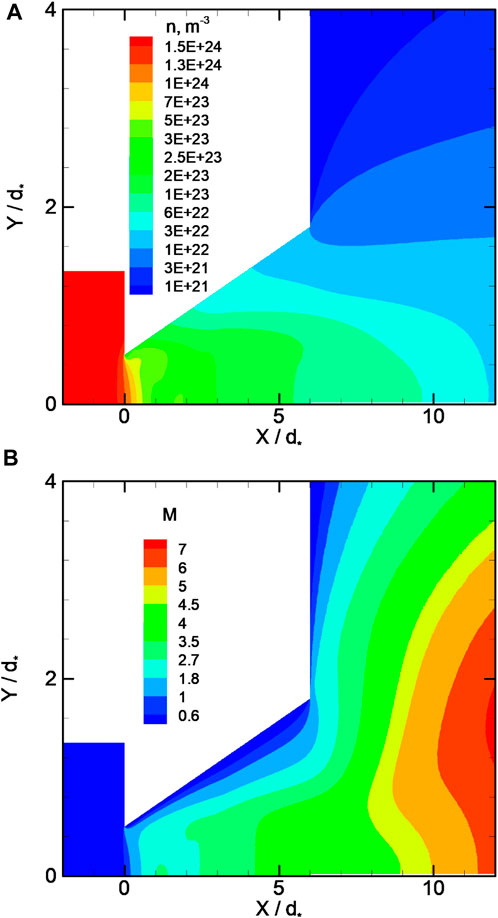
FIGURE 2. Distribution of fields inside nozzle (DSMC simulations, case 2). Number density (A) and Mach number (B).

FIGURE 3

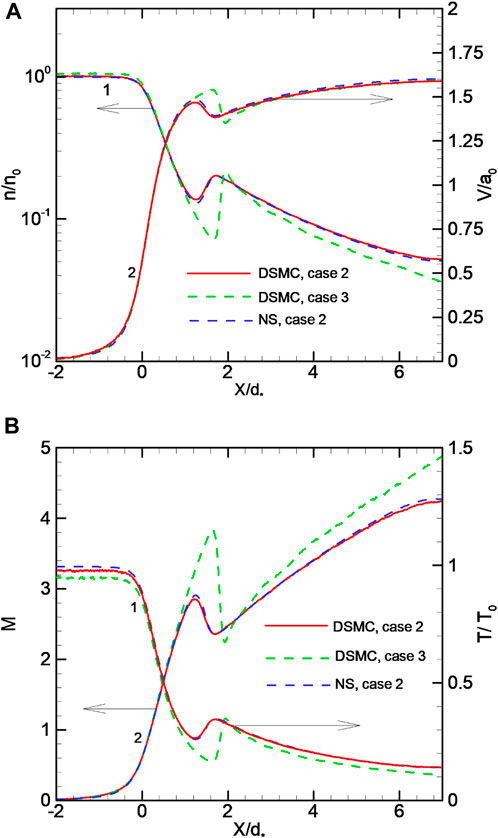
FIGURE 3. Number density (1) and velocity (2) (A); temperature (1) and Mach number (2) (B) distributions along the flow axis for cases 2 and 3. a₀ is the sound velocity in the chamber.

First, an oblique shock is formed inside the conical nozzle (Ivanov et al., 1999). A sharp expansion of the flow directly behind the throat and further interaction of the flow with the wall leads to the appearance of a positive pressure gradient along the wall near the throat. A local increase in pressure near the surface leads to the formation of a shock wave. With the increase in chamber pressure, the intersection zone of shock with the flow axis shifts toward the nozzle outlet (Figure 3). The intensity of shock also increases. In cases 2 and 3 (inside the nozzle, cases 1 and 2 are identical), for which the stagnation pressure in the chamber differs by the factor of 3, the ratio of the Mach numbers on the axis behind and before shock is approximately 1.22 (case 2) and 1.78 (case 3), respectively. After the shock, the axial parameters inside the nozzle vary monotonically; the density and temperature decrease, while the velocity and Mach number increase. In the general case, shock reflected from the axis can reach the nozzle wall, be reflected from it, and “return” to the downstream axis.

Second, the flow in the near-wall region is affected by the boundary conditions on the wall. In the axial region, the temperature decreases with increasing distance from the throat, except at the vicinity of the shock. There is practically no temperature gradient along the wall surface. The gas temperature is close to the wall temperature. At the wall, the gas decelerates and a subsonic flow region is formed. The sound line starts at the top of the throat and closes at the nozzle edge.

Despite the rather high values of the Reynolds number, there is no region of one-dimensional isentropic expansion, and viscous effects manifest themselves in the entire region of the flow through the nozzle.

For the Re_∗ numbers given in Table 1, the flow regime through the nozzle is close to hydrodynamic. This makes it possible to carry out a calculation using the NS equations and compare the modeling results obtained by different approaches. The axial distributions of the parameters obtained by solving the NS equation for case 2 are shown in Figure 3, and an almost complete agreement of the results is seen.

3.2 Expanding jet flow

The flow in a supersonic underexpanded jet for high Reynolds numbers Re_L has been widely studied (Dulov and Lukyanov, 1984; Avduevski et al., 1989; Rebrov, 2001; Franquet et al., 2015; Sutton and Biblarz, 2017). Depending on the value of Re_L, the flow in the jet expansion region can be laminar or turbulent. In the initial section behind the nozzle, a barrel shock is formed, which confines the region of free expansion of the jet. At small expansion ratio values, the jet consists of some periodically repeating structures, such as the barrels (Mach diamonds). This mode is characterized by a regular reflection of a barrel shock from the axis (no Mach disk). The pressure ratio increases above a certain value n_∗, which leads to the appearance of a central shock wave, the Mach disk. An increase in n leads to the gradual vanishing of all barrels, except the first one. The shock wave structure includes the barrel shock, Mach disk, and reflected oblique shock (Supplementary Figure S3A). The distance to the Mach disk at high Reynolds numbers Re_L can be estimated using the Lewis–Carlson expression (Lewis and Carlson, 1964) as follows:

$x_c/d_a=0.69{\mathrm{M}}_a\sqrt{\gamma n},(11)$

where M_a is the Mach number at the nozzle outlet. Equation 11 is the result of experimental data processing for nitrogen, helium, and carbon dioxide jets. For sound outflow through an orifice in the hydrodynamic regime, the following expression (Ashkenas and Sherman, 1965) can be used:

$x_c/d_{\ast }=0.67\sqrt{N}.(12)$

The last equation is convenient because it does not require a knowledge of the parameters in a nozzle outlet section.

With a significant decrease in the Re_L number down to approximately 100, two trends are observed. The first trend is in the thickening of the barrel shocks and Mach disk, as well as the jet gas and ambient gas mixing layer at the jet boundary. The flow is restructured from the laminar regime to the scattering regime (Muntz et al., 1970), in which the observed flow in the far field of the jet acquires a diffusion character.

The second trend is in the evolution of a shock wave structure. In the experiments with a decrease in Re_L below a certain value (e.g., Re_L ≈ 350 for CO₂), a transition to a quasi-regular reflection of an incident oblique shock, the so-called X-shaped configuration, is observed (Kisliakov et al., 1975; Rebrov, 2001) (Supplementary Figure S3B). In the region of the X-shaped configuration, there is a sharp increase in density that is relative to the maximum, which is possible for a direct shock in an inviscid gas.

Herein, we present the simulation results of an underexpanded jet outflow for extremely low Re_L (Re_L ≤ 30, Table 1).

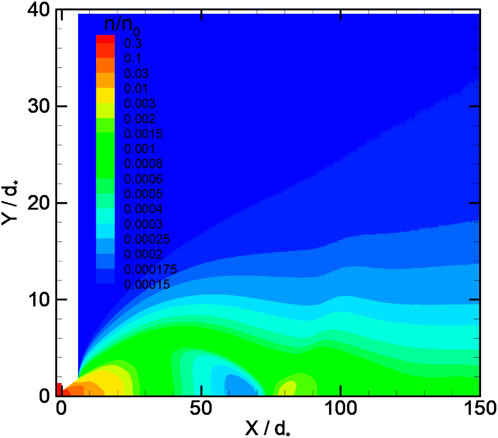
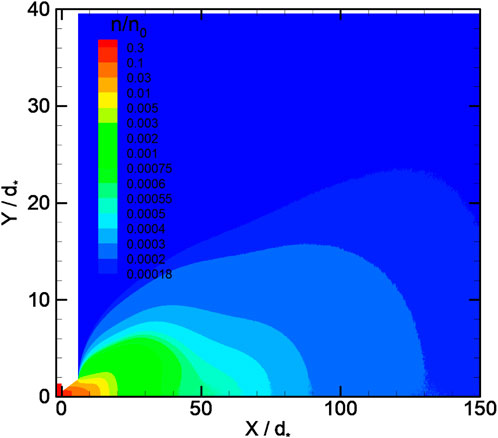
For case 3, Re_L = 30 (Kn_L = 0.033), the density field is shown in Figure 4. The formation of a shock structure is clearly seen (Supplementary Figure S3C). The jet core is confined by the oblique shock. Shock is smeared (Figures 4, 5, 6) and located close to the jet axis at a distance that is less than Y < 10d_∗ = 2.8d_a. The influence of the reflected shock on the flow is limited by the radial coordinate Y ∼ 20d_∗. In the expansion region, the density minimum is close to the environment density. A minimum on temperature distribution and maximum on Mach number distribution along the axis are observed in the region before the shock–axis intersection region. The temperature and density minima and Mach number maximum positions do not coincide. According to the data presented in Figure 6, the Mach number reaches its maximum value on axis M$\sim 22$ at the position X/d_∗ ∼ 50, then decreases to value M$\sim 3$ behind the shock. The flow behind the shock on the jet centerline is supersonic. The maximal value of M does not exceed 5. The oscillations are typical for the axial pressure distribution. The pressure change in the shock region exceeds two orders of magnitude. Starting from X/d_∗ ∼ 150, the pressure changes slightly. The density, velocity, and temperature changes in the expansion region are also non-monotonic (Supplementary Figure S4). The density in the shock–axis intersection region increases by an order of magnitude, and the velocity undergoes a smaller change, decreasing by 10%.

FIGURE 4

FIGURE 4. Number density field for case 3.

FIGURE 5

FIGURE 5. Number density distribution in the longitudinal direction for case 3.

FIGURE 6

FIGURE 6. Mach number and pressure distributions along the flow axis for case 3.

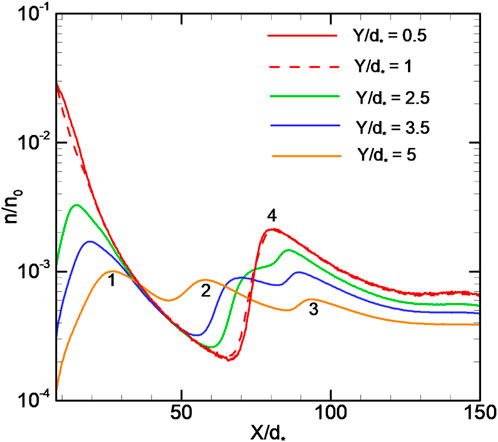
Due to rarefaction, the shock waves are smearing and no more the infinitely thin layers. For the considered flow case, the presence of a small radius Mach disk (Supplementary Figure S3A) is questionable. The shock wave configuration obtained in the simulations is very close to the X-shaped configuration, as previously described by Kisliakov et al. (1975) and Rebrov (2001) (Supplementary Figure S3B). The latter assumes an absence of the Mach disk, a quasi-regular intersection of the incident oblique shock with the flow axis and supersonic flow behind the X-point. A reflection of the incident shock from an axis should lead to the presence of the two density maxima of the longitudinal distribution near the axis that correspond to the incident and reflected shock, respectively. In Figure 5, at the coordinates Y/d_∗ = 3.5 and 5, three density maxima are observed. The first (number 1 in the figure) corresponds to the density change when the line with Y/d_∗ = 3.5 or 5 intersects the beginning of the oblique shock layer near the nozzle. The other two maxima (2 and 3) are the aforementioned line intersections at the end of the incident shock and reflected shock (near the interaction region), respectively. As Y/d_∗ decreases, starting from Y/d_∗ ∼ 1.5, maxima 2 and 3 degenerate into one maximum 4. For Y/d_∗ = 0.5 and 1, the density distributions in the shock region on the jet centerline practically coincide, demonstrating only one density maximum.

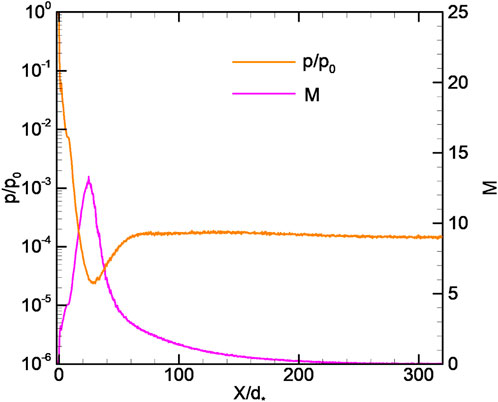
One of the goals of this work was to analyze the possibility of using the empirical equations for estimating the location of the intersection of shock and the axis. The location of shock may be predicted by using equation (11) or (12). The corresponding lines (marked as L1, L2, and A) are depicted in Figure 6 (also see Supplementary Figure S4). Equation 11 requires nozzle outlet parameters M_a and p_a. For the considered cases, such parameters vary by the radial coordinates at the nozzle exit. The parameters can be estimated as axial parameters (line L1 in Figure 6) or averaged parameters (line L2). The shock location can be defined as the position of the maximal density gradient within the shock. Equation 12, which is valid for sound outflow in the hydrodynamic regime, underestimates a shock location coordinate. The same situation exists with the assessment by (11) using the average parameters at the nozzle outlet (line A). On the contrary, the assessment by (11), with the use of axial parameters, overestimates a shock location coordinate (Supplementary Figure S4). It can be seen that all the shock location predictions are not satisfactory for the considered parameters’ range.

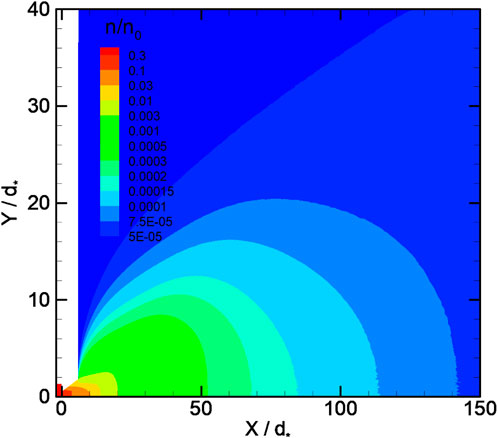
With a threefold decrease in the Reynolds number to Re_L = 9.9 (Kn_L = 0.1, case 2), the flow pattern changes significantly. The shock structure is no longer observed (Figure 7). However, the isolines of the parameters are significantly deformed in relation to the case Re_L → 0. The deformation of the isolines is the most pronounced for the density field (Figure 7). Thus, we can conclude that a smeared and degenerate shock wave structure exists for this situation. This statement somewhat corrects the conclusion (Dulov and Lukyanov, 1984) about the complete degeneration of such a structure at Re_L = 10. A plateau is observed on the axial density distribution corresponding to the coordinates 40 < X/d_∗ < 60 (Supplementary Figure S5), which can be identified with the interaction of smeared oblique shock with the flow axis. The Mach number reaches its maximum value M$\sim 13$ at the location X/d_∗ ∼ 30 (Figure 8). Furthermore, the Mach number, without experiencing oscillations, decreases monotonically to zero at the boundary of the computational domain. The pressure in the jet becomes equal to the pressure of the background starting from X/d_∗ ∼ 100, and the density and temperature reach their asymptotic values at X/d_∗ ∼ 200 (Supplementary Figure S5). For this case, we can only conventionally discuss the position of shock on the axis and identify it with a plateau on the axial density distribution.

FIGURE 7

FIGURE 7. Number density field for case 2.

FIGURE 8

FIGURE 8. Mach number and pressure distributions along the flow axis for case 2.

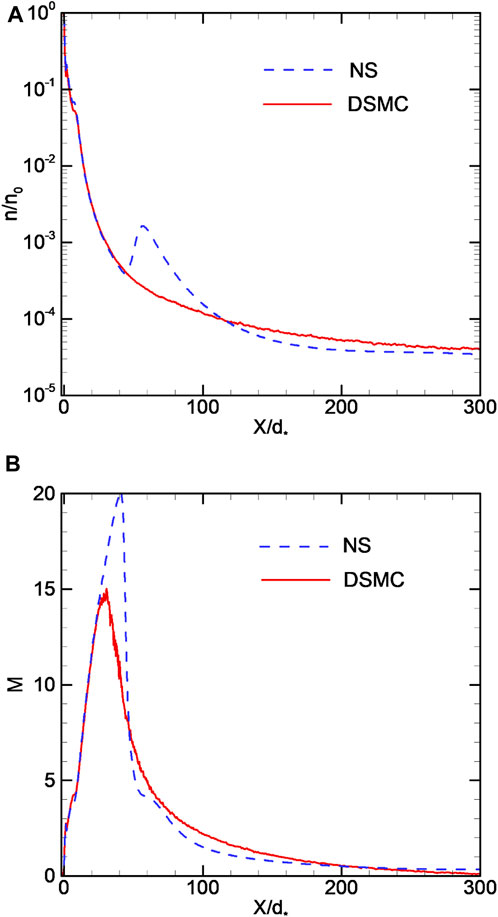
Further reduction of the Reynolds number to Re_L = 5 (Kn_L = 0.2, case 1) leads to a complete shock wave degeneration (Figure 9). Density field isolines’ deformation is no longer observed. In contrast to the outflow into vacuum, the Mach number and temperature fields have a maximum and minimum, respectively, but no oscillations of the parameters are observed. The gas dynamic parameters’ axial distributions are shown in Figure 10, Supplementary Figure S6. The plateau on the density distribution disappears, which confirms the complete degeneration of the shock waves. The distance to shock may be estimated by (11) or (12), but it does not make sense for this case.

FIGURE 9

FIGURE 9. Number density field for case 1.

FIGURE 10

FIGURE 10. Mach number and pressure distributions along the flow axis for case 1.

The change in the shock wave structure in a strongly underexpanded jet at low Re_L numbers can be clearly seen in Supplementary Figure S7. In case 1, the density decreases monotonically; in case 2, a step appears on the density distribution; and in case 3, the structure shown in Supplementary Figure S3B becomes pronounced.

3.3 Relevancy analysis of calculations based on Navier–Stokes equations

The calculations for all the cases were performed on the basis of the NS equations as well. The corresponding computational parameters and boundary conditions are described in Section 2.3.

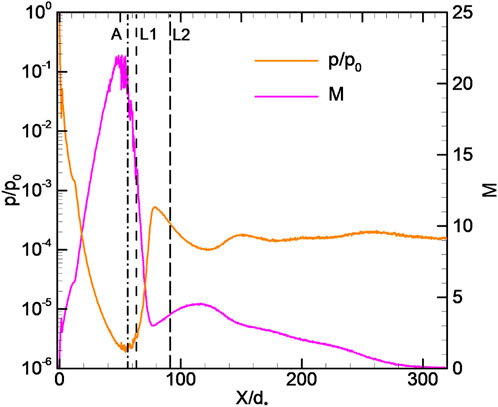
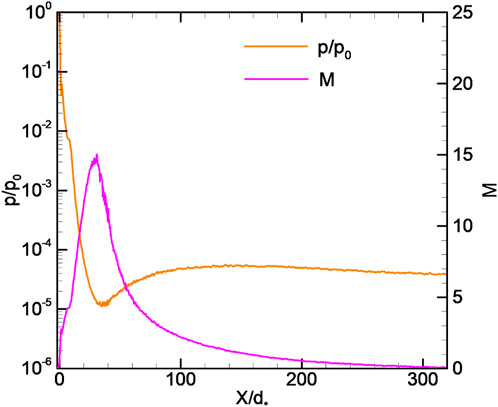
Figures 11A, B show the axial parameters’ distributions in the jet, which include the flow deceleration region, for case 1 (Re_L = 5, Kn_L = 0.2). In the initial part of the jet, the solutions based on the NS and DSMC methods coincide with each other. However, the NS approach predicts a larger size for the initial jet region up to the point where the flow deceleration begins, which corresponds to the maximum velocity in the jet. Accordingly, the Mach number limiting values achievable in the jet, predicted on the basis of the NS equations, turn out to be higher, and the limiting density and temperature values are lower in relation to that predicted by the DSMC method. The thickness of the layer in which the flow deceleration occurs turns out to be smaller than that predicted by the NS equations. This conclusion is consistent with the one proposed by Greenshields and Reese (2007) and Scanlon et al. (2015), where the discrepancies between the experimental data and NS solution for the problem of the shock wave thickness determination in a rarefied gas are discussed. A larger density gradient in the shock wave obtained from solving the NS equations, with respect to the numerical solution of the Boltzmann equation or the DSMC results for Mach number M ≫ 1, was also observed in the study conducted by Shoev et al. (2020) and Poleshkin and Kudryavtsev (2023). The density distribution described by the NS equations clearly shows a low-intensity jump, which is not typical for the considered case (Re_L = 5 and Kn_L = 0.2), corresponding to the scattering regime (Dulov and Lukyanov, 1984; Avduevski et al., 1989). As discussed previously, the shock wave degenerates with Reynolds number reduction. Case 1 corresponds to the intermediate situation when it is completely smeared when simulated within the DSMC method, but not yet smeared when simulated by NS equations. Thus, in this case, there is a qualitative difference between the results of the methods used.

FIGURE 11

FIGURE 11. Number density (A) and Mach number (B) distributions along the flow axis for case 1.

As Re_L increases, the situation changes (Supplementary Figure S8). At Re_L = 30, there is a qualitative agreement between the results of different methods. Both methods reproduce the shock structure that is typical for the considered parameters. However, as previously discussed, NS predicts higher Mach numbers.

The reason for the discrepancy between the NS equations and DSMC method solutions can be related with the high degree of non-equilibrium flows within the shock layers. Supplementary Figure S9 shows the distributions of the translational temperature components on the axis for cases 1 and 3. In case 1, the translational non-equilibrium turns out to be high and reaches the values R_n = (T_x − T_y)/T ∼ 50% in the jet deceleration region, where T_x and T_y are the x- and y-temperature components that are the mean values of the corresponding molecular kinetic energy components, determined by the molecular velocity components v_x and v_y, respectively. Within the shock layer for case 3, similar to the previous case, R_n increases up to $\sim 40-50\%$. The distribution function in a rarefied shock layer can significantly differ from the Maxwellian one (Bykov and Lukyanov, 1998). The condition for the correct use of NS equations is some relatively small deviations from the equilibrium state (Cercignani, 1975).

4 Conclusion

The DSMC and NS simulations of the underexpanded jet outflow from a conical nozzle into the background was performed for low Reynolds number values, 5 ≤ Re_L ≤ 30, responsible for the jet–ambient gas interaction regime. In the indicated range of Re_L, a drastic change in the flow structure in the expansion region outside the nozzle was observed. The flow at Re_L = 30 contained a shock structure that is typical for a highly underexpanded jet. Such a structure was somewhat smeared. With the Reynolds number decreasing, the shock structure was significantly smeared. Nevertheless, a weak trail of shocks were preserved even at Re_L = 9.9. At Re_L = 5, shocks completely degenerate. For such a regime, the results of DSMC and NS are qualitatively different; an approach based on the solution of NS equations continues the shock wave structure prediction. At Re_L = 30, a qualitative agreement and satisfactorily quantitative agreement in the results within the shock layer region were observed.

The flow inside the conical nozzle had a complex structure that was affected by internal shock and the presence of the flow-limiting surface. For the considered Re_∗ range, 800 < Re_∗ ≤ 2500, the nozzle flow showed a pronounced 2D structure. The axial distribution of the parameters calculated by the DSMC and NS approaches was in perfect agreement with each other.

The presence of a complex shock structure both in the nozzle and jet expansion region, with sufficiently non-linear behavior of gas dynamic parameters, should be taken into account when studying condensation and other relaxation processes and when interpreting the corresponding experimental results.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

NB: conceptualization, methodology, formal analysis, visualization, validation, manuscript writing—original draft, review, and editing. YG: supervision, methodology, conceptualization, and manuscript writing—review and editing. SF: validation, formal analysis, visualization, and manuscript writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

The work was completely performed at the Novosibirsk State University using the computational capabilities of the Peter the Great St.Petersburg Polytechnic University with the financial support of the Russian Science Foundation (grant no. 22-11-00080).

Acknowledgments

The computational resources were provided by the supercomputer center of Peter the Great St. Petersburg Polytechnic University. The authors would like to sincerely acknowledge their colleagues from the Novosibirsk State University—Alexander Zarvin and Kirill Dubrovin—for their fruitful discussions.

Conflict of interest

Author YG was employed by the company Soft-Impact, Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2023.1216927/full#supplementary-material

References

Ashkenas, H., and Sherman, F. S. (1965). “Structure and utilization of supersonic free jets in low density wild tunnels,” in Rarefied gas dynamics: Proc. Of 4th int symp. Editor J. H. de Leeuw (N.Y.: Academic Press), 84–105.

Google Scholar

Avduevski, V. S., Ashratov, E. A., Ivanov, A. V., and Pirumov, U. G. (1989). Gas dynamics of supersonic non-isobaric jets. Moscow: Mashinistroenie.

Google Scholar

Bird, G. A. (1994). Molecular gas dynamics and the direct simulation of gas flows. Oxford: Clarenton Press.

Google Scholar

Bird, G. A. (2013). The DSMC method. United States: CreateSpace Independent Publishing Platform.

Google Scholar

Bykov, N. Y., and Gorbachev, Y. E. (2019). Cluster formation in copper vapor jet expanding into vacuum: the direct simulation Monte Carlo. Vacuum 163, 119–127. doi:10.1016/j.vacuum.2019.02.007

CrossRef Full Text | Google Scholar

Bykov, N. Y., and Lukyanov, G. A. (1998). Structure and parameters of the shock layer formed when a supersonic underexpanded jet interacts with a counterpropagating hypersonic flow in the transition regime. Tech. Phys. 43, 755–760. doi:10.1134/1.1259069

CrossRef Full Text | Google Scholar

Bykov, N. Y., Safonov, A. I., Leshchev, D. V., Starinsky, S. V., and Bulgakov, A. V. (2019). The gas-jet method of deposition of nanostructured silver films. Tech. Phys. 64, 776–789. doi:10.1134/S1063784219060045

CrossRef Full Text | Google Scholar

Bykov, N. Y., and Zakharov, V. V. (2022). Rarefied gas mixtures with large species mass ratio: outflow into vacuum. Phys. Fluids 34, 057106. doi:10.1063/5.0089628

CrossRef Full Text | Google Scholar

Cai, G., Liu, L., He, B., Ling, G., Weng, H., and Wang, W. (2022). A review of research on the vacuum plume. Aerospace 9, 706. doi:10.3390/aerospace9110706

CrossRef Full Text | Google Scholar

Cercignani, C. (1975). Theory and application of the Boltzmann equation. Edinburgh and London: Scottish Academic Press.

Google Scholar

Dubrovin, K. A., Zarvin, A. E., Kalyada, V. V., and Yaskin, A. S. (2022). Influence of the outflow initial parameters on the transverse dimensions of underxpanded argon jets in presence of condensation. Vacuum 207, 111651. doi:10.1016/j.vacuum.2022.111651

CrossRef Full Text | Google Scholar

Dulov, V. G., and Lukyanov, G. A. (1984). Gas dynamics of outflow processes. Novosibirsk: Nauka.

Google Scholar

Franquet, E., Perrier, V., Gibout, S., and Bruel, P. (2015). Free underexpanded jets in a quiescent medium: A review. Prog. Aerosp. Sci. 77, 25–53. doi:10.1016/j.paerosci.2015.06.006

CrossRef Full Text | Google Scholar

George, J. D. (2000). A combined CFD-DSMC method for numerical simulation of nozzle plume flows. Ithaca: Cornell University.

Google Scholar

Greenshields, C. J., and Reese, J. M. (2007). The structure of shock waves as a test of brenner’s modifications to the Navier-Stokes equations. J. Fluid Mech. 580, 407–429. doi:10.1017/S0022112007005575

CrossRef Full Text | Google Scholar

Greenshields, C. J., Weller, H. G., Gasparini, L., and Reese, J. M. (2009). Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows. Int. J. Numer. methods fluids 63, 1–21. doi:10.1002/fld.2069

CrossRef Full Text | Google Scholar

Hagena, O. F. (1987). Condensation in free jets: comparison of rare gases and metals. Z Phys D - Atoms, Mol. Clust. 4, 291–299. doi:10.1007/BF01436638

CrossRef Full Text | Google Scholar

Hagena, O. F. (1980). Nucleation and growth of clusters in expanding nozzle flows. Surf. Sci. 106, 101–116. doi:10.1016/0039-6028(81)90187-4

CrossRef Full Text | Google Scholar

Ivanov, M. S., Markelov, G. N., Ketsdever, A. D., and Wadsworth, D. C. (1999). Numerical study of cold gas micronozzle flows. AIAA 1999. doi:10.2514/6.1999-166

CrossRef Full Text | Google Scholar

Kashkovsky, A. V., Kudryavtsev, A. N., and Shershnev, A. A. (2023). Numerical investigation of the rarefied supersonic underexpanded jet structure using the dsmc method. Thermophys. Aeromechanics 30, 29–36. doi:10.1134/s0869864323010043

CrossRef Full Text | Google Scholar

Kisliakov, N. I., Rebrov, A. K., and Sharafutdinov, R. G. (1975). On the structure of low-density high-pressure jets behind a supersonic nozzle. Appl. Mech. Theor. Phys. 1975, 42–52.

Google Scholar

Lewis, C. H., and Carlson, D. J. (1964). Normal shock location in underexpanded gas and gas-particle jets. AIAA 2, 776–777. doi:10.2514/3.2409

CrossRef Full Text | Google Scholar

Micci, M. M., and Ketsdever, A. D. (Editors) (2000). “Micropropulsion for small spacecraft,” Progress in astronautics and aeronautics (Reston, VA: American Institute of Aeronautics and Astronautics).

Google Scholar

Muntz, E. P., Hamel, B. B., and Maguire, B. L. (1970). Some characteristics of exhaust plume rarefaction. AIAA J. 8, 1651–1658. doi:10.2514/3.5960

CrossRef Full Text | Google Scholar

Poleshkin, S. O., and Kudryavtsev, A. N. (2023). Investigation of shock wave internal structure with different kinetic models. AIP Conf. Proc. 2504, 030097. doi:10.1063/5.0132379

CrossRef Full Text | Google Scholar

Rebrov, A. K., Chekmarev, S. F., and Sharafutdinov, R. G. (1971). The effect of sparsity on the structure of a free nitrogen jet. Appl. Mech. Tech. Phys. 1971, 136–144.

Google Scholar

Rebrov, A. K. (2001). Free jets in vacuum technologies. J. Vac. Sci. Tech. A 19, 1679–1687. doi:10.1116/1.1382649

CrossRef Full Text | Google Scholar

Scanlon, T., White, C., Borg, M. K., Cassineli, P. R., Farbar, E., Boyd, I. D., et al. (2015). Open-source direct simulation Monte Carlo chemistry modeling for hypersonic flows. AIAA 53, 1670–1680. doi:10.2514/1.J053370

CrossRef Full Text | Google Scholar

Schwartzentruber, T. E., and Boyd, I. D. (2015). Progress and future prospects for particle-based simulation of hypersonic flow. Prog. Aerosp. Sci. 72, 66–79. doi:10.1016/j.paerosci.2014.09.003

CrossRef Full Text | Google Scholar

Sharipov, F. (2004). Numerical simulation of rarefied gas flow through a thin orifice. J. Fluid Mech. 518, 35–60. doi:10.1017/S0022112004000710

CrossRef Full Text | Google Scholar

Shoev, G. V., Timokhin, M. Y., and Bondar, Y. A. (2020). On the total enthalpy behavior inside a shock wave. Phys. Fluids 32, 041703. doi:10.1063/5.0005741

CrossRef Full Text | Google Scholar

Starinskiy, S. V., Safonov, A. I., Shukhov, Y. G., Sulyeva, V. S., Korolkov, I. V., Volodin, V. A., et al. (2022). Nanostructured silver substrates produced by cluster-assisted gas jet deposition for surface-enhanced Raman spectroscopy. Vacuum 199, 110929. doi:10.1016/j.vacuum.2022.110929

CrossRef Full Text | Google Scholar

Suss, A., Mary, I., Garrec, T. L., and Mariél, S. (2023). A hybrid lattice Boltzmann - Navier-Stokes method for unsteady aerodynamic and aeroacoustic computations. J. Comput. Phys. 485, 112098. doi:10.1016/j.jcp.2023.112098

CrossRef Full Text | Google Scholar

Sutton, G. P., and Biblarz, O. (2017). Rocket propulsion elements. ninth edition. United States: Wiley.

Google Scholar

Tcheremissine, F. G. (2023). Solution of the Boltzmann equation in the continuum flow regime. Comput. Math. Math. Phys. 63, 319–331. doi:10.1134/S0965542523020057

CrossRef Full Text | Google Scholar

Varoutis, S., Valougeorgis, D., Sazhin, O., and Sharipov, F. (2008). Rarefied gas flow through short tubes into vacuum. J. Vac. Sci. Technol. A A 26, 228–238. doi:10.1116/1.2830639

CrossRef Full Text | Google Scholar

Volchkov, V. V., Ivanov, A. V., Kisliakov, N. I., Rebrov, A. K., Sukhnev, V. A., and Sharafutdinov, R. G. (1973). Low density jets behind the sonic nozzle at high pressure drops. Appl. Mech. Theor. Phys. 1973, 64–73.

Google Scholar