Inclined colloidal drops: Evaporation kinetics and pattern formation

The drying of solute-laden drops is ubiquitous in everyday life, from paints and printers to the raindrops drying on our windows. Nonetheless, scientific interest has primarily focused on understanding the evaporation kinetics on flat surface, with the key parameter of substrate inclination only recently started being addressed. This work focuses on the influence of moderate substrate inclinations at 20° and 40° on the evaporation kinetics and associated deposit patterns of colloidal drops. Inclination altered the shape of the drops which formed a lower contact angle at the upper side of the drop (rear edge) and larger contact angle at the lower side (front edge). As evaporation rate is a function of contact angle, which in turn is a function of inclination, the evaporation lifetime was extended by 43% and 61% for 20° and 40°, respectively, compared to a flat drop. A theoretical approximation of the evaporative flux across the liquid-vapour interface of the drops showed the contribution of each edge to the evaporation kinetics. These differences in the evaporative fluxes altered the internal flows within the drop and in turn the coffee-ring formation mechanism. The particle deposit shape at the two edges for each drop was visualised which combined with the theoretical arguments allowed the proposition of the particle deposition mechanism in inclined drops: inclination added a gravitationally-driven velocity flow component within the drops, which is perpendicular and hence negligible in flat drops. This additional flow hindered or enhanced the number of particles arriving at the rear and front edges of the inclined drops, respectively, and hence influenced the dimensions of the coffee-ring patterns. Eventually, the particle deposits grew sufficiently tall to effectively stagnate the outward flow which resulted in enhanced particle accumulation at the interior of the drops as inclination increased.

Introduction

The evaporation of sessile drops has been widely studied in a variety of contexts due to its importance in many applications, such as disease diagnosis (Fang et al., 2006; Gorr et al., 2013; Askounis et al., 2016), forensic tests (Brutin et al., 2011; Smith et al., 2020) and inkjet printing (Meyer et al., 2017; Thokchom et al., 2017) to name a few. In most of these cases, the free evaporation of a single drop evaporating on a flat surface is dominated by its contact angle (Gleason et al., 2016), with numerous external parameters affecting the process, such as substrate heating (Parsa et al., 2015; Kita et al., 2016), humidity (Bou Zeid and Brutin, 2013; Brutin, 2013), wettability (Stauber et al., 2015; Günay et al., 2021), etc., thoroughly explored.

During the drying of a sessile drop on a flat surface, the evaporation flux is higher at the edge of the drop which is replenished by inducing an outward flow from the drop’s centre to the edge (Deegan et al., 1997). This flow is also capable of carrying and depositing solute at the periphery of the drop resulting in ring-like patterns, in a phenomenon aptly described as “coffee-ring” effect in Deegan and co-workers’ seminal work (Deegan et al., 2000). A wide range of different factors affecting the phenomenon have since been reported as a means to either promote or suppress the coffee-ring (Mampallil and Eral, 2018; Parsa et al., 2018; Wilkinson et al., 2021). Some of these various factors include: ambience conditions [e.g., pressure (Askounis et al., 2014), relative humidity (Brutin, 2013)], solute [e.g., size (Parsa et al., 2017b), concentration (Brutin, 2013)], base fluid [e.g., fluid composition (Parsa et al., 2017a), surfactants (Shao et al., 2019)] and substrate [e.g., elasticity (Chen et al., 2020), temperature (Li et al., 2015; Parsa et al., 2015), wettability (Patil et al., 2016; Zhang et al., 2020)].

In real life, however, many drops are positioned at an incline, may they be raindrops on plant leaves or engineered surfaces. These inclined drops are elongated by gravity, i.e., spherical cap assumption becomes invalid, even at small Bond numbers (e.g., $Bo=0.21$) (Kim et al., 2017; Thampi and Basavaraj, 2020), with a lower contact angle at the top edge and a higher angle at the bottom edge. In the last few years, the topic of the evaporation of inclined drops started attracting scientific attention. Increasing drop inclination to 90° was reported to lead to faster evaporation kinetics (Kim et al., 2017; Dhar et al., 2020; Tredenick et al., 2021) and irregular coffee-ring patterns (Mondal et al., 2018; Gopu et al., 2020; Logesh Kumar et al., 2021) due to the opposing flows driven by capillary and sedimentation. Nonetheless, the exact pattern formation mechanism remains unclear with parameters such as evaporation rate and drop volume yielding contradictory results (Du and Deegan, 2015; Kim et al., 2021). Additionally, in most studies a wide range of angles was studied but moderate ones 0°–40° remain largely unresolved.

Further research into the parameters affecting the dynamics of drop evaporation and the associated coffee-ring effect on flat and inclined substrates as numerous technological applications such as photonic crystals (Winhard et al., 2021) depend on them. In this work, we focused on the evaporation process of aqueous colloidal drops in the unresolved inclination range of 0°–40°. We started by observing the evaporation of a drop on a flat surface, as a baseline. Then, we followed the evaporation of drops on 20° and 40° inclined substates and compared their evaporation kinetics against the baseline. Next, we described mathematically how the evaporation flux across the liquid-air interface was altered by each inclination and discuss its link to the evaporation process. Lastly, we imaged the coffee-ring patterns the drops left behind and proposed a mechanism describing the underlying physics.

Methods

Solution and deposition

Stock suspension containing 1 μm polystyrene colloidal particles (Polybead, Polyscience, United States) was diluted in deionised water to desired concentration of 0.1% w/w. Before use, the suspension was sonicated for at least 10 min to ensure stable and uniform particle dispersion. The density of the particles is 1.05 g/cm³ and do not sediment at slower timescale than the evaporation of the drops. Smooth hydrophilic glass substrates were ultrasonically cleaned in deionised water and ethanol for at least 10 min prior to each experiment. The substrates were then dried by compressed air. 9 μl drops were gently deposited by a micropipette onto substrates with the inclination angles, α, of 0, 20 and 40°. The experiments were conducted under controlled ambient conditions of 23 ± 0.5°C temperature and 65 ± 5% relative humidity. A CCD camera and a led-light were employed to capture the evolution over time of the side-view of the drying drops. The temporal evolution of drop profiles (i.e., volume, base diameter, contact angle) were acquired with the conic section method (tangent method) using the drop shape analysis software (DSA4, KRÜSS GmbH).

Characterisation

The final deposition patterns of dried drops were imaged by a laser scanning confocal microscope (LSCM, OLS-5000, Olympus, Japan) and were post-processed.

Results and discussion

Inclination and evaporation kinetics

Figure 1 shows the temporal evolution of drop shape at substrate inclination angles, $\alpha$, of 0°, 20°, and 40°. The symmetrical shape of the drop placed on the flat surface ($\alpha$ = 0°) deformed when the surface was inclined, forming the asymmetrical drop shape at $\alpha$ = 20° and 40°.

FIGURE 1

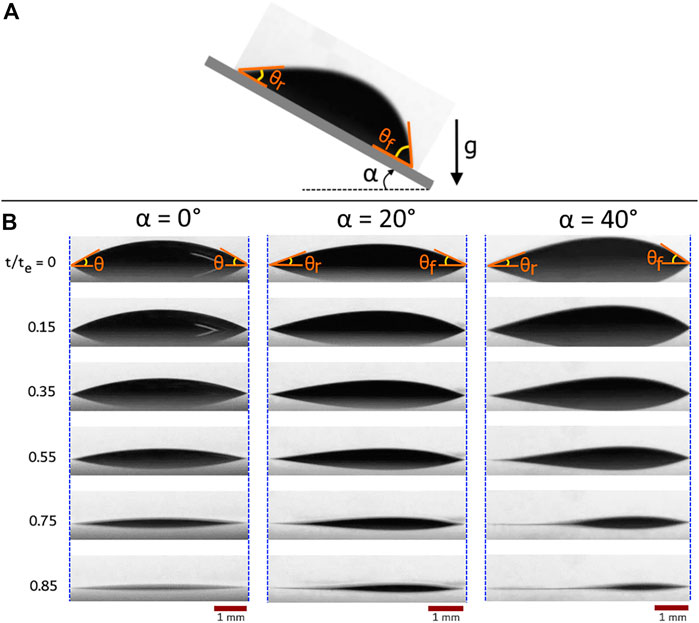
FIGURE 1. (A) A colloidal sessile drop deposited on a solid surface inclined by $\alpha$. The gravity direction is denoted by g. (B) Snapshots of colloidal drops evaporating at 0°, 20°, and 40° inclination with corresponding mean contact angle, $\theta$, rear contact angle, ${\theta }_r$, and front contact angle, ${\theta }_f$. $t/t_e$ is the normalised evaporation time by total evaporation time, $t_e$, for each drop. $t_e$ at 0°, 20°, and 40° inclination is 2,108, 2,924 and 3,604 s, respectively.

On the flat surface, the drying drop follows the constant contact radius (CCR) evaporation mode during which the contact base remains constant, and the contact angle decreases linearly (Figure 1). No initial spreading was observed for the flat drop, but inclined drops had an initial spreading because of the action of gravity upon deposition (Figure 1). This spreading leads to the largest base for $\alpha$ = 40°, which is a first indication of the effect of inclination. At $\alpha$ = 20° and 40°, the contact line and the contact angle on the front side are different than the rear side of the drops. Initially, both drops dry under the CCR mode. However, later, the contact line at the rear edge depins, and the contact angle remains relatively constant while the base diameter decreases (Figure 1). At the front edge, the drop follows the CCR mode until full evaporation. Due to the difference in the behaviour of contact angle and contact line at the two sides of the drops, the drying of inclined drops start with CCR and then transition to mixed mode. As shown in Figure 1, the depinning of the contact line at the rear edge occurs for $t/t_e=$ 0.8 and 0.6 for $\alpha$ = 20° and 40°, respectively. In other words, the higher the $\alpha$, the shorter is the pinning duration of the contact line. This also affects the transition time from CCR to mixed mode. The temporal evolution of the base diameter of each drop is presented in Figure 2A. The kinetics of the contact angle on the lower and upper sides of the inclined drops, front (${\theta }_f$) and rear (${\theta }_r$) angles, respectively, are compared to the mean contact angle, $\theta$, of the flat drop in Figure 2B.

FIGURE 2

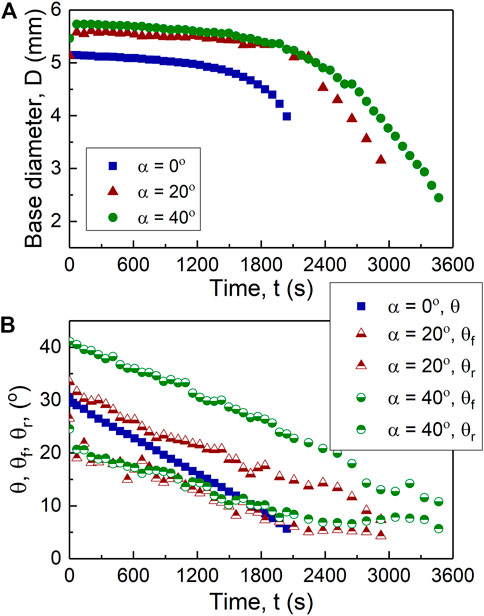
FIGURE 2. Temporal evolution of the drying 0.1% w/w microspheres drops at 0°, 20°, and 40° inclination: (A) base diameter, and (B) mean contact angle, $\theta$, rear contact angle, ${\theta }_r$, and front contact angle, ${\theta }_f$.

Figure 3 shows that the temporal evolution of volume is mainly linear for all three cases due to their evaporation mainly under the CCR regime. Additionally, this figure demonstrates the inversely linear relationship between the evaporation time and substrate inclination, $\alpha$. In particular, increasing $\alpha$ to 20° (triangles) decreases the evaporation time by 43%. Further increase of $\alpha$ to 40° (squares) leads to a further decrease of the evaporation time by 18% or 61% compared to the 20° and flat drop, respectively.

FIGURE 3

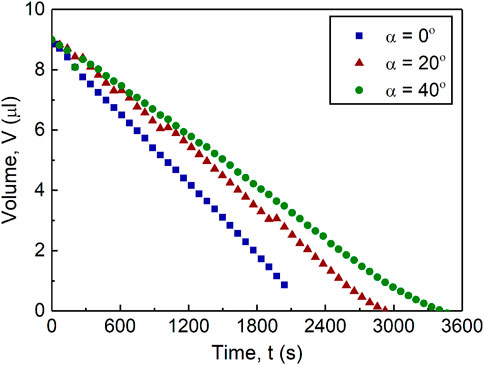
FIGURE 3. Drop volume of the drying 0.1% w/w microspheres drops drying at 0°, 20°, and 40° inclination over time.

These differences in the evaporation kinetics may be attributed to the different and asymmetrical distribution of evaporation flux along the contact line between the front and rear edges. For an evaporating drop in a quasi-steady state, the evaporative flux is given (Dhar et al., 2020):

$J\left(\theta \right)=J_o\left(0.27{\theta }^2+1.3\right)\left[0.6381-0.2239{\left(\theta -\frac{\pi }{4}\right)}^2\right]{\left[1-{\left(\frac{r}{R}\right)}^2\right]}^{\left(\frac{\theta }{4}-\frac{1}{2}\right)}(1)$

where $R$ is the drop radius, and $r$ is the distance from the drop apex towards the edge.

As Eq. 1 is valid for a symmetric, spherical cap sessile drop at $\alpha$ = 0°, we obtain the ratio of evaporative flux which incorporates the effect of $\alpha$ as:

$\frac{J\left({\theta }_a\right)}{J\left({\theta }_0\right)}=\frac{\left(0.27{\theta }_{\alpha }^2+1.3\right)\left[0.6381-0.2239{\left({\theta }_{\alpha }-\frac{\pi }{4}\right)}^2\right]{\left[1-{\left(\frac{r}{R}\right)}^2\right]}^{\left(\frac{{\theta }_{\alpha }}{4}-\frac{1}{2}\right)}}{\left(0.27{\theta }_0^2+1.3\right)\left[0.6381-0.2239{\left({\theta }_0-\frac{\pi }{4}\right)}^2\right]{\left[1-{\left(\frac{r}{R}\right)}^2\right]}^{\left(\frac{{\theta }_0}{4}-\frac{1}{2}\right)}}(2)$

where ${\theta }_0$ is the drop contact angle at $\alpha$ = 0°, and ${\theta }_{\alpha }$ corresponds to the effective contact angle at each $\alpha$.

The plot of Eq. 2 for each inclined drop is depicted in Figure 4 as a function of the normalised radius at $\alpha$ = 20° and 40°. At both inclinations, the maximum $\frac{J\left({\theta }_a\right)}{J\left({\theta }_0\right)}$ appears at the rear edge of the drops, i.e., $\frac{r}{R}\sim -0.999$, with slightly different values of $1.400$ and 1.34 for 20° and 40°, respectively. However, the minima of $\frac{J\left({\theta }_a\right)}{J\left({\theta }_0\right)}$ appear at different positions depending on inclination. At $\alpha$ = 20°, the minimum value of $\frac{J\left({\theta }_a\right)}{J\left({\theta }_0\right)}\sim 0.951$ appears at $\frac{r}{R}\sim -0.467$, whereas at $\alpha$ = 40°, the minimum value of $\frac{J\left({\theta }_a\right)}{J\left({\theta }_0\right)}\sim 0.735$ at the front edge, $\frac{r}{R}\sim 0.999$. This indicates that the minimum at the apex of the symmetric drop shifts due to the asymmetrical shape of the inclined drops, in agreement with the literature (Dhar et al., 2020). The depression of the evaporative flux is stronger in the 40° case, starting at $\frac{r}{R}\sim 0.572$ and continues to the edge $\frac{r}{R}\sim 0.999$ whereas in the 20° case, the depression occurs over an almost three times smaller distance from $\frac{r}{R}\sim$ 0.865 to the edge $\frac{r}{R}\sim$ 0.999. Further, after $\frac{r}{R}\sim 0.873$ the evaporative flux in the 40° drops decays much faster than in the 20° and should have a considerable effect on the evaporation kinetics.

FIGURE 4

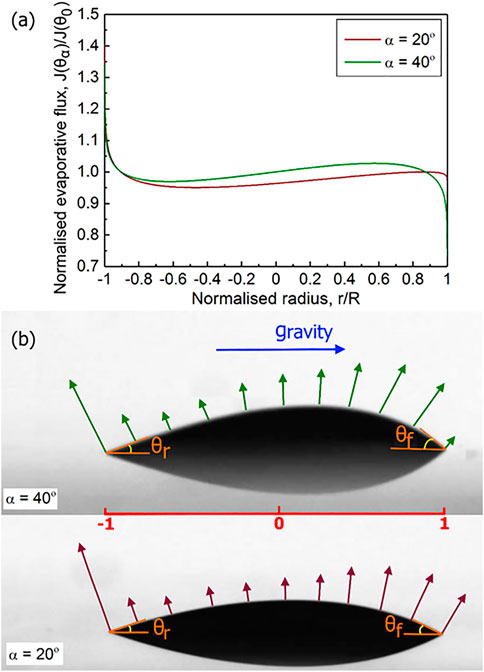
FIGURE 4. (A) Normalised evaporative flux of the 0.1% microspheres drops drying at 20° and 40° inclination versus the normalised radius. (B) Schematic illustration of the distribution of the evaporative flux magnitude at the inclinations of 20° and 40°. The length of arrows corresponds to the calculated evaporative flux magnitudes $J\left({\theta }_{20}\right)$ and $J\left({\theta }_{40}\right)$.

In Figure 4B, we visualise the evaporative flux distribution in the exemplary 20° and 40° drops, where the length of the arrows is indicative of the magnitude of evaporative flux depicted in Figure 4A.

Inclination and coffee-ring formation mechanism

Figure 5 depicts the differences in the particle deposition patterns for each case. At $\alpha$ = 0°, the deposition pattern is highly symmetrical with a pronounced ring forming at the contact line and some deposition at the interior (Figure 5A). Increasing inclination to 20° yielded the asymmetric pattern in Figure 5B with the rear and front edges (top and bottom sides) being thinner than the flat equivalent, which is quantified by LCSM below. Notably, a particle-free area formed at the centre of the drop, potentially due to the interplay between the enhanced outward fluid flow carrying particles to the rear edge of the drop, where evaporation flux is higher, and the diminished flow towards the front edge, where evaporation flux is lower; as shown in Figure 4. Further increasing the inclination to 40° yielded the completely different asymmetric deposit pattern in Figure 5C. Here, the actual rear and front edges of the ring-like deposits are thinner, and the interior seems to be more densely covered by particles with some streaks resembling the rear edge, which may have formed during the retraction of the rear edge at the later stages of evaporation. The effect of inclination on the width of the ring-like deposits and the particle deposition at the interior is further demonstrated in the insets Figure 5. However, these images provide little evidence on the influence of gravity on particle motion. Hence, in what follows, we imaged and measured the highlighted areas (insets) of the deposits in Figure 5 with high resolution LCSM. These observations should enable us to determine the influence of gravity on particle motion and propose an accurate particle deposition mechanism.

FIGURE 5

FIGURE 5. Deposit patterns left behind the drying of 0.1% w/w microspheres drops at (A) 0°, (B) 20°, and (C) 40° inclinations. Insets show a magnification of the deposit patterns at the top and bottom of each case. The scale bar for all insets corresponds to 500 μm.

Figures 6A–C shows the shape of the ring deposits at the rear side of the drops with increasing inclination from 0° to 40° and the corresponding height profiles, which quantify the dimensions of these deposits, are compared in Figure 6D. The ring on the flat substrate appears rather symmetrical with a slightly steeper edge toward the interior followed by randomly distributed particles at the interior, as reported previously (Askounis et al., 2014). As inclination increases, the ring deposit at the rear edge becomes thinner and slightly shorter and the amount of randomly distributed particles at the interior increases, as demonstrated at the bottom part of Figures 6A–C and quantified in the right side of the corresponding height profiles (noisy region in Figure 6D). At the front side, Figures 6E–G, the ring deposits simultaneously become thinner and taller with increasing inclination from 0° to 40°. Notably, there appears to be little particle distribution at the interior in the 20° case (top part of Figure 6F) and substantially more at 40° (top part of Figure 6G).

FIGURE 6

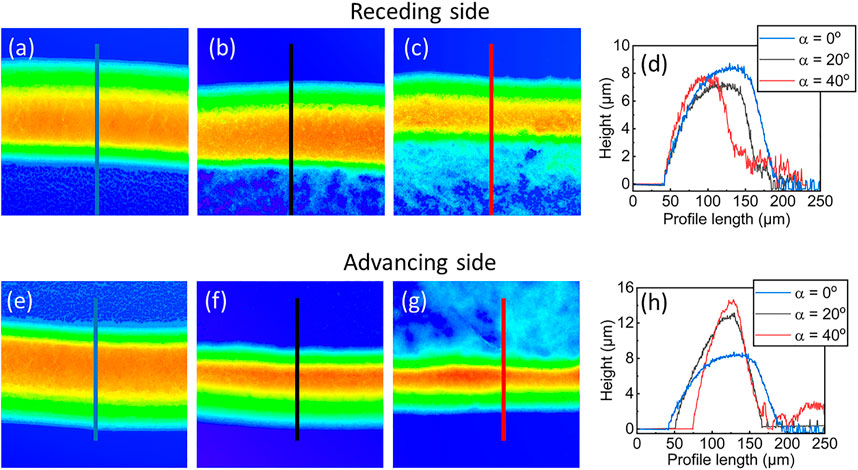
FIGURE 6. (A–C) Topography images by LSCM at the rear side with increasing inclination from left to right and (D) corresponding height profiles. (E–G) Topography images by LSCM at the front side with increasing inclination from left to right and (H) corresponding height profiles.

These differences in particle distribution unveiled at the contact line of the drops allows us to postulate the following deposition mechanism (Figure 7): First, we assume a wedge at the edge of the drop such that evaporative flux, J, and induced outward flow, I, are linearly related, as we described previously (Askounis et al., 2011). The particles are large enough and hence they should be subjected to the action of gravity in the form of sedimentation velocity, $u_g$, which in the inclined cases has an angular component acting at the same direction and same plane as I and should influence the deposit formation.

FIGURE 7

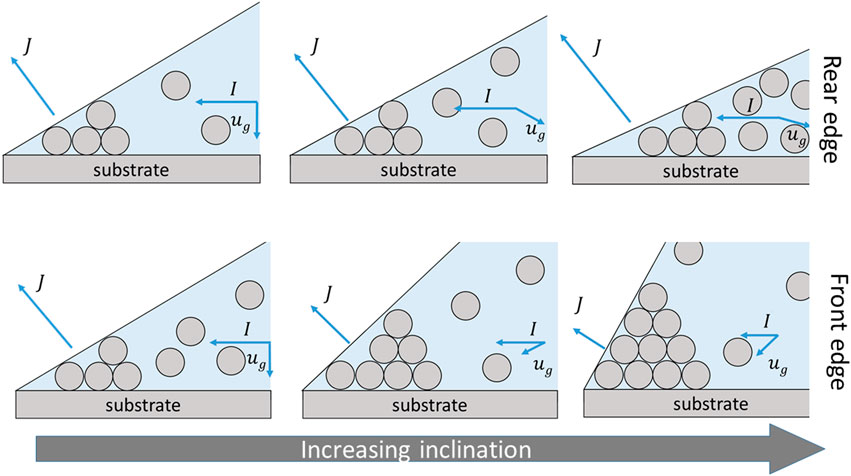
FIGURE 7. Schematic illustrating how inclination affects the mechanism of particle deposition at the rear and front sides of a drop, top and bottom row respectively, for increasing inclination from left to right. In all cases, the deposit becomes large enough to stagnate the flows carrying particles.

On one hand, inclination resulted in smaller drop contact angles at the rear edge and hence a higher evaporation flux (Stauber et al., 2015), which induced a stronger outward flow and in turn carried particles faster at the contact line. At the same time, the smaller contact angle results in less available volume for particle deposition at the wedge. We may surmise, at present, that the particle deposit became sufficiently tall enough, at this side of the drop, to substantially interfere with the outward flow and effectively stagnate the liquid supply, leading to an abrupt depinning of the contact line. This depinning should leave behind a thinner and slightly shorter ring followed by an increasing particle accumulation at the interior, similar to our previous observation for flat nanocolloidal drops (Askounis et al., 2011), albeit here depending on inclination angle (Figure 6D).

At the front edge, inclination led to larger contact angles and hence a weaker outward flow resulting in smaller number of particles arriving at the contact line and the formation of taller and thinner deposits (Figure 6G). Hence, the stagnation of the flow due to the deposit build-up should appear later compared to the rear edge and yield the different particle distribution at the interior of the 40° case (Figure 6G).

The afore mentioned potential mechanism is depicted in Figure 7. In our mechanism so far, gravity only plays an indirect role by altering the shape of the drops. In turn, the shape alters the evaporation kinetics and the corresponding outward flow and particle deposition pattern. However, we should also consider gravity which should have a component acting parallel to the flow, as illustrated in Figure 7. $u_g$ countered the action of I at the rear side while enhanced it at the front side, resulting in the observed asymmetric particle deposits in Figure 6.

Conclusion

The effect of two different degrees of moderate degrees of inclination, namely, 20° and 40°, on both the evaporation kinetics and the resulting deposit pattern of colloidal drops were investigated. Increasing inclination was found to considerably extend the lifetime of the drops by altering the contact angle at their rear (top) and front (bottom) edges. The evaporation kinetics were quantified by calculating the evaporative flux as a function of contact angle normalised against the flat drop. Furthermore, the particle deposits were measured, and their shape was found to be highly dependent on a combination of the evaporation kinetics, the effect of gravity on particle motion and the available space at the edge of the drops. These findings enabled us to propose a comprehensive mechanism describing the deposit formation for each case. This fundamental work could lead to applications, in the future, to exploit the evaporation kinetics in microscale cooling systems, or the associated coffee-ring effect in patterning applications such forensics or biomedical diagnosis.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AA designed and conducted the experiments; MP and AA performed the post-processing of the experimental data; MP and AA analysed the data and discussed the results; MP and AA wrote the manuscript; All authors have given approval to the final version of the manuscript.

Acknowledgments

This study was supported by the Open Access Fund at the Northumbria University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Askounis, A., Orejon, D., Koutsos, V., Sefiane, K., and Shanahan, M. E. R. (2011). Nanoparticle deposits near the contact line of pinned volatile droplets: Size and shape revealed by atomic force microscopy. Soft Matter 7, 4152–4155. doi:10.1039/C1SM05241A

CrossRef Full Text | Google Scholar

Askounis, A., Sefiane, K., Koutsos, V., and Shanahan, M. E. R. (2014). The effect of evaporation kinetics on nanoparticle structuring within contact line deposits of volatile drops. Colloids Surf. A Physicochem. Eng. Asp. 441, 855–866. doi:10.1016/j.colsurfa.2012.10.017

CrossRef Full Text | Google Scholar

Askounis, A., Takata, Y., Sefiane, K., Koutsos, V., and Shanahan, M. E. R. (2016). Biodrop” evaporation and ring-stain deposits: The significance of DNA length. Langmuir 32, 4361–4369. doi:10.1021/acs.langmuir.6b00038

PubMed Abstract | CrossRef Full Text | Google Scholar

Bou Zeid, W., and Brutin, D. (2013). Influence of relative humidity on spreading, pattern formation and adhesion of a drying drop of whole blood. Colloids Surf. A Physicochem. Eng. Asp. 430, 1–7. doi:10.1016/j.colsurfa.2013.03.019

CrossRef Full Text | Google Scholar

Brutin, D. (2013). Influence of relative humidity and nano-particle concentration on pattern formation and evaporation rate of pinned drying drops of nanofluids. Colloids Surf. A Physicochem. Eng. Asp. 429, 112–120. doi:10.1016/j.colsurfa.2013.03.012

CrossRef Full Text | Google Scholar

Brutin, D., Sobac, B., Loquet, B., and Sampol, J. (2011). Pattern formation in drying drops of blood. J. Fluid Mech. 667, 85–95. doi:10.1017/S0022112010005070

CrossRef Full Text | Google Scholar

Chen, Y., Askounis, A., Koutsos, V., Valluri, P., Takata, Y., Wilson, S. K., et al. (2020). On the effect of substrate viscoelasticity on the evaporation kinetics and deposition patterns of nanosuspension drops. Langmuir 36, 204–213. doi:10.1021/acs.langmuir.9b02965

PubMed Abstract | CrossRef Full Text | Google Scholar

Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G. G., Nagel, S. R., and Witten, T. A. (1997). Capillary flow as the cause of ring stains from dried liquid drops. Nature 389, 827–829. doi:10.1038/39827

CrossRef Full Text | Google Scholar

Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G., Nagel, S. R., and Witten, T. A. (2000). Contact line deposits in an evaporating drop. Phys. Rev. E 62, 756–765. doi:10.1103/PhysRevE.62.756

PubMed Abstract | CrossRef Full Text | Google Scholar

Dhar, P., Dwivedi, R. K., and Harikrishnan, A. R. (2020). Surface declination governed asymmetric sessile droplet evaporation. Phys. Fluids 32, 112010. doi:10.1063/5.0025644

CrossRef Full Text | Google Scholar

Du, X., and Deegan, R. D. (2015). Ring formation on an inclined surface. J. Fluid Mech. 775, R3. doi:10.1017/jfm.2015.312

CrossRef Full Text | Google Scholar

Fang, X., Li, B., Petersen, E., Seo, Y.-S., Samuilov, V. A., Chen, Y., et al. (2006). Drying of DNA droplets. Langmuir 22, 6308–6312. doi:10.1021/la060479u

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleason, K., Voota, H., and Putnam, S. A. (2016). Steady-state droplet evaporation: Contact angle influence on the evaporation efficiency. Int. J. Heat. Mass Transf. 101, 418–426. doi:10.1016/j.ijheatmasstransfer.2016.04.075

CrossRef Full Text | Google Scholar

Gopu, M., Rathod, S., Namangalam, U., Pujala, R. K., Kumar, S. S., and Mampallil, D. (2020). Evaporation of inclined drops: Formation of asymmetric ring patterns. Langmuir 36, 8137–8143. doi:10.1021/acs.langmuir.0c01084

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorr, H. M., Zueger, J. M., McAdams, D. R., and Barnard, J. A. (2013). Salt-induced pattern formation in evaporating droplets of lysozyme solutions. Colloids Surf. B Biointerfaces 103, 59–66. doi:10.1016/j.colsurfb.2012.09.043

PubMed Abstract | CrossRef Full Text | Google Scholar

Günay, A. A., Kim, M. K., Yan, X., Miljkovic, N., and Sett, S. (2021). Droplet evaporation dynamics on microstructured biphilic, hydrophobic, and smooth surfaces. Exp. Fluids 62, 153–214. doi:10.1007/S00348-021-03242-3

CrossRef Full Text | Google Scholar

Kim, J. Y., Gonçalves, M., Jung, N., Kim, H., and Weon, B. M. (2021). Evaporation and deposition of inclined colloidal droplets. Sci. Rep. 11, 17784. doi:10.1038/s41598-021-97256-w

CrossRef Full Text | Google Scholar

Kim, J. Y., Hwang, I. G., and Weon, B. M. (2017). Evaporation of inclined water droplets. Sci. Rep. 7, 42848. doi:10.1038/srep42848

PubMed Abstract | CrossRef Full Text | Google Scholar

Kita, Y., Askounis, A., Kohno, M., Takata, Y., Kim, J., and Sefiane, K. (2016). Induction of Marangoni convection in pure water drops. Appl. Phys. Lett. 109, 171602. doi:10.1063/1.4966542

CrossRef Full Text | Google Scholar

Li, Y., Lv, C., Li, Z., Quéré, D., and Zheng, Q. (2015). From coffee rings to coffee eyes. Soft Matter 11, 4669–4673. doi:10.1039/C5SM00654F

PubMed Abstract | CrossRef Full Text | Google Scholar

Logesh Kumar, P., Thampi, S. P., and Basavaraj, M. G. (2021). Patterns from drops drying on inclined substrates. Soft Matter 17, 7670–7681. doi:10.1039/D1SM00714A

CrossRef Full Text | Google Scholar

Mampallil, D., and Eral, H. B. (2018). A review on suppression and utilization of the coffee-ring effect. Adv. Colloid Interface Sci. 252, 38–54. doi:10.1016/j.cis.2017.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, S., Pham, D. V., Merkulov, S., Weber, D., Merkulov, A., Benson, N., et al. (2017). Soluble metal oxo alkoxide inks with advanced rheological properties for inkjet-printed thin-film transistors. ACS Appl. Mater Interfaces 9, 2625–2633. doi:10.1021/ACSAMI.6B12586

CrossRef Full Text | Google Scholar

Mondal, R., Semwal, S., Kumar, P. L., Thampi, S. P., and Basavaraj, M. G. (2018). Patterns in drying drops dictated by curvature-driven particle transport. Langmuir 34, 11473–11483. doi:10.1021/acs.langmuir.8b02051

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsa, M., Boubaker, R., Harmand, S., Sefiane, K., Bigerelle, M., and Deltombe, R. (2017a). Patterns from dried water-butanol binary-based nanofluid drops. J. Nanoparticle Res. 19, 268. doi:10.1007/s11051-017-3951-2

CrossRef Full Text | Google Scholar

Parsa, M., Harmand, S., Sefiane, K., Bigerelle, M., and Deltombe, R. (2017b). Effect of substrate temperature on pattern formation of bidispersed particles from volatile drops. J. Phys. Chem. B 121, 11002–11017. doi:10.1021/acs.jpcb.7b09700

CrossRef Full Text | Google Scholar

Parsa, M., Harmand, S., Sefiane, K., Bigerelle, M., and Deltombe, R. (2015). Effect of substrate temperature on pattern formation of nanoparticles from volatile drops. Langmuir 31, 3354–3367. doi:10.1021/acs.langmuir.5b00362

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsa, M., Harmand, S., and Sefiane, K. (2018). Mechanisms of pattern formation from dried sessile drops. Adv. Colloid Interface Sci. 254, 22–47. doi:10.1016/j.cis.2018.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Patil, N. D., Bange, P. G., Bhardwaj, R., and Sharma, A. (2016). Effects of substrate heating and wettability on evaporation dynamics and deposition patterns for a sessile water droplet containing colloidal particles. Langmuir 32, 11958–11972. doi:10.1021/acs.langmuir.6b02769

CrossRef Full Text | Google Scholar

Shao, X., Duan, F., Hou, Y., and Zhong, X. (2019). Role of surfactant in controlling the deposition pattern of a particle-laden droplet: Fundamentals and strategies. Adv. Colloid Interface Sci. 275, 102049. doi:10.1016/J.CIS.2019.102049

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, F. R., Nicloux, C., and Brutin, D. (2020). A new forensic tool to date human blood pools. Sci. Rep. 10, 8598–8612. doi:10.1038/s41598-020-65465-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Stauber, J. M., Wilson, S. K., Duffy, B. R., and Sefiane, K. (2015). Evaporation of droplets on strongly hydrophobic substrates. Langmuir 31, 3653–3660. doi:10.1021/ACS.LANGMUIR.5B00286

PubMed Abstract | CrossRef Full Text | Google Scholar

Thampi, S. P., and Basavaraj, M. G. (2020). Beyond coffee rings: Drying drops of colloidal dispersions on inclined substrates. ACS Omega 5, 11262–11270. doi:10.1021/acsomega.9b04310

PubMed Abstract | CrossRef Full Text | Google Scholar

Thokchom, A. K., Zhou, Q., Kim, D.-J., Ha, D., and Kim, T. (2017). Characterizing self-assembly and deposition behavior of nanoparticles in inkjet-printed evaporating droplets. Sens. Actuators B Chem. 252, 1063–1070. doi:10.1016/j.snb.2017.06.045

CrossRef Full Text | Google Scholar

Tredenick, E. C., Forster, W. A., Pethiyagoda, R., van Leeuwen, R. M., and McCue, S. W. (2021). Evaporating droplets on inclined plant leaves and synthetic surfaces: Experiments and mathematical models. J. Colloid Interface Sci. 592, 329–341. doi:10.1016/j.jcis.2021.01.070

CrossRef Full Text | Google Scholar

Wilkinson, J., Tam, C., Askounis, A., and Qi, S. (2021). Suppression of the coffee-ring effect by tailoring the viscosity of pharmaceutical sessile drops. Colloids Surf. A Physicochem. Eng. Asp. 614, 126144. doi:10.1016/j.colsurfa.2021.126144

CrossRef Full Text | Google Scholar

Winhard, B. F., Haugg, S., Blick, R., Schneider, G. A., and Furlan, K. P. (2021). Direct writing of colloidal suspensions onto inclined surfaces: Optimizing dispense volume for homogeneous structures. J. Colloid Interface Sci. 597, 137–148. doi:10.1016/j.jcis.2021.03.017

CrossRef Full Text | Google Scholar

Zhang, H., Kita, Y., Zhang, D., Nagayama, G., Takata, Y., Sefiane, K., et al. (2020). Drop evaporation on rough hot-spots: Effect of wetting modes. Heat. Transf. Eng. 41, 1654–1662. doi:10.1080/01457632.2019.1640458

CrossRef Full Text | Google Scholar