A force controlled tribometer for pre-sliding measurements at the nanometer scale

In the pre-sliding friction regime, interfaces partially stick and partially slip. The pre-slip is thought to be locally initiated at regions of the interface where the ratio of shear stress to normal stress exceeds a critical value. The displacements involved in pre-slip can be limited to the nanoscale, especially for stiff interfaces. Furthermore, little is known experimentally about the interplay between surface topography, pre-sliding behavior and wear. In this work, we introduce a pre-sliding tribometer that enables the study of how the pre-sliding friction at various types of ball-on-flat interfaces evolves as a function of wear. Polytetrafluoroethylene-on-silicon (PTFE-on-Si) pre-sliding measurements covering interfacial displacements up to 50 nm, conducted with the new instrument, show good agreement with Mindlin theory predictions, without adjustable parameters.

1 Introduction

The rapid shrinkage of the feature size in micro-electro-mechanical systems (MEMS), optical devices and integrated circuits (IC) translates into increasingly high demands on the performance of the positioning systems used in their manufacturing. In such systems, whenever the sample and its carrier are not perfectly flat and parallel as these surfaces are brought together, relative motion between the surfaces will be resisted by friction at the interface. The frictional stress causes strain which can hamper the positioning accuracy and repeatability (Garcia and Sniegowski, 1995; Kolesar et al., 2004; Iwasaki et al., 2012; Kim et al., 2012). In both MEMS and IC industries positioning accuracy and repeatability are crucial, while the widely-used silicon based materials have high stiffness which implies that the transition from static to dynamic friction involves small deformations. As the device feature size decreases down to the nanometer scale, friction behavior at this scale can lead to control errors and instability. To solve these problems, a better understanding of the friction behavior of macroscopic multi-asperity interfaces subjected to nanometer scale deformations is required.

In pre-sliding, as the applied tangential force approaches the maximum static or dynamic friction force, part of the contact area undergoes slip (Parlitz et al., 2004). Interestingly, this gradual onset of sliding observed in various experiments (Sahli et al., 2018; Weber et al., 2019; Willemet et al., 2021; Farain and Bonn, 2022) contrasts with the instability that governs the onset of sliding observed (Ben-David et al., 2010a; Ben-David et al., 2010b) and predicted (Barras et al., 2019; Schär et al., 2021) in larger systems, such as in earthquakes, where bulk elastic interactions play a more dominant role. Pre-sliding friction behavior was described empirically by the Dahl model, where the relation between tangential force and displacement smoothly transitions from elastic sticking to dissipative sliding as the applied force approaches the dynamic friction force. Subsequent sophistications of the Dahl model, such as the LuGre model, the Leuven model and the GMS model, include more parameters to capture the velocity dependence and hysteresis of the friction force (Bo and Pavelescu, 1982; Canudas-de-Wit, 1998; Swevers et al., 2000; Carbone and Mangialardi, 2008; Lukovic, 2019).

Through analytics, Mindlin (1949) found that the ratio between normal and tangential stiffness of a linearly elastic and ideally smooth sphere-on-flat contact between identical materials follows the relation: ${\mathit{k}}_{\perp }∕{\mathit{k}}_{\parallel }=\left(\mathbf{2}-\mathit{v}\right)∕\left(\mathbf{2}-\mathbf{2}\mathit{v}\right)$, where $\mathit{v}$ is the Poisson ratio of the material. This relation could be extended to multi-asperity contacts through Persson theory and computer simulations (Berthoud and Baumberger, 1998; Campañá et al., 2011; Yastrebov et al., 2015). Beyond the elastic response of the multi-asperity contacts, pre-slip has also been investigated analytically (Cattaneo, 1938; Johnson, 1985) and numerically. Boundary Element Method calculations have been developed to enable calculation of the pre-slip that results from an externally applied force under the assumption that the local friction coefficient equals the global friction coefficient (Mishra et al., 2019). This assumption was recently verified experimentally through the use of shear stress sensitive fluorescent molecular probes (Hsu et al., 2022).

It has been challenging to investigate pre-sliding at small displacement scales experimentally. Corwin et al. (2004) observed pre-sliding displacements up to 300 nm for polysilicon interfaces, depending on the surface treatment. Al-Bender and De Moerlooze (2010) developed a displacement controlled tribometer for pre-sliding measurements in which the pre-sliding distance, i.e., the distance by which the interface can be deformed before gross sliding occurs, is approximately 40 µm. Similar pre-sliding distances were observed by Hwang and Zum Gahr (2003).

In the context of precision positioning, pre-sliding behavior of stiff materials under sub-Newton loads leading to nanometer scale displacements is of interest. However, nanometer scale displacement has been difficult to study experimentally because most commercial tribometers lack the required precision to observe nanoscale pre-sliding at multi-asperity interfaces (Dion et al., 2013). Furthermore, pre-sliding behavior is expected to be influenced significantly by wear: during the manufacturing of MEMS and IC’s, the surfaces of positioning devices encounter fresh, previously untouched sample surfaces as the products are manufactured. Therefore, there is a great need for the experimental study of the interplay between non-linear pre-sliding behavior at the nanoscale and wear caused by contact with previously untouched surface (Hsia et al., 2020).

In this work, a force controlled tribometer is introduced, which can measure non-linear, pre-sliding friction behavior at interfaces with tangential stiffness as high as 10⁵ Nm⁻¹. The tribometer employs an interferometer for measuring interfacial displacement with nanometer precision. The tribometer is also designed to enable “non-repeated” wear experiments in which the slider contacts a fresh, unworn counter surface in every pre-sliding cycle through an automated positioning system.

The presented tribometer therefore enables in-depth study of the pre-sliding behavior and its dependence on topography and wear under industrially relevant conditions. We present PTFE-on-Si pre-sliding measurements and experimentally confirm the normal force dependent tangential interface stiffness predicted by Mindlin theory, without adjustable parameters.

2 Concept and design of the pre-sliding tribometer

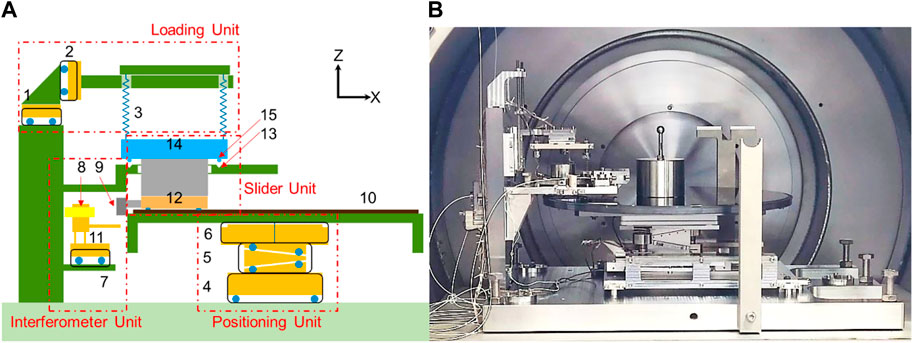
Figure 1 shows a schematic of the pre-sliding tribometer. The tribometer can be subdivided into four units: 1) Loading stages that provide normal and tangential load at the interface through compliant springs. 2) Positioning stages that move a flat sample carrier between pre-sliding cycles so as to enable non-repeated friction experiments (see above). 3) An interferometer that measures the displacement of the slider with respect to the sample carrier during pre-sliding and 4) a slider that hosts three immobilized balls that form a plane paralleled the sample carrier surface.

FIGURE 1

FIGURE 1. The pre-sliding tribometer. (A) Schematic of the setup. (B) picture of the setup.

The loading unit of the tribometer consists of three components: a tangential actuator (Part 1), a normal actuator (Part 2) and a set of three parallel springs (Part 3) whose total design stiffness is 150 Nm⁻¹ (50 Nm⁻¹ stiffness for each spring). All actuators are driven by stick-slip piezo units. The tangential actuator can provide a lateral displacement over a range of 18 mm and the normal actuator can provide a normal displacement over a range of 21 mm. These two actuators both have a resolution of 1 nm (which translates into 0.15 µN through the stiffness of the three parallel springs) and a repeatability of 50 nm (7.5 µN when multiplied with the parallel spring stiffness). This design enables the simultaneous lateral and normal loading of the interface. The three springs have fixed hinge supports attached to the platform of normal and tangential actuators and fixed to the slider unit. The springs are evenly distributed over the slider with 60° angles between the attachment points. This design guarantees that normal and tangential load are evenly transferred through displacement of the actuators. Based on the fact that the slip distances of interest are at the nanometer scale while the loading stages travel in the millimeter range, it is reasonable to treat the slider end of the springs as fixed. By controlling the position of the actuator platform, the normal force F_N and tangential force F_T exerted at the interface can be controlled in the range of F_N = 7.5–2000 mN and F_T = −30 to 30 mN, respectively.

The positioning unit consists of three actuators that control the movement of the sample carrier in X (Part 4) and Z (Part 5) directions as well as the rotation of the sample carrier around the Z-axis (Part 6). The sample carrier (Part 10) with a diameter of 300 mm is placed on top of the actuators. These three degrees of freedom enable the slider to contact the carrier at any desired position for pre-sliding experiments in a non-repeated fashion as described above and in (Hsia et al., 2020; Hsia et al., 2022). Up to 101,326 unique spots on a single sample can be visited. A 1 kg dead weight is placed on top of the center of the sample to avoid relative displacement between the sample and the actuator platform.

The interferometer unit contains a sensor actuator (Part 7) and a laser head (Part 8) which illuminates a retro-reflector (Part 9). The laser head is mounted on a compliant stand (Part 11) with intrinsic stiffness in X direction K_X = 5∙10³ Nm⁻¹. During measurements, the stand (Part 11) is brought into contact with the sample carrier (Part 10) with a pre-load of approximately 1 N by moving the sensor actuator. This contact is made to ensure that the laser head follows the movement of the sample carrier and can record the relative displacement between the slider and the sample carrier. The laser head is a Michelson interferometer which embeds a beam splitter. The retro-reflector is clamped on the slider and stretches toward the sensor head to shorten the interferometer working distance and improve the signal amplitude. The 3 mm diameter retro-reflector has a corner cube geometry and is coated with silver to boost its reflection.

The slider unit contains a puck which hosts three ball holders (Part 12), an interferometer retro-reflector (Part 9) and a puck clamp (Part 14). The three ball holders are embedded with respect to the +X-axis on 60, 180 and 300° locations on the X-Y plane. The apices of the three balls form a plane which is parallel to the puck finish. The puck is then aligned to be parallel to the sample surface. To align the puck clamp parallel to the sample, three identical adjustment pins (Part 15) pointing in the –Z direction are located at the same angles as the balls on the puck clamp. On the frame, three V-grooves (Part 13) are placed with the same X-Y position to host the pins. Each V-groove contains two separate copper blocks which form a 90° groove. For each block (6 in total), a unique positive voltage ranging from 0.15 V to 4.98 V (in detail: 0.15 V; 0.31 V; 0.62 V; 1.24 V; 2.49 V; 4.98 V) is applied and the puck clamp is grounded. By measuring the total series voltage, all possible contact combinations between adjustment pins and V-groove blocks can be deciphered.

Control software was developed to operate the system in a fully automated manner. Normal and tangential load as a function of time and test cycle can be applied during pre-sliding experiments through automated control of the movement of the loading stages. In between the pre-sliding cycles, the software automatically separates the tribopairs and displaces the sample carrier such that the next pre-sliding cycle is conducted at a previously untouched location on the sample. The software also synchronizes the data received from stages and interferometer with its internal clock (5 kHz) such that synchronized force-displacement data can be obtained.

3 Materials and methods

The slider samples used in this study were 3.18 mm diameter PTFE spheres (Goodfellow, FP30-SP-000120). The root mean square (rms) surface roughness of the spheres is approximately 0.46 µm, as measured through optical profilometry (Keyence VK-X1100) on a 30 μm² × 30 μm² area after removing the spherical curvature. The sample was a 300 mm diameter double side polished silicon wafer (UniveristyWafer, Test Grade). The rms surface roughness of the wafer is less than 5 nm as measured by AFM (Bruker Dimension Icon) on a 30 μm² × 30 μm² area. The PTFE ball has a reduced modulus of 592 ± 47 MPa as measured via nanoindentation (FemtoTools FT-I04). This translates into a shear modulus of 203 ± 16 MPa (Landau et al., 1960) using the PTFE Poisson ratio ν₁ = 0.46 provided by the supplier (Goodfellow). The <100> silicon wafer has a reduced modulus of 151 ± 17 GPa as measured via nanoindentation (FemtoTools FT-I04) and calculated shear modulus of 59 ± 7 GPa using the Poisson ratio ν₂ = 0.278 (Gan et al., 1996).

Three PTFE spheres were clamped into the ball holders on the puck (Part 12) and slid against the Si wafer. First, the normal actuator (Part 2) will move up to compensate the gravitational force exerted on the slider. When the electronic contacts in the V-grooves on the puck clamp indicated that the gravitational force acting on the puck was (almost fully) carried by the loading springs, the normal actuator was stopped. Next, the Z positioning actuator raised the sample carrier to create contact between the plane formed by 3-ball apices and the Si wafer. This contact was again detected via the V-grooves. By further moving the sample carrier up, the normal force exerted at the PTFE-on-Si interface was increased. When the normal load exerted at the interface increased to 7.5 mN, the Z positioning actuator stopped moving and the normal load actuator resumed moving downward until the intended normal load was reached. Through this loading sequence, vibrations generated by the Z positioning actuator movement were minimized and only allowed to influence the contacts at small normal loads. The tangential load was subsequently applied by moving the lateral load stage thus tilting the three loading springs in the X-Z plane. The maximum tilting angle was 0.5° which leads to a 0.88% normal load variation which is ignored.

Pre-sliding experiments were performed in a non-repeated sliding fashion because the wear behavior of the slider can be strongly influenced by wear debris if the sliding is repeated on the same spot (Hsia et al., 2020). The 3-ball puck was thus lifted from the sample surface after each pre-sliding measurement. Subsequently the sample carrier was rotated by 0.18° before contact was made again between the 3-ball puck and a previously untouched area on the Si wafer sample. Furthermore, to increase the total number of “landing sites” on the sample for long wear experiments, the 3-ball puck could be placed at different radial distances from the center of the wafer sample. After all the sites on a single circumference have been visited, the X positioning actuator will move the sample carrier 0.35 mm in the X direction such that the slider can make contact with previously untouched areas on the wafer sample. The minimal distance between two contact spots on the wafer thus was 0.35 mm in the axial direction and 0.32 mm in the radial direction. The tilt of the sample surface with respect to the 3-ball puck was minimized to ensure all three balls came into contact with the sample surface within 50 µm normal displacement of the Z positioning actuator. The misalignment between the 3-ball puck and the sample surface can maximally result in a lateral force variation per contact of 0.7 µN which is negligible compared to the imposed tangential forces in this study.

4 Results

In the PTFE-on-Si pre-sliding measurements, the interface was sequentially loaded in the +X,-X and +X directions to ensure that pre-slip could be identified by comparing the measured displacements at 0 tangential force, F_T = 0 (Figure 2A). Pre-sliding measurements were conducted at normal loads of 75, 150, 225 and 300 mN. The tangential force amplitude was fixed at 5 mN, while the tangential loading rate was 7.5 mN/s. In response to the tangential loading, tangential displacements up to about 50 nm could be observed, which is far below the range of displacements observed in previous pre-sliding experiments (Hwang and Zum Gahr, 2003; Al-Bender and De Moerlooze, 2010). It can be seen that most of the tangential displacement is recoverable and thus elastic, while partial slip at the nanometer scale takes place. The pre-sliding response can be described reasonably well by the analytical model developed by Cattaneo and Mindlin (Johnson, 1985). From the pre-sliding force-distance curves (Figure 2A), a pre-sliding distance as well as a tangential interface stiffness could be extracted. Both quantities show a systematic dependence on normal force. The pre-sliding displacement was measured by subtracting the displacements measured before tangentially loading the interface, and after tangentially loading up to 5 mN in the +X direction and then returning to 0 applied tangential load. Impressively, pre-sliding displacements of just a few nanometers were reliably detectable for the macroscopically loaded PTFE-on-Si contacts. The pre-sliding displacement decreased from 8 nm at a normal load of F_N = 75 mN to just 4 nm at a normal load of F_N = 300 mN, i.e., more pre-sliding occurs at a lower normal load. These nanometer scale pre-sliding displacements were in fact predicted by Cattaneo and measured experimentally at the micrometer scale in the classical works of Johnson (1955), but so far never observed experimentally at the nanometer scale. The analytical prediction of the relative tangential displacement that remains after the contact is tangentially loaded and unloaded is given by Johnson (1985) and Mindlin et al. (1952):

${\delta }_{slip}=\frac{3\mu F_N}{16a}\left(\frac{2-{\nu }_1}{G_1}+\frac{2-{\nu }_2}{G_2}\right)\left[{2\left(1-\frac{F_T}{2\mu F_N}\right)}^{\frac{2}{3}}-{\left(1-\frac{F_T}{\mu F_N}\right)}^{\frac{2}{3}}-1\right](1)$

where, ${\mathit{\delta }}_{\mathit{s}\mathit{l}\mathit{i}\mathit{p}}$ is the tangential displacement induced by partial slip, or pre-sliding. ${\mathit{F}}_{\mathit{T}}$ and $\mathit{a}$ are the maximum applied tangential load and Hertzian contact radius, respectively. $\mathit{\mu }{\mathit{F}}_{\mathit{N}}$ is the maximum friction force. $\mathit{\nu }$ and $\mathit{G}$ are Poisson ratios and shear moduli of elasticity of the two contacting materials. Although we observe smaller slip distances than expected at the low normal loads, the overall scale and trend of the experimentally observed slip distances is consistent with the analytical predictions.

FIGURE 2

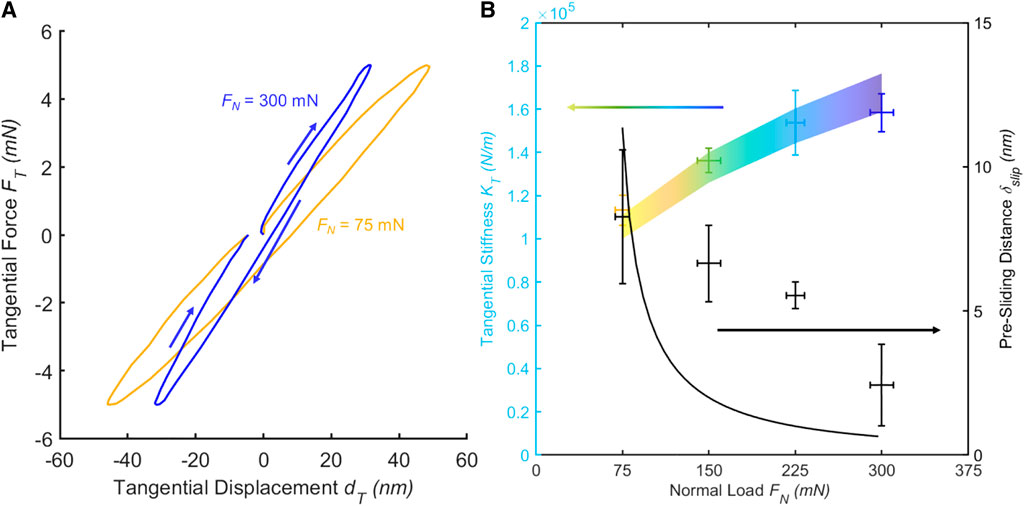
FIGURE 2. (A) Pre-sliding hysteresis curve measured at a 3-PTFE-balls/Si interface at 75 mN and at 300 mN collective normal load. (B) Tangential stiffness and pre-sliding distance of the 3-PTFE-balls/Si interface at different normal loads. Datapoints represent experiments while the colored areas represent theory predictions from Eq. 1 and Eq. 2 using the parameters and their uncertainty provided in the Materials and Methods section. For the friction coefficient, we used $\mathit{\mu }$ = 0.07. The error bars indicate the standard deviation obtained from five independent pre-sliding experiments, each conducted on different PTFE and Si samples.

To derive the tangential interface stiffness, a linear fit was made to the force-distance curves at absolute tangential forces ${\mathit{F}}_{\mathit{T}}$ in the range 1–4 mN on both onward and backward sections. The tangential stiffness increases systematically with normal load (Figure 2B) from (1.13 ± 0.07) × 10⁵ N/m (1.58 ± 0.09) × 10⁵ N/m. We compared the measured tangential interface stiffness to an independent Mindlin theory prediction. The tangential interface stiffness, ${\mathit{K}}_{\mathit{T}}$, is approximated under the assumption of elastic contact of ideally smooth sphere-on flat interfaces with very small partial slip (Johnson, 1985):

$K_T=\frac{F_T}{{\delta }_{elastic}}=\frac{8a}{\left(\frac{2-{\nu }_1}{G_1}+\frac{2-{\nu }_2}{G_2}\right)}(2)$

Full agreement between the experiments and the independent Mindlin theory predictions is observed (Figure 2B). In addition to the pre-sliding displacements and the tangential interface stiffness, the area within the force-distance hysteresis loop can be extracted from the measurements. This area indicates how much energy is dissipated during the pre-sliding experiment through friction and wear, and can also be viewed as the toughness of the interface. We found dissipated energies ranging from about 138 pJ to 57 pJ for the normal forces ranging from 75 mN to 300 mN, respectively: More energy is dissipated during the low normal force hysteresis loops because those involve more pre-sliding.

5 Discussion

The newly-developed force controlled pre-sliding tribometer measures nanometer scale pre-sliding displacement. Nanometer slip distances were observed at macroscopic multi-asperity PTFE-on-Si contacts as those contacts were deformed tangentially by up to 50 nm. These measurements address pre-sliding behavior at a length scale that was previously not accessible (Hwang and Zum Gahr, 2003; Al-Bender and De Moerlooze, 2010), thus enabling future experimental investigation of many pre-sliding contacts (Berthoud and Baumberger, 1998; Campañá et al., 2011) in the context of stiff interfaces.

The surface topography of mating materials is known to influence the interfacial tangential stiffness (Wang et al., 2010). In our experiments, interlocking friction is not expected to occur as the surface slopes on the Si wafer are very low (Peng et al., 2022). Instead, slip likely takes place through the transfer of nanometrically thin PTFE films (Makinson and David, 1964). The local ratio of tangential to normal stress controls the elastic or slip displacement that occurs locally (Cattaneo, 1938; Johnson, 1985; Bazrafshan et al., 2020; Hsu et al., 2022). By applying Mindlin theory, we neglected the effect of surface topography on pre-sliding. This is a reasonable approximation because in this study the experimentally applied normal loads results in a large fraction (∼0.5) of real to nominal contact area for the PTFE-on-Si contacts studied here, as was previously shown using fluorescence microscopy imaging of PTFE-on-glass contacts (Weber, 2017). In future experiments, the ratio of real to nominal contact area can be reduced through an appropriate choice of contacting materials and conditions (Hsia et al., 2021) and the interplay between surface topography and pre-sliding behavior can be investigated systematically.

For interfaces between materials stiffer than those studied here, the average size of individual contact junctions will be smaller. This means that the contact stress exerted at contact junctions decreases from a maximal value, potentially of the order of the material hardness, to zero, from the center of the contact junction to the edge of the contact junction within a nanometer scale distance (Pham-Ba and Molinari, 2021). Thus pre-sliding behavior, that is sensitive to the geometry of individual contact junctions will occur at an even smaller length scale than that observed here. Future improvements in the present pre-sliding instrument may enable such pre-sliding observations in stiffer contacts.

6 Conclusion

A newly-designed pre-sliding tribometer is described and its working mechanism is explained. Through interferometry, nanometer scale tangential displacement at PTFE-on-Si interfaces is recorded, far beyond the precision of previous pre-sliding measurements. The experimental data reveals the evolution of pre-sliding distances, tangential interface stiffness and pre-sliding energy dissipation as a function of different loading conditions: pre-sliding distances decrease with increasing normal load while tangential interface stiffness increases with increasing normal load. Good agreement between the experimental results and the tangential stiffness of sphere-on-flat contacts from Mindlin theory, without adjustable parameters, was obtained. In future work, the instrument will be used to the study the interplay between wear caused by non-repeated sliding and pre-sliding behavior, which is important in the context of precision positioning applications.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SF and BW devised the project. JD carried out the experiment and analyzed the data with the aid of BW. JD and BW wrote the original manuscript. SF and BW reviewed the manuscript.

Funding

This project received financial support from the Dutch Research Council (Project No. VI.Veni.192.177).

Acknowledgments

The authors gratefully acknowledge the contributions made by many co-workers at AMOLF, Philips Engineering Solutions (PES) and ARCNL: Jeroen Dekkers, Thanh Ngo and Rens Verhees from PES for preparing the concept and detailed design of the instrument; Marco Konijnenburg from the software engineering department at AMOLF for developing the software with which the instrument is controlled; Duncan Verheijde from the electronics engineering department at AMOLF for his help in developing the contact grooves and synchronization; Iliya Cerjak from the mechanical engineering department at AMOLF for his help in designing machine parts; Mark Mol from ARCNL for technical support; Olaf Janssen, Menno Borsboom, Wouter van der Weijden, Niels Winkelaar, Wessel Zwart, Ricardo Eliazer, Mark Willemse and Jan van der Linden from the precision manufacturing department at AMOLF for manufacturing the custom parts of the instrument. This work has been carried out at the Advanced Research Center for Nanolithography (ARCNL), a public-private partnership of the University of Amsterdam (UvA), the Vrije Universiteit Amsterdam, the Dutch Research Council (NWO) and the semiconductor equipment manufacturer ASML.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Bender, F., and De Moerlooze, K. (2010). On the relationship between normal load and friction force in pre-sliding frictional contacts. Part 1: Theoretical analysis. Wear 269 (3-4), 174–182. doi:10.1016/j.wear.2010.02.010

CrossRef Full Text | Google Scholar

Barras, F., Aldam, M., Roch, T., Brener, E., Bouchbinder, E., and Molinari, J. (2019). Emergence of cracklike behavior of frictional rupture: The origin of stress drops. Phys. Rev. X 9 (4), 041043. doi:10.1103/physrevx.9.041043

CrossRef Full Text | Google Scholar

Bazrafshan, M., de Rooij, M., de Vries, E., and Schipper, D. (2020). Evaluation of pre-sliding behavior at a rough interface: Modeling and experiment. J. Appl. Mech. 87 (4). doi:10.1115/1.4045900

CrossRef Full Text | Google Scholar

Ben-David, O., Cohen, G., and Fineberg, J. (2010a). The dynamics of the onset of frictional slip. Science 330 (6001), 211–214. doi:10.1126/science.1194777

PubMed Abstract | CrossRef Full Text | Google Scholar

Ben-David, O., Rubinstein, S., and Fineberg, J. (2010b). Slip-stick and the evolution of frictional strength. Nature 463 (7277), 76–79. doi:10.1038/nature08676

PubMed Abstract | CrossRef Full Text | Google Scholar

Berthoud, P., and Baumberger, T. (1998). Shear stiffness of a solid–solid multicontact interface. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 454, 1615–1634. doi:10.1098/rspa.1998.0223

CrossRef Full Text | Google Scholar

Bo, L., and Pavelescu, D. (1982). The friction-speed relation and its influence on the critical velocity of stick-slip motion. Wear 82 (3), 277–289. doi:10.1016/0043-1648(82)90223-x

CrossRef Full Text | Google Scholar

Campañá, C., Persson, B., and Müser, M. (2011). Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys. Condens. Matter 23 (8), 085001. doi:10.1088/0953-8984/23/8/085001

PubMed Abstract | CrossRef Full Text | Google Scholar

Canudas-de-Wit, C. (1998). Comments on "A new model for control of systems with friction. IEEE Trans. Automatic Control 43 (8), 1189–1190. doi:10.1109/9.704999

CrossRef Full Text | Google Scholar

Carbone, G., and Mangialardi, L. (2008). Analysis of the adhesive contact of confined layers by using a Green's function approach. J. Mech. Phys. Solids 56 (2), 684–706. doi:10.1016/j.jmps.2007.05.009

CrossRef Full Text | Google Scholar

Cattaneo, C. (1938). Sul contatto di due corpi elasticie: Distribution locale degli sforzi. Reconditi dell Acad. Naz. Lincei 27, 474–478.

Google Scholar

Corwin, A. D., Street, M. D., Carpick, R. W., Ashurst, W. R., and de Boer, M. P. (2004). “Pre-sliding tangential deflections can govern the friction of MEMS devices,” in ASME/STLE 2004 international joint Tribology conference. Parts A and B.

CrossRef Full Text | Google Scholar

Dion, J., Chevallier, G., Penas, O., and Renaud, F. (2013). A new multicontact tribometer for deterministic dynamic friction identification. Wear 300 (1-2), 126–135. doi:10.1016/j.wear.2013.01.100

CrossRef Full Text | Google Scholar

Farain, K., and Bonn, D. (2022). Non-monotonic dynamics in the onset of frictional slip. Tribol. Lett. 70 (2), 57. doi:10.1007/s11249-022-01598-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Gan, L., Xiang, M., Zhou, L., Wagner, D., Klein, W., and Nathans, J. (1996). POU domain factor Brn-3b is required for the development of a large set of retinal ganglion cells. Proc. Natl. Acad. Sci. 93 (9), 3920–3925. doi:10.1073/pnas.93.9.3920

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, E., and Sniegowski, J. (1995). Surface micromachined microengine. Sensors Actuators A Phys. 48 (3), 203–214. doi:10.1016/0924-4247(95)00999-x

CrossRef Full Text | Google Scholar

Hsia, F., Elam, F., Bonn, D., Weber, B., and Franklin, S. (2020). Wear particle dynamics drive the difference between repeated and non-repeated reciprocated sliding. Tribol. Int. 142, 105983. doi:10.1016/j.triboint.2019.105983

CrossRef Full Text | Google Scholar

Hsia, F., Franklin, S., Audebert, P., Brouwer, A., Bonn, D., and Weber, B. (2021). Rougher is more slippery: How adhesive friction decreases with increasing surface roughness due to the suppression of capillary adhesion. Phys. Rev. Res. 3 (4), 043204. doi:10.1103/physrevresearch.3.043204

CrossRef Full Text | Google Scholar

Hsia, F., Hsu, C., Peng, L., Elam, F., Xiao, C., Franklin, S., et al. (2022). Contribution of capillary adhesion to friction at macroscopic solid–solid interfaces. Phys. Rev. Appl. 17 (3), 034034. doi:10.1103/physrevapplied.17.034034

CrossRef Full Text | Google Scholar

Hsu, C., Hsia, F., Weber, B., de Rooij, M., Bonn, D., and Brouwer, A. (2022). Local shearing force measurement during frictional sliding using fluorogenic mechanophores. J. Phys. Chem. Lett. 13, 8840–8844. submitted. doi:10.1021/acs.jpclett.2c02010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, D., and Zum Gahr, K. (2003). Transition from static to kinetic friction of unlubricated or oil lubricated steel/steel, steel/ceramic and ceramic/ceramic pairs. Wear 255 (1-6), 365–375. doi:10.1016/s0043-1648(03)00063-2

CrossRef Full Text | Google Scholar

Iwasaki, M., Seki, K., and Maeda, Y. (2012). High-precision motion control techniques: A promising approach to improving motion performance. IEEE Ind. Electron. Mag. 6 (1), 32–40. doi:10.1109/mie.2012.2182859

CrossRef Full Text | Google Scholar

Johnson, K. (1985). Contact mechanics. Cambridge: Cambridge University Press, 216–220.

Google Scholar

Johnson, K. (1955). Surface interaction between elastically loaded bodies under tangential forces. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 230 (1183), 531–548.

Google Scholar

Kim, H., Yoo, S., and Kim, D. (2012). Nano-scale wear: A review. Int. J. Precis. Eng. Manuf. 13 (9), 1709–1718. doi:10.1007/s12541-012-0224-y

CrossRef Full Text | Google Scholar

Kolesar, E., Odom, W., Jayachandran, J., Ruff, M., Ko, S., Howard, J., et al. (2004). Design and performance of an electrothermal MEMS microengine capable of bi-directional motion. Thin Solid Films 447-448, 481–488. doi:10.1016/j.tsf.2003.07.011

CrossRef Full Text | Google Scholar

Landau, L., Lifshitz, E., Sykes, J., Reid, W., and Dill, E. (1960). Theory of elasticity: Vol. 7 of course of theoretical physics. Phys. Today 13 (7), 44–46. doi:10.1063/1.3057037

CrossRef Full Text | Google Scholar

Lukovic, M. (2019). The influence of surface temperature on the coefficient of static friction. Phys. Teach. 57 (9), 636–638. doi:10.1119/1.5135798

CrossRef Full Text | Google Scholar

Makinson, K., and David, T. (1964). The friction and transfer of polytetrafluoroethylene. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 281 (1384), 49–61. doi:10.1103/PhysRevE.107.024801

CrossRef Full Text | Google Scholar

Mindlin, R. (1949). Compliance of elastic bodies in contact. J. Appl. Mech. 16 (3), 259–268. doi:10.1115/1.4009973

CrossRef Full Text | Google Scholar

Mindlin, R., Mason, W., Osmer, T., and Deresiewicz, H. (1952). “Effects of an oscillating tangential force on the contact surfaces of elastic spheres,” in Proceedings of the first US national congress of applied mechanics, 203–208.

Google Scholar

Mishra, T., de Rooij, M., Shisode, M., Hazrati, J., and Schipper, D. (2019). An analytical model to study the effect of asperity geometry on forces in ploughing by an elliptical asperity. Tribol. Int. 137, 405–419. doi:10.1016/j.triboint.2019.05.015

CrossRef Full Text | Google Scholar

Parlitz, U., Hornstein, A., Engster, D., Al-Bender, F., Lampaert, V., Tjahjowidodo, T., et al. (2004). Identification of pre-sliding friction dynamics. Chaos Interdiscip. J. Nonlinear Sci. 14 (2), 420–430. doi:10.1063/1.1737818

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, L., Hsia, F., Woutersen, S., Bonn, M., Weber, B., and Bonn, D. (2022). Nonmonotonic friction due to water capillary adhesion and hydrogen bonding at multiasperity interfaces. Phys. Rev. Lett. 129 (25), 256101. doi:10.1103/physrevlett.129.256101

PubMed Abstract | CrossRef Full Text | Google Scholar

Pham-Ba, S., and Molinari, J. (2021). Creation and evolution of roughness on silica under unlubricated wear. Wear 472-473, 203648. doi:10.1016/j.wear.2021.203648

CrossRef Full Text | Google Scholar

Sahli, R., Pallares, G., Ducottet, C., Ben Ali, I., Al Akhrass, S., Guibert, M., et al. (2018). Evolution of real contact area under shear and the value of static friction of soft materials. Proc. Natl. Acad. Sci. 115 (3), 471–476. doi:10.1073/pnas.1706434115

PubMed Abstract | CrossRef Full Text | Google Scholar

Schär, S., Albertini, G., and Kammer, D. (2021). Nucleation of frictional sliding by coalescence of microslip. Int. J. Solids Struct. 225, 111059. doi:10.1016/j.ijsolstr.2021.111059

CrossRef Full Text | Google Scholar

Swevers, J., Al-Bender, F., Ganseman, C., and Projogo, T. (2000). An integrated friction model structure with improved presliding behavior for accurate friction compensation. IEEE Trans. Automatic Control 45 (4), 675–686. doi:10.1109/9.847103

CrossRef Full Text | Google Scholar

Wang, Z., Wang, W., Wang, H., Zhu, D., and Hu, Y. (2010). Partial slip contact analysis on three-dimensional elastic layered half space. J. Tribol. 132 (2). doi:10.1115/1.4001011

CrossRef Full Text | Google Scholar

Weber, B. (2017). Sliding friction: From microscopic contacts to Amontons’ law. Amsterdam: Ph.D. University of Amsterdam.

Google Scholar

Weber, B., Suhina, T., Brouwer, A., and Bonn, D. (2019). Frictional weakening of slip interfaces. Sci. Adv. 5 (4), eaav7603. doi:10.1126/sciadv.aav7603

PubMed Abstract | CrossRef Full Text | Google Scholar

Willemet, L., Kanzari, K., Monnoyer, J., Birznieks, I., and Wiertlewski, M. (2021). Initial contact shapes the perception of friction. Proc. Natl. Acad. Sci. 118 (49), e2109109118. doi:10.1073/pnas.2109109118

PubMed Abstract | CrossRef Full Text | Google Scholar

Yastrebov, V., Anciaux, G., and Molinari, J. (2015). From infinitesimal to full contact between rough surfaces: Evolution of the contact area. Int. J. Solids Struct. 52, 83–102. doi:10.1016/j.ijsolstr.2014.09.019

CrossRef Full Text | Google Scholar