The numerical simulation of nanosecond-pulsed discharge-assisted ignition in lean-burn natural gas HCCI engines

A plasma-assisted internal combustion engine model is established based on detailed plasma kinetics, combustion kinetics, and physical compression/expansion processes. The effects of nanosecond repetitively pulsed discharge (NRPD) on plasma-assisted ignition characteristics of mixtures under different fuel concentrations are studied under HCCI engine-relevant conditions. The coupled plasma and chemical kinetic model are validated with experiments. The comparison between NRPD and thermal ignition with a certain amount of input energy is carried out, and the results show that the former can ignite a mixture owing to the kinetic effect of nonequilibrium plasma, but the latter cannot ensure ignition. Path flux analysis shows that excited states and electrons react with fuel, providing O and H directly, increasing the possibility of ignition at a low temperature. The effect of NRPD on combustion performance under various equivalence ratios (φ) is investigated. It was found that in ICEs with NRPD, the ignition delay time under the lean-burn condition (φ = 0.5) is the shortest among three demonstrative cases. Even though the leaner mixture case with φ = 0.2 is more favorable for the production of O and OH during the discharge, after discharge, the heat release in case 2 with φ = 0.5 dramatically increases, resulting in the temperature exceeding that in the ultra-lean case. As the piston moves up, the higher amounts of CH₃, HO₂, and H₂O₂ as well as higher temperature for the lean-burn (φ = 0.5) case lead to the rapid increase of OH and O, which accelerates the consumption of methane and finally the earliest hot ignition near TDC. Finally, a series of parameter studies are performed to show the effects of E/N, current density, φ, and discharge timing on the ignition process. The results suggest that discharge parameters E/N and current density together with discharge timings and equivalence ratios can improve ignitability in internal combustion engines.

1 Introduction

With the increasingly stringent fossil fuel supply and pollutant emissions from classical internal combustion engines (ICEs), the new advanced combustion technologies such as homogeneous charge compression ignition (HCCI) (Saxena and Bedoya, 2013) and spark assisted compression ignition (SACI) (Persson et al., 2007) attract great attentions. Among these strategies, high compression ratio and lean-burn are usually used to improve fuel economy and reduce emissions (Persson et al., 2007; Ju et al., 2011; Saxena and Bedoya, 2013). However, they may suffer from flammability limits and unstable combustion (Cho and He, 2007; Ju et al., 2011). The mechanism of a spark plug on ignition is to form a thermal equilibrium arc, whereas most of the discharge power is expended in heating spark plug electrodes (Shiraishi et al., 2009; Schenk et al., 2015), and only the remaining energy is deposited into mixture via thermal ionization and Joule heating. To overcome this problem and achieve successful ignition in lean fuel/air mixture, especially in ICEs, a reliable ignition strategy, that is, nonequilibrium plasma-assisted ignition/combustion (PAI/PAC) technology is proposed (Bellenoue et al., 2007; Cathey et al., 2007; Cathey et al., 2008; Shiraishi et al., 2009; Singleton et al., 2010; Zhu et al., 2017).

The novel promising ignition systems characterized by nonequilibrium plasma can be created by corona discharge (Bellenoue et al., 2007), nanosecond repetitively pulsed discharge (NRPD) (Cathey et al., 2007), and gliding arc discharge (Zhu et al., 2017). Among them, NRPD is the one with a smaller proportion of energy thermalization which has been demonstrated great potential to achieve stable combustion in lean-burn gasoline engines (Cathey et al., 2007). The experimental results showed significant advantages of NRPD over spark ignition (SI) for extending the flammability limit in ICEs (Shiraishi et al., 2009). In a single-cylinder engine with NRPD-assisted ignition, the ignition delay time was three to four orders of magnitude shorter and approximately 13–17% narrower of combustion duration compared with spark discharge (Shiraishi et al., 2009). A faster flame propagation assisted by NRPD was also observed (Cathey et al., 2008; Singleton et al., 2010). Another advantage may stem from less specific fuel consumption, NOx emission (Tropina et al., 2014), and knocking (Stepanyan et al., 2013) under the usage of nonequilibrium plasma. It was found that nonequilibrium discharge energy of 50 mJ/cm³ can cause a 600 K reduction in ignition temperature, while if the energy is used for heating, the ignition temperature reduction is only 20 K (Stepanyan et al., 2013). The aforementioned experiments revealed the potential of nonequilibrium plasma discharge in engines from the viewpoint of the experiment; however, the detailed physical interpretation for the guidance of the NRPD application in ICEs is still limited.

Numerical simulations are needed to reveal the mechanism of NRPD in depth and find the level where the discharge parameters can be used to control combustion phasing. To date, there are abundant zero-dimension (0D) and a few higher dimensional numerical simulations about nonequilibrium plasma discharge (Hagelaar and Pitchford, 2005; Konstantinovskii et al., 2005; Kosarev et al., 2008; Popov, 2008; Shi et al., 2008; Schulz and Menon, 2009; Uddi et al., 2009; Zhu et al., 2013; Ju and Sun, 2015a; Ju and Sun, 2015b; Lefkowitz et al., 2015; Defilippo and Chen, 2016; Ju et al., 2016; Yang et al., 2016; Mao and Chen, 2018; Mao et al., 2019a; Mao et al., 2022), which are listed in Table 1.

TABLE 1

TABLE 1. Summary of simulations involving nonequilibrium plasma.

Uddi et al. (2009) studied the O atom concentrations of air, CH₄/air, and C₂H₄/air in the process of single pulse nanosecond discharge by two-photon laser-induced fluorescence technology and established the nonequilibrium plasma-assisted combustion mechanism. They found that the O atom is the key particle for plasma ignition and flame propagation speed improvement. Ju et al. (2016) further found the existence of O(1D) provides a low-temperature oxidation path of fuel in plasma-assisted combustion of CH₄/air and C₂H₄/air by coupling ZDPlasKin and SENKIN. Similarly, Mao et al. (2019a) found O(1D) has a higher potential to accelerate radical production in the chain branching reactions only at a low temperature. As temperature rises, the positive effect of O on ignition enhancement dominates because O atom concentration dramatically increases. In the ultra-lean mixture, most of O(1D) is consumed in the collision with O₂ and N₂, so the influence of O(1D) on ignition can be ignored (Popov, 2008). Moreover, Popov (2011) showed the kinetic effect of singlet oxygen molecule O₂(a¹Δ_g) is weakened in hydrocarbon/air mixture, while the generation efficiency of O atom during discharge is high. Thus, the kinetic enhancement effect of O is larger than that of O₂(a¹Δ_g). Recently, Mao et al. (2019b) used a hybrid repetitive nanosecond and DC discharge to adjust the electric field strength for the selectivity of excitation of reactants and maximize ignition enhancement. Results showed that the reduced electric field strength E/N (ratio of electric field strength and gas number density) is efficient in controlling active species production. However, there are only a few works on plasma-assisted ignition/combustion in ICEs to reveal the kinetic enhancement pathways and discharge parameter effect on the ignition process.

Due to the complexity of detailed plasma/chemistry kinetics in ICEs, some researchers used a simplified discharge process, such as the addition of radicals O and H (Filimonova et al., 2018; Filimonova et al., 2020). Filimonova et al. (2018) simulated nanosecond streamer discharges in the HCCI engine by using an external source in terms of a fixed specific deposited energy. Then, the calculated concentrations of O, H, and C₃H₇ were added into C₃H₈/air. They compared the effect of discharge parameters on low/high temperatures of a lean propane-air mixture and suggested the pressure rise rate and other combustion characteristics are largely determined by the moment of discharge initiation and the specific energy input. However, neglecting the effect of E/N and energy deposited channel may result in a large discrepancy in ignition timing and heat release rate compared with a comprehensive plasma ignition kinetic model involving various excited species and plasma reactions.

In this work, a CH₄/air plasma kinetic mechanism is developed and validated based on experimental results first. This model couples the plasma kinetics (Pancheshnyi et al., 2008), combustion dynamics (Kee et al., 1996), and compression/expansion process of ICEs (Zhang et al., 2015). Electron energy distribution function (EEDF) and electron energy loss fraction are calculated to analyze discharge energy deposition distribution. Then, the effects of NRPD on combustion phasing, heat release rate, and species formation under ICE-related conditions are investigated and compared with equilibrium discharge. The pathway flux analysis (PFA), rate of production (ROP) of plasma/chemical reactions, and crucial radicals are analyzed to show how the plasma expands combustion limitation within lean-burn conditions. Finally, a parametric study of E/N, current density, equivalence ratio (φ), and discharge timing on ignition timing is carried out for a better understanding of combustion phasing and heat release control under lean-burn conditions in ICEs.

2 Kinetic mechanism, numerical method, and model validation

2.1 Kinetic mechanism

A PAI mechanism of CH₄/air is developed based on the air plasma kinetic model (Defilippo and Chen, 2016) and GRI Mech 3.0 (Smith et al., 2021), including 103 species, 64 electron collision reactions, and 1843 chemical reactions. The relaxation of excited states, electron impact dissociation CH₄, electron-ion recombination reactions, charge exchange reactions, and attachment reactions are involved. The collisions between electrons and products are ignored due to the low concentrations. Also, super-elastic collisions and electron-electron collisions are neglected due to the lower electron-to-gas fraction (N_e/N_gas∼10⁻⁶) (Hagelaar and Pitchford, 2005). The rate constants of electron impact reactions are computed by solving the Boltzmann equation based on the corresponding collision cross-sections using BOLSIG+ (Hagelaar and Pitchford, 2005), where the collision cross sections of O₂ and N₂ are taken from Phelps (Phelps database, 2020) and SIGLO (SIGLO database, 2020) databases, respectively, and the dissociation collision cross sections of CH₄ are computed according to Janev and Reiter (2002). Table 2 lists all species in the kinetic mechanism for plasma-assisted combustion CH₄/air. Here, O₂(A3) is the group of O₂(A³Σ_u⁺, A^’3Δ_u, c¹Σ_u⁻), owing to their similar excitation energies and shorter lifetimes (Defilippo, 2013). The states of N₂(A³Σ_u⁺,v = 0–4), N₂(A³Σ_u⁺,v = 5–9), and N₂(A³Σ_u⁺,v = 10-) are integrated into N₂(A³Σ_u⁺) based on an approximation of fast collisional energy exchange among them (Mao et al., 2016). In addition, N₂(B^’3Σ_u⁻) and N₂(W³Δ_u) are substituted by N₂(B³Π_g) due to their short lifetime and immediately convert to N₂(B³Π_g) (Popov, 2008). Similarly, N₂(a^’1Σ_u⁻) is the group of N₂(a^’1Σ_u⁻), N₂(a¹Π_g), and N₂(w¹Δ_u) (Defilippo, 2013) and N₂(C³Π_u) is the group of N₂(C³Π_u), N₂(E³Σ_g⁺), and N₂(a^’’1Σ_g⁺). The electronically excited CH₄ is no longer included in this mechanism due to all excitation states of methane finally leading to dissociation (Fuss et al., 2010).

TABLE 2

TABLE 2. Particles included in the detailed kinetic mechanism.

2.2 Numerical method

For plasma kinetics modeling, the following Eqs 1–5 are solved. In energy conservation, Eq. 5, the temperature rising caused by Joule heating is considered by the penultimate term.

$\frac{\mathrm{d}\left[N_i\right]}{\mathrm{d}\mathit{t}}={\displaystyle \sum _{j=1}^{j_{\max }}{\mathit{Q}}_{ij}\left(t\right)},(1)$

$aA+bB\to cC+dD,(2)$

$R_j=k_j{\left[A\right]}^a{\left[B\right]}^b,(3)$

$Q_A=-aR,Q_B=-bR,Q_C=cR,Q_D=dR,(4)$

$\frac{N_{gas}}{\gamma -1}\frac{\mathrm{d}{T}_{gas}}{\mathrm{d}t}={\displaystyle \sum _{j=1}^{j_{\max }}\pm \delta \epsilon \cdot R_j+P_{elast}\cdot \left[N_e\right]}+Q_{src},(5)$

where [N_i] is the number density for specie i, Q_ij is the rate of production for specie i in reaction j, and k_j and R_j are the rate constant and the reaction rate for reaction j, respectively. δε is the heat release from enthalpy change, which is neglected in plasma kinetics.

The pressure and temperature in realistic ICEs vary with the movement of the piston. This physical compression/expansion process is modeled through source terms and inserted into the respective species and energy equations (Zhang et al., 2015). Assuming that the compression/expansion process is locally isentropic and adiabatic, the source term can be found in Appendix A. The evolution of mass fractions for specie k and temperature yields

$\frac{\mathrm{d}\rho {\mathit{Y}}_k}{\mathrm{d}\mathit{t}}=W_k{\omega }_k+S_{\rho }{\mathit{Y}}_k,k=\mathrm{1,2},\cdots ,N_s,(6)$

$\frac{\mathrm{d}\rho c_{p}T}{\mathrm{d}\mathit{t}}+{\displaystyle \sum _{k=1}^{N_s}\rho h_k}{\omega }_k=\frac{\mathrm{d}P}{\mathrm{d}\mathit{t}},(7)$

where Y_k, ω_k, and h_k are the mass fraction, chemical reaction rate, and specific enthalpy for specie k, respectively. S_ρ is the density change due to compression/expansion processes, ρ is the mixture density, c_p is the specific heat at constant pressure, and P is the pressure. The whole N_s+2 ordinary differential equations are computed by Chemkin-III.

In this article, the discharge frequency is 1 MHz lasting for 5 crank angle degree (CAD) (around 700 pulses) (Filimonova et al., 2020). The plasma-assisted combustion solver deals with both plasma kinetics and combustion kinetics simultaneously during each pulse duration, as shown in Figure 1. Within each discharge time step, the component concentration and temperature are calculated by plasma kinetics solver ZDPlasKin at first and then used in Chemkin solver for the combustion process. After that, all the parameters are returned to the plasma kinetics solver again. The whole process repeats until the end of discharge. Although the reduced field strength is 0 Td in the time gap between voltage pulses, both plasma kinetics and combustion kinetics are considered in the period. After a series of time-dependence tests, the time step size is restricted to 10⁻⁹ s, which are not shown for brevity.

FIGURE 1

FIGURE 1. Schematic diagram of the 0D plasma-assisted combustion/ignition process.

2.3 Model validation

The PAI kinetic model of CH₄/air mixture is validated by comparison with the results of time-dependent O atom concentration measured by two-photon absorption laser–induced fluorescence (TALIF) during single-pulse nanosecond discharge in air and CH₄/air mixtures (Uddi et al., 2009), as shown in Figure 2. Consistent with the experiment, the voltage of nanosecond pulse discharge is reduced to a square wave with a pulse duration of 25 ns. The initial temperature is 300 K, pressure of 60 Torr, and equivalence ratio of 1. Figure 2 shows a good agreement between simulation and experiment, especially the peak value after discharge and the attenuation process of O atoms for both cases, indicating that plasma chemical processes are well described by the present model.

FIGURE 2

FIGURE 2. Temporal evolution of O atom mole fraction in air and CH₄/air mixtures.

The cylinder pressure and temperature traces in pure compression/expansion without ignition and with ignition in ICEs are validated and compared with Chemkin-Pro in Figures 3A,B, respectively. The initial CH₄/air mixture is φ = 0.5 under a temperature of 300 K and pressure of 1 atm. The engine parameters are derived from experiments (Wang et al., 2019), where the bore is 105 mm, stroke 125 mm, connecting rod length is 210 mm, compression ratio is 16, and engine speed is 1200 r/min. For ignition the case, the initial temperature is 430 K and pressure of 1.2 atm. It is seen that the cylinder pressure, temperature, and piston compression/expansion cycles are well captured by the current model, which will be used in the following simulations.

FIGURE 3

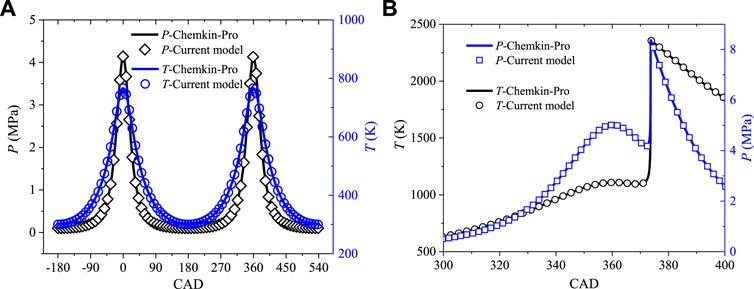
FIGURE 3. Cylinder pressure and temperature traces in pure compression/expansion processes without ignition (A) and with ignition (B) from the current model and Chemkin-Pro.

3 Initial conditions

Three cases are carried out to study the effect of nonequilibrium plasma on lean CH₄/air mixture under ICEs conditions, including fuel-lean and stoichiometric ones, as shown in Table 3. Here, the stoichiometric condition represents high load in comparison with the lean conditions (φ = 0.2, 0.5) of idle and/or economical cruising modes. Normally, a CH₄/air mixture with the equivalence ratio of 0.2 is too lean to be ignited, while a high voltage nanosecond pulsed discharge can be used to stabilize ultra-lean methane flames across a wide range of equivalence ratios (φ = 0.06–0.3) (Starikovskiy and Aleksandrov, 2013). All cases start with the thermal dynamic condition of 300 K and 1 atm at the bottom dead center (BDC), namely 180 CAD. Also, the repetitive rate of discharge voltage is 1 MHz, and the pulse duration is 25 ns (Filimonova et al., 2018). Within one pulse, the reduced electric field is fixed at 100 Td (Filimonova et al., 2018), while in the pulse interval, no electric field is imposed (E/N = 0 Td).

TABLE 3

TABLE 3. Initial parameters of simulation cases.

4 Results and discussion

4.1 Electron energy distribution function and energy loss fraction

EEDF presents the proportion of electrons in different energy levels to the total number of electrons. Figure 4 shows the normalized EEDF for lean CH₄/air mixture (φ = 0.5) computed by Boltzmann solver BOLSIG+ (Hagelaar and Pitchford, 2005) under various E/N. It is seen that energy deposited channels vary with a series of E/N. The electron temperature is defined as 2/3 times of mean electron energy. With reduced electric field increasing, the proportion of electrons with higher energies increases, resulting in the shift of energy distribution towards the right. Thus, electron temperature increases with the increment of E/N, leading to the energy deposition direction change accordingly.

FIGURE 4

FIGURE 4. Normalized EEDF with electron energy in the lean CH₄/air mixture.

Figure 5 shows the electron energy loss fractions as a function of E/N in a lean CH₄/air mixture. It is found that at lower E/N (<8 Td), most of the energy is used to excite the vibrationally excited states of CH₄ and O₂. N₂(vib) accounts for a major fraction of all excited states for E/N between 10 Td and 100 Td. As E/N increases, the discharge energy is deposited into the excitation and dissociation of N₂, and O₂ grows and decreases at a higher electric field. When E/N is close to 10³ Td, most of the electron energy is spent on electron impact ionization. Under the condition of moderate E/N marked by the gray region, vibrationally and electronically excited N₂ are of great significance, and, thus, they are included in the current plasma mechanism. Furthermore, the quenching reactions of N₂ electronically excited states through N₂^* + O₂ => N₂ + 2O are also included to consider fast gas heating process (Popov, 2001).

FIGURE 5

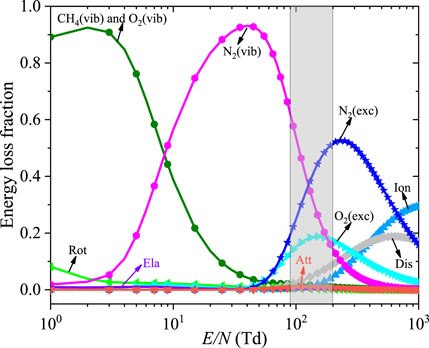
FIGURE 5. Evolution of energy loss fractions with E/N. Rot: rotational excited states of O₂ and N₂; Att: electron attachment reactions of CH₄ and O₂; Ela, Dis, and Ion represent the elastic collision, dissociation, and ionization in CH₄/air plasma, respectively.

4.2 The comparison between nanosecond repetitively pulsed discharge and thermal ignition

In order to compare the combustion-assisted effect of nonequilibrium plasma from NRPD (case 2) and equilibrium plasma from thermal ignition (case 4), which can be simplified to a constant high-temperature heat source in Eq. 7. In addition, all the initial thermodynamic conditions, total discharge energy, discharge timing, and discharge duration are identical. The discharge power density is calculated as follows (Mao et al., 2019b):

$p=j\times E=e{n}_e{v}_{dr}\times E,(8)$

where e is the elementary charge, n_e is the electron number density, and v_dr is the drift velocity.

Figure 6 shows the cylinder pressure and temperature profiles with motor run, NRPD, and thermal ignition (TI). It is seen that NRPD can achieve successful ignition, and both temperature and pressure peaks are near the top dead center (TDC), while TI with only thermal effect is considered unable to ignite the mixture successfully. The maximum temperature of TI is only 124 K higher than that of motor run at TDC. This phenomenon is consistent with previous experiments in ICEs (Cathey et al., 2007; Shiraishi et al., 2009). It implies that the kinetic effect of NRPD plays a more important role in the ignition process.

FIGURE 6

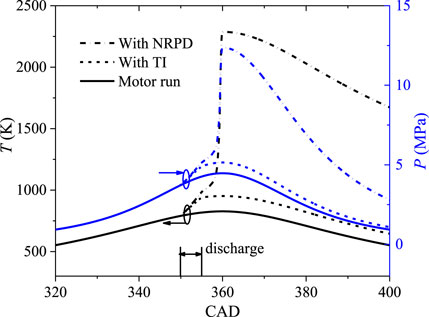
FIGURE 6. Cylinder pressure and temperature profiles under motor run, NRPD, and equilibrium discharge.

4.3 Ignition process under different equivalence ratios

Figure 7 presents the time evolution of partial active species in the first discharge pulse. The initial condition of case 2 is employed. Among excited states, N₂(vib1) dominates during the entire discharge process since more energy is deposited into the N₂ vibrational excitation channel, as shown in Figure 5. N₂(vib1) and O₂(vib1) accumulate gradually during discharge due to their longer lifetimes. N₂(A³Σ_u⁺), O, and H increase at first and then decrease after the dashed vertical line. During the first pulse, the temperature increases by about 0.1 K and the temperature rising rate is around 10⁵ K/s. The fast-heating effect is relatively weakened compared to Popov (2001). This can be attributed to the lower concentration of N₂ electrically excited states caused by a small proportion of discharge energy deposited into N₂^* and lower current density.

FIGURE 7

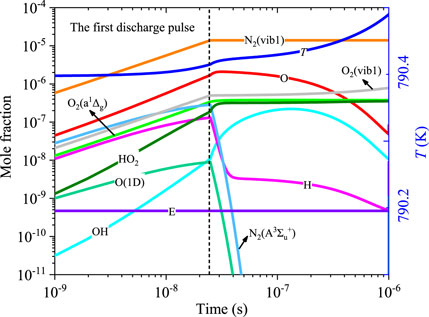
FIGURE 7. Temporal evolutions of N₂(vib1), O₂(vib1), O₂(a¹Δ_g), O(1D), N₂(A³Σ_u⁺), O, H, HO₂, E, and OH for φ = 0.5 in the first discharge pulse.

It is well recognized that one of the advantages of nonequilibrium plasma is that it can produce high-energy electrons, excited-state species, and active radicals (Ju et al., 2016), (Starikovskiy and Aleksandrov, 2013). Here, we further examine the performance of NRPD at different φ of CH₄/air mixtures under typical HCCI engine conditions with detailed plasma kinetics and combustion kinetics. The initial setups of cases 1–3 are shown in Table 3.

Figure 8 shows temperature and total heat release rate as a function of CAD for cases 1–3. The corresponding specific discharge energy inputs for the three cases are p = 1.9 J/cm³. In the current cases, the electron densities are specified as 1.61 × 10¹¹ cm⁻³, 1.6 × 10¹¹ cm⁻³ and 1.58 × 10¹¹ cm⁻³, respectively, for φ = 0.2, φ = 0.5 and φ = 1.0 and kept as constant during each simulation. The current lean and ultra-lean mixtures with φ = 0.5 and 0.2 cannot be ignited upon compression without discharge. It is found that THRR goes up and down periodically from 350 CAD to 355 CAD due to cycled discharge pulses, and the mixture is not ignited immediately at the end of discharge since the global temperature is rather low. As the piston moves up, the temperature of case 2 exceeds the others at about 356.8 CAD, and the ignition occurs first. The ignition timing is defined as when the peak of OH concentration is reached. For cases 1 and 2, heat is released dramatically around TDC, while for the super lean case 3, the ignition is prolonged, and only a small portion of heat is released in the whole cycle. It is expected that the slow heat release rate will lead to a lower thermal efficiency (Filimonova et al., 2020) in real engines. In contrast, the heat release peak is much higher as φ increases from lean to stoichiometry condition in Figure 7.

FIGURE 8

FIGURE 8. Evolution of temperature and HRR with a crank angle degree for cases 1–3.

Figure 9 shows the HRR of the highest three exothermic reactions (R116, R119, and R168) from the end of discharge to 357.5 CAD. It is seen that the HRR of the three reactions plays a critical role in heat release at a low temperature, and the total heat release rate increases dramatically after an initial reduction because of the completion of discharge. The higher HRR of the three reactions in case 2 leads to the temperature rising, directly exceeding that in case 3 at 356.8 CAD (T = 1030 K). However, care should be taken that the pressure, temperature, and species quantities play important roles in reaction evolution such that the leading reactions just after discharge can be totally different when the thermal dynamic states change dramatically.

FIGURE 9

FIGURE 9. HRR of main exothermic reactions and temperature from 355 to 357.5 CAD for cases 2 and 3.

PFA can be used to reveal the production/consumption contribution rate of other species to a certain species. The detailed PFA of excited species and radicals integrated from initial time to the end of discharge for case 2 is shown in Figure 10. It is found that over 95% of N₂(vib1) is produced by electron impact with nitrogen molecules and the relaxation of higher vibrational level N₂(vib2) (vibrational–vibrational, VV), while it is almost consumed by relaxation reactions through vibrational–translational (VT) exchange in Figure 10A. Figure 10B shows that about 96.3% of O₂(vib1) is produced during vibrationally excited species N₂(v) quenching processes, but most of them will continue to be consumed by VT relaxation reactions. The results indicate that N₂(vib1) and O₂(vib1) with lower vibrational levels have a minor kinetic effect on fuel decomposition through chemical reaction pathways.

FIGURE 10

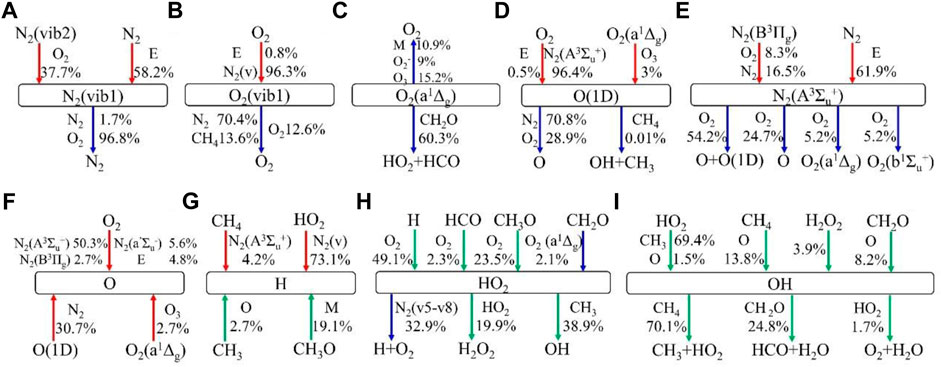
FIGURE 10. Path fluxes of production and consumption of (A) N₂(vib1), (B) O₂(vib1), (C) O₂(a¹Δ_g), (D) O(1D), (E) N₂(A³Σ_u⁺), (F) O, (G) H, (H) HO_2, and (I) OH at the end of discharge for case 2. The red lines are plasma excitation reactions, blue lines are plasma quenching reactions, and green lines are combustion reactions. For one subfigure, all percentages do not sum to 1 exactly due to some minor proportions in other reactions.

Figure 10C shows that 60.3% of O₂(a¹Δ_g) is consumed through reaction O₂(a¹Δ_g) + CH₂O => HO₂ + HCO, prompting CH₂O decomposing to HCO. In Figure 10E, most of N₂(A³Σ_u⁺) is generated from higher excited level N₂(B³Π_g) and electron impact. Abundant N₂(A³Σ_u⁺) is consumed to promote O, O(1D), and O₂ excited states.

Different from the finding of Mao et al. (2019b), where O(1D) was mainly produced by electron impact with O₂, the existence of N₂(A³Σ_u⁺) leads to O₂ dissociation, contributing to the most excitation of O(1D), as shown in Figure 10D. More than 99% of O(1D) is consumed to produce O by quenching channels of O(1D) + N₂ => O + N₂ and O(1D) + O₂ => O + O₂, while little O(1D) reacts with CH₄ to initiate chain branching reactions (Popov, 2008). Figure 10F shows that electronically excited states of N₂ and O(1D) contribute 58.4% and 30.7% of O production, respectively. Abundant O will accelerate the chain branching reaction O + CH₄ = CH₃ + OH and promote radical production (Mao et al., 2019a). In Figure 9G, higher vibrational levels of N₂, such as N₂(vib5-8), show a significant contribution to H formation by dissociating HO₂, leading to the cancellation of chain termination, which plays a crucial role in the radical pool. The existence of N₂(a^’1Σ_u⁻) contributes 4.2% of H via dissociating CH₄. It is well recognized that at low temperature, accumulated HO₂ not only dominates H but contributes H₂O₂ and OH production, as shown in Figures 10H,I. Abundant O, H, and OH radicals produced during discharge, directly and indirectly, are in favor of CH₄ consumption (Mao et al., 2016).

We further examine the fuel and oxidizer intermediates conversion to explain the earliest ignition event in case 2. Figure 11 shows the evolution of O, H, OH, CH₃, HO_2, and H₂O₂ mole fractions for cases 1–3 from the last third discharge pulse to 358 CAD. It can be found that at the end of discharge, O and OH concentrations of case 3 are larger than those of the other cases in Figures 11B,C, indicating the significant kinetic effect of NRPD in a leaner mixture. In contrast, CH₃ and HO₂ accumulation in case 2 are the highest in Figures 11D,E.

FIGURE 11

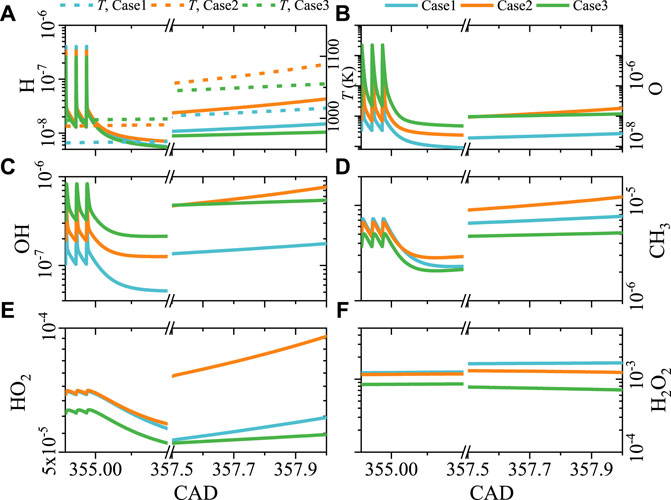
FIGURE 11. Evolution of (A) H, (B) O, (C) OH, (D) CH₃, (E) HO₂, and (F) H₂O₂ mole fractions after discharge.

With the piston moving up to TDC, the temperature of case 2 exceeds the other cases at 356.8 CAD, as shown in Figure 8, and the concentrations of radicals O and OH in case 2 also overwhelms those in case 3 at about 357.5 CAD in Figures 11B,C. The higher O and OH concentrations in case 2 will promote CH₄ oxidation. Figure 12 shows the rate of production (ROP) in terms of O and OH at this moment. ROP is defined as the species O production rate in each reaction related to O. As temperature increases, the oxygen atom from H + O₂ = O + OH, and OH generated from H₂O₂ decomposition via R85 H₂O₂(+M) = 2OH(+M) as well as HO₂ and CH₃ oxidation through R119 HO₂ + CH₃ = OH + CH₃O dominant.

FIGURE 12

FIGURE 12. Normalized ROP of (A) O and (B) OH for case 2 at 357.5 CAD.

It can also be seen that at 357.5 CAD, concentrations of CH₃, HO_2, and H₂O₂ for case 2 in Figures 11D–F as well as temperature are larger than those in cases 1 and 3, leading to the rapid increase of OH and O and then a quick consumption of methane. Finally, the higher temperature and radical concentrations in case 2 lead to the advanced ignition before TDC.

5 Parameter sensitivity

In HCCI engines, ultra-lean premixed combustion suffers from combustion instability and even misfires. Therefore, the influences of different parameters such as E/N, current density, φ, and discharge timing (t_dis) on the performance of combustion characteristics are investigated to clarify how to extend the flammability and improve flame stability with the method of plasma in such engines.

The variety of E/N has shown the resulted different electron energy deposited channels in Figure 5. In this section, a range of E/N from 90 to 150 Td is carried out with the other identical initial conditions in case 2. Figure 13 shows ignition timing and maximum temperature (T_max) under different E/N. The ignition timing is defined as when the maximum of OH is achieved. As expected, the ignition timing advances with E/N increasing. For E/N < 100 Td, the ignition takes place before TDC, while for E/N > 130 Td, the mixture is ignited before the end of discharge. Correspondingly, T_max increases with E/N increasing due to the increased input energy, while too high a temperature may result in higher NOx emission. The later ignition timing at lower E/N will decrease heat efficiency. For E/N of 90 Td, when the electron density is increased to 2.0 × 10¹¹ cm⁻³, represented by the red star in Figure 13, the ignition timing is shortened by around 15 CAD at 360 CAD compared with ignition timing of 375 CAD when the density is 1.6 × 10¹¹ cm⁻³. The results imply that an E/N with a suitable electron density is necessary for controlling ignition timing.

FIGURE 13

FIGURE 13. Ignition timing and maximum combustion temperature under different E/N.

The current density effect is examined in Figure 14 with the same initial condition of case 2 except for initial electron density varying in the range of 0.22–0.48 A/cm². Similar to Figure 13, the combustion timing and T_max increase with the increase in current density since a larger current density involves more radicals and more deposited discharge energy into the treated mixture (Aleksandrov et al., 2010). A low current density of 0.22 A/cm² retards the ignition timing to around 375 CAD. Larger E/N is used to shorten the ignition delay time, as marked by the red star where E/N increased from 100 Td to 112 Td. The conclusion is consistent with previous findings that increasing discharge voltage and energy can lead to successful ignition by nonequilibrium plasma for severe conditions (Shiraishi et al., 2009; Schenk et al., 2015).

FIGURE 14

FIGURE 14. Ignition timing and maximum combustion temperature as a function of current density.

Figure 15 depicts the combustion performance dependence of φ under the same condition as case 2. It is seen that the ignition timing varies monotonically as φ increases with the shortest ignition delay residing in φ = 0.4. The underlying reason is discussed in Section 4.3. For φ = 0.4–0.9, the combustion phase is slightly delayed with φ increasing due to the lower radical concentrations such as O and OH after discharge. At ultra-lean such as φ = 0.2, the ignition timing is postponed to the expansion stroke and increasing electron density from 1.6 × 10¹¹ to 2.8 × 10¹¹ cm⁻³ lead to the combustion phase close to TDC. Furthermore, increasing the E/N from 100 to 112 Td at φ = 0.9 can also make the combustion phase in advance.

FIGURE 15

FIGURE 15. Ignition timing as a function of φ.

To choose the optimal mode of engine operation, a series of moments of discharge initiation is performed to investigate the dependence of discharge timing on ignition timing in Figure 16 under the same initial conditions as case 2, except for discharge timing (t_dis). It can be found that the evolution of the combustion phase with discharge timing is nonmonotonic. When the discharge is initiated at 340 CAD, the ignition occurs earliest. However, the combustion phase far away from TDC can lead to lower energy efficiency. According to Figure 14, the ignition timing can be adjusted by changing E/N. Here, for the case with discharge timing of 340 CAD, a reduced E/N from 100 to 96 Td can be used to postpone ignition and retard the combustion to TDC, as marked by the red star symbol in Figure 16. The reduced E/N, meaning lower input energy, will reduce minimum ignition energy, maximum combustion temperature and further NOx emission. Thus, the matching between discharge timing and E/N is desired.

FIGURE 16

FIGURE 16. Ignition timing as a function of discharge timing.

6 Conclusion

The nanosecond pulse discharge plasma-assisted ignition of CH₄/air is simulated by coupling detailed plasma kinetics and combustion kinetics under conditions related to HCCI engines, taking into account the volume change due to piston movement and compared with equilibrium heating. The calculation includes stoichiometric, lean, and super-lean fuel conditions. The rate of production and path flux analysis of key radicals are analyzed to show the plasma enhancement effect on ignition. Finally, the influence of discharge parameters E/N, current density, φ, and discharge timing on combustion characteristics are studied. The main conclusions are as follows:

1) For the lean CH₄/air mixture under HCCI engine-related conditions, the comparison between NRPD and equilibrium discharge strategies suggests that under the same input energy, NRPD enables the ignition during the expansion stroke, while equilibrium discharge only leads to a certain temperature rising without successful ignition. It suggests that the NRPD offers an efficient probability for chemical selectivity.

2) With plasma-assisted, the leaner mixture is favorable for O and OH production. N₂ electronically excited states not only contribute O and H atoms but also excited species such as O(1D), while most of the plasma generated radical O(1D) is consumed in the de-excitation reaction with N₂ and O₂ molecules and does not react for CH₄ oxidation. Although N₂(vib1) and O₂(vib1) are almost quenched during VT relaxation, the higher vibrationally excited levels N₂(vib5-8) play a more important role in HO₂ dissociation, ceasing chain-termination reactions.

3) With the compression/expansion effect involved, the ignition delay time for case 2 (φ = 0.5) is the shortest compared with case 3 (φ = 0.2) and case 1 (φ = 1.0) under the same discharge energy. The reason is that in case 2, the reactions involving HO₂ + CH₃ = OH + CH₃O and HCO + O₂ = HO₂ + CO dominate heat release after discharge such that the global temperature of case 2 exceeds that of case 3. As the piston moves up approaching TDC, the higher amounts of CH₃, HO_2, and H₂O₂ for case 2 and temperature are larger, leading to a rapid increase of OH and O and then a quick consumption of methane. Finally, the higher temperature and radical concentrations in case 2 lead to the earliest hot ignition.

4) The discharge parameters E/N and current density can be modified for the improvement of the maximum combustion temperature and ignition timing for higher efficiency. The coupling of discharge timing and E/N can achieve lower pollutant emission as well.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FZ and JZ contributed to the conception and design of the study. YB conducted the simulation and wrote the first draft of the manuscript. FZ and SZ contributed to manuscript revision. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51876139) and Special funds for the construction of innovative provinces in Hunan (Grant No. 2019RS 2028).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aleksandrov, N. L., Kindysheva, S. V., Nudnova, M. M., and Starikovskiy, A. Y. (2010). Mechanism of ultra-fast heating in a non-equilibrium weakly ionized air discharge plasma in high electric fields. J. Phys. D. Appl. Phys. 43, 255201. doi:10.1088/0022-3727/43/25/255201

CrossRef Full Text | Google Scholar

Bansal, G., Mascarenhas, A., and Chen, J. H. (2015). Direct numerical simulations of autoignition in stratified dimethyl-ether (DME)/air turbulent mixtures. Combust. Flame 162, 688–702. doi:10.1016/j.combustflame.2014.08.021

CrossRef Full Text | Google Scholar

Bellenoue, M., Labuda, S., Ruttun, B., and Sotton, J. (2007). Spark plug and corona abilities to ignite stoichiometric and lean methane/air mixture. Combust. Sci. Technol. 179, 477–496. doi:10.1080/00102200600637584

CrossRef Full Text | Google Scholar

Cathey, C., Cain, J., Hai, W., Gundersen, M. A., Carter, C., Ryan, M., et al. (2008). OH production by transient plasma and mechanism of flame ignition and propagation in quiescent methane–air mixtures. Combust. Flame 154, 715–727. doi:10.1016/j.combustflame.2008.03.025

CrossRef Full Text | Google Scholar

Cathey, C. D., Tang, T., Shiraishi, T., Urushihara, T., Kuthi, A., and Gundersen, M. A. (2007). Nanosecond plasma ignition for improved performance of an internal combustion engine. IEEE Trans. Plasma Sci. 35, 1664–1668. doi:10.1109/tps.2007.907901

CrossRef Full Text | Google Scholar

Cho, H. M., and He, B. Q. (2007). Spark ignition natural gas engines—a review. Energy Convers. Manag. 48, 608–618. doi:10.1016/j.enconman.2006.05.023

CrossRef Full Text | Google Scholar

Defilippo, A. C., and Chen, J. Y. (2016). Modeling plasma-assisted methane–air ignition using pre-calculated electron impact reaction rates. Combust. Flame 172, 38–48. doi:10.1016/j.combustflame.2016.07.005

CrossRef Full Text | Google Scholar

Defilippo, A. C. (2013). Microwave-assisted ignition for improved internal combustion engine efficiency. Berkeley: Ph.D. thesis, University of California.

Google Scholar

Filimonova, E. A., Bocharov, A. N., and Bityurin, V. A. (2018). Influence of a non-equilibrium discharge impact on the low temperature combustion stage in the HCCI engine. Fuel 228, 309–322. doi:10.1016/j.fuel.2018.04.124

CrossRef Full Text | Google Scholar

Filimonova, E. A., Dobrovolskaya, A. S., Bocharov, A. N., Bityurin, V. A., and Naidis, G. V. (2020). Formation of combustion wave in lean propane-air mixture with a non-uniform chemical reactivity initiated by nanosecond streamer discharges in the HCCI engine. Combust. Flame 215, 401–416. doi:10.1016/j.combustflame.2020.01.029

CrossRef Full Text | Google Scholar

Fuss, M. C., Muñoz, A., Oller, J. C., Blanco, F., Hubin-Franskin, M. J., Almeida, D., et al. (2010). Electron–methane interaction model for the energy range 0.1–10000 eV. Chem. Phys. Lett. 486, 110–115. doi:10.1016/j.cplett.2009.12.097

CrossRef Full Text | Google Scholar

Hagelaar, G. J. M., and Pitchford, L. C. (2005). Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 14, 722–733. doi:10.1088/0963-0252/14/4/011

CrossRef Full Text | Google Scholar

Janev, R. K., and Reiter, D. (2002). Collision processes of CH_y and CH_y⁺ hydrocarbons with plasma electrons and protons. Phys. Plasmas 9, 4071–4081. doi:10.1063/1.1500735

CrossRef Full Text | Google Scholar

Ju, Y., Lefkowitz, J. K., Reuter, C. B., Won, S. H., Yang, X., Yang, S., et al. (2016). Plasma assisted low temperature combustion. Plasma Chem. Plasma process. 36, 85–105. doi:10.1007/s11090-015-9657-2

CrossRef Full Text | Google Scholar

Ju, Y., Sun, W., Burke, M. P., Gou, X., and Chen, Z. (2011). Multi-timescale modeling of ignition and flame regimes of n-heptane-air mixtures near spark assisted homogeneous charge compression ignition conditions. Proc. Combust. Inst. 33, 1245–1251. doi:10.1016/j.proci.2010.06.110

CrossRef Full Text | Google Scholar

Ju, Y., and Sun, W. (2015). Plasma assisted combustion: Dynamics and chemistry. Prog. Energy Combust. Sci. 48, 21–83. doi:10.1016/j.pecs.2014.12.002

CrossRef Full Text | Google Scholar

Ju, Y., and Sun, W. (2015). Plasma assisted combustion: Progress, challenges, and opportunities. Combust. Flame 162, 529–532. doi:10.1016/j.combustflame.2015.01.017

CrossRef Full Text | Google Scholar

Kee, R. J., Rupley, F. M., Meeks, E., and Miller, J. A. (1996). Chemkin-III: a Fortran chemical kinetics package for the analysis of gas-phase chemical and plasma kinetics. SAND 96-8216, UC405.

Google Scholar

Konstantinovskii, R. S., Shibkov, V. M., and Shibkova, L. V. (2005). Effect of a gas discharge on the ignition in the hydrogen-oxygen system. Kinet. Catal. 46, 775–788. doi:10.1007/s10975-005-0136-2

CrossRef Full Text | Google Scholar

Kosarev, I. N., Aleksandrov, N. L., Kindysheva, S. V., Starikovskaia, S. M., and Starikovskii, A. Y. (2008). Kinetics of ignition of saturated hydrocarbons by nonequilibrium plasma: CH₄-containing mixtures. Combust. Flame 154, 569–586. doi:10.1016/j.combustflame.2008.03.007

CrossRef Full Text | Google Scholar

Lefkowitz, J. K., Peng, G., Rousso, A., and Ju, Y. (2015). Species and temperature measurements of methane oxidation in a nanosecond repetitively pulsed discharge. Phil. Trans. R. Soc. A 373, 20140333. doi:10.1098/rsta.2014.0333

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, X., and Chen, Q. (2018). Effects of vibrational excitation on nanosecond discharge enhanced methane–air ignition. AIAA J. 56, 4312–4320. doi:10.2514/1.j057304

CrossRef Full Text | Google Scholar

Mao, X., Chen, Q., Rousso, A. C., Chen, T. Y., and Ju, Y. (2019). Effects of controlled non-equilibrium excitation on H₂/O₂/He ignition using a hybrid repetitive nanosecond and DC discharge. Combust. Flame 206, 522–535. doi:10.1016/j.combustflame.2019.05.027

CrossRef Full Text | Google Scholar

Mao, X., Li, G., Chen, Q., and Zhao, Y. (2016). Kinetic effects of nanosecond discharge on ignition delay time. Chin. J. Chem. Eng. 24, 1719–1727. doi:10.1016/j.cjche.2016.05.014

CrossRef Full Text | Google Scholar

Mao, X., Rousso, A., Chen, Q., and Ju, Y. (2019). Numerical modeling of ignition enhancement of CH₄/O₂/He mixtures using a hybrid repetitive nanosecond and DC discharge. Proc. Combust. Inst. 37, 5545–5552. doi:10.1016/j.proci.2018.05.106

CrossRef Full Text | Google Scholar

Mao, X., Zhong, H., Zhang, T., Starikovskiy, A., and Ju, Y. (2022). Modeling of the effects of non-equilibrium excitation and electrode geometry on H₂/air ignition in a nanosecond plasma discharge. Combust. Flame 240, 112046. doi:10.1016/j.combustflame.2022.112046

CrossRef Full Text | Google Scholar

Pancheshnyi, S., Eismann, B., Hagelaar, G. J. M., and Pitchford, L. C. (2008). Toulouse, France: University of Toulouse, LAPLACE, CNRS-UPS-INP. http://www.zdplaskin.laplace.univ-tlse.fr.Computer code ZDPlasKin.

Google Scholar

Persson, H., Hultqvist, A., Johansson, B., and Remon, A., Investigation of the early flame development in spark assisted HCCI combustion using high speed chemiluminescence imaging, SAE Technical Paper Series, Paper No. 2007-01- 0212.

Google Scholar

Phelps database. www.lxcat.net (Accessed Jul 1, 2020).

Popov, N. A. (2008). Effect of a pulsed high-current discharge on hydrogen-air mixtures. Plasma Phys. Rep. 34, 376–391. doi:10.1134/s1063780x08050048

CrossRef Full Text | Google Scholar

Popov, N. A. (2011). Effect of singlet oxygen O₂(a¹Δ_g) molecules produced in a gas discharge plasma on the ignition of hydrogen-oxygen mixtures. Plasma Sources Sci. Technol. 21, 045002. doi:10.1088/0963-0252/20/4/045002

CrossRef Full Text | Google Scholar

Popov, N. A. (2001). Investigation of the mechanism for rapid heating of nitrogen and air in gas discharges. Plasma Phys. Rep. 27, 886–896. doi:10.1134/1.1409722

CrossRef Full Text | Google Scholar

Saxena, S., and Bedoya, I. D. (2013). Fundamental phenomena affecting low temperature combustion and HCCI engines, high load limits and strategies for extending these limits. Prog. Energy Combust. Sci. 39, 457–488. doi:10.1016/j.pecs.2013.05.002

CrossRef Full Text | Google Scholar

Schenk, A., Rixecker, D. G., and Bohne, S. (2015). Results from Gasoline and CNG Engine Tests with the Corona Ignition System EcoFlash. Paper No. W4A.4, 27–30. Argonne, IL: Third Laser Ignition Conference.

PubMed Abstract | Google Scholar

Schulz, J., and Menon, S. (2009). in Large-Eddy Simulation of Pulsed Arc Discharges in Supersonic Flow, 40th AIAA Plasmadynamics & Lasers Conference, AIAA 2009–4072.

Shi, F., Wang, D., and Ren, C. (2008). Simulations of atmospheric pressure discharge in a high-voltage nanosecond pulse using the particle-in-cell Monte Carlo collision model in noble gases. Phys. Plasmas 15, 063503. doi:10.1063/1.2927437

CrossRef Full Text | Google Scholar

Shiraishi, T., Urushihara, T., and Gundersen, M. (2009). A trial of ignition innovation of gasoline engine by nanosecond pulsed low temperature plasma ignition. J. Phys. D. Appl. Phys. 42, 135208. doi:10.1088/0022-3727/42/13/135208

CrossRef Full Text | Google Scholar

Shiraishi, T., Kakuho, A., Urushihara, T., Cathey, C., Tang, T., Gundersen, M., et al. (2009). A study of volumetric ignition using high-speed plasma for improving lean combustion performance in internal combustion engines. SAE Int. J. Engines 1, 399–408. doi:10.4271/2008-01-0466

CrossRef Full Text | Google Scholar

SIGLO database. www.lxcat.net (Accessed Jul 1, 2020).

Singleton, D., Pendleton, S. J., and Gundersen, M. A. (2010). The role of non-thermal transient plasma for enhanced flame ignition in C₂H₄–air. J. Phys. D. Appl. Phys. 44, 022001. doi:10.1088/0022-3727/44/2/022001

CrossRef Full Text | Google Scholar

Smith, G. P., Golden, D. M., Frenklach, M., Moriarty, N. W., Eiteneer, B., Goldenberg, M., et al. (2021). http://www.me.berkeley.edu/gri_mech/ (Accessed June 01, 2021).

Starikovskiy, A., and Aleksandrov, N. (2013). Plasma-assisted ignition and combustion. Prog. Energy Combust. Sci. 39, 61–110. doi:10.1016/j.pecs.2012.05.003

CrossRef Full Text | Google Scholar

Stepanyan, S. A., Boumehdi, M. A., Vanhove, G., and Starikovskaia, S. M. (2013). “Time-resolved electric field measurements in nanosecond surface dielectric discharge. Comparison of different polarities. Ignition of combustible mixtures by surface discharge in a rapid compression machine,” in AIAA Aerospace Sciences Meeting Including the New Horizons Forum & Aerospace Exposition, AIAA 2013–1053.

CrossRef Full Text | Google Scholar

Tropina, A. A., Kuzmenko, A. P., Marasov, S. V., and Vilchinsky, D. V. (2014). Ignition system based on the nanosecond pulsed discharge. IEEE Trans. Plasma Sci. 42, 3881–3885. doi:10.1109/tps.2014.2339654

CrossRef Full Text | Google Scholar

Uddi, M., Jiang, N., Mintusov, E., Adamovich, I. V., and Lempert, W. R. (2009). Atomic oxygen measurements in air and air/fuel nanosecond pulse discharges by two photon laser induced fluorescence. Proc. Combust. Inst. 32, 929–936. doi:10.1016/j.proci.2008.06.049

CrossRef Full Text | Google Scholar

Wang, Y., Wang, H., and Yao, M. (2019). Effects of low-temperature reforming products of PRF50 on combustion and emission characteristics in an HCCI engine. Appl. Therm. Eng. 151, 451–458. doi:10.1016/j.applthermaleng.2019.01.088

CrossRef Full Text | Google Scholar

Yang, S., Xiang, G., Yang, V., Sun, W., Nagaraja, S., Lefkowitz, J. K., et al. (2016). Nanosecond pulsed plasma activated C₂H₄/O₂/Ar mixtures in a flow reactor. J. Propuls. Power 32, 1240–1252. doi:10.2514/1.b36060

CrossRef Full Text | Google Scholar

Zhang, F., Yu, R., and Bai, X. (2015). Direct numerical simulation of PRF70/air partially premixed combustion under IC engine conditions. Proc. Combust. Inst. 35, 2975–2982. doi:10.1016/j.proci.2014.09.004

CrossRef Full Text | Google Scholar

Zhu, J., Gao, J., Ehn, A., Alden, M., Larsson, A., Kusano, Y., et al. (2017). Spatiotemporally resolved characteristics of a gliding arc discharge in a turbulent air flow at atmospheric pressure. Phys. Plasmas 24, 013514. doi:10.1063/1.4974266

CrossRef Full Text | Google Scholar

Zhu, Y., Wu, Y., Li, Y., and Jia, M. (2013). Modelling of plasma aerodynamic actuation driven by nanosecond SDBD discharge. J. Phys. D. Appl. Phys. 46, 355205. doi:10.1088/0022-3727/46/35/355205

CrossRef Full Text | Google Scholar

Appendix A

To obtain the temporal evolution of temperature and pressure during compression and expansion strokes without combustion, the energy conservation equation is simplified to Eq. A9 in a 0D model along with state Eq. A10:

$\rho c_p\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}=\frac{\mathrm{d}P}{\mathrm{d}\mathit{t}},(\mathrm{A9})$

$P=\rho R_{g}T.(\mathrm{A10})$

Eq. A10 can be rearranged as follows:

$\frac{\mathrm{d}P}{\mathrm{d}\mathit{t}}=\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}}{R}_{g}T+\rho R_g\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}.(\mathrm{A11})$

Combining Eqs. A9 and A11, the time derivative of temperature can be expressed as follows:

$\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}=\frac{R_{g}T}{\rho c_p-\rho R_g}\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}},(\mathrm{A12})$

where dρ/dt is associated with piston motion. In order to mimic the pressure variation resulting from the compression/expansion process, a mass (density) source term is inserted into the continuity equation as follows under the assumption of a homogenous mixture.

$\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}}=S_{\rho }=-\frac{{\rho }_0{V}_0}{V^2}\frac{\mathrm{d}V}{\mathrm{d}\mathit{t}},(\mathrm{A13})$

$\frac{\mathrm{d}V}{\mathrm{d}\mathit{t}}=\frac{\mathrm{d}}{\mathrm{d}\mathit{t}}(V_c+X\frac{\pi D^2}{4})=\frac{\pi D^2}{4}\frac{\mathrm{d}X}{\mathrm{d}\mathit{t}},(\mathrm{A14})$

where V and X are the volume of the engine cylinder and position of the piston, respectively, as a function of engine parameters. Subscript 0 denotes the initial field.

$\frac{\mathrm{d}X}{\mathrm{d}\mathit{t}}=R\omega \sin \theta +R^2\omega \sin \theta \cos \theta \frac{1}{\sqrt{L_{rod}^2-{(R\sin \theta )}^2}},(\mathrm{A15})$

where $\omega =2\pi \times \text{rpm}$, $\theta ={\theta }_0+\omega t$, R is the radius of crank offset, L_rod is the connecting rod length, and rpm is the engine speed.

To calculate the combustion process during the compression/expansion strokes, chemical source terms should be added to equations Eqs A9 and A11 which can be rearranged to yield the following:

$\frac{\mathrm{d}\rho c_{p}T}{\mathrm{d}\mathit{t}}=c_{p}T\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}}+\rho c_p\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}=\frac{\mathrm{d}P}{\mathrm{d}\mathit{t}}-{\displaystyle \sum _{k=1}^{N_s}\rho h_k}{\omega }_k,(\mathrm{A16})$

$\frac{\mathrm{d}P}{\mathrm{d}\mathit{t}}=R_{g}T\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}}+\rho R_g\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}+\rho T\frac{\mathrm{d}{R}_g}{\mathrm{d}\mathit{t}},(\mathrm{A17})$

where dρ/dt is the same as Appendix A.

From the aforementioned two equations, the new energy equation is obtained as follows:

$\frac{\mathrm{d}T}{\mathrm{d}\mathit{t}}=\frac{1}{\rho c_p-\rho R_g}\left[(R_{g}T-c_{p}T)\frac{\mathrm{d}\rho }{\mathrm{d}\mathit{t}}+\rho \frac{\mathrm{d}{R}_g}{\mathrm{d}\mathit{t}}T-{\displaystyle \sum _{k=1}^{N_s}\rho h_k}{\omega }_k\right],(\mathrm{A18})$

where MW_k and Y_k are molar mass and mass fraction of specie k, respectively, and dR_g/dt is calculated as follows:

$\frac{\mathrm{d}{R}_g}{\mathrm{d}\mathit{t}}=R\frac{\mathrm{d}}{\mathrm{d}\mathit{t}}\left(\frac{1}{M{W}_{mix}}\right)=R{\displaystyle \sum _{k=1}^{N_s}\frac{1}{M{W}_k}\frac{\mathrm{d}{Y}_k}{\mathrm{d}\mathit{t}}}.(\mathrm{A19})$