Zintl Phase Compounds Mg3Sb2−xBix (x = 0, 1, and 2) Monolayers: Electronic, Phonon and Thermoelectric Properties From ab Initio Calculations

The Mg₃Sb_2−xBi_x family has emerged as the potential candidates for thermoelectric applications due to their ultra-low lattice thermal conductivity (${\kappa }_L$) at room temperature (RT) and structural complexity. Here, using ab initio calculations of the electron-phonon averaged (EPA) approximation coupled with Boltzmann transport equation (BTE), we have studied electronic, phonon and thermoelectric properties of Mg₃Sb_2−xBi_x (x = 0, 1, and 2) monolayers. In violation of common mass-trend expectations, increasing Bi element content with heavier Zintl phase compounds yields an abnormal change in ${\kappa }_L$ in two-dimensional Mg₃Sb_2−xBi_x crystals at RT (∼0.51, 1.86, and 0.25 W/mK for Mg₃Sb₂, Mg₃SbBi, and Mg₃Bi₂). The ${\kappa }_L$ trend was detailedly analyzed via the phonon heat capacity, group velocity and lifetime parameters. Based on quantitative electronic band structures, the electronic bonding through the crystal orbital Hamilton population (COHP) and electron local function analysis we reveal the underlying mechanism for the semiconductor-semimetallic transition of Mg₃Sb_2-−xBi_x compounds, and these electronic transport properties (Seebeck coefficient, electrical conductivity, and electronic thermal conductivity) were calculated. We demonstrate that the highest dimensionless figure of merit ZT of Mg₃Sb_2−xBi_x compounds with increasing Bi content can reach ∼1.6, 0.2, and 0.6 at 700 K, respectively. Our results can indicate that replacing heavier anion element in Zintl phase Mg₃Sb_2−xBi_x materials go beyond common expectations (a heavier atom always lead to a lower ${\kappa }_L$ from Slack’s theory), which provide a novel insight for regulating thermoelectric performance without restricting conventional heavy atomic mass approach.

Introduction

The term Zintl phase was firstly proposed by F. Laves (Kauzlarich et al., 2007; Kauzlarich et al., 2016), as a German scientist, indicating a collection of materials within the general class of intermetallics, and the compounds can be understood by a formal electron transfer from a positively-charged metal to a negatively-charged element. In particular, the rich chemistry and evolution of structural complexity of Zintl phase compounds become a series of promising thermoelectric (TE) materials because of their “phonon-glass electron-crystal (PGEC)” (Shuai et al., 2017; Rowe, 2018) structures. The ideal concept presents that a high-performance TE material should have an excellent electrical conductivity of crystals, but also have a higher phonon-scattering rate like glass, where the cation region act as “phonon-glass” and the anion region play as “electron crystal” to alter phonon thermal and electrical transport properties. More interestingly, the structural complexity of Zintl phase compounds is mainly manifested in the diversity of anionic frameworks composed of internal covalent bonds, and the anionic framework can be roughly divided into zero-dimensional (0D) cluster, one-dimensional (1D) chain, two-dimensional (2D) planar, and complex three-dimensional (3D) network structures in accordance with the spatial extension. The 0D cluster structures include Sr₃AlSb₃ (Zevalkink et al., 2013) and Yb₁₄MnSb₁₁ (Brown et al., 2006), and Yb₁₄MnSb₁₁ in the high temperature region can reach 1, in which the maximum Seebeck coefficient of Sr₃AlSb₃ is 500 μV K⁻¹ in the medium temperature region. Herein, the figure of merit defined as $ZT$ ($ZT=\sigma S^{2}T/({\kappa }_e+{\kappa }_L)$), where $\sigma$ stands for the electrical conductivity, $S$ represents the Seebeck coefficient, and $T$ is the Kelvin temperature. ${\kappa }_e$ and ${\kappa }_L$ are the electronic and the lattice thermal conductivities, respectively. Next, Sr3GaSb3 (Zevalkink et al., 2012) and A₅Sn₂As₆ (A = Sr and Eu) (Wang et al., 2012) represent the 1D chain structures, where the maximum $ZT$ of Sr₃TGaSb₃ at 1000 K can exceed 0.9 by doping with Zn element. Meanwhile, the 2D planar structures incorporate BaGa₂Pn₂ (A = P, As) (He et al., 2010) and YbGd₂Sb₂ (Xia and Bobev, 2007). The representative of the 3D network structures is skutterudite (CoSb3) (Shi et al., 2005; Liu et al., 2020), which is a near-ideal “PGEC” with the higher $S$ (200 μV K⁻¹) and power factor ($\sigma S^2$) (30 μW cm⁻¹ K⁻¹), while the higher lattice thermal conductivity would suppress its TE performance.

Recently, the Mg₃Sb_2−xBi_x compounds have become one of the most widely studied TE materials owing to their abundant and inexpensive constituent elements. Experimental measurements and theoretical calculations suggested that the $ZT$ of Mg₃Sb₂ can reach 1 in the high temperature region, and it has simple synthesis, a high melting point, and excellent mechanical stability (Ohno et al., 2018; Shi et al., 2018). It is worth noting that Mg₃(SbBi)₂ alloys would reduce the effective mass of Mg₃Sb₂ and further help to increase the carrier mobility (Imasato et al., 2018). Meanwhile, it was reported that increasing the Bi content in N-type Mg₃Sb_2−xBi_x compounds can significantly improve the low-temperature $ZT$ value (Imasato et al., 2018; Shu et al., 2019), which is even comparable to N-type Bi₂Te₃. However, it was designed and shown that a $ZT$ of 1.85 for Mg_3.195Mn_0.05Sb_1.5Bi_0.49Te_0.01 at 723 K can reach 1.85 (Chen et al., 2018), which is still lower than that of a class of superior TE materials such as SnSe (∼2.8 at 773 K) (Zhao et al., 2014; Zhao et al., 2016; Chang et al., 2018). The above studies mainly focus on the TE transport properties of 3D Zintl phase Mg₃Sb_2−xBi_x (x = 0, 1, and 2) family. According to the 2D quantum confinement effect (Hicks and Dresselhaus, 1993; Zeng et al., 2018), we know that decreasing dimension in 3D materials can not only reduce the ${\kappa }_L$ but also avoid appearing the poor TE performance in some crystalline orientations. The previous work suggested that the ZT value of 2D Mg₃Sb₂ can increase to 2.5 at 900 K, and the near record-high value is larger than that of 3D structure (Huang et al., 2019). The TE performance of 3D Zintl phase Mg₃Sb_2−xBi_x compounds, as a typical layered TE materials family, may be further enhanced through the dimensionality reduction approach. Yet, few 2D Zintl phase Mg₃Sb_2−xBi_x compounds have been studied, and it is necessary to further explore the behind mechanism for the excellent TE performance.

In this work, we performed the first-principles calculations combining with the BTE and the EPA approximation (as a more predictive approach than the deformation potential approximation method) (Samsonidze and Kozinsky, 2018) to systematically calculate and detailedly analyze the phonon thermal and TE transport properties of 2D Mg₃Sb_2−xBi_x within a wide range of temperature. It is found that, through our theoretical calculations, 2D Mg₃Sb_2−xBi_x (x = 0, 1, and 2) compounds possess an abnormal ${\kappa }_L$ trend (${\kappa }_L^{M{g}_{3}SbBi}>{\kappa }_L^{M{g}_{3}S{b}_2}>{\kappa }_L^{M{g}_{3}B{i}_2}$), which violates the common theory (Heavier atomic mass in similar materials usually corresponds to lower ${\kappa }_L$). We elucidate the reason why this anomaly occurs in 2D Mg₃Sb_2−xBi_x structures by quantitatively comparing the phonon heat capacity, the phonon group velocities, the phonon lifetime, the anharmonicity, the transferred and shared charge, and the characteristics of bonds. Meanwhile, we further calculated the electrical transport properties in 2D Mg₃Sb_2−xBi_x including the $\sigma$, $S$, ${\kappa }_e$, and TE performance as a function of chemical potential with respect to the Fermi energy under different temperatures. Our results will provide a theoretical basis for accelerating TE application of 2D Zintl phase materials and pave a new way for predicting and exploring the ultra-high TE performance in PGEC family materials.

Computational Details

The phonon thermal and electrical transport properties have been calculated by the plane-wave pseudopotential approach within the density functional theory (DFT) (Hohenberg and Kohn, 1964), which is employed in the Vienna Ab-initio Simulation Package (VASP) (Kresse and Furthmüller, 1996) software along with projector augmented-wave (PAW) potential (Bliichl, 1994). To ensure the good convergence of electrons and ions during structural optimizations, the plane-wave cutoff energy of the 2D Mg₃Sb_2−xBi_x compounds was set as 500 eV, and a Monkhorst-Pack k-point grid of 15 × 15 × 1 was used to ensure accurate calculation. A Hellmann-Feynman force convergence threshold of 10^–4 eV A⁻¹ was adopted, and the energy convergence threshold between the two steps was set to be 10^–6 eV. To avoid the effect of the interaction between adjacent layers, 2D Mg₃Sb_2−xBi_x unit cells were added a 20 Å thickness of vacuum slab along the out-of-plane direction. We next calculated the electronic band structures using the Perdew, Burke, and Ernzerhof (PBE) functional (Perdew et al., 1996) and the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional (Paier et al., 2006), and different functionals are designed to obtain accurate band results for 2D Mg₃Sb_2−xBi_x materials. The ${\kappa }_L$ is computed by solving the linearized BTE as implemented in ShengBTE software (Li et al., 2014), then considering Born effective charges and dielectric constants effect in the selected compounds. Meanwhile, electronic transport coefficients are calculated exactly by solving semi-classical BTE within the EPA approximation (fully first-principles computations of electron-phonon interactions) as described detailedly (see Supplementary material) in the excellent work (Samsonidze and Kozinsky, 2018).

Results and Discussions

Herein, 2D Mg₃Sb_2−xBi_x (x = 0, 1, and 2) compounds belong to a typical hexagonal structure with the space group P3m1 (No. 156) which is made up of the cationic layer of Mg²⁺ and the anionic layer of [Mg₂(Sb_2−xBi_x)]²⁻ as shown in Figure 1. It has been found that the bonds between ionic Mg²⁺ layers and covalent [Mg₂(Sb_2−xBi_x)]²⁻ layers can be broken to produce a corresponding 2D materials (Gorai et al., 2016; Zhang et al., 2018). Figures 1A, B represents schematic illustration of 2D Mg₃Sb_2−xBi_x (x = 0, 1, and 2), and their calculated lattice constants within the PBE-level are 4.736 Å, 4.794 Å, and 4.843 Å, respectively, which are close to the lattice parameters for corresponding 3D Mg₃Sb₂ (4.573 Å) (Huang et al., 2019) and 3D Mg₃Bi₂ (4.666 Å) (Zhang and Iversen, 2019). Meanwhile, during the structural relaxation of 2D Mg₃Sb_2−xBi_x, we did not consider the too weak van der Waals effect, which has been reported and investigated in previous work (Zhang et al., 2018). Meanwhile, we also present the first Brillouin zone path (Γ-M-K-Γ) with high-symmetry points, named Γ (0, 0, 0), M (1/2, 0, 0), and K (1/3, 1/3, 0), as illustrated in Figure 1C. It is obviously seen that two cases of Mg atoms exist in the primitive cell of 2D Mg₃Sb_2−xBi_x, named by Mg1 and Mg2 (see the inset of the Figures 2B, D, F. Interestingly, between Mg and Sb atoms interactions caused by the corresponding electrical properties has been confirmed, which can occur in a Mg-Sb bonding interaction for the all Mg1 and Mg2 cases in N-type doping Mg₃Sb₂ (Sun et al., 2019). Therefore, it should be noted that the bonding characteristic in 2D Mg₃Sb_2−xBi_x compounds may directly determine their electronic and phononic structures and thus play a crucial role in the calculations of TE properties.

FIGURE 1

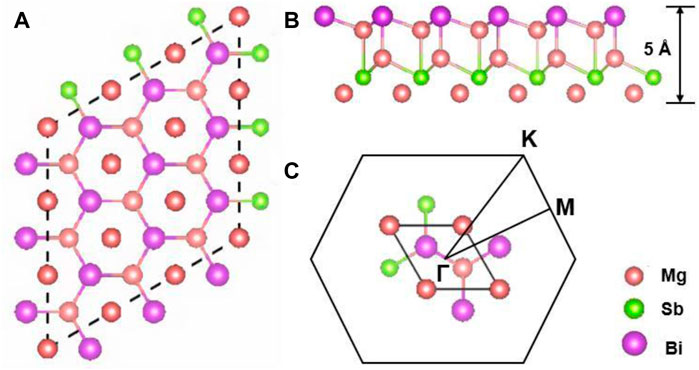
FIGURE 1. Schematic illustration of 2D Mg₃Sb_2−xBi_x in a 5 × 5 × 1 supercell: (A) top view and (B) side view; Mg, Sb ,and Bi are represented orange, green and purple, respectively. (C) The corresponding primitive cell and the first Brillouin zone path with high-symmetry points in 2D Mg₃Sb_2−xBi_x compounds.

FIGURE 2

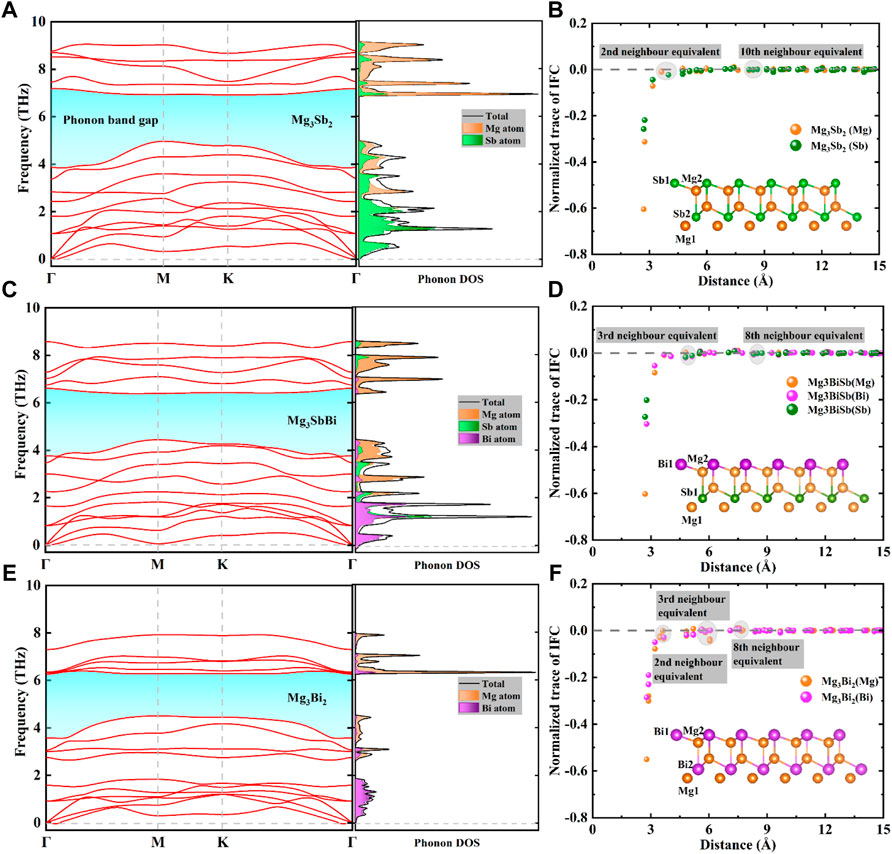
FIGURE 2. Calculated phonon dispersion curves and atom-projected density of states (DOS) for (A) 2D Mg₃Sb₂, (C) 2D Mg₃SbBi and (E) 2D Mg₃Bi₂. The colored shapes highlight phonon band gaps in these compounds. Normalized trace of interatomic force constant (IFC) tensors as a function of atomic distances of (B) 2D Mg₃Sb₂, (D) 2D Mg₃SbBi and (F) 2D Mg₃Bi₂, respectively.

The 2D Mg₃Sb_2−xBi_x family has five atoms in the primitive cell, and the corresponding phonon dispersion curves and phonon harmonicity results are depicted in Figure 2. We found that the above compounds have not imaginary vibrational frequency in the phonon dispersion curves, indicating the dynamic stability of the 2D Mg₃Sb_2−xBi_x compounds in this study (Chang et al., 2021). Meanwhile, it can be seen from Figure 2 that the mixing of acoustic phonons and low-frequency optical phonons exist a stronger phonon scattering processes, which indicates a lower ${\kappa }_L$ in these materials. From Figures 2A, C, F, it can be clearly observed that the region of colored phonon band-gap (Significant dispersion in the high-frequency optical phonons) are gradually decreased with increasing Bi atom content, and these optical phonons in the current compounds holds non-zero phonon group velocities and then has a certain contribution to phonon heat transport. We further track the phenomenon by comparing atom-projected phonon DOS of the Mg, Sb, and Bi atoms in these related compounds, as depicted in Figures 2A, C, E. The total phonon DOS of Mg₃Sb₂ and Mg₃SbBi monolayers decomposes into two separate regions: Mg-site mainly dominated between 6 and 9 THz, and Sb/Bi-sites mainly dominated below ∼3 THz. Surprisingly, for Mg₃Bi₂ monolayer, the total phonon DOS decomposes into three separate regions: Mg1-site mainly dominated between 6 and 8 THz, Mg2-site mainly dominated between 2 and five THz, and Bi-sites mainly dominated below ∼2 THz. The above results show that all of phonon vibration frequencies would be more compressed with increasing Bi atomic mass, which benefits for becoming high-performance TE materials, while it is not enough to explain the anomalous ${\kappa }_L$ changes in 2D Mg₃Sb_2−xBi_x compounds by the increased Bi atomic mass. Therefore, it is urgent to study the interatomic force constants (IFCs) effect in Mg₃Sb_2−xBi_x family, which can directly determine phonon heat conduction behavior.

Figures 2B, D, F show the presence of long-ranged interaction among these compounds, and to further compare and analyze the IFCs between Mg atom and Sb/Bi atoms, traces of IFC tensors are normalized by the trace values of the self-interacting IFC tensor in the above compounds. For instance, second-nearest neighbours, separated by ∼4 Å (including Mg1-Sb1, Mg1-Sb2, and Mg1-Mg2, etc.,), have interactions that are comparable to those of tenth-nearest neighbours, spaced ∼9 Å apart, and much weaker than first-neighbours interactions in Figure 2B. Clearly, there are very similar phenomenon for normalized trace of IFC in 2D Mg₃SbBi and Mg₃Bi₂ structures, excepting for the reduced distances at same nearest neighbours cases by the increased Bi content. Herein, we calculate the IFC tensor on the basis of first-principles calculations as follow (Lee et al., 2014; Li et al., 2020a; Li et al., 2020b):

$\frac{{\partial }^{2}E}{\partial R_I\partial R_J}=\left[\begin{array}{ccc}\frac{{\partial }^{2}E}{\partial R_x\partial R_x}& \frac{{\partial }^{2}E}{\partial R_x\partial R_y}& \frac{{\partial }^{2}E}{\partial R_x\partial R_z}\\ \frac{{\partial }^{2}E}{\partial R_y\partial R_x}& \frac{{\partial }^{2}E}{\partial R_y\partial R_y}& \frac{{\partial }^{2}E}{\partial R_y\partial R_z}\\ \frac{{\partial }^{2}E}{\partial R_z\partial R_x}& \frac{{\partial }^{2}E}{\partial R_z\partial R_y}& \frac{{\partial }^{2}E}{\partial R_z\partial R_z}\end{array}\right],(1)$

where $E$ and $R_{\alpha }$ represent energy and atomic position along $\alpha$ direction, respectively. By computing the trace of IFC tensors, we can assess bonding stiffness regardless of crystal structure or coordinate system:

$Trace of IFC=\frac{{\partial }^{2}E}{\partial R_x\partial R_x}+\frac{{\partial }^{2}E}{\partial R_y\partial R_y}+\frac{{\partial }^{2}E}{\partial R_z\partial R_z},(2)$

Finally, the normalization is calculated by the trace value of self-interaction force constants:

$Normalized trace of IFC=\frac{\frac{{\partial }^{2}E}{\partial R_{0,x}\partial R_{n,x}}+\frac{{\partial }^{2}E}{\partial R_{0,y}\partial R_{n,y}}+\frac{{\partial }^{2}E}{\partial R_{0,z}\partial R_{n,z}}}{\frac{{\partial }^{2}E}{\partial R_{0,x}\partial R_{0,x}}+\frac{{\partial }^{2}E}{\partial R_{0,y}\partial R_{0,y}}+\frac{{\partial }^{2}E}{\partial R_{0,z}\partial R_{0,z}}}.(3)$

In addition, to describe accurately the related IFCs in the calculation of ${\kappa }_L$, we choose a cutoff distance of the tenth-nearest neighbor in 2D Mg₃Sb_2−xBi_x family. We need to point out that Mg1 atom exists at the octahedral site surrounded by 6 corresponding atoms, which would provide 2 electrons to the [Mg₂(Sb_2−xBi_x)]²⁻ network, while Mg2 atom exists at the tetrahedral site surrounded by 4 corresponding atoms. In terms of its configuration, a detailed chemical bonding analysis of 3D Mg₃Sb₂ has been reported that the two different Mg atom sites present a similar bonding character responding to the transferred charges of +1.51 and +1.47, respectively (Zhang et al., 2019), and exists dominantly ionic bonds with partial covalent bonds in 3D Mg₃Sb₂ system (Zhang et al., 2018). These results offers a rational explanation of the relation to phonon heat conduction properties of 3D Mg₃Sb_2−xBi_x family. To deeply understand bonding character and quantify the bond hierarchy strengths of a pair of atoms in 2D Mg₃Sb_2−xBi_x compounds, we next compute and analyze the transferred and shared charges and COHP along with integrated “-COHP” (ICOHP) for the nearest-neighbor atom in the following section.

Based on the more accurate second- and third-order IFCs from the normalized trace of IFC data, we firstly calculate the ${\kappa }_L$ of the selected three Zintl-phase compounds as shown in Figure 3A. Each material would demonstrate roughly the common ${\kappa }_L$ ∼ 1/T behavior. Meanwhile, it is well known that the calculation of ${\kappa }_L$ is more sensitive to the selection of q-mesh grids, and we set a q-mesh grid of 100 × 100 × 1 to solve phonon BTE and then obtain the convergence of ${\kappa }_L$. Because of the symmetry of 2D Mg₃Sb_2−xBi_x, the ${\kappa }_L$ along two in-plane directions shows isotropy, so only a value are depicted. As seen from Figure 3A , 2D Mg₃SbBi alloy holds a higher lattice thermal conductivity, while its average atomic mass is between those of 2D Mg₃Sb₂ and 2D Mg₃Bi₂. For instance, our calculated ${\kappa }_L$ of Mg₃Sb₂, Mg₃SbBi, and Mg₃Bi₂ monolayers at 300 K are 0.51, 1.86, and 0.25 W/mK, respectively, which may originate from a smaller displacement and the mass difference (related to bonding strength) caused by a heavier atom (Li and Mingo, 2014; Yang et al., 2020). As presented in the inset of Figure 3A, we further study the ${\kappa }_L$ changes between the relaxation time approximation (RTA) and the iteratively solving (ITE) methods among the three materials, and the RTA results are below the ITE data, indicating the main function of the Umklapp processes in phonon heat conduction behavior. To deeply understand the behind mechanism of the intriguing phenomena, we perform a detailed analysis on phonon frequency-dependent cumulative ${\kappa }_L$, decomposing ${\kappa }_L$ to three separate parts (phonon heat capacity, group velocity, and phonon lifetime), and phonon anharmonicity information, as presented in Figures 3B–G.

FIGURE 3

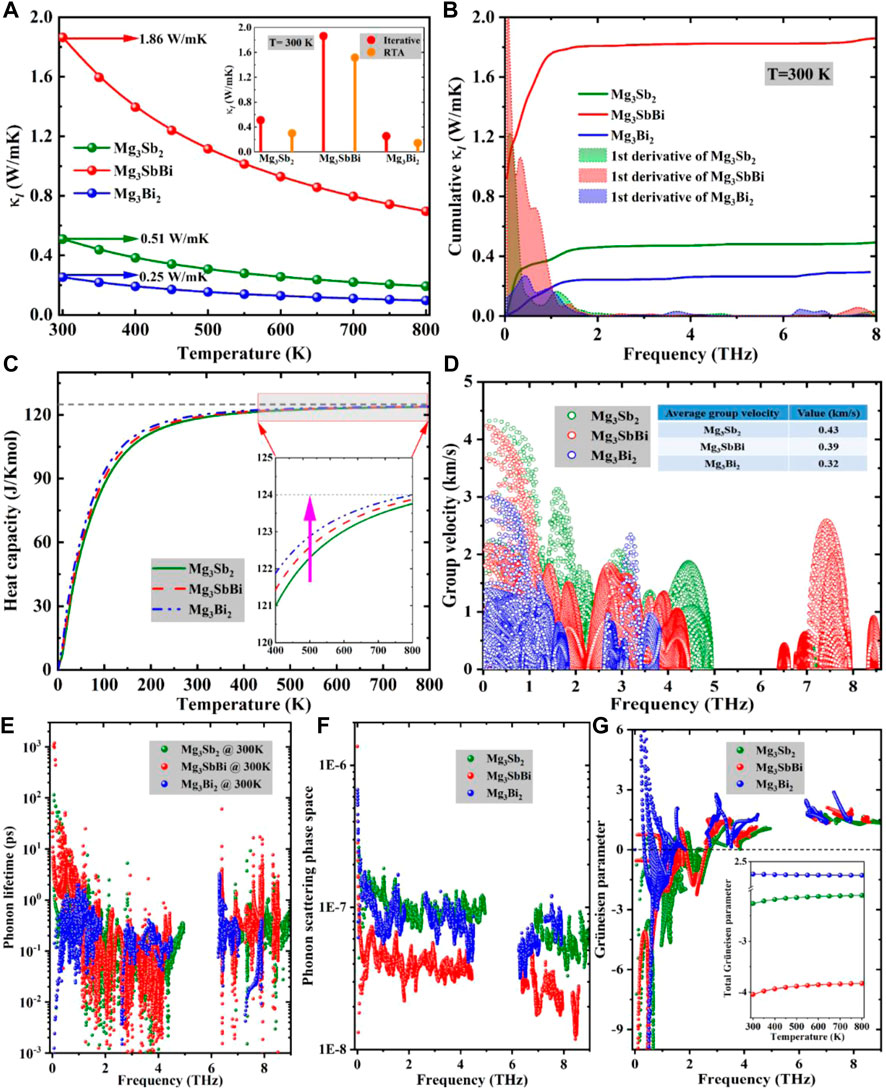
FIGURE 3. (A) Calculated ${\kappa }_L$ of 2D Mg₃Sb_2−xBi_x with respect to the temperature ranging from 300 to 800 K. (B) Cumulative ${\kappa }_L$ of these compounds and their derivatives versus phonon frequency at 300 K. (C) Calculated changes of phonon heat capacity of the above compounds as a function of temperature. The phonon frequency-dependent behavior of (D) the phonon group velocities, (E) phonon lifetime, (F) phonon scattering phase space, and (G) Grüneisen parameters in 2D Mg₃Sb_2−xBi_x.

Obviously, with the increase of cumulative ${\kappa }_L$ can become negligible above a frequency value of ∼2 THz among the three 2D Zintl phase compounds, suggesting the major contribution of the lower optical and acoustic phonons to ${\kappa }_L$ (Figure 2). What we need to notice is that 2D Mg₃SbBi and 2D Mg₃Bi₂ exist two relatively small shape areas (blue and red marked) between 6 and 8 THz, because the higher optical phonons would be compressed and then benefit three-phonon scattering processes. To further check the contribution of all phonons vibrations to the calculated ${\kappa }_L$, the phonon heat capacity (C_v) of among 2D Mg₃Sb₂, 2D Mg₃SbBi and 2D Mg₃Bi₂ with respect to temperature were obtained and illustrated in Figure 3B, which agree well with the previous experimental data by using the PPMS measurement (Xin et al., 2018). The C_v (obeying ${\kappa }_L\propto$ C_v) of these compounds at temperatures within the range of 400–800 K are very close (∼122 J/K mol) to each other for all the three materials, and obey the classical limit of Dulong-Petit law (Fitzgerel and Verhoek, 1960) as shown in the inset of Figure 3C. Therefore, these tiny difference in C_v are not the primary cause of the anomalous ${\kappa }_L$ trend in 2D Mg₃Sb_2−xBi_x systems. For three compounds, the phonon group velocity (v_g) as a function of frequency is plotted in Figure 3D, and it can be seen that the group velocity of 2D Mg₃Sb₂ is higher than that of 2D Mg₃Bi₂, closing to that of 2D Mg₃SbBi in the cutoff frequency below 1.5 THz, which suggests the calculated ${\kappa }_L$ of 2D Mg₃Sb₂ and 2D Mg₃SbBi might be roughly close (following the rule ${\kappa }_L\propto$ v_g). On average level, we show that the average group velocities of 2D Mg₃Sb_2−xBi_x are 0.43, 0.39, and 0.32 km/s, respectively. However, it is clearly observed in Figure 3D that the three v_g data exist similar distribution, excepting for having the significant differences (the non-negligible velocities for Mg₃SbBi) around a frequency ranging between 6.5 and 8 THz, while the changes are consistent with the above the slope of phonon dispersion curves.

Interestingly, none of the C_v and the v_g can explain the relatively higher ${\kappa }_L$ of 2D Mg₃SbBi compared to 2D Mg₃Sb₂ systems. Therefore, we can conclude that the abnormal ${\kappa }_L$ trends in the three materials must lie in the unusual phonon lifetimes (τ) as plotted in Figure 3E. The calculated τ of 2D Mg₃SbBi were considerably larger than those of the other two materials in the lower- (0–2 THz) and higher-frequency (6–8 THz) regions, which might be because of the suppressed three-phonon scattering processes in 2D Mg₃SbBi, caused by the alloying (a mass difference occurring in [Mg₂(SbBi)]²⁻). Obviously, these variation trends of the τ in Mg₃Sb_2−xBi_x were consistent with the cumulative ${\kappa }_L$ results as seen in Figure 3B. In the light of the theory of lattice dynamics, the calculated τ is strongly dependent on three-phonon scattering phase space (P₃) and Grüneisen parameter (γ), as presented in Figures 3F, G. Herein, the P₃ is defined as (Lindsay and Broido, 2008; Peng et al., 2016; Yang et al., 2020):

$P_3=\frac{2}{3\Theta }\left(P_3^{+}+\frac{1}{2}{P}_3^{-}\right),(4)$

$P_3^{\pm }={\displaystyle \sum _{\lambda }{\displaystyle \int d\mathit{q}{D}_{\lambda }^{\pm }}}\left(\mathit{q}\right),(5)$

$D_{\lambda }^{\pm }\left(\mathit{q}\right)={\displaystyle \sum _{{\lambda }^{\prime }{\lambda }^{\prime \prime }}{\displaystyle \int d{\mathit{q}}^{\prime }\delta }}\left({\omega }_{\lambda }\left(\mathit{q}\right)\pm {\omega }_{{\lambda }^{\prime }}\left({\mathit{q}}^{\prime }\right)-{\omega }_{{\lambda }^{\prime \prime }}\left(\mathit{q}\pm {\mathit{q}}^{\prime \prime }-\mathit{G}\right)\right),(6)$

where $\Theta$ represents a normalization factor, $D_{\lambda }^{\pm }\left(\mathit{q}\right)$ represents two types of three-phonon scattering channels, and it is also the two phonon DOS and momentum conservation were imposed on ${\mathit{q}}^{\prime \prime }$ (Okubo and Tamura, 1983). From Figure 3F, it is shown that the P₃ of 2D Mg₃SbBi is smaller than these of the other two compounds in the entire phonon frequency ranges, which suggests that phonons in 2D Mg₃SbBi have less phonon scattering channels, leading to relatively larger τ (Figure 3E) compared to 2D Mg₃Sb₂ and 2D Mg₃Bi₂ materials. The other important factor that the number of phonons scattering channels determined exists the strength of phonon anharmonicity, quantitatively described by the γ, which characterizes how many phonon frequencies vary with the crystal volume. As revealed in the inset of Figure 3G, the calculated total γ for 2D Mg₃SbBi is ∼ −4.0, which is lower than that of 2D Mg₃Sb₂ (γ= ∼ −2.1) and 2D Mg₃Bi₂ (γ= ∼ 2.2) at the temperature ranging from 300 to 800 K. Consequently, anomalously increase of the ${\kappa }_L$ from 2D Mg₃Sb₂, 2D Mg₃SbBi, and 2D Mg₃Bi₂ has been demonstrated by breaking up into the relative contribution of the C_v, v_g, and τ as discussed above.

It is well known that the superior TE performance in a material results from an intrinsic ultra-low ${\kappa }_L$, from the above phonon heat conduction results, and it is very necessary to confirm the potential TE transport properties from 2D Mg₃Sb₂ to 2D Mg₃Bi₂. We firstly calculated the electronic band structures in 2D Mg₃Sb_2−xBi_x using the two function potentials as plotted in Figures 4A–C, which can directly explain the reason for the high TE performance of a material. Since Sb and Bi atoms possessed the same outermost valence electrons (including 3p and 2s), the slope of these band structures would be very similar. Meanwhile, the calculated band-gaps with PBE and HSE06 potentials are 0.17 and 0.56 eV for 2D Mg₃Sb₂. Therefore, to obtain more accurate values, we carried out the HSE06 to correct the band structures, and a negative band-gap was occurred in 2D Mg₃Bi₂ (Figure 4C). In addition, we found that the valence band maximum is located at Γ point for all of the selected compounds, due to the domination of Mg-Sb/Bi bonding interactions (Sun et al., 2019; Wood et al., 2020), while location of the conduction band minimum are between Γ and M paths, the same Γ point, and around Γ point for 2D Mg₃Sb₂, 2D Mg₃SbBi, and 2D Mg₃Bi₂, respectively. To further characterize and explore the behind mechanism of chemical-bonding properties in 2D Mg₃Sb_2−xBi_x, we also calculated the ELF and COHP with integrated pCOHP (-pCOHP) as plotted in Figures 4D–I. Meanwhile, three ELF values of 0, 0.5, and 1.0 reflect non-localized electrons (none-charge density), completely delocalized electrons (electron gas–like pair phenomenon), and fully localized electrons (the occurrence probability of the electrons), respectively (Silvi and Savin, 1994; Yue et al., 2017; Wu et al., 2020). It can be clearly seen that the value of the ELF between Mg atoms and Sb/Bi atoms gradually decrease with increasing Bi element in 2D Mg₃Sb_2−xBi_x systems, suggesting a weaker covalent bond in 2D Mg₃Bi₂ and then proved its semi-metallic feature. The lower value of ELF in Mg₃Bi₂ monolayer also confirms the weaker and lower shared charges as listed in Table 1 in the material compared to the other two structures which have higher shared electrons and stronger covalent bonding. The corresponding charges changes in the family of Mg₃Sb_2−xBi_x monolayers were calculated through the density-derived electrostatic and chemical (DDEC6) approach as implemented in CHARGEMOL package (Manz and Limas, 2016). Meanwhile, the higher ELF values in Mg₃Sb₂ and Mg₃SbBi monolayers also verify the higher transferred charges as seen in Table 1 since a higher ELF usually suggests a higher concentration of localized electrons in both Mg₃Sb₂ and Mg₃SbBi compared to Mg₃Bi₂ monolayers. From Table 1, our analysis shows that the higher difference in electronegativity between two atoms enhances the transferred electrons which is illustrated in 2D Mg₃Sb₂ with higher difference in electronegativity between Mg and Sb atoms (higher transferred charge) compared to 2D Mg₃Bi₂ with lower difference in electronegativity between Mg and Bi atoms (lower transferred charge). On the other hand, the value of Mg-Sb atoms around the ELF distribution in 2D Mg₃SbBi is much larger when compared 2D Mg₃Sb₂ and the results is in agreement with the corresponding calculations as depicted in Figures 4G,H. Herein, the negative value on the abscissa represents antibonding interactions, otherwise represents bonding interactions in the three “-pCOHP” curves. Meanwhile, the absolute ICOHP (defined as $ICOHP=\underset{-\infty }{\overset{E}{{\displaystyle \int }}}pCOHP\left(E\right)dE$) serves as an indicator toward the bond strength, which can indicate the d₁ interaction trends in 2D Mg₃Sb_2−xBi_x (Mg₃SbBi > Mg₃Sb₂ > Mg₃Bi₂), and it is consistent with the ${\kappa }_L$ changes. However, comparing for d₁ interactions in these compounds, we found that the absolute ICOHP for d₂ is always smaller. Typically, a weaker bond might cause phonons rattling behavior, leading the phonon modes softened, which supports the above ${\kappa }_L$ results.

FIGURE 4

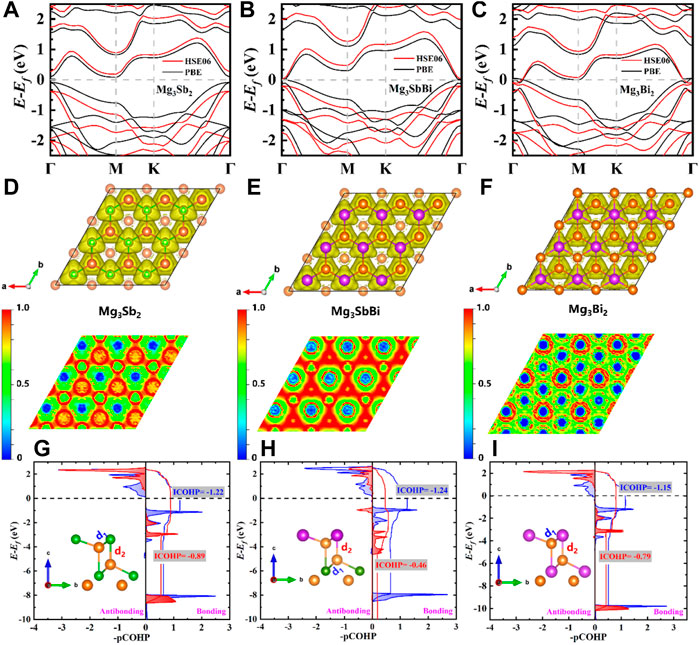
FIGURE 4. Calculated electronic band structures of (A) 2D Mg₃Sb₂, (B) 2D Mg₃SbBi, and (C) 2D Mg₃Bi₂ by using HSE06 (solid red lines) and PBE function potentials (solid black lines), and the Fermi-level (E_f) is set to 0 eV. Top view (upper) and the corresponding slice projection along (001) plane (down) of 2D Mg₃Sb_2−xBi_x electron localization function (ELF) for (D) 2D Mg₃Sb₂, (E) 2D Mg₃SbBi, and (F) 2D Mg₃Bi₂, respectively. Calculated the projected Crystal Orbital Hamilton Population (pCOHP) curves of 2D Mg₃Sb_2−xBi_x pairwise interactions (including d₁ and d₂) versus energy for (G) 2D Mg₃Sb₂, (H) 2D Mg₃SbBi, and (I) 2D Mg₃Bi₂. Herein, the bond behind mechanism of both d₁ and d₂ was investigated and studied by the standalone computer program Local Orbital Basis Suite towards Electronic-Structure Reconstruction (LOBSTER) program (Maintz et al., 2016).

TABLE 1

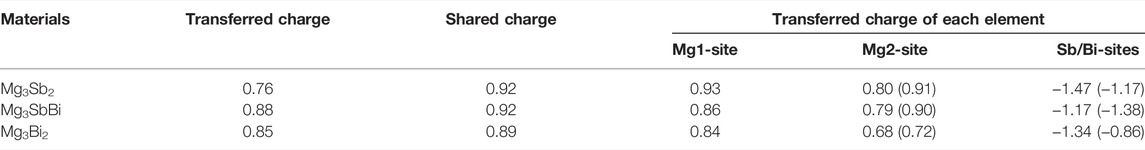
TABLE 1. Comparison of transferred and shared charges ($\left|e\right|$) and the corresponding transferred charge ($\left|e\right|$) of each element in 2D Mg₃Sb₂, (h) 2D Mg₃SbBi, and (i) 2D Mg₃Bi₂.

Usually, the several approaches, including the constant relaxation time approximation (Singh and Mazin, 1997; Madsen, 2006; Madsen and Singh, 2006; Yang et al., 2008), the deformation potential approximation (Sjakste et al., 2006; Murphy-Armando et al., 2010; Wang et al., 2011), and Wannier interpolation (Giustino et al., 2007; Bernardi et al., 2014; Qiu et al., 2015), can directly determine the electronic transport coefficients by solving the BTE theory. Herein, we used the EPA method to compute the corresponding parameters ($S$, $\sigma$, and ${\kappa }_e$) for the family of 2D Mg₃Sb_2−xBi_x compounds, which was widely verified in the previous work (Nam et al., 2021; Biele and D'Agosta, 2022). For the above compounds, we presented the variation of $S$ versus on the values of μ at three different temperatures in Figure 5A. It is cleared from the figure that the maximum value of the $S$ are 900 μV/K (Mg₃Sb₂), 750 μV/K (Mg₃SbBi), and 650 μV/K (Mg₃Bi₂) at 300 K, respectively, which are superior to those of some commercial TE materials such as SnSe (∼500 μV/K) (Zhang and Zhao, 2015)and Bi₂Te₃ (∼200 μV/K) (Poudel et al., 2008), suggesting the high-performance TE candidate materials for P/N-type doping 2D Mg₃Sb_2−xBi_x. Meanwhile, there are two notable peaks around the μ−E_f value of ∼0 Ry, characterizing the $S$ curves, and the calculated $S$ would be decreased rapidly when beyond the ranges. The negative $S$ values of the three studied compound are smaller than that of the corresponding positive values at ∼ 0 Ry region, and the discrepancy can be understood by the above band structures (mainly attributing to the band-gaps) as displayed in Figures 4A–C. By increasing Bi content from 2D Mg₃Sb₂ to 2D Mg₃Bi₂, the bandgap decrease gradually and thereby the absolute value of the maximum $S$ decreases as well. As illustrated in Figure 5B, because of the similar electronic band structures among the three compounds, the $\sigma$ curves represents a close slope at different temperatures. Moreover, we can see that the calculated $\sigma$ values almost roughly increase with increasing the value of μ for all studied materials, while it is opposite for the $S$, indicating the two coefficients coupled unfavorably for enhancing TE performance. Furthermore, the maximum $\sigma$ values for negative chemical and positive chemical potentials in the family of 2D Mg₃Sb_2−xBi_x compounds are almost equal at 300 K, 500 K, and 700 K.

FIGURE 5

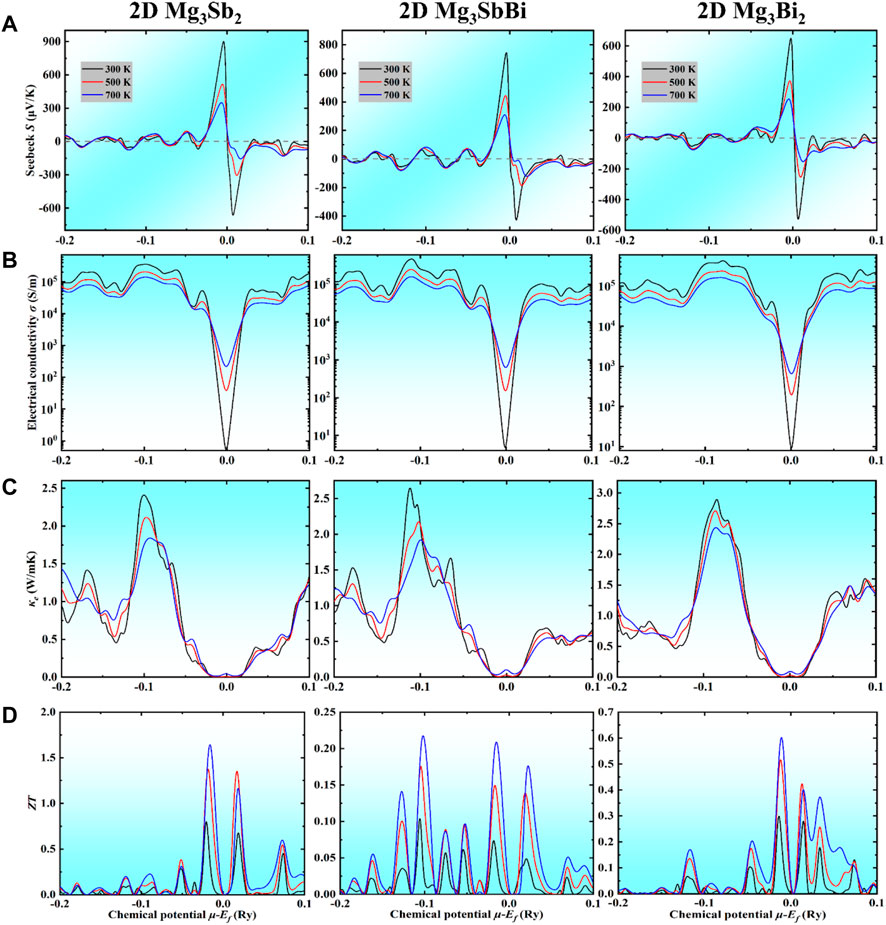
FIGURE 5. Calculated TE transport coefficients for the 2D Mg₃Sb_2−xBi_x family as a function of chemical potential (μ) shifted with respect to the E_f at 300 K, 500 K, and 700 K, respectively. (A) Seebeck coefficient, (B) electrical conductivity, (C) electronic thermal conductivity, and (D) the corresponding ZT. Herein, the negative and positive (μ−E_f) represent the corresponding P-type and N-type samples doped, respectively.

It is well known that the trends of ${\kappa }_e$ is tied to the $\sigma$ curves, and Figure 5C shows the variation of ${\kappa }_e$ with response to the μ−E_f at different temperatures. Interestingly, we can observe that the maximum values of the ${\kappa }_e$ for negative μ region are 2.4 W/mK (2D Mg₃Sb₂), 2.6 W/mK (2D Mg₃SbBi), and 2.8 W/mK (2D Mg₃Bi₂), while for positive chemical potential region these are 1.9 W/mK (2D Mg₃Sb₂), 0.8 W/mK (2D Mg₃SbBi), and 1.6 W/mK (2D Mg₃Bi₂) at 300 K, respectively, where the calculated ${\kappa }_e$ data is close to several commercial TE materials such as SnSe (∼2 W/mK) (Wang et al., 2015) and Bi₂Te₃ (∼1 W/mK) (Hicks and Dresselhaus, 1993). The results indicates that the N-type doping 2D Mg₃Sb_2−xBi_x composition may possess a higher TE performance compared with the corresponding P-type doping samples. Based on the phonon thermal transport and electronic transport properties computed above, we show the ZT of 2D Mg₃Sb_2−xBi_x compounds as a function of the μ−E_f at three typical temperatures (300 K, 500 K, and 700 K) as seen in Figure 5D. Obviously, the ZT in the three studied materials exhibit different trends, and the maximum ZT at 700 K can reach about 1.6 (2D Mg₃Sb₂), 0.2 (2D Mg₃SbBi), and 0.6 (2D Mg₃Bi₂), respectively. It can been clearly observed in Figure 5D that the TE performance of N-type doping is inferior to that of P-type doping for 2D Mg₃SbBi and 2D Mg₃Bi₂ compounds, while it is opposite for 2D Mg₃Sb₂, and the behavior has been mainly dominated by Bi element content and then changing electronic band engineering.

Conclusion

In summary, we have systematically investigated the TE transport properties of the family of Mg₃Sb_2−xBi_x (x = 0, 1, and 2) monolayers. Our results present that the three typical materials possess extremely lower lattice thermal conductivities, including 2D Mg₃Sb₂ (∼0.51 W/mK), 2D Mg₃SbBi (∼1.86 W/mK), and 2D Mg₃Bi₂ (∼0.25 W/mK) at 300 K, respectively, while a heavier atomic mass in a compound usually possesses a lower ${\kappa }_L$ on the basis of the conventional (Keyes’ and Slack’s) theory. By decomposing the ${\kappa }_L$, it is concluded that the abnormal phenomenon is mainly due to the effect of phonon lifetime, which is significantly larger in Mg₃SbBi alloying system. Meanwhile, all these samples exhibit a transformation from semiconductor to semimetallic with increasing Bi element content, indicating a heavier compound having a narrower band-gap. Moreover, coupling with the ${\kappa }_L$ above, we further obtained that the maximum ZT values of 1.6, 0.2, and 0.6 at 700 K are founded in N-type doping 2D Mg₃Sb₂, P-type doping 2D Mg₃SbBi, and P-type doping 2D Mg₃Bi₂, respectively. All the results of the analysis above suggest that increasing Bi element to Zintl phase 2D Mg₃Sb_2−xBi_x alloy, which is beneficial to the reduction of the electronic thermal conduct ivies, might not necessarily improve the TE performance and offer a novel regulation approach which can be generalized in other Zintl phase monolayer compounds. Therefore, to obtain the optimal ZT in 2D Mg₃Sb_2−xBi_x alloys, both Sb and Bi element contents (except for x = 0, 1, and 2) need be further demonstrated by coupling theoretical calculations and experimental measurements.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

ZC, JM, KY, XZ, and DT designed research. ZC: Conceptualization, Software, Formal analysis, Writing—original draft and editing, Data curation. KY, MA-F, and MH: Formal analysis, Writing—review and editing. JZ, YG, and HS performed the part calculations. All authors analyzed data and discussed results.

Funding

This work was supported by the National Natural Science Foundation of China [Grant Nos 51720105007, 52076031, 11602149, 51806031, 52176166) and the Fundamental Research Funds for the Central Universities [DUT19RC(3)006], and the computing resources from the Supercomputer Center of Dalian University of Technology. Research reported in this publication was supported in part by the U.S. National Science Foundation (Award Number 1905775, 2030128).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2022.876655/full#supplementary-material

References

Bernardi, M., Vigil-Fowler, D., Lischner, J., Neaton, J. B., and Louie, S. G. (2014). Ab InitioStudy of Hot Carriers in the First Picosecond after Sunlight Absorption in Silicon. Phys. Rev. Lett. 112, 257402. doi:10.1103/physrevlett.112.257402

PubMed Abstract | CrossRef Full Text | Google Scholar

Biele, R., and D'agosta, R. (2022). Transport Coefficients of Layered TiS 3. Phys. Rev. Mater. 6, 014004. doi:10.1103/physrevmaterials.6.014004

CrossRef Full Text | Google Scholar

Bliichl, P. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50, 17953–17979.

Google Scholar

Brown, S. R., Kauzlarich, S. M., Gascoin, F., and Snyder, G. J. (2006). Yb14MnSb11: New High Efficiency Thermoelectric Material for Power Generation. Chem. Mater. 18, 1873–1877. doi:10.1021/cm060261t

CrossRef Full Text | Google Scholar

Chang, C., Wu, M., He, D., Pei, Y., Wu, C.-F., Wu, X., et al. (2018). 3D Charge and 2D Phonon Transports Leading to High Out-Of-Plane ZT in N-type SnSe Crystals. Science 360, 778–783. doi:10.1126/science.aaq1479

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, Z., Yuan, K., Sun, Z., Zhang, X., Gao, Y., Qin, G., et al. (2021). Ultralow Lattice thermal Conductivity and Dramatically Enhanced Thermoelectric Properties of Monolayer InSe Induced by an External Electric Field. Phys. Chem. Chem. Phys. 23, 13633–13646. doi:10.1039/d1cp01510a

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Wu, H., Cui, J., Xiao, Y., Zhang, Y., He, J., et al. (2018). Extraordinary Thermoelectric Performance in N-type Manganese Doped Mg3Sb2 Zintl: High Band Degeneracy, Tuned Carrier Scattering Mechanism and Hierarchical Microstructure. Nano Energy 52, 246–255. doi:10.1016/j.nanoen.2018.07.059

CrossRef Full Text | Google Scholar

Fitzgerel, R. K., and Verhoek, F. H. (1960). The Law of Dulong and Petit. . Chem. Educ. 37 (10), 545–549. doi:10.1021/ed037p545

CrossRef Full Text | Google Scholar

Giustino, F., Cohen, M. L., and Louie, S. G. (2007). Electron-phonon Interaction Using Wannier Functions. Phys. Rev. B 76, 165108. doi:10.1103/physrevb.76.165108

CrossRef Full Text | Google Scholar

Gorai, P., Toberer, E. S., and Stevanović, V. (2016). Computational Identification of Promising Thermoelectric Materials Among Known quasi-2D Binary Compounds. J. Mater. Chem. A. 4, 11110–11116. doi:10.1039/c6ta04121c

CrossRef Full Text | Google Scholar

He, H., Stearrett, R., Nowak, E. R., and Bobev, S. (2010). Baga2Pn2 (Pn = P, as): New Semiconducting Phosphides and Arsenides with Layered Structures. Inorg. Chem. 49, 7935–7940. doi:10.1021/ic100940b

PubMed Abstract | CrossRef Full Text | Google Scholar

Hicks, L. D., and Dresselhaus, M. S. (1993). Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys. Rev. B 47, 12727–12731. doi:10.1103/physrevb.47.12727

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871. doi:10.1103/physrev.136.b864

CrossRef Full Text | Google Scholar

Huang, S., Wang, Z., Xiong, R., Yu, H., and Shi, J. (2019). Significant Enhancement in Thermoelectric Performance of Mg3Sb2 from Bulk to Two-Dimensional Mono Layer. Nano Energy 62, 212–219. doi:10.1016/j.nanoen.2019.05.028

CrossRef Full Text | Google Scholar

Imasato, K., Kang, S. D., Ohno, S., and Snyder, G. J. (2018). Band Engineering in Mg3Sb2 by Alloying with Mg3Bi2 for Enhanced Thermoelectric Performance. Mater. Horiz. 5, 59–64. doi:10.1039/c7mh00865a

CrossRef Full Text | Google Scholar

Kauzlarich, S. M., Brown, S. R., and Jeffrey Snyder, G. (2007). Zintl Phases for Thermoelectric Devices. Dalton Trans., 2099–2107. doi:10.1039/b702266b

PubMed Abstract | CrossRef Full Text | Google Scholar

Kauzlarich, S. M., Zevalkink, A., Toberer, E., and Snyder, G. J. (2016). Zintl Phases: Recent Developments in Thermoelectrics and Future Outlook.

Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

Lee, S., Esfarjani, K., Luo, T., Zhou, J., Tian, Z., and Chen, G. (2014). Resonant Bonding Leads to Low Lattice thermal Conductivity. Nat. Commun. 5, 3525–3528. doi:10.1038/ncomms4525

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Liu, P.-F., Zhang, C., Shi, X., Jiang, S., Chen, W., et al. (2020a). Lattice Vibrational Modes and Phonon thermal Conductivity of Single-Layer GaGeTe. J. Materiomics 6, 723–728. doi:10.1016/j.jmat.2020.04.005

CrossRef Full Text | Google Scholar

Li, J., Yang, J., Shi, B., Zhai, W., Zhang, C., Yan, Y., et al. (2020b). Ternary Multicomponent Ba/Mg/Si Compounds with Inherent Bonding Hierarchy and Rattling Ba Atoms toward Low Lattice thermal Conductivity. Phys. Chem. Chem. Phys. 22, 18556–18561. doi:10.1039/d0cp02792h

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Carrete, J., A. Katcho, N. N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comp. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2014). Lattice Dynamics and thermal Conductivity of Skutterudites CoSb 3 and IrSb 3 from First Principles: Why IrSb 3 Is a Better thermal Conductor Than CoSb 3. Phys. Rev. B 90, 094302. doi:10.1103/physrevb.90.094302

CrossRef Full Text | Google Scholar

Lindsay, L., and Broido, D. A. (2008). Three-phonon Phase Space and Lattice thermal Conductivity in Semiconductors. J. Phys. Condens. Matter 20, 165209. doi:10.1088/0953-8984/20/16/165209

CrossRef Full Text | Google Scholar

Liu, Z.-Y., Zhu, J.-L., Tong, X., Niu, S., and Zhao, W.-Y. (2020). A Review of CoSb 3-based Skutterudite Thermoelectric Materials. J. Adv. Ceramics, 1–27. doi:10.1007/s40145-020-0407-4

CrossRef Full Text | Google Scholar

Madsen, G. K. H. (2006). Automated Search for New Thermoelectric Materials: the Case of LiZnSb. J. Am. Chem. Soc. 128, 12140–12146. doi:10.1021/ja062526a

PubMed Abstract | CrossRef Full Text | Google Scholar

Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comp. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007

CrossRef Full Text | Google Scholar

Maintz, S., Deringer, V. L., Tchougréeff, A. L., and Dronskowski, R. (2016). LOBSTER: A Tool to Extract Chemical Bonding from Plane‐wave Based DFT. Wiley Online Library.

Google Scholar

Manz, T. A., and Limas, N. G. (2016). Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology. RSC Adv. 6, 47771–47801. doi:10.1039/c6ra04656h

CrossRef Full Text | Google Scholar

Murphy-Armando, F., Fagas, G., and Greer, J. C. (2010). Deformation Potentials and Electron−Phonon Coupling in Silicon Nanowires. Nano Lett. 10, 869–873. doi:10.1021/nl9034384

PubMed Abstract | CrossRef Full Text | Google Scholar

Nam, H. N., Suzuki, K., Nguyen, T. Q., Masago, A., Shinya, H., Fukushima, T., et al. (2021). Low-temperature Acanthite-like Phase of Cu $ _ {2} $ S: A First-Principles Study on Electronic and Transport Properties. arXiv preprint arXiv:2110.09117.

Google Scholar

Ohno, S., Imasato, K., Anand, S., Tamaki, H., Kang, S. D., Gorai, P., et al. (2018). Phase Boundary Mapping to Obtain N-type Mg3Sb2-Based Thermoelectrics. Joule 2, 141–154. doi:10.1016/j.joule.2017.11.005

CrossRef Full Text | Google Scholar

Okubo, K., and Tamura, S.-I. (1983). Two-phonon Density of States and Anharmonic Decay of Large-Wave-Vector LA Phonons. Phys. Rev. B 28, 4847–4850. doi:10.1103/physrevb.28.4847

CrossRef Full Text | Google Scholar

Paier, J., Marsman, M., Hummer, K., Kresse, G., Gerber, I. C., and Ángyán, J. G. (2006). Screened Hybrid Density Functionals Applied to Solids. J. Chem. Phys. 124, 154709. doi:10.1063/1.2187006

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, B., Zhang, H., Shao, H., Xu, Y., Zhang, X., and Zhu, H. (2016). Low Lattice thermal Conductivity of Stanene. Sci. Rep. 6 (1), 1–10. doi:10.1038/srep20225

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Poudel, B., Hao, Q., Ma, Y., Lan, Y., Minnich, A., Yu, B., et al. (2008). High-thermoelectric Performance of Nanostructured Bismuth Antimony telluride Bulk Alloys. Science 320, 634–638. doi:10.1126/science.1156446

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, B., Tian, Z., Vallabhaneni, A., Liao, B., Mendoza, J. M., Restrepo, O. D., et al. (2015). First-principles Simulation of Electron Mean-Free-Path Spectra and Thermoelectric Properties in Silicon. Epl 109, 57006. doi:10.1209/0295-5075/109/57006

CrossRef Full Text | Google Scholar

Rowe, D. M. (2018). Thermoelectrics Handbook: Macro to Nano. CRC Press.

Google Scholar

Samsonidze, G., and Kozinsky, B. (2018). Accelerated Screening of Thermoelectric Materials by First‐Principles Computations of Electron-Phonon Scattering. Adv. Energ. Mater. 8, 1800246. doi:10.1002/aenm.201800246

CrossRef Full Text | Google Scholar

Shi, X., Wang, X., Li, W., and Pei, Y. (2018). Advances in Thermoelectric Mg3Sb2and its Derivatives. Small Methods 2, 1800022. doi:10.1002/smtd.201800022

CrossRef Full Text | Google Scholar

Shi, X., Zhang, W., Chen, L. D., and Yang, J. (2005). Filling Fraction Limit for Intrinsic Voids in Crystals: Doping in Skutterudites. Phys. Rev. Lett. 95, 185503. doi:10.1103/physrevlett.95.185503

PubMed Abstract | CrossRef Full Text | Google Scholar

Shu, R., Zhou, Y., Wang, Q., Han, Z., Zhu, Y., Liu, Y., et al. (2019). Mg3+ δ Sb X Bi2− X Family: A Promising Substitute for the State-Of-The-Art N-type Thermoelectric Materials Near Room Temperature. Adv. Funct. Mater. 29, 1807235. doi:10.1002/adfm.201807235

CrossRef Full Text | Google Scholar

Shuai, J., Mao, J., Song, S., Zhang, Q., Chen, G., and Ren, Z. (2017). Recent Progress and Future Challenges on Thermoelectric Zintl Materials. Mater. Today Phys. 1, 74–95. doi:10.1016/j.mtphys.2017.06.003

CrossRef Full Text | Google Scholar

Silvi, B., and Savin, A. (1994). Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 371, 683–686. doi:10.1038/371683a0

CrossRef Full Text | Google Scholar

Singh, D. J., and Mazin, I. I. (1997). Calculated Thermoelectric Properties of La-Filled Skutterudites. Phys. Rev. B 56, R1650–R1653. doi:10.1103/physrevb.56.r1650

CrossRef Full Text | Google Scholar

Sjakste, J., Tyuterev, V., and Vast, N. (2006). Ab Initiostudy ofΓ−Xintervalley Scattering in GaAs under Pressure. Phys. Rev. B 74, 235216. doi:10.1103/physrevb.74.235216

CrossRef Full Text | Google Scholar

Sun, X., Li, X., Yang, J., Xi, J., Nelson, R., Ertural, C., et al. (2019). Achieving Band Convergence by Tuning the Bonding Ionicity in N‐type Mg 3 Sb 2. J. Comput. Chem. 40, 1693–1700. doi:10.1002/jcc.25822

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F. Q., Zhang, S., Yu, J., and Wang, Q. (2015). Thermoelectric Properties of Single-Layered SnSe Sheet. Nanoscale 7, 15962–15970. doi:10.1039/c5nr03813h

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Xia, S.-Q., and Tao, X.-T. (2012). A5Sn2As6 (A = Sr, Eu). Synthesis, Crystal and Electronic Structure, and Thermoelectric Properties. Inorg. Chem. 51, 5771–5778. doi:10.1021/ic300308w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Wang, S., Obukhov, S., Vast, N., Sjakste, J., Tyuterev, V., et al. (2011). Thermoelectric Transport Properties of Silicon: Toward Anab Initioapproach. Phys. Rev. B 83, 205208. doi:10.1103/physrevb.83.205208

CrossRef Full Text | Google Scholar

Wood, M., Imasato, K., Anand, S., Yang, J., and Snyder, G. J. (2020). The Importance of the Mg-Mg Interaction in Mg3Sb2-Mg3Bi2 Shown through Cation Site Alloying. J. Mater. Chem. A. 8, 2033–2038. doi:10.1039/c9ta11328b

CrossRef Full Text | Google Scholar

Wu, Y., Ma, C., Chen, Y., Mortazavi, B., Lu, Z., Zhang, X., et al. (2020). New Group V Graphyne: Two-Dimensional Direct Semiconductors with Remarkable Carrier Mobilities, Thermoelectric Performance, and thermal Stability. Mater. Today Phys. 12, 100164. doi:10.1016/j.mtphys.2019.100164

CrossRef Full Text | Google Scholar

Xia, S.-Q., and Bobev, S. (2007). Cation−Anion Interactions as Structure Directing Factors: Structure and Bonding of Ca2CdSb2 and Yb2CdSb2. J. Am. Chem. Soc. 129, 4049–4057. doi:10.1021/ja069261k

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, J., Li, G., Auffermann, G., Borrmann, H., Schnelle, W., Gooth, J., et al. (2018). Growth and Transport Properties of Mg3X2 (X = Sb, Bi) Single Crystals. Mater. Today Phys. 7, 61–68. doi:10.1016/j.mtphys.2018.11.004

CrossRef Full Text | Google Scholar

Yang, J., Li, H., Wu, T., Zhang, W., Chen, L., and Yang, J. (2008). Evaluation of Half-Heusler Compounds as Thermoelectric Materials Based on the Calculated Electrical Transport Properties. Adv. Funct. Mater. 18, 2880–2888. doi:10.1002/adfm.200701369

CrossRef Full Text | Google Scholar

Yang, Z., Yuan, K., Meng, J., Zhang, X., Tang, D., and Hu, M. (2020). Why thermal Conductivity of CaO Is Lower Than that of CaS: a Study from the Perspective of Phonon Splitting of Optical Mode. Nanotechnology 32, 025709. doi:10.1088/1361-6528/abbb4c

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, S.-Y., Qin, G., Zhang, X., Sheng, X., Su, G., and Hu, M. (2017). Thermal Transport in Novel Carbon Allotropes with S P 2 or S P 3 Hybridization: An Ab Initio Study. Phys. Rev. B 95, 085207. doi:10.1103/physrevb.95.085207

CrossRef Full Text | Google Scholar

Zeng, J., He, X., Liang, S.-J., Liu, E., Sun, Y., Pan, C., et al. (2018). Experimental Identification of Critical Condition for Drastically Enhancing Thermoelectric Power Factor of Two-Dimensional Layered Materials. Nano Lett. 18, 7538–7545. doi:10.1021/acs.nanolett.8b03026

PubMed Abstract | CrossRef Full Text | Google Scholar

Zevalkink, A., Pomrehn, G., Takagiwa, Y., Swallow, J., and Snyder, G. J. (2013). Thermoelectric Properties and Electronic Structure of the Zintl-phase Sr3AlSb3. ChemSusChem 6, 2316–2321. doi:10.1002/cssc.201300518

PubMed Abstract | CrossRef Full Text | Google Scholar

Zevalkink, A., Zeier, W. G., Pomrehn, G., Schechtel, E., Tremel, W., and Snyder, G. J. (2012). Thermoelectric Properties of Sr3GaSb3 - a Chain-Forming Zintl Compound. Energy Environ. Sci. 5, 9121–9128. doi:10.1039/c2ee22378c

CrossRef Full Text | Google Scholar

Zhang, J., Song, L., Sist, M., Tolborg, K., and Iversen, B. B. (2018). Chemical Bonding Origin of the Unexpected Isotropic Physical Properties in Thermoelectric Mg3Sb2 and Related Materials. Nat. Commun. 9 (1), 1–10. doi:10.1038/s41467-018-06980-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., and Iversen, B. B. (2019). Fermi Surface Complexity, Effective Mass, and Conduction Band Alignment in N-type Thermoelectric Mg3Sb2 - xBix from First Principles Calculations. J. Appl. Phys. 126, 085104. doi:10.1063/1.5107484

CrossRef Full Text | Google Scholar

Zhang, J., Song, L., and Iversen, B. B. (2019). Insights into the Design of Thermoelectric Mg3Sb2 and its Analogs by Combining Theory and experiment. npj Comput. Mater. 5, 1–17. doi:10.1038/s41524-019-0215-y

CrossRef Full Text | Google Scholar

Zhang, X., and Zhao, L.-D. (2015). Thermoelectric Materials: Energy Conversion between Heat and Electricity. J. Materiomics 1, 92–105. doi:10.1016/j.jmat.2015.01.001

CrossRef Full Text | Google Scholar

Zhao, L.-D., Lo, S.-H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow thermal Conductivity and High Thermoelectric Figure of merit in SnSe Crystals. Nature 508, 373–377. doi:10.1038/nature13184

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L.-D., Tan, G., Hao, S., He, J., Pei, Y., Chi, H., et al. (2016). Ultrahigh Power Factor and Thermoelectric Performance in Hole-Doped Single-crystal SnSe. Science 351, 141–144. doi:10.1126/science.aad3749

PubMed Abstract | CrossRef Full Text | Google Scholar