
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Mech. Eng., 08 July 2022
Sec. Solid and Structural Mechanics
Volume 8 - 2022 | https://doi.org/10.3389/fmech.2022.861554
This article is part of the Research TopicHydromechanical Instabilities in Geomaterials: Advances in Numerical Modeling and Experimental TechniquesView all 7 articles
 Qi Liu
Qi Liu J. Carlos Santamarina*
J. Carlos Santamarina*Single and multi-phase fluids fill the pore space in sediments; phases may include gases (air, CH4, CO2, H2, and NH3), liquids (aqueous solutions or organic compounds), and even ice and hydrates. Fluids can experience instabilities within the pore space or trigger instabilities in the granular skeleton. Then, we divided fluid-driven instabilities in granular media into two categories. Fluid instabilities at constant fabric take place within the pore space without affecting the granular skeleton; these can result from hysteresis in contact angle and interfacial tension (aggravated in particle-laden flow), fluid compressibility, changes in pore geometry along the flow direction, and contrasting viscosity among immiscible fluids. More intricate fluid instabilities with fabric changes take place when fluids affect the granular skeleton, thus the evolving local effective stress field. We considered several cases: 1) open-mode discontinuities driven by drag forces, i.e., hydraulic fracture; 2) grain-displacive invasion of immiscible fluids, such as desiccation cracks, ice and hydrate lenses, gas and oil-driven openings, and capillary collapse; 3) hydro-chemo-mechanically coupled instabilities triggered by mineral dissolution during the injection of reactive fluids, from wormholes to shear band formation; and 4) instabilities associated with particle transport (backward piping erosion), thermal changes (thermo-hydraulic fractures), and changes in electrical interparticle interaction (osmotic-hydraulic fractures and contractive openings). In all cases, we seek to identify the pore and particle-scale positive feedback mechanisms that amplify initial perturbations and to identify the governing dimensionless ratios that define the stable and unstable domains. A [N/m] Contact line adhesion
Contrary to the generalized use of equivalent continuum models, instabilities often emerge and determine the macroscale response of granular materials. They can result from mechanical actions (e.g., shear and compaction bands) or from coupled processes such as hydro-mechanically coupled hydraulic fractures or chemo-mechanically coupled contraction cracks. Multi-phase fluids add additional mechanisms that can result in pore-scale and macro-scale instabilities, from Haines jumps to segregated ice lenses and giant desiccation cracks.
Instabilities can determine deformation and pressure fields and control fluid transport and the “geo-plumbing” of the formation. Furthermore, instabilities affect the upscaling of laboratory results to the field and all engineering analyses and designs such as foundations, subsurface structures, resource recovery and geological storage.
At the macro-scale, instabilities imply a non-convex potential energy surface (Kochmann and Bertoldi, 2017). At the particle/pore-scale, instabilities involve positive feedback mechanisms that exacerbate the effects of initial perturbations.
Table 1 compiles observed/reported fluid-driven instabilities that take place at constant fabric or cause fabric changes. The following sections analyze the evolution of such fluid-driven instabilities in granular materials to identify underlying pore and particle scale processes. We conducted cast analyses within the framework of particle/pore scale dimensionless ratios to identify the governing parameters that define stable and unstable regimes.
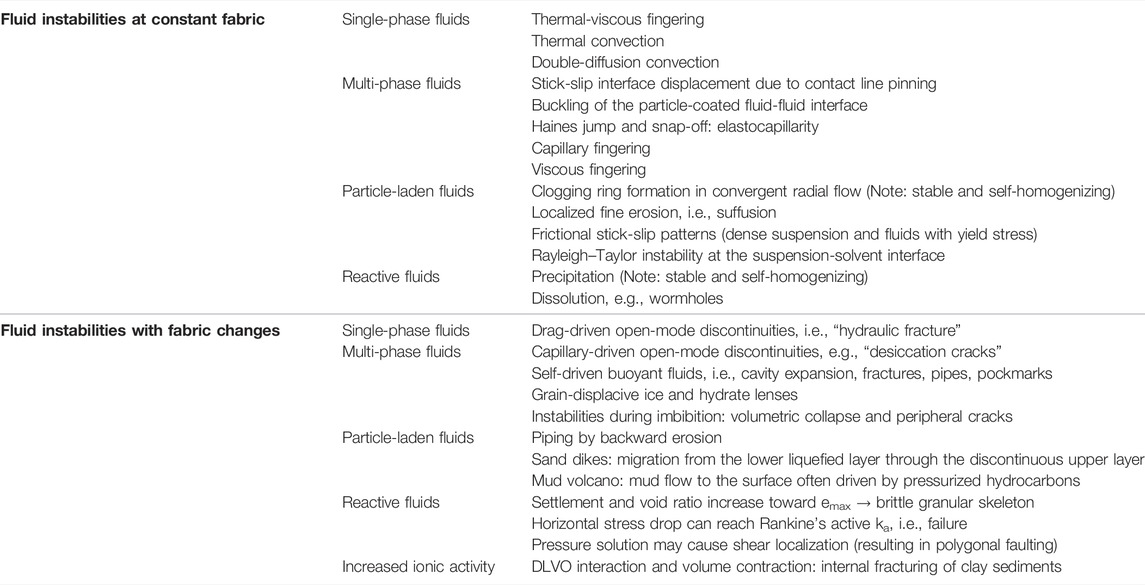
TABLE 1. Fluid-driven instabilities in granular materials. Examples are organized into instabilities 1) at constant fabric and 2) with fabric changes.
We first consider the various forms of instabilities that emerge during fluid invasion/flow through a rigid porous medium, i.e., without mechanical coupling. We explore single and multi-phase fluids, particle-laden fluids, and reactive fluids.
The pore space in sediments is often occupied by more than one fluid. Multi-phase fluids affect unsaturated soil behavior, oil and gas recovery, energy chemical geostorage, CO2 geostorage, and the remediation of ground contaminated with light non-aqueous phase liquids (LNAPLs) or dense non-aqueous phase liquids (DNAPLs). The various phases may include gases (air, CH4, CO2, H2, NH3), liquids (aqueous solutions and organic compounds), and even ice and hydrates.
Interfacial tension. A molecule at the interface between two fluids experiences different intermolecular forces than the same molecule in the bulk fluid (Figure 1). This asymmetry manifests as a surface tension between the phases. Dissolved salts, surfactants, and suspended colloids affect the surface tension; the Gibbs adsorption isotherm relates the interfacial tension under thermodynamic equilibrium
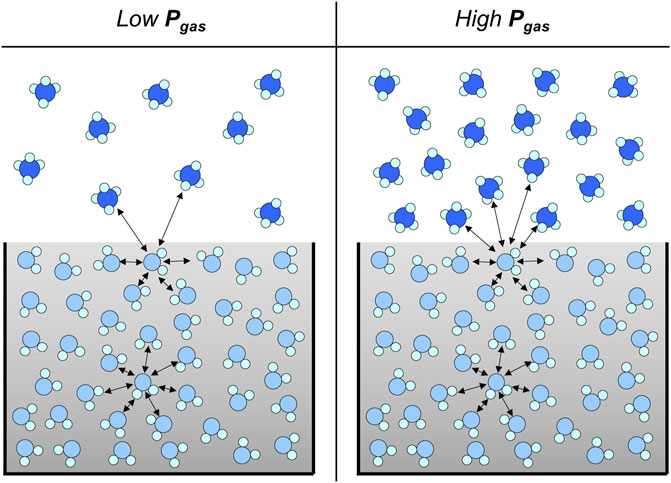
FIGURE 1. Interfacial tension. Intermolecular forces at the interface between a liquid and a gas to demonstrate that the interfacial tension decreases with increasing gas pressure.
Fluid interfaces contract and extend as they traverse the converging-diverging pore geometry in soils. Thus, we should consider the transient state of the interface instead of the equilibrium state in the analysis of multi-phase fluid flow (Jang et al., 2016; Liu et al., 2021). Time-dependent adsorption/desorption of surfactants or colloidal particles (e.g., nanoparticles, bacteria, and asphaltenes) controls interfacial tension during interface expansion and contraction. The Langmuir model provides the simplest description of adsorption and desorption kinetics (Langmuir, 1918; Chang and Franses, 1992; He et al., 2015). The adsorption energy increases with particle size; therefore, particles larger than >10 nm tend to experience irreversible adsorption into the interface in contrast to surfactants (Hua et al., 2016). Figure 2 shows the interfacial tension hysteresis loop of a surfactant solution and a nanofluid droplet in a decane bath (silica nanoparticles: d = 76 nm; surfactant: CTAB). Surfactant-coated interfaces exhibit higher hysteresis compared to particle-coated interfaces; in both cases, the interfacial tension increases during rapid droplet expansion.
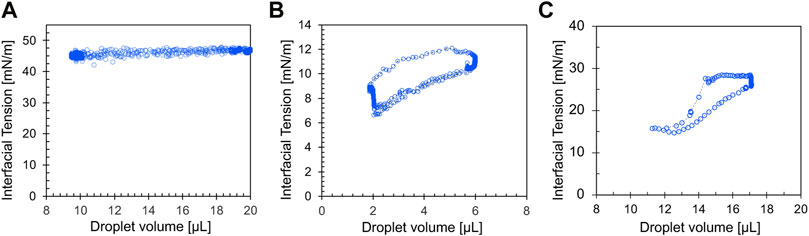
FIGURE 2. Interfacial tension hysteresis. (A) Water droplet in decane. (B) CTAB solution droplet in decane. (C) Nanofluid droplet in decane. (Benitez, 2022).
Contact angle. Young’s equation predicts the contact angle

FIGURE 3. Contact angle: the effect of contact line adhesion on contact angle hysteresis. (A) Young’s contact angle. (B) Advancing contact angle. (C) Receding contact angle.
In contrast to the single thermodynamic contact angle predicted by Young’s equation, interfaces can exhibit a range of contact angles between two asymptotic values: the advancing contact angle
The three phases, L-V-S, meet at the contact line. The contact line adhesion A acts against the intended motion and it can be estimated from the advancing and receding contact angles (Figures 3B,C):
The experimentally measured lateral adhesion force between a liquid droplet and a solid shows the maximum static adhesion followed by a reduced kinetic adhesion, which is remarkably analogous to solid-solid friction (Gao et al., 2018). Surfactants and particles adsorbed at the interface result in complex interface-substrate interaction which alters the contact line pinning.
Non-convex displacement-dependent capillary pressure. The varying pore geometry along the invasion path, transient contact angle behavior, and hysteretic interfacial tension result in non-convex capillary pressure vs. displacement signatures.
1) Varying pore-geometry along the invasion path. Consider the displacement of a wetting liquid by a non-wetting fluid across a pore constriction with a sinusoidal geometry as illustrated in Figure 4A (viscosity and gravity effects are negligible for small capillary and Bond numbers). The pressure difference between the wetting and the non-wetting fluids Δu(x) at position x is a function of the surface tension
where
2) Contact line pinning and sliding. Typically, the contact line remains pinned onto the pore wall until it reaches the asymptotic contact angle; thereafter, the contact line slides and the advancing contact angle remains constant (Figure 5A). For nanoparticle coated fluid interfaces, they may reach a peak contact angle followed by a pronounced post-peak relaxation to a lower contact angle during steady displacement (Figures 5B,C).
3) Buckling of nanoparticle coated interfaces. The particle surface coverage increases as the interface area decreases across a pore constriction; eventually, a particle shell forms and interfacial tension reverses to compression (Liu et al., 2021). At some point, the shell may buckle or crumple. The buckling resistance is determined by particle-particle and particle-interface interactions. And boundary conditions affect buckling patterns (Meyer et al., 2006; Liu et al., 2021).

FIGURE 4. Haines jumps. (A) Elastic and capillary interactions. Pore scale mechanisms: (B) soft fluid by entrapped gas bubble; (C) deformable soft matrix; (D) interacting menisci (modified from Sun and Santamarina, 2019b).
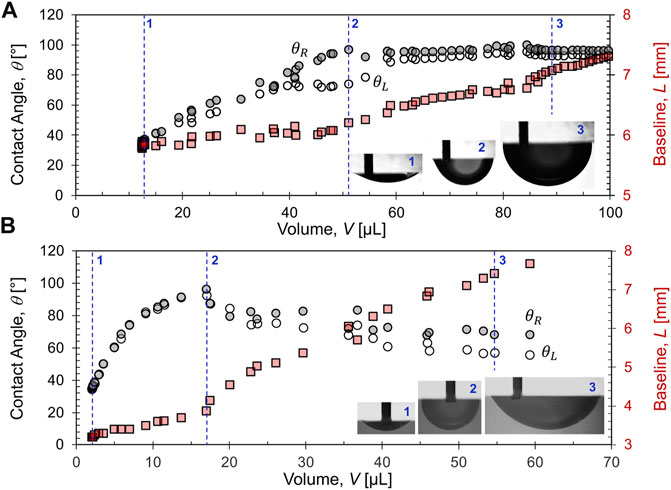
FIGURE 5. Contact line sliding and jumping. (A) Oil droplet in DI water. (B) Oil droplet in nanofluid (data from Sun et al., 2022).
Soft-system response → Instabilities (Haines jumps and snap-offs). The system deforms in response to changes in capillary pressure. Common causes for a soft system response include 1) the presence of entrapped gas, 2) interacting menisci, and 3) a deformable solid matrix (Figure 4—Note: a deformable solid matrix implies mechanical coupling with the mineral skeleton). Then, displacement-dependent capillarity couples with pressure-dependent volume change to cause “jump” instabilities similar to frictional stick-slip (Sun and Santamarina, 2019b). The sudden local jump of the fluid interface—often known as a Haines jump—causes a transient pressure change and fluid redistribution (Morrow and Szabo, 1970; Gauglitz and Radke, 1989; Berg et al., 2013).
The actual system volume response
A jump will occur during either advancing or receding when the resultant ΔP-vs-
A system with an elastocapillary number Nec<1 is prone to Haines instabilities.
Wetting fluids transported along corners and crevices or left behind during sudden jumps, i.e., “snap-off,” may accumulate at pore throats to form plugs that split the traversing non-wetting fluid (Figure 6). Snap-offs and plugs result in foam generation inside the porous medium (Lenormand et al., 1983; Peña et al., 2009).
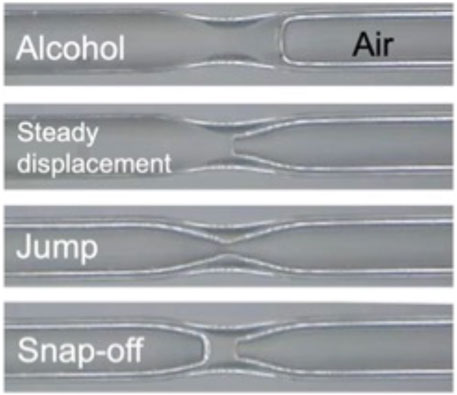
FIGURE 6. Changes in pore geometry along the advancing path: jumps and snap-offs (Jang et al., 2016).
Viscous and capillary fingers. Immiscible fluid displacement is controlled by capillary force FC, viscous force FD, and the buoyant force Fb. Critical dimensionless numbers are the capillary number, the viscous ratio and the Bond number (Chatzis and Morrow, 1984; Lenormand et al., 1988; Dawson and Roberts, 1997; Ferer et al., 2004; Santamarina and Jang, 2011; Zhao et al., 2016; see Zhao et al., 2019 for pore-scale modeling methods):
Patterns observed during immiscible fluid invasion (i.e., non-wetting) fall into domains defined by these dimensionless numbers: stable displacement takes place at large M and Ca; viscous fingering at small M and large Ca; and capillary fingering at large M and small Ca (Figure 7). The Rayleigh-Taylor instability, observed when a lighter fluid ascends through a heavier fluid, develops at large Bond numbers. Different invasion modes lead to distinct fluid pressure fields: the pressure drop occurs mainly in the more viscous phase, i.e., the invading phase in stable displacement or the defending phase in viscous fingering; on the other hand, the viscous pressure drop is negligible compared to the capillary pressure difference between the fluids in the capillary fingering regime (An et al., 2020).
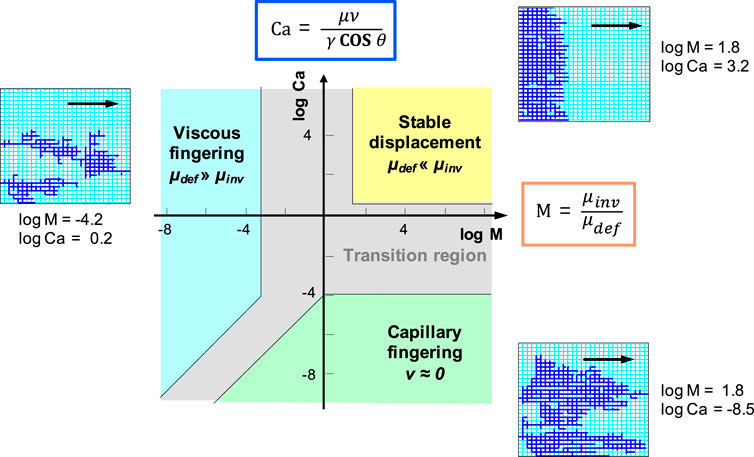
FIGURE 7. Mixed fluid instabilities at constant fabric. Regimes for viscous fingering, capillary fingering, and stable displacement in the space defined by the capillary number Ca and viscous ratio M (Schematic representation—after Lenormand et al., 1988. Pore network simulations are conducted by Sheng Dai.).
Viscous fingering can also occur in a single phase fluid due to thermal effects, such as during the injection of a hot liquid (low viscosity) into a porous medium saturated with the same liquid at low temperature (higher viscosity)Note: invasion regularizes as temperature homogenizes) (Helfrich, 1995; Islam and Azaiez, 2010). Thermal viscous fingering may be accompanied by convective currents triggered by the fluid’s thermal expansion and density changes.
Inherent pore size variability results in preferential flow pathways across sediments; in fact, as few as 10% of pores may be responsible for more than 50% of the total flow rate (Jang et al., 2011). Note: Flow channeling is even more pronounced in fractures and fractured rock masses (National Academies of Sciences, Engineering, and Medicine, 2020; Cardona et al., 2021). These preferential flow paths will also deliver the majority of the reactants to cause either dissolution or precipitation within the soil mass.
Precipitation is a self-homogenizing process: it reduces transport along preferential flow paths and reactive fluids deviate to other pathways. On the other hand, dissolution tends to localize due to positive feedback; preferential flow channels enlarge and lead to increased flow focusing and “wormhole” formation (Menke et al., 2017; Derr et al., 2020). Wormholes affect dam stability (Romanov et al., 2003), CO2 sequestration (Kim and Santamarina, 2015), groundwater transport in karst terrain (Dreybrodt, 1990), and acid stimulation of oil reservoirs (Fredd and Scott Fogler, 1998; Al-Arji et al., 2021). In the absence of advection, diffusive reactant transport promotes homogeneous dissolution.
The previous discussion suggests that dissolution topologies in rigid porous media such as in rocks depend on three concurrent processes: diffusion, advection, and chemical reaction. Two dimensionless ratios combine the three time scales for advection tadv, diffusion tdiff, and reaction tr for a channel length Lch:
where the process parameters are the kinetic rate of the reaction k [1/s], the average pore velocity v [m/s] and the diffusion coefficient D [m2/s]. The Pe-Da diagram in Figure 8 captures the space for the various dissolution topologies: compact dissolution, conical wormhole, dominant wormhole, ramified wormhole, and uniform dissolution regimes. Low advection velocities—long tadv and small Pe—allow reactant consumption near the inlet and instabilities cannot develop; conversely, very high advection velocities—short tadv, high Pe and small Da—carry reactants throughout the porous medium from inlet to outlet and favors a stable homogeneous dissolution. Wormholes develop with intermediate flow rates—large Da and Pe-—so that reactants act preferentially along flow channels. Finally, we note that extensive dissolution in granular materials will cause fabric changes, as discussed later in this manuscript.
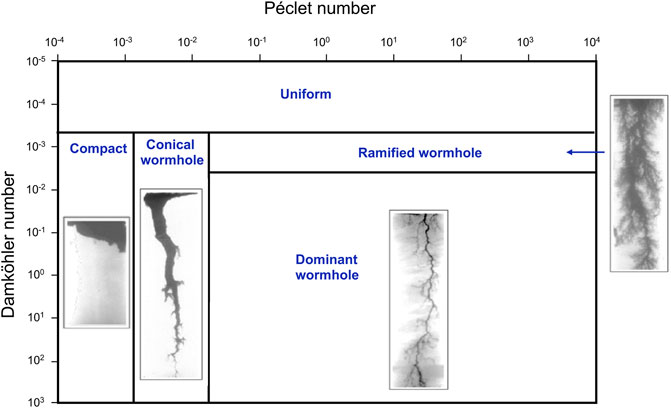
FIGURE 8. Dissolution regimes without fabric changes. Instabilities in the space defined by Péclet and Damköhler numbers (modified by Golfier et al., 2002; images from Fredd, 2000).
Particle-laden fluids are common in nature (e.g., ground water flow) and frequently used in engineered applications (tremie submerged construction, drilling muds, and well stimulation and proppants).
Particle inclusion changes the liquid density, rheology, and interfacial properties. Density triggers convective fingers in water columns, as seen during the release of mine waste slurries in large water bodies (Rayleigh-Taylor instability; Lange et al., 1998; Völtz et al., 2002).
The suspension viscosity increases with a higher mineral volume fraction and more frequent inter-particle interactions result in fluids with yield stress; then, instabilities readily emerge. For example, air injection into dense granular suspensions results in bubble migration with frictional stick-slip characteristics and viscous fingering (Sandnes et al., 2011).
A particle embedded in a moving fluid experiences buoyant weight FB, drag FD, inertia against motion changes FI, and electrical interaction with pore walls Fwall (it combines van der Waals and electrostatic forces, including hydrophobic adhesion forces). These forces combine to produce self-stabilizing clogging rings in convergent radial flow (negative feedback during fluid extraction), and fingered erosion during outward fluid flow (positive feedback during fluid injection) (Valdes and Santamarina, 2006; Valdes and Carlos Santamarina., 2007; Liu et al., 2019). The dimensionless ratios between interacting forces define the various particle migration regimes in terms of the particle size d, obstacle size D, particle and fluid mass densities
Clogged pore constrictions alter flow in nearby open paths, affect retardation, and may promote neighboring clogging. Experimental observations show that the probability of neighboring clogging is much higher than the probability of independent clogging (Liot et al., 2018; Van Zwieten et al., 2018; Liu et al., 2019).
Under mixed-phase conditions, particle-laden fluids may experience preferential particle accumulation at the interface with other immiscible fluids, e.g., hydrophobic nanoparticles suspended in water. This situation may stabilize interfaces and hinder coalescence (e.g., Pickering emulsions) or prompt pore-scale interfacial instabilities such as interface buckling and the stick-slip response of the contact line, as reviewed earlier. Under radial flow conditions (fluid injection), particle bands develop away from the injection point due to gravity and inertia; additional injection can break the particle bands and form erosion fingers (Kim et al., 2017).
Pressure gradients, capillarity, mineral dissolution, and various forms of flow localization in rigid porous media may collude with the granular nature of soils and sediments to give rise to mechanically coupled instabilities that cause fabric changes. At the macroscale, mechanical coupling implies changes in effective stress. At the particle scale, these instabilities reflect the interplay between particle level forces. The following sections analyze fluid-driven instabilities with fabric changes and the underlying forces; given the wide range of possible interactions, the list is limited to frequently encountered field conditions.
The effective stress principle σ’ = σ-u anticipates a gradient in effective stress when there is a fluid pressure gradient dσ’/dx = −du/dx. At the particle level, the flowing fluid gradually transfers its pressure as viscous drag onto the particles; hence, pressure decreases and interparticle skeletal forces accumulate in the direction of fluid flow. Then, the ab initio formation of a fluid-driven open mode discontinuity involves the following sequence of events: fluid injection at a point causes radial fluid flow; drag forces push particles away from the injection point, i.e., cavity expansion; tangential extension and the particles’ relative displacement result in a surface imperfection that facilitates preferential fluid flow; arising tangential drag forces cause further interparticle separation (Figure 9C). The positive feedback built into this sequence of events leads to the development of open-mode discontinuities, including planar “hydraulic fractures” (Shin and Santamarina, 2010; 2011b; Carrillo and Bourg, 2021) as well as tubular pipes (Cartwright and Santamarina, 2015). Note: the term “open-mode discontinuity” is preferred instead of “fracture” in the context of granular materials, i.e., without cohesion; moreover, models that are based on classical fracture mechanics are inadequate for the analysis of open mode discontinuities in granular materials.
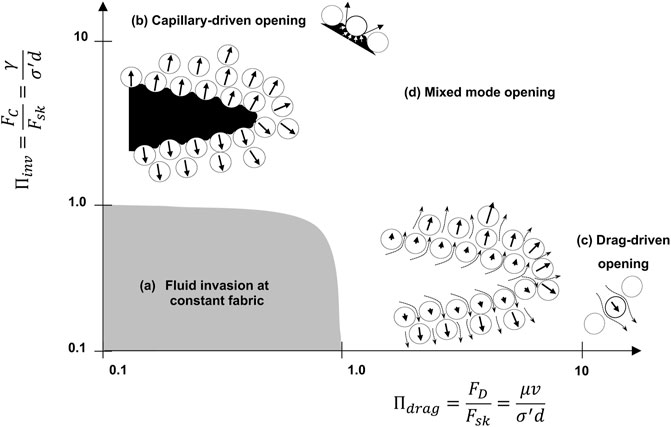
FIGURE 9. Grain-displacive open-mode discontinuities. (A) Fluid invasion without fabric changes. (B) Capillary-driven opening: surface tension and the difference in fluid pressures across the fluid interface are responsible for the resulting particle forces. (C) Drag-driven opening: drag forces push particles and accumulate away from the opening. (D) Mixed mode opening.
Particles experience two forces in single-phase fluid flow (without changes in pore fluid chemistry): the skeletal force
Therefore, high invasion velocity v, low effective stress σ’ and small grain size d favor the development of drag-driven open-mode discontinuities.
Earthquakes are natural triggers of fluid-driven localizations. When saturated loose sands liquefy during an earthquake, the liquefied layer typically forms at a depth 5 m < z < 20 m, i.e., sufficiently deep to be contractive but shallow enough so that the dynamic strain exceeds the elastic threshold strain (Ishihara, 1993; 1997). During liquefaction, the effective stress vanishes and the pore fluid pressure reaches the overburden stress (Ishihara, 1993; Lee and Santamarina, 2007). The excess pore pressure may gradually drain through the upper unliquefied layer or trigger a vertical open-mode discontinuity for rapid drainage; in fact, the aligned sand boils often observed on grassy fields reveal the underlying open discontinuity that links the liquefied layer to the surface (Chameau et al., 1991; Bardet and Kapuskar, 1993; Schneider and Mayne, 2000; Sukkarak et al., 2021).
Immiscible fluids experience capillarity in the pore space of granular materials, and the wetting fluid is at a lower pressure than the non-wetting fluid, Δu = un-uw. The granular skeleton picks up the pressure difference in terms of a change in effective stress (hence, Bishop’s model). At the particle scale, the capillary force acting on a particle FC = πd⋅γ can significantly alter the preexisting effective stress dependent particle forces Fsk = σ′d2, where d is the particle diameter and γ the interfacial tension. The ratio between these two forces
defines two distinct invasion regimes (Figure 9 - Shin and Santamarina, 2011b; see also Holtzman et al., 2012; Carrillo and Bourg, 2021):
1) pore-invasive
2) grain-displacive
In general, invasion is grain-displacive in fine-grained sediments at low effective stress. Still, other forms of mixed-fluid instabilities can take place in coarse-grained sediments, but these are mechanically decoupled from the granular skeleton (refer to “fluid-driven instabilities at constant fabric” described in the previous section).
The concepts of interfacial tension, contact angle, and capillary pressure explored earlier for immiscible fluids can be extended to analyze other systems, including water-ice (i.e., frozen ground engineering) and water-hydrates (i.e., hydrates bearing sediments). Often, the immiscible fluid invades the boundary and remains as a continuous phase. However, ice, hydrate, and gas bubbles, may nucleate inside the porous. Examples of gas nucleation include exsolution during depressurization (e.g., sampling marine sediments), water cavitation (e.g., rapid shear induced dilation under undrained conditions), or heat-induced phase transformation. Boundary invasion or internal nucleation may result in the same degree of saturation, yet there are salient differences in other macroscale physical properties such as the capillarity pressure vs. degree of saturation, relative permeabilities, bulk stiffness, consolidation, and shear strength (Sills et al., 1991; Rebata-Landa and Santamarina, 2012; Jang and Santamarina, 2014).
Desiccation cracks: non-wetting air invasion into a water-saturated sediment. Consider a clay bed sedimented from a slurry. The supernatant water evaporates until the air-water interface reaches the sediment surface. Further evaporation requires the interface to go down, but the air-water clings onto the water-wet mineral grains, dragging them down (internally, the water experiences suction and the effective stress increases). Eventually, the sediment will resist further compaction, and additional suction causes the air-water interface to invade the sediment, starting at the largest pores (often associated with surface defects). At the invaded defect, suction causes particle displacement normal to and away from the air-water interface. Thus particles displace away from each other at the tip, further air invasion takes place, and eventually forms a desiccation crack (Figures 10A,B; Shin and Santamarina, 2011b; 2011a; Cordero et al., 2017). Desiccation cracks may also nucleate and grow within the sediment, i.e., beneath the surface, when suction triggers gas exsolution or cavitation within the sediment (Figure 10C - Zhao and Santamarina, 2020).
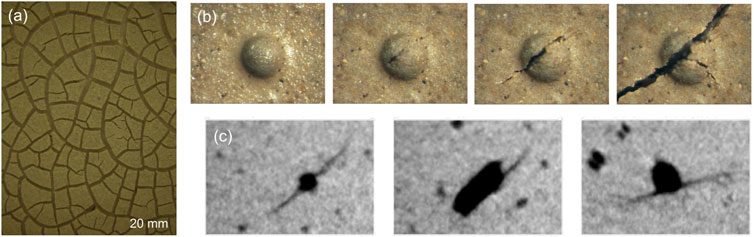
FIGURE 10. Grain-displacive non-wetting fluid invasion: desiccation cracks. (A) Surface desiccation cracks (Shin and Santamarina, 2011b). (B) Crack initiation at a surface defect during drying (Shin and Santamarina, 2011a). (C) Internal desiccation cracks observed using X-ray micro CT (Zhao and Santamarina, 2020).
Non-wetting buoyant fluid columns. Buoyant oil or gas with a density ρb may mobilize long column heights H; then, the capillary pressure at the top of the column is
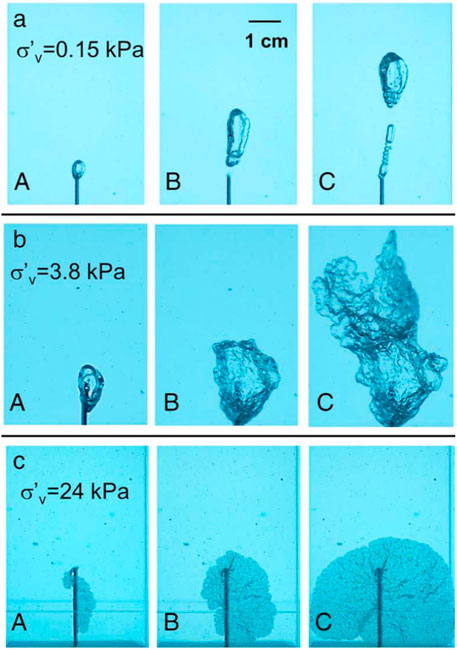
FIGURE 11. Grain-displacive gas migration in a transparent fine-grained granular medium at different vertical effective stress levels: (A) bubble at
Non-wetting ice and hydrate growth in sediments - The local effective stress. Ice and hydrates require the proper pressure and temperature conditions for phase stability; in addition, hydrate formation is typically gas-limited. When appropriate, both ice and hydrate nucleate on mineral surfaces (heterogeneous nucleation) and grow into the pore space until they reach the surrounding pore walls. Further growth of the non-wetting ice or hydrate phases is either pore invasive
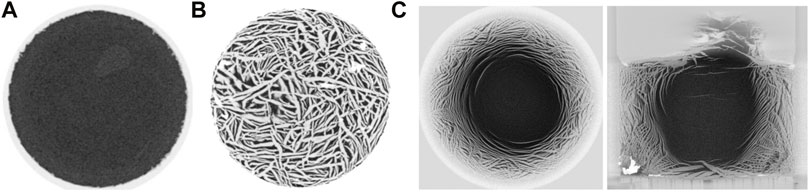
FIGURE 12. Frozen soil. (A) Pore invasive ice formation in sand (no lenses). Grain-displacive ice lenses in (B) bentonite paste and in (C) kaolinite paste (Viggiani et al., 2015).
The onion-like topology of ice lenses in Figure 12C suggests that the growth of grain-displacive instabilities reflects the evolving local effective stress. To test this hypothesis, we prepared cylindrical disk specimens using water saturated kaolinite paste; after consolidation to

FIGURE 13. Grain-displacive ice lens formation is affected by and eventually affects the local effective stress (Note: this observation applies to all fluid-driven instabilities that affect fabric). (A) Ice lens nucleates and grows at the tip of the wedge when the tip is under tension. (B) Ice lenses grow at various locations at a distance from the tip when the tip is under compression. Sketches on the left show the experimental configurations (Yun, 2005).
Wetting fluid imbibition: capillary contraction. Spontaneous water imbibition into a dry or partially saturated hydrophilic soil tends to cause volume contraction as capillary forces pull particles towards the invading water front. Potential instabilities include peripheral open-mode discontinuities surrounding the area subjected to wetting, and pronounced volume collapse (e.g., collapsible loess—combines cementation dissolution and loss of suction at interparticle contacts—Barden, McGown and Collins, 1973; Houston et al., 1988; Rinaldi et al., 2001; Lourenco et al., 2012; Bruchon et al., 2013; Li et al., 2016). On the other hand, partially saturated, dense soils and soils with swelling minerals may swell when water content increases (Berney, 2004).
Reactive fluids traverse the granular medium, causing either mineral dissolution or precipitation. Precipitation is self-homogenizing because transmissivity decreases more rapidly along the more conductive pathways (i.e., negative feedback); overall, precipitation produces a marked increase in stiffness, dilative tendency, and strength (by either adding cohesion or increasing the friction angle —Jung et al., 2012).
On the other hand, post-depositional dissolution is significantly more complex. Initially, dissolution evolves as predicted in the dimensionless Pe-Da space for rigid porous media (Figure 8). Rather than wormhole formation (limited by arching instability), grain dissolution readily affects interparticle coordination and forces, triggers fabric rearrangement, and the void ratio evolves towards a stress-dependent terminal value closer to emax. Consequently, both hydraulic and mechanical properties are affected; in particular, there is an increased contractive tendency (Cha and Santamarina, 2014). Furthermore, experimental and discrete element DEM simulation results show that 1) the horizontal stress ratio ko decreases during dissolution and it can reach the active value ka (i.e., internal shear failure), often followed by horizontal stress recovery; 2) the anisotropy in coordination reaches a maximum as the stress ratio approaches ka, and 3) there is a marked difference in the internal fabric between the initial and post-dissolution conditions even if boundary stresses return to similar values (Shin and Santamarina, 2009; Cha and Santamarina, 2016, 2019a).
Minerals dissolve preferentially at grain contacts under high stress. Solutes diffuse towards the pore space and reprecipitate on unstressed grain surfaces nearby. (Note: this phenomenon is known as pressure solution Weyl, 1959; Rutter, 1983; Etheridge et al., 1984; Fowler and Yang, 1999; Croizé et al., 2010). Pressure-dependent mineral dissolution adds additional complexity: strong force chains in the granular skeleton collude with force-dependent dissolution to create the positive feedback dissolution that promotes the emergence of shear localization as the stress ratio (or force anisotropy) reaches failure conditions under zero lateral strain and constant vertical stress boundary conditions (Cha and Santamarina, 2019b). In the shear band, the porosity is higher and the coordination number is lower than in the surrounding soil mass, strong force chains form and grains experience faster dissolution (Figure 14). Shear discontinuities triggered by mineral dissolution may explain the non-tectonic origin of polygonal faults observed in marine sediments and lacustrine deposits (Cartwright and Dewhurst, 1998; Shin et al., 2008).
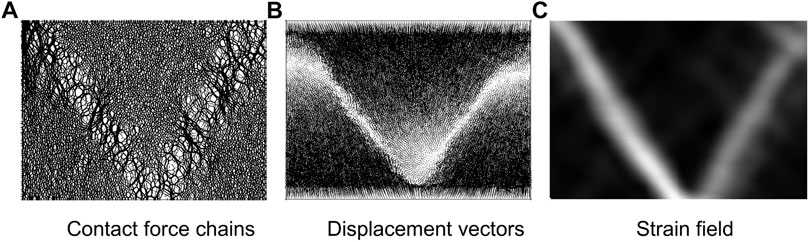
FIGURE 14. Shear bands during dissolution. Pressure solution creates the positive feedback mechanism that leads to shear band formation (modified from Cha and Santamarina, 2019b).
Flowing fluids can remove and drag grains away. Particle deposition takes place downstream as the flow velocity decreases and its carrying capacity diminishes. The geological record has extensive evidence of sediment erosion-and-deposition phenomena, including: cm-scale sand boils downstream of eroding dams; km-scale mud volcanoes (e.g., Lusi—Indonesia); pipes; and sand dikes observed in marine seismic sections (Hovland et al., 2002; Chand et al., 2012; Moss et al., 2012).
At low fine content, the overburden load is carried by the skeleton-forming coarse grains, and load-free fine particles can be detached and dragged away (Skempton and Brogan, 1994; Moffat et al., 2011). In this case, particle erosion is accompanied by an increase in hydraulic conductivity but without volume change (Suffusion—Fannin et al., 2015). Soils sensitive to suffusion fall under the GF(F), G(F), G(G), GS(S), S(F), or S(S) groups in the Revised Soil Classification System (See Castro et al., 2022). At the macroscale, the feedback mechanism in suffusion resembles dissolution channeling, yet mass removal takes place as grains rather than dissolved species.
On the other hand, energy-intensive erosion may gradually destabilize the load carrying skeleton, causing significant volumetric contraction and even skeletal collapse (suffosion). Regressive or backward erosion piping is a major concern in dam stability (a potential mechanism behind the Teton dam’s failure—Sherard, 1987). It requires long seepage pathways to minimize the gradient at the exit or filters against clay cores to prevent fine migration (Li and Jonathan Fannin, 2008; Chang and Zhang, 2013; Hendron, 2013; Robbins and Van Beek, 2015; Santamarina et al., 2019).
All forms of energy are coupled, including thermal, chemical, hydraulic, and mechanical THCM (Mitchell, 1991). Under the right boundary conditions, mechanically-coupled processes can eventually cause instabilities in granular media. Two examples follow:
1) Thermo-hydro-mechanical THM coupling: thermal water expansion can build up pore pressure and cause a hydraulic fracture if the rate of heating is higher than the rate of pore water pressure dissipation; both are diffusion processes, therefore the ratio
2) Chemo-hydro-mechanical CHM coupling: A diffusing salt front causes a pressure front that precedes it. The pressure front can produce a hydraulic fracture, followed by surface contraction cracks above it (recently observed by Mengwei Liu in our laboratory). These CHM-driven instabilities result from changes in electrical interparticle forces (van der Waals, double layer, osmotic) and may emerge in high specific surface fine-grained clayey sediments. By contrast, the dissolution-based instabilities described earlier apply to coarse-grained sediments such as silts and sands.

FIGURE 15. Thermo-hydro fractures. (A) Extensively fractured kaolinite paste after heating in microwave oven (scale = 1 mm). (B) Natural thermo-hydro fracture (scale = 25 m–Madain Saleh, Saudi Arabia).
The previous sections identified a wide range of localizations and described the underlying positive feedback mechanisms conducive to instabilities. Table 2 summarizes the critical dimensionless ratios involved in these processes. In all cases, we focused on pore and particle scale phenomena to analyze the initiation and evolution of instabilities.
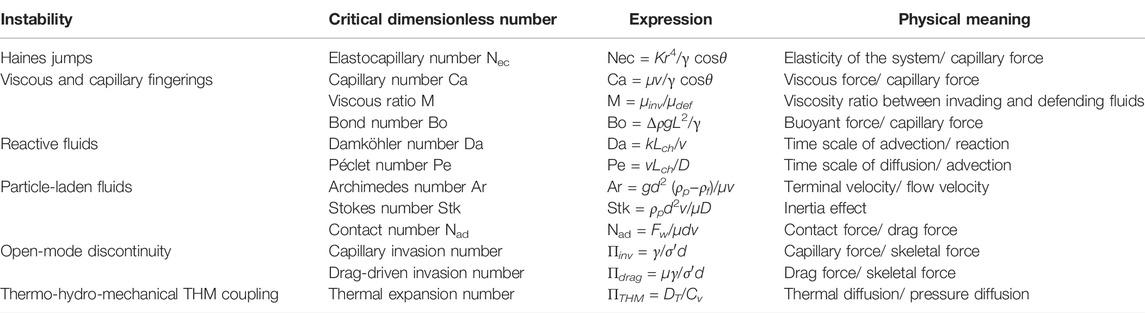
TABLE 2. Pore/particle scale dimensionless ratios that define the domains for fluid-driven instabilities. The selected ratios presented here resemble the analysis in the text.
Forces. The magnitude of interparticle forces is a function of grain-size; therefore, grain-size plays a central role in defining the space for various instabilities. Table 3 lists interparticle forces and corresponding equations for first-order estimates. We can see that grain weight FW, buoyancy and inertia relate to volume f (d3), the force acting on a grain that is part of a load carrying skeleton Fsk scales with its area f (d2), while drag FD, capillary FC, and electrical interactions are proportional to size f(d). These equations define straight lines in log-log plots; therefore, the different forces intersect at specific particle sizes. For example, self-weight and the capillary force are equal at d ≈ 2 mm; self-weight prevails for larger particles while capillarity gains relevance for finer soils. Similarly, we can anticipate that electrical interactions gain relevance for high specific surface submicron particles and vanish in silts and sands.

TABLE 3. Particle-level forces. They scale with d, d2+, and d3. The ratio between the skeletal force and all other forces confirms the importance of the particle buoyant weight in coarse-grained sediments and of capillary, drag, and electrical forces on phenomena that take place in fine-grained sediments (Mitchell, 1976; Santamarina, 2003).
Instability, nucleation, and growth. Scaling analyses and dimensionless ratios hide the intricate physical details at the pore/grain scales that eventually lead to macroscale instabilities. Localizations start at nucleation sites that are typically associated with the inherent variability in granular materials. For example, liquefaction and shear band formation are delayed in homogeneous sands compared to heterogeneous specimens at the same density (Frost et al., 2019). Similarly, desiccation cracks start at surface or subsurface imperfections, or “dimples” (see Figure 11), and dissolution wormholes evolve from the preferential conduction paths initially present in the porous network. In fact, numerical simulations that capture natural variability systematically render more “natural” results (e.g., a porosity random field with or without spatial correlation).
After nucleation, positive feedback mechanisms sustain further growth. For example, there are pronounced differences in the interparticle forces around an open-mode discontinuity triggered by viscous forces (hydraulic fracture) and by capillary forces (e.g., desiccation crack or ice lens). Yet, particle forces cause unloading and extension at the opening tip in both cases, which favors water invasion (in hydraulic fractures) and interface invasion (in desiccation cracks and ice lenses). Therefore, macroscale simulations require particularly sensitive relations between the permeability and void ratio (hydraulic fracture), or the entry pressure and void ratio (in desiccation cracks).
We can extend this discussion to all forms of fluid-driven granular instabilities; analysis and simulations must capture the governing conditions in terms of dimensionless ratios, recognize the local pore and grain-scale processes, identify the source of positive feedback, and select constitutive relations with high sensitivity to local changes.
Local vs. global instabilities. The evolution of local instabilities may cease and not evolve into large scale instabilities. For example, 1) the contact line displacement for a liquid advancing on a flat surface consists of numerous local stick-slip events, yet the macro-scale movement and front geometry may appear smooth (high frequency jumps are aliased in most observations); 2) pore-scale Haines jumps do not necessarily define macroscale invasion patterns; and 3) viscous fingers reach a characteristic length scale. On the other hand, dissolution wormholes can grow beyond the scale of the engineering problem under consideration. In some cases, the upscaling of local instabilities to global instabilities will depend on global properties such as spatial variability in grain size, pore size, mineralogy, and contact forces.
Fluid-driven instabilities are ubiquitous in soils and sediments. However, they are often overlooked in the interpretation of laboratory studies as well as in analytical solutions and numerical simulations. These instabilities can emerge across scales and are readily observed in millimeter-scale microfluidic chips to kilometer-scale features in the geological record.
Some fluid-driven instabilities take place within the pore space without affecting the granular skeleton. These instabilities are driven by differences in viscosity between the invading and the defending fluids, interfacial tension, and capillarity and cause characteristic invasion patterns. Pore-scale capillary instabilities result from a combination of hysteresis in contact angle and interfacial tension, elastic deformations, and the longitudinal pore geometry. Sudden jumps in fluid interfaces and associated snap-offs cause rapid redistribution of phases. Particle-laden fluids may also cause instabilities in rigid porous media.
More intricate instabilities take place when fluids affect the granular skeleton. In general, hydro-thermo-chemo-mechanically coupled processes affect the sediment structure and can cause instabilities under certain conditions.
Fluid-driven instabilities coupled with fabric changes can be generated by viscous forces in single-phase fluid injection (hydraulic fracture) or by capillary forces produced by an immiscible fluid (grain-displacive invasion: desiccation cracks, ice and hydrate lenses, gas and oil-driven openings, and capillary collapse). The marked differences between viscosity and capillarity-driven open-mode discontinuities require careful analysis prior to numerical modeling.
Mineral dissolution caused by the injection of reactive fluids evolves as a function of the interplay between various rates (advection, diffusion, and reaction), the spatial distribution of reactive minerals, and the granular skeleton response during dissolution. Instabilities include wormhole formation and the emergence of shear bands (even in sediments under zero lateral strain conditions).
Other fluid-driven instabilities in granular materials are associated with particle transport (piping erosion), thermal changes (thermo-hydraulic fractures), and changes in electrical interparticle interaction (osmotic-hydraulic fractures and contractive openings).
In all cases, instabilities involve some form of positive feedback mechanism; conversely, self-homogenizing processes tend to be stabilizing for fluid flow and granular stability. The types of instabilities and their evolving topologies can be systematically organized in the space defined by dimensionless ratios of time (or rate), length scales, and forces (or pressure and stress).
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
G. Abelskamp edited the manuscript. M. Benitez obtained the hysteretic interfacial tension and contact angle data. Support for this research was provided by the KAUST Endowment.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Al-Arji, H., Al-Azman, A., Le-Hussain, F., and Regenauer-Lieb, K. (2021). Acid Stimulation in Carbonates: A Laboratory Test of a Wormhole Model Based on Damköhler and Péclet Numbers. J. Petroleum Sci. Eng. 203, 108593. doi:10.1016/J.PETROL.2021.108593
Al-Sahhaf, T., Elkamel, A., Suttar Ahmed, A., and Khan, A. R. (2005). The Influence of Temperature, Pressure, Salinity, and Surfactant Concentration on the Interfacial Tension of the N-Octane-Water System. Chem. Eng. Commun. 192, 667–684. doi:10.1080/009864490510644
An, S., Erfani, H., Godinez‐Brizuela, O. E., and Niasar, V. (2020). Transition From Viscous Fingering to Capillary Fingering: Application of GPU‐Based Fully Implicit Dynamic Pore Network Modeling. Water Resour. Res. 56 (12), e2020WR028149. doi:10.1029/2020WR028149
Andújar Márquez, J., Martínez Bohórquez, M., and Gómez Melgar, S. (2016). Ground Thermal Diffusivity Calculation by Direct Soil Temperature Measurement. Application to Very Low Enthalpy Geothermal Energy Systems. Sensors 16, 306. doi:10.3390/s16030306
Bachu, S., and Bennion, D. B. (2009). Interfacial Tension between CO2, Freshwater, and Brine in the Range of Pressure from (2 to 27) MPa, Temperature from (20 to 125) °C, and Water Salinity from (0 to 334 000) mg·L−1. J. Chem. Eng. Data 54, 765–775. doi:10.1021/je800529x
Barden, L., McGown, A., and Collins, K. (1973). The Collapse Mechanism in Partly Saturated Soil. Eng. Geol. 7, 49–60. doi:10.1016/0013-7952(73)90006-9
Bardet, J. P., and Kapuskar, M. (1993). Liquefaction Sand Boils in San Francisco during 1989 Loma Prieta Earthquake. J. Geotech. Engrg. 119, 543–562. doi:10.1061/(asce)0733-9410(1993)119:3(543)
Berg, S., Ott, H., Klapp, S. A., Schwing, A., Neiteler, R., Brussee, N., et al. (2013). Real-time 3D Imaging of Haines Jumps in Porous Media Flow. Proc. Natl. Acad. Sci. U.S.A. 110, 3755–3759. doi:10.1073/pnas.1221373110
Berney, E. S. (2004). A Partially Saturated Constitutive Theory for Compacted Fills. Available at: https://apps.dtic.mil/sti/citations/ADA425462 (Accessed April 26, 2022).doi:10.21236/ada425462
Bruchon, J.-F., Pereira, J.-M., Vandamme, M., Lenoir, N., Delage, P., and Bornert, M. (2013). Full 3D Investigation and Characterisation of Capillary Collapse of a Loose Unsaturated Sand Using X-Ray CT. Granul. Matter 15, 783–800. doi:10.1007/s10035-013-0452-6
Cardona, A., Finkbeiner, T., and Santamarina, J. C. (2021). Natural Rock Fractures: From Aperture to Fluid Flow. Rock Mech. Rock Eng. 54, 5827–5844. doi:10.1007/s00603-021-02565-1
Carrillo, F. J., and Bourg, I. C. (2021). Capillary and Viscous Fracturing during Drainage in Porous Media. Phys. Rev. E 103, 063106. doi:10.1103/PhysRevE.103.063106
Cartwright, J. A., and Dewhurst, D. N. (1998). Layer-bound Compaction Faults in Fine-Grained Sediments. Geol. Soc. Am. Bull. 110, 1242–1257. doi:10.1130/0016-7606(1998)110<1242:lbcfif>2.3.co;2
Cartwright, J., and Santamarina, C. (2015). Seismic Characteristics of Fluid Escape Pipes in Sedimentary Basins: Implications for Pipe Genesis. Mar. Petroleum Geol. 65, 126–140. doi:10.1016/j.marpetgeo.2015.03.023
Castro, G. M., Park, J., and Santamarina, J. C. (2022). Revised Soil Classification System RSCS: Implementation and Engineering Implications. Submitt. Publ.
Cha, M., and Santamarina, J. C. (2014). Dissolution of Randomly Distributed Soluble Grains: Post-dissolution K0-Loading and Shear. Géotechnique 64, 828–836. doi:10.1680/geot.14.p.115
Cha, M., and Santamarina, J. C. (2016). Hydro-chemo-mechanical Coupling in Sediments: Localized Mineral Dissolution. Geomechanics Energy Environ. 7, 1–9. doi:10.1016/j.gete.2016.06.001
Cha, M., and Santamarina, J. C. (2019a). Localized Dissolution in Sediments under Stress. Granul. Matter 21, 79. doi:10.1007/s10035-019-0932-4
Cha, M., and Santamarina, J. C. (2019b). Pressure-dependent Grain Dissolution Using Discrete Element Simulations. Granul. Matter 21, 101. doi:10.1007/s10035-019-0960-0
Chameau, J. L., Clough, G. W., Reyna, F., and Frost, J. D. (1991). Liquefaction Response of San Francisco Bayshore Fills. Bull. Seismol. Soc. Am. 81, 1998–2018. doi:10.1785/BSSA0810051998
Chand, S., Thorsnes, T., Rise, L., Brunstad, H., Stoddart, D., Bøe, R., et al. (2012). Multiple Episodes of Fluid Flow in the SW Barents Sea (Loppa High) Evidenced by Gas Flares, Pockmarks and Gas Hydrate Accumulation. Earth Planet. Sci. Lett. 331-332, 305–314. doi:10.1016/j.epsl.2012.03.021
Chang, C. H., and Franses, E. I. (1992). Modified Langmuir-Hinselwood Kinetics for Dynamic Adsorption of Surfactants at the Air/water Interface. Colloids Surfaces 69, 189–201. doi:10.1016/0166-6622(92)80230-Y
Chang, D. S., and Zhang, L. M. (2013). Extended Internal Stability Criteria for Soils under Seepage. Soils Found. 53, 569–583. doi:10.1016/j.sandf.2013.06.008
Chatzis, I., and Morrow, N. R. (1984). Correlation of Capillary Number Relationships for Sandstone. Soc. Pet. Eng. J. 24, 555–562. doi:10.2118/10114-pa
Cordero, J. A., Useche, G., Prat, P. C., Ledesma, A., and Santamarina, J. C. (2017). Soil Desiccation Cracks as a Suction-Contraction Process. Géotechnique Lett. 7, 279–285. doi:10.1680/jgele.17.00070
Croizé, D., Renard, F., Bjørlykke, K., and Dysthe, D. K. (2010). Experimental Calcite Dissolution under Stress: Evolution of Grain Contact Microstructure during Pressure Solution Creep. J. Geophys. Res. 115 (B9). doi:10.1029/2010JB000869
Dai, S., Santamarina, J. C., Waite, W. F., and Kneafsey, T. J. (2012). Hydrate Morphology: Physical Properties of Sands with Patchy Hydrate Saturation. J. Geophys. Res. 117, B11205. doi:10.1029/2012JB009667
Dawson, H. E., and Roberts, P. V. (1997). Influence of Viscous, Gravitational, and Capillary Forces on DNAPL Saturation. Groundwater 35, 261–269. doi:10.1111/j.1745-6584.1997.tb00083.x
de Gennes, P.-G. (1985). Wetting: Statics and Dynamics. Rev. Mod. Phys. 57, 827–863. doi:10.1103/revmodphys.57.827
Derr, N. J., Fronk, D. C., Weber, C. A., Mahadevan, A., Rycroft, C. H., and Mahadevan, L. (2020). Flow-Driven Branching in a Frangible Porous Medium. Phys. Rev. Lett. 125, 158002. doi:10.1103/PhysRevLett.125.158002
Dreybrodt, W. (1990). The Role of Dissolution Kinetics in the Development of Karst Aquifers in Limestone: a Model Simulation of Karst Evolution. J. Geol. 98, 639–655. doi:10.1086/629431
Eral, H. B., ’t Mannetje, D. J. C. M., and Oh, J. M. (2013). Contact Angle Hysteresis: A Review of Fundamentals and Applications. Colloid Polym. Sci. 291, 247–260. doi:10.1007/s00396-012-2796-6
Etheridge, M. A., Wall, V. J., Cox, S. F., and Vernon, R. H. (1984). High Fluid Pressures During Regional Metamorphism and Deformation: Implications for Mass Transport and Deformation Mechanisms. J. Geophys. Res. 89, 4344–4358. doi:10.1029/jb089ib06p04344
Fannin, R. J., Arulrajah, A., Slangen, P., Evans, R., Arulrajah, A., and Evans, R. (2015). Discussion: On the Distinct Phenomena of Suffusion and Suffosion. Geotech. Lett. 5, 129–130. doi:10.1680/jgele.15.0001710.1680/geolett.15.00017
Ferer, M., Ji, C., Bromhal, G. S., Cook, J., Ahmadi, G., and Smith, D. H. (2004). Crossover from Capillary Fingering to Viscous Fingering for Immiscible Unstable Flow: Experiment and Modeling. Phys. Rev. E 70, 16303. doi:10.1103/PhysRevE.70.016303
Fowler, A. C., and Yang, X. (1999). Pressure Solution and Viscous Compaction in Sedimentary Basins. J. Geophys. Res. 104, 12989–12997. doi:10.1029/1998jb900029
Fredd, C. N. (2000). Dynamic Model of Wormhole Formation Demonstrates Conditions for Effective Skin Reduction During Carbonate Matrix Acidizing. SPE Permian Basin Oil Gas. Recover. Conf. Proc. doi:10.2118/59537-ms
Fredd, C. N., and Fogler, H. S. (1998). Influence of Transport and Reaction on Wormhole Formation in Porous Media. AIChE J. 44, 1933–1949. doi:10.1002/aic.690440902
Frost, J. D., Roy, N., Chen, C.-C., Park, J.-Y., Jang, D.-J., Lu, Y., et al. (2019). Quantitative Analysis of Microstructure Properties and Their Influence on Macroscale Response. KSCE J. Civ. Eng. 23, 3777–3792. doi:10.1007/S12205-019-0713-Y
Gao, N., Geyer, F., Pilat, D. W., Wooh, S., Vollmer, D., Butt, H.-J., et al. (2018). How Drops Start Sliding over Solid Surfaces. Nat. Phys. 14, 191–196. doi:10.1038/nphys4305
Gauglitz, P. A., and Radke, C. J. (1989). Dynamics of Haines Jumps for Compressible Bubbles in Constricted Capillaries. AIChE J. 35, 230–240. doi:10.1002/aic.690350207
Gibbs, J. W. (1878). On the Equilibrium of Heterogeneous Substances. Am. J. Sci. s3-16, 441–458. doi:10.2475/ajs.s3-16.96.441
Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., and Quintard, M. (2002). On the Ability of a Darcy-Scale Model to Capture Wormhole Formation during the Dissolution of a Porous Medium. J. Fluid Mech. 457, 213–254. doi:10.1017/S0022112002007735
He, Y., Yazhgur, P., Salonen, A., and Langevin, D. (2015). Adsorption-desorption Kinetics of Surfactants at Liquid Surfaces. Adv. Colloid Interface Sci. 222, 377–384. doi:10.1016/j.cis.2014.09.002
Helfrich, K. R. (1995). Thermo-viscous Fingering of Flow in a Thin Gap: A Model of Magma Flow in Dikes and Fissures. J. Fluid Mech. 305, 219–238. doi:10.1017/S0022112095004605
Hendron, A. (2013). Improving Dam Safety with Lessons Learned from Case Histories of Dam Failures and Unacceptable Dam Performance. Karl Terzaghi Lect.
Holtzman, R., Szulczewski, M. L., and Juanes, R. (2012). Capillary Fracturing in Granular Media. Phys. Rev. Lett. 108, 264504. doi:10.1103/PhysRevLett.108.264504
Houston, S. L., Houston, W. N., and Spadola, D. J. (1988). Prediction of Field Collapse of Soils Due to Wetting. J. Geotechnical Eng. 114114, 401–458. doi:10.1061/(asce)0733-9410(1988)114:1(40)
Hovland, M., Gardner, J. V., and Judd, A. G. (2002). The Significance of Pockmarks to Understanding Fluid Flow Processes and Geohazards. Geofluids 2, 127–136. doi:10.1046/j.1468-8123.2002.00028.x
Hua, X., Bevan, M. A., and Frechette, J. (2016). Reversible Partitioning of Nanoparticles at an Oil-Water Interface. Langmuir 32, 11341–11352. doi:10.1021/ACS.LANGMUIR.6B02255
Ishihara, K. (1993). Liquefaction and Flow Failure during Earthquakes. Géotechnique 43, 351–451. doi:10.1680/geot.1993.43.3.351
Ishihara, K. (1997). Soil Behaviour in Earthquake Geotechnics. Choice Rev. Online 34, 5113. doi:10.5860/choice.34-5113
Islam, M. N., and Azaiez, J. (2010). Miscible Thermo-Viscous Fingering Instability in Porous Media. Part 1: Linear Stability Analysis. Transp. Porous Med. 84, 821–844. doi:10.1007/s11242-010-9555-2
Jang, J., Narsilio, G. A., and Santamarina, J. C. (2011). Hydraulic Conductivity in Spatially Varying Media-A Pore-Scale Investigation. Geophys. J. Int. 184, 1167–1179. doi:10.1111/j.1365-246X.2010.04893.x
Jang, J., and Santamarina, J. C. (2014). Evolution of Gas Saturation and Relative Permeability during Gas Production from Hydrate-Bearing Sediments: Gas Invasion vs. Gas Nucleation. J. Geophys. Res. Solid Earth 119, 116–126. doi:10.1002/2013JB010480
Jang, J., Sun, Z., and Santamarina, J. C. (2016). Capillary Pressure across a Pore Throat in the Presence of Surfactants. Water Resour. Res. 52, 9586–9599. doi:10.1002/2015WR018499
Jung, J.-W., Santamarina, J. C., and Soga, K. (2012). Stress-strain Response of Hydrate-Bearing Sands: Numerical Study Using Discrete Element Method Simulations. J. Geophys. Res. 117, 4202. doi:10.1029/2011JB009040
Kim, J., Xu, F., and Lee, S. (2017). Formation and Destabilization of the Particle Band on the Fluid-Fluid Interface. Phys. Rev. Lett. 118, 074501. doi:10.1103/PhysRevLett.118.074501
Kim, S., and Santamarina, J. C. (2015). Reactive Fluid Flow in CO 2 Storage Reservoirs: A 2‐D Pore Network Model Study. Greenh. Gas. Sci. Technol. 5, 462–473. doi:10.1002/ghg.1487
Kochmann, D. M., and Bertoldi, K. (2017). Exploiting Microstructural Instabilities in Solids and Structures: From Metamaterials to Structural Transitions. Appl. Mech. Rev. 69 (5). doi:10.1115/1.4037966
Lange, A., Schröter, M., Scherer, M. A., Engel, A., and Rehberg, I. (1998). Fingering Instability in a Water-Sand Mixture. Eur. Phys. J. B 4, 475–484. doi:10.1007/s100510050405
Langmuir, I. (1918). The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 40, 1361–1403. doi:10.1021/ja02242a004
Lee, J.-S., and Santamarina, J. C. (2007). Seismic Monitoring Short-Duration Events: Liquefaction in 1gmodels. Can. Geotech. J. 44, 659–672. doi:10.1139/T07-020
Lei, L., and Santamarina, J. C. (2018). Laboratory Strategies for Hydrate Formation in Fine‐Grained Sediments. J. Geophys. Res. Solid Earth 123, 2583–2596. doi:10.1002/2017JB014624
Lenormand, R., Touboul, E., and Zarcone, C. (1988). Numerical Models and Experiments on Immiscible Displacements in Porous Media. J. Fluid Mech. 189, 165–187. doi:10.1017/s0022112088000953
Lenormand, R., Zarcone, C., and Sarr, A. (1983). Mechanisms of the Displacement of One Fluid by Another in a Network of Capillary Ducts. J. Fluid Mech. 135, 337–353. doi:10.1017/S0022112083003110
Li, M., and Fannin, R. J. (2008). Comparison of Two Criteria for Internal Stability of Granular Soil. Can. Geotech. J. 45, 1303–1309. GIF. doi:10.1139/T08-046/ASSET/IMAGES/T08-046IE17H
Li, P., Vanapalli, S., and Li, T. (2016). Review of Collapse Triggering Mechanism of Collapsible Soils Due to Wetting. J. Rock Mech. Geotechnical Eng. 8, 256–274. doi:10.1016/j.jrmge.2015.12.002
Liot, O., Singh, A., Bacchin, P., Duru, P., Morris, J. F., and Joseph, P. (2018). Pore Cross-Talk in Colloidal Filtration. Sci. Rep. 8, 12460. doi:10.1038/s41598-018-30389-7
Liu, Q., Sun, Z., and Santamarina, J. C. (2021). Self-assembled Nanoparticle-Coated Interfaces: Capillary Pressure, Shell Formation and Buckling. J. Colloid Interface Sci. 581, 251–261. doi:10.1016/j.jcis.2020.07.110
Liu, Q., Zhao, B., and Santamarina, J. C. (2019). Particle Migration and Clogging in Porous Media: A Convergent Flow Microfluidics Study. J. Geophys. Res. Solid Earth 124, 9495–9504. doi:10.1029/2019JB017813
Menke, H. P., Bijeljic, B., and Blunt, M. J. (2017). Dynamic Reservoir-Condition Microtomography of Reactive Transport in Complex Carbonates: Effect of Initial Pore Structure and Initial Brine pH. Geochimica Cosmochimica Acta 204, 267–285. doi:10.1016/j.gca.2017.01.053
Meyer, E. E., Rosenberg, K. J., and Israelachvili, J. (2006). Recent Progress in Understanding Hydrophobic Interactions. Proc. Natl. Acad. Sci. U.S.A. 103, 15739–15746. doi:10.1073/pnas.0606422103
Mitchell, J. K. (1991). Conduction Phenomena: From Theory to Geotechnical Practice. Géotechnique 41, 299–340. doi:10.1680/geot.1991.41.3.299
Mitchell, J. K. (1976). Fundamental of Soil Behaviour. Hoboken, New Jersey, United States: John Wiley & Sons.
Moffat, R., Fannin, R. J., and Garner, S. J. (2011). Spatial and Temporal Progression of Internal Erosion in Cohesionless Soil. Can. Geotech. J. 48, 399–412. doi:10.1139/t10-071
Morrow, N. R., and Szabo, J. O. (1970). Physics and Thermodynamics of Capillary Action in Porous Media. Ind. Eng. Chem. 62, 32–56. doi:10.1021/ie50726a006
Moss, J. L., Cartwright, J., and Moore, R. (2012). Evidence for Fluid Migration Following Pockmark Formation: Examples from the Nile Deep Sea Fan. Mar. Geol. 303-306, 1–13. doi:10.1016/j.margeo.2012.01.010
Mulligan, C. N., Yong, R. N., and Gibbs, B. F. (2001). Surfactant-enhanced Remediation of Contaminated Soil: a Review. Eng. Geol. 60, 371–380. doi:10.1016/S0013-7952(00)00117-4
National Academies of Sciences and Medicine, E (2020). Characterization, Modeling, Monitoring, and Remediation of Fractured Rock. Washington, D.C., United States: National Academies Press.
Peña, T. J., Carvalho, M. S., and Alvarado, V. (2009). Snap-off of a Liquid Drop Immersed in Another Liquid Flowing through a Constricted Capillary. AIChE J. 55, 1993–1999. doi:10.1002/aic.11839
Rebata-Landa, V., and Santamarina, J. C. (2012). Mechanical Effects of Biogenic Nitrogen Gas Bubbles in Soils. J. Geotech. Geoenviron. Eng. 138, 128–137. doi:10.1061/(asce)gt.1943-5606.0000571
Robbins, B. A., and Van Beek, V. M. (2015). Backward Erosion Piping: A Historical Review and Discussion of Influential Factors. Assoc. State Dam Saf. Off. Dam Saf. 2, 919–938.
Romanov, D., Gabrovšek, F., and Dreybrodt, W. (2003). Dam Sites in Soluble Rocks: A Model of Increasing Leakage by Dissolutional Widening of Fractures beneath a Dam. Eng. Geol. 70, 17–35. doi:10.1016/S0013-7952(03)00073-5
Rutter, E. H. (1983). Pressure Solution in Nature, Theory and Experiment. J. Geol. Soc. 140, 725–740. doi:10.1144/gsjgs.140.5.0725
Sandnes, B., Flekkøy, E. G., Knudsen, H. A., Måløy, K. J., and See, H. (2011). Patterns and Flow in Frictional Fluid Dynamics. Nat. Commun. 2, 288. doi:10.1038/ncomms1289
Santamarina, J. C., and Jang, J. (2011). Energy Geotechnology: Implications of Mixed Fluid Conditions. Available at: https://egel.kaust.edu.sa/Documents/Papers/Santamarina_2010a.pdf (Accessed September 29, 2019).
Santamarina, J. C. (2003). Soil Behavior at the Microscale: Particle Forces. Geotechnical-Special-Publication, 25–56. doi:10.1061/40659(2003)2
Santamarina, J. C., Torres-Cruz, L. A., and Bachus, R. C. (2019). Why Coal Ash and Tailings Dam Disasters Occur. Science. 364, 526–528. doi:10.1126/SCIENCE.AAX1927
Schneider, J. A., and Mayne, P. W. (2000). “Liquefaction Response of Soils in Mid-America Evaluated by Seismic Cone Tests,” in Innovations and Applications In Geotechnical Site Characterization (Denver, CO: Geo), 1–16.
Sherard, J. L. (1987). Lessons from the Teton Dam Failure. Eng. Geol. 24, 239–256. doi:10.1016/0013-7952(87)90064-0
Shin, H., Santamarina, J. C., and Cartwright, J. A. (2008). Contraction-driven Shear Failure in Compacting Uncemented Sediments. Geol 36, 931–934. doi:10.1130/g24951a.1
Shin, H., and Santamarina, J. C. (2011a). Desiccation Cracks in Saturated Fine-Grained Soils: Particle-Level Phenomena and Effective-Stress Analysis. Géotechnique 61, 961–972. doi:10.1680/geot.8.P.012
Shin, H., and Santamarina, J. C. (2010). Fluid-driven Fractures in Uncemented Sediments: Underlying Particle-Level Processes. Earth Planet. Sci. Lett. 299, 180–189. doi:10.1016/J.EPSL.2010.08.033
Shin, H., and Santamarina, J. C. (2009). Mineral Dissolution and the Evolution of K0. J. Geotech. Geoenviron. Eng. 135, 1141–1147. doi:10.1061/(ASCE)GT.1943-5606.0000053
Shin, H., and Santamarina, J. C. (2011b). Open-mode Discontinuities in Soils. Géotechnique Lett. 1, 95–99. doi:10.1680/geolett.11.00014
Sills, G. C., Wheeler, S. J., Thomas, S. D., and Gardner, T. N. (1991). Behaviour of Offshore Soils Containing Gas Bubbles. Géotechnique 41, 227–241. doi:10.1680/geot.1991.41.2.227
Skempton, A. W., and Brogan, J. M. (1994). Experiments on Piping in Sandy Gravels. Géotechnique 44, 449–460. doi:10.1680/geot.1994.44.3.449
Sparks, A. D. W., Gallipoli, D., Augarde, C. E., Toll, D. G., Fisher, P. C., and Congreve, A. (2012). Formation and Evolution of Water Menisci in Unsaturated Granular Media. Géotechnique 62, 1143–1144. doi:10.1680/geot.12.D.004
Sukkarak, R., Tanapalungkorn, W., Likitlersuang, S., and Ueda, K. (2021). Liquefaction Analysis of Sandy Soil during Strong Earthquake in Northern Thailand. Soils Found. 61, 1302–1318. doi:10.1016/j.sandf.2021.07.003
Sun, Z., Liu, Q., Benitez, M. D., and Santamarina, J. C. (2022). Invasion Patterns Induced by Nanoparticle-Coated Interfaces. Under Prep.
Sun, Z., and Santamarina, J. C. (2019a). Grain‐Displacive Gas Migration in Fine‐Grained Sediments. J. Geophys. Res. Solid Earth 124, 2274–2285. doi:10.1029/2018JB016394
Sun, Z., and Santamarina, J. C. (2019b). Haines Jumps: Pore Scale Mechanisms. Phys. Rev. E 100, 023115. doi:10.1103/physreve.100.023115
Valdes, J. R., and Carlos Santamarina, J. (2007). Particle Transport in a Nonuniform Flow Field: Retardation and Clogging. Appl. Phys. Lett. 90, 244101. doi:10.1063/1.2748850
Valdes, J. R., and Santamarina, J. C. (2006). Particle Clogging in Radial Flow: Microscale Mechanisms. SPE J. 11, 193–198. doi:10.2118/88819-PA
Van Zwieten, R., Van De Laar, T., Sprakel, J., and Schroën, K. (2018). From Cooperative to Uncorrelated Clogging in Cross-Flow Microfluidic Membranes. Sci. Rep. 8, 5687. doi:10.1038/s41598-018-24088-6
Viggiani, G., Andò, E., Takano, D., and Santamarina, J. C. (2014). Laboratory X-Ray Tomography: A Valuable Experimental Tool for Revealing Processes in Soils. Geotech. Test. J. 38, 20140060–20140071. doi:10.1520/GTJ20140060
Völtz, C., Pesch, W., and Rehberg, I. (2002). Rayleigh-Taylor Instability in a Sedimenting Suspension. Phys. Rev. E 65, 011404. doi:10.1103/PhysRevE.65.011404
Weyl, P. K. (1959). Pressure Solution and the Force of Crystallization: a Phenomenological Theory. J. Geophys. Res. 64, 2001–2025. doi:10.1029/jz064i011p02001
Young, T. (1805). III. An Essay on the Cohesion of Fluids. Phil. Trans. R. Soc. 95, 65–87. doi:10.1098/rstl.1805.0005
Yun, T. S. (2005). Mechanical and Thermal Study of Hydrate Bearing Sediments. PhD Thesis.Available at: https://libproxy.kaust.edu.sa/login?url=https://www.proquest.com/dissertations-theses/mechanical-thermal-study-hydrate-bearing/docview/304999500/se-2?accountid=78788.
Zhao, B., MacMinn, C. W., and Juanes, R. (2016). Wettability Control on Multiphase Flow in Patterned Microfluidics. Proc. Natl. Acad. Sci. U.S.A. 113, 10251–10256. doi:10.1073/pnas.1603387113
Zhao, B., MacMinn, C. W., Primkulov, B. K., Chen, Y., Valocchi, A. J., Zhao, J., et al. (2019). Comprehensive Comparison of Pore-Scale Models for Multiphase Flow in Porous Media. Proc. Natl. Acad. Sci. U.S.A. 116, 13799–13806. doi:10.1073/pnas.1901619116
Zhao, B., and Santamarina, J. C. (2020). Desiccation Crack Formation beneath the Surface. Géotechnique 70, 181–186. doi:10.1680/jgeot.18.T.019
Ah [J] Hamaker constant in van der Waals interaction
A [N/m] contact line adhesion
Ar [] Archimedes number
Bo [] bond number
C [mol/L] concentration
cv [m2/s] pressure diffusion coefficient
Ca [] capillary number
d [m] diameter
D [m2/s] diffusion coefficient
DT [m2/s] thermal diffusion coefficient
Da [] Damköhler number
e [] void ratio
F [N] force (c: capillary; b: buoyant; D: drag; sk: skeletal; W: grain weight; EI: electrical interaction; wall: wall interaction; Th: thermo-elastic)
g [m/s2] standard gravity
G [Pa/m3] stiffness (sk: skeleton)
H [m] height
k [1/s] kinetic rate of reaction
K [Pa/m3] system stiffness
k0 [] lateral earth pressure coefficient at rest
L [m] characteristic length
Lch [m] channel length
LL [] liquid limit
M [] viscous ratio
Nad [] contact number
Nec [] elastocapillary number
u [Pa] fluid pressure (w: wetting phase; n: non-wetting phase)
Pe [] Péclet number
r [m] pore radius
Stk [] Stokes number
t [s] time scale (adv: advection; diff: diffusion; r: reaction; in: inertia)
V [m3] volume
W [] water content
z [m] depth
v [m/s] fluid flow velocity
Δu [Pa] capillary pressure
γ [N/m] interfacial tension (VS.: vapor-solid; LS: liquid-solid; LV: liquid-vapor)
θ [°] contact angle (a: advancing; r: receding)
μ [Pa.s] viscosity (inv: invading phase; def: defending phase)
ρ [kg/m3] density (b: buoyant; w: water; p: particle; f: fluid)
Keywords: multi-phase fluid, capillary phenomena, reactive flow, particle-laden flow, instability, THCM coupling
Citation: Liu Q and Santamarina JC (2022) Fluid-Driven Instabilities in Granular Media: From Viscous Fingering and Dissolution Wormholes to Desiccation Cracks and Ice Lenses. Front. Mech. Eng 8:861554. doi: 10.3389/fmech.2022.861554
Received: 24 January 2022; Accepted: 26 May 2022;
Published: 08 July 2022.
Edited by:
Giulio Sciarra, Ecole Centrale de Nantes, FranceReviewed by:
Alexandre Guevel, Duke University, United StatesCopyright © 2022 Liu and Santamarina. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. Carlos Santamarina, Y2FybG9zLnNhbnRhbWFyaW5hQGthdXN0LmVkdS5zYQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.