- 1State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, China
- 2John and Willie Leone Family Department of Energy and Mineral Engineering, The Pennsylvania State University, University Park, PA, United States
Due to inherent heterogeneity of geomaterials, rock mechanics involved with extensive lab experiments and empirical correlations that often lack enough accuracy needed for many engineering problems. Machine learning has several characters that makes it an attractive choice to reduce number of required experiments or develop more effective correlations. The timeliness of this effort is supported by several recent technological advances. Machine learning, data analytics, and data management have expanded rapidly in many commercial sectors, providing an array of resources that can be leveraged for subsurface applications. In the last 15 years, deep learning in the form of deep neural networks, has been used very effectively in diverse applications, such as computer vision, seismic inversion, and natural language processing. Despite the remarkable success in these and related areas, deep learning has not yet been widely used in the field of scientific computing specially when it comes to subsurface applications due to the lack of large amount of data to train algorithms. In this paper, we review such efforts and try to envision future game-changing advances that may impact this field.
Introduction
Laboratory experiments have been the main and direct approach for measurements of different mechanical and petrophysical properties of porous rocks such as Young’s modulus, permeability, and tortuosity. However, laboratory experiments are costly and often time-demanding due to the extensive sample preparations and expensive instrumentations required. In addition, laboratory experiments of large-scale problems require rigorous understanding of the underlying physics of the system and variables that can potentially affect the process of interest. Thus, such laboratory experiments may not provide accurate predictions for multiphysics problems unless a rigorous workflow have been developed. For instance, predicting the influence of morphology and mineralogy of porous media and materials on the deformation-dependent properties by performing laboratory experiments is currently extremely challenging due to the necessity of calibrating various parameters.
However nowadays, we are at the beginning of an exciting era in which we have not only sophisticated experimental instruments, but also rapidly advancing computer technology. As a branch of artificial intelligence that aims for program machines to perform their jobs more skillfully, machine learning has come a long way as computer science continues to evolve. Compared to the result that obtained from laboratory experiments and exhaustive computational simulations, the advantage of machine learning-based approximation solutions is that data-driven learning methods exploit large data sets to identify otherwise unknown relations, thus creating efficient and invertible maps between input and output parameters (Gu et al., 2018; Liang et al., 2018; Mozaffar et al., 2019). Due to its inherent ability to analyze complex data, machine learning methods have emerged as a new paradigm in scientific research and engineering applications (Liu et al., 2020a). Although these techniques and some of these algorithms were available in the past, but recent advances in processing and storage of data and reduction in their costs have made these techniques very attractive to study engineering problems.
Many scholars apply machine learning methods to their research fields, such as signal processing, biomedicine, complex dynamic systems (Brunton et al., 2016), multi-physical phenomena (Rudy et al., 2017), etc. Some commonly used machine learning methods include Perceptron (Rosenblatt, 1958), Genetic Programming (Goldberg, 1989; Banzhaf et al., 1998), Kernel and Nearest-Neighbor Nonparametric Regression (Dudani, 1976; Altman, 1992), Linear Statistical Models (Neter et al., 1996), Adaptive Boosting Algorithm (Freund and Schapire, 1997; Hastie et al., 2009), Support-Vector Machines (Cortes and Vapnik, 1995; Tefas et al., 2002; Veropoulos et al., 2016) and Artificial Neural Network (Ivakhnenko, 1971; Rumelhart et al., 1986; Widrow, 1987; Ge et al., 2004; Hinton and Salakhutdinov, 2006; Li et al., 2019). Rosenblatt (Rosenblatt, 1958) built the perceptron model and described the process of learning behavior in detail which is considered as the precursor to modern artificial network models (Cortes and Vapnik, 1995). Genetic Programming draws on the principles of biological evolution in nature, simulates the operation of genetics in the data set containing feasible solutions to continuously generate new data sets, and finally globally searches for the optimal solution that meets the requirements (Banzhaf et al., 1998). K-nearest neighbor algorithm follows the principle that the minority obeys the majority: classify the target samples with the K samples that are most similar to the target samples in the feature space. We could use distance function to weight the evidence to make the results more accurate (Dudani, 1976). Although the calculation result of this method is easy to fluctuate with the value of K and the calculation amount is large, it is suitable for solving Nonparametric regression problems. On the contrary, Linear Statistical Models cannot handle such problems (Neter et al., 1996). In addition, machine learning methods can also be used for classification problems. After Freund (Freund and Schapire, 1997) introduced their Adaptive Boosting Algorithm, Boosting has been a very successful technique for solving classification questions by reducing multi-class classification problem to two-class problems. Hastie (Hastie et al., 2009) proposed the SAMME algorithm based on the AdaBoost algorithm. The proposed new algorithm combines weak classifiers and puts more weight on the misclassified data points so that it can achieve higher classification accuracy. Through non-linearly mapping input vectors to a high dimension feature space and constructing a linear decision surface with special properties, Support-Vector Machines could solve two-group classification problems well. This method is very advantageous while dealing with non-separable training data (Cortes and Vapnik, 1995) and has been successfully applied to a number of applications, ranging from face recognition (Tefas et al., 2002) to biological data processing for medical diagnosis (Veropoulos et al., 2016). In addition to the various methods mentioned above, Artificial Neural Networks have gradually developed into an important branch in the field of machine learning (Li et al., 2019). From “Perceptron” (Rosenblatt, 1958) to “MADLINE” (Widrow, 1987) to “restricted Boltzmann machine” (Hinton and Salakhutdinov, 2006), with the use of nonlinear functions (Ivakhnenko, 1971) and back-propagation algorithms (Rumelhart et al., 1986), ANN could train a multilayer neural network with a central layer to convert high-dimensional data to low-dimensional codes by extensive tunable parameters through multi-layer network structure which will obtain the nonlinear relationship contained in a large amount of training data and generally receive good classification and regression accuracy.
As engineering researchers, we focus on the application of machine learning method in engineering and mechanics. Further, we investigate the feasibility of machine learning in processing mechanical response data of materials and reveal complex mechanical mechanisms. In fact, a considerable number of computational mechanics researchers have already done this work (Ge et al., 2004; Li et al., 2019), and we will show it as much as possible in the following sections. The results presented will help researchers in the engineering field to choose appropriate machine learning methods to achieve faster convergence speed and solution accuracy when dealing with some specific problems, and to save computational costs to a certain extent. In addition, this paper can provide some help in the selection of input parameters of the model, in order to make predictions more concisely on the premise of ensuring accuracy. For a more intuitive display, we briefly list some common machine learning methods and their typical references as shown in Table 1.
Rock mechanics
Due to the high degree of variability in natural materials and the physical environment in which they are located, rock mechanical behavior always exhibits a high degree of nonlinearity. In practice, experience knowledge and numerical modeling methods have been important tools for understanding rock mass behavior and predicting its response to its environment and changes in situ stress conditions (Morgenroth et al., 2019). But from previous applications, we can know that it is often difficult to integrate all the data collected into empirical and numerical models effectively. Furthermore, frequent use of extrapolation and interpolation techniques are also likely to distort the data. Since the 1990s, scholars have noticed the advantages of new computer science research methods applied to the simulation of rock mechanical behavior. By integrating machine learning into the rock mechanics, we could obtain more meaningful conclusions from data which are collected relatively inexpensively (Zhou and Wu, 1994). As a result, we use computers to find patterns in data, not “manipulate” data. In this part, we will review the application of machine learning in rock mechanics as well as future opportunities for data-driven approaches.
Rock mass properties
Sklavounos and Sakellariou (Sklavounos and Sakellariou, 1995) reported a neural network to classify rock masses. Along with this research, five criteria include strength of intact rock, drill core quality, joint spacing, joint condition, groundwater conditions were scaled to [0, 1] to become the “content” of the input neurons, and then some non-linear transformation is completed to obtain the desirable output results which is the classification of rock masses. This is a simple application of an earlier neural network to rock classification. In addition, some scholars apply machine learning methods to the estimation of some rock mechanics parameters that are difficult to obtain directly such as the UCS and swing quality of rocks. The reason is that standard cores cannot always be extracted from weak, highly fractured, thinly bedded, foliated and/or block-in-matrix rocks. Zorlu et al. (Zorlu et al., 2008) constructed 138 rock databases containing uniaxial compressive strength and petrographic properties for training with a sandstone uniaxial compressive strength prediction model. They used two predictive models including artificial neural networks and linear regression to learn from different types of sandstone data and found that packing density, concavo–convex type grain contact and content quartz had a greater impact on determining the uniaxial compressive strength of sandstone. According to the training results of the model, the equation for predicting the uniaxial compressive strength of sandstone is given as follows
where UCSn is the normalized uniaxial compressive strength; PDn is the normalized packing density; CCn is the normalized concavo–convex type grain contact; Qn is the normalized quartz content. Yagiz et al. (Yagiz et al., 2012) utilized backpropagation algorithm for ANN modeling and used hyperbolic tangent sigmoidal activation function for feedforward artificial neural network architecture
They used the model and the existing rock properties to estimate the UCS and E of the rock and adjusted the input rock parameters according to the accuracy of the prediction results. By comparison, it is more accurate to use four-cycle slake durability index normalized as input variable than the two-cycle one. The rest of the input variables also include dry unit weight normalized, Schmidt hardness normalized, effective porosity normalized, and P‐wave velocity normalized. Tiryaki et al. (Tiryaki, 2008) utilized multiple nonlinear regression, ANN methods and regression tree models to do the similar research like (Yagiz et al., 2012). Their results indicated that regression trees method performed best when compared to multiple nonlinear regression. This is because the individual relationship between the output quantities such as UCS and E and the input quantities tends to be nonlinear, while the property of the double logarithmic model of the multiple nonlinear regression model is still linear. In Samani et al. (Samani and Bafghi, 2012) study, the relationship between stone geotechnical parameters and the sawing rate of stones via diamond wire sawing was analyzed using an artificial network model. The study was prone to adopting the percentage of Silica, the coefficient of water absorption, the UCS, and abrasive hardness as the proper parameters for this accurate network. But their findings cannot be extrapolated to other types of ores. Other scholars have focused on the improvement of machine learning methods. Cervan et al. (Ceryan et al., 2012) introduced generalized regression neural networks to predict UCS of rocks. This method is based on non-parametric kernel regression, uses sample data as the posterior probability verification condition and performs non-parametric estimation, and finally calculates the correlation density function between the dependent and independent variables in the network from the training samples. While this method had strong capability of generalization, it is possible of getting trapped in local minima and subjectivity in the determination of model parameters and structure. Liu et al. (Liu et al., 2015) used extreme learning machine to estimate the UCS of rocks because of its good generalization ability, which figured out that The ELM approach can perform much better than the RBF-NN and the BP-NN in modeling the rock parameter problems, this is because the connection weight value between the input layer and the hidden layer is random and will not be changed after setting, which reduces the calculation amount of backpropagation. Also, the ELM performs equivalently to the GRNN (generalized regression neural network) and the SVM (support vector machines) in estimation of the UCS of rocks and takes much less time than the GRNN. Kumar et al. (Rajesh Kumar et al., 2013) innovatively used various physical parameters of the drill bit during the drilling process, including the equivalent sound level as the input of the network. Then, the rock properties derived from their neural network prediction model can be linked to drilling parameters. Mahmoodzadeh et al. (Mahmoodzadeh et al., 2022) finished an excellent work. Based on 244 datasets intact Sandstone which included three input parameters of uniaxial compressive strength (UCS), uniaxial tensile strength (UTS), and minimum principal stress (σ3). They compared the pros and cons of four machine learning techniques: Gaussian Process Regression (GPR), Support Vector Regression (SVR), Decision Tree (DT), and Long Short-Term Memory (LSTM), in building cohesion (C) and friction angle (φ) prediction models. Their results show that the LSTM model produced the most accurate results (as shown in Figure 1). Some statistical evaluation shown as follows
where
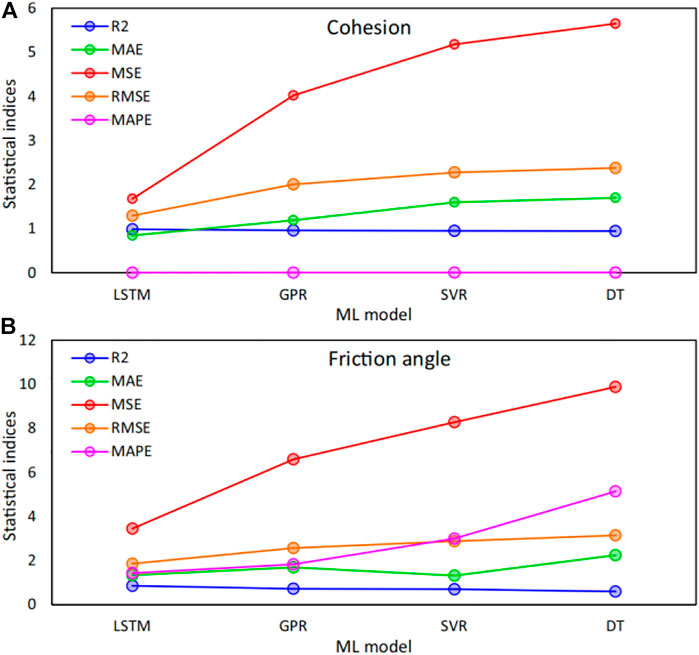
FIGURE 1. Evaluation indices results of the ML models (Mahmoodzadeh et al., 2022).
Garg et al. (Garg et al., 2022) also conducted a similar comparative analysis of different machine learning techniques. The object of prediction is the compressive strength of concrete. The evaluation criteria included Correlation Coefficient (CC), Root Mean Square Error (RMSE), Variance Account For (VAF), Nash -Sutcliffe Efficiency (NSE), and RMSE deviation from observation’s standard deviation ratio (RSR). Studies have shown that Support Vector Machine predicts better than Gaussian Process Regression for this problem.
It is worth noting that the shear behavior of rock is one of the most important characteristics of rock, which is more practical than UCS. This property of rock is usually characterized by shear strength. Under the existing laboratory conditions, the shear strength of rock is usually determined by direct shear test and triaxial compression test. Many scholars have used direct shear tests based on constant normal load or constant normal stiffness to study the main factors controlling the shear behavior of rocks. These factors cover roughness of discontinuity roughness, infilling conditions, rock stiffness, and initial stress (Papaliangas et al., 1993; Indraratna et al., 1999). Neto et al. (Dantas Neto et al., 2021) listed existing models that describe the overall shear stress-shear displacement behavior of rocks and pointed out that these analytical models are not suitable for test results under varying boundary conditions associated with normal stiffness. And proposed to use neural network model to solve this problem. The selected neural network model is similar to the above-including input layer, hidden layer and output layer. The more important thing is the selection of input layer parameters. After a lot of trial calculations and parameter value changes, the final input layer parameters include stiffness and initial normal stress acting on the joint surface), JRC, uniaxial compressive strength and basic friction angle of the intact rock, and the horizontal displacement. The correlation coefficient between the shear stress and dilation output by the model and the test sample reached 0.99 which shows that the model had good capability of predicting the shear behavior of rock. Matos et al. (Matos et al., 2019) pointed out the same problem. The author argued that previous analytical models that predicted the shear behavior of unfilled rock joints could not take into account the uncertainties inherent in the rock formation process. As an improvement, they used the First-Order Takagi-Sugeno fuzzy controller to incorporate the existing uncertain variables into the prediction model, and trained the prediction model based on the results of 44 direct shear tests. The input parameters of the model remain the same as (Dantas Neto et al., 2021). Their predictions showed that the model can be used to define the shear behavior of rock sections. Hasanipanah et al. (Hasanipanah et al., 2021) investigated the feasibility of Kriging model in predicting the complex nonlinear relationship of rock joints shear strength. In their article, the Kriging model is improved by some typical nonlinear functions to enhance its predictive ability; including second-order, third-order, exponential, logarithmic and so on. Their results showed that Kriging models augmented with logistic and hyperbolic tangents provided more accurate predictions by comparison. Azar (Fathipour-Azar, 2022) chose the ensemble ML approach of stacked generalization to estimate the shear strength of rock discontinuities. It used a meta-model to combine several heterogeneous basic AI and ML models, where the meta-model is linear regression, and the basic model is stacking ensemble framework SVM-M5P-RF. The ensemble ML approach included three input parameters, respectively normal stress, compressive strength ratio of joint walls and joint roughness coefficient, this analytical model is more robust in predicting shear strength compared to individual SVM, M5P and RF methods. Zhang et al. (Zhang et al., 2021) focused his research on the optimization of the prediction model; deep learning technology was applied to the multiple layer perceptron (MLP) neural network model to reduce possible accuracy problems, and the Harris hawks optimization (HHO) algorithm was used to develop The DMLP model has been further optimized. The optimized HHO-DMLP model is used to predict the friction angle, and the sample data are derived from datasets in different regions of the world. The training results can obtain friction angle prediction results with considerable accuracy. It is worth noting that for larger number of datasets, conventional training methods (SVM, RF) are less reliable and may even overfit.
In the machine learning methods mentioned above, the work performed by scholars is all data-driven, that is, establishing a data-to-data connection and striving to ensure the correctness of this connection, which is not only related to the algorithm, but also related to the training samples. However, before the emergence of machine learning, many fields have accumulated a large number of physical models in the long-term development process. Solving these physical models can make accurate predictions, but the more complex physical models are, the more difficult it is to solve (Li and Chen, 2022). As a result, some scholars (Raissi et al., 2018) began to combine data-driven machine learning methods with physical models, such as applying neural networks to the problem of solving partial differential equations, and named them “Physics-informed Neural Networks.” This method can be applied to modeling and calculation in the fields of physics and engineering, which has great potential for development. Moreover, these physical equations are often followed in the training samples of traditional machine learning methods, and it is also a waste of resources to not reflect them in the algorithm in a sense. This method is widely used in the field of fluid mechanics. As a typical porous medium, the fluid exchange process of rock in the ground is very complicated. Some scholars try to use this method to solve these problems. We will show their results in the following pages. Deng et al. (Deng and Pan, 2021) adopted the concept and workflow of the deep physics-informed neural networks to solve Spontaneous imbibition (as shown in Figure 2). This is because the traditional method is very complicated to solve the spontaneous imbibition governing equation, whether it is a self-similar solution controlled by an ordinary differential equation or a transient solution. They adopted the well-established PINN framework obtained by the former, used the one-dimensional unsteady state immiscible, incompressible horizontal flow equations as the main loss function and performed a detailed sensitivity analysis based on them, including sampling resolution, activation functions, neural network initialization, and loss function selection. The results demonstrated the effectiveness of the method, and they also point out that since PINN is always in the form of forward computation, the method is suitable for situations with different types of boundary conditions.
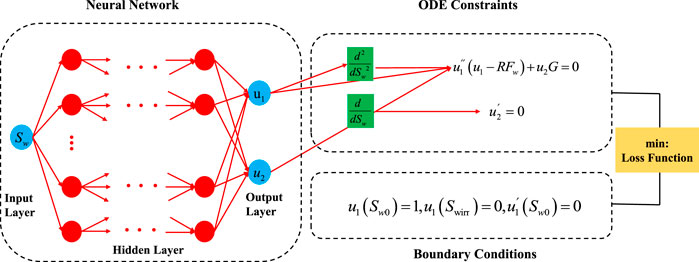
FIGURE 2. PINN configuration for transient spontaneous imbibition solutions (Deng and Pan, 2021).
Haghighat et al. (Haghighat et al., 2021) applied PINN to solve the equations of coupled flow and deformation of single-phase and multi-phase flows in fluid flow problems in porous media. They chose the dimensionless form of the coupling relationship of porous media under single-phase or two-phase flow conditions in the loss function, thus avoiding the unstable optimization problem that may be caused by multiple differential relationships. Moreover, the classical strain splitting algorithm for pore mechanics is abandoned, and fixed stress splitting is adopted, which improves the convergence and robustness of PINN. At the end of the article, they also pointed out that the training speed of the PINN model is slow and its computational speed is not competitive with conventional FEM methods. But the advantage of PINN lies in its ability to deal with the inverse problem obtained by combining the training samples. The following paper investigates the feasibility of the PINN method to solve the problem of gas drainage of a water-filled porous medium by Almajid et al. (Almajid and Abu-Alsaud, 2021). The results of this study can be used to improve the performance of reservoir simulators. In their research, the continuity hyperbolic PDE was used as the loss function, and the availability of observed data, the trainability of the multiphase flow parameters, etc. were used as the performance evaluation criteria of the PINN model. Accuracy issues of PINN models with and without observational data are compared. Furthermore, differences between artificial neural networks with and without physical properties for specific research topics are explored. The results indicated that the PINN model can greatly improve the accuracy through observational data; without observational data, the PINN model can only provide some trend changes for reference. When the constants were included in the observations we provided, only the predictions of the PINN model achieved acceptable accuracy. The above research indeed proves the superiority of the PINN model, which has a broad application prospect in solving the problems related to porous media such as rocks in the field of petroleum engineering.
Back-analysis
In the field of rock engineering, the displacement inverse analysis method has attracted widespread attention. It uses the measured displacement at the engineering site or simulation data as the basic information to reverse the mechanical parameters of the actual rock mass, and the initial in-situ stress of the formation, etc. The workload of solving the inverse problem is huge, but the benefits it brings are also considerable. We could use the result of back analysis as the basic parameters of numerical simulation, which is the most commonly used research methods in rock mechanics. These parameters are more meaningful than those obtained from conventional rock mechanics tests because the inverse analysis comprehensively considers various influencing factors brought about by rock characteristics, structures and even construction (Vardakos. et al., 2007).
In order to improve the efficiency and reliability of back analysis calculation work, some scholars have introduced machine learning methods into back analysis work. Wang et al. (Wang et al., 2015) and Wang et al. (Wang et al., 2000) respectively analyzed the feasibility of neural network and genetic algorithm in inverse analysis problem with examples. In order to ensure the uniqueness of the solution, the number of unknowns for inverse analysis using the neural network should be lower than the number of inputs. Due to the limited input, the elastic modulus and the internal friction angle are the two most sensitive rock mechanics parameters for inverse analysis (Wang et al., 2015)
where
The genetic algorithm can process multiple individuals in the training sample at the same time, that is, evaluate multiple solutions in the search space, reducing the risk of falling into the local optimal solution, which makes it more robust. Because of this advantage, the genetic algorithm can use the data with noisy to search for the Poisson’s ratio of the rock mass (Wang et al., 2000). Jin et al. (Jin et al., 2006) used Fast Lagrangian Analysis of Continuum to obtain the mapping relationship of stress-stress field-rock mechanics parameters at special points as a learning sample and adopted radial basis function networks to carry out inverse analysis on three rock mechanical parameters, namely bulk modulus, shear modulus and density, which had significant influence on the initial in-situ stress field. Their research showed high computational accuracy. Song et al. (Song et al., 2015) introduced a new Difference Evolution and Extreme Learning Machine method to back analyze the parameters of rocks. The sample parameter relationship between forward analysis and back analysis is shown in Figure 3. They utilized three-dimensional numerical simulation and monitoring data to create training and testing samples, which were trained by ELM. Considering the global optimization property of DE and simple structure of ELM, this method achieved a high calculation speed and reasonable result. Gu et al. (Gu et al., 2015) pointed out the deficiencies of conventional back-analysis methods, especially for special geographical locations such as dams. The integrated deformation modulus inversed by the conventional inversion method didn’t meet the actual situation. Thus, they proposed a partition inverse analysis method based on chaotic genetic algorithm to solve this problem. First is to divide the region to identify different displacement measurement data and finite element calculation results (input), and then obtain a more realistic inversion result. Finally, the project case verified the feasibility and validity of the proposed method. Zheng et al. (Zheng et al., 2013) also considered Back-analysis problems associated with dams. But the focus of their analysis is on the static and creep properties of rock-fill material in the reverse analysis, and on the choice of type of SVM model.
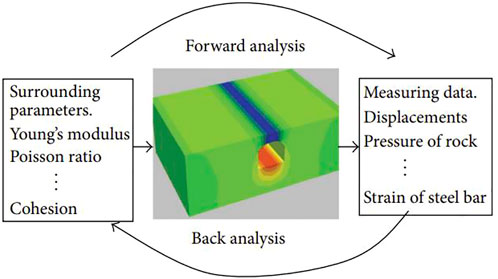
FIGURE 3. The forward and back analysis of geotechnical engineering (Song et al., 2015).
Existing inverse analysis methods are usually only applicable to limited engineering fields or at the same geological conditions. Therefore, the future development direction should be changed to a more applicable and wider range of back-analysis methods.
Determining constitutive behaviors
Theoretically, identifying the constitutive equations of geological materials is also very important, even more than mechanical parameters and the reason is as follows. The constitutive model cannot reflect the actual behavior of geological materials, and even the precise mechanical parameters cannot describe the actual engineering behavior. However, the identification of constitutive models is a complicated problem that cannot be solved well using a traditional method because of such factors as the formulation complexity, idealization of material behavior, and excessive empirical parameters (Adeli, 2013). Previous studies (Papaliangas et al., 1993; Sklavounos and Sakellariou, 1995; Indraratna et al., 1999; Wang et al., 2000; Jin et al., 2006; Vardakos. et al., 2007; Tiryaki, 2008; Zorlu et al., 2008; Ceryan et al., 2012; Samani and Bafghi, 2012; Yagiz et al., 2012; Rajesh Kumar et al., 2013; Zheng et al., 2013; Gu et al., 2015; Liu et al., 2015; Song et al., 2015; Wang et al., 2015; Raissi et al., 2018; Matos et al., 2019; Almajid and Abu-Alsaud, 2021; Dantas Neto et al., 2021; Deng and Pan, 2021; Haghighat et al., 2021; Hasanipanah et al., 2021; Zhang et al., 2021; Fathipour-Azar, 2022; Garg et al., 2022; Li and Chen, 2022; Mahmoodzadeh et al., 2022) have shown that machine learning methods can provide new ideas for rock mechanics problems, and this issue is no exception (Ghaboussi and Sidarta, 1998; Jaksa. and Maier., 2009). In these cases, as an important branch of machine learning methods, the use of artificial neural networks is the most common because of its high generalization. Tan et al. (Tan and Wang, 2001) employed radial basis function neural network (RBFNN) to obtain rock constitutive equation based on stress-strain relationship of rock under different confining pressures in previous literature. Part of this data is used to train the network and the other part is used as validation, and their research shows that predicting constitutive equations using neural networks is feasible and reliable. Peng et al. (Peng et al., 2008) and Li et al. (Li et al., 2008) did a similar job. They separately predicted the elastoplastic constitutive model of moderate sandy clay and sand based on their own experimental data. Thus, if one ANN model can approach the experimental curve of one geomaterial very well, this ANN model can well describe the constitutive relationship of the geomaterial. However, it is worth noting that the input layers of the above studies are in all knowledge of stress-strain curves, which cannot well reflect the influence of the loading history on the stress-strain relationship of rock materials (Wei, 2018). Therefore, in order to better describe the influence of various relative factors on the mechanical behavior of geotechnical materials, scholars have added more inputs when using neural networks. He et al. (Shouling et al., 2009) attempted to model the nonlinear elastic behavior of fiber-lime reinforced soil under multi-axial shear loading using a neural network firstly. In their study, five inputs comprise the confining pressure, the principal strain, curing period of soil, contents of fiber, and lime; the output is designated as the principal stress. The training samples of the network come from 30 groups of 34 triaxial shear tests, and the remaining four groups verify the reliability of the artificial neural network model. Yazdani et al. (Yazdani et al., 2013) used Taguchi method for sensitivity analysis of constitutive models and adopted genetic algorithm to fit the computed numerical results and observed data of the soil model. Their results reveal that the stress-strain relationship of this material depends mainly on the parameters of soil cohesion and internal friction angle. Rashidian et al. (Rashidian and Hassanlourad, 2014) constructed an ANN (as shown in Figure 4) to examine mechanical behavior of carbonate soils with a structure of 5-10-2. They used relative density, axial strain, maximum void ratio, calcium carbonate content, and confining pressure as input neurons. The stress-strain curve predicted by the model is highly consistent with the experimental result. Kohestani et al. (Kohestani and Hassanlourad, 2016) continued research work in this area. They exploited ANN and SVM to model the mechanical behavior of different carbonate soils. Compared with (Rashidian and Hassanlourad, 2014), they added the minimum void ratio as an input parameter. In their test, the errors of predictions were accumulated as the entire stress paths were predicted incrementally, but it still yielded good compatibility with the experimental data results used for testing.
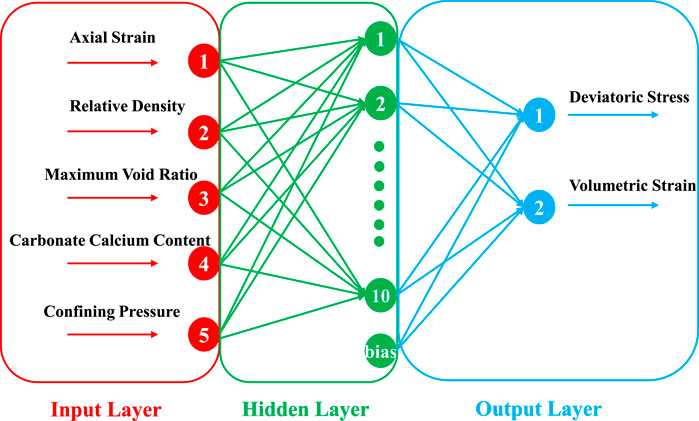
FIGURE 4. Architecture of used ANN (Rashidian and Hassanlourad, 2014).
In order to accurately describe the constitutive theory of unsaturated soils, Johari et al. (Johari et al., 2011) used genetic algorithm to optimize the weight of neural network, and obtains an ensemble algorithm for modeling unsaturated soils. The optimized neural network structure is 8-5-3. The eight input neurons include eight initial parameters such as initial gravimetric water content, initial dry density, and the three output neurons are deviatoric stress, suction and volumetric strain respectively. The results of 15 groups of comprehensive triaxial tests are used as training samples, and the prediction results revealed good compatibility with the other three groups of experimental results.
To sum up, in the problem of predicting the constitutive relationship of materials, the machine learning method represented by artificial neural network can always produce more comprehensive results, but it needs the support of new data with more complex conditions.
Rock mass stability research
Due to the fractal self-similarity of rock mechanics information, engineers always hope to predict the overall information of rock mass from local information to avoid potential problems in engineering, like the instability of tunnel caused by tunnel surrounding rock distortion. Many scholars have made efforts in this regard. Li et al. (Li et al., 2005) deployed the grey GM (1,1) model to predict surrounding rock displacement based on the convergence-time sequence of rocks, and they used n small interval trapezoidal area to replace the area of [k, k+1] interval and GM (1,1) function curve envelope which will improve the precision and adaptability of the model. Li et al. (Li et al., 2006) discussed the internal relationship between monitor data and the artificial neural network in displacement prediction. Their results show that the prediction values by BP neural network agree well with the measured ones, but Long-term forecasts with less measured data can significantly reduce the accuracy of forecasts. Yao et al. (Yao et al., 2010) pointed out that SVM could provide accurate displacement prediction of tunnel surrounding rock, and they used shuffled complex evolution algorithm to select the appropriate parameters for SVM which offered robust and flexible effect during analysis (as shown in Figure 5).
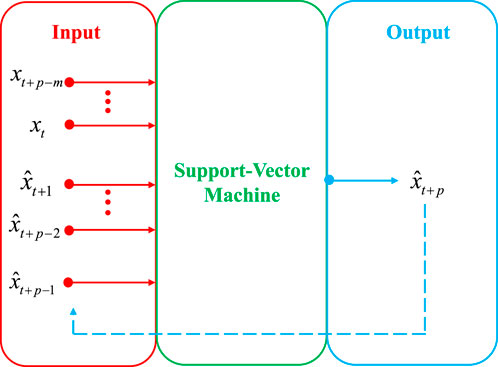
FIGURE 5. The prediction process of MS based on SVM (Yao et al., 2010).
Based on SVM Yao et al. (Yao et al., 2014) introduced a forgetting factor to adjust the weights between new and old data, which could treat the time-varying features of rock displacement well. Also, they compared the performance of the SVMFF (Support-Vector Machine forgetting factor) with that of ANNFF (Artificial neural networks forgetting factor) using RMSE (Eq. 7). As a result, SVMFF can provide a better performance in most situations than ANNFF (as shown in Figure 6).
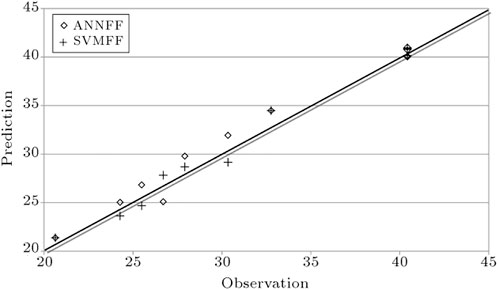
FIGURE 6. Comparison between the prediction errors of SVMFF and ANNFF (Yao et al., 2014).
Wu et al. (Wu et al., 2014) came to a similar conclusion without considering the forgetting factor (as shown in Figure 7).
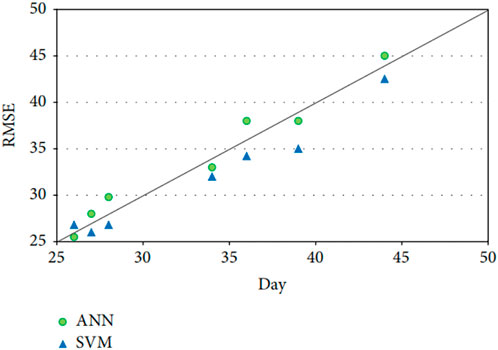
FIGURE 7. Comparison between the predicting errors of SVM and ANN (Wu et al., 2014).
On the basis of the above rock displacement, we can continue to investigate the stability of the rock mass, mainly for slope stability and rockbrust. The stability of the slopes generally exists due to the combined effects of geology, hydrology, and soil parameters (Diganta and Arunav, 2017; Das et al., 2020). We naturally associate it with the powerful ability of machine learning methods, especially artificial neural networks, to predict multi-factor problems. Rockburst is the rapid release of accumulated elastic energy of hard and brittle surrounding rock in a high stress state under the action of excavation or other load disturbances, resulting in dynamic instability disasters such as rock spalling, fragmentation and ejection (Roohollah and Abbas, 2019). Depending on its characteristics of suddenness and great damage, scholars expect to make effective predictions to prevent threats to construction workers. Because of the complexity of rockburst mechanism and its influencing factors, rockburst prediction methods based on machine learning methods have been rapidly developed similarly. Feng et al. obtained the time series of the mechanical behavior of the rock through measurement and used the obtained historical information to find out the relationship between the values at different times to make predictions at the next time, and his research results are applied to earthquake magnitude series (Feng et al., 1996), real-time roof pressure prediction in coal mines (Feng et al., 1997) and rockburst possibility prediction (Feng and Wang, 1994). But it’s worth noting that this section appears to have more to do with external factors. For example, no matter how hard the rock is, it is difficult to resist the erosion of rain. We are further trying to find a corresponding relationship of failure in engineering design. So in this part, we just briefly introduce the parameter selection for model training. When predicting slope stability, Chakraborty et al. (Goswami and Chakraborty, 2017) and Lu et al. (Lu and Rosenbaum, 2003) all used the height of the slope (H), cohesion (C), angle of internal friction (φ), slope inclination (β), unit weight of soil (γ), and coefficient of pore water pressure (ru) as input parameters. Compared with (Lu and Rosenbaum, 2003; Goswami and Chakraborty, 2017), Erzin et al. (Erzin and Cetin, 2014) established a network model that omits the pore water pressure input. Faradonbeh et al. (Roohollah and Abbas, 2019) used the maximum tangential stress, uniaxial tensile strength, uniaxial compressive strength, and elastic energy index as input variables when predicting rockburst. Meanwhile, they adopted RMSE (Eq. 7) to evaluate the selected emotional neural network (ENN), gene expression programming (GEP), and decision tree-based C4.5 algorithm. The above network models for slope stability and rockburst prediction have shown high accuracy after being trained by training samples.
Fracture mechanics
As we mentioned in the previous section, machine learning methods in rock mechanics are often used to capture nonlinear complex relationships between data. Correspondingly, there are also complicated engineering problems in fracture mechanics that often involve nonlinear complex relationships between high-dimensional data. The more common ones include fracture toughness measurements, problems of crack propagation, crack identification, etc. Commonly used machine learning methods include support vector machine (Deng et al., 2013), neural network (Aldakheel et al., 2021), Bayesian optimization and reinforcement learning (Alipour et al., 2021; Fuchs et al., 2021), etc.
First, the literature reports related to metal materials are carried out. Due to the variety of sample sizes, it is impractical to perform all finite element simulations for different sample sizes to accurately analyze their fracture toughness. Liu et al. [854] introduced regression tree and artificial neural network to solve this problem. They performed data-heavy finite element analysis to provide training data for the predictive model. The inputs to the model are four constants related to the sample size, and the output is a quantity related to the crack tip plane-strain stress intensity factor and indentation load. Their results indicate that artificial network models can achieve relatively high prediction accuracy with a relatively simple structure. Daghigh et al. (Daghigh et al., 2020) applied the decision tree regressor and adaptive boosting regressor machine learning methods to effectively predict fracture toughness properties of multiscale bio-nano-composites based on the limited number of training data obtained from these impact tests and finite element analysis. Their results indicates that ML predictions could provide a way to assist in the prediction and optimization of fracture toughness by varying compositions.
Rock fracture toughness is one of the important mechanical parameters in geomechanics to describe the characteristics of resisting the crack initiation and propagation in rock masses (Liu et al., 2017) (Wang et al., 2016). Fracture toughness also becomes an important factor in designing hydraulic fractures due to its dominant role in height growth and fracture propagation (Zia et al., 2018). Wang et al. (Wang et al., 2021a) was the first to introduce machine learning methods into the prediction of rock fracture toughness. The training datasets are all based on the cracked chevron notched Brazilian disc specimen. Most of them come from numerical simulations (as shown in Figures 8, 9), and a small part comes from literature research. They constructed decision regression tree, random regression forest, extra regression tree and fully-connected neural network to predict rock fracture toughness. Their prediction results indicate that the regression-tree-based ensemble method has higher ability; also, higher number of neurons in different layers, which will improve the accuracy of ANN predictions.
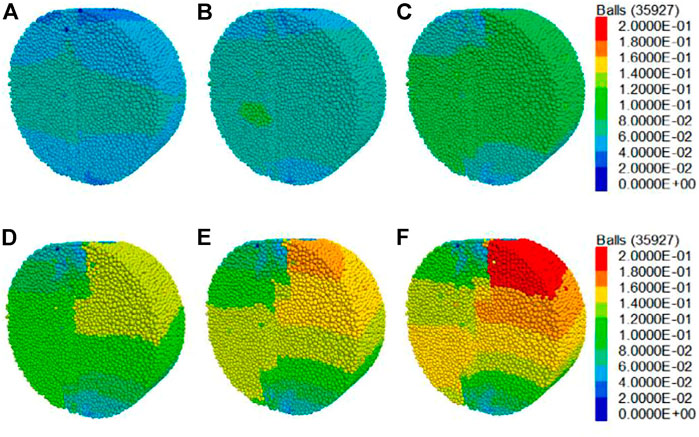
FIGURE 8. Numerical displacement fields of the ISRM-suggested CCNBD testing specimen at the different failure stages by 3D particle-based discrete element method (Wang et al., 2021a).
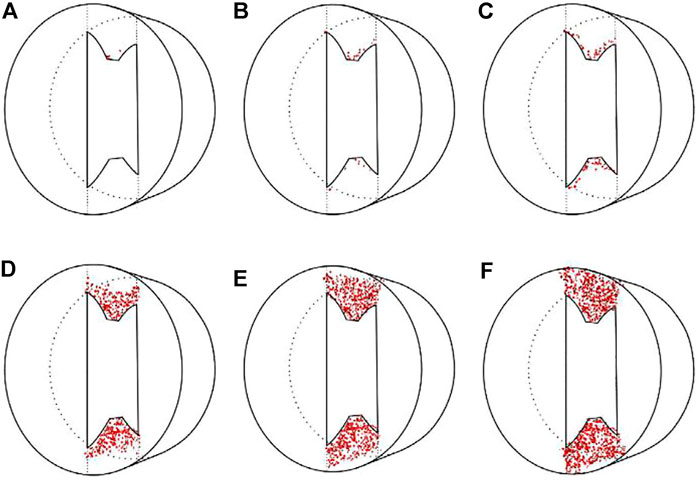
FIGURE 9. 3-D numerical particle-based discrete element method progressive fracture process of the ISRM-suggested CCNBD testing specimens at different failure stages (Wang et al., 2021a).
In the context of the complex and nonlinear nature of PNCs fracture toughness, Hamdia et al. (Hamdia et al., 2015) employed artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) to predict the fracture energy of polymer nanocomposites. Considering the uncertainty of single neural network modeling that may cause instability of parameter sensitivity analysis (Cherkassky et al., 2006), Cao et al. (Cao et al., 2017) developed a neural network ensemble-based parameter sensitivity analysis paradigm which could make decisions about parameter sensitivity by synthesizing sensitivity analysis results of individual neural networks. They figured out that tensile strength and modulus of elasticity are the critical parameters in the fracture failure of the notched concrete beam. Mahmoodzadeh et al. (Mahmoodzadeh et al., 2022) has confirmed the superiority of the LSTM model. On this basis, Duyen et al. (Nguyen-Le et al., 2020) used predicted different changes that are computed by hidden Markov model to improve the out consequences which trained by LSTM model. This model is trained using experimental data from a 4-point shear beam. When the amount of training sample data is large (335), the error between the prediction result of the model and the test sample is only 1.199%, better than the prediction results only using the LSTM model (1.370%). ML are also used in the determination of representative volume elements for microstructurally small cracks. Due to the high computational cost of the finite element method in multi-scale analysis problems, Karen et al. (DeMille and Spear, 2022) used the existing finite element simulation results as training data for CNNs (Convolutional neural networks), and the RVEMSC is predicted with comprise? microstructural and geometrical information local to the given crack-front point as input. Although CNNs are not found to be accurate enough to replace all FE simulations, but it’s a rapid screening tool for improving the efficiency of the FE-based RVEMSC determination framework. Support Vector Regression is widely used in the analysis related to non-deterministic damage prediction. Feng et al. (Feng et al., 2021a) reported that as part of machine learning aided-computer aided engineering, extended support vector regression can identify relationships between input variables such as conditions of initial crack, external loading conditions, and structural damage evolutions. The resulting dataset can be used to predict the probability of structural failure. Feng et al. (Feng et al., 2021b) improved algorithm based on previous work, and they eliminated the influences of random outliers so that the training robustness and computational adaptability of the proposed regression model can be reinforced. The effectiveness of this improvement was verified by experiments and numerical simulations.
Pore-scale analysis
Digital rock modeling provides a controllable environment and a straightforward variables variation to produce accurate results quickly and economically. Modeling digital rocks at the pore scale requires image acquisition which is achieved by imaging the pore space of the rocks of interest, analyzing them digitally through a series of image processing steps, and modeling the physics using the various available numerical tools, which allows deciphering the relationship between pore characteristics and fluid flow properties as well as the mechanical properties (Goral et al. (Goral et al., 2020)). Pore scale models used for fluid flow simulation require three-dimensional representation of the rock sample of interest while computing mechanical properties requires a detailed geometry and a high-resolution mesh with millions of mesh elements, leading to computationally expensive simulations. Despite the recent advances in digital rock modeling techniques and the hardware capabilities as well as the computational power, there are still limiting factors to the ability of such techniques to tackle large-scale problems.
Fluid flow simulations using digital rock samples can be performed using various techniques that try to balance between accuracy and speed at the cost of the level of details required. Pore Network Models (PNM), for instance, have been widely used to estimate the permeability of porous rocks (Blunt, 2001; Joekar-Niasar et al., 2008). PNM decompose the complex pore space significantly and replace it with a ball-and-stick network to reduce the computational cost while providing velocity and pressure field averaged over a simplified geometry. Blunt (Blunt, 2017) argued that conventional PNM have some challenges in simulating imbibition and residual trapping of CO2 which plays an important role in the assessment of long-term storage capacity and safety of geological sequestration. On the contrary, direct flow simulations such as finite method solutions and Lattice Boltzmann Methods (LBM) solve Navier Stokes equation (NVE) explicitly using the original complex geometry which provides the highest level of accuracy and details (Wang et al., 2021b). Given the level of details involved in such simulations, the associated computational cost is rather significant due to the methods being either time-dependent, nonlinear, or iterative. Lattice Boltzmann Methods is a time-dependent method while Navier Stokes equation is both time-dependent and nonlinear.
The size of the sample is perhaps the foremost limiting factor in most numerical simulation techniques. X-ray micro-Computed Tomography (μ-CT) images of a typical rock sample of 1 cm in diameter has dimensions of 2500 × 2500 × 5000 voxels, with a resolution of few micrometers (Soulaine et al., 2016; Wang et al., 2019b). Fluid flow simulation using finite methods solutions and Lattice Boltzmann Methods, however, are usually restricted to a maximum model size of 3003 voxels, above which the simulation is no longer efficient (Raeini et al., 2014). Such numerical simulation tools require scalability and parallelization of the algorithm on high-performance computers (HPC) clusters to yield relatively fast and efficient estimation of the properties of interest. Incorporating mechanical behavior of porous rocks along with fluid flow simulation rises the computational cost markedly which is caused by the increase in the complexity of the meshing and reservoir heterogeneity (Li et al., 2022). Machine leaning shows potential in overcoming the limitation of the choosing between higher resolution or larger field of view by enhancing the quality of the 2D slices to achieve better segmentation and phase labeling (Figure 10). User-biases also imposes a significant challenge in image processing. During image segmentation to distinguish pores from grains, user-biases are shown to affect the physical accuracy of the petrophysical results (Garfi et al., 2020). Leu et al. (Leu et al., 2014) performed sensitivity analysis of the method of segmentation on the permeability on a digital rock sample. The results showed discrepancy in permeability values obtained from different segmentation methods due to the dissimilar labeling of pores and grains. User-biased segmentation method that require manual determination of the threshold value fail to produce reliable phase labeling results (Figure 11) which yield inaccurate property estimation (Iassonov et al., 2009).

FIGURE 10. Using machine learning algorithms, a larger field of view and a higher resolution can be achieved simultaneously by enhancing the available micro-CT images and thus achieve a bigger sample (Da Wang et al., 2021).
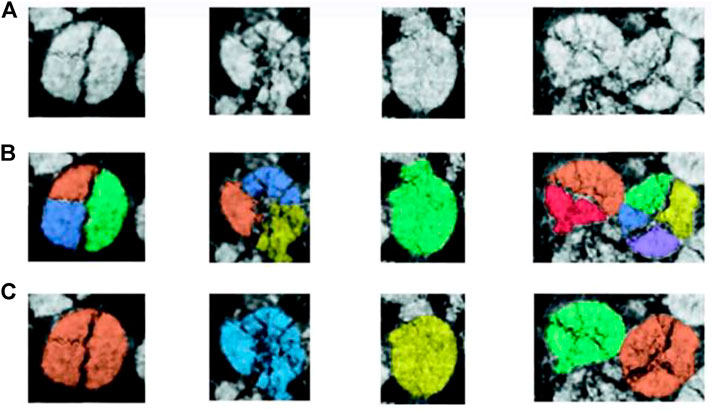
FIGURE 11. Comparison between different segmentation methods including traditional (B) and machine learning assisted methods (C) shows user-bias in labeling original data (A) when using traditional segmentation methods. Each color represents different particle (Jiang et al., 2020).
Machine Learning could potentially provide a breakthrough by surpassing the limitations imposed by traditional pore scale imaging and modeling techniques. The use of machine learning algorithms eliminates the need to decide between higher accuracy or larger field of view as automated thresholding and image optimization can be easily achieved using the various algorithms of machine learning.
Considering the different available structures of machine learning algorithm, estimation of mechanical and petrophysical properties of complex geometries such as porous rocks are easily attainable (Figure 12). Machine learning algorithm differ based on the structure and application and include Artificial neural networks (ANNs), Deep neural networks (DNNs), and Convolutional neural networks (CNNs). ANNs are composed of dense neural network blocks that take a number of inputs and use weights, biases, and an activation energy to output the outcome through a series of hidden layers. ANNs are used to correlate geometrical properties, for example, such as porosity and surface area to permeability of porous rocks (Iassonov et al., 2009). DNNs involve more than one hidden layer. Unlike ANNs which use the weighted sum of the inputs CNNs use convolution operations. CNN are useful for automated segmentation and flow field and petrophysical properties prediction.
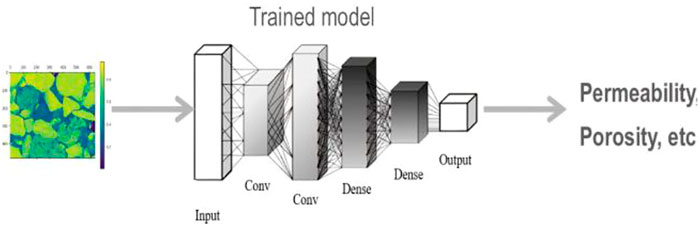
FIGURE 12. A trained machine learning model takes 2D slices of the geometry as an input and estimate the property of interest without the lengthy and biased image processing (Araya-Polo et al., 2020).
Machine learning has been widely used for various applications. Hadi and Nygaard (Hadi and Nygaard, 2018) presented a machine learning algorithm based on Artificial Neural Networks (ANNs) to derive an empirical correlation to estimate shear velocity from conventional logs. Saad et al. (Saad et al., 2018) developed a physics-based machine learning algorithm that uses rock density, porosity, and mineralogy to predict its Young’s modulus. Araya-Polo et al. (Araya-Polo et al., 2020) utilized deep neural networks (DNNs) to provide a quick estimation of rock permeability from thin-section images of various samples with different grains’ size ranging from samples with very fine to very coarse grains. Their results show acceptable agreement with laboratory-measured permeability with an average error of 11.69%. Bekele (Bekele, 2020) employed DNNs to predict two-dimensional deformation in an idealized poroelastic model. The algorithm was tested against the analytical solution of Barry and Mercer’s source problem with time-dependent fluid injection and extraction. The results show a good agreement with the vertical and horizontal deformation, but higher error was noticed for the predicted pore pressure. With the vast amount of data available in the form of X-ray images of real and synthetic rocks, as well as the ability to generate synthetic digital rock samples (Al Balushi and Dahi Taleghani, 2020), machine learning continues to become increasingly prevalent as there is a potential to advance and improve all aspects of the data-driven workflow which would lead to faster simulations and obtaining higher image quality.
Conclusion
We have presented an overview of advances in using various machine learning techniques in different aspects of rock mechanics. Some of these efforts were specifically engaged in predicting rock failure characteristics while other were focused on mechanical and petrophysical behavior of rock during its service life. Although most of the initial works were focused on the behavior of rock masses but these techniques found better applications in microscale or digital rock analysis due to the lack of data. One of the main barriers in further development of machine learning techniques in rock mechanics is limited datasets which is mainly driven by lengthy and expensive nature of rock mechanics tests. Hence using micro CT scan images is one of the solutions to fill this gap to populate large number of data required for training neural networks.
Author contributions
HY: part of original writing, literature review. AT: Review and revision, advising. FA: part of original writing, literature review. HW: Article modification, literature review.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adeli, H. (2013). Neural networks in civil engineering: 1989–2000. Computer-Aided Civ. Infrastructure Eng. 16 (2), 126–142. doi:10.1111/0885-9507.00219
Al Balushi, F., and Dahi Taleghani, A. (2020). “Numerical generation of stress-dependent permeability curves,” in 54th US Rock Mechanics/Geomechanics Symposium.
Aldakheel, F., Satari, R., and Wriggers, P. (2021). Feed-forward neural networks for failure mechanics problems. Appl. Sci. 11 (2021), 6483. doi:10.3390/app11146483
Alipour, M., Esatyana, E., Sakhaee-Pour, A., Sadooni, F., and Al-Kuwari, H. (2021). Characterizing fracture toughness using machine learning. J. Pet. Sci. Eng. 200 (2021), 108202. doi:10.1016/j.petrol.2020.108202
Almajid, M. M., and Abu-Alsaud, M. O. (2021). Prediction of porous media fluid flow using physics informed neural networks. J. Petroleum Sci. Eng. 208 (2022), 109205. doi:10.1016/j.petrol.2021.109205
Altman, N. S. (1992). An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 46, 175. doi:10.2307/2685209
Araya-Polo, M., Alpak, F. O., Hunter, S., Hofmann, R., and Saxena, N. (2020). Deep learning–driven permeability estimation from 2D images. Comput. Geosci. 24 (2), 571–580. doi:10.1007/s10596-019-09886-9
Banzhaf, W., Nordin, P., Keller, R. E., and Francone, F. (1998). Genetic programming: An introduction. San Francisco: Morgan Kaufmann.
Blunt, M. J. (2001). Flow in porous media—Pore-network models and multiphase flow. Curr. Opin. colloid & interface Sci. 6 (3), 197–207. doi:10.1016/s1359-0294(01)00084-x
Blunt, M. J. (2017). Multiphase flow in permeable media: A pore-scale perspective. United states: Cambridge University Press.
Brunton, S. L., Proctor, J. L., and Kutz, J. N. (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. U. S. A. 113, 3932–3937. doi:10.1073/pnas.1517384113
Cao, M., Pan, L., Gao, Y., Novak, D., Ding, Z. C., Lehky, D., et al. (2017). Neural network ensemble-based parameter sensitivity analysis in civil engineering systems. Neural comput. Appl. 28 (7), 1583–1590. doi:10.1007/s00521-015-2132-4
Ceryan, N., Okkan, U., and Kesimal, A. (2012). Application of generalized regression neural networks in predicting the unconfined compressive strength of carbonate rocks. Rock Mech. Rock Eng. 45, 1055–1072. doi:10.1007/s00603-012-0239-9
Cherkassky, V., Krasnopolsky, V., Solomatine, D., and Valdes, J. (2006). Computational intelligence in Earth sciences and environmental applications: Issues and challenges. Neural Netw. 19 (2), 113–121. doi:10.1016/j.neunet.2006.01.001
Cortes, C., and Vapnik, V. (1995). Support-vector networks. Mach. Learn. 20, 273–297. doi:10.1007/bf00994018
Da Wang, Y., Blunt, M. J., Armstrong, R. T., and Mostaghimi, P. (2021). Deep learning in pore scale imaging and modeling. Earth-Science Rev. 215, 103555. doi:10.1016/j.earscirev.2021.103555
Daghigh, V., Lacy, T. E., Daghigh, H., Gu, G., Baghaei, K. T., Horstemeyer, M. F., et al. (2020). Machine learning predictions on fracture toughness of multiscale bio-nano-composites. J. Reinf. Plast. Compos. 39 (2020), 587–598. doi:10.1177/0731684420915984
Dantas Neto, S. A., Indraratna, B., Fortuna Oliveira, D. A., and de Assis, A. P. (2021). Modelling the shear behaviour of clean rock discontinuities using artificial neural networks. Rock Mech. Rock Eng. 50 (7), 1817–1831. doi:10.1007/s00603-017-1197-z
Das, S. K., Biswal, R. K., Sivakugan, N., and Das, B. (2020). Classification of slopes and prediction of factor of safety using differential evolution neural networks. Environ. Earth Sci. 64 (1), 201–210. doi:10.1007/s12665-010-0839-1
DeMille, K., and Spear, A. (2022). Convolutional neural networks for expediting the determination of minimum volume requirements for studies of microstructurally small cracks, Part I: Model implementation and predictions. Comput. Mater. Sci. 207 (2022), 111290. doi:10.1016/j.commatsci.2022.111290
Deng, L., and Pan, Y. (2021). Application of physics-informed neural networks for self-similar and transient solutions of spontaneous imbibition. J. Pet. Sci. Eng. 203 (2021), 108644. doi:10.1016/j.petrol.2021.108644
Deng, N. Y., Tian, Y. J., and Zhang, C. H. (2013). Support vector machines optimization based theory, algorithms, and extensions. CRC Press.
Diganta, G., and Arunav, C. (2017). Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 10 (17), 385. doi:10.1007/s12517-017-3167-x
Dudani, S. A. (1976). The distance-weighted k-nearest-neighbor rule. IEEE T Syst. Man. Cy 17, 325327.
Erzin, Y., and Cetin, T. (2014). The prediction of the critical factor of safety of homogeneous finite slopes subjected to earthquake forces using neural networks and multiple regressions. Geomech. Eng. 6 (1), 1–15. doi:10.12989/gae.2014.6.1.001
Fathipour-Azar, H. (2022). Stacking ensemble machine learning-based shear strength model for rock discontinuity. Geotech. Geol. Eng. (Dordr). 40 (6), 3091–3106. doi:10.1007/s10706-022-02081-1
Feng, X. T., Seto, M., and Katsuyama, K. (1997). Neural dynamic modelling on earthquake magnitude series. Geophys. J. Int. 128, 547–556. doi:10.1111/j.1365-246x.1997.tb05317.x
Feng, X. T., and Wang, L. N. (1994). Rockburst prediction based on neural networks. Trans. Nonferrous Metals Soc. China 1994 (1), 7–14.
Feng, X. T., Wang, Y. J., and Yao, J. G. (1996). A neural network model for real-time roof pressure prediction in coal mines. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 33, 647–653. doi:10.1016/0148-9062(96)00010-1
Feng, Y., Wang, Q., Wu, D., Gao, W., and Tin-Loi, F. (2021). Stochastic nonlocal damage analysis by a machine learning approach. Comput. Methods Appl. Mech. Eng. 372 (2020), 113371. doi:10.1016/j.cma.2020.113371
Feng, Y., Wang, Q., Wu, D., Luo, Z., Chen, X., Zhang, T., et al. (2021). Machine learning aided phase field method for fracture mechanics. Int. J. Eng. Sci. 169 (2021), 103587. doi:10.1016/j.ijengsci.2021.103587
Freund, Y., and Schapire, R. E. (1997). A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 55, 119–139. doi:10.1006/jcss.1997.1504
Fuchs, A., Heider, Y., Wang, K., Sun, W., and Kaliske, M. (2021). DNN2: A hyper-parameter reinforcement learning game for self-design of neural network based elasto-plastic constitutive descriptions. Comput. Struct. 249 (2021), 106505. doi:10.1016/j.compstruc.2021.106505
Garfi, G., John, C. M., Berg, S., and Krevor, S. (2020). The sensitivity of estimates of multiphase fluid and solid properties of porous rocks to image processing. Transp. Porous Media 131 (3), 985–1005. doi:10.1007/s11242-019-01374-z
Garg, A., Aggarwal, P., and Aggarwal, Y. (2022). Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr. 30 (1), 33–42.
Ge, H. W., Liang, Y. C., Liu, W., and Gu, X. J. (2004). Applications of artificial neural networks and genetic algorithms to rock mechanics. Chin. J. Rock Mech. Eng. 9, 15421550.
Ghaboussi, J., and Sidarta, D. E. (1998). New nested adaptive neural networks (NANN) for constitutive modeling. Comput. Geotechnics 22, 29–52. doi:10.1016/s0266-352x(97)00034-7
Goldberg, D. E. (1989). Optimization,and machine learning. New York: Addison-Wesley.Genetic algorithms in search
Goral, J., Andrew, M., Olson, T., and Deo, M. (2020). Correlative core-to pore-scale imaging of shales. Mar. Petroleum Geol. 111, 886–904. doi:10.1016/j.marpetgeo.2019.08.009
Goswami, D., and Chakraborty, A. (2017). Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 10 (17), 385–7511. doi:10.1007/s12517-017-3167-x
Gu, G. X., Chen, C. T., and Buehler, M. J. (2018). De novo composite design based on machine learning algorithm. Extreme Mech. Lett. 18, 19–28. doi:10.1016/j.eml.2017.10.001
Gu, H., Wu, Z., Huang, X., and Song, J. (2015). Zoning modulus inversion method for concrete dams based on chaos genetic optimization algorithm. Math. Problems Eng. 2015, 1–9. doi:10.1155/2015/817241
Hadi, F. A., and Nygaard, R. (2018). “Shear wave prediction in carbonate reservoirs: Can artificial neural network outperform regression analysis?,” in 52nd US Rock Mechanics/Geomechanics Symposium.
Haghighat, E., Amini, D., and Juanes, R. (2021). Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training. Comput. Methods Appl. Mech. Eng. 397 (2022), 115141. doi:10.1016/j.cma.2022.115141
Hamdia, K. M., Lahmer, T., Nguyen-Thoi, T., and Rabczuk, T. (2015). Predicting the fracture toughness of PNCs: A stochastic approach based on ANN and ANFIS. Comput. Mat. Sci. 102, 304–313. doi:10.1016/j.commatsci.2015.02.045
Hasanipanah, M., Meng, D., Keshtegar, B., Trung, N. T., and Thai, D. K. (2021). Nonlinear models based on enhanced kriging interpolation for prediction of rock joint shear strength. Neural comput. Appl. 33 (9), 4205–4215. doi:10.1007/s00521-020-05252-4
Hastie, T., Rosset, S., Zhu, J., and Zou, H. (2009). Multi-class adaboost. Stat. Interface 2, 349–360. doi:10.4310/sii.2009.v2.n3.a8
Hinton, G. E., and Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science 313, 504–507. doi:10.1126/science.1127647
Iassonov, P., Gebrenegus, T., and Tuller, M. (2009). Segmentation of X‐ray computed tomography images of porous materials: A crucial step for characterization and quantitative analysis of pore structures. Water Resour. Res. 45 (9). doi:10.1029/2009wr008087
Indraratna, B., Haque, A., and Aziz, N. (1999). Shear behaviour of idealized infilled joints under constant normal stiffness. Geotechnique 49 (3), 331–355. doi:10.1680/geot.1999.49.3.331
Jiang, Z., Li, J., Yang, Y., Mu, L., Wei, C., Yu, X., et al. (2020). Machine-learning-revealed statistics of the particle-carbon/binder detachment in lithium-ion battery cathodes. Nat. Commun. 11 (1), 2310–2319. doi:10.1038/s41467-020-16233-5
Jin, Chang-Yu., Ma, Zhen-Yue., Zhang, Yun-Liang., Sha, Rui-Hua., and Chen, Qing-Fa. (2006). Application of neural network to back analysis of mechanical parameters and initial stress field of rock masses. Rock Soil Mech. 27, 12631266.
Joekar-Niasar, V., Hassanizadeh, S. M., and Leijnse, A. (2008). Insights into the relationships among capillary pressure, saturation, interfacial area and relative permeability using pore-network modeling. Transp. Porous Media 74 (2), 201–219. doi:10.1007/s11242-007-9191-7
Johari, A., Javadi, A. A., and Habibagahi, G. (2011). Modelling the mechanical behaviour of unsaturated soils using a genetic algorithm-based neural network. Comput. Geotechnics 38 (1), 2–13. doi:10.1016/j.compgeo.2010.08.011
Kohestani, V. R., and Hassanlourad, M. (2016). Modeling the mechanical behavior of carbonate sands using artificial neural networks and support vector machines. Int. J. Geomech. 16 (1), 04015038. doi:10.1061/(asce)gm.1943-5622.0000509
Leu, L., Berg, S., Enzmann, F., Armstrong, R. T., and Kersten, M. (2014). Fast X-ray micro-tomography of multiphase flow in berea sandstone: A sensitivity study on image processing. Transp. Porous Media 105 (2), 451–469. doi:10.1007/s11242-014-0378-4
Li, J., Zhang, D., Wang, N., and Chang, H. (2022). Deep learning of two-phase flow in porous media via theory-guided neural networks. SPE J. 27 (02), 1176–1194. doi:10.2118/208602-pa
Li, X. D., Zhang, G. Y., Xiang, F. P., Wang, J. T., and Xu, H. (2008). Normalization characteristic of sands under triaxial compression and numerical modeling method. Chin. J. Rock Mech. Eng. 27 (A1), 3082–3087.
Li, X. H., Zhao, Y., Jin, X. G., Lu, Y. Y., and Wang, X. F. (2005). Application of grey majorized model in tunnel surrounding rock displacement forecasting. Lect. Notes Comput. Sci. 3611, 584–591. doi:10.1007/11539117_83
Li, X., Yan, Z. M., and Liu, Z. L. (2019). Combination and application of machine learning and computational mechanics. Chin. Sci. Bull. 64, 635–648. doi:10.1360/n972019-00005
Li, Y. S., Li, X. P., and Zhang, C. L. (2006). Displacement prediction method of surrounding rock in tunnel based on bp neural network. Chin. J. Rock Mech. Eng. 25 (A1), 2969–2973.
Li, Y., and Chen, S. (2022). Physics-informed neural networks:recent advances and prospects. Comput. Sci. 49 (4), 254–262.
Liang, L., Liu, M., Martin, C., and Sun, W. (2018). A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 15, 20170844. doi:10.1098/rsif.2017.0844
Liu, X., Athanasiou, C. E., Padture, N. P., Sheldon, B. W., and Gao, H. (2020). A machine learning approach to fracture mechanics problems. Acta Mat. 190 (2020), 105–112. doi:10.1016/j.actamat.2020.03.016
Liu, X., Athanasiou, C., Padture, N., Sheldon, B. W., and Gao, H. (2020). A machine learning approach to fracture mechanics problems. Acta Mater. 190 (2020), 105–112. doi:10.1016/j.actamat.2020.03.016
Liu, Y., Dai, F., Fan, P., Xu, N., and Dong, L. (2017). Experimental investigation of the influence of joint geometric configurations on the mechanical properties of intermittent jointed rock models under cyclic uniaxial compression. Rock Mech. Rock Eng. 50 (6), 1453–1471. doi:10.1007/s00603-017-1190-6
Liu, Z. B., Shao, J. F., Xu, W. Y., and Wu, Q. (2015). Indirect estimation of unconfined compressive strength of carbonate rocks using extreme learning machine. Acta Geotech. 10, 651–663. doi:10.1007/s11440-014-0316-1
Lu, P., and Rosenbaum, M. (2003). Artificial neural networks and grey systems for the prediction of slope stability. Nat. Hazards 30 (3), 383–398. doi:10.1023/b:nhaz.0000007168.00673.27
Mahmoodzadeh, A., Mohammadi, M., Salim, S., Farid Hama Ali, H., Hashim Ibrahim, H., Nariman Abdulhamid, S., et al. (2022). Machine learning techniques to predict rock strength parameters. Rock Mech. Rock Eng. 55 (3), 1721–1741. doi:10.1007/s00603-021-02747-x
Matos, Y., Dantas, S., and Barreto, G. (2019). Predicting the shear strength of unfilled rock joints with the first-order takagi-sugeno fuzzy approach. Soils Rocks 42 (1), 21–29. doi:10.28927/sr.421021
Mohamed A. Shahin., , Jaksa., Mark B., and Maier., Holger R. (2009). Recent advances and future challenges for artificial neural systems in geotechnical engineering applications. Adv. Artif. Neural Syst., 1–9. doi:10.1155/2009/308239
Morgenroth, J., Khan, U. T., and Perras, M. A. (2019). An overview of opportunities for machine learning methods in underground rock engineering design. Geosciences 9 (12), 504. doi:10.3390/geosciences9120504
Mozaffar, M., Bostanabad, R., Chen, W., Ehmann, K., Cao, J., and Bessa, M. (2019). Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. U. S. A. 116, 26414–26420. doi:10.1073/pnas.1911815116
Kutner, M. H., Nachtsheim, C. J., Neter, J., and Li, W. (1996). Applied linear statistical models. Chicago: Irwin.
Nguyen-Le, D., Tao, Q., Nguyen, V., Abdel-Wahab, M., and Nguyen-Xuan, H. (2020). A data-driven approach based on long short-term memory and hidden Markov model for crack propagation prediction. Eng. Fract. Mech. 235 (2020), 107085. doi:10.1016/j.engfracmech.2020.107085
Papaliangas, T., Hencher, S. R., Manolopoulos, S., and Manolopoulou, S. (1993). The effect of frictional fill thickness on the shear strength of rock discontinuities. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 30 (2), 81–91. doi:10.1016/0148-9062(93)90702-f
Peng, X. H., Wang, Z. C., Luo, T., Yu, M., and Luo, Y. S. (2008). An elasto-plastic constitutive model of moderate sandy clay based on BC-RBFNN. J. Central South Univ. Technol. (S1), 47–50.
Raeini, A. Q., Blunt, M. J., and Bijeljic, B. (2014). Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. water Resour. 74, 116–126. doi:10.1016/j.advwatres.2014.08.012
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2018). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045
Rajesh Kumar, B., Vardhan, H., Govindaraj, M., and Vijay, G. S. (2013). Regression analysis and ANN models to predict rock properties from sound levels produced during drilling. Int. J. Rock Mech. Min. Sci. (1997). 58, 61–72. doi:10.1016/j.ijrmms.2012.10.002
Rashidian, V., and Hassanlourad, M. (2014). Application of an artificial neural network for modeling the mechanical behavior of carbonate soils. Int. J. Geomech. 14, 142–150. doi:10.1061/(asce)gm.1943-5622.0000299
Roohollah, S. F., and Abbas, T. (2019). Long-term prediction of rockburst hazard in deep underground openings using three robust data mining techniques. Eng. Comput. 35, 659–675. doi:10.1007/s00366-018-0624-4
Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408. doi:10.1037/h0042519
Rudy, S. H., Brunton, S. L., Proctor, J. L., and Kutz, J. N. (2017). Data-driven discovery of partial differential equations. Sci. Adv. 3, e1602614. doi:10.1126/sciadv.1602614
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0
Saad, B., Negara, A., and Syed Ali, S. (2018). “Digital rock physics combined with machine learning for rock mechanical properties characterization,” in Abu Dhabi International Petroleum Exhibition & Conference.
Samani, H. Y., and Bafghi, A. R. Y. (2012). Prediction of the sawing quality of Marmarit stones using the capability of artificial neural network. Int. J. Numer. Anal. Methods Geomech. 36, 881–891. doi:10.1002/nag.1033
Shouling, He., and Jiang, Li. (2009). Modeling nonlinear elastic behavior of reinforced soil using artificial neural networks. Appl. Soft Comput. 9, 954–961. doi:10.1016/j.asoc.2008.11.013
Sklavounos, P., and Sakellariou, M. (1995). “Intelligent classification of rock masses,” in WIT transactions on information and communication technologies (Billerica, MA, USA: WIT Press), 8.
Song, Z. P., Jiang, A. N., and Jiang, Z. B. (2015). Back analysis of geomechanical parameters using hybrid algorithm based on difference evolution and extreme learning machine. Math. Problems Eng. 2015, 1–11. doi:10.1155/2015/821534
Soulaine, C., Gjetvaj, F., Garing, C., Roman, S., Russian, A., Gouze, P., et al. (2016). The impact of sub-resolution porosity of x-ray microtomography images on the permeability. Transp. Porous Media 113 (1), 227–243. doi:10.1007/s11242-016-0690-2
Tan, Y. L., and Wang, C. Q. (2001). A fast approaching model for rock constitutive equation by radial basis function neural network. Chin. J. Geotechnical Eng. 23, 14–17.
Tefas, A., Kotropoulos, C., and Pitas, I. (2002). Enhancing the performance of elastic graph matching for face authentications by using Support Vector Machines, ACAI99.
Tiryaki, B. (2008). Predicting intact rock strength for mechanical excavation using multivariate statistics, artificial neural networks, and regression trees. Eng. Geol. 99, 51–60. doi:10.1016/j.enggeo.2008.02.003
Vardakos., Sotirios S., Gutierrez, Marte S., and Barton., Nick R. (2007). Back-analysis of Shimizu Tunnel No.3 by distinct element modeling. Tunn. Undergr. Space Technol. 22, 401–413. doi:10.1016/j.tust.2006.10.001
Veropoulos, K., Cristianini, N., and Campbell, C. (2016). The application of support vector machines to medical decision support: A case study, ACAI99.
Wang, D. G., Liu, Y. X., and Li, S. J. (2000). Genetic algorithms for inverse analysis of isplacements in geotechnical engineerin. Chin. J. Rock Mech. Eng. 19 (A1), 979–982.
Wang, Y. D., Chung, T., Armstrong, R. T., McClure, J. E., and Mostaghimi, P. (2019b). Computations of permeability of large rock images by dual grid domain decomposition. Adv. Water Resour. 126, 1–14. doi:10.1016/j.advwatres.2019.02.002
Wang, Y. D., Chung, T., Armstrong, R. T., and Mostaghimi, P. (2021). ML-LBM: Predicting and accelerating steady state flow simulation in porous media with convolutional neural networks. Transp. Porous Media 138 (1), 49–75. doi:10.1007/s11242-021-01590-6
Wang, Y., Zhang, X., and Liu, X. (2021). Machine learning approaches to rock fracture mechanics problems: Mode-I fracture toughness determination. Eng. Fract. Mech. 253 (2021), 107890. doi:10.1016/j.engfracmech.2021.107890
Wang, Y., Zhou, X., and Xu, X. (2016). Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics. Eng. Fract. Mech. 163, 248–273.
Wang, Z. B., Ma, F. H., and Zhang, B. X. (2015). Intelligent displacement back analysis of surrounding rock parameters of the mined subway tunnel in changchun. J. Water Resour. Archit. Eng. 13 (5), 122–126.
Wei, Gao. (2018). A comprehensive review on identification of the geomaterial constitutive model using the computational intelligence method. Adv. Eng. Inf. 38, 420–440. doi:10.1016/j.aei.2018.08.021
Widrow, B. (1987). “Piscataway,” in Proceedings of the IEEE First International Conference on Neural Networks, 143157
Wu, Q. D., Yan, B., Zhang, C., Wang, L., Ning, G., and Yu, B. (2014). Displacement prediction of tunnel surrounding rock: A comparison of support vector machine and artificial neural network. Math. Problems Eng. 2014 (1), 1–6. doi:10.1155/2014/351496
Yagiz, S., Sezer, E. A., and Gokceoglu, C. (2012). Artificial neural networks and nonlinear regression techniques to assess the influence of slake durability cycles on the prediction of uniaxial compressive strength and modulus of elasticity for carbonate rocks. Int. J. Numer. Anal. Methods Geomech. 36, 1636–1650. doi:10.1002/nag.1066
Yao, B., Yao, J., Zhang, M., and Yu, L. (2014). Improved support vector machine regression in multi-step-ahead prediction for rock displacement surrounding a tunnel. Sci. Iran. 21 (4), 1309–1316.
Yao, B. Z., Yang, C. Y., Yao, J. B., and Sun, J. A. (2010). Tunnel surrounding rock displacement prediction using support vector machine. Int. J. Comput. Intell. Syst. 3, 843. doi:10.2991/ijcis.2010.3.6.14
Yazdani, M., Daryabari, A., Farshi, A., and Talatahari, S. (2013). Application of Taguchi method and genetic algorithm for calibration of soil constitutive models. J. Appl. Math. 2013 (8), 258721(1-11). doi:10.1155/2013/258721
Zhang, H., Nguyen, H., Bui, X. N., Pradhan, B., Asteris, P. G., Costache, R., et al. (2021). A generalized artificial intelligence model for estimating the friction angle of clays in evaluating slope stability using a deep neural network and harris hawks optimization algorithm. Eng. Comput., 1–14. doi:10.1007/s00366-020-01272-9
Zheng, D. J., Cheng, L., Bao, T. F., and Lv, B. (2013). Integrated parameter inversion analysis method of a CFRD based on multi-output support vector machines and the clonal selection algorithm. Comput. Geotech. 47, 68–77. doi:10.1016/j.compgeo.2012.07.006
Zhou, Y. X., and Wu, X. P. (1994). Use of neural networks in the analysis and interpretation of site investigation data. Comput. Geotechnics 16, 105–122. doi:10.1016/0266-352x(94)90017-5
Zia, H., Lecampion, B., and Zhang, W. (2018). Impact of the anisotropy of fracture toughness on the propagation of planar 3D hydraulic fracture. Int. J. Fract. 211 (1-2), 103–123. doi:10.1007/s10704-018-0278-7
Keywords: rock mechanics, machine learining, deep learning, artificial neural network, failure, pore scale analysis
Citation: Yu H, Taleghani AD, Al Balushi F and Wang H (2022) Machine learning for rock mechanics problems; an insight. Front. Mech. Eng 8:1003170. doi: 10.3389/fmech.2022.1003170
Received: 25 July 2022; Accepted: 22 August 2022;
Published: 17 October 2022.
Edited by:
Li Li, Huazhong University of Science and Technology, ChinaReviewed by:
Zarghaam Rizvi, University of British Columbia, Okanagan Campus, CanadaAman Garg, The Northcap University, India
Copyright © 2022 Yu, Taleghani, Al Balushi and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arash Dahi Taleghani, YXVkNDQwQHBzdS5lZHU=
 Hao Yu
Hao Yu Arash Dahi Taleghani
Arash Dahi Taleghani Faras Al Balushi2
Faras Al Balushi2