Adjustable Magnetic-Control Design of a Metasurface for Sound Insulation

Magnetic field is one efficient approach to realize non-contact control of materials. Here, we propose a type of membrane-based metasurface consisting of several parts of magnetorheological films embedded with magnetic particles, which enable non-contact control of sound insulation through magnetic field. The abundant degree of freedoms in membrane-type metamaterials are explored by considering composite structures. Through numerical calculations, we have investigated the effect of magnetic field excitation and film composition on the acoustic properties and the performance for sound insulation. We find an optimized model for better adjustability, wider acoustic band, and more balanced performance.

Introduction

In recent years, artificial acoustic metamaterials have significantly expanded the horizon of acoustic materials, helical-structured metamaterials, PT-symmetric acoustics, acoustic cloaking, the acoustic Meta‐Skin Insulator, etc, leading to many novel phenomena (Christensen et al., 2007; Li et al., 2009; Liang et al., 2010; Boechler et al., 2011; Zhang et al., 2011; Zhu et al., 2011; Chen et al., 2014a; Zhou et al., 2014; Zhu et al., 2014; Molerón and Daraio, 2015; Zhu et al., 2016a; Cummer et al., 2016; Ma and Sheng, 2016; Yang and Sheng, 2017; Tang et al., 2018; Tong et al., 2020; Zeng et al., 2021). The single layer of acoustic metamaterials, i.e., acoustic metasurfaces, can manipulate the phase and amplitude of sound in unprecedented ways and enable many interesting applications like anomalous refraction and reflection, radiation control, acoustic holography, acoustic absorption, etc (Lee et al., 2010; Liang and Li, 2012; Mei et al., 2012; Zhao et al., 2013a; Zhao et al., 2013b; Li et al., 2013; Li et al., 2014; Tang et al., 2014; Xie et al., 2014; Kaina et al., 2015; Xiao et al., 2015; Yuan et al., 2015; Gao et al., 2016; Assouar et al., 2018). Mechanisms of exotic elastic metamaterials have also been investigated (Akl and Baz, 2012; Chen et al., 2014b; Bergamini et al., 2014; Wang et al., 2014; Zhu et al., 2016b; Chen et al., 2017a). In this work, we focus on membrane-type metamaterials as they have excellent sound isolation and absorption properties with regard to low-frequency noise ranging from 50 to 1000 Hz (Yang et al., 2010). Their average transmission loss may exceed 40 dB. Moreover, they are light in weight and easy to prepare. Membrane-type materials use resonance as a means to absorb sound waves at some frequencies (Du et al., 2001). Negative effective parameters have also been achieved by membrane-type materials (Yang et al., 2013). Recently, external static magnetic force has been applied to harness the geometric nonlinearity of membrane structures so as to tune the transmission spectrum both theoretically and experimentally (Chen et al., 2017b). However, the abundant degrees of freedoms in the structure design of the membrane-type metasurfaces for adjustable magnetic control have not been fully explored yet.

Magnetic Acoustic Metamaterial Models and Theory

Theoretical Model for the Monolayer Magnetoacoustic Metamaterial

In the past decade, researchers have proposed to realize active acoustic metamaterials with magnetorheological films (Chen et al., 2017b; Domel et al., 2018). Such a metamaterial is composed of magnetorheological film, aluminum and lead mass block (Figures 1A–D). For the magnetorheological film, the Young’s modulus changes with magnetic field, thus the resonance frequency also varies accordingly, leading to the active control functionality.

FIGURE 1

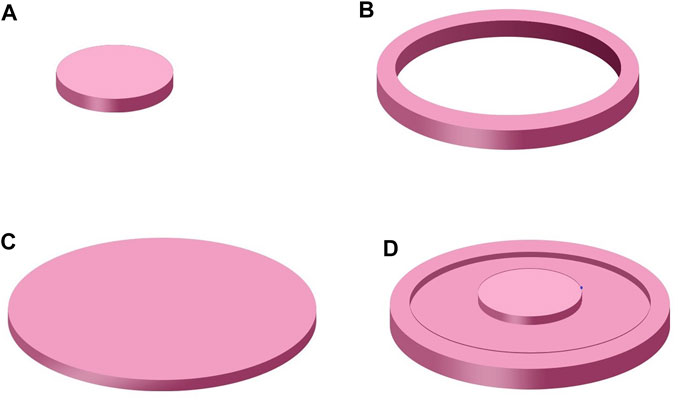
FIGURE 1. Diagrams of various parts of an active acoustic material film: (A) additional mass block, (B) aluminum frame, (C) magnetic film, and (D) overview of the whole film.

To achieve better performances in sound insulation at low frequencies, a local resonance of the system at low frequencies is realized by attaching a mass block of lead to the magnetic film. The inertial force generated by the additional mass is added to the vibration equation of the film as an external incentive force. The equation describing free vibrations of the film structure with the added mass is (Sun et al., 2010)

${\epsilon }_r=\frac{du}{dr}+\frac{1}{2}{\left(\frac{dw}{dr}\right)}^2(1)$

${\epsilon }_{\theta }=\frac{u}{r}(2)$

where ${\epsilon }_r$ is the radial strain, ${\epsilon }_{\theta }$ is the circumferential strain, $\text{u}$ and $\text{w}$ are the radial and out-of-plane displacements of the membrane, respectively. Due to the axial symmetry, the balance equation in circumferential direction is automatically satisfied. Meanwhile, the relation between the bending angle and the deflection is introduced by $\text{sinθ}=-\frac{dw}{dr}$. The equilibrium equations are:

$2\pi r{\sigma }_{r}t\frac{dw}{dr}=-\pi R_1^2{P}_m(3)$

$\frac{d}{dr}\left(r{\sigma }_r\right)-{\sigma }_{\theta }=0(4)$

The free vibration characteristic equation of the membrane-type acoustic metamaterial is

$\left[\mathrm{K}+K_{f-{\omega }^2}\mathrm{M}\right]\left[\tilde{q}\right]=0,(5)$

where M and K denote the mass matrix and stiffness matrix, respectively, $K_f$ denotes the stiffness matrix for the pre-stressed material, ω is the natural angular frequency of the system, and $\tilde{q}$ an eigenvector.

When an incident plane wave propagates normal to the surface, it first interacts with the magnetic film and additional mass block. For this mass-weighted film, the surface-averaged Green function of Equation is (Chen et al., 2017b)

$\langle G_m\rangle =\frac{\langle W\rangle }{\langle {\delta }_P\rangle }={\displaystyle \sum _{i=1}\frac{S{\langle W_i\left(r,H\right)\rangle }^2}{{\displaystyle \iint \rho W_i^{2}dS·\left({\omega }_i^2\left(H\right)-{\omega }^2\right)}}}.(6)$

Here ⟨W⟩ is the surface-averaged displacement of the membrane-type structure, ${\delta }_P$ is the sound pressure variation through the structure, $S$ is the relevant area, $\rho$ is the local surface density, $W_i$ is the ith eigenmodes, and ${\omega }_i$ is the relevant angular eigenfrequency. When the magnetic field is imposed, both the eigenmodes and the eigenfrequencies will be changed accordingly.

The effect of a mass block can be analyzed by using the equivalent-lumped-element method (Du et al., 2001). The equivalent masses of the film and the mass block at the center of the circle are denoted $M_1$ and $M_2$, and the equivalent elasticity coefficient of the film is denoted $K_1$. The natural frequency of the system is then

$f=\frac{1}{2\pi }\sqrt{\frac{K_1}{M_1+M_2}}.(7)$

From Eq. 5, the natural frequency of the initial system is reduced by adding the mass block. By increasing the mass, the sound insulation effect of the model system at low frequencies becomes better. For this reason, we chose to use blocks of lead.

The Young’s modulus E of magnetorheological films varies with the volume fraction of ferromagnetic particles φ, the strength of the magnetic field $H_0$, the vacuum permeability ${\mu }_0$, relative permeability ${\mu }_m$ and constant D. An expression for E is given by the linear magnetic dipole model (Feng et al., 2015),

$\Delta E=3\phi H_0{\mu }_0{\mu }_{m}D.(8)$

From Eq. 8, it is clear that the Young’s modulus of a magnetorheological film can be conveniently changed by adjusting the volume fraction of magnetic particles in the magnetorheological film, and hence the working frequency of the active acoustic material is altered accordingly.

The unit cell of the monolayer active acoustic metamaterial comprises a magnetron film, aluminum frame, and lead mass block. The unit cell is exposed to air. At the upper boundary of the air layer, an incoming plane-wave is incident at a pressure of 1 Pa; at the lower boundary of the air layer, a set of outgoing plane waves are emitted. In this manner, the performance of the unit cell with regard to sound insulation can be calculated from the changes in sound pressure of these incoming and outgoing waves.

The acoustic properties of the metamaterials were numerically analyzed using the frequency mode of the acoustic-solid coupling module implemented in COMSOL Multiphysics 5.4. The structural size of the cell is as follows: film thickness d = 1 mm, radius r = 15 mm, frame thickness ${\mathit{d}}_1=3\text{mm}$, inner diameter ${\mathit{r}}_1=15\text{mm}$, ${\mathit{r}}_2=17\text{mm}$, mass block radius ${\mathbf{r}}_3=6\text{mm}$, and thickness ${\mathit{d}}_2=2\text{mm}$. The support frame of the unit cell is chosen as aluminum. The membrane-type film is made of magnetorheological material. And the mass block is made of lead. The material parameters of aluminum are: density ρ = 2,700 $\text{kg}/{\text{m}}^3$, Young’s modulus E = 70 GPa, and Poisson’s ratio ν = 0.33. The parameters for the magnetorheological material are: density ρ = 2,100 $\text{kg}/{\text{m}}^3$, Young’s modulus E = 6.5 MPa, and Poisson’s ratio ν = 0.45. Table 1 gives the dependence of the Young’s modulus of the material on the magnetic field strength over the range of 0–300 kA/m for a 188 KPa pre-stressing of the magnetron film used in this study.

TABLE 1

TABLE 1. Young’s modulus for various magnetically controlled films produced under the same prestressing from different magnetic field strengths.

Composite Magnetic Control Metasurface Film

We note that there are abundant degrees of freedoms to be explored in the magnetic membrane-type metasurface design. In this work, we consider a kind of composite magnetic membrane-type metasurface that are composed of multiple films instead of only one film. Compared to the previously investigated simple single-film structure, the multiple film design in principle can realize controllable broadband sound insulation by tuning the independent resonances of each film.

The composite magnetic membrane-type metamaterial is composed of one circular film and two annular films (Figures 2, 3), which are interposed by two aluminum spacers, yielding the sequence of film-1-aluminum-film-2-aluminum-film-3. The whole structure is embedded in an aluminum frame. The structural size of the composite membrane-type metamaterial is the same as that of the previously investigated simple membrane-type metamaterial with only one film.

FIGURE 2

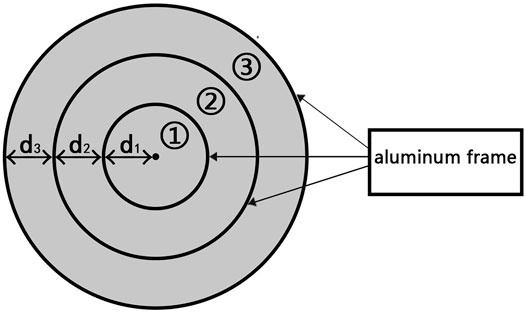
FIGURE 2. Diagram of the model for a concentric circular single-layer composite magnetic control metasurface. Areas labeled ①, ②, and ③, are film positions; the thick black lines are fixed frames made of aluminum.

FIGURE 3

FIGURE 3. Composite structure of the metasurface model used in the study.

The acoustic properties of the metamaterials were numerically analyzed using the frequency mode of the acoustic-solid coupling module implemented in COMSOL Multiphysics 5.4. The structural size of the cell is as follows: film thickness d = 1 mm, radius ${\mathit{d}}_1$ = ${\mathit{d}}_2$ = ${\mathit{d}}_3$ = 5 mm, Young’s modulus ${\mathit{E}}_1$, ${\mathit{E}}_2$ and ${\mathit{E}}_3$, they are adjustable. The material parameters of aluminum frames are: thickness d = 1 mm, height h = 1 mm, density ρ = 2,700 $\text{kg}/{\text{m}}^3$, Young’s modulus E = 70 GPa, and Poisson’s ratio ν = 0.33.

Simulation Analysis of the Models

Simulation of the Monolayer Magnetron Film

Figure 4 shows the performance curves for the sound insulation of the single-film active acoustic metamaterial under different magnetic fields, i.e., 0 kA/m (3.52 MPa), 100 kA/m (3.91 MPa), 200 kA/m (4.65 MPa), and 300 kA/m (5.55 MPa). With increasing magnetic field strength, the Young’s modulus of the magnetorheological film increases, and the maximum peak frequency (216 Hz, 224 Hz, 244 Hz, 270 Hz) of the active acoustic material increases. The peak value (74.7 dB, 78.3 dB, 85.3 dB, 119.1 dB) for sound insulation increases too. We get better sound insulation performance. The working bandwidth also turns wider, and hence sound insulation in the low-frequency range is improved. By adding a magnetic field, controlling adjustments can be made in the peak value of sound insulation for the film material. Non-contact active control of noise is thereby realized, along with a broader frequency range and better performance for sound insulation of the film material.

FIGURE 4

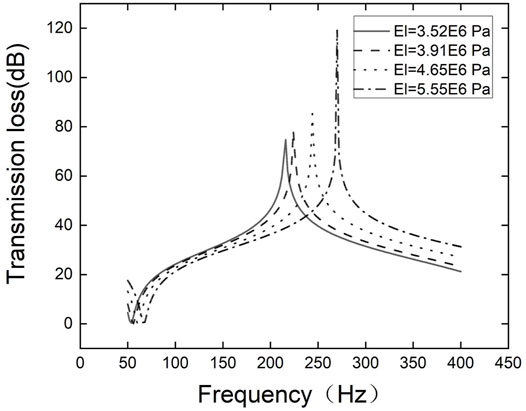
FIGURE 4. Performance curves for sound insulation of films of the same material for various magnetic field strengths.

Simulation Analysis of the Composite Magnetic Membrane-type Metasurface

Comparison of Film Arrays With Various Modulations in Young’s Modulus

Figures 5A–C shows the performance curves of various films with regard to sound insulation. The Young’s modulus of the three films are 2 MPa, 16 MPa, and 32 MPa, respectively, which are produced under a magnetic field of 200 kA/m. Figure 5D shows the performance curves of the three-film membrane-type metamaterials.

FIGURE 5

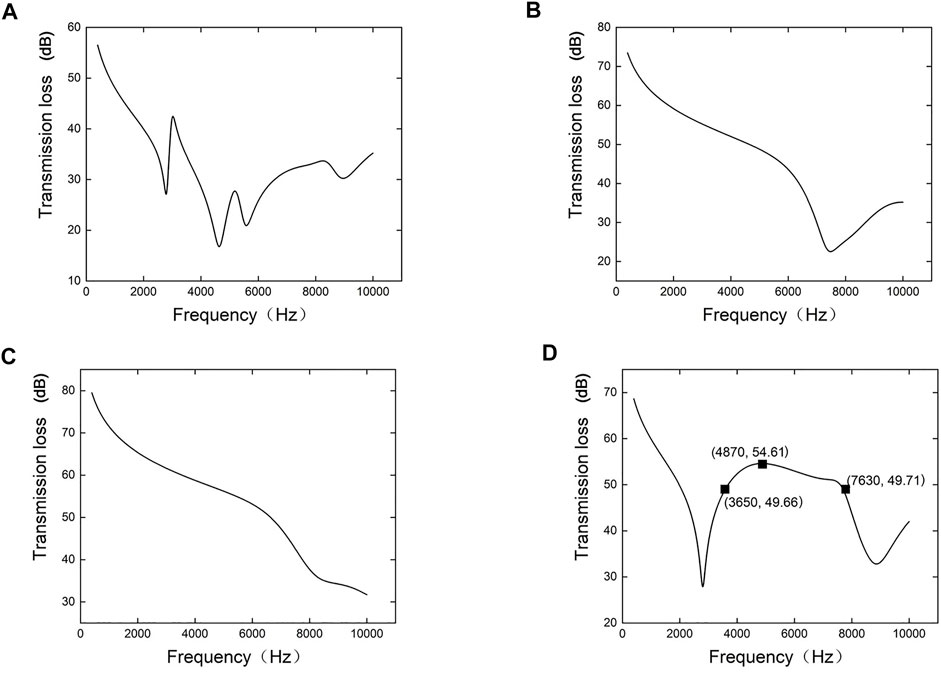
FIGURE 5. Young’s modulus of three films are: (A) all 2 MPa, (B) all 16 MPa, (C) 32 MPa, (D) in sequence 2 MPa, 16 and 32 MPa.

Comparing with the previous cases where the films have exactly the same Young’s moduli, we find that when the three films’ Young’s moduli are different, a more stable sound insulation effect is achieved in a larger bandwidth. To be more specific, the working bandwidth for the regime with sound insulation effect of maximum −5 dB is found to be 3,980 Hz (Figure 5D), which is much bigger than those observed in Figure 4. We find that the working bandwidth of sound insulation is greatly broadened and produces a better effect for sound insulation. Therefore, this multi-film design solves the issue of narrow working bandwidth for single-film magnetic control films.

Investigation on Different Film Combinations for the Designed Three-Film Metasurface on the Performance for Sound Insulation

With regard to sound insulation, next we discuss the performance of three-film metasurface comprising three films with different Young’s modulus (Figure 6). Under a 200 kA/m magnetic field excitation, the Young’s modulus for films labeled ①, ②, and ③ are: 2, 14, and 28 MPa (Figure 6A); 2, 12, and 24 MPa (Figure 6B); 2, 10, and 20 MPa. Figure 6C: 2, 8, and 16 MPa (Figure 6D); and 2, 30 and 60 MPa (Figure 6E).

FIGURE 6

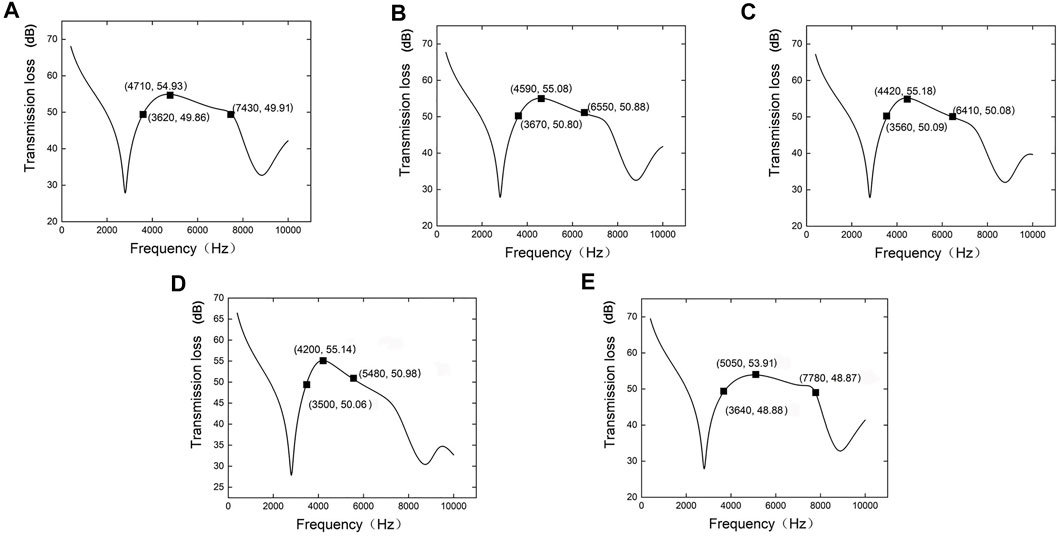
FIGURE 6. Performance curves for sound insulation of the three-film system for which the Young’s moduli of the films ①, ②, and ③ are: (A) 2 MPa, 14 MPa, and 28 MPa, (B) 2 MPa, 12 MPa, and 24 MPa; (C) 2 MPa, 10 MPa, and 20 MPa; (D) 2 MPa, 8 MPa, and16 MPa; and (E) 2 MPa, 30 and 60 MPa.

By comparing Figures 6A–E with Figure 5D, we find that by tuning the Young’s moduli in different films, a distinct modulation is achieved in the sound insulation effect. The bandwidths relating to the maximum −5 dB working range are, in sequential order, 3,810 Hz, i.e., 3,620–7,430 Hz, 2,880 Hz, i.e., 3,670–6,550 Hz, 2,580 Hz, i.e., 3,560–6,140 Hz, 1,980 Hz, i.e., 3,500–5,480 Hz, and 4,140 Hz, i.e., 3,640–7,780 Hz, respectively, whereas that observed in Figure 5D is 3,980 Hz. Clearly, with a decreasing contrast in Young’s moduli for different films, the working bandwidth of the three-film metasurface gradually diminishes.

Influence of the Magnetic Field for the Designed Three-Film Metasurface on the Performance for Sound Insulation

The magnetic field excitation is also a major influence factor on magnetically controlled films and, in particular, on the performance of such films for sound insulation.

For reference, we utilize the performance curves obtained under a 200-kA/m magnetic field for the three-film metasurface with Young’s moduli of 2, 16, and 32 MPa (Figure 5D). Retaining the same film conditions, we adjust the intensity of the magnetic field to obtain the performance curves for sound insulation (Figures 7A,B), for which the Young’s modulus were 0.02, 0.16, and 0.32 MPa under a 20-kA/m magnetic field, and 10, 80, and 160 MPa under a 890-kA/m magnetic field.

FIGURE 7

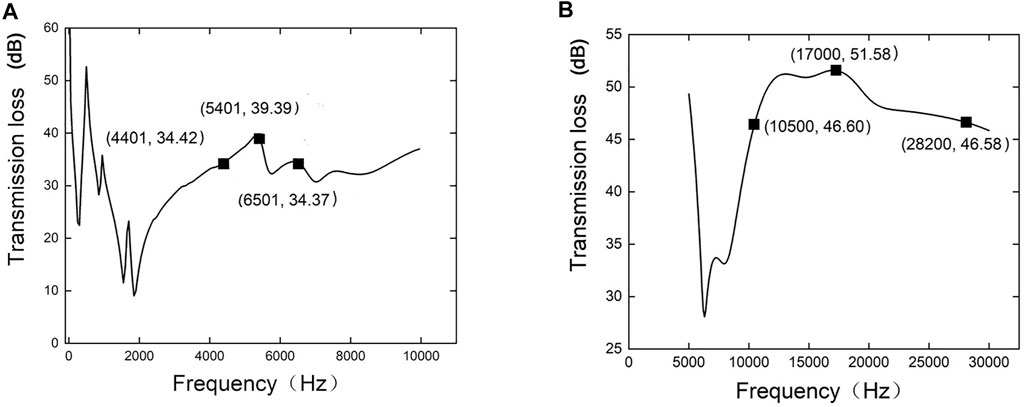
FIGURE 7. Performance curves for sound insulation for two different magnetic field strength: (A) 20 kA/m and (B)890 kA/m.

In comparing Figure 5D with Figures 7A,B, the maximum −5-dB working bandwidth for sound insulation is 1,200 Hz, i.e., 4,401–6,501 Hz (Figure 7A) and 1,7700 Hz, i.e., 10,500–28,200 Hz (Figure 7B). Clearly, reducing the magnetic field intensity narrows the working frequency band and decreases the frequency of the peak; conversely, increasing the magnetic field intensity widens the working frequency band and raises the frequency of the peak. That is, by adjusting magnetic field strength, an adjustable working frequency band can be obtained, and this modulation is achieved through non-contact means. The results also show that this three-film metasurface is suitable for high frequency applications, whereas for low frequency, applying a mass block is better than implementing modulations in the magnetic field strength.

Summary and Discussion

The acoustic characteristics and sound-insulation performance of multi-film composite metasurfaces with magnetic control are designed and analyzed. Compared with the single-film structure, multi-film magnetic metasurfaces have a wider working bandwidth and offer a better performance with regard to sound insulation. Together, they improve the performance of magnetron films and also broaden their range of application.

This work proves that magnetic field is one efficient approach to realize non-contact control of materials. The magnetic field is controllable and adjustable. And the adjustment effect is evident. We can get the desired changes by adjusting the magnetic field parameters.

We also have other ways to realize magnetic adjustment. For example, we can use Niobium metal to make materials. Nb has diamagnetism and superconductivity at a certain temperature. At the temperature, we can realize non-contact control of materials. Adjusting the magnetic field can control the parameters of the materials. Changing the temperature can also realize the switch of the magnetic control function. This idea has rich application prospect.

Our work shows that the use of film combination can greatly improve the overall performance of membrane-type metamaterials. This enhancement can also be considered in the other fields of acoustics and acoustic applications to achieve a better performance beyond a single film structure.

Data Availability Statement

The raw data supporting the conclusion of this will be made available by the authors, without undue reservation.

Author Contributions

PX conducted the simulations. PX, YL, and XL contributed to the writing. XL conceived and led the project.

Funding

This work was supported by the National key R & D program of China (No. 2020YFA0211400), State Key Program of National Natural Science of China (No. 11834008), National Natural Science Foundation of China (No. 12174192, No. 11774167), State Key Laboratory of Acoustics, Chinese Academy of Science (No. SKLA202008), Key Laboratory of Underwater Acoustic Environment, Chinese Academy of Sciences (No. SSHJ-KFKT-1701).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akl, W., and Baz, A. (2012). Analysis and Experimental Demonstration of an Active Acoustic Metamaterial Cell. J. Appl. Phys. 111 (4), 044505–045059. doi:10.1063/1.3686210

CrossRef Full Text | Google Scholar

Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic Metasurfaces. Nat. Rev. Mater. 3 (12), 460–472. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

Bergamini, A., Delpero, T., Simoni, L. D., Lillo, L. D., Ruzzene, M., and Ermanni, P. (2014). Phononic crystal with Adaptive Connectivity. Adv. Mater. 26, 1343–1347. doi:10.1002/adma.201305280

PubMed Abstract | CrossRef Full Text | Google Scholar

Boechler, N., Theocharis, G., and Daraio, C. (2011). Bifurcation-based Acoustic Switching and Rectification. Nat. Mater 10 (9), 665–668. doi:10.1038/nmat3072

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Liu, P., Hou, Z., and Pei, Y. (2017). Magnetic-control Multifunctional Acoustic Metasurface for Reflected Wave Manipulation at Deep Subwavelength Scale. Sci. Rep. 7 (1), 851–852. doi:10.1038/s41598-017-09652-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Xu, X., Ai, S., Chen, H., Pei, Y., and Zhou, X. (2014). Active Acoustic Metamaterials with Tunable Effective Mass Density by Gradient Magnetic fields. Appl. Phys. Lett. 105, 071913. doi:10.1063/1.4893921

CrossRef Full Text | Google Scholar

Chen, Y., Hu, G., and Huang, G. (2017). A Hybrid Elastic Metamaterial with Negative Mass Density and Tunable Bending Stiffness. J. Mech. Phys. Sol. 105 (5), 179–198. doi:10.1016/j.jmps.2017.05.009

CrossRef Full Text | Google Scholar

Chen, Y., Liu, H., Reilly, M., Bae, H., and Yu, M. (2014). Enhanced Acoustic Sensing through Wave Compression and Pressure Amplification in Anisotropic Metamaterials. Nat. Commun. 5, 5247. doi:10.1038/ncomms6247

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen, J., Fernandez-Dominguez, A. I., De Leon-Perez, F., Martin-Moreno, L., and Garcia-Vidal, F. J. (2007). Collimation of Sound Assisted by Acoustic Surface Waves. Nat. Phys 3, 851–852. doi:10.1038/nphys774

CrossRef Full Text | Google Scholar

Cummer, S. A., Christensen, J., and Alù, A. (2016). Controlling Sound with Acoustic Metamaterials. Nat. Rev. Mater. 1 (3), 16001. doi:10.1038/natrevmats.2016.1

CrossRef Full Text | Google Scholar

Domel, A. G., Saadat, M., Weaver, J. C., Haj-Hariri, H., Bertoldi, K., and Lauder, G. V. (2018). Shark Skin-Inspired Designs that Improve Aerodynamic Performance. J. R. Soc. Interf. 15 (139), 20170828. doi:10.1098/rsif.2017.0828

CrossRef Full Text | Google Scholar

Du, G., Zhu, Z., and Gong, X. (2001). Acoustic Foundation. Nanjing: Nanjing University Press, 221.

Google Scholar

Feng, J., Xuan, S., Liu, T., Ge, L., Yan, L., Zhou, H., et al. (2015). The Prestress-dependent Mechanical Response of Magnetorheological Elastomers. Smart Mater. Struct. 24 (9), 085032–0850329. doi:10.1088/0964-1726/24/8/085032

CrossRef Full Text | Google Scholar

Gao, H., Gu, Z.-m., Liang, B., Zou, X.-y., Yang, J., Yang, J., et al. (2016). Acoustic Focusing by Symmetrical Self-Bending Beams with Phase Modulations. Appl. Phys. Lett. 108, 073501. doi:10.1063/1.4941992

CrossRef Full Text | Google Scholar

Kaina, N., Lemoult, F., Fink, M., and Lerosey, G. (2015). Negative Refractive index and Acoustic Superlens from Multiple Scattering in Single Negative Metamaterials. Nature 525 (7567), 77–81. doi:10.1038/nature14678

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G., and Kim, C. K. (2010). Composite Acoustic Medium with Simultaneously Negative Density and Modulus. Phys. Rev. Lett. 104 (5), 0543011. doi:10.1103/PhysRevLett.104.054301

CrossRef Full Text | Google Scholar

Li, J., Fok, L., Yin, X., Bartal, G., and Zhang, X. (2009). Experimental Demonstration of an Acoustic Magnifying Hyperlens. Nat. Mater 8 (12), 931–934. doi:10.1038/nmat2561

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Jiang, X., Li, R.-q., Liang, B., Zou, X.-y., Yin, L.-l., et al. (2014). Experimental Realization of Full Control of Reflected Waves with Subwavelength Acoustic Metasurfaces. Phys. Rev. Appl. 2, 064002. doi:10.1103/PhysRevApplied.2.064002

CrossRef Full Text | Google Scholar

Li, Y., Liang, B., Gu, Z.-m., Zou, X.-y., and Cheng, J.-c. (2013). Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci. Rep. 3, 2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, B., Guo, X. S., Tu, J., Zhang, D., and Cheng, J. C. (2010). An Acoustic Rectifier. Nat. Mater 9 (12), 989–992. doi:10.1038/nmat2881

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., and Li, J. (2012). Extreme Acoustic Metamaterial by Coiling up Space. Phys. Rev. Lett. 108 (11), 114301. doi:10.1103/PhysRevLett.108.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, G., and Sheng, P. (2016). Acoustic Metamaterials: from Local Resonances to Broad Horizons. Sci. Adv. 2 (2), e1501595. doi:10.1126/sciadv.1501595

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, J., Ma, G., Yang, M., Yang, Z., Wen, W., and Sheng, P. (2012). Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat. Commun. 3 (2), 756–762. doi:10.1038/ncomms1758

PubMed Abstract | CrossRef Full Text | Google Scholar

Molerón, M., and Daraio, C. (2015). Acoustic Metamaterial for Subwavelength Edge Detection. Nat. Commun. 6 (1), 8037. doi:10.1038/ncomms9037

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J.-y., Hu, J.-l., He, X.-t., and Zheng, Z.-l. (2010). A Theoretical Study of a Clamped Punch-Loaded Blister Configuration: The Quantitative Relation of Load and Deflection. Int. J. Mech. Sci. 52, 928–936. doi:10.1016/j.ijmecsci.2010.03.009

CrossRef Full Text | Google Scholar

Tang, H., Chen, Z., Tang, N., Li, S., Shen, Y., Peng, Y., et al. (2018). Acoustic Metasurfaces: Hollow‐Out Patterning Ultrathin Acoustic Metasurfaces for Multifunctionalities Using Soft fiber/Rigid Bead Networks. Adv. Funct. Mater. 28 (36), 1870251. doi:10.1002/adfm.201870251

CrossRef Full Text | Google Scholar

Tang, K., Qiu, C., Ke, M., Lu, J., Ye, Y., and Liu, Z. (2014). Anomalous Refraction of Airborne Sound through Ultrathin Metasurfaces. Sci. Rep. 4, 6517. doi:10.1038/srep06517

PubMed Abstract | CrossRef Full Text | Google Scholar

Tong, L., Xiong, Z., Shen, Y. X., Peng, Y. G., Huang, X. Y., Ye, L., et al. (2020). Metasurfaces: An Acoustic Meta‐Skin Insulator. Adv. Mater. 32, 2002251. doi:10.1002/adma.202002251

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Casadei, F., Shan, S., Weaver, J. C., and Bertoldi, K. (2014). Harnessing Buckling to Design Tunable Locally Resonant Acoustic Metamaterials. Phys. Rev. Lett. 113, 014301. doi:10.1103/PhysRevLett.113.014301

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, S., Ma, G., Li, Y., Yang, Z., and Sheng, P. (2015). Active Control of Membrane-type Acoustic Metamaterial by Electric Field. Appl. Phys. Lett. 106 (3), 091904–0919045. doi:10.1063/1.4913999

CrossRef Full Text | Google Scholar

Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B.-I., and Cummer, S. A. (2014). Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, M., Ma, G., Yang, Z., and Sheng, P. (2013). Coupled Membranes with Doubly Negative Mass Density and Bulk Modulus. Phys. Rev. Lett. 110 (13), 134301. doi:10.1103/physrevlett.110.134301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, M., and Sheng, P. (2017). Sound Absorption Structures: From Porous Media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 47 (1), 83–114. doi:10.1146/annurev-matsci-070616-124032

CrossRef Full Text | Google Scholar

Yang, Z., Dai, H. M., Chan, N. H., Ma, G. C., and Sheng, P. (2010). Acoustic Metamaterial Panels for Sound Attenuation in the 50-1000 Hz Regime. Appl. Phys. Lett. 96 (4), 041906. doi:10.1063/1.3299007

CrossRef Full Text | Google Scholar

Yuan, B., Cheng, Y., and Liu, X. (2015). Conversion of Sound Radiation Pattern via Gradient Acoustic Metasurface with Space-Coiling Structure. Appl. Phys. Express 8, 027301. doi:10.7567/APEX.8.027301

CrossRef Full Text | Google Scholar

Zeng, L.-S., Shen, Y.-X., Fang, X.-S., Li, Y., and Zhu, X.-F. (2021). Experimental Realization of Ultrasonic Retroreflection Tweezing via Metagratings. Ultrasonics 117, 106548. doi:10.1016/j.ultras.2021.106548

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Xia, C., and Fang, N. (2011). Broadband Acoustic Cloak for Ultrasound Waves. Phys. Rev. Lett. 106, 024301. doi:10.1103/PhysRevLett.106.024301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, J., Li, B., Chen, Z. N., and Qiu, C.-W. (2013). Redirection of Sound Waves Using Acoustic Metasurface. Appl. Phys. Lett. 103, 151604. doi:10.1063/1.4824758

CrossRef Full Text | Google Scholar

Zhao, J., Li, B., Chen, Z., and Qiu, C.-W. (2013). Manipulating Acoustic Wavefront by Inhomogeneous Impedance and Steerable Extraordinary Reflection. Sci. Rep. 3, 2537. doi:10.1038/srep02537

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, X., Assouar, M. B., and Oudich, M. (2014). Acoustic Superfocusing by Solid Phononic Crystals. Appl. Phys. Lett. 105, 233506. doi:10.1063/1.4904262

CrossRef Full Text | Google Scholar

Zhu, R., Chen, Y. Y., Barnhart, M. V., Hu, G. K., Sun, C. T., and Huang, G. L. (2016). Experimental Study of an Adaptive Elastic Metamaterial Controlled by Electric Circuits. Appl. Phys. Lett. 108, 011905. doi:10.1063/1.4939546

CrossRef Full Text | Google Scholar

Zhu, X., Li, K., Zhang, P., Zhu, J., Zhang, J., Tian, C., et al. (2016). Implementation of Dispersion-free Slow Acoustic Wave Propagation and Phase Engineering with Helical-Structured Metamaterials. Nat. Commun. 7, 11731. doi:10.1038/ncomms11731

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X., Liang, B., Kan, W., Zou, X., and Cheng, J. (2011). Acoustic Cloaking by a Superlens with Single-Negative Materials. Phys. Rev. Lett. 106 (1), 014301. doi:10.1103/PhysRevLett.106.014301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X., Ramezani, H., Shi, C., Zhu, J., and Zhang, X. (2014). PT-symmetric Acoustics. Phys. Rev. X 4 (3), 031042. doi:10.1103/physrevx.4.031042

CrossRef Full Text | Google Scholar