Phononic Crystal Sensors: A New Class of Resonant Sensors—Chances and Challenges for the Determination of Liquid Properties

Resonant mechanical sensors are often considered as mass balance, which responds to an analyte adsorbed on or absorbed in a thin sensitive (and selective) layer deposited on the surface of the resonant device. In a more general sense, the sensor measures properties at the interface of the mechanical resonator to the medium under inspection. A phononic crystal (PnC) sensor employs mechanical resonance as well; however, the working principle is fundamentally different. The liquid medium under inspection becomes an integral part of the PnC sensor. The liquid-filled compartment acts as a mechanical resonator. Therefore, the sensor probes the entire liquid volume within this compartment. In both sensor concepts, the primary sensor value is a resonant frequency. To become an attractive new sensing concept, specifically as a bio and chemical sensor, the PnC sensor must reach an extraordinary sensitivity. We pay attention to the liquid viscosity, which is an important factor limiting sensitivity. The main part of our analysis has been performed on 1D PnC sensors, since they underlie the same material-related acoustic dissipation mechanisms as 2D and 3D PnC sensors. We show that an optimal relation of frequency shift to bandwidth and amplitude of resonance is the key to an enhanced sensitivity of the sensor-to-liquid analyte properties. We finally address additional challenges of 2D and 3D PnC sensor design concept. We conclude that the sensor should seek for a frequency resolution close to 10⁻⁶ the probing frequency, or a resolution with speed of sound approaching 1 mm s⁻¹, taking water-based analytes as an example.

Introduction

Mechanical Resonant Sensors: A Short Review

Mechanical resonant sensors apply a mechanical element vibrating at one of its eigenfrequencies. They consequently become sensitive to variations in those properties, which define the respective eigenfrequencies. The smaller the devices, the more susceptible they are to perturbations by external parameters. The dominating concept of resonant sensors recognizes a change in mass of the resonator due to adsorption of molecules on the resonator surface. Therefore, the sensor has often been called microbalance. The reality is much more fascinating; hence, the validity of this most simple understanding must be carefully verified (Lucklum and Hauptmann, 2006).

Modern concepts employ microelectromechanical systems (MEMSs) and nanoelectromechanical systems (NEMSs). Most fascinating demonstrations of those sensors are tight-knit with single nanoparticle detection (Ekinci et al., 2004a). The principle has been employed for mass sensing (Yang et al., 2006) down to a single proton (Chaste et al., 2012). NEMSs have proven their potential as an ultrasensitive mass spectrometer as well. They can measure the mass of individual molecules in real time and solve the problem of selectivity by discrimination via their molecular mass (Naik et al., 2009; Hanay et al., 2012). However, this exceptional resolution requires experimental conditions currently available in research labs only. Furthermore, Dohn et al. (Dohn et al., 2010), Hana et al. (Hanay et al., 2015), and just recently Orhan et al. (Orhan et al., 2020) have addressed the position-dependent sensitivity of the NEMS device. This behavior results from the nonuniform vibration profile of the flexural modes in cantilevers or doubly clamped beams commonly used in NEMSs. The authors have suggested their exploitation for the so-called inertial imaging. By contrast, Sansa et al. have introduced a single-mode nanoresonator, where the stiff sensing platform is supported by four beams and performs in an in-plane translation mode. Consequently, the frequency shift induced by an adsorbed particle remains independent of the landing position (Sansa et al., 2020).

One important aspect of enhanced sensitivity is the improvement of the relation of mechanical energy stored in the resonator to mechanical energy lost to the system. The measurement of tiny changes in the corresponding frequency requires a high Q-factor of resonance, which is defined as the ratio of energy stored and dissipated per cycle. It can be measured as the ratio of the resonator’s resonant frequency, f_res, and the full width frequency at half-maximum, f_FWHM:

$Q=\frac{f_{res}}{f_{FWHM}}.(1)$

Considering different loss mechanisms,

$Q^{-1}={\displaystyle \sum Q_i^{-1}}.(2)$

The index i reflects different mechanisms, including those based on material properties. We specifically call viscosity and thermoelastic losses (Pitarresi and Patterson, 2003; Greene et al., 2008) of all materials involved in vibration, losses depending on the degree of confinement of mechanical energy within the vibrating body, support (tether, anchor) losses, or, more general, acoustic wave propagation leaving the vibrating body (Lochon et al., 2006). For those reasons, all the above experiments have used almost purely elastic materials like SiC (Ekinci et al., 2004a; Yang et al., 2006) or a carbon nanotube (Chaste et al., 2012) and have been performed in vacuum. Ekinci et al. have analyzed that the viscous regime for a small, for example, a 1 GHz nanomechanical resonance takes place at a gas pressure above the atmospheric pressure (Ekinci et al., 2004b). Chapellier et al. reported about a quartz cantilever vibrating in its length-extension mode in the low-MHz range, reaching an experimentally determined Q-factor exceeding 200,000 in vacuum but reaching only 60,000 at atmospheric pressure (Chapellier et al., 2018). Fischeneder et al. have introduced an AFM cantilever with a tuneable Q-factor to enable speed measurements with a high local resolution (Fischeneder et al., 2018). Reviews by Fanget et al. on bacteria detection and antibiotic susceptibility testing (Fanget et al., 2011) and just very recently McGinn (McGinn et al., 2020) and Guruprasad (Guruprasad and Shetha, 2020) provide an overview of gas sensors based on gravimetric detection.

Mechanical Sensors for Liquids

When working in a liquid environment, one faces a dramatically changed situation. The liquid amplifies several loss mechanisms; hence, the resonance peaks get significantly broader and the respective Q-factors of cantilevers lower to 200 or even below (see, e.g., Kucera et al., 2014; Ruiz-Díez et al., 2019). The frequency readings become less accurate. The two most important reasons are viscous and acoustic losses, reflecting acoustic energy dissipation in the liquid and acoustic energy radiation into the liquid (Ruiz-Díez et al., 2015). A clever trick going around this problem is to encapsulate the liquid within a channel in a cantilever (Burg et al., 2007) or double-sided clamped beam (Barton et al., 2010) surrounded by vacuum. For liquid sensor applications of MEMS cantilever resonators, we refer to 2020 reviews by Alunda et al. about AFM (Alunda and Lee, 2020), Pujol-Vila et al. (Pujol-Vila et al., 2020) about bacteria, and simulative considerations by Rezaee (SoltanRezaee and Bodaghi, 2020).

The device with the longest tradition and a very successful example of mechanical resonant sensors is the so-called quartz crystal microbalance (QCM) in gases (Sauerbrey, 1959) and liquids (Kanazawa and Gordon, 1985) with various applications, just recently (Dirri et al., 2019; Migoń et al., 2020; Seed et al., 2020; Wang, 2020) among others. A thin quartz crystal plate vibrates in its thickness-shear mode; hence, the viscosity of the liquid (together with its density) facing the quartz crystal surface is the most important parameter defining an acoustic energy loss. The Q-factor of a bare 5 MHz QCM sensor reaches 100,000 and decreases to about 3,300 and less with single-side contact to water. The penetration depth of shear waves in Newtonian liquids (Stokes boundary layer ($\sqrt{2\eta /\left(\omega \mathit{\varrho }\right)}$) is in the order of ¼ ($1/\left(\sqrt{2}\pi \right)$ of its wavelength; hence, the Q-reduction is a measure of energy dissipation in a liquid layer very thin compared to the typical height of the liquid in a measurement cell, even in microfluidic systems. This is an important methodical difference to the PnC sensors. Losses caused by liquid shear viscosity are the most obvious mechanism. Loss factors outgoing this value indicate the activation of other, typically relaxation processes.

(Bio)chemical sensitivity requires surface modifications of the device surface to achieve sensitivity and selectivity to the compound of interest (Pohanka, 2018; Meng et al., 2019; Mujahid et al., 2019). The sensitive layers often introduce own viscous and thermoelastic loss mechanisms in addition to the pure mass effect. They appear as a complex acoustic load impedance acting at the quartz crystal surface. When the analyte interacts with the immobilized molecules, the acoustic load changes and carries much more information than only a mass increase. Many articles (Rajakovic et al., 1991; Lin and Ward, 1995; Dormack et al., 1997; McHale et al., 2000; Voinova et al., 2002; Ellis and Thompson, 2010; Ellis and Thompson, 2011) among them demonstrate that the idiom microbalance should not be reduced to a mass balance. One technique among others (Eichelbaum et al., 1999; Schröder et al., 2001; Borngräber et al., 2002) to reveal this hidden information is measuring frequency shift and acoustic energy dissipation known as QCM-D (Rodahl et al., 1995; Stengel et al., 2005; da Silva et al., 2020; Yongabi et al., 2020; Adamczyk et al., 2020). We here refer to an own publication giving deeper insights into the physics behind (Lucklum and Hauptmann, 2003).

Phononic Crystals for Mechanical Sensors

A fascinating idea to reduce radiation losses of resonant sensors is the exploitation of phononic crystals. A phononic crystal (PnC), an engineered material characterized by a periodic array of scattering inclusions in a homogeneous host matrix, exhibits bandgaps, where propagation of acoustic waves is forbidden or, in practice, at least significantly decreased; for example, this property has been employed in tethers of MEMS resonators by incorporating a PnC. It reduces anchor losses when designing the bandgap around the resonant frequency of the resonator. Sorenson at al. have employed coupled ring linear acoustic bandgap (LAB) structures as support elements. These structures are a compact solution for the integration with high-frequency MEMS devices. The third-order lateral extension mode of the AlN-on-Si resonator at 213 MHz falls into the LAB from 210 to 223 MHz. It reduces anchor losses of the MEMS resonators and demonstrates a Q enhancement of 82% compared to an equivalent device using simple tethers (Sorenson et al., 2011). Binci et al. have applied a similar structure to piezoelectric-on-silicon lamb mode resonators. Experiments prove an enhancement in Q by a factor of three to almost 5,400 (Binci et al., 2016). Chen at al. have utilized a 2D-PnC within the support of a rectangular AT-cut quartz crystal plate to trap acoustic energy and to reduce anchor losses (Chen et al., 2015). Bao et al. have introduced a multistage PnC structure for anchor-loss reduction of thin-film piezoelectric-on-silicon MEMS resonators and have achieved a maximum Q of the resonators of about 10,000 at 110 MHz, equivalent to an enhancement by 19.4 times (Bao et al., 2018). Wu et al. reported a spurious mode free AlN lamb wave resonator (LWR) having a Q of 1,893 at 1.02 GHz in air, which is a 45% improvement over the LWR with simple beam tethers. Here, a 1D gourd-shape PnC with a large phononic bandgap acts as a tether. The large ratio of the resistance at parallel to the resistance at series resonance of almost 50 dB indicates a high figure of merit (FOM) (Wu et al., 2016). Lin et al. (2014) designed, fabricated, and characterized an AlN lamb wave resonator equipped with two PnC strip tethers. The PnC is composed of six cross unit cells. Their experiments show a 50% improvement in Q over an identical resonator utilizing the uniform beam tethers, if the resonant frequency falls in the acoustic bandgap (Lin et al., 2014). Ardito et al. (2016) have studied an AlN contour-mode resonator having the PnC next to the anchor. The Q-factor numerically reaches 105 when inserting 5 × 3 PnCs, which is an improvement by almost 300 times. Anchor losses no more dominate the Q (Ardito et al., 2016). Very recently, Gao et al. (2021) have exploited the surface phononic crystal (SPC) concept for SPC resonators operating in a liquid (Gao et al., 2021). They show the velocity of Rayleigh waves in the proposed sensor can be reduced to a value lower than the sound velocity in water, thereby suppressing the propagation of acoustic waves and hence eliminating acoustic radiation. They report an improvement of Q by 15 times compared to a conventional Rayleigh wave resonator. QCM arrays also employ PnCs. Here, the phononic crystal structure has a complete bandgap covering the resonant frequency of the QCM. Acoustic interference between two QCMs (Chen et al., 2013) or in QCM arrays (Chen et al., 2011) can be avoided.

Phononic Crystals for Liquid Sensors

Our first phononic crystal sensors have applied a conceptually very different approach (Lucklum and Li, 2009). In contrast to the majority of resonant sensors, the PnC sensor does not only inspect the interface between the (solid) resonator and a thin interfacial liquid overlayer. The acoustic wave penetrates the analyte and travels through the whole analyte body, thereby probing its acoustic properties in the entire volume. The promising feature of phononic crystals, where a liquid becomes an integral part of the PnC, is the existence of modes, which cause a characteristic discontinuity in the bandgap. Such a transmission gap is usually very narrow. Since the dimensions of those irregularities correspond to the acoustic wavelength, phononic crystal sensors should become possible in a wide range of constructional elements like pipelines or microfluidic channels.

To become a sensor, the defect mode must be related to properties of the material the applicant is interested in. These properties include intrinsic material parameters (density, viscosity, elastic moduli, and speed of sound), geometric values (layer thickness and acoustic path length), and secondary values, like concentration of a toxic component in a solution or a virus in a buffer or the conversion rate in a chemical reactor or thermodynamic values related to the Gibbs free energy.

The most developed devices comprise a defect in an otherwise regular PnC structure. Classical engineering materials surrounding the defect cannot realize boundary condition as PnCs can do. In this way, the PnC can support a high Q of the cavity resonance. The Q-factor can be as high as 20,000 or 50,000 when neglecting liquid viscosity. However, the Q-factor becomes an independent measure of liquid properties as well. Moreover, the PnC provides more freedom in the design of coupling conditions to the (usually exploited) electromechanical transducer(s) generating and detecting the acoustic waves. PnC sensors can be designed to fit the experimental conditions, for example, typical dimensions of microfluidic channels or reactors in the lower mm- or upper µm range require frequencies in the range of 100 kHz–10 MHz fitting well to classical ultrasonic transducers (Lucklum and Vellekoop, 2016). Even nanofluidic resonators with the respective GHz acoustic frequencies are feasible. At those frequencies, we can note an overlap with photonic crystals and the possibility of the so-called phononic crystal sensors providing access to a parallel investigation of matter with optical and acoustic fields (Lucklum et al., 2013; Amoudache et al., 2014; Huang et al., 2020).

The Concept of Phononic Crystal Sensors

Basics of the Method

The capability to control and manipulate the propagation of acoustic waves is an inherent advantage of a phononic crystal (PnC). The PnC sensor applies this advantage to achieve a high-quality factor of resonance of a liquid-filled cavity. In other words, the PnC sensor combines the measurement of a resonant frequency of a mechanical resonator as applied for acoustic microsensors with the wave propagation through the medium as applied for ultrasonic sensors. It uses the frequency of a well-separated transmission mode through the PnC sensor while keeping the separation of acoustic transducer and analyte. The value of interest changes one or more of the inherent resonant parameters in a distinct manner.

The principle applies the fundamental relation among speed of sound v, acoustic wavelength λ, and frequency f:

$v= \lambda \cdot f.(3)$

Resonance, for example, in a one-dimensional cavity, appears, if its thickness, h, is

$h=n\frac{\lambda }{2},(4)$

where n is the overtone number, being 1, 2, 3. The resonant frequency becomes

$f_{res}=n\frac{v}{2h}.(5)$

This simple equation is valid only if the boundaries of the cavity are fully reflective. The acoustic impedances, Z, of two materials facing each other define the reflection coefficient, R:

$R=\frac{Z_2-Z_1}{Z_2+Z_1}.(6)$

R approaches 1 or −1 with a large acoustic contrast between the two materials, that is, a large difference between their acoustic impedances. For example, the interface between a semi-infinite layer of water having a characteristic acoustic impedance of 1.5 10⁶ N m⁻³ and a semi-infinite layer of air or tungsten (W) with an acoustic impedance of 414 N m⁻³ or 104 10⁶ N m⁻³ would result in a reflection coefficient of R_air-H2O = −0.999 and R_W-H2O = 0.972, respectively. The water–air interface behaves almost ideal, whereas the water–W interface has already a little transparency.

The Role of Material Properties

The problem becomes more involved, if the materials are not ideal, if they dissipate acoustic energy. Polymers are typical representatives of viscoelastic materials. The Maxwell model and the Kelvin–Voigt model are often applied to express viscoelastic properties (Ferry, 1980). The wave propagation in a viscoelastic phononic crystal is a prospective challenge (Lou et al., 2018). Elastic and viscous properties can be considered by a complex format of the eigenvector (Wang et al., 2020; Li et al., 2021a; Li et al., 2021b), or, as done here, by a complex format of speed of sound or acoustic impedance:

$v\to v^{\prime }+j v^{″}\cdot Z_c\to {Z^{\prime }}_c+j {Z^{″}}_c,(7)$

where the imaginary parts reflect material-related losses. $j=\sqrt{-1}$.

Metals behave almost ideal, $v_m^{\prime }$ is about 10⁵ larger than $v_m^{″}$. In the case of a longitudinal wave in a liquid, ${\mathit{v}}^{″}$ takes into account the longitudinal and shear viscosity of the liquid, μ and η, the thermal conductivity, τ, as well as the density, ρ, the specific heat at constant pressure, C_p, and the ratio of specific heats, γ (Holmes et al., 2011):

${v^{\prime }}_A=\frac{\text{π }f}{{\rho }_A {v^{\prime }}_A}\left({\mu }_A+\frac{4}{3}{\eta }_A+\frac{\gamma -1}{C_{\text{p}A}}{\tau }_A\right).(8)$

We have introduced the index, A, which represents the liquid analyte the sensor has been developed for. Z_1,2 in Eq. 6 must be extended with respect to Eq. 7. The speed of sound, v_A, or the acoustic impedance, Z_A, now contain two independent information. Note, both R′ and R′′ have become complex functions of Z₁′, Z₁′′, Z₂′ and Z₂′′.

The correlation between the frequency of the cavity mode and its bandwidth and material parameters of a liquid confined in the cavity is the basic idea behind the application of phononic crystals as a sensor platform. Lucklum et al., 2012; Zubtsov et al., 2012; Oseev et al., 2013; Salman et al., 2014; Li et al., 2015; Wang et al., 2016; Villa-Arango et al., 2017a; Villa-Arango et al., 2017b; Lucklum and Vellekoop, 2017; Oseev et al., 2017; Lucklum and Vellekoop, 2018; Villa-Arango et al., 2018; Cicek et al., 2019; Lucklum and Vellekoop, 2019; Mukhin et al., 2019; Mukhin and Lucklum, 2019; Wasmer et al., 2019 referred to recently published articles applying this methodology. We also want to refer to a different kind of PnC sensor with incidence normal on the periodic structure [(Zubtsov et al., 2012), (Lucklum et al., 2012), (Lanoy et al., 2018)].

It might be less motivating to develop or use a liquid sensor just for the determination of its sound velocity. Both real and imaginary parts of speed of sound have very favorable relations to really interesting properties of a liquid analyte. Among others, we mention here the concentration of a component in a liquid mixture, the conversion rate during a (bio)chemical reaction, or much more involved properties related to conformation changes of proteins in real samples like blood or processes like enzymatic catalysis. A fundamental requirement is always a sufficient large dependence of sound velocity on these properties. Figure 1 demonstrates an example: a binary mixture of water and alcohol. The speed of sound depends on the concentration; we use the molar ratio x₂ of 1-propanol (Kuhnkies and Schaaffs, 1963). The sensitivity of the PnC sensor becomes concentration-dependent with its maximum at low alcohol concentrations. The function has a maximum at x₂ = 0.056; hence, the sensor sensitivity approaches zero, and the sensor is “deaf” here. We have successfully applied our sensor to technical products, for example, for the analysis of gasoline (Oseev et al., 2013; Oseev et al., 2018).

FIGURE 1

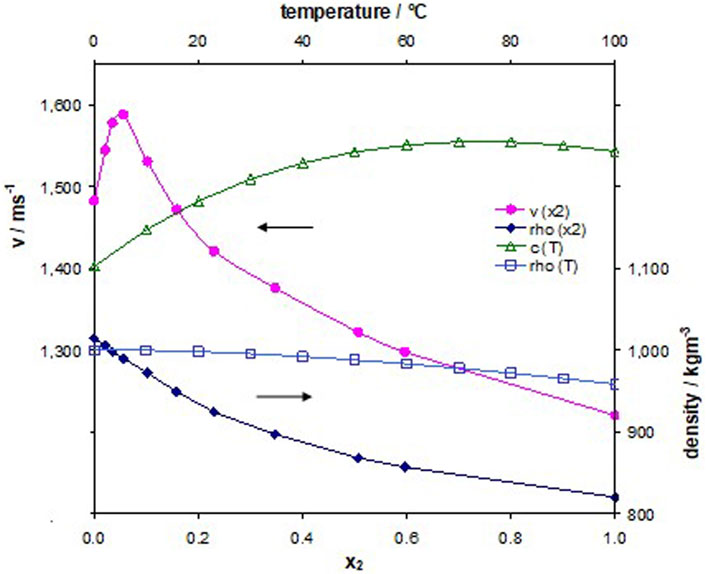
FIGURE 1. The lower abscissa shows the relationship between speed of sound and density of a water-1-propanol-mixture vs. the molar ratio of 1-propanol. The upper abscissa shows the relation of speed of sound and density of water vs temperature.

The list of articles reporting such dependencies is very long. We refer to only two 2021 articles. The first introduces an open-access database of nanofluids, including speed of sound and viscosity (Mondejar et al., 2021). The second analyzes the long-time stability of density and sound velocity measurement of the well-known commercial DSA 5000 density meter (Wagner et al., 2021). Both articles prove the actuality of sound velocity research.

The Task of the Phononic Crystal

The major task of the phononic crystal (PnC) is the enhancement of the Q-factor of the cavity resonator, Eq. 1.

We start with semi-infinite layers of air or tungsten (W) confining a 500-µm thin layer of water (H₂O)¹. Figure 2 presents the magnitude and phase of the reflection coefficient, R, (Eq. 6), at the (lower) H₂O–air or H₂O–W interface. The effective acoustic impedance, Z_a, of H₂O–air or H₂O–W has been calculated with Eq. 9:

$Z_{a_{i,i-1}}=\frac{Z_{ai}+Z_{ai-1}}{1+\frac{Z_{ai}\cdot Z_{ai-1}}{Z_{ci}^2}}\text{with}{Z}_{ai}=\text{j}{Z}_{ci}\cdot \text{tan}\left(\omega \frac{{\rho }_i}{Z_{ci}}{h}_i\right)Z_{ci}={\rho }_i{v}_i,(9)$

where Z_ci is the characteristic impedance of the material, and i, ρ_i, v_i, and h_i are its density, speed of sound, and thickness, respectively. In the case of an infinite layer thickness, Z_ai = Z_ci holds.

FIGURE 2

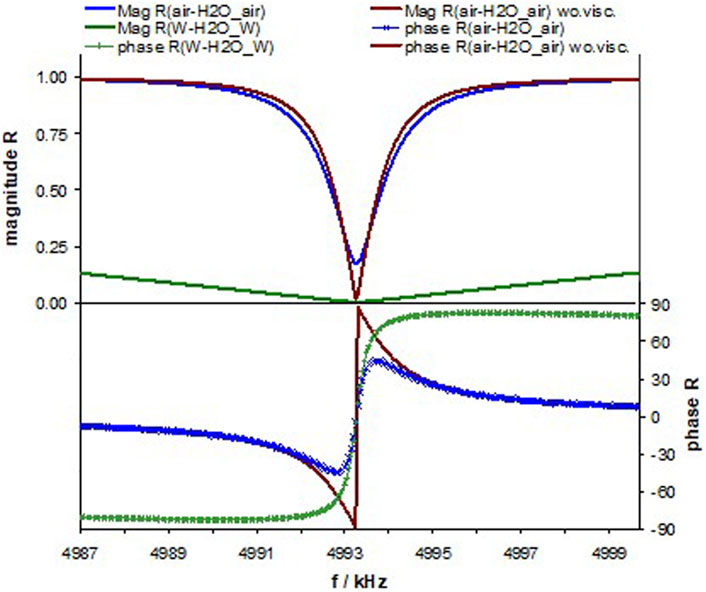
FIGURE 2. Magnitude and phase of the reflection coefficient, R, at the interface of a single water layer to either semi-infinite metal plates (green) or air (blue), both with viscosity, and air–H₂O–air without viscosity (brown).

Mag (R) decreases up to a certain frequency, further on called resonant frequency of the cavity, f_cav, and increases again above f_cav. Mag (R) behaves approximately symmetric in a small frequency range around f_cav. It approaches 0 at the air–water interface only, if the viscosity of water is set to zero. The viscosity of air can be neglected, since it does not much influence the results. When replacing air by W, the viscosity of water becomes negligible. The difference is caused by the Q-factor of the cavity resonance, which is only 90 for W in contrast to 3.375 for air. The phase plot supports the above findings. Without viscosity, we note a phase shift of π at f_cav; with viscosity, the phase shift is much smoother.

A very conservative estimation of the accessible accuracy in the frequency measurement, Δf, assumes 100 measurement points within f_FWHM. The hypothetical freestanding water layer would allow for a frequency resolution of 15 Hz or 3 ppm. The determination of sound velocity in this layer would provide the required accuracy.

Results

Reference

Next, we make a step toward a realistic 1D PnC design. The PnC now consists of Fe- and Al-plates. Each plate has a thickness of 200 µm. Figure 3 shows the reflection coefficient, R, of the corresponding regular PnC with 19 Fe-plates and 18 Al-plates. Fe-plates always face the water bath and later on, the analyte layer. Figure 3 shows 9 minima, followed by the bandgap reaching from 5.5 to 10.5 MHz. Figure 3, and the following have been calculated using the impedance concept in propagation problems based on a chain matrix technique (Lucklum et al., 1997), that is, a repeated application of Eq. 9. All extrema have been calculated with an accuracy of 1 Hz.

FIGURE 3

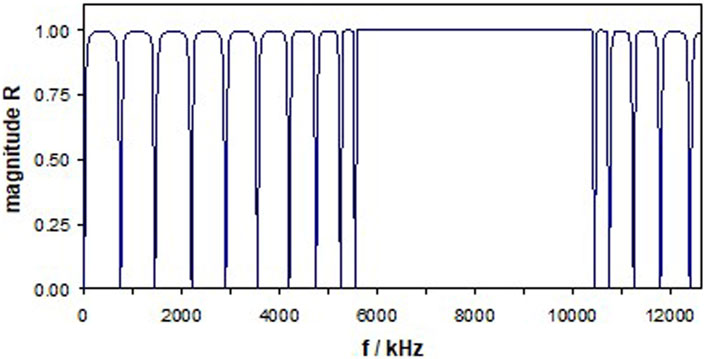
FIGURE 3. Frequency dependence of the magnitude of the reflection coefficient, R, of a regular one-dimensional phononic crystal (1D-PnC). The PnC consists of 19 layers of Fe (steel) and 18 layers of Al and faces semi-infinite layers of H₂O.

The PnC Sensor

In the sensor arrangement, the analyte layer replaces the central inner Al-plate. The analyte is always pure water kept at 20°C. An optimized PnC sensor design consists of 210 µm metal plates. The analyte layer has a thickness of 153.2 µm to realize f_cav ≈ 5 MHz. The 9PnC (see below) features a bandgap from 5 to 9.5 MHz.

Role and Appearance of Viscosity

We start the analysis with two single Fe-plates confining the analyte layer and proceed with adding in step-by-step one Al- and one Fe-plate on each side. We call these arrangements 1, 3, 5, 7, and 9PnC and present magnitude and phase of the reflection coefficient of the PnC to water.

If we do not consider the viscosity of the analyte, we note the increase of the frequency at the minimum of Mag R(f) and the decrease of f_FWHM with an increasing number of plates, Figure 4. We call the respective frequency f_res, just in contrast to f_cav, which is independent of the number of plates. Mag R_min approaches 0. The phase φ_max (not shown) reaches 90°, whereas φ_min gets 90°only if all v_i′′ (Eq. 7), including those of the metals, are set to 0.

FIGURE 4

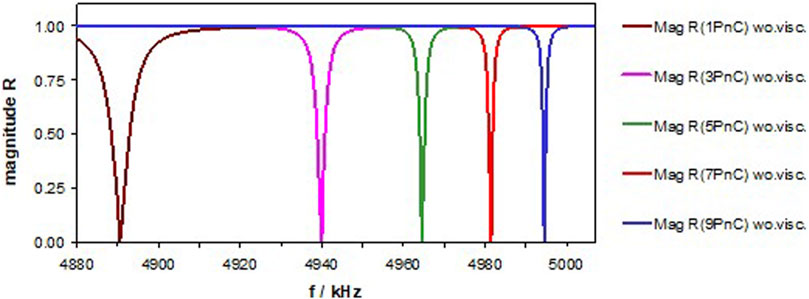
FIGURE 4. Magnitude of R at the interface between the xPnC and semi-infinite water. x represents the number of metal layers: the left and right of the central H₂O layer. The viscosity of this H₂O layer is assumed to be 0 (wo. visc.).

Figure 5 shows the same arrangement, now considering all viscous losses attenuating the longitudinal wave. Similar to Figure 4, we note the increase of f_res and the decrease of f_FWHM with an increasing number of plates. The most obvious difference is the decreasing Mag R_min in the upper part of the diagram with an increasing number of metal plates. The magnitude at f_res decreases linearly with frequency, which seems to correspond well with Eq. 8. Only Mag R_min of the 3PnC deviates by 12%. The lower part of Figure 5 shows the phase of the reflection coefficient, φ. The zero crossing of φ takes place at f_res. φ_min and φ_max have a frequency difference between 1.8 kHz (1PnC) and 660 Hz (9PnC).

FIGURE 5

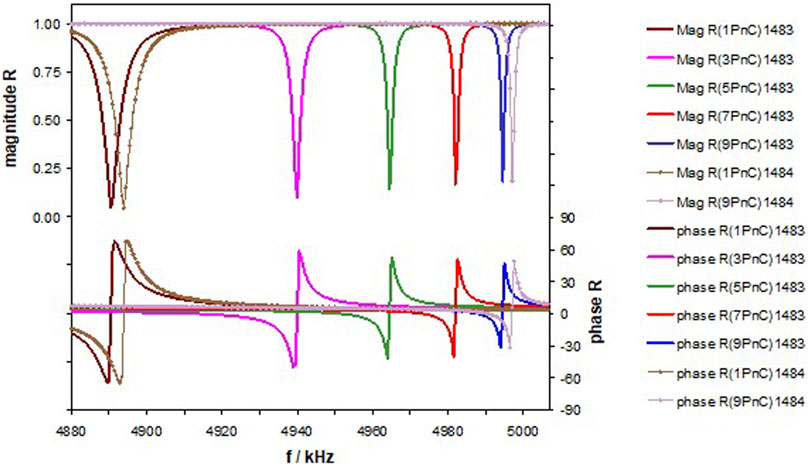
FIGURE 5. Magnitude and phase of R at the interface between the xPnC and semi-infinite water. All viscosities have been considered. The sound velocity of the liquid is 1,483 m s⁻¹. We further present two examples of magnitude and phase of R for 1,484 m s⁻¹ to demonstrate the sensor sensitivity.

Unfortunately, one cannot use the entire bandgap for liquid sensor purposes. On the one hand, f_FWHM decreases and the Q-factor of the liquid resonance increases when departing from the bandgap edge. On the other hand, as this becomes a limiting factor, Mag R_min increases and the peak disappears more and more. From the measurement point of view, Mag R_min should be smaller than 0.5 (a rule of thumb). Since the peak reappears when Mag R_min approaches the higher edge of the bandgap, this finding cannot be attributed to the frequency dependence of v′′, Eq. 8.

Figure 5 also contains the PnC sensor response to a shift in speed of sound of the analyte by 1 ms⁻¹ of the 1PnC and the 9PnC. Table 1 summarizes the respective f_res, f_FWHM, Q, and the figure of merit, FOM_v

$FO{M}_v=\frac{\Delta f_{res}}{\Delta v_{sA} f_{FWHM}}.(10)$

TABLE 1

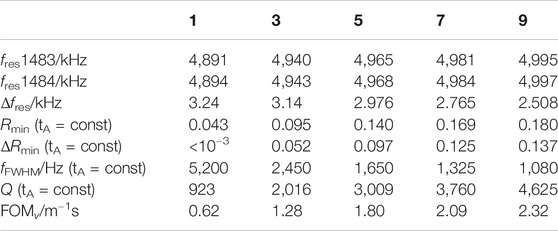
TABLE 1. Characteristic values of the 1, 3, 5, 7, and 9PnC at a constant analyte layer thickness of 153 µm.

For comparison, we have modified the thickness of the analyte layer, t_A, to realize the same f_res for all numbers of layers. Figure 6 demonstrates Mag R(f) in a reduced frequency range. The required liquid cavity thicknesses are specified in the legend (inside the diagram). Note that the minima do not change monotonically with the number of layers.

FIGURE 6

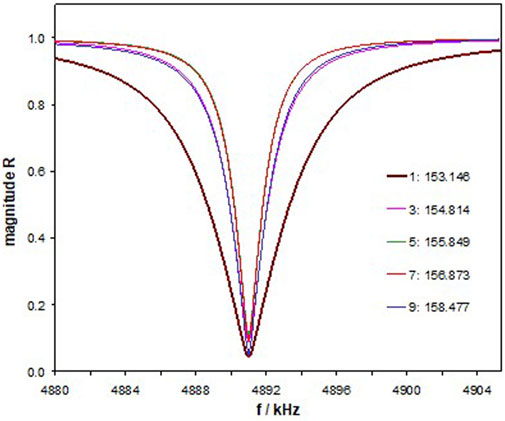
FIGURE 6. Magnitude of R for the xPnC with a modified analyte layer thickness to realize the same f_res. The respective thicknesses (in µm) are noted in the legend (inside the diagram).

We compare ΔR_min, f_FWHM, and Q of the two approaches in Figure 7 and have summarized the data in Table 2, where t_A replaces f_res. One can note two observations. Although the frequency dependence of v′′ vanishes, all values still depend on the number of layers. Specifically, Mag R_min and Q are maximal for the 5-layer arrangement. As the first hypothesis, we attribute this finding to a difference in the effective path length of the probing acoustic wave in the liquid cavity, since, as demonstrated already, the viscosity of the analyte donates the largest amount to the overall acoustic losses. The (almost linear) slope does not only reflect Eq. 8. Further research is required to prove that this hypothesis may also cause the deviation of 12% in Figure 4. This knowledge is important to recalculate the viscosity of an unknown analyte.

FIGURE 7

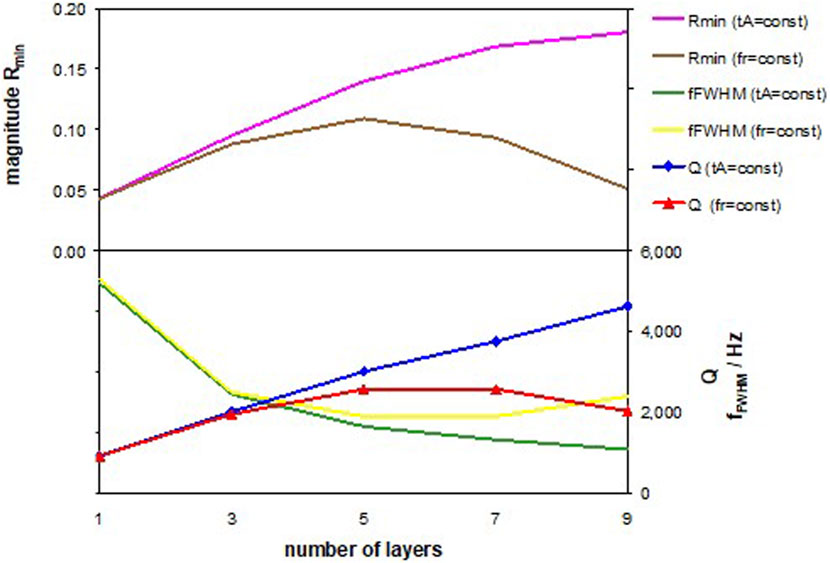
FIGURE 7. Dependence of the characteristic PnC-values R_min, f_FWHM, and Q on the number of layers for two setups: at constant analyte, layer thickness, t_A, and at constant resonance frequency, f_res.

TABLE 2

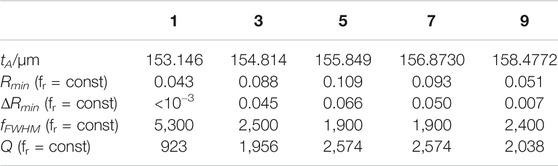
TABLE 2. Characteristic values of the 1, 3, 5, 7, and 9PnC at a constant resonant frequency of 4,891 kHz.

Other Properties Influencing the 1D Performance of the PnC Sensor

Surface roughness and deviations from parallelism have a similar effect on the sensor transfer function although the physics behind is different. The two interfaces to the liquid analyte have the largest impact. The 1D approach considers the effect of roughness with integration over a set of different cavity layer thicknesses. The consequence of a statistical variation of the analyte layer up to 10 nm is an increase of Mag R_min from 0.18 to 0.23 and a decrease of the Q-factor from 4.500 to 3.400.

The much larger effect has an indirect nature. Depending on hydrophobicity or hydrophilicity of the solid surface, a rough hydrophobic surface may cause trapping of air and a significant difference in density of an equivalent layer representing the rough interface. The effect is similar to an additional layer of a different material or the adsorption of foreign molecules.

Parallelism concerns most of all the interfaces of the analyte layer, too. The reflection coefficient, Eq. 6, can be considered by effective impedance, $Z_{i\theta }=Z_i/\text{cos}\left(\theta \right)$. Since θ is very small, cos(θ) approaches 1. However, due to the large aspect ratio between the diameter and thickness of the analyte layer in a real PnC, the cavity thickness itself may become different. For example, an analyte layer having a diameter of 10 mm and a maximal allowed difference in the layer thickness of 10 nm would require a maximal deviation from parallelism of only 6^.10⁻⁵ degrees.

Cross-Sensitivities

The physical value with the highest cross-sensitivity is temperature. Figure 1 therefore also depicts the dependence of sound velocity and density of water on temperature (Seitenubersicht and Sitemap, 1983; Bilaniuk and Wong, 1993). Table 3 summarizes the consequences for the response of the 9PnC. The sensor responses to a virtual increase of the sound velocity by 1 ms⁻¹ (second line) is only slightly larger than the frequency shift, which considers the respective necessary changes in the speed of sound and the density of a real analyte with temperature (line 3); here, water (Figure 1) is shown in line 3. The bottom line provides the values for a change in the analyte temperature of 1 K.

TABLE 3

TABLE 3. Characteristic values of the 9PnC to temperature.

For comparison, a highly diluted water–alcohol mixture causes a 3 mm s⁻¹/ppm shift of the sound velocity. The large dependence of the sensor response on temperature or more exactly, on the analyte temperature, has important consequences for any experimental setup. 7 kHz/K at room temperature almost requires an extraordinary high-level temperature control. A realistic solution is a second channel with a reference liquid that is implemented in a real 3D-PnC microfluidic sensor. The dependence on the temperature of the semi-infinite water facing the PnC can be neglected.

By contrast, a secondary cross-sensitivity must be considered: heat generation due to acoustic energy dissipation caused by liquid viscosity. Indeed, the PnC sensor can be redesigned to become a (differential) calorimeter. Bian et al. have recently reported another interesting concept, a band gap manipulation, via thermal-sensitive viscoelastic materials (Bian et al., 2020).

Pressure also changes the speed of sound. We refer to Belogol'skii et al. who measured the sound velocity in distilled water in the pressure range 0.1–60 MPa and in the temperature range 0–40°C. The equation has been derived by the least-square processing of experimental data (Sekoyan et al., 1999). The importance of the pressure dependence has to be considered in relation to the intended resolution in the speed of sound. A rough estimation shows that a pressure change of 1 kPa, which corresponds to a water column of 10 cm, would cause a frequency change of 150 Hz. In other words, a microfluidic system design must incorporate high stability of pressure as well.

Additional Challenges of 2D and 3D PnC Sensors

The above reported problems persist in 2D and 3D PnCs. New challenges appear due to the finite size in two or all three directions. They also exist in real 1D PnCs. For example, the lateral dimensions of the electromechanical transducers are finite; hence, they do not excite perfectly longitudinal waves. The lateral dimensions of the plates are limited as well, for example, because of the high requirements regarding temperature and temperature fields.

The 2D and 3D PnC designs offer many more degrees of freedom. 3D printing technologies extend the technological capabilities (Lucklum and Vellekoop, 2017; Aravantinos-Zafiris et al., 2021). Numerous articles especially report about PnC important features like wave-guiding and acoustic energy concentration. One additional material property to be considered is the shear viscosity of the liquid. The majority of cavity modes own in-plane displacement fields at certain parts of the solid–liquid interface. Recently, we have introduced the exploitation of the axisymmetric (radial) cavity mode for PnC sensors (Mukhin and Lucklum, 2020; Gueddida et al., 2021). This mode is free of in-plane displacement and results in an improved Q-factor of the cavity resonance. The additional task of the PnC surrounding the circular analyte-filled cavity is the excitation and detection of this mode by typically planar transducers.

The second important challenge is acoustic energy radiation in unwanted directions. 2D PnCs avoid this phenomenon by appropriate boundary conditions. A real PnC sensor may feature a circular defect, which extends to a (microfluidic) capillary perpendicular to the classical 2D-design. This approach avoids the need of transducers at the ends of the capillary or more involved microfluidic systems. However, a liquid-filled capillary may provide unwanted waveguide properties. The 3D PnC has the capability to overcome this problem. We have found a solution based on a combination of a 2D and a 1D PnC. A major task of the 2D design is the focusing of the planar wave into the capillary including conversion into the axisymmetric mode and vice versa. The major task of the 1D PnC is the suppression of wave propagation of this mode along the capillary. We refer to an upcoming article for details and solutions.

Conclusion

Phononic crystals can become an attractive alternative sensor solution in the field of chemical and biosensors. Their unique feature is the determination of the sound velocity of liquid analytes, a volumetric property related to many interesting physical and (bio) chemical values. The crucial point is a high-accuracy measurement. The first task of the phononic crystal is to support a high-Q liquid cavity resonance. This resonance should be located at the edge of the bandgap of the PnC. We have discussed, based on a one-dimensional model, that it requires a high-level control of secondary values, first of all temperature and pressure. Chance and challenge are the important factors of liquid viscosity: chance, since viscosity is an independent material property of significant worth, and challenge, since viscosity dissipates acoustic energy and lowers the Q and hence the figure of merit of this sensor concept. The further development of PnC sensors as 2D or 3D structures does not reduce the importance of our findings; however, new engineering challenges must be solved to optimize the overall sensor design.

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The work has been performed within the project “Tubular Bell” supported by the National French Agency ANR-18-CE92-0023 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under grants VE 483/2-1 and LU 605/22-1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

AFM, atomic force microscopy; FOM, Figure Of Merit; LWR, Lamb wave resonator; MEMS, microelectromechanical systems; NEMSs, nanoelectromechanical systems; PnC, phononic crystal; QCM, quartz crystal Microbalance; SH, horizontally polarized shear waves.

Footnotes

¹We neglect experimental counter-arguments here.

References

Adamczyk, Z., Sadowska, M., and Żeliszewska, P. (2020). Applicability of QCM-D for Quantitative Measurements of Nano- and Microparticle Deposition Kinetics: Theoretical Modeling and Experiments. Anal. Chem. 92, 5087–15095. doi:10.1021/acs.analchem.0c03115

PubMed Abstract | CrossRef Full Text | Google Scholar

Alunda, B. O., and Lee, Y. J. (2020). Review: Cantilever-Based Sensors for High Speed Atomic Force Microscopy. Sensors 20, 47841–47939. doi:10.3390/s20174784

PubMed Abstract | CrossRef Full Text | Google Scholar

Amoudache, S., Pennec, Y., Djafari Rouhani, B., Khater, A., Lucklum, R., and Tigrine, R. (2014). Simultaneous Sensing of Light and Sound Velocities of Fluids in a Two-Dimensional phoXonic crystal with Defects. J. Appl. Phys. 115, 134503 1–8. doi:10.1063/1.4870861

CrossRef Full Text | Google Scholar

Aravantinos-Zafiris, N., Lucklum, F., and Sigalas, M. M. (2021). Complete Phononic Band Gaps in the 3D Yablonovite Structure with Spheres. Ultrasonics 110, 106265. doi:10.1016/j.ultras.2020.106265

PubMed Abstract | CrossRef Full Text | Google Scholar

Ardito, R., Cremonesi, M., D’Alessandro, L., and Frangi, A. (2016). “Application of Optimally-Shaped Phononic Crystals to Reduce Anchor Losses of MEMS Resonators,” in 2016 IEEE International Ultrasonics Symposium (IUS) (Tours: IEEE), 74313715.

Google Scholar

Bao, F.-H., Bao, L.-L., Li, X.-Y., Ammar Khan, M., Wu, H.-Y., Qin, F., et al. (2018). Multi-stage Phononic crystal Structure for Anchorloss Reduction of Thin-Film Piezoelectric-On-Silicon Microelectromechanical-System Resonator. Appl. Phys. Expr. 11, 067201 1–5. doi:10.7567/apex.11.067201

CrossRef Full Text | Google Scholar

Barton, R. A., Ilic, B., Verbridge, S. S., Cipriany, B. R., Parpia, J. M., and Craighead, H. G. (2010). Fabrication of a Nanomechanical Mass Sensor Containing a Nanofluidic Channel. Nano Lett. 10, 2058–2063. doi:10.1021/nl100193g

PubMed Abstract | CrossRef Full Text | Google Scholar

Bian, Z., Yang, S., Zhou, X., and Hui, D. (2020). Band gap Manipulation of Viscoelastic Functionally Graded Phononic crystal. Nanotechn. Rev. 9, 515–512. doi:10.1515/ntrev-2020-0042

CrossRef Full Text | Google Scholar

Bilaniuk, N., and Wong, G. S. K. (1993). Speed of Sound in Pure Water as a Function of Temperature. J. Acoust. Soc. Am. 93, 1609–1612. doi:10.1121/1.406819

CrossRef Full Text | Google Scholar

Binci, L., Tu, C., Zhu, H., and Lee, J. E.-Y. (2016). Planar Ring-Shaped Phononic crystal Anchoring Boundaries for Enhancing the Quality Factor of Lamb Mode Resonators. Appl. Phys. Lett. 109, 203501 1–4. doi:10.1063/1.4967794

CrossRef Full Text | Google Scholar

Borngräber, R., Schröder, J., Lucklum, R., and Hauptmann, P. (2002). Is an Oscillator-Based Measurement Adequate in a Liquid Environment? IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 49, 1254–1259. doi:10.1109/tuffc.2002.1041542

CrossRef Full Text | Google Scholar

Burg, T. P., Godin, M., Knudsen, S. M., Shen, W., Carlson, G., Foster, J. S., et al. (2007). Weighing of Biomolecules, Single Cells and Single Nanoparticles in Fluid. Nature 446, 1066–1069. doi:10.1038/nature05741

PubMed Abstract | CrossRef Full Text | Google Scholar

Chapellier, P., Lavenus, P., Dulmet, B., and Le Traon, O. (2018). “A High Q Length-Extension Mode Quartz Resonator for MEMS Oscillator and Time-Frequency Applications,” in 2018 European Frequency and Time Forum (EFTF) (Turin, Italy: IEEE), 20–23.

Google Scholar

Chaste, J., Eichler, A., Moser, J., Ceballos, G., Rurali, R., and Bachtold, A. (2012). A Nanomechanical Mass Sensor with Yoctogram Resolution. Nat. Nanotech 7, 301–304. doi:10.1038/nnano.2012.42

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y.-Y., Huang, L.-C., Wu, T.-T., and Sun, J.-H. (2011). “Isolation of Bulk Acoustic Waves in a Sensor Array with Phononic Crystals,” in 2011 IEEE International Ultrasonics Symposium (Orlando, FL, USA: IEEE), 2487–2490.

CrossRef Full Text | Google Scholar

Chen, Y.-Y., Lin, Y.-R., Wu, T. T., and Pao, S.-Y. (2015). “Anchor Loss Reduction of Quartz Resonators Utilizing Phononic Crystals,” in 2015 IEEE International Ultrasonics Symposium (IUS) (Taipei, Taiwan: IEEE), 1–4.

CrossRef Full Text | Google Scholar

Chen, Y. Y., Huang, L. C., Wang, W. S., Lin, Y. C., Wu, T. T., Sun, J. H., et al. (2013). Acoustic Interference Suppression of Quartz crystal Microbalance Sensor Arrays Utilizing Phononic Crystals. Appl. Phys. Lett. 102, 153514 1–5. doi:10.1063/1.4802781

CrossRef Full Text | Google Scholar

Cicek, A., Trak, D., Arslan, Y., Korozlu, N., Kaya, O. A., and Ulug, B. (2019). Ultrasonic Gas Sensing by Two-Dimensional Surface Phononic Crystal Ring Resonators. ACS Sens 4, 1761–1765. doi:10.1021/acssensors.9b00865

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva, A. C., da Silva, R. A., Souza, M. J. P. G., Montoya, P. M., Bentini, R., Augusto, T., et al. (2020). Electrochemical Quartz crystal Microbalance with Dissipation Investigation of Fibronectin Adsorption Dynamics Driven by Electrical Stimulation onto a Conducting and Partially Biodegradable Copolymer. Biointerphases 15, 021003 1–11. doi:10.1116/1.5144983

CrossRef Full Text | Google Scholar

Dirri, F., Palomba, E., Longobardo, A., Zampetti, E., Saggin, B., and Scaccabarozzi, D. (2019). A Review of Quartz crystal Microbalances for Space Applications. Sensors Actuators A: Phys. 287, 48–75. doi:10.1016/j.sna.2018.12.035

CrossRef Full Text | Google Scholar

Dohn, S., Schmid, S., Amiot, F., and Boisen, A. (2010). Position and Mass Determination of Multiple Particles Using Cantilever Based Mass Sensors. Appl. Phys. Lett. 97, 044103 1–3. doi:10.1063/1.3473761

CrossRef Full Text | Google Scholar

Dormack, A., Prucker, O., Rühe, J., and Johannsmann, D. (1997). Swelling of a Polymer brush Probed with a Quartz crystal Resonator. Phys. Rev. E 56, 680–689. doi:10.1103/PhysRevE.56.680

CrossRef Full Text | Google Scholar

Eichelbaum, F., Borngräber, R., Schröder, J., Lucklum, R., and Hauptmann, P. (1999). Interface Circuits for quartz-crystal-microbalance Sensors. Rev. Sci. Instrum. 70, 2750–2755. doi:10.1063/1.1149788

CrossRef Full Text | Google Scholar

Ekinci, K. L., Huang, X. M. H., and Roukes, M. L. (2004). Ultrasensitive Nanoelectromechanical Mass Detection. Appl. Phys. Lett. 84, 4469–4471. doi:10.1063/1.1755417

CrossRef Full Text | Google Scholar

Ekinci, K. L., Yang, Y. T., and Roukes, M. L. (2004). Ultimate Limits to Inertial Mass Sensing Based upon Nanoelectromechanical Systems. J. Appl. Phys. 95, 2682–2689. doi:10.1063/1.1642738

CrossRef Full Text | Google Scholar

Ellis, J. S., and Thompson, M. (2011). Conformational States of Nucleic Acid-Peptide Complexes Monitored by Acoustic Wave Propagation and Molecular Dynamics Simulation. Chem. Sci. 2, 237–255. doi:10.1039/c0sc00423e

CrossRef Full Text | Google Scholar

Ellis, J. S., and Thompson, M. (2010). Viscoelastic Modeling with Interfacial Slip of a Protein Monolayer Electrode-Adsorbed on an Acoustic Wave Biosensor. Langmuir 26, 11558–11567. doi:10.1021/la100798c

PubMed Abstract | CrossRef Full Text | Google Scholar

Fanget, S., Hentz, S., Puget, P., Arcamone, J., Matheron, M., Colinet, E., et al. (2011). Gas Sensors Based on Gravimetric Detection-A Review. Sensors Actuators B: Chem. 160, 804–821. doi:10.1016/j.snb.2011.08.066

CrossRef Full Text | Google Scholar

Ferry, J. D. (1980). Viscoelastic Properties of Polymers. 3rd edn. New York: Wiley.

Fischeneder, M., Oposich, M., Schneider, M., and Schmid, U. (2018). Tuneable Q-Factor of MEMS Cantilevers with Integrated Piezoelectric Thin Films. Sensors 18, 1–12. doi:10.3390/s18113842

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, F., Bermak, A., Benchabane, S., Robert, L., and Khelif, A. (2021). Acoustic Radiation-free Surface Phononic crystal Resonator for In-Liquid Low-Noise Gravimetric Detection. Microsyst. Nanoeng. 7, 8 1–10. doi:10.1038/s41378-020-00236-9

CrossRef Full Text | Google Scholar

Greene, R. J., Patterson, E. A., and Rowlands, R. E. (2008). Thermoelastic Stress Analysis. Springer Handbook of Experimental Solid Mechanics, 743–768. doi:10.1007/978-0-387-30877-7_26

CrossRef Full Text

Gueddida, A., Pennec, Y., Zhang, V., Lucklum, F., Vellekoop, M., Mukhin, N., et al. (2021). “Tubular Phononic Crystal Sensor,” in 2020 IEEE SENSORS (Rotterdam, Netherlands: IEEE).

Google Scholar

Guruprasad, B., and Shetha, M. S. (2020). Design and Fabrication of Cantilever MEMS Sensor Model for Electro-Chemical Gas Sensor. Int. J. Eng. Res. Techn. 9, 704–715. doi:10.17577/ijertv9is070262

CrossRef Full Text | Google Scholar

Hanay, M. S., Kelber, S. I., O'Connell, C. D., Mulvaney, P., Sader, J. E., and Roukes, M. L. (2015). Inertial Imaging with Nanomechanical Systems. Nat. Nanotech 10, 339–344. doi:10.1038/nnano.2015.32

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanay, M. S., Kelber, S., Naik, A. K., Chi, D., Hentz, S., Bullard, E. C., et al. (2012). Single-protein Nanomechanical Mass Spectrometry in Real Time. Nat. Nanotech 7, 602–608. doi:10.1038/nnano.2012.119

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmes, M. J., Parker, N. G., and Povey, W. J. W. (2011). Temperature Dependence of Bulk Viscosity in Water Using Acoustic Spectroscopy. J. Phys. Conf. Ser. 269, 1–7. doi:10.1088/1742-6596/269/1/012011

CrossRef Full Text | Google Scholar

Huang, N.-N., Chung, Y.-C., Chiu, H.-T., Hsu, J.-C., Lin, Y.-F., Kuo, C.-T., et al. (2020). Dual Photonic–Phononic Crystal Slot Nanobeam with Gradient Cavity for Liquid Sensing. Crystals 10, 421 1–16. doi:10.3390/cryst10050421

CrossRef Full Text | Google Scholar

Kanazawa, K. K., and Gordon, J. G. (1985). Frequency of a Quartz Microbalance in Contact with Liquid. Anal. Chem. 57, 1770–1771. doi:10.1021/ac00285a062

CrossRef Full Text | Google Scholar

Kucera, M., Wistrela, E., Pfusterschmied, G., Ruiz-Díez, V., Manzaneque, T., Sánchez-Rojas, J. L., et al. (2014). Characterization of a Roof Tile-Shaped Out-Of-Plane Vibrational Mode in Aluminumnitride-Actuated Self-Sensing Micro-resonators for Liquid Monitoring Purposes. Appl. Phys. Lett. 104, 1–5. doi:10.1063/1.4882177

CrossRef Full Text | Google Scholar

Kuhnkies, R., and Schaaffs, W. (1963). Untersuchungen an adiabatisch und isotherm aufgenommenen Schallkennlinien binärer Mischungen. Acustica 13, 407.

Google Scholar

Lanoy, M., Bretagne, A., Leroy, V., and Tourin, A. (2018). A Phononic Crystal-Based High Frequency Rheometer. Crystals 8, 1–7. doi:10.3390/cryst8050195

CrossRef Full Text | Google Scholar

Li, F.-L., Zhang, C., and Wang, Y.-S. (2021). Analysis of the Effects of Viscosity on the SH-Wave Band-Gaps of 2D Viscoelastic Phononic Crystals by Dirichlet-To-Neumann Map Method. Int. J. Mech. Sci. 195, 106225. doi:10.1016/j.ijmecsci.2020.106225

CrossRef Full Text | Google Scholar

Li, J., Yang, P., Ma, Q., and Xia, M. (2021). Complex Band Structure and Attenuation Performance of a Viscoelastic Phononic crystal with Finite Out-Of-Plane Extension. Acta Mechanica 2021. doi:10.1007/s00707-021-02969-8

CrossRef Full Text | Google Scholar

Li, P., Li, F., Liu, Y., Shu, F., Wu, J., and Wu, Y. (2015). Temperature Insensitive Mass Sensing of Mode Selected Phononic crystal Cavity. J. Micromech. Microeng. 25, 125027. doi:10.1088/0960-1317/25/12/125027

CrossRef Full Text | Google Scholar

Lin, C. M., Hsu, J. C., Senesky, D. G., and Pisano, A. P. (2014). “Anchor Loss Reduction in AlN Lamb Wave Resonators Using Phononic Crystal Strip Tethers,” in 2014 IEEE International Frequency Control Symposium (FCS) (Taipei, Taiwan: IEEE), 1–5.

CrossRef Full Text | Google Scholar

Lin, Z., and Ward, M. D. (1995). The Role of Longitudinal Waves in Quartz Crystal Microbalance Applications in Liquids. Anal. Chem. 67, 685–693. doi:10.1021/ac00100a001

CrossRef Full Text | Google Scholar

Lochon, F., Dufour, I., and Rebière, D. (2006). A Microcantilever Chemical Sensors Optimization by Taking into Account Losses. Sensors Actuators B: Chem. 118, 292–296. doi:10.1016/j.snb.2006.04.034

CrossRef Full Text | Google Scholar

Lou, J., He, L., Yang, J., Kitipornchai, S., and Wu, H. (2018). Wave Propagation in Viscoelastic Phononic crystal Rods with Internal Resonators. Appl. Acoust. 141, 382–392. doi:10.1016/j.apacoust.2018.07.029

CrossRef Full Text | Google Scholar

Lucklum, F., and Vellekoop, M. J. (2016). “3D Phononic-Fluidic Cavity Sensor for Resonance Measurements of Volumetric Fluid Properties,” in 2016 IEEE SENSORS (Orlando, FL, USA: IEEE), 1–3.

Google Scholar

Lucklum, F., and Vellekoop, M. J. (2018). Bandgap Engineering of Three-Dimensional Phononic Crystals in a Simple Cubic Lattice. Appl. Phys. Lett. 113, 201902. doi:10.1063/1.5049663

CrossRef Full Text | Google Scholar

Lucklum, F., and Vellekoop, M. J. (2017). Design and Fabrication Challenges for Millimeter-Scale Three-Dimensional Phononic Crystals. Crystals 11, 348. doi:10.3390/cryst7110348

CrossRef Full Text | Google Scholar

Lucklum, F., and Vellekoop, M. J. (2019). “Ultra-sensitive and Broad Range Phononic-Fluidic Cavity Sensor for the Determination of Mass Fractions in Aqueous Solutions,” in 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII) (Berlin, Germany: IEEE), 885–888.

Google Scholar

Lucklum, R., Behling, C., Cernosek, R. W., and Martin, S. J. (1997). Determination of Complex Shear Modulus with Thickness Shear Mode Resonators. J. Phys. D: Appl. Phys. 30, 346–356. doi:10.1088/0022-3727/30/3/006

CrossRef Full Text | Google Scholar

Lucklum, R., and Hauptmann, P. (2006). Acoustic Microsensors-The challenge behind Microgravimetry. Anal. Bioanal. Chem. 384, 667–682. doi:10.1007/s00216-005-0236-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucklum, R., and Hauptmann, P. (2003). Transduction Mechanism of Acoustic-Wave Based Chemical and Biochemical Sensors. Meas. Sci. Techn. 14, 1854–1864. doi:10.1088/0957-0233/14/11/002

CrossRef Full Text | Google Scholar

Lucklum, R., and Li, J. (2009). Phononic Crystals for Liquid Sensor Applications. Meas. Sci. Technol. 20, 124014. doi:10.1088/0957-0233/20/12/124014

CrossRef Full Text | Google Scholar

Lucklum, R., Zubtsov, M., and Ke, M. (2012). Liquid Sensor Utilizing a Regular Phononic Crystal with Normal Incidence of Sound. IEEE Trans. Ultrason. Ferroelectr., Freq. Contr. 59, 463–471. doi:10.1109/tuffc.2012.2216

CrossRef Full Text | Google Scholar

Lucklum, R., Zubtsov, M., and Oseev, A. (2013). Phoxonic Crystals-A New Platform for Chemical and Biochemical Sensors. Anal. Bioanal. Chem. 405, 6497–6509. doi:10.1007/s00216-013-7093-9

PubMed Abstract | CrossRef Full Text | Google Scholar

McGinn, C. K., Lamport, Z. A., and Kymissis, I. (2020). Review of Gravimetric Sensing of Volatile Organic Compounds. ACS Sens. 5, 1514–1534. doi:10.1021/acssensors.0c00333

PubMed Abstract | CrossRef Full Text | Google Scholar

McHale, G., Lücklum, R., Newton, M. I., Cowen, J. A., and Hauptmann, P. (2000). Influence of Viscoelasticity and Interfacial Slip on Acoustic Wave Sensors. J. Appl. Phys. 88, 7304–7312. doi:10.1063/1.1326855

CrossRef Full Text | Google Scholar

Meng, Z., Stolz, R. M., Mendecki, L., and Mirica, K. A. (2019). Electrically-Transduced Chemical Sensors Based on Two-Dimensional Nanomaterials. Chem. Rev. 119, 478–598. doi:10.1021/acs.chemrev.8b00311

PubMed Abstract | CrossRef Full Text | Google Scholar

Migoń, D., Wasilewski, T., and Suchy, D. (2020). Application of QCM in Peptide and Protein-Based Drug Product Development. Molecules 25, 39501–39518. doi:10.3390/molecules25173950

CrossRef Full Text | Google Scholar

Mondejar, M. E., Regidor, M., Krafczyk, J., Ihmels, C., Schmid, B., Kontogeorgis, G. M., et al. (2021). An Open-Access Database of the Thermophysical Properties of Nanofluids. J. Mol. Liquids 333, 115140. doi:10.1016/j.molliq.2020.115140

CrossRef Full Text | Google Scholar

Mujahid, A., Afzal, A., and Dickert, F. L. (2019). An Overview of High Frequency Acoustic Sensors-QCMs. SAWs FBARs-Chemical Biochem. Appl. Sensors 19, 1–29. doi:10.3390/s19204395

CrossRef Full Text | Google Scholar

Mukhin, N., Kutia, M., Oseev, A., Steinmann, U., Palis, S., and Lucklum, R. (2019). Narrow Band Solid-Liquid Composite Arrangements: Alternative Solutions for Phononic Crystal-Based Liquid Sensors. Sensors 19, 3743 1–15. doi:10.3390/s19173743

CrossRef Full Text | Google Scholar

Mukhin, N., and Lucklum, R. (2019). QCM Based Sensor for Detecting Volumetric Properties of Liquids. Curr. Appl. Phys. 19, 679–682. doi:10.1016/j.cap.2019.03.017

CrossRef Full Text | Google Scholar

Mukhin, N., and Lucklum, R. (2020). “Tube Liquid Resonant Sensor Based on a Combination of 2D and 1FD Phononic Crystals,” in 27th Int. Congr. Sound Vibrat (Prague: Proc in print), 12–16.

Google Scholar

Naik, A. K., Hanay, M. S., Hiebert, W. K., Feng, X. L., and Roukes, M. L. (2009). Towards Single-Molecule Nanomechanical Mass Spectrometry. Nat. Nanotech 4, 445–450. doi:10.1038/nnano.2009.152

PubMed Abstract | CrossRef Full Text | Google Scholar

Orhan, E., Yuksel, M., Ari, A. B., Yanik, C., Hatipoglu, U., Murat Yagci, A., et al. (2020). Performance of Nano-Electromechanical Systems as Nanoparticle Position Sensors. Front. Mech. Eng. 6, 1–9. doi:10.3389/fmech.2020.00037

CrossRef Full Text | Google Scholar

Oseev, A., Lucklum, R., l Zubtsov, M., Schmidt, M.-P., Mukhin, N. V., and Hirsch, S. (2017). SAW-based Phononic Crystal Microfluidic Sensor-Microscale Realization of Velocimetry Approaches for Integrated Analytical Platform Applications. Sensors 17, 2187 1–12. doi:10.3390/s17102187

CrossRef Full Text | Google Scholar

Oseev, A., Mukhin, N., Lucklum, R., Zubtsov, M., Schmidt, M. P., Fomin, A., et al. (2018). Study of Liquid Resonances in Solid-Liquid Composite Periodic Structures (Phononic Crystals) – Theoretical Investigations and Practical Application for In-Line Analysis of Conventional Petroleum Products. Sens. Actuators B 257, 469–477. doi:10.1016/j.snb.2017.10.144

CrossRef Full Text | Google Scholar

Oseev, A., Zubtsov, M., and Lucklum, R. (2013). Gasoline Properties Determination with Phononic crystal Cavity Sensor. Sens. Actuators B 189, 208–212. doi:10.1016/j.snb.2013.03.072

CrossRef Full Text | Google Scholar

Pitarresi, G., and Patterson, E. A. (2003). A Review of the General Theory of Thermoelastic Stress Analysis. J. Strain Anal. Eng. Des. 38, 405–417. doi:10.1243/03093240360713469

CrossRef Full Text | Google Scholar

Pohanka, M. (2018). Overview of Piezoelectric Biosensors. Immunosensors DNA Sensors Their Appl. Mater. 11, 1–13. doi:10.3390/ma11030448

PubMed Abstract | CrossRef Full Text | Google Scholar

Pujol-Vila, F., Villa, R., and Alvarez, M. (2020). Nanomechanical Sensors as a Tool for Bacteria Detection and Antibiotic Susceptibility Testing. Front. Mech. Eng. 6, 44–18. doi:10.3389/fmech.2020.00044

CrossRef Full Text | Google Scholar

Rajakovic, L. V., Cavic-Vlasak, B. A., Ghaemmaghami, V., Kallury, K. M. R., Kipling, A. L., and Thompson, M. (1991). Mediation of Acoustic Energy Transmission from Acoustic Wave Sensors to the Liquid Phase by Interfacial Viscosity. Anal. Chem. 63, 615–621. doi:10.1021/ac00006a012

CrossRef Full Text | Google Scholar

Rodahl, M., Höök, F., Krozer, A., Brzezinski, P., and Kasemo, B. (1995). Quartz crystal Microbalance Setup for Frequency and Q‐factor Measurements in Gaseous and Liquid Environments. Rev. Scientific Instr. 66, 3924–3930. doi:10.1063/1.1145396

CrossRef Full Text | Google Scholar

Ruiz-Díez, V., Hernando-García, J., Manzaneque, T., Kucera, M., Schmid, U., and Sánchez-Rojas, J. L. (2015). Viscous and Acoustic Losses in Length-Extensional Microplate Resonators in Liquid media. Appl. Phys. Lett. 106, 083510. doi:10.1063/1.4913885

CrossRef Full Text | Google Scholar

Ruiz-Díez, V., Toledo, J., Hernando-García, J., Ababneh, A., Seidel, H., and Sánchez-Rojas, J. L. (2019). A Geometrical Study on the Roof Tile-Shaped Modes in AlN-Based Piezoelectric Microcantilevers as Viscosity-Density Sensors. Sensors 19, 1–11. doi:10.3390/s19030658

CrossRef Full Text | Google Scholar

Salman, A., Adem Kaya, O., and Cicek, A. (2014). Determination of Concentration of Ethanol in Water by a Linear Waveguide in a 2-dimensional Phononic crystal Slab. Sens. Actuators A. 208, 50–55. doi:10.1016/j.sna.2013.12.037

CrossRef Full Text | Google Scholar

Sansa, M., Defoort, M., Brenac, A., Hermouet, M., Banniard, L., Fafin, A., et al. (2020). Optomechanical Mass Spectrometry. Nat. Comm. 11, 1–7. doi:10.1038/s41467-020-17592-9

CrossRef Full Text | Google Scholar

Sauerbrey, G. N. (1959). Verwendung von Schwingquarzen zur Wagung dunner Schichten und zur Mikrowagung. Z. Physik 155, 206–222. doi:10.1007/bf01337937

CrossRef Full Text | Google Scholar

Schröder, J., Borngräber, R., Lucklum, R., and Hauptmann, P. (2001). Network Analysis Based Interface Electronics for Quartz crystal Microbalance. Rev. Sci. Instr. 72, 2537–2545. doi:10.1063/1.1370560

CrossRef Full Text | Google Scholar

Seed, C. M., Acharya, B., and Krim, J. (2020). Continuum Model Analysis of QCM Nanotribological Data to Obtain Friction Coefficients for 304SS Contacts Lubricated by Water and TiO2 Nanoparticle Suspensions. Front. Mech. Eng. 8, 1–10. doi:10.3389/fmech.2020.00072

CrossRef Full Text | Google Scholar

Seitenubersicht and Sitemap (1983). Wasser und seine Eigenschaften: Dichte, Dichtetabelle, Anleitung für eine einfache Dichtemessung und -berechnung, Mengeneinheiten für Wasser, Dichteanomalie. Available at: http://www.wissenschaft-technik-ethik.de/wasser_dichte.html.

Google Scholar

Sekoyan, S. S., Samorukova, L. M., Stefanov, S. R., and Levtsov, V. I. (1999). Pressure Dependence of the Sound Velocity in Distilled Water. Meas. Tech. 42, 406–413. doi:10.1007/BF02504405

CrossRef Full Text | Google Scholar

SoltanRezaee, M., and Bodaghi, M. (2020). Simulation of an Electrically Actuated Cantilever as a Novel Biosensor. Sci. Rep. 10, 3385. doi:10.1038/s41598-020-60296-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorenson, L., Fu, J. L., and Ayazi, F. (2011). “One-dimensional Linear Acoustic Band gap Structures for Performance Enhancement of AlN On-Si Micromechanical Resonators,” in 2011 16th Int. Solid-State Sensors, Actuators and Microsystems Conference (Beijing: IEEE), 918–921.

Google Scholar

Stengel, G., Höök, F., and Knoll, W. (2005). Viscoelastic Modeling of Template-Directed DNA Synthesis. Anal. Chem. 77, 3709–3714. doi:10.1021/ac048302x

PubMed Abstract | CrossRef Full Text | Google Scholar

Villa-Arango, S., Betancur, D., Torres, R., and Kyriacou, P. (2018). Use of Transient Time Response as a Measure to Characterize Phononic Crystal Sensors. Sensors 18, 3618. doi:10.3390/s18113618

PubMed Abstract | CrossRef Full Text | Google Scholar

Villa-Arango, S., Betancur Sánchez, D., Torres, R., Kyriacou, P., and Lucklum, R. (2017). Differential Phononic Crystal Sensor: Towards a Temperature Compensation Mechanism for Field Applications Development. Sensors 17, 1960. doi:10.3390/s17091960

PubMed Abstract | CrossRef Full Text | Google Scholar

Villa-Arango, S., Torres Villa, R., Kyriacou, P. A., and Lucklum, R. (2017). Fully-disposable Multilayered Phononic crystal Liquid Sensor with Symmetry Reduction and a Resonant Cavity. Measurement 102, 20–25. doi:10.1016/j.measurement.2017.01.051

CrossRef Full Text | Google Scholar

Voinova, M. V., Jonson, M., and Kasemo, B. (2002). 'Missing Mass' Effect in Biosensor's QCM Applications. Biosens. Bioelectron. 17, 835–841. doi:10.1016/s0956-5663(02)00050-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner, Z., Bendová, M., Rotrekl, J., Sýkorová, A., Čanji, M., and Parmar, N. (2021). Density and Sound Velocity Measurement by an Anton Paar DSA 5000 Density Meter: Precision and Long-Time Stability. J. Mol. Liquids 329, 115547. doi:10.1016/j.molliq.2021.115547

CrossRef Full Text | Google Scholar

Wang, C., Cai, F., Li, F., Meng, L., Li, J., Wu, J., et al. (2016). A Highly Sensitive Compact Liquid Sensor Based on Slotted Phononic crystal Plates. Lab. Chip 16, 4595–4600. doi:10.1039/c6lc01151a

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L. (2020). Metal-organic Frameworks for QCM-Based Gas Sensors: A Review. Sensors Actuators A: Phys. 307, 111984. doi:10.1016/j.sna.2020.111984

CrossRef Full Text | Google Scholar

Wang, T. T., Laude, V., Kadic, M., Wang, Y.-F., and Wang, Y-S. (2020). Complex-eigenfrequency Band Structure of Viscoelastic Phononic Crystals. Appl. Sci. 9, 1–11.

Google Scholar

Wasmer, P., Bulling, J., and Prager, J. (2019). “Ultrasonic Sensor Based on Phononic Crystals,” in Proc. 23rd Int. Congr. Acoustics (Aachen, Germany: Beitrag zu einem Tagungsband), 9–13.

Google Scholar

Wu, G., Zhu, Y., Merugu, S., Wang, N., Sun, C., and Gu, Y. (2016). GHz Spurious Mode Free AlN Lamb Wave Resonator with High Figure of merit Using One Dimensional Phononic crystal Tethers. Appl. Phys. Lett. 109, 013506 1–4. doi:10.1063/1.4955410

CrossRef Full Text | Google Scholar

Yang, Y. T., Callegari, C., Feng, X. L., Ekinci, K. L., and Roukes, M. L. (2006). Zeptogram-Scale Nanomechanical Mass Sensing. Nano Lett. 6, 583–586. doi:10.1021/nl052134m

PubMed Abstract | CrossRef Full Text | Google Scholar

Yongabi, D., Khorshid, M., Gennaro, A., Jooken, S., Duwé, S., Deschaume, O., et al. (2020). QCM-D Study of Time-Resolved Cell Adhesion and Detachment: Effect of Surface Free Energy on Eukaryotes and Prokaryotes. ACS Appl. Mater. Inter. 12, 18258–18272. doi:10.1021/acsami.0c00353

CrossRef Full Text | Google Scholar

Zubtsov, M., Lucklum, R., Ke, M., Oseev, A., Grundmann, R., Henning, B., et al. (2012). 2D Phononic crystal Sensor with normal Incidence of Sound. Sens. Actuators A. 186, 118–124. doi:10.1016/j.sna.2012.03.017

CrossRef Full Text | Google Scholar