Thermoelectric Properties of Arsenic Triphosphide (AsP3) Monolayer: A First-Principles Study

Recently, monolayer of triphosphides (e.g., InP₃, SnP₃, and GaP₃) attracts much attention due to their good thermoelectric performance. Herein, we predict a novel triphosphide monolayer AsP₃ and comprehensively investigate its thermoelectric properties by combining first-principles calculations and semiclassical Boltzmann transport theory. The results show that AsP₃ monolayer has an ultralow thermal conductivity of 0.36 and 0.55 Wm K⁻¹ at room temperature along the armchair and zigzag direction. Surprisingly, its maximum Seebeck coefficient in the p-type doping reaches 2,860 µVK⁻¹. Because of the ultralow thermal conductivity and ultrahigh Seebeck coefficient, the thermoelectric performance of AsP₃ monolayer is excellent, and the maximum ZT of p-type can reach 3.36 at 500 K along the armchair direction, which is much higher than that of corresponding bulk AsP₃ at the same temperature. Our work indicates that the AsP₃ monolayer is the promising candidate in TE applications and will also stimulate experimental scientists’ interest in the preparation, characterization, and thermoelectric performance tuning.

Introduction

Thermoelectric (TE) materials are regarded as potential candidates to alleviate the energy and environment crisis by recycling waste heat (Elsheikh et al., 2014; Champier, 2017; Gao et al., 2016). However, TE technology is currently facing two crucial issues: high production cost and low conversion efficiency (El Chaar et al., 2011). For the conversion efficiency of a TE material, it is characterized by the dimensionless figure of merit ZT = S²σT/κ (Ding et al., 2016; Gandi and Schwingenschlögl, 2014), where S is the Seebeck coefficient, σ is the electronic conductivity, T is the absolute temperature, and κ is the thermal conductivity, respectively. Over the past few decades, great progress has been achieved in enhancing the ZT values through certain strategies (Ouyang et al., 2019; Gayner and Kar, 2016), such as nanostructuring, quantum confinement, and the “phonon-glass electron-crystal” (Zhang et al., 2020; Hicks and Dresselhaus, 1993a; Hicks and Dresselhaus, 1993b). Therefore, searching “electronic crystal-phonon glass” thermoelectric materials has great significance (Jiang et al., 2019). Due to the development of nanotechnology, new thermoelectric materials are constantly being discovered in recent years. Phosphorene sheds light on two-dimensional (2D) layered materials in TE applications (Fei et al., 2014). However, the chemical degradation upon exposure to ambient conditions seriously limits its practical application (Wood et al., 2014). Scientists make great effort to find novel materials with puckered layered structure similar to phosphorene, which can not only retain the excellent electronic properties of phosphorene, but also overcome the chemical instability. Very recently, 2D triphosphides which include a combination of phosphorus and selective elements from Group III, IV, and V attract much attention because of their outstanding thermoelectric performance. For example, Ouyang et al. (2018) predicted the ZT value up to 2.06 along the armchair direction of InP₃ monolayer at room temperature. Zhu et al. (2019) indicated that the ZT value of monolayer SnP₃ was 3.46 along the armchair direction at 500 K. Single-layer SbP₃ (Sun et al., 2020) and GeP₃ (Jing et al., 2017) are also predicted as good TE materials.

In this work, utilizing first-principles calculations and the Boltzmann transport equation, we explore stability, phonon/electron, and TE properties of the AsP₃ monolayer. Our calculated results show that the AsP₃ monolayer exhibits ultrahigh Seebeck coefficient and ultralow thermal conductivity, and the maximum ZT of p-type AsP₃ monolayer can reach 3.36 at 500 K along the armchair direction. This work reveals that AsP₃ is a promising candidate for TE applications.

Methods

The TE properties of single-layer AsP₃ are calculated using the first-principles and density functional theory (DFT) as performed in the Vienna ab initio simulation package (VASP) (Blöchl, 1994). We set up a vacuum layer with a thickness of 20 Å along the z-direction and use the vdW-DF2 method to correct interaction force between the layers (Klimeš et al., 2009). The generalized gradient approximation (GGA) and the Perdew−Burke−Ernzerhof (PBE) are adopted for processing the exchange-correlation functional (Perdew et al., 1996; Kresse and Furthmüller, 1996). A plane wave basis with a cutoff energy of 500 eV and a 6 × 6 × 1-k-mesh are used for the structural relaxation of the Brillouin zone (BZ). The convergence criterion for complete relaxation of all geometric structures is that the total energy change is <10⁻⁷ eVÅ⁻¹ and the residual force is <0.01 eVÅ⁻¹.

The Boltzmann transport theory and rigid band approximation are used to evaluate the electronic transport properties, which are carried out in the BoltzTrap software with a dense k-mesh 40 × 40 × 1 (Madsen and Singh, 2006). This method has achieved good agreement between theoretical calculations and experiments for many TE materials (Bilc et al., 2006; Xu et al., 2010; Parker and Singh, 2010). For the phonon transport properties, it can be obtained by solving the Boltzmann transport equation in the ShengBTE packages with 50 × 50 × 1 k-points (Li et al., 2014). The phonon dispersions and the harmonic second-order interaction force constants (2nd IFCs) are calculated by using VASP and PHONOPY software (Togo and Tanaka, 2015), in which the 3 × 3 × 1 k-mesh within 4 × 4 × 1 supercell is adopted. The third-order IFCs (3rd IFCs) is obtained by using the 3 × 3 × 1 supercell with the finite-difference method (Li et al., 2012), which considers the interaction including the seventh nearest neighbor atoms.

Results and Discussion

Atomic and Electronic Structures

Based on calculations of the first-principles, the AsP₃ monolayer exhibits a hexagonal honeycomb configuration with space group $P\overline{3}m1$ (No. 164), as shown in Figures 1A–C. A unit cell for AsP₃ monolayer is constituted by two As and six P atoms, and the optimized lattice constants a = 6.62 Å. More calculated parameters are summarized in Table 1. Interestingly, the AsP₃ monolayer has an obvious anisotropic structure, thus we will explore its TE performance in the armchair and zigzag direction.

FIGURE 1

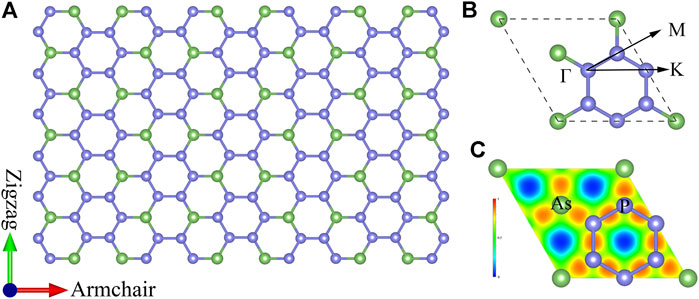
FIGURE 1. (A) Top view of atomic structure, (B) corresponding first Brillouin zone path, and (C) electronic local function for monolayer AsP₃.

TABLE 1

TABLE 1. Calculated lattice constants (l_a), bond lengths of P–P (l_P–P) and X–P (l_X–P), and bandgap based on PBE and HSE06.

We study the electrical band structures as well as the corresponding density of states (DOS) of AsP₃ monolayer, as presented in Figure 2A. We find that the AsP₃ monolayer is an indirect bandgap semiconductor, its valence band maximum (VBM) is locating at the Γ point, whereas the conduction band minimum (CBM) is located between the Γ and M points. The accurate bandgap of 2.28 eV is obtained by using the Herd–Scuseria–Emzerhof hybrid functional (HSE06) (Heyd et al., 2003). In the vicinity of Fermi level, the two highest valence bands (VBs) exhibit overlap at the Γ point, which benefits their electrical transport characteristics (Ding et al., 2018). The DOS further demonstrates that the edges of the VB and CB are mainly coming from the P atoms, which can also be observed in Figure 2B, where the partial charge density provides that the charge is mainly concentrated near P atoms. Meantime, a peak shape of DOS is acquired in monolayer AsP₃, which is regarded as the electronic transmission characteristic of high TE performance (Peng et al., 2014).

FIGURE 2

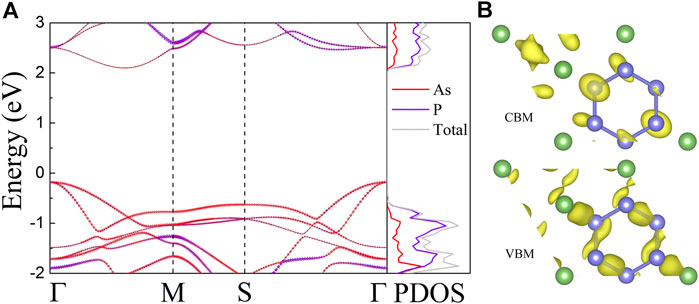
FIGURE 2. (A) Calculated orbital-resolved band structures and corresponding DOS of AsP₃ monolayer. The contribution from As (red) and p (purple) atoms weight the colors of band structures. (B) The partial charge densities of DOS.

Electrical Transport Properties

Based on the deformation potential (DP) theory (Bardeen and Shockley, 1950), the carrier mobility of AsP₃ monolayer can be calculated by the formula:

${\mu }_{2D}=\frac{2e{\hslash }^3{C}_{2D}}{3{\kappa }_{B}T{\left|m^{\ast }\right|}^2{E}_l^2},(1)$

where m*, κ_B, E_l, and C_2D are the effective mass, the Boltzmann constant, the DP constant, and the 2D elastic constants, respectively. These parameters and the relaxation time $\left(\tau =\text{μm}\ast /e\right)$ are given in Table 2. One can see clearly that the hole mobility is significantly higher than the electron mobility. Besides, the flatter conduction bands provide a greater effective mass m* of electron doping, which demonstrates a larger Seebeck coefficient S because it is proportional to m* (Gao et al., 2018).

TABLE 2

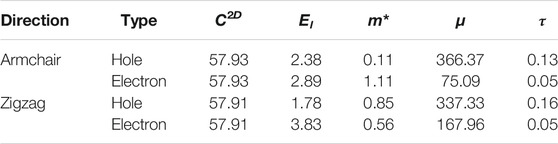
TABLE 2. Calculated elastic modulus C^2D (J m⁻²), DP constant E_l (eV), effective mass m* (m_e), carrier mobility μ (cm⁻² V⁻¹ s⁻¹), and relaxation time τ (ps) for electron and hole in AsP₃ monolayer at 300 K.

We obtain the electrical transport properties of AsP₃ monolayer via calculating the semiclassical Boltzmann transport equation (May et al., 2009), involving Seebeck coefficient S, electrical conductivity σ, electrical thermal conductivity κ_e, and power factor (PF), which are important parameters for evaluating the TE properties. The rigid band approximation theory is adopted to simulate the influence of doping on electron transport. It is assumed that the band structure of the n-type and p-type systems does not change in shape under light doping, whereas the Fermi level moves up and down (Singh, 2007; Parker and Singh, 2011). Positive and negative μ correspond to the n-type and p-type doping. Here, the S, σ, and PF concerning chemical potential μ can be computed by employing the Fermi–Dirac distribution function f_μ (Parker and Singh, 2011) as:

${\sigma }_{\alpha \beta }\left(T,\mu \right)=\frac{1}{V}{\displaystyle \int {\displaystyle {\sum }_{\alpha \beta }\left(\epsilon \right)}\left[-\frac{\partial f_{\mu }\left(T,\epsilon \right)}{d\epsilon }\right]d\epsilon },(2)$

$S_{\alpha \beta }\left(T,\mu \right)=\frac{1}{eTV{\sigma }_{\alpha \beta }\left(T,\mu \right)}{\displaystyle \int {\displaystyle {\sum }_{\alpha \beta }\left(\epsilon \right)\left(\epsilon -\mu \right)\left[-\frac{\partial f_{\mu }\left(T,\epsilon \right)}{d\epsilon }\right]d\epsilon }},(3)$

where V is the volume of the primitive cell, and the transport distribution function ${\displaystyle \sum }_{\alpha \beta }\left(\epsilon \right)$ is written as follows:

${\displaystyle {\sum }_{\alpha \beta }\left(\epsilon \right)}=\frac{e^2}{N_0}{\displaystyle {\sum }_{i,q}\tau v_{\alpha }\left(i,q\right)v_{\beta }\left(i,q\right)\frac{\delta \left(\epsilon -{\epsilon }_{i,q}\right)}{d\epsilon }},(4)$

where N₀ is the number of q points sampling, τ is the electronic relaxation time, and ν is electronic velocity.

Figures 3A,B are the Seebeck coefficient S of AsP₃ monolayer as a function of µ. The downward trend of the S with the temperature gradually slows down as the temperature increases. Surprisingly, the AsP₃ monolayer shows ultrahigh S compared to other triphosphates with high TE performance (InP₃ (Ouyang et al., 2018), SnP₃ (Zhu et al., 2019), and CaP₃ (Zhu et al., 2020a)). At room temperature, the S of AsP₃ monolayer reaches 2,860 µVK⁻¹ along the zigzag direction and 2,800 µVK⁻¹ along the armchair direction. The double degeneracy of the valence band at the Г point and the steep electronic density of states near the Fermi level effectively increase the S.

FIGURE 3

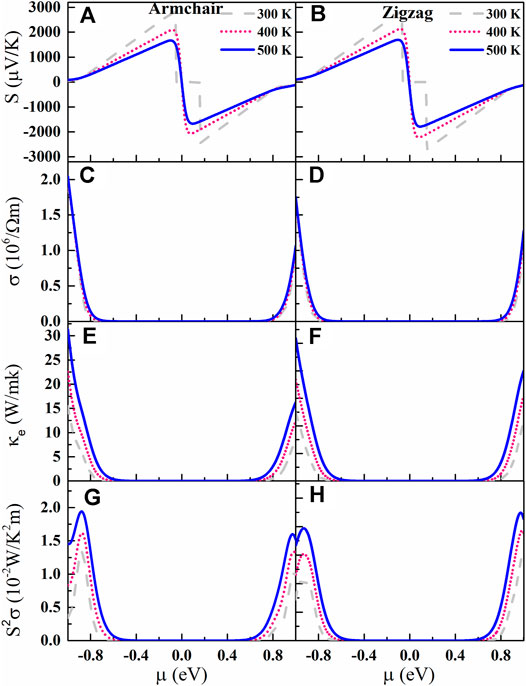
FIGURE 3. (A)–(H) Seebeck coefficients, electrical conductivity, electrical thermal conductivity, and power factor vs. chemical potential µ at different temperatures (300, 400, and 500 K).

The electrical conductivity σ vs. μ is shown in Figures 3C,D. It is found that the p-type σ is visibly larger than that of the n-type for AsP₃ monolayer, due to the higher mobility and relaxation time of hole. Since electrons submit the Fermi–Dirac distribution, the gradient of σ around VBM and CBM tends to be flat with increasing temperature. According to the Wiedemann–Franz law, the κ_e is proportional to the σ: κ_e= LσT, where L is the Lorenz number $\left(L={\pi }^2{\kappa }_B^2/3e^2\right)$ (Jonson and Mahan, 1980). As shown in Figures 3E,F, the κ_e of the AsP₃ monolayer increases with rising temperature. The influence of p-type doping on the κ_e is greater than that of n-type doping, which is related to its larger p-type σ.

Based on the obtained S and σ, we calculate the PF as shown in Figures 3G,H. Similar to σ, the PF of p-type AsP₃ monolayer is significantly higher than that of n-type, which means that it is a potential p-type TE material.

Phonon Transport Properties

The phonon spectrum and projected density of state (PhDOS) of the AsP₃ monolayer are illustrated in Figure 4A. No virtual phonon modes are observed in phonon dispersion, which indicates that the AsP₃ monolayer is dynamically stable. The phonon spectrum of AsP₃ contains three phonon branches (ZA, TA, and LA) and twenty-one optical branches. The low-frequency optical branch and the acoustic branch of the AsP₃ monolayer are softened and overlapped, leading to the strong acoustic–optic interaction (Gao et al., 2018). Besides, the flat-frequency band over the entire frequency range can lead to smaller phonon group velocity (Ma et al., 2016; Ma et al., 2018). It can be seen from the corresponding PhDOS that the phonon mode mainly contains As atoms in the low-frequency region (below 3 THz), while the high-frequency region (over 12 THz) is contributed by the P atom.

FIGURE 4

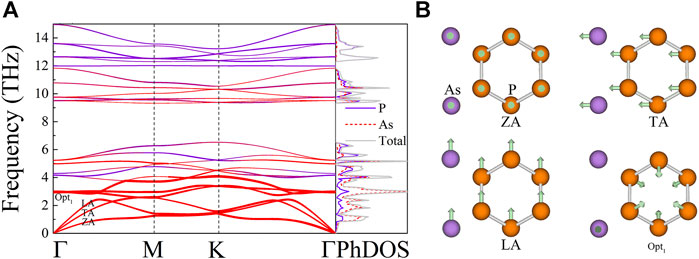
FIGURE 4. (A) Phonon spectra and phonon density of states (PhDOS) for AsP₃, (B) the corresponding vibrational modes of the acoustic phonon branches (ZA, TA, and LA), and the lowest optical branch (Opt₁) near and at the Γ point.

Figure 4B depicts the corresponding vibration modes near the Γ point of the acoustic branch (ZA, TA, and LA) and the lowest optical branch (Opt₁) to display the characteristics of the phonon mode more intuitively. It can be seen that the vibration of the three-phonon branch occurs along the in-plane (TA and LA) or outside the plane (ZA), which is a property of natural vibration. Interestingly, it is observed that As atoms of the Opt₁ branch have in-plane opposite motions relative to their adjacent As atoms, while P atoms have in-plane antiphase motions. This phenomenon can significantly block heat transport, thereby reducing the thermal conductivity of the lattice (Ding et al., 2015).

Based on the 2nd and 3rd IFCs, the κ_l is calculated by the self-consistent iterative method. The calculation formula of κ_l is as follows:

${\kappa }_{l,\alpha \beta }={\displaystyle {\sum }_{q,\lambda }{C}_V\left(q,\lambda \right)v^{\alpha }\left(q,\lambda \right)v^{\beta }\left(q,\lambda \right){\tau }_{q,\lambda }},(5)$

where C_V, ν, and τ_qλ are phonon model specific heat, group velocity, and relaxation time, respectively. As shown in Figure 5A, we plot the κ_l of AsP₃ monolayer vs. temperature. The inherent κ_l is obviously proportional to 1/T, which is attributed to the inherent enhancement of phonon–phonon scattering (Liu et al., 2018). Excitingly, the AsP₃ monolayer shows ultralow thermal conductivity. At room temperature, κ_l along the armchair direction (0.36 Wm⁻¹ K⁻¹) is lower than that along the zigzag direction (0.55 Wm⁻¹ K⁻¹). We explore the relationship between κ_l and frequency to describe the contribution of different phonons. Figure 5B shows that acoustic branches (below 2 THz) along armchair (zigzag) direction contribute about 75% (86%) to κ_l.

FIGURE 5

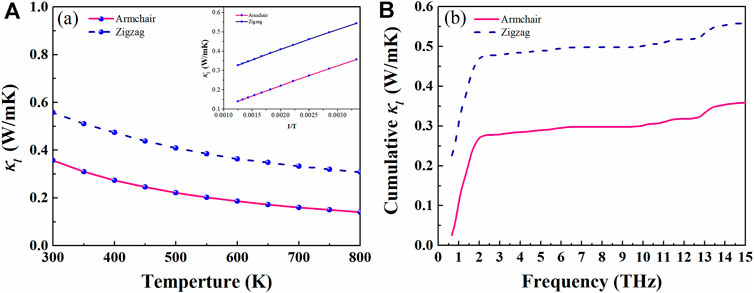
FIGURE 5. Lattice thermal conductivity of AsP₃ as a function of temperature (A) and frequency (B). The insets of (A) is lattice thermal conductivity as a function of T⁻¹.

The phonon group velocity is an important coefficient to evaluate the heat transferability, which can be obtained by the following equation:

$v=\frac{d\omega \left(q\right)}{dq}.(6)$

The corresponding group velocity of AsP₃ monolayer is plotted in Figure 6A. We can see that the group velocity in the low-frequency area is distinctly larger than that of the high-frequency area. It exhibits a smaller average group velocity about 1.91 km s⁻¹, which is related to the flat phonon dispersions and low cutoff frequency.

FIGURE 6

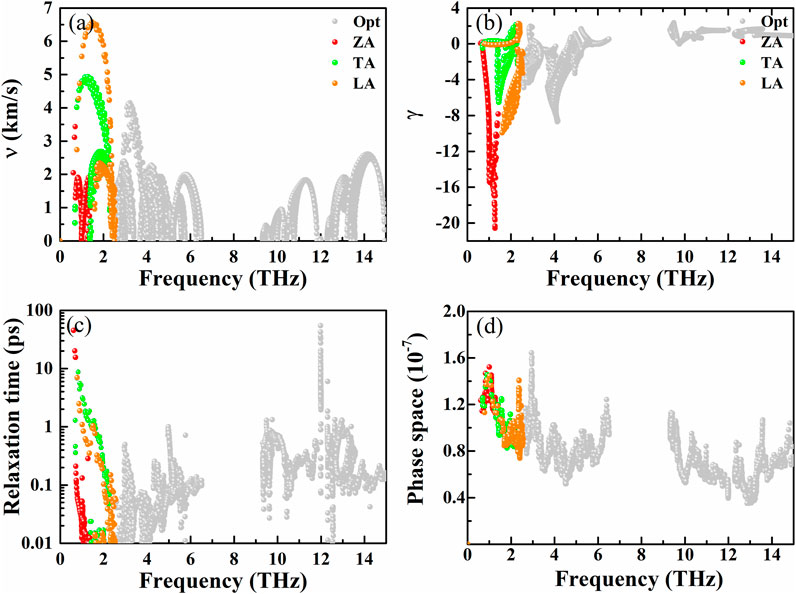
FIGURE 6. (A) Phonon group velocity, (B) Grüneisen parameters, (C) phonon relaxation time, and (D) three-phonon scattering phase space as a function of frequency for AsP₃, respectively.

To determine the other origin of ultralow κ_l of AsP₃ monolayer, we calculate the Grüneisen parameter γ, which can be used to describe the anharmonic interaction of crystals. It can be described by the following equation:

${\gamma }_{\lambda }\left(q\right)=-\frac{V}{{\omega }_{\lambda }\left(q\right)}\frac{\partial {\omega }_{\lambda }\left(q\right)}{\partial V}.(7)$

Generally, the larger |γ| represents the stronger anharmonicity and the lower κ_l. As presented in Figure 6B, one can see a larger |γ| in the low-frequency region, and the average of |γ| is about 16.17, indicating the existence of strong phonon–phonon scattering.

Figure 6C is the phonon relaxation time vs. frequency of AP₃ monolayer. At 300 K, our calculated phonon relaxation time of AsP₃ monolayer (4.3 ps) can be compared with the single-layer KAgS (4.05 ps) (Zhu et al., 2020b), which is an important factor for the low κ_l of AsP₃ monolayer. The three-phonon scattering phase space (P₃) is the available space for the three-phonon scattering process (Li and Mingo, 2015), which can further analyze the source of lower κ_l. As shown in Figure 6D, the AsP₃ monolayer possesses a larger P₃ over the entire frequency region, which allows stronger phonon–phonon scattering and weaker heat transport.

Thermoelectric Figure of Merit

Combining the electrical transport coefficients and thermal conductivity, we can estimate the ZT values of AsP₃, as displayed in Figure 7. The p-type doped AsP₃ monolayer exhibits a higher ZT than the n-type one, which is caused by larger PF of p-type. The maximum ZT values of p-type doped AsP₃ monolayer at 500 K can reach 3.36 and 2.92 along the armchair and zigzag direction, while corresponding ZT values at 300 K is 2.22 and 1.84, much higher than that of bulk AsP₃ (∼0.5 at 300 K) (Duan et al., 2019), which is mainly caused by the larger S and lower κ_l of AsP₃ single-layered structure by dimensionality reduction. The maximum ZT value of AsP₃ monolayer at 500 K is comparable with other 2D triphosphides, such as n-type doped InP₃ (ZT = 3.23) (Ouyang et al., 2018), p-type doped SnP₃ (ZT = 3.46) (Zhu et al., 2019), and p-type doped SbP₃ (ZT = 3.5) (Sun et al., 2020). Besides, the maximum ZT values can be achieved when the carrier concentration is between 1 × 10¹⁰ and 10¹¹ cm⁻². Generally speaking, if the ZT value is close to 3, it is deemed a good TE material (Harman et al., 2002), therefore AsP₃ monolayer can be a potential candidate for TE applications.

FIGURE 7

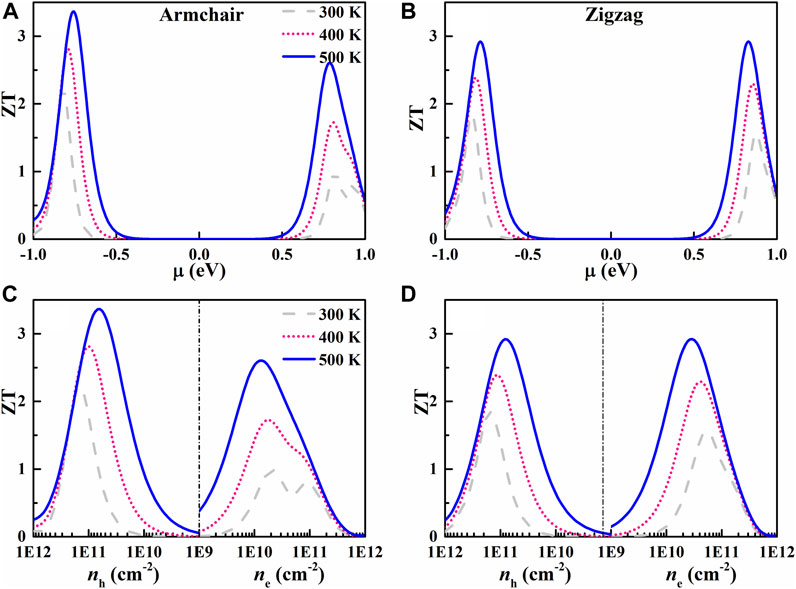
FIGURE 7. ZT as a function of the chemical potential (A) and carrier concentration (B) of the AsP₃ monolayer.

Conclusion

In conclusion, we investigate the TE performance of AsP₃ monolayer by a highly precise first-principles method. The calculated results show that AsP₃ monolayer is an indirect bandgap semiconductor with a bandgap of 2.28 eV. It also possesses excellent Seebeck coefficients and electrical conductivity. Due to its lower values of phonon velocities (1.91 km s⁻¹), larger Grüneisen parameters |γ| (16.17), as well as shorter phonon relaxation time (4.30 ps), AsP₃ monolayer exhibits ultralow κ_l 0.36 Wm⁻¹ K⁻¹ (0.55 Wm⁻¹ K⁻¹) at room temperature in the armchair (zigzag) direction. At 500 K, the maximum ZT of the AsP₃ monolayer can reach up to 3.36 (armchair direction) and 3.08 (zigzag direction) by the optimal p-type doping. These results prove the huge advantages of AsP₃ single-layer film in high-efficiency conversion of heat energy.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

GX established the theoretical models and supervised the project, and LF and HY performed the calculations and data analysis.

Funding

This work was financially supported by National Natural Science Foundation of China (NSFC) (Grant No. 11874145 and 11474243).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bardeen, J., and Shockley, W. (1950). Deformation Potentials and Mobilities in Non-polar Crystals. Phys. Rev. 80, 72–80. doi:10.1103/physrev.80.72

CrossRef Full Text | Google Scholar

Bilc, D. I., Mahanti, S. D., and Kanatzidis, M. G. (2006). Electronic Transport Properties of PbTe and AgPb_mSbTe_2+m Systems. Phys. Rev. B 74, 125202. doi:10.1103/physrevb.74.125202

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

Champier, D. (2017). Thermoelectric Generators: A Review of Applications. Energ. Convers. Manage. 140, 167–181. doi:10.1016/j.enconman.2017.02.070

CrossRef Full Text | Google Scholar

Ding, G., Gao, G. Y., Huang, Z., Zhang, W., and Yao, K. (2016). Thermoelectric Properties of monolayerMSe2(M = Zr, Hf): Low Lattice thermal Conductivity and a Promising Figure of merit. Nanotechnology 27, 375703. doi:10.1088/0957-4484/27/37/375703

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, G., Wang, C., Gao, G., Yao, K., Dun, C., Feng, C., et al. (2018). Engineering of Charge Carriers via a Two-Dimensional Heterostructure to Enhance the Thermoelectric Figure of merit. Nanoscale 10, 7077–7084. doi:10.1039/c7nr09029c

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Xu, B., Lin, Y., Nan, C., and Liu, W. (2015). Lattice Vibration Modes of the Layered Material BiCuSeO and First Principles Study of its Thermoelectric Properties. New J. Phys. 17, 083012. doi:10.1088/1367-2630/17/8/083012

CrossRef Full Text | Google Scholar

Duan, S., Cui, Y., Chen, X., Yi, W., Liu, Y., and Liu, X. (2019). Ultrahigh Thermoelectric Performance Realized in Black Phosphorus System by Favorable Band Engineering through Group VA Doping. Adv. Funct. Mater. 29, 1904346. doi:10.1002/adfm.201904346

CrossRef Full Text | Google Scholar

El Chaar, L., lamont, L. A., and El Zein, N. (2011). Review of Photovoltaic Technologies. Renew. Sustain. Energ. Rev. 15, 2165–2175. doi:10.1016/j.rser.2011.01.004

CrossRef Full Text | Google Scholar

Elsheikh, M. H., Shnawah, D. A., Sabri, M. F. M., Said, S. B. M., Hassan, M. H., Ali Bashir, M. B., et al. (2014). A Review on Thermoelectric Renewable Energy: Principle Parameters that Affect Their Performance. Renew. Sust. Energ. Rev. 30, 337–355. doi:10.1016/j.rser.2013.10.027

CrossRef Full Text | Google Scholar

Fei, R., Faghaninia, A., Soklaski, R., Yan, J.-A., Lo, C., and Yang, L. (2014). Enhanced Thermoelectric Efficiency via Orthogonal Electrical and thermal Conductances in Phosphorene. Nano Lett. 14, 6393–6399. doi:10.1021/nl502865s

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandi, A. N., and Schwingenschlögl, U. (2014). WS2As an Excellent High-Temperature Thermoelectric Material. Chem. Mater. 26, 6628–6637. doi:10.1021/cm503487n

CrossRef Full Text | Google Scholar

Gao, H. B., Huang, G. H., Li, H. J., Qu, Z. G., and Zhang, Y. J. (2016). Development of Stove-Powered Thermoelectric Generators: A Review. Appl. Therm. Eng. 96, 297–310. doi:10.1016/j.applthermaleng.2015.11.032

CrossRef Full Text | Google Scholar

Gao, Z., Liu, G., and Ren, J. (2018). High Thermoelectric Performance in Two-Dimensional Tellurium: An Ab Initio Study. ACS Appl. Mater. Inter. 10, 40702–40709. doi:10.1021/acsami.8b11836

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Z., Tao, F., and Ren, J. (2018). Unusually Low thermal Conductivity of Atomically Thin 2D Tellurium. Nanoscale 10, 12997–13003. doi:10.1039/c8nr01649f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gayner, C., and Kar, K. K. (2016). Recent Advances in Thermoelectric Materials. Prog. Mater. Sci. 83, 330–382. doi:10.1016/j.pmatsci.2016.07.002

CrossRef Full Text | Google Scholar

Harman, T. C., Taylor, P. J., Walsh, M. P., and LaForge, B. E. (2002). Quantum Dot Superlattice Thermoelectric Materials and Devices. Science 297, 2229–2232. doi:10.1126/science.1072886

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060

CrossRef Full Text | Google Scholar

Hicks, L. D., and Dresselhaus, M. S. (1993a). Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys. Rev. B 47, 12727–12731. doi:10.1103/physrevb.47.12727

CrossRef Full Text | Google Scholar

Hicks, L. D., and Dresselhaus, M. S. (1993b). Thermoelectric Figure of merit of a One-Dimensional Conductor. Phys. Rev. B 47, 16631–16634. doi:10.1103/physrevb.47.16631

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, X., Zhu, L., Li, B., and Yao, K. (2019). Thermoelectric Properties of Monolayer α-Te: Low Lattice thermal Conductivity and Extremely High Dimensionless Figure of merit. Phys. Let. A. 384, 126222. doi:10.1016/j.physleta.2019.126222

CrossRef Full Text | Google Scholar

Jing, Y., Ma, Y., Li, Y., and Heine, T. (2017). GeP3: A Small Indirect Band Gap 2D Crystal with High Carrier Mobility and Strong Interlayer Quantum Confinement. Nano Lett. 17, 1833–1838. doi:10.1021/acs.nanolett.6b05143

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonson, M., and Mahan, G. D. (1980). Mott’s Formula for the Thermopower and the Wiedemann-Franz Law. Phys. Rev. B 21, 4223–4229. doi:10.1103/physrevb.21.4223

CrossRef Full Text | Google Scholar

Klimeš, J., Bowler, D. R., and Michaelides, A. (2009). Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201. doi:10.1088/0953-8984/22/2/022201

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

Li, W., Carrete, J., A. Katcho, N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Li, W., Lindsay, L., Broido, D. A., Stewart, D. A., and Mingo, N. (2012). Thermal Conductivity of Bulk and Nanowire Mg₂Si_xSn_1−x Alloys from First Principles. Phys. Rev. B 86, 174307. doi:10.1103/physrevb.86.174307

CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2015). Ultralow Lattice thermal Conductivity of the Fully Filled Skutterudite YbFe₄Sb₁₂ Due to the Flat Avoided-Crossing Filler Modes. Phys. Rev. B 91, 144304. doi:10.1103/physrevb.91.144304

CrossRef Full Text | Google Scholar

Liu, P. F., Bo, T., Xu, J., Yin, W., Zhang, J., Wang, F., et al. (2018). First-principles Calculations of the Ultralow thermal Conductivity in Two-Dimensional Group-IV Selenides. Phys. Rev. B 98, 235426. doi:10.1103/physrevb.98.235426

CrossRef Full Text | Google Scholar

Ma, D., Ding, H., Meng, H., Feng, L., Shiomi, J., and Yang, N. (2016). Nano-cross-junction Effect on Phonon Transport in Silicon Nanowire Cages. Phys. Rev. B 94, 165434. doi:10.1103/physrevb.94.165434

CrossRef Full Text | Google Scholar

Ma, D., Wan, X., and Yang, N. (2018). Unexpected thermal Conductivity Enhancement in Pillared Graphene Nanoribbon with Isotopic Resonance. Phys. Rev. B 98, 245420. doi:10.1103/physrevb.98.245420

CrossRef Full Text | Google Scholar

Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007

CrossRef Full Text | Google Scholar

May, A. F., Toberer, E. S., Saramat, A., and Snyder, G. J. (2009). Characterization and Analysis of Thermoelectric Transport in N-type Ba₈Ga1_6-xGe_30+x. Phys. Rev. B 80, 125205. doi:10.1103/physrevb.80.125205

CrossRef Full Text | Google Scholar

Ouyang, T., Jiang, E., Tang, C., Li, J., He, C., and Zhong, J. (2018). Thermal and Thermoelectric Properties of Monolayer Indium Triphosphide (InP3): a First-Principles Study. J. Mater. Chem. A. 6, 21532–21541. doi:10.1039/c8ta07012a

CrossRef Full Text | Google Scholar

Ouyang, Y., Zhang, Z., Li, D., Chen, J., and Zhang, G. (2019). Emerging Theory, Materials, and Screening Methods: New Opportunities for Promoting Thermoelectric Performance. Annalen Der Physik 531, 1800437. doi:10.1002/andp.201800437

CrossRef Full Text | Google Scholar

Parker, D., and Singh, D. J. (2010). High-temperature Thermoelectric Performance of Heavily Doped PbSe. Phys. Rev. B 82, 035204. doi:10.1103/physrevb.82.035204

CrossRef Full Text | Google Scholar

Parker, D., and Singh, D. J. (2011). Potential Thermoelectric Performance from Optimization of Hole-Doped Bi₂Se₃. Phys. Rev. X 1, 021005. doi:10.1103/physrevx.1.021005

CrossRef Full Text | Google Scholar

Peng, H., Kioussis, N., and Snyder, G. J. (2014). Elemental Tellurium as a Chiral P-type Thermoelectric Material. Phys. Rev. B 89, 195206. doi:10.1103/physrevb.89.195206

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, D. J. (2007). Electronic and Thermoelectric Properties of CuCoO₂: Density Functional Calculations. Phys. Rev. B 76, 085110. doi:10.1103/physrevb.76.085110

CrossRef Full Text | Google Scholar

Sun, Z., Yuan, K., Chang, Z., Bi, S., Zhang, X., and Tang, D. (2020). Ultra-low thermal Conductivity and High Thermoelectric Performance of Two-Dimensional Triphosphides (InP3, GaP3, SbP3 and SnP3): a Comprehensive First-Principles Study. Nanoscale 12, 3330–3342. doi:10.1039/c9nr08679j

PubMed Abstract | CrossRef Full Text | Google Scholar

Togo, A., and Tanaka, I. (2015). First Principles Phonon Calculations in Materials Science. Scripta Materialia 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021

CrossRef Full Text | Google Scholar

Wood, J. D., Wells, S. A., Jariwala, D., Chen, K.-S., Cho, E., Sangwan, V. K., et al. (2014). Effective Passivation of Exfoliated Black Phosphorus Transistors against Ambient Degradation. Nano Lett. 14, 6964–6970. doi:10.1021/nl5032293

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., Zheng, Y., and Zheng, J. C. (2010). Thermoelectric Transport Properties of PbTe under Pressure. Phys. Rev. B 82, 195102. doi:10.1103/physrevb.82.195102

CrossRef Full Text | Google Scholar

Zhang, Z., Ouyang, Y., Cheng, Y., Chen, J., Li, N., and Zhang, G. (2020). Size-dependent Phononic thermal Transport in Low-Dimensional Nanomaterials. Phys. Rep. 860, 1–26. doi:10.1016/j.physrep.2020.03.001

CrossRef Full Text | Google Scholar

Zhu, X.-L., Liu, P.-F., Wu, Y.-Y., Zhang, P., Xie, G., and Wang, B.-T. (2020a). Significant Enhancement of the Thermoelectric Properties of CaP3 through Reducing the Dimensionality. Mater. Adv. 1, 3322–3332. doi:10.1039/d0ma00603c

CrossRef Full Text | Google Scholar

Zhu, X.-L., Liu, P.-F., Zhang, J., Zhang, P., Zhou, W.-X., Xie, G., et al. (2019). Monolayer SnP3: an Excellent P-type Thermoelectric Material. Nanoscale 11, 19923–19932. doi:10.1039/c9nr04726c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X.-L., Yang, H., Zhou, W.-X., Wang, B., Xu, N., and Xie, G. (2020b). KAgX (X = S, Se): High-Performance Layered Thermoelectric Materials for Medium-Temperature Applications. ACS Appl. Mater. Inter. 12, 36102–36109. doi:10.1021/acsami.0c08843

PubMed Abstract | CrossRef Full Text | Google Scholar