Interactions Between Dynamic Softening and Strengthening Mechanisms During Hot Forging of a High-Strength Steel

Open-die forging is a critical step in the manufacture of large numbers of components used in the transportation and energy industries. Dynamic recrystallization, dynamic transformation, and dynamic precipitation take place during the hot deformation process and significantly affect microstructure conditioning, which ultimately influences the service properties of the component. In the present work, using a Gleeble 3800 thermomechanical simulator, the open-die forging of a large-size ingot made of a modified AISI 6140 medium carbon high-strength steel is investigated. Deformation temperatures ranging from 950°C to 1,250°C and strain rates ranging from 0.01 to 1 s⁻¹, representative of the actual process, are considered in the analysis. The generated true stress–true strain curves are used as a basis for the development of a constitutive model predicting the occurrence of softening and strengthening phenomena as a function of thermomechanical conditions. The corresponding activation energy is determined to be about 374 kJ mol⁻¹ and is compared against the values reported in the literature for other high-strength steels. Dynamic recrystallization kinetics is studied using the t₅₀ model, and the influence of temperature and strain rate is quantified and discussed. The interaction between dynamic precipitation and dynamic recrystallization is discussed, and the deformation conditions under which such interactions occur are determined. The thermomechanical results are validated by microstructure examination, including laser confocal microscopy, field emission scanning electron microscopy, transmission electron microscopy, and energy-dispersive spectroscopy. The present study focuses on reproducing the deformation cycle applied during the open-die forging process of a vanadium-containing high-strength steel used in the industry with special attention to the interaction between dynamic recrystallization and precipitation processes.

Introduction

High-strength medium carbon steels are characterized by their excellent mechanical properties along with good formability and low cost (Titov et al., 2017; Ebrahimi et al., 2017). Turbine and transmission shafts are good examples of direct applications of these types of steels. They are produced through ingot casting, followed by open-die forging and quench and temper processes. The cast ingots are generally reheated to temperatures above 1,200°C before open-die forging operations are initiated. The latter consist of a series of biaxial compression hits that form the final geometry of the component. Major microstructural changes are also produced during the open-die forging process. These include the closing down of the solidification porosities as well as the breakdown of the coarse columnar dendritic as-cast structure into much finer equiaxed grains through the recrystallization process (Chadha et al., 2016; Han et al., 2015). However, these steels are also characterized by their high strength, which is mostly obtained through a judicious control of their composition and the formation of very fine precipitates that control the grain size and provide strong work hardening properties. The open-die forging process is essentially a thermomechanical process in which temperature, and strain and strain rates are key processing parameters that determine the evolution of the microstructure, particularly recrystallization, precipitation, and phase transformation processes in the steels.

In recent years, the demand for ever larger components has been increasing steadily, resulting in the presence of nonuniform microstructures from the surface to the center of the forged component. Such microstructure gradients render the properties overly variable, which may sometimes result in entire components being scrapped (Bouissa et al., 2020). It is therefore important to quantify the impact of hot forging parameters on microstructural changes and to optimize the thermomechanical processing parameters. The determination of constitutive equations relating the above processing parameters to microstructure evolution phenomena is a critical step in the development of microstructure-based numerical simulation models of large-size forgings (Sanrutsadakorn et al., 2013; Wang et al., 2014; Han et al., 2015; Chadha et al., 2016; Bitterlin et al., 2018).

Constitutive modeling of the flow curve is the first and most important step in quantifying the microstructure evolution through mathematical formulations. Recrystallization, precipitation, and phase transformation occurring at high temperatures are generally diffusion-controlled processes; and as a result, exponential or hyperbolic sine equations have been used to model different alloys (Sanrutsadakorn et al., 2013; Wang et al., 2014; Chadha et al., 2016; Bitterlin et al., 2018). Specifically, the workability of various steels can be compared by determining the deformation activation energy and using the Zener–Hollomon parameter (Z); the result of this comparison can then be used as a tool for optimum material selection for target applications. In addition to flow curve modeling, the kinetics of phase transformation, static recovery (SRV) and recrystallization (SRX), and dynamic recovery (DRV) and dynamic recrystallization (DRX) under different hot working conditions can be modeled using the Avrami formalism (Jonas et al., 2009; Quelennec et al., 2010; Chen et al., 2012; Kim and Park, 2015; Yang et al., 2019). Furthermore, the kinetics of all the above phenomena, particularly DRV and DRX, may be significantly influenced by the presence of titanium, niobium, or vanadium. These elements induce the formation of very fine precipitates on the boundary and avoid grain growth. It is very important to mention that although the influence of titanium and niobium on DRX and DRV has been extensively studied (Vervynckt et al., 2011; Knyazyuk et al., 2020; Gramlich et al., 2020), significantly less data are, however, available on the influence of vanadium carbonitride precipitation on phase transformation and recrystallization kinetics and their mutual interactions during high temperature deformation of medium carbon low alloy steels (Wu et al., 2011). This could mainly be attributed to the fact that titanium and niobium are mostly used in rolled products, while vanadium is mostly used in forged specialty steels.

With the use of thermodynamic modeling software, Thermo-Calc, a strong affinity of vanadium for carbon and nitrogen, was revealed, which resulted in the formation of vanadium carbonitrides [V(C, N)] that strengthen the matrix and increase yield strength. Phase transformation and DRX have also been reported as being accelerated and delayed, because of the presence of vanadium in the chemical composition (Sourmail et al., 2017). Other researchers have also reported the dynamic precipitation of vanadium carbonitrides at grain boundaries and sub-grain boundaries of austenite under specific hot deformation conditions (Mirzaee et al., 2012; Xiao et al., 2015). Such a precipitation could have a delaying effect on the mobility of austenite grains and thus slow down the kinetics of DRX (Humphreys et al., 2012). Vervynckt et al. (2011) quantified the Zener pining force and compared it with the recrystallization force, and then they discussed the interaction between both forces on microstructure evolution. As reported very recently by Sourmail (Sourmail et al., 2021), the presence of vanadium impacts the evolution of the retained austenite and carbides during the tempering process of such steels. Fully understanding the role played by this element during hot deformation is therefore critically important.

The kinetics of DRX has been analyzed by different methods, but in the literature (Jonas et al., 2009; Quelennec et al., 2010), the general process has involved building the associated DRV curve mathematically from the experimental curve and then separating both softening mechanisms in order to quantify the DRX-ed curves. Specifically, a t₅₀ constant represents the time required to reach 50% of recrystallization based on the Avrami model. Chen et al. studied the kinetics of DRX in a 42CrMo steel (Chen et al., 2012) and used true strain and critical strain instead of time to model DRX. They found that DRX was accelerated when higher temperatures and/or low strain rates were employed. Kim and Park (2015) studied the DRX kinetics of a vanadium microalloyed steel and used the ${\epsilon }_{1\text{/}2}$ method (i.e., strain at which 50% of recrystallization is reached) to model the flow curve. The preceding therefore illustrates that the determination of the critical deformation conditions for the initiation of DRX is an important step in the development of a kinetic model. These conditions are mostly found by using the double-derivative method developed by Jonas et al. (2013). Specifically, the method allows to find the critical strain necessary to activate the DRX softening mechanism. Ghosh et al. (2013a) later reported that the double-derivative method may also be used to find the critical condition for the formation of Widmanstätten ferrite in hot deformed austenite at temperatures well above Ae₃. This phenomenon is known as dynamic transformation (DT) and was originally reported by Yada et al. (2000).

The present work inscribes in the above context and aims to determine the constitutive behavior of a vanadium-containing medium carbon steel simulating the open-die forging operations of components used in the transportation industry. Flow curves were analyzed and corrected for adiabatic heating and frictional effects to increase the accuracy of the constitutive equations. The kinetics of DRX was determined, and the interaction between DRX and vanadium precipitates was studied using the critical stress, ${\sigma }_c$, for DRX. This value was then used to estimate the DRX force and was compared with the Zener pinning force. Furthermore, the deformation energy was determined and correlated with the Zener–Hollomon parameter. The results of the present work will contribute to a better understanding of the role of vanadium in microstructure evolution during the forging and heat treatments of these alloys.

Experimental Procedure

AISI 6140 steel was provided by Finkl Steel, Québec, Canada. The chemical composition of the steel is given in Table 1. Ae₃ at 787°C was calculated with Thermo-Calc. Samples were cut from a slice of a 40-metric-ton heat-treated ingot. The geometry of the samples was cylindrical, with a height of 15 mm and a diameter of 10 mm. Isothermal compression tests were carried out on a DSI Gleeble 3800 thermomechanical simulator. Four deformation temperatures were used, 1,250°C, 1,150°C, 1,050°C, and 950°C, along with four different strain rates, 0.01, 0.1, 0.5, and 1 s⁻¹. Thermocouples were welded to monitor the temperature evolution during tests, and nickel-based paste was applied on the two ends of the samples to reduce friction. The samples were heated at a rate of 2°C s⁻¹ until reaching the austenitization temperature of 1,250°C, and then held for 5 min for homogenization, after which a cooling rate of 1°C s⁻¹ was used until the deformation temperature was attained. A deformation of 0.8 was then applied, and the specimen was immediately air quenched (Figure 1). The diameter and height of the specimens were measured at different locations after deformation in order to determine the barreling severity and correct the stress strain curves for the frictional effect. The samples were then cut in half in the direction parallel to the deformation axis for metallographic preparation and microstructural examination purposes.

TABLE 1

TABLE 1. Chemical composition of the investigated steel (wt%).

FIGURE 1

FIGURE 1. Thermomechanical scheme of the experimental procedure.

The surface of the samples was polished up to 1,200 grit with silicon carbide paper. Polishing was then continued with a 1-μm diamond paste, followed by a 0.05-μm paste. The samples were etched with Villela etchant (1 g of picric acid, 5 ml of HCl, and 100 ml of ethanol). The etched microstructures were observed with laser confocal microscopy.

Results and Discussion

Constitutive Modeling

In order to predict the flow curves, the Zener–Hollomon parameter, which considers the variations of both strain rate and temperature, was used (Chadha et al., 2016):

$Z=\dot{\mathit{ϵ}}\text{exp}\left(\frac{Q}{RT}\right)(1)$

where $\dot{\mathit{ϵ}}$ is the strain rate, Q is the activation energy of deformation (J mol⁻¹), and R is the universal gas constant (8.314 J mol⁻¹ K⁻¹). The activation energy Q was determined using the Arrhenius constitutive equation. The Arrhenius model is used to relate the flow stress, strain rate, and deformation temperature during hot deformation (Wang et al., 2014; Han et al., 2015; Chadha et al., 2016; Bitterlin et al., 2018):

$\dot{\mathit{ϵ}}=AF\left(\sigma \right)\exp \left(-\frac{Q}{RT}\right)(2)$

with

$F\left(\sigma \right) = {\sigma }^{n_1}$ (ασ ≤ 0.8)

$F\left(\sigma \right) =\exp \left(\beta \sigma \right)$ (ασ ≥ 1.2)

$F\left(\sigma \right) ={\left[\text{sinh }\left(\alpha \sigma \right)\right]}^{\text{n}}$ (for all σ)

where A, n₁, $\beta$, α, and n are material constants.

For the sake of simplicity, the hyperbolic-sine equation is used in the present work, as it provides very good accuracy for all stress values. Then, taking the logarithm of Eq. 2 from both sides leads to

$\text{ln}\dot{\mathit{ϵ}}=\text{ln} A+n \text{ln }\left[\text{sinh}\left(\text{ασ}\right)\right]-\frac{Q}{RT}(3)$

From Equation 3, the above-mentioned material constants can be found using linear regression. n₁ and $\beta$ are provided by plotting an Ln $\sigma$ vs. Ln $\dot{\mathit{ϵ}}$ and a $\sigma$ vs. ln $\dot{\mathit{ϵ}}$ graph. α can then be calculated by using $\alpha =\beta /{\text{n}}_1$ (Chadha et al., 2016; Bitterlin et al., 2018). By differentiation of Eq. 3, n and Q could be determined:

$n= \frac{\partial ln\dot{\mathit{ϵ}}}{\partial \left[\ln \text{sinh}\left(\text{ασ}\right)\right]}(4)$

$Q=nR\frac{\partial \ln \left[\text{sinh}\left(\text{ασ}\right)\right]}{\partial \left(1/T\right)}(5)$

Hence, by plotting ln $\left[\text{sinh}\left(\text{ασ}\right)\right]$ vs. ln $\dot{\mathit{ϵ}}$ and ln $\left[\text{sinh}\left(\text{ασ}\right)\right]$ vs. 1/T, the values of n and Q can be determined from the slopes of the curves. To increase the level of accuracy and cover the entire spectrum of flow curves, a 0.05 step was considered from 0 to 0.8 strain.

Finally, the combination of the Zener–Hollomon parameter (Eq. 1) and the hyperbolic sine (Eq. 2) gives the flow stress as follows:

$\sigma =\frac{1}{\alpha }\text{ln}\left[{\left(\frac{Z}{A}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}+{\left\{{\left(\frac{Z}{A}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}+1\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right](6)$

Figure 2 summarizes the type of curves obtained to determine the constants n₁, β, n, and Q for a strain of 0.2.

FIGURE 2

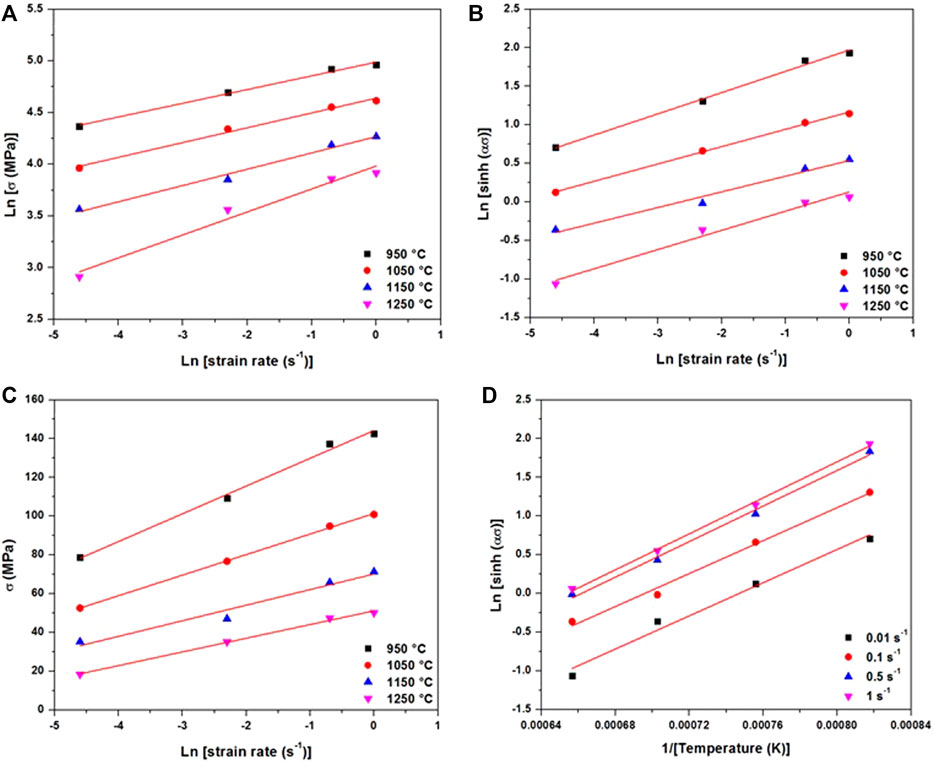
FIGURE 2. Type of curves used to calculate constants of the hyperbolic sine constitutive equations for strain = 0.2.

Based on the above analysis, the constant α was determined to be 0.018 MPa⁻¹. It is higher than the one reported for a superaustenitic stainless steel with 0.012 MPa⁻¹ (Han et al., 2015) and a nickel modified 4330 with 0.015 MPa⁻¹ (Bitterlin et al., 2018), meaning that the presence of vanadium increases the value of the stress multiplier α. The opposite tendency is observed for the exponent n, as it is equal to 3.72 for the studied steel and lies between 4.2 and 4.6 for the 4330 and the superaustenitic stainless steel, respectively. In order to validate the developed constitutive model, two more compression tests (975°C with a strain rate of 2 s⁻¹ and 1,125°C and strain rate of 0.05 s⁻¹) were conducted, and the results are shown in Figure 3. A variation of 5–10 MPa between the experimental and predicted curves is observed, indicating that the developed model accurately predicts the AISI 6140 flow behavior (Figure 3).

FIGURE 3

FIGURE 3. Comparison of predicted and experimental flow curves.

Friction Correction

In order to minimize the friction effect, a nickel-based lubricant and tungsten thin foil were used between the dies and the samples. As reported by Li et al. (2009), despite optimizing the lubricant application and effect during hot compression, the friction cannot be totally eliminated, and the stress–strain curves need to be corrected accordingly to avoid the introduction of errors in the development of the constitutive equations. In the present study, a mathematical model involving geometrical features of the sample was used to reveal a much clearer steady state on the flow curves and to isolate the pure material effect. The friction was corrected using Han et al. (2015):

${\sigma }^{\ast }=\frac{\sigma }{1 + \frac{2}{3\sqrt{3}} \mu \frac{r_0}{h_0} \text{exp}\left(\frac{3\mathit{ϵ}}{2}\right)}(7)$

where ${\sigma }^{\ast }$ is the true stress after friction correction; σ is a measured true stress; r₀ and h₀ are respectively the initial radius and height of the sample; and μ is the friction coefficient, which represents the resistance of the material to the deformation, as reported by Li et al. (2009):

$\mu =\frac{\frac{r}{h} B}{\frac{4}{\sqrt{3}} - \frac{2B}{3\sqrt{3}}}(8)$

where r and h are the final radius and height of the sample after compression and B is the barreling factor considering the barreling effect of the deformation on the sample and is given by Li et al. (2009):

$B=4\frac{\Delta R_s}{R_s}\frac{h}{\Delta h}(9)$

where ΔR_s is the difference between the maximum radius and the minimum radius and Δh is the difference between the initial height and the final height of the sample.

Figure 4 shows the effect of friction correction using the above equations. The application of a friction correction model translates into a drop in the stress values and leads to clearer steady states and a more precise material behavior prediction. It should be noted that the influence of deformation conditions in terms of increasing the specimen temperature (i.e., adiabatic heating) was also calculated during the present study. The methodology was similar to that reported by Chadha et al. (2016), and it was found that for the deformation conditions used in the present study, adiabatic heating had a very minor incidence on the deformation temperature.

FIGURE 4

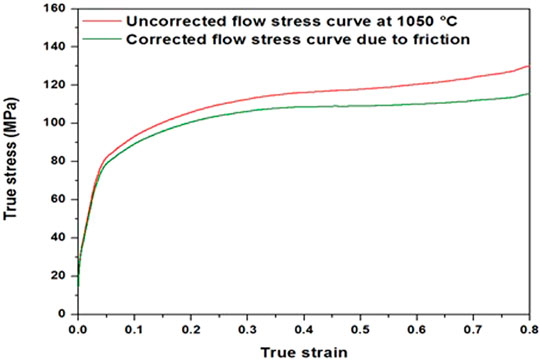
FIGURE 4. Effect of the application of the average friction coefficient model. The curve showing lower stress is the friction-corrected curve, whereas the curve showing higher stress is the experimental row curve.

Flow Curve Analysis

Experimental flow curves show both work hardening and softening behaviors. The softening behaviors are identified as DRV and DRX because flow curves show a maximum before experiencing a drop in stress values. The typical behavior of the dynamically recrystallized curve of a steel is composed of a linear elastic portion followed by plastic deformation work hardening zone until reaching a maximum value. Then, a drop in stress occurs, indicating that a softening mechanism has become macroscopically visible; and finally, the steady state is reached, where all the previously mentioned mechanisms are in equilibrium and balance each other. Low temperatures and high deformation rates promote the work hardening behavior, whereas high temperature and low strain rate promote DRX, as shown in Figure 5. The maximum stress (σ_p) is also affected by the processing conditions, decreases with increasing temperature, and increases with increasing strain rate.

FIGURE 5

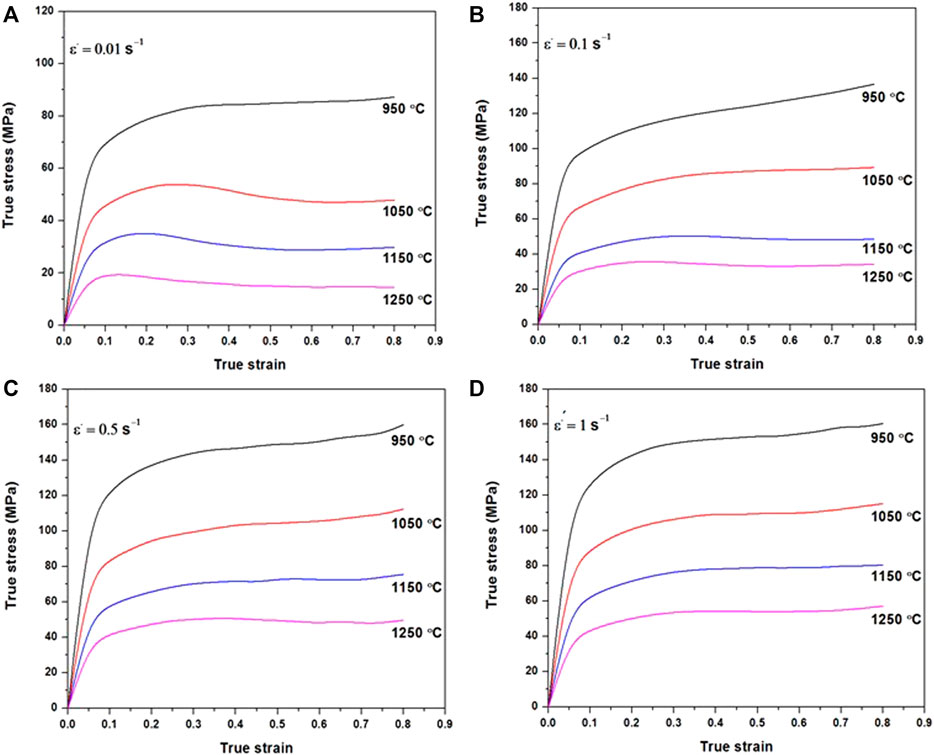
FIGURE 5. Flow curves of 6140 under hot compression process. (A) Strain rate 0.01 s⁻¹, (B) strain rate 0.01 s⁻¹, (C) strain rate 0.01 s⁻¹, and (D) strain rate 0.01 s⁻¹.

Good workability can be defined as the ability to reach recrystallization during deformation without the presence of instabilities such as cracks. The above results also reveal that the investigated material is more adapted to hot working than to cold working, as lower testing temperatures show a strong work hardening behavior and the need to use low strain rates. Applying the constitutive modeling model allows the calculation of deformation energy, which is an indication of a steel’s workability. Han et al. (2015) calculated a deformation energy of 577.8 kJ mol⁻¹ for a superaustenitic stainless steel; Sanrutsadakorn et al. (2013) calculated it as 348.1 kJ mol⁻¹ for an AISI 4340, and Bitterlin et al. (2018) reported a deformation energy of 367.9 kJ mol⁻¹ for an AISI 4330 modified with nickel. In our case, a deformation energy of 374 kJ mol⁻¹ was determined based on the above-reported hot deformation results, indicating a much better workability than a stainless steel, but a somewhat higher deformation energy than the 4330 and the 4340. This indicates that the presence of vanadium decreases the high-temperature workability of this steel. This information is quite important from an industrial point of view when it comes to designing optimum open-die forging schedules for large-size ingots made of this steel.

Dynamic Recrystallization Kinetics

From all the experiments, only those conducted at higher temperatures and lower strain rates showed a behavior that is characteristic of DRX occurrence. This is because DRX is a thermally activated softening mechanism. The calculation of the kinetics of DRX involves the theoretical construction of the dynamically recovered (DRV-ed) curve as a point of reference to quantify the kinetics of recrystallization. The amount of softening is defined as follows:

$X=\frac{{\sigma }_{DRV}-{\sigma }_{DRX}}{{\sigma }_{SAT}-{\sigma }_{SS}}(10)$

where ${\sigma }_{DRV}$ is the mathematically calculated stress, ${\sigma }_{DRX}$ is the experimental stress, ${\sigma }_{SAT}$ is the saturation state of the recovered curve, and ${\sigma }_{SS}$ is the steady-state stress in the experimental curve. Critical conditions for DRX must be calculated in order to apply the kinetic model. To this end, the double-derivative method was used (Jonas et al., 2013), and the results indicate that both DRX and DT occur during open-die forging of the investigated alloy. The double minima shown in Figure 6 are representative of the critical condition required to reach DRX and DT. The first minimum is identified as the onset of DT, and the second is indicative of the occurrence of DRX (Ghosh et al., 2013b). An analysis of the critical conditions calculated with the double-derivative method shows that a true strain of 0.1 is needed to activate DT, and a true strain of 0.2 is needed for DRX. The analysis also shows that the critical condition for the onset of DT is constant over the temperatures and strain rates used in the present investigation. Moreover, the critical condition for DRX decreases with increasing temperature. A comparison of the results with those reported by Ghosh et al. (2013a) on four different steels showed a similar tendency for the critical strains, thereby confirming that the investigated AISI 6140 vanadium alloy is influenced by the same tendency. With regard to the influence of deformation conditions on the impact of DT, Jonas et al. (2013) studied the effect of DT on the mean flow stress at several temperatures. As ferrite is softer than austenite, its formation through the DT mechanism naturally leads to the softening of the material. In their research, Jonas et al. concluded that 0.2–0.4 MPa of softening is produced per percentage of ferrite. They also showed that at least 35% of ferrite is needed to detect a drop in the required load. In our study, we only detected the presence of Widmanstätten ferrite in the matrix, indicating that the presence of vanadium seems to have promoted the formation of this type of ferrite instead of the allotriomorphic one, as observed in C–Mn steels.

FIGURE 6

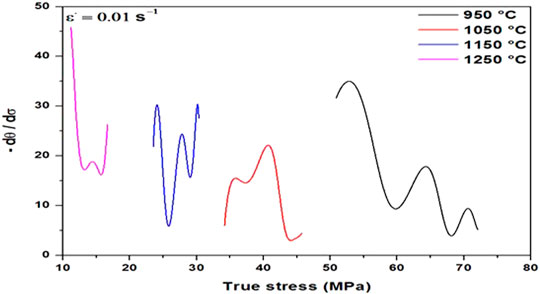
FIGURE 6. Double-derivative method for the 6140. It shows the presence of a double minima indicating both presence of dynamic recrystallization and dynamic transformation for all temperatures and strain rate 0.01 s⁻¹.

In order to determine the DRX kinetics, the critical condition was set at 0% of recrystallization, and the recrystallization progress is calculated as the difference between DRV and DRX curves. This method also requires the calculation of σ_SAT and σ_ss. The recovery curve was constructed by assuming that the flow curves of non-recrystallized regions can be described by the following equation (Jonas et al., 2009; Quelennec et al., 2010):

$\frac{d\rho }{d\epsilon }=a-\tau \sqrt{\rho }(11)$

In the above equation, $\rho$ is the dislocation density, $\mathit{ϵ}$ is the strain, a is the athermal work hardening rate, and $\tau$ is the recovery rate. By integrating (11), the following equation is obtained, describing the dynamically recovered curve:

$\sigma =\sqrt{\left({\sigma }_{SAT}^2-\left({\sigma }_{SAT}^2-{\sigma }_0^2\right)\text{exp}\left(-r\mathit{ϵ}\right)\right)}(12)$

where ${\sigma }_0$ is the yield stress and ${\sigma }_{SAT}$ is the saturation stress of the recovery curve and is given by

${\sigma }_{SAT}=M{\alpha }_{DRX}{\mu }_{i}b\sqrt{\frac{a}{\tau }}(13)$

where M is the Taylor factor, ${\alpha }_{DRX}$ is a material constant and is set to 0.5, ${\mu }_i$ is the shear modulus, and b is the Burgers vector. ${\mu }_i$ and b are temperature-dependent (Ghosh et al., 2013b). By employing $\sigma =M{\alpha }_{DRX}{\mu }_{i}b\sqrt{\rho }$, and taking into consideration that

$\frac{d\rho }{d\mathit{ϵ}} ={\left(M{\alpha }_{DRX}{\mu }_{i}b\right)}^{-2}\frac{d{\sigma }^2}{d\mathit{ϵ}}=2 {\left(M{\alpha }_{DRX}{\mu }_{i}b\right)}^{-2}\sigma \frac{d\sigma }{d\mathit{ϵ}}(14)$

(12) can be rewritten as

$2\theta \sigma =\tau {\sigma }_{SAT}^2-\tau {\sigma }^2(15)$

with $\theta = \frac{d\sigma }{d\mathit{ϵ}}$. Plotting 2$\theta \sigma$ vs. ${\sigma }^2$ gives the values of “−$\tau$” as the slope of the curve and with “a” as the vertical intercept as $\tau {\sigma }_{SAT}^2=\text{ a}$.

By applying the above methodology, all the parameters of the model were determined; and the recovery curve, reconstituted using Eq. 12, was separated from the stress–strain curve in order to quantify only the DRX kinetics. An illustrative example is presented in Figure 7 for the tests carried out at 1,150°C. On the basis of the above analysis, the DRX kinetics were extracted from the stress–strain curves, and the results are shown in Figures 8A,B. It can be seen that increasing the forging temperature accelerates DRX kinetics. A similar tendency is observed for the strain rate, although the strain rate seems to have a more significant impact on the DRX kinetic promotion than does the temperature parameter. Bitterlin et al. (2018) reported that increasing the strain rate had a negative impact on the kinetics for a similar steel. The main difference in chemical composition between the investigated steel and the one by Bitterlin et al. is in the presence of a higher amount of vanadium in ours. The presence of vanadium is probably the main reason for the observed behavior, indicating a possible occurrence of dynamic precipitation (Mirzaee et al., 2012) in the present steel.

FIGURE 7

FIGURE 7. Calculated recovery curve superimposed with experimental curve.

FIGURE 8

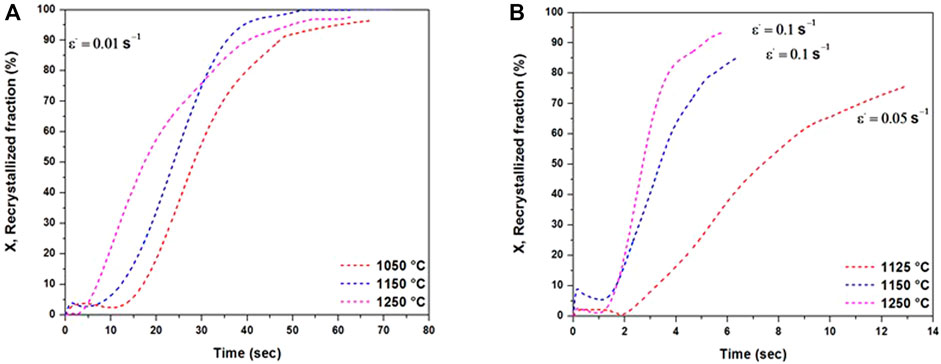
FIGURE 8. Kinetic of dynamic recrystallization for AISI. (A) Strain rate 0.01 s⁻¹. (B) Strain rate 0.1 and 0.05 s⁻¹.

In order to model the evolution of the recrystallized fraction, the Avrami model was used (Jonas et al., 2009; Quelennec et al., 2010):

$X=1- \text{exp}\left(-k{t}^{n_{DRX}}\right)=1-\text{exp}\left(-0.693 {\left(\frac{t}{t_{50}}\right)}^{n_{DRX}}\right)(16)$

where X is the fraction of recrystallization, k is the Avrami constant, and n_DRX is the Avrami exponent.

DRX kinetics for a strain rate of 0.01 s⁻¹ shows a t₅₀ value neighboring 20 s. In contrast, with a strain rate of 0.1 s⁻¹, t₅₀ drops to values ∼3 s. Based on the results reported in Figure 8, increasing the strain rate and decreasing the forging temperature lead to partially recrystallized microstructures, as shown in Figure 8B for the samples deformed at 1,150°C and a strain rate of 0.1 s⁻¹. Similar results were reported by Jonas et al. (2009) and confirm that the presence of vanadium-delayed DRX by about one-third of an order of magnitude. The incubation time for DRX increased with decreasing temperature and increasing strain rate, further confirming that DRX is a thermally activated process.

Modeling Deformation Energy

The deformation energy was considered as the area under the flow curve (Poliak and Jonas, 1996):

$-W_{def}= \underset{0}{\overset{\mathit{ϵ}}{{\displaystyle \int }}}\sigma d\mathit{ϵ}(17)$

The scale of W_def is in MPa. Each curve was fitted with a 12th-order polynomial, and the area under the curve was evaluated using Matlab. Figure 9 shows the evolution of W_def with lnZ, where a linear correlation between the deformation energy and the Zener–Hollomon parameter can be observed. With the use of regression analysis, the following relation was determined with an R² value of 97.5%:

$W_{def}= -9.1035\text{ln}Z+224.7(18)$

FIGURE 9

FIGURE 9. Deformation energy versus the Zener–Hollomon parameter.

The above finding is an interesting practical tool for comparison between hot forging process parameters and the Zener–Hollomon parameter.

Interaction Between Dynamic Recrystallization and Precipitates

The DRX driving force is given by the relation:

$F_{DRX}= \frac{1}{2} {\mu }_i{b}^2\Delta \rho (19)$

[Vervynckt et al., 2011]where ${\mu }_i$ is the shear modulus, which is 4 × 10⁴ MPa for steel (Vervynckt et al., 2011; Wu et al., 2011). b is the temperature-dependent Burgers vector (Ghosh et al., 2013b). $\Delta \rho$, which represents the dislocation density, can be estimated using the following equation proposed by Dutta et al. (2001):

$\Delta \rho = \frac{\left(\sigma -{\sigma }_c\right)}{M{\alpha }_{\text{IP}}{\mu }_{i}b}(20)$

where $\sigma$ is the applied stress; ${\sigma }_c$ is the critical stress for the onset of DRX; M is the Taylor factor, which is 3.1 for austenite; and ${\alpha }_{\text{IP}}$ is a constant taken as 0.15 (Vervynckt et al., 2011; Wu et al., 2011; Dutta et al., 2001). Initially, ${\sigma }_c$ was taken as ${\sigma }_0$ (yield stress) by Wu, Vervynkt, and Dutta; but here, we take ${\sigma }_c$ to more properly isolate the dislocation density responsible for the DRX.

To study the interaction between DRX and precipitate, it is important to quantify the Zener pinning force due to the presence of the precipitates. As reported by Vervynckt et al. (2011), the presence of precipitates hinders the movement of the grain boundaries and as a result delays or could even stop the recrystallization process. Under these conditions, the Zener pinning force Z_p could be estimated using Eq. 21:

$Z_p=\frac{3}{2}\frac{\gamma f}{r_p}(21)$

where $\gamma$ is the grain boundary energy (0.75 J mol⁻¹ in austenite), f is the precipitate volume fraction estimated with the Thermo-Calc thermodynamic database, and r_p is the average precipitate radius that was estimated with the Hitachi SU8230FEG-SEM at very high magnification and was found to be about 100 nm.

A calculation was made for a 950°C temperature and a strain rate of 0.01 s⁻¹, and a Z_p value of 0.0112 MPa was determined. In comparison with a Mn–Cu–V weathering steel, Wu et al. (2011) calculated a Z_p value of 1.46 MPa for 950°C 0.1 s⁻¹. That means that according to Eq. 21, either the volume fraction increases with increasing strain rate or the radius of the particles decrease with increasing strain rate. Research on a magnesium alloy by Wu et al. (2020) showed that an increasing strain rate increases the precipitate size and decreases its volume fraction. Liu et al. (2020a) reported that increasing the deformation increases the carbide size. It must also be noted that Z_p is constant for a given temperature and strain rate. A comparison between Z_p and the recrystallization driving force plotted based on the combination is reported in Figure 10. It can be seen that under the considered experimental conditions, the Zener pinning force is significantly greater than the recrystallization driving force. This finding explains the absence of any apparent DRX behavior on the flow stress curve, which is characterized by the presence of only a work hardening behavior. Hence, forging at 950°C and a strain rate of 0.01 s⁻¹ would not result in grain refinement in the investigated steel, further confirming the role played by the presence of vanadium. Finally, Eq. 21 also shows that increasing the volume fraction of precipitates and reducing the precipitates’ radius would both increase the Zener pinning force and, therefore, increase the grain boundary pinning process. The above analyses are in agreement with those reported by Singh et al. and Springer et al., who found that Z_p increased with deformation and related it to a more homogeneously distributed precipitation under deformation (Springer and Prahl, 2018; Singh et al., 2019).

FIGURE 10

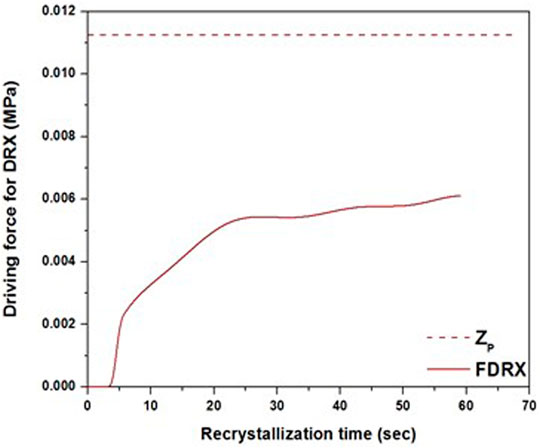
FIGURE 10. Comparison between Zener force (Zp) and dynamic recrystallization (DRX) force (FDRX) for 950°C strain rate 0.01 s⁻¹.

Microstructural Validation

To validate and confirm the hot deformation results with regard to the occurrence or absence of recrystallization, DT, and the presence of fine precipitates, a combination of optical microscopy, field emission gun–scanning electron microscopy (FEG-SEM), and electron backscatter diffraction (EBSD) was used; and the findings are discussed in the following paragraphs. An optical metallographic examination of the as-received material revealed a bainitic microstructure (Figure 11A) with homogeneously distributed precipitates (Figure 12A). In the case of the sample deformed at 950°C 1 s⁻¹ (Figure 11B), where the material shows only work hardening behavior, the microstructure showed an elongated grain, and there were no traces of recrystallization. It must be noted that revealing the microstructure of the deformed sample was quite tedious due to the presence of a large number of dislocations and deformation bands. In contrast, for samples deformed at 1,250°C and 1,050°C and at a strain rate of 0.01 s⁻¹, DRX occurred; and as shown in Figures 11C,D, fine recrystallized grains could be seen, in agreement with the flow curves (Figure 5A). The main difference between these two deformed microstructures is at the grain refinement level. The grain is more refined for 1,050°C than for 1,250°C. This is mainly due to the fact that at 1,250°C, the grain growth occurs very fast and actually could take place during deformation (Liu et al., 2020b). Figures 12, 13 show illustrative examples of the SEM and EBSD images of samples deformed under different deformation conditions. An analysis of the results using the double-derivative method (Figure 6) indicated that DT could occur under specific deformation conditions. From a microstructural perspective, the results, reported in Figure 12C, for the sample deformed at 1,050°C 0.01 s⁻¹ shows the presence of very fine ferrite needles originating from austenite grain boundaries. These needles are characteristic of Widmanstätten ferrite, as also reported by other researchers (Ghosh et al., 2016; Grewal et al., 2016), thereby confirming the formation of dynamically transformed austenite at temperatures well above Ae₃ in the present investigation. In contrast, no presence of Widmanstätten ferrite was observed at 950°C or 1,250°C, as shown in Figures 12B,D. For comparison, the SEM image of the as-received material is also shown in Figure 11A.

FIGURE 11

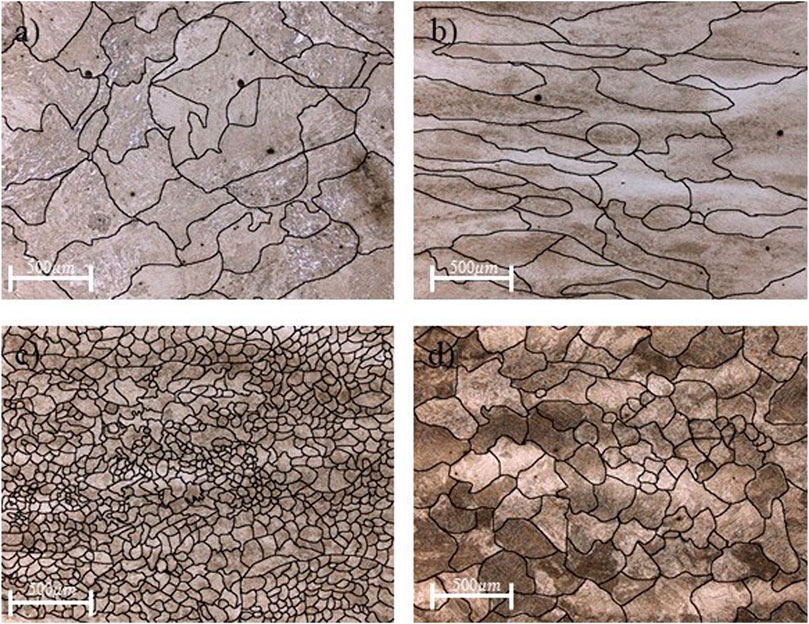
FIGURE 11. Optical micrography of (A) as-received material, (B) deformed at 950°C 0.01 s⁻¹, (C) deformed at 1,050°C 0.01 s⁻¹, and (D) deformed at 1,250°C 0.01 s⁻¹, etched with Nital 3%.

FIGURE 12

FIGURE 12. Scanning electron microscopy (SEM) micrography of (A) as-received material, (B) deformed at 950°C 0.01 s⁻¹, (C) deformed at 1,050°C 0.01 s⁻¹, and (D) deformed at 1,250°C 0.01 s⁻¹.

FIGURE 13

FIGURE 13. Electron backscatter diffraction EBSD) measurement of specimen deformed at 1,250°C 0.01 s⁻¹.

The SEM analysis (Figure 14) of the samples deformed at 950°C clearly revealed the presence of very fine vanadium-rich precipitates, which is in accordance with the thermodynamic modeling (Figure 15); and mechanical testing results confirm that the presence of precipitates at 950°C will result in considerable delays in recrystallization, as already discussed in the above section. Finally, the microstructure of the samples deformed at 1,250°C 0.01 s⁻¹ show precipitate-free recrystallized features, and the EBSD measurement indicates random textures of deformed austenite (Figure 13), which further confirms the mechanical testing results.

FIGURE 14

FIGURE 14. Vanadium participates in sample 950°C 0.01 s⁻¹.

FIGURE 15

FIGURE 15. Thermo-Calc result of sample at 950°C for single-point equilibrium.

Summary and Conclusion

The evolution of the microstructure of a vanadium alloyed medium carbon steel (modified AISI 6140) was investigated to simulate the open-die forging process of large-size components. Specifically, the present study focused on interactions between recrystallization, phase transformation, and precipitation. A combination of mechanical testing, thermodynamic analysis, and microstructural examination was used for the analysis. Results show that both work hardening and DRX softening mechanisms occur under conditions representing the open-die forging of large-size blocks. A constitutive model was developed using a hyperbolic sine Arrhenius type equation, and a deformation energy of 374 kJ was determined for the investigated steel. A comparison with other steel deformation energy leads to the conclusion that vanadium decreases the workability of the ingot. The deformation energy was correlated with the Zener–Hollomon parameter, and a relationship was determined between deformation energy and Z. The deformation energy was then directly linked to the strain rate and the temperature. DRX kinetics was studied using the t₅₀ method, and it was shown that the kinetics was promoted by high temperatures and high strain rates. It was also shown that up to a strain rate limit, there is no efficient recrystallization. The obtained results also reveal that under some forging conditions, the Zener pinning force was higher than the DRX force, indicating that precipitates interact with DRX by delaying it. The deformation conditions for the operation of each mechanism were determined, and a microstructure investigation confirmed the occurrence of DT, DRX, and precipitation for specific forging conditions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MK is the main author of this research. He did all the experiments and the models developed in this article. MJ is in charge of the project and gave access to devices to do the experiments. DS is the engineer in charge of the Gleeble 3800 where compression test was made. J-BM is from Finkl Steel and provided all the materials.

Conflict of Interest

J-BM was employed by the company Finkl Steel.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bitterlin, M., Shahriari, D., Lapierre-Boire, L.-P., Morin, J.-B., and Jahazi, M. (2018). Hot Deformation Behavior of a Nickel-Modified AISI 4330 Steel. ISIJ Int. 58 (9), 1711–1720. doi:10.2355/isijinternational.isijint-2018-034

CrossRef Full Text | Google Scholar

Bouissa, Y., Bohlooli, N., Shahriari, D., Champliaud, H., Morin, J.-B., and Jahazi, M. (2020). FEM Modeling and Experimental Validation of Quench-Induced Distortions of Large Size Steel Forgings. J. Manufacturing Process. 58, 592–605. doi:10.1016/j.jmapro.2020.08.042

CrossRef Full Text | Google Scholar

Chadha, K., Shahriari, D., and Jahazi, M. (2016). Constitutive Modelling of Ingot Breakdown Process of Low alloy Steels. Int. J. Ital. Assoc. Metall. 4, 5–12.

Google Scholar

Chen, M.-S., Lin, Y. C., and Ma, X-S. (2012). The Kinetics of Dynamic Recrystallization of 42CrMo Steel. Mater. Sci. Eng. A 556, 260–266. doi:10.1016/j.msea.2012.06.084

CrossRef Full Text | Google Scholar

Dutta, B., Palmiere, E. J., and Sellars, C. M. (2001). Modelling the Kinetics of Strain Induced Precipitation in Nb Microalloyed Steels. Acta Materialia 49 (5), 785–794. doi:10.1016/s1359-6454(00)00389-x

CrossRef Full Text | Google Scholar

Ebrahimi, G. R., Momeni, A., Kazemi, S., and Alinejad, H. (2017). Flow Curves, Dynamic Recrystallization and Precipitation in a Medium Carbon Low alloy Steel. Vacuum 142, 135–145. doi:10.1016/j.vacuum.2017.05.010

CrossRef Full Text | Google Scholar

Ghosh, C., Aranas, C., and Jonas, J. J. (2016). Dynamic Transformation of Deformed Austenite at Temperatures above the Ae3. Prog. Mater. Sci. 82, 151–233. doi:10.1016/j.pmatsci.2016.04.004

CrossRef Full Text | Google Scholar

Ghosh, C., Basabe, V. V., and Jonas, J. J. (2013a). Determination of the Critical Strains for the Initiation of Dynamic Transformation and Dynamic Recrystallization in Four Steels of Increasing Carbon Contents. Steel Res. Int. 84 (5), 490–494. doi:10.1002/srin.201200188

CrossRef Full Text | Google Scholar

Ghosh, C., Basabe, V. V., Jonas, J. J., Kim, Y.-M., Jung, I.-H., and Yue, S. (2013b). The Dynamic Transformation of Deformed Austenite at Temperatures above the Ae3. Acta Materialia 61 (7), 2348–2362. doi:10.1016/j.actamat.2013.01.006

CrossRef Full Text | Google Scholar

Gramlich, A., Schäfers, H., and Krupp, U. (2020). Influence of Alloying Elements on the Dynamic Recrystallization of 4 wt.-% Medium Manganese Steels. Materials (Basel) 13 (22), 5178. doi:10.3390/ma13225178

PubMed Abstract | CrossRef Full Text | Google Scholar

Grewal, R., Aranas, C., Chadha, K., Shahriari, D., Jahazi, M., and Jonas, J. J. (2016). Formation of Widmanstätten Ferrite at Very High Temperatures in the Austenite Phase Field. Acta Materialia 109, 23–31. doi:10.1016/j.actamat.2016.02.062

CrossRef Full Text | Google Scholar

Han, Y., Wu, H., Zhang, W., Zou, D., Liu, G., and Qiao, G. (2015). Constitutive Equation and Dynamic Recrystallization Behavior of As-Cast 254SMO Super-austenitic Stainless Steel. Mater. Des. 69, 230–240. doi:10.1016/j.matdes.2014.12.049

CrossRef Full Text | Google Scholar

Humphreys, J., Rollett, A., and Rohrer, G. S. (2012). Recrystallization and Related Annealing Phenomena. Elsevier.

Google Scholar

Jonas, J. J., Ghosh, C., Quelennec, X., and Basabe, V. V. (2013). The Critical Strain for Dynamic Transformation in Hot Deformed Austenite. ISIJ Int. 53 (1), 145–151. doi:10.2355/isijinternational.53.145

CrossRef Full Text | Google Scholar

Jonas, J. J., Quelennec, X., Jiang, L., and Martin, É. (2009). The Avrami Kinetics of Dynamic Recrystallization. Acta materialia 57 (9), 2748–2756. doi:10.1016/j.actamat.2009.02.033

CrossRef Full Text | Google Scholar

Kim, K. W., and Park, J. K. (2015). A Study of the Dynamic Recrystallization Kinetics of V-Microalloyed Medium Carbon Steel. J. Mater. Sci. 50 (18), 6142–6153. doi:10.1007/s10853-015-9171-1

CrossRef Full Text | Google Scholar

Knyazyuk, T. V., Novoskoltsev, N. S., Zisman, A. A., and Khlusova, E. I. (2020). Influence of Niobium Microalloying on the Kinetics of Static and Dynamic Recrystallization during Hot Rolling of Medium-Carbon High-Strength Steels. Inorg. Mater. Appl. Res. 11 (6), 1325–1332. doi:10.1134/s207511332006009x

CrossRef Full Text | Google Scholar

Li, Y. P., Onodera, E., Matsumoto, H., and Chiba, A. (2009). Correcting the Stress-Strain Curve in Hot Compression Process to High Strain Level. Metall. Mat Trans. A. 40 (4), 982–990. doi:10.1007/s11661-009-9783-7

CrossRef Full Text | Google Scholar

Liu, D., Ding, H., Hu, X., Han, D., and Cai, M. (2020a). Dynamic Recrystallization and Precipitation Behaviors during Hot Deformation of a κ-carbide-bearing Multiphase Fe-11Mn-10Al-0.9C Lightweight Steel. Mater. Sci. Eng. A 772, 138682. doi:10.1016/j.msea.2019.138682

CrossRef Full Text | Google Scholar

Liu, Z.-b., Tu, X., Wang, X.-h., Liang, J.-x., Yang, Z.-y., Sun, Y.-q., et al. (2020b). Carbide Dissolution and Austenite Grain Growth Behavior of a New Ultrahigh-Strength Stainless Steel. J. Iron Steel Res. Int. 27, 732–741. doi:10.1007/s42243-020-00429-6

CrossRef Full Text | Google Scholar

Mirzaee, M., Keshmiri, H., Ebrahimi, G. R., Momeni, A., and Reza, G. (2012). Dynamic Recrystallization and Precipitation in Low Carbon Low alloy Steel 26NiCrMoV 14-5. Mater. Sci. Eng. A 551, 25–31. doi:10.1016/j.msea.2012.04.063

CrossRef Full Text | Google Scholar

Poliak, E. I., and Jonas, J. J. (1996). A One-Parameter Approach to Determining the Critical Conditions for the Initiation of Dynamic Recrystallization. Acta Materialia 44 (1), 127–136. doi:10.1016/1359-6454(95)00146-7

CrossRef Full Text | Google Scholar

Pratap Singh, A., Singh, B., and Saxena, K. K. (2019). Precipitation Behaviour of Microalloyed Steel during Hot Deformation. Mater. Today Proc. 18, 4821–4825. doi:10.1016/j.matpr.2019.07.471

CrossRef Full Text | Google Scholar

Quelennec, X., Martin, E., Jiang, L., and Jonas, J. J. (2010). Work Hardening and Kinetics of Dynamic Recrystallization in Hot Deformed Austenite. J. Phys. Conf. Ser. 240, 012082. doi:10.1088/1742-6596/240/1/012082

CrossRef Full Text | Google Scholar

Sanrutsadakorn, A., Uthaisangsuk, V., Suranuntchai, S., and Thossatheppitak, B. (2013). “Constitutive Modeling of Flow Behaviour of AISI 4340 Steel under Hot Working Conditions,” in Applied Mechanics and Materials (Bächau, Switzerland: Trans Tech Publications), 863–869.

Google Scholar

Sourmail, T., Garcia-Mateo, C., Caballero, F. G., Cazottes, S., Epicier, T., Danoix, F., et al. (2017). The Influence of Vanadium on Ferrite and Bainite Formation in a Medium Carbon Steel. Metall. Mat Trans. A. 48 (9), 3985–3996. doi:10.1007/s11661-017-4188-5

CrossRef Full Text | Google Scholar

Sourmail, T., Otter, L., Collin, S., Billet, M., Philippot, A., Cristofari, F., et al. (2021). Direct and Indirect Decomposition of Retained Austenite in Continuously Cooled Bainitic Steels: Influence of Vanadium. Mater. Characterization 173, 110922. doi:10.1016/j.matchar.2021.110922

CrossRef Full Text | Google Scholar

Springer, P., and Prahl, U. (2018). Pinning Effect of Strain Induced Nb(C,N) on Case Hardening Steel under Warm Forging Conditions. J. Mater. Process. Tech. 253, 121–133. doi:10.1016/j.jmatprotec.2017.11.008

CrossRef Full Text | Google Scholar

Titov, V. I., Tarasenko, L. V., and Utkina, A. N. (2017). Effect of Alloying Elements on the Composition of Carbide Phases and Mechanical Properties of the Matrix of High-Carbon Chromium-Vanadium Steel. Phys. Met. Metallogr. 118 (1), 81–86. doi:10.1134/s0031918x17010070

CrossRef Full Text | Google Scholar

Vervynckt, S., Verbeken, K., Thibaux, P., and Houbaert, Y. (2011). Recrystallization–precipitation Interaction during Austenite Hot Deformation of a Nb Microalloyed Steel. Mater. Sci. Eng. A 528 (16-17), 5519–5528. doi:10.1016/j.msea.2011.03.087

CrossRef Full Text | Google Scholar

Wang, J., Ma, W.-l., Chu, Z., and Zhang, Q. (2014). Constitutive Model for F45V Microalloyed Forging Steel at High Temperature. J. Iron Steel Res. Int. 21 (4), 464–468. doi:10.1016/s1006-706x(14)60072-8

CrossRef Full Text | Google Scholar

Wu, H., Du, L., and Liu, X. (2011). Dynamic Recrystallization and Precipitation Behavior of Mn-Cu-V Weathering Steel. J. Mater. Sci. Tech. 27 (12), 1131–1138. doi:10.1016/s1005-0302(12)60008-5

CrossRef Full Text | Google Scholar

Wu, Q., Yan, H., Chen, J., and Xia, W. (2020). The Interactions between Dynamic Precipitates and Dynamic Recrystallization in Mg-5Zn-1Mn Alloys during Hot Compression. Mater. Characterization 160, 110131. doi:10.1016/j.matchar.2020.110131

CrossRef Full Text | Google Scholar

Xiao, H., Tang, B., Liu, C., and Gao, Y. (2015). Dynamic Precipitation in a Mg–Gd–Y–Zr alloy during Hot Compression. Mater. Sci. Eng. A 645, 241–247. doi:10.1016/j.msea.2015.08.022

CrossRef Full Text | Google Scholar

Yada, H., Li, C-M., and Yamagata, H. (2000). Dynamic γ→ α Transformation during Hot Deformation in Iron–Nickel–Carbon Alloys. ISIJ Int. 40 (2), 200–206. doi:10.2355/isijinternational.40.200

CrossRef Full Text | Google Scholar

Yang, Q., Ji, C., and Zhu, M. (2019). Modeling of the Dynamic Recrystallization Kinetics of a Continuous Casting Slab under Heavy Reduction. Metallurgical Mater. Trans. A 50 (1), 357–376. doi:10.1007/s11661-018-5005-5

CrossRef Full Text | Google Scholar

Nomenclature

Z Zener–Hollomon parameter (s⁻¹)

$\dot{\mathit{\epsilon }}$ strain rate (s⁻¹)

Q Deformation energy (J mol⁻¹)

R Gas constant (8.314 J mol⁻¹ K⁻¹)

T Absolute temperature (K)

$\mathit{\sigma }$ Stress (MPa)

$\mathit{\epsilon }$ Strain

${\mathit{\sigma }}_{\text{c}}$ Critical stress (MPa)

${\mathit{\epsilon }}_{\text{c}}$ Critical STRAIN

M Taylor factor

$\mathit{\mu }$ Friction coefficient

${\mathit{\sigma }}_{DRV}$ Dynamic recovery stress (MPa)

${\mathit{\sigma }}_{DRX}$ Experimental stress (MPa)

${\mathit{\sigma }}_{SAT}$ Saturation stress without DRX (MPa)

${\mathit{\sigma }}_{SS}$ Permanent regime of experimental curve (MPa)

${\mathit{\sigma }}_0$ Yield stress (MPa)

A Material constant (s⁻¹)

n Stress exponent

$\mathit{\alpha }$ Stress multiplier (MPa⁻¹)

$\mathit{\beta }$ Material constant

n₁ Material constant

t Time (s)

t₅₀ Time at 50% of recrystallization

B Barreling factor

${\mathit{\mu }}_i$ Shear modulus (MPa)

${\mathit{\alpha }}_{DRX}$ Material constant for DRX kinetic

${\mathit{\alpha }}_{\text{IP}}$ Material constant for interaction between precipitate and DRX

$\mathit{\gamma }$ Grain boundary energy (J mol⁻¹)

b Burgers vector (m)

r Precipitate radius (m)

f Precipitate volume fraction

W_def Deformation energy (MPa)

$\mathit{\rho }$ Dislocation density (m⁻²)

R_s Radius of the sample (m)

H Height of the sample (m)

ΔR_s Difference between the maximum radius and the minimum radius of the sample (m)

Δh Difference between the initial height and the final height of the sample (m)

a Athermal work hardening rate

$\mathit{\tau }$ Recovery rate

r₀ Initial radius of the sample (m)

h₀ Initial height of the sample (m)

${\mathit{\sigma }}^{\ast }$ Stress without friction (MPa)

r_p Precipitate radius (m)