Separate and Combined Effects of Geometrical and Mechanical Properties Changes Due to Aging on the Femoral Strength in Men and Women

Aging, from 40 to +80 years old, causes geometrical and mechanical properties changes in the proximal femur. The subperiosteal width expands faster in men compared to women during aging, while the cortical thickness varies unequally in each sector and differently between men and women. Another change which occurs during aging is bone mechanical properties such as stiffness and ultimate strains. Numerical analysis allows us to study the potential effects of each of the age-dependent changes on the fracture forces separately and combined. We investigated the effects of the geometrical and bone mechanical properties changes due to aging on the femoral strength during a common falling scenario using a transverse isotropic continuum damage model. First, the femur model was adapted from a previously developed human body model named THUMS v4.02. Then, three sets of models were developed to address each of the changes separately and combined for both sexes. We found that the fracture forces in women are on average 1500 N less than in men of the same age. The age-dependent geometrical changes increased the fracture forces in men (25 N/decade), whereas it reduced the fracture forces by 116 N/decade in women. The mechanical properties changes reduced the fracture forces in men more than in women (354.5 N/ decade vs. 225.4 N/decade). When accounting for both geometrical and mechanical properties changes due to aging, the fracture forces decreased by 10.7% of the baseline in women per decade compared to 7.2% per decade in men.

Introduction

Adults older than 65 are at risk of a fall, and this risk increases as they get older (Ambrose et al., 2013). During 2014, 25% of older adults in the United States experienced falling at least once (Bergen et al., 2016). Falls are the leading cause of accidental death and nonfatal injuries in this age group (Burns et al., 2016). Nonfatal and fatal falls cost $50 billion, and falling is the costliest nonfatal injury in the US (Florence et al., 2018). Houry et al. (2016) estimated growth in the population of older adults, which without preventive plans, could lead to a 100% increase in the number of injuries caused by a fall in the year 2030.

Falls, commonly to the sideways, cause more than 95% of all hip fractures (Hayes et al., 1993; Parkkari et al., 1999; Nasiri Sarvi and Luo 2017). Hip fractures lead to hospitalization and cause long-term consequences on mobility and independence of the patients (Florence et al., 2018). Elderly women are at a higher risk of hip fracture comparing to men at a similar age (Courtney et al., 1995; Silva 2007; Ito et al., 2011), and the fracture risk increases exponentially as men and women get older (Beck et al., 2000; Ito et al., 2011).

The geometry of the bone, bone mechanical properties, and loading mode are three factors that affect the femoral strength (Silva 2007). The first two factors are changing with aging, and the loading mode represents an extrinsic factor. The geometrical parameters of the bone, such as the cortical thickness, cortical cross-sectional area, and cross-sectional moment of inertia, are negatively correlated with aging (Ito et al., 2011). In other words, the endosteal resorption and periosteal expansion cause geometrical changes of the bone. In general, the cross-sectional area of the femoral neck is larger in men comparing to women; and these differences increase as they get older (Beck et al., 2000; Carpenter et al., 2011). Several studies suggested that the cortical thicknesses are changing dissimilarly in each quadrant of the femoral neck (Mayhew et al., 2005; Poole et al., 2010; Johannesdottir et al., 2011; Poole et al., 2012; Carballido-Gamio et al., 2013; Johannesdottir et al., 2013). A longitudinal study by Johannesdottir et al. (2013) suggested that the average superior cortical thickness gets thinner at a higher rate than the inferior thickness in a 5-year period for both sexes. Moreover, the thickness decreases slower in men comparing to women. Similar behavior was reported in several cross-sectional studies (Poole et al., 2010; Ito et al., 2011; Johannesdottir et al., 2011; Khoo et al., 2019). Mayhew et al. (2005) have reported the corresponding cortical thicknesses in 16 sectors of the femoral neck. The average superior cortical thickness decreases with aging in men and women (Poole et al., 2010; Ito et al., 2011; Johannesdottir et al., 2011; Khoo et al., 2019), while the average inferior cortical thickness remains constant with aging. Mechanical properties of the cortical and trabecular bone are changing with age, and these changes are site-dependent (Osterhoff et al., 2016). Unlike as observed for vertebrae, trabecular bone in the femur merely has a minor contribution to the biomechanical strength of the whole-bone compared to the cortical bone (Holzer et al., 2009; Osterhoff et al., 2016). In the femoral neck, the cortical bone loses stiffness in terms of Young’s and shear modulus by 3 and 4% per decade of age, respectively. Ultimate strains decrease about 5–10% of the initial value per decade while yield properties of the bone do not change significantly with age (Reilly et al., 1974; Reilly and Burstein 1975; Martin 1993; Dokko et al., 2009; Kutz 2009; Mirzaali et al., 2016; Osterhoff et al., 2016). Those changes, combined, cause a transition from a ductile bone to a more brittle one with age (Ott et al., 2010). Trabecular bone is experiencing similar mechanical properties changes in the femoral neck where the modulus is decreasing approximately 5% per decade (Mosekilde et al., 1987; Kutz, 2009). In contrary to the geometrical changes, mechanical properties changes of bone are sex-independent (Martin 1993; Morgan and Bouxsein 2008; Osterhoff et al., 2016).

Several whole-bone experiments and finite element models are designed to investigate the aging effect on the femoral strength. Age, sex, bone mineral density (BMD), loading rate, loading configuration, and individual geometrical characteristics are widely used to explain the variation of the femoral strength in test subjects (Silva 2007; Morgan and Bouxsein 2008; Dragomir-Daescu et al., 2011; Grassi et al., 2012; Panyasantisuk et al., 2018). A recent study by Dragomir-Daescu et al. (2018) has concluded that the aBMD, sex, and age are sufficient parameters to clinically evaluate the femoral strength. In addition to them, they also explored the effect of loading rate and neck-shaft angle. They discovered that the inclusion of the two latter variables would not considerably improve the prediction of the femoral strength (Dragomir-Daescu et al., 2018). Several other clinical and whole-bone experiments indicate the effect of bone size and mechanical properties of the bone on the femoral strength (Bouxsein 2006; Morgan and Bouxsein 2008).

The majority of current computational studies on the strength of femur are focused on developing subject-specific finite element models, which are typically using isotropic mechanical properties to evaluate the femur strength (Dall’Ara et al., 2013; Rezaei et al., 2017). While those models are capable of predicting the subject-specific femoral strength accurately, they are not developed to predict the effect of changes that occur to the bone of average men and women due to aging. There has been no work published so far to the best of authors’ knowledge, which explicitly studies the separate and combined effects of the geometrical and mechanical properties changes due to aging in each of the sexes. Moreover, many studies (Reilly et al., 1974; Reilly and Burstein 1975; Ashman et al., 1984; Cezayirlioglu et al., 1985; Rho et al., 1995; Derikx et al., 2011; Mirzaali et al., 2016; Falcinelli and Whyne 2020) have shown that the yield and ultimate strains of the cortical bone are asymmetric which in turn could affect the femoral strength predictions and fracture initiation. The subject-specific models are also getting computationally expensive to the extent that it becomes impractical to implement them into whole-body models. In the current study, we aim to investigate the separate and combined effect of geometrical and mechanical properties changes on fall-induced femur fractures using a transverse isotropic continuum damage model. Simultaneously, it is intended to keep the simplicity of the model while improving the accuracy of bone modeling to allow direct application of this method in the whole-body models. We applied the geometrical and mechanical properties change for 4 decades of age, from 40 to 80 years old with the aim to evaluate the effect of each of the age-dependent changes on the femoral strength.

Materials and Methods

Three distinct sets of numerical models were developed to investigate the separated and combined effects of key changes in the geometry and mechanical properties on the strength of femur. The first set accounted only for age-dependent geometrical changes (GeomAge), the second set accounted only for age-dependent mechanical properties changes (MechAge), and the third set accounted for both changes in 4 decades of age (MechGeomAge), from 40 to 80 years old.

Baseline Model

The geometry of the baseline model for 40 years old men and women was obtained from the total human model for safety (THUMS) v4.02. It represents the 50th percentile adult man with the height and weight of 77 and 1.75 m, respectively (Iwamoto et al., 2002). Albeit, the initial model needed several modifications to represent elderly men and women. Foremost, the cortical thickness was uniform around the femoral neck in the initial model, whereas the cortical thickness naturally varies in each sector of the femoral neck (Mayhew et al., 2005; Johannesdottir et al., 2013; Khoo et al., 2019). Additionally, the subperiosteal width of the narrowest point of the neck is different among men and women (Beck et al., 2000; Duan et al., 2003), which indicated the significance of developing two distinctive baseline models for men and women.

The geometry of the initial THUMS model is based on a healthy man, and the subperiosteal width is in close agreement with the reported value from the national health and nutrition examination survey (NHANES III) database (Beck et al., 2000; Duan et al., 2003). On the other hand, the baseline model for women required scaling down to the representative subperiosteal width following the NHANES III (Beck et al., 2000). The homogenous scaling factor for this adjustment was around 0.859. Afterward, the baseline model for men and women was adjusted for the corresponding cortical thickness in each sector of the femoral neck. The cortical thicknesses in each sector were calculated using the combination of the average cortical thicknesses for each age group from the NHANES III database (Beck et al., 2000; Duan et al., 2003) and the relative thicknesses in each sector of the femoral neck from the study by Mayhew et al. (2005). Since the average inferior cortical thicknesses in the study by Mayhew et al. (2005) was not in agreement with similar studies (see Supplementary Material), we decided to transform the reported cortical thicknesses of each sector $\left(d_{secto{r}_i}\right)$ to a relative thickness by dividing those thicknesses by the maximum reported thickness $\left(D_{Ma{x}_{reported}}\right)$. Then, we used the average of the relative cortical thicknesses and the NHANES III average cortical thicknesses $\left(D_{avg, NHANES III}\right)$ for each age group to evaluate the new maximum cortical thickness $\left(D_{Ne{w}_{Max}}\right)$ (Eq. 1):

$d_{avg,NHANES III}=D_{Ne{w}_{Max}}\frac{\left(\Sigma \left(\frac{d_{\sec to{r}_i}}{D_{Ma{x}_{reported}}}\right)\right)}{16}(1)$

Finally, the relative cortical thicknesses of each sector were transformed back to absolute thicknesses using the new maximum thickness (Beck et al., 2000; Mayhew et al., 2005; Figures 1A,B).

FIGURE 1

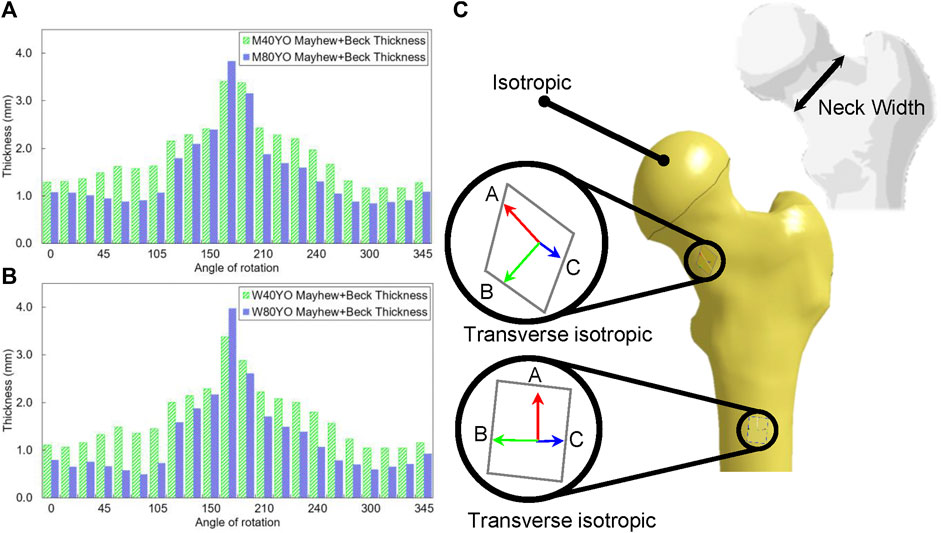
FIGURE 1. The cortical thickness changes for (A) men and (B) women in 40 and 80 years old was estimated using the combination of Beck et al. (2000) and Mayhew et al. (2005), (Angle of rotation was assumed in such a way that the posterior of the femoral neck corresponds to 270°), (C) transverse plane of the shaft and neck (Plane’s normal is in red), the femoral head was assumed to be isotropic.

The mechanical properties of both cortical and trabecular bones were modified. The material model of the cortical bone was altered to a transverse isotropic continuum damage model since it better can represent the cortical bone than an isotropic model (Reilly et al., 1974; Reilly and Burstein 1975; Dong and Guo 2004; de Bakker et al., 2009)^; and it accounts for the asymmetric yield and ultimate strains (Reilly et al., 1974; Reilly and Burstein 1975; Ashman et al., 1984; Cezayirlioglu et al., 1985; Rho et al., 1995; Derikx et al., 2011; Falcinelli and Whyne 2020; Mirzaali et al., 2016) in tension, compression, and shear in respective directions. Mechanical properties of the cortical bone were adapted from the experiments by Reilly et al. (1974) and Reilly and Burstein (1975, Table 1). Those properties were assumed to be similar for both men and women.

TABLE 1

TABLE 1. Mechanical properties used for the healthy 40 years old subject. See Figure 1C for material directions.

The transverse isotropic elastic model was combined with a linear damage model. Six damage parameters were applied independently to the stiffness parameters in respective directions. The damage initiates as an element reaches the yield strain in the respective direction. Subsequently, it linearly decreases the stiffness in the corresponding direction until the ultimate strain is reached. In each timestep, the damage parameters were automatically calculated using Eq. 2:

$d_k=\max \left(d_k;D_k^c{\left(\frac{{\mathit{ϵ}}_k-{\mathit{ϵ}}_k^s}{{\mathit{ϵ}}_k^c-{\mathit{ϵ}}_k^s}\right)}_{+}\right)(2)$

where${\left(\right)}_{+}$is the positive part of: ${\left(\mathrm{x}\right)}_{+}=\{\begin{array}{c}\mathrm{x}\\ 0\end{array} \begin{array}{c}\mathrm{if}\mathrm{x}>0\\ \mathrm{if}\mathrm{x}<0\end{array}$; ${\mathrm{ϵ}}_{\mathrm{k}}^{\mathrm{s}}$ and ${\mathrm{ϵ}}_{\mathrm{k}}^{\mathrm{c}}$ are yield and ultimate strains in the respective directions. Thexstiffness parameters were set to 1% of their initial value as the strain reaches its ultimate value. It adequately secured the integrity of the mesh. Moreover, it alleviated the demand for a smoother mesh, which might increase the computational costs for the whole-body model. The update to the mechanical properties of the trabecular bone was limited to the stiffness and ultimate strain values. The material model remained isotropic elastic-plastic with continuum damage mechanics.

The geometry of the cortical bone was divided into two distinct sections. The shaft and neck region were assumed to be transverse isotropic. The principal axis of the transverse plane is respectively along the shaft and neck hollow (Figure 1C). Contrary to the shaft and neck, the femoral head typically undergoes multidirectional loading; therefore, it was assumed to have an isotropic continuum damage model with similar mechanical properties to the average value of the shaft and neck regions. The cortical bone was meshed with selectively reduced hexahedron elements, and the trabecular bone was meshed using tetrahedron elements (average dimension of elements 1.7 mm, and the total number of 32,823 nodes and 127,821 elements). A convergence study on the mesh was performed using a one-step division of the cortical bone elements, and remeshing of the trabecular bone according to the new surrounding cortical bone elements. It was found that the maximum forces differed approximately 10% and the refined model was utilized in this study.

Aging Effects

Two geometrical parameters were varied in the GeomAge set, which corresponds to the subperiosteal expansion and the endocortical resorption. Two distinct models were developed for men and women since those changes are different between sexes. First, the subperiosteal width of the baseline model was scaled to the corresponding width for each decade (Beck et al., 2000; Duan et al., 2003). The width was increased by 0.08 and 0.028 mm/year for men and women, respectively (Duan et al., 2003). Afterward, the cortical thickness of each sector of the femoral neck was modified to the corresponding thicknesses obtained from the combination of the NHANES III database Beck et al., (2000) and Mayhew et al. (2005) as explained for the baseline models. The cortical thickness of the femoral neck was assumed to be constant along the neck axis in each sector. Moreover, it changed linearly during aging. The angle in Figures 1A,B corresponds to the rotation in the clockwise direction, starting from the superior surface of the femur.

In the MechAge set, mechanical properties of the bone, such as stiffness, were changed due to aging. The Young’s and shear modulus of the cortical bone was reduced by 3 and 4% per decade of age, respectively (Burstein et al., 1976). The ultimate strain was decreased by 10% of the initial value per decade, and yield properties were remained constant during aging (Reilly et al., 1974; Reilly and Burstein 1975; Martin 1993; Dokko et al., 2009; Kutz 2009; Mirzaali et al., 2016). Likewise, the modulus of elasticity and yield stresses of the trabecular bone were reduced 17 and 1.09 MPa, respectively, per decade of age (Mosekilde et al., 1987; Keaveny, 1998). The changes were assumed to be linear and the same for all directions. It is noteworthy that the age in the current study is a representative age which means the bone strength of a 40 years-old osteoporotic subject is substantially comparable with an older representative age group in the current simulations.

The geometry from the GeomAge set was combined with the corresponding mechanical properties from the MechAge set to produce the MechGeomAge set. Since the GeomAge consisted of both sexes, the MechGeomAge could explore the potential differences between men and women as well. The MechGeomAge conveniently represented the general aging effects on the femur for both men and women.

Fall Simulations

The femur was positioned in the sideways fall experimental setup in all three sets. Initially, the femoral shaft was rotated 10° with respect to the horizontal plane, and the femoral neck was rotated internally to 15° (Courtney et al., 1994; Dragomir-Daescu et al., 2011). Next, the length of the femoral shaft in the GeomAge, MechAge, and MechGeomAge sets was adjusted according to Dragomir-Daescu et al. (2011). Nodes at the distal of the shaft were constrained to an external revolute joint in the coronal plane (Altai et al., 2019; Figure 2). Finally, a displacement rate of 100 mm/s was applied to the femoral head using a cement pad. The cement pad was free to move in the vertical direction, according to Dragomir-Daescu et al. (2011), while a fully constrained pad was added to the trochanteric area of the femur. Later, the force-displacement curves and the corresponding fracture regions were compared to the experimental results (Courtney et al., 1995; Dragomir-Daescu et al., 2011) in order to verify the results. The maximum force in the force-displacement curve, which will be denoted as fracture forces, was compared to demonstrate the effect of each of the changes separately and combined. For additional verification, the age-based fracture forces from similar experimental setups were pooled to compare with the results of the MechGeomAge sets. All simulations were done using LS-Dyna 971 R8.0.0 (LSTC 2016), and each sideways fall simulation took about 7 h to complete on four cores.

FIGURE 2

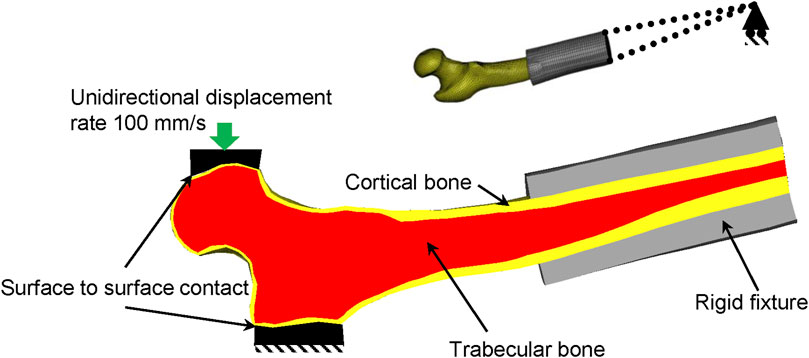
FIGURE 2. The proximal section of the femur was positioned in the sideways fall configuration. The rigid fixture was connected to external nodes of the distal femur that could rotate in the sagittal plane. The displacement was applied to the femoral head.

Results

The geometrical changes due to aging in the femoral neck affect the fracture forces differently for men and women (Figure 3). Combination of subperiosteal expansion and endocortical resorption caused a slight increase in fracture forces in men, whereas it caused a decrease in women (Figure 3). The fracture forces increased by 25 N per decade, 0.5% of the baseline, for men, while it decreased by 116 N per decade, 3% of the baseline, for women.

FIGURE 3

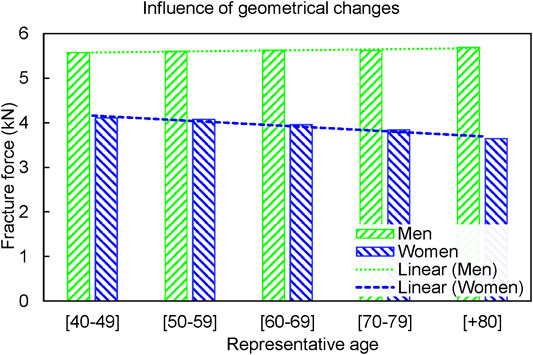
FIGURE 3. The fracture forces in GeomAge set slightly increased (25 N per decade) for men, and it reduced by 116 N per decade for women.

The changes in mechanical properties due to aging progressively reduced the fracture forces in both men and women (Figure 4). However, the fracture forces reduced differently in men compared to women. While the fracture force decreased 354.5 N per decade, 7% of the baseline, for men, it decreased 225.4 N, 5.7% of the baseline, for Women. It is noteworthy that the geometry was kept intact for various ages in the MechAge set.

FIGURE 4

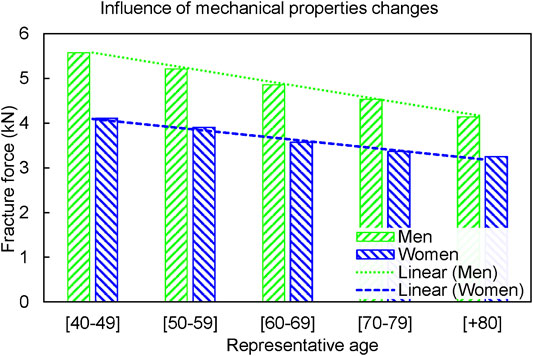
FIGURE 4. The fracture forces in the MechAge set reduced by 354.5 N per decade for men and 225.4 N per decade for women.

Similar to the MechAge, the fracture forces decreased with aging for both men and women in the MechGeomAge set (Figure 5). In general, women had a lower fracture force comparing to men of a similar age, whereas both men and women experienced a similar trend in the age-dependent fracture forces. The fracture forces decreased by 373.3 N per decade, 7.2% of the baseline, and 368.1 N per decade, 10.7% of the baseline, for men and women, respectively.

FIGURE 5

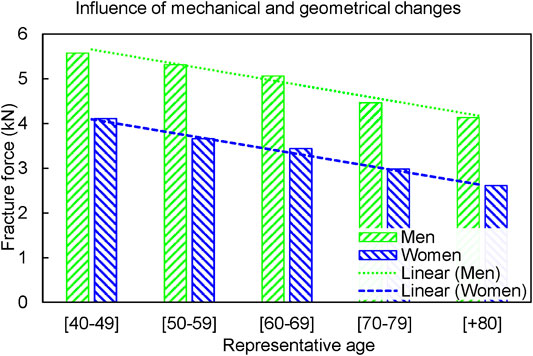
FIGURE 5. The combined changes (MechGeomAge set) reduced the fracture forces in both men and women. The fracture forces reduced by 373.3 N per decade for men and 368.1 N per decade for women.

Force-displacement curves from the simulations of the MechGeomAge set were compared to the experimental results (Courtney et al., 1995; Dragomir-Daescu et al., 2011). Several key characteristics of the force-displacement curves were similar for the experimental results and simulations (Figure 6A). The general shape of the simulation curves was similar to the experiments even though there were apparent differences between each of the simulations and the experimental results (Figure 6A). Apart from the similarities in the force-displacement curves, the resultant age-dependent fracture forces remained within the experimental fracture forces (Figures 6B,C). Furthermore, the fracture region was also similar between the experiment (Dragomir-Daescu et al., 2011) and simulations. The maximum force in the simulation curves typically corresponded to a fracture in the superior and superoanterior sections of the femoral neck. The fracture pattern was similar to those reported in the experiment (Dragomir-Daescu et al., 2011; Figure 7). This fracture region varied slightly between the sexes and various ages (Figure 6).

FIGURE 6

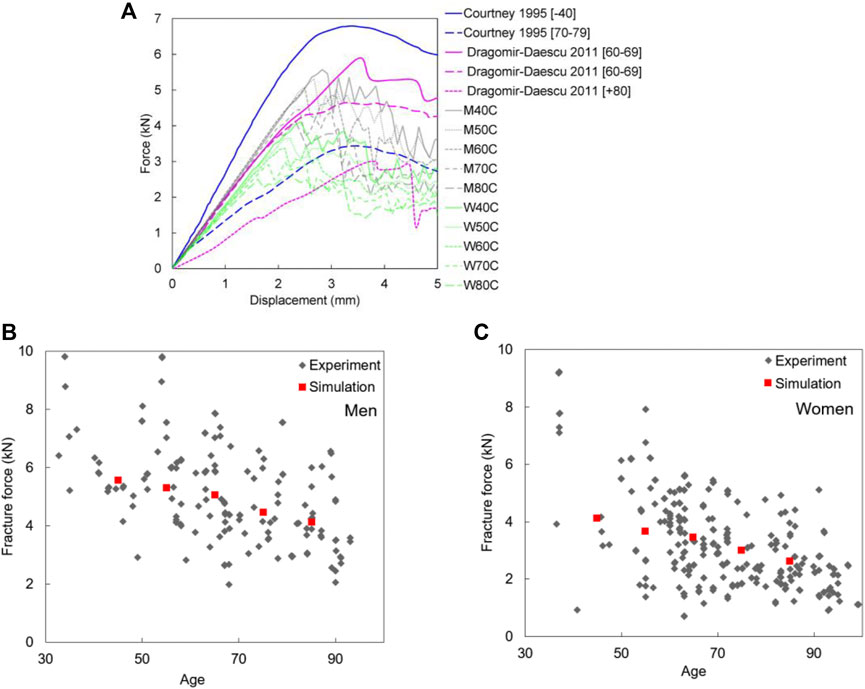
FIGURE 6. (A) Comparison of experimental force-displacement curves of a similar test setup with simulation results of MechGeomAge set (Courtney et al., 1995; Dragomir-Daescu et al., 2011); Pooled maximum fracture forces data (grey) (de Bakker et al., 2009; Op Den Buijs and Dragomir-Daescu 2011; Rezaei and Dragomir-Daescu 2015; Kroker et al., 2017; Rezaei et al., 2017; Dragomir-Daescu et al., 2018; Patton et al., 2019) for (B) men and (C) women compared to the simulation results (red) for the combined changes (MechGeomAge set).

FIGURE 7

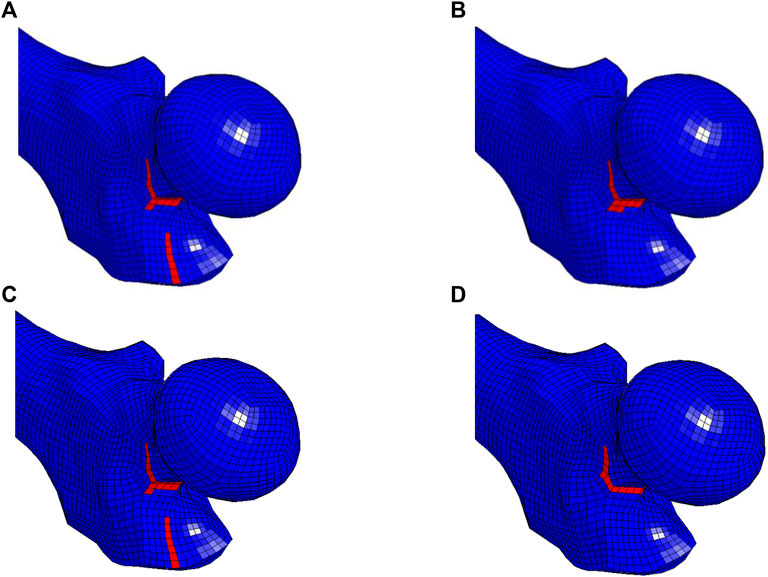
FIGURE 7. Initial fracture pattern results from the instance that the force-displacement curve reached the global maximum in the (A) 40 years old and (B) 80 years old men, (C) 40 years old, and (D) 80 years old women simulation. The initial pattern slightly changed due to aging in men and women.

Discussions

Aging causes two major changes in the femoral neck, geometrical and mechanical properties. Numerical simulations made it possible to split the effect of the geometrical and mechanical properties due to aging. In this study, we conducted a distinct series of simulations to investigate the potential effect of each of those changes separately and combined. In order to account for the asymmetry of the yield and ultimate strains as well as Young’s and shear modulus, we implemented a transverse isotropic continuum damage model for the cortical bone. Overall, the fracture forces decreased with aging when accounting for both geometrical and mechanical properties changes in men and women. Likewise, the fracture forces reduced with aging in men and women when accounting for only the mechanical properties changes. However, the geometrical changes caused a diverging effect on the fracture forces in each of the sexes with a slight increase in men and a decrease in women with aging.

The geometrical changes in the femoral neck consist of the changes in cortical thickness, cortical cross-sectional area, and moment of inertia. Ito et al. (2011) investigated the changes happening in a longitudinal two-year cohort study and found a significant reduction of cortical cross-sectional area and moment of inertia in women. Manske et al. (2006) showed that the failure load is associated with the cortical cross-sectional area and moment of inertia. Although cortical cross-sectional area and moment of inertia were not directly changed in this study, these changes were indirectly altered. The subperiosteal expansion increases the moment of inertia, which acts in favor of increasing the bone’s fracture force. Conversely, the endocortical resorption decreases the cortical thickness, which leads to a thinner loading area and, consequently, a lower fracture force (Duan et al., 2003; de Bakker et al., 2009). Thus, these two geometrical changes are essentially working against each other. The results of the GeomAge set indicated that the subperiosteal expansion is the dominant factor in men, and it assists the bone to maintain its strength during aging; whereas the rate of reduction of the cortical thickness dominates the changes in the neck region in women; and it causes a decrease in the fracture forces. Moreover, women experienced lower fracture forces compared to men at a similar age when accounting for age-dependent geometrical changes. This difference between the fracture forces increased in the later years. A possible explanation for these differences might be that the cortical thickness is changing dissimilarly in the corresponding sectors among men and women (Mayhew et al., 2005; Johannesdottir et al., 2013). This inhomogeneous change leads to a thicker cortical thickness for men compared to women, which itself increases the load-bearing capacity of the bone. Additionally, the widening of the neck width amplifies the effect of greater cortical thickness in men.

Despite the geometrical changes, the variations in the mechanical properties of the cortical and trabecular bone due to aging affect men and women in an analogous way (Seeman 2001; Morgan and Bouxsein 2008; Keaveny et al., 2010). Decreases in the modulus and ultimate strain make the bone more brittle and reduce the toughness of compact bone (Burstein et al., 1976; Martin 1993; Zioupos and Currey 1998; Villette and Phillips 2018), which could explain the reduction of the fracture forces. Another important finding is that the size of the bone has a key role in the reduction rate of fracture forces due to aging. In other words, the fracture forces decreased 5.7% from the baseline for women as a result of the mechanical properties changes due to aging, compared to men, for which it decreased 7% of the baseline.

Accounting for both mechanical and geometrical changes due to aging, the fracture forces reduced for both men and women. Women experienced a lower fracture force (average of all age groups: 3359 N) and a higher reduction rate (10.7% of the baseline) compared to men (4909 N, 7.2%). This finding is consistent with previous research, which found a smaller fracture force for women compared to men in general (Kanis et al., 1990; Rosen et al., 1999; Bauer et al., 2006; Dragomir-Daescu et al., 2011; Nasiri and Luo 2016; Nasiri Sarvi and Luo 2017; Dragomir-Daescu et al., 2018; Kleiven 2020). Rezaei and Dragomir-Daescu (2015), in an experimental study, suggested 640.3 N and 859.3 N per decade decrease in the fracture forces for men and women, respectively. Lang et al. (2012), in a 5-years longitudinal study, found 122 N and 164 N decrease per 5 years in fracture forces for men and women, using FE modeling. Similarly, Keaveny et al. (2010) predicted 547 N and 607 N decrease per decade in the fracture forces for men and women (10 and 13% decrease of the baseline). The absolute decrease in the fracture forces in the current study was 373.3 N for men and 368.1 N for women. Despite the differences in these absolute values, the percentage of change per decade is in agreement with those studies.

In the current study, THUMS v4.02 was used to acquire the geometry of the femur. In the baseline model, we aimed to modify the primary model to address the shortcomings of the current model. Afterward, we investigated the potential effects of the major aging changes of the geometry and mechanical properties on the fracture forces of the femur. Meanwhile, the findings of the current study are subject to several limitations. First, the model was simplified at the structural and material properties level, although several previous studies were focused on sophisticated CT image-based modeling of the femur. At the structural level, the accuracy of the cortical thickness estimation could be improved using a recently developed cortical bone mapping (CBM) technique (Treece and Gee, 2015; Treece and Gee, 2018; Schileo et al., 2020). Similarly, it can be used to follow the age-dependent changes to the cortical bone with a higher resolution. At the material properties level, the mechanical properties were applied homogenously to the bone even though the CT images have shown the inhomogeneity of those properties. A similar approach of CT-based models could be used to assign heterogeneous mechanical properties to the cortical and trabecular bones using bone mineral density or porosity (Bayraktar et al., 2004; Hansen et al., 2008; Ariza et al., 2015; Grassi et al., 2016; Enns-Bray et al., 2018). It has been shown that the ultimate strain can benefit from a similar density-based power law (Dragomir-Daescu et al., 2011), although numerous CT-based models have implemented the uniform asymmetric strain limits and have shown accurate results when comparing to the experiments (Bayraktar et al., 2004; Grassi et al., 2016). Despite the benefits of a higher resolution femur model and the improved accuracy of these models, this approach could be computationally expensive for implementing in the whole-body models. The fracture criteria for the damage model of the current study were asymmetric, transverse isotropic, and uncoupled. A possible improvement in the damage model could be made using the continuum damage model proposed by Hambli (2013). The proposed damage model was asymmetric and coupled; however, it lacks the transverse isotropic/orthotropic material properties and fracture criteria. Another limitation of this work is that the interindividual differences such as neck-shaft angle and neck length, which could play a role in the femoral strength, were not studied. A recent study by Dragomir-Daescu et al. (2018) suggested that at least neck-shaft angle is not improving the prediction of the femoral strength as much as sex, age and BMD do. The simplifications of the current study, especially in the homogenous material properties of the bone, could adversely affect the slope of the force-displacement curves in Figure 6A, and the limited range of the fracture forces in Figures 6B,C. Also, the smaller difference between the slopes of the most compliant and stiffest models compared to the experiments can have been affected by using average geometry for each age group instead of subject-specific geometries. Part of the wide range of the fracture forces for each decade of age in Figure 6B for men and Figure 6C for women corresponds to the quality of the tested bone such as T-score or BMD. The age in the current study refers to a healthy adult in each decade of age, and a wider range could be achieved for each age group if the mechanical properties of different age group were assigned to all GeomAge models. Finally, having a larger number of experimental force-displacement curves would offer a better validation of the model. Despite these limitations, the current model uses minor modifications to the primary THUMS v4.02 model, which enables the direct application of it in a whole-body model. Moreover, the simplicity of the model does not interfere with the accuracy.

Conclusion

Aging changes the geometry of the femoral neck, and it affects the mechanical properties of the bone. In the current study, those changes were explored separately and combined to demonstrate the possible effect of both changes in altering the femoral strength during aging. The results of the current study suggest that the fracture forces reduced in both men and women when accounting for both mechanical and geometrical changes due to aging. The geometrical changes due to aging counteracted some of the adverse effects of the mechanical changes in men, whereas it adversely affected the fracture forces in women.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

PS and SK designed the study. PS performed and analyzed the finite element simulations, wrote the original draft. SK performed supervision, funding acquisition, writing review, and editing. All authors critically reviewed and revised the manuscript.

Funding

This study was supported by a grant from “BVFF—Bana väg för framtiden” (BVFF number 2016-025) and the Center for Biomechanical Modeling and Experimentation (BioMEx) at KTH—Royal Institute of Technology.

Conflict of Interest

SK has a financial interest in a company aiming to produce safety flooring (Igelkott Golv AB), and both he and the company may benefit from the results of this research.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the center for High-Performance Computing (PDC).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.691171/full#supplementary-material

Abbreviations

THUMS, total human model for safety; BMD, bone mineral density; GeomAge, simulation set for the geometrical changes due to aging; MechAge, simulation set for the mechanical properties changes due to aging; MechGeomAge, simulation set for the geometrical and mechanical properties changes; NHANES III, National Health and Nutrition Examination Survey; ${\mathrm{ϵ}}_{\mathrm{k}}^{\mathrm{s}}$, yield strains; ${\mathrm{ϵ}}_{\mathrm{k}}^{\mathrm{c}}$, ultimate strains; $d_{secto{r}_i}$, cortical thicknesses of each sector; $D_{Ma{x}_{reported}}$, maximum reported thickness in Mayhew et al. (2005); $D_{avg, NHANES III}$, NHANES III average cortical thicknesses; $D_{Ne{w}_{Max}}$, new maximum cortical thickness; $d_k$, damage parameter in the respective direction.

References

Altai, Z., Qasim, M., Li, X., and Viceconti, M. (2019). The Effect of Boundary and Loading Conditions on Patient Classification Using Finite Element Predicted Risk of Fracture, Clin. Biomech., 68. 137–143. doi:10.1016/j.clinbiomech.2019.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ambrose, A. F., Paul, G., and Hausdorff, J. M. (2013). Risk Factors for Falls Among Older Adults: A Review of the literatureMaturitas. Elsevier.

Ariza, O., Gilchrist, S., Widmer, R. P., Guy, P., Ferguson, S. J., Cripton, P. A., et al. (2015). Comparison of Explicit Finite Element and Mechanical Simulation of the Proximal Femur during Dynamic Drop-tower Testing, J. Biomech., 48. 224–232. doi:10.1016/j.jbiomech.2014.11.042

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashman, R. B., Cowin, S. C., Van Buskirk, W. C., Rice, J. C., and Rice+, J. C. (1984). A Continuous Wave Technique for the Measurement of the Elastic Properties of Cortical Bone, J. Biomech., 17. 349–361. doi:10.1016/0021-9290(84)90029-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauer, J. S., Kohlmann, S., Eckstein, F., Mueller, D., Lochmüller, E.-M., and Link, T. M. (2006). Structural Analysis of Trabecular Bone of the Proximal Femur Using Multislice Computed Tomography: a Comparison with Dual X-ray Absorptiometry for Predicting Biomechanical Strength In Vitro. Calcif Tissue Int. 78 (2), 78–89. doi:10.1007/s00223-005-0070-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayraktar, H. H., Morgan, E. F., Niebur, G. L., Morris, G. E., Wong, E. K., and Keaveny, T. M. (2004). Comparison of the Elastic and Yield Properties of Human Femoral Trabecular and Cortical Bone Tissue. J. Biomech. 37 (1), 27–35. doi:10.1016/s0021-9290(03)00257-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, T. J., Looker, A. C., Ruff, C. B., Sievanen, H., and Wahner, H. W. (2000). Structural Trends in the Aging Femoral Neck and Proximal Shaft: Analysis of the Third National Health and Nutrition Examination Survey Dual-Energy X-Ray Absorptiometry Data, J. Bone Miner Res., 15. , 2297–2304. doi:10.1359/jbmr.2000.15.12.2297

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergen, G., Stevens, M. R., and Burns, E. R. (2016). Falls and Fall Injuries Among Adults Aged ≥65 Years - United States, 2014, MMWR Morb. Mortal. Wkly. Rep., 65. 993–998. doi:10.15585/mmwr.mm6537a2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouxsein, M. L. (2006). Biomechanics of Osteoporotic Fractures. Bmm, 4. 143–154. doi:10.1385/bmm:4:3:143

CrossRef Full Text | Google Scholar

Burns, E. R., Stevens, J. A., and Lee, R. (2016). The Direct Costs of Fatal and Non-fatal Falls Among Older Adults - United States. J. Saf. Res. 58, 99–103. doi:10.1016/j.jsr.2016.05.001

CrossRef Full Text | Google Scholar

Burstein, A., Reilly, D., and Martens, M. (1976). Aging of Bone Tissue. J. Bone Jt. Surg. 58 (1), 82–86. doi:10.2106/00004623-197658010-00015

CrossRef Full Text | Google Scholar

Carballido-Gamio, J., Harnish, R., Saeed, I., Streeper, T., Sigurdsson, S., Amin, S., et al. (2013). Structural Patterns of the Proximal Femur in Relation to Age and Hip Fracture Risk in Women, Bone, 57. 290–299. doi:10.1016/j.bone.2013.08.0171

PubMed Abstract | CrossRef Full Text | Google Scholar

Carpenter, R. D., Sigurdsson, S., Zhao, S., Lu, Y., Eiriksdottir, G., Sigurdsson, G., et al. (2011). Effects of Age and Sex on the Strength and Cortical Thickness of the Femoral Neck. Bone 48 (4), 741–747. doi:10.1016/j.bone.2010.12.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Cezayirlioglu, H., Bahniuk, E., Davy, D. T., and Heiple, K. G. (1985). Anisotropic Yield Behavior of Bone under Combined Axial Force and Torque, J. Biomech., 18. 61–69. doi:10.1016/0021-9290(85)90045-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Courtney, A. C., Wachtel, E. F., Myers, E. R., and Hayes, W. C. (1995). Age-related Reductions in the Strength of the Femur Tested in a Fall-Loading Configuration. J. Bone Jt. Surg. 77 (3), 387–395. doi:10.2106/00004623-199503000-00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Courtney, A. C., Wachtel, E. F., Myers, E. R., and Hayes, W. C. (1994). Effects of Loading Rate on Strength of the Proximal Femur. Calcif Tissue Int. 55 (1), 53–58. doi:10.1007/bf00310169

PubMed Abstract | CrossRef Full Text | Google Scholar

Dall'Ara, E., Luisier, B., Schmidt, R., Kainberger, F., Zysset, P., and Pahr, D. (2013). A Nonlinear QCT-Based Finite Element Model Validation Study for the Human Femur Tested in Two Configurations In Vitro. Bone 52 (1), 27–38. doi:10.1016/j.bone.2012.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

de Bakker, P. M., Manske, S. L., Ebacher, V., Oxland, T. R., Cripton, P. A., and Guy, P. (2009). During Sideways Falls Proximal Femur Fractures Initiate in the Superolateral Cortex: Evidence from High-Speed Video of Simulated Fractures, J. Biomech., 42. Elsevier, 1917–1925. doi:10.1016/j.jbiomech.2009.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Derikx, L. C., Vis, R., Meinders, T., Verdonschot, N., and Tanck, E. (2011). Implementation of Asymmetric Yielding in Case-specific Finite Element Models Improves the Prediction of Femoral Fractures, Computer Methods Biomech. Biomed. Eng., 14. 183–193. doi:10.1080/10255842.2010.542463

PubMed Abstract | CrossRef Full Text | Google Scholar

Dokko, Y., Ito, O., and Co, P. S. G. (2009). Development of Human Lower Limb and Pelvis FE Models for Adult and the Elderly. SAE Int. doi:10.4271/2009-01-0396

CrossRef Full Text | Google Scholar

Dong, X. N., and Guo, X. E. (2004). The Dependence of Transversely Isotropic Elasticity of Human Femoral Cortical Bone on Porosity. J. Biomech. 37 (8), 1281–1287. doi:10.1016/j.jbiomech.2003.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Dragomir-Daescu, D., Op Den Buijs, J., McEligot, S., Dai, Y., Entwistle, R. C., Salas, C., et al. (2011). Robust QCT/FEA Models of Proximal Femur Stiffness and Fracture Load during a Sideways Fall on the Hip, Ann. Biomed. Eng., 39. 742–755. doi:10.1007/s10439-010-0196-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Dragomir-Daescu, D., Rossman, T. L., Rezaei, A., Carlson, K. D., Kallmes, D. F., Skinner, J. A., et al. (2018). Factors Associated with Proximal Femur Fracture Determined in a Large Cadaveric Cohort, Bone, 116. 196–202. doi:10.1016/j.bone.2018.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, Y., Beck, T. J., Wang, X.-F., and Seeman, E. (2003). Structural and Biomechanical Basis of Sexual Dimorphism in Femoral Neck Fragility Has its Origins in Growth and Aging, J. Bone Miner Res., 18. 1766–1774. doi:10.1359/jbmr.2003.18.10.1766

PubMed Abstract | CrossRef Full Text | Google Scholar

Enns-Bray, W. S., Bahaloo, H., Fleps, I., Ariza, O., Gilchrist, S., Widmer, R., et al. (2018). Material Mapping Strategy to Improve the Predicted Response of the Proximal Femur to a Sideways Fall Impact, J. Mech. Behav. Biomed. Mater., 78. 196–205. doi:10.1016/j.jmbbm.2017.10.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Falcinelli, C., and Whyne, C. (2020). Image-based Finite-Element Modeling of the Human Femur. Computer Methods Biomech. Biomed. Eng., 1–24.

Google Scholar

Florence, C. S., Bergen, G., Atherly, A., Burns, E., Stevens, J., and Drake, C. (2018). Medical Costs of Fatal and Nonfatal Falls in Older Adults, J. Am. Geriatr. Soc., 66. 693–698. doi:10.1111/jgs.15304

PubMed Abstract | CrossRef Full Text | Google Scholar

Grassi, L., Schileo, E., Taddei, F., Zani, L., Juszczyk, M., Cristofolini, L., et al. (2012). Accuracy of Finite Element Predictions in Sideways Load Configurations for the Proximal Human Femur, J. Biomech., 45. 394–399. doi:10.1016/j.jbiomech.2011.10.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Grassi, L., Väänänen, S. P., Ristinmaa, M., Jurvelin, J. S., and Isaksson, H. (2016). How Accurately Can Subject-specific Finite Element Models Predict Strains and Strength of Human Femora? Investigation Using Full-Field Measurements, J. Biomech., 49. 802–806. doi:10.1016/j.jbiomech.2016.02.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Hambli, R. (2013). A Quasi-Brittle Continuum Damage Finite Element Model of the Human Proximal Femur Based on Element Deletion. Med. Biol. Eng. Comput. 51 (1–2), 219–231. doi:10.1007/s11517-012-0986-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, U., Zioupos, P., Simpson, R., Currey, J. D., and Hynd, D. (2008). The Effect of Strain Rate on the Mechanical Properties of Human Cortical Bone. J. Biomechanical Eng. Am. Soc. Mech. Eng. 130 (1), 011011. doi:10.1115/1.2838032

CrossRef Full Text | Google Scholar

Hayes, W. C., Myers, E. R., Morris, J. N., Gerhart, T. N., Yett, H. S., and Lipsitz, L. A. (1993). Impact Near the Hip Dominates Fracture Risk in Elderly Nursing home Residents Who Fall, Calcif Tissue Int. 52. 192–198. doi:10.1007/bf00298717

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzer, G., Von Skrbensky, G., Holzer, L. A., et al. Skrbensky, G. Von., Holzer, L. A., et al. (2009). Hip Fractures and the Contribution of Cortical versus Trabecular Bone to Femoral Neck Strength. J. Bone Mineral Res. 24 (3), 468–474. doi:10.1359/jbmr.081108

PubMed Abstract | CrossRef Full Text | Google Scholar

Houry, D., Florence, C., Baldwin, G., Stevens, J., and McClure, R. (2016). The CDC Injury Center's Response to the Growing Public Health Problem of Falls Among Older Adults, Am. J. Lifestyle Med. 10. 74–77. doi:10.1177/1559827615600137

CrossRef Full Text | Google Scholar

Ito, M., Nakata, T., Nishida, A., and Uetani, M. (2011). Age-related Changes in Bone Density, Geometry and Biomechanical Properties of the Proximal Femur: CT-based 3D Hip Structure Analysis in normal Postmenopausal Women. Bone 48 (3), 627–630. doi:10.1016/j.bone.2010.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Iwamoto, M., Kisanuki, Y., Watanabe, I., Furusu, K., and Miki, K. (2002). Development of a Finite Element Model of the Total Human Model for Safety (THUMS) and Application to Injury Reconstruction. Munich, Germany: International Research Council on Biomechanics of Injury, 31–42.

Johannesdottir, F., Aspelund, T., Reeve, J., Poole, K. E., Sigurdsson, S., Harris, T. B., et al. (2013). Similarities and Differences between Sexes in Regional Loss of Cortical and Trabecular Bone in the Mid-femoral Neck: The AGES-Reykjavik Longitudinal Study, J. Bone Miner Res., 28. 2165–2176. doi:10.1002/jbmr.1960

PubMed Abstract | CrossRef Full Text | Google Scholar

Johannesdottir, F., Poole, K. E. S., Reeve, J., Siggeirsdottir, K., Aspelund, T., Mogensen, B., et al. (2011). Distribution of Cortical Bone in the Femoral Neck and Hip Fracture: A Prospective Case-Control Analysis of 143 Incident Hip Fractures; the AGES-REYKJAVIK Study, Bone, 48. 1268–1276. doi:10.1016/j.bone.2011.03.776

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanis, J. A., Aaron, J. E., Evans, D., Thavarajah, M., and Beneton, M. (1990). Bone Loss and Age-Related Fractures. Exp. Gerontol. 25 (3–4), 289–296. doi:10.1016/0531-5565(90)90064-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Keaveny, T. M., Kopperdahl, D. L., Melton, L. J., Hoffmann, P. F., Amin, S., Riggs, B. L., et al. (2010). Age-dependence of Femoral Strength in white Women and Men. J. Bone Mineral Res. 25 (5), 994–1001. doi:10.1002/jbmr.231

CrossRef Full Text | Google Scholar

Keaveny, T. M. (1998). “Cancellous bone.” Handbook Of Biomaterial Properties. Boston, MA: Springer US, 15–23. doi:10.1007/978-1-4615-5801-9_2

CrossRef Full Text

Khoo, B. C. C., Brown, K., Lewis, J. R., Perilli, E., and Prince, R. L. (2019). Ageing Effects on 3-Dimensional Femoral Neck Cross-Sectional Asymmetry: Implications for Age-Related Bone Fragility in Falling, J. Clin. Densitom., 22. 153–161. doi:10.1016/j.jocd.2018.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Kleiven, S. (2020). Hip Fracture Risk Functions for Elderly Men and Women in Sideways Falls, J. Biomech., 105. 109771. doi:10.1016/j.jbiomech.2020.109771

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroker, A., Plett, R., Nishiyama, K. K., McErlain, D. D., Sandino, C., and Boyd, S. K. (2017). Distal Skeletal Tibia Assessed by HR-pQCT Is Highly Correlated with Femoral and Lumbar Vertebra Failure Loads, J. Biomech., 59. 43–49. doi:10.1016/j.jbiomech.2017.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutz, M. (2009). Biomedical Engineering and Design Handbook. Editor M. Kutz (New York: McGraw-HillMcGraw-Hill), Vol. 1.

Lang, T. F., Sigurdsson, S., Karlsdottir, G., Oskarsdottir, D., Sigmarsdottir, A., Chengshi, J., et al. (2012). Age-related Loss of Proximal Femoral Strength in Elderly Men and Women: The Age Gene/Environment Susceptibility Study - Reykjavik, Bone50. 743–748. doi:10.1016/j.bone.2011.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

LSTC (2016). Ls-Dyna Keyword User’s Manual Ls-Dyna R9.0.

Manske, S. L., Liu-Ambrose, T., de Bakker, P. M., Liu, D., Kontulainen, S., Guy, P., et al. (2006). Femoral Neck Cortical Geometry Measured with Magnetic Resonance Imaging Is Associated with Proximal Femur StrengthOsteoporos. Int. 17. 1539–1545. doi:10.1007/s00198-006-0162-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, B. (1993). Aging and Strength of Bone as a Structural Material, Calcif Tissue Int., 53. S34–S40. doi:10.1007/bf01673400

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayhew, P. M., Thomas, C. D., Clement, J. G., Loveridge, N., Beck, T. J., Bonfield, W., et al. (2005). Relation between Age, Femoral Neck Cortical Stability, and Hip Fracture Risk. The Lancet 366 (9480), 129–135. doi:10.1016/s0140-6736(05)66870-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Mirzaali, M. J., Schwiedrzik, J. J., Thaiwichai, S., Best, J. P., Michler, J., Zysset, P. K., et al. (2016). Mechanical Properties of Cortical Bone and Their Relationships with Age, Gender, Composition and Microindentation Properties in the Elderly. Bone 93, 196–211. doi:10.1016/j.bone.2015.11.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Morgan, E. F., and Bouxsein, M. L. (2008). “Biomechanics of Bone and Age-Related Fractures,” in “Biomechanics of Bone and Age-Related Fractures.” Principles Of Bone Biology. Editors J. P. Bilezikian, L. G. Raisz, and T. J. Martin (Academic Press), 29–51. doi:10.1016/b978-0-12-373884-4.00024-0

CrossRef Full Text | Google Scholar

Mosekilde, L., Mosekilde, L., and Danielsen, C. C. (1987). Biomechanical Competence of Vertebral Trabecular Bone in Relation to Ash Density and Age in normal Individuals. Bone 8 (2), 79–85. doi:10.1016/8756-3282(87)90074-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Nasiri, M., and Luo, Y. (2016). Study of Sex Differences in the Association between Hip Fracture Risk and Body Parameters by DXA-Based Biomechanical Modeling, Bone. 90. 90–98. doi:10.1016/j.bone.2016.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Nasiri Sarvi, M., and Luo, Y. (2017). Sideways Fall-Induced Impact Force and its Effect on Hip Fracture Risk: a Review. Osteoporos. Int. 28 (10), 2759–2780. doi:10.1007/s00198-017-4138-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Op Den Buijs, J., and Dragomir-Daescu, D. (2011). Validated Finite Element Models of the Proximal Femur Using Two-Dimensional Projected Geometry and Bone Density. Computer Methods Programs Biomed. 104 (2), 168–174. doi:10.1016/j.cmpb.2010.11.008

CrossRef Full Text | Google Scholar

Osterhoff, G., Morgan, E. F., Shefelbine, S. J., Karim, L., McNamara, L. M., and Augat, P. (2016). Bone Mechanical Properties and Changes with Osteoporosis. Injury 47 (Suppl. 2), S11–S20. doi:10.1016/s0020-1383(16)47003-8

CrossRef Full Text | Google Scholar

Ott, I., Kienzler, R., and Schröder, R. (2010). Aging in the Cortical Bone: a Constitutive Law and its Application, Arch. Appl. Mech., 80. 527–541. doi:10.1007/s00419-009-0381-35

CrossRef Full Text | Google Scholar

Panyasantisuk, J., Dall'Ara, E., Pretterklieber, M., Pahr, D. H., and Zysset, P. K. (2018). Mapping Anisotropy Improves QCT-Based Finite Element Estimation of Hip Strength in Pooled Stance and Side-Fall Load Configurations. Med. Eng. Phys. 59. 36–42. doi:10.1016/j.medengphy.2018.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Parkkari, J., Kannus, P., Palvanen, M., Natri, A., Vainio, J., Aho, H., et al. (1999). Majority of Hip Fractures Occur as a Result of a Fall and Impact on the Greater Trochanter of the Femur: A Prospective Controlled Hip Fracture Study with 206 Consecutive Patients, Calcif Tissue Int. 65. 183–187. doi:10.1007/s002239900679

PubMed Abstract | CrossRef Full Text | Google Scholar

Patton, D. M., Bigelow, E. M. R., Schlecht, S. H., Kohn, D. H., Bredbenner, T. L., and Jepsen, K. J. (2019). The Relationship between Whole Bone Stiffness and Strength Is Age and Sex Dependent, J. Biomech., 83. 125–133. doi:10.1016/j.jbiomech.2018.11.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Poole, K. E., Mayhew, P. M., Rose, C. M., Brown, J. K., Bearcroft, P. J., Loveridge, N., et al. (2010). Changing Structure of the Femoral Neck across the Adult Female Lifespan, J. Bone Miner Res., 25. 482–491. doi:10.1359/jbmr.090734

PubMed Abstract | CrossRef Full Text | Google Scholar

Poole, K. E. S., Treece, G. M., Mayhew, P. M., Vaculík, J., Dungl, P., Horák, M., et al. (2012). “Cortical Thickness Mapping to Identify Focal Osteoporosis in Patients with Hip Fracture.” PLoS ONE. Editor X.-M. Shi (San Francisco, CA, United States: Public Library of Science), 7, e38466. doi:10.1371/journal.pone.00384666

CrossRef Full Text

Reilly, D. T., Burstein, A. H., and Frankel, V. H. (1974). The Elastic Modulus for Bone, J. Biomech., 7. 271–275. doi:10.1016/0021-9290(74)90018-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Reilly, D. T., and Burstein, A. H. (1975). The Elastic and Ultimate Properties of Compact Bone Tissue. J. Biomech. 8 (6), 393–405. doi:10.1016/0021-9290(75)90075-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Rezaei, A., and Dragomir-Daescu, D. (2015). Femoral Strength Changes Faster with Age Than BMD in Both Women and Men: A Biomechanical Study. J. Bone Miner Res. 30 (12), 2200–2206. doi:10.1002/jbmr.2572

PubMed Abstract | CrossRef Full Text | Google Scholar

Rezaei, A., Giambini, H., Rossman, T., Carlson, K. D., Yaszemski, M. J., Lu, L., et al. (2017). Are DXA/aBMD and QCT/FEA Stiffness and Strength Estimates Sensitive to Sex and Age? Ann. Biomed. Eng., 45. 2847–2856. doi:10.1007/s10439-017-1914-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Rho, J. Y., Hobatho, M. C., and Ashman, R. B. (1995). Relations of Mechanical Properties to Density and CT Numbers in Human Bone, Med. Eng. Phys., 17. 347–355. doi:10.1016/1350-4533(95)97314-f

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosen, C. J., Glowacki, J., and Bilezikian, J. P. (1999). in The Aging Skeleton. Editors C. Rosen, J. Glowacki, and J. P. Bilezikian (Elsevier).

Schileo, E., Pitocchi, J., Falcinelli, C., and Taddei, F. (2020). Cortical Bone Mapping Improves Finite Element Strain Prediction Accuracy at the Proximal Femur. Bone 136, 115348. doi:10.1016/j.bone.2020.115348

PubMed Abstract | CrossRef Full Text | Google Scholar

Seeman, E. (2001). During Aging, Men Lose Less Bone Than Women Because They Gain More Periosteal Bone, Not Because They Resorb Less Endosteal Bone. Calcif Tissue Int. 69 (4), 205–208. doi:10.1007/s00223-001-1040-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Silva, M. J. (2007). Biomechanics of Osteoporotic Fractures. Injury 38 (3), 69–76. doi:10.1016/j.injury.2007.08.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Treece, G., and Gee, A. (2018). “Cortical Bone Mapping: Measurement and Statistical Analysis of Localised Skeletal Changes.” Current Osteoporosis Reports, 1. Switzerland: Springer Nature.

Treece, G. M., and Gee, A. H. (2015). Independent Measurement of Femoral Cortical Thickness and Cortical Bone Density Using Clinical CT, Med. Image Anal., 20. 249–264. doi:10.1016/j.media.2014.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Villette, C. C., and Phillips, A. T. M. (2018). Rate and Age-dependent Damage Elasticity Formulation for Efficient Hip Fracture Simulations. Med. Eng. Phys. 61. 1–12. doi:10.1016/j.medengphy.2018.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Zioupos, P., and Currey, J. D. (1998). Changes in the Stiffness, Strength, and Toughness of Human Cortical Bone with Age, Bone, 22. 57–66. doi:10.1016/s8756-3282(97)00228-7

PubMed Abstract | CrossRef Full Text | Google Scholar