
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mech. Eng., 17 May 2021
Sec. Biomechanical Engineering
Volume 7 - 2021 | https://doi.org/10.3389/fmech.2021.685519
This article is part of the Research TopicBiomechanics and MechanobiologyView all 6 articles
Recently, various researches have revealed the importance of the investigations performed for evaluating mechanical properties and damages of the brain tissues while dealing with the production of surgical ligaments and helmets. Therefore, it is vital to study the structure of the brain both experimentally and numerically. By experimental tests, despite being costly, it is almost impossible to establish stress distribution in micro scale, which causes injury. Micromechanical predictions are effective ways to assess brain behavior. They can be applied to compensate for some experimental test limitations. In this work, a numerical study of the axonal injury in different heterogeneous porcine brain parts with different axon distributions under quasi-static loading is provided. In order to produce a heterogeneous structure, axons are distributed in regular, semi-regular, and irregular patterns inside the representative volume element. To accurately examine the brain tissue time-dependent behavior, a visco-hyperelastic constitutive model is developed. Also, axonal damage is studied under different conditions by applying different levels of load and rate. Because of geometrical complexities, a self-consistent method was applied to study the damage in higher volume fractions of the axon. The results reveal that the regions of the brain enjoying a regular axon distribution would have higher strength. In addition, among the two influential load and loading rate parameters, the brain tissue in all regions shows more sensitivity toward the applying load.
Any alteration in brain function, caused by an external force is defined as traumatic brain injury (TBI) (Menon et al., 2010). Direct impact effect of external force, quick acceleration (Smith and Meaney, 2000) and deceleration, infiltration of external objects such as gunshot and exposure to the blast wave (Chafi et al., 2010) would lead to TBI (Maas et al., 2008). TBI could be called one of the well-known public health problems. Every year, 1.7 million people experience TBI (Langlois et al., 2006). Falls resulting in 35.2% of TBIs come first when discussing the causes of TBI, motor vehicle traffic, struck by/against events, and assaults is on the next place (Faul et al., 2002–2006). Since TBI leads to both death and disability of individuals, and it is also more common among the youth (75% in males), it imposes high costs on society (Maas et al., 2008). Axonal damage due to brain impact and TBI can cause axonal death and disorientation (Peter and Mofrad, 2012). In most cases, symptoms of brain injury are invisible to the eye (Tanielian et al., 2008). Hence, to get a better explanation of the nature of TBI, simulation of the injury under different conditions could be helpful. Considering the vast studies performed on damage, their impact on mechanics and the advances made in finite element (FE) simulation in recent years, assuming the brain tissue as a mechanical matter, computer simulations could be employed to study TBI.
Dealing with brain tissues, material properties and injury criteria (i.e. mechanical behavior of the tissue) are the two most important parameters to be considered. Recently, several procedures have been provided to study the mechanical properties of the brain tissue. Atomic force microscopy (AFM) (Magdesian et al., 2012) is one of the most vastly used devices to characterize the brain tissue, especially single neuron mechanical behavior (Bernick et al., 2011). Magdesian et al. (Magdesian et al., 2012), performed an experimental test on a single neuron employing AFM. They found out that the axons have time dependent behavior. In another study, critical pressure to axonal injury and reversibility of the damage were investigated in hippocampal axons and dorsal root ganglion (DRG) (Harper and Lawson, 1985; Caffrey et al., 1992) neurons under gradual forces. Apart from AFM, Micropipette Aspiration (Schmid-Schönbein et al., 1981), Scanning Force Microscopy (SFM) (Christ et al., 2010), Transmission Electron Microscopy (TEM) (Labus and Puttlitz, 2016), Magnetic Resonance Elastography (MRE) (Anderson et al., 2016; Testu et al., 2017; Schmidt et al., 2018; Weickenmeier et al., 2018), as well as Digital Image Correlation (DIC) technique (Libertiaux et al., 2011) are other common devices used for studying mechanical behavior of the brain tissue.
Considering the experimental test limitations such as preparing the sample and the lack of access to the test setups, numerical methods have been developed to predict the mechanical behavior of the material. Therefore, many different constitutive models were presented to study brain tissue in macro and micro scales. Wright et al. (Wright et al., 2013) performed a macroscale simulation of brain tissue using MRI data while applying an acceleration curve on the model. They found out that rotational acceleration has a more sensible effect than translational acceleration on injury response.
Additionally, by employing numerical methods, researchers were able to provide a detailed record of the phenomenon happening in different conditions, while there was a huge difficulty for in vitro experiments. While performing micro scale experimental tests on the tissue is still challenging (Abolfathi et al., 2009; Karami et al., 2009; Yousefsani et al., 2018), characterization of a single neuron (Goriely et al., 2015) is one of the most common micro scale simulations of the brain tissue. Abolfathi et al. (Abolfathi et al., 2009) implemented numerical tests to study axonal undulation and neuron volume fraction impacts on brain tissue mechanical properties. It is found out that undulation has a significant effect on material stiffness in the axon longitudinal direction, while axon volume fraction has an overall influence on the tissue behavior.
Based on a similar structure of brain tissue and composites, common concepts, algorithms, and failure metrics of micromechanics could be considered in biomechanics for modeling the tissue. Representative volume element (RVE) is a helpful tool to simulate and study the effective properties of a macroscopic material (KAZEMPOUR et al., 2018; Sheidaei et al., 2019). Appropriate selection of the RVE size is an important factor to have an accurate effective behavior prediction (Hashin, 1983). In such a system, strain (Bain and Meaney, 2000; Ganpule et al., 2013) and strain energy (Goriely et al., 2015) are two micromechanical parameters which could be employed to predict the brain injury level. The unknown coefficients of the employed constitutive model could be determined through optimization functions (Kazempour et al., 2019), while these functions are also beneficial for studying and unraveling the problems of human body tissues (Chavoshnejad et al., 2018).
Miller et al. (Miller et al., 1998) considered strain, stress, and negative pressure parameters as the necessary injury criteria to determine more vulnerable regions of white and gray brain tissue matters. In fact, when a point is damaged, its surrounding area experiences higher loads, which results in a higher risk of injuries. This necessitates a damage function that can model the axonal injuries more realistically. Goriely et al. (Goriely et al., 2015) advantaging from continuum theories, presented a damage criterion for axons which is a function of strain energy or strain. To wrap it up, studies performed on conventional injuries made a great deal of effort to demonstrate vulnerable regions of the tissue, however, they mostly fail to provide damage distribution, damage initiation and injury evolution.
In this study, the RVE definition was employed to micromechanically study the brain tissue. Axons and Extra Cellular Matrix (ECM) are considered as the constituent parts of the tissue in the RVE. A visco-hyperelastic constitutive model presenting damage function has been utilized as the material model [cf. Goriely et al. (Goriely et al., 2015)]. The model along with the injury criteria is assigned to the RVE. Therefore, a VUMAT ABAQUS subroutine including damage parameters, i.e. two viscoelastic terms and a hyperelastic term, has been developed to define the RVE behavior. Axons were distributed irregularly in a 3D RVE, and were analyzed under different strain and strain rates. Since irregular distribution would lead to geometrical complexity, the issue is resolved employing the self-consistent approximation method. The damage and material models are found to be suitable for studying the mechanical behavior of the brain tissue, while the accuracy of RVE simulation could be enhanced by taking advantage of the abovementioned technique.
Due to the dimensions of axons compared to the tissue level of the brain, numerical analysis of the tissue including all of its components would lead to high computational costs. Representative Volume Element (RVE) is one of the micromechanical applicable tools to decrease the computational costs of the numerical simulations while records macro scale behavior. RVE is the smallest size of a heterogeneous material which is large enough to describe the material behavior in macro size (Kanit et al., 2003). To this aim, axons, and Extra Cellular Matrix (ECM) are simulated in a 3D RVE to study axonal injury. Considering the geometrical complexity, for studying the axonal injury, undulated axons were distributed in the RVE.
Since the distribution of axons in various regions of the brain tissue has both regular and irregular patterns, the corresponding isotropic and anisotropic behavior of these parts should be carefully observed. It is worth mentioning that the regions of brain with regular axonal distribution can be divided into two completely regular and semi-regular parts. In the former, axons are aligned with each other and in the latter, anisotropic behavior would be predictable.
To simulate all the three different regions (two with anisotropic behavior and one being isotropic), a computational MATLAB script has been developed to distribute the axons in the RVE. The volume fraction of the axons, reference axon distances and shape as well as RVE dimensions Minimum distances between axons are given as an input to the script, using random rotational and translational matrixes, it creates the axons, and checks the intersection between them. Finally, reference axon coordinates, translation and rotation matrixes would be saved as output files. Figure 1 shows the construction of the RVEs in different regions of the brain.
In the current investigation, axonal damage rate in three different parts of the brain is studied. To reduce the calculation expenses, Representative Volume Element (RVE) has been defined and used. Therefore, the RVE size is required. The importance of true size specification of RVE is the prevention of probable influences of its geometric dimensions on the deduced results which is in contradiction with the definition of RVE. Diverse constitutional models are presented to predict the behavioral traits of brain and other soft tissues in which elastic, viscoelastic, hyperelastic and visco-hyperelastic (Miller, 1999; Sahoo et al., 2014; Samadi-Dooki et al., 2018; Voyiadjis and Samadi-Dooki, 2018; Kazempour et al., 2019; Chavoshnejad et al., 2020) models can be mentioned. In the current study, the elastic constitutional model is utilized to examine the RVE size, thereafter isotropic and anisotropic behavior in different parts of brain are thoroughly investigated. First, it is assumed that the RVE has an orthotropic elastic behavior and the required loadings were exerted accordingly.
where
After obtaining the optimum size for RVE and examining its behavior in various alignments, a visco-hyperelastic model and offered damage model by Goriely et al. (Goriely et al., 2015) are used to study the axonal damage. Assuming an isotropic nature (Wang and Wineman, 1972) for axon, strain energy
Where
where
Since the responses vary in different physical conditions such as variation of the strain rate, temperature, strain levels, and other parameters, a visco-hyperelastic constitutive model has been developed to consider the time-dependent behavior of the brain tissue. Similarly, the stress is also divided into two time-dependent and elastic parts (Holzapfel, 2000).
Where
Bergström and Boyce (Bergström and Boyce, 1998) studies showed that quasi-static stress equations could also be applied for deviatoric part of the viscous response.
As for the strain energy function, Neo-Hookean strain energy model (Eq. 9) is employed to include deviatoric parts of both the elastic and viscous stresses. It is noteworthy that Neo-Hookean coefficients have different values for each of the elastic and viscous parts. Moreover, for the viscous part of the stress, as mentioned earlier, two relaxation time constants are assumed so as to account for both fast and slow loading velocities.
where
where
Since, a self-consistent approximation is used to increase the volume fraction of the axon, for the RVEs that are used in anisotropic regions, an anisotropic behavior for the ECM is employed. Eq. 12 shows the behavior of the anisotropic regions.
where
Note that invariant
Similarly, time-dependent parameters are added to the anisotropic model. Therefore, the stress is calculated using Eq. 6 and Eq. 7. Although stresses in isotropic and anisotropic models could be obtained by the same logic, the difference comes from the point that the anisotropic model has invariant
The models are implemented in VUMAT subroutines for a stress analysis in ABAQUS. Therefore, discretization of the models is needed in small time increments. Eq. 6 could be discretized the following way,
Considering Eq. 10 and assuming the small time increments, the numerical stress relation could be obtained.
Where Eq. 16 is a recursive relation to calculate the stress in every time increment based on the strain in the current time increment and the previous one's. In order to implement Eq. 16 in VUMAT subroutine, Cauchy stress must be calculated (Holzapfel, 2000).
Using the provided derivation and separation relations by Holzapfel (Holzapfel, 2000), Cauchy stress would be obtained as:
It is noteworthy that in the isotropic model, all of the
One of the forms of traumatic brain injury is Diffuse Axonal Injury (DAI) (Faul and Coronado, 2015), that occurs when the brain rapidly moves in the skull. Axons are the long connecting fibers which would suffer a cut in high accelerations and decelerations. Many parts of the brain are vulnerable to such an injury, therefore investigation of the DAI in different parts of the brain becomes of a high importance. Goriely et al. (Goriely et al., 2015) in 2015 studied axonal damage and presented damage criteria based on strain energy.
where
where
Likewise the equation of Goriely et al. (Goriely et al., 2015), the proposed damage variable is a function of initial damage
where
In order to construct the geometric model of RVE in ABAQUS software, a python script has been written in which reference axonal coordinates, generated translation and rotation matrixes by MATLAB script is read. Through this script, axons would be created, and dispersed in the RVE. In further steps, python code specifies appropriate material for the axon and ECM, distinguishes the existent contacts and creates a complete connection among them. For the geometric discretization of ECM and axons, C3D4 and C3D8 elements have been employed respectively.
To move forward, a tensile load needed to be exerted, hence, a loading model presented by Shaoning has been used. In this model, three orthogonal facets have symmetric boundary conditions being constrained in normal direction to the same face and one of three remained faces is subjected to a vertical tension. Zero boundary conditions in various loadings have been demonstrated in Table 1 employing notations given in Figure 2. Subsequently each RVE is studied while subjected to two loading modes with different sizes and rates. In order to exert shear load, one of the faces is fully constrained and the corresponding free parallel face is loaded in the shear direction. Following various tests and for providing homogeneous results on macroscopic level, volume averaging is used in microscopic scale. The volume average stress and strain are obtained according to Eq. 25:
Where
Due to the geometrical intricacies of the RVE, increasing axonal volume fraction leads to the rise of calculation expenses. Indeed, this increase makes axons geometrically closer to each other leading to geometrical complexity then discretization and RVE meshing problems would be generated. To solve this problem, a self-consistent method should be applied. Regarding self-consistency theory, heterogeneous composites are able to be simulated by homogeneous material, in this manner, average mechanical constants for homogenous material should be presented. In the aforementioned method, homogenized coefficients of a heterogeneous composite would be applied on the basis matrix. In case of further axonal distribution in this matrix, the increase in volume fraction will be closely observed. In order to apply self-consistency estimation, PSO function is exerted in a MATLAB code form. Normal and shear stresses according to time are introduced as input data to the function. By employing an optimization function, a homogenized basis matrix on the fitted graphs by a second axonal distribution is obtained, based on which a new RVE with higher volume fraction is created. Subsequently, the MATLAB code runs the python code in which ABAQUS software begins to analyze the matrix structural model by using the VUMAT subroutine. Finally, after finishing the analysis, a python code gives a time correspondent stress chart. MATLAB reads the python output for the produced homogenized matrix coefficients and compares them with heterogeneous composite data. This procedure goes on until the graphs fully fit each other with acceptable tolerances. Appendix Figure A1 briefly demonstrates the applied procedure.
In this section, proceeding to the selection of RVE size, as an important parameter affecting the whole results, their behavior has been analyzed. The resultant isotropic or anisotropic behaviors have been validated through various distributions of the axons in the medium. Consequently, the effect of volume fraction is also investigated to see whether it implies any changes in the predicted behavior of the RVE.
Following the validation of the selected RVE size, a more real condition has been applied to the model (i.e. the material and damage criteria). Considering a more practical situation, the effects of volume fractions, loading rates, and loads have been studied on the damage propagation.
Mechanical properties should be independent of RVE size. A wrong decision of the RVE size would lead to less independence of mechanical properties. Therefore, RVE size would be concerned as one of the most important parameters in predicting effective attributes of heterogeneous materials. Considering the impact of boundary conditions on the results, on one hand, calculation of the outputs by using a smaller RVE size could not be acceptable. On the other hand, by enlarging the RVE, the calculation expenses will grow dramatically, therefore, RVEs are generated in different sizes (500, 700, 900, 1100 micrometers) with volume fraction of 5%. The applied attributes of RVEs are displayed in the Table 2. Subsequently, studying RVEs according to the elastic model, the optimum size has been selected through analyzing their effective elastic modulus (further details are provided in the following sections). The effective elastic modulus for various sizes of RVEs with the same volume fraction quantity are displayed in Figure 3.
According to Figure 3, increasing RVE size to more than 900 mM brings no significant changes in the results, indicating an appropriate RVE size equal to 900 mM, in this study. It can also be understood that the results are independent of RVEs size, and the 900 mM RVE size leads to an optimized computation expense.
Due to the random distribution of axons, for RVE creation, it is necessary to examine their behavior, especially for irregular and semi-regular distribution sections. Thus, an orthotropic behavior is considered for the RVEs with a size of 900 mM, summarized in Table 3.
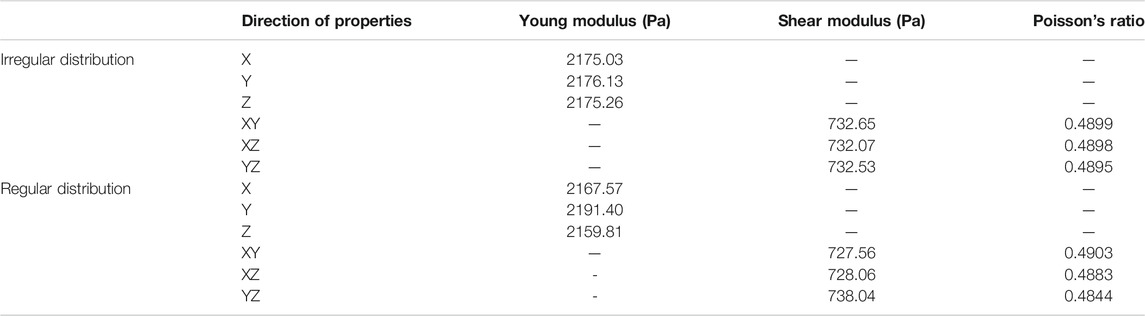
TABLE 3. Material coefficients of the orthotropic assumption for the RVE considering different distribution of axons.
According to the obtained results for loading RVEs in various directions, RVEs with irregular distribution have an isotropic response and RVEs with regular distribution show anisotropic behavior. Therefore, the mechanical behavior of the RVEs with isotropic behavior is predictable by two tests and the behavior of the RVEs which behave anisotropically could be predicted by six tests.
Due to the anisotropic behavior of the RVE with regular distribution, subsequent studies for these regions are performed with anisotropic constitutive models. However, in order to ensure the isotropic behavior of the RVEs with the irregular distribution of the axons, it is necessary to examine the other two conditions. The effect of different random distributions on mechanical behavior and the study of the RVE in different volume fractions are the states which should be considered for the investigation. In order to investigate the effects of different random distributions, three RVEs with various distributions were created and studied in 5% axonal volume fractions. The results show independent behavior of the axonal distribution for the RVEs (Table 4).
Axonal volume fraction influence on isotropic behavior is also studied by the creation of three RVEs with volume fraction of 5, 10, and 15%, subjected to a tensile strain of 3%. RVEs were subjected to static loading. In order to increase the volume fraction, self-consistent approximation was used. The results show that enhancing axons volume fraction leads to an increase in the effective elastic modulus. Table 5 presents the results of the effects of volume fraction on the mechanical properties of the RVE. As can be seen in Table 4, elastic modulus in different volume fractions is almost equal for perpendicular directions, which again confirms the isotropic behavior of the representative volume element.
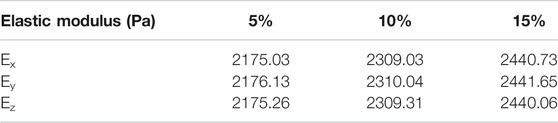
TABLE 5. Homogenized elastic modulus for different VF for orthotropic model in irregular distribution.
In Figure 4, 3% strain is applied to the RVE as a static load. The results show that axons experience higher stresses than ECM. Therefore, axons play a more important role in the brain injury investigation compared to ECM. It can be interpreted that the micromechanical study of the stress distribution in the brain tissue is one of the most important issues in the TBI study. Assuming the elastic behavior in this section, the importance of micromechanical analysis is shown. Therefore, in this study, for achieving a more realistic result, a visco-hyperelastic model is developed.
Javid et al. (Javid et al., 2014) performed an experimental test on the brain tissue in which mechanical properties of axon and ECM were presented separately. In the present study, the outcomes of these tests were used to extract the coefficients of the visco-hyperelastic model. To evaluate the developed constitutive model, a RVE with 52.7% axonal volume fraction is generated. In the next step, 3% strain is applied on the created RVE and the results were compared with the experimental outcomes represented by Javid et al. (Javid et al., 2014). The results are highly consistent with the experimental results and could be used in the present study. Table 6 indicates the obtained material coefficients of the RVE components. For a better illustration, the results obtained by Javid et al. (Javid et al., 2014) along with the mean volumetric stress of the RVE calculated in the present study are demonstrated in Figure 5.
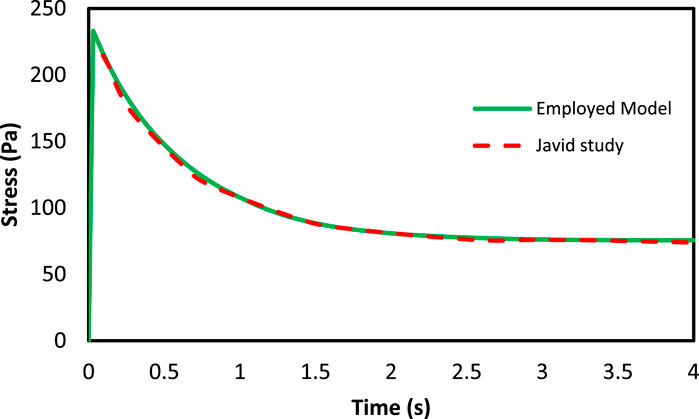
FIGURE 5. The mean volumetric stress of RVE in axons direction with 52.7% axons volume fraction under 3% strain.
In order to investigate axonal damage in different regions of the brain, RVEs were created with different volume fractions in different axonal distributions. RVEs were subjected to two various strains in two different loading rates, and the RVEs responses were evaluated with respect to time. Strain loads of 10 and 15% were applied in tensile and shear modes at times of 0.5 and 1s in a quasi-static manner on the RVEs. Figure 6 shows the loading conditions.
It is also important to note that micromechanical analysis is time-consuming, especially in quasi-static and dynamic loadings, in which the used constitutive model has a time-dependent behavior. In the present study, due to intangible variation of stress over time after 6 s, the analysis was performed up to 6 s. In Figure 7, the variations of the mean volumetric stress in the loading direction are illustrated for 15% volume fraction of axons under 15% tensile strain in a region with irregular distribution.
Figure 7 demonstrate the variations of the mean stress of the RVE versus time with volume fraction of 15% in the region with a semi-regular distribution. As can be seen, the stress increases up to the 0.5 and 1 s at different loading rates. Due to the viscous behavior in the RVE, when the strain reaches a constant value, a decrease in stress would be observed. Moreover, due to the loading rate behavior in the brain tissue (Pervin and Chen, 2009), increasing the loading rate leads to a firmer response in the tissue (Rashid et al., 2014). It should be noted that in accidents, the loading rate on the brain tissues is usually high, which indicates that the brain tissue is more vulnerable. These figures present a suitable response of the rate dependency of the developed constitutive model which could be very useful when studying the rate dependency of the brain tissue.
Figure 8 shows the mean volumetric stress of the axons against time for axons in both non-damaged and damaged states. It is found out that in damage presence, the experienced stresses by the axons are reduced, indicating a decrease in their stiffness and strength. Moreover, Figure 9 shows the maximum experienced stress by the axons in both damaged and non-damaged modes. According to the figure, the RVE with regular distribution of axons expresses higher stiffness than the semi-regular and irregular distribution modes. Stress also drops in the regular, semi-regular and irregular distribution mode by 10.7, 9.9, and 7.8%, respectively. Due to the full axon alignment along the loading direction in regular distribution, the largest reduction would occur in this section coming from a higher strain energy experienced by the axons.
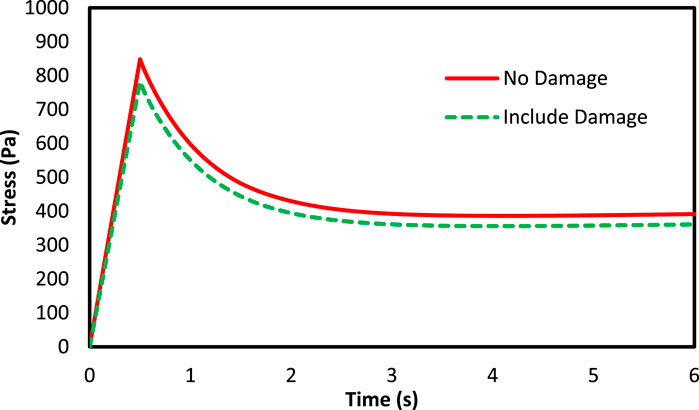
FIGURE 8. Stress variation of the axons with 5% VF under 15% strain for both damage and non-damage modes.
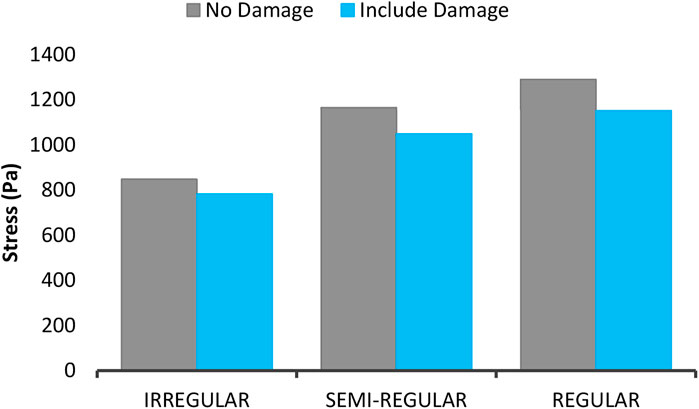
FIGURE 9. The maximum mean stress of the axons with 5% VF under 15% strain for three types of distribution in both damage and non-damage modes.
According to the damage model presented in Eqs 23, 24, due to the dependency of the damage on the strain energy, the damage starts to grow from the loading onset. Therefore, the damage amount could be compared between loading, loading rate and different volume fraction. Figure 10A shows the stress of the axons and the RVE at 10% volume fraction and 15% strain load, and different loading rates in the non-applied mode of the damage model. The results show that the experienced stress by the axons is higher than that of ECM (Karami et al., 2009). In addition, as the strain rate rises, the rate of increase in the maximum experienced stress in the axons grows greater than that of ECM, indicating an increase in crash vulnerability (Figure 10B). Moreover, the following figure shows the experienced stress in the RVE at 10% strain and 10% volume fraction in the non-applied state of the damage model. According to Figure 11, studying different distributions of axons would reveal that the RVE with regular distribution shows a higher stiffness due to the axon presence in loading direction. This suggests that those regions in the brain in which the axons have a more regular orientation express stiffer behavior.
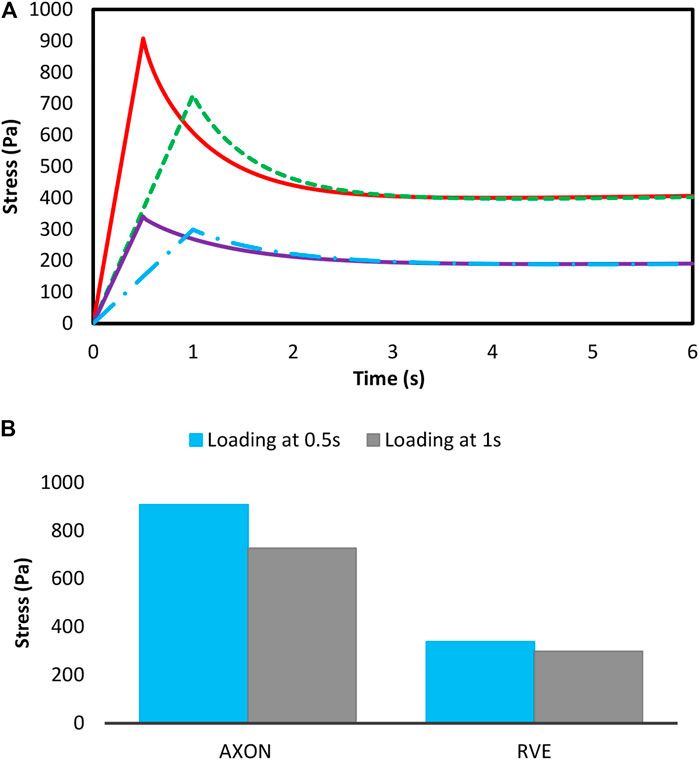
FIGURE 10. (A) Mean stress—(B) The maximum mean stress in the axons and RVE with 10% VF subjected to 15% strain in different loading rates in non-damage mode.
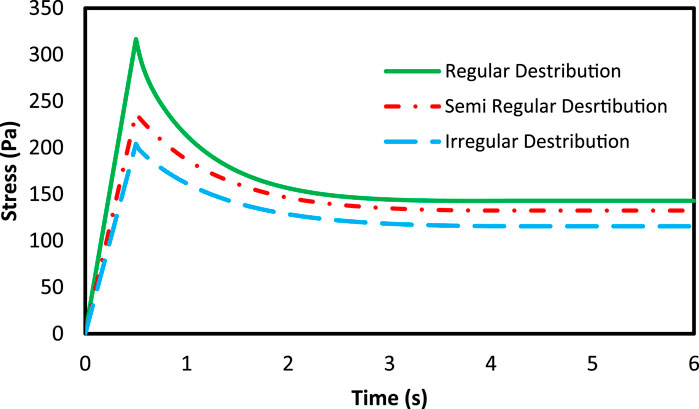
FIGURE 11. The mean stress of the RVE with 10% VF in three types of axonal distribution under 10% strain.
In addition, by increasing the loading rate, regions of the brain which have a more regular axon distribution reveal a higher raise in the stiffness. Figure 12 displays the maximum mean experienced stress for three different axon distributions, 10% strain load and 10% volume fraction at two different loading rates. According to the figure, in all loading rates, brain tissue regions having a regular axonal distribution express larger stiffness. In addition, at higher loading rates, the damage amount increases, indicating the sensitivity of the brain tissue to the loading rate.
Figure 13 shows the changes in the maximum experienced mean stress by the axons at 15% load and 5 and 10% volume fraction in the presence of the damage model, and without the model. As shown in the figure, by rising the axon volume fraction, the brain tissue in all regions shows stiffer behavior. Moreover, in constant loading, by increasing volume fraction, stress-drops rate decreases during injury, indicating a grow in tissue stiffness in all areas (Karami et al., 2009; Karami and Shankar, 2011). In addition, in a constant volume fraction, in the brain regions where axons have a more regular distribution, by applying the damage model, the stress-drop rate increases. This phenomenon indicates more energy is required to apply a constant strain to these areas. According to Eqs 23, 24, the damage parameter is a function of strain energy. An enhancement in absorbed strain energy leads to an increase in the damage coefficient, and subsequently in the stress reduction. However, the areas of the tissue having a regular distribution of axons still show higher strength in case of injury. It should be noted that due to the low volume fraction of axons and the proximity of the axon properties and ECM, the variation rate in tissue behavior is not noticeable.
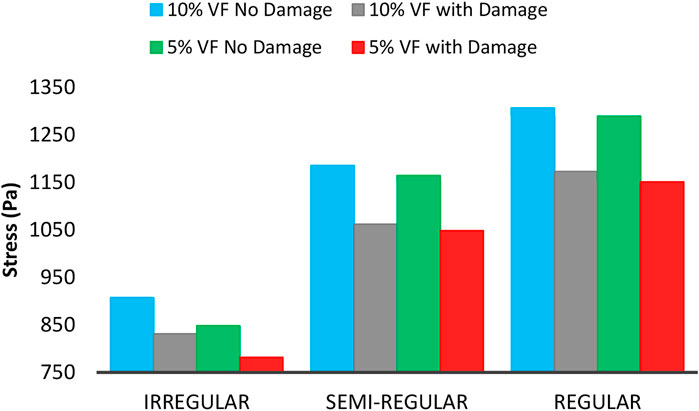
FIGURE 13. Maximum mean experienced stress by axons with 5 and 10% VF under 15% strain including the damage and non-damage modes.
Figure 14 shows the maximum experienced mean stress by axons at 5% volume fraction, 10 and 15% strain. As can be seen, the experienced stress by axons increases in all axonal distributions while enhancing the load. Furthermore, the rate of increase for the brain tissue is higher when dealing with the regular distribution of axons, which indicates higher stiffness in these areas. Moreover, as the load increases, the drop amount in stress increases in all areas, indicating a rise in axonal damage.
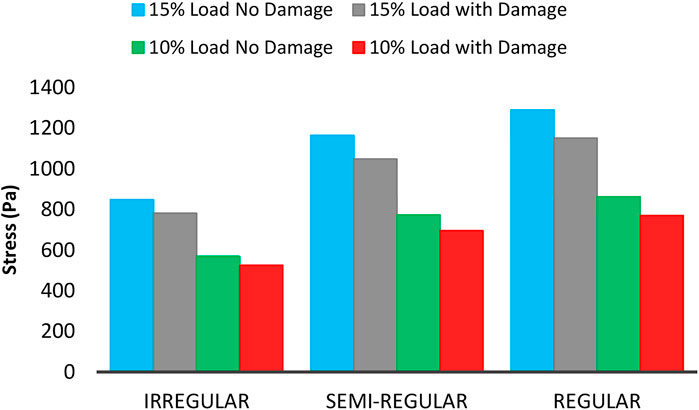
FIGURE 14. Maximum mean experienced stress by axons with 5% VF under 10 and 15% strain including the damage and non-damage modes.
Figure 15 and Figure 16 show the von Mises stress distribution on the axons and the homogenized stress for the ECM, respectively. The RVE is under the strain of 15%, which shows the volume fraction of 5% in 0.5 s for the irregular distribution of axons. According to the following figure, the maximum average stress on the ECM is approximately 291 Pa, while the experienced stress at the same time for the axons is between 693 and 1353 Pa. It is clear that the stress observed in ECM is less than that of axon, confirming previous results under different loading conditions. It can be concluded that axons experience more stress, and are more vulnerable. Karami et al. (Karami et al., 2009) and Javid et al. (Javid et al., 2014) also came at the same conclusion. Moreover in all experiments, the experienced stress in neurons is higher than that in ECM (Abolfathi et al., 2009).
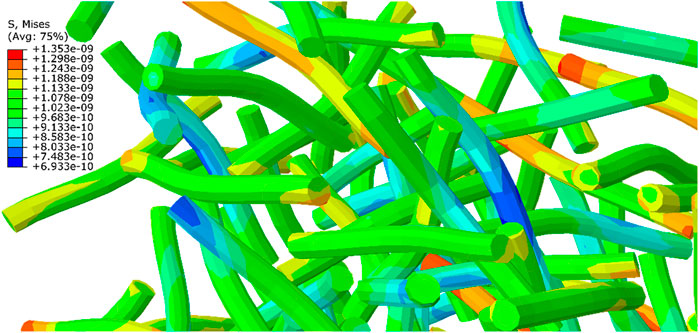
FIGURE 15. Distribution of the maximum stress on axons of a RVE with 5% volume fraction on which 15% strain is applied at 0.5 s (the results should be multiplied by 1e12 Pa).
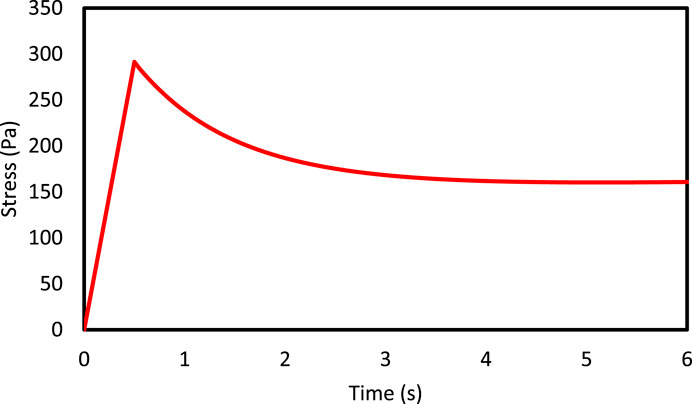
FIGURE 16. The mean volumetric stress of an RVE with 5% volume fraction of neuron, 15% strain is applied at 0.5 s.
In the present study, the brain tissue behavior and axonal damage extent in different loads, volume fractions and loading rates were investigated for different parts of the brain tissue in regular and irregular axonal distributions. For this purpose, a MATLAB code was developed which creates axons in different distributions; then, the generated coordinates by the Python code were entered into ABAQUS, and the aforementioned analysis was performed on the tissue in this software. It should be noted that due to the small size of the axons at the tissue level, RVE definition has been used to analyze the tissue. Subsequently, the elastic model has been utilized to investigate the optimal RVE size, and avoid the effects of boundary conditions. Furthermore, the amount of tissue anisotropy has been studied in different distributions. For this, a visco-hyperelastic model has been developed to examine the load to texture, loading rates and different volume fractions. It is found out that by increasing the loading rate, the experienced stress by axons increases, indicating that the tissue is vulnerable to high loading rates. Moreover, as the load increases, the experienced stress by the axons rises, while the amount of tissue sensitivity to the load becomes much greater than the loading rate. In regular axon distribution, for instance, a 1.5 times increase in load, causes the maximum experienced stress increase by 1.33 times, while by doubling the loading rate, the enhancement of the axonal stress would be 1.17 times higher. This shows the importance of efforts to reduce the load on the brain tissue. In addition, the experienced stress by axons under the same loading conditions is greater than the ECM, which emphasizes the necessity of the existence of DAI. The results of this study could be useful in the production of helmets, surgical robots, and all the tools which are used for preventing or treating the brain injuries.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
MK: Methodology, Software, Validation, Writing—original draft. AK: Validation, Writing—original draft. MB: Conceptualization, Methodology, Writing, review and editing, Supervision. YR: Conceptualization, Methodology, Writing, review and editing, Supervision. MB: Methodology, Software, review and editing, Supervision.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
fx1
Abolfathi, N., Naik, A., Sotudeh Chafi, M., Karami, G., and Ziejewski, M. (2009). A Micromechanical Procedure for Modelling the Anisotropic Mechanical Properties of Brain White Matter. Comp. Methods Biomech. Biomed. Eng. 12 (3), 249–262. doi:10.1080/10255840802430587
Anderson, A. T., Van Houten, E. E., McGarry, M. D., Paulsen, K. D., Holtrop, J. L., Sutton, B. P., et al. (2016). Observation of Direction-dependent Mechanical Properties in the Human Brain with Multi-Excitation MR Elastography. J. Mech. Behav. Biomed. Mater. 59, 538–546. doi:10.1016/j.jmbbm.2016.03.005
Bain, A. C., and Meaney, D. F. (2000). Tissue-level Thresholds for Axonal Damage in an Experimental Model of Central Nervous System White Matter Injury. J. biomechanical Eng. 122 (6), 615–622. doi:10.1115/1.1324667
Bergström, J., and Boyce, M. (1998). Constitutive Modeling of the Large Strain Time-dependent Behavior of Elastomers. J. Mech. Phys. Sol. 46 (5), 931–954. doi:10.1016/s0022-5096(97)00075-6
Bernick, K. B., Prevost, T. P., Suresh, S., and Socrate, S. (2011). Biomechanics of Single Cortical Neurons. Acta Biomater. 7 (3), 1210–1219. doi:10.1016/j.actbio.2010.10.018
Caffrey, J., Eng, D., Black, J., Waxman, S., and Kocsis, J. (1992). Three Types of Sodium Channels in Adult Rat Dorsal Root Ganglion Neurons. Brain Res. 592 (1-2), 283–297. doi:10.1016/0006-8993(92)91687-a
Chafi, M., Karami, G., and Ziejewski, M. (2010). Biomechanical Assessment of Brain Dynamic Responses Due to Blast Pressure Waves. Ann. Biomed. Eng. 38 (2), 490–504. doi:10.1007/s10439-009-9813-z
Chavoshnejad, P., Ayati, M., Abbasspour, A., Karimpur, M., George, D., Rémond, Y., et al. (2018). Optimization of Taylor Spatial Frame Half-Pins Diameter for Bone Deformity Correction: Application to Femur. Proc. Inst. Mech. Eng. H: J. Eng. Med. 232 (7), 673–681. doi:10.1177/0954411918783782
Chavoshnejad, P., More, S., and Razavi, M. J. (2020). From Surface Microrelief to Big Wrinkles in Skin: A Mechanical In-Silico Model. Extreme Mech. Lett. 36, 100647. doi:10.1016/j.eml.2020.100647
Christ, A. F., Franze, K., Gautier, H., Moshayedi, P., Fawcett, J., Franklin, R. J., et al. (2010). Mechanical Difference between White and Gray Matter in the Rat Cerebellum Measured by Scanning Force Microscopy. J. Biomech. 43 (15), 2986–2992. doi:10.1016/j.jbiomech.2010.07.002
Faul, M., and Coronado, V. (2015). “Epidemiology of Traumatic Brain Injury,” in Handbook of Clinical Neurology (Elsevier), 3–13. doi:10.1016/b978-0-444-52892-6.00001-5
Faul, M., Xu, L., Wald, M., Coronado, V., and Dellinger, A. M. (2002–2006). Traumatic Brain Injury in the United States: National Estimates of Prevalence and Incidence. Inj. Prev. 16 (Suppl. 1), A268.
Fereidoonnezhad, B., O’Connor, C., and McGarry, J. P. (2020). A New Anisotropic Soft Tissue Model for Elimination of Unphysical Auxetic Behaviour. J. Biomech. 111, 110006. doi:10.1016/j.jbiomech.2020.110006
Ganpule, S., Alai, A., Plougonven, E., and Chandra, N. (2013). Mechanics of Blast Loading on the Head Models in the Study of Traumatic Brain Injury Using Experimental and Computational Approaches. Biomech. Model. mechanobiology 12 (3), 511–531. doi:10.1007/s10237-012-0421-8
Goriely, A., Budday, S., and Kuhl, E. (2015). “Neuromechanics: from Neurons to Brain,” in Advances in Applied Mechanics (Elsevier), 79–139. doi:10.1016/bs.aams.2015.10.002
Harper, A., and Lawson, S. (1985). Conduction Velocity Is Related to Morphological Cell Type in Rat Dorsal Root Ganglion Neurones. J. Physiol. 359 (1), 31–46. doi:10.1113/jphysiol.1985.sp015573
Hashin, Z. (1983). Analysis of Composite Materials—A Survey. J. Appl. Mech. 50 (3), 481–505. doi:10.1115/1.3167081
Holzapfel, A. G. (2000). Nonlinear Solid Mechanics: A Continuum Approach for Engineering. 1st Edn. Chichester, United Kingdom: John Wiley & Sons Ltd.
Horgan, C. O., and Murphy, J. G. (2009). On the Volumetric Part of Strain-Energy Functions Used in the Constitutive Modeling of Slightly Compressible Solid Rubbers. Int. J. Sol. Structures 46 (16), 3078–3085. doi:10.1016/j.ijsolstr.2009.04.007
Javid, S., Rezaei, A., and Karami, G. (2014). A Micromechanical Procedure for Viscoelastic Characterization of the Axons and ECM of the Brainstem. J. Mech. Behav. Biomed. Mater. 30, 290–299. doi:10.1016/j.jmbbm.2013.11.010
Kanit, T., Forest, S., Galliet, I., Mounoury, V., and Jeulin, D. (2003). Determination of the Size of the Representative Volume Element for Random Composites: Statistical and Numerical Approach. Int. J. Sol. structures 40 (13-14), 3647–3679. doi:10.1016/s0020-7683(03)00143-4
Karami, G., Grundman, N., Abolfathi, N., Naik, A., and Ziejewski, M. (2009). A Micromechanical Hyperelastic Modeling of Brain White Matter under Large Deformation. J. Mech. Behav. Biomed. Mater. 2 (3), 243–254. doi:10.1016/j.jmbbm.2008.08.003
Karami, G., and Shankar, S. (2011). “A Multiscale Analysis of the White Brain Material with Axons as Bidirectional Orientated Fibers,” in SIMULIA Customer Conference, 1–14doi:10.21236/ada548703
Kazempour, M., Bagherian, A., Sheidaei, A., Baniassadi, M., Baghani, M., Rémond, Y., et al. (2018). in Stem Cells and Regenerative Medicine: Proceedings of the 8th International China-Europe Symposium (Wuhan, China: IOS Press).
Kazempour, M., Baniassadi, M., Shahsavari, H., Remond, Y., and Baghani, M. (2019). Homogenization of Heterogeneous Brain Tissue under Quasi-Static Loading: a Visco-Hyperelastic Model of a 3D RVE. Biomech. Model. Mechanobiology 18 (4), 969–981. doi:10.1007/s10237-019-01124-6
Labus, K. M., and Puttlitz, C. M. (2016). An Anisotropic Hyperelastic Constitutive Model of Brain White Matter in Biaxial Tension and Structural–Mechanical Relationships. J. Mech. Behav. Biomed. Mater. 62, 195–208. doi:10.1016/j.jmbbm.2016.05.003
Langlois, J. A., Rutland-Brown, W., and Thomas, K. E. (2006). Traumatic Brain Injury in the United States; Emergency Department Visits, Hospitalizations, and Deaths. Atlanta, GA: Centers for Disease Control and Prevention .National Center for Injury Prevention and Control. doi:10.1037/e721222007-001
Libertiaux, V., Pascon, F., and Cescotto, S. (2011). Experimental Verification of Brain Tissue Incompressibility Using Digital Image Correlation. J. Mech. Behav. Biomed. Mater. 4 (7), 1177–1185. doi:10.1016/j.jmbbm.2011.03.028
Maas, A. I., Stocchetti, N., and Bullock, R. (2008). Moderate and Severe Traumatic Brain Injury in Adults. Lancet Neurol. 7 (8), 728–741. doi:10.1016/s1474-4422(08)70164-9
Magdesian, M. H., Sanchez, F. S., Lopez, M., Thostrup, P., Durisic, N., Belkaid, W., et al. (2012). Atomic Force Microscopy Reveals Important Differences in Axonal Resistance to Injury. Biophysical J. 103 (3), 405–414. doi:10.1016/j.bpj.2012.07.003
Menon, D. K., Schwab, K., Wright, D. W., and Maas, A. I. (2010). Position Statement: Definition of Traumatic Brain Injury. Arch. Phys. Med. Rehabil. 91 (11), 1637–1640. doi:10.1016/j.apmr.2010.05.017
Miller, K. (1999). Constitutive Model of Brain Tissue Suitable for Finite Element Analysis of Surgical Procedures. J. Biomech. 32 (5), 531–537. doi:10.1016/s0021-9290(99)00010-x
Miller, R. T., Margulies, S. S., Leoni, M., Nonaka, M., Chen, X., Smith, D. H., et al. (1998). Finite Element Modeling Approaches for Predicting Injury in an Experimental Model of Severe Diffuse Axonal Injury. SAE Tech. Paper 107 (6), 2798–2810. doi:10.4271/983154
Pervin, F., and Chen, W. W. (2009). Dynamic Mechanical Response of Bovine Gray Matter and White Matter Brain Tissues under Compression. J. Biomech. 42 (6), 731–735. doi:10.1016/j.jbiomech.2009.01.023
Peter, S. J., and Mofrad, M. R. (2012). Computational Modeling of Axonal Microtubule Bundles under Tension. Biophysical J. 102 (4), 749–757. doi:10.1016/j.bpj.2011.11.4024
Rashid, B., Destrade, M., and Gilchrist, M. D. (2014). Mechanical Characterization of Brain Tissue in Tension at Dynamic Strain Rates. J. Mech. Behav. Biomed. Mater. 33, 43–54. doi:10.1016/j.jmbbm.2012.07.015
Sahoo, D., Deck, C., and Willinger, R. (2014). Development and Validation of an Advanced Anisotropic Visco-Hyperelastic Human Brain FE Model. J. Mech. Behav. Biomed. Mater. 33, 24–42. doi:10.1016/j.jmbbm.2013.08.022
Samadi-Dooki, A., Voyiadjis, G. Z., and Stout, R. W. (2018). A Combined Experimental, Modeling, and Computational Approach to Interpret the Viscoelastic Response of the White Matter Brain Tissue during Indentation. J. Mech. Behav. Biomed. Mater. 77, 24–33. doi:10.1016/j.jmbbm.2017.08.037
Schmid-Schönbein, G., Sung, K., Tözeren, H., Skalak, R., and Chien, S. (1981). Passive Mechanical Properties of Human Leukocytes. Biophysical J. 36 (1), 243–256. doi:10.1016/s0006-3495(81)84726-1
Schmidt, J., Tweten, D., Badachhape, A., Reiter, A., Okamoto, R., Garbow, J., et al. (2018). Measurement of Anisotropic Mechanical Properties in Porcine Brain White Matter Ex Vivo Using Magnetic Resonance Elastography. J. Mech. Behav. Biomed. Mater. 79, 30–37. doi:10.1016/j.jmbbm.2017.11.045
Sheidaei, A., Kazempour, M., Hasanabadi, A., Nosouhi, F., Pithioux, M., Baniassadi, M., et al. (2019). Influence of Bone Microstructure Distribution on Developed Mechanical Energy for Bone Remodeling Using a Statistical Reconstruction Method. Maths. Mech. Sol. 24 (10), 3027–3041. doi:10.1177/1081286519828418
Smith, D. H., and Meaney, D. F. (2000). Axonal Damage in Traumatic Brain Injury. The neuroscientist 6 (6), 483–495. doi:10.1177/107385840000600611
Tanielian, T., Haycox, L. H., Schell, T. L., Marshall, G. N., Burnam, M. A., Eibner, C., et al. (2008). Invisible Wounds of War. Summary and Recommendations for Addressing Psychological and Cognitive Injuries. Santa Monica, CA: RAND Corporation. doi:10.7249/mg720.1
Testu, J., McGarry, M., Dittmann, F., Weaver, J., Paulsen, K., Sack, I., et al. (2017). Viscoelastic Power Law Parameters of In Vivo Human Brain Estimated by MR Elastography. J. Mech. Behav. Biomed. Mater. 74, 333–341. doi:10.1016/j.jmbbm.2017.06.027
Voyiadjis, G. Z., and Samadi-Dooki, A. (2018). Hyperelastic Modeling of the Human Brain Tissue: Effects of No-Slip Boundary Condition and Compressibility on the Uniaxial Deformation. J. Mech. Behav. Biomed. Mater. 83, 63–78. doi:10.1016/j.jmbbm.2018.04.011
Wang, H. C., and Wineman, A. S. (1972). A Mathematical Model for the Determination of Viscoelastic Behavior of Brain In Vivo—I Oscillatory Response. J. Biomech. 5 (5), 431–446. doi:10.1016/0021-9290(72)90002-4
Weickenmeier, J., Kurt, M., Ozkaya, E., Wintermark, M., Pauly, K. B., and Kuhl, E. (2018). Magnetic Resonance Elastography of the Brain: a Comparison between Pigs and Humans. J. Mech. Behav. Biomed. Mater. 77, 702–710. doi:10.1016/j.jmbbm.2017.08.029
Whitford, C., Movchan, N. V., Studer, H., and Elsheikh, A. (2018). A Viscoelastic Anisotropic Hyperelastic Constitutive Model of the Human Cornea. Biomech. Model. mechanobiology 17 (1), 19–29. doi:10.1007/s10237-017-0942-2
Wright, R. M., Post, A., Hoshizaki, B., and Ramesh, K. T. (2013). A Multiscale Computational Approach to Estimating Axonal Damage under Inertial Loading of the Head. J. neurotrauma 30 (2), 102–118. doi:10.1089/neu.2012.2418
Yousefsani, S. A., Shamloo, A., and Farahmand, F. (2018). Micromechanics of Brain White Matter Tissue: A Fiber-Reinforced Hyperelastic Model Using Embedded Element Technique. J. Mech. Behav. Biomed. Mater. 80, 194–202. doi:10.1016/j.jmbbm.2018.02.002
Keywords: visco-hyperelastic, traumatic brain injury (TBI), diffuse axonal injury (DAI), FEM, axonal damage
Citation: Kazempour M, Kazempour A, Baniassadi M, Remond Y and Baghani M (2021) Numerical Investigation of Axonal Damage for Regular and Irregular Axonal Distributions. Front. Mech. Eng 7:685519. doi: 10.3389/fmech.2021.685519
Received: 25 March 2021; Accepted: 03 May 2021;
Published: 17 May 2021.
Edited by:
Masoumeh Ozmaian, University of Texas at Austin, United StatesReviewed by:
Behrooz Fereidoonnezhad, National University of Ireland Galway, IrelandCopyright © 2021 Kazempour, Kazempour, Baniassadi, Remond and Baghani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mostafa Baghani, YmFnaGFuaUB1dC5hYy5pcg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.