A Nitric Oxide–Modulated Variable-Order Fractional Maxwell Viscoelastic Model of Cerebral Vascular Walls

It is well known that the mechanical behavior of arterial walls plays an important role in the pathogenesis of vascular diseases. Most studies existing in the literature focus on the mechanical interactions between the blood flow and wall’s deformations. However, in the brain, the smaller vessels experience not only oscillatory forces due to the pulsatile blood flow but also structural and morphological changes controlled by the surrounding brain cells. In this study, the mechanical deformation of the cerebral arterial wall caused by the pulsatile blood flow and the dynamics of the neuronal nitric oxide (NO) is investigated. NO is a small diffusive gaseous molecule produced by the endothelial cells and neurons, which is involved in the regulation of cerebral blood flow and pressure. The cerebral vessel is assumed to be a hollow axial symmetric cylinder whose wall thickness is much smaller than the cylinder’s radius and longitudinal length is much less than the propagating wavelength. The wall is an isotropic, homogeneous linear viscoelastic material described by an NO-modulated variable-order fractional Maxwell model. A fractional telegraph equation is obtained for the axial component of the displacement. Patterns of wall’s deformation are investigated through numerical simulations. The results suggest that a significantly decreased inactivation of the neuronal NO may cause a reduction in the shear stress at the blood-vessel interface, which could lead to a decrease in the production of shear-induced endothelial NO and neurovascular disease.

Introduction

Cerebral vasculature plays a critical role in brain’s metabolism and neurovascular conditions. The literature abounds with studies of cerebral blood flow and its interactions with the vasculature and brain cells [reviews of models and computer simulations can be found in chapter 4 of Drapaca and Sivaloganathan (2019)]. Recent advancements in technology have allowed researchers to gain invaluable knowledge about the intricate chemo-mechanical connections among neurons, glial, vascular, and blood cells. It is now acknowledged that the neurons and glial cells control the cerebral blood flow through the chemo-mechanical activation of the cells within the vascular wall (Attwell et al., 2010).

One of the many particles that facilitate the chemo-mechanical communications among the brain cells, blood, and the vascular wall is the nitric oxide (NO). A small diffusive gaseous molecule, the cerebral NO is mainly produced by shear-induced mechanotransduction at the blood-vessel interface (Sriram et al., 2016) and by synthesis reactions within the endothelial cells of the blood vessels and neurons (Forstermann and Sessa, 2012). NO diffuses and is removed from brain through some specialized chemical processes (Palacios-Callender et al., 2007; Unitt et al., 2010; Santos et al., 2011; Santos et al., 2012; Helms et al., 2016). In its role as a neuro-glial-vascular messenger, NO controls the cerebral blood flow and the release of neurotransmitters (Huang, 1999; Iadecola, 2004; Attwell et al., 2010; Contestabile et al., 2012; Iadecola, 2017). The regulation of the blood flow in brain is achieved through vasomotor mechanisms in which both the neuronal and endothelial NO are involved (Cockcroft, 2005; Metea and Newman, 2006; Attwell et al., 2010; Atochin and Huang, 2011; Petzold and Murthy, 2011; Contestabile et al., 2012; Lourenco et al., 2014; Haselden et al., 2020). However, throughout the entire cardiovascular system, the endothelial NO usually acts as a vasodilator (Attwell et al., 2010; Schuler et al., 2014). While the cerebral NO activity causes the local vasodilatation of downstream cerebral vessels at the neuro-glial-vascular unit site, the NO diffusion within the vascular wall relaxes the smooth muscle cells leading to the so-called remote vasodilation due to the propagation of muscle’s relaxation to the upstream arteries via the intercellular communications among endothelial and smooth muscle cells (Freed and Gutterman, 2017) facilitated by vascular gap junctions (Iadecola, 2004; Iadecola, 2017). Impaired cerebral NO production and/or decay can signal the presence of a neurovascular disease (Parker and Parks, 1995; Maurer et al., 2000; Wilkinson et al., 2004; Unitt et al., 2010; Santos et al., 2011; Haselden et al., 2020).

Although the NO-modulated vasodilation contributes to the mechanical deformation of the vascular walls of intracerebral vessels, existing mathematical models and corresponding numerical simulations of blood flow interacting with the deformable vascular wall do not account for it since their focus is the mechanics of big arteries in the presence of the pulsatile blood flow. The arteries are usually modeled as anisotropic, incompressible, nonlinear elastic materials whose constitutive stress-strain relationships may also incorporate collagen fibers’ orientations and waviness, and/or the activation of smooth muscle cells (see Ebrahimi, 2009; Holzapfel and Ogden, 2010; Kim and Wagenseil, 2014; Espinosa et al., 2018 and references within). For instance, muscle activation has been modeled using 1) the (original or modified) Hill model (Hill, 1938), 2) an elastic strain-energy function dependent on the concentration of free intracellular calcium (Rachev and Hayashi, 1999), 3) a strain-energy function dependent on the chemical kinetics of the smooth muscle (Stalhand et al., 2008), and 4) a lumped Hodgkin-Huxley-like electrical circuit of the smooth muscle cell membrane coupled with a fluid compartment model describing the mass balances of considered ions and a contractile kinematics model regulated by intracellular calcium (Yang et al., 2003). Given the viscoelastic behavior of constituent cells (Kasza et al., 2007) of the blood vessels (and biological tissues, in general), the vascular wall has also been modeled as a viscoelastic material (Toth et al., 1998; Orosz et al., 1999; Holzapfel et al., 2002; Hodis and Zamir, 2008; Ebrahimi, 2009). Since these models do not incorporate the NO influence on the vascular wall, they are not able to predict neurovascular pathologies in which NO plays a critical role. Furthermore, the coupling of most of the above models with the cerebral NO dynamics will probably increase the already large number of model parameters that are practically impossible to find in a living brain with minimally invasive procedures using present-day technologies.

The aim of this study is to propose a novel mechanical model for cerebral arterioles that accounts for changes in the wall’s mechanical behavior due to the NO-activated vascular cells and has few parameters. Orosz et al. (1999) used stress-relaxation measurements in cerebral arteries of human cadavers to show that four- and five-element generalized Maxwell viscoelastic models provide more accurate descriptions of the vascular wall mechanics than the two-element Maxwell viscoelastic model. One way to obtain a linear viscoelastic constitutive law with fewer parameters that perform as well as (or better) a spring-dashpot model with many elements is to use an integral formulation instead of the differential operator representation commonly associated with rheological (spring-dashpot) models. Integral constitutive laws admit equivalent differential formulations only for certain expressions of their relaxation functions (Gurtin and Sternberg, 1965; Drapaca et al., 2007). It was observed experimentally that relaxation functions represented as power functions of negative fractional exponents accurately describe the fading memory of many viscoelastic materials, including polymers and soft biological tissues (Nutting, 1921; Gemant, 1935; Gemant, 1936; Scott Blair and Coppen, 1939; Scott Blair and Coppen, 1942; Nutting, 1943; Guttinger, 1966; Caputo and Mainardi, 1971; Bagley and Torvik, 1983a; Bagley and Torvik, 1983b; Koeller, 1984; Torvik and Bagley, 1984; Suki et al., 1994; Mainardi, 2010). Integral constitutive laws with decaying fraction power-law relaxation functions have equivalent differential representations like those used in classic rheological models where integer-order derivatives were replaced by fractional-order derivatives (convolutions between decaying fraction power functions and integer-order derivatives). These fractional viscoelastic models are causal at zero time (Bagley and Torvik, 1983b; Torvik and Bagley, 1984) and can be derived from molecular theories that incorporate the molecular complexity of various polymers (Bagley and Torvik, 1983b; Suki et al., 1994). In this context, the fractional order of the strain history models the “contribution of the long-chain molecules to the macroscopic stress” (Suki et al., 1994). Also, Suki et al. (1994) noticed the structural similarities between the lung tissue and some polymers and showed that a fractional viscoelastic model can successfully predict the viscoelastic behavior of lung tissue. Given that lungs are highly vascularized, it is reasonable to assume that a fractional viscoelastic model could be employed in studies of blood vessels mechanics.

Therefore, this study proposes a new NO-modulated variable-order fractional Maxwell viscoelastic model for the cerebral vascular wall and investigates its predictions through numerical simulations. The suggested constitutive equation is a generalization of the (constant order) fractional Maxwell viscoelastic model (see, for instance, Mainardi, 2010). The classic (first-order) Maxwell viscoelastic model has been previously used in the literature to model vascular walls (see, for instance, Hodis and Zamir, 2008), and therefore, this is the model which was chosen to be generalized here. According to Lorenzo and Hartley (2002), variable-order fractional operators are suitable in modeling, for instance, the fading memory characteristic of viscoelastic materials and the order memory which records the order in which memories are recalled [a recent review of applications of variable-order fractional operators can be found in Patnaik et al. (2020)]. In the model proposed here, the neuronal NO dynamics controls the order memory. With only three parameters, the proposed model can account for vessel’s mechanics and the fact that the order memory of chemo-mechanical events is essential to the proper functionality of the constituent cells of the vascular wall. Lastly, the vascular wall is assumed to be isotropic and homogeneous.

As in Hodis and Zamir (2008), it is further assumed that the cerebral vessel is a hollow axial symmetric cylinder whose wall thickness is much smaller than the cylinder’s radius, and longitudinal length is much less than the propagating wavelength. These assumptions together with the new constitutive equation led to a variable-order fractional telegraph equation for the unknown axial displacement of the vessel’s wall. By assuming that the blood-vessel interface was exposed to the pulsatile blood flow and the vessel-tissue interface was tethered (Hodis and Zamir, 2008), an initial-boundary value problem was obtained and solved using the separation of variables method and finite difference schemes. The assumption of a tethered vessel-tissue interface is supported by experiments performed using high-resolution ultrasonic scanning that shows significantly larger longitudinal displacements of the wall’s middle layers than the corresponding displacements of the wall’s outer layers (Persson et al., 2003; Cinthio et al., 2006). Lastly, the variable fractional order was taken to be proportional to the concentration of neuronal NO. Two cases of neuronal NO synthesis (NOS) were considered: 1) a stepwise activation of NO with drastically decreased NO inactivation and 2) a dynamic activation of NO (Hall and Garthwaite, 2006). Case 1 may not be physiological because the main neuronal NOS activation matches the short pulsatile Ca²⁺- calmodulin binding activation in dendritic spines (Hall and Garthwaite, 2006), and thus, this case may model impaired neuronal NO dynamics. Indeed, the temporal variation of NO resembles a stepwise function when the NO inactivation is drastically reduced by either brain ischemia (Santos et al., 2011) or the inhibition of cytochrome c oxidase (COX) (Palacios-Callender et al., 2007; Unitt et al., 2010). Brains of Alzheimer disease (AD) patients may suffer from a COX inhibition and thus an accumulation of NO (primarily in the temporal cortex and hippocampus) because a selective defect of COX causing a significant reduction in COX activity was found in AD brains (Parker and Parks, 1995; Maurer et al., 2000). Numerical simulations generated in MATLAB show smaller displacements within the vascular wall in the case of stepwise NOS than in the case of dynamic NOS. Also, the shear stress at the bloodvessel interface is smaller in the case of stepwise neuronal NOS. Since the production of shear-induced endothelial NO is proportional to the shear stress at the inner boundary of the vessel’s wall (Sriram et al., 2016), it follows that less endothelial NO will be produced in this case which could ultimately lead to neurovascular disease. Thus, the model could be used as a complementary clinical tool for early detection of disease and intervention (Alzheimer, for instance).

The study is structured as follows. The proposed mathematical model and the initial-boundary value problem under investigation are presented in Mathematical Model. The corresponding semi-analytic solution is given in Semi-Analytic Solution. Numerical simulations are shown in Results, which is followed by the last section containing a discussion of the results and final conclusions.

Mathematical Model

The vessel is modeled as a hollow horizontal axial symmetric circular cylinder of radius $\mathit{a}$ and thickness $\mathit{h}$ (Figure 1). As in Hodis and Zamir (2008), it is assumed that the vessel’s wall is made of a homogeneous, linear viscoelastic material that is tethered at the outer boundary (the wall-tissue interface) and exposed to oscillations caused by the heart pulsations at its inner boundary (the blood-wall interface). In addition, it is assumed that the spatial variations of the oscillations can be neglected in a first approximation because they are of the same order of magnitude as the propagating wavelength (which is approximately $10\mathit{ m}$ at a frequency of $1\mathit{ Hz}$ in the systemic circulation) while the vessel’s length is much smaller than the wavelength. Thus, only the time variations of the oscillations at the inner boundary of the vessel’s wall will contribute to the wall’s deformation. If $\left(\mathbf{r,\theta ,x}\right)$ are the cylindrical coordinates, then the modeling assumptions made so far reduce the equation of motion which is relevant to the work presented here to the following equation (Hodis and Zamir, 2008):

$\mathit{\rho }\frac{{\partial }^2\mathit{\xi }}{\partial {\mathit{t}}^2}=\frac{\partial {\mathit{\sigma }}_{\mathit{rx}}}{\partial \mathit{r}}+\frac{{\mathit{\sigma }}_{\mathit{rx}}}{\mathit{r}},(1)$

for $\left(\mathit{r,t}\right)\in \left(\mathit{a,a+h}\right)\mathbf{\times }\left[\mathit{0,T}\right]$. In Eq. 1, $\mathit{\rho }$ is the mass density, $\mathit{\xi }\left(\mathit{r},\mathit{t}\right)$ is the axial displacement of a material point of the vessel’s wall, and ${\mathit{\sigma }}_{\mathit{rx}}\left(\mathit{r},\mathit{t}\right)$ is the shear stress of a wall’s point. Lastly, because the wall thickness $\mathit{h}$ is usually much smaller than the radius $\mathit{a}$, the curvature term ${\mathit{\sigma }}_{\mathit{rx}}/\mathit{r}$ is smaller than the other terms of Eq. 1, and thus, it can be neglected. Therefore, Eq. 1 reduces to (Hodis and Zamir, 2008):

$\mathit{\rho }\frac{{\mathbf{\partial }}^2\mathit{\xi }}{\partial {\mathit{t}}^{\mathbf{2}}}=\frac{\partial {\mathit{\sigma }}_{\mathit{rx}}}{\partial \mathit{r}}.(2)$

FIGURE 1

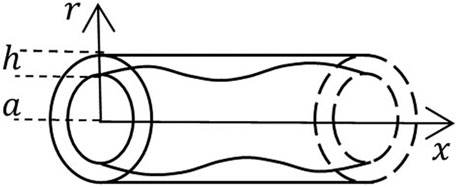
FIGURE 1. A schematic of the geometric domain occupied by a vessel of radius $\mathit{a}$ and wall thickness $\mathit{h}$. The model assumes a hollow horizontal axial symmetric circular cylinder whose wall has a fixed outer boundary and an oscillatory inner boundary.

In this study, it is assumed that the mechanical behavior of the vessel’s wall is described by the constitutive equation of a variable-order fractional Maxwell linear viscoelastic material:

${\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}{\mathit{\sigma }}_{\mathit{rx}}=\mathit{E}\left({\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}{\mathit{\epsilon }}_{\mathit{rx}}-\frac{{\mathit{\sigma }}_{\mathit{rx}}}{{\mathit{\mu }}_{\mathit{\alpha }}}\right),(3)$

where, based on the model’s assumptions, the infinitesimal strain ${\mathit{\epsilon }}_{\mathit{rx}}$ reduces to:

${\mathit{\epsilon }}_{\mathit{rx}}=\frac{\partial \mathit{\xi }}{\partial \mathit{r}}.(4)$

The constitutive Eq. 3 has three physical parameters: $\mathit{E}$, the modulus of elasticity, ${\mathit{\mu }}_{\mathit{\alpha }}$, and $\mathit{\alpha }\left(\mathit{t}\right),0<\mathit{\alpha }\left(\mathit{t}\right)\le 1$. Without loss of generality, it is assumed further that ${\mathbf{\epsilon }}_{\mathit{rx}}\left(\mathit{r},0+\right)\mathbf{=0}$ and ${\mathbf{\sigma }}_{\mathit{rx}}\left(\mathit{r,0+}\right)\mathbf{=0}$ (Bazhlekova and Bazhlekov, 2017). Lastly, the variable-order fractional derivative used in Eq. 3 is as follows (see for instance Ramirez and Coimbra, 2010; Moghaddam and Machado, 2017):

${\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}\mathit{\phi }\left(\mathit{t}\right)=\{\begin{array}{c}\frac{1}{\mathit{\Gamma }\left(1-\mathit{\alpha }\left(\mathit{t}\right)\right)}{\displaystyle \underset{0}{\overset{\mathit{t}}{\int }}\frac{{\mathit{\phi }}^{\left(\mathit{m}\right)}\left(\mathit{s}\right)\mathit{ds}}{{\left(\mathit{t}-\mathit{s}\right)}^{\mathit{\alpha }\left(\mathit{t}\right)}}},\mathbf{i}\mathbf{f}\mathit{m}-1<\mathit{\alpha }\left(\mathit{t}\right)<\mathit{m},\mathbf{\forall }\mathit{t}>0\\ {\mathit{\phi }}^{\left(\mathit{m}\right)}\left(\mathit{t}\right),\mathbf{i}\mathbf{f}\mathit{\alpha }\left(\mathit{t}\right)=\mathit{m},\forall \mathit{t}>0\\ \frac{1}{\mathit{\Gamma }\left(-\mathit{\alpha }\left(\mathit{t}\right)\right)}\underset{0}{\overset{\mathit{t}}{{\displaystyle \int }}}\frac{\mathit{\phi }\left(\mathit{s}\right)\mathit{ds}}{{\left(\mathit{t}-\mathit{s}\right)}^{1+\mathit{\alpha }\left(\mathit{t}\right)}},\mathbf{i}\mathbf{f}\mathit{\alpha }\left(\mathit{t}\right)<0,\forall \mathit{t}>0\end{array},(5)$

where$\mathit{m}\in \left\{\mathrm{1,2,3}\dots \right\},$ $\mathit{\phi }\left(\mathit{t}\right)$ is an arbitrary, continuously ${\mathit{m}}^{\text{th}}$-order differentiable function whose ${\mathit{m}}^{\text{th}}$-order derivative is denoted by ${\mathit{\phi }}^{\left(\mathit{m}\right)}\left(\mathit{t}\right)$ such that ${\mathit{\phi }}^{\left(\mathit{k}\right)}\left(0+\right)=0,\mathit{k}\in \left\{\mathrm{0,1},\dots \mathit{m}-1\right\}$, $\mathit{\alpha }\left(\mathit{t}\right)$ is a continuously differentiable function, and $\mathit{\Gamma }\left(\mathit{z}\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\mathbf{y}}^{\mathbf{z-1}}\mathbf{exp}\left(-\mathit{y}\right)\mathit{dy}\left(\mathbf{Re}\left(\mathit{z}\right)>0\right)}$ is the gamma function. For $\mathit{\alpha }\left(\mathit{t}\right)$ constant, the fractional derivative given by Eq. 5 reduces to the Caputo fractional derivative (see, for instance, Caputo and Mainardi, 1971).

According to Ramirez and Coimbra (2010), Eq. 5 is desirable in modeling of physical processes since a physical interpretation of the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)\in \left(\mathbf{0,1}\right)$ can be provided in this case: the order of a variable-order model describing the dynamics of a viscoelastic oscillator in stationary motion is a normalized phase shift. Since Eq. 5 preserves the well-known formula of calculating the integer-order derivative of a monomial (Samko and Ross, 1993), the following property holds for nonconstant analytic functions satisfying the zero initial conditions mentioned above (Theorem 1, pg. 82 in West et al., 2003):

${\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}{\partial }_{\mathit{t}}^{\mathit{\beta }\left(\mathit{t}\right)}\mathit{\phi }\left(\mathit{t}\right)={\partial }_{\mathit{t}}^{\mathit{\beta }\left(\mathit{t}\right)}{\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}\mathit{\phi }\left(\mathit{t}\right)={\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)+\mathit{\beta }\left(\mathit{t}\right)}\mathit{\phi }\left(\mathit{t}\right),(6)$

Equation 6 yields ${\partial }_{\mathit{t}}^{\mathit{\alpha }\left(\mathit{t}\right)}{\partial }_{\mathit{t}}^{-\mathit{\alpha }\left(\mathit{t}\right)}\mathit{\phi }\left(\mathit{t}\right)=\mathit{\phi }\left(\mathit{t}\right).$

From Eq. 5 and the zero initial conditions satisfied by ${\mathit{\epsilon }}_{\mathit{rx}}$ and ${\mathit{\sigma }}_{\mathit{rx}}$, it follows that Eq. 3 becomes the fractional Maxwell model for $\mathit{\alpha }\left(\mathit{t}\right)$ a constant in the interval $\left(\mathrm{0,1}\right)$ and reduces to the classic Maxwell model for $\mathit{\alpha }\left(\mathit{t}\right)=1,\mathbf{\forall }\mathit{t}>0.$ Note that in the classic Maxwell model parameter ${\mathit{\mu }}_{\mathit{\alpha }}$ becomes the viscosity denoted by $\mathit{\mu }$. When the fractional order is a constant $\mathit{\alpha }\in \left(\mathrm{0,1}\right)$, properties of the (Caputo) fractional derivative Eq. 5 and the Laplace transform can be combined to obtain the following expressions for the creep compliance $\mathit{J}$ and relaxation modulus $\mathit{G}$ (Mainardi, 2010; Bazhlekova and Bazhlekov, 2017):

$\mathit{J}\left(\mathit{t}\right)=\frac{1}{\mathit{E}}\left(\frac{\mathit{g}}{\mathit{\Gamma }\left(1+\mathit{\alpha }\right)}{\mathit{t}}^{\mathit{\alpha }}+1\right),\mathit{G}\left(\mathit{t}\right)=\mathit{E}{\mathit{E}}_{\mathit{\alpha }}\left(-\mathit{g}{\mathit{t}}^{\mathit{\alpha }}\right),(7)$

where $\mathit{g}=\mathit{E}/{\mathit{\mu }}_{\mathit{\alpha }}$ and the Mittag-Leffler function is, by definition, ${\mathit{E}}_{\mathit{\alpha }}\left(\mathit{z}\right)={\displaystyle \sum _{\mathit{k}=0}^{\infty }\frac{{\mathit{z}}^{\mathit{k}}}{\mathit{\Gamma }\left(\mathit{\alpha k}+1\right)}}$ . Figure 2 shows plots of dimensionless material functions $\mathit{EJ}$ and $\mathit{G}/\mathit{E}$ given by Eq. 7 versus the dimensionless time $\overline{\mathit{t}}=\mathit{t}/\mathit{T}$ for various values of $\mathit{\alpha }$. Thus, the material functions for a variable order $\mathit{\alpha }\left(\mathit{t}\right)\in \left(\mathrm{0,1}\right)$ will combine the behavior of multiple material functions shown in Figure 2.

FIGURE 2

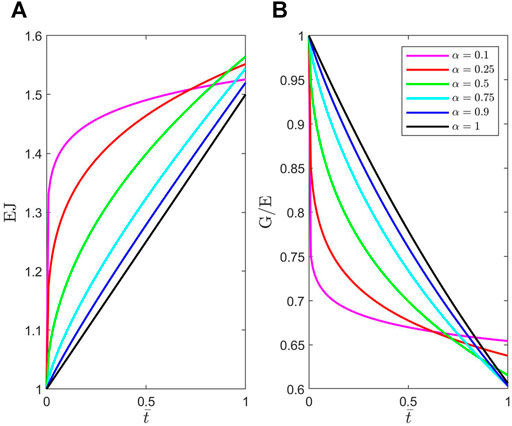
FIGURE 2. Plots of dimensionless material functions (A) $\mathit{EJ}$ and (B) $\mathit{G}/\mathit{E}$ given by Eq. 7 versus the dimensionless time $\overline{\mathit{t}}$ for various constant values of $\mathit{\alpha }\in \mathbf{(}\mathrm{0,1})$.

Replacing Eq. 4 in Eq. 3, applying operator ${\partial }_{\mathit{t}}^{-\mathit{\alpha }\left(\mathit{t}\right)}$ to Eq. 3, and using Eq. 6 give:

${\mathit{\sigma }}_{\mathit{rx}}=\mathit{E}\left(\frac{\partial \mathit{\xi }}{\partial \mathit{r}}-\frac{1}{{\mathit{\mu }}_{\mathit{\alpha }}}{\partial }_{\mathit{t}}^{-\mathit{\alpha }\left(\mathit{t}\right)}{\mathit{\sigma }}_{\mathit{rx}}\right).(8)$

Differentiating Eq. 8 with respect to the spatial variable $\mathit{r}$ and using Eq. 2 yield:

$\frac{\mathbf{\partial }{\mathit{\sigma }}_{\mathit{rx}}}{\partial \mathit{r}}=\mathit{ E}\left(\frac{{\partial }^2\mathit{\xi }}{\partial {\mathit{r}}^2}-\frac{\mathit{\rho }}{{\mathit{\mu }}_{\mathit{\alpha }}}{\partial }_{\mathit{t}}^{2-\mathit{\alpha }\left(\mathit{t}\right)}\mathit{\xi }\right).(9)$

Lastly, by replacing Eq. 9 in Eq. 2 the following equation is obtained:

$\frac{{\partial }^2\mathit{\xi }}{\partial {\mathit{t}}^2}+\mathit{g}{\partial }_{\mathit{t}}^{2-\mathit{\alpha }\left(\mathit{t}\right)}\mathit{\xi }=\frac{\mathit{E}}{\mathit{\rho }}\frac{{\partial }^2\mathit{\xi }}{\partial {\mathit{r}}^2},(10)$

Eq. 10 is a variable-order fractional telegraph equation (or two-term time-variable fractional diffusion-wave equation).

The initial and boundary conditions are as follows:

$\mathit{\xi }\left(\mathit{r},0\right)=0,\frac{\partial \mathit{\xi }}{\partial \mathit{t}}\left(\mathit{r},0\right)={\mathit{\xi }}_0\mathit{\omega ,}(11)$

$\mathit{\xi }\left(\mathit{a},\mathit{t}\right)={\mathit{\xi }}_0\mathbf{sin}\mathit{\omega t},\mathit{\xi }\left(\mathit{a}+\mathit{h},\mathit{t}\right)=0.(12)$

It is assumed that the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)\in \left(\mathrm{0,1}\right)$ models the temporal effects of the neuronal NO on the vessel’s wall. At this incipient stage, the shape of $\mathit{\alpha }\left(\mathit{t}\right)$ is considered to look like the temporal profile of the concentration of neuronal NO. Hall and Garthwaite (2006) proposed two models of neuronal NO dynamics: 1) stepwise activation of NO and 2) dynamic activation of NO. Both models include the NO inactivation. The equation of the first model is as follows:

$\frac{\mathit{d}\left[\mathit{NO}\right]}{\mathit{dt}}={\mathit{\nu }}_1-\frac{{\mathit{V}}_{\mathit{max}}\left[\mathit{NO}\right]}{{\mathit{K}}_{\mathit{m}}+\left[\mathit{NO}\right]},$

whose approximate analytic solution for zero initial condition is (Mehala and Rajendran, 2014) as follows:

$\left[\mathit{NO}\right]\left(\mathit{t}\right)=\frac{{\mathit{\nu }}_1}{\mathit{\kappa }}\left(1-\mathbf{exp}\left(-\mathit{\kappa t}\right)\right).(13)$

The equation of the second model is as follows:

$\frac{\mathit{d}\left[\mathit{NO}\right]}{\mathit{dt}}={\mathit{\nu }}_1\left(1-\mathbf{exp}\left(-{\mathit{k}}_1\mathit{t}\right)\right)\mathbf{exp}\left(-{\mathit{k}}_2\mathit{t}\right)-\frac{{\mathit{V}}_{\mathit{max}}\left[\mathit{NO}\right]}{{\mathit{K}}_{\mathit{m}}+\left[\mathit{NO}\right]}$

whose approximate analytic solution for zero initial condition is (Mehala and Rajendran, 2014) as follows:

$\left[\mathit{NO}\right]\left(\mathit{t}\right)={\mathit{\nu }}_1\left(\frac{-\mathbf{exp}\left(-{\mathit{k}}_2\mathit{t}\right)}{{\mathit{k}}_2-\mathit{\kappa }}+\frac{-\mathbf{exp}\left(-\left({\mathit{k}}_1+{\mathit{k}}_2\right)\mathit{t}\right)}{{\mathit{k}}_1+{\mathit{k}}_2-\mathit{\kappa }}+\mathbf{exp}\left(-\mathit{\kappa t}\right)\left(\frac{1}{{\mathit{k}}_2-\mathit{\kappa }}-\frac{1}{{\mathit{k}}_1+{\mathit{k}}_2-\mathit{\kappa }}\right)\right).(14)$

Here, $\left[\mathit{NO}\right]$ is the concentration of NO, ${\mathit{\nu }}_1$ is the constant rate of NOS, ${\mathit{V}}_{\mathit{max}}$ is the maximum rate at saturating concentration of NO, ${\mathit{K}}_{\mathit{m}}$ is the concentration of NO at which the reaction rate is $\frac{{\mathit{V}}_{\mathit{max}}}{2}$, ${\mathit{k}}_1$ and ${\mathit{k}}_2$ are constant kinetic parameters, and $\mathit{\kappa }={\mathit{V}}_{\mathit{max}}/{\mathit{K}}_{\mathit{m}}$. The values in Table 1 were chosen such that the numerical solutions to the above differential equations for $\left[\mathit{NO}\right]$ and the corresponding approximate analytic solutions agree (Mehala and Rajendran, 2014). Figures 3A,B show plots of the NO concentrations given by Eqs 13, 14, respectively, while Figures 3C,D show two proposed profiles for the variable order $\mathit{\alpha }\left(\mathit{t}\right)\in \left(\mathrm{0,1}\right)$ which are obtained by simply multiplying the NO concentrations shown in Figures 3A,B by a factor of ${10}^2$. The scaling factor was chosen as follows. As seen in Figures 3A,B, the maximum concentrations of NO are in the low picomolar rage, while physiological values are in the low nanomolar range (Hall and Garthwaite, 2006). A mere multiplication of the NO concentrations by ${10}^2$ brings the maximum values within the physiological range for the NO concentrations. Since these scaled concentrations are still less than $1\mathit{ nM}$, they can be used as expressions for $\mathit{\alpha }\left(\mathit{t}\right).$ Another advantage of this scaling factor is that significant differences are observed between the displacements and the shear stresses at the blood-vessel interface corresponding to the two profiles of $\mathit{\alpha }\left(\mathit{t}\right)$ shown in Figures 3C,D (see later).

TABLE 1

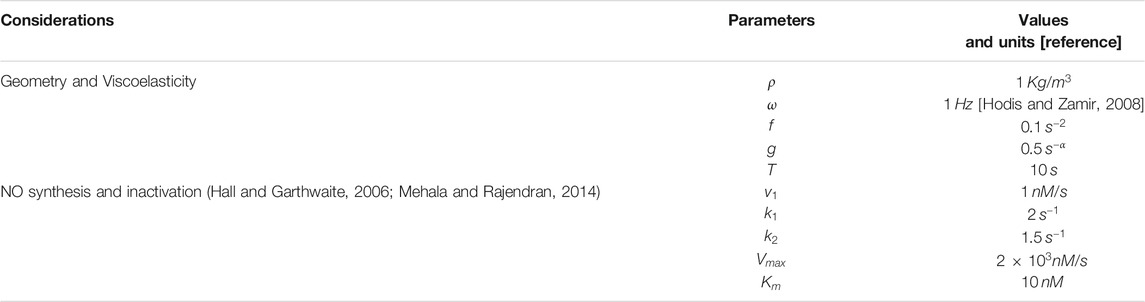
TABLE 1. List of parameters with corresponding values and units. Due to a lack of experimental data, the value of $T$ was fixed first, and then, the values of $f$ and $g$ were chosen such that a semi-analytic solution could be found for the initial boundary value problem Eqs 15–17. The normalized value of the wall’s density was chosen for mathematical simplicity.

FIGURE 3

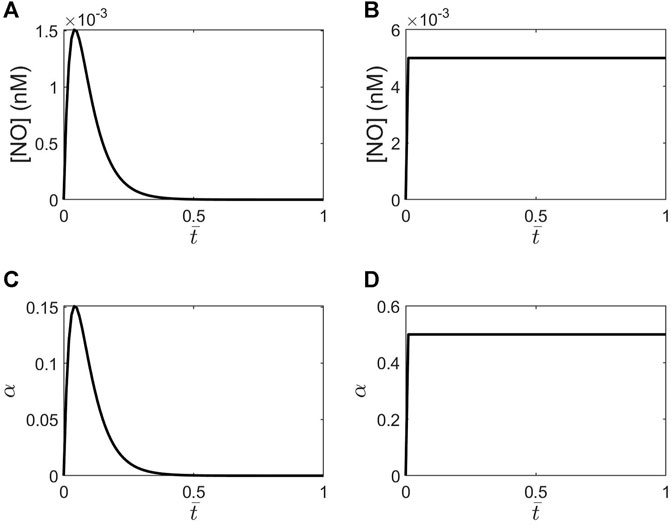
FIGURE 3. Plots of NO concentrations versus the dimensionless time $\overline{\mathit{t}}$ for (A) the dynamic synthesis of NO (Eq. 14) and (B) the stepwise synthesis of NO (Eq. 13). The proposed shapes for the variable order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the two cases of NOS (A) and (B) are shown in plots (C) and (D), respectively.

The aim of the study is to find a semi-analytic solution to the initial-boundary value problem (10–12) for two variable orders given by scaled Eqs 13, 14. The first step is to formulate a corresponding non-dimensional problem. By introducing the dimensionless quantities:

$\overline{\mathit{r}}=\frac{\mathit{r}-\mathit{a}}{\mathit{h}},\hspace{1em}\overline{\mathit{t}}=\frac{\mathit{t}}{\mathit{T}},\hspace{1em}\overline{\mathit{\xi }}=\frac{\mathit{\xi }}{{\mathit{\xi }}_0},$

the initial-boundary value problem (10–12) transforms into the following dimensionless form:

$\frac{{\partial }^{\mathbf{2}}\overline{\mathit{\xi }}}{\partial {\overline{\mathit{t}}}^{\mathbf{2}}}+\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}\overline{\mathit{\xi }}=\mathit{f}{\mathit{T}}^{\mathbf{2}}\frac{{\partial }^{\mathbf{2}}\overline{\mathit{\xi }}}{\partial {\overline{\mathit{r}}}^{\mathbf{2}}},\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)\in {\left(\mathbf{0,1}\right)}^{\mathbf{2}},(15)$

$\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\mathbf{0}\right)=\mathbf{0},\frac{\partial \overline{\mathit{\xi }}}{\partial \overline{\mathit{t}}}\left(\overline{\mathit{r}},\mathbf{0}\right)=\mathit{\omega T, }(16)$

$\overline{\mathit{\xi }}\left(\mathbf{0},\overline{\mathit{t}}\right)=\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right),\overline{\mathit{\xi }}\left(\mathbf{1},\overline{\mathit{t}}\right)=\mathbf{0.}(17)$

In Eq. 15, $\mathit{f}=\mathit{E}/\left(\mathit{\rho }{\mathit{h}}^{\mathbf{2}}\right)$. The solution for problem (15–17) is presented in the next section.

Semi-Analytic Solution

A classic approach of solving initial-boundary value problems for partial differential equations is used. Look for a solution to problem (15–17) of the form:

$\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\mathit{V}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)+\mathit{W}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right),(18)$

such that $\mathit{V}\left(\mathbf{0},\overline{\mathit{t}}\right)=\overline{\mathit{\xi }}\left(\mathbf{0},\overline{\mathit{t}}\right)=\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right),\mathit{V}\left(\mathbf{1},\overline{\mathit{t}}\right)=\overline{\mathit{\xi }}\left(\mathbf{1},\overline{\mathit{t}}\right)=\mathbf{0}$ and $\frac{{\partial }^{\mathbf{2}}\mathit{V}}{\partial {\overline{\mathit{r}}}^{\mathbf{2}}}=\mathbf{0}$. It is straightforward to solve for $\mathit{V}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)$ and find that:

$\mathit{V}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\left(\mathbf{1}-\overline{\mathit{r}}\right)\sin \left(\mathit{\omega T}\overline{\mathit{t}}\right).(19)$

Combining Eqs 18, 19 yields:

$\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\left(\mathbf{1}-\overline{\mathit{r}}\right)\mathbf{sin}\left(\mathit{\omega }\mathit{T}\overline{\mathit{t}}\right)+\mathit{W}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right).(20)$

By substituting Eq. 20 in problem (15–17), the following initial-boundary value problem for $\mathit{W}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)$ is obtained:

$\frac{{\partial }^{\mathbf{2}}\mathit{W}}{\partial {\overline{\mathit{t}}}^{\mathbf{2}}}+\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}\mathit{W}=\mathit{f}{\mathit{T}}^{\mathbf{2}}\frac{{\partial }^{\mathbf{2}}\mathit{W}}{\partial {\overline{\mathit{r}}}^{\mathbf{2}}}+\left(1-\overline{\mathit{r}}\right)\left[{\left(\mathit{\omega T}\right)}^{\mathbf{2}}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)-\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}\left(\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)\right)\right],(21)$

$\mathit{W}\left(\overline{\mathit{r}},\mathbf{0}\right)=\mathbf{0},\frac{\partial \mathit{W}}{\partial \overline{\mathit{t}}}\left(\overline{\mathit{r}},\mathbf{0}\right)=\mathit{\omega T}\overline{\mathit{r}}\mathit{,}(22)$

$\mathit{W}\left(\mathbf{0},\overline{\mathit{t}}\right)=\mathbf{0},\mathit{W}\left(\mathbf{1},\overline{\mathit{t}}\right)=\mathbf{0.}(23)$

The first step in solving problem (21–23) is to look for a solution to the corresponding homogeneous equation:

$\frac{{\partial }^{\mathbf{2}}\mathit{W}}{\partial {\overline{\mathit{t}}}^{\mathbf{2}}}+\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}\mathit{W}=\mathit{f}{\mathit{T}}^{\mathbf{2}}\frac{{\partial }^{\mathbf{2}}\mathit{W}}{\partial {\overline{\mathit{r}}}^{\mathbf{2}}}.(24)$

The method of separation of variables suggests looking for a solution of the form $\mathit{W}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\mathit{F}\left(\overline{\mathit{t}}\right)\mathit{G}\left(\overline{\mathit{r}}\right)$. Then, Eq. 24 and the boundary conditions (Eq. 23) yield the following Sturm-Liouville problem for $\mathit{G}\left(\overline{\mathit{r}}\right)$:

$\mathit{f}{\mathit{T}}^{\mathbf{2}}\frac{{\mathit{d}}^{\mathbf{2}}\mathit{G}}{\mathit{d}{\overline{\mathit{r}}}^{\mathbf{2}}}-\mathit{\lambda G}=\mathbf{0},\hspace{1em}\mathit{G}\left(\mathbf{0}\right)=\mathit{G}\left(\mathbf{1}\right)=\mathbf{0}(25)$

Thus, the eigenfunctions satisfying problem (25) are ${\mathit{G}}_{\mathit{n}}\left(\overline{\mathit{r}}\right)=\mathbf{sin}\left(\mathit{n\pi }\overline{\mathit{r}}\right),\mathit{n}\in \left\{\mathbf{1,2,3}\dots \right\},$ and the corresponding eigenvalues are ${\mathit{\lambda }}_{\mathit{n}}=-{\left(\mathit{n\pi T}\right)}^{\mathbf{2}}\mathit{f}, \mathit{n}\in \left\{\mathbf{1,2,3}\dots \right\}$. The solution to problem (21, 22) is thus of the form:

$\mathit{W}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)={\displaystyle \sum _{\mathit{n}=\mathbf{1}}^{\infty }{\mathit{A}}_{\mathit{n}}\left(\overline{\mathit{t}}\right)\sin \left(\mathit{n\pi }\overline{\mathit{r}}\right)}.(26)$

Substituting Eq. 26 in problem (21, 22) and using the half-range Fourier sine series expansions of the functions $1-\overline{\mathit{r}}$ and $\overline{\mathit{r}}$ yield the following initial value problem for ${\mathit{A}}_{\mathit{n}}\left(\overline{\mathit{t}}\right),\mathit{n}\in \left\{\mathbf{1,2,3}\dots \right\}$:

$\frac{{\mathit{d}}^{\mathbf{2}}{\mathit{A}}_{\mathit{n}}}{\mathit{d}{\overline{\mathit{t}}}^{\mathbf{2}}}+\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\mathit{A}}_{\mathit{n}}=-\mathit{f}{\left(\mathit{n\pi T}\right)}^{\mathbf{2}}{\mathit{A}}_{\mathit{n}}+\frac{\mathbf{2}}{\mathit{n\pi }}\left[{\left(\mathit{\omega T}\right)}^{\mathbf{2}}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)-\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}\left(\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)\right)\right],(27)$

${\mathit{A}}_{\mathit{n}}\left(\mathbf{0}\right)=\mathbf{0},\mathit{ }\frac{\mathit{d}{\mathit{A}}_{\mathit{n}}}{\mathit{d}\overline{\mathit{t}}}\left(\mathbf{0}\right)=\mathbf{2}\mathit{\omega T}\frac{{\left(-\mathbf{1}\right)}^{\mathit{n}+\mathbf{1}}}{\mathit{n\pi }}.(28)$

Let

${\mathit{Z}}_{\mathit{n}}\left(\overline{\mathit{t}}\right)={\mathit{A}}_{\mathit{n}}\left(\overline{\mathit{t}}\right)+\frac{\mathbf{2}}{\mathit{n\pi }}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right),\mathit{n}\in \left\{\mathbf{1,2,3}\dots \right\}.(29)$

By replacing expression (29) in problem (27, 28), the following problem for the unknown function ${\mathit{Z}}_{\mathit{n}}\left(\overline{\mathit{t}}\right),\mathit{n}\in \left\{\mathbf{1,2,3}\dots \right\}$ is obtained:

$\frac{{\mathit{d}}^{\mathbf{2}}{\mathit{Z}}_{\mathit{n}}}{\mathit{d}{\overline{\mathit{t}}}^2}+\mathit{B}{\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left(\overline{\mathit{t}}\right)}{\mathit{Z}}_{\mathit{n}}+{\mathit{C}}_{\mathit{n}}{\mathit{Z}}_{\mathit{n}}={\mathit{D}}_{\mathit{n}}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right),(30)$

${\mathit{Z}}_{\mathit{n}}\left(\mathbf{0}\right)=\mathbf{0},\frac{\mathit{d}{\mathit{Z}}_{\mathit{n}}}{\mathit{d}\overline{\mathit{t}}}\left(\mathbf{0}\right)={\mathit{F}}_{\mathit{n}},(31)$

where $\mathit{B}=\mathit{g}{\mathit{T}}^{\mathit{\alpha }\left(\overline{\mathit{t}}\right)},{\mathit{C}}_{\mathit{n}}={\left(\mathit{n\pi }\mathit{T}\right)}^{\mathbf{2}}\mathit{f},{\mathit{D}}_{\mathit{n}}=\mathbf{2}\mathit{n\pi }{\mathit{T}}^{\mathbf{2}}\mathit{f}$, and ${\mathit{F}}_{\mathit{n}}=\mathbf{2}\mathit{\omega T}\frac{{\left(-\mathbf{1}\right)}^{\mathit{n}+\mathbf{1}}+\mathbf{1}}{\mathit{n\pi }}$. Once the solution to the initial value problem (30, 31) is found, Eqs 20, 26, and 29 can be combined to find the solution to the original problem (15–17):

$\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\left(\mathbf{1}-\overline{\mathit{r}}\right)\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)+{\displaystyle \sum _{\mathit{n}=1}^{\infty }\left[{\mathit{Z}}_{\mathit{n}}\left(\overline{\mathit{t}}\right)-\frac{2}{\mathit{n\pi }}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)\right]\mathbf{sin}\left(\mathit{n\pi }\overline{\mathit{r}}\right)},(32)$

Thus, the last step is finding a solution to problem (30, 31). If the fractional order is a constant $\mathit{\alpha }\in \left(\mathrm{0,1}\right)$, then a closed-form solution of problem (30, 31) can be obtained by using either the Laplace transform method (Gorenflo et al., 2014) or an operational method proposed by Luchko and Garenflo (1999) (it is worth noticing here that the Laplace transform method belongs to the class of operational methods). Not only that this analytic solution is cumbersome and difficult to implement in a computer program but also may not be generalizable to the case of variable fractional order. Therefore, looking for a numerical solution to problem (Eqs 30, 31) is a better approach. Eq. 30 is a linear multi-term fractional differential equation which for a constant fractional order $\mathit{\alpha }\in \left(\mathrm{0,1}\right)$, can be solved numerically using the elegant explicit, implicit, and predictor-corrector methods involving product-integration rules proposed by Garrappa (2018). For the variable-order fractional differential Eq. 30, the finite difference schemes given by Moghaddam and Machado (2017) can be used. Thus, in this study, the second-order derivative of Eq. 20 will be approximated by a center difference scheme, and the variable-order fractional derivative will be approximated by the forward difference scheme proposed in theorem 3.1 of Moghaddam and Machado (2017). For the sake of completeness, the numerical discretization of Eq. 30 is presented further.

Let $\mathbf{0}=\overline{{\mathit{t}}_{\mathbf{0}}}<\overline{{\mathit{t}}_{\mathbf{1}}}<\dots <\overline{{\mathit{t}}_{\mathit{N}}}=\mathbf{1}$ be an equally spaced discretization of the interval $\left[\mathbf{0,1}\right]$ of constant step size $\Delta \overline{\mathit{t}}=\mathbf{1}/\mathit{N}$. Denoting by ${\mathit{Z}}_{\mathit{n}}^{\mathit{k}}={\mathit{Z}}_{\mathit{n}}\left(\overline{{\mathit{t}}_{\mathit{k}}}\right),\mathit{k}\in \left\{\mathbf{0,1},\dots ,\mathit{N}\right\},\mathit{n}\text{fixed}$, and ${\mathit{\alpha }}^{\mathit{k}}=\mathit{\alpha }\left(\overline{{\mathit{t}}_{\mathit{k}}}\right),\mathit{k}\in \left\{\mathbf{0,1},\dots ,\mathit{N}\right\}$, the numerical approximations of the derivatives in Eq. 30 can be written as:

$\frac{{\mathit{d}}^{\mathbf{2}}{\mathit{Z}}_{\mathit{n}}}{\mathit{d}{\overline{\mathit{t}}}^{\mathbf{2}}}\left({\overline{\mathit{t}}}_{\mathit{k}+\mathbf{1}}\right)\approx \frac{{\mathit{Z}}_{\mathit{n}}^{\mathit{k}+\mathbf{2}}-\mathbf{2}{\mathit{Z}}_{\mathit{n}}^{\mathit{k}+\mathbf{1}}+{\mathit{Z}}_{\mathit{n}}^{\mathit{k}}}{\Delta {\overline{\mathit{t}}}^{\mathbf{2}}},(33)$

${\partial }_{\overline{\mathit{t}}}^{\mathbf{2}-\mathit{\alpha }\left({\overline{\mathit{t}}}_{\mathit{k}+\mathbf{1}}\right)}{\mathit{Z}}_{\mathit{n}}\left({\overline{\mathit{t}}}_{\mathit{k}+\mathbf{1}}\right)\approx \frac{\Delta {\overline{\mathit{t}}}^{-\mathbf{2}+{\mathit{\alpha }}^{\mathit{k}+1}}}{\mathbf{\Gamma }\left(1+{\mathit{\alpha }}^{\mathit{k}+1}\right)}{\displaystyle \sum _{\mathit{j}=\mathbf{0}}^{\mathit{k}}{\mathit{\psi }}_{\mathbf{2},\mathit{k},\mathit{j}}\left({\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}+\mathbf{2}}-\mathbf{2}{\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}+\mathbf{1}}+{\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}}\right)},(34)$

where ${\mathit{\psi }}_{2,\mathit{k},\mathit{j}}={\left(\mathit{j}+\mathbf{1}\right)}^{{\mathit{\alpha }}^{\mathit{k}+\mathbf{1}}}-{\mathit{j}}^{{\mathit{\alpha }}^{\mathit{k}+\mathbf{1}}}$ (Moghaddam and Machado, 2017). The truncation error of scheme Eq. 33 is of order $\mathit{O}\left(\Delta {\overline{\mathit{t}}}^{\mathbf{2}}\right)$, while for scheme Eq. 34, it is of order $\mathit{O}\left(\Delta \overline{\mathit{t}}\right)$. By replacing approximations Eqs 33, 34 in problem (30, 31), the following explicit scheme is obtained:

${\mathit{Z}}_{\mathit{n}}^0=\mathbf{0},{\mathit{Z}}_{\mathit{n}}^1={\mathit{F}}_{\mathit{n}}\Delta \overline{\mathit{t}}$

${\mathit{Z}}_{\mathit{n}}^{\mathit{k}+2}-\mathbf{2}{\mathit{Z}}_{\mathit{n}}^{\mathit{k}+1}+{\mathit{Z}}_{\mathit{n}}^{\mathit{k}}+\mathit{B}\frac{\Delta {\overline{\mathit{t}}}^{{\mathit{\alpha }}^{\mathit{k}+1}}}{\Gamma \left(1+{\mathit{\alpha }}^{\mathit{k}+1}\right)}{\displaystyle \sum _{\mathit{j}=0}^{\mathit{k}}{\mathit{\psi }}_{2,\mathit{k},\mathit{j}}\left({\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}+2}-2{\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}+1}+{\mathit{Z}}_{\mathit{n}}^{\mathit{k}-\mathit{j}}\right)+{\mathit{C}}_{\mathit{n}}\Delta {\overline{\mathit{t}}}^2{\mathit{Z}}_{\mathit{n}}^{\mathit{k}+1}}={\mathit{D}}_{\mathit{n}}\Delta {\overline{\mathit{t}}}^2\mathbf{sin}\left(\mathit{\omega T}{\overline{\mathit{t}}}_{\mathit{k}+1}\right),\mathit{k}\in \left\{\mathrm{0,1},\dots ,\mathit{N}-2\right\}.(35)$

The semi-analytic solution to problem (15–17) is then obtained by replacing the discrete solution (35) for $\mathit{n}\in \left\{\mathrm{1,2},\dots .\right\}$ in Eq. 32.

The shear stress distribution within the vessel’s wall is obtained from the dimensionless form of Eq. 2 by integration (Hodis and Zamir, 2008):

${\overline{\mathit{\sigma }}}_{\mathit{rx}}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)=\frac{1}{\mathit{f}{\mathit{T}}^2}{\displaystyle \underset{0}{\overset{\overline{\mathit{r}}}{\int }}\frac{{\partial }^2\overline{\mathit{\xi }}\left(\tilde{\mathit{r}},\overline{\mathit{t}}\right)}{\partial {\overline{\mathit{t}}}^2}\mathit{d}\tilde{\mathit{r}}+{\overline{\mathit{\sigma }}}_{\mathit{rx}}\left(\mathbf{0},\overline{\mathit{t}}\right)},(36)$

where the following non-dimensionalization was used for the shear stress: ${\overline{\mathit{\sigma }}}_{\mathit{rx}}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)={\mathit{\sigma }}_{\mathit{rx}}\left(\mathit{r},\mathit{t}\right)/\left(\frac{\mathit{E}{\mathit{\xi }}_{\mathbf{0}}}{\mathit{h}}\right)$. By replacing Eq. 32 in Eq. 36, the following expression for the shear stress at the blood-vessel interface is obtained:

${\mathit{\tau }}_{\mathit{w}}\equiv {\overline{\mathit{\sigma }}}_{\mathit{rx}}\left(\mathbf{0},\overline{\mathit{t}}\right)={\displaystyle \sum _{\mathit{n}=1}^{\infty }\frac{-1}{\mathit{n\pi f}{\mathit{T}}^2}\left[\frac{{\mathit{d}}^2{\mathit{Z}}_{\mathit{n}}\left(\overline{\mathit{t}}\right)}{\mathit{d}{\overline{\mathit{t}}}^2}-\frac{2{\mathit{\omega }}^2{\mathit{T}}^2}{\mathit{n\pi }}\mathbf{sin}\left(\mathit{\omega T}\overline{\mathit{t}}\right)\right]}(37)$

Results

Numerical scheme Eq. 35 was implemented in MATLAB, and plots of the distributions of dimensionless displacements within the vessel’s wall (Eq. 32) and the dimensionless shear stress at the blood-vessel interface (Eq. 37) were generated for two expressions of the variable fractional order: the stepwise NOS and the dynamic NOS. The values of the parameters used in the numerical simulations are given in Table 1. Numerical simulations used a step size $\Delta \overline{\mathit{t}}=0.00025$ and $20$ terms of the Fourier series in Eq. 32.

Figure 4 shows temporal profiles of the dimensionless axial displacement $\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)\mathit{ }$at various radial locations inside the vascular wall and for constant fractional orders. These plots were generated using MATLAB’s function MT_FDE_PI12_PC developed by Garrappa which is an implementation of the predictor-corrector scheme proposed by Garrappa (2018). The same results are obtained with the forward scheme Eq. 35 when $\mathit{\alpha }$ is constant. This agreement of numerical solutions validates scheme Eq. 35. The plots of Figure 4 show that while the amplitudes of the oscillations are approaching zero as $\overline{\mathit{r}}\to 1$ for all values of $\mathit{\alpha }$, the decaying in amplitude decreases faster as $\mathit{\alpha }$ increases. The solutions for constant fractional orders provide a first glimpse into the shapes of the displacements for variable fractional orders since these are expected to be a combination of the behaviors of the solutions for constant $\mathit{\alpha }$.

FIGURE 4

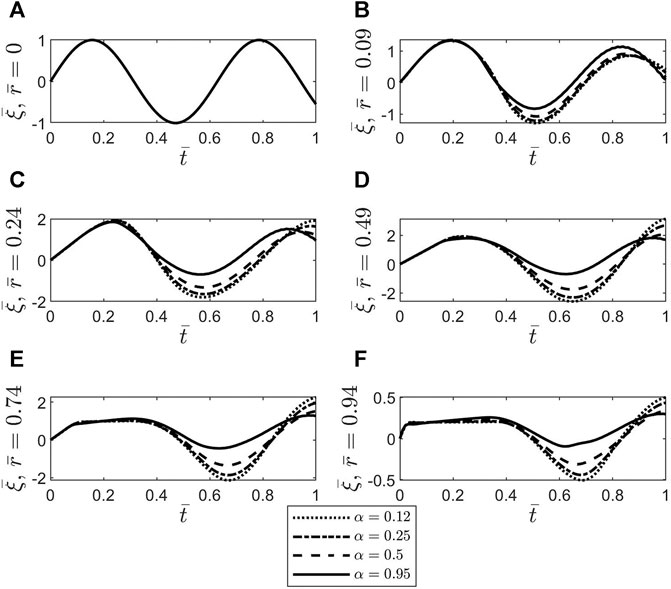
FIGURE 4. Plots of the dimensionless axial displacement $\overline{\mathit{\xi }}$ versus the dimensionless time $\overline{\mathit{t}}$ at various dimensionless radial locations $\overline{\mathit{r}}$ within the vascular wall (A) r^―=0, (B) r^―=0.09, (C) r^―=0.24, (D) r^―=0.49, (E) r^―=0.74, and (F) r^―=−0.94 and for various constant values of $\mathit{\alpha }\in \left(\mathrm{0,1}\right).$

Figures 5, 6 show spatio-temporal variations of the dimensionless axial displacement $\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)\mathit{ }$ for the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of decaying dynamic NOS (Figure 5) and to the case of stepwise NOS (Figure 6). The amplitude of the oscillations appears to be bigger in the dynamic NOS case than in the stepwise NOS case. This is confirmed in Figure 7 which shows temporal profiles of the dimensionless axial displacement at various radial locations inside the vascular wall which was extracted from the surfaces presented in Figures 5, 6. Since the results in Figure 7 resemble those in Figure 4, it can be concluded that the solutions for variable fractional orders are plausible. According to Figures 3C,D, the maximum value of $\mathit{\alpha }\left(\mathit{t}\right)$ for the case of dynamic NOS is 0.15 which is smaller than the almost constant value of 0.5 that $\mathit{\alpha }\left(\mathit{t}\right)$ in the case of stepwise NOS. The results in Figure 7 confirmed what was already known from Figure 4, namely that the amplitude of oscillations corresponding to the higher values of $\mathit{\alpha }\left(\mathit{t}\right)$ is smaller than the one corresponding to lower values of $\mathit{\alpha }\left(\mathit{t}\right)$.

FIGURE 5

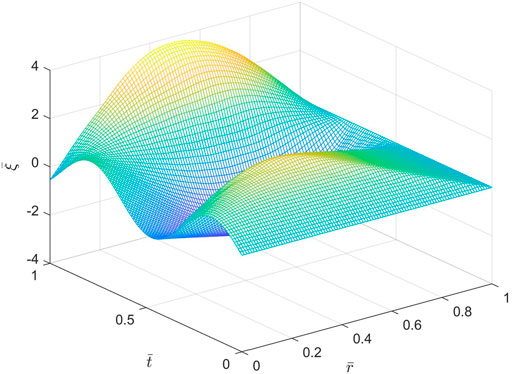
FIGURE 5. Spatio-temporal variations of the dimensionless axial displacement $\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)$ for the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of dynamic NOS.

FIGURE 6

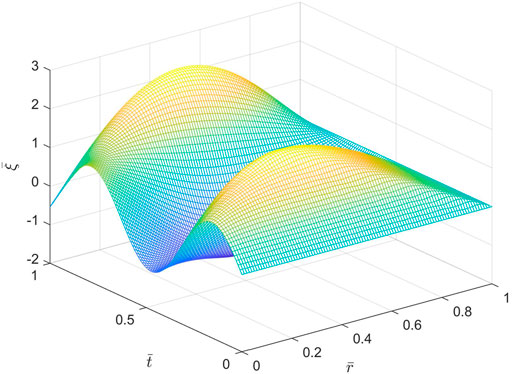
FIGURE 6. Spatio-temporal variations of the dimensionless axial displacement $\overline{\mathit{\xi }}\left(\overline{\mathit{r}},\overline{\mathit{t}}\right)$ for the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of stepwise NOS.

FIGURE 7

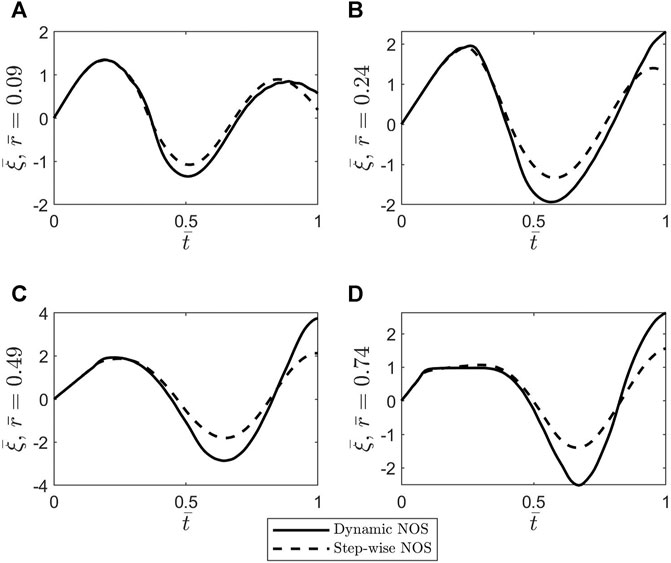
FIGURE 7. Plots of the dimensionless axial displacement $\overline{\mathit{\xi }}$ versus the dimensionless time $\overline{\mathit{t}}$ at various dimensionless radial locations $\overline{\mathit{r}}$ within the vascular wall (A) r^―=0.09, (B) r^―=0.24, (C) r^―=0.49, and (D) r^―=0.74 for the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of dynamic NOS (solid line) and to the case of stepwise NOS (dashed line).

To better understand the differences noticed between the oscillatory patterns corresponding to the two cases of stepwise NOS and dynamic NOS, the dimensionless shear stress at the blood-vessel interface was calculated using Eq. 37 and MATLAB’s built-in function gradient. The results of this comparison are shown in Figure 8. The amplitude of the shear stress is bigger in the case of dynamic NOS which was expected given that the amplitude of the axial displacement is also bigger in this case. By varying the scaling factor of order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of stepwise neuronal NOS, the difference between the shear stresses at the inner boundary of the vessel wall corresponding to the two cases 1) vanishes when the fractional order of the stepwise neuronal NOS gets smaller and 2) is almost unchanged when the fractional order of the stepwise neuronal NOS approaches 1. The possible implications of this finding will be discussed in the next section.

FIGURE 8

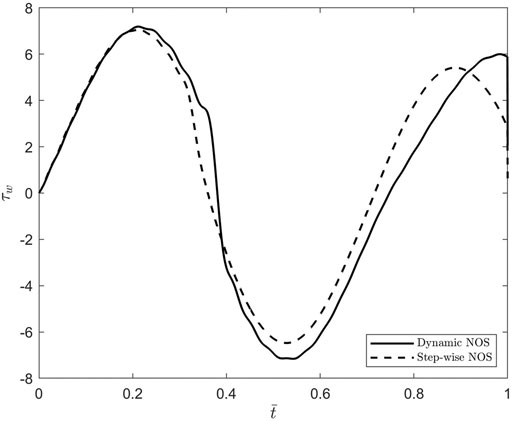
FIGURE 8. Plots of the dimensionless shear stress at the bloodvessel interface ${\mathit{\tau }}_{\mathit{w}}\mathit{ }$versus the dimensionless time $\overline{\mathit{t}}$ for the variable fractional order $\mathit{\alpha }\left(\mathit{t}\right)$ corresponding to the case of dynamic NOS (solid line) and to the case of stepwise NOS (dashed line).

Discussion

The main contribution of this study is modeling the wall of a cerebral blood vessel using an NO-modulated variable-order fractional Maxwell viscoelastic model. The variable fractional order is assumed to be proportional to the neuronal NO dynamics, and thus, the order memory introduced by this choice guides the pattern of the fading memory of this viscoelastic material. Two cases of NOS are considered: a stepwise activation of NO and a dynamic activation of NO. Following the approach of Hodis and Zamir (2008), a variable-order fractional telegraph equation for the axial displacement of the wall was obtained which was solved under the assumptions that the outer boundary of the vascular wall was tethered, and the inner boundary of the wall was exposed to the pulsatile blood flow. Numerical simulations were created in MATLAB using numerical scheme (Eq. 35) and Garrappa’s function MT_FDE_PI12_PC (Garrappa, 2018) for constant fractional orders. The function MT_FDE_PI12_PC was used to validate scheme (Eq. 35) in the case of constant fractional orders. The main finding of these simulations is that a significantly decreased inactivation of the neuronal NO causes a reduction in the shear stress at the blood-vessel interface which could lead to a decrease in the production of shear-induced endothelial NO and ultimately to neurovascular disease.

Testing the computer code for various values of the parameters $\mathit{f},\mathit{ g},$ and $\mathit{T}$ which are present in the coefficients of Eq. 15 showed that both approaches, scheme (Eq. 35) and MT_FDE_PI12_PC, were sensitive to these parameters for variable and constant fractional orders. These numerical schemes are stable only for narrow ranges of $\mathit{f},\mathit{ g},$ and $\mathit{T}$. These parameters couple mechanical parameters $\mathit{E},\mathit{ }{\mathit{\mu }}_{\mathit{\alpha }}$, wall thickness $\mathit{h}$, and the characteristic time $\mathit{T}$. Thus, if these narrow ranges of $\mathit{f},\mathit{ g},$ and $\mathit{T}$ are subsets of their corresponding physiological ranges, this stability issue could be disregarded. However, for $\mathit{E}=6\mathit{ }\times {10}^5\mathit{N}/{\mathit{m}}^2$, ${\mathit{\mu }}_{\mathit{\alpha }}=1.5\mathit{ }\times {10}^5\mathit{Kg}/\left(\mathit{m}\times {\mathit{s}}^{2-\mathit{\alpha }}\right)$ derived from Hodis and Zamir (2008) for arteries and $\left(\mathit{\alpha }=1\right)$, a wall thickness $\mathit{h}={10}^{-3}\mathit{ m}$ measured in human intracranial arteries in vivo (Yuan et al., 2021), and a more accurate value of the wall density $\mathit{\rho }\approx 1.1\mathit{ }\times {10}^3\frac{\mathit{Kg}}{{\mathit{m}}^3}$ (IT’IS Foundation, 2021), the following values are obtained: $\mathit{f}=5.45\times {10}^8\mathit{ }{\mathit{s}}^{-2}$ and $\mathit{g}=4\mathit{ }{\mathit{s}}^{-\mathit{\alpha }}$. These values, together with the chosen $\mathit{T}=10\mathit{ s}$, make Eq. 15 stiff since the order of magnitude of the coefficient of the right-hand side term is much bigger than the magnitudes of the coefficients of the left-hand-side terms. For a smaller wall thickness which is more appropriate for an intracerebral arteriole which experiences NO-modulated vasodilation, the order of magnitude of the coefficient of the right-hand-side term of Eq. 15 becomes even bigger. The proposed numerical schemes are unstable for a stiff Eq. 15, and a mere decrease of the step size $\Delta \overline{\mathit{t}}$ does not resolve this issue. Finding algorithms for stiff variable-order fractional differential equations is an open problem in numerical analysis. Nevertheless, for a characteristic time $\mathit{T}$ of order of $\mathit{ms}$ which may be more suitable for NO dynamics in vivo (Hall and Garthwaite, 2006), a possibly lower value of $\mathit{E}$ corresponding to cerebral arterioles (Medical Physiology, 2021), and a more realistic value of the wall density, the numerical stiffness can be avoided, and thus, the presented results will hold.

Emerging imaging techniques could help validate the proposed model in animal models and thus make the model relevant to clinical applications. For instance, a multimodal in vivo magnetic resonance (MR)/electron paramagnetic resonance (EPR) spectroscopy/fluorometry could be used to visualize NO production and spatio-temporal distribution (Sharma et al., 2014). Also, intravascular optical coherence tomography could be used for the in vivo real-time estimation of the vascular stiffness (Potlov et al., 2020). By combining these imaging techniques and the high-resolution ultrasonic scanning of Persson et al. (2003) and Cinthio et al. (2006) for the visualization of wall’s longitudinal displacements, the cerebral NO dynamics and vascular wall mechanics may be investigated simultaneously. This approach can be used to estimate $\mathit{\alpha }\left(\mathit{t}\right), \mathit{f},\mathit{ g},$ and $\mathit{T}$ and validate the mathematical model proposed here. If a significant decrease in the neuronal NO inactivation is observed, then the model’s prediction could suggest the use of a preventive therapy [such as NO inhalation proposed by Terpolilli et al. (2016)] to reduce imminent brain damage.

Until the above-mentioned imaging techniques are adapted and approved for clinical applications, animal models can be used to find healthy physiological ranges for the model’s parameters and investigate the potential of using these parameters as biomarkers. For example, animal models of cerebral ischemia have shown that the decreasing amount of endothelial NO will act as a protective agent for a few minutes after the injury, while the amount of neuronal NO will increase causing neuronal injury (Huang, 1999; Wei et al., 1999). If the production of shear-induced endothelial NO mediated by the blood flow ceases to happen following ischemia, then the stepwise concentration of neuronal NO is a consequence of the significantly decreased NO inactivation caused by ischemia (Santos et al., 2011) and thus, according to the prediction made by the proposed model, may contribute to the reduction of the localized endothelial NO produced by the lower shear stress in the vessel wall at its inner boundary. Thus, the model’s prediction may explain the interplay between the endothelial and neuronal NO seen in cerebral ischemia. Lastly, model’s parameters estimated using the multimodal in vivo imaging techniques mentioned above could suggest the presence of cerebral ischemia and thus be used as a complementary diagnostic tool.

Improving the mathematical model may provide more sensitive biomarkers and helps avoiding the numerical stiffness issue mentioned earlier. According to Iadecola (2004), the NO-modulated local vasodilation of the intracerebral arterioles and capillaries propagates upstream in the vascular network which causes an increase of blood flow in the upstream arteries that leads to increased shear stress at the blood-vessel interface and thus an increase in the amount of shear-induced endothelial NO and a further flow-mediated vasodilation. The proposed model represents the blood flow as an inner boundary condition, and thus, this mechanism of global production of shear-induced endothelial NO is not accounted for. Thus, the decrease in the local production of the shear-induced endothelial NO due to a stepwise neuronal NOS predicted by the model proposed in this study might not be significant enough to cause adverse effects if the cerebral blood flow is intact. Coupling the deformation of the vessel’s wall and the blood flow and incorporating in the model the mechanism described above should provide a better prediction of the amount of shear-induced endothelial NO and the possible role that the neuronal NO dynamics may play in this process. Introducing more detailed information about the complex, multi-layered structure of the vascular wall could also enhance the accuracy of model’s predictions. Lastly, the full three-dimensional fluid-structure interaction problem should be formulated and solved since the simplifying assumptions made by Hodis and Zamir (2008) and implemented here that reduced the model to a one-dimensional problem might not be valid for cerebral arterioles given the overly complex geometry of the cerebral vascular network (Reina-De La Torre et al., 1998). The parameters of this enhanced mathematical model could be found either from in vitro/in situ measurements or from in vivo, real-time observations using medical imaging techniques.

In conclusion, the study proposes a novel NO-modulated variable-order fractional Maxwell viscoelastic model of the cerebral arterioles and investigates the effects of the neuronal NOS on the mechanical behavior of the vessel’s wall. Numerical simulations show how neuronal NO dynamics influence the deformation and shear stress within the vascular wall. A generalization of this model to a three-dimensional geometry and the incorporation of the blood flow into the model should provide a better understanding of the coupling between NO dynamics and mechanical damage and their combined role in neurovascular diseases.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

CD stated the problem under investigation, proposed the mathematical model and its semi-analytic solution, implemented code in MATLAB, generated results, and wrote the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Attwell, D., Buchan, A. M., Charpak, S., Lauritzen, M., MacVicar, B. A., and Newman, E. A. (2010). Glial and Neuronal Control of Brain Blood Flow. Nature 468, 232–243. doi:10.1038/nature09613

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagley, R. L., and Torvik, P. J. (1983b). A Theoretical Basis for the Application of Fractional Calculus to Viscoelasticity. J. Rheology 27, 201–210. doi:10.1122/1.549724

CrossRef Full Text | Google Scholar

Bagley, R. L., and Torvik, P. J. (1983a). Fractional Calculus - A Different Approach to the Analysis of Viscoelastically Damped Structures. AIAA J. 21, 741–748. doi:10.2514/3.8142

CrossRef Full Text | Google Scholar

Bazhlekova, E., and Bazhlekov, I. (2017). Stokes' First Problem for Viscoelastic Fluids with a Fractional Maxwell Model. Fractal Fract 1, 7. doi:10.3390/fractalfract1010007

CrossRef Full Text | Google Scholar

Blair, G. W. S., and Caffyn, J. (1942). The Classification of the Rheological Properties of Industrial Materials in the Light of Power-Law Relations between Stress, Strain and Time. J. Sci. Instrum. 19, 88–93. doi:10.1088/0950-7671/19/6/303

CrossRef Full Text | Google Scholar

Caputo, M., and Mainardi, F. (1971). A New Dissipation Model Based on Memory Mechanism. Pageoph 91, 134–147. doi:10.1007/bf00879562

CrossRef Full Text | Google Scholar

Cinthio, M., Ahlgren, Å. R., Bergkvist, J., Jansson, T., Persson, H. W., and Lindström, K. (2006). Longitudinal Movements and Resulting Shear Strain of the Arterial wall. Am. J. Physiology-Heart Circulatory Physiol. 291 (1), H394–H402. doi:10.1152/ajpheart.00988.2005

CrossRef Full Text | Google Scholar

Cockcroft, J. (2005). Exploring Vascular Benefits of Endothelium-Derived Nitric Oxide. Am. J. Hypertens. 18, 177–183. doi:10.1016/j.amjhyper.2005.09.001

CrossRef Full Text | Google Scholar

Contestabile, A., Monti, B., and Polazzi, E. (2012). Neuronal-glial Interactions Define the Role of Nitric Oxide in Neural Functional Processes, Curr. Neuropharmacology 10, no. 4, 303–310. doi:10.2174/157015912804143522

PubMed Abstract | CrossRef Full Text | Google Scholar

Drapaca, C. S., and Sivaloganathan, S. (2019). Mathematical Modelling and Biomechanics of the Brain. New York, USA: Fields Institute Monographs, Springer Science+Business Media, LLC. doi:10.1007/978-1-4939-9810-4

CrossRef Full Text | Google Scholar

Drapaca, C. S., Sivaloganathan, S., and Tenti, G. (2007). Nonlinear Constitutive Laws in Viscoelasticity. Maths. Mech. Sol. 12, 475–501. doi:10.1177/1081286506062450

CrossRef Full Text | Google Scholar

Ebrahimi, A. P. (2009). Mechanical Properties of normal and Diseased Cerebrovascular System. J. Vasc. Interv. Neurol. 2 (2), 155–162.

Google Scholar

Forstermann, U., and Sessa, W. C. (2012). Nitric Oxide Synthases: Regulation and Function. Eur. Heart J. 33, 829–837. doi:10.1093/eurheartj/ehr304

PubMed Abstract | CrossRef Full Text | Google Scholar

Freed, J. K., and Gutterman, D. D. (2017). Communication Is Key: Mechanisms of Intercellular Signaling in Vasodilation. J. Cardiovasc. Pharmacol. 69 (5), 264–272. doi:10.1097/FJC.0000000000000463

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabriela Espinosa, M., Catalin Staiculescu, M., Kim, J., Marin, E., and Wagenseil, J. E. (2018). Elastic Fibers and Large Artery Mechanics in Animal Models of Development and Disease. J. Biomech. Eng. 140 (2), 0208031–02080313. doi:10.1115/1.4038704

CrossRef Full Text | Google Scholar

Garrappa, R. (2018). Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 6, 16. doi:10.3390/math6020016

CrossRef Full Text | Google Scholar

Gemant, A. (1936). A Method of Analyzing Experimental Results Obtained from Elasto‐Viscous Bodies. Physics 7, 311–317. doi:10.1063/1.1745400

CrossRef Full Text | Google Scholar

Gemant, A. (1935). Compressional Waves in media with Complex Viscosity. Physics 6, 363–365. doi:10.1063/1.1745278

CrossRef Full Text | Google Scholar

Gorenflo, R., Kilbas, A. A., Mainardi, F., and Rogosin, S. V. (2014). Mittag-Leffler Functions, Related Topics and Applications. New York, USA: Springer-Verlag. doi:10.1007/978-3-662-43930-2_6

CrossRef Full Text | Google Scholar

Gurtin, M., and Sternberg, E. (1965). On the Linear Theory of Viscoelasticity. Archive Rational Mech. Anal. 11, 291–356.

Google Scholar

Guttinger, W. Generalized Functions and Dispersion Relations in Physics. Fortschritte der Physik 14, 483–602. doi:10.1002/prop.19660140114

CrossRef Full Text | Google Scholar

Hall, C. N., and Garthwaite, J. (2006). Inactivation of Nitric Oxide by Rat Cerebellar Slices. J. Physiol. 577 (2), 549–567. doi:10.1113/jphysiol.2006.118380

CrossRef Full Text | Google Scholar

Haselden, W. D., Kedarasetti, R. T., and Drew, P. J. (2020). Spatial and Temporal Patterns of Nitric Oxide Diffusion and Degradation Drive Emergent Cerebrovascular Dynamics. Plos Comput. Biol. 16 (7), e1008069. doi:10.1371/journal.pcbi.1008069

PubMed Abstract | CrossRef Full Text | Google Scholar

Helms, C. C., Liu, X., and Kim-Shapiro, D. B. (2017). Recent Insights into Nitrite Signaling Processes in Blood. Biol. Chem. 398, 319–329. doi:10.1515/hsz-2016-0263

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, A. V. (1938). The Heat of Shortening and the Dynamic Constants of Muscle. Proc. R. Soc. Lond. B 126, 136–195. doi:10.1098/rspb.1938.0050

CrossRef Full Text | Google Scholar

Hodis, S., and Zamir, M. (2008). Solutions of the Maxwell Viscoelastic Equations for Displacement and Stress Distributions within the Arterial wall. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 78, 021914. doi:10.1103/PhysRevE.78.021914

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzapfel, G. A., Gasser, T. C., and Stadler, M. (2002). A Structural Model for the Viscoelastic Behavior of Arterial walls: Continuum Formulation and Finite Element Analysis. Eur. J. Mech. - A/Solids 21, 441–463. doi:10.1016/s0997-7538(01)01206-2

CrossRef Full Text | Google Scholar

Holzapfel, G. A., and Ogden, R. W. (2010). Constitutive Modelling of Arteries. Proc. R. Soc. A. 466, 1551–1597. doi:10.1098/rspa.2010.0058

CrossRef Full Text | Google Scholar

Huang, P. L. (1999). Neuronal and Endothelial Nitric Oxide Synthase Gene Knockout Mice. Braz. J. Med. Biol. Res. 32, 1353–1359. doi:10.1590/s0100-879x1999001100005

CrossRef Full Text | Google Scholar

Iadecola, C. (2004). Neurovascular Regulation in the normal Brain and in Alzheimer's Disease. Nat. Rev. Neurosci. 5, 347–360. doi:10.1038/nrn1387

PubMed Abstract | CrossRef Full Text | Google Scholar

Iadecola, C. (2017). The Neurovascular Unit Coming of Age: a Journey through Neurovascular Coupling in Health and Disease. Neuron 96, 17–42. doi:10.1016/j.neuron.2017.07.030

PubMed Abstract | CrossRef Full Text | Google Scholar

IT’IS Foundation (2021). Tissue Properties Database: Density. Available at: https://itis.swiss/virtual-population/tissue-properties/database/density/. Zurich: Zurich43.

Google Scholar

Kasza, K. E., Rowat, A. C., Liu, J., Angelini, T. E., Brangwynne, C. P., Koenderink, G. H., et al. (2007). The Cell as a Material. Curr. Opin. Cel Biol. 19, 101–107. doi:10.1016/j.ceb.2006.12.002

CrossRef Full Text | Google Scholar

Kim, J., and Wagenseil, J. E. (2014). Bio-chemo-mechanical Models of Vascular Mechanics. Ann. Biomed. Eng. 43, 1477–1487. doi:10.1007/s10439-014-1201-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Koeller, R. C. (1984). Applications of Fractional Calculus to the Theory of Viscoelasticity. ASME J. Appl. Mech. 51, 299–307. doi:10.1115/1.3167616

CrossRef Full Text | Google Scholar

Lorenzo, C. F., and Hartley, T. T. (2002). Variable Order and Distributed Order Fractional Operators. NASA/TM-2002-211376, New York, USA: Springer Link. doi:10.1023/A:1016586905654

CrossRef Full Text | Google Scholar

Lourenço, C. F., Santos, R. M., Barbosa, R. M., Cadenas, E., Radi, R., and Laranjinha, J. (2014). Neurovascular Coupling in hippocampus Is Mediated via Diffusion by Neuronal-Derived Nitric Oxide. Free Radic. Biol. Med. 73, 421–429. doi:10.1016/j.freeradbiomed.2014.05.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Luchko, Y., and Gorenflo, R. (1999). An Operational Method for Solving Fractional Differential Equations with the Caputo Derivatives. Acta Mathematica Vietnamica 24 (2), 207–233.

Google Scholar

Mainardi, F. (2010). Fractional Calculus and Waves in Linear Viscoelasticity. London, UK: Imperial College Press.

Google Scholar

Maurer, I., Zierz, S., and Moller, H.-J. (2000). A Selective Defect of Cytochrome C Oxidase Is Present in Brain of Alzheimer Disease Patients. Neurobiol. Aging 21, 455–462. doi:10.1016/s0197-4580(00)00112-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Medical Physiology, 3rd Edition: Elastic Properties of Blood Vessels (2021). https://doctorlib.info/physiology/medical/104.html. Chicago: Doctorlib.

Google Scholar

Mehala, N., and Rajendran, L. (2014). Analytical Solutions of Nonlinear Differential Equations in the Mathematical Model for Inactivation of Nitric Oxide by Rat Cerebellar Slices. Ajac 05, 908–919. doi:10.4236/ajac.2014.514099

CrossRef Full Text | Google Scholar

Metea, M. R., and Newman, E. A. (2006). Glial Cells Dilate and Constrict Blood Vessels: A Mechanism of Neurovascular Coupling. J. Neurosci. 26 (11), 2862–2870. doi:10.1523/jneurosci.4048-05.2006

CrossRef Full Text | Google Scholar

Moghaddam, B. P., and Machado, J. A. T. (2017). Extended Algorithms for Approximating Variable Order Fractional Derivatives with Applications. J. Sci. Comput. 71, 1351–1374. doi:10.1007/s10915-016-0343-1

CrossRef Full Text | Google Scholar

N. Atochin, D., and L. Huang, P. (2011). Role of Endothelial Nitric Oxide in Cerebrovascular Regulation. Cpb 12 (9), 1334–1342. doi:10.2174/138920111798280974

CrossRef Full Text | Google Scholar

Nutting, P. G. (1921). A Study of Elastic Viscous Deformation. Proc. Amer. Soc. Test. Mater. 21, 1162–1171. doi:10.2307/3407697

CrossRef Full Text | Google Scholar

Nutting, P. G. (1943). A General Stress-Strain-Time Formula. J. Franklin Inst. 235, 513–524. doi:10.1016/s0016-0032(43)91483-8

CrossRef Full Text | Google Scholar

Orosz, M., Molnarka, G., Toth, M., Nadasy, G. L., and Monos, E. (1999). Viscoelastic Behavior of Vascular wall Simulated by Generalized Maxwell Models – a Comparative Study. Med. Sci. Monit. 5 (3), 549–555.

Google Scholar

Palacios-Callender, M., Hollis, V., Mitchison, M., Frakich, N., Unitt, D., and Moncada, S. (2007). Cytochrome C Oxidase Regulates Endogenous Nitric Oxide Availability in Respiring Cells: a Possible Explanation for Hypoxic Vasodilation. Proc. Natl. Acad. Sci. 104 (47), 18508–18513. doi:10.1073/pnas.0709440104

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, W. D., and Parks, J. K. (1995). Cytochrome C Oxidase in Alzheimer's Disease Brain. Neurology 45, 482–486. doi:10.1212/wnl.45.3.482

PubMed Abstract | CrossRef Full Text | Google Scholar

Patnaik, S., Hollkamp, J. P., and Semperlotti, F. (2020). Applications of Variable-Order Fractional Operators: a Review, Proc. R. Soc. A. 476, 20190498. doi:10.1098/rspa.2019.0498

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, M., Rydén Ahlgren, Å., Jansson, T., Eriksson, A., Persson, H. W., and Lindström, K. (2003). A New Non-invasive Ultrasonic Method for Simultaneous Measurements of Longitudinal and Radial Arterial wall Movements: First In Vivo Trial. Clin. Physiol. Funct. Imaging 23 (5), 247–251. doi:10.1046/j.1475-097x.2003.00504.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Petzold, G. C., and Murthy, V. N. (2011). Role of Astrocytes in Neurovascular Coupling. Neuron 71, 782–797. doi:10.1016/j.neuron.2011.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Potlov, A. Y., Proskurin, S. G., and Frolov, S. V. (2020). Young’s Modulus Evaluation for the Blood Vessel walls Using Intravascular Optical Coherence Tomography, 2020 International Conference on e-Health and Bioengineering (EHB), Iasi, Romania, Oct. 2020 1–4. doi:10.1109/EHB50910.2020.9280242

CrossRef Full Text | Google Scholar

Rachev, A., and Hayashi, K. (1999). Theoretical Study of the Effects of Vascular Smooth Muscle Contraction on Strain and Stress Distributions in Arteries. Ann. Biomed. Eng. 27, 459–468. doi:10.1114/1.191

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramirez, L. E. S., and Coimbra, C. F. M. (2010). On the Selection and Meaning of Variable Order Operators for Dynamic Modeling. Int. J. Differential Equations 2010, 1–16. doi:10.1155/2010/846107

CrossRef Full Text | Google Scholar

Reina-De La Torre, F., Rodriguez-Baeza, A., and Sahuquillo-Barris, J. (1998). Morphological Characteristics and Distribution Pattern of the Arterial Vessels in Human Cerebral Cortex: a Scanning Electron Microscope Study. Anat. Rec. 251, 87–96. doi:10.1002/(sici)1097-0185(199805)251:1<87::aid-ar14>3.0.co;2-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Samko, S. G., and Ross, B. (1993). Integration and Differentiation to a Variable Fractional Order. Integral Transforms Spec. Functions 1 (4), 277–300. doi:10.1080/10652469308819027

CrossRef Full Text | Google Scholar

Santos, R. M., Lourenço, C. F., Ledo, A., Barbosa, R. M., and Laranjinha, J. (2012). Nitric Oxide Inactivation Mechanisms in the Brain: Role in Bioenergetics and Neurodegeneration, Int. J. Cel Biol., 2012, 1, 13. doi:10.1155/2012/391914

CrossRef Full Text | Google Scholar

Santos, R. M., Lourenço, C. F., Pomerleau, F., Huettl, P., Gerhardt, G. A., Laranjinha, J., et al. (2011). Brain Nitric Oxide Inactivation Is Governed by the Vasculature. Antioxid. Redox Signaling 14 (6), 1011–1021. doi:10.1089/ars.2010.3297

CrossRef Full Text | Google Scholar

Schuler, D., Sansone, R., Freudenberger, T., Rodriguez-Mateos, A., Weber, G., Momma, T. Y., et al. (2014). Measurement of Endothelium-dependent Vasodilation in Mice-Brief Report, Atvb 34, no. 12, 2651–2657. doi:10.1161/ATVBAHA.114.304699

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott Blair, G. M., and Coppen, F. M. V. (1939). The Subjective Judgement of the Elastic and Plastic Properties of Soft Bodies; the "differential Thresholds" for Viscosities and Compression Moduli. Proc. R. Soc. Lond. B 128, 109–125. doi:10.1098/rspb.1939.0046

CrossRef Full Text | Google Scholar

Sharma, R., Seo, J.-W., and Kwon, S. (2014). In VivoImaging of Nitric Oxide by Magnetic Resonance Imaging Techniques. J. Nanomater. 2014, 1–13. doi:10.1155/2014/523646

CrossRef Full Text | Google Scholar

Sriram, K., Laughlin, J. G., Rangamani, P., and Tartakovsky, D. M. (2016). Shear-induced Nitric Oxide Production by Endothelial Cells. Biophysical J. 111, 208–221. doi:10.1016/j.bpj.2016.05.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Stålhand, J., Klarbring, A., and Holzapfel, G. A. (2008). Smooth Muscle Contraction: Mechanochemical Formulation for Homogeneous Finite Strains. Prog. Biophys. Mol. Biol. 96, 465–481. doi:10.1016/j.pbiomolbio.2007.07.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Suki, B., Barabasi, A. L., and Lutchen, K. R. (1994). Lung Tissue Viscoelasticity: a Mathematical Framework and its Molecular Basis. J. Appl. Physiol. 76 (6), 2749–2759. doi:10.1152/jappl.1994.76.6.2749

CrossRef Full Text | Google Scholar

Terpolilli, N. A., Feiler, S., Dienel, A., Müller, F., Heumos, N., Friedrich, B., et al. (2016). Nitric Oxide Inhalation Reduces Brain Damage, Prevents Mortality, and Improves Neurological Outcome after Subarachnoid Hemorrhage by Resolving Early Pial Microvasospasms. J. Cereb. Blood Flow Metab. 36 (12), 2096–2107. doi:10.1177/0271678X15605848

CrossRef Full Text | Google Scholar

Torvik, P. J., and Bagley, R. L. (1984). On the Appearance of the Fractional Derivative in the Behavior of Real Materials. ASME J. Appl. Mech. 51, 294–298. doi:10.1115/1.3167615

CrossRef Full Text | Google Scholar

Tóth, M., Nádasy, G. L., Nyáry, I., Kerényi, T., Orosz, M., Molnárka, G., et al. (1998). Sterically Inhomogenous Viscoelastic Behavior of Human Saccular Cerebral Aneurysms. J. Vasc. Res. 35 (5), 345–355. doi:10.1159/000025604

CrossRef Full Text | Google Scholar

Unitt, D. C., Hollis, V. S., Palacios-Callender, M., Frakich, N., and Moncada, S. (2010). Inactivation of Nitric Oxide by Cytochrome C Oxidase under Steady-State Oxygen Conditions. Biochim. Biophys. Acta (Bba) - Bioenerg. 1797, 371–377. doi:10.1016/j.bbabio.2009.12.002

CrossRef Full Text | Google Scholar

Wei, G., Dawson, V. L., and Zweier, J. L. (1999). Role of Neuronal and Endothelial Nitric Oxide Synthase in Nitric Oxide Generation in the Brain Following Cerebral Ischemia. Biochim. Biophys. Acta (Bba) - Mol. Basis Dis. 1455, 23–34. doi:10.1016/s0925-4439(99)00051-4

CrossRef Full Text | Google Scholar

West, B. J., Bologna, M., and Grigolini, P. (2003). Physics of Fractal Operators. USA: Springer-Verlag New York.

Google Scholar

Wilkinson, I. B., Franklin, S. S., and Cockcroft, J. R. (2004). Nitric Oxide and the Regulation of Large Artery Stiffness. Hypertension 44, 112–116. doi:10.1161/01.HYP.0000138068.03893.40

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Clark, J. W., Bryan, R. M., and Robertson, C. (2003). The Myogenic Response in Isolated Rat Cerebrovascular Arteries: Smooth Muscle Cell Model. Med. Eng. Phys. 25, 691–709. doi:10.1016/S1350-4533(03)00100-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, S., Jordan, L. C., Davis, L. T., Cogswell, P. M., Lee, C. A., Patel, N. J., et al. (2021). A Cross‐sectional, Case‐control Study of Intracranial Arterial wall Thickness and Complete Blood Count Measures in Sickle Cell Disease. Br. J. Haematol. 192 (4), 769–777. doi:10.1111/bjh.17262

CrossRef Full Text | Google Scholar