- 1Laboratory for Surface Technology and Tribology, University of Twente, Enschede, Netherlands
- 2Department of Mechanical Engineering, Semarang State Polytechnic, Semarang, Indonesia
- 3Orthopaedic and Traumatology Department, Prof. Dr. R. Soeharso Orthopedic Hospital Surakarta, Surakarta, Indonesia
- 4Laboratory for Engineering Design and Tribology, University of Diponegoro, Semarang, Indonesia
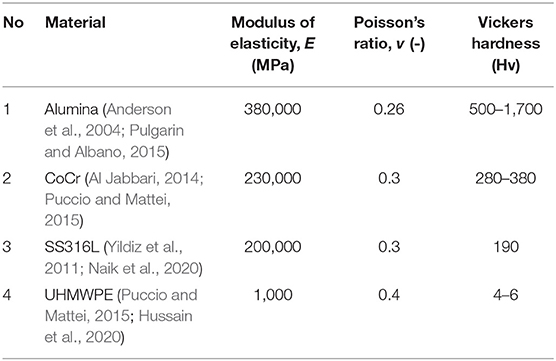
The wear of hip prosthesis due to applied load and sliding distance during the patient's daily activity cannot be avoided. Wear causes osteolysis or metallosis due to the wear debris produced by the wear process. Several methods were used to reduce wear in metal-on-metal hip prostheses. One of the efforts performed to reduce wear was the differential-hardness concept. Based on the literature, the fine surface roughness of the femoral head are the reason why the hip prosthesis with differential-hardness reduces wear. Besides, the differential-hardness will contribute to the difference of modulus elasticity then influenced the contact stress on the surface contact. According to Archard's wear law, wear on the material pair is affected by contact stress. Therefore, the analysis of contact stress on the hip prosthesis with differential-hardness is important to investigate. The investigation performed by the static contact of two-dimensional axisymmetric with frictionless by using finite element simulation. The simulated models are the alumina vs. alumina, alumina vs. SS316L, CoCr vs. CoCr, CoCr vs. SS316L, and SS316L vs. UHMWPE. The purpose of this study is to determine the contact stress on the surface contact due to differential-hardness of the femoral head and cup. The results of simulations show that the differential-hardness marked by differences in the modulus of elasticity can reduce the contact stress on the surface contact if compare with the similar hardness.
Introduction
Wear on the hip prosthesis is a common problem and it cannot be avoided. The wear debris from plastic material in metal-on-plastic (MoP) of hip prosthesis caused osteolysis (Ma et al., 1983; Livermore et al., 1990; Kabo et al., 1993), whereas wear debris from metal material in metal-on-metal (MoM) of hip prosthesis caused metallosis (Willis-Owen et al., 2011; Pesce et al., 2013). In the other hand, the biomaterial debris generated from the wear can lead to the aseptic loosening (Yang et al., 2007; Babic et al., 2020). This study will be focused on the MoM hip prosthesis. Various methods are used to reduce wear on the MoM hip prosthesis, from hip design to implant material selection. One way to reduce wear on the MoM hip prosthesis is differential-hardness (DH) (Firkins et al., 2001; Barnes et al., 2008a). Differential-hardness is means that the hardness of femoral head different with the hardness of cup. The use of DH can reduce the metal particle in the hip prosthesis (Barnes et al., 2008b; Le Duff et al., 2014). Further, the DH have been a tribological recommendation to optimize wear of hip prosthesis (Le Duff et al., 2014; Fisher et al., 2016).
Several studies on DH hip prosthesis have shown that the DH of implant materials can decrease wear. Firkins et al. demonstrated that hip prostheses with DH could decrease wear rates (Firkins et al., 2001). Their research showed that the ceramic-on-metal (CoM) hip prosthesis was able to reduce wear rates by about 100 times lower than the MoM hip prosthesis. According to Firkins, the ceramic femoral head has a better initial surface finish than other metals, which may have contributed to reduced wear. This is supported by the initial surface roughness of the ceramic femoral head being lower than the metal head. Barnes et al. also conducted a similar study on differences in the hardness of implant materials, which reduced the wear rate (Barnes et al., 2008a). Tests were carried out on three types of hip prostheses, namely MoM, DH MoM, and DH CoM. The results showed that the lowest wear rates were ranging from DH CoM, DH MoM, and MoM, respectively. Based on Barnes work, MoM with the similar hardness showed a larger wear surface area than DH MoM. Femoral heads having similar hardness show a greater increase in surface roughness compared to femoral heads with differential hardness. This may be the cause of greater wear on MoM with similar hardness than the DH MoM hip prosthesis.
Both studies show that differences in material hardness can reduce wear rates. These researches show the reasons of decreasing in wear rates in DH MoM and CoM from the point of view of the surface roughness. In addition to this factor, the contact stress factor on the contact surface also affects wear. This is based on Archard's wear law (Archard, 1953; Kauzlarich and Williams, 2001) according to Equation (1) which shows that contact stress is directly proportional to linear wear, where hW, kW, p, and L are linear wear (mm), specific wear rate (mm3/Nm), contact stress (N/mm2), and sliding distance (mm), respectively.
Based on our literature survey, the investigation of contact stress based on finite element simulation in the DH bearing is rare. Most researcher investigated the MoM hip prosthesis with similar hardness. Uddin et al. predicted the wear of MoM hip prosthesis. Their research investigated the contact stress cobalt chrome (CoCr) vs. cobalt chrome by using finite element simulation (Uddin and Zhang, 2013). Gao et al. investigated a “pre-worn” bearing surface geometry to reduce the wear of MoM hip replacements by numerical wear simulation (Gao et al., 2018). The material pairs used in their research are CoCr. Jangid et al. simulated some materials to investigate the effect of material to wear in the artificial hip joint (Jangid et al., 2019). Their research simulated some material couples by using finite element simulation. One of the case material couple simulated using Ansys software is CoCr alloy and Ti6Al4V for cup and femoral head component, respectively. However, the concern of this research is not in MoM materials, where it investigated mixed material couples. The last conclusion showed that least wear when using the CoCr alloy on the ultra-high molecular weight polyethylene (UHMWPE) material.
Therefore, the contact stress on the contact surface between the head and cup in the hip prosthesis with DH is necessary to analyze. This research contributes to providing information on the contact stress of metal on metal with differential-hardness of the materials. This research has been initiated by investigation of the contact stress on the liner and cup surface by using finite element simulation (Saputra et al., 2016, 2017). The objective of this study is to determine the contact stress on the surface contact due to the DH MoM hip prosthesis. The contact stress is obtained from contact simulation using Abaqus finite element software.
Materials and Equipment
The implant materials commonly used for hip prostheses are CoCr, Stainless steel 316L (SS316L) and UHMWPE. In the DH MoM hip prosthesis, the material used is a combination of Alumina, CoCr, and SS316L materials. For contact simulation purposes, the material properties used are Alumina (Anderson et al., 2004), CoCr (Puccio and Mattei, 2015), SS316L (Yildiz et al., 2011), and UHMWPE (Puccio and Mattei, 2015) as shown in Table 1. Surface roughness is not discussed in this study, because based on Equation (1), surface roughness is included in the specific wear rate variable obtained from the experiment. The contact simulation in this study was carried out using Abaqus software (Hibbitt et al., 2012). The simulation were run on a computer with an AMD Athlon processor with Radeon Graphics running at 2.40 MHz using 4 GB of RAM, and running at Windows 10.
Methods
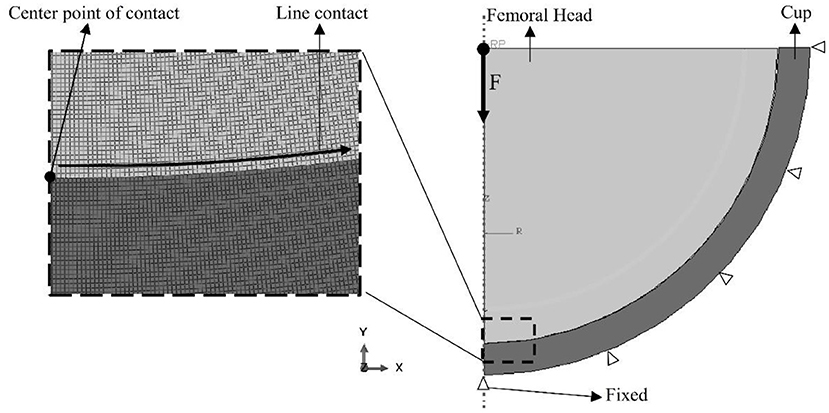
To simplify, the contact simulation is performed by modeling the static contact of two-dimensional axisymmetric with frictionless. The two-dimensional axisymmetric contact model proved enough efficient than a three-dimensional model (Dosaev et al., 2019). The contact model is composed of head and cup components with materials adopted in Table 1. The simulated models are the alumina vs. alumina (AA), alumina vs. SS316L (AS), CoCr vs. CoCr (CC), CoCr vs. SS316L (CS), and SS316L vs. UHMWPE (SU). The all geometry models is shown in detail in Figure 1. The diameter of the femoral head and cup are 45 and 45.2 mm respectively, while the cup thickness is 2.4 mm. The simulation was carried out by applied load 3,000 N at the midpoint of the femoral head, which it was adopted from the literatures (Paul, 1976; Bartel et al., 1985; Dowson et al., 1993; International Standard, 2014). The outer surface of the cup is fixed so that it cannot move toward the -x and -y axes. The elements used were a 4-node bilinear axisymmetric quadrilateral, reduced integration, hourglass control (CAX4R) (Hibbitt et al., 2012). The number of elements used is 153,789 elements, the meshing density can be seen in Figure 1. After completed simulation, then the collection of data is carried out to obtain the maximum value of contact stress at the contact center point and the distribution of contact stress along the contact area. Both types of data are used to predict initial wear based on Archard's wear law (Archard, 1953; Kauzlarich and Williams, 2001).
Figure 2 shows the contact stress maximum on the liner surface of the single mobility model as a function of load for Hertz theory (Johnson, 1985), Bartel theory (Bartel et al., 1985) and present Finite Element (FE). In the present FE, the contact stress maximum was obtained at the center point of the liner surface. Comparison of the results of contact stress maximum between the theory of conformal contact and the finite element simulation were conducted as verification. Based on this comparison, it can be seen that the contact stress maximum of the present FE shows a good agreement with Bartel theory. The deviation of the contact stress maximum between the present FE and Bartel theory is about 5.7% at the load equal 3,000 N. However, the contact stress maximum of Hertz theory was not showing a good agreement with Bartel theory and FE present. The deviation of the contact stress maximum between the present FE and Hertz theory is about 167.7% at load equal to 3,000 N. It verified that Hertz theory is not recommended for the conformal contact case with high load (Bartel et al., 1985).
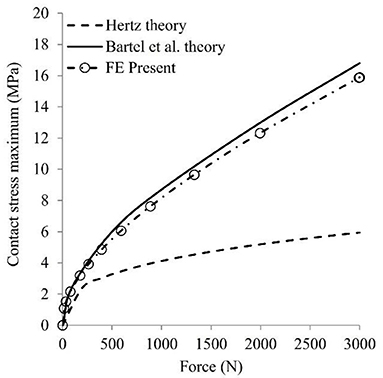
Figure 2. The comparison of the contact stress on the liner surface as a function of load for Bartel theory (Bartel et al., 1985), Hertz theory (Johnson, 1985), and FE present.
Results
The results of simulation are presented in a graph of contact stress, force and contact radius. Figure 3A shows the contact stress as a function of force on the cup surface of the AA, AS, CC, CS, and SU models. The contact stress maximum is obtained at the center of the cup surface, which it is the center point of contact interaction between the femoral head and cup. The maximum contact stress is obtained from AA, AS, CC, CS, and SU models. The contact stress for all models are presented together in Figure 3A. To simplify investigation, the SS316L is used as control variable or base variable. The results show the contact stress at the AA model larger than the AS model with deviation of about 15%. The contact stress at the CC model larger than the CS model with deviation 3%. While, the contact stress at the CS model larger than the SU model with deviation 87%. If compare the deviation between the AA-AS model, the CC-CS model and the CS-SU model, so that the deviation of the CS-SU model more large than the CC-CS model. Based on Figure 3A, the high contact stress occur at the AA model, while the low contact stress occur at the SU model.
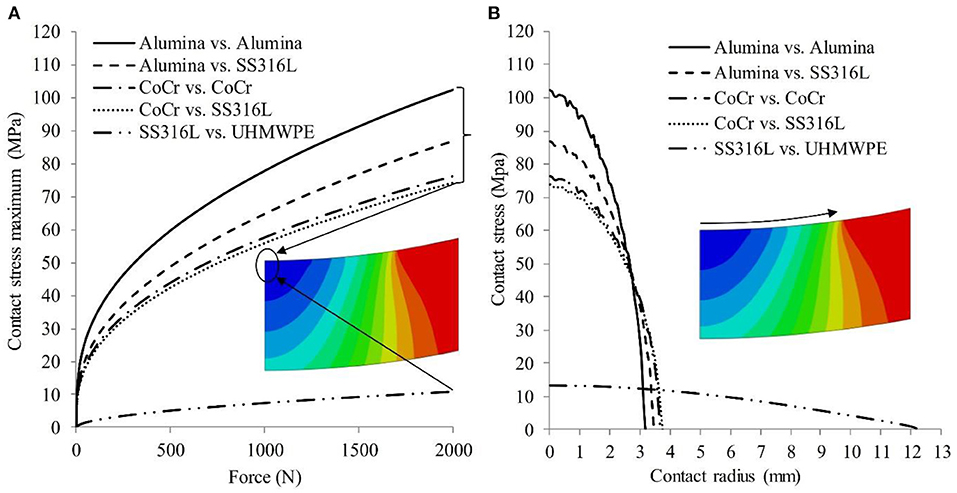
Figure 3. (A) The contact stress of AA, AS, CC, CS, and SU models as a function of Force and (B) the contact stress of AA, AS, CC, CS, and SU models as a function of contact radius.
Figure 3B shows the distribution of contact stress as a function of contact radius. This figure shows the distribution of contact stress and contact radius formed on the cup surface, where the distribution of contact stress is marked with a color contour. The contact stress is obtained along the contact area starting from the center point of the contact to the contour end of the contact stress. The results show the contact radius at the AA model is smaller than the AS model with deviation of about 9%. The contact radius at the CC model is smaller than the CS model with deviation of about 1%. While, the contact radius at the CS model is smaller than the SU model with deviation about 69%. Based on Figure 3B, the high contact radius occur at the SU model, while the low contact radius occur at the AA model. The contour of contact stress for CC and CS model as example can be seen in Figure 4.
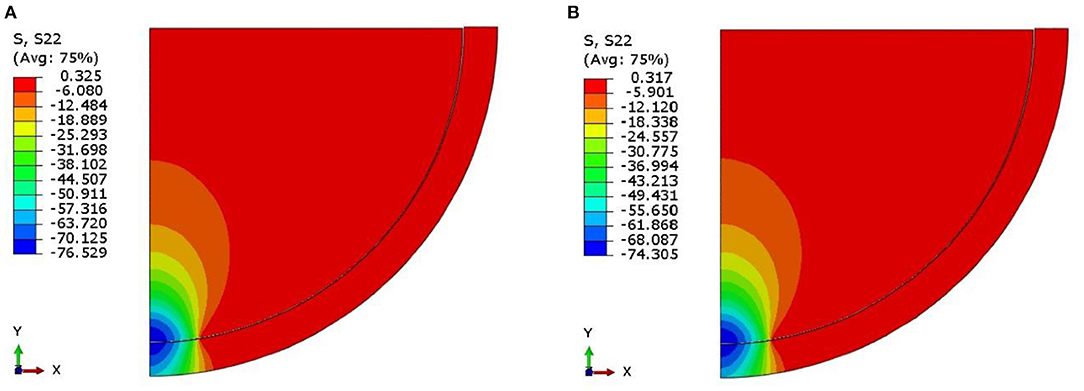
Figure 4. The examples of contact stress distribution of (A) CoCr vs. CoCr model and (B) CoCr vs. SS316L model.
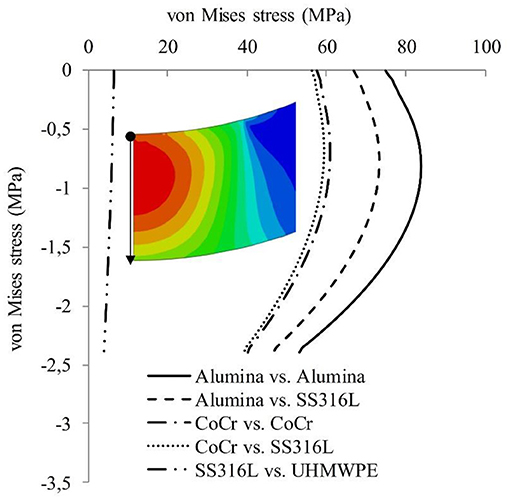
Further, the von Mises stress along the thickness of the cup to predict the yield level of the material against the loading conditions is investigated. The von Mises stress in Figure 5 is obtained from the center point of the contact to the end of cup thickness. Figure 5 shows the von Mises stress of AA, AS, CC, CS, and SU model. The results show the von Mises stress of AA model is higher than AS model with deviation of 12%. The von Mises stress of the CC model is higher than the CS model with deviation of about 2%. While, the von Mises stress of the CS model is higher than the SU model with the deviation of about 89%. The Figure 5 shows the high von Mises stress occur at the AA model, while the low von Mises stress occur at the SU model. Figure 5 show the von Mises stress along the cup thickness for AA until SU model is decrease. It shows that the differential hardness reducing the von Mises. The contour of von Mises stress for CC and CS model can be seen in Figure 6.
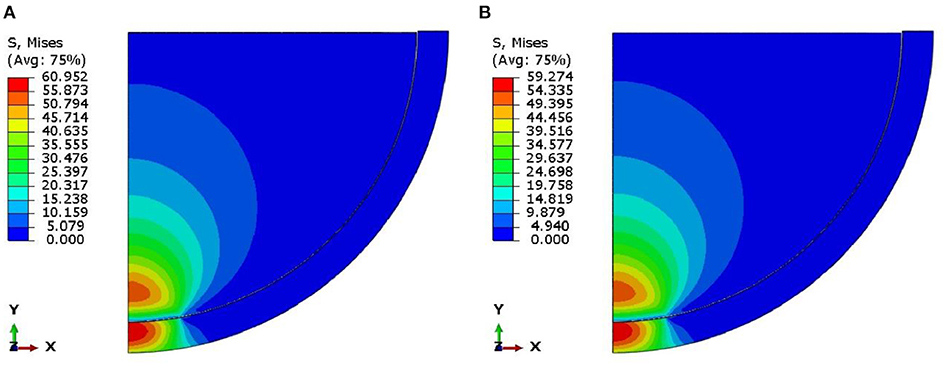
Figure 6. The examples of von Mises stress of (A) CoCr vs. CoCr model and (B) CoCr vs. SS316L model.
Discussions
The results of simulation have been presented in results section, and then the analysis is carried out related to these data. This research only observe the contact stress on the cup surface due to DH of material. The wear calculation of cup surface due to DH material is not performed in this research. In the next research, the wear on the cup may be calculated using Saputra wear model (Saputra et al., 2019). The wear calculation to involve the lubrication, it may be calculated using Ruggiero wear model (Ruggiero and Sicilia, 2020).
Based on the deviation of contact stress on each cup surface of the AA, AS, CC, CS, and SU models, the decreasing of contact stress of the AA model to the AS model, and from the CC model to the CS model is low. It means that the decreasing wear due to contact stress of the AA model to AS model, and the CC model to CS model is low. In fact, the experimental wear data presented by Barnes et al. (2008a) and Firkins et al. (2001) showed a very significant decrease in wear. This shows that the surface roughness factor is more dominant in the wear process than the contact stress factor. Based on the research of Svahn et al., the surface roughness has a strong influence on wear rate (Svahn et al., 2003). Although his research is not specific about hip, the authors argue that his research is relevant because it has similarities in MoM contact interactions. Al-Samarai et al. concluded that the surface roughness have correlation to specific wear rate (Al-Samarai et al., 2012). This is also supported by the theory of Jin et al. (1997) and the experiments of Chan et al. (1999) that the surface roughness of MoM can be reduced by increasing lubrication. It means that the process of decreasing wear on the hip prosthesis DH MoM is more dominantly influenced by the low surface roughness of the head.
Based on the deviation comparison the AS - CS models, the AS model deviation is quite significant. It is due to the large difference in the modulus of elasticity in the AS model, i.e., 180,000 MPa. Whereas, in the CS model, the difference is slight, i.e., 30,000 MPa. Based on this analysis, it can be concluded that the wear decrease due to differential-hardness is strongly influenced by the difference in modulus of elasticity. The greater the difference in modulus of elasticity, the greater the decrease in wear on the cup surface. It means that the modulus elasticity has correlations with hardness. Based on literature, the hardness of a material be inclined to increase with an increase in the elastic modulus (Lan and Venkatesh, 2014). Although the contact stress of DH MoM is relatively low compared to wear from the experimental results of Barnes and Firkin, contact stress still has a significant contribution in determining wear. How significant is the contribution of contact stress in calculating wear, further research needs to perform.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
ES contributed to the simulation. IB contributed to medicine. JJ contributed as the second mentor. EH contributed as primary mentor. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors fully acknowledged the Directorate of Research and Community Services, Republic of Indonesia for the approved fund with Grant No. 225-102/UN7.6.1/PP/2020.
References
Al Jabbari, Y. S. (2014). Physico-mechanical properties and prosthodontic applications of Co-Cr dental alloys: a review of the literature. J. Adv. Prosthodont. 6, 138–145. doi: 10.4047/jap.2014.6.2.138
Al-Samarai, R. A., Haftirman Ahmad, K. R., and Al-Douri, Y. (2012). Evaluate the effects of various surface roughness on the tribological characteristics under dry and lubricated conditions for Al-Si Alloy. J. Surf. Eng. Mater. Adv. Technol. 2, 167–173. doi: 10.4236/jsemat.2012.23027
Anderson, I. A., Bowden, M., and Wyatt, T. P. (2004). Stress analysis of hemispherical ceramic hip prosthesis bearings. Med. Eng. Phys. 27, 115–122. doi: 10.1016/j.medengphy.2004.09.018
Archard, J. F. (1953). Contact and rubbing of flat surfaces. J. Appl. Phys. 24, 981–988. doi: 10.1063/1.1721448
Babic, M., Veric, O., Bozic, Z., and Susic, A. (2020). Finite element modelling and fatigue life assessment of a cemented total hip prosthesis based on 3D scanning. Eng. Failure Anal. 113:104536. doi: 10.1016/j.engfailanal.2020.104536
Barnes, C. L., DeBoer, D., Corpe, R. S., Nambu, S., Carroll, M., and Timmerman, I. (2008a). Wear performance of large-diameter differential-hardness hip bearings. J. Arthroplasty 23, 56–60. doi: 10.1016/j.arth.2008.05.021
Barnes, C. L., Nambu, S., Carroll, M., Timmerman, I., and Svarczkopf, T. (2008b). Differential hardness bearings in hip arthroplasty. J. Surg. Orth. Adv. 17, 40–44.
Bartel, D. L., Burstein, A. H., Toda, M. D., and Edwards, D. L. (1985). The effect of conformity and plastic thickness on contact stresses in metal-backed plastic implants. J. Biomech. Eng. 107,193–199. doi: 10.1115/1.3138543
Chan, F. W., Bobyn, J. D., Medley, J. B., and Krygier, J. J. (1999). Simulator wear of metal-metal hip implants under adverse load conditions, in Proceedings of the 45th Orthopaedic Research Society (Anaheim, California), 310.
Dosaev, M., Samsonov, V., and Bekmemetev, V. (2019). Comparison between 2D and 3D simulation of contact of two deformable axisymmetric bodies. Int. J. Nonlinear Sci. Numerical Simul. 21, 123–133. doi: 10.1515/ijnsns-2018-0157
Dowson, D., Jobbins, B., and Seyed-Harraf, A. (1993). An evaluation of the penetration of ceramic femoral heads into polythene acetabular cups. Wear 162–164, 880–889. doi: 10.1016/0043-1648(93)90090-9
Firkins, P. J., Tipper, J. L., Ingham, E., Stone, M. H., Farrar, R., and Fisher, J. (2001). A novel low wearing differential hardness, ceramic-on-metal hip joint prosthesis. J. Biomech. 34, 1291–1298. doi: 10.1016/S0021-9290(01)00096-3
Fisher, J., Jin, Z., Tipper, J., Stone, M., and Ingham, E. (2016). Tribology of alternative bearings. Clin Orthop Relat Res. 453, 25–34. doi: 10.1097/01.blo.0000238871.07604.49
Gao, L., Hua, Z., and Hewson, R. (2018). Can a “pre-worn” bearing surface geometry reduce the wear of metal-on-metal hip replacements? - A numerical wear simulation study. Wear 406–407, 13–21. doi: 10.1016/j.wear.2018.03.010
Hibbitt, D., Karlsson, B., and Sorensen, P. (2012). Abaqus Documentation. Dassault Systèmes, Providence, RI, United States.
Hussain, M., Naqvi, R. A., Abbas, N., Khan, S. M., Nawaz, S., Hussain, A., et al. (2020). Ultra-high-molecular-weight-polyethylene (UHMWPE) as a promising polymer material for biomedical applications: a concise review. Polymers. 12:323. doi: 10.3390/polym12020323
International Standard (2014). Implant for surgery-Wear of total hip-joint prostheses, Part 1: Loading and displacement parameters for wear-testing machines and corresponding environmental conditions for test (ISO Standard No. 14242-1:2014). Available online at: https://www.iso.org/standard/63073.html (accessed March 30, 2021).
Jangid, V., Singh, A. K., and Mishra, A. (2019). Wear simulation of artificial hip joints: effect of materials. Mater. Today 18, 3867–3875. doi: 10.1016/j.matpr.2019.07.326
Jin, Z. M., Dowson, D., and Fisher, J. (1997). Analysis of fluid film lubrication in artificial joint replacements with surfaces of high elastic modulus. Proc. Ins. Mech. Eng. H 211, 247–256. doi: 10.1243/0954411971534359
Kabo, J. M., Gebhard, J. S., Loren, G., and Amstutz, H. C. (1993). In vivo wear of polyethylene acetabular components. J. Bone Joint Surg. Br. 75, 254–258. doi: 10.1302/0301-620X.75B2.8444946
Kauzlarich, J. J., and Williams, J. A. (2001). Archard wear and component geometry. Proc. Ins. Mech. Eng. J J. Eng. Tribol. 215, 387–403. doi: 10.1243/1350650011543628
Lan, H., and Venkatesh, T. A. (2014). On the relationships between hardness and the elastic and plastic properties of isotropic power-law hardening materials. Philos. Magazine 94, 35–55. doi: 10.1080/14786435.2013.839889
Le Duff, M. J., Johnson, A. J., and Amstutz, H. C. (2014). Do hardened femoral heads reduce blood metal ion concentrations after hip resurfacing?. Hip Int. 24, 327–332. doi: 10.5301/hipint.5000139
Livermore, J., Ilstrup, D., and Morrey, B. (1990). Effect of femoral head size on wear of the polyethylene acetabular component. J. Bone Joint Surg. Am. 72, 518–528. doi: 10.2106/00004623-199072040-00008
Ma, S. M., Kabo, J. M., and Amstutz, H. C. (1983). Frictional torque in surface and conventional hip replacement. J. Bone Joint Surg. Am. 65, 366–370. doi: 10.2106/00004623-198365030-00012
Naik, R. P., Kumar, U.A , and Pappula, L. (2020). Experimental investigation on surface roughness, hardness and mrr of stainless steel 316L in EDM with distilled water as electrolyte using Taguchi method. Int. J. Sci. Res. Sci. Eng. Technol. 7, 274–280. doi: 10.32628/IJSRSET20722
Paul, J. P. (1976). Force actions transmitted by joints in the human body. Proc. Royal Soc. B 192, 163–172. doi: 10.1098/rspb.1976.0004
Pesce, V., Maccagnano, G., Vicenti, G., Notarnicola, A., Lovreglio, P., and Soleo, L. (2013). First case report of vanadium metallosis after ceramic-on-ceramic total hip arthroplasty. J. Biol. Regul. Homeost Agents 27, 1063–1068.
Puccio, F. D., and Mattei, L. (2015). Biotribology of artificial hip joints. World J. Orthop. 6, 77–94. doi: 10.5312/wjo.v6.i1.77
Pulgarin, H. L. C., and Albano, M. P. (2015). Sintering and microstructure of Al2O3 and Al2O3-ZrO2 Ceramics. Proc. Mater. Sci. 8, 180–189. doi: 10.1016/j.mspro.2015.04.062
Ruggiero, A., and Sicilia, A. (2020). Lubrication modeling and wear calculation in artificial hip joint during the gait. Tribol. Int. 142:105993. doi: 10.1016/j.triboint.2019.105993
Saputra, E., Anwar, I. B., Ismail, R., Jamari, J., and Heide, E. V. D. (2016). Finite element study of contact pressure distribution on inner and outer liner in the bipolar hip prosthesis. AIP Conf. Proc. 1725:20075. doi: 10.1063/1.4945529
Saputra, E., Anwar, I. B., Ismail, R., Jamari, J., and Heide, E. V. D. (2017). Study of unipolar and bipolar hip prostheses using finite element simulation: contact stress analysis. Key Eng. Mater. 739, 96–102. doi: 10.4028/www.scientific.net/KEM.739.96
Saputra, E., Anwar, I. B., Jamari, J., and van der Heide, E. (2019). A wear formulation of total hip prosthesis for salat activity. Int. Rev. Mech. Eng. 13:16340. doi: 10.15866/ireme.v13i1.16340
Svahn, F., Kassman, A., and Wallen, E. (2003). The influence of surface roughness on friction and wear of machine element coatings. Wear 254, 1092–1098. doi: 10.1016/S0043-1648(03)00341-7
Uddin, M. S., and Zhang, L. C. (2013). Predicting the wear of hard-on-hard hip joint prostheses. Wear 301, 192–200. doi: 10.1016/j.wear.2013.01.009
Willis-Owen, C. A., Keene, G. C., and Oakeshott, R. D. (2011). Early metallosis-related failure after total knee replacement: a report of 15 cases. J. Bone Joint Surg. Br. 93, 205–209. doi: 10.1302/0301-620X.93B2.25150
Yang, S.-Y., Yu, H., Gong, W., Wu, B., Mayton, L., Costello, R., et al. (2007). Murine model of prosthesis failure for the long-term study of aseptic loosening. J. Orthop. Res. 25, 603–611. doi: 10.1002/jor.20342
Keywords: alumina, contact stress, differential-hardness, finite element simulation, hip prosthesis
Citation: Saputra E, Budiwan Anwar I, Jamari J and Heide Evd (2021) Reducing Contact Stress of the Surface by Modifying Different Hardness of Femoral Head and Cup in Hip Prosthesis. Front. Mech. Eng. 7:631940. doi: 10.3389/fmech.2021.631940
Received: 21 November 2020; Accepted: 08 April 2021;
Published: 14 May 2021.
Edited by:
Alessandro Ruggiero, University of Salerno, ItalyReviewed by:
Linmao Qian, Southwest Jiaotong University, ChinaVladimir Ivanovich Pakhaliuk, Sevastopol State University, Russia
Copyright © 2021 Saputra, Budiwan Anwar, Jamari and Heide. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eko Saputra, ZWtvLnNhcHV0cmFAcG9saW5lcy5hYy5pZA==
 Eko Saputra
Eko Saputra Iwan Budiwan Anwar
Iwan Budiwan Anwar J. Jamari
J. Jamari Emile van der Heide
Emile van der Heide