Low-Frequency Broadband Acoustic Metasurface Absorbing Panels

A broadband sound absorption attained by a deep-subwavelength structure is of great interest to the noise control community especially for extremely low frequencies (20–100 Hz) in room acoustics. Coupling multiple different resonant unit cells has been an effective strategy to achieve a broadband sound absorption. In this paper, we report on an analytical, numerical and experimental study of a low-frequency broadband (50–63 Hz, one third octave band), high absorption (average absorption coefficient $\approx$93%), near-omnidirectional (0–75°) acoustic metasurface absorber composed of four coupled unit cells at a thickness of 15.4 cm (1/45 of the wavelength at 50 Hz). To further broaden the bandwidth (50–100 Hz, one octave band), a design with 19 unit cells coupled in a supercell is analytically studied to achieve an average absorption coefficient of 85% for a wide angle range (0–75°) at a thickness of 20 cm (1/34 of wavelength at 50 Hz). Two additional degrees of freedom, the lateral size of supercell and the number of unit cells in the supercell, are demonstrated to facilitate such a causally optimal design which is close to the ideally causal optimality. The proposed design methodology may solve the long-standing issue for low frequency absorption in room acoustics.

Introduction

A sound absorber with a broadband and high absorption at a deep-subwavelength scale is of great interest in many occasions, such as room acoustics (Cox and D’Antonio, 2016), automobiles and aerospace engineering (Nark et al., 2018). A particular interest is to realize the so-called modal equalization (i.e., absorbing the normal mode frequencies of a room which usually fall below 100 Hz) (Fuchs et al., 2001; Błaszak, 2008; Rivet et al., 2012; Lau and Powell, 2018) for improving sound generation and speech interpretation. However, this is hindered by the inability of conventional sound absorbing materials to effectively remove low frequency sound (Yang and Sheng, 2017).

The emergence of acoustic metamaterials (Ma and Sheng, 2016; Ge et al., 2018) and acoustic metasurfaces (Assouar et al., 2018; Gerard and Jing, 2019) has enabled novel methods to design acoustic functional devices and has facilitated the development of new sound absorbing structures. To achieve the deep-subwavelength scale, one strategy is to use a very thin decorated membrane (Mei et al., 2012; Yang et al., 2015). In such a design, however, a uniform and controlled tension of the membranes is needed, which leads to fabrication challenges and durability issues. Another strategy is to modify the geometry of the conventional Helmholtz resonator (HR) and the microperforated panel (MPP) (Maa, 1998) into space-coiling structures (Cai et al., 2016; Li and Assouar, 2016; Huang et al., 2018), embedded-neck structures (Simon, 2018; Huang et al., 2019) or multi-coiled structures (Donda et al., 2019). Under the condition of impedance match or critical coupling (Romero-García et al., 2016a; Romero-García et al., 2016b), these designs can achieve a perfect sound absorption. Both the strategies above, however, have relatively narrow absorption bandwidth, which inevitably hinders practical applications. Some designs improve the bandwidth of single/identical resonator by tailoring the damping, such as increasing the intrinsic material damping (Leroy et al., 2015) or utilizing a heavily overdamped condition (Lee and Iizuka, 2018). Such designs, however, are either impractical or can hardly be applied to airborne sound absorption without a sacrifice of thickness (Romero-Garciá et al., 2016a).

To maximize the bandwidth of acoustic absorbers, a combination of different resonators (Kim et al., 2006; Kim, 2010; Wang and Huang, 2011; Li et al., 2016; Jiménez et al., 2017; Peng et al., 2018; Liu et al., 2019; Mosa et al., 2019; Zhu et al., 2019; Huang and et al., 2020) has been proposed as an effective design strategy. However, their corresponding thicknesses along the propagating direction are either thick or left with a potential for improvement. It is thus reasonable to ask: How much potential is there left for improvement? Or, for a target absorption spectrum, what is the minimum sample thickness required? These questions were addressed recently by (Yang et al., 2017) in which a target absorption is attained with the minimum sample thickness as dictated by the law of causality. However, the sponge, which is not desired in harsh environment, is needed to achieve a causally optimal design for a broadband design, by remediating the negative absorption effects resulting from using a small, finite number of resonators. In addition, the examples demonstrated in that study pertain to broadband absorption at mid to high frequency ranges. To design a causally optimal sound absorber which can achieve a broadband, near-omnidirectional high absorption at extremely low frequencies is still a largely unsolved issue. Though this issue was partially addressed by (Donda et al., 2019), the design therein was neither broadband nor demonstrated to be causally optimal.

To address the foregoing issues, this paper provides a framework to design a metasurface sound absorbing panel which is composed of non-uniform unit cells with different embedded necks in a supercell. In the design procedure, three degrees of freedom (DOFs), which are the lateral size of the unit cells, the number of unit cells and the lateral size of the supercell, are crucial factors to provide a broad range of surface impedance for a target absorption spectrum. Constrained by a desired absorption spectrum, a supercell at a minimum thickness is designed with the aid of optimization based on the Genetic algorithm (GA). Besides, the roles of different couplings (the interference coupling in the far field, the evanescent wave coupling, and the acoustic-structure interaction) on the absorption are separately evaluated.

The paper is structured as follows: In Theoretical Model, the metasurface geometry and the corresponding theoretical model are presented, along with the causal optimality recently introduced to sound absorption. In Design for 50–63 Hz (One-Third Octave) Absorption Without Optimization, a design with a validation of simulation and experimental results is presented. To form the desired absorption spectrum over 50–63 Hz, a fairly weak coupling between unit cell is assumed and each unit cell is thus designed independently (Ni, 2017; Peng et al., 2018) to have a perfect absorption (an impedance-matching condition) at its specified resonant frequency. At each peak of the absorption spectrum, the absorption is solely contributed from one resonator. Design for 50–63 Hz (One-Third Octave) Absorption With Optimization presents a design where the lateral sizes of unit cells are demonstrated to be instrumental to reducing the thickness by means of GA-based optimization. The thickness of the optimized structure is reduced by 23% without sacrificing the absorption performance. At the two center peaks of the absorption spectrum, the strong coupling, in which more than one resonator is excited, is observed. This leads to a new avenue to designing a deep-subwavelength sound absorber. The strong coupling is briefly explained as the far field coupling (Lepetit and Kanté, 2014) with the Hamiltonian from the coupled-mode theory (Suh et al., 2004; Verslegers et al., 2012). In The Coupling Through the Evanescent Wave and Acoustic-Structure Interaction, the evanescent wave coupling and the acoustic-structure interaction are separately evaluated for the validation of the assumptions made in Theoretical Model for Supercell With Different Unit Cells. In Design for 50–100 Hz (One Octave) Absorption With Optimization, a judicious tuning of a supercell’s lateral size and the number of unit cells in a supercell, combined with the careful design of the lateral sizes of unit cells, is demonstrated to jointly facilitate a causally optimal (Yang et al., 2017) absorber covering 50–100 Hz. The causally optimal absorber is further compared with an ideal absorber at an ideally minimum thickness. Conclusion concludes the paper.

Theoretical Model

Description of Metasurface Geometry

Figure 1A shows the proposed metasurface with 2-dimensional periodic array of supercells. Figure 1B shows one supercell with different deep-subwavelength resonant units with embedded cylindrical necks. The incident pressure is $p_{\text{in}}=P_{\text{in}}{e}^{-j\left(k_{x}x+k_{y}y-k_{z}z\right)}$, in which $k_x=k\sin {\theta }_{\text{in}}\cos {\phi }_{\text{in}}$, $k_y=k\sin {\theta }_{\text{in}}\sin {\phi }_{\text{in}}$ and $k_z=\cos {\theta }_{\text{in}}$. ${\theta }_{\text{in}}$ is the polar angle of incidence and ${\phi }_{\text{in}}$ is the azimuthal angle of incidence. $k=\omega /c_0$. The time dependence $e^{j\omega t}$ is dropped for simplicity.

FIGURE 1

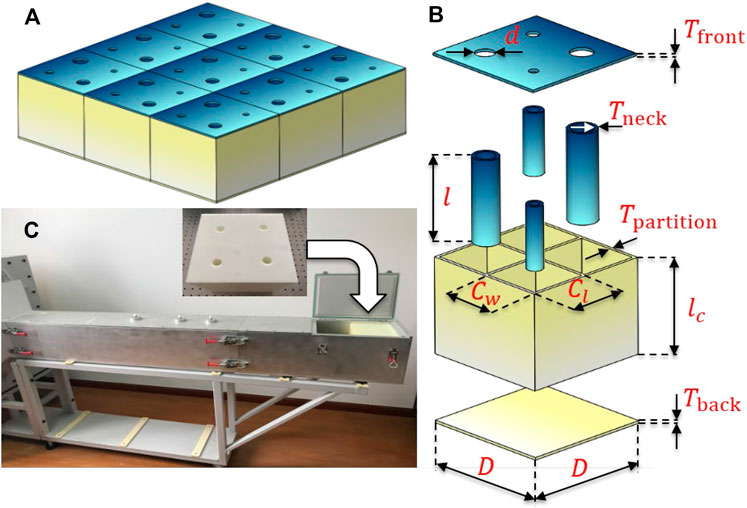
FIGURE 1. (A) Schematic of a metasurface absorber with nine supercells. (B) The explosive view of one supercell with four different unit cells. The thickness of the front panel, $T_{\text{front}}$, the thicknesses of the necks’ walls, $T_{\text{neck}}$, and the thicknesses of partitions, $T_{\text{partition}}$, are all set as 5 mm, according to our experimental trials, to mitigate the coupling effect between neighboring air domains through the shared partitions so that the assumption of acoustically rigid boundaries in the analytical and numerical models is genuinely valid. The thickness of the back panel $T_{\text{back}}$, is 2 mm. The diameter of the neck is $d$, the length of the neck is $l_n=l+T_{\text{front}}$, the lateral size of a unit cell is $S\left(C_w\times C_l\right)$, the length of the cavity is $l_c$, and the side length of a supercell is $D$. (C) The photograph of the experimental set-up for measuring absorption using the two microphones method. The lateral size of the impedance tube is $20\text{cm}\times 20\text{cm}$.

Theoretical Model for a Single Resonant Unit Cell With the Embedded Neck

The Stinson’s model (Stinson and Shaw, 1985; Stinson, 1991; Huang et al., 2019), which is valid for a broad range of frequencies, is used to model the narrow neck with the visco-thermal loss effect taken into account. Therefore, we have the impedance for the cylindrical neck with a circular cross-section (Huang et al., 2019),

$Z_n=-{\rho }_0{c}_0\frac{2j\sin \left(\frac{k_c{l}_n}{2}\right)}{\sqrt{\left(\gamma -\left(\gamma -1\right){\psi }_h\right){\psi }_v}},(1)$

where ${\rho }_0$, $c_0$ and $\gamma$ are density, speed of sound and the ratio of specific heats of air. The values are taken as 1.21 $\text{kg}/{\text{m}}^3$, 343.2 $\text{m}/\text{s }$and 1.4. $k_c= k\sqrt{\gamma -\left(\gamma -1\right){\psi }_h/{\psi }_v}$, ${\psi }_v=J_2\left(k_{v}d/2\right)/J_0\left(k_{v}d/2\right)$ and ${\psi }_h=J_2\left(k_{h}d/2\right)/J_0\left(k_{h}d/2\right)$ refer to the complex wave number, the viscous function and the thermal function of the embedded neck (Huang et al., 2019). $k_v$ and $k_h$ the viscous wave number and the thermal wave number: $k_v^2= -j\omega \left({\rho }_0/\eta \right), k_h^2= -j\omega \left({\rho }_0{C}_p/K\right).$$\eta$, $C_p$ and $K$ are the dynamic viscosity of air, the specific heat at constant pressure and the fluid thermal conductivity, of which the values are taken as $1.825\times {10}^{-5}\text{kg}/\left(\text{m}\cdot \text{s}\right)$, 1,007 $\text{J}/\left(\text{kg}\cdot \text{K}\right)$ and $0.02514\text{W}/\left(\text{m}\cdot \text{K}\right)$. All the geometric symbols are referred to Figure 1B. This model, which takes thermal loss into account for the long neck, has been well validated against experimental results recently (Huang et al., 2019). Note that the conventional HR model (Panton and Miller, 1975) is only a special model derived from this generalized model (Weston, 1953; Stinson and Shaw, 1985; Maa, 1998).

For resonant unit cells whose dimensions are all much smaller than the working wavelength, the impedance for the irregular-shape cavity resulted from the embedded neck can be approximated as (Huang et al., 2019),

$Z_c=-\frac{jS{\rho }_0{c}_0^2}{\omega V},(2)$

where $\omega$ is the angular frequency. $S$ and $V$ are the lateral area and the volume of the cavity. $V=S{l}_c-\pi {\left(\left(d/2\right)+T_{\text{neck}}\right)}^{2}l$. Under this scenario, it is the volume of the cavity that plays the important role. It is reasonable to neglect the thermal and viscous loss here since the dimensions of the cavity are much larger than the boundary layer thickness for the frequencies of interest.

The overall impedance of the resonator can be approximated as the sum of the impedances of the neck and cavity, which reads (Huang et al., 2019),

$Z=Z_n+Z_c+2\sqrt{2\omega {\rho }_0\eta }+j\omega {\rho }_0\delta ,(3)$

where the subscript n represents the neck and c represents the cavity. $2\sqrt{2\omega {\rho }_0\eta }$ is the resistance correction. $\delta =\left[1+\left(1-1.25\right)\epsilon \right]\times \left(4/3\pi \right)d$ is the mass end correction in which $\epsilon =d/\min \left(C_w,C_l\right)$ is the ratio of the neck’s diameter to the narrower side of the cavity.

Theoretical Model for Supercell With Different Unit Cells

When a supercell of the panel is composed of M different unit cells in parallel, its absorption performance can be characterized by a mean specific acoustic admittance or a mean specific acoustic impedance at normal incidence (Zwikker and Kosten, 1949),

$\frac{1}{Z_{\text{tot}}}={\displaystyle {\sum }_1^M\frac{{\varnothing }_N}{Z_N},}(4)$

where $Z_N$ is the specific acoustic impedance for resonator N in which end corrections of the neck to both the waveguide and the cavity are considered. ${\varnothing }_N$ is the surface porosity, ${\varnothing }_N=\pi {\left(d_N/2\right)}^2/D^2$. Note that the far field interference coupling (e.g., constructive and destructive interference) among the reflected propagating waves from the individual unit cells (Huang et al., 2020) is implicitly included in Eq. 4. The sound absorption coefficient can be subsequently calculated by (Uno, 2010),

$\alpha \left(f,{\theta }_{\text{in}}\right)=\frac{4\mathrm{Re}\left(Z_{\text{tot}}\right){\rho }_0{c}_0\cos {\theta }_{\text{in}}}{{\left\{{\rho }_0{c}_0+\mathrm{Re}\left(Z_{\text{tot}}\right)\cos {\theta }_{\text{in}}\right\}}^2+{\left\{\mathrm{Im}\left(Z_{\text{tot}}\right)\cos {\theta }_{\text{in}}\right\}}^2},(5)$

For normal incidence, a perfect absorption requires an impedance match between the panel and the air,

$\text{Re}\left(Z_{\text{tot}}\right)={\rho }_0{c}_0(\mathrm{6a})$

$\text{Im}\left(Z_{\text{tot}}\right)=0(\mathrm{6b})$

Although this method is physically straightforward, computationally inexpensive and accurate for our deep-subwavelength structures, several underlying assumptions and limitations need to be noted. First, Eq. 5 can be assumed to be independent (Wang et al., 2014) of the azimuthal angle $\phi$ if the lateral size of the supercell is deep-subwavelength. Otherwise, an asymmetric absorption (Lee and Iizuka, 2019; Wang et al., 2019) would be observed because of the geometric asymmetry, when the incident wave is from the same polar angle but different azimuthal angles. Second, this frequently used method is an approximation in terms of the accuracy of the mean specific impedance. Eq. 4 is based on the assumptions (Zwikker and Kosten, 1949) that lateral sizes of necks are considerably smaller than the wavelength and the lateral size of the supercell is sufficiently small, at which the pressure is constant over the surface and the volume displacement is additive. These assumptions can also be understood in a mathematical manner: Only the fundamental mode wave dominates the scattering field and thus needs to be considered, when $\lambda \ge 2D$ (Kim, 2010), regardless of the angle of incidence. When these assumptions are invalid, the coupled-mode theory (Wang et al., 2019) and radiation impedance method (Kim et al., 2006; Lee and Iizuka, 2019) can be used, which either implicitly or explicitly take into account the coupling of evanescent waves between unit cells. Third, the acoustic-structure interaction is neglected. The second and third assumptions will be carefully examined in this study.

Throughout this paper we will use a figure of merit ${\alpha }_{\text{avg}, \theta }^{f_1\sim f_2}$ to characterize and evaluate the absorption performance of the sound absorbing panel, which is the average absorption coefficient from $f_1$ to $f_2$ at the incident angle $\theta$.

Causal Optimality in Sound Absorption

An absorber can be regarded as causally optimal when its thickness reaches the minimum limitation dictated by the principle of causality (Yang et al., 2017):

$T\ge \frac{1}{4{\pi }^2}\frac{B_{\text{eff}}}{B_0}\left|\underset{0}{\overset{\infty }{{\displaystyle \int }}}\text{In}\left[1-A\left(\lambda \right)\right]d\lambda \right|=T_{\min },(7)$

where $\lambda$ is the wavelength in air, $A\left(\lambda \right)$ is the absorption as a function of the wavelength, $B_{\text{eff}}$ is the effective bulk modulus of the absorber in the static limit, and $B_0$ is the bulk modulus of the air. $B_{\text{eff}}$ can be calculated as $B_0/{\varphi }_V$ , in which volume porosity ${\varphi }_V\equiv V_{\text{air}}/V_{\text{tot}}$ is the volume fraction of the air domain considering $B_{\text{solid}}\gg B_{\text{air}}$.

Results and Discussion

Design for 50–63 Hz (One-Third Octave) Absorption Without Optimization

Motivated by the application of modal frequency absorption, four different resonant unit cells arranged in a supercell, with parameters listed in Table 1, are realized, with ${\alpha }_{\text{avg},0^{°}}^{50\sim 63\text{Hz}}\approx 93\%$ for the analytical prediction and simulation, and ${\alpha }_{\text{avg},0^{°}}^{48\sim 61\text{Hz}}\approx 93\%$ for the experiment, as shown in Figure 2A. The total thickness is 19 cm, which is around 1/36 of the wavelength at 50 Hz. Its absorption performance over 50–63 Hz as a function of the angle of incidence is also shown in Figures 2B–F. The analytical model is based on Eq. 5, while details of the sample fabrication and experimental setup are provided in Supplementary Appendix A. Details of the first type of numerical model can be found in Supplementary Appendix B. The first type of numerical model is distinct from the second type of numerical model, which will be discussed in The Coupling Through the Evanescent Wave and Acoustic-Structure Interaction. The average absorption coefficient over 50–63 Hz is observed to be around 90% for angles of incidence smaller than 60°, because of the subwavelength size of the supercell. For angles of incidence larger than 60°, the absorption drops, likely due to an impedance mismatch. Interestingly, starting from around 50°, only three absorption peaks appears instead of four peaks in the absorption spectrum, which is a signature of coupling between two unit cells (Li et al., 2016) and this phenomenon is resulted from a coalescence of eigenstates (Ding et al., 2016; Wang et al., 2019) as the incident angle changes.

TABLE 1

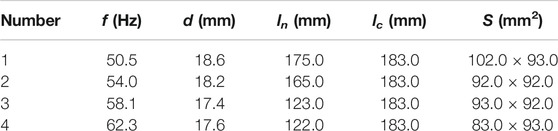
TABLE 1. Geometric parameters of the metasurface absorber with four different unit cells without optimization. The lateral size of the supercell is 20 cm $\times$ 20 cm. The overall thickness of the absorber is 19 cm. Its volume porosity is 80%.

FIGURE 2

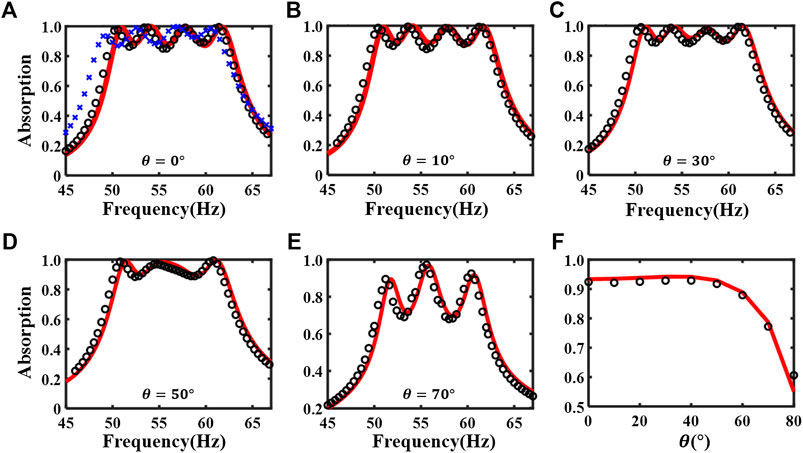
FIGURE 2. (A) The theoretical (red solid line), the first type of numerical (black circles) and experimental (blue crosses) absorption coefficient at normal incidence for the non-optimized metasurface absorber. (B–E) The theoretical and numerical absorption coefficient for the angles of incidence ${10}^{°}$, ${30}^{°}$,${50}^{°}$, and ${70}^{°}$. (F) The theoretical and numerical average absorption coefficient over 50–63 Hz vs. angle of incidence.

The design principle of this absorber is described as follows. The lateral size of the supercell is fixed as $20\text{cm}\times 20\text{cm}$, matching the size of our existing impedance tube (Figure 1C). The suitable number of unit cells in a supercell, which depends on the Q factor of unit cells and the desired 50–63 Hz absorption spectrum, is chosen as four. Additional unit cells are needed, if their Q factor is larger (Donda et al., 2019). To form a continuously high absorption spectrum, each unit cell is designed to have a perfect absorption, following Eq. 6, at a specific frequency inside the targeted absorption spectrum. The frequencies at which the perfect absorption occur are nearly equally spaced. By assuming a weak coupling effect between unit cells at these perfect absorption frequencies, each unit cell can thus be designed independently. During this design process, the lateral size of each unit cell is assigned without being optimized. In Figure 3A, the absorption coefficients of the supercells with only one individual unit cell are plotted as mark lines (blue diamonds, green circles, magenta points and black crosses), while that of the supercell with all unit cells is plotted as red solid line. For example, the curve for “unit cell one” is a plot of $Z_{\text{tot}}\left(f\right)=Z_1\left(f\right)/{\varnothing }_1$, with ${\varnothing }_1=\pi {\left(d_1/2\right)}^2/{\left(20 \text{cm}\right)}^2$. It is noted that the peaks of the red solid line, which indicates the near-perfect absorption of the supercell, matches well with peaks of the individual unit cells, which to a certain extent supports the assumption of the weak coupling between unit cells. It is, however, still too early to claim from these analytical results in Figure 3A that these near-perfect absorption points are contributed solely from individual unit cells operating independently. The underlying physical behavior will be revealed in the next paragraph by means of finite element method (FEM) simulations. Two important points of this trial-and-error design strategy should be mentioned. First, how large the cross-sectional area is assigned to each cavity is roughly proportional to the target wavelength because of the fact that a larger volume of cavity is required for a smaller resonant frequency. For example, unit cell one which targets the lowest frequency has a cavity with the largest cross-sectional area. The best assignment of cross-sectional area to each cavity, however, is not investigated here but will be discussed in Design for 50–63 Hz (One-Third Octave) Absorption With Optimization. Second, the design of a long and embedded neck plays a critical role in minimizing the thickness of the unit cell for the longest wavelength and thus the overall thickness of the supercell, because a large phase delay is correlated with a long neck (Huang et al., 2019). During the design of unit cell one, the neck length $l$ and the length of its cavity $l_c$ can be obtained by solving 6a and 6b, whereas $d$ is parametrically swept and the cross-sectional area is set as $93 \text{mm}\times 102 \text{mm}$. One set of $l$ and $l_c$ is chosen, in which $l$ is as close as possible to $l_c$ but a clearance between $l$ and $l_c$ is left to ensure that the mass end correction is physically meaningful. The concept of curved necks (Huang et al., 2019), which is capable of further shrinking the total thickness, is not used here though, considering the fabrication complexity.

FIGURE 3

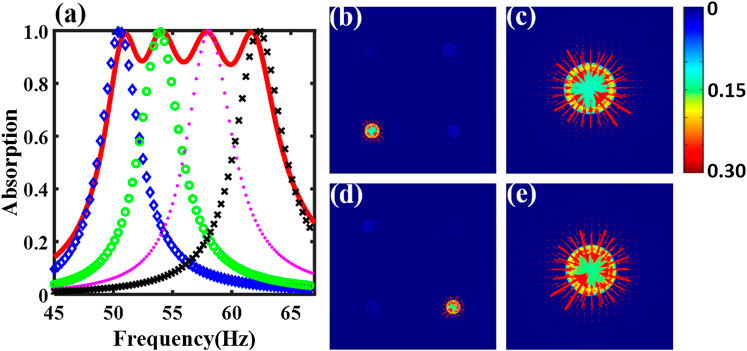
FIGURE 3. (A) The theoretical absorption coefficient of the non-optimized supercell (red solid line) and individual unit cells (blue diamonds, green circles, magenta points and black crosses are for unit cell one, two, three, and four respectively). The curve for “unit cell N” is an absorption spectrum for a metasurface in which only unit cell N can interact with the incident sound and all the other unit cells are blocked at the front panel. N = 1, 2, 3, 4. Sound intensity maps of the non-optimized supercell at (B) 53.6 Hz and (D) 57.8 Hz, respectively. The bottom-left unit cell of (B) and the bottom-right unit cell of (D) are enlarged, as shown in (C) and (E), respectively. The incident pressure is normalized to 1 Pa. Color bar ($\text{w}/{\text{m}}^2$): component of the sound intensity vector that are perpendicular to the supercell surface, i.e.,$I_z$. Arrow: components of the sound intensity vector that are parallel to the supercell surface, i.e., $I_x$ and $I_y$. The size of the arrows is proportional to the magnitude of the intensity.

To gain insights concerning how the supercell is behaving at these near-perfect absorption frequencies, the sound intensity fields just above the supercell surface are drawn at the resonant frequencies of two selected unit cells (53.6 and 57.8 Hz) using COMSOL in Figures 3B–E. At these resonant frequencies, the sound intensity is observed to be highly concentrated and drawn to the only unit cell whose mode is excited. Instead of “penetrating” the entire supercell and being absorbed by all the unit cells at a similar amount, the sound energy is dissipated mostly by one resonating unit cell while other unit cells behave in a way as if they were “sealed.” This is a clear signature of the weak coupling between the resonant unit cells at the resonant frequencies, and thus it confirms the validity to design each unit cell independently for a near-perfect absorption.

Design for 50–63 Hz (One-Third Octave) Absorption With Optimization

In the previous section, the achieved design for the desired absorption spectrum has room to shrink the thickness, considering several deficiencies during the design methodology. First, by assuming a weak coupling between unit cells, all unit cells in the previous section are designed independently to realize near-perfect absorption at their individual resonant frequencies to form a continuously high absorption spectrum. A better assignment of the contribution from all unit cells to the total absorption at each individual frequency of interest is left to be resolved. Second, the assignment of the cross-sectional area to each cavity follows an empirical idea: Generally, a larger cross-sectional area is required for a lower frequency if the cavities are required to have the same depth. A better assignment of cross-sectional areas also needs to be proposed. To address the two concerns above, the lateral areas of unit cells are assigned as additional variables to be treated in GA, while the thickness of the absorber is to be optimized for the same absorption spectrum, i.e., ${\alpha }_{\text{avg},0^{°}}^{50\sim 63\text{Hz}}\ge 93\%$. The details of variables, constraints and the object function are listed in Supplementary Appendix C. Note that the area of supercell, instead of being a variable in the next section, is also fixed to be 20 cm by 20 cm which is the size of our impedance tube.

Figure 4 shows the absorption performance of the optimized design, which is 15.4 cm (1/44.5 of the wavelength at 50 Hz) and is 23% thinner than the non-optimized one, with the geometric parameters listed in Table 2. However, its average absorption performance is not sacrificed as shown from the comparison of two designs’ performance in Table 3. Note that the average frequency range for the analytical predictions and the numerical results is 50–63 Hz, while that for the experiment is 48–61 Hz because of the small frequency shift as shown in Figures 2A,4A. The larger mismatch between the experimental result and the analytical prediction of the optimized design, compared with that of the non-optimized design, can be reasonably explained by a larger fabrication error, as shown in Supplementary Appendix A. The maximum tolerance is 0.4 mm for the optimized sample, which is larger than that of the previous unoptimized sample, which is 0.1 mm.

FIGURE 4

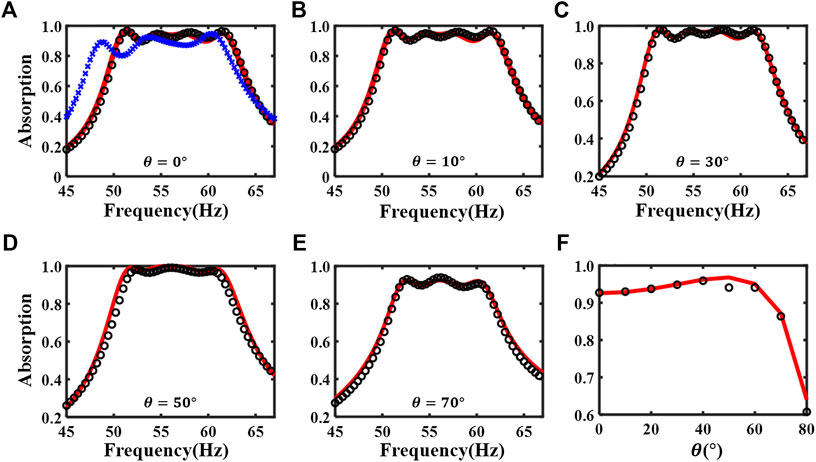
FIGURE 4. (A) The theoretical (red solid line), the first type of numerical (black circles) and experimental (blue cross) absorption coefficient at normal incidence for the optimized metasurface absorber. (B–E) The theoretical and numerical absorption coefficient for the angles of incidence ${10}^{°}$, ${30}^{°}$, ${50}^{°}$, and ${70}^{°}$. (F) The theoretical and numerical average absorption coefficient over 50–63 Hz vs. angle of incidence.

TABLE 2

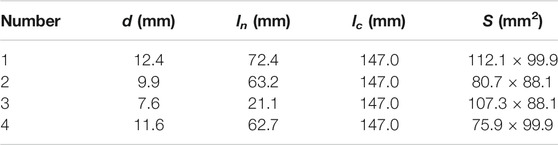
TABLE 2. Geometric parameters of the optimized metasurface absorber composed of four different unit cells. The lateral size of the supercell is $20 \text{cm}\times 20 \text{cm}$. The overall thickness of the absorber is 15.40 cm. Its volume porosity is 84%.

TABLE 3

TABLE 3. Comparison of the absorption performance between the non-optimized (design A) and the optimized (design B) absorber. “Theory” and “Simulation” refer to the average absorption coefficients over 50–63 Hz based on the analytical model and the first type of numerical result, while “Experiment” refers to the average absorption coefficient over 48–61 Hz based on the experimental result. ${\varphi }_V$ and $T$ are the volume porosity and total thickness of the design. $T_{\text{min}}$ is the minimum thickness dictated by the principle of causality (i.e., Eq. 7).

Next, we will uncover how the supercell thickness can be reduced while the absorption performance is maintained. In contrast to the fairly weak coupling between unit cells demonstrated from the previous design at these near-perfect absorption points, a strong coupling, at which more than one unit cells jointly contribute to the total absorption, is observed as shown in Figure 5A. The intensity plots for the middle two peaks of the absorption curve (i.e., 54.4 and 57.8 Hz) are used to further shed light on the strong coupling. As shown in Figures 5B–D, two different unit cells are excited simultaneously and strongly coupled to work as energy sinks at 54.4 Hz. At 57.8 Hz, this phenomenon is not as pronounced as that at 54.4 Hz because the portion of absorption from one of the unit cells is large, as shown in Figures 5E–G. Theoretically speaking, the strong coupling is the interference of the reflected propagating waves from the simultaneously excited unit cells. The total reflected propagating wave is a linear combination of the reflected propagating waves from all the individual unit cells. Interference, a fundamental wave phenomenon, happens among these reflected propagating waves, which creates the ripples in the absorption spectrum of the supercell and even changes the number of absorption peaks (Figure 4F). Consequently, each individual unit cell is not required to satisfy the near-perfect absorption requirement (Huang et al., 2020) like shown in Figure 3. Moreover, the assignment of cross-sectional areas to these non-uniform cavities is judiciously tuned thanks to the assistance of GA. As shown in Table 2, for the unit cell one, which corresponds to the lowest resonant frequency, its cross-sectional area is $112.1 \text{mm}\times 99.9 \text{mm}$, which is 18% larger than that of the non-optimized design, i.e., $102.0 \text{mm}\times 93.0 \text{mm}$, while its neck and cavity lengths are shortened. Benefiting from the strong coupling and well-designed non-uniform cavities, the thickness of supercell, which is highly dependent on the neck and cavity lengths of unit cell with the lowest resonant frequency, is decreased from 19 to 15.4 cm by 23%. This can be well explained from the perspective of the causality constraint (Eq. 7): The larger the volume porosity is, the smaller the minimum thickness is. Our optimized design, which has shorter embedded necks and thus a larger volume porosity, has a smaller actual thickness $T$ and a smaller causally minimum thickness $T_{\text{min}}$ as well, as shown in Table 3.

FIGURE 5

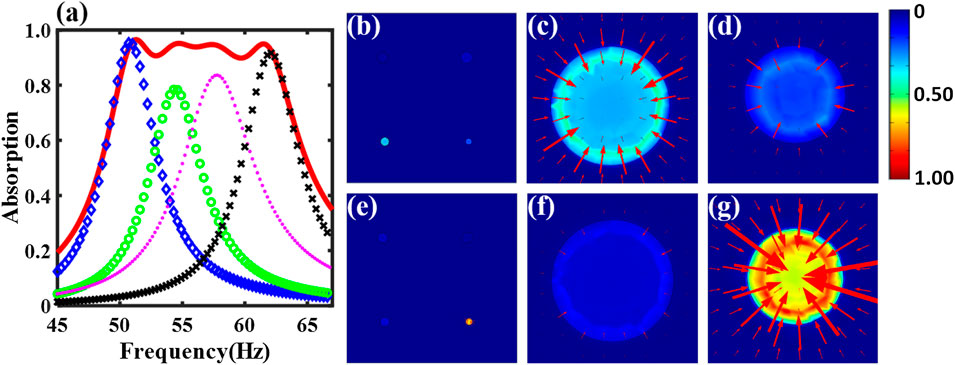
FIGURE 5. (A) The theoretical absorption coefficient of the optimized supercell (red solid line) and individual unit cells (blue diamonds, green circles, magenta points and black crosses are for unit cell one, two, three, and four respectively). The curve for “unit cell N” is an absorption spectrum for a metasurface in which only unit cell N can interact with the incident sound and all the other unit cells are blocked at the front panel. N = 1, 2, 3, 4. Sound intensity maps of the optimized supercell at (B) 54.4 Hz and (E) 57.8 Hz, respectively. The bottom-left unit cell and the bottom-right unit cell of (B) are enlarged, as shown in (C) and (D), respectively. The bottom-left unit cell and the bottom-right unit cell of (E) are enlarged, as shown in (F) and (G), respectively. The incident pressure is normalized to 1 Pa. Color bar ($\text{w}/{\text{m}}^2$): component of the sound intensity vector that are perpendicular to the supercell surface, i.e.,$I_z$. Arrow: components of the sound intensity vector that are parallel to the supercell surface, i.e., $I_x$ and $I_y$. The size of the arrows is proportional to the magnitude of the intensity.

The Hamiltonian from the coupled-mode theory (Suh et al., 2004; Verslegers et al., 2012) is likely another way to interpret the interference coupling in the far field (Lepetit and Kanté, 2014; Huang et al., 2020). Taking the system at the second absorption peak (i.e., at 54.4 Hz) of normal incidence as an example, two resonators are effectively excited so that the four-state system can be reduced to a two-state system at this frequency. This two-state system is coupled to one port since here only the plane wave mode exists in the far field under the cutoff frequency of the waveguide. Thus, the effective Hamiltonian of this two-states, one-port open system is written as (Suh et al., 2004; Verslegers et al., 2012; Lepetit and Kanté, 2014),

$H_{\text{eff}}=\left(\begin{array}{cc}{\Omega }_2+j{\delta }_2& \kappa \\ \kappa & {\Omega }_3+j{\delta }_3\end{array}\right)+j\left(\begin{array}{cc}{\gamma }_2& \sqrt{{\gamma }_2{\gamma }_3}\\ \sqrt{{\gamma }_2{\gamma }_3}& {\gamma }_3\end{array}\right),(8)$

where ${\text{Ω}}_n$, ${\delta }_n$ and ${\gamma }_n$ are the resonance frequency, the intrinsic loss rate and the radiation leakage rate to the port for the $n^{\text{th}}$ resonator. $\kappa$ is the near filed coupling which, in this case, is the evanescent wave (Yang et al., 2017) on the surface of the absorber panel. Since the off-diagonal terms represent the coupling effect between resonators, there are two kinds of couplings (Lepetit and Kanté, 2014) in the open system, i.e., the near field coupling $\kappa$ and the far field coupling $\sqrt{{\gamma }_2{\gamma }_3}$. The near field coupling exists when the resonant modes belong to different closely distributed resonators, while the far field coupling exists when the modes have the same symmetry. The near field coupling, however, in this case is negligible, though they satisfy the condition above. This is because that the analytical model (Eq. 4), which does not consider the effect of coupling of the evanescent wave by means of self-energy term (Yang et al., 2017), still matches well with the numerical simulation in which the near field coupling is considered. Therefore, it is the interference coupling in the far field (Huang et al., 2020) that likely results in the total absorption of the supercell, which cannot be obtained by simply the summation of absorptions from each individual unit cell. We also note that, different from the closed system (Ding et al., 2016) in which the coupling term is resulted from the near field coupling, our system is an open system in which the radiation leakage $\gamma$ can also become the off-diagonal elements but result in the coupling effect in the far field. Instead of the manipulation of near field coupling (Yang et al., 2017) in their open system, our improved design benefits from the far field coupling under the framework of the Hamiltonian, which similarly, is illustrated as the coherent coupling effect (Huang et al., 2020) by designing a larger number of imperfect absorbers to enhance sound absorption.

The Coupling Through the Evanescent Wave and Acoustic-Structure Interaction

Besides the interference coupling in the far field, there also exists two types of coupling mechanisms in our absorber within the frequency range of interest: the evanescent wave coupling on the top surface via air and the acoustic-structure interaction between cavities through partitions. In Figures 2,4, the first type of simulations has considered evanescent wave coupling but not the acoustic-structure interaction. To consider the acoustic-structure interaction, the second type of simulations is performed using the Thermoviscous Acoustic-Solid Interaction Module of COMSOL Multiphysics 5.4 with detailed settings in Supplementary Appendix B. The coupling effects that each model takes into account are summarized in Table 4. The absorption coefficient curves of different models for the non-optimized and the optimized design are plotted in Figures 6A–F. As shown in Table 4, the difference between the theoretical model and the first type of numerical simulation is that the former does not consider the evanescent waves while the latter does. The difference between the first and second type of numerical model is that the former does not consider the acoustic-structure interaction while the latter does. This means that we can separately evaluate the validation of the assumptions that are made in Theoretical Model for Supercell With Different Unit Cells about the evanescent wave and acoustic-structure interaction by comparing the results in Figure 6.

TABLE 4

TABLE 4. The coupling effects that each model takes into account. By comparing the corresponding curves in Figure 6, the evanescent wave coupling and the acoustic-structure interaction can be separately evaluated for the validation of the assumptions that are made in the Theoretical Model for Supercell With Different Unit Cells.

FIGURE 6

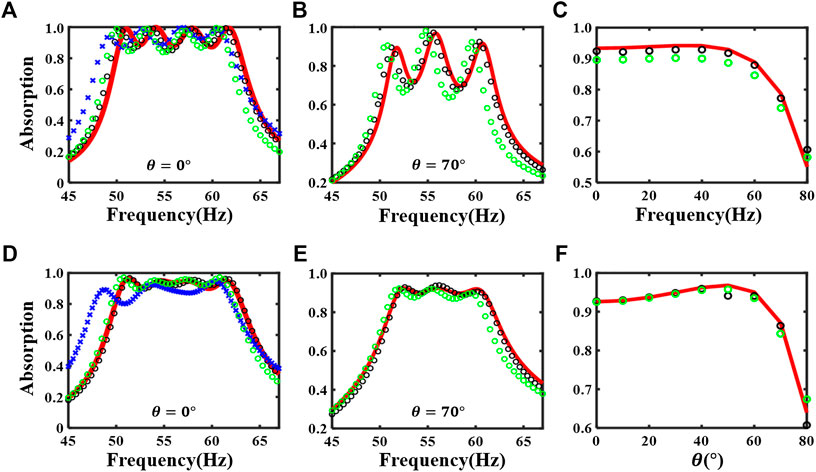
FIGURE 6. (A) The theoretical (red solid line), the first type of numerical (black circles), the second type of numerical (green circles) and experimental (blue cross) absorption coefficient at normal incidence. (B) The theoretical and the two types of numerical absorption coefficient for the angle of incidence ${70}^{°}$. (C) The theoretical and the two types of numerical average absorption coefficient over 50–63 Hz vs. angle of incidence. (A-C) and (D-F) are for the non-optimized and the optimized metasurface absorber, respectively.

One observation of Figure 6 is that the positions of the peaks of the first type of numerical results are all slightly down-shifted from the theoretical predictions because of the coupling by the evanescent waves. This observation is consistent with the one in the supplementary material of (Yang et al., 2017) and shows that the coupling by the evanescent waves is negligible.

Another observation of Figure 6 is the redshift of the second type of numerical results compared with the first type of numerical results. This is consistent with the redshift of the experimental results compared with the first type of numerical results, and this is resulted from the relatively weak acoustic-structure interaction through the partitions. The weak acoustic-structure interaction could be explained as follows: First, whether the structural resonance happens within the frequency of interest is examined. We numerically calculate the modal frequencies of the whole structure. For the normal incidence case, the bottom surface and four side surfaces are assumed as fixed to mimic the boundary conditions in a waveguide. For the oblique incident cases, the bottom surface is assigned as fixed and the four side surfaces are assigned as the Floquet periodic condition. In all these cases, the lowest modal frequencies are around 800 Hz, which are beyond of the range of our interest. This means that no structural resonance occurs within the frequency range of interest so that the interaction between the neighboring cavities through the partition can be approximated as a transmission problem involving only acoustic waves. In this case, we can estimate the effect of the 5 mm partition by calculating its plane wave pressure transmission coefficient (material properties are in Supplementary Appendix A), which is approximately 8% at 50 Hz when the wave diction is perpendicular to the partition. This means that the impedance and the thickness of the partition are large enough that the transmission through the partition at the frequency range of interest is reasonably small. Thus, the acoustic-structure interaction manifests itself as a small sound transmission through the partition in our case, which effectively makes the cavity less stiff and consequently results in the redshift of the resonant frequency.

Based on the above analysis and observation, the analytical model, which does not consider the acoustic-structure interaction as well as the evanescent coupling, is acceptable as a simple model to design the absorber, as long as structural resonance is not excited and the impedance and thickness of the partition are large enough to effectively reduce the sound transmission.

Design for 50–100 Hz (One Octave) Absorption With Optimization

The optimized metasurface absorber, which benefits from the strong coupling between unit cells with judiciously designed cavities, is further explored to realize 50–100 Hz absorption. The lateral size of the supercell for an optimal design will be discussed below, instead of being assumed as $20 \text{cm}\times 20\text{cm}$. For this reason, the experimental validation is not conducted in the section. The absorption performance of a resonator is conventionally (Uno, 2010) characterized by its maximum absorption cross section, which is in fact the lateral size of the supercell at which the perfect absorption condition (i.e., Eq. 6) is satisfied. The lateral size is also recently demonstrated to be directly related to the effective porosity (Wang and Huang, 2011; Peng et al., 2018) and thus the impedance matching condition in Eq. 6a. Besides, the number of unit cells, which is a bridge between the absorption ability (e.g., bandwidth) of a single unit cell and the overall absorption of the supercell, is an additional important variable not well discussed in previous literatures.

With the above concerns, GA is used as an efficient tool to seek an optimal design which satisfies ${\alpha }_{\text{avg},0^{°}}^{50\sim 100\text{Hz}}\ge 85\%$, in which the two additional variables (the lateral size of supercell D and the number of unit cells M), are incorporated. The details of variables, constraints and the object function are listed in Supplementary Appendix D. An optimal design, at a thickness of 20 cm (which is 1/34.3 of the wavelength at 50 Hz) and a lateral size of 78.84 cm $\times$ 78.84 cm, is achieved with all the other parameters listed in Table 5. Within the supercell, there are 19 different unit cells whose lateral sizes are well tuned. Figure 7A shows the analytically predicted absorption for the supercell and individual unit cells. The analytical model is valid since the dimensions of the supercell satisfy the assumptions discussed in Theoretical Model for Supercell With Different Unit Cells. The FEM validation is not provided here since the existing computation resource in our lab is insufficient for this design with 19 unit cells. The analytical prediction, however, has been proven to be accurate in previous two designs. The average absorption coefficient over 50–100 Hz as a function of angle of incidence is plotted in Figure 7F and remains above 85% until 75°, which again demonstrates its near-omnidirectional absorption capability. The absorptions at 10, 30, 50, and 70° are plotted in Figures 7C–E, respectively.

TABLE 5

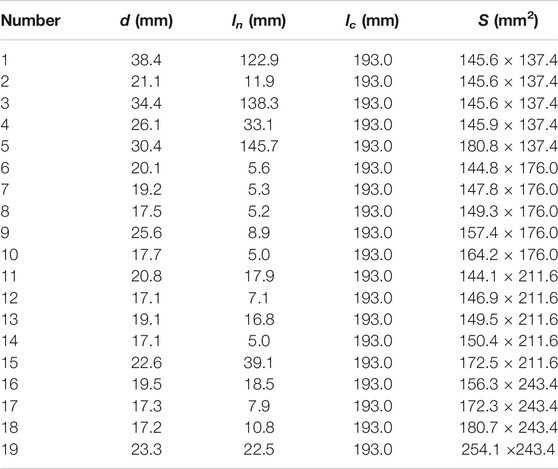
TABLE 5. Geometric parameters of an optimized metasurface absorber composed of 19 different unit cells. The lateral size of the supercell is 78.84 cm $\times$ 78.84 cm. The overall thickness of the absorber is 20 cm. Its volume porosity is 90%.

FIGURE 7

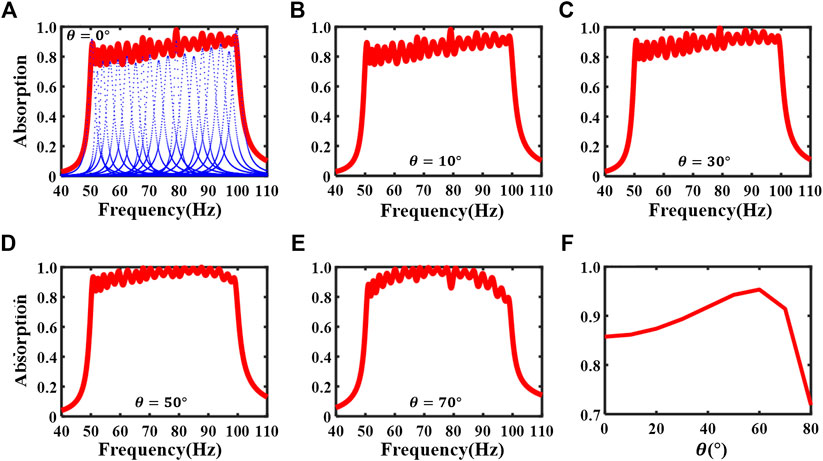
FIGURE 7. (A) The absorption coefficient of the optimized supercell (red solid line) and individual unit cells (blue points lines) at normal incidence. (B–E) The theoretical absorption coefficients for the angles of incidence ${10}^{°}$, ${30}^{°}$,${50}^{°}$, and ${70}^{°}$. (F) The theoretical average absorption coefficient over 50–100 Hz vs. angle of incidence.

It is noted that the achieved design is causally optimal: If we insert the achieved absorption spectrum (the red curve in Figure 8) of our design and the corresponding volume porosity (90% for this design) into Eq. 7, $d_{\text{min}}$ is calculated as 20 cm, which is precisely the thickness of our design.

FIGURE 8

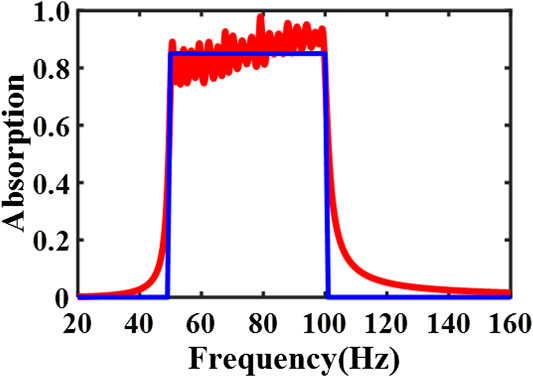
FIGURE 8. The absorption coefficient of the optimized supercell (red solid line) and the ideal absorber (blue solid line) at normal incidence. The optimal thickness for the optimized design is 20 cm. The optimal thickness for the ideal design is 16.9 cm when the volume porosity is set as one and the achieved absorption spectrum exactly matches with the desired one (85% over 50–100 Hz) in Eq. 7.

Next, we will uncover how the two additional design variables, like the geometric parameters of all unit cells, play critical roles in reaching the causally optimal design (the minimum thickness) for a desired absorption spectrum. For the lateral size of supercell being a suitable value, on one hand, it should be as large as possible so that the lateral size of unit cells can be larger and therefore the thickness of all unit cells can be smaller to meet the design objective. On the other hand, it cannot be too large because that will result in an impedance-mismatch for individual unit cells and thus a drop of absorption coefficient. The number of unit cells should also be properly chosen. If the number of unit cells is too small, it would be insufficient to achieve such a broad absorption spectrum by coupling. However, if the number of unit cells is too large and the thickness is preserved, it would call for an increased lateral size of the supercell, which would result in a reduction of the impedance match and the absorption performance. Similarly, for such a case of a large number of unit cells, if the lateral size of the supercell is chosen to be preserved for the desired absorption performance, it would result in an increase in the thickness of the supercell.

In addition, we would like to further comment on the impact of the causality constraint on guiding the thinnest design of the linear and passive absorber for a desired absorption spectrum. First, it is not difficult to design an absorber which is causally optimal as indicated in the supplemental material of reference (Yang et al., 2017): The MPP or sponge can easily become causally optimal if the desired absorption is not required to be high over a broad low frequency range. However, it is hard to realize a high absorption at such a low-frequency and broad range as presented in the paper, i.e., 50–100 Hz. Second, as shown in Eq. 7, the optimal thickness not only relies on the achieved absorption spectrum, but also is highly dependent on the volume porosity. The larger the volume porosity is, the smaller the optimal thickness is. In other words, a better space utilization makes an absorber thinner. A higher volume porosity ($\ge$95%) can be achieved by making the partitions between the unit cells as thin as 1 mm, at which the partitions may not be treated as ideally rigid anymore. Third, designing an absorber whose absorption spectrum is as close as possible to the desired one is crucial to shrink the minimum thickness, especially for low frequencies. As shown in Figure 8, the absorption spectrum of an ideal absorber, whose absorption spectrum exactly matches with the desired one (85% over 50–100 Hz in this case), is plotted as a benchmark. The proposed design exhibits an absorption performance fairly close to the desired one with little unwanted absorption outside the frequency range of interest. This is due to the fine manipulation of acoustic surface impedance and the absorption spectrum by utilizing unit cells with large Q factors. The optimal thickness of the ideal absorber is 16.9 cm by substituting a volume porosity of 100% and the desired absorption spectrum (the blue curve in Figure 7) into Eq. 7. Thus, our 20 cm design is not only causally optimal, but is also close to the ideal design. This is benefited from an adequate tuning range of acoustic impedances, which is provided by the three DOFs during the design of supercell, to simultaneously shape the absorption spectrum and to maintain a high volume porosity. The three DOFs in fact provide a similar functionality as the sponge does in (Yang et al., 2017) where lateral sizes of unit cells are uniform, and the lateral size of the supercell as well as the number of unit cells are fixed.

Conclusion

This paper analytically, numerically and experimentally studies a low-frequency broadband (50–63 Hz, one third octave band), high absorption (average absorption coefficient $\approx$93%), near-omnidirectional ($0^{°}$–${75}^{°}$) acoustic metasurface absorber composed of four coupled unit cells at a thickness of only 15.4 cm (1/45 of the wavelength at 50 Hz), in which the suitable assignment of lateral size to each unit cell plays a critical role in reducing the overall thickness. The interference coupling in the far field, the evanescent wave coupling, and the acoustic-structure interaction are discussed. Furthermore, to realize a broadband and near-perfect absorption at an optimal thickness, the lateral size of supercell and the number of unit cells in the supercell are also judiciously engineered. Taking all these new degrees of freedom into account and with the assistance of GA, a causally optimal acoustic absorber, which is a broadband (50–100 Hz, one octave band), high-absorption (average absorption coefficient 85%), near-omnidirectional ($0^{°}$–${75}^{°}$) and deep-subwavelength (1/34 of wavelength at 50 Hz), is proposed. Our future work is to experimentally validate the proposed design for 50–100 Hz and further push the design of absorbers to the ideal one by means discussed in this paper. We believe that our design philosophy, in which three degrees of freedom are proven to be critical in reaching a causally optimal thickness, would offer a gateway to designing broadband sound absorbers with different formats of unit cells (MPP, HRs, space-coiling structures, etc.) and to meet the long-standing need in room acoustics.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JJ and DL contributed equally to this work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

YL acknowledges support from the National Natural Science Foundation of China under Grant No. 11704284.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2020.586249/full#supplementary-material

References

Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic metasurfaces. Nat Rev Mater 3 (12), 460–472. doi:10.1038/s41578-018-0061-4

31123431CrossRef Full Text | Google Scholar

Błaszak, M. A. (2008). Acoustic design of small rectangular rooms : normal frequency statistics. Appl. Acoust. 69, 1356–1360. doi:10.1016/j.apacoust.2007.10.005

CrossRef Full Text | Google Scholar

Cai, X., Guo, Q., Hu, G., and Yang, J. (2016). Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators. Appl. Phys. Lett. 105 (12), 121901. doi:10.1063/1.4895617

CrossRef Full Text | Google Scholar

Cox, T., and D’Antonio, P. (2016). Acoustic absorbers and diffusers: theory, design and application. 3rd Edn. Boca Raton, FL: CRC Press.

Google Scholar

Ding, K., Ma, G., Xiao, M., Zhang, Z. Q., and Chan, C. T. (2016). Emergence, coalescence, and topological properties of multiple exceptional points and their experimental realization. Phys. Rev. X 6 (2), 1–13. doi:10.1103/PhysRevX.6.021007

CrossRef Full Text | Google Scholar

Donda, K., Zhu, Y., Fan, S.-W., Cao, L., Li, Y., and Assouar, B. (2019). Extreme low-frequency ultrathin acoustic absorbing metasurface. Appl. Phys. Lett. 115 (17), 173506. doi:10.1063/1.5122704

CrossRef Full Text | Google Scholar

Fuchs, H. V., Zha, X., Zhou, X., and Drotleff, H. (2001). Creating low-noise environments in communication rooms, Appl. Acoust. 62, 1375–1396. doi:10.1016/s0003-682x(01)00008-1

CrossRef Full Text | Google Scholar

Ge, H., Yang, M., Ma, C., Lu, M.-H., Chen, Y.-F., Fang, N., et al. (2018). Breaking the barriers: advances in acoustic functional materials. Natl. Sci. Rev. 5 (2), 159–182. doi:10.1093/nsr/nwx154

CrossRef Full Text | Google Scholar

Gerard, N. J. R. K., and Jing, Y. (2019). Loss in acoustic metasurfaces : a blessing in disguise. MRS Commun. 10 (1), 32–41. doi:10.1557/mrc.2019.148

CrossRef Full Text | Google Scholar

Huang, S., Fang, X., Wang, X., Assouar, B., Cheng, Q., and Li, Y. (2018). Acoustic perfect absorbers via spiral metasurfaces with embedded apertures. Appl. Phys. Lett. 113 (23), 233501. doi:10.1063/1.5063289

CrossRef Full Text | Google Scholar

Huang, S., Fang, X., Wang, X., Assouar, B., Cheng, Q., and Li, Y. (2019). Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 145 (1), 254–262. doi:10.1121/1.5087128

CrossRef Full Text | Google Scholar

Huang, S., Liu, T., Zhou, Z., Wang, X., Zhu, J., and Li, Y. (2020). Extreme sound confinement from quasibound states in the continuum. Phys. Rev. Appl. 14 (2), 1. doi:10.1103/physrevapplied.14.021001

CrossRef Full Text | Google Scholar

Huang, S., Zhou, Z., Li, D., Liu, T., Wang, X., Zhu, J., et al. (2020). Compact broadband acoustic sink with coherently coupled weak resonances. Sci. Bull. 65 (5), 373–379. doi:10.1016/j.scib.2019.11.008

CrossRef Full Text | Google Scholar

Jiménez, N., Romero-García, V., Pagneux, V., and Groby, J.-P. (2017). Rainbow-trapping absorbers: broadband, perfect and asymmetric sound absorption by subwavelength panels for transmission problems. Sci. Rep. 7 (1), 13595. doi:10.1038/s41598-017-13706-4

CrossRef Full Text | Google Scholar

Kim, S., Kim, Y.-H., and Jang, J.-H. (2006). A theoretical model to predict the low-frequency sound absorption of a Helmholtz resonator array. J. Acoust. Soc. Am. 119 (4), 1933–1936. doi:10.1121/1.2177568

CrossRef Full Text | Google Scholar

Kim, Y.-H. (2010). “Essentials of acoustics in a closed space,” in Sound propagation: an impedance based approach (Singapore: John Wiley & Sons), Chap. 5, Vol. 9, 323–334.

CrossRef Full Text | Google Scholar

Lau, S.-K., and Powell, E. A. (2018). Effects of absorption placement on sound field of a rectangular room: a statistical approach. J. Low Freq. Noise Vib. Act. Contr. 37 (2), 394–406. doi:10.1177/1461348418780027

CrossRef Full Text | Google Scholar

Lee, T., and Iizuka, H. (2018). Heavily overdamped resonance structurally engineered in a grating metasurface for ultra-broadband acoustic absorption. Appl. Phys. Lett. 113 (10), 101903. doi:10.1063/1.5047798

CrossRef Full Text | Google Scholar

Lee, T., and Iizuka, H. (2019). Acoustic resonance coupling for directional wave control: from angle-dependent absorption to asymmetric transmission. New J. Phys. 21 (4), 043030. doi:10.1088/1367-2630/ab130d

CrossRef Full Text | Google Scholar

Lepetit, T., and Kanté, B. (2014). Controlling multipolar radiation with symmetries for electromagnetic bound states in the continuum. Phys. Rev. B 90 (24), 1–4. doi:10.1103/PhysRevB.90.241103

CrossRef Full Text | Google Scholar

Leroy, V., Strybulevych, A., Lanoy, M., Lemoult, F., Tourin, A., and Page, J. H. (2015). Superabsorption of acoustic waves with bubble metascreens. Phys. Rev. B 91 (2). doi:10.1103/PhysRevB.91.020301

CrossRef Full Text | Google Scholar

Li, J., Wang, W., Xie, Y., Popa, B.-I., and Cummer, S. A. (2016). A sound absorbing metasurface with coupled resonators. Appl. Phys. Lett. 109 (9), 091908. doi:10.1063/1.4961671

CrossRef Full Text | Google Scholar

Li, Y., and Assouar, B. M. (2016). Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 108 (6), 063502. doi:10.1063/1.4941338

CrossRef Full Text | Google Scholar

Liu, C. R., Wu, J. H., Chen, X., and Ma, F. (2019). A thin low-frequency broadband metasurface with multi-order sound absorption. J. Phys. D Appl. Phys. 52 (10), 105302. doi:10.1088/1361-6463/aafaa3

CrossRef Full Text | Google Scholar

Maa, D.-Y. (1998). Potential of microperforated panel absorber. J. Acoust. Soc. Am. 104 (5), 2861–2866. doi:10.1121/1.423870

CrossRef Full Text | Google Scholar

Ma, G., and Sheng, P. (2016). Acoustic metamaterials: from local resonances to broad horizons. Sci. Adv. 2 (2), e1501595. doi:10.1126/sciadv.1501595

CrossRef Full Text | Google Scholar

Mei, J., Ma, G., Yang, M., Yang, Z., Wen, W., and Sheng, P. (2012). Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 3. doi:10.1038/ncomms1758

CrossRef Full Text | Google Scholar

Mosa, A. I., Putra, A., Ramlan, R., Prasetiyo, I., and Esraa, A.-A. (2019). Theoretical model of absorption coefficient of an inhomogeneous MPP absorber with multi-cavity depths. Appl. Acoust. 146, 409–419. doi:10.1016/j.apacoust.2018.11.002

CrossRef Full Text | Google Scholar

Nark, D. M., Jones, M. G., and Sutliff, D. L. (2018). “Broadband inlet liner design for the DGEN aero-propulsion research turbofan,” 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, Georgia, June 25–29, 2018.

CrossRef Full Text | Google Scholar

Ni, S. (2017). Sound-proof sandwich panel design via metamaterial concept. PhD dissertation. Raleigh (NC): North Carolina State University.

CrossRef Full Text | Google Scholar

Panton, R. L., and Miller, J. M. (1975). Resonant frequencies of cylindrical Helmholtz resonators. J. Acoust. Soc. Am. 57 (6), 1533–1535. doi:10.1121/1.380596

CrossRef Full Text | Google Scholar

Peng, X., Ji, J., and Jing, Y. (2018). Composite honeycomb metasurface panel for broadband sound absorption. J. Acoust. Soc. Am. 144 (4), EL255–EL261. doi:10.1121/1.5055847

CrossRef Full Text | Google Scholar

Rivet, E., Boulandet, R., Lissek, H., and Rigas, I. (2012). Study on room modal equalization at low frequencies with electroacoustic absorbers, Acoustics 2012, Nantes, France, Apr 2012. hal-00810955, pp. 2851–2856.

CrossRef Full Text | Google Scholar

Romero-Garciá, V., Theocharis, G., Richoux, O., Merkel, A., Tournat, V., and Pagneux, V. (2016a). Perfect and broadband acoustic absorption by critically coupled sub-wavelength resonators. Sci. Rep. 6 (1), 19519. doi:10.1038/srep19519

CrossRef Full Text | Google Scholar

Romero-García, V., Theocharis, G., Richoux, O., and Pagneux, V. (2016b). Use of complex frequency plane to design broadband and sub-wavelength absorbers. J. Acoust. Soc. Am. 139 (6), 3395–3403. doi:10.1121/1.4950708

CrossRef Full Text | Google Scholar

Simon, F. (2018). Long elastic open neck acoustic resonator for low frequency absorption. J. Sound Vib. 421, 1–16. doi:10.1016/j.jsv.2018.01.044

CrossRef Full Text | Google Scholar

Stinson, M. R. (1991). The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am. 89 (2), 550–558. doi:10.1121/1.400379

CrossRef Full Text | Google Scholar

Stinson, M. R., and Shaw, E. A. G. (1985). Acoustic impedance of small, circular orifices in thin plates. J. Acoust. Soc. Am. 77 (6), 2039–2042. doi:10.1121/1.391776

CrossRef Full Text | Google Scholar

Suh, W., Wang, Z., and Fan, S. (2004). Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities. IEEE J. Quant. Electron. 40 (10), 1511–1518. doi:10.1109/JQE.2004.834773

CrossRef Full Text | Google Scholar

Uno, I. (2010). “Mathematical supplement,” in Noise reduction analysis (Sudbury, MA: Jones & Barlett Publishers), Chap. 4, Vol. 5, 133–135.

CrossRef Full Text | Google Scholar

Verslegers, L., Yu, Z., Ruan, Z., Catrysse, P. B., and Fan, S. (2012). From electromagnetically induced transparency to superscattering with a single structure: a coupled-mode theory for doubly resonant structures. Phys. Rev. Lett. 108 (8), 1–5. doi:10.1103/PhysRevLett.108.083902

CrossRef Full Text | Google Scholar

Wang, C., and Huang, L. (2011). On the acoustic properties of parallel arrangement of multiple micro-perforated panel absorbers with different cavity depths. J. Acoust. Soc. Am. 130 (1), 208–218. doi:10.1121/1.3596459

CrossRef Full Text | Google Scholar

Wang, C., Huang, L., and Zhang, Y. (2014). Oblique incidence sound absorption of parallel arrangement of multiple micro-perforated panel absorbers in a periodic pattern. J. Sound Vib. 333 (25), 6828–6842. doi:10.1016/j.jsv.2014.08.009

CrossRef Full Text | Google Scholar

Wang, X., Fang, X., Mao, D., Jing, Y., and Li, Y. (2019). Extremely asymmetrical acoustic metasurface mirror at the exceptional point. Phys. Rev. Lett. 123 (21), 214302. doi:10.1103/PhysRevLett.123.214302

CrossRef Full Text | Google Scholar

Weston, D. E. (1953). The theory of the propagation of plane sound waves in tubes. Proc. Phys. Soc. B 66 (8), 695–709. doi:10.1088/0370-1301/66/8/310

CrossRef Full Text | Google Scholar

Yang, M., Chen, S., Fu, C., and Sheng, P. (2017). Optimal sound-absorbing structures. Mater. Horiz. 4 (4), 673–680. doi:10.1039/c7mh00129k

CrossRef Full Text | Google Scholar

Yang, M., Meng, C., Fu, C., Li, Y., Yang, Z., and Sheng, P. (2015). Subwavelength total acoustic absorption with degenerate resonators. Appl. Phys. Lett. 107 (10), 104104. doi:10.1063/1.4930944

CrossRef Full Text | Google Scholar

Yang, M., and Sheng, P. (2017). Sound absorption structures: from porous media to acoustic metamaterials keynote topic. Annu. Rev. Mater. Res. 47 (1), 83–114. doi:10.1146/annurev-matsci-070616-124032

CrossRef Full Text | Google Scholar

Zhu, Y., Donda, K., Fan, S., Cao, L., and Assouar, B. (2019). Broadband ultra-thin acoustic metasurface absorber with coiled structure. APEX 12, 114002. doi:10.7567/1882-0786/ab494a

CrossRef Full Text | Google Scholar

Zwikker, C., and Kosten, C. W. (1949). “Absorption by resonators,” in Sound absorbing materials (New York, NY: Elsevier), 127–163.

CrossRef Full Text | Google Scholar