Ratio of Loss and Storage Moduli Determines Restitution Coefficient in Low-Velocity Viscoelastic Impacts

Impact tests are an important tool to analyze dynamic material properties of viscoelastic media in technology and biology. In this context, rigorous contact mechanical models of the collision problem are necessary to adequately interpret data from impact experiments. It is shown here theoretically that the coefficient of restitution in these types of testing is mainly a function of one specific material property, namely, the ratio between the loss and storage moduli of the viscoelastic probe at the characteristic timescale of the impact. Explicit dependencies of the restitution coefficient on factors like impact velocity, impactor shape, general material rheology, and functional grading—beyond the fact that those may influence the impact duration and the dynamic modulus associated with it—are weak.

Introduction

Impact tests are considered as a fast and simple method to gain insights about the material behavior of viscoelastic media—for example, rubber or soft tissues like articular cartilage—under dynamic loading.

In the simplest case, only the rebound velocity (or some directly related measure, e.g., the rebound height) of a rigid impactor is determined. In technical contexts, this testing procedure is often referred to as the determination of the “rebound elasticity” of the material [see, e.g., the industrial standard DIN EN ISO, 8307 (2018)]. However, how the so-obtained coefficient of restitution (COR) generally relates to the viscoelastic rheology, or put bluntly, what kind of material property the “rebound elasticity” actually represents, remains unclear.

Biological tissues, especially in joints, are often subject to impact loading, for example, during sporting activities or accidents. Therefore, impact tests are also performed on these tissues to analyze material properties and to determine damage thresholds. For this purpose, Burgin and Aspden (2007) constructed a drop tower, which was later developed further by Kang et al. (2017). In this regard, Burgin et al. (2014) pointed out that the material behavior of articular cartilage under impact loading is quite different from the one under slow loading conditions. Ozcan et al. (2011) used the frequency response function in impact tests with a hammer to characterize frequency-dependent material properties of the human liver.

Contact mechanics models of viscoelastic impacts have a long history. In solving the impact problem, these models, obviously, heavily rely on the solutions of the contact problem. For linear materials, the latter ones are obtained based on the correspondence between linearly elastic and linearly viscoelastic boundary value problems established by Lee (1955). Although the correspondence principle strictly only holds, if the regions of boundary themselves do not change in time (this is generally not the case for dynamic contact problems, when the contact area is not known a priori), Lee and Radok (1960) were able to show that the correspondence solution of the viscoelastic Hertzian problem is consistent with all boundary conditions, if the contact radius is a non-decreasing function of time. If the contact radius possesses a single maximum (this is the case for the impact problem), the solution needs to be adjusted, as was acknowledged by Lee and Radok in their paper. The corrected contact solution for the restitution phase (when the contact radius is decreasing in time) has been presented by Hunter (1960) (for the Hertzian case) and Graham (1965) and Ting (1966) (for arbitrary convex, axisymmetric profile geometries).

Hunter also applied his contact solution to analyze the respective contact-impact problem. Bassi (1978) was the first to examine the problem, to which extent impact characteristics (for the linear impact onto an incompressible Kelvin solid, see Impact Onto an Incompressible Kelvin Solid) allow for the determination of dynamic material properties. The linear impact problem for viscoelastic materials (i.e., the impact of a rigid flat cylindrical punch onto a viscoelastic medium) has been also studied by Butcher and Segalman (2000), Schwager and Pöschel (2007), and Argatov (2013). For the impact of a sphere onto a Kelvin solid (see Impact of a Paraboloid), Kuwabara and Kono (1987) proposed a model, later studied in detail by Ramírez et al. (1999), in which the simple form of the equation of motion during the compression phase (when the contact radius is increasing) is also used for the restitution. This, from a contact mechanics perspective, is slightly erroneous (as pointed out above) but allows for a mathematically simple treatment of the impact. A contact mechanically more rigorous solution of this problem was given by Willert et al. (2017). Selyutina et al. (2015) and Springhetti and Selyutina (2018) theoretically studied the impact response of articular cartilage on the basis of a quasi-linear Kelvin material model. The impact problem for a quasi-linear standard solid has been analyzed by Argatov et al. (2016).

In the present manuscript, it is analyzed in detail whether the primary result of a viscoelastic impact test, the COR, can be directly related to a specific material property and how this relation is in turn affected by the shape of the impactor (flat punch or spherical), the general material rheology, and functional grading—as biomaterials usually are graded media. For this purpose, the low-velocity (i.e., quasi-static) central normal impact of a rigid body with mass m and initial velocity v₀ onto an incompressible viscoelastic half-space is studied. First, in Impact Onto an Incompressible Kelvin Solid, the simplest viscoelastic material, the Kelvin solid with complete decoupling of elastic and viscous properties, is considered, and the known respective impact solutions are briefly summed up. To capture the influence of material rheology, a more general material model is considered in Influence of Material Rheology, first in a rigorous way and after that in an approximate sense, which demonstrates that the COR indeed is bound to a specific material property. Influence of Viscoelastic Grading is devoted to the effect of graded viscoelasticity.

Impact Onto an Incompressible Kelvin Solid

The arguably minimal model of a viscoelastic material is the Kelvin solid with shear modulus G_∞ and shear viscosity η. The complex dynamic modulus in this case simply reads as

$\begin{array}{ll}\widehat{G}(\omega )=G_{\infty }+i\eta \omega ,& (1)\end{array}$

with the angular frequency of oscillation ω and the imaginary unit i. In the following, the known solutions for the impact of a cylindrical flat punch with radius a, and a sphere (approximated in the vicinity of the contact as a paraboloid) with radius R onto such a material, occupying a half-space, are briefly recapitulated.

Impact of a Cylindrical Flat Punch

In case of the impact of a rigid, cylindrical punch, the impact solution can be looked up in Butcher and Segalman (2000), Schwager and Pöschel (2007), Argatov (2013), and Willert (2020). It only depends on a nondimensional damping parameter

$\begin{array}{ll}2D:=\frac{\eta {\omega }_0}{G_{\infty }}=\frac{Im\left\{\widehat{G}({\omega }_0)\right\}}{Re\left\{\widehat{G}({\omega }_0)\right\}},{\omega }_0:=\sqrt{\frac{8a{G}_{\infty }}{m}}.& (2)\end{array}$

Note that ω₀ is the characteristic angular frequency of the elastic problem. “Im” and “Re” denote the imaginary and real parts of a complex quantity, respectively. Hence, D is given by the ratio of the loss and storage moduli at the characteristic frequency scale of the impact problem.

The COR for weak damping is given by Argatov (2013).

$\begin{array}{ll}\epsilon =exp\left[-\frac{2D}{\sqrt{1-D^2}}arctan\left(\frac{\sqrt{1-D^2}}{D}\right)\right],D<1,& (3)\end{array}$

whereas for strong damping (Willert, 2020)

$\begin{array}{ll}\epsilon =exp\left[-\frac{2D}{\sqrt{D^2-1}}artanh\left(\frac{\sqrt{D^2-1}}{D}\right)\right],D>1.& (4)\end{array}$

Impact of a Paraboloid

For a spherical impactor, contact mechanically rigorous modeling is slightly more complicated than in the previous case, because the contact radius is not prescribed by the radius of the flat punch and therefore increasing and decreasing during the impact. Hence, compression and restitution must be considered separately. A self-consistent model of the impact is most conveniently implemented within the framework of the “method of dimensionality reduction” (MDR; Popov and Heß, 2015; Popov et al., 2018). In the model by Kuwabara and Kono (1987), the simple form of the equation of motion for compression is also used for the restitution phase. It has been shown recently by the author in the monograph (Willert, 2020) that both models differ only slightly from each other. Also, both agree well with experimental results by Van Zeebroeck et al. (2003) on impacts with rubber and various biomaterials.

The impact duration and thus the characteristic frequency for the elastic problem were given by Hertz in his classical paper (Hertz, 1882). Hence, the nondimensional damping parameter, in analogy to Equation, reads (omitting numerical factors of the order of one)

$\begin{array}{ll}2D=\eta {\left(\frac{R{v}_0}{m^2{G}_{\infty }^3}\right)}^{1/5}.& (5)\end{array}$

Figure 1 shows the COR as a function of the damping parameter for the flat punch and the spherical impactor. The curves are practically the same. Hence, the explicit dependence of the COR on the impactor shape is very weak. However, the shape obviously influences the damping parameter and therefore, implicitly, the impact solution. Especially note that the damping parameter for the spherical impactor depends on the impact velocity, so the COR is velocity dependent. This is not the case for the linear contact with a cylindrical punch, where the characteristic frequency is strictly a system property.

FIGURE 1

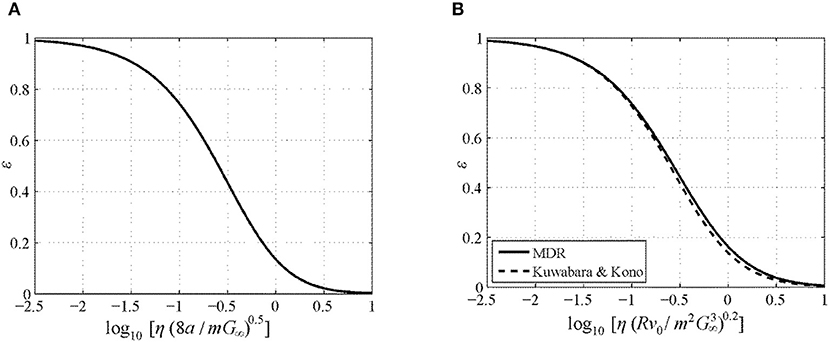
Figure 1. Coefficient of restitution as a function of the governing damping parameter for the impact onto an incompressible Kelvin solid. (A) Impact of a cylindrical flat punch. (B) Impact of a paraboloid; solid line, contact mechanically rigorous model implemented within the method of dimensionality reduction (MDR); dashed line, Kuwabara–Kono model.

Influence of Material Rheology

The fact that model predictions based on the Kelvin solid agree well with experimental data raises an interesting question: If, obviously, no real viscoelastic material exhibits such a trivial rheology, as suggested by the Kelvin model, how is it possible for the latter to accurately predict real impact behavior? Although the answer is quite simple, to demonstrate it, we have to briefly look into more general rheological models.

Rheological Models in Linear Viscoelasticity

The rheological behavior of “real” linearly viscoelastic materials is often captured in terms of a Prony series. In case of a generalized Maxwell model, the time-dependent shear modulus reads

$\begin{array}{ll}G\left(t\right)={\tilde{G}}_{\infty }+{\displaystyle \sum _{i=1}^N}{G}_{i}exp\left(-\frac{t}{{\tau }_i}\right),& (6)\end{array}$

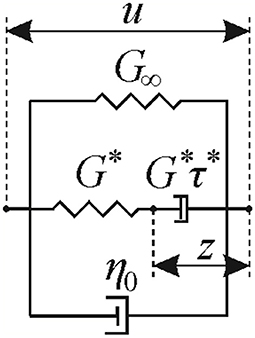
with several different relaxation times τ_i (usually arranged in a logarithmic scale) and associated moduli G_i. If the problem of interest itself has an inherent timescale τ^* (for impact problems, this is the impact duration), it seems reasonable to assume that all relaxation processes faster than τ^* run infinitely fast and all slower than τ^* run infinitely slow (note that relaxation times in a Prony series are usually listed in a logarithmic scale). As under this assumption a Maxwell element of the Prony series with very slow relaxation degenerates to a spring, and one with very fast relaxation degenerates to a dashpot, we arrive at the following rheological model (see Figure 2): a Maxwell element in parallel with a Kelvin element. The modulus and viscosity of the Kelvin element are given by summing up the fast and slow relaxation processes,

$\begin{array}{l}{G}_{\infty }:={\tilde{G}}_{\infty }+{\displaystyle \sum _{{\tau }_i\gg \tau *}}{G}_i,\\ {\eta }_0:={\displaystyle \sum _{{\tau }_i\ll \tau *}}{G}_i{\tau }_i.& (7)\end{array}$

Hence, the complex dynamic modulus is

$\begin{array}{ll}\widehat{G}(\omega )=G_{\infty }+G^{*}\frac{{(\omega {\tau }^{*})}^2}{1+{(\omega {\tau }^{*})}^2}+i\left[{\eta }_0\omega +G^{*}\frac{\omega {\tau }^{*}}{1+{(\omega {\tau }^{*})}^2}\right].& (8)\end{array}$

Now, why is the Kelvin solid such a convenient model? Because for harmonic loading with angular frequency ω, owing to Equation (1), any linearly viscoelastic material can be interpreted as a Kelvin solid, with the elastic modulus and viscosity given by the storage and loss modulus at ω! Loading under impact is not exactly harmonic but can be approximated well enough by harmonic functions; see, for example, the work of Hunter (1957) on the Hertzian impact problem. Note that exactly sinusoidal indentation has been studied in detail by Argatov (2012) and that harmonic loading is also used in models of impact tests (Ruta and Szydło, 2005).

FIGURE 2

Figure 2. Rheological model for the Kelvin–Maxwell solid. Notations are given in the text.

Solution of the Impact Problem for the Kelvin–Maxwell Solid

Let us analyze the consequences of this idea in case of the Kelvin–Maxwell solid introduced above. For simplicity, the impact of a rigid flat cylindrical punch with radius a and mass m is considered, as it has been shown before that the impactor shape is of secondary importance. The system of equations of motion for the outer and inner degrees of freedom of the rheological element shown in Figure 2, u and z, reads

$\begin{array}{l}0=m\ddot{u}+8{\eta }_{0}a\stackrel{\bullet }{u}+8G_{\infty }au+8G^{*}a(u-z),\\ 0={\tau }^{*}\stackrel{\bullet }{z}+z-u.& (9)\end{array}$

Written in proper nondimensional variables, the problem only depends on the following parameters:

$\begin{array}{ll}{\delta }_0:={\eta }_0\sqrt{\frac{8a}{G_{\infty }m}},{\delta }^{*}:=G^{*}{\tau }^{*}\sqrt{\frac{8a}{G_{\infty }m}},\gamma :=\frac{G_{\infty }}{G^{*}}.& (10)\end{array}$

In Figure 3 the COR—obtained by explicit solution of Equation —is shown in contour lines as a function of the governing parameters for

$\begin{array}{ll}\gamma {\delta }^{*}\equiv 1\iff {\tau }^{*}\equiv \sqrt{\frac{m}{8G_{\infty }a}}& (11)\end{array}$

in a logarithmic scale.

FIGURE 3

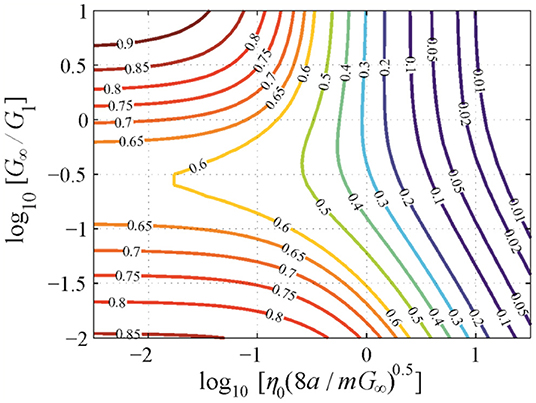
Figure 3. Contour line diagram of the coefficient of restitution as a function of the governing nondimensional parameters for the impact of a cylindrical flat punch onto a Kelvin–Maxwell solid.

Approximate Solution via the Solution for the Kelvin Solid

These results can be reproduced in a very simple way, based on the idea laid out above: If, for harmonic loading, a viscoelastic material can always be considered a Kelvin solid, and loading during impact is close to harmonic, it should be possible to obtain the impact solution for an arbitrary viscoelastic rheology based on the closed-form analytic solution for the Kelvin solid in Equations (3) and (4). For the Kelvin–Maxwell solid, Equation (2) suggests the following form for the damping parameter D:

$\begin{array}{ll}2D=\frac{Im\left\{\widehat{G}({\omega }_0)\right\}}{Re\left\{\widehat{G}({\omega }_0)\right\}},{\omega }_0{\tau }^{*}=1,& (12)\end{array}$

which has been proposed recently by the author in the context of a three-element standard solid (Willert, 2020), that is, the ratio of loss and storage moduli at the characteristic frequency of the elastic problem. This form, however, only provides good results, if the impact duration does not deviate too strongly from the elastic case. A significant improvement can be achieved if the actual timescale of the viscoelastic problem is used, that is,

$\begin{array}{ll}2D=\frac{Im\left\{\widehat{G}({\omega }^{*})\right\}}{Re\left\{\widehat{G}({\omega }^{*})\right\}},{\omega }^{*}=\frac{\pi }{T},& (13)\end{array}$

where the impact duration T for the calculation has been taken from the exact solution of the problem (see Solution of the Impact Problem for the Kelvin–Maxwell Solid).

Figure 4 shows the coefficients of restitution obtained by this simple procedure—calculating the damping ratio according to Equation or and applying the analytical solution for the Kelvin solid—in the same fashion as in Figure 3. Usage of the modified damping parameter in Equation results in very good agreement with the exact solution. This strongly supports the idea that the general material behavior in viscoelastic impacts is of secondary importance; the main influencing factor is the ratio of loss and storage moduli at the timescale of the impact. Hence, this quantity can be determined in a stable way measuring only the COR.

FIGURE 4

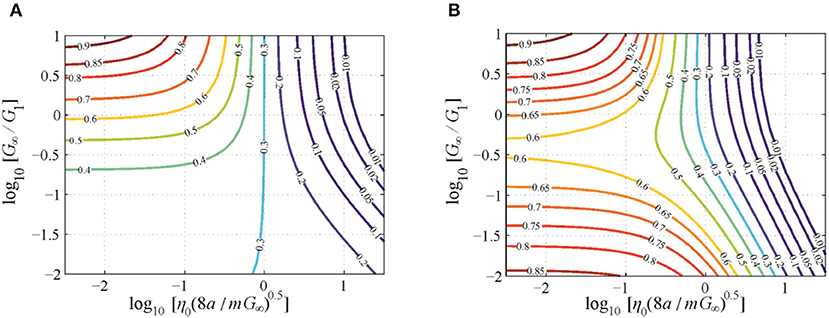
Figure 4. Contour line diagrams of the coefficient of restitution as a function of the governing nondimensional parameters for the impact of a cylindrical flat punch onto a Kelvin–Maxwell solid; approximate solutions based on the solution for the Kelvin solid. (A) Based on Equation (12) for the damping parameter D. (B) Based on Equation (13) for the damping parameter.

Influence of Viscoelastic Grading

Besides viscoelasticity or poroelasticity, most biomaterials exhibit functional grading. Whether and how this influences the applicability of the idea described above shall be discussed in the following.

Correspondence Principle in Graded Viscoelasticity

All hitherto given viscoelastic contact (or contact-impact) solutions are based on the elastic-viscoelastic correspondence principle. Already Hashin (1965), as early as in 1965, considered the viscoelastic correspondence for heterogeneous (composite) materials. Only roughly 40 years later did Paulino and Jin (2001) and Mukherjee and Paulino (2003) show that the correspondence principle applies also to graded viscoelastic materials, if the spatial and temporal variations of the moduli are separable, that is, if every point exhibits the same stress relaxation behavior in time. Additionally, Jin (2006) pointed out that in case of two-phase graded composites, for the relaxation functions to be separable, the relaxation behavior in shear and dilatation must be the same.

Impact Onto a Power-Law Graded Kelvin Solid

So let us consider the impact of a rigid flat cylindrical punch onto a power-law graded Kelvin solid with the depth- and time-dependent shear and bulk moduli,

$\begin{array}{l}G(z,t)=G_0{z}^q\left[1+\tau \delta (t)\right],\\ K(z,t)=K_0{z}^q\left[1+\tau \delta (t)\right],& (14)\end{array}$

with exponent q of the power-law grading, some characteristic time τ and the Dirac δ function. The static Poisson ratio is

$\begin{array}{ll}\nu :=\frac{3K_0-2G_0}{6K_0+2G_0}\approx 0.5,& (15)\end{array}$

because the material is considered to be incompressible. The elastic solution of the contact problem was given by Booker et al. (1985a),

$\begin{array}{ll}{F}_{el}=2c_N(q)a^{1+q}d:=k(q)d,& (16)\end{array}$

where c_N is a lengthy expression, which can be constructed from the fundamental solution in Booker et al. (1985b).

As the viscoelastic correspondence principle holds for this problem, the equation of motion reads

$\begin{array}{ll}m\ddot{d}+k(q)\tau \dot{d}+k(q)d=0,& (17)\end{array}$

and is thus formally the same as in the homogeneous case. Hence, also for graded viscoelastic materials, the COR is determined by the ratio of the loss and storage moduli at the timescale of the impact—at least, if the relaxation functions in shear and dilatation are separable and identical in form. Nonetheless, grading obviously affects the contact stiffness and therefore the impact duration.

Discussion

As has been shown, the COR mainly depends on a ratio of moduli. To determine the values of the moduli themselves, one has to consider at least one dimensional property of the impact, for example, the impact duration or the maximum indentation depth. However, the relation between these quantities and the dynamic modulus seems to exhibit a slightly stronger explicit dependence on the material rheology than the restitution coefficient itself. For the flat cylindrical punch, a decent estimate for the absolute value of the dynamic modulus (showing a relative error of <10% for the Kelvin–Maxwell solid with γδ^* ≡ 1 and not too small values of the restitution coefficient, ε ≥ 0.3) is given by

$\begin{array}{ll}\left|\widehat{G}({\omega }^{*})\right|\approx \frac{{\pi }^2}{T^2}\frac{m}{8a},& (18)\end{array}$

with the impact duration T.

All results presented are strictly valid only for incompressible media. Although many technological and biological materials can in good approximation be considered to be incompressible, there is, of course, no physical necessity to neglect dilatation. However, it has been shown recently by the author that the effect of compressibility in viscoelastic impacts is often very small (Willert, 2020). Moreover, the restriction to quasi-static processes, which requires the impact velocity to be much smaller than the smallest speed of wave propagation in the deformable material, poses a serious constraint of the calculations and considerations presented above, especially for very soft materials, as in this case wave propagation can be a significant source of energy dissipation (Hunter, 1957; Roylance, 1973).

To obtain a general linearly viscoelastic material model, which is nonetheless manageable in terms of the material parameters used, the analyzed Kelvin–Maxwell solid neglects the finite character of the relaxation processes that are either much faster or much slower than the impact itself. Thus, the results obtained can probably only serve as a “zero-order” approximation for “real” general linearly viscoelastic media (whose sets of material parameters, though, are usually unmanageable with respect to comprehensive analysis).

In sinusoidal indentation, the behavior is characterized by incomplete storage and loss moduli (Argatov, 2012). Their use may well be appropriate also for the analysis of the impact problem.

Conclusions

The low-velocity impact of a rigid impactor onto a linearly viscoelastic flat has been studied within the framework of viscoelastic contact mechanics. It is found that the COR in this impact configuration is mainly a simple, unique, decreasing function of the ratio of the loss and storage moduli at the impact timescale. The explicit dependencies of the COR on the profile shape of the impactor, the general material rheology, and material grading (at least, if the relaxation behavior in shear and dilatation are the same)—beyond the fact that all these quantities may influence the impact timescale and the loss and storage moduli associated with it—are very weak. Therefore, as a simple and good approximation for the impact solution, the closed-form analytical solution for the impact of a flat cylindrical punch on a Kelvin solid can be used. Contact mechanically semi-rigorous approaches, like the Kuwabara–Kono model for parabolic impact, can also often be used. The obtained results will help to appropriately interpret impact test measurements on soft materials like rubber or articular cartilage.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Argatov, I. I. (2012). Sinusoidally-driven flat-ended indentation of time-dependent materials: asymptotic models for low and high rate loading. Mech. Mater. 48, 56–70. doi: 10.1016/j.mechmat.2011.12.010

CrossRef Full Text | Google Scholar

Argatov, I. I. (2013). Mathematical modeling of linear viscoelastic impact: application to drop impact testing of articular cartilage. Tribol. Int. 63, 213–225. doi: 10.1016/j.triboint.2012.09.015

CrossRef Full Text | Google Scholar

Argatov, I. I., Selyutina, N. S., and Mishuris, G. S. (2016). Impact problem for the quasi-linear viscoelastic standard solid model. J. Strain Anal. Eng. Design 51, 294–303. doi: 10.1177/0309324715610027

CrossRef Full Text | Google Scholar

Bassi, A. C. (1978). Dynamic modulus of rubber by impact and rebound measurements. Polymer Eng. Sci. 18, 750–754. doi: 10.1002/pen.760181004

CrossRef Full Text | Google Scholar

Booker, J. R., Balaam, N. P., and Davis, E. H. (1985a). The behaviour of an elastic non-homogeneous half-space. Part II–circular and strip footings. Int. J. Num. Anal. Methods Geomech. 9, 369–381. doi: 10.1002/nag.1610090406

CrossRef Full Text | Google Scholar

Booker, J. R., Balaam, N. P., and Davis, E. H. (1985b). The behaviour of an elastic non-homogeneous half-space. Part I–line and point loads. Int. J. Num. Anal. Methods Geomech. 9, 353–367. doi: 10.1002/nag.1610090405

CrossRef Full Text | Google Scholar

Burgin, L. V., and Aspden, R. M. (2007). A drop tower for controlled impact testing of biological tissues. Med. Eng. Phys. 29, 525–530. doi: 10.1016/j.medengphy.2006.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Burgin, L. V., Edelsten, L., and Aspden, R. M. (2014). The mechanical and material properties of elderly human articular cartilage subject to impact and slow loading. Med. Eng. Phys. 36, 226–232. doi: 10.1016/j.medengphy.2013.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Butcher, E. A., and Segalman, D. J. (2000). Characterizing damping and restitution in compliant impacts via modified K-V and higher-order linear viscoelastic models. J. Appl. Mech. 67, 831–834. doi: 10.1115/1.1308578

CrossRef Full Text | Google Scholar

DIN EN ISO 8307 (2018). Flexible Cellular Polymeric Materials - Determination of Resilience by Ball Rebound.

Graham, G. A. C. (1965). The contact problem in the linear theory of viscoelasticity. Int. J. Eng. Sci. 3, 27–46. doi: 10.1016/0020-7225(65)90018-2

CrossRef Full Text | Google Scholar

Hashin, Z. (1965). Viscoelastic behavior of heterogeneous media. J. Appl. Mech. 32, 630–636. doi: 10.1115/1.3627270

CrossRef Full Text | Google Scholar

Hertz, H. (1882). Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 92, 156–171.

Google Scholar

Hunter, S. C. (1957). Energy absorbed by elastic waves during impact. J. Mech. Phys. Solids 5, 162–171. doi: 10.1016/0022-5096(57)90002-9

CrossRef Full Text | Google Scholar

Hunter, S. C. (1960). The Hertz problem for a rigid spherical indenter and a viscoelastic half-space. J. Mech. Phys. Solids 8, 219–234. doi: 10.1016/0022-5096(60)90028-4

CrossRef Full Text | Google Scholar

Jin, Z. H. (2006). Some notes on the linear viscoelasticity of functionally graded materials. Math. Mech. Solids 11, 216–224. doi: 10.1177/1081286504040401

CrossRef Full Text | Google Scholar

Kang, W., Chen, Y. C., Bagchi, A., and O'Shaughnessy, T. J. (2017). Characterization and detection of acceleration-induced cavitation in soft materials using a drop-tower-based integrated system. Rev. Sci. Instruments 88:125113. doi: 10.1063/1.5000512

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuwabara, G., and Kono, K. (1987). Restitution coefficient in a collision between two spheres. Jap. J. Appl. Phys. 26, 1230–1233. doi: 10.1143/JJAP.26.1230

CrossRef Full Text | Google Scholar

Lee, E. H. (1955). Stress analysis in visco-elastic bodies. Q. Appl. Math. 13, 183–190 doi: 10.1090/qam/69741

CrossRef Full Text | Google Scholar

Lee, E. H., and Radok, J. R. M. (1960). The contact problem for viscoelastic bodies. J. Appl. Mech. 27, 438–444. doi: 10.1115/1.3644020

CrossRef Full Text | Google Scholar

Mukherjee, S., and Paulino, G. H. (2003). The elastic-viscoelastic correspondence principle for functionally graded materials, revisited. J. Appl. Mech. 70, 359–363. doi: 10.1115/1.1533805

CrossRef Full Text | Google Scholar

Ozcan, M. U., Ocal, S., Basdogan, C., Dugusoy, G., and Tokat, Y. (2011). Characterization of frequency-dependent material properties of human liver and its pathologies using an impact hammer. Med. Image Anal. 15, 45–52. doi: 10.1016/j.media.2010.06.010

CrossRef Full Text | Google Scholar

Paulino, G. H., and Jin, Z. H. (2001). Correspondence principle in viscoelastic functionally graded materials. J. Appl. Mech. 68, 129–132. doi: 10.1115/1.1331286

CrossRef Full Text | Google Scholar

Popov, V. L., and Heß, M. (2015). Method of Dimensionality Reduction in Contact Mechanics and Friction. Berlin; Heidelberg; Springer Verlag.

Google Scholar

Popov, V. L., Willert, E., and Heß, M. (2018). Method of dimensionality reduction in contact mechanics and friction: a user's handbook. iii. viscoelastic contacts. Facta Univ. Ser. Mech. Eng. 16, 99–113. doi: 10.22190/FUME180327013P

CrossRef Full Text | Google Scholar

Ramírez, R., Pöschel, T., Brilliantov, N. V., and Schwager, T. (1999). Coefficient of restitution of colliding viscoelastic spheres. Phys. Rev. E 60, 4465–4472. doi: 10.1103/PhysRevE.60.4465

PubMed Abstract | CrossRef Full Text | Google Scholar

Roylance, D. (1973). Wave propagation in a viscoelastic fiber subjected to transverse impact. J. Appl. Mech. 40, 143–148. doi: 10.1115/1.3422914

CrossRef Full Text | Google Scholar

Ruta, P., and Szydło, A. (2005). Drop-weight test based identification of elastic half-space model parameters. J Sound Vibrat. 282, 411–427. doi: 10.1016/j.jsv.2004.02.052

CrossRef Full Text | Google Scholar

Schwager, T., and Pöschel, T. (2007). Coefficient of restitution and linear-dashpot model revisited. Granul. Matter 9, 465–469. doi: 10.1007/s10035-007-0065-z

CrossRef Full Text | Google Scholar

Selyutina, N. S., Argatov, I. I., and Mishuris, G. S. (2015). On application of Fung's quasi-linear viscoelastic model to modeling of impact experiments for articular cartilage. Mech. Res. Commun. 67, 24–30. doi: 10.1016/j.mechrescom.2015.04.003

CrossRef Full Text | Google Scholar

Springhetti, R., and Selyutina, N. S. (2018). Viscoelastic modeling of articular cartilage under impact loading. Meccanica 53, 519–530. doi: 10.1007/s11012-017-0717-y

CrossRef Full Text | Google Scholar

Ting, T. C. T. (1966). The contact stresses between a rigid indenter and a viscoelastic half-space. J. Appl. Mech. 33, 845–854. doi: 10.1115/1.3625192

CrossRef Full Text | Google Scholar

Van Zeebroeck, M., Tijskens, E., VanLiedekerke, P., Deli, V., DeBaerdemaeker, J., Ramon, H., et al. (2003). Determination of the dynamical behaviour of biological materials during impact using a pendulum device. J. Sound Vibrat. 266, 465–480. doi: 10.1016/S0022-460X(03)00579-0

CrossRef Full Text | Google Scholar

Willert, E. (2020). Stoßprobleme in Physik, Technik und Medizin: Grundlagen und Anwendungen. Berlin: Springer Vieweg.

Google Scholar

Willert, E., Kusche, S., and Popov, V. L. (2017). The influence if viscoelasticity on velocity-dependent restitutions in the oblique impact of spheres. Facta Univ. Ser. Mech. Eng. 15, 269–284. doi: 10.22190/FUME170420006W

CrossRef Full Text | Google Scholar