- Hopkinson Lab, Department of Engineering, University of Cambridge, Cambridge, United Kingdom
This work contains an analysis of the existence of critical phenomena in MILD combustion systems through an exploration of classical results from high-energy asymptotics theory for extinction conditions of non-premixed flames and well-stirred reactors. Through the derivation of an expression linking burning rate to Damköhler number, the criteria for a folded S-Shaped Curve, representative of a combustion system with sudden extinction and ignition behavior, was derived. This theory is discussed in detail, with particular focus on the limitations of the global chemistry it presents. The conditions reported by various previously-published numerical and experimental investigations are then discussed in the context of this theory. Of these investigations, those with the highest level of preheat and dilution had monotonic rather than folded S-Shaped Curves, indicating a lack of sudden extinction phenomena. It suggests that MILD combustion systems are those which lack sudden ignition and extinction behavior, therefore exhibiting a smooth, stretched S-Shaped Curve rather than a folded one with inflection points. The results suggest that the delineation between folded versus monotonic S-Shaped Curves may provide a useful alternative definition of MILD combustion.
1. Introduction
Analyses mapping the transition between fully burning, partially burning, and chemically frozen states are crucial to the understanding of ignition and extinction behavior in general combustion systems. The examination of these critical phenomena is essential considering the practical applications relying on the successful occurrence or avoidance of ignition and extinction events. Detailing these behaviors in complex systems, such as those involving preheat and dilution as in the MILD regime, is of particular importance. Ignition may be achieved through a supply of heat or fuel-attacking radicals to a combustible mixture; in the case of hot product dilution, both are relevant and, from the results in Sidey et al. (2014), have a significant effect on a systems autoignition and propagation behavior. In conventional systems, with the supply of heat and/or oxidation initiation radicals, if the rate of heat addition or chain-branching radical production dominates, thermal runaway will occur, and the system mixture will ignite. Conversely, if the rate of cooling or deactivating and quenching reactions dominate, the mixture will not successfully combust. From this, it follows that extinction must then occur through the removal of heat or chain-branching radicals. This may be achieved in numerous ways, including the mixing with a cold or inert gas or reduction in mixture equivalence ratio or pressure, as discussed in Law (2006).
Observable from the results of the jet in cross-flow experiment presented in Sidey and Mastorakos (2015) and autoignition and propagation results presented in Sidey et al. (2014), the high temperature and reactive species concentration in burned product oxidiser dictates that MILD combustion systems may be dominated by autoignition behavior. MILD system reactants are preheated and, in the cases discussed throughout this work, in the presence of chain-branching radicals through mixing with hot combustion products. Mixing with hot products dilutes the reactants such that, in the absence of the heat or radicals supplied through this mixing, the reactants would be unable to initiate thermal runaway. Any ignition attempt with a similar concentration of fresh reactants diluted with a cold, inert gas (say, CO2) would be unsuccessful because the system would lack the ability for sufficient heat and radical production to reach feedback combustion conditions. Once reactant mixtures diluted with hot combustion products autoignite, they continue to burn in an autoignition regime continually supplied with hot combustion products either through an external or internal recirculation system. The ability of a flame to propagate, as opposed to autoignite, in a premixed system heavily diluted with hot, reactive gas is discussed in Sidey et al. (2014). Due to this constant supply of heat and, in some cases, combustion radical species, required as parameters of the MILD combustion systems presented in this work, all of which are adiabatic and well-mixed, it follows that conventional extinction conditions cannot occur.
The lack of conventional extinction behavior in MILD combustion systems was addressed theoretically by Cavaliere and de Joannon (2004) through the examination of a well-stirred reactor (WSR). The working temperature of a WSR, TWSR, and the initial temperature of its reactants, T° are reported in Figure 1, from Cavaliere and de Joannon (2004), as a function of reactant O2 mole fraction, XO2. The system, designated as atmospheric CH4-air in stoichiometric quantities with a residence time, τres, of 1 s, ignites from a weakly burning state at Tsi, the system self-ignition temperature. This self-ignition, or autoignition, temperature is not a fundamental system parameter and is instead dependent on reactor and mixture characteristics, but is well defined for a WSR with a known τres and reactants of known composition. The behavior of the system working temperature, TWSR, is heavily dependent on XO2. Specifically, as dilution increases, and thus XO2 decreases, TWSR is reduced. Cavaliere and de Joannon take T° = 1100K as a specific example in Figure 1; for the most highly diluted case, the temperature rise during combustion, ΔT, is very low. This case, adhering to the conditions very high reactant preheat temperature and very low combustion temperature rise, exemplifies the Cavaliere and de Joannon definition of MILD combustion. The relationship between TWSR and T° in Figure 1 provides a comparison between the peak temperature of the system and its reaction timescale, linked to T°. Through this graphical analysis, known as an S-Shaped Curve analysis, the criticality characteristics of a system may be assessed. Conventional S-Shaped Curves are characterized by a weakly burning lower branch, intensely burning high temperature branch, and an unstable region connecting the two; these curves are referred to as “folded” (Figure 1, XO2 = 0.1, 0.2). As the peak temperature, or burning rate, of an intensely burning system on a folded S-Shaped Curve is decreased, extinction will occur when conditions of the unstable region are reached. Alternatively, systems which do not exhibit this sudden extinction behavior are described by smooth or monotonic S-Shaped Curves in which intensely and weakly burning branches are connected and no unstable region exists. In Figure 1, Cavaliere and de Joannon demonstrate that MILD combustion systems, defined by a high preheat temperature and low temperature rise during combustion, may approach fully-stable, monotonic S-Shaped Curve behavior and therefore may not extinguish as conventional systems do.
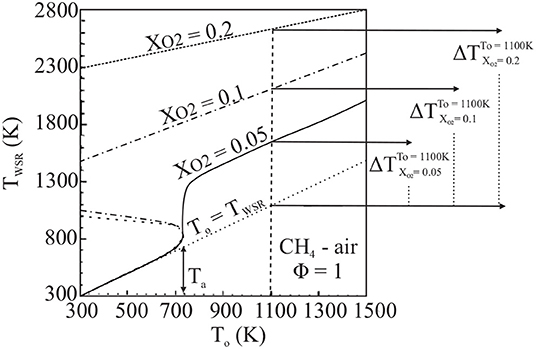
Figure 1. WSR behavior as a function of dilution (XO2) demonstrating conventional folded (XO2 = 0.1, 0.2) and smooth (MILD condition, XO2 = 0.05) S-Shaped Curves, from Cavaliere and de Joannon (2004).
The absence of sudden extinction behavior in combustion systems with reactants mixed extensively with preheated diluent, either inert or reacting, has been observed experimentally and theoretically. Libby and Williams (1983) reported on the smooth transition between thin and diffuse reaction zones of premixed laminar flames resulting from counterflowing reactants and combustion products at high rates of strain. Smooke et al. (1991), in a study investigating fresh premixed CH4-air reactants counterflowing against hot combustion products, observed that cases in which the burned product temperature was above 1480 K, no extinction strain rate could be reached experimentally or numerically. Similarly, Darabiha et al. (1988); Darabiha and Candel (1992) reported similar behavior in both C3H8-air and H2-air systems and suggested that the dissolution of conventional extinction and ignition behavior occurs when the hot stream temperature nears the adiabatic flame temperature of the cold reactants. This is in agreement with (Libby and Williams, 1983), who suggested that reaction zone and extinction behavior transitions occur when the hot product streams in such systems are cooled from their adiabatic flame temperature. Mastorakos et al. (1995) studied the effect of simultaneous preheat and dilution on turbulent counterflow flames experimentally by flowing either pure fuel or premixed fuel and air against hot combustion products from a second premixed flame. They reported that, even at very high strain rates, preheated and diluted flames would not extinguish, a finding consistent with theoretical work by Bray et al. (1996). Bray et al. investigated the extinction behavior of counterflow flames in which the opposing streams had unequal enthalpies. They found that, if an opposing stream was heated extensively, the mean reaction rate of the system in question was always above zero at its stagnation point. In practice, this means that sudden extinction phenomenon disappeared if one opposing stream, even if inert, was heated above a critical temperature within the range of hot combustion products. Choi and Katsuki (2002) also commented on the unusual extinction characteristics arising from extensive preheat and dilution, reporting that combustion reactions occur even with air excessively diluted with a preheated inert gas. Medwell et al. (2007) investigated flames produced with a heated and diluted co-flow apparatus with OH, formaldehyde, and temperature monitoring. Their work reported areas of distributed combustion zones with increased co-flow hot product concentration. As in the case of dilution with an inert gas in the Bray et al. and Mastorakos et al. studies, the presence of radical species in the initial reactant concentration was not necessary for the dissolution of conventionally observed extinction behavior. The high preheat temperature of the inert diluent initiates chain-branching reactions and the production of autoignition radicals upon mixing with the oxidiser and fuel.
With a focus primarily on the temperature of the hot overflowing stream rather than composition, many of these studies have not extensively investigated the critical phenomenon physics linked to reactive diluent, such as in the counterflow cases discussed in Sidey and Mastorakos (2016). Considering the lack of sudden extinction behavior due to preheat alone, the addition of radical species in the reactant composition at the system's boundary condition would exacerbate the ability of the system to react even at very high rates of strain. Coriton et al. (2010) and Coriton et al. (2013) investigated the effect of hot product stoichiometry and flame heat loss on laminar counterflow flames and observed that a regime without sudden extinction behavior occurs when sufficient oxidizing species are present in the hot combustion product stream. They identified the role of key radical pools in extinction behavior and concluded that the thickening of the heat release rate profile under MILD conditions was due to a shift in OH and O production rates. In this study, the absence of an abrupt extinction event in the highly diluted cases was attributed to sustained concentrations of OH and O in counterflow reaction zone in contrast to the depleted H, OH, and O concentrations leading to abrupt extinction in conventional flames. While the depletion of key CH4 attacking radicals such as H, OH, and O would lead to extinction, this effect must be coupled with temperature; the production of both heat and chain-branching intermediate species are intrinsically linked in systems diluted with preheated gas. In the presence of high temperatures, these radicals are produced immediately and, through further oxidation reactions, the radicals themselves lead to increased temperatures through a positive feedback process. The absence of these radicals may be due to quenching, competing weakly- or non-exothermic reactions, or simply a reduction in system temperature.
Despite the observation of the lack of extinction behavior in systems involving extensive dilution, the fundamental nature of this behavior is not strongly linked with the conditions of the MILD regime. This work aims to extend conventional extinction and ignition analysis specifically to MILD combustion processes to assess the existence of sudden limit phenomena in heavily diluted and preheated combustion systems with a simplified analysis.
Not only do we believe this work provides a link between the work of Cavaliere and de Joannon (2004) and the combustion analyses presented in Law (2006), but also presents the ideal that the presence of a classical extinction point may be used as a tool to delineate MILD combustion regimes. A mathematical analysis for investigating the presence of critical phenomena in simplified combustion systems from Law (2006) will be presented.
The capability of heavily diluted combustible mixtures, both from the non-premixed and premixed studies in Sidey and Mastorakos (2016) and Sidey et al. (2014) respectively, to exhibit sudden limit phenomena based on the presented analysis will be assessed. Finally, the conditions for critical phenomena will be discussed in comparison with previous studies and generalized for the MILD regime.
2. Critical Phenomena in Conventional Combustion Systems
The ignitability of a combustion system is often evaluated through the comparison of burning rate and a metric indicative of the residence time available for reaction, usually Damköhler number, Da:
Damköhler number is a non-dimensionalized number indicative of time available for a reaction to proceed at a specified rate. As Damköhler number tends to ∞, τm must be very large and/or τc very small, indicating that the system must have reached an equilibrium state with a very fast reaction occurring in a long flow timespan. Conversely, a null Damköhler number describes a system with a very short residence time and comparatively long reaction time; the system is chemically frozen. In counterflow non-premixed systems, the flow may be characterized by the strain rate, A, a parameter describing the velocity gradient between the counterflowing streams. Systems with high rates of strain have very low associated reaction zone residence times, making them analogous to low Damköhler number systems. Low rates of strain allow for relatively long residence times allowing reactions to proceed, often to completion. Low strain rate counterflowing systems have a high Damköhler number.
A comparison of system burning rate or maximum temperature (indicative of burning rate) with Damköhler number results in an S-Shaped Curve, similar to that discussed with (Cavaliere and de Joannon, 2004) shown in Figure 2. As discussed briefly with Figure 1, S-Shaped Curves typically appear folded (Figure 2, left): a low Damköhler number and low temperature branch associated with frozen or weakly-reacting cases, a high temperature and high Damköhler number branch associated with fully burning cases, and an unstable region connecting the two branches. The inflection points on the S-Shaped Curve, or the points at which the upper and lower branches connect to the unstable transition region, are critical Damköhler numbers at which system ignition and extinction occur (DaI and DaE, respectively). A system's behavior may, under certain conditions, be appear as a smooth S-Shaped Curve on the burning rate–Damköhler number plot (Figure 2, right). These system lack critical points and, rather, transition smoothly from a frozen to burning state. As mentioned, these systems do not have a defined extinction Damköhler number or strain rate, but instead transition smoothly to a frozen, non-reacting state as residence time in comparison with reaction time becomes relatively small.
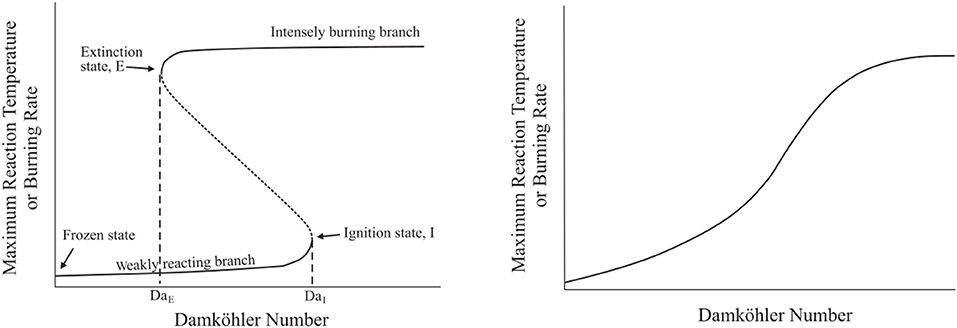
Figure 2. Folded (left) vs. smooth S-Shaped Curves detailing the transitions between weakly reacting, unstable, and fully burning branches in a combustion system. Adapted from Law (2006).
Through the analysis of simplified combustion systems, one may derive the criteria for the existence of critical points on the S-Shaped Curve in terms of system parameters such as preheat temperature. Furthermore, considering the unconventional extinction behavior of MILD combustion systems, reported in the work discussed in Sidey et al. (2014), and the regime definition involving preheat temperature (Cavaliere and de Joannon, 2004), it is important to investigate the applicability of this analysis to the MILD regime.
2.1. Condition for a Folded S-Shaped Curve
In order to investigate the existence of critical points, an assessment of the operation limits of two simplified combustion systems must be performed, beginning with an adiabatic thermal explosion. The energy and species governing equations for such a system, a lean, homogeneous body of gas at T° which ignites adiabatically after time t, with one-step global Arrhenius kinetics, are as follows, from Law (2006):
The fuel reaction rate, , of Equations (2) and (3) is assumed to be of the Arrhenius form with the pre-exponential factor composed of B, the collision frequency factor, and cF, the fuel concentration. By stoichiometrically weighting both temperature and fuel concentration ( and ) to apply a coupling function, Equations (2) and (3) can be expressed as follows:
with the coupling function, Ξ stemming from the following linear combination:
The resulting conserved scalar balance equation is:
Integrating Equation (7), recalling that , gives:
This result, linking the stoichiometrically weighted temperature with fuel concentration is useful when considering the energy balance in the second simplified combustion system: a well-stirred reactor (WSR) or Longwell bomb (Longwell and Weiss, 1955). Recall that through the analysis of a WSR system, an S-Shaped Curve was derived in Cavaliere and de Joannon (2004). The WSR energy balance, which relates the initial system and flame or reaction zone temperature, Tf, on the LHS to the reaction characteristics, assumed to be one-step Arrhenius, on the RHS. Note that because the WSR involves a changing flow, constant pressure system, Equation (9) differs from Equation (2) in that it requires cp rather than cv.
With the substitution of non-dimensional stoichiometrically weighted temperature () and fuel concentration (1), Equation (9) becomes:
The term , presented in reciprocal form on the LHS of Equation 10, is a form of Damköhler number, characterizing the residence time in relation to the reaction time. Equation 10 expresses the convective transport (LHS, controlled by Da) and chemical release (RHS, controlled by the Arrhenius one-step reaction term or burning rate) in the WSR. As discussed by Law (2006), this analysis may be extended to general reaction zones treated as a WSR - an assumption applicable the cases presented in this work considering the rigorous mixing and WSR-like behavior of the MILD regime. It is important to note that the precise definition of Damköhler number, whether it be strain rate, initial temperature, or collisional Damköhler number, is immaterial as long as it describes the ratio of transport or residence time to reaction time of the system.
After the derivation of the relationship between the chemical (burning rate) and diffusion terms of a generalized reaction zone, the existence of critical points of ignition and extinction may be determined. Graphically, critical points on S-Shaped Curve are points where the slope on the Da − Tf curve are vertical, or infinite. Mathematically, this condition may be expressed as:
Taking the natural logarithm of Equation (10) gives:
Followed by the derivative:
Applying the above to the critical points and substituting in Equation (11) gives:
In Equation (14), the first term in the LHS describes effects due to system preheat whereas the second term in the LHS describes the effects due to composition reflected in . If the critical point is the system ignition point (), the system preheat temperature term dominates as is likely to be close to . For extinction (), is likely close to and the composition term will heavily influence Equation (14) as opposed to the smaller preheat temperature term. This implies that reaching the ignition state is directly affected by the heat loss of the system whereas the extinction state is affected by the composition of the system or, rather, the ability of the system to sustain chain-branching and propagating reactions.
Equation (14) may be rearranged to give a general expression for the critical temperature (both ignition and extinction) in quadratic form:
Solving Equation 16 for the root gives:
which, through the substitution of , leads to the following quadratic equation and the determination of as a root:
only exists, from Equation (19), if the term under the square root is positive. This means that, in order for a combustion system to behave with critical extinction or ignition phenomena, the system must meet the condition:
This condition is useful when considering the definition of the MILD combustion regime. It links the system preheat temperature, T°, and composition, the non-dimensionalizing terms of (cp and YF), to the activation energy of the system, , as criteria for critical phenomena manifested as inflection points on a folded S-Shaped Curve. This means that the limit phenomena of a system may be estimated solely by its composition and preheat characteristics, two already well-defined MILD parameters. If the condition outlined by Equation (20) is not fulfilled, the S-Shaped Curve cannot contain any inflection points and the system will not exhibit any sudden extinction behavior.
3. Critical Phenomena in the MILD Regime
3.1. Laminar Counterflow CH4-Hot Product Flames
This result may be easily applied to combustion systems meeting MILD criteria by considering counterflow flames with hot combustion product as an oxidiser presented in Sidey and Mastorakos (2016) and mixtures of varying dilution in Sidey et al. (2014). This analysis may begin with the assumption that a reduced global one-step methane reaction, given below with a corresponding activation temperature, Ta, is suitable to approximate MILD system chemistry.
This assumption carries implications for the present analysis. Obviously considering the results of Sidey and Mastorakos (2016) and Sidey et al. (2014), the presence of hot combustion products in MILD systems affects the activation temperature. In particular, the presence of radical species in the oxidiser may significantly encourage ignition. The effects of radical species are not included in the global, one-step reaction considered here. This analysis is therefore limited in its application, and may only be used as an exercise to understand the behavior of some MILD systems rather than a rigorous chemical tool.
Note that the use of this chemistry in this work is not a statement that complex chemistry is not required for MILD combustion. However, many complex combustion phenomena may be adequately understood through a 1-step chemistry description, including the well-known bending behavior of turbulent flame speed vs. turbulent intensity in Nivarti and Cant (2017). This does not mean that complex chemistry is not needed to understand the details of such phenomenon, but that the high activation energy concept still has usefulness in characterizing combustion from a theoretical perspective. While performing a series of calculations with complex chemistry we would locate the transition from sudden extinction to no sudden extinction more accurately in parameter space in this work, the transition distance is not substantially large. Further, considering the development of 1-step models tune activation energy in order to describe global combustion parameters like flame speed or extinction strain rate, a global chemistry framework is appropriate within the context of this work.
Recalling the definitions of the stoichiometrically weighted non-dimensionalized temperature terms, Equation (20) may be written as:
First considering the CH4-hot product flames, q = 50100 KJ/kg and values for cp, T°, and YF, given in Table 1, are obtained from the composition of the MILD counterflow systems presented in Sidey and Mastorakos (2016). Note that the value for YF is taken to be YF, stoic from the reaction of CH4 and hot products, assumed to be H2O, CO2, N2, and O2. T° is taken to be the equilibrium mixing, or frozen, temperature of CH4 and hot combustion products mixed in stoichiometric quantities. As the conditions in Table 1 and Ta the one-step reaction of methane (Reaction 21) are substituted into (Equation 20), it becomes clear that, for extensively preheated and diluted systems, the condition in Equation (20) is not satisfied. This result is presented graphically in Figure 3. The equality in Equation (20) is plotted as a solid line in Figure 3: any system operating above this line will have a folded S-Shaped Curve while anything below it does not meet the aforementioned condition and will have a monotonic S-Shaped Curve.
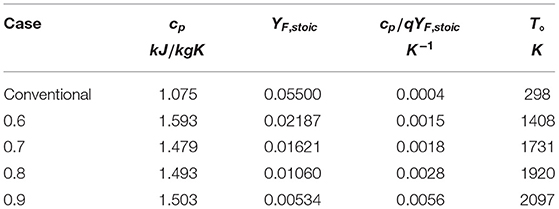
Table 1. Quantities relating to the counterflow systems in Sidey and Mastorakos (2016) relevant to the critical phenomena condition (Equation 20).
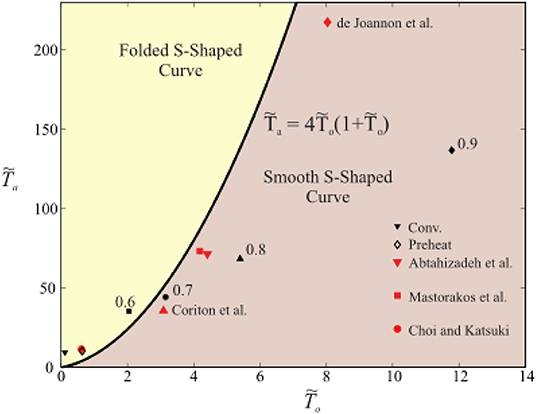
Figure 3. A plot of the function defining the requirement for the existence of critical points or a folded S-Shaped Curve in a CH4 combustion system, Equation (20), and points from CH4/hot product simulations presented in Sidey et al. (2014) and highly diluted cases from Coriton et al. (2010), Abtahizadeh et al. (2012), Mastorakos et al. (1995), Choi and Katsuki (2002), and de Joannon et al. (2012).
Note that each of the cases examined in this analysis will have a curve, although they do not differ from each other significantly. The conventional, non-preheated, stoichiometric, CH4-air system, marked “Conv.,” and a preheated, stoichiometric, CH4-air system, marked “Preheat,” both lie within the folded S-Shaped Curve region on Figure 3. The CH4 heavily diluted MILD combustion systems, or cases with Φ = 0.7, 0.8, and0.9 hot combustion products as an oxidiser, approximated through this analysis do not have folded S-Shaped Curves. This analysis is extended to similar counterflow non-premixed and premixed studies in the literature, with each symbol marked with its respective reference. The most heavily diluted cases presented by de Joannon et al. (2012) (preheated and diluted CH4/N2 and air), Mastorakos et al. (1995) (CH4-vitiated air at 1,750 K), Coriton et al. (2010) (CH4/air and 2,200 K hot products), and Abtahizadeh (Abtahizadeh et al., 2012) (CH4-vitiated air at 1415 K) all lie within the region of monotonic S-Shaped Curves in agreement with the findings reported in their associated references. The Choi and Katsuki (2002) case (CH4-vitiated air, diluted 20–50% by mole fraction) lies in the folded S-Shaped Curve region. This is due to the relatively low initial temperature of the oxidiser, To, and low level of dilution in comparison with the other studies presented here. However, Choi and Katsuki (2002) still reported on the absence of typical extinction behavior at these conditions. This discrepancy may be associated with the approximations made in this analysis, particularly the estimation of YF, stoic from values reported in the literature.
These results suggest that systems with extensive hot product recirculation do not extinguish suddenly even under heavily strained conditions. Instead, they would exhibit smooth transition behavior between intensely burning and near-frozen states. This behavior is dependent on both preheat temperature and dilution, evidenced by the typical extinction behavior of the case with preheated, undiluted air as an oxidiser (“Preheat”). This is approximately consistent with estimations made by Smooke et al. (1991) and Mastorakos et al. (1995) that no extinction behavior occurs when a hot product stream is heated above 1,480 K or 1,550 K, respectively.
The above quantification of the boundary separating the folded vs. monotonic behavior is sensitive mostly to the value used for activation energy, Ta. An increase or decrease of Ta by 10% does not change the results presented here. In other words, each study presented in Figure 3 remains in either the folded or smooth s-shaped curve area of the figure if the Ta were altered by 10%. Sensitivity analysis shows that a 20-25% variation in Ta may result in substantial enough changes to make a particular estimate of an experimental condition to jump from a non-folded to a folded regime. But such large uncertainties in the activation energy in the fuels used here are not expected, given the usual accuracy in the empirical 1-step models concerning flame speed or extinction strain rate.
This is in agreement with the numerical result discussed in Sidey and Mastorakos (2016); heavily diluted and preheated counterflow flames do not exhibit critical extinction behavior even at very high strain rates. The results may be viewed in the context of this analysis by plotting the inverse of strain rate, 1/A, a metric indicative of residence versus reaction time, or Damköhler number, and maximum temperature. In Figure 4, the S-Shaped Curves of CH4 (left) and kerosene (right) conventional and MILD counterflow flames are plotted. For the CH4-oxidant systems where an extinction strain rate does exist (CH4 burning with air, Φ = 0.6, 0.7 hot products), the S-Shaped Curve is folded with multiple solutions on distinct burning and weakly reaction branches. The unsteady region connecting the two branches is not plotted as it does not exert a physical presence within the system, and the intensely burning branch simply jumps to a frozen solution when sudden extinction occurs. These results are in partial agreement with those arising from the analysis based on Equation (20), with error in the prediction of Φ = 0.7 case behavior likely due to the assumption of a global one-step reaction and estimation of Ta. The highly diluted (Φ = 0.8, 0.9 hot product oxidiser) cases do not show any sudden extinction behavior and, as predicted by Figure 3, exhibit monotonic S-Shaped Curves devoid of unsteady regions.
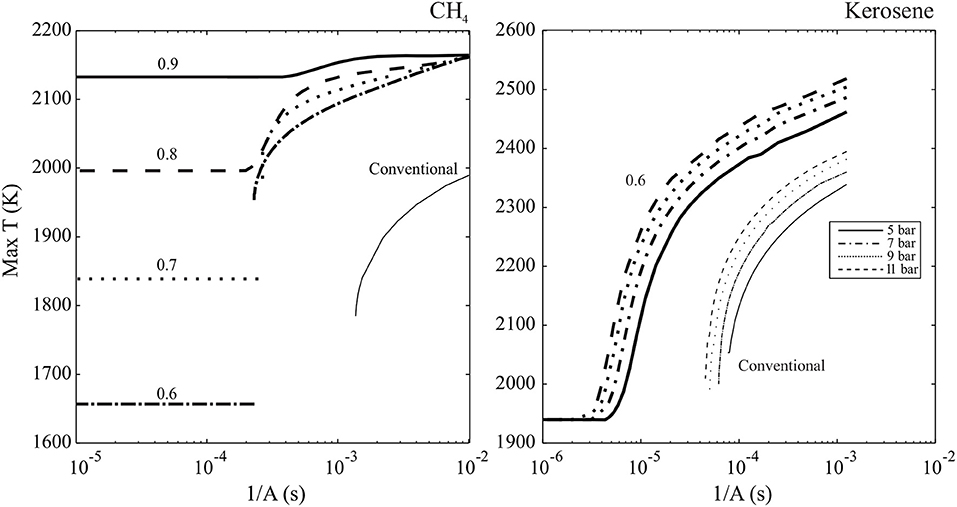
Figure 4. Maximum temperature of methane (Left) and kerosene (Right) counterflow MILD (bold, marked with equivalence ratio of hot combustion product oxidiser) and conventional flames varying with strain rate, A, from Sidey et al. (2016) and Sidey and Mastorakos (2015).
Similarly to CH4 conventional flames, kerosene flames with air as an oxidiser suddenly extinguish at a specified strain rate, and therefore have a folded S-Shaped Curve. S-Shaped Curves for MILD kerosene counterflow flames at above atmospheric pressures are all smooth, indicating that there is an absence of extinction behavior in MILD kerosene systems and that this behavior is not pressure dependent. Based on results for CH4 systems, it is reasonable to expect that, with estimates of kerosene Ta and T°, cp, and YF, stoic for kerosene-0.6 hot products counterflow flames, these systems would not meet the conditions for a folded S-Shaped Curve and therefore lie below the function plotted on Figure 3.
3.2. Premixed CH4-Air-Hot Product Reactants of Varying Dilution, ζ
This analysis may also be applied to the mixtures of CH4, air, and hot combustion products, the composition of which is designated by a dilution variable, defined in Sidey and Mastorakos (2016). Although the autoignition and premixed flame systems presented in Sidey et al. (2014) are fundamentally inapplicable to a discussion on extinction considering they are unstrained, the mixtures of varying dilution studied in these systems is. If in a strained system, these mixtures are representative of cases in which fresh reactants are mixed hot combustion products in varying degrees, similar to those discussed in Mastorakos et al. (1995), Smooke et al. (1991), Darabiha et al. (1988), and Darabiha and Candel (1992).
As explained in detail in Sidey et al. (2014), these mixtures are obtained by mixing cold, fresh reactants of a specified equivalence ratio (Φ = 0.6, 1.0, and 1.3 from Sidey et al. (2014), with the addition of Φ = 0.7, 0.8, and0.9 allowing for a comparison with the lean counterflow flame cases discussed here) adiabatically with hot combustion products from a premixed flame of the same equivalence ratio. The result is a series of CH4-air-hot product mixtures of varying dilution, ζ. A low ζ defines a mixture of mostly fresh reactants while high ζ indicates a high fraction of hot combustion products: ζ = 0.2 is defined as a mixture of 20% hot combustion products and 80% cold reactants.
The mixture preheat temperature, T°, is plotted against XO2 in Figure 5 for each dilution case. The two are linked such that as the fraction of hot combustion products in the mixture, or ζ, increases, XO2 is reduced and the bulk temperature of the mixture increases. For low levels of dilution, each case satisfies the condition for critical points on the S-Shaped Curve (Equation 20). However, as T° increases and O2 available for reaction is reduced, the critical points on each mixture's S-Shaped Curve disappear, marked with a transition from a bold, patterned to dotted line in Figure 5. The point of this transition is marked with a “⋆” symbol for each case. The conditions at which the loss of critical points is estimated by this analysis are summarized in Table 2. Note that both T° and composition (YF and XO2) affect the existence of sudden extinction behavior for each dilution case. Despite this, each equivalence ratio case seems to transition into a region characterized by smooth S-Shaped Curves at a dilution ratio of ζ = 0.7or0.8, or, rather, a hot product fraction of 70–80% by mass. If considering the suggestion by Darabiha et al. (1988) and Darabiha and Candel (1992) that sudden extinction events cease to occur when preheat temperature approaches adiabatic flame temperature, it is worthwhile to note that the S-Shaped Curves of the mixtures in Figure 5 become smooth within 550 K of each case's adiabatic flame temperature or around 1,400 K.
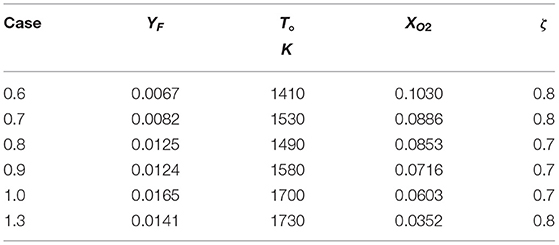
Table 2. Dilution characteristics for which the condition in Equation (20) is not met and diluted mixtures are described by smooth S-Shaped Curves (see Figure 5).
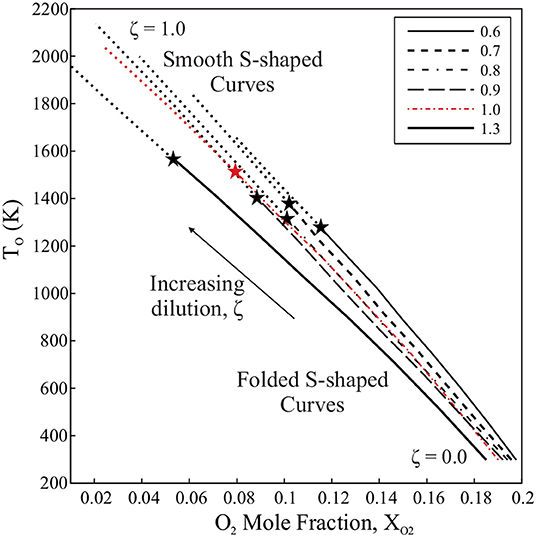
Figure 5. S-Shaped Curve behavior for mixtures of increasing hot product dilution, ζ based on the mixing procedure of Sidey et al. (2014). Patterned, bold lines mark regions where mixtures satisfy the condition for a folded S-Shaped Curve, while dotted lines regions where mixtures fail to satisfy Equation 20, suggesting smooth S-Shaped Curve behavior. The “⋆” symbols mark the point of transition from folded to smooth S-Shaped Curves.
It is also worthwhile to note that, in Sidey et al. (2014), premixed flame simulations failed to converge due to a tendency of the diluted mixture to autoignite at the cold boundary at a dilution ratio varying from ζ = 0.6to0.7. This limit coincides with the emergence of elongated ignition events visible in the PFR results, also in Sidey et al. (2014). From these comparisons, it is clear that a shift in autoignition, propagation, and limit phenomena behavior all seem to occur in agreement with the non-existence of critical points on a diluted and preheated system's S-Shaped Curve as predicted by the condition in Equation (20).
4. Discussion
In this work, the existence of sudden limit behavior in highly preheated and diluted systems is investigated. The lack of sudden extinction phenomena of combustion systems involving significant dilution and subsequent mixing with hot combustion products has been reported in numerical and experimental investigations, including Libby and Williams (1983), Smooke et al. (1991), Darabiha et al. (1988), Darabiha and Candel (1992), Bray et al. (1996), and Mastorakos et al. (1995). Its understanding and prediction is not only useful for the application of such concepts in practical devices, but for further definition of the MILD combustion regime and is perhaps most accessible through S-Shaped Curve theory. Through the derivation of an expression linking burning rate to Damköhler number in a WSR, the criteria for a folded S-Shaped Curve, representative of a combustion system with sudden extinction and ignition behavior, was developed in Law (2006). This condition, , was used to assess the existence of a folded vs. monotonic S-Shaped Curve in the non-premixed counterflow CH4-air cases in Sidey et al. (2014). The simulation results agreed well with predicted S-Shaped Curve behavior, with the exception of the case in which fuel was burned in Φ = 0.7 hot combustion product oxidiser, although this is likely due to the estimation of CH4 activation temperature, Ta, through a global one-step oxidation reaction. The limits of the existence of critical points on the S-Shaped Curve agreed well with estimations made by Smooke et al. (1991) and Mastorakos et al. (1995). Although these results are of interest, they should not be taken as a rigorous explanation of the MILD regime as the chemical complexity of systems involving hot combustion products has been significantly simplified with the assumption of a one-step, global reaction. Despite this, within strict limitations, this analysis provides interesting insight into the limit behavior of MILD systems.
Mixtures of varying dilution based on those examined in unstrained premixed systems in Sidey et al. (2014) were also investigated in this analysis. Although no specific mixture temperature, T°, or O2 content, XO2, was found to be transition point from folded to smooth S-Shaped Curve behavior, the S-Shaped Curve behavior of all the cases investigated here became monotonic at a once diluted with 70-80% hot combustion products (ζ = 0.7, 0.8). Although this result is not directly applicable to unstrained premixed configurations which do not allow for extinction behavior, it is worthwhile to note that this limit of folded S-Shaped Curve behavior coincides well with the limit of the mixture's ability to support a freely propagating laminar flame. Furthermore, the emergence of monotonic S-Shaped Curve behavior coincides with the elongation of a mixture's primary autoignition event in a premixed system.
Supported by results from Sidey and Mastorakos (2016) and Sidey et al. (2014), it may be assumed that, as acknowledged by Cavaliere and de Joannon (2004), the MILD regime is characterized by a monotonic S-Shaped Curve. This result is accurately predicted by the (Liñán, 1974) analysis assessing the existence of turning points in a system's S-Shaped Curve. This theoretical result validates the numerical and experimental observation that MILD systems do not undergo sudden extinction behavior, even at very high rates of strain.
5. Conclusions
The lack of sudden extinction behavior and the ignition tendencies in heavily preheated and diluted strained non-premixed systems and unstrained premixed systems raises questions about critical phenomena in the MILD combustion regime. This work presents an analysis based on the existence of critical phenomena in conventional combustion systems, manifested as a folded S-Shaped Curve on a burning rate vs. Damköhler number plot. This analysis is limited in its application as it is unable to capture the effect of complex chemistry introduced by the presence of radical species in MILD systems. However, it provides a useful context as a first step for considering such systems and, although it over simplifies the definition of activation temperature, provides interesting insight into preheated and diluted combustion. It shows that, for heavily diluted and preheated CH4 combustion systems, sudden extinction phenomena cannot occur and the system behavior is described by a monotonic S-Shaped Curve.
The choice of employing simple chemistry should be thought of as a choice to use high-activation energy concepts as a useful tool for as characterizing combustion from a theoretical perspective. This adds an important perspective for understanding MILD combustion; if one employs this high-activation energy theory to various experimental configurations reported in the literature as MILD, one sees that these studies fall in a different part of the catastrophe surface. Within this analysis, critical phenomena of the mixtures investigated here ceased to exist at a level of dilution which corresponded to the point at which the mixtures were deemed to become MILD according to the autoignition and premixed flame analysis in Sidey et al. (2014). It follows that the extinction vs. no extinction behavior presented here may be used as a tool to delineate MILD combustion regimes from conventional ones.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
JS-G contributed to the theoretical development and writing of this work. EM contributed to the theoretical development and background of this work.
Funding
JS-G would like to acknowledge funding by Rolls-Royce Canada, the Cambridge Overseas Trust, Jesus College Cambridge, and the National Research Council of Canada. The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^Recall that, from Equation (8), . Further, through the application of conservation of energy across a flame with no heat loss and constant cp, cp(Tad−T°) = qYF and, non-dimensionalized, ).
References
Abtahizadeh, E., van Oijen, J., and de Goey, P. (2012). Numerical study of MILD combustion with entrainment of burned gas into oxidizer and/or fuel streams. Combust. Flame 159, 2155–2165. doi: 10.1016/j.combustflame.2012.02.004
Bray, K. N. C., Champion, M., and Libby, P. A. (1996). Extinction of premixed flames in turbulent counterflowing streams with unequal enthalpies. Combust. Flame 107, 53–64.
Cavaliere, A., and de Joannon, M. (2004). MILD combustion. Prog. Energy Combust. Sci. 30, 329–366. doi: 10.1016/j.pecs.2004.02.003
Choi, G., and Katsuki, M. (2002). Chemical kinetic study on the reduction of nitric oxide in highly preheated air combustion. Proc. Combust. Inst. 29, 1165–1171. doi: 10.1016/S1540-7489(02)80147-X
Coriton, B., Frank, J. H., and Gomez, A. (2013). Effects of strain rate, turbulence, reactant stoichiometry and heat losses on the interaction of turbulent premixed flames with stoichiometric counterflowing combustion products. Combust. Flame 160, 2442–2456. doi: 10.1016/j.combustflame.2013.05.009
Coriton, B., Smooke, M. D., and Gomez, A. (2010). Effect of the composition of the hot product stream in the quasi-steady extinction of strained premixed flames. Combust. Flame 157, 2155–2164. doi: 10.1016/j.combustflame.2010.05.002
Darabiha, N., and Candel, S. (1992). The influence of the temperature on extinction and ignition limits of strained hydrogen-air diffusion flames. Combust. Sci. Technol. 86, 67–85.
Darabiha, N., Candel, S., Giovangigli, V., and Smooke, M. D. (1988). Extinction of strained premixed propane-air flames with complex chemistry. Combust. Sci. Technol. 60, 267–285.
de Joannon, M., Sorrentino, G., and Cavaliere, A. (2012). MILD combustion in diffusion-controlled regimes of hot diluted fuel. Combust. Flame 159, 1832–1839. doi: 10.1016/j.combustflame.2012.01.013
Libby, P. A., and Williams, F. A. (1983). Strained premixed laminar flames under nonadiabatic conditions. Combust. Sci. Technol. 31, 1–42.
Liñán, A. (1974). The asymptotic structure of counterflow diffusion flames for large activation energies. Acta Astronaut. 1, 1007–1039.
Longwell, J. P., and Weiss, M. A. (1955). High temperature reaction rates in hydrocarbon combustion. J. Ind. Eng. Chem. 47, 1634–1643.
Mastorakos, E., Taylor, A. M. K. P., and Whitelaw, J. H. (1995). Extinction of turbulent counterflow flames with reactants diluted by hot products. Combust. Flame 102, 101–114.
Medwell, P. R., Kalt, P. A. M., and Dally, B. B. (2007). Simultaneous imaging of OH, formaldehyde, and temperature of turbulent nonpremixed jet flames in a heated and diluted coflow. Combust. Flame 148, 48–61. doi: 10.1016/j.combustflame.2006.10.002
Nivarti, G., and Cant, S. (2017). Direct numerical simulation of the bending effect in turbulent premixed flames. Proc. Combust. Inst. 36, 1903–1910. doi: 10.1016/j.proci.2016.07.076
Sidey, J., Gordon, R., and Mastorakos, E. (2014). Simulations of autoignition and laminar premixed flames in methane/air mixutres diulted with hot products. Combust. Sci. Technol. 186, 453–465. doi: 10.1080/00102202.2014.883217
Sidey, J., and Mastorakos, E. (2015). Visualization of MILD combustion from jets in cross-flow. Proc. Combust. Inst. 35, 3537–3545. doi: 10.1016/j.proci.2014.07.028
Sidey, J. A., Giusti, A., and Mastorakos, E. (2016). Simulations of laminar non-premixed flames of kerosene with hot combustion products as oxidiser. Combust. Theory Model. 20, 958–973. doi: 10.1080/13647830.2016.1201146
Sidey, J. A., and Mastorakos, E. (2016). Simulations of laminar non-premixed flames of methane with hot combustion products as oxidiser. Combust. Flame 163, 1–11. doi: 10.1016/j.combustflame.2015.07.034
Smooke, M., Crump, J., Seshadri, K., and Giovangigli, V. (1991). Comparison between experimental measurements and numerical calculations of the structure of counterflow, diluted, methane-air, premixed flames. Proc. Combust. Inst. 23, 463–470. doi: 10.1016/S0082-0784(06)80292-4
Westbrook, C. K., and Dryer, F. L. (1981). Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 27, 31–43.
Nomenclature
Keywords: MILD combustion, extinction, limit phenomena, S-shaped curve, hot product dilution
Citation: Sidey-Gibbons JAM and Mastorakos E (2020) MILD Combustion Limit Phenomena. Front. Mech. Eng. 5:72. doi: 10.3389/fmech.2019.00072
Received: 01 May 2019; Accepted: 24 December 2019;
Published: 21 January 2020.
Edited by:
Mara de Joannon, Istituto di ricerche sulla combustione (IRC), ItalyReviewed by:
Amir Mardani, Sharif University of Technology, IranGiancarlo Sorrentino, University of Naples Federico II, Italy
Copyright © 2020 Sidey-Gibbons and Mastorakos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jenni A. M. Sidey-Gibbons, amFtczRAY2FtLmFjLnVr
†These authors have contributed equally to this work
 Jenni A. M. Sidey-Gibbons
Jenni A. M. Sidey-Gibbons Epaminondas Mastorakos
Epaminondas Mastorakos