High-Pressure Pool-Boiling Heat Transfer Enhancement Mechanism on Sintered-Particle Wick Surface

We experimentally study high-pressure pool-boiling heat transfer enhancement using a copper sintered-particle wick structure in water. The wicks are fabricated using the multi-step sintering process using 200 μm sintered copper powder. Thermophysical properties of water change at elevated pressure, therefore changing the bubble dynamics. For the single-layer wick, Critical Heat Fluxes (CHF) of 179.63, 182.42, and 198.16 W/cm² are found at 0, 103.4, and 206.8 kPa, respectively. The maximum CHF is found at 206.8 kPa with the wick superheat of 9.9 K. A 110% enhancement is found in the CHF for 206.8 kPa, compared to 0 kPa. We observed a CHF 1.8 times higher compared to the plain surface at 0 kPa. The maximum Heat Transfer Coefficient (HTC) of 252.46 W/cm² K is found at a heat flux of 100 W/cm² and a pressure of 206.8 kPa. The high-pressure pool-boiling result for the single-layer wick shows that the heat transfer coefficient is enhanced by 100% compared to 0 kPa. We suggest the reasons for enhancement of the pool-boiling performance is primarily due to high rate of bubble generation, high bubble release frequency, and reduced thermal-hydraulic length modulation, and enhanced thermal conductivity due to the sintered wick layer. Our analysis suggests that the Rayleigh-critical wavelength decreases by 4.67% with varying pressure, which may cause the bubble pinning between the sintered particles and prevents bubble coalescence. Similarly, the role of pressure in enhancing heat transfer compared to the effect of the wicking layer is also analyzed and found that the critical flow length, λ_u reduces by three times for 200 μm diameter particles. We suggest that the porous wick layer provides a capillary-assist to liquid flow effect, and delays the surface dry out. The pressure and surface modification amplify the boiling heat transfer performance. All these reasons may contribute to the CHF and HTC enhancement in the wicking layer at high-pressure.

Highlights

- Mechanisms of heat transfer enhancement at high-pressure pool-boiling on the wick surface.

- The surface modification at elevated pressure improves the boiling heat transfer performance by a factor of four compared to a plain surface.

- The critical heat flux at elevated pressure is found to be 1.8 times higher than one at 0 kPa.

- Pinning mechanism and capillary-driven flow effects explain the CHF enhancement mechanism.

- Pressure reduces the modulation wavelength by three times.

Introduction

There is a need to improve advanced thermal management systems reliability and prevent premature failure in space applications, including efficient electricity production, water desalination, smart buildings, and food production. Due to the excessive generation of heat in electronic devices, two-phase liquid-vapor phase-change heat transfer has been received considerable interest in electronics cooling to transfer a large amount of heat in a small thermal resistance. Nucleate pool-boiling is a simple, efficient, and reliable cooling approach. However, the real technical challenges lie in the reduced heat transfer performance, i.e., Heat Transfer Coefficient (HTC), and limited Critical Heat Flux (CHF).

Zuber initially developed the theory for the Critical Heat Flux using hydrodynamic instability model for an infinite plain surface (Zuber, 1959). The Zuber ${q^{″}}_{CHF}$ is,

$\begin{array}{ll}{q^{″}}_{CHF}=\frac{\Pi }{24}{{\rho }_g}^{1/2}{h}_{lg}{\left[g\sigma \left({\rho }_l-{\rho }_g\right)\right]}^{1/4}& (1)\end{array}$

And the modulation wavelength λ_m is,

$\begin{array}{ll}{\lambda }_m=9{\left[\frac{\sigma }{g({\rho }_l-{\rho }_g)}\right]}^{1/2}& (2)\end{array}$

where, σ is the surface tension, h_lg is the enthalpy of vaporization, g is the gravitational acceleration, ρ_l and ρ_g are the densities of the liquid and vapor, respectively.

The CHF, expressed in Equation (1), shows that the maximum limit of pool-boiling heat transfer depends on the properties of the water and the modulation wavelength. The thermo-physical properties of water i.e., the specific volume, surface tension, and the latent heat of vaporization change at high-pressure, which can have a significant impact on the boiling performance. The latent heat of vaporization and the specific volume of water change with increasing pressure as shown in Figure 1. In the literature, many experimental studies have reported enhancement in the pool-boiling performance at elevated pressures (Semeria, 1963; Bobrovich and Mamontova, 1965; Nishikawa et al., 1982; Sakashita and Ono, 2009). The pool-boiling behavior has been studied at high-pressures (up to 7 MPa) on a horizontal surface (normal direction of the surface is aligned with the direction of the gravitational acceleration). The results showed that the pressure affects the size of the nucleating bubbles, whereas the bubble departure frequency of the coalesced bubbles does not change (Sakashita, 2011). In the following year, a direct correlation between pressure and the nucleation site densities was found (Sakashita, 2011). A significant enhancement in the performance of pool-boiling has also been reported at low pressure for the microporous surfaces (Rainey et al., 2003a) and the square pin-finned surfaces (Rainey et al., 2003b). The bubble detachment frequency was noticed at high-pressure and found a negligible effect at high heat fluxes on a rectangular horizontal heating surface. However, a small variation has been observed in the averaged values of data at elevated pressures (Bobrovich and Mamontova, 1965). Similar observations have been made in the high -pressure pool-boiling experiment on the horizontal upward facing surface (Sakashita and Ono, 2009). A systematic study was carried out for the nucleation site densities at a high-pressure pool-boiling experiment and reported that the nucleation site density increases in proportion of 1.5th of the pressure. Many surface modification methods have been employed to enhance the performance of the pool-boiling heat transfer and understand CHF enhancement mechanism including surface roughness (Jones et al., 2009), micro/nanostructured surfaces (Jo et al., 2012), wettability (Takata et al., 2003, 2006; Nam and Ju, 2008; Betz et al., 2010, 2011, 2013; Jo et al., 2016; Marcel et al., 2017), addition of nanoparticles (Trisaksri and Wongwises, 2009), extended surfaces like microchannels (Jaikumar and Kandlikar, 2015a,b), porous coatings (Hwang and Kaviany, 2006), and modulated wick surface (Nasersharifi et al., 2018).

FIGURE 1

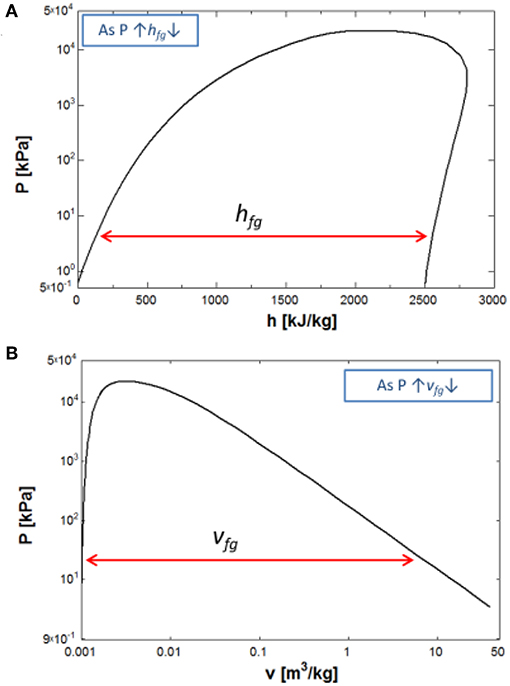
Figure 1. The effect of pressure on the thermophysical properties of water. (A) The latent heat of vaporization. (B) The specific volume of water.

The surface roughness improved the performance of the pool-boiling heat transfer with the increased number of active nucleation site densities and the decreased size of cavities (Jones et al., 2009). The varied wettability surface featured with combining hydrophilic (gives an advantage in supplying liquid to the heated surface) and hydrophobic (activates nucleation at lower wall superheat) surfaces, enhanced the CHF and the HTC during the pool-boiling (Betz et al., 2013). The Graphene Oxide (GO) coated surface was tested in the high-pressure pool-boiling experimental arrangement and found 51.5% enhancement at 412 kPa compared to the plain surface. The bubble size on the GO coated surface was found significantly smaller than the bubble size on the plain surface. The non-homogenous nanostructure (mixed wettability) was attributed with the pinning effect, enhanced the HTC (Li and Betz, 2017). The pool-boiling performance on the microporous coating has been examined due to the increased active nucleation site density from the direct visualizations (Chang and You, 1997). The enhancement in the nucleate boiling behavior has been studied for the square fin array and microporous coatings. The CHF enhancement has featured to the surface area enhancement, fin efficiency, increased number of nucleation site density, vapor bubble departure resistance, and re-wetting liquid flow resistance (Rainey and You, 2000). The modulated porous-layer coatings were investigated and found an enhancement in the pool-boiling CHF nearly three times over that of a plain surface, mainly decreasing hydrodynamic-instability wavelength (Liter and Kaviany, 2001). The nucleate pool-boiling behavior was examined by studying the various boiling parameters including increased active nucleation site density, decreased bubble size and increased departure frequency on the microporous surfaces (Kim et al., 2002). The pool-boiling performance has been investigated on thin uniform porous coatings of different copper particle diameters and wick layers. They found that a thin uniform coating significantly influences the hydrodynamic instabilities by decreasing the critical Rayleigh-Taylor wavelength (Hwang and Kaviany, 2006; Hwang et al., 2015). The heat transfer enhancement by evaporation momentum force was studied by directing the bubble interface motion over the heated surface (Kandlikar, 2013). The enhancement in the CHF has reported for the bi-porous sintered copper coatings in FC-72 (Byon et al., 2013). They found that the CHF is primarily a function of the particle size to cluster size ratio (d/D) and independent of the coating thickness. The saturated pool-boiling heat transfer performance has performed on the multilevel modulated wicks, i.e., single-layer, columnar, and mushroom post wicks structure for n-pentane (Nasersharifi et al., 2018). In the mushroom wick, the critical heat flux has determined for a pitch distance of 3.5 mm. Further reduction of the pitch distance, 1 mm, a 250% of enhancement in the critical heat flux was found. The capillary performance of 3D printed wick structures for the sintered powder, screen mesh, and composites wick structures was studied in the two-phase heat transfer process (Jafari et al., 2018).

In this work, we explore the impact of pressure on the performance of 200 μm copper sintered particle wick structures in a pool-boiling system. The objective of the present study is to understand the coupled effect of high-pressure and the wick structure in the pool-boiling performance. The dynamic bubble behavior has also studied at elevated pressure with the wick structure. We discuss the possible reasons for the enhancement in the result and discussion section.

Experimental

Wick Structure Fabrications

We fabricated the single-layer wick structure using a sintering process. The detailed sintering process is found in the previous work (Nasersharifi et al., 2018), and the key approach is shown in Figure 2. The commercially available 200 μm-diameter copper powder was used in the sintering process (particle size distribution is 177–250 μm). The wick was sintered on a polished surface of 1 cm diameter and 2.54 cm long copper rod. The copper surface was cleaned using isopropanol solution before sintering. The fabrication was done in the stainless-steel mold cavity. The cylindrical-shaped mold was machined 200 microns deeper than the copper rod with a ±50 μm tolerance. The copper substrate was placed into the mold, and the copper particles were spread uniformly into the mold cavity, controlling the layers of the wick. The mold filled with the particles was kept in the furnace filled with Argon gas flow with 50 sccm at 950°C for 2 h. The fabricated wick layer was allowed to cool naturally at the ambient condition with the cooling rate of 5–10°C per minute. The fabricated wick layer on the copper rod was released from the mold cavity and examined the surface quality in the confocal microscope (Leica VZ700 C). The zoomed top view of the single-layer wick is shown in Figure 3. A copper heating block of 1′′ (2.541 cm) in diameter and 2′′ (2.508 cm) long was machined to insert the Cartridge heater. A thermally conductive paste, OMEGABONDTM 201 (Two-part epoxy: very high thermal conductivity) from Omega Engineering, Inc., was applied at the interface between the wick structure and the copper heating block. The wick structure with the copper heating block was kept in an oven at 125°C for 4 h to ensure the copper blocks get appropriately fixed. The cured copper heating block was assembled with a cylindrical Teflon block with the 500 W capacity of the Cartridge heating rod. The heating block was insulated with the Polytetrafluoroethylene (PTFE) surface. The heater block assembly was demonstrated in research work (Dahariya and Betz, 2019). A high-temperature copper sealant (ULTRA COPPER GASKET MAKER) was used to avoid any water leakage from the gap between the copper heating block and the insulated surface. The gap was carefully filled with the sealant. Three holes were drilled at 3, 9, and 15 mm from the tip of the copper surface to accommodate thermocouples for measuring the surface temperature and heat flux. A thermal paste was applied on the thermocouple tips to ensure minimal thermal resistances between the thermocouples and the copper rod. Three K-type thermocouples (0.3175 cm diameter) were used to measure the surface temperature. A thermocouple was also placed inside the boiling chamber to measure the temperature of the working fluid, i.e., water. The contact angles of the plain and wick surfaces were measured using a Goniometer, which were 80.52 and 100.96°, respectively as shown in Figure 3, indicating that the wick increases the contact angle by 25%. The wick surface was kept at 125°C for 48 h in the oven to oxidize the surface and the contact angle was measured again. After the surface treatment, the contact angle was 98.53°. The detailed measurement procedure of the wick structure is found in the previous work (Albu et al., 2019), and only the measured thickness, pore size, porosity, and permeability of the wick structure are given here. The wick thickness was approximately the size of the sintered copper particle diameter, i.e., 200 μm. The measured effective pore size and porosity were 109–117 μm and 0.25, respectively. The measured permeability was 7.05 × 10⁻¹¹ m².

FIGURE 2

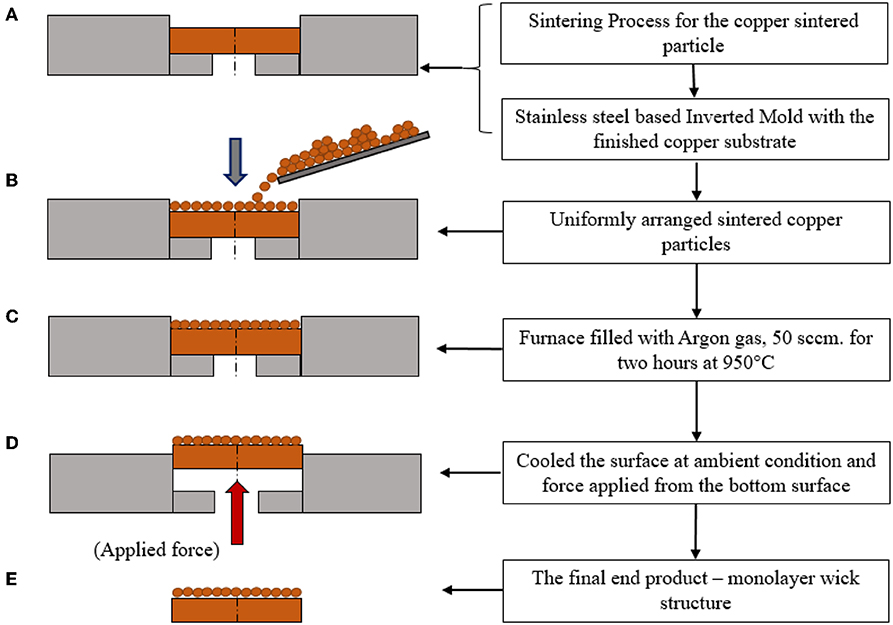
Figure 2. The process flow chart of the sintering process for the wick structure using the copper sintered particles. (A) An assembly of the machined smoothed polished copper surface with a stainless steel mold. (B) Poured and uniformly distributed sintered copper particles in the pocket of mold and the copper substrate. (C) The entire assembly kept in the furnace filled with Argon gas, 50 sccm (cubic centimeter per minute) for 2 h at 950°C. (D) Finally, the surface is allowed to cool at ambient condition. (E) The end product of the single-layer wick structure.

FIGURE 3

Figure 3. The zoomed top view of copper substrates and the contact angle measurement using the Goniometer. (A) The smoothed polished copper surface of diameter ~1 cm with contact angle 80.52° and (B) the mono layer wick structure of 200 μm sintered copper particles with contact angle 100.96°. The base width of the bubble is also shown.

Experimental Method and Procedure

A similar pool-boiling experimental setup was used for the high-pressure pool-boiling heat transfer measurements (Li and Betz, 2017). The schematic of the experimental setup is shown in Figure 4. The wick surface with the PTFE block was placed in a closed stainless-steel boiling vessel with a capacity of 1.5 L, filled with deionized water. The boiling tests were performed at different gauge pressures. The pressure inside the boiling vessel was maintained using the LF (Low flow) low pressure, Precision Back Pressure Regulator valve manufactured by Equilibar. The water was boiled for an hour to remove any gas. The water was boiled until it the saturation temperature of 100, 121, and 135°C at 0, 103.4, and 206.8 kPa, respectively. A cartridge water heater of 250 W was immersed in the vessel. A 1,500 W power supply (INPUT rating 100–240 V, ~19 A, 50/60 Hz, manufactured by GDK Lambda) was used to provide the required heat flux to the 1 cm² of surface area. A data acquisition system (OMEGA OM-USB-TC-AI) was used to record the surface and water temperatures, and monitor the pressure inside the water pool during the boiling. The surface temperature T_s, was extrapolated using three data points to the specified locations. Fourier's law of heat conduction was used to calculate the heat flux. The superheat was determined by calculating a difference of the surface temperature and the saturated water temperature, ΔT = T_s – T_sat. During the high-pressure pool-boiling experiments, initially, the pressure was measured inside the chamber using a pressure transducer. The boiling process was visualized using the SONY Cyber-shot DSC-RX100M6 camera. The boiling data were taken at an interval of 10–12 min when the system reaches a steady-state. The measurements for the surface temperature, T_s, and the saturated water temperature, T_sat were recorded for a minute (60 data points) for each heat flux with a scan rate of 1 Hz. The averages of the measured temperatures were used to extrapolate the surface temperature. The same test procedure was followed in the previous work (Dahariya and Betz, 2019). The CHF was determined as the maximum heat flux provided to the surface corresponding to the last observed steady surface temperature. Beyond the maximum heat flux, a dramatic increase in the surface temperature was noticed. The HTC was determined from the ratio of the heat flux q″ and the degree of superheat (T_s – T_sat) shown in Figure 6.

FIGURE 4

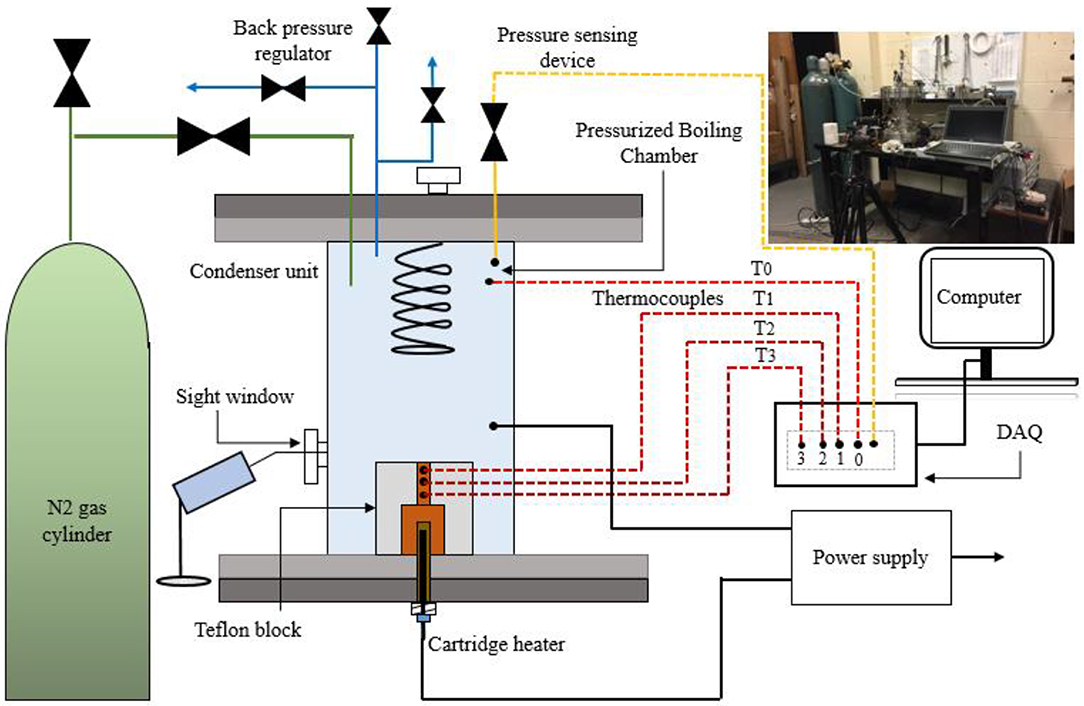
Figure 4. The schematic of high-pressure pool-boiling experimental setup chamber with the data acquisition system, back pressure regulator valve, nitrogen gas cylinder, power supply, heater arrangement, and the sight window with the camera for bubble visualization during boiling. The image of the initial setup of high-pressure pool-boiling is also shown at the top right.

In the uncertainty analysis, the error in the thermocouples, the pressure transducer, and losses in the heat flux measurement were considered. The uncertainty in the measurements and the error analysis were shown in Dahariya and Betz (2019). The uncertainty was determined for the measured heat flux. The uncertainty at the onset and 30 W/cm² was determined to be 14.43 and 0.65%, respectively. The uncertainties were also calculated for high-pressure experimental data. For the measured heat flux of 45 W/cm², the uncertainty was 18.62 and 16.45% at 103.4 and 206.8 kPa, respectively.

Results

The high-pressure pool-boiling results are shown in Figure 5, which compares the boiling performance of the plain surface to the single-layer wick surface. The results are shown for the single-layer wick surface at three different elevated pressures: 0, 103.4, and 206.8 kPa. The boiling curve is drawn for the heat flux q″, and degree of superheat ΔT = T_s – T_sat as shown in Figure 5. For the plain surface, q_CHF = 102.14 W/cm² was found at ΔT = 22.87 K. The result agrees well to previous work, which found 85 W/cm² at 28 K (Li and Betz, 2017), within the uncertainty, ±15 W/cm². The difference in CHF can be related to the different surface roughness. For the plain surface, the CHF are 118.23 and 130.24 W/cm² at 103.4 and 206.8 kPa, respectively. Li and Betz (2017) reported pool-boiling results at high-pressure on the Graphene Oxide (GO) coated surface with CHF of 80, 90, and 105 W/cm² at 0, 103.4, and 206.8 kPa, respectively. The enhanced CHF at elevated pressure was reported due to change in the bubble dynamics and pinning mechanisms. At high-pressure, the thermophysical properties of water i.e., the specific volume and the latent heat of vaporization, decrease. The effect of change in the property of water was observed in the bubble departure size and the bubble departure frequency, which influence the boiling performance (Dahariya and Betz, 2019). A 46% of reduction in the bubble size was found from 0 to 620.5 kPa with 10–12% of an error margin. Further enhancement in the CHF is found in the single-layer wick surface. The slope of the boiling curve for the wick structure shown in Figure 5 is higher than the plain surface. The measured CHF for the single-layer wick is 179.63, 182.42, and 198.16 W/cm² at 0, 103.4, and 206.8 kPa, respectively. For the single-layer wick, the maximum heat flux, 198.16 W/cm² is obtained at 9.89 K of superheat for 206.8 kPa. At the gauge pressure of 0 kPa, the CHF is 1.75 times higher for the wick surface as compared to the plain surface at 0 kPa. A significant reduction in the degree of superheat is also noticed for the single-layer wick at the given heat flux compared to the plain surface. For the wick surface, the maximum heat flux is obtained at ΔT = 9.87 K for 206.8 kPa. Whereas, the maximum CHF is obtained for the plain surface at 16.79 K. The degree of superheat value is comparatively smaller than the plain surface, which enhances the HTC. Twenty percent enhancement of the CHF was reported for the wick structure (200 μm wick) with n-pentane as the working fluid (Nasersharifi et al., 2018). The low wick superheat was related to the increased effective thermal conductivity. In the boiling curve, the boiling onset is as important as determining the CHF. The HTC is determined with a ratio of heat flux and the wick superheat. Figures 6, 7 show the HTC as a function of the superheat and the heat flux, respectively. The coupled effect of the surface modification of the wick layer and increasing pressure enhances the HTC. For the plain surface, the heat transfer performance curve exhibits enhancement of 75% at 206.8 kPa compared to 0 kPa. The maximum HTC is observed at a degree of superheat around 6 and 16 K for the wick surface and the plain surface, shown in Figure 6. The wick layer reduces the degree of superheat by 2.5 times. The maximum HTC, 252.46 W/cm² K is observed for the heat flux at 100 W/cm² for 206.8 kPa shown in Figure 6. The heat transfer performance enhances 100% compared to 0 kPa. The enhancement is obtained due to the low superheat and a different boiling behavior which is explained in the next section. At high heat flux, the HTC further decreases. For the other two pressures 0 and 130.4 kPa, the maximum HTC has found ~145 and 195 kW/m² K at 150 W/cm² of heat flux shown in Figure 7. The difference in the HTC can be related to a change in the boiling behavior at higher pressure. Figure 8 shows the boiling images of the wick surface at different heat fluxes for the two pressures. Figures 8(1a–f) show the recorded boiling images for 0 kPa and Figures 8(2a–f) show the boiling images for 206.8 kPa.

FIGURE 5

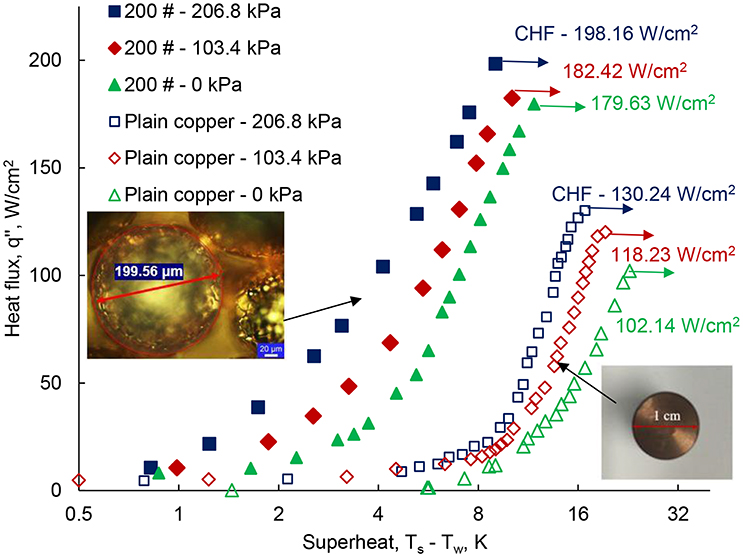
Figure 5. The high-pressure pool-boiling curves for plain surface and 200 μm single-layer wick surface for three different gauge pressures; 0, 103.4, and 206.8 kPa. The critical heat flux for each condition is reported for the plain copper and the wick surface.

FIGURE 6

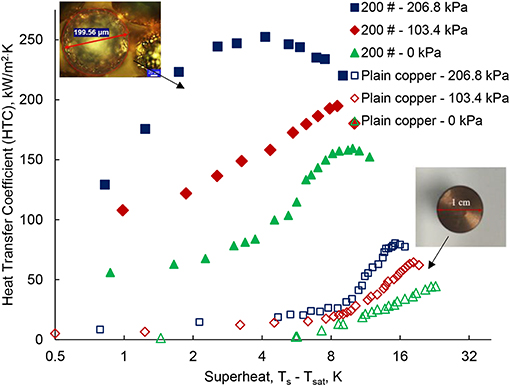
Figure 6. The performance of high-pressure pool-boiling data for three different gauge pressures; 0, 103.4, and 206.8 kPa. Heat Transfer Coefficient (HTC), kW/m² K. vs. Superheat T_s – T_sat (K).

FIGURE 7

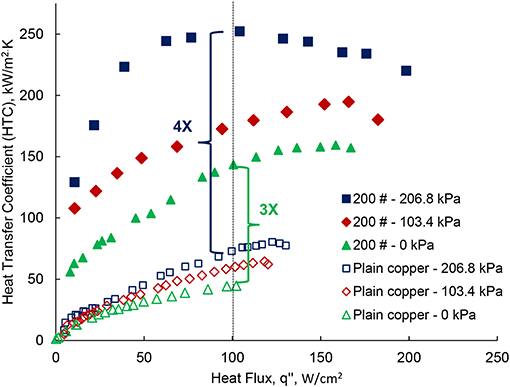
Figure 7. The performance of high-pressure pool-boiling for three different gauge pressures; 0, 103.4, and 206.8 kPa. Heat Transfer Coefficient (HTC) in kW/m² K vs. Heat Flux (q″) in W/cm².

FIGURE 8

Figure 8. The recorded nucleate pool-boiling images for the 200 μm mono layer wick structure are shown in 1(a–f) at 0 kPa at different heat fluxes. The high-pressure boiling images at 206.8 kPa for the single-layer wick are shown in 2(a–f) for different heat fluxes.

The bubble nucleation begins at a heat flux of 5–10 W/cm² and a degree of superheat of 0.5–1.0 K, which is similar to the plain surface (Dahariya and Betz, 2019). The bubble departure size is ~3 mm as shown in Figure 8(1a). The nucleate boiling is observed up to the heat flux of 100 W/cm². The results suggest that the boiling on the wick extends the nucleate boiling region (supports nucleation) for a longer duration. At high heat flux >100 W/cm², the bubble starts merging to the neighboring bubbles, leading to boiling in the form of slugs or columns which can be seen in the boiling images shown in Figure 8. The effect of pressure on the bubble size is observed at 206.8 kPa is shown in Figures 8(2a–f). The bubble size reduces significantly from 3 to 1 mm, which is two times lower than at 0 kPa. At higher heat fluxes, boiling occurs in the form of jets and generates more vapor from the surface in the bulk fluid. The jets start forming at a low heat flux of 21.72 W/cm², which is shown in the boiling pictures. The results show that the boiling occurs on the wick surface through the liquid-vapor jets. As the heat flux increases, the jets start merging and reaches to a maximum limit of the nucleate boiling heat transfer.

Discussion

During pool-boiling, nucleate boiling plays a vital role in the heat transfer process, and the cavity size behavior at saturation point is also essential to study. Hsu's theory states that the size of active cavities is dependent on the surface wettability, thermal boundary layer, and the properties of the water is expressed in Equation (3)

$\begin{array}{ll}\left\{r_{max},r_{min}\right\}=\frac{\delta }{2C_1}\left[1-\frac{{\theta }_{sat}}{{\theta }_w}\pm \sqrt{{\left(1-\frac{{\theta }_{sat}}{{\theta }_w}\right)}^2-\frac{4A{C}_3}{\delta {\theta }_w}}\right]& (3)\end{array}$

where δ is the thickness of boundary layer in microns. C₁ = (1 + cos )/sin, C₃ = (1 + cos ), is the wetting angle, A = 2σT_sat/ρ_gh_lg, θ_w = T_w − T_sat. T_w is the surface temperature, T_sat is the saturation temperature of the water, ρ_g is the density of vapor, and h_lg is the latent heat of vaporization.

From Hsu's correlation, it was found that pressure affects the active cavity size (Hsu, 1962). A detailed study was performed for the performance of high-pressure pool-boiling heat transfer and the pressure effect on the boiling parameters e.g., nucleation size densities, bubble departure size, and bubble departure frequency (Dahariya and Betz, 2019). The pressure effect on the boiling performance for the plain surface was studied at a micron level for saturated conditions. The pressure activates nucleation sites for micron size cavities and helps increase the range of active cavity sizes, resulting in a greater number of nucleation sites. The experimental results also showed that at a low wall superheat, the size range of active nucleation sites is wider than at atmospheric pressure. A similar trend is observed in the wick structure for the nucleation site density shown in Figure 8. The active nucleation site density increases significantly at high-pressure and can be compared with the results at 0 kPa. The coupled effect of the pressure and the surface features on the wick surface could be the main reason for the increased number of nucleation sites on the wick surface.

From the bubble visualization, it is also noticed that pressure affects the bubble departure size. The size of the bubble departure decreases. The change in the bubble departure size can be quantified by the pressure effect using the Fritz correlation (Fritz and Ende, 1936), expressed in Equation (4),

$\begin{array}{ll}{D}_d=0.0208\varphi {\left[\frac{\sigma }{g({\rho }_l-{\rho }_g)}\right]}^{1/2}& (4)\end{array}$

where σ is the surface tension of the water, g is the acceleration of the gravity, ϕ is the wetting angle, ρ_l and ρ_g is the density of the liquid and vapor, respectively.

For example, the bubble departure diameter decreases from 4.5 to 4.00 mm for the pressure ranging, 0–620.5 kPa, respectively, using Fritz's correlation. Similarly, the bubble departure diameter for the wick surface at 0 kPa, is comparatively smaller than the plain surface that can be seen in the boiling pictures. The cavity size could be the main reason for the small bubble departure size. At high-pressure, the bubble departure size reduces further due to the pressure effect which also affects the bubble departure frequency. The smaller bubbles lift at a faster rate and transport heat through bubbles from the surface to the fluid. The higher bubble frequency rate can be related to the change in the thermophysical properties of water at high-pressure. For example, the surface tension of water is 0.0589 and 0.052 N/m at 0 and 206.8 kPa, respectively. At high-pressure, 11.7% of change has noticed in the surface tension of the water. Similarly, a 2.6% change is seen in the difference in the density of water and vapor—the total percentage of change in the property of water could be the result of bubble departure size change.

The increased active nucleation site densities can explain the heat transfer performance for the wick surface at high-pressure. Based on the micro convection theory (Foster, 1959) the HTC depends on the boiling parameters, i.e., bubble departure diameter, bubble departure frequency, and the bubble nucleation site density. The correlation for the HTC is expressed in Equation (5),

$\begin{array}{ll}HTC=2{(2\Pi k_l{\rho }_l{c}_{pl})}^{1/2}{D_d}^2{f}^{1/2}{{\eta }^{\prime }}_a& (5)\end{array}$

where k_l is the conductivity of the liquid, c_pl is the specific heat of the liquid, ρ_l is the density of the liquid, D_d is the bubble departure diameter, f is detachment frequency, and ${{\eta }_a}^{\prime }$ is the active nucleation site density.

The HTC is directly proportional to the nucleation site density. The results shown in Figure 6, show that the high-pressure pool-boiling has a different boiling behavior. The onset point of wall superheat is smaller than at 0 kPa. It indicates that the boiling starts at a low wall superheat, ΔT = T_s – T_sat. As already discussed in the previous section; the pressure activates the nucleation sites at the micron size scale. The number of active nucleation sites on the wick surface at 206.8 kPa is significantly higher than at 0 kPa as shown in Figure 8. The enhanced heat transfer performance with the surface modifications, and the pressure is shown in Figure 7. The HTC is enhanced three times compared to the plain surface by the surface modification. We further increase the HTC four times compared to the plain surface by varying the system pressure and with the surface modification. This shows there is a coupled effect of surface modification and system pressure. The possible reasons for the boiling performance enhancement by pressure could be an increased number of active nucleation sites and available surface area for heat transfer due to the wick, which may support to bubble nucleation. Also, the sintered wick increases the effective thermal conductivity of the surface (Nasersharifi et al., 2018). The increased effective thermal conductivity of the single-layer wick increases the heat flux per unit square of the heating surface. Therefore, the HTC is enhanced!

Explaining the dry out mechanism in the pool-boiling heat transfer is still under discussion. However, Zuber's was the first to describe the dry out mechanism responsible for CHF for the infinite plain surface (Zuber, 1959). He emphasized the roles of the critical Rayleigh-Taylor wavelength in the CHF mechanisms. According to the Rayleigh-Taylor theory of instabilities, the CHF depends on ${({\lambda }_{RT})}^{-1/2}$, where λ_RT is the wavelength, which is a function of the property of water. The wavelength at the onset of hydrodynamic instabilities can be reduced by varying two parameters: changing the thermophysical properties of water by varying pressure or employing porous-layer coatings on the surface. The pool-boiling mechanisms on the plain surface and the wick surface are shown in Figure 9. For the plain surface, the CHF occurs at high heat flux when the bubbles start merging, and the vapor columns of liquid-vapor jets start forming.

FIGURE 9

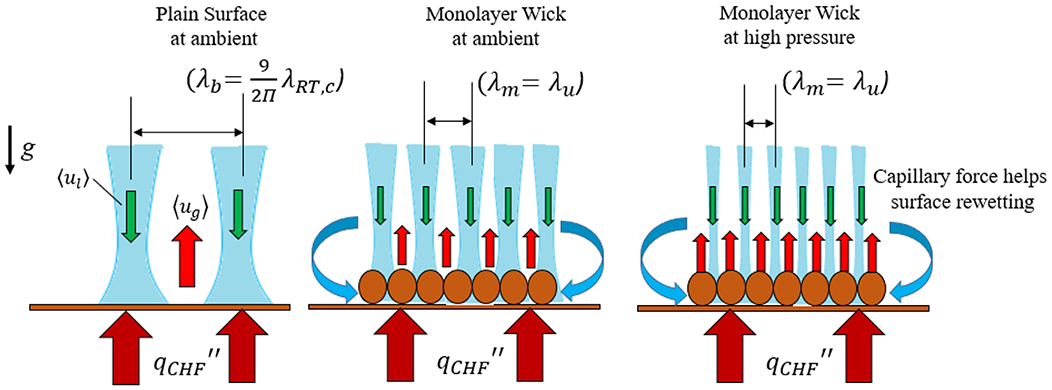
Figure 9. Comparison of high-pressure pool-boiling mechanism for the plain surface and the single-layer wick surface. The critical heat flux, wick geometries, counter flow of the liquid-vapor jets, hydrodynamic instability wavelength are also shown. The role of capillary force in rewetting the wick surface is shown.

Further increase of the heat flux, resulting the increased number of continuous jet columns. The process continues until the two neighboring vapor column jets start interacting and reaches to the critical velocity of the vapor. When the system reaches to a critical point, the system becomes unstable and the surface temperature drops. Due to the porous structure, the bubbles start pinning between the wick and the nucleate boiling begins at a low wall superheat. The bubble pinning prevents the merging of the jet columns with the neighboring jets and controls the liquid-vapor phase separation. Pressure has more effect in the liquid-vapor phase separation by decreasing the modulation wavelength λ_m and is seen in Figure 9.

Based on the classical theory of hydrodynamic liquid-choking limit, the modulation in the porous layer coating separates the liquid-vapor by pumping liquid through the capillary action from the surface to an evaporation sites (Liter and Kaviany, 2001). The theory also hypothesized that the counter motion of the fluids causes a viscous-drag resistance in the liquid. Based on the assumptions, the CHF is determined as a function of the fluid properties, coating material properties, and the macro and pore-scale geometries of the coating is expressed in Equation (6). For a uniform thin porous-layer layer, the critical flux is,

$\begin{array}{ll}\frac{q_{CHF,u}}{\frac{\Pi }{24}{{\rho }_g}^{1/2}\Delta h_{lg}{\left[\sigma g({\rho }_l-{\rho }_g)\right]}^{1/4}}=\frac{3{\left[\frac{\sigma }{g({\rho }_l-{\rho }_g)}\right]}^{1/4}}{{{\lambda }_u}^{1/2}}& (6)\end{array}$

And,

$\begin{array}{ll}{\lambda }_u={\left(\frac{\Pi }{5.88{\epsilon }^n}\right)}^{2}d& (7)\end{array}$

where ϵ is the porosity, and d is the diameter of the copper particle.

The given correlation depends on the constant empirical parameter n is shown in Equation (7). The critical heat flux is calculated for the uniform thin porous-layer coating using Equation (6), with ϵ = 0.4 and n = 1.2, and diameter d = 200 μm. The predicted critical heat flux for 0, 130.4, and 206.8 kPa is found 178.76, 230.05, and 255.94 kW/m², respectively. The enhanced CHF is 1.5 times as high as the plain surface. The measured CHF, 179.63 KW/m² at 0 kPa agrees well with the predicted value. However, the values at higher pressure are over predicted with the measured CHF, 182.42, and 198.16 kW/m² for 130.4, and 206.8 kPa, respectively. The enhanced CHF suggests that the pressure may have a significant effect on the modulation wavelength. Calculating the modulation wavelength for pressure ranging 0–206.8 kPa, λ_m varies from 22.5 to 21.45 mm. It reduces the distance of the pinned liquid-vapor jets by 4.67%. The significant change in the pitch distance has observed in the boiling pictures. It indicates that there is a liquid-vapor phase separation that occurs at the solid/liquid interface of the wick which impacts the heat transfer performance significantly. If we calculate the flow critical length scale for 200 μm particle diameter and the porosity ϵ ranging 0.4–0.5, λ_u lies between 8.6 and 2.5 mm. This reduces λ_u by three times. The analysis suggests that the porous structure also play an important role in the CHF enhancement by a factor of ${\left(\frac{{\lambda }_m}{{\lambda }_u}\right)}^{1/2}$. Finally, an optimized wick design (pore spacing and vapor departure sites) is needed to maximize the CHF using different sizes of sintered particles.

Conclusions

High-pressure pool-boiling performance is studied for the single-layer sintered copper powder wick surfaces using water as a working fluid. The wick structures are fabricated using a multi-step sintering process with 200 μm copper particles, and it increases the contact angle by 25%. The performance of the heat transfer is compared to a plain surface. The results found that the critical heat flux for the single-layer wick surface is 1.75 times higher than that of a plain surface at 0 kPa. However, the critical heat flux is only 1.1 times higher than at 206.8 kPa for the wick surface. The heat transfer performance enhancement is related to the possible decrease in the hydrodynamic instability and the capillary effect in rewetting the surface. We also found that pressure has an impact on the modulation wavelength. It reduces by 4.67% for the pressure ranging 0–206.8 kPa and controls the liquid-vapor phase separation at the solid-liquid interface with a bubble pinning effect. The wick surface also decreases the wall superheat by three-folds. The maximum heat transfer coefficient, 252.46 W/cm² K is found at 100 W/cm² of heat flux for 206.8 kPa. The high-pressure pool-boiling result shows that the HTC is enhanced by 100% as compared to 0 kPa. The surface modification increases the HTC by three times as compared to a plain surface. However, the pressure further amplifies the performance by four times compared to a plain surface demonstrating a coupled effect between pressure and surface modification. The HTC enhancement is related to the increased number of nucleation sites, enhanced effective thermal conductivity, and increased evaporation surface area. Overall, the surface modification and the pressure amplify the performance of pool-boiling heat transfer and dissipates a large amount of heat passively at a low wall superheat.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

SD built the experimental setup, performed the experiments, analyzed the data, and wrote the manuscript. NP assisted in sample manufacturing and assisted with conducting experiments. ME fabricated the wick samples. GH and AB supervised the project and contributed to the final version of the manuscript.

Funding

This work was supported by the NASA Cooperative Agreement Notice, Grant Number 80NSSC18M0030, the United States of America.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would also like to acknowledge Eric Wagner for providing training for using the machine shop at Kansas State University. We thank Brady Brooks for proofreading the article and assisting with running the experiments.

References

Albu, N., Keese, J., and Hwang, G. (2019). “Bimodal, thin wick structures for high heat flux two-phase thermal control systems,” in 49th International Conference on Environmental Systems (ICES-2019–ES-206) (Boston, MA).

Google Scholar

Betz, A. R., Jenkins, J., Kim, C. -J., and Attinger, D. (2011). “Nano-engineered surfaces with heterogeneous wettability for boiling heat transfer enhancement,” in Paper Presented at ASME 2011 9th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM 2011 (Edmonton, AB).

Google Scholar

Betz, A. R., Jenkins, J., Kim, C. -J., and Attinger, D. (2013). Boiling heat transfer on superhydrophilic, superhydrophobic, and superbiphilic surfaces. Int. J. Heat Mass Transf. 57, 733–741. doi: 10.1016/j.ijheatmasstransfer.2012.10.080

CrossRef Full Text | Google Scholar

Betz, A. R., Xu, J., Qiu, H., and Attinger, D. (2010). Do surfaces with mixed hydrophilic and hydrophobic areas enhance pool-boiling? Appl. Phys. Lett. 97:141909. doi: 10.1063/1.3485057

CrossRef Full Text | Google Scholar

Bobrovich, G. I., and Mamontova, N. N. (1965). A study of the mechanism of nucleate boiling at high heat fluxes. Int. J. Heat Mass Transf. 8, 1421–1424. doi: 10.1016/0017-9310(65)90131-6

CrossRef Full Text | Google Scholar

Byon, C., Choi, S., and Kim, S. J. (2013). Critical heat flux of bi-porous sintered copper coatings in FC-72. Int. J. Heat Mass Transf. 65, 655–661. doi: 10.1016/j.ijheatmasstransfer.2013.06.029

CrossRef Full Text | Google Scholar

Chang, J. Y., and You, S. M. (1997). Enhanced boiling heat transfer from microporous surfaces: effects of a coating composition and method. Int. J. Heat Mass Transf. 40, 4449–4460. doi: 10.1016/S0017-9310(97)00057-4

CrossRef Full Text | Google Scholar

Dahariya, S., and Betz, A. R. (2019). High-pressure pool boiling: mechanism for heat transfer enhancement and comparison to existing models. Int. J. Heat Mass Transf. 141, 696–706. doi: 10.1016/j.ijheatmasstransfer.2019.07.016

CrossRef Full Text | Google Scholar

Foster, D. E. (1959). Heat transfer to a boiling liquid-mechanism and correlation. J. Heat Transf. 81, 43–53. doi: 10.1115/1.4008129

CrossRef Full Text | Google Scholar

Fritz, W., and Ende, W. (1936). Maximum volume of vapor bubbles. Phys. Zeitscher. 37, 391–395

Hsu, Y. Y. (1962). On the size range of active nucleation cavities on a heating surface. J. Heat Transf. 84, 207–213. doi: 10.1115/1.3684339

CrossRef Full Text | Google Scholar

Hwang, G., Park, C., and Kaviany, M. (2015). “High-heat-flux distributed capillary artery evaporators,” in Handbook of Porous Media (Boca Raton, FL: CRC Press), 615–648.

Hwang, G.-S., and Kaviany, M. (2006). Critical heat flux in thin, uniform particle coatings. Int. J. Heat Mass Transf. 49, 844–849. doi: 10.1016/j.ijheatmasstransfer.2005.09.020

CrossRef Full Text | Google Scholar

Jafari, D., Wits, W. W., and Geurts, B. J. (2018). Metal 3D-printed wick structures for heat pipe application: capillary performance analysis. Appl. Therm. Eng. 143, 403–414. doi: 10.1016/j.applthermaleng.2018.07.111

CrossRef Full Text | Google Scholar

Jaikumar, A., and Kandlikar, S. G. (2015a). Enhanced pool-boilingfor electronics cooling using porous fin tops on open microchannels with FC-87. Appl. Therm. Eng. 91, 426–433. doi: 10.1016/j.applthermaleng.2015.08.043

CrossRef Full Text | Google Scholar

Jaikumar, A., and Kandlikar, S. G. (2015b). Enhanced pool-boilingheat transfer mechanisms for selectively sintered open microchannels. Int. J. Heat Mass Transf. 88, 652–661. doi: 10.1016/j.ijheatmasstransfer.2015.04.100

CrossRef Full Text | Google Scholar

Jo, H., Kim, S., Kim, H., and Kim, M. H. (2012). Nucleate boiling performance on nano/microstructures with different wetting surfaces. Nanoscale Res. Lett. 7:242. doi: 10.1186/1556-276X-7-242

PubMed Abstract | CrossRef Full Text | Google Scholar

Jo, H., Park, H. S., and Kim, M. H. (2016). Single bubble dynamics on hydrophobic-hydrophilic mixed surfaces. Int. J. Heat Mass Transf. 93, 554–565. doi: 10.1016/j.ijheatmasstransfer.2015.09.031

CrossRef Full Text | Google Scholar

Jones, B. J., McHale, P., and Garimella, S. V. (2009). The influence of surface roughness on nucleate pool-boilingheat transfer. J. Heat Transf. 131:121009. doi: 10.1115/1.3220144

CrossRef Full Text | Google Scholar

Kandlikar, S. G. (2013). Controlling bubble motion over heated surface through evaporation momentum force to enhance pool-boilingheat transfer. Appl. Phys. Lett. 102:051611. doi: 10.1063/1.4791682

CrossRef Full Text | Google Scholar

Kim, J. H., Rainey, K. N., You, S. M., and Pak, J. Y. (2002). Mechanism of nucleate boiling heat transfer enhancement from microporous surfaces in saturated FC-72. J. Heat Transf. 124, 500–506. doi: 10.1115/1.1469548

CrossRef Full Text | Google Scholar

Li, N., and Betz, A. R. (2017). Boiling performance of graphene oxide coated copper surfaces at high-pressures. J. Heat Transf. 139:111504. doi: 10.1115/1.4036678

CrossRef Full Text | Google Scholar

Liter, S. G., and Kaviany, M. (2001). Pool-boiling CHF enhancement by modulated porous-layer coating: theory and experiment. Int. J. Heat Mass Transf. 44, 4287–4311. doi: 10.1016/S0017-9310(01)00084-9

CrossRef Full Text | Google Scholar

Marcel, C., Clausse, A., Frankiewicz, C., Betz, A., and Attinger, D. (2017). Numerical investigation into the effect of surface wettability in pool-boiling heat transfer with a stochastic-automata model. Int. J. Heat Mass Transf. 111, 657–665. doi: 10.1016/j.ijheatmasstransfer.2017.04.035

CrossRef Full Text | Google Scholar

Nam, Y., and Ju, Y. S. (2008). Bubble nucleation on hydrophobic islands provides evidence to anomalously high contact angles of nanobubbles. Appl. Phys. Lett. 93:103115. doi: 10.1063/1.2981572

CrossRef Full Text | Google Scholar

Nasersharifi, Y., Kaviany, M., and Hwang, G. (2018). Pool-boiling enhancement using multilevel modulated wick. Appl. Therm. Eng. 137, 268–276. doi: 10.1016/j.applthermaleng.2018.03.073

CrossRef Full Text | Google Scholar

Nishikawa, K., Fujita, Y., Ohta, H., and Hitaka, S. (1982). Effects of system pressure and surface roughness on nucleate boiling heat transfer. Unknown J. 42, 95–123.

Google Scholar

Rainey, K. N., and You, S. M. (2000). Pool-boilingheat transfer from plain and microporous, square pin-finned surfaces in saturated FC-72. J. Heat Transf. 122, 509–516. doi: 10.1115/1.1288708

CrossRef Full Text | Google Scholar

Rainey, K. N., You, S. M., and Lee, S. (2003a). Effect of pressure, subcooling, and dissolved gas on pool-boiling heat transfer from microporous surfaces in FC-72. J. Heat Transf. 125, 75–83. doi: 10.1115/1.1527890

CrossRef Full Text | Google Scholar

Rainey, K. N., You, S. M., and Lee, S. (2003b). Effect of pressure, subcooling, and dissolved gas on pool-boiling heat transfer from microporous, square pin-finned surfaces in FC-72. Int. J. Heat Mass Transf. 46, 23–35. doi: 10.1016/S0017-9310(02)00257-0

CrossRef Full Text | Google Scholar

Sakashita, H. (2011). Bubble growth rates and nucleation site densities in saturated pool-boiling of water at high-pressures. J. Nucl. Sci. Technol. 48, 734–743. doi: 10.1080/18811248.2011.9711756

CrossRef Full Text | Google Scholar

Sakashita, H., and Ono, A. (2009). Boiling behaviors and critical heat flux on a horizontal plate in saturated pool-boiling of water at high-pressures. Int. J. Heat Mass Transf. 52, 744–750. doi: 10.1016/j.ijheatmasstransfer.2008.06.040

CrossRef Full Text | Google Scholar

Semeria, R. (1963). High-speed cinematography and pool-boiling under high-pressure. La Houlle Blanche 6, 679–687. doi: 10.1051/lhb/1963048

CrossRef Full Text | Google Scholar

Takata, Y., Hidaka, S., and Kohno, M. (2006). “Enhanced nucleate boiling by superhydrophobic coating with checkered and spotted patterns,” in Paper Presented at Proceedings of the Sixth International Conference on Boiling Heat Transfer Spoleto (New York, NY).

Takata, Y., Hidaka, S., Masuda, M., and Ito, T. (2003). Pool-boiling on a superhydrophilic surface. Int. J. Energy Res. 27, 111–119. doi: 10.1002/er.861

CrossRef Full Text | Google Scholar

Trisaksri, V., and Wongwises, S. (2009). Nucleate pool-boiling heat transfer of TiO2–R141b nanofluids. Int. J. Heat Mass Transf. 52, 1582–1588. doi: 10.1016/j.ijheatmasstransfer.2008.07.041

CrossRef Full Text | Google Scholar

Zuber, N. (1959). Hydrodynamic aspects of boiling heat transfer (thesis). University of California, Los Angeles, CA, United States.

Google Scholar

Nomenclature