Effect of Canyons on a Fire Propagating Laterally Over Slopes

In this paper, the problem related with a fire front propagating laterally on a slope with a nearby canyon is presented. The presence of the canyon can modify the intensity of the fire and create a difficult situation for elements involved in fire suppression. When a fire propagating laterally in a slope enters the canyon, a rapid increase in the fire's rate of spread occurs and a strong convective activity is generated due to the burning inside the canyon. The convective flow generated will then induce a change in the propagation of the fire in the slope. In certain conditions the rate of spread and the intensity of the fire will be strongly increased. This type of extreme fire behavior is referred to as eruptive fire behavior (or blow-up), and usually happens over slopes or in canyon configurations. In this study, we analyzed the results of laboratory-scale experiments that model a fire spreading latterly over a slope and then enter a canyon that is embedded in the slope. Three configuration parameters were used in the experiments. The first is the inclination α of the slope, the second is the orientation γ of the axis of the canyon and the third is the angle β of the ignition line. The fire spread is very complex and dynamic resulting in situations in which very high values of the ROS can be reached for several configurations, creating dangerous situations for firefighters.

Introduction

Forest fires are a phenomenon that can be characterized by a great level of destruction of material and human assets. In the worst cases, forest fires may cause accidents and fatalities among firefighters and civilians. Many of these accidents and fatalities are associated with canyons. Accidents involving firefighters related to forest fires are often due to insufficient knowledge about fire and its behavior, especially in the case of Extreme Fire Behavior (EFB) (Viegas, 2006, 2012; Werth et al., 2011).

In 2013, in Portugal at Serra do Caramulo, several firefighters were fighting a flank fire on a sloped terrain with a nearby canyon (Viegas et al., 2013). When the fire entered the bottom of the canyon the behavior of the fire was modified dramatically. Several firefighters were hurt by the fire and two of them lost their lives. This particular accident motivated us to study the change of the fire behavior over slopes when the flank fire enters canyons, with the aim to improve the safety of the teams involved in the suppression of wildfires in similar conditions.

Static and Dynamic Fire Behavior

Most fire behavior models are based on the assumption that the fire propagation properties are quasi static and can be determined from three groups of essential factors: topography, fuel and meteorology, which are called the “fire triangle” (Byram, 1959). Recognizing that in the general case the convective flow induced by the fire modifies its behavior in the course of time, even in the case of permanent boundary conditions, Viegas (2006) proposed, as an alternative to this classic formulation, the concept of “square of fire,” adding a fourth factor: time. According to this concept the fire behavior is dynamic in the sense that it changes in the course of time even with permanent boundary conditions.

Designating by R_o the basic rate of spread (ROS) of a fire line spreading on a horizontal surface in the absence of wind we can define the non-dimensional rate of spread R' by:

$\begin{array}{l}{R}^{{}^{\prime }}=\frac{R}{R_o}\end{array}$

Viegas (2006) showed that only if R' ≈ 1 the behavior of a fire can be considered as static as its properties remain constant.

If the value of R' is large, the acceleration of the fire front can be quite large and lead to what we designate as Extreme Fire Behavior that is normally associated to rapid changes of the ROS and to large values of fire line intensity.

As a reference, a fire spreading in a shrub fuel bed with a load of 1.5 kg, a typical value of R_o is of the order of 50 m.h⁻¹ (≈0.014 m.s⁻¹). The corresponding value of the fire line intensity is 5,625 kW/m. This intensity was determined according to Byram (1959).

In the present study we consider the ranges of values of R' that are shown in Table 1 to differentiate various fire behavior regimes. In Table 1 we included the reference values of fire line intensity and estimated flame length as an indication of the meaning of these limits.

TABLE 1

Table 1. Classes of fire behavior regime.

Fires spreading on slopes have been studied by several authors, namely by Dupuy (1995), Dupuy and Maréchal (2011), Dupuy et al. (2011), and Silvani et al. (2012), with it found that fire induced convection becomes dominant for values of slope angle α > 30°.

Fire spread in canyons is of particular relevance in fire safety analysis as a large number of fatalities are related to this type of terrain configuration (cf. Viegas, 2005; Schemel et al., 2008; Viegas and Simeoni, 2011; Lahaye et al., 2018). This type of fires was extensively studied by Viegas and Pita (2004) and Dold and Zinoviev (2009). The steady increase of the ROS of the fire front, even in the absence of wind or any other contributing factor was also reported in Pyne et al. (1996) and Dold (2010). The designation of “eruptive” fire behavior was coined in Viegas and Pita (2004), to designate this type of fire behavior. Viegas (2005, 2006) proposed a mathematical model to predict the ROS of the head fire in canyons. According to this model the presence of the flame induces a local enhancement of the flow velocity around the fire front that produces an increase in its ROS in the course of time. The positive feedback between both processes leads to a gradual increase of R' that can reach quite high values.

The merging of two fire fronts that was studied in Viegas et al. (2012), Sharples et al. (2013), and Raposo et al. (2015, 2018), also exhibits a behavior similar to a fire eruption leading to extremely high values of R' and are accompanied by very strong convective effects.

To the knowledge of the present authors, the problem of fires spreading in slopes with embedded or nearby canyons, which is the object of the present paper, is not reported in the literature. As described above, the problem of fire spread on slopes was studied quite extensively both empirically and using analytical and numerical models. The spread of fires in canyons was studied as well but the interaction between fires spreading on a slope with a nearby canyon that is relevant for applications, was not considered before. As pointed out by Silvani et al. (2012) even in the absence of wind, heat transfer is not only achieved by radiation, but also by convection, therefore the presence of fire inside or near the canyon modifies the flame geometry and the spread of the fire. Depending on the slope angle, the orientation of the canyon axis and the inclination of the fire front, as a result of this complex interaction very high values of the ROS can be achieved due to the presence of the canyon.

The main objective of this paper is a detailed and exhaustive analysis of the phenomenon has an interaction on lateral spread of fire on a slope with a canyon. The intent is to understand the variation of fire propagation velocity and direction and the values of the fire intensity, and contribute toward the increase of scientific knowledge in this case of EFB. Different ignition angles will be tested to evaluate their influence on the development in the forest fires. The acquisition of images in the visible and infrared range to determine the velocity and direction of fire propagation, the flame geometry and the energy release rate are purposed in this work. This study also aims to propose behavior models and operation rules to personal safety when people fight against forest fires on slopes with canyons, based on previous studies and in the research that will be carried out.

Methodology

Definition of the Problem

The geometry of a canyon embedded in a slope is described schematically in Figure 1. Let us consider an absolute reference frame O_oX_oY_oZ_o in which the horizontal datum plane is defined by the axis X_o and Y_o. A second reference frame is defined by O₁X₁Y₁Z₁ in which the axis OX₁ is parallel to OX_o and the axis OY₁ is rotated by an angle α in relation to OX_o. Henceforth this angle will be designated as slope angle.

FIGURE 1

Figure 1. The variation of test table geometry.

Rotating the system of axis O₁ X₁ Y₁ Z₁ by an angle γ around axis OZ we can define a new system OXYZ that is shown in Figure 1 in which OZ ≡ OZ₁.

The surface of the slope is a square ABCD in which A≡O. The canyon is embedded in this slope in the rectangle CEFG as shown in Figure 1. The canyon has two lateral faces of equal slope and therefore its section has a constant triangular shape. The base of the canyon is HI, that is designated as its “axis” and is parallel to OY. More details on the canyon geometry are given in the next section.

In this study we consider a linear fire front AJ that is spreading across the surface of the ground. The angle between this line and OX axis is β, as indicated in Figure 1. Henceforth, this is designated as Line i. In the present study the following values of β were used: 0, 10, and 20°.

Experimental Setup

For the experimental study an original test table (Figure 2) was built. The test table has a burn area of 3 × 3 m² and one embedded canyon of 0.94 × 2.34 m². The test table permits an angle change of the slope (α) between 0 and 45° and the orientation of the canyon axis (γ) between 0 and 360°, as demonstrated in Figure 1. It also allows for a change in the canyon configuration, but in these tests only the configuration shown in Figure 3 was used.

FIGURE 2

Figure 2. Table of laboratory tests.

FIGURE 3

Figure 3. Technical drawing of the canyon configuration.

The canyon that was used in the tests is a “U shape” canyon with the dimensions shown in Figure 3, with an approximately 38° in the lateral slopes and 40° in the entrance of the canyon. The depth of the canyon is 0.35 m and its length is 2.34 m. Figure 3 exhibits the technical drawing of the canyon configuration.

Methods

In all experiments the fuel bed was composed of a layer of Pinus pinaster dead needles with a load of 0.6 kg.m⁻² (on a dry basis) that covered the entire surface of the slope and the canyon.

The conditions of fuel load and bulk density were controlled during the preparation of the fuel bed; air temperature, relative humidity and fuel moisture (m_f) were monitored. The time between preparation of the fuel bed and burning did not exceed 10 min to avoid changes in moisture content of the fuel in contact with ambient air.

The fuel moisture content (m_f) is a critical factor that has significant effects on the combustion process. According to Byram (1959) and Pyne et al. (1996), the fuel moisture content determines the possibility of a forest fuel to ignite and what proportion of it is available for the combustion process. In each test the fuel moisture content was measured twice: at the beginning of the preparation of the fuel bed and immediately before each test. The value presented in Table 2 corresponds to the one measured immediately before the test. A moisture analyser (A&D ML50) was used for the measurement. This machine enables the quantification of water inside the fuel in a drying period of 10 min.

TABLE 2

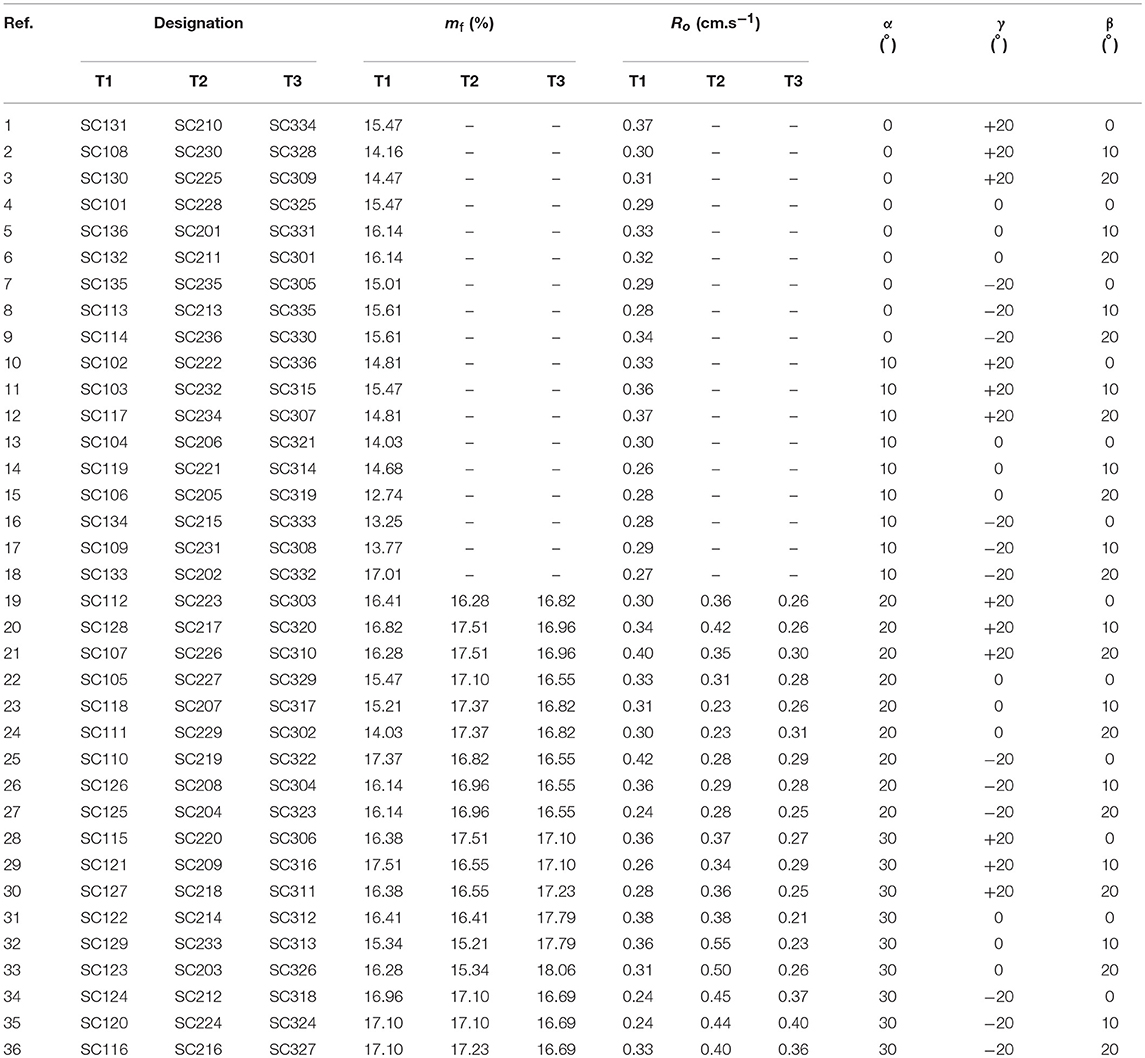
Table 2. Data of the tests performed (for experiments with slope angles of α = 20° and α = 30° three tests were performed).

The tests were monitored using a photographic camera (Canon EOS 550D), two video cameras—one in the frontal plane (Sony AVCHD MPEG2 SD) and one in the lateral plane (Sony HD DCR-SR87). An infrared camera (FLIR SC660) was used to record all tests in the range of 300–1,500°C, with a rate of acquisition of 15 Hz. Before each test a reference test to determine the basic ROS (R_o) was performed using a horizontal table of 1 × 1 m² with the same fuel cover.

We analyzed the infrared recorded images to obtain the fire contour at pre-defined times. The time between frames was adapted for each test, in order to determine the evolution of the fire front, following the methodology referred in Raposo (2016). In order to have an overall assessment of the fire front evolution during the experiment and also to analyse the spatial distribution of temperature along the fuel bed, infrared images (IR) from each experiment were recorded. Using IR methodology, the position of the fire perimeter at given time frames was assessed and from these images the ROS at various positions of the fire perimeter. The threshold of 350°C was used to avoid the obstruction of the view by the plume of the fire. The adjustment of this threshold can be set even after the recording of the images. Any digital frame of the video of the IR camera is stored on the PC hard disk frame, with the name corresponding to time t, then each frame is imported. In this program, a specifically written application allows the capture of the fire line in the image and for each point, the Cartesian coordinates of the frame are converted into true physical Cartesian coordinates in the plane of the combustion table. This conversion encompasses a simple but non-trivial image calibration technique in which the camera is assimilated to a pin-hole optical system without aberration. Eventually, the fire line is described by an ordered set of points, in the OXY Cartesian system defined above. The program computes the average and instantaneous values of ROS at each point of the fire line and the isochrones of the fire perimeter.

As the IR recording was continuous it was possible to estimate the local value of the ROS at any point of the fuel bed or at any time. This feature was used to determine the value of ROS at predefined distances along the reference lines mentioned below to allow the estimation of average values of ROS at given locations and their standard deviation.

These tests were performed with four different slope angles (α): 0, 10, 20, and 30° and for three values of the orientation of the canyon axis (γ): −20, 0, and 20° (Figure 4).

FIGURE 4

Figure 4. Effect of the inclination of the axis of the canyon (γ): (A) −20° (Test SC124); (B) 0° (Test SC122); (C) +20° (Test SC115).

For each angle of slope and rotation of the table, three angles (β) of ignition line were used (0, 10, and 20°).

Data of the tests performed, are presented in Table 2. In order to reduce uncertainty three replications (T1, T2, and T3) were performed for each set of parameters for α = 20° and α = 30°. Preliminary tests with α = 0° and α = 10° showed that for these low values of slope R' was always lower than 2 and therefore only one test was performed for these slope angles.

As an example, in Figure 5 the isochrones of one of the tests (SC324) are shown together with some reference lines that were used to analyse the spread of the fire. Line a (yellow line) is along the center of the table; Line b (green line) is at mid distance between line a and the left border of the canyon (FG); Line c (blue line) is along the waterline of the canyon (HI); Line d (orange line) is along the propagation of the head fire that coincides with the maximum slope direction of the plane OXY. Lines a, b and c are all parallel to OY axis.

FIGURE 5

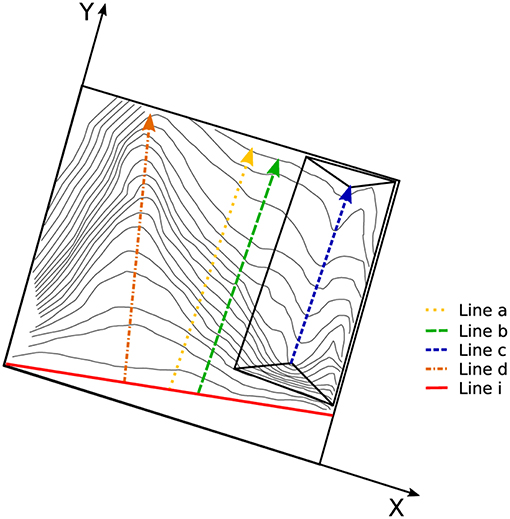
Figure 5. The measurement directions of the fire propagation. The isochrones correspond to test SC324 (α = 30°, γ = −20°, β = 10°).

Results and Discussion

Overall Fire Behavior Regimes

In the present analysis we considered a non-dimensional rate of spread (R'), defined by equation (1) to allow the extension of the results to other fuel bed properties. In order to assess the overall danger associated to the problem of a flank fire entering in the canyon for the set of conditions that were analyzed in the present study we analyzed the maximum local value of R' along each line of reference mentioned above. The results are shown graphically in Table 3, using the color codes for each Class of fire behavior as defined in Table 1.

TABLE 3

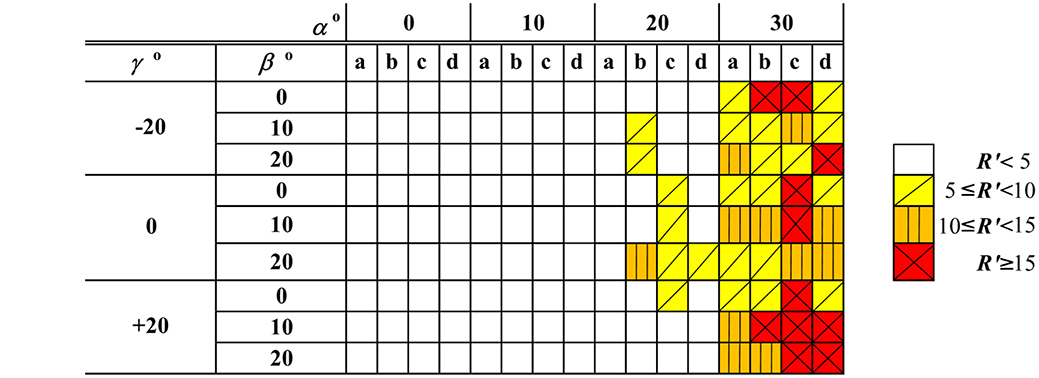
Table 3. Distribution of the class of FB according to the maximum local value of R' along the reference lines.

As can be seen in Table 3 for α ≤ 10° the fire behavior is only in Classes 1 and 2. For α = 20°, Class 3 is observed only along lines b, c, and d, near or inside the canyon, for some sets of values of β and of γ. Class 4 regime was only observed along line b for γ = 0° and β = 20°.

For α = 30°, Class 3 regime is observed in all cases. Class 4 regime occurs in most situations for lines b and c. Class 5 regime is also observed along these lines and along line d as well for some sets of values of the control parameters.

We can conclude that besides the interior of the canyon its vicinity (near line b) is a potentially dangerous area to stay and to operate in the case of a fire spreading in the geometric conditions that were considered. This was actually the case in the accident that was mentioned above that occurred in Portugal.

Linear Ignition With β = 0°

In the previous analysis we indicated that the maximum value of R' along a reference line was in a certain range of values, without actually stating the location where this maximum value occurs. Although we have this information in our database, it would require much more space to present it. In order to illustrate the variation of R' along the reference lines, as an example, we present part of the results for β = 0°.

Effect of Slope Angle

To analyse the effect of slope angle α we consider the evolution of R' along line b for γ = −20° for four values of α, that are shown in Figure 6. Each data point in this figure corresponds to the local average value from three replications that were performed for α = 20° and α = 30°. The corresponding bars represent the confidence intervals for a 90% level. As can be seen, the values of R' are in generally lower than 3 for α ≤ 20°. The case of α = 30° is of particular interest as the value of R' increases initially, then it decreases to values lower than one and increases up to 8, corresponding to Class 3 regime.

FIGURE 6

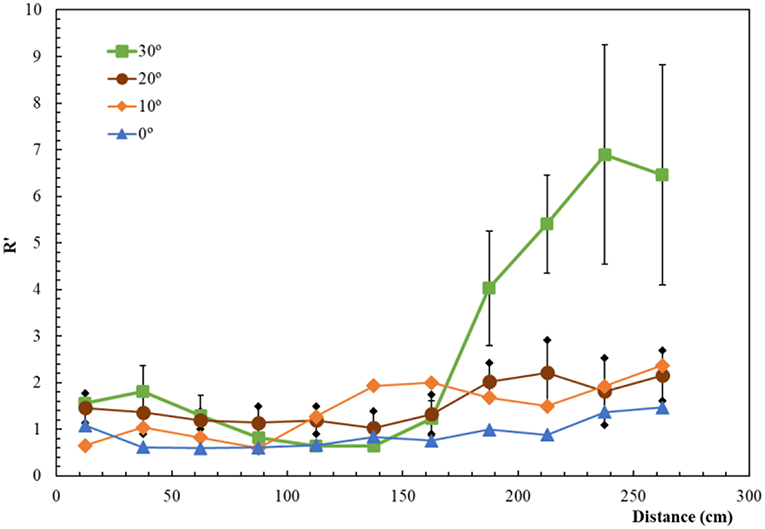
Figure 6. Mean values of R' along line b for tests with β = 0° and γ = −20° for various of slope angle α. The error bars correspond to a level of confidence of 90%.

Effect of Canyon Axis Inclination

In order to analyse the effect of the inclination angle γ of the axis of the canyon we consider the case of slope angle α = 30°. The results are shown in Figure 7 for each line a, b, c and d. The scale of R' is the same in the four figures to facilitate a comparison.

FIGURE 7

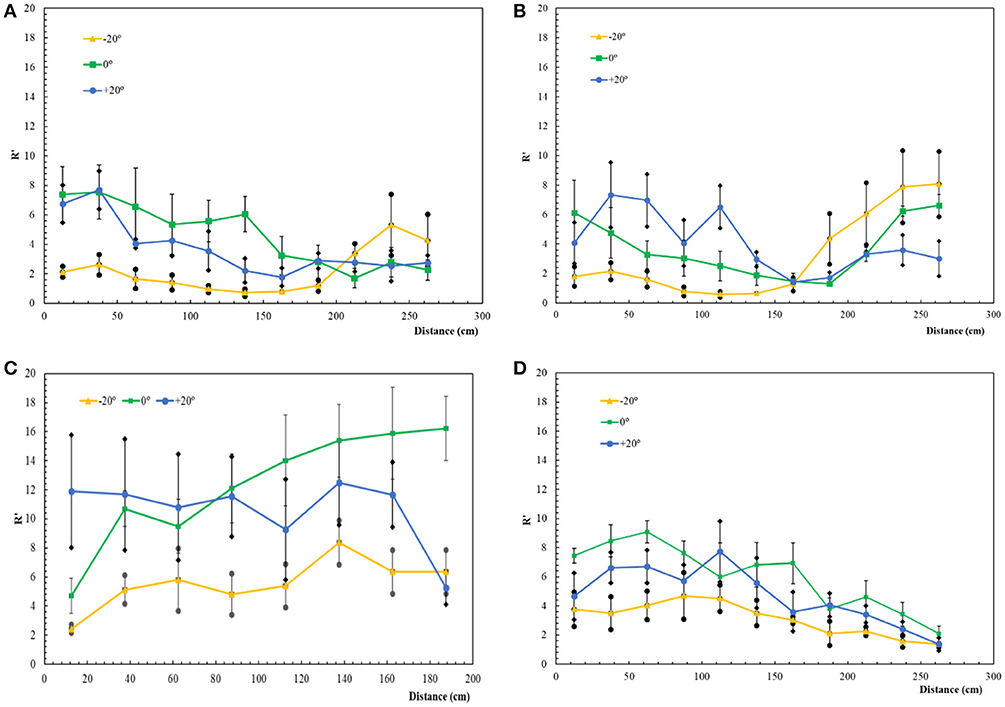
Figure 7. Mean value of R' for tests with α = 30° and β = 0°–(A) Line a; (B) Line b; (C) Line c; (D) Line d. The error bars correspond to a level of confidence of 90%.

In line a (Figure 7A) the value of R' is always lower than 10 but the effect of angle γ can be observed. The case of γ = 0° registers the higher values of R' in the lower part of the slope but the difference between the three cases of inclination angle γ is reduced in its upper part. In Figure 7B the results for line b, near the canyon are shown. In this case the values of R' are also lower than 10 and an influence of angle γ can be observed. In the first part of the slope the values of R' decrease with distance but are larger for larger values of γ. In the upper part of the slope the values of R' increase due to the proximity of the canyon, but the opposite occurs in the upper part of the slope. The increase of R' for the case of γ = 0° is particularly noteworthy as it is directly influenced by the fire eruption in the canyon as line b is parallel to the maximum slope direction.

The results for line c in the bottom of the canyon are shown in Figure 7C. There is a marked influence of the inclination angle γ: for γ = −20° the fire behavior is almost always in Class 2. For γ = +20° the value of R' is practically constant along line b and of the order of 12. For γ = 0° the value of R' increases along line c reaching Class 5.

The results for line d of maximum slope are shown in Figure 7D. The values of R' decrease along the slope for the three values of γ. The values of R' are higher for γ = 0° and decrease symmetrically with γ.

Conclusions

In this paper the complex situation of a linear fire line spreading on a slope in the vicinity of an embedded canyon was analyzed in a laboratory simulation. Three geometrical parameters were considered in the study: the slope of the fuel bed α, the inclination angle of the axis γ of the canyon and the orientation of the ignition line β.

The spread of the fire in this terrain configuration can create very high risk situations for firefighters due to the potential increase of the ROS. In order to assess this potential of having areas of very high fire line intensity, we defined five Classes of fire behavior according to the maximum local values of the non-dimensional ROS R'.

In the overall analysis it was verified that for slope angles α ≤ 10° the fire behavior is always Classes 1 or 2 and therefore not considered very dangerous. For α = 20°, we may have fire behavior of Class 3 or even of Class 4 in some configurations. For α = 30°, fire behavior is mostly in Class 3 but quite often it reaches Classes 4 and 5, especially for γ = +20°, making this range of configurations the most dangerous.

More detailed results were presented for the ignition line configuration corresponding to β = 0°. It was observed that the orientation angle of the canyon axis has a complex influence on fire spread along the reference lines. Analysis of the ROS along line b for γ = −20° indicate that the value of R' remains below 2 in average for α ≤ 20° but can reach a value of 7 for α = 30°.

The results for α = 30° show that for lines a, b and d the fire behavior is always in Classes 1 to 3 for each orientation of the canyon axis. For line c, when γ = −20° the fire behavior is in Classes 2 and 3 but when γ = +20° the fire behavior is in Classes 3 and 4. In this line, for γ = 0° initially the fire behavior starts in Class 3 but along the distance inside the canyon the ROS increases and we have Classes 4 and 5, being dangerous situations for the firefighters.

Analysis of the ROS along the line a and b for γ = −20° show that the value of R' is below 2 in average at the base of the slope but can reach a value >5 when the fire enters the canyon and it influences the adjacent points. For line c when γ = 0° the canyon axis is aligned with the maximum slope and the eruptive effect occurs. For γ = −20° and γ = +20° the waterline is not aligned with maximum slope and the convective flow is affected, therefore the values of R' are lower but are higher in line c. For line d the fire has an acceleration initially but then the value of R' decreases for all values of γ. It is observed that the presence of the canyon interferes with the direction of propagation when the fire spreads with a higher ROS in the direction of the canyon's waterline affecting the adjacent points.

In the future, we intend to insert pitot tubes to the test table to analyze the convective flow and use thermocouples to measure the transfer of heat by radiation, for the different slope angles and to model this complex problem numerically.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

We would like to thank the FCT-Foundation for Science and Technology for the Ph.D. Grants (SFRH/BD/138235/2018 and SFRH/BD/140923/2018) and for the Projects FIREWHIRL (PTDC/EMS-ENE/2530/2014), FIRESTORM (PCIF/GFC/0109/2017), and RENATURE (CENTRO-01-0145-FEDER-000007) that allowed this work to be performed.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to express our gratitude to Gonçalo Rosa and Nuno Luís for their support in laboratory tests. We also would like to express our appreciation to Doctor Aileen Gracias for reviewing our paper.

References

Byram, G.M. (1959). “Combustion of forest fuels,” in Forest Fire Control and Use, Vol. 3, eds K. P. Davis (New York, NY: McGraw-Hill, 61–89.

Google Scholar

Dold, J. (2010). “Flow attachment in eruptive fire growth,” in VI International Conference on Forest Fire Research (Coimbra).

Google Scholar

Dold, J. W., and Zinoviev, A. (2009). Fire eruption through intensity and spread rate interaction mediated by flow attachment. Combust. Theory Model. 13, 763–793. doi: 10.1080/13647830902977570

CrossRef Full Text | Google Scholar

Dupuy, J.-L., and Maréchal, J. (2011). Slope effect on laboratory fire spread: contribution of radiation and convection to fuel bed preheating. Int. J. Wildl. Fire 20, 289–307. doi: 10.1071/WF09076

CrossRef Full Text | Google Scholar

Dupuy, J. L. (1995). Slope and fuel load effects on fire behavior: laboratory experiments in pine needles fuel beds. Int. J. Wildland Fire 5, 153–164.

Google Scholar

Dupuy, J. L., Maréchal, J., Portier, D., and Valette, J. C. (2011). The effects of slope and fuel bed width on laboratory fire behaviour. Int. J. Wildland Fire 20, 272–288. doi: 10.1071/WF09075

CrossRef Full Text | Google Scholar

Lahaye, S., Sharples, J., Matthews, S., Heemstra, S., Price, O., and Badlan, R. (2018). How do weather and terrain contribute to firefighter entrapments in Australia? Int. J. Wildland Fire 27, 85–98. doi: 10.1071/WF17114

CrossRef Full Text | Google Scholar

Pyne, S. J., Andrews, P. L., and Laven, R. D. (1996). Introduction to Wildland Fire. New York, NY: John Wiley and Sons.

Google Scholar

Raposo, J. R., Cabiddu, S., Viegas, D. X., Salis, M., and Sharples, J. (2015). Experimental analysis of fire spread across a two-dimensional ridge under wind conditions. Int. J. Wildland Fire 24:1008. doi: 10.1071/WF14150

CrossRef Full Text | Google Scholar

Raposo, J. R., Viegas, D. X., Xie, X., Almeida, M., Figueiredo, A. R., Porto, L., et al. (2018). Analysis of the physical processes associated with junction fires at laboratory and field scales. Int. J. Wildland Fire 27, 52–68. doi: 10.1071/WF16173

CrossRef Full Text | Google Scholar

Raposo, J. R. N. R. (2016). Extreme Fire Behaviour Associated to Merging of Two Linear Fire Fronts. Coimbra: University of Coimbra.

Google Scholar

Schemel, C. F., Simeoni, A., Biteau, H., Rivera, J. D., and Torero, J. L. (2008). A calorimetric study of wildland fuels. Exp. Ther. Fluid Sci. 32, 1381–1389. doi: 10.1016/j.expthermflusci.2007.11.011

CrossRef Full Text | Google Scholar

Sharples, J. J., Towers, I. N., Wheeler, G., Wheeler, V., and Mccoy, J. A. (2013). “Modelling fire line merging using plane curvature flow,” in 20th International Congress on Modelling and Simulation (Coimbra).

Google Scholar

Silvani, X., Morandini, F., and Dupuy, J.-L. (2012). Effects of slope on fire spread observed through video images and multiple-point thermal measurements. Exp. Ther. Fluid Sci. 41, 99–111. doi: 10.1016/j.expthermflusci.2012.03.021

CrossRef Full Text | Google Scholar

Viegas, D. X. (2005). A mathematical model for forest fires blowup. Combust. Sci. Technol. 177, 27–51. doi: 10.1080/00102200590883624

CrossRef Full Text | Google Scholar

Viegas, D. X. (2006). Parametric study of an eruptive fire behaviour model. Int. J. Wildland Fire 15, 169–177. doi: 10.1071/WF05050

CrossRef Full Text | Google Scholar

Viegas, D. X. (2012). “Extreme fire behaviour,” in Forest Management: Technology, Practices and Impact, eds A. C. B. Cruz and R. E. G. Correa (New York, NY: Nova Science Publishers, Inc., 1–56.

Google Scholar

Viegas, D. X., and Pita, L. P. (2004). Fire spread in canyons. Int. J. Wildland Fire 13, 253–274. doi: 10.1071/WF03050

CrossRef Full Text | Google Scholar

Viegas, D. X., Raposo, J. R., Davim, D. A., and Rossa, C. G. (2012). Study of the jump fire produced by the interaction of two oblique fire fronts. Part 1. Analytical model and validation with no-slope laboratory experiments. Int. J. Wildland Fire 21, 843–856. doi: 10.1071/WF10155

CrossRef Full Text | Google Scholar

Viegas, D. X., Ribeiro, L. M., Almeida, M. A., Oliveira, R., Viegas, M. T. P., Reva, V., et al. (2013). Os Grandes Incêndios Florestais e os Acidentes Mortais Ocorridos em 2013. Coimbra: University of Coimbra.

Viegas, D. X., and Simeoni, A. (2011). Eruptive behaviour of forest fires. Fire Technol. 47, 303–320. doi: 10.1007/s10694-010-0193-6

CrossRef Full Text | Google Scholar

Werth, P. A., Potter, B. E., Clements, C. B., Finney, M. A., Goodrick, S. L., Alexander, M. E., et al. (2011). Synthesis of Knowledge of Extreme Fire Behavior. Vol. 1. Portland, OR: USDA.

Google Scholar