Jacqueline Krim- Physics Department, North Carolina State University, Raleigh, NC, United States
Studies of the fundamental origins of friction have progressed rapidly in recent years, yielding valuable information on the relative contributions of electronic, magnetic, electrostatic, and phononic dissipative mechanisms. The field is now moving toward design of active control method for nano and/or meso scale friction, including the use of magnetic and electric fields external to the contact. These methods constitute an area of rapidly growing interest, as they address one of tribology's present day grand challenges: achieving in situ control of friction levels without removing and replacing lubricant materials situated within inaccessible confines of a contact. In this review, 25 examples of electromagnetic tuning of friction are overviewed, with examples spanning atomic to macro scale systems to demonstrate the variety and versatility of approaches that have been reported in the literature. Applications include, but are not limited to triboelectric generators, geological drilling, automotive braking and efficiency, spacecraft systems, biological systems, and magnetic spintronics. Experimental methods for measuring the impact of electric or magnetic fields on friction include AFM, SFA, QCM, pin-on-disk, hard disk head-on-substrate, MEMS and NEMS based tribometers, and optical spectroscopies. Computational and theoretical approaches include analytic, equilibrium and non-equilbrium Monte Carlo simulations.
Introduction and Overview
Studies of how friction originates at the atomic scale have advanced rapidly in recent years, (Krim, 2012) from passive investigations of model systems (Müser et al., 2001) to active control and custom design of adaptive lubricant systems (Wu et al., 2015; Berman et al., 2018). Control and manipulation of adhesion and friction at a sliding contact is essential for progress in a wide variety of applications spanning nanoscale to macroscale applications. Achieving in situ control of friction levels without removing and replacing lubricant materials situated within inaccessible confines of a contact constitutes a current grand challenge in the field of nanotribology. The overarching goal is to successfully switch and/or adjust materials at the molecular level so as to reversibly and non-invasively tune friction levels. Externally applied electric or magnetic fields constitute a particularly promising, and rapidly growing, means to achieve to such “active” or “smart” control of friction at a molecular level in a field that has come to be known as “tribotronics” (Glavatskih and Höglund, 2008).
Figure 1 depicts a molecular level schematic, including possible nanoparticle or molecular additives to the bulk lubricant, of the Stribeck curve (Lu et al., 2006), which is a plot of a lubricated contact's friction coefficient μ = Ff/N vs. the quantity ηv/N. The friction force Ff is defined as the force that resists sliding, and the quantities η, v and N are, respectively, the lubricant viscosity, the sliding speed and the applied load. The friction coefficient is a non-linear function of the load, lubricant viscosity and lubricant entrainment speed and the curve is divided into three regions: full solid on solid contact (boundary lubrication), partial contact (mixed lubrication), and zero contact (hydrodynamic lubrication). For fixed viscosity and load, the friction coefficient is notably independent of velocity in the boundary lubrication regime where it is comparable to “Coulomb,” or dry-contact, friction. This is because the contacting asperities in the boundary lubrication regime support the full load of the solids pressed into contact. As the velocity increases, there is a progressive transition to a “Stokes” regime of hydrodynamic lubrication characterized by linear dependence of friction on velocity, with the solid surfaces fully separated by the intervening lubricant.
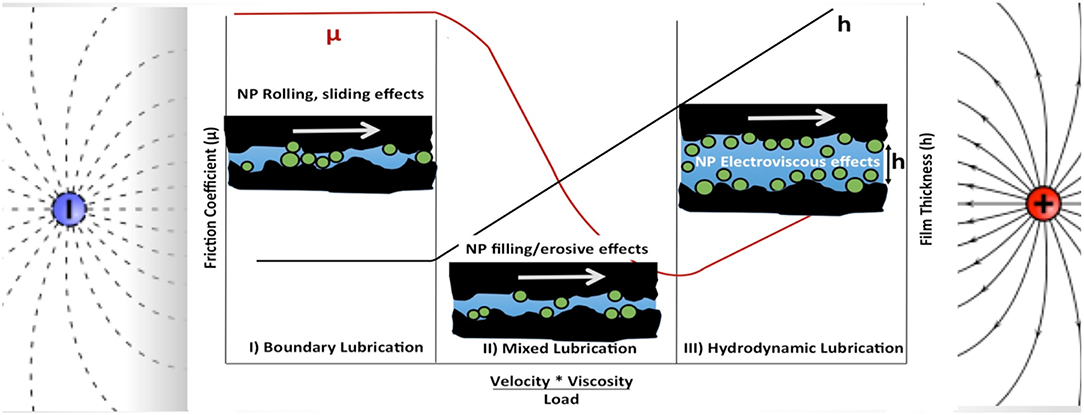
Figure 1. Schematic of a Stribeck curve for a lubricated contact in the presence of an external field. [Adapted from Curtis et al. (2017)], and licensed with permission from Creative Commons 4.0 (http://creativecommons.org/licenses/by/4.0) An applied field can be employed to tune the properties of the lubricant, to additives or nanoparticles within the lubricant, to boundary layers that form between the wall and the lubricant and/or to the solid-solid contacting asperities.
Active control of friction can be achieved by field-induced changes to lubricants, to lubricant additives, to boundary layers and/or to the contacting solids themselves. In this review, 25 examples of tuning of friction by means of an external electric or magnetic field are overviewed, with examples spanning atomic to macroscale systems. The goal is not to present a comprehensive list of all publications in this rapidly growing area, but rather to demonstrate the variety and versatility of approaches reported on in the literature. Examples are divided into 4 sections: (I) Field induced changes to bulk lubricants (Boulware et al., 2010a,b; Démery and Dean, 2010; De Vicente et al., 2011; Tusch et al., 2014; Ashtiani et al., 2015; Kabeel et al., 2015; Rodriguez-López et al., 2015; Vlachová et al., 2015; Zhao et al., 2017; Pardue et al., 2018; Acharya et al., 2019) (II) Field induced changes to solid contacts (Gabureac et al., 2004; Highland and Krim, 2006; Park et al., 2006, 2007; Socoliuc et al., 2006; Qi et al., 2008; Pierno et al., 2010; Kisiel et al., 2011; Krim et al., 2011; Altfeder and Krim, 2012; Benassi et al., 2014; Mao et al., 2017; Popov et al., 2017; Benad et al., 2018; Popov and Li, 2018; Rajauria et al., 2018; Wolloch et al., 2018); (III) Field induced changes to surface boundary layers (Zhu et al., 1994; Coffey and Krim, 2005; Ismail et al., 2009; Drummond, 2012; Wolter et al., 2012; Wei et al., 2013; de Wijn et al., 2014, 2016; Kreer, 2016; Zeng et al., 2017; Fredricks et al., 2019); and (IV) Ionic liquid systems (Wanless et al., 1994; Sweeney et al., 2012; Hausen et al., 2013; Fedorov and Kornyshev, 2014; Li et al., 2014; Fajardo et al., 2015; Kong et al., 2016; David et al., 2017; Zhou and Qu, 2017; Pilkington et al., 2018; Pivnic et al., 2018).
The majority of the examples presented here parameterize friction in terms of either the friction coefficient μ = Ff/N or shear stress τ = Ff/A, where A is the true are of contact between the opposing surfaces. Fluid viscosity and diffusion coefficients are also in some cases utilized as parameters to document friction levels. The latter quantity is closely linked to frictional drag forces of an object through that material. Friction coefficients are generally employed for cases of dry contact measurements performed in the boundary lubrication regime of lubricated contacts. In the hydrodynamic lubrication regime it is meanwhile more common to parameterize friction in terms of the shear stress, which for contacts separated by an average distance h, is linear in the velocity gradient as τ = Ff/A = ηv/h.
Experimental methods employed in the various examples include Atomic Force Microscopy (AFM), Surface Forces Apparatus (SFA), Quartz Crystal Microbalance (QCM), optical spectroscopies and wide range of tribometer systems comprised of macroscale, microscale and/or nanoscale components. In practice, magnetic fields are applied by either positioning samples directly within the interior regions of a solenoid or within the uniform field regions of Helmholtz coils, which consist of two electromagnets aligned on the same axis. Electric fields are meanwhile applied through direct application of a bias voltage across the sliding contacts, or alternatively by positioning working, counter, and quasireference electrodes close to the contacts. The experimental literature therefore generally reports magnetic fields in units of Tesla while electric field control of friction is generally reported in terms of potential difference in Volts applied at or near the contact.
Computational and theoretical methods employed analytic, finite element, and both equilibrium and non-equilbrium Monte Carlo approaches. External fields are modeled either by performing the study within a force field or by adjusting materials' properties to reflect the presence of an external field.
Section I. Field Induced Changes to Bulk Lubricants and Lubricant Additives
Example 1: Improved Tribological Performance of Magnetorheological Fluids Comprised of Magnetic Particles in Oil Associated With Nanodiamond Additives (Zhao et al., 2017)
Magnetorheological fluids are liquids whose viscosity increases significantly in the presence of an applied magnetic field (De Vicente et al., 2011; Ashtiani et al., 2015). In their most common form, they are comprised of magnetizable microparticles dispersed into a carrier fluid and held in suspension with the aid of stabilizing additives. When an external field is applied, the particles transform from random individual particles into chains aligned along the field direction and, within milliseconds, become semisolid materials. The transformation is fast, reversible and continuously adjustable. The actively controllable nature of the fluid, as well as it low energy consumption, has given rise to a wide range of applications in machinery manufacturing, auto parts, precision machining, aerospace, biomedical, and other applications. Magnetorheological brakes and tunable clutches are commonplace in automotive industry applications, where applying the field substantially increases the friction.
Despite widespread commercial availability, settlement of the particles, instabilities in the friction, and insufficiently high shear stresses remain problematic for some applications. Of these, a weak response to the applied field, as well as instabilities in the friction and shear stress levels are the greatest challenges that inhibit widespread and broader commercial use of these materials. To address these challenges, Zhao et al. (2017) performed a study of the impact of dispersing nanodiamonds on the performance of a conventional magnetorheological fluid. In particular, the researchers compared the shear stress and viscosity of fluids in fields ranging from 0 to 0.76 T in the presence and absence of 2% suspensions of 90 nm diameter nanodiamonds. The carrier fluid consisted of a 75% slurry of 2.75 μm carbonyl iron power Fe(CO)5 and stabilizers dispersed in a synthetic mineral oil carrier fluid. The external magnetic field was applied by positioning the sample within a solenoid coil.
In zero magnetic field, the nanodiamonds were reported to have no significant effects. However, when magnetic fields were applied, the nanodiamonds were reported to abrade the surfaces, enhancing the ability of the metallic particles to lock to the walls. This in turn increased the shear stress values by up to a factor of 5, from several hundred Pa in the absence of a field to nearly 105 Pa at the highest field strengths studied. The nanodiamonds were also reported to assist in preventing settlement of the magnetic particles. It was therefore concluded that nanodiamonds as additives provide a straightforward and low cost approach to improved settling stability along with significant improvements in shear strength. The results are depicted schematically in Figure 2.
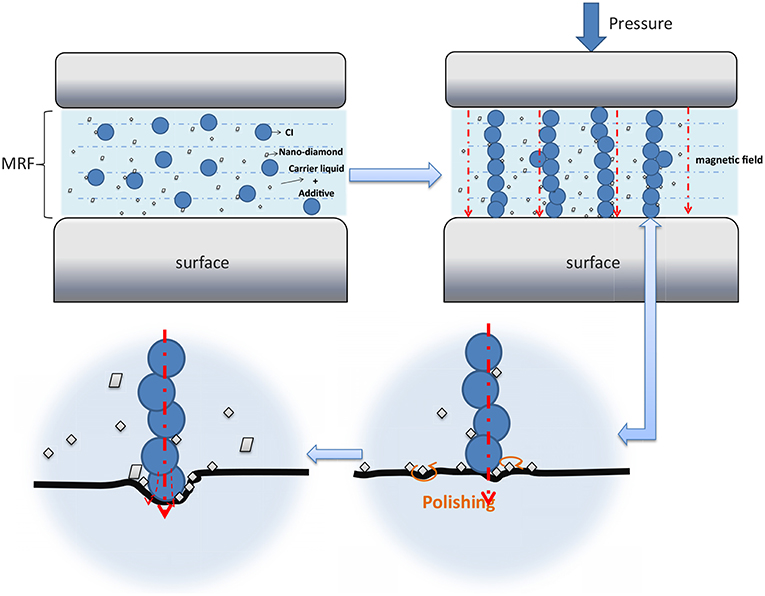
Figure 2. Schematic of the underlying mechanism explaining nanodiamond enhancement of magnetorheologial performance. Polishing mechanisms in the presence of the field enable higher wall friction levels, giving rise to higher shear strengths when the field is applied. Reprinted with permission from Zhao et al. (2017).
Example 2: Experimental Studies of Magnetic Field Dependent Friction for Two Particles in Water, Enabling an Analysis Method for Treating More Complex Systems (Tusch et al., 2014)
Fundamental studies of the underlying mechanisms of magentorheological fluids require a detailed understanding of the response of individual particles in the suspension to the applied magnetic field. Single particle treatments are relatively straightforward. However, they are insufficient to capture the more complex behavior of actual suspensions of many particles. Tusch et al. (2014) reported an experimental study of magnetic field manipulation of a two-particle system, along with an analysis that provides a simplified approach that is extendable to more complex systems. The study consisted of two 2.8 μm beads suspended in water in a periodic time dependent external magnetic field that varied between 0.15 and 0.45 mT. Diffusion coefficients of the particles, which are a measure of the hydrodynamic friction, were measured by analyzing the time response to the applied field. The analysis was performed within a framework of stochastic thermodynamics using a hydrodynamic model.
Two different estimation methods for the system's dissipation were performed. The first was referred to as “energy based” and was based on interaction potentials measured for the two particle system. The second was referred to as “information based” and relied exclusively on the positions and trajectories of the particles. The latter was obtained by video microscopy of projections of the Brownian motion of the two beads onto their container's bottom wall. The authors found the latter approach to be simpler to implement and also, and more importantly, of general applicability to more complex systems. The energy-based approach was found to be too cumbersome and/or or prohibitive difficulty to be extended to complex systems. Overall, the authors concluded that information-based estimates “are attractive since they are simple to implement and do not require any knowledge of the dynamics of the system, a definitive advantage for many experimental applications.” They also suggested that the approach could be useful for microrheology studies of biological systems and for analysis of small chemical or biochemical reactors.
Example 3: Liquid Oxygen as a Magnetorheological Fluid for Cryogenic and Space Applications and Mechanical Systems With no Moving Parts (Boulware et al., 2010a,b; Kabeel et al., 2015)
Commercial magnetorheological fluids, such as those reported on in Examples 1 and 2, perform well in many industrial applications. But they cannot be used in cryogenic applications where the carrier fluids are solid and the colloidal suspensions are immobile. Moreover, in space applications there are many components whose lifetime is limited by wear associated with moving parts in rubbing contact. This challenge is particularly inhibiting for applications such as satellites since testing on earth only approximates the extreme mechanical conditions during launch and the extreme environmental conditions in space. Repair after launch is generally not feasible. One proposed solution to this technical need is the development of liquid oxygen as working magnetorheological fluid. Unlike the vast majority of magenetorheological fluids, which freeze at cryogenic temperatures, oxygen remains liquid. Since it is already used extensively for life support systems and propellents in space systems, it is an ideal candidate for use as a magnetic fluid in such systems for magnetorheological purposes. Since liquid oxygen exhibits strong paramagnetic susceptibility, it can be used as the working fluid in a cryogenic magnetic fluid system designed so as to have no mechanically moving parts, and thus no wear.
Boulware et al. have reported a number of experimental and theoretical studies to develop a basic understanding of the dynamics of liquid oxygen subjected to external magnetic fields of up to 1.1T (Boulware et al., 2010a,b). Its paramagnetic susceptibility increases as temperature decreases associated with a reduction in thermal energy that allows polar molecules to more readily align with an externally applied magnetic field. Since it is a paramagnetic fluid, it is however far weaker than the common ferrofluids employed for room temperature applications. Theoretical treatments are however more straightforward from the point of view that the system is comprised of only one component.
The researchers performed both experimental and theoretical studies of the dynamics of a slug liquid oxygen within a solenoid when subjected to an external magnetic field. The dynamics were monitored by recording pressure changes in a closed volume on both sides of the slug as oxygen molecules, which are oblong in shape, reoriented in response to the applied field. The researchers modeled the system by incorporating viscous, magnetic, and pressure forces into an equation of motion. They next employed a one-dimensional discretized algorithm to solve coupled Navier-Stokes and Maxwell's equations for the equation of motion. Overall, their combined experimental and theoretical approach successfully established liquid oxygen as a viable candidate for a moving part free magnetorhological system in cryogenic applications.
Example 4: Colloidal Stability and Magnetic Field-Induced Ordering of Iron Particles in silicon Oil and Hydrocarbons Studied With a Quartz Crystal Microbalance (Rodriguez-López et al., 2015)
Real time monitoring of the rheological properties of a magnetorheological fluid are of particular importance for advancing both applied and fundamental knowledge. QCM is a technique that provides such real time measurements, yielding nanoscale results that have been routinely linked to macroscale friction coefficients (Vlachová et al., 2015; Pardue et al., 2018). Rodriguez-López et al. employed the technique for in situ and real time measurements of fluid shear stress as a function of applied magnetic fields ranging from 0 to 0.02T. The researchers studied silicon oil and hydrocarbon carrier fluids with 5 and 32% respective volume fractions of 5–10 μm iron microparticles, and were the first to successfully use a QCM for measures of shear stress in a magnetorheological slurry.
QCM studies were reported for both particle sedimentation under gravity and the impact of externally applied magnetic fields on the shifts of resonance frequency and dissipation factor. As expected, interactions among particles and also interactions between the iron particles and the resonator surface increased when magnetic fields were applied. The increase was attributed to increased contact stiffness between the particles and the surface. QCM data are also reflective of a lubricant's shear loss modulus G” and shear storage modulus G', providing a means for the researchers to compare the results with theoretical predictions of system behavior.
In particular, they performed a finite element modeling study examining both cases of free settling of particles and particle alignment under the action of the magnetic field. The modeling was performed by utilizing realistic materials values for the QCM, and high shear loss values for the viscous fluid (G” = 25 MPa). The particles were modeled as viscoelastic structures (G' = G” = 5 MPa for settling particles; G' = 50 MPa, G” = 5 MPa for the particles in a magnetic field) forming within the fluid and acting in combination with the fluid itself. The basic model was in agreement with the trends observed in the frequency and dissipation QCM data.
Example 5: Tuning Friction Through Electric Field Manipulation of Charged Silica and Alumina Nanoparticles in Aqueous Lubricant Suspensions (Acharya et al., 2019)
Magnetorheological fluids require at least one of the constituents of a lubricant to be magnetic, so as to response to an externally applied magnetic field. In an analogous fashion, electrically charged constituents of a lubricant will respond to externally applied electric fields. Nanoparticles in suspension are often electrically charged either intrinsically or by design. The study of their motion through active external control by electrical fields is rapidly growing, and active colloids are emerging as an area of widespread applications. In separate studies, nanoparticles have been demonstrated as lubricant additives capable of producing significant reductions or increases in the friction coefficients of the materials that they are added to.
Acharya et al. have recently reported the first use of active colloids for tuning friction at material-nanoparticle-liquid interfaces. Static, and also low frequency (0.6–50 mHz), electric fields of magnitude 100 N/C were applied to suspensions of either negatively charged TiO2 (40 nm diameter; −33 mV zeta potential) or positively charged Al2O3 (30 nm diameter; +61 mV zeta potential) nanoparticles suspended in water. The fields resulted in electrophoretic forces, which were employed to reposition the particles relative to a planar platinum surface of a quartz crystal microbalance, which was then used to monitor friction levels. Friction levels were reported in terms of the damping levels of the surrounding suspension on the oscillatory motion of the QCM electrode. The field was produced by biasing the sensing electrode of the QCM with respect to a grounded Pt electrode positioned nearby within the surrounding suspension. The authors report successful active electrotunable control of friction, and studied the response as a function of the applied field's frequency. Kinetic effects corresponding to nanoparticle repositioning at the interface were reported to occur at glasslike time scales and the studies also reported that nanoparticles manipulated by electric fields can act as “cantilever-free” atomic force probes capable of “tapping mode” exploration of interfacial properties in addition to being manipulated purely for the purpose of adjusting interfacial friction. In particular, features attributed to field-induced reorientation of water layers were identified in the friction data.
Example 6: Monte Carlo Simulation of Drag Forces in Classical Fields (Démery and Dean, 2010)
Démery and Dean (2010) performed Monte Carlo simulations of inclusions (point defects and or small objects that are otherwise recognizably distinct from the substance they are embedded in) moving at constant velocity in the presence of an external field. They found, as anticipated, that the defects experienced frictional drag forces that depended on both the field dynamics and how the inclusion coupled to the field. Changes in friction were manifested by changes in the diffusion constants of the inclusion moving within a surrounding material. The authors used their results to predict frictional drag levels exerted on the inclusions such as proteins in lipid membranes associated with protein interactions with membrane height and composition fluctuations. The forces on a point-like magnetic field moving within an Ising ferromagnet were also investigated, and were well-explained by these results. The theory is potentially applicable to soft materials such as those described in Example 5.
The authors argue that a rich phenomenology can arise from their relatively straightforward analysis because a wide range of field theories is available to describe soft materials. They also suggested directions for future investigations, including interacting fields, extensions to more realistic dynamics and possible experiments where their predictions could be tested. In particular, they suggested using optical tweezers to pull an inclusion, such as a colloid, through a binary fluid mixture close to the critical point.
Section II. Field Induced Changes to Solid Contacts.
Example 7: Control of Friction at an AFM Contact With a Semiconductor by Tuning Bias Levels and Charge Density Levels (Park et al., 2006, 2007; Qi et al., 2008)
Park et al. successfully controlled charge carrier densities to tune friction levels, utilizing semiconducting contacts, by applying external bias voltages to vary doping levels, and thus the mobile charge concentrations of the systems studied (Park et al., 2006, 2007; Qi et al., 2008) (Figure 3). In a first study, the researchers demonstrated electronic control of friction by employing a friction force microscope with a conductive titanium nitride coated tip in sliding contact with an oxygen passivated Si(100) wafer. The wafer was patterned with arrays of 2 μm-wide highly doped p-type strips with a period of 30 μm in a nearly intrinsic n-type substrate. Increased friction levels were observed only in the highly doped p regions and were observed to increase with tip-sample bias voltage, contact strain, and velocity. The increases friction levels could not be attributed to wear or surface damage.
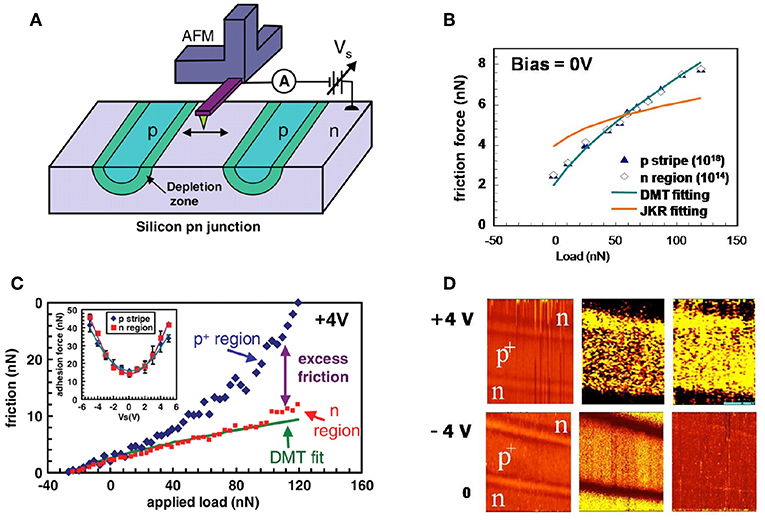
Figure 3. (A) Schematic of AFM measurements on a silicon pn junction device. (B) In the absence of an external bias voltage the friction force vs. load curve for p-type and n-type regions of the surface are indistinguishable. Application of positive (C) or negative (C,D) bias voltages allows the friction to be tuned. The excess friction in the presence of an external bias is attributed to static charge and triboelectric effects. Reprinted with permission from Park et al. (2006) (A,C); and Park et al. (2007).
The researchers also later investigated electronic contributions to friction at a semiconducting n-type GaAs surface covered by an approximately 1 nm thick oxide layer (Qi et al., 2008). The friction force microscope tip in this case had a 50 nm radius and was coated with Pt. Charge accumulation or depletion was induced by the application of forward or reverse bias voltages and substantial changes in friction levels were observed. The friction levels could be quantitatively explained by modeling the forces exerted by the trapped charges on the surfaces that were triboelectrically generated.
Example 8: Control of Friction Through Magnetic Levitation and Surface Charge Densities at a Contact Between a Magnetic AFM Tip and a Superconducting YBCO Sample (Altfeder and Krim, 2012)
As demonstrated by Example 7, and confirmed by recent theory (Wolloch et al., 2018), surface charge distributions are known to play a major and dominant role in friction and adhesion and can be are highly dynamic in nature in the presence of an external field. For insulating surfaces, tribo-generated static electricity moreover can be the dominant contribution to friction. An example of this is reported in Altfeder et al. who performed a magnetic probe microscopy study of levitation and atomic-scale friction for and Fe film coated AFM tip sliding on YBCO between 65 and 293 K. The study was therefore performed in a temperature range that passed through the superconducting transition temperature Tc = 92.5 K of the YBCO sample. The friction coefficient was observed to be constant at μk = 0.19 when the sample was in a superconducting state and exhibited no correlation with the strength of superconducting levitation forces. The friction coefficient abruptly began to increase with temperature as the sample passed into the normal phase, progressively increasing and nearly doubling, to μk = 0.33 at room temperature. The results were attributed to contact electrification and static electricity giving rise to increased friction levels in the non-superconducting phase, which for the sample studied was believed to be semiconducting in nature. As such, friction measurements provide a means to test theories of superconductivity that predict thin superconducting or semiconducting surface regions above Tc.
Example 9: Magnetic Field Dependence of Friction of Adsorbed Layers on Superconductors (Highland and Krim, 2006)
The density of charge carriers in a superconducting materials can be varied by applying an external magnetic field to the material so as to drive the material from a superconducting into a normal state.
Highland and Krim employed this approach to study sliding friction levels in nitrogen, water, and superheated helium films adsorbed on Pb(111) substrates with a quartz crystal microbalance by positioning the sample chamber within a solenoid coil and applying a weak magnetic field close to the superconducting transition to, respectively, drive the system in and out of the superconducting state. Reductions in friction upon entry into the superconducting state were reported to be larger for nitrogen than helium, consistent with theory based on polarizability of the adsorbed layers and were successfully interpreted in terms of conduction electron contributions to friction. The Highland and Krim studies were performed in conditions that suppressed competing mechanisms for friction, allowing electronic effects to be resolved. In general, however, such effects are quite small relative to alternate mechanisms (phononic, static electricity, etc.). Independent efforts to observe conduction electron friction have variously encountered high background levels of phonon friction which prevented them from being resolved (Pierno et al., 2010), or required non-contact conditions to minimize contributions from competing mechnisms (Kisiel et al., 2011).
In addition to reporting friction levels in the presence and absence of the external magnetic field, the researchers also observed that the repetitive cycling of an externally applied magnetic field in and of itself impacted friction levels as compared to measurements performed in static field conditions. This phenomenon remains unexplained, but is potentially attributed to either “noise” induced by abrupt changes in field (Examples 11, 12) and/or molecular film reorientations associated with the changing field (Examples 18,19).
Example 10: Tuning Friction Through Magnetic Field Induced Changes to Contact Geometry: Magnetostriction of Nanoscale Ni-Ni Contacts (Gabureac et al., 2004)
Gabureac et al. report studies of nickel nanocontacts in the presence of an applied magnetic field.
They observed significant changes in resistance depending on the angle between the applied field and the contact direction. The changes are consistent with modifications of the contact geometry induced by magnetostriction, which is a property of ferromagnetic materials whereby they change their shape or dimensions during the process of magnetization. The studies were performed at field strengths ranging from 0 to 1T for Ni-Ni nanocontacts in close proximity.
The authors point out that a small 100 μm diameter Ni magnet shrinks in the direction of magnetization by 5 nm, which is a very large effect when considering atomic scale nanocontacts. While they do not specifically report friction levels associated with the varying contact levels resulting from the applied magnetic fields, they point out that such effects are likely to be ubiquitous in systems employing externally applied fields, and must be accounted for to properly design and control mechanical systems via electronic methods.
They conclude by emphasizing the importance of magnetomechanical effects in measuring magnetoresistance in nanocontacts and argue that the effects are extremely difficult to avoid. This in turn impacts studies of the electrical resistance of nanocontacts. The same would therefore be applicable to nanoscale studies of the impact of magnetic fields on tribocontacts.
Example 11: Microscale Motion Control With Magnetic Fields Applied to Ferromagnetic Films (Benassi et al., 2014)
Benassi et al. report a theoretical study of actuation and control that is applicable to motion and friction control in micromechanical systems. The work is motivated by the fact that recent progress in friction reduction associated with lowering commensurability of contacting crystal lattices lacks versatility in terms of modifying and/or controlling friction. To circumvent this lack of versatility, they propose to tune the material properties with external control parameters, and note that the example of an external field applied to an ionic liquid is a promising example of such control.
In particular, they propose a non-contact motion control technique based on the introduction of a tunable magnetic interaction. As a specific example, they suggest coating two non-contacting bodies with ferromagnetic films.
The researchers demonstrate that wear-free motion control in these systems can be achieved by means of interacting magnetic domains arising at the surface below the Curie temperature. Their hypothesis is that the size, shape, and ordering of such domains is easily controlled with an external magnetic field, allowing a flexible and reversible means to tune system tribological properties. Given that typical domain sizes are on the order of nm to tens of μm, the approach is well-suited for integration into micron scale devices, and the domain behavior could be tailored through proper design and preparation of the ferromagnetic coatings, external magnetic fields and the distance between the plates.
Example 12: Electrostatically Tunable Adhesion Via Oscillation Induced Reductions in Contact Hysteresis at a Head-Disk Interface (Rajauria et al., 2018)
Rajauria et al. have recently studied the impact of vibrations induced by an external field on a high speed sliding interface, namely a recording head-disk contact moving in close proximitry at high speeds on the order of 5–40 m/s. Contact hysteresis between sliding interfaces is a common phenomenon that has a major impact on the tribological performance of a head-disk system. The majority of studies of contact hysteresis have been performed with AFM at very slow speeds on the order of μm/s. Additional methods that perform measurements at higher speed are therefore of interest.
The researchers employed commercially available hard disk drives to perform the studies. Such systems are of particular interest, since the sliding speeds are high, while the gap sizes between the contacts are of nm extent. The primary result was to demonstrate that out-of-plane oscillations induced by AC voltages applied between the head and the disk are able to completely suppress contact hysteresis, and thus tune the friction and adhesion levels. They noted that this is a dynamic effect associated with the time for contacts to grow and adhere, since the electrostatic force arising from the applied DC or AC voltage is attractive.
It should also be noted here that a large number of studies have examined active control of friction through externally applied vibrations (Socoliuc et al., 2006; Krim et al., 2011; Mao et al., 2017; Popov et al., 2017; Benad et al., 2018; Popov and Li, 2018), and in many cases the vibrations wree induced by electromagnetic fields (Socoliuc et al., 2006; Krim et al., 2011). The two approaches to tuning friction therefore have some overlap.
Section III. Field Induced Changes to Surface Boundary Layers
Example 13: Influence of Electrochemical Potentials on the Friction and Wear of Iron and Iron Oxides in Aqueous Systems. A Microscopic Study of Macroscale Rubbing Contacts (Zhu et al., 1994)
Bias potential dependence of friction is a common phenomenon in the literature for rubbing contacts that contain iron, particularly in the presence of water. In a 1994 study, Zhu et al. explored the chemical nature of the boundary layer films that form under such conditions, which in turn have a strong impact on friction levels. They studied the influence of electrochemical potentials on both friction and wear, for iron/iron, and iron oxide/alumina oxide rubbing contacts that were lubricated with aqueous fluids. They employed impedance spectroscopy and Fourier transform infrared micro spectroscopy to explore friction and wear of the rubbing contacts in well-defined conditions as a function of the applied bias voltage. The researchers measured friction coefficients with a macroscale tribometer comprised of a reciprocating hemispherical pin with stroke length 0.3 mm at a frequency of 10 Hz. The pin was pressed into contact with a flat surface that was fully immersed in a cell filled with an aqueous electrolyte employed as the lubricant. The pin and flat were both connected to an external potentiostat and otherwise electrically grounded. A reference electrode and Pt counterelectrode were also immersed in the cell within close proximity to the contact, to facilitate potential control in cases where both the pin and flat were conducting.
The researchers concluded that the observed changes in friction and wear were attributable to two primary mechanisms: (1) Changes in electrostatic repulsion associated with changes to the double layer charge and (2) surface redox reactions. They also modeled the electric double layer effect and found a significant dependence of the friction coefficient on surface bias potential for ratios of the applied contact pressure to inter-surface pressure falling below an approximate factor of 10. In addition, they also observed that the decreased friction levels at positive electrode potentials were attributable to the formation of FeOOH on the metal surfaces. Positive electrode potentials also produced iron (II) carboxylate on the surfaces when octanoic acid was present, causing a significant reduction in friction.
Example 14: Switching on a Lubricant at Sliding Contact Lubricated by Aqueous Solutions: A Pin on Disc Study (Ismail et al., 2009)
Ismail et al. (2009) reviewed the bias voltage dependence of a number of macroscale systems comprised of steel contacts lubricated by water, and found a general trend for systems containing octanoate. In particular, friction coefficients were collectively reported to drop from approximately 0.4 to 0.15 for bias voltages, respectively, tuned between −1.0 and +1.0 V.
The authors then reported their own investigation of alkaline aqueous-based solutions, employing a macroscale pin-on-disk setup with a bias voltage that spanned ±1V. They observed that friction was reduced in octanoate solutions under negative electrochemical bias due to a production of a low friction tribochemical layer (iron octanoate). They noted the usefulness for industrial applications of mastering the capability of switching friction between two known values by varying the bias voltage, namely high and low values for cathodic and anodic potentials. They also reported that the tribochemical layer reduced wear of both pin and disk and that in general NaOH tests yielded much higher friction coefficients and more corrosion for the same applied potentials.
Example 15: Tuning Macroscale Friction Employing Polyelectrolyte Brushes and Fluid Counterions (Wei et al., 2013)
Some of the lowest known friction coefficients, μ < 0.001, occur in aqueous systems at biological interfaces. These include the vitreous body of eyes and synovial joints such as hip, knees, and fingers. The exceptional tribological performance of such systems is associated with the presence of phospholipids, hyaluronan, lubricins, and bottle-brush-like glycoproteins in synovial fluids. Hyalluronan and glycoproteins are biopolyelectrolytes whose side chains contain large amounts of sulfonic and carboxylic groups. The charged nature of these biomacromolecules and their brush-like structures are thought to underlie their superior lubricating properties (Kreer, 2016). In particular, they respond to electrostatic interactions via swelling–collapse transitions of end-tethered polymer chains and osmotic pressures within the brushes. Polyelectrolyte brushes are fully stretched when they are immersed in pure water, allowing water molecules to fully penetrate them. But when they are immersed in an electrolyte solution, strong electrostatic screening occurs causing the water to be expelled and the brushes to collapse (Figure 4) The various configurations are associated with significantly different friction levels, and have been the topic of much interest in the nanotribology community.
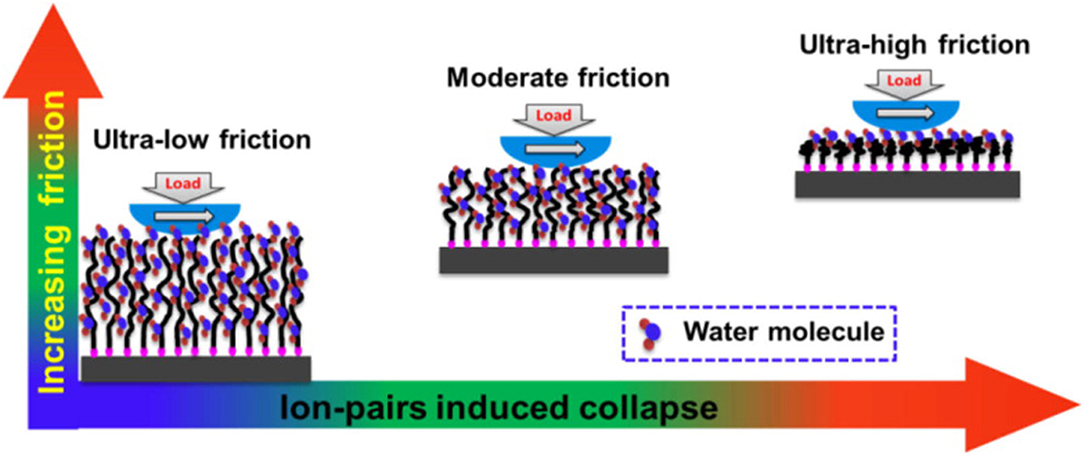
Figure 4. Schematic of the dependence of friction on the stretching of polyelctrolyte brushes. Reprinted with permission from Wei et al. (2013). Copyright 2013 American Chemical Society. Externally applied fields and/or changes in the electrolyte counterions or pH can modify the brush configuration because the brushes are electrically charged. Water molecules fully penetrate the brushes when they are fully stretched and friction coefficients are ultra-low, of order μ = 10−3. Water molecules are completely expelled from the brushes when they are fully compressed and friction levels are high, of order μ = 1.
Wei et al. for example reported significant tuning of friction levels in polymer brushes linked to swelling and collapse of the polymers (Wei et al., 2013). Friction coefficients were measured in macroscale setups, employing a pin-on-disk configuration (Figure 4). The pin, which was not coated with a polymer brush, was prepared from a commercial silicon elastomer kit mixture poured into a mold to produce an elastomeric poly-(dimethylsiloxane) (PDMS) hemisphere. The disks were comprised of silicon and were prepared with surface treatments that initiated growth and attachment of the polyelectrolyte brushes. The conformation of the brushes was characterized by both AFM and measurements with a QCM positions in situ to monitor liquid dynamic response. Superior lubrication with friction coefficients μ < 0.001 was associated with the fully extended swollen polymers, while completely collapsed configurations exhibited high friction coefficients close to μ = 1. Intermediate configurations with intermediate friction coefficients were also achieved for partially collapsed configurations.
The authors achieved the dramatic range of friction levels by exchanging counterions in the surrounding liquid, which tuned the system's electrochemical properties. For the case of cationic brushes with quaternary ammonium groups, they successfully tuned friction coefficients in a progressive manner between approximately 0.001 and 1 by exchanging the counterions in the surrounding liquid progressively in series, as Cl− < ClO < PF < TFSI−. For the case of anionic brushes they achieved tuning of the friction levels by employing oppositely charged surfactants (tetraalkylammonium) with varying hydrophobic tail lengths, multivalent metal ions, and protons. The increases in friction observed for cationic brushes were successfully explained to result from a collapse configuration induced by ion-pairing interactions. The increases in friction observed for anionic brushes were linked to the length of hydrophobic tails of surfactants, and the associated hydrophobicity induced by electrostatic interactions between the surfactants and polymer chains.
Example 16: Surface Forces Apparatus Study of Electric Field Induced Reductions to Friction in Polyelectrolyte Coatings (Drummond, 2012)
Drummond reported in 2012 a careful investigation of the impact of an external electric field applied to polymer brush materials attached to both contacts in a crossed-mica surface configuration of a Surface Forces Apparatus (Drummond, 2012). Drummond hypothesized that external electric fields would produce far more rapid changes in molecular configuration than methods that alter the properties of the surrounding electrolyte solution, for example the counterion exchange method described in Example 15. Drummond further hypothesized that coating both surfaces with a polyelctrolyte brush could result in lower friction levels than coating just one surface.
Samples were prepared by attaching polymer brushed to the surfaces of atomically uniform cleaved mica substrates. In particular, the mica surfaces were coated by self-assembly of amphiphilic diblock polystyrene-polyacrylic acid co- polymers (PS36 -b-PAA125) from aqueous solution at pH 10, and both atomic force microscopy and quartz crystal microbalance methods were employed to monitor the degree of adsorption and structure. The mica surfaces themselves were curved and attached to the front surfaces of the two crossed cylinder silica disks pressed into sliding contact by a SFA. The posterior surfaces of such disks are commonly coated with silver films in a SFA, allowing a means to apply a bias voltage across the sliding contacts.
Drummond applied AC electric fields by applying bias voltages in the form of square waves with frequencies ranging between 200 and 1,000 Hz and amplitudes of up to 20 V peak to peak. The intensity of the applied field was proposed to determine the degree of interpenetration between polymer brushes in contact, and explored the speed of the dynamical responses of the polymer by examining the friction reduction vs. applied frequency. Friction levels were observed to drop by several orders of magnitude, to below the detection level of the instrument, when fields were applied. The response was fast and reversible for externally applied fields up to 450 Hz, and the electrically extended brushed were observed to resist collapse under application of a normal load.
Example 17: A Reversibly Electrocontrollable Polymer Brush for Electroswitchable Friction (Zeng et al., 2017)
Zeng et al. (2017), reported success at developing electrically switchable friction, defined as friction that can be reversibly manipulated by an external electric field,via an electro-controllable polymer branched brush. They grafted the electro-controllable polymer branched brush, poly-sodium allyloxy hydroxypropyl sulfonate (poly-AHPS), onto an electrically conductive indium tin oxide (ITO) glass, and observed two friction states: (1) stretched polymer brush arrays when negatively charged and (2) rolled polymer knolls when positively charged and two substantially different friction levels. The range of the change in friction, although modest, could be tuned by sandwiching polar, or non-polar molecules between the brushes. The authors proposed that the systems is useful for automatic control of friction, and could find wide application in automatization, intelligent manipulation and actuators, and micro-electro-mechanical systems.
Example 18: Theoretical Model of Electrochemical Control of Nanoscopic Friction and Effects of Molecule Anchoring (de Wijn et al., 2014, 2016)
The majority of published studies of electrotuning of friction are experimental in nature, and there is a great need for detailed theoretical understanding of the mechanisms. In one such study, de Wijn et al. reported a theoretical model of nanoscopic friction under electrochemical conditions that models an AFM tip sliding along an adsorbed layers of polar molecules. The system is representative of systems such as water on platinum, where electric fields control the orientation of the molecules with respect to the substrate (see also Example 5, where flipping of water by an external field is observed to impact friction levels.). They concluded that the dependence of the friction force on the electric field was determined by the interplay of two dissipative mechanisms (1) the rotation of the dipoles and (2) slipping motion of the tip over potential barriers presented by the molecular surface. They moreover developed a strategy for custom design of how friction depends on the external field. The strategy was based on the competition between long-range electrostatic interactions and short-range chemical interactions that are present between the polar molecules adsorbed on the surface and the AFM tip.
In a follow-up publication they explored the effects of anchoring the molecules, and how it impacts friction levels near bias voltages that are sufficiently large to cause them to reorient, employing the same strategy involving the long-range electrostatic interactions and short-range chemical interactions. The authors also derived a dispersion relation for phononic vibrations of the surface molecules and showed how it could be used to understand important features of the frictional response. Both molecules that rotate about their center of mass and molecules anchored on one side were considered. As might be expected, the variation of friction with external electrical fields was strongly influenced by how the adsorbed molecules were anchored to the surface. The work thus revealed unique theoretical insights into how molecular anchoring can be used for custom design of electrolyte-based lubricants with specific responses to external electric fields.
Example 19: Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules (Fredricks et al., 2019)
In a manner analogous to polar surface molecules being reoriented by an external field, magnetic molecular adlayers can be reoriented by an external magnetic field. Fredricks et al. employed a QCM to study sliding friction levels of thin (1–2 monolayers) and thick (~10 monolayers) oxygen films adsorbed on nickel and gold at 47.5 K. The magnetic fields were applied by positioning the sample chamber and its surrounding within the uniform field regions of Helmholtz coils. The measurements were performed at a temperature close to that where oxygen adlayers lying flat on the surface are readily reoriented to a more compressed and upright position. Weak fields, in combination with the ferromagnetic nature of nickel, are therefore sufficient to reorient the adlayers. As is the case for Example 18, changes in orientation and corrugation are known to have a great impact on phononic friction levels (Coffey and Krim, 2005; Krim, 2012). Friction levels are therefore tuned in association with reorientation of the molecules.
The researchers observed experimentally that friction levels for the thin (thick) films in the presence of a weak magnetic field were observed to be approximately 30% (50%) lower than those recorded in the absence of the external field for films adsorbed on nickel, but increased for adsorbed layers on gold. Magnetically induced structural reorientation (magnetostriction) and/or realignment of adlayer spins, which, respectively, reduced structural phononic mechanisms and magnetic interfacial corrugation and commensurability, were suggested as the most likely mechanisms underlying the observed field-induced reductions in friction. The work demonstrated the role of magnetic effects in a model system that is highly amenable to future theoretical studies (Wolter et al., 2012).
Section IV. Ionic Liquid Systems
In 2008, when Glavatskih and Höglund first suggested the expression “tribotronics,” (Glavatskih and Höglund, 2008) they envisioned one approach to active control of friction could be through the possible use of electrorheological fluids. Electrical bias of the surfaces in tribological contact lubricated by polar liquids would in this case allow the composition, structure and boundary film formation attributes to be varied. Ideally this would be performed in a tunable and reversible manner. Experiments performed under electrochemical conditions using molten salts or electrolyte solutions constitute physical realizations of this approach (Figure 5). Ionic liquids are molten salts whose melting points below room temperature (Fedorov and Kornyshev, 2014). Their low melting points are the results of weak electrostatic interactions between the ions, which also hinders their ordering into a crystalline solid lattice. Weakened electrostatic forces are achieved by incorporating at least one large and organic ionic species, which increases the distance between neighboring charged centers. Studies of IL's as lubricants have been rapidly increasing in recent years. This section presents a selection of results from the current literature.
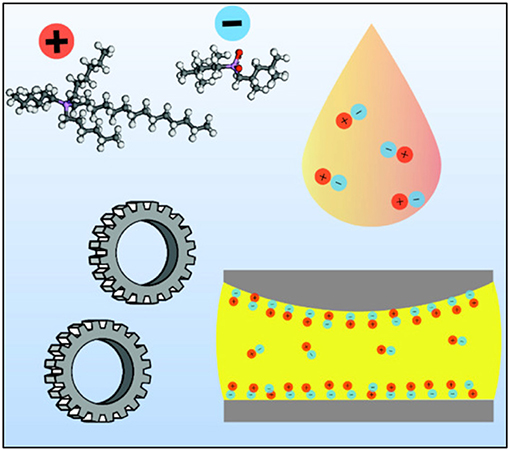
Figure 5. Schematic of ionic liquid as a lubricant additive. Externally applied electric fields reposition the charged constituents within the confines of a contact. Reprinted with permission from Zhou and Qu (2017).
Example 20: Ball on Disk Studies of Ionic Liquid Lubrication at Electrified Interfaces (Kong et al., 2016)
Kong et al. (2016) have reported on the tribological performance of ionic liquids at electrified interfaces with a macroscale stainless steel ball on stainless steel disk reciprocating tribometer. They varied the bias voltage from 0 to 10V, and measured friction coefficients as a function of the applied bias. Three ionic liquids were studied: 1-Ethyl-3-methylimidazolium tetrafluoroborate ([C2MIM][BF4]), 1-Butyl-3-methylimidazolium tetrafluoroborate ([C4MIM][BF4]), and 1-Hexyl-3-methylim- idazolium tetrafluoroborate ([C6MIM][BF4]) (Purity: 99%). These were characterized by a fixed anionic structure and cationic backbone with different alkyl side chain lengths.
They observed the friction coefficient to increase by almost a factor of two under the applied bias voltage, from about 0.08 to 0.014 for the shortest side chain length studied. The effect was less pronounced for the longer chain lengths. They attributed the difference in response to either the greater flexibility of the longer side chains or possibly differences in electrical conductivity. The latter could potentially impact the strength of the response to the applied field.
Example 21: Control of Nanoscale Friction on Gold Surfaces in Ionic Liquids and Electrolytes via Electric Potential-Induced Changes to the Surface Chemistry, Structure, and/or Lubricant Layers (Wanless et al., 1994; Sweeney et al., 2012; Hausen et al., 2013)
Sweeney et al. and also Hausen et al. have measured friction coefficients for nanoscale contacts on gold surfaces in an AFM lubricated by an ionic liquid or electrolyte under an applied bias voltage (Sweeney et al., 2012; Hausen et al., 2013). The AFM instruments in these studies employed tips and contacts that were immersed directly in a surrounding liquid, and electric fields were applied to the contacts by positioning working, counter and quasireference electrodes close to the contacts (Wanless et al., 1994). While both groups studied gold surfaces, Hausen et al. focused on changes to the surface structure and chemistry of the gold surface as well as changes to the electrolyte induced by the external field. Sweeney et al. focused on how changes to an ionic liquid surrounding the contact impacted friction levels.
Hausen et al. utilized a Au(100) surface and a silicon AFM tip immersed in perchloric acid. and the potential was varied between 0 and +1.45 V. Reversible surface oxidation occurs at 1.2V, with a corresponding increase in friction coefficient. The researchers also succeeded to reversibly induce surface reconstruction and oxidation by varying the bias between −0.12V and +0.5V for contacts immersed in 0.05 M H2SO4. The friction coefficients in the latter study varied between 0.02 and 0.04, respectively for the reconstructed and oxidized surfaces.
Sweeney et al. studied an ionic liquid system consisted of 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl) trifluorophosphate (1/2Py1;4_FAP) confined between silica colloid probes or sharp silica tips and a Au(111) substrate (Sweeney et al., 2012). The bias voltage was varied between −2 and+1.5V, and friction coefficients varied, respectively, in the range of approximately 0.15 to 0.7. The researchers explained the results as evidence for the confined ion layer between the two surfaces changing from cation-enriched (at negative potentials) to anion-enriched (at positive potentials) when the bias was varied. Tuning frictional forces reversibly at the molecular level was therefore achieved without changing the substrates and employing a self-replenishing boundary lubricant of low vapor pressure.
Example 22: AFM and Neutron Reflectance Studies of an Ionic Liquid Lubricant Enabling Superlubricity to be Switched on and off in situ Using an Electrical Potential (Li et al., 2014; Pilkington et al., 2018)
Li et al. (2014) have reported on the tribological performance of ionic liquid lubrication of a silica tip sliding on a graphite surface, and report friction coefficients falling below 0.01 in the low friction state (Li et al., 2014).
The researchers applied a +1.5 V potential to the graphite surface, which changed the ion composition of the boundary layer and thus the lubricity. At positive potentials, when the interfacial ion layer was anion rich, and the friction fell below the detection limits of the instrument, thus the term superlubricity. The ionic liquid used for these studies was 1-hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate ([HMIm] FAP), a material that is chemically stable to both air and water. Later studies by (Pilkington et al., 2018) have directly detected the response of ionic liquids to applied fields by means of a neutron reflectance technique (Pilkington et al., 2018).
Example 23: Molecular Dynamics Simulations of Friction Force Microscopy of Ionic Liquid Lubricated Contacts (Fajardo et al., 2015; Pivnic et al., 2018)
Fajardo et al. employed molecular dynamics simulations and a coarse-grained model of ionic liquids, to study mechanisms of electrotunable friction for ionic liquids confined between planar substrates. Their model employed parameters to simulate the ionic liquid 1-butyl-3-methylimidazo- lium hexafluoro phosphate, BMIM+PF6– confined between mica surfaces. Their modeling effort focussed on the shape and the intramolecular charge distribution of the ions, and how it impacted frictional drag forces. As expected, externally applied electric fields were found to induce significant structural changes in the film, which in turn gave rise to modification of friction forces.
A major conclusion of the study was the authors' finding that although only a specific system was modeled, the results were applicable to a wide range of ionic system lubricants. In particular, they found that an electric-field-induced shift of the slippage plane from the solid–liquid interface to the interior of the film was common. Quoting their summary, two generic trends were in evidence: (Fajardo et al., 2015)
(1). “The friction force reaches a maximum as a function of surface charge. This maximum corresponds to the charge at which the slippage plane shifts one layer away from the solid– liquid interface to the boundary between the counterion- and co-ion-rich layers.”
(2). “The nanoscale film will exhibit the electrostriction/ electroswelling effect, which will be asymmetric with respect to the sign of the surface charge, as long as the cations and anions have different molecular shapes, chemical structures, and intramolecular charge distributions.”
Pivnic et al. (2018) also employed molecular dynamics simulations and a course-grained model to examine a tip-substrate geometry lubricated by one layer of an ionic liquid (Pivnic et al., 2018). Their work revealed the dependence of the friction force on the electrode surface charge density to be dependent on the motion of the confined liquid relative to the substrate and tip. This in turn was found to be dependent on two primary factors: (1) the strengths of the ion–substrate and ion–tip interactions, and (2) the degree of commensurability between characteristic ion dimensions and that of the substrate and tip surface lattices.
Example 24: Impact of Surface Roughness on Ionic Lubricant Tribological Performance (David et al., 2017)
David et al. (2017) studied the impact of surface roughness on electrotuning by means of ionic liquids, noting that most prior studies examined atomically smooth surfaces while in practice most contacting surfaces were rough. Their studies were performed by means of non-equilibrium molecular dynamics for a range of increasingly rough surfaces. Surface roughness was introduced in the form of a periodic array of parallel troughs with rectangular cross sections. The dimensions of the troughs were varied in order to change the degree of roughness.
The researchers found friction to depend on both the direction of shear (parallel or perpendicular to the troughs) as well as the roughness, and increased with roughness for the specific systems studied. The friction force was observed to display a maximum at a specific surface charge density. Strengthening of the substrate–liquid dispersion interactions acted to shift this maximum toward lower surface charge levels. The authors also noted that surface roughness has also been reported in the literature to decrease friction in systems that exhibit roughness profiles distinct from that which they modeled. The sensitive dependence on roughness therefore presents both a challenge and opportunity for custom atomic scale design of ionic lubricant systems.
Example 25: Ionic Liquids as Lubricant Additives: A Review (Zhou and Qu, 2017)
The majority of studies of ionic liquids as lubricants have studied pure (neat) fluids or as base fluids for lubricants. The lubricating features nonetheless have been commonly attributed to boundary layer formation of adlayers whose structures are controlled by the external field. The use of ionic fluids as an additive is increasingly growing as an area of research since a breakthrough in achieving miscibility in non-polar hydrocarbon oils was achieved in the past few years. Small quantities of ionic liquids added to a base fluid appear to be equally effective as lubrication by the pure ionic liquid. Zhou and Qu (2017) provide a review of how ionic liquids have recently been used as additives, including an effort to correlate lubricity with cationic and anionic structures, oil-solubility, and other relevant physicochemical properties.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by National Science Foundation Award Number DMR1535082.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Acharya, B., Seed, C. M., Brenner, D. W., Smirnov, A. I., and Krim, J. (2019). Tuning friction at material-nanoparticle-liquid interfaces with an external electric field. arXiv:1901.10512.
Altfeder, I., and Krim, J. (2012). Temperature dependence of nanoscale friction for Fe on YBCO. J. Appl. Phys. 111:094916. doi: 10.1063/1.4717983
Ashtiani, M., Hashemabadi, S. H., and Ghaffari, A. (2015). A review on the magnetorheological fluid preparation and stabilization. J. Mag. Mag. Mater. 374, 716–730. doi: 10.1016/j.jmmm.2014.09.020
Benad, J., Nakano, K., Popov, V. L., and Popov, M. (2018). Active control of friction by transverse oscillations. Friction. 7, 74–85 doi: 10.1007/s40544-018-0202-1
Benassi, A., Schwenk, J., Marioni, M. A., Hug, H. J., and Passerone, D. (2014). Microscale motion control through ferromagnetic films. Adv. Mater. Interfaces 1:1400023. doi: 10.1002/admi.201400023
Berman, D., Erdemir, A., and Sumant, A. V. (2018). Approaches for achieving superlubricity in two-dimensional materials. ACS Nano 12, 2122–2137. doi: 10.1021/acsnano.7b09046
Boulware, J. C., Ban, H., Jensen, S., and Wassom, S. (2010a). Experimental studies of the pressures generated by a liquid oxygen slug in a magnetic field. J. Mag. Mag. Mater. 322, 1752–1757. doi: 10.1016/j.jmmm.2009.12.022
Boulware, J. C., Wassom, S., Jensen, S., and Ban, H. (2010b). “The magnetohydrodynamic response of liquid oxygen: experimentation and simulation,” in AIP Conference Proceedings (Tuscon, AZ), 1554–1561. doi: 10.1063/1.3422336
Coffey, T., and Krim, J. (2005). Impact of substrate corrugation on the sliding friction levels of adsorbed films. Phys. Rev. Lett. 95:076101. doi: 10.1103/PhysRevLett.95.076101
Curtis, C. K., Marek, A., Smirnov, A. I., and Krim, J. (2017). A comparative study of the nanoscale and macroscale tribological attributes of alumina and stainless steel surfaces immersed in aqueous suspensions of positively or negatively charged nanodiamonds. Beilstein J. Nanotechnol. 8, 2045–2059. doi: 10.3762/bjnano.8.205
David, A., Fajardo, O. Y., Kornyshev, A. A., Urbakh, M., and Bresme, F. (2017). Electrotunable lubricity with ionic liquids: the influence of nanoscale roughness. Faraday Discuss. 199, 279–297. doi: 10.1039/C6FD00244G
De Vicente, J., Klingenberg, D. J., and Hidalgo-Alvarez, R. (2011). Magnetorheological fluids: a review. Soft Matt. 7, 3701–3710. doi: 10.1039/c0sm01221a
de Wijn, A. S., Fasolino, A., Filippov, A. E., and Urbakh, M. (2014). Nanoscopic friction under electrochemical control. Phys. Rev. Lett. 112:055502. doi: 10.1103/PhysRevLett.112.055502
de Wijn, A. S., Fasolino, A., Filippov, A. E., and Urbakh, M. (2016). Effects of molecule anchoring and dispersion on nanoscopic friction under electrochemical control. J. Phys. 112:055502. doi: 10.1088/0953-8984/28/10/105001.
Démery, V., and Dean, D. S. (2010). Drag forces in classical fields. Phys. Rev. Lett. 104:080601. doi: 10.1103/PhysRevLett.104.080601
Drummond, C. (2012). Electric-field-induced friction reduction and control. Phys. Rev. Lett. 109:154302. doi: 10.1103/PhysRevLett.109.154302
Fajardo, O. Y., Bresme, F., Kornyshev, A. A., and Urbakh, M. (2015). Electrotunable friction with ionic liquid lubricants: how important is the molecular structure of the ions?. J. Phys. Chem. Lett. 6:3998–4004. doi: 10.1021/acs.jpclett.5b01802
Fedorov, M. V., and Kornyshev, A. A. (2014). Ionic liquids at electrified interfaces. Chem. Rev. 114, 2978–3036. doi: 10.1021/cr400374x
Fredricks, Z. B., Stevens, K. M., Kenny, S., Acharya, B., and Krim, J. (2019). Tuning nanoscale friction by applying weak magnetic fields to reorient adsorbed oxygen molecules. Condensed Matt. 4:1. doi: 10.3390/condmat4010001
Gabureac, M., Viret, M., Ott, F., and Fermon, C. (2004). Magnetoresistance in nanocontacts induced by magnetostrictive effects. Phys. Rev. B. 69:100401. doi: 10.1103/PhysRevB.69.100401
Glavatskih, S., and Höglund, E. (2008). Tribotronics—towards active tribology. Tribol. Int. 41, 934–939. doi: 10.1016/j.triboint.2007.03.001
Hausen, F., Zimmet, J. A., and Bennewitz, R. (2013). Surface structures and frictional properties of Au (100) in an electrochemical environment. Surface Sci. 607, 20–24. doi: 10.1016/j.susc.2012.08.009
Highland, M., and Krim, J. (2006). Superconductivity dependent friction of water, nitrogen, and superheated He films adsorbed on Pb (111). Phys. Rev. Lett. 96:226107. doi: 10.1103/PhysRevLett.96.226107
Ismail, M. N., Harvey, T. J., Wharton, J. A., Wood, R. J., and Humphreys, A. (2009). Surface potential effects on friction and abrasion of sliding contacts lubricated by aqueous solutions. Wear 267, 1978–1986. doi: 10.1016/j.wear.2009.06.007tt
Kabeel, A. E., El-Said, E. M., and Dafea, S. A. (2015). A review of magnetic field effects on flow and heat transfer in liquids: present status and future potential for studies and applications. Renew. Sustain. Energy Rev. 45:830–837. doi: 10.1016/j.rser.2015.02.029
Kisiel, M., Gnecco, E., Gysin, U., Marot, L., Rast, S., and Meyer, E. (2011). Suppression of electronic friction on Nb films in the superconducting state. Nat. Mater. 10:119. doi: 10.1038/nmat2936
Kong, L., Huang, W., and Wang, X. (2016). Ionic liquid lubrication at electrified interfaces. J. Phys. 49:225301. doi: 10.1088/0022-3727/49/22/225301
Kreer, T. (2016). Polymer-brush lubrication: a review of recent theoretical advances. Soft Matt. 12, 3479–3501. doi: 10.1039/C5SM02919H
Krim, J. (2012). Friction and energy dissipation mechanisms in adsorbed molecules and molecularly thin films. Adv. Phys. 61, 155–323. doi: 10.1080/00018732.2012.70640
Krim, J., Yu, P., and Behringer, R. P. (2011). Stick–slip and the transition to steady sliding in a 2d granular medium and a fixed particle lattice. Pure Appl. Geophys. 168:2259–2275. doi: 10.1007/s00024-011-0364-5
Li, H., Wood, R. J., Rutland, M. W., and Atkin, R. (2014). An ionic liquid lubricant enables superlubricity to be “switched on” in situ using an electrical potential. Chem. Commun. 50, 4368–4370. doi: 10.1039/c4cc00979g
Lu, X., Khonsari, M. M., and Gelinck, E. R. (2006). The Stribeck curve: experimental results and theoretical prediction. J. Tribol. 128, 789–794. doi: 10.1115/1.2345406
Mao, X., Popov, V. L., Starcevic, J., and Popov, M. (2017). Reduction of friction by normal oscillations. II. In-plane system dynamics. Friction 5, 194–206. doi: 10.1007/s40544-017-0146-x
Müser, M. H., Wenning, L., and Robbins, M. O. (2001). Simple microscopic theory of amontons's laws for static friction. Phys. Rev. Lett. 86:1295. doi: 10.1103/PhysRevLett.86.1295
Pardue, T. N., Acharya, B., Curtis, C. K., and Krim, J. (2018). A tribological study of γ-Fe 2 O 3 nanoparticles in aqueous suspension. Tribol. Lett. 66:130. doi: 10.1007/s11249-018-1083-1
Park, J. Y., Ogletree, D. F., Thiel, P. A., and Salmeron, M. (2006). Electronic control of friction in silicon pn junctions. Science 313:186. doi: 10.1126/science.1125017
Park, J. Y., Qi, Y., Ogletree, D. F., Thiel, P. A., and Meron, S. (2007). Influence of carrier density on the friction properties of silicon p n junctions. Phys. Rev. B. 76:064108. doi: 10.1103/PhysRevB.76.064108
Pierno, M., Bruschi, L., Fois, G., Mistura, G., Boragno, C., de Mongeot, F. B., et al. (2010). Nanofriction of neon films on superconducting lead. Phys. Rev. Lett. 105:016102. doi: 10.1103/PhysRevLett.105.016102
Pilkington, G. A., Harris, K., Bergendal, E., Reddy, A. B., Palsson, G. K., Vorobiev, A., et al. (2018). Electro-responsivity of ionic liquid boundary layers in a polar solvent revealed by neutron reflectance. J. Chem. Phys. 148:193806. doi: 10.1063/1.5001551
Pivnic, K., Fajardo, O. Y., Bresme, F., Kornyshev, A. A., and Urbakh, M. (2018). Mechanisms of electrotunable friction in friction force microscopy experiments with ionic liquids. J. Phys. Chem. 122, 5004–5012. doi: 10.1021/acs.jpcc.8b00516
Popov, M., and Li, Q. (2018). Multimode active control of friction, dynamic ratchets and actuators. Phys. Mesomech. 21, 24–31. doi: 10.1134/s1029959918010046
Popov, M., Popov, V. L., and Popov, N. V. (2017). Reduction of friction by normal oscillations. I. Influence of contact stiffness. Friction 5, 45–55. doi: 10.1007/s40544-016-0136-4.
Qi, Y., Park, J. Y., Hendriksen, B. L., Ogletree, D. F., and Salmeron, M. (2008). Electronic contribution to friction on GaAs: an atomic force microscope study. Phys. Rev. B. 77:184105. doi: 10.1103/PhysRevB.77.184105
Rajauria, S., Ruiz, O., Canchi, S. V., Schreck, E., and Dai, Q. (2018). Electrostatically tunable adhesion in a high speed sliding interface. Phys. Rev. Lett. 120:026101. doi: 10.1103/PhysRevLett.120.026101
Rodriguez-López, J., Castro, P., de Vicente, J., Johannsmann, D., Elvira, L., Morillas, J. R., et al. (2015). Colloidal stability and magnetic field-induced ordering of magnetorheological fluids studied with a quartz crystal microbalance. Sensors 15, 30443–30456. doi: 10.3390/s151229808
Socoliuc, A., Gnecco, E., Maier, S., Pfeiffer, O., Baratoff, A., Bennewitz, R., et al. (2006). Atomic-scale control of friction by actuation of nanometer-sized contacts. Science 313, 207–210. doi: 10.1126/science.1125874
Sweeney, J., Hausen, F., Hayes, R., Webber, G. B., Endres, F., Rutland, M. W., et al. (2012). Control of nanoscale friction on gold in an ionic liquid by a potential-dependent ionic lubricant layer. Phys. Rev. Lett. 109:155502. doi: 10.1103/PhysRevLett.109.155502
Tusch, S., Kundu, A., Verley, G., Blondel, T., Miralles, V., Démoulin, D., et al. (2014). Energy versus information based estimations of dissipation using a pair of magnetic colloidal particles. Phys. Rev. Lett. 9:112. doi: 10.1103/PhysRevLett.112.180604
Vlachová, J., König, R., and Johannsmann, D. (2015). Stiffness of sphere–plate contacts at MHz frequencies: dependence on normal load, oscillation amplitude, and ambient medium. Beilstein J. Nanotechnol. 6:845. doi: 10.3762/bjnano.6.87
Wanless, E. J., Senden, T. J., Hyde, A. M., Sawkins, T. J., and Heath, G. A. (1994). A new electrochemical cell for atomic force microscopy. Rev. Sci. Instrum. 65, 1019–1020. doi: 10.1063/1.1145108
Wei, Q., Cai, M., Zhou, F., and Liu, W. (2013). Dramatically tuning friction using responsive polyelectrolyte brushes. Macromolecules 46, 9368–9379. doi: 10.1021/ma401537j
Wolloch, M., Levita, G., Restuccia, P., and Righi, M. C. (2018). Interfacial charge density and its connection to adhesion and frictional forces. Phys. Rev. Lett. 121:026804. doi: 10.1103/PhysRevLett.121.026804
Wolter, B., Yoshida, Y., Kubetzka, A., Hla, S. W., von Bergmann, K., and Wiesendanger, R. (2012). Spin friction observed on the atomic scale. Phys. Rev. Lett. 109:116102. doi: 10.1103/PhysRevLett.109.116102r
Wu, Y., Wei, Q., Cai, M., and Zhou, F. (2015). Interfacial friction control. Adv. Mater. Interfaces 2:1400392. doi: 10.1002/admi.201400392
Zeng, H., Zhang, Y., Mao, S., Nakajima, H., and Uchiyama, K. (2017). A reversibly electro-controllable polymer brush for electro-switchable friction. J. Mater. Chem. 5, 5877–5881. doi: 10.1039/C7TC01624G
Zhao, M., Zhang, J., Yao, J., and Peng, Z. (2017). Effects of nano-diamond on magnetorheological fluid properties. Nano 12:1750119. doi: 10.1142/S1793292017501193
Zhou, Y., and Qu, J. (2017). Ionic liquids as lubricant additives: a review. ACS Appl. Mater. Interface. 9, 3209–3222. doi: 10.1021/acsami.6b12489
Keywords: tribotronics, magnetorheology, nanoparticles, electrotuning friction, nanotribology, ionic liquids
Citation: Krim J (2019) Controlling Friction With External Electric or Magnetic Fields: 25 Examples. Front. Mech. Eng. 5:22. doi: 10.3389/fmech.2019.00022
Received: 07 December 2018; Accepted: 10 April 2019;
Published: 21 May 2019.
Edited by:
Roman Pohrt, Technische Universität Berlin, GermanyReviewed by:
Martin H. Müser, Saarland University, GermanyValentin L. Popov, Technische Universität Berlin, Germany
Alexander Filippov, Donetsk Institute for Physics and Engineering, Ukraine
Copyright © 2019 Krim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jacqueline Krim, jkrim@ncsu.edu