Insight on intrusion behavior of compacted bentonite with accessory-mineral ring: a modelling approach

Investigating the intrusion behavior of buffer/backfill materials is a critical aspect in the design of high-level radioactive waste (HLW) disposal repositories. This study proposes an intrusion model that accounts for the influence of the accessory-mineral ring and refines it by incorporating the specimen saturation process. The results show that the model demonstrated good agreement with the measured values after 30 days, but less accurate prior to this time. After incorporating a correction for the specimen’s saturation process, the model could well predict the measured values throughout the whole intrusion process. Additionally, the study suggests that predictions under parallel montmorillonite plates may be lower compared to non-parallel plates. The accessory-mineral ring significantly inhibits bentonite intrusion, and its restraining effect increases with the ring’s width. Compared to the smooth acrylic fissures, the irregular fractures in actual disposal repositories further limit bentonite intrusion. Fracture water seepage restricts bentonite intrusion in the upper part of the specimen while promoting it in the lower part, and also enhances the inhibiting effect of the accessory-mineral ring. The extent of this effect depends on the water flow velocity. Furthermore, increasing temperature promotes bentonite intrusion.

1 Introduction

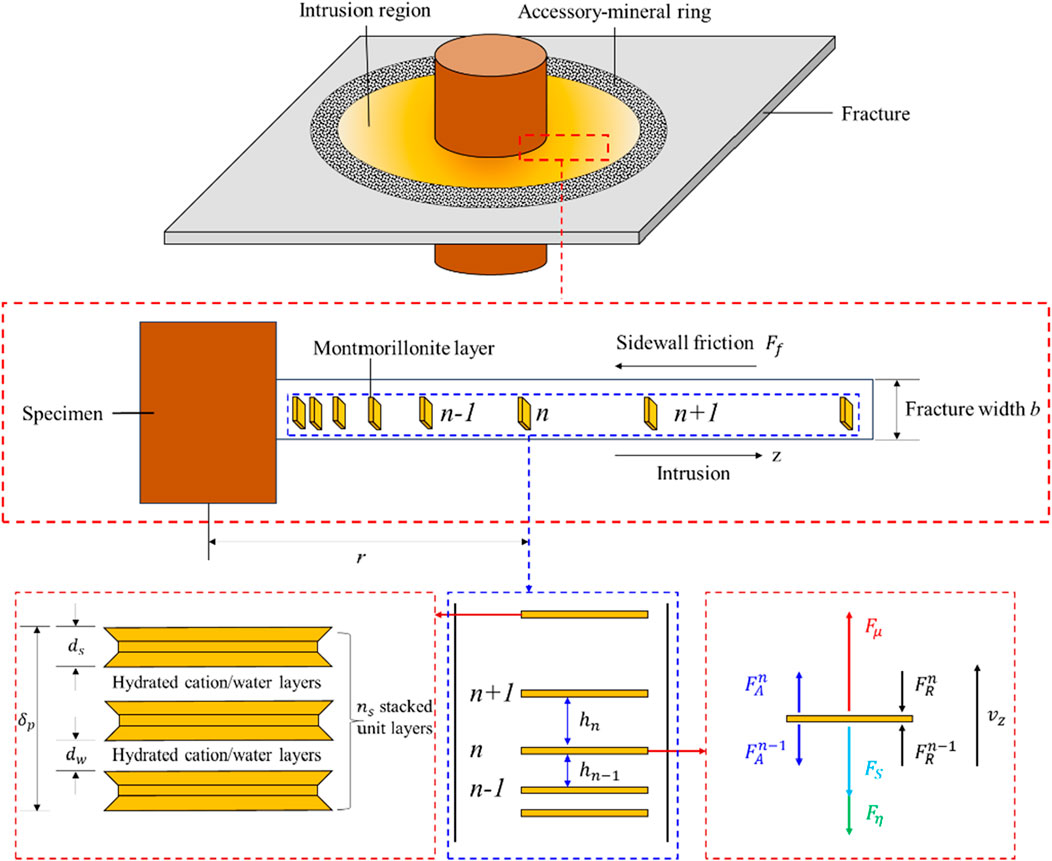
Currently, the safe disposal of high-level radioactive waste (HLW) remains a significant global challenge (Baik et al., 2007; Liu et al., 2009; Wen, 2006). One widely accepted and practical approach is deep geological disposal, where the waste is placed in deep underground repositories and surrounded by buffer/backfill materials to ensure long-term or permanent isolation from the surrounding environment and human populations (Figure 1). After comprehensive comparisons of various materials, highly compacted bentonites-based materials are widely selected as the candidate buffer/backfill materials to be placed between the surrounding rock and canisters, due to their low permeability, good swelling properties, suitable thermal conductivity, and strong adsorption capacity (Yang et al., 2024; Hasan et al., 2024). Research has shown that the fractures of varying sizes, whether naturally occurring or induced by construction activities, are commonly present in the surrounding rock (Nguyen et al., 2009). These fractures can serve as pathways for groundwater flow. During the long-term operation of a repository, the compacted bentonite absorbs water, causing it to swell and extrude into these fractures. More importantly, the bentonite that extrudes into the fractures will continue to swell, and under the influence of groundwater in fracture, it can form colloids (or adsorb radionuclides) and migrate outward with the percolating flow (Wu et al., 2024a), resulting in an erosion effect (Borrelli et al., 2013) (Figure 1). Consequently, this intrusion/erosion process may lead to the migration and leakage of radionuclides with the bentonite colloids, reducing the buffering performance of the engineered barrier layer and compromising the safety and reliability of the disposal repository. Therefore, studying the intrusion process and mechanisms of bentonite in fractures within the surrounding rock is crucial for the design and safe operation of engineered barrier systems in radioactive waste disposal. This research holds significant practical engineering value.

Figure 1

Figure 1. Schematic diagram of bentonite intrusion and erosion.

Research shows that the intrusion process of bentonite into the surrounding rock fractures exhibits typical rheological characteristics, with distinct zones along the intrusion path, including solid bentonite, gel, and sol regions (Xu, 2017). To study the intrusion behavior of bentonite, Pusch (1983) designed an experimental setup consisting of two concentric granite rings to simulate the fractures in the surrounding rock, and conducted intrusion tests with MX80 bentonite. The results showed that the intrusion distance was proportional to the logarithm of time. Kanno and Wakamatsu (1991), using the gap between two acrylic plates to simulate surrounding rock fractures, found that the intrusion distance of Kunigel V1 bentonite was proportional to the square root of time. Subsequently, using the same experimental apparatus, they observed that as the bentonite proportion and fracture width increased, the intrusion rate also increased (Kanno et al., 1999). Huang and Chen (2019) conducted experimental studies on the intrusion process of GMZ bentonite and found that the intrusion distance increased with the dry density of the bentonite and the fracture width. Reid et al. (2015) found that at the intrusion edge, montmorillonite particles, driven by their diffusion dynamics, continuously diffused into the fracture water. Due to the extremely low volume fraction of montmorillonite at the boundary, the diffusion force of montmorillonite was insufficient to transport the accessory minerals present in the bentonite, such as quartz and feldspar (Bai et al., 2021; Wu et al., 2024b). Consequently, these accessory minerals were left behind at the intrusion edge. As montmorillonite particles were progressively depleted from the edge, the accumulation of accessory minerals increased, forming a distinct layer of dark-colored, ring-shaped material—referred to as the accessory-mineral ring.

Regarding modeling approaches, a solid particle diffusion model was established to simulate the distribution of the dry density of bentonite within fractures (Kanno et al., 2011). This model typically assumes no-slip boundary conditions for the fracture sidewalls, which may lead to an overestimation of the theoretical intrusion rate. Xu et al. (2022) proposed a model to describe the one-dimensional intrusion behavior of bentonite throughout the entire intrusion process. However, this model did not consider the influence of the accessory-mineral ring. A later intrusion model that incorporated the accessory-mineral ring showed that it inhibited bentonite intrusion (Ye et al., 2022). Despite this improvement, the model still could not capture the evolution of the intrusion distance over time. In summary, a comprehensive model that accurately describes the full process of intrusion, including the effects of the accessory-mineral ring, is still lacking.

In this study, a bentonite intrusion model was developed, accounting for accessory-mineral ring. It was subsequently validated based on intrusion tests by Xu et al. (2022) and corrected considering specimen saturation process. Finally, the influences of unparallel montmorillonite plates, accessory-mineral ring, irregular fractures, seepage water and temperature on bentonite intrusion were discussed.

2 Intrusion model

2.1 Model development

2.1.1 For pure montmorillonite

Generally, montmorillonite particles have irregular shapes and varying sizes. During their hydration and expansion process, they rotate and move in an irregular manner. To simplify the problem, this study assumes a highly idealized scenario to highlight the key features of the intrusion issue (Xu et al., 2022). As shown in Figure 2, it is assumed that montmorillonite consists of plate-like particles made up of one or more layers, all with identical size and properties. When these particles move through a two-dimensional fracture, they align strictly in a face-to-face arrangement, forming a columnar phase. This means that only the face-to-face distance h between the montmorillonite particles changes over time and space, while the edge-to-edge distance remains constant during the intrusion process. By performing a force analysis on the montmorillonite particle n along the z-axis, the motion equation can be derived using Newton’s second law,

$F_n=F_{n1}+F_{n2}=ma(1)$

where, a is the acceleration, m is the mass of the particle, F_n is the net force acting on the particle, F_n1 is the internal net force, which includes the viscous drag force F_η, the combination of the gravitational force and buoyant force F_s, the diffusional driving force F_μ, the van der Waals’ force F_A, as well as the diffuse double layer force F_R. F_n2 is the external net force, including the sidewall friction force F_f. Thus, the internal F_n1 and external net F_n2 force acting on one single particle located at the intrusion radius r can be written as,

$F_{n1}=-F_S-F_{\eta }+F_{\mu }+{\displaystyle \sum _i}{F}_A^i-{\displaystyle \sum _i}{F}_R^i(2)$

${F_n}_2=-\frac{2S_p}{2\pi rb}{F}_f=-\frac{S_p}{\pi rb}{F}_f(3)$

where, the summation over i includes all the nearest neighbors, b is the fracture width, S_p is the bottom surface area of montmorillonite layers.

Figure 2

Figure 2. Dynamic force balance diagram of montmorillonite particles.

Combinations of Equations 1–3 yield,

$F_n=-F_S-F_{\eta }+F_{\mu }+{\displaystyle \sum _i}{F}_A^i-{\displaystyle \sum _i}{F}_R^i-\frac{S_p}{\pi rb}{F}_f=ma(4)$

Under steady-state conditions, where acceleration is negligible (a ≈0) and the net force F_n equals zero, Equation 4 simplifies to:

$F_n=-F_S-F_{\eta }+F_{\mu }+{\displaystyle \sum _i}{F}_A^i-{\displaystyle \sum _i}{F}_R^i-\frac{S_p}{\pi rb}{F}_f=0(5)$

For this two-dimensional model, it is assumed that only the nearest neighbors interact with each other, as illustrated in Figure 2, which shows the forces acting on the nth particle. Therefore, Equation 5 can be rewritten as,

$F_n=-F_S-F_{\eta }+F_{\mu }+\left(F_A^n-F_A^{n-1}\right)-\left(F_R^n-F_R^{n-1}\right)-\frac{S_p}{\pi rb}{F}_f=0(6)$

where the superscript “n” denotes the interaction forces between the nth and the n+1 particles, and similar meaning remains for the superscript “n-1”.

In Equation 6, both the van der Waals force F_A and the double-layer repulsive force F_R are expressed in discrete form and need to be converted into the continuous form,

$F_A^n-F_A^{n-1}=\left(z_n-z_{n-1}\right)\frac{F_A^n-F_A^{n-1}}{z_n-z_{n-1}}=\left(h+{\delta }_p\right)\frac{\mathrm{\partial }{F}_A}{\mathrm{\partial }\varphi }\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }z}(7)$

$F_R^n-F_R^{n-1}=\left(z_n-z_{n-1}\right)\frac{F_R^n-F_R^{n-1}}{z_n-z_{n-1}}=\left(h+{\delta }_p\right)\frac{\mathrm{\partial }{F}_R}{\mathrm{\partial }\varphi }\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }z}(8)$

where, δ_p is the thickness of a single unit montmorillonite particle (Figure 2), Φ is the volume fraction of montmorillonite particles and can be written as (Liu, 2013; Sun et al., 2015),

$\varphi =\frac{n_s{d}_s}{{\delta }_p+h}=\frac{n_s{d}_s}{n_s{d}_s+\left(n_s-1\right)d_w+h}(9)$

where, n_s is the number of unit layers of montmorillonite particle, d_s is the thickness of a single unit montmorillonite layer.

Additionally, the specific forms of the various forces in Equation 6 can be converted through the following steps.

Firstly, According to Hamaker-De Boer theory, Van der Waals force F_A could be written as (Komine and Ogata, 2003),

$F_A=\frac{A_H{S}_p}{6\pi }\left[\frac{1}{h^3}-\frac{2}{{\left(h+{\delta }_p\right)}^3}+\frac{1}{{\left(h+2{\delta }_p\right)}^3}\right](10)$

where, A_H is the Hamaker constant.

Then, according to the DLVO theory, the double layer force F_R could be expressed as (Sridharan and Jayadeva, 1982),

$F_R=2cRT{S}_p\left(\cosh {\zeta }^m-1\right)(11)$

where, R is the gas constant, c is the cation concentration, ζ^m is the dimensionless potential at the midpoint of two plates.

For the viscous drag force F_η, it is primarily caused by the relative motion between the montmorillonite particles and the fluid. Its expression is given by (Petsev et al., 1993; Hubbard and Douglas, 1993),

$F_{\eta }=f{v}_z(12)$

where, f is a proportional coefficient of the fluid and particles.

The diffusion driving force F_μ can be derived from the chemical potential gradient, which causes particles to diffuse from regions of higher particle concentration to regions of lower concentration. On average, for a single particle, the diffusion driving force can be expressed as (Hiemenz, 1986),

$F_{\mu }=-k_{B}T\frac{\mathrm{\partial }\mathit{ln}\varphi }{\mathrm{\partial }z}=\frac{-k_{B}T}{\varphi }\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }z}(13)$

where, k_B is the Boltzmann constant, T is the absolute temperature.

The sidewall friction force F_f could be written as,

$F_f=2\pi r{\delta }_p\mu {\sigma }_r(14)$

where, μ is the friction coefficient between the sidewall and soil particles and is determined as 0.034 and 0.1 for the non-accessory-mineral and accessory-mineral ring, respectively (Ye et al., 2022), σ_r is the swelling pressure acting on the sidewall of the intrusion region.

In addition, the particle flux J (J = Φv_z) should satisfy the following continuity equation,

$\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}=-\frac{\mathrm{\partial }J}{\mathrm{\partial }z}(15)$

Substituting Equations 7–15 into Equation 6 yields the intrusion model (Equation 16),

$\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}=F_S\nabla \left(\frac{\varphi }{f}\right)+\nabla \left({\mu }_f\varphi \right)+\nabla \left(D\nabla \varphi \right)(16)$

where, μ_f is the friction factor by sidewall, and written as (Equation 17)

${\mu }_f=\frac{2\mu {\delta }_p{S}_p{\sigma }_r}{bf}(17)$

and D is the diffusion coefficient, and expressed as (Equation 18),

$D=\frac{k_{B}T-\left(h+{\delta }_p\right)\varphi \left(\frac{\mathrm{\partial }{F}_A}{\mathrm{\partial }\varphi }-\frac{\mathrm{\partial }{F}_R}{\mathrm{\partial }\varphi }\right)}{f}(18)$

It should be noted that under real conditions, particles may exhibit irregularities in size, properties, and arrangements, particularly during the hydration and swelling process. However, the assumption of a columnar phase remains plausible when the volume fraction of particles is sufficiently large, such that, if rigid, the particles cannot rotate freely without colliding with their neighbors. Although particles may jitter due to diffusion-driven motion, they will predominantly align in parallel when their distance is smaller than the diameter of the montmorillonite particles (Liu et al., 2009). For example, with 200 nm-sized particles and a thickness of 1 nm, free rotation could occur when the average distance is around 200 nm, corresponding to a volume fraction of approximately 0.005. At this point, the model’s validity begins to diminish. However, at such large distances, the van der Waals and double-layer forces acting on the particles are negligible compared to the dominant diffusion-driven forces, allowing the latter to govern the behavior. Therefore, the model can still be useful for describing montmorillonite expansion at low volume fractions.

In addition, it should be emphasized that Equation 6 is specifically focused solely on montmorillonite and does not take into account the influence of accessory minerals present in bentonite. The following discussion will address the impact of the accessory mineral and its ring on bentonite intrusion.

2.1.2 Considering accessory mineral and its ring effects

2.1.2.1 Accessory mineral

According to the literature (Liu et al., 2011) and the present study, the accessory mineral primarily affects the lateral wall friction and viscous forces. The sidewall friction has been analyzed above and will not be discussed further here. The following section will focus on the impact of accessory minerals on the viscous force.

The research suggests that the proportion α of accessory minerals significantly influences the viscous force, primarily by altering the friction coefficient f between montmorillonite particles and the fluid (Liu, 2013) (Equation 19),

$f=\left[6\pi \eta \frac{\frac{d_s}{2}\sqrt{\frac{4S_p}{\pi d_s^2}-1}}{{\tan }^{-1}\sqrt{\frac{4S_p}{\pi d_s^2}-1}}+\frac{\eta }{k}\frac{1-\frac{\varphi }{n_s\beta }}{\frac{\varphi }{n_s\beta }}{S}_p{d}_s\right]n_s(19)$

where, k is the intrinsic permeability, η is viscosity of water, β is the montmorillonite proportion in bentonite.

Based on Kozeny–Carman equation, the permeability k could be written as (Kozeny, 1927)

$k=\frac{1}{k_0{\tau }^2}\frac{1}{a_p^2}\frac{{\left(1-\phi \right)}^3}{{\phi }^2}(20)$

where, a_p is the specific surface area per unit volume, φ is the volume fraction of bentonite, k₀τ² is the pore shape factor.

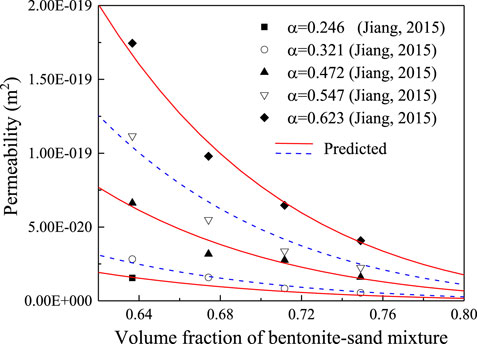
Assuming that the accessory mineral in the bentonite is spherical in shape, a_p can be expressed as (Karnland et al., 2006),

$a_p=\frac{2}{d_s}\beta =\frac{2}{d_s}\left(1-\alpha \right)(21)$

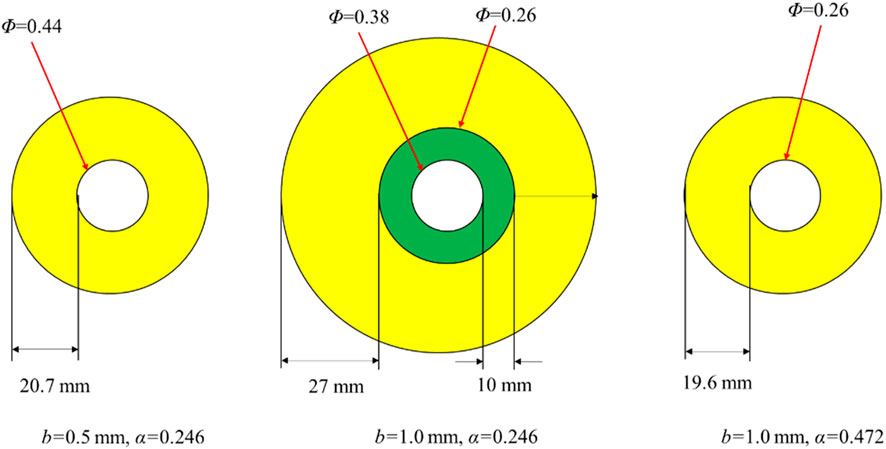
To determine the pore shape factor k₀τ² in Equation 20, the relationship between permeability k of GMZ bentonite–sand material specimens and the proportion of accessory minerals α was borrowed from Jiang (Jiang, 2015). The following values for the pore shape factor were selected for different proportions of accessory minerals: 4.66 for α = 0.246, 3.70 for α = 0.321, 2.36 for α = 0.472, 1.99 for α = 0.547, and 1.83 for α = 0.623. Using this data, Equation 20 can effectively predict the permeability of the bentonite, as shown in Figure 3. By fitting the pore shape factors k₀τ² and the proportion of accessory minerals α, the quantitative relationship between k₀τ² and α can be derived,

$k_0{\tau }^2=17.67{\left(\alpha -0.246\right)}^2-14.17\left(\alpha -0.246\right)+4.66(22)$

Figure 3

Figure 3. Evolutions of permeability with volume fraction of bentonite.

2.1.2.2 Accessory-mineral ring

The proportion of accessory minerals in the accessory-mineral ring and montmorillonite volume fraction at the boundary between the non-accessory and accessory-mineral rings are the two key factors, which influence the intrusion of bentonite (Ye et al., 2022). It is found that in the initial intrusion stage, the proportion of accessory minerals in the accessory mineral ring is the same as that in the non-accessory mineral ring, and at this point, the friction coefficients in both the accessory mineral ring and the non-accessory mineral ring are identical, with a value of 0.39. As the bentonite intrudes into the fractures, montmorillonite at the intrusion edge gradually diffuses into the fracture water, causing the accumulation of accessory minerals at the intrusion edge. This accumulation leads to an increase in both the width of the accessory-mineral ring and the proportion of accessory minerals. However, once the intrusion reaches a certain level, the pore structure formed by the accessory minerals in the ring begins to inhibit further diffusion of the montmorillonite, resulting in a decrease or even cessation of montmorillonite diffusion. This is reflected in the stabilization of the accessory mineral ring width, which also means that the proportion of accessory minerals within the ring no longer changes. According to the research by Xu et al. (2022), the friction coefficient of the accessory-mineral ring is directly related to the proportion of accessory minerals, and increases approximately linearly with the increasing proportion to the accessory minerals. Therefore, once the width of the accessory mineral ring stabilizes, the friction coefficient of the ring will also stabilize. For the stage prior to the stabilization of width of accessory-mineral ring, according to relevant literature (Kanno et al., 1999; Ye et al., 2022), the relationship between the width l₂ of the accessory mineral ring and time is described by k₁ $\sqrt{d}$, where d represents time and k₁​ is a constant. The area of the accessory mineral ring is approximately 2πrk₁ $\sqrt{d}$, where r is the intrusion radius. Additionally, studies have shown that the diffusion rate of montmorillonite is positively correlated with the soil-water contact area at the intrusion edge (Borrelli et al., 2013). Assuming the diffusion rate of montmorillonite remains constant during this stage, the area of accessory minerals in the accessory mineral ring will follow a linear relationship with time, described by 2πrk₂d, where k₂​ is a constant. Thus, the proportion of accessory minerals in the ring could be described by k₂ ${/k}_1\sqrt{d}$. It can be inferred that the trend of changes in the proportion of accessory minerals, as well as the friction coefficient in the ring over time are consistent with the trend in the width of the accessory mineral ring, with a rapid increase initially, followed by stabilization.

Regarding the volume fraction Φ of montmorillonite at the interface of the two regions, according to the intrusion model (Equations 23, 24) in the steady state (Ye et al., 2022), Φ can be approximated as shown in Equation 25. Additionally, the friction coefficient of accessory-mineral ring and the montmorillonite volume fraction at the boundary between the two regions in the steady state are determined as 0.1 and 0.15, respectively.

$l_1=\frac{3.57b}{2{\mu }_1}\left({\rho }_1-{\rho }_2\right)(23)$

$l_2=\frac{3.57b}{2{\mu }_2}\left({\rho }_2-{\rho }_3\right)(24)$

$\varphi \approx k_3{l}_2{\mu }_2=k_3{l}_2{k}_4{l}_2=k_5{l}_2^2(25)$

where, l₁ is the width of non-accessory-mineral ring, l₂ is the width of accessory-mineral ring, μ₁ is the friction coefficient in the non-accessory-mineral ring, μ₂ is the friction coefficient in the accessory-mineral ring, ρ₁ is the dry density of montmorillonite at the intrusion port, ρ₂ is dry density of montmorillonite at the boundary between the non-accessory and accessory-mineral rings, ρ₂ is dry density of montmorillonite at the intrusion edge, k₃, k₄, k₅ are constants. Thus, the trend of change in Φ over time is also consistent with the trend in the width of the accessory mineral ring, with an initial rapid increase followed by stabilization.

In conclusion, according to the relationship between the width of accessory-mineral ring and the friction coefficient of the accessory mineral ring, as well as the montmorillonite volume fraction at the interface, time-dependent curves for the friction coefficient of the accessory mineral ring and the montmorillonite volume fraction at the interface are obtained under different fracture widths, as shown in Figure 4.

Figure 4

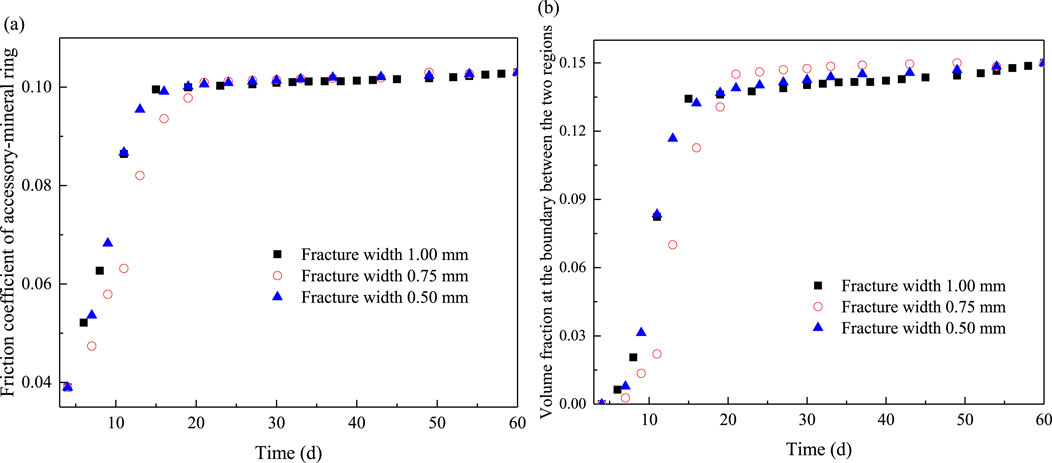
Figure 4. Evolutions of friction coefficient of accessory-mineral ring (A) and volume fraction of montmorillonite at the two-region boundary (B) with time.

2.2 Model verification and correction

2.2.1 Model verification

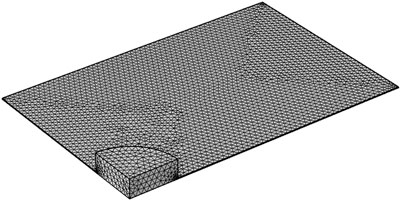
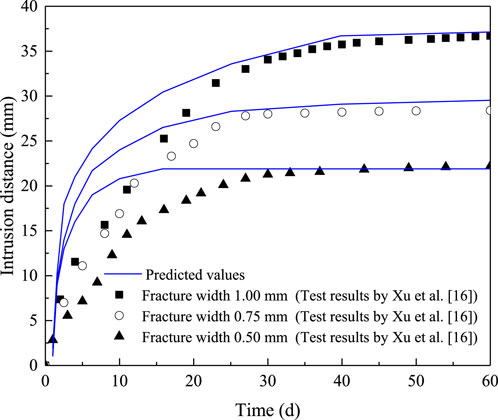
In order to reduce the computational workload, this study focuses on modeling and calculations within a quarter of the region. As shown in Figure 5, a fracture intersects the specimen hole with 0.15 m × 0.1 m geometry was modeled and implemented using the COMSOL Multiphysics. The boundary condition was set as zero flux. The mesh consists of 18,195 domain elements, 10,726 boundary elements, and 458 edge elements. The volume fraction at the specimen hole and fracture were set to 0.48 and 0, respectively. The constitutive model developed in this study was implemented into the coefficient form of the partial differential equation module, with the parameters as shown in Table 1. Then, the intrusion distance vs time curves for under different fracture widths are obtained, as shown in Figure 6. It can be observed in Figure 6 that the model accurately predicts the intrusion distance after 30 days. However, there is a noticeable discrepancy in the predictions for the period prior to 30 days. This discrepancy can be attributed to the fact that the model assumes the specimen to be fully saturated, whereas in the two-dimensional intrusion experiment conducted in this study, the bentonite material undergoes slow hydration. During the early stages of the test, the material remains unsaturated, resulting in a lower swelling force compared to its saturated state. Consequently, the model overestimates the intrusion distance in the initial phase when compared to the experimental data.

Figure 5

Figure 5. Modelling for the bentonite intrusion.

Table 1

Table 1. Parameters used in the model (Sun et al., 2015).

Figure 6

Figure 6. Evolutions of intrusion distance of bentonite with time.

2.2.2 Model correction considering the saturation process of the specimen

To address the discrepancy between the predicted and measured values for the period prior to 30 days, the intrusion model is enhanced by incorporating the effects of unsaturated conditions. According to previous studies (Vanapalli et al., 2001; Schanz and Al-Badran, 2014), as the degree of saturation increases, the swelling pressure of bentonite follows an S-shaped growth trend. In this study, it is assumed that during the early stages of the two-dimensional intrusion tests, the soil undergoes uniform hydration. Based on this assumption, the swelling pressure of the bentonite increases in an S-shaped manner over time. in this manner, Equations 13, 14 are updated accordingly as (Equations 26, 27),

${\mu }_f=\frac{2\mathrm{s}\mu {\delta }_p{S}_p{\sigma }_r}{af}(26)$

$D=\frac{k_{B}T-\left(h+{\delta }_p\right)\varphi \left(\frac{\mathrm{\partial }s\left(F_A-\mathrm{\partial }{F}_R\right)}{\mathrm{\partial }\varphi }\right)}{f}(27)$

where, s represents the ratio of non-saturated to saturated swelling pressure, which exhibits an S-shaped growth trend as time increases. Through comparison, the logistic model is selected, and its expression is written as (Equation 28),

$s=1-\frac{1}{1+{\left(\frac{t}{p}\right)}^q}(28)$

where, t represents time, p and q are constants related to the fracture width a and proportion of accessory minerals α and their expressions are expressed as (Equations 29, 30),

$p=24.32+17.13a-16.51\left(\alpha -0.246\right)+18.56a^2-0.56{\left(\alpha -0.246\right)}^2-9.3a\left(\alpha -0.246\right)(29)$

$q=4.98+1.67a-4.73\left(\alpha -0.246\right)+3.56a^2+2.11{\left(\alpha -0.246\right)}^2-1.06a\left(\alpha -0.246\right)(30)$

According to Equation 23, s increases with the increase in fracture width, and decreases with the increase in proportion of accessory minerals. Explanation to this observation is given as follows:

The contact area between soil and water at the intrusion boundary is a direct factor influencing s, but its essence depends on the volume fraction of montmorillonite in the intrusion zone. According to Figure 3, a higher volume fraction results in lower permeability of montmorillonite, which in turn makes it less prone to hydration, leading to a decrease in s. Based on the model developed in this study, the volume distribution of montmorillonite in the intrusion zone is obtained, as shown in Figure 7. It can be observed in Figure 7 that the volume fraction of montmorillonite in the intrusion zone with a fracture width of 1 mm is generally lower than that with a fracture width of 0.5 mm, which helps explain the increase in s with the widening of the fracture. Additionally, Figure 7 also shows that for the case with α = 0.472, the volume fraction of montmorillonite at the extrusion mouth is 0.38, which is lower than that with α = 0.246, where the montmorillonite volume fraction is 0.26. According to the above conclusions, s should be expected to increase as α increases. However, further analysis shows that for the case with α = 0.472, the area where the montmorillonite volume fraction exceeds 0.26 accounts for only 12.9% of the total intrusion area, which can be neglected. In contrast, the area with a montmorillonite volume fraction below 0.26 is 2.6 times larger than that with α = 0.246. This indicates that a larger area of low montmorillonite volume fraction accelerates the hydration process. Therefore, s should decrease with the increase in the proportion of accessory minerals.

Figure 7

Figure 7. Details for bentonite intrusion based on calculated results.

Finally, by substituting Equations 21–25 into Equation 12, the predicted intrusion distance, the width of the accessory mineral ring and the dry density of specimen, considering the unsaturated effects, can be obtained, as shown in Figure 8. It can be observed in Figure 8 that intrusion distance initially increases significantly and then gradually slows down. This observation is inconsistent with that by Liu et al. (2009), who found that the bentonite would expand indefinitely, with the intrusion distance increasing without limit. The difference in this study may be attributed to the inclusion of sidewall friction effects in the model. As the bentonite intrudes into the fracture, the intrusion area will increase, which increases the sidewall force, thereby limiting further intrusion. Additionally, Figure 8 demonstrates the corrected intrusion model provides a good prediction of the intrusion distance and the width of the accessory mineral ring. This comparison further highlights the importance of considering the influence of sidewall friction in modeling the intrusion process.

Figure 8

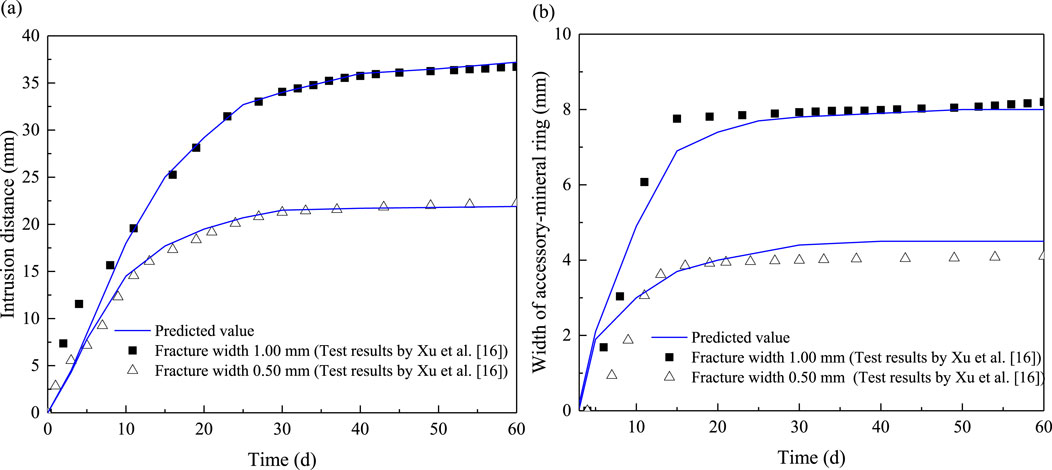
Figure 8. Comparison of the predicted intrusion distance (A) and width of accessory-mineral ring (B) with measured values.

3 Discussion

3.1 Comparison of the scenario of parallel and non-parallel montmorillonite plates

It is important to acknowledge that under real conditions, particles may not always align perfectly in a parallel arrangement. To explore how irregular arrangements could influence the combined van der Waals and double-layer forces, one potential scenario was considered, as shown in Figure 9. For comparison, it was assumed that h₁ = 0.5 × (h₂ + h₃). According to Equations 10, 11, the combined forces F_c of van der Waals and the double-layer decreases significantly with increasing the distance h between two montmorillonite plate, with the decrease rate slowing at larger distances. Thus, it can be deduced that F_c1 < 0.5 × (F_c2 + F_c3). This implies that the values predicted in this study, based on idealized assumptions, would be lower than those observed under real conditions.

Figure 9

Figure 9. Comparison of the combined forces of van der Waals as well as the double-layer based on idealized assumptions and real conditions.

3.2 The influence of accessory-mineral ring on the intrusion of bentonite

According to the proposed intrusion model, the predicted intrusion distances with and without accessory-mineral ring under the fracture width of 1 mm are presented in Figure 10. It can be observed in Figure 10 that the intrusion distance without accessory-mineral ring is clearly higher than that with accessory-mineral ring. The difference between the two increases significantly and then gradually with time. This trend corresponds well with the observed increase in the width of the accessory-mineral ring (Figure 6). Furthermore, it can be concluded that the accessory-mineral ring plays a significant role in effectively restraining the intrusion of bentonite. The degree of its influence becomes more pronounced as the width of the accessory-mineral ring increases, suggesting that a wider ring provides greater resistance to intrusion.

Figure 10

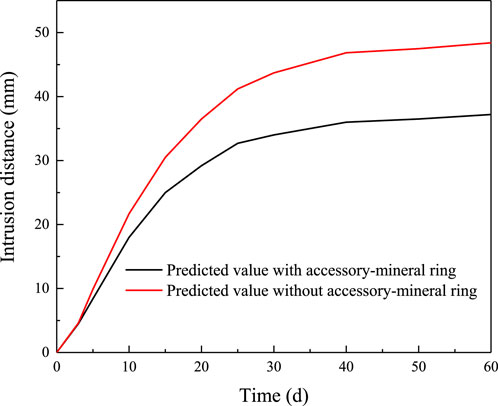
Figure 10. Predicted intrusion distances with and without accessory-mineral ring under the fracture width of 1 mm.

3.3 The influence of irregular fractures on the intrusion of bentonite

The tests conducted by Ye et al. (2022) used smooth acrylic plates to simulate the regular fractures, whereas actual disposal repositories typically contain numerous irregular fractures (Nguyen et al., 2009). Since irregular fractures can be considered as a combination of several regular smooth fractures, the test results obtained from smooth surface fractures can still reflect the intrusion behavior in irregular fractures. However, there are still certain differences between the two, mainly related to the effect of irregular fractures on the expansion driving force of bentonite. As shown in Figure 11, irregular fractures can be simplified as a structure composed of three connected smooth fractures. At the junctions of the fractures, ideally, the montmorillonite layers would change accordingly with the direction of the fracture, so the expansion driving force F_s of bentonite would remain unaffected (Figure 11A), and the model proposed in this study would still be applicable. However, in practical scenarios, the montmorillonite layers may only deviate by a certain angle, or even not deviate at all (Figure 11B). Since bentonite needs to migrate along the fracture, the expansion driving force of montmorillonite will be partially reduced. The maximum reduction factor is given by cos(α), where α is the angle between the two fracture segments. Meanwhile, according to research by Reid et al. (2015), the irregular fractures favor the accumulation of accessory minerals, promoting the development of mineral rings, which in turn inhibit the intrusion of bentonite. Above all, it is clear that, compared to regular fractures, the intrusion of bentonite in irregular fractures is subject to varying degrees of suppression. Further tests may be conducted in the future to verify this effect.

Figure 11

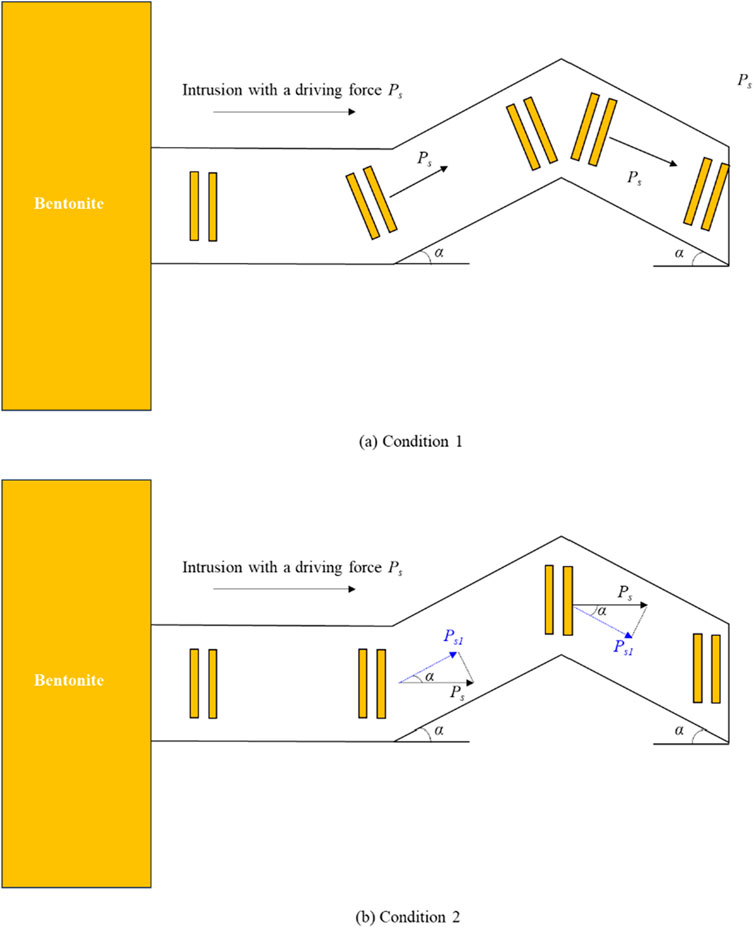
Figure 11. Diagram of bentonite intrusion into irregular fracture. (A) Condition 1. (B) Condition 2.

3.4 The influence of seepage water on the intrusion of bentonite

This study focuses on the intrusion behavior of bentonite under static water conditions. However, in actual disposal repository, bentonite intrusion is also influenced by the flow of fracture water. On one hand, fracture water flow exerts a seepage force in the direction of water flow, while the swelling pressure of bentonite acts in opposite and same directions in the upper and bottom parts of the intrusion region, respectively (Figure 12). As a result, compared to static water conditions, the intrusion in the upper part is reduced and in the bottom part is increased. To quantitatively analyze the influence of seepage water on the intrusion, a new intrusion model was established considering the influence of seepage force (F_w).

Figure 12

Figure 12. Comparison of the predicted intrusion distance with and without seepage water.

Specifically, for the upper part, the forces balance model can be written as (Equation 31),

$F_n=-F_S+F_w-F_{\eta }+F_{\mu }+\left(F_A^n-F_A^{n-1}\right)-\left(F_R^n-F_R^{n-1}\right)-\frac{S_p}{\pi rb}{F}_f=0(31)$

For the bottom part, the forces balance model can be written as (Equation 32),

$F_n=-F_S-F_w-F_{\eta }+F_{\mu }+\left(F_A^n-F_A^{n-1}\right)-\left(F_R^n-F_R^{n-1}\right)-\frac{S_p}{\pi rb}{F}_f=0(32)$

By following the model derivation steps outlined in Section 2.1, the new intrusion models for the upper and bottom part can be expressed as (Equations 33, 34),

$\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}=\left(F_S-F_w\right)\nabla \left(\frac{\varphi }{f}\right)+\nabla \left({\mu }_f\varphi \right)+\nabla \left(D\nabla \varphi \right)(33)$

$\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}=\left(F_S+F_w\right)\nabla \left(\frac{\varphi }{f}\right)+\nabla \left({\mu }_f\varphi \right)+\nabla \left(D\nabla \varphi \right)(34)$

According to the research by Börgesson and Sandén (2006), the hydraulic conductivity of the bentonite is so low that water flow into the clay is sufficiently stopped and keep a high hydraulic gradient in the clay. Consequently, the seepage force may be 100 times greater than that of gravitational force (Xu et al., 2022). In this study, by setting F_w = 100F_s, the predicted intrusion distance in the upper and bottom parts is 34.5 and 39.9 mm, respectively. These values represent a decrease of 2.5 mm in the upper region and an increase of 2.9 mm in the bottom region, compared to the predictions under static water conditions.

It should be noted that the seepage water will also lead to the loss of montmorillonite, which may decrease the intrusion distance. When the accessory-mineral ring is not considered, the influence extent is primarily governed by the fracture water flow velocity. Specifically, when the flow velocity increases from 1 m/year to 100 m/year, the predicted intrusion distance of bentonite decreases from 10 m to 1 m (Moreno et al., 2011). However, the more montmorillonite loss will cause more accessory minerals left at the intrusion edge (Reid et al., 2015). This may increase the width of the accessory mineral ring and the proportion of accessory minerals, which is higher than under static water conditions, thus further inhibiting bentonite intrusion. Overall, a more detailed quantitative analysis of the influence of mass loss and the accessory-mineral ring on the bentonite intrusion is necessary and will be the focus of future investigations.

3.5 Influence of temperature on bentonite intrusion

In the deep geological disposal repository, due to the impact of radionuclide decay heat, the temperature of bentonite continuously increases, potentially exceeding 100°C. Research indicates that the swelling pressure of bentonite increases as temperature rises, which may consequently alter its intrusion behavior. Therefore, it is crucial to analyze the impact of temperature on the intrusion characteristics of bentonite in detail. This section will focus on investigating how temperature influences bentonite intrusion behavior, which is essential for improving the design and safety assessment of high-level radioactive waste disposal sites.

Temperature influences various forces acting on bentonite, except for gravitational and buoyant forces. Specifically, the following forces are affected:

The viscosity of water η, which is used to calculate the viscous drag force F_η, is temperature-dependent and can be expressed as a function of temperature (T) (Bai et al., 2020; Zhou et al., 2024) (Equation 35),

$\eta =0.66{\left(T-227\right)}^{-1.55}(35)$

For Equation 13 used to calculate the diffusional driving force F_μ, the temperature variable T is already included.

The van der Waals force F_A, which is determined by the Hamaker constant A_H, varies with temperature. The temperature dependence of A_H can be expressed as (Liu et al., 2009) (Equation 36),

$A_H=2.5k_{B}T(36)$

For Equation 10 used to calculate the diffuse double layer force F_A, the dimensionless potential ζ^m at the midpoint of montmorillonite plates is temperature-dependent and can be expressed as (Equation 37),

${\zeta }^m={\sinh }^{-1}\left[2\sinh {\zeta }_{\infty }^m+\frac{4}{\kappa h}\left(\frac{{\zeta }_{\infty }^h}{2}\right)\right](37)$

where, ζ_∞^m and ζ_∞^h can be written as (Equations 38, 39),

${\zeta }_{\infty }^m=4{\tanh }^{-1}\left[\tanh \frac{{\zeta }_{\infty }^0}{4}\exp \left(\frac{-\kappa h}{2}\right)\right](38)$

and

${\zeta }_{\infty }^h=4{\tanh }^{-1}\left[\tanh \frac{{\zeta }_{\infty }^0}{4}\exp \left(-\kappa h\right)\right](39)$

where, ζ_∞^m and κ can be described by (Equations 40, 41),

${\zeta }_{\infty }^0=2{\tanh }^{-1}\left(\frac{\lambda F{\theta }^0}{2{\epsilon }_0{\epsilon }_r\kappa RT}\right)(40)$

and

$\kappa =\sqrt{\frac{2F^{2}c{\lambda }^2}{{\epsilon }_0{\epsilon }_{r}RT}}(41)$

where, F is the Faraday constant, λ is the average valence of cation, θ₀ is the density of surface charge, ε₀ is the vacuum permittivity, ε_r is the relative permittivity. ε_r is temperature-dependent and can be expressed as (García-García et al., 2006) (Equation 42),

${\epsilon }_r=0.0022T^2-1.708T+391.2(42)$

Based on the above analysis of the temperature effects on the forces acting on the montmorillonite, the relationship between the intrusion distance and the temperature is derived and presented in Figure 13. It can be observed in Figure 13 that the intrusion distance increases by 11.3% at T = 80°C, compared to that at T = 20°C.

Figure 13

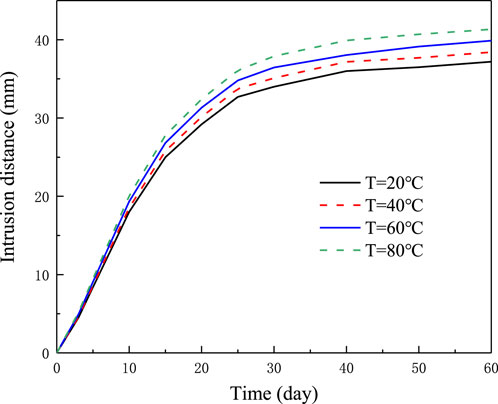
Figure 13. Predicted intrusion distance with time under various temperatures for the fracture width of 1 mm.

4 Conclusion

In this paper, a bentonite intrusion model was developed, accounting for the influence of accessory-mineral ring, and subsequently validated and corrected considering specimen saturation process. Additionally, the influences of unparallel montmorillonite plates, accessory-mineral ring, irregular fractures, seepage water and temperature on bentonite intrusion were discussed. The following conclusions were drawn:

1) The proposed intrusion model’s predictions were in good agreement with the measured values after 30 days, but less accurate prior to this time. With saturation process of specimen being considered, the model could well predict the measured values in the full process of intrusion.

2) The value predicted in this study, based on idealized assumptions, may be lower than that observed under real conditions.

3) The accessory-mineral ring plays a significant role in restraining the intrusion of bentonite, and its influence degree becomes more pronounced as the width of the accessory-mineral ring increases.

4) In comparison to the smooth acrylic fissures, the irregular fractures in the actual disposal repository will decrease the expansion force of bentonite and promote the development of mineral rings, both of which restrict the intrusion of bentonite.

5) Fracture water seepage restricts bentonite intrusion in the upper part of the specimen, while promoting it at the bottom. Additionally, fracture water seepage increases the width and proportion of accessory minerals, further impeding bentonite intrusion. The influence extent depends on the water velocity.

6) The predicted intrusion distance increases with increasing temperature.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LX: Conceptualization, Data curation, Investigation, Methodology, Supervision, Visualization, Writing–original draft. JY: Writing–review and editing. YY: Resources, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors LX, JY, and YY were employed by Ningbo Rail Transit Group Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Nie, Q., Wu, H., and Hou, J. (2021). The attachment-detachment mechanism of ionic/nanoscale/microscale substances on quartz sand in water. Powder. Technol. 394, 1158–1168. doi:10.1016/j.powtec.2021.09.051

CrossRef Full Text | Google Scholar

Bai, B., Xu, T., Nie, Q., and Li, P. (2020). Temperature-driven migration of heavy metal Pb2+ along with moisture movement in unsaturated soils. Int. J. Heat. Mass. Tran. 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Baik, M. H., Cho, W. J., and Hahn, P. S. (2007). Erosion of bentonite particles at the interface of a compacted bentonite and a fractured granite. Eng. Geol. 91 (2-4), 229–239. doi:10.1016/j.enggeo.2007.02.002

CrossRef Full Text | Google Scholar

Börgesson, L., and Sandén, T. (2006). “Piping and erosion in buffer and backfill materials,” in Current knowledge.

Google Scholar

Borrelli, R. A., Thivent, O., and Ahn, J. (2013). Parametric studies on confinement of radionuclides in the excavated damaged zone due to bentonite type and temperature change. Phys. Chem. Earth. 65, 32–41. doi:10.1016/j.pce.2013.05.013

CrossRef Full Text | Google Scholar

García-García, S., Jonsson, M., and Wold, S. (2006). Temperature effect on the stability of bentonite colloids in water. Interf. Sci. 298 (2), 694–705. doi:10.1016/j.jcis.2006.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasan, K., Jaya, R. P., and Yahaya, F. M. (2024). Application of bentonite in cement-based composites: a review of current status, challenges and future prospects. J. Build. Eng. 98, 111171. doi:10.1016/j.jobe.2024.111171

CrossRef Full Text | Google Scholar

Hiemenz, P. C. (1986). Principles of colloid and surface chemistry. New York and Basel: Marcel Dekker, Inc.

Google Scholar

Huang, Y. Y., and Chen, B. (2019). Intrusion behaviors of highly compacted bentonite into host-rock fractures in a HLW disposal repository. Chin. J. Rock. Mech. Eng. 38 (12), 2561–2569. doi:10.13722/j.cnki.jrme.2019.0198

CrossRef Full Text | Google Scholar

Hubbard, J. B., and Douglas, J. F. (1993). Hydrodynamic friction of arbitrarily shaped Brownian particles. Phys. Rev. E, 47 (5), R2983. doi:10.1103/PhysRevE.47.R2983

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Z. (2015). Study on the optimum ratio determination for highly compacted GMZ01 bentonite-sand mixtures. Shanghai, China: Tongji University (Master's dissertation).

Google Scholar

Kanno, T., Iwata, Y., and Sugino, H. (2011). Modelling of bentonite swelling as solid particle diffusion. Clay. Sci. Eng., 561–570.

Google Scholar

Kanno, T., and Wakamatsu, H. (1991). “Experimental study on bentonite gel migration from a deposition hole,” in Proceedings of the third international conference on nuclear fuel reprocessing and waste management.

Google Scholar

Kanno, T., Wakamatsu, K., and Sugino, H. (1999). “Evaluation of extrusion and erosion of bentonite buffer,” in Proc 7th int conf on radioactive waste management and environmental remediation (ICEM’99).

Google Scholar

Karnland, O., Olsson, S., and Nilsson, U. (2006). Mineralogy and sealing properties of various bentonites and smectite-rich clay materials (No. SKB-TR--06-30). Swedish Nuclear Fuel and Waste Management Co.

Google Scholar

Kozeny, J. (1927). Ueber kapillare leitung des wassers im boden. Akad. Wiss. Wien 136, 271–306.

Google Scholar

Komine, H., and Ogata, N. (2003). New equations for swelling characteristics of bentonite-based buffer materials. Can. Geotech. J. 40, 460–475. doi:10.1139/t02-115

CrossRef Full Text | Google Scholar

Liu, L., Moreno, L., and Neretnieks, I. (2009). A dynamic force balance model for colloidal expansion and its DLVO-based application. Langmuir 25 (2), 679–687. doi:10.1021/la8026573

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L. C. (2013). Prediction of swelling pressures of different types of bentonite in dilute solutions. Colloid. Surf. A 434 (Complete), 303–318. doi:10.1016/j.colsurfa.2013.05.068

CrossRef Full Text | Google Scholar

Liu, L. C., Neretnieks, I., and Moreno, L. (2011). Permeability and expansibility of natural bentonite mx-80 in distilled water. Phys. Chem. Earth. 36 (17-18), 1783–1791. doi:10.1016/j.pce.2011.07.009

CrossRef Full Text | Google Scholar

Moreno, L., Liu, L., and Neretnieks, I. (2011). Erosion of sodium bentonite by flow and colloid diffusion. Phys. Chem. Earth. 36 (17-18), 1600–1606. doi:10.1016/j.pce.2011.07.034

CrossRef Full Text | Google Scholar

Nguyen, T. S., Börgesson, L., Chijimatsu, M., Hernelind, J., Jing, L., Kobayashi, A., et al. (2009). A case study on the influence of THM coupling on the near field safety of a spent fuel repository in sparsely fractured granite. Environ. Geol. 57, 1239–1254. doi:10.1007/s00254-008-1565-9

CrossRef Full Text | Google Scholar

Petsev, D. N., Starov, V. M., and Ivanov, I. B. (1993). Concentrated dispersions of charged colloidal particles: sedimentation, ultrafiltration and diffusion. Colloid. Surf. A 81, 65–81. doi:10.1016/0927-7757(93)80235-7

CrossRef Full Text | Google Scholar

Pusch, R. (1983). Stability of bentonite gels in crystalline rock–physical aspects. SKBF/SKB Tech. Rep.

Google Scholar

Reid, C., Lunn, R., El Mountassir, G., and Tarantino, A. (2015). A mechanism for bentonite buffer erosion in a fracture with a naturally varying aperture. Mineral. Mag. 79 (6), 1485–1494. doi:10.1180/minmag.2015.079.6.23

CrossRef Full Text | Google Scholar

Schanz, T., and Al-Badran, Y. (2014). Swelling pressure characteristics of compacted Chinese Gaomiaozi bentonite GMZ01. Soils. Found. 54 (4), 748–759. doi:10.1016/j.sandf.2014.06.026

CrossRef Full Text | Google Scholar

Sridharan, A., and Jayadeva, M. S. (1982). Double layer theory and compressibility of clays. Geotechnique 32, 133–144. doi:10.1680/geot.1983.33.4.461

CrossRef Full Text | Google Scholar

Sun, D. A., Zhang, L., Li, J., and Zhang, B. (2015). Evaluation and prediction of the swelling pressures of gmz bentonites saturated with saline solution. Appl. Clay. Sci. 105 (mar), 207–216. doi:10.1016/j.clay.2014.12.032

CrossRef Full Text | Google Scholar

Vanapalli, S. K., Fredlund, D. G., and Pufahl, D. E. (2001). Influence of soil structure and stress history on the soil-water characteristics of a compacted till. Géotechnique 51 (6), 573–576. doi:10.1680/geot.51.6.573.40456

CrossRef Full Text | Google Scholar

Wen, Z. J. (2006). Physical property of China’s buffer material for high-level radioactive waste repositories. Chin. J. Rock. Mech. Eng. 25 (4), 794–800. doi:10.3321/j.issn:1000-6915.2006.04.014

CrossRef Full Text | Google Scholar

Wu, H., Bai, B., and Liu, J. (2024a). Temperature-driven coupled transport of pollutants and suspended particles established by granular thermodynamics. Int. J. Heat Mass Transf. 228, 125645. doi:10.1016/j.ijheatmasstransfer.2024.125645

CrossRef Full Text | Google Scholar

Wu, H., Bai, B., and Zhou, R. (2024b). A coupled transport model of pollutants-suspended particles in saturated porous media based on granular thermodynamics. Chem. Eng. Res. Des. 203, 442–452. doi:10.1016/j.cherd.2024.01.059

CrossRef Full Text | Google Scholar

Xu, L. B., Ye, W. M., Liu, Z. R., Wang, Q., and Chen, Y. G. (2022). Extrusion behavior of bentonite-based materials considering pore size and sand content effects. Construc. Build. Mater. 347, 128580. doi:10.1016/j.conbuildmat.2022.128580

CrossRef Full Text | Google Scholar

Xu, Y. F. (2017). Mechanisms and models for bentonite erosion used for geologic disposal of high level radioactive waste: a review. Adv. Earth. Sci. 32 (10), 1050. doi:10.11867/j.issn.1001-8166.2017.10.1050

CrossRef Full Text | Google Scholar

Yang, G. S., Bai, B., Chen, W. X., Mao, H. T., Liu, Z. H., and Lan, X. L. (2024). Experimental study on heat conduction and water migration of composite bentonite samples. Chin. J. Geotech. Eng. 46 (S2), 161–165. doi:10.11779/CJGE2024S20024

CrossRef Full Text | Google Scholar

Ye, W. M., Xu, L. B., Wang, Q., and Chen, Y. G. (2022). Bentonite-sand mixture intrusion process and its model in rock fissures with consideration of lateral wall friction. Chin. J. Geotech. Eng. 4, 044.

Google Scholar

Zhou, R., Bai, B., Chen, L., Zong, Y., and Wu, N. (2024). A granular thermodynamic constitutive model considering THMC coupling effect for hydrate-bearing sediment. Ocean. Eng. 310, 118689. doi:10.1016/j.oceaneng.2024.118689

CrossRef Full Text | Google Scholar