A comprehensive review of yttrium aluminum nitride: crystal structure, growth techniques, properties, and applications

YAlN has emerged as a wide band gap semiconductor with high potential to compete with ScAlN in industrial applications. Theoretical predictions about YAlN’s material properties have been the main motivation for conducting experimental investigations and verify simulated results. However, several challenges have been faced in experimental studies on YAlN that contradict theoretical data, especially when trying to reach higher alloy concentrations. This work presents a systematic review analyzing different material properties including structural characterization, elastic properties, and thermal features. It combines all available experimental data on the growth and reported material parameters, such as band gap, lattice parameters, and electrical properties with the aim of introducing a new motivation to further study YAlN’s potential in various fields of device applications. The review provides a comprehensive overview on the current state of knowledge on YAlN, highlighting the discrepancies between theoretical predictions and experimental results. By providing information from multiple studies, this work offers valuable insights into the challenges and opportunities associated with YAlN development, paving the way for future research directions and potential industrial applications of this promising wide band gap semiconductor.

1 Introduction

Over many years, group III-nitrides have been widely used in various types of electronic and optoelectronic devices. These materials are semiconductors with direct band gaps ranging from 0.7 eV for InN to 6.2 eV for AlN (Monemar et al., 2005; Edgar et al., 1990). Due to the great number of possible applications, group III-nitrides have gained significant attention in recent years. The possibility of forming ternary alloys, such as AlGaN or AlInN, allows for the tuning of the band gap of these compounds, making them potential candidates for optical applications (Pelá et al., 2011). One of the outstanding materials within the group III-nitrides is AlN, which due to its notable properties has been extensively utilized in acoustic, electronic, and optical devices. AlN owns a wide band gap (6.2 eV) (Edgar et al., 1990), high spontaneous polarization and break down voltage (1.351 $\frac{\mathrm{C}}{{\mathrm{m}}^2}$ and 4–10 $\frac{\text{MV}}{\text{cm}}$, respectively) (Dreyer et al., 2016; Ruemenapp and Peier, 1999), high thermal conductivity (321 $\frac{\mathrm{W}}{\mathrm{m}.\mathrm{K}}$) (Cheng et al., 2020), and high thermal stability (T_m = 2200°C) (Berger, 1996). Due to its widespread use, numerous theoretical and experimental studies have been conducted on AlN.

One of the most important physical properties of AlN for applications is piezoelectricity. Piezoelectric materials are crucial components in microelectromechanical systems (MEMS) and are widely utilized in acoustic devices (BAW and SAW), radio frequency (RF) systems, and sensors. Beside AlN, a variety of piezoelectric materials exists, including lead zirconated titanite (PZT), quartz (SiO₂), zinc oxide (ZnO), and lithium niobite (LiNbO₃). Despite its lower piezoelectric coefficient, AlN has been extensively employed in device applications. The primary reasons for this preference include its high stiffness and sound velocity in addition to its ease of growth, high thermal stability, and compatibility with CMOS technology (Shelton et al., 2009). However, the relatively low piezoelectric coefficient of AlN (d₃₃ $\cong$ 5 $\frac{\text{pC}}{\mathrm{N}}$) remains a significant limitation for further improving device efficiency (Zhang M. et al., 2015).

In 2009, Akiyama et al. (2009) demonstrated that alloying AlN with the transition metal nitride ScN can significantly enhance its piezoelectric properties. For Al_0.6Sc_0.4N, an increase in the piezoelectric coefficient d₃₃ of up to 25 $\frac{\text{pC}}{\mathrm{N}}$ (approximately 400% improvement) was reported (Akiyama et al., 2009). This discovery opened up potential applications for Sc_xAl_1-xN alloys in various acoustic devices. Furthermore, in 2019, Fichtner et al. reported the first observation of ferroelectric properties in Sc_xAl_1-xN thin films (Fichtner et al., 2019). This discovery provides a wide range of potential applications for ferroelectric nitrides, such as non-volatile memory devices, ferroelectric resistive memory, and optical and tunable microwave components (Setter et al., 2006). Due to its high potential for device applications, numerous theoretical and experimental studies have been conducted on Sc_xAl_1-xN. Various growth techniques have been employed to produce this ternary alloy, such as sputtering (Akiyama et al., 2009), metal organic chemical vapor deposition (MOCVD) (Leone et al., 2019), and molecular beam epitaxy (MBE) (Hardy et al., 2017). Despite its outstanding properties and high potential in electromechanical devices, a significant drawback for the commercial implementation of Sc_xAl_1-xN is the high cost Sc, a rare earth material. Consequently, extensive researches have been undertaken to identify potential substitutes for Sc in this alloy system. One promising alternative of ScN as an alloying element for AlN is Yttrium Nitride (YN). Y belongs to the same group in the periodic table of elements as Sc, resulting in similar electronic configuration of their outer most shell, with Y having only one higher principle quantum number. This similarity leads to comparable chemical properties for both elements and their compounds. Notably, the cost of Y is approximately 100 times lower than that of Sc (ISE, 2024), making it a more economically viable option. Furthermore, Y has already found widespread use in industrial products, such as application of Y₂O₃ in LEDs, which could facilitate its implementation in commercial devices (Loewen, 2024). Theoretical and experimental studies have been conducted to investigate the structure and material properties of Y_xAl_1-xN. Computational predictions suggest that Y_xAl_1-xN exhibits similar trends in band gap, electrical, and optical parameters as Sc_xAl_1-xN (Žukauskaitė, 2012). From a structural perspective and based on thermodynamic calculations, Y_xAl_1-xN is expected to maintain its wurtzite structure up to a Y concentration of approximately x = 0.75. This high stability of the wurtzite phase could potentially lead to further enhanced piezoelectric coefficients, thus offering greater potential for applications in acoustic devices (Zukauskaite et al., 2012; Manna et al., 2017; Xie et al., 2020).

Despite the rapid progress in studies concerning Y_xAl_1-xN, to the best of the author’s knowledge, there has been no systematic review article that consolidates all available data on this material. This review article aims to provide a comprehensive and detailed overview of the advancements made in the research of Y_xAl_1-xN in recent years. The first three sections will discuss theoretical calculations and predictions related to the formation, structural, elastic, and thermal properties of Y_xAl_1-xN. Following this, various methods developed for the growth of Y_xAl_1-xN will be examined, along with experimental structural parameters. In section five, the article will present available data on material properties such as band gap, permittivity, piezoelectric coefficient, and spontaneous polarization. The subsequent section will explore potential device applications, and finally, the last section will summarize all data and discussions. This comprehensive review seeks to serve as a valuable resource for researchers and engineers interested in Y_xAl_1-xN and its applications.

2 From AlN to YN: structural analysis

AlN and YN are binary compounds composed of nitrogen atoms bonded to metal atoms (Al or Y). In binary compounds, nitrogen and metal atoms form stacks of monolayers (Sahin et al., 2009). However, in the alloys like Y_xAl_1-xN, the metal atoms (Y and Al) distribute randomly in the metal monolayers, with nitrogen atoms binding to either Al or Y atoms to form the crystal lattice. These compounds are referred to as ternary or pseudo binary systems. A ternary compound is made up of three different elements. Thus, it can apply to YAlN or ScAlN as they consist three distinct elements. On the other hand, a pseudo binary compound is a compound which is treated as a binary system, although it involves more than two elements. This approach is often utilized in order to simplify the properties by reducing the system into two effective components, in this case Y(Sc)N and AlN. Thus, the alloy can be viewed as a mixture of two binary nitrides. In this work, the alloy is referred to as a ternary system, and the fraction of Y is denoted by x, with the ratio of Y to Al atoms equal to $\frac{x}{1-x}.$

AlN crystallizes in the hexagonal wurtzite structure (P6₃mc space group) under ambient conditions (Siegel et al., 2006). The electronic configuration of Al ($1s^{2}2s^{2}2p^{6}3s^{2}3p^1$) and N ($1s^{2}2s^{2}2p^3$) atoms play a crucial role in bond formation. During AlN crystal formation, Al atoms undergo $3s{p}^3$ hybridization, while N excites to $2s^2{p}^3$ hybridization state (Cunha et al., 2022). This results in covalent bonds between the semi-complete sublevels of Al and N atoms, as well as an additional ionic bond between the complete sublevel of the N and the empty sublevel of Al. The covalent bonds in AlN have a length of $l_1=1.89\AA$ and form a tetrahedron with the angle of $110.5°$. The ionic bond has the length of $l_2=1.92\AA$, with an angle of $107.7°$ between the covalent and ionic bonds. Each N atom binds with four Al atoms, creating another tetrahedron and forming the wurtzite crystal structure. The unit cell of AlN consists of 14 N and Al atoms (Cunha et al., 2022). A schematic of the wurtzite unit cell of AlN is shown in Figure 1.

Figure 1

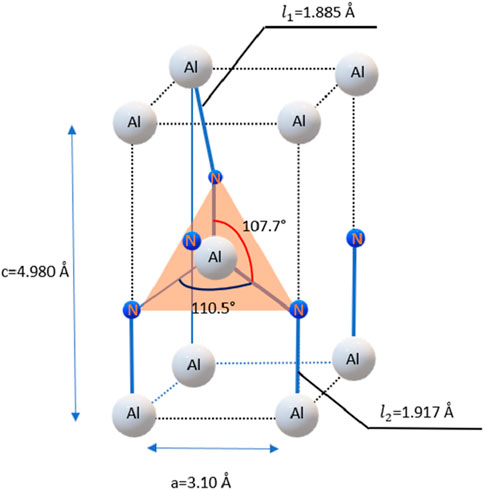
Figure 1. Crystal structure and lattice parameters of AlN. The lattice parameters and bond lengths are taken from (Cunha et al., 2022).

Additional to the stable wurtzite structure, theoretical studies have investigated the properties of rock salt, zinc blende, and layered hexagonal AlN (Ahmed and Sharma, 2021; Louhibi-Fasla et al., 2014). For small layer thicknesses of a few monolayers, calculations suggest that layered hexagonal AlN has a lower configuration energy compared to other structures (Louhibi-Fasla et al., 2014). This layered hexagonal form was experimentally observed by Tsipas et al in 2013 (Tsipas et al., 2013). Zinc blende AlN is stable only at very small thicknesses before transforming to the wurtzite structure (Hultman et al., 1992). Simulations predict a direct band gap of 3.44 eV (at Γ point) for layered hexagonal AlN (Bacaksiz et al., 2015), while the Zinc blende structure shows a bandgap of approximately 3.24 eV (Γ-X) at zero pressure (Silva et al., 2005). Ueno et al. (1992) has demonstrated that under high pressure (22.0 GPa), wurtzite AlN can transform into the cubic rock salt phase [NaCl (B1)]. In high pressure condition, AlN exhibits a band gap of 4.04 eV (Γ-X) (Ahmed and Sharma, 2021). The properties of different AlN structures are summarized in Table 1, providing a comprehensive overview of the material’s structural variations and their associated electronic properties.

Table 1

Table 1. Structural properties and band gap of different crystal structures of AlN and YN.

Transition metal nitrides have various commercial applications, with ScN receiving significant attentions in recent years due to its potential in semiconductor technologies (Eklumd et al., 2016; Adamski et al., 2019). Given the electronic similarities between Sc and Y atoms, similar potential is expected for YN. The high thermal stability and melting temperature of transition metal nitrides also enable the formation of single crystals through annealing (Hultman, 2000). Theoretical calculations have predicted several interesting properties for YN, including strong anisotropic mechanical and electronic characteristics, as well as ferroelastic properties (Xu et al., 2018). Density Functional Theory (DFT) calculations indicate that the formation enthalpy of rock salt YN is lower than that of its hexagonal structure (Rowberg et al., 2021), suggesting that YN is expected to crystallize in the rock salt phase under ambient conditions. In its rock salt structure, YN exhibits an indirect band gap in the range of 0.9–1.3 eV (Rowberg et al., 2021; Liu et al., 2014; Ramirez-Montes et al., 2016). The calculated lattice parameter for rock salt YN is $a=4.88\AA$ (Rowberg et al., 2021). Notably, like ScN, YN is highly unstable in the wurtzite structure (Rowberg et al., 2021).

The first reports on the synthesis of YN dates back to 1950s, when Kempter et al. (1957) described the production of YN powder by converting metallic Y to YH₂ and then heating it up to 900°C in nitrogen environment. In recent years, researchers have reported growing YN on various substrates using techniques such as magnetron sputtering and metal organic chemical vapor deposition (Gregoire et al., 2008; Leone et al., 2023). However, the growth of YN has consistently presented challenges due to the high degree of oxidation observed in thin layers (Žukauskaitė, 2012; Leone et al., 2023). This oxidation issue results in n-type conduction in YN layers, more pronounced compared to that observed in ScN thin films (Rowberg et al., 2021; Biswas and Saha, 2019; Deng et al., 2015). To address this oxidation problem, researchers have found that using a protective passivation layer is important for YN applications. Specifically, the use of AlN as a passivation layer has shown positive results in reducing oxidation of YN thin layers (Gregoire et al., 2008). Despite the experimental instability of YN in structures other than rock salt, theoretical studies have investigated the structural parameters of alternative crystalline phases for YN, including wurtzite, zinc blende, and layered hexagonal phases (Mancera et al., 2003; Rowberg et al., 2021). The structural parameters for these different phases of YN, along with corresponding data for AlN, are summarized in Table 1.

DFT calculations have provided valuable insights into the mixing enthalpies and phase stability of Y_xAl_1-xN alloys across different compositions (Žukauskaitė, 2012; Manna et al., 2017; Xie et al., 2020). The calculations reveal that the wurtzite phase of Y_xAl_1-xN remains stable up to a high Y concentration of x = 0.75. Manna et al. (2017) calculated a temperature-composition phase diagram for the full range of Y_xAl_1-xN compositions, indicating a region between x = 0.2 and x = 0.9 were mixing enthalpies are not achievable under thermodynamic equilibrium. It is hypothesized that non-equilibrium growth techniques, such as reactive DC magnetron sputtering, could potentially overcome these thermodynamic limitations and enable the growth of compositions within this range.

The predictions for potential applications of wurtzite Y_xAl_1-xN, such as high piezoelectric coefficient $d_{33}$ with increasing Y content, provide strong motivation for thorough studies on the structural properties and type of phase transition of these alloys at high concentrations. The transition from wurtzite to the rock salt structure in materials like AlN and YN has been extensively studied both theoretically and experimentally. Corll initially described this transition using a continual deformation model (Corll, 1967), while Sowa later developed a more general crystallographic model that explained the transformation mechanism without breaking any bonds (Sowa, 2001). Several advanced models have since been generated from both experimental and theoretical data (Knudson and Gupta, 1998; Tolbert and Alivisatos, 1995; Wilson and Madden, 2002). In the wurtzite structure, two key structural parameters are the internal parameter $u$, which indicates the relative positions of metal and nitrogen atoms, and the $\frac{c}{a}$ ratio of lattice parameters. During the transition from wurtzite to rock salt, the internal parameter changes from approximately 0.38–0.50, while the $\frac{c}{a}$ ratio changes from about 1.6 to 1. This transformation process results in an intermediate layered hexagonal phase. In this intermediate structure, atoms are located in lateral planes, and the bond angles between the metal and nitrogen atoms in this plane is 60°. The final transition from the layered hexagonal to the rock salt phase involves a change in bond angles from 60° to 90°, with atoms moving horizontally within the lateral planes (Wilson and Madden, 2002). Based on calculations shown in Figure 2 for the mixing enthalpy of AlN and YN, the formation of a layered hexagonal intermediate lattice has not been predicted for Y_xAl_1-xN. Due to lack of experimental data at high Y concentrations, it has not been possible to draw conclusions about the formation of an intermediate phase and the nature of the phase transition in this system. In contrast, for Sc_xAl_1-xN, many studies initially predicted the formation of a layered hexagonal structure during the phase transition (Farrer and Bellaiche, 2002; Talley et al., 2018; Zhang et al., 2013; Furuta et al., 2021). However, recent experimental data have shown that the phase transition in Sc_xAl_1-xN occurs at around x = 0.45–0.5, with the crystalline structure changing directly from wurtzite to rock salt without an intermediate phase (Mihalic et al., 2023). Interestingly, as seen in Figure 2, the mixing enthalpies of different structures of Y_xAl_1-xN have close values in the range $x$ = 0.65 to $x$ = 0.80. This suggests that in this composition range, various growth parameters that can affect film strain, particularly the choice of the substrate and buffer layer, may have a significant effect on the resulting crystal structure (Afshar et al., 2024).

Figure 2

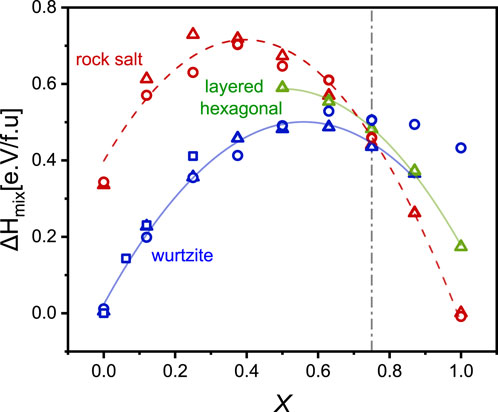
Figure 2. Mixing enthalpies of wurtzite (blue symbols), layered hexagonal (green symbols), and rock salt (red symbols) structures of Y_xAl_1-xN acquired from different literature (Zukauskaite et al., 2012; Manna et al., 2017; Xie et al., 2020). Lines are polynomial fits to the data point for guiding the eye.

During the formation of Y_xAl_1-xN, beside Al atoms, Y atoms, which have an atomic radius approximately 1.3 times larger than Al ($\left.r_Y=212\text{\hspace{0.17em}pm},r_{Al}=118\text{\hspace{0.17em}pm}\right)$ (Clementi et al., 1967) are incorporated into the crystal lattice. As the Y concentration ($x$) increases, more Y atoms participate in the lattice, leading to an increase in the bond length between metal and nitrogen atoms and consequently, an expansion of the lattice parameters (Žukauskaitė, 2012; Ramirez-Montes et al., 2016). The calculation of lattice parameters for wurtzite Y_xAl_1-xN and their comparison with Vegard’s law has been performed for both $a$ and $c$ lattice parameters (Žukauskaitė, 2012; Manna et al., 2017; Xie et al., 2020; Mayrhofer et al., 2015a; Assali et al., 2021), as illustrated in Figure 3A. Ramirez-Montes et al. (2016) simulated the $a$ and $c$ lattice parameters of wurtzite Y_xAl_1-xN and reported behavior similar to that of the lattice parameters in rock salt Y_xAl_1-xN. They calculated bowing parameters of - 0.262 Å for the $a$ lattice parameter, and - 0.483 Å for the $c$ lattice parameter in wurtzite Y_xAl_1-xN. Interestingly, the lattice parameters of wurtzite Y_xAl_1-xN exhibit less deviation from Vegard’s law compared to the rock salt structure. This smaller deviation is attributed to the closer values of lattice constants in the wurtzite structure of binary compounds (AlN and YN) compared to their rock salt counter parts (Ramirez-Montes et al., 2016).

Figure 3

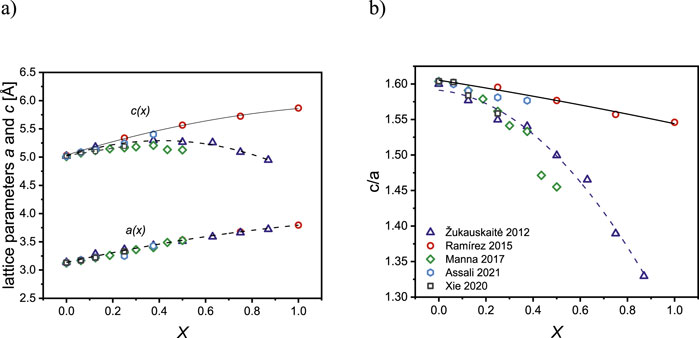
Figure 3. (A) Theoretical lattice parameters, and (B) their ratios for wurtzite Y_xAl_1-xN reported by Ramirez-Montes et al. (2016) (red circles), Zukauskaite et al. (2012) (blue triangles), Manna et al. (2017) (green rhombus), Assali et al. (2021) (blue rhombus), and Xie et al. (2020) (black squares). Dashed lines are the polynomial fits to the data ponits assuming a phase transition from wurtzite to rock salt, and solid lines are the polynomial fit to the data points provided by Ramirez et al. with the assumption of the stability of the wurtzite structure in the whole concentration range.

For alloys that maintain the wurtzite structure throughout the entire composition range, such as Ga_xAl_1-xN and In_xAl_1-xN, both lattice parameters $a$ and $c$ rise with increasing alloy concentration (Ambacher et al., 2021). For alloys that undergo phase transition, like Sc_xAl_1-xN, the behavior of the lattice parameters differs significantly. In these cases, the $c$ lattice parameter initially increases but begins to decrease as the phase transition approaches. At this critical point, the formation of an intermediate layered hexagonal structure is predicted, while the $a$ lattice parameter increases in a manner similar to that observed in the rock salt structure. The structural transition from wurtzite (β-ZnS) to layered hexagonal (lh-MgO) and rock salt (NaCl) structures is characterized by a continuous decrease in the ratio of the lattice parameters, $\frac{c}{a}$ (Ambacher et al., 2021).

The calculated $c$ to $a$ ratio for wurtzite Y_xAl_1-xN are illustrated in Figure 3B. The data points from Ramirez-Montes et al. (2016)’s calculations show only a slight decrease in the $\frac{c}{a}$ ratio, which is attributed to their assumption of a stable wurtzite structure across the entire concentration range. In contrast, calculations by Zukauskaite et al. (2012) indicate a more significant decrease of $\frac{c}{a}$ ratio, dropping from 1.603 for AlN to 1.39 for Y_0.75Al_0.25N. For rock salt Y_xAl_1-xN, the ratio of the lattice parameters in an unstrained lattice reduces to $\frac{a_{\parallel }}{a_{\perp }}=1$. However, there is currently no experimental data available to validate theoretical prediction regarding the phase transition of Y_xAl_1-xN.

The highest reported Y concentration in sputtered Y_xAl_1-xN films is around x = 0.7 to x = 0.8 (Afshar et al., 2024). However, experimental studies have faced challenges in maintaining a high-quality wurtzite structure above x = 0.4, with possible amorphization occurring at higher concentration (Afshar et al., 2024), a discrepancy that has not been fully addressed in theoretical predictions. As shown in Figure 2, calculations consistently predict the wurtzite phase to be stable for x < 0.7, while above x = 0.75, the rock salt structure becomes energetically favorable. Previous research conducted by our group has identified amorphization as a limiting factor for maintaining Y_xAl_1-xN at concentrations close to the predicted phase transition. This issue posed significant challenges in achieving the desired structural integrity at higher Y concentrations. These findings highlight both the potential and challenges in synthesizing Y_xAl_1-xN alloys across a wide composition range, emphasizing the need for further research to bridge the gap between theoretical predictions and experimental realities.

For the cubic rock salt structure, the calculated lattice parameter for AlN is 4.085 Å (Ahmed and Sharma, 2021) and for YN is 4.88 Å (Rowberg et al., 2021). To the authors’ knowledge, the only available data for rock salt Y_xAl_1-xN over the entire compositional range are those obtained by Ramirez-Montes et al. (2016), where they compared the calculated $a$ lattice parameters of the rock salt phase with the predictions from Vegard’s law. Their results showed that the equilibrium lattice parameters vary non-linearly with Y concentration ($x$), deviating from Vegard’s law with an upward bowing parameter of - 0.203 Å. The calculated data for the binary compounds (AlN and YN) showed good agreement with the experimental values.

3 Elastic properties of Y_xAl_1-xN

The knowledge of mechanical and elastic parameters is crucial for understanding different physical phenomena, such as stiffness, stability, elastic anisotropy, and properties relevant to device application like electroacoustic devices. The relation between stress and strain in a crystal is defined by the Hook’s law, expressed as in Equation 1:

$\mathit{\epsilon }=\mathit{S}\mathit{\sigma }(1)$

where $S$ is the elastic compliance. This equation can also be written in terms of elastic stiffness, $C$ as in Equation 2:

$\mathit{\sigma }=\mathit{C}\mathit{\epsilon }(2)$

Given the elastic properties of crystals are directionally dependent, it is essential to define a standard orthogonal system. For hexagonal crystals, the standard axes are defined as $x:\left[2\overline{11}0\right],y:\left[01\overline{1}0\right]$, and $z:\left[0001\right]$ (Nye, 1985; Tromans, 2011) The elastic coefficients are described using Voigt’s notation as $S_{mn},C_{mn}\left(m,n=1,\dots ,6\right)$ (Voigt, 1910). Using this notation, the Hook’s law can be rewritten as shown in Equation 3:

${\mathit{\sigma }}_{\mathit{m}}={\displaystyle \sum _{\mathit{n}}}{\mathit{C}}_{\mathit{m}\mathit{n}}{\mathit{\epsilon }}_{\mathit{n}}(3)$

For describing the elastic properties in hexagonal crystals, only 5 independent stiffness coefficients are required due to their transverse isotropy, which means the elastic properties remain invariant under rotation around the z-axis (Mouhat and Coudert, 2014). This leads to equalities such as $C_{11}=C_{22},C_{44}=C_{55}$, $C_{13}=C_{22}$, and $C_{66}=\frac{1}{2}\left(C_{11}-C_{12}\right)$. Various studies have reported calculated elastic constants for different concentrations of wurtzite Y_xAl_1-xN, summarized in Table 2. Among the elastic coefficients, $C_{11}$ shows the highest value. As the concentration of Y atoms in the crystal increases, the values of $C_{11},C_{12},C_{33},$ and $C_{44}$ decreases, while $C_{13}$ increases. Based on the Born mechanical stability criteria and the calculated elastic coefficients, wurtzite Y_xAl_1-xN is considered mechanically stable (Nye, 1985). Using the elastic coefficients and Voigt-Reus-Hill approximation (Hill, 1952; Reuss, 1929), polycrystalline elastic moduli, such as bulk or shear modulus can be calculated.

Table 2

Table 2. Calculated stiffness coefficients for Y_xAl_1-xN.

For hexagonal crystals, these parameters can be calculated using stiffness coefficients (Nye, 1985). Several theoretical calculations are available for bulk and shear moduli of wurtzite Y_xAl_1-xN (Ramirez-Montes et al., 2016; Assali et al., 2021; Laidoudi et al., 2022). All data show a decrease of the elastic moduli as the Y concentration increases, which is a result of the change in the bond angels. The only available data on the elastic properties of rock salt Y_xAl_1-xN is the bulk modulus provided by Ramirez-Montes et al. (2016). Based on the available data, the bulk modulus of the rock salt structure has higher values compared to the hexagonal Y_xAl_1-xN. The higher coordination number and structural uniformity of the rock salt crystal are the main reasons for these higher values (Ambacher et al., 2023). However, in both crystal systems, the lattice softening occurs as Y content increases. Similar behavior has also been reported for Sc_xAl_1-xN (Ambacher et al., 2023). Figure 4 represents the bulk modulus of hexagonal and rock salt structures of Y_xAl_1-xN as a function of Y concentration.

Figure 4

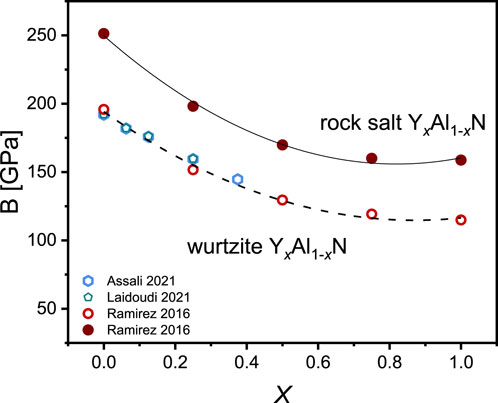
Figure 4. Theoretical bulk modulus of wurtzite and rock salt Y_xAl_1-xN reported by Ramirez-Montes et al. (2016) (filled and unfilled red circles), Assali et al. (2021) (blue rhombus), and Laidoudi et al. (2026) (green rhombus).

Further understanding of the elastic properties of Y_xAl_1-xN can be achieved by calculating the elastic compliance coefficients, which allows for the determination of useful elastic properties such as Young’s modulus, shear modulus, and Poisson’s ratio. The relationship between stiffness and compliance coefficients was established by Wei et al. (2019). Using this relationship and the stiffness coefficients calculated by Assali et al. (2021), the compliance coefficients of Y_xAl_1-xN were calculated and are shown in Figure 5. Notably, within the studied concentration range (x < 0.4), no extreme changes in compliance coefficients were observed, suggesting that the alloy is still far from its structural phase transition point. For Sc_xAl_1-xN, Ambacher et al. (2023) observed an extreme change in $S_{33}$ as the alloy approached the wurtzite to rock salt phase transition. The alloying process involves competition between Al and Y (or Sc) atoms for binding with nitrogen, which intensifies as the concentration of alloying atoms increases. Near the critical composition for structural transition, the crystal becomes highly sensitive to external forces, manifesting as extreme changes in elastic coefficients (Ambacher et al., 2023).

Figure 5

Figure 5. Calculated compliance coefficients of wurtzite Y_xAl_1-xN based on the stiffness coefficients simulated by Assali et al. (2021).

Young’s modulus is a material-specific property defined as the ratio of tensile stress $\left(\sigma \right)$ to tensile strain $\left(\epsilon \right)$, providing information about the materials’ deformability. In a crystal system, the Young’s modulus for an arbitrary crystal plane $E_{hkil},$ is defined as the ratio of stress to strain in the direction normal to the crystal plane $\left(hkil\right)$. The directional dependence of Young’s modulus in a hexagonal crystal system can be calculated using the compliance coefficients, $S_{mn},$ and as a function of the angle $\left(\theta \right)$ between the normal to the crystal plane and the axis [0001]. In hexagonal crystals, Young’s modulus is independent of the azimuth angle $\left(\phi \right)$ due to the six-fold rotation axis along [0001] (Gorodtsov and Lisovenko, 2019). This symmetry results in $E_{hkil}$ being solely dependent on the polar angle $\theta$. The polar angle can be defined using the following Equation 4 (Zhang et al., 2007):

$\mathbf{cos}\left(\mathit{\theta }\right)=\frac{\frac{\mathit{a}}{\mathit{c}}\mathit{l}}{\sqrt{{\mathit{h}}^{\mathbf{2}}+\frac{{\left(\mathit{h}+\mathbf{2}\mathit{k}\right)}^{\mathbf{2}}}{\mathbf{3}}+{\left(\frac{\mathit{a}}{\mathit{c}}\mathit{l}\right)}^{\mathbf{2}}}}(4)$

where $a$ and $c$ are lattice parameters, and $h,k,$ and $l$ are Miller-Bravis indices of the crystal plane.

Using the equations provided in previous studies (Zhang et al., 2007), a polar representation of the directional dependence of Young’s modulus can be generated for hexagonal crystals. These structures exhibit both rotational symmetry and mirror symmetry with respect to the [0001] axis, allowing the polar representation of elastic properties be limited to the interval $\theta =\left[0°,90°\right]$. The directional dependency of other elastic properties, such as Shear’s modulus and Poisson’s ratio, can also be calculated using the compliance coefficients and considering the symmetries in hexagonal structures. Utilizing the equations given in referenced works for directionally dependent elastic properties in hexagonal crystals (Tromans, 2011; Zhang et al., 2007), and employing the compliance coefficients derived from the stiffness coefficients simulated by Assali et al. (2021), the Young’s modulus, Shear’s modulus, and Poisson’s ratio of wurtzite Y_xAl_1-xN were calculated and are presented in Figures 6A–C. The elastic modulus of AlN in each graph are calculated based on different data sets of elastic coefficients, and the average values are depicted (Assali et al., 2021; Kazan et al., 2007; McNeil et al., 1993; Tsubouchi and Mikoshiba, 1985). The shade around the values related to AlN are the error range resulted from using various reported data sets, showing a deviation of approximately 5% between different calculations and experimental values. This error bar can also be expected for the calculated values related to Y_xAl_1-xN. The elastic modulus of Y_xAl_1-xN exhibit a softening of the crystal structure as the number of Y atoms increases, a trend also observed in wurtzite Sc_xAl_1-xN (Ambacher et al., 2023). Additionally, anisotropies are evident in the elastic’s moduli. For Young’s modulus, higher values are observed in the [01–10] direction for $x$ = 0, 0.0625, and 0.125. As the concentration increases to $x$ = 0.25 and 0.375, the value in the [0001] becomes larger. A similar trend is observed for the Shear’s modulus. However, considering the possible errors resulted from the simulation of elastic coefficient, these results need further investigation. For having a better conclusion on the behavior of elastic modulus, comparison between different simulated and experimental data is of great importance. Notably, the symmetrical behavior of Young’s modulus becomes more pronounced at higher concentrations. Poisson’s ratio, which describes the ratio of transverse strain to axial strain under uniaxial stress, shows high anisotropy in hexagonal crystal across the entire concentration range, as illustrated in Figure 6C. From $x$ = 0 to 0.25, the Poisson’s ratio exhibits higher values along the [01–10] axis, while at $x$ = 0.375, an opposite behavior is observed. These trends in elastic properties are similar to those reported for Sc_xAl_1-xN (Ambacher et al., 2023), suggesting commonalities in the mechanical behavior of these III-nitride alloys.

Figure 6

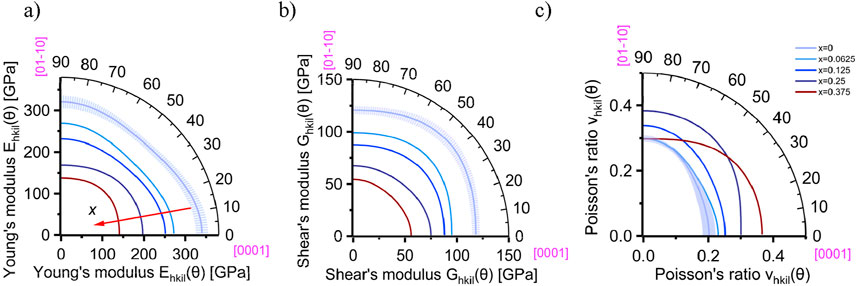
Figure 6. Calculated directional dependent elastic properties. (A) Young’s modulus, (B) Shear’s modulus, and (C) Poisson’s ratio of Y_xAl_1-xN represented in polar coordinates. The calculations for AlN were done using the elastic data set of stiffness coefficients simulated by Assali et al. (2021), Kazan et al. (2007), McNeil et al. (1993), and Tsubouchi and Mikoshiba, (1985) and the average value for each parameter, along with error bars is shown. The calculations for YAlN were done using the elastic data set of stiffness coefficients simulated by Assali et al. (2021).

Assali et al. (2021) have calculated the mass density and directional-dependent sound velocities in Y_xAl_1-xN crystals. The general relation between the sound velocities and stiffness coefficients is given by the following Equation 5, as (Ledbetter, 2006):

${\mathit{v}}_{\mathit{m}\mathit{n}}\left(\mathit{x}\right)=\sqrt{\frac{{\mathit{C}}_{\mathit{m}\mathit{n}}\left(\mathit{x}\right)}{\mathit{\rho }\left(\mathit{x}\right)}}(5)$

Where $\rho \left(x\right)$ is the crystal’s mass density. Sound velocity in different crystal directions is crucial for acoustic devices, making polar representation of longitudinal $\left(v_l\right)$, transversal $\left(v_t\right)$, and quasi-transversal $\left(v_{qt}\right)$ velocities particularly useful. This visualization helps in understanding the anisotropic nature of sound propagation in Y_xAl_1-xN crystals, essential for designing and optimizing acoustic devices. Figure 7 shows the polar representation of these sound velocities, calculated based on the data sets provided by Assali et al. (2021) for Y_xAl_1-xN. The calculations related to AlN are done using different sets of data for elastic coefficients and the average values are shown in the graphs, with the shaded area showing the error related to calculations based on different reported values (Kazan et al., 2007; McNeil et al., 1993; Assali et al., 2021; Tsubouchi and Mikoshiba, 1985). In the case of Y_xAl_1-xN, since the number of elastic data available is very limited, the calculations were done only using one data set (Assali et al., 2021). However, based on the different reported values for AlN, an error bar of approximately 5% can also be expected for the data related to Y_xAl_1-xN. The longitudinal sound velocities exhibit the highest value for all concentrations in Y_xAl_1-xN alloys. As Y concentration increases, all sound velocities decrease due to crystal softening. The longitudinal velocity ($v_l$) consistently shows the highest value along the [0001] axis. For transversal sound velocity, values in the basal plane exceed those along the c-axis [(0001)]. Notably, at 45°, the quasi-transversal sound velocity decreases significantly with increasing alloy concentration, indicating strong directional dependency.

Figure 7

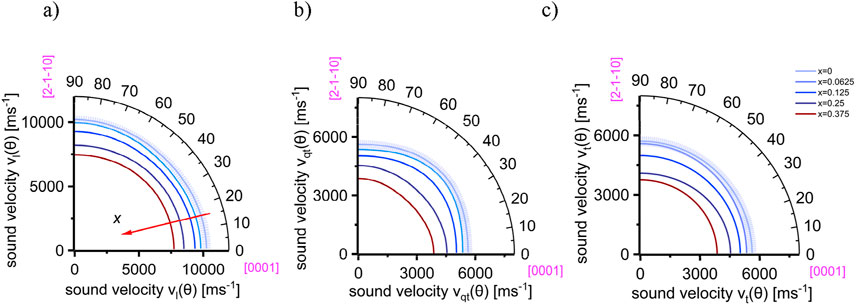
Figure 7. Calculated directional dependent sound velocities. (A) Longitudinal, (B) quasi-transversal, and (C) transversal sound velocities in Y_xAl_1-xN at different alloy concentrations. The calculations for AlN were done using the elastic data set of stiffness coefficients simulated by Assali et al. (2021), Kazan et al. (2007), McNeil et al. (1993), and Tsubouchi and Mikoshiba, (1985) and the average value for each parameter, along with error bars is shown. The calculations for YAlN were done using the elastic data set of stiffness coefficients simulated by Assali et al. (2021).

Generally, wurtzite Sc_xAl_1-xN exhibits higher sound velocities than wurtzite Y_xAl_1-xN for the same values of x. This difference is due to Y’s larger atomic volume, resulting in longer bond lengths between Y and Al or N atoms, leading to more pronounced softening. Additionally, Y’s higher atomic mass increases mass densities, directly affecting crystal sound velocities as per Equation 9.

Compared to Sc_xAl_1-xN, there are fewer available data sets and first-principle studies on Y_xAl_1-xN, particularly regarding different structural phases and near the phase transition point. This limitation hinders comprehensive comparisons. More simulated data, especially near the predicted structural phase transition and considering various possible lattices, would enhance understanding of Y_xAl_1-xN’s elastic properties. Such knowledge is crucial for applications in devices like resonators and actuators, highlighting the need for further research in this area to fully exploit the potential of Y_xAl_1-xN in technological applications.

4 Thermal conductivity

In crystals, the heat conduction is a temperature-dependent random process that can be divided into two parts: conduction by electrons and phonons. In metals, thermal conduction is dominant by the electronic part, which originates from the high density of electrons in metals and the fact that the Fermi velocity of electrons is much higher compared to sound velocities. In semiconductors, heat conduction is dominated by phonons and depends on the mean free path of the phonons, which can be affected by two major parameters: geometry and scattering from other phonons (Kittel and Holcomb, 2005). Phonon-related thermal conductivity depends on the average speed of the collective lattice vibrations and the average phonon mean free path, and is given by the following Equation 6, as:

$\mathit{k}=\frac{\mathbf{1}}{\mathbf{3}}{\mathit{C}}_{\mathit{V}}\mathit{v}\mathit{l}(6)$

where $k$ is the thermal conductivity, $C_V$ is the volumetric heat capacity, $v$ is the average phonon velocity, and $l$ is the phonon mean free path (Kittel and Holcomb, 2005).

Debye temperature is a material property in solids that determines the maximum vibration frequency of phonons. It is related to the elastic properties of crystals via sound velocities. The average Debye velocity is connected to the crystal’s elastic properties through a set of equations (Anderson, 1963) as is shown in Equations 7a–7c,

${\mathit{v}}_{\mathit{m}}\left(\mathit{x}\right)=\frac{\mathbf{1}}{{}^{\mathbf{3}}\sqrt{\frac{1}{3}\left(\frac{1}{{\mathit{v}}_{\mathit{l}}^{\mathbf{3}}\left(\mathit{x}\right)}+\frac{2}{{\mathit{v}}_{\mathit{s}}^{\mathbf{3}}\left(\mathit{x}\right)}\right)}}(\mathrm{7a})$

${\mathit{v}}_{\mathit{s}}\left(\mathit{x}\right)=\sqrt{\frac{\mathit{G}\left(\mathit{x}\right)}{\mathit{\rho }\left(\mathit{x}\right)}}(\mathrm{7b})$

${\mathit{v}}_{\mathit{l}}\left(\mathit{x}\right)=\sqrt{\frac{\mathit{B}\left(\mathit{x}\right)+\frac{\mathbf{4}}{\mathbf{3}}\mathit{G}\left(\mathit{x}\right)}{\mathit{\rho }\left(\mathit{x}\right)}}(\mathrm{7c})$

in which the first equation defines the average Debye velocity ($v_m$) in terms of longitudinal ($v_l$) and shear ($v_s$) sound velocities, and subsequent equations express $v_s$ and $v_l$ in terms of shear modulus ($G$), bulk modulus ($B$), and density ($\rho$).

The Debye temperatures is a crucial parameter for determining important thermal properties such as specific heat ($C_v\left(x\right)$), melting temperature ($T_m\left(x\right)$), and minimum thermal conductivity, $(k_{\mathit{min}}\left(T,x\right)$). The Debye temperature of Y_xAl_1-xN can be calculated as a function of elastic properties (Debye velocity) for each alloy concentration using a formula that incorporate Planck’s constant ($h=6.6261\times {10}^{-34}J.S$), Boltzmann’s constant ($k_B=1.3806\times {10}^{-23}\frac{J}{K}$ ), the number of atoms in the unit cell ($n$), which is equal to 4 for wurtzite and 8 for rock salt structures, Avogadro’s number ($N_A$), mass density ($\rho \left(x\right)$), and the atomic masses of Y, Al, and N ($m_Y,m_{Al},m_N$), and can be represented as following in Equation 8 (Kittel and Holcomb, 2005),

${\mathit{T}}_{\mathit{D}}\left(\mathit{x}\right)=\frac{\mathit{h}}{{\mathit{k}}_{\mathit{B}}}{}^{\mathbf{3}}\sqrt{\frac{\mathbf{3}}{\mathbf{4}\mathit{\pi }}\frac{\mathit{n}{\mathit{N}}_{\mathit{A}}\mathit{\rho }\left(\mathit{x}\right)}{{\mathit{m}}_{\mathit{Y}}\mathit{x}+{\mathit{m}}_{\mathit{A}\mathit{l}}\left(\mathbf{1}-\mathit{x}\right)+{\mathit{m}}_{\mathit{N}}}}{\mathit{v}}_{\mathit{m}}\left(\mathit{x}\right)(8)$

Assali et al. (2021) have calculated the Debye temperature of Y_xAl_1-xN, finding that it decreases with increasing alloy composition, from approximately 920 K for AlN to 500 K for Y_0.375Al_0.625N. This decrease is attributed to the change in the bond angels which results in the bond softening and increased freedom of phonon vibrations at lower temperatures.

Various models have been proposed to understand and predict thermal conductivity in materials. Kittel modeled the phonon-deviated thermal conductivity by assuming the mean free path of phonons equals the bond length (Kittel and Holcomb, 2005). Cahill et al. (1992) took a quantum mechanical approach, dividing the sample into regions of size of $\frac{\lambda }{2}$, and oscillation frequencies defined by $\omega =\frac{2\pi v}{\lambda }$ and lifetime of $\tau =\frac{\pi }{\omega }$. This model allows for the calculation of temperature-dependent thermal conductivity. In materials with high disorder, such as sputtered films with columnar structures where phonon heat transport is limited, a diffusive thermal conductivity model can be applied. This model considers heat transport as a random walk process resulting from atomic vibrations rather than phonon propagation (Allen and Feldman, 1993). Using this approach, Agne et al. (2018) established a relationship between a material’s eleastic properties and its minimum diffusive thermal conductivity.

Tran et al. (2023) have experimentally measured the thermal conductivity of wurtzite Y_xAl_1-xN and Sc_xAl_1-xN for concentrations up to x = 0.2. Both alloys demonstrated a similar decreasing trend in thermal conductivity as the alloy concentration increased, which is attributed to enhanced phonon-alloy scattering. Notably, Y_xAl_1-xN exhibited lower thermal conductivity compared to Sc_xAl_1-xN, a result of the further intensified phonon-alloy scattering due to the larger atomic size of Y relative to Sc.

Using the elastic property data sets for Y_xAl_1-xN provided by Assali et al. (2021), the minimum and minimum diffusive thermal conductivities of wurtzite Y_xAl_1-xN were calculated. Figure 8 illustrates the calculated values for minimum and diffusive thermal conductivities, as well as experimental values at room temperature, as a function of alloy composition (Tran et al., 2023). As evident in Figure 8, the diffusive thermal conductivity shows a higher incorporation compared to the minimum thermal conductivity, which is attributed to the high degree of disorder and alloy-phonon scatterings in Y_xAl_1-xN. This behavior aligns with similar observation reported by Ambacher et al for Sc_xAl_1-xN (Ambacher et al., 2023).

Figure 8

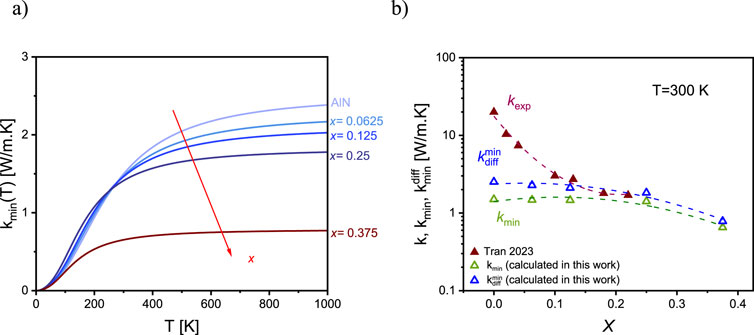
Figure 8. (A) Minimum thermal conductivity of Y_xAl_1-xN as a function of temperature. (B) Experimentally measured thermal conductivity of Y_xAl_1-xN at room temperature by Tran et al. (2023) along with the calculated minimum and minimum diffusive thermal conductivity at room temperature. The calculations were done using elastic data sets provided by Assali et al. (2021).

The observed reduction in both theoretical and experimental results, with the increase in alloy composition, can be a significant drawback for device applications, especially at higher Y concentration, where efficient heat dissipation becomes crucial. However, modern thermal management techniques offer potential solutions to mitigate this issue. Advanced material design strategies can be employed to enhance thermal properties while maintaining desired electrical and optical characteristics. In this case, Nano-structuring approaches or engineered interfaces can be utilized to manipulate phonon transport and potentially improve thermal conductivity (Dhumal et al., 2023). These innovative techniques can help reduce heating during device operation, thereby expanding the potential applications of Y_xAl_1-xN alloys in high-performance electronic and optoelectronic devices.

5 Growth methods of Y_xAl_1-xN

5.1 Sputter deposition

The growth process is crucial for achieving high-quality films suitable for various device applications. Up to date, several different growth techniques have been reported for the synthesis of Y_xAl_1-xN, including sputter deposition, MOCVD, and MBE (Zukauskaite et al., 2012; Leone et al., 2023; Wang et al., 2023a). Among these methods, sputter deposition has been the most widely employed technique for experimental studies on Y_xAl_1-xN thin films.

Sputter deposition is a versatile and widely used technique in the semiconductor industry, offering significant advantages for growing materials with very high melting temperatures, such as YN. The success of sputter deposition in producing high-quality Sc_xAl_1-xN samples in the expected wurtzite phase has made it a promising method for achieving high-quality Y_xAl_1-xN films, given the similarities between these two alloy systems. To optimize the quality of the sputtered Y_xAl_1-xN crystals, several key parameters can be tuned, including the powers applied to the material targets, sputtering pressure, type and ratio of sputtering gases, gas flow rates, and substrate temperature. For alloys such as Y_xAl_1-xN, the alloy concentration can be either tuned by controlling the powers applied on the separate material targets, or by using alloyed target materials with defined ratios. Independent control of target powers allows for precise adjustment of the desired alloy concentration.

One advantage of sputtering compared to other growth methods is the possibility of material growth at very low or room temperature, which cannot be offered by techniques such as MOCVD. This makes sputtering suitable for large-scale production lines and industrial applications. However, growth at room temperature may result in the lower crystalline quality of the films (Žukauskaitė, 2012). Moreover, the harsh plasma environment and high growth rate, especially at low temperatures, can result in high amounts of stress in the thin films, potentially affecting layers quality and decreasing device lifetime (Pandit et al., 2024).

The effects of different sputtering parameters have been extensively studied for the growth of Sc_xAl_1-xN (ZhangY. et al., 2015; Rez-Campos et al., 2018), providing valuable insights that can be applied to Y_xAl_1-xN. For Sc_xAl_1-xN, it has been observed that the choice of substrates has a significant impact on film quality (Kobayashi et al., 2024; Mayrhofer et al., 2015b). Drawing from the experiences of Sc_xAl_1-xN, similar optimization strategies can be applied for the growth of Y_xAl_1-xN.

The sputter growth of Y_xAl_1-xN has been reported and studied by several research groups (Žukauskaitė, 2012; Mayrhofer et al., 2015a; Solonenko et al., 2023; Pandit et al., 2023; Afshar et al., 2024). The first sputtered Y_xAl_1-xN films were investigated in 2012 by Zukauskaite et al. (2012), who reported the growth of Y_xAl_1-xN up to $x$ = 0.22 on Si (100) and Al₂O₃ (0001) substrates using a mixture of Ar and N₂ plasma. Their study revealed that higher growth temperature, up to 900°C, led to improved structural quality of the thin films. The measured band gap of these samples showed good agreement with the predicted values, ranging from 6.2 eV for AlN to 4.5 eV for Y_0.22Al_0.75N. Lattice parameters $a$ and $c$ and their ratios were reported for samples up to $x$ = 0.13, aligning well with simulated values. However, a significant drop in crystal quality was observed at x = 0.22, making it impossible to extract lattice parameters from XRD results. Notably, this concentration is still far from the predicted alloy concentration for the phase transition to rock salt structure.

In 2015, Mayrhofer et al. (2015a) studied the properties of Y_xAl_1-xN films grown by sputtering technique on silicon substrates, addressing the oxidation problems of the layers. They used a 250 nm thin TiN capping layer to prevent oxidation and formation of yttrium hydroxide groups. The study investigated the effect of various sputtering parameters, including applied power on the Y target, Ar to N₂ ratio, and growth temperature on film quality. Comparing growth temperatures of 250°C and 800°C, they reported improved crystal quality in samples grown at higher temperatures. The lattice parameter $c$ was extracted from the symmetric (0002) XRD reflection of Y_xAl_1-xN and compared with DFT calculated data. However, no experimental data for lattice parameter $a$ was provided. The reported lattice parameter $c$ values were lower than the simulated ones, but good agreement was observed considering the strain applied to the films during the growth. It’s worth noting that experimental data points in this work were only available up to approximately $x$ = 0.11.

The growth of sputtered Y_xAl_1-xN with higher Y concentrations was reported for the first time in 2023 by Pandit et al. (2023) and Solonenko et al. (2023). Pandit et al used single alloyed targets with different Y and Al combinations, prepared by arc melting methods, to grow samples on p-type Si (100) substrates. They successfully grew wurtzite Y_xAl_1-xN up to x = 0.20, though no systematic study on the effect of growth parameters were reported. XRD results showed the presence of (10–10) axis crystals at high concentrations, especially at x = 0.12. Scanning electron microscopy revealed columnar growth and hexagonal structure of the films, with x = 0.12 sample showing a high number of abnormally oriented grains. One of the most significant findings by Pandit et al. (2023) is the oxidation resistance of samples with $x$ = 0.15 and 0.2, even at temperatures around 700°C. This is particularly noteworthy because Y_xAl_1-xN typically has a higher oxygen affinity compared to Sc_xAl_1-xN, which can lead to rapid oxidation upon air exposure-a major drawback for device applications. While aluminum oxide (Al₂O₃) is known to be passivative (Gorobez et al., 2021), oxidation in transition metals tends to be diffusive, allowing oxygen to penetrate deeper into the sample (Smeltzer and Young, 1975). The observed oxidation resistance is therefore a promising result, motivating further investigation into the potential use of Y_xAl_1-xN in various applications. The study highlights the importance of crystal quality and reducing defects and dangling bonds in Y_xAl_1-xN to further decrease oxidation susceptibility. This underscored the need for continuous research focused on enhancing the crystal quality of the layers.

Another study on sputter growth of Y_xAl_1-xN was conducted in 2023 by Solonenko et al. (2023), who reported for the first time the growth of wurtzite Y_xAl_1-xN up to x = 0.29. They mentioned the use of an AlN seed layer to improve crystal quality in the samples. The growth process utilized two separate Al and Y sputtering targets, with silicon serving as the substrate for the films. XRD analysis revealed a shift in peak positions, indicating changes in lattice parameters as a function of Y concentration. A significant decrease in the intensity of symmetric XRD peaks was observed at higher alloy concentrations, which was interpreted as a decline in crystal quality at higher $x$ values. Additionally, the coexistence of different crystalline phases was noted. The research determined the lattice parameters c and a of the samples up to x = 0.29. However, they observed a deviation between the measured values and theoretical predictions. This discrepancy might be attributed to significant strain in the layers. The presence of strain could be a result of the lattice mismatch between the Y_xAl_1-xN films and the underlying substrate or seed layer.

In one of our recent works (Afshar et al., 2024) we reported the growth of wurtzite Y_xAl_1-xN up to x = 0.37 on sapphire substrates. The successful measurement of the lattice parameters $c$ and $a$ of wurtzite Y_xAl_1-xN up to this concentration was possible, which was achieved using a growth technique involving the stacking of buffer layers to gradually decrease strain in the layers. This method has previously proved successful for the growth of similar materials, such as Sc_xAl_1-xN (Moe et al., 2023; Beaucejour et al., 2022). This approach allowed for the growth of Y_xAl_1-xN films with higher alloy concentration than previously reported using lower growth temperatures (450°C). However, above x = 0.37, an abrupt decrease in crystal quality was observed. Based on various measurements, including XRD, AFM, and band gap analysis, this decline in quality was interpreted as a possible amorphization of the layers at higher Y concentrations. This amorphization of Y_xAl_1-xN was proposed as a primary limitation for achieving high alloy concentration before reaching the theoretically predicted structural phase transition to the rock salt structure. Notably, this phenomenon appears to be a material-specific property of Y_xAl_1-xN, as it was not observed in similar alloys such as Sc_xAl_1-xN.

The lattice parameters determined from various experimental results are summarized in Figures 9A, B. The FWHM of the rocking curve scans performed on Y_xAl_1-xN are shown in Figure 9C, from which, an abrupt decrease in the quality can be observed as the Y content increases. For the achieved alloy concentrations, the experimental data generally align with the theoretical results presented in Figure 3. Fitting functions defining the relationship between $a$ and $c$ lattice parameters of wurtzite Y_xAl_1-xN and the alloy concentration x was defined previously in our recent work (Afshar et al. 2024). Comparing the available experimental data on the lattice parameters with simulated values also highlights the huge range of alloy concentrations that has not been explored experimentally yet.

Figure 9

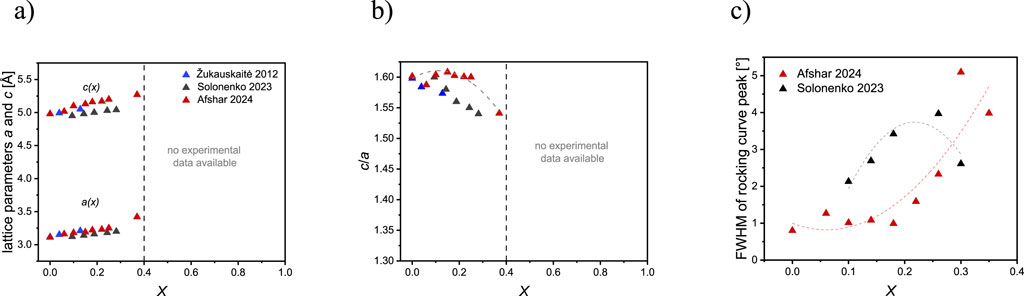
Figure 9. (A) Experimental lattice parameters, and (B) lattice parameters’ ratios for wurtzite Y_xAl_1-xN reported by Zukauskaite et al. (2012) (blue), Solonenko et al. (2023) (black), and Afshar et al. (2024) (red). (C) FWHM of the rocking curve scan on Y_xAl_1-xN reported by Afshar et al. (2024) and Solonenko et al. (2023).

5.2 Metal organic chemical vapor deposition (MOCVD)

Metal Organic Chemical Vapor Deposition (MOCVD) is a widely used growth method for both research and industrial production of thin films. This method involves the introduction of metalorganic precursors into a heated reactor, where they react on the substrate surface to form a solid thin film. The precursors are carried by gases, such as hydrogen (H₂) and nitrogen (N₂) into the reactor, where they undergo chemical reactions that result in the deposition of the desired material while gaseous byproducts are removed from the chamber. Several factors affect the quality of the films grown using MOCVD, including pressure, reactor temperature, and gas flow rates. Precise control over these parameters is essential, as they significantly influence the crystalline quality of the films (Stringfellow, 2012).

The MOCVD growth technique provides controlled reaction kinetics along with high substrate temperature, enabling the formation of highly ordered films on large substrates. This capability makes MOCVD an attractive method for industrial applications, particularly in sectors requiring uniform and high-quality thin films. However, achieving the desired material stoichiometry in alloy systems can be challenging, as it requires the precise control over growth parameters. This is especially true for materials with high melting temperature, which finding suitable precursors and achieving optimal gas pressures can complicate the growth process. Moreover, the high temperature required for MOCVD growth, often exceeding 1000°C, can limit the choice of substrate (An et al., 2021).

The growth of Y_xAl_1-xN using metal organic chemical vapor deposition was first achieved in 2023 by Leone et al. (2023). They investigated the effect of growth temperature on film quality, using either GaN or AlN wurtzite buffer layers. Samples with concentrations ranging from $x$ = 0.15 to $x$ = 0.41, and $x$ = 1 were grown. For most samples, especially those with $x$ > 0.3, cubic inclusions in the films were observed. Sever oxidation was reported, particularly for YN samples. To protect against oxidation, a thick AlN on top of the Y_xAl_1-xN films was suggested. Even at lower Y concentrations, XRD reflections related to Y₂O₃ were observed, possibly due to oxygen contaminations in the growth chamber from organic compounds in gases or precursors. Similar to sputtered samples, the percentage of Y at which cubic inclusions were observed was far below theoretical predictions for phase transition, highlighting growth difficulties regardless of technique. In 2024, Streicher et al reported the growth of YAlN/GaN heterostructures using MOCVD, focusing on low Y concentrations from $x$ = 0.033 to 0.09 (Streicher et al., 2024). They successfully protected layers from oxidation by capping them with amorphous SiN_x without breaking vacuum. No cubic phases were observed at these concentrations, corroborated by the presence of a 2DEG at the buffer-barrier interface. This group also reported successful growth of Sc_xAl_1-xN/GaN heterostructures by MOCVD (Streicher et al., 2022).

5.3 Molecular beam epitaxy (MBE)

Molecular Beam Epitaxy (MBE) is a sophisticated thin film growth technique renowned for its ability to produce high-purity epitaxial layers with precise control over composition and thickness, providing high purity deposition. This method involves the evaporation of ultra-pure elemental or molecular sources in an ultra-high vacuum (UHV) environment, typically ranging from 10⁻⁸ to 10⁻¹² Torr. The evaporated atoms or molecules travel towards the heated substrate and they get condensate and form epitaxial layers through a process of atomic-layer deposition (Wang and Wu, 2023).

In the MBE process, the key parameters affecting the growth include substrate temperature and atomic beam flux and can be finely tuned to produce high-quality films with minimal defects. This high precision makes MBE a valuable tool in various research areas. However, this high precision comes with certain limitations. In this method, the growth rates are typically slow, which can make it unsuitable for large-scale production. Additionally, the requirement of UHV chambers necessitates expensive components and skilled operators, contributing to higher overall costs (Vishwanath et al., 2018). Despite these challenges, MBE still remains a critical technique in research for having a deep understanding of specific material properties.

The only reported growth of Y_xAl_1-xN using molecular beam epitaxy (MBE) was achieved in 2023 by Wang et al. (2023b). They successfully grew a single concentration of Y (x = 0.07) by MBE on a GaN template and conducted studies on the band alignment and ferroelectricity of Y_0.07Al_0.93N (Wang et al., 2023a; Wang et al., 2023b). This research represents a significant milestone as it is the first and only study to report ferroelectricity in Y_xAl_1-xN.

The discussed growth methods used for the growth Y_xAl_1-xN layers and their advantages and disadvantages are summarized in Table 3. Despite the theoretically predicted high potential of Y_xAl_1-xN for applications, especially at high Y content, no systematic studies have been conducted on the growth of high concentration Y near the phase transition point to gain better insight into the structural behavior of this material. These findings underscore the challenges associated with growth and characterization of high-quality Y_xAl_1-xN films, particularly at elevated Y concentrations. They highlight the need for careful consideration of growth conditions, substrate effect, and characterization methods when interpreting experimental results. Further investigations will be essential to reconcile these differences and achieve a more comprehensive understanding of the structural evolution of Y_xAl_1-xN alloys across a wide range of compositions.

Table 3

Table 3. Summary of comparison between different growth methods used for YAlN.

6 Material properties

6.1 Piezoelectricity

As mentioned in Section 1, high piezoelectricity has been one of the main motivations for studying transition metal nitrides. The discovery of elevated piezoelectricity in Sc_xAl_1-xN in 2009 (Akiyama et al., 2009) shifted attentions toward the high potential of transition metal nitrides for high-frequency applications. Studies on alloying of Sc and III-N groups, such as GaN and AlN, have reported increases in the piezoelectric coefficient d₃₃ (Uehara et al., 2019). Tasnádi et al. (2010) demonstrated that the increase in d₃₃ of Sc_xAl_1-xN is a quantum mechanical intrinsic property arising from the softening of the material, specifically the decrease in the stiffness coefficient $C_{33}$. This softening is related to the metastable condition of the alloy and its tendency towards a structural phase transition from wurtzite to rock salt. Consequently, as the material approaches the phase transition point, it becomes softer, resulting in a higher d₃₃ value. Since the stability of wurtzite Y_xAl_1-xN was predicted up to $x$ = 0.75 (Zukauskaite et al., 2012), higher softening and consequently higher d₃₃ values are expected as the composition approaches the phase transition point. Several studies have reported d₃₃ values for sputtered Y_xAl_1-xN films (Mayrhofer et al., 2015a; Pandit et al., 2023; Schlögl et al., 2022; Afshar et al., 2024). However, due to the limitations in growth process discussed in previous sections, improved piezoelectric coefficients have only been reported up to $x$ = 0.2 (Pandit et al., 2024).

The first piezoelectric measurement on Y_xAl_1-xN was reported in 2015 by Mayrhofer et al. (2015a). They measured the d₃₃ of sputtered films, finding large deviations from theoretical predictions. They reported d₃₃ of 3.2 $\frac{\text{pC}}{\mathrm{N}}$ for $x$ = 0.01, increasing to 3.7 $\frac{\text{pC}}{\mathrm{N}}$ at $x$ = 0.06. This unexpected deviation from theoretical values may be due to insufficient structural quality of the films. Poor crystal quality can also lead to high incorporation of oxygen atoms after exposure to atmospheric conditions, significantly affecting piezoelectric properties, as observed for AlN (Farrell et al., 2008). Solonenko et al. (2023) also reported experimental d₃₃ values for sputtered Y_xAl_1-xN, but found no increase compared to AlN values, possibly due to lack of structural qualities or high strain in their films. In 2023, Schlögl et al. (2022) demonstrated for the first time an elevated d₃₃ of 7.79 $\frac{\text{pC}}{\mathrm{N}}$ for Y_0.09Al_0.91N, although they reported 2%–3% oxygen incorporation in their films. In the same year, Pandit et al. (2023), Pandit et al. (2024) reported a systematic increase of d₃₃ in Y_xAl_1-xN films up to $x$ = 0.2, with a value of 12 $\frac{\text{pC}}{\mathrm{N}}$ for Y_0.2Al_0.8N, in good agreement theoretical values. Afshar et al. (2024) reported d₃₃ values for sputtered Y_xAl_1-xN that agreed well with theoretical values up to x = 0.18, after which a drop was observed, attributed to decreased crystal quality at higher concentrations. The fit functions to the experimental and simulated d₃₃ values of Sc_xAl_1-xN and Y_xAl_1-xN are summarized in Figure 10A. The data related to Y_xAl_1-xN are plotted based on the equation defining the relation between d₃₃ and Y concentration provided by Afshar et al. (2024), and data related to Sc_xAl_1-xN are acquired by fitting a polynomial function to the data points reported by Akiyama et al. (2009). Based on available data and theoretical predictions, Y_xAl_1-xN is expected to show the highest piezoelectric potential close to its structural phase transition. However, difficulties in growing high-quality films at high alloy concentrations have limited verification of the theoretical predictions.

Figure 10

Figure 10. Comparison of available data points for material properties of Y_xAl_1-xN and Sc_xAl_1-xN: (A) d₃₃, (B) band gap, (C) relative permittivity at low frequency range, and (D) relative permittivity at high frequency (optical) range. Red stars in graphs (A–C) represent experimental data from Afshar et al. (2024). Graph (A): red triangles: experimental data for Y_xAl_1-xN from Pandit et al. (2024), blue circles: experimental data for Sc_xAl_1-xN by Akiyama et al. (2009). Graph (B): blue filled triangles: experimental data for Y_xAl_1-xN from Leone et al. (2023), black open triangles: theoretical data for Y_xAl_1-xN from Ramirez-Montes et al. (2016), blue circles, experimental data for Sc_xAl_1-xN from Baeumler et al. (2019). Graph (C): red triangles: experimental data for Y_xAl_1-xN from Sedrine et al. (2015), blue circles: experimental data for Sc_xAl_1-xN from Baeumler et al. (2019). Graph (D): blue circles: experimental data for Sc_xAl_1-xN from Akiyama et al. (2013). In all graphs red and black dashed lines are the exponential fits to the data points related to Y_xAl_1-xN and Sc_xAl_1-xN, respectively.

Tholander et al. (2016) have studied the electric and structural properties of Y_xIn_1-xN, predicting that it crystallizes in the wurtzite structure up to x = 0.5 before transition to rock salt crystal. They reported an increase in d₃₃ to 23.31 $\frac{\text{pC}}{\mathrm{N}}$ for Y_0.5In_0.5N, which is highly comparable to Sc_xAl_1-xN. However, due to the scarcity of indium (Pecharsky and Geschneider, 2024, Accessed 24 July 2024), and its high demand in electronic devices (Lasky, 2015), Y_xAl_1-xN may be a more sustainable long-term alternative. For Y_xAl_1-xN, Tholander et al initially predicted d₃₃ values far below those of Sc_xAl_1-xN, attributing this to a large volume mismatch between the Y and Al atoms (Tholander et al., 2013). However, experimental data provided by Pandit et al. (2023) contradicts this assumption, at least up to x = 0.2. Their findings suggest that the volume mismatch effect may not be as significant as initially predicted for lower Y concentrations. Nonetheless, as the number of Y atoms in the crystal increases, the effect of volume mismatch could become more pronounced.

6.2 Ferroelectricity

Prior to the finding of ferroelectricity in Sc_xAl_1-xN (Fichtner et al., 2019), this phenomenon has been primarily observed in limited materials, such as oxide perovskites (Cohen, 1992). However, the application of oxide materials in electronic devices is challenging due to the difficulties in deposition as thin films, diffusion of toxic materials, and high number of oxygen vacancies that can significantly affect device performance (Lee et al., 2023). Ferroelectric nitrides offer several advantages, including low operating voltage, high Curie temperature, large electromechanical response, and high compatibility with industrial semiconductor technologies (Wang et al., 2023a). From a crystallographic perspective, ferroelectric materials belong to 10 different polar point groups (Shahrokhi et al., 2020; Shi et al., 2016). Conventional group III-nitrides do not exhibit ferroelectricity, as the orientation of their spontaneous polarization cannot be switched (Bernardini et al., 1997). In a conventional wurtzite ferroelectric material, the structure should have the ability of transition between metal polar and nitrogen polar phases. This transition occurs through a change in the internal parameter, with an intermediate layered hexagonal phase forming during the ferroelectric switching process. In an ideal wurtzite structure, the internal parameter, $u$, has the value of approximately 0.375. During ferroelectric switching, this value changes to 0.5 for the intermediate layered hexagonal phase. At this point metal and nitrogen atoms occupy the same crystalline plane. After switching is complete, the $u$ value reverts to 0.375. This process allows for the reversal of polarization direction, which is a key characteristic of ferroelectric materials. Since ferroelectric switching requires a transition between wurtzite and layered hexagonal structures, the barrier energy for this process can be determined by calculating the difference of formation energy between these two structures. In Sc_xAl_1-xN, as the Sc content increases, a change in the average bond angels occurs, leading to an increase in the internal lattice parameter and flattening of the equilibrium energy diagrams due to competition between wurtzite and layered hexagonal structures (Fichtner et al., 2019; Ambacher et al., 2023). This small energy difference between the two structures enables polarization switching due to application of an external voltage (Tasnádi et al., 2010). Considering the similarities of Y_xAl_1-xN and Sc_xAl_1-xN, ferroelectric properties are also expected for Y_xAl_1-xN. Due to Y_xAl_1-xN’s lower stiffness and higher bond length, lower coercive fields may be achievable, which is one of the most critical parameters for ferroelectric materials. The small difference in formation enthalpy between wurtzite and layered hexagonal structures of Y_xAl_1-xN, especially at higher Y concentrations, suggests that ferroelectricity in Y_xAl_1-xN is energetically possible, as shown in Figure 2.

For practical applications, a low coercive field is desirable. Additionally, high insulation properties, typically characterized by wide band gaps, are necessary for the switching process. While AlN possesses a conventional wurtzite structure and a wide band gap, its very strong bonding between nitrogen and aluminum atoms and the bond angels close to an ideal wurtzite structure, results in the expectation of extremely large coercive fields. This high coercive field requirement can lead to a material breakdown before switching occurs, a limitation also observed in GaN (Moriwake et al., 2020).

Reported coercive fields of Sc_xAl_1-xN typically range around 6 $\frac{\text{MV}}{\text{cm}}$ (Gund et al., 2021); (Fichtner et al., 2019). However, for certain applications, such as non-volatile memory devices, lower coercive fields in the range of 100 $\frac{\text{kV}}{\text{cm}}$ are desired to ensure reliable switching with the constraints of device miniaturization and power consumption (Choi et al., 2022). To date, only one study has reported ferroelectricity in Y_xAl_1-xN layers grown by MBE on GaN, with a low concentration of x = 0.07 (Wang et al., 2023a). This work reported coercive fields of around 6 $\frac{\text{MV}}{\text{cm}}$, and remnant polarization of approximately 130 $\frac{\mu \mathrm{C}}{{\text{cm}}^2}$, comparable to values reported for Sc_xAl_1-xN at similar concentration range (Wang et al., 2023b). As demonstrated by Yassine et al. (2022) for Sc_xAl_1-xN, structural properties and defects, such as strain and surface morphology, strongly influence ferroelectric properties. Therefore, optimizing the growth process to achieve high-quality crystals is crucial for realizing ferroelectricity in Y_xAl_1-xN. Further experimental data, especially at higher Y concentrations is significantly demanded for future studies on the polarization behavior of Y_xAl_1-xN and its potential industrial applications.

6.3 Band gap, optical, and dielectric properties

For a better understanding of the optical properties of Y_xAl_1-xN, calculating the electronic band structure and the density of states is crucial. The tunable band gap of Y_xAl_1-xN and Sc_xAl_1-xN provides a significant benefit for the application of these material in different fields, such as photovoltaics, optoelectronics, and sensor technologies. The calculated band structure of Y_xAl_1-xN shows significant changes with increasing Y content. Ramirez-Montes et al. (2016) calculated the band structure of wurtzite and rock salt Y_xAl_1-xN, finding that rock salt AlN and YN both exhibit indirect band gaps of ($\mathrm{\Gamma }\to X$) of 5.917 eV and 1.229 eV, respectively. For intermediate concentrations ($x$ = 0.25, 0.5, and 0.75), direct band gaps ($\mathrm{\Gamma }\to \mathrm{\Gamma }$) of 2.692 eV, 1.385 eV, and 0.885 eV were obtained. Assuming a rock salt structure across the entire concentration range, a transition from indirect to direct and back to indirect band gap occurs. For wurtzite Y_xAl_1-xN, a direct band gap was observed for concentrations $x$ = 0, 0.5, and 0.75, while indirect band gaps were reported for $x$ = 0.25 (3.885 eV at $\to \mathrm{\Gamma }$ ) and x = 1 (3.606 eV at $M\to \mathrm{\Sigma }$). Xie et al. (2020) calculated the band structure of Y_xAl_1-xN up to x = 0.25, reporting a direct band gap of 4.028 eV for AlN, followed by a transition to indirect band gaps 3.421 eV, 3.091 eV, and 2.712 eV for Y_xAl_1-xN at Y concentrations x = 0.0625, 0.125, and 0.25, respectively. The low band gap values reported in this study are attributed to the use of the Generalized Gradient Approximation (GGA) calculation method, which is known to significantly underestimate band gaps (Xie et al., 2020). Despite this limitation, the results still demonstrate a clear decreasing trend in band gaps as Y concentration increases.

There are some experimental data available on the optical band gap Y_xAl_1-xN from various studies (Zukauskaite et al., 2012; Leone et al., 2023; Afshar et al., 2024). The calculated experimental data show good agreement with theoretically predicted band gaps. As expected, a decreasing trend can be observed as the Y concentration increases, which is similar to the band gap behavior of Sc_xAl_1-xN (Baeumler et al., 2019). The experimental band gaps of Y_xAl_1-xN and Sc_xAl_1-xN, and comparison with the theoretical data are shown in Figure 10B. As can be seen in this figure, Y_xAl_1-xN and Sc_xAl_1-xN show similar band gap trends, with the values of Y_xAl_1-xN being slightly lower at the same concentrations compared to Sc_xAl_1-xN. This difference is due to different bond length in the crystal. Larger, i.e., weaker, bonds in Y_xAl_1-xN results in lower energy gap values (Miglio et al., 2017).

Another way to study the optical properties of Y_xAl_1-xN is through the dielectric function, which is needed for understanding its potential in various applications, including semiconductor lasers, ultraviolet photodetectors, and conductive optically transparent layers. The interaction of the crystal and light in the macroscopic range is defined by the dielectric function, which consists of imaginary and real parts as a function of frequency $\omega$. These components depend on several atomic and structural properties of the crystal, such as electronic band structures, conduction, and valance bands. The real part of the dielectric function represents the material’s dispersive properties and is related to atomic polarization after interaction with electromagnetic waves. It allows for the calculation of the material’s effect on the phase velocity of electromagnetic waves. Conversely, the imaginary part quantifies energy loss in the electromagnetic wave due to the material’s absorptive properties, such as electronic transitions and phonon interactions. The real and imaginary parts of the dielectric function are interconnected through Kramers–Kronig relations (Kronig, 1926).

By having the dielectric function of the material, several optical properties such as refractive index, absorption, and loss function can be calculated. Xie et al. (2020) have calculated the dielectric functions and other optical parameters of Y_xAl_1-xN for several alloy concentrations. The real part of dielectric function shows an increasing trend with increasing Y concentration. This increase in the dielectric function indicates an increase in the density of states and a band gap reduction as the number of Y atoms increase, which agrees with other studies (Xie et al., 2020). The absorption edge and band gap of Y_xAl_1-xN exhibits a red shift with increasing Y concentration, with absorption in the visible region observed at $x$ = 0.25, consistent with a decrease in the material’s band gap. These results align with the experimentally determined refractive index and extinction coefficient of sputtered Y_xAl_1-xN ($x$ = 0–0.22) reported by Sedrine et al. (2015). The high-frequency dielectric constant of Y_xAl_1-xN for this range are shown in Figure 10C.

Additional to the dielectric function of Y_xAl_1-xN at high frequency (visible range), information about the dielectric coefficient in the low frequency range (kHz-GHz) is crucial for understanding several properties of the material such as capacitive behavior and carrier dynamics, which are important for potential applications in power electronics, RF filters, and communication systems. Daoust et al. (2022) have simulated the static relative permittivity of Y_xAl_1-xN for x = 0.06 and 0.25, while Mayrhofer et al. (2015a) have experimentally measured the relative permittivity of Y_xAl_1-xN, up to x = 0.11. A recent study (Afshar et al., 2024) has reported the measured relative permittivity of Y_xAl_1-xN up to x = 0.28, showing good agreement with previously reported experimental data by Mayrhofer et al. (2015a), and demonstrating good insulating properties. The experimental data show higher values compared to the simulated data and are also higher than the values reported for Sc_xAl_1-xN (Akiyama et al., 2013). The deviation between simulated and experimental relative permittivity may be due to the underestimation of dielectric properties by DFT + U method (Lee et al., 2018; Lee et al., 2011). The predicted relative permittivity of Y_xAl_1-xN up to x = 0.3 based on the equation provided by Afshar et al. (2024), along with the permittivity of Sc_xAl_1-xN based on the fit function on the experimental data reported by Akiyama et al. (2013) are illustrated in Figure 10D. Having comprehensive data on various material properties of Y_xAl_1-xN provides the opportunity to study its potential for different application devices, which will be discussed in the following section.

7 Potential device applications

7.1 Acoustic resonators

The discussed properties of Y_xAl_1-xN in Section 6 highlights its possible application in high-frequency and high-power acoustic devices especially due to its predicted high piezoelectric coefficient. High-frequency and high-power acoustic devices such as surface acoustic wave devices (SAW) have significant application in next-generation telecommunication as sensors and high frequency filters. They are widely used in mobile devices, such as smartphones, GPS systems, and Wi-Fi modules, and are ideal for their low cost and small size, but can be used only for low frequencies (30 MHz to 2–3 GHz) (Mandal and Banerjee, 2022). One of the important components of a SAW device is the piezoelectric materials, on top of which the IDT is applied. Materials with higher piezoelectricity exhibit higher coupling coefficients leading to strong interaction between the acoustic waves and the electrical field resulting in higher efficiency in term of energy transfer. This makes transition metal nitrides, such as Y_xAl_1-xN a potential candidate to be considered for such applications. Assali et al. (2021) have calculated the electromechanical coupling of Y_xAl_1-xN-based surface acoustic filters with c-place sapphire as the substrate. They have demonstrated the possibility of improvement of electromechanical coupling coefficient of approximately 650%, and increase of the quality factor of approximately 6% compared to AlN-based devices in the frequency range of 0.8 GHz up to 1.2 GHz.

Bulk acoustic waves devices (BAWs) are particularly promising for future communication systems due to their ability to operate at frequencies exceeding 10 GHz (Vinita et al., 2024). The efficiency of BAW devices is often quantified by the coupling coefficient, which measures how effectively input electrical energy is converted to acoustic energy. This coefficient is influenced by various factors, including electrode geometry, piezoelectric material crystalline orientation, and film stress (Zhang et al., 2023; Vu et al., 2022). For BAW devices, the coupling coefficient can be expressed as a function of material-specific parameters (Dou et al., 2023):

${\mathit{k}}_{\mathbf{33}}^{\mathbf{2}}=\frac{{\mathit{e}}_{\mathbf{33}}^{\mathbf{2}}}{{\mathit{\epsilon }}_{\mathbf{0}}{\mathit{\epsilon }}_{\mathbf{33}}{\mathit{C}}_{\mathbf{33}}}(9)$

Where $e_{33}$ is the piezoelectric coefficient, ${\epsilon }_0$ is vacuum permittivity, ${\epsilon }_{33}$ is relative permittivity, and $C_{33}$ is the stiffness coefficient. Using simulated data on piezoelectric constants and elastic coefficients provided by Assali et al. (2021), and dielectric constant equations reported by Afshar et al. (2024) for Y_xAl_1-xN as a function of Y concentration, the coupling coefficient for Y_xAl_1-xN-based BAWs is calculated. The calculation results are shown in Figure 11A. The results show improved coupling coefficient compared to AlN, especially at higher Y concentrations, which is attributed to higher piezoelectric coefficients. However, it should be additionally noted that these calculations were performed only considering the material properties. In application devices, the effect of other factors, such as size and shape of the device, can have an impact on the actual values of measured $k_{33}^2$ (Muller and Dubios, 2008).

Figure 11

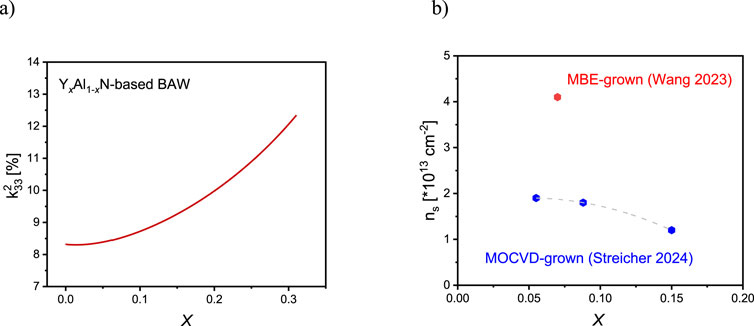
Figure 11. (A) Coupling coefficient of Y_xAl_1-xN-based bulk acoustic wave devices calculated from the experimental and simulated data sets taken from references (Afshar et al., 2024; Assali et al., 2021). (B) Experimentally measured sheet carrier density at the interface of YAlN/GaN heterostructure grown by MOCVD (Streicher et al., 2024) and MBE (Wang et al., 2023b).

The comparable coupling coefficients of Y_xAl_1-xN with what has been previously reported for Sc_xAl_1-xN (Schneider et al., 2017), combined with the lower production costs of Y-based devices, highlight the promising potential of Y_xAl_1-xN and underscores the need for further research into Y_xAl_1-xN-based devices. Pandit et al. (2024) have recently reported the fabrication of a bulk acoustic resonator based on Y_0.2Al_0.8N, demonstrating approximately 16% increase in the electromechanical coupling coefficient compared to AlN. This experimental result provides concrete evidence supporting the calculated predictions regarding the high potential of Y_xAl_1-xN as RF-resonators.

7.2 High electron mobility transistors (HEMTs)

In recent years, Gallium Nitride (GaN) based electronic devices have made significant contributions to high-power applications and sustainable energy solutions due to their exceptional efficiency. This advancement is primarily attributed to the development of High-Electron-Mobility Transistors (HEMTs), which exploit the unique properties of noncentrosymmetric crystal lattices in heterostructures. The critical parameters of the crystals used in HEMT heterostructures include wide band gap, spontaneous polarization, piezoelectric polarization, and band offset between the barrier and channel layers. In these structures, the material with the lower band gap typically serves as the channel layer, while the higher band gap material acts as the barrier. The combination of band offset and polarization gradient leads to charge accumulation at the interface of the heterostructure. Depending on the polarization direction, this accumulation can result in either electron or hole accumulation (Ambacher et al., 1999). The most common heterostructures in GaN technology focus on electron accumulation, referred to as the two-dimensional electron gas (2DEG). The quantity of charges accumulated in this region is determined by the total polarization gradient and is known as sheet electron density, denoted as n_s. It describes the number of charge carriers per unit area in a two-dimensional electron gas. Most of the time, higher sheet carrier density results in lower channel resistance, typically measured in ohm per square (Ω/□), and better performance of the HEMT (Li et al., 2020). Lower channel resistance enables higher channel currents, enhanced output power, and improved energy efficiency. Moreover, sheet resistance can provide invaluable insight into the quality of the material specifically in the case of semiconductor layers for which doping has been done.

Theoretically, AlN/GaN HEMTs have shown exceptional performance potential. However, practical implementation faces challenges due to the significant lattice mismatch between AlN barrier and GaN channel in the lateral plane. This mismatch limits the critical thickness of the barrier layer to approximately 3-4 nm, beyond which cracks begin to form, negatively impacting device performance (Storm et al., 2013). To reduce this lattice mismatch, Ga is added to AlN. GaAlN/GaN HEMTs have been extensively studied and become widely adopted in industry. These state-of-the-art transistor devices can operate at high power levels. The sheet carrier density in these devices typically ranges from 5 $\times$ 10¹² cm⁻² to early 2 $\times$ 10¹³ cm⁻², depending on the alloy composition of the barrier and a possible AlN spacer layer. Recent research has explored the potential of ScN alloyed with AlN to enhance polarization gradients and introduce piezoelectric polarization (Ambacher et al., 2021). Sc_xAl_1-xN/GaN heterostructures have demonstrated higher polarization gradients compared to Ga_xAl_1-xN/GaN heterostructures, potentially resulting in increased sheet carrier density and high-power output (Streicher et al., 2022; Krause et al., 2023). Key advantages of Sc_xAl_1-xN/GaN heterostructures include higher sheet carrier density confined as 2DEG and potential for lattice matching to GaN, removing the limitations caused by a critical barrier thickness (Dinh et al., 2023). Studies have reported sheet carrier densities up to $5.26\times {10}^{13}\mathrm{c}{\mathrm{m}}^{-2}$ and Hall mobility of 910$\mathrm{c}{\mathrm{m}}^2{\mathrm{V}}^{-1}$ for MBE-grown Sc_0.2Al_0.8N/GaN heterostructures (Frei et al., 2019).

In recent years, research has focused on the growth of Y_xAl_1-xN/GaN heterostructures, showing type-I band alignment with a valance band offset of - 0.1 eV and a conduction band offset of 2.2 eV (Streicher et al., 2024; Wang et al., 2023b). The experimentally reported sheet carrier density in GaN-based heterostructures of Y_xAl_1-xN are shown in Figure 11B. Streicher et al. (2024) and Wang et al. (2023b) have both demonstrated a well-defined confinement of the two-dimensional electron gas at the Y_xAl_1-xN/GaN interface, grown by MOCVD and MBE, respectively. Streicher et al. (2024) have reported that the 2DEG remains unaffected by oxidation over time due to the high protection provided by an amorphous SiN_x capping layer, while Wang et al. (2023b) have capped their layers with 2 nm GaN. Although the measured sheet carrier densities deviate from the simulated values, still an improvement compared to the state-of-the-art GaAlN/GaN is proven. The low sheet resistivity of 150 Ω/□ achieved for this heterostructure is also a significant improvement compared to the previous values reported for Sc_xAl_1-xN/GaN and Ga_xAl_1-xN/GaN (Streicher et al., 2024). Electrical measurements have shown low leakage currents and the absence of unwanted donors, indicating that Y_xAl_1-xN/GaN is a potential candidate for next-generation power electronic devices.

7.3 Further application fields

Based on the material properties of Y_xAl_1-xN, several other applications are expected from this alloy system, which have not been explored thoroughly by experimental means. Some research groups have reported the potential of Y_xAl_1-xN and its tunable band gap in optical devices, such as solar blind ultraviolet photodetectors (Huang et al., 2023; Jiang et al., 2024). Huang et al and Jiang et al have reported the use of Y_xAl_1-xN with specific absorption cut-off edge as solar blind detector, exhibiting good performance (Huang et al., 2023; Jiang et al., 2024). These studies have shown promising results for the application of Y_xAl_1-xN as optical sensors, which is also encouraging for the application of other rare earth materials in this field of technology. Additionally, ferroelectric properties observed in Y_xAl_1-xN allows for a wide application, such as ferroelectric self-power photovoltaic and energy efficient memory devices. For having an insight over the full capacity of Y_xAl_1-xN for such applications, several researches have to be invested on this novel material.

8 Conclusion

Transition metal nitrides, specifically Y_xAl_1-xN and Sc_xAl_1-xN, represent a class of novel materials with promising properties that are anticipated to play a significant role in future semiconducting devices. This study provides a comprehensive review of the structural, elastic, optical, electronic, and thermal properties of the ternary alloy system Y_xAl_1-xN, drawing from both simulated and experimental data. The structural analysis highlights the similarities between the structural characteristics and elastic parameters of Y_xAl_1-xN and Sc_xAl_1-xN. Alongside, optical and electronic properties of Y_xAl_1-xN and Sc_xAl_1-xN are also compared, further highlighting the similarities of the two alloy systems and emphasizing on the potential of Y_xAl_1-xN. Based on the available elastic properties, the thermal conductivity of Y_xAl_1-xN is evaluated and the limitation caused by insufficient thermal conductivity are discussed. In the following chapters, this study reviews the reported growth methods for the synthesis of Y_xAl_1-xN and the pros and cons are described. Additionally, the structural data, especially lattice parameters calculated from experimental results are summarized. By studying different material properties, such as electrical and optical parameters, this review also delves into the potential applications of Y_xAl_1-xN, such as acoustic resonators and high electron mobility transistors, by examining calculated sound velocities, elastic moduli, coupling coefficients, and carrier densities. A comparative analysis with Sc_xAl_1-xN, a reference material with well-documented and analogous properties, was conducted for each material property. A significant obstacle in advancing the understanding of Y_xAl_1-xN properties is the scarcity of experimental and simulated data. One of the critical challenges identified in experimental research is the oxidation and instability of films with high Y concentrations, which persist regardless of the growth methods employed. Therefore, systematic research, particularly focused on optimizing the growth processes of Y_xAl_1-xN, is imperative for a more detailed exploration of its material parameters. The data available thus far indicate that Y_xAl_1-xN exhibits behavior remarkably similar to Sc_xAl_1-xN, which serves as a compelling incentive for the research community to dedicate further time and resources to a wide array of studies on Y_xAl_1-xN. This investment is crucial for unlocking the full potential of these materials in various advanced technological applications.

Author contributions

NA: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Validation, Visualization, Writing–original draft, Writing–review and editing. MY: Conceptualization, Methodology, Resources, Writing–review and editing. OA: Conceptualization, Funding acquisition, Resources, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors would like to thank to Gips-Schüle foundation and the German Science Foundation (DFG) who supported this work (Project No. AM 105/53-1). The authors would like to acknowledge the support of the library of the University of Freiburg for open access publication of this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adamski, N. L., Dreyer, C. E., and Van de Walle, C. G. (2019). Giant polarization charge density at lattice-matched GaN/ScN interfaces. Appl. Phys. Lett. 115 (23). doi:10.1063/1.5126717

CrossRef Full Text | Google Scholar

Afshar, N., Yassine, M., Yassine, A., Maier, N., and Ambacher, O. (2024). Electrical and structural characterization of YAlN at high alloy concentrations. J. Appl. Phys. 136 (18). doi:10.1063/5.0241907

CrossRef Full Text | Google Scholar

Agne, M. T., Hanus, R., and Snyder, G. J. (2018). Minimum thermal conductivity in the context of diffuson-mediated thermal transport. Energy Environ. Sci. 11 (3), 609–616. doi:10.1039/C7EE03256K

CrossRef Full Text | Google Scholar

Ahmed, B., and Sharma, B. I. (2021). Structural and electronic properties of AlN in rock salt, zinc blende, and wurtzite phase: a DFT study. Dig. J. Nanomater. Biostructures 16 (1), 125–133. doi:10.15251/djnb.2021.161.125

CrossRef Full Text | Google Scholar

Akiyama, M., Kamohara, T., Kano, K., Teshigahara, A., Takeuchi, Y., and Kawahara, N. (2009). Enhancement of piezoelectric response in scandium aluminum nitride alloy thin films prepared by dual reactive cosputtering. Adv. Mater. 21 (5), 593–596. doi:10.1002/adma.200802611

PubMed Abstract | CrossRef Full Text | Google Scholar

Akiyama, M., Umeda, K., Honda, A., and Nagase, T. (2013). Influence of scandium concentration on power generation figure of merit of scandium aluminum nitride thin films. Appl. Phys. Lett. 102 (2). doi:10.1063/1.4788728

CrossRef Full Text | Google Scholar

Allen, P. B., and Feldman, J. L. (1993). Thermal conductivity of disordered harmonic solids. Phys. Rev. B 48 (17), 12581–12588. doi:10.1103/PhysRevB.48.12581

PubMed Abstract | CrossRef Full Text | Google Scholar

Ambacher, O., Christian, B., Feil, N., Urban, D. F., Elsässer, C., Prescher, M., et al. (2021). Wurtzite ScAlN, InAlN, and GaAlN crystals, a comparison of structural, elastic, dielectric, and piezoelectric properties. J. Appl. Phys. 130 (4). doi:10.1063/5.0048647

CrossRef Full Text | Google Scholar

Ambacher, O., Mihalic, S., Yassine, M., Yassine, A., Afshar, N., and Christian, B. (2023). Review:Structural, elastic, and thermodynamic properties of cubic and hexagonal Sc _x Al _1-x N crystals. J. Appl. Phys. 134. doi:10.1063/5.0170742

CrossRef Full Text | Google Scholar

Ambacher, O., Smart, J., Shealy, J. R., Weimann, N. G., Chu, K., Murphy, M., et al. (1999). Two-dimensional electron gases induced by spontaneous and piezoelectric polarization charges in N- and Ga-face AlGaN/GaN heterostructures. J. Appl. Phys. 85 (6), 3222–3233. doi:10.1063/1.369664

CrossRef Full Text | Google Scholar

An, J., Dai, L. F., and Zheng, J. (2021). Parameter study of the high temperature MOCVD numerical model for AlN growth using orthogonal test design. Sci. Rep. 11 (8877), 8877. doi:10.1038/s41598-021-87554-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, O. L. (1963). A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 24 (7), 909–917. doi:10.1016/0022-3697(63)90067-2

CrossRef Full Text | Google Scholar

Assali, A., Laidoudi, F., Serhane, R., Kanouni, F., and Mezilet, O. (2021). Highly enhanced electro-acoustic properties of YAlN/sapphire based surface acoustic wave devices for next generation of microelectromechanical systems. Mater. Commun. 26, 102067. doi:10.1016/j.mtcomm.2021.102067

CrossRef Full Text | Google Scholar

Bacaksiz, C., Sahin, H., Ozaydin, H. D., Horzum, S., Senger, R. T., and Peeters, F. M. (2015). Hexagonal AlN:Dimensional-crossover-driven band-gap transition. Phys. Rev. B 19 (8), 085430. doi:10.1103/PhysRevB.91.085430

CrossRef Full Text | Google Scholar

Baeumler, M., Lu, Y., Kurz, N., Kirste, L., Prescher, M., Christoph, T., et al. (2019). Optical constants and band gap of wurtzite Al _1-x Sc _x N/Al₂O₃ prepared by magnetron sputter epitaxy for scandium concentrations up to x=0.41. J. Appl. Phys. 126 (4). doi:10.1063/1.5101043

CrossRef Full Text | Google Scholar

Beaucejour, R., D'Agati, M., Kalyan, K., and Olson, R. H. (2022). Compensation of the stress gradient in physical vapor deposited Al_1−xSc_xN films for microelectromechanical systems with low out-of-plane bending. Micromachines 13 (8), 1169. doi:10.3390/mi13081169

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, L. I. (1996). Semiconductor materials. London: Taylor and Francis Inc.

Google Scholar

Bernardini, F., Fiorentini, V., and Vanderbilt, D. (1997). Spontaneous polarization and piezoelectric constants of III-V nitrides. Phys. Rev. B 56 (16), R10024–R10027. doi:10.1103/PhysRevB.56.R10024

CrossRef Full Text | Google Scholar

Biswas, B., and Saha, B. (2019). Development of semiconducting ScN. Phys. Rev. Mater. 3 (2), 020301. doi:10.1103/PhysRevMaterials.3.020301

CrossRef Full Text | Google Scholar

Cahill, D. G., Watson, S. K., and Pohl, R. O. (1992). Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46 (10), 6131–6140. doi:10.1103/PhysRevB.46.6131

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Z., Koh, Y. R., Mamun, A., Shi, J., Bai, T., Huynh, K., et al. (2020). Experimental observation of high intrinsic thermal conductivity of AlN. Phys. Rev. Mater. 4 (4), 044602. doi:10.1103/PhysRevMaterials.4.044602

CrossRef Full Text | Google Scholar

Choi, H. S., Li, S., Park, I. H., Liew, W. H., Kwon, K. C., Wang, L., et al. (2022). Tailoring the coercive field in ferroelectric metal-free perovskites by hydrogen bonding. Nat. Commun. 13 (794), 794. doi:10.1038/s41467-022-28314-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Clementi, E., Raimondi, D. L., and Reinhardt, W. P. (1967). Atomic screening constants from SCF functions. II. Atoms with 37 to 86 electrons. J. Chem. Phys. 47 (4), 1300–1307. doi:10.1063/1.1712084

CrossRef Full Text | Google Scholar

Cohen, R. E. (1992). Origin of ferroelectricity in perovskite oxides. Nature 358, 136–138. doi:10.1038/358136a0

CrossRef Full Text | Google Scholar

Corll, J. A. (1967). Effect of pressure on the elastic parameters and structure of CdS. Phys. Rev. 157 (3), 623–626. doi:10.1103/PhysRev.157.623

CrossRef Full Text | Google Scholar

Cunha, C. L., Pimenta, T. C., and Fraga, M. A. (2022). “Development and applications of aluminum nitride thin film technology,” in Thin film deposition-fundamentals, processes, and applications (London: IntechOpen). doi:10.5772/intechopen.106288

CrossRef Full Text | Google Scholar

Daoust, P., Desjardins, P., Maust, R. A., and Côté, M. (2022). Longitudinal piezoelectric, elastic, and dielectric properties of rare-earth aluminum nitride alloys determined by density-functional perturbation theory. Phys. Rev. Mater. 6 (3), 034405. doi:10.1103/PhysRevMaterials.6.034405

CrossRef Full Text | Google Scholar

Deng, R., Ozsdolay, B. D., Zheng, P. Y., Khare, S. V., and Gall, D. (2015). Optical and transport measurement and first-principles determination of the ScN band gap. Phys. Rev. B 91 (4), 045104. doi:10.1103/PhysRevB.91.045104

CrossRef Full Text | Google Scholar

Dhumal, A. R., Kulkarni, A. P., and Ambhore, N. H. (2023). A comprehensive review on thermal management of electronic devices. J. Eng. Appl. Sci. 70 (140), 140. doi:10.1186/s44147-023-00309-2

CrossRef Full Text | Google Scholar

Dinh, D. V., Lähnemann, J., Geelhaar, L., and Brandt, O. (2023). Lattice parameters of Sc_xAl_1−xN layers grown on GaN(0001) by plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 122 (15). doi:10.1063/5.0137873

CrossRef Full Text | Google Scholar

Dou, W., Zhou, D., Qin, R., Yang, Y., Guo, H., Mu, Z., et al. (2023). Super-high-frequency bulk acoustic resonators based on aluminum scandium nitride for wideband applications. nanomaterials 13 (20), 2737. doi:10.3390/nano13202737

PubMed Abstract | CrossRef Full Text | Google Scholar

Dreyer, C. E., Janotti, A., Van de Walle, C. G., and Vanderbilt, D. (2016). Correct implementation of polarization constants in wurtzite materials and impact on III-nitrides. Phys. Rev. X 6 (2), 021038. doi:10.1103/PhysRevX.6.021038

CrossRef Full Text | Google Scholar

Edgar, J. H., Yu, A. U., and Rys, A. (1990). Low temperature metal-organic chemical vapor deposition of aluminum nitride with nitrogen trifluoride as the nitrogen source. This Solid Films 189, L11–L14. doi:10.1016/0040-6090(90)90469-T

CrossRef Full Text | Google Scholar

Eklumd, P., Kerdsongpanya, S., and Alling, B. (2016). Transition-metal-nitride-base thin films as novel energy harvesting materials. R. Soc. Chem. 4, 3905–3914. doi:10.1039/C5TC03891J

CrossRef Full Text | Google Scholar

Farrell, R., Pagan, V. R., Kabulski, A., Kuchibhatl, S., Harman, J., Kasarla, K. R., et al. (2008). High temperature annealing studies on the piezoelectric properties of thin aluminum nitride films Pittsburgh, PA, and morgantown, WV (United States): national energy technology lab (NETL). doi:10.2172/1015474

CrossRef Full Text | Google Scholar

Farrer, N., and Bellaiche, L. (2002). Properties of hexagonal ScN versus wurtzite GaN and InN. Phys. Rev. B 66 (20), 201203. doi:10.1103/PhysRevB.66.201203

CrossRef Full Text | Google Scholar

Fichtner, S., Wolf, N., Lofink, F., Kienl, L., and Wagner, B. (2019). AlScN: a III-V semiconductor based ferroelectric. J. Appl. Phys. 125 (11). doi:10.1063/1.5084945

CrossRef Full Text | Google Scholar

Frei, K., Trejo-Hernandez, R., Schütt, S., Kirste, L., Prescher, M., Aidam, R., et al. (2019). Investigation of growth parameters for ScAlN-barrier HEMT structures by plasma-assisted MBE. Jpn. J. Appl. Phys. 58, SC1045. doi:10.7567/1347-4065/ab124f

CrossRef Full Text | Google Scholar

Furuta, K., Hirata, K., Anggraini, S. A., Akiyama, M., Uehara, M., and Yamada, H. (2021). First-principles calculations of spontaneous polarization in ScAlN. J. Appl. Phys. 130 (2). doi:10.1063/5.0051557

CrossRef Full Text | Google Scholar

Gorobez, J., Maack, B., and Nilius, N. (2021). Growth of self-passivating oxide layers on aluminum—pressure and temperature dependence. PSS 258 (5). doi:10.1002/pssb.202000559

CrossRef Full Text | Google Scholar

Gorodtsov, V. A., and Lisovenko, D. S. (2019). Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals. Mech. Mater. 134, 1–8. doi:10.1016/j.mechmat.2019.03.017

CrossRef Full Text | Google Scholar

Gregoire, J. M., Kirby, S. D., Scopelianos, G. E., Lee, F. H., and Bruce van Dover, R. (2008). High mobility single crystalline ScN and single orientation epitaxial YN on sapphire via magnetron sputtering. J. Appl. Phys. 104 (7). doi:10.1063/1.2996006

CrossRef Full Text | Google Scholar

Gund, V., Davaji, B., Lee, H., Casamento, J., Xing, H. G., Jena, D., et al. (2021). “Towards realizing the low-coercive field operation of sputtered ferroelectric Sc_xAl_1-xN,” in 21st international conference on solid-state sensors, actuators and microsystems (transducers) (Orlando; FL, USA). doi:10.1109/Transducers50396.2021.9495515

CrossRef Full Text | Google Scholar

Hardy, M. T., Downey, B. P., Nepal, N., Storm, D. F., Katzer, D. S., and Meyer, D. J. (2017). Epitaxial ScAlN grown by molecular beam epitaxy on GaN and SiC substrates. Appl. Phys. Lett. 110 (16). doi:10.1063/1.4981807

CrossRef Full Text | Google Scholar

Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 65, 349–354. doi:10.1088/0370-1298/65/5/307

CrossRef Full Text | Google Scholar

Huang, L., Huang, S., Lin, J., Wang, Z., Chen, Z., Zheng, W., et al. (2023). Band gap engineering of AlYN films for solar-blind ultraviolet photodetection. ACS Appl. Electron. Mater. 5 (2), 1106–1113. doi:10.1021/acsaelm.2c01581

CrossRef Full Text | Google Scholar

Hultman, L. (2000). Thermal stability of nitride thin films. Vacuum 57 (1), 1–30. doi:10.1016/S0042-207X(00)00143-3

CrossRef Full Text | Google Scholar

Hultman, L., Benhenda, S., Radnoczi, G., Sundgren, J. E., Greene, J. E., and Petrov, I. (1992). Interfacial reactions in single-crystal-TiN(100)/Al/polycrystalline-TiN multilayer thin films. Thin Solid Films 215 (2), 152–161. doi:10.1016/0040-6090(92)90430-J

CrossRef Full Text | Google Scholar

ISE (2024). “Current prices of rare earths,” in Institut für seltene erden und metalle AG. Retrieved on July 22nd 2024 from.

Google Scholar

Jiang, X., Wu, Y., Qi, J., Liu, Y., Wang, Y., Zhou, B., et al. (2024). Preparation and deep-UV solar-blind photovoltaic performance of AlYN-based MSM detector. IEEE Sensors J. 24, 25581–25589. doi:10.1109/JSEN.2024.3418585

CrossRef Full Text | Google Scholar

Kazan, M., Moussaed, E., Nader, R., and Masri, P. (2007). Elastic constants of aluminum nitride. PSS 4 (1), 204–207. doi:10.1002/pssc.200673503

CrossRef Full Text | Google Scholar

Kempter, C. P., Krikorian, N. H., and McGuire, J. C. (1957). The crystal structure of yttrium nitride. J. Phys. Chem. 61 (9), 1237–1238. doi:10.1021/j150555a023

CrossRef Full Text | Google Scholar

Kittel, C., and Holcomb, D. F. (2005). Introduction to solid state physics. Am. J. Phys. 35, 547–548. doi:10.1119/1.1974177

CrossRef Full Text | Google Scholar

Knudson, M. D., and Gupta, Y. M. (1998). Real-time observation of a metastable state during the phase transition in shocked cadmium sulfide. Phys. Rev. Lett. 81 (14), 2938–2941. doi:10.1103/PhysRevLett.81.2938

CrossRef Full Text | Google Scholar

Kobayashi, A., Honda, Y., Maeda, T., Okuda, T., Ueno, K., and Fujioka, H. (2024). Structural characterization of epitaxial ScAlN films grown on GaN by low-temperature sputtering. Appl. Phys. Express 17, 011002. doi:10.35848/1882-0786/ad120b

CrossRef Full Text | Google Scholar

Krause, S., Streicher, I., Waltereit, P., Kirste, L., Brückner, P., and Leone, S. (2023). AlScN/GaN HEMTs grown by metal-organic chemical vapor deposition with 8.4 W/mm output power and 48% power added efficiency at 30GHz. IEEE Electron Device Lett. 44 (1), 17–20. doi:10.1109/LED.2022.3220877

CrossRef Full Text | Google Scholar

Kronig, R. de L. (1926). On the theory of dispersion of X-rays. J. Opt. Soc. Am. 12 (6), 547–557. doi:10.1364/JOSA.12.000547

CrossRef Full Text | Google Scholar

Laidoudi, F., Kanouni, F., Assali, A., Caliendo, C., Amara, S., Nezzari, H., et al. (2022). Thickness shear SMR resonator based on yttrium-doped AlN for high sensitive liquid sensors. Sensors Actuators A:Physical 333, 113238. doi:10.1016/j.sna.2021.113238

CrossRef Full Text | Google Scholar

Lasky, R. (2015). Indium and Gallium: playing important roles in LED lighting and the 2014 nobel prize in physics. Indium Corp. Available at: https://www.indium.com/blog/indium-and-gallium-playing-important-roles-in-led-lighting-and-the-2014-nobel-prize-in-physics.php.

Google Scholar

Ledbetter, H. (2006). Sound velocities, elastic constants: temperature dependence. Mater. Sci. Eng. A 442 (1-2), 31–34. doi:10.1016/j.msea.2006.04.147

CrossRef Full Text | Google Scholar

Lee, B., Lee, C. K., Hwang, C. S., and Han, S. (2011). Influence of exchange-correlation functionals on dielectric properties of rutile TiO₂. Curr. Appl. Phys. 11 (1), S293–S296. doi:10.1016/j.cap.2010.11.104

CrossRef Full Text | Google Scholar

Lee, J., Yang, K., Kwon, J. Y., Kim, J. E., Han, D. I., Lee, D. H., et al. (2023). Role of oxygen vacancies in ferroelectric or resistive switching hafnium oxide. Nano Converg. 10 (55), 55. doi:10.1186/s40580-023-00403-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M., Youn, Y., Yim, K., and Han, S. (2018). High-throughput ab initio calculations on dielectric constant and band gap of non-oxide dielectrics. Sci. Rep. 8 (14794), 14794. doi:10.1038/s41598-018-33095-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Leone, S., Ligl, J., Manz, C., Kirste, L., Fuchs, T., Menner, H., et al. (2019). Metal-organic chemical vapor deposition of AluminumScandium nitride. PSS 14 (1). doi:10.1002/pssr.201900535

CrossRef Full Text | Google Scholar

Leone, S., Streicher, I., Prescher, M., Stranák, P., and Kirste, L. (2023). Metal-organic chemical vapor deposition of aluminum yttrium nitride. PSS 17 (10). doi:10.1002/pssr.202300091

CrossRef Full Text | Google Scholar

Li, J. Z., Li, J., Lin, J. Y., and Jian, H. X. (2020). Correlation between sheet carrier density-mobility product and persistent photoconductivity in AlGaN/GaN modulation doped heterostructures. MRS Internet J. Nitride Semicond. Res. 5, 626–632. doi:10.1557/S1092578300004853

CrossRef Full Text | Google Scholar

Liu, J., Li, X., Zhang, H., Yin, W., Zhang, H., Peng, P., et al. (2014). Electronic structures and optical properties of two-dimensional scn and YN nanosheets. J. Appl. Phys. 115 (9). doi:10.1063/1.4867515

CrossRef Full Text | Google Scholar

Loewen, E. (2024). Standford advanced matterials. Available at: https://stanfordmaterials.com/blog/yttrium-properties-and-applications.html.

Google Scholar

Louhibi-Fasla, S., Achour, H., Kefif, K., and Ghalem, Y. (2014). First-principles study of high-pressure phases of AlN. Phys. Procedia 55, 324–328. doi:10.1016/j.phpro.2014.07.047

CrossRef Full Text | Google Scholar

Mancera, L., Rodriguez, J. A., and Taheuchi, N. (2003). First principles calculations of the ground state properties and structural phase transformation in YN. J. Phys. Condens. Matter 15, 2625–2633. doi:10.1088/0953-8984/15/17/316

CrossRef Full Text | Google Scholar

Mandal, D., and Banerjee, S. (2022). Surface acoustic wave (SAW) sensors: physics, materials, and applications. Sensors 22 (3), 820. doi:10.3390/s22030820

PubMed Abstract | CrossRef Full Text | Google Scholar

Manna, S., Brennecka, G. L., Stevanović, V., and Ciobanu, C. V. (2017). Tuning the piezoelectric and mechanical properties of the AlN system via alloying with YN and BN. J. Appl. Phys. 122 (10). doi:10.1063/1.4993254

CrossRef Full Text | Google Scholar

Mayrhofer, P. M., Riedl, H., Euchner, H., Stöger-Pllach, M., Mayrhofer, P. H., Bittner, A., et al. (2015a). Microstructure and piezoelectric response of Y _x Al _1-x N thin films. Acta Mater. 100, 81–89. doi:10.1016/j.actamat.2015.08.019

CrossRef Full Text | Google Scholar

Mayrhofer, P. M., Persson, A. P. O., Bittner, A., and Schmid, U. (2015b). Properties of Sc_xAl_1-xN (x = 0.27) thin films on sapphire and silicon substrates upon high temperature loading. Microsyst. Technol. 22, 1679–1689. doi:10.1007/s00542-015-2798-7

CrossRef Full Text | Google Scholar

McNeil, L. E., Grimsditch, M., and French, R. H. (1993). Vibrational spectroscopy of aluminum nitride. J. Am. Ceram. Soc. 76 (5), 1132–1136. doi:10.1111/j.1151-2916.1993.tb03730.x

CrossRef Full Text | Google Scholar

Miglio, A., Heinrich, C. P., Hautier, W., Tremel, G., and Zeier, W. G. (2017). Local bonding influence on the band edge and band gap formation in quaternary chalcopyrites. Adv. Sci. 4 (9), 1700080. doi:10.1002/advs.201700080

PubMed Abstract | CrossRef Full Text | Google Scholar

Mihalic, S., Wade, E., Lüttich, C., Hörich, F., Sun, C., Christian, B., et al. (2023). Structural properties and epitaxial relation of cubic rock salt Sc _x Al _1-x N/ScN/Si. J. Appl. Phys. 134 (15). doi:10.1063/5.0169741

CrossRef Full Text | Google Scholar

Moe, C. G., Leathersich, J., Carlstrom, D., Bi, F., Kim, D., and Shealy, J. B. (2023). Metal–organic chemical vapor deposition-grown AlScN for microelectromechanical-based acoustic filter applications. PSS 220 (16), 2200849. doi:10.1002/pssa.202200849

CrossRef Full Text | Google Scholar

Monemar, B., Paskov, P. P., and Kasic, A. (2005). Optical properties of InN-the band gap question. Superlattices Microstruct. 38, 38–56. doi:10.1016/j.spmi.2005.04.006

CrossRef Full Text | Google Scholar

Moriwake, H., Yokoi, R., Taguchi, A., Ogawa, T., Fisher, C. A. J., Kuwabara, A., et al. (2020). A computational search for wurtzite-structured ferroelectrics with low coercive voltages. Apl. Mater. 8 (12). doi:10.1063/5.0023626

CrossRef Full Text | Google Scholar

Mouhat, F., and Coudert, F. X. (2014). Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90 (22), 224104. doi:10.1103/PhysRevB.90.224104

CrossRef Full Text | Google Scholar

Muller, C., and Dubios, M. A. (2008). Effect of size and shape on the performances of BAW resonators: a model and its applications. Beijing: IEEE, 1552–1556. doi:10.1109/ULTSYM.2008.0378

CrossRef Full Text | Google Scholar

Nye, J. F. (1985). Physical properties of crystals:their representation by tensors and matrices. Clarendon Press.

Google Scholar

Pandit, S., Schneider, M., Berger, C., and Schmid, U. (2024). Compressive stress reduction in sputter-deposited yttrium aluminum nitride (Y _0.2 Al _0.8 N) thin films for BAW resonators with high electromechanical coupling. Sensors Actuators A Phys. 376 (115638), 115638. doi:10.1016/j.sna.2024.115638

CrossRef Full Text | Google Scholar

Pandit, S., Schneider, M., Schwarz, S., and Schmid, U. (2023). Enhancement of piezoelectric response in yttrium aluminum nitride (Y_xAl_1-xN) thin films. Adv. Eng. Mater. 25 (22). doi:10.1002/adem.202300940

CrossRef Full Text | Google Scholar

Pecharsky, V. K., and Geschneider, K. A. (2024). Rare-earth Elem. Available at: https://www.britannica.com/science/rare-earth-element (Accessed July 24, 2024).

Google Scholar

Pelá, R. R., Caetano, C., Marques, M., Ferreira, L. G., Furthmüller, J., and Teles, L. K. (2011). Accurate band gaps of AlGaN, InGaN, and AlInN alloys calculations based on LDA-1/2 approach. Appl. Phys. Lett. 98 (15). doi:10.1063/1.3576570

CrossRef Full Text | Google Scholar

Ramirez-Montes, L., Lopez-Perez, W., Gonzalez-Garcıa, A., and Gonzalez-Hernandez, R. (2016). Structural, optoelectronic, and thermodynamic properties of Y _x Al _1-x N semiconducting alloys. J. Mater. Sci. 51, 2817–2829. doi:10.1007/s10853-015-9590-z

CrossRef Full Text | Google Scholar

Reuss, A. (1929). Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 9 (1), 49–58. doi:10.1002/zamm.19290090104

CrossRef Full Text | Google Scholar

Rez-Campos, A.Pe ́, Sinusı ́a Lozano, M., Garcia-Garcia, F. J., Chen, Z., and Iriarte, G. F. (2018). Synthesis of ScAlN thin films on Si (100) substrates at room temperature. Microsyst. Technol. 24, 2711–2718. doi:10.1007/s00542-017-3660-x

CrossRef Full Text | Google Scholar

Rowberg, A. J. E., Mu, S., Swift, M. W., and Van de Walle, C. G. (2021). Structural, electronic, and polarization properties of YN and LaN. Phys. Rev. Mater. 5 (9), 094602. doi:10.1103/PhysRevMaterials.5.094602

CrossRef Full Text | Google Scholar

Ruemenapp, T., and Peier, D. (1999). “Dielectric breakdown in aluminum nitride,” in Eleventh international symposium on high voltage engineering (London). doi:10.1049/cp:19990870

CrossRef Full Text | Google Scholar

Sahin, H., Cahangirov, S., Bekaroglu, E., Akturk, E., Senger, R. T., Ciraci, S., et al. (2009). Monolayer honeycomb structures of group-IV elements and III-V binary compounds: first-principles calculations. Phys. Rev. B 80 (15), 155453. doi:10.1103/PhysRevB.80.155453

CrossRef Full Text | Google Scholar

Schlögl, M., Schneider, M., and Schmid, U. (2022). Piezoelectricity in Y_0.09 Al_0.91 N thin films. Mater. Sci. Engineering:B 276, 115543. doi:10.1016/j.mseb.2021.115543

CrossRef Full Text | Google Scholar

Schneider, M., DeMiguel-Ramos, M., Flewitt, A. J., Iborra, E., and Schmid, U. (2017). Scandium aluminium nitride-based film bulk acoustic resonators. Proceedings 1 (4), 305. doi:10.3390/proceedings1040305

CrossRef Full Text | Google Scholar

Sedrine, N. B., Zukauskaite, A., Birch, J., Hultman, L., and Darakchieva, V. (2015). Infrared dielectric functions and optical phonons of wurtzite Y_xAl_1−xN (0 ⩽ x ⩽ 0.22). Jpn. J. Appl. Phys. 48. doi:10.1088/0022-3727/48/41/415102

CrossRef Full Text | Google Scholar

Setter, N., Damjanovic, D., Eng, L., Fox, G., Gevorgian, S., Hong, S., et al. (2006). Ferroelectric thin films: review of materials, properties, and applications. J. Appl. Phys. 100 (5). doi:10.1063/1.2336999

CrossRef Full Text | Google Scholar

Shahrokhi, S., Gao, W., Wang, Y., Anandan, P. R., Rahaman, Md. Z., Singh, S., et al. (2020). Emergence of ferroelectricity in halide perovskites. Small Methods 4 (8). doi:10.1002/smtd.202000149

CrossRef Full Text | Google Scholar

Shelton, S., Chan, M., Park, H., Horsley, D., Boser, B., Izyumin, I., et al. (2009). “CMOS-compatible AlN piezoelectric micromachined ultrasonic transducers,” in IEEE international ultrasonic symposium (Rome). doi:10.1109/ULTSYM.2009.5441602

CrossRef Full Text | Google Scholar

Shi, P. P., Tang, Y. Y., Li, P. F., Liao, W. Q., Wang, Z. X., Ye, Q., et al. (2016). Symmetry breaking in molecular ferroelectrics. Chem. Soc. Rev. 45 (14), 3811–3827. doi:10.1039/C5CS00308C

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegel, A., Parlinski, K., and Wdowik, U. D. (2006). Ab initiocalculation of structural phase transitions in AlN crystal. Phys. Rev. B 74 (10), 104116. doi:10.1103/PhysRevB.74.104116

CrossRef Full Text | Google Scholar

Silva, A. F. da, Souza Dantas, N., de Almeida, J. S., Ahuja, R., and Persson, C. (2005). Electronic and optical properties of wurtzite and zinc-blende TlN and AlN. J. Cryst. Growth 281 (1), 151–160. doi:10.1016/j.jcrysgro.2005.03.021

CrossRef Full Text | Google Scholar

Smeltzer, W. W., and Young, D. J. (1975). Oxidation properties of transition metals. Prog. Solid State Chem. 10 (1), 17–54. doi:10.1016/0079-6786(75)90003-5

CrossRef Full Text | Google Scholar

Solonenko, D., Strube, J., Fammels, J., Fissltheler, E., Röbisch, V., Howell, K., et al. (2023). AlYN thin films with high Y content: microstructure and performance. PSS 17 (10). doi:10.1002/pssr.202300193

CrossRef Full Text | Google Scholar

Sowa, H. (2001). On the transition from the wurtzite to the NaCl type. Found. Adv. 57 (2), 176–182. doi:10.1107/S0108767300014902

PubMed Abstract | CrossRef Full Text | Google Scholar

Storm, D. F., Deen, D. A., Katzer, D. S., Mayer, D. J., Binari, S. C., Gougousi, T., et al. (2013). Ultrathin-barrier AlN/GaN heterostructures grown by rf plasma-assisted molecular beam epitaxy on freestanding GaN substrates. J. Cryst. Growth 380, 14–17. doi:10.1016/j.jcrysgro.2013.05.029

CrossRef Full Text | Google Scholar

Streicher, I., Leone, S., Kirste, L., Manz, C., Straňák, P., Prescher, M., et al. (2022). Enhanced AlScN/GaN heterostructures grown with a novel precursor by metal–organic chemical vapor deposition. PSS 17 (2). doi:10.1002/pssr.202200387

CrossRef Full Text | Google Scholar

Streicher, I., Straňák, P., Kirste, L., Prescher, M., Müller, S., and Leone, S. (2024). Two-dimensional electron gases in AlYN/GaN heterostructures grown by metal-organic chemical vapor deposition. Apl. Mater. 12 (5). doi:10.1063/5.0203156

CrossRef Full Text | Google Scholar

Stringfellow, G. B. (2012). Organometallic vapor-phase epitaxy: theory and practice. Elsevier Science.

Google Scholar

Talley, K. R., Millican, S. L., Mangum, J., Siol, S., Musgrave, C. B., Gorman, B., et al. (2018). Implications of heterostructural alloying for enhanced piezoelectric performance of (Al,Sc)N. Phys. Rev. Mater. 2 (6), 063802. doi:10.1103/PhysRevMaterials.2.063802

CrossRef Full Text | Google Scholar

Tasnádi, F., Alling, B., Höglund, C., Wingqvist, G., Birch, J., Hultman, L., et al. (2010). Origin of the anomalous piezoelectric response in wurtzite Sc _xAl _1-xN alloys. Phsical Rev. Lett. 104 (13), 137601. doi:10.1103/PhysRevLett.104.137601

PubMed Abstract | CrossRef Full Text | Google Scholar

Tholander, C., Abrikosov, I. A., Hultman, L., and Tasnádi, F. (2013). Volume matching condition to establish the enhanced piezoelectricity in ternary (Sc,Y)_0.5(Al,Ga,In)_0.5 alloys. Phys. Rev. B 87 (9), 094107. doi:10.1103/PhysRevB.87.094107

CrossRef Full Text | Google Scholar

Tholander, C., Birch, J., Tasnádi, F., Hultman, L., Palisaitis, J., Persson, P. O. Å., et al. (2016). Ab initio calculations and experimental study of piezoelectric Y _x in _1-x N thin films deposited using reactive magnetron sputter epitaxy. Acta Mater. 105, 199–206. doi:10.1016/j.actamat.2015.11.050

CrossRef Full Text | Google Scholar

Tolbert, S. H., and Alivisatos, A. P. (1995). The wurtzite to rock salt structural transformation in CdSe nanocrystals under high pressure. J. Chem. Phys. 102 (11), 4642–4656. doi:10.1063/1.469512

CrossRef Full Text | Google Scholar

Tran, D. Q., Tasandi, F., Zukauskaite, A., Birch, J., Darakchieva, V., and Paskov, P. P. (2023). Thermal conductivity of Sc _x Al _1-x N and Y _x Al _1-x N alloys. Appl. Phys. Lett. 122 (18). doi:10.1063/5.0145847

CrossRef Full Text | Google Scholar

Tromans, D. (2011). Elastic anisotropy of HCP metal crystals and polycrystals. Int. J. Recent Res. Appl. Stud. 6 (462).

Google Scholar

Tsipas, P., Kassavetis, S., Tsoutsou, D., Xenogiannopoulou, E., Golias, E., Giamini, S. A., et al. (2013). Evidence for graphite-like hexagonal AlN nanosheets epitaxially grown on single crystal Ag(111). Appl. Phys. Lett. 103 (25). doi:10.1063/1.4851239

CrossRef Full Text | Google Scholar

Tsubouchi, K., and Mikoshiba, N. (1985). Zero-temperature-coefficient SAW devices on AlN epitaxial films. IEEE 32 (5): 634–644. doi:10.1109/T-SU.1985.31647

CrossRef Full Text | Google Scholar

Uehara, M., Mizuno, T., Aida, Y., Yamada, H., Umeda, K., and Akiyama, M. (2019). Increase in the piezoelectric response of scandium-doped Gallium nitride thin films sputtered using a metal interlayer for piezo MEMS. Appl. Phys. Lett. 114 (1). doi:10.1063/1.5066613

CrossRef Full Text | Google Scholar

Ueno, M., Onodera, A., Shimomura, O., and Takemura, K. (1992). X-Ray observation of the structural phase transition of aluminum nitride under high pressure. Phys. Rev. B 45 (17), 10123–10126. doi:10.1103/PhysRevB.45.10123

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinita, P. D., Islam, Sk. M., and Singh, J. (2024). Bulk acoustic wave resonators for sensing applications: a review. Sensors Actuators A Phys. 378, 115839. doi:10.1016/j.sna.2024.115839

CrossRef Full Text | Google Scholar

Vishwanath, S., Dang, P., and Xing, H. G. (2018). “Chapter 20 - challenges and opportunities in molecular beam epitaxy growth of 2D crystals: an overview,” in Molecular beam epitaxy (Elsevier), 443–485. doi:10.1016/B978-0-12-812136-8.00017-7

CrossRef Full Text | Google Scholar

Voigt, W. (1910). Lehrbuch der Kristallphysik. Springer Nature. Leipzig.

Google Scholar

Vu, L., Shuai, Y., Huang, S., Zhu, D., Wang, Y., Luo, W., et al. (2022). Area dependence of effective electromechanical coupling coefficient induced by on-chip inductance in LiNbO₃-based BAW resonators. Electronics 11 (23), 4032. doi:10.3390/electronics11234032

CrossRef Full Text | Google Scholar

Wang, D., Mondal, S., Kezer, P., Hu, M., Liu, J., Wu, Y., et al. (2023b). Band alignment and charge carrier transport properties of YAlN/III-nitride heterostructures. Appl. Surf. Sci. 637 (15), 157893. doi:10.1016/j.apsusc.2023.157893

CrossRef Full Text | Google Scholar

Wang, D., Mondal, S., Liu, J., Hu, M., Wang, P., Yang, S., et al. (2023a). Ferroelectric YAlN grown by molecular beam epitaxy. Appl. Phys. Lett. 123 (3). doi:10.1063/5.0159562

CrossRef Full Text | Google Scholar

Wang, F., and Wu, J. (2023). Modern ion plating technology. Amsterdam: Elsevier Inc. doi:10.1016/C2019-0-03578-9

CrossRef Full Text | Google Scholar

Wei, J., Zhou, W., Li, S., Shen, P., Ren, S., Hu, A., et al. (2019). Modified embedded atom method potential for modeling the thermodynamic properties of high thermal conductivity beryllium oxide. ACS Omega 4 (4), 6339–6346. doi:10.1021/acsomega.9b00174

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, M., and Madden, P. A. (2002). Transformations between tetrahedrally and octahedrally coordinated crystals: the wurtzite → rocksalt and blende → rocksalt mechanisms. J. Physics:Condensed Matter 14, 4629–4643. doi:10.1088/0953-8984/14/18/301

CrossRef Full Text | Google Scholar

Xie, Y., Cai, Y., Liu, Y., Zhao, Y., Guo, S., Sun, C., et al. (2020). Electronic structure and optical properties of YAlN: a first principle study. PSS 27 (5). doi:10.1002/pssb.201900678

CrossRef Full Text | Google Scholar

Xu, B., Xiang, H., Yin, J., Xia, Y., and Liu, Z. (2018). A two-dimensional tetragonal yttrium nitride monolayer: a ferroelastic semiconductor with switchable anisotropic properties. Nanoscale 10 (1), 215–221. doi:10.1039/C7NR05679F

PubMed Abstract | CrossRef Full Text | Google Scholar

Yassine, M., Nair, A., Fammels, J., Wade, E., Fu, Z., Kirste, L., et al. (2022). Influence of structural properties on the ferroelectric behavior of hexagonal AlScN. J. Appl. Phys. 132 (11). doi:10.1063/5.0103578

CrossRef Full Text | Google Scholar

Zhang, J.-M., Zhang, Y., Xu, K.-W., and Ji, V. (2007). Young's modulus surface and Poisson's ratio curve for cubic metals. J. Phys. Chem. Solids 68 (4), 503–510. doi:10.1016/j.jpcs.2007.01.025

CrossRef Full Text | Google Scholar

Zhang, S., Holec, D., Fu, W. Y., Humphreys, C. J., and Moram, M. A. (2013). Tunable optoelectronic and ferroelectric properties in Sc-based III-nitrides. J. Appl. Phys. 114 (13). doi:10.1063/1.4824179

CrossRef Full Text | Google Scholar

Zhang, Y., Zhu, W., Zhou, D., and Yang, C. (2015). Effects of sputtering atmosphere on the properties of c-plane ScAlN thin films prepared on sapphire substrate. J. Mater. Sci. Mater. Electron. 26, 472–478. doi:10.1007/s10854-014-2423-z

CrossRef Full Text | Google Scholar

Zhang, Z., Xuan, W., Jiang, H., Xie, W., Li, Z., Dong, S., et al. (2023). High electromechanical coupling coefficient of longitudinally excited shear wave resonator based on optimized bragg structure. Micromechanics 14 (11), 2086. doi:10.3390/mi14112086

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang M., M., Yang, J., Si, C., Han, G., Zhao, Y., and Ning, J. (2015). Research on the piezoelectric properties of AlN thin films for MEMS applications. Micromachines 6 (9), 1236–1248. doi:10.3390/mi6091236

CrossRef Full Text | Google Scholar

Žukauskaitė, A. (2012). Metastable YAlN and ScAlN thin films: growth and characterization. Linköping: Linköping University Institute of Technology. Dissertation.

Google Scholar

Zukauskaite, A., Tholander, C., Palisaitis, J., Persson, P., Darakchieva, D., Sedrine, N. B., et al. (2012). Y_x Al _1-x N thin films. J. Phys. D Appl. Phys. 45 (42), 422001. doi:10.1088/0022-3727/45/42/422001

CrossRef Full Text | Google Scholar