Study on acoustic emission characteristics under compression and fractal dimension of pore structure of polyvinyl alcohol fiber engineered cementitious composites

Fiber adding to engineered cementitious composites (ECC) can effectively improve the performance of material. This study used the acoustic emission (AE) technique to study the influence of polyvinyl alcohol (PVA) fibre content on compressive strength and damage evolution of ECC and used the fractal theory to analyse the pore structure of PVA-ECC, which innovatively explored the mechanical properties and durability of PVA-ECC from macro and micro perspectives. In terms of mechanical properties, the compressive strength of ECC with 1% PVA volume content was the highest. PVA changed the compression damage mechanism of ECC, showing a decrease in internal tensile cracking and an increase in shear cracking through RA-AF values. ECC developed from brittle damage to ductile damage. In terms of microstructure and durability, ECC with 1% PVA volume content had the best impermeability and pore structure fractal characteristics, and PVA had a great influence on the fractal characteristics of transition pores and capillary pores. The fractal dimension had a good correlation with porosity, total pore volume, most probable aperture, compressive strength and chloride diffusion coefficient, indicating that the mechanical strength and impermeability of ECC were closely related to the complex spatial structure and distribution characteristics of pores. The fractal dimension can be used to comprehensively characterise the mechanical properties and durability of ECC.

1 Introduction

Cementitious materials remain important civil engineering materials in modern construction. The high strength, ductility, and durability of these materials can ensure the safety and stability of structures (Sun, et al., 2023; Yang, et al., 2024). Ordinary cementitious materials are brittle (Rajput and Iqbal, 2017; Wagh, et al., 2024). Currently, various fiber materials incorporating can improve the mechanical properties of cementitious materials to some extent, such as steel fiber, polypropylene fiber, PVA fibers, basalt fibers, etc., (Li B. et al., 2023; Zhao, et al., 2024). Rahmani et al. (2012) studied the effect of cellulose, polypropylene and steel fibers on the impact resistance of cementitious materials, with the addition of steel fibers having the most significant effect of increasing the average number of failure blows by 375%. Li J. Y. et al. (2023) tested the tensile and compressive properties of polypropylene fiber concrete at room temperature and after high temperatures. When fiber content is low, polypropylene fibers significantly improve the mechanical properties of concrete after high temperature. However, with the increase of fiber content, compressive strength after high temperature shows a tendency to increase first and then decrease at the same temperature. Shen et al. (2024) used SHPB equipment to conduct mechanical property experiments on steel-polypropylene fiber-reinforced concrete after high temperatures. It is found that the dynamic compressive strength of hybrid fiber concrete with optimum admixture increases by 97.1% compared to C40 plain concrete at 800°C temperature group.

PVA fibers are advantageous for practical engineering applications due to their high toughness, good affinity with cementitious materials and low production cost (Sundar et al., 2017; Zhang et al., 2024). PVA-ECC is a polymer composite material. Stukhlyak et al. (2015) proposed a multi-scale analysis method for composite materials and believed that the self-organizing system of materials and the interaction between different deformation scales are factors that cannot be ignored in evaluating material properties. Therefore, for polymer composites, the deformation and crack characteristics are analyzed from macro-scale, meso-scale and micro-scale. The initiation of initial crack is controlled by the micro-scale mechanism, and the propagation of crack is defined by the macro-scale fracture mechanism. In the study of macroscopic mechanical properties of PVA-ECC, Zhang et al. (2019) concluded that PVA fibers can improve the impact resistance and tensile properties of cementitious materials through drop-weight tests and uniaxial tensile tests. Farhan and Jagdish (2021) replaced cement with fly ash and iron slag, and used PVA fiber as an additive with contents of 0%, 2%, and 3%. Compared with the concrete without PVA fibers, the compressive strength, flexural strength, and split tensile strength of the concrete containing PVA fibers are improved, and the mechanical property indexes are optimal when the additives are 3%. Wu et al. (2024) analyzed the effect of steel-PVA hybrid fibers on the flexural properties of slab concrete by three-point bending test, the development of cracks in concrete by using DIC technique and SEM experiments, and the evolution of cracks based on fractal theory quantitatively. It is concluded that the steel-PVA hybrid fibers increase the proportional ultimate strength and residual flexural strength of the concrete. The presence of PVA fibers further reduce the rate of crack development and crack area compared to steel fiber reinforced concrete. The best flexural properties of concrete are achieved when the steel fiber content is 1.0% and PVA fiber content is 0.2%.

In the study of micro crack propagation and damage evolution of PVA-ECC, AE technology is widely used in experimental studies of concrete. AE signals can quantitatively or qualitatively analyze the pressure damage process and damage evolution of materials (Lockner, 1993; Nair and Cai, 2010; Bi et al., 2020; Zhang and Li, 2020; Lyu, et al., 2024). Huang et al. (2019) have analyzed the compression damage characteristics of PVA fiber concrete after high temperature using acoustic emission technology. The results showed that the fibres resulted in a wider distribution of energy count rates in the specimens, with relatively small peak energy count rates, and it was concluded that PVA fibres could improve the high temperature resistance of the concrete by comparing it with the reference concrete. Chen et al. (2022) implemented preloading of concrete with and without added cementitious materials at different ages with different strengths, and studied the law of the effect of early damage on long-term strength of concrete based on the AE technique. It was found that the pozzolanic effect of cementitious materials and hydrates produced C-S-H gels to fill the pores and repair the early damage caused by preloading. The addition of cementitious materials resulted in higher compressive strength of 270 days age specimens than ordinary concrete. Chen et al. (2023) classified and localized cracks in corroded concrete columns under eccentric loading by the AE technique, and proposed a simple four-step method of crack identification based on the results of GMM calculations, which provided a quantitative analysis of the proportion of tensile and shear cracks in compressive damage.

In the study of microporous structure of PVA-ECC, Chen et al. (2021) measured the effective chloride diffusion coefficients of cement mortars at different water-cement ratios. It was found that higher water-cement ratios led to a porous structure, which increased the chloride diffusion coefficient in cement mortar. He et al. (2023) found that the dielectric constant can characterize water-cement ratio of plastic concrete, while water-cement ratio affects the microporous structure of concrete. The changes in pore structure of material have impact on mechanical properties, durability, etc (Fan et al., 2022). With the development of high-performance concrete and indepth study of the pore structure of the material, traditional pore structure parameters, such as porosity, pore volume and pore size distribution are unable to quantitatively characterise the complexity of the pores. Scholars have established a variety of fractal models of concrete pore structure to describe the complexity of pore structure in terms of the size of fractal dimension, and the relationship between microscopic pore structure and macroscopic mechanical properties has been established through the fractal dimension. Liu et al. (2023) determined the compressive strength and pore structure parameters of steel-PVA hybrid fibre concrete with different dosage, and calculated the fractal dimension under different pore size distributions based on the thermodynamic fractal model. The article concluded that the fractal dimension was consistent with the change rule of compressive strength affected by the fibres, and the fractal dimension of gel pores and capillary pores varied greatly. Li et al. (2024) concluded that the pore structure of steel fibre ground polymer recycled concrete had significant fractal characteristics. The fractal dimension was negatively correlated with porosity and most probable aperture, positively correlated with curvature coefficient, and positively correlated with cubic compressive strength, split tensile strength and flexural strength. Zhao J. et al. (2023) calculated the fractal dimension of pore structure of basalt-polypropylene fibre concrete based on optical method, and found that fractal dimension had a strong correlation with porosity, spacing coefficient, compressive strength, and splitting tensile strength. The fractal dimension can reflect the complexity of material pore structure and the influence of pore structure on mechanical properties. Jin et al. (2017), Zarnaghi et al. (2018), and Lv et al. (2019) found a linear relationship between the fractal dimension and strength of concrete.

Most current research of PVA-ECC focuses on the effects of fiber content on mechanical properties, such as compressive, flexural, tensile, and macroscopic damage characteristics. However, fewer studies investigate the stages of internal crack development and pore structure characteristics under different PVA contents. Based on the AE technology, this paper investigated the characteristic parameters of AE and the development of tensile cracks and shear cracks in specimens with different PVA content, and analysed the influence of PVA on the uniaxial compression damage characteristics of ECC. The pore structure parameters and chloride diffusion coefficient were obtained through mercury intrusion porosimetry (MIP) tests and chloride penetration tests, and the influence of PVA fibre on the fractal characteristics of pore structure was analysed based on fractal theory. The correlations between fractal dimensions and mechanical parameters, pore structure parameters, and chloride diffusion coefficient were also analysed. This study aims to provide a theoretical basis for the application of PVA fibers in ECC from micro and macro perspective.

2 Test

2.1 Test materials

In these tests, the cements are sulfoaluminate double fast cement of strength 42.5. Fly ash is the first grade low calcium fly ash with the specific surface area of 420 m²/kg. Silica ash has a specific surface area of 2000 m²/kg. Fine quartz sand specification are 100–200 mesh, which came from Anhui Fengyang County Shengli Quartz Sand Factory. High-efficiency polycarboxylic acid water reducing agents were produced by Zhengzhou Xinghui Chemical Raw Material Company, while retarders from Shandong Zhongda New Material Company and dilatants from CNBM Zhongyan Technology Co, as shown in Table 1. PVA fibers were produced at the Shangwanwei raw material plant. The PVA parameters are shown in Table 2.

Table 1

Table 1. Chemical composition of material (%).

Table 2

Table 2. Related parameters of PVA fibers.

The PVA-ECC substrate formulation is shown in Table 3. PVA fibers are added in volume fractions of 0%, 0.5%, 1.0%, 1.5%, and 2.0%, corresponding to specimen numbers P0, P0.5, P1, P1.5, P2, as shown in Table 4.

Table 3

Table 3. Mix ratio of base materials.

Table 4

Table 4. PVA fiber content and number.

2.2 Specimens preparation

There are two specimen standards for this test, as shown in Figure 1. One is a cube with a size of 100 mm × 100 mm ×100 mm, which is used for uniaxial compression tests and AE tests. There are 3 groups of P0-P2, a total of 15 groups of specimens. The other is a flat cylinder with a diameter of 100 mm and a thickness of 50 mm P0-P2 are 4 groups, a total of 20 groups of specimens. Three groups were used for chloride penetration tests, and one group was used for MIP tests.

Figure 1

Figure 1. Three-dimensional dimensioned sample of the specimens. (A)Cubic specimen (B)Flat cylinder specimen.

Firstly, dry materials such as cement, fly ash, silica ash, quartz sand, expansion agent, etc.,. were put into the mixer for stirring for 1.5 min, and the dry materials were stirred evenly. Subsequently, water was poured into the mixer in batches, and PVA fibers were gradually poured evenly. Water reducing agents were poured according to the wetting degree of materials in mixer. After all the materials were stirred evenly, the mixer was closed, and the stirred cement paste was put out for use.

Pour half of the cement paste into mold, then put it on the vibration table, open the vibration table to discharge air in cement paste, and then pour the other half of the cement paste into mold. Repeat above vibration process to make the cement paste more even. Finally, the cement paste was wrapped with preservative film together with the mold. The purpose was to allow the cement paste to continue hydration heat reaction in curing film, thereby effectively inhibiting the generation of microcracks. These were placed in the standard curing room with indoor temperature of 20°C ± 2°C, humidity of 95%, and curing for 28 days.

After standard curing, the specimens were polished to make the surface smooth and flat. The six surfaces of cube specimens and the upper and lower surfaces of flat cylinders were polished using 20 mesh coarse sandpaper.

2.3 Test methods and equipments

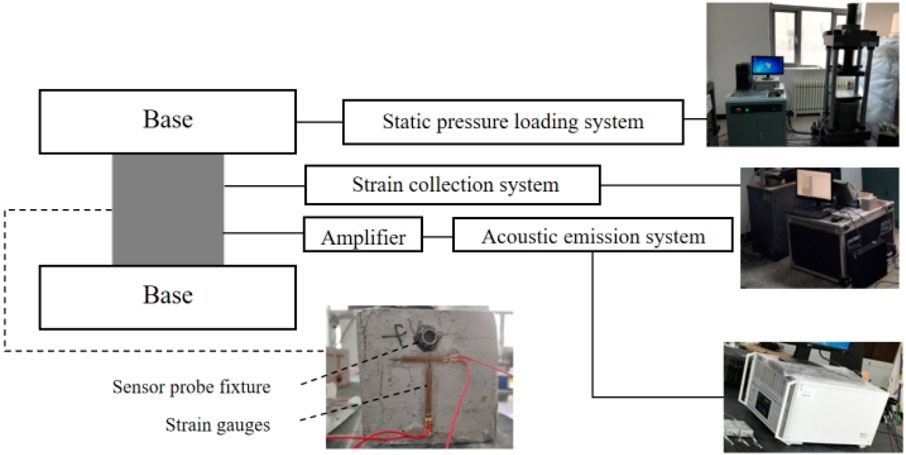
2.3.1 Uniaxial compression and acoustic emission test

For the static loading device, we adopted a micro-controlled electro-hydraulic servo rigidity test press, capable of a maximum test force of 2t and an internal piston range of 100 mm. The strain gauges with a width of 3 mm were selected, and two opposite sides were selected from four sides of the specimen. Floating ash on the surface was erased, and strain gauges were pasted on two opposite sides of the specimen in a positive T and inverted T fashion.

The multi-channel acoustic emission detection system was produced by American Physical Acoustics Company, as shown in Figure 2. Experimental acoustic signals were set to a thresh-old value of 40 dB. Add 2/4/6-AST amplifier. The function was to expand the signals collected by sensor and then transmit it to host computer, which made the test results more accurate. Ring sensor fixtures were specially made. Before the test, ring fixtures were fixed on the surface of specimen with glue. During the test, sensor probe was smeared with coupling agent such as vaseline and then put into the fixture. It can ensure that the probe is fixed, in good contact with cementitious specimen, and not damaged.

Figure 2

Figure 2. Schematic diagram of uniaxial compression and acoustic emission test.

2.3.2 Chlorine penetration test

The tests were conducted using NEL method proposed by Lu (1997) from Tsinghua University. The test instruments were NEL-VJH intelligent vacuum water saturator for concrete and NELD-CCM540 chloride diffusion coefficient tester for cement produced by Beijing NELD Company. According to “The method for determining the chloride diffusion coefficient for cement mortar” (JC/T1086-2008), the specimens were placed in a vacuum environment and soaked with NaCl solution to fully saturate specimens with salt, so that the specimens contained only one conductive ion, chloride ion. After that, the specimen was fixed between electrodes and a DC voltage of 1V–10 V was applied. The conductivity was derived from voltage values and electric current values of the specimens, then the chloride diffusion coefficient was derived from the Nernst-Einstein equation with Equation 1. The resistance of material to chloride penetration was evaluated according to the magnitude of diffusion coefficient.

$D_i=\frac{RT{\sigma }_i}{Z_i^2{F}^2{C}_i}(1)$

where $D_i$ = chloride diffusion coefficient, which is the number of chloride ions passing per unit time per unit area (10⁻¹² m²/s); $R$ = 8.314 (J/mol·K), gas constant; $T$ = absolute temperature (K); ${\sigma }_i$ = particle bias conductivity (S/m); $Z_i$ = particle charge or valence; $F$ = 96,500 (c/mol), Faraday’s constant; $C_i$ = particle concentration, which is chloride ion concentration of the salt solution used (mol/L).

2.3.3 MIP test

MIP tests adopted Micromeritic AutoPore IV 9510 automatic mercury porosimeter produced by American Mac company, which could measure the pore size range of 3–360000 nm. The specimens were crushed into particles less than 14 mm in diameter and height. The particles were cleaned and subsequently dried at 60°C for 24 h. Then the dried particles were sealed with expansion agent matched by mercury porosimeter, and the pore structure characteristic parameters were measured according to the Washburn equation (Washburn, 1921). As shown in Equation 2:

$d_p=-\frac{4\gamma \cos \theta }{p}(2)$

Where $d_p$ = pore diameter; $\gamma$ = 0.485N/m, surface tension of mercury; $\theta =130°$, contact angle; $p$ = externally applied pressure, test setting 0.1–61000 psia.

3 Results and discussion

3.1 Stress-strain curves and AE ringing counts

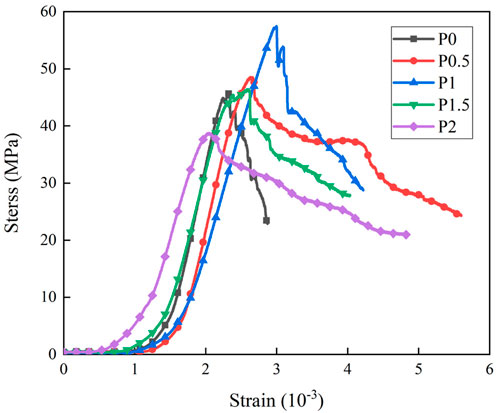
AE characteristic parameters can reflect the evolution of internal cracks during the damage process of cementitious, rock and other materials. In this paper, ringing counts and cumulative ringing counts are selected to analyse the AE characteristics. Ringing counts refers to the number of oscillations exceeding threshold, which can reflect the intensity and frequency of AE signals. Compressive damage of the specimen is a continuous development process. The speed and strength of internal crack development can be known by the response of ringing counts (Dong, et al., 1995; Ji, et al., 2000). Uniaxial compression tests were carried out on 5 groups of specimens, and stress-strain curves were obtained. As shown in Figure 3, the compressive strength increased first and then decreased with the increase of PVA content. When volume fraction of PVA was 1%, the compressive strength was 57.49MPa, reaching the maximum value, which was 25.6% higher than that of the reference specimen P0. When volume fraction of PVA was 2%, the compressive strength was 15.2% lower than that of the reference specimen P0, indicating that more fibers would reduce the strength of materials.

Figure 3

Figure 3. Stress-strain curves of test specimens with different PVA content.

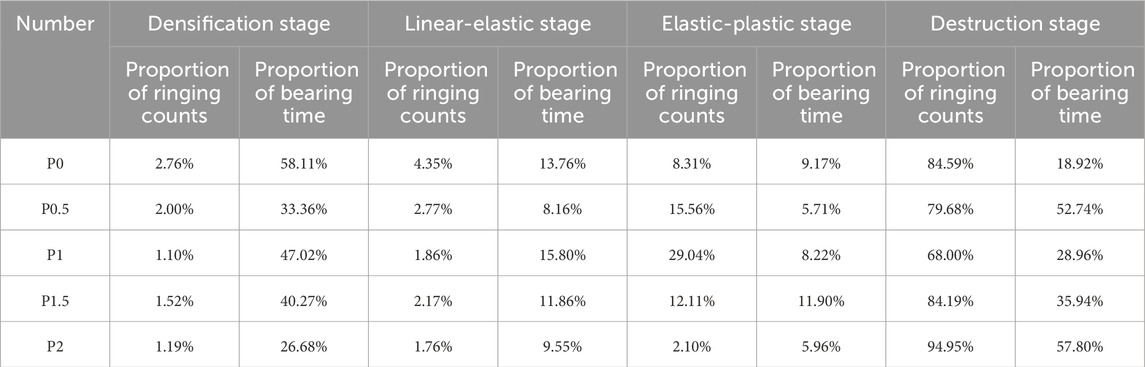
Figure 4 shows the stress-time-ringing counts-cumulative ringing counts curves of PVA-ECC specimens. According to the change of stress curve slope, compression damage process can be divided into different stages (Zhou et al., 2020). In this paper, it was divided into densification stage, linear-elastic stage, elastic-plastic stage and destruction stage. Table 5 shows the proportion of load duration and AE ringing counts in each stage.

Stage I: The densification stage is defined as the period from the beginning of loading to 30% of peak stress. At the initial stage of loading, original pores and initial defects in specimen began to be continuously compressed. The stress increased nonlinearly, and the growth rate gradually accelerated. Ringing counts were few and sparse, signal intensity was weak, and there were no obvious cracks propagation. PVA reduced the proportion of bearing time and ringing count in densification stage to varying degrees, which was due to the filling of PVA to reduce internal microcracks of ECC.

Stage II: The linear-elastic stage occurs from 30% to 80% of peak stress. At this stage, specimen began to bear pressure, stress curve increased linearly, and ringing counts gradually became dense and increased. That indicated meso-cracks in the material began to develop, but macro-cracks had not yet occurred.

Stage III: The elastic-plastic stage spans from 80% to 100% of peak stress. The stress growth rate slowed down until it reached the maximum strength. Ringing counts increased sharply at the peak stress, and cumulative ringing counts curve increased exponentially. It showed that the meso-cracks inside specimen expanded to outer surface, and the surfaces of specimen began to show cross-connected interconnecting macro-cracks. Accumulated deformation energy inside the specimen was released in form of strain waves, and AE signals were frequent. PVA began to play a role in toughness, and played a bridging and crack resistance effect on the cracking damage of specimen, which increased AE events. The proportion of ringing counts of P0.5, P1 and P1.5 were greater than that of P0.

Stage IV: The destruction stage refers to the decrease from 100% of peak stress to 50%. The test set automatically stopped when it dropped to 50% of the peak stress. P0 showed obvious brittle damage after the peak, and stress curve decreased almost linearly. PVA-ECC showed strong ductility characteristics after the peak, and the time proportion of destruction stage with PVA was 28.96%–57.8%, which was 53%–205% higher than that of P0. This demonstrated that PVA fibers increased residual stress post-damage, changing the damage mode from brittle to ductile and maintaining a certain bearing capacity after damage. The ringing counst in destruction stage accounted for 68%–94.95%. After peak stress, the increase of each ringing count represented that specimen had new macro cracks, AE signal intensity increased, and the bearing capacity of specimen decreased rapidly. Ringing counts of P1 still surged in post-peak stage, indicating that its post-peak bearing capacity was large. P2 had the largest proportion of ringing counts in post-peak stage, indicating that its ductility was the largest.

Figure 4

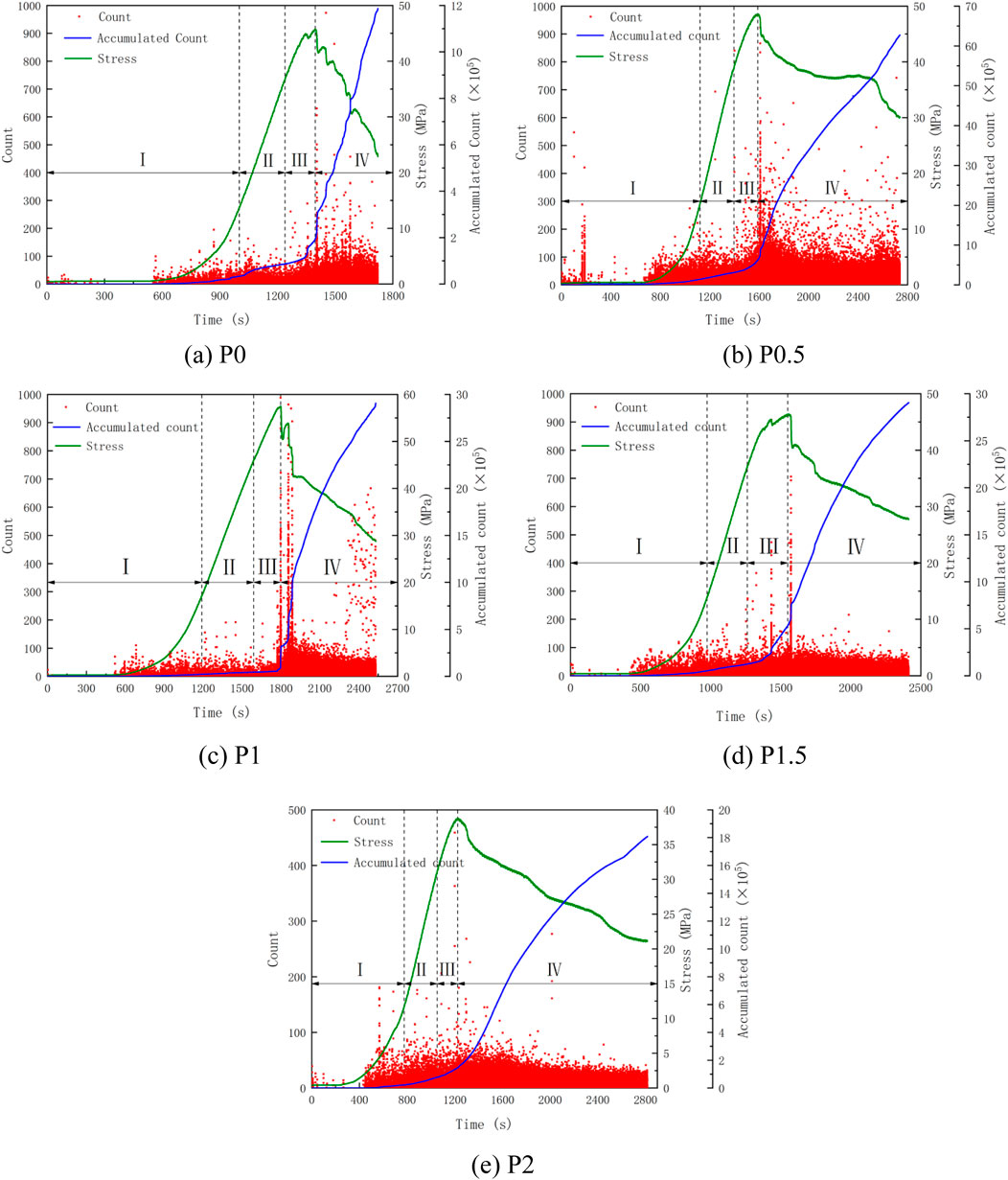
Figure 4. Stress-time-ringing counts-cumulative ringing counts curves. (A) P0. (B) P0.5. (C) P1. (D) P1.5. (E) P2.

Table 5

Table 5. Proportion of ringing counts and bearing time in each stage of the loading process.

3.2 RA-AF distribution characteristics based on Gaussian mixture model

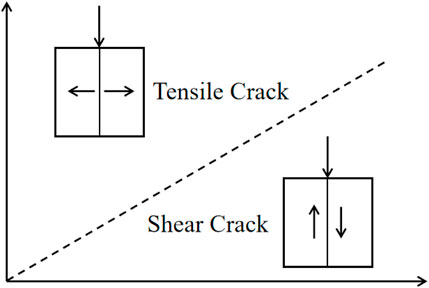
Tensile damage and shear damage mainly occur during the compression damage process of PVA-ECC. The RA-AF value in AE parameters can characterize tensile cracks and shear cracks. RA is the ratio of rise time to amplitude, and AF is the ratio of ringing count to duration. The study found that (Reboul, et al., 2020) AE signal waveform change gradient under tensile damage is large and signal frequency is high, and the performance is higher AF value and lower RA value; on the contrary, AE signals under shear damage show lower AF values and higher RA values. However, there is no accurate standard for the evaluation of RA and AF values, and the slope method with k as diagonal is commonly used. This method considers that crack above the slash is a tensile crack, and crack below the slash is a shear crack, as shown in Figure 5.

Figure 5

Figure 5. Crack damage type based on RA-AF.

Since the RA-AF threshold of ECC is usually difficult to unify, it is difficult to accurately classify the crack types only by slope method. In recent years, scholars have introduced Gaussian Mixture Model (GMM) to cluster RA-AF values. Based on the probability model, GMM classifies data by probability distribution, and calculates m single Gaussian models under different weight coefficients, and uses the Expectation-Maximization (EM) algorithm to fit m mixed Gaussian distributions. The expression of single Gaussian model is shown in Equation 3 (Luo, et al., 2024; Shi, et al., 2024):

$N_i\left(\overrightarrow{x}|\overrightarrow{u},\sum _i\right)=\frac{\exp \left[-\frac{1}{2}{\left(\overrightarrow{x}-\overrightarrow{u}\right)}^T{\left(\sum _i\right)}^{-1}\left(\overrightarrow{x}-\overrightarrow{u}\right)\right]}{2{\pi }^{\frac{D}{2}}{\left|\sum _i\right|}^{\frac{1}{2}}}(3)$

where $\overrightarrow{u}$ = the average vector of $D\times 1$; ${\sum }_i$ = the covariance matrix of $D\times D$.

The GMM expression is calculated by weighting single Gaussian model, as shown in Equation 4:

$p\left(x_i\right)={\displaystyle \sum _{i=1}^m}{\alpha }_{i}N\left(x|u_i,\sum _i\right)(4)$

where $m$ = the number of models; ${\alpha }_i$ = the weight of mixed model; $N\left(x|u_i,{\sum }_i\right)$ = the $i$ th single Gaussian model density function.

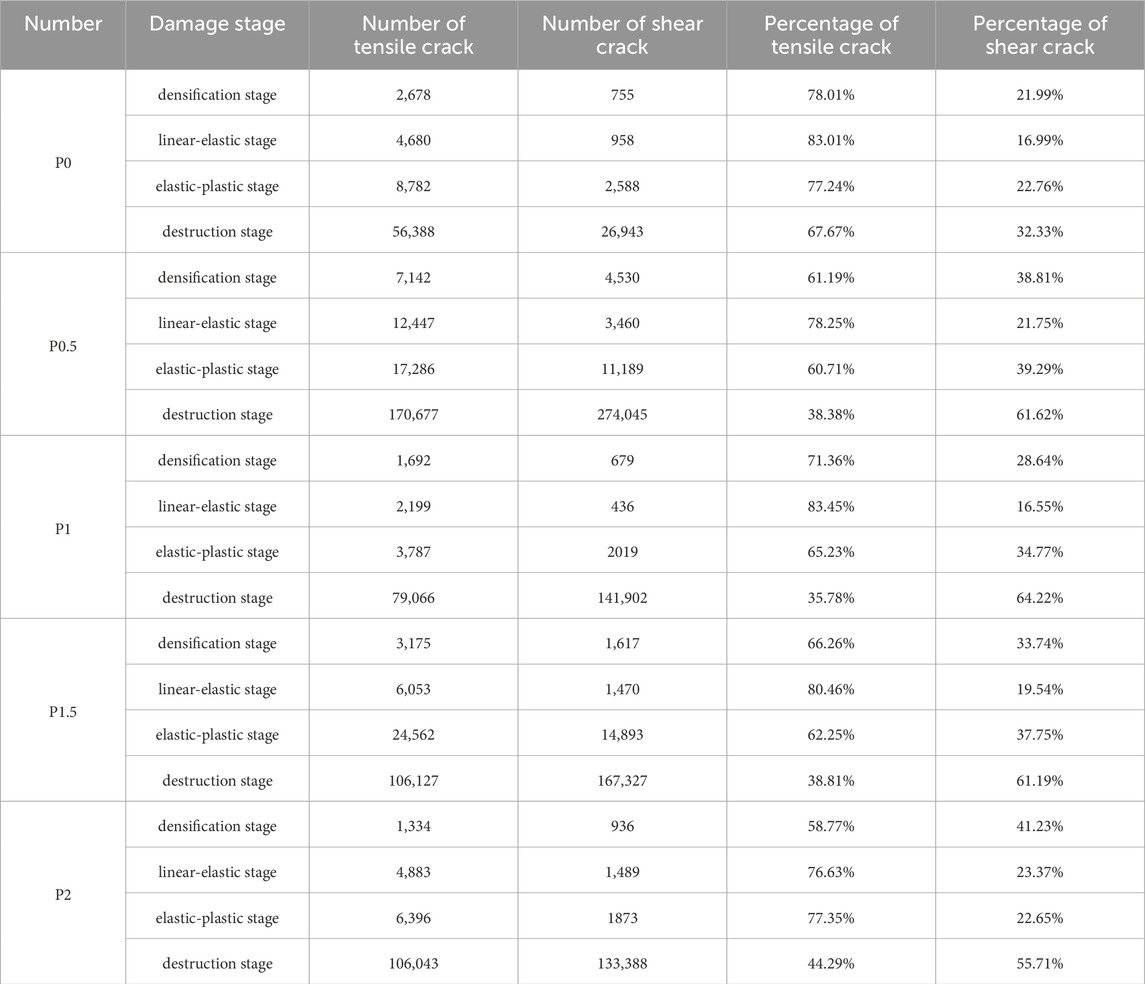
The crack propagation types of PVA-ECC under uniaxial compression are classified by GMM model. Figure 6 describes the distribution of RA-AF and the proportion of tensile cracks and shear cracks under five PVA contents. It can be seen from (a) that ECC without PVA were dominated by tensile damage during the damage process, and tensile cracks account for 70%. The addition of PVA changed the propagation mode of internal cracks in ECC. The proportion of shear cracks in PVA-ECC under uniaxial compression exceeded 50%, and the proportion of shear cracks increased first and then decreased with the increase of PVA contents. When PVA content was 1%, the proportion of shear cracks was the largest, reaching 62.57%.

Figure 6

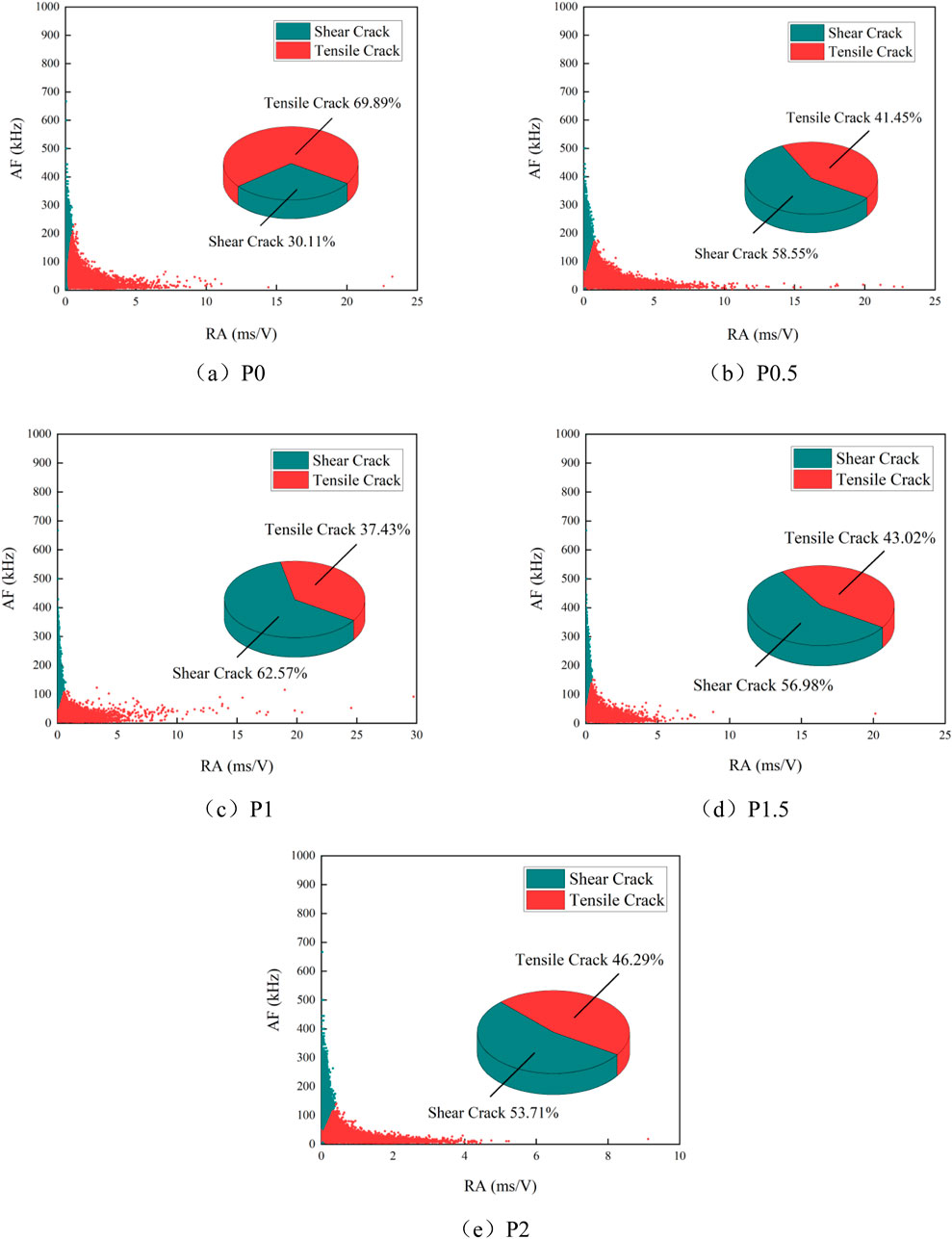
Figure 6. RA-AF scatter plot and the proportion of tensile cracks and shear cracks. (A) P0. (B) P0.5. (C) P1. (D) P1.5. (E) P2.

The compression of ECC first led to tensile stress, which caused micro-cracks to form in the interior. As shown in Table 6, in densification stages, linear-elasticity stages, and elastic-plastic stages, the number of cracks was small, and the internal cracks were mostly caused by tensile damage. When stress reached the maximum value, the number of cracks increased sharply after the specimen was destroyed, which was consistent with AE event signal activity. In destruction stage, the proportion of shear cracks increased, which was due to the bridging effect of PVA, so that the bite force at crack propagation increased, and internal shear stress of the specimen increased. After shear stress bears part of stress, the degree of crack tensile cracking decreased. The damage mode transited from tensile damage to shear damage. The specimen was not split by a single vertical crack, but formed a multi-directional irregular shear crack, which inhibited the formation of interconnecting cracks and the release of deformation energy. PVA changed internal compression damage mechanism of specimen and improved tensile, shear and fracture toughness of ECC.

Table 6

Table 6. The number and proportion of tensile cracks and shear cracks in each damage stage.

3.3 Chloride diffusion coefficient

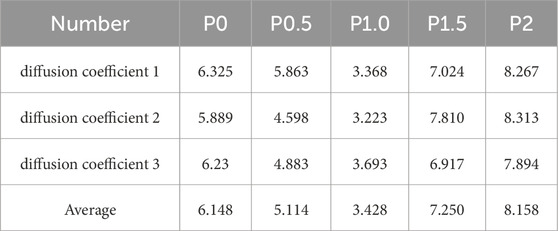
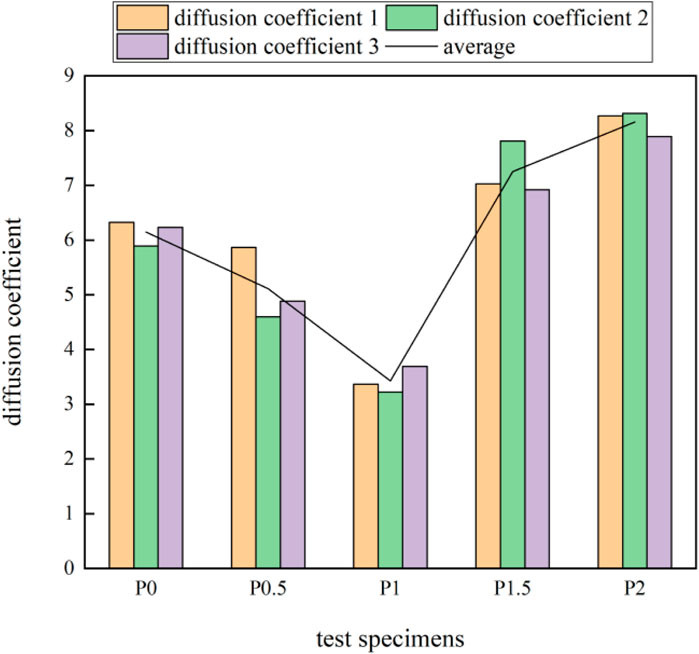
Chlorine penetration tests were carried out on ECC with different fiber content. Three tests were carried out on the same batch of specimens to take the average value to obtain the chloride diffusion coefficient of the material as shown in Table 7 and Figure 7. The chloride diffusion coefficients show firstly decrease and then increase with increasing PVA fiber content. When PVA fiber content is 1%, the chloride diffusion coefficient is the smallest, which decreases by 44.2% compared with the baseline specimen P0, and the specimen has the best impermeability performance.

Table 7

Table 7. Chloride diffusion coefficients (10⁻¹²) of the materials.

Figure 7

Figure 7. Chloride diffusion coefficients of PVA-ECC.

3.4 Pore structure parameters

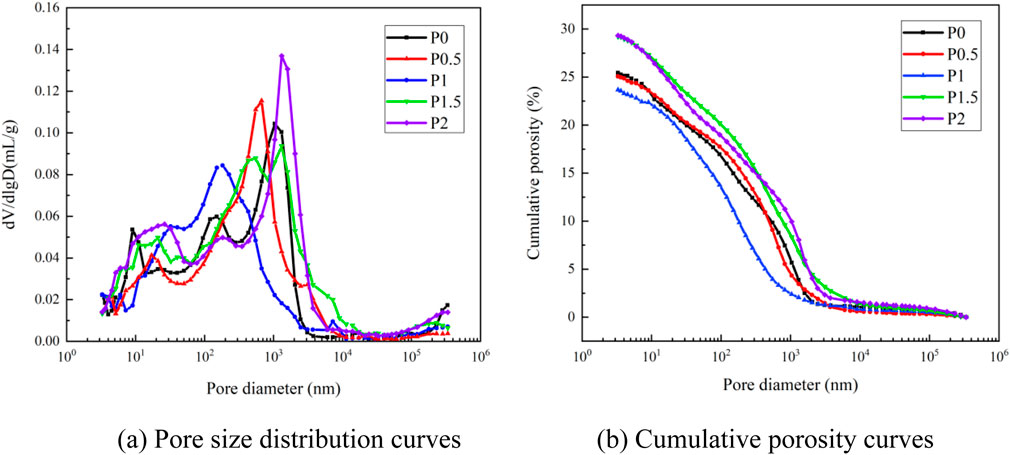
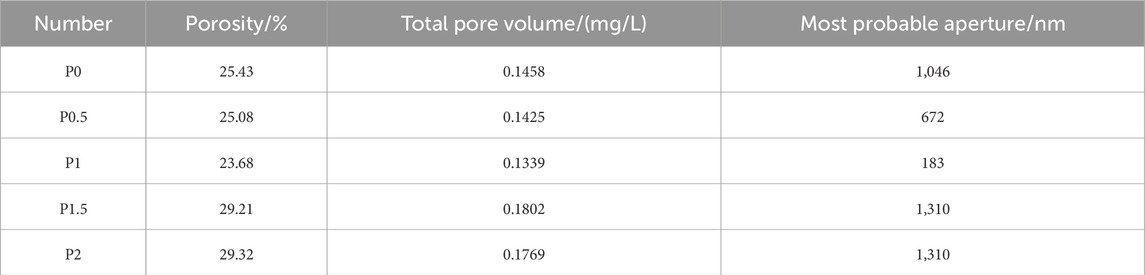
Among the pore structure parameters, porosity, total pore volume and most probable aperture are important parameters affecting the macroscopic properties of concrete (Li, et al., 2024). Figure 8A depicts the pore size distribution curves. Most probable aperture is the pore size with the highest probability of occurrence, which corresponds to the peak of distribution density in pore size distribution curve. From (a), it is clear that P1 has the smallest most probable aperture. Figure 8B depicts the cumulative porosity curves, where P1 porosity is the smallest at 23.68%. Table 8 shows the measured values of porosity, total pore volume, and most probable aperture for five groups of specimens in MIP tests. It can be seen that porosity, total pore volume and most probable aperture of PVA-ECC show a pattern of firstly decreasing and then increasing with increasing PVA content. The pore structure is optimal at 1% PVA fiber content, suggesting that a moderate amount of PVA fibers improves pore structure and increases compactness, reducing initial defects. However, excessive PVA fibers are difficult to disperse, forming groups that negatively affect fluidity, adhesion, and polymerization, increasing internal porosity and microscopic defects, thus adversely affecting pore size distribution and compressive strength.

Figure 8

Figure 8. MIP results of PVA-ECC. (A) Pore size distribution curves (B) Cumulative porosity curves.

Table 8

Table 8. Pore structure parameters.

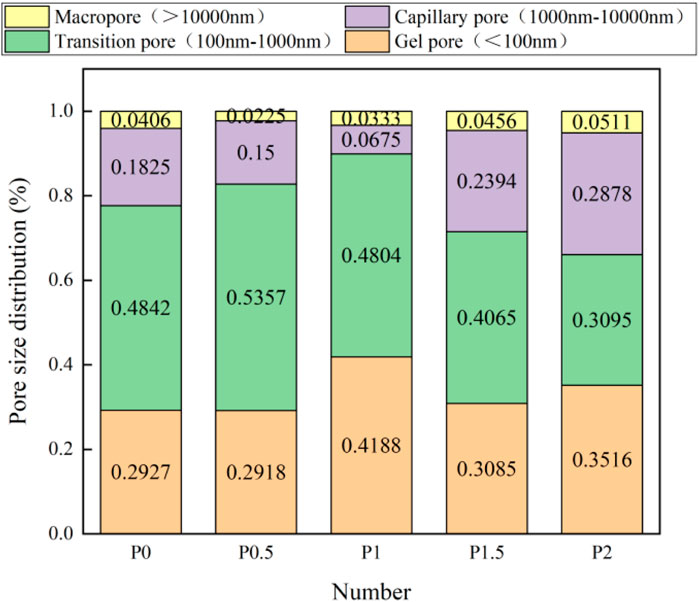
The pore sizes are categorized into four ranges: gel pores (<100 nm), transition pores (100–1,000 nm), capillary pores (1,000–10000 nm), and macropores (>10,000 nm) (Zhao Y. C. et al., 2023). The percentage of different pore size ranges in total pore volume is shown in Figure 9.

Figure 9

Figure 9. The percentage of different pore size ranges to the total pore volume.

Gel pores are harmless or less harmful pores, which are mainly formed by cement hydration reaction and gas produced by water evaporation during mixing. Transition pores, capillary pores and macropores are harmful pores. Transition pores are generated by the gap between cement particles. Capillary pores are the voids left by cementitious particles that are not filled by hydration products. Macropores are mainly cracks caused by uneven distribution of aggregates in materials. Harmful pores affect the mechanical properties and durability of ECC. It was found that PVA mainly affected the number of gel pores and capillary pores. Appropriate amount of PVA increased the number of gel pores and decreased the number of capillary pores. Excessive fibers led to poor dispersion of the material, resulting in uneven distribution between aggregates, which made the number of capillary pores and macropores increase.

3.5 Fractal dimension of pore structure

Fractal theory effectively analyzes the pore size distribution of materials, characterizing the pore structure (Winslow, 1985; Xuan, et al., 2018). Menger sponge model and thermodynamic-based fractal model were used to calculate the fractal dimension. The Menger sponge model assumes a square unit cell with side length R, which is divided equally into n small cubes with r. The contents were obtained by the residual relative volume formula (Wei, et al., 2007), as shown in Equations 5-7:

$V=1-P={\left(r/R\right)}^{3-D}(5)$

$\lg \left(1-P\right)=\left(3-D\right)\lg \left(r/R\right)(6)$

$D=3-\frac{\lg \left(1-P\right)}{\lg \left(r/R\right)}(7)$

where D = fractal dimension; p = material porosity, which is the cumulative percentage of mercury that entering material at a given pressure value in mercury compression experiments; r = corresponding pore size at pressure value; R = maximum pore size. R/R responds to the pore size distribution of material. A larger fractal dimension D indicates a more complex pore space and better pore structure of material.

Zhang and Li (1995) proposed thermodynamic fractal model based on the principle of energy conservation, which suggests that the work done by external environment on mercury in MIP test is equal to the increase in surface energy of the mercury that enters pores. Its expression is Equation 8:

${\int }_0^{V}P\mathrm{d}V=-{\int }_0^{\delta }\sigma \cos \sigma \mathrm{d}S(8)$

where p = the pressure applied when pressing mercury. V = the amount of mercury pressed in specimen. S = the pore surface area.

Pore specific surface area, pore size and mercury intake are correlated by fractal analysis, and after quantitative analysis, the relationship is expressed as shown in Equation 9:

${\displaystyle \sum _{i=1}^n}{P}_i\Delta V_i=C^{\prime }{r}_n^{2-D}{V}_n^{D/3}(9)$

where $P_i$ = Pressure at $i$ th pressurization, (Pa); $\Delta V_i$ = Mercury feed at the $i$ th pressing of mercury, (m³); $r_n$ = Pore size at $n$ th pressing of mercury, (m); $V_n$ = Cumulative mercury feed at stage $n$, (m³); $C^{\prime }$ = Constant factor; $D$ = Fractal dimensions based on thermodynamic relations.

We demand $W_n={\displaystyle {\sum }_{i=1}^n}{P}_i\Delta V_i$, $Q_n=V_n^{1/3}/r_n$, logarithmic conversion is performed to obtain Equation 10:

$\lg \left(W_n/r_n^2\right)=D\lg Q_n+\lg C^{\prime }(10)$

The five groups fractal dimensions of specimens were calculated based on two fractal models, and the relationship curves for P0 were fitted. As shown in Figure 10, the fractal curves based on thermodynamic relationship present a high degree of linear correlation, and the correlation coefficients R² are all greater than 0.999, indicating that this model can more accurately reflect the fractal characteristics of pore size distribution of PVA-ECC. Fractal dimensions increased and then decreased with the increase of PVA contents. The larger fractal dimension is, the more complex internal structure of pores is, and the more reasonable pore size distribution is.

Figure 10

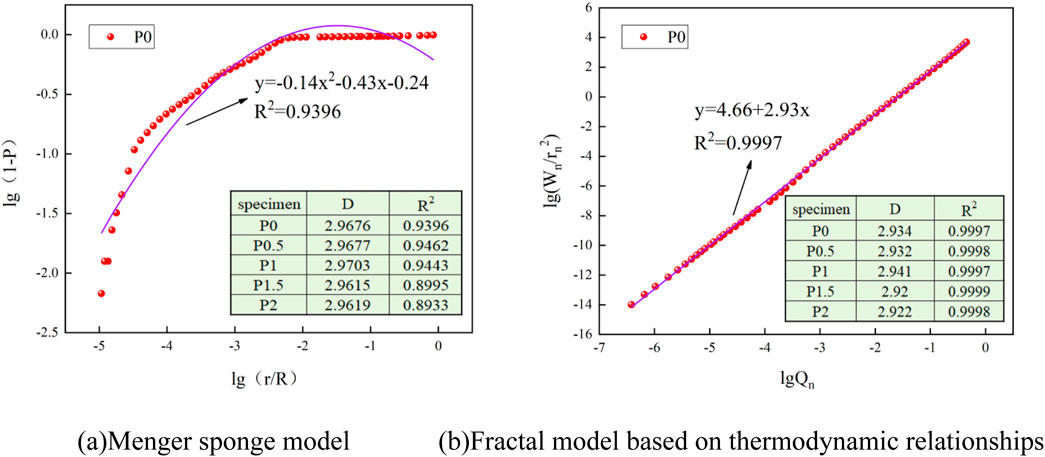
Figure 10. Fractal dimension of PVA-ECC. (A) Menger sponge model (B) Fractal model based on thermodynamic relationships.

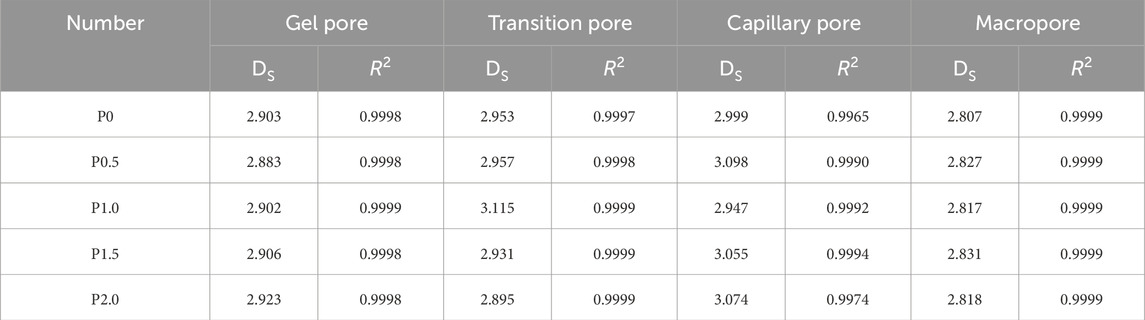
In order to further study the effect of PVA on pore size distribution, the fractal dimensions of gel pores, transition pores, capillary pores and macropores of five groups of specimens were calculated in Table 9. According to three-dimensional Euclidean space, the fractal dimension D of ECC is between 2 and 3. The transition pores and capillary pores in table have D_S>3. At present, scholars believe that this is due to the presence of ink bottle-shaped pores in cementitious materials (Zeng, et al., 2010; Lee and Jacobsen, 2011). Ink bottle-shaped pores are usually formed by evaporation of water during hardening process of cementitious materials. In MIP test, only when the intrusion pressure is large, mercury will enter the small pore. At this time, the small pore volume is recorded, but it is actually the total volume of large pore and small pore in the ink bottle-shaped pore. According to the data of Table 9, it is speculated that PVA cause ink bottle-shaped pores in specimen.

Table 9

Table 9. Fractal dimension of different pore size range.

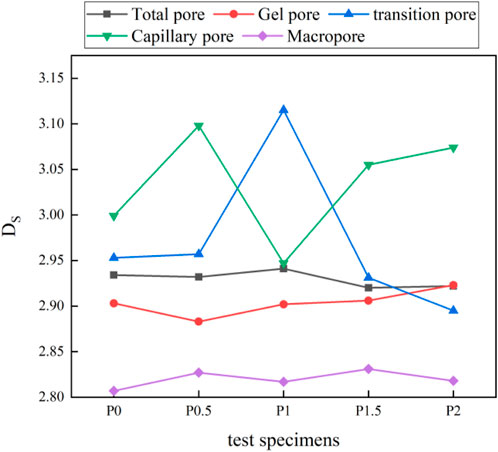
Figure 11 describes the change of fractal dimension of each pore range under different PVA content. PVA had a great influence on the fractal characteristics of transition pores and capillary pores, and had little influence on the fractal characteristics of gel pores and macropores. This was because the fiber diameter was in range of capillary pore diameter, and the most probable apertures in five groups of specimens were in range of transition pores and capillary pores. Therefore, the fiber had a great influence on the spatial structure distribution of transition pores and capillary pores.

Figure 11

Figure 11. The variation law of fractal dimension in each pore size range.

3.6 The correlation between fractal dimension and pore structure parameters

Studies have shown that the fractal dimension of fiber reinforced concrete has a certain correlation with pore structure parameters and mechanical parameters (Li, et al., 2024; Zhao J. et al., 2023). Figure 12 shows the relationship between porosity, total pore volume, most probable aperture of P0, P0.5, P1, P1.5, P2 and their fractal dimension. It can be found that the porosity, total pore volume, and most probable aperture of PVA-ECC have a strong negative correlation with the fractal dimension, and the correlation coefficients R² are 0.970, 0.981, and 0.863 respectively. The porosity, total pore volume and most probable aperture decrease with the increase of fractal dimension. Fractal dimension can be used to comprehensively characterize pore structure characteristics. The larger fractal dimension leads to the higher complexity of internal pore structure space and the higher ability of pore size occupying the space. This also leads to a smaller most probable aperture, which avoids development of the internal connected pore size to the larger pore size, and reduces the probability and proportion of the larger pore size, while makes the overall porosity and total pore volume lower.

Figure 12

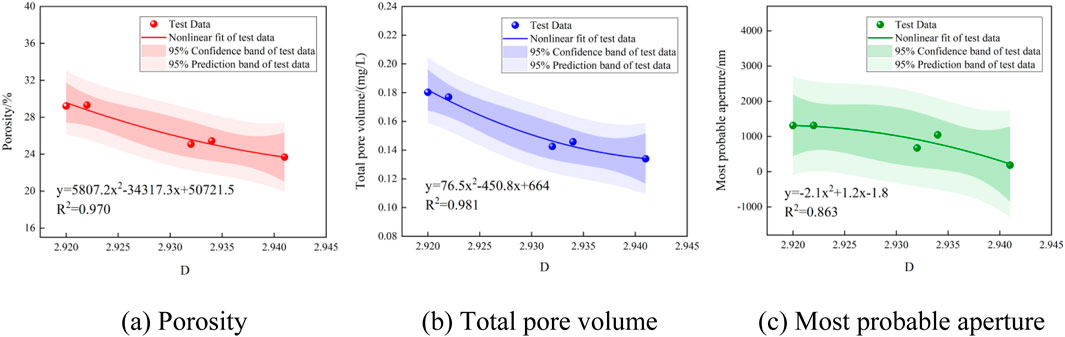
Figure 12. The correlation between fractal dimension and pore structural parameters. (A) Porosity (B) Total pore volume (C) Most probable aperture.

3.7 The correlation between fractal dimension and compressive strength, chloride diffusion coefficient

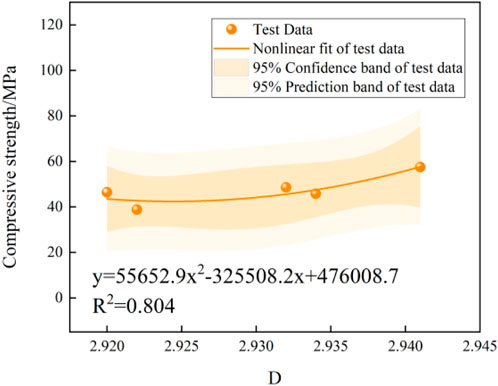
Figure 13 depicts the correlation between fractal dimension and compressive strength. The correlation coefficient R² is 0.804. Compressive strength has a good positive correlation with fractal dimension, and increases with the increase of fractal dimension. The increase in fractal dimension represents a higher spatial complexity of the pore structure, which indicates an increase in multidirectionality of the initial defects, inhomogeneity and asymmetry of the fracture structure. During initial deformation stage, the internal stresses have not been concentrated due to the randomness of initial defect distribution. During loading process, some of the initial defects and cracks are compacted, while others are “activated” and gradually evolve into connected cracks, resulting in internal stress concentrations. The fractal dimension, representing the spatial complexity of microstructure, is closely related to this “competition” between compact deformation and crack evolution. When fractal dimension is large, it is difficult to form connecting cracks within structure, and stress concentration phenomenon is not easy to occur, while the compressive capacity of specimen is improved to a certain extent.

Figure 13

Figure 13. The correlation between fractal dimension and compressive strength.

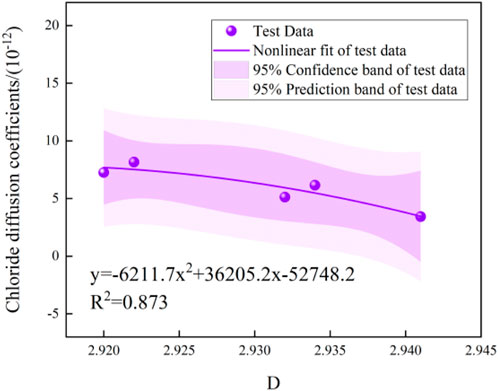
Figure 14 depicts the correlation between fractal dimension and chloride diffusion coefficient. The correlation coefficient R² is 0.873. Chloride diffusion coefficient has a good negative correlation with fractal dimension, and decreases with the increase of fractal dimension. With spatial structure becoming complex, the interconnecting pores become less, and the ions is more difficult to flow between pores, so that chloride diffusion coefficient becomes lower, and the impermeability of material is improved.

Figure 14

Figure 14. The correlation between fractal dimension and chloride diffusion coefficient.

Fractal dimension indicates that the mechanical strength and impermeability of ECC are closely related to the pore structure characteristics. The fractal dimension can be used to assess or predict the mechanical strength, impermeability and microstructure of PVA-ECC in advance, and to make a comprehensive evaluation of the mechanical properties and durability of material.

4 Conclusion

In this paper, the influences of PVA on compressive damage mechanism and pore structure fractal characteristics of ECC are obtained through experimental research. The conclusions are as follows:

(1) When volume fraction of PVA is less than 2%, the compressive strength increases first and then decreases with increase of PVA. and the peak point appears when the fiber content is 1%. The uniaxial compression damage of specimen can be divided into four stages: densification stage, linear-elastic stage, elastic-plastic stage and destruction stage. The number of AE ringing counts is small in densification stage and linear elastic stage, reflecting the compaction of initial pores and the generation of meso-cracks; It increases exponentially in elastic-plastic stage, reflecting the expansion of internal cracks to the surface to form macro-cracks. PVA increase the toughness of ECC and slow down the decrease of post-peak stress curve, while prolong post-peak bearing time and activate AE signals. ECC develops from brittle damage to ductile damage.

(2) The characteristics of RA-AF are analyzed by GMM model. In compression damage, the proportion of tensile cracks in P0 is 70%, the proportion of shear cracks in PVA-ECC is more than 50%, and the proportion of shear cracks increases first and then decreases with the increase of PVA content. The bridging effect of PVA transforms internal tensile stress of ECC into shear stress, which inhibits the generation of penetrating cracks. The effect of PVA on proportion of shear cracks is consistent with the effect on compressive strength. PVA change the compression damage mechanism and improve the compressive capacity of ECC.

(3) The chloride diffusion coefficient decreases first and then increases with the increase of PVA. Chloride diffusion coefficient of P1 is the smallest, which is 44.2% lower than that of reference specimen P0, and the impermeability of P1 is the best. The porosity, total pore volume and most probable aperture of PVA-ECC decrease first and then increase with the increase of PVA content. When PVA content is 1%, the number and volume of pores are the least, and ECC is the most dense. The influence of PVA on pore structure parameters and chloride diffusion coefficient is consistent. The pore size can be divided into four distribution ranges: gel pores (<100 nm), transition pores (100nm–1000 nm), capillary pores (1,000nm–10000 nm) and macropores (>10000 nm). PVA mainly affects the proportion of gel pores and capillary pores.

(4) The fractal model based on thermodynamic relationship can better characterize the fractal characteristics of PVA-ECC. Fractal dimension increases first and then decreases with the increase of PVA content, and P1 has the best fractal characteristics. In pore size distribution, due to the size characteristics of fiber diameter and most probable aperture, PVA has a great influence on the fractal characteristics of transition pores and capillary pores, and has little influence on the fractal characteristics of gel pores and macropores.

(5) Porosity, total pore volume and most probable aperture of PVA-ECC have a strong negative correlation with fractal dimension. Fractal dimension can be used to comprehensively characterize the pore structure characteristics of materials. Compressive strength of PVA-ECC has a good positive correlation with fractal dimension, and chloride diffusion coefficient has a good negative correlation with fractal dimension. The fractal dimension shows that mechanical strength and impermeability of cementitious materials are closely related to the complex spatial structure and distribution characteristics of pores.

This study simultaneously analyzes the effect of PVA fiber content on the structure and properties of ECC from both macro and micro perspectives. The mechanical strength, impermeability, pore size distribution, and fractal characteristics of PVA-ECC with 1% volumetric content are best in the range of 0%–2% PVA content. The fractal characteristics of materials are closely related to their mechanical properties and durability, and fractal dimension can be used as one of indicators to comprehensively evaluate the mechanical properties and durability of ECC. This paper provides a reference for practical engineering applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Conceptualization, Funding acquisition, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. XH: Formal Analysis, Project administration, Validation, Writing–review and editing. YZ: Data curation, Investigation, Resources, Writing–review and editing. YQ: Data curation, Investigation, Methodology, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funding by Hebei Technology Innovation Center for Multi-Hazard Resilience and Emergency Handling of Engineering Structures (Grant No. FZ246304).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bi, H., Li, H., Zhang, W., Wang, L., Zhang, Q., Cao, S., et al. (2020). Evaluation of the acoustic emission monitoring method for stress corrosion cracking on aboveground storage tank floor steel. Int. J. Press. Vessels Pip. 179, 104035. doi:10.1016/j.ijpvp.2019.104035

CrossRef Full Text | Google Scholar

Chen, J. L., Wang, J. D., He, R., Shu, H., and Fu, C. (2021). Experimental study on effective chloride diffusion coefficient of cement mortar by different electrical accelerated measurements. Crystals 11, 240. doi:10.3390/cryst11030240

CrossRef Full Text | Google Scholar

Chen, Z. G., He, R., and Jin, X. Y. (2022). Study of the healing effect of concrete with supplementary cementitious materials after early-age damage by acoustic emission technique. Appl. Sci. 12, 5871. doi:10.3390/app12125871

CrossRef Full Text | Google Scholar

Chen, Z. G., Zhang, G. Y., He, R., Tian, Z., Fu, C., and Jin, X. (2023). Acoustic emission analysis of crack type identification of corroded concrete columns under eccentric loading: a comparative analysis of RA-AF method and Gaussian mixture model. Case Stud. Constr. Mater. 18, e02021. doi:10.1016/j.cscm.2023.e02021

CrossRef Full Text | Google Scholar

Dong, Y. L., Xie, H. P., and Zhao, P. (1995). Experimental study on complete damage process of concrete under compression. J. Exp. Mech. 2 (10), 95–102. (in Chinese).

Google Scholar

Fan, X. C., Ge, T., and Liang, T. F. (2022). Fractal theory of cracks in hybrid steel fiber ultra-high performance concrete beams. Bull. Chin. Ceram. Soc. 41 (5), 1578–1588. (in Chinese). doi:10.16552/j.cnki.issn1001-1625.20220410.002

CrossRef Full Text | Google Scholar

Farhan, M., and Jagdish, C. (2021). A study based upon the effect of polyvinyl alcohol fiber, iron slag and fly ash over the strength aspects of geo-polymer concrete. IOP Conf. Ser. Earth Environ. Sci. 889, 012051. doi:10.1088/1755-1315/889/1/012051

CrossRef Full Text | Google Scholar

He, R., Nantung, T., Olek, J., and Lu, N. (2023). Use of dielectric constant for determination of water-to-cement ratio (W/C) in plastic concrete: part 2 comparison determined W/C values by ground penetrating radar (GPR) and microwave oven drying measurements. ES Mater. Manuf. 22, 874. doi:10.30919/esmm5f874

CrossRef Full Text | Google Scholar

Huang, J. S., Yang, D. Y., Zhu, Z. D., Wang, T. Z., and Wang, T. Q. (2019). Study on acoustic emission characteristics of polyvinyl alcohol fiber concrete under compression damage after high temperature. Concrete 351, 47–51. (in Chinese). doi:10.3969/j.issn.1002-3550.2019.01.012

CrossRef Full Text | Google Scholar

Ji, H. G., Zhang, T. S., Cai, M. F., and Zhang, Z. Y. (2000). Experimental study on concrete damage by dynamic measurement of acoustic emission. Chin. J. Rock Mech. Eng. 2 (19), 165–168. (in Chinese).

Google Scholar

Jin, S., Zhang, J., and Han, S. (2017). Fractal analysis of relation between strength and pore structure of hardened mortar. Constr. Build. Mater. 135, 1–7. doi:10.1016/j.conbuildmat.2016.12.152

CrossRef Full Text | Google Scholar

Lee, S. F., and Jacobsen, S. (2011). Study of interfacial microstructure, fracture energy, compressive energy and debonding load of steel fiber-reinforced mortar. Mater. Struct. 44 (8), 1451–1465. doi:10.1617/s11527-011-9710-4

CrossRef Full Text | Google Scholar

Li, B., Zheng, W. B., and Zhang, Y. (2023). Study on the compressive stress-strain curve and performance of low-slump polypropylene fiber concrete after high temperature. Appl. Sci. 13, 7222. doi:10.3390/app13127222

CrossRef Full Text | Google Scholar

Li, J. Y., Chen, L., Luo, J. W., Zhu, Y. P., Fan, X. M., and Hu, G. C. (2023). Study on mechanical properties and microstructure of steel-polypropylene fiber coal gangue concrete. Front. Mater. 10, 1281372. doi:10.3389/fmats.2023.1281372

CrossRef Full Text | Google Scholar

Li, Z. J., Liu, X., Zhao, C. Y., Wang, C., and Tian, X. (2024). Pore structure and mechanical properties of steel fiber reinforced geopolymer recycled aggregate concrete. Acta Mater. Compos. Sin. 41. (in Chinese). doi:10.13801/j.cnki.fhclxb.20240023.002

CrossRef Full Text | Google Scholar

Liu, M. Y., Gong, S. Y., Cao, Z. Y., Fan, P., and Zhang, W. X. (2023). Research on mechanical properties and pore structure of steel-polyvinyl alcohol fiber concrete. Industr. Build. Suppl. 53, 623–627. (in Chinese).

Google Scholar

Lockner, D. (1993). The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Min. Sci. and Geomechanics Abstr. 30 (7), 883–899. doi:10.1016/0148-9062(93)90041-B

CrossRef Full Text | Google Scholar

Lu, X. Y. (1997). Application of the Nernst-Einstein equation to concrete. Cem. Concr. Res. 27 (2), 293–302. doi:10.1016/S0008-8846(96)00200-1

CrossRef Full Text | Google Scholar

Luo, T., Huang, C. L., Zhang, T. Q., and Jin, F. (2024). Analysis of acoustic emission characteristics during the splitting tensile failure process of rock filled concrete. Water Resour. Hydropower Eng. 55 (1), 40–50. (in Chinese). doi:10.13928/j.cnki.wrahe.2024.01.004

CrossRef Full Text | Google Scholar

Lv, Q., Qiu, Q., Zheng, J., Wang, J., and Zeng, Q. (2019). Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 228, 116986. doi:10.1016/j.conbuildmat.2019.116986

CrossRef Full Text | Google Scholar

Lyu, X., Li, W. J., Hu, H., Ding, X. Z., and Hu, X. C. (2024). Cracking characteristics evaluation for reinforcement basalt fiber reactive powder concrete beam using acoustic emission. Front. Mater. 11, 1346140. doi:10.3389/fmats.2024.1346140

CrossRef Full Text | Google Scholar

Nair, A., and Cai, C. S. (2010). Acoustic emission monitoring of bridges: review and case studies. Eng. Struct. 32 (6), 1704–1714. doi:10.1016/j.engstruct.2010.02.020

CrossRef Full Text | Google Scholar

Rahmani, T., Kiani, B., Shekarchi, M., and Safari, A. (2012). Statistical and experimental analysis on the behavior of fiber reinforced concretes subjected to drop weight test. Constr. Build. Mater. 37, 360–369. doi:10.1016/j.conbuildmat.2012.07.068

CrossRef Full Text | Google Scholar

Rajput, A., and Iqbal, M. A. (2017). Impact behavior of plain, reinforced and prestressed concrete targets. Mater. Des. 114, 459–474. doi:10.1016/j.matdes.2016.10.073

CrossRef Full Text | Google Scholar

Reboul, N., Grazide, C., Roy, N., and Ferrier, E. (2020). Acoustic emission monitoring of reinforced concrete wall-slab connections. Constr. Build. Mater. 259, 119661. doi:10.1016/j.conbuildmat.2020.119661

CrossRef Full Text | Google Scholar

Shen, X. G., Li, X., Liu, L., Chen, X. Z., and Du, J. (2024). Research on mechanical properties of steel-polypropylene fiber-reinforced concrete after high-temperature treatments. Appl. Sci. 14, 3861. doi:10.3390/app14093861

CrossRef Full Text | Google Scholar

Shi, Z. X., Chen, X. D., Ning, Y. J., and Tian, H. X. (2024). Study on crack propagation of rubber self-compacting concrete based on RA-AF characteristics. J. Civ. Environ. Eng. 46 (5), 175–183. (in Chinese). doi:10.11835/j.issn.2096-6717.2023.048

CrossRef Full Text | Google Scholar

Stukhlyak, P. D., Buketov, A. V., Panin, S. V., Maruschak, P. O., Moroz, K. M., Poltaranin, M. A., et al. (2015). Structural fracture scales in shock-loaded epoxy composites. Phys. Mesomech. 18 (1), 58–74. doi:10.1134/S1029959915010075

CrossRef Full Text | Google Scholar

Sun, Y., Liu, S. H., Jia, Y., Zhu, A. L., Wang, L. J., and He, W. (2023). A cross-scale finite element analysis of concrete-faced rockfill dam. Phys. Chem. Earth. 130, 103375. doi:10.1016/j.pce.2023.103375

CrossRef Full Text | Google Scholar

Sundar, K. S., Pazhani, K. C., and Ravisankar, K. (2017). Fracture behaviour of fibre reinforced geopolymer concrete. Curr. Sci. 113, 116–122. doi:10.18520/cs/v113/i01/116-122

CrossRef Full Text | Google Scholar

Wagh, M., Waghe, U., Bahrami, A., Ansari, K., Özkılıç, Y. O., and Nikhade, A. (2024). Experimental investigation of mechanical and durability performances of self-compacting concrete blended with bagasse ash, metakaolin, and glass fiber. Front. Mater. 11, 1351554. doi:10.3389/fmats.2024.1351554

CrossRef Full Text | Google Scholar

Washburn, E. W. (1921). Note on a method of determining the distribution of pore sizes in a porous material. Proc. Natl. Acad. Sci. 7, 115–116. doi:10.1073/pnas.7.4.115

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, J. X., Yu, Q. J., Zeng, X. X., and Bai, R. Y. (2007). Fractal dimension of pore structure of concrete. J. South China Univ. Technol. Nat. Sci. Ed. 35 (2), 121–124. (in Chinese). doi:10.3321/j.issn:1000-565X.2007.02.026

CrossRef Full Text | Google Scholar

Winslow, D. N. (1985). The fractal nature of the surface of cement paste. Cem. and Concr. Res. 15 (5), 817–824. doi:10.1016/0008-8846(85)90148-6

CrossRef Full Text | Google Scholar

Wu, J. J., Zhang, W. J., Han, J. H., Liu, Z. Y., Liu, J., and Huang, Y. F. (2024). Experimental study on the flexural performance of steel-polyvinyl alcohol hybrid fiber-reinforced concrete. Materials 17, 3099. doi:10.3390/ma17133099

PubMed Abstract | CrossRef Full Text | Google Scholar

Xuan, W. H., Chen, X. D., Yang, G., Dai, F., and Chen, Y. (2018). Impact behavior and microstructure of cement mortar incorporating waste carpet fibers after exposure to high temperatures. J. Clean. Prod. 187, 222–236. doi:10.1016/j.jclepro.2018.03.183

CrossRef Full Text | Google Scholar

Yang, W. D., Liu, H. X., and Wang, H. S. (2024). Experimental study on mechanical properties of basalt fiber reinforced nano-SiO₂ concrete after high temperature. Front. Mater. 11, 1415144. doi:10.3389/fmats.2024.1415144

CrossRef Full Text | Google Scholar

Zarnaghi, V. N., Fouroghi-Asl, A., Nourani, V., and Ma, H. (2018). On the pore structures of lightweight self-compacting concrete containing silica fume. Constr. Build. Mater. 193, 557–564. doi:10.1016/j.conbuildmat.2018.09.080

CrossRef Full Text | Google Scholar

Zeng, Q., Li, K., Fen-Chong, T., and Dangla, P. (2010). Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surf. Sci. 257 (3), 762–768. doi:10.1016/j.apsusc.2010.07.061

CrossRef Full Text | Google Scholar

Zhang, B. Q., and Li, S. F. (1995). Determination of the surface fractal dimension for porous media by mercury porosimetry. Industrial and Eng. Chem. Res. 34 (4), 1383–1386. doi:10.1021/ie00043a044

CrossRef Full Text | Google Scholar

Zhang, J., Bai, P. C., Yan, C. W., Liu, S. G., and Wang, X. X. (2019). Experimental investigation on relations between impact resistance and tensile properties of cement-based materials reinforced by polyvinyl alcohol fibers. Appl. Sci. 9, 4434. doi:10.3390/app9204434

CrossRef Full Text | Google Scholar

Zhang, X., and Li, B. (2020). Damage characteristics and assessment of corroded RC beam-column joint under cyclic loading based on acoustic emission monitoring. Eng. Struct. 205, 110090. doi:10.1016/j.engstruct.2019.110090

CrossRef Full Text | Google Scholar

Zhang, Y. H., Sun, Y. H., Zhong, W. L., and Fan, L. F. (2024). A real-time study on the cracking characteristics of polyvinyl alcohol fiber-reinforced geopolymer composites under splitting tensile load based on high-speed digital image correlations. Buildings 14, 1986. doi:10.3390/buildings14071986

CrossRef Full Text | Google Scholar

Zhao, J., Li, X. F., and Guo, L. (2023). Study on fractal dimension and mechanical properties of basalt polypropylene fiber concrete pore structure. Compos. Mater. Sci. Eng. 8, 78–84. (in Chinese). doi:10.19936/j.cnki.2096-8000.20230828.012

CrossRef Full Text | Google Scholar

Zhao, Q. M., Chen, L., Wang, X. Y., Zhang, S. R., and Li, F. (2024). Study on the modification effect and mechanism of composite solid waste and steel fiber on the mechanical properties of concrete. Front. Mater. 11, 1431648. doi:10.3389/fmats.2024.1431648

CrossRef Full Text | Google Scholar

Zhao, Y. C., Yi, J., and Li, Y. (2023). Impermeability of polyvinyl alcohol fiber cementitious composites. Sichuan Build. Mater. 49 (6), 18–21. (in Chinese). doi:10.3969/j.issn.1672-4011.2023.06.007

CrossRef Full Text | Google Scholar

Zhou, X. Y., Yang, D. Y., Li, Y. S., Zhu, C. X., Wang, T. Z., Lv, J. F., et al. (2020). Study on mechanical properties and damage evolution of multi-size polypropylene fiber reinforced concrete. China Concr. Cem. Prod. 4, 49–53. (in Chinese). doi:10.19761/j.1000-4637.2020.04.049.05

CrossRef Full Text | Google Scholar