Manifestations in nature of self-controlled quasi-stationary nuclear fusion into magnetized low-temperature hydrogen plasma

This paper examines the characteristics of nuclear reactions occurring in low-temperature magnetized deuterium plasma. It is demonstrated that considering the ionization-recombination dynamics of deuterium atoms in this plasma allows for the potential realization of efficient nuclear fusion at low thermal energies $kT\approx 10-20eV$. The study shows that these processes are linked to the formation of coherent correlated states of deuterons, accompanied by the generation of giant energy fluctuations $\delta E\ge 10-50keV$ during each recurring ionization event of deuterium atoms. These findings align with known anomalies in the solar atmosphere, such as the sharp temperature increase above the Sun’s surface and the observed excess concentration of helium-3 ions in the solar wind. Furthermore, this process may explain well-documented experimental results, such as neutron generation during electric discharges in gas.

1 Introduction

Conventional understanding holds that efficient nuclear fusion is only feasible in high-temperature plasma, with temperatures $kT\ge 10-20keV$, or through the use of particle beams of similar or greater energy. The significant technological challenges associated with achieving such conditions and developing corresponding thermonuclear systems have driven interest in finding more optimal methods for facilitating low-energy nuclear reactions (LENR).

The operating principle behind LENR systems typically involves mechanisms that reduce the Coulomb barrier between interacting nuclei by stimulating various effects within a condensed matrix. These effects include enhanced electron screening, pycnonuclear fusion driven by strong lattice deformation, or processes such as proton-to-neutron conversion within the reaction zone. Despite this, such systems still require substantial external control and complex techniques to sustain and manage LENR, often resulting in low overall efficiency.

2 Characteristics of formation of giant ion energy fluctuations in stationary low-temperature magnetized hydrogen plasma

This work proposes a significantly more efficient mechanism for inducing self-similar, self-controlled unlimited in time nuclear fusion, achieved through short-term, highly frequent giant energy fluctuations of particles within low-temperature plasma, under the influence of an external stationary magnetic field.

The physical mechanism driving these fluctuations is linked to the formation of coherent correlated states (CCS) among interacting particles. These states are characterized by both exceptionally large (giant) and long-lasting fluctuations in the energy and momentum of the particles involved. The behavior of such states can be described using the modified Schrödinger-Robertson uncertainty relations (Schrödinger, 1930; Robertson, 1930; Dodonov et al., 1980; Dodonov and Manko, 1988; Dodonov et al., 1993; Vysotskii and Vysotskyy, 2023; Vysotskii and Vysotskyy, 2015a; Vysotskii and Vysotskyy, 2017; Vysotskii and Vysotskyy, 2019; Vysotskii and Vysotskyy, 2020; Vysotskii and Vysotskyy, 2015b),

$\begin{array}{l}\delta p\delta q\ge \frac{\mathrm{\hslash }}{2\sqrt{1-r_{pq}^2}}\equiv {\mathrm{\hslash }}_{eff}/2,{\mathrm{\hslash }}_{eff}=\mathrm{\hslash }/\sqrt{1-r_{pq}^2}\equiv G_{pq}\mathrm{\hslash },r_{pq}=\frac{<qp>+<pq>}{2\sqrt{<p^2><q^2>}};\\ \delta E\delta t\ge \frac{\mathrm{\hslash }}{2\sqrt{1-r_{Et}^2}}\equiv {\mathrm{\hslash }}_{eff}/2,{\mathrm{\hslash }}_{eff}=\mathrm{\hslash }/\sqrt{1-r_{Et}^2}\equiv G_{Et}\mathrm{\hslash },r_{Et}=\frac{<Et>+<tE>}{2\sqrt{<E^2><t^2>}},\end{array}(1)$

which generalize the standard Heisenberg uncertainty relations under condition $r\ne 0$.

In these modified relations, the parameter r represents the correlation coefficient, which ranges $\left|r\right|\le 1$, indicating the degree of mutual coherence and correlation between dynamic variables such as momentum and coordinate (p and q), or energy and time (E and t). Another important characteristic is the correlation efficiency coefficient G $=1/\sqrt{1-r^2}$ , which falls within the interval $1\le G\le \infty$.

As demonstrated in previous works (Dodonov et al., 1980; Dodonov and Manko, 1988; Dodonov et al., 1993; Vysotskii and Vysotskyy, 2023), if a tunable oscillator is in an excited state prior to the formation of CCS, where its energy satisfies the condition E$\left(n\right)=\mathrm{\hslash }\omega \left(n+1/2\right)\approx kT$ , the formation of CCS results in fluctuations whose amplitude takes the form $\delta E^{\left(\min \right)}\approx G^{2}kT$. The simplest method of CCS formation involves altering the parameters of an equivalent harmonic oscillator, which corresponds to the state of a particle within a potential well.

Earlier studies (Dodonov et al., 1980; Dodonov and Manko, 1988; Dodonov et al., 1993) established that the correlation coefficient (Equation 1) r

$r=\text{Re}\left\{{\epsilon }^{*}\frac{d\epsilon }{dt}\right\}/\left|{\epsilon }^{*}\frac{d\epsilon }{dt}\right|(2)$

can be computed by solving the classical oscillator equation with a variable frequency

$\frac{d^2\epsilon }{d{t}^2}+{\omega }^2\left(t\right)\epsilon =0(3)$

under the initial conditions

$\epsilon \left(0\right)=1,{\left.\frac{d\epsilon }{dt}\right|}_0=i(4)$

In these (Equations 3, 4) $\omega \left(t\right)$ is oscillator dimensionless nonstationary frequency, normalized to its initial frequency ${\omega }_0=\omega \left(0\right)$; t is dimensionless (normalized to ${\omega }_0^{-1}$) time; $\epsilon \left(t\right)$ is the dimensionless (normalized to $q_0=\sqrt{\mathrm{\hslash }/M{\omega }_0}$) complex coordinate of the particle.

One of the most practical models for a controlled nonstationary oscillator involves the motion of a particle with charge Q and mass M in a magnetic field H (Dodonov et al., 1980; Dodonov and Manko, 1988). In this system, all parameters of particle motion - such as the eigenfunctions ${\phi }_n\left(q\right)$, frequency ${\omega }_H=QH/Mc$, and energy spectrum $E_n=\mathrm{\hslash }\omega \left(n+1/2\right)$ - align with the mathematical framework of a harmonic oscillator. Each abrupt application of the magnetic field induces the formation of a coherent correlated state among the ions within the field’s range. This process is discussed in detail in reference (Vysotskii and Vysotskyy, 2023), while other applications of CCS in quantum systems are explored in works (Vysotskii and Vysotskyy, 2015a; Vysotskii and Vysotskyy, 2017; Vysotskii and Vysotskyy, 2019; Vysotskii and Vysotskyy, 2020; Vysotskii and Vysotskyy, 2015b).

The dynamics of the magnetic field switching on over a characteristic time τ is well approximated by the simple function

$\mathrm{\omega }\left(t\right)={\mathrm{\omega }}_0\left\{1+\left(g-1\right)\left[1-e^{-t/\mathrm{\tau }}\right]\right\},g={\mathrm{\omega }}_{\max }/{\mathrm{\omega }}_{\min }(5)$

The dependence of the coefficient of correlation efficiency G on time after increasing the base frequency of oscillations by g times relative to the initial value ${\mathrm{\omega }}_{\min }$ is shown in Figure 1.

Figure 1

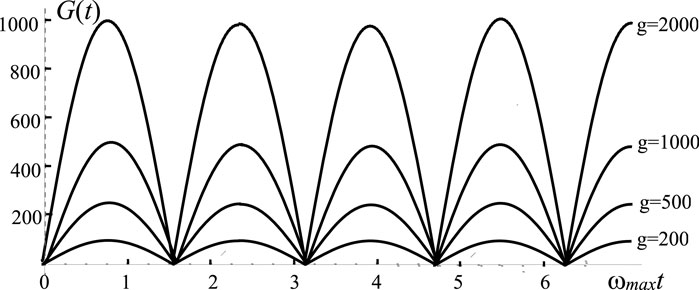
Figure 1. Non-stationary dynamics of the correlation efficiency coefficient G(t) after an increase in the base oscillating frequency $\mathrm{\omega }\left(t\right)$ (Equation 5) by a factor of g relative to the value ${\mathrm{\omega }}_0$.

A significant increase in the correlation coefficient G results in a corresponding large amplification in both the amplitude and the duration of the energy fluctuations.

One potential method for estimating the impact of CCS on tunneling effects and subsequent nuclear transformations involves a formal substitution of the expression $\mathrm{\hslash }\to {\mathrm{\hslash }}^{*}\equiv \mathrm{\hslash }/\sqrt{1-r^2}\equiv G\mathrm{\hslash }$ in the equation for tunneling probability. The direct application of this substitution in the formula for the tunneling probability within the barrier region L(E) near a nucleus of radius R,

$\begin{array}{l}{D}_{r\ne 0}\approx \exp \left\{-\frac{2\sqrt{1-r^2}}{\mathrm{\hslash }}{\displaystyle \underset{R}{\overset{R+L\left(E\right)}{\int }}}\sqrt{2\mu \left\{V\left(q\right)-E\right\}}dq\right\}=\\ ={\left(D_{r=0}\right)}^{\sqrt{1-r^2}}\equiv {\left(D_{r=0}\right)}^{1/G}\to 1at\left|r\right|\to 1andG\to \infty \end{array}(6)$

aligns well with independent rigorous quantum mechanical calculations. Here μ is the reduced mass of the nucleus.

In the low-temperature magnetized hydrogen plasma (or hot hydrogen gas) discussed later, the lifetime of such a correlated state is limited by the mean free path time of the proton or deuteron before it undergoes a collision with another atom or nucleus in a given plasma (Nguyen-Kuok, 2017; Francis, 1960; Chu and Lu, 2020; Fueno et al., 1960; Mizuno et al., 2006):

$\Delta t_{ion}^{\left(corr\right)}\approx <l>/v_i\approx \sqrt{{\left(k{T}_i\right)}^3{M}_i}/4\mathrm{\pi }{n}_i{e}^4\mathrm{\Lambda },(7)$

where Λ ≈ 10 is the standard Coulomb logarithm which determines the ratio of the impact parameters during the collision of particles in plasma, $<l>$ - mean free path of a particle (proton or deuteron) in a plasma, $v_i\approx \sqrt{k{T}_i/M_i}$ is the isothermal velocity of the particle in this plasma.

In these collisions, the coherent superposition of eigenfunctions is disrupted, resulting in the cessation of giant energy oscillations which greatly increase the probability (Equation 6) of the tunnel effect and the probability of the corresponding nuclear fusion.

It should be noted that a similarly significant increase in the probability of the tunneling effect, leading to a comparable rise in the probability of nuclear fusion in cooled deuterium gas under the influence of a magnetic field, had previously been observed in experiments (Mizuno et al., 2006).

These studies were conducted using a reactor tube (Pyrex glass tube) with an outer diameter of 6 mm, an inner diameter of 3 mm, and a length of 100 mm, filled with deuterium gas at a pressure of 3 atm. The tube was placed inside a solenoid connected to a direct current power source, and both the reactor tube and solenoid were cooled with liquid nitrogen. Three identical neutron detectors (2 cm in diameter, 10 cm in length) were positioned 20 cm from the reactor tube. The detectors were calibrated using a standard Cf²⁵² neutron source with an activity of 2.58·10⁴ decay/s, placed at the location of the reactor tube during calibration. A typical count under these conditions was 5 ± 1 count/s from the standard neutron source.

The initial conditions of a typical experiment corresponded to a constant magnetic field of 8 kG within the reactor tube. Under these conditions, a background neutron flux with very low intensity $P_0\approx 0.008\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}/\mathrm{s}$, close to the natural background level, was detected. This background was also recorded when the solenoid current was absent.

During rapid changes in the solenoid current, the magnetic field increased to 10 kG. Such changes in the field resulted in a short-term increase in neutron flux intensity by a factor of 500–1000 compared to the initial natural background. These neutrons were produced in the reaction $d+d=H{e}^3+n$, whose initial probability in the cooled deuterium gas, with a low natural concentration of ionized deuterium atoms (deuterons) and in the presence of a constant magnetic field, was very small.

From these data, it follows that during the magnetic field variation, the neutron channel intensity of nuclear fusion in the cold deuterium gas corresponded to a value of $d{N}_n/dt\approx \left(1.3-2\right)\cdot {10}^5$ reaction/s. A similar short-term and substantial increase in neutron count rate occurred when the power supply was initially connected to the solenoid, creating a magnetic field of 8 kG, as well as in other modes of rapid current changes.

These results are in good agreement with the model of coherent correlated states and large energy fluctuations in nonstationary harmonic oscillators, which, in this system, are formed based on the relatively small number of ionized deuterium atoms in the reactor tube during magnetic field changes in the solenoid. A detailed analysis of the implementation of this nuclear fusion mechanism, taking into account the solenoid parameters (including the influence of solenoid inductance on the dynamics of magnetic field changes), is provided in (Vysotskii and Vysotskyy, 2020). No other hypothetical mechanism can explain the short-term occurrence of nuclear fusion, accompanied by neutron generation, in strongly cooled deuterium gas during rapid magnetic field variations.

At first glance, it might appear that in a harmonic oscillator driven by the interaction between a charged particle and a constant magnetic field, such an effect would only occur during the short initial period $\Delta t_{ion}^{\left(corr\right)}$ immediately following the activation of the magnetic field, and would not continue in stationary systems with a constant magnetic field.

To reproduce this effect, the magnetic field would need to be switched off and then rapidly reactivated. Given the significant technological challenges posed by the requirement for very frequent on/off switching of a strong magnetic field, it might seem that such a system for stimulating nuclear fusion is not feasible.

However, a more detailed analysis reveals a fundamentally different mechanism for self-controlled, repeated switching on and off of the interaction between the charge and the constant magnetic field. This mechanism arises from the natural alternation between recombination and ionization processes in a stationary low-temperature hydrogen gas or plasma, which causes the particle’s charge Q(t) to switch on and off autonomously. This dynamic corresponds to a transition from the standard interpretation of oscillator frequency in a variable magnetic field ${\omega }_H\left(t\right)=QH\left(t\right)/Mc$ to a different scenario ${\omega }_H\left(t\right)=Q\left(t\right)H/Mc$, where the magnetic field is constant but the charge is variable.

By incorporating this natural microdynamics of each plasma ion and gas atom, the system allows for very frequent charge switching. This, in turn, leads to pulsed activation of the interaction between the ion and the magnetic field, facilitating the short-term formation of CCS and enabling nuclear fusion.

The parameters of the microdynamics of changes in the charge state of atoms and iones are determined by well-known and frequently used characteristic times (Nguyen-Kuok, 2017; Francis, 1960; Chu and Lu, 2020; Fueno et al., 1960) that are associated with specific processes in plasma physics.

a) The lifetime of a neutral hydrogen or deuterium atom before its ionization (Nguyen-Kuok, 2017) is equal to

$\begin{array}{ll}\hfill <t_{atom}>& =1/<{\sigma }_{ion}\left(v_e\right)v_e>n_e=\left\{C_H{n}_e{\left(k{T}_e\right)}^{3/2}\sqrt{\frac{8}{\pi m_e}}\left(\frac{V_i}{k{T}_e}+2\right)\right.\hfill \\ \hfill & {\left.\exp \left(-\frac{V_i}{k{T}_e}\right)\right\}}^{-1}\hfill \end{array}(8)$

Here $V_i\approx 13.6eV$ is the ionization potential of an atom; ${С}_H\approx 6\cdot {10}^{-18}$ cm²/eV is a parameter depending on the structure of the cross section ${\sigma }_{ion}\left(v\right)$ of the hydrogen ionization process (Nguyen-Kuok, 2017).

Using this data, it is possible to estimate the typical average lifetime of a hydrogen or deuterium atom in the plasma,

$<t_{atom}>\approx \frac{\left({10}^8-{10}^9\right)}{n_e}\approx {10}^{-7}-{10}^{-10}s,(9)$

based on the plasma temperature $k{T}_e=10-20$ eV and the electron (ion) concentration $n_i=n_e={10}^{16}-{10}^{18}$ cm^-3.

b) The average time for an atom of hydrogen or deuterium to become ionized corresponds to the transient period during which the frequency of the equivalent harmonic oscillator (3) changes. The specific value ${\tau }_{ion}$ is determined by the speed of those electrons from the plasma composition incident on the atom, whose energy exceeds the ionization potential, as well as by their distance from the atom, at which the moving electron can affect the state of the atom. This value in plasma is determined with acceptable accuracy by the Debye screening radius $R_D=\sqrt{k{T}_e/4\pi n_e{e}^2}$. In the case when the electron energy ${\epsilon }_e\gg V_i$, the value ${\tau }_{ion}$ is determined by the relation

${\tau }_{ion}\approx R_D/v_e=\sqrt{m_e/4\pi n_e{e}^2}(10)$

This time (Equation 10) is relatively short, ${\tau }_{ion}\approx 2\cdot \left({10}^{-13}-{10}^{-14}\right)$ s in plasma with the parameters $k{T}_e=10-20eV,n_e={10}^{16}-{10}^{18}c{m}^{-3}$.

c) The average duration of the ionized state, during which each atom remains as a proton or deuteron in the plasma before undergoing recombination and returning to its neutral state, is given by (Nguyen-Kuok, 2017; Francis, 1960; Chu and Lu, 2020; Fueno et al., 1960)

$\begin{array}{c}\hfill <t_{ion}>=n_e{n}_i/n_a{n}_e^2<{\sigma }_i\left(v\right)v_e>=K<t_{atom}>,\\ \hfill & K=n_{i,e}/n_a=n_i/\left(n_{a0}-n_i\right)\hfill \end{array}(11)$

This duration (Equation 11) is much longer compared to the lifetime (Equation 9) of the atom $<t_{atom}>$ in its neutral state, as predicted by the Saha equation,

$K\approx 4\frac{{\left(m_{e}k{T}_e/2\right)}^{3/2}}{{\mathrm{\hslash }}^3{n}_{a0}}\exp \left(-V_i/k{T}_e\right)\gg 1(12)$

This solution $K\gg 1$ holds within the considered temperature range $k{T}_e\approx 10-20eV$, under the condition that the total particle concentration in the plasma $n_{a0}\ll {10}^{24}$ cm³ is much lower than in a solid state.

From the condition $K\gg 1$, it follows that the average time $<t_{ion}>$ for which hydrogen and its isotopes exist as free nuclei and free electrons in the plasma is significantly longer than their corresponding lifetime as neutral atoms $<t_{atom}>$. Therefore, the time required for subsequent ionization of atoms in the plasma is much shorter.

To estimate $\Delta t_{ion}^{\left(corr\right)}$ (7) in CCS, the replacement T_i → G²T_i should be applied. This modification leads to a substantial increase in the lifetime of the CCS. In particular, for plasma parameters $k{T}_i\approx 10-20eV$ and n_i = 10¹⁴–10¹⁸ cm^-3, the time $\Delta t_{ion}^{\left(corr\right)}$ increases from 10^–7 – 10^–11 s for the uncorrelated state to $\Delta t_{ion}^{\left(corr\right)}\approx {10}^{-3}-{10}^{-1}$ s for the values <G> ≈ 300–800. This time is 10⁵–10⁷ times longer than the oscillation period of the harmonic oscillator corresponding to the proton cyclotron frequency in a magnetic field of strength H = 3000 Oe.

In conducting these calculations, it is also important to account for the fact that the probability $P_{diss}$ of hydrogen molecules or their isotopes dissociating into atoms under the given plasma conditions $kT\approx \left(2-4\right){\epsilon }_{diss}$ is nearly 1.

From these considerations, it follows that under the specified plasma parameters, coherent correlated states of hydrogen isotope ions will persist throughout the period prior to recombination.

The dynamics of these processes (Equations 8–11) are illustrated in Figure 2.

Figure 2

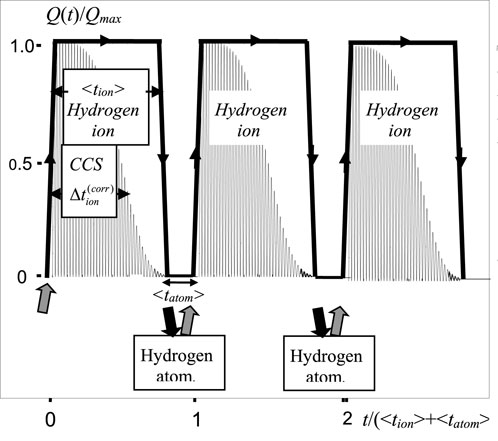
Figure 2. Dynamics of successive ionization cycles of atoms, the process of CCS formation, and subsequent ion recombination in a constant magnetic field.

It is of great significance that the process of alternating ionization and recombination of any atom in a plasma can continue for an unlimited amount of time without the need for any external control.

From these estimates, it follows that the relative proportion of nuclei in the plasma that, at any given moment, are in a coherent correlated state (CCS) and characterized by anomalously large energy fluctuations, corresponds to the efficiency coefficient for utilizing low-temperature plasma in nuclear fusion:

$\eta =P_{diss}\Delta t_{ion}^{\left(corr\right)}/\left(<t_{ion}>+<t_{atom}>\right)(13)$

Based on the estimates above, the quantity $\eta$ (Equation 13), which depends on plasma temperature and density, is $\eta \ge 0.3-0.5$.

Efficient nuclear fusion in such nuclei, driven by giant energy fluctuations $\delta E\ge 10-50keV$ in low-temperature plasma, can occur over an unlimited period and does not require additional energy input, provided an external magnetic field is present. The presence of these energy fluctuations allows nuclear fusion involving hydrogen isotopes:

$d+d=\left\{\begin{array}{l}H{e}^3+n\\ H^3+p\\ H{e}^4\end{array}\right.(14)$

and also with the participation of heavier nuclei.

3 Possible realization of nuclear fusion in low-temperature magnetized plasma in nature and space

The processes described above may not only be implemented under terrestrial laboratory conditions but also occur naturally in space and stars. One such phenomenon is the generation of neutrons during a lightning discharge, which corresponds to nuclear fusion (Equation 14) involving deuterons present in the air near the lightning’s path. A typical structure of the neutron flux observed during a lightning discharge is shown in Figure 3 (Kuzhevskij, 2004).

Figure 3

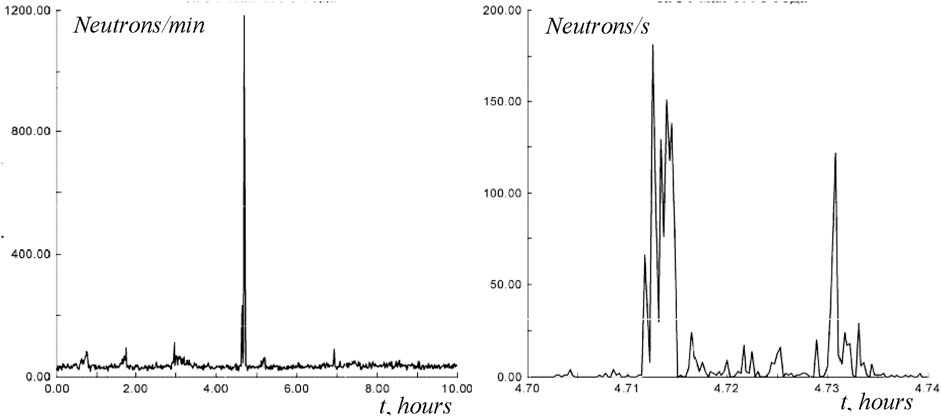
Figure 3. Neutron registration during natural lightning on 31 May 1998 (Kuzhevskij, 2004). The figure on the right shows an enlarged section of the left figure.

Under normal pressure and temperature, the density of water vapor in the atmosphere is about $\rho =5\cdot {10}^{-4}g/c{m}^3.$ The concentration of heavy water molecules (HDO and D₂O) in this vapor, under the same conditions, is approximately $n_{HDO}\approx {10}^{15}c{m}^{-3}$. The intense ultraviolet radiation generated by the lightning discharge causes these molecules to dissociate, releasing free deuterium atoms and ions. To initiate reaction (14), a large energy $E_D\ge 5-10keV$ is required for deuterons to overcome the Coulomb barrier.

In previous studies (Babich and Roussel-Dupre, 2007; Babich, 2019), the low efficiency and practical impossibility of directly accelerating heavy ions in the electric field of a lightning discharge to energies required for nuclear fusion and neutron generation were well established. This limitation arises because the maximum achievable energy of deuterons in the lightning plasma is restricted by charge exchange reactions $D^{+}+N_2=D+N_2^{+}$ that occur as these ions collide with nitrogen molecules in the dense lower atmosphere. To achieve nuclear fusion under these conditions, an unrealistically strong electric field of approximately $\epsilon >\left(0.55-1.74\right)\cdot {10}^{6}V/cm$ for the $d+d=H{e}^3+n$ reaction and $\epsilon >\left(0.44-1.52\right)\cdot {10}^{6}V/cm$ for $N^{14}+H^2=n+O^{15}$ reaction would be required. These fields are far beyond what is observed during lightning discharges.

As a result, it is generally accepted that the primary mechanism for neutron generation during thunderstorms is photonuclear reactions, which require gamma photons with energies of approximately $E_{\gamma }>10.55MeV$. However, it is challenging to explain the production of such a large number of gamma photons during a lightning event.

These complex issues can be effectively addressed by considering that all the necessary conditions for CCS formation and the subsequent stimulation of nuclear fusion involving deuterons are met during a lightning discharge.

Typical lightning discharge currents range from 10⁴ A to 10⁵ A, with a duration of approximately 10^–4 s. This current generates a strong magnetic field $H\ge {10}^{3}Oe$ in the surrounding air, sufficient to establish CCS in a region with a radius of 10–20 cm around the discharge. The relatively long duration of the discharge allows for numerous ionization-recombination cycles of deuterium atoms, facilitating effective nuclear fusion and neutron generation.

Another possible application of the CCS concept is related to the unique anomalies observed in the solar atmosphere. It is well-known that the temperature at the visible surface of the Sun (the photosphere) is approximately 5700 K. Above the photosphere lies a thin layer of the chromosphere, about 1000 km thick. Near the outer surface of this layer, at the base of the solar corona, the temperature dramatically increases to approximately $\left(1.5-2\right)\cdot {10}^{6}K$ within a range of 100–300 km. This phenomenon contradicts the fundamental laws of thermodynamics.

The literature provides little explanation for this anomaly–a sharp rise in the temperature of gas and low-temperature plasma above the relatively cool solar surface. Traditional attempts to explain these observations have largely revolved around hypotheses suggesting the possibility of “transit” mechanisms that transfer energy, with minimal losses, from the core of the Sun to regions far beyond its surface, through a much colder near-surface medium. However, no convincing evidence has been presented to substantiate such a mechanism.

It has long been established that accounting for all possible “transit” energy transfer mechanisms can explain no more than 3.5% of the energy observed in the solar corona, as recorded by numerous astronomical measurements. The sources and mechanisms responsible for the remaining 96.5% of the corona’s energy remain largely unknown. The most significant challenge is identifying a mechanism capable of maintaining the corona’s high temperature consistently throughout the solar cycle (Zaitsev et al., 2021; Selhorst et al., 2005).

Reliable astronomical observations reveal that frequent vertical ejections of gas and plasma, including atoms and ions with strong internal magnetic fields, occur from the photosphere. These events are classified as Type II spicules, and their formation is driven by rapid reconnections of the magnetic field. Inside these spicules, circulating magnetic fields with strengths $H\approx 2-3kOe$ are observed. Figure 4 shows images of these spicules, along with a diagram illustrating the anomalous temperature rise above the solar surface.

Figure 4

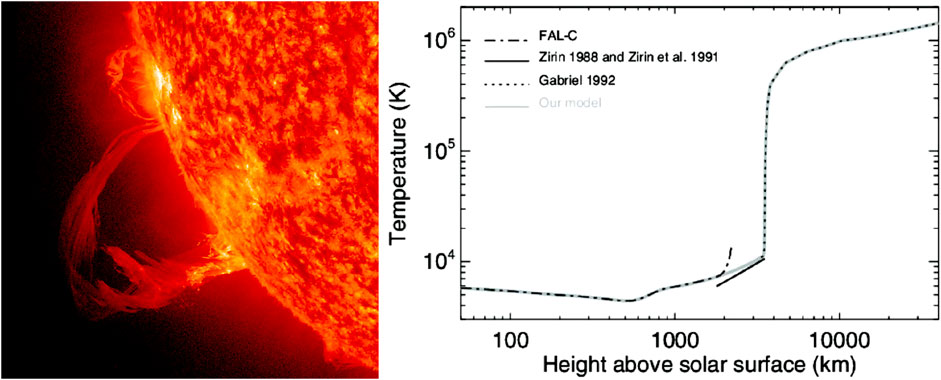
Figure 4. Photograph of solar spicules and the altitude distribution of solar gas temperature in the lower part of the solar atmosphere (Selhorst et al., 2005; NASA, 2024).

The action of the magnetic fields on the low-temperature plasma generates stable jets that are tightly confined within magnetic flux tubes, allowing the plasma to move freely along the tube axes. These magnetic flux tubes form at the boundaries of large-scale photospheric structures known as supergranules, where counter-streaming plasma flows exist, and extended regions of intense magnetic fields are generated. In these regions, the Kruskal-Schwarzschild instability conditions are satisfied, and the zone itself is divided into a system of magnetic tubes.

At any given moment, there are approximately 10⁶ spicules on the surface of the Sun, covering roughly 1% of its surface area. These spicules travel at initial speeds of 50–100 km/s, have diameters ranging from 200 to 2000 km, and possess an average lifetime of 5–7 min. They extend from the chromosphere to the lower solar corona, reaching heights of up to $\left(6-10\right)\cdot {10}^3$ km. The plasma temperature in the visible portion of the spicules, which exits the chromosphere, reaches approximately $T\approx \left(1.5-2\right)\cdot {10}^{6}K$.

The schematic representation of the circulating magnetic field and the direction of plasma flows forming the spicules in the solar atmosphere (at the boundary between the photosphere, chromosphere, and corona) is shown in Figure 5.

Figure 5

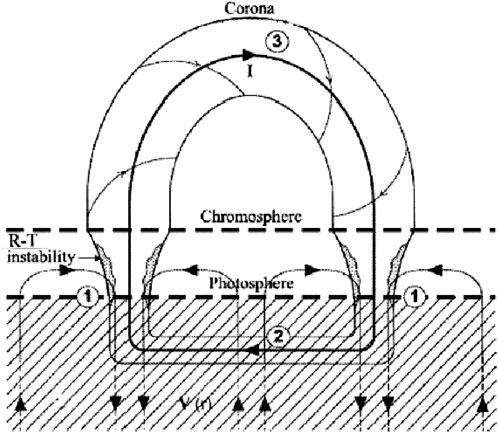
Figure 5. Scheme of spicule formation on the solar surface (Erdèlyi and Ballai, 2007).

In some cases, the energy associated with the vertical injection of these spicules is substantial enough to allow them to overcome the Sun’s gravitational field. These vertical flows contribute to coronal mass ejections into space, which, when directed towards Earth, are detected and can result in geomagnetic storms.

The typical composition at the base of the spicule tubes in the photosphere consists of “standard” low-temperature solar gas, primarily hydrogen, $H{e}^4/H=0.24700$; $H{e}^3/H={10}^{-5}$; $H^2/H=\left(2.579\right)\cdot {10}^{-5}$ with an initial total concentration of hydrogen atoms and ions $n_{a0}\approx {10}^{16}-{10}^{17}c{m}^{-3}$. A straightforward analysis indicates that the volumes contained within these magnetized spicules provide an ideal environment for nuclear reactions facilitated by the formation of CCS. The strong magnetic fields present, coupled with the appropriate concentration of hydrogen isotopes, support the possibility of nuclear fusion. The rapid heating of spicules caused by nuclear fusion would contribute significantly to the heating of the solar atmosphere. Consequently, it can be proposed that each spicule acts as a long-lasting, self-regulating nuclear fusion reactor.

Another unresolved enigma of the solar atmosphere is the anomalously high concentration of the He³ isotope relative to He⁴ in plasma jets originating from spicules with high vertical velocities. These jets, reaching Earth, display He³/He⁴ ratios 10–20 times greater than the typical solar composition, where He³/He⁴ ≈ 0.008. This peculiar phenomenon could be explained by nuclear reactions $d+d=H{e}^3+n$ involving He³, facilitated by the formation of CCS within these spicules.

It is plausible that similar processes manifest in other natural phenomena.

3 Conclusion

This paper presents a mechanism for an alternative form of nuclear fusion that does not require high plasma temperatures or high-energy particle accelerators.

The fundamental basis of this mechanism is the process of creating coherent correlated states of deuterons, each of which, during its formation through the ionization of atoms, exists in a magnetized plasma in the form of a nonstationary harmonic oscillator. The efficiency of this process corresponds to the Schrödinger-Robertson uncertainty relations (Equation 1). These relations are based on the foundational ideas and fundamental equations of quantum mechanics and serve as a direct generalization of the Heisenberg uncertainty principle for ordinary (incoherent) states, which are one of the cornerstones of modern nuclear physics and technology. Both sets of relations are derived from the same equations; however, in the derivation of the Heisenberg-Robertson uncertainty relations, certain mathematical simplifications are made. Historically, the Heisenberg uncertainty principle has been widely used in the analysis and optimization of various nuclear and atomic processes for nearly 100 years since its discovery in 1927, while the Schrödinger-Robertson uncertainty relations, after their discovery in 1930, were almost forgotten and have only begun to be actively investigated in the last 20–30 years. One of the reasons for this disparity is that any coherent correlated state of a quantum system, after its formation, rapidly relaxes into a normal uncorrelated superposition state due to the dephasing influence of environmental fluctuations on the system. If this short initial time interval is ignored, there is no need to consider the Schrödinger-Robertson uncertainty relations when optimizing any system.

However, this situation fundamentally changes when analyzing and optimizing rapidly changing quantum processes, whose characteristic time period of change is shorter than the duration of the coherent correlated states’ existence.

The proposed nuclear fusion process arises from the self-regulated formation of giant fluctuations in particle energy, driven by the establishment of coherent correlated states of deuterium or hydrogen in the presence of an external, constant, or slowly varying magnetic field. This process hinges on the alternating microdynamics of ionization and recombination within atoms. With each act of ionization, a CCS is formed, resulting in large energy fluctuations with significant durations.

This process is self-regulating, as it occurs primarily during the initial stages of ionization. As the plasma heats rapidly, the time between recombination and subsequent ionization increases, leading to a reduction in the average energy output and a corresponding decrease in plasma temperature. This, in turn, shortens the time before the next recombination event. Once recombination occurs, a new cycle of plasma heating begins. The described self-regulating nuclear fusion mechanism does not require external control and can persist for extended periods.

It should also be noted that without initial (start-up) heating of the gas, this self-regulating process is impossible. This is due to the fact that at very low temperatures, there will be very few ions in the gas volume, and the energy released in fusion reactions involving these ions will be insufficient for the subsequent self-heating of the system, taking into account the inevitable “loss” of part of this energy beyond the confines of the small reactor tube. For this reason, in the aforementioned experiment (Mizuno et al., 2006), the conditions for the onset of such a self-regulating fusion process were not fulfilled.

This analysis demonstrates that the same self-regulating nuclear fusion mechanism may occur not only under controlled laboratory conditions but also in natural environments. In particular, this model provides a plausible explanation for neutron generation during lightning discharges in the Earth’s atmosphere.

Previously, nuclear fusion was thought to occur exclusively in the core of the Sun, where temperature and pressure are extreme. However, the analysis presented in this paper suggests that fusion reactions can continue indefinitely near the Sun’s surface, specifically in its atmosphere, due to the presence of strong magnetic fields. These exoenergetic fusion reactions are consistent with the puzzling phenomenon of the solar atmosphere’s extreme heating above the Sun’s relatively cool surface.

Furthermore, the nuclear reactions leading to the formation of He³ isotopes offer an explanation for the elevated concentrations of He³ observed in particle streams emitted from the Sun and subsequently detected on Earth.

We conclude that nuclear fusion in magnetized low-temperature plasma holds potential for the development of safe and inexpensive energy sources.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

VV: Writing–original draft, Writing–review and editing. MV: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Babich, L. P. (2019). Thunderstorm neutrons. Phys. Uspekhi 62, 976–999. doi:10.3367/ufne.2018.12.038501

CrossRef Full Text | Google Scholar

Babich, L. P., and Roussel-Dupre, R. A. (2007). Origin of neutron flux increases observed in correlation with lightning. J. Geophys. Res. 112, D13303. doi:10.1029/2006jd008340

CrossRef Full Text | Google Scholar

P. K. Chu, and X. Lu (2020). “Low temperature plasma technology: methods and applications,” (Boca Raton: CRC Press). doi:10.1201/b15153

CrossRef Full Text | Google Scholar

Dodonov, V. V., Klimov, A. B., and Manko, V. I. (1993). Physical effects in correlated quantum states. Squeezed Correl. States Quantum Syst. Commack, N. Y Nova Sci. 295, 61–107.

Google Scholar

Dodonov, V. V., Kurmishev, E. V., and Manko, V. I. (1980). Generalized uncertainty relation and correlated coherent states. Phys. Lett. A 79, 150–152. doi:10.1016/0375-9601(80)90231-5

CrossRef Full Text | Google Scholar

Dodonov, V. V., and Manko, V. I. (1988). Invariants and correlated states of nonstationary systems. Commack, New York. Nova Sci. 183, 103–261.

Google Scholar

Erdèlyi, R., and Ballai, I. (2007). Heating of the solar and stellar coronae: a review. Astron. Nachrichten 328 (8), 726–733. doi:10.1002/asna.200710803

CrossRef Full Text | Google Scholar

Francis, G. (1960) “Ionization phenomena in gases,”. Academic Press.

Google Scholar

Fueno, T., Eyring, H., and Ree, T. (1960). Three-body recombination of gaseous ions. Can. J. Chem. 38, 1693–1701. doi:10.1139/v60-235

CrossRef Full Text | Google Scholar

Kuzhevskij, B. M. (2004). Generation of neutrons in lightning. MSU Bull. (5), 14–16.

Google Scholar

Mizuno, T., Akimoto, T., Takahashi, A., Celani, F., and Celani, F. (2006). ’Neutron emission from D₂ gas in magnetic fields under low temperature’. Condens. Matter Nucl. Sci., 312–323. doi:10.1142/9789812774354_0025

CrossRef Full Text | Google Scholar

NASA (2024). Solar dynamics observatory (SDO) gallery. Available at: https://sdo.gsfc.nasa.gov/gallery/main/item/118.

Google Scholar

Nguyen-Kuok, S. (2017). “Theory of low-temperature plasma physics,”. Cham: Springer. doi:10.1007/978-3-319-43721-7

CrossRef Full Text | Google Scholar

Robertson, H. P. (1930). A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. A 35, 667.

Google Scholar

Schrödinger, E. (1930). Heisenbergschen unschärfeprinzip. Ber. Kgl. Akad. Wiss., Berl. S24, 29.

Google Scholar

Selhorst, C. L., Valio, A. B. M., and Costa, J. E. R. (2005). Solar atmospheric model with spicules applied to radio observation. Astronomy Astrophysics 433 (1), 365–374. doi:10.1051/0004-6361:20042043

CrossRef Full Text | Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2015a). Coherent correlated states of interacting particles – the possible key to paradoxes and features of LENR. Curr. Sci. 108 (4), 30.

Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2015b). Formation of correlated states and optimization of nuclear reactions for low-energy particles at nonresonant low-frequency modulation of a potential well. J. Exp. Theor. Phys. 120 (2), 246–256. doi:10.1134/s1063776115020235

CrossRef Full Text | Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2017). Formation of correlated states and tunneling for a low energy and controlled pulsed action on particles. J. Exp. Theor. Phys. 125 (8), 195–209. doi:10.1134/s106377611707024x

CrossRef Full Text | Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2019). Features of correlated states and a mechanism of self-similar selection of nuclear reaction channels involving low-energy charged particles. J. Exp. Theor. Phys. 128 (6), 856–864. doi:10.1134/s1063776119040125

CrossRef Full Text | Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2020). “Universal mechanism of LENR in physical and biological systems on the base of coherent correlated states of interacting particles,” in Cold fusion: advances in condensed matter nuclear science. (Amsterdam: Elsevier), 333–370. doi:10.1016/B978-0-12-815944-6.00017-8

CrossRef Full Text | Google Scholar

Vysotskii, V. I., and Vysotskyy, M. V. (2023). Self-controlled flashing nuclear fusion in stationary magnetized low-temperature plasma. Fusion Sci. Technol. 79 (5), 537–552. doi:10.1080/15361055.2022.2151284

CrossRef Full Text | Google Scholar

Zaitsev, V. V., Stepanov, A. V., and Kronshtadtov, P. V. (2021). Type-II spicules as important sources of both heating and sustain the mass loss of solar corona. Geomagnetism Aeronomy 61, 1116–1121. doi:10.1134/s0016793221080235

CrossRef Full Text | Google Scholar