Temperature-tunable topological zero-refraction acoustic metamaterials

Zero-refractive index metamaterials have a wide range of applications in directional transmission and wave-front shaping due to their unusual acoustic properties. However, for most given acoustic topological metamaterials, the operating frequency is relatively fixed and the effect of temperature on their topological properties is rarely considered. Therefore, temperature-controlled tunable topological zero-refraction acoustic metamaterials are proposed in this paper. Firstly, a metamaterial with quadruple degenerate Dirac-like points at the center of the Brillouin zone is constructed, and the influence of temperature on the Dirac-like points is analyzed. The results show that the topological bandgap frequency range is more sensitive to temperature. The existence of pseudospin-polarized edge state is demonstrated by analysing the band structure of supercells with different topological phase phonon crystal. The topological zero-refraction property of the edge states outcoupled into free space is numerically demonstrated, and the non-contact active control of their operating frequencies can be realized by temperature. This study can provide a corresponding reference for the intelligent control of near-zero refractive index acoustic topological materials in elastic wave collimation and acoustic communication.

1 Introduction

Topological phases and topological phase transitions of matter have been extensively studied in condensed matter physics due to their fundamental property of being insensitive to continuous perturbations of material parameters. At the same time, a class of metamaterials with non-trivial topological properties, known as topological metamaterials (Hasan and Kane, 2010; Qi and Zhang, 2011) has sparked significant scientific interest. Materials having topological characteristics exhibit several innovative qualities (He et al., 2019; Zhang et al., 2018a; Lin et al., 2023), such as backscattering suppression at boundaries and lossless transport, which have great potential for applications in electronics, acoustics, and mechanical systems.

In studying 2D phononic crystals, the initial method for determining their topological properties was to introduce an external magnetic field to break the time-reversal symmetry, resulting in the quantum Hall effect. Fleury et al. (2014) suggested putting a flow field into an acoustic system composed of an annular resonant cavity to accomplish the nonreciprocal transmission of acoustic waves. The proposed method provides a novel solution to solve the problem of breaking the time-reversal symmetry of fluid acoustic systems. Yang et al. (Xue et al., 2022) introduced a background flow velocity field to construct an equivalent magnetic field in a two-dimensional air acoustic system, successfully broking the time-reversal symmetry of the phononic crystal system, realizing the analogy of quantum Hall effect in acoustics for the first time, and theoretically investigating the quantum Hall effect acoustic edge states and their properties such as backscattering suppression, immunodeficiency, and disorder. Although topological edge states for acoustic analogy can be established by introducing background rotational flow velocity fields, temporal and spatial modulations, their implementation still faces some harsh operating conditions until He et al. proposed a method to simulate the quantum spin Hall effect in acoustics, which achieved acoustic pseudo spin topological edge states based on acoustic quantum spin Hall effect analogy by modulating the acoustic quadruple Dirac degenerate band inversion through adjusting the filling material (He et al., 2016). Zhang et al. (2017) constructed quadruple degeneracy points in honeycomb lattice phononic crystal based on energy band folding. The topological phase transition between pseudo spin dipole and quadrupole modes was induced by breaking the spatial symmetry of the system, achieving robust transmission characteristics of unidirectional and path reconfigurable pseudo spin edge states. Then, Chen et al. (2018) introduced the one-dimensional topological structures into the field of elastic waves. They achieved band inversion by adjusting the stiffness coefficients of springs in a one-dimensional spring oscillator system based on the SSH model, distinguished different topological phases by calculating the winding number, and constructed topologically protected interface states. These topological edge protection properties are independent of boundary defects and material impurities, which has attracted high attention to the exploration of acoustic metamaterials in precise control of elastic waves (Zhu et al., 2018), topological valley transmission (Deng et al., 2024; Cai et al., 2023). Acoustic delay lines (Wang J. Q. et al., 2022), elastic energy harvesters (Tan et al., 2024; Yuan et al., 2024), etc.

In addition to topological transport, the non-reflective topological refraction properties of phononic crystals (Wang B. B. et al., 2022; Huang et al., 2021) have also attracted widespread attention for their ability to effectively address the terminal impedance mismatch problem between the domain wall and external space. According to the momentum conservation theory, acoustic topological refraction can be evaluated quantitatively (Zhang et al., 2018b), and experiments show that the refraction direction of the valley edge state is determined by the projection of the valley K and K′(Lu et al., 2017a). Zhang (Zhang et al., 2018b) investigated the topological directional refraction of edge states with different valley polarizations. This valley-polarized edge state ensures nonreflective external coupling from the topological interface to free space, with near-perfect efficiency and high stability. Li (Ye et al., 2017) proposed a valley-Hall-like photonic insulator based on a C3v Kagome split ring that explores the refraction of edge states from the interface to the background space at the Zigzag termination. This provides a new method for controlling terahertz wave propagation and promotes potential applications in directional collimation, beam splitting, and negative refraction imaging. Lu (Lu et al., 2018) constructed pure S0-mode valley topological phononic crystal plates and realized valley refraction with different directionality by changing the material properties of the terminals. It provides a way to study the symmetric modes of Lamb waves alone, which has potential applications in fast and accurate ultrasonic nondestructive testing. However, for elastic systems, the topological refraction phenomenon is closely related to the existence of edge states in a single bandgap and does not have the property of bandgap adjustability after the structural design is completed, which cannot satisfy the requirements of different operating environments, limiting the range of applications.

Given the materials and structures utilized in practical engineering, environmental temperature variations during operation are unavoidable, and alterations in material properties and structural rigidity significantly influence the structure’s dynamic properties. Furthermore, current research indicates that the thermal setting impacts the spread and topological characteristics of acoustic waves. However, these studies primarily focus on how the thermal environment alters the materials’ physical attributes, with a lesser number examining how thermal stresses affect the band properties of acoustic topological insulators. Consequently, two-dimensional two-component honeycomb phononic crystals constructed by tungsten-epoxy resin are studied in this paper, analyzing numerically the progression of their band properties under thermal stress. Pseudospin-polarized edge states are obtained at the interface of two phononic crystals with different topological phases, and the topological zero-refraction property of the edge states outcoupled into free space is numerically demonstrated, which proves that the topological zero-refraction is independent of the angle and direction of incidence. The frequency range of the topological state can be changed by the temperature, which realizes the non-contact active regulation of the topological zero-refraction property.

2 Band structure and topological phase transition

The honeycomb solid phononic crystal unit proposed in this paper is depicted in Figure 1A, in which the purple border represents metallic tungsten, and the gray area is epoxy. The primitive cell structure is illustrated in the inset. This formation is a standard hexagonal honeycomb lattice, made up of six metallic arms (each side length l = 24 mm and width t) along with six extra counterweights (rectangles of length h = 10.11 mm, width w) located at the vertices of the hexagon, and the lattice constant $a_s=\sqrt{3}l$. The selected material parameters are as follows: the mass density of tungsten ${\rho }_{\text{Tun}}=19100\text{kg}/{\mathrm{m}}^3$, Young’s modulus ${\mathrm{E}}_{\text{Tun}}=391.18\text{GPa}$, and the Poisson’s ratio $v_{\text{Tun}}=0.35$; the mass density of epoxy ${\rho }_{\mathrm{Exp}}=1180\text{kg}/{\mathrm{m}}^3$, Young’s modulus ${\mathrm{E}}_{\mathrm{Exp}}=0.559\text{GPa}$, and the Poisson’s ratio $v_{\mathrm{Exp}}=0.368$. The solid mechanics module of COMSOL Multiphysics is employed to calculate the band structure and displacement field distribution of this phononic crystal. The Floquet periodic boundary conditions is applied to the single cell (supercell) obtained by scanning the first Brillouin zone to solve the bulk (edge) band dispersion relationship.

Figure 1

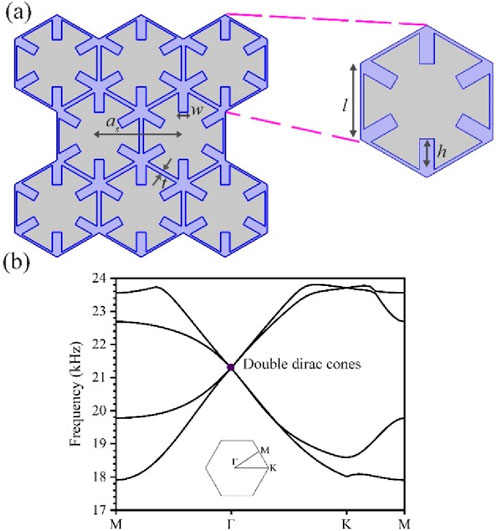
Figure 1. (A) Schematic diagram of phononic crystal structure. (B) Band diagram of phononic crystal at t = 0.18 mm, w = 3.98 mm.

Figure 1B illustrates the dispersion relation of the honeycomb lattice phononic crystal at t = 0.18 mm and w = 3.98 mm. Observations show the phononic crystal’s bandgap close at 21.3 kHz, creating a quadruple accidentally degenerate Dirac point (purple point). Altering the structural parameters can open the quadruple accidental degeneracy of Dirac points, forming a topologically complete bandgap. Figures 2A, B illustrate the single-cell band structures of phonon crystal I (PC I, t = 0.36 mm, w = 3.98 mm) and phonon crystal II (PC II, t = 0.06 mm, w = 3.4 mm), with their double degenerate eigenstates at the Γ-point are marked by blue and red dots. To further characterize the topology of PC I and PC II, k⋅p perturbation theory (Lu et al., 2017b; Yan et al., 2018) is utilized to compute their topological invariants. The effective Hamiltonian near the Г-point for in-plane polarizer elastic waves in the designed honeycomb lattice phononic crystal structure can be expressed as (Mei et al., 2012):

$H_{ij}^{eff}=H_{ij}^{\prime }+{\sum }_{\alpha }\frac{H_{i\alpha }^{\prime }{H}_{\alpha j}^{\prime }}{{\epsilon }_i-{\epsilon }_{\alpha }}(1)$

where i, j = 1, 2, 3, 4, ${\epsilon }_{1,2}={\epsilon }_p$ and ${\epsilon }_{3,4}={\epsilon }_d$ are the eigenfrequencies of four eigenstates at the Γ point. $H_{ij}^{\prime }$ is the first order perturbation term and $H_{i\alpha }^{\prime }{H}_{\alpha j}^{\prime }$ comes from the second order perturbation. On the basis p+, d+, p-, d-, the effective Hamiltonian of Equation 1 can be rewritten as:

$H^{\text{eff}}\left(\mathbf{k}\right)=\left(\begin{array}{cccc}M-B{k}^2& A{k}_{+}& 0& 0\\ A^{*}{k}_{-}& -M-B{k}^2& 0& 0\\ 0& 0& M-B{k}^2& A{k}_{-}\\ 0& 0& A{k}_{+}& -M+B{k}^2\end{array}\right)(2)$

Figure 2

Figure 2. Dispersion relations of (A) PC I and (B) PC II.

Where $k_{\pm }=k_x\pm i{k}_y,M=\left({\epsilon }_d-{\epsilon }_p\right)/2$, is the difference of frequency between d and p eigenstates around the Γ-point. Parameter A is determined by the off-diagonal elements of the first-order perturbation. Parameter B comes from the second-order perturbation term, and is typically negative. The effective Hamiltonian quantity in Equation 2 can be used as the elastic counterpart of the quantum spin Hall effect. The pseudospin Chern numbers in the elastic wave systems can be calculated by

$C_s=\pm \frac{1}{2}\left[\text{sgn}\left(M\right)+\text{sgn}\left(B\right)\right](3)$

It can be seen from Equation 3 that the sign of M directly determines the pseudospin Chern number. The corresponding displacement field distributions of these double degenerate eigenstates are displayed in the inset of Figure 2. The results show that for the PC I structure, the frequency of the pseudo-spin dipole mode (p-state) is above that of the pseudo-spin quadrupole mode (d-state), and hence $M=\left({\epsilon }_d-{\epsilon }_p\right)/2<0$ with the corresponding pseudospin Chern numbers $C_s=\pm 1$, which implies that the bandgap is topologically non-trivial band. For the PC II structure, $M=\left({\epsilon }_d-{\epsilon }_p\right)/2>0$ with the d-type states exceed the p-type states, we obtain the pseudospin Chern numbers $C_s=0$, which implies that the bandgap is topologically trivial band. Thus, topological phase transitions from non-trivial states to trivial states occurred in these two types of phononic crystal structures.

3 The influence of temperature on the topological band structure

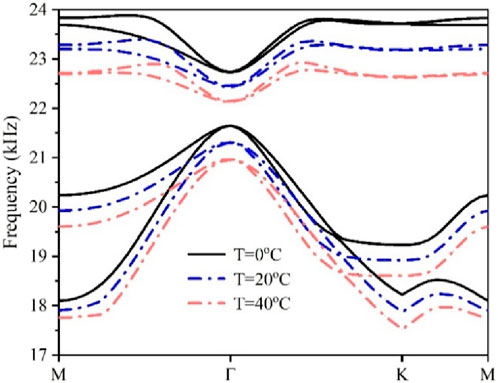
Traditional acoustic metamaterials lack adjustable bandgap characteristics after structural creation, making them unable to meet different operating conditions and limiting their potential applications. Since temperature is easy to precisely control, altering the topological frequency through temperature adjustment is a feasible option. Figure 3 depicts the band structure of the phononic crystal I under varying temperature conditions. Observations show a reduction in its bandgap frequency with rising temperatures. Specifically, the frequency of its bandgap drops from 21.65 kHz-22.73 kHz to 20.97 kHz-22.13 kHz as the temperature rises from 0°C to 40°C. Consequently, this enables the adjustment of the topology frequency through temperature modifications.

Figure 3

Figure 3. Band gap structure of PC I at different temperatures.

Vibration theory suggests that the modal characteristics of the phononic crystal structure can be solved through the subsequent equation

$\left(\mathbf{K}-{\omega }^2\mathbf{M}\right)\mathrm{U}=0(4)$

wherein K represents the entire structural rigidity matrix, M denotes the mass matrix, and U signifies the vector of vibration modes.

Under the thermal environment, the structure modal state is primarily influenced by how material parameters fluctuate with temperature and the internal thermal stresses caused by the thermal environment. Upon thermal loading of the phononic crystal structure, the change of the mass matrix M in Equation 4 can be negligible, while the structural material parameters undergo significant changes with increasing temperature. Taking into account the impact of temperature, the structural stiffness matrix can be expressed as:

${\mathbf{K}}_T={\int }_{\mathrm{\Omega }}{\mathbf{B}}^{\mathrm{T}}{\mathbf{D}}^T\mathbf{B}\mathrm{d}\mathrm{\Omega }(5)$

where B represents the geometric matrix and D denotes the elastic matrix linked to the material’s elastic modulus E and Poisson’s ratio c.

On the other hand, fluctuations in temperature induce thermal stresses inside the structure, factors that should be considered in its stiffness matrix, which can then be described as follows:

${\mathbf{K}}_{\sigma }={\int }_{\mathrm{\Omega }}{\mathbf{G}}^{\mathrm{T}}\mathrm{S}\mathbf{G}\mathrm{d}\mathrm{\Omega }(6)$

Here, G represents the matrix for strain-displacement and S denotes the matrix for structural thermal stress. To address the structural modal parameters within the thermal environment, it’s crucial to consider the alterations in material parameters due to the thermal environment and the effects of thermal stresses on the stiffness matrix. Combining Equations 5, 6, the complete stiffness matrix K for the structure under thermal environment conditions is.

$\mathbf{K}={\mathbf{K}}_T+{\mathbf{K}}_{\sigma }(7)$

where ${\mathbf{K}}_T$ represents the matrix of structural stiffness and ${\mathbf{K}}_{\sigma }$ represents the matrix of thermal stress.

In Equation 7, the structural stiffness matrix ${\mathbf{K}}_T$ is related to the physical properties of the structure. As the temperature rises, the elasticity modulus of the metal tungsten diminishes, leading to a downward trend in the overall stiffness matrix. The thermal stress stiffness matrix ${\mathbf{K}}_{\sigma }$ is related to the form of thermal stresses in the structure. Under conditions of tensile thermal stress, ${\mathbf{K}}_{\sigma }$ is positive and the inherent frequency of the structural formation rises. Conversely, under compressive thermal stress, ${\mathbf{K}}_{\sigma }$ turns negative and the natural frequency tends to diminish.

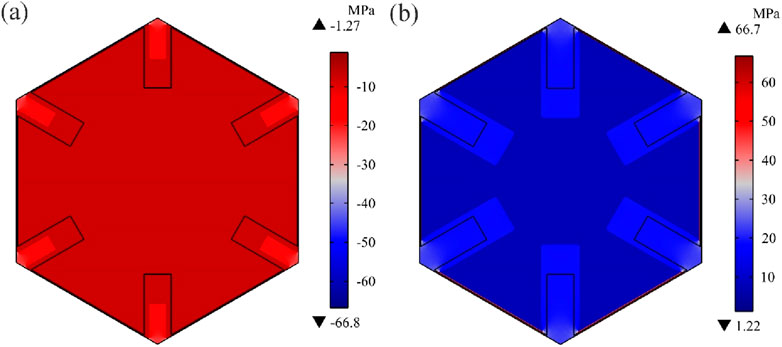
Following the preceding analysis, the distribution of compressive stress in phononic crystal II across various temperatures was analyzed, as depicted in Figure 4. At a temperature of T = 0^oC, a negative compressive stress signifies tensile stress, making ${\mathbf{K}}_{\sigma }$ is positive and the structure’s natural frequency ascends; However, at T = 40^oC, the compressive stress becomes positive, while the natural frequency tends to decline. This is consistent with the effect of temperature on the bandgap structure in Figure 3. Conclusively, by adjusting the temperature, the total stiffness of the structure can be modulated effectively, and then the band structure can be adjusted. There exists an inverse relationship between the structure’s inherent frequency and temperature.

Figure 4

Figure 4. (A) Compressive stress distribution at T = 0°C and (B) T = 40°C.

4 The influence of temperature on the frequency range of topological channel transmission

Excitation and outcoupling of topological edge states play a crucial role in achieving protected refractions. The body-boundary correspondence principle posits that topological edge states are present at the interface of supercells composed of phononic crystals with two different topological properties. Figure 5A displays a supercell consisting of 8 PC I structures and 8 PC II structures, in which the boundaries are indicated by red dashed lines. Through the finite element method, Floquet boundary conditions are applied to both the upper and lower sides of the supercell to obtain the dispersion diagram at varied temperatures, as shown in Figures 5B, C, with the gray region denoting the bulk state and the red and blue lines indicate the edge states. The range of 21.67 kHz–22.46 kHz at 20°C, and 21.04 kHz–21.66 kHz at 60°C, suggests that temperature fluctuations can manipulate the topological bandgaps. Figure 5D displays the in-plane displacement field distributions for eigenmodes of the edge states at points A and B. Observation reveals that the maxima of their displacement amplitudes are mainly concentrated at the interface between the two phononic crystal structures and decay rapidly to the two sides of the body, suggesting that these topological fringe states can be well localized at the interface. The enlarged view in Figure 5D plots the velocity field at points A (wave vector $k_x=-0.02\times \left(2\pi /a\right)$) and B (wave vector $k_x=0.02\times \left(2\pi /a\right)$). Since the opposite velocity directions of points A and B approximate angular momentum, there is a similar quantum spin Hall effect for pseudo-spin up and pseudo-spin down states in electronic systems. It is worth noting that the velocity fields and pseudo-spin directions of point A contrast with those at point B. Consequently, the intersection point at an identical frequency on the boundary represents two distinct pseudo-spin states. The pair of interdependent pseudo-spin edge states share identical velocity magnitudes and divergent orientations, facilitating the transmission of dependent pseudo-spin acoustic waves.

Figure 5

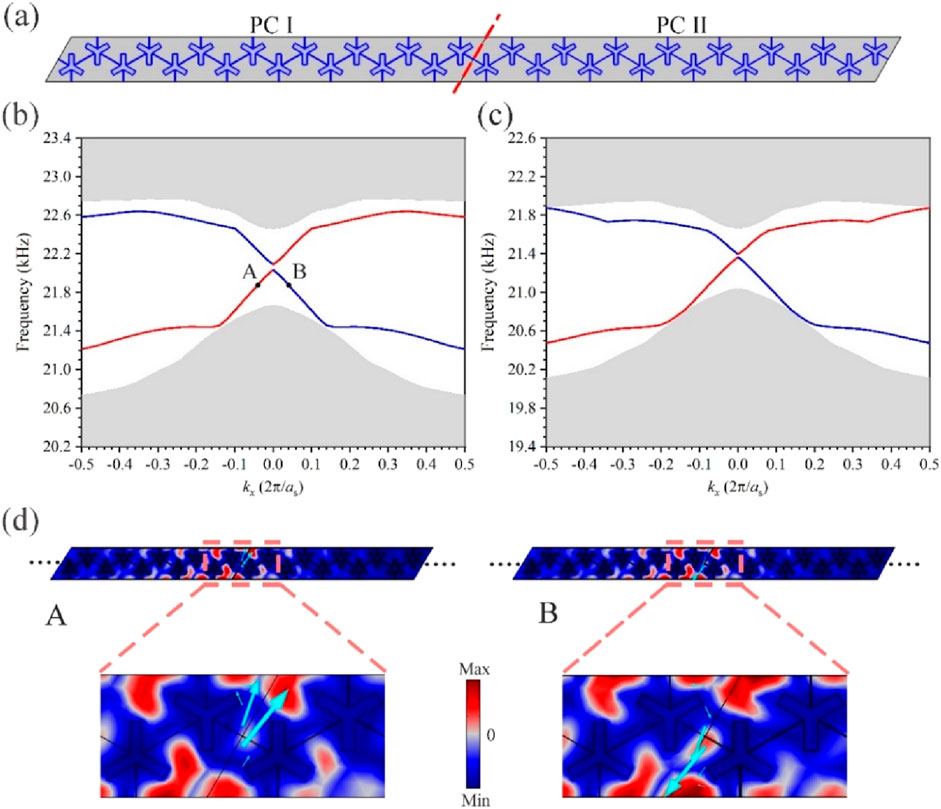
Figure 5. (A) The supercell structure is composed of 10 Type-I (Δh = −1 mm) structures and 10 Type-II (Δh = 1 mm) structures; (B, C) Projected band structures at 20°C and 60°C. (D) E (wave vector $k_x=-0.02\times \left(2\pi /a\right)$, left), F (wave vector $k_x=0.02\times \left(2\pi /a\right)$ , right) two points are in the velocity field of the edge state, with the same eigenfrequencies of points A and B.

Subsequently, the impact of temperature on the topological bandgap received additional examination, as depicted in Figure 6. Observations indicate an increase in compressive stress within supercells as temperature rises and a decrease in the structure’s total stiffness, leading to a shift in both the upper and lower boundary frequencies of the topological channel to lower frequencies. The results suggest that altering the temperature could enable the modulation of the elastic wave topological transmission state without physical contact.

Figure 6

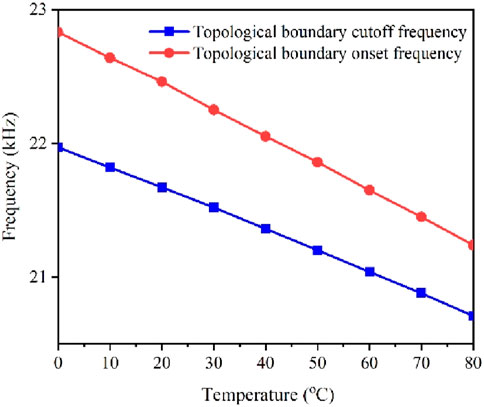
Figure 6. Relationship between temperature and the onset and cut-off frequencies of the topological bandgap.

5 Tunable topological zero-refraction insulators

Investigating the topological refractive characteristics of elastic valley projection edge states outcoupling into free space, a topological waveguide consisting of PC Ⅰ and PC Ⅱ with a zigzag-type boundary at the outgoing end surrounded by water is constructed as shown in Figure 7. For an in-depth examination of the coupling characteristics between solid waveguides and liquid materials, a discussion on the topological refractive qualities of the valley edge states into water is undertaken. Figure 7A illustrates the displacement field and acoustic pressure field distributions of the topological waveguide submerged in water, under an excitation frequency of f = 21.8 kHz at 20^oC. It is noteworthy that the elastic wave propagates along the normal of the terminals after passing through the topological waveguide, suggesting a typical zero refraction.

Figure 7

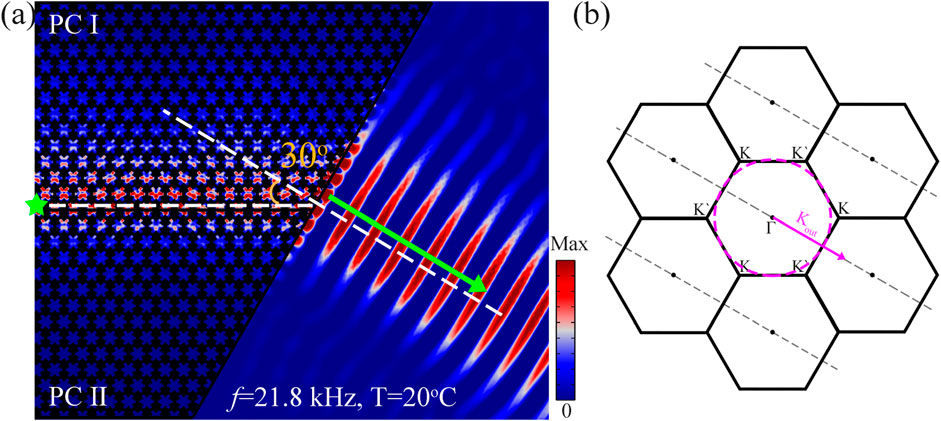
Figure 7. (A) Displacement field and acoustic pressure field distributions in water. (B) The equifrequency curve analysis in water.

To better analyze the negative refraction behavior, the equifrequency curve examining the coupling between the edge states and free space in wave vector space is performed, as shown in Figure 7B. The black solid hexagon denotes the first Brillouin zone, the purple-red dashed circle depicts the equifrequency curve of longitudinal waves in free space, and the black dashed line represents the normal to the zigzag terminal, k_l and k_t denote the wave vectors of longitudinal and transverse waves in free space, respectively. The topological edge states propagating from left to right are projected from the K′valley and follow the conservation of the wave vector components parallel to the zigzag termination when leaving the phononic crystal. Therefore, the refracted wave vector K_out in free space should be satisfied:

${\mathrm{K}}_{\text{out}}\cdot {\mathbf{e}}_{\text{zig}}=\mathrm{K}\cdot {\mathbf{e}}_{\text{zig}}(8)$

Here, e_zig represents the unit vector along the terminal boundary of the phononic crystal, $\left|\mathrm{K}\right|=\frac{2}{3}\times \frac{2\pi }{a_{\mathrm{s}}}$ denotes the magnitude of the incident wave vector K. The equifrequency curve of the longitudinal wave in free space is determined by the following equation:

$\left|{\mathrm{K}}_{\text{out}}\right|=\frac{2\pi f}{c_l\left(c_t\right)}(9)$

where f represents the incident wave frequency, c_l and c_t denotes the longitudinal wave and transverse wave velocities in free space. As depicted in Figure 7B, based on the above phase matching condition, the terminal normal intersects with the equifrequency curve at the frequency f = 21.8 kHz, which further confirms the negative refraction phenomenon of in-plane bulk elastic waves after leaving the phononic crystal. Thus, based on Equations 8, 9, this negative refraction angle γ can be determined by the following equation:

$\left|{\mathrm{K}}_{\text{out}}\right|\cdot \cos \left(90°+\gamma \right)=\left|\mathrm{K}\right|\cdot \cos 90°(10)$

Therefore, γ = 0^o can be obtained from Equation 10 when the frequency f = 21.8 kHz, and the theoretical predictions are in good agreement with the simulation results.

According to the phase-matching condition, the edge state of incident pseudo-spin polarization is locked at the Г-point and its wave vector is independent of the angle concerning the normal of the zigzag termination. The direction of the outgoing beam depends on the intersection of the black dashed lines in Figure 7B intersecting with the equifrequency curves in free space. We further investigate the topological edge state transmission at different incidence angles. The corresponding total displacement field distributions of the topological waveguide at incident angles α = 60^o and α = 90^o are given in Figure 8. These results indicate that in any direction of the topological interface, this externally coupled edge state always refracts at zero angle, exhibiting as an elastic near-zero refractive index metamaterial. This topological solid phononic crystal structure opens a new avenue for designing collimators in fluid environments using the topological refraction effect of elastic waves.

Figure 8

Figure 8. Topological zero refraction at incidence angles of (A) 60° and (B) 90°, respectively.

Subsequently, the coupling between the designed topological waveguide and different background media is analyzed and its topological zero-refraction properties are verified in different fluid and solid environments. Figure 9 investigates and analyzes the topological refraction properties of the pseudo-spin edge state from topological waveguide into the polyurethane background medium at 20°C. Unlike acoustic waves in the fluid domain, refracted waves can be divided into longitudinal and transverse components after leaving the waveguide based on the vector characteristics of in-plane body elastic waves. The total displacement field distribution as well as the longitudinal and transverse polarization displacement gradient fields of the edge state entering polyurethane at f = 21.8 kHz are given in Figures 9A–C, respectively. It can be observed that after passing through the topological straight waveguide, the refracted waves all propagate along the terminal normal, exhibiting zero-angle refraction characteristics. In order to accurately explain the refracted longitudinal and transverse wave modes, the outcoupling of the edge states was analyzed by equifrequency curve, as shown in Figure 9D. The presence of longitudinal (ΓA) and transverse (ΓB) modes in the polyurethane background medium, respectively, and their refractive angles γalso satisfy the phase matching condition ${\mathrm{K}}_{\text{out}}\cdot {\mathbf{e}}_{\text{zig}}=\mathrm{K}\cdot {\mathbf{e}}_{\text{zig}}$, which can be calculated as ${\gamma }_{\mathrm{\Gamma }\mathrm{A}}={\gamma }_{\mathrm{\Gamma }\mathrm{B}}=0°$. The theoretical predictions are in good agreement with the simulation results in Figures 9B, C. The above results confirm that topological zero refraction can be achieved by in-plane bulk elastic waves within such elastic solid systems in different fluid and solid environments.

Figure 9

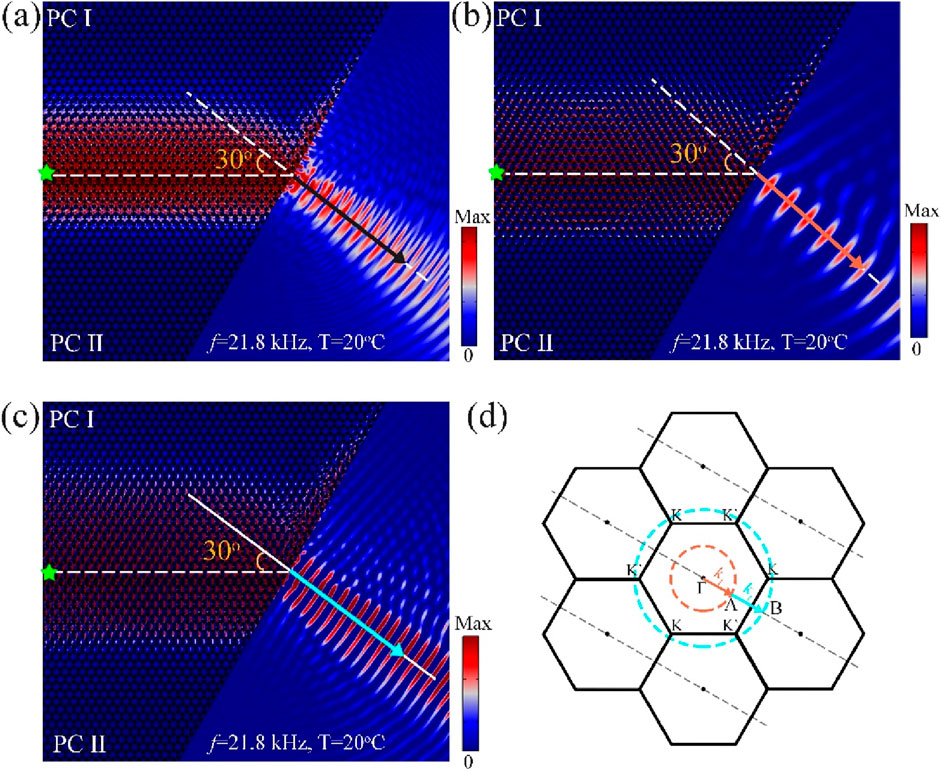
Figure 9. Topological refraction properties of pseudo-spin edge states from topological waveguide into the polyurethane background medium. (A) The total displacement field distributions at f = 21.8 kHz. (B, C) The real longitudinal and transverse polarized displacement gradient field, respectively. (D) The corresponding k-space analysis on the out-coupling of the edge states through the zigzag termination at f = 21.8 kHz. The Brillouin zone is depicted by the black solid line. The red-orange (cyan) dashed circles indicate the dispersions of longitudinal (transverse) waves in polyurethane.

Then, we investigated the effect of temperature on the topological zero refraction characteristics. The acoustic response of the topological acoustic system in different background media at different temperatures and an excitation frequency of 21.2 kHz was calculated, as shown in Figure 10. At the temperature of 20°C, the topological refraction characteristics under both water and polyurethane background media become chaotic and irregular [as shown in Figures 10A, C]. Then, we increase the temperature to 60°C, and the acoustic system in both background media can present clear topological zero refraction characteristics [Figures 10B, D]. This shows that the increase in temperature can change the topological characteristics of the acoustic system. The topological zero refraction transmission frequency range can be effectively controlled by temperature to meet the noise and vibration control requirements in different environments.

Figure 10

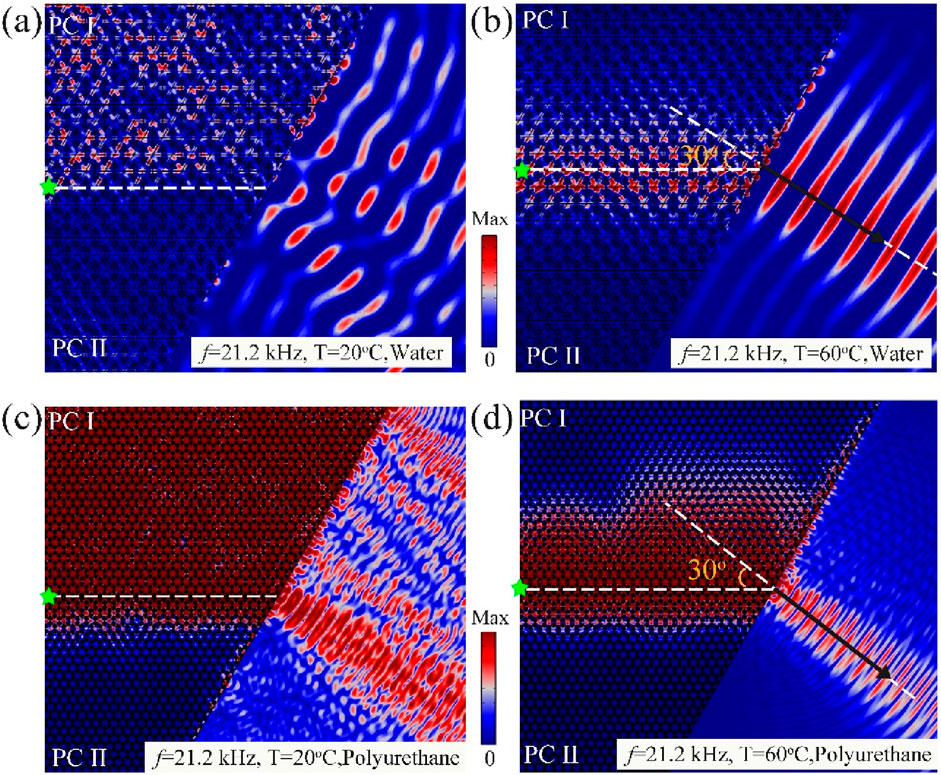
Figure 10. Topological refractive properties in different background media at different temperatures. (A, B) Displacement field and acoustic pressure field distributions in water at 20°C and 60°C, respectively. (C, D) Displacement field and acoustic pressure field distributions in polyurethane at 20°C and 60°C, respectively.

6 Conclusion

In this paper, topologically protected edge states of bulk elastic waves are realized in a two-dimensional two-component phononic crystal, and the effect of temperature on the topological bandgap and topological zero-refraction properties are analyzed and discussed. First, the effect of temperature on the band structure of acoustic wave crystals is investigated by numerical calculations and theoretical analysis. Then, the refractive properties of the edge state outcoupled to free space are investigated, and it is found that the topological zero-refraction properties are independent of the incident angle and exhibit metamaterial properties with near-zero refractive index. Finally, some numerical examples demonstrate the modulation of the topological zero-refraction transmission frequency achieved by controlling the temperature. This research can be used to flexibly control and direct acoustic waves, providing a corresponding reference for underwater communication and intelligent control of vibration, among others.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YC: Conceptualization, Writing–original draft. TS: Writing–review and editing. ZW: Funding acquisition, Writing–review and editing. ZZ: Funding acquisition, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Industrial Science and Technology Research Project of Henan Province (242102210095), the Doctoral Research Fund of Zhengzhou University of Light Industry (2020BSJJ029), Key Research and Development Special Project of Henan Province (221111210500), Government Collaborative Innovation Projects of Jiangsu Provincial Department of Science and Technology (BZ2023023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, C. X., He, G. C., Zheng, Z. F., Qin, Y., and Yin, J. F. (2023). Ultra-wideband valley transmission on elastic topological phononic crystals. Results Phys. 50, 106570. doi:10.1016/j.rinp.2023.106570

CrossRef Full Text | Google Scholar

Chen, H., Nassar, H., and Huang, G. L. (2018). A study of topological effects in 1D and 2D mechanical lattices. J. Mech. Phys. Solids 117, 22–36. doi:10.1016/j.jmps.2018.04.013

CrossRef Full Text | Google Scholar

Deng, C. X., Yang, Y. Q., Li, J., Zhang, X., Yu, Y. J., Lu, Q., et al. (2024). Asymmetric transport in sonic valley Hall insulators. Phys. Rev. Appl. 21, 034048. doi:10.1103/PhysRevApplied.21.034048

CrossRef Full Text | Google Scholar

Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R., and Alù, A. (2014). Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519. doi:10.1126/science.1246957

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasan, M. Z., and Kane, C. L. (2010). Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

He, C., Ni, X., Ge, H., Sun, X. C., Chen, Y. B., Lu, M. H., et al. (2016). Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12, 1124–1129. doi:10.1038/NPHYS3867

CrossRef Full Text | Google Scholar

He, M. Y., Sun, H. M., and He, Q. L. (2019). Topological insulator: spintronics and quantum computations. Front. Phys. 14, 43401. doi:10.1007/s11467-019-0893-4

CrossRef Full Text | Google Scholar

Huang, H. B., Huo, S. Y., and Chen, J. J. (2021). Subwavelength elastic topological negative refraction in ternary locally resonant phononic crystals. Int. J. Mech. Sci. 198, 106391. doi:10.1016/j.ijmecsci.2021.106391

CrossRef Full Text | Google Scholar

Lin, Z. K., Wang, Q., Liu, Y., Xue, H. R., Zhang, B. L., Chong, Y. D., et al. (2023). Topological phenomena at defects in acoustic, photonic and solid-state lattices. Nat. Rev. Phys. 5, 483–495. doi:10.1038/s42254-023-00602-2

CrossRef Full Text | Google Scholar

Lu, J., Qiu, C., Ye, L., Fan, X., Ke, M., Zhang, F., et al. (2017a). Observation of topological valley transport of sound in sonic crystals. Arxiv 13 (16), 369–374. doi:10.1038/nphys3999

CrossRef Full Text | Google Scholar

Lu, J. Y., Qiu, C. Y., Deng, W. Y., Huang, X. Q., Li, F., Zhang, F., et al. (2018). Valley topological phases in bilayer sonic crystals. Phys. Rev. Lett. 120, 116802. doi:10.1103/PhysRevLett.120.116802

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, J. Y., Qiu, C. Y., Ye, L. P., Fan, X. Y., Ke, M. Z., Zhang, F., et al. (2017b). Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 13, 369–374. doi:10.1038/NPHYS3999

CrossRef Full Text | Google Scholar

Mei, J., Wu, Y., Chan, C. T., and Zhang, Z. Q. (2012). First-principles study of Dirac and Dirac-like cones in phononic and photonic crystals. Phys. Rev. B 86, 035141. doi:10.1103/PhysRevB.86.035141

CrossRef Full Text | Google Scholar

Qi, X. L., and Zhang, S. C. (2011). Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

Tan, M. T., Sun, X. W., Liu, Y. H., Gao, X. L., Hu, L. W., and Song, T. (2024). Selective topological valley transport of elastic waves in a Bragg-type phononic crystal plate. J. Appl. Phys. 135, 243107. doi:10.1063/5.0216068

CrossRef Full Text | Google Scholar

Wang, B. B., Jia, D., Ge, Y., Yuan, S. Q., and Sun, H. X. (2022). Acoustic suppressed topological refraction in valley sonic crystals. New J. Phys. 24, 113033. doi:10.1088/1367-2630/aca21d

CrossRef Full Text | Google Scholar

Wang, J. Q., Zhang, Z. D., Yu, S. Y., Ge, H., Liu, K. F., Wu, T., et al. (2022). Extended topological valley-locked surface acoustic waves. Nat. Commun. 13, 1324. doi:10.1038/s41467-022-29019-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, H. R., Yang, Y. H., and Zhang, B. L. (2022). Topological acoustics. Nat. Rev. Mater. 7, 974–990. doi:10.1038/s41578-022-00465-6

CrossRef Full Text | Google Scholar

Yan, M., Lu, J. Y., Li, F., Deng, W. Y., Huang, X. Q., Ma, J. H., et al. (2018). On-chip valley topological materials for elastic wave manipulation. Nat. Mater. 17, 993–998. doi:10.1038/s41563-018-0191-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, L. P., Qiu, C. Y., Lu, J. Y., Wen, X. H., Shen, Y. Y., Ke, M., et al. (2017). Observation of acoustic valley vortex states and valley-chirality locked beam splitting. Phys. Rev. B 95, 174106. doi:10.1103/PhysRevB.95.174106

CrossRef Full Text | Google Scholar

Yuan, W. T., Zhang, Y. X., Pan, Y. D., Huang, Y., Zhao, J. F., Yang, F., et al. (2024). Topological rainbow trapping, concentration and guiding in graded elastic valley phononic crystal plate. Eng. Struct. 304, 117596. doi:10.1016/j.engstruct.2024.117596

CrossRef Full Text | Google Scholar

Zhang, Z. W., Tian, Y., Cheng, Y., Wei, Q., Liu, X. J., and Christensen, J. (2018a). Topological acoustic delay line. Phys. Rev. Appl. 9, 034032. doi:10.1103/PhysRevApplied.9.034032

CrossRef Full Text | Google Scholar

Zhang, Z. W., Tian, Y., Wang, Y. H., Gao, S. X., Cheng, Y., Liu, X. J., et al. (2018b). Directional acoustic antennas based on valley-Hall topological insulators. Adv. Mater. 30, 1803229. doi:10.1002/adma.201803229

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z. W., Wei, Q., Cheng, Y., Zhang, T., Wu, D. J., and Liu, X. J. (2017). Topological creation of acoustic pseudospin multipoles in a flow-free symmetry-broken metamaterial lattice. Phys. Rev. Lett. 118, 084303. doi:10.1103/PhysRevLett.118.084303

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y. F., Hu, J., Fan, X. D., Yang, J., Liang, B., Zhu, X. F., et al. (2018). Fine manipulation of sound via lossy metamaterials with independent and arbitrary reflection amplitude and phase. Nat. Commun. 9, 1632. doi:10.1038/s41467-018-04103-0

PubMed Abstract | CrossRef Full Text | Google Scholar