- 1Zhejiang Hongtu Traffic Construction Co., Ltd., Hangzhou, China
- 2College of Civil Engineering and Architecture, Zhejiang University, Hangzhou, China
- 3College of Civil Engineering and Architecture, Quzhou University, Quzhou, China
Glass transition is one of the most crucial physical properties for polymerical materials. As a typical complex polymerical material, the glass transition phenomenon in asphalt binder is directly related to their temperature-related properties. To investigate the glass transition characteristics, this study delves into the glass transition temperature of asphalt binder based on molecular dynamics simulations. It is found that the calculation range for the glass transition temperature sits between 100 and 400 K. The evolution of asphalt binder structure is influenced by different cooling rates, where lower cooling rates allow sufficient microstructural rearrangement, resulting in a smaller volume at the lower temperature. Model size is closely associated with the glass transition region. As the size increases, the transition region significantly expands. Increasing the model size also reduces volume fluctuations after isothermal relaxation, providing more stable volume changes. It is observed that higher cooling rates with a model size over 100 Å can well reproduce the glass transition process of asphalt binders. This work provides atomic-scale insights for the glass transition phenomenon in asphalt binder, which could be beneficial for the design of high-performance asphalt binder.
1 Introduction
The Nobel laureate in Physics, P.W. Aderson, proposed in 1995 that “the deepest and most interesting unresolved issue in solid-state theory may be the nature of glass and the glass transition” (Couzin, 2005). By lowering the temperature, polymers undergo a significant decrease in properties such as Young’s modulus and viscosity, while their structure remains largely unchanged (remaining in an amorphous state). The study of glass transition has a history of nearly 80 years. Despite a substantial amount of experimental, theoretical, and simulation research, the fundamental question regarding the nature of the glassy state remains unanswered (Anderson and Marasteanu, 1999; Zhang and Greenfield, 2007a; You et al., 2020; Khan et al., 2021; Cui B. et al., 2022; Cui W. et al., 2022; Lu et al., 2022; Liu et al., 2017). To date, no single theory has been able to explain all the phenomena associated with the glass transition, and existing theories only align with experimental or simulation results within certain specific ranges of supercooling and specific systems. In recent years, with a deepening understanding of the intrinsic relationship between material microstructures and properties, Molecular Dynamics (MD) simulations have played a crucial role in studying the glass transition phenomenon (Rigby and Roe, 1987), simulating the relationship between the specific volume and temperature of polymers during the cooling process can effectively uncover underlying mechanisms behind the glass transition. However, due to the femtosecond-scale timestep used in MD simulations, the cooling rate differs significantly from experiments, potentially by up to 1012 times (Bulacu and van der Giessen, 2007). Despite this challenge, research indicates that MD simulations are still able to effectively capture the glass transition phenomenon in polymers (Khan et al., 2021; Godey et al., 2018; Yao, et al., 2022; Berthier and Reichman, 2023; Lunkenheimer et al., 2023; Kang et al., 2019).
Based on the movement of constituent molecules, rheological behavior can be generally categorized into three states and two transitions, i.e., glassy state, glass transition, rubbery (high elasticity) state, flow transition, and flow state (Wang et al., 2020). Molecular dynamics simulation can provide motion details of asphalt molecules, clearly delineating the differences in movement between the glassy and rubbery states, capturing the transition of molecules from a free state to a “frozen” state. Some studies consider the critical temperature at which a system transitions from the rubbery state to the glass transition region as the glass transition temperature
As a typical polymerical material, asphalt binder exhibits temperature-dependent performance in terms of cracking, rutting, and low durability. In winter and cold regions, asphalt binder requires a good low-temperature performance and relaxation capability to prevent damage (Debbarma et al., 2022; Tabatabaee et al., 2012; Kriz et al., 2011; Amoussou et al., 2016; Krishnan and Rajagopal, 2005; Hu et al., 2022). At high temperatures, asphalt transitions from a solid amorphous glassy state to a viscous isotropic liquid state. Upon cooling, the liquid asphalt gradually transitions to the glassy state. Clearly, the temperature that determines the transition of the asphalt’s mechanical state from viscoelastic to glassy affects its toughness, deformation, physical properties, and rheological behavior, thereby is crucial for their engineering applications. At the microscopic level,
Different calculation methods based on MD simulations have been developed to calculate
2 Materials and methods
The selection of initial configurations is crucial for an in-depth study of the glassy state. In this work, we adopted a four-component asphalt molecule model proposed by Li and Greenfield (2014), as shown in Figure 1A. Using the Materials Studio software, we employed a random walk algorithm to establish the amorphous molecular model of asphalt, as depicted in Figure 1B. The initial density of the model was set to 1.0 g/cm3, and the initial temperature was set to 300 K. Asphalt molecules were randomly placed into a periodic cell with initial dimensions of 75 × 75 × 75 Å3 at fixed proportions, refer to our previous work for more details (Pang et al., 2023). The molecular structure of asphalt is quite complex, and during the modeling process, the relative positions of the molecules are irregular. The model was first optimized through energy minimization and relaxation processes. In this work, the Consistent Valence Force Field (CVFF) was utilized to describe the atomic interactions within the asphalt system. The long-range van der Waals interactions were represented using the Lennard-Jones (LJ) potential with a cutoff distance set to 12.5 Å. Additionally, the Particle-Particle-Particle-Mesh (PPPM) algorithm was employed to compute long-range electrostatic interactions, with an accuracy set to 10–4. A series of structural relaxation simulations were conducted on the model under canonical (NVT), isothermal-isobaric (NPT), and microcanonical (NVE) ensembles, each for relaxation periods of 0.5 ns, 1 ns, and 0.5 ns, respectively. During relaxation, the pressure was set to a constant 1 atm, and the temperature was maintained at 300 K. Following structural relaxation, the equilibrium density of the asphalt was approximately 0.96 g/cm3 (Zhang and Greenfield, 2007b), close to experimental data ranging from 0.95 to 1.05 g/cm3. Subsequently, under a pressure of 1 atm, a cooling cycle was applied to the asphalt model. Initially, the model was heated to 400 K in the NPT ensemble for 1 ns and then maintained at a constant temperature for 0.5 ns, followed by cooling to 100 K. The initial temperature cooling interval was set to 20 K. After 15 cooling cycles, the system temperature reached 100 K. With the decrease in temperature, the volume or density change curve of the sample was obtained to determine the glass transition temperature (Yao et al., 2022; Schawe, 2022). As the volume and density exhibit similar variation curves, this study chose the volume parameter to fit the glass transition temperature.
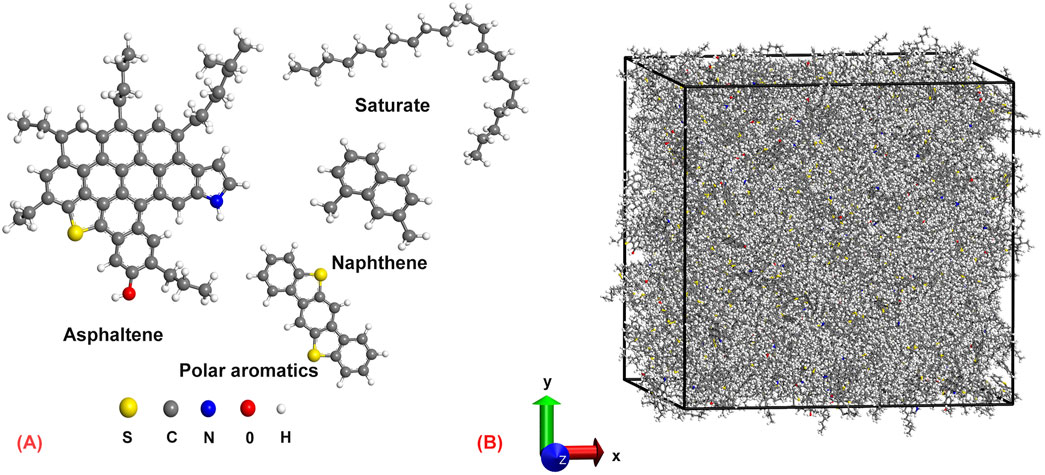
Figure 1. Schematic view of the simulation model. (A) Four representative molecules of the asphalt binder; (B) Molecular structure of asphalt binder.
3 Results and discussion
3.1 Glass transition temperature calculation
Figure 2A shows the volume change trend of the asphalt binder model during a stepwise cooling process. Considering a constant volume expansion coefficient for the model in the glassy and rubbery states (i.e., the volume changes linearly with temperature), the intersection temperature of the two fitted lines from the corresponding low-temperature and high-temperature regions (LL fit and HL fit) represents
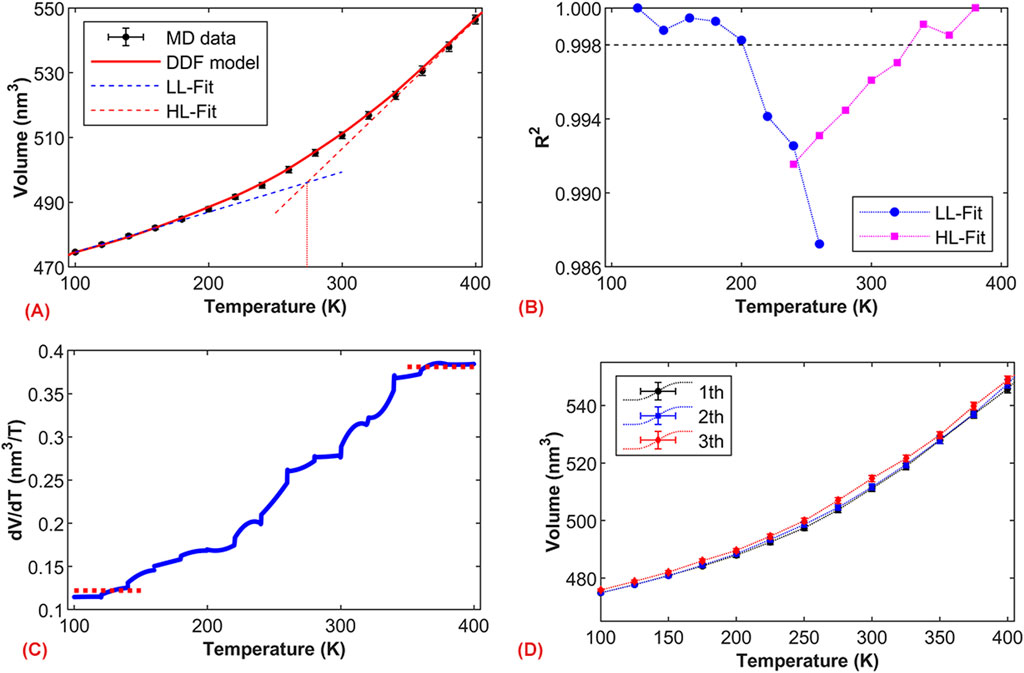
Figure 2. Molecular dynamics simulation and calculation of glass transition temperature. (A) Volume-temperature relationship graph; (B) Comparison of the coefficient of determination R2 for linear fits, where LL-Fit and HL-Fit represent linear fits in the low-temperature and high-temperature regions, respectively; (C) Rate of change of volume with temperature based on the DDF model; (D) Volume-temperature relationship graphs under different simulation processes.
From Figure 2A, it is evident that the value of
Due to the different motion characteristics of molecules during the cooling and heating processes, molecular systems typically exhibit hysteresis effects in their thermal and volumetric properties during the glassy state transition (Minisini and Soldera, 2023). Hence, it is necessary to explore the influence of the simulation process on
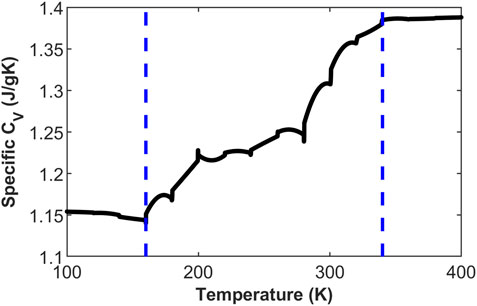
The glass transition region of the system can be identified from the volume-temperature curve. Based on the results from Figure 2A, the deviation from linear behavior in the volume-temperature relationship occurs between 180 K and 340 K, corresponding to the beginning and end of the glassy state transition, respectively. This can be expressed as
The above defines the transition range of the glassy state from a molecular thermodynamic perspective (volume and energy), and similarly, in molecular dynamics, it is possible to capture the differences between the asphalt glassy state and rubbery state. Figure 4 depicts the mean square displacement (MSD) plot from MD simulations under the NPT ensemble for asphalt components in the rubbery state (400 K) and glassy state (100 K) with a 0.5 ns timescale. It is evident that the motion of asphalt at the two temperatures is entirely different. At 400 K, the components of asphalt are nearly in a flowing state, especially the saturated components, which undergo extensive motion within the system. Conversely, at 100 K, the asphalt components are only engaged in localized vibrations. This demonstrates the transition of asphalt components from a free-flowing state to a “frozen state.”
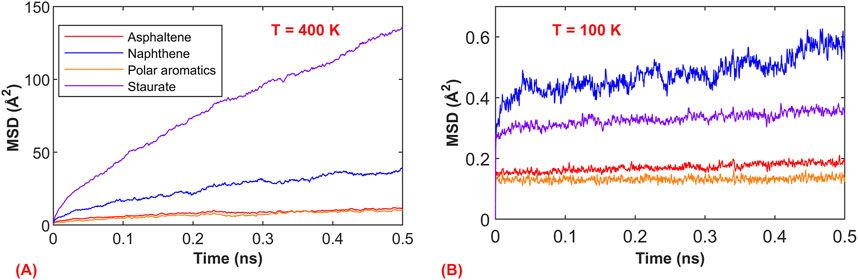
Figure 4. Molecular motion simulation results of asphalt components. (A) Mean square displacement (MSD) at the rubbery state (400 K); (B) Mean square displacement (MSD) at the glassy state (100 K).
3.2 Cooling rate
Since the glass transition phenomenon is directly related to molecular motion, and molecular motion is temperature-dependent, it is necessary to examine the effect of cooling rates on the glassy state transition. For macroscopic-scale experiments, the formation of the glassy state requires a relatively rapid cooling rate. Asphalt molecules, unable to rearrange slowly during cooling, consequently form the glassy state. Typically, the standard cooling rate for experiments is 20 K/min. In contrast, for different simulation systems, MD simulations currently employ cooling rates of 20 K or 25 K per cycle. Due to the disparity in time scales, the cooling rate in MD simulations differs by approximately 1012 orders of magnitude from experimental cooling rates. Considering that the simulated cooling time for each cycle in this study is 100 ps, the corresponding cooling rate is 0.2 K/ps. To further examine the potential impact of cooling rates, five different cooling rates were selected, including 0.05, 0.10, 0.15, 0.20, and 0.25 K/ps.
The volume-temperature relationships of asphalt at different cooling rates are compared in Figure 5A, and the nonlinear trends indicate the presence of the glass transition phenomenon. As expected, the cooling rate has a more pronounced effect on the volume at lower temperatures. Specifically, at cooling rates of 0.20 and 0.25 K/ps, the volumes almost overlap within the range of 100–400 K. However, when cooling rate below 0.15 K/ps, a significant decrease in volume is observed in the lower temperature region (under 250 K). This result suggests that when cooling rate below 0.15 K/ps, asphalt molecules undergo more thorough microstructural adjustments, leading to an overall decrease in volume. To compare the effects of different cooling rates, we statistically analyzed the fitted data within the low-temperature ranges of 100–140 K and 100–180 K (corresponding to the high-temperature ranges of 360–400 K and 320–400 K). As shown in Figure 5B, at around 270 K, the fittings under cooling rates of 0.20 and 0.25 K/ps maintain good consistency, while due to more thorough microstructural relaxation at lower cooling rates, the simulated system exhibits a slightly lower value. Based on five simulation calculations, the average
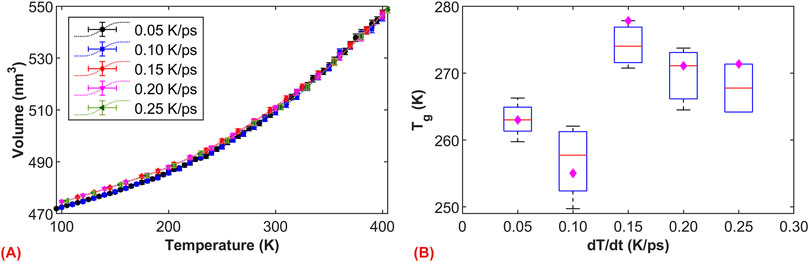
Figure 5. The effect of cooling rate on the glass transition. (A) Volume-temperature curves of asphalt under different cooling rates; (B) Relationship between glass transition temperature and cooling rate. The magenta diamonds represent the fitting at temperatures 100–160 K and 340–400 (K)
To investigate the influence of cooling rate on the structure of asphalt, we selected the same model and examined the aggregation of asphalt at 100 K under different cooling rates (0.05 and 0.25 K/ps). We define free volume as the sum of the regions within which each atom can move freely. According to the coordination number, we define the polyhedron for each atom, and the volume of this polyhedron represents the free movement region of the atom. Figure 6A shows the trend of free volume variation with temperature at different cooling rates, when the cooling rate was 0.20 K/ps, the decrease in free volume is slightly larger, confirming that slow cooling leads to more complete molecular rearrangement, resulting in more uniform system molecules. Figure 6B displays the x-y direction view of the model, from which it is observed that under slow cooling conditions, the asphalt has sufficient time to rearrange, forming larger aggregations and local voids, resulting in a relatively dense system. On the other hand, it illustrates that under rapid cooling conditions, the asphalt does not have enough time to rearrange, leading to a more dispersed system and consequently a relatively larger volume at low temperatures. This observation aligns with the previous volume calculation results.
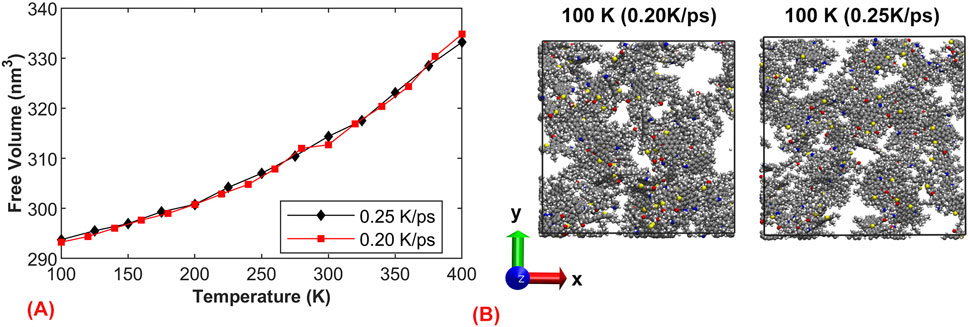
Figure 6. The effect of cooling rate on the structure of asphalt.: (A) Curve of Free Volume with Temperature; (B) Asphalt structure at 100 K under two cooling rates of 0.20 and 0.25 K/ps.
3.3 Model size
The transition of an amorphous solid (glass transition) is directly related to the motion of different molecules, and the model size affects the number of molecules, their aggregation, and kinetic behavior. To further investigate
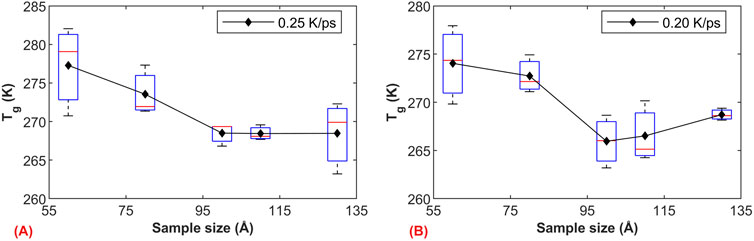
Figure 7. The influence of model size on
Based on the simulation results, we further investigated the influence of model size on the glass transition region. Figure 8A illustrates the volume-temperature curves for models of 50 Å under two cooling rates. Due to the relatively small model size, the sensitivity of volume to temperature increases (microscopic pressure and temperature control exhibit relatively large fluctuations), resulting in a relatively large standard deviation for each volume data point. As the model size increases to 50 Å, the fluctuation in volume during the relaxation phase notably decreases, as shown in Figure 8B. Apart from volume fluctuations, we observed a good consistency in the volume of the simulated systems under both cooling rates. The graph clearly demonstrates the close relationship between the glass transition region and the model size. Specifically, when the model size is 50 Å, the glass transition region is small, but it significantly widens when the size increases to 100 Å. This phenomenon is possibly due to the larger molecular weight in larger models, leading to more complex entanglement between molecules and longer relaxation times, thus resulting in a wider glass transition region.
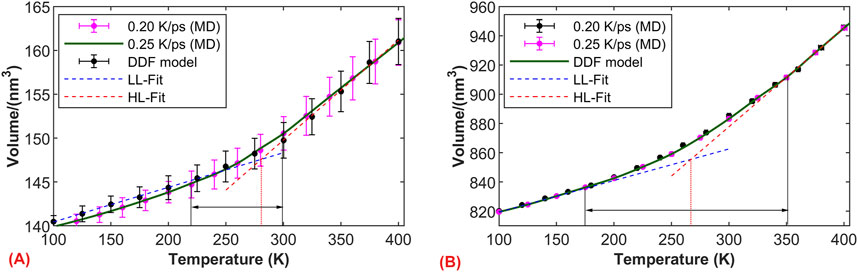
Figure 8. Influence of temperature on the glass transition region. Volume-temperature curves under two cooling rates: (A) model size of 50 × 50 × 50 Å; (B) model size of 100 × 100 × 100 Å.
4 Conclusion
Based on molecular dynamics (MD) simulations, this study thoroughly explores the glass transition of asphalt binder. By selecting the intermediate temperature of the glass transition region as the glass transition temperature (
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
YF: Conceptualization, Project administration, Writing–review and editing. YP: Writing–original draft, Writing–review and editing. JZ: Writing–review and editing. YN: Writing–review and editing. HL: Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Zhejiang Hongtu Transportation Construction Co., Ltd., and the ZJU-ZCCC Institute of Collaborative Innovation (No. ZDJG2021003).
Acknowledgments
The authors acknowledge the support of ZheJiang University, YP, JZ, YN, Researchers Supporting Project number (ZDJG2021003).
Conflict of interest
Author YF was employed by Zhejiang Hongtu Traffic Construction Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from Zhejiang Hongtu Transportation Construction Co., Ltd. The funder had the following involvement in the study: study design, analysis, and decision to publish.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amoussou, R. I. H. D. T., Tanoue, H., Sasaki, M., and Shigeishi, M. (2016). Hydrothermal recovery of asphalt from asphalt concrete. Constr. Build. Mater. 125, 1196–1204. doi:10.1016/j.conbuildmat.2016.07.129
Anderson, D. A., and Marasteanu, M. O. (1999). Physical hardening of asphalt binders relative to their glass transition temperatures. Transp. Res. Rec. J. Transp. Res. Board 1661, 27–34. doi:10.3141/1661-05
Apostolidis, P., Elwardany, M., Porot, L., Vansteenkiste, S., and Chailleux, E. (2021). Glass transitions in bituminous binders. Mater. Struct. 54, 132. doi:10.1617/s11527-021-01726-6
Berthier, L., and Reichman, D. R. (2023). Modern computational studies of the glass transition. Nat. Rev. Phys. 5, 102–116. doi:10.1038/s42254-022-00548-x
Bulacu, M., and van der Giessen, E. (2007). Molecular-dynamics simulation study of the glass transition in amorphous polymers with controlled chain stiffness. Phys. Rev. E 76, 011807. doi:10.1103/PhysRevE.76.011807
Couzin, J. (2005). How much can human life span Be extended? Science 309, 83. doi:10.1126/science.309.5731.83
Cui, B., Wang, H., Gu, X., and Hu, D. (2022). Study of the inter-diffusion characteristics and cracking resistance of virgin-aged asphalt binders using molecular dynamics simulation. Constr. Build. Mater. 351, 128968. doi:10.1016/j.conbuildmat.2022.128968
Cui, W., Huang, W., Hassan, H. M. Z., Cai, X., and Wu, K. (2022). Study on the interfacial contact behavior of carbon nanotubes and asphalt binders and adhesion energy of modified asphalt on aggregate surface by using molecular dynamics simulation. Constr. Build. Mater. 316, 125849. doi:10.1016/j.conbuildmat.2021.125849
Debbarma, K., Debnath, B., and Sarkar, P. P. (2022). A comprehensive review on the usage of nanomaterials in asphalt mixes. Constr. Build. Mater. 361, 129634. doi:10.1016/j.conbuildmat.2022.129634
Godey, F., Fleury, A., Ghoufi, A., and Soldera, A. (2018). The extent of the glass transition from molecular simulation revealing an overcrank effect. J. Comput. Chem. 39, 255–261. doi:10.1002/jcc.25069
Godey, F., Fleury, A., and Soldera, A. (2019). Local dynamics within the glass transition domain. Sci. Rep. 9, 9638. doi:10.1038/s41598-019-45933-2
He, L., Li, G., Lv, S., Gao, J., Kowalski, K. J., Valentin, J., et al. (2020). Self-healing behavior of asphalt system based on molecular dynamics simulation. Constr. Build. Mater. 254, 119225. doi:10.1016/j.conbuildmat.2020.119225
Hu, D., Gu, X., Wang, G., Zhou, Z., Sun, L., and Pei, J. (2022). Performance and mechanism of lignin and quercetin as bio-based anti-aging agents for asphalt binder: a combined experimental and ab initio study. J. Mol. Liq. 359, 119310. doi:10.1016/j.molliq.2022.119310
Ji, W. M., and Zhang, L. W. (2019). Diamond nanothread reinforced polymer composites: ultra-high glass transition temperature and low density. Compos. Sci. Technol. 183, 107789. doi:10.1016/j.compscitech.2019.107789
Kang, Y., Zhou, D., Wu, Q., Liang, R., Shangguan, S., Liao, Z., et al. (2019). Molecular dynamics study on the glass forming process of asphalt. Constr. Build. Mater. 214, 430–440. doi:10.1016/j.conbuildmat.2019.04.138
Khabaz, F., and Khare, R. (2015). Glass transition and molecular mobility in styrene-butadiene rubber modified asphalt. J. Phys. Chem. B 119, 14261–14269. doi:10.1021/acs.jpcb.5b06191
Khan, R. A. A., Chen, X., Qi, H.-K., Huang, J.-H., and Luo, M.-B. (2021). A novel shift in the glass transition temperature of polymer nanocomposites: a molecular dynamics simulation study. Phys. Chem. Chem. Phys. 23, 12216–12225. doi:10.1039/d1cp00321f
Krishnan, J. M., and Rajagopal, K. R. (2005). On the mechanical behavior of asphalt. Mech. Mater. 37, 1085–1100. doi:10.1016/j.mechmat.2004.09.005
Kriz, P., Stastna, J., and Zanzotto, L. (2011). Glass transition and phase stability in asphalt binders. Road Mater. Pavement Des. 9, 37–65. doi:10.1080/14680629.2008.9690158
Li, D. D., and Greenfield, M. L. (2014). Chemical compositions of improved model asphalt systems for molecular simulations. Fuel 115, 347–356. doi:10.1016/j.fuel.2013.07.012
Li, G., Tan, Y., Fu, Y., Liu, P., Fu, C., and Oeser, M. (2022). Density, zero shear viscosity and microstructure analysis of asphalt binder using molecular dynamics simulation. Constr. Build. Mater. 345, 128332. doi:10.1016/j.conbuildmat.2022.128332
Liu, J., Liu, Q., Wang, S., Zhang, X., Xiao, C., and Yu, B. (2021). Molecular dynamics evaluation of activation mechanism of rejuvenator in reclaimed asphalt pavement (RAP) binder. Constr. Build. Mater. 298, 123898. doi:10.1016/j.conbuildmat.2021.123898
Liu, J., Sun, Y., Wang, W., and Chen, J. (2017). Using the viscoelastic parameters to estimate the glass transition temperature of asphalt binders. Constr. Build. Mater. 153, 908–917. doi:10.1016/j.conbuildmat.2017.07.120
Lu, P., Ma, Y., Ye, K., and Huang, S. (2022). Analysis of high-temperature performance of polymer-modified asphalts through molecular dynamics simulations and experiments. Constr. Build. Mater. 350, 128903. doi:10.1016/j.conbuildmat.2022.128903
Lunkenheimer, P., Loidl, A., Riechers, B., Zaccone, A., and Samwer, K. (2023). Thermal expansion and the glass transition. Nat. Phys. 19, 694–699. doi:10.1038/s41567-022-01920-5
Luo, L., Chu, L., and Fwa, T. F. (2021). Molecular dynamics analysis of oxidative aging effects on thermodynamic and interfacial bonding properties of asphalt mixtures. Constr. Build. Mater. 269, 121299. doi:10.1016/j.conbuildmat.2020.121299
Minisini, B., and Soldera, A. (2023). Volumetric and energetic properties of polystyrene and polyethylene oxide affected by thermal cycling. Macromol. theory simulations 32, 2300008. doi:10.1002/mats.202300008
Nikookar, M., Omidkhah, M. R., Pazuki, G. R., and Mohammadi, A. H. (2022). An insight into molecular weight distributions of asphaltene and asphalt using Gel Permeation Chromatography. J. Mol. Liq. 362, 119736. doi:10.1016/j.molliq.2022.119736
Pang, Y., Sun, L., Zhan, H., Zheng, X., Zhang, J., Bian, C., et al. (2023). Assessing the impact of ultra-thin diamond nanothreads on the glass transition temperature of a bituminous binder. Nanoscale Adv. 5, 6724–6735. doi:10.1039/d3na00622k
Rigby, D., and Roe, R. J. (1987). Molecular dynamics simulation of polymer liquid and glass. I. Glass transition. J. Chem. Phys. 87, 7285–7292. doi:10.1063/1.453321
Schawe, J. E. K. (2022). The influence of hydrogen bonds on the glass transition in amorphous binary systems. J. Mol. Liq. 368, 120598. doi:10.1016/j.molliq.2022.120598
Soenen, H., Besamusca, J., Fischer, H. R., Poulikakos, L. D., Planche, J.-P., Das, P. K., et al. (2013). Laboratory investigation of bitumen based on round robin DSC and AFM tests. Mater. Struct. 47, 1205–1220. doi:10.1617/s11527-013-0123-4
Sun, D., Lin, T., Zhu, X., Tian, Y., and Liu, F. (2016). Indices for self-healing performance assessments based on molecular dynamics simulation of asphalt binders. Comput. Mater. Sci. 114, 86–93. doi:10.1016/j.commatsci.2015.12.017
Tabatabaee, H. A., Velasquez, R., and Bahia, H. U. (2012). Predicting low temperature physical hardening in asphalt binders. Constr. Build. Mater. 34, 162–169. doi:10.1016/j.conbuildmat.2012.02.039
Tayfun, U., Kanbur, Y., Abaci, U., Guney, H. Y., and Bayramli, E. (2015). Mechanical, flow and electrical properties of thermoplastic polyurethane/fullerene composites: effect of surface modification of fullerene. Compos. Part B Eng. 80, 101–107. doi:10.1016/j.compositesb.2015.05.013
Wang, D., Cannone Falchetto, A., Riccardi, C., and Wistuba, M. P. (2020). Investigation on the low temperature properties of asphalt binder: glass transition temperature and modulus shift factor. Constr. Build. Mater. 245, 118351. doi:10.1016/j.conbuildmat.2020.118351
Yang, L., Zhou, D., and Kang, Y. (2020). Rheological properties of graphene modified asphalt binders. Nanomater. (Basel) 10, 2197. doi:10.3390/nano10112197
Yao, H., Dai, Q., and You, Z. (2016). Molecular dynamics simulation of physicochemical properties of the asphalt model. Fuel 164, 83–93. doi:10.1016/j.fuel.2015.09.045
Yao, H., Liu, J., Xu, M., Ji, J., Dai, Q., and You, Z. (2022). Discussion on molecular dynamics (MD) simulations of the asphalt materials. Adv. Colloid Interface Sci. 299, 102565. doi:10.1016/j.cis.2021.102565
You, L., Spyriouni, T., Dai, Q., You, Z., and Khanal, A. (2020). Experimental and molecular dynamics simulation study on thermal, transport, and rheological properties of asphalt. Constr. Build. Mater. 265, 120358. doi:10.1016/j.conbuildmat.2020.120358
Zhang, L., and Greenfield, M. L. (2007a). Analyzing properties of model asphalts using molecular simulation. Energy and Fuels 21, 1712–1716. doi:10.1021/ef060658j
Zhang, L., and Greenfield, M. L. (2007b). Relaxation time, diffusion, and viscosity analysis of model asphalt systems using molecular simulation. J. Chem. Phys. 127, 194502. doi:10.1063/1.2799189
Zhang, R., Du, F., Jariyavidyanont, K., Zhuravlev, E., Schick, C., and Androsch, R. (2022). Glass transition temperature of poly(d,l-lactic acid) of different molar mass. Thermochim. Acta 718, 179387. doi:10.1016/j.tca.2022.179387
Keywords: asphalt binder, glass transition temperature, molecular dynamics simulation, data driven, cooling rate, model size
Citation: Fang Y, Pang Y, Zhang J, Nie Y and Lu H (2024) Glass transition temperature of asphalt binder based on atomistic scale simulation. Front. Mater. 11:1485669. doi: 10.3389/fmats.2024.1485669
Received: 24 August 2024; Accepted: 14 October 2024;
Published: 23 October 2024.
Edited by:
Wenwu Xu, San Diego State University, United StatesCopyright © 2024 Fang, Pang, Zhang, Nie and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yingying Pang, eWluZ2VyQHpqdS5lZHUuY24=
 Yongwei Fang1
Yongwei Fang1 Yingying Pang
Yingying Pang Jiandong Zhang
Jiandong Zhang Hongquan Lu
Hongquan Lu