Broadband acoustic pseudospin topological states based on the reverse spin-orbit coupling in generalized insulators

Acoustic topological insulators have the excellent characteristic of the pseudospin-dependent one-way transmission of sound edge states immune to backscattering. We realize the broadband acoustic pseudospin topological edge states with subwavelength generalized topological insulators, which is achieved by reverse pseudospin-orbit coupling. The subwavelength band and broadband nontrivial bandgap can be achieved by adjusting the topological structure of the scatterers and introducing resonators. The results demonstrate that the resonator can significantly reduce the frequencies of p-states and d-states by introducing resonance scattering; the scattering size and rotation angles change the frequencies of p-states and d-states in opposite directions by adjusting the distribution of the sound field. Then, we experimentally realize the pseudospin-dependent one-way transmission of sound edge states along the interface separating phononic crystals with distinct topological phases. Our research provides a systematic scheme for the design of acoustic topological insulators with versatile applications.

1 Introduction

Topological insulators emerging in electronic systems represent a new state of matter, which is an insulator in the bulk, while a conductor on the surface is protected by time-reversal symmetry. They have attracted extensive attention in condensed matter physics (Kane and Mele, 2005; Qi and Zhang, 2011; Hasan and Kane, 2010; Yang et al., 2015; Haldane and Raghu, 2008; Nanthakumar et al., 2019). Topological insulators exhibit the quantum spin Hall effect (QSHE), which is the consequence of the spin-orbit interaction of a particle (an electron) with its motion (Kane and Mele, 2005; Nanthakumar et al., 2019; Andrei Bernevig et al., 2006). The surface (or edge) states at the interfaces of topological insulators lead to a conducting state with the property of robust one-way propagation without backscattering (Christiansen et al., 2019). Inspired by the exciting physical properties, the concept of topological states has recently been extended to classical waves in artificial periodical structures, such as the electromagnetic waves in photonic crystals and acoustic waves in phononic crystals (PCs) (Chen et al., 2021; Wu and Hu, 2015; He et al., 2016; Jia et al., 2019; Lee and Iizuka, 2019; Chen et al., 2020; Chen W. J. et al., 2014).

The crucial condition to achieve the QSHE is Kramers degeneracy for the fermions system (Zhang X. et al., 2018). The key physics realizing an analog QSHE in bosonic systems, therefore, is to create a double Dirac cone, where a Kramers doublet exists in the form of double-degenerated states named pseudospin up and pseudospin down (He et al., 2016). For photonics, the polarization degrees of freedom, including transverse electric (TE) polarization and transverse magnetic (TM) polarization, can be utilized to construct the polarization-based Kramers doublet (Khanikaev et al., 2013; Ma et al., 2015). In addition, using two pairs of degenerate Bloch modes based on the symmetry of the space point group can also achieve a double cone induced by the accidental degeneracy of the double-degenerated states (Wu and Hu, 2015; Xu et al., 2016; Li and Mei, 2015; Sakoda, 2012). In the acoustic systems, however, due to the lack of various polarization, the main method of realizing an acoustic analog QSHE is the hybridization of the Bloch modes related to lattice symmetry (Nanthakumar et al., 2019; He et al., 2016; Jia et al., 2019; Lee and Iizuka, 2019; Chen et al., 2020; Jia et al., 2018; Dai et al., 2017; Chen Z. G. et al., 2014).

Recent research on the realization of a double Dirac cone in the center of the first Brillouin zone (FBZ) takes two approaches. The first approach involves folding the deterministic Dirac cones located at the FBZ corners of the honeycomb lattice into the FBZ center of an enhanced triangular lattice, thereby creating a double Dirac cone. This process is also referred to as the band folding mechanism (Wu and Hu, 2015; Huang et al., 2024). In this folding process, the FBZ of the honeycomb lattice is folded twice, and correspondingly, the band number has doubled, by which the band structure of the triangular lattice becomes more complicated. The double Dirac cone in the FBZ center is associated with the primitive honeycomb lattice. The approach to opening nontrivial bandgaps and generating edge states involves lifting the degeneracy associated with the double Dirac cones. This is achieved by breaking the symmetry of the honeycomb lattice by concentrating or distracting the elements for the ampliative triangular lattice (Wu and Hu, 2015; Zhang et al., 2017; Lu et al., 2014; Tirth et al., 2024).

The second approach is to tailor the coupling strength between the sound field and the structures under the protection of the high lattice symmetry of C_6(v) to realize an accidental double Dirac cone in the FBZ center (Wen et al., 2018; Zhang et al., 2023; Wang et al., 2023). Compared with band folding, this approach of adjusting the sound field to achieve accidental double Dirac cones is simpler, more flexible, and highly operable. Consequently, it offers numerous adjusting factors that can be used to effectively break the degeneracy of the double Dirac cone. Furthermore, the scattering mechanisms, including Bragg scattering and local resonance in acoustic topological insulators, can affect the frequency of the topological edge states (Yu et al., 2019; Ni et al., 2023; Yves et al., 2022). However, there is a lack of systematic research on the methods for realizing and breaking an accidental double Dirac cone, especially on the influence of the coupling among these parameters after the introduction of resonance scattering. This research gap may hinder the engineering application of the acoustic topological insulator.

In this article, we utilize the construction method of generalized acoustic topological insulators to realize the broadband acoustic pseudospin topological edge states at a subwavelength scale based on double degenerate modal similarity and reverse reconstruction of spin-orbit coupling. The effects of three major degrees of freedom are systematically analyzed on the scattering intensity of the adjacent scatterers of the PCs, including the size, orientation, and resonance element embedding in the scatterers. Subsequently, the influences of the collaborative coupling effect on bandgaps in which the topological edge states appear are discussed. The results demonstrate that collaborative coupling of the parameters can not only achieve the accidental degeneracy of the double Dirac cone but also adjust the frequency of the two double degeneracy points and the width of the complete bandgap between the two double degenerate points. Furthermore, we study the edge states at the interfaces separated by two sonic crystals with distinct topological phases, and the sound transmission of topological insulators protected by topology is realized. Our work provides a theoretical basis for the design of acoustic topological insulators and may pave the foundation for applying acoustic communication based on acoustic topological insulators.

2 Materials and methods

2.1 Materials

Figure 1A illustrates a schematic diagram of a triangular lattice cell composed of a rotatable hexagonal rod (orange) without cavities in air (blue) with C_6v point-group symmetry (six-fold rotational symmetry and six-fold mirror symmetry). The lattice constant is a. The parameters of the hexagonal rod include the radius of the inscribed circle R and the rotation angle of the rod θ relative to the Y-axis. The scatterer is manufactured with polylactic acid, which has a density of ρ = 1250 kg/m³ and a longitudinal wave velocity of c_l = 1788 m/s. The density and sound velocity of air are ρ₀ = 1.25 kg/m³ and c₀ = 344 m/s, respectively. Due to the large impedance difference between the scatterer and the matrix, the shear modes inside the scatterer rod can be ignored. Thus, the boundary of the scatterer rod can be considered a hard boundary.

Figure 1

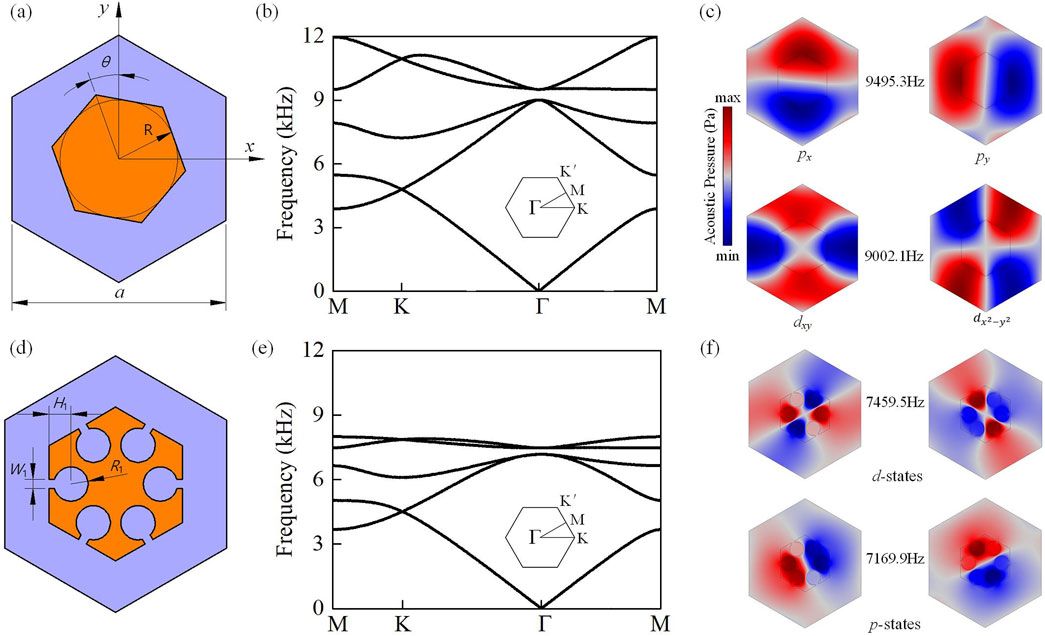
Figure 1. (A) The schematic diagram of a triangular lattice cell without resonators. (B) Band structure of the unit cell in (A). The parameters include the lattice constant a = 40 mm, R = 0.22a, and θ = 0°. The insert illustrates the FBZ. (C) The pressure distributions of the four degenerate Bloch states at the Γ point, which can be represented by $p_x$, $p_y$, $d_{xy}$, and $d_{x^2-y^2}$ according to the symmetry. The dark red and dark blue colors indicate maximum and minimum values. (D) The schematic diagram of a compound cell with resonators. (E) The band structure of the unit cell in (D). (F) The pressure distributions of the four degenerate Bloch states at the Γ point.

2.2 Methods

The simulations are accomplished using the finite element method available in COMSOL Multiphysics commercial software. The pressure acoustic module is employed to visualize the modal characteristics and propagating features of acoustic waves. The materials involved in the simulations are air and polylactic acid, which are used in manufacturing the scatterers. Due to the large mismatch between the acoustic impedances of the two materials, the scatterer is considered a rigid body in the calculations. The mesh has a free triangular type, and the largest element size is less than 1/15 of the shortest incident wavelength. The boundaries of the cell are applied with the floquet conditions. For the simulation of wave transmission, the sound source of the structure adopts the background-pressure field with a width of 4a, while the perfectly matched layers are imposed around the structure. When calculating the transmission loss, the integral path for the entrance is the boundary between the background-pressure field and the structure, and that of the exit is located 0.5 mm outside the structure. The thermoviscous acoustics domain is utilized to analyze the effects of viscous and thermal losses caused by scatterers. The viscous boundary-layer thickness is defined at the maximum value under study. The viscous-boundary-layer thickness, ε_visc, is set by ${\epsilon }_{\text{visc}}=\sqrt{2\mu /\omega {\rho }_0}$, where μ and ω are the dynamic viscosity and angular frequency, respectively.

3 Results

3.1 Degenerate states

Figure 1B displays the band structure of the primary triangular lattice cell with the parameters containing lattice constant a = 40 mm, radius R = 0.16a, and the rotation angle θ = 0°. Owing to the C_6v point-group symmetry, it exhibits two double degenerate points at the frequency 9002.1 Hz and 9495.3 Hz at the FBZ center. The four eigenstates of the two double degenerate points are shown in Figure 1C, represented by the pressure field distributions. According to group theory, these eigenstates can be described by Bloch basis functions, and the two double-degenerated states correspond to E₁ and E₂ irreducible representations (Sakoda, 2012; Chen Z. G. et al., 2014).

Due to the symmetry, the sound pressure eigenstates are similar to the p/d orbital of the electron, and the pseudospin dipole states and quadrupole states can be expressed by $p_x/p_y$ and $d_{x^2-y^2}/d_{xy}$ (Lee and Iizuka, 2019). Here, p_x obeys the symmetry ${\sigma }_x/{\sigma }_y=-1/+1$; p_y obeys the symmetry ${\sigma }_x/{\sigma }_y=-1/+1$; d_xy obeys the symmetry ${\sigma }_x/{\sigma }_y=-1/-1$; and $d_{x^2-y^2}$ obeys the symmetry ${\sigma }_x/{\sigma }_y=+1/+1$; where σ_x,y = +1, −1 means the even or odd symmetry along the X- or Y-axis of the unit cell, respectively (He et al., 2016). To simplify the representation, the pseudospin dipole and quadrupole states are represented as p-states and d-states, respectively.

Six identical Helmholtz resonators are added to the hexagonal rod, distributed along the mid-line of each side of the hexagon rod to form a compound cell, as shown in Figure 1D. In addition to lattice parameters a = 40 mm, radius of inscribed circle R = 0.22a, and rotation angle θ = 0°, the parameters of resonator I include the cavity radius R₁ = 2.5 mm, cavity width W₁ = 1.2 mm, and cavity depth H₁ = 2.9 mm of the resonator. Compared with the original band structure without resonators, the frequencies of double degeneracy points at the FBZ center are reduced to 7169.9 Hz and 7459.5 Hz, respectively, as shown in Figure 1E. Note that the resonant frequency can be approximated by the theoretical formula $f_r=\frac{c}{2\pi }\sqrt{\frac{W_1}{Sl}}$ (Lee and Iizuka, 2019), where c represents the velocity of sound, S is the cavity area, and l = H₁ − R₁ is the length of the neck. Figure 1F shows the eigenmode distribution of the degeneracy points after the introduction of the resonator. Compared with Figure 1E, the frequencies of the p-states and d-states are significantly reduced, and the modes at the degeneracy points have reversed.

3.2 Topological phases

In addition to the traditional method of realizing an acoustic topological insulator composed of different topological phases of the same SC, based on the modal characteristics of p-states and d-states, the reverse spin-orbit coupling of the degenerate states with similar modal characteristics can also be used to realize the acoustic topological insulator, that is, the generalized acoustic topological insulator (Zhang et al., 2023; Huang et al., 2022), as shown in Figure 2A. Figure 2B shows the influence on the size of the scatterer. When the radius R increases from 0.215a to 0.275a, the eigenfrequency of the p-states increases, while the eigenfrequency of the d-states decreases because the coupling strength between the adjacent scatterers changes during the process of scatterer augmentation. When radius R = 0.24a, the p-states and d-states obtain the same frequency to form an accidental double Dirac cone at the FBZ center. In addition, the results demonstrate that the band structure can be reversed by different sizes of scatterers due to the significantly slower velocity of longitudinal acoustic waves in an air background than that within the scatterers.

Figure 2

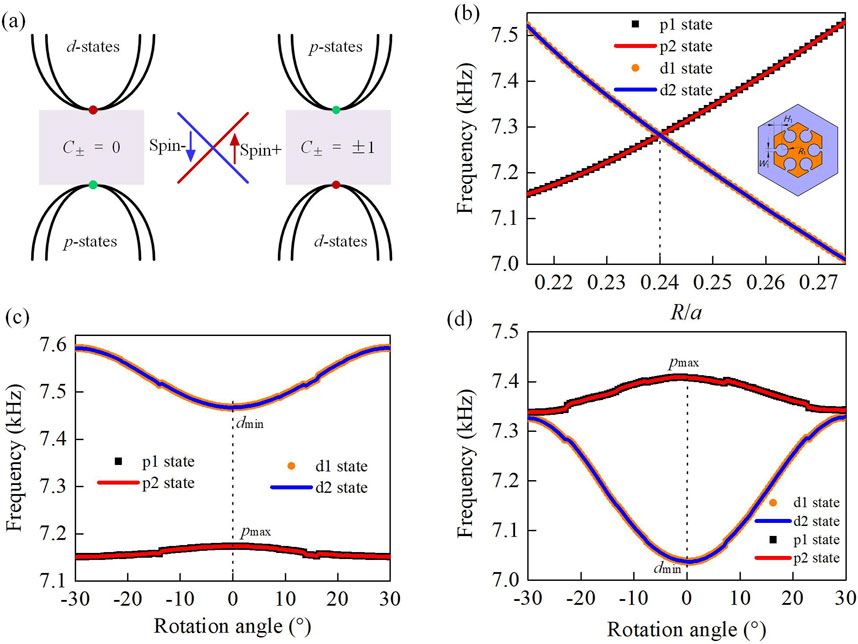
Figure 2. (A) The schematic of the generalized acoustic topological insulator. (B) The relationships between the scatterer size and the frequency of degenerate states. The dotted black line and the solid red line represent the p1 and p2 states, respectively, and the dotted orange line and the solid blue line denote the d1 and d2 states, respectively. (C) The effect of rotation angle on degenerate states is associated with the parameters of R = 0.22a and Resonator I. (D) The influence of rotation angles on degenerate states, which are controlled by the parameters of R = 0.265a and Resonator II.

In order to prove that the band inversion implies a topological phase transition, we calculate the topological invariant Z₂ based on the $k\cdot p$ perturbation theory (Wang et al., 2023; Mei et al., 2012). The eigenstates at the $\mathrm{\Gamma }$ point can be expressed as ${\left(\left|p_x\right.\rangle ,\left|p_y\right.\rangle ,\left|d_{x^2-y^2}\right.\rangle ,\left|d_{xy}\right.〉\right)}^T$.The effective Hamiltonian around the $\mathrm{\Gamma }$ point is described as $H_{mm}^{eff}=H_{mn}^{\prime }+{\sum }_{\alpha }\frac{H_{m\alpha }^{\prime }{H}_{\alpha n}^{\prime }}{{\epsilon }_m-{\epsilon }_{\alpha }}\left(m,n=1,2,3,4\right)$, where ${\epsilon }_{1,2}={\epsilon }_p$ and ${\epsilon }_{3,4}={\epsilon }_d$ are the eigenfrequencies of four states around the $\mathrm{\Gamma }$ point (Zhang et al., 2017). According to the effective Hamiltonian in the vicinity of the $\mathrm{\Gamma }$ point, the spin Chern numbers can be calculated as $C_{\pm }=\pm \frac{1}{2}\left[\text{sgn}\left(M\right)+\text{sgn}\left(B\right)\right]$ (He et al., 2016; Zhang et al., 2017). Here, M represents the eigenfrequency difference between p-states and d-states at the $\mathrm{\Gamma }$ point, described as $M=\frac{{\epsilon }_d-{\epsilon }_p}{2}$. B comes from the second-order perturbation $H_{m\alpha }^{\prime }{H}_{\alpha n}^{\prime }$ and is typically negative. Thus, for R = 0.22a with the d-states above the p-states, the spin Chern numbers are $C_{\pm }=0$, which indicates the band gap is trivial. When R = 0.26a, the d-states are below the p-states with $M=\frac{{\epsilon }_d-{\epsilon }_p}{2}<0$, and the spin Chern numbers are $C_{\pm }=\pm 1$, which means the band gap is nontrivial. Therefore, when R increases from 0.215a to 0.275a, the bandgap between p-states and d-states changes from topologically trivial to topologically nontrivial. The transition point corresponds to the case where two double degeneracy points in the FBZ center form an accidental quadruple degeneracy point with R = 0.24a. Note that although the compound cell has C_6v symmetry, the symmetry axis of the pseudospin dipole modes and the pseudospin quadrupole modes are changed due to the coupling effect of local resonance and Bragg scattering, which affects the sound field distribution.

The effect of rotation angle θ on the double degenerate points is then analyzed with the lattice constant a = 40 mm and the radius R = 0.22a. In one rotation period, as shown in Figure 2C, p-states are below d-states. The eigenfrequencies of the p-states and d-states exhibit the characteristics of nonlinear variation, and the p-states have a minimum value p_min, while the d-states have a maximum value d_max. When $\left|\theta \right|$ = 30°, the p-states and the d-states have the largest frequency differences, which are 7148.1 Hz and 7585.2 Hz, respectively. Therefore, the rotation angle θ can change the bandgap between the two double degenerate points and increases with the absolute value of the rotation angle $\left|\theta \right|$ during a rotation period. The spin Chern number $C_{\pm }=0$ indicates that the bandgap between the two double degenerate states is topologically trivial.

The phononic crystal formed by the composite scatterers (R = 0.22a and θ = 30°) with resonator I is named PC-A. It is worth noting that the p_min and d_max are the eigenfrequency values of p-states and d-states with R = 0.22a. When the radius R increases, the p-states and d-states will overlap, and even the eigenfrequency of the p-states is higher than that of the d-states so that the spin number is $C_{\pm }=\pm 1$, and the corresponding bandgap becomes topologically nontrivial. The phononic crystal consisting of scatterers (R = 0.265a and θ = 0°) with resonator II is named PC-B. Figure 2D shows the relationship between the rotation angles and frequencies of degenerate states, with the inscribed radius of scatterer R = 0.265a and the parameters of resonator II (cavity radius R₂ = 2.6 mm, slot width W₂ = 2 mm, and slot length H₂ = 3.4 mm) embedded in the scatterer. When the rotation angle is θ = 0°, the eigenfrequencies of the two double degeneracy points are 7037 Hz and 7408 Hz, respectively. As illustrated in the upper and lower panels of Figure 2D, the frequency of p-states is higher than that of d-states, and thus the spin Chen number is $C_{\pm }=\pm 1$.

4 Discussion

4.1 Dispersion relationship of supercell

In order to verify the interface separating phononic crystals with distinct topological phases and support the pseudospin-dependent, one-way transmission of sound edge states, a ribbon-shaped supercell is constructed in Figure 3A, in which the upper and lower layers are PC-B, and the middle layer is PC-A. Each layer contains 10 cells, and the size of the supercell is 30 × 1 cell. Floquet periodic boundary conditions are applied to the left and right boundaries of the supercell, and continuous boundary conditions are applied to the upper and lower boundaries of the supercell. The numerical calculation results in Figure 3B demonstrate that an overlapping bulk bandgap can be found in the range from 7140 Hz to 7400 Hz. The bandgap is spanned by topological edge states as indicated by the red and blue double-degenerated curves, which correspond to two sets of edge states with opposite group velocities (Zhang et al., 2017). Note that the Bloch states of PC-A and PC-B are not exactly the same, which is also the reason for the existence of a bandgap in the edge states. However, this bandgap can be reduced by adjusting the parameters of the scatterer (Yves et al., 2017).

Figure 3

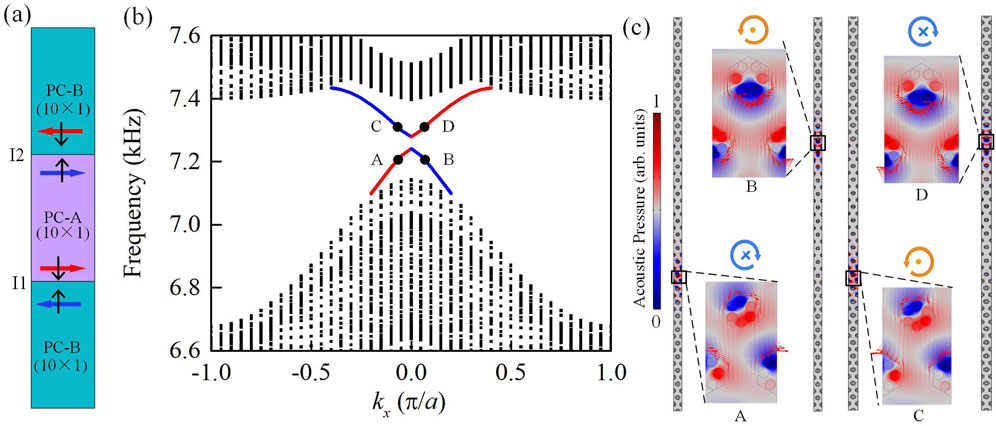
Figure 3. (A) The schematic diagram of a supercell composed of PC-B and PC-A. (B) The dispersion relationship of the supercell. (C) Acoustic pressure field distribution of the pseudospin-dependent one-way edge modes localized at the interface of the supercell, corresponding to the points A, B, C, and D in (B).

Figure 3C displays the distributions of the pressure field at points A and B with k = ±0.05π/a. The distributions are highly localized at the interfaces separating distinct topological phases. The sound intensity distribution (red arrow) shows that there are two opposite sound energy vortices near the interface between PC-A (PC-B) and PC-B(PC-A), separating phononic crystals with distinct topological phases, in which the chirality of the energy vortex corresponds to pseudospin states. The intensity exhibits a nonzero clockwise (anticlockwise) acoustic energy flow for the pseudospin-down (pseudospin-up) state, which is even averaged over time. Thus, four transmission channels on two interfaces are found: the lower interface I1 contains a forward-moving edge state with pseudospin down (clockwise) and a backward-moving edge state with pseudospin up (anticlockwise); the converse applies to the upper interface I2. Note that the transmission channels for sound are split in a time-reversal-invariant fashion without backscattering, which demonstrates that the counter propagations of acoustic energy at the sample edge associated with the two pseudospin states are independent. This independence serves as a mark of the quantum spin Hall effect state. Therefore, the robust one-way acoustic transmission protected by the topology can be achieved based on the collaborative coupling of multiple parameters.

4.2 One-way sound transmission

We construct a sound field composed of PC-A and PC-B to illustrate pseudospin-dependent unidirectional sound transmission, as shown in Figure 4A, where the field size of PC-A and PC-A are both 11 cells × 8 cells separated by a zigzag interface. The plane line source is located at the incident port on the left side of the sound field, and the perfect matching layer is added around the sound field except the incident port and the exit port. When the excitation frequency is 7400 Hz within the range of edge states, the sound field is well localized along the interface, as shown in Figure 4A.

Figure 4

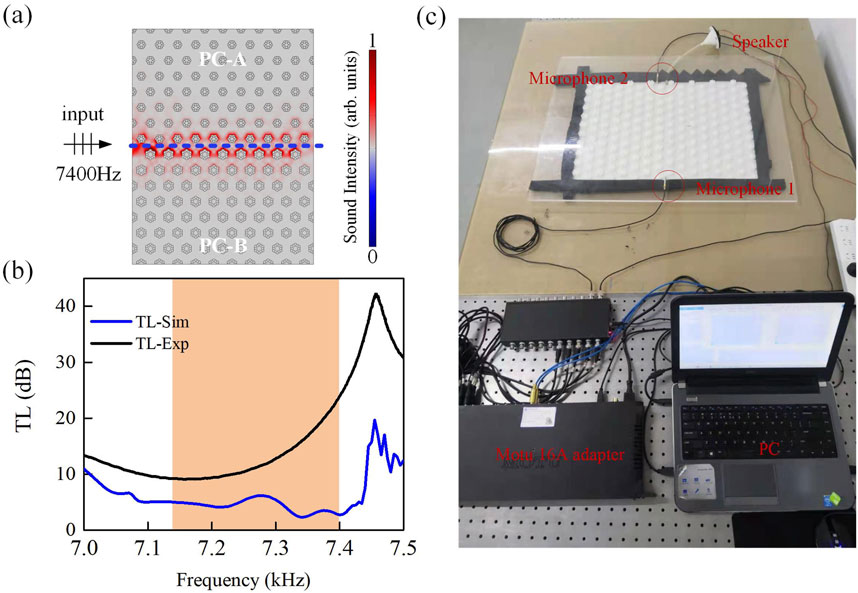
Figure 4. (A) The distribution of sound pressure with an excitation frequency of 7400 Hz. The blue dotted line represents the position of the interface. (B) The transmission loss along the interface. The solid blue and black lines represent the numerically calculated transmission loss, TL-Sim, and the experimental transmission loss, TL-Exp. (C) The setup of the experiment.

The transmission loss (TL) is also used to quantify the one-way propagation characteristic dependent on pseudospin, which is defined as $\text{TL}=10\log \left(P_{in}/P_{out}\right)$. Here, $P_{in}$ and $P_{out}$ denote the acoustic effect at the inlet and outlet along the interface, respectively. The acoustic effect is calculated by the following equations: $P_{in}=\int p_0^2/2\rho c$, $P_{out}=\int {\left|p_c\right|}^2/2\rho c$. The numerically calculated TL is TL-Sim, represented by the blue line, as shown in Figure 4B. The results indicate that the TL is less than 10 dB in the edge states frequency range from 7140 Hz to 7400 Hz, denoted by the area shaded in orange.

Experimental verification of one-way sound transmission is further carried out, and the experimental configuration is illustrated in Figure 4C. The input and output of the microphones are acquired by an adapter (Motu-16A) and processed by MATLAB software, and the experiments are conducted by a loudspeaker. The samples consisting of 176 scatterers and a baseplate are fabricated using polylactic acid via 3D printing. The scatterer has a height of 8 mm and is placed in a waveguide formed by the baseplate and a plexiglass plate. The two-dimensional approximation is applicable because the planar waveguide supports the propagating mode uniformly along the scatterer axis for the wavelengths under consideration. Ribbon-shaped sound-absorbing foam is mounted around the surroundings of the samples to minimize the background noise from boundary reflections (Zhang Z. et al., 2018). The experimental results TL-Exp illustrated in Figure 4B with a solid black line are in good agreement with the numerical results. However, the TL of the experiment is larger than that of the simulation, which is mainly due to the leakage of acoustic energy caused by the gap between the plexiglass plate and the scatterers during the experiment.

5 Conclusion

In conclusion, we demonstrate the pseudospin-dependent one-way acoustic transmission of edge states along the interface based on generalized acoustic topological insulators in numerical calculations and experimental studies. Subwavelength and broadband topological edge states can be achieved by introducing resonant elements and changing the topology structure of the cells. Our research provides a theoretical basis for the design of acoustic topological insulators and paves the way for the development of directional transmission acoustic functional devices.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CL: conceptualization, methodology, writing–original draft. YL: formal analysis, software, validation, writing–review and editing. ZH: validation, writing–review and editing. WG: writing–review and editing. ZH: supervision, writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Aeronautical Science Foundation of China under Grant No. 20220015070001.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andrei Bernevig, B., Hughes, T. L., and Zhang, S.-C. (2006). Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Chen, T., Ding, W., Zhang, J., Huang, W., and Zhu, J. (2020). Double topological edge states investigation in sonic metamaterials. Phys. Lett. A 384, 126510. doi:10.1016/j.physleta.2020.126510

CrossRef Full Text | Google Scholar

Chen, W. J., Jiang, S. J., Chen, X. D., Zhu, B., Zhou, L., Dong, J. W., et al. (2014a). Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 5782. doi:10.1038/ncomms6782

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Meng, F., and Huang, X. (2021). Creating acoustic topological insulators through topology optimization. Mech. Syst. Signal P. R. 146, 107054. doi:10.1016/j.ymssp.2020.107054

CrossRef Full Text | Google Scholar

Chen, Z. G., Ni, X., Wu, Y., He, C., Sun, X. C., Zheng, L. Y., et al. (2014b). Accidental degeneracy of double Dirac cones in a phononic crystal. Sci. Rep. 4, 4613. doi:10.1038/srep04613

PubMed Abstract | CrossRef Full Text | Google Scholar

Christiansen, R. E., Wang, F., Stobbe, S., Sigmund, O., Engheta, N., Noginov, M. A., et al. (2019). Acoustic and photonic topological insulators by topology optimization. DTU Orbit.

CrossRef Full Text | Google Scholar

Dai, H., Liu, T., Jiao, J., Xia, B., and Yu, D. (2017). Double Dirac cone in two-dimensional phononic crystals beyond circular cells. J. Appl. Phys. 121, 135105. doi:10.1063/1.4979852

CrossRef Full Text | Google Scholar

Haldane, F. D., and Raghu, S. (2008). Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904. doi:10.1103/physrevlett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasan, M. Z., and Kane, C. L. (2010). Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

He, C., Ni, X., Ge, H., Sun, X. C., Chen, Y. B., Lu, M. H., et al. (2016). Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12, 1124–1129. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

Huang, Z., Cervera, F., Wu, J. H., Ibarias, M., Liu, C., García-Chocano, V. M., et al. (2024). Topological transmission in Suzuki-phase sonic crystals. Phys. Rev. Appl. 21, 054003. doi:10.1103/physrevapplied.21.054003

CrossRef Full Text | Google Scholar

Huang, Z., Wu, J. H., Lei, Y. Z., Liu, C. R., and Ma, F. Y. (2022). Multi-band acoustic topological insulator. Mater. Today Phys. 27, 100793. doi:10.1016/j.mtphys.2022.100793

CrossRef Full Text | Google Scholar

Jia, D., Sun, H., Xia, J., Yuan, S., Liu, X., and Zhang, C. (2018). Acoustic topological insulator by honeycomb sonic crystals with direct and indirect band gaps. New J. Phys. 20, 093027. doi:10.1088/1367-2630/aae104

CrossRef Full Text | Google Scholar

Jia, D., Sun, H.-x., Yuan, S.-q., Zhang, C., and Liu, X.-j. (2019). Pseudospin-dependent acoustic topological insulator by airborne sonic crystals with a triangular lattice. Appl. Phys. Express 12, 044003. doi:10.7567/1882-0786/ab0468

CrossRef Full Text | Google Scholar

Kane, C. L., and Mele, E. J. (2005). Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801. doi:10.1103/physrevlett.95.226801

PubMed Abstract | CrossRef Full Text | Google Scholar

Khanikaev, A. B., Mousavi, S. H., Tse, W. K., Kargarian, M., MacDonald, A. H., and Shvets, G. (2013). Photonic topological insulators. Nat. Mater 12, 233–239. doi:10.1038/nmat3520

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T., and Iizuka, H. (2019). Bragg scattering based acoustic topological transition controlled by local resonance. Phys. Rev. B 99, 064305. doi:10.1103/physrevb.99.064305

CrossRef Full Text | Google Scholar

Li, Y., and Mei, J. (2015). Double Dirac cones in two-dimensional dielectric photonic crystals. Opt. Express 23, 12089. doi:10.1364/oe.23.012089

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, J., Qiu, C., Xu, S., Ye, Y., Ke, M., and Liu, Z. (2014). Dirac cones in two-dimensional artificial crystals for classical waves. Phys. Rev. B 89, 134302. doi:10.1103/physrevb.89.134302

CrossRef Full Text | Google Scholar

Ma, T., Khanikaev, A. B., Mousavi, S. H., and Shvets, G. (2015). Guiding electromagnetic waves around sharp corners: topologically protected photonic transport in metawaveguides. Phys. Rev. Lett. 114, 127401. doi:10.1103/physrevlett.114.127401

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, J., Wu, Y., Chan, C. T., and Zhang, Z. Q. (2012). First-principles study of Dirac and Dirac-like cones in phononic and photonic crystals. Phys. Rev. B 86, 035141. doi:10.1103/physrevb.86.035141

CrossRef Full Text | Google Scholar

Nanthakumar, S. S., Zhuang, X., Park, H. S., Nguyen, C., Chen, Y., and Rabczuk, T. (2019). Inverse design of quantum spin hall-based phononic topological insulators. J. Mech. Phys. Solids 125, 550–571. doi:10.1016/j.jmps.2019.01.009

CrossRef Full Text | Google Scholar

Ni, X., Yves, S., Krasnok, A., and Alu, A. (2023). Topological metamaterials. Chem. Rev. 123, 7585–7654. doi:10.1021/acs.chemrev.2c00800

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, X.-L., and Zhang, S.-C. (2011). Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110. doi:10.1103/revmodphys.83.1057

CrossRef Full Text | Google Scholar

Sakoda, K. (2012). Opt. Express. 20, 99925. doi:10.1364/OE.20.009925

CrossRef Full Text

Tirth, S., Christian, B., Vittorio, P., and Florian, M. (2024). Rev. Mod. Phys. 96, 021002. doi:10.1103/RevModPhys.96.021002

CrossRef Full Text

Wang, Y., Wang, H. X., Liang, L., Zhu, W., Fan, L., Lin, Z. K., et al. (2023). Hybrid topological photonic crystals. Nat. Commun. 14, 4457. doi:10.1038/s41467-023-40172-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, X., Qiu, C., Lu, J., He, H., Ke, M., and Liu, Z. (2018). Acoustic Dirac degeneracy and topological phase transitions realized by rotating scatterers. J. Appl. Phys. 123, 091703. doi:10.1063/1.5004073

CrossRef Full Text | Google Scholar

Wu, L. H., and Hu, X. (2015). Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901. doi:10.1103/physrevlett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., Wang, H. X., Xu, Y. D., Chen, H. Y., and Jiang, J. H. (2016). Accidental degeneracy in photonic bands and topological phase transitions in two-dimensional core-shell dielectric photonic crystals. Opt. Express 24, 18059. doi:10.1364/oe.24.018059

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Gao, F., Shi, X., Lin, X., Gao, Z., Chong, Y., et al. (2015). Topological acoustics. Phys. Rev. Lett. 114, 114301. doi:10.1103/physrevlett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Z., Ren, Z., and Lee, J. (2019). Phononic topological insulators based on six-petal holey silicon structures. Sci. Rep. 9, 1805. doi:10.1038/s41598-018-38387-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Yves, S., Fleury, R., Lemoult, F., Fink, M., and Lerosey, G. (2017). Topological acoustic polaritons: robust sound manipulation at the subwavelength scale. New J. Phys. 19, 075003. doi:10.1088/1367-2630/aa66f8

CrossRef Full Text | Google Scholar

Yves, S., Ni, X., and Alu, A. (2022). Topological sound in two dimensions. Ann. N. Y. Acad. Sci. 1517, 63–77. doi:10.1111/nyas.14885

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Xiao, M., Cheng, Y., Lu, M. H., and Christensen, J. (2018a). Commun. Phys. 1, 1. doi:10.1038/s42005-018-0094-4

CrossRef Full Text

Zhang, X., Zangeneh-Nejad, F., Chen, Z. G., Lu, M. H., and Christensen, J. (2023). A second wave of topological phenomena in photonics and acoustics. Nature 618, 687–697. doi:10.1038/s41586-023-06163-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Tian, Y., Cheng, Y., Wei, Q., Liu, X., and Christensen, J. (2018b). Topological acoustic delay line. Phys. Rev. Appl. 9, 034032. doi:10.1103/physrevapplied.9.034032

CrossRef Full Text | Google Scholar

Zhang, Z., Wei, Q., Cheng, Y., Zhang, T., Wu, D., and Liu, X. (2017). Topological creation of acoustic pseudospin multipoles in a flow-free symmetry-broken metamaterial lattice. Phys. Rev. Lett. 118, 084303. doi:10.1103/physrevlett.118.084303

PubMed Abstract | CrossRef Full Text | Google Scholar