- 1Department of Engineering Mechanics, Dalian University of Technology, Dalian, China
- 2DUT-BSU Joint Institute, Dalian University of Technology, Dalian, China
- 3Department of Orthopedics, Dalian Municipal Central Hospital Affiliated of Dalian University of Technology, Dalian, China
- 4School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, United Kingdom
- 5Faculty of Mechanics and Mathematics, Belarusian State University, Minsk, Belarus
Metamaterials are artificially created materials or structures with properties not found in nature. They encompass electromagnetic, acoustic, and mechanical metamaterials, which are particularly significant in applied engineering. Mechanical metamaterials exhibit unique mechanical properties such as vanishing shear modulus, negative Poisson’s ratio, negative compressibility, etc. This paper reviews the most commonly used mechanical metamaterials and discusses their applications in the field of applied engineering, specifically in vibration isolation, energy absorption, and vibration reduction. The prospects for future developments in this field are also presented.
1 Introduction
Metamaterials are artificially created materials or structures with properties not found in nature. With advancements in metamaterial research, various types have emerged, including electromagnetic metamaterial, acoustic metamaterial, mechanical metamaterial, etc., as shown in Figure 1.
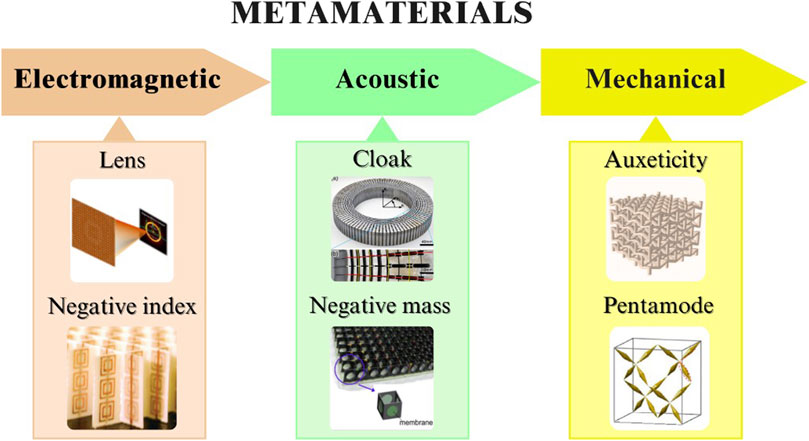
Figure 1. Types of metamaterials. Adapted with permission from (Monteverde et al., 2001). Copyright 2001, The American Association for the Advancement of Science; Adapted with permission from (Park et al., 2011). Copyright 2011, American Physical Society; Adapted with permission from (Chen et al., 2017). Copyright 2017, American Physical Society; Adapted with permission from (Yuan et al., 2019). Copyright 2019, American Physical Society; Reproduced under the terms of the CC-BY license from (Zou et al., 2023). Copyright 2023, The Authors. Published by MDPI; Reproduced under the terms of the CC-BY license from (Galea Mifsud et al., 2024). Copyright 2024, The Authors. Published by MDPI.
Veselago (1968) first proposed the concept of metamaterials and introduced the theoretical concept of materials with inverse physical characteristics, such as a negative refractive index, negative permittivity, and permeability. A significant advancement in metamaterials occurred in 1999 when physicist John Pendry published a theoretical paper proposing the creation of non-magnetic thin sheets of metal that respond to microwave radiation with effective magnetic permeability (Pendry et al., 1999). Further contributions were made by Dr. Smith in 2004, who developed a metamaterial capable of refracting electromagnetic radiation (Smith et al., 2004). Additionally, optical transformation was proposed to control wave propagation using metamaterials (Leonhardt, 2006).
Electromagnetic metamaterials are artificially engineered to have distinct electromagnetic properties not seen in natural materials. They are created by arranging small structures in a specific manner to control the behavior of electromagnetic waves. The first work on electromagnetic metamaterials was conducted in the early 1990s by John Pendry and his colleagues (Pendry et al., 1999). They proposed a new type of material that could have a negative dielectric constant and permeability, allowing it to refract light in a way that was not possible with natural materials. These materials are designed to transcend the limitations of natural materials exhibiting unique properties, such as the negative refractive index (Smith et al., 2000; Chang et al., 2024), cloaking (Shin et al., 2012; Fujii et al., 2013; Jung et al., 2021), superlensing (Aydin and Ozbay, 2007; Haxha et al., 2018; Yuan et al., 2019), etc.
Acoustic metamaterials are artificially designed materials that manipulate sound waves in unique ways. Similar to electromagnetic metamaterials, subwavelength structures are arranged in acoustic metamaterials to create desired acoustic properties. The first experimental implementation of an acoustic metamaterial was a 2D photonic crystal demonstrating negative refraction of acoustic waves (Zhang and Liu, 2004). This experiment showed that the refracted wave possessed a negative refractive index within a certain frequency range. Additional research has demonstrated that locally resonant structures can exhibit a negative mass density during acoustic resonance (Huang and Sun, 2009; Chen H. et al., 2015; He et al., 2023). The development of acoustic metamaterials has led to the discovery of various properties including negative reflection index (Zhang and Liu, 2004; Brunet et al., 2015; Park and Lee, 2019; Wang et al., 2021; Kuci et al., 2024), sound absorption (Yang et al., 2015a; 2015b; Cummer et al., 2016; He et al., 2024), cloak (Chen et al., 2017; Jin et al., 2019), etc.
Artificial structures with unique mechanical properties, determined by the composition of the material and the geometry of the elements, are known as mechanical metamaterials. They are part of the family of metamaterials, which encompass concepts in electromagnetism, acoustics, and mechanics. Similarities between acoustic and mechanical metamaterials include their capacity to manipulate waves, exhibit negative properties, and create band gaps. Mechanical metamaterials are designed to overcome the limitations of conventional materials such as metals and composites in mechanical properties. These properties come from the principle of the interaction of waves with periodic structures. Although composite structures in mechanics are not new, 3D methods for designing such artificial microstructures are just beginning to be developed, especially for unusual macroscopic properties. Mechanical metamaterials possess superior mechanical properties, such as negative Poisson’s ratio (i.e., auxetics) (Hewage et al., 2016; Dudek et al., 2020; Mizzi et al., 2020; Lim, 2024), vanishing shear modulus, (Christensen et al., 2015; Dudek et al., 2020; Lymperopoulos and Theotokoglou, 2022; Wei et al., 2023), negative stiffness (Hewage et al., 2016; Gao et al., 2021; Zhang K. et al., 2023), negative compressibility (Dudek et al., 2020; Grima-Cornish et al., 2020), etc. Researchers have applied these unique properties for various applications. To enhance sound absorption and mechanical properties, lightweight multifunctional microlattices have been fabricated using 3D printing with digital light processing (Li et al., 2023a). Li et al. (2023b) introduced an interpenetrating hollow micro-lattice metamaterial, which interweaves hollow octet-truss and hollow rhombic dodecahedron-like truss structures. The metamaterial exhibits high strain recovery after cyclic compression and excellent sound absorption properties. Due to coherent coupling effects and weak resonances, porous multifunctional metamaterials operate effectively at low frequencies, offering high sound absorption, deformation resistance, and impact resistance (Li et al., 2022). Xu et al. (2024) proposed a new Buffer Lander-leg with a Yoshimura core. It is based on the Buckling Restrain conducted a numerical study on an enhanced periodic auxetic metamaterial for vibration isolation. Pyskir et al. (2019) conducted a numerical study on an enhanced periodic auxetic metamaterial for vibration isolation, demonstrating increased band gap width and range resulting from geometric modifications inspired by rotating squares. The width and position of the band gap are notably improved through modifications to the unit cell design, with pre-compression exerting influence on the band gap.
Therefore, this paper focuses on reviewing auxetic mechanical metamaterials and their structures. It provides a comprehensive overview of recent advancements and potential applications in fields such as vibration reduction, energy absorption, and vibration isolation.
2 Types of auxetic mechanical metamaterial
Poisson’s ratio is a measure of deformation that describes the tendency of a material to expand in directions perpendicular to the direction of compression. It is defined as the ratio of lateral strain to axial strain. Three basic elastic constants are important from an engineering perspective: Young’s modulus (
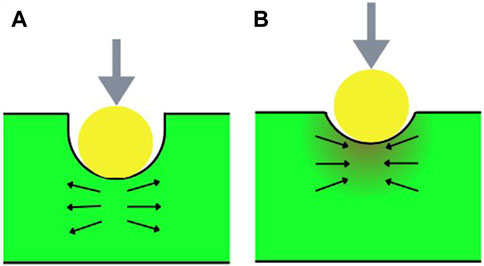
Figure 2. Deformation diagram of (A) non-auxetic material and (B) auxetic material. Reproduced under the terms of the CC-BY license from (Kolken and Zadpoor, 2017). Copyright 2017, The Authors. Published by RSC Advances.
Therefore, an auxetic metamaterial is characterized by a negative Poisson’s ratio, meaning that when stretched in one direction, it contracts in the other two perpendicular directions. In other words, the material becomes larger under tension and smaller under compression. Auxetic metamaterials can be divided into several groups based on the deformation, such as origami-kirigami structure, chiral/anti-chiral structure, rotating unit structure, re-entrant structure, etc.
2.1 Origami-kirigami structure
Origami, a traditional Japanese art form, involves the folding of paper (Chen Y. et al., 2015). The auxetic principle, which is employed in the design of origami structures, involves the folding of a 2D flat structure into a 3D structure to increase the degrees of freedom. Origami-based mechanical metamaterials can be classified into two categories: rigid and deformable structures. The demanded rigid structures include Miura origami, Ron Resch, tubular origami structures, etc. The demanded deformable structures include Miura origami, Kresling origami, curved origami, etc., as shown in Figure 3.
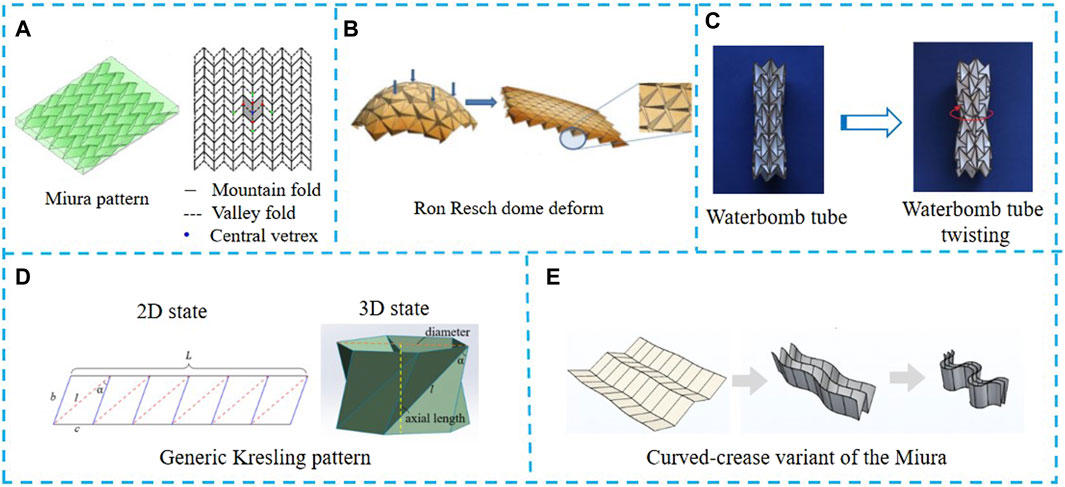
Figure 3. Types of origami metamaterials. (A) Miura origami. Reproduced under the terms of the CC-BY-NC-SA license from (Lv et al., 2014). Copyright 2014, The Authors. Published by Springer Nature. (B) Ron Resch origami. Reproduced under the terms of the CC-BY-NC-SA license from (Lv et al., 2014). Copyright 2014, The Authors. Published by Springer Nature. (C) Origami tubular structures. Reproduced under the terms of the CC-BY license from (Feng et al., 2018). Copyright 2018, The Authors. Published by Springer Nature. (D) Kresling origami. Reproduced under the terms of the CC-BY license from (Ye et al., 2022). Copyright 2022, The Authors. Published by MPDI. (E) Curved origami. Adapted with permission from (Karami et al., 2024). Copyright 2024, American Physical Society.
The Miura geometry is composed of a set of identical rigid parallelogram faces connected by edges capable of folding into “mountain” and “valley” folds (Zhou et al., 2016). The planar state of Miura origami can be described by two quantities: Poisson’s ratio, describing the relationship between deformations in orthogonal directions; stretching rigidity, characterizing the planar mechanical stiffness (Wei et al., 2013). 3D Miura metamaterials can be created by repeating multilevel M-V (mountain–valley stacking) or V-V (valley–valley stacking) unit cells in all three orthogonal directions. The properties are allowed to emerge by origami metamaterials. Metamaterials with V-V stacked configurations exhibit larger volume changes and higher tensile stiffness compared to M-V stacked configurations, displaying negative Poisson’s ratios in all three orthogonal planes (Zhou et al., 2016).
Ron Resch origami, developed through various folding modes, exhibits multiple degrees of freedom. Tachi (2013) proposed 3D origami mosaic creation system builds upon Resch’s patterns by enabling the shaping of 3D surfaces from sheet material through a folding process. To achieve the required geometric parameters, the configuration is modified by determining the coordinates of the vertices to meet unfolding requirements, while also limiting the fold angle (
Origami tubular structures are 3D formations created by folding thin sheets of paper. One of the key advantages of this type of structure lies in its polygonal cross-section (Filipov et al., 2016). The properties of origami tubes are like a “zipper” when folded according to the Miura pattern, resulting in various mesh configurations (Filipov et al., 2015). Feng et al. (2018) have explored the twisting motion of 3D tubular mechanical metamaterials inspired by the water bomb origami technique. Meticulous kinematic analysis has established that the initial torsion imparts a rigid origami motion to the structure. Moreover, it has been demonstrated that continuous torsion enhances the strength of the tube.
Kresling origami is characterized by its formation into a cylindrical shape comprised of triangulated cells. These cylindrical structures exhibit properties such as axial extensibility, tunable stiffness, multistability, and bistability. In their studies, Kidambi and Wang (2020) investigated the deployment dynamics of Kresling structures with varying geometries and operational strategies. The study found that dynamic deployment is sensitive to initial conditions and small geometric changes. Furthermore, the research revealed the influence of specific geometrical configurations on the stiffness of different axial and off-axis deformation modes, indicating the potential of Kresling-based structures for deployable systems with customizable characteristics. Ye et al. (2022) examined the geometry and radial closure ability of Kresling designs, particularly focusing on their application in valves. Through their research, they developed a new bending pattern termed RC-ori, which effectively eliminates torsion. Their findings revealed that there was negligible change in the open area as the component approached complete folding, thereby emphasizing the effectiveness of this innovative design for microflow control valves.
Curved origami refers to origami characterized by curved folds and/or panels (Zhai et al., 2021). It involves the creation of 3D surfaces that are developable but contain areas of non-zero principal curvature. Lee et al. (2018) provided an analytical model for origami with curved folds, avoiding the need for surface discretization. Karami et al. (2024) introduced a variant of the Miura origami tessellation known as curvilinear-fold tessellation. Zhai et al. (2020) described a family of curved origami-based metamaterials for in situ stiffness manipulation. These metamaterials demonstrated unique functionalities, including curved gripping with fast or precise negative stiffness modes, as well as in situ switching between zero stiffness vibration isolation mode and a positive stiffness responsive mode.
Kirigami is a derivative that incorporates cutting into the folding process. The auxetic principle of kirigami structures is akin to the rotating rigid structure, as both involve rotating blocks around a connecting hinge (Wang et al., 2020). A new shape is formed by cutting or carving a continuous flat sheet to initiate a kirigami structure, which then undergoes a new structural configuration through stretching, folding, or other external stimuli. Precise control of differentiated material structures is facilitated by fractal cuts. The structures are classified into hierarchical and alternating motifs (Cho et al., 2014). Flexible shapes can be achieved through fractal-cut kirigami. In hierarchical kirigami metamaterials, structures are constructed using rectangular and square-cut units (Tang and Yin, 2017). Kunin et al. (2016) presented the static and dynamic elastic response of fractal materials. Materials deform when “rigid” elements are rotated rather than deformed; static and dynamic properties can be manipulated by controlling the cutting pattern and its hierarchies. Periodic parallel cuts are employed in ribbon kirigami to enhance its tensile strength. This is achieved through bending the highly reliable ribbons formed by these cuts. Ribbon kirigami exhibits multistability under tension. Yu et al. (2023) investigated the demonstration of multistable behavior in kirigami by replacing one of the main cuts. Furthermore, Wang et al. (2020) considered the normalized stiffness and tensile behavior of planar ribbon kirigami, noting that not all configurations contribute to the normalized extensibility, resulting in a decrease in normalized stiffness.
Hybrid mechanical metamaterials based on origami and kirigami are artificial materials that utilize origami and kirigami folding and cutting techniques to simultaneously manipulate thin materials, as shown in Figure 4.

Figure 4. Hybrid mechanical metamaterials based on origami and kirigami (A) zigzag stripes inspired by the Miura pattern. Reproduced under the terms of the CC-BY-NC license from (Eidini and Paulino, 2015) Copyright 2015, The Authors. Published by American Association for the Advancement of Science. (B) Nano-metamaterial based on cutting and folding. Reproduced under the terms of the CC-BY-NC license from (Liu et al., 2018). Copyright 2018, The Authors. Published by American Association for the Advancement of Science.
Applying these principles, artificial structures with unique properties are created using hybrid origami and kirigami mechanical metamaterials. The technique of employing complex zigzag stripes was inspired by the Miura pattern, yielding zigzag metamaterials with a single degree of freedom possessing identical kinematics (Eidini and Paulino, 2015). Novelino et al. (2020) introduced a model of Kresling origami with folds replaced by cuts. Hybrid mechanical metamaterials based on origami and kirigami allow for rapid shape changes and instantaneous fixation of the metamaterial’s shape without affecting its mechanical properties. At the nanoscale, the fabrication of 3D nanostructures is facilitated by hybrid metamaterials combining origami and kirigami, preserving their diversity and functionality. Folding, bending, and twisting were achieved through cutting and external stimuli (Liu et al., 2018).
2.2 Chiral and anti-chiral structure
Chiral metamaterials are a class of auxetic structures characterized by their lack of symmetry for their mirror images, similar to the relationship between left and right hands (Lakes, 1991; Prall and Lakes, 1997; Grima et al., 2008b). The structural evolution of different types of chiral mechanical metamaterials can be classified into three categories: chiral, anti-chiral, and meta-chiral (Wu et al., 2019) A 2D chiral structure is composed of a honeycomb pattern featuring central cylinders (i.e., nodes) connected by elastic tangential links (i.e., ligaments). A 2D chiral structure is formed by a honeycomb structure consisting of central cylinders (i.e., nodes), which are connected by elastic tangential links (i.e., ligaments). Balan P et al. (2023) demonstrated that these chiral blocks can flexibly fold or unfold due to the rotational motion of the cylinders when subjected to mechanical loads. In contrast, an anti-chiral structure positions the central cylinders on one side of the ligaments (Wang et al., 2020). The meta-chiral structure is unique in that it combines elements of both chiral and anti-chiral configurations: some nodes are attached to one side of the ligaments as in chiral structures, while other nodes are attached to the opposite side, as in anti-chiral structures (Grima et al., 2008a).
Chiral, anti-chiral, and meta-chiral structures are divided into systems having three (tri-), four (tetra-), and six (hexa-) edges attached to each node, as shown in Figure 5.
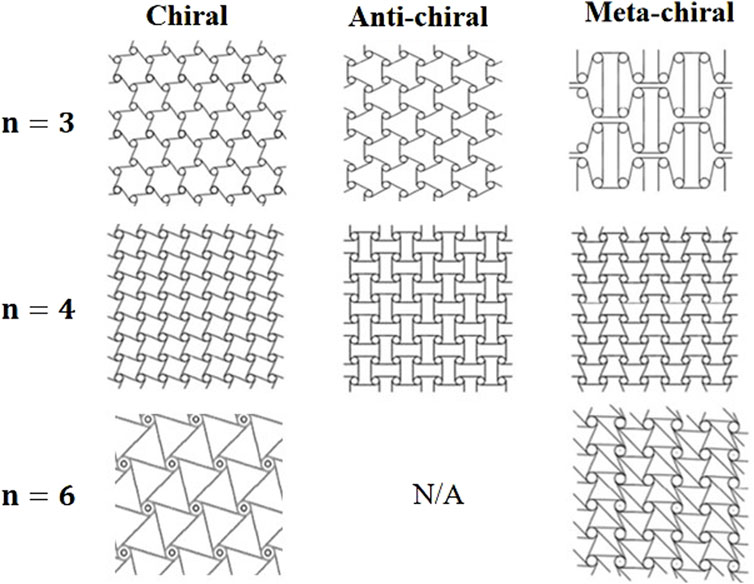
Figure 5. Classification of chiral, anti-chiral, and meta-chiral structures according to their edges. Reproduced under the terms of the CC-BY license from (Wu et al., 2019) Copyright 2019, The Authors. Published by Elsevier; Reproduced under the terms of the CC-BY license from (Bacigalupo et al., 2019). Copyright 2019, The Authors. Published by Frontiers.
Chiral and anti-chiral auxetic metamaterials exhibit enhanced mechanical properties, including negative Poisson’s ratio, high compressibility, negative thermal expansion behavior, etc. (Wu et al., 2018; 2019; Yu et al., 2018). Lightweight chiral materials and structures provide benefits such as impact energy absorption, vibration suppression, vibration attenuation, sound absorption, electromagnetic stealth, thermal insulation, zero thermal expansion, etc. (Wu et al., 2019; Balan P et al., 2023).
The vibration damping capabilities of tetra-chiral unit cells, both with and without internal resonators, were analyzed and compared using Bloch’s theorem and the finite element method (Zhu et al., 2016). An experimental evaluation was conducted on an auxetic damper composed of a counter tetra-chiral honeycomb structure with cylinders filled with metal rubber particles (Ma et al., 2013). Wu et al. (2018) investigated anti-tetra-chiral structures with elliptical nodes undergoing deformation under uniaxial tensile loading. They provided a more accurate analysis of the Poisson’s ratio and in-plane tensile modulus by considering the ligament thickness. Ye et al. (2021) proposed a comprehensive interactive progressive method for energy absorption during the development of chiral mechanical metamaterials, leveraging the rotational mechanism of negative Poisson’s ratio metamaterials. Pan et al. (2023) reported on a chiral lattice with ring nodes subjected to quasi-static single-layer compression, finding that this structure allows energy absorption in the out-of-plane direction.
Hierarchical structures represent a novel class of 2D auxetic metamaterials capable of exhibiting a negative Poisson’s ratio at various levels of compressive strain (Mousanezhad et al., 2015). These structures consist of unit cells formed by hierarchical honeycombs. As the structural hierarchy increases, the hexagonal honeycomb cell evolves see Figure 6.
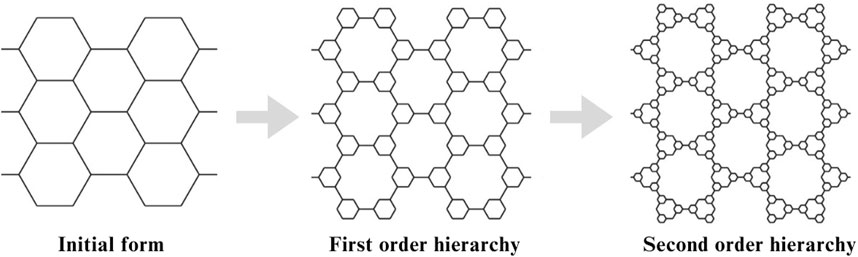
Figure 6. Development of hexagonal honeycomb cell. Reproduced under the terms of the CC-BY license from (Mousanezhad et al., 2015). Copyright 2015, The Authors. Published by Springer Nature.
Hierarchical structures possess properties such as specific stiffness, buckling strength, negative Poisson’s ratio, and enhanced stiffness (Ajdari et al., 2012; Mousanezhad et al., 2016; 2015). It is shown that hierarchical chiral structures can improve the impact energy absorption capacity of chiral structures (Lu et al., 2019). The Poisson’s ratio of these structures decreases under uniaxial compression due to hierarchy-dependent elastic instability from the early stages of deformation, resulting in auxeticity at later deformation stages (Mousanezhad et al., 2015). The mechanical properties of hierarchical metamaterials, including the Poisson’s ratio, can be precisely controlled and significantly modified through small adjustments in design parameters (Dudek et al., 2022).
2.3 Rotating unit structure
A rotating unit structure is based on the arrangement of rigid squares connected at the vertices by hinges (Grima and Evans, 2000). The united structure was based on the idealized geometry of “rotating triangles” and “rotating squares” (Grima and Evans, 2006). The isotropic design of rigid squares and rotating triangles ensures a constant Poisson ratio of −1.0, independent of the direction of loading (Grima and Evans, 2006; 2000). Plewa et al. (2023) presented a structure composed of rigid squares hinged together, enabling isotropic expansion and contraction under loads, allowing the system to exhibit auxetic behavior. Similarly, Grima et al. (2012) introduced a novel model based on scalene rigid triangles that rotate relative to each other. The extent of the auxetic behavior in this model depends on the shape of the triangles and their connections. Grima et al. (2004) introduced a model using rigid rectangles, where systems can exhibit both positive and negative Poisson ratios depending on the angle between the rectangles. The extent of auxetic behavior is determined by the system’s geometry and its deformation characteristics. The rigid rectangle model is divided into two types of systems.
Type
Lim (2023) introduced a system comprising rhombuses and right triangles based on the tangram principle. Their findings demonstrated that axial Poisson’s ratio and dimensionless Young’s moduli depend on the shapes and separation angles of the rigid elements, which define the dimensions of the metamaterial unit cell. In cases where the Poisson’s ratio is −1 under tension along any axis, the Young’s moduli are equal, increasing monotonically with the shape descriptors of the rigid blocks. Galea et al. (2023) investigated structures with uniformly sized perforations in three planes, achieving a negative Poisson’s ratio of approximately −0.5 and demonstrating a range of anisotropic Poisson’s ratios and Young’s moduli with diamond-shaped perforations.
2.4 Re-entrant structure
The re-entrant structure is called periodically connected hexagonal elements in which the interior angles of the polygon are greater than
Star-shaped re-entrant structures were proposed by Theocaris et al. (1997). These star-shaped building blocks were divided into the periodic structures named Star-3, Star-4, and Star-6, or collectively Star-n (Grima et al., 2005). Zhang et al. (2019a) introduced an innovative hierarchical metamaterial characterized by a return planar lattice structure incorporating a star-shaped sub-cell. This design exhibits specific stiffness and auxetic properties, elucidating its hierarchical porosity and multi-level tunable parameters. Ai and Gao (2018) developed a model to predict the effective Young’s moduli and negative Poisson’s ratios of 2D periodic star-shaped lattice return structures with orthotropic symmetry.
3 Applications of the auxetic mechanical metamaterials in different engineering problems
Auxetic metamaterials, due to their unique properties, play a significant role in various engineering applications. In structures subjected to moving loads such as vehicles and buildings, vibration can be reduced by these metamaterials (Pyskir et al., 2021; Zhang et al., 2022; Ma et al., 2023). With the development of technology and increasing requirements for various engineering systems, there is an increasing demand for metamaterials, especially in the fields such as defense, biomedical engineering, and aviation. To increase passenger comfort and protect equipment from wear and tear, auxetic metamaterials can also help. The importance of these materials lies in their ability to effectively address vibration and energy absorption, making them an essential element of modern engineering applications (Pan and Zhang, 2020).
3.1 Application in vibration isolation problems
Auxetic metamaterials are characterized by the unique property of a negative Poisson’s ratio, indicating that these materials contract in the transverse direction when compressed in the axial direction. Consequently, these materials exhibit both static and dynamic properties, such as the capability to create a wide and low-frequency bandgap. This bandgap at relatively low frequencies contributes to vibration attenuation and subsequent vibration isolation. The vibration isolation characteristics of metamaterials are determined by the presence of bandgap regions (Moscatelli et al., 2019). The mechanisms underlying the formation of bandgaps can be attributed to Bragg scattering and/or local resonance.
A hybrid meta-structure consisting of re-entrant and anti-chiral metamaterials using rubber layers coated with elastic mass inclusions at circular nodes has been developed to optimize wave-damping characteristics (Qi et al., 2019). This design provides bandgaps in the mid-low frequency range that are not present in the re-entrant honeycomb structure. The deformation of the intermediate thin bundles and the contact between the cells, without completely closing the holes, are facilitated by the rotating squares mechanism, combined with bending induced by pre-compression. This modification enhances the bandgap width and position, consequently, the vibration isolation, by favoring a heterogeneous stress field (Pyskir et al., 2019). Pyskir et al. (2021) further developed this model by incorporating an auxetic reinforced metamaterial featuring resonant inclusions (Figure 7). These modifications significantly reduce vibration transmission within the bandgap frequency ranges and increase the width of the bandgap, particularly at low frequencies. The continuous characteristics of the bandgap facilitate effective isolation.
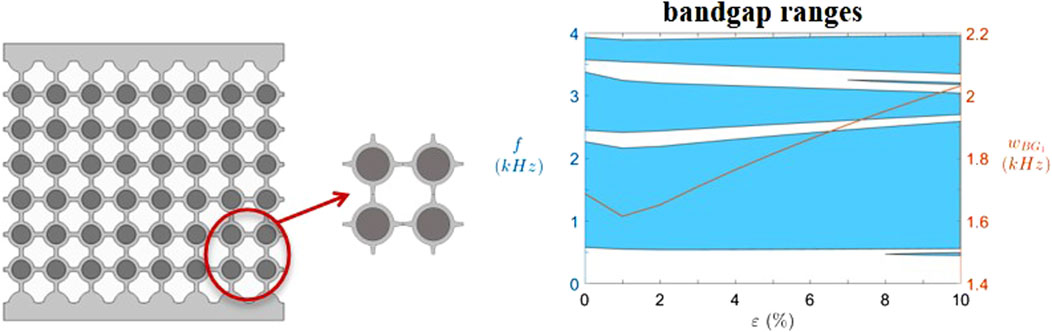
Figure 7. Example of bandgap expansion in rotating and bending squares with auxetic-reinforced metamaterial and resonant inclusions. Reproduced under the terms of the CC-BY license from (Pyskir et al., 2021). Copyright 2021, The Authors. Published by MDPI.
The integration of origami into vibration isolation systems as a negative stiffness module shows promise for enhancing isolation effectiveness. However, significant challenges in engineering applications arise from the intricate mathematical modeling and the pronounced nonlinear mechanical properties of origami. Liu et al. (2022) addressed these issues by utilizing Tachi-Miura origami as a corrective mechanism for negative stiffness, resulting in the development of an origami-type isolator denoted as HSLDS/QZS. Superior vibration isolation characteristics were attained through dynamic characterization under base excitation and force excitation with reduced permeability.
A 3D chiral mechanical metamaterial achieves a low-frequency bandgap, facilitated by the tactile and descriptive shape of the chiral block joint. This bandgap is enabled without altering the relative density of the material (Zhao et al., 2022). Zhang et al. (2022) presented a method for tuning the vibration isolation ability and collision resistance characteristics of a model of bifunctional hierarchical metamaterials. This method changes the band gaps by varying the thickness of self-similar small squares and connecting edges. Tao et al. (2022) proposed a model consisting of a re-entrant honeycomb structure with hierarchical characteristics achieved by attaching small re-entrant structural units to the nodes of traditional re-entrant structures. The developed re-entrant honeycomb structure with hierarchical characteristics can open several bandgaps, especially in the low-frequency region. Compressive or tensile stress applied to the overall structure effectively improves the frequency, width, and attenuation strength of the bandgap. Ma et al. (2023) presented a model of hierarchical honeycombs with re-entrant structures, where the joints of the three walls are replaced by square unit cells. The introduction of square unit cells allowed for an expanded band gap, especially in the low-frequency range and increased their number.
Conventional metamaterials with a negative Poisson’s ratio can be joined using re-entrant metamaterials with similar properties, using annular rings as connecting elements. This allows the bandgap to vary in different assemblies. Damping the particles improves their damping characteristics, resulting in better vibration isolation at low and medium frequencies (Gao et al., 2023).
Reconfiguring a bistable honeycomb mechanical metamaterial, developed by combining re-entrant structures and cosine-shaped beams, enables the manipulation of elastic wave propagation at sub-wavelength scales and affects the value of Poisson’s ratio (Xiao et al., 2024). Although this configuration exhibits distinctive elastic vibration characteristics, enabling the manipulation of elastic wave propagation through local resonance mechanisms, the overall stiffness of the periodic structure is reduced by the low stiffness of the material. This can result in reduced load-carrying capacity, deformation, and damage, as well as changes in vibration isolation properties.
3.2 Application in vibration reduction problems
Materials with high specific strength and damping characteristics are crucial for effective vibration reduction. These materials convert vibrational energy into thermal energy, thereby reducing the amplitude and impact of vibrations on structures. Qin and Yang (2019) proposed a method for the topological optimization of metamaterials to enhance vibration suppression. Their method demonstrated a
In designing structures for vibration reduction, methods such as vibration isolation, vibration absorption, and damping are employed. The vibration reduction is characterized by the properties of wave attenuation in the low-frequency range. Chen et al. (2020) introduced a model of a 3D auxetic metamaterial with a double arrowhead, exhibiting a combination of lightweight, high specific strength, and high damping characteristics.
For instrumentation and acoustic stealth in submersible vehicles, it is crucial to employ a flange that supports the main engine and can be fabricated using local methods while being situated closer to the vibration source. Zhuang et al. (2024) developed a novel metamaterial flange featuring rectangular star-shaped unit cells with horizontal ligaments, which exhibit a high load-bearing capacity. This design effectively mitigates vibrations across a broad spectrum of low to medium frequencies, achieving both a 36.5% reduction in weight and enhanced engine support.
The vibration reduction efficiency of mechanisms is influenced by the support provided by honeycomb sandwich foundations with re-entrant structures (Pan and Zhang, 2020). This efficiency is dependent on internal geometric parameters, such as the initial tilt angle of the mechanism. Therefore, the support from a honeycomb sandwich foundation enhances vibration transmission reduction, contingent upon the initial angle and geometric parameters. Chen et al. (2021) revealed the impact of fiber stacking angles on the vibration damping properties of a carbon fiber-reinforced polymer three-dimensional double-arrow model, highlighting its lightweight, high specific strength, and high damping characteristics. A change in the angle of the star in a chiral star-shaped composite mechanical metamaterial, which is formed by combining a chiral lattice structure and star-shaped honeycombs, also results in the position and width of the band gap being affected, enabling the achievement of low-frequency vibration suppression (Zhang et al., 2023).
Given the use of spindles across various fields, including industrial production and medical equipment, achieving vibration reduction is essential for ensuring stable and accurate operation. Kim et al. (2022) developed spindle holders based on re-entrant hexagon-type auxetic structures, manufactured using various additive manufacturing processes, to enhance vibration reduction. Consequently, auxetic carbon fiber-reinforced polymer and titanium holders, due to their superior damping characteristics, effectively achieve vibration reduction over a wide frequency range.
3.3 Application in energy absorption problems
To characterize energy absorption, it is essential to understand total energy absorption, specific energy absorption, and dimensionless equivalent plateau stress. Avoiding materials with low modulus of elasticity and low strength is crucial, as these can lead to material failure (Zhang et al., 2019b; Wang Y. et al., 2020; Guo et al., 2020).
Determining the main characteristics of out-of-plane compression in auxetic structures is critical, particularly in studying the effects of compression velocity, structural parameters, and configurations on energy absorption rates. Lu et al. (2019) compared the dynamic properties of anti-tetra-chiral, hexachiral, and hierarchical chiral structures under out-of-plane loading. The ligament length, node radius, ligament thickness, and the level of the structural hierarchy were varied under various conditions of external impact compression. Their findings indicated that hierarchical chiral structures, due to cell wall strengthening, exhibit better compression stability and energy absorption capacity compared to unit cells. At the same time, anti-tetra-chiral structures generated higher plateau stress and demonstrated better energy absorption efficiency compared to hexachiral structures. Among re-entrant, arrowhead, and anti-tetra-chiral structures, the highest energy absorption was observed in the arrowhead structure (Najafi et al., 2019).
Despite the significant potential of auxetic metamaterials for energy absorption, they face several limitations, including low elastic modulus, low strength, high cost, and inefficient fabrication processes. Wang et al. (2020) proposed a cross-chiral structure derived from the transformation of a cubic lattice with zero Poisson’s ratio by adjusting the tilt angle of the struts. This model exhibited anisotropy with increased Young’s moduli and negative Poisson’s ratio in the principal directions, although the properties deteriorated in off axial direction. Nonetheless, the structure demonstrated outstanding specific moduli and specific strength, and could absorb energy effectively at ultralow relative densities
In recent years, significant research has focused on the development of auxetic re-entrant metamaterials. Guo et al. (2020) proposed a re-entrant cylindrical shell for testing under various crushing speeds, demonstrating elevated plateau stress and specific energy absorption at higher velocities. However, energy absorption is compromised by the instability of auxetic lattice cylindrical shells during crushing, leading to inward concavity and structural twisting. Qi et al. (2020) explored circular re-entrant structures by replacing conventional re-entrant honeycomb inclined cell walls with double arc-shaped walls. This design exhibits non-uniform auxetic deformation prior to compaction under quasi-static loading, achieving superior compressive strength and specific energy absorption compared to typical re-entrant honeycombs. Auxetic “multi-lattice” composite structures, composed of 3D re-entrant lattice structures simulated by particle and fiber-reinforced composites, demonstrate higher strength, stiffness, and energy absorption capacity than pure 3D re-entrant structures (Sahariah et al., 2022). The mechanical properties can be tuned through the 3D structure formed by rotating and connecting 2D cells with a re-entrant hexagonal honeycomb. This configuration enables control and determination of both the peak force and specific energy absorption of the lattice (Teng et al., 2022). In regular re-entrant honeycomb geometries, dividing inclined struts into two sections without altering mass enhances energy absorption capabilities by introducing nodes with lower rotational stiffness (Choudhry et al., 2022). Alomarah et al. (2023) introduced an auxetic metamaterial in the shape of a butterfly, featuring vertical and inclined walls akin to re-entrant honeycombs, which exhibit excellent specific energy absorption per unit volume and mass in compression in any direction. Based on deep learning technology, Zhang and Ma (2024) predicted the energy absorption properties of a re-entrant honeycomb structure featuring an internal arc, extending the parameter range beyond that of the validation set.
Sandwich structures, characterized by low mass, high rigidity, and significant strength, combined with other auxetic structures, demonstrate unique properties in energy absorption (Tan et al., 2020). Zhao et al. (2021) investigated a sandwich beam model featuring a star-triangular honeycomb core, which exhibits superior bending resistance and higher energy absorption capabilities compared to sandwich beams with star-shaped and re-entrant hexagonal cores. Sadegh Ebrahimi et al. (2022) developed and compared four types of hybrid metamaterial structures by integrating cellular, re-entrant, and star-shaped elementary cells, among which the compressive strength, constant stress, and energy absorption are predominantly higher in the structure in the form of a re-entrant star. Hierarchical honeycombs also exhibit excellent energy absorption properties and relatively stable bearing capacities (Huang et al., 2021). Structures composed of composite cellular metamaterials in hierarchical cellular shapes, filled with polyurethane foam, demonstrate high specific strength, rigidity, and energy absorption capabilities (Usta et al., 2021a).
A 3D auxetic structure, based on a hybrid of S-shaped unit cells with repeated insertion, is noted for its high stress concentration (Khadem-Reza et al., 2022). However, due to the destructive interaction of S-shaped and re-entrant unit cells, it demonstrates the lowest energy absorption. Etemadi et al. (2024) demonstrated an auxetic metamaterials by inducing curvature at the sharp corners of a re-entrant cell and replacing straight struts with curved ones. This approach reduces stress concentration on the structure, resulting in significantly improved energy absorption capabilities and specific energy absorption of the formed structures.
3.4 Application in energy harvesting problems
The increasing demand for energy harvesting and storage is of significant interest, particularly due to its applications in nanodevices, sensor networks, health monitoring systems, and intelligent transportation systems. Energy storage emerges as a logical solution to mitigate the need for frequent battery and wiring replacements in remote and mobile electronic devices, thereby providing consistent power to numerous distributed sensor nodes. Among various energy generation methodologies, Piezoelectric Energy Harvesting is recognized as a popular and simple method to supply operating power for electronic devices (Wei and Jing, 2017). However, a major limitation of current energy harvesting methods is their reliance on the resonant frequencies of ambient vibrations, which are often random and broadband.
To address this problem, researchers have proposed the use of honeycomb sandwich panels with auxetic core and face sheets, based on the theory of higher-order shear-deformable plates (Khorshidi et al., 2022). This design achieves higher deflection and improved energy harvesting capability with lower stiffness. By increasing the angle of inclination of the auxetic cell panels, higher power output can be obtained at the expense of reduced stiffness, thereby enabling the structure to support greater loads and harvest more energy. Additionally, increasing the aspect ratio of the cells can further enhance energy harvesting by lowering the resonant frequency and increasing power output. Hosseinkhani et al. (2022) demonstrated that the efficiency of energy transformation in piezoelectric storage devices is significantly improved by employing meta-lattice structures. The integration of auxetic patterns into an ideal crystal creates functionalized defects that disrupt periodicity and form additional band passages above the main band gap. This leads to a substantial enhancement in the performance of the energy harvesting system, with improvements ranging from 1.29 to 5.26 times across different designs.
3.5 Application in impact-resistant problems
Impact-resistant devices play a crucial role in various engineering fields, including aviation, shipbuilding, and the automotive industry. Therefore, these structures must exhibit flexible tuning properties and efficient mechanical behavior (Yang et al., 2023). Auxetic metamaterials characterized by their unique properties such as a negative Poisson’s ratio and low stiffness. Nevertheless, low stiffness may be a limiting factor in their use in applications where high levels of stiffness, strength, hardness, and energy absorption capacity are required simultaneously. To address these limitations, auxetic lattice structures are often combined with nearly incompressible soft materials to create high-performance composites (Li et al., 2020). These auxetic lattice-reinforced composites exhibit notable properties such as high stiffness, energy absorption, and impact resistance. The negative Poisson’s ratio of the auxetic reinforcements induces a state of biaxial compression within the matrix, enhancing the material’s overall performance.
Origami metamaterials and corrugated metamaterials with a negative Poisson’s ratio can be utilized to mitigate impact effects. By transforming the impulse process into a quasi-static process, these materials enable the sustained application of a stable impact force, which significantly reduces both the maximum impact force and displacement (Zhang et al., 2024).
Sandwich panels, characterized by their high specific strength, stiffness, adaptability, and impact resistance, are widely used in aerospace, marine, land transportation, and military applications Sandwich panels with auxetic configurations offer significant advantages, including enhanced stability under large deformations and high impact energies (Usta et al., 2021b). The impact resistance of these structures can be further improved by adjusting parameters such as the face sheet stacking sequence, laminate thickness, and the internal angle of the core cell walls.
4 Summary and future perspective
In conclusion, it can be noted that auxetic metamaterials are increasingly being used in the field of applied engineering. Their unique properties make it possible to improve the ability of energy absorption, vibration isolation, vibration reduction, etc., under various load conditions. However, the boundaries of research have not yet been reached, and further efforts are required to improve the characteristics of auxetic metamaterials in the field of applied engineering.
(1) The application of additive manufacturing processes to create new metamaterials designed for local or global control of mechanical properties such as mass, stiffness, damping, energy absorption, etc., is a promising field of research.
(2) The structures of metamaterials should be optimized to improve the geometry and reduce the cost of production. This may include the development of more efficient design algorithms based on computer modeling and machine learning, as well as the use of new materials and manufacturing technologies. Such improvements will make it possible to create more compact, lightweight, and cheap auxetic metamaterials, which will expand their application in engineering.
(3) It is necessary to continue studying hybrid structures of metamaterials combining various unit cells capable of providing improved properties of compressive strength, vibration reduction, energy absorption, etc. Further research is required to optimize the structures and materials used in hybrid systems.
Author contributions
VS: Conceptualization, Writing–original draft. HW: Conceptualization, Writing–original draft, Writing–review and editing. YL: Funding acquisition, Resources, Writing–review and editing. YC: Writing–review and editing. MZ: Funding acquisition, Writing–review and editing. YL: Conceptualization, Funding acquisition, Resources, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (12211530062), the DUT-BSU Joint Institute Fund (ICR2303) and the Fundamental Research Funds for the Central Universities, China (DUT23YG217).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ai, L., and Gao, X. L. (2018). An analytical model for star-shaped re-entrant lattice structures with the orthotropic symmetry and negative Poisson’s ratios. Int. J. Mech. Sci. 145, 158–170. doi:10.1016/j.ijmecsci.2018.06.027
Ajdari, A., Jahromi, B. H., Papadopoulos, J., Nayeb-Hashemi, H., and Vaziri, A. (2012). Hierarchical honeycombs with tailorable properties. Int. J. Solids Struct. 49, 1413–1419. doi:10.1016/j.ijsolstr.2012.02.029
Alomarah, A., Yuan, Y., and Ruan, D. (2023). A bio-inspired auxetic metamaterial with two plateau regimes: compressive properties and energy absorption. Thin-Walled Struct. 192, 111175. doi:10.1016/j.tws.2023.111175
Attard, D., and Grima, J. N. (2008). Auxetic behaviour from rotating rhombi. Phys. Status Solidi B Basic Res. 245, 2395–2404. doi:10.1002/pssb.200880269
Attard, D., Manicaro, E., and Grima, J. N. (2009). On rotating rigid parallelograms and their potential for exhibiting auxetic behaviour. Phys. Status Solidi B Basic Res. 246, 2033–2044. doi:10.1002/pssb.200982034
Aydin, K., and Ozbay, E. (2007). Left-handed metamaterial based superlens for subwavelength imaging of electromagnetic waves. Appl. Phys. A Mater Sci. Process 87, 137–141. doi:10.1007/s00339-006-3817-4
Bacigalupo, A., Lepidi, M., Gnecco, G., Vadalà, F., and Gambarotta, L. (2019). Optimal design of the band structure for beam lattice metamaterials. Front. Mater 6. doi:10.3389/fmats.2019.00002
Balan, P. M., Mertens A, J., and Bahubalendruni, M. V. A. R. (2023). Auxetic mechanical metamaterials and their futuristic developments: a state-of-art review. Mater Today Commun. 34, 105285. doi:10.1016/j.mtcomm.2022.105285
Brunet, T., Merlin, A., Mascaro, B., Zimny, K., Leng, J., Poncelet, O., et al. (2015). Soft 3D acoustic metamaterial with negative index. Nat. Mater 14, 384–388. doi:10.1038/nmat4164
Chang, Q., Wang, Z., Liu, X., Saito, N., and Fan, T. (2024). A solid-solution approach for high frequency 3-dimensional isotropic negative-refractive-index metamaterials based on microwave ceramics. Ceram. Int. 50, 772–780. doi:10.1016/j.ceramint.2023.10.158
Chen, H., Zhai, S., Ding, C., Luo, C., and Zhao, X. (2015a). Acoustic metamaterial with negative mass density in water. J. Appl. Phys. 118. doi:10.1063/1.4929569
Chen, Y., Peng, R., and You, Z. (2015b). Origami of thick panels. Sci. (1979) 349 (349), 396–400. doi:10.1126/science.aab2870
Chen, Y., Zheng, M., Liu, X., Bi, Y., Sun, Z., Xiang, P., et al. (2017). Broadband solid cloak for underwater acoustics. Phys. Rev. B 95, 180104. doi:10.1103/PhysRevB.95.180104
Chen, Y. L., Wang, D. W., and Ma, L. (2021). Vibration and damping performance of carbon fiber-reinforced polymer 3D double-arrow-head auxetic metamaterials. J. Mater Sci. 56, 1443–1460. doi:10.1007/s10853-020-05366-z
Chen, Y. L., Wang, X. T., and Ma, L. (2020a). Damping mechanisms of CFRP three-dimensional double-arrow-head auxetic metamaterials. Polym. Test. 81, 106189. doi:10.1016/j.polymertesting.2019.106189
Chen, Z., Wu, X., Xie, Y. M., Wang, Z., and Zhou, S. (2020b). Re-entrant auxetic lattices with enhanced stiffness: a numerical study. Int. J. Mech. Sci. 178, 105619. doi:10.1016/j.ijmecsci.2020.105619
Cho, Y., Shin, J. H., Costa, A., Kim, T. A., Kunin, V., Li, J., et al. (2014). Engineering the shape and structure of materials by fractal cut. Proc. Natl. Acad. Sci. U. S. A. 111, 17390–17395. doi:10.1073/pnas.1417276111
Choudhry, N. K., Panda, B., and Kumar, S. (2022). In-plane energy absorption characteristics of a modified re-entrant auxetic structure fabricated via 3D printing. Compos B Eng. 228, 109437. doi:10.1016/j.compositesb.2021.109437
Christensen, J., Kadic, M., Kraft, O., and Wegener, M. (2015). Vibrant times for mechanical metamaterials. MRS Commun. 5, 453–462. doi:10.1557/mrc.2015.51
Cummer, S. A., Christensen, J., and Alù, A. (2016). Controlling sound with acoustic metamaterials. Nat. Rev. Mater 1, 16001. doi:10.1038/natrevmats.2016.1
Dudek, K. K., Attard, D., Gatt, R., Grima-Cornish, J. N., and Grima, J. N. (2020). The multidirectional auxeticity and negative linear compressibility of a 3D mechanical metamaterial. Materials 13, 2193. doi:10.3390/ma13092193
Dudek, K. K., Martínez, J. A. I., Ulliac, G., and Kadic, M. (2022). Micro-scale auxetic hierarchical mechanical metamaterials for shape morphing. Adv. Mater. 34, e2110115. doi:10.1002/adma.202110115
Eidini, M., and Paulino, G. H. (2015). Unraveling metamaterial properties in zigzag-base folded sheets. Sci. Adv. 1, e1500224. doi:10.1126/sciadv.1500224
Etemadi, E., Zamani, A. M. M., Scarpa, F., Zeeshan, M., Hosseinabadi, M., and Hu, H. (2024). Modified re-entrant auxetic metamaterials with energy absorption enhancement. Mater Today Commun. 38, 108079. doi:10.1016/j.mtcomm.2024.108079
Evans, K. E., and Alderson, A. (2000). Auxetic materials: functional materials and structures from lateral thinking. Adv. Mater. 12, 617–628. doi:10.1002/(sici)1521-4095(200005)12:9<617::aid-adma617>3.0.co;2-3
Feng, H., Ma, J., Chen, Y., and You, Z. (2018). Twist of tubular mechanical metamaterials based on waterbomb origami. Sci. Rep. 8, 9522. doi:10.1038/s41598-018-27877-1
Filipov, E. T., Paulino, G. H., and Tachi, T. (2016). Origami tubes with reconfigurable polygonal cross-sections. Proc. R. Soc. A Math. Phys. Eng. Sci. 472, 20150607. doi:10.1098/rspa.2015.0607
Filipov, E. T., Tachi, T., Paulino, G. H., and Weitz, D. A. (2015). Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl. Acad. Sci. U. S. A. 112, 12321–12326. doi:10.1073/pnas.1509465112
Fujii, G., Watanabe, H., Yamada, T., Ueta, T., and Mizuno, M. (2013). Level set based topology optimization for optical cloaks. Appl. Phys. Lett. 102. doi:10.1063/1.4812471
Galea, R., Farrugia, P. S., Dudek, K. K., Attard, D., Grima, J. N., and Gatt, R. (2023). A novel design method to produce 3D auxetic metamaterials with continuous pores exemplified through 3D rotating auxetic systems. Mater Des. 226, 111596. doi:10.1016/j.matdes.2023.111596
Galea Mifsud, R., Muscat, G. A., Grima-Cornish, J. N., Dudek, K. K., Cardona, M. A., Attard, D., et al. (2024). Auxetics and FEA: modern materials driven by modern simulation methods. Materials 17, 1506. doi:10.3390/ma17071506
Gao, R., Guo, S., Tian, X., and Liu, S. (2021). A negative-stiffness based 1D metamaterial for bidirectional buffering and energy absorption with state recoverable characteristic. Thin-Walled Struct. 169, 108319. doi:10.1016/j.tws.2021.108319
Gao, X., Wei, J., Huo, J., Wan, Z., and Li, Y. (2023). The vibration isolation design of a Re-entrant negative Poisson’s ratio metamaterial. Appl. Sci. Switz. 13, 9442. doi:10.3390/app13169442
Gibson, L. J., Ashby, M. F., Schajer, G. S., and Robertson, C. I. (1982). The mechanics of two-dimensional cellular materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 382, 25–42. doi:10.1098/rspa.1982.0087
Grima, J. N., Alderson, A., and Evans, K. E. (2004). Negative Poisson’s ratios from rotating rectangles. Comput. Methods Sci. Technol. 10, 137–145. doi:10.12921/cmst.2004.10.02.137-145
Grima, J. N., Chetcuti, E., Manicaro, E., Attard, D., Camilleri, M., Gatt, R., et al. (2012). “On the auxetic properties of generic rotating rigid triangles,” in Proceedings of the royal society A: mathematical, physical and engineering sciences (Royal Society), 810–830. doi:10.1098/rspa.2011.0273
Grima, J. N., and Evans, K. E. (2000). Auxetic behavior from rotating squares. J. Mater Sci. Lett. 19, 1563–1565. doi:10.1023/A:1006781224002
Grima, J. N., and Evans, K. E. (2006). Auxetic behavior from rotating triangles. J. Mater Sci. 41, 3193–3196. doi:10.1007/s10853-006-6339-8
Grima, J. N., Farrugia, P. S., Gatt, R., and Attard, D. (2008a). On the auxetic properties of rotating rhombi and parallelograms: a preliminary investigation. Phys. Status Solidi B Basic Res. 245, 521–529. doi:10.1002/pssb.200777705
Grima, J. N., Gatt, R., Alderson, A., and Evans, K. E. (2005). On the potential of connected stars as auxetic systems. Mol. Simul. 31, 925–935. doi:10.1080/08927020500401139
Grima, J. N., Gatt, R., and Farrugia, P. S. (2008b). On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi B Basic Res. 245, 511–520. doi:10.1002/pssb.200777704
Grima-Cornish, J. N., Grima, J. N., and Attard, D. (2020). A novel mechanical metamaterial exhibiting auxetic behavior and negative compressibility. Materials 13, 79. doi:10.3390/ma13010079
Guo, Y., Zhang, J., Chen, L., Du, B., Liu, H., Chen, L., et al. (2020). Deformation behaviors and energy absorption of auxetic lattice cylindrical structures under axial crushing load. Aerosp. Sci. Technol. 98, 105662. doi:10.1016/j.ast.2019.105662
Guo, Z., and Xiao, J. (2024). In-plane impact dynamics of thickness gradient honeycomb structures with negative Poisson’s ratio multi-arc concave cells. Mech. Adv. Mater. Struct. 31, 2386–2397. doi:10.1080/15376494.2022.2158405
Haxha, S., AbdelMalek, F., Ouerghi, F., Charlton, M. D. B., Aggoun, A., and Fang, X. (2018). Metamaterial superlenses operating at visible wavelength for imaging applications. Sci. Rep. 8, 16119. doi:10.1038/s41598-018-33572-y
He, C., Li, Z., Wu, G., and Tao, M. (2024). Fractal acoustic metamaterials with near-zero index and negative properties. Appl. Acoust. 217, 109825. doi:10.1016/j.apacoust.2023.109825
He, F., Shi, Z., Zhang, Z., Qian, D., and Feng, X. (2023). Antioptimization of mass-in-mass acoustic metamaterials based on interval analysis. Mech. Syst. Signal Process 205, 110855. doi:10.1016/j.ymssp.2023.110855
Hewage, T. A. M., Alderson, K. L., Alderson, A., and Scarpa, F. (2016). Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative Poisson’s ratio properties. Adv. Mater. 28, 10323–10332. doi:10.1002/adma.201603959
Hosseinkhani, A., Ebrahimian, F., Younesian, D., and Moayedizadeh, A. (2022). Defected meta-lattice structures for the enhanced localized vibrational energy harvesting. Nano Energy 100, 107488. doi:10.1016/j.nanoen.2022.107488
Huang, H. H., and Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 11, 013003. doi:10.1088/1367-2630/11/1/013003
Huang, W., Zhang, Y., Xu, Y., Xu, X., and Wang, J. (2021). Out-of-plane mechanical design of bi-directional hierarchical honeycombs. Compos B Eng. 221, 109012. doi:10.1016/j.compositesb.2021.109012
Jin, Y., Fang, X., Li, Y., and Torrent, D. (2019). Engineered diffraction gratings for acoustic cloaking. Phys. Rev. Appl. 11, 011004. doi:10.1103/PhysRevApplied.11.011004
Jung, M., Heo, N., Park, J., and Yoo, J. (2021). Multi-directional cloaking structure design using topology optimization. J. Electromagn. Waves Appl. 35, 1008–1019. doi:10.1080/09205071.2020.1866683
Karami, A., Reddy, A., and Nassar, H. (2024). Curved-Crease origami for morphing metamaterials. Phys. Rev. Lett. 132, 108201. doi:10.1103/PhysRevLett.132.108201
Khadem-Reza, L., Etemadi, E., Abbaslou, M., and Hu, H. (2022). Design of novel 3D auxetic structures based on S-shaped unit-cells. Smart Mater Struct. 31, 075024. doi:10.1088/1361-665X/ac7681
Kidambi, N., and Wang, K. W. (2020). Dynamics of Kresling origami deployment. Phys. Rev. E 101, 063003. doi:10.1103/PhysRevE.101.063003
Kim, J., Hegde, H., Kim, H. Y., and Lee, C. B. (2022). Spindle vibration mitigation utilizing additively manufactured auxetic materials. J. Manuf. Process 73, 633–641. doi:10.1016/j.jmapro.2021.11.051
Kolken, H. M. A., and Zadpoor, A. A. (2017). Auxetic mechanical metamaterials. RSC Adv. 7, 5111–5129. doi:10.1039/c6ra27333e
Kuci, X., Geers, M. G. D., and Kouznetsova, V. G. (2024). Towards design of a gradient locally resonant acoustic metasurface for negative reflection. J. Mech. Phys. Solids 187, 105632. doi:10.1016/j.jmps.2024.105632
Kunin, V., Yang, S., Cho, Y., Deymier, P., and Srolovitz, D. J. (2016). Static and dynamic elastic properties of fractal-cut materials. Extreme Mech. Lett. 6, 103–114. doi:10.1016/j.eml.2015.12.003
Lakes, R. (1991). Deformation mechanisms in negative Poisson’s ratio materials: structural aspects. J. Mater. Sci. 26, 2287–2292. doi:10.1007/bf01130170
Lee, T. U., You, Z., and Gattas, J. M. (2018). Elastica surface generation of curved-crease origami. Int. J. Solids Struct. 136–137, 13–27. doi:10.1016/j.ijsolstr.2017.11.029
Leonhardt, U. (2006). Optical conformal mapping. Science 312 (5781), 1777–1780. doi:10.1126/science.1126493
Li, T., Liu, F., and Wang, L. (2020). Enhancing indentation and impact resistance in auxetic composite materials. Compos B Eng. 198, 108229. doi:10.1016/j.compositesb.2020.108229
Li, Z., Li, X., Chua, J. W., Lim, C. H., Yu, X., Wang, Z., et al. (2023a). Architected lightweight, sound-absorbing, and mechanically efficient microlattice metamaterials by digital light processing 3D printing. Virtual Phys. Prototyp. 18. doi:10.1080/17452759.2023.2166851
Li, Z., Li, X., Wang, X., Wang, Z., and Zhai, W. (2023b). Interpenetrating hollow microlattice metamaterial enables efficient sound-absorptive and deformation-recoverable capabilities. ACS Appl. Mater Interfaces 15, 24868–24879. doi:10.1021/acsami.3c02498
Li, Z., Li, X., Wang, Z., and Zhai, W. (2022). Multifunctional sound-absorbing and mechanical metamaterials via a decoupled mechanism design approach. Mater Horiz. 65, 75–87. doi:10.1039/d2mh00977c
Lim, T. C. (2023). Auxetic properties of a tangram-inspired metamaterial. Eng. Res. Express 5, 015063. doi:10.1088/2631-8695/acc1c5
Lim, T. C. (2024). A mechanical metamaterial with adjustable positive to negative Poisson’s ratio based on rotating trapeziums and triangles. Philos. Mag. 104, 300–320. doi:10.1080/14786435.2023.2293929
Liu, S., Peng, G., and Jin, K. (2022). Towards accurate modeling of the Tachi-Miura origami in vibration isolation platform with geometric nonlinear stiffness and damping. Appl. Math. Model 103, 674–695. doi:10.1016/j.apm.2021.11.012
Liu, Z., Du, H., Li, J., Lu, L., Li, Z.-Y., and Fang, N. X. (2018). Nano-kirigami with giant optical chirality. Sci. Adv. 4, eaat4436. doi:10.1126/sciadv.aat4436
Lu, Q., Qi, D., Li, Y., Xiao, D., and Wu, W. (2019). Impact energy absorption performances of ordinary and hierarchical chiral structures. Thin-Walled Struct. 140, 495–505. doi:10.1016/j.tws.2019.04.008
Lv, C., Krishnaraju, D., Konjevod, G., Yu, H., and Jiang, H. (2014). Origami based mechanical metamaterials. Sci. Rep. 4, 5979. doi:10.1038/srep05979
Lymperopoulos, P. N., and Theotokoglou, E. E. (2022). Numerical investigation of pentamode mechanical metamaterials. WSEAS Trans. Appl. Theor. Mech. 17 (17.7), 47–55. doi:10.37394/232011.2022.17.7
Ma, N., Han, Q., Han, S., and Li, C. (2023). Hierarchical re-entrant honeycomb metamaterial for energy absorption and vibration insulation. Int. J. Mech. Sci. 250, 108307. doi:10.1016/j.ijmecsci.2023.108307
Ma, Y., Scarpa, F., Zhang, D., Zhu, B., Chen, L., and Hong, J. (2013). A nonlinear auxetic structural vibration damper with metal rubber particles. Smart Mater Struct. 22, 084012. doi:10.1088/0964-1726/22/8/084012
Mizzi, L., Salvati, E., Spaggiari, A., Tan, J. C., and Korsunsky, A. M. (2020). Highly stretchable two-dimensional auxetic metamaterial sheets fabricated via direct-laser cutting. Int. J. Mech. Sci. 167, 105242. doi:10.1016/j.ijmecsci.2019.105242
Monteverde, M., Núñez-Regueiro, M., Rogado, N., Regan, K. A., Hayward, M. A., He, T., et al. (2001). Pressure dependence of the superconducting transition temperature of magnesium diboride. Sci. (1979) 292, 75–77. doi:10.1126/science.1059775
Moscatelli, M., Ardito, R., Driemeier, L., and Comi, C. (2019). Band-gap structure in two- and three-dimensional cellular locally resonant materials. J. Sound. Vib. 454, 73–84. doi:10.1016/j.jsv.2019.04.027
Mousanezhad, D., Babaee, S., Ebrahimi, H., Ghosh, R., Hamouda, A. S., Bertoldi, K., et al. (2015). Hierarchical honeycomb auxetic metamaterials. Sci. Rep. 5, 18306. doi:10.1038/srep18306
Mousanezhad, D., Haghpanah, B., Ghosh, R., Hamouda, A. M., Nayeb-Hashemi, H., and Vaziri, A. (2016). Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: a simple energy-based approach. Theor. Appl. Mech. Lett. 6, 81–96. doi:10.1016/j.taml.2016.02.004
Najafi, M., Ahmadi, H., and Liaghat, G. (2019). Experimental investigation on energy absorption of auxetic structures. Mater Today Proc. 34, 350–355. doi:10.1016/j.matpr.2020.06.075
Novelino, L. S., Ze, Q., Wu, S., Paulino, G. H., and Zhao, R. (2020). Untethered control of functional origami microrobots with distributed actuation. Proc. Natl. Acad. Sci. 117, 24096–24101. doi:10.1073/pnas.2013292117
Pan, K., and Zhang, W. (2020). Dynamic modeling and vibration reduction analysis of a negative Poisson’s ratio honeycomb foundation support. Proc. - 2020 5th Int. Conf. Mech. Control Comput. Eng. ICMCCE 2020, 524–527. doi:10.1109/ICMCCE51767.2020.00120
Pan, Y., Zhang, X. G., Han, D., Li, W., Xu, L. F., Zhang, Y., et al. (2023). The out-of-plane compressive behavior of auxetic chiral lattice with circular nodes. Thin-Walled Struct. 182, 110152. doi:10.1016/j.tws.2022.110152
Park, C. M., and Lee, S. H. (2019). Zero-reflection acoustic metamaterial with a negative refractive index. Sci. Rep. 9, 3372. doi:10.1038/s41598-019-40184-7
Park, C. M., Park, J. J., Lee, S. H., Seo, Y. M., Kim, C. K., and Lee, S. H. (2011). Amplification of acoustic evanescent waves using metamaterial slabs. Phys. Rev. Lett. 107, 194301. doi:10.1103/PhysRevLett.107.194301
Pendry, J. B., Holden, A. J., Robbins, D. J., and Stewart, W. J. (1999). Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 47, 2075–2084. doi:10.1109/22.798002
Plewa, J., Płońska, M., and Junak, G. (2023). Auxetic behaviour of rigid connected squares. Materials 16, 5306. doi:10.3390/ma16155306
Prall, D., and Lakes, R. S. (1997). Properties of a chiral honeycomb with a Poisson’s ratio of - 1. Int. J. Mech. Sci. 39, 305–314. doi:10.1016/s0020-7403(96)00025-2
Pyskir, A., Collet, M., Dimitrijevic, Z., and Lamarque, C.-H., 2019. Numerical optimization of a prestressed auxetic metamaterial for vibration isolation.
Pyskir, A., Collet, M., Dimitrijevic, Z., and Lamarque, C. H. (2021). Enhanced vibration isolation with prestressed resonant auxetic metamaterial. Materials 14, 6743. doi:10.3390/ma14226743
Qi, C., Jiang, F., Remennikov, A., Pei, L. Z., Liu, J., Wang, J. S., et al. (2020). Quasi-static crushing behavior of novel re-entrant circular auxetic honeycombs. Compos B Eng. 197, 108117. doi:10.1016/j.compositesb.2020.108117
Qi, D., Yu, H., Hu, W., He, C., Wu, W., and Ma, Y. (2019). Bandgap and wave attenuation mechanisms of innovative reentrant and anti-chiral hybrid auxetic metastructure. Extreme Mech. Lett. 28, 58–68. doi:10.1016/j.eml.2019.02.005
Qin, H., and Yang, D. (2019). Vibration reduction design method of metamaterials with negative Poisson’s ratio. J. Mater Sci. 54, 14038–14054. doi:10.1007/s10853-019-03903-z
Sadegh Ebrahimi, M., Hashemi, R., and Etemadi, E. (2022). In-plane energy absorption characteristics and mechanical properties of 3D printed novel hybrid cellular structures. J. Mater. Res. Technol. 20, 3616–3632. doi:10.1016/j.jmrt.2022.08.064
Sahariah, B. J., Namdeo, A., and Khanikar, P. (2022). Composite-inspired multilattice metamaterial structure: an auxetic lattice design with improved strength and energy absorption. Mater Today Commun. 30, 103159. doi:10.1016/j.mtcomm.2022.103159
Seetoh, I. P., Liu, X., Markandan, K., Zhen, L., and Lai, C. Q. (2021). Strength and energy absorption characteristics of Ti6Al4V auxetic 3D anti-tetrachiral metamaterials. Mech. Mater. 156, 103811. doi:10.1016/j.mechmat.2021.103811
Shen, J., Liu, K., Zeng, Q., Ge, J., Dong, Z., and Liang, J. (2021). Design and mechanical property studies of 3D re-entrant lattice auxetic structure. Aerosp. Sci. Technol. 118, 106998. doi:10.1016/j.ast.2021.106998
Shin, D., Urzhumov, Y., Jung, Y., Kang, G., Baek, S., Choi, M., et al. (2012). Broadband electromagnetic cloaking with smart metamaterials. Nat. Commun. 3, 1213. doi:10.1038/ncomms2219
Smith, D. R., Padilla, W. J., Vier, D. C., Nemat-Nasser, S. C., and Schultz, S. (2000). Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84, 4184–4187. doi:10.1103/physrevlett.84.4184
Smith, D. R., Pendry, J. B., and Wiltshire, M. C. K. (2004). Metamaterials and negative refractive index. Sci. (1979) 305, 788–792. doi:10.1126/science.1096796
Tachi, T. (2013). Designing freeform origami tessellations by generalizing resch’s patterns. J. Mech. Des. 135. doi:10.1115/1.4025389
Tan, H. L., He, Z. C., Li, E., Tan, X. W., Cheng, A. G., and Li, Q. Q. (2020). Energy absorption characteristics of three-layered sandwich panels with graded re-entrant hierarchical honeycombs cores. Aerosp. Sci. Technol. 106, 106073. doi:10.1016/j.ast.2020.106073
Tang, Y., and Yin, J. (2017). Design of cut unit geometry in hierarchical kirigami-based auxetic metamaterials for high stretchability and compressibility. Extreme Mech. Lett. 12, 77–85. doi:10.1016/j.eml.2016.07.005
Tao, Z., Ren, X., Sun, L., Zhang, Y., Jiang, W., Zhao, A. G., et al. (2022). A novel re-entrant honeycomb metamaterial with tunable bandgap. Smart Mater Struct. 31, 095024. doi:10.1088/1361-665x/ac812b
Teng, X. C., Ren, X., Zhang, Y., Jiang, W., Pan, Y., Zhang, X. G., et al. (2022). A simple 3D re-entrant auxetic metamaterial with enhanced energy absorption. Int. J. Mech. Sci. 229, 107524. doi:10.1016/j.ijmecsci.2022.107524
Theocaris, P. S., Stavroulakis, G. E., and Panagiotopoulos, P. D. (1997). Negative Poisson’s ratios in composites with star-shaped inclusions: a numerical homogenization approach. Archive Appl. Mech. (Ingenieur Archiv) 67, 274–286. doi:10.1007/s004190050117
Usta, F., Scarpa, F., Türkmen, H. S., Johnson, P., Perriman, A. W., and Chen, Y. (2021a). Multiphase lattice metamaterials with enhanced mechanical performance. Smart Mater Struct. 30, 025014. doi:10.1088/1361-665X/abd15d
Usta, F., Türkmen, H. S., and Scarpa, F. (2021b). Low-velocity impact resistance of composite sandwich panels with various types of auxetic and non-auxetic core structures. Thin-Walled Struct. 163, 107738. doi:10.1016/j.tws.2021.107738
Veselago, V.-G. (1968). THE ELECTRODYNAMICS OF SUBSTANCES WITH SIMULTANEOUSLY NEGATIVE VALUES OF ɛ AND μ. Sov. Phys. Uspekhi 10 (4), 509–514. doi:10.1070/pu1968v010n04abeh003699
Wang, J., Allein, F., Boechler, N., Friend, J., and Vazquez-Mena, O. (2021). Design and fabrication of negative-refractive-index metamaterial unit cells for near-megahertz enhanced acoustic transmission in biomedical ultrasound applications. Phys. Rev. Appl. 15, 024025. doi:10.1103/PhysRevApplied.15.024025
Wang, Q., Li, Z., Zhang, Y., Cui, S., Yang, Z., and Lu, Z. (2020c). Ultra-low density architectured metamaterial with superior mechanical properties and energy absorption capability. Compos B Eng. 202, 108379. doi:10.1016/j.compositesb.2020.108379
Wang, S., Deng, C., Ojo, O., Akinrinlola, B., Kozub, J., and Wu, N. (2022). Design and modeling of a novel three dimensional auxetic reentrant honeycomb structure for energy absorption. Compos Struct. 280, 114882. doi:10.1016/j.compstruct.2021.114882
Wang, Y., Wang, C., and Tan, H. (2020a). Geometry-dependent stretchability and stiffness of ribbon kirigami based on large curvature curved beam model. Int. J. Solids Struct. 182 (183), 236–253. doi:10.1016/j.ijsolstr.2019.08.007
Wang, Z., Luan, C., Liao, G., Liu, J., Yao, X., and Fu, J. (2020b). Progress in auxetic mechanical metamaterials: structures, characteristics, manufacturing methods, and applications. Adv. Eng. Mater 22. doi:10.1002/adem.202000312
Wei, C., and Jing, X. (2017). A comprehensive review on vibration energy harvesting: modelling and realization. Renew. Sustain. Energy Rev. 74, 1–18. doi:10.1016/j.rser.2017.01.073
Wei, Z., Hu, Z., Zhu, R., Chen, Y., and Hu, G. (2023). A transformable anisotropic 3D penta-mode metamaterial. Mater Des. 234, 112306. doi:10.1016/j.matdes.2023.112306
Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y., and Mahadevan, L. (2013). Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110, 215501. doi:10.1103/PhysRevLett.110.215501
Wu, W., Hu, W., Qian, G., Liao, H., Xu, X., and Berto, F. (2019). Mechanical design and multifunctional applications of chiral mechanical metamaterials: a review. Mater Des. 180, 107950. doi:10.1016/j.matdes.2019.107950
Wu, W., Song, X., Liang, J., Xia, R., Qian, G., and Fang, D. (2018). Mechanical properties of anti-tetrachiral auxetic stents. Compos Struct. 185, 381–392. doi:10.1016/j.compstruct.2017.11.048
Xiao, B., Liu, Y., Xu, W., Wei, R., Chen, M., and Jiang, H. (2024). A bistable honeycomb mechanical metamaterial with transformable Poisson’s ratio and tunable vibration isolation properties. Thin-Walled Struct. 198, 111718. doi:10.1016/j.tws.2024.111718
Xu, Y., Huang, H., Zhang, C., and Fu, R. (2024). Energy absorption behaviors of a novel buffer lander-leg with Yoshimura core. Chin. J. Aeronautics 37, 333–342. doi:10.1016/j.cja.2023.09.028
Yang, K., Rao, L., Hu, L., Pan, F., Yin, Q., and Chen, Y. (2023). Flexible, efficient and adaptive modular impact-resistant metamaterials. Int. J. Mech. Sci. 239, 107893. doi:10.1016/j.ijmecsci.2022.107893
Yang, M., Ma, G., Yang, Z., and Sheng, P. (2015a). Subwavelength perfect acoustic absorption in membrane-type metamaterials: a geometric perspective. EPJ Appl. Metamaterials 2, 10. doi:10.1051/epjam/2015017
Yang, M., Meng, C., Fu, C., Li, Y., Yang, Z., and Sheng, P. (2015b). Subwavelength total acoustic absorption with degenerate resonators. Appl. Phys. Lett. 107. doi:10.1063/1.4930944
Ye, M., Gao, L., Wang, F., and Li, H. (2021). A novel design method for energy absorption property of chiral mechanical metamaterials. Materials 14, 5386. doi:10.3390/ma14185386
Ye, S., Zhao, P., Zhao, Y., Kavousi, F., Feng, H., and Hao, G. (2022). A novel radially closable tubular origami structure (RC-ori) for valves. Actuators 11, 243. doi:10.3390/act11090243
Yu, X., Zhou, J., Liang, H., Jiang, Z., and Wu, L. (2018). Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review. Prog. Mater Sci. 94, 114–173. doi:10.1016/j.pmatsci.2017.12.003
Yu, Y., Yin, Y., Bai, R., Hu, Y., Li, B., Wang, M. Y., et al. (2023). Reprogrammable multistable ribbon kirigami with a wide cut. Appl. Phys. Lett. 123. doi:10.1063/5.0157978
Yuan, G., Rogers, K. S., Rogers, E. T. F., and Zheludev, N. I. (2019). Far-field superoscillatory metamaterial superlens. Phys. Rev. Appl. 11, 064016. doi:10.1103/PhysRevApplied.11.064016
Zhai, Z., Wang, Y., Lin, K., Wu, L., and Jiang, H. (2020). In situ stiffness manipulation using elegant curved origami. Sci. Adv. 6, eabe2000. doi:10.1126/sciadv.abe2000
Zhai, Z., Wu, L., and Jiang, H. (2021). Mechanical metamaterials based on origami and kirigami. Appl. Phys. Rev. 8. doi:10.1063/5.0051088
Zhang, J., and Ma, P. (2024). Energy absorption properties of a novel auxetic honeycomb based on deep learning technology. Acta Mech. 235, 4473–4488. doi:10.1007/s00707-024-03960-9
Zhang, K., Qi, L., Zhao, P., Zhao, C., and Deng, Z. (2023a). Buckling induced negative stiffness mechanical metamaterial for bandgap tuning. Compos Struct. 304, 116421. doi:10.1016/j.compstruct.2022.116421
Zhang, L., Bai, Z., and Chen, Y. (2022a). Dual-functional hierarchical mechanical metamaterial for vibration insulation and energy absorption. Eng. Struct. 271, 114916. doi:10.1016/j.engstruct.2022.114916
Zhang, L., Yang, D., Li, Q., and Qiu, J. (2024). Accessing quasi-static impact process by 3D-NPR corrugated metamaterials. Int. J. Mech. Sci. 274, 109310. doi:10.1016/j.ijmecsci.2024.109310
Zhang, W., Yin, S., Yu, T. X., and Xu, J. (2019a). Crushing resistance and energy absorption of pomelo peel inspired hierarchical honeycomb. Int. J. Impact Eng. 125, 163–172. doi:10.1016/j.ijimpeng.2018.11.014
Zhang, W., Zhao, S., Sun, R., Scarpa, F., and Wang, J. (2019b). In-plane mechanical behavior of a new star-re-entrant hierarchical metamaterial. Polym. (Basel) 11, 1132. doi:10.3390/polym11071132
Zhang, X., and Liu, Z. (2004). Negative refraction of acoustic waves in two-dimensional phononic crystals. Appl. Phys. Lett. 85, 341–343. doi:10.1063/1.1772854
Zhang, Y., Ren, X., Jiang, W., Han, D., Yu Zhang, X., Pan, Y., et al. (2022b). In-plane compressive properties of assembled auxetic chiral honeycomb composed of slotted wave plate. Mater Des. 221, 110956. doi:10.1016/j.matdes.2022.110956
Zhang, Y., Wang, L., Ding, Q., Han, H., Xu, J., Yan, H., et al. (2023b). Low-frequency property and vibration reduction design of chiral star-shaped compositive mechanical metamaterials. Mech. Adv. Mater. Struct. 30, 3749–3763. doi:10.1080/15376494.2022.2081751
Zhao, P., Zhang, K., Qi, L., and Deng, Z. (2022). 3D chiral mechanical metamaterial for tailored band gap and manipulation of vibration isolation. Mech. Syst. Signal Process 180, 109430. doi:10.1016/j.ymssp.2022.109430
Zhao, X., Wei, L., Wen, D., Zhu, G., Yu, Q., and Ma, Z. D. (2021). Bending response and energy absorption of sandwich beams with novel auxetic honeycomb core. Eng. Struct. 247, 113204. doi:10.1016/j.engstruct.2021.113204
Zhou, X., Zang, S., and You, Z. (2016). Origami mechanical metamaterials based on the Miura-derivative fold patterns. Proc. R. Soc. A Math. Phys. Eng. Sci. 472, 20160361. doi:10.1098/rspa.2016.0361
Zhu, D., Huang, X., Hua, H., and Zheng, H. (2016). Vibration isolation characteristics of finite periodic tetra-chiral lattice coating filled with internal resonators. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 230, 2840–2850. doi:10.1177/0954406215602913
Zhuang, Y., Li, Q., Yang, D., and Geng, X. (2024). Vibration suppression of power cabin for underwater vehicle based on mechanical metamaterial flanges. Ocean. Eng. 310, 118540. doi:10.1016/j.oceaneng.2024.118540
Keywords: mechanical metamaterial, negative Poisson’s ratio, vibration isolation, energy absorption, vibration reduction
Citation: Siniauskaya V, Wang H, Liu Y, Chen Y, Zhuravkov M and Lyu Y (2024) A review on the auxetic mechanical metamaterials and their applications in the field of applied engineering. Front. Mater. 11:1453905. doi: 10.3389/fmats.2024.1453905
Received: 24 June 2024; Accepted: 26 July 2024;
Published: 06 August 2024.
Edited by:
Fuyin Ma, Xi’an Jiaotong University, ChinaReviewed by:
Zhendong Li, Central South University, ChinaDeqing Yang, Shanghai Jiao Tong University, China
Copyright © 2024 Siniauskaya, Wang, Liu, Chen, Zhuravkov and Lyu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yadong Liu, ZG9jdG9yeWFkb25nQDE2My5jb20=; Yongtao Lyu, eW9uZ3Rhb2x1QGRsdXQuZWR1LmNu
 Volha Siniauskaya
Volha Siniauskaya Hao Wang
Hao Wang Yadong Liu
Yadong Liu Yuhang Chen
Yuhang Chen Michael Zhuravkov5
Michael Zhuravkov5 Yongtao Lyu
Yongtao Lyu