- 1Paul Scherrer Institute, Center for Photon Science, Villigen, Switzerland
- 2Paul Scherrer Institute, Center for Neutron and Muon Sciences, Villigen, Switzerland
Frustrated magnets with ordered magnetic spiral phases that spontaneously break inversion symmetry have received significant attention from both fundamental and applied sciences communities due to the experimental demonstration that some of these materials can couple to the lattice and induce electric polarization. In these materials, the common origin of the electric and magnetic orders guarantees substantial coupling between them, which is highly desirable for applications. However, their low-magnetic ordering temperatures (typically
1 Introduction
The spiral is a common pattern in nature and can be found in items as diverse as snail shells, pea tendrils, galaxies, and DNA. One of the distinctive characteristics of spirals is the presence of chirality, a term introduced by Lord Kelvin for describing objects that cannot be superimposed on their mirror image (Thomson, 1894; Kelvin, 1904). Chirality is of enormous importance in biology, chemistry, and physics (Wagnière, 2007; Lee and Yang, 1956; Lee et al., 1957; Balents and Fisher, 1996; Emori et al., 2013; Everschor-Sitte et al., 2018; Taguchi et al., 2001; Tokura et al., 2014), with various definitions used across different (sub)disciplines (Simonet et al., 2012; Fecher et al., 2022; Cheong and Xu, 2022). In the context of spin networks, which includes the magnetic spirals discussed in this mini-review, the word chirality is usually employed as a synonym of helicity, a vector quantity (
2 Status and challenges for magnetoelectric magnetic spirals
For a large number of insulating spiral magnets, the generation of polarization is believed to originate from spin-orbit (SO) splitting on the magnetic ions (Katsura et al., 2005; Mostovoy, 2006; Sergienko and Dagotto, 2006); this exchange coupling can result in polar charge displacements when the magnetic order exhibits non-vanishing torques
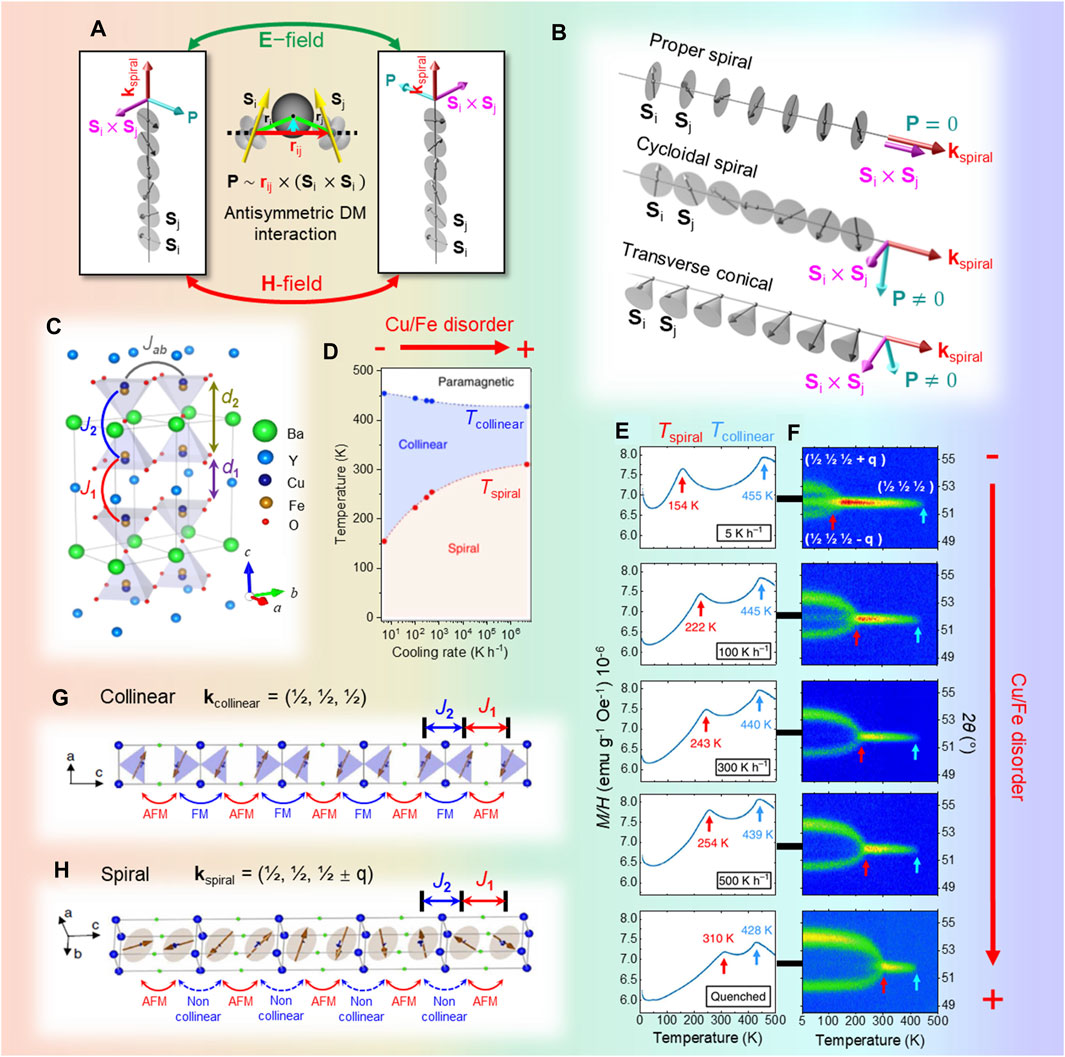
Figure 1. (A) Illustration of the coupling between magnetic chirality and electrical polarization driven by the antisymmetric Dzyaloshinskii–Moriya (DM) interaction under electric
Despite their promising multifunctionalities, three main shortcomings have hindered the implementation of magnetic spirals able to create polarization (henceforth magnetoelectric spirals) in real devices. One of them is that they do not have a net magnetization M, a characteristic that makes the magnetic detection of the spiral rotation sense, directly related to P, more difficult than the M sense in ferromagnets. A more favorable situation is found in transverse conical cycloids, characterized by a ferromagnetic (FM) component perpendicular to the cycloid rotation plane that guarantees the simultaneous presence of spontaneous M and P (Figure 1B) (Yamasaki et al., 2006; White et al., 2012). Unfortunately, conical magnets are often not stable in the absence of a magnetic field (Murakawa et al., 2008; Kitagawa et al., 2010; Ramakrishnan et al., 2019). Another important drawback is the low polarization values reported for ME spirals, typically far below 1
3 Stabilizing magnetic spirals far beyond RT
3.1 Chemical disorder as a tool for
Recently, an unexpected knob for controlling both the ordering temperature and periodicity of a magnetic spiral has emerged: chemical disorder. The positive impact of this variable on
To understand this surprising behavior, it is worth mentioning that the magnetic order expected from the Goodenough–Kanamori–Anderson (GKA) superexchange rules, consistent with the NN exchanges calculated using density functional theory (DFT) (Morin et al., 2015), is not a spiral but a collinear antiferromagnetic (AFM) arrangement described by the propagation vector
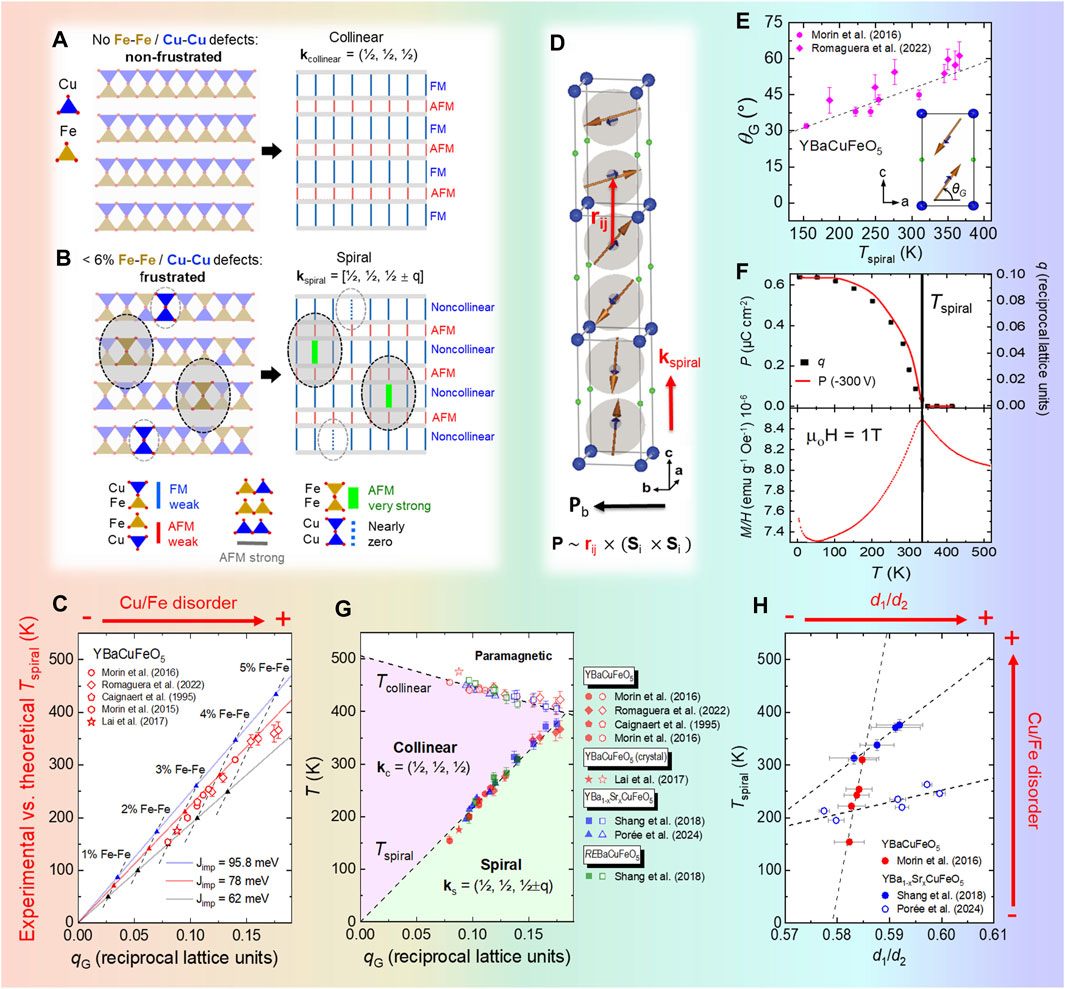
Figure 2. (A, B) Scheme of Cu/Fe disorder’s impact on the magnetic order in YBaCuFeO5. Perfect Cu/Fe order (A) leads to collinear AFM order, while introducing AFM Fe–Fe “defects” (B) leads to frustrated exchanges, causing spiral order. (C) Linear correlation between
The emergence of a stable spiral phase in a material without any obvious source of magnetic frustration and the huge, positive impact of the Cu/Fe chemical disorder on the spiral ordering temperature were both puzzling and difficult to conciliate with traditional magnetic frustration mechanisms. Interestingly, both observations could be recently rationalized in terms of a novel, disorder-based frustration mechanism based on the gigantic impact of a few Fe–Fe “defects” occupying the bipyramidal units (Scaramucci et al. (2018, 2020)). Such defects are energetically very expensive, but their presence in small amounts (together with the same number of Cu–Cu defects to preserve electric neutrality) cannot be disregarded in real samples, in particular in those with large amounts of Cu/Fe disorder (Figures 2A, B). As mentioned previously, the bipyramidal units are preferentially occupied by Cu–Fe pairs, whose NN exchange
Within this model, both
An important question, not addressed by this theoretical model, is the relationship between
3.2 Adding A-cation substitutions
Although reaching high
A particularly interesting characteristic of the two spiral tuning mechanisms described in the previous sections—Cu/Fe disorder and
As shown in Figures 1D, E, the increase in
3.3 Adding B-cation substitutions
Although 400 K is a value comfortably far from RT, a relevant question is whether magnetic spirals with higher
In the case of B-cation substitutions with a 1:1 B:B′ ratio, much easier to model theoretically than solid solutions, the theory developed by Scaramucci and co-workers provides some guidelines for material design. In addition to respecting electric neutrality, BB’-cation pair candidates should have comparable sizes in order to promote the presence of B-site disorder and display affinity for the square-pyramidal coordination. They should also comply with the premises of the random magnetic exchanges model, which requires having a single direction with weak, alternating FM and AFM exchanges, along with the experimental possibility of replacing the weak FM bonds with a small amount of strongly frustrating AFM defects. This scenario is realized in AA’CuFeO5 layered perovskites, where the exchanges are very strong in the ab plane, weak FM
4 Next steps and perspectives
4.1 Polarization, magnetization, and magnetoelectric coupling
Despite the huge progress in
Although AA’CuFeO5-layered perovskites were believed to be purely AFM, the recent report of weak ferromagnetism (WFM) in YBaCuFeO5 ceramic samples coexisting with the spiral modulation suggests that the ground-state magnetic order of these materials could be conical (Lyu et al., 2022). Since the measurements were performed on ceramic samples, the direction of the WFM component and its degree of coupling with the cycloid orientation, directly linked to P, are unknown. However, its appearance precisely at the onset of the spiral magnetic order strongly suggests the existence of some type of coupling between the spiral and WFM components. As ferromagnets respond strongly to external magnetic fields, this observation is extremely interesting because it could facilitate the detection and manipulation of the spiral rotation plane—and hence the polarization direction—with magnetic fields.
4.2 Beyond layered perovskites
The disorder-based local magnetic frustration mechanism proposed by Scaramucci and co-workers was initially developed for the layered perovskite YBaCuFeO5. However, it could, with some modifications, also be relevant for other materials with different crystal structures. Possible material candidates could be identified among frustrated magnets with chemical disorders and incommensurate spiral phases stable up to medium-to-high temperatures whose origin is not understood. The hexaferrite
5 Concluding remarks
To conclude, we believe that the results summarized in this mini-review will be of interest to the community interested in magnetoelectric material research. On one side, they demonstrate that magnetic spirals, a class of magnetic textures rarely stable above 100 K, where the magnetoelectric coupling can be very strong, can be engineered in AA’CuFeO5-layered perovskites in such a way that they survive up to 400 K, i.e., safely far from RT. On the other hand, they provide a theoretical framework that rationalizes these experimental findings and a set of empirical rules to tune the spiral ordering temperature that can be used for the design of other materials with improved functional properties. This eliminates one of the main obstacles to the integration of spiral magnets in real-life devices and suggests that technological applications based on magnetoelectric spirals could become reality in the not-too-distant future.
Author contributions
AR: conceptualization, visualization, writing–original draft, and writing–review and editing. MM: conceptualization, supervision, writing–original draft, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The previous work of the authors reported in this mini-review was supported by the following funding agencies: AR: Spanish Ministerio de Ciencia, Innovación y Universidades (project nos. MAT2015-68760-C2-2, RTI2018-098537-B-C21, PID2021-124734OB-C22, and FPI grant no. PRE2018-084769, co-funded by ERDF (from EU)), and Severo Ochoa Program for Centers of Excellence in R
Acknowledgments
The previous work of the authors reported in this mini-review benefited from fruitful discussions with A. Scaramucci, M. Müller, Ch. Mudry, N. Spaldin, M. Morin, T. Shang, V. Poree, E. Razzoli, H. Ueda, M. Ciomaga-Hatnean, J.L. García-Muñoz, and J. Herrero-Martín. The authors also acknowledge the allocation of beam time at several neutron and synchrotron X-ray large-scale facilities: SINQ and SLS (Villigen, Switzerland); ILL (Grenoble, France); Alba (Bellaterra, Spain), which was crucial for the above-mentioned work.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arkenbout, A. H., Palstra, T. T. M., Siegrist, T., and Kimura, T. (2006). Ferroelectricity in the cycloidal spiral magnetic phase of MnWO4. Phys. Rev. B 74, 184431–184438. doi:10.1103/PhysRevB.74.184431
Atanassova, Y., Popov, V., Bogachev, G., Iliev, M., Mitros, C., Psycharis, V., et al. (1993). Raman-active and infrared-active phonons in YBaCuFeO5 - experiment and lattice dynamics. Phys. Rev. B 47, 15201–15207. doi:10.1103/PhysRevB.47.15201
Babkevich, P., Poole, A., Johnson, R. D., Roessli, B., Prabhakaran, D., and Boothroyd, A. T. (2012). Electric field control of chiral magnetic domains in the high-temperature multiferroic CuO. Phys. Rev. B 85, 134428–134433. doi:10.1103/PhysRevB.85.134428
Balents, L., and Fisher, M. A. (1996). Chiral surface states in the bulk quantum hall effect. Phys. Rev. Lett. 76, 2782–2785. doi:10.1103/PhysRevLett.76.2782
Cabrera, I., Kenzelmann, M., Lawes, G., Chen, Y., Chen, W. C., Erwin, R., et al. (2009). Coupled magnetic and ferroelectric domains in multiferroic ni3v2o8. Phys. Rev. Lett. 103, 087201–087204. doi:10.1103/PhysRevLett.103.087201
Caignaert, V., Mirebeau, I., Bourée, F., Nguyen, N., Ducouret, A., Greneche, J. M., et al. (1995). Crystal and magnetic structure of YBaCuFeO5. J. Solid State Chem. 114, 24–35. doi:10.1006/jssc.1995.1004
Cheong, S.-W., and Xu, X. (2022). Magnetic chirality. npj Quantum Mater. 7, 40–45. doi:10.1038/s41535-022-00447-5
Cox, D., Takei, W., and Shirane, G. (1963). A magnetic and neutron diffraction study of the cr2o3-fe2o3 system. J. Phys. Chem. Solids 24, 405–423. doi:10.1016/0022-3697(63)90199-9
Dey, D., Nandy, S., Maitra, T., Yadav, C., and Taraphder, A. (2018). Nature of spiral state and absence of electric polarisation in sr-doped YBaCuFeO5 revealed by first-principle study. Sci. Rep. 8, 2404–2412. doi:10.1038/s41598-018-20774-7
Diko, P., Duvignaud, P., Lanckbeen, A., Van Moer, A., Naessens, G., and Deltour, R. (1993). Influence of iron doping on the microstructure of YBa2(Cu1−xFex)3O7−δ ceramics. J. Am. Ceram. Soc. 76, 2859–2864. doi:10.1111/j.1151-2916.1993.tb04027.x
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E., and Beach, G. S. D. (2013). Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Matter. 12, 611–616. doi:10.1038/NMAT3675
Er-Rakho, L., Michel, C., Lacorre, P., and Raveau, B. (1988). YBaCuFeO5+δ: a novel oxygen-deficient perovskite with a layer structure. J. Solid State Chem. 73, 531–535. doi:10.1016/0022-4596(88)90141-7
Everschor-Sitte, K., Masell, J., Reeve, R. M., and Kläui, M. (2018). Perspective: magnetic skyrmions—overview of recent progress in an active research field. J. Appl. Phys. 124, 240901–240918. doi:10.1063/1.5048972
Fecher, G., Kübler, J., and Felser, C. (2022). Chirality in the solid state: chiral crystal structures in chiral and achiral space groups. Materials 15, 5812–5844. doi:10.3390/ma15175812
Fiebig, M., Lottermoser, T., Meier, D., and Trassin, M. (2016). The evolution of multiferroics. Nat. Rev. Mater. 1, 16046–16060. doi:10.1038/natrevmats.2016.46
Finger, T., Senff, D., Schmalzl, K., Schmidt, W., Regnault, L. P., Becker, P., et al. (2010). Electric-field control of the chiral magnetism of multiferroic MnWO4 as seen via polarized neutron diffraction. Phys. Rev. B 81, 054430–054435. doi:10.1103/PhysRevB.81.054430
Johnson, R. D., Chapon, L. C., Khalyavin, D. D., Manuel, P., Radaelli, P. G., and Martin, C. (2012). Giant improper ferroelectricity in the ferroaxial magnet CaMn7O12. Phys. Rev. Lett. 108, 067201–067205. doi:10.1103/PhysRevLett.108.067201
Katsura, H., Nagaosa, N., and Balatsky, A. V. (2005). Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 95, 057205. doi:10.1103/PhysRevLett.95.057205
Kawamura, Y., Kai, T., Satomi, E., Yasui, Y., Kobayashi, Y., Sato, M., et al. (2010). High-temperature multiferroic state of RBaCuFeO5 (R = Y, Lu, and Tm). J. Phys. Soc. Jpn. 79, 073705. doi:10.1143/JPSJ.79.073705
Kelvin, L. (1904). Baltimore lectures on molecular dynamics and wave theory of light. Warehouse, London, UK: C. J. Clay and Sons, Cambridge University Press.
Kimura, T. (2007). Spiral magnets as magnetoelectrics. Annu. Rev. Mater. Res. 37, 387–413. doi:10.1146/annurev.matsci.37.052506.084259
Kimura, T. (2012). Magnetoelectric hexaferrites. Annu. Rev. Condens. Matter Phys. 3, 93–110. doi:10.1146/annurev-conmatphys-020911-125101
Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T.-h., and Tokura, Y. (2003). Magnetic control of ferroelectric polarization. Nature 426, 55–58. doi:10.1038/nature02018
Kimura, T., Lashley, J. C., and Ramirez, A. P. (2006). Inversion-symmetry breaking in the noncollinear magnetic phase of the triangular-lattice antiferromagnet CuFeO2. Phys. Rev. B 73, 220401. doi:10.1103/PhysRevB.73.220401
Kimura, T., Lawes, G., Goto, T., Tokura, Y., and Ramirez, A. P. (2005). Magnetoelectric phase diagrams of orthorhombic rMnO3 (r = gd, tb, and dy). Phys. Rev. B 71, 224425. doi:10.1103/PhysRevB.71.224425
Kimura, T., Sekio, Y., Nakamura, H., Siegrist, T., and Ramirez, A. P. (2008). Cupric oxide as an induced-multiferroic with high-TC. Nature Mater. 7, 291–294. doi:10.1038/nmat2125
Kitagawa, Y., Hiraoka, Y., Honda, T., Ishikura, T., Nakamura, H., and Kimura, T. (2010). Low-field magnetoelectric effect at room temperature. Nat. Mater. 9, 797–802. doi:10.1038/nmat2826
Klyndyuk, A. I., and Chizhova, E. A. (2006). Properties of RBaCuFeO5+δ (R = Y, La, Pr, Nd, Sm-Lu). Inorg. Mater 42, 550–561. doi:10.1134/S0020168506050189
Kundys, B., Maignan, A., and Simon, C. (2009). Multiferroicity with high in ceramics of the YBaCuFeO5 ordered perovskite. Appl. Phys. Lett. 94, 072506. doi:10.1063/1.3086309
Kurumaji, T., Seki, S., Ishiwata, S., Murakawa, H., Kaneko, Y., and Tokura, Y. (2013). Magnetoelectric responses induced by domain rearrangement and spin structural change in triangular-lattice helimagnets NiI2 and CoI2. Phys. Rev. B 87, 014429. 014429–014437. doi:10.1103/PhysRevB.87.014429
Kurumaji, T., Seki, S., Ishiwata, S., Murakawa, H., Tokunaga, Y., Kaneko, Y., et al. (2011). Magnetic-field induced competition of two multiferroic orders in a triangular-lattice helimagnet MnI2. Phys. Rev. Lett. 106, 167206–167209. doi:10.1103/PhysRevLett.106.167206
Lai, C.-H., Wang, C.-W., Wu, H.-C., Liang, Y.-H., Studer, A. J., Chen, W.-T., et al. (2024). Tunable magnetic structures in the helimagnet YBa(Cu2−xFex)2O5. Phys. Rev. Matter. 8, 054404. doi:10.1103/PhysRevMaterials.8.054404
Lai, Y.-C., Du, C.-H., Lai, C.-H., Liang, Y.-H., Wang, C.-W., Rule, K. C., et al. (2017). Magnetic ordering and dielectric relaxation in the double perovskite YBaCuFeO5. J. Phys. Condens. Matter 29, 145801. doi:10.1088/1361-648X/aa5708
Lai, Y.-C., Shu, G.-J., Chen, W.-T., Du, C.-H., and Chou, F.-C. (2015). Self-adjusted flux for the traveling solvent floating zone growth of YBaCuFeO5 crystal. J. Cryst. Growth 413, 100–104. doi:10.1016/j.jcrysgro.2014.12.020
Lawes, G., Harris, A. B., Kimura, T., Rogado, N., Cava, R. J., Aharony, A., et al. (2005). Magnetically driven ferroelectric order in ni3v2o8. Phys. Rev. Lett. 95, 087205–087208. doi:10.1103/PhysRevLett.95.087205
Lee, T., Oehme, R., and Yang, C. (1957). Remarks on possible noninvariance under time reversal and charge conjugation. Phys. Rev. B 106, 340–345. doi:10.1103/PhysRev.106.340
Lee, T., and Yang, C. (1956). Question of parity conservation in weak interactions. Phys. Rev. B 104, 254–258. doi:10.1103/PhysRev.104.254
Liang, X., Matyushov, A., Hayes, P., Schell, V., Dong, C., Chen, H., et al. (2021). Roadmap on magnetoelectric materials and devices. IEEE Trans. Magnetics 57, 1–57. doi:10.1109/TMAG.2021.3086635
Luo, S., and Wang, K. (2018). Giant dielectric permittivity and magneto-capacitance effect in YBaCuFeO5. Scr. Mater. 146, 160–163. doi:10.1016/j.scriptamat.2017.11.032
Lyu, J., Morin, M., Shang, T., Fernández-Díaz, M. T., and Medarde, M. (2022). Weak ferromagnetism linked to the high-temperature spiral phase of YBaCuFeO5. Phys. Rev. Res. 4, 023008. doi:10.1103/PhysRevResearch.4.023008
Marelli, E., Lyu, J., Morin, M., Leménager, M., Shang, T., Yüzbasi, N., et al. (2024). Cobalt-free layered perovskites RBaCuFeO5+δ (R = 4f lanthanide) as electrocatalysts for the oxygen evolution reaction. EES. Catal. 2, 335–350. doi:10.1039/D3EY00142C
Meyer, C., Hartmann-Boutron, F., Gros, Y., and Strobel, P. (1990). Mössbauer study of YBaCuFeO5+δ -site assignments of the metallic ions. Solid State Comm. 76, 163–168. doi:10.1016/0038-1098(90)90535-J
Mombru, A., Christides, C., Lappas, A., Prassides, K., Pissas, M., Mittros, C., et al. (1994). Magnetic structure of the oxygen-deficient perovskite YBaCuFeO5+δ. Inorg. Chem. 33, 1255–1258. doi:10.1021/ic00085a008
Mombru, A., Prassides, K., Christides, C., Erwin, R., Pissas, M., Mitros, C., et al. (1998). Neutron powder diffraction study (T = 4.2-300 K) and polarization analysis of YBaCuFeO5+δ. J. Phys. Condes. Matter 10, 1247–1258. doi:10.1088/0953-8984/10/6/008
Momozawa, N., Yamaguchi, Y., Takei, H., and Mita, M. (1985). Magnetic structure of (Ba1−xSrx)2Zn2Fe12O22. J. Phys. Soc. Jpn. 54, 771–780. doi:10.1143/JPSJ.54.771
Morin, M., Canévet, E., Raynaud, A., Bartkowiak, M., Sheptyakov, D., Ban, V., et al. (2016). Tuning magnetic spirals beyond room temperature with chemical disorder. Nat. Commun. 7, 13758–13764. doi:10.1038/ncomms13758
Morin, M., Scaramucci, A., Bartkowiak, M., Pomjakushina, E., Deng, G., Sheptyakov, D., et al. (2015). Incommensurate magnetic structure, Fe/Cu chemical disorder, and magnetic interactions in the high-temperature multiferroic YBaCuFeO5. Phys. Rev. B 91, 064408. doi:10.1103/PhysRevB.91.064408
Mostovoy, M. (2006). Ferroelectricity in spiral magnets. Phys. Rev. Lett. 96, 067601. doi:10.1103/PhysRevLett.96.067601
Mukherjee, S., Shimamoto, K., Windsor, Y. W., Ramakrishnan, M., Parchenko, S., Staub, U., et al. (2018). Multiferroic phase diagram of E-type RMnO3 films studied by neutron and x-ray diffraction. Phys. Rev. B 98, 174416. doi:10.1103/PhysRevB.98.174416
Murakawa, H., Onose, Y., Ohgushi, K., Ishiwata, S., and Tokura, Y. (2008). Generation of electric polarization with rotating magnetic field in helimagnet ZnCr2Se4. J. Phys. Soc. Jpn. 77, 043709. doi:10.1143/JPSJ.77.043709
Porée, V., Gawryluk, D., Shang, T., Rodríguez-Velamazán, J., Casati, N., Sheptyakov, D., et al. (2024) “YBa1−xSrxCuFeO5 layered perovskites: exploring the magnetic order beyond the paramagnetic-collinear-spiral triple point. doi:10.48550/arXiv.2402.04816
Ramakrishnan, M., Constable, E., Cano, A., Mostovoy, M., White, J., Gurung, N., et al. (2019). Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212. doi:10.1038/s41563-018-0275-2
Romaguera, A., Zhang, X., Fabelo, O., Fauth, F., Blasco, J., and García-Muñoz, J. (2022). Helimagnets by disorder: its role on the high-temperature magnetic spiral in the YBaCuFeO5 perovskite. Phys. Rev. Res. 4, 043188. doi:10.1103/PhysRevResearch.4.043188
Romaguera, A., Zhang, X., Fabelo, O., Fauth, F., Blasco, J., and García-Muñoz, J. (2023). Magnetic properties of highly ordered single crystals with layered YBaCuFeO5 structure. EPJ Web Conf. 286, 05005. doi:10.1051/epjconf/202328605005
Ruiz-Aragón, M. J., Morán, E., Amador, U., Martínez, J. L., Andersen, N. H., and Ehrenberg, H. (1998). Low-temperature magnetic structure of YBaCuFeO5 and the effect of partial substitution of yttrium by calcium. Phys. Rev. B 58, 6291–6297. doi:10.1103/PhysRevB.58.6291
Sando, D., Agbelele, A., Rahmedov, D., Liu, J., Rovillain, P., Toulouse, C., et al. (2013). Crafting the magnonic and spintronic response of BiFeO3 films by epitaxial strain. Nat. Mater. 12, 641–646. doi:10.1038/NMAT3629
Scaramucci, A., Shinaoka, H., Mostovoy, M. V., Lin, R., Mudry, C., and Müller, M. (2020). Spiral order from orientationally correlated random bonds in classical XY models. Phys. Rev. Res. 2, 013273. doi:10.1103/PhysRevResearch.2.013273
Scaramucci, A., Shinaoka, H., Mostovoy, M. V., Müller, M., Mudry, C., Troyer, M., et al. (2018). Multiferroic magnetic spirals induced by random magnetic exchanges. Phys. Rev. X 8, 011005. doi:10.1103/PhysRevX.8.011005
Scott, J. (2013). Room-temperature multiferroic magnetoelectrics. NPG Asia Mater. 5, e72. doi:10.1038/am.2013.58
Seki, S., Kurumaji, T., Ishiwata, S., Matsui, H., Murakawa, H., Tokunaga, Y., et al. (2010). Cupric chloride CuCl2 as an S =1/2 chain multiferroic. Phys. Rev. B 82, 064424. doi:10.1103/PhysRevB.82.064424
Seki, S., Yamasaki, Y., Soda, M., Matsuura, M., Hirota, K., and Tokura, Y. (2008). Correlation between spin helicity and an electric polarization vector in quantum-spin chain magnet LiCu2O2. Phys. Rev. Lett. 100, 127201. doi:10.1103/PhysRevLett.100.127201
Sergienko, I. A., and Dagotto, E. (2006). Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 73, 094434–094438. doi:10.1103/PhysRevB.73.094434
Shang, T., Canévet, E., Morin, M., Sheptyakov, D., Fernández-Díaz, M. T., Pomjakushina, E., et al. (2018). Design of magnetic spirals in layered perovskites: extending the stability range far beyond room temperature. Sci. Adv. 4, eaau6386. doi:10.1126/sciadv.aau6386
Sharma, M., and Maitra, T. (2023). Orbitally driven spin reorientation in Mn-doped YBaCuFeO5. J. Phys. Chem. Solids 181, 111494. doi:10.1016/j.jpcs.2023.111494
Simonet, V., Loire, M., and Ballou, R. (2012). Magnetic chirality as probed by neutron scattering. Eur. Phys. J. Spec. Top. 213, 5–36. doi:10.1140/epjst/e2012-01661-8
Spaldin, N. A., and Ramesh, R. (2019). Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212. doi:10.1038/s41563-018-0275-2
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N., and Tokura, Y. (2001). Spin chirality, berry phase, and anomalous hall effect in a frustrated ferromagnet. Science 291, 2573–2576. doi:10.1126/science.1058161
Taniguchi, K., Abe, N., Takenobu, T., Iwasa, Y., and Arima, T. (2006). Ferroelectric polarization flop in a frustrated magnet MnWO4 induced by a magnetic field. Phys. Rev. Lett. 97, 097203. 097203–097206. doi:10.1103/PhysRevLett.97.097203
Tokura, Y., Seki, S., and Nagaosa, N. (2014). Multiferroics of spin origin. Rep. Prog. Phys. 77, 076501. doi:10.1088/0034-4885/77/7/076501
Wagnière, G. (2007). On chirality and the universal asymmetry: reflections on image and mirror image. Zürich, CH: Wiley.
White, J. S., Honda, T., Kimura, K., Kimura, T., Niedermayer, C., Zaharko, O., et al. (2012). Coupling of magnetic and ferroelectric hysteresis by a multicomponent magnetic structure in Mn2GeO4. Phys. Rev. Lett. 108, 077204. doi:10.1103/PhysRevLett.108.077204
Yamasaki, Y., Miyasaka, S., Kaneko, Y., He, J.-P., Arima, T., and Tokura, Y. (2006). Magnetic reversal of the ferroelectric polarization in a multiferroic spinel oxide. Phys. Rev. Lett. 96, 207204. doi:10.1103/PhysRevLett.96.207204
Yasui, Y., Kihara, S., Ikeda, K., and Banshodani, T. (2024). Doping effect on magnetic properties of high-temperature multiferroic compound YBaCuFeO5. AIP Adv. 14. doi:10.1063/9.0000741
Zhang, X., Romaguera, A., Falbelo, O., Fauth, F., Herrero-Martín, J., and García-Muñoz, J. L. (2021). Tuning the tilting of the spiral plane by Mn doping in YBaCuFeO5 multiferroic. Acta Mater 206, 116608. doi:10.1016/j.actamat.2020.116608
Zhang, X., Romaguera, A., Sandiumenge, F., Fabelo, O., Blasco, J., Herrero-Martín, J., et al. (2022). Magnetic properties of a highly ordered single crystal of the layered perovskite YBaCuFe0.95Mn0.05O5. J. Magn. Magn. Mater. 551, 169165. doi:10.1016/j.jmmm.2022.169165
Keywords: layered perovskite, chemical disorder, frustrated magnetism, spiral magnetic order, magnetoelectric coupling
Citation: Romaguera A and Medarde M (2024) Room temperature magnetoelectric magnetic spirals by design. Front. Mater. 11:1448765. doi: 10.3389/fmats.2024.1448765
Received: 13 June 2024; Accepted: 29 July 2024;
Published: 19 August 2024.
Edited by:
Nicole Benedek, Cornell University, United StatesReviewed by:
Kemp Plumb, Brown University, United StatesCopyright © 2024 Romaguera and Medarde. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arnau Romaguera, YXJuYXUucm9tYWd1ZXJhLWNhbXBzQHBzaS5jaA==; Marisa Medarde, bWFyaXNhLm1lZGFyZGVAcHNpLmNo
 Arnau Romaguera
Arnau Romaguera Marisa Medarde
Marisa Medarde