- School of Transportation Science and Engineering, Jilin Jianzhu University, Changchun, China
The aggregate gradation of asphalt mixture is one of the most important factors affecting the service life of asphalt pavement. In order to study the gradation of asphalt mixture with the best comprehensive performance, this study puts forward a new method of mineral aggregate gradation optimization based on the fuzzy analytic hierarchy process and comprehensive evaluation method, aiming at the multi-level and multi-index evaluation of the road performance of asphalt mixture. First, the orthogonal test design method is applied to design nine target gradations with coarse aggregate (>4.75 mm) and fine aggregate (<4.75 mm) of AC-20 (asphalt concrete) mixture serving as two factors and the upper, middle, and lower positions of the gradation curve as three levels, and then the road performance test research is carried out. Second, a comprehensive model for evaluation of road performance of mineral aggregate gradation is established. A fuzzy complementary judgment matrix is constructed, and the index weights of each level and the hierarchical total ranking weight are calculated. Then, the membership function is introduced into the comprehensive evaluation model for the road performance of mineral aggregate gradation, and the membership values of each index of asphalt mixture road performance are obtained. Finally, the fuzzy comprehensive evaluation method is used to find out the comprehensive evaluation value of the road performance of the nine graded asphalt mixtures, and the mineral aggregate gradation is optimized. The research results show that the 1# gradation of the asphalt mixture has the highest comprehensive road performance evaluation value, and the combination of the fuzzy hierarchical analysis process and comprehensive evaluation method can more objectively and comprehensively evaluate the comprehensive road performance of the asphalt mixture and provide a useful reference for the optimal selection of asphalt mixture mineral gradation.
1 Introduction
The performance of asphalt pavements will inevitably degrade gradually due to all the year round exposure to traffic loads and environmental factors (Chen et al., 2020). In addition, mineral aggregate gradation has an important influence on the tensile strength, fatigue resistance, deformation resistance at high temperature, crack resistance at low temperature, and water damage resistance of the asphalt mixture (Tayfur et al., 2007; Moghaddam et al., 2011; Li et al., 2020; Zhai, et al., 2019). Due to the wide gradation range of the specifications and the differences in climatic conditions and materials in each region, it is often impossible to completely apply the specification in gradation design. The orthogonal test design method deals with multi-factor tests, which can infer better test conditions through fewer test times and provide more comprehensive test results (Lu and Zhang, 2018). For the multi-index orthogonal test of asphalt mixture, the comprehensive scoring method and comprehensive balance method are often used to transform it into a single-index test problem for comprehensive optimization, and the results often lose comprehensiveness because of the differences in each index (Hu et al., 2021; Cheng et al., 2019).
In recent years, scholars around the world have used mathematics and machine algorithms to optimize mineral aggregate gradation. Pan et al. (2020) developed a gradation segregation model based on the fractal dimension to evaluate the variability of reclaimed asphalt pavement (RAP) gradation and then proposed an optimized gradation design method based on Mohr–Coulomb theory to reduce the variability of RAP gradation. Xue and Jiang (2022) used the discrete element method to obtain the interlock-coarse gradation of the AC-20 asphalt mixture and determined the interlock-dense gradation, and compared with the specific gradation, the Marshall stability, dynamic stability, shear strength, and splitting strength of the AC-20 asphalt mixture with interlocking dense gradation are all improved. Sivilevičius et al. (2011) constructed the models of constrained and unconstrained non-linear optimization to choose the best HMA mixture gradation. Sebaaly et al. (2018) developed simple multilayer perceptron structure artificial neural network (ANN) models and used a non-linear constrained genetic algorithm to call the ANN model to optimize the aggregate gradation of the asphalt mixture. Wang et al. (2021) proposed a gradation optimization method based on the fractal theory method and trial calculation method, and the gradation obtained by the two methods was simulated based on particle flow code in two dimension (PFC2D); the results showed that the asphalt mixture with optimized gradation based on the fractal theory method had higher strength and better stability. Most of these gradation optimization methods are based on the performance of the asphalt mixture, but the results obtained are different. In order to solve the problems encountered when using the conventional methods mentioned above, this article takes the AC-20 asphalt mixture as an example, uses the fuzzy analytic hierarchy process and fuzzy comprehensive evaluation method to fully characterize multiple factors and indicators of asphalt mixture road performance, conducts fuzzy comprehensive evaluation on the experimental results of asphalt mixture road performance of nine mineral aggregate gradations, and selects the mineral aggregate gradation with the best comprehensive performance.
Fuzzy analytic hierarchy process and fuzzy comprehensive evaluation, as fundamental fuzzy mathematical methods, have certain universality and scalability, and are widely used in various fields (Xu et al., 2023; Li et al., 2023; Arman, 2023). However, few studies have comprehensively applied the two methods to the optimization of asphalt mixture gradation. This paper proposes a mineral aggregate gradation optimization method that is suitable for the results of multi-index orthogonal experiments of asphalt mixtures by combining the fuzzy analytic hierarchy process and fuzzy comprehensive evaluation method. The application of fuzzy mathematical methods has established a theoretical foundation for the analysis of multi-index orthogonal test results of asphalt mixtures, enriching the multi-index evaluation system of asphalt mixtures. First, on the basis of completion of the road performance tests of asphalt mixture with nine mineral aggregate gradations designed by the orthogonal test, the road performance evaluation model of the asphalt mixture with mineral aggregate gradation is constructed. Second, by constructing the fuzzy complementary judgment matrix, consistency test, and calculating the index weights, the total ranking weight of the comprehensive evaluation index of aggregate gradation road performance is calculated. Finally, on the basis of completion of the evaluation object, evaluation index, membership function, and fuzzy comprehensive evaluation matrix, the fuzzy comprehensive evaluation values of nine mineral aggregate graded asphalt mixtures are calculated, the comprehensive road performance ranking is determined, and the best mineral aggregate gradation is presented.
2 Methodology
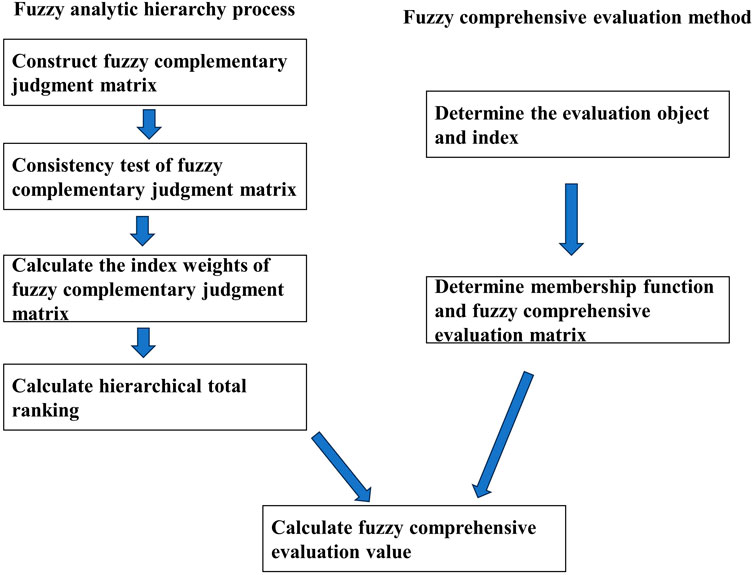
The method flow of this study is shown in Figure 1.
2.1 Fuzzy analytic hierarchy process
In the 1970s, Saaty T. L., an American expert in operational research, put forward a systematic decision analysis method combining qualitative and quantitative analyses, namely, the analytic hierarchy process (Saaty, 1990). However, the traditional analytic hierarchy process has some problems, such as difficulty in testing the consistency of the judgment matrix, the complexity of adjustment, and the lack of scientificity. Meanwhile, due to the uncertainty of human thinking, ignoring the fuzziness of human behavior may lead to mistakes in decision (Ahmed and Kilic, 2019; Jaganathan et al., 2007; Zhang et al., 2021). Therefore, in view of the fuzziness of the target to be evaluated, this paper introduces the fuzzy mathematical analysis method into the analytic hierarchy process and establishes a multi-level comprehensive evaluation model.
2.1.1 Establish hierarchical analytic structure model
The fuzzy analytic hierarchy process can be used to construct a multi-level hierarchical analytic structure model according to the different attributes of the problem to be evaluated. The basic principle is to decompose first and then synthesize, select some factors and indexes related to the target to be evaluated, and then construct a hierarchical analytic structure model according to the relative importance and affiliation between the factors and indexes (Han et al., 2020).
2.1.2 Construct fuzzy complementary judgment matrix
When the multi-level analytic structure model is established, for the factors or indexes of the same level, the target or factors of the previous level need to be used as a criterion for two comparisons, and the importance of the indexes can be assigned by the “0.1–0.9” comparison scale. A comparison scale
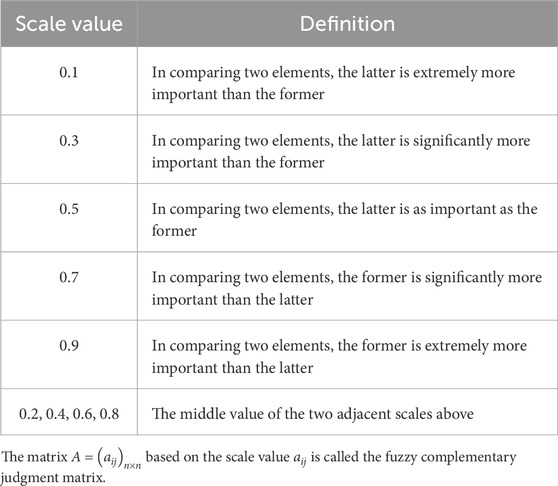
Table 1. Scale value and definition (Xie and Liu, 2006).
2.1.3 Consistency test of the fuzzy complementary judgment matrix
After constructing the fuzzy complementary judgment matrix, it is necessary to check its consistency, and if Equation 1 is not satisfied, the non-consistency matrix needs to be transformed into a new fuzzy consistency judgment matrix by Equation 2 (Xu, 2001).
where i = 1, 2, … , n; j = 1, 2, … , n; k = 1, 2, … , n.
2.1.4 Calculate the index weights of the fuzzy complementary judgment matrix
By comparing the relative importance between two elements, the fuzzy complementary judgment matrix
where i = 1, 2, … , n; j = 1, 2, … , n.
2.1.5 Calculate hierarchical total ranking
Assume that there are K layers in an evaluation index system and in order to determine the ranking weight of each element in the Kth layer corresponding to the relative importance of the target layer, it is necessary to multiply the weight of each element layer by layer, as shown in Equation 4.
2.2 Fuzzy comprehensive evaluation method
2.2.1 Determine the evaluation object and index
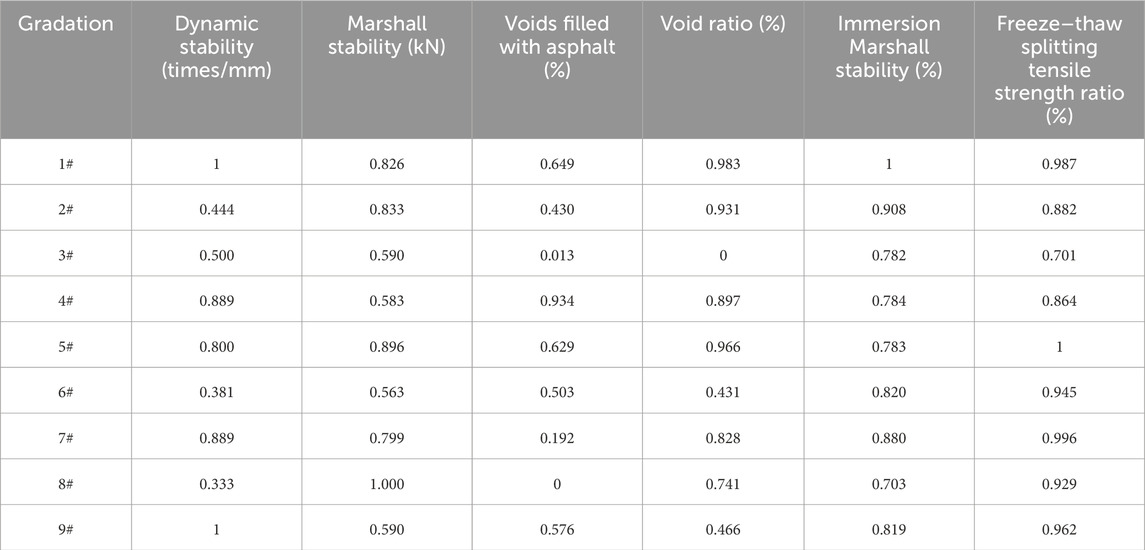
In order to evaluate the comprehensive road performance of the AC-20 asphalt mixture, it is necessary to determine the evaluation object and evaluation index of the evaluation model first. The road performance test results of nine mineral aggregate gradations are taken as the evaluation object, and the evaluation index set is composed of six indexes, namely, dynamic stability, Marshall stability, voids filled with asphalt, void ratio, immersion Marshall stability, and freeze–thaw splitting tensile strength ratio.
2.2.2 Determine membership function and fuzzy comprehensive evaluation matrix
Since different evaluation indexes have different representational meanings and dimensions, if the indexes are to be comparable with each other, the indexes can be standardized. According to the Technical Specification for Construction of Highway Asphalt Pavements (JTG F40-2004, 2004) of China, the evaluation index properties can be divided into maximal, intermediate, and minimal indexes. The Marshall stability is not less than 8 kN, the dynamic stability is not less than 2,400 times/mm, the immersion Marshall stability is not less than 85%, and the freeze–thaw splitting tensile strength ratio must be at least 80%: these four indexes can be regarded as maximum indexes. The recommended range of void ratio is 3%–6%, and that of effective asphalt saturation is 55%–70%, which can be regarded as intermediate indexes.
Dynamic stability, Marshall stability, immersion Marshall stability, and freeze–thaw splitting tensile strength ratio are all maximum indexes, and the membership function is shown in Equation 5.
Void ratio and voids filled with asphalt are intermediate indexes, and their membership function is shown in Equation 6.
where i = 1, 2, … , 9; j = 1, 2, … , 6; k is the middle value of the recommended range in the specification (JTG F40-2004, 2004).
Through the above membership function equation to obtain the membership value of each evaluation index for the road performance, the fuzzy comprehensive evaluation matrix R can be established.
2.2.3 Calculate fuzzy comprehensive evaluation value
According to the fuzzy comprehensive evaluation matrix and the hierarchical total ranking weight, the fuzzy comprehensive evaluation value F can be determined, as shown in the following equation.
3 Engineering example
3.1 Raw material test
The Jicao Expressway is located in the transitional zone from the hinterland of Changbai Mountain in central and southern Jilin Province to the Songnen Plain. It belongs to a seasonal frozen soil area, and the road surface damage caused by repeated freeze–thaw cycles is severe, requiring high road performance. The Jicao Expressway used the modified AC-20 asphalt mixture as the middle layer material of asphalt pavement, coarse aggregate and fine aggregate were used as andesite, and the filler was andesite mineral powder. The technical performance test results of raw materials are shown in Tables 2, 3.
3.2 Design and synthesis of mineral aggregate gradation
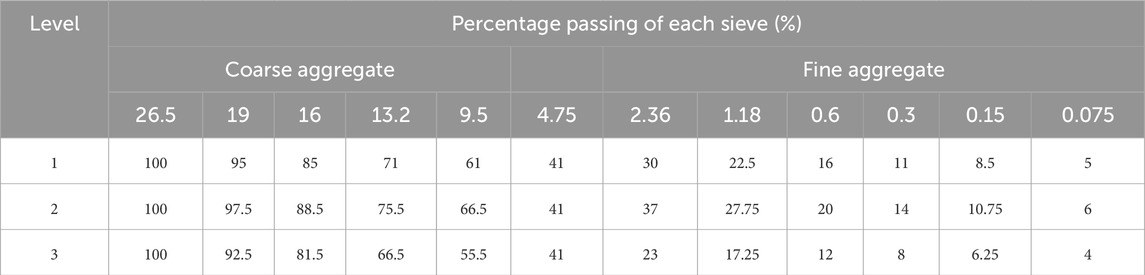
In this paper, within the range of gradation given in the specification (JTG F40-2004, 2004), the 4.75-mm sieve is used as the dividing sieve, and coarse aggregate (>4.75 mm) and fine aggregate (<4.75 mm) are two factors affecting the road performance of asphalt mixture, and each factor selects three levels, namely, middle, upper, and lower positions of the gradation curve, with the middle position being the middle value of the gradation range, the upper position being the bisector of the upper limit and middle of the gradation range, and the lower position being the bisector of the middle and the lower limit of the gradation range, as shown in Table 4. For two factors and three levels, nine initial design gradations were obtained by using the L9 (34) orthogonal table (Zhu, 2010), and then the synthetic gradations were calculated according to the design gradations and aggregate sieving results, as shown in Table 5.
According to the Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering (JTG, E20-2011, 2011) of China, the density test (T 0706-2011) and Marshall stability test (T 0709-2011) of the asphalt mixture composed of nine synthetic gradations were carried out. The test results showed that the best oil–stone ratio of asphalt mixture specimens of nine gradations was close to 5.3%. Therefore, in order to avoid the influence of oil–stone ratio factor on the road performance of the asphalt mixture, the oil–stone ratio of nine gradations was taken as 5.3%. Under the optimal oil–stone ratio conditions, Marshall stability and immersion Marshall test (T 0709-2011), rutting test (T 0719-2011), and freeze–thaw splitting test (T 0729-2011) were carried out according to specification (JTG, E20-2011, 2011), and the test results of asphalt mixture road performance indexes were obtained as shown in Table 6.
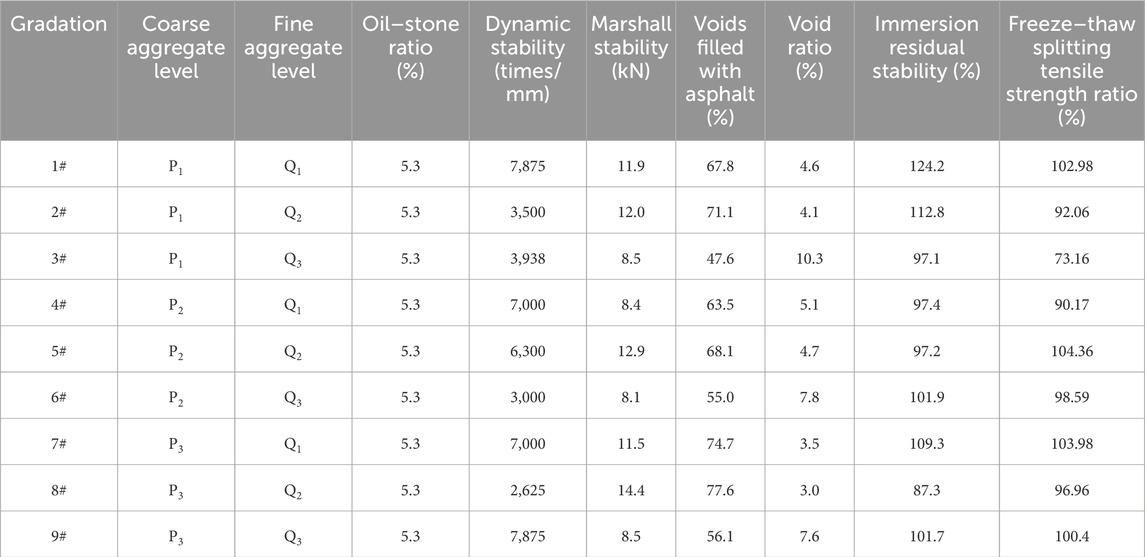
Table 6. Road performance test results of AC-20 (Zhu, 2010).
3.3 Establish the comprehensive evaluation model for road performance
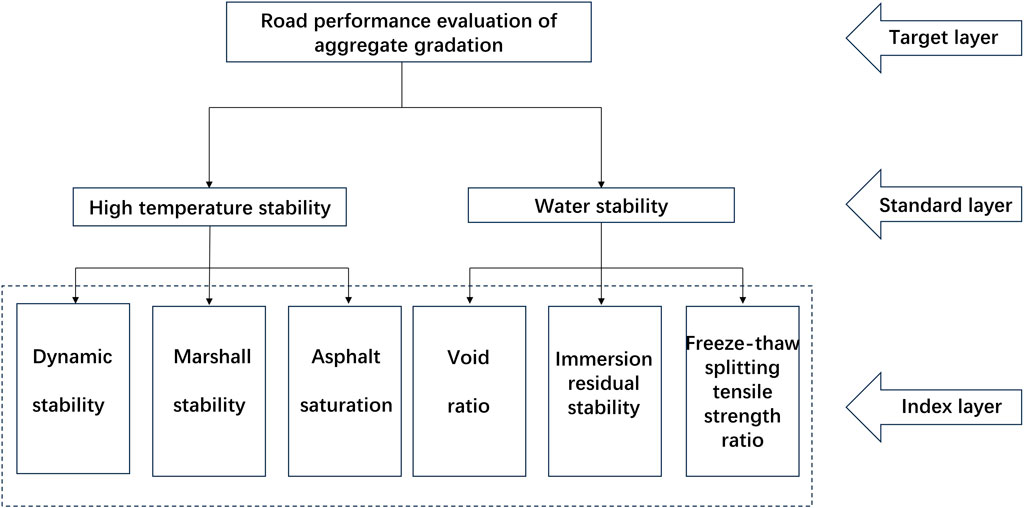
The AC-20 asphalt mixture as the pavement middle layer material, its high-temperature stability, and water stability should be the primary considerations. Therefore, this paper uses the principle of the analytic hierarchy process, takes the road performance of mineral aggregate gradation as the target layer (L), takes the high-temperature stability and water stability of the asphalt mixture as the two major factors in the standard layer (M), and the dynamic stability, Marshall stability, voids filled with asphalt, void ratio, immersion Marshall stability, and freeze–thaw splitting tensile strength ratio of six indexes included in the index layer (N) so as to construct a comprehensive evaluation model of mineral aggregate gradation road performance, as shown in Figure 2.
3.4 Determine the fuzzy complementary judgment matrix and the evaluation index weight
According to the comprehensive evaluation model of mineral aggregate gradation road performance established in Figure 1, consulting with road industry experts and using the 0.1–0.9 scale method in Table 1, a fuzzy judgment matrix for the target layer based on two factors in the criterion layer is constructed as shown in A1. The fuzzy judgment matrix for high-temperature stability based on three indicators, namely, dynamic stability, Marshall stability, and effective asphalt saturation, is constructed as shown in A2. The fuzzy judgment matrix for water stability based on three indicators, namely, porosity, immersion Marshall stability, and freeze–thaw splitting tensile strength ratio, is constructed as shown in A3.
3.5 Consistency test of the judgment matrix
Because the second-order matrix itself has consistency, it is not necessary to check the consistency of A1, but only to check the consistency of A2 and A3. The transformed consistent complementary judgment matrices are as follows.
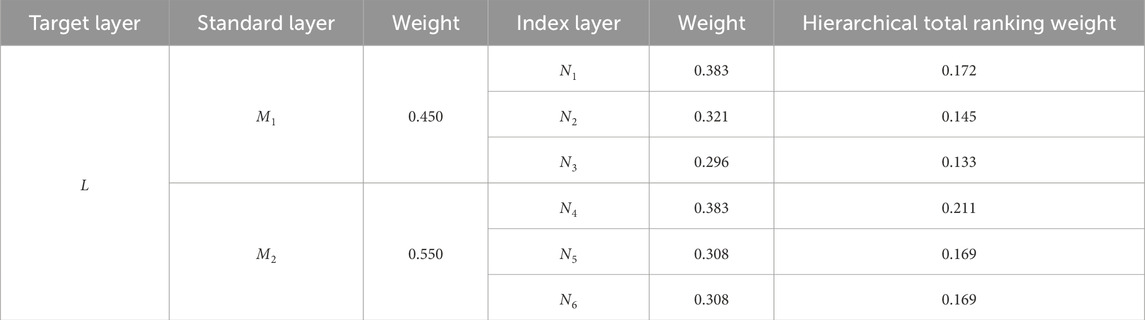
By substituting A1, as well as the transformed A2 and A3 consistent complementary judgment matrices, into Formula 3, the weights of each evaluation factor can be obtained. Then, according to Formula 4, the ranking weight vector of the evaluation indicators relative to the overall goal can be obtained. The specific data are shown in Table 7.
3.6 Fuzzy comprehensive evaluation
After determining the hierarchical total ranking weight of the index layer, the aggregate gradation is optimized by combining fuzzy comprehensive evaluation, and the membership values of each index in nine gradations are calculated according to Equations 5, 6, as shown in Table 8. Calculate the average membership value of six indexes under different factors and levels, and obtain the change relationship diagram between each index and factor and level, as shown in Figures 3A–C, 4A–C.
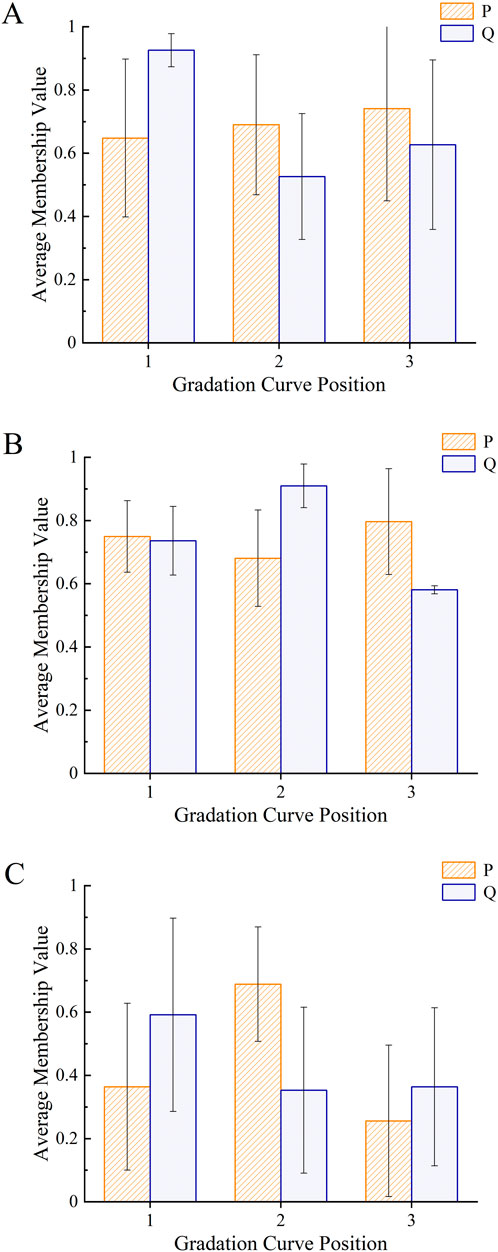
Figure 3. Influence of gradation curve position on high-temperature stability. (A) Dynamic stability. (B) Marshall stability. (C) Voids filled with asphalt.
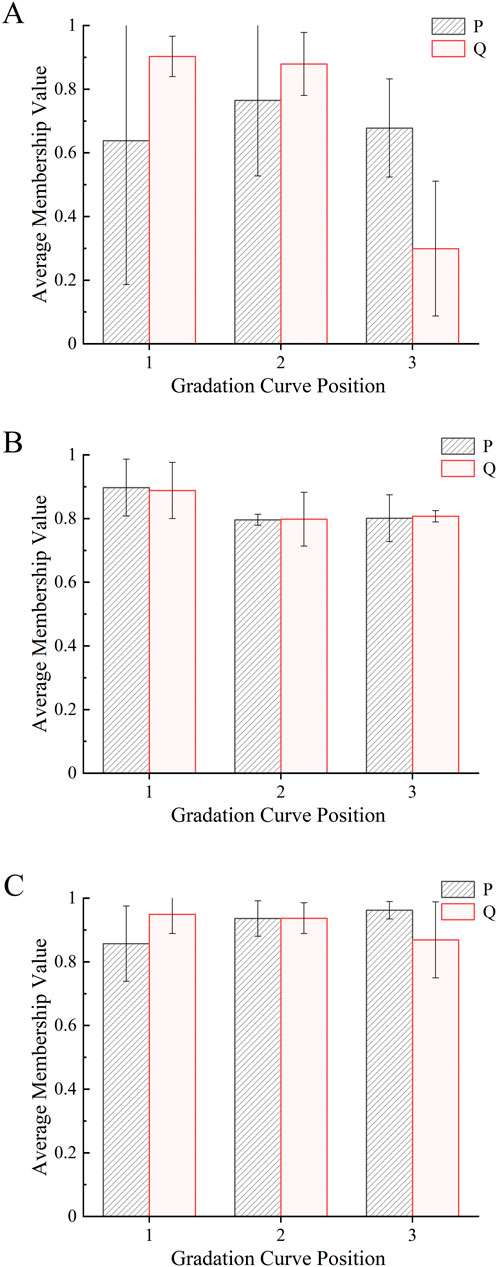
Figure 4. Influence of gradation curve position on water stability. (A) Void ratio. (B) Immersion Marshall stability. (C) Freeze–thaw splitting tensile strength ratio.
As can be seen from Figure 3A, the dynamic stability of mineral aggregate gradation obtained by combining the lower position of the coarse aggregate gradation curve with the middle position of the fine aggregate gradation curve (P3Q1) is better, and the asphalt mixture composed of it has higher rutting resistance under high temperature. A large amount of coarse aggregates bear the main load, while the fine aggregates in the middle fill the pores. These two types of aggregates are mutually embedded and squeezed, forming a good skeleton structure with high resistance to shear slip and compression deformation. Therefore, it has high dynamic stability, fewer ruts, and good high-temperature stability. As can be seen from Figure 3B, the combination of the lower position of the coarse aggregate gradation curve and the upper position of the fine aggregate gradation curve (P3Q2) gives the best Marshall stability of the mineral aggregate gradation, so the strength of the asphalt mixture is higher. Because the structural changes of fine aggregates can better affect the Marshall stability of asphalt mixtures, Q2 has more fine aggregates and bears stronger extrusion pressure during the experimental process, resulting in higher stability (Xu et al., 2008). As can be seen from Figure 3C, the voids filled with asphalt of mineral aggregate gradation formed by the upper position of the coarse aggregate gradation curve and the middle position of the fine aggregate gradation curve (P2Q1) is the closest to the median, and the asphalt mixture is more durable.
It can be seen from Figure 4A that the combination of the void ratio closest to the median is the upper position of the coarse aggregate gradation curve and the middle position of the fine aggregate gradation curve (P2Q1), and the asphalt mixture formed by its mineral aggregate gradation has better water resistance and plastic deformation resistance. Figures 4B, C show that the mineral aggregate gradation formed by the combination of middle position of coarse aggregate gradation curve and middle position of fine aggregate gradation curve (P1Q1) and middle position of coarse aggregate gradation curve and lower position of fine aggregate gradation curve (P1Q3) has the best immersion Marshall stability and freeze–thaw splitting tensile strength ratio, and asphalt mixture has the best water stability. An appropriate proportion of coarse and fine aggregates can improve the water resistance of asphalt mixtures, reduce the likelihood of water loss and damage, and avoid cracking and damage.
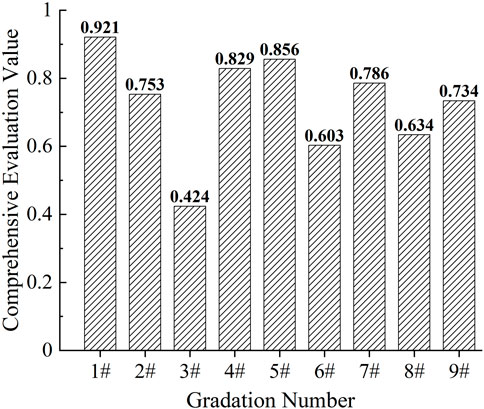
According to Equation 7, the fuzzy comprehensive evaluation value F of nine gradations can be obtained as shown in Figure 5.
From Figures 3, 4, it can be seen that the evaluation of high-temperature stability and water stability of asphalt mixture needs single-index analysis, and the optimal combination scheme determined by different indexes is different. However, the fuzzy comprehensive evaluation method can be used to obtain the membership value of each index of each gradation, and finally the gradation with the best comprehensive performance of asphalt mixture can be determined by the fuzzy comprehensive evaluation value. According to the maximum membership principle of fuzzy theory, it can be seen from Figure 5 that the comprehensive road performance of nine gradations is ranked as 1# > 5#>4# > 7#>2# > 9#>8# > 6#>3#, so the best aggregate gradation is the 1# gradation.
The use of the fuzzy analytic hierarchy process and comprehensive evaluation method can enable us to have better grading selection. By selecting a better grading, we can improve the material performance, save costs and resources, improve construction quality, and extend project life, thereby promoting the development and progress of engineering and materials fields. Therefore, precise selection and optimization of gradation have important practical significance and value.
4 Conclusion
This article is based on the Jicao Expressway project to conduct research on the optimal gradation of intermediate layer asphalt mixtures and proposes a theoretical system suitable for gradation optimization analysis. First, the Marshall stability test, immersion Marshall test, rutting test, and freeze–thaw splitting test were conducted on nine experimental groups to obtain the road performance indicators of asphalt mixture. Then, the fuzzy analytic hierarchy process and fuzzy comprehensive evaluation method were used to evaluate the road performance of nine graded asphalt mixtures and select the gradation ratio. The main conclusions are as follows.
(1) This study established a multi-level evaluation model for the performance of AC-20 asphalt mixture pavement using the analytic hierarchy process (AHP). Six indicators affecting the two factors were determined with the high temperature stability and water stability of the intermediate layer as the primary consideration factors. The relative importance and membership relationship between each factor and indicator were fully considered, improving the objectivity and accuracy of the comprehensive evaluation of asphalt mixture pavement performance.
(2) Using fuzzy mathematics theory and analytic hierarchy process to calculate the evaluation index weight of asphalt mixture road performance and determining the index weight vector through the fuzzy consistent judgment matrix can reduce the subjective one-sidedness of the traditional expert scoring method. The membership function is introduced, and the membership value is calculated, which solves the incomparability between indexes. The proposed evaluation system and weight determination method provide a theoretical basis for subsequent research on the road performance of asphalt mixtures.
(3) This study solves the problem of only obtaining the optimal combination scheme for a single indicator and is unable to obtain the optimal gradation for comprehensive road performance. Based on the fuzzy analytic hierarchy process and comprehensive evaluation method, the optimal gradation for the AC-20 asphalt mixture mineral aggregate is proposed as the 1 # gradation, providing a reference for the selection of asphalt mixture gradation in research.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
FZ: conceptualization, methodology, and writing–review and editing. SZ: data curation, formal analysis, investigation, methodology, and writing–original draft. WC: resources, validation, writing–original draft, and writing–review and editing. HR: resources, validation, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research leading to these results received funding from the Jilin Provincial Science and Technology Development Project under Grant Agreement No (20240304141SF).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, F., and Kilic, K. (2019). Fuzzy Analytic Hierarchy Process: a performance analysis of various algorithms. Fuzzy Sets Syst. 362, 110–128. doi:10.1016/j.fss.2018.08.009
Arman, H. (2023). Fuzzy analytic hierarchy process for pentagonal fuzzy numbers and its application in sustainable supplier selection. J. Clean. Prod. 409, 137190. doi:10.1016/j.jclepro.2023.137190
Chen, A., Zhao, Y., Li, P., Li, Y., Mohammed, M., and Guo, P. (2020). Crack propagation prediction of asphalt pavement after maintenance as a function of initial cracks distribution. Constr. Build. Mater. 231, 117157. doi:10.1016/j.conbuildmat.2019.117157
Cheng, Y., Li, L., Zhou, P., Zhang, Y., and Liu, H. (2019). Multi-objective optimization design and test of compound diatomite and basalt fiber asphalt mixture. Materials 12 (9), 1461. doi:10.3390/ma12091461
Han, Y., Zhou, R., Geng, Z., Bai, J., Ma, B., and Fan, J. (2020). A novel data envelopment analysis cross-model integrating interpretative structural model and analytic hierarchy process for energy efficiency evaluation and optimization modeling: application to ethylene industries. J. Clean. Prod. 246, 118965. doi:10.1016/j.jclepro.2019.118965
Hu, J., Ma, T., Zhu, Y., Huang, X., Xu, J., and Chen, L. (2021). High-viscosity modified asphalt mixtures for double-layer porous asphalt pavement: design optimization and evaluation metrics. Constr. Build. Mater. 271, 121893. doi:10.1016/j.conbuildmat.2020.121893
Jaganathan, S., Erinjeri, J. J., and Ker, J.-i. (2007). Fuzzy analytic hierarchy process based group decision support system to select and evaluate new manufacturing technologies. Int. J. Adv. Manuf. Technol. 32, 1253–1262. doi:10.1007/s00170-006-0446-1
JTG E20-2011 (2011). Standard test methods of bitumen and bituminous mixtures for Highway engineering. Beijing, China: China Ministry of Communications.
JTG F40-2004 (2004). Technical specification for construction of Highway asphalt pavements. Beijing, China: China Ministry of Communications.
Li, P., Su, J., Ma, S., and Dong, H. (2020). Effect of aggregate contact condition on skeleton stability in asphalt mixture. Int. J. Pavement Eng. 21 (2), 196–202. doi:10.1080/10298436.2018.1450503
Li, X., Chen, D., Fu, J., Liu, S., and Geng, X. (2023). Construction and application of fuzzy comprehensive evaluation model for rockburst based on microseismic monitoring. Appl. Sci. 13 (21), 12013. doi:10.3390/app132112013
Lu, X., and Zhang, S. (2018). Study on influencing factors of performance indexes of AC-20 modified asphalt mixture based on orthogonal experimental design. Highway 11, 177–181.
Moghaddam, T. B., Karim, M. R., and Abdelaziz, M. (2011). A review on fatigue and rutting performance of asphalt mixes. Sci. Res. Essays 6 (4), 670–682.
Pan, Y., Li, J., Yang, T., Liu, G., Zhou, J., Guo, P., et al. (2020). Optimization of gradation design of recycled asphalt mixtures based on fractal and Mohr-Coulomb theories. Constr. Build. Mater. 248, 118649. doi:10.1016/j.conbuildmat.2020.118649
Saaty, T. L. (1990). How to make a decision: the analytic hierarchy process. Eur. J. operational Res. 48 (1), 9–26. doi:10.1016/0377-2217(90)90057-I
Sebaaly, H., Varma, S., and Maina, J. W. (2018). Optimizing asphalt mix design process using artificial neural network and genetic algorithm. Constr. Build. Mater. 168, 660–670. doi:10.1016/j.conbuildmat.2018.02.118
Sivilevičius, H., Podvezko, V., and Vakrinienė, S. (2011). The use of constrained and unconstrained optimization models in gradation design of hot mix asphalt mixture. Constr. Build. Mater. 25 (1), 115–122. doi:10.1016/j.conbuildmat.2010.06.050
Tayfur, S., Ozen, H., and Aksoy, A. (2007). Investigation of rutting performance of asphalt mixtures containing polymer modifiers. Constr. Build. Mater. 21 (2), 328–337. doi:10.1016/j.conbuildmat.2005.08.014
Wang, Z., Liang, Q., Yan, F., and Bian, G. (2021). Strength improvement of cement emulsified asphalt mixture through aggregate gradation design. Constr. Build. Mater. 299, 124018. doi:10.1016/j.conbuildmat.2021.124018
Xie, J., and Liu, C. (2006). Fuzzy mathematical method and its application. Wu Han: Huazhong University of Science and Technology Press.
Xu, H., Tan, Y., Li, X., and Tian, Y. (2008). Research on the relationship between Marshall stability and grading curve characteristics of asphalt mixtures. Highway, 213–217.
Xu, S. l., Yeyao, T., and Shabaz, M. (2023). Multi-criteria decision making for determining best teaching method using fuzzy analytical hierarchy process. Soft Comput. 27 (6), 2795–2807. doi:10.1007/s00500-022-07554-2
Xue, J., and Jiang, Y. (2022). Gradation optimization and evaluation of AC-20 mixtures based on interlock-dense theory. Constr. Build. Mater. 350, 128893. doi:10.1016/j.conbuildmat.2022.128893
Xu, Z. (2001). An algorithm for fuzzy complementarity judgment matrix sorting. J. Syst. Eng. 16 (4), 311–314. doi:10.3969/j.issn.1000-5781.2001.04.012
Zhai, Y., Zhang, B., Wang, F., Zhong, Y., and Li, X. (2019). Composite dielectric model of asphalt mixtures considering mineral aggregate gradation. J. Mater. Civ. Eng. 31 (6), 04019091. doi:10.1061/(asce)mt.1943-5533.0002642
Zhang, Z., Liu, P., Rochlani, M., Falla, G. C., Leischner, S., and Oeser, M. (2021). A fuzzy comprehensive evaluation method to select the optimal mineral filler for optimization of the performance of asphalt mastics. Constr. Build. Mater. 298, 123847. doi:10.1016/j.conbuildmat.2021.123847
Keywords: AC-20 asphalt mixture, fuzzy hierarchical analysis process, fuzzy comprehensive evaluation method, gradation optimization, orthogonal design
Citation: Zhu F, Zhang S, Chen W and Rong H (2024) Gradation optimization of AC-20 asphalt mixture based on the fuzzy analytic hierarchy process and comprehensive evaluation method. Front. Mater. 11:1423835. doi: 10.3389/fmats.2024.1423835
Received: 26 April 2024; Accepted: 12 September 2024;
Published: 27 September 2024.
Edited by:
Hugo M. R. D. Silva, University of Minho, PortugalReviewed by:
Hasanain Radhi Radeef, University of Technology Malaysia, MalaysiaAhmed Hemida, Louisiana State University, United States
Copyright © 2024 Zhu, Zhang, Chen and Rong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hua Rong, MTcxODYxMzkwM0BxcS5jb20=
 Fu Zhu
Fu Zhu Shengyu Zhang
Shengyu Zhang