
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 04 July 2024
Sec. Structural Materials
Volume 11 - 2024 | https://doi.org/10.3389/fmats.2024.1407922
This article is part of the Research Topic Static and Dynamic Performance Analysis of Structures and Materials Under Complex Loads and Environmental Excitation View all 10 articles
 Juan Guo1,2
Juan Guo1,2 Weifeng Liu1
Weifeng Liu1 Jianbo Guo1
Jianbo Guo1 Hongfa Yu1*
Hongfa Yu1* Haiyan Ma1*
Haiyan Ma1* Jun Yan3
Jun Yan3 Qinghua Tao1
Qinghua Tao1 Weiquan Gao1
Weiquan Gao1 Meng Zhang1
Meng Zhang1 Fang Wang1,2
Fang Wang1,2The harsh geological conditions in the northwest region of China, characterized by widespread saline-alkali soil rich in alkali ions, pose a high risk of Alkali-Silica reaction (ASR) in concrete, particularly due to the presence of ASR-active natural river sands. To address ASR hazards, locally applied concrete often employs High-Performance concrete (HPC) prepared with high proportions of mineral admixtures. In this paper, the alkali content is controlled by adding mixed water with NaOH to the initial configuration of concrete, and three different alkali content states are set up. A 1 mol/L NaOH solution was used to simulate alkaline conditions, and HPC specimens were immersed for an extended period to investigate the effects of equivalent alkali content, immersion time, concrete strength, and admixture on the flexural mechanical properties of HPC under the condition of long-term alkali immersion. Results indicate that, the strength grade was positively correlated with the flexural strength of HPC, but the alkali content was negatively. Initial immersion significantly enhances strength, followed by a gradual decline after long-term immersion. Among three types of admixture addition methods, the impact on flexural strength of HPC immersed in alkaline solution for 10 years follows the order: Double doped air entraining agent and rust inhibitor is greater than single doped air entraining agent is greater than single doped rust inhibitor. In the process of macroscopic test, it is difficult to observe the variation rule of stress and strain in detail, only the final aggregate failure mode can be analyzed. In order to analyze the strain change of the specimen and the failure process of the aggregates more accurately, a three-dimensional random aggregate concrete mesoscopic model was established, and equations relating microhardness to the mechanical properties of concrete components were derived from statistical analysis, providing a basis for parameter selection in the model. Results demonstrate that with increasing strength, the occurrence time of initial cracks is delayed, and the ratio of cracks bypassing aggregates (cracks develop along the ITZ between aggregate and mortar until complete failure) decreases, and the ratio of cracks penetrating aggregates (cracks develop directly through aggregates in an almost vertical direction) increases.
In the northwest region of China, salt lakes and saline-alkali soils contain high concentrations of chlorides, sulfates, and alkali metal ions, which greatly predispose concrete to alkali-aggregate reaction (AAR). Aggregates, serving as the framework of concrete, typically consist of minerals containing silica dioxide such as chalcedony, quartz, and chert. These mineral components are prone to undergo ASR with alkalis (Na2O, K2O) in cement, resulting in the formation of expansive alkali-silicate gel, thus leading to concrete deterioration (Zhou, 2011).
Over the past half-century, more than 20 countries have incurred significant losses due to the damage inflicted on buildings by ASR (Tang et al., 2022; Mong et al., 2002; E Grattan-Bellew et al., 1998). Numerous experiments have been conducted to investigate the impact of ASR on concrete strength. Cavalcanti (Cavalcanti, 1986) studied the extent of strength, durability, and harmful cracking effects of concrete under long-term ASR. Sanchez et al. (Crouch and Wood, 1990; Kubo and Nakata, 2012; Sanchez, 2014) found that the tensile strength and elastic modulus of concrete are more affected by ASR than compressive strength. Nixon et al. (Nixon and Bollinghaus, 1985; Smaoui et al., 2004) demonstrated that high expansion levels have a significant impact on compressive strength. At low expansion levels (0.05%) and high expansion levels (0.2–0.3%), the tensile strength decreased by 12%–70% and 50%–70%, respectively.
Currently, the main methods to suppress ASR include the use of inactive aggregates, controlling moisture, managing total alkali content in concrete, and adding inhibitory materials and chemical admixtures (Ding et al., 2008; Jan et al., 2013; Liu et al., 2015). According to Qian’s research (Qian et al., 1994), as the content of slag and fly ash in concrete increases, the expansion decreases, and the inhibition effect on ASR strengthens. The optimal inhibition effect on ASR is achieved when the addition reaches 30%. Moreover, studies have pointed out that the key role of fly ash lies in alleviating or preventing the chemical reaction of reactive aggregates. Chen’s research (Chen et al., 1993) indicates that the effective addition of silica fume is about 10%–15%, but it can only delay the occurrence of ASR without complete inhibition. Duyhai et al. (Choi and Choi, 2015; Vo et al., 2020) explored the effect of slag content on inhibiting ASR in highly alkaline reactive aggregates and found a positive correlation. The use of admixtures to suppress ASR can be traced back to as early as 1951 (McCoy and Caldwell, 1951). Due to not requiring changes in construction conditions and even possibly improving the performance of concrete, this method has received considerable attention. Shayan and Ivanusec (Shayan and Ivanusec, 1989) explored the influence of adding NaOH on the mechanical properties of mortar containing non-reactive and reactive aggregates and ultimately found that adding NaOH led to a decrease in mortar strength, with similar trends observed in both types of concrete. This is because the addition of NaOH undergoes significant chemical reactions with cement, affecting the performance of concrete. In general, high alkaline conditions are detrimental to the strength of concrete (Qian, 1996).
Wu Z et al. (Wu, 2000) summarized the definition of HPC. In addition to cement, aggregate and water, low water-binder ratio, sufficient mineral admixtures and high-efficiency admixtures were used, and stricter quality management was adopted. Concrete with excellent mechanical properties, durability and good impact resistance can be called High-Performance Concrete (HPC).
HPC inherently exhibits a suppression effect on ASR due to its internal incorporation of large quantities of mineral admixtures such as slag, fly ash (FA), and silica fume (SF). Marzouk and Langdon (Marzouk and Langdon, 2003), in their exploration of the influence of alkaline aggregates on the mechanical properties of HPC and Ordinary Portland Cement (OPC), immersed concrete specimens separately in NaOH solution at 80°C or distilled water for 12 weeks. They found that high alkaline environments significantly affected the strength of OPC but had minimal impact on both low and high alkali-reactive HPC. Fares and Khan (Fares and Khan, 2013) investigated the inhibitory effects of two-phase and three-phase blended materials on ASR, including FA and SF. The results indicated that the inhibitory effect of single addition SF (15% content) or single addition FA (45% content) on ASR was not as good as the combined addition of FA + SF (10% FA and 10% SF).
Yu et al. (Yu et al., 2003) investigated the compressive strength of OPC20 and OPC30 after 270 days of exposure in the saline soil environment of Qinghai Chaerhan Salt Lake, and found that they were reduced by 41%–65% and 18%–23%.
Wang et al. (Wang, 1993) found that the compressive strength of high-strength and high-density concrete with a water-binder ratio of 0.22–0.26 and a strength grade of C50 mixed with 10% silica fume increased by 18.5%–27.3% after immersion in salt lake alkaline solution for 3 years, indicating that HPC showed better corrosion resistance in the face of long-term corrosion.
Zhang et al. (Zhang, 2014) found that the relative dynamic elastic modulus of OPC30 and OPC50 increased to 110% and 109% after 550 days immersion in salt lake alkaline solution, and decreased to 90% and 104% respectively after 1,550 days of immersion in salt lake alkaline solution. The relative dynamic elastic modulus of HPC with strength grade of C65 (10% silica fume +45% slag), C70 (10% silica fume +27% fly ash) and C80 (10% silica fume) were still in the growth stage at 1,550 days, and increased by about 110%–120%.
Gao et al. (Gao et al., 2019) studied the compressive strength of HPC exposed to salt lake alkaline solution for 1 year and 1.5 years. It was found that the compressive strength of HPC with the strength grade C50 (12% fly ash +20% slag +3% silica fume) increased by 35% and 27%.
At present, the research on the mechanical properties of HPC in salt lake alkali corrosion environment has not been more than 5 years, so it is urgent to study its durability and long-term strength change in a longer time span, which has important scientific value for the technical development and engineering application of HPC in salt lake environment.
With the continuous progress of computer technology, the strict requirements of traditional tests and high cost have prompted researchers to start exploring in the direction of numerical simulation. At present, breakthrough progress has been made in many fields, for example, Xiang et al. (Xiang and Liew, 2013) proposed a computational framework for transverse compression of microtubules using Cauchy-Born rules, and used atomistic-continuum simulation and mesh-free method to calculate the high-order gradient continuum theory format, and deeply studied the elastic properties and mechanical response of microtubules under transverse compression.
In the field of concrete, it has been widely used to analyze the mechanical response of concrete under load, such as cracking and failure mode. Compared with the test, numerical simulation has many advantages, which can more intuitively observe the stress and strain changes of the specimen, the specific failure process of aggregate, the crack propagation and damage mechanism. It has important research value and significance.
Xu et al. (Xu et al., 2011) employed a novel algorithm to determine the stacking problem between ellipsoidal and ellipsoidal aggregate models and investigated the influence of aggregate shape on aggregate packing behavior in concrete. Fang et al. (Fang et al., 2013) proposed an efficient three-dimensional aggregate growth and determination algorithm based on vector growth and judgment criteria. They generated spatial octahedral aggregate models with random shape characteristics and successfully applied them to static and dynamic microscopic mechanical simulation of concrete.
Zhang et al. (Zhang et al., 2021) discussed the influence of porosity characteristics on the compressive strength of coral aggregates and developed a series of algorithms considering the real mesoscopic characteristics of coral aggregates based on two-dimensional XCT images. Wu (Wu et al., 2021a; Wu et al., 2022) established particle generation algorithms and vector growth algorithms that can generate three-dimensional particle systems assembled from irregularly shaped and sized particles. They obtained convex-concave particles with different shapes and sizes, which are more in line with engineering reality compared to previous simulations that could only model regular geometric shapes or simple polyhedra particles. To address the issue of particle volume fraction in the model being smaller than the actual fraction, they proposed using the gravity compaction algorithm in the PFC3D program and a spatial translation/rotation algorithm from literature to analyze the distribution of aggregates in concrete models.
Wu et al. (Wu et al., 2021b), through numerical simulation and comparison with experimental results, found that coral aggregate concrete (CAC) with larger aggregate volumes and smaller MAS values experienced faster failure processes. They also demonstrated that the proposed three-dimensional random mesoscopic modeling method, considering the random characteristics of aggregate shape and spatial distribution, exhibits high reliability in simulating and analyzing the compression performance of CAC. This method can provide further insights into the mixture design, performance research, and prediction of CAC. Li (Li et al., 2023) utilized the 3D random aggregate concrete mesoscopic model to simulate the uniaxial compressive mechanical properties of HPC specimens under long-term corrosion conditions and found that the failure morphology was in good agreement with the compressive strength.
Chen (Chen et al., 2023) studied the change of bearing capacity of reinforced cage specimens and ordinary specimens with different eccentricity and width-thickness ratio, and discussed the law of reinforcement effect of reinforced cage using the finite element analysis method. And found that when the width-thickness ratio is 22.5 and the eccentricity is small, the reinforcement cage greatly improves the ultimate bearing capacity of the CFSST column, however, this enhancement decreases with the increase of eccentricity.
Currently, there is a lack of research on the mechanical properties of HPC containing alkali-reactive aggregates and high proportions of mineral admixtures under prolonged exposure to alkaline solution environments. Therefore, this study aims to investigate the flexural mechanical properties of HPC with ASR inhibition measures under prolonged immersion in alkaline solution and analyze the mesoscopic mechanisms of fracture failure.
The cement used is P.II 52.5 cement and P.O 42.5 cement produced by Gansu Qilianshan Cement Group Co., Ltd. The main physical and mechanical properties of this type of cement are shown in Table 1. The chemical composition and alkali content of the main raw materials are shown in Tables 2 and 3, respectively. Fly ash is produced by Gansu Yongdeng Liandian Fly Ash Co., Ltd. Ground granulated blast furnace slag: S95 grade product from Gansu Xiangyang Trading Co., Ltd.’s slag mill, with a specific surface area of 330 m2/kg. Silica fume: Product from Qinghai Blue Sky Environmental Protection Technology Co., Ltd., with a SiO2 content of 90.51% and a specific surface area of 26,200 m2/kg. Fine aggregate: River sand from Ledu, Qinghai, with a bulk density of 1,639 kg/m3, fineness modulus of 2.87, and classified as medium sand with specific parameter indexes shown in Table 4. The coarse aggregate for C40∼45 consists of granite crushed stone from Xining, with a maximum particle size of 31.5 mm. It contains 2.9% needle-like particles, and it has a continuous grading from 5mm to 31.5 mm. The SO42- content is 0.02%, and the Cl- content is 0.0063%. For C50∼60, the coarse aggregate also comprises granite crushed stone from Xining, with a maximum particle size of 20 mm. It contains 2.6% needle-like particles, and it has a continuous grading from 5mm to 20 mm. The SO42- content is 0.02%, and the Cl- content is 0.0057%. For specific parameter details, please refer to Table 4. High-efficiency water reducer: PJ-FDN polycarboxylate-based high-efficiency water reducer from Xining Yangjian Waterproofing Additives Co., Ltd., liquid form, recommended dosage of 1.5%, water reduction rate of over 25%, K2O content of 0.000562%, Na2O content of 0.427518%, solid content greater than 9.5%, and Cl- content of 0.037909%. Air-entraining agent: Product from Xining Yangjian Waterproofing Additives Co., Ltd., with K2O content of 0.000562%, Na2O content of 0.390312%, SO42- content less than 0.105%, and Cl- content of 0.016994%. FDN steel anti-corrosion agent: Product from Xining Yangjian Waterproofing Additives Co., Ltd., with a solid content of 30%, K2O content of 0.131472%, Na2O content of 0.080336%, SO42- content less than 0.1145%, and Cl- content of 0.648371%. Water: Drinking water that meets national standards.

Table 1. Physical mechanical properties of cement (Yan et al., 2022).
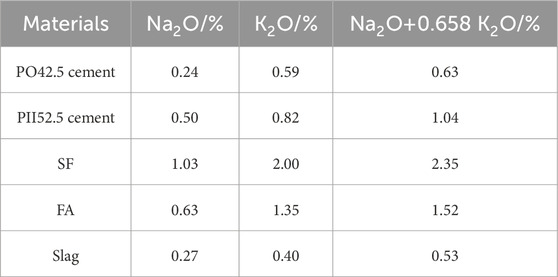
Table 3. Alkali active ingredients of main materials (Yan et al., 2022).

Table 4. Basic parameters of aggregate (Yan et al., 2022).
According to the CECS53: 93 standard, the alkali content of concrete raw materials refers to the content of equivalent sodium oxide in raw materials, measured as a percentage of weight. Equivalent sodium oxide content refers to the sum of sodium oxide and 0.658 times of potassium oxide. When calculating the alkali content (kg/m3) of concrete, the equivalent alkali content of cement is counted as 100% of the equivalent alkali content, the equivalent alkali content of mineral admixture = 15% of the equivalent alkali of fly ash +50% of the equivalent alkali of slag +50% of the equivalent alkali of silica fume, the equivalent alkali content of admixture = 100% of the equivalent alkali of admixture. The equivalent alkali content of each component including mixed water multiplied by the corresponding amount (kg/m3), and then all the alkali content of each components are added as the alkali content of concrete (kg/m3). The equivalent alkali content of concrete refers to the percentage of the alkali content of concrete divided by the mass of unit volume concrete.
The paper presents four different concrete mix designs for varying strength grades, and for the C50 strength grade, three types of admixture addition methods are employed. To investigate the influence of total alkali content in concrete on its physical mechanical properties under high-concentration alkali exposure, various equivalent alkali contents are designed based on the aforementioned six concrete mixtures. Specifically, specimens labeled as −0 represent the original equivalent alkali content of the materials, termed as low alkali state; whereas specimens labeled as −1 and −2 have NaOH added to the mixing water to increase the equivalent alkali content, referred to as medium alkali state and high alkali state, respectively. The detailed information regarding the equivalent alkali content and material usage for each mix design can be found in Table 5. Additionally, Table 6 provides detailed specifications of important indicators such as slump, water-cement ratio, expansion degree, and air content for each mix design.
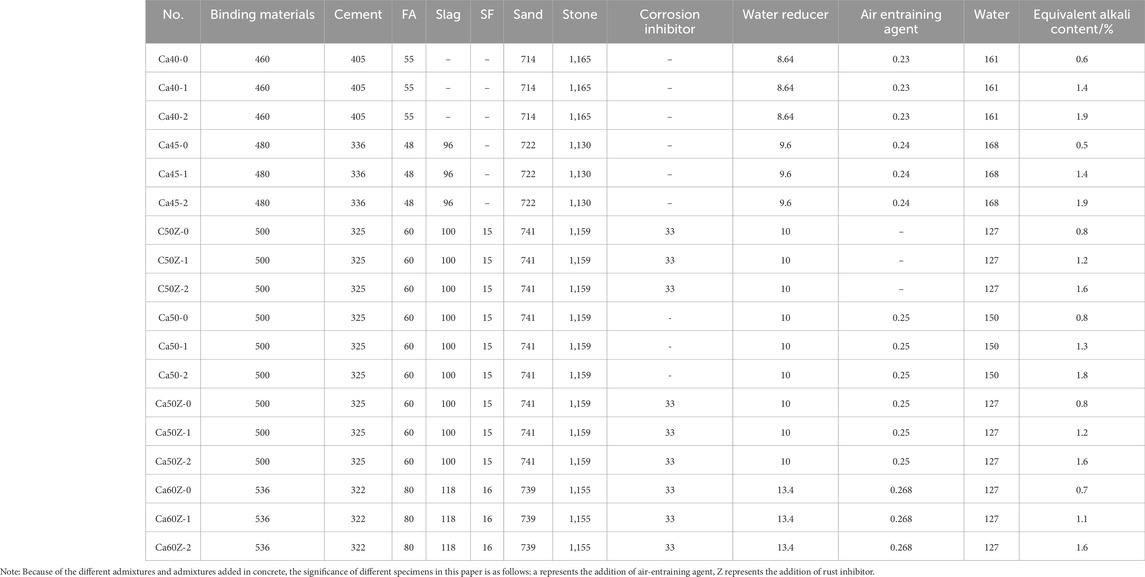
Table 5. The mix proportion and material consumption of concrete/kg (YAN et al., 2022).
The corrosion medium used in this experiment is a standard alkaline solution, specifically employed for ASR testing. Following ASTM standards, a solution of 1 mol/L NaOH concentration is utilized, and all concrete specimens are fully immersed in the solution. Figure 1 illustrates the preparation process of concrete specimens 10 years ago.

Figure 1. HPC preparation process 10 years ago (Yan et al., 2022). (A) Vibrating, (B) Mold release, (C) Immersion, (D) Immersing device, (E) Temperature controller.
The concrete specimens immersed in alkaline solution for 10 years are highly valuable, and it is crucial to ensure adequate spacing between specimens in the immersion environment. To fully utilize the immersion space and obtain as many different mechanical properties as possible, the specimens used in this experiment have dimensions of 515 mm × 100 mm × 100 mm. All the specimens were made in the same batch and began to immerse. They are all immersed in standard alkaline solution (1 mol/L NaOH) for durations of 0 days, 28 days, 182 days, 365 days and 3,650 days. When the required immersion time was reached, some specimens were taken out for testing and the rest continued to immerse. The flexural test is conducted using four-point loading, with the loading points illustrated in Figure 2. After completing the flexural test, the remaining portions of the specimens are subjected to other mechanical property tests.
According to the Standard for Testing Methods of Physical and Mechanical Properties of Concrete (Ministry of Housing and Urban-Rural Development of the OPeople’s Republic of China, 2019), the flexural strength of concrete specimens can be calculated by Eq. 1:
Where,
During the specimen preparation process, the specimens were first cut into approximately 3 mm thick slices using a precision automatic cutting machine. Subsequently, they were polished using 240-grit and 600-grit sandpaper. During the polishing process, a figure “8” motion was used to pre-polish, aiming to remove any damage zones that could cause polishing errors. Next, the specimens were embedded in epoxy resin within a metallographic mold. The epoxy resin mixture was injected into the mold using a vacuum drying oven to ensure complete sealing of the specimens. After sealing, the back of the specimens was polished to ensure uniform force application during polishing. Manual pre-polishing was performed to remove the resin layer from the front surface, ensuring a resin impregnation depth of 0.1 mm and avoiding excessive resin thickness during pre-polishing. Ultrasonic cleaning with anhydrous ethanol was then conducted, followed by formal polishing using a UNIPOL-12000M automatic pressure grinding and polishing machine (as shown in Figure 3A). Diamond polishing compounds of varying particle sizes were used for polishing, ranging from large to small. The final polished samples retained a thin layer of resin protection on the surface, exhibiting a mirror-like finish. The polished samples were dried in a vacuum drying oven for more than 48 h to evaporate the anhydrous ethanol and prevent contamination of the hardness tester. Microhardness testing was performed using an HVS-1000MZ hardness tester (as shown in Figure 3B), employing a 136° inverted pyramid diamond indenter. Indentations were made on the specimen surface under the applied test load, and Vickers hardness values were calculated accordingly.

Figure 3. Microhardness specimen preparation and testing equipment. (A) UNIPOL-12000M automatic pressure grinding and polishing machine, (B) HVS-1000MZ hardness tester.
After applying a certain test load with the diamond indenter, the length of the indentation diagonal is calculated using the arithmetic mean method. Based on this, the indentation surface area is calculated, and subsequently, the Vickers hardness value is determined. The specific calculation formula is shown as Eq. 2:
Where, HV is the Vickers hardness (MPa), F is the test load (N) (the test load is determined based on the clarity of the indentation, typically ranging from 20 μm to 60μm, and in this study, a test load of 0.490N was used under a ×400 magnification), S is the surface area of the indentation (mm2), d is the arithmetic mean of the diagonals of the indentation (mm), θ is the included angle of the diamond indenter (°), which is 136° in this study.
The long-term immersion of HPC in standard alkali solution can lead to changes in its strength, which is a key indicator for assessing its durability. Systematic studies on the strength variation of HPC specimens at different immersion ages provide valuable insights into their performance under various environmental conditions. This research helps to determine the corrosion resistance of HPC in harsh environments such as brine, providing comprehensive information and basis for evaluating its durability.
The flexural strength of HPC immersed in 38°C standard alkali solution for 10 years was tested, and the flexural strength of 0 days and 3,650 days was recorded. The resistance coefficient proposed in reference (Gao, 2018) can effectively assess the strength changes of HPC after long-term immersion, thus providing a more comprehensive and accurate evaluation of the material’s durability. The specific calculation formula is shown as Eq. 3:
Where,
Table 7 summarizes the initial strength, strength after 10 years immersion, and corresponding corrosion resistance coefficients of specimens with different strength levels under low alkali and medium alkali conditions. For HPC with varying alkali content, the flexural strength generally exhibits an increasing trend with higher strength grades. Furthermore, comparison between HPC specimens with different admixture at C50 strength level reveals that air-entraining agent and corrosion inhibitor can enhance the flexural strength of HPC. It is noteworthy that although both air-entraining agent and corrosion inhibitor improve the flexural performance of HPC, after 10 years of immersion, the HPC with air-entraining agent demonstrates superior flexural performance.
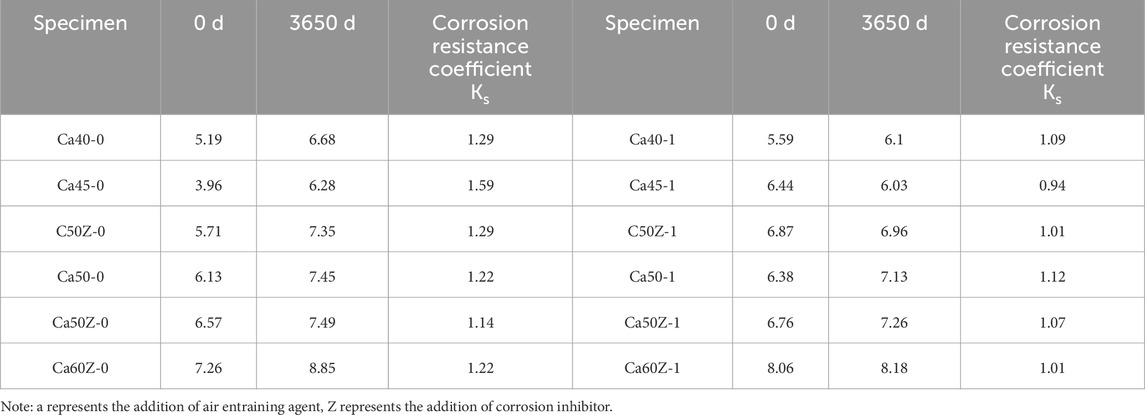
Table 7. Comparison of initial flexural strength and flexural strength immersed in standard alkali solution for 10 years of HPC (MPa).
Furthermore, the corrosion resistance coefficients in Table 7 are generally greater than 1, indicating a widespread increase in flexural strength of HPC under long-term ASR inhibition. A comparison of corrosion resistance coefficients between low alkali and medium alkali states of HPC reveals that the corrosion resistance coefficient under low alkali conditions is typically greater than that under medium alkali conditions. The corrosion resistance coefficient under low alkali conditions is around 1.2, while that under medium alkali conditions is slightly higher than 1. Further analysis indicates that before immersion in alkali solution, the difference in flexural strength between low alkali and medium alkali states of HPC is small, and the flexural strength of HPC under medium alkali conditions is relatively higher. However, after 10 years of immersion in alkali solution, the flexural strength of HPC under medium alkali conditions is affected by factors such as expansion rate and damage, resulting in slightly lower strength of specimens under medium alkali conditions. Additionally, long-term immersion of HPC in standard alkali solution leads to the formation of ASR corrosion products, which fill and divide cracks. Although this increases the porosity, the corrosion products fill the pores, resulting in a reduction in crack size, thereby improving the flexural strength of HPC to some extent.
This study conducted experimental tests on the flexural strength of HPC under medium alkali conditions immersed in alkali solution for 0 days, 28 days, 182 days, 365 days, and 3650 days, and the results are shown in Table 8.
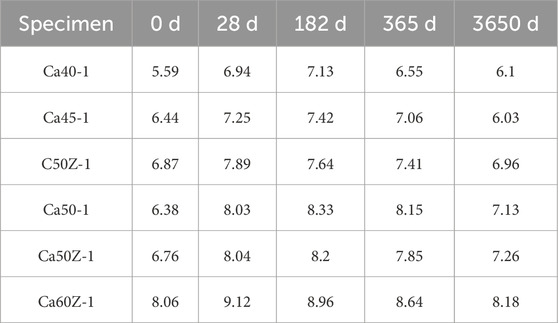
Table 8. The change of flexural strength of HPC in medium alkali state with the immersing time (MPa).
Based on the experimental data in Table 8, curves depicting the flexural strength and relative flexural strength of HPC under medium alkali conditions over time of alkali immersion were plotted as shown in Figures 4, 5. From the observations in Figure 4, it can be inferred that the flexural strength of HPC under medium alkali conditions generally increases with increasing strength grade during different immersion periods. With prolonged immersion time, the flexural strength of HPC exhibits a trend of initially increasing and then decreasing: at 28 days of immersion, the flexural strength of HPC is generally higher compared to the initial strength, during the period from 28 days to 182 days of immersion, the flexural strength of most strength grades of HPC continues to increase but gradually levels off, after 365 days of immersion, the flexural strength of HPC is lower than that at 182 days, however, between 365 days and 3650 days of immersion, the flexural strength of HPC continues to decrease but remains higher than the initial flexural strength before immersion. This indicates that during prolonged alkali immersion, HPC with ASR inhibition measures experiences a significant increase in flexural strength at the initial stage of immersion, followed by corrosion-induced damage. Nonetheless, the ultimate flexural mechanical performance still exhibits an improvement in durability characteristics.
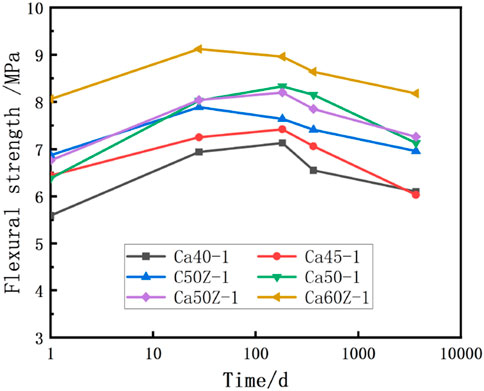
Figure 4. The change of flexural strength of HPC in medium alkali state with the immersing time of alkali solution.
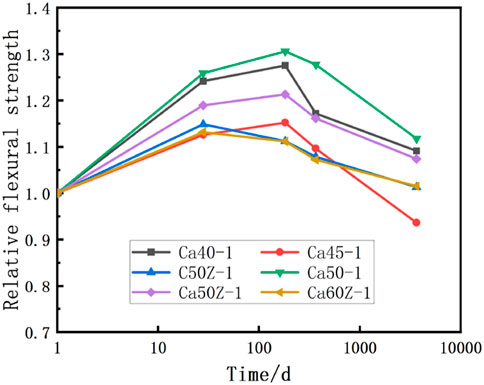
Figure 5. The change of the relative flexural strength of HPC in alkali state with the immersion time of alkali solution.
By comparing the flexural strengths of C50Z-1, Ca50-1, and Ca50Z-1 at different time intervals, it was found that the addition of air-entraining agent and corrosion inhibitor can improve the flexural performance of HPC. During the immersion period of 28 days to 365 days in alkali solution, the HPC with only air-entraining agent showed higher flexural strength compared to that with only corrosion inhibitor. After immersion for 3650 days, HPC with both additives maintained higher long-term flexural performance, indicating that the combination of air-entraining agent and corrosion inhibitor can synergistically enhance the stability of long-term flexural performance in alkali solution immersion.
In Figure 5, the relative flexural strength of Ca50-1 specimens is significantly higher than other mix proportions at each time interval, demonstrating a notable performance advantage. This also suggests that the effect of air-entraining agent on resisting ASR in HPC is stronger than that of corrosion inhibitor. Additionally, the relative flexural strength of Ca60Z-1 remains relatively stable over time, indicating that long-term immersion in alkali solution has the least impact on its flexural mechanical performance.
This study analyzed the flexural strength of specimens with different alkali contents immersed in standard alkali solution for 10 years, and the relevant data were summarized in Table 9. The relative residual flexural strength represents the ratio of the flexural strength of HPC under medium and high alkali conditions to that under low alkali conditions.
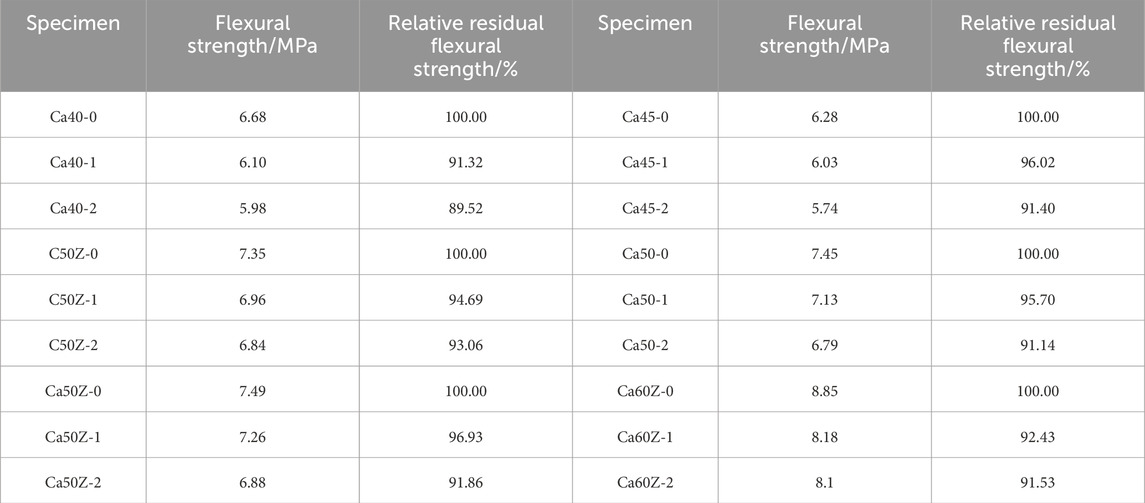
Table 9. The effect of alkali content on the flexural strength of HPC after immersing in standard alkali solution for 10 years.
According to the relevant data from Table 9 and Figure 6 is plotted below. In the graph, the horizontal axis labels 0, 1, and two represent the HPC specimens under low, medium, and high alkali conditions, respectively. By observing the data in the graph, it facilitates a better analysis of the trends and characteristics of the experimental results, thereby gaining deeper insights into the tendencies and features of the experiment.
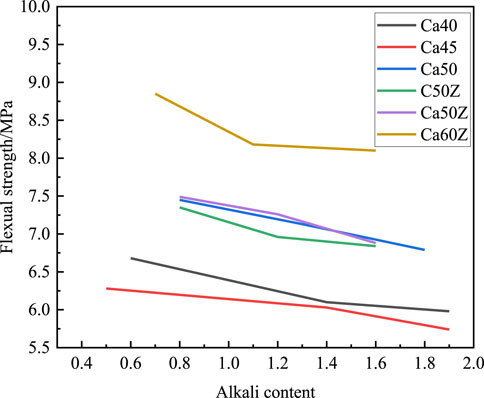
Figure 6. The effect of alkali content on the flexural strength of HPC after 10 years of immersion in standard alkali solution.
Based on the observation of Figure 6, it is evident that HPC under different alkali content states generally exhibits an increasing trend in flexural strength as their respective strength grades increase. However, with the increase in alkali content, the flexural strength of HPC gradually decreases. Under medium alkali conditions, the relationship between flexural strength and strength grade is not significant, with a decrease ranging from 3.07% to 8.68%. Specifically, the Ca40 specimens show the highest decrease in flexural strength at 8.68%, while the Ca50Z specimens exhibit the lowest decrease at only 3.07%. Conversely, under high alkali conditions, the relative residual flexural strength of specimens across different strength grades remains at around 92%. This indicates that although the flexural strength of HPC generally increases with the increase in concrete strength grade, excessively high alkali content also leads to a certain degree of performance reduction.
The flexural strength is an important index to measure the flexural failure resistance of materials, which can be used to evaluate the performance of concrete beam-column members. At the same time, the actual flexural failure of concrete is also closely related to its seismic and other properties (Chen et al., 2019). Therefore, it is of great engineering significance to study the flexural strength of concrete. Figure 7 illustrates the flexural failure modes of Ca40 specimens with different alkali contents. In the early stages of the test, tensile deformation was observed at the bottom of the specimen, while compressive deformation was evident at the top. Due to the excellent performance of high-performance concrete, cracks typically exhibited small extension trends during the test. As the load continued to increase, cracks at the center of the specimen gradually expanded, forming distinct tensile failure characteristics. The expansion of cracks led to gradual loss of connection among the concrete inside the specimen, ultimately resulting in its failure. Upon reaching the failure point, noticeable fragmentation and collapse occurred at the center of the specimen, with cracks extending across the entire cross-section, exhibiting clear brittle failure characteristics.
Furthermore, HPC specimens with different alkali contents exhibited similar characteristics in the flexural test: there were distinct nearly vertical main cracks near the center of the specimen, causing the concrete to fracture into two parts. Upon studying the cross-section of the HPC specimens, it was observed that the fracture surface was relatively smooth. Statistical analysis of the damage to the aggregates revealed (yellow circles in Figure 7 represent cracks bypassing the aggregates, while red circles represent cracks penetrating the aggregates) that the alkali content had minimal influence on the damage pattern of the aggregates within the specimens. Approximately 64.9% of the cracks in Ca40 specimens penetrated the aggregates (there is a relatively smooth section of the aggregate in the final failure surface). This is mainly due to the excellent mix design of HPC and the tight bond between aggregates and mortar induced by various admixtures. As a result, cracks directly penetrated through them, leading to a relatively smooth fracture surface.
Figure 8 illustrates the failure modes of HPC specimens with different strength grades under low alkali conditions. There were no significant differences in the overall failure modes of specimens with different strength grades, which still exhibited a single main crack near the center of the specimen. Some specimens experienced slight damage during immersion in the alkali solution, resulting in minor spalling of the concrete surface during the loading test. However, the overall fracture surfaces appeared relatively smooth.
Compared to admixtures, the strength has a significant influence on the internal crack propagation characteristics of HPC. With the increase in strength grade, the probability of interface failure between aggregate and mortar decreases. Consequently, the proportion of cracks bypassing aggregates (there are grooves or protrusions of aggregate in the final failure surface) and causing aggregate detachment gradually reduces. When the strength grade reaches C50 and C60, the proportion of cracks penetrating aggregates is 80.4% and 83.3% respectively, with the majority of aggregates being directly split, resulting in smooth fracture surfaces.
With the advancement of computer technology, scholars have established various random aggregate models of different shapes and dimensions to simulate the distribution of coarse aggregates in concrete. Since Wittmann’s pioneering work (Wittmann et al., 1985) using 2D circular aggregate models to study the influence of coarse aggregates on the micro-mechanical properties of concrete, the understanding of aggregate shapes has deepened. As a result, random aggregate models have gradually evolved from regular geometric bodies to random-shaped particles, transitioning from two-dimensional planes to three-dimensional space. Common random aggregate models include two-dimensional spheres, ellipses, and polygons, as well as three-dimensional spheres, ellipsoids, and regular polyhedra [(Häfner et al., 2006; Wriggers and Moftah, 2006; Lu et al., 2010)]. In this study, based on random quadrilaterals in a plane, a spatial random octahedra matrix is generated. Then, a 3D random convex polyhedron aggregate model with controllable shape and size is obtained by using the random growth algorithm. The modeling process is described in the following text.
(1) Generating Planar Random Quadrilaterals
To ensure the randomness of the aggregate model shapes, a random quadrilateral is established in the plane as the projection surface of the aggregate model. Specifically, a circle with a radius of R = 0.5D is generated in the XOY plane, where D is the determined aggregate diameter. Within this circle, a random quadrilateral ABCD is determined as the inscribed shape, roughly as shown in Figure 9A.
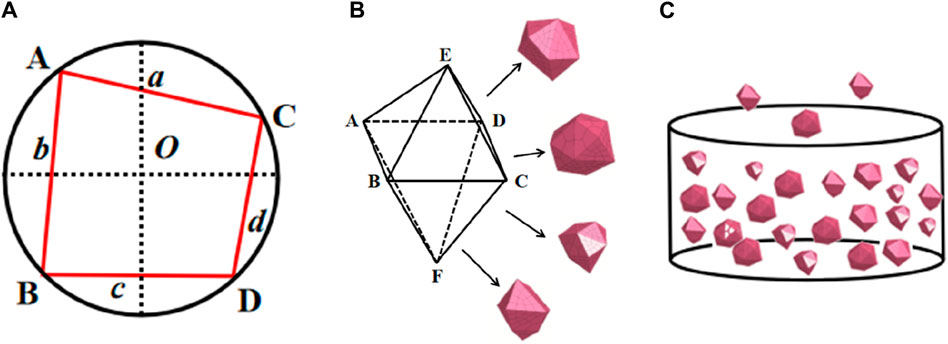
Figure 9. Modeling process of three-dimensional random aggregate concrete meso-model. (A) Generating Planar Random Quadrilaterals, (B) The spatial random octahedron generates a 3D random convex polyhedron by growth algorithm, (C) Aggregate Placement.
(2) The spatial random octahedron matrix generates a 3D random convex polyhedron by growth algorithm.
An appropriate aggregate center point O is determined in the XOY plane, and a spatial random octahedron is established as the base of the aggregate model. After that, a random growth algorithm is used to obtain 3D random convex polyhedron aggregate model with controllable shape and size. As seen in Figure 9B, the three-dimensional random model closely resembles real aggregates in terms of edge and corner features, demonstrating the authenticity and reliability of this aggregate model.
(3) Aggregate Placement
During aggregate placement, the Fuller grading curve is used to determine the gradation relationship of random polyhedral aggregates in the mesoscopic model of concrete to meet the gradation requirements of coarse aggregates. An aggregate library is established based on the grading curve, and random center coordinates for aggregates are determined. Aggregates are then selected from the library based on these coordinates and placed within the designated area. Subsequently, the coordinates of the placed aggregates are checked against the boundary: if all vertexes of the aggregates are within the area, the placement is valid; if any vertexes are outside the area, indicating invalid placement, the aggregates are removed, and new center coordinates are determined for re-placement. During aggregate placement, the spatial “limited translation” and “random placement” algorithms proposed in reference (Fang et al., 2013) are utilized, combined with criteria for aggregate intersection and boundary intrusion, to adjust the spatial positions of aggregates. This process ultimately yields a three-dimensional random aggregate model that meets the desired aggregate volume fraction.
After completing the aggregate placement, referring to the mesoscopic model established by Wu et al. (Wu et al., 2021c) based on the finite element method, the ITZ is treated as a continuum damage-plasticity model. The material identification algorithm [(Fang and Zhang, 2012; Fang et al., 2016; Mao et al., 2019)] is used to identify coarse aggregates, mortar, and ITZ in the three-dimensional mesoscopic model. Subsequently, the mapping algorithm [(Fang and Zhang, 2012; Fang et al., 2016; Mao et al., 2019)] is employed to mesh the model, generating finite element meshes for different components, the mesh type is hexahedral mesh, the characteristic mesh size is 2mm, and the element number is 643,750, as shown in Figure 10. From the figure, it can be observed that after concealing the mortar and ITZ in the central part of the specimen, the distribution of aggregates appears completely random.
In this paper, the model of aggregate is selected as HJC model, and the model of mortar and ITZ is selected as K&C model. The HJC model needs to obtain the elastic modulus, mass density, Poisson’s ratio and compressive strength of the aggregate. Because this paper uses the REL3 version of the K&C model, compared with other versions, it has the function of automatically determining the material parameters. It only needs to input the initial parameters such as uniaxial compressive strength, uniaxial tensile strength and elastic modulus, other parameters of concrete can be automatically calculated.
In this paper, the parameters of the model are determined by the microhardness as the medium, and the relationship between the microhardness and the meso-components of the concrete is acquired by means of statistics. The microhardness of each component of HPC required in this paper is obtained through experiments, and finally the mechanical parameters of each component of HPC are obtained. Details are shown in Section 4.2.
In order to obtain the mechanical parameters of each mesoscopic component of HPC, the microhardness test was carried out in this paper. According to the calculation formula for microhardness in Section 2.4.4, the microhardness variation with position near the coarse aggregate can be obtained (Figure 11). In the figure, the initial phase with relatively high microhardness corresponds to the aggregate, the lowest point in the curve represents the microhardness of the ITZ, and the subsequent relatively flat segment corresponds to the microhardness of the matrix. By conducting parallel measurements of 10 sets of data near the same aggregate and taking the average, the specific microhardness values for Ca40-0, Ca50-0, and Ca60Z-0 components are presented in Table 10.
Due to limitations in size and testing conditions, the mechanical properties of mortar and the interface transition zone (ITZ) have not been accurately determined. Therefore, this study first obtained the microhardness values of various components inside concrete, including the matrix, aggregate, and ITZ, through experiments. Then, based on the work of Diao et al. (Diao, 2021) and Liu et al. (Liu and Jia, 1995), relationships between the macroscopic mechanical properties such as compressive strength fc, splitting tensile strength fst, and elastic modulus Ec of concrete and microhardness were established.
Through data fitting analysis, it was found that there is a linear relationship between the microhardness HV of the matrix and the splitting tensile strength fst-mor of mortar, and a quadratic function relationship between the compressive strength fc of the matrix and its microhardness. The relationship between the compressive strength fc and the static modulus of elasticity Ec of the matrix is linear. The static modulus of elasticity Ec of the matrix has a power function relationship with the elastic modulus Ec-mor of mortar, and the elastic modulus Ec-mor of mortar has a power function relationship with the compressive strength fc-mor of mortar, as shown in Figure 12. By using the experimentally measured microhardness of the matrix, the mechanical properties of the mortar components can be subsequently determined.
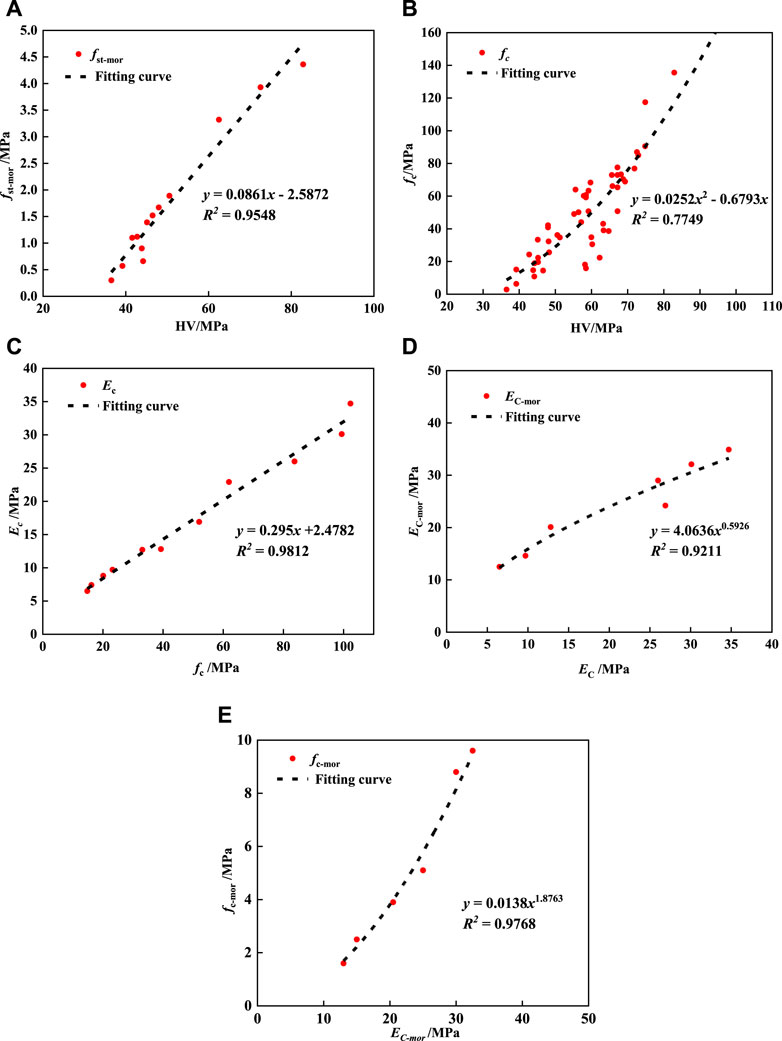
Figure 12. Relationship between the macroscopic mechanical properties of mortar and HV of matrix. (A) Relationship between HV and fst-mor of matrix, (B) Relationship between HV and fc of matrix, (C) The relationship between fc and Ec of matrix, (D) The relationship between Ec and Ec-mor, (E) Relationship between Ec-mor and fc-mor.
Figure 13 illustrates the relationship between the microhardness of the ITZ and its mechanical properties. From the graph, it is evident that the microhardness of the ITZ exhibits an exponential relationship with its splitting tensile strength, and the splitting tensile strength of the ITZ has an exponential relationship with its compressive strength. Since the ITZ can be considered as the weaker mortar component, the relationship between Ec-ITZ and fc can be referenced from Figure 12C.
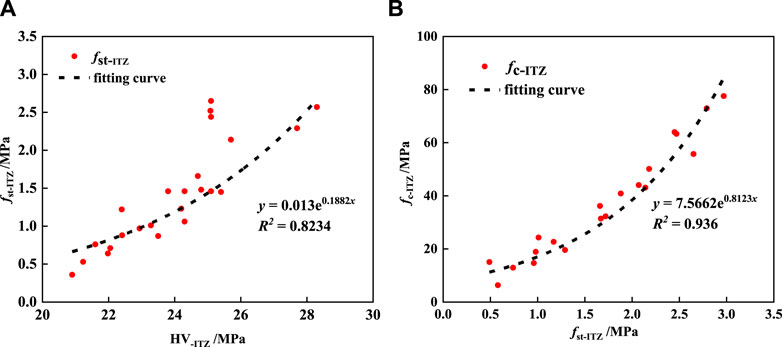
Figure 13. Relationship between the macroscopic mechanical properties of ITZ and HV. (A) Relationship between HV-ITZ and fst-ITZ, (B) Relationship between fst-ITZ and fc-ITZ.
In this study, the mortar and ITZ are modeled using the K&C model, which includes three strength failure surfaces: the initial yield surface, the ultimate strength surface, and the residual strength surface. This model can simulate the changes of the strengthening surface between the initial yield surface and the ultimate strength surface, as well as the softening surface between the ultimate strength surface and the residual strength surface (Liu and Jia, 1995). By utilizing the aforementioned relationships between microhardness and the mechanical properties of each component, the material parameters of mortar and ITZ can be calculated, as detailed in Table 11.
The aggregate is modeled using the HJC model, which comprises a state equation, a yield surface equation, and a damage evolution model, as illustrated in Figure 14. Specific material parameters are selected based on references (Li et al., 2023), with an elastic modulus E = 66GPa, mass density ρ = 2780 kg/m3, Poisson’s ratio μ = 0.15, and compressive strength fc = 50 MPa.
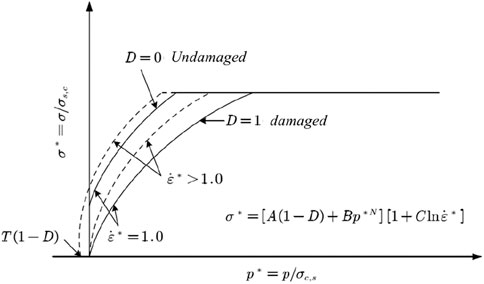
Figure 14. The yield surface equation of HJC model (Qin et al., 2014).
Based on the modeling method and process described in Section 4.1, a 515 mm × 100 mm × 100 mm prismatic concrete specimen model was established with a mesh size of 2mm, resulting in a total of 645,060 elements. The aggregate volume fraction is 46%. Distributed displacement loads were applied along the Z-axis to simulate the mesosfailure mechanism of HPC in flexural experiments (Figure 15). From the simulated results, stress is concentrated between the two loading points, and cracks gradually propagate upwards in this region. Eventually, the overall failure process is consistent with the simulation results, with most of the aggregates along the failure surface being split, forming relatively smooth fracture surfaces.
By referring to the relevant articles (Liu et al., 2021; Guo et al., 2022; Li et al., 2023), it can be found that the simulation effect is better when the error between the experiment and the simulation results is less than 10%.
Table 12 summarizes the experimental and simulated flexural strengths, the error is within 10%, indicating that this model can effectively simulate the flexural mechanical properties of HPC containing ASR inhibitors under long-term alkali immersion.
Figure 16 depicts the failure process of three different strength HPC specimens, Ca40-0, Ca50-0, and Ca60Z-0. The maximum effective strain was adjusted to 0.003. From the figure, it can be observed that cracks in all specimens generally develop from bottom to top. Cracks first appear in Ca40-0 at 0.002 s, then propagate rapidly upwards, bypassing the bottom aggregates and directly penetrating some aggregates in the middle of the specimen by 0.008s, forming the main crack. In contrast, cracks in Ca50-0 and Ca60Z-0 form later due to directly penetrating the bottom aggregates, but the main cracks also form at 0.008 s. With subsequent loading, the cracks gradually widen, leading to the final failure mode consistent with the actual scenario. Specifically, with increasing strength, the proportion of cracks penetrating aggregates increases. Almost no cracks bypassing aggregates were observed in Ca50-0 and Ca60Z, indicating that using the three-dimensional random aggregate mesoscopic model and associating microhardness with the mechanical parameters of concrete components to obtain model parameters can effectively simulate the flexural failure mode of HPC.
Figure 17 illustrates the failure process of coarse aggregates in the Ca40-0 model, where most aggregates exhibit splitting failure. As shown in the figure, as the loading time progresses, cracks make contact with the aggregates at 0.002s, followed by the appearance of fine cracks in the aggregates at 0.004 s. With further loading, the cracks continue to expand, penetrating the aggregates almost vertically, widening the cracks on both sides, and squeezing the aggregates sideways, ultimately resulting in a relatively smooth fracture surface. A small portion of cracks bypassing the aggregates can be observed. At 0.004s, the crack penetrates the ITZ and reaches the aggregates. Subsequently, instead of continuing to propagate in the original direction, the crack propagates along the ITZ between the aggregates and the mortar until complete failure occurs, causing the detachment of the aggregates from the mortar. The final failure surface exhibits protruding aggregates or retained aggregate voids.
Based on the investigation of the mechanical properties and microfailure mechanisms of HPC containing ASR inhibition measures under long-term alkali immersion, the specific conclusions are as follows.
(1) With the increase in strength grade, the flexural strength of HPC generally shows an increasing trend, but as the alkali content rises, the flexural strength gradually decreases. Air-entraining agents perform better in resisting ASR under long-term alkali immersion compared to corrosion inhibitor.
(2) In standard alkali solution, the flexural strength of HPC in the middle alkali state generally increases with the increase in strength grade during different immersion periods. The immersion time has an impact on the flexural strength of HPC with different strength grades. Initially, immersion can significantly enhance the flexural strength, but prolonged immersion leads to a gradual decrease in strength, albeit still maintained at a relatively high level.
(3) HPC specimens of different strength grades and alkali contents exhibit similar fracture characteristics in flexural tests, mainly characterized by a single primary crack formed between loading points and eventually extending to the specimen section.
(4) The three-dimensional random aggregate mesoscopic concrete model was used to simulate the flexural failure mode of HPC. Results demonstrate that with increasing strength, the occurrence time of initial cracks is delayed, and the ratio of cracks bypassing aggregates (cracks develop along the ITZ between aggregate and mortar until complete failure) decreases, and the ratio of cracks penetrating aggregates (cracks develop directly through the aggregates in an almost vertical direction) increases.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
JuG: Data curation, Formal Analysis, Investigation, Software, Writing–original draft, Writing–review and editing. WL: Formal Analysis, Investigation, Methodology, Software, Writing–review and editing. JiG: Funding acquisition, Resources, Software, Writing–review and editing. HY: Funding acquisition, Methodology, Resources, Writing–review and editing. HM: Funding acquisition, Methodology, Resources, Writing–review and editing. JY: Methodology, Resources, Writing–original draft. QT: Formal Analysis, Investigation, Writing–review and editing. WG: Formal Analysis, Investigation, Writing–review and editing. MZ: Investigation, Writing–review and editing. FW: Formal Analysis, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Major State Basic Research Development Program of China (973 Program) (Grant Nos. 2015CB655102), (Grant Nos. 2009CB623200), Qinghai Provincial Department of Science and Technology (Grant Nos. 2013-G-Q006A), and Lanzhou-Xinjiang High-speed Railway Xining Railway Station Comprehensive Renovation Project (2010-001).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Cavalcanti, A. J. C. T. (1986). “Alkali-aggregate reaction at moxoto dam, Brazil,” in Proceedings of the 7th international conference on alkali-aggregate reaction in concrete (Canada: Noyes Publication), 168–172. doi:10.1016/S0963-8695(97)88915-3
Chen, H., Soles, J. A., and Malhotra, V. M. (1993). Investigations of supplementary cementing materials for reducing alkali-aggregate reactions. Cem. Concr. Compos. 15 (1-2), 75–84. doi:10.1016/0958-9465(93)90039-C
Chen, J., Shi, H., Li, J., Guo, M., Ding, F., Shao, Z., et al. (2023). Mechanical properties of CFSST with steel reinforcement cage under biaxial eccentric compression. J. Constr. Steel Res. 204, 107853. doi:10.1016/j.jcsr.2023.107853
Chen, J., Zhao, C., Ding, F., and Xiang, P. (2019). Experimental study on the seismic behavior of precast concrete column with grouted corrugated sleeves and debonded longitudinal reinforcements. Adv. Struct. Eng., 1369–4332.
Choi, Y. C., and Choi, S. (2015). Alkali–silica reactivity of cementitious materials using ferro-nickel slag fine aggregates produced in different cooling conditions. Constr. Build. Mater. 99, 279–287. doi:10.1016/j.conbuildmat.2015.09.039
Crouch, R. S., and Wood, J. G. M. (1990). Damage evolution in AAR affected concretes. Eng. Fract. Mech. 35, 211–218. doi:10.1016/0013-7944(90)90199-q
Diao, Y. (2021). Research on macroscopic mechanical properties of concrete interfacial transition zone and its relationship with microstructure. Nanjing Univ. Aeronautics Astronautics.
Ding, J., Bai, Y., and Cai, Y. (2008). Suppressing effect of lithium slag on alkalisilica reaction and separation of its self-expansion. J. Hohai Univ. Nat. Sci. 36 (6), 824–827.
E Grattan-Bellew, P., J Beaudoin, J., and Vallée, V.-G. (1998). Effect of aggregate particle size and composition on expansion of mortar bars due to delayed ettringite formation. Cem. Concr. Res. 28 (8), 1147–1156. doi:10.1016/S0008-8846(98)00084-2
Fang, Q., and Zhang, J. (2012). “Three-dimensional numerical modelling of concrete-like materials subjected to dynamic loadings,” in Advances in protective structures (Boca Raton: CRC Press), 33–64.
Fang, Q., Zhang, J., Huan, Y., et al. (2013). The investigation into three-dimensional mesoscale modelling of fully-graded concrete. Eng. Mech. 30 (1), 14–30. (in Chinese).
Fang, Q., Zhang, J., Zhang, Y., Gong, Z., Chen, L., and Liu, J. (2016). 3D numerical investigation of cement mortar with microscopic defects at high strain rates. J. Mater Civ. Eng. ASCE28 28 (3), 1–10. doi:10.1061/(asce)mt.1943-5533.0001436
Fares, G., and Khan, M. I. (2013). HPC composites formulated to counteract early ASR expansion. J. ofF Mater. Civ. Eng. 25 (12), 1951–1958. doi:10.1061/(asce)mt.1943-5533.0000790
Gao, P. (2018). Study on durability of subway concrete structures under high salty soil in high altitude region of northwest China. Nanjing Univ. Aeronautics Astronautics.
Gao, P., Yu, H., Wen, J., et al. (2019). Effect of air-entraining agent on mitigating alkali-silica reactions under high-altitude alkaline environment. J. Chin. Ceram. Soc. 47 (5), 625–631.
Guo, J., Zhang, J., Yu, H., Ma, H., and Wu, Z. (2022). Experimental and 3D mesoscopic investigation of uniaxial compression performance on basic magnesium sulfate cement-coral aggregate concrete (BMSC-CAC). Compos. Part B Eng. 236, 109760. doi:10.1016/J.COMPOSITESB.2022.109760
Häfner, S., Eckardt, S., Luther, T., and Könke, C. (2006). Mesoscale modeling of concrete: geometry and numerics. Comput. Struct. 84 (7), 450–461. doi:10.1016/j.compstruc.2005.10.003
Jan, L., Thomas, M. D. A., Sellevold, E. J., Pedersen, B., Andiç-Çakır, Ö., Justnes, H., et al. (2013). Alkali-silica reaction (ASR)-performance testing: influence of specimen pre-treatment, exposure conditions and prism size on alkali leaching and prism expansion. Cem. Concr. Res. 53 (11), 68–90. doi:10.1016/j.cemconres.2013.05.017
Kubo, Y., and Nakata, M. (2012). “Effect of reactive aggregate on mechanical properties of concrete affected by alkali-silica reaction,” in Proceedings of the 14th International Conference on Alkali–Aggregate Reaction in Concrete, Austin, May 20–25th 2012. (electronic).
Li, L., Ma, H., Yu, H., Zhang, J., Cheng, M., Wu, Z., et al. (2023). Attack resistance mechanism, uniaxial compressive mechanical properties and meso-simulation of high-performance concrete exposed to brine in salt lake for 10 years. Constr. Build. Mater. 407, 133520. doi:10.1016/j.conbuildmat.2023.133520
Liu, S. H., Bracci, J. M., Mander, J. B., and Hurlebaus, S. (2015). Performance of D-regions affected by alkali-silica reaction: experimental and analytical study. ACI Mater. J. 4 (112), 501–511. doi:10.1061/(ASCE)ST.1943-541X.0001847
Liu, H., and Jia, F. (1995). Effect of fine aggregate on elastic modulus of mortar and concrete. concrete (1), 12–18.
Liu, T., Ma, H., Wu, Z., et al. (2021). Study on impact compressive properties of basic magnesium sulfate cement concrete. J. Build. Mater. 24 (03), 562–570.
Lu, Y., Song, Z., and Tu, Z. (2010). Analysis of dynamic response of concrete using a mesoscale model incorporating 3D effects. Int. J. Prot. Struct. 1 (2), 197–217. doi:10.1260/2041-4196.1.2.197
Ma, H., Xu, W., and Li, Y. (2016). Random aggregate model for mesoscopic structures and mechanical analysis of fully-graded concrete. Comput. Struct. 177, 103–113. doi:10.1016/j.compstruc.2016.09.005
Mao, L., Hu, Z., Xia, J., Feng, G. l., Azim, I., Yang, J., et al. (2019). Multi-phase modelling of electrochemical rehabilitation for ASR and chloride affected concrete composites. Compos. Struct. 207, 176–189. doi:10.1016/j.compstruct.2018.09.063
Marzouk, H., and Langdon, S. (2003). The effect of alkali -aggregate reactivity on the mechanical properties of high and normal strength concrete. Cem. Concr. Compos. 25 (4-5), 549–556. doi:10.1016/s0958-9465(02)00094-x
McCoy, W. J., and Caldwell, A. G. New approach to inhibiting alkali-aggregate reaction expansion, A. C. I, 1951,22(9):693- 706.
Ministry of Housing and Urban-Rural Development of the OPeople’s Republic of China (2019). GB/T 50081-2019 Standard for test methods of concrete physical and mechanical properties. Beijing: China Architecture and Building Press.
Mong, X., Xu, Z., and Tang, M. (2002). Review of alkali-aggregate reaction and its research progress. J. Mater. Sci. Eng. (01), 128–132. (in Chinese).
Nixon, P. J., and Bollinghaus, R. (1985). The effect of alkali aggregate reaction on the tensile strength of concrete, Durab. Build. Mater. 2 (3), 243–248.
Qian, C. X., Guo, H. D., and Tang, M. S. (1994). Mechanism of mineral admixture suppressing alkali-silica reaction: Part I, Corrosion degree of reactive aggregate in blended cement pastes and its correlations with expansion value and electric resistance change. Cem. Concr. Res. 24 (16), 1111–1120. doi:10.1016/0008-8846(94)90035-3
Qin, F., Kong, X. Z., and Wu, H. (2014). Determination of HOLMQUIST-JOHNSON-COOK CONSITIUTIVE model parameters of rock. Eng. Mech. 31 (03), 197–204. doi:10.6052/j.issn.1000-4750.2012.10.0780
Sanchez, L. F. M. (2014). Contribution to the assessment of damage in aging concrete infrastructures affected by alkali-aggregate reaction (Québec: Department of Geology and Geological Engineering, Université Laval). PhD thesis.
Shayan, A., and Ivanusec, I. (1989). “Influence of NaOH on mechanical properties of cement paste and mortar with and without reactive aggregate,” in Proceedings of the8th intonational conference on alkali-aggregate reaction in concrete (Japan: Kyoto).
Smaoui, N., Bérubé, M. A., Fournier, B., and Bissonnette, B. (2004). Influence of specimen geometry, orientation of casting plane, and mode of concrete consolidation on expansion due to ASR. Cem. Concr. Aggreg. 26 (2), 1–13. doi:10.1520/cca11927
Tang, M., Xu, Z., Deng, M., Lv, Y., Han, S., and Lan, X. (2022) Alkali aggregate reaction of concrete in China. J. Build. Mater. 1998 (01), 10–16. (in Chinese).
Vo, D., Hwang, C., Tran Thi, K. D., Yehualaw, M. D., and Chen, W. C. (2020). Effect of fly ash and reactive MgO on the engineering properties and durability of high-performance concrete produced with alkali-activated slag and recycled aggregate. J. Mater. Civ. Eng. 32 (11). doi:10.1061/(ASCE)MT.1943-5533.0003420
Wang, F. (1993). “A Study on corrosion and destruction of concrete under natural condition of Caerhan,” in Proc. 3rd Beijing Int. Symp. On cem. And concr (Beijing: IEEE), 811–815.
Wittmann, F. H., Roelfstra, P. E., and Sadouki, H. (1985). Simulation and analysis of composite structures. Mater. Sci. Eng. 68 (2), 239–248. doi:10.1016/0025-5416(85)90413-6
Wriggers, P., and Moftah, S. O. (2006). Mesoscale models for concrete: homogenisation and damage behaviour. Finite Elem. Analysis Des. 42 (7), 623–636. doi:10.1016/j.finel.2005.11.008
Wu, Z. (2000). High performance concrete--green high performance concrete. China Concr. Cem. Prod. (01), 3–6.
Wu, Z., Zhang, J., Fang, Q., Yu, H., and Ma, H. (2021a). Mesoscopic modelling of concret-e material under static and dynamic loadings: a review. Constr. Build. Mater. 278, 122419. doi:10.1016/j.conbuildmat.2021.122419
Wu, Z., Zhang, J., and Yu, H. (2021c). Three-dimensional mesoscopic investigation on quasi-static compressive properties of coral aggregate concrete. ACI Mater. J. 118 (4), 121–132.
Wu, Z., Zhang, J., and Yu, H. (2022). Mesoscopic particulate system assembled from three-dimensional irregular particles. Adv. Powder Technol. 33 (5), 103580. doi:10.1016/j.apt.2022.103580
Wu, Z., Zhang, J., Yu, H., Ma, H., and Fang, Q. (2021b). 3D mesoscopic analysis on the compressive behavior of coral aggregate concrete accounting for coarse aggregate volume and maximum aggregate size. Compos. Struct. 273, 114271. doi:10.1016/j.compstruct.2021.114271
Xiang, P., and Liew, K. M. (2013). A computational framework for transverse compression of microtubules based on a higher-order Cauchy–Born rule. Comput. Methods Appl. Mech. Eng. 254, 14–30. doi:10.1016/j.cma.2012.10.013
Xu, W., Chen, H., and Lv, Z. (2011). An overlapping detection algorithm for random sequential packing of elliptical particles. Phys. A Stat. Mech. its Appl. 390 (13), 2452–2467. doi:10.1016/j.physa.2011.02.048
Yan, J., Yu, H., Zhang, W., Zahng, L., Ma, H., Gong, X., et al. (2022). Expansion and mechanical properties of high-performance concrete with ASR inhibition measures exposed to alkaline solution at 38℃ for 10 years. Constr. Build. Mater. 353, 129044. doi:10.1016/j.conbuildmat.2022.129044
Yu, H., Hua, P., Qu, W., Sun, W., and Yan, L. (2003). Field exposure experiment of anti-corrosion concrete pole in northwest salt lake area. China Concr. Cem. Prod. (6), 23–26. (in chinese).
Zhang, J., Wu, Z., Zhang, Y., Fang, Q., Yu, H., and Jiang, C. (2021). Mesoscopic characteristics and macroscopic mechanical properties of coral aggregates. Constr. Build. Mater. 309, 125125. doi:10.1016/j.conbuildmat.2021.125125
Zhang, L. (2014). Research on durability of reinforced concrete structure based on the correlation between field exposure test and indoor durability test. Nanjing: Nanjing University of Aeronautics and Astronautics.
Keywords: ASR inhibition measures, HPC, prolonged alkaline solution immersion, flexural strength, numerical simulation
Citation: Guo J, Liu W, Guo J, Yu H, Ma H, Yan J, Tao Q, Gao W, Zhang M and Wang F (2024) The flexural mechanical properties and mesoscopic mechanisms of fracture failure of HPC with ASR inhibition measures under prolonged alkaline solution immersion. Front. Mater. 11:1407922. doi: 10.3389/fmats.2024.1407922
Received: 27 March 2024; Accepted: 04 June 2024;
Published: 04 July 2024.
Edited by:
Ping Xiang, Central South University, ChinaReviewed by:
Piotr Smarzewski, Military University of Technology in Warsaw, PolandCopyright © 2024 Guo, Liu, Guo, Yu, Ma, Yan, Tao, Gao, Zhang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongfa Yu, eXVob25nZmFAbnVhYS5lZHUuY24=; Haiyan Ma, bWFoYWl5YW5AbnVhYS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.