Effect of cyclic compression on the micromechanical properties of a Zr-based metallic glass

In this study, the effect of cyclic compression on the micromechanical properties of a Zr-based metallic glass (MG) was investigated via nanoindentation. Cyclic compression significantly softened the surface of the sample, with a maximum hardness loss of 19.93%. The number of cyclic compression passes had a greater effect on the hardness of the sample than the cyclic compression load. The elastic modulus exhibited a nonlinear variation upon increasing the cyclic loading or number of passes at a lower loading rate due to the coupling effect of loading rate and cyclic compression treatment. Then, the serration behavior and strain rate sensitivity analysis were applied. The calculated m-values obtained for MGs were all negative and gradually tended to zero upon further cyclic compression treatment. This demonstrated the weakening effect of cyclic compression on the strain rate sensitivity of MG, and the underlying mechanism was discussed. This study provides a process reference for studying the fatigue failure behaviors of MGs from the perspective of mechanical properties, which is useful for understanding their fatigue generation.

Introduction

Due to their amorphous structures, metallic glasses (MGs) exhibit excellent mechanical and physical properties, such as high strength, high hardness, and wear resistance (Hufnagel et al., 2016; Lai et al., 2019; Yang et al., 2019; Tao et al., 2022; Zhang et al., 2023). However, at room temperature, they undergo non-uniform and highly localized deformation in a narrow region called the shear band. MGs usually fail catastrophically along the shear band once the stress reaches its yield limit, thus exhibiting almost zero plasticity, which seriously hampers their industrial applications. Much work has been conducted to study the plasticity of MGs to overcome this bottleneck.

The effect of cold rolling on the plasticity of MGs was studied by Park et al. (2014), who obtained a tensile plasticity of 0.8% by applying a thickness reduction ratio of 20%. They reported that cold rolling introduced a shear-softening zone in the sample that contained a large free volume that readily underwent plastic flow. During tensile tests, the free volume-rich region easily underwent shear band nucleation, resulting in a large number of branching shear bands that could accommodate more plastic deformation. This ultimately manifested in an enhanced macro-plasticity in the MGs. Zhou et al. reported that pre-plastic deformation (PPD) improved the mechanical properties of MGs (Zhou et al., 2022). This enhancement was related to Poisson’s ratio, where PPD treatment in MGs with a high Poisson’s ratio triggered the generation of multiple shear bands and enhanced their compression plasticity, while those with a low Poisson’s ratio showed worse performance after PPD treatment. Gu et al. used pre-compression to increase the plasticity of MGs from 2.8% to 6.7% (Gu et al., 2014; Gu et al., 2014). They attributed this improvement in plasticity to the excess free volume generated by the shear stresses from deformation. In addition to the research mentioned above, shot peening, severe plastic deformation, and other methods have also been adopted to explore the plastic deformation of MGs (Lee et al., 2010; Fornell et al., 2014; Gao et al., 2016; Guo et al., 2018; Ma et al., 2019; Li et al., 2020; Phan et al., 2021). The essence of all of the abovementioned methods was microstructural modulation by applying an external stress. However, this applied stress is almost always a single stress, which impelled us to investigate the effect of alternating stress on the plasticity of MGs.

The application of alternating stresses is usually realized by cyclic compression, and studies of MGs have mainly focused on their fatigue damage. For example, Greer et al. analyzed the effect of cyclic compression on the onset of failure in a Zr-based MG (Louzguine-Luzgin et al., 2014). They proposed that stress inversion accelerated the concentration of shear events in the shear zone, leading to a reduction in the fatigue resistance of MGs. By analyzing the impact of free volume on the compression fatigue of MGs, Zhang et al. found that a lower free volume suppressed the formation of new shear bands under cyclic loading. This enhanced the fatigue endurance limit and fatigue ratio of the samples (Wang et al., 2019). However, in early reports, researchers focused more on crack initiation process due to cyclic loading and the morphological characteristics of sample failure, to determine the cause of fatigue failure and elucidate the failure mechanism. However, the understanding of the evolution of the structural and mechanical properties of MGs during cyclic loading was insufficient. Although some scholars have used numerical simulations (Ye et al., 2016; Li et al., 2019) to attempt to elucidate the atomic mechanism by which cyclic compression leads to elastic softening, they still lack strong experimental support. It is difficult to determin the evolution of the micromechanical properties of MGs during resistance to fatigue damage, which requires further research to better understand the fatigue damage mechanism of MGs.

In this paper, nanoindentation was adopted to investigate the effects of the number of cyclic compression passes and loads on the micromechanical properties of a Zr-based MG. The characteristics of the micromechanical response of MGs under cyclic compression were analyzed, and potential response mechanisms were also discussed.

Materials and methods

The master alloy Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 (at%) was prepared under a high-purity argon atmosphere (99.99%) by fusing pure element components by arc melting. The ingot was poured and repeatedly melted to ensure uniformity, and then sucked into a water-cooled copper mold. Finally, a cylindrical rod with a diameter (d) of 5 mm was obtained (Li et al., 2019). The experimental samples were cut from the cylindrical rod with a height of 3 mm. Prior to the experiment, the sample’s top surface was ground with sandpaper and then polished with 40 nm SiO₂ suspension, as shown in Figure 1A. The cyclic loading tests were performed by a QBG-200 high-frequency fatigue testing machine (produced by Changchun Qianbang Equipment Co., Ltd.) The stress ratio $R={\sigma }_{\min }/{\sigma }_{\max }$ was kept constant at 0.1.

Figure 1

Figure 1. (A) The picture of samples, (B) nanoindentation device.

Previous report has given the research on the fatigue failure of Zr-based MG (Wang et al., 2005). Although the yield strength of Zr-based MG reaches 1.8 GPa, its fatigue endurance limit is very low, about 615 MPa. They reported that the origin of fatigue failure cracks is the porosities and inclusions in the casting process, and analyzed the fatigue fracture morphology. It is found that there are obvious melting fields in the fracture area, which indicates that the fracture generates high temperature instantaneously. This study gives us inspiration to carry out elastic cyclic loading in the range of fatigue limit and study its effect on the mechanical properties of materials. Therefore, two loads (200 and 400 MPa) within the fatigue endurance limit range were selected. On the other hand, according to this report, when the loading load is 800 MPa, the fatigue life reaches about 100,000 times, so the lower number of cycles may not bring significant changes in the result, so 10,000 and 40,000 cycles are chosen. The corresponding samples were labeled 200C1, 200C4, and 400C1. The load frequency was 90 Hz. Samples were subjected to nanoindentation testing after cyclic compression treatment. Nanoindentation experiments were conducted at room temperature using a Nano Indenter G200 equipped with a Berkovich diamond indenter, Figure 1B, with indentations performed in a load-controlled mode. The loading rates were 0.5, 1, and 5 mN/s, and the maximum load was 50 mN. Each test is repeated at least 5 times. To prevent the indentations from influencing each other, they were spaced 50 µm apart. To eliminate thermal impacts, thermal drift was kept at 0.05 nm/s.

Results and discussion

(1) HARDNESS ANALYSIS

Figure 2A shows the correlation between the number of cyclic compression passes and the microhardness under three different loading rates.

Figure 2

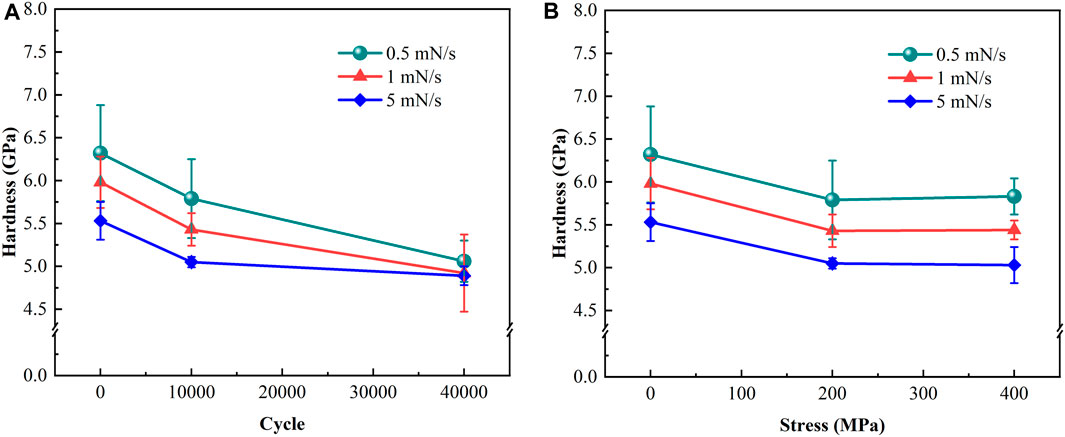
Figure 2. (A) Relationship between the number of cyclic compression passes and hardness at different loading rates for as cast, 200C1 and 200C4 samples; (B) Relationship between the cyclic compression load and the hardness at different loading rates for as cast, 200C1 and 400C1 samples.

The microhardness of the samples at all three loading rates was negatively correlated with the number of passes. Below 10,000 cyclic compression passes, the hardness decreased upon increasing the loading rate under the same conditions. The microhardness was significantly affected by the number of passes at a loading rate of 0.5 mN/s. The microhardness of the as-cast sample was 6.32 GPa, which then decreased to 5.79 GPa when the sample was treated with 10,000 cyclic compression passes. When the cyclic compression passes reached 40,000, the microhardness dropped significantly to 5.06 GPa, representing the maximum hardness reduction rate of 19.93%. When the loading rate was increased to 1 mN/s, the influence of cyclic compression passes was weakened. The hardness was 5.98, 5.43, and 4.92 GPa for as cast, 200C1 and 200C4 samples, showing a significant decrease in microhardness with the number of passes. The blue line shows that the microhardness was 5.53, 5.05, and 4.89 GPa, respectively, as the number of cyclic compression passes increased at a constant loading rate of 5 mN/s. When the number of cyclic compression passes exceeded 10,000, the rate of hardness reduction gradually leveled off. Similarly, when the loading rate surpassed 1 mN/s, the impact of the loading rate on hardness was greatly diminished after 40,000 cycles.

Figure 2B shows the relationship between the load during cyclic compression and hardness at different loading rates. At a constant loading rate of 0.5 mN/s, the microhardness of the as-cast sample was 6.32 GPa, but when the load was increased to 200 MPa, the microhardness decreased to 5.79 GPa. As the cyclic compression load increased to 400 MPa, its hardness showed an extremely small change to 5.83 GPa. There was a clear negative correlation between hardness and the load during cyclic compression. The hardness substantially decreased when the cyclic compressive load exceeded 200 MPa, and this negative correlation weakened considerably when the loading rate exceeded 1 mN/s. At a loading rate of 1 mN/s, the corresponding hardness values for the two-stage increase in the cyclic compression load from 0 to 200 MPa and then to 400 MPa were 5.98, 5.43, and 5.44 GPa. When the load reached 5 mN/s, the corresponding hardness values were 5.53, 5.05, and 5.03 GPa, respectively, representing a much slower decrease.

In MGs, shear transformation zones (STZs) are the fundamental plastic flow units, where shear band nucleation itself is considered to originate from cooperative STZ activation (Chen et al., 2016; Zhao et al., 2017). Therefore, at a low loading rate, atoms have sufficient time to undergo diffusive relaxation processes, thereby increasing the hardness or flow stress. When the loading rate was increased, the local atomic relaxation diffusion time decreased, and the STZ was continuously activated to form a shear band nucleus. Plastic flow was shared by multiple shear bands, and the flow stress or hardness was weakened.

On the other hand, Applying stress below the yield strength of the MG may still lead to permanent structural changes at the atomic scale (Albano and Falk, 2005; Ogata et al., 2006). When the sample was subjected to cyclic compression treatment, cyclic stresses could induce excess free volume. At the same loading rate, the shear bands were more easily nucleated, providing more shear bands that could accommodate plastic deformation, accompanied by lower flow stress and a comparable decrease in hardness.

Freels et al. (2011) also studied the cyclic compression behavior of Cu based MG. They found that cyclic compression could induce shear bands or mixed-mode cracks at pre-existing defects on the surface. With further cyclic loading, the cracks gradually expanded in the normal direction along the loading direction. They presented the process of crack expansion under cyclic compression until sample failure, helping us to understand how fatigue failure of MGs occurs. However, we do not have access to whether the mechanical properties of the samples changed before the cracks were generated. Our study provides a perspective to study the evolution of mechanical properties during early fatigue loading of samples. This means that, under cyclic loading, the MGs first soften before cracking occurs, which is an unavoidable process.

(2) ELASTIC MODULUS ANALYSIS

Figure 3A shows that the elastic modulus was strongly correlated with the number of cyclic compression passes at different loading rates. At a loading rate of 0.5 mN/s, as the number of cyclic compression passes increased from 0 to 10,000, the elastic modulus decreased from 98.05 to 94.81 GPa. However, at 40,000 passes, it increased to 111.59 GPa. At a loading rate of 1 mN/s, the elastic modulus decreased as the number of passes increased to 40,000 from 100.57 to 93.45 GPa. A similar trend was observed when the loading rate was 5 mN/s. The elastic modulus of Zr-based MGs was positively correlated with the loading rate when the number of cyclic compression passes was below 10,000.

Figure 3

Figure 3. (A) Relationship between the number of cyclic compression passes and elastic modulus at different loading rates for as cast, 200C1 and 200C4 samples; (B) Relationship between the load during cyclic compression and elastic modulus at different loading rates for as cast, 200C1 and 400C1 samples.

The same negative correlation was observed between the cyclic compression load and elastic modulus at loading rates of 1 mN/s and 5 mN/s, as shown in Figure 3B. At a loading rate of 1 mN/s, the elastic modulus decreased from 100.57 to 97.76 GPa for cyclic compression loads of 0 MPa, 200 MPa, and 400 MPa, respectively. A similar trend in the elastic modulus was observed at a loading rate of 5 mN/s, with corresponding elastic modulus values of 112.35, 110.54, and 106.09 GPa, respectively. This negative correlation was invalid at a loading rate of 0.5 mN/s, where the corresponding elastic modulus values were 98.05, 94.81, and 98.02 GPa for cyclic compression loads of 0 MPa, 200 MPa, and 400 MPa, respectively.

The anomalous enhancement in the elastic modulus be interpreted from the view of inherent atomic-scale structure. As we know, the uniaxial compressive stress can be decomposed into two different stresses in the maximum shear plane, i.e., shear stress and hydrostatic pressure with an equal magnitude. Lee et al. have previously reported the effect of compressive stress on the structure of MGs from the view of inherent atomic-scale structure (Lee et al., 2007). On the one hand, they found that with increasing shear strain, the fraction of densely packed polyhedral within the MG decreases, while the fraction of loosely packed polyhedral increases, implying an increase in the free volume of the MG. On the other hand, they analyzed the relationship between hydrostatic pressure and rate change in the free-energy barrier for nucleation and the nucleation rate of nanocrystals, finding that hydrostatic pressure favors the nucleation of nanocrystal in MGs with a lower packing density. In a word, during uniaxial compression, shear stress promotes the creation of free volume and lowers the diffusion energy barrier of atoms in the local region, which in turn leads to an increase in the rate of nanocrystal nucleation under hydrostatic pressure.

For this study, the increase in free volume of in nucleation rate of nanocrystal due to cyclic compressive stress are in a competing relationship, At the beginning of loading, the hydrostatic pressure in the cyclic stress has a very small and almost negligible effect on the nucleation rate increase, which gradually strengthens with the increase of loads or the number of cycles. The sample structure tends to produce a critical state of local ordering as the number of cycles or loading amplitude increases. During nanoindentation, the loading rate of 0.5 mN/s provided a more than sufficient time for the structural relaxation of the sample, in which atoms tended to undergo localized ordered, and the spacing between atoms decreased. This ultimately exhibited an anomalous increase in the elastic modulus.

(3) P-H CURVE ANALYSIS

The load-depth curves of different samples were analyzed to understand the deformation behavior during nanoindentation of the Zr-based MG. Figure 4A depicts the representative load-depth (P-h) curves of various samples at a maximum indentation load of 50 mN and a loading rate of 0.5 mN/s.

Figure 4

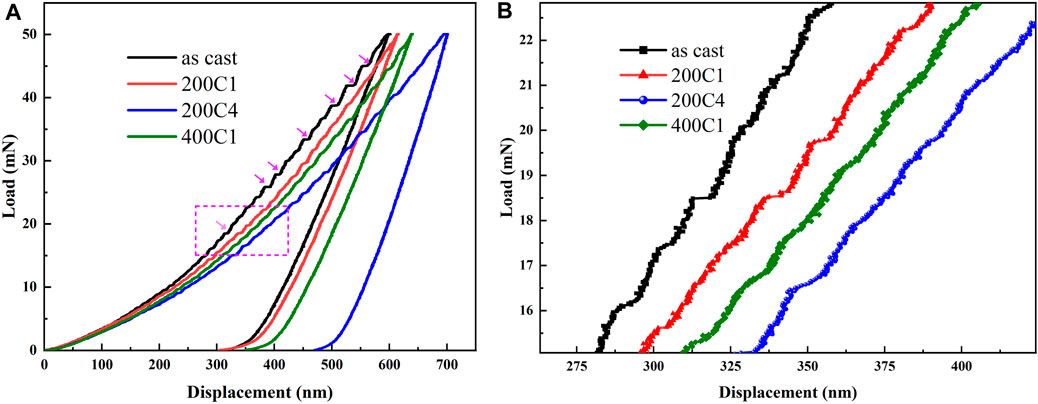
Figure 4. (A) Representative load-depth curves of different samples, where the arrow indicates a typical serrated shape. (B) Enlarged view of the marked area on the loading curve in (A).

The local enlarged view is presented in Figure 4B, in which the P-h curve of the as-cast sample showed an ideal stair-step-like serration. Then, it substantially transformed into ripple-shaped or even slightly uneven curves as the number of cyclic compression passes increased from 0 to 40,000. Similarly, an increase in the stress amplitude also weakened the serrations in the P-h curves. The pop-in event was attributed to plastic flow in the MG, which was confined in the tiny space along the indenter tip (Schuh and Nieh, 2003; Packard and Schuh, 2007). Plastic flow in MGs often occurs in the form of shear bands, where more obvious serration indicates the generation of larger scale shear bands, meaning that the plastic flow is more localized. In contrast, cyclic compression treatment significantly weakened the serration in the P-h curves, suggesting that it is beneficial to the plastic deformation ability of MGs.

Relative to the indentation depth of 600.17 nm in the as-cast sample, after cyclic compression, the maximum indentation depth increased significantly from 615.47 nm to 701.65 nm as the number of cyclic compression passes increased from 10,000 to 40,000. This means that the sample underwent softening during cyclic compression, corresponding to the hardness results.

Discrete displacement bursts during the nanoindentation of MGs are called pop-in events and occur due to the nucleation and propagation of shear bands, with each pop-in corresponding to a single shear event (Wright et al., 2001; Packard and Schuh, 2007; Brechtl et al., 2020). The more pronounced step-like serration in the as-cast samples implies that the shear bands formed during the indentation process accommodated more plastic strain. Conversely, this indicates that a single shear band can accommodate less plastic deformation. As mentioned earlier, cyclic compression generates a large free volume, leading to easier activation of STZ, and lowering the stress threshold for the emergence of shear bands. Under the same loading conditions, the treated samples can generate more shear bands to accommodate the resulting plastic strain. Thus, the plastic strain accommodated by a single shear band decreased. In other words, the region of the MGs that can accommodate plastic deformation increased and strain localization decreased.

The nature of elastic-plastic deformation beneath the indenter can be evaluated using the h_f/h_max ratio (Herbert et al., 2018), which lies between 0 and 1. h_max is the maximum indentation depth during indentation, and h_f is the residual depth after indentation. A ratio of 0 implies complete elastic deformation, while a ratio of one indicates complete plastic deformation. Figure 5 shows the h_f/h_max ratio of different samples.

Figure 5

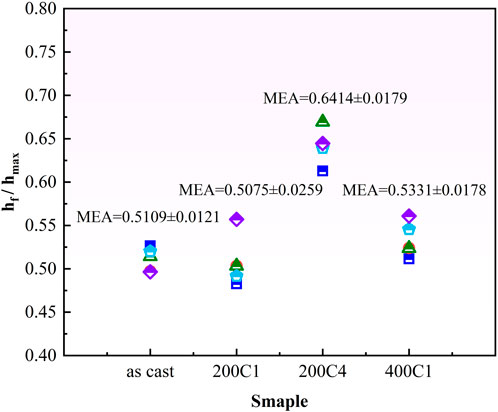
Figure 5. The h_f/h_max ratios of different samples, each feature identification point represents one test data.

For the as-cast sample, the mean h_f/h_max value was 0.5109 ± 0.0121, indicating elastic-plastic deformation. The average value of the ratio remained almost constant (0.5075 ± 0.0259) after 10,000 cyclic compression passes under 200 MPa cyclic compressive stress. The ratio then became 0.6414 ± 0.0179, and a significant increase was observed when the cyclic compression passes increased to 40,000, indicating more plastic during the indentation process. When the cyclic compressive stress amplitude was varied, the h_f/h_max ratio changed in a similar trend. In addition, the h_f/h_max ratio can be used to identify the reliability of the calculated hardness values obtained from nanoindentation tests. When the ratio was greater than 0.7, pileup during indentation may provide an incorrect estimate of H due to an erroneous contact area deduced from indentation load-depth data (Guillonneau et al., 2019). Obviously, all h_f/h_max ratios in this study were less than 0.7, implying that the previous hardness results were accurate.

(4) STRAIN RATE SENSITIVITY ANALYSIS

The strain rate sensitivity, m, was also taken into account to better understand the rate-dependent deformation mechanism. Rate jumps were done to estimate the strain rate sensitivity (m), as shown in Eq. 1 (Dhale et al., 2022):

$m=\frac{\partial \ln H}{\partial \ln \dot{\epsilon }}(1)$

where H is the hardness derived from the constant-strain-rate experiments, $\dot{\epsilon }$ is the indentation strain rate applied during the experiment, given as Eq. 2 (Pan et al., 2008):

$\dot{\epsilon }=\frac{1}{h}\frac{dh}{dt}=\frac{1}{2}\frac{\dot{P}}{P}(2)$

Figure 6 shows the variation in ln(Hardness) with ln(strain rate) for different numbers of cyclic compression passes. The m value of each sample is shown by the fitted curves’ slopes. The linear fits’ slopes yielded m = −0.05634, −0.05687, −0.0129, and −0.06139 for the as-cast, 200C1, 200C4, and 400C1 samples, respectively. These changes in m imply a correlation between cyclic compression and the strain rate sensitivity of MGs, particularly the number of cyclic compression passes.

Figure 6

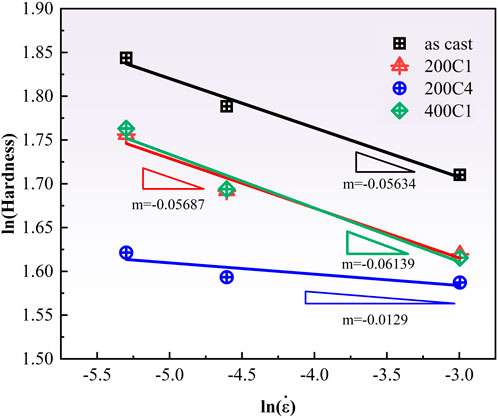
Figure 6. Variations of ln(Hardness) with ln(strain rate) for different specimens to determine the strain rate sensitivity values.

The positive and negative values of m reflect the different deformation mechanisms of the material. Resistance to local plastic deformation is frequently implied by a positive and high value of m combined with large strain hardening. For MGs, m = 1 indicates a Newtonian fluid above the glass transition temperature T_g. Because shear band-mediated flow dominates the strain rate sensitivity of MGs, the strain rate sensitivity usually becomes negative at room temperature or below the T_g. The differences in local flow during the indentation of the samples in different treatment states were also evidenced by the serration of the P-h curves in Figure 4. Similar negative values of m were also reported by Bhattacharyya et al. (2007), who investigated the strain rate sensitivity of MGs in different structural states, including as-cast, structurally-relaxed, and shot-peened states. They found that all of the strain rate sensitivity m values were negative and depended on the structural state of the MGs. For the shot-peened sample, with the highest free volume content, the value of m was the closest to zero. These results lend great support to our own research.

The strain rate sensitivity of MGs is a result of the mismatch between the intrinsic strain rate and the applied strain rate. It is widely recognized that the free volume content is an important parameter for characterizing the structural state of MGs. The shear strain rate of MGs is related to the free volume content, where a larger free volume content results in a higher intrinsic shear strain rate(Van Steenberg et al., 2007). When the indenter was loaded, the shear stresses produced in the sample drove the atoms to move. As the loading rate exceeded the intrinsic strain rate, the atom movement rate is insufficient to achieve stress relaxation, and further deformation requireed higher stresses, thus exhibiting strain rate dependence. In contrast, in this paper, cyclic compressive loading introduced a large amount of free volume within the MG, which increased the intrinsic strain rate level of the sample. When applying the same loading rate, the time required for atomic relaxation decreased, resulting in a decrease of the strain rate dependence. As shown in Figure 2, the hardness values of the samples at different strain rates showed little difference after 40, 000 loading cycles under 200 MPa.

Conclusion

In this paper, the effect of cyclic compression on the micromechanical properties of a Zr-based MG was investigated using nanoindentation, aiming to investigate the evolution of micromechanical properties of MGs during resistance to fatigue damage, and to provide experimental support for the understanding of fatigue damage mechanisms in MGs. The following conclusions are drawn from this study:

(1) Cyclic compression treatment significantly reduced the surface microhardness of MGs. The maximum hardness reduction reached 19.93% because cyclic compression could induce excess free volume. This made it easier to form multiple shear bands in MGs, which means that atoms are more likely to flow, exhibiting a decrease in hardness.

(2) The elastic modulus of the samples was also changed by cyclic compression, which introduced a large amount of free volume that increased the atomic spacing and decreased the elastic modulus. Specifically, loading to 400 MPa or 40,000 cycles led to an anomalous enhancement in the elastic modulus of the MGs when the loading rate was 0.5 mN/s. This was attributed to the combined effect of an increase in the localized nucleation rate due to cyclic compression and a lower indentation loading rate.

(3) The serration behavior and strain rate sensitivity analysis indicated that the deformation mechanism of the sample during indentation was shear band-dominated flow, as indicated by the negative m-value. In addition, the cyclic compression treatment significantly reduced the strain rate sensitivity of the MGs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Data curation, Methodology, Writing–original draft. HZ: Investigation, Methodology, Writing–original draft. HS: Data curation, Methodology, Writing–review and editing. AW: Methodology, Supervision, Writing–review and editing. YL: Conceptualization, Funding acquisition, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Science and Technology Project of Hebei Education Department (No. QN2023156), the Key Project of the Natural Science Foundation of Hebei Province (Basic Discipline Research) (No. A2023210064), and the National Natural Science Foundation of China (Grant Nos 12272392 and No.11790292).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albano, F., and Falk, M. L. (2005). Shear softening and structure in a simulated three-dimensional binary glass. J. Chem. Phys. 122 (15), 154508. doi:10.1063/1.1885000

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhattacharyya, A., Singh, G., Prasad, K. E., Narasimhan, R., and Ramamurty, U. (2015). On the strain rate sensitivity of plastic flow in metallic glasses. Mater. Sci. Eng. A 625, 245–251. doi:10.1016/j.msea.2014.12.004

CrossRef Full Text | Google Scholar

Brechtl, J., Wang, Z., Xie, X., Qiao, J. W., and Liaw, P. K. (2020). Relation between the defect interactions and the serration dynamics in a zr-based bulk metallic glass. Appl. Sci. 10 (11), 3892. doi:10.3390/app10113892

CrossRef Full Text | Google Scholar

Chen, Z. Q., Huang, L., Huang, P., Xu, K., Wang, F., and Lu, T. (2016). Clarification on shear transformation zone size and its correlation with plasticity for Zr-based bulk metallic glass in different structural states. Mater. Sci. Eng. A 677, 349–355. doi:10.1016/j.msea.2016.09.054

CrossRef Full Text | Google Scholar

Dhale, K., Banerjee, N., Outeiro, J., and Singh, R. K. (2022). Investigation of the softening behavior in severely deformed micromachined sub-surface of Zr-based bulk metallic glass via nanoindentation. J. Non-Crystalline Solids 576, 121280. doi:10.1016/j.jnoncrysol.2021.121280

CrossRef Full Text | Google Scholar

Fornell, J., Concustell, A., Greer, A. L., Suriñach, S., Baró, M., and Sort, J. (2014). Effects of shot peening on the nanoindentation response of Cu_47.5Zr_47.5Al₅ metallic glass. J. alloys Compd. 586, S36–S40. doi:10.1016/j.jallcom.2012.12.051

CrossRef Full Text | Google Scholar

Freels, M., Wang, G. Y., Zhang, W., Liaw, P., and Inoue, A. (2011). Cyclic compression behavior of a Cu–Zr–Al–Ag bulk metallic glass. Intermetallics 19 (8), 1174–1183. doi:10.1016/j.intermet.2011.03.023

CrossRef Full Text | Google Scholar

Gao, M., Dong, J., Huan, Y., Wang, Y. T., and Wang, W. H. (2016). Macroscopic tensile plasticity by scalarizating stress distribution in bulk metallic glass. Sci. Rep. 6 (1), 21929. doi:10.1038/srep21929

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, J., Song, M., Ni, S., Liao, X., and Guo, S. (2014). Improving the plasticity of bulk metallic glasses via pre-compression below the yield stress. Mater. Sci. Eng. A 602, 68–76. doi:10.1016/j.msea.2014.02.065

CrossRef Full Text | Google Scholar

Guillonneau, G., Wheeler, J. M., Wehrs, J., Philippe, L., Baral, P., Höppel, H. W., et al. (2019). Determination of the true projected contact area by in situ indentation testing. J. Mater. Res. 34 (16), 2859–2868. doi:10.1557/jmr.2019.236

CrossRef Full Text | Google Scholar

Guo, W., Yamada, R., and Saida, J. (2018). Rejuvenation and plasticization of metallic glass by deep cryogenic cycling treatment. Intermetallics 93, 141–147. doi:10.1016/j.intermet.2017.11.015

CrossRef Full Text | Google Scholar

Herbert, E. G., Hackney, S. A., Dudney, N. J., and Phani, P. S. (2018). Nanoindentation of high-purity vapor deposited lithium films: the elastic modulus. J. Mater. Res. 33 (10), 1335–1346. doi:10.1557/jmr.2018.83

CrossRef Full Text | Google Scholar

Hufnagel, T. C., Schuh, C. A., and Falk, M. L. (2016). Deformation of metallic glasses: recent developments in theory, simulations, and experiments. Acta Mater. 109, 375–393. doi:10.1016/j.actamat.2016.01.049

CrossRef Full Text | Google Scholar

Lai, L., He, R., Ding, K., Liu, T., Liu, R., Chen, Y., et al. (2019). Ternary Co-Mo-B bulk metallic glasses with ultrahigh strength and good ductility. J. Non-Crystalline Solids 524, 119657. doi:10.1016/j.jnoncrysol.2019.119657

CrossRef Full Text | Google Scholar

Lee, J. C., Park, K. W., Kim, K. H., Fleury, E., Lee, B. J., Wakeda, M., et al. (2007). Origin of the plasticity in bulk amorphous alloys. J. Mater. Res. 22 (11), 3087–3097. doi:10.1557/jmr.2007.0382

CrossRef Full Text | Google Scholar

Lee, M. H., Das, J., Lee, K. S., Kühn, U., and Eckert, J. (2010). Effect of prestraining on the deformation and fracture behavior of Zr₄₄Ti₁₁Cu_{9. 8}Ni_{10. 2}Be₂₅. Intermetallics 18 (10), 1902–1907. doi:10.1016/j.intermet.2010.02.031

CrossRef Full Text | Google Scholar

Li, S., Huang, P., and Wang, F. (2019). Rejuvenation saturation upon cyclic elastic loading in metallic glass. Comput. Mater. Sci. 166, 318–325. doi:10.1016/j.commatsci.2019.05.007

CrossRef Full Text | Google Scholar

Li, Y. S., Wei, Y. P., Zhang, K., Zhang, Y. T., Wang, Y., Tang, W. Q., et al. (2019). Rejuvenation, embryonic shear bands and improved tensile plasticity of metallic glasses by nanosecond laser shock wave. J. Non-Crystalline Solids 513, 76–83. doi:10.1016/j.jnoncrysol.2019.02.031

CrossRef Full Text | Google Scholar

Li, Y. S., Zhang, K., Wang, Y., Tang, W. Q., Zhang, Y. T., Wei, B. C., et al. (2020). Abnormal softening of Ti-metallic glasses during nanosecond laser shock peening. Mater. Sci. Eng. A 773, 138844. doi:10.1016/j.msea.2019.138844

CrossRef Full Text | Google Scholar

Louzguine-Luzgin, D. V., Louzguina-Luzgina, L. V., Ketov, S. V., Zadorozhnyy, V. Y., and Greer, A. L. (2014). Influence of cyclic loading on the onset of failure in a Zr-based bulk metallic glass. J. Mater. Sci. 49, 6716–6721. doi:10.1007/s10853-014-8276-2

CrossRef Full Text | Google Scholar

Ma, C., Suslov, S., Ye, C., and Dong, Y. (2019). Improving plasticity of metallic glass by electropulsing-assisted surface severe plastic deformation. Mater. Des. 165, 107581. doi:10.1016/j.matdes.2019.107581

CrossRef Full Text | Google Scholar

Ogata, S., Shimizu, F., Li, J., Wakeda, M., and Shibutani, Y. (2006). Atomistic simulation of shear localization in Cu–Zr bulk metallic glass. Intermetallics 14 (8-9), 1033–1037. doi:10.1016/j.intermet.2006.01.022

CrossRef Full Text | Google Scholar

Packard, C. E., and Schuh, C. A. (2007). Initiation of shear bands near a stress concentration in metallic glass. Acta Mater. 55 (16), 5348–5358. doi:10.1016/j.actamat.2007.05.054

CrossRef Full Text | Google Scholar

Pan, D., Inoue, A., Sakurai, T., and Chen, M. W. (2008). Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl. Acad. Sci. 105 (39), 14769–14772. doi:10.1073/pnas.0806051105

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J. M., Lim, K. R., Park, E. S., Hong, S., Park, K. H., Eckert, J., et al. (2014). Internal structural evolution and enhanced tensile plasticity of Ti-based bulk metallic glass and composite via cold rolling. J. alloys Compd. 615, S113–S117. doi:10.1016/j.jallcom.2014.01.075

CrossRef Full Text | Google Scholar

Phan, A. D., Zaccone, A., Lam, V. D., and Wakabayashi, K. (2021). Theory of pressure-induced rejuvenation and strain hardening in metallic glasses. Phys. Rev. Lett. 126 (2), 025502. doi:10.1103/physrevlett.126.025502

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuh, C. A., and Nieh, T. G. (2003). A nanoindentation study of serrated flow in bulk metallic glasses. Acta mater. 51 (1), 87–99. doi:10.1016/s1359-6454(02)00303-8

CrossRef Full Text | Google Scholar

Tao, K., Li, F. C., Liu, Y. H., Pineda, E., Song, K., and Qiao, J. (2022). Unraveling the microstructural heterogeneity and plasticity of Zr₅₀Cu₄₀Al₁₀ bulk metallic glass by nanoindentation. Int. J. Plasticity 154, 103305. doi:10.1016/j.ijplas.2022.103305

CrossRef Full Text | Google Scholar

Van Steenberge, N., Sort, J., Concustell, A., Das, J., Scudino, S., Suriñach, S., et al. (2007). Dynamic softening and indentation size effect in a Zr-based bulk glass-forming alloy. Scr. Mater. 56 (7), 605–608. doi:10.1016/j.scriptamat.2006.12.014

CrossRef Full Text | Google Scholar

Wang, X. D., Ren, X. C., Qu, R. T., and Zhang, Z. (2019). Compression-compression fatigue behavior of a Zr-based metallic glass with different free volume contents. J. Alloys Compd. 810, 151924. doi:10.1016/j.jallcom.2019.151924

CrossRef Full Text | Google Scholar

Wang, G. Y., Liaw, P. K., Peker, A., Yang, B., Benson, M. L., Yuan, W., et al. (2005). Fatigue behavior of Zr–Ti–Ni–Cu–Be bulk-metallic glasses. Intermetallics. 13 (3–4), 429–435. doi:10.1016/j.intermet.2004.07.037

CrossRef Full Text | Google Scholar

Wright, W. J., Saha, R., and Nix, W. D. (2001). Deformation mechanisms of the Zr₄₀Ti₁₄Ni₁₀Cu₁₂Be₂₄ bulk metallic glass. Mater. Trans. 42 (4), 642–649. doi:10.2320/matertrans.42.642

CrossRef Full Text | Google Scholar

Yang, G. N., Shao, Y., and Yao, K. F. (2019). Understanding the fracture behaviors of metallic glasses—an overview. Appl. Sci. 9 (20), 4277. doi:10.3390/app9204277

CrossRef Full Text | Google Scholar

Ye, Y. F., Wang, S., Fan, J., Liu, C., and Yang, Y. (2016). Atomistic mechanism of elastic softening in metallic glass under cyclic loading revealed by molecular dynamics simulations. Intermetallics 68, 5–10. doi:10.1016/j.intermet.2015.09.003

CrossRef Full Text | Google Scholar

Zhang, M., Wang, Y., Ding, G., Zheng, R., Wei, R., Zhang, G., et al. (2023). Biocompatible superhydrophobic surface on Zr-based bulk metallic glass: fabrication, characterization, and biocompatibility investigations. Ceram. Int. 49 (15), 25549–25562. doi:10.1016/j.ceramint.2023.05.095

CrossRef Full Text | Google Scholar

Zhao, P., Li, J., Hwang, J., and Wang, Y. (2017). Influence of nanoscale structural heterogeneity on shear banding in metallic glasses. Acta Mater. 134, 104–115. doi:10.1016/j.actamat.2017.05.057

CrossRef Full Text | Google Scholar

Zhou, C., Zhang, H., Yuan, X., Song, K., and Liu, D. (2022). Applicability of pre-plastic deformation method for improving mechanical properties of bulk metallic glasses. Materials 15 (21), 7574. doi:10.3390/ma15217574

PubMed Abstract | CrossRef Full Text | Google Scholar