Rheological behavior of the synovial fluid: a mathematical challenge

Background: Synovial fluid (SF) is often used for diagnostic and research purposes as it reflects the local inflammatory environment. Owing to its complex composition, especially the presence of hyaluronic acid, SF is usually viscous and non-homogeneous. The presence of high-molar-mass hyaluronan in this fluid gives it the required viscosity for its function as a lubricant. Viscosity is the greatest major hydraulic attribute of the SF in articular cartilage.

Methods: Empirical modeling of previously published results was performed. In this study, we explored the flow of a non-Newtonian fluid that could be used to model the SF flow. Analyzing the flow in a simple geometry can help explain the model’s efficacy and assess the SF models. By employing some viscosity data reported elsewhere, we summarized the dynamic viscosity values of normal human SF of the knee joints in terms of time after injecting hyaluronidase (HYAL) at 25°C. The suggested quadratic behavior was obtained through extrapolation. For accurate diagnosis or prediction, the comparison between three specific parameters (a_i, t₀, and ln η₀) was made for normal and pathological cases under the same experimental conditions for treatment by addition of HYAL and for investigation of the rheological properties. A new model on the variation of viscosity on the SF of knee joints with time after injection of HYAL with respect to normal and postmortem samples at different velocity gradients was proposed using data previously reported elsewhere.

Results: The rheological behavior of SF changes progressively over time from non-Newtonian to a Newtonian profile, where the viscosity has a limiting constant value (η₀) independent of the gradient velocity at a unique characteristic time (t₀ ≈ 8.5 h). The proposed three-parameter model with physical meaning offers insights into future pathological cases. The outcomes of this work are expected to offer new perspectives for diagnosis, criteria, and prediction of pathological case types through comparisons with new parameter values treated under the same experimental conditions as HYAL injection. This study also highlights the importance of HYAL treatment for better intra-assay precision.

Highlights

► Synovial fluid is a challenging matrix to analyze.

► Based on the proposed model, hyaluronidase treatment offers better intra-assay precision. We recommend hyaluronidase treatment of the synovial fluid for osteoarthritis biomarker research.

Introduction

The movements of the knee joints need an effective and efficient lubrication mechanism, which is ensured by hyaluronic acid (HA) in the synovial fluid (SF); the SF is an extracellular biofluid existing in the synovial joints of living beings. Synovial or diarthrodial joints are the most sophisticated joints in the body; unlike fibrous or cartilaginous joints, each bone end in the synovial joints is covered by an independent layer of hyaline cartilage (Johnston, 1955a; Johnston, 1955b; Johnston, 1955c; Freemont and Denton, 2010; Perkasan and Saju, 2016).

Viscosity is the most important hydraulic fluid characteristic of the SF from articular cartilage, where its significant amount is affected by pressure, temperature, and joint movements. When the SF and especially HA with hyaluronidase (HYAL) or another affection is assimilated, the viscosity loses its abnormal rheological character over time and becomes constant for any shear velocity value.

HA is also known as sodium hyaluronate or hyaluronan and is a natural linear polysaccharide having high molecular weight (Kogan et al., 2007). In the joints, HA plays important roles in protecting the articular cartilage and transporting nutrients to the cartilage. In patients with rheumatoid arthritis (RA), it has been reported that HA acts as an anti-inflammatory substance by preventing the attachment of inflammatory mediators to the synovial tissues (Miyazaki et al., 1983; Mendichi and Soltes, 2002; Brouwers et al., 2022). The high levels of high-molar-mass HA in the SF offer essential lubrication to the joints and work as shock absorbers, diminishing the friction between the moving cartilage and bones as well as minimizing joint tearing (Herschel and Bulkley, 1926; Johnston, 1955a; Johnston, 1955b; Johnston, 1955c; Ibrahim et al., 2019). Under inflammatory arthritic disease conditions, such as RA or osteoarthritis, the high molar mass of HA is degraded by reactive oxygen species (ROS), which alters its viscosity and reduces its lubricant and shock absorbing properties, leading to deteriorated joint motions and pain (Herschel and Bulkley, 1926; Johnston, 1955a; Johnston, 1955b; Johnston, 1955c; Ibrahim et al., 2019). Excellent outcomes have been achieved for better biocompatibility and corrosion performance as well (Mansoorianfar et al., 2020). There are studies on the physiological characteristics of HA as well as the latest innovations in biotechnological manufacturing and formulations of HA-based tools for biomedical use (Arulmoli et al., 2016; Bowman et al., 2018; Chircov et al., 2018; Yasin et al., 2022).

Since the SF is a macromolecular solution of HA and a dialysate of blood plasma, its rheological behavior is highly non-linear and therefore difficult to characterize quantitatively. As such, the dynamic interactions between these two biorheologically complex materials offer challenging biomechanics problems. The SF is also a difficult biological matrix to analyze because of its complex non-Newtonian nature. Indeed, a few reports on the analysis of SF from non-inflammatory conditions have shown that technical issues can occur when analyzing untreated SF (Moreno et al., 2000; Ekmann et al., 2010; Jayadev et al., 2012). For instance, it was shown via the Luminex assay that treating SF with HYAL improves cytokine recovery in polystyrene but not magnetic beads (Jayadev et al., 2012). In addition, HYAL treatment is routinely performed before proteomic and metabolomic analyses (Mateos et al., 2012; Jónasdóttir et al., 2017). However, to date, there are no reports on the importance of HYAL treatment that is not routinely used in arthritis research. For example, HYAL treatment is not mentioned in more than half of the abovementioned studies that have investigated the SF in inflammatory joint diseases (Shen et al., 2010; Yoon et al., 2014; Barden et al., 2016; Rao et al., 2017; Snelling et al., 2017; Mustonen et al., 2019; Yamin et al., 2019; Church et al., 2020).

Inflammatory arthritis is characterized by an expanded volume of SF, while the quantity of HA is often decreased. This results in typically diminished shear viscosity. However, in traumatic osteoarthritis, the volume of HA expands and results in excess viscous fluid. Frequently, this increase in volume would be even but may not be equivalent in magnitude to that of inflammatory arthritis (Siala et al., 2018). Research on the viscosity of normal SF has been the subject of numerous published works (Ragan, 1946; Freemont and Denton, 2010; Fu et al., 2019). The rheological behavior of the SF is responsible for its deformation under shear stress and is of utmost importance in the calculation of the gap necessary to sustain a specific load in such a system. Accordingly, the most relevant metrics of the SF as a joint lubricant in this study are as follows:

- τ: shear stress;

- Vg: viscosity gradient or shear rate;

- τ₀: produced stress;

- n: flow behavior index, with K as the flow reliability index;

- i: number of velocity gradients (Vg);

- η₀: zero viscosity;

- η: viscosity

The rheological properties of the SF, HA, and HYAL have been separately investigated in literature and compared to classical rheological models because of their complex non-Newtonian natures (Ibrahim et al., 2019; Stanciu et al., 2020; Stanciu and Ouerfelli, 2020; More et al., 2020; Stanciu and Ouerfelli, 2021). However, the drawbacks that need to be addressed in these works are the poor assay repeatability and potentially inefficient use of precious samples. Owing to its viscosity, handling SF in a laboratory setting is challenging. Similarly, modeling of rheological properties based on addition of HYAL to SF has not been addressed in literature to the best of our knowledge. To overcome this problem, SF was treated with HYAL (Ibrahim et al., 2019; More et al., 2020), but we identify the lack of a reliable third-order polynomial model as a knowledge gap as well as the motivation for this study. Thus, the following are the contributions of the present study:

• an expression for the impact on SF upon treatment with HYAL based on simulation of joint lubrication behaviors using data from published studies;

• variation of viscosity with time after injection of HYAL into the SF from the knee joints at different velocity gradients on normal and postmortem samples;

• we present a novel standardization model of the effects of HYAL for the evaluation and possible prediction of different types of synovial liquid adjustments in several types of arthritis using newly obtained parameter values from treated pathological cases;

• the proposed modeling is expected to be a potential guide for clinical decision-making, laying the groundwork for future studies aimed at unraveling the complexities of joint health.

The results of this study expand upon some perspectives concerning the diagnosis and criteria for certain clinical cases. We also offer a model for comparison with pathological cases. In this study, we explore the flow of a non-Newtonian fluid that could be utilized to model the SF flow. Analyzing the flow in a simple geometry can help explain the model’s efficacy and also assess the SF model. By employing viscosity data reported in literature (Johnston, 1955c), we summarize the dynamic viscosity values of normal human SF of the knee joints in terms of time after injection of HYAL at 25°C. The suggested quadratic behaviors are obtained by extrapolation. For accurate diagnosis or prediction, comparisons are provided between three specific parameters (a_i, t₀, and ln η₀) for both normal and pathological cases under the same experimental conditions of treatment through the addition of HYAL and investigation of the rheological properties.

Methods

This study employs the results published previously by other authors (Johnston, 1955a; Johnston, 1955b; Johnston, 1955c). The apparatus utilized by Johnston (1955a, 1955b, 1955c) consisted of a horizontal capillary tube (length: 16 cm; internal diameter: 0–3 mm) linked to two vertical tubes of length 5 cm and internal diameter 1 mm increasing to cups with internal diameter 0–5 cm. A cross tube (internal diameter: 1 mm) with a tap linked the two limbs to form a U-shaped tube (Supplementary Figure S1) (Johnston, 1955a; Johnston, 1955b; Johnston, 1955c). Different calibrations, reproducibility experiments, accuracies, and suitable liquids are described in detail in the original experimental work (Johnston, 1955c). The slopes of the line plots of the applied pressures versus reciprocal flow times for the SF and water from consecutive standardization runs were used to calculate the relative shear viscosities (Johnston, 1955a; Johnston, 1955b; Johnston, 1955c). To the best of our knowledge, since there are no offsets in the present setup from that used in Johnston’s work, we used the available data for the current investigation (Ibrahim et al., 2019; More et al., 2020).

Figure 1

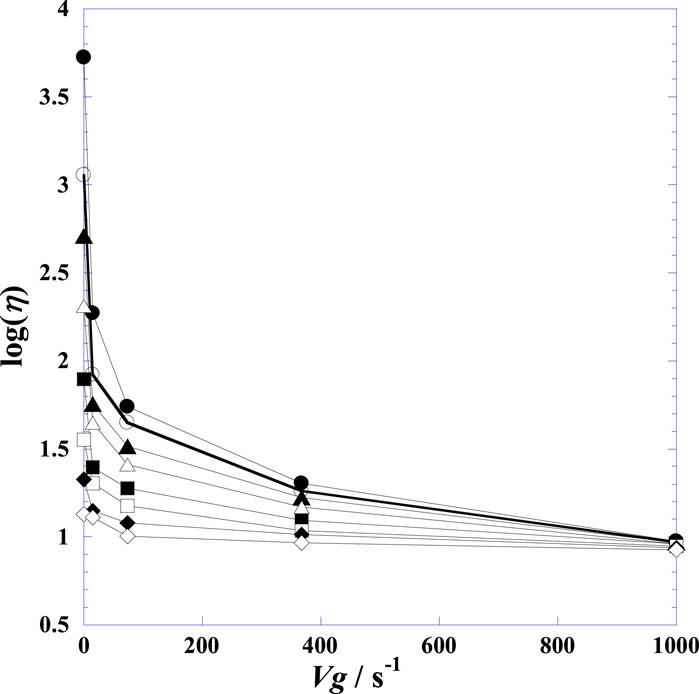
Figure 1. Displays the variation of the decimal logarithm of shear viscosity log(η) with the velocity gradient (Vg) at fixed times after injection of hyaluronidase at 25°C on a normal human Post-mortem synovial fluid of knee joints. (●): t = 0.0 h; (○): t = 1.25 h; (▲): t = 2.00 h; (∆): t = 3.0 h; (■): t = 4.25 h; (□): t = 5.50 h; (♦): t = 6.50 h; (◊): t = 7.50 h.

Results and discussion

Mathematical formulation

We explore the flow of a non-Newtonian fluid that could then be utilized to model the SF flow. The SF flow equations are not amenable to easy mathematical investigation since the actual geometry of the area where the flow occurs is complex. As such, analyzing the flow in a simple geometry can help explain the model’s efficacy for subsequently assessing the SF model.

Analysis

Supplementary Figure S2 displays the decrease in shear viscosity with time at different velocity gradients, as modified from Johnston (1955c). It was observed that the shear viscosities at elevated velocity gradients were practically unaffected for some time, while the viscosities at low velocity gradients decreased rapidly. The viscosity at infinite velocity gradient did not show any clear decline up to 7.5 h after the addition of HYAL; however, throughout this period, the zero viscosity of the velocity gradient decreased exponentially from 5,300 to 13.50 cP (Johnston, 1955c). Moreover, the viscosities cause non-Newtonian flows to become Newtonian flows like that of water, indicating that HYAL induces its full effects after nearly 8.5 h. This model can be compared with other data from various synovial joint disorders (caused by arthritis, joint trauma diseases, and aging) to determine the degree of synovial lubrication; here, we developed a mathematical model to analyze the lubricant composition of the SF in whole human knee joints by expanding upon the approaches reported in previous studies and utilizing relevant published functional parameters (Blewis et al., 2007; Chhimwal et al., 2023). By employing viscosity data reported earlier (Johnston, 1955c), we summarize in Table 1 the dynamic viscosities of normal human SF of the knee joints in terms of time after injection of HYAL at 25°C. Table 1 shows that the viscosity decreases with HYAL treatment time at each fixed velocity and that the viscosity decreases with the velocity gradient at each fixed time.

Figure 2

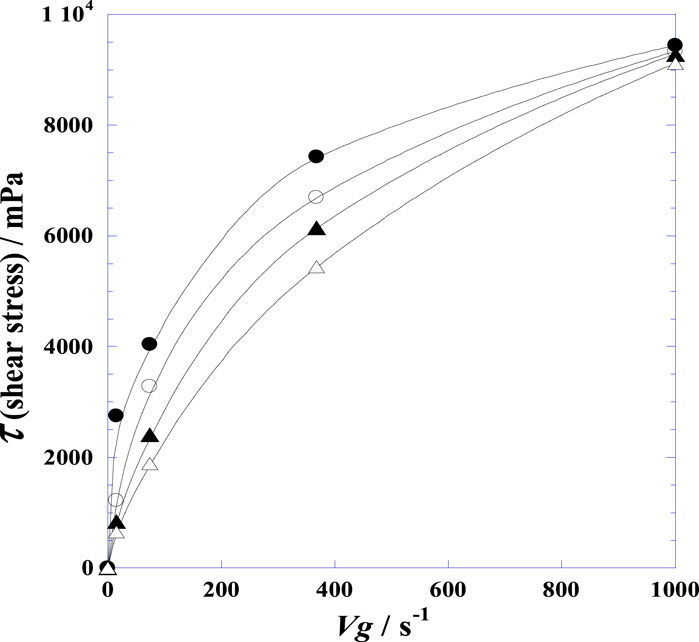
Figure 2. Variation of the shear stress (τ) of the synovial fluid of the knee joints of normal postmortem samples with velocity gradient (Vg) at four fixed instances after injection of hyaluronidase at 25°C. (●): t = 0.0 h; (○): t = 1.25 h; (▲): t = 2.00 h; (∆): t = 3.0 h.

Table 1

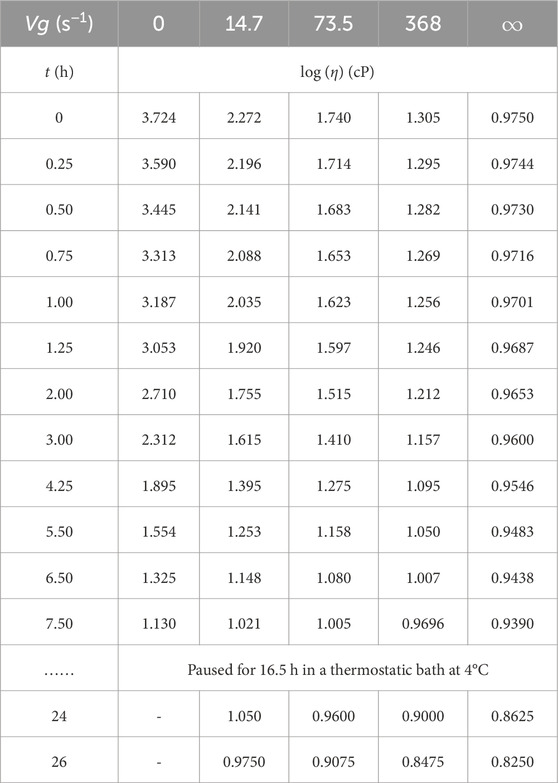
Table 1. Decimal logarithm of the viscosity (log η) with time (t) at different fixed velocity gradients (Vg) after injection of hyaluronidase at 25°C into synovial fluid of the knee joints (i.e., for normal postmortem PM3 as per Johnston (1955c)).

Table 2 indicates positive correlations for the different velocity gradients, showing the results of non-parametric tests for statistical dependence as well as Spearman’s correlation test (Taylor, 1987) wherein the null hypothesis was the independence of two variables. This test revealed that there was a causal correlation and significant association between the different velocity gradients of the SF over different time instances of HYAL application.

Table 2

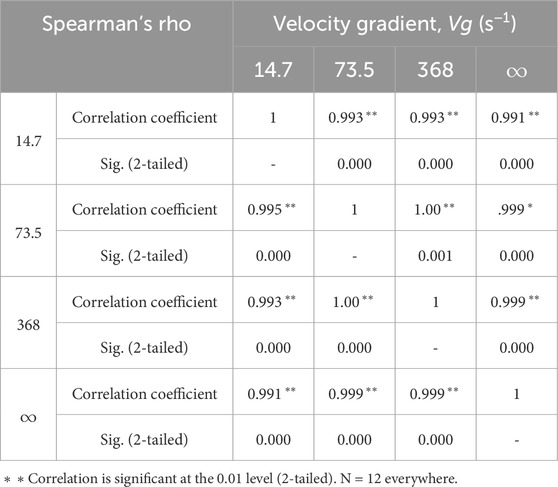
Table 2. Correlation coefficients between the different velocity gradients of the synovial fluid for different HYAL application times.

Figure 1 shows the variation in viscosity of the SF (in terms of log (η/cP)) against the gradient velocity (Vg) over time (t). The curves clearly demonstrate that the viscosity decreases with the velocity gradient. Further, this decrease is more accentuated upon initial addition of HYAL and flattens gradually with time. The rationale behind choosing a second-order polynomial model with three adjustable parameters (Ai, Bi, and Ci) for fitting the curves in Supplementary Figure S2 is that such models can be used in situations where the relationships between the study and explanatory variables are curvilinear. Sometimes a non-linear relationship over a small range of the explanatory variable can also be modeled using polynomials. It is worth noting here that the viscosities at high velocity gradients are not influenced initially for some time. The viscosity for the infinite velocity gradient did not begin decreasing until 7.5 h after the addition of HYAL.

Abnormal viscosity behavior of the sample: governing equations

The SF is a viscous and non-Newtonian fluid that exhibits shear-thinning effects (Schurz and Ribitsch, 1987), and its viscosity decreases with increasing shear rate. At high shear rates, the SF behaves more like a fluid with low viscosity; at low shear rates, actions such as walking or standing on one leg can contextually exhibit higher viscosities. Within the scope of the current study, we simulate cartilage tissues experiencing static compressive loads, for which the shear rates are expected to be very low; hence, we assume a constant corresponding viscosity value of 1 Pa∙s for the SF. This value of viscosity for static loading has also been used in previous studies (Persson et al., 2017; Wu and Ferguson, 2017; Liao et al., 2020).

Given the above conditions, Figure 2 displays the differences in the shear stress (τ = η·Vg) of the SF with velocity gradient (Vg) for four fixed instances of time (from 0 to 3.0 h). The convex curvatures in Figure 2 demonstrate that the SF possesses rheological attributes with shear thinning or pseudoplastic behaviors, confirming that the SF has non-Newtonian characteristics. Nevertheless, the curvatures diminish over time, showing that the SF with added HYAL has the characteristics of a fluid with Newtonian (linear) behaviors. The rheological properties highlight the classical non-Newtonian power–law model, such as the usual Ostwald–de Waele and Herschel–Bulkley models expressed by Eqs. (1, 2) (Herschel and Bulkley, 1926; Goodwin et al., 2000; Hron et al., 2010):

$\tau =K·{Vg}^n(1)$

$\tau ={\tau }_0+K·{Vg}^n(2)$

where τ is the shear stress, Vg is the viscosity gradient or shear rate, τ₀ is the produced stress, n is the flow behavior index, and K is the flow reliability index.

In this case, the value of n is less than unity, and the power law indicates that the effective viscosity would diminish considerably with increasing shear rates; this requires a fluid with very high viscosity at standoff and very low viscosity as the shear rate tends to infinity, while a non-abnormal fluid has both maximum and minimum effective viscosity values that depend on the physical and chemical properties at the molecular level.

The diminishing curvature of the flow behavior index (n) curve with time is shown in Figure 3, where the index increases from a value of about 0.3 to almost 1; this means that as more time elapses, the SF with added HYAL tends to increasingly approach Newtonian behavior (n = 1). By extrapolation on Figure 3, it can be concluded that the non-Newtonian character of the SF is destroyed after more than 8 h upon addition of HYAL. The details of the logarithmic technique, derivation operations, and mathematical methods of determining the current and variable flow behavior indexes are available in previous works (Stanciu et al., 2020; Stanciu and Ouerfelli, 2020, 2021).

Figure 3

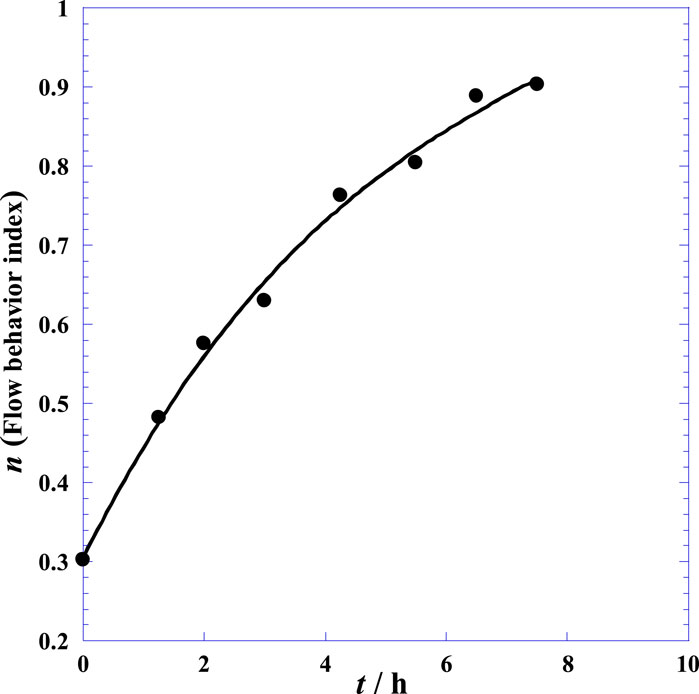
Figure 3. Variation of the flow behavior index (n) with time (t) of the synovial fluid of the knee joints of normal postmortem samples after injection of hyaluronidase at 25°C (Eq. (1)).

Contribution to modeling the viscosity overtime after HYAL injection

Suggested quadratic behavior analysis of the model

Starting from the similar simple shapes of different curves in Supplementary Figure S2 and plotting the variation of log η versus time (t) following the injection of HYAL into the SF (Johnston, 1955c), the current study suggests a simple second-order polynomial model with three adjustable free parameters (A_i, B_i, and C_i) as follows:

$Y=A_i\times x^2+B_i\times x+C_i(3)$

where Y denotes log η and x is the time t after the injection of HYAL; the subscript i indicates the index of the velocity gradient Vg.

We note that the trends of the scatter points of different curves in Supplementary Figure S2 can lead to mathematical behaviors other than quadratic ones, like the logarithmic function. Nevertheless, we already have an implicit logarithmic dependence (Y = log η) that can cause complications with the double-logarithm dependence for easy manipulation of this mathematical form. This dependence hides the viscosity–temperature dependence in the case of either the Arrhenius or Vogel–Fulcher–Tammann behavior (Stanciu et al., 2020; Stanciu and Ouerfelli, 2020, 2021).

Non-linear regression provides optimal values of the parameters (A_i, B_i, and C_i) at different velocity gradients (Vg), and the corresponding fitted data are given in Table 3. From Table 3 and Figure 4, it is noted that the coefficient A_i decreases with the velocity gradient Vg while the absolute value of B_i increases with Vg. Good dependence between all the polynomial constants (A_i, B_i, and C_i) with the velocity gradient (Vg) is remarkable. Therefore, a simple expression for A_i as a function of Vg is suggested in Eq. 4 as follows:

$A_i=\frac{1}{{\left(4.1102+0.091967·V_g\right)}^{2.5}}(4)$

Table 3

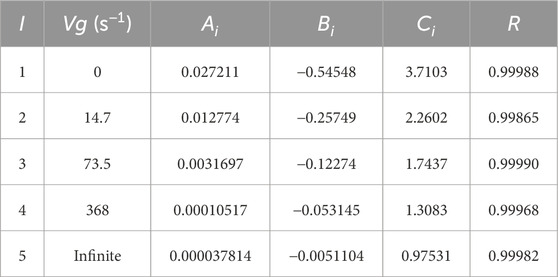
Table 3. Adjustable parameter values (A_i, B_i, and C_i) at different velocity gradients (Vg) of Eq. (3) and correlation coefficients corresponding to the non-linear regression method.

Figure 4

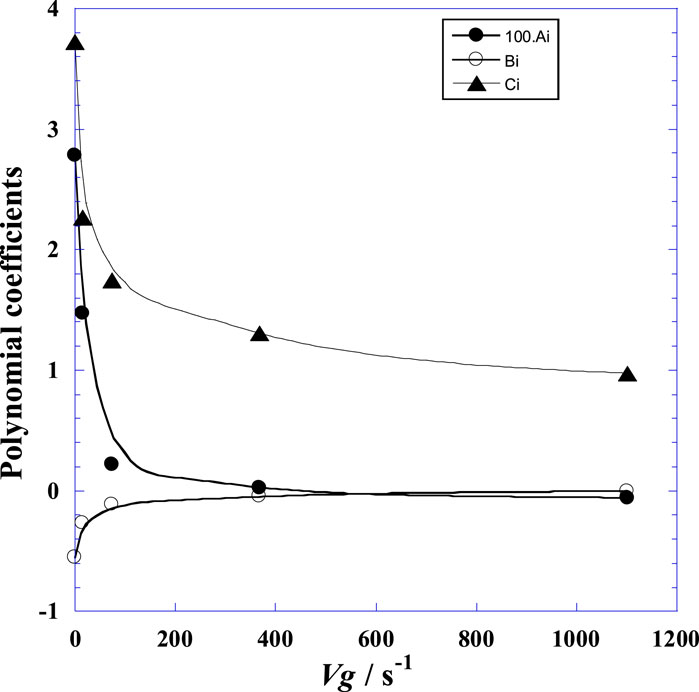
Figure 4. Variation of the adjustable parameter values (A_i, B_i, and C_i) of Eq. (3) versus the velocity gradient (Vg) at 25°C.

Likewise, we see that C_i increases with Vg similar to A_i. Figure 5 shows the mutual correlations between the polynomial coefficients A_i, B_i, and C_i of Eq. (3). From the quasilinear dependence between B_i and C_i as indicated by Figure 5C, a mutual linear correlation can be expressed by Eq. 5 as follows

$C_{i=}-4.927\times B_i+1.030(5)$

with a reliable correlation coefficient of R = 0.99781.

Figure 5

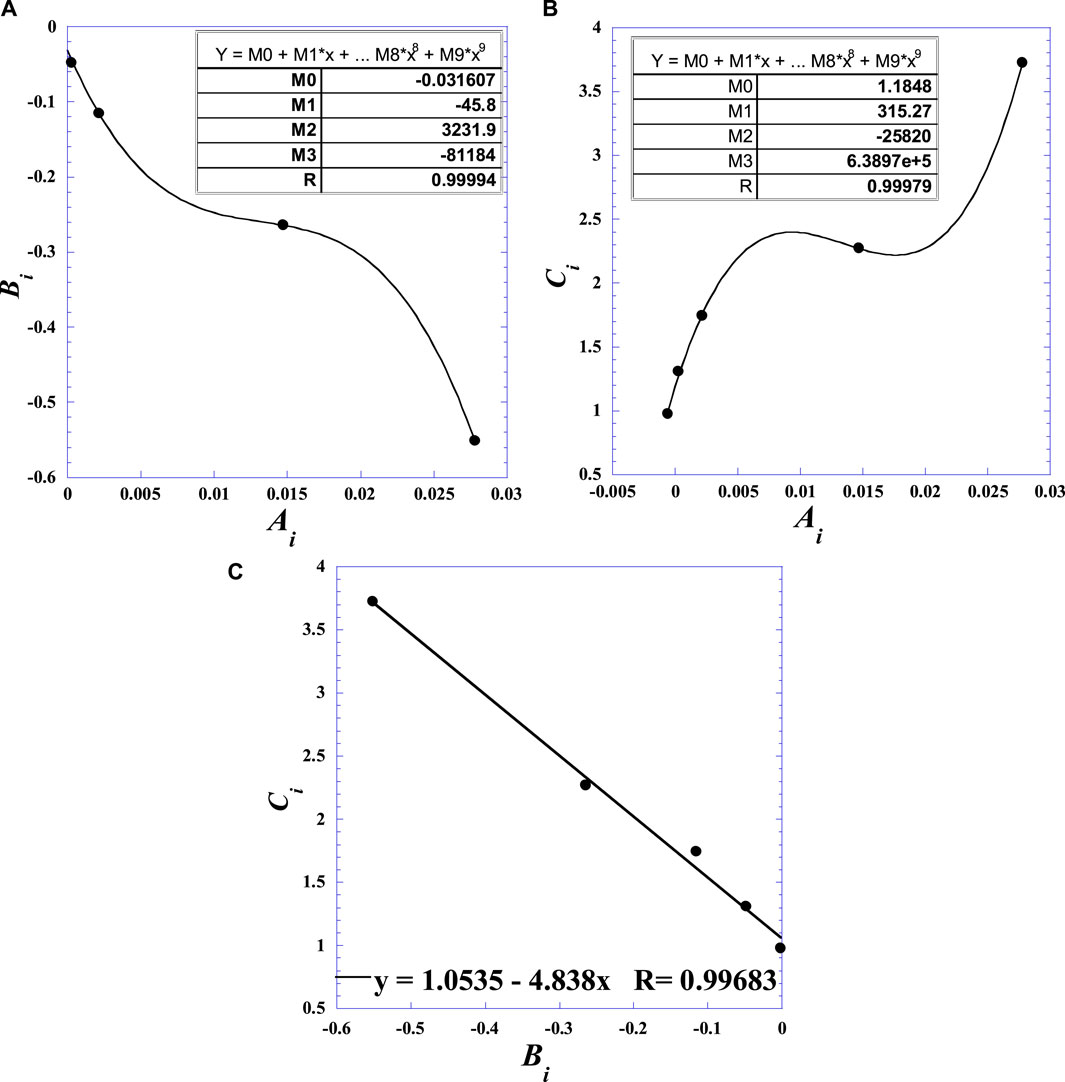
Figure 5. Mutual correlations between the polynomial coefficients (A_i, B_i, and C_i) of Eq. (3): (A) non-linear dependence between B_i and A_i; (B) non-linear dependence between A_i and C_i; (C) quasi-linear dependence between B_i and C_i.

However, by extrapolating this model to time t greater than the studied durations (Supplementary Figure S2), a quasi-unique point D (x₀,y₀) independent of the velocity gradient was observed, characterizing the specific experimental conditions mentioned above and as detailed in the original work (Johnston, 1955c).

Figure 6 indicates that the viscosity decreases with time after HYAL treatment at different velocity gradients (4.7, 73.5, 368, and infinite) and that the viscosity decreases when the velocity is high; the highest viscosity is observed with a velocity gradient of 4.7, and the lowest viscosity is obtained with infinite velocity. At the fixed point indicated by the arrow, the SF becomes a non-Newtonian fluid (i.e., it loses its rheological properties), and this result is in accordance with the findings of another study (Rebenda et al., 2020). In normal cases, the viscosity of the SF is high, and the environment inside the joint limits movements because of the high friction of the SF. When the velocity increases, the SF becomes less viscous and more fluid; this easily facilitates mechanical movement of the joint as the friction is reduced (Schmidt et al., 2007).

Figure 6

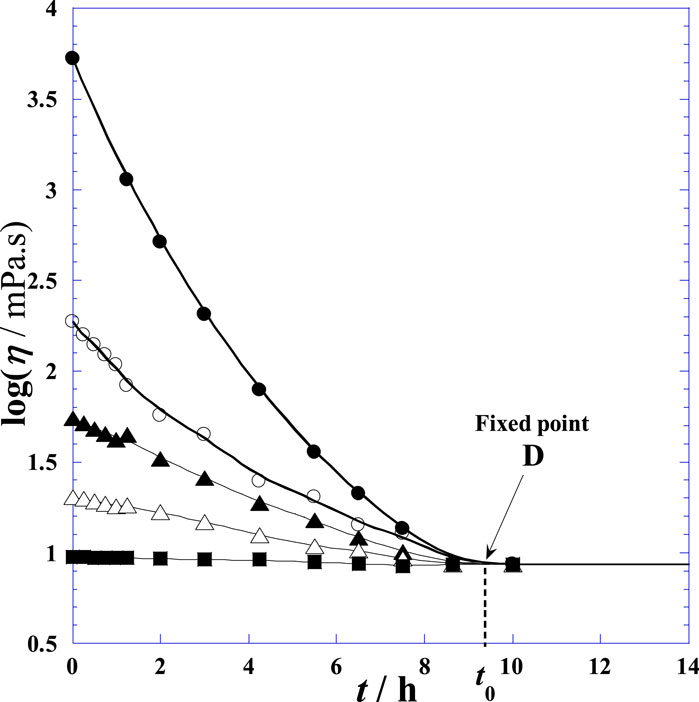
Figure 6. Variation of the shear viscosity of the synovial fluid of the knee joints of normal postmortem samples versus time (t) at different velocity gradients upon treatment with hyaluronidase at 25°C. (●): Vg = zero velocity; (○): Vg = 14.7 s⁻¹; (▲): Vg = 73.5 s⁻¹; (∆): Vg = 368 s⁻¹; (■): infinite velocity gradient.

The fixed points D (x₀,y₀) can be determined as follows:

$Y_0=A_i·x_0^2+B_i·x_0+C_i(6)$

Regardless of the values of Vg represented by the index i, the following equation can be written:

$\frac{{\partial A}_i}{{\partial V}_g}.x_0^2+\frac{{\partial B}_i}{{\partial V}_g}.x_0+\frac{{\partial C}_i}{{\partial V}_g}=0(7)$

Solving Eq. (7), we obtain the Eq. 8 expressed as follows

$x_0=\frac{-\frac{{\partial B}_i}{{\partial V}_g}\pm \sqrt{{\left(\frac{{\partial B}_i}{{\partial V}_g}\right)}^2-4\frac{{\partial A}_i}{{\partial V}_g}.\frac{{\partial C}_i}{{\partial V}_g}}}{2A_i}(8)$

By inserting this obtained value (x₀) into Eq. (6), the value of y₀ was deduced. Then, the coordinates of the fixed point D (x₀ = 8.657 ± 0.1581, y₀ = 0.9365 ± 0.0023) were obtained. Given that the fixed point is independent of the velocity gradient Vg, Eq. (3) can be rewritten as follows:

$(9)$

where only the a_i coefficients are variables dependent on the velocity gradient Vg.

Comparing Eqs. (3) and (9), the following relationships we can write in Eqs 10, 11

$\left\{\begin{array}{l}{A}_i=a_i\ge 0\\ C_i=a_i{x}_0^2+y_0^2\\ B_i=-2a_i{x}_0\end{array}\right.>0(10)$

where

$x_0=\frac{-B_i}{2A_i}(11)$

At the fixed point D, all curves of Figure 6 exhibit the same horizontal tangent with null values of all derivative functions (common minimum). Physically, this instantaneous constancy of log η = 0.9365 versus time indicates that the fluid system shows Newtonian behaviors at and after the critical time t₀ = 9.657 h. Note that t₀ and ln η₀ are specific to the clinical conditions presented in the original work by Johnston (1955c) and fluctuate between the (t₀, ln η₀) values of the pathological (disease) and normal human cases, reflecting the candidate state (disease or normal); this can be used in the future to differentiate between different conditions like arthritis, osteoarthritis, and other joint pains in light of the newly obtained parameter values. Moreover, the variation of a_i versus Vg in Eq. (12) can also be used as a test to determine the patient’s state as a more detailed diagnostic. The variations of the parameter values are also interesting for the diagnosis and classification of RA. For accurate diagnosis or prediction, comparisons between the three specific parameters (a_i, t₀, and ln η₀) under normal and pathological disease conditions can be made under identical experimental conditions of addition of HYAL and investigation of the rheological properties. The aforementioned deductions show that HYAL practically digests the SF such that the viscosity becomes constant (log η₀) and independent of the velocity gradient (Vg); this outcome is in agreement with the results reported by other researchers, where the SF shows a shear-thinning rheology and thickens with increasing HA concentrations (Romanishina et al., 2017; Ruggiero and Sicilia, 2020; Ozan et al., 2021).

From Eq. (4), by expressing A_i = a_i as a function of the velocity gradient, the proposed model for the experiment described above can be summarized in Eq. 12 and Eq. 13 as follows:

$\left\{\begin{array}{l}\mathit{log}\eta =a_i{\left(t-t_0\right)}^2+\mathit{log}{\eta }_{0}fort\le t_0\\ \mathit{log}\eta =\mathit{log}{\eta }_0=Constantfort\ge t_0\\ a_i=\frac{1}{{\left(4.1102+0.091967·V_g\right)}^{2.5}}\end{array}\right.(12)$

where t is expressed in h, Vg in h⁻¹, and

$\left\{\begin{array}{l}{t}_0=\left(8.657\pm 0.158\right)h\\ \mathit{log}{\eta }_0=0.9365\pm 0.0023\end{array}\right.(13)$

It is remarkable that the second-degree-polynomial-dependence of a_i on Vg has an R-square value of 0.99951, which is similar to the results obtained by other investigators (Pouran et al., 2018; Estell et al., 2021; Fontanella et al., 2022; Si et al., 2022; Dogru et al., 2023; Garcia et al., 2023; Jahangir et al., 2023; Pellicore et al., 2023; Tang et al., 2023; Wang et al., 2023). By considering the divergence of the model in Eq. (12), it is advisable to consider a very low non-zero value of Vg ≈ 0.1 s⁻¹ instead of Vg = 0 and a finite value of Vg ≈ 600 s⁻¹ instead of infinity at the extreme limits of the domain of Vg.

Lastly, it is noteworthy that a minimum number of parameters were chosen that could be easily used to identify their physical significances and quadratic behaviors. Nevertheless, considering the strong curvatures especially at low values of the velocity gradient (Figure 6), it is noted that this model cannot force a feeble discrepancy between the experiments and estimations for both the curvature and convergence at the limits of the degradation domain of the SF. Finally, to obtain excellent agreement under special conditions, the choice of a decimal degree slightly greater than two is proposed for Eq. (2). In fact, it is observed that the a_i values calculated using Eq. (2) do not exactly match with those in Table 3 calculated using Eq. (3); hence, optimal values were determined specific to the experimental conditions so as to minimize discrepancy and optimize concordance (Table 4; Supplementary Figure S3).

Table 4

Table 4. Comparisons between the adjustable parameter values (A_i) at different velocity gradients (Vg) of Eq. (3) and those estimated using Eq. (12), along with specific optimized values.

Parameter values and possibility of diagnosis

Note that t₀ and ln η₀ are specific to the clinical conditions presented in the original work by Johnston (1955c) and fluctuate between the (t₀, ln η₀) values associated with the pathological (disease) and normal human cases, reflecting that the patient state (disease or normal) may be used to further differentiate between different types of diseases. The variation of the a_i parameter versus Vg in Eq. (12) can additionally be used to test the patient state as a more detailed diagnostic. The variations of the three parameters proposed in this work could enable correct diagnosis and classification of RA and rheumatic disorders or even differential diagnoses for non-inflammatory synovitis and osteoarthritis. To enable such diagnoses or predictions, comparisons between the three parameters a_i, t₀, and ln η₀ can be made for the normal and pathological cases must under the same experimental conditions of addition of HYAL and investigation of the rheological properties.

Conclusion and future directions

The governing equations for the partial differential equations related to the SF were effectively solved to obtain insights into the viscous flow along the articular surfaces of the knee joints. Because of its non-Newtonian nature, HA alters the reactivity of the SF even though it constitutes only a small percentage of the SF. These findings are relevant not only to the flow of the SF but also to the chemical interactions of HA with polymeric fluids. The flow of a shear-thinning and chemically reactive fluid that can be used to represent the flow of the SF is a major focus of the present study. The most important results of this study are as follows:

- development of a mathematical model on the variation of viscosity over time after injection of HYAL into the SF of the knee joints of normal postmortem samples at different velocity gradients reported previously;

- the rheological behavior of the SF switches gradually over time from a non-Newtonian to Newtonian profile, where the viscosity takes a constant value (η₀) regardless of the gradient velocity at a unique characteristic time (t₀ ≈ 8.5 h);

- the proposed three-parameter model (a_i, t₀, and lnη₀) will be useful for comparing the incremental values in future pathological cases, where the values of these three characteristic parameters would exhibit certain variations;

- the proposed approach can offer new perspectives for the diagnosis, criteria, and prediction of different types of pathological cases when treated under the same experimental conditions, such as HYAL injection, and the newly obtained parameter values can be extended for new treatment cases.

- application of the proposed model to future studies of different pathological cases can provide possible information and predictions for comparisons with various synovial disorders by means of the three specific parameters (a_i, t₀, and ln η₀), while allowing classification of rheumatic disorders or even differential diagnoses for non-inflammatory synovitis and osteoarthritis.

To determine the lubrication conditions of the joints and their possible health implications, it would be significant to have information on the viscosity and velocity of the SF and its modeling. The proposed modeling approach is thus expected to potentially guide clinical decision making while laying the groundwork for future studies aimed at unraveling the complexities of joint health.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and any further inquiries may be directed to the corresponding author.

Author contributions

NV: Funding acquisition, Project administration, Resources, Validation, Visualization, Writing–original draft, Writing–review and editing. NO: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. EM: Conceptualization, Data curation, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. KA: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. LS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. DC: Supervision, Validation, Visualization, Funding acquisition, Writing–review and editing. DM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project was funded by Lucian Blaga University of Sibiu through a research grant (no. LBUS - IRG - 09-2023).

Acknowledgments

We are grateful to Drs. A.T. Al-Khaldi, S.S. Al-Jameel, F.S. Alshehri, H.M. Almuzafar, and A.M. Homeida (IAU, College of Science, Dammam, KSA) for the fruitful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Abbreviations

τ, shear stress; η, shear viscosity; Vg, velocity gradient; HYAL, hyaluronidase; HA, hyaluronic acid; SF, synovial fluid; PM, postmortem.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2024.1386694/full#supplementary-material

References

Arulmoli, J., Wright, H. J., Phan, D. T. T., Sheth, U., Que, R. A., Botten, G. A., et al. (2016). Combination scaffolds of salmon fibrin, hyaluronic acid, and laminin for human neural stem cell and vascular tissue engineering. Acta Biomater. 43, 122–138. doi:10.1016/j.actbio.2016.07.043

PubMed Abstract | CrossRef Full Text | Google Scholar

Barden, A. E., Moghaddami, M., Mas, E., Phillips, M., Cleland, L. G., and Mori, T. A. (2016). Specialised pro-resolving mediators of inflammation in inflammatory arthritis. Prostagl. Leukot. Essent. Fat. Acids 107, 24–29. doi:10.1016/j.plefa.2016.03.004

CrossRef Full Text | Google Scholar

Blewis, M., Nugent-Derfus, G., Schmidt, T., Schumacher, B., and Sah, R. (2007). A model of synovial fluid lubricant composition in normal and injured joints. Eur. Cell. Mater. 13, 26–39. doi:10.22203/ecm.v013a03

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowman, S., Awad, M. E., Hamrick, M. W., Hunter, M., and Fulzele, S. (2018). Recent advances in hyaluronic acid based therapy for osteoarthritis. Clin. Transl. Med. 7, 6–11. doi:10.1186/s40169-017-0180-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Brouwers, H., von Hegedus, J. H., van der Linden, E., Mahdad, R., Kloppenburg, M., Toes, R., et al. (2022). Hyaluronidase treatment of synovial fluid is required for accurate detection of inflammatory cells and soluble mediators. Arthritis Res. Ther. 24, 18. doi:10.1186/s13075-021-02696-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Chhimwal, J., Jangid, P., Kumar, D., Kumar, V., and Kumar, R. (2023). To study and develop the mathematical models to review the properties of synovial fluids. Mater. Today Proc., 2214–7853. doi:10.1016/j.matpr.2023.01.246

CrossRef Full Text | Google Scholar

Chircov, C., Grumezescu, A. M., and Bejenaru, L. E. (2018). Hyaluronic acid-based scaffolds for tissue engineering. Rom. J. Morphol. Embryol. 59, 71–76.

PubMed Abstract | Google Scholar

Church, L. D., Schmidt, T., Berthold, E., Arve-Butler, S., Gullstrand, B., Mossberg, A., et al. (2020). Children with oligoarticular juvenile idiopathic arthritis have skewed synovial monocyte polarization pattern with functional impairment—a distinct inflammatory pattern for oligoarticular juvenile arthritis. Arthritis Res. Ther. 22 (1), 186. doi:10.1186/s13075-020-02279-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Dogru, S., Dai, Z., Alba, G. M., Simone, N. J., and Albro, M. B. (2023). Computational and experimental characterizations of the spatiotemporal activity and functional role of TGF-β in the synovial joint. J. Biomech. 156, 111673. doi:10.1016/j.jbiomech.2023.111673

PubMed Abstract | CrossRef Full Text | Google Scholar

Ekmann, A., Rigdal, M. L., and Gröndahl, G. (2010). Automated counting of nucleated cells in equine synovial fluid without and with hyaluronidase pretreatment. Vet. Clin. Pathol. 39 (1), 83–89. doi:10.1111/j.1939-165x.2009.00203.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Estell, E. G., Murphy, L. A., Gangi, L. R., Shah, R. P., Ateshian, G. A., and Hung, C. T. (2021). Attachment of cartilage wear particles to the synovium negatively impacts friction properties. J. Biomech. 127, 110668. doi:10.1016/j.jbiomech.2021.110668

PubMed Abstract | CrossRef Full Text | Google Scholar

Fontanella, C. G., Belluzzi, E., Pozzuoli, A., Favero, M., Ruggieri, P., Macchi, V., et al. (2022). Mechanical behavior of infrapatellar fat pad of patients affected by osteoarthritis. J. Biomech. 131, 110931. doi:10.1016/j.jbiomech.2021.110931

PubMed Abstract | CrossRef Full Text | Google Scholar

A. J. Freemont, and J. Denton (2010). “CHAPTER 30 - synovial fluid,” Winifred gray, gabrijela kocjan, diagnostic cytopathology. 3rd Edn (Churchill Livingstone: London, UK), 809–817. doi:10.1016/B978-0-7020-3154-0.00030-2

CrossRef Full Text | Google Scholar

Fu, J., Ni, M., Chai, W., Li, X., Hao, L., and Chen, J. (2019). Synovial fluid viscosity test is promising for the diagnosis of periprosthetic joint infection. J. Arthroplasty 34 (6), 1197–1200. doi:10.1016/j.arth.2019.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, S. A., Johnson, A. K., Brown, S. R., Washabaugh, E. P., Krishnan, C., and Palmieri-Smith, R. M. (2023). Dynamic knee stiffness during walking is increased in individuals with anterior cruciate ligament reconstruction. J. Biomech. 146, 111400. doi:10.1016/j.jbiomech.2022.111400

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodwin, J. W., Goodwin, J., and Hughes, R. W. (2000). Rheology for chemists. 2nd ed. Cambridge, UK: Royal Society of Chemistry.

Google Scholar

Herschel, W. H., and Bulkley, R. (1926). Konsistenzmessungen von Gummi-Benzollösungen. Kolloid Zeitschrift39 39, 291–300. doi:10.1007/bf01432034

CrossRef Full Text | Google Scholar

Hron, J., Malek, J., Pustejovska, P., and Rajagopa, K. R., (2010). On the modeling of the synovial fluid. Advances in Tribology 2010, 1–12. doi:10.1155/2010/104957

CrossRef Full Text | Google Scholar

Ibrahim, M. G., Hasona, W. M., and ElShekhipy, A. A. (2019). Concentration-dependent viscosity and thermal radiation effects on MHD peristaltic motion of Synovial Nanofluid: applications to rheumatoid arthritis treatment. Comput. Meth Prog. Bio170 170, 39–52. doi:10.1016/j.cmpb.2019.01.001

CrossRef Full Text | Google Scholar

Jahangir, S., Esrafilian, A., Ebrahimi, M., Stenroth, L., Alkjær, T., Henriksen, M., et al. (2023). Sensitivity of simulated knee joint mechanics to selected human and bovine fibril-reinforced poroelastic material properties. J. Biomech. 160, 111800. doi:10.1016/j.jbiomech.2023.111800

PubMed Abstract | CrossRef Full Text | Google Scholar

Jayadev, C., Rout, R., Price, A., Hulley, P., and Mahoney, D. (2012). Hyaluronidase treatment of synovial fluid to improve assay precision for biomarker research using multiplex immunoassay platforms. J. Immunol. Methods 386 (1–2), 22–30. doi:10.1016/j.jim.2012.08.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, J. P. (1955a). The sedimentation behaviour of mixtures of hyaluronic acid and albumin in the ultracentrifuge. Biochem. J. 59, 620–626. doi:10.1042/bj0590620

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, J. P. (1955b). A comparison of the properties of hyaluronic acid from normal and pathological human synovial fluids. Biochem. J. 59, 626–633. doi:10.1042/bj0590626

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, J. P. (1955c). The viscosity of normal and pathological human synovial fluids. Biochem. J. 59, 633–637. doi:10.1042/bj0590633

PubMed Abstract | CrossRef Full Text | Google Scholar

Jónasdóttir, H. S., Brouwers, H., Kwekkeboom, J. C., van der Linden, H. M. J., Huizinga, T., Kloppenburg, M., et al. (2017). Targeted lipidomics reveals activation of resolution pathways in knee osteoarthritis in humans. Osteoarthr. Cartil. 25 (7), 1150–1160. doi:10.1016/j.joca.2017.01.018

CrossRef Full Text | Google Scholar

Kogan, G., Šoltés, L., Stern, R., and Gemeiner, P. (2007). Hyaluronic acid: a natural biopolymer with a broad range of biomedical and industrial applications. Biotechnol. Lett. 29, 17–25. doi:10.1007/s10529-006-9219-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, J., Smith, D. W., Miramini, S., Gardiner, B. S., and Zhang, L. (2020). A coupled contact model of cartilage lubrication in the mixed-mode regime under static compression. Tribol. Int. 145, 106185. doi:10.1016/j.triboint.2020.106185

CrossRef Full Text | Google Scholar

Mansoorianfar, M., Mansourianfar, M., Fathi, M., Bonakdar, S., Ebrahimi, M., Mohammadi Zahrani, E., et al. (2020). Surface modification of orthopedic implants by optimized fluorine-substituted hydroxyapatite coating: enhancing corrosion behavior and cell function. Ceram. Int. 46 (2), 2139–2146. doi:10.1016/j.ceramint.2019.09.197

CrossRef Full Text | Google Scholar

Mateos, J., Lourido, L., Fernández -Puente, P., Calamia, V., Fernández -López, C., Oreiro, N., et al. (2012). Differential protein profiling of synovial fluid from rheumatoid arthritis and osteoarthritis patients using LC–MALDI TOF/TOF. J. Proteome 75 (10), 2869–2878. doi:10.1016/j.jprot.2011.12.042

CrossRef Full Text | Google Scholar

Mendichi, R., and Soltes, L. (2002). Hyaluronan molecular weight and polydispersity in some commercial intra-articular injectable preparations and in synovial fluid. Inflamm. Res. 51, 115–116. doi:10.1007/pl00012388

PubMed Abstract | CrossRef Full Text | Google Scholar

Miyazaki, M., Sato, S., and Yamaguchi, T. (1983). “Analgesic and antiinflammatory action of hyaluronic sodium,” in Japan Pharmacological Conference. Tokyo.

Google Scholar

More, S., Kotiya, A., Kotia, A., Ghosh, S. K., Spyrou, L. A., and Sarris, I. E. (2020). Rheological properties of synovial fluid due to viscosupplements: a review for osteoarthritis remedy. Comput. Methods Programs Biomed. 196, 105644. doi:10.1016/j.cmpb.2020.105644

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno, M. J., Clayburne, G., and Schumacher, H. R. (2000). Processing of noninflammatory synovial fluids with hyaluronidase for cytospin preparations improves the accuracy of differential counts. Diagn Cytopathol. 22 (4), 256–258. doi:10.1002/(sici)1097-0339(200004)22:4<256::aid-dc13>3.0.co;2-g

PubMed Abstract | CrossRef Full Text | Google Scholar

Mustonen, A. M., Käkelä, R., Lehenkari, P., Huhtakangas, J., Turunen, S., Jouk- ainen, A., et al. (2019). Distinct fatty acid signatures in infrapatellar fat pad and synovial fluid of patients with osteoarthritis versus rheumatoid arthritis. Arthritis Res. Ther. 21 (1), 124. doi:10.1186/s13075-019-1914-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozan, S. C., Labrosse, G., and Uguz, A. K. (2021). A model of synovial fluid with a hyaluronic acid source: a numerical challenge. Fluids 6, 152. doi:10.3390/fluids6040152

CrossRef Full Text | Google Scholar

Pellicore, M. J., Gangi, L. R., Murphy, L. A., Lee, A. J., Jacobsen, T., Kenawy, H. M., et al. (2023). Toward defining the role of the synovium in mitigating normal articular cartilage wear and tear. J. Biomech. 148, 111472. doi:10.1016/j.jbiomech.2023.111472

PubMed Abstract | CrossRef Full Text | Google Scholar

Perkasan, D., and Saju, Dr. K. K. (2016). Review of tribological characteristics of synovial fluid. Procedia Techn 25, 1170–1174.

Google Scholar

Persson, B. N. J., Kovalev, A., and Gorb, S. N. (2017). Simple contact mechanics model of the vertebrate cartilage. Soft Matter 13, 6349–6362. doi:10.1039/c7sm00753a

PubMed Abstract | CrossRef Full Text | Google Scholar

Pouran, B., Arbabi, V., Bajpayee, A. G., van Tiel, J., Töyräs, J., Jurvelin, J. S., et al. (2018). Multi-scale imaging techniques to investigate solute transport across articular cartilage. J. Biomech. 78, 10–20. doi:10.1016/j.jbiomech.2018.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Ragan, C. (1946). Viscosity of normal human synovial fluid. Proc. Soc. Exp. Biol. Med. 63 (3), 572–575. doi:10.3181/00379727-63-15677

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, D. A., Gurish, M. F., Marshall, J. L., Slowikowski, K., Fonseka, C. Y., Liu, Y., et al. (2017). Pathologically expanded peripheral T helper cell subset drives B cells in rheumatoid arthritis. Nature 542 (7639), 110–114. doi:10.1038/nature20810

PubMed Abstract | CrossRef Full Text | Google Scholar

Rebenda, D., Vrbka, M., Čípek, P., Toropitsyn, E., Nečas, D., Pravda, M., et al. (2020). On the dependence of rheology of hyaluronic acid solutions and frictional behavior of articular cartilage. Mater. (Basel) 13 (11), 2659. doi:10.3390/ma13112659

CrossRef Full Text | Google Scholar

Romanishina, T. A., Romanishina, S. A., Deeva, V. S., and Slobodyan, S. M. (2017). “Numerical modeling of synovial fluid layer,” in Proceedings of the 2017 IEEE international young scientists forum on applied physics and engineering (YSF), Lviv, Ukraine, 143–14653.

CrossRef Full Text | Google Scholar

Ruggiero, A., and Sicilia, A. (2020). Lubrication modeling and wear calculation in artificial hip joint during the gait. Tribol. Int. 142, 105993. doi:10.1016/j.triboint.2019.105993

CrossRef Full Text | Google Scholar

Schmidt, T. A., Gastelum, N. S., Nguyen, Q. T., Schumacher, B. L., and Sah, R. L. (2007). Boundary lubrication of articular cartilage: role of synovial fluid constituents. Arthritis & Rheumatism 56, 882–891. doi:10.1002/art.22446

CrossRef Full Text | Google Scholar

Schurz, J., and Ribitsch, V. (1987). Rheology of synovial fluid. Biorheology 24, 385–399. doi:10.3233/bir-1987-24404

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, H., Goodall, J. C., and Hill Gaston, J. S. (2010). Frequency and phenotype of T helper 17 cells in peripheral blood and synovial fluid of patients with reactive arthritis. J. Rheumatol. 37 (10), 2096–2099. doi:10.3899/jrheum.100146

PubMed Abstract | CrossRef Full Text | Google Scholar

Si, Y., Tan, Y., Gao, L., Li, R., Zhang, C., Gao, H., et al. (2022). Mechanical properties of cracked articular cartilage under uniaxial creep and cyclic tensile loading. J. Biomech. 134, 110988. doi:10.1016/j.jbiomech.2022.110988

PubMed Abstract | CrossRef Full Text | Google Scholar

Siala, M., Rihl, M., Sellami, H., Znazen, A., Sassi, N., Laadhar, L., et al. (2018). Detection of Shigella spp. nucleic acids in the synovial tissue of Tunisian rheumatoid arthritis patients and other forms of arthritis by quantitative real-time polymerase chain reaction. Rheumatol. Int. 38, 1009–1016. doi:10.1007/s00296-018-3939-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Snelling, S. J. B., Bas, S., Puskas, G. J., Dakin, S. G., Suva, D., Finckh, A., et al. (2017). Presence of IL-17 in synovial fluid identifies a potential inflammatory osteoarthritic phenotype. PLoS One 12 (4), e0175109. doi:10.1371/journal.pone.0175109

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanciu, I., Messaâdi, A., Díez-Sales, O., Al-Jameel, S. S., Mliki, E., Herráez, J. V., et al. (2020). Novel equation correlating the rheological properties of some commercial tomato ketchups. J. Biochem. Technol. 11 (3), 102–114.

Google Scholar

Stanciu, I., and Ouerfelli, N. (2020). An extended Casson equation for rheological properties of soybean oil at different temperatures and atmospheric pressure. J. Biochem. Technol. 11 (3), 52–57.

Google Scholar

Stanciu, I., and Ouerfelli, N. (2021). Application extended vogel-tammann-fulcher equation for soybean oil. Orient. J. Chem. 37, 1287–1294. doi:10.13005/ojc/370603

CrossRef Full Text | Google Scholar

Tang, T. Q., Rooman, M., Shah, Z., Khan, S., Vrinceanu, N., Alshehri, A., et al. (2023). Numerical study of magnetized Powell–Eyring hybrid nanomaterial flow with variable heat transfer in the presence of artificial bacteria: applications for tumor removal and cancer cell destruction. Front. Mater. 10. doi:10.3389/fmats.2023.1144854

CrossRef Full Text | Google Scholar

Taylor, J. M. G. (1987). Kendall’s and spearman’s correlation coefficients in the presence of a Blocking variable. Biometrics 43, 409–416. doi:10.2307/2531822

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Li, X., Zhang, T., Li, J., Viellehner, J., Komnik, I., et al. (2023). Effects of soft tissue artifacts on the calculated kinematics of the knee during walking and running. J. Biomech. 150, 111474. doi:10.1016/j.jbiomech.2023.111474

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., and Ferguson, S. J. (2017). The influence of cartilage surface topography on fluid flow in the intra-articular gap. Comput. Methods Biomech. Biomed. Eng. 20, 250–259. doi:10.1080/10255842.2016.1215438

CrossRef Full Text | Google Scholar

Yamin, R., Berhani, O., Peleg, H., Aamar, S., Stein, N., Gamliel, M., et al. (2019). High percentages and activity of synovial fluid NK cells present in patients with advanced stage active rheumatoid arthritis. Sci. Rep. 9 (1), 1351. doi:10.1038/s41598-018-37448-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Yasin, A., Ren, Y., Li, J., Sheng, Y., Cao, C., and Zhang, K. (2022). Advances in hyaluronic acid for biomedical applications. Front. Bioeng. Biotechnol. 10, 910290. doi:10.3389/fbioe.2022.910290

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon, B. R., Yoo, S. J., Choi, Y. H., Chung, Y. H., Kim, J., Yoo, I. S., et al. (2014). Functional pheno-type of synovial monocytes modulating inflammatory T-cell responses in rheumatoid arthritis (RA). PLoS One 9 (10), e109775. doi:10.1371/journal.pone.0109775

PubMed Abstract | CrossRef Full Text | Google Scholar