Programmable mechanical metamaterials: basic concepts, types, construction strategies—a review

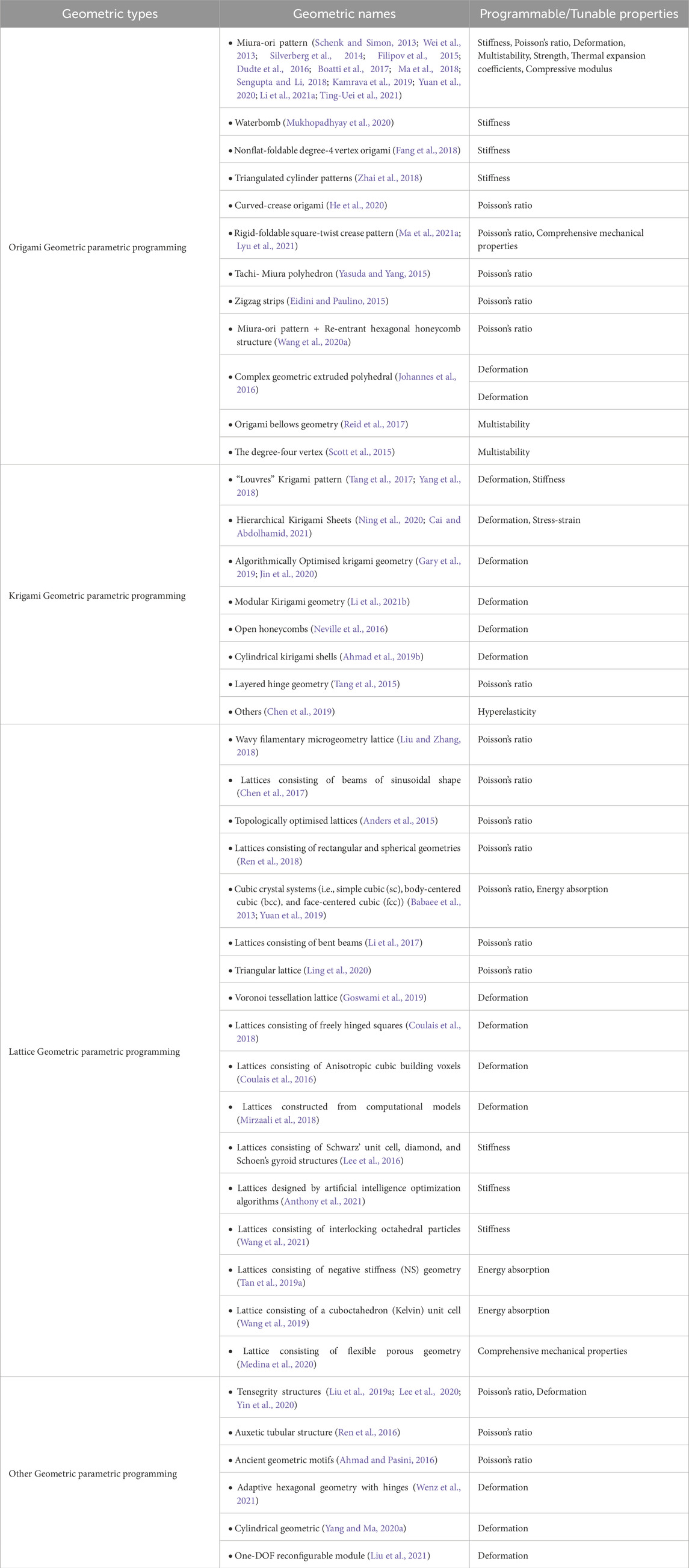
Metamaterials have been a hot topic over the past 2 decades, involving scientific research directions in materials, engineering, and physics. Among them, programmable mechanical metamaterials are an emerging class of metamaterials that offer intelligent programming and control of diverse mechanical properties, such as stiffness, damping, thermal expansion, and shape memory behavior. Meanwhile, it can be rationally designed to have specific geometric architectures and programming strategies in response to different types of external stimuli, such as temperature, electric and magnetic fields, and mechanical loads. These intelligent mechanical properties have a wide range of potential applications due to their uniqueness and controllability, including soft robotics, adaptive structures, and wearable devices. Thus, the programming strategies to achieve them are particularly critical. Combined with related programmable thinking concepts, this paper briefly reviews programming strategies for programmable mechanical metamaterials, including geometric, structural, and external driving force programming. Meanwhile, this paper presents the principles of programming strategies classified according to different programmable mechanical properties (e.g., programmable stiffness, deformation, multistability) and looks ahead to the challenges and opportunities for future research.

1 Introduction

People’s tireless exploration of metamaterials has promoted its rapid development for a long time. Related research has been growing exponentially in recent years. The metamaterial is an emerging class of artificial composite materials with unique properties not found in traditional natural materials (Shelby et al., 2001; Smith et al., 2004). Metamaterials do not differ significantly in composition from traditional materials; their unique characteristics primarily arise from complex artificial structures (Liua and Zhang, 2011). Specifically, metamaterials can modulate various physical quantities through the combinatorial arrangement of various periodic or non-periodic geometrical unit cells (Rodger, 2001; Shalaev, 2007; Grima and Caruana-Gauci, 2011). This modulation can also involve microscopic size tailoring, resulting in never-before-seen, novel, or even extreme physical properties of materials (Zheludev and Kivshar, 2012; Martin, 2013).

Professor Rodger M. Walser first introduced the concept of metamaterials in 2001 (Rodger, 2001). Then, professors R. A. Shelby and D. R. Smith demonstrated that the novel properties of metamaterials are real by actually producing metamaterials with a negative refractive index (Shelby et al., 2001). Currently, electromagnetic metamaterial is the most fully developed class of metamaterials. It has produced numerous research applications, for example, lenses that break traditional diffraction limits (Hou-Tong Padilla et al., 2006), electromagnetic cloaks of invisibility (Adrian, 2006), and new antennas (Yuandan and Tatsuo, 2012). In addition, metamaterials also exhibit novel optical, acoustic, thermal, and mechanical properties (Nicholas et al., 2006). Optical metamaterials refer to artificial structural materials composed of metallodielectric subwavelength building blocks (Soukoulis and Martin, 2011). It can realize various innovative optical properties, such as negative refractive index (Pendry, 2000; Hoffman et al., 2007; Tsakmakidis et al., 2007; Valentine et al., 2008), tunable negative refractive index (Shalaev, 2007), and enhanced nonlinear optical properties (Soukoulis and Martin, 2011). Current applications include optical tunneling devices (Silveirinha and Engheta, 2006) and cloaking devices (Soukoulis and Martin, 2011). Acoustic and thermal metamaterials are fundamentally similar in principle to electromagnetic and optical metamaterials and can accomplish novel physical properties by manipulating and controlling acoustic or thermal conductivity (StevenChristensen and Alu, 2016), for example, acoustic metamaterials with diffraction, negative refraction (Nicholas et al., 2006; Lee et al., 2009), transformation acoustics (Cummer and Schurig, 2007) properties, and thermal metamaterials with thermal stealth properties (Xu et al., 2014).

It is worth noting the mechanical metamaterials, which can achieve many mechanical properties of materials that do not exist in nature (Zheng et al., 2014; Amir, 2016; Yu et al., 2018). This is a relatively new branch of metamaterial research (Amir, 2016). Such as superstretchability (Jiang and Wang, 2016), negative compressibility (Nicolaou and Motter, 2012; Yi et al., 2014; Rod Lakes and Wojciechowski, 2023), negative stiffness (Correa et al., 2015; Hewage et al., 2016; Lakes et al., 2023), superstrength (Zheng et al., 2016), negative Poisson’s ratio (Bertoldi et al., 2010; Babaee et al., 2013; Grima et al., 2016; Kolken and Zadpoor, 2017; Jiang et al., 2018), tunable stiffness (Yu et al., 2018), superfluidity (Kadic et al., 2012; Kadic et al., 2014), nonlinear behavior (Xiaoyan and Huajian, 2016). These properties facilitate the development of a variety of applications, such as special dampers (Jiang and Wang, 2016), robotics (Bartlett et al., 2015), bionic soft mechanical applications (Wang et al., 2014), and mechanical stealth devices (Bueckmann et al., 2014). Additionally, topological mechanical metamaterials also belong tomechanical metamaterials (Nash et al., 2015; Paulose et al., 2015; Li et al., 2020; Paulose et al., 2023). Although mechanical metamaterials have many novel properties, they also have certain limitations. Metamaterials are composed of homogenized structure unit cells, and their overall properties are relatively single and passive, which is relatively insufficient in today’s computing and intelligent era. Along with the emergence of coded metamaterials and programmable electromagnetic metamaterials (Liu and Cui, 2017; Bao and Cui, 2019), the programming design through computational logic systems can allow mechanical metamaterials to become more intelligent, active, and controllable based on their unconventional physical properties (Zheludev, 2010; Florijn et al., 2014; Jascha et al., 2017; Shah et al., 2021). Therefore, the programming and intelligence of mechanical metamaterials have gradually started to explode in recent years, enabling numerous excellent properties such as programmable stiffness (Mukhopadhyay et al., 2020), Poisson’s ratio (He et al., 2020), multistability (Kamrava et al., 2019), energy absorption (Tan et al., 2019a), thermal expansion coefficient (Peng Yong et al., 2021), hyperelasticity (Chen et al., 2019), and deformation (Ye et al., 2021).

Previously, related reviews have been conducted for programmable mechanical metamaterials (Bertoldi et al., 2017; Kadic et al., 2019). For example, Xianglong Yu et al. (Yu et al., 2018), Emilio Barchiesi et al. (Barchiesi et al., 2019), Jae-Hwang Lee et al. (Lee et al., 2012) reviewed the mechanical properties characterization of metamaterials; Katia Bertoldi et al. (Bertoldi et al., 2017) introduced programmable kirigami, origami, and bistable metamaterials and made a future vision for programmable mechanical metamaterials with mechanical information storage and retrieval properties; Zian Jian et al. (Jia et al., 2020), Amir A. Zadpoor (Amir, 2016) offered a brief summary of programmable lattice metamaterials in mechanical properties; Ahmad Rafsanjani et al. (Ahmad et al., 2019a) provided a brief review of the development of programmable robots built on flexible mechanical metamaterials; Pengcheng Jiao et al. (Jiao and Alavi, 2021) discussed the development trend of smart mechanical metamaterials; Jixiang Qi et al. (Qi et al., 2022), S. Macrae Montgomery et al. (Macrae Montgomery et al., 2020) summarized the principles of construction and fabrication of active mechanical metamaterials. These review papers supply a good reference for researchers and practitioners in various industries.

Here, this paper furnishes a brief review of programmable mechanical metamaterials’ basic concepts, classification, and construction strategies, mainly from the perspective of programming thinking and logic (controlled mechanical systems for logical flow). Sections 2–5 introduce the construction strategies of programmable origami and kirigami mechanical metamaterials, programmable lattice, other geometrically structured mechanical metamaterials, and typical programmable hierarchical mechanical metamaterials, respectively. Section 6 focuses on the construction strategy based on external driving force programming. Section 7 supplements several unique programmable mechanical metamaterials (e.g., bistable structural programming, artificial intelligence parameter-optimized structural programming), discusses the insufficiency of current programmable mechanical metamaterial construction strategies and predicts possible future direction of development.

2 Basic concepts, building blocks, classification

This section discusses the development of programmable thinking in materials and the concept, building blocks and classification of programmable mechanical metamaterials.

2.1 A brief development of programmable thinking

In the field of physical sciences, the concept of programmable thinking was initially applied to the study of programmable matter. Toffoli (White et al., 2011) described programmable matter as early as 1991, which can be assembled into blocks of various sizes, dynamically reconfigured into any uniform, polynomially interconnected fine-grained computational network (Tommaso and Norman, 1991), interactively driven, observed, analyzed, and modified in real-time (Tommaso and Norman, 1991).

Later, as programmable thinking was introduced into materials research, intelligent materials began to emerge. For example, Ion et al. (Ion et al., 2016; Ion et al., 2017) proposed a digital mechanical metamaterial, which can control mechanical signal propagation through the transformation and arrangement of unit cells with different functions; E. Hawkes et al. (Hawkes et al., 2010) proposed a programmable substance (Figure 1A) that can achieve a specific shape or stiffness by programming properties according to commands; Tiejun Cui et al. (Cui et al., 2014; Bao and Cui, 2019) proposed a programmable electromagnetic metamaterial (Figure 1B) consisting of unit cells with “0” or “1” states controlled by biased diodes. Arranging these unit cells through field-programmable gate array (FPGA) hardware can realize the programming control of electromagnetic waves; Teunis van Manen et al. (van Manen et al., 2018) considered that stress gradient, compressive in-plane stresses, and time sequence could be programmed based on related parameters (such as stiffness ratio and thickness ratio) to achieve the purpose of controlling plane material deformation (bending, buckling); Farhang Momeni et al. (Momeni et al., 2017) and S. Tibbits et al. (Raviv et al., 2014; Tibbits, 2014) argue that 4D printing is achieved through a combination of programming strategies, stimulus source (such as water and heat), stimuli-responsive materials, geometric structures, and other elements.

Figure 1

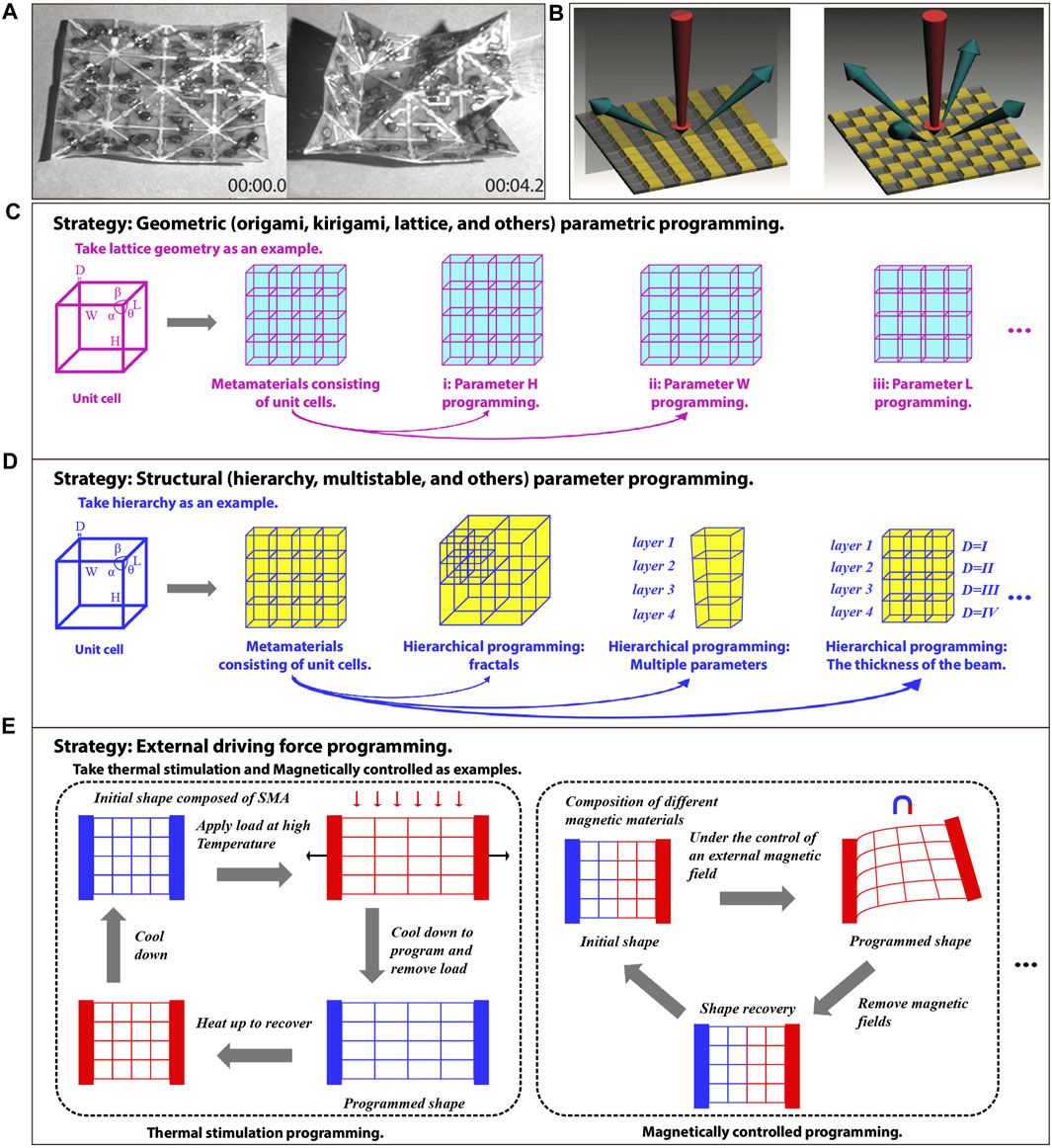
Figure 1. Development of programmable thinking in materials and Programming construction strategy of Mechanical metamaterials. (A) Programmable matter (Reproduced with permission from (Hawkes et al., 2010). Copyright 2010, PNAS). (B) Programmable electromagnetic metamaterials (Reproduced with permission from (Cui et al., 2014). Copyright 2014, CIOMP). (C) Programming of unit cells geometric parameters (e.g., length, width, height). (D) Programming of structural parameters (e.g., fractal hierarchy). (E) Programming construction strategy of external driving force (e.g., thermal stimulation, magnetic control).

In addition, a variety of strategies (e.g., programming strategies based on geometry (Liu et al., 2017; Kanik et al., 2019; Xu et al., 2019), multi-material (Wu et al., 2016), thermal expansion stress difference (Yun et al., 2020), sequential self-folding (Mao et al., 2015), spatio-temporal (Nojoomi et al., 2018; Guseinov et al., 2020), and transition temperature (Lendlein, 2018) modulation) also highlight the important role of programmable thinking in the construction of new materials.

2.2 Definition

Programmable mechanical metamaterials refer to: using programmable thinking through the computational control of “information parameters” to construct metamaterials with controllable (Florijn et al., 2016; Tang et al., 2017; Zhang et al., 2019; Zhang et al., 2019; Xin et al., 2020), tunable (Ning et al., 2020; Wu et al., 2021), and programmable (Abdullah et al., 2020; Jin et al., 2020; Shi et al., 2021) mechanical properties. Specifically, on one hand, it is constructed from unit cells with the same or different ‘geometric parameters’. These unit cells can be dynamically distributed, arranged, and assembled in different computing networks, arrays, spaces, and subdivisions through a programming system, thereby achieving the purpose of controlling the propagation of mechanical signals (Liu et al., 2023). The elements can interact and drive each other (Liu et al., 2023). On the other hand, it can also integrate external driving forces and use logical operations to control mechanical properties (Liu et al., 2023).

2.3 Programming elements and strategies

Programming Elements of programmable mechanical metamaterials:

• Programmable thinking is the guiding principle in the design of mechanical metamaterials. Firstly, it can be considered as a combination of code (unit cells) and operations (distribution rules), enabling parameterized programming through modulation of relevant “information parameters” (${\epsilon }_y=f\left({\epsilon }_x\right)$) (Wenz et al., 2021). Secondly, it can also be seen as a controlled mechanical operating system with logical flow attributes $\left(if-then-else\right)$ (Wenz et al., 2021).

• The “information parameters” refer to the objects of manipulation and can be primarily categorized into three parts: a. Geometric parameters of unit cells: encompassing various geometric properties of different types, such as kirigami, origami, lattices, tensioned structures, and double holes. b. Structural parameters: related to the arrangement of unit cells in space, including hierarchical structures, algorithm-optimized structures, and multi-stable structures. c. External driving force: mainly indicating external forces applied to the material, such as manual forces, water, light, heat, electricity, magnetism, and aerodynamics.

• Model characterization: Programmable mechanical metamaterials require theoretical mechanical and mathematical models to characterize the relationships between the different elements.

• Simulation and experiment: Verification of mechanical properties requires material simulation and experimental verification.

Based on the programming elements, the construction strategy can be broadly described as (Figures 1C–E):

• Programmable thinking is applied in two scenarios (Wang et al., 2020; Liu et al., 2021; Liu et al., 2023): a. The mechanical performance depends on geometric or structural parameters. In other words, once the metamaterial is manufactured, its mechanical properties remain fixed. Different metamaterials exhibit distinct mechanical behaviors, which are determined by their respective micro-geometry or microstructural parameters. For example, in the subsequent introduction of specific content, programmable mechanical metamaterials based on kirigami (Section 3), origami (Section 3), lattice (Section 4), and hierarchical structure (Section 5) belong to this kind. This scenario corresponds to the first type of programmable thinking (${\epsilon }_y=f\left({\epsilon }_x\right)$). b. The mechanical performance is controlled by external driving force. The geometry or structure of the metamaterial will change under the driving control of thermal, magnetic, pneumatic, etc. methods (Section 6). Accompanying this change in geometry or structure, the mechanical properties of the metamaterial will also change in a controlled manner, thus enabling real-time programming and control of the mechanical properties of the metamaterial. At the same time, this is also the application manifestation of the second type of programmable thinking $\left(if-then-else\right)$.

• According to the above, programming strategies can be divided into:a. The main idea is programming strategies with geometric unit cells or structural combinations, such as geometric parametric programming, topological geometry programming, and structural parametric programming. b. External driving force programming.

2.4 Classification

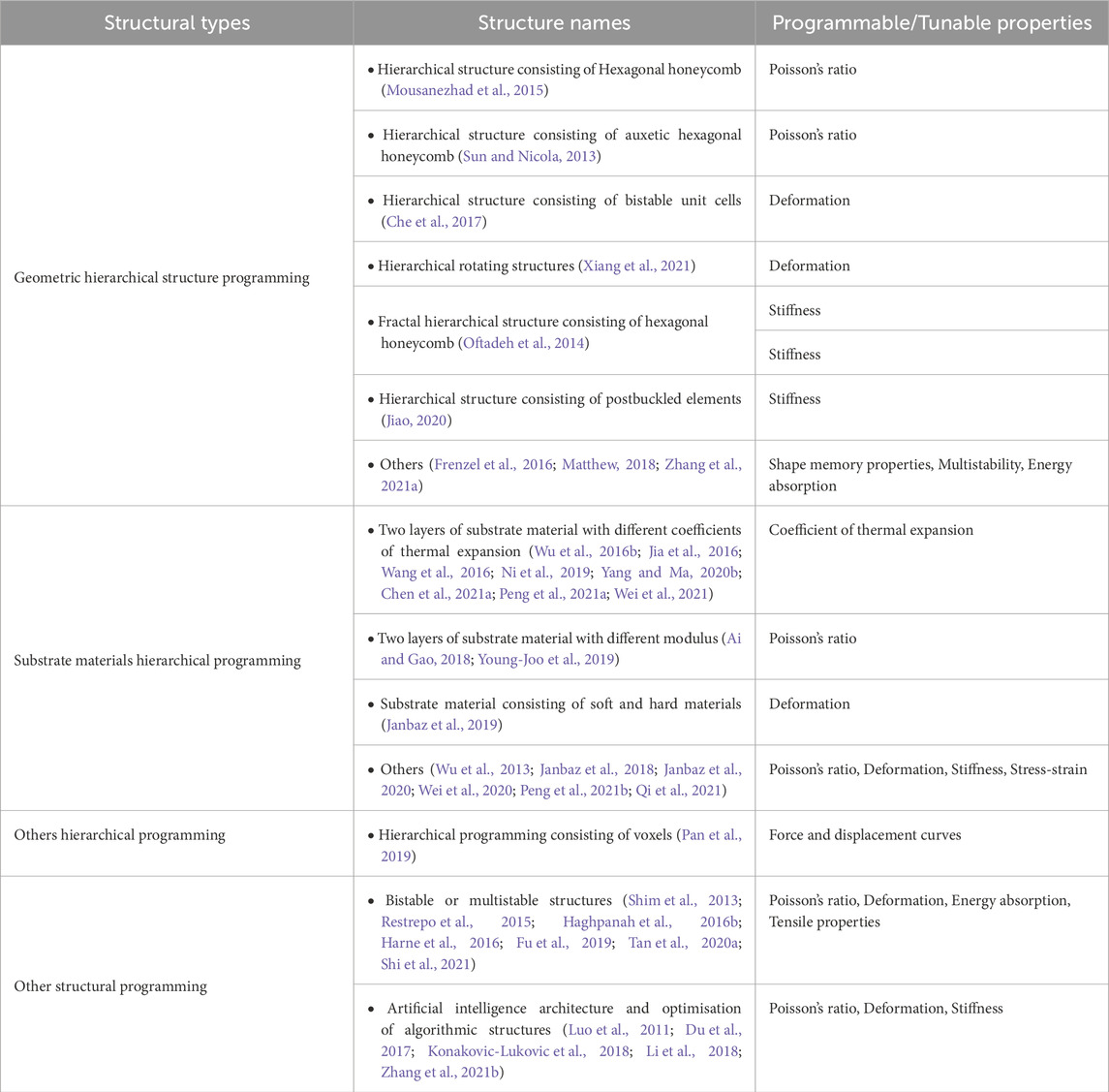
There are many classification criteria for programmable mechanical metamaterials. For example, according to dimensions, they can be divided into two-dimensional programmable mechanical metamaterials (Seffen, 2006; Chiang, 2019; Park et al., 2019; Bai et al., 2022) and three-dimensional programmable mechanical metamaterials (Babaee et al., 2013; Jiang and Wang, 2016; Kadic et al., 2019). Here, since this paper mainly focuses on the introduction of programming strategies for programmable mechanical metamaterials, this article will classify them according to programming strategies: geometric or structural programming, and external driving force programming. Firstly, according to the geometry, programmable mechanical metamaterials are divided into three main categories: those based on Origami and kirigami geometry (Bertoldi et al., 2017; Tang et al., 2017), those based on lattice geometry (Florijn et al., 2014; Haghpanah et al., 2016a; Jin et al., 2020), and those based on other geometry. This segment accounts for the vast majority of the number of programmable mechanics metamaterials. In addition, according to structure, programmable mechanical metamaterials are divided into two main categories: hierarchical structural programming (Bauer et al., 2017; Matthew, 2018), multistable structural programming (Bertoldi et al., 2017; Che et al., 2017; Kadic et al., 2019). Finally, programmable mechanical metamaterials based on the external driving force programming are also a significant category.

It should be noted that when introducing programming strategies based on origami, kirigami, lattices, and typical hierarchical structures, this article mainly focuses on the introduction of geometric or structural parameter programming, supplemented by external driving force programming strategies. A discussion of geometric or structural parameters is supplemented when introducing programming strategies based on typical external driving force.

3 Origami, kirigami geometry or structural programming

Origami is the folding of two-dimensional materials to create three-dimensional objects and its ability to produce highly complex geometric objects through the seemingly simple operation of folding flat sheets of paper (Chen et al., 2015; Kamrava et al., 2017). On the other hand, Kirigami is a modification of origami, adding cuts to origami and thus expanding the range of three-dimensional objects that can be constructed (Wang et al., 2017). Programming of origami and kirigami geometries is an essential way of constructing metamaterials, such as Miura origami (Schenk and Simon, 2013). In addition, auxiliary means can also be used - programming on demand by applying external driving force (which leads to rigid/non-rigid origami motion) (see Section 6 for details).

3.1 Origami geometry or structural programming

3.1.1 Programmable stiffness

Based on origami self-locking or interlocking mechanisms, multiple stiffness programming of metamaterials can be achieved using geometric, structural, and external force modulation (assisted) strategies. For example, geometric parameter programming realizes stiffness conversion, origami layered structure programming realizes stiffness grading, and on-demand strain regulation programming realizes tunable stiffness. Figure 2A shows a tubular metamaterial constructed based on Waterbomb origami (Mukhopadhyay et al., 2020). Applying force/displacement to the end can cause rigid origami motion (near-zero stiffness) and non-rigid origami motion (high stiffness) (Mukhopadhyay et al., 2020). Among them, the critical transition point $L_{cr}$ is generated by the stop of rigid motion (self-locking mechanism) due to the contact of vertices inside the metamaterial Figure 2A(i) (Mukhopadhyay et al., 2020). This phenomenon has a significant stiffness transition, and thus, by controlling the occurrence of a critical point $L_{cr}$ during motion through geometric parameters ($m,n,\alpha$)and external forces/displacements, a sudden and abrupt increase in stiffness can be programmed (Figure 2A(ii)) (Mukhopadhyay et al., 2020); Figure 2B presents a metamaterial constructed based on a nonflat-foldable degree-4 vertex origami (single-collinear, SC) (Fang et al., 2018). Combined with the parametric tuning of sector angles ${\gamma }_1,{\gamma }_2$ (Figure 2B(i), especially the concatenation of SC unit cells with different collinear crease thicknesses into geometrically heterogeneous multilayer structures (see Section 5 for hierarchical programming), Four stiffness segments (Figure 2B(ii)) and eight target stiffnesses with locking configurations (Figure 2B(iii)) based on FPR (flexible photosensitive resin) substrate materials can be implemented programmatically (Fang et al., 2018); Figure 2C presents a design of an on-demand deployable tunable stiffness metamaterial consisting of Triangulated cylinder patterns (Figure 2C(i) (Zhai et al., 2018). By manually unfolding or folding the geometry as needed to adjust the angles of $\alpha$ and $\beta$, the metamaterial can be converted between near-zero and high stiffness (Figure 2C(ii-iii)) (Zhai et al., 2018).

Figure 2

Figure 2. Origami metamaterial with programmable stiffness. (A) Geometric parameters programming (Reproduced with permission from (Mukhopadhyay et al., 2020). Copyright 2020, Elsevier): (i) unit cells and parameter characterization (top), rigid, non-rigid motion (bottom), III is a schematic representation of the metamaterial at the transition critical point $L_{cr}$; (ii) Stiffness variation curves with m as the variable (top) and α as the variable (bottom) under axial force loading. (B) Hierarchical programming (Reproduced with permission from (Fang et al., 2018). Copyright 2018, Wiley): (i) unit cells parameter characterization (top) and physical schematic (bottom); (ii) Programmable four-stiffness segments and variation curves; (iii) Multi-objective stiffness programming for different configurations represented by the equivalent spring model. (C) On-demand programming (Reproduced with permission from (Zhai et al., 2018). Copyright 2018, PNAS): (i) unit cell ∆ABC and parametric characterization; (ii) low stiffness (left), high stiffness (right) paper folded triangular cylinder and metamaterial (middle); (iii) Low (left) and high (right) stiffness folding deployment of metamaterials with paper and rubber bands as the substrate material. (D) Others: Metamaterials proposed by (i) Jiayao Ma et al. (Reproduced with permission from (Ma et al., 2018). Copyright 2018, Elsevier), (ii) Lin Yuan et al. (Reproduced with permission from (Yuan et al., 2020). Copyright 2020, Elsevier), (iii) Mark Schenk et al. (Reproduced with permission from (Schenk and Simon, 2013). Copyright 2013, PNAS), (iv) Evgueni T. Filipov et al. (Reproduced with permission from (Filipov et al., 2015). Copyright 2015, PNAS), (v) Sattam Sengupta et al. (Reproduced with permission from (Sengupta and Li, 2018). Copyright 2018, SAGE), respectively.

Other metamaterials with graded stiffness (Figure 2D(i) (Ma et al., 2018) (Figure 2D(ii)) (Yuan et al., 2020), tunable stiffness (Figure 2D(iii)) (Schenk and Simon, 2013) (Figure 2D(iv)) (Filipov et al., 2015) (Figure 2D(v)) (Sengupta and Li, 2018) can also be realized by using Miura-ori and applying the above strategy.

3.1.2 Programmable poisson’s ratio

Based on origami geometry, metamaterials can be programmed to achieve tunable Poisson’s ratio properties. Such as geometric and structural parameter programming to realize “+” and “-”Poisson’s ratio conversion, manual strain programming to realize adjustable Poisson’s ratio. Y.L. He et al. demonstrates a three-dimensional metamaterial constructed from curved-crease origami (CCO) (He et al., 2020). The initial angle $\alpha =65°$ remains unchanged, and when the aspect ratio $c_1:c_2$ is lower than about $2:3$, the Poisson’s ratio $V_{HB}$ of metamaterials changes from “+” to “-” (He et al., 2020). Similarly, the Poisson’s ratios ($V_{HB}$, $V_{HL}$, $V_{HW}$) of metamaterials can be positively or negatively interconverted in different directions in increasing or decreasing form through the modulation of geometrical parameters (e.g., initial angle $\alpha$, layered incremental angular difference $∆\alpha$) (He et al., 2020). Figure 3A(i) presents a two-dimensional metamaterial constructed from Miura-ori origami (Figure 3A(ii)), exhibiting equal but opposite sign in-plane and out-of-plane Poisson’s ratios (Wei et al., 2013). When stretched along the x-axis, the material demonstrates a negative Poisson’s ratio behavior (Figure 3A(iii)), whereas when subjected to symmetric bending moments at the boundaries $x=\pm L$, it shows a positive Poisson’s ratio behavior (Figure 3A(iv)) (Wei et al., 2013). Therefore, the metamaterial can realize “+” and “-” Poisson’s ratio tuning by external driving force.

Figure 3

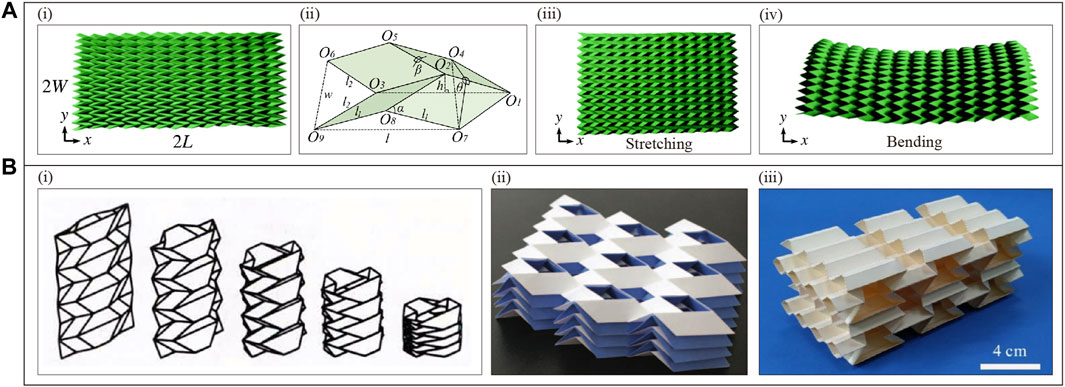
Figure 3. Origami metamaterial with programmable Poisson’s ratio. (A). External driving force modulation (Reproduced with permission from (Wei et al., 2013). Copyright 2013, American Physical Society): (i) a metamaterial consisting of 13 × 1 3 unit cells, where $\alpha =45°,l_1=l_2=l_3$, the plate dimension is 2L by 2W. (ii) Unit cell and parametric characterization. (iii) Schematic diagram of stretching along the x-axis. (iv) Schematic diagram of applying a symmetrical bending moment to the boundary $x=\pm L$. (B) Others: metamaterials proposed by (i) H. Yasuda et al. (Reproduced with permission from (Yasuda and Yang, 2015). Copyright 2015, American Physical Society), (ii) Maryam Eidini et al. (Reproduced with permission from (Eidini and Paulino, 2015). Copyright 2015, American Association for the Advancement of Science), and (iii) Hairui Wang et al. (Reproduced with permission from (Wang et al., 2020). Copyright 2020, Elsevier), respectively.

Numerous metamaterials with the same properties are also realized using the above strategy, for example, those constructed by using Rigid-foldable square-twist crease pattern (Lyu et al., 2021), Tachi-Miura polyhedron (Figure 3B(i) (Yasuda and Yang, 2015), Zigzag strips (Figure 3B(ii)) (Eidini and Paulino, 2015), and Re-entrant hexagonal honeycomb structure (Figure 3B(iii)) (Wang Hairui et al., 2020), respectively.

3.1.3 Programmable deformation

Based on origami geometry, metamaterials with programmable deformation properties can be realized. For example, angular parameters are programmed to control the deformation shape, and numerical optimization algorithms are programmed to control the curvature deformation. Figure 4A reveals a metamaterial consisting of a complex geometric extruded polyhedra (Figure 4A(i) (Johannes et al., 2016). Eqs 1–4 quantify the geometric deformation of the metamaterial in terms of vectors and internal volumes, respectively:

${\mathbf{P}}_1=\left[L,0,0\right],(1)$

${\mathbf{P}}_2=\left[L\cos \left({\gamma }_3\right),L\sin \left({\gamma }_3\right),0\right],(2)$

${\mathbf{P}}_3=\left[L\cos \left({\gamma }_2\right),L\delta ,L\sqrt{1-{\cos }^2\left({\gamma }_2\right)-{\delta }^2}\right],(3)$

$v_{\mathit{int}}=\left|{\mathbf{P}}_3\bullet \left({\mathbf{P}}_1\times {\mathbf{P}}_2\right)\right|+2L\left(‖{\mathbf{P}}_3\times {\mathbf{P}}_1‖+‖{\mathbf{P}}_1\times {\mathbf{P}}_2‖+‖{\mathbf{P}}_2\times {\mathbf{P}}_3‖\right).(4)$

Figure 4

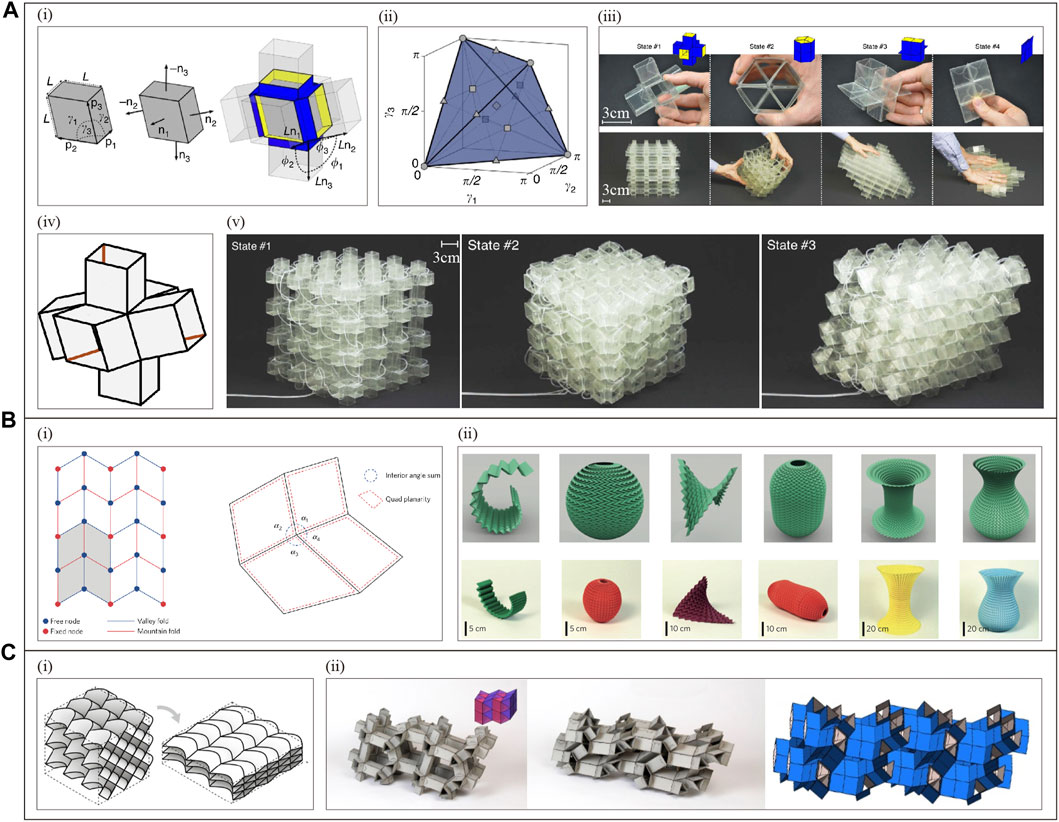
Figure 4. Origami metamaterial with programmable deformation. (A) Geometric parametric programming(Reproduced with permission from (Johannes et al., 2016). Copyright 2016, Nature Publishing Group): (i) The unit cell (left) and its deformation modes (middle, right); (ii) All achievable angular combinations based on ${\mathrm{\gamma }}_1,{\mathrm{\gamma }}_2,{\mathrm{\gamma }}_3$; (iii) Programmed states #1, #2, #3, and #4 achieved by manual loading; (iv) Inflatable loads are applied at the orange hinge positions of each unit cell; (v) A metamaterial composed of 96 unit cells with airbags connected by inflatable tubes. (B) Numerical optimization algorithm programming(Reproduced with permission from (Dudte et al., 2016). Copyright 2016, Nature Publishing Group): (i) Pattern of mountain/valley fold orientation and fixed/free nodes for numerical optimization method. Gray represents a unit cell; (ii) Deformation simulation (top) and real object (bottom) with programmable curvature. (C). Others: (i) metamaterials designed by Ting-Uei Lee et al. (Reproduced with permission from (Ting-Uei et al., 2021). Copyright 2021, Elsevier), (ii) Johannes T. B Overvelde et al. (Reproduced with permission from (Overvelde et al., 2017). Copyright 2017, Nature Publishing Group), respectively.

Here, $\delta =\left[\cos \left({\gamma }_1\right)-\cos \left({\gamma }_2\right)\cos \left({\gamma }_3\right)\right]∕\sin \left({\gamma }_3\right)$, therefore, changing the angles ${\gamma }_1,{\gamma }_2,{\gamma }_3$ can regulate its deformation state (Figure 4A(ii)) (Johannes et al., 2016). Among them, state #1 deformation is the smallest and state #4 is the largest (Figure 4A(iii)) (Johannes et al., 2016). At the same time, various deformations such as states #one to three can also be realized by applying an external inflatable load in a distributed driving manner (Figure 4A(iv-v)) (Johannes et al., 2016). Figure 6B displays a metamaterial constructed based on Miura-ori origami (Figure 4B(i) (Dudte et al., 2016). Using Kawasaki’s theorem and a numerical optimization algorithm based on this theorem, metamaterials can achieve deformations with controlled curvature properties (Figure 4B(ii)) (Dudte et al., 2016).

Using the above strategies, metamaterials with programmable force and displacement properties (Figure 4C(i) (Ting-Uei et al., 2021), reconfigurable deformation properties (Figure 4C(ii)) (Overvelde et al., 2017), the programmable behavior of a mechanical bit used for robots (Treml et al., 2018) and the fast shape changing and instantaneous shape locking (Novelino et al., 2020) were also realized based on Miura-ori pattern, Complex geometric extruded polyhedral and Bistable origami, respectively.

3.1.4 Programmable multistable

Metamaterials with various mechanical multistable properties can be realized through origami geometric parameters and unit cell arrangement (structure) strategies, for example, programmable bistable, tristable, and global multistable metamaterials. Figure 5A presents a metamaterial constructed based on Miura-ori strings (Figure 5A(i), which can be programmed to achieve unit cells (Figure 5A(ii)) with monostable, semi-bistable and bistable states by controlling the angles ${\alpha }_1$ and ${\alpha }_2$ (Kamrava et al., 2019). The number of Miura-ori (n) in an angle chord is also a critical programming parameter for it (Figure 5A(iii)). Figure 5A(iv) offers a configuration of this metamaterial: each orthogonal direction contains 12 star-shaped cells ($n=4$) in series (36 in total), with 15 design parameters, programmable to achieve three Behavior (Kamrava et al., 2019). In addition, based on Origami bellows geometry, the degree-four vertex geometry and hypar origami also realizes metamaterials with programmable bistable properties (Reid et al., 2017), global multistable properties (Scott et al., 2015) and multistable properties (Liu et al., 2019), respectively.

Figure 5

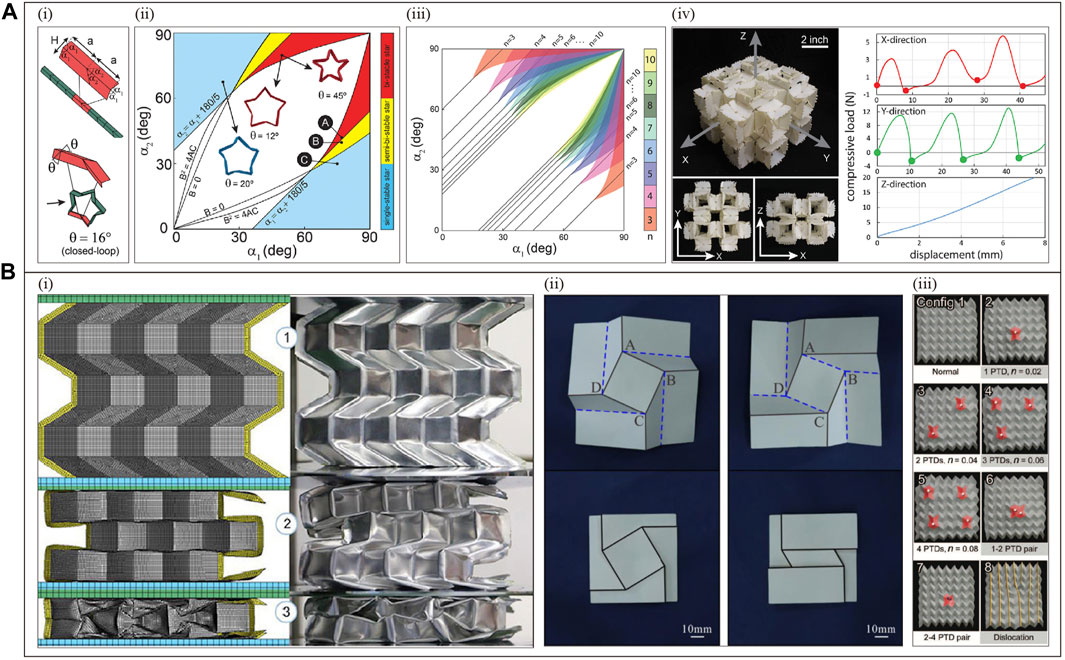
Figure 5. Origami metamaterials with programmable multistability and other properties. (A) Geometry and structural parameters programming multistability (Reproduced with permission from (Kamrava et al., 2019). Copyright 2019, Wiley): (i) Miura-ori structure (top) and metamaterial unit cells (bottom); (ii) Stability analysis diagram of star unit cells with different ${\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2$. The blue, yellow, and red regions correspond to monostable, semi-bistable, and bistable behaviors, respectively; (iii) Bistable and semi-bistable behaviors corresponding to different (n); (iv) The real metamaterial (left) and the programmable multistability curve (right). (B) Other properties of geometric programming: (i) Compression simulation diagram (left) and physical diagram (right) of metamaterial proposed by Zhejian Li et al. (Reproduced with permission from (Li et al., 2021). Copyright 2020, Elsevier). (ii) Metamaterials proposed by Jiayao Ma et al. (Reproduced with permission from (Ma et al., 2021). Copyright 2021, Elsevier). (iii) Schematic diagram of different programming configurations of metamaterials proposed by Jesse L. Silverberg et al. (Reproduced with permission from (Silverberg et al., 2014). Copyright 2014, American Association for the Advancement of Science).

3.1.5 Other programmable mechanical properties

In addition to stiffness, Poisson’s ratio, deformation, and multi-stability properties, other programmable mechanical properties can be achieved using origami geometric and structural strategies. Figure 5B(i-iii) shows that based on Miura-ori origami, Rigid-foldable square-twist crease pattern, bistable Miura-ori unit cells can respectively achieve graded compressive strength (Li et al., 2021), comprehensive mechanical properties (Ma et al., 2021), and compressive modulus with reversible adjustment (Silverberg et al., 2014).

3.2 Kirigami geometry or structural programming

3.2.1 Programmable deformation

Using kirigami geometry, multiple programmable deformations of metamaterials can be achieved. For example, geometric parameters are used to program the deformation, unit cells (with the same mechanical properties but different deformation) are arranged to program special patterns, and optimization algorithms are used to program the deformation. A metamaterial constructed from the “Louvres” Krigami pattern is designed in Figure 6A (Tang et al., 2017). Figure 6A(i-ii) exhibits that due to the compressive force P and the notch breaking the original geometric symmetry, the center of gravity shifts down and is not aligned with the neutral plane (dotted line), and the generated bending moment M can guide different buckling behaviors to make the unit cell locally bend clockwise and counterclockwise in a controlled manner (Tang et al., 2017). Thus, the change in kiri-kirigami morphology can be programmed by controlling the homogeneous or heterogeneous tilt direction of the unit cells (Figure 6A(iii)) (Tang et al., 2017). Figure 6B presents a metamaterial constructed based on Hierarchical Kirigami Sheets (Figure 6B(i) (Ning et al., 2020). By adjusting the geometric parameters (e.g., ${\delta }_1,{\delta }_2,l,t$), multiple sets of unit cells can be made to have a similar stress-strain response but different fractions of the void area due to buckling, for example, the combination: ${\delta }_1^{\left(1\right)}/l=0.1375,{\delta }_2^{\left(1\right)}/l=0.075,{\gamma }^{\left(1\right)}=0°$ and ${\delta }_1^{\left(2\right)}/l=0.15,{\delta }_2^{\left(2\right)}/l=0.075,{\gamma }^{\left(2\right)}=90°$ (Figure 6B(ii)) (Ning et al., 2020). Therefore, metamaterials can be programmed to achieve complex deformable patterns, such as text and flowers, through unit cell arrangement programming (Figure 6B(iii)) (Ning et al., 2020). Figure 8C shows a metamaterial with an array of notches embedded in an elastic polyester plastic sheet (Figure 6C(i) (Jin et al., 2020). In combination with ${\delta }_1$ and $H$ parameter modulation and heterogeneous unit cell programming configurations, simple macroscopic deformation of metamaterials can be achieved under external aerodynamic loading (Figure 6C(ii)) (Jin et al., 2020). However, more complex shape simulations can be completed by the programming of the Nelder–Mead simplex algorithm and the Melder–Nelson algorithm (Figure 6C(iii) (Jin et al., 2020).

Figure 6

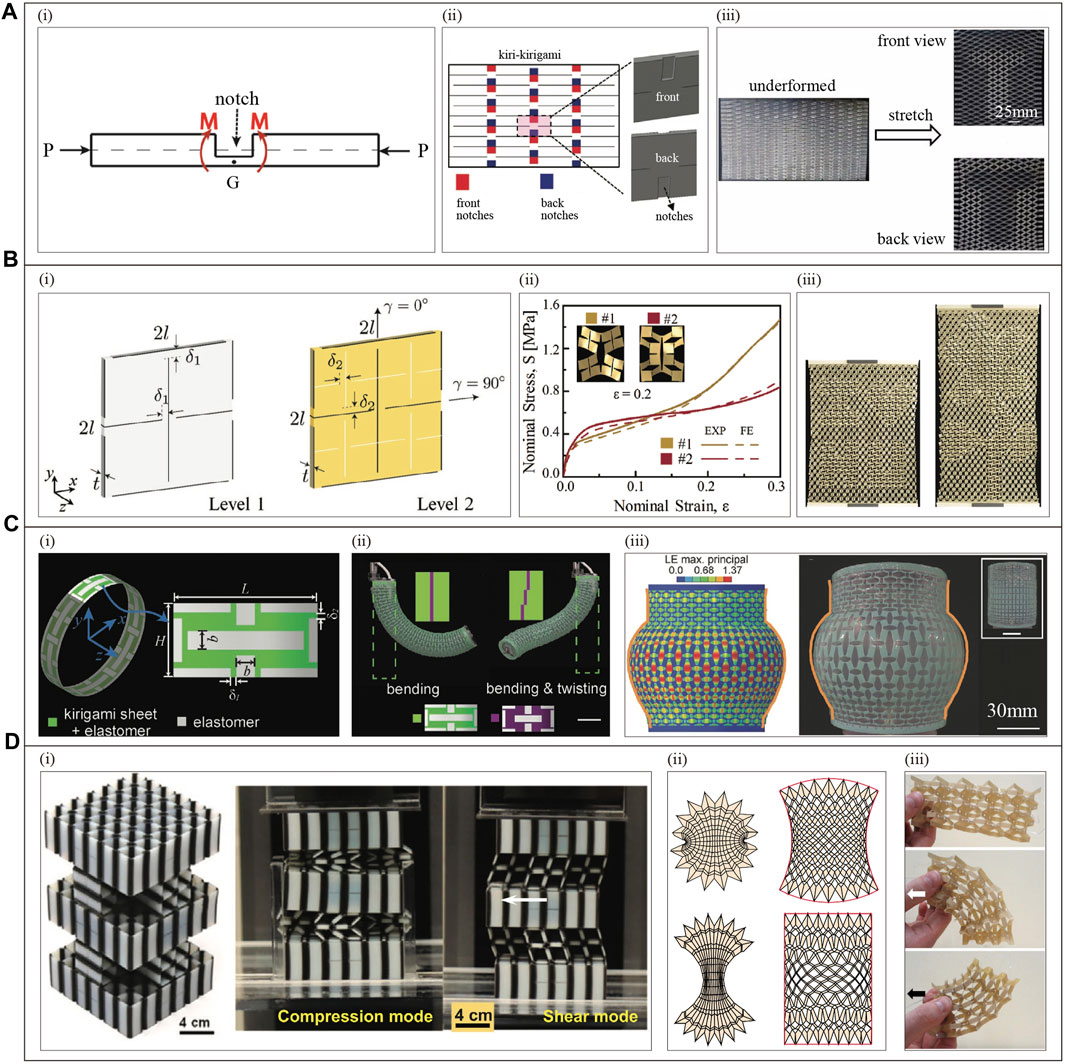
Figure 6. Kirigami metamaterials with programmable deformation and other properties. (A) Geometric parameters programming deformation(Reproduced with permission from (Tang et al., 2017). Copyright 2017, Wiley): (i) Geometric parameters of unit cell; (ii) Arrangement of unit cell;(iii) Programmable deformation imitating the letter “T”. (B) Deformations programmed by the unit cell arrangement(Reproduced with permission from (Ning et al., 2020). Copyright 2019, Wiley): (i) Schematic diagram of the unit cells and parameters. (ii) Stress-strain response of two different configurations of unit cells at 0.2 strain. (iii) Programmed realization of the text and flower pattern (parameters: ${\mathrm{\delta }}_1^{\left(1\right)}/\mathrm{l}=0.125,{\mathrm{\delta }}_2^{\left(1\right)}/\mathrm{l}=0.0525,{\mathrm{\gamma }}^{\left(1\right)}=0°$ and ${\mathrm{\delta }}_1^{\left(2\right)}/\mathrm{l}=0.15,{\mathrm{\delta }}_2^{\left(2\right)}/\mathrm{l}=0.0525,{\mathrm{\gamma }}^{\left(2\right)}=90°$). (C) Optimization algorithm to program deformation(Reproduced with permission from (Jin et al., 2020). Copyright 2020, Wiley): (i) unit cell and parametric characterization, (ii) Distributed programming of two unit cells for ${\mathrm{\delta }}_1/\mathrm{L}=0.03$ and ${\mathrm{\delta }}_1/\mathrm{L}=0.18$ to achieve bending deformation. (iii) When the pneumatic pressure is at p = 6.4 kPa, an optimization algorithm is applied to program the simulated tank shape. (D) Other programmable deformations: metamaterials designed by (i) Yanbin Lin et al. (Reproduced with permission from (Li et al., 2021). Copyright 2021, Wiley), (ii) Gary P. T. Choi et al. (Reproduced with permission from (Gary et al., 2019). Copyright 2019, Nature Publishing Group), and (iii) Robin M. Neville et al. (Reproduced with permission from (Neville et al., 2016). Copyright 2016, Nature Publishing Group), respectively.

In addition, based on Modular Kirigami geometry (Figure 6D(i) (Li et al., 2021), Algorithmically Optimised krigami geometry (Figure 6D(ii) (Gary et al., 2019), Open honeycombs (Figure 6D(iii)) (Neville et al., 2016), Cylindrical kirigami shells (Ahmad et al., 2019b), programmable deformation features are also implemented separately.

3.2.2 Other programmable mechanical properties

Other mechanical properties can be achieved with programmable kirigami metamaterials. For example, References (Yang et al., 2018) demonstrates a metamaterial constructed based on a paper-cut geometry similar to Figure 6A (Yang et al., 2018). Using the bistability property, this metamaterial can achieve a symmetric configuration transition of stiffness from 100% to 0% by adjusting the unit cell geometry parameters ${\mathcal{l}}_c∕{\mathcal{l}}_x,{\mathcal{l}}_c∕{\mathcal{l}}_y$ (Yang et al., 2018). In addition, based on Hierarchical Kirigami Sheets (Cai and Abdolhamid, 2021), Kirigami MGs (Chen et al., 2019), and Layered hinge geometry (Tang et al., 2015), it is possible to achieve metamaterials with programmable Poisson’s ratio, programmable stress-strain relation.

4 Lattice and other geometric or structural programming

In addition to origami and kirigami geometries, lattices, honeycombs, and other geometries are also important sources for building programmable mechanical metamaterials.

4.1 Lattice geometry or structural programming

4.1.1 Programmable poisson’s ratio

Poisson’s ratio can be programmed based on lattice geometry strategies, such as geometric parameter tuning Poisson’s ratio, topological shape programming Poisson’s ratio, and topologically optimized geometry or structure programming Poisson’s ratio. Jianxing Liu et al. produces a triangular, honeycomb, square metamaterial constructed based on Wavy filamentary microgeometry (Liu and Zhang, 2018). In triangular metamaterials, when the slope $\tan {\theta }_0$ remains unchanged, by changing the width ratio $\left(w_2/w_1\right)$ and length ratio $\left(L_2/\left(L_1+L_2\right)\right.$, the Poisson’s ratio can be controlled transition between −0.2 and −1.0 (Liu and Zhang, 2018). Similarly, Poisson’s ratio can be programmed to switch between positive and negative by manipulating $\left(\tan {\theta }_0\right)$, $\left(w_2/w_1\right)$, $\left(L_{sample}/H_{sample}\right)$ of honeycomb and square metamaterials (Liu and Zhang, 2018). Figure 7A presents a metamaterial constructed based on beams of sinusoidal shape (Figure 7A(i) (Chen et al., 2017). By programming half wave-length $n$ (Figure 7A(ii)), especially the topological geometry (Figure 7A(iii)), the metamaterial Poisson’s ratio can be adjusted as needed (Chen et al., 2017). Figure 7B represents a digital system metamaterial (Anders et al., 2015). Topological optimization of its microstructure by nonlinear geometric modeling can lead to different linear and nonlinear Poisson ratios (Figure 7B(i) (Anders et al., 2015). Figure 7B(ii) reveals that the Poisson’s ratio can be tuned between −0.8 and 0.8 using this method (Anders et al., 2015).

Figure 7

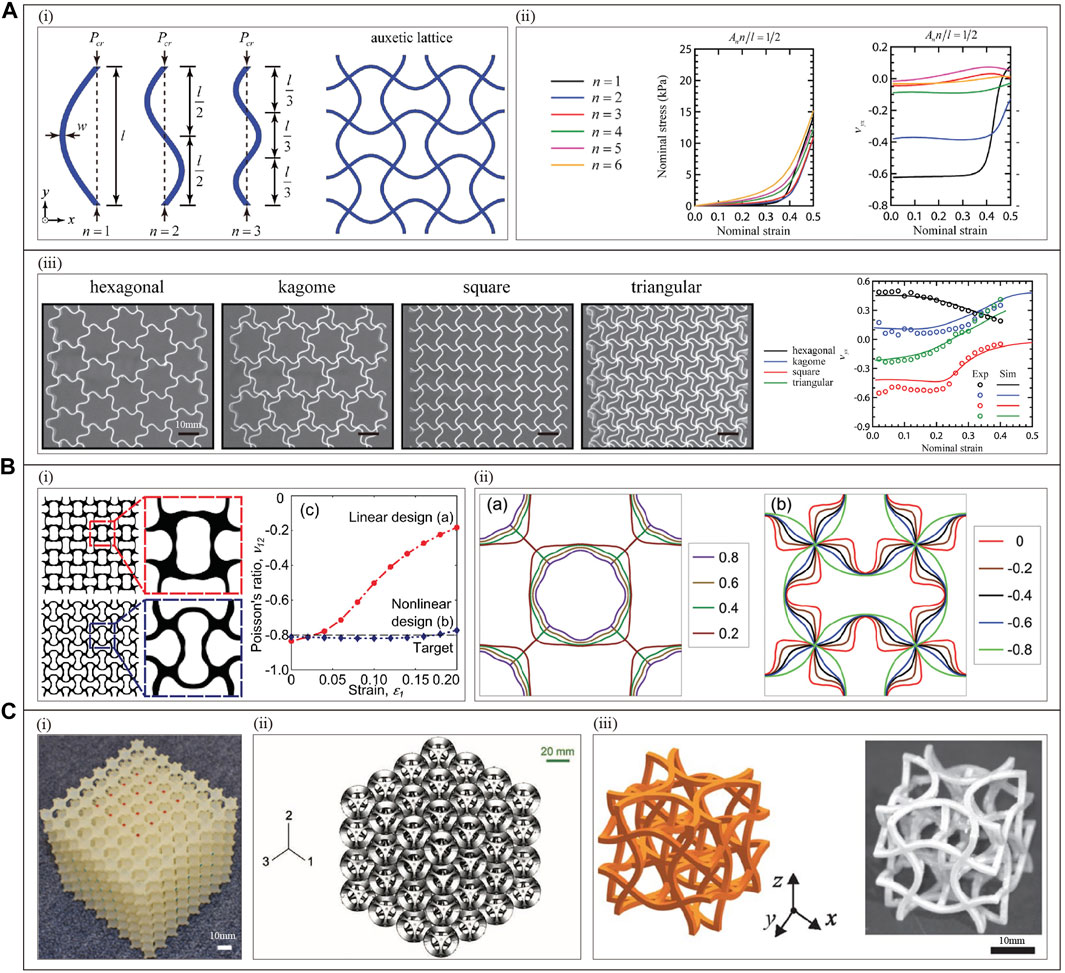
Figure 7. Lattice metamaterials with programmable Poisson’s ratio. (A) Topological lattice programming (Reproduced with permission from (Chen et al., 2017). Copyright 2017, American Physical Society): (i) Unit cells and parameters (left), metamaterials (right). (ii) Influence of half wavelength n on Poisson’s ratio. (iii) hexagonal, kagome, square, triangular metamaterials (left) and corresponding Poisson’s ratio changes (right). (B) Topology optimization programming (Reproduced with permission from (Anders et al., 2015). Copyright 2015, Wiley): (i) Geometrically nonlinear modeling topology optimization (left) and its Poisson’s ratio variation (right). (ii) Tunable range of Poisson’s ratio under both topology optimizations. (C) Others: metamaterials designed by (i) Xin Ren et al. (Reproduced with permission from (Ren et al., 2018). Copyright 2018, Elsevier), (ii) Sahab Babaee et al. (Reproduced with permission from (Babaee et al., 2013). Copyright 2013, Wiley), and (iii) Tiantian Li et al. (Reproduced with permission from (Li et al., 2017). Copyright 2017, Nature Publishing Group), respectively.

In addition, using the above construction methods, the metamaterials designed based on rectangular and spherical geometries (Figure 7C(i)) (Ren et al., 2018), cubic crystal systems (i.e., simple cubic (sc), body-centered cubic (bcc), and face-centered cubic (fcc)) (Figure 7C(ii)) (Babaee et al., 2013), bent beams (Figure 7C(iii)) (Li et al., 2017), and triangular geometry (Ling et al., 2020), respectively, also realized the programming regulation of Poisson’s ratio.

4.1.2 Programmable deformation

The lattice geometry strategy can realize the deformation control of metamaterials, for example, geometry and structure parameters can be programmed to realize shape controllability, geometric parameters combined with a self-locking mechanism can be programmed to realize multi-step path deformation, and heterogeneous voxel structure programming can realize controllable local patterns. Figure 8A displays a soft metamaterial (Architected Soft Machines, ASM) based on Voronoi tessellation (Goswami et al., 2019). Metamaterials can be programmed to bend 45° or 90°, respectively, when the thickness of the beam is distributed with a 0.5–1.0 mm lateral gradient (Figure 8A(i) or an orthogonal gradient (Figure 8A(ii)), respectively (Goswami et al., 2019). Similarly, by programming beam orientation (Figure 8A(iii)), unit cell size (Figure 8A(iv)), complex deformation behavior similar to a hand can be achieved (Goswami et al., 2019). Figure 10B(i) presents a metamaterial constructed based on freely hinged squares (Coulais et al., 2018). Setting the thickness $t_{\alpha }=1.0mm,t_{\beta }=2.0mm$ of the hinge beam can realize two-step path deformation (Coulais et al., 2018). First, the α hinge bucks at 4% strain under compression, triggering the first-step path deformation, while the thicker $\beta$ hinge does not buckle (Coulais et al., 2018). Up to 49% strain, the metamaterial forms self-contact, completing the first deformation (Figure 8B(ii)) (Coulais et al., 2018). Then, further compression leads to buckling of the $\beta$ hinge, starting the second step of path deformation until the structure is fully compressed (Figure 8B(iii-iv)) (Coulais et al., 2018). Therefore, based on the self-locking mechanism, by controlling the hinge thickness $t_{\alpha },t_{\beta }$ and the number of hinges, metamaterials can be programmed to achieve more complex multi-step paths (Coulais et al., 2018). Figure 8C designs a metamaterial based on anisotropic cubic building voxels (Figure 8C(i) (Coulais et al., 2016). Its voxels have axially aligned soft deformation patterns that can lead to elongated (+) or flattened (−) shapes (Coulais et al., 2016). Thus, a “smiley face”-like patterned texture (Figure 8C(iii)) can be achieved by a programmed arrangement of voxels (Figure 8C(ii)) (Coulais et al., 2016). In addition, the metamaterial shown in Figure 8D is also programmed based on computational models to achieve controllable shape matching properties (Mirzaali et al., 2018); Metamaterial with pattern transformation also can be programmed by geometric parameters (Chen and Jin, 2018).

Figure 8

Figure 8. Lattice metamaterials with programmable deformation, stiffness, and energy absorption. (A) Geometry parameter programming deformation (Reproduced with permission from (Goswami et al., 2019). Copyright 2019, Wiley): (i) Simulation diagram of ASM beam with thickness gradient (increasing linearly from 0.5 mm to 1 mm) and stress distribution. (ii) Simulation and experimental demonstration of ASM, exhibiting 90° bending deformation. (iii) Experimental diagram of ASM with inclined beam configuration, undergoing compression with θ twisted from 0° to 40°. (iv) Voronoi heterolattice programming for complex hand deformation. (B) Self-locking mechanism programmed for multi-step path deformation (Reproduced with permission from (Coulais et al., 2018). Copyright 2018, Nature Publishing Group): (i) Two-step path simulation diagram: The red and blue long lines depict the development of self-contact networks during the deformation process. In the initial step, the α-hinge (shown as red dots) undergoes folding, leading to self-contact between the connected squares aloang the red lines and initiating the first-stage topological transformation. Subsequently, in the second step, the β-hinge (indicated by blue dots) folds, facilitating self-contact between the squares connected by the blue lines. (ii-iii) Show physical images. (iv) Display the graph of compression force vs. engineering strain. (C) Voxel programming patterned textures (Reproduced with permission from (Coulais et al., 2016). Copyright 2016, Nature Publishing Group): (i) undeformed voxels (left), flattened (−) or elongated (+) states (right) (Liu and Zhang, 2018). (ii) Unit cells in different deformation states (Liu and Zhang, 2018). (iii) Programmable “smiley face” pattern (Liu and Zhang, 2018). (D) Others with programmable deformation: metamaterials designed by M. J Mirzaali et al. (Reproduced with permission from (Mirzaali et al., 2018). Copyright 2018, Nature Publishing Group); (E) Geometric parameters to modulate stiffness (Reproduced with permission from (Lee et al., 2016). Copyright 2016, Nature Publishing Group): (i) Metamaterials. (ii) E/S ratio as a function of aspect ratio. (iii) E/S ratio as a function of volume fraction. (F) Artificial intelligence-optimized structural design to regulate stiffness (Reproduced with permission from (Anthony et al., 2021). Copyright 2021, Elsevier): (i) Unit cells (left, middle), which are tiled and blue arrows indicate loading or shock loads (right). (ii) Comparison of the results of 2500 generative designs and 15,000 random designs satisfying the manufacturing constraints, the results of genetic algorithm generative designs are generally better than random designs. (G) Interlocking lattice to achieve adjustable stiffness (Reproduced with permission from (Wang et al., 2021). Copyright 2021, Nature Publishing Group): (i) unit cell (left) and interlocking unit cell (right). (ii) Soft state. (iii) high stiffness state.

4.1.3 Programmable stiffness

Lattice geometry programming can also realize stiffness regulation, such as geometric parameters to regulate stiffness, artificial intelligence algorithm programming stiffness, self-locking mechanism programming to achieve adjustable stiffness. Figure 8E exhibits a metamaterial constructed from Schwarz’ unit cell, diamond, and Schoen’s gyroid structures (Figure 8E(i) (Lee et al., 2016). The metamaterial can be controlled to display different E/S ratios (ratio of Young’s modulus to shear modulus) when the aspect ratio $\alpha$ is at 1.0, 2.0, 10, respectively (Figure 8E(ii)) (Lee et al., 2016). Similarly, the E/S ratio can be adjusted by programming the volume fraction $\phi$ (Figure 8E(iii)) (Lee et al., 2016). Figure 8F(i) presents a lattice structure designed using an artificial intelligence-based optimization algorithm (Anthony et al., 2021). To begin with, the approach entails training a Convolutional Neural Network (CNN) to forecast the effective stiffness and wave speed of the unit cell design. Subsequently, a Genetic Algorithm (GA) is employed, using the CNN as its evaluation function, to produce metamaterials exhibiting exceptional effective stiffness and wave speed (depicted in Figure 8F(ii)) (Anthony et al., 2021). This methodology showcases the effectiveness of combining Machine Learning (ML) and GA in attaining optimal stiffness designs for metamaterials, even in scenarios with intricate nonlinear constraints (Anthony et al., 2021). Figure 8G demonstrates a metamaterial constructed based on interlocking octahedral particles (Figure 8G(i)) (Wang et al., 2021). By applying variable compression at the boundary to trigger interlocking between unit cells, metamaterials can be controlled to switch between low stiffness (Figure 8G(ii)) and high stiffness (Figure 8G(iii)) (Wang et al., 2021).

4.1.4 Programmable energy absorption and other mechanical properties

The lattice geometry also offers great ability in programming energy absorption. Xiaojun Tan et al. presents a unit cell constructed based on negative stiffness (NS) geometry (Tan et al., 2019a). In this metamaterial, the energy absorption per volume $W_V$, energy absorption per mass $W_m$, and energy absorption efficiency $\eta$ can be adjusted with increasing or decreasing controlled programming of $h/L$ (vertex height to length ratio of the bending beam) and $t/L$ (in-plane thickness to length ratio), respectively (Tan et al., 2019a).

In addition, energy absorption can also be programmed by lattice density (Yuan et al., 2019) and volume (Wang et al., 2019). At the same time, programmable comprehensive mechanics capability can also be achieved based on flexible porous geometry and deflated continuation algorithm (Medina et al., 2020).

4.2 Other geometric programming

In addition to the aforementioned geometries, other geometries (such as tensegrity (Fraternali et al., 2014; Wang et al., 2020; Intrigila et al., 2023)) can also construct metamaterials with various properties. Tensegrity metamaterials mainly adjust the mechanical properties by exploiting the tunable nonlinear mechanical behaviour of the constituent tensegrity units (Micheletti et al., 2023).

4.2.1 Programming Poisson’s ratio

The tensegrity programming strategy can achieve tunable Poisson’s ratio. Xu Yin et al. shows a metamaterial constructed based on truncated regular octahedral tensegrities (TROTs) (Yin et al., 2020). The metamaterial Poisson’s ratio v or stress-strain can be programmed by the initial twist angle ${\alpha }_0$, the residual chord prestress $q_s$ [ (Yin et al., 2020)]. In addition, Reference (Micheletti et al., 2023) proposed two tensegrity structures: the “six-node” and the “eight-node” units. By adjusting its prestress, bistable and multistable reprogramming characteristics can be achieved. Meanwhile, programmable Poisson’s ratio properties were also achieved based on Auxetic tubular structure (Ren et al., 2016), Ancient geometric motifs (Ahmad and Pasini, 2016) and other tensioned monolithic structures (Liu et al., 2019).

4.2.2 Programmable deformation

Figure 9A(i) presents a metamaterial unit cell with programmable displacement behavior based on adaptive hexagonal geometry with hinges (Wenz et al., 2021). By manipulating the parameters $\alpha ,\beta ,t_2$, this unit cell can realize the transformation of Poisson’s ratio from positive to negative values, accompanied by the deformation characteristics of expansion and contraction (Figure 9A(ii)) (Wenz et al., 2021). Therefore, based on the series and parallel connection of unit cells, local protrusions of metamaterials can be achieved by controlling the local deformation behavior (Wenz et al., 2021). This phenomenon offers the possibility of realizing complex nonlinear system behavior similar to earthworm movement (Figure 9A(iii)) (Wenz et al., 2021). In addition, programmable shape features are also implemented based on tensegrity (Figure 9B) (Lee et al., 2020), Cylindrical geometric (Yang and Ma, 2020a), and One-DOF reconfigurable module (Liu et al., 2021).

Figure 9

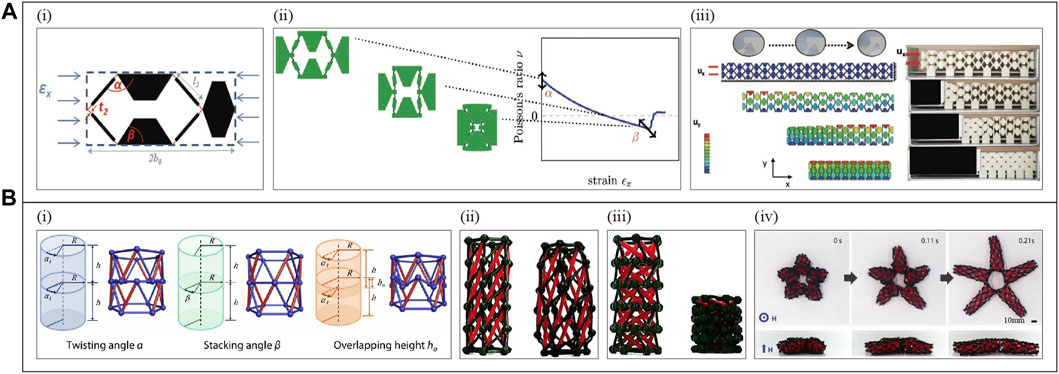
Figure 9. Metamaterials with programmable displacement behavior and programmable deformation properties based on other geometric constructions. (A) Metamaterials with programmable displacement behavior (Reproduced with permission from (Wenz et al., 2021). Copyright 2021, Wiley): (i) Unit cell and parametric characterization. (ii) Deformation state (left) versus parameters (right) for positive to negative Poisson’s ratio. (iii) Metamaterial motion simulation (displacement ${\mathrm{U}}_{\mathrm{x}}$ increases from top to bottom) (left) and physical map (right). (B) Tensegrity programming deformation (Reproduced with permission from (Lee et al., 2020). Copyright 2020, American Association for the Advancement of Science): (i) Main controllable parameters. (ii) Expansion deformation. (iii) Compression deformation. (iv) Programmable “starfish” deformation.

5 Typical hierarchical programming

Hierarchical structure strategy entails employing configurations comprising two or more layers of heterogeneous unit cells to attain programmable control over the mechanical properties of metamaterials. This strategy can be classified into two types: geometric hierarchical and substrate material hierarchical. Geometric heterogeneity-based hierarchical programming involves regulating the mechanical properties through layered structures with varying geometric parameters. On the other hand, substrate material-based hierarchical programming involves combining layers of materials with different mechanical properties to achieve programmable control over the mechanical properties. Voxel programming also falls under hierarchical programming, which uses arrangements of different performance-based elements to modulate metamaterial properties. However, voxel programming involves a larger amount of programming information, as it designs using basic units (in large numbers), while hierarchical programming uses several or multiple groups of basic units (in smaller quantities) for programming.

5.1 Geometric hierarchical programming

5.1.1 Programmable poisson’s ratio

Based on the geometric hierarchical structure, the Poisson’s ratio of metamaterials can be programmed and controlled, such as the hierarchical arrangement of heterogeneous unit cells to achieve a tunable Poisson’s ratio. Figure 10A presents a metamaterial based on hexagonal honeycomb (Figure 10A(i) (Mousanezhad et al., 2015). Figure 10A(ii) shows that by varying the first level hierarchy parameter ${\gamma }_1$, the Poisson’s ratio can be controlled to switch between positive and negative at different strains (Mousanezhad et al., 2015). In contrast, smaller Poisson’s ratios and more complex regulation of Poisson’s ratios can be achieved through the combined regulation of the first- and second-level hierarchical parameters ${\gamma }_1,{\gamma }_2$ (Figure 10A(iii)) (Mousanezhad et al., 2015). In addition, tunable Poisson’s ratio properties were also achieved based on the auxetic hexagonal honeycomb (Sun and Nicola, 2013).

Figure 10

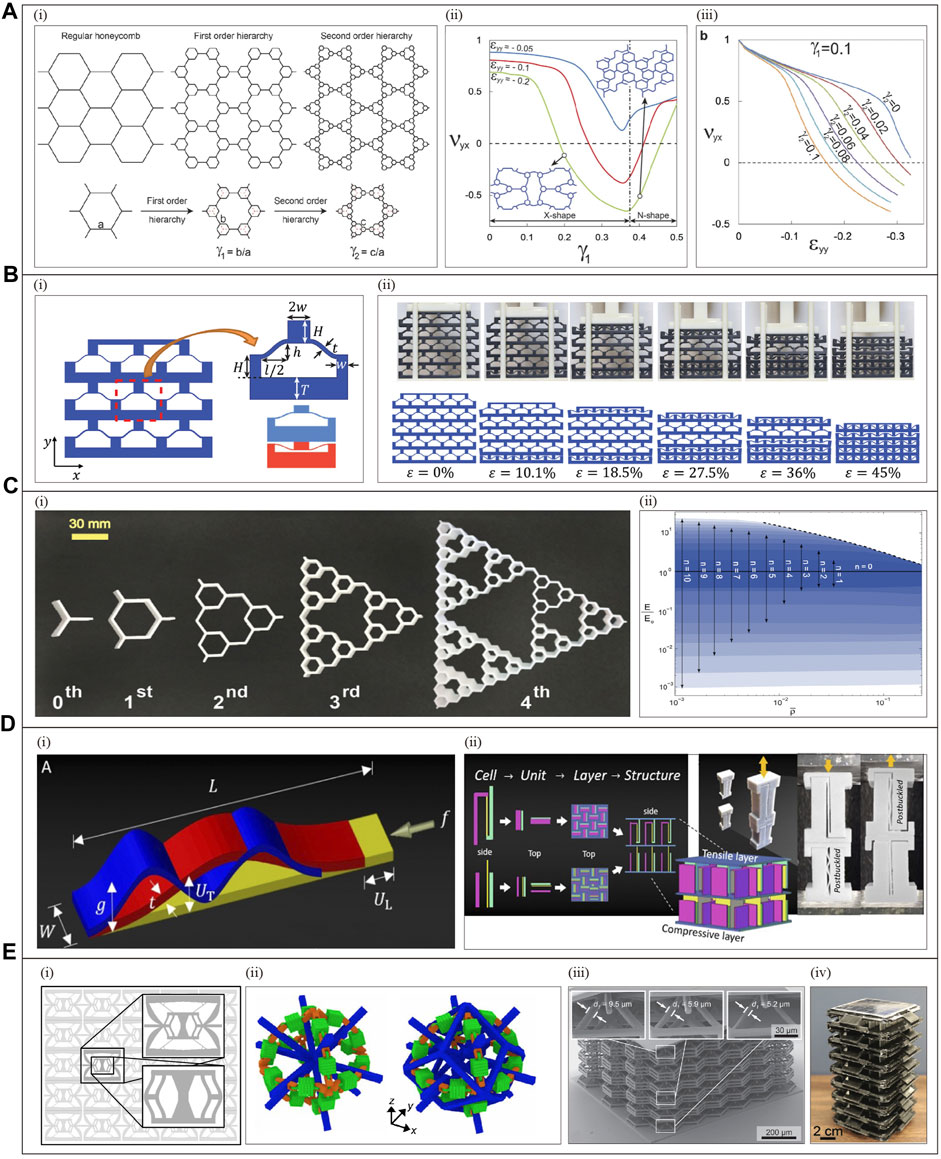
Figure 10. Hierarchical metamaterial with programmable Poisson’s ratio and other properties. (A)Two-order hierarchy programming Poisson’s ratio(Reproduced with permission from (Mousanezhad et al., 2015). Copyright 2015, Nature Publishing Group): (i) Hierarchical structure and characterization of key parameters. (ii)When the y-axis direction is compressed by $5\%,10\%,20\%$, the Poisson’s ratio variation curve with ${\mathrm{\gamma }}_1$. (iii) Curve of Poisson’s ratio variation with ${\mathrm{\gamma }}_2$when ${\mathrm{\gamma }}_1=0.1$is fixed; (B)Hierarchical programming deformation sequences(Reproduced with permission from (Che et al., 2017). Copyright 2017, ASME): (i) Unit cells and parameters. (ii) Two stable states of the unit cell. (iii) Experiments (top) and simulations (bottom) for programming the deformation sequence by manipulating the thickness parameter $\mathrm{t}$of the beam; (C)Fractal hierarchy programming modulus of elasticity(Reproduced with permission from (Oftadeh et al., 2014). Copyright 2014, American Physical Society): (i) Unit cells and hierarchical structures. (ii) The curve of elastic modulus as a function of P and n, the dotted line is the ultimate elastic modulus of the layered honeycomb at a specific relative density; (D)Hierarchical structural programming stiffness(Reproduced with permission from (Jiao, 2020). Copyright 2020, AIP PUBLISHING): (i) post-buckling beam-related parameters and different post-buckling deformation configurations (yellow, red, blue) with different geometric ratios. (ii) Unit cell design principles (left) and real objects (right); (E)Geometric hierarchy programming multistability and energy absorption properties: metamaterials designed by (i) Matthew F. Berwind et al (Reproduced with permission from (Matthew, 2018). Copyright 2018, Wiley), (ii) Hang Zhang et al(Reproduced with permission from (Zhang et al., 2021). Copyright 2021, American Association for the Advancement of Science), (iii) Tobias Frenzel et al(Reproduced with permission from (Frenzel et al., 2016). Copyright 2016,Wiley)and Yuzhen Chen et al(Reproduced with permission from (Chen and Jin, 2021). Copyright 2021,Wiley), respectively.

5.1.2 Programmable deformation

Programmable deformation characteristics can be achieved based on geometric hierarchy, such as the hierarchical arrangement of heterogeneous unit cells to achieve programmable deformation sequences, and hierarchical structures with different unit cell parameters programmed to control multi-step deformation paths. Figure 10B exhibits a metamaterial constructed from bistable unit cells (Figure 10B(i-ii)) (Che et al., 2017). By programming the beam parameters ($t=0.96mm,1.15mm,1.08mm,1.02mm,0.90mm$) of different layers of unit cells, controllable and deterministic complex deformation sequences can be realized under different axial strains (Figure 10B(iii)) (Che et al., 2017). Xiang Li et al. presents a metamaterial based on Hierarchical rotating structures, which can achieve a controlled multi-step deformation path by manipulating the angular parameters $\theta$ and $\alpha$ (Xiang et al., 2021). It shows a two-step path deformation ($\theta =25°,\alpha =35°$) with the first step deformation occurring at a strain of about 0.17, where θ is closed, and α is open (Xiang et al., 2021). When θ closes, the stress increases abruptly and, as compression continues, α closes at a strain of approximately 0.31 and a second deformation step topology occurs (Xiang et al., 2021).

5.1.3 Programmable stiffness and other properties

The geometric hierarchical structure strategy can also realize the programming control of the stiffness of metamaterials. Such as fractal structure to realize elastic modulus control, and hierarchical structure programming to realize stiffness control. Figure 10C designs a metamaterial based on hexagonal honeycomb Figure 10C(i) (Oftadeh et al., 2014). It can achieve a wide range of effective elastic modulus by adjusting the relative density p and the layered betweenness n (Figure 10C(ii)) (Oftadeh et al., 2014). At the same time, the highest in-plane stiffness at a given weight ratio can be achieved by optimizing the structural configuration (Oftadeh et al., 2014). Figure 10D presents a metamaterial composed of post-buckled elements Figure 10D(i) arranged in a layered structure (Figure 10D(ii)) (Jiao, 2020). By adjusting the geometric ratios $R_{gt}=g/t$ and $R_{lw}=L/W$, it is possible to tune the deformation configuration of the beams, leading to either an increase or decrease in tensile and compressive stiffness ($K_T$ and $K_C$) (Jiao, 2020). Specifically, when the values of t and W are kept constant, increasing L and g results in a decrease in stiffness, whereas decreasing L leads to an increase in stiffness (Jiao, 2020).

Furthermore, using the above strategies, metamaterials with programmable shape memory (Figure 10E(i) (Matthew, 2018), multi-stability (Figure 10E(ii)) (Zhang Hang et al., 2021), and shock energy absorption properties (Figure 10E(iii-iv)) (Frenzel et al., 2016; Chen and Jin, 2021) were also realized.

5.2 Hierarchical programming of constituent materials

5.2.1 Programmable coefficient of thermal expansion

By employing a composite layered design of the substrate materials, it becomes feasible to regulate the thermal expansion coefficient of the metamaterial. For example, by combining two layers of substrate materials with distinct thermal expansion coefficients and adjusting geometric parameters, the metamaterial can be programmed to exhibit positive and negative thermal expansion coefficient conversion. Yong Peng et al. illustrates a metamaterial unit constructed using such substrate materials (Peng et al., 2021). By controlling the ratio of thermal expansion coefficients ${\alpha }_1/{\alpha }_2$ of the two layers, as it increases from 0.2 to 10, the thermal expansion coefficient $∆S$ of the metamaterial can be changed from positive to negative (Peng et al., 2021). Meanwhile, In this metamaterials, based on the regulation of ${\alpha }_1/{\alpha }_2$, combined with the angle ${\phi }_1$ and the height ratio $S_1/S_2$, a broader range of positive and negative thermal expansion coefficient adjustments can be achieved (Peng et al., 2021). Figure 11A(i-ii) also depicts a metamaterial composed of two layers of base materials with different thermal expansion coefficients (Wang et al., 2016). However, unlike the previous case, the initial compositions of these two base materials are the same, and the variation in thermal expansion coefficients is achieved by introducing different volume concentrations of copper nanoparticles into one of the materials (Figure 11A(iii)) (Wang et al., 2016). Meanwhile, geometric parameters such as beam width and thickness can also program the thermal expansion coefficient of this metamaterial (Figure 11A(iv)) (Wang et al., 2016). In addition, references (Wu et al., 2016; Jia et al., 2016; Boatti et al., 2017; Ni et al., 2019; Yang and Ma, 2020b; Chen et al., 2021; Wei et al., 2021) also implement programmable thermal expansion coefficients using the above strategy.

Figure 11

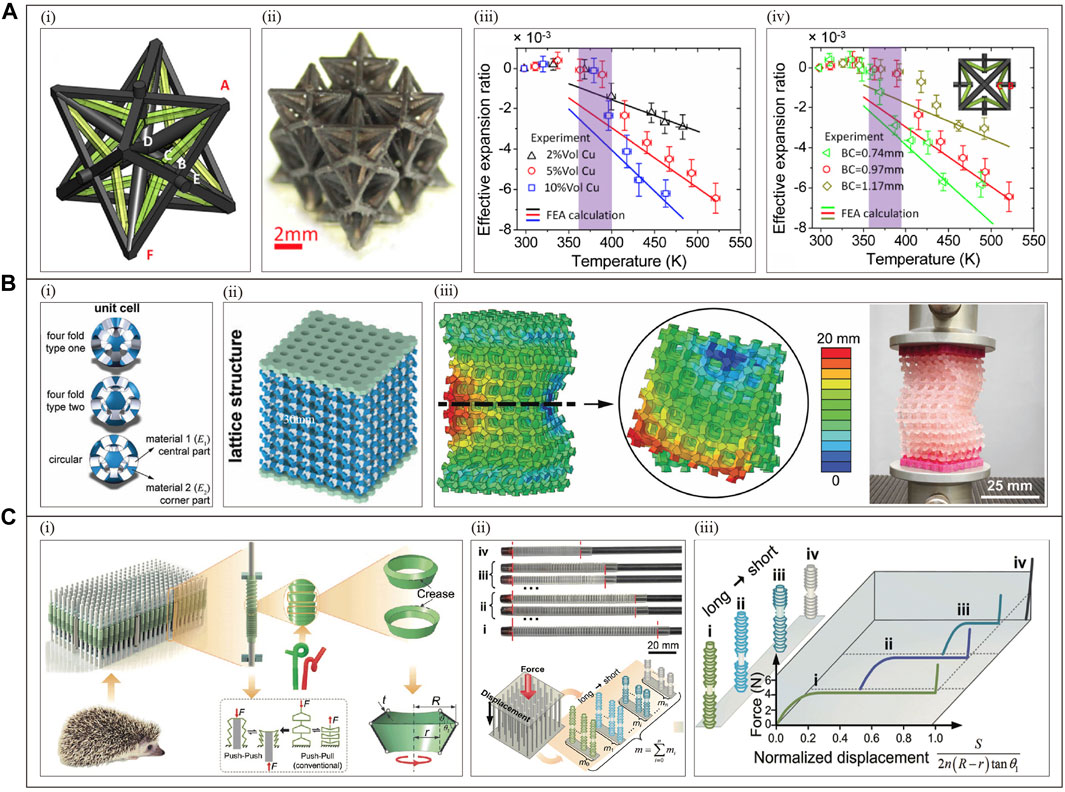
Figure 11. Hierarchical metamaterials (programmable coefficient of thermal expansion and other properties). (A) Substrate material composition programming thermal expansion coefficient (Reproduced with permission from (Wang et al., 2016). Copyright 2016, American Physical Society): (i) The unit cell consists of PEGDA (black) and Reinforced PEGDA (green) doped with copper nanoparticles. (ii) Physical objects. (iii) The effect of volume change of reinforced copper nanoparticles on the effective expansion ratio. (iv) The effect of the length change of the beam BC on the effective expansion rate; (B) Deformation controlled by layered programming of substrate materials (Reproduced with permission from (Janbaz et al., 2019). Copyright 2019, The Royal Society of Chemistry): (i) Three unit cells with different geometric designs, consisting of two layers of materials. (ii) Schematic diagram of metamaterials. (iii) Simulations (left) and real objects (right) of metamaterials with rotational and wavy deformations. (C) Voxel programming force and displacement curves (Reproduced with permission from (Pan et al., 2019). Copyright 2019,Wiley): (i) Schematic diagram of the construction: the array structure consists of multiple parallel multistable voxels, the idea is derived from the Atelerix albiventris (left). The multistable voxel consists of a hollow multistable structure and an internally linked guide rod, which can change the state by loading and inversion loading, and the multistable structure consists of bistable units connected in series (middle). Bistable unit and geometric parameters (right); (ii) Different initial lengths correspond to different steady states with different force and displacement profiles. Here, four typical initial lengths are used as examples. (iii) Schematic illustration of the strategy for programming loading curves by adjusting the initial length of multistable voxels.

5.2.2 Programmable poisson’s ratio and other properties

By designing multi-layered substrate materials, it is feasible to manipulate the Poisson’s ratio of the metamaterial (Ai and Gao, 2018; Janbaz et al., 2020). Young-Joo Lee et al. portrays a metamaterial constructed using two layers of substrate materials with different moduli (Young-Joo et al., 2019). This metamaterial has one combination (PDMS - soft, with TPU) where the Poisson’s ratio can be adjusted to switch between positive and negative values (Young-Joo et al., 2019). Furthermore, in this metamaterial, by adjusting geometric parameters such as rib width, unit width, and unit height, the Poisson’s ratio can also be significantly controlled (Young-Joo et al., 2019).

Programmable deformation properties can also be achieved through the programming strategies described above. Figure 11B(i–ii) demonstrates a metamaterial based on flexible and stiff materials (Janbaz et al., 2019). It allows for controlled deformation behavior through composite programming of dual material spatial distribution and geometric design (four-fold type one, four-fold type two, circular) (Figure 11B(iii) (Janbaz et al., 2019). In addition, more complex deformation programming can also be achieved through the layering and geometric design of hydrogels (Wu et al., 2013; Wei et al., 2020), LCE (Peng et al., 2021). Likewise, critical stress and strain (Janbaz et al., 2018), variable stiffness (Qi et al., 2021) can also be programmed to control.

5.3 Voxel programming

Voxels correspond to 3D unit cell programming, while 2D unit cell programming is called pixels. Pixel or voxel programming means: programmed construction of metamaterials by on-demand spatial arrangement of unit cells with different mechanical properties. Figure 11C shows a 3D metamaterial constructed based on multi-stable voxels (formed by series-connected bistable units) (Pan et al., 2019). The different lengths of the multi-stable voxels represent various stable states, which arise from the series connection of bistable units (Pan et al., 2019). A multi-stable voxel with n bistable units has $2^n$ stable states and $n+1$ stable lengths (Figure 11C(iv)), generating $n+1$ different force-displacement curves (Pan et al., 2019). Therefore, by arranging these voxels to form predefined gradients, the force-displacement curves of the metamaterial can be programmed (Pan et al., 2019). For instance, considering m voxels, when a rigid plate is compressed, the total loading curve is the superposition of the loading curves of m voxels, and the force-displacement curve of the metamaterial can be programmed by assigning initial lengths to the voxels (programmable quantities of $2^{m\bullet n+1}$) (Figure 11C(v)) (Pan et al., 2019).

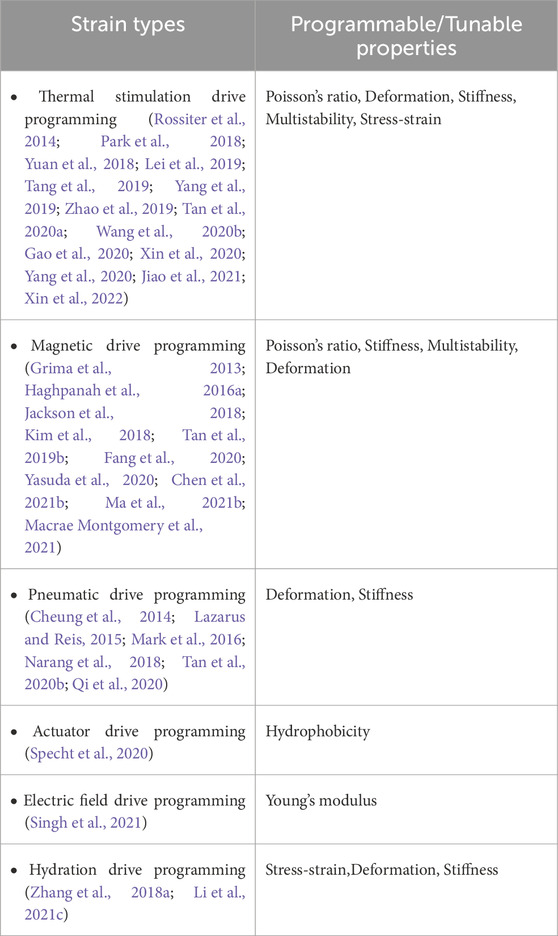
6 External driving force programming

The previously mentioned strategy has already introduced the concept of external driving force programming. External driving force programming refers to the following: Firstly, it involves combining geometric and structural design to programmable control the mechanical properties of the metamaterial using base materials that are sensitive to external factors such as light, etc. And can undergo shape changes. Secondly, it can also be achieved by combining magnetic control, pneumatic control, or other methods with geometric and structural design to programmable control the mechanical properties. Most importantly, unlike the pre-programming strategy, the external driving force programming strategy allows real-time programmability.

6.1 Thermal drive programming

6.1.1 Programmable poisson’s ratio

Thermal stimuli-responsive materials, such as Shape Memory Polymers (SMPs), can undergo various deformation states, including bending, curling, and swelling, when subjected to temperature stimulation. By utilizing SMPs as substrate materials, real-time tunable Poisson’s ratio properties can be achieved by programming the external stimulus. Figure 12A showcases a metamaterial (Figure 12A(i) with the unique ability to adjust its Poisson’s ratio through geometric parameters, specifically the unit cell center angle (Figure 12A(ii)) (Xin et al., 2020). Consequently, employing SMPs programmed to tune the geometrical parameters enables this metamaterial to exhibit a wide range of Poisson’s ratios, following the outlined strategy (Xin et al., 2020):

• During the heating stage, when the metamaterial is subjected to an external tensile load and the temperature surpasses its glass transition temperature (${>T}_g$), the shape memory polymer (SMP) substrate material transitions from a glassy state to a highly elastic state. The random molecular chains (soft segments) elongate, leading to deformation in the metamaterial, and the central angle of the unit changes from $2\theta \left(2\alpha \right)$ to $2{\theta }^{\prime }\left(2{\alpha }^{\prime }\right)$.

• During the cooling stage, the external tensile load is maintained, and the temperature is cooled to room temperature (${<T}_g$). The orientation of molecular chains becomes fixed, and internal stress is frozen.

• During the unloading stage, the load is removed, and the metamaterial is fixed in this temporary shape, causing the central angle of the unit to change from $2{\theta }^{\prime }\left(2{\alpha }^{\prime }\right)$ to $2{\theta }^{″}\left(2{\alpha }^{″}\right)$.

• During the re-heating stage, as the temperature increases (${<T}_g$), the molecular chains return to their random state, causing the metamaterial to revert to its original shape. Consequently, the central angle of the unit is restored from $2{\theta }^{″}\left(2{\alpha }^{″}\right)$ to $2\theta \left(2\alpha \right)$.

Figure 12

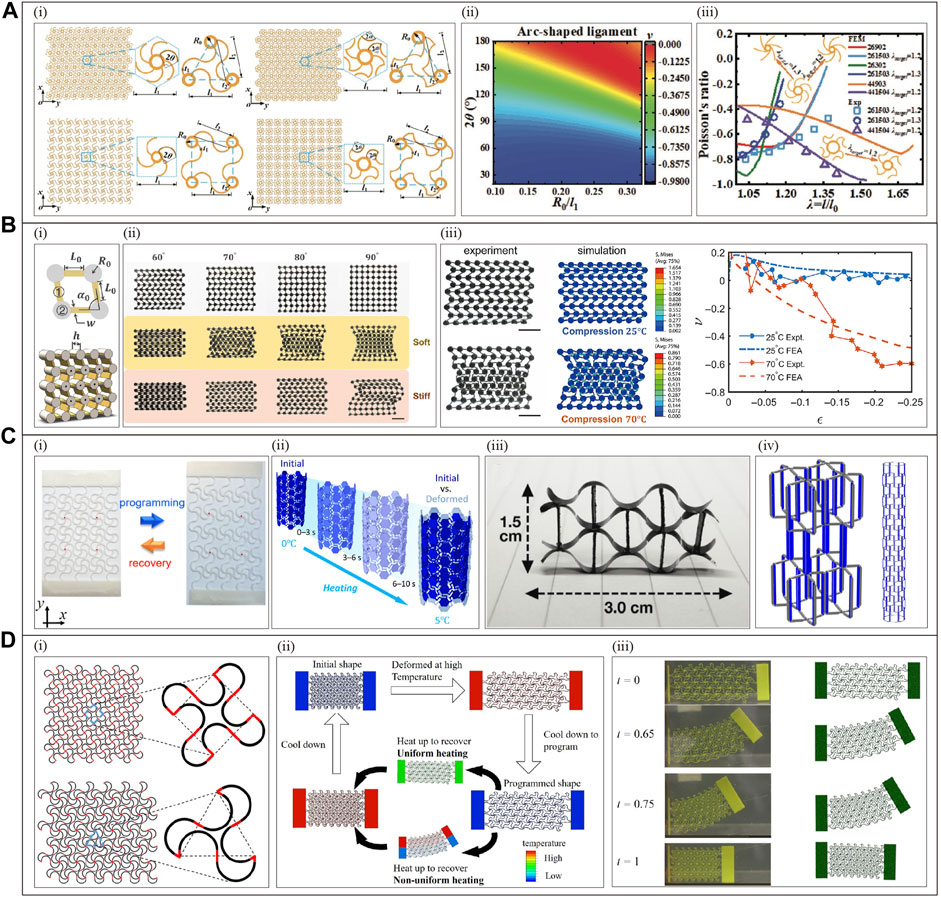
Figure 12. Thermally driven metamaterial with programmable Poisson’s ratio and deformation. (A) Thermal stimulus-responsive materials combined with geometric parameter programming for Poisson’s ratio (Reproduced with permission from (Xin et al., 2020). Copyright 2020,Wiley): (i) Hexa-chiral (top) and tetra-chiral (bottom) metamaterials featuring arc-shaped ligaments and crescent-shaped ligaments. (ii) The impact of geometric parameters on the Poisson’s ratio of arc-shaped tetra-chiral metamaterials. (iii) Different ${\mathrm{\lambda }}_{\text{target}}$ configurations correspond to different Poisson’s ratios. (B) Programmable Poisson’s ratio based on the hierarchical design of thermally responsive materials and conventional materials (Reproduced with permission from (Zhao et al., 2019). Copyright 2019, American Physical Society): (i) Unit cell and geometric parameters. (ii) Tunable Poisson’s ratio phenomenon. (iii) Based on the hierarchical design of soft and hard heterogeneous materials, metamaterials show tunable Poisson’s ratio properties at different temperatures, physical image (left), finite element simulation (middle), Poisson’s ratio line graph (right); (C) Other metamaterials with programmable Poisson’s ratio: (i) Ming Lei et al. (Reproduced with permission from (Lei et al., 2019). Copyright 2019, American Chemical Society), (ii) Pengcheng Jiao et al. (Reproduced with permission from (Jiao et al., 2021). Copyright 2021, MDPI), (iii) Dace Gao et al. (Reproduced with permission from (Gao et al., 2020). Copyright 2020, The Royal Society of Chemistry), (iv) Haedong Park et al. (Reproduced with permission from (Park et al., 2018). Copyright 2018,Wiley)designed metamaterials, respectively; (D) Deformation achieved by the uneven temperature programming (Reproduced with permission from (Wang et al., 2020). Copyright 2020, American Chemical Society): (i) Rectangular (top) and triangular (bottom) horseshoe lattices and their unit cells. (ii) Program control cycle based on shape memory function: the deformation state is regulated by applying non-uniform temperature in the recovery step. (iii) Non-uniform temperature programming to control bending deformation, t is the height of the metamaterial intruding into the hot water tank.

Therefore, the metamaterial temperature is raised above $T_g$ and stretched to the programmed setting of multiple deformations ${\lambda }_{target}$ (Xin et al., 2020). Then, cooled and unloaded to fix various programmed configurations (mainly changes in geometric parameters $2\theta \left(2\alpha \right)$), the new configuration can achieve a variety of different auxetic properties than the original configuration (Figure 12A(iii)) (Xin et al., 2020). Figure 12B(i) offers a metamaterial whose Poisson’s ratio can be tuned by a layered design of soft and hard substrate materials (Figure 12B(ii)) (Zhao et al., 2019). Specifically, a hierarchical design (SMPs are distributed at the unit cell marker ①, and rubber materials are distributed at the unit cell marker ②) based on SMPs (different elastic moduli of materials at different temperatures) and rubber materials (with constant material modulus) found that: Compression at 25°C has a positive Poisson’s ratio, while at 70°C, the Poisson’s ratio is negative (Figure 12B(iii)) (Zhao et al., 2019). This shows that the metamaterial can program the Poisson’s ratio in real-time by temperature (Zhao et al., 2019). In addition, Figure 12C(i-iv) also implements the ability of Poisson’s ratio to be programmed and tuned in real-time, respectively (Park et al., 2018; Lei et al., 2019; Gao et al., 2020; Jiao et al., 2021).

6.1.2 Programmable deformation

Programmable deformation properties can be achieved based on thermally stimulated responsive material programming. For example, thermally stimulated responsive materials are used as hinges to achieve deformation programming, and inhomogeneous temperature stimulated programming to control deformation. Nan Yang et al. designs a metamaterial based on ring-shaped origami unit cells, whose deformation mechanism is controlled by the local deformation angle $\theta$ (Yang et al., 2020). The deformation state (outward or inward) formed by each $\theta$ angle can be represented by “0,1″in this metamaterial (Yang et al., 2020). Meanwhile, this deformed state can be further controlled by thermal stimulation through the distribution of $\gamma$-shaped SMA hinges (Yang et al., 2020). Therefore, based on thermal stimulation, more complex shape programming can be achieved by controlling the “0,1” states (e.g., programmed to 100 or 000) of each $\theta$ angle of the quarter cells (Yang et al., 2020). Figure 12D proposes a metamaterial constructed based on the horseshoe lattice (Figure 12D(i) and the substrate material of SMPs (Wang et al., 2020). Its programming logic is similar to Figure 12A. But the difference is that the metamaterial can deform on demand (Figure 12D(iii)) by inhomogeneous heating (Figure 12D(ii)) (Wang et al., 2020). Moreover, applying the same strategy, programmable deformation properties are also achieved in Figure 13A(i-ii), respectively (Yuan et al., 2018; Tang et al., 2019).

Figure 13

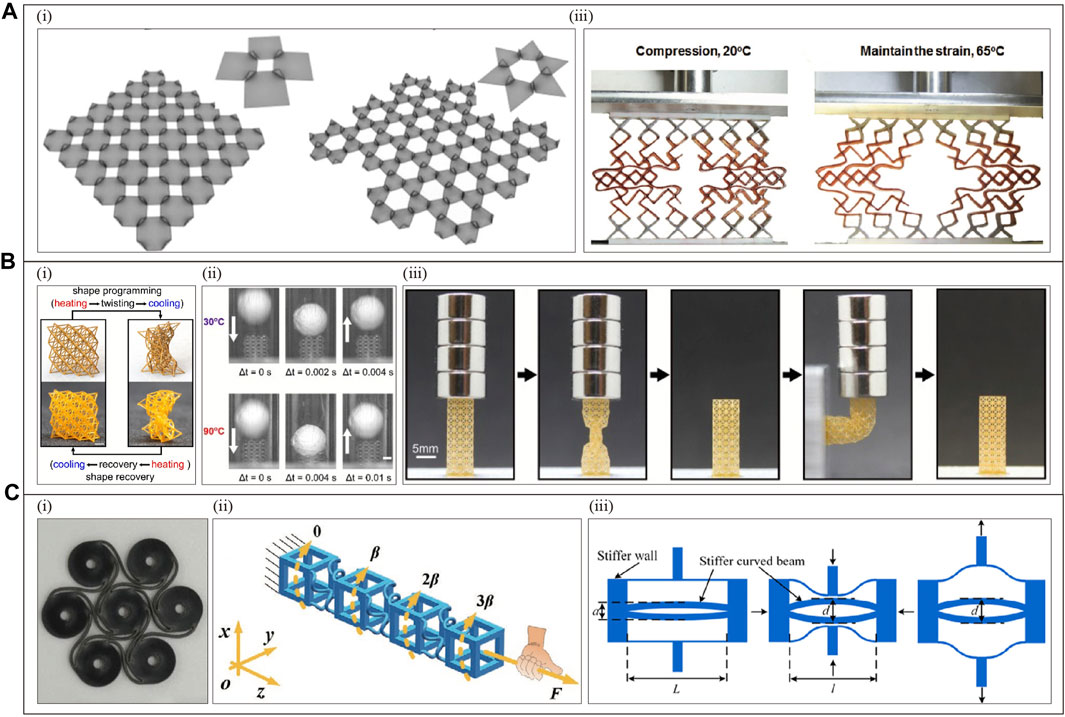
Figure 13. Thermally driven metamaterials with programmable deformation, stiffness, and other properties. (A) Other metamaterials with programmable deformation: (i) Yichao Tang et al. (Reproduced with permission from (Tang et al., 2019). Copyright 2019,PNAS), and (ii) Chao Yuan et al. (Reproduced with permission from (Yuan et al., 2018). Copyright 2018,Wiley) designed metamaterials, respectively. (B) Glass and rubber state conversion programming for adjustable stiffness(Reproduced with permission from (Yang et al., 2019). Copyright 2019, The Royal Society of Chemistry): (i) Programming flow. (ii) Stiffness changes of metamaterials with different temperatures under shock loading. (iii) When the stiffness remains constant, the metamaterial can achieve different shapes through temperature programming: the sample is in its original shape and subjected to a load (left one); the sample is programmed into different geometric shapes and subjected to the same load (left two); after heating, it returns to its original shape (left three); the sample is reprogrammed into a curved shape and subjected to the same load (left four); after heating, it returns to its original shape (left five). (C) Other properties: metamaterials designed by (i) Jonathan Rossiter et al(Reproduced with permission from (Rossiter et al., 2014). Copyright 2014, IOP Publishing Ltd.), (ii) Xiaozhou Xin et al(Reproduced with permission from (Xin et al., 2022). Copyright 2021, Wiley), and (iii) Xiaojun Tan et al(Reproduced with permission from (Tan et al., 2020a). Copyright 2019, Elsevier), respectively.

6.1.3 Programmable stiffness and other properties

The tunable stiffness properties are also achieved by the above methods. Figure 13B(i) illustrates a metamaterial based on SMPs and microlattice structure (Yang et al., 2019). Figure 13B(ii) displays that it has two states of high and low stiffness under temperature stimuli of 30°C and 90°C, which utilizes the two states of the substrate material (SMP) under temperature stimulation (glass and rubbery state) (Yang et al., 2019). Meanwhile, Figure 13B(iii) demonstrates that the metamaterial can program the shape by temperature stimulation as required while the stiffness remains constant (Yang et al., 2019). Furthermore, adjustable stiffness characteristics are also implemented respectively in Figure 13Bi (Rossiter et al., 2014). Moreover, applying a strategy similar to Figure 12A, Figure 13C(ii-iii) also achieves programmable stress-strain (Xin et al., 2022) and multistability properties (Tan et al., 2020a), respectively.

6.2 Magnetic drive programming

6.2.1 Programmable poisson’s ratio

Magnetic materials controlled by a magnetic field can achieve different states. Therefore, employing magnetic materials as substrate materials or incorporating them into the substrate materials enables the geometric or structural changes of metamaterials to be controlled by external magnetic fields. Poisson’s ratio can be programmed by this method. Figure 14A(i) exhibits a metamaterial constructed by embedding an electromagnetic switch into a honeycomb structure (Haghpanah et al., 2016a). Figure 14A(ii-iii) demonstrates that active control of Poisson’s ratio can be achieved by electromagnetically switching (activating or deactivating) the mode of the unit cell geometry (Haghpanah et al., 2016a). Specifically, Figure 14A(iv) illustrates that by deactivating the electromagnets on the diagonal of the sample, the Poisson’s ratio of the metamaterial can switch from 0.15 to 0.5 under axial compression (Haghpanah et al., 2016a). In contrast, the Poisson’s ratio value will be close to one by deactivating all electromagnets (Haghpanah et al., 2016a). Besides, Figure 14B(i-ii) also achieves tunable Poisson’s ratio properties using similar strategies, respectively (Grima et al., 2013; Ma et al., 2021).

Figure 14

Figure 14. Magnetically actuated metamaterials (tunable Poisson’s ratio and stiffness). (A) Electromagnetic switch real-time programming to control Poisson’s ratio(Reproduced with permission from (Haghpanah et al., 2016a). Copyright 2015, Wiley): (i) Metamaterial. (ii) Unit cell geometry (left) and tessellation (right). (iii) electromagnetic switch deactivation (top) and activation (bottom). (iv) Poisson’s ratio curve: the green line represents the programmable response of the metamaterial: When the magnet is in active mode, there is a small expansion laterally. At a strain of $0.4\times {10}^{-3}$, the metamaterial diagonal magnets are deactivated and the metamaterial follows an intermediate response. When the strain is $0.7\times {10}^{-3}$, all magnets are deactivated and the metamaterial transitions to a nearly incompressible state; (B) Other magnetically driven metamaterials with tunable Poisson’s ratio and stiffness: (i) Joseph N Grima et al.(Reproduced with permission from (Grima et al., 2013). Copyright 2013, IOP Publishing Ltd.), (ii) Chunping Ma et al. (Reproduced with permission from (Ma et al., 2021). Copyright 2020, American Chemical Society),(iii) S. Macrae Montgomery et al.(Reproduced with permission from (Macrae Montgomery et al., 2021). Copyright 2020, Wiley) designed metamaterials, respectively; (C) Real-time programming of physical binary unit cells to control stiffness(Reproduced with permission from (Chen et al., 2021). Copyright 2021, Nature Publishing Group): (i) m-bits unit cell and its electromagnetic field (left), compression test (right). (ii) Two states of m-bits: the magnetic lid and the stopper are lowered (raised) in the closed (open) state. (iii) The stiffness modulus can change with the ON and OFF states. (iv) The effective stiffness modulus as a function of the number ratio of unit cells with the ON state. (D) Magnetic fluid and polymer lattice programming to achieve tunable stiffness(Reproduced with permission from (Jackson et al., 2018). Copyright 2018, American Association for the Advancement of Science): (i) Polymeric cubooctahedral unit cells. (ii-iii) Magnetic fluid filling. (iv) The effective stiffness of the cubooctahedral lattice as a function of the magnetic field strength shows a 35% increase in stiffness from 0 to 0.11 T (E) Magnetic composites are programmed to achieve multi-stable properties(Reproduced with permission from (Tan et al., 2019b). Copyright 2019, Elsevier): (i) unit cells. (ii) unit cells with two steady states. (iii) magnetron metamaterials with multiple steady states under loading experiments. (F) Other programmable multistable: metamaterials were designed by (i) H. Yasuda et al. (Reproduced with permission from (Yasuda et al., 2020). Copyright 2020, American Physical Society) and (ii) Hongbin Fang et al. (Reproduced with permission from (Fang et al., 2020). Copyright 2019, IOP Publishing Ltd.), respectively.

6.2.2 Programmable stiffness

The geometric or structural changes of the metamaterial can be programmed by the composite configuration of magnetic and conventional materials, which can accomplish the tunable stiffness. Figure 14C proposes a metamaterial consisting of a physical binary element (m-bits) unit cell (Figure 14C(i) composed of magnetic materials and conventional materials (Chen et al., 2021). Figure 14C(ii) reveals that this unit cell can switch between two stable geometrical states (ON and OFF) under the influence of an electromagnetic field (Chen et al., 2021). Through this switching, the unit cell stiffness can be adjusted in a controlled manner (Figure 14C(iii)) (Chen et al., 2021). Also, the metamaterial stiffness can increase linearly with the percentage ”ξ” of the number of unit cell (ON), which demonstrates strong programmable stiffness properties (Figure 14C(iv)) (Chen et al., 2021). Figure 14D(i–iii) offers a metamaterial constructed by filling a magnetic fluid into a cuboctahedral lattice (Jackson et al., 2018). By programming domination of the external magnetic field, its stiffness can be varied by about 35 percent increase (Figure 14D(iv)) (Jackson et al., 2018). Furthermore, Figure 14B(iii) also implements programmable stiffness using the analogous design (Macrae Montgomery et al., 2021).

6.2.3 Programmable multistability and deformation

By the composite of magnetic materials and conventional materials, metamaterials can be adjusted by external magnetic fields to achieve multistable properties. Figure 14E(i) presents a metamaterial unit cell consisting of a system of magnets (Tan et al., 2019b). This metamaterial can transition between stable states through a load of the external magnetic field (Tan et al., 2019b). And the number of stable states is determined by the number of unit cells connected in series (Tan et al., 2019b). For example, Figure 14E(ii) exhibits that a single unit cell has two stable states, while Figure 14E(iii) shows that a metamaterial composed of multiple unit cells has multiple stable states (Tan et al., 2019b). Using this approach, Figure 14F(i–ii) also implement programmable multi-stable characteristics (Fang et al., 2020; Yasuda et al., 2020), respectively. Additionally, controlled deformation properties of metamaterials also have been achieved. Figure 15A(i) produces a magnetic ink composite metamaterial consisting of a silicone rubber soft material and neodymium-iron-boron (NdFeB) alloy (Kim et al., 2018). By programming the magnetic orientation of the ink, it can achieve controllable shape changes, such as complex three-dimensional deformation (Figure 15A(ii)) and motion (Figure 15A(iii)) (Kim et al., 2018).

Figure 15

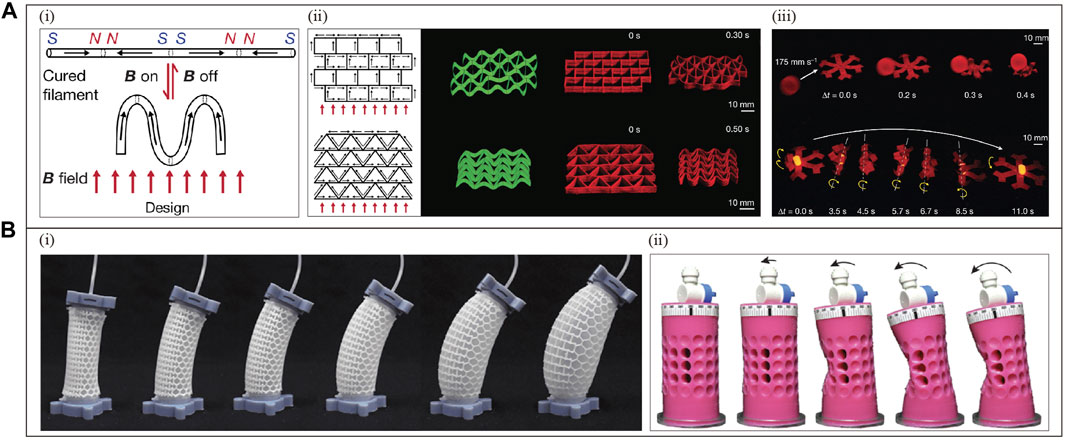
Figure 15. Magnetically actuated and pneumatic metamaterials with programmable deformation. (A) Magnetic composite material realizes programmable deformation (Reproduced with permission from (Kim et al., 2018). Copyright 2018, Nature Publishing Group): (i) Programming example: Under the influence of B (200 mT) magnetic field, unit cells can be transformed between straight and M-shaped lines. (ii-iii) 3D complex deformation and motion. (B) Other pneumatic actuation programming: metamaterials were proposed by (i) Pan Qi et al. (Reproduced with permission from (Qi et al., 2020). Copyright 2020, Science China Press and Springer-Verlag GmbH Germany), and (ii) Arnaud Lazarus et al. (Reproduced with permission from (Lazarus and Reis, 2015). Copyright 2015, Wiley), respectively.

6.3 Pneumatic drive programming

Pneumatics can realize sophisticated programmed control of metamaterial deformation. Andrew G. Mark et al. introduces a programmable robot motion based on an Auxetic metamaterial (Mark et al., 2016). When inflated, the Auxetic metamaterial shrinks laterally under compressive forces, and the conventional material expands laterally (Mark et al., 2016). The alternating sliding of the two parts of material along the channel can lead to the continuous advancement of the programmed robot (Mark et al., 2016). Using the same strategy, Figure 15B(i–ii) also implements programmed deformation and pattern-transforming, respectively (Lazarus and Reis, 2015; Qi et al., 2020). Likewise, the stiffness can also be programmed to be controlled under pneumatic actuation (Cheung et al., 2014; Narang et al., 2018; Tan et al., 2020b).

7 Discussion

7.1 Other programming strategies

Multistable structures, artificial intelligence, and actuator programming strategies are also extremely promising directions in the future (related methods have been mentioned above, here only are summarized).

Multistable structures have been recognized as an efficient approach to achieving programmability in mechanical metamaterials (Liu et al., 2021). It has two or more stable states, and different states can achieve unequal mechanical properties (Pan et al., 2019). First, based on this structure, the metamaterial can be programmed to transition between two or more states on-demand using logical thinking.

Furthermore, the spatial distribution programming based on unit cells with different stable states can also realize the regulation of mechanical properties. Currently, it has achieved various properties, e.g., programmable energy absorption (Restrepo et al., 2015; Harne et al., 2016; Fu et al., 2019; Shi et al., 2021), deformation (Haghpanah et al., 2016b), negative Poisson’s ratio (Shim et al., 2013) and tensile properties (Tan et al., 2020a). Optimization algorithm or artificial intelligence programming refers to attaining better mechanical properties using the optimization design of geometry or structure (Li et al., 2023). Presently, this strategy has accomplished diversified abilities, such as tunable Poisson’s ratio (Konakovic-Lukovic et al., 2018), deformation (Luo et al., 2011; Zhang et al., 2021), negative Poisson’s ratio (Li et al., 2018), and shear stiffness (Du et al., 2017).

In addition, the emergence of programmable mechanical metamaterials based on cellular automata combined with energy storage calculations heralds major progress in a new generation of materials with advanced computing capabilities. For example, digital recognition functions have been realized through single mechanical actuators (Liu et al., 2023); as well as directly embodying the key elements of computing power and intelligence, namely, perception, decision-making and command, directly in the mechanical field, thus getting rid of the tradition of additional computers and large electronic devices rely (Zhang et al., 2023). There are multitudinous other ways of external driving force programming (Nick et al., 2020), such as actuator programming to achieve tunable hydrophobicity (Specht et al., 2020), electric field-driven programming for achieving tunable Young’s modulus (Singh et al., 2021), Tunable stress-strain curves realized by hydraulic-driven programming (Zhang et al., 2018), tunable stiffness and deformable metamaterials (Li et al., 2021).

7.2 Summary of strategies based on common geometry, structure and external driving force

This subsection summarizes the typical geometric, structural, and types of external driving force covered throughout the text (Tables 1–3). concurrently, an enumerated introduction is also given to their corresponding purposes.

Table 1

Table 1. Summary of common geometry.

Table 2

Table 2. Summary of typical structure.

Table 3

Table 3. Summary of typical external driving force.

7.3 Challenges and limitations

7.3.1 Intelligent limitations of strategies

Although current strategies have certain logical operation capabilities (pre-programming: geometric or structural parameter programming) and autonomous feedback capabilities (external driving force programming), their level of intelligence is still low. This is specifically reflected in the following aspects.

First, the geometric or structural programming strategy only obtains the corresponding mechanical performance parameters by simply changing the geometric or structural parameters. And it also can be based on the unit cells with different mechanical performance parameters, they are arranged on demand to simply control the propagation of mechanical signals. This approach cannot create metamaterials with complex mechanical properties. For example, a piece of metamaterial can have multiple mechanical properties at the same time and has the property of converting mechanical properties in real time in the same dimension. Hence, the programming strategy should adopt more artificial intelligence-related technologies and methods. Artificial intelligence has a convoluted system that can imitate human intelligent thinking to make various behaviors and calculations, including various methods, such as language recognition, image recognition, and natural language processing (Guo et al., 2016). Although some metamaterials have used artificial intelligence as the strategies (Anthony et al., 2021), such methods are more about applying artificial intelligence to the generation process of geometry or structure rather than programming the process of building metamaterials. If artificial intelligence algorithms are applied to the programming and construction of metamaterials, can metamaterials be as smart as robots in the future? People can achieve many functions and effects like robots just from the perspective of material design.

Second, geometric, or structural programming can also be called pre-programming; once fabricated, the mechanical properties cannot be regulated by adjusting its geometric or structural parameters. It can only operate according to pre-programmed logic and exhibit corresponding mechanical properties. It cannot achieve the real-time programming. External driving force programming can achieve real-time programming through some methods. However, this is achieved by relying on external driving forces rather than the metamaterial itself. So, is it possible to look for some methods in the metamaterial itself that enables real-time programming? At present, we have not seen any relevant scholars put forward some feasible methods.

Third, external driving force programming means that the mechanical properties of metamaterials can be adjusted in real-time according to external stimuli. Through this strategy, metamaterials can realize simple interactive feedback of stimulation (Chen et al., 2021). However, its intelligence level is still some distance from 4D materials (Momeni et al., 2017), programmable electromagnetic metamaterials (Liu and Cui, 2017; Bao and Cui, 2019), programmable planar soft matter (van Manen et al., 2018), and programmable DNA materials (Zhang et al., 2018; Albrecht et al., 2023). Simultaneously, numerous external stimuli (e.g., pneumatics, actuator drives) require many complex devices to control, which make metamaterials sometimes look more like “machines” than “materials”. At present, no scholar has given a more precise explanation. Regardless of whether external driving forces will become the main development direction of real-time programming of programmable mechanical metamaterials. More types of external driving forces should be explored and discovered.

7.3.2 Geometry types restrictions and scale restrictions

The general understanding in modern materials science about the composition of matter is as follows: Specific quantities and types of atoms can combine into molecules through certain bonding mechanisms, and a large number of atoms or molecules can come together in specific spatial arrangements to form various unique materials (Bohr, 1961). Due to the interactions between atoms within molecules, the physical and chemical properties of molecules depend not only on the types and numbers of constituent atoms but also on their structure (Bohr, 1961). The properties of materials are influenced not only by the types and structures of atoms or molecules but also by the arrangement and bonding of atoms or molecules (Van Melsen and Andrew, 2004). At the same time, electrons play a crucial role in determining the properties of materials. Their directional motion generates electric current, and under the influence of external electric and magnetic fields, their trajectories and states can be altered as needed (Van Melsen and Andrew, 2004).

Therefore, from the perspective of materials science, the three main construction strategies (geometric programming, structural programming, and external driving force programming) of programmable mechanical metamaterials are also derived from the above basic cognitive logic. Although more and more new mechanical metamaterials have been proposed in recent years (Bai et al., 2022; Farzaneh et al., 2022; Ma et al., 2022; Mehboob et al., 2022; Pagliocca et al., 2022; Wagner et al., 2022; Yang et al., 2022; Zhang et al., 2023; Liang et al., 2023; Sundararaman et al., 2023; Tian et al., 2023; Wang et al., 2023), the construction of metamaterials is currently unable to reach the atomic or molecular scale. At present, most metamaterials are still large in scale and more like “building structures” and “products” and cannot be used as “materials” for the design and manufacture of various applications. This is a question worthy of consideration and breakthrough in the future.

Although Table 1 and 2 lists numerous geometric or structural types for achieving various programmable mechanical properties, it is far from enough. Need to explore more geometry or structure (such as hypercube) to develop more prosperous programmable mechanical properties (such as programmable tensile strength and compressive strength).

8 Conclusion

The main construction strategies of programmable mechanical metamaterials can be divided into geometric parameters, structural parameters, and external driving force programming. Whether it is geometry or external driving force programming, the core is the adjustment of geometry. In fact, the difference is that geometric or structural programming depends on designing the geometry or structure to determine the mechanical properties of the metamaterial, while external driving force programming controls the state of the geometry or structure through external driving forces. Currently, most research focuses on achieving many programmable properties by manipulating geometric or structural parameters, while artificial intelligence or optimization algorithm programming is a relatively new approach. It is foreseeable that artificial intelligence and computational science will become the mainstream of programmable mechanical metamaterials in the future. The resulting smart applications will further eliminate dependence on additional computers and large-scale electronics. In addition, new smart materials with novel programmable mechanical properties based on new geometries or structures are also an important direction for future development. More novel mechanical properties will greatly promote the continuous progress of science and technology.

Author contributions

CL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XZ: Funding acquisition, Writing–review and editing. JC: Writing–review and editing. YL: Visualization, Writing–review and editing. JZ: Investigation, Writing–review and editing. SQ: Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdullah, A. M., Li, X., PaulBraun, V. J. A. R., and Jimmy Hsia, K. (2020). Kirigami-Inspired self-assembly of 3D structures. Adv. Funct. Mater. 30 (14), 1909888. doi:10.1002/adfm.201909888

CrossRef Full Text | Google Scholar

Adrian, C. (2006). Physics: voila! Cloak of invisibility unveiled. Science 314 (5798), 403. doi:10.1126/science.314.5798.403

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, R., Bertoldi, K., and André, R. (2019a). Programming soft robots with flexible mechanical metamaterials. Sci. ROBOTICS 4 (29), eaav7874. doi:10.1126/scirobotics.aav7874

CrossRef Full Text | Google Scholar

Ahmad, R., Jin, L., Deng, B., and Bertoldi, K. (2019b). Propagation of pop ups in kirigami shells. Proc. Natl. Acad. Sci. U. S. A. 116 (17), 8200–8205. doi:10.1073/pnas.1817763116

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, R., and Pasini, D. (2016). Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mech. Lett. 9, 291–296. doi:10.1016/j.eml.2016.09.001

CrossRef Full Text | Google Scholar

Ai, L., and Gao, X.-L. (2018). Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion. Int. J. Mech. Sci. 135, 101–113. doi:10.1016/j.ijmecsci.2017.10.042

CrossRef Full Text | Google Scholar

Albrecht, C., Blank, K., Mio, L., Hirler, S., Mai, T., Gilbert, I., et al. (2023). DNA: a programmable force sensor. Science 301 (5631), 367–370. doi:10.1126/science.1084713

PubMed Abstract | CrossRef Full Text | Google Scholar

Amir, A. (2016). Mechanical meta-materials. Mater. HORIZONS 3 (5), 371–381. doi:10.1039/c6mh00065g

CrossRef Full Text | Google Scholar

Anders, C., Wang, F., Jensen, J. S., Sigmund, O., and Lewis, J. A. (2015). Topology optimized architectures with programmable Poisson's ratio over large deformations. Adv. Mater. 27 (37), 5532–5527. doi:10.1002/adma.201502485

CrossRef Full Text | Google Scholar

Anthony, P., White, B. C., Jensen, S. C., and Boyce, B. L. (2021). Pragmatic generative optimization of novel structural lattice metamaterials with machine learning. Mater. Des. 203, 109632. doi:10.1016/j.matdes.2021.109632

CrossRef Full Text | Google Scholar

Babaee, S., Shim, J., Weaver, J. C., Chen, E. R., Patel, N., and Bertoldi, K. (2013). 3D soft metamaterials with negative Poisson's ratio. Adv. Mater. 25 (36), 5044–5049. doi:10.1002/adma.201301986

PubMed Abstract | CrossRef Full Text | Google Scholar

Bai, Y., Liu, C., Li, Y., Li, J., Qiao, L., Zhou, J., et al. (2022a). Programmable mechanical metamaterials with tailorable negative Poisson’s ratio and arbitrary thermal expansion in multiple thermal deformation modes. ACS Appl. Mater. Interfaces 14 (31), 35905–35916. doi:10.1021/acsami.2c08270

PubMed Abstract | CrossRef Full Text | Google Scholar

Bai, Y., Wang, H., Xue, Y., Pan, Y., Kim, J. T., Ni, X., et al. (2022b). A dynamically reprogrammable surface with self-evolving shape morphing. Nature 609, 701–708. doi:10.1038/s41586-022-05061-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Bao, L., and Cui, T. J. (2019). Tunable, reconfigurable, and programmable metamaterials. Microw. Opt. Technol. Lett. 62 (1), 9–32. doi:10.1002/mop.32164

CrossRef Full Text | Google Scholar

Barchiesi, E., Spagnuolo, M., and Placidi, L. (2019). Mechanical metamaterials: a state of the art. Math. Mech. Solids 24 (1), 212–234. doi:10.1177/1081286517735695

CrossRef Full Text | Google Scholar

Bartlett, N. W., Tolley, M. T., Overvelde, J. T., Weaver, J. C., Mosadegh, B., Bertoldi, K., et al. (2015). A 3D-printed, functionally graded soft robot powered by combustion. Science 349 (6244), 161–165. doi:10.1126/science.aab0129

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauer, J., Meza, L. R., Schaedler, T. A., Schwaiger, R., Zheng, X., Valdevit, L., et al. (2017). Nanolattices: an emerging class of mechanical metamaterials. Adv. Mater. 29 (40), 1701850. doi:10.1002/adma.201701850

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertoldi, K., Reis, P. M., Stephen, W., and Mullin, T. (2010). Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 22 (3), 361–366. doi:10.1002/adma.200901956

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertoldi, K., Vitelli, V., Christensen, J., and Martin van Hecke, (2017). Flexible mechanical metamaterials. Nat. Rev. Mater. 2 (11), 17066. doi:10.1038/natrevmats.2017.66

CrossRef Full Text | Google Scholar

Boatti, E., Vasios, N., and Bertoldi, K. (2017). Origami metamaterials for tunable thermal expansion. Adv. Mater. 29 (26), 1700360. doi:10.1002/adma.201700360

PubMed Abstract | CrossRef Full Text | Google Scholar

Bohr, N. (1961). Atomic theory and the description of nature. CUP Arch. 1.

Google Scholar

Bueckmann, T., Thiel, M., Kadic, M., Schittny, R., and Wegener, M. (2014). An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun. 5, 4130. doi:10.1038/ncomms5130

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, J., and Abdolhamid, A. (2021). Hierarchical kirigami-inspired graphene and carbon nanotube metamaterials: tunability of thermo-mechanic properties. Mater. Des. 206, 109811. doi:10.1016/j.matdes.2021.109811

CrossRef Full Text | Google Scholar

Che, K., Yuan, C., Wu, J., Jerry Qi, H., and Meaud, J. (2017). Three-dimensional-Printed multistable mechanical metamaterials with a deterministic deformation sequence. J. Appl. MECHANICS-TRANSACTIONS ASME 84 (1), 011004. doi:10.1115/1.4034706

CrossRef Full Text | Google Scholar

Chen, J., Xu, W., Wei, Z., Wei, K., and Yang, X. (2021a). Stiffness characteristics for a series of lightweight mechanical metamaterials with programmable thermal expansion. Int. J. Mech. Sci. Int. J. Mech. Sci. 202, 106527. doi:10.1016/j.ijmecsci.2021.106527

CrossRef Full Text | Google Scholar

Chen, S. H., Chan, K. C., Han, D. X., Zhao, L., and Wu, F. F. (2019). Programmable super elastic kirigami metallic glasses. Mater. Des. 169, 107687. doi:10.1016/j.matdes.2019.107687

CrossRef Full Text | Google Scholar

Chen, T., Pauly, M., and Reis, P. M. (2021b). A reprogrammable mechanical metamaterial with stable memory. Nature 589 (7842), 386–390. doi:10.1038/s41586-020-03123-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., and Jin, L. (2021). Reusable energy-absorbing architected materials harnessing snapping-back buckling of wide hyperelastic columns. Adv. Funct. Mater. 31 (31). doi:10.1002/adfm.202102113

CrossRef Full Text | Google Scholar

Chen, Y., and Jin, L. (2018). Geometric role in designing pneumatically actuated pattern-transforming metamaterials. EXTREME Mech. Lett. 23, 55–66. doi:10.1016/j.eml.2018.08.001

CrossRef Full Text | Google Scholar

Chen, Y., Li, T., Scarpa, F., and Wang, L. (2017). Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys. Rev. Appl. 7 (2), 024012. doi:10.1103/PhysRevApplied.7.024012

CrossRef Full Text | Google Scholar

Chen, Y., Peng, R., and Zhong, Y. (2015). Origami of thick panels. Science 349 (6246), 396–400. doi:10.1126/science.aab2870

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheung, K. C., Tachi, T., Calisch, S., and Miura, K. (2014). Origami interleaved tube cellular materials. Smart Mater. Struct. 23 (9), 094012. doi:10.1088/0964-1726/23/9/094012

CrossRef Full Text | Google Scholar

Chiang, Y. C. (2019). Programming flat-to-synclastic reconfiguration. Archidoct 6, 64–79.

Google Scholar

Correa, D. M., Klatt, T., Cortes, S., Haberman, M., Kovar, D., and Seepersad, C. (2015). Negative stiffness honeycombs for recoverable shock isolation. Papid Prototyp. J. 21 (2), 193–200. doi:10.1108/RPJ-12-2014-0182

CrossRef Full Text | Google Scholar

Coulais, C., Sabbadini, A., Vink, F., and Martin, van H. (2018). Multi-step self-guided pathways for shape-changing metamaterials. Nature 561, 512–515. doi:10.1038/s41586-018-0541-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Coulais, C., Teomy, E., de Reus, K., yair, S., and Martin van Hecke, (2016). Combinatorial design of textured mechanical metamaterials. Nature 535 (7613), 529–532. doi:10.1038/nature18960

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding metamaterials, digital metamaterials and programmable metamaterials. LIGHT-SCIENCE Appl. 3 (e218), e218. doi:10.1038/lsa.2014.99

CrossRef Full Text | Google Scholar

Cummer, S. A., and Schurig, D. (2007). One path to acoustic cloaking. New J. Phys. 9 (45), 45. PII S1367-2630(07)37675-1. doi:10.1088/1367-2630/9/3/045

CrossRef Full Text | Google Scholar

Du, Y., Li, H., Luo, Z., and Tian, Q. (2017). Topological design optimization of lattice structures to maximize shear stiffness. Adv. Eng. Softw. 112, 211–221. doi:10.1016/j.advengsoft.2017.04.011

CrossRef Full Text | Google Scholar

Dudte, L. H., Vouga, E., Tachi, T., and Mahadevan, L. (2016). Programming curvature using origami tessellations. Natures Mater. 15 (5), 583–588. doi:10.1038/NMAT4540

PubMed Abstract | CrossRef Full Text | Google Scholar

Eidini, M., and Paulino, G. H. (2015). Unraveling metamaterial properties in zigzag-base folded sheets. Sci. Adv. 1 (8), e1500224. doi:10.1126/sciadv.1500224

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, H., Chang, T.-S., and Wang, K. W. (2020). Magneto-origami structures: engineering multi-stability and dynamics via magnetic-elastic coupling. SMART Mater. Struct. 29 (1), 015026. doi:10.1088/1361-665X/ab524e

CrossRef Full Text | Google Scholar

Fang, H., Chu, S.-C. A., Xia, Y., and Wang, K. (2018). Programmable self-locking origami mechanical metamaterials. Mech. Metamaterials, Adv. Mater. 30 (15), 1706311. doi:10.1002/adma.201706311

CrossRef Full Text | Google Scholar

Farzaneh, A., Pawar, N., Portela, C. M., and Hopkins, J. B. (2022). Sequential metamaterials with alternating Poisson’s ratios. Nat. Commun. 13 (1), 1041. doi:10.1038/s41467-022-28696-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Filipov, E. T., Tachi, T., and Paulino, G. H. (2015). Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. PNAS 112 (40), 12321–12326. doi:10.1073/pnas.1509465112

PubMed Abstract | CrossRef Full Text | Google Scholar

Florijn, B., Coulais, C., and Martin van Hecke, (2016). Programmable mechanical metamaterials: the role of geometry. Soft matter 12 (42), 8736–8743. doi:10.1039/c6sm01271j

PubMed Abstract | CrossRef Full Text | Google Scholar

Florijn, B., Coulais, C., and Martin van Hecke, (2014). Programmable mechanical metamaterials. Phys. Rev. Lett. 113 (17), 175503. doi:10.1103/PhysRevLett.113.175503

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraternali, F., Carpentieri, G., Amendola, A., Skelton, R. E., and Nesterenko, V. F. (2014). Multiscale tunability of solitary wave dynamics in tensegrity metamaterials. Appl. Phys. Lett. 105 (20). doi:10.1063/1.4902071

CrossRef Full Text | Google Scholar

Frenzel, T., Findeisen, C., Kadic, M., Gumbsch, P., and Wegener, M. (2016). Tailored buckling microlattices as reusable light-weight shock absorbers. Absorbers 28 (28), 5865–5870. doi:10.1002/adma.201600610

CrossRef Full Text | Google Scholar

Fu, K., Zhao, Z., and Jin, L. (2019). Programmable granular metamaterials for reusable energy absorption. Adv. Funct. Mater. 29 (32), 1901258. doi:10.1002/adfm.201901258

CrossRef Full Text | Google Scholar

Gao, D., Lin, M.-F., Xiong, J., Li, S., Shi, N., Liu, Y., et al. (2020). Photothermal actuated origamis based on graphene oxide–cellulose programmable bilayers. Nanoscale Horizons 5 (4), 730–738. doi:10.1039/c9nh00719a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gary, P. T., Choi, L. H., and Mahadevan, D. L. (2019). Programming shape using kirigami tessellations. Nat. Mater. 18 (9), 999+. doi:10.1038/s41563-019-0452-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Goswami, D., Liu, S., Pal, A., Silva, L. G., and Martinez, R. V. (2019). 3D-architected soft machines with topologically encoded motion. Adv. Funct. Mater. 29 (24), 1808713. doi:10.1002/adfm.201808713

CrossRef Full Text | Google Scholar

Grima, J. N., Caruana-Gauci, R., Dudek, M. R., Wojciechowski, K. W., and Gatt, R. (2013). Smart metamaterials with tunable auxetic and other properties. SMART Mater. Struct. 22 (8), 084016. doi:10.1088/0964-1726/22/8/084016

CrossRef Full Text | Google Scholar

Grima, J. N., and Caruana-Gauci, R. (2011). Materials that push back. Nat. Mater. 11 (7), 565–566. doi:10.1038/nmat3364

PubMed Abstract | CrossRef Full Text | Google Scholar

Grima, J. N., Mizzi, L., Azzopardi, K. M., and Gatt, R. (2016). Auxetic perforated mechanical metamaterials with randomly oriented cuts. Adv. Mater. 28 (2), 385–389. doi:10.1002/adma.201503653

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Liu, Y., Ard, O., Lao, S., Wu, S., and Michael, S. (2016). Deep learning for visual understanding: a review. NEUPOCOMPUTING 187, 27–48. doi:10.1016/j.neucom.2015.09.116

CrossRef Full Text | Google Scholar

Guseinov, R., McMahan, C., Pérez, J., Daraio, C., and Bickel, B. (2020). Programming Temporal morphing of self-actuated shells. Nat. Commun. 11 (1), 237. doi:10.1038/s41467-019-14015-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Haghpanah, B., Ebrahimi, H., Mousanezhad, D., Hopkins, J., and Vaziri, A. (2016a). Programmable elastic metamaterials. Adv. Eng. Mater. 18 (4), 643–649. doi:10.1002/adem.201500295

CrossRef Full Text | Google Scholar

Haghpanah, B., Salari-Sharif, L., Pourrajab, P., Hopkins, J., and Valdevit, L. (2016b). Multistable shape-reconfigurable architected materials. Adv. Mater. 28 (36), 7915–7920. doi:10.1002/adma.201601650

PubMed Abstract | CrossRef Full Text | Google Scholar

Harne, R. L., Wu, Z., and Wang, K. W. (2016). Designing and harnessing the metastable states of a modular metastructure for programmable mechanical properties adaptation. J. Mech. Des. 138 (2), 021402. doi:10.1115/1.4032093

CrossRef Full Text | Google Scholar

Hawkes, E., An, B., Benbernou, N. M., Tanaka, H., Kim, S., Demaine, E. D., et al. (2010). Programmable matter by folding. Proc. Of Natl. Acad. Of Sci. Of U. S. A. 107 (28), 12441–12445. doi:10.1073/pnas.0914069107

PubMed Abstract | CrossRef Full Text | Google Scholar

He, Y. L., Zhang, P. W., You, Z., Li, Z. Q., Wang, Z. H., and Shu, X. F. (2020). Programming mechanical metamaterials using origami tessellations. Compos. Sci. Technol. 189, 108015. doi:10.1016/j.compscitech.2020.108015

CrossRef Full Text | Google Scholar

Hewage, T. A. M., Alderson, K. L., and Scarpa, F. (2016). Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative Poisson's ratio properties. Adv. Mater. 28 (46), 10323–10332. doi:10.1002/adma.201603959

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, A. J., Alekseyev, L., Howard, S. S., Franz, K. J., Wasserman, D., Podolskiy, V. A., et al. (2007). Negative refraction in semiconductor metamaterials. Nat. Mater. 6 (12), 946–950. doi:10.1038/nmat2033

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou-Tong Padilla, C., Zide, W. J., Gossard, J. M. O., Taylor, A. C., Averitt, A. J., and Richard, D. (2006). Active terahertz metamaterial devices. Nature 444 (7119), 597–600. doi:10.1038/nature05343

PubMed Abstract | CrossRef Full Text | Google Scholar

Intrigila, C., Micheletti, A., Nodargi, N. A., and Bisegna, P. (2023). Mechanical response of multistable tensegrity-like lattice chains. Addit. Manuf. 74, 103724. doi:10.1016/j.addma.2023.103724

CrossRef Full Text | Google Scholar

Ion, A., Frohnhofen, J., Wall, L., Kovacs, R., Alistar, M., Lindsay, J., et al. (2016). “Metamaterial mechanisms, UIST 2016,” in PROCEEDINGS OF THE 29TH ANNUAL SYMPOSIUM ON USER INTERFACE SOFTWARE AND TECHNOLOGY, Tokyo Japan, October, 2016, 529–539. doi:10.1145/2984511.2984540

CrossRef Full Text | Google Scholar

Ion, A., Wall, L., Kovacs, R., and Baudisch, P. (2017). “Digital mechanical metamaterials,” in PROCEEDINGS OF THE 2017 ACM SIGCHI CONFERENCE ON HUMAN FACTORS IN COMPUTING SYSTEMS (CHI'17), Denver Colorado USA, May, 2017, 977–988. doi:10.1145/3025453.3025624

CrossRef Full Text | Google Scholar

Jackson, J. A., Messner, M. C., Dudukovic, N. A., Smith, W. L., Bekker, L., Moran, B., et al. (2018). Field responsive mechanical metamaterials. Science 4 (12), eaau6419. eaau6419. doi:10.1126/sciadv.aau6419

PubMed Abstract | CrossRef Full Text | Google Scholar

Janbaz, S., Bobbert, F. S. L., Mirzaali, M. J., and Zadpoor, A. A. (2019). Ultra-programmable buckling-driven soft cellular mechanisms. Mater. Horizons 6 (6), 1138–1147. doi:10.1039/c9mh00125e

CrossRef Full Text | Google Scholar

Janbaz, S., McGuinness, M., and Amir, A. (2018). Multimaterial control of instability in soft mechanical metamaterials. Phys. Rev. Appl. 9 (6), 064013. doi:10.1103/PhysRevApplied.9.064013

CrossRef Full Text | Google Scholar

Janbaz, S., Narooei, K., van Manen, T., and Zadpoor, A. A. (2020). Strain rate–dependent mechanical metamaterials. Sci. Adv. 6 (25), eaba0616. eaba0616. doi:10.1126/sciadv.aba0616

PubMed Abstract | CrossRef Full Text | Google Scholar

Jascha, U., Le Ferrand, H., Ermanni, P., André, R., and Arrieta, A. F. (2017). Programmable snapping composites with bio-inspired architecture. BIOINSPIRATION BIOMIMETICS 12 (2), 1–11. doi:10.1088/1748-3190/aa5efd

CrossRef Full Text | Google Scholar

Jia, L., Gu, T., Shan, S., Kang, S. H., Weaver, J. C., and Bertoldi, K. (2016). Harnessing buckling to design architected materials that exhibit effective negative swelling. Adv. Mater. 28 (31), 6619–6624. doi:10.1002/adma.201600812

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, Z., Fan, L., Jiang, X., and Wang, L. (2020). Engineering lattice metamaterials for extreme property, programmability, and multifunctionality. J. Appl. Phys. 127 (15). doi:10.1063/5.0004724

CrossRef Full Text | Google Scholar

Jiang, Y., Liu, Z., Matsuhisa, N., Qi, D., Wan, R., Yang, H., et al. (2018). Auxetic mechanical metamaterials to enhance sensitivity of stretchable strain sensors. Adv. Mater. 30 (12), 1706589. doi:10.1002/adma.201706589

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., and Wang, Q. (2016). Highly-stretchable 3D-architected mechanical metamaterials. Sci. Rep. 6, 34147. doi:10.1038/srep34147

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, P., and Alavi, A. H. (2021). Artificial intelligence-enabled smart mechanical metamaterials: advent and future trends. Int. Mater. Rev. 66 (6), 365–393. doi:10.1080/09506608.2020.1815394

CrossRef Full Text | Google Scholar

Jiao, P., Hong, L., Wang, J., Yang, J., Zhu, R., Lajnef, N., et al. (2021). Self-triggered thermomechanical metamaterials with asymmetric structures for programmable response under thermal excitations. Materials 14 (9), 2177. doi:10.3390/ma14092177

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, P. (2020). Hierarchical metastructures with programmable stiffness and zero Poisson’s ratio. Apl. Mater. 8 (5), 051109. doi:10.1063/5.0003655

CrossRef Full Text | Google Scholar

Jin, L., Antonio, E. F., Deng, B., Ahmad, R., and Bertoldi, K. (2020). Kirigami-Inspired inflatables with programmable shapes. Adv. Mater. 32 (33), 2001863. doi:10.1002/adma.202001863

PubMed Abstract | CrossRef Full Text | Google Scholar

Johannes, T., Overvelde, B., Shevchenko, Y., Becerra, S. A., Whitesides, G. M., Weaver, J. C., et al. (2016). A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929. doi:10.1038/ncomms10929

PubMed Abstract | CrossRef Full Text | Google Scholar

Kadic, M., Buckmann, T., Schittny, R., Gumbsch, P., and Wegener, M. (2014). Pentamode metamaterials with independently tailored bulk modulus and mass density. Phys. Rev. Appl. 2 (5), 054007. doi:10.1103/PhysRevApplied.2.054007

CrossRef Full Text | Google Scholar

Kadic, M., Buckmann, T., Stenger, N., Thiel, M., and Wegener, M. (2012). On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 100 (19), 191901. doi:10.1063/1.4709436

CrossRef Full Text | Google Scholar

Kadic, M., Milton, G. W., Martin van Hecke, , and Wegener, M. (2019). 3D metamaterials. Nat. Rev. Phys. 1 (3), 198–210. doi:10.1038/s42254-018-0018-y

CrossRef Full Text | Google Scholar

Kamrava, S., Ghosh, R., Wang, Z., and Vaziri, A. (2019). Origami-Inspired cellular metamaterial with anisotropic multi-stability. Adv. Eng. Mater. 21 (2), 1800895. doi:10.1002/adem.201800895

CrossRef Full Text | Google Scholar

Kamrava, S., Mousanezhad, D., Hamid, E. 1, Ghosh, R., and Vaziri, A. (2017). Origami-based cellular metamaterial with auxetic, bistable, and self-locking properties. Sci. Rep. 7, 46046. doi:10.1038/srep46046

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanik, M., Orguc, S., Varnavides, G., Kim, J., Benavides, T., Gonzalez, D., et al. (2019). Strain-programmable fiber-based artificial muscle. Science 365 (6449), 145–150. doi:10.1126/science.aaw2502

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y., Yuk, H., Zhao, R., Chester, S. A., and Zhao, X. (2018). Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 558 (7709), 274–279. doi:10.1038/s41586-018-0185-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolken, H. M. A., and Zadpoor, A. A. (2017). Auxetic mechanical metamaterials. RSC Adv. 7 (9), 5111–5129. doi:10.1039/c6ra27333e

CrossRef Full Text | Google Scholar

Konakovic-Lukovic, M., Julian, P., Keenan, C., and Mark, P. (2018). Rapid deployment of curved surfaces via programmable auxetics. ACM Trans. Graph. 37 (4), 106. doi:10.1145/3197517.3201373

CrossRef Full Text | Google Scholar

Lakes, R. S., Lee, T., Bersie, A., and Wang, Y. C. (2023). Extreme damping in composite materials with negative-stiffness inclusions. Nature 410 (6828), 565–567. doi:10.1038/35069035

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazarus, A., and Reis, P. M. (2015). Soft actuation of structured cylinders through auxetic behavior. Adv. Eng. Mater. 17 (6), 815–820. doi:10.1002/adem.201400433

CrossRef Full Text | Google Scholar

Lee, H., Jang, Y., Choe, J. K., Lee, S., Song, H., Jin, P., et al. (2020). 3D-printed programmable tensegrity for soft robotics. Sci. robotics 5 (45), eaay9024. aay9024. doi:10.1126/scirobotics.aay9024

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J.-H., Singer, J. P., and Thomas, E. L. (2012). Micro-/Nanostructured mechanical metamaterials. Adv. Mater. 24 (36), 4782–4810. doi:10.1002/adma.201201644

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S. H., Choon, M. P., Yong, M. S., Wang, Z. G., and Kim, C. K. (2009). Acoustic metamaterial with negative modulus. J. Physics-Condensed Matter 21 (17), 175704. doi:10.1088/0953-8984/21/17/175704

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, W., Kang, D.-Y., Song, J., Moon, J. H., and Kim, D. (2016). Controlled unusual stiffness of mechanical metamaterials. Sci. Rep. 6, 20312. doi:10.1038/srep20312

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, M., Hong, W., Zhao, Z., Hamel, C., Chen, M., Lu, H., et al. (2019). 3D printing of auxetic metamaterials with digitally reprogrammable shape. ACS Appl. Mater. Interfaces 11 (25), 22768–22776. doi:10.1021/acsami.9b06081

PubMed Abstract | CrossRef Full Text | Google Scholar

Lendlein, A. (2018). Fabrication of reprogrammable shape-memory polymer actuators for robotics. Sci. ROBOTICS 3 (18), eaat9090. doi:10.1126/scirobotics.aat9090

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Luo, Z., Gao, L., and Walker, P. (2018). Topology optimization for functionally graded cellular composites with metamaterials by level sets. Comput. Methods Appl. Mech. Eng. 328, 340–364. doi:10.1016/j.cma.2017.09.008

CrossRef Full Text | Google Scholar

Li, S., Deng, B., Grinthal, A., Schneider-Yamamura, A., Kang, J., Martens, R. S., et al. (2021c). Liquid-induced topological transformations of cellular microstructures. Nature 592 (7854), 386–391. doi:10.1038/s41586-021-03404-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, T., Hu, X., Chen, Y., and Wang, L. (2017). Harnessing out-of-plane deformation to design 3D architected lattice metamaterials with tunable Poisson’s ratio. Sci. Rep. 7 (8949), 8949. doi:10.1038/s41598-017-09218-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Yu, S., Liu, H., Lu, M., and Chen, Y. (2020). Topological mechanical metamaterials: a brief review. Curr. Opin. Solid State and Mater. Sci. 24 (5), 100853. doi:10.1016/j.cossms.2020.100853

CrossRef Full Text | Google Scholar

Li, Y., Zhang, Q., Hong, Y., and Yin, J. (2021b). 3D transformable modular kirigami based programmable metamaterials. Adv. Funct. Mater. 31 (43), 2105641. doi:10.1002/adfm.202105641

CrossRef Full Text | Google Scholar

Li, Z., Gao, W., Wang, M. Y., Wang, C. H., and Luo, Z. (2023). Three-dimensional metamaterials exhibiting extreme isotropy and negative Poisson's ratio. Int. J. Mech. Sci. 259, 108617. doi:10.1016/j.ijmecsci.2023.108617

CrossRef Full Text | Google Scholar

Li, Z., Yang, Q., Fang, R., Chen, W., and Hong, H. (2021a). Origami metamaterial with two-stage programmable compressive strength under quasi-static loading. Int. J. Mech. Sci. 189, 105987. doi:10.1016/j.ijmecsci.2020.105987

CrossRef Full Text | Google Scholar

Liang, K., Wang, Y., Luo, Y., Takezawa, A., Zhang, X., and Kang, Z. (2023). Programmable and multistable metamaterials made of precisely tailored bistable cells. Mater. Des. 227, 111810. doi:10.1016/j.matdes.2023.111810

CrossRef Full Text | Google Scholar

Ling, B., Wei, K., Wang, Z., Yang, X., Qu, Z., and Fang, D. (2020). Experimentally program large magnitude of Poisson’s ratio in additively manufactured mechanical metamaterials. Int. J. Mech. Sci. 173, 105466. doi:10.1016/j.ijmecsci.2020.105466

CrossRef Full Text | Google Scholar

Liu, C., Qiu, S., Zhang, X., and Chen, Z. (2023a). Research on interdisciplinary design thinking and methods based on programmable mechanical metamaterials. Buildings 13 (4), 933. doi:10.3390/buildings13040933

CrossRef Full Text | Google Scholar

Liu, J., and Zhang, Y. (2018). A mechanics model of soft network materials with periodic lattices of arbitrarily shaped filamentary microstructures for tunable Poisson’s ratios. J. Appl. MECHANICS-TRANSACTIONS ASME 85 (5), 051003. doi:10.1115/1.4039374

CrossRef Full Text | Google Scholar

Liu, K., Tachi, T., and Paulino, G. (2019b). Invariant and smooth limit of discrete geometry folded from bistable origami leading to multistable metasurfaces. Nat. Commun. 10, 4238. doi:10.1038/s41467-019-11935-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K., Wu, J., Paulino, G. H., and Jerry Qi, H. (2017). Programmable deployment of tensegrity structures by stimulus-responsive polymers. Sci. Rep. 7 (3511), 3511. doi:10.1038/s41598-017-03412-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K, Zegard, T., Pratapa, P. P., and Paulino, G. H., Unraveling tensegrity tessellations for metamaterials with tunable stiffness and bandgaps, J. Mech. Phys. Solids, vo.131, pp.147–166. 2019a. doi:10.1016/j.jmps.2019.05.006

CrossRef Full Text | Google Scholar

Liu, S., and Cui, T. J. (2017). Concepts, working principles, and applications of coding and programmable metamaterials. Adv. Opt. Mater. 5 (22), 1700624. doi:10.1002/adom.201700624

CrossRef Full Text | Google Scholar

Liu, W., Jiang, H., and Chen, Y. (2021). 3D programmable metamaterials based on reconfigurable mechanism modules. Adv. Funct. Mater. 32, 2109865. doi:10.1002/adfm.202109865

CrossRef Full Text | Google Scholar

Liu, Z., Fang, H., Xu, J., and Wang, K.-W. (2023b). Cellular automata inspired multistable origami metamaterials for mechanical learning. Adv. Sci. 10, 2305146. doi:10.1002/advs.202305146

CrossRef Full Text | Google Scholar

Liua, Y., and Zhang, X. (2011). Metamaterials: a new frontier of science and technology. Chem. Soc. Rev. 40 (5), 2494–2507. doi:10.1039/c0cs00184h

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Z., Luo, Q., Tong, L., Gao, W., and Song, C. (2011). Shape morphing of laminated composite structures with photostrictive actuators via topology optimization. Compos. Struct. 93 (2), 406–418. doi:10.1016/j.compstruct.2010.09.001

CrossRef Full Text | Google Scholar

Lyu, S., Qin, B., Deng, H., and Ding, X. (2021). Origami-based cellular mechanical metamaterials with tunable Poisson’s ratio: construction and analysis. Int. J. Mech. Sci. 212, 106791. doi:10.1016/j.ijmecsci.2021.106791

CrossRef Full Text | Google Scholar

Ma, C., Chang, Y., Wu, S., and Zhao, R. R. (2022). Deep learning-accelerated designs of tunable magneto-mechanical metamaterials. ACS Appl. Mater. Interfaces 14 (29), 33892–33902. doi:10.1021/acsami.2c09052

CrossRef Full Text | Google Scholar

Ma, C., Wu, S., Qiji, Z., Xiao, K., Zhang, R., Jerry Qi, H., et al. (2021b). Magnetic multimaterial printing for multimodal shape transformation with tunable properties and shiftable mechanical behaviors. ACS Appl. Mater. INTERFACES 13 (11), 12639–12648. doi:10.1021/acsami.0c13863

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Song, J., and Chen, Y. (2018). An origami-inspired structure with graded stiffness. Int. J. Mech. Sci. 136, 134–142. doi:10.1016/j.ijmecsci.2017.12.026

CrossRef Full Text | Google Scholar

Ma, J., Zang, S., Feng, H., Chen, Y., and Zhong, Y. (2021a). Theoretical characterization of a non-rigid-foldable square-twist origami for property programmability. Int. J. Mech. Sci. 189, 105981. doi:10.1016/j.ijmecsci.2020.105981

CrossRef Full Text | Google Scholar

Macrae Montgomery, S., Wu, S., Xiao, K., Armstrong, C. D., Cole, Z., Qiji, Z., et al. (2021). Magneto-mechanical metamaterials with widely tunable mechanical properties and acoustic bandgaps. Adv. Funct. Mater. 31 (3), 2005319. doi:10.1002/adfm.202005319

CrossRef Full Text | Google Scholar

Macrae Montgomery, S., Xiao, K., Armstrong, C. D., and Qi, H. J. (2020). Recent advances in additive manufacturing of active mechanical metamaterials. Curr. Opin. Solid State and Mater. Sci. 24 (5), 100869. doi:10.1016/j.cossms.2020.100869

CrossRef Full Text | Google Scholar

Mao, Y., Yu, K., Isakov, M. S., Wu, J., Dunn, M. L., and Jerry Qi, H. (2015). Sequential self-folding structures by 3D printed digital shape memory polymers. Sci. Rep. 5, 13616. doi:10.1038/srep13616

PubMed Abstract | CrossRef Full Text | Google Scholar

Mark, A. G., Palagi, S., Tian, Q., and Fischer, P. (2016). “Auxetic metamaterial simplifies soft robot design,” in 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, May 2016, 16–21.

CrossRef Full Text | Google Scholar

Martin, W. (2013). Metamaterials beyond optics. Science 342 (6161), 939–940. doi:10.1126/science.1246545

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthew, F. (2018). Berwind, alec kamas, and christoph eberl, A hierarchical programmable mechanical metamaterial unit cell showing metastable shape memory. Adv. Eng. Mater. 20 (11), 1800771. doi:10.1002/adem.201800771

CrossRef Full Text | Google Scholar

Medina, E., Farrell, P. E., Bertoldi, K., and Rycroft, C. H. (2020). Navigating the landscape of nonlinear mechanical metamaterials for advanced programmability. Phys. Rev. B 101 (6), 064101. doi:10.1103/PhysRevB.101.064101

CrossRef Full Text | Google Scholar

Mehboob, A., Mehboob, H., Nawab, Y., and Hwan Chang, S. (2022). Three-dimensional printable metamaterial intramedullary nails with tunable strain for the treatment of long bone fractures. Mater. Des. 221, 110942. doi:10.1016/j.matdes.2022.110942

CrossRef Full Text | Google Scholar

Micheletti, A., dos Santos, F. A., and Guest, S. D. (2023). Prestrain-induced bistability in the design of tensegrity units for mechanical metamaterials. Appl. Phys. Lett. 18 Sept. 123 (12), 121702. doi:10.1063/5.0160023

CrossRef Full Text | Google Scholar

Mirzaali, M. J., Janbaz, S., Strano, M., Vergani, L., and Zadpoor, A. A. (2018). Shape-matching soft mechanical metamaterials. Sci. Rep. 8 (965), 965. doi:10.1038/s41598-018-19381-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Momeni, F., SeyedMehdi, M. H. N., Liu, X., and Ni, J. (2017). A review of 4D printing. Mater. Des. 122, 42–79. doi:10.1016/j.matdes.2017.02.068

CrossRef Full Text | Google Scholar

Mousanezhad, D., Babaee, S., Ebrahimi, H., Ghosh, R., Hamouda, A. S., Bertoldi, K., et al. (2015). Hierarchical honeycomb auxetic metamaterials. Sci. Rep. 5 (1), 18306. doi:10.1038/srep18306

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukhopadhyay, T., Ma, J., Feng, H., Hou, D., Gattasd, J. M., Chen, Y., et al. (2020). Programmable stiffness and shape modulation in origami materials: emergence of a distant actuation feature. Appl. Mater. Today 19 (100537), 100537. doi:10.1016/j.apmt.2019.100537

CrossRef Full Text | Google Scholar

Narang, Y. S., Vlassak, J. J., and Howe, R. D. (2018). Mechanically versatile soft machines through laminar jamming. Adv. Funct. Mater. 28 (17), 1707136. doi:10.1002/adfm.201707136

CrossRef Full Text | Google Scholar

Nash, L. M., Kleckner, D., Read, A., Vitelli, V., AriTurnerIrvine, M. W. T. M., and Irvine, W. T. M. (2015). Topological mechanics of gyroscopic metamaterials. Natl. Acad. Of Sci. Of U. S. A. 112 (47), 14495–14500. doi:10.1073/pnas.1507413112

PubMed Abstract | CrossRef Full Text | Google Scholar

Neville, R. M., Scarpa, F., and Pirrera, A. (2016). Shape morphing Kirigami mechanical metamaterials. Sci. Rep. 6, 31067. doi:10.1038/srep31067

PubMed Abstract | CrossRef Full Text | Google Scholar

Ni, X., Guo, X., Li, J., Huang, Y., Zhang, Y., and Rogers, J. A. (2019). 2D mechanical metamaterials with widely tunable unusual modes of thermal expansion. Adv. Mater. 31 (48), 1905405. doi:10.1002/adma.201905405

CrossRef Full Text | Google Scholar

Nicholas, F., Dongjuan, Xi., Jianyi, Xu., Muralidhar, A., Werayut, S., Cheng, S., et al. (2006). Ultrasonic metamaterials with negative modulus. Nat. Mater. 5 (6), 452–456. doi:10.1038/nmat1644

PubMed Abstract | CrossRef Full Text | Google Scholar

Nick, Z. H., Tabor, C. E., and Harne, R. L. (2020). Liquid metal microchannels as digital sensors in mechanical metamaterials. Extreme Mech. Lett. 40, 100871. doi:10.1016/j.eml.2020.100871

CrossRef Full Text | Google Scholar

Nicolaou, G., and Motter, E. (2012). Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 11 (7), 608–613. doi:10.1038/NMAT3331

PubMed Abstract | CrossRef Full Text | Google Scholar

Ning, An, AugustZhou, G. J., Rafsanjani, A., Bertoldi, K., and Bertoldi, K. (2020). Programmable hierarchical kirigami. Adv. Funct. Mater. 30 (6), 1906711. doi:10.1002/adfm.201906711

CrossRef Full Text | Google Scholar

Nojoomi, A., Arslan, H., Lee, K., and Yum, K. (2018). Bioinspired 3D structures with programmable morphologies and motions. Nat. Commun. 9, 3705. doi:10.1038/s41467-018-05569-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Novelino, L. S., Ze, Q., Paulino, G. H., and Zhao, R. (2020). Untethered control of functional origami micro-robots with distributed actuation. Proc. Natl. Acad. Sci. 117 (39), 24096–24101. doi:10.1073/pnas.2013292117

PubMed Abstract | CrossRef Full Text | Google Scholar

Oftadeh, R., Haghpanah, B., Vella, D., Boudaoud, A., and Vaziri, A. (2014). Optimal fractal-like hierarchical honeycombs. Phys. Rev. Lett. 113 (10), 104301. doi:10.1103/PhysRevLett.113.104301

PubMed Abstract | CrossRef Full Text | Google Scholar

Overvelde, J. T. B., Weaver, J. C., Hoberman, C., and Bertoldi, K. (2017). Rational design of reconfigurable prismatic architected materials. Nature 541 (7637), 347–352. doi:10.1038/nature20824

PubMed Abstract | CrossRef Full Text | Google Scholar

Pagliocca, N., Uddin, K. Z., Anni, I. A., Shen, C., Youssef, G., and Koohbor, B. (2022). Flexible planar metamaterials with tunable Poisson’s ratios. Mater. Des. 215, 110446. doi:10.1016/j.matdes.2022.110446

CrossRef Full Text | Google Scholar

Pan, F., Li, Y., Li, Z., Yang, J., Liu, B., and Chen, Y. (2019). 3D pixel mechanical metamaterials. Adv. Mater. 31 (25), 1900548. doi:10.1002/adma.201900548

CrossRef Full Text | Google Scholar

Park, H., Kwon, H., An, Y., Woong-Ryeol, Y., Moon, M., and Hur, K. (2018). Mechanical metamaterials with ThermoresponsiveSwitching between positive and negative Poisson's ratios. Rapid Res. Lett. 12 (5), 1800040. doi:10.1002/pssr.201800040

CrossRef Full Text | Google Scholar

Park, Y., Vella, G., and Loh, K. (2019). Bio-Inspired active skins for surface morphing. Sci. Rep. 9, 18609. doi:10.1038/s41598-019-55163-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Paulose, J., Chen, B.G., and Vincenzo, V. (2015). Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 11 (2), 153–156. doi:10.1038/NPHYS3185

CrossRef Full Text | Google Scholar

Paulose, J., Meeussen, A. S., and Vitelli, V. (2023). Selective buckling via states of self-stress in topological metamaterials. Proc. Of Natl. Acad. Of Sci. Of U. S. A. 112 (25), 7639–7644. doi:10.1073/pnas.1502939112

PubMed Abstract | CrossRef Full Text | Google Scholar

Pendry, J. B. (2000). Negative refraction makes a perfect lens. Phys. Rev. Lett. 85 (18), 3966–3969. doi:10.1103/PhysRevLett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, X., Xiao, K., Roach, D. J., Wang, Y., Hamel, C. M., Lu, C., et al. (2021b). Integrating digital light processing with direct ink writing for hybrid 3D printing of functional structures and devices. Addit. Manuf. 40, 101911. doi:10.1016/j.addma.2021.101911

CrossRef Full Text | Google Scholar

Peng, Y., Wei, K., Mei, M., Yang, X., and Fang, D. (2021a). Simultaneously program thermal expansion and Poisson’s ratio in three dimensional mechanical metamaterial. Compos. Struct. 262 (113365), 113365. doi:10.1016/j.compstruct.2020.113365

CrossRef Full Text | Google Scholar

Qi, G. 1, Chen, Z., Cheng, J., Zhang, B., Zhang, Y.-F., Li, H., et al. (2021). 3D printing of highly stretchable hydrogel with diverse UV curable polymers. Sci. Adv. 7 (2), eaba4261. eaba4261. doi:10.1126/sciadv.aba4261

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, J., Chen, Z., Jiang, P., Hu, W., Wang, Y., Zhao, Z., et al. (2022). Recent progress in active mechanical metamaterials and construction principles. Adv. Sci. 9 (1), 2102662. doi:10.1002/advs.202102662

CrossRef Full Text | Google Scholar

Qi, P. A. N., Chen, S. T., Chen, F. F., and Zhu, X. Y. (2020). Programmable soft bending actuators with auxetic metamaterials. Sci. CHINA-TECHNOLOGICAL Sci. 63 (12), 2518–2526. doi:10.1007/s11431-020-1741-2

CrossRef Full Text | Google Scholar

Raviv, D., Zhao, W., McKnelly, C., Papadopoulou, A., Kadambi, A., Shi, B., et al. (2014). Active printed materials for complex self-evolving deformations. Sci. Rep. 4, 7422. doi:10.1038/srep07422

PubMed Abstract | CrossRef Full Text | Google Scholar

Reid, A., Lechenault, F., Rica, S., and Adda-Bedia, M. (2017). Geometry and design of origami bellows with tunable response. Phys. Rev. E 95 (1), 013002. doi:10.1103/PhysRevE.95.013002

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, X., Shen, J., Ghaedizadeh, A., Tian, H., and Yi, M. (2016). A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 25 (6), 065012. doi:10.1088/0964-1726/25/6/065012

CrossRef Full Text | Google Scholar

Ren, X., Shen, J., Tran, P., Ngo, T. D., and Yi Min, X. (2018). Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial. Mater. Des. 139, 336–342. doi:10.1016/j.matdes.2017.11.025

CrossRef Full Text | Google Scholar

Restrepo, D., Mankame, N. D., and Zavattieri, P. D. (2015). Phase transforming cellular materials. Extreme Mech. Lett. 4, 52–60. doi:10.1016/j.eml.2015.08.001

CrossRef Full Text | Google Scholar

Rodger, M. (2001). Walser. Electromagnetic metamaterials. Proc. SPIE 4467, 1–15.

Google Scholar

Rod Lakes, K. W., and Wojciechowski, K. W. (2023). Negative compressibility, negative Poisson's ratio, and stability. Phys. Status solidi B-Basci solid State Phys. 245 (3), 545–551. doi:10.1002/pssb.200777708

CrossRef Full Text | Google Scholar

Rossiter, J., Takashima, K., Scarpa, F., Walters, P., and Mukai, T. (2014). Shape memory polymer hexachiral auxetic structures with tunable stiffness. Smart Mater. Struct. 23 (4), 045007. doi:10.1088/0964-1726/23/4/045007

CrossRef Full Text | Google Scholar

Schenk, M., and Simon, D. (2013). Geometry of miura-folded metamaterials. Proc. Natl. Acad. Sci. U. S. A. 110 (9), 3276–3281. doi:10.1073/pnas.1217998110

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, W., Menaut, R., Chen, B.G., and Martin van Hecke, (2015). Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114 (5), 055503. doi:10.1103/PhysRevLett.114.055503

PubMed Abstract | CrossRef Full Text | Google Scholar

Seffen, K. A. (2006). Mechanical memory metal: a novel material for developing morphing engineering structures. Scr. Mater. 55, 411–414. doi:10.1016/j.scriptamat.2006.03.028

CrossRef Full Text | Google Scholar

Sengupta, S., and Li, S. (2018). Harnessing the anisotropic multistability of stacked-origami mechanical metamaterials for effective modulus programming. J. INTELLIGENT MATERIAL Syst. Struct. 29 (14), 2933–2945. doi:10.1177/1045389X18781040

CrossRef Full Text | Google Scholar

Shah, D. S., Yang, E. J., Yuen, M. C., Huang, E. C., and Kramer-Bottiglio, R. (2021). Jamming skins that control system rigidity from the surface. Adv. Funct. Mater. 31 (1), 2006915. doi:10.1002/adfm.202006915

CrossRef Full Text | Google Scholar

Shalaev, V. M. (2007). Optical negative-index metamaterials. Nat. Photonics 1 (1), 41–48. doi:10.1038/nphoton.2006.49

CrossRef Full Text | Google Scholar

Shelby, R. A., Smith, D. R., and Schultz, S. (2001). Experimental verification of a negative index of refraction. Science 292 (5514), 77–79. doi:10.1126/science.1058847

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Mofatteh, H., Mirabolghasemi, A., Desharnais, G., and Akbarzadeh, A. (2021). Programmable multistable perforated shellular. Adv. Mater. 33 (42), 2102423. doi:10.1002/adma.202102423

CrossRef Full Text | Google Scholar

Shim, J., Shan, S., Koˇsmrlj, A., SungKang, H. E. R., Weaver, J. C., Bertoldi, K., et al. (2013). Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials. SOFT MATTER 9 (34), 8198–8202. doi:10.1039/c3sm51148k

CrossRef Full Text | Google Scholar

Silveirinha, M., and Engheta, N. (2006). Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near- zero materials. Phys. Rev. Lett. 97 (15), 157403. doi:10.1103/PhysRevLett.97.157403

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverberg, J. L., Evans, A. A., McLeod, L., Hayward, R. C., Hull, T., Santangelo, C. D., et al. (2014). Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345 (6197), 647–650. doi:10.1126/science.1252876

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., Mukhopadhyay, T., Adhikari, S., and Bhattacharya, B. (2021). Voltage-dependent modulation of elastic moduli in lattice metamaterials: emergence of a programmable state-transition capability. Int. J. Solids Struct. 208, 31–48. doi:10.1016/j.ijsolstr.2020.10.009

CrossRef Full Text | Google Scholar

Smith, D. R., Pendry, J. B., and Wiltshire, M. C. K. (2004). Metamaterials and negative refractive index. Science 305 (5685), 788–792. doi:10.1126/science.1096796

PubMed Abstract | CrossRef Full Text | Google Scholar

Soukoulis, M., and Martin, W. (2011). Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5 (9), 523–530. doi:10.1038/NPHOTON.2011.154

CrossRef Full Text | Google Scholar

Specht, M., Berwind, M., and Eberl, C. (2020). Adaptive wettability of a programmable metasurface. Adv. Eng. Mater. 23 (2), 2001037. doi:10.1002/adem.202001037

CrossRef Full Text | Google Scholar

StevenChristensen, A. J., and Alu, A. (2016). Controlling sound with acoustic metamaterials. Nature 1 (3), 16001. doi:10.1038/natrevmats.2016.1

CrossRef Full Text | Google Scholar

Sun, Y., and Nicola, P. (2013). Hierarchical fibers with a negative Poisson’s ratio for tougher composites. MATERIALS 6 (2), 699–712. doi:10.3390/ma6020699

PubMed Abstract | CrossRef Full Text | Google Scholar

Sundararaman, V., O’Donnell, M. P., Chenchiah, I. V., Clancy, G., and Weaver, P. M. (2023). Stiffness tailoring in sinusoidal lattice structures through passive topology morphing using contact connections. Mater. Des. 226, 111649. doi:10.1016/j.matdes.2023.111649

CrossRef Full Text | Google Scholar

Tan, X., Chen, S., Wang, B., Tang, J., Wang, L., Zhu, S., et al. (2020b). Real-time tunable negative stiffness mechanical metamaterial. Extreme Mech. Lett. 41, 100990. doi:10.1016/j.eml.2020.100990

CrossRef Full Text | Google Scholar

Tan, X., Chen, S., Zhu, S., Wang, B., Xu, P., Yao, K., et al. (2019a). Reusable metamaterial via inelastic instability for energy absorption. Int. J. Mech. Sci. 155, 509–517. doi:10.1016/j.ijmecsci.2019.02.011

CrossRef Full Text | Google Scholar

Tan, X., Wang, B., Yao, K., Zhu, S., Chen, S., Xu, P., et al. (2019b). Novel multi-stable mechanical metamaterials for trapping energy through shear deformation. Int. J. Mech. Sci. 164, 105168. doi:10.1016/j.ijmecsci.2019.105168

CrossRef Full Text | Google Scholar

Tan, X., Wang, B., Yao, Y., Yao, K., Kang, Y., Zhu, S., et al. (2020a). Programmable Buckling-based negative stiffness metamaterial. Mater. Lett. 262, 127072. 127072. doi:10.1016/j.matlet.2019.127072

CrossRef Full Text | Google Scholar

Tang, Y., Li, Y., Hong, Y., Shu, Y., and Yin, J. (2019). Programmable active kirigami metasheets with more freedom of actuation. Proc. Natl. Acad. Sci. U. S. A. 116 (52), 26407–26413. doi:10.1073/pnas.1906435116

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, Y., Lin, G., Han, L., Qiu, S., Yang, S., and Yin, J. (2015). Design of hierarchically cut hinges for highly stretchable and reconfigurable metamaterials with enhanced strength. Adv. Mater. 27 (44), 7181–7190. doi:10.1002/adma.201502559

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, Y., Lin, G., Yang, S., Yun, K. Y., Kamien, R. D., and Yin, J. (2017). Programmable kiri-kirigami metamaterials. Adv. Mater. 29 (10), 160462. doi:10.1002/adma.201604262

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, Y., Chen, K., Zheng, H., Kripalani, D. R., Zeng, Z., Jarlöv, A., et al. (2023). Additively manufactured dual-faced structured fabric for shape-adaptive protection. Adv. Sci. 10, 2301567. doi:10.1002/advs.202301567

CrossRef Full Text | Google Scholar

Tibbits, S. (2014). 4D PRINTING: MULTI-MATERIAL SHAPE CHANGE. Archit. Des. 84 (1), 116–121. doi:10.1002/ad.1710

CrossRef Full Text | Google Scholar

Ting-Uei, L., Yan, C., Heitzmann, M. T., and Gattas, J. M. (2021). Compliant curved-crease origami-inspired metamaterials with aprogrammable force-displacement response. Mater. Des. 207, 109859. doi:10.1016/j.matdes.2021.109859

CrossRef Full Text | Google Scholar

Tommaso, TOFFOLI, and Norman, MARGOLUS (1991). PROGRAMMABLE MATTER: CONCEPTS AND REALIZATION. Phys. D. 47 (1-2), 263–272. doi:10.1016/0167-2789(91)90296-L

CrossRef Full Text | Google Scholar

Treml, B., Gillman, A., Buskohl, P., and Vaia, R. (2018). Origami mechanologic. Proc. Natl. Acad. Sci. 115, 6916–6921. doi:10.1073/pnas.1805122115

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsakmakidis, L., Boardman, D., and Ortwin, H. (2007). ‘Trapped rainbow’ storage of light in metamaterials. Nature 450 (7168), 397–401. doi:10.1038/nature06285

PubMed Abstract | CrossRef Full Text | Google Scholar

Valentine, J. Z., Shuang, Z., Ulin-Avila, T., Genov, E., Bartal, D. A., and Zhang, G. (2008). Xiang. Three-dimensional optical metamaterial with a negative refractive index. Nature 455 (7211), 376–U32. doi:10.1038/nature07247

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Melsen, J., and Andrew, G. (2004). From atomos to atom: the history of the concept atom. Massachusetts, United States: Courier Corporation.

Google Scholar

van Manen, T., Janbaz, S., and Amir, A. (2018). Programming the shape-shifting of flat soft matter. Mater. TODAY 21 (2), 144–163. doi:10.1016/j.mattod.2017.08.026

CrossRef Full Text | Google Scholar

Wagner, M. A., Schwarz, F., Huber, N., Geistlich, L., Galinski, H., and Spolenak, R. (2022). Deformation-induced topological transitions in mechanical metamaterials and their application to tunable non-linear stiffening. Mater. Des. 221, 110918. doi:10.1016/j.matdes.2022.110918

CrossRef Full Text | Google Scholar

Wang, D., Xu, H., Wang, J., Jiang, C., Zhu, X., Qi, G., et al. (2020b). Design of 3D printed programmable horseshoe lattice structures based on a phase-evolution model. ACS Appl. Mater. INTERFACES 12 (9), 22146–22156. doi:10.1021/acsami.0c04097

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F., Guo, X., Xu, J., Zhang, Y., and Chen, C. Q. (2017). Patterning curved three- dimensional structures with programmable kirigami designs. J. Appl. MECHANICS-TRANSACTIONS ASME 84 (6), 061007. doi:10.1115/1.4036476

CrossRef Full Text | Google Scholar

Wang, H., Zhao, D., Jin, Y., Wang, M., Mukhopadhyay, T., and Zhong, Y. (2020a). Modulation of multi-directional auxeticity in hybrid origami metamaterials. Appl. Mater. Today 20, 100715. doi:10.1016/j.apmt.2020.100715

CrossRef Full Text | Google Scholar

Wang, Q., Gossweiler, G. R., Craig, S. L., and Zhao, X. (2014). Cephalopod-inspired design of electro-mechano-chemically responsive elastomers for on-demand fluorescent patterning. Nat. Commun. 5, 4899. doi:10.1038/ncomms5899

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Jackson, J. A., Qi, Ge, Hopkins, J. B., Spadaccini, C. M., and Fang, N. X. (2016). Lightweight mechanical metamaterials with tunable negative thermal expansion. Phys. Rev. Lett. 117 (17), 175901. doi:10.1103/PhysRevLett.117.175901

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Meng, Z., and Chang, Q. (2023). Robotic materials transformable between elasticity and plasticity. Adv. Sci. 10, 2206637. doi:10.1002/advs.202206637

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Li, L., Douglas, H., Andrade, J. E., and Daraio, C. (2021). Structured fabrics with tunable mechanical properties. Nature 596 (7871), 238–243. doi:10.1038/s41586-021-03698-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Ramirez, B., Carpenter, K., Naify, C., Hofmann, D. C., and Daraio, C. (2019). Architected lattices with adaptive energy absorption. Extreme Mech. Lett. 33, 100557. doi:10.1016/j.eml.2019.100557

CrossRef Full Text | Google Scholar

Wang, Y., Zhao, W., Rimoli, J. J., Zhu, R., and Hu, G. (2020c). Prestress-controlled asymmetric wave propagation and reciprocity-breaking in tensegrity metastructure. Extreme Mech. Lett. 37, 100724. doi:10.1016/j.eml.2020.100724

CrossRef Full Text | Google Scholar

Wei, K., Xiao, X., Xu, W., Han, Z., Wu, Y., and Wang, Z. (2021). Large programmable coefficient of thermal expansion in additively manufactured bi-material mechanical metamaterial. VIRTUAL Phys. Prototyp. 16, S53–S65. doi:10.1080/17452759.2021.1917295

CrossRef Full Text | Google Scholar

Wei, Y.-L., Yang, Q.-S., Ma, L.-H., Tao, R., and Shang, J.-J. (2020). Design and analysis of 2D/3D negative hydration expansion Metamaterial driven by hydrogel. Mater. Des. 196, 109084. doi:10.1016/j.matdes.2020.109084

CrossRef Full Text | Google Scholar

Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y., and Mahadevan, L. (2013). Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110 (21), 215501. doi:10.1103/PhysRevLett.110.215501

PubMed Abstract | CrossRef Full Text | Google Scholar

Wenz, F., Schmidt, I., Alexander, L., Tobias, L., Baumann, S., Andrae, H., et al. (2021). Designing shape morphing behavior through local programming of mechanical metamaterials. Adv. Mater. 33 (37), 2008617. doi:10.1002/adma.202008617

CrossRef Full Text | Google Scholar

White, P. J., Revzen, S., Thorne, C. E., and Yim, M. (2011). A general stiffness model for programmable matter and modular robotic structures. Robotica 29, 103–121. doi:10.1017/S0263574710000743

CrossRef Full Text | Google Scholar

Wu, J., Yuan, C., Ding, Z., Isakov, M., Mao, Y., Wang, T., et al. (2016a). Multi-shape active composites by 3D printing of digital shape memory polymers. Sci. Rep. 6 (24224), 24224. doi:10.1038/srep24224

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L., Li, B., and Zhou, J. (2016b). Isotropic negative thermal expansion metamaterials. ACS Appl. Mater. INTERFACES 8 (27), 17721–17727. doi:10.1021/acsami.6b05717

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, R., PeterRoberts, C. E., Lyu, S., Zheng, F., Soutis, C., Diver, C., et al. (2021). Lightweight self-forming super-elastic mechanical metamaterials with adaptive stiffness. Adv. Funct. Mater. 31 (06), 2008252. doi:10.1002/adfm.202008252

CrossRef Full Text | Google Scholar

Wu, Zi L., Moshe, M., Greener, J., Therien-Aubin, H., Nie, Z., Sharon, E., et al. (2013). Three-dimensional shape transformations of hydrogel sheets induced by small-scale modulation of internal stresses. Nat. Commun. 4, 1586. doi:10.1038/ncomms2549

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, L., Fan, R., Fan, Z., and Lu, Y. (2021). Programmable mechanical metamaterials based on hierarchical rotating structures. Int. J. Solids Struct. 216, 145–155. doi:10.1016/j.ijsolstr.2021.01.028

CrossRef Full Text | Google Scholar

Xiaoyan, Li., and Huajian, G. (2016). Smaller and stronger. Nat. Mater. 15 (4), 373–374. doi:10.1038/nmat4591

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, X., Liu, L., Liu, Y., and Leng, J. (2022). 4D pixel mechanical metamaterials with programmable and reconfigurable properties. Adv. Funct. Mater. 32 (6), 2107795. doi:10.1002/adfm.202107795

CrossRef Full Text | Google Scholar

Xin, X., Liu, L., Liu, Y., and Leng, J. (2020). 4D printing auxetic metamaterials with tunable, programmable, and reconfigurable mechanical properties. Adv. Funct. Mater. 30 (43), 2004226. doi:10.1002/adfm.202004226

CrossRef Full Text | Google Scholar

Xu, H., Shi, X., Gao, F., Sun, H., and Zhang, B. (2014). Ultrathin three-dimensional thermal cloak. Phys. Rev. Lett. 112 (5), 054301. doi:10.1103/PhysRevLett.112.054301

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, T., Zhang, J., Salehizadeh, M., Onaizah, O., and Diller, E. (2019). Millimeter-scale flexible robots with programmable three-dimensional magnetization and motions. Sci. Robotics 4 (29), eaav4494. eaav4494. doi:10.1126/scirobotics.aav4494

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Boorugu, M., Dopp, A., Ren, J., Martin, R., Han, D., et al. (2019). 4D printing reconfigurable, deployable and mechanically tunable metamaterials. Mater. HORIZONS 6 (6), 1244–1250. doi:10.1039/c9mh00302a

CrossRef Full Text | Google Scholar

Yang, H., and Ma, L. (2020a). 1D and 2D snapping mechanical metamaterials with cylindrical topology. Int. J. Solids Struct. 204, 220–232. doi:10.1016/j.ijsolstr.2020.08.023

CrossRef Full Text | Google Scholar

Yang, H., and Ma, L. (2020b). 1D to 3D multi-stable architected materials with zero Poisson's ratio and controllable thermal expansion. Mater. Des. 188, 108430. doi:10.1016/j.matdes.2019.108430

CrossRef Full Text | Google Scholar

Yang, K., Sun, Y., Yao, Y., and Zhu, W. (2022). A universal strategy for flexible, efficient and programmable crashworthiness under quasi-static and dynamic loadings based on plastic deformation of metals. Mater. Des. 222, 111027. doi:10.1016/j.matdes.2022.111027

CrossRef Full Text | Google Scholar

Yang, N., Zhang, M., and Zhu, R. (2020). 3D kirigami metamaterials with coded thermal expansion properties. EXTREME Mech. Lett. 40, 100912. doi:10.1016/j.eml.2020.100912

CrossRef Full Text | Google Scholar

Yang, Yi, Dias, M. A., and Holmes, D. P. (2018). Multistable kirigami for tunable architected materials. Phys. Rev. Mater. 2 (11), 110601. doi:10.1103/PhysRevMaterials.2.110601

CrossRef Full Text | Google Scholar

Yasuda, H., Korpas, L. M., and Raney, J. R. (2020). Transition waves and formation of domain walls in multistable mechanical metamaterials. Phys. Rev. Appl. 13 (5), 054067. doi:10.1103/PhysRevApplied.13.054067

CrossRef Full Text | Google Scholar

Yasuda, H., and Yang, J. (2015). Reentrant origami-based metamaterials with negative Poisson’s ratio and bistability. Phys. Rev. Lett. 114 (18), 185502. doi:10.1103/PhysRevLett.114.185502

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, T., Lee, Y.-C., Liu, H., Zhang, X., Cui, J., Mondoa, C., et al. (2021). Morphing pasta and beyond. Sci. Adv. 7 (19), eabf4098. doi:10.1126/sciadv.abf4098

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi, M., Xie, X. Y., Shen, J., Yan, X., Ghaedizadeh, A., Rong, J., et al. (2014). Designing orthotropic materials for negative or zero compressibility. Int. J. solids Struct. 51 (23-24), 4038–4052. doi:10.1016/j.ijsolstr.2014.07.024

CrossRef Full Text | Google Scholar

Yin, X., Gao, Z.-Y., Zhang, S., Zhang, L.-Y., and Xu, G. K. (2020). Truncated regular octahedral tensegrity-based mechanical metamaterial with tunable and programmable Poisson's ratio. Int. J. Mech. Sci. 167, 105285. doi:10.1016/j.ijmecsci.2019.105285

CrossRef Full Text | Google Scholar

Young-Joo, L., Lim, S.-M., Yi, S.-M., Lee, J., Kang, S., Gwang-Mook, C., et al. (2019). Auxetic elastomers: mechanically programmable meta-elastomers with an unusual Poisson’s ratio overcome the gauge limit of a capacitive type strain sensor. Extreme Mech. Lett. 31, 100516. doi:10.1016/j.eml.2019.100516

CrossRef Full Text | Google Scholar

Yu, X., Zhou, J., Liang, H., Jiang, Z., and Lingling, W. (2018). Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review. Prog. Mater. Sci. 94, 114–173. doi:10.1016/j.pmatsci.2017.12.003

CrossRef Full Text | Google Scholar

Yuan, C., Mu, X., Dunn, C. K., Haidar, J., Wang, T., and Jerry Qi, H. (2018). Thermomechanically triggered two-stage pattern switching of 2D lattices for adaptive structures. Adv. Funct. Mater. 28 (18), 1705727. doi:10.1002/adfm.201705727

CrossRef Full Text | Google Scholar

Yuan, L., Dai, H., Song, J., Ma, J., and Chen, Y. (2020). The behavior of a functionally graded origami structure subjected to quasi-static compression. Mater. Des. 189, 108494. doi:10.1016/j.matdes.2020.108494

CrossRef Full Text | Google Scholar

Yuan, S., Chua, C. K., and Zhou, K. (2019). 3D-Printed mechanical metamaterials with high energy absorption. Adv. Mater. Technol. 4 (3), 1800419. doi:10.1002/admt.201800419

CrossRef Full Text | Google Scholar

Yuandan, D., and Tatsuo, I. (2012). Metamaterial-based antennas. Proc. Of IEEE 100 (7), 2271–2285. doi:10.1109/JPROC.2012.2187631

CrossRef Full Text | Google Scholar

Yun, L., Pang, W., Li, X., Goswami, S., Xu, Z., David Stroman, , et al. (2020). Laser-Induced graphene for electrothermally controlled, mechanically guided, 3D assembly and human-soft actuators interaction. Adv. Mater. 32 (17), 1908475. doi:10.1002/adma.201908475

CrossRef Full Text | Google Scholar

Zhai, Z., Wang, Y., and Jiang, H. (2018). Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. PNAS 115 (9), 2032–2037. doi:10.1073/pnas.1720171115

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Guo, X., Wu, J., Fang, D., and Zhang, Y. (2018a). Soft mechanical metamaterials with unusual swelling behavior and tunable stress-strain curves. Sci. Adv. 4 (6), eaar8535. eaar8535. doi:10.1126/sciadv.aar8535

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Wu, J., Fang, D., and Zhang, Y. (2021a). Hierarchical mechanical metamaterials built with scalable tristable elements for ternary logic operation and amplitude modulation. Sci. Adv. 7 (9), eabf1966. doi:10.1126/sciadv.abf1966

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., Zhao, S., Sun, R., Scarpa, F., and Wang, J. (2019b). In-plane mechanical behavior of a new star-Re-entrant hierarchical metamaterial. Polymers 11 (7), 1132. doi:10.3390/polym11071132

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Ye, H., Nan, W., Tao, R., and Luo, Z. (2021b). Design optimization of multifunctional metamaterials with tunable thermal expansion and phononic bandgap. Mater. Des. 209, 109990. doi:10.1016/j.matdes.2021.109990

CrossRef Full Text | Google Scholar

Zhang, Y., Bo, L., Zheng, Q. S., Genin, M., and Chen, C. Q. (2019a). Programmable and robust static topological solitons in mechanical metamaterials. Nat. Commun. 10 (5605), 5605. doi:10.1038/s41467-019-13546-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Deshmukh, A., and Wang, K.-W. (2023b). Embodying multifunctional mechano-intelligence in and through phononic metastructures harnessing physical reservoir computing. Adv. Sci. 10, 2305074. doi:10.1002/advs.202305074

CrossRef Full Text | Google Scholar

Zhang, Y., Tu, J., Wang, D., Zhu, H., Maity, S. K., Qu, X., et al. (2018b). Programmable and multifunctional DNA-based materials for biomedical applications. Adv. Mater. 30 (24), 1703658. doi:10.1002/adma.201703658

CrossRef Full Text | Google Scholar

Zhang, Z., Song, B., Fan, J., Wang, X., Wei, S., Fang, R., et al. (2023a). Design and 3D printing of graded bionic metamaterial inspired by pomelo peel for high energy absorption. Chin. J. Mech. Eng. Addit. Manuf. Front. 2 (1), 100068. doi:10.1016/j.cjmeam.2023.100068

CrossRef Full Text | Google Scholar

Zhao, Z., Yuan, C., Lei, M., Yang, L., Zhang, Q., Chen, H., et al. (2019). Three-dimensionally printed mechanical metamaterials with thermally tunable auxetic behavior. Phys. Rev. Appl. 11 (4), 044074. doi:10.1103/PhysRevApplied.11.044074

CrossRef Full Text | Google Scholar

Zheludev, N. I. (2010). The road ahead for metamaterials. Science 328 (5978), 582–583. doi:10.1126/science.1186756

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheludev, N. I., and Kivshar, Y. S. (2012). From metamaterials to metadevices. Nat. Mater. 11 (11), 917–924. doi:10.1038/NMAT3431

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, X., Lee, H., Weisgraber, T. H., Shusteff, M., DeOtte, J., Duoss, E. B., et al. (2014). Ultralight, ultrastiff mechanical metamaterials. Science 344 (6190), 1373–1377. doi:10.1126/science.1252291

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, X., Smith, W., Jackson, J., Moran, B., Cui, H., Chen, D., et al. (2016). Spadaccini, Multiscale metallic metamaterials. Nat. metamaterials 15 (10), 1–7. doi:10.1038/NMAT4694

PubMed Abstract | CrossRef Full Text | Google Scholar