Modern quantum materials

Quantum phenomena, including entanglement, superposition, tunneling, and spin–orbit interactions, among others, are foundational to the development of recent innovations in quantum computing, teleportation, encryption, sensing, and new modalities of electronics, such as spintronics, spin-orbitronics, caloritronics, magnonics, twistronics, and valleytronics. These emerging technologies provide disruptive influences to global commercial markets. These remarkable advances in quantum technologies are nearly always enabled by the discovery of materials and their quantum behaviors. Such advances are governed by quantum principles that are strongly influenced by environmental, physical, topological, and morphological conditions such as very small length scales, short time durations, ultrahigh pressures, ultralow temperatures, etc., which lead to quantum behaviors that manifest as quantum tunneling, entanglement, superpositioning, superfluidity, low-dimensional, high-temperature and high-pressure superconductivity, quantum fluctuations, Bose–Einstein condensates, topological effects, and other phenomena that are not yet fully understood nor adequately explored. Here, we provide a review of quantum materials developed up to 2023. Remarkable advances in quantum materials occur daily, and therefore, by the time of publication, new and exciting breakthroughs will have occurred that are regrettably not covered herein.

1 Introduction

The widely venerated Richard Feynman once explained to a layperson that electrons participate in all chemical bonds, determining not only classical properties such as hardness, density, malleability, and color but also adhering to quantum principles that often give rise to rather weird behaviors. Some of these weird behaviors appear in common water.

For example, upon freezing, water takes on six-sided fractalized crystalline structures (Harvey. 2017; Wikipedia, 2022b) where each molecule’s H⁺ ions bond to an average of ∼17.6% more partners, giving rise to an increase in volume of ∼9% (Jain, 2014). This increased volume lowers the density of water and allows ice to float in water. The large expansion of freezing water exerts extreme pressures on its container walls, in some cases beyond 1 GPa, depending upon the specific phase of ice¹, leading to the commonly experienced fracturing of thick iron pipes in winter climes.

In this frozen state, ice was long thought to form a thin layer of liquid water under the application of pressure, for example, under ice skates, allowing for the astonishing exploits of Bobby Orr and others on the ponds of North America (Schwegler et al., 2008). In recent years, this description of slippery ice has proven incomplete, as illuminated by the work of² Canale et al. (2019) andBonn (2020).

To this day, water continues to offer weird quantum surprises; for example, common water consists of two hydrogen cations and an oxygen anion that take on spin isomerisms of ortho- and para-forms. Ortho-water has both hydrogen ion magnetic spins aligning parallel (↑↑), whereas para-water has hydrogen spins aligning antiparallel (↓↑) (Beduz et al., 2012). However, unlike spin isomers of hydrogen gas molecules (i.e., H⁺ ions in H₂), water spin isomers experience electric dipoles, giving rise to properties like ferroelectricity. An orthorhombic, low-temperature form of hexagonal ice has been shown to be ferroelectric and described as ice XI, which is considered a stable configuration of ice I_h (Iedema et al., 1998).

We comment on quantum water merely to demonstrate that even materials that we consider common offer quantum weirdness. Other quantum behaviors discussed in this article include quantum tunneling, spin–orbit interactions, entanglement, superpositioning, and other phenomena.

In preparing this manuscript, we have noted that during the last several years, the term “quantum materials” has evolved into a universally accepted term of the quantum lexicon; however, an equally accepted definition of quantum materials (QMs) has remained elusive. Although many definitions have been proffered by practitioners who describe QMs within the frameworks of their own experiences, our field continues to grapple with a degree of self-identity.

We proffer a definition of QMs that we hope captures both breadth and specificity:

Quantum materials are those whose properties cannot be thoroughly explained within the framework of classical deterministic theories where individual particles through electron confinement, collective quasiparticle excitations, and many-body interactions, express their quantum behavior as superconductivity, quantum fluctuations, entanglement and superposition, quantum tunneling, and superfluidity, among other phenomena; these effects often occur at nanoscales, ultralow temperatures, ultrahigh pressures, or ultrashort time durations.

The broad goals of the present article are to provide insight into the complex and rich field of quantum materials, reflecting some of the recently recognized challenges and successes. This review is presented for those new to the field, for example, scholars considering quantum materials as a future research topic or perhaps as a component to their formal education or those wishing to expose themselves to new opportunities made available by our increasingly quantum society.

We aim to cast quantum materials in the context of phenomena that are actively explored in practical quantum technologies. These phenomena include coherence of qubits, fidelity of quantum states, quantum error-correction stratagems, and implementation of powerful quantum algorithms, all essential to realizing practical quantum computing, quantum information, and quantum communication technologies. Alternatively, and of equal import, is the development of long-lived superposition states that enable encryption and ultra-secure communication, quantum teleportation, sensing, and other quantum applications.

The extraordinary extension of performance of modern electronics includes the development of spintronics (Žutić et al., 2004), spin-orbitronics (Manchon et al., 2015), caloritronics (Bauer et al., 2012), magnonics (Kruglyak et al., 2010), twistronics (Hennighausen and Kar, 2021), and valleytronics (Schaibley et al., 2016), and the other “-ics” unintentionally omitted that are emerging every day. Such advances are nearly always enabled by newly discovered materials and their quantum behaviors. Such remarkable advances in technologies not only positively influence society but are also governed by quantum principles that are strongly impacted by environmental, physical, topological, and morphological conditions. For example, at very small length scales, short time durations, ultrahigh pressures, and ultralow temperatures, etc., quantum behaviors manifest as quantum tunneling, entanglement, superpositioning, superfluidity, low-dimensional, high-temperature and high-pressure superconductivity, quantum fluctuations, Bose–Einstein condensates, topological effects, and other phenomena that are not yet fully understood nor adequately explored.

Figure 1 illustrates a depiction of correlations among select quantum phenomena (i.e., entanglement, superposition, tunneling, and spin–orbit interactions) correlated with recently developed materials that effectively illustrate quantum behaviors, with technologies such as quantum computing (Nielsen and Chuang, 2000), teleportation (Bennett et al., 1993), encryption (Gisin et al., 2002; Pirandola et al., 2020), sensing (Degen et al., 2017), and new modalities of electronics that provide effective driving forces to global markets. The international business community responds to these opportunities with investments in quantum materials due to their promise of considerable financial returns. We will address these relationships and others in greater detail in forthcoming sections.

Figure 1

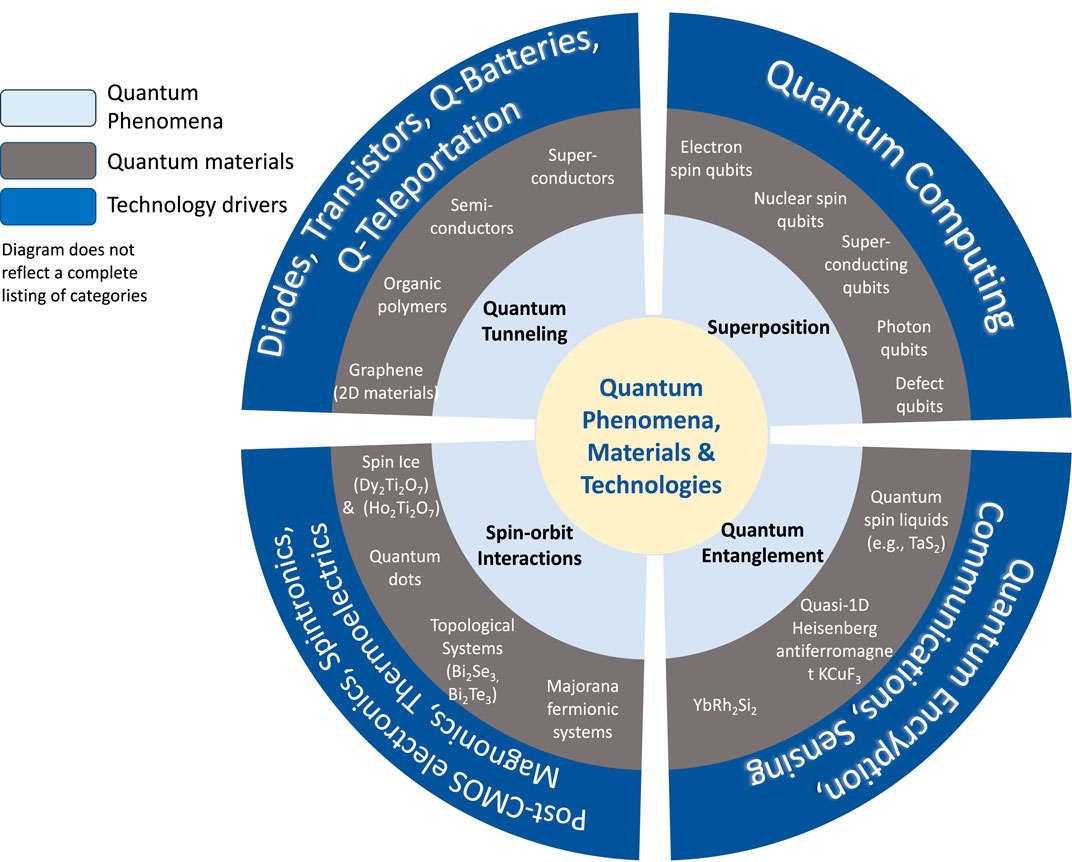
Figure 1. Illustration depicting correlations among select quantum phenomena (i.e., entanglement, superposition, tunneling, and spin–orbit interactions) with recently developed materials that effectively illustrate the quantum behaviors of burgeoning quantum technologies.

In its entirety, this perspective on quantum materials applies to emerging quantum technologies and their societal impact.

We begin this article with a discussion of the evolution of quantum mechanics, both in the early part of the twentieth century (i.e., the first quantum revolution) and later (the second quantum revolution), with the latter being defined here in the context of influences upon quantum advances related to emerging quantum technologies depicted in Figure 1 that promise to strongly influence the global society of the twenty-first century.

2 The first quantum revolution

To fully understand the state of today’s modern sciences and technologies, one must first understand the history of society’s transition from classical to quantum science. The evolution of basic physics and chemistry, and to a lesser extent health sciences, engineering, and mathematics, during the last century to today are presented and discussed.

Figures 2, 3 present timelines of major events of the twentieth and twenty-first centuries that have contributed to what we refer to as the quantum revolution(s).

Figure 2

Figure 2. A brief review of the first quantum revolution defined by the seminal contributions made by principals from 1900 to c. 1927. Photographs from top to bottom: Planck, Einstein, Bohr, de Broglie, Heisenberg, Schrodinger, and Dirac.

Figure 3

Figure 3. (A) The second quantum revolution is defined by the seminal contributions made by principals in advancing quantum theory in entanglement and superposition over the period of 1935–1994. Photographs from top to bottom include Podolsky, Rosen, Bell, Stanislaw, Benioff, Feynman, Deutsch, Bennett, and Shor. The timeline presented defines major events in the quantum revolution influencing the future of quantum computing, teleportation, and encryption. (B) The second quantum revolution continues with seminal contributions made by principals in quantum computing, information sciences, teleportation, and quantum communication from 1995 to the present. Photographs from top to bottom include Lloyd, Grover, DiVincenzo, Nakamura, Tsai, Pan, Hanson, Awschalom, Aspect, Clauser, and Zeilinger.

At the time of the first quantum revolution (see Figure 2), circa 1900, experimental techniques had advanced to a degree of accuracy and precision that provoked some in the scientific community to challenge the veracity of classical theories of the age.

2.1 Quantization of radiation

One such phenomenon was that of black body radiation, a problem that in 1859 was described by Kirchhoff as: “…how does the intensity of the electromagnetic radiation emitted by a black body depend on the frequency of the radiation and the temperature of the body?” (Wikipedia, 2022d).

This problem had been explored experimentally, but no theory was proffered that adequately matched the known data of the time. For example, circa 1900, Wien’s law (Wien, 1897) correctly predicted behavior at low wavelengths, that is, λ < 0.1 μm, but failed at higher wavelengths, while the Rayleigh–Jeans law (Pais, 1979-10) agreed with results at higher wavelengths, that is, λ > 0.4 μm, but failed at the lower wavelengths; the later providing its λ⁻⁴ dependence based on classical physical arguments derived from the equipartition theorem. Over the ultraviolet bands, that is, 0.1 < λ < 0.4 μm, no theory adequately predicted the electromagnetic radiation emitted by black bodies; this was referred to as the “ultraviolet catastrophe” (Ehrenfest, 1911).

Max Planck, having just been named Kirchhoff’s successor at the Friedrich Wilhelm Universität, took up this challenge. Employing Boltzmann’s statistical interpretation of the second law of thermodynamics, he developed what is now known as Planck’s Law. Planck’s Law specifically states that electromagnetic energy can only be emitted in quantized fragments, defined as hv, where h is a constant of action, 6.62607015×10⁻³⁴ m² kg/s or J^.s, to become known as Planck’s constant, and ν is the frequency of the thermal radiation.

Planck empirically obtained an expression (Eq. (1)) for black body spectral radiance (B) expressed in terms of wavelength (where λ = c/v):

$B_{\mathit{v}}\left(T\right)=\frac{2h{\mathit{v}}^3}{c^2}\frac{1}{e^{h\mathit{v}/kT}-1},(1)$

where B_v(T) is the spectral radiance density of frequency ν at thermal equilibrium of temperature T; h is Planck’s constant; c is the speed of light in free space; and k is Boltzmann’s constant.

At the time of his breakthrough, Planck did not believe his theory captured physical reality and thought that h served as nothing more than a mathematical convenience. Notwithstanding his lack of self-confidence, Planck's work grew in relevance and import, eventually being recognized as the first pillar of quantum physics. Planck was subsequently awarded the 1918 Nobel Prize in physics.

Another who took up the mantle to challenge foundational canons of classical physics was a then largely unknown, third-class patent clerk, Albert Einstein. Armed with only thought experiments, that is, gedankenexperiments, Einstein dared to challenge some of the most established tenets of science, including those of the illustrious Sir Isaac Newton.

2.2 Quantization of electromagnetic energy: The photoelectric effect

In 1905, since declared Einstein’s “annus mirabilis” or miraculous year, he published four articles that ushered in a new era of scientific enlightenment (Einstein, 1905a; Einstein, 1905b; Einstein, 1905c; Einstein, 1905d).

His first published work, “On a Heuristic Point of View about the Creation and Conversion of Light” (Einstein, 1905a), employed Planck’s proposed quanta of electromagnetic energy to solve the paradox of the photoelectric effect.

The photoelectric effect, first reported in c. 1880s, refers to the emission of electrons when light is incident upon a material’s surface. Electrons emitted in this manner are identified as photoelectrons. By proposing a theory that electrons can only escape the surface of a material when light of a discrete energy strikes the surface, as opposed to a flux or polychromatic intensity of light, Einstein provided a second key pillar to early quantum physics. His treatment of light as quanta would usher in the treatment of light as particles, later to be known as photons.

This work led to Einstein receiving the 1921 Nobel Prize in physics (delayed by WWI) and established the quantization of light, much as Plank provided the quantization of black body radiation. Robert Millikan, who experimentally confirmed Einstein’s theory, as well as accurately measured the electron’s mass and charge, was awarded the Nobel Prize in physics in 1923.

Einstein’s second article, “Investigations on the Theory of Brownian Movement” (Einstein, 1905b), led to the confirmation of the existence of atoms and their approximate size. Some argue this work could well have earned him the Nobel because the existence of atoms at that time was not universally accepted, and this work placed both the existence and the approximate size of atoms on a firm footing.

His third article, and arguably the most bold and influential work of 1905, was his introduction of special relativity that challenged the pedagogy of Newtonian mechanics. This article, “On the Electrodynamics of Moving Bodies” (Einstein, 1905c), reconciled Maxwell’s equations for electricity and magnetism with the laws of Newtonian mechanics by introducing major changes to the interpretation as relative speed approaches the speed of light. This became known as Einstein’s Special Theory of Relativity. It is here that Einstein introduces a theory of time, distance, mass, and energy that are consistent with Maxwell’s electromagnetism but omits the force of gravity, which would appear in his later opus on the General Theory of Relativity (Einstein, 1905e). An essential component of this third article is Einstein’s proposal that the speed of light is a fundamental constant of nature for all reference frames (i.e., independent of the state of motion of the light-emitting body). Einstein’s embrace of the foundational import of the speed of light as a fundamental constant will be revisited in our discussion of entanglement, which challenges this principle. As a result of this third article, the symmetries of spacetime were augmented by internal symmetries. The world view of modern theoretical physics can be traced back to the fundamental postulate that physical phenomena do not change just because you happen to be moving instead of standing still. As reported by Jackson, “Asking about the impact of special relativity on theoretical physics, is like asking about the impact of Shakespeare on the English language” (Jackson, 1987).

In his fourth and final article of 1905, entitled “Does the Inertia of a Body Depend Upon its Energy Content?” (Einstein, 1905d), Einstein introduces his mass-energy equivalence theory, providing what is inarguably the most famous equation in human history: E = mc² (Wikipedia, 2022c). This equation states that the energy of a body at rest equals its mass times the speed of light squared. Because the speed of light, or c, is 299,792,458 m/s, the amount of potential energy that is available is enormous. This would be confirmed in later years through the development of atomic bombs and nuclear reactors.

2.3 Quantization of electronic angular momentum

Circa 1911–1912, soon after earning his Ph.D. under the tutelage of Christian Christiansen at the University of Copenhagen, Niels Bohr joined the renowned experimentalist Ernest Rutherford at Victoria University of Manchester. For his first assignment, Rutherford challenged Bohr to bring stability to his (Rutherford’s) planetary model of the atom that had recently eclipsed the “plum pudding” model of J.J. Thomas (the discoverer of the electron). Although popular, Rutherford’s atomic model came under attack for a critical flaw, whereupon orbiting negatively charged electrons would lose energy and spiral inward, ultimately crashing into the positively charged nucleus and annihilating the atom. It is noteworthy that both Joseph Larmor and Jean Perrin had proposed planetary atomic models (DBpedia, 2023) earlier than Rutherford, but Rutherford’s model was more widely accepted and attributed to him.

In a series of three articles published in 1913 (Bohr, 1913a; Bohr, 1913b; Bohr, 1913c), Bohr’s proposed model of the atom ushered in another quantum milestone. Bohr’s model, similar to Rutherford’s (and others), had a positively charged centrally-located nucleus with orbiting negatively charged electrons. However, he confined electrons to discrete orbits defined by their quantized angular momentum and energy by applying Plank’s constant.

A key attribute of the Bohr model is its ability to explain the spectral emission lines of hydrogen, that is, the Balmer series, using discrete transitions of electrons between quantized orbits. These stable orbits, labeled stationary orbits, are maintained at discrete energies from the nucleus. The electron cannot have any other orbit in between these discrete orbits; those energies are forbidden. Electrons only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency, ν, determined by the energy difference of the orbital levels in accordance with the relation, for example, ΔE = E₂ − E₁ = hv, where h is Planck’s constant. The energy level of such orbits became the principal quantum number, n. This work led to Bohr receiving the 1922 Nobel Prize in physics.

The seminal works of Planck, Einstein, and Bohr provided quantization of black body radiation, light, and electron angular momentum, respectively, and allowed the photon and electron to assume particle-like behavior in contradiction to the accepted Maxwellian doctrine.

This particle-dominated interpretation of quantum physics continued until circa 1923, whereupon Louis de Broglie, son of Victor Duc de Broglie and Pauline d’Armaillé, put forth the disruptive theory of matter waves, postulating that quantum particles exhibit wave-like characteristics (Broglie, 1924); a theory he derived from Einstein’s Special Theory of Relativity and subsequently earned him the (singular) 1929 Nobel Prize in physics.

2.4 Equivalence of matrix and wave mechanical quantum theories: enter the Copenhagen Interpretation

During 1925–1926, quantum theory entered into a time of rapid evolution and conflict, whereupon a dual theoretic framework that included the work of Heisenberg, Born, and Jordan, championing particle-like behavior and matrix mechanics (Heisenberg, 1925) and Schrödinger, building upon the work of de Broglie, advocated for wave-like behavior of quantum particles described by wave mechanics (Schrodinger, 1926). For his contributions, Heisenberg was solely awarded the 1934 Nobel in physics, while Born was solely awarded the same prize much later in 1954 for his lifetime contributions to quantum mechanics.

In 1927, Dirac stunned the physics community by introducing relativity to Schrödinger’s electron wavefunction equation. This led to what is known as the Dirac Equation, which provided a more accurate description of the behavior of the hydrogen atom and predicted electron spin, magnetic monopoles, and antimatter, among other surprises (Dirac, 1926; Dirac, 1927). Dirac shared the 1933 Nobel Prize in physics with Schrödinger.

Shortly thereafter, an important contribution was made by a young Hungarian mathematician, physicist, computer scientist pioneer, engineer, and polymath, Jancsi “Johnny” von Neuman, who was the first to prove the mathematical equivalence of Heisenberg’s matrix and Schrödinger’s wave mechanical quantum theories³ (Maeda, 1937), During his lifetime, von Neuman made numerous seminal contributions to quantum physics, mathematics, economics, game theory, cellular automata, early digital computer development in hardware, software, and information theory, among others (Macrae, 1992).

Finally, of relevance to this article, the concept of electron spin, that is, the fourth quantum number, was first proposed by Kronig in 1925 while a graduate student at Columbia University. His concept was soundly criticized by a visiting Wolfgang Pauli leading to Kronig opting not to publish. Several months later, Goudsmit and Uhlenbeck of Leiden developed a comparable theory that was also criticized by a visiting Pauli, but their advisor Ehrenfest, being favorably impressed, immediately submitted the work for publication (Uhlenbeck and Goudsmit, 1926). Goudsmit and Uhlenbeck have since been attributed as the discoverers of electron spin. Perhaps due to confusion over credit, no Nobel Prize was ever awarded for the discovery of spin. This is considered a considerable oversight by the physics community due to the immense significance and impact of spin (Commins, 2012).

The Copenhagen Interpretation dominates much of the twenty-first century’s discourse on quantum mechanics.

This theory evolved to accommodate both wave and particle views of quantum systems, perhaps in response to von Neuman’s rigorous proof of equivalence. Although the Copenhagen Interpretation is largely attributed to Niels Bohr, its most recognized champion, it represents a plurality of views attributed to Bohr, his colleagues, and students at the Institute of Theoretical Physics of the University of Copenhagen, an institute founded by Bohr in 1921 that continues to provide leadership to the quantum community. Common themes of the Copenhagen Interpretation include the idea that quantum mechanics is inherently indeterministic and obeys the principle of complementarity; that is, quantum particles have certain complementary properties that cannot be simultaneously observed and measured. In Bohr’s view, the behavior of quantum particles cannot be separated from the influence of measurement; hence, one must consider the particle under study together with its measurement in order to obtain a comprehensive description. Either one, without the other, provides an incomplete picture of reality.

3 The second quantum revolution

The second quantum revolution (see Figure 3A,B), as defined here, begins with the controversial 1935 publication by Einstein, Podolsky, and Rosen (henceforth EPR). EPR challenged the completeness provided by the state of quantum mechanics at that time (Einstein et al., 1935-05).

3.1 The Einstein–Podolsky–Rosen (EPR) paradox

EPR specifically describes a pair of particles in an entangled state and asserts that if the position of the first particle is measured, the result would allow for the prediction of the second particle’s position with absolute certainty. Alternatively, if the momentum of the first particle is measured, then the momentum of the second particle could be similarly predicted with certainty. EPR argues that no action taken on the first particle could instantaneously affect the other because that would require information to be transmitted faster than the speed of light, which is forbidden by Einstein’s Special Theory of Relativity. In short, physics is local and deterministic.

From this, they developed the EPR criterion:

“If, without in any way disturbing a system, we can predict with certainty (i.e. with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.” (Commins, 2012).

However, in accordance with Heisenberg’s Uncertainty Principle, those observables are incompatible, and therefore, quantum theory does not provide a complete description of reality.

Schrödinger first employed the word Verschränkung, translated from German as entanglement, to describe correlations between two distant particles in a letter to Einstein (c. 1935). He expanded upon this concept in a later publication (Schrödinger, 1935).

Like Einstein, Schrödinger was dissatisfied with the idea of transmission of information exceeding the speed of light. Einstein famously ridiculed entanglement as “spukhafte Fernwirkung” or “spooky action at a distance.”

3.2 De Broglie–Bohm theory

In 1951, 16 years after the publication of EPR, David Bohm proposed a variant to the EPR thought experiment in which the measurement of a variety of discrete possible outcomes, unlike position and momentum, were considered (Bohm and Aharonov, 1957).

The EPR–Bohm thought experiment employed an electron–positron pair. In that experiment, the electron is sent to destination A, where it is observed, somewhat famously, by Alice, and the positron is sent to destination B, where it is observed by her equally famous colleague Bob. According to quantum mechanics, the emitted pair contributes to a quantum state called a spin singlet. A spin singlet refers to a set of particles whose net angular momentum is zero; that is, its overall spin quantum number, s, is zero. As a result, only one spectral line is emitted from this singlet, and the particles are said to be entangled.

This can be viewed as a quantum superposition of two states. In state 1, the electron has its spin aligned upward ↑, and the positron has its spin aligned downward ↓. In state 2, the electron has spin ↓ and the positron spin ↑. Because it is in a state of superposition, it is impossible without measurement to know the definite spin state of either particle. This is akin to Schrödinger’s famous cat, who is both dead and alive until its box is opened to confirm its state of livelihood.

Alice now measures the spin of the electron, whereupon she obtains one of two possible outcomes ↑ or ↓. If she measures ↑, the quantum state of the system has collapsed into state 1, and if Bob subsequently measures the spin of the positron, there is a 100% probability that he will obtain ↓. Similarly, if Alice measures electron spin ↓, Bob measures positron spin ↑.

The de Broglie–Bohm theory is an interpretation of quantum mechanics that postulates that the configuration of particles exists before measurement. Furthermore, the evolution over time of such quantum particles is governed by the time-dependent Schrödinger equation.

The theory is deterministic and explicitly nonlocal and depends on the configuration of particles under consideration. Measurements represent a particular case of quantum processes described by the theory of standard quantum predictions adherent to the Copenhagen Interpretation.

Physicists who support the de Broglie–Bohm theory maintain that the underlying probabilistic behavior of the Universe represents deterministic foundations validated by hidden variables.

Although the motivation for the introduction of a hidden variable stems in large part from the pursuit to validate quantum mechanics’ determinism, some indeterministic theories attempt to explain the underlying reality of quantum mechanics employing hidden variables, for example, Nelson’s stochastic mechanics (Nelson et al., 1986).

3.3 Bell’s local realism

The principle of locality evolved out of classical field theories and proposes that an object is influenced only by its immediate surroundings and interacts with other objects directly through fields between those objects.

As such, the formalization of locality states that if there are two observables, each existing within two distinct but localized regions of spacetime, they must commute. Alternatively, a solution to field equations is considered local only if the underlying equations are covariant or locally Lorentz invariant⁴ (Wikipedia, 2022e),

In 1964, John Stewart Bell formulated the Bell inequality, sometimes known as Bell’s theorem, which, if violated, indicates that quantum mechanics violates local realism, which relates to the value of unmeasured quantities (Bell, 1964). Oddly, Bell’s initial motivation was to establish determinism in physics, but the result has proven quite the opposite.

3.4 Hidden variables

The consequence of Bell’s theorem is that quantum mechanics is incompatible with local hidden-variable theories. Hidden variables, in this context, possess properties related to quantum particles that are undetectable by measurement. They are local but do not agree with conventional quantum mechanics pedagogy, and if they do—then they are not local (Bell, 1987).

Specifically, Bell deduced that if measurements were performed on entangled particles, then the assumption that outcomes would depend upon hidden variables implies mathematical constraints on how measurements correlate. Bell showed that quantum mechanics predict correlations that violate this inequality and that no local hidden-variable theories can reproduce statistical predictions of quantum mechanics.

Entering the 1970s, optical experiments had advanced to a degree that allowed robust testing of Bell’s theorem. Kocher and Commins demonstrated that an atomic cascade of calcium atoms was a practical source of polarized correlated photons (Kocher and Commins, 1967). This research catalyzed the team of Freedman and Clauser to measure linearly polarized correlated photons emitted in such a cascade (Freedman and Clauser, 1972). By employing a generalization of Bell’s inequality, they showed that the existence of local hidden variables imposed restrictions upon observed correlations in conflict with predictions of quantum mechanics. Their findings supported a quantum mechanical description of the Universe violating these restrictions to an unprecedented statistical accuracy against the existence of local hidden variables.

Aspect et al. followed in 1982, measuring linearly polarized entangled-photon pairs using time-varying analyzers and acousto-optical switching supporting a violation of Bell’s inequality to a statistical accuracy greater than five standard deviations (Aspect et al., 1982).

Zeilinger’s group further advanced experimental work in multiparticle violations of Bell’s inequalities (Greenberger et al., 1990) and provided important foundational contributions to quantum teleportation (Bouwmeester et al., 1997a).

As a result of their seminal contributions, Aspect, Clauser, and Zeilinger shared in the 2022 Nobel Prize in physics “for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science” (Nobel Prize, 2022).

From these studies and others, it has been shown that the only manner in which hidden variables can explain predictions of quantum physics is if they are inherently nonlocal, or in other words, entangled particles are able to interact instantaneously across immense distances (Mermin, 1993). This profound declaration provides guardrails for much of the present and future development of modern quantum theories, models, and technologies.

4 Early concepts of quantum computers and information theory

Circa 1960, Feynman reasoned that because classical physics is local, causal, and deterministic, classical computers are only adequate in solving problems of similar character. However, where quantum systems are inherently nonlocal sand indeterministic, he proffered one must bring to bear computers of similar nondeterministic properties, that is, quantum computers, to solve quantum problems (Feynman, 1982).

This concept was embodied in the work of Paul Benioff, who laid the foundation of quantum computing with his work (Benioff, 1980) describing a quantum mechanical model of Turing Machines⁵ (Wikipedia, 2023), based on Schrödinger’s formulism that was motivated in part by the classical description of reversible Turing machines by Charles Bennett of IBM (Bennett, 1973).

However, identifying Benioff’s work as the launch point of quantum computing and bestowing upon him the title “Father of quantum computing” would not be without challenge.

David Deutsch, circa 1985, described Bennioff’s work as “quantum kinematics and dynamics, but effectively classical…” (Deutsch, 1985) Deutsch further defined a universal quantum computer as being capable of “perfectly simulating every finite, realizable physical system…with high but not perfect accuracy” (Deutsch, 1985). In that same article, he introduced the first quantum algorithm designed to run on a quantum computer and proposed the use of entangled states as quantum keys. These contributions have led many to assign Deutsch the mantle of “Father of Quantum Computing” (Quantumzeitgeist, 2022).

In 1988, Yamamoto and Igeta proposed the first physical validation of a quantum computer incorporating Feynman’s controlled NOT (CNOT) gate (Igeta and Yamamoto, 1988). Their approach was the forerunner of modern quantum computers and networking protocols using photons to transmit qubits and atoms to perform two-qubit operations.

4.1 The DiVincenzo criteria

Moving from theoretical to experimental manifestations of quantum computers, DiVincenzo published an article in 1996 entitled: “Topics in Quantum Computing” (DiVincenzo, 2000), where he outlined five requirements for creating a tangible quantum computer. His criteria have guided much of the experimental research developing quantum computers ever since, allowing for the realization of the ambitions of many quanta computational theorists (Pérez-Delgado and Kok, 2011-01). These requirements have been canonized as the DiVincenzo criteria and state that a quantum computer must consist of the following:

1. A scalable physical system with well-characterized qubits,

2. The ability to initialize the state of the qubits to a simple fiducial state,

3. A universal set of quantum gates,

4. Long relevant decoherence times, much longer than the gate-operation times, and

5. A qubit-specific measurement system (Bohm and Aharonov, 1957).

4.2 Development of qubits

In accordance with DiVincenzo’s first and second criteria, qubits must be initialized to a well-defined and understood (fiducial) state.

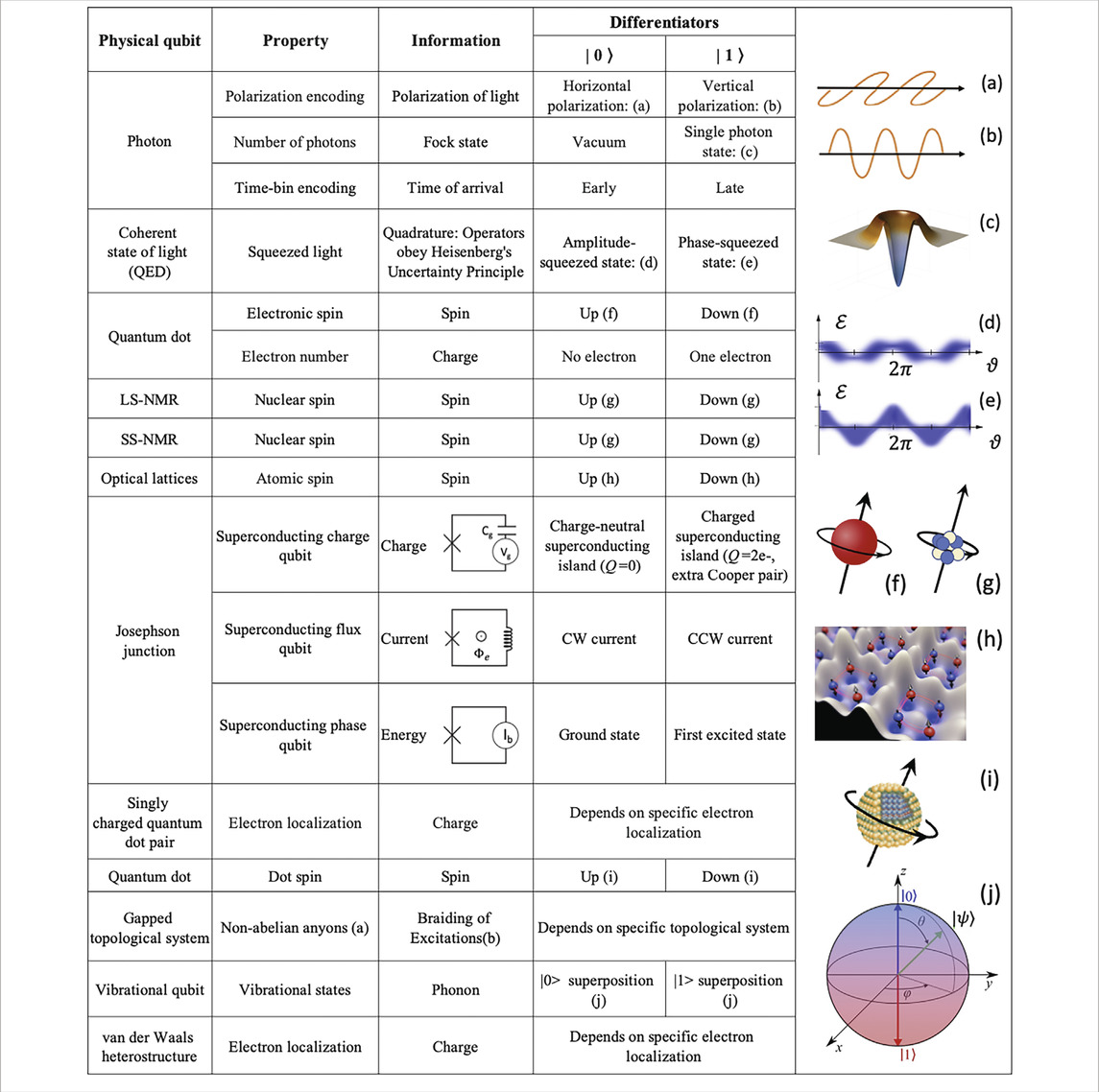
By definition, a qubit is a basic unit of quantum information that can be any two-level, that is, two-state, system that can exist in superposition. (The name qubit was contrived in 1995 by Schumacher, who shares credit with his colleague Wootters (Schumacher, 1995).) Further, whereas in a classical system, a bit would exist in a well-defined state of “1” or “0,” the qubit may exist as a “1” or “0” or a superposition of both states. This quantum mechanical property is described using a geometrical representation of the pure state space in Hilbert space, referred to as a Bloch sphere (see Figure 4).

Figure 4

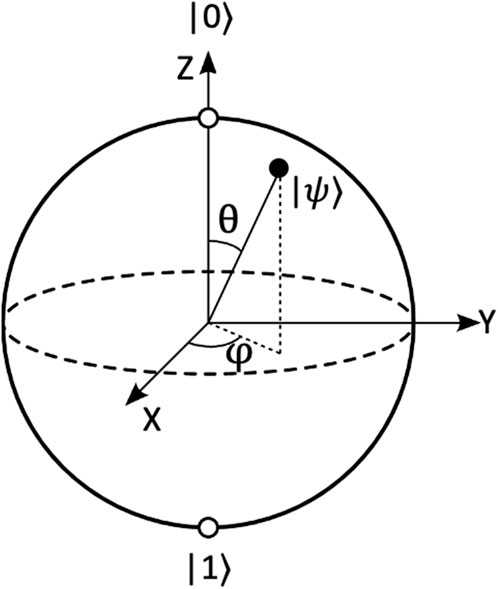
Figure 4. Bloch sphere representation of the pure state space of a two-level quantum mechanical system such as a qubit.

For a two-dimensional Hilbert space, the space of all such states is the complex vector. The north and south poles of the Bloch sphere are assigned to standard quantum basis vectors, |0⟩ and |1⟩, respectively. When applied to an electron qubit, the poles would correspond to spin-up ↑ and spin-down ↓ states of the electron, respectively. The points on the surface of the sphere correspond to pure states of the system, whereas the interior points correspond to mixed states.

In further consideration of an electron as a qubit, under the application of a magnetic field, the electron spin will polarize down ↓, while after exposure to microwave energy, the spin aligns up ↑. If the microwave pulse is terminated between transitions, the spin may exist in a state of superposition (Eq. (2)), such that:

${\displaystyle \sum _x}\psi \left(x\right)\left|x⟩\right.〉(2)$

where $\psi \left(x\right)$ represents the electron wavefunction, summing over all infinite terms. This equation completely describes the quantum state of the electron. A qubit having both position and spin would be described as Eq. (3):

${\displaystyle \sum _x}\psi +\left(x\right)\left|x,\uparrow ⟩\right.〉+\psi -\left(x\right)\left|x,\downarrow ⟩\right.〉(3)$

If one generalizes this term for a particle that can be in any one of infinitely many discrete positions, the superposition principle informs Eq. (4):

${\displaystyle \sum _x}{\psi }_n\left|n⟩\right.〉(4)$

This expression gives rise to the state vector in Hilbert space, an infinite-dimensional complex vector space. The sum of the state’s absolute squares of the amplitudes must sum to unity (Eq. (5)) (Wikipedia, 2022g).

${\displaystyle \sum }{\psi }_n^{*}{\psi }_n=1(5)$

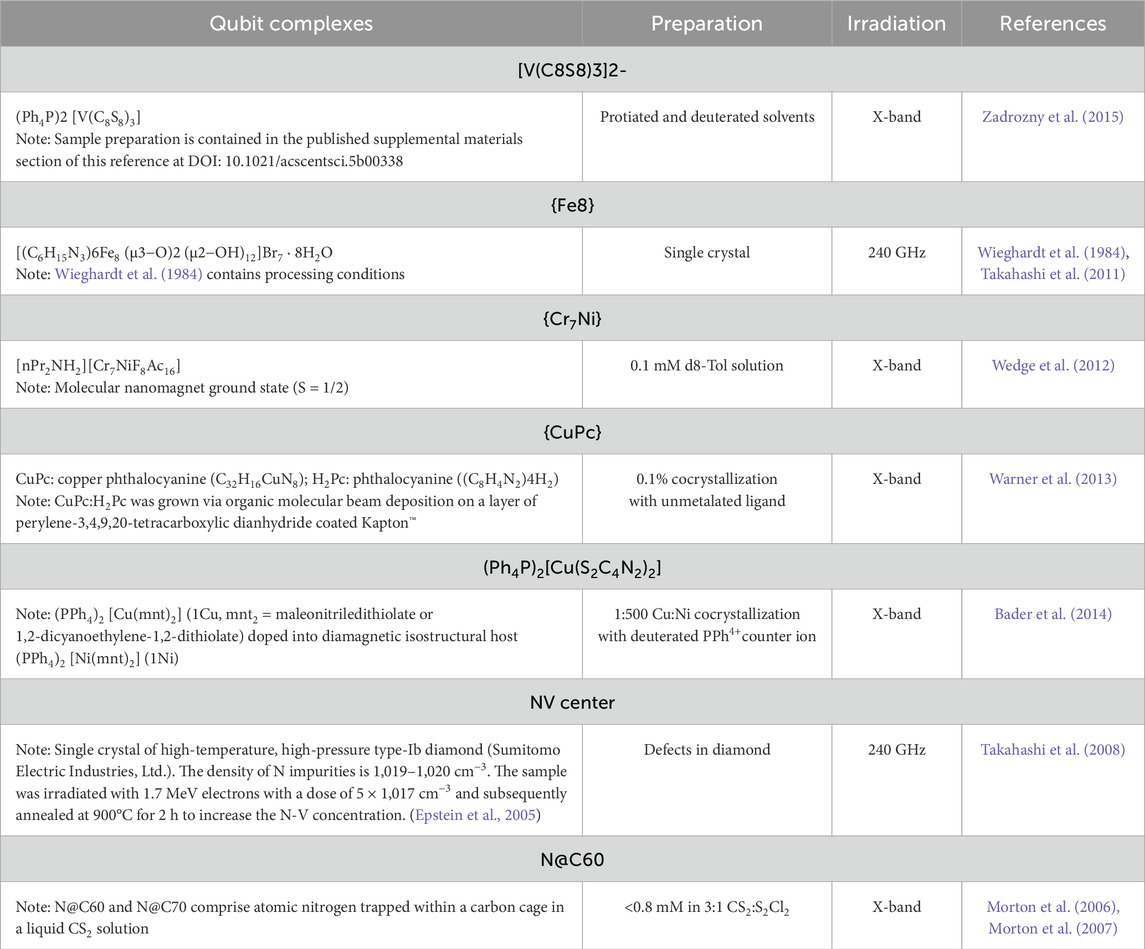
Researchers have implemented qubits as several physical manifestations, including:

• Photonic qubits,

• Spin qubits (including spin–orbit qubit),

• Superconducting qubits as charge, flux, and phase qubits,

• Vibrational qubits,

• Topological qubits, that is, anyons,

• Trapped ions,

• among other variants.

A key attribute of qubits is their coherence, or rather, their ability to retain quantum information. The loss of such information is referred to as decoherence. If qubits remain perfectly isolated from their environment, then coherence will be maintained for prolonged periods. However, as soon as a qubit is allowed to interact with its environment, quantum decoherence occurs. The rate of decoherence depends upon the degree of coupling by the qubit to its environment and its intrinsic stability to encode quantum information. As with any quantum-coupled system, entanglements are generated between the system and its environment and its measurement (i.e., in accordance with the Copenhagen Interpretation).

Guided by the DiVincenzo criteria, the development of modern quantum computers has been enabled by the rapid advance of qubit modalities and their coherence and subsequent computational fidelities. We delve more deeply into these concepts later in this article.

To better understand the differences between quantum annealing and gate-based adiabatic quantum computers (AQC), problems must be expressed in terms of quantum gates and associated quantum circuitry.

4.3 Quantum logic gates

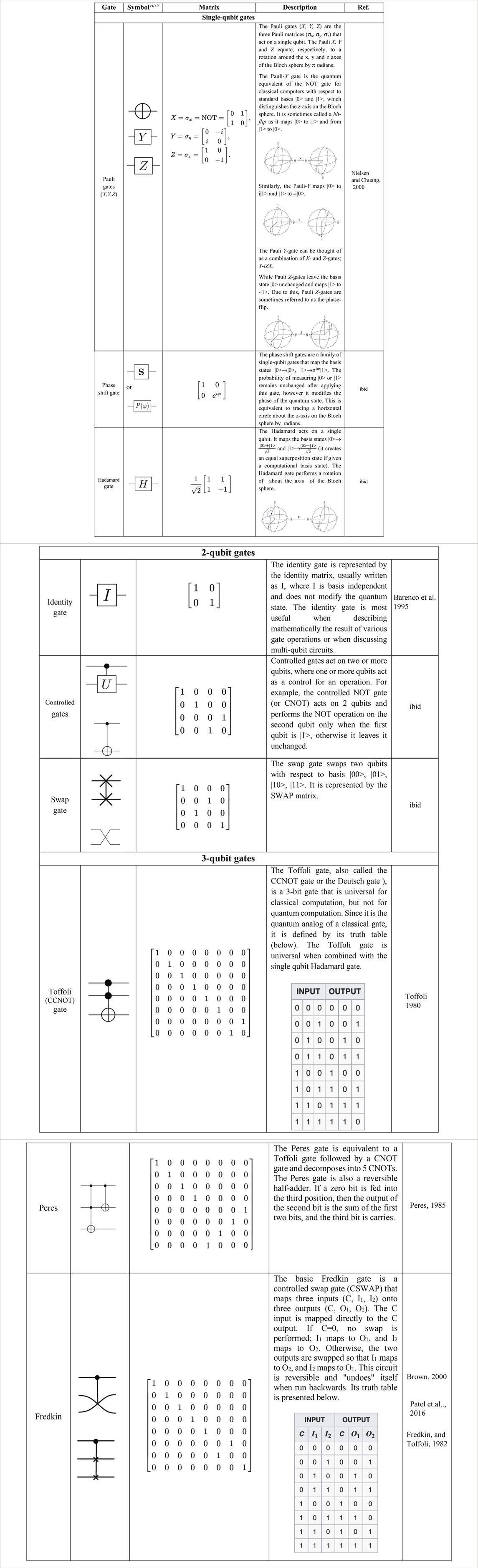
Although this article focuses predominantly on quantum materials, a brief review of quantum logic gates and circuitry is called for to provide the reader with the necessary background in quantum information theory to appreciate the overall import and impact of QMs.

Unlike many classical logic gates, all quantum logic gates are reversible. It is possible to perform classical computing operations using only reversible gates. For example, the reversible Toffoli gate can implement all Boolean functions, often at the cost of having to use ancilla bits. The Toffoli gate has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits.

Quantum logic gates are represented by unitary matrices, such that a gate that acts on n is represented by the unitary matrix, and the set of all such gates with group operation of matrix multiplication represents the symmetry group U (2ⁿ). The quantum states that gates act upon are unit vectors in 2ⁿ complex dimensions, with complex Euclidean norm (the 2-norm) (Nielsen and Chuang, 2000; Yanofsky and Mannucci, 2013). The basis vectors, that is, eigenstates, are possible outcomes when measured, and a quantum state is a linear combination of such measurements. Although common quantum gates operate on vector spaces of one or two qubits, quantum gates are now being developed to act on three or more qubits.

Figure 5 presents a list of some common gates categorized as operating on one, two, and three (or more) qubits. Further, Table 1 provides a further subset of these gates in which details such as symbols, permutation matrices, operational descriptions, and, when appropriate, truth tables are presented. Even though quantum logic gates belong to continuous symmetry groups, their implementation as hardware is inexact and introduces errors that lead to the degradation of quantum-state fidelities. When error-correction stratagems are employed, gates are further restricted to finite sets (Bennett, 1973; Williams and Clearwater, 1998).

Figure 5

Figure 5. Some popular gates as Clifford and non-Clifford classification. The reader is directed to the text for further description.

Table 1

Table 1. Expanded properties of some common quantum gates.

Progress has been made on some gate classifications (Grier and Schaeffer, 2022). For example, Bouland et al. (2016) classified all 2-qubit commuting Hamiltonians, while Childs et al. (2010) characterized all 2-qubit Hamiltonians that are restricted to circuits over two qubits. Bouland and Aaronson (2014) completed a classification for linear optics of 2-mode beam splitters, while Amy et al. (2020) provided a classification for Clifford + T circuits based on elements appearing as unitary matrices.

In Figure 5, some popular gates are presented as Clifford and non-Clifford. In quantum computing and information theory, Clifford gates are elements of the Clifford group, a set of transformations that normalize the n-qubit Pauli group. The concept was introduced by Gottesman and is named after the mathematician William Clifford (Gottesman, 1998a). Quantum circuits that consist of Clifford gates can be readily simulated with a classical computer due to the Gottesman–Knill theorem (GKT)⁷.

Clifford gates are further notable in that they are pivotal to the development of a universal quantum computer. For instance, the stabilizer formalism that tracks state evolution through conjugated Pauli elements is the foundation of several quantum error-correction stratagems (Gottesman, 2010).

There have been many variants involving entangling two-qubit gates with superconducting qubits.

The gates can be classified into two classes. One class contains gates that rely on the dynamical flux-tunability of either the underlying qubits or some separate sub-circuitry. This class includes the direct-resonant iSWAP (Bialczak et al., 2010; Dewes et al., 2012) and the higher-level resonance-induced dynamical c-phase (DP) (DiCarlo et al., 2009; Barends et al., 2014a) gates.

The second class contains gates in which the qubits have fixed frequencies and microwave activation sources. The gates in this class include the resonator side-band-induced iSWAP (Leek et al., 2009), the cross-resonance (CR) gate (Chow et al., 2012), the Bell–Rabi gate (Poletto et al., 2012), the microwave activated phase gate (Chow et al., 2013), and the driven resonator induced c-phase (RIP) (Cross and Gambetta, 2015).

5 Quantum Annealers, Analog Quantum Simulators, and Universal Quantum Computers

There are three different types of quantum computers: quantum annealers (adiabatic quantum computers, or AQCs), analog quantum simulators (AQS; or analog quantum computers), and universal quantum computers.

Quantum annealers are defined as generic solvers of optimization problems such as QUBO⁸ problems (Wikipedia, 2022f). Researchers are actively defining ways to improve design efficiencies and application value. Notwithstanding such timely advances, quantum annealing is projected to remain the least powerful and most inflexible of the present quantum computing paradigms.

In contrast, analog quantum simulators (or analog quantum computer) are asserted as powerful and flexible quantum computing platforms. They are anticipated to be employed to solve some of the most challenging problems in drug design, biochemistry, and quantum theory.

Finally, universal quantum computing is the ultimate manifestation of analog quantum computers that will access arrays of upward of 10⁶ entangled qubits. The principal idea behind universal computing is to vector computational power to the most thought-provoking problems of yet unimagined complexity (Essential, 2022).

5.1 Quantum annealers and adiabatic quantum processors

In our physical or classical experiences, we observe that time-evolving systems attempt to attain a minimum free energy. For example, in the case of metallurgy, temperature and time are used in concert to create time-varying thermal gradients to enhance atomic mobility, allowing for grain size refinement (e.g., via Ostwald ripening) and the annihilation of defects leading to desired morphologies and microstructures.

Quantum annealing originated from theoretical research performed in the 1980s and 1990s (Apolloni et al., 1988; Apolloni et al., 1989; Ray et al., 1989) and replaces time-varying thermal gradients described in our metallurgy example with quantum thermal fluctuations. Its central importance is in addressing problems of system optimization where energy minimization of a problem-specific Hamiltonian is employed. For our purposes, quantum annealing is analogous to adiabatic quantum computations (analog quantum computers) that rely on the adiabatic theorem to perform calculations (Farhi et al., 2000).

When considering the minimization of a target variable, the fundamental goal is to guide the system to avoid local minima and attain the global minimum. D-Wave Systems of Canada has made quantum annealing computers available to commercial markets. Their platforms also run Qbsolv, which is open-source software that solves quadratic unconstrained binary optimization (QUBO) problems on D-Wave’s quantum processors (D-Wave Initiates Open Quantum Software Environment, 2022a). D-Wave employs superconducting phase qubits for their quantum annealing computers (Harris et al., 2010a; Next Big Future, 2022). Figure 6 is a photograph of D-Wave Systems’ chip designed to operate as a 128-qubit superconducting adiabatic quantum optimization processor (QCI, 2022).

Figure 6

Figure 6. Photograph of a 128-qubit superconducting adiabatic quantum chip constructed by D-Wave Systems, Inc. (Used with permission of D-Wave Systems, Inc. under Creative Commons Attribution 4.0 International License).

In superconducting qubit modalities, electron wavefunctions allow for quantum tunneling through potential barriers instead of electrons imagined as particles jumping over such barriers governed by classical mechanics. Such quantum annealing processes take place over relatively long time durations. If a too-slow tempering is applied, a greater cost is incurred in terms of computing power, working memory, and processing time (Wikipedia, 2022a).

In quantum annealing, the system begins in the lowest energy eigenstate of the initial problem-specific Hamiltonian. Ideally, it stays in the minimum energy state throughout the quantum annealing so that by the end of the process, it is in the minimum energy state of the Hamiltonian and, therefore, has an answer to the problem at hand. For this reason, prolonged qubit coherence is required.

A classical Hamiltonian is a mathematical representation of a physical system in terms of its energies. One can input any particular state of the system, and the Hamiltonian returns the energy for that state. For most non-convex Hamiltonians, finding the minimum energy state is an NP-hard⁹ problem that classical computers cannot solve efficiently.

For a quantum system, the Hamiltonian maps certain states, called eigenstates, to energies. Only when the system is in an eigenstate of the Hamiltonian is its energy well defined and called an eigenenergy. The collection of eigenstates with defined eigenenergies makes up the eigenspectrum. In quantum annealing, for every unique problem, there is a unique Hamiltonian and a unique eigenspectrum. A plot illustrating quantum annealing as eigenenergies versus time is plotted in Figure 7 (Dwavesys, 2022).

Figure 7

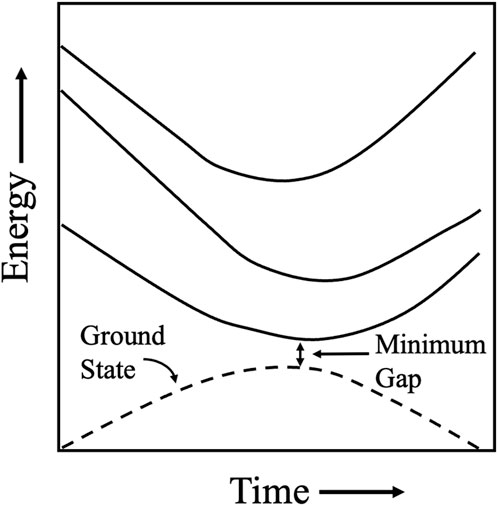
Figure 7. A schematic illustrating quantum annealing as eigenenergies versus time. The ground state is at the bottom of the energy axis, and the excited states appear above. During the anneal the first excited state approaches the ground state and diverges. The minimum distance between the ground state and the first excited state in the anneal defines the minimum gap. Adapted from: https://docs.dwavesys.com/docs/latest/c_gs_2.html# eigenspectrum accessed Dec. 23, 2022.

As the problem-specific Hamiltonian is introduced, other energy levels shift closer to the ground state, increasing the likelihood that a transition to an excited state occurs. Certain external conditions induce these transitions, including thermal fluctuations of the physical system brought on by coupling to its environment or running the annealing process too quicky. An annealing process that is isolated from external influences allows the Hamiltonian to evolve slowly; this is called an adiabatic process. Because no computation exists in perfect isolation, quantum annealing can be thought of as a close approximation of an adiabatic quantum computers (AQC). The most difficult problem in terms of quantum annealing stems from systems that possess very low minimum gaps where inadvertent jumps may take place.

D-Wave Systems believes the combination of quantum annealing, gate-based quantum computing, and classical machines is what business users will require in the coming decades to solve mixed integer problems to enable rapid drug design and development and chemical process optimization, logistics, scheduling, and related optimization problems.

5.2 Gate-based analog quantum computers

Several leading electronics companies, such as Google, IBM, and Intel, have built analog quantum computers based on gate-model designs.

These devices typically function at very low temperatures, requiring expensive and large He³⁺ dilution refrigeration instrumentation to minimize the deleterious influence of heat upon qubit coherence.

In analog quantum computers, processing power increases relative to classical computers, where n is the number of qubits. So, if the platform has three qubits, a processing power enhancement of 2³, or 8x, results relative to a classical computer. Google’s Sycamore, with 53 qubits, or 2⁵³∼9¹⁵ (Nielsen and Chuang, 2000) over classical computers. In 2019, Google claimed that the Sycamore would take 200 s to complete a calculation that a supercomputer of that day would take 10,000 years to complete, thus claiming to have achieved quantum supremacy¹⁰ (Harrow and Montanaro, 2017; Kan, 2019). IBM countered that the task would have only taken a mere 2.5 days on a classical platform (On Quantum Supremacy, 2019). Since then, Google has pursued several validation experiments of Sycamore’s computational power and utility, including:

• In 2020, a Google research team reported the results of the application of a variational quantum eigensolver (Peruzzo et al., 2014) that approximated the binding energy of H⁺ ion chains in diazene by application of the Hartree–Fock formulism performed on Sycamore¹¹.

• In April 2021, researchers working on Sycamore reported the simulation of anyon interferometry and braiding statistics of topologically ordered states demonstrating long-range entangled properties (Satzinger et al., 2021).

• In July 2021, a Google collaboration using Sycamore reported on the many-body localization configuration of up and down spins stimulated with a laser to achieve a periodically driven floquet system. Because no energy was absorbed from the laser, the system remained in a protracted eigenstate such that it represented a time crystal¹² (Zakrzewski, 2012; Wolchover, 2021; Mi et al., 2022).

• In 2022, Sycamore was used to simulate traversable wormhole dynamics (Jafferis et al., 2022).

All major quantum-dot cellular automata (QCA) companies are striving to scale up their quantum computational platforms with the ultimate goal of attaining a mega-qubit computer.

As illustrated in Figure 8, the growth of the quantum annealer product market is driven by D-Wave Systems. From 2007 to 2022, D-Wave Systems experienced near-exponential growth, with platforms boasting qubits of 128 in 2007 (D-Wave 1) to 5,640 in 2020 (Advantage). D-Wave expects to launch its next Advantage-2 machine with over 7,000 qubits, featuring a new connectivity topology, in 2024. In 2011, D-Wave began selling its platforms to U.S. government agencies, organizations, and NGOs, including Low-Cost Mission Operations (LCMO), Google, NASA, and the Los Alamos National Lab (LANL).

Figure 8

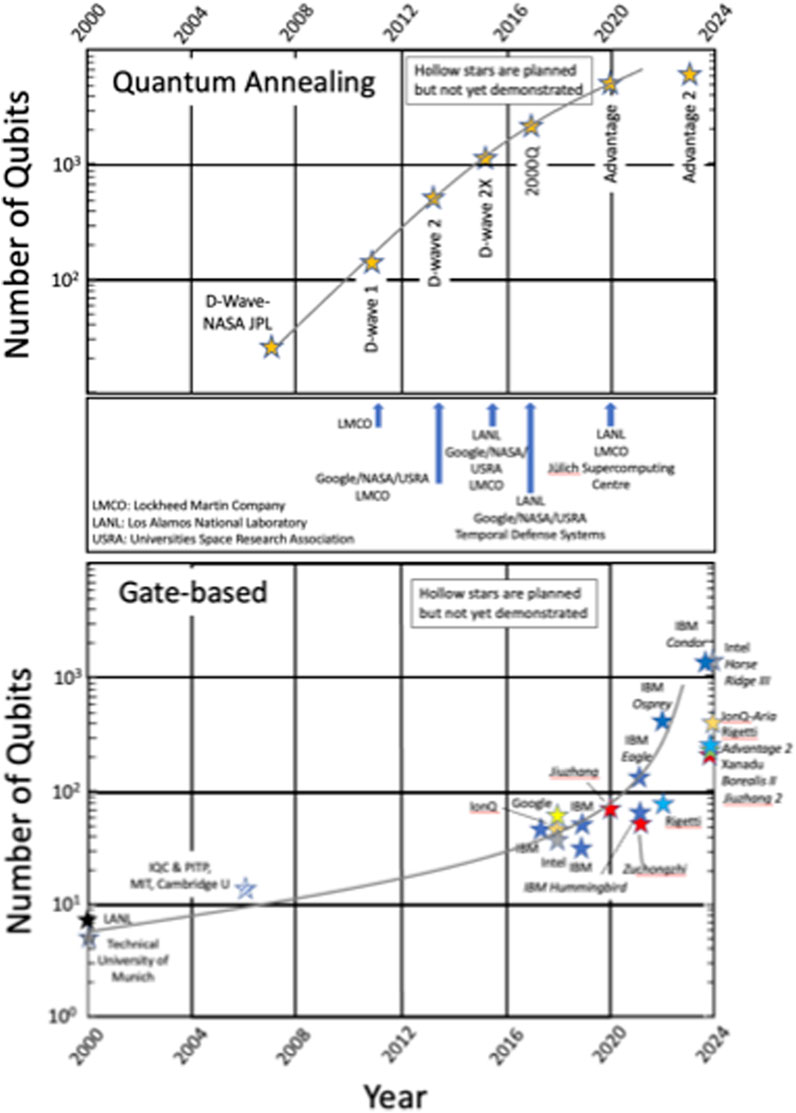
Figure 8. A comprehensive illustration of the time evolution of qubit-based quantum annealing (top) and AQCs (bottom) quantum computational platforms up to 2022 (and projected beyond). Industrial sources are denoted for each, and, in some cases, industrial buyers are noted (middle).

Figure 8 presents the evolution of quantum computer advances as a function of the number of incorporated qubits. We note that the number of qubits does not necessarily translate to the number of active qubits in coherence or perfect fidelity. Here, advances in quantum annealing demonstrated by D-Wave Systems are presented in the top panel, whereas gate-based quantum computer advances are presented in the bottom panel for the many companies participating in this market segment. Further, the commercialization of D-Wave Systems’ products is reflected beneath the top panel. We remind the reader that gate-based quantum computers are referred to here as analog quantum computers or analog quantum computers.

The first generation of analog quantum computers occurred in 1998 with the introduction of the first working 2-qubit quantum computer based on a liquid-state nuclear magnetic resonance (LS-NMR) qubit modality that employed a solution of chloroform molecules (Chuang I. L. et al., 1998). Soon afterward, circa 2000, researchers demonstrated a 5-qubit (Vandersypen et al., 2000) NMR quantum computer using perfluorobutadienyl complexes and a 7-qubit (Knill et al., 2000) NMR quantum computer using transcrotonic acid with a second 7-qubit NMR quantum computer. Vandersypen et al. (2001) demonstrated using a perfluorobutadienyl iron complex with two inner carbon ions.

The first 12-qubit quantum computer was demonstrated by researchers at the Institute for Quantum Computing and the Perimeter Institute for Theoretical Physics in Waterloo in collaboration with MIT and Cambridge University (Science Daily, 2006).

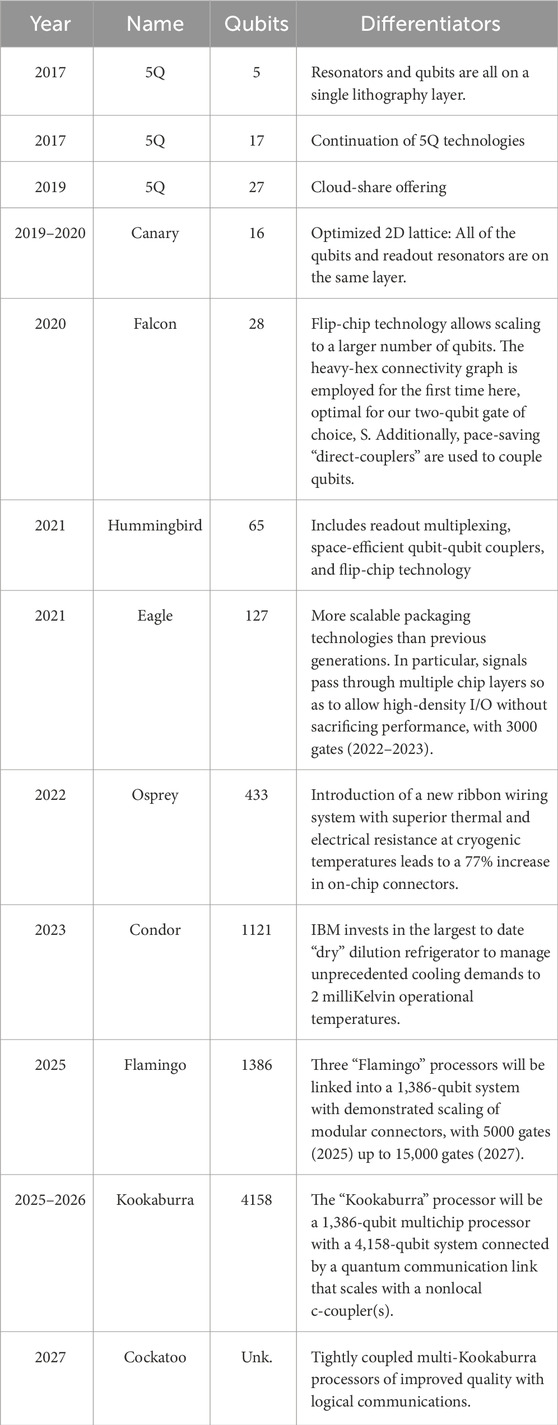
The years 2017–2019 saw a plethora of activity in large-qubit AQC platforms from Google, IBM, Intel, and IonQ. The evolution of IBM platforms is presented in Table 2 with details of their designation, number of qubits, and other differentiators.

Table 2

Table 2. Evolution of qubit technology.

In late 2022, IBM released Osprey, a 433-transmonic-based qubit analog quantum computers boasting a new ribbon wiring modality, depicted in Figure 9A, with enhanced electrical and thermal resistance at cryogenic temperatures, leading to a 77% increase in on-chip connections to replace their famous “chandelier” design as depicted in Figure 9B (SCL, 2022).

Figure 9

Figure 9. The Osprey cryogenic “ribbon” wiring system of enhanced electrical and thermal resistance leads to a 77% increase in on-chip connectivity. (Photograph courtesy of Connie Zhou, (Hu, 2022)). (B) The quantum “chandelier” of IBM is prior art. (Photograph courtesy of Peter Garritano, (Brooks, 2024)).

While IBM and Google invested in superconducting qubits (i.e., transmons and other forms), IonQ adopted trapped-ion technology (Maunz, 2016). Their work consisted specifically of a laser-cooled 32 × 1 (Ma X. S. et al., 2012) Yb⁺ ion-chain trapped above a microfabricated chip. Each physical qubit was encoded in ²S_1/2 electronic ground-state hyperfine “clock” states, |0>≡ |F = 0; m_F = 0>, |1>≡ |F = 1; m_F = 0, with a qubit frequency splitting of ω₀ = 2π ×12.642820424 (4) GHz. The qubits have a measured decoherence time in excess of 2.75 s, limited by the stability of the external magnetic field, and an average single-shot detection fidelity of >99.5% (Egan et al., 2020; Wikipedia, 2022c).

Other key players in quantum computational platforms are Xanadu (photonic qubits), Rigetti (superconducting qubits), Intel (“hot” silicon spin qubits (Petit et al., 2020)), Baidu (superconducting qubits), and Google and Microsoft (topological qubit). Note: The qubit modality is presented in parentheses after each company.

Finally, we report the demonstrations and breakthroughs by Chinese scientists in this realm of quantum physics. Competition in quantum computing between the United States and China, the two dominant global economies, and other international players has resulted in an expansion of the international market size in quantum technologies from USD 10 B in 2021 (Quantum Technology Market Size, 2022b). In addition to the investments made in the private sector, the U.S. government has invested billions in quantum projects sponsored by the Department of Energy (DOE), the Defense Advanced Research Projects Agency (DARPA), and the National Security Agency (NSA), among others.

The Chinese government has kept pace with domestic investments in quantum computing with the creation of a National Laboratory for Quantum Information Science (Quantumcomputing, 2022). Additionally, Alibaba has invested USD 15 B to establish the Academy for Discovery, Adventure, Momentum, and Outlook, which includes new research laboratories in China, the United States, Russia, Israel, and Singapore (Techinasia, 2022).

Representing China’s advances, in 2019, Jiuzhang became the first photonic quantum computer to claim quantum supremacy. Jiuzhang was developed by researchers at the University of Science and Technology of China (USTC) led by Pan and Lu (Conover, 2020-12). Previously, quantum supremacy had been achieved by Google’s Sycamore based on superconducting qubits (Kan, 2019).

In December 2020, USTC announced that Jiuzhang performed a Gaussian boson sampling in 200 s. The USTC group estimated that it would take 2.5 billion years for the Sunway to perform the same calculation (Ball, 2020-12; Letzter, 2020).

5.3 Universal quantum computer (a quantum turing machine)

A universal quantum computer, sometimes referred to as a quantum Turing machine (QTM), harnesses the power of quantum computation by implementation of quantum algorithms. QTMs relate to the classical, or probabilistic, Turing machine by application of the transition matrix. A transition matrix is a square matrix whose elements are probabilistic values of each transition in a Markov chain (Asmussen, 2003; Lawler, 2006). As shown by Fortnow (2003) in the QTM example, a transition matrix is one in which its product with a matrix representing a classical machine delivers the probability matrix of the quantum machine. [NEW- https://en.wikipedia.org/wiki/Quantum_Turing_machine#cite_ref-transition_3-0].

The first description of a quantum mechanical model of a Turing machine was by Benioff in a pair of papers published in 1980 and 1982 (Benioff, 1980; 1982). Deutsch (1985) further suggested that quantum gates could function in a similar fashion to traditional digital computing binary gates.

IBM’S Condor, debuted in December of 2023, sports a quantum processor with 1,121 superconducting qubits, a 50% increase in qubit density with over a mile of high-density cryogenic flex wiring within its single dilution refrigerator. The Condor is believed to be the world’s first universal quantum computer [NEW- https://en.wikipedia.org/wiki/IBM_Condor. Accessed July 22, 2024].

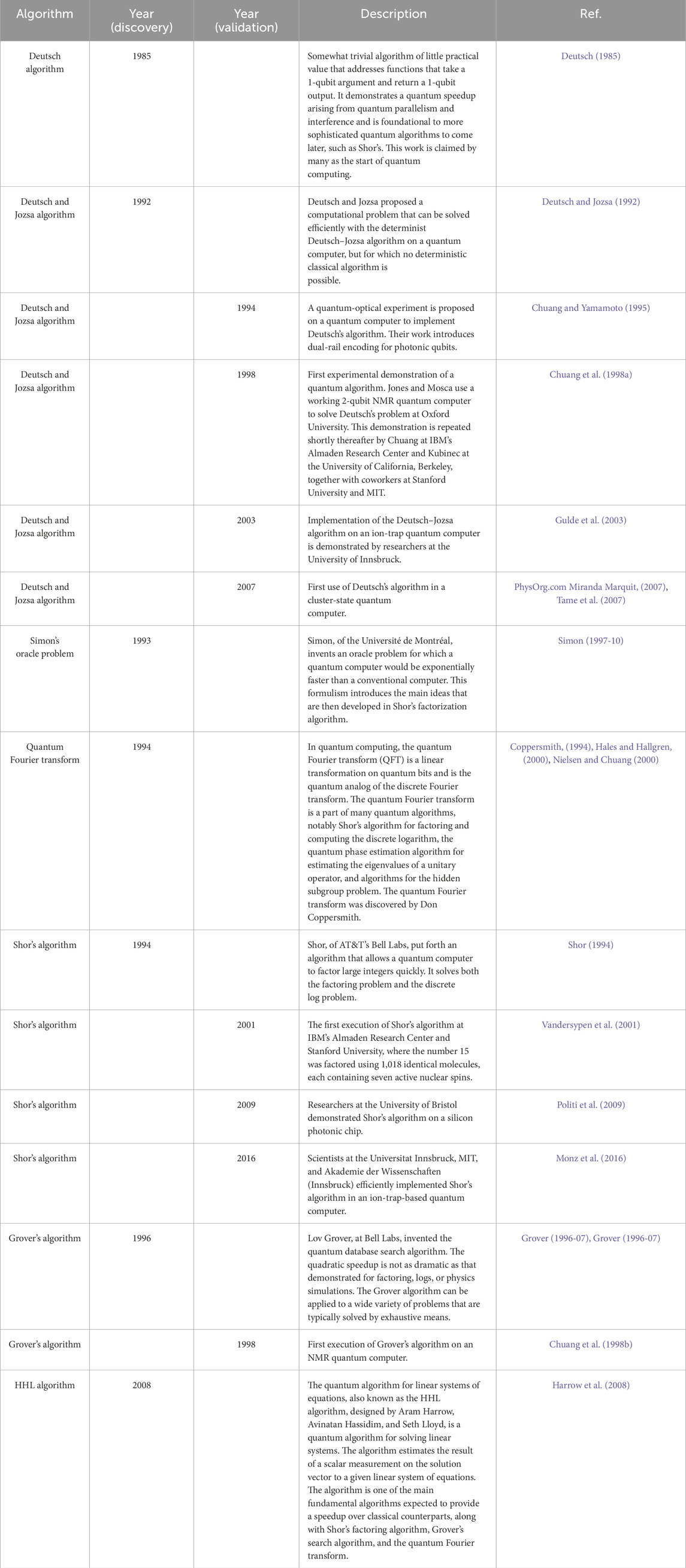
6 Quantum algorithms

Table 3 lists the major milestones in quantum algorithms that have occurred over the past 3 decades. Deutsch’s algorithm, reported in 1985, has been labeled by some as the start of quantum computing. However, this algorithm is overly simplistic, addressing functions of 1-qubit arguments and returning 1-qubit outputs; it finds little practical utility. As an extension of this work, in 1992, Deutsch and co-author Jozsa produced the landmark Deutsch–Jozsa algorithm (Deutsch and Jozsa, 1992), which is the first example of a quantum algorithm that is exponentially faster than any deterministic classical algorithm. In 1998, 2003, and 2007, teams of researchers validated the Deutsch–Jozsa algorithm in the laboratory using NMR, ion traps, and entangled-photon clusters, respectively (Kan, 2019; Ball, 2020-12; Letzter, 2020; Deutsch and Jozsa, 1992; Chuang and Yamamoto, 1995; Gulde et al., 2003).

Table 3

Table 3. Evolution of popular quantum algorithms (theory and experimental validation).

In 1994, Peter Shor of MIT, employing Coppersmith’s recently developed quantum Fourier transform, conceived a quantum algorithm that calculates prime factors of large numbers vastly more efficiently than classical computers (Simon, 1997-10). Researchers have since experimentally validated Shor’s algorithm. Specifically, validation was provided by a team featuring researchers from IBM and Stanford University employing spin-1/2 nuclei in a perfluorobutadienyl iron complex using room temperature liquid-state nuclear magnetic resonance; a team from the Centre for Quantum Photonics (Bristol, United Kingdom) carried out an elegant experiment on an integrated silica-on-silicon waveguide that guided four single-photon qubits; and a team of scientists at the Universitat Innsbruck, MIT, and the Akademie der Wissenschaften (Innsbruck) efficiently implemented Shor’s algorithm using an ion-trap-based quantum computer by effectively controlling seven qubits and four cache-qubits, together with implementation of generalized arithmetic operations, known as modular multipliers (Coppersmith, 1994; Shor, 1994; Hales and Hallgren, 2000).

In 1996, Lov Grover of AT&T Bell Labs conceived a quantum database search algorithm that presents a quadratic “speedup” for a variety of problems that are typically performed by brute force (Grover, 1996-07). In 1998, the first quantum computer, that is, a 2-qubit LS-NMR machine, demonstrated the Grover algorithm. Unlike other quantum algorithms, which may provide exponential speedup over classical machines, Grover’s algorithm provides only a quadratic speedup. However, even a quadratic speedup can be applied to increase the speed of broad classes of searches (Nielsen and Chuang, 2000).

7 Select quantum phenomena and technologies

In this section, we return to Figure 1 and more deeply examine select quantum phenomena related to emerging quantum technologies; these include entanglement and superposition, cavity- and circuit-based quantum electrodynamics, teleportation, tunneling, and spin–orbit interactions.

7.1 Entanglement and superposition

Quantum entanglement describes the state of two or more particles connected even when separated by vast distances. In principle, under these conditions, if one changes the properties of one particle, typically by measurement of one of its intrinsic properties such as spin or polarization, the properties of the entangled partner(s) change instantly. In theory, this would be the case even if the entangled particles are on opposite sides of the Universe—some ninety-two billion light years apart (Bars and Terning, 2018).

Entangled qubits become a system with a single quantum state. If you measure one qubit (i.e., collapse its superposition to a single state), you will have the same impact on other entangled qubits in the system.

Einstein rejected this phenomenon because such transmission of information, being spontaneous across vast distances, violates his prized fundamental constant—the speed of light (c), a concept he introduced in 1905 as a fundamental constraint upon all physical systems.

However, entanglement has since been extensively studied, and findings have brought into question the speed of light as a fundamental constant. Recently, Yin et al. investigated the continuous violation of the Bell inequality and concluded that the lower bound of the speed of light was as much as four orders of magnitude (×10,000) its value if Earth’s speed in an inertial reference frame is less than 10⁻³ times the speed of light (Yin et al., 2013).

Because the speed of light, as a constraint on physical systems, has been a pillar of physics since 1905 (Einstein, 1905f), any rigorous theory proposing a change c, supported by careful experimentation and withstanding rigorous peer review, would indeed be widely heralded.

Notwithstanding debates challenging the speed of light, entanglement continues to create opportunities in applied physics and engineering, specifically, for example, in enhancing the security of communications through quantum encryption. In this example, one considers a particle of an entangled pair to be sent as an encryption key. If a malign actor intercepts the transmission, this triggers an instant change in the remote quantum state of an entangled particle’s quantum state, resulting in the detection of the eavesdropping attempt (Ekert et al., 1994).

The state of superposition just introduced will next be discussed in greater detail. The state of superposition creates a near-infinite range of possibilities, a smearing of classical determinism. Quantum superposition is a theory that quantum particles simultaneously exist in a multiplicity of quantum states. This phenomenon is responsible for numerous properties that are key features of quantum theory, including quantum interference (Anderson and Kasevich, 1998), entanglement, and teleportation (Pirandola et al., 2015).

The in-phase summation of delocalized wavefunctions is responsible for quantum coherence, a feature of quantum states (Baumgratz et al., 2014), as well as providing the underlying foundations for ultrafast quantum algorithms such as the Deutsch–Jozsa algorithm (Deutsch and Jozsa, 1992), the Shor algorithm (Shor, 1997), the Grover algorithm (Grover, 1996), quantum cryptography (Gisin N. et al., 2002), and quantum metrology (Giovannetti et al., 2011), among others.

7.2 Quantum teleportation

Quantum teleportation describes the communication of quantum information from source to target locations without this information being classically transferred between sites. It is noteworthy that matter and energy cannot be teleported without passing through an intermediate location. However, teleportation of quantum states is indeed possible: only quantum states are teleported—physical matter remains at the source and must be already present at the target location.

In this context, classical communications include, for example, conventional radio frequency (RF) wireless systems. The quantum state in classical communication is irrelevant because the information transfer is intrinsically decoherent.

However, in 1993, Bennett et al. (1993) proposed that a quantum state of a particle could be transferred to a distant particle without physical displacement of either particle or the classical communication of information by electromagnetic signals or other means. This has become the basis of quantum teleportation that has since been explored theoretically and experimentally (Bouwmeester et al., 1997b; Werner, 2001).

Specifically, quantum teleportation has been verified in laboratories using a wide variety of qubit modalities including photonic qubits (Bouwmeester et al., 1997c; Boschi et al., 1998; Kim et al., 2001; Ursin et al., 2004; Jin et al., 2010; Ma X. S. et al., 2012; Yin et al., 2012) (as single rail (Giacomini et al., 2002; Lombardi et al., 2002) and dual rail (Fattal et al., 2004; Metcalf et al., 2014) as well as time-bin (Marcikic et al., 2003; de Riedmatten et al., 2004; Landry et al., 2007)), spin-orbital (Wang et al., 2015), nuclear magnetic resonance (Nielsen et al., 1998), optical modes (Furusawa et al., 1998; Bowen et al., 2003; Zhang et al., 2003; Takei et al., 2005a; Takei et al., 2005b; Yonezawa et al., 2007; Yukawa et al., 2008; Lee et al., 2011; Takeda et al., 2013), atomic ensembles (Sherson et al., 2006; Chen et al., 2008; Bao et al., 2012; Krauter et al., 2013), trapped atoms (Barrett et al., 2004; Riebe et al., 2004; Riebe et al., 2007; Olmschenk et al., 2009; Nölleke et al., 2013), and various other solid-state systems (Gao et al., 2013; Steffen et al., 2013; Bussières et al., 2014a; Pfaff et al., 2014).

Due to the successes of quantum teleportation experiments, it has rapidly become a keystone to quantum information networks. It contributes meaningfully to a variety of quantum information protocols, including quantum repeaters (Briegel et al., 1998), quantum teleportation networks (Xu et al., 2016), quantum gate teleportation (Pan et al., 1998; Gottesman and Chuang, 1999; Raussendorf and Briegel, 2001; Makino et al., 2016; Su et al., 2016; Bouchard et al., 2017), and quantum computation and communication systems (Pan et al., 2012; Pirandola et al., 2015; Xia et al., 2017).

However, the further realization of a global quantum network, the ultimate prize of this community, will require demonstrated high-fidelity quantum teleportation over great distances. Teleportation employing optical fibers in tandem with free-space channels (Bouwmeester et al., 1997d; Landry et al., 2007; Ma et al., 2012; Yin et al., 2012; Sun Q.-C. et al., 2016; Valivarthi et al., 2016) is typically limited to 100 s of kilometers due to degradation of signal fidelity by environmentally induced interference or loss of photons within the optical fibers (Ursin et al., 2007). Next, we delve deeper into advances in optical-fiber- and free-space-based quantum teleportation efforts.

Proposed in 1984, quantum key distribution (QKD) allows two users to exchange provably secure keys via a potentially insecure quantum channel (Bennett and Brassard, 1984). On the application front, however, the operating distance of practical fiber-based QKD systems is limited to about 150 km (Lo et al., 2014), mainly due to the high background noise of practical single-photon detectors (Hadfield, 2009; Eisaman et al., 2011) and inefficient finite-key security analysis (Scarani and Renner, 2008; Tomamichel et al., 2012; Lim et al., 2014).

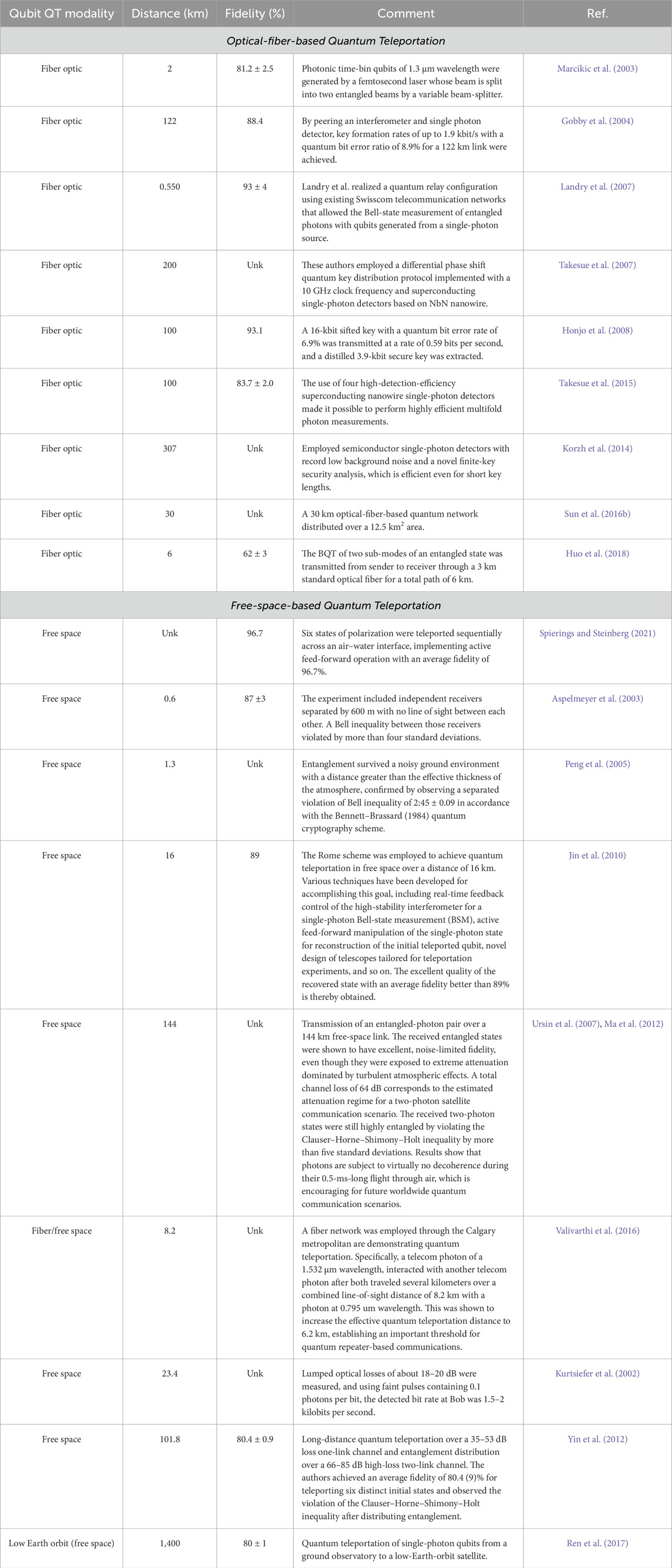
7.2.1 Optical-fiber-based quantum teleportation

Figure 4 presents the major demonstrations of fiber optic- and free space-based quantum teleportation. Presented are the distance traveled prior to qubit decoherence with measured fidelities together with commentary providing key insights to details of the experiments. Quantum key distribution (QKD) offers an unconditionally secure means of communication based on the laws of quantum mechanics. A major challenge in realizing a practical QKD system is to attain a 40 dB channel loss: This is required for global scale QKD networks using communication satellites.

As early as 2003, Marcikic et al. (2003) reported on a demonstration of probabilistic quantum teleportation of photonic time-bin qubits of 1.3 µm wavelength generated by a femtosecond laser whose beam is split into two entangled beams by a variable beam-splitter. The 1.3 µm photons were teleported onto photons of 1.55 µm wavelength from one location to another, separated by 55 m but connected by 2 km of standard optical telecommunications fiber. The overall mean fidelity was 81.2% ± 2.5%, a value six standard deviations greater than the maximum fidelity of 66.7% achievable using the best protocols using classical decoherent photon transmissions.

In 2004, Gobby et al. demonstrated a QKD over standard telecom fiber exceeding 100 km (Gobby et al., 2004). By peering an interferometer and single-photon detector, key formation rates of up to 1.9 kbit/s with a quantum bit error ratio of 8.9% for a 122 km link were achieved.

In 2007, Landry et al. realized a quantum relay configuration using existing Swisscom telecommunication networks that allowed the Bell-state measurement of entangled photons with a fidelity of 93% ± 4%: Qubits were generated from a single-photon source (Landry et al., 2007).

Further advances were introduced by Takesue et al. in 2007, who reported the first QKD experiment in which secure keys were distributed at a 12.1 bit/s secure key rate with a 42 dB channel loss over 200 km of optical fiber. These authors employed a differential phase shift quantum key distribution protocol implemented with a 10 GHz clock frequency and superconducting single-photon detectors based on NbN nanowires (Takesue et al., 2007).

In 2008, Honjo et al. reported the entanglement-based QKD experiment over a 100-km optical fiber. They employed superconducting single-photon detectors based on NbN nanowires that provided high-speed single-photon detection for the 1.5-µm telecom band, an efficient entangled-photon pair source that consists of a fiber-coupled periodically poled lithium niobate waveguide and ultralow loss filters, and planar light wave circuit Mach–Zehnder interferometers (MZIs) with ultra-stable operation. Experiments verified a 16-kbit sifted key with a quantum bit error rate of 6.9% at a rate of 0.59 bits per second, from which a distilled 3.9-kbit secure key was extracted (Honjo et al., 2008).

Long-distance transmission of quantum information using quantum repeaters (Briegel et al., 1998; Sangouard et al., 2011) requires the efficient distribution of entanglement between remote nodes of a network (Kimble, 2008). In 2014, Bussières et al. (2014b) demonstrated quantum teleportation of the polarization state of a telecom-wavelength photon onto the state of a solid-state quantum memory. Entanglement was established between a rare-earth-ion-doped crystal storing a single photon that was polarization-entangled with a flying telecom-wavelength photon (Clausen et al., 2011; Saglamyurek et al., 2011). The latter was jointly measured with another flying polarization qubit to be teleported, which heralds the teleportation. The fidelity of the qubit retrieved from the memory was shown to be greater than the maximum fidelity achievable without entanglement, even when the combined distances traveled by the two flying qubits was 25 km along standard optical fiber.

In 2015, Korzh et al., for the first time, presented a compact and autonomous QKD system that was capable of distributing provably secure cryptographic keys over 307 km of optical fiber. This was achieved by using semiconductor single-photon detectors with record low background noise (Korzh et al., 2014) and a novel finite-key security analysis, which is efficient even for short key lengths. This demonstrates the feasibility of practical long-distance QKD based on standard fiber-optic telecom components.

Quantum teleportation over optical fibers remains challenging due to the very poor efficiencies of telecom-band single-photon detectors. Motivated to overcome this impediment, Takesue et al. (2015) reported the successful quantum teleportation over optical fiber using four high-detection-efficiency superconducting nanowire single-photon detectors that made it possible to perform highly efficient multifold photon measurements, allowing confirmation of successful teleportation over 100 km of fiber with an average fidelity of 83.7% ± 2.0%.

By 2016, Sun et al. reported the construction of a 30 km optical-fiber-based quantum network distributed over a 12.5 km² area. This network with active stabilization displayed a unique robustness against environmental noise. Both quantum-state and process-tomography measurements and independent statistical testing confirmed the quantum nature of quantum teleportation over this network (Sun QC. et al., 2016).

Soon after, Huo et al. experimentally demonstrated deterministic quantum teleportation of an optical coherent state through fiber channels (Huo et al., 2018), whereupon two sub-modes of an entangled state were transmitted from sender to receiver through a 3 km fiber. The deterministic teleportation of optical modes over the fiber channel of 6 km was realized with a fidelity of 62% ± 3% for the retrieved quantum state, which surpassed the classical limit of 50%.

7.2.2 Free-space-based quantum teleportation

Although quantum teleportation (Marcikic et al., 2003; Ursin et al., 2004) and entanglement distribution (Zhang et al., 2008; Dynes et al., 2009; Lambert H. N. J. et al., 2020) over moderate distances have been realized using optical fibers, decoherence inherent to optical fibers necessitates the use of quantum repeaters^203−brieg in order to realize teleportation over larger distances. However, the practical utilization of quantum repeaters remains experimentally challenging (Yuan et al., 2008).

Free-space channels, first used for quantum key demonstrations (Kurtsiefer et al., 2002), offer a promising approach because degradation of fidelity is much less through the high orbit atmosphere. Further, ultra-long-distance quantum communication can be achieved on a global scale with the use of satellites.

Previous long-distance demonstrations (see Table 4) include using free-space distribution of entangled-photon qubits over distances of 600 m (Aspelmeyer et al., 2003), 1,300 m (Peng et al., 2005), 16,000 m (Jin et al., 2010), 23,400 m (Kurtsiefer et al., 2002), and 97,000 m (Fedrizzi et al., 2009).

Table 4

Table 4. Major demonstrations in quantum teleportation.

Quantum teleportation of entangled multiphoton qubits was demonstrated over 101.8 km via a two-link free-space channel with an average fidelity of 80.4 ± 0.9% (Yin et al., 2012).

A key experimental demonstration of entangled-photon quantum key distribution over 144 km was carried out by the Zeilinger group of the University of Vienna, where the local state was at the Canary Island of La Palma, and the receiver was located at the Tenerife Ground Station of the European Space Agency. Photons were sent over an optical free-space link (Ursin et al., 2007;Ma et al., 2012).

In 2017, Ren et al. of the University of Science and Technology of China reported the quantum teleportation of single-photon qubits from a ground observatory to a low-Earth-orbit satellite through an uplink channel over distances of up to 1,400 km (Ren et al., 2017). Successful quantum teleportation of six input states in mutually unbiased bases with an average fidelity of 80 ± 1% was demonstrated. Quantum teleportation through space is particularly attractive because degradation from the molecular scattering of entangled particles is lessoned. Such a demonstration of reliable and ultra-long-distance quantum teleportation from ground-to-satellite uplink marks an essential step in realizing a global quantum internet.

7.2.2.1 Time-bin qubits

Qubits encoded by the time of arrival of individual photons are referred to as time-bin qubits (TBQ) (Brendel et al., 1999). TBQs are useful for fiber networks due to their simplicity of generation, interfacing with quantum devices, and independence of dynamic polarization transformations experienced in the use of standard optical fibers. Individual telecom-band photons with a ∼1.5 μm wavelength are ideal qubits due to their ability to travel over long optical fibers or free space.

Valivarthi et al. (2020) reported on the utility of time-bin qubits and their freedom from polarization transformations typically unique to standard optical fibers. The growing availability of sources and detectors of individual telecom-bands has further accelerated progress toward quantum networks and associated technologies, such as quantum memories (Lvovsky et al., 2009), quantum transducers (Lambert N. J. et al., 2020), or quantum nondestructive measurement devices (Braginsky and Khalili, 1996).

Quantum teleportation has been advanced via various photon teleportation modalities. In recent years, such advancement has manifested as bidirectional quantum teleportation (BQT) that has attracted much attention from the scientific community, where it finds utility in quantum-secure direct communication (QSDC) (Li et al., 2013), quantum remote control (Huelga et al., 2002), and cryptographic switching (Srinatha et al., 2014).

Whereas standard quantum teleportation modalities, that is, unidirectional teleportation, realize quantum communication from one party to another, BQT provides an exchange of quantum information between two or more sites. In an ideal version of BQT, parties share maximally entangled qubits and teleport from source to target(s), employing standard quantum teleportation two or more times through redundant or multiple channels (Siddiqui and Wilde, 2022).

7.2.2.2 BQT protocols

Several protocols now exist for BQT involving two participants (Hassanpour and Houshmand, 2016; Sang, 2016; Sadeghi Zadeh et al., 2017; Zhou R. G. et al., 2019; Zhou et al., 2020) and three participants (Yan, 2013; Duan Y. J. et al., 2014; Choudhury and Dhara, 2016; Hong, 2016; Li and Jin, 2016; Yang et al., 2016) using various types of entangled states as quantum channels, including EPR states (Rigolin, 2005), GHZ states (Dong and Teng, 2008; Espoukeh and Pedram, 2014), GHZ-like states (Nandi and Mazumdar, 2014; Yuan, 2015; Zhang et al., 2016), W states (Cao and Song, 2007; Zuo et al., 2009), W-like states (Man et al., 2007), and cluster states (Liu and Zhou, 2014; Li et al., 2016; Sisodia and Pathak, 2018).

In 2013, Yan (Yan, 2013) proposed a protocol for BQT using a six-qubit cluster state as the quantum channel to realize deterministic bidirectional quantum-controlled teleportation of an arbitrary single-qubit state where a source A transmits an arbitrary single-qubit state to a receiver B, while simultaneously the receiver transmits an arbitrary single B qubit state to the original source A mediated by a controller C.

Duan et al. (Duan et al., 2014a) proposed another protocol for BQT in which two participants, A and B, share two three-qubit GHZ (Karlsson and Bourennane, 1998) (Greenberger–Horne–Zeilinger) states as the quantum channel where they mutually transmit two-qubit entangled states to one another. This is believed to be the first protocol for BQT of arbitrary two-qubit states.

An improved BQT protocol, based on a quantum channel of a six-qubit cluster state, was proposed by Zhou R. G. et al. (2019). In their protocol, source A transmits an unknown three-qubit entangled state to receiver B and, at the same time, B transmits an arbitrary single-qubit state to A by utilizing GHZ-state measurement, Bell-state measurement, single-qubit von Neumann measurement, and unitary operations. These authors argue that their approach has advantages in higher intrinsic efficiency than other protocols.

Verma has proposed an improved protocol for asymmetric bidirectional quantum teleportation by using a quantum channel composed of two three-qubit GHZ states based on local CNOT gate operations, Bell-state measurements, GHZ-state measurements, and unitary operations (Verma, 2020). He claims, compared with previous BQT protocols, such as Zhou et al. (Zhou R. G. et al., 2019), that this protocol reduces operational complexity, requires less consumption of quantum and classical resources, and possesses a higher intrinsic efficiency.

7.2.2.3 BQT under water and during inclement weather

Mastriani et al., among others, have explored BQT, and other quantum tunneling (QT) demonstrations, in theory and practical experiments, under water and during inclement weather (Arnon and Kedar, 2009; Bouchard et al., 2018; Iyengar et al., 2020; Sitharama Iyengar et al., 2020; Tarantino et al., 2020; Mastriani et al., 2021a; Mastriani et al., 2021b). These authors recently evaluated the performance of a bidirectional teleportation protocol (Cong et al., 2017; Yang et al., 2017; Zhou R.-G. et al., 2019; Chen et al., 2020) employing six or more qubits (using the IBM Q Experience quantum processor) where they explored the viability of BQT in a specific scenario in which two submerged submarines, on opposite sides of the ocean, serve as source and target with an optical geostationary satellite generating and distributing optical qubits. As such, optical qubits are transmitted to buoys located on the sea surface and linked to the submerged submarines. Results demonstrated a low margin of error, implying a high presence of decoherence and sensitivity to flip errors even in quantum circuits consisting of a few-gates.

Because quantum technologies based on superconducting qubits lose quantum information at environmental temperatures due to decoherence in a non-adiabatic situation, practical underwater quantum communications are exclusively reserved for optical circuit-based entangled photons (Mastriani et al., 20215).

Mastriani et al. also provided seminal contributions to understanding the role of quantum Fourier transforms in entanglement and quantum Fourier transform (QFT) (Nielsen and Chuang, 2000; Weinstein et al., 2001) by spectral analysis, whereas traditional approaches adhere to temporal approaches. Mastriani et al. conjecture that this approach will advance fault-tolerant protocols for use in quantum computing and quantum communication technologies (Mastriani et al., 2021a; Mastriani et al., 2021b).

Chakravartula et al. demonstrated in simulation the quantum teleportation of entangled pairs of photons generated from a mode-locked laser source through spontaneous four-wave mixing across an air–water interface. One of the pair was sent wirelessly to an underwater receiver. Six states of polarization were teleported sequentially, implementing active feed-forward operation with an average fidelity of 96.7% (Chakravartula et al., 2020).

7.3 Quantum tunneling

Quantum tunneling is a phenomenon in which quantum particles, such as electrons, pass through a barrier, such as an electric potential. The strangeness of this phenomenon is that it occurs when the particle does not possess sufficient energy to overcome the barrier according to the laws of classical mechanics. Tunneling is exclusively a consequence of the quantum wave nature of matter, whereupon the wave function describing the state of a particle, in accordance with Schrödinger’s wave equation, has a non-zero probability of transitioning through a barrier that decreases exponentially with the barrier’s height and width as well as the particle’s mass. Tunneling is most prominently observed in particles of low mass, such as electrons or protons, in situations where barrier thicknesses are ∼3 nm for electrons and ∼0.1 nm for protons (Wikipedia, 2022). A schematic illustration that captures the underlying physics is presented in Figure 10.

Figure 10

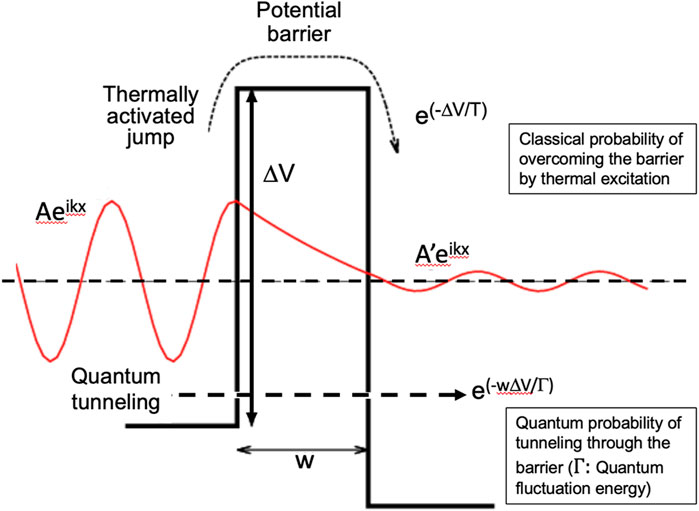
Figure 10. A schematic of an electronic barrier (center, solid line) with an electron approaching from the left (depicted by a sine wave, $\mathrm{A}{\mathrm{e}}^{\text{ikx}}$). The probabilities of transitioning over (classically by thermal activation, $e^{\left(-\frac{∆V}{T}\right)}$) or tunneling through (quantum mechanically, $e^{\left(-\frac{w∆V}{\mathrm{\Gamma }}\right)}$) are provided.

While the laws of quantum mechanics allow for tunneling, researchers cannot exactly explain what happens while the particle experiences tunneling. A topic of continued debate is the speed of the particle during tunneling. Some argue it is instantaneous, while others contend it is finite but may exceed the speed of light. The articles by Spierings and Steinberg (2020); Spierings and Steinberg (2021), Kuzmanović et al. (2022), Sainadh et al. (2020), and Pollak (2017a), Pollak (2017b), and Dumont et al. (2020), among others, are enlightening in this respect.

Quantum tunneling is integral to understanding many modern technologies, including (i) nuclear fusion (Balantekin and Takigawa, 1998), where quantum tunneling increases the probability of atomic nuclei overcoming Coulombic forces to achieve thermonuclear fusion; (ii) solid-state electronics, such as tunnel diodes, where a tunneling-induced “negative” differential resistance allows the function of oscillators, amplifiers, switches, frequency converters, and detectors at microwave frequencies (Fink, 1975); and, (iii) radioactive decay of atomic nuclei. In the latter, the nuclei experience the formation of a potential barrier originating from the equilibrium condition created by the balance of short-range nuclear forces (attraction) and Coulombic forces (repulsion). Alpha particles, emitted during tunneling from unstable nuclei, produce stable atoms. The first interpretation of alpha decay employing quantum tunneling was proffered by Gamow (1928) and independently by Gurney and Condon (1928).

The quantum tunneling effect was first proposed in theory by Hund while calculating the ground state of the double-well potential (Hund, 1927; Merzbacher, 2002). And, from the work of Gamow, Born realized the enormous potential for tunneling to be applied to many physical systems (Razavy, 2003; Wikipedia et al., 2023).

Tunneling further influenced many applications, ranging from the advent of the scanning tunneling microscope to quantum computing. The first experimental suggestion of tunneling-related anomalies was from Earhart (c. 1901), who discovered an unexpected conduction regime while investigating the conduction of gases between closely spaced electrodes, later known as the space charge regime. Circa 1911, Rother refined Earhart’s experiments, allowing for the measurement of field emission currents (Cuff, 1993). Quantum tunneling, within the framework of Fowler–Nordheim tunneling (Fowler and Nordheim, 1928-05), is now the understood mechanism for electrons transitioning through a space charge barrier. Millikan and Lauritsen (1928) and Oppenheimer (1928) contributed to the understanding of this and related phenomena.

Table 5 presents a listing of technologies in which quantum tunneling plays an enabling role. The table is segmented into categories of quantum tunneling (QT) and superconducting tunneling junctions (SQT). Here, one sees the important role of QT in electronics (diodes, transistors, flash memory), nuclear reactions (alpha decay, nuclear fusion), biology, and microscopy. Magnetic tunnel junctions (MTJs) find utility in specialized applications such as magnetic field sensors, magnetic memory, memristors, spin valves, and other spintronic components. Superconducting tunnel junctions (STJs) are used in highly sensitive magnetometers, single-photon detectors, astronomical imaging, quantum computers, and fast logic elements.

Table 5

Table 5. Applications of quantum tunneling and superconducting tunnel junctions.

Table 6

Table 6. Applications of spin-orbitronic devices.

7.4 Spin–orbit coupling (SOC)

Spin–orbit coupling (SOC), sometimes referred to more generally as spin–orbit interactions, is a relativistic interaction of a particle’s spin angular momentum with its orbital angular momentum (see Figure 11A,B) or its spin with its electrostatic and/or its electrodynamic environment(s) (see Figure 11C,D). It can manifest as one of several effects that occur on electronic (<0.01 nm), atomic (0.01 < d < 0.1 nm), or multi-ionic (i.e., the atomic lattice, 0.1 nm < d ∼1 nm)) length scale. For this reason, SOC often brings about some confusion among novices and even expert practitioners (Scitechdaily, 2022).

Figure 11

Figure 11. (A) The proton’s point of view (POV) of the electron orbit and its intrinsic spin moment. (B) The electron’s POV of the orbiting ion and the induced orbital moment. (C) Ion’s POV of an electron traversing a lattice of periodic potential. (D) Electron’s POV of the ions’ crystal fields acting upon the electron. Adapted from: ps://scitechdaily.com/scientists-strengthen-spin-orbit-qubits-in-milestone-critical-for-scale-up-of-quantum-computers.

In one case, considering the electron’s atomic energy levels, due to electromagnetic interaction between the electron’s magnetic dipole, its orbital motion, and electrostatic fields induced by the positively charged nucleus, the atom’s spectral lines split. Such behavior has also become known as the Balmer series, the same Balmer series that Niels Bohr brought clarity to in his seminal articles of 1913, whereupon he introduced the concept of stationary orbits and the principle of quantized orbital energy (i.e., the principal quantum number, n).

Another SOC effect derives from the interplay between angular momentum and the strong nuclear force within the nucleus that leads to a shift in energy levels observed in the nucleus shell model (Haxel et al., 1949; Mayer, 1949). SOC is also responsible for the origin of magnetocrystalline anisotropy that gives rise to the spin-Hall effect, which is of value to spintronics and a plethora of other magnetic phenomena.

Here, we restrict our discussions to SOC phenomena involving electronic and ionic systems that impact many of the quantum technologies discussed in this review (Spavieri and Mansuripur, 2015; Wikipedia, 2022). As previously mentioned, SOC-induced electron energy splitting, that is, ∆ℰ, and its influence upon the Balmer series first addressed by Bohr, was later advanced by Thomas using Bohr’s atomic model in conjunction with

Schrödinger’s wave mechanics and relativistic kinematics (Thomas, 1926; Thomas, 1927). This result agreed with later predictions by Dirac’s relativistic quantum field theory (c. 1928) (Mansuripur, 2015). These foundational contributions were used in practical technologies such as spin-orbitronics (bib_wikipedia_2022j).

7.5 Spin-orbit technologies

Spin-orbitronic devices are relatively new to the quantum electronic lexicon, encapsulating the influence of SOC in determining the performance of some modern electronic components. Table 6 provides a listing of spin orbitronic technologies, including: embedded magnetoresistive random-access memory (eMRAM), spin–orbit torque MRAM (SOT-MRAM), resistive switching RAM (RRAM), spin-torque nanooscillators, and STT-based synapses, neurons, and the neuromorphic computing.

We next examine spin-transfer torque (STT), an effect where the orientation of a free magnetic layer in a magnetic tunnel junction is manipulated using spin-polarized currents (SPC). When an SPC is injected into this magnetic free layer, the angular momentum is transferred to the layer thus reversing its orientation, providing a bistable state useful for memory and logic devices.

Spin-transfer torque magnetic random-access memory, that is, STT-MRAM, is a nonvolatile memory that operates under sub-nanosecond and sub-picojoule conditions and provides major advantages over charge-based memories such as SRAM and DRAM (Krizakova et al., 2022a; Wikipedia, 2022). Industrial production of this memory technology was first demonstrated by Hitachi, which produced a 32-Mbit STT-RAM in 2009 (Session 8-4, 2023). The commercialization of these technologies will be addressed in Section 9.

Spin-transfer torque arises from the transfer of electron spin angular momentum to the orbital angular momentum of the lattice (see Figure 11B). When the current density is sufficiently high, the magnetization rotates. This has been experimentally demonstrated in cases when the thickness of the magnetic material is of the order of hundreds of nanometers or less. Such nanoscale devices, known as spin-torque nanooscillators (STNOs), generate high-frequency voltage signals in the GHz range. STNOs have abundant potential as RF signal generators, modulators, and RF detectors.

Recently, spin–orbit torque (SOT) has been proposed to switch the magnetization of the free magnetic layer in MTJs at lower power and faster speeds (Miron et al., 2011; Liu et al., 2012a; Liu et al., 2012b; Cai et al., 2017; Li et al., 2019). SOT provides versatility in the manipulation of magnetization using electric currents, leading to novel spintronic performance and devices. It is based on spin-transfer effects, like STT-MRAM; however, the source of spins is the lattice of the SOT layer via intrinsic SOC, and, therefore, there is no need for SPCs (Antaios, 2023).

SOT can be generated from several sources, including the use of heavy metal (large Z and hence large orbital momentum) layers such as Pt^368−liu or Ta^370−liu or by means of the Rashba effect¹³ stemming from the breaking of crystal inversion symmetry. Several investigators have shown SOT efficiency can be further improved by engineering interface structure and chemistry (Fan et al., 2013; Fan et al., 2014; Nan et al., 2015), electric field tuning (Yan Y. et al., 2016; Fan et al., 2016), ferroelectric polarization (Lin et al., 2018), or by the introduction of materials possessing higher SOT efficiencies (Valenzuela and Tinkham, 2006; Ando and Saitoh, 2010; Pai et al., 2012; Jamali et al., 2015; Akyol et al., 2016).

7.5.1 Spin-torque nanooscillators

Spin-torque nanooscillators (STNOs) are highly tunable by both currents and magnetic fields and, as such, have advantages over standard voltage-controlled oscillators (VCOs). While the frequency variation in VCOs is only ∼20% of the carrier frequency (i.e., 1–3 GHz), STNOs can be tuned by current over several GHz and magnetic fields up to 40 GHz (Zeng et al., 2013).

STNOs are also among the smallest of microwave oscillators, operating over broad temperatures while biased using low voltages. Additionally, STNOs can be readily integrated using complementary metal-oxide semiconductor (CMOS) protocols for on-wafer systems. All these advantages make STNOs promising for microwireless communications, array transmitters, microwave sources, on-chip clocks, and massively-parallel microwave signal processors (Albertsson et al., 2019).

After the initial seminal works by Slonczewski (1996) and Berger (1996), Kiselev et al. performed systematic experiments on microwave emissions from magnetic nanostructures (Kiselev et al., 2003). Since then, many different STNO configurations have been studied that are distinguished principally by device topology, including spacer layers, patterning geometries, and magnetic configurations.

A unique type of STNO was developed, whereupon magnetic precession is caused by spin currents generated by the spin-Hall effect (Hirsch, 1999; Sinova et al., 2015). This device is called the spin-Hall nano-oscillator (SHNO). SHNOs (Liu et al., 2013; Duan Z. et al., 2014; Demidov et al., 2014; Dürrenfeld et al., 2017; Demidov et al., 2022) have advantages over STNOs in that multiple SHNOs can be integrated into a common spin-Hall material and controlled simultaneously by a single in-plane current allowing long-range synchronization (Awad et al., 2017; Zahedinejad et al., 2020; Zahedinejad et al., 2022). Additionally, a gated structure is readily incorporated in a three-terminal SHNO topology (Liu et al., 2012c; Albertsson et al., 2019; Tarequzzaman et al., 2019), allowing for an individual oscillator to be independently controlled by a common gate voltage (Liu et al., 2017; Fulara et al., 2020b; Choi et al., 2022).

As the spin-orbitronic version of STNOs, SHNOs have been developed for neuromorphic computing (Zahedinejad et al., 2020). However, the relationship between damping and SOT-induced in-plane torque in perpendicular magnetic anisotropy (PMA) systems is asymmetrical, and challenges exist in artificial neuron-based PMA-based SHNOs (Fulara et al., 2019).

STT-based spintronic devices have demonstrated commercial success as mass-produced eMRAM (e = embedded) alternatives to existing Flash-embedded memories (Sato et al., 2018a). Due to superior performance, SOT-based spin-orbitronic devices are expected to extend nonvolatile memory technologies. Additionally, as artificial intelligence, quantum computing, and “big data” evolve to play ever greater roles in daily life, new opportunities will exist for nonvolatile spin-orbitronic devices.

7.5.2 STT-based neuromorphic technologies

Neuromorphic computing embraces aspects of biological processes, including brain communication and computation, by employing electronic circuits as analogs to biologic neural networks. Neuromorphic computing offers advantages over conventional von Neumann systems in energy efficiency, processing speed, and the ability to learn. Neuromorphic computing is particularly well suited to solving problems in artificial intelligence. The creation and integration of artificial synapses and neurons are required in order to realize the goal of a neuromorphic computer. Artificial synapses require multilevel differentiated nonvolatile states. One modality that allows the storage of such synaptic weights is the memristor. Any effective memristor-based technology must contain a high density of devices assembled using standard complementary metal-oxide semiconductor (CMOS) protocols employing compatible materials and back-end processes. Neuromemristive systems¹⁴ (Wikipedia, 2022) facilitate neuroplasticity¹⁵. i.e., the brain’s ability to alter its structure and function in response to stimuli, while neuromorphic engineering centers on mimicking the brain’s behavior. For example, a neuromemristive system may replace details of a cortical microcircuit with an abstract neural network (Merkel and Kudithipudi, 2014).

Alternative paths have been proffered. For example, in 2022, MIT researchers developed an integration-friendly technology using inorganic materials compatible with conventional silicon processing (Onen et al., 2022). Those CMOS-friendly materials included WO₃ as the channel material, nanoporous proton-conducting phosphosilicate glass (PSG) as the protonic solid electrolyte (SE), and Pd as the hydrogen reservoir and controlling gate. The basic operating principles of the device rely on the modulation of the channel conductance via electrochemically controlled intercalation of protons within the WO₃ channel (Yao et al., 2020;Onen et al., 2021).

Three-terminal protonic programmable resistors, having self-aligned gate structures with Pd layers, use PSG layers as etch masks. The geometry of the Au channel electrodes and the Pd layer are tailored to avoid charging and minimize deleterious capacitance, thus maximizing device energy efficiency. As a result, devices show excellent energy efficiency under ultrafast operation. Energy consumption during transients was measured to be ∼2.5 fJ per pulse. Under intense electric fields, ultrafast modulation of nanoscale protonic programmable resistors has shown exceptional energy efficiency. SOT-induced multilevel magnetization switching, as well as the conventional synaptic function of spike-timing-dependent plasticity (STDP), was experimentally demonstrated by Cao al. in 2019 (Cao et al., 2019). Other effective strategies include fine-magnetic domain wall switching in antiferromagnetic (AFM) (Wadley et al., 2016; Olejník et al., 2017; Shi et al., 2020) or AFM/FM (Liu et al., 2020; Yun et al., 2020) heterostructures, where many 100-nm-sized binary domains are affixed to AFM layers that are reversed independently under application of applied currents (Fukami et al., 2016; Kurenkov et al., 2017;Yan et al., 2021).

7.5.2.1 Advances in neuromorphic computing

Neuromorphic computing uses hardware based on artificial neurons and synapses. Table 7 provides an evolutionary history of neuromorphic computing over the last 2 decades, tracking the major advances in these areas by major universities and organizations. The most common neuromorphic hardware is spiking neural networks (SNN). Artificial synaptic devices connect SNNs with analog circuitry to transfer signals that mimic brain functions. Instead of encoding data through binary systems of 0–1 s, SNNs encode analog signals (Techtarget, 2022). Neuromorphic computers are non-von Neumann systems¹⁶ inspired by principles that mimic biological neural activity and are particularly well suited for solving problems related to artificial intelligence, among others. Artificial neurons and synapses have been demonstrated using memristors (Maan et al., 2016), spintronic memories, threshold switches, transistors (Zhou and Ramanathan, 2015), and other electronic components. In particular, artificial synapses require multilevel, nonvolatile states to store information. Although spin-orbitronic devices show superior performance over proposed systems such as memristors, the characteristic bistable nature of MTJs makes them difficult to employ as multilevel synapses.

Table 7

Table 7. Evolution of neuromorphic computing.

Memristive devices rely on electronic spin and polarization. These memristor devices can be categorized further as spintronic memristors and spin-transfer torque (STT) memristors. In spintronic memristors, the path of the spin of electrons alters the magnetization state of the device, which consequently changes its resistance. Meanwhile, in STT memristors, the comparative magnetization of the two electrodes affects the magnetic state of the tunnel junction, which, in turn, changes its resistance. Because these devices operate under differing physical principles, their memristive behavior is markedly different (Maan et al., 2016).

8 Qubit modalities

As previously stated, a qubit represents quantum information as a 0 or 1, or both. It is difficult to envision the simultaneous existence of a 0 and 1, a phenomenon called superposition. A superposition of 0 and 1 means the quantum state is made up of part 0 and part 1. The superposition state can be expressed as ∣0⟩∣0⟩ and ∣1⟩∣1⟩ or ∣0⟩+∣1⟩∣0⟩+∣1⟩. A qubit can be established using any two-level quantum system. There are many ways to establish qubits. Some are presented in Table 8 and are described below.

Table 8

Table 8. Types and properties of popular qubit systems.

Before we progress further in describing qubits, we introduce key terms, such as relaxation time T₁ and dephasing time T₂. Both T₁ and T₂ are together referred to as decoherence times. T₁ describes how long the phase of a qubit remains intact. For example, it is the transition time between state |+⟩ and state |-⟩, that is (Eqs. 6 and 7):

$\left|+⟩\right.〉=\frac{1}{\sqrt{2}}\left(\left|\left|0\right.⟩\right.+\left|\left|1\right.⟩\right.\right)(6)$

$\left|-⟩\right.〉=\frac{1}{\sqrt{2}}\left(\left|\left|0\right.⟩\right.-\left|\left|1\right.⟩\right.\right).(7)$

Similarly, T₂ is not the time after which an initial state |+⟩ switches to state |−⟩ but rather the time after which these states effectively disentangle. Figure 12A depicts the exponential decay typical of relaxation time T₁, while oscillations defining a Gaussian decay envelope allow the determination of the dephasing time T₂^*. Figure 21, introduced and discussed later in the text, provides a compilation of coherence times of charge qubits according to material system and coherence type.

Figure 12

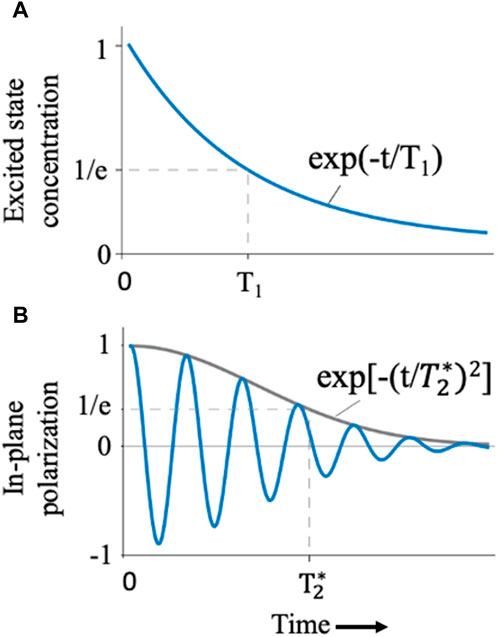
Figure 12. (A) Exponential decay typical for relaxation processes, reflecting the relaxation time T₁. (B) Oscillations with a Gaussian decay envelope measuring the inhomogeneous dephasing time T₂^*in the time domain. The ^*implies a Ramsey experiment (see text for details).

The inhomogeneous dephasing time T^*₂ implies a Ramsey experiment¹⁷. A T^*₂ Ramsey experiment measures the dephasing time, T^*₂, of a qubit and the qubit’s detuning, which is a measure of the difference between the qubit’s resonant frequency and the frequency of the rotation pulses being used to perform the Ramsey experiment. Ideally, this detuning would be 0, meaning pulses are perfectly tailored to address each qubit without enacting any unintended interactions with neighboring qubits. In practice, qubits drift, and the pulse parameters must be adjusted. Retuning qubits and pulses requires the running of a T^*₂ Ramsey experiment to measure the size of the qubit detuning.

8.1 Photon (boson) qubits

One of the most effective means of transmitting quantum information is the encoding of photon polarization (see Table 8). Such encoding requires two distinct optical modes. This is referred to as dual-rail encoding¹⁸. The photon state is an eigenstate, that is, a single Fock state¹⁹; dual-rail qubits are states that do not evolve under propagation. Alternatively, if one considers the electromagnetic field as encoded as two distinct Fock states, then this entails the use of a single optical mode and is referred to as single rail encoding (Lund and Ralph, 2002)¹⁸. In these cases, optical modes are a superposition of eigenstates and experience phase evolution under propagation.

8.1.1 Time bin qubits

Time-bin qubits, originally developed in 1999 by Brendel et al. (1999) propagate over long distances along optical fibers with unusually robust fidelity. In 2013, Humphreys et al. developed a technique for optical quantum computing using time-bin qubits (Humphreys et al., 2013). This concept allows photonic quantum computing using a single optical path and greatly reduces system complexity. In that same year, Donohue et al. demonstrated an ultrafast measurement technique for time-bin qubits that enables high data rates with minimal errors (Donohue et al., 2013). Humphreys et al. also showed the use of time-bin qubits enabling linear optic quantum computing (LOQC) (Knill et al., 2001) in a single spatial mode, further minimizing complexity. Together, these developments are foundational in realizing practical quantum information systems using photonic qubits.

Additionally, the photonic temporal degree of freedom is one of the most promising quantum communication modalities over fiber and free-space channel networks. Bouchard et al. demonstrated the feasibility of picosecond time-bin states of light for applications in quantum communications. With the ability to measure time-bin superpositions with superb phase stability, they helped realize efficient quantum key distribution protocols such as BB84 (Bouchard et al., 2022).

Gündoğan et al. demonstrated the first solid-state spin-wave optical quantum memory with on-demand readout using a full atomic frequency comb in a Pr³⁺:Y₂SiO₅ crystal. These authors stored weak coherent pulses with a signal-to-noise ratio greater than 10:1. Narrow-band spectral filtering based on spectral hole burning in a second Pr³⁺:Y₂SiO₅ crystal was shown effective in filtering out excess noise to a level of 2.0 ± 0.3×10⁻³ photons per pulse. These authors also reported spin-wave storage of photonic time-bin qubits, demonstrating that spin-wave memory operates in the quantum regime (Gündoğan et al., 2015).

8.1.2 Advances in squeezed light

Shahmoon et al. calculated the entanglement between a short pulse of resonant squeezed light (SL) and a two-level atom in free space. They found that the squeezing phase, that is, the phase of the EM field and the atomic superposition phase, determine the performance of atom-pulse mode entanglement and gate errors (Shahmoon et al., 2009).

Callus and Kok (2021) demonstrated how to create maximal entanglement between two qubits encoded in two spectrally distinct solid-state quantum emitters embedded in a waveguide interferometer. Their method does not require identical emitters, accommodates a degree of spectral variation arising from slight deviations introduced during fabrication, and creates entanglement with a concurrence²¹ above 99% in the event of scattering losses and detector inefficiencies.

Ortu et al. demonstrated long-duration quantum memories for photonic qubits and achieved long-distance quantum networks by mapping optical states onto coherent spin-waves (Ortu et al., 2022). However, this approach suffers from readout noise caused by spin-wave manipulation. A dynamical decoupling technique and small magnetic fields were employed to achieve storage of six temporal modes for 20 ms, 50 ms, and 100 ms in a Eu³⁺:Y₂SiO₅ crystal based on an atomic frequency comb-type memory (Grover, 1996-07c). The quantum coherence of this memory was verified by storing two time-bin qubits for 20 ms with an average memory output fidelity of 85% ± 2%.

8.2 Superconductor qubits

Superconducting qubits are characterized as employing Josephson junctions (JJs). A JJ is an electrical component that exists as a weak-link circuit between two superconductive leads on either side of a thin layer of insulator material a few atoms in thickness (see Figure 13). The resulting JJ device exhibits the Josephson Effect²², producing a supercurrent. The condensate wave function on either side of the junction is weakly correlated, having different superconducting phases. Current through the JJ occurs by quantum tunneling (discussed earlier), creating a nonlinear inductance that allows for a qubit design that behaves as an anharmonic oscillator of quantized energy levels (Strogatz, 2004).

Figure 13

Figure 13. (A) Schematic of a Josephson junction (JJ), (B) scanning electron microscopy image of a JJ (used with permission of Angstrom Engineering), and (C) circuit element representation.

8.2.1 Charge qubits

The simplest superconducting qubit is the “Cooper-pair box,” more generally referred to as the superconducting “charge” qubit (see Figure 14A). The charge qubit, first described in theory by Büttiker (1987), was demonstrated experimentally a decade later by Bouchiat et al. (1998). Its time-domain quantum dynamic behavior was described by Nakamura et al. (1999) (Martinis, 2009; Siddiqi, 2021).

Figure 14

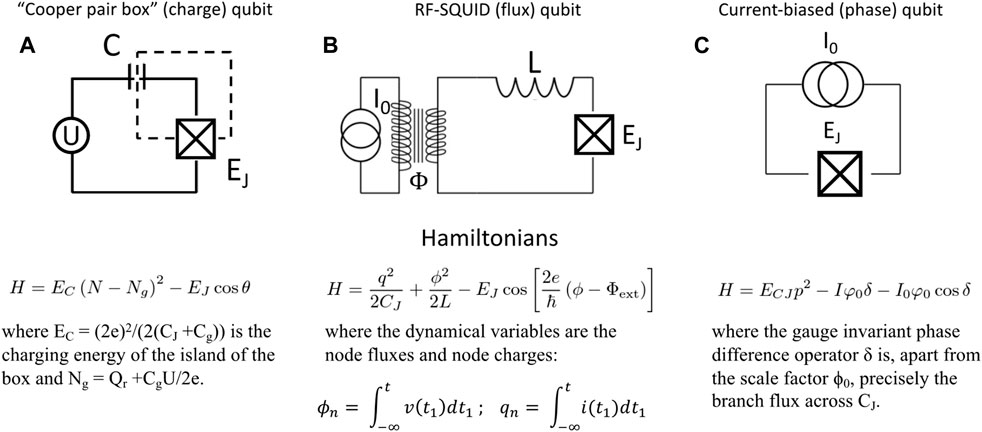
Figure 14. A simple circuit diagram of each superconducting qubit with their Hamiltonian and other key parameters. This figure was constructed in part from data presented in Wikipedia (2022m) and Devoret et al. (2004).

In superconducting quantum computing, a charge qubit is formed by an infinitesimal superconducting island (denoted in its circuit diagram of Figure 14A as the dashed box) coupled by a JJ to a superconducting reservoir (Makhlin et al., 2001). The charge qubit’s basis states are charge states, that is, states that represent the presence or absence of excess Cooper pairs in the islands. The state of the qubit is determined by the number of Cooper pairs that have tunneled across the junction. The quantum superposition of charge states can be achieved by tuning the gate voltage that controls the chemical potential of the island. The qubit is typically read out by electrostatically coupling the island to a sensitive RF single-electron transistor.

Charge qubits are fabricated using techniques like those used in microelectronics. The devices are usually made on silicon wafers employing electron beam lithography and physical vapor deposition. Typical coherence times for a charge qubit are on the order of a few microseconds (Houck et al., 2009-02). However, recent works using transmons²³ have demonstrated dramatic enhancements in coherence times.

The transmon’s enhanced coherence derives from a reduced sensitivity to charge noise originating from an increase in the ratio of Josephson energy to charging energy using a shunting capacitor. Planar on-chip transmon qubits have coherence times of approximately 30 μs–40 μs (Barends et al., 2013-08), with recent work approaching ∼100 μs attained by replacing the superconducting transmission line cavity with a three-dimensional superconducting cavity (Paik et al., 2011-12; Rigetti et al., 2012-09). Replacement of niobium with tantalum in the transmon device leads to coherence times as high as 300 μs (Place et al., 2021-03; Wikipedia, 2022).

Chow et al. describe a route toward a logical memory with superconducting transmons employing a rotated surface code (RSC). Quantum error correction, necessary to realize scalable quantum computers, is theoretically possible with an error rate below the threshold. Two-dimensional surface coding permits relatively high fault-tolerant thresholds at the ∼1% level and only requires a latticed network of qubits with nearest-neighbor interactions. These authors describe single- and two-qubit gate tune-up procedures simultaneously benchmarking pairs of two-qubit gates (Chow et al., 2015). While there are many approaches to achieving quantum fault tolerance, one of the most promising is the two-dimensional (2D) surface code (Bravyi and Kitaev, 1998; Kitaev, 2003; Raussendorf and Harrington, 2007; Fowler A. G. et al., 2012). This code has a high tolerance to errors, or threshold (approximately 6.7 × 10⁻³), requires only nearest-neighbor qubit interactions, and has simple error syndrome extraction circuits (Dennis et al., 2002) and a suite of fault-tolerant logic based on transversal gates, code deformation (Raussendorf et al., 2007), or lattice surgery (Horsman et al., 2012). To realize this code, coupling between data qubits and the syndromes was induced by using a quantum bus (Majer et al., 2007; Sillanpaa et al., 2007) where each bus couples to four data qubits and each qubit couples to two buses, allowing a tiling that achieves the connectivity required for the RSC (Chow et al., 2014). IBM uses coplanar waveguide microwave resonators for buses. An example of a connected multi-qubit device consisting of eight transmon qubits, four quantum buses, and eight readout resonators allowing for studying both Z and X parity checks is presented as the optical micrograph of Figure 15 (Gambetta et al., 2017-01).

Figure 15

Figure 15. A device consisting of eight transmon qubits, four quantum busses, and eight readout resonators (i.e., 8Q/4B/8) fabricated at IBM (Gambetta et al., 2017). Inset shows an optical micrograph of an individual transmon qubit. Used with permission of IBM under Creative Commons Attribution 4.0 International License.

Figure 14A The circuit schematic of the superconducting charge qubit is also known as the “Cooper-pair box.” The dashed square denotes the superconducting island. Beneath is its Hamiltonian, where E_C is the charging energy, the JJ capacitance is C_j, and the gate capacitor is C_g. N is the number of Cooper pairs to tunnel through the junction. The quantum superposition of charge states is achieved by tuning the gate voltage that controls the chemical potential of the island. (b) The circuit schematic of the flux qubit is also known as the RF-superconducting quantum interference device (SQUID) qubit. Its Hamiltonian is presented below the image with key parameters defined. (c) The circuit schematic of the phase qubit is also known as the current-biased qubit. Its Hamiltonian is presented below the image, where the gauge invariant phase difference operator is equivalent to the flux across the JJ.

Wang et al. of the Beijing Academy of Quantum Information Sciences produced a transmonic chip that contained five independent transmons, four independent quarter-wave resonators for measuring the intrinsic Q factor of the resonator, and three additional transmons for testing resistance. The Purcell effect²⁴ limited transmon temporal decoherence to over 2 milliseconds. The coupling strength between the readout resonator and transmons was 50 MHz × 2π. The measured T₁ and T₂* were 50 μs and 75 μs, respectively (Wang C. et al., 2022).

8.2.2 Flux qubits

Flux qubits, also known as persistent-current qubits or SQUID qubits, are micron-sized loops of superconducting material that are spatially divided by JJs (see Figure 14B). The flux qubit was first proposed by Orlando et al. (1999) and fabricated shortly thereafter. In fabrication, the JJ parameters are engineered so that a persistent current flows continuously when an external magnetic flux is applied. Only an integer number of flux quanta are allowed to penetrate the superconducting ring, resulting in clockwise or counterclockwise supercurrents in the loop to compensate a non-integer external flux bias. When the applied flux through the loop is close to a half-integer number of flux quanta, the two lowest energy eigenstates of the loop will be a quantum superposition of the clockwise and counterclockwise currents (Wikipedia, 2022).

The two lowest energy eigenstates differ only by the relative quantum phase between the composing current-direction states. Higher energy eigenstates correspond to much larger (macroscopic) persistent currents that induce an additional flux quantum to the qubit loop, which is well separated energetically from the lowest two eigenstates. This separation, known as the qubit nonlinearity, allows operations with the two lowest eigenstates, thus effectively creating the necessary two-level system for qubit operation.

Computational operations are performed by pulsing the qubit with microwave radiation that has an energy comparable to that of the gap between the energy of the two basis states. Properly selected pulse durations and amplitudes can put the qubit into a quantum superposition of the two basis states, while subsequent pulses can manipulate the probability weighting that the qubit will be measured in either of the two basis states, thus performing a computational operation (Paladino et al., 2014).

8.2.3 Phase qubits

The phase qubit is also a superconducting device based on a superconductor–insulator–superconductor JJ (Nielsen and Chuang, 2000) closely related to the previously mentioned flux qubit and charge qubit. The major distinction among the three is the ratio of Josephson energy to charging energy, that is, the required energy for one Cooper pair to charge the total capacitance of the circuit (see Figure 14C) (You and Nori, 2007-01).

For a phase qubit, this ratio is on the order of 10⁶, which allows for macroscopic bias currents through the JJ. For flux qubits, it is on the order of 10¹, which allows for mesoscopic supercurrents on the order of 300 nA. For charge qubits, it is on the order of < 10⁰, whereupon only a few Cooper pairs tunnel through and charge the Cooper-pair box. However, transmons (Koch et al., 2007-10; Fink, 2010; Schreier et al., 2008-05b) can have very low charging energy due to the circuit’s large shunt capacitance and, therefore, have a ratio on the order of 10–100 (Eng et al., 2015).

8.3 Electron spin qubits

Spin is an effective and popular way of encoding quantum information, is a common qubit modality, and manifests in several systems.

8.3.1 Quantum-dot spin qubits

An electrostatic quantum dot typically consists of a stacked heterostructure that is designed to create quantum confinement in three dimensions by combining electric fields and topological constraints. Stano and Loss provide an excellent review of the performance metrics of spin qubits in gated semiconducting quantum-dot nanostructures (Stano and Loss, 2022).

The electron is quantum-confined at the interface between the active materials. For these spins to be considered as potential qubits, it is necessary to be able to isolate a single spin, establish entanglement between pairs, and ultimately read the quantum-encoded information. Moreover, all these tasks must be performed with sufficient spatiotemporal precision to avoid degradation to quantum fidelity from environmental influence (Escalera-Moreno et al., 2018).

As previously discussed, the strength of spin–orbit interactions is an important factor influencing the coherence of select qubit modalities and is key in the development of quantum-dot spin qubits. In one such case, researchers have found larger than expected spin–orbit interactions at the surface of silicon where electrons are confined as if they existed within quantum dots (Q-dots) (Osika et al., 2022).

An interesting and potentially valuable finding was the manipulation of electron spin bound to a single phosphorus (P) donor ion in silicon that was measured with fidelities greater than 99% (Muhonen J. T. et al., 2014; Watson et al., 2015), which is above the threshold for coded quantum error correction (Raussendorf et al., 2007; Wang D. S. et al., 2011). One of the main sources of error during single-shot spin readout is the relaxation of spins prior to measurement (Baart et al., 2016). The spin relaxation time, T₁, also represents an upper bound to the spin coherence time, T₂, where T₂ < 2T₁ (Tyryshkin et al., 2012). Watson et al. (2017) showed that electrons bound to 2P and 3P donor dots can have spin relaxation times up to 16 times greater than those of 1P donors because of higher confinement potential. This agrees with the theoretical work of Hsueh et al. (2014). Enhanced spin relaxation times, combined with high signal-to-noise single-electron transistor charge sensors, allow for a fidelity of 99.8% in the sequential readout of two donor-bound electron spin qubits.

The isolation of qubits from noise sources, such as surrounding nuclear spins and spin–electric susceptibility (Balasubramanian et al., 2009; Kuhlmann et al., 2013; Muhonen J. T. et al., 2014; Reed et al., 2016), has enabled extensions of quantum coherence times. The possibility of achieving enhanced quantum coherence was doubted due to background charge fluctuations (Paladino et al., 2014; Bermeister et al., 2014; Huang and Hu, 2014). Still, a sizeable spin–electric coupling will be needed in multiple-qubit systems to support single-spin and spin–spin interactions (Tokura et al., 2006;Trif et al., 2008; Hu et al., 2012).

Yoneda et al., and references contained therein, reported on single-electron spin qubits with an isotopically enriched phase coherence time of 20 μs (Veldhorst et al., 2014; Eng et al., 2015) and fast electrical control speed of up to 30 MHz mediated by extrinsic spin–electric coupling. Using rapid spin rotation, they revealed that the free-evolution dephasing is caused by charge noise—rather than conventional magnetic noise—as highlighted by a 1/f spectrum extending over 7 decades of frequency. The qubit exhibits superior performance with single-qubit gate fidelities exceeding 99.9% on average, offering a path to large-scale spin-qubit systems with controllable fault tolerance (Yoneda et al., 2018).

8.3.2 Molecular spin qubits

Molecular nanomagnets have many intrinsic low-energy states that can be used to define qubits and allow quantum computation with embedded quantum error correction (Chiesa et al., 2020). The magnetic materials community has witnessed a dramatic increase in molecular magnetism research activity, including advances in phase coherence of spin qubits from a few microseconds to a few milliseconds.

The method of Chiesa et al. (2020), using a sequence of RF pulses to actuate error corrections, has been applied to a simple s = 3/2 molecule and scaling to larger spin systems.

Transition-metal complexes offer a unique potential as tunable qubits, in some cases, challenge solid-state systems. Zadrozny et al. harnessed molecular design to create a series of qubits, for example, (Ph₄P)₂ [V(C₈S₈)₃], with T₂ values of 1–4 μs at 80 K in protiated and deuterated environments (Zadrozny et al., 2015). Through chemical tuning of nuclear spins in the vanadium environment, these authors realized a T₂ of ∼1 ms for the species (d20-Ph₄P)₂ [V(C₈S₈)₃]. This T₂ value surpasses the performance of other coordination complexes by more than an order of magnitude.

Einstein–Podolsky–Rosen (EPR) data reveal the electronic role of ligands in interacting with cations. However, pulsed EPR measurements specifically reveal decoherence is strongly influenced by nuclear spins in protiated and deuterated solvents.

The results illustrated in Figure 16 and presented in Table 9 show improvements in transition-metal complexes with coherence times appropriate for more advanced quantum interactive polynomial (QIP) applications, including creating hybrid electronuclear quantum memory (Morton et al., 2008) with ⁵¹V nuclear spin.

Figure 16

Figure 16. Comparison of T₂ values of [V(C₈S₈)₃]²⁻ with other molecular and solid-state electronic spin-qubit systems. Data listed are referenced by Zadrozny et al. (2015). This figure is modified and reproduced with permission of the American Chemical Society under Creative Commons Attribution 4.0 International License.

Table 9

Table 9. Examples of molecular qubits.

8.3.3 2-Dimensional spin qubits systems

Trauzettal et al. proposed a route to form spin qubits as graphene quantum dots, allowing for the lifting of the well-known valley degeneracy experienced in graphene (Trauzettel et al., 2007). These authors showed that this problem can be avoided in quantum dots based on ribbons of graphene with armchair boundaries. A new feature of these proposed spin qubits is that an array formed of such qubits allows the coupling of any two via Heisenberg exchange if others are decoupled by detuning.

Wang et al. integrated hexagonal boron nitride (hBN) capacitors with aluminum JJs to realize transmon qubits with coherence times reaching 25 μs, consistent with the hBN loss tangent inferred from resonator measurements. The hBN PPC (polypropylene carbonate) reduces the qubit feature size by approximately two orders of magnitude compared to conventional all-aluminum coplanar transmons. These results establish hBN as a promising dielectric for building high-coherence quantum circuits with substantially reduced form factor and a reduction in deleterious qubit crosstalk (Wang J. I. et al., 2022).

The discovery of atom-like spin emitters associated with defects in wide bandgap semiconductors presents further opportunities for versatile qubits. Research activities in this area have focused on defects in hBN because hBN contains a high density of nuclear spins that are expected to create a strong, incoherent spin bath, resulting in poor coherence of spins. New 2D-WBG materials as qubit candidates are the subject of ongoing research. Defo et al. present a method for rapid estimation of the zero-phonon line (ZPL), a key property of atomic qubits in WBG materials (Kuate Defo et al., 2021). Their approach to calculating ZPL employs Janak’s theorem²⁵ and converges more rapidly than the standard method (∆SCF)²⁶. They apply this and related theoretical techniques to the case of singly charged calcium vacancies in SiS₂, which they propose as a qubit material. This work could assist in accelerating high-throughput searches for 2D materials with unique potential for quantum sensing and quantum computing applications.

Point defects and defect complexes in AlN have been studied by Varley et al. for potential as single-spin centers and solid-state qubits similar to those observed in diamond and SiC, finding that isolated anion vacancies (V_N) meet many of the criteria for an individually addressable quantum system (Varley et al., 2016). However, since these states reside near the conduction-band, studies have focused on how properties can be tuned by complexing vacancies with near-neighbor substitutional impurities. Transition-metal dopants Ti and Zr favorably substitute on the Al site, form complexes with V_N, and possess the desired electronic and optical properties, such as charge and spin states, binding energies, and optical excitation energies, making this material a practical individually addressable solid-state qubits host.

Koehl et al. have endeavored to identify and develop robust quantum systems (Koehl et al., 2011) that can be readily manipulated for use in advanced information and communication technologies (Awschalom and Flatte, 2007) by building upon recent results of nitrogen-vacancy (NV) centers in diamond that have attracted interest based on atomic-scale electronic spin states that can be used as individual addressable, solid-state qubits, even under ambient conditions (Jelezko et al., 2004). These attractive quantum properties have motivated others to identify similar defects in other 2D semiconductor systems, as they may offer an expanded functionality not available to NV-diamond (Weber et al., 2010).

Notably, defects in silicon carbide (SiC) have been suggested as a potential qubit candidate owing to a combination of theoretical predictions and experimental magnetic resonance studies (Baranov et al., 2005; Son et al., 2006; Baranov et al., 2011; Gali, 2011; Ruskov and Tahan, 2012; Mizuochi et al., 2022; Son et al., 2022). Koehl et al. demonstrated several defect spin states in 4H-SiC that can be optically addressed and coherently controlled in the time domain at temperatures that approached ambient (∼300 K). Using conventional optical and microwave techniques, they studied the spin-1 ground state of each of four inequivalent forms of neutral carbon–silicon divacancies, as well as a pair of defect spin states of unidentified origin. These defects are optically active near telecommunication bands (Saleh and Teich, 1991) and are found in a host material for which industrial-scale crystal growth capacity already exists (Powell et al., 2006) and has undergone advanced microfabrication process refinement (Zetterling, 2002). Additionally, they possess desirable spin coherence properties that are comparable to those of NV-diamond systems, making them promising candidates for various photonic, spintronic, and quantum information applications that merge quantum degrees of freedom with classical electronic and optical technologies.

8.4 Nuclear spin qubits

8.4.1 Nuclear spin-enabled NMR quantum computers

The spin states of nuclei within molecules were suggested as qubits and probed through nuclear magnetic resonances as early as 1993 (Lloyd, 1993; DiVincenzo, 1995a; DiVincenzo, 1995b).

Manipulation of nuclear spins as qubits using liquid state NMR was introduced independently circa 1996–1997 by Cory, Fahmy and Havel (Cory et al., 1996; Cory et al, 1997) and Gershenfeld and Chuang (1997; 1998).

Initial NMR approaches employed spins of a collective of atoms or molecules in the liquid state known as liquid state NMR or LSNMR. Menicucci and Caves (2002) proffer that all experiments to date involving LSNMR ensemble quantum computing have not demonstrated quantum entanglement, a requirement for quantum computation. Research has since evolved towards solid state NMR (SSNMR) as a more viable method for quantum computation. SSNMR allows the precise localization and measurement of qubits thus alleviating the requirement of measuring an ensemble. IBM researchers reported in 2001 the first implementation of Shor’s algorithm in a 7-qubit NMR quantum computer (Vandersypen, 2001).

8.4.2 Nitrogen-vacancy (NV) centers

Single defects in diamond, especially negatively charged NV centers, have shown unusual potential as qubit systems. It has been shown that their coherence properties are strongly improved by growing ultrapure diamond with low concentrations of parasitic spins. Wood et al. demonstrated quantum control of a single NV center within diamond at 200,000 rpm, a rotational period comparable to NV spin coherence times of $T_2^{HE}$ = 177 ± 24 μs, ($T_2^{XY8-1}$ = 323 ± 21 μs, and $T_2^{XY8-4}$ = 462 ± 130 μs for the Hahn echo, XY8-1, and XY8-4 pulse sequences, respectively) (Wood et al., 2022). Stroboscopic imaging of individual NV centers shows rapid circular motion in addition to rotation with demonstrated control and readout of qubit quantum states under microwave excitation. Using spin-echo interferometry of such qubits, these authors were able to detect modulation of the NV Zeeman shift arising from the rotating NV axis under DC magnetic fields. These authors and others established single NV qubits in the physically rotating frame as a path forward for Jakobi et al. to demonstrate single-qubit diamond-based rotational sensors (Jakobi et al., 2016).

Coherently coupled pairs of NV defect electron spins in diamond promise further advances. Scalable registers of spin qubits are essential to advancing quantum interactive polynomials (QIPs). Ion implantation is a plausible technique to produce defect pairs in close enough proximity to allow spin coupling via dipolar interaction. Residual radiation-induced defects, resulting in degraded qubit performance, is a principal hindrance.

Alternatively, Dréau et al. used the electronic spin of a single NV defect in diamond to observe the real-time evolution of neighboring single nuclear spins under ambient conditions (Dréau et al., 2013). Using a diamond sample with a natural abundance of C, these authors demonstrated high-fidelity initialization and single-shot readout of an individual C nuclear spin (Hennighausen and Kar, 2021). By including the intrinsic N nuclear spin of the NV defect in the quantum register (Schaibley et al., 2016), they reported the simultaneous observation of quantum jumps linked to both nuclear-spin species, providing an efficient initialization of two qubits. These results provide a viable path forward for diamond-based quantum information processing that includes active feedback in quantum error correction and tests of quantum correlations with solid-state single spins at room temperature.

Jahnke et al. reported a high-quality ¹²C-enriched polycrystalline chemical vapor-deposited diamond with properties comparable to single crystals. Single NVs in the grains of this material show extremely long electron spin coherence times of greater than 2 ms (Jahnke et al., 2012).

Coherent manipulation of an individual electron spin and nearby individual nuclear spins create a controllable quantum register. Using optical and microwave excitations to control electron spin associated with NV color centers in diamond, Dutt et al. demonstrated robust initialization of electron and nuclear-spin qubits and transfer of arbitrary quantum states between them at room temperature. Nuclear-spin qubits were isolated from the electron spin even during optical polarization and measurement of their electronic state (Dutt et al., 2007).

8.5 Topological qubits

8.5.1 Non-Abelian anyons

A topological quantum computer (TQC) was proposed by Kitaev in 1997 that employs anyons²⁷ as qubits (Kitaev, 1997), which are quasiparticles in two-dimensional systems whose world lines wrap around one another to form braids in three-dimensional spacetime (i.e., one temporal plus two spatial dimensions). Figures 17A–C depict topological qubits (i.e., anyons) and their functions, including braiding (i.e., computation) and fusion (i.e., measurement). Braids form logic gates that are largely impervious to small perturbations that normally would compromise coherence in other qubit modalities, leading to computational errors (Pachos, 2012; Topological Quantum Computer, 2023). Anyons appear as quasiparticles in fractional quantum Hall states and as excitations in some frustrated quantum magnetic systems (Wilczek, 2006).

Figure 17

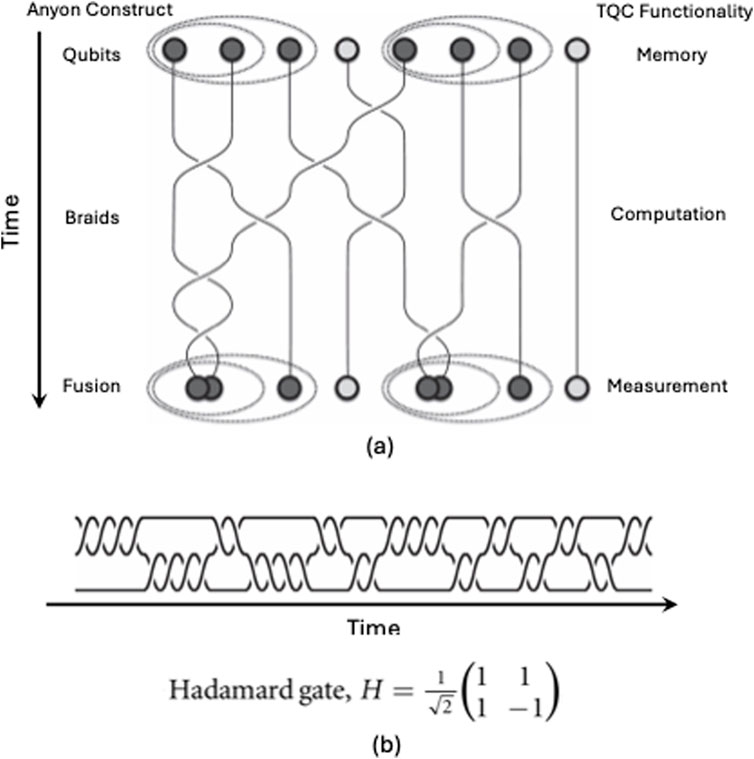
Figure 17. (A) illustrates two qubits composed of four non-Abelian anyons acting as memory units. These anyons are shown to demonstrate braiding, or the mapping out of paths, in three-dimensional spacetime as a means to implement logic gates and execute computations. Panel (B) is an example of anyon braiding approximating the Hadamard gate. Upon braiding, multiple anyons behave as one larger composite anyon. These fused anyons contain quantum information reflecting braiding operations. (Field and Simula, 2018; Nayak et al., 2008).

The exchange statistics of quantum Hall states are typically Abelian. However, Moore et al. proposed that anyons can be realized in fractional quantum Hall states (Moore and Read, 1991; Wen and Xiao-Gang, 1991) that are described by non-Abelian statistics²⁸; these are Ising anyons²⁹ and Fibonacci anyons³⁰.

While early on, non-Abelian anyons were considered a mathematical conception, Alexei Kitaev showed in 2003 that non-Abelian anyons could be used to construct a topological quantum computer (Kitaev, 2003). It was 10 years before Willett et al. presented the first experimental evidence of non-Abelian anyons (Willett et al., 2013).

As a rule, in a system with non-Abelian anyons, there are composite particles whose statistics are not uniquely determined by the statistics of their components but rather as quantum superposition. If the overall statistics of the fusion of several anyons are known, there remains ambiguity in the fusion of the subsets of these anyons, and each possibility is a unique quantum state. These multiple states provide a Hilbert space on which quantum computations can be performed (Nayak et al., 2008;Wikipedia, 2022).

8.5.2 Quasiparticle braiding

An example of an anyon derives from the fractional quantum Hall state at 1/3 filling. One can envision these quasiparticles as one-third of a composite boson, consisting of an electron with three bound flux quanta. Therefore, they have an effective fractional charge of e/3, and the phase addition that one expects to result from braiding two of them is 2π/3 (Arovas et al., 1984). While the e/3 charge has been firmly established for more than 20 years, the experimental detection of anyonic statistics—the fractional phase—has been somewhat elusive.

8.5.3 Majorana zero modes

Majorana zero modes are fermionic operators ($\left.\gamma \right)$. It is important that MZMs be spatially localized for Majorana fermions to be interpreted as Ising anyons and acquire particle-like behavior. Such MZMs are decoupled from local fluctuations and are predicted to obey non-Abelian exchange statistics. Therefore, qubits encoded by such MZMs would not only have decoherence that is exponentially suppressed by the physical separation between MZMs but would also allow topologically protected gate operations through braiding. The built-in topological qubit protection is unique; however, clear experimental evidence for the existence of non-Abelian low-energy modes in solid-state devices has proven elusive (Microsoft, 2022; Wikipedia, 2022).

8.6 Vibrational qubits

In an ideal three-dimensional crystal, phonons play a role analogous to photons but propagate at much lower velocities. In fact, the phonon-photon analogy is also supported in semiconductor crystal systems where conduction and valence bands play a role, like the quantum electrodynamic (QED) vacuum, where quasi-free electrons and holes propagate according to quadratic dispersion, scattering off acoustic phonons that possess linear dispersion. Thus, the behavior of QED repeats itself in the behavior of electronic and hole quasiparticles in solid and phonon vibrations within crystals (Ruskov and Tahan, 2012).

Mortezapour et al. investigated the dynamics of coherence and entanglement of vibrating qubits of a single trapped-ion qubit inside a perfect cavity and used it to construct bipartite systems made of two such subsystems, taken as identical and noninteracting (Mortezapour et al., 2018). These authors found that qubit phonons led to the prolonging of initial coherence in both single-qubit and two-qubit systems. They showed how photon–phonon correlations between cavity and vibrational modes stored in single-qubit systems are strongly affected by the initial state of the qubit. Such results provide insights into how phonon qubit systems maintain quantum information compared to systems of stationary qubits.

Specifically, the evolution of two-qubit coherence for various intensities of the cavity and vibrational modes for stationary qubits (column I) and vibrating qubits (column II) are shown to evolve in time in Figure 18. As can be seen in column I, an increase in the intensity of the cavity mode suppresses the decay of coherence during time evolution. Alternatively, column II displays the vibration of qubits inducing rapid oscillations and prolonging coherence compared to stationary qubits. The more intense the qubit vibrational mode, the slower the decay of two-qubit coherence, a behavior resembling that of single-qubit coherence. These results provide evidence that coherence and entanglement are, in general, quantum effects of a different nature when seen within the same composite system (Hanson et al., 2007).

Figure 18

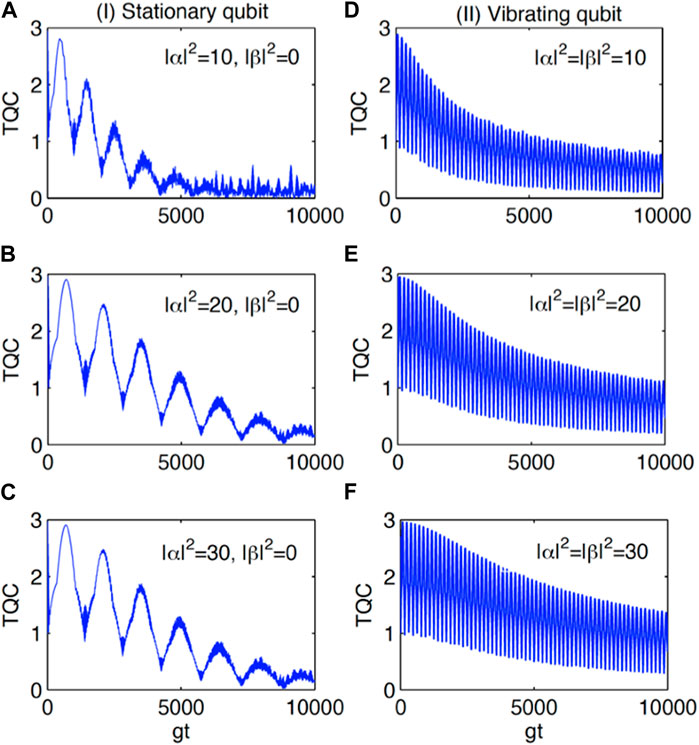
Figure 18. The dynamic behavior of two-qubit coherence (TQC) for different intensities of cavity and vibrational modes. Column (I) for stationary qubits and column (II) for vibrating qubits. Symbols depicted within each panel are defined and discussed in Mortezapour et al. (2018).

Theoretical predictions support the need for quantum gate fidelities of 99.99% in order for error-correction codes to be effective. In 2012, Berrios et al. tested fidelities for a CNOT gate executed by ultrafast laser pulses interacting with vibrational modes of SCCl2 (i.e., the molecule SCC_F: thiophosgene thiocarbonyl chloride) to be effective. These authors included all vibrational states, even those that did not encode desired qubits but were close enough in energy to interfere with a population transferred by laser pulses. They pursued two approaches: (1) optimal control theory that determined the best possible pulse and (2) a constrained physical model that calculated the most likely pulse. Optimal control theory found pulses with fidelities >99.99%, more than the quantum error-correction threshold for 8×10⁴ iterations, and 99.92% after the 8×10⁴ iterations for most likely pulses. Both calculations converged as an inverse power law toward a fidelity of 100%. The principal finding was that fidelities necessary for quantum error correction are certainly attainable with qubit-encoded molecular vibrations (Berrios et al., 2012).

Ruskov and Tahan explored the possibility of strongly coupling semiconductor qubit states to Si-etched nanomechanical resonators. These systems are relevant to qubit transduction, as an auxiliary technology for quantum information processing, for qubit characterization, and for quantum-enabled devices. Specifically, these authors considered systems where cavity phonons interacted with qubit states over a frequency band of 1–10 GHz (Ruskov and Tahan, 2012).

Gollub et al. analyzed the effects of molecular properties on the structure of quantum gates and the complexity of the resulting mechanisms with the goal of rating a molecule’s suitability for molecular quantum computing (Gollub et al., 2006). A primary property of molecular vibration is its anharmonicity³¹ and its extension to multimode systems, whereupon the mode coupling must also be accounted for. Characteristic properties are tuned in a parametrized two-dimensional model system, and their effects upon quantum gates are explored. These authors found that the interplay of anharmonicity and coupling is of prime importance to basic control of all systems.

Key findings included the complexity of the optimized quantum gate laser fields that depended on gate length, among other parameters. For converged runs with equal gate lengths, very similar or even identical laser fields are found suitable. Calculations demonstrated that it was possible to implement highly efficient elementary global quantum gates, that is, CNOT, NOT, and Hadamard gates, for all symmetric, asymmetric, anharmonic, and coupled 2D systems (Gollub et al., 2006).

Recently, Troppmann et al. explored the possibility of quantum computing with molecular vibrations in a 2D model of acetylene, finding that specifically shaped femtosecond-laser pulses in the IR represented global quantum gates and could be acquired by optimal control theory. Leakage from the qubit basis used for quantum computation and the influence of dark, non-IR-active modes coupled via anharmonic resonances was proven to be an essential variable. In a 3D-model, it was further demonstrated that selective preparation of a vibrational eigenstate in near anharmonic resonance was essential. A Hadamard gate was realized in that work; this is the first step in the preparation of a Bell state³².

8.7 Trapped-ion qubits

Ions can be confined and suspended in a vacuum using electromagnetic fields. Under such circumstances, qubits are stored as stable electronic states, and quantum information is transferred through a collective of quantized motion of ions in a trap interacting via Coulombic forces. Lasers are useful in inducing coupling between such qubits for single-qubit systems or coupling between internal qubits and external motional states for entangled qubits (Nielsen and Chuang, 2000).

Trapped ions are one of the most promising qubit modalities for realizing useful quantum computers. They exhibit properties necessary for building such systems that have very few fundamental limitations to achieve sufficiently high gate fidelities. The single- and two-qubit gate fidelities demonstrated in small-scale systems, combined with the ion’s long coherence times, exceed the capabilities of many other proposed modalities. However, to build a useful quantum simulator that outperforms current classical machines and therefore achieves “quantum advantage;” the system size must be scaled to at least a few tens of qubits without compromising the precision of operation (Bruzewicz et al., 2019a).

The fundamental operations in quantum computing have been demonstrated with very high accuracy in trapped-ion systems. Promising schemes to scale the system to necessarily larger numbers of qubits include transporting ions to spatially distinct locations in an array of ion traps and building larger, entangled states via photonically connected networks of remotely entangled ion chains. This makes the trapped-ion quantum computer modality one of the most promising for a scalable universal quantum computer (Friis et al., 2018-04; Monz et al., 2011;Paul, 1990).

Ionic qubit states can be prepared using a process called optical pumping. In such a process, a laser couples the ion to excited states that eventually decay to one state that is not coupled to the laser. Once the ion reaches that state, it has no excited levels to couple in the presence of the laser and, therefore, remains in that particular state. If the ion decays to one of the other states, the laser will continue to excite the ion until it decays to a state that does not interact with the laser. This initialization process is standard in many experiments and can be performed with exceptionally high fidelity (>99.9%) (Schindler et al., 2013).

Figures 19A–C depict states of preparation, control, and detection of trapped-ion optical qubits. Here, the ion is seen to be quickly optically pumped to the |1⟩ state by coupling the long-lived |0⟩ state to an auxiliary state |e⟩_SP that rapidly decays. The qubit is further controlled by directly coupling the |0⟩ and |1⟩ states using a narrow electric quadrupole transition, while readout is achieved by photo-transitioning |1⟩ → |e⟩_R and collecting scattered fluorescence (Bruzewicz et al., 2019).

Figure 19

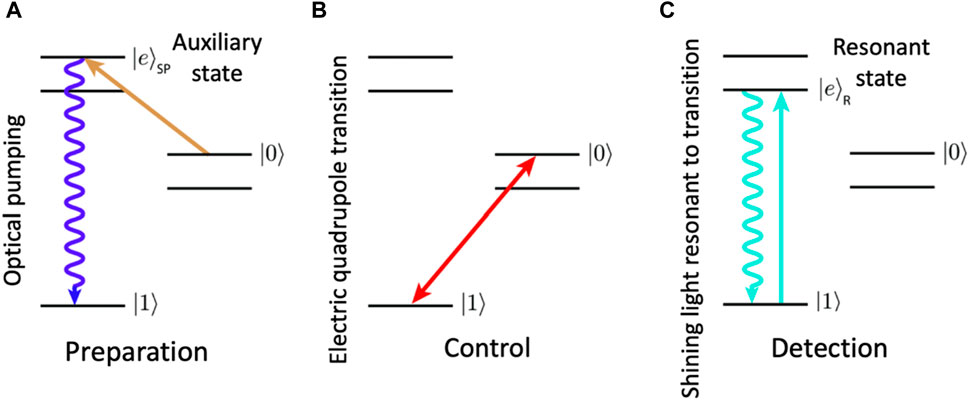
Figure 19. Depiction of state preparation, control, and detection in trapped-ion optical qubits as discussed by Bruzewicz et al. (2019). (A) The ion is initially pumped to the |1⟩ state by coupling the long-lived |0⟩ state to an auxiliary state |e⟩SP that rapidly decays. (B) Qubit control is achieved by directly coupling the |0⟩ and |1⟩ states using a narrow electric quadrupole transition. (C) Detection is achieved by light resonant on the broad transition |1⟩ → |e⟩R and collecting the resulting scattered fluorescence photons. There is no similar transition |0⟩ → |e⟩R, so the |0⟩ state appears dark in contrast. Rights to reproduce strictly adhere to those granted by arXiv.org as agreed upon by the original authorsSimplified depiction of state preparation, control, and detection in trapped-ion optical qubits. (A) (Initiation) The ion can be quickly optically pumped to the |1⟩ state by coupling the long-lived |0⟩ state to an auxiliary state |e⟩_SP that rapidly decays. (B) Qubit control is achieved by directly coupling the |0⟩ and |1⟩ states using a narrow electric quadrupole transition. (C) Detection is achieved by shining light resonant on the broad transition |1⟩ → |e⟩_R and collecting the resulting scattered fluorescence photons. There is no similar transition |0⟩ → |e⟩_R, so the |0⟩ state appears dark.

Figures 20A–C depict an assembly of a macroscale ion trap with “blade”-shaped electrodes wherein the dashed area in (a) translates to the dashed area in (b). The blade ion trap in the ultrahigh vacuum reveals needle-type electrodes separated by mere millimeters. Finally, nine calcium-43 ions confined in an ion trap appear to be approximately 10 µm apart, scattering 397 nm laser light at an effective temperature of ∼1 mK (Ion Trap QuantumComputing, 2023).

Figure 20

Figure 20. (A) Assembly of a macroscale ion trap with “blade”-shaped electrodes (Credit: Sarah Woodrow for photograph, University of Oxford, Department of Physics). The dashed area in (A) is the dashed area in (B). (B) “Blade” ion trap in an ultrahigh vacuum system. The tips of the needle electrodes are separated by 2.3 mm (Credit: David Nadlinger for photograph, Department of Physics, University of Oxford). (C) An image of nine calcium-43 ions confined in an ion trap about 10 µm apart scattering 397 nm laser light at an effective temperature of ∼1 mK.

9 Qubit and gate coherence and fidelity

An expansive and informative review of superconducting qubits and their properties has been published by Siddiqi (2021); from this, we learn much.

Contemporary superconducting qubits combine one or a few Al/AlO_x/Al Josephson junctions (JJs), which function as a nonlinear inductance (Tinkham, 2004), with other reactive elements—comprising thin-film Al, Nb, NbN, NbTiN, Ta, or TiN, for example—to form a circuit where the potential energy surface has at least two bound states. The minimalist realization of such an anharmonic oscillator is a single Josephson tunnel junction formed by two planar superconducting electrodes separated by an insulating layer.

The geometric self-capacitance shunts the kinetic inductance associated with Cooper pairs tunneling across the barrier to yield a resonance frequency typically in the microwave frequency range, and individual quantum levels can be readily detected using microwave spectroscopy (Martinis et al., 1985; Martinis et al., 2020). Coupling the JJ circuit to a microwave resonator for control and readout robustly yields long-lived charge-based and flux-based qubits in which the lowest two energy levels form the “0” and “1” states of a physical qubit (Koch et al., 2007-10; You et al., 2007). In these circuits, the junction provides the anharmonicity needed to selectively address the 0–1 transition. JJs can be constructed by sandwiching two superconducting reservoirs around any structure that allows the condensate wavefunction to deviate from its surrounding bulk value, but the tunnel-junction geometry with an insulating barrier has thus far been the most widely used (Van Duzer and Turner, 1998) in electronic circuits, given the attractive features of a robust sinusoidal dependence of the supercurrent on the junction phase difference (Golubov et al., 2004) and the absence of electronic states below the superconducting energy gap. To tune the qubit parameters and drive quantum-state transitions, JJs can be readily integrated into superconducting loops or can be contacted with isolated submicron superconducting islands, enabling control via an external magnetic or electric field, respectively (Makhlin et al., 2001; Wendin and Shumeiko, 2007; Krantz et al., 2019;Kjaergaard et al., 2020). The values begin around 10 ns of inhomogeneous dephasing time in early experiments with qubits in GaAs. Echo techniques extend the coherence by orders of magnitude, as can different material choices. The coherence times published during 2021 span six orders of magnitude, depending on the qubit type, material, and protection measures.

The relaxation times are often comparable to coherence times, unlike spin qubits, where they can be advanced to far longer amplitudes. Therefore, relaxation is a bigger issue for charge qubits, even in single-qubit experiments. Second, unlike spin qubits, the echo techniques do not prolong coherence. Third, there is much less variation among the published data despite an upward trend in T₂^*. As the charge–qubit dephasing time, T₂^*, is related to charge noise, a clear trend would indicate an improvement in the available samples and devices concerning charge noise. Finally, one would expect no apparent difference between devices made in Si and III–V materials concerning charge–qubit coherence.

In Figure 21A–D, different coherence times, T₂, measured using different measurement techniques, are presented for various qubit systems being of discrete category on the horizontal axis. These figures depict data extracted from Stano and Loss (2022) and presented in a different format for ease of identifying trends in the format of this review. The keys that define these data are presented in Tables 10, 11. Table 12 presents a summary of key decoherence mechanisms, their origins, and viable mitigation strategies summarized from the work of Siddiqi (2021) including: two-level system defects, quasiparticles and phonons, and 1/f magnetic flux noise. The next several sections present discussion o f coherence mechanisms of different qubit modalities.

Figure 21

Figure 21. (A) T₂^*, inhomogeneous dephasing time, also called free induction decay (FID) time. (B) $T_2^{Echo}$, coherence time measured under a Hahn echo. (C) $T_2^{DynD}$, coherence time measured under dynamical decoupling. (D) $T_2^{Rabi}$, decay of coherent Rabi oscillations. In each panel, the horizontal axis uses the qubit type as a discrete category. All data colors reflect the qubit material and are defined in Table 10.

Table 10

Table 10. Identifiers and descriptions employed in Figure 21 and Figure 24.

Table 11

Table 11. Symbol key to Figure 21 and Figure 24.

Table 12

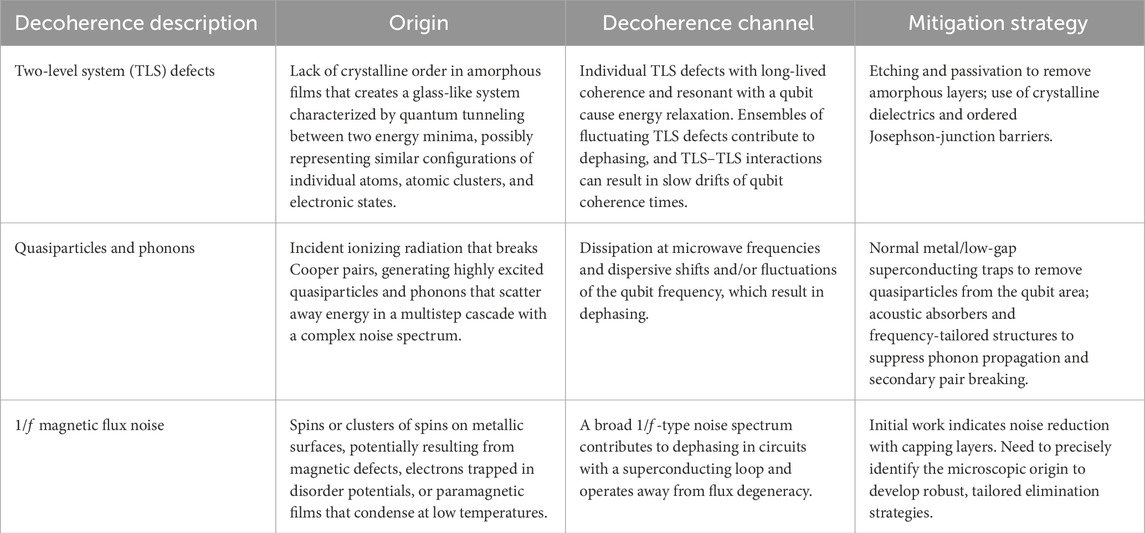
Table 12. Summary of key decoherence mechanisms, their origins, and viable mitigation strategies (Siddiqi, 2021).

9.1 Coherence of charge qubits

We end the overview of coherence times by examining charge qubits. As already mentioned, we include them even though they implement qubits that do not rely on spin. The reason is a close relationship between the devices in which the two types of experiment are typically done and the techniques used: for example, the measurement of spin is done indirectly, converting different spin states to different charge states, which are then detected.

All types of coherence times of charge qubits, including the relaxation time, are gathered in Figure 21. In the three panels of the figure, the same data are shown according to the publication date, the device material, and the coherence type. One can see several differences compared with spin qubits. First, the relaxation times are often comparable to coherence times, unlike for most spin qubits, where they can be pushed to the longest scale by far. Therefore, relaxation is a bigger issue for charge qubits, even in single-qubit experiments. Second, unlike for spin qubits, the echo techniques do not prolong coherence substantially. Third, there is much less variation among the data: despite an upward trend in T₂^* over time, the increase is not marked. As the charge–qubit dephasing time T₂^* is directly related to charge noise, a clear trend would indicate an overall improvement of the available samples and devices concerning the level of charge noise. Finally, as one would expect based on the nuclear-spin noise being irrelevant for charge qubits, there is no apparent difference between devices made in Si and III–V materials concerning charge–qubit coherence.

The increased capacitance influences the anharmonicity and the difference in energy between successive excitations and charge dispersion. The advantage of transmons derives from predicting that as E_j/E_c increases, the charge dispersion decreases exponentially, while anharmonicity decreases as a power law.

9.2 Coherence of semiconducting qubits

Gate-controlled semiconductor spin qubits are considered an attractive platform for massively-scalable quantum information systems due to their relatively small form factor and fast processing times (Chatterjee et al., 2021). A primary source of decoherence for spin qubits is the hyperfine interaction between electron spins and randomly fluctuating nuclear spins of their semiconductor lattice, leading to magnetic noise that causes unwanted qubit rotation (Hanson et al., 2007). A proven effective mitigation strategy for this noise source has been the use of group-IV semiconductors as opposed to group III–V semiconductor compounds. This allows for the development of nuclear-spin-free hosts that have been shown to extend coherence times by more than four orders of magnitude (Stano and Loss, 2022).

Reaching two-qubit gate fidelities greater than 99% has been a long-standing goal for semiconductors and other spin-qubit modalities. Such qubits are promising for scaling as they leverage mature semiconductor processing technologies (Zwerver et al., 2022). A spin-based quantum processor in silicon with single-qubit and two-qubit gate fidelities, all of which are >99.5% extracted from gate-set tomography, is an important step in the evolution of this technology (McArdle et al., 2020).

Electron spin qubits in silicon (Veldhorst et al., 2014; Veldhorst et al., 2015; Zajac et al., 2016; Vandersypen et al., 2017; Yoneda et al., 2018; Jones et al., 2018; Li et al., 2018; Petit et al., 2020; Yang et al., 2020) are particularly promising for a large-scale quantum computer owing to their nanofabrication capability, but the two-qubit gate fidelity has been limited to 98% owing to the slow operation (Huang et al., 2019).

Noiri et al. employed a micromagnet-induced gradient field applied to silicon spin qubits creating fast electrical control of tuning two-qubit coupling. This allowed a demonstration of a two-qubit gate fidelity of 99.5% with single-qubit gate fidelities of 99.8%. These authors realized Deutsch–Jozsa and Grover search algorithms with high success rates using a universal gate set. These results demonstrated universal gate fidelity beyond the fault-tolerance threshold and may enable scalable silicon quantum computers (Noiri et al., 2022).

Universal quantum logic operations were demonstrated using a pair of ion-implanted ³¹P donor nuclei in a silicon nanoelectronic device. A nuclear two-qubit controlled-Z gate was obtained by imparting a geometric phase to a shared electron spin4 and used to prepare entangled Bell states with fidelities up to 94.2 $\pm$ 2.7%. The quantum operations were precisely characterized using gate-set tomography (GST) (Nielsen et al., 2021), yielding one-qubit average gate fidelities up to 99.95 $\pm$ 2.0%, two-qubit average gate fidelity of 99.37 $\pm$ 11.0% and two-qubit preparation/measurement fidelities of 98.95 $\pm$ 4.0%. These three metrics indicated that nuclear spins in silicon are approaching the performance demanded in fault-tolerant quantum processors (Fowler A. G. et al., 2012). Entanglement between the two nuclei and the shared electron was demonstrated by producing a Greenberger–Horne–Zeilinger three-qubit state with 92.5 $\pm$ 1.0% fidelity.

Because electron spin qubits in semiconductors can be further coupled to other electrons (Harvey-Collard et al., 2017; He et al., 2019; Madzik et al., 2021) or physically shuttled across different locations (Hensen et al., 2020; Yoneda et al., 2021), these results establish a viable route for scalable quantum information processing using donor nuclear and electron spins (Mądzik et al., 2022).

The use of couplers to control two-qubit interactions has also improved operational fidelity in many-qubit systems by reducing parasitic overcrowding (Yan et al., 2018). Nonetheless, two-qubit gate errors continue to limit the capability of near-term quantum applications. This limitation derives from dispersive approximations that do not fully incorporate three-body dynamics. Using an approach that systematically extends dispersive approximations to exploit couplers was recently employed by Sung et al. and demonstrated CZ and ZZ-free iSWAP gates with two-qubit fidelities of 99.76 $\pm$ 0.07% and 99.87 $\pm$ 0.23%, respectively (Sung et al., 2021).

One attractive feature of spin qubits is their compact size. Protection schemes based on local encodings in decoherence-free subspaces are particularly interesting because such encodings do not require a qualitative scale-up in qubit size, as opposed to global, for example, topological, encodings.

9.3 Coherence of topological qubits

Hybrid semiconductor–superconductor devices, based on novel materials (and/or processing technologies), can be engineered into topological phases that, in turn, can be used as protected qubit encodings (Sato et al., 2009; Alicea, 2010; Sau et al., 2010). For example, a quasi-one-dimensional semiconductor with strong spin–orbit coupling and large Lande g-factor can, when in proximity to an S-wave superconductor, becomes a topological superconductor with localized Majorana zero modes (MZMs)³³ at its terminations (Lutchyn et al., 2010; Oreg et al., 2010; Hell et al., 2017). MZMs are decoupled from local fluctuations and obey non-Abelian anyonic exchange statistics. Hence, qubits encoded as MZMs experience exponentially reduced decoherence in the physical space between MZMs but would allow topologically protected gate operations through braiding (Stanescu, 2016).

Recent experiments have focused on 1D-systems (e.g., nanowires) with strong spin–orbit interaction, proximity-coupled to an S-wave superconductor, taking the form of heavy-element semiconductors such as InAs and InSb, coupled to Al and NbTiN as superconductors. However, disorder at the semiconductor–superconductor interface remains a source of subgap states that yield subgap conductance and degrade the hard superconducting gap that serves to protect against thermal quasiparticle excitation (Takei et al., 2013). Hence, the engineering of interface chemistry and structure remains a principal challenge in eliminating scattering and disorder that leads to topological qubit decoherence and less-than-ideal gate fidelity (Akhmerov et al., 2011; Krogstrup et al., 2015). Figure 22A illustrates frequency scans of simulated time evolution for a single qubit. The figure shows scans of the population of the |0⟩ state (as n₀) as a function of simulated time t and frequency ω on the “ibmq_armonk device” (Team, 2020; Das et al., 2021). The time t is equal to the number of gates times τ multiplied by the scaling factor 0.015. The oscillatory behavior reveals non-Markovian effects, with the oscillations becoming less pronounced at higher frequencies. We begin with a single-qubit system with the Hamiltonian matrix H(ω) = ωσ_z, where we use atomic units with ħ = 1, and σ_z is the Pauli-Z matrix. If one allows the system to relax without applying any gates, this becomes a T₁ experiment, measuring the relaxation time for an excited state. However, the noise sources here, represented by the non-vanishing memory kernel, generate non-Markovian behavior.

Figure 22

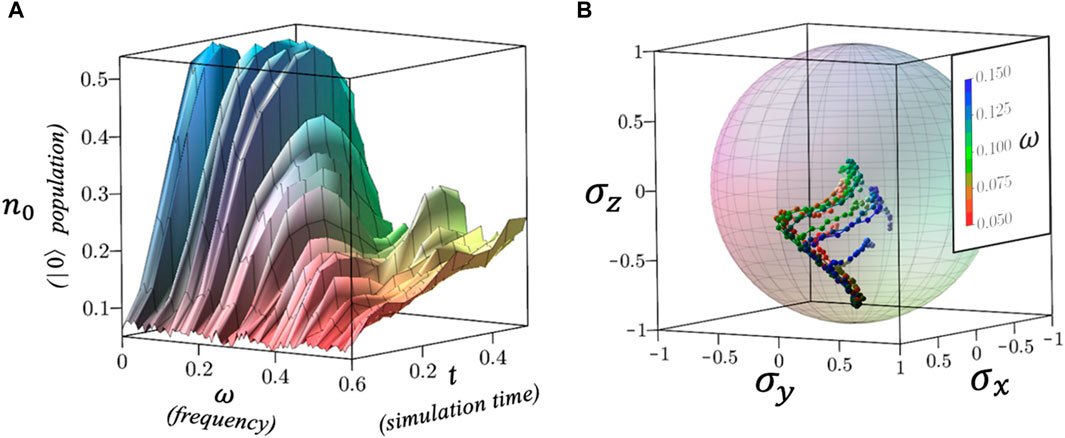
Figure 22. (A) Frequency scans of simulated time evolution for a single qubit. Scans of the population of the |0⟩ state (n₀) as a function of simulated time t and frequency ω on the IBM Q Armonk device (i.e., ibmq_armonk). The time t is equal to the number of gates times τ multiplied by the scaling factor 0.015. The oscillatory behavior reveals non-Markovian effects, with oscillations becoming less pronounced at higher ω. (B) Single-qubit state trajectories with respect to simulated time for a range of ω. Scan of several trajectories, represented in a Bloch sphere for a single-qubit device for a range of frequencies 0.05<ω < 0.15 at increments of 0.01. σ_i represents the expectation with respect to that operator as a function of time.

In Figure 22, the non-Markovian behavior is evident from the oscillations in the population of the ground state, which reveal a memory dependence beyond the pure decay of Markovian dynamics. Furthermore, the oscillations are more pronounced at lower frequencies, indicating a bath with colored noise (Smart et al., 2022). Scans of several trajectories represented in the Bloch sphere for a single-qubit device for a range of frequencies represent the expectation with respect to that operator (${\sigma }_x,{\sigma }_y,{\sigma }_z$) as a function of time (Figure 22B). Each simulation has an equal number of gate applications and changes only the frequency ω in the propagation with time step τ. We can also observe how the quantum-state vector moves within the Bloch sphere at different frequencies. A slow precession around the axis corresponding to H is observed for frequencies in the high region of the spectral density and does not allow for coupling between the bath and the system. However, the system can be strongly pulled around the Bloch sphere for frequencies that couple to the bath, resulting in various trajectories through the state space (Scholarpedia, 2022).

Figure 23 depicts advances in qubit coherence times for various qubit modalities from ∼2000 to ∼2015, including charge (McDermott, 2009; Siddiqi, 2021), quantronium (Metcalfe et al., 2007), flux (Yan F. et al., 2016), 2D transmon and fluxonium (Manucharyan et al., 2009), and 3D transmon qubits (Oliver and Welander, 2013). The transmon, developed by Schoelkopf and coworkers, significantly reduced the charge sensitivity of the Cooper-pair box by adding a shunt capacitor that later advanced microsecond times to the cavity-QED architecture (Koch et al., 2007-10; Houck et al., 2008). Bylander et al. increased T² above 20 μs with a persistent-current flux qubit in a 2D geometry using dynamical decoupling (Bylander et al., 2011), and a 3D-cavity approach developed by Paik et al. (2011) was employed by Rigetti et al. (2012-09) to further increase T² to ∼100 μs. A five-orders-of magnitude increase in coherence time has defined a “Moore’s Law” equivalence for quantum coherence (Steffen, 2011), approaching levels required for a class of fault-tolerant quantum error-correction codes (DiVincenzo, 2009; Fowler et al., 2009; Fowler A. G. et al., 2012).

Figure 23

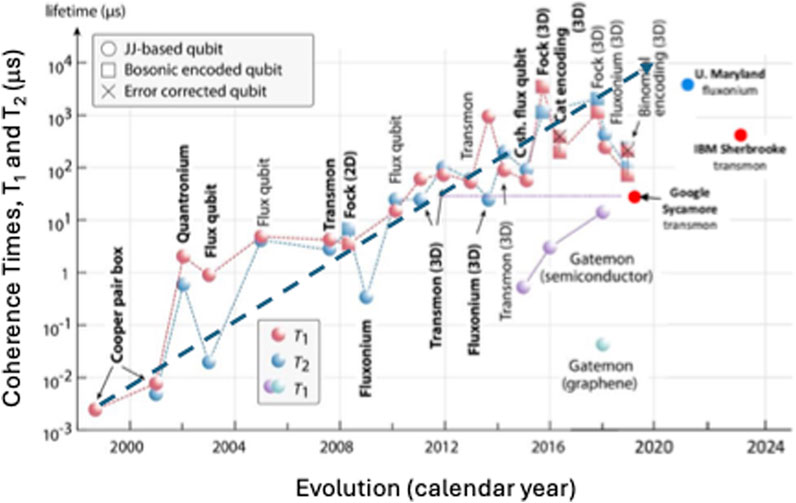
Figure 23. Superconducting qubit relaxation and coherence times (bold font indicates first demonstration of modality) are shown to increase logarithmically over time. Improvements are attributed to both innovations in materials science as well as device topologies (Kjaergaard et al., 2020). Reproduced with permission of the Annual Review with proper attribution.

Fault-tolerant quantum computers that can solve hard problems rely on quantum error correction (Nielsen and Chuang, 2000). One of the most promising error-correction codes is the surface code (Fowler A. G. et al., 2012), which requires universal gate fidelities exceeding an error-correction threshold of 99% (Wang D. S. et al., 2011). Among the many qubit platforms, only superconducting circuits (Barends et al., 2014b), trapped ions (Ballance et al., 2016), and NV centers in diamond (Rong et al., 2015) have met this high standard at the time of this publication.

9.4 The role of SOC in coherence

In spin–orbit qubits, information is stored between orbital and spin degrees of freedom. It is the strength of the coupling between the spin and orbital electronic and magnetic states that keeps the qubit stable and less prone to decoherence brought on by noise. Kobayashi et al. substantially lengthened the length of time that a spin–orbit qubit³⁴ in silicon can retain quantum information (van Der Heijden et al., 2018; Kobayashi et al., 2021; Scitechdaily, 2022). Although spin–orbit qubits have been investigated for over a decade, recent studies have demonstrated coherence times 10,000 times longer than previously recorded, making them an ideal candidate for scaling up silicon quantum computers. Van der Heijden et al. investigated the spin–orbit coupling of a boron atom in silicon focused on applying fast readout of the spin state of two boron atoms in a compact circuit hosted in a transistor, enabling rapid qubit manipulation and coupling over large distances (Van der Heijden et al., 2014;Zwerver et al., 2022).

Weber et al. also highlighted the role of spin–orbit coupling in qubits in silicon, focusing on phosphorus atom qubits (Weber et al., 2018). Their research revealed that spin–orbit coupling of the phosphorus electron spin to the induced electric fields extended spin lifetimes to minutes. The SOC interaction also allows coupling to other quantum systems, making the prospects for hybrid quantum systems possible.

Bommer et al. recently carried out a study investigating spin–orbit interaction in Majorana nanowires. By encoding quantum information into the topological property of Majorana zero modes, the decoherence error can be resolved from a fundamental device level. However, the creation of Majoranas relies on magnetic fields, which are typically incompatible with superconductivity. To overcome this limitation is to leverage the presence of spin–orbit interactions. Spin–orbit interaction materials experience weak magnetic fields required for Majoranas, thus allowing for superconductivity.

The study carried out by Bommer and his colleagues shows that superconductivity and spin–orbit interaction can exist simultaneously, unveiling that spin–orbit interaction protects superconductivity in Majorana nanowires (Bommer et al., 2019).

9.5 Control of qubit fidelity

High-fidelity control of qubits is of paramount importance to achieving robust fault tolerance and reliable quantum computation. This central tenet is required for effective fault tolerance and is expressed in terms of an error threshold; a common target is <1% error threshold of the surface code (Raussendorf and Harrington, 2007; Fowler A. G. et al., 2012). Reaching two-qubit gate fidelities greater than 99% has been a long-standing goal for semiconductors and the greater realm of spin-qubit modalities. Such qubits are promising for scaling as they leverage the mature semiconductor processing technologies developed over the last several decades (Zwerver et al., 2022).

The use of couplers to control two-qubit interactions has improved operational fidelity in many-qubit systems by reducing parasitic and frequency overcrowding. Nonetheless, two-qubit gate errors continue to limit the capability of near-term quantum applications. This limitation, in part, derives from the existing tunable coupler topologies that are based on dispersive approximations that do not fully incorporate three-body dynamics. Using an approach that systematically extends dispersive approximations to exploit engineered coupler structures, Sung et al. have demonstrated CZ and ZZ-free iSWAP gates with two-qubit interaction fidelities of 99.76 $\pm$ 0.07% and 99.87 $\pm$ 0.23%, respectively (Sung et al., 2021).

9.6 Superconducting qubit fidelity

The number of nodes in a quantum circuit determines the dimension of the quantum system, the size of inductors and JJs fixes the potential, and the capacitance values define the kinetic energy of the quantum state. The ability to independently control these three aspects of quantum states allows one to construct superconducting circuits that satisfy these requirements for intrinsic noise protection and, ultimately, coherence and fidelity.

The development and design of protected superconducting qubits now evolve along three main paths: (i) Josephson-junction arrays based on multimode circuits (Gyenis et al., 2021), (ii) compact few-mode circuits (Kringhøj et al., 2018), and (iii) driven systems (Chow et al., 2010; Wu et al., 2021a). These efforts can be further categorized as presented in Table 13.

Table 13

Table 13. Strategies for enhancing qubit coherence.

Operation fidelity is a dimensionless figure of merit, allowing the comparison of diverse qubits. Using randomized benchmarking (Epstein et al., 2014), one can extract the gate errors independently of the measurement errors, even if the former are orders of magnitude smaller than the latter. Although it is not strictly correct, the fidelity is used to judge the progress toward error-correction thresholds required for fault-tolerant quantum computing. The problem is that the fidelity, as defined below, is not the error parameter entering the threshold theorem. The two parameters can differ by orders of magnitude in the unfavorable way: whereas the fidelity extracted by the randomized benchmarking can be low, the error rate can remain much larger (Sanders et al., 2015; Blume-Kohout et al., 2017). For all these reasons, evaluating the gate fidelities is popular, and impressive values have been reached.

Figure 24 shows the published fidelities of the gates, measurements, and initializations, respectively. For gates (Figure 24A), electron spin-½ qubits previously reached fidelities well above 99.9%. The use of both natural and isotopically purified silicon was essential for this achievement. Recently, a new record of 99.99% was set by hole-doped germanium (Lawrie et al., 2021a). There is notable progress in almost every qubit category, and increasing the fidelity of single-qubit gates is one of the most impressive achievements within the spin-qubit field.

Figure 24

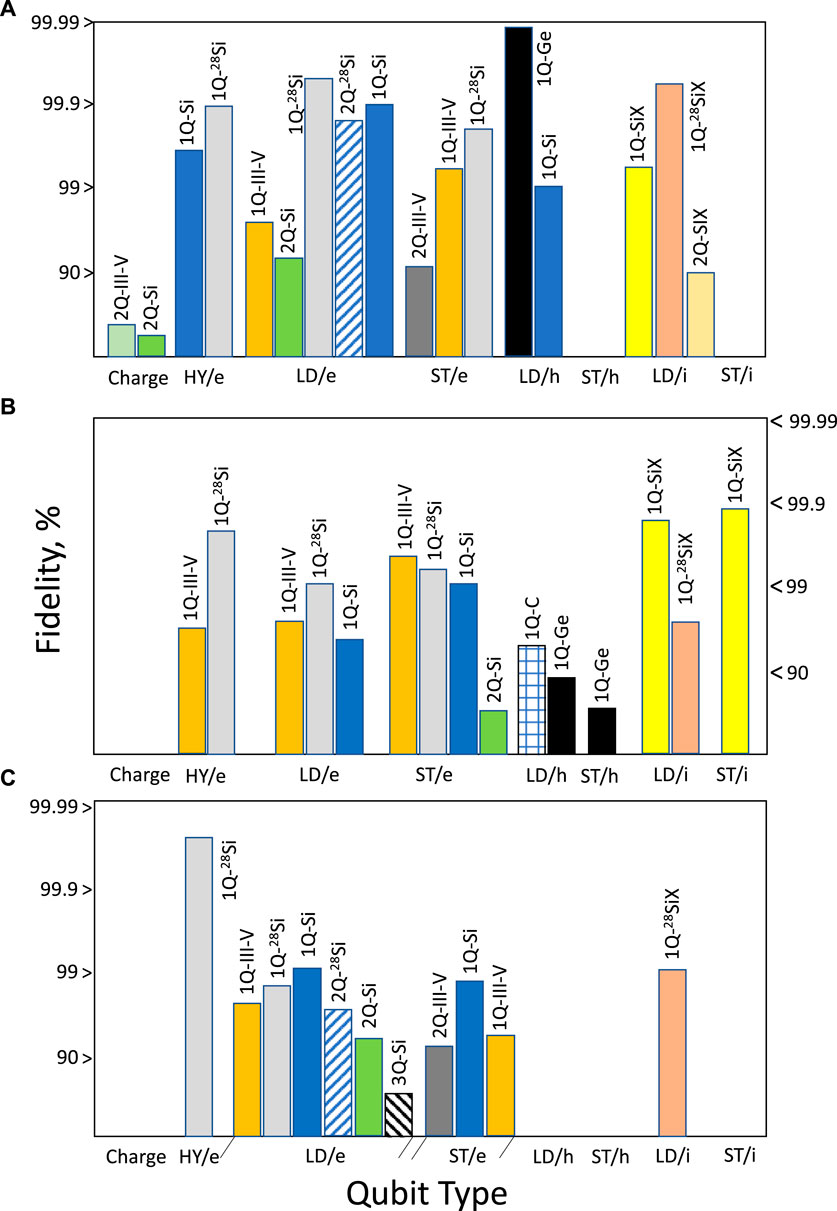
Figure 24. Fidelities are shown for (A) gates, (B) measurements, and (C) initializations. In all panels, the horizontal axis shows the qubit type. The vertical axis shows the fidelity in percent. The data color indicates the material defined in the supplemental documents in Stano and Loss (2022). LD/e, ST/e, LD/h, LD/i, and ST/i qubit types are defined in Table 11. 1Q, one-qubit gate; 2Q, two-qubit gate; 3Q, three-qubit gate.

Figure 24 also shows measurement fidelities. Until recently, the infidelities remained above a few percent. Relying on a “latched” readout in the Pauli spin blockade (Broome et al., 2017a; Nakajima et al., 2017), the fidelities above 99% were achieved with a singlet–triplet algorithm: for example, initializing all individual qubits into single-qubit fiducial states, and then entangling them with gates into the desired entangled multi-qubit state, such as one of the two-qubit Bell states or the three-qubit Greenberger–Horne–Zeilinger (GHZ) state.

Shunting the circuit with a large capacitance leads to an electrostatic energy that is significantly reduced relative to the JJ (E_j/E_c >> 1). The sensitivity of the qubit frequency to the charge noise is suppressed. In this regime, the qubit is called a transmon.

Stano and Loss published an excellent review of performance metrics for qubit/gate fidelities and coherence times, among other properties (Stano and Loss, 2022). Of the plethora of data presented by these authors, we reproduce a subset here as Figures 21, 24.

9.7 Qubit, gate, and system fidelities

Figures 24A–C show published fidelities of gates, measurements, and initializations, respectively. For the gates shown in Figure 20A, electron spin-½ qubits reached fidelities above 99.9%. Using natural and isotopically purified forms of Si was required for this achievement. These values were further enhanced using a hole in Ge (Lawrie et al., 2021b), leading to fidelities of 99.99%. Figure 24B shows measurement fidelities. Until recently, infidelities remained above a few percent. Relying on a latched readout in the Pauli spin blockade (Broome et al., 2017b; Nakajima et al., 2017b), fidelities above 99% were achieved for singlet–triplet qubits. Higher fidelities for impurity spins require exceptionally long lifetimes. In all fidelity categories presented in Figure 24, that is, gates, measurements, and initializations, infidelities remain one to two orders of magnitude above single-qubit systems. Concerning initializations, the more-qubit infidelities are initializations into a nontrivial state achieved through the application of a simple quantum algorithm. For example, initializing all individual qubits into a single-qubit state and then entangling them with gates into the desired entangled multi-qubit state, such as one of the two-qubit Bell states or the three-qubit Greenberger–Horne–Zeilinger (GHZ) state. Figure 25A is a schematic of a harmonic oscillator, where energy levels are equally spaced and un-addressable. When a JJ is added to the circuit (b), a nonlinear component is introduced in the form of a non-dissipative, nonlinear inductance. A two-level system (TLS) of eigenfunctions in a double-well potential is characterized by the strain-dependent asymmetry energy ε and the tunnel coupling Δ (see Figure 25C). The image in (c) depicts a material schematic of the JJ where superconducting electrodes sandwich an insulator. A classic example is Al/Al₂O₃/Al. The tunneling of individual atoms between two configurations (Phillips, 1987; Agarwal et al., 2013), displacements of dangling bonds, and hydrogen defects (Holder et al., 2013) are depicted in the image. Near the interface of the superconducting electrodes, TLSs may also arise from bound electron/hole Andreev states (Faoro et al., 2005) or Kondo-fluctuators (Faoro and Ioffe, 2007).

Figure 25

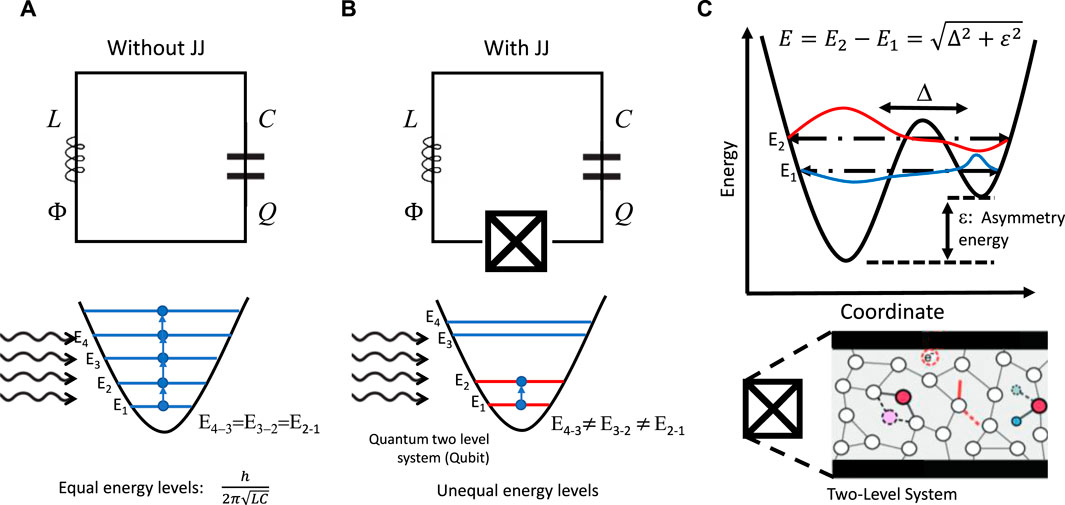
Figure 25. (A) Schematic of a harmonic oscillator where energy levels are equally spaced and un-addressable. (B) A Josephson Junction (JJ) is added to the circuit, introducing a nonlinear component in the form of a non-dissipative, nonlinear inductance. (C) The upper illustration of a TLS sketch of eigenfunctions in a double-well potential that is characterized by the strain-dependent asymmetry energy (ε) and the tunnel coupling (Δ). The lower image in (C) depicts a material schematic of the JJ where superconducting electrodes are on either side of an insulator. A classic example is the Al/Al₂O₃/Al system.

We next turn to qubit energy relaxation. For spin qubits, for example, in considering two-electron singlet and triplet states, relaxation times are the main limitation to spin fidelity (Barthel et al., 2009; IBM, 2016; IMEC, 2023). Because of this, there are numerous values of relaxation time for singlet–triplet qubits, either explicitly reported or implicitly inferred by many experiments, for example, using Pauli spin blockade for determining spin characteristics. The use of impurities focused on isolating qubits from such reservoirs that electrons do not escape hence conserving dipole momentum. As such, qubits couple weakly to phonons, and decrease transition energies, typically using lower magnetic fields and thus setting fundamental limitations upon quantum computations (Shrivastava, 1983; Khaetskii and Nazarov, 2001).

10 Sources, impact, and mitigation of noise

10.1 Two-level system defects

Consider first the case where a TLS is coupled to a qubit with strength g, such that g is larger than the decoherence rate of both the TLS and the qubit. In this regime, the TLS acts as a random qubit that can swap information with the quantum circuit (see Figure 25).

Phase qubits consist of a JJ and a shunt capacitor, both with lateral dimensions on the order of microns, and therefore have large areas of amorphous regions with many TLS defects. Naturally, smaller junctions have fewer defects. When such defects are exposed to intense electric fields, they give rise to classic TLS physics, including strong electromagnetic coupling among distinct TLS defects (Simmonds et al., 2004; Martinis et al., 2005). The signatures of strong EM coupling can be observed in the time domain, where beating is seen when driving coherent Rabi oscillations as a significant source of decoherence.

Best practices to improve coherence include improved shielding, which involves effective cryosinking and the use of nested radiation shields at infrared frequencies. Further, traps for both quasiparticles and phonons at the quantum-chip level must be developed. Such structures can be based on either microscopic defects or lithographically defined structures (Levenson-Falk et al., 2014; Wang et al., 2014; Taupin et al., 2016).

Engineered structures can incorporate a normal metal (Riwar et al., 2016) or lower-gap superconductor regions (Aumentado et al., 2004; Riwar and Catelani, 2019; Martinis, 2021) to trap quasiparticles, as well as circuits for active pumping using pulses (Gustavsson et al., 2016) or voltage-biased tunnel junctions (Marín-Suárez et al., 2020). Traps for phonons can be constructed using absorptive materials (Henriques et al., 2019) or by harnessing phonon bandgap and band-stop structures designed to stop phonon recombination (Rostem et al., 2018). The main intrinsic source of decoherence in superconducting qubits is 1/f noise (Paladino et al., 2002).

10.2 1/f noise

Types of 1/f³⁵ noise typically found in quantum circuits include charge fluctuations (Christensen et al., 2019), magnetic flux noise (Anton et al., 2012; Kumar et al., 2016), and fluctuations of the supercurrent in Josephson junctions (Constantin and Yu, 2007; Schreier et al., 2008). Background charge noise severely limits coherence in conventional Cooper-pair box-type qubits. The transmon qubit was designed to mitigate this noise source (Stanescu, 2016).

Flux qubits operate with a large shunting capacitor or in a regime where a charge is highly delocalized, rendering phase a good quantum number and obtaining immunity to charge fluctuations. Operating in this regime leads to a sensitivity to magnetic fluctuations. Flux noise is common to all qubits that use a loop for magnetic bias and limit coherence. One typically operates at a point of degeneracy where the energy is insensitive to flux for fixed-frequency qubits. This noise spans DC to 10 GHz, including operations at low temperatures.

Critical current noise is currently the least deleterious of noise sources, especially for submicron junctions, and limits dephasing times when the coherence time exceeds milliseconds (Anton et al., 2012). The precise mechanism of 1/f noise remains elusive. A theoretic explanation that produces 1/f noise (Van Harlingen et al., 2004) is obtained by hopping between two wells in a double-well potential. Assuming a distribution of barrier heights for the hopping process yields 1/f-type behavior. For charge noise and critical current noise, most models include some type of electronic traps that arise from structural disorder. In the case of critical current noise, one imagines that tunneling electrons become trapped at varying times.

Generalized filter-transfer functions as noise spectral filters (Lutchyn et al., 2010; Oreg et al., 2010) are particularly effective. Compact-protected circuits have only a few degrees of freedom and are examples of local decoherence-free subspaces. Protection of these qubits arises because the low-energy performance of the circuit is approximated as an effective Hamiltonian with parity symmetry, such as Cooper-pair or fluxon³⁶ symmetry.

Finally, systems experiencing continuous high-intensity drive conditions have also demonstrated protection against various noise sources where the interaction of the driving field and the qubit leads to beneficial properties.

QP tunneling across a JJ can cause qubit excitation (or relaxation) and result in bit flip even while driving E_j/E_c >> 1, exponentially suppressing qubit sensitivity to charge parity and background charge fluctuations. For superconducting order fluctuations to efficiently trap quasiparticles, it is necessary to enhance frequency to increase the probability of shallow trap QP recombination.

The total number of nodes in a quantum circuit determines the dimensionality of the quantum system, while its inductance determines its kinetic energy, and its capacitance determines its potential energy.

The ability to independently control dimensionality and kinetic and potential energies allows one to create superconducting circuits that satisfy requirements for intrinsic noise protection and conditions that provide acceptable coherence and fidelity.

It has been shown that some qubit modalities allow for protected gate operations (Brooks et al., 2013a; Klots and Ioffe, 2021), which are crucial for fault-tolerant quantum computations.

The development and design of protected superconducting qubits has evolved along three main paths: JJ arrays based on multimode circuits (Kitaev, 2003; Ioffe et al., 2002; Ioffe and Feigel’man, 2002; Douçot and Vidal, 2002; Gladchenko et al., 2009; Douçot and Ioffe, 2012; Bell et al., 2014a), compact few-mode circuits (Brooks et al., 2013b; Kalashnikov et al., 2020; Smith et al., 2020), and driven systems (Bell et al., 2014b; Mirrahimi et al., 2014; Ofek et al., 2016; Puri et al., 2017; Didier et al., 2019b; Mundada et al., 2020; Campagne-Ibarcq et al., 2020; Grimm et al., 2020; Wu et al., 2021b; Huang et al., 2021). These efforts are further categorized as presented in Table 14.

Table 14

Table 14. Noise mechanisms in superconducting qubits.

A logical qubit may be constructed by assembling a set of noisy cells to reduce the total effect of local errors along the chain, a type of global encoding. This approach to noise protection is based upon the concept of topological ground-state degeneracy³⁷.

Alternatively, compact-protected circuits are individual qubits with degrees of freedom in local decoherence-free subspaces (DFS)³⁸. These circuits require extreme conditions, such as large inductances and minimal parasitic capacitance. Protection in such compact qubits arises from the low-energy behavior of the circuit that is approximated by a Hamiltonian with parity symmetry, such as Cooper pair or fluxon (i.e., a quasiparticle of electric or magnetic flux) symmetry (Hsieh et al., 2019). Finally, systems under continuous driving fields can also show protection against noise sources (Vool and Devoret, 2017; Indico, 2022).

11 Quantum technology drivers, key players, and markets

Quantum technologies driving the development of QMs are rich and diverse and include quantum computers, cybersecurity, transportation, finance, navigation, materials discovery (biology, drug discovery, electronic materials, etc.), communication, and novel electronics, among others. Some of these will be reviewed briefly here in the context of private sector players and market dynamics. More detailed technical descriptions have appeared elsewhere in this perspective.

11.1 Quantum technology drivers

Quantum computers, due to their immense potential to impact international science and technology markets, have been a key focus of this review. Quantum computing is currently a topic of intense interest among scientific, communication, and business communities because of its potential to disrupt existing classical performance standards and metrics.

Quantum computers exist as variants of simulators, quantum annealers, and analog quantum computers. We will consider each of these in turn and by global region.

11.1.1 North American region

11.1.1.1 Quantum annealing.

Quantum annealing is generally used to solve combinatorial optimization problems such as machine learning, portfolio optimization, route optimization, etc. D-Wave Systems, a Canadian company founded in 1999, was the first to introduce a quantum annealing approach as a quantum solver. In 2011, the world’s first commercial quantum annealing machine, operating with 128 qubits, was developed by D-Wave with a price tag of approximately USD 10,000,000. In 2019, D-Wave announced the release of Pegasus, which was a quantum processor chip consisting of 5,000 low-noise qubits. D-Wave Systems has since been a major player in quantum computing markets, providing quantum annealing platforms to commercial customers. Their platforms operate using Qbsolv, which is open-source software that solves QUBO problems on D-Wave’s quantum processors (D-Wave Initiates Open Quantum Software Environment, 2022b). D-Wave exclusively employs superconducting phase qubits for their quantum annealers (Harris et al., 2010b). As illustrated in Figure 8, the growth of the quantum annealer product market is dominated by D-Wave Systems’ products. D-Wave launched its Advantage- 2 machine in 2024, which has more than 1,200 qubits and 10,000 couplers. D-Wave began selling its platforms to U.S. government agencies, organizations, and NGOs, including LCMO, Google, NASA, and LANL, as early as 2011.

11.1.1.2 Gate-based analog quantum computers.

Research in superconducting quantum computing is conducted by companies such as Google (Globe News Wire, 2023), IBM (Globe News Wire, 2023), IMEC (Castelvecchi, 2017), BBN Technologies (IBM, 2016), Rigetti (IMEC, 2023), and Intel (Ryan et al., 2017). Many recently developed quantum processing units, or quantum chips (QPUs), utilize superconducting architectures. These devices function at very low temperatures and require expensive and large He³⁺ dilution refrigeration to minimize the deleterious influence of environmental heat upon qubit coherence.

The years 2017–2019 saw a plethora of activity in large-qubit AQC platforms from industrial leaders Google, IBM, Intel, and IonQ, among others. Other key players in quantum computational platform development employ different qubit modalities, for example: Xanadu, photonic qubits; Rigetti, superconducting qubits (Rigetti Launches Quantum Cloud Services, 2018); Intel, “hot” silicon spin qubits; Baidu, superconducting qubits; and Google and Microsoft, topological qubits.

All major AQC companies are striving to scale up their quantum computational platforms with the goal of attaining a mega-qubit computer.

In addition to the investments made by private sector players, the U.S. government has invested billions in quantum technologies sponsored by the Department of Energy (DOE), the Defense Advanced Research Projects Agency (DARPA), and the National Security Agency (NSA), among others.

11.1.2 Asia–Pacific Region

11.1.2.1 Quantum annealing.

Although D-Wave dominates the North American region, it is not alone in the market space of quantum annealers.

In 2018, NEC Corporation introduced the world’s first LHZ³⁹unit cell machine, facilitating scaling to a fully connectorized architecture using superconducting parametron⁴⁰ qubits. NEC demonstrated a quantum annealer using a four-qubit Lechner, Hauke, and Zoller (LHZ) scheme with circuit coupling technology. NEC has achieved a first-time demonstration by successfully solving small-scale combinatorial optimization problems via quantum annealing using their LHZ approach. NEC’s LHZ-based machine is resistant to noise and remains capable of scaling up to a fully connectorized quantum annealing architectures while maintaining prolonged quantum superposition states.

In another first-time demonstration, NEC developed a three-dimensional topology that efficiently connects several LHZ unit cells arranged in a tile pattern with external devices. NEC is currently working to develop a quantum annealing machine using superconducting parametrons in a project commissioned by the New Energy and Industrial Technology Development Organization with the target of realizing quantum annealing machines by the end of 2023 (Intel Invests US$50 Million to Advance Quantum Computing, 2022).

Tohoku University and NEC have started joint research on computer systems using an 8-qubit quantum annealing machine developed by NEC and sponsored by Japan’s National Institute of Advanced Industrial Science and Technology (Petit et al., 2020).

Also, in the Asia–Pacific Region, an Australian quantum computing company, Silicon Quantum Computing Pty Limited (SQC), in 2017 embarked to create and commercialize a quantum computer in conjunction with the Australian Centre of Excellence for Quantum Computation and Communication Technology. Their goal is to produce a silicon-based 10-qubit prototype device. As well as developing its own proprietary technology and intellectual property, SQC continues to lead efforts to build and develop a silicon quantum computing industry to influence global markets.

11.1.2.2 Gate-based analog quantum computers.

In the Asia-Pacific Region, demonstrations and breakthroughs by Chinese scientists in quantum physics have been impressive. Competition in quantum computing between the U.S. and China, the two dominant global economies, and other international players has resulted in the expansion of the international market size from USD 10 B in 2021 to a projected USD 44 B by 2028, growing at a compounded annual growth rate (CAGR) of 30.2% over this forecasted period (see Table 15) (HPC, 2022)

Table 15

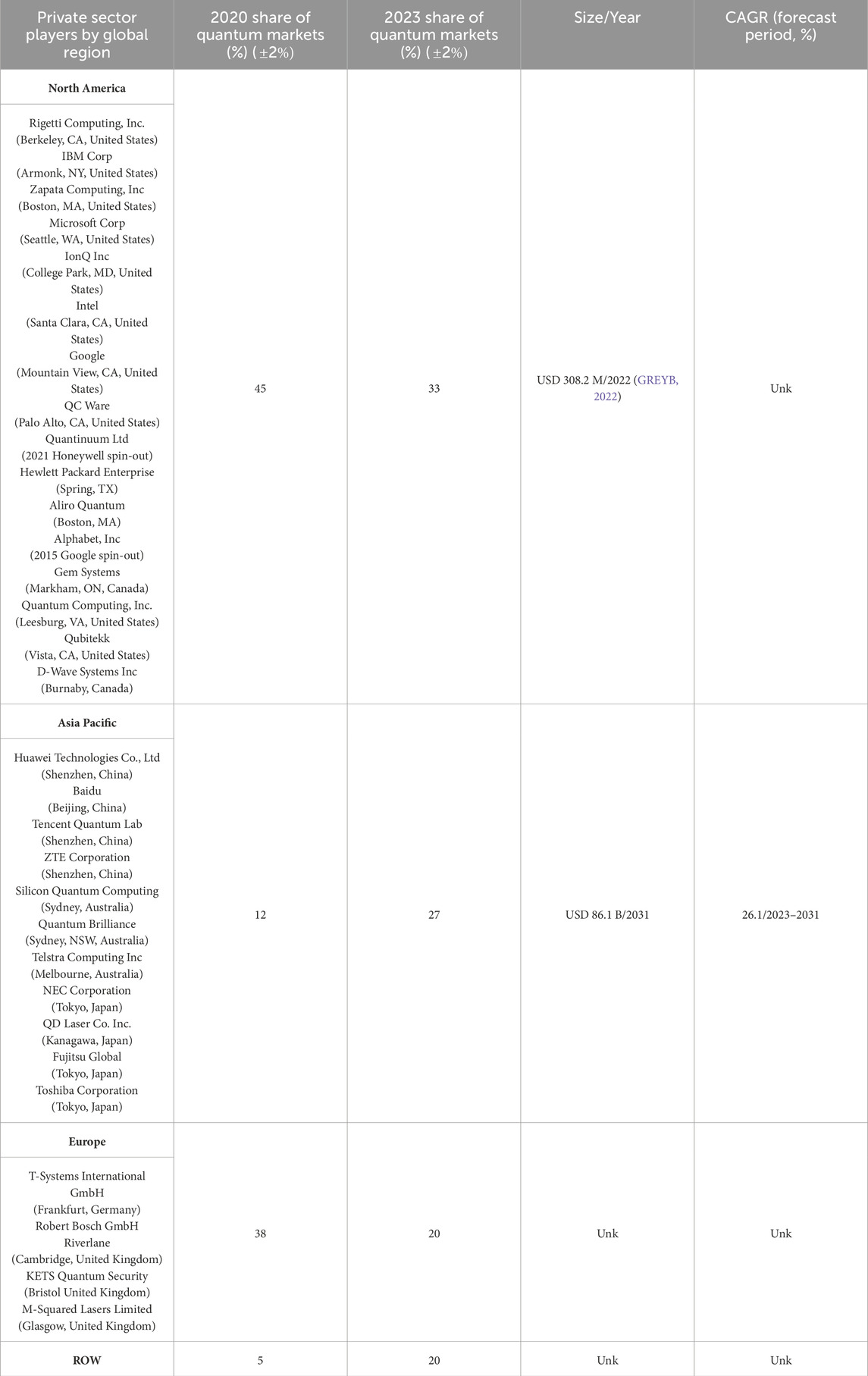
Table 15. Global regions of quantum computing market share, commercial players, and market dynamics.

The Chinese government has kept pace, making domestic investments in quantum research and advanced technologies in defense, security, and artificial intelligence of around $15 billion. (Note, this figure is disputed as high by many international experts). Notwithstanding the disagreement, it is widely believed that Chinese state funding in quantum S&T exceeds the combined investments of the total of EU and US commitments. Amongst the various projects and initiatives is the National Laboratory for Quantum Science in Hefei; the largest quantum research facility in the world, at thirty-seven hectares (370,000 m² or ∼4 million sq. ft.) (Davey, 2023). Additionally, Alibaba has invested USD 15 B in the establishment of DAMO (i.e., the Academy for Discovery, Adventure, Momentum, and Outlook) that includes seven new research laboratories in China, the United States, Russia, Israel, and Singapore (Quantum Technology Market Size, 2022a).

China’s advances include Jiuzhang, the first photonic quantum computer to claim quantum supremacy (2019). Previously, quantum supremacy had been achieved by Google’s Sycamore based on superconducting qubits (Quantum Computing, 2022). Jiuzhang is reported to have a Hilbert space that is 10 billion times greater than that of the superconductor-based Sycamore processor and, as such, is harder to simulate classically (Techinasia, 2022). The Asia–Pacific quantum technology market is expected to experience significant growth, with a CAGR of 26.1% from 2022 to 2031. The total addressable market for this period is projected to reach USD 86.1 B. This growth is driven by the increasing demand for reliable network and computing solutions, the growing government and private funding for quantum technologies, rising investments in research and development, and the expanding applications of quantum technology across market sectors (see Table 16). Recent breakthroughs by Chinese scientists have identified the path forward for space-based quantum communication and teleportation, necessary developments for the creation of a quantum internet. Although the Asia–Pacific Region only accounts for 12% of the total market share of the quantum computer market in 2020, it increased dramatically to 27% in 2023 while North American and European Regions shares reduce commensurately.

Table 16

Table 16. State of quantum markets and projections.

11.1.3 European region

11.1.3.1 EuroQCI

Since 2019, all 27 EU member States signed the EuroQCI (QCI-Quantum Communication Infrastructure) Declaration, agreeing to work collectively with the European Commission and the European Space Agency toward the development of a quantum communication infrastructure covering the entire EU (Kan, 2019). The EuroQCI is planned as a secure quantum communication infrastructure composed of a terrestrial segment relying on fiber communications networks linking strategic sites at national and cross-border levels and a space segment based on satellites. It will be an integral part of the new EU space-based secure communication system spanning the whole EU, including its overseas territories.

The EuroQCI will safeguard sensitive data and critical infrastructures by integrating quantum-based systems into existing communication infrastructures, providing an additional security layer based on quantum physics. It will reinforce the protection of Europe’s governmental institutions, their data centers, hospitals, energy grids, etc., becoming one of the integral pillars of the EU’s Cybersecurity Strategy for the coming decades.

The EuroQCI was initially launched in 2019, and work has continued under the supervision of the European Commission. The terrestrial segment is implemented by the Member States, and the space segment is implemented by the ESA.

For the terrestrial segment, the EuroQCI’s first implementation phase started in January 2023 with the support of the Commission’s Digital Europe Program, with a focus on:

• A set of industrial projects with the aim of developing Europe’s quantum communication ecosystem and industry.

• National projects allowing Member States to design and build the national quantum communication networks that will form the basis of the terrestrial segment.

• Establishing coordination and support action to act as a link between all projects, facilitate collaboration, and identify standardization protocols.

These first projects will make it possible to take steps toward services establishing a highly secure way of delivering encryption key material.

Alongside this, the Connecting Europe Facility (CEF) will provide funding for projects developing cross-border links between national networks and interconnections with the EuroQCI’s space component.

11.1.3.2 EuroQCI satellite constellation

For the space segment, the EU Commission is currently working with ESA on the specifications of a first-generation constellation of EuroQCI satellites. This will build on the first prototype satellite, Eagle1, developed by ESA and an industrial consortium, and due to be launched in late 2024. More recently, several European countries have joined to form the European High Performance Computing Joint Undertaking (EuroHPC JU) to build state-of-the-art quantum computers by circa 2023 as accelerators interconnected with the Joint Undertaking’s supercomputers, forming “hybrid” machines that blend the best of quantum and classical computing technologies (Letzter, 2020). In 2022, the EuroHPC JU announced six sites across the EU will be home to the first European quantum computers, which will be integrated into EuroHPC supercomputers. These newly acquired quantum computers will be located at sites in Czechia, Germany, Spain, France, Italy, and Poland. In total, €100 million, with 50% coming from the EU and 50% from 17 of the EuroHPC JU-participating countries, has been invested. Its substantial computing capacity will address complex simulation and optimization problems, especially in materials development, drug discovery, weather forecasting, transportation, and other real-world problems of import to industry and society. A specific aim is to deliver the first computer with quantum acceleration by 2025. Table 15 also lists individual companies that have been notably active in promoting meaningful investments in quantum technologies. Further, this table provides a listing of the top seven countries leading investments in quantum technologies. Here, we list only publicized investments made by government agencies and institutions and not those made by private companies. The latter are difficult to quantify as many companies do not make public such data, while in other countries, such as China, commercial industry is heavily subsidized by the central government, making it difficult to parse such investments. These investments also do not include the collective investments by the EU and other collaborative Member States. Nonetheless, Table 17 reflects the major investments and the seriousness of high-income countries toward quantum technology and its potential. Noteworthy investments include the timely multibillion-dollar investments by the United States, China, Germany, the United Kingdom, and France.

Table 17

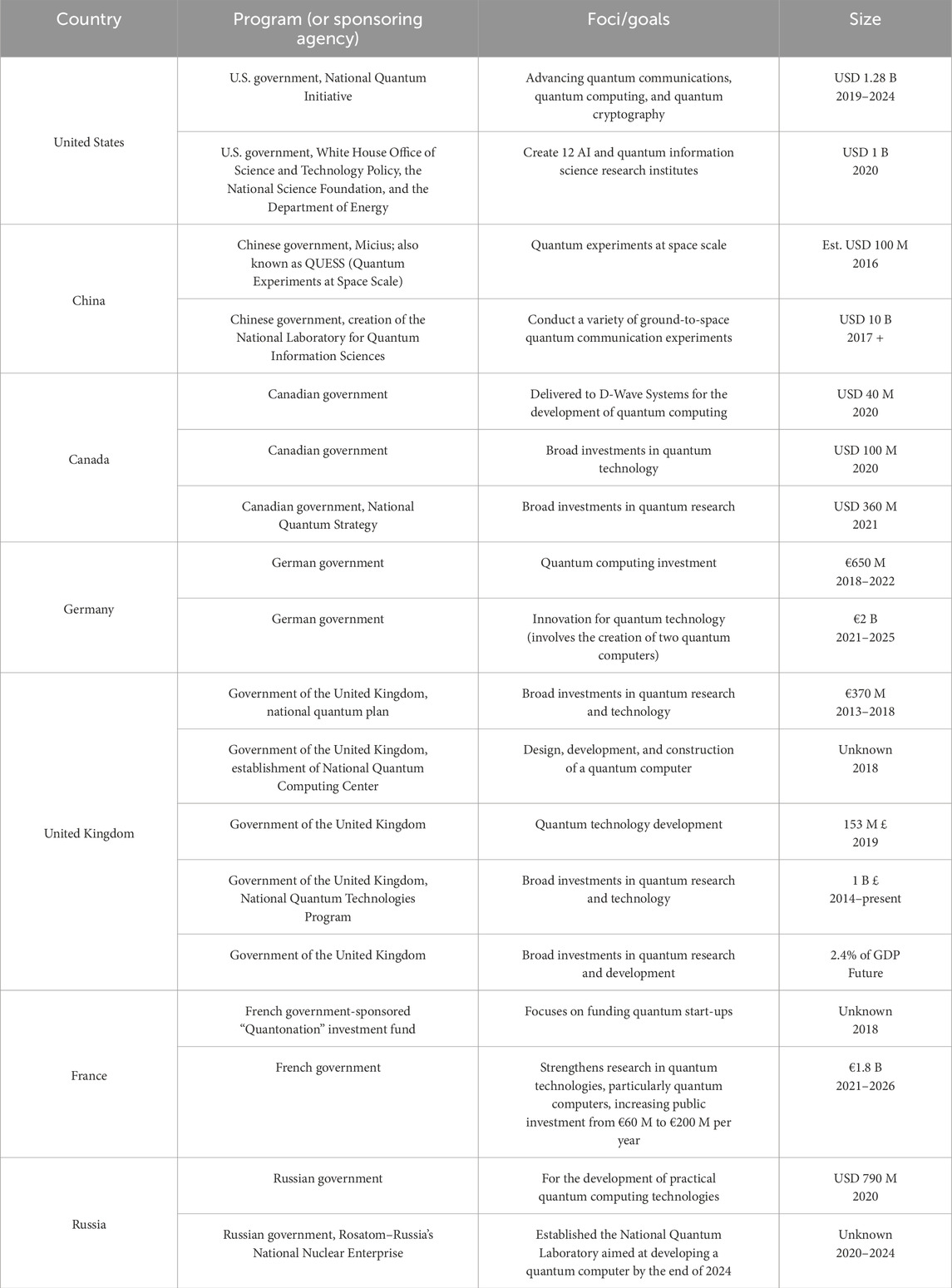
Table 17. Countries making major investments in quantum technologies (industrial contributions omitted) (Digital Strategy, 2022a).

11.2 Market size and dynamics

Table 15 presents the 2020 market share for quantum computing revenues for major global regions. One sees that among these, North America maintains a dominant market position with 45%, followed by Europe at 38% and Asia Pacific at 12%. Noteworthy, the 2023 forecast reveals a dramatic increase in the Asia–Pacific share to 27%, with North America at 33% and Europe falling to 20%.

Table 16 provides a breakdown of market segments by other quantum technologies.

In 2021, the global quantum computing market was valued at USD 472 million. The market was anticipated to expand at a 30.2% CAGR from USD 472 million in 2021 to USD 1,765 million by 2026. The early utilization of quantum computing was in the medical and defense section, trailed by finance and banking, which are projected to drive the market’s worldwide expansion. Geographically, North America held the highest market share, that is, approximately 45% of the global quantum computing market. Whereas the Europe and Asia–Pacific regions held approximately 38% and 12%, respectively (see Table 15) (Innovationcloud, 2022). We next examine other important quantum technologies, beginning with cybersecurity.

11.2.1 Cybersecurity

Security in communications touches many aspects of society, including financial and banking services. For example, price derivatives employ a highly computation-intensive calculation scheme known as Monte Carlo. This simulation model found its inception during World War II’s Manhattan Project where it played an essential role in accurately accounting for neutron scattering and absorption during nuclear fission. Because computational speed is often a limiting factor in the efficiency and timeliness of financial transactions, quantum computing schemes and algorithms enhance trading efficiency.

In cybersecurity, the generation of random numbers is of great value. These are generated by quantum calculations and are integral to cryptography. Quantum-secure communications enable an entirely secure exchange of quantum encryption keys. The quantum key distribution (QKD) allows someone to securely distribute encryption keys. QKDs will remain secure even from future code-breaking quantum efforts.

Quantum communications are of great interest to commercial, military, and intelligence communities. Many other quantum applications that have been proposed but not yet matured will be enabled by future entangled quantum networks (Digital Strategy, 2022b).

According to verified market research, the quantum cryptography market size was valued in 2021 at USD 102.34 M and is projected to reach USD 476.83 M by 2030, growing at a CAGR of 18.7% from 2022 to 2030 (GREYB, 2022).

11.2.2 Quantum teleportation

Quantum teleportation is defined as the transfer of information from one particle (source) to its entangled partner (target). The connection between entangled pairs of particles has a minimum amount of entanglement needed to successfully perform quantum teleportation. Researchers have performed many demonstrations of this type over the past decade. Famously, a research group from China teleported a photon from Earth to a satellite orbiting 1,400 km (defined as “low Earth orbit”). Quantum Experiments at Space Scale (i.e., QUESS) is a Chinese research project in the field of quantum teleportation. Tiangong-2, China’s second Space Laboratory module, was launched in 2016. Tiangong-2 carries out Space-Earth quantum key distribution and laser communications experiments (Science the Wire, 2022). A satellite, nicknamed Mozi, is operated by the Chinese Academy of Sciences, as well as ground stations in China (Google, 2022; Tiangong-2 takes China one step closer to space station, 2018). Quantum teleportation is the lynchpin on the path towards a quantum internet. The quantum communication market size was estimated at 570 M$ in 2022 and projected to grow to 8.3 B$ by 2032 with a compound annual growth rate (CAGR) of 29.3% during the forecast period of 2023–2032. Security issues, increasing cyber threats, government initiatives, and quantum technology advances are key market drivers. [NEW-https://www.marketresearchfuture.com/reports/quantum-communication-market-12240. Accessed 7/23/2024].

11.2.3 Transportation and logistics

Transportation and logistics pose optimization challenges in identifying the most efficient routes by considering variables such as route conditions, vehicle performance, driver capabilities, etc. Multiple constraints increase the computational complexity of the calculations that are well-managed by quantum computers and, in particular, quantum annealers.

11.2.4 Molecular simulation and drug design

Physicists, chemists, and materials scientists endeavor to solve problems that often involve molecular simulations, including machine learning-based refinements. As molecules become increasingly large and more complex, the number of possible configurations grows exponentially, necessitating quantum computers. Examples of such problems include drug design, materials discovery, and optimized manufacturing processes involving thousands of individual steps to identify which complex processes play the most important roles in determining performance and the most affordable and efficient processes (First Quantum Satellite SuccessfullyLaunched, 2016).

11.2.5 Ultra-precise quantum clocks

Atomic clocks are the bedrock of GPS⁴¹ (or GNSS⁴²) systems that allow for highly accurate operations affecting commerce (e.g., trucking, trains, airfreight, shipping containers in the management/telematics of just-in-time supply chain management); maritime industries navigation (e.g., automatic identification system); mobile telecommunication networks (4G, 5G, and 6G); agricultural management in planting, watering, and fertilizing of crops; commercial air travel (e.g., air traffic management systems); building and construction industries, and banks and financial institutions that rely on global positioning system (GPS) for precise time-stamping of transactions, etc. The atomic clock market is estimated at 509 M$ in 2024 and projected to reach 782 M$ by 2031, growing at a compound annual growth rate (CAGR) of 6.3% over this period.

Quantum-based atomic clocks, whose origins date to the 1950s, are now routinely integrated into satellites providing GPS functions. In an atomic clock, a large group of atoms, often cesium or rubidium atoms, is excited by sequential microwave pulses. These EM waves trigger atoms to oscillate, whereupon these atomic oscillations are used to define a highly precise time interval; that is, a second is defined as a finite number of atomic oscillations. It is noteworthy that the second has been defined by NIST as “the duration of 9,192,631,770 periods of transitions between two hyperfine levels of the caesium-133 isotope” (Wall, 2016). However, recent demonstrations of atomic clock functions exploit the principles of quantum entanglement to greatly reduce sources of noise and produce much more accurate clocks. A perfect, noiseless comparison is impossible to achieve as the probabilistic nature of quantum mechanics allows for some intrinsic noise associated with any experiment (Innovationcloud, 2022). Work aggressively continues along these lines.

11.2.6 Ergotropy and Quantum Batteries

Puliyil et al. provided connections between the laws of thermodynamics and quantum information theory to propose a concept called ergotropy that represents the amount of work one can extract from a system while maintaining constant entropy (Puliyil et al., 2022). This requires a phenomenon called genuine multipartite entanglement, where a collective of particles behaves as a single unit. The difference between work extraction from individual parts and work extraction from a collective is an ergotropic gap.

Ergotropy is foundational to new quantum batteries (QB). In one manifestation, QBs are microcavities where the active material consists of organic molecules dispersed in a matrix where each molecule exists in a quantum superposition. If they collectively maintain coherence, the total system behaves cooperatively, giving rise to ultrafast charging that is proportional to the number of molecular units. This, in turn, gives rise to a counterintuitive behavior where the recharging time is inversely related to the battery capacity, leading to the charging power being both sizeable and increasing with battery mass (Malia et al., 2022). In the future, this type of device may prove disruptive to wireless charging, solar cells, and electric vehicle markets.

11.2.7 Quantum materials institutes (QMIs)

To meet quantum technology demands, QMIs have formed all over the world, and top-tier research institutes and universities lead such efforts. To manage the potential runaway expenses and bring to bear the necessary diversity in human talent and tools, QMIs tend to exist as large consortia, combining universities, national laboratories, and large and small businesses, often funded, in part or in whole, by local and/or national governments.

It is only because industry and governments are confident of substantial return on investments that we move forward aggressively as a society in pursuit of quantum materials, science, and technologies.

The study of QMs is a nontrivial exercise and requires concerted and coordinated efforts in theory, simulation, materials processing in 0-D, 1-D, 2-D, and 3-D, and the employment of powerful characterization tools such as electron microscopy, neutron scattering, synchrotron spectroscopies, and x-ray scattering techniques, in addition to sophisticated low-temperature transport measurements and high-pressure studies (among other highly specialized techniques). Taken together, these efforts can quickly escalate to tens or even hundreds of millions of dollars (euros, yen, pounds, yuan, krona…etc.) of investment in the necessary tools, staffing, and infrastructure.

Although universities and national laboratories account for many of the fundamental breakthroughs in QMs, such technological centers often find it challenging to translate such innovations to industrial companies, which are better prepared to create products and technologies to address real-world problems.

The need for partnerships between university hubs, national laboratories, and companies that focus on QM business-oriented opportunities has become undeniably important.

11.2.8 Quantum-based electronics

In earlier sections, we covered several subfields of electronics and devices that rely on novel quantum materials in great detail. Here, we very briefly cover a subset of these materials and devices where market information is available.

To this end, we examine spin-transfer torque magnetic random-access memory, that is, STT-MRAM. STT-MRAM is a nonvolatile memory that operates under sub-nanosecond and sub-picojoule conditions, providing major advantages over charge-based memories such as SRAM and DRAM (Puliyil et al., 2022; Quach et al., 2022). STT-RAM is a type of magnetoresistance RAM or MRAM.

This technology was first demonstrated as a viable commercial product by Hitachi, which produced a 32-Mbit STT-RAM in 2009 (Krizakova et al., 2022). By 2011, Qualcomm presented a 1 Mbit embedded STT-MRAM that was manufactured in TSMC’s 45 nm LP technology (Wikipedia, 2022). In 2012, Everspin released the first commercially available DDR3 dual in-line memory module, which had a capacity of 64 Mb (Takemura et al., 2009). In 2019, Everspin started production for 28 nm 1 Gb STT-MRAM chips (Kim et al., 2011). Also in 2019, Intel demonstrated an STT-MRAM for L4-cache (Likharev and Semenov, 1991; Everspin, 2012). STT-MRAM continues to demonstrate more competitive operation speed, resistance consistency, and energy efficiency with excellent endurance (Everspin, 2019).

The MRAM market is projected to reach USD 7.2 B by 2027, growing at a CAGR of 32.7% over the analysis period of 2020–2027. China, the world’s second-largest economy, is forecasted to reach a projected market size of USD 2.2 B by 2027 at a CAGR of 42.4% over the same analysis period (Tomshardware, 2022).

12 Challenges and outlook

The ultimate success of quantum technologies will rely on several concomitant achievements. Let us focus merely on quantum computing because many of the challenges that exist for market adoption by QC are faced by other quantum technologies.

First, all quantum technologies are based on quantum mechanics that we know to be inherently indeterministic in nature, and, therefore, problems are merely presented with degrees of probability as opposed to classical computers that deliver unambiguous solutions. As a result, quantum computers are highly specialized instruments that offer advantages for application to certain specialized problems.

Also, as we have described, QCs employ fragile qubits that are highly susceptible to decoherence from environmental factors, such as electrical, mechanical, and thermal noise, among other factors (e.g., 1/f noise) that can cause the collapse of the state function and create errors (Cao et al., 2020).

Because of these errors, it is estimated that 1,000 physical qubits are needed to make a single logical error-free qubit, a goal that has yet to be achieved. Hence, a commercially viable quantum computer is projected to require 200 logical qubits or some 200,000 physical qubits (Globe News Wire, 2023).

Figure 26 depicts market demands and challenges to market insertion. Market demands have been discussed obliquely thus far and include the need for early adoption by the finance and banking sectors with the continued adoption by medical, biomedical, and defense sectors. These can be enhanced by the formation of strategic alliances and the continued rise in commercial investment.

Figure 26

Figure 26. Illustrative depiction of market demands and challenges to insertion for quantum computing and related technologies. Information was accrued from https://www.greyb.com/blog/quantum-computing-market-research.

Challenges to insertion are more difficult to articulate because they expand over broad technical categories that include system architecture and topologies such as multiplexing and pipelining and the integration of quantum and classical components and subsystems, some of which require ultralow temperatures and others are ill-suited for such environs.

Physical challenges relate to the fragility of qubits, noise mitigation, and environmental controls. All play into error-correction stratagems and algorithms. Such constraints require innovative developments in fabrication processes, new materials, and software. Even the ability to measure a qubit’s state accurately and reliably is a nontrivial exercise.

Additionally, the worldwide quantum workforce is presently ill-prepared to address the needs of the marketplace today or in the near future. The quantum workforce lacks individuals who are properly educated in the necessary physics, engineering, and materials science capable of supporting quantum technologies. This has led to a reluctance toward market insertion and adoption (Entanglementtech, 2022).

Finally, a fissure has formed between laboratories performing breakthrough research, investment firms, and the corporate ecosystem that is retarding the growth of global quantum markets. This fissure is widened by barriers to effective communication and knowledge transfer, leading to mistrust among these key stakeholders.

The concepts and information communicated here are indeed challenging for the scientific layperson to grasp. Notwithstanding, we have endeavored to provide a prospectus that includes historical, foundational physics, innovative materials science, and applications-oriented insights that will guide the reader in obtaining a deeper appreciation and knowledge of quantum science and technologies.

Author contributions

VH: Conceptualization, Writing–original draft, Writing–review and editing. PA: Conceptualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Ice exhibits at least eighteen phases depending on temperature and pressure. When water is quenched, up to three types of amorphous ice can form depending on its history of pressure and temperature.

²In 2020, the simultaneous measurement of rheological and surface kinetical properties of the lubricating layer forming on the surface of ice revealed that its viscous and elastic behavior depends upon both its intrinsic character upon melting as well as its interaction with the incident skating blades. The findings suggest that lubrication and concomitant wear of the ice surface leads to the formation of a third layer that forms between the layer of ice and water. Few materials form such viscoelastic, liquid–solid layers in response to friction and wear as those observed in ice. This interpretation provides important missing pieces in the quest to better understand water and ice.

³von Neumann was the first to establish a rigorous mathematical framework for quantum mechanics, known as Dirac–von Neumann axioms, in his 1932 text Mathematical Foundations of Quantum Mechanics. He realized (c. 1926) that a state of a quantum system could be represented by a point in complex Hilbert space as infinite-dimensional, even for a single particle. In this formalism, observable quantities such as position or momentum are represented as linear operators acting on the Hilbert space associated with the quantum system. Quantum mechanics was hence reduced to the mathematics of Hilbert spaces and the linear operators acting on them. This new mathematical formulation included the formulations of both Heisenberg and Schrödinger as special cases. Remarkably, in this work, von Neumann also foundationally addressed issues that would appear years later, such as determinism versus non-determinism, hidden-variable theory, and Bell’s theorem together with the experiments of Aspect (c. 1982) that support today’s interpretation of quantum physics, including the validity of nonlocality in apparent violation of special relativity.

⁴A physical quantity is said to be Lorentz covariant if it transforms under a given representation of the Lorentz group. According to the representation theory of the Lorentz group, these quantities are built out of scalars, four-vectors, four-tensors, and spinors. A Lorentz covariant scalar (e.g., the spacetime interval) remains the same under Lorentz transformations and is said to be a Lorentz invariant (i.e., they transform under the trivial representation).

⁵A Turing machine is an idealized model of a central processing unit (CPU) that controls all data manipulation done by a computer, with the canonical machine using sequential memory to store data. Typically, the sequential memory is represented as a tape of infinite length on which the machine can perform read and write operations. In the context of formal language theory, a Turing machine (automaton) can enumerate some arbitrary subset of valid strings of an alphabet. A set of strings that can be enumerated in this manner is called a recursively enumerable language. The Turing machine can equivalently be defined as a model that recognizes valid input strings rather than enumerating output strings.

⁶The notation for quantum gates was first suggested by several leaders of the community, including Adriano Barenco, Charles Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, and Harald Weinfurter. Their contributions built on the notations introduced by Feynman (1985).

⁷The GKT states that quantum circuits can be simulated efficiently on classical computers using 1. Preparation of qubits in computational basis states; 2. the use of Clifford gates; and 3. measurements in the computational basis, enabling the use of standard algorithms for assessing entanglement and quantum error correction.

⁸Quadratic unconstrained binary optimization (QUBO) is a combinatorial optimization problem with a wide range of applications from finance and economics to artificial intelligence and machine learning.

⁹In computational complexity, NP-hardness, that is, nondeterministic polynomial-time hardness, is the defining property of a class of problems solvable by a nondeterministic Turing machine (TM) in polynomial time. The proof is described, for example, in Sipser (1997).

¹⁰The goal of all international efforts in quantum computing is to demonstrate “quantum supremacy,” defined as attaining a programmable quantum device that can solve a problem that no classical computer can solve in any reasonable amount of time. Quantum supremacy involves both the engineering of a quantum computer and designing a theoretic task that can be solved by that quantum computer at a superpolynomial speedup over the best-known classical algorithm—“On ‘Quantum Supremacy,’” IBM Research Blog, 22 October 2019.

¹¹The Hartree–Fock method is typically used to numerically solve the time-independent Schrödinger equation for multi-electron atoms (or molecules) as described by the Born–Oppenheimer approximation.

¹²A time crystal is a quantum system of particles whose lowest energy state is one in that the particles are in a repetitive motion that does not lose energy to the environment and come to rest because it is already in its quantum ground state. The motion of the particles does not represent kinetic energy; it has “motion without energy.” The atoms in a time crystal are arranged periodically in both space and time.

¹³The Rashba effect, also called the Bychkov–Rashba effect, is a momentum–dependent splitting of spin bands in bulk crystals and low- dimensional condensed– matter systems. The splitting results from the combined effect of spin–orbit interaction and asymmetry of the crystal potential, in the direction perpendicular to the two–dimensional plane. This effect can drive a wide variety of novel physical phenomena, especially manipulating electron spins by electric fields. An example of a physical phenomenon that can be explained by the Rashba effect is the anisotropic magnetoresistance (AMR), Majorana fermions, and topological p–wave superconductors. (Adapted from: https://en.wikipedia.org/wiki/Rashba_effect accessed 7/1/2023).

¹⁴Neuromemristive systems (NMSs) are brain-inspired, adaptive computer architectures based on emerging resistive memory technologies (i.e., memristors).

¹⁵Neuroplasticity is the ability of the nervous system to change its activity in response to intrinsic or extrinsic stimuli by reorganizing its structure, functions, or connections upon injury.

¹⁶A non-von Neumann architecture attempts to eliminate redundant load-and-store operations by performing numerical and logical operations on memory elements for the calculation of nondeterministic polynomial time (i.e., NP-Hard) problems.

¹⁷A $T_2^{*}$ Ramsey experiment consists of an $\frac{X}{2}$ pulse, bringing the qubit to the equator on the Bloch sphere, followed by a delay of variable duration, during which the qubit precesses about the Z-axis on the equator. A Z rotation is then applied through 2π∗t detuning. Finally, another $\frac{X}{2}$ pulse is applied, which, if the precession from the delay and the manual Z rotation offset each other perfectly, should land the qubit in the excited state. When the precession from the delay and the Z rotation do not offset each other perfectly, the qubit does not land perfectly in the excited state, and the state visibility oscillates, creating fringes. While this is happening, dephasing also causes the state to contract toward the center of the Bloch sphere, away from its surface. This causes the amplitude of the fringes to decay in time, so we expect an exponentially decaying sinusoidal waveform as a function of the delay time. The time decay constant is calculated from these fringes (https://forest-benchmarking.readthedocs.io/en/latest/examples/qubit_spectroscopy_t2.html accessed 7/1/23).

¹⁸A qubit can be encoded in terms of probability amplitudes corresponding to the photon occupation of two modes of some degree of freedom of the optical field. This is referred to as dual- rail encoding.

¹⁹A Fock state is an element of Fock space with a well-defined number of particles. The Fock states of bosons and fermions obey relations with respect to the Fock space creation and annihilation operators. When the number of particles is variable, one constructs the Fock space as the direct sum of the tensor product Hilbert spaces for each particle number.

²⁰Sponsored by the European Commission on Future and Emerging Technologies.

²¹Concurrence is a scalar function defining an entanglement monotone, i.e.that is, a way of measuring entanglement, for bipartite density matrices describing the mixed states of a two-qubit system.

²²The Josephson effect is an example of a macroscopic quantum phenomenon that occurs when two superconducting materials are separated by a small distance or across a thin layer, whereupon a current is produced that flows continuously without voltage bias (known as a Josephson junction). Josephson junctions play important roles in SQUIDs, qubits, and RSFQ (rapid single flux quantum (RSFQ) electronics, among other technologies.

²³A transmon is a type of superconducting charge qubit that was designed to have reduced sensitivity to charge noise. Its name is an abbreviation of the “transmission line shunted plasma oscillation qubit”. This consists of a Cooper-pair box where two superconductors are capacitively shunted in order to decrease the sensitivity to charge noise, while maintaining a sufficient anharmonicity for selective qubit control. It was first developed by Robert J. Schoelkopf, Michel Devoret, and Steven M. Girvin.

²⁴The Purcell effect is the enhancement of a quantum system's spontaneous emission rate by its environment. Edward Mills Purcell (c. 1940s) discovered the enhancement of spontaneous emission rates of atoms when they are incorporated into a resonant cavity. The magnitude of the enhancement is given by the Purcell factor is:. ${\mathit{F}}_p=\frac{3}{{4\pi }^2}{\left(\frac{{\lambda }_{\text{free}}}{n}\right)}^3\frac{Q}{V}$, where λ free is the vacuum wavelength, n is the refractive index of the cavity material (so λ free/n is the wavelength inside the cavity), and Q and V are the cavity quality factor and mode volume, respectively. (see: "Purcell Factor - Qwiki". Retrieved 2023-04-16.)

²⁵Janak’s theorem allows a calculation of charge transition levels by analyzing the Kohn–Sham eigenvalues of density-functional theory without needing to explicitly compare differently charged systems. Specifically, the eigenvalue is the derivative of the total energy with respect to the occupation of a state.

²⁶The $\Delta$SCF approximation is a density-functional method closely resembling standard density-functional theory (DFT), the only difference being that in $\Delta$SCF, one or more electrons are placed in higher-lying Kohn–Sham orbitals instead of placing all electrons in the lowest possible orbitals as one does when calculating the ground-state energy within standard DFT.

²⁷An anyon is a type of quasiparticle that occurs in two-dimensional systems that are classified as Abelian or non-Abelian. Abelian anyons play a major role in explaining the fractional quantum Hall effect.

²⁸Non-Abelian anyonic statistics are higher-dimensional representations of the braid group. Anyonic statistics are not to be confused with parastatistics, which describe the statistics of particles whose wave functions are higher-dimensional representations of the permutation group.

²⁹The Ising anyon model is a model of non-Abelian anyons that represent a path to experimental verification that arises by Majorana zero modes (MZM) and consists of three types of particles including vacuum (1), anyon and ($\sigma$), and fermion ($\psi$), that obey the fusion rules: $\sigma \times \sigma =1+\psi ; \sigma \times \psi =\sigma \mathrm{and} \psi \times \psi =1$, respectively.

³⁰The Fibonacci model for topological quantum computing is based on the fusion rules for a Majorana fermion as described above. The particles described as Fibonacci anyons correspond, in theory, to collectivities of electrons, as in the quantum Hall effect. Fusion rules for such quasiparticles were conjectured by Moore and Read [see G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991).] as part of a larger conjecture that links the fractional quantum Hall effect with braiding associated via conformal field theory with Chern–Simons theory. (Note: The Chern–Simons theory is a 3-dimensional topological quantum field theory first proffered by mathematical physicist Albert Schwarz and further developed by Edward Witten. In condensed-matter physics, Chern–Simons theory describes the topological order in fractional quantum Hall effect states).

³¹Anharmonicity derives from atoms in molecules that vibrate about their equilibrium positions and plays a role in lattice and molecular vibrations in quantum oscillations, as in quantum computers. When these vibrations have small amplitudes, they can accurately be described as harmonic oscillators. However, when vibrational amplitudes become large, for example, at high temperatures, anharmonicity becomes nonnegligible. Under such circumstances, anharmonicity not only makes the potential experienced by each oscillator more complex but also introduces meaningful coupling between oscillators. Accurate anharmonic vibrational energies can then be obtained by solving anharmonic vibrational equations for atoms within mean-field theory, possibly using Møller–Plesset perturbation theory.

³²A Bell state is an entangled and normalized basis vector of two qubits. Their normalization implies that the overall probability is in one of the mentioned states is: $〈\mathrm{\Phi }|\mathrm{\Phi }〉=1$. Because of entanglement, the measurement of one qubit will “collapse” the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell states the two qubits were in initially. Bell states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding Bell states is useful in the analysis of quantum communication, among other quantum technologies, such as superdense coding and quantum teleportation.

³³Majorana zero modes (MZM) are a mathematical construct that allows electrons to be described as composed of two halves. From a quantum computing perspective, if an electron can be split into two parts, then the information it encodes as a qubit will be protected from local perturbations. Furthermore, MZMs realize a representation of non-Abelian braid groups that enable topological quantum computation, wherein the storage and manipulation of information occur in decoherence-free degrees of freedom.

³⁴Spin–orbit qubits are a class of spin qubits characterized by strong large spin–orbit coupling. In spin–orbit qubits, information is stored on both the spin of the electron as well as its orbit. The strength of the coupling between spin and orbital moments maintains the qubit stability and makes it less prone to being compromised by electrical noise and environmental factors.

³⁵1/f noise refers to the phenomenon of the spectral density, S(f), of a stochastic process, having the form $S\left(f\right)=\frac{C}{f^{\alpha }}$ , where f is the frequency on an interval bounded away from both zero and infinity, with $1\le$ $\alpha \le 1.5$, and C is a constant. 1/f noise is an intermediate between the well-understood white noise with no correlation in time and Brownian motion noise. Brownian motion is the integral of white noise, and integration of a signal increases the exponent α by 2, whereas the inverse operation of differentiation decreases it by 2. 1/f noise cannot be obtained by simple integration or differentiation of signals. Also, there are no simple linear stochastic differential equations generating signals with 1/f noise. 1/f fluctuations are widely found in nature and have been observed and reported for more than 8 decades (http://www.scholarpedia.org/article/1/f_noise).

³⁶A fluxon (i.e., Josephson vortex) is made of circulating supercurrents and has no normal core in the tunneling barrier. Supercurrents circulate around the center of a fluxon, which is situated within the Josephson barrier.

³⁷Topological degeneracy is an effect that occurs when the ground state of a gapped many-body Hamiltonian becomes degenerate in the limit of large systems such that degeneracy cannot be lifted by local perturbations.

³⁸A decoherence-free subspace (DFS) is a subspace of a Hilbert space that is invariant to non-unitary dynamics. DFSs can also be characterized as a special class of quantum error-correcting codes. In the latter, they are passive error-preventing codes because these subspaces are encoded with information that will not require active stabilization. These subspaces prevent destructive environmental interactions by isolating quantum information.

³⁹LHZ is an abbreviation for a technique proposed by Lechner, Hauke, and Zoller. As the number of qubits increases, it becomes difficult to directly connect each qubit to each other qubit with hardware. To solve this problem, the software company ParityQC and LHZ proposed a transformation that enables fully connected qubits to be obtained using qubits that are physically connected to only their nearest neighbors.

⁴⁰A superconducting parametron is a superconducting resonant circuit composed of Josephson junctions and capacitors that oscillate with different phases; it is used as a qubit. The lifetime of the qubit is an order of magnitude longer than that of flux qubits.

⁴¹The global positioning system (GPS), originally Navstar GPS, is a satellite-based radio navigation system owned by the United States government and operated by the United States Space Force.

⁴²Global navigation satellite system (GNSS) is a general term describing any satellite constellation that provides positioning, navigation, and timing (PNT) services on a global or regional basis.

References

Agarwal, K., Martin, I., Lukin, M. D., and Demler, E. (2013). Polaronic model of two-level systems in amorphous solids. Phys. Rev. B 87, 144201. doi:10.1103/physrevb.87.144201

CrossRef Full Text | Google Scholar

Akhmerov, A. R., Dahlhaus, J. P., Hassler, F., Wimmer, M., and Beenakker, C. W. J. (2011). Quantized conductance at the Majorana phase transition in a disordered superconducting wire. Phys. Rev. Lett. 106 (5), 057001. doi:10.1103/physrevlett.106.057001

PubMed Abstract | CrossRef Full Text | Google Scholar

Akyol, M., Jiang, W., Yu, G., Fan, Y., Gunes, M., Ekicibil, A., et al. (2016). Effect of heavy metal layer thickness on spin-orbit torque and current-induced switching in Hf| CoFeB| MgO structures. Appl. Phys. Lett. 109 (2). doi:10.1063/1.4958295

CrossRef Full Text | Google Scholar

Albertsson, D. I., Zahedinejad, M., Åkerman, J., Rodriguez, S., and Rusu, A. (2019). Compact macrospin-based model of three-terminal spin-Hall nano oscillators. IEEE Trans. Magn. 55, 1–8. doi:10.1109/tmag.2019.2925781

CrossRef Full Text | Google Scholar

Alicea, J. (2010). Majorana fermions in a tunable semiconductor device. Phys. Rev. B 81 (12), 125318. doi:10.1103/physrevb.81.125318

CrossRef Full Text | Google Scholar

Amunts, K., Ebell, C., Muller, J., Telefont, M., Knoll, A., and Lippert, T. (2016). The human brain project: creating a european research infrastructure to decode the human brain. Neuron 92 (3), 574–581. doi:10.1016/j.neuron.2016.10.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Amy, M., Glaudell, A. N., and Ross, N. J. (2020). Number-theoretic characterizations of some restricted Clifford+ T circuits. Quantum 4, 252. doi:10.22331/q-2020-04-06-252

CrossRef Full Text | Google Scholar

Anderson, B. P., and Kasevich, M. A. (1998). Macroscopic quantum interference from atomic tunnel arrays. Science 282 (5394), 1686–1689. doi:10.1126/science.282.5394.1686

PubMed Abstract | CrossRef Full Text | Google Scholar

Ando, K., and Saitoh, E. (2010). Inverse spin-Hall effect in palladium at room temperature. J. Appl. Phys. 108 (11). doi:10.1063/1.3517131

CrossRef Full Text | Google Scholar

Antaios (2023). Antaios. Available at: https://antaios.fr/-SOT-MRAM-#:∼:text=SOT%20is%20based%20on%20spin,via%20the%20spin%2Dorbit%20interaction (Accessed September 1, 22).

Google Scholar

Anton, S. M., Müller, C., Birenbaum, J. S., O’Kelley, S. R., Fefferman, A. D., Golubev, D. S., et al. (2012). Pure dephasing in flux qubits due to flux noise with spectral density scaling as 1/f α. Phys. Rev. B 85 (22), 224505. doi:10.1103/physrevb.85.224505

CrossRef Full Text | Google Scholar

Apolloni, B., Carvalho, M. C., and De Falco, D. (1989). Quantum stochastic optimization. Stoc. Proc. Appl. 33 (2), 233–244. doi:10.1016/0304-4149(89)90040-9

CrossRef Full Text | Google Scholar

Apolloni, B., Cesa-Bianchi, N., and De Falco, D. (1988). “A numerical implementation of quantum annealing,” in Stochastic processes, physics and geometry, proceedings of the ascona-locarno conference.

Google Scholar

Arnon, S., and Kedar, D. (2009). Non-line-of-sight underwater optical wireless communication network. J. Opt. Soc. Am. A 26, 530. doi:10.1364/josaa.26.000530

PubMed Abstract | CrossRef Full Text | Google Scholar

Ariyoshi, S., Matsuo, H., Otani, C., Sato, H., Shimizu, H. M., and Kawase, K. (2005). “Characterization of an STJ-based direct detector of submillimeter waves,” in IEEE Transactions on Applied Superconductivity, Vol. 15 (2), 920–923. doi:10.1109/TASC.2005.850119

CrossRef Full Text | Google Scholar

Arovas, D., Schrieffer, J. R., and Wilczek, F. (1984). Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723. doi:10.1103/physrevlett.53.722

CrossRef Full Text | Google Scholar

Asmussen, S. R. (2003). “Markov Chains”. Applied Probability and Queues. Stochastic Modelling and Applied Probability 51, 3–8. doi:10.1007/0-387-21525-5_1

CrossRef Full Text | Google Scholar

Aspect, A., Dalibard, J., and Roger, G. (1982). Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49 (25), 1804–1807. doi:10.1103/physrevlett.49.1804

CrossRef Full Text | Google Scholar

Aspelmeyer, M., Bohm, H. R., Gyatso, T., Jennewein, T., Kaltenbaek, R., Lindenthal, M., et al. (2003). Long-distance free-space distribution of quantum entanglement. Science 301, 621–623. doi:10.1126/science.1085593

PubMed Abstract | CrossRef Full Text | Google Scholar

Aumentado, J., Keller, M. W., Martinis, J. M., and Devoret, M. H. (2004). Nonequilibrium quasiparticles and 2e periodicity in single-Cooper-pair transistors. Phys. Rev. Lett. 92, 066802. doi:10.1103/physrevlett.92.066802

PubMed Abstract | CrossRef Full Text | Google Scholar

Awad, A. A., Dürrenfeld, P., Houshang, A., Dvornik, M., Iacocca, E., Dumas, R. K., et al. (2017). Long-range mutual synchronization of spin Hall nano-oscillators. Nat. Phys. 13, 292–299. doi:10.1038/nphys3927

CrossRef Full Text | Google Scholar

Awschalom, D. D., and Flatte, M. E. (2007). Challenges for semiconductor spintronics. Nat. Phys. 3, 153–159. doi:10.1038/nphys551

CrossRef Full Text | Google Scholar

Baart, T. A., Shafiei, M., Fujita, T., Reichl, C., Wegscheider, W., and Vandersypen, L. M. K. (2016). Single-spin CCD. Nat. Nanotechnol. 11 (4), 330–334. doi:10.1038/nnano.2015.291

PubMed Abstract | CrossRef Full Text | Google Scholar

Bader, K., Dengler, D., Lenz, S., Endeward, B., Jiang, S.-D., Neugebauer, P., et al. (2014). Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 5, 5304. doi:10.1038/ncomms6304

PubMed Abstract | CrossRef Full Text | Google Scholar

Balantekin, A. B., and Takigawa, N. (1998). Quantum tunneling in nuclear fusion. Rev. Mod. Phys. 70 (1), 77–100. doi:10.1103/revmodphys.70.77

CrossRef Full Text | Google Scholar

Balasubramanian, G., Chan, I. Y., Kolesov, R., Al-Hmoud, M., Tisler, J., Shin, C., et al. (2008). Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 455, 648–651. doi:10.1038/nature07278

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasubramanian, G., Neumann, P., Twitchen, D., Markham, M., Kolesov, R., Mizuochi, N., et al. (2009). Ultralong spin coherence time in isotopically engineered diamond. Nat. Mat. 8, 383–387. doi:10.1038/nmat2420

PubMed Abstract | CrossRef Full Text | Google Scholar

Ball, P. (2020). Physicists in China challenge Google’s 'quantum advantage. Nature 588 (7838), 380. Bibcode:2020Natur.588.380B. doi:10.1038/d41586-020-03434-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A., and Lucas, D. M. (2016). High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504. doi:10.1103/physrevlett.117.060504

PubMed Abstract | CrossRef Full Text | Google Scholar

Bao, X. H., Xu, X. F., Li, C. M., Yuan, Z. S., Lu, C. Y., and Pan, J. W. (2012). Quantum teleportation between remote atomicensemble quantum memories. Proc. Natl. Acad. Sci. U. S. A. 109, 20347–20351. doi:10.1073/pnas.1207329109

PubMed Abstract | CrossRef Full Text | Google Scholar

Baranov, P. G., Bundakova, A. P., Soltamov, A. A., Orlinskii, S. B., Borovykh, I. V., Zondervan, R., et al. (2011). Silicon vacancy in SiC as a promising quantum system for single-defect and single-photon spectroscopy. Phys. Rev. B 83, 125203. doi:10.1103/physrevb.83.125203

CrossRef Full Text | Google Scholar

Baranov, P. G., Il’in, I. V., Mokhov, E. N., Muzafarova, M. V., Orlinskii, S. B., and Schmidt, J. (2005). EPR identification of the triplet ground state and photoinduced population inversion for a Si-C divacancy in silicon carbide. JETP Lett. 82, 441–443. doi:10.1134/1.2142873

CrossRef Full Text | Google Scholar

Barenco, A., Bennett, C. H., Cleve, R., DiVincenzo, D. P., Margolus, N., Shor, P., et al. (1995). Elementary gates for quantum computation. Am. Phys. Soc. (APS) 52 (5), 3457–3467. doi:10.1103/physreva.52.3457

PubMed Abstract | CrossRef Full Text | Google Scholar

Barends, R., Kelly, J., Megrant, A., Sank, D., Jeffrey, E., Chen, Y., et al. (2013). Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111 (8), 080502. doi:10.1103/physrevlett.111.080502

PubMed Abstract | CrossRef Full Text | Google Scholar

Barends, R., Kelly, J., Megrant, A., Veitia, A., Sank, D., Jeffrey, E., et al. (2014a). Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503. doi:10.1038/nature13171

PubMed Abstract | CrossRef Full Text | Google Scholar

Barends, R., Kelly, J., Megrant, A., Veitia, A., Sank, D., Jeffrey, E., et al. (2014b). Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503. doi:10.1038/nature13171

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrett, M. D., Chiaverini, J., Schaetz, T., Britton, J., Itano, W. M., Jost, J. D., et al. (2004). Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739. doi:10.1038/nature02608

PubMed Abstract | CrossRef Full Text | Google Scholar

Bars, I., and Terning, J. (2018) Extra dimensions in space and time. Springer, 27.

Google Scholar

Barthel, C., Reilly, D. J., Marcus, C. M., Hanson, M. P., and Gossard, A. C. (2009). Rapid single-shot measurement of a singlet–triplet qubit. Phys. Rev. Lett. 103, 160503. doi:10.1103/PhysRevLett.103.160503

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauer, G. E., Saitoh, E., and Van Wees, B. J. (2012). Spin caloritronics. Nat. Mater. 11 (5), 391–399. doi:10.1038/nmat3301

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumgratz, T., Cramer, M., and Plenio, M. B. (2014). Quantifying coherence. Phys. Rev. Lett. 113 (14), 140401. doi:10.1103/physrevlett.113.140401

PubMed Abstract | CrossRef Full Text | Google Scholar

Beduz, C., Carravetta, M., Chen, J. Y. C., Concistrè, M., Denning, M., Frunzi, M., et al. (2012). Quantum rotation of ortho and para-water encapsulated in a fullerene cage. Proc. Natl. Acad. Sci. 109 (32), 12894–12898. doi:10.1073/pnas.1210790109

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, J. S. (1964). On the einstein podolsky rosen paradox. Phys. Phys. Fiz. 1 (3), 195–200. doi:10.1103/physicsphysiquefizika.1.195

CrossRef Full Text | Google Scholar

Bell, J. S. (1987). Speakable and unspeakable in quantum mechanics. Cambridge University Press, 65.

Google Scholar

Bell, M. T., Paramanandam, J., Ioffe, L. B., and Gershenson, M. E. (2014a). Protected Josephson rhombus chains. Phys. Rev. Lett. 112 (16), 167001. doi:10.1103/physrevlett.112.167001

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, M. T., Paramanandam, J., Ioffe, L. B., and Gershenson, M. E. (2014b). Protected Josephson rhombus chains. Phys. Rev. Lett. 112 (16), 167001. doi:10.1103/physrevlett.112.167001

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, R. P. (1959). The tunnel effect correction for parabolic potential barriers. Trans. Faraday Soc. 55, 1–4. doi:10.1039/tf9595500001

CrossRef Full Text | Google Scholar

Bell, R. P. (1980). The tunnel effect in chemistry. London: Chapman & Hall. (Ronald.

Google Scholar

Benioff, P. (1980). The computer as a physical system: a microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 22, 563–591. doi:10.1007/bf01011339

CrossRef Full Text | Google Scholar

Benioff, P. (1982). Quantum mechanical hamiltonian models of turing machines. J. Stat. Phys. 29 (3), 515–546. doi:10.1007/BF01342185

CrossRef Full Text | Google Scholar

Benjamin, B. V., Gao, P., McQuinn, E., Choudhary, S., Chandrasekaran, A. R., Bussat, J. M., et al. (2014). Neurogrid: a mixed-analog-digital multichip system for large-scale neural simulations. Proc. IEEE 102 (5), 699–716. doi:10.1109/jproc.2014.2313565

CrossRef Full Text | Google Scholar

Bennett, C. H. (1973). Logical reversibility of computation. IBM J. Res. Dev. 17 (6), 525–532. doi:10.1147/rd.176.0525

CrossRef Full Text | Google Scholar

Bennett, C. H., and Brassard, G. (1984). in Proceedings of IEEE international conference on computer, systems & signal processing (IEEE), 175–179.

Google Scholar

Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., and Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70 (13), 1895–1899. doi:10.1103/physrevlett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, L. (1996). Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54 (13), 9353–9358. doi:10.1103/physrevb.54.9353

PubMed Abstract | CrossRef Full Text | Google Scholar

Bermeister, A., Keith, D., and Culcer, D. (2014). Charge noise, spin-orbit coupling, and dephasing of single-spin qubits. Appl. Phys. Lett. 105, 192102. doi:10.1063/1.4901162

CrossRef Full Text | Google Scholar

Berrios, E., Gruebele, M., Shyshlov, D., Wang, L., and Babikov, D. (2012). High fidelity quantum gates with vibrational qubits. J. Phys. Chem. A 116 (46), 11347–11354. doi:10.1021/jp3055729

PubMed Abstract | CrossRef Full Text | Google Scholar

Bez, R., Fantini, P., and Pirovano, A. (2019). “Historical review of semiconductor memories,” in Woodhead Publishing Series in Electronic and Optical Materials, Semiconductor Memories and Systems. Editors A. Redaelli, and F. Pellizzer (Woodhead Publishing), 1–26.

Google Scholar

Bialczak, R. C., Ansmann, M., Hofheinz, M., Lucero, E., Neeley, M., O’Connell, A. D., et al. (2010). Quantum process tomography of a universal entangling gate implemented with Josephson phase qubits. Nat. Phys. 6, 409–413. doi:10.1038/nphys1639

CrossRef Full Text | Google Scholar

Biedenharn, L., Lieb, E., Simon, B., and Wilczek, F. (1990). The ancestry of the anyon. Phys. Today 43 (8), 90–91. doi:10.1063/1.2810672

CrossRef Full Text | Google Scholar

Binnig, G., and Rohrer, H. (1986). Scanning tunneling microscopy. IBM J. Res. Dev. 30 (4), 355–369. doi:10.1016/0039-6028(83)90716-1

CrossRef Full Text | Google Scholar

Blume-Kohout, R., Gamble, J. K., Nielsen, E., Rudinger, K., Mizrahi, J., Fortier, K., et al. (2017). Demonstration of qubit operations below a rigorous fault tolerance threshold with gate set tomography. Nat. Commun. 8, 14485. doi:10.1038/ncomms14485

PubMed Abstract | CrossRef Full Text | Google Scholar

Boahen, K., Gao, P., McQuinn, E., Choudhary, S., Chandrasekaran, A. R., Bussat, J. M., et al. (2014). Neurogrid: a mixed-analog-digital multichip system for large-scale neural simulations. Proc. IEEE 102 (5), 699–716. doi:10.1109/jproc.2014.2313565

CrossRef Full Text | Google Scholar

Bohm, D., and Aharonov, Y. (1957). Discussion of experimental proof for the paradox of einstein, rosen, and podolsky. Phys. Rev. 108 (4), 1070–1076. doi:10.1103/physrev.108.1070

CrossRef Full Text | Google Scholar

Bohr, N. (1913a). I. On the constitution of atoms and molecules. Phil. Mag. 26, 1–25. doi:10.1080/14786441308634955

CrossRef Full Text | Google Scholar

Bohr, N. (1913b). On the constitution of atoms and molecules. Part II: systems containing only a single nucleus. Phil. Mag. 26 (153), 476–502. doi:10.1080/14786441308634993

CrossRef Full Text | Google Scholar

Bohr, N. (1913c). On the constitution of atoms and molecules. Part III: systems containing several nuclei. Phil. Mag. 26 (155), 857–875. doi:10.1080/14786441308635031

CrossRef Full Text | Google Scholar

Bommer, J. D. S., Zhang, H., Gül, Ö., Nijholt, B., Wimmer, M., Rybakov, F. N., et al. (2019). Spin-orbit protection of induced superconductivity in Majorana nanowires. Phys. Rev. Lett. 122, 187702. doi:10.1103/PhysRevLett.122.187702

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonn, D. (2020). The physics of ice skating. Available at: https://www.nature.com/articles/d41586-019-03833-5.

Google Scholar

Boschi, D., Branca, S., De Martini, F., Hardy, L., and Popescu, S. (1998). Experimental realization of teleporting an unknown pure quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 80, 1121–1125. doi:10.1103/physrevlett.80.1121

CrossRef Full Text | Google Scholar

Bouchard, F., England, D., Bustard, P. J., Heshami, K., and Sussman, B. (2022). Quantum communication with ultrafast time-bin qubits. PRX Quantum 3 (1), 010332. doi:10.1103/prxquantum.3.010332

CrossRef Full Text | Google Scholar

Bouchard, F., Fickler, R., Boyd, R. W., and Karimi, E. (2017). High-dimensional quantum cloning and applications to quantum hacking. Sci. Adv. 3 (2), e1601915. doi:10.1126/sciadv.1601915

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchard, F., Sit, A., Hufnagel, F., Abbas, A., Zhang, Y., Heshami, K., et al. (2018). Quantum cryptography with twisted photons through an outdoor underwater channel. Opt. Express 26 (17), 22563–22573. doi:10.1364/oe.26.022563

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchiat, V., Vion, D., Joyez, P., Esteve, D., and Devoret, M. H. (1998). Quantum coherence with a single Cooper pair. Phys. Scr. 1998 (T76), 165. doi:10.1238/physica.topical.076a00165

CrossRef Full Text | Google Scholar

Bouland, A., and Aaronson, S. (2014). Generation of universal linear optics by any beam splitter. Phys. Rev. A 89 (6), 062316. doi:10.1103/physreva.89.062316

CrossRef Full Text | Google Scholar

Bouland, A., Mančinska, L., and Zhang, X. (2016). Complexity classification of two-qubit commuting Hamiltonians. arXiv preprint arXiv:1602.04145.

Google Scholar

Bouwmeester, D., Pan, J. W., Mattle, K., Eibl, M., Weinfurter, H., and Zeilinger, A. (1997a). Experimental quantum teleportation. Nature 390, 575–579. doi:10.1038/37539

CrossRef Full Text | Google Scholar

Bouwmeester, D., Pan, J. W., Mattle, K., Eibl, M., Weinfurter, H., and Zeilinger, A. (1997b). Experimental quantum teleportation. Nature 390 (6660), 575–579. doi:10.1038/37539

CrossRef Full Text | Google Scholar

Bouwmeester, D., Pan, J. W., Mattle, K., Eibl, M., Weinfurter, H., and Zeilinger, A. (1997c). Experimental quantum teleportation. Nature 390, 575–579. doi:10.1038/37539

CrossRef Full Text | Google Scholar

Bouwmeester, D., Pan, J. W., Mattle, K., Eibl, M., Weinfurter, H., and Zeilinger, A. (1997d). Experimental quantum teleportation. Nature 390, 575–579. doi:10.1038/37539

CrossRef Full Text | Google Scholar

Bowen, W. P., Treps, N., Buchler, B. C., Schnabel, R., Ralph, T. C., Bachor, H. A., et al. (2003). Experimental investigation of continuousvariable quantum teleportation. Phys. Rev. A 67, 032302. doi:10.1103/physreva.67.032302

CrossRef Full Text | Google Scholar

Braginsky, V. B., and Khalili, F. Y. (1996). Quantum nondemolition measurements: the route from toys to tools. Rev. Mod. Phys. 68 (1), 1–11. doi:10.1103/revmodphys.68.1

CrossRef Full Text | Google Scholar

Bravyi, S. B., and Kitaev, A. Y. (1998). Quantum codes on a lattice with boundary. Preprint at arXiv:quant-ph/9811052v1.

Google Scholar

Brendel, J., Gisin, N., Tittel, W., and Zbinden, H. (1999). Pulsed energy-time entangled twin-photon source for quantum communication. Phys. Rev. Lett. 82 (12), 2594–2597. doi:10.1103/physrevlett.82.2594

CrossRef Full Text | Google Scholar

Briegel, H. J., Dür, W., Cirac, J. I., and Zoller, P. (1998). Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81 (26), 5932–5935. doi:10.1103/physrevlett.81.5932

CrossRef Full Text | Google Scholar

Broglie, L. D. (1924). XXXV. A tentative theory of light quanta. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 47 (278), 446–458. doi:10.1080/14786442408634378

CrossRef Full Text | Google Scholar

Brooks, P., Kitaev, A., and Preskill, J. (2013a). Protected gates for superconducting qubits. Phys. Rev. A 87 (5), 052306. doi:10.1103/physreva.87.052306

CrossRef Full Text | Google Scholar

Brooks, P., Kitaev, A., and Preskill, J. (2013b). Protected gates for superconducting qubits. Phys. Rev. A 87 (5), 052306. doi:10.1103/physreva.87.052306

CrossRef Full Text | Google Scholar

Brooks, M. (2024). Quantum computing is taking on its biggest challenge: noise, MIT Technology Review.

Broome, M. A., Watson, T., Keith, D., Gorman, S., House, M., Keizer, J., et al. (2017a). High-fidelity single-shot singlet–triplet readout of precision-placed donors in silicon. Phys. Rev. Lett. 119, 046802. doi:10.1103/physrevlett.119.046802

PubMed Abstract | CrossRef Full Text | Google Scholar

Broome, M. A., Watson, T., Keith, D., Gorman, S., House, M., Keizer, J., et al. (2017b). High-fidelity single-shot singlet–triplet readout of precision-placed donors in silicon. Phys. Rev. Lett. 119, 046802. doi:10.1103/physrevlett.119.046802

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, J. (2000). The quest for the quantum computer. New York: Simon and Schuster.

Google Scholar

Bruzewicz, C. D., Chiaverini, J., McConnell, R., and Sage, J. M. (2019). Trapped-ion quantum computing: progress and challenges. Appl. Phys. Rev. 6 (2), 021314. doi:10.1063/1.5088164

CrossRef Full Text | Google Scholar

Bussières, F., Clausen, C., Tiranov, A., Korzh, B., Verma, V. B., Nam, S. W., et al. (2014a). Quantum teleportation from a telecomwavelength photon to a solidstate quantum memory. Nat. Phot. 8, 775–778. doi:10.1038/nphoton.2014.215

CrossRef Full Text | Google Scholar

Bussières, F., Clausen, C., Tiranov, A., Korzh, B., Verma, V. B., Nam, S. W., et al. (2014b). Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat. Photonics 8 (10), 775–778. doi:10.1038/nphoton.2014.215

CrossRef Full Text | Google Scholar

Büttiker, M. (1987). Zero-current persistent potential drop across small-capacitance Josephson junctions. Phys. Rev. B 36 (7), 3548–3555. doi:10.1103/physrevb.36.3548

CrossRef Full Text | Google Scholar

Bylander, J., Gustavsson, S., Yan, F., Yoshihara, F., Harrabi, K., Fitch, G., et al. (2011). Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nat. Phys. 7 (7), 565–570. doi:10.1038/nphys1994

CrossRef Full Text | Google Scholar

Cai, K., Yang, M., Ju, H., Wang, S., Ji, Y., Li, B., et al. (2017). Electric field control of deterministic current-induced magnetization switching in a hybrid ferromagnetic/ferroelectric structure. Nat. Mater. 16 (7), 712–716. doi:10.1038/nmat4886

PubMed Abstract | CrossRef Full Text | Google Scholar

Callus, E., and Kok, P. (2021). Cumulative generation of maximal entanglement between spectrally distinct qubits using squeezed light. Phys. Rev. A 104 (5), 052407. doi:10.1103/physreva.104.052407

CrossRef Full Text | Google Scholar

Campagne-Ibarcq, P., Eickbusch, A., Touzard, S., Zalys-Geller, E., Frattini, N. E., Sivak, V. V., et al. (2020). Quantum error correction of a qubit encoded in grid states of an oscillator. Nature 584 (7821), 368–372. doi:10.1038/s41586-020-2603-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Canale, L., Comtet, J., Niguès, A., Cohen, C., Clanet, C., Siria, A., et al. (2019). Nanorheology of interfacial water during ice gliding. Phys. Rev. X 9 (4), 041025. doi:10.1103/physrevx.9.041025

CrossRef Full Text | Google Scholar

Cao, H. J., and Song, H. S. (2007). Teleportation of a single qubit state via unique W state. Int. J. Theor. Phys. 46, 1636–1642. doi:10.1007/s10773-006-9301-2

CrossRef Full Text | Google Scholar

Cao, Y., Rushforth, A., Sheng, Y., Zheng, H., and Wang, K. (2019). Tuning a binary ferromagnet into a multistate synapse with spin–orbit-torque-induced plasticity. Adv. Funct. Mater. 29 (25), 1808104. doi:10.1002/adfm.201808104

CrossRef Full Text | Google Scholar

Cao, Y., Xing, G., Lin, H., Zhang, N., Zheng, H., and Wang, K. (2020). Prospect of spin-orbitronic devices and their applications. IScience 23 (10), 101614. doi:10.1016/j.isci.2020.101614

PubMed Abstract | CrossRef Full Text | Google Scholar

Castelvecchi, D. (2017). Quantum computers ready to leap out of the lab in 2017. Nature 541 (7635), 9–10. doi:10.1038/541009a

PubMed Abstract | CrossRef Full Text | Google Scholar

Catelani, G., Nigg, S. E., Girvin, S. M., Schoelkopf, R. J., and Glazman, L. I. (2012). Decoherence of superconducting qubits caused by quasiparticle tunneling. Phys. Rev. B 86 (18), 184514. doi:10.1103/physrevb.86.184514

CrossRef Full Text | Google Scholar

Catelani, G., Schoelkopf, R. J., Devoret, M. H., and Glazman, L. I. (2011). Relaxation and frequency shifts induced by quasiparticles in superconducting qubits. Phys. Rev. B 84 (6), 064517. doi:10.1103/physrevb.84.064517

CrossRef Full Text | Google Scholar

Chakravartula, V., Samiappan, D., Kumar, R., and Manjari, A. P. (2020). Implementation of quantum teleportation of photons across an air–water interface. Opt. Quantum Electron. 52, 1–10. doi:10.1007/s11082-020-02449-8

CrossRef Full Text | Google Scholar

Chatterjee, A., Stevenson, P., De Franceschi, S., Morello, A., de Leon, N. P., and Kuemmeth, F. (2021). Semiconductor qubits in practice. Nat. Rev. Phys. 3 (3), 157–177. doi:10.1038/s42254-021-00283-9

CrossRef Full Text | Google Scholar

Chen, J., Li, D., Liu, M., and Yang, Y. (2020). Bidirectional quantum teleportation by using a four-qubit GHZ state and two bell states. IEEE Access 8, 28925–28933. doi:10.1109/access.2020.2971973

CrossRef Full Text | Google Scholar

Chen, Y. A., Chen, S., Yuan, Z. S., Zhao, B., Chuu, C. S., Schmiedmayer, J., et al. (2008). Memorybuiltin quantum teleportation with photonic and atomic qubits. Nat. Phys. 4, 103–107. doi:10.1038/nphys832

CrossRef Full Text | Google Scholar

Chiesa, A., Macaluso, E., Petiziol, F., Wimberger, S., Santini, P., and Carretta, S. (2020). Molecular nanomagnets as qubits with embedded quantum-error correction. J. Phys. Chem. Lett. 11 (20), 8610–8615. doi:10.1021/acs.jpclett.0c02213

PubMed Abstract | CrossRef Full Text | Google Scholar

Childs, A. M., Leung, D., Mančinska, L., and Ozols, M. (2010). Characterization of universal two-qubit Hamiltonians. arXiv preprint arXiv:1004.1645.

Google Scholar

Choi, J. G., Park, J., Kang, M. G., Kim, D., Rieh, J. S., Lee, K. J., et al. (2022). Voltage-driven gigahertz frequency tuning of spin Hall nano-oscillators. Nat. Commun. 13, 3783. doi:10.1038/s41467-022-31493-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Choudhury, B. S., and Dhara, A. (2016). A bidirectional teleportation protocol for arbitrary two-qubit state under the supervision of a third party. Int. J. Theor. Phys. 55, 2275–2285. doi:10.1007/s10773-015-2865-y

CrossRef Full Text | Google Scholar

Chow, J. M., DiCarlo, L., Gambetta, J. M., Motzoi, F., Frunzio, L., Girvin, S. M., et al. (2010). Optimized driving of superconducting artificial atoms for improved single-qubit gates. Phys. Rev. A 82 (4), 040305. doi:10.1103/physreva.82.040305

CrossRef Full Text | Google Scholar

Chow, J. M., Gambetta, J. M., Córcoles, A. D., Merkel, S. T., Smolin, J. A., Rigetti, C., et al. (2012). Universal quantum gate set approaching fault-tolerant thresholds with superconducting qubits. Phys. Rev. Lett. 109, 060501. doi:10.1103/PhysRevLett.109.060501

PubMed Abstract | CrossRef Full Text | Google Scholar

Chow, J. M., Gambetta, J. M., Cross, A. W., Merkel, S. T., Rigetti, C., and Steffen, M. (2013). Microwave-activated conditional-phase gate for superconducting qubits. New J. Phys. 15, 115012. doi:10.1088/1367-2630/15/11/115012

CrossRef Full Text | Google Scholar

Chow, J. M., Gambetta, J. M., Magesan, E., Abraham, D. W., Cross, A. W., Johnson, B. R., et al. (2014). Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. Commun. 5, 4015. doi:10.1038/ncomms5015

PubMed Abstract | CrossRef Full Text | Google Scholar

Chow, J. M., Srinivasan, S. J., Magesan, E., Córcoles, A. D., Abraham, D. W., Gambetta, J. M., et al. (2015). Characterizing a four-qubit planar lattice for arbitrary error detection. Quantum Inf. Comput. XIII 9500, 315–323. doi:10.1117/12.2192740

CrossRef Full Text | Google Scholar

Christensen, B. G., Wilen, C. D., Opremcak, A., Nelson, J., Schlenker, F., Zimonick, C. H., et al. (2019). Anomalous charge noise in superconducting qubits. Phys. Rev. B 100, 140503. doi:10.1103/physrevb.100.140503

CrossRef Full Text | Google Scholar

Chuang, I. L., Gershenfeld, N., and Kubinec, M. (1998a). Experimental implementation of fast quantum searching. Phys. Rev. Lett. 80 (15), 3408–3411. doi:10.1103/physrevlett.80.3408

CrossRef Full Text | Google Scholar

Chuang, I. L., Gershenfeld, N., and Kubinec, M. (1998b). Experimental implementation of fast quantum searching. Phys. Rev. Lett. Am. Phys. Soc. 80 (15), 3408–3411. doi:10.1103/physrevlett.80.3408

CrossRef Full Text | Google Scholar

Chuang, I. L., and Yamamoto, Y. (1995). Simple quantum computer. Phys. Rev. A 52 (5), 3489–3496. doi:10.1103/physreva.52.3489

PubMed Abstract | CrossRef Full Text | Google Scholar

Clausen, C., Usmani, I., Bussières, F., Sangouard, N., Afzelius, M., de Riedmatten, H., et al. (2011). Quantum storage of photonic entanglement in a crystal. Nature 469, 508–511. doi:10.1038/nature09662

PubMed Abstract | CrossRef Full Text | Google Scholar

Commins, E. D. (2012). Electron spin and its history. Annu. Rev. Nucl. Part. Sci. 62, 133–157. doi:10.1146/annurev-nucl-102711-094908

CrossRef Full Text | Google Scholar

Cong, L., Wei, Z., Hua-bo, L., and Si-meng, W. (2017). Bidirectional quantum teleportation controlled by single-qutrit state. Acta Phot. Sin. 46 (5), 0527002.

Google Scholar

Conover, E. (2020). The new light-based quantum computer Jiuzhang has achieved quantum supremacy. Sci. News. Retrieved 2020-12-19. doi:10.1126/science.abe8770

CrossRef Full Text | Google Scholar

Constantin, M., and Yu, C. C. (2007). Microscopic model of critical current noise in Josephson junctions. Phys. Rev. Lett. 99, 207001. doi:10.1103/physrevlett.99.207001

PubMed Abstract | CrossRef Full Text | Google Scholar

Coppersmith, D. (1994). An approximate Fourier transform useful in quantum factoring. Technical Report RC19642, IBM. arXiv:quant-ph/0201067.

Google Scholar

Cory, D. G., Fahmy, A. F., and Havel, T. F. (1996). “Nuclear magnetic resonance spectroscopy: an experimentally accessible paradigm for quantum computing,” in Proceedings of the Fourth Workshop on Physics and Computation. Editors T. Toffoli, B. Biafore, and J. Leao (New England Complex Systems Institute), 87–91.

Google Scholar

Cory, D. G., Fahmy, A. F., and Havel, T. F. (1997). Ensemble quantum computing by NMR spectroscopy. Proceedings of the National Academy of Sciences 94 (5), 1634–1639. doi:10.1073/pnas.94.5.1634

PubMed Abstract | CrossRef Full Text | Google Scholar

Cross, A. W., and Gambetta, J. M. (2015). Optimized pulse shapes for a resonator-induced phase gate. Phys. Rev. A 91, 032325. doi:10.1103/physreva.91.032325

CrossRef Full Text | Google Scholar

CT (2022a). Quantum hardware noise and advanced control. Available at: https://www.ct.imm.cnr.it/?q=articles/quantum-hardware-noise-and-advanced-control.

Google Scholar

CT (2022b). Quantum hardware noise and advanced control. Available at: https://www.ct.imm.cnr.it/?q=articles/quantum-hardware-noise-and-advanced-control.

Google Scholar

Cuff, T. M. (1993). THE STM (scanning tunneling microscope) the forgotten contribution of Robert francis Earhart to the discovery of quantum tunneling.

Google Scholar

Danon, J., Chatterjee, A., Gyenis, A., and Kuemmeth, F. (2021). Protected solid-state qubits. Appl. Phys. Lett. 119 (26), 260502. doi:10.1063/5.0073945

CrossRef Full Text | Google Scholar

Das, N., Paul, G., and Majumdar, R. (2021). Quantum secure direct communication with mutual authentication using a single basis. Int. J. Theor. Phys. 60, 4044–4065. doi:10.1007/s10773-021-04952-4

CrossRef Full Text | Google Scholar

Davey, R. (2023). How is China investing in qantum technology? Available at: https://www.azoquantum.com/Article.aspx?ArticleID=435 (Accessed July 19, 2024).

DBpedia (2023). Bohr model. Available at: https://dbpedia.org/page/Bohr_model (Accessed March 1, 2023).

Google Scholar

Degen, C. L., Reinhard, F., and Cappellaro, P. (2017). Quantum sensing. Rev. Mod. Phys. 89 (3), 035002. doi:10.1103/revmodphys.89.035002

CrossRef Full Text | Google Scholar

De Graaf, S. E., Faoro, L., Burnett, J., Adamyan, A. A., Ya Tzalenchuk, A., Kubatkin, S. E., et al. (2018). Suppression of low-frequency charge noise in superconducting resonators by surface spin desorption. Nat. commun. 9 (1), 1143. doi:10.1038/s41467-018-03577-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Demidov, V. E., Urazhdin, S., Ulrichs, H., Tiberkevich, V., Slavin, A., Baither, D., et al. (2022). Magnetic nano-oscillator driven by pure spin current. Nat. Mat. 11 (2012), 1028–1031. doi:10.1038/nmat3459

PubMed Abstract | CrossRef Full Text | Google Scholar

Demidov, V. E., Urazhdin, S., Zholud, A., Sadovnikov, A. V., and Demokritov, S. O. (2014). Nanoconstriction-based spin-Hall nano-oscillator. Appl. Phys. Lett. 105, 172410. doi:10.1063/1.4901027

CrossRef Full Text | Google Scholar

Dennis, E., Kitaev, A., Landahl, A., and Preskill, J. (2002). Topological quantum memory. J. Math. Phys. 43, 4452–4505. doi:10.1063/1.1499754

CrossRef Full Text | Google Scholar

de Riedmatten, H., Marcikic, I., Tittel, W., Zbinden, H., Collins, D., and Gisin, N. (2004). Long distance quantum teleportation in a quantum relay configuration. Phys. Rev. Lett. 92, 047904. doi:10.1103/physrevlett.92.047904

PubMed Abstract | CrossRef Full Text | Google Scholar

Deutsch, D. (1985). Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. A 400 (1818), 97–117. doi:10.1098/rspa.1985.0070

CrossRef Full Text | Google Scholar

Deutsch, D., and Jozsa, R. (1992). Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 439 (1907), 553–558. doi:10.1098/rspa.1992.0167

CrossRef Full Text | Google Scholar

Devoret, M. H., Wallraff, A., and Martinis, J. M. (2004). Superconducting qubits: a short review.

Google Scholar

Dewes, A., Ong, F. R., Schmitt, V., Lauro, R., Boulant, N., Bertet, P., et al. (2012). Characterization of a two-transmon processor with individual single-shot qubit readout. Phys. Rev. Lett. 108, 057002. doi:10.1103/PhysRevLett.108.057002

PubMed Abstract | CrossRef Full Text | Google Scholar

DiCarlo, L., Chow, J. M., Gambetta, J. M., Bishop, L. S., Johnson, B. R., Schuster, D. I., et al. (2009). Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244. doi:10.1038/nature08121

PubMed Abstract | CrossRef Full Text | Google Scholar

Didier, N., Sete, E. A., Combes, J., and da Silva, M. P. (2019a). AC flux sweet spots in parametrically modulated superconducting qubits. Phys. Rev. Appl. 12 (5), 054015. doi:10.1103/physrevapplied.12.054015

CrossRef Full Text | Google Scholar

Didier, N., Sete, E. A., Combes, J., and da Silva, M. P. (2019b). AC flux sweet spots in parametrically modulated superconducting qubits. Phys. Rev. Appl. 12 (5), 054015. doi:10.1103/physrevapplied.12.054015

CrossRef Full Text | Google Scholar

Didier, N., Sete, E. A., Combes, J., and da Silva, M. P. (2019c). AC flux sweet spots in parametrically modulated superconducting qubits. Phys. Rev. Appl. 12 (5), 054015. doi:10.1103/physrevapplied.12.054015

CrossRef Full Text | Google Scholar

Digital Strategy (2022a). Digital strategy. Available at: https://digital-strategy.ec.europa.eu/en/policies/european-quantum-communication-infrastructure-euroqci.

Google Scholar

Digital Strategy (2022b). Digital strategy. Available at: https://digital-strategy.ec.europa.eu/en/policies/quantum.

Google Scholar

Dirac, P. A. M. (1926). On the theory of quantum mechanics. Proc. R. Soc. Lond. Ser. A, Contain. Pap. a Math. Phys. Character 112 (762), 661–677. doi:10.1098/rspa.1926.0133

CrossRef Full Text | Google Scholar

Dirac, P. A. M. (1927). The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. Ser. A, Contain. Pap. a Math. Phys. Character 114 (767), 243–265. doi:10.1098/rspa.1927.0039

CrossRef Full Text | Google Scholar

DiVincenzo, D. (1995a). A two-bit gates are universal for quantum computation. Phys. Rev. A. 51 (2), 1015–1022. doi:10.1103/PhysRevA.51.1015

PubMed Abstract | CrossRef Full Text | Google Scholar

DiVincenzo, D. (1995b). Quantum computation. Science 270 (5234).

CrossRef Full Text | Google Scholar

DiVincenzo, D. P. (2000). The physical implementation of quantum computation. Fortschritte der Physik Prog. Phys. 48 (9), 771–783. doi:10.1002/1521-3978(200009)48:9/11<771::aid-prop771>3.0.co;2-e

CrossRef Full Text | Google Scholar

DiVincenzo, D. P. (2009). Fault-tolerant architectures for superconducting qubits. Phys. Scr. 2009 (T137), 014020. doi:10.1088/0031-8949/2009/t137/014020

CrossRef Full Text | Google Scholar

Dong, J., and Teng, J. F. (2008). Controlled teleportation of an arbitrary n-qudit state using nonmaximally entangled GHZ states. Eur. Phys. J. D 49, 129–134. doi:10.1140/epjd/e2008-00141-0

CrossRef Full Text | Google Scholar

Donohue, J. M., Agnew, M., Lavoie, J., and Resch, K. J. (2013). Coherent ultrafast measurement of time-bin encoded photons. Phys. Rev. Lett. 111 (15), 153602. doi:10.1103/physrevlett.111.153602

PubMed Abstract | CrossRef Full Text | Google Scholar

Douçot, B., and Ioffe, L. B. (2012). Physical implementation of protected qubits. Rep. Prog. Phys. 75 (7), 072001. doi:10.1088/0034-4885/75/7/072001

PubMed Abstract | CrossRef Full Text | Google Scholar

Douçot, B., and Vidal, J. (2002). Pairing of Cooper pairs in a fully frustrated Josephson-junction chain. Phys. Rev. Lett. 88 (22), 227005. doi:10.1103/physrevlett.88.227005

PubMed Abstract | CrossRef Full Text | Google Scholar

Dréau, A., Spinicelli, P., Maze, J. R., Roch, J. F., and Jacques, V. (2013). Single-shot readout of multiple nuclear spin qubits in diamond under ambient conditions. Phys. Rev. Lett. 110 (6), 060502. doi:10.1103/physrevlett.110.060502

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, Y. J., Zha, X. W., Sun, X. M., and Xia, J. F. (2014a). Bidirectional quantum-controlled teleportation via a maximally seven-qubit entangled state. Int. J. Theor. Phys. 53, 2697–2707. doi:10.1007/s10773-014-2065-1

CrossRef Full Text | Google Scholar

Duan, Z., Smith, A., Yang, L., Youngblood, B., Lindner, J., Demidov, V. E., et al. (2014b). Nanowire spin torque oscillator driven by spin orbit torques. Nat. Commun. 5, 5616. doi:10.1038/ncomms6616

PubMed Abstract | CrossRef Full Text | Google Scholar

Dumont, R. S., Rivlin, T., and Pollak, E. (2020). The relativistic tunneling flight time may be superluminal, but it does not imply superluminal signaling. New J. Phys. 22 (9), 093060. doi:10.1088/1367-2630/abb515

CrossRef Full Text | Google Scholar

Dürrenfeld, P., Awad, A. A., Houshang, A., Dumas, R. K., and Åkerman, J. (2017). A 20 nm spin Hall nano-oscillator. Nanoscale 9, 1285–1291. doi:10.1039/c6nr07903b

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutt, M. G., Childress, L., Jiang, L., Togan, E., Maze, J., Jelezko, F., et al. (2007). Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316 (5829), 1312–1316. doi:10.1126/science.1139831

PubMed Abstract | CrossRef Full Text | Google Scholar

D-Wave Initiates Open Quantum Software Environment (2022a). D-wave systems. Archived from the original on 8 march 2021.

Google Scholar

D-Wave Initiates Open Quantum Software Environment (2022b). D-wave systems. Archived from the original on 8 march 2021. Retrieved 24 Dec 2022.

Google Scholar

Dwavesys (2022). Dwavesys. Available at: https://docs.dwavesys.com/docs/latest/c_gs_2.html#eigenspectrum (Accessed December 23, 22).

Google Scholar

Dynes, J. F., Takesue, H., Yuan, Z. L., Sharpe, A. W., Harada, K., Honjo, T., et al. (2009). Efficient entanglement distribution over 200 kilometers. Opt. Express 17, 11440–11449. doi:10.1364/oe.17.011440

PubMed Abstract | CrossRef Full Text | Google Scholar

Egan, L., Debroy, D. M., Noel, C., Risinger, A., Zhu, D., Biswas, D., et al. (2020). Fault-tolerant operation of a quantum error-correction code. arXiv preprint arXiv:2009.11482.

Google Scholar

Ehrenfest, P. (1911). Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?” [In which features of the light quantum hypothesis does thermal radiation play an essential role?]. Ann. Phys. 341 (11), 91–118. doi:10.1002/andp.19113411106

CrossRef Full Text | Google Scholar

Einstein, A. (1905a). Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” (On a Heuristic Point of View about the Creation and Conversion of Light). Ann. Phys. 17 (6), 132–148. doi:10.1515/9783112596609

CrossRef Full Text | Google Scholar

Einstein, A. (1905b). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen” (Investigations on the theory of Brownian Movement). Ann. Phys. 17 (4), 549–560.

CrossRef Full Text | Google Scholar

Einstein, A. (1905c). Zur elektrodynamik bewegter körper” (on the electrodynamics of moving bodies). Ann. Phys. 17 (10), 891–921. doi:10.1007/978-3-662-48039-7_4

CrossRef Full Text | Google Scholar

Einstein, A. (1905d). Does the inertia of a body depend upon its energy-content. Ann. Phys. 18 (13), 639–641. doi:10.1002/andp.19053231314

CrossRef Full Text | Google Scholar

Einstein, A. (1905e). Die Grundlage der allgemeinen Relativitatstheorie (The basis of the general theory of relativity). Ann. Phys. 49, 769. doi:10.1007/978-3-662-48039-7_12

CrossRef Full Text | Google Scholar

Einstein, A. (1905f). Zur elektrodynamik bewegter körper. Ann. Phys. 17 (10), 890–921. doi:10.1002/andp.19053221004

CrossRef Full Text | Google Scholar

Einstein, A., Podolsky, B., and Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete?” (PDF). Phys. Rev. 47 (10), 777–780. doi:10.1103/PhysRev.47.777

CrossRef Full Text | Google Scholar

Eisaman, M. D., Fan, J., Migdall, A., and Polyakov, S. V. (2011). Invited review article: single-photon sources and detectors. Rev. Sci. Instrum. 82, 071101. doi:10.1063/1.3610677

PubMed Abstract | CrossRef Full Text | Google Scholar

Ekert, A. K., Huttner, B., Palma, G. M., and Peres, A. (1994). Eavesdropping on quantum-cryptographical systems. Phys. Rev. A 50 (2), 1047–1056. doi:10.1103/physreva.50.1047

PubMed Abstract | CrossRef Full Text | Google Scholar

Eng, K., Ladd, T. D., Smith, A., Borselli, M. G., Kiselev, A. A., Fong, B. H., et al. (2015). Isotopically enhanced triple-quantum-dot qubit. Sci. Adv. 1, e1500214. doi:10.1126/sciadv.1500214

PubMed Abstract | CrossRef Full Text | Google Scholar

Entanglementtech (2022). Entanglementtech. Available at: https://entanglementtech.com/.

Google Scholar

Epstein, J. M., Cross, A. W., Magesan, E., and Gambetta, J. M. (2014). Investigating the limits of randomized benchmarking protocols. Phys. Rev. A 89, 062321. doi:10.1103/physreva.89.062321

CrossRef Full Text | Google Scholar

Epstein, R. J., Mendoza, F. M., Kato, Y. K., and Awschalom, D. D. (2005). Anisotropic interactions of a single spin and dark-spin spectroscopy in diamond. Nat. Phys. 1 (2), 94–98. doi:10.1038/nphys141

CrossRef Full Text | Google Scholar

Escalera-Moreno, L., Baldoví, J. J., Gaita-Arino, A., and Coronado, E. (2018). Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: a critical perspective. Chem. Sci. 9 (13), 3265–3275. doi:10.1039/c7sc05464e

PubMed Abstract | CrossRef Full Text | Google Scholar

Espoukeh, P., and Pedram, P. (2014). Quantum teleportation through noisy channels with multi-qubit GHZ states. Quantum inf. Process. 13 (8), 1789–1811. doi:10.1007/s11128-014-0766-2

CrossRef Full Text | Google Scholar

Essential (2022). The 3 essential types of quantum computing-and their applications. Available at: http://brainstormingbox.org/the-3-essential-types-of-quantum-computing-and-their-applications/ (Accessed December 23, 2022).

Google Scholar

Estimates (2022). Estimates made from. Available at: https://www.researchnester.com/reports/quantum-computing-market/4910.

Google Scholar

Everspin (2012). Everspin ships first ST-MRAM memory with 500X performance of flash. Computerworld (Accessed February 5, 2023).

Google Scholar

Everspin (2019). Everspin enters pilot production phase for the world’s First 28 nm 1 Gb STT-MRAM component | Everspin. Available at: www.everspin.com (Accessed June 25, 2019).

Google Scholar

Fan, X., Celik, H., Wu, J., Ni, C., Lee, K. J., Lorenz, V. O., et al. (2014). Quantifying interface and bulk contributions to spin–orbit torque in magnetic bilayers. Nat. Commun. 5 (1), 3042. doi:10.1038/ncomms4042

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, X., Wu, J., Chen, Y., Jerry, M. J., Zhang, H., and Xiao, J. Q. (2013). Observation of the nonlocal spin-orbital effective field. Nat. Commun. 4 (1), 1799. doi:10.1038/ncomms2709

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Kou, X., Upadhyaya, P., Shao, Q., Pan, L., Lang, M., et al. (2016). Electric-field control of spin–orbit torque in a magnetically doped topological insulator. Nat. Nanotechnol. 11 (4), 352–359. doi:10.1038/nnano.2015.294

PubMed Abstract | CrossRef Full Text | Google Scholar

Faoro, L., Bergli, J., Altshuler, B. L., and Galperin, Y. M. (2005). Models of environment and T1 relaxation in Josephson charge qubits. Phys. Rev. Lett. 95, 046805. doi:10.1038/srep237868

PubMed Abstract | CrossRef Full Text | Google Scholar

Faoro, L., and Ioffe, L. B. (2007). Microscopic origin of critical current fluctuations in large, small, and ultra-small area Josephson junctions. Phys. Rev. B 75, 132505. doi:10.1103/physrevb.75.132505

CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., Gutmann, S., and Sipser, M. (2000). Quantum computation by adiabatic evolution. arXiv:quant-ph/0001106v1.

Google Scholar

Farquhar, E., and Hasler, P. (2006). “A field programmable neural array,” in IEEE international symposium on circuits and systems, 4114–4117. doi:10.1109/ISCAS.2006.1693534

CrossRef Full Text | Google Scholar

Fattal, D., Diamanti, E., Inoue, K., and Yamamoto, Y. (2004). Quantum teleportation with a quantum dot single photon source. Phys. Rev. Lett. 92, 037904. doi:10.1103/physrevlett.92.037904

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedrizzi, A., Ursin, R., Herbst, T., Nespoli, M., Prevedel, R., Scheidl, T., et al. (2009). High-fidelity transmission of entanglement over a high-loss free-space channel. Nat. Phys. 5, 389–392. doi:10.1038/nphys1255

CrossRef Full Text | Google Scholar

Fell, J., and Axmacher, N. (2011). The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 12, 105–118. doi:10.1038/nrn2979

PubMed Abstract | CrossRef Full Text | Google Scholar

Feynman, R. (1982). Simulating physics with computers. Int. J. Theor. Phys. 21 (6/7), 467–488. doi:10.1007/BF02650179

CrossRef Full Text | Google Scholar

Feynman, R. P. (1986). Quantum mechanical computers. Found. Phys. 16 (6), 507–531. doi:10.1007/bf01886518

CrossRef Full Text | Google Scholar

B. Field, and T. Simula (2018). Introduction to topological quantum computation with non-Abelian anyons. Quantum Sci. Technol.3, 045004.

CrossRef Full Text | Google Scholar

D. G. Fink (1975). Electronic engineers handbook (New York, NY: McGraw Hill).

Google Scholar

Fink, J. M. (2010). Quantum nonlinearities in strong coupling circuit QED (Ph.D.). Zürich, Switzerland: ETH Zurich.

Google Scholar

First Quantum Satellite Successfully Launched (2016) Archived from the original on 18 march 2018. Austrian Academy of Sciences.

Google Scholar

Fortnow, L. (2003). One complexity theorist’s view of quantum computing. Theor. Comput. Sci. 292 (3), 597–610. doi:10.1016/S0304-3975(01)00377-2

CrossRef Full Text | Google Scholar

Fortunebusinessinsights (2022). Fortunebusinessinsights. Available at: https://www.fortunebusinessinsights.com/quantum-computing-market-104855.

Google Scholar

Fowler, A. G., Mariantoni, M., Martinis, J. M., and Cleland, A. N. (2012a). Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324. doi:10.1103/physreva.86.032324

CrossRef Full Text | Google Scholar

Fowler, A. G., Stephens, A. M., and Groszkowski, P. (2009). High-threshold universal quantum computation on the surface code. Phys. Rev. A 80 (5), 052312. doi:10.1103/physreva.80.052312

CrossRef Full Text | Google Scholar

Fowler, A. G., Whiteside, A. C., and Hollenberg, L. C. (2012b). Towards practical classical processing for the surface code: timing analysis. Phys. Rev. A 86 (4), 042313. doi:10.1103/physreva.86.042313

PubMed Abstract | CrossRef Full Text | Google Scholar

Fowler, R. H., and Nordheim, Dr. L. (1928). Electron emission in intense electric fields” (PDF). Proc. R. Soc. A 119 (781), 173–181. doi:10.1098/rspa.1928.0091

CrossRef Full Text | Google Scholar

Fredkin, E., and Toffoli, T. (1982). Conservative logic. Int. J. Theor. Phys. 21 (3–4), 219–253. doi:10.1007/BF01857727

CrossRef Full Text | Google Scholar

Freedman, S. J., and Clauser, J. F. (1972). Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28 (14), 938–941. doi:10.1103/physrevlett.28.938

CrossRef Full Text | Google Scholar

Friis, N., Marty, O., Maier, C., Hempel, C., Holzäpfel, M., Jurcevic, P., et al. (2018). Observation of entangled states of a fully controlled 20-qubit system. Phys. Rev. X 8 (2), 021012. doi:10.1103/physrevx.8.021012

CrossRef Full Text | Google Scholar

Fukami, S., Zhang, C., DuttaGupta, S., Kurenkov, A., and Ohno, H. (2016). Magnetization switching by spin–orbit torque in an antiferromagnet–ferromagnet bilayer system. Nat. Mater. 15 (5), 535–541. doi:10.1038/nmat4566

PubMed Abstract | CrossRef Full Text | Google Scholar

Fulara, H., Zahedinejad, M., Khymyn, R., Awad, A., Muralidhar, S., Dvornik, M., et al. (2019). Spin-orbit torque–driven propagating spin waves. Sci. Adv. 5, eaax8467. doi:10.1126/sciadv.aax8467

PubMed Abstract | CrossRef Full Text | Google Scholar

Fulara, H., Zahedinejad, M., Khymyn, R., Dvornik, M., Fukami, S., Kanai, S., et al. (2020a). Giant voltage-controlled modulation of spin Hall nano-oscillator damping. Nat. Commun. 11, 4006. doi:10.1038/s41467-020-17833-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fulara, H., Zahedinejad, M., Khymyn, R., Dvornik, M., Fukami, S., Kanai, S., et al. (2020b). Giant voltage-controlled modulation of spin Hall nano-oscillator damping. Nat. Commun. 11, 4006. doi:10.1038/s41467-020-17833-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Furusawa, A., Sørensen, J. L., Braunstein, S. L., Fuchs, C. A., Kimble, H. J., and Polzik, E. S. (1998). Unconditional quantum teleportation. Science 282, 706–709. doi:10.1126/science.282.5389.706

PubMed Abstract | CrossRef Full Text | Google Scholar

Gali, A. (2011). Time-dependent density functional study on the excitation spectrum of point defects in semiconductors. Phys. Status Solidi B 248, 1337–1346. doi:10.1002/pssb.201046254

CrossRef Full Text | Google Scholar

Gambetta, J. M., Chow, J. M., and Steffen, M. (2017). Building logical qubits in a superconducting quantum computing system. Springer Sci. Bus. Media LLC 3 (1), 2. doi:10.1038/s41534-016-0004-0

CrossRef Full Text | Google Scholar

Gamow, G. (1928). Zur quantentheorie des atomkernes. Z. für Phys. 51 (3-4), 204–212. doi:10.1007/bf01343196

CrossRef Full Text | Google Scholar

Gao, W. B., Fallahi, P., Togan, E., Delteil, A., Chin, Y., Miguel-Sanchez, J., et al. (2013). Quantum teleportation from a propagating photon to a solidstate spin qubit. Nat. Commun. 4, 2744. doi:10.1038/ncomms3744

PubMed Abstract | CrossRef Full Text | Google Scholar

Geerlings, K. L. (2013). Improving coherence of superconducting qubits and resonators. Yale University.

Google Scholar

Gershenfeld, N. A., and Chuang, I. L. (1997). Bulk spin-resonance quantum computation. Science 275 (5298), 350–356. doi:10.1126/science.275.5298.350

PubMed Abstract | CrossRef Full Text | Google Scholar

Gershenfeld, N. A., and Chuang, I. L. (1998). Quantum computing with molecules. Sci. Am. 278 (6), 66–71. doi:10.1038/scientificamerican0698-66

PubMed Abstract | CrossRef Full Text | Google Scholar

Gertler, J. M., Baker, B., Li, J., Shirol, S., Koch, J., and Wang, C. (2021). Protecting a bosonic qubit with autonomous quantum error correction. Nature 590 (7845), 243–248. doi:10.1038/s41586-021-03257-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Giacomini, S., Sciarrino, F., Lombardi, E., and De Martini, F. (2002). Active teleportation of a quantum bit. Phys. Rev. A 66, 030302. doi:10.1103/physreva.66.030302

CrossRef Full Text | Google Scholar

Giovannetti, V., Lloyd, S., and Maccone, L. (2011). Advances in quantum metrology. Nat. photonics 5 (4), 222–229. doi:10.1038/nphoton.2011.35

CrossRef Full Text | Google Scholar

Gisin, N., Ribordy, G., Tittel, W., and Zbinden, H. (2002). Quantum cryptography. Rev. Mod. Phys. 74 (1), 145–195. doi:10.1103/revmodphys.74.145

CrossRef Full Text | Google Scholar

Gladchenko, S., Olaya, D., Dupont-Ferrier, E., Douçot, B., Ioffe, L. B., and Gershenson, M. E. (2009). Superconducting nanocircuits for topologically protected qubits. Nat. Phys. 5 (1), 48–53. doi:10.1038/nphys1151

CrossRef Full Text | Google Scholar

Globe News Wire (2023). Globe news wire. Available at: https://www.globeewswire.com/news-release/2022/10/10/2531311/0/en/Global-Magneto-Resistive-RAM-MRAM-Market-to-Reach-7-2-Billion-by-2027.html2/7/23.

Google Scholar

Gobby, C., Yuan, A., and Shields, A. J. (2004). Quantum key distribution over 122 km of standard telecom fiber. Appl. Phys. Lett. 84 (19), 3762–3764. doi:10.1063/1.1738173

CrossRef Full Text | Google Scholar

Gollub, C., Troppmann, U., and de Vivie-Riedle, R. (2006). The role of anharmonicity and coupling in quantum computing based on vibrational qubits. New J. Phys. 8 (4), 48. doi:10.1088/1367-2630/8/4/048

CrossRef Full Text | Google Scholar

Golubov, A. A., Kupriyanov, M. Y., and Il’ichev, E. (2004). The current-phase relation in Josephson junctions. Rev. Mod. Phys. 76, 411–469. doi:10.1103/revmodphys.76.411

CrossRef Full Text | Google Scholar

Google (2022). Google. Available at: https://www.google.com/search?q=quantum+cryptography+market+size&rlz=1C5CHFA_enUS943US965&oq=quantum+qencryption+market&aqs=chrome.2.69i57j0i22i30l2j0i390l4.16316j0j7&sourceid=chrome&ie=UTF-8.

Google Scholar

Gottesman, D. (1998a). Theory of fault-tolerant quantum computation. Phys. Rev. A 57 (1), 127–137. doi:10.1103/physreva.57.127

CrossRef Full Text | Google Scholar

Gottesman, D. (1998b). The Heisenberg representation of quantum computers. arXiv:quant-ph/9807006v1.

Google Scholar

Gottesman, D. (2010). An introduction to quantum error correction and fault-tolerant quantum computation. In Quantum information science and its contributions to mathematics. Proc. Symposia Appl. Math. 68, 13–58.

CrossRef Full Text | Google Scholar

Gottesman, D., and Chuang, I. L. (1999). Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402 (6760), 390–393. doi:10.1038/46503

CrossRef Full Text | Google Scholar

Green, T. J., Sastrawan, J., Uys, H., and Biercuk, M. J. (2013). Arbitrary quantum control of qubits in the presence of universal noise. New J. Phys. 15, 095004. doi:10.1088/1367-2630/15/9/095004

CrossRef Full Text | Google Scholar

Green, T. J., Uys, H., and Biercuk, M. J. (2012). High-order noise filtering in nontrivial quantum logic gates. Phys. Rev. Lett. 109, 020501. doi:10.1103/physrevlett.109.020501

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenberger, D. M., Horne, M. A., Shimony, A., and Zeilinger, A. (1990). Bell’s theorem without inequalities. Am. J. Phys. 58 (12), 1131–1143. doi:10.1119/1.16243

CrossRef Full Text | Google Scholar

GREYB (2022). Quantum computing market research. Available at: https://www.greyb.com/blog/quantum-computing-market-research/.

Google Scholar

Grier, D., and Schaeffer, L. (2022). The classification of Clifford gates over qubits. Quantum 6, 734. doi:10.22331/q-2022-06-13-734

CrossRef Full Text | Google Scholar

Grimm, A., Frattini, N. E., Puri, S., Mundhada, S. O., Touzard, S., Mirrahimi, M., et al. (2020). Stabilization and operation of a Kerr-cat qubit. Nature 584 (7820), 205–209. doi:10.1038/s41586-020-2587-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Grover, L. K. (1996). “A fast quantum mechanical algorithm for database search,” in Proceedings of the twenty-eighth annual ACM symposium on theory of computing. STOC ’96 (Philadelphia, Pennsylvania, USA: Association for Computing Machinery), 212–219. arXiv:quant-ph/9605043. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

Grover, L. K. (1996). in Proceedings of the twenty-eighth annual ACM symposium on theory of computing (New York: ACM), 212–219.

CrossRef Full Text | Google Scholar

Gulde, S., Riebe, M., Lancaster, G. P. T., Becher, C., Eschner, J., Häffner, H., et al. (2003). Implementation of the Deutsch–Jozsa algorithm on an ion-trap quantum computer. Nature 421 (6918), 48–50. doi:10.1038/nature01336

PubMed Abstract | CrossRef Full Text | Google Scholar

Gündoğan, M., Ledingham, P. M., Kutluer, K., Mazzera, M., and De Riedmatten, H. (2015). Solid-state spin-wave quantum memory for time-bin qubits. Phys. Rev. Lett. 114 (23), 23s0501. doi:10.1103/physrevlett.114.230501

CrossRef Full Text | Google Scholar

Gurney, R. W., and Condon, E. U. (1928). Wave mechanics and radioactive Disintegration. Nature 122 (3073), 439. doi:10.1038/122439a0

CrossRef Full Text | Google Scholar

Gustavsson, S., Yan, F., Catelani, G., Bylander, J., Kamal, A., Birenbaum, J., et al. (2016). Suppressing relaxation in superconducting qubits by quasiparticle pumping. Science 354, 1573–1577. doi:10.1126/science.aah5844

PubMed Abstract | CrossRef Full Text | Google Scholar

Gyenis, A., Di Paolo, A., Koch, J., Blais, A., Houck, A. A., and Schuster, D. I. (2021). Moving beyond the transmon: noise-protected superconducting quantum circuits. PRX Quantum 2 (3), 030101. doi:10.1103/prxquantum.2.030101

CrossRef Full Text | Google Scholar

Hadfield, R. H. (2009). Single-photon detectors for optical quantum information applications. Nat. Phot. 3, 696–705. doi:10.1038/nphoton.2009.230

CrossRef Full Text | Google Scholar

Hales, L., and Hallgren, S. (2000). “An improved quantum Fourier transform algorithm and applications,” in Proceedings 41st annual symposium on foundations of computer science, 515–525. doi:10.1109/SFCS.2000.892139

CrossRef Full Text | Google Scholar

Hamilton, C. A., Kautz, R. L., Steiner, R. L., and Lloyd, F. L. (1985). A practical Josephson voltage standard at 1 V. IEEE Electron Device Lett. 6 (12), 623–625. doi:10.1109/edl.1985.26253

CrossRef Full Text | Google Scholar

Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S., and Vandersypen, L. M. (2007). Spins in few-electron quantum dots. Rev. Mod. Phys. 79 (4), 1217–1265. doi:10.1103/revmodphys.79.1217

CrossRef Full Text | Google Scholar

Harris, R., Johansson, J., Berkley, A. J., Johnson, M. W., Lanting, T., Han, S., et al. (2010a). Experimental demonstration of a robust and scalable flux qubit. Phys. Rev. B 81 (13), 134510. doi:10.1103/PhysRevB.81.134510

CrossRef Full Text | Google Scholar

Harris, R., Johansson, J., Berkley, A. J., Johnson, M. W., Lanting, T., Han, S., et al. (2010b). Experimental demonstration of a robust and scalable flux qubit. Phys. Rev. B 81 (13), 134510. doi:10.1103/PhysRevB.81.134510

CrossRef Full Text | Google Scholar

Harrow, A. W., Hassidim, A., and Lloyd, S. (2008). Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103 (15), 150502. arXiv:0811.3171. doi:10.1103/physrevlett.103.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrow, A. W., and Montanaro, A. (2017). Quantum computational supremacy. Nature 549 (7671), 203–209. doi:10.1038/nature23458

PubMed Abstract | CrossRef Full Text | Google Scholar

Harvey, A. H. (2017). “Properties of ice and supercooled water,” in CRC handbook of chemistry and physics. Editors W. M. Haynes, D. R. Lide, and T. J. Bruno 97th ed. (Boca Raton, FL: CRC Press).

Google Scholar

Harvey-Collard, P., Jacobson, N. T., Rudolph, M., Dominguez, J., Ten Eyck, G. A., Wendt, J. R., et al. (2017). Coherent coupling between a quantum dot and a donor in silicon. Nat. Commun. 8, 1029. doi:10.1038/s41467-017-01113-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Hassanpour, S., and Houshmand, M. (2016). Bidirectional teleportation of a pure EPR state by using GHZ states. Quantum Inf. Process. 15 (2), 905–912. doi:10.1007/s11128-015-1096-8

CrossRef Full Text | Google Scholar

Haxel, O., Jensen, J. H. D., and Suess, H. E. (1949). On the“ magic numbers” in nuclear structure. Phys. Rev. 75 (11), 1766. doi:10.1103/physrev.75.1766.2

CrossRef Full Text | Google Scholar

He, Y., Gorman, S. K., Keith, D., Kranz, L., Keizer, J. G., and Simmons, M. Y. (2019). A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375. doi:10.1038/s41586-019-1381-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Heisenberg, W. (1925). Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. für Phys. 33, 879–893. doi:10.1007/bf01328377

CrossRef Full Text | Google Scholar

Hell, M., Leijnse, M., and Flensberg, K. (2017). Two-dimensional platform for networks of Majorana bound states. Phys. Rev. Lett. 118 (10), 107701. doi:10.1103/physrevlett.118.107701

PubMed Abstract | CrossRef Full Text | Google Scholar

Hennighausen, Z., and Kar, S. (2021). Twistronics: a turning point in 2D quantum materials. Electron. Struct. 3 (1), 014004. doi:10.1088/2516-1075/abd957

CrossRef Full Text | Google Scholar

Henriques, F., Valenti, F., Charpentier, T., Lagoin, M., Gouriou, C., Martínez, M., et al. (2019). Phonon traps reduce the quasiparticle density in superconducting circuits. Appl. Phys. Lett. 115, 212601. doi:10.1063/1.5124967

CrossRef Full Text | Google Scholar

Hensen, B., Wei Huang, W., Yang, C. H., Wai Chan, K., Yoneda, J., Tanttu, T., et al. (2020). A silicon quantum-dot-coupled nuclear spin qubit. Nat. Nanotechnol. 15, 13–17. doi:10.1038/s41565-019-0587-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirsch, J. E. (1999). Spin Hall effect. Phys. Rev. Lett. 83, 1834–1837. doi:10.1103/physrevlett.83.1834

CrossRef Full Text | Google Scholar

Holder, A. M., Osborn, K. D., Lobb, C. J., and Musgrave, C. B. (2013). Bulk and surface tunneling hydrogen defects in alumina. Phys. Rev. Lett. 111, 065901. doi:10.1103/physrevlett.111.065901

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, W. Q. (2016). Asymmetric bidirectional controlled teleportation by using a seven-qubit entangled state. Int. J. Theor. Phys. 55, 384–387. doi:10.1007/s10773-015-2671-6

CrossRef Full Text | Google Scholar

Honjo, T., Nam, S. W., Takesue, H., Zhang, Q., Kamada, H., Nishida, Y., et al. (2008). Long-distance entanglement-based quantum key distribution over optical fiber. Opt. Express 16 (23), 19118–19126. doi:10.1364/oe.16.019118

PubMed Abstract | CrossRef Full Text | Google Scholar

Horsman, C., Fowler, A., Devitt, S., and Meter, R. V. (2012). Surface code quantum computing by lattice surgery. New J. Phys. 14, 123011. doi:10.1088/1367-2630/14/12/123011

CrossRef Full Text | Google Scholar

Houck, A. A., Koch, J., Devoret, M. H., Girvin, S. M., and Schoelkopf, R. J. (2009). Life after charge noise: recent results with transmon qubits. Quantum Inf. Process. 8 (2–3), 105–115. doi:10.1007/s11128-009-0100-6

CrossRef Full Text | Google Scholar

Houck, A. A., Schreier, J. A., Johnson, B. R., Chow, J. M., Koch, J., Gambetta, J. M., et al. (2008). Controlling the spontaneous emission of a superconducting transmon qubit. Phys. Rev. Lett. 101 (8), 080502. doi:10.1103/physrevlett.101.080502

PubMed Abstract | CrossRef Full Text | Google Scholar

HPC (2022). HPC wire. Available at: https://www.hpcwire.com/off-the-wire/nec-develops-unit-cell-key-to-scaling-fully-connected-quantum-annealing-architecture/.

Google Scholar

Hsieh, W. T., Bell, M., Lu, W. S., Zhang, W., Kamenov, P., Kalashnikov, K., et al. (2019). Symmetry protected qubits through fluxon pairing. APS March Meet. Abstr. 2019, A29–A005.

Google Scholar

Hsueh, Y. L., Büch, H., Tan, Y., Wang, Y., Hollenberg, L. C., Klimeck, G., et al. (2014). Spin-lattice relaxation times of single donors and donor clusters in silicon. Phys. Rev. Lett. 113 (24), 246406. doi:10.1103/physrevlett.113.246406

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, C. (2022). IBM’s biggest quantum chip yet could help solve the trickiest math problems. Pop. Sci.

Google Scholar

Hu, X., Liu, Y., and Nori, F. (2012). Strong coupling of a spin qubit to a superconducting stripline cavity. Phys. Rev. B 86, 035314. doi:10.1103/physrevb.86.035314

CrossRef Full Text | Google Scholar

Huang, P., and Hu, X. (2014). Electron spin relaxation due to charge noise. Phys. Rev. B 89, 195302. doi:10.1103/physrevb.89.195302

CrossRef Full Text | Google Scholar

Huang, W., Yang, C. H., Chan, K. W., Tanttu, T., Hensen, B., Leon, R. C. C., et al. (2019). Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536. doi:10.1038/s41586-019-1197-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z., Mundada, P. S., Gyenis, A., Schuster, D. I., Houck, A. A., and Koch, J. (2021). Engineering dynamical sweet spots to protect qubits from 1/f noise. Phys. Rev. Appl. 15 (3), 034065. doi:10.1103/physrevapplied.15.034065

CrossRef Full Text | Google Scholar

Huelga, S. F., Plenio, M. B., and Vaccaro, J. A. (2002). Remote control of restricted sets of operations: teleportation of angles. Phys. Rev. A 65 (4), 042316. doi:10.1103/physreva.65.042316

CrossRef Full Text | Google Scholar

Humphreys, P. C., Metcalf, B. J., Spring, J. B., Moore, M., Jin, X. M., Barbieri, M., et al. (2013). Linear optical quantum computing in a single spatial mode. Phys. Rev. Lett. 111 (15), 150501.

PubMed Abstract | CrossRef Full Text | Google Scholar

Hund, F. (1927). Zur deutung der molekelspektren. i. Z. für Phys. 40 (10), 742–764. doi:10.1007/bf01400234

CrossRef Full Text | Google Scholar

Huo, M., Qin, J., Cheng, J., Yan, Z., Qin, Z., Su, X., et al. (2018). Deterministic quantum teleportation through fiber channels. Sci. Adv. 4 (10), eaas9401. doi:10.1126/sciadv.aas9401

PubMed Abstract | CrossRef Full Text | Google Scholar

IBM (2016). IBM makes quantum computing available on IBM Cloud. Available at: www-03.ibm.com (Accessed May 4, 2016).

Google Scholar

Iedema, M. J., Dresser, M. J., Doering, D. L., Rowland, J. B., Hess, W. P., Tsekouras, A. A., et al. (1998). Ferroelectricity in water ice. J. Phys. Chem. B 102 (46), 9203–9214. doi:10.1021/jp982549e

CrossRef Full Text | Google Scholar

Igeta, K., and Yamamoto, Y. (1988). “Quantum mechanical computers with single atom and photon fields,” in International Conference on Quantum Electronics. Editors H. Inaba, T. Yajima, and T. Ikegami (Optica Publishing Group), TuI4.

Google Scholar

IMEC (2023). IMEC enters the race to unleash quantum computing with silicon qubits. Available at: www.imec-int.com (Accessed March 10, 2023).

Google Scholar

Indico (2022). Indico. Available at: https://indico.fnal.gov/event/44309/contri-butions/191634/attachments/132006/162964/AMatos_DechorenceMechs.pdf (Accessed June 1, 2022).

Google Scholar

Innovationcloud (2022). Innovationcloud. Available at: https://innovationcloud.com/blog/what-is-quantum-technology-and-how-it-will-impact-our-future.html.

Google Scholar

Intel Invests US$50 Million to Advance Quantum Computing (2022). Intel newsroom. Intel Newsroom.

Google Scholar

Ioffe, L. B., and Feigel’man, M. V. (2002). Possible realization of an ideal quantum computer in Josephson junction array. Phys. Rev. B 66 (22), 224503. doi:10.1103/physrevb.66.224503

CrossRef Full Text | Google Scholar

Ioffe, L. B., Feigel’man, M. V., Ioselevich, A., Ivanov, D., Troyer, M., and Blatter, G. (2002). Topologically protected quantum bits using Josephson junction arrays. Nature 415 (6871), 503–506. doi:10.1038/415503a

PubMed Abstract | CrossRef Full Text | Google Scholar

Iogansen, L. V. (1964). The possibility of resonance transmission of electrons in crystals through a system of barriers. Sov. Phys. JETP 18 (1), 146–150.

Google Scholar

Ion Trap Quantum Computing (2023). Ion trap quantum computing. Available at: https://www.physics.ox.ac.uk/research/group/ion-trap-quantum-computing (Accessed April 2, 23).

Google Scholar

Iyengar, S. S., Kumar, K. J., and Mastriani, M. (2020). Bidirectional teleportation for underwater quantum communications. arXiv preprint arXiv:2009.04241.

Google Scholar

Jackson, J. D. (1987). The impact of special relativity on theoretical physics. Phys. Today 40 (5), 34–42. doi:10.1063/1.881108

CrossRef Full Text | Google Scholar

Jafferis, D., Zlokapa, A., Lykken, J. D., Kolchmeyer, D. K., Davis, S. I., Lauk, N., et al. (2022). Traversable wormhole dynamics on a quantum processor. Nature 612 (7938), 51–55. doi:10.1038/s41586-022-05424-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Jahnke, K. D., Naydenov, B., Teraji, T., Koizumi, S., Umeda, T., Isoya, J., et al. (2012) Long coherence time of spin qubits in $^{12} $ C enriched polycrystalline CVD diamond. arXiv preprint arXiv:1206.4260.

Google Scholar

Jain, B. K. (2009). Digital electronics - a modern approach by B K jain.

Google Scholar

Jain, S. (2014). Fundamentals of physical geology. New Delhi, India: Springer India.

Google Scholar

Jaklevic, R. C., Lambe, J., Silver, A. H., and Mercereau, J. E. (1964). Quantum interference effects in Josephson tunneling. Phys. Rev. Lett. 12 (7), 159–160. doi:10.1103/physrevlett.12.159

CrossRef Full Text | Google Scholar

Jakobi, I., Momenzadeh, S. A., De Oliveira, F. F., Michl, J., Ziem, F., Schreck, M., et al. (2016). Efficient creation of dipolar coupled nitrogen-vacancy spin qubits in diamond. J. Phys. Conf. Ser. 752 (1), 012001. doi:10.1088/1742-6596/752/1/012001

CrossRef Full Text | Google Scholar

Jamali, M., Lee, J. S., Jeong, J. S., Mahfouzi, F., Lv, Y., Zhao, Z., et al. (2015). Giant spin pumping and inverse spin Hall effect in the presence of surface and bulk spin− orbit coupling of topological insulator Bi2Se3. Nano Lett. 15 (10), 7126–7132. doi:10.1021/acs.nanolett.5b03274

PubMed Abstract | CrossRef Full Text | Google Scholar

Jelezko, F., Gaebel, T., Popa, I., Gruber, A., and Wrachtrup, J. (2004). Observation of coherent oscillations in a single electron spin. Phys. Rev. Lett. 92, 076401. doi:10.1103/physrevlett.92.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, X. M., Ren, J. G., Yang, B., Yi, Z. H., Zhou, F., Xu, X. F., et al. (2010). Experimental freespace quantum teleportation. Nat. Phot. 4, 376–381. doi:10.1038/nphoton.2010.87

CrossRef Full Text | Google Scholar

Jones, C., Fogarty, M. A., Morello, A., Gyure, M. F., Dzurak, A. S., and Ladd, T. D. (2018). Logical qubit in a linear array of semiconductor quantum dots. Phys. Rev. X 8, 021058. doi:10.1103/physrevx.8.021058

CrossRef Full Text | Google Scholar

Kalashnikov, K., Hsieh, W. T., Zhang, W., Lu, W. S., Kamenov, P., Di Paolo, A., et al. (2020). Bifluxon: fluxon-parity-protected superconducting qubit. PRX Quantum 1 (1), 010307. doi:10.1103/prxquantum.1.010307

CrossRef Full Text | Google Scholar

Kan, M. (2019). Google claims quantum computing achievement, IBM says not so fast. PCMAG.

Google Scholar

Kane, B. E. (1998). A silicon-based nuclear spin quantum computer. nature 393 (6681), 133–137. doi:10.1038/30156

CrossRef Full Text | Google Scholar

Karlsson, A., and Bourennane, M. (1998). Quantum teleportation using three-particle entanglement. Phys. Rev. A 58, 4394–4400. doi:10.1103/physreva.58.4394

CrossRef Full Text | Google Scholar

Khaetskii, A. V., and Nazarov, Y. V. (2001). Spin-flip transitions between Zeeman sublevels in semiconductor quantum dots. Phys. Rev. B 64, 125316. doi:10.1103/PhysRevB.64.125316

CrossRef Full Text | Google Scholar

Kim, J. P., Kim, T., Wuyang, H., Rao, H. M., Kangho, L., Zhu, X., et al. (2011) “San diego, CA, USA,” in A 45nm 1Mb embedded STT-MRAM with design techniques to minimize read-disturbance. 2011 Symposium on VLSI circuits (VLSIC). ieeexplore.ieee.org. Qualcomm Inc. Archived from the original on 1 July 2017. Retrieved 2/5/2023.

Google Scholar

Kim, Y. H., Kulik, S. P., and Shih, Y. (2001). Quantum teleportation of a polarization state with a complete bell-state measurement. Phys. Rev. Lett. 86, 1370–1373. doi:10.1103/physrevlett.86.1370

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimble, H. J. (2008). The quantum internet. Nature 453, 1023–1030. doi:10.1038/nature07127

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiselev, S. I., Sankey, J. C., Krivorotov, I. N., Emley, N. C., Schoelkopf, R. J., Buhrman, R. A., et al. (2003). Microwave oscillations of a nanomagnet driven by a spin-polarized current. nature 425 (6956), 380–383. doi:10.1038/nature01967

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitaev, A. Y. (2003). Fault-tolerant quantum computation by anyons. Ann. Phys. 303 (1), 2–30. doi:10.1016/s0003-4916(02)00018-0

CrossRef Full Text | Google Scholar

Kitaev, A. (1997). Fault-tolerant quantum computation by anyons. Ann. Phys. 303 (1), 2–30. doi:10.1016/S0003-4916(02)00018-0

CrossRef Full Text | Google Scholar

Kjaergaard, M., Schwartz, M. E., Braumüller, J., Krantz, P., Wang, J. I. J., Gustavsson, S., et al. (2020). Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369–395. doi:10.1146/annurev-conmatphys-031119-050605

CrossRef Full Text | Google Scholar

Klots, A. R., and Ioffe, L. B. (2021). Set of holonomic and protected gates on topological qubits for a realistic quantum computer. Phys. Rev. B 104 (14), 144502. doi:10.1103/physrevb.104.144502

CrossRef Full Text | Google Scholar

Knill, E., Laflamme, R., Martinez, R., and Tseng, C. H. (2000). An algorithmic benchmark for quantum information processing. Nature 404, 368–370. doi:10.1038/35006012

PubMed Abstract | CrossRef Full Text | Google Scholar

Knill, E., Laflamme, R., and Milburn, G. J. (2001). A scheme for efficient quantum computation with linear optics. Nature 409 (6816), 46–52. doi:10.1038/35051009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kobayashi, T., Salfi, J., Chua, C., Van Der Heijden, J., House, M. G., Culcer, D., et al. (2021). Engineering long spin coherence times of spin–orbit qubits in silicon. Nat. Mater. 20 (1), 38–42. doi:10.1038/s41563-020-0743-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, J., Yu, T. M., Gambetta, J., Houck, A. A., Schuster, D. I., Majer, J., et al. (2007). Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76 (4), 042319. doi:10.1103/physreva.76.042319

CrossRef Full Text | Google Scholar

Kocher, C., and Commins, E. (1967). Polarization correlation of photons emitted in an atomic cascade. Phys. Rev. Lett. - Phys. Rev. Lett. 18, 575–577. doi:10.1103/PhysRevLett.18.575

CrossRef Full Text | Google Scholar

Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G., and Awschalom, D. D. (2011). Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479 (7371), 84–87. doi:10.1038/nature10562

PubMed Abstract | CrossRef Full Text | Google Scholar

Korzh, B., Walenta, N., Lunghi, T., Gisin, N., and Zbinden, H. (2014). Free-running InGaAs single photon detector with 1 dark count per second at 10% efficiency. Appl. Phys. Lett. 104, 081108. doi:10.1063/1.4866582

CrossRef Full Text | Google Scholar

Krantz, P., Kjaergaard, M., Yan, F., Orlando, T. P., Gustavsson, S., and Oliver, W. D. (2019). A quantum engineers guide to superconducting qubits. Appl. Phys. Rev. 6, 021318. doi:10.1063/1.5089550

CrossRef Full Text | Google Scholar

Krauter, H., Salart, D., Muschik, C. A., Petersen, J. M., Shen, H., Fernholz, T., et al. (2013). Deterministic quantum teleportation between distant atomic objects. Nat. Phys. 9, 400–404. doi:10.1038/nphys2631

CrossRef Full Text | Google Scholar

Kringhøj, A., Casparis, L., Hell, M., Larsen, T. W., Kuemmeth, F., Leijnse, M., et al. (2018). Anharmonicity of a superconducting qubit with a few-mode Josephson junction. Phys. Rev. B 97 (6), 060508. doi:10.1103/physrevb.97.060508

CrossRef Full Text | Google Scholar

Krizakova, V., Perumkunnil, M., Couet, S., Gambardella, P., and Garello, K. (2022). Spin-orbit torque switching of magnetic tunnel junctions for memory applications. J. Magnetism Magnetic Mater. 562, 169692. doi:10.1016/j.jmmm.2022.169692

CrossRef Full Text | Google Scholar

Krogstrup, P., Ziino, N. L. B., Chang, W., Albrecht, S. M., Madsen, M. H., Johnson, E., et al. (2015). Epitaxy of semiconductor–superconductor nanowires. Nat. Mater. 14 (4), 400–406. doi:10.1038/nmat4176

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruglyak, V. V., Demokritov, S. O., and Grundler, D. (2010). Magnonics. J. Phys. D Appl. Phys. 43 (26), 264001. doi:10.1088/0022-3727/43/26/264001

CrossRef Full Text | Google Scholar

Kuate Defo, R., Nguyen, H., Ku, M. J., and Rhone, T. D. (2021). Methods to accelerate high-throughput screening of atomic qubit candidates in van der Waals materials. J. Appl. Phys. 129 (22), 225105. doi:10.1063/5.0048833

CrossRef Full Text | Google Scholar

Kuhlmann, A. V., Houel, J., Ludwig, A., Greuter, L., Reuter, D., Wieck, A. D., et al. (2013). Charge noise and spin noise in a semiconductor quantum device. Nat. Phys. 9, 570–575. doi:10.1038/nphys2688

CrossRef Full Text | Google Scholar

Kumar, P., Sendelbach, S., Beck, M., Freeland, J., Wang, Z., Wang, H., et al. (2016). Origin and reduction of 1/f magnetic flux noise in superconducting devices. Phys. Rev. Appl. 6, 041001. doi:10.1103/physrevapplied.6.041001

CrossRef Full Text | Google Scholar

Kurenkov, A., DuttaGupta, S., Zhang, C., Borders, W. A., Fukami, S., and Ohno, H. (2017). “Spin-orbit torque memristor, operated by pulsed currents,” in JSAP annual meetings extended abstracts the 64th JSAP spring meeting 2018 (The Japan: Society of Applied Physics), 2150.

Google Scholar

Kurtsiefer, C., Zarda, P., Halder, M., Weinfurter, H., Gorman, P. M., Tapster, P. R., et al. (2002). Quantum cryptography: a step towards global key distribution. Nature 419, 450. doi:10.1038/419450a

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuzmanović, M., Dvir, T., Leboeuf, D., Ilić, S., Haim, M., Möckli, D., et al. (2022). Tunneling spectroscopy of few-monolayer NbSe 2 in high magnetic fields: triplet superconductivity and Ising protection. Phys. Rev. B 106 (18), 184514. doi:10.1103/physrevb.106.184514

CrossRef Full Text | Google Scholar

Kwiat, P. G., Berglund, A. J., Altepeter, J. B., and White, A. G. (2000). Experimental verification of decoherence-free subspaces. Science 290 (5491), 498–501. doi:10.1126/science.290.5491.498

PubMed Abstract | CrossRef Full Text | Google Scholar

Ladd, T. D., Jelezko, F., Laflamme, R., Nakamura, Y., Monroe, C., and O’Brien, J. L. (2010). Quantum computers. Nature 464, 45–53. doi:10.1038/nature08812

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambert, H. N. J., Rueda, A., Sedlmeir, F., and Schwefel, H. G. (2020a). Quantum information technologies: coherent conversion between microwave and optical photons—an overview of physical implementations (adv. Quantum technol. 1/2020). Adv. Quantum Technol. 3, 1900077. doi:10.1002/qute.202070011

CrossRef Full Text | Google Scholar

Lambert, N. J., Rueda, A., Sedlmeir, F., and Schwefel, H. G. (2020b). Coherent conversion between microwave and optical photons—an overview of physical implementations. Adv. Quantum Technol. 3 (1), 1900077. doi:10.1002/qute.201900077

CrossRef Full Text | Google Scholar

Landry, O., van Houwelingen, J. A. W., Beveratos, A., Zbinden, H., and Gisin, N. (2007). Quantum teleportation over the Swisscom telecommunication network. J. Opt. Soc. Am. B 24, 398–403. doi:10.1364/josab.24.000398

CrossRef Full Text | Google Scholar

Lawler, G. F. (2006). Introduction to stochastic processes. 2nd ed. New York: Chapman & Hall/CRC Press. doi:10.1201/9781315273600

CrossRef Full Text

Lawrie, W. I. L., Rimbach-Russ, M., Riggelen, F. V., Hendrickx, N. W., Snoo, S. D., Sammak, A., et al. (2023). Simultaneous single-qubit driving of semiconductor spin qubits at the fault-tolerant threshold. Nat. Commun. 14 (1), 3617

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawrie, W. I. L., Russ, M., van Riggelen, F., Hendrickx, N. W., de Snoo, S. L., Sammak, A., et al. (2021) Simultaneous driving of semiconductor spin qubits at the fault-tolerant threshold. arXiv preprint arXiv:2109.07837.

Google Scholar

Lee, H. Y., Chen, P. S., Wu, T. Y., Chen, Y. S., Wang, C. C., Tzeng, P. J., et al. (2008). “Low power and high-speed bipolar switching with a thin reactive Ti buffer layer in robust HfO2 based RRAM,” in 2008 IEEE international electron devices meeting, 1–4.

CrossRef Full Text | Google Scholar

Lee, N., Benichi, H., Takeno, Y., Takeda, S., Webb, J., Huntington, E., et al. (2011). Teleportation of nonclassical wave packets of light. Science 332, 330–333. doi:10.1126/science.1201034

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. H. (2003) The design of CMOS radio-frequency integrated circuits (PDF). Cambridge University Press.

Google Scholar

Leek, P. J., Filipp, S., Maurer, P., Baur, M., Bianchetti, R., Fink, J. M., et al. (2009). Using sideband transitions for two-qubit operations in superconducting circuits. Phys. Rev. B 79, 180511. doi:10.1103/physrevb.79.180511

CrossRef Full Text | Google Scholar

Letzter, R. (2020). China claims fastest quantum computer in the world. Lives Sci. 11.

Google Scholar

Levenson-Falk, E. M., Kos, F., Vijay, R., Glazman, L., and Siddiqi, I. (2014). Single-quasiparticle trapping in aluminum nanobridge Josephson junctions. Phys. Rev. Lett. 112, 047002. doi:10.1103/physrevlett.112.047002

PubMed Abstract | CrossRef Full Text | Google Scholar

Levy, J. (2002). Universal quantum computation with spin-1/2 pairs and Heisenberg exchange. Phys. Rev. Lett. 89 (14), 147902. doi:10.1103/physrevlett.89.147902

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, R., Petit, L., Franke, D. P., Dehollain, J. P., Helsen, J., Steudtner, M., et al. (2018). A crossbar network for silicon quantum dot qubits. Sci. Adv. 4, eaar3960. doi:10.1126/sciadv.aar3960

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Edmonds, K. W., Liu, X., Zheng, H., and Wang, K. (2019). Manipulation of magnetization by spin–orbit torque. Adv. Quantum Technol. 2 (1-2), 1800052. doi:10.1002/qute.201800052

CrossRef Full Text | Google Scholar

Li, Y. H., and Jin, X. M. (2016). Bidirectional controlled teleportation by using nine-qubit entangled state in noisy environments. Quantum Inf. Process. 15 (2), 929–945. doi:10.1007/s11128-015-1194-7

CrossRef Full Text | Google Scholar

Li, Y. H., Li, X. L., Nie, L. P., and Sang, M. H. (2016). Quantum teleportation of three and four-qubit state using multi-qubit cluster states. Int. J. Theor. Phys. 55, 1820–1823. doi:10.1007/s10773-015-2821-x

CrossRef Full Text | Google Scholar

Li, Y. H., Li, X. L., Sang, M. H., Nie, Y. Y., and Wang, Z. S. (2013). Bidirectional controlled quantum teleportation and secure direct communication using five-qubit entangled state. Quantum inf. Process. 12, 3835–3844. doi:10.1007/s11128-013-0638-1

CrossRef Full Text | Google Scholar

Lidar, D. A., Chuang, I. L., and Whaley, K. B. (1998). Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 81 (12), 2594–2597. doi:10.1103/physrevlett.81.2594

CrossRef Full Text | Google Scholar

Likharev, K. K., and Semenov, V. K. (1991). RSFQ logic/memory family: a new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1 (1), 3–28. doi:10.1109/77.80745

CrossRef Full Text | Google Scholar

Lilienfeld, J. E. (1930). Method and apparatus for controlling electric current. U. S. Pat. no. 1 745, 175.

Google Scholar

Lim, C. C. W., Curty, M., Walenta, N., Xu, F., and Zbinden, H. (2014). Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307. doi:10.1103/physreva.89.022307

CrossRef Full Text | Google Scholar

Lin, W., Pollard, S. D., Guo, R., Yoong, H. Y., Chen, S., Wang, H., et al. (2018). Tuning of current-induced effective magnetic field through Rashba effect engineering in hybrid multiferroic structures. NPG Asia Mater. 10 (8), 740–748. doi:10.1038/s41427-018-0069-7

CrossRef Full Text | Google Scholar

Liu, L., Lee, O. J., Gudmundsen, T. J., Ralph, D. C., and Buhrman, R. A. (2012a). Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 109 (9), 096602. doi:10.1103/physrevlett.109.096602

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Pai, C. F., Li, Y., Tseng, H. W., Ralph, D. C., and Buhrman, R. A. (2012b). Spin-torque switching with the giant spin Hall effect of tantalum. Science 336 (6081), 555–558. doi:10.1126/science.1218197

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Pai, C. F., Ralph, D. C., and Buhrman, R. A. (2012c). Magnetic oscillations driven by the spin Hall effect in 3-terminal magnetic tunnel junction devices. Phys.Rev. Lett. 109, 186602. doi:10.1103/physrevlett.109.186602

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, R. H., Chen, L., Urazhdin, S., and Du, Y. W. (2017). Controlling the spectral characteristics of a spin-current auto-oscillator with an electric field. Phys. Rev. Appl. 8, 021001. doi:10.1103/physrevapplied.8.021001

CrossRef Full Text | Google Scholar

Liu, R. H., Lim, W. L., and Urazhdin, S. (2013). Spectral characteristics of the microwave emission by the spin Hall nano-oscillator. Phys. Rev. Lett. 110, 147601. doi:10.1103/physrevlett.110.147601

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., and Hersam, M. C. (2019). 2D materials for quantum information science. Nat. Rev. Mater 4, 669–684. doi:10.1038/s41578-019-0136-x

CrossRef Full Text | Google Scholar

Liu, X. H., Edmonds, K. W., Zhou, Z. P., and Wang, K. Y. (2020). Tuning interfacial spins in antiferromagnetic–ferromagnetic–heavy-metal heterostructures via spin-orbit torque. Phys. Rev. Appl. 13 (1), 014059. doi:10.1103/physrevapplied.13.014059

CrossRef Full Text | Google Scholar

Liu, Z. M., and Zhou, L. (2014). Quantum teleportation of a three-qubit state using a five-qubit cluster state. Int. J. Theor. Phys. 53, 4079–4082. doi:10.1007/s10773-014-2158-x

CrossRef Full Text | Google Scholar

Lloyd, S. (1993). A potentially realizable quantum computer. Science. 261 (5128), 1569–1571. doi:10.1126/science.261.5128.1569

PubMed Abstract | CrossRef Full Text | Google Scholar

Lo, H.-K., Curty, M., and Tamaki, K. (2014). Secure quantum key distribution. Nat. Phot. 8, 595–604. doi:10.1038/nphoton.2014.149

CrossRef Full Text | Google Scholar

Locatelli, N., Cros, V., and Grollier, J. (2022). Spin-torque building blocks. Nat. Mat. 13 (2014), 11–20. doi:10.1038/nmat3823

PubMed Abstract | CrossRef Full Text | Google Scholar

Lombardi, E., Sciarrino, F., Popescu, S., and De Martini, F. (2002). Teleportation of a vacuumonephoton qubit. Phys. Rev. Lett. 88, 070402. doi:10.1103/physrevlett.88.070402

PubMed Abstract | CrossRef Full Text | Google Scholar

Loss, D., and DiVincenzo, D. P. (1998). Quantum computation with quantum dots. Phys. Rev. A 57 (1), 120–126. doi:10.1103/physreva.57.120

CrossRef Full Text | Google Scholar

Lund, A. P., and Ralph, T. C. (2002). Nondeterministic gates for photonic single-rail quantum logic. Phys. Rev. A 66 (3), 032307. doi:10.1103/physreva.66.032307

CrossRef Full Text | Google Scholar

Lutchyn, R. M., Sau, J. D., and Sarma, S. D. (2010). Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105 (7), 077001. doi:10.1103/physrevlett.105.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lvovsky, A. I., Sanders, B. C., and Tittel, W. (2009). Optical quantum memory. Nat. photonics 3 (12), 706–714. doi:10.1038/nphoton.2009.231

CrossRef Full Text | Google Scholar

Ma, X.-S., Herbst, T., Scheidl, T., Wang, D., Kropatschek, S., Naylor, W., et al. (2012). Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269–273. doi:10.1038/nature11472

PubMed Abstract | CrossRef Full Text | Google Scholar

Maan, A. K., Jayadevi, D. A., and James, A. P. (2016). A survey of memristive threshold logic circuits. IEEE Trans. Neural Netw. Learn. Syst. 28 (99), 1734–1746. doi:10.1109/TNNLS.2016.2547842

PubMed Abstract | CrossRef Full Text | Google Scholar

Macrae, N. (1992). “John von Neumann: The Scientific Genius Who Pioneered the Modern Computer, Game Theory,” in Nuclear deterrence, and much more (Pantheon Press).

Google Scholar

Mądzik, M. T., Asaad, S., Youssry, A., Joecker, B., Rudinger, K. M., Nielsen, E., et al. (2022). Precision tomography of a three-qubit donor quantum processor in silicon. Nature 601, 348–353. doi:10.1038/s41586-021-04292-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Madzik, M. T., Laucht, A., Hudson, F. E., Jakob, A. M., Johnson, B. C., Jamieson, D. N., et al. (2021). Conditional quantum operation of two exchange-coupled single-donor spin qubits in a MOS-compatible silicon device. Nat. Commun. 12, 181. doi:10.1038/s41467-020-20424-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Maeda, F. (1937). Mathematical foundations of quantum mechanics. Journal of science of the Hiroshima university, series A (mathematics, physics, chemistry), 191–213.

Google Scholar

Majer, J., Chow, J. M., Gambetta, J. M., Koch, J., Johnson, B. R., Schreier, J. A., et al. (2007). Coupling superconducting qubits via a cavity bus. Nat. Lond. 449, 443–447. doi:10.1038/nature06184

PubMed Abstract | CrossRef Full Text | Google Scholar

Makhlin, Y., Schoen, G., and Shnirman, A. (2001). Quantum state engineering with Josephson-junction devices. Rev. Mod. Phys. 73 (2), 357–400. doi:10.1103/revmodphys.73.357

CrossRef Full Text | Google Scholar

Makino, K., Hashimoto, Y., Yoshikawa, J. I., Ohdan, H., Toyama, T., van Loock, P., et al. (2016). Synchronization of optical photons for quantum information processing. Sci. Adv. 2 (5), e1501772. doi:10.1126/sciadv.1501772

PubMed Abstract | CrossRef Full Text | Google Scholar

Malia, B. K., Wu, Y., Martínez-Rincón, J., and Kasevich, M. A. (2022). Distributed quantum sensing with mode-entangled spin-squeezed atomic states. Nature 612 (7941), 661–665. doi:10.1038/s41586-022-05363-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Man, Z. X., Xia, Y. J., and An, N. B. (2007). Quantum teleportation of an unknown N-Qubit W-Like state. JETP Lett. 85, 662–666. doi:10.1134/s0021364007120168

CrossRef Full Text | Google Scholar

Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M., and Duine, R. A. (2015). New perspectives for Rashba spin–orbit coupling. Nat. Mater. 14 (9), 871–882. doi:10.1038/nmat4360

PubMed Abstract | CrossRef Full Text | Google Scholar

Mansuripur, M. (2015). Origin of the spin–orbit interaction. Phys. Scr. 90, 085501. doi:10.1088/0031-8949/90/8/085501

CrossRef Full Text | Google Scholar

Manucharyan, V. E., Koch, J., Glazman, L. I., and Devoret, M. H. (2009). Fluxonium: single cooper-pair circuit free of charge offsets. Science 326 (5949), 113–116. doi:10.1126/science.1175552

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcikic, I., de Riedmatten, H., Tittel, W., Zbinden, H., and Gisin, N. (2003). Longdistance teleportation of qubits at telecommunication wavelengths. Nature 421, 509–513. doi:10.1038/nature01376

PubMed Abstract | CrossRef Full Text | Google Scholar

Marín-Suárez, M., Peltonen, J. T., and Pekola, J. P. (2020). Active quasiparticle suppression in a non-equilibrium superconductor. Nano Lett. 20, 5065–5071. doi:10.1021/acs.nanolett.0c01264

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinis, J. M. (2009). Superconducting phase qubits. Quantum inf. Process. 8 (2), 81–103. doi:10.1007/s11128-009-0105-1

CrossRef Full Text | Google Scholar

Martinis, J. M. (2021). Saving superconducting quantum processors from decay and correlated errors generated by gamma and cosmic rays. npj Quantum Inf. 7, 90. doi:10.1038/s41534-021-00431-0

CrossRef Full Text | Google Scholar

Martinis, J. M., Cooper, K. B., McDermott, R., Steffen, M., Ansmann, M., Osborn, K. D., et al. (2005). Decoherence in Josephson qubits from dielectric loss. Phys. Rev. Lett. 95, 210503. doi:10.1103/physrevlett.95.210503

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinis, J. M., Devoret, M. H., and Clarke, J. (1985). Energy-level quantization in the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett. 55, 1543–1546. doi:10.1103/physrevlett.55.1543

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinis, J. M., Devoret, M. H., and Clarke, J. (2020). Quantum Josephson junction circuits and the dawn of artificial atoms. Nat. Phys. 16, 234–237. doi:10.1038/s41567-020-0829-5

CrossRef Full Text | Google Scholar

Mastriani, M., Iyengar, S. S., and Kumar, L. (2021). Satellite quantum communication protocol regardless of the weather. Opt. Quantum Electron. 53 (4), 181. doi:10.1007/s11082-021-02829-8

CrossRef Full Text | Google Scholar

Maunz, P. L. W. (2016). High optical access trap 2.0. Sandia Natl. Lab. Rep. No. SAND2016-0796R. doi:10.2172/1237003

CrossRef Full Text | Google Scholar

Mayer, M. G. (1949). On closed shells in nuclei. II. Phys. Rev. 75 (12), 1969. doi:10.2172/4410667

CrossRef Full Text | Google Scholar

Maze, J. R., Stanwix, P. L., Hodges, J. S., Hong, S., Taylor, J. M., Cappellaro, P., et al. (2008). Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644–647. doi:10.1038/nature07279

PubMed Abstract | CrossRef Full Text | Google Scholar

McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C., and Yuan, X. (2020). Quantum computational chemistry. Rev. Mod. Phys. 92, 015003. doi:10.1103/revmodphys.92.015003

CrossRef Full Text | Google Scholar

McDermott, R. (2009). Materials origins of decoherence in superconducting qubits. IEEE Trans. Appl. Supercond. 19 (1), 2–13. doi:10.1109/tasc.2008.2012255

CrossRef Full Text | Google Scholar

Menicucci, N. C., and Caves, C. M. (2002). Local realistic model for the dynamics of bulk-ensemble NMR information processing. Phys. Rev. Lett. 88 (16), 167901. doi:10.1103/PhysRevLett.88.167901

PubMed Abstract | CrossRef Full Text | Google Scholar

Merkel, C., and Kudithipudi, D. (2014). “Neuromemristive extreme learning machines for pattern classification,” in 2014 IEEE computer society annual symposium on VLSI (IEEE), 77–82.

CrossRef Full Text | Google Scholar

Mermin, N. D. (1993). Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 65 (3), 803–815. arXiv:1802.10119. Bibcode:1993RvMP. doi:10.1103/RevModPhys.65.803

CrossRef Full Text | Google Scholar

Merzbacher, E. (2002). The early history of quantum tunneling. Phys. Today 55 (8), 44–49. doi:10.1063/1.1510281

CrossRef Full Text | Google Scholar

Metcalf, B. J., Spring, J. B., Humphreys, P. C., Thomas-Peter, N., Barbieri, M., Kolthammer, W. S., et al. (2014). Quantum teleportation on a photonic chip. Nat. Phot. 8, 770–774. doi:10.1038/nphoton.2014.217

CrossRef Full Text | Google Scholar

Metcalfe, M., Boaknin, E., Manucharyan, V., Vijay, R., Siddiqi, I., Rigetti, C., et al. (2007). Measuring the decoherence of a quantronium qubit with the cavity bifurcation amplifier. Phys. Rev. B 76 (17), 174516. doi:10.1103/physrevb.76.174516

CrossRef Full Text | Google Scholar

Mi, X., Ippoliti, M., Quintana, C., Greene, A., Chen, Z., Gross, J., et al. (2022). Time-crystalline eigenstate order on a quantum processor. Nature 601 (7894), 531–536. doi:10.1038/s41586-021-04257-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Microsoft (2022). News microsoft. Available at: https://news.microsoft.com/source/features/innovation/azure-quantum-majorana-topological-qubit/#:∼:text=The%20ability%20to%20create%20and,information%2C%20called%20a%20topological%20qubit.

Google Scholar

Millikan, R. A., and Lauritsen, C. C. (1928). Relations of field-currents to thermionic-currents. PNAS 14 (1), 45–49. doi:10.1073/pnas.14.1.45

PubMed Abstract | CrossRef Full Text | Google Scholar

Miron, I. M., Garello, K., Gaudin, G., Zermatten, P. J., Costache, M. V., Auffret, S., et al. (2011). Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476 (7359), 189–193. doi:10.1038/nature10309

PubMed Abstract | CrossRef Full Text | Google Scholar

Mirrahimi, M., Leghtas, Z., Albert, V. V., Touzard, S., Schoelkopf, R. J., Jiang, L., et al. (2014). Dynamically protected cat-qubits: a new paradigm for universal quantum computation. New J. Phys. 16 (4), 045014. doi:10.1088/1367-2630/16/4/045014

CrossRef Full Text | Google Scholar

Mizuochi, N., Yamasaki, S., Takizawa, H., Morishita, N., Ohshima, T., Itoh, H., et al. (2022). Continuous-wave and pulsed EPR study of the negatively charged silicon vacancy with S53/2 and C3v symmetry in n-type 4H-SiC. Phys. Rev. B 66, 235202. doi:10.1103/physrevb.66.235202

CrossRef Full Text | Google Scholar

Modha, D., Arthur, J. V., Alvarez-Icaza, R., Cassidy, A. S., Sawada, J., Akopyan, F., et al. (2014). A million spiking-neuron integrated circuit with a scalable communication network and interface. Science. 345 (6197), 668–673. doi:10.1126/science.1254642

PubMed Abstract | CrossRef Full Text | Google Scholar

Monz, T., Nigg, D., Martinez, E. A., Brandl, M. F., Schindler, P., Rines, R., et al. (2016). Realization of a scalable Shor algorithm. Science 351 (6277), 1068–1070. arXiv:1507.08852. doi:10.1126/science.aad9480

PubMed Abstract | CrossRef Full Text | Google Scholar

Monz, T., Schindler, P., Barreiro, J., Chwalla, M., Nigg, D., Coish, W., et al. (2011). 14-Qubit entanglement: creation and coherence. Phys. Rev. Lett. 106 (13), 130506. doi:10.1103/physrevlett.106.130506

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, G., and Read, N. (1991). Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 360 (2–3), 362–396. doi:10.1016/0550-3213(91)90407-O

CrossRef Full Text | Google Scholar

Mortezapour, A., Naeimi, G., and Franco, R. L. (2018). Coherence and entanglement dynamics of vibrating qubits. Opt. Commun. 424, 26–31. doi:10.1016/j.optcom.2018.04.044

CrossRef Full Text | Google Scholar

Morton, J. J., Tyryshkin, A. M., Brown, R. M., Shankar, S., Lovett, B. W., Ardavan, A., et al. (2008). Solid-state quantum memory using the 31P nuclear spin. Nature 455 (7216), 1085–1088. doi:10.1038/nature07295

CrossRef Full Text | Google Scholar

Morton, J. J. L., Tyryshkin, A. M., Ardavan, A., Porfyrakis, K., Lyon, S. A., and Briggs, G. A. D. (2006). Electron spin relaxation of N@C60 in CS2. J. Chem. Phys. 124, 014508. doi:10.1063/1.2147262

PubMed Abstract | CrossRef Full Text | Google Scholar

Morton, J. J. L., Tyryshkin, A. M., Ardavan, A., Porfyrakis, K., Lyon, S. A., and Briggs, G. A. D. (2007). Environmental effects on electron spin relaxation in N@C60. Phys. Rev. B Condens. Matter Mat. Phys. 76, 085418. doi:10.1103/physrevb.76.085418

CrossRef Full Text | Google Scholar

Muhonen, J. T., Dehollain, J. P., Laucht, A., Hudson, F. E., Kalra, R., Sekiguchi, T., et al. (2014). Storing quantum information for 30 seconds in a nanoelectronic device. Nat. Nanotechnol. 9 (12), 986–991. doi:10.1038/nnano.2014.211

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, C., Cole, J. H., and Lisenfeld, J. (2019). Towards understanding two-level-systems in amorphous solids: insights from quantum circuits. Rep. Prog. Phys. 82 (12), 124501. doi:10.1088/1361-6633/ab3a7e

PubMed Abstract | CrossRef Full Text | Google Scholar

Mundada, P. S., Gyenis, A., Huang, Z., Koch, J., and Houck, A. A. (2020). Floquet-engineered enhancement of coherence times in a driven fluxonium qubit. Phys. Rev. Appl. 14 (5), 054033. doi:10.1103/physrevapplied.14.054033

CrossRef Full Text | Google Scholar

Nakajima, T., Delbecq, M. R., Otsuka, T., Stano, P., Amaha, S., Yoneda, J., et al. (2017). Robust single-shot spin measurement with 99.5% fidelity in a quantum dot array. Phys. Rev. Lett. 119, 017701. doi:10.1103/physrevlett.119.017701

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, Y., Pashkin, Y. A., and Tsai, J. S. (1999). Coherent control of macroscopic quantum states in a single-Cooper-pair box. nature 398 (6730), 786–788. doi:10.1038/19718

CrossRef Full Text | Google Scholar

Nan, T., Emori, S., Boone, C. T., Wang, X., Oxholm, T. M., Jones, J. G., et al. (2015). Comparison of spin-orbit torques and spin pumping across NiFe/Pt and NiFe/Cu/Pt interfaces. Phys. Rev. B 91 (21), 214416. doi:10.1103/physrevb.91.214416

CrossRef Full Text | Google Scholar

Nandi, K., and Mazumdar, C. (2014). Quantum teleportation of a two qubit state using GHZ-like state. Int. J. Theor. Phys. 53, 1322–1324. doi:10.1007/s10773-013-1928-1

CrossRef Full Text | Google Scholar

Nayak, C., Simon, S. H., Stern, A., Freedman, M., and Sarma, S. D. (2008). Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80 (3), 1083–1159. doi:10.1103/revmodphys.80.1083

CrossRef Full Text | Google Scholar

Nelson, E. (1986). “Stochastic processes in classical and quantum systems: proceedings of the 1st ascona-como international conference, held in ascona, ticino (Switzerland), june 24–29, 1985,” in Stochastic processes in classical and quantum systems. Editors S. Albeverio, G. Casati, and D. Merlini (Berlin: Springer-Verlag), 262, 438–469. doi:10.1007/3-540-17166-5

CrossRef Full Text | Google Scholar

N.I.C.E. Workshop, 2014(2014). Towards intelligent computing with neuromemristive circuits and systems - feb.

Google Scholar

Next Big Future (2022). Robust and scalable flux qubit, archived 2013-08-16 at the wayback machine.

Google Scholar

Nielsen, E., Gamble, J. K., Rudinger, K., Scholten, T., Young, K., and Blume-Kohout, R. (2021). Gate set tomography. Quantum 5, 557. doi:10.22331/q-2021-10-05-557

CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2000). Quantum computation and quantum information. Cambridge Univ. Press.

Google Scholar

Nielsen, M. A., Knill, E., and Laflamme, R. (1998). Complete quantum teleportation using nuclear magnetic resonance. Nature 396, 52–55. doi:10.1038/23891

CrossRef Full Text | Google Scholar

Nigg, D., Mueller, M., Martinez, E. A., Schindler, P., Hennrich, M., Monz, T., et al. (2014). Quantum computations on a topologically encoded qubit. Science 345 (6194), 302–305. doi:10.1126/science.1253742

PubMed Abstract | CrossRef Full Text | Google Scholar

Nobel Prize (2022). Nobel prize. Available at: https://www.nobelPrize.org/Prizes/lists/all-nobel-Prizes.

Google Scholar

Noiri, A., Takeda, K., Nakajima, T., Kobayashi, T., Sammak, A., Scappucci, G., et al. (2022). Fast universal quantum gate above the fault-tolerance threshold in silicon. Nature 601, 338–342. doi:10.1038/s41586-021-04182-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Nölleke, C., Neuzner, A., Reiserer, A., Hahn, C., Rempe, G., and Ritter, S. (2013). Efficient teleportation between remote singleatom quantum memories. Phys. Rev. Lett. 110, 140403. doi:10.1103/physrevlett.110.140403

PubMed Abstract | CrossRef Full Text | Google Scholar

Obrien, J. L., Furusawa, A., and Vuc kovic, J. (2022). Photonic quantum technologies. Nat. Phot. 3, 687–695. doi:10.1038/nphoton.2009.229

CrossRef Full Text | Google Scholar

Ofek, N., Petrenko, A., Heeres, R., Reinhold, P., Leghtas, Z., Vlastakis, B., et al. (2016). Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536 (7617), 441–445. doi:10.1038/nature18949

PubMed Abstract | CrossRef Full Text | Google Scholar

Olejník, K., Schuler, V., Martí, X., Novák, V., Kašpar, Z., Wadley, P., et al. (2017). Antiferromagnetic CuMnAs multi-level memory cell with microelectronic compatibility. Nat. Commun. 8 (1), 15434. doi:10.1038/ncomms15434

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliver, W., and Welander, P. (2013). Materials in superconducting quantum bits. MRS Bull. 38 (10), 816–825. doi:10.1557/mrs.2013.229

CrossRef Full Text | Google Scholar

Olmschenk, S., Matsukevich, D. N., Maunz, P., Hayes, D., Duan, L. M., and Monroe, C. (2009). Quantum teleportation between distant matter qubits. Science 323, 486–489. doi:10.1126/science.1167209

PubMed Abstract | CrossRef Full Text | Google Scholar

Onen, M., Emond, N., Li, J., Yildiz, B., and Del Alamo, J. A. (2021). CMOS-compatible protonic programmable resistor based on phosphosilicate glass electrolyte for analog deep learning. Nano Lett. 21 (14), 6111–6116. doi:10.1021/acs.nanolett.1c01614

PubMed Abstract | CrossRef Full Text | Google Scholar

Onen, M., Emond, N., Wang, B., Zhang, D., Ross, F. M., Li, J., et al. (2022). Nanosecond protonic programmable resistors for analog deep learning. Science 377 (6605), 539–543. doi:10.1126/science.abp8064

PubMed Abstract | CrossRef Full Text | Google Scholar

On Quantum Supremacy (2019). IBM research blog.

Google Scholar

Oppenheimer, J. R. (1928). Three notes on the quantum theory of aperiodic effects. Phys. Rev. 31 (1), 66–81. doi:10.1103/PhysRev.31.66

CrossRef Full Text | Google Scholar

Oreg, Y., Refael, G., and Von Oppen, F. (2010). Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105 (17), 177002. doi:10.1103/physrevlett.105.177002

PubMed Abstract | CrossRef Full Text | Google Scholar

Orlando, T. P., Mooij, J. E., Tian, L., Van Der Wal, C. H., Levitov, L. S., Lloyd, S., et al. (1999). Superconducting persistent-current qubit. Phys. Rev. B 60 (22), 15398–15413. doi:10.1103/physrevb.60.15398

CrossRef Full Text | Google Scholar

Ortu, A., Holzäpfel, A., Etesse, J., and Afzelius, M. (2022). Storage of photonic time-bin qubits for up to 20 ms in a rare-earth doped crystal. npj Quantum Inf. 8, 29. doi:10.1038/s41534-022-00541-3

CrossRef Full Text | Google Scholar

Osika, E. N., Kocsis, S., Hsueh, Y. L., Monir, S., Chua, C., Lam, H., et al. (2022). Spin-photon coupling for atomic qubit devices in silicon. Phys. Rev. Appl. 17 (5), 054007. doi:10.1103/physrevapplied.17.054007

CrossRef Full Text | Google Scholar

Pachos, J. K. (2012). Introduction to topological quantum computation. Cambridge, UK: Cambridge University Press.

Google Scholar

Paconsulting (2022). Paconsulting. Available at: https://www.paconsulting.com/insights/what-is-quantum-technology/#:∼:text=Quantum%20technology%20is%20a%20class,quantum%20entanglement%20and%20quantum%20superposition.

Google Scholar

Page, C. C., Moser, C. C., Chen, X., and Dutton, P. L. (1999). Natural engineering principles of electron tunnelling in biological oxidation–reduction. Nature 402 (6757), 47–52. doi:10.1038/46972

PubMed Abstract | CrossRef Full Text | Google Scholar

Pai, C. F., Liu, L., Li, Y., Tseng, H. W., Ralph, D. C., and Buhrman, R. A. (2012). Spin-transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101 (12), 122404. doi:10.1063/1.4753947

CrossRef Full Text | Google Scholar

Paik, H., Schuster, D. I., Bishop, L. S., Kirchmair, G., Catelani, G., Sears, A. P., et al. (2011). Observation of high coherence in Josephson junction qubits measured in a three-dimensional circuit QED architecture. Phys. Rev. Lett. 107 (24), 240501. doi:10.1103/physrevlett.107.240501

PubMed Abstract | CrossRef Full Text | Google Scholar

Paik, H., Schuster, D. I., Bishop, L. S., Kirchmair, G., Catelani, G., Sears, A. P., et al. (2011). Observation of high coherence in Josephson junction qubits measured in a three-dimensional circuit QED architecture. Phys. Rev. Lett. 107 (24), 240501. doi:10.1103/physrevlett.107.240501

PubMed Abstract | CrossRef Full Text | Google Scholar

Pais, A. (1979). Einstein and the quantum theory. Rev. Mod. Phys. 51 (4), 863–914. doi:10.1103/RevModPhys.51.863

CrossRef Full Text | Google Scholar

Paladino, E., Faoro, L., Falci, G., and Fazio, R. (2002). Decoherence and 1/f noise in Josephson qubits. Phys. Rev. Lett. 88 (22), 228304. doi:10.1103/physrevlett.88.228304

PubMed Abstract | CrossRef Full Text | Google Scholar

Paladino, E., Galperin, Y., Falci, G., and Altshuler, B. (2014). 1/f noise: implications for solid-state quantum information. Rev. Mod. Phys. 86, 361–418. doi:10.1103/revmodphys.86.361

CrossRef Full Text | Google Scholar

Pan, J. W., Bouwmeester, D., Weinfurter, H., and Zeilinger, A. (1998). Experimental entanglement swapping: entangling photons that never interacted. Phys. Rev. Lett. 80 (18), 3891–3894. doi:10.1103/physrevlett.80.3891

CrossRef Full Text | Google Scholar

Pan, J. W., Chen, Z. B., Lu, C. Y., Weinfurter, H., Zeilinger, A., and Żukowski, M. (2012). Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84 (2), 777–838. doi:10.1103/revmodphys.84.777

CrossRef Full Text | Google Scholar

Patel, R. B., Ho, J., Ferreyrol, F., Ralph, T. C., and Pryde, G. J. (2016). A quantum Fredkin gate. Sci. Adv. 2 (3), e1501531. doi:10.1126/sciadv.1501531

PubMed Abstract | CrossRef Full Text | Google Scholar

Paul, W. (1990). Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 62 (3), 531–540. doi:10.1103/revmodphys.62.531

CrossRef Full Text | Google Scholar

Peng, C.-Z., Yang, T., Bao, X. H., Zhang, J., Jin, X. M., Feng, F. Y., et al. (2005). Experimental free-space distribution of entangled photon pairs over 13 km: towards satellite-based global quantum communication. Phys. Rev. Lett. 94, 150501. doi:10.1103/physrevlett.94.150501

PubMed Abstract | CrossRef Full Text | Google Scholar

Peres, A. (1985). Reversible logic and quantum computers. Phys. Rev. A 32 (6), 3266–3276. doi:10.1103/physreva.32.3266

PubMed Abstract | CrossRef Full Text | Google Scholar

Pérez-Delgado, C. A., and Kok, P. (2011). Quantum computers: definition and implementations. Phys. Rev. A 83 (1), 012303. doi:10.1103/PhysRevA.83.012303

CrossRef Full Text | Google Scholar

Peruzzo, A., McClean, J., Shadbolt, P., Yung, M. H., Zhou, X. Q., Love, P. J., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213. doi:10.1038/ncomms5213

PubMed Abstract | CrossRef Full Text | Google Scholar

Petit, L., Eenink, H. G. J., Russ, M., Lawrie, W. I. L., Hendrickx, N. W., Philips, S. G. J., et al. (2020). Universal quantum logic in hot silicon qubits. Nature 580, 355–359. doi:10.1038/s41586-020-2170-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Pfaff, W., Hensen, B. J., Bernien, H., van Dam, S. B., Blok, M. S., Taminiau, T. H., et al. (2014). Unconditional quantum teleportation between distant solidstate quantum bits. Science 345, 532–535. doi:10.1126/science.1253512

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillips, W. A. (1987). Two-level states in glasses. Rep. Prog. Phys. 50, 1657–1708. doi:10.1088/0034-4885/50/12/003

CrossRef Full Text | Google Scholar

PhysOrg.com Miranda Marquit (2007). First use of Deutsch’s Algorithm in a cluster state quantum computer.

Google Scholar

Pickett, M. D., Medeiros-Ribeiro, G., and Williams, R. S. (2012). A scalable neuristor built with Mott memristors. Nat. Mater. 12 (2), 114–117. doi:10.1038/nmat3510

PubMed Abstract | CrossRef Full Text | Google Scholar

Pirandola, S., Andersen, U. L., Banchi, L., Berta, M., Bunandar, D., Colbeck, R., et al. (2020). Advances in quantum cryptography. Adv. Opt. Photonics 12 (4), 1012–1236. doi:10.1364/aop.361502

CrossRef Full Text | Google Scholar

Pirandola, S., Eisert, J., Weedbrook, C., Furusawa, A., and Braunstein, S. L. (2015a). Advances in quantum teleportation. Nat. Phot. 9, 641–652. doi:10.1038/nphoton.2015.154

CrossRef Full Text | Google Scholar

Place, A. P. M., Rodgers, L. V. H., Mundada, P., Smitham, B. M., Fitzpatrick, M., Leng, Z., et al. (2021). New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 12 (1), 1779. doi:10.1038/s41467-021-22030-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Poletto, S., Gambetta, J. M., Merkel, S. T., Smolin, J. A., Chow, J. M., Córcoles, A. D., et al. (2012). Entanglement of two superconducting qubits in a waveguide cavity via monochromatic two-photon excitation. Phys. Rev. Lett. 109, 240505. doi:10.1103/PhysRevLett.109.240505

PubMed Abstract | CrossRef Full Text | Google Scholar

Politi, A., Matthews, J. C., and O’Brien, J. L. (2009). Shor’s quantum factoring algorithm on a photonic chip. Science 325 (5945), 1221. arXiv:0911.1242. doi:10.1126/science.1173731

PubMed Abstract | CrossRef Full Text | Google Scholar

Pollak, E. (2017a). Transition path time distribution, tunneling times, friction, and uncertainty. Phys. Rev. Lett. 118 (7), 070401. doi:10.1103/physrevlett.118.070401

PubMed Abstract | CrossRef Full Text | Google Scholar

Pollak, E. (2017b). Quantum tunneling: the longer the path, the less time it takes. J. Phys. Chem. Lett. 8 (2), 352–356. doi:10.1021/acs.jpclett.6b02692

PubMed Abstract | CrossRef Full Text | Google Scholar

Poon, C.-S., and Zhou, K. (2011). Neuromorphic silicon neurons and large-scale neural networks: challenges and opportunities. Front. Neurosci. 5, 108. doi:10.3389/fnins.2011.00108

PubMed Abstract | CrossRef Full Text | Google Scholar

Powell, A., Jenny, J., Muller, S., McD. Hobgood, H., Tsvetkov, V., Lenoard, R., et al. (2006). Growth of sic substrates. Syst. 16, 751–777. doi:10.1142/s0129156406004016

CrossRef Full Text | Google Scholar

Prenat, G., Jabeur, K., Di Pendina, G., Boulle, O., and Gaudin, G. (2015). Beyond STT-MRAM, spin orbit torque RAM SOT-MRAM for high speed and high reliability applications. Spintronics-based Computing, 145–157.

CrossRef Full Text | Google Scholar

Pufall, M. R., Rippard, W. H., Csaba, G., Nikonov, D. E., Bourianoff, G. I., and Porod, W. (2015). Physical implementation of coherently coupled oscillator networks. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 76–84. doi:10.1109/jxcdc.2015.2468070

CrossRef Full Text | Google Scholar

Puliyil, S., Banik, M., and Alimuddin, M. (2022). Thermodynamic signatures of genuinely multipartite entanglement. Phys. Rev. Lett. 129 (7), 070601. doi:10.1103/physrevlett.129.070601

PubMed Abstract | CrossRef Full Text | Google Scholar

Puri, S., Boutin, S., and Blais, A. (2017). Engineering the quantum states of light in a Kerr-nonlinear resonator by two-photon driving. npj Quantum Inf. 3 (1), 18. doi:10.1038/s41534-017-0019-1

CrossRef Full Text | Google Scholar

QCI (2022). We believe that quantum computing, and all of its power, should be made accessible to all businesses, not just an elite quantum workforce. Available at: https://www.quantumcomputinginc.com/blog/quantum-annealing-gate/ (Accessed December 22, 22).

Google Scholar

Quach, J. Q., McGhee, K. E., Ganzer, L., Rouse, D. M., Lovett, B. W., Gauger, E. M., et al. (2022). Superabsorption in an organic microcavity: toward a quantum battery. Sci. Adv. 8 (2), eabk3160. doi:10.1126/sciadv.abk3160

PubMed Abstract | CrossRef Full Text | Google Scholar

Quantum Computing (2022). Quantum computing. Available at: https://quantumcomputing.com/whurley/china-goes-big-with-92-acre-10-billion-quantum-research-center.

Google Scholar

Quantum Technology Market Size (2022a). Growth to reach CAGR 30.2 % by 2028 provided by: market research store.

Google Scholar

Quantum Technology Market Size (2022b). Quantum technology market size & growth to reach CAGR 30.2 % by 2028 provided by: market research store (Accessed December 30, 22).

Google Scholar

Quantumzeitgeist (2022). David deutsch the father of quantum computing but who is he. Available at: https://www.economist.com/technology-quarterly/2017/03/09/david-deutsch-father-of-quantum-computing (Accessed December 5, 2022).

Google Scholar

Raussendorf, R., and Briegel, H. J. (2001). A one-way quantum computer. Phys. Rev. Lett. 86 (22), 5188–5191. doi:10.1103/physrevlett.86.5188

PubMed Abstract | CrossRef Full Text | Google Scholar

Raussendorf, R., and Harrington, J. (2007). Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504. doi:10.1103/physrevlett.98.190504

PubMed Abstract | CrossRef Full Text | Google Scholar

Raussendorf, R., Harrington, J., and Goyal, K. (2007a). Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9 (6), 199. doi:10.1088/1367-2630/9/6/199

CrossRef Full Text | Google Scholar

Ray, P., Chakrabarti, B. K., and Chakrabarti, A. (1989). Sherrington-Kirkpatrick model in a transverse field: absence of replica symmetry breaking due to quantum fluctuations. Phys. Rev. B 39 (16), 11828–11832. doi:10.1103/PhysRevB.39.11828

PubMed Abstract | CrossRef Full Text | Google Scholar

Razavy, M. (2003). Quantum theory of tunneling. World Sci. 4–462. doi:10.1142/9789812564887

CrossRef Full Text | Google Scholar

Reed, M. D., Maune, B., Andrews, R., Borselli, M., Eng, K., Jura, M., et al. (2016). Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402. doi:10.1103/physrevlett.116.110402

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, J. G., Xu, P., Yong, H. L., Zhang, L., Liao, S. K., Yin, J., et al. (2017). Ground-to-satellite quantum teleportation. Nature 549, 70–73. doi:10.1038/nature23675

PubMed Abstract | CrossRef Full Text | Google Scholar

Riebe, M., Chwalla, M., Benhelm, J., Häffner, H., Hänsel, W., Roos, C. F., et al. (2007). Quantum teleportation with atoms: quantum process tomography. New J. Phys. 9, 211. doi:10.1088/1367-2630/9/7/211

CrossRef Full Text | Google Scholar

Riebe, M., Häffner, H., Roos, C. F., Hänsel, W., Benhelm, J., Lancaster, G. P. T., et al. (2004). Deterministic quantum teleportation with atoms. Nature 429, 734–737. doi:10.1038/nature02570

PubMed Abstract | CrossRef Full Text | Google Scholar

Rigetti, C., Gambetta, J. M., Poletto, S., Plourde, B. L. T., Chow, J. M., Córcoles, A. D., et al. (2012). Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Am. Phys. Soc. (APS). 86 (10), 100506. doi:10.1103/physrevb.86.100506

CrossRef Full Text | Google Scholar

Rigetti Launches Quantum Cloud Services (2018). Announces $1Million challenge. HPCwire. Retrieved 2022-09-31.

Google Scholar

Rigolin, G. (2005). Quantum teleportation of an arbitrary two-qubit state and its relation to multipartite entanglement. Phys. Rev. A 71 (3), 032303. doi:10.1103/physreva.71.032303

CrossRef Full Text | Google Scholar

Ristè, D., Bultink, C. C., Tiggelman, M. J., Schouten, R. N., Lehnert, K. W., and DiCarlo, L. (2013). Millisecond charge-parity fluctuations and induced decoherence in a superconducting transmon qubit. Nat. Commun. 4 (1), 1913. doi:10.1038/ncomms2936

PubMed Abstract | CrossRef Full Text | Google Scholar

Riwar, R.-P., and Catelani, G. (2019). Efficient quasiparticle traps with low dissipation through gap engineering. Phys. Rev. B 100, 144514. doi:10.1103/physrevb.100.144514

CrossRef Full Text | Google Scholar

Riwar, R.-P., Hosseinkhani, A., Burkhart, L. D., Gao, Y. Y., Schoelkopf, R. J., Glazman, L. I., et al. (2016). Normal-metal quasiparticle traps for superconducting qubits. Phys. Rev. B 94, 104516. doi:10.1103/physrevb.94.104516

CrossRef Full Text | Google Scholar

Rong, X., Geng, J., Shi, F., Liu, Y., Xu, K., Ma, W., et al. (2015). Experimental fault-tolerant universal quantum gates with solid-state spins under ambient conditions. Nat. Commun. 6, 8748. doi:10.1038/ncomms9748

PubMed Abstract | CrossRef Full Text | Google Scholar

Rostem, K., de Visser, P. J., and Wollack, E. J. (2018). Enhanced quasiparticle lifetime in a superconductor by selective blocking of recombination phonons with a phononic crystal. Phys. Rev. B 98, 014522. doi:10.1103/physrevb.98.014522

CrossRef Full Text | Google Scholar

Ruiz, A. D. L. F. (2014). Quantum annealing. arXiv preprint arXiv:1404.2465. doi:10.48550/arXiv.1404.2465

CrossRef Full Text | Google Scholar

Ruskov, R., and Tahan, C. (2012). Coherent phonons as a new element of quantum computing and devices. J. Phys. Conf. Ser. 398 (1), 012011. doi:10.1088/1742-6596/398/1/012011

CrossRef Full Text | Google Scholar

Ryan, C. A., Johnson, B. R., Ristè, D., Donovan, B., and Ohki, T. A. (2017). Hardware for dynamic quantum computing. Rev. Sci. Instrum. 88 (10), 104703. doi:10.1063/1.5006525

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadeghi Zadeh, M. S., Houshmand, M., and Aghababa, H. (2017). Bidirectional teleportation of a two-qubit state by using eight-qubit entangled state as a quantum channel. Int. J. Theor. Phys. 56, 2101–2112. doi:10.1007/s10773-017-3353-3

CrossRef Full Text | Google Scholar

Saglamyurek, E., Sinclair, N., Jin, J., Slater, J. A., Oblak, D., Bussières, F., et al. (2011). Broadband waveguide quantum memory for entangled photons. Nature 469, 512–515. doi:10.1038/nature09719

PubMed Abstract | CrossRef Full Text | Google Scholar

Sainadh, U. S., Sang, R. T., and Litvinyuk, I. V. (2020). Attoclock and the quest for tunnelling time in strong-field physics. J. Phys. Photonics 2 (4), 042002. doi:10.1088/2515-7647/aba009

CrossRef Full Text | Google Scholar

Saleh, B. E. A., and Teich, M. C. (1991). Fundamentals of photonics Ch.22. Wiley.

Google Scholar

Sanders, Y. R., Wallman, J. J., and Sanders, B. C. (2015). Bounding quantum gate error rate based on reported average fidelity. New J. Phys. 18, 012002. doi:10.1088/1367-2630/18/1/012002

CrossRef Full Text | Google Scholar

Sang, M. H. (2016). Bidirectional quantum teleportation by using five-qubit cluster state. Int. J. Theor. Phys. 55, 1333–1335. doi:10.1007/s10773-015-2774-0

CrossRef Full Text | Google Scholar

Sangouard, N., Simon, C., de Riedmatten, H., and Gisin, N. (2011). Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80. doi:10.1103/revmodphys.83.33

CrossRef Full Text | Google Scholar

Sato, H., Honjo, H., Watanabe, T., Niwa, M., Koike, H., Miura, S., et al. (2018a). “14ns write speed 128Mb density Embedded STT-MRAM with endurance>1010 and 10yrs retention@85C using novel low damage MTJ integration process,” in IEEE international electron devices meeting (IEDM), San Francisco, CA, USA, 2018, 27IEEE international electron devices meeting (IEDM), San Francisco, CA, USA, 2018 (IEEE), 2.1–27.2.4. doi:10.1109/IEDM.2018.8614606

CrossRef Full Text | Google Scholar

Sato, M., Takahashi, Y., and Fujimoto, S. (2009). Non-Abelian topological order in s-wave superfluids of ultracold fermionic atoms. Phys. Rev. Lett. 103 (2), 020401. doi:10.1103/physrevlett.103.020401

PubMed Abstract | CrossRef Full Text | Google Scholar

Satzinger, K. J., Liu, Y., Smith, A., Knapp, C., Newman, M., Jones, C., et al. (2021). Realizing topologically ordered states on a quantum processor. Science 374 (6572), 1237–1241. doi:10.1126/science.abi8378

PubMed Abstract | CrossRef Full Text | Google Scholar

Sau, J. D., Lutchyn, R. M., Tewari, S., and Sarma, S. D. (2010). Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104 (4), 040502. doi:10.1103/physrevlett.104.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

Scarani, V., and Renner, R. (2008). Quantum cryptography with finite resources: unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 100, 200501. doi:10.1103/physrevlett.100.200501

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaibley, J. R., Yu, H., Clark, G., Rivera, P., Ross, J. S., Seyler, K. L., et al. (2016). Valleytronics in 2D materials. Nat. Rev. Mater. 1 (11), 1–15. doi:10.1038/natrevmats.2016.55

CrossRef Full Text | Google Scholar

Schindler, P., Nigg, D., Monz, T., Barreiro, J. T., Martinez, E., Wang, S. X., et al. (2013). A quantum information processor with trapped ions. New J. Phys. 15 (12), 123012. doi:10.1088/1367-2630/15/12/123012

CrossRef Full Text | Google Scholar

Scholarpedia (2022). Scholarpedia. Available at: http://www.scholarpedia.org/article/1/f_noise.

Google Scholar

Schreier, J. A., Houck, A. A., Koch, J., Schuster, D. I., Johnson, B. R., Chow, J. M., et al. (2008) Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77 (18), 180502. doi:10.1103/physrevb.77.180502

CrossRef Full Text | Google Scholar

Schrodinger, E. (1926). Quantisierung als eigenwertproblem. Ann. Phys. 384 (4), 361–376. doi:10.1002/andp.19263840404

CrossRef Full Text | Google Scholar

Schrödinger, E. (1935). Discussion of probability relations between separated systems. Proc. Camb. Philosophical Soc. 31, 555–563. doi:10.1017/s0305004100013554

CrossRef Full Text | Google Scholar

Schumacher, B. (1995). Quantum coding. Phys. Rev. A 51 (4), 2738–2747. doi:10.1103/physreva.51.2738

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwegler, E., Sharma, M., Gygi, F., and Galli, G. (2008). Melting of ice under pressure. Proc. Natl. Acad. Sci. 105 (39), 14779–14783. doi:10.1073/pnas.0808137105

PubMed Abstract | CrossRef Full Text | Google Scholar

SCI (2023). 33525 stj detectors. Available at: https://sci.esa.int/web/sci-fmi/-/33525-stj-detectors (Accessed March 20, 23).

Google Scholar

Science Daily (2006). 12-qubits reached in quantum information quest.

Google Scholar

Science the Wire (2022). Science the wire. Available at: https://science.thewire.in/the-sciences/quantum-entanglement-applications-qkd/.

Google Scholar

Scitechdaily (2022). Scientists strengthen spin-orbit qubits in milestone critical for scale up of quantum computers. Available at: https://scitechdaily.com/scientists-strengthen-spin-orbit-qubits-in-milestone-critical-for-scale-up-of-quantum-computers/.

Google Scholar

SCL (2022). Schr dinger s cat einstein s dice and the chandelier a novice s guide to quantum computers. Available at: https://www.scl.org/articles/10503-schr-dinger-s-cat-einstein-s-dice-and-the-chandelier-a-novice-s-guide-to-quantum-computers (Accessed December 28, 22).

Google Scholar

Sengupta, A., Panda, P., Wijesinghe, P., Kim, Y., and Roy, K. (2016). Magnetic tunnel junction mimics stochastic cortical spiking neurons. Sci. Rep. 6, 30039. doi:10.1038/srep30039

PubMed Abstract | CrossRef Full Text | Google Scholar

Session 8-4 (2023). 32-Mb 2T1R SPRAM with localized bi-directional write driver and ’1'/'0' dual-array equalized reference cell. vlsisymposium.org. Archived from the original on 5 Feb 2023.

Google Scholar

Shahmoon, E., Levit, S., and Ozeri, R. (2009). Qubit coherent control with squeezed light fields. arXiv preprint arXiv:0901.2824.

Google Scholar

Shao, Q., Yu, G., Lan, Y. W., Shi, Y., Li, M. Y., Zheng, C., et al. (2016). Strong Rashba-Edelstein effect-induced spin–orbit torques in monolayer transition metal dichalcogenide/ferromagnet bilayers. Nano Lett. 16 (12), 7514–7520. doi:10.1021/acs.nanolett.6b03300

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharad, M., Augustine, C., Panagopoulos, G., and Roy, K. (2012). Proposal for neuromorphic hardware using spin devices. arXiv:1206.3227.

Google Scholar

Sherson, J. F., Krauter, H., Olsson, R. K., Julsgaard, B., Hammerer, K., Cirac, I., et al. (2006). Quantum teleportation between light and matter. Nature 443, 557–560. doi:10.1038/nature05136

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Lopez-Dominguez, V., Garesci, F., Wang, C., Almasi, H., Grayson, M., et al. (2020). Electrical manipulation of the magnetic order in antiferromagnetic PtMn pillars. Nat. Electron. 3 (2), 92–98. doi:10.1038/s41928-020-0367-2

CrossRef Full Text | Google Scholar

Shor, P. W. (1994). “Algorithms for quantum computation: discrete logarithms and factoring,” in Proceedings 35th annual symposium on foundations of computer science. IEEE Comput. Soc. Press, 124–134. doi:10.1109/sfcs.1994.365700

CrossRef Full Text | Google Scholar

Shor, P. W. (1997). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509. doi:10.1137/s0097539795293172

CrossRef Full Text | Google Scholar

Shrivastava, K. N. (1983). Theory of spin–lattice relaxation. Phys. Stat. Solidi B 117, 437–458. doi:10.1002/pssb.2221170202

CrossRef Full Text | Google Scholar

Siddiqi, I. (2021). Engineering high-coherence superconducting qubits. Nat. Rev. Mater 6, 875–891. doi:10.1038/s41578-021-00370-4

CrossRef Full Text | Google Scholar

Siddiqui, A. U., and Wilde, M. M. (2022). The SWAP imposter: bidirectional quantum teleportation and its performance. arXiv preprint arXiv:2210.10882.

Google Scholar

Sillanpaa, M. A., Park, J. I., and Simmonds, R. W. (2007). Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nat. Lond. 449, 438–442. doi:10.1038/nature06124

PubMed Abstract | CrossRef Full Text | Google Scholar

Simmonds, R. W., Lang, K. M., Hite, D. A., Nam, S., Pappas, D. P., and Martinis, J. M. (2004). Decoherence in Josephson phase qubits from junction resonators. Phys. Rev. Lett. 93 (7), 077003. doi:10.1103/physrevlett.93.077003

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon, D. R. (1997). On the power of quantum computation. SIAM J. Comput. 26 (5), 1474–1483. doi:10.1137/S0097539796298637

CrossRef Full Text | Google Scholar

Sinova, J., Valenzuela, S. O., Wunderlich, J., Back, C. H., and Jungwirth, T. (2015). Spin Hall effects. Rev. Mod. Phys. 87, 1213–1260. doi:10.1103/revmodphys.87.1213

CrossRef Full Text | Google Scholar

Sipser, M. (1997). Introduction to the theory of computation. Boston: PWS Pub. Co.

Google Scholar

Sisodia, M., and Pathak, A. (2018). Comment on “quantum teleportation of eight-qubit state via six-qubit cluster state”. Int. J. Theor. Phys. 57, 2213–2217. doi:10.1007/s10773-018-3746-y

CrossRef Full Text | Google Scholar

Sitharama Iyengar, S., Latesh Kumar, K. J., and Mastriani, M. (2020). Bidirectional teleportation for underwater quantum communications. arXiv e-prints, arXiv-2009.

Google Scholar

Slavin, A., and Tiberkevich, V. (2009). Nonlinear auto-oscillator theory of microwave generation by spin-polarized current. IEEE Trans. Magn. 45, 1875–1918. doi:10.1109/tmag.2008.2009935

CrossRef Full Text | Google Scholar

Slonczewski, J. C. (1996). Current-driven excitation of magnetic multilayers. J. Magnetism Magnetic Mater. 159 (1-2), L1–L7. doi:10.1016/0304-8853(96)00062-5

CrossRef Full Text | Google Scholar

Smart, S. E., Hu, Z., Kais, S., and Mazziotti, D. A. (2022). Relaxation of stationary states on a quantum computer yields a unique spectroscopic fingerprint of the computer’s noise. Commun. Phys. 5 (1), 28. doi:10.1038/s42005-022-00803-8

CrossRef Full Text | Google Scholar

Smith, W. C., Kou, A., Xiao, X., Vool, U., and Devoret, M. H. (2020). Superconducting circuit protected by two-Cooper-pair tunneling. npj Quantum Inf. 6 (1), 8. doi:10.1038/s41534-019-0231-2

CrossRef Full Text | Google Scholar

Soare, A., Ball, H., Hayes, D., Sastrawan, J., Jarratt, M. C., McLoughlin, J. J., et al. (2014). Experimental noise filtering by quantum control. Nat. Phys. 10, 825–829. doi:10.1038/nphys3115

CrossRef Full Text | Google Scholar

Son, N. T., Carlsson, P., ul Hassan, J., Janzén, E., Umeda, T., Isoya, J., et al. (2006). Divacancy in 4H-SiC. Phys. Rev. Lett. 96, 055501. doi:10.1103/physrevlett.96.055501

PubMed Abstract | CrossRef Full Text | Google Scholar

Son, N. T., Zolnai, Z., and Janzen, E. (2022). Silicon vacancy related TV2a center in 4H-SiC. Phys. Rev. B 68, 205211. doi:10.1103/physrevb.68.205211

CrossRef Full Text | Google Scholar

Spagnolo, M., Morris, J., Piacentini, S., Antesberger, M., Massa, F., Crespi, A., et al. (2022). Experimental photonic quantum memristor. Nat. Photonics 16 (4), 318–323. doi:10.1038/s41566-022-00973-5

CrossRef Full Text | Google Scholar

Spavieri, G., and Mansuripur, M. (2015). Origin of the spin–orbit interaction. Phys. Scr. 90 (8), 085501. doi:10.1088/0031-8949/90/8/085501

CrossRef Full Text | Google Scholar

Spierings, D. C., and Steinberg, A. M. (2020). Measuring the time tunneling particles spend in the barrier. Opt. Opto-Atomic, Entanglement-Enhanced Precis. Metrology II 11296, 45–52. doi:10.1117/12.2552583

CrossRef Full Text | Google Scholar

Spierings, D. C., and Steinberg, A. M. (2021). Tunneling takes less time when it’s less probable. arXiv preprint arXiv:2101.12309.

Google Scholar

Srinatha, N., Omkar, S., Srikanth, R., Banerjee, S., and Pathak, A. (2014). The quantum cryptographic switch. Quantum inf. Process. 13, 59–70. doi:10.1007/s11128-012-0487-3

CrossRef Full Text | Google Scholar

Stanescu, T. D. (2016). Introduction to topological quantum matter & quantum computation. CRC Press.

Google Scholar

Stano, P., and Loss, D. (2022). Review of performance metrics of spin qubits in gated semiconducting nanostructures. Nat. Rev. Phys. 4, 672–688. doi:10.1038/s42254-022-00484-w

CrossRef Full Text | Google Scholar

Steffen, L., Salathe, Y., Oppliger, M., Kurpiers, P., Baur, M., Lang, C., et al. (2013). Deterministic quantum teleportation with feedforward in a solid-state system. Nature 500, 319–322. doi:10.1038/nature12422

PubMed Abstract | CrossRef Full Text | Google Scholar

Steffen, M. (2011). Superconducting qubits are getting serious. Physics 4, 103. doi:10.1103/physics.4.103

CrossRef Full Text | Google Scholar

Strogatz, S. (2004). Sync: the emerging science of spontaneous order.

Google Scholar

Su, X., Tian, C., Deng, X., Li, Q., Xie, C., and Peng, K. (2016). Quantum entanglement swapping between two multipartite entangled states. Phys. Rev. Lett. 117 (24), 240503. doi:10.1103/physrevlett.117.240503

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Q.-C., Mao, Y. L., Chen, S. J., Zhang, W., Jiang, Y. F., Zhang, Y. B., et al. (2016). Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Phot. 10, 671–675. doi:10.1038/nphoton.2016.179

CrossRef Full Text | Google Scholar

Sung, Y., Ding, L., Braumüller, J., Vepsäläinen, A., Kannan, B., Kjaergaard, M., et al. (2021). Realization of high-fidelity cz and z z-free iswap gates with a tunable coupler. Phys. Rev. X 11 (2), 021058. doi:10.1103/physrevx.11.021058

CrossRef Full Text | Google Scholar

Liu, M. (2024). Synopsys: eMRAM for low-power SoCs in advanced process nodes. Available at: https://www.synopsys.com/designware-ip/technical-bulletin/emram-low-power-advanced-nodes.html (Accessed July 24, 2024).

Google Scholar

Takahashi, S., Hanson, R., van Tol, J., Sherwin, M. S., and Awschalom, D. D. (2008). Quenching spin decoherence in diamond through spin bath polarization. Phys. Rev. Lett. 101, 047601. doi:10.1103/physrevlett.101.047601

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, S., Tupitsyn, I. S., van Tol, J., Beedle, C. C., Hendrickson, D. N., and Stamp, P. C. E. (2011). Decoherence in crystals of quantum molecular magnets. Nature 476, 76–79. doi:10.1038/nature10314

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeda, S., Mizuta, T., Fuwa, M., van Loock, P., and Furusawa, A. (2013). Deterministic quantum teleportation of photonic quantum bits by a hybrid technique. Nature 500, 315–318. doi:10.1038/nature12366

PubMed Abstract | CrossRef Full Text | Google Scholar

Takei, N., Aoki, T., Koike, S., Yoshino, K. i., Wakui, K., Yonezawa, H., et al. (2005b). Experimental demonstration of quantum teleportation of a squeezed state. Phys. Rev. A 72, 042304. doi:10.1103/physreva.72.042304

CrossRef Full Text | Google Scholar

Takei, N., Yonezawa, H., Aoki, T., and Furusawa, A. (2005a). Highfidelity teleportation beyond the nocloning limit and entanglement swapping for continuous variables. Phys. Rev. Lett. 94, 220502. doi:10.1103/physrevlett.94.220502

PubMed Abstract | CrossRef Full Text | Google Scholar

Takei, S., Fregoso, B. M., Hui, H. Y., Lobos, A. M., and Sarma, S. D. (2013). Soft superconducting gap in semiconductor Majorana nanowires. Phys. Rev. Lett. 110 (18), 186803. doi:10.1103/physrevlett.110.186803

PubMed Abstract | CrossRef Full Text | Google Scholar

Takemura, R., Kawahara, T., Miura, K., Yamamoto, H., Hayakawa, J., Matsuzaki, N., et al. (2009). “32-mb 2t1r spram with localized bi-directional write driver and ‘1’/‘0’dual-array equalized reference cell,” in 2009 symposium on VLSI circuits (IEEE), 84–85.

Google Scholar

Takesue, H., Dyer, S. D., Stevens, M. J., Verma, V., Mirin, R. P., and Nam, S. W. (2015). Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors. Optica 2 (10), 832–835. doi:10.1364/optica.2.000832

CrossRef Full Text | Google Scholar

Takesue, H., Nam, S. W., Zhang, Q., Hadfield, R. H., Honjo, T., Tamaki, K., et al. (2007). Quantum key distribution over a 40-dB channel loss using superconducting single-photon detectors. Nat. photonics 1 (6), 343–348. doi:10.1038/nphoton.2007.75

CrossRef Full Text | Google Scholar

Tame, M. S., Prevedel, R., Paternostro, M., Böhi, P., Kim, M. S., and Zeilinger, A. (2007). Experimental realization of Deutsch’s algorithm in a one-way quantum computer. Phys. Rev. Lett. 98 (14), 140501. doi:10.1103/physrevlett.98.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarantino, S., Da Lio, B., Cozzolino, D., and Bacco, D. (2020). Feasibility study of quantum communications in aquatic scenarios. Optik 216, 164639. doi:10.1016/j.ijleo.2020.164639

CrossRef Full Text | Google Scholar

Tarequzzaman, M., Böhnert, T., Decker, M., Costa, J. D., Borme, J., Lacoste, B., et al. (2019). Spin torque nano-oscillator driven by combined spin injection from tunneling and spin Hall current. Commun. Phys. 2, 20. doi:10.1038/s42005-019-0119-7

CrossRef Full Text | Google Scholar

Taupin, M., Khaymovich, I. M., Meschke, M., Mel’nikov, A. S., and Pekola, J. P. (2016). Tunable quasiparticle trapping in Meissner and vortex states of mesoscopic superconductors. Nat. Commun. 7, 10977. doi:10.1038/ncomms10977

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, J. (2004). Modern physics for scientists and engineers. Prentice Hall, 479.

Google Scholar

Team, I. Q. (2020). ibmq_armonk v1.1.5. Available at: https://quantum-computing.ibm.com.

Google Scholar

Techinasia (2022). Techinasia. Available at: https://www.techinasia.com/alibaba-15bn-damo (Accessed December 30, 22).

Google Scholar

Toffoli, T. (1980). “An adapted and condensed version: Toffoli, Tommaso (1980),” in Reversible computing (PDF). Automata, languages and programming, seventh colloquium. Editors J. W. de Bakker, and J. van Leeuwen (Noordwijkerhout, Netherlands: Springer Verlag), 632–644. doi:10.1007/3-540-10003-2_104

CrossRef Full Text | Google Scholar

Techtarget (2022). Techtarget. Available at: https://www.techtarget.com/searchenterpriseai/definition/neuromorphic-computing.

Google Scholar

Thomas, L. H. (1926). The motion of the spinning electron Nature, 117–514.

Google Scholar

Thomas, L. H. (1927). I.The kinematics of an electron with an axis. Mag 3, 1–22. doi:10.1080/14786440108564170

CrossRef Full Text | Google Scholar

Tiangong-2 takes China one step closer to space station (2018). chinaspacereport. Archived from the original.

Google Scholar

Tinkham, M. (2004). Introduction to superconductivity. 2nd edn. Dover.

Google Scholar

Tokura, Y., Van der Wiel, W. G., Obata, T., and Tarucha, S. (2006). Coherent single electron spin control in a slanting Zeeman field. Phys. Rev. Lett. 96, 047202. doi:10.1103/physrevlett.96.047202

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomamichel, M., Lim, C. C. W., Gisin, N., and Renner, R. (2012). Tight finite-key analysis for quantum cryptography. Nat. Commun. 3, 634. doi:10.1038/ncomms1631

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomshardware (2022). Tomshardware. Available at: https://www.tomshardware.com/news/intel-demonstrates-stt-mram-for-l4-cache#:∼:text=Intel%20researchers%20have%20demonstrated%202MB,step%20forward%20for%20the%20technology (Accessed September 1, 2023).

Google Scholar

Topological Quantum Computer (2023). Topological quantum computer. Available at: https://en.wikipedia.org/wiki/Topological_quantum_computer (Accessed April 22, 23).

Google Scholar

Tougaw, P. D., and Lent, C. S. (1994). Logical devices implemented using quantum cellular automata. J. Appl. Phys. 75 (3), 1818–1825. doi:10.1063/1.356375

CrossRef Full Text | Google Scholar

Trauzettel, B., Bulaev, D., Loss, D., and Burkard, G. (2007). Spin qubits in graphene quantum dots. Nat. Phys. 3, 192–196. doi:10.1038/nphys544

CrossRef Full Text | Google Scholar

Trebst, S., Troyer, M., Wang, Z., and Ludwig, A. W. (2008). A short introduction to Fibonacci anyon models. Prog. Theor. Phys. Suppl. 176, 384–407. doi:10.1143/ptps.176.384

CrossRef Full Text | Google Scholar

Trif, M., Golovach, V. N., and Loss, D. (2008). Spin dynamics in InAs nanowire quantum dots coupled to a transmission line. Phys. Rev. B 77, 045434. doi:10.1103/physrevb.77.045434

CrossRef Full Text | Google Scholar

Trixler, F. (2013). Quantum tunnelling to the origin and evolution of life. Curr. Org. Chem. 17 (16), 1758–1770. doi:10.2174/13852728113179990083

PubMed Abstract | CrossRef Full Text | Google Scholar

Troppmann, U., Tesch, C. M., and de Vivie-Riedle, R. (2003). Preparation and addressability of molecular vibrational qubit states in the presence of anharmonic resonance. Chem. Phys. Lett. 378 (3-4), 273–280. doi:10.1016/s0009-2614(03)01266-1

CrossRef Full Text | Google Scholar

Tsunegi, S., Taniguchi, T., Miwa, S., Nakajima, K., Yakushiji, K., Fukushima, A., et al. (2018). Evaluation of memory capacity of spin torque oscillator for recurrent neural networks. Jpn. J. Appl. Phys. 57, 120307. doi:10.7567/jjap.57.120307

CrossRef Full Text | Google Scholar

Tucker, J. (1979). Quantum limited detection in tunnel junction mixers. IEEE J. Quantum Electron. 15 (11), 1234–1258. doi:10.1109/jqe.1979.1069931

CrossRef Full Text | Google Scholar

Tyryshkin, A. M., Tojo, S., Morton, J. J., Riemann, H., Abrosimov, N. V., Becker, P., et al. (2012). Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11 (2), 143–147. doi:10.1038/nmat3182

PubMed Abstract | CrossRef Full Text | Google Scholar

Uhlenbeck, G., and Goudsmit, S. (1926). Spinning electrons and the structure of spectra. Nature 117, 264–265. doi:10.1038/117264a0

CrossRef Full Text | Google Scholar

Ursin, R., Jennewein, T., Aspelmeyer, M., Kaltenbaek, R., Lindenthal, M., Walther, P., et al. (2004). Quantum teleportation across the danube. Nature 430, 849. doi:10.1038/430849a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ursin, R., Tiefenbacher, F., Schmitt-Manderbach, T., Weier, H., Scheidl, T., Lindenthal, M., et al. (2007). Entanglement-based quantum communication over 144 km. Nat. Phys. 3, 481–486. doi:10.1038/nphys629

CrossRef Full Text | Google Scholar

Van Duzer, T., and Turner, C. W. (1981). Principles of superconductive devices and circuits. 2nd edn. Prentice Hall.

Google Scholar

Valenzuela, S. O., and Tinkham, M. (2006). Direct electronic measurement of the spin Hall effect. Nature 442 (7099), 176–179. doi:10.1038/nature04937

PubMed Abstract | CrossRef Full Text | Google Scholar

Valery, J. A., Chowdhury, S., Jones, G., and Didier, N. (2022). Dynamical sweet spot engineering via two-tone flux modulation of superconducting qubits. PRX Quantum 3 (2), 020337. doi:10.1103/prxquantum.3.020337

CrossRef Full Text | Google Scholar

Valivarthi, R., Davis, S. I., Peña, C., Xie, S., Lauk, N., Narváez, L., et al. (2020). Teleportation systems toward a quantum internet. PRX Quantum 1 (2), 020317. doi:10.1103/prxquantum.1.020317

CrossRef Full Text | Google Scholar

Valivarthi, R., Puigibert, M. G., Zhou, Q., Aguilar, G. H., Verma, V. B., Marsili, F., et al. (2016). Quantum teleportation across a metropolitan fibre network. Nat. Phot. 10, 676–680. doi:10.1038/nphoton.2016.180

CrossRef Full Text | Google Scholar

van Der Heijden, J., Kobayashi, T., House, M. G., Salfi, J., Barraud, S., Laviéville, R., et al. (2018). Readout and control of the spin-orbit states of two coupled acceptor atoms in a silicon transistor. Sci. Adv. 4 (12), eaat9199. doi:10.1126/sciadv.aat9199

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Heijden, J., Salfi, J., Mol, J. A., Verduijn, J., Tettamanzi, G. C., Hamilton, A. R., et al. (2014). Probing the spin states of a single acceptor atom. Nano Lett. 14 (3), 1492–1496. doi:10.1021/nl4047015

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandersypen, L., Steffen, M., Breyta, G., Yannoni, C. S., Sherwood, M. H., and Chuang, I. L. (2001). Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887. doi:10.1038/414883a

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandersypen, L. M., Steffen, M., Breyta, G., Yannoni, C. S., Cleve, R., and Chuang, I. L. (2000). Experimental realization of an order-finding algorithm with an NMR quantum computer. Phys. Rev. Lett. 85 (25), 5452–5455. doi:10.1103/physrevlett.85.5452

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandersypen, L. M. K., Bluhm, H., Clarke, J. S., Dzurak, A. S., Ishihara, R., Morello, A., et al. (2017). Interfacing spin qubits in quantum dots and donors—hot, dense and coherent. npj Quantum Inf. 3, 34. doi:10.1038/s41534-017-0038-y

CrossRef Full Text | Google Scholar

Van Harlingen, D. J., Plourde, B. L. T., Robertson, T. L., Reichardt, P. A., and Clarke, J. (2004). Decoherence in flux qubits due to 1/f noise in Josephson junctions. Boston, MA: Springer US, 171–184.

CrossRef Full Text | Google Scholar

Varley, J. B., Janotti, A., and Van de Walle, C. G. (2016). Defects in AlN as candidates for solid-state qubits. Phys. Rev. B 93 (16), 161201. doi:10.1103/physrevb.93.161201

CrossRef Full Text | Google Scholar

Veldhorst, M., Hwang, J. C. C., Yang, C. H., Leenstra, A. W., de Ronde, B., Dehollain, J. P., et al. (2014). An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotech. 9, 981–985. doi:10.1038/nnano.2014.216

PubMed Abstract | CrossRef Full Text | Google Scholar

Veldhorst, M., Yang, C. H., Hwang, J. C. C., Huang, W., Dehollain, J. P., Muhonen, J. T., et al. (2015). A two-qubit logic gate in silicon. Nature 526, 410–414. doi:10.1038/nature15263

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, V. (2020). Bidirectional quantum teleportation by using two GHZ-states as the quantum channel. IEEE Commun. Lett. 25 (3), 936–939. doi:10.1109/lcomm.2020.3036587

CrossRef Full Text | Google Scholar

Vool, U., and Devoret, M. (2017). Introduction to quantum electromagnetic circuits. Int. J. Circuit Theory Appl. 45 (7), 897–934. doi:10.1002/cta.2359

CrossRef Full Text | Google Scholar

Wadley, P., Howells, B., Železný, J., Andrews, C., Hills, V., Campion, R. P., et al. (2016). Electrical switching of an antiferromagnet. Science 351 (6273), 587–590. doi:10.1126/science.aab1031

PubMed Abstract | CrossRef Full Text | Google Scholar

Waldrop, M. M. (2013). Neuroelectronics: smart connections. Nature 503 (7474), 22–24. doi:10.1038/503022a

PubMed Abstract | CrossRef Full Text | Google Scholar

Wall, M. (2016). China Launches pioneering ’hack-proof’ quantum-communications satellite. Space.com. Purch.

Google Scholar

Wang, C., Gao, Y. Y., Pop, I. M., Vool, U., Axline, C., Brecht, T., et al. (2014). Measurement and control of quasiparticle dynamics in a superconducting qubit. Nat. Commun. 5, 5836. doi:10.1038/ncomms6836

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Li, X., Xu, H., Li, Z., Wang, J., Yang, Z., et al. (2022a). Towards practical quantum computers: transmon qubit with a lifetime approaching 0.5 milliseconds. npj Quantum Inf. 8, 3. doi:10.1038/s41534-021-00510-2

CrossRef Full Text | Google Scholar

Wang, D. S., Fowler, A. G., and Hollenberg, L. C. (2011). Surface code quantum computing with error rates over 1%. Phys. Rev. A 83 (2), 020302. doi:10.1103/physreva.83.020302

CrossRef Full Text | Google Scholar

Wang, J. I., Yamoah, M. A., Li, Q., Karamlou, A. H., Dinh, T., Kannan, B., et al. (2022b). Hexagonal boron nitride as a low-loss dielectric for superconducting quantum circuits and qubits. Nat. Mater. 21 (4), 398–403. doi:10.1038/s41563-021-01187-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X. L., Cai, X. D., Su, Z. E., Chen, M. C., Wu, D., Li, L., et al. (2015). Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516–519. doi:10.1038/nature14246

PubMed Abstract | CrossRef Full Text | Google Scholar

Warner, M., Din, S., Tupitsyn, I. S., Morley, G. W., Stoneham, A. M., Gardener, J. A., et al. (2013). Potential for spin-based information processing in a thin-film molecular semiconductor. Nature 503, 504–508. doi:10.1038/nature12597

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, T. F., Weber, B., House, M. G., Büch, H., and Simmons, M. Y. (2015). High-fidelity rapid initialization and read-out of an electron spin via the single donor D− charge state. Phys. Rev. Lett. 115 (16), 166806. doi:10.1103/physrevlett.115.166806

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, T. F., Weber, B., Hsueh, Y. L., Hollenberg, L. C., Rahman, R., and Simmons, M. Y. (2017). Atomically engineered electron spin lifetimes of 30 s in silicon. Sci. Adv. 3 (3), e1602811. doi:10.1126/sciadv.1602811

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, B., Hsueh, Y. L., Watson, T. F., Li, R., Hamilton, A. R., Hollenberg, L. C. L., et al. (2018). Spin–orbit coupling in silicon for electrons bound to donors. npj Quantum Inf. 4, 61. doi:10.1038/s41534-018-0111-1

CrossRef Full Text | Google Scholar

Weber, J. R., Koehl, W. F., Varley, J. B., Janotti, A., Buckley, B. B., Van de Walle, C. G., et al. (2010). Quantum computing with defects. Proc. Natl. Acad. Sci. U. S. A. 107, 8513–8518. doi:10.1073/pnas.1003052107

PubMed Abstract | CrossRef Full Text | Google Scholar

Wedge, C. J., Timco, G. A., Spielberg, E. T., George, R. E., Tuna, F., Rigby, S., et al. (2012). Chemical engineering of molecular qubits. Phys. Rev. Lett. 108, 107204. doi:10.1103/physrevlett.108.107204

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinstein, Y. S., Pravia, M. A., Fortunato, E. M., Lloyd, S., and Cory, D. G. (2001). Implementation of the quantum Fourier transform. Phys. Rev. Lett. 86, 1889–1891. doi:10.1103/physrevlett.86.1889

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, X. G. (1991). Non-Abelian statistics in the fractional quantum Hall states. Phys. Rev. Lett. 66 (6), 802. doi:10.1103/PhysRevLett.66.802

PubMed Abstract | CrossRef Full Text | Google Scholar

Wendin, G., and Shumeiko, V. S. (2007). Quantum bits with Josephson junctions (review article). Low. Temp. Phys. 33, 724–744. doi:10.1063/1.2780165

CrossRef Full Text | Google Scholar

Werner, R. F. (2001). All teleportation and dense coding schemes. J. Phys. A Math. Gen. 34 (35), 7081–7094. doi:10.1088/0305-4470/34/35/332

CrossRef Full Text | Google Scholar

Wieghardt, K., Pohl, K., Jibril, I., and Huttner, G. (1984). Hydrolysis products of the monomeric amine complex (C6H15N3)FeCl3: the structure of the octameric iron(III) cation of [(C6H15N3)6Fe8(µ3–O)2(µ 2–OH)12]Br7 · 8H2O. Angew. Chem. Int. Edn Engl. 23, 77–78. doi:10.1002/anie.198400771

CrossRef Full Text | Google Scholar

Wien, W. (1897). XXX. On the division of energy in the emission-spectrum of a black body. Series 43 (262), 214–220. doi:10.1080/14786449708620983

CrossRef Full Text | Google Scholar

Wikipedia (2022). Adiabatic quantum computation. Available at: https://en.wikipedia.org/wiki/Adiabatic_quantum_computation (Accessed December 28, 22).

Google Scholar

Wikipedia (2022b). Ice. Available at: https://en.wikipedia.org/wiki/Ice#cite_ref-Physics_of_Ice_6-0 (Accessed December 31, 2022).

Google Scholar

Wikipedia (2022c). List of quantum processors. Available at: https://en.wikipedia.org/wiki/List_of_quantum_processors#cite_note-IonQ32-22 (Accessed December 29, 22).

Google Scholar

Wikipedia (2022d). Max_Planck. Available at: https://en.wikipedia.org/wiki/Max_Planck (Accessed February 12, 2022).

Google Scholar

Wikipedia (2022e). Principle of locality. Available at: https://en.wikipedia.org/wiki/Principle_of_locality (Accessed December 5, 2022).

Google Scholar

Wikipedia (2022f). Quadratic unconstrained binary optimization. Available at: https://en.wikipedia.org/wiki/Quadratic_unconstrained_binary_optimization (Accessed December 23, 2022).

Google Scholar

Wikipedia (2022g). Quantum superposition. Available at: https://en.wikipedia.org/wiki/Quantum_superposition (Accessed December 30, 22).

Google Scholar

Wikipedia (2022h). Flux qubit. Available at: https://en.wikipedia.org/wiki/Flux_qubit.

Google Scholar

Wikipedia (2022i). Neuromorphic engineering. Available at: https://en.wikipedia.org/wiki/Neuromorphic_engineering#cite_note-Maan_1%E2%80%9313-6.

Google Scholar

Wikipedia (2022j). Orbit interaction. Available at: https://en.wikipedia.org/wiki/Spin%E2%80%93orbit_interaction (Accessed June 22, 2023).

Google Scholar

Wikipedia (2022k). Quantum tunnelling. Available at: https://en.wikipedia.org/wiki/Quantum_tunnelling (Accessed January 16, 23).

Google Scholar

Wikipedia (2022l). Spin transfer torque. Available at: https://en.wikipedia.org/wiki/Spin-transfer_torque (Accessed July 1, 23).

Google Scholar

Wikipedia (2022m). Superconducting quantum computing. Available at: https://en.wikipedia.org/wiki/Superconducting_quantum_computing.

Google Scholar

Wikipedia (2022n). Topological quantum computer. Available at: https://en.wikipedia.org/wiki/Topological_quantum_computer.

Google Scholar

Wikipedia (2022o). Transmon. Available at: https://en.wikipedia.org/wiki/Transmon#cite_note-4.

Google Scholar

Wikipedia (2022p). Anyon. Available at: https://en.wikipedia.org/wiki/Anyon#cite_note-24.

Google Scholar

Wikipedia Romeira, B., and Figueiredo, J. (2023). Quantum tunnelling. Available at: https://en.wikipedia.org/wiki/Quantum_tunnelling (Accessed January 16, 23).

Google Scholar

Wikipedia (2023). Turing machine. Available at: https://en.wikipedia.org/wiki/Turing_machine (Accessed May 7, 23).

Google Scholar

Wilczek, F. (2006). From electronics to anyonics. Phys. World 19, 22–23. doi:10.1088/2058-7058/19/1/31

CrossRef Full Text | Google Scholar

Willett, R. L., Nayak, C., Shtengel, K., Pfeiffer, L. N., and West, K. W. (2013). Magnetic-field-tuned aharonov-bohm oscillations and evidence for non-abelian anyons at ν= 5/2. Phys. Rev. Lett. 111 (18), 186401. doi:10.1103/physrevlett.111.186401

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, C. P., and Clearwater, S. H. (1998). Explorations in quantum computing. Santa Clara: Telos.

Google Scholar

Wolchover, N. (2021). Eternal change for No energy: a time crystal finally made real. Quanta Mag.

Google Scholar

Wood, B. D., Stimpson, G. A., March, J. E., Lekhai, Y. N. D., Stephen, C. J., Green, B. L., et al. (2022). Long spin coherence times of nitrogen vacancy centers in milled nanodiamonds. Phys. Rev. B 105 (20), 205401. doi:10.1103/physrevb.105.205401

CrossRef Full Text | Google Scholar

Wu, Y., Bao, W.-Su, Cao, S., and Jian-Wei, P. (2021). Qubits meet materials science. Nat. Rev. Mater 6, 869. doi:10.1038/s41578-021-00378-w

CrossRef Full Text | Google Scholar

Wu, Y., Bao, W.-Su, Cao, S., and Pan, J.-W. (2021a). Qubits meet materials science. Nat. Rev. Mater 6, 869. doi:10.1038/s41578-021-00378-w

CrossRef Full Text | Google Scholar

Xia, X. X., Sun, Q. C., Zhang, Q., and Pan, J. W. (2017). Long distance quantum teleportation. Quantum Sci. Technol. 3 (1), 014012. doi:10.1088/2058-9565/aa9baf

CrossRef Full Text | Google Scholar

Xu, J. S., Yung, M. H., Xu, X. Y., Tang, J. S., Li, C. F., and Guo, G. C. (2016). Robust bidirectional links for photonic quantum networks. Sci. Adv. 2 (1), e1500672. doi:10.1126/sciadv.1500672

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Q., Zheng, G., Wang, Y. X., Zoller, P., Clerk, A. A., and Jiang, L. (2022). Autonomous quantum error correction and fault-tolerant quantum computation with squeezed cat qubits. arXiv preprint arXiv:2210.13406.

Google Scholar

Yan, A. (2013). Bidirectional controlled teleportation via six-qubit cluster state. Int. J. Theor. Phys. 52, 3870–3873. doi:10.1007/s10773-013-1694-0

CrossRef Full Text | Google Scholar

Yan, F., Gustavsson, S., Kamal, A., Birenbaum, J., Sears, A. P., Hover, D., et al. (2016b). The flux qubit revisited to enhance coherence and reproducibility. Nat. Commun. 7, 12964. doi:10.1038/ncomms12964

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, F., Krantz, P., Sung, Y., Kjaergaard, M., Campbell, D. L., Orlando, T. P., et al. (2018). Tunable coupling scheme for implementing high-fidelity two-qubit gates. Phys. Rev. Appl. 10 (5), 054062. doi:10.1103/physrevapplied.10.054062

CrossRef Full Text | Google Scholar

Yan, Y., Wan, C., Zhou, X., Shi, G., Cui, B., Han, J., et al. (2016a). Strong electrical manipulation of spin–orbit torque in ferromagnetic heterostructures. Adv. Electron. Mater. 2 (10), 1600219.doi:10.1002/aelm.201600219

CrossRef Full Text | Google Scholar

Yan, Z., Yun, J. J., Sui, W. B., Xi, L., Xie, Z. T., Cao, J. W., et al. (2021). Current switching of interface antiferromagnet in ferromagnet/antiferromagnet heterostructure. Appl. Phys. Lett. 118 (3), 032402. doi:10.1063/5.0039074

CrossRef Full Text | Google Scholar

Yang, C. H., Leon, R. C. C., Hwang, J. C. C., Saraiva, A., Tanttu, T., Huang, W., et al. (2020). Operation of a silicon quantum processor unit cell above one kelvin. Nature 580, 350–354. doi:10.1038/s41586-020-2171-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, G., Lian, B. W., Nie, M., and Jin, J. (2017). Bidirectional multi-qubit quantum teleportation in noisy channel aided with weak measurement. Chin. Phys. B 26 (4), 040305. doi:10.1088/1674-1056/26/4/040305

CrossRef Full Text | Google Scholar

Yang, Y. Q., Zha, X. W., and Yu, Y. (2016). Asymmetric bidirectional controlled teleportation via seven-qubit cluster state. Int. J. Theor. Phys. 55, 4197–4204. doi:10.1007/s10773-016-3044-5

CrossRef Full Text | Google Scholar

Yanofsky, N. S., and Mannucci, M. (2013). Quantum computing for computer scientists. Cambridge University Press.

Google Scholar

Yao, X., Klyukin, K., Lu, W., Onen, M., Ryu, S., Kim, D., et al. (2020). Protonic solid-state electrochemical synapse for physical neural networks. Nat. Commun. 11 (1), 3134. doi:10.1038/s41467-020-16866-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, J., Cao, Y., Yong, H. L., Ren, J. G., Liang, H., Liao, S. K., et al. (2013). Lower bound on the speed of nonlocal correlations without locality and measurement choice loopholes. Phys. Rev. Lett. 110 (26), 260407. doi:10.1103/physrevlett.110.260407

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, J., Ren, J. G., Lu, H., Cao, Y., Yong, H. L., Wu, Y. P., et al. (2012). Quantum teleportation and entanglement distribution over 100kilometre freespace channels. Nature 488, 185–188. doi:10.1038/nature11332

PubMed Abstract | CrossRef Full Text | Google Scholar

Yogendra, K., Fan, D., Jung, B., and Roy, K. (2016). Magnetic pattern recognition using injection-locked spin-torque nano-oscillators. IEEE Trans. Electron Devices 63, 1674–1680. doi:10.1109/ted.2016.2523423

CrossRef Full Text | Google Scholar

Yoneda, J., Huang, W., Feng, M., Yang, C. H., Chan, K. W., Tanttu, T., et al. (2021). Coherent spin qubit transport in silicon. Nat. Commun. 12, 4114. doi:10.1038/s41467-021-24371-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoneda, J., Takeda, K., Otsuka, T., Nakajima, T., Delbecq, M. R., Allison, G., et al. (2018). A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotech 13, 102–106. doi:10.1038/s41565-017-0014-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yonezawa, H., Braunstein, S. L., and Furusawa, A. (2007). Experimental demonstration of quantum teleportation of broadband squeezing. Phys. Rev. Lett. 99, 110503. doi:10.1103/physrevlett.99.110503

PubMed Abstract | CrossRef Full Text | Google Scholar

You, J. Q., Hu, X., Ashhab, S., and Nori, F. (2007). Low-decoherence flux qubit. Phys. Rev. B 75, 140515. doi:10.1103/physrevb.75.140515

CrossRef Full Text | Google Scholar

You, J. Q., and Nori, F. (2007). Superconducting circuits and quantum information. Phys. Today 58 (11), 42–47. arXiv:quant-ph/0601121. doi:10.1063/1.2155757

CrossRef Full Text | Google Scholar

Yuan, W. (2015). Quantum teleportation of an arbitrary three-qubit state using GHZ-like states. Int. J. Theor. Phys. 54, 851–855. doi:10.1007/s10773-014-2279-2

CrossRef Full Text | Google Scholar

Yuan, Z.-S., Chen, Y. A., Zhao, B., Chen, S., Schmiedmayer, J., and Pan, J. W. (2008). Experimental demonstration of a BDCZ quantum repeater node. Nature 454, 1098–1101. doi:10.1038/nature07241

PubMed Abstract | CrossRef Full Text | Google Scholar

Yukawa, M., Benichi, H., and Furusawa, A. (2008). Highfidelity continuousvariable quantum teleportation toward multistep quantum operations. Phys. Rev. A77, 022314. doi:10.1103/physreva.77.022314

CrossRef Full Text | Google Scholar

Yun, J., Bai, Q., Yan, Z., Chang, M., Mao, J., Zuo, Y., et al. (2020). Tailoring multilevel-stable remanence states in exchange-biased system through spin-orbit torque. Adv. Funct. Mat. 30, 1909092. doi:10.1002/adfm.201909092

CrossRef Full Text | Google Scholar

Zadrozny, J. M., Niklas, J., Poluektov, O. G., and Freedman, D. E. (2015). Millisecond coherence time in a tunable molecular electronic spin qubit. ACS central Sci. 1 (9), 488–492. doi:10.1021/acscentsci.5b00338

PubMed Abstract | CrossRef Full Text | Google Scholar

Zahedinejad, M., Awad, A. A., Muralidhar, S., Khymyn, R., Fulara, H., Mazraati, H., et al. (2020). Two-dimensional mutually synchronized spin Hall nano-oscillator arrays for neuromorphic computing. Nat. Nanotechnol. 15, 47–52. doi:10.1038/s41565-019-0593-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zahedinejad, M., Fulara, H., Khymyn, R., Houshang, A., Dvornik, M., Fukami, S., et al. (2022). Memristive control of mutual spin Hall nano-oscillator synchronization for neuromorphic computing. Nat. Mat. 21, 81–87. doi:10.1038/s41563-021-01153-6

CrossRef Full Text | Google Scholar

Zajac, D. M., Hazard, T. M., Mi, X., Nielsen, E., and Petta, J. R. (2016). Scalable gate architecture for a one-dimensional array of semiconductor spin qubits. Phys. Rev. Appl. 6, 054013. doi:10.1103/physrevapplied.6.054013

CrossRef Full Text | Google Scholar

Zakrzewski, J. (2012). Viewpoint: crystals of Time physics.aps.org. APS Phys. Archived Orig. 2 Febr., 2017. doi:10.1103/Physics.5.116

CrossRef Full Text | Google Scholar

Zeng, Z., Finocchio, G., and Jiang, H. (2013). Spin transfer nano-oscillators. Nanoscale 5 (6), 2219–2231. doi:10.1039/c2nr33407k

PubMed Abstract | CrossRef Full Text | Google Scholar

C. M. Zetterling (2002). Process technology for silicon carbide devices (Institution of Electrical Engineers).

Google Scholar

Zhang, B., Liu, X. T., Wang, J., and Tang, C. J. (2016). Quantum teleportation of an arbitrary N-qubit state via GHZ-like states. Int. J. Theor. Phys. 55, 1601–1611. doi:10.1007/s10773-015-2798-5

CrossRef Full Text | Google Scholar

Zhang, L., Zhou, J., Li, H., Shen, L., and Feng, Y. P. (2021). Recent progress and challenges in magnetic tunnel junctions with 2D materials for spintronic applications. Appl. Phys. Rev. 8 (2), 021308. doi:10.1063/5.0032538

CrossRef Full Text | Google Scholar

Zhang, Q., Takesue, H., Nam, S. W., Langrock, C., Xie, X., Baek, B., et al. (2008). Distribution of time-energy entanglement over 100 km fiber using super-conducting single photon detectors. Opt. Express 16, 5776–5781. doi:10.1364/oe.16.005776

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, T. C., Goh, K. W., Chou, C. W., Lodahl, P., and Kimble, H. J. (2003). Quantum teleportation of light beams. Phys. Rev. A 67, 033802. doi:10.1103/physreva.67.033802

CrossRef Full Text | Google Scholar

Zhou, R. G., Li, X., Qian, C., and Ian, H. (2020). Quantum bidirectional teleportation 2↔ 2 or 2↔ 3 Qubit teleportation protocol via 6-Qubit entangled state. Int. J. Theor. Phys. 59, 166–172. doi:10.1007/s10773-019-04306-1

CrossRef Full Text | Google Scholar

Zhou, R. G., Xu, R., and Lan, H. (2019). Bidirectional quantum teleportation by using six-qubit cluster state. Ieee Access 7, 44269–44275. doi:10.1109/access.2019.2901960

CrossRef Full Text | Google Scholar

Zhou, R.-G., Zhang, Y. N., Xu, R., Qian, C., and Hou, I. (2019c). Asymmetric bidirectional controlled teleportation by using nine-qubit entangled state in noisy environment. IEEE Access 7, 75247–75264. doi:10.1109/access.2019.2920094

CrossRef Full Text | Google Scholar

Zhou, Y., and Ramanathan, S. (2015). Mott memory and neuromorphic devices. Proc. IEEE 103 (8), 1289–1310. doi:10.1109/JPROC.2015.2431914

CrossRef Full Text | Google Scholar

Zmuidzinas, J., and Richards, P. L. (2004). Superconducting detectors and mixers for millimeter and submillimeter astrophysics. Proc. IEEE 92 (10), 1597–1616. doi:10.1109/jproc.2004.833670

CrossRef Full Text | Google Scholar

Zuo, X., Liu, Y., Zhang, W., and Zhang, Z. (2009). Simpler criterion on W state for perfect quantum state splitting and quantum teleportation. Sci. China Ser. G Phys. Mech. Astronomy 52 (12), 1906–1912. doi:10.1007/s11433-009-0305-9

CrossRef Full Text | Google Scholar

Žutić, I., Fabian, J., and Sarma, S. D. (2004). Spintronics: fundamentals and applications. Rev. Mod. Phys. 76 (2), 323–410. doi:10.1103/revmodphys.76.323

CrossRef Full Text | Google Scholar

Zwerver, A. M. J., Krähenmann, T., Watson, T. F., Lampert, L., George, H. C., Pillarisetty, R., et al. (2022). Qubits made by advanced semiconductor manufacturing. Nat. Electron 5, 184–190. doi:10.1038/s41928-022-00727-9

CrossRef Full Text | Google Scholar