Free vibration analysis of functionally graded graphene platelet-reinforced metal foam doubly curved panel

In this research, free vibration characteristics of functionally graded metal foam doubly curved panels reinforced with graphene platelets and with porosities have been surveyed. Halpin Tsai's approach is utilized for extracting the effective Young modulus of porous metal foam nanocomposite and also the effective density of nanocomposite porous doubly curved shell panel is estimated by using an extended rule of mixture. The FSDT hypothesis is utilized for determining the displacement field and the Finite element and Hamilton principle are utilized for deriving the mass and stiffness matrices of the structure. Finally, the influences of several variables such as porosity distribution, porosity coefficient, GPL dispersion pattern, the weight fraction of Nanofillers, and span angles on the free vibrations characteristics of doubly curved shell panels with FG porosities and reinforced by graphene platelet have been reported in detail.

1 Introduction

Composite materials, including functionally graded materials (FGMs), play a pivotal role in various industries due to their unique combination of properties, such as high strength-to-weight ratio and corrosion resistance (Hucke, 1971; Shen and Bever, 1972; Mahamood et al., 2017). The importance of composites lies in their ability to provide enhanced performance compared to traditional materials. To ensure their effectiveness, researchers employ rigorous evaluation methods to assess material properties. These methods include mechanical testing, non-destructive testing, and advanced analytical techniques (Voigt, 1889; Hill, 1965; Halpin and Tsai, 1969; Mori and Tanaka, 1973; Wakashima and Tsukamoto, 1991). Understanding and optimizing these properties are crucial for developing lightweight and durable structures in the aerospace, automotive, and construction industries. Researchers study composite structures (Wattanasakulpong and Chaikittiratana, 2015; Sobhani et al., 2021; Civalek et al., 2022) even in nanoscience (Saffari et al., 2017; Penna et al., 2021; Penna et al., 2022; Lovisi, 2023; Penna, 2023) to push the boundaries of material science, aiming for innovations that improve efficiency, sustainability, and overall performance in diverse applications (Dastjerdi et al., 2020a; Dastjerdi et al., 2020b).

Nowadays, scholars are evaluating the performance of structures that are made of polymeric and metallic nanocomposite in practical applications subjected to various loadings. Also, some of these structures have been employed in various industries like aerospace, marine, automobile, etc. One of the most important characteristics of these structures is their low weight in connection with high stiffness. On the other hand, adding the nanoparticles to the matrix (polymer or metal) does not change the weight of the structure considerably but it can more significantly increase its stiffness. It is mentioned that these nanoparticles may decrease the stiffness of structures. Since, the nanoparticles have a high level of energy and if their weight fraction is more than a certain amount in the matrix, the nanoparticles stick together and agglomeration will occur. There are many investigations about determining the maximum weight fraction of various nanofillers. Two famous examples of nanoparticle reinforcement which recently attracted the attention of researchers are carbon nanotubes (CNTs) and graphene platelets (GPLs). Since many studies have been conducted into structures that are reinforced with these nanoparticles, studies are considered which are related to the free vibration characteristics of shell-type structures reinforced by GPLs. Babaei et al. (Mollaei et al., 2023) presented free vibrations of functionally graded graphene reinforced composite (FG-GPL RC) cylindrical shell panels employing three-dimensional FEM. Hamilton principle was applied to obtain the governing equations. Amirabadi et al. (Amirabadi et al., 2022) employed third-order shear deformation theory (TSDT) combined with generalized differential quadrature (GDQ) procedure to predict the free vibration behavior of rotating FG- GPL conical shells for various boundary conditions. Dynamic characteristics of FG-GPL shells with piezoelectric patches assuming nonlinear behavior for electro-elastic coupling were presented by Rao et al. (Rao et al., 2018). Nguyen Van Do and Hyung Lee (Van Do and Lee, 2020a) evaluated static bending and natural frequencies of FG-GPL RC cylindrical shell panels employing FSDT and utilizing the isogeometric method. Applying classical shell theory and the Rayleigh-Ritz technique, the free vibration response of sandwich FG-GPL cylindrical shells was studied by Permoon, Farsadi, and Askarian (Permoon et al., 2023). Dynamic characteristics of an FG-GPL conical structure applying Jacobi-Ritz solution were presented by Zhao et al. (Zhao et al., 2023). Free vibration characteristics of rotating 2D FG-GPL conical shells supporting an elastic medium employing FSDT were presented by Amirabadi et al. (Amirabadi et al., 2021). Mohammadi et al. (Mohammadi, 2023) applied isogeometric procedure and higher order shear deformation theory (HSDT) to evaluate free vibrations of trapezoidally corrugated FG-GPL RC laminated cylindrical panels. Mohammadi, Shojaei, and Kiani (Mohammadi et al., 2023) presented an isogeometric method for free vibrations of FG-GPL panel-type structures based on the Kirchhoff–Love shell hypothesis. Liu et al. employing an analytical model (Amirabadi et al., 2023) presented 3D buckling and free vibration behavior of pre-stressed FG-GPL RC cylinders. Dong et al. (Dong et al., 2022) combined GDQM and trigonometric expansion analysis to evaluate the vibration behavior of FG-GPL RC conical shells assuming the ring as a frequency controller based on FSDT. Dong et al. (Dong et al., 2018a) performed an investigation about the influences of rotation and axial force simultaneously on the geometrically nonlinear free vibrations of FG-GPL RC cylinders applying Donnell's theory and an analytical solution. Based on HSDT, the natural frequency characteristics of FG-GPL cylindrical and spherical shell-type panels by employing isogeometric solution were presented by Nguyen Van Do and Hyung Lee (Van Do and Lee, 2020b). Liu et al. (Liu et al., 2021) used three-dimensional elasticity assumptions and an analytical layer-wise solution for the investigation of free vibration characteristics of FG GPL spherical shells. Traveling wave evaluation of a rotating FG-GPL RC cylinder for several boundary conditions according to Donnell shell theory was conducted by Qin et al. (Qin et al., 2019). Utilizing FSDT as a theory and using GDQM as a solution, natural frequencies of FG-GPL cylinders resting on various types of elastic foundations for different BCs were presented by Sobhani et al. (Sobhani et al., 2023a). Sobhani and Avcar (Sobhani and Avcar, 2022) examined various nanofiller materials' effects on the free vibration of cylindrical shells employing FSDT and using GDQM as a numerical solution.

Free vibrations characteristic of FG-GPL doubly curved shell structures have been studied in few articles. The differences between these works are usually in methodology. In detail, Wang et al. (Wang et al., 2018) introduced an analytical model for obtaining natural frequencies of FG doubly curved panels reinforced by GPLs based on HSDT. Free vibration responses of FG GPLs doubly curved shells based on HSDT were presented by Adamian (Adamian et al., 2020). Employing FSDT and Ritz solution, free vibrations of FG-GPL doubly curved panels were presented by Esmaili et al. (Esmaeili et al., 2022). In another investigation by considering the same hypothesis and solution, they (Esmaeili and Kiani, 2022) studied thermal induced vibration responses of GPL RC doubly curved panels. Free vibrations of FG-GPL RC doubly curved shell-type structures in thermal conditions employing Reddy’s HSDT and using an analytical model were developed by Shen et al. (Shen et al., 2019). Sobhi, Ashraf, and Zenkour (Sobhy and Zenkour, 2019) proposed an analytical model for free vibration analysis of FG-GPL RC doubly-curved panels supported on elastic foundations based on an HSDT.

The weight of the structure is too prominent in the aerospace industry and the low weight of the structure can be useful for other applications where saving energy is important. One of the ways to decrease the weight of a structure is BY creating pores in it; the stiffness of the structure also will decrease. To compensate for the decrease in stiffness of the structures, these structures can be reinforced with nanoparticles. Hence, scholars have examined the various types of structures which were fabricated by FG porous material reinforced by nanoparticles. Due to there being many investigations in this field, we review the articles which are related to the vibration behavior of shell structures made of FG porous material reinforced by GPLs. In detail, Bahaadini et al. (Bahaadini et al., 2019) proposed an analytical model for obtaining natural frequencies of FG-GPL RC conical shells with FG porosities employing Love’s first approximation assumptions. Ye and Wang (Ye and Wang, 2021) employed the Galerkin method to study the resonance phenomenon in an FG- GPL cylinder with FG porosities based on Donnell’s nonlinear assumptions. Wang et al. (Wang et al., 2019) conducted an investigation into the nonlinear vibrations of a porous cylinder reinforced with GPLs nanofillers by employing the Galerkin approach and Donnell nonlinear hypothesis. Moradi Dastjerdi and Behdinan (Moradi-Dastjerdi and Behdinan, 2021) presented an axisymmetric meshless model according to moving least squares approximations for obtaining the stress waves in porous cylindrical shells reinforced by GPL nanofillers exposed to thermal conditions. Nonlinear free vibrations of FG-GPL imperfect cylinders with FG porosities employing FSDT were performed by means of an analytical model by Salehi et al. (Salehi et al., 2023). Nejadi et al. (Nejadi et al., 2021) presented a GDQM numerical model as a semi-analytical formulation for free vibrations of sandwich cylinders based on FSDT and by assuming porosity and GPL sense on transfering fluid flow. Zhou et al. (Zhou et al., 2021) employ Reddy theory and the standard Lagrange model to illustrate free vibrations of FG GPL cylinders with FG porosities under supersonic load. Ton-That et al. (Ton-That et al., 2021) reported the nonlinear forced vibrations of FG-GPL cylinders with FG porosity effects by applying nonlinear Donnell assumptions and the Galerkin solution. Ebrahimi et al. (Ebrahimi et al., 2019) presented an analytical model for free vibration analysis of FG –GPL cylinders with FG porosities employing the FSDT as a theory. Pourjabari et al. (Pourjabari et al., 2019) analytically reported the free and forced vibrations characteristic of the FG-GPL cylinders in a micro sense employing modified strain gradient theory. Free vibrations of FG-GPL cylinders considering various FG porosity patterns were presented by Barati and Zenkour (Barati and Zenkour, 2019). Kiarasi et al. (Kiarasi et al., 2021) utilized FEM as a numerical solution and two-dimensional axisymmetric elasticity as an accurate theory to study the free vibrations of FG-GPL RC joined conical–cylindrical structure considering FG porosities. Zhang et al. (Zhang et al., 2023) examined free vibrations characteristic of FG-GPL joined hemispherical–cylindrical–hemispherical structure with FG porosities by using 3D elasticity based on FEM. Cho (Cho, 2023) applied FSDT and two-dimensional FE solution to present free vibration characteristics of FG –GPL cylindrical panels with FG porosities. Twinkle and Pitchaimani (Twinkle and Pitchaimani, 2021) examined the influence of FG-GPL reinforcement and FG porosities on the free vibrations and stability of porous GPL-reinforced cylindrical shell panels according to HSDT and utilizing Galerkin solution. Salehi et al. (Salehi et al., 2023) proposed a novel analytical model for geometrically nonlinear vibrations of FG-GPL RC imperfect cylinders with FG porosities employing FSDT. A novel analytical model for investigating the traveling wave vibrations of rotating FG GPL joined conical-cylindrical structures considering FG porosities applying Donnell’s assumptions was reported by Chai and Wang (Chai and Wang, 2022).

The above literature review shows that in the most of investigations, structures with simple shapes and governing equations like cylindrical and conical shells have been considered, and free vibrations of porous metal foam FG-GPL doubly curved panels have not been investigated so far. In this investigation, FSDT as a theory and FEM as a numerical solution are applied to investigate the natural frequency characteristics of porous FG-GPL metal foam doubly curved panels. Four distinct porosity distributions combined with five different GPL dispersion functions are assumed through the thickness of the structures. The porosity distributions are assumed with symmetric, asymmetric, and uniform patterns through the thickness of the structure. Two distributions of porosity are employed for a symmetric pattern. In one of them, the pores are mainly concentrated at the upper and lower surfaces of the doubly curved shell panel and in the other, the concentration of pores at the upper and lower surfaces of the structure is too low. In asymmetric porosity distribution, the number of pores at the structure’s thickest point is low and the number of pores gradually increases from the structure’s least to most thick points. Five distinct GPL dispersion functions are supposed via the thickness of the shell panel: GPLX, GPLO, GPLA, GPLV, and GPLUD. The effect of various variables including porosity distribution, porosity coefficient, GPL dispersion pattern, weight fraction of GPLs, and span angles on the free vibration characteristics of FG porous nanocomposite structure have been studied. In Section 2, the effective mechanical properties of the structure are presented by proposing the Halpin-Tsai model and extension rule of mixture. Then, in Section 3, the finite element procedure and Rayleigh-Ritz method are utilized for extracting the stiffness and mass matrix of FG porous doubly curved panel reinforced with GPLs.Finally, in Section 4 the numerical results of the natural frequencies of the structures are presented and discussed in detail. The most prominent finding results are presented in the conclusion section.

2 Governing equations of porous FG-GPL RC doubly curved shell panel

2.1 Description of the Geometry

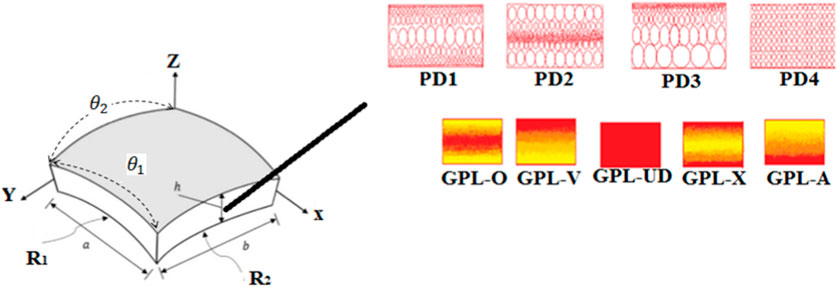
Figure 1 denotes the geometrical parameters of the FG porous metal foam doubly-curved panel reinforced by GPLs, where h is the thickness of the shell structure, R₁ and R₂ are the radiuses of curvature, ${\theta }_1$ and ${\theta }_2$ represent the span angles of a doubly curved shell, respectively. Also, four distinct porosity patterns combined with five GPL dispersion functions are depicted in Figure 1.

FIGURE 1

FIGURE 1. The schematic of FG porous nanocomposite doubly curved shell panel.

2.2 Obtaining the equal mechanical properties of FG porous doubly curved panel reinforced with graphene platelet:

Four different porosity functions are supposed via the thickness of the doubly curved panel. (See Figure 1) and their relation to changing mechanical properties including Young modulus and density along the structure thickness is shown in Eqs 1–4. Besides, five GPL dispersion functions through the thickness of a doubly curved panel are shown in Figure 1; Eq. 16 (Anirudh et al., 2019; Li and Zheng, 2020; Moradi-Dastjerdi and Behdinan, 2020; Zhao et al., 2020).

Nonlinear symmetric porosity function 1:

$\left\{\begin{array}{l}E\left(\mathrm{\Upsilon }\right)=E^{*}\left[1-e_0^1\cos \left(\pi \mathrm{\Upsilon }\right)\right]\\ G\left(\mathrm{\Upsilon }\right)=G^{*}\left[1-e_0^1\cos \left(\pi \mathrm{\Upsilon }\right)\right]\\ \rho \left(\mathrm{\Upsilon }\right)={\rho }^{*}\left[1-e_0^1\cos \left(\pi \mathrm{\Upsilon }\right)\right]\end{array}\right.(1)$

where $\mathrm{\Upsilon }$ = z/h

Nonlinear symmetric porosity function 2:

$\left\{\begin{array}{l}E\left(\mathrm{\Upsilon }\right)=E^{*}\left[e_0^2\left(1-\cos \left(\pi \mathrm{\Upsilon }\right)\right)\right]\\ G\left(\mathrm{\Upsilon }\right)=G^{*}\left[e_0^2\left(1-\cos \left(\pi \mathrm{\Upsilon }\right)\right)\right]\\ \rho \left(\mathrm{\Upsilon }\right)={\rho }^{*}\left[e_m^2\left(1-\cos \left(\pi \mathrm{\Upsilon }\right)\right)\right]\end{array}\right.(2)$

Nonlinear asymmetric porosity function 3:

$\left\{\begin{array}{l}E\left(\mathrm{\Upsilon }\right)=E^{*}\left[e_0^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+\pi /4\right)\right)\right]\\ G\left(\mathrm{\Upsilon }\right)=G^{*}\left[e_0^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+\pi /4\right)\right)\right]\\ \rho \left(\mathrm{\Upsilon }\right)={\rho }^{*}\left[e_m^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+\pi /4\right)\right)\right]\end{array}\right.(3)$

Uniform porosity pattern 4:

$\left\{\begin{array}{l}E=E^{*}{e}_0^4\\ G=G^{*}{e}_0^4\\ \rho ={\rho }^{*}{e}_m^4\end{array}\right.(4)$

΄Where $E^{*}$, $G^{*}$, and ${\rho }^{*}$ are the corresponding material properties of nanocomposite doubly curved panels reinforced with GPL nanofillers but without internal cavities. Also, $e_0^1$, $e_0^2,e_0^3$, and $e_0^4$ (the amounts of them are between zero and one) represents the coefficients of porosity for distribution functions 1, 2, 3, and 4, respectively. $e_m^1,e_m^2,e_m^3$, and $e_m^4$ are related to the mass density coefficient for patterns 1, 2, 3, and 4, respectively.

Mass density and modules of elasticity for open-cell metal foam such as used in this research are dependent as presented in the below Eq. (Gibson and Ashby, 1982; Ashby et al., 2000; Asgari et al., 2022).

$\frac{E\left(\mathrm{\Upsilon }\right)}{E^{*}}={\left(\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }^{*}}\right)}^2(5)$

Eq. 4 is utilized to denote the dependency between the mass density and porosity coefficients for each porosity function as following relations:

$\begin{array}{ll}1-e_m^1\cos \left(\pi \mathrm{\Upsilon }\right)& =\sqrt{1-e_0^1\mathit{cos}\left(\pi \mathrm{\Upsilon }\right)}\hfill \\ {e_m}^2\left(1-\cos \left(\pi \mathrm{\Upsilon }\right)\right)& =\sqrt{e_0^2\left(1-\mathit{cos}\left(\pi \mathrm{\Upsilon }\right)\right)}\hfill \\ e_m^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+pi/4\right)\right)& =\sqrt{e_0^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+pi/4\right)\right)}\hfill \\ e_m^4& =\sqrt{e_0^4}\hfill \end{array}(6)$

For comparing the stiffness of different distributions, the analyses should be implemented for the shells with identical masses. Hence, it is supposed that the mass of doubly curved shell panels with different porosity functions and nanofiller dispersion functions are similar:

$\begin{array}{l}\hfill {\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\sqrt{1-e_0^1\mathit{cos}\left(\pi \mathrm{\Upsilon }\right)}\mathrm{d}\Upsilon ={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\sqrt{e_0^2\left(1-\mathit{cos}\left(\pi \mathrm{\Upsilon }\right)\right)}d\mathrm{\Upsilon }\\ \hfill & ={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\sqrt{e_0^3\left(1-\cos \left(\pi \mathrm{\Upsilon }/2+pi/4\right)\right)}d\mathrm{\Upsilon }=\sqrt{e_0^4}\hfill \end{array}(7)$

Based on Eq. 7, the amounts of $e_0^2,e_0^3$ and $e_0^4$ may be evaluated with a known value of $e_0^1$. Details of these coefficients are presented in Table 1. When $e_0^1$ reaches 0.6, $e_0^2$ (=0.9612) is near to the upper bound. This justifies the selection of $e_0^1$ ∈ [0,0.6] hereafter.

TABLE 1

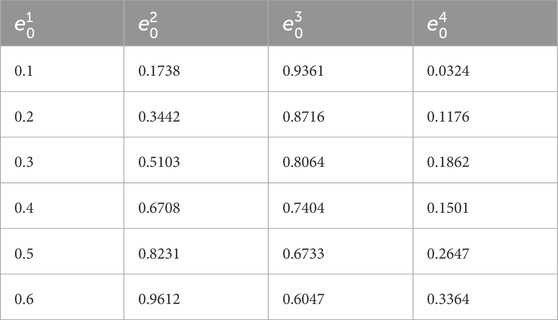
TABLE 1. Porosity coefficients for various patterns (Dong et al., 2018b; Yang et al., 2018).

The Young’s modulus of the doubly curved panel fabricated by metallic nanocomposite without porosity based on the Halpin-Tsai micromechanics model (Choi and Lakes, 1995; Liu, 1997; Arshid et al., 2020; Arshid et al., 2021; Ebrahimi et al., 2021) is calculated as the following:

$E^{*}=\frac{3}{8}\left(\frac{1+{\epsilon }_L^{GPL}{\eta }_L^{GPL}{V}_{GPL}}{1-{\eta }_L^{GPL}{V}_{GPL}}\right)E_m+\frac{5}{8}\left(\frac{1+{\epsilon }_W^{GPL}{\eta }_W^{GPL}{V}_{GPL}}{1-{\eta }_W^{GPL}{V}_{GPL}}\right)(8)$

in which

${\epsilon }_L^{GPL}=\frac{2l_{GPL}}{t_{GPL}}(9)$

${\epsilon }_W^{GPL}=\frac{2w_{GPL}}{t_{GPL}}(10)$

${\eta }_L^{GPL}=\frac{E_{GPL}-E_m}{E_{GPL}+{\epsilon }_L^{GPL}{E}_m}(11)$

${\eta }_W^{GPL}=\frac{E_{GPL}-E_m}{E_{GPL}+{\epsilon }_W^{GPL}{E}_m}(12)$

The mechanical properties of GPLs are shown with subscripts of GPL. Additionally, the subscripts of m are utilized for showing the corresponding mechanical properties of matrix material. The volume amount of nanofillers is indicated with $V_{GPL}$. $l_{GPL}$, $w_{GPL}$, and $t_{GPL}$ symbols are hired for showing the length, width, and thickness of nanofillers, respectively (Arshid et al., 2020; Zhao et al., 2020; Ebrahimi et al., 2021).

According to the rule of mixture, mass density and Poisson's ratio of the shell are obtained as below Eqs (Guo et al., 2021; Babaei, 2022):

${\rho }^{*}={\rho }_{GPL}{V}_{GPL}+{\rho }_m\left(1-V_{GPL}\right)(13)$

$v^{*}=v_{GPL}{V}_{GPL}+v_m\left(1-V_{GPL}\right)(14)$

Accordingly, the shear modulus of the shell is expressed below:

$G^{*}=\frac{E^{*}}{2\left(1+v^{*}\right)}(15)$

Also, the $V_{GPL}$ for various GPL dispersion functions varies through the shell’s thickness and may be obtained by using the below Eq (see also Figure 1):

$V_{GPL}\left(z\right)=\left\{\begin{array}{l}\begin{array}{l}{t}_{i1}\left[1-\cos \left(\pi \mathrm{\Upsilon }\right)\right]GPL-X\\ t_{i2}\left[\cos \left(\pi \mathrm{\Upsilon }\right)\right]GPL-O\\ t_{i3}GPL-UD\\ t_{i4}\left[1-\cos \left(\frac{\pi }{4}-\frac{\pi }{2}\mathrm{\Upsilon }\right)\right]GPL-A\end{array}\\ t_{i5}\left[\cos \left(\frac{\pi }{4}-\frac{\pi }{2}\mathrm{\Upsilon }\right)\right]GPL-V\end{array}\right\}(16)$

Where $t_{i1},t_{i2},t_{i3},t_{i4}$, and $t_{i5}$ denote the upper limit of the $V_{GPL}$, and subscript i =1, 2, 3, and 4 denote corresponding parameters for porosity functions 1, 2, 3, and 4 within each pattern. $V_{GPL}^T$ is the total volume amount of nanofillers and it is obtained by substituting the GPLs weight fraction ${\Delta }_{GPL}$ into Eq. 16. Hence, $t_{i1},t_{i2},t_{i3},t_{i4}$, and $t_{i5}$ may be obtained by Eq. 18 (Esmaeili et al., 2022).

$V_{GPL}^T=\frac{{\Delta }_{GPL}{\rho }_m}{{\Delta }_{GPL}{\rho }_m+{\rho }_{GPL}-{\Delta }_{GPL}{\rho }_{GPL}}(17)$

$V_{GPL}^T{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }_c}d\mathrm{\Upsilon }=\left\{\begin{array}{l}{t}_{i1}{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left[1-\cos \left(\pi \mathrm{\Upsilon }\right)\right]\frac{\rho \left(\varsigma \mathrm{\Upsilon }\right)}{{\rho }_c}d\psi \\ t_{i2}{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left[\cos \left(\pi \mathrm{\Upsilon }\right)\right]\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }_c}d\psi \\ t_{i3}{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }_c}d\mathrm{\Upsilon }\\ t_{i4}{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left[1-\cos \left(\frac{\pi }{4}-\frac{\pi }{2}\mathrm{\Upsilon }\right)\right]\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }_c}d\mathrm{\Upsilon }\\ t_{i5}{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}}\left[\cos \left(\frac{\pi }{4}-\frac{\pi }{2}\mathrm{\Upsilon }\right)\right]\frac{\rho \left(\mathrm{\Upsilon }\right)}{{\rho }_c}d\mathrm{\Upsilon }\end{array}\right.(18)$

2.3 FSDT shell theory equations

FSDT shell theory is hired to present the displacements of doubly curved shell panels as follows:

$\begin{array}{ll}\mathrm{u}& ={\mathrm{u}}_0+\mathrm{z}\alpha \hfill \\ \mathrm{v}& ={\mathrm{v}}_0+\mathrm{z}\beta \hfill \\ \mathrm{w}& ={\mathrm{w}}_0\hfill \end{array}(19)$

In Eq. 2, u, v, and w, are displacements along the x, y, and z axes, respectively, while ${\mathrm{u}}_0$, ${\mathrm{v}}_0$, and ${\mathrm{w}}_0$ are the same displacements at the mid-plane of the shell. Also, $\alpha$ and $\beta$ are normal transverse rotations around y and x, respectively. Hence, the strain field of the doubly curved shell panel is as follows:

$\begin{array}{ll}{\epsilon }_x& ={\epsilon }_x^0+\mathrm{z}{k}_x,{\epsilon }_y={\epsilon }_y^0+\mathrm{z}{k}_y\\ {\gamma }_{xy}& ={\gamma }_{xy}^0+\mathrm{z}{k}_{xy},{\gamma }_{xz}={\gamma }_{xz}^0,{\gamma }_{yz}={\gamma }_{yz}^0\end{array}(20)$

where

$\begin{array}{ll}{\epsilon }_x^0& =\frac{\partial u_0}{\partial x}-\frac{w}{R_1},{\epsilon }_y^0=\frac{\partial v_0}{\partial y}-\frac{w}{R_2}\\ k_{\mathrm{x}}& =\frac{\partial \alpha }{\partial x},k_y=\frac{\partial \beta }{\partial y},k_{xy}=\frac{\partial \alpha }{\partial y}+\frac{\partial \beta }{\partial x}\\ {\gamma }_{xz}^0& =\frac{\partial w}{\partial x}+\alpha ,{\gamma }_{yz}^0=\frac{\partial w}{\partial y}+\beta ,{\gamma }_{xy}^0=\frac{\partial v_0}{\partial x}+\frac{\partial u_0}{\partial y}-2\frac{w}{R_{12}}\end{array}(21)$

Therefore, the matrix form of Eq. 21 will be as:

$\begin{array}{l}\left[\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\end{array}\right]=\left\{\begin{array}{l}{\epsilon }_x^0\\ {\epsilon }_y^0\\ {\gamma }_{xy}^0\end{array}\right\}+z\left\{\begin{array}{l}{k}_x\\ k_y\\ k_{xy}\end{array}\right\}=\left[\begin{array}{ccccc}\frac{\partial }{\partial x}& 0& -\frac{1}{R_1}& z\frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial y}& -\frac{1}{R_2}& 0& z\frac{\partial }{\partial y}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& \frac{-2}{R_{12}}& \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]\left[\begin{array}{c}{u}_0\\ v_0\\ w_0\\ \alpha \\ \beta \end{array}\right]=d_{1}Q\\ \left\{\begin{array}{c}{\gamma }_{xz}^0\\ {\gamma }_{yz}^0\end{array}\right\}=\left[\begin{array}{ccccc}0& 0& \frac{\partial }{\partial x}& 1& 0\\ 0& 0& \frac{\partial }{\partial y}& 0& 1\end{array}\right]\left[\begin{array}{c}{u}_0\\ v_0\\ w_0\\ \alpha \\ \beta \end{array}\right]=d_{2}Q\end{array}(22)$

where

$\begin{array}{ll}\hfill Q& =\left[\begin{array}{l}{u}_0\\ v_0\\ w_0\\ \alpha \\ \beta \end{array}\right],d_1=\left[\begin{array}{ccccc}\frac{\partial }{\partial x}& 0& -\frac{1}{R_1}& z\frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial y}& -\frac{1}{R_2}& 0& z\frac{\partial }{\partial y}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& \frac{-2}{R_{12}}& \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right],\hfill \\ d_2\hfill & =\left[\begin{array}{ccccc}0& 0& \frac{\partial }{\partial x}& 1& 0\\ 0& 0& \frac{\partial }{\partial y}& 0& 1\end{array}\right]\hfill \end{array}$

$\left\{\begin{array}{c}{\epsilon }_x^0\\ {\epsilon }_y^0\\ {\gamma }_{xy}^0\end{array}\right\}=\left[\begin{array}{ccccc}\frac{\partial }{\partial x}& 0& -\frac{1}{R_1}& 0& 0\\ 0& \frac{\partial }{\partial y}& -\frac{1}{R_2}0& 0& 0\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& \frac{-2}{R_{12}}& 0& 0\end{array}\right]\left[\begin{array}{c}{u}_0\\ v_0\\ w_0\\ \alpha \\ \beta \end{array}\right]=d_{3}Q$

$\left\{\begin{array}{c}{k}_x\\ k_y\\ k_{xy}\end{array}\right\}=\left[\begin{array}{ccccc}0& 0& 0& \frac{\partial }{\partial x}& 0\\ 0& 0& 0& 0& \frac{\partial }{\partial y}\\ 0& 0& 0& \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]\left[\begin{array}{c}{u}_0\\ v_0\\ w_0\\ \alpha \\ \beta \end{array}\right]=d_{4}Q$

where

$d_3=\left[\begin{array}{ccccc}\frac{\partial }{\partial x}& 0& -\frac{1}{R_1}& 0& 0\\ 0& \frac{\partial }{\partial y}& -\frac{1}{R_2}0& 0& 0\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& \frac{-2}{R_{12}}& 0& 0\end{array}\right],d_4=\left[\begin{array}{ccccc}0& 0& 0& \frac{\partial }{\partial x}& 0\\ 0& 0& 0& 0& \frac{\partial }{\partial y}\\ 0& 0& 0& \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]$

The constitutive relations of a porous FG-GPL doubly curved shell panel are:

$\begin{array}{l}\left\{\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right\}=\left[\begin{array}{ccc}{C}_{11}& C_{12}& 0\\ C_{12}& C_{22}& 0\\ 0& 0& C_{66}\end{array}\right]\left\{\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\end{array}\right\}\\ \left\{\begin{array}{c}{\tau }_{xz}\\ {\tau }_{yz}\end{array}\right\}=\left[\begin{array}{cc}{C}_{44}& 0\\ 0& C_{55}\end{array}\right]\left\{\begin{array}{c}{\gamma }_{xz}\\ {\gamma }_{yz}\end{array}\right\}\\ C_{11}=C_{22}=\frac{E^{*}}{1-{v^{*}}^2},C_{12}=\frac{v^{*}{E}^{*}}{1-{v^{*}}^2},C_{44}=C_{55}=C_{66}=G^{*}\end{array}(23)$

By integrating the stress field along the thickness direction, resultant moment and force will be:

$\begin{array}{l}\left\{\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right\}={\displaystyle {\int }_{\raisebox{1ex}{$-h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right]dz,\left\{\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right\}={\displaystyle {\int }_{\raisebox{1ex}{$-h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right]zdz\\ \left\{\begin{array}{c}{Q}_x\\ Q_y\end{array}\right\}={\mathrm{K}}^2{\displaystyle {\int }_{\raisebox{1ex}{$-h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[\begin{array}{c}{\tau }_{xz}\\ {\tau }_{yz}\end{array}\right]dz\end{array}(24)$

In Eq. 24, K is the shear correction factor and equals 5/6.

Simplified form of Eq. 24 is as follows:

$\left[\begin{array}{c}\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\\ M_x\\ M_y\end{array}\\ M_{xy}\\ Q_x\\ Q_y\end{array}\right]=\left[\begin{array}{cccccccc}{A}_{11}& A_{12}& 0& B_{11}& B_{12}& 0& 0& 0\\ A_{12}& A_{22}& 0& B_{12}& B_{22}& 0& 0& 0\\ 0& 0& A_{66}& 0& 0& B_{66}& 0& 0\\ B_{11}& B_{12}& 0& D_{11}& D_{12}& 0& 0& 0\\ B_{12}& B_{22}& 0& D_{12}& D_{22}& 0& 0& 0\\ 0& 0& B_{66}& 0& 0& D_{66}& 0& 0\\ 0& 0& 0& 0& 0& 0& K^2{A}_{44}& 0\\ 0& 0& 0& 0& 0& 0& 0& K^2{A}_{55}\end{array}\right]\left\{\begin{array}{c}{\epsilon }_x^0\\ {\epsilon }_y^0\\ {\gamma }_{xy}^0\\ k_x\\ k_y\\ k_{xy}\\ {\gamma }_{xz}^0\\ {\gamma }_{yz}^0\end{array}\right\}(25)$

where:

$\left(A_{ij},B_{ij},D_{ij}\right)={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{C}_{ij}\left(1,z,z^2\right)dz(26)$

The strain and kinetic energies of the doubly curved panel may be presented as the below Eqs.

$\begin{array}{l}\hfill \begin{array}{c}\delta U={\delta U}_1=\frac{1}{2}\iiint {\epsilon }^T\sigma dV\\ \hfill & =\iint \left\{\begin{array}{c}{N}_x{\epsilon }_x^0+N_y{\epsilon }_y^0+N_{xy}{\gamma }_{xy}^0+M_x{K}_x+M_y{K}_y+\\ M_{xy}{K}_{xy}+Q_x{\gamma }_{xz}+Q_y{\gamma }_{yz}\end{array}\right\}\hfill \\ \hfill & dxdy=\int \left(\left({\left(d_{3}Q\right)}^T{A}^T+{\left(d_{4}Q\right)}^T{B}^T\right)\left(d_3\delta Q\right)\right)\hfill \\ \hfill & +\left({\left(d_{3}Q\right)}^T{B}^T+{\left(d_{4}Q\right)}^T{D}^T\right)\left(d_4\delta Q\right)+{\left(d_{2}Q\right)}^T{e}^T\hfill \\ \hfill & \left(d_2\delta Q\right)dxdy\hfill \\ \delta T={\int }_{-\frac{h}{2}}^{\frac{h}{2}}\rho \left(\ddot{u}\delta u+\ddot{v}\delta v+\ddot{w}\delta w\right)dV\end{array}\end{array}(27)$

where:

$\begin{array}{l}\begin{array}{ll}\left\{\begin{array}{l}\delta u=\delta u_0+{z\delta }_{\alpha }\\ \delta v=\delta v_0+{z\delta }_{\beta }\\ \delta w={\delta w}_0\end{array}\right.& \left\{\begin{array}{l}\ddot{u}=\frac{{\partial }^2{u}_0}{\partial t^2}+z\frac{{\partial }^2\alpha }{\partial t^2}\\ \ddot{v}=\frac{{\partial }^2{v}_0}{\partial t^2}+z\frac{{\partial }^2\beta }{\partial t^2}\\ \ddot{w}=\frac{{\partial }^2{w}_0}{\partial t^2}\end{array}\right.\end{array}\\ \delta T=\int {\int }_{-\frac{h}{2}}^{\frac{h}{2}}\rho \left(\left(\frac{{\partial }^2{u}_0}{\partial t^2}+z\frac{{\partial }^2\alpha }{\partial t^2}\right)\left(\delta u_0+{z\delta }_{\alpha }\right)\right)\\ \hfill & +\left(\frac{{\partial }^2{v}_0}{\partial t^2}+z\frac{{\partial }^2\beta }{\partial t^2}\right)\left(\delta v_0+{z\delta }_{\beta }\right)+\frac{{\partial }^2{w}_0}{\partial t^2}{\delta w}_{0}dzdA\hfill \end{array}(28)$

Replacing Eqs 27, 28 Hamilton’s principle, we have:

$\begin{array}{l}\hfill {\int }_{t_1}^{t_2}\left[{\iint }_{-\frac{h}{2}}^{\frac{h}{2}}\rho \left(\left(\frac{{\partial }^2{u}_0}{\partial t^2}+z\frac{{\partial }^2\alpha }{\partial t^2}\right)\left(\delta u_0+{z\delta }_{\alpha }\right)\right)\right]\\ \hfill & +\left(\frac{{\partial }^2{v}_0}{\partial t^2}+z\frac{{\partial }^2\beta }{\partial t^2}\right)\left(\delta v_0+{z\delta }_{\beta }\right)+\frac{{\partial }^2{w}_0}{\partial t^2}{\delta w}_{0}dzdA\hfill \\ \hfill & +\int \left(\left({\left(d_{3}Q\right)}^T{A}^T+{\left(d_{4}Q\right)}^T{B}^T\right)\left(d_3\delta Q\right)+\left({\left(d_{3}Q\right)}^T{B}^T+{\left(d_{4}Q\right)}^T{D}^T\right)\right)\hfill \\ \hfill & \left(d_4\delta Q\right)+{\left(d_{2}Q\right)}^T{e}^T\left(d_2\delta Q\right)dxdydt=0\hfill \end{array}(29)$

2.4 FEM solution of governing equations:

In this section, for solving the governing motion equations of the shell, the graded FE method is used. In conventional FEM, the material property is constant through the element. In GFEM, to treat the material heterogeneity, in addition to the displacement field, the material properties of the FG-GPL porous doubly curved structure could also be determined from their nodal values. This approach leads to a smooth change of the properties along the structure and also obtains more precise results than discretizing the structure into elements with constant properties. By using the interpolation functions of cubic ten nodded triangular element, the displacement field, and material properties of individual element $\left(e\right)$ in terms of the nodal displacement vector q, nodal elasticity modulus $E_i$ and mass density ${\rho }_i$ and shape function matrix $\mathrm{\Psi }$ are as:

$\begin{array}{l}{Q}^{\left(e\right)}=\left(\left(\begin{array}{ccc}{\mathrm{\Psi }}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathrm{\Psi }}_1\end{array}\right)\dots \left(\begin{array}{ccc}{\mathrm{\Psi }}_{10}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathrm{\Psi }}_{10}\end{array}\right)\right)\left\{\begin{array}{c}{u}_{01}\\ v_{01}\\ w_{01}\\ {\alpha }_1\\ {\beta }_1\\ ⋮\\ u_{010}\\ v_{010}\\ w_{010}\\ {\alpha }_{10}\\ {\beta }_{10}\end{array}\right\}=\mathrm{\Psi }q\left(\mathrm{e}\right)\\ E^{*}={\displaystyle \sum _{i=1}^{10}}{E}_i{\psi }_i=\mathrm{\Psi }\mathbf{\Xi },\rho *={\displaystyle \sum _{i=1}^{10}}{\rho }_i{\psi }_i=\mathrm{\Psi }\mathfrak{R}\end{array}(30)$

where ${\mathrm{\Psi }}_n,\mathrm{n}=1,2,\dots ,10$ are the approximation functions and presented in the Appendix. $u_{0i}$, $v_{0i}$, $w_{0i}$, ${\alpha }_i$ and ${\beta }_i$ are nodal DOFs, $\mathbf{\Xi }$ and $\mathfrak{R}$ are respectively vectors containing elasticity modulus and mass density of each node, and are as:

$\begin{array}{l}\psi =\left[\begin{array}{cccccccccc}{\psi }_1& {\psi }_2& {\psi }_3& {\psi }_4& {\psi }_5& {\psi }_6& {\psi }_7& {\psi }_8& {\psi }_9& {\psi }_{10}\end{array}\right],\\ \mathbf{\Xi }={\left[\begin{array}{cccccccccc}{E}_1& E_2& E_3& E_4& E_5& E_6& E_7& E_8& E_9& E_{10}\end{array}\right]}^T\\ \mathfrak{R}={\left[\begin{array}{cccccccccc}{\rho }_1& {\rho }_2& {\rho }_3& {\rho }_4& {\rho }_5& {\rho }_6& {\rho }_7& {\rho }_8& {\rho }_9& {\rho }_{10}\end{array}\right]}^T\end{array}(31)$

Substituting Eqs 30, 31 in Eq. 29 can be rewritten as

$\begin{array}{l}\hfill {\int }_{{\mathrm{\Omega }}_0^e}\left[\left({\left(d_3\mathrm{\Psi }\right)}^T{A}^T{d}_3\mathrm{\Psi }+{\left(d_4\mathrm{\Psi }\right)}^T{B}^T{d}_3\mathrm{\Psi }+{\left(d_3\mathrm{\Psi }\right)}^T{B}^T{d}_4\mathrm{\Psi }\right)\right]\\ \hfill & +{\left(d_4\mathrm{\Psi }\right)}^T{D}^T{d}_4\mathrm{\Psi }+{\left(d_2\mathrm{\Psi }\right)}^T{e}^T{d}_2\mathrm{\Psi }q+{\mathrm{\Psi }}^{T}I\mathrm{\Psi }\ddot{q}dxdy=0\hfill \end{array}(32)$

where $d_2\mathrm{\Psi }=B_2,d_3\mathrm{\Psi }=B_3,d_4\mathrm{\Psi }=B_4$.

${\int }_{{\mathrm{\Omega }}_0^e}\left[\left({B_3}^T{A}^T{B}_3+{B_4}^T{B}^T{B}_3+{B_3}^T{B}^T{B}_4+{B_4}^T{D}^T{B}_4+{B_2}^T{e}^T{B}_2\right)q+{\mathrm{\Psi }}^{T}I\mathrm{\Psi }\ddot{q}\right]dxdy=0(33)$

Rearranging Eq. 33, the FE model of porous FG-GPL RC doubly curved panel element will be as follows:

$\begin{array}{ll}{\left(k_1+k_2+k_3\right)}^{\left(e\right)}{q}^{\left(e\right)}+M^e{\ddot{q}}^{\left(e\right)}& =0\\ k_1^e& ={\int }_{{\mathrm{\Omega }}_0^e}\left[{B_3}^T{A}^T+{B_4}^T{B}^T\right]B_{3}dxdy\\ k_2^e& ={\int }_{{\mathrm{\Omega }}_0^e}\left[{B_3}^T{B}^T+{B_4}^T{D}^T\right]B_{4}dxdy\\ k_3^e& ={\int }_{{\mathrm{\Omega }}_0^e}\left[{B_2}^T{e}^T{B}_2\right]dxdy\\ M^e& ={\int }_{{\mathrm{\Omega }}_0^e}{\mathrm{\Psi }}^{T}I\mathrm{\Psi }dxdy\end{array}(34)$

Where in Eq. 34 and mass matrix of element, [I] may be evaluated as:

$\mathrm{I}=\left[\begin{array}{ccccc}{\mathrm{I}}_0& 0& 0& {\mathrm{I}}_1& 0\\ 0& {\mathrm{I}}_0& 0& 0& {\mathrm{I}}_1\\ 0& 0& {\mathrm{I}}_0& 0& 0\\ {\mathrm{I}}_1& 0& 0& {\mathrm{I}}_2& 0\\ 0& {\mathrm{I}}_1& 0& 0& {\mathrm{I}}_2\end{array}\right](35)$

where ${\mathrm{I}}_{\mathrm{i}},\mathrm{i}=0,1,2$ are

$\left\{\begin{array}{c}{\mathrm{I}}_0\\ {\mathrm{I}}_1\\ {\mathrm{I}}_2\end{array}\right\}={\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left\{\begin{array}{c}1\\ z\\ z^2\end{array}\right\}\rho dz(36)$

By assembly of mass, stiffness, and force matrices of each element, the FE motion equations of the FG-GPL RC doubly curved panel are as

$\left(k_1+k_2+k_3\right)q+M\ddot{q}=0(37)$

The natural frequency problem of the structure may be derived by the solution of the eigenvalue model as follows:

$\left(\left(k_1+k_2+k_3\right)-M{\omega }^2\right)q=0(38)$

where $\omega$ is the circular natural frequency and q is the mode shapes of free vibrations.

The shell is fully clamped at its all edges as:

$u_0,v_0,w_0,\alpha ,\beta =0(39)$

3 Numerical results and discussion

In this part, natural frequencies of FG-GPL porous doubly curved shell panels examined by changing the volume weight fraction of nanofillers, nanofiller dispersion pattern, porosity distribution, and porosity coefficient are investigated in detail. The shell is fully clamped on its four edges.

3.1 Validation

To validate the obtained results of the present research, the first six natural frequencies of isotropic homogenous doubly curved shell panels with clamped edges are extracted employing commercial FEM software ANSYS-WORKBENCH, and the results are compared with the results of the present research. Therefore, one may consider e0=0 and ${\Delta }_{GPL}=0wt\%$ . Also, the dimensions and material properties of the shell are chosen as the following: Geometry: R1=0.225 m, R2=0.4 m, h=0.025m, ${\theta }_1=120°,{\theta }_2=60°$ and Mechanical properties: E=200 GPa, $\mathrm{\upsilon }=0.3,\mathrm{\rho }=7800kg/m^3$

A comparison of the results of the present research with natural frequencies of ANSYS WORKBENCH is presented in Table 2, and it indicates excellent concordance between the results.

TABLE 2

TABLE 2. Comparison of results of present research with natural frequencies of ANSYS WORKBENCH.

3.2 Natural frequencies of FG porous doubly curved shell panel reinforced by GPLs

The influence of coefficients of porosity and distributions of porosity, GPL pattern, and weight fraction of nanofillers and span angles on the natural frequency characteristics of an FG-GPL porous doubly curved shell panel is investigated in this section. Therefore, the below material properties and dimensions are employed:

Geometry: R1=0.225 m, R2=0.4 m, h=0.025m, ${\theta }_1=120°,{\theta }_2=60°$.

Material property: $E_m$ = 130GPa, ${\rho }_m$ = 8960 kg/m3, ${\upsilon }_m$ = 0.34 for copper²⁸, and $E_{GPL}$ = 1.01 TPa, ${\rho }_{GPL}$ = 1062.5 kg/m3, ${\upsilon }_{GPL}$ =0.186 , $w_{GPL}$ = 1.5 μm, $l_{GPL}$ = 2.5 μm, $t_{GPL}$ = 1.5 nm for GPLs (Arshid et al., 2020; Zhao et al., 2020; Ebrahimi et al., 2021).

Table 3 describes the influences of nanofiller patterns on the free vibrations of the porous FG-GPL doubly curved shell panel (${\theta }_1=120°$, PD1,e₀=0.2, ${\Delta }_{GPL}=0.05wt\%$). As it is obvious in this table, the maximum and minimum fundamental frequencies belong to GPLX and GPL-UD, respectively. Concentrating more nanofiller near the upper and lower surfaces of the doubly curved shell panel will result in more stiffness of the shell and consequently higher natural frequencies will be obtained. In addition, for uniform dispersion of nanofillers along the thickness of the structure, the minimum stiffness of the shell and also the lowest natural fundamental frequencies will be created. Also, the results of this table indicate that fundamental frequencies for GPL-A and GPL-V have approximately the same values. Comparing the results of Table 3 shows that the maximum difference between the fundamental frequencies with the change of nanofiller distributions is about 13%. In addition, the results of this table denote that by increasing the span angle ${\theta }_2$ from 60 $°$ to 150 $°$ the natural frequency of the shell rose considerably, by 30%. This is due to the fact that by increasing the span angle, the ratio of stiffness to the mass of the shell increases. The influences of various porosity distributions are reported in Table 4 (${\theta }_1=120°$, GPLX,e₀=0.2, ${\Delta }_{GPL}=0.05wt\%$). The maximum and minimum fundamental frequencies are estimated for PD1 and PD3, respectively. This means that PD1 provides higher rigidity for the shell while PD3 leads to a lower stiffness of the doubly curved shell panel. Comparing the results of Table 4 shows that the maximum difference between fundamental frequencies considering the effect of porosity distributions is about 43%. Also, the results of this table denote that when the distribution of pores is symmetric and their size is more around the mid-pane of the shell, the stiffness of the shell is greater and for the asymmetric distribution of pores, the stiffness of the shell will be lower. The impacts of the weight fraction of nanofillers on the natural frequencies of the porous FG-GPL structure (${\theta }_1=120°$, GPLX, e₀=0.2, PD1) is reported in Table 5. By changing the weight fraction of nanofillers from 0 to 1%, the fundamental frequencies of doubly curved shell panels considerably increase (approximately 80%). The impact of porosity coefficient on the free vibrations characteristics of porous FG-GPL doubly curved shell (${\theta }_1=120°$, GPLX, ${\Delta }_{GPL}=0.05wt\%$, PD1) are indicated in Table 6. This table denotes that by increasing the porosity of the shell, the fundamental frequencies of FG-GPL porous doubly curved shell panels for PD1 decrease by approximately 22%. This is due to the fact that both the mass and stiffness of the structure decrease as the size of pores increases, the decrease of the mass of the shell is more remarkable than its stiffness. Comparing the results of Tables 3–6 illustrates that the natural frequencies are less influenced by GPL distribution than other parameters affecting the frequency of the shell. The first six free vibrations mode shapes of porous FG-GPL doubly curved shell panels for different span angles ${\theta }_2=60°,90°$, and $150°$ are shown in Figures 2–4. As it can be seen in these figures, it is obvious that by increasing the span angle of the doubly curved shell panel, higher free vibration mode shapes with more strain energies are obtained.

TABLE 3

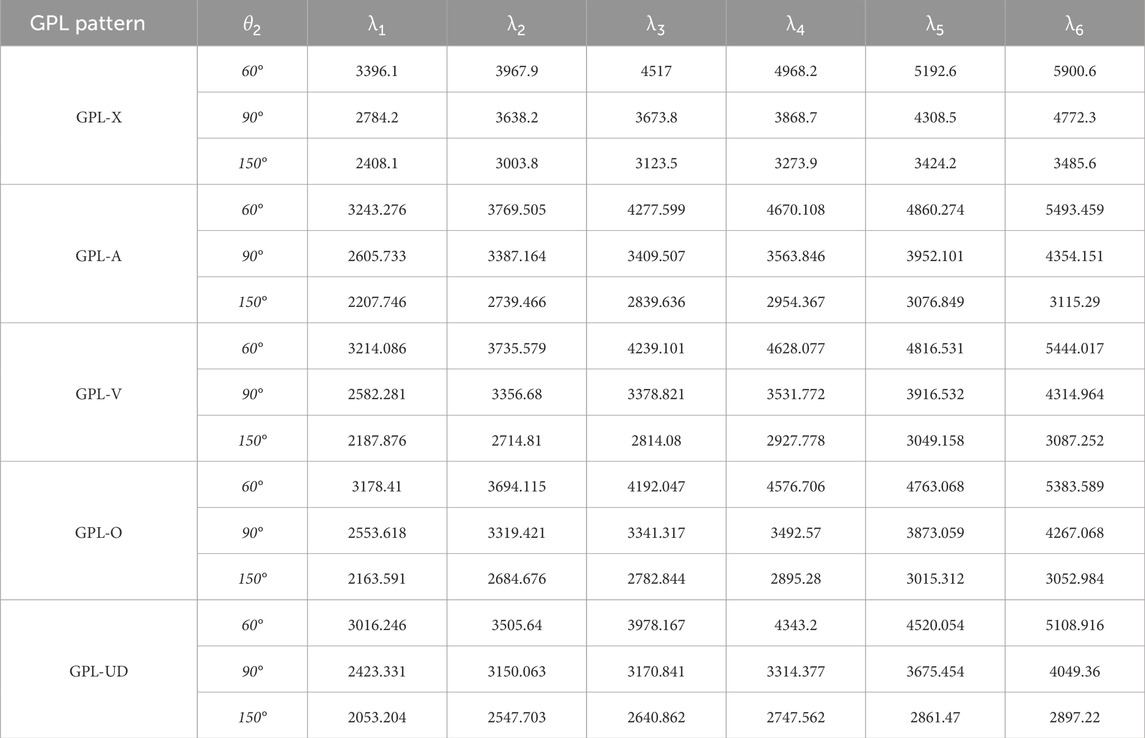
TABLE 3. Natural frequencies of FG- porous doubly curved panel reinforced by graphene nanoparticles for various span angles and GPL pattern (${\theta }_1=120°$, PD1,e₀=0.2, ${\Delta }_{GPL}=0.05wt\%$).

TABLE 4

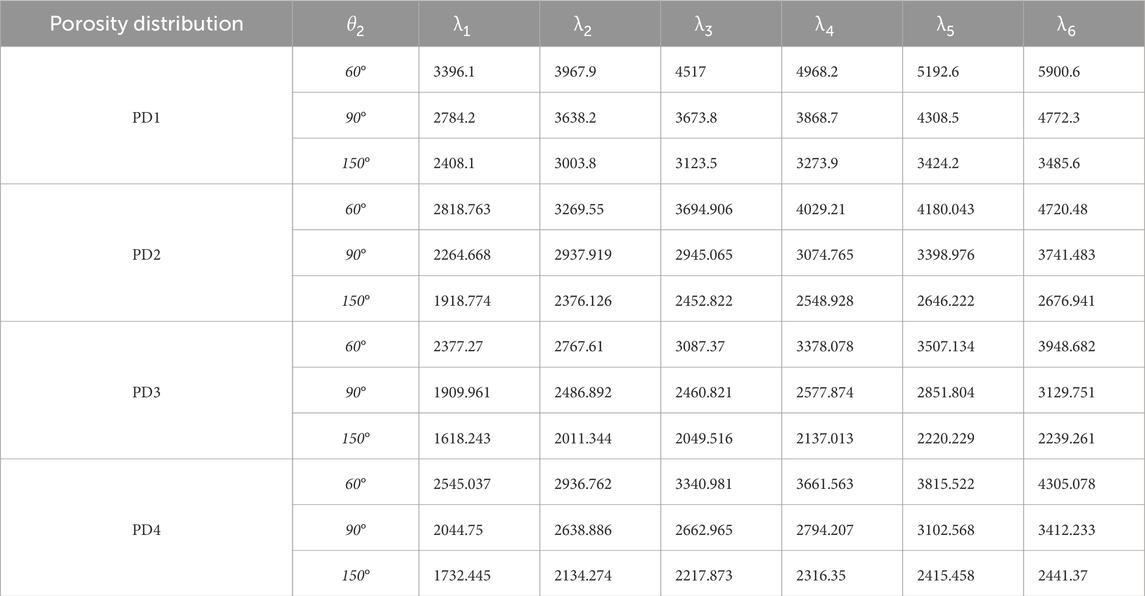
TABLE 4. Natural frequencies of FG- porous doubly curved panel reinforced by graphene nanoparticles for various span angles and porosity distribution (${\theta }_1=120°$, GPLX,e₀=0.2, ${\Delta }_{GPL}=0.05wt\%$).

TABLE 5

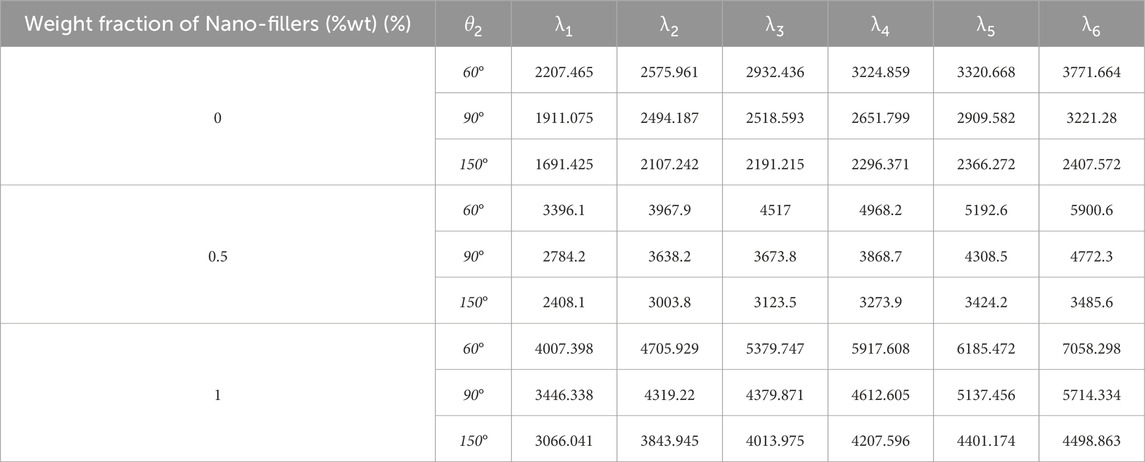
TABLE 5. Natural frequencies of FG- porous doubly curved panel reinforced by graphene nanoparticles for various span angles and weight fraction of nanofiller ( ${\theta }_1=120°$, GPLX, e₀=0.2, PD1).

TABLE 6

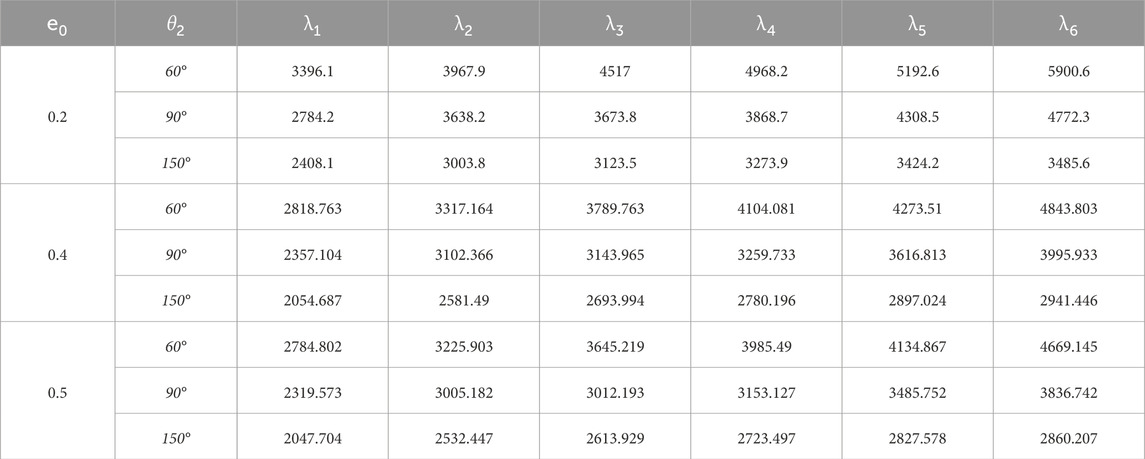
TABLE 6. Natural frequencies of FG- porous doubly curved panel reinforced by graphene nanoparticles for various span angles and porosity coefficients (${\theta }_1=120°$, GPLX, ${\Delta }_{GPL}=0.05wt\%$, PD1).

FIGURE 2

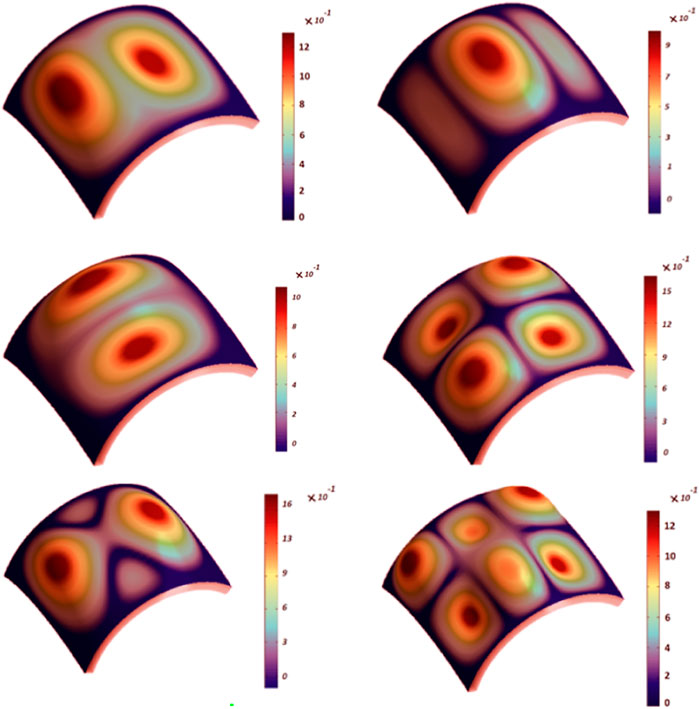
FIGURE 2. The first six mode shapes of FG-GPL porous doubly curved panel (GPLX, ${\Delta }_{GPL}=0.05wt\%$, PD1, e0=0.2, R1=0.225 m, R2=0.4 m, ${\mathrm{\theta }}_1={120}^0,{\mathrm{\theta }}_2={60}^0$).

FIGURE 3

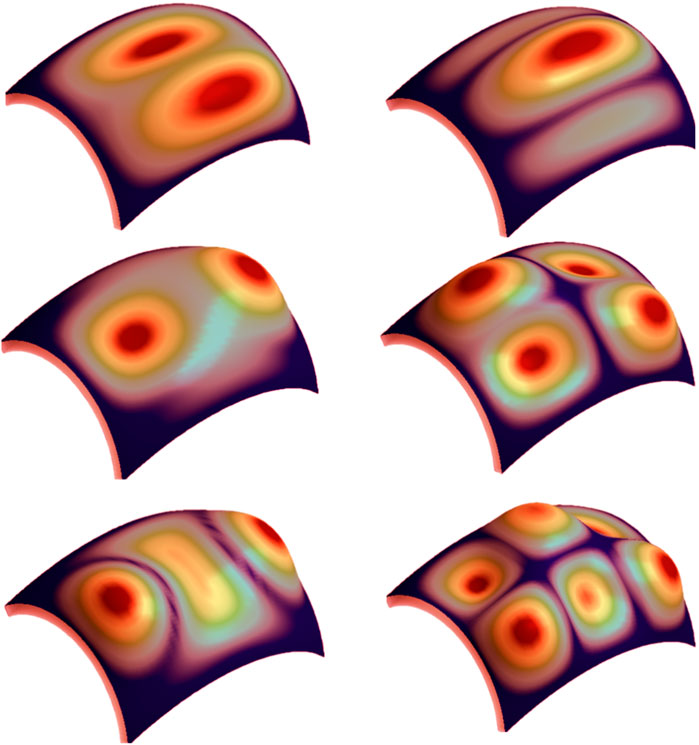
FIGURE 3. The first six mode shapes of FG-GPL porous doubly curved panel (GPLX, ${\Delta }_{GPL}=0.05wt\%$, PD1, e0=0.2, R1=0.225 m, R2=0.4 m, ${\mathrm{\theta }}_1={120}^0,{\mathrm{\theta }}_2={90}^0$).

FIGURE 4

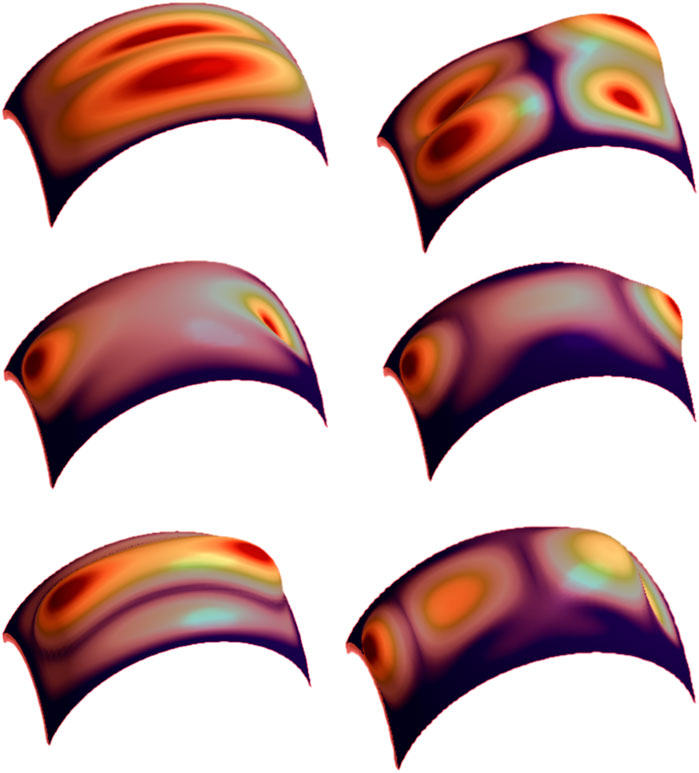
FIGURE 4. The first six buckling mode shapes of FG-GPL porous doubly curved panel (GPLX, ${\Delta }_{GPL}=0.05wt\%$, PD1, e0=0.2, R1=0.225 m, R2=0.4 m, ${\mathrm{\theta }}_1={120}^0,{\mathrm{\theta }}_2={150}^0$).

4 Conclusion

Free vibration characteristics of FG porous metal foam doubly curved shell panel reinforced by GPLs nanofillers have been surveyed in this research. Four distinct porosity functions and five GPL distributions are considered across the shell thickness. Applying FSDT and employing FEM based on the Hamilton principle, the governing motion equations of the shell are derived. The effects of GPL patterns, the weight fraction of nanofillers, porosity coefficient, and pattern and span angles on the free vibration responses of FG-GPL doubly curved panels with FG porosities have been examined. The main results are as:

a) Maximum and minimum fundamental frequencies are obtained for GPL-X and GPL-UD, respectively.

b) The fundamental frequencies of GPL-A and GPL-V are approximately identical.

c) The maximum and minimum fundamental frequencies of the shell have been obtained for PD1 and PD3.

d) By changing ${\Delta }_{GPL}$ from 0 to 1%, the fundamental frequencies of the structure remarkably increase (approximately 80%).

e) By growing the size of the porosity of the structure, the fundamental frequencies of the shell decrease by 22%.

f) The natural frequencies are less influenced by GPL distribution than other parameters (about 13%).

g) By increasing the span angle ${\theta }_2$ from 60 $°$ to 150 $°$, the fundamental frequencies remarkably are enhanced by 30%.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Li-Li Zhang: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Writing original draft, Writing–review & editing. Li-Cai Zhao: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft, Writing–review & editing. Song-Jun Lang: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Writing–original draft, Writing–review & editing. Kamran Asemi: Conceptualization, Investigation, Methodology, Supervision, Validation, Writing–review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author L-CZ was employed by Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adamian, A., Hosseini Safari, K., Sheikholeslami, M., Habibi, M., Al-Furjan, M. S. H., and Chen, G. (2020). Critical temperature and frequency characteristics of GPLs-reinforced composite doubly curved panel. Appl. Sci. 10 (9), 3251. doi:10.3390/app10093251

CrossRef Full Text | Google Scholar

Amirabadi, H., Farhatnia, F., and Civalek, Ӧ. (2021). Frequency response of rotating two-directional functionally graded GPL-reinforced conical shells on elastic foundation. J. Braz. Soc. Mech. Sci. Eng. 43 (7), 349. doi:10.1007/s40430-021-03058-6

CrossRef Full Text | Google Scholar

Amirabadi, H., Farhatnia, F., Eftekhari, S. A., and Hosseini-Ara, R. (2022). Free vibration analysis of rotating functionally graded GPL-reinforced truncated thick conical shells under different boundary conditions. Mech. Based Des. Struct. Mach. 50 (11), 3821–3852. doi:10.1080/15397734.2020.1822183

CrossRef Full Text | Google Scholar

Amirabadi, H., Farhatnia, F., Eftekhari, S. A., and Hosseini-Ara, R. (2023). Wave propagation in rotating functionally graded GPL-reinforced cylindrical shells based on the third-order shear deformation theory. Waves Random Complex Media 33 (2), 345–371. doi:10.1080/17455030.2021.1880031

CrossRef Full Text | Google Scholar

Anirudh, B., Ganapathi, M., Anant, C., and Polit, O. (2019). A comprehensive analysis of porous graphene-reinforced curved beams by finite element approach using higher-order structural theory: bending, vibration and buckling. Compos. Struct. 222, 110899. doi:10.1016/j.compstruct.2019.110899

CrossRef Full Text | Google Scholar

Arshid, E., Amir, S., and Loghman, A. (2020). Static and dynamic analyses of FG-GNPs reinforced porous nanocomposite annular micro-plates based on MSGT. Int. J. Mech. Sci. 180, 105656. doi:10.1016/j.ijmecsci.2020.105656

CrossRef Full Text | Google Scholar

Arshid, E., Amir, S., and Loghman, A. (2021). Thermal buckling analysis of FG graphene nanoplatelets reinforced porous nanocomposite MCST-based annular/circular microplates. Aerosp. Sci. Technol. 111, 106561. doi:10.1016/j.ast.2021.106561

CrossRef Full Text | Google Scholar

Asgari, G. R., Arabali, A., Babaei, M., and Asemi, K. (2022). Dynamic instability of sandwich beams made of isotropic core and functionally graded graphene platelets-reinforced composite face sheets. Int. J. Struct. Stab. Dyn. 22 (08), 2250092. doi:10.1142/s0219455422500924

CrossRef Full Text | Google Scholar

Ashby, M. F., Evans, T., Fleck, N. A., Hutchinson, J., Wadley, H., and Gibson, L. (2000). Metal foams: a design guide. Oxford, United Kingdom: Butterworth-Heinemann.

Google Scholar

Babaei, H. (2022). Thermomechanical analysis of snap-buckling phenomenon in long FG-CNTRC cylindrical panels resting on nonlinear elastic foundation. Compos. Struct. 286, 115199. doi:10.1016/j.compstruct.2022.115199

CrossRef Full Text | Google Scholar

Bahaadini, R., Saidi, A. R., Arabjamaloei, Z., and Ghanbari-Nejad-Parizi, A. (2019). Vibration analysis of functionally graded graphene reinforced porous nanocomposite shells. Int. J. Appl. Mech. 11 (07), 1950068. doi:10.1142/s1758825119500686

CrossRef Full Text | Google Scholar

Barati, M. R., and Zenkour, A. M. (2019). Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech. Adv. Mater. Struct. 26 (18), 1580–1588. doi:10.1080/15376494.2018.1444235

CrossRef Full Text | Google Scholar

Chai, Q., and Wang, Y. Q. (2022). Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Eng. Struct. 252, 113718. doi:10.1016/j.engstruct.2021.113718

CrossRef Full Text | Google Scholar

Cho, J. R. (2023). Free vibration analysis of functionally graded porous cylindrical panels reinforced with graphene platelets. Nanomaterials 13 (9), 1441. doi:10.3390/nano13091441

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, J., and Lakes, R. (1995). Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson's ratio. Int. J. Mech. Sci. 37, 51–59. doi:10.1016/0020-7403(94)00047-n

CrossRef Full Text | Google Scholar

Civalek, Ö., Dastjerdi, S., and Akgöz, B. (2022). Buckling and free vibrations of CNT-reinforced cross-ply laminated composite plates. Mech. Based Des. Struct. Mach. 50 (6), 1914–1931. doi:10.1080/15397734.2020.1766494

CrossRef Full Text | Google Scholar

Dastjerdi, S., Akgöz, B., and Civalek, Ö. (2020a). On the effect of viscoelasticity on behavior of gyroscopes. Int. J. Eng. Sci. 149, 103236. doi:10.1016/j.ijengsci.2020.103236

CrossRef Full Text | Google Scholar

Dastjerdi, S., Akgöz, B., Civalek, Ö., Malikan, M., and Eremeyev, V. A. (2020b). On the non-linear dynamics of torus-shaped and cylindrical shell structures. Int. J. Eng. Sci. 156, 103371. doi:10.1016/j.ijengsci.2020.103371

CrossRef Full Text | Google Scholar

Dong, Y., Gao, Y., Zhu, Q., Moradi, Z., and Safa, M. (2022). TE-GDQE implementation to investigate the vibration of FG composite conical shells considering a frequency controller solid ring. Eng. Analysis Bound. Elem. 138, 95–107. doi:10.1016/j.enganabound.2022.01.017

CrossRef Full Text | Google Scholar

Dong, Y. H., He, L. W., Wang, L., Li, Y. H., and Yang, J. (2018b). Buckling of spinning functionally graded graphene reinforced porous nanocomposite cylindrical shells: an analytical study. Aerosp. Sci. Technol. 82, 466–478. doi:10.1016/j.ast.2018.09.037

CrossRef Full Text | Google Scholar

Dong, Y. H., Zhu, B., Wang, Y., Li, Y. H., and Yang, J. (2018a). Nonlinear free vibration of graded graphene reinforced cylindrical shells: effects of spinning motion and axial load. J. Sound Vib. 437, 79–96. doi:10.1016/j.jsv.2018.08.036

CrossRef Full Text | Google Scholar

Ebrahimi, F., Mohammadi, K., Barouti, M. M., and Habibi, M. (2021). Wave propagation analysis of a spinning porous graphene nanoplatelet-reinforced nanoshell. Waves random complex media 31 (6), 1655–1681. doi:10.1080/17455030.2019.1694729

CrossRef Full Text | Google Scholar

Ebrahimi, F., Seyfi, A., Dabbagh, A., and Tornabene, F. (2019). Wave dispersion characteristics of porous graphene platelet-reinforced composite shells. Struct. Eng. Mech. Int'l J. 71 (1), 99–107. doi:10.12989/sem.2019.71.1.099

CrossRef Full Text | Google Scholar

Esmaeili, H. R., and Kiani, Y. (2022). Vibrations of graphene platelet reinforced composite doubly curved shells subjected to thermal shock. Mech. Based Des. Struct. Mach. 52, 650–679. doi:10.1080/15397734.2022.2120499

CrossRef Full Text | Google Scholar

Esmaeili, H. R., Kiani, Y., and Beni, Y. T. (2022). Vibration characteristics of composite doubly curved shells reinforced with graphene platelets with arbitrary edge supports. Acta Mech. 233 (2), 665–683. doi:10.1007/s00707-021-03140-z

CrossRef Full Text | Google Scholar

Gibson, I. J., and Ashby, M. F. (1982). The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A. Math. Phys. Sci. 382 (1782), 43–59. doi:10.1098/rspa.1982.0088

CrossRef Full Text | Google Scholar

Guo, H., Yang, T., Żur, K. K., Reddy, J. N., and Ferreira, A. J. M. (2021). “Effect of thermal environment on nonlinear flutter of laminated composite plates reinforced with graphene nanoplatelets,” in Modeling and computation in vibration problems, volume 1: numerical and semi-analytical methods (Bristol, United Kingdom: IOP Publishing).

CrossRef Full Text | Google Scholar

Halpin, J. C., and Tsai, S. W. (1969). Effects of environmental factors on composite materials.

Google Scholar

Hill, R. (1965). A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13 (4), 213–222. doi:10.1016/0022-5096(65)90010-4

CrossRef Full Text | Google Scholar

Hucke, E. E. (1971). “Preliminary reports,” in Memoranda and Technical Notes of the ARPA Materials Summer Conference Held at Woods Hole Volume 1, Massachusetts, July 1971. & MICHIGAN UNIV ANN ARBOR DEPT OF MATERIALS AND METALLURGICAL ENGINEERING.

Google Scholar

Kiarasi, F., Babaei, M., Mollaei, S., Mohammadi, M., and Asemi, K. (2021). Free vibration analysis of FG porous joined truncated conical-cylindrical shell reinforced by graphene platelets. Adv. nano Res. 11 (4), 361–380. doi:10.12989/anr.2021.11.4.361

CrossRef Full Text | Google Scholar

Li, Z., and Zheng, J. (2020). Nonlinear stability of the encased functionally graded porous cylinders reinforced by graphene nanofillers subjected to pressure loading under thermal effect. Compos. Struct. 233, 111584. doi:10.1016/j.compstruct.2019.111584

CrossRef Full Text | Google Scholar

Liu, D., Zhou, Y., and Zhu, J. (2021). On the free vibration and bending analysis of functionally graded nanocomposite spherical shells reinforced with graphene nanoplatelets: three-dimensional elasticity solutions. Eng. Struct. 226, 111376. doi:10.1016/j.engstruct.2020.111376

CrossRef Full Text | Google Scholar

Liu, G. R. (1997). A step-by-step method of rule-of-mixture of fiber-and particle-reinforced composite materials. Compos. Struct. 40 (3-4), 313–322. doi:10.1016/s0263-8223(98)00033-6

CrossRef Full Text | Google Scholar

Lovisi, G. (2023). Application of the surface stress-driven nonlocal theory of elasticity for the study of the bending response of FG cracked nanobeams. Compos. Struct. 324, 117549. doi:10.1016/j.compstruct.2023.117549

CrossRef Full Text | Google Scholar

Mahamood, R. M., Akinlabi, E. T., Mahamood, R. M., and Akinlabi, E. T. (2017). Types of functionally graded materials and their areas of application. Funct. graded Mater., 9–21. doi:10.1007/978-3-319-53756-6_2

CrossRef Full Text | Google Scholar

Mohammadi, H. (2023). “Isogeometric free vibration analysis of trapezoidally corrugated FG-GRC laminated panels using higher-order shear deformation theory,” in Structures (vol. 48) (Amsterdam, Netherlands: Elsevier), 642–656.

CrossRef Full Text | Google Scholar

Mohammadi, H., Shojaee, M., and Kiani, Y. (2023). A simplified isogeometric approach for vibrational analysis of nanocomposite panels with a free-form curve. Thin-Walled Struct. 183, 110426. doi:10.1016/j.tws.2022.110426

CrossRef Full Text | Google Scholar

Mollaei, S., Babaei, M., and Asemi, K. (2023). Torsional buckling of functionally graded graphene reinforced composite laminated cylindrical panel. Archive Appl. Mech. 93 (2), 427–435. doi:10.1007/s00419-022-02132-2

CrossRef Full Text | Google Scholar

Moradi-Dastjerdi, R., and Behdinan, K. (2020). Stability analysis of multifunctional smart sandwich plates with graphene nanocomposite and porous layers. Int. J. Mech. Sci. 167, 105283. doi:10.1016/j.ijmecsci.2019.105283

CrossRef Full Text | Google Scholar

Moradi-Dastjerdi, R., and Behdinan, K. (2021). Stress waves in thick porous graphene-reinforced cylinders under thermal gradient environments. Aerosp. Sci. Technol. 110, 106476. doi:10.1016/j.ast.2020.106476

CrossRef Full Text | Google Scholar

Mori, T., and Tanaka, K. (1973). Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta metall. 21 (5), 571–574. doi:10.1016/0001-6160(73)90064-3

CrossRef Full Text | Google Scholar

Nejadi, M. M., Mohammadimehr, M., and Mehrabi, M. (2021). Free vibration and stability analysis of sandwich pipe by considering porosity and graphene platelet effects on conveying fluid flow. Alexandria Eng. J. 60 (1), 1945–1954. doi:10.1016/j.aej.2020.11.042

CrossRef Full Text | Google Scholar

Penna, R. (2023). Bending analysis of functionally graded nanobeams based on stress-driven nonlocal model incorporating surface energy effects. Int. J. Eng. Sci. 189, 103887. doi:10.1016/j.ijengsci.2023.103887

CrossRef Full Text | Google Scholar

Penna, R., Feo, L., and Lovisi, G. (2021). Hygro-thermal bending behavior of porous FG nano-beams via local/nonlocal strain and stress gradient theories of elasticity. Compos. Struct. 263, 113627. doi:10.1016/j.compstruct.2021.113627

CrossRef Full Text | Google Scholar

Penna, R., Feo, L., Lovisi, G., and Fabbrocino, F. (2022). Application of the higher-order Hamilton approach to the nonlinear free vibrations analysis of porous FG nano-beams in a hygrothermal environment based on a local/nonlocal stress gradient model of elasticity. Nanomaterials 12 (12), 2098. doi:10.3390/nano12122098

PubMed Abstract | CrossRef Full Text | Google Scholar

Permoon, M. R., Farsadi, T., and Askarian, A. R. (2023). Vibration analysis of sandwich cylindrical shells made of graphene platelet polymer–viscoelastic–ceramic/metal FG layers. Funct. Compos. Struct. 5 (1), 015004. doi:10.1088/2631-6331/acbd28

CrossRef Full Text | Google Scholar

Pourjabari, A., Hajilak, Z. E., Mohammadi, A., Habibi, M., and Safarpour, H. (2019). Effect of porosity on free and forced vibration characteristics of the GPL reinforcement composite nanostructures. Comput. Math. Appl. 77 (10), 2608–2626. doi:10.1016/j.camwa.2018.12.041

CrossRef Full Text | Google Scholar

Qin, Z., Safaei, B., Pang, X., and Chu, F. (2019). Traveling wave analysis of rotating functionally graded graphene platelet reinforced nanocomposite cylindrical shells with general boundary conditions. Results Phys. 15, 102752. doi:10.1016/j.rinp.2019.102752

CrossRef Full Text | Google Scholar

Rao, M. N., Schmidt, R., and Schröder, K. U. (2018). “Forced vibration analysis of FG-graphene platelet reinforced polymer composite shells bonded with piezoelectric layers considering electroelastic nonlinearities,” in Smart materials, adaptive structures and intelligent systems (vol. 51944, p. V001T03A006) (American Society of Mechanical Engineers).

CrossRef Full Text | Google Scholar

Saffari, S., Hashemian, M., and Toghraie, D. (2017). Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects. Phys. B Condens. Matter 520, 97–105. doi:10.1016/j.physb.2017.06.029

CrossRef Full Text | Google Scholar

Salehi, M., Gholami, R., and Ansari, R. (2023). Analytical solution approach for nonlinear vibration of shear deformable imperfect FG-GPLR porous nanocomposite cylindrical shells. Mech. Based Des. Struct. Mach. 51 (4), 2177–2199. doi:10.1080/15397734.2021.1891096

CrossRef Full Text | Google Scholar

Shen, H. S., Xiang, Y., and Fan, Y. (2019). Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments. Nanotechnol. Rev. 8 (1), 467–483. doi:10.1515/ntrev-2019-0042

CrossRef Full Text | Google Scholar

Shen, M., and Bever, M. B. (1972). Gradients in polymeric materials. J. Mater. Sci. 7, 741–746. doi:10.1007/bf00549902

CrossRef Full Text | Google Scholar

Sobhani, E., Arbabian, A., Civalek, Ö., and Avcar, M. (2021). The free vibration analysis of hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells. Eng. Comput. 38, 3125–3152. doi:10.1007/s00366-021-01453-0

CrossRef Full Text | Google Scholar

Sobhani, E., and Avcar, M. (2022). The influence of various nanofiller materials (CNTs, GNPs, and GOPs) on the natural frequencies of Nanocomposite Cylindrical Shells: a comparative study. Mater. Today Commun. 33, 104547. doi:10.1016/j.mtcomm.2022.104547

CrossRef Full Text | Google Scholar

Sobhani, E., Koohestani, M., Civalek, Ö., and Avcar, M. (2023a). Natural frequency investigation of graphene oxide powder nanocomposite cylindrical shells surrounded by Winkler/Pasternak/Kerr elastic foundations with a focus on various boundary conditions. Eng. Analysis Bound. Elem. 149, 38–51. doi:10.1016/j.enganabound.2023.01.012

CrossRef Full Text | Google Scholar

Sobhani, E., Masoodi, A. R., and Civalek, Ö. (2023b). On vibrational-based numerical simulation of a jet engine cowl shell-like structure. Mech. Adv. Mater. Struct. 30 (19), 4016–4027. doi:10.1080/15376494.2022.2087241

CrossRef Full Text | Google Scholar

Sobhy, M., and Zenkour, A. M. (2019). Vibration analysis of functionally graded graphene platelet-reinforced composite doubly-curved shallow shells on elastic foundations. Steel compos. Struct. 33 (2), 195–208. doi:10.12989/scs.2019.33.2.195

CrossRef Full Text | Google Scholar

Ton-That, H. L., Nguyen-Van, H., and Chau-Dinh, T. (2021). A novel quadrilateral element for analysis of functionally graded porous plates/shells reinforced by graphene platelets. Archive Appl. Mech. 91, 2435–2466. doi:10.1007/s00419-021-01893-6

CrossRef Full Text | Google Scholar

Twinkle, C. M., and Pitchaimani, J. (2021). Free vibration and stability of graphene platelet reinforced porous nano-composite cylindrical panel: influence of grading, porosity and non-uniform edge loads. Eng. Struct. 230, 111670. doi:10.1016/j.engstruct.2020.111670

CrossRef Full Text | Google Scholar

Van Do, V. N., and Lee, C. H. (2020a). Bézier extraction based isogeometric analysis for bending and free vibration behavior of multilayered functionally graded composite cylindrical panels reinforced with graphene platelets. Int. J. Mech. Sci. 183, 105744. doi:10.1016/j.ijmecsci.2020.105744

CrossRef Full Text | Google Scholar

Van Do, V. N., and Lee, C. H. (2020b). Static bending and free vibration analysis of multilayered composite cylindrical and spherical panels reinforced with graphene platelets by using isogeometric analysis method. Eng. Struct. 215, 110682. doi:10.1016/j.engstruct.2020.110682

CrossRef Full Text | Google Scholar

Voigt, W. (1889). Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 274 (12), 573–587. doi:10.1002/andp.18892741206

CrossRef Full Text | Google Scholar

Wakashima, K., and Tsukamoto, H. (1991). Mean-field micromechanics model and its application to the analysis of thermomechanical behaviour of composite materials. Mater. Sci. Eng. A 146 (1-2), 291–316. doi:10.1016/0921-5093(91)90284-t

CrossRef Full Text | Google Scholar

Wang, A., Chen, H., Hao, Y., and Zhang, W. (2018). Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results Phys. 9, 550–559. doi:10.1016/j.rinp.2018.02.062

CrossRef Full Text | Google Scholar

Wang, Y. Q., Ye, C., and Zu, J. W. (2019). Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 85, 359–370. doi:10.1016/j.ast.2018.12.022

CrossRef Full Text | Google Scholar

Wattanasakulpong, N., and Chaikittiratana, A. (2015). Flexural vibration of imperfect functionally graded beams based on Timoshenko beam theory: Chebyshev collocation method. Meccanica 50, 1331–1342. doi:10.1007/s11012-014-0094-8

CrossRef Full Text | Google Scholar

Yang, J., Chen, D., and Kitipornchai, S. (2018). Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 193, 281–294. doi:10.1016/j.compstruct.2018.03.090

CrossRef Full Text | Google Scholar

Ye, C., and Wang, Y. Q. (2021). Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: internal resonances. Nonlinear Dyn. 104 (3), 2051–2069. doi:10.1007/s11071-021-06401-7

CrossRef Full Text | Google Scholar

Zhang, D., Wang, Y., and Li, L. (2023). Free vibration response of FG porous joined hemispherical–cylindrical–hemispherical shell vessels reinforced by graphene platelet. Int. J. Struct. Stab. Dyn. 23 (03), 2350025. doi:10.1142/s0219455423500256

CrossRef Full Text | Google Scholar

Zhao, J., Fan, G., Guan, J., Li, H., Liu, J., Xie, Z., et al. (2023). Free vibration and dynamic analysis on free-constrained layer of graphene based on composite conical shell via Jacobi-Ritz method. Int. J. Struct. Stab. Dyn. doi:10.1142/s0219455424500238

CrossRef Full Text | Google Scholar

Zhao, S., Yang, Z., Kitipornchai, S., and Yang, J. (2020). Dynamic instability of functionally graded porous arches reinforced by graphene platelets. Thin-Walled Struct. 147, 106491. doi:10.1016/j.tws.2019.106491

CrossRef Full Text | Google Scholar

Zhou, X., Wang, Y., and Zhang, W. (2021). Vibration and flutter characteristics of GPL-reinforced functionally graded porous cylindrical panels subjected to supersonic flow. Acta Astronaut. 183, 89–100. doi:10.1016/j.actaastro.2021.03.003

CrossRef Full Text | Google Scholar

Appendix A

${\psi }_1=\frac{\left(x_{23}\left(y-y_3\right)-y_{23}\left(x-x_3\right)\right)\left(x_{49}\left(y-y_9\right)-y_{49}\left(x-x_9\right)\right)\left(x_{58}\left(y-y_8\right)-y_{58}\left(x-x_8\right)\right)}{\left(x_{23}{y}_{13}-y_{23}{x}_{13}\right)\left(x_{49}{y}_{16}-y_{49}{x}_{16}\right)\left(x_{58}{y}_{18}-x_{58}{r}_{18}\right)}$

${\psi }_2=\frac{\left(x_{31}\left(y-y_1\right)-y_{31}\left(x-x_1\right)\right)\left(x_{74}\left(y-y_4\right)-y_{74}\left(x-x_4\right)\right)\left(x_{65}\left(y-y_5\right)-y_{65}\left(x-x_5\right)\right)}{\left(x_{31}{y}_{21}-y_{31}{x}_{21}\right)\left(x_{74}{y}_{24}-y_{74}{x}_{24}\right)\left(x_{65}{y}_{25}-y_{65}{x}_{25}\right)}$

${\psi }_3=\frac{\left(x_{21}\left(y-y_1\right)-y_{21}\left(x-x_1\right)\right)\left(x_{69}\left(y-y_9\right)-y_{69}\left(x-x_9\right)\right)\left(x_{78}\left(y-y_8\right)-y_{78}\left(x-x_8\right)\right)}{\left(x_{21}{y}_{31}-y_{21}{x}_{31}\right)\left(x_{69}{y}_{39}-y_{69}{x}_{39}\right)\left(x_{78}{y}_{38}-y_{78}{x}_{38}\right)}$

${\psi }_4=\frac{\left(x_{85}\left(y-y_5\right)-y_{85}\left(x-x_5\right)\right)\left(x_{32}\left(y-y_2\right)-y_{32}\left(x-x_2\right)\right)\left(x_{31}\left(y-y_1\right)-y_{31}\left(x-x_1\right)\right)}{\left(x_{85}{y}_{45}-y_{85}{x}_{45}\right)\left(x_{32}{y}_{41}-y_{32}{x}_{41}\right)\left(x_{31}{y}_{41}-y_{31}{x}_{41}\right)}$

${\psi }_5=\frac{\left(x_{31}\left(y-y_1\right)-y_{31}\left(x-x_1\right)\right)\left(x_{74}\left(y-y_4\right)-y_{74}\left(x-x_4\right)\right)\left(x_{32}\left(y-y_2\right)-y_{32}\left(x-x_2\right)\right)}{\left(x_{31}{y}_{51}-y_{31}{x}_{51}\right)\left(x_{74}{y}_{54}-y_{74}{x}_{54}\right)\left(x_{32}{y}_{52}-y_{32}{x}_{52}\right)}$

${\psi }_6=\frac{\left(x_{12}\left(y-y_2\right)-y_{12}\left(x-x_2\right)\right)\left(x_{47}\left(y-y_7\right)-y_{47}\left(x-x_7\right)\right)\left(x_{13}\left(y-y_3\right)-y_{13}\left(x-x_3\right)\right)}{\left(x_{12}{y}_{62}-y_{12}{x}_{62}\right)\left(x_{23}{y}_{63}-y_{23}{x}_{63}\right)\left(x_{13}{y}_{63}-y_{13}{x}_{63}\right)}$

${\psi }_7=\frac{\left(x_{96}\left(y-y_6\right)-y_{96}\left(x-x_6\right)\right)\left(x_{12}\left(y-y_2\right)-y_{12}\left(x-x_2\right)\right)\left(x_{13}\left(y-y_3\right)-y_{13}\left(x-x_3\right)\right)}{\left(x_{96}{y}_{76}-y_{96}{x}_{76}\right)\left(x_{12}{y}_{72}-y_{12}{x}_{72}\right)\left(x_{13}{y}_{73}-y_{13}{x}_{73}\right)}$

${\psi }_8=\frac{\left(x_{69}\left(y-y_9\right)-y_{96}\left(x-x_9\right)\right)\left(x_{21}\left(y-y_1\right)-y_{21}\left(x-x_1\right)\right)\left(x_{23}\left(y-y_3\right)-y_{23}\left(x-x_3\right)\right)}{\left(x_{69}{y}_{89}-y_{69}{x}_{89}\right)\left(x_{21}{y}_{81}-y_{21}{x}_{81}\right)\left(x_{23}{y}_{83}-y_{23}{x}_{83}\right)}$

${\psi }_9=\frac{\left(x_{58}\left(y-y_8\right)-y_{58}\left(x-x_8\right)\right)\left(x_{23}\left(y-y_3\right)-y_{23}\left(x-x_3\right)\right)\left(x_{21}\left(y-y_1\right)-y_{13}\left(x-x_1\right)\right)}{\left(x_{58}{y}_{98}-y_{58}{x}_{98}\right)\left(x_{23}{y}_{93}-y_{23}{x}_{93}\right)\left(x_{21}{y}_{91}-y_{21}{x}_{91}\right)}$

${\psi }_{10}=\frac{\left(x_{31}\left(y-y_1\right)-y_{31}\left(x-x_1\right)\right)\left(x_{32}\left(y-y_2\right)-y_{32}\left(x-x_2\right)\right)\left(x_{21}\left(y-y_1\right)-y_{21}\left(x-x_1\right)\right)}{\left(x_{31}{y}_{10-1}-y_{31}{x}_{10-1}\right)\left(x_{32}{y}_{10-2}-y_{32}{x}_{10-2}\right)\left(x_{21}{y}_{10-1}-y_{21}{x}_{10-1}\right)}$